Đề tuyển sinh vào lớp 10 môn Toán năm 2023 – 2024 sở GD&ĐT Bình Dương
Giới thiệu đến quý thầy, cô giáo và các em học sinh đề chính thức kỳ thi tuyển sinh vào lớp 10 Trung học Phổ thông môn Toán năm học 2023 – 2024 sở Giáo dục và Đào tạo tỉnh Bình Dương; kỳ thi được diễn ra vào sáng thứ Sáu ngày 02 tháng 06 năm 2023. Mời bạn đọc đón xem!
Chủ đề: Đề thi vào 10 môn Toán năm 2023-2024
Môn: Môn Toán
Thông tin:
Tác giả:
Tài liệu liên quan:
Preview text:
https://thcs.toanmath.com/de-thi-tuyen-sinh-lop-10-mon-toan ĐÁP ÁN: Bài 1 (2 điểm). 1) Giải phương trình 2
x + x − 6 = 0.
∆ = 25 > 0 phương trình có hai nghiệm phân biệt 1 − + 5 1 − − 5 x = = 2; x = = 3 − . 1 2 2 2
Tập nghiệm phương trình là S = {2;− } 3 .
2) Giải phương trình x − 3 x = 4.
Đặt t = x (x ≥ 0,t ≥ 0) phương trình trở thành 2t − 3t − 4 = 0 . Ta có 1− ( 3)
− − 4 = 0 nên phương trình có hai nghiệm t = 1
− (loại), t = 4 (nhận). 1 2
Với t = 4 ⇒ x = 4 ⇔ x =16.
Tập nghiệm phương trình là S = { } 16 . x − y = 1 −
3) Giải hệ phương trình 2x + 3y = 8 x − y = 1 − 3 x − 3y = 3 − 5 x = 5 x =1 x =1 ⇔ ⇔ ⇔ ⇔ 2x 3y 8 2x 3y 8 2x 3y 8 2 3y 8 + = + = + = + = y = 2
Tập nghiệm hệ phương trình là S = ( { 1;2)}. Bài 2 (1,5 điểm).
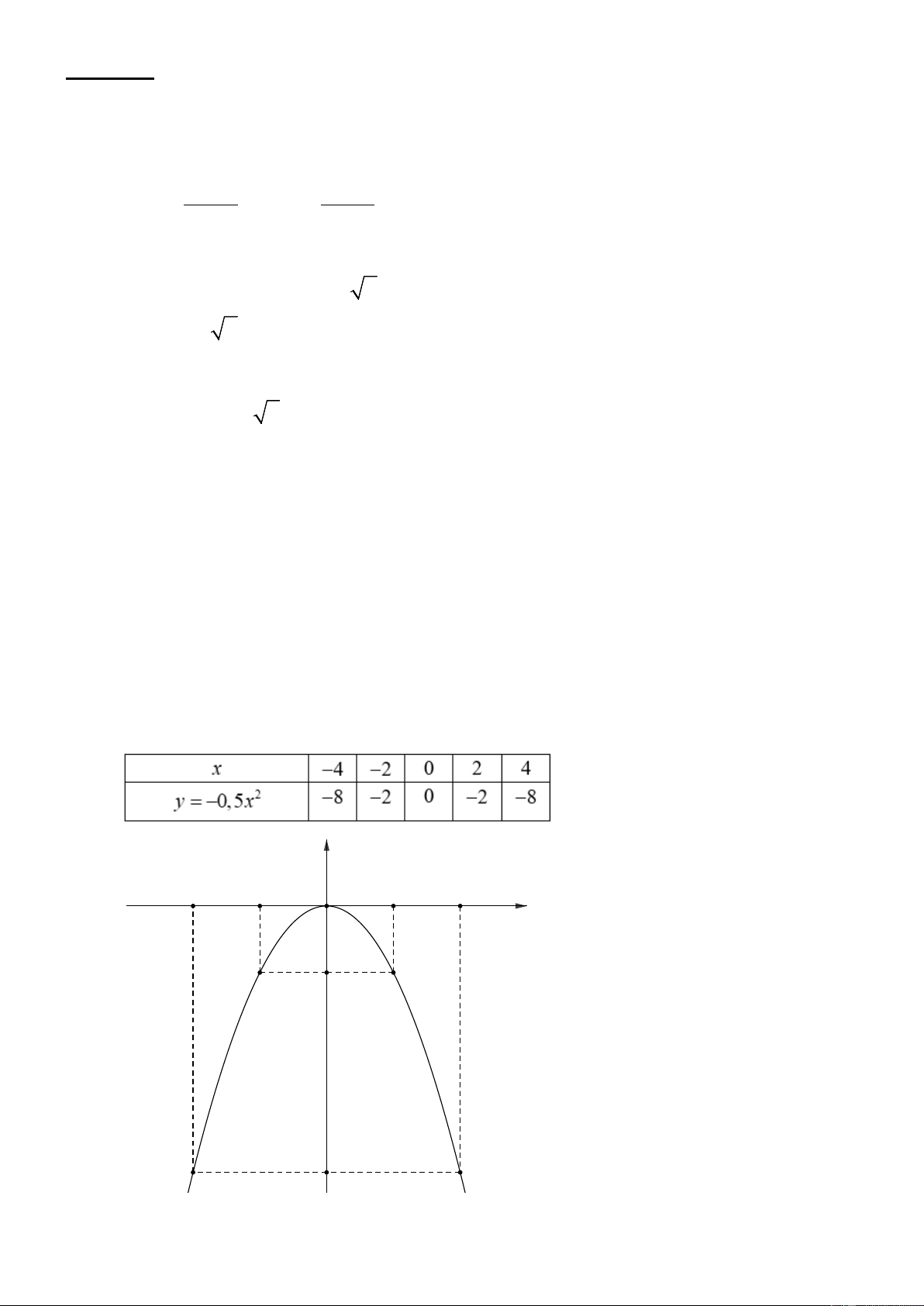
1) Vẽ đồ thị của hàm số 2 y = 0, − 5x . y -4 -2 O 2 4 x -2 -8
2) (d : y = ax + b vuông góc với (d): y = 0, − 5x + 2 nên có . a ( 0, − 5) = 1 − ⇔ a = 2. 1 )
(d : y = 2x + b tiếp xúc 2 (P) : y = 0,
− 5x nên phương trình 1 ) 2 2 0,
− 5x = 2x + b ⇔ 0,
− 5x − 2x − b = 0 có nghiệm kép nên ∆ = 4 − 2b = 0 ⇔ b = 2 .
Vậy phương trình đường thẳng (d : y = 2x + 2. 1 ) Bài 3 (1,5 điểm). 1) Phương trình 2 2
x − 2(m +1)x + m + m = 0 có hai nghiệm phân biệt khi 2 2 ′
∆ = m + 2m +1− m − m = m +1> 0 ⇔ m > 1 − . Vậy m > 1 − thì phương trình 2 2
x − 2(m +1)x + m + m = 0 có hai nghiệm phân biệt. 2) 2 2
x − 2(m +1)x + m + m = 0 x + x 1 2 m = −1 x x 2(m 1) + = + 2 Ta có 1 2 ⇔ 2 ⇒ 2
x .x = m + m x + x x + x 1 2 1 2 1 2 x x = −1 + − 1 1 2 2 2
(x + x )2 − 2 x + x − 4x x = 0 là hệ thức liên hệ giữa x và x mà không phụ 1 2 ( 1 2) 1 2 1 2
thuộc vào tham số m. Bài 4 (1,5 điểm).
Gọi giá tiền niêm yết (khi chưa giảm giá) của một cái quạt máy và một ấm đun siêu tốc
là x, y(x > 0, y > 0) (đồng).
Ta có phương trình x + y = 630000.
Giá tiền quạt máy sau khi giảm giá là x −15%x = 85%x = 0,85x.
Giá tiền ấm siêu tốc sau khi giảm giá là y −12%y = 88%y = 0,88y .
Ta có phương trình 0,85x + 0,88y = 543000 .
x + y = 630000 Giải hệ
0,85x + 0,88y = 543000
x + y = 630000
0,88x + 0,88y = 554400 ⇔ ⇔
0,85x + 0,88y = 543000
0,85x + 0,88y = 543000 0,03x =11400 x = 380000 x = 380000 ⇔ ⇔ x y 630000 380000 y 630000 + = + = y = 250000
Vậy giá tiền niêm yết (khi chưa giảm giá) của một cái quạt máy và một ấm đun siêu tốc
là 380000 (đồng) và 250000 (đồng). Bài 5 (3,5 điểm).
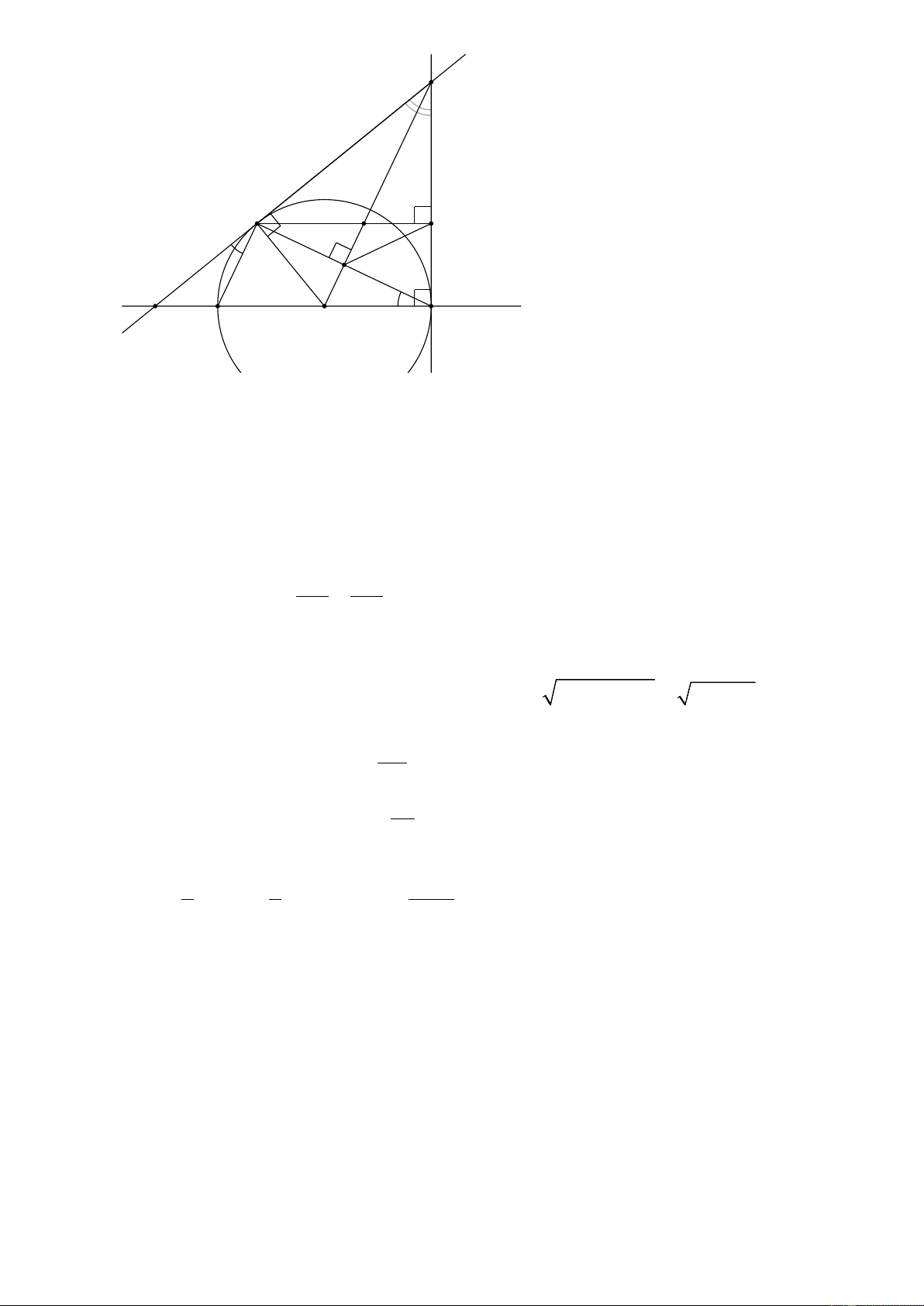
1) Ta có CH ⊥ BD ⇒ H nhìn CD dưới một góc vuông (1)
Theo tính chất hai tiếp tuyến cắt nhau CD và BD, ta có DC = DB Hai bán kính OC = OB
⇒ OD là trung trực của BC ⇒ OD ⊥ CB
⇒ N nhìn CD dưới một góc vuông (2)
Từ (1) và (2) ⇒ tứ giác CNHD nội tiếp được trong đường tròn. D 1 2 C H M N E A O B
2) Theo tính chất hai tiếp tuyến cắt nhau CD và BD, ta có DC = DB, ta có = D D 1 2
Theo tính chất tiếp tuyến và giả thiết, ta có góc =
COD DMH (cùng phụ với hai góc bằng nhau = D D ) 1 2 Mặt khác =
DMH CMO (đối đỉnh) ⇒ = COD CMO ∆COM có =
COM CMO ⇒ cân tại C ⇒ CM = CO .
3) ∆EAC và ∆ECB có góc E chung và góc =
ECA CBA (cùng chắn cung AC)
⇒ đồng dạng ⇒ EA EC 2 = ⇒ E . A EB = EC . EC EB
4) Hình nón được tạo bởi tam giác vuông DNB quay quanh DN
⇒ bán kính r = NB và chiều cao h = ND .
Theo Pitago cho tam giác vuông BOD: 2 2
OD = OB + BD = 36 + 64 =10cm .
Theo hệ thức lượng trong tam giác vuông BOD, ta có: 6.8
BN.OD = O . B BD ⇒ BN = = 4,8cm . 10 Và 2 64
BD = DN.DO ⇒ DN = = 6,4cm 10
Thể tích của hình nón tạo thành 1 2 1 2 6144
V = π.r .h = π.(4,8) .6,4 = π ≈154,4156( 3 cm ) . 3 3 125
Trường THPT Tân Bình − Bình Dương.
Giáo viên: Lê Hành Pháp.
Document Outline
- de-tuyen-sinh-vao-lop-10-mon-toan-nam-2023-2024-so-gddt-binh-duong
- TS TOAN 10 BINH DUONG 2024
- ĐÁP ÁN: