Đề tuyển sinh vào lớp 10 môn Toán năm 2023 – 2024 sở GD&ĐT Hải Phòng

SỞ GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI TUYỂN SINH VÀO LỚP 10 THPT HẢI PHÒNG
NĂM HỌC 2023 – 2024
ĐỀ THI MÔN: TOÁN ĐỀ CHÍ NH THỨC
Thời gian làm bài: 120 phút (không kể thời gian phát đề)
(Đề thi gồm 02 trang, 06 bài) Bài 1. (1,5 điểm) Cho các biểu thức: A = − − ( − )2 3 8 50 2 1 ;  3 x + 6 x  x − 9 B =  + : với x≥ 0; x ≠ 4; 9 x ≠ . x − 4 x − 2 x −   3
a) Rút gọn biểu thức A và B.
b) Tìm x sao cho A − 2B = 3. Bài 2. (1,5 điểm)
2(x − 3) + 3(3x + y) = 11 −
1. Giải hệ phương trình ( .  x − 3 
) − 2(3x + y) = 5
2. Một quyển vở giá 14 000 đồng, một hộp bút giá 30 000 đồng. Minh muốn mua 01 hộp bút và một số quyển vở. a) Gọi x (x ∗
∈  ) là số quyển vở Minh mua, y là số tiền cần trả khi mua x quyển vở
và 01 hộp bút. Hãy biểu diễn y theo x.
b) Nếu Minh có 300 000 đồng để mua vở và 01 hộp bút thì Minh mua được tối đa bao nhiêu quyển vở? Bài 3. (2,5 điểm)
1. Cho phương trình 2 x − (m − ) 2 2
1 x + m − 9 = 0 ( )
1 ( x là ẩn, m là tham số). a) Giải phương trình ( ) 1 khi m = 3 − .
b) Tìm các giá trị của m để phương trình ( )
1 có hai nghiệm phân biệt 1x, 2x thỏa mãn
điều kiện x − x = 2m −10 1 2 .
2. Một trường học có mảnh vườn hình chữ nhật chu vi là 100m. Nhà trường tiến hành
mở rộng mảnh vườn đó bằng cách tăng chiều dài thêm 5m và chiều rộng thêm 4m, khi đó diện tích tăng thêm 2
240m .Tính chiều dài và chiều rộng của mảnh vườn trước khi mở rộng. Bài 4. (0,75 điểm)
Một chi tiết máy gồm một phần có dạng hình trụ, phần còn lại có dạng
hình nón với các kích thước như hình 1. Biết rằng phần hình trụ có chu vi đáy
là 37,68cm. Tính thể tích của chi tiết máy đó (lấy π ≈ 3, ;
14 kết quả làm tròn
đến chữ số thập phân thứ 2). Trang 1/7 Hình 1 Bài 5. (3,0 điểm)
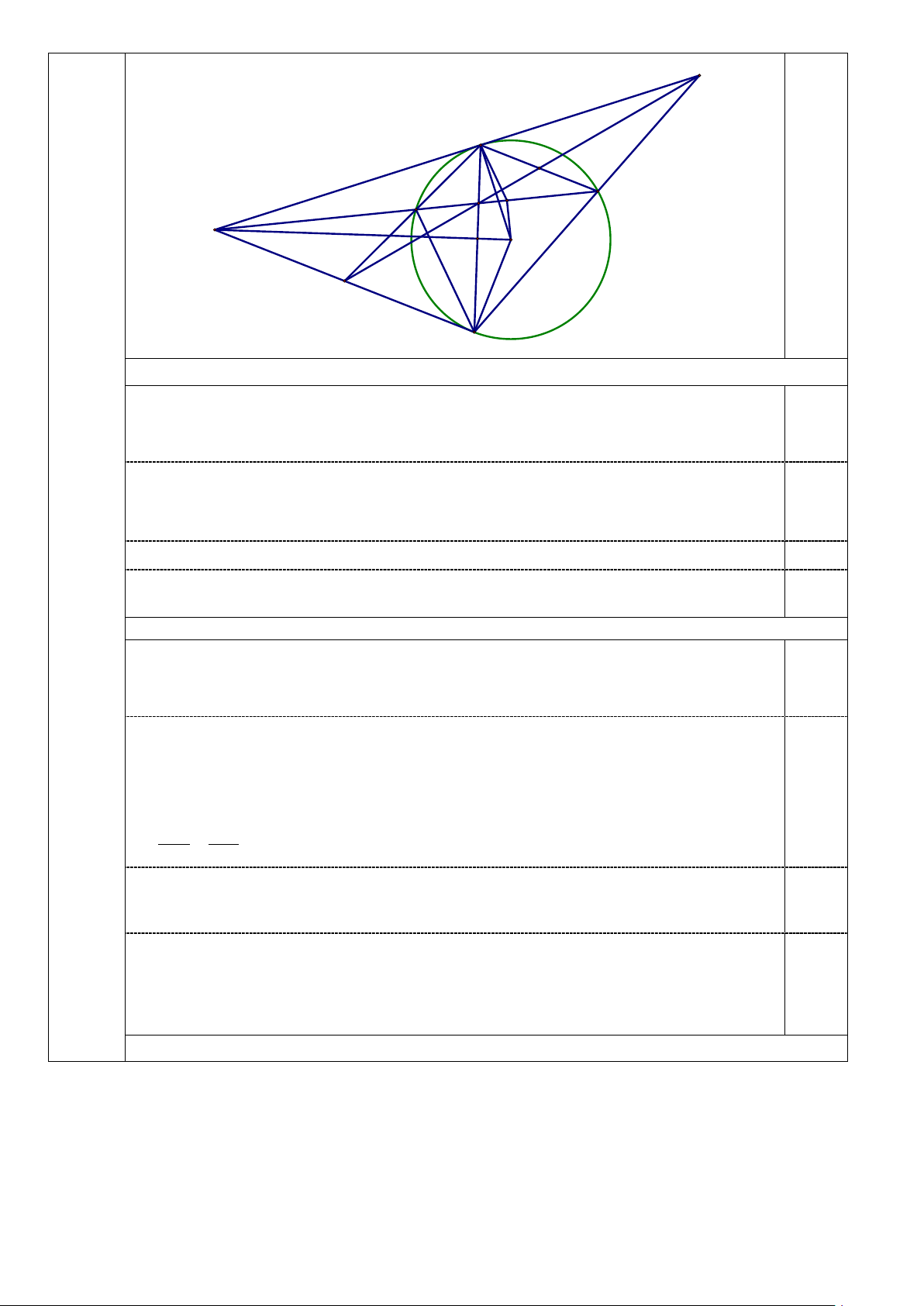
Cho đường tròn (O;R) và điểm A sao cho OA > 2R, vẽ hai tiếp tuyến AB, AC của đường
tròn (B, C là các tiếp điểm), kẻ dây cung BD song song với AC. Đường thẳng AD cắt (O;R) tại
điểm E (E ≠ D). Gọi I là trung điểm của DE.
a) Chứng minh năm điểm A, B, I , O, C cùng thuộc một đường tròn.
b) Đường thẳng BC cắt OA, AD lần lượt tại H và K. Gọi F là giao điểm của BE và AC.
Chứng minh AK.AI = AH .AO và tam giác AFE đồng dạng với tam giác BFA.
c) Chứng minh ba đường thẳng AB, CD, FK đồng quy. Bài 6. (0,75 điểm)
Cho các số thực a,b thoả mãn: a > 0, b > 0 và (a + b)3 = ( 2 2
2 1− a − b ).
Tìm giá trị nhỏ nhất của biểu thức 1 1 M = + . 2 2 ab a + b ----------- HẾT -----------
- Thí sinh làm bài trên giấy thi, không sử dụng tài liệu.
- Cán bộ coi thi không giải thích gì thêm. Trang 2/7
SỞ GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI TUYỂN SINH VÀO LỚP 10 THPT HẢI PHÒNG
Năm học 2023 – 2024
HDC ĐỀ CHÍNH THỨC
HƯỚNG DẪN CHẤM VÀ BIỂU ĐIỂM MÔN TOÁN (gồm 04 trang) Bài Đáp án Điểm a. (1,0 điểm)
A = 6 2 − 5 2 − 2 −1 0,25
= 2 − 2 +1 (vì 2 −1 > 0 ) =1 0,25 Với x
≥ 0, x ≠ 4, x≠ 9 ta có :  3( x + 2)
x  ( x − 3)( x + 3) B =  +  : 0,25 1 
( x − 2)( x + 2) x − 2 x − 3  (1,5đ) 3+ x 1 1 = ⋅ = . 0,25 x − 2 x + 3 x − 2 b. (0,5 điểm) Để 2
A − 2B = 3 ⇔ 1−
= 3 ⇒ x − 2 − 2 = 3 x − 6 ⇔ 2 x = 2 ⇔ x =1 0,25 x − 2
⇔ x =1 (thoả mãn).
Vậy x =1 thì A − 2B = 3. 0,25 1. (0,75 điểm)
2(x −3) + 3(3x + y) = 11 − (   x − 3 
) − 2(3x + y) = 5 0,25
4(x − 3) + 6(3x + y) = 22 −   7( x − 3) = 7 − ⇔  ⇔  3
 (x − 3) − 6(3x + y) =15 (  x − 3 
)− 2(3x + y) = 5 x − 3 = 1 − x = 2 x = 2 ⇔ ( ⇔  ⇔ 0,25  x 3  ) 2(3x y) 5 (  2 3  ) 2(3.2 y) 5  − − + = − − + = 6 + y = 3 − 2 (1,5đ) x = 2 ⇔  y = 9 − 0,25
Vậy hệ phương trình có nghiệm duy nhất là ( ;x y) = (2; 9 − ). 2. (0,75 điểm)
a) Công thức tính y theo x là y =14000x +30000. 0,25
b) Theo đề bài ta có: 14000x + 30000 ≤ 300000 0,25 Giải được 135 x ≤ ≈ 19,29 7 0,25
Vậy bạn Minh mua tối đa được 19 quyển vở. 1a. (0,5 điểm) Với m = 3 − phương trình ( ) 1 có dạng 2 x + 8x = 0. 0,25 x = 0 x = 0
⇔ x(x + 8) = 0 ⇔ ⇔   3 x + 8 = 0 x = 8 − 0,25
(2,5đ) Vậy khi m = 3,
− phương trình có nghiệm là x = 0; x = 8 − . 1b. (1,0 điểm) Có ∆ = −  (m − ) 2 2 2 2 '
1  − m + 9 = m − 2m +1− m + 9 = 2 − m +10.  0,25 Phương trình ( )
1 có hai nghiệm phân biệt x ,
⇔ ∆ > ⇔ − m + > ⇔ m < 1 2 x ' 0 2 10 0 5 Trang 3/7
x + x = 2 m −  1 2 1 2 ( ) ( ) Theo hệ thức Vi-ét  2 x x = m − 9 3  0,25 1 2 ( )
Theo đề bài ta có: x − x = 2m −10, kết hợp với (2) ta được x = 2m − 6; x = 4 1 2 1 2
Thay x = 2m − 6; x = 4 vào (3) ta được: ( m − ) 2 2 2
6 4 = m − 9 ⇔ m −8m +15 = 0 . 1 2 0,25
Giải được m = 3 (thoả mãn), m = 5 (loại)
Vậy với m = 3 phương trình ( )
1 có hai nghiệm phân biệt x , x thỏa mãn 1 2 0,25
x − x = 2m −10. 1 2 2. (1,0 điểm)
Gọi chiều dài của vườn ban đầu là x(m), chiều rộng của vườn ban đầu là y(m)
(ĐK: 0 < y < x < 50 )
Vì chu vi của vườn ban đầu là 100m nên ta có phương trình: 0,25
2(x + y) =100 ⇔ x + y = 50 ( ) 1
Chiều dài của vườn sau khi mở rộng là: (x + 5) (m)
Chiều rộng của vườn sau khi mở rộng là: ( y + 4) (m) 0,25
Khi đó diện tích vườn trường đã tăng thêm 2
240m nên ta có phương trình:
(x +5)( y + 4)− xy = 240 (2) x + y = 50
Từ (1) và (2) ta có hệ phương trình: (  x + 5 
)( y + 4) − xy = 240 0,25 Giải hệ phương trình.
Giải hệ phương trình ta được: x = 30; y = 20 (thoả mãn điều kiện).
Vậy chiều dài của vườn ban đầu là 30m, chiều rộng của vườn ban đầu là 20m. 0,25 (0,75 điểm)
Độ dài bán kính đáy của phần hình trụ là: 37,68 R ≈ ≈ 6(cm) 0,25 2.3,14
Thể tích của phần có dạng hình trụ là: 4 2 2 3
V = π R .2R ≈ 3,14.6 . 2.6 ≈1356,48(cm ) 1 ( )
(0,75đ) Thể tích của phần có dạng hình nón là: 0,25 1 2 1 2 3
V = π R .R ≈ .3,14.6 .6 ≈ 226,08(cm ) 2 3 3
Thể tích của chi tiết máy đó là: 3
V = V +V ≈1582,56( m c ) 0,25 1 2 Vẽ hình đúng cho câu a) 0,25 Trang 4/7 J B G I D E K A O H F C a. (1,0 điểm) Xét (O) có:
+ DE là dây không đi qua tâm O và I là trung điểm của DE 0,25
⇒ OI ⊥ DE tại I (quan hệ vuông góc giữa đường kính và dây) ⇒  0 AIO = 90
+ AB, AC là tiếp tuyến của đường tròn (O)
⇒ AB ⊥ OB, AC ⊥ OC (tính chất tiếp tuyến). 0,25 ⇒  =  0 ABO ACO = 90 . ⇒  =  =  0 ABO ACO AIO = 90 0,25 Hay năm điểm ,
A B, I, O, C cùng thuộc một đường tròn đường kính AO 0,25
( quỹ tích cung chứa góc). b. (1,0 điểm) Xét ( ;
O R) có AB = AC (tính chất hai tiếp tuyến cắt nhau)
Mà OB = OC = R ⇒ OA là đường trung trực của BC 0,25 5
⇒ OA ⊥ BC tại H ⇒  0 AHK = 90 (3,0đ) Xét A ∆ HK và A ∆ IO có:  =  0 AHK AIO = 90 (cmt)  HAK chung 0,25 ⇒ A ∆ HK # A
∆ IO (g.g) AH AK ⇒ =
⇒ AK.AI = AH.A . O AI AO Ta có: BD // ( ) ⇒  =  AC gt BDE FAE (so le trong) 0,25 Mà  = 
BDE FBA (cùng chắn  EB của ( ; O R) ) ⇒  =  FAE FB . A Xét A ∆ FE và B ∆ FA có:  AFE chung  0,25 =  FAE FBA (cmt) ⇒ A ∆ FE# B
∆ FA(g.g) c. (0,75 điểm) Trang 5/7 Ta có: A ∆ FE# B ∆ FA (cmt) FE FA 2 ⇒ = ⇒ FA = F . B FE. FA FB Xét F ∆ EC và F ∆ CB có:  EFC chung  = 
FCE FBC (cùng chắn  EC của ( ; O R) ) 0,25 ⇒ F ∆ EC# F
∆ CB (g.g) FE FC 2 ⇒ = ⇒ FC = F . B FE. FC FB Mà 2 FA = F . B FE (cmt) nên 2 2
FA = FC ⇒ FA = FC
⇒ F là trung điểm của đoạn thẳng AC .
Gọi G là giao điểm của FK và BD
Ta có: BG // FC (gt) BG KG ⇒ =
(hệ quả định lí Ta-lét) FC KF
DG // AF (gt) GD KG ⇒ =
(hệ quả định lí Ta-lét) 0,25 FA KF Suy ra BG GD =
mà AF = CF nên BG = DG FC FA
⇒ G là trung điểm của đoạn thẳng B . D
Kéo dài AB cắt DC tại J. Gọi G ' là giao điểm của JF và BD . Xét J
∆ AF có: BG ' // AF (gt) BG ' JG ' ⇒ =
( hệ quả định lí Ta-lét) AF JF Xét J
∆ FC có: DG '//CF (gt) DG ' JG ' ⇒ =
( hệ quả định lí Ta-lét) CF JF 0,25 Suy ra BG ' DG ' =
mà AF = CF nên BG ' = DG ' AF CF
hay G ' là trung điểm BD ⇒ G' ≡ G ⇒ F ,K ,J thẳng hàng
Suy ra: ba đường thẳng AB, CD, FK đồng quy tại J. (0,75 điểm)
Ta có: (a + b)3 = ( 2 2
− a − b ) ⇔ (a + b)3 + ( 2 2 2 1 2 a + b ) = 2
Vì a > 0, b > 0 ta có ( 2 2
2 a + b ) ≥ (a + b)2 (theo AM – GM)
⇒ (a + b)3 + (a + b)2 ≤ 2 0,25
⇔ (a + b)3 + (a + b)2 − 2 ≤ 0 ⇔ (a + b − ) (a + b)2 1
+ 2(a + b) + 2 ≤ 0  
⇔ a + b −1≤ 0 ( vì (a + b)2 + 2(a + b) + 2 > 0 với a > 0,b > 0 ) 6 ⇔ a + b ≤1.
(0,75đ) Chứng minh bất đẳng thức phụ sau: 1 1 4 + ≥
(x > 0, y > 0) (∗) x y x + y Ta có: 1 1 4 + ≥
⇔ (x + y)2 ≥ 4xy ⇔ (x − y)2 ≥ 0 (luôn đúng) x y x + y
Áp dụng bất đẳng thức (∗) , ta được: 0,25 1 1 4 1 1 4 + ≥ ⇔ + ≥
≥ 4 (vì a + b ≤1) 2 2 2 2 2 2 2ab a + b
a + b + 2ab 2ab a + b (a +b)2
Với a > 0, b > 0 ta có 1
1≥ a + b ≥ 2 ab ⇒1≥ 4ab ⇒ ≥ 2 0,25 2ab Trang 6/7 1 1  1 1  1 ⇒ M = + = + + ≥ 4 + 2 ⇔ M ≥   6 2 2 2 2 ab a + b
 2ab a + b  2ab
Dấu “ =” xảy ra khi và chỉ khi 1 a = b = 2
Vậy giá trị nhỏ nhất của M là 6 khi 1 a = b = . 2 * Chú ý:
- Trên đây chỉ trình bày một cách giải, nếu học sinh làm cách khác mà đúng thì cho điểm tối đa ứng
với điểm của câu đó. - Trong một câu:
+ Có nhiều ý mà các ý phụ thuộc nhau, học sinh làm phần trên sai phần dưới đúng thì không cho điểm.
+ Có nhiều ý mà các ý không phụ thuộc nhau, học sinh làm đúng ý nào thì cho điểm ý đó.
- Bài hình học, học sinh vẽ hình sai phần nào thì trừ 0,25 điểm phần đó. Riêng điều kiện OA > 2R ,
nếu học sinh vẽ không đúng tỉ lệ và không ảnh hưởng đến kết quả thì vẫn cho đủ điểm.
Họ và tên thí sinh:.................................................................................... Số báo danh:.................
Cán bộ coi thi số 1: ........................................ Cán bộ coi thi số 2: .......................................... Trang 7/7