Đề tuyển sinh vào lớp 10 môn Toán năm 2023 – 2024 sở GD&ĐT Phú Thọ

Giới thiệu đến quý thầy, cô giáo và các em học sinh đề chính thức kỳ thi tuyển sinh vào lớp 10 Trung học Phổ thông môn Toán năm học 2023 – 2024 sở Giáo dục và Đào tạo tỉnh Phú Thọ; đề thi có đáp án trắc nghiệm và lời giải chi tiết tự luận. Mời bạn đọc đón xem!

39 20 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề thi vào 10 môn Toán năm 2023-2024

Môn: Môn Toán

Thông tin:

6 trang 8 tháng trước

Tác giả:

Profile Vũ Hường
TRƯỜNG THCS VĂN LANG
TỔ TOÁN - TIN
ĐÁP ÁN THAM KHẢO MÔN TOÁN VÀO 10
TỈNH PHÚ THỌ
NĂM HỌC 2023- 2024
I. PHẦN TRẮC NGHIỆM
1
2
3
4
5
6
7
8
9
10
11
12
C
B
A
A
B
D
C
B
C
D
A
D
II. PHẦN TỰ LUẬN
Câu 1:
a) Khi
(thỏa mãn điều kiện xác định) thì giá trị biểu thức
5 16 4 5.4 4 24
8
41 3
16 1
A
++
= == = =
−
−
Vậy với
16a =
thì
8A =
.
b) Với
0; 1; 4a aa> ≠≠
11
.
12
aa
B
a aa
−

= +

−−

( )
( )
1
11
.
22
1
aa
aa
aa
aa
−
−+
= =
−−
−
c) Với
0; 1; 4
a aa> ≠≠
ta có:
5 41
.0 . 0
12
a
AB
aa
+
<⇔ <
−−
( )(
)
1 20aa⇔ − −<
(vì
5 40a +>
)
1 21 4aa⇔< < ⇔< <
Vì
a ∈
nên
{ }
2;3a ∈
Vậy
{
}
2;3a
∈
Câu 2:
a) Vì
( ) ( )
2
1; 2 :M P y ax∈=
nên:
2
.1 2 2aa=⇔=
Với
( )
2
2 :2a Py x=⇒=
PT hoành độ giao điểm của
( ) ( )
,dP
là
( )( )
22
1
2 3 1 2 3 1 0 12 1 0
1
2
x
x x xx x x
x
=
= −⇔ − += ⇔ − − = ⇔
=
Với
12xy=⇒=
;
11
22
xy=⇒=
Vậy tọa độ giao điểm của
(
)
d
và
( )
P
là
( )
11
1; 2 ; ;
22
AB



.
b) Xét hệ phương trình:
3 5 15
39
xy m
xy m
+= +
+= +
226 3
39 26
x m xm
xy m y m
=+=+

⇔⇔

+= + = +

Xét
( )
(
) ( )
2
2
2 1 3 2 6 2 3 1 2 10 11
5 33
2
2 22
Q xy x m m m m m
Qm
= − −= + + − + −= + +

⇒ = + − ≥−


Từ đó suy ra
3
min
2
Q = −
khi
5
2
m
= −
Câu 3.
a) Do
AB CD
tại O nên
90 1POD BOC A OC

Xét
()O
có
0
90MCD DM PC
tại M
0
90PMD
Xét tứ giác
OMPD
có
0
90POD PMD 
tứ giác
OMPD
nội tiếp
b) Từ
0
1 BOJ 90
Xét
()O
có
0
90AMB
( Góc nội tiếp chắn nửa đường tròn)
Xét
OJB
và
BMA
có:
BOJ 90BMA

OBJ MBA
( góc chung).
Do đó
2
( . ) . . .2 2 .
BJ BA
BOJ BMA g g BJ BM BO BA R R R
BO BM
 ”
c) Xét
()O
có
BMD BAC
( tính chất góc nội tiếp)
IMQ IAQ

tứ giác
AMIQ
nội tiếp
180 90 180 90
IQA AMI IQA IQA

 
Xét
AOC
có
90 ;AOC OA OC R

AOC
vuông cân tại O
0
45 45OAC IAQ

Xét
AQI
có
90 ; 45IQA IAQ


AQI
vuông cân tại Q
d) Tứ giác
AOJM
nội tiếp nên
MJC MAQ
mà
AMQ CMB
( tính chất góc nội
tiếp)
Do đó
. ..
MJ MA
MJC MAQ g g MJ MQ MA MC
MC MQ
 ”
2
0
1 12
. . . sin . . .sin 45 .
2 2 44
MQJ
MA MC
S MJ MQ MQJ MA MC

Gọi
X
là điểm chính giữa của cung nhỏ AC
MA MC XA X C 
(không đổi )
2
2
( 2 1)
2
.
44 2
MQJ
XA XC
R
S

( không đổi)
Dấu bằng xảy ra
MX
M là điểm chính giữa cung nhỏ AC
Vậy
2
( 2 1)
max
2
MQJ
R
S
. Khi M là điểm chính giữa cung nhỏ AC
Câu 4.
22
3
23
8 13 11 1 3 2xx x
xx

− +=++ −


(ĐKXĐ:
0x ≠
)
PT đã cho
(
)
( )
( )
( )
( )
(
)
22
3
32 2
3
32 2
3
8 13 11 2 3 3 2
8 13 11 2 3 3 2
8 15 6 1 3 2 1 3 2 0
xx x x x
xxx x x
x xx x x x
⇔ − + =++ −
⇔ − + =++ −
⇔ − + + + + −− − =
( ) ( )
( ) ( )
( )
( ) ( )
( )
( ) ( )
( )
( ) ( )
( )
3
2
2
2
2
22
3
3
2
2
2
22
3
3
321 3 2
18 1 0
21 213 2 3 2
3
1 8 11 0
21 213 2 3 2
xx x
xx
x xx x
x
xx
x xx x

+ −− −

⇔ − ++ =
− + − −+ −

+

⇔− + + =

− + − −+ −


( )
( )
( ) ( ) ( )
(
)
( ) ( )
( )
( ) ( )
( )
( ) ( )
( )
2
2
22
3
3
2
2
2
22
3
3
22
2
3
2
2
2
22
3
3
3 21 213 2 3 2
18 1 0
21 213 2 3 2
1 1 1 41
3 2 2 1 12
2 4 33
1 8 1. 0
21 213 2 3 2
x x xx x
xx
x xx x
xx x
xx
x xx x

++−+− −+ −

⇔− + =

− + − −+ −




−+ − + − +






⇔− + =
− + − −+ −
Dễ thấy
( )
( ) ( )
( )
22
2
3
2
2
22
3
3
1 1 1 41
3 2 2 1 12
2 4 33
0, 0
21 213 2 3 2
xx x
x
x xx x


−+ − + − +






> ∀≠
− + − −+ −
Từ đó suy ra
( ) (
)
2
1
1 8 1 0 1;
8
xx x

− + =⇒∈ −


Vậy tập nghiệm
1
1;
8
S

= −


_______HẾT________
| 1/6
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

TRƯỜNG THCS VĂN LANG ĐÁP ÁN THAM KHẢO MÔN TOÁN VÀO 10 TỔ TOÁN - TIN TỈNH PHÚ THỌ NĂM HỌC 2023-2024
I. PHẦN TRẮC NGHIỆM 1 2 3 4 5 6 7 8 9 10 11 12 C B A A B D C B C D A D II. PHẦN TỰ LUẬN Câu 1:
a) Khi a =16 (thỏa mãn điều kiện xác định) thì giá trị biểu thức 5 16 4 5.4 4 24 A + + = == = = 8 16 −1 4 −1 3
Vậy với a =16 thì A = 8.
b) Với a > 0;a ≠ 1;a ≠ 4  1 1  a (1 1 − − + a a a ) = + 1  . a − a B = . =
a 1− a a − 2 a (1− a ) a − 2 a − 2
c) Với a > 0;a ≠1;a ≠ 4 ta có: 5 a + 4 1 . A B < 0 ⇔ .
< 0 ⇔ ( a − )1( a − 2) < 0 (vì 5 a + 4 > 0) a −1 a − 2
⇔ 1 < a < 2 ⇔ 1 < a < 4
Vì a ∈ nên a∈{2; } 3 Vậy a ∈{2; } 3 Câu 2:
a) Vì M ( )∈(P) 2 1;2
: y = a x nên: 2 .1 a = 2 ⇔ a = 2
Với a = ⇒ (P) 2 2 : y = 2x
PT hoành độ giao điểm của (d ),(P)là x = 1 2 2 2x 3x 1 2x 3x 1 0
(x )1(2x )1 0  = − ⇔ − + = ⇔ − − = ⇔ 1 x =  2
Với x =1⇒ y = 2; 1 1 x = ⇒ y = 2 2
Vậy tọa độ giao điểm của (d ) và (P) là A( ) 1 1 1;2 ;B ;   . 2 2   
b) Xét hệ phương trình: 3
x + y = 5m +15 2x = 2m + 6 x = m + 3  ⇔  ⇔ 
x + y = 3m + 9
x + y = 3m + 9 y = 2m + 6 Xét
Q = xy − 2x −1 = (m + 3)(2m + 6) − 2(m + 3) 2
−1 = 2m +10m +11 2  5  3 3 ⇒ Q = 2 m + − ≥ −  2    2 2 Từ đó suy ra 3 minQ = − khi 5 m = − 2 2 Câu 3.
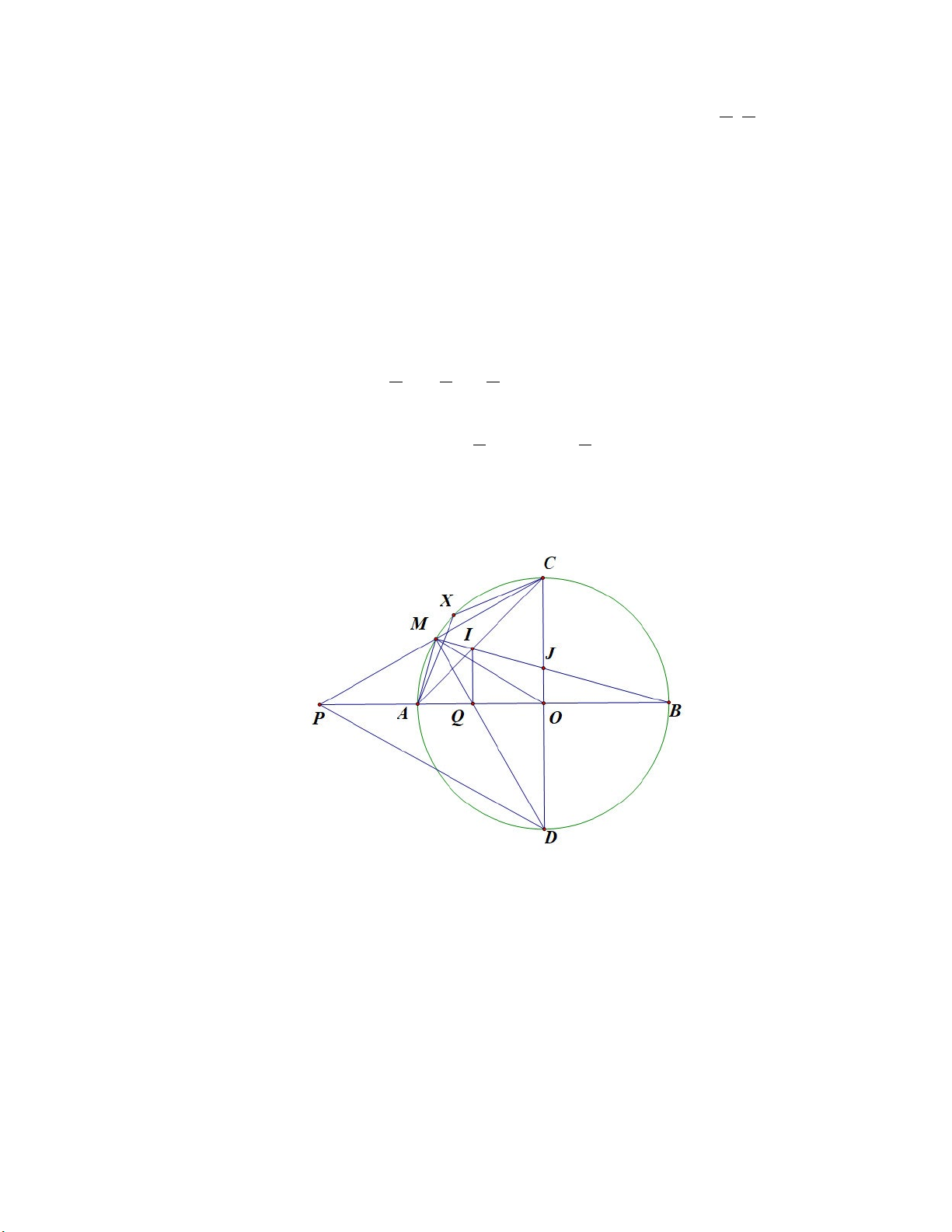
a) Do AB CD tại O nên    POD BOC AOC 90     1 Xét (O) có  0
MCD  90  DM PC tại M  0  PMD  90
Xét tứ giác OMPD có   0
POD PMD  90  tứ giác OMPD nội tiếp b) Từ    0 1  BOJ  90 Xét (O) có  0
AMB  90 ( Góc nội tiếp chắn nửa đường tròn) Xét OJ B  và BMA có:   BOJ BMA 90    
OBJ  MBA ( góc chung). Do đó BJ BA 2 BOJ” BM
A (g.g)  
BJ.BM BO.BA  .2 R R  2R . BO BM c) Xét (O) có  
BMD  BAC ( tính chất góc nội tiếp)    IMQ  IAQ
 tứ giác AMIQ nội tiếp        IQA AMI 180 IQA 90 180 IQA 90         Xét AOC có  AOC 90 
;OA OC R A
OC vuông cân tại O  0  OAC 45 IAQ 45     Xét AQI có    IQA 90 ;IAQ 45    A
QI vuông cân tại Q
d) Tứ giác AOJM nội tiếp nên  
MJC MAQ mà  
AMQ CMB ( tính chất góc nội tiếp) Do đó  ”   MJ MA MJC MAQ g.g    MJ.MQ  . MA MC MC MQ 1  1
2 MA MC 2 0 S
 .MJ.MQ.sin MQJ  . . MA MC. sin 45  . MQJ 2 2 4 4
Gọi X là điểm chính giữa của cung nhỏ AC MA MC XA XC (không đổi )
2 XA XC 2 2 R ( 2  1) S  .  ( không đổi) MQJ 4 4 2
Dấu bằng xảy ra M X  M là điểm chính giữa cung nhỏ AC Vậy 2 R ( 2  1) max S
. Khi M là điểm chính giữa cung nhỏ AC MQJ 2 Câu 4. 2 2  3  3 2
8x −13x +11 = + 1+ 3x −  
2 (ĐKXĐ: x ≠ 0) x x  PT đã cho ⇔ x( 2 8x −13x + ) 11 = 2 + (x + 3) 3 2 3x − 2 3 2
⇔ 8x −13x +11x = 2 + (x + 3) 3 2 3x − 2 ⇔ ( 3 2
8x −15x + 6x + ) 1 + (x + 3)( 3 2
2x −1− 3x − 2) = 0
(x + 3)(2x − )3 1 − ( 2 3x − 2  2 ) (x )1 (8x )1   ⇔ − + + = 0 (2x − )2 1 + (2x − ) 3 2 3 1 3x − 2 + ( 2 3x − 2)2   ( )2  x + x 1 (8x ) ( 3) 1 1  ⇔ − + + = 0   (  2x − )2 1 + (2x − ) 3 2 3 1 3x − 2 + ( 2 3x − 2)2   
(x +3)+(2x − )2 1 + (2x − ) 3 2  3
1 3x − 2 + 3x − 2 2  ( 2 )2 (x ) 1 (8x ) 1  ⇔ − + = 0   (  2x − )2 1 + (2x − ) 3 2 3 1 3x − 2 + ( 2 3x − 2)2    2 2    3 2 1
x − + ( x − ) 1  1  41 3 2 2 1 + 12     x − +   (      x ) 2 4 3 3 2 1 (8x ) 1 .   ⇔ − + = 0 (2x − )2 1 + (2x − ) 3 2 3 1 3x − 2 + ( 2 3x − 2)2 2 2    3 2 1
x − + ( x − ) 1  1  41 3 2 2 1 + 12     x − +  2  4   3  3  Dễ thấy   > 0, x ∀ ≠ 0 (2x − )2 1 + (2x − ) 3 2 3 1 3x − 2 + ( 2 3x − 2)2
Từ đó suy ra (x )2 ( x )  1 1 8 1 0 x 1;  − + = ⇒ ∈  − 8   Vậy tập nghiệm  1 S 1;  =  − 8   _______HẾT________
Document Outline

  • Doc1
  • ĐÁP ÁN THAM KHẢO TOÁN VÀO 10 NĂM 2023-2024 (1)