Đề vào lớp 10 môn Toán (chuyên) 2022 – 2023 trường chuyên Nguyễn Trãi – Hải Dương

SỞ GIÁO DỤC VÀ ĐẠO TẠO
KỲ THI TUYỂN SINH LỚP 10 HẢI DƯƠNG
THPT CHUYÊN NGUYỄN TRÃI NĂM HỌC 2022 -2023 ĐỀ CHÍ
Môn thi: TOÁN (Chuyên) NH THỨC
Thời gian làm bài : 150 phút, không tính thời gian phát đề (Đề thi có 01 trang) Câu 1 (2,0 điểm).    + + +  a. So sánh biểu thức x x 2 x 3 x 2 A=1− :  + +   với 5 − .
x 1  x 5 x 6 x 2 3 x  + − + − −     2 2024 2023
b. Tính giá trị của biểu thức
4x (x +1) − 2x + 2x +1 B = tại 1 3 x = − . 2 2x + 3x 2 3 − 2 2 3 + 2 Câu 2 (2,0 điểm). a. Giải phương trình: x −1 3x −1+ = 3x +1 4x 
x + y + xy = 8
b. Giải hệ phương trình:  1 1 1 + =  2 2
 x + 2x y + 2y 4 Câu 3 (2,0 điểm). a. Tìm các cặp số nguyên ( ; x y) thỏa mãn phương trình 2 2 2
y − 5y + 62 = (y − 2)x + (y − 6y + 8)x .
b. Cho đa thức P(x) với các số nguyên thỏa mãn P(2021).P(2022) = 2023. Chứng minh rằng
đa thức P(x) − 2024 không có nghiệm nguyên. Câu 4 (3,0 điểm).
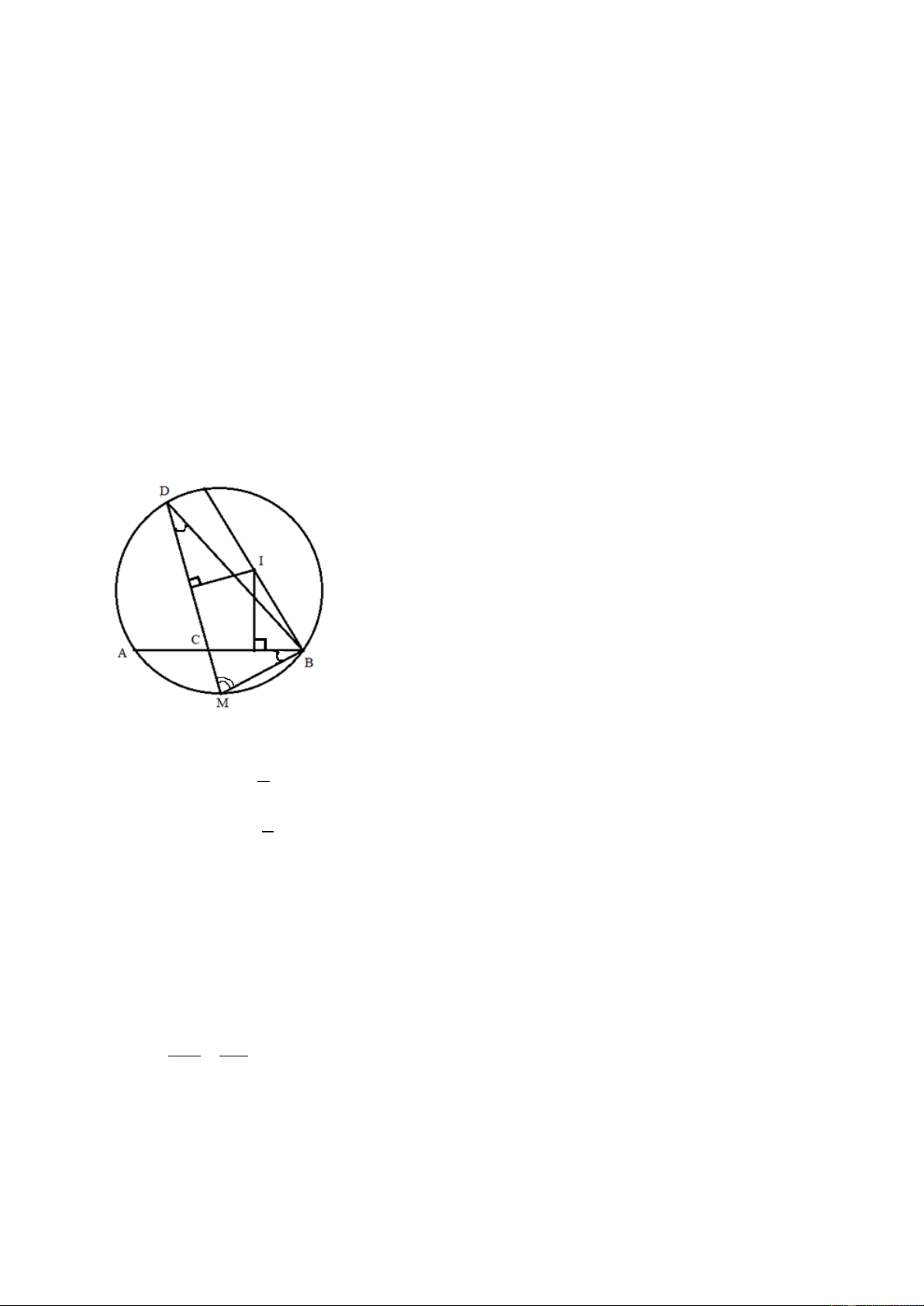
1. Cho đường tròn (O) và dây cung AB không đi qua tâm O. Gọi M là điểm chính giữa của
cung nhỏ AB; D là 1 điểm thay đổi trên cung lớn AB (D khác A và B); DM cắt AB tại C.
a. Chứng minh rằng MB.BD = MD.BC;
b. Chứng minh rằng MB là tiếp tuyến của đường tròn ngoại tiếp tam giác BCD và khi điểm D
thay đổi thì tâm đường tròn ngoại tiếp tam giác BCD nằm trên một đường thẳng cố định.
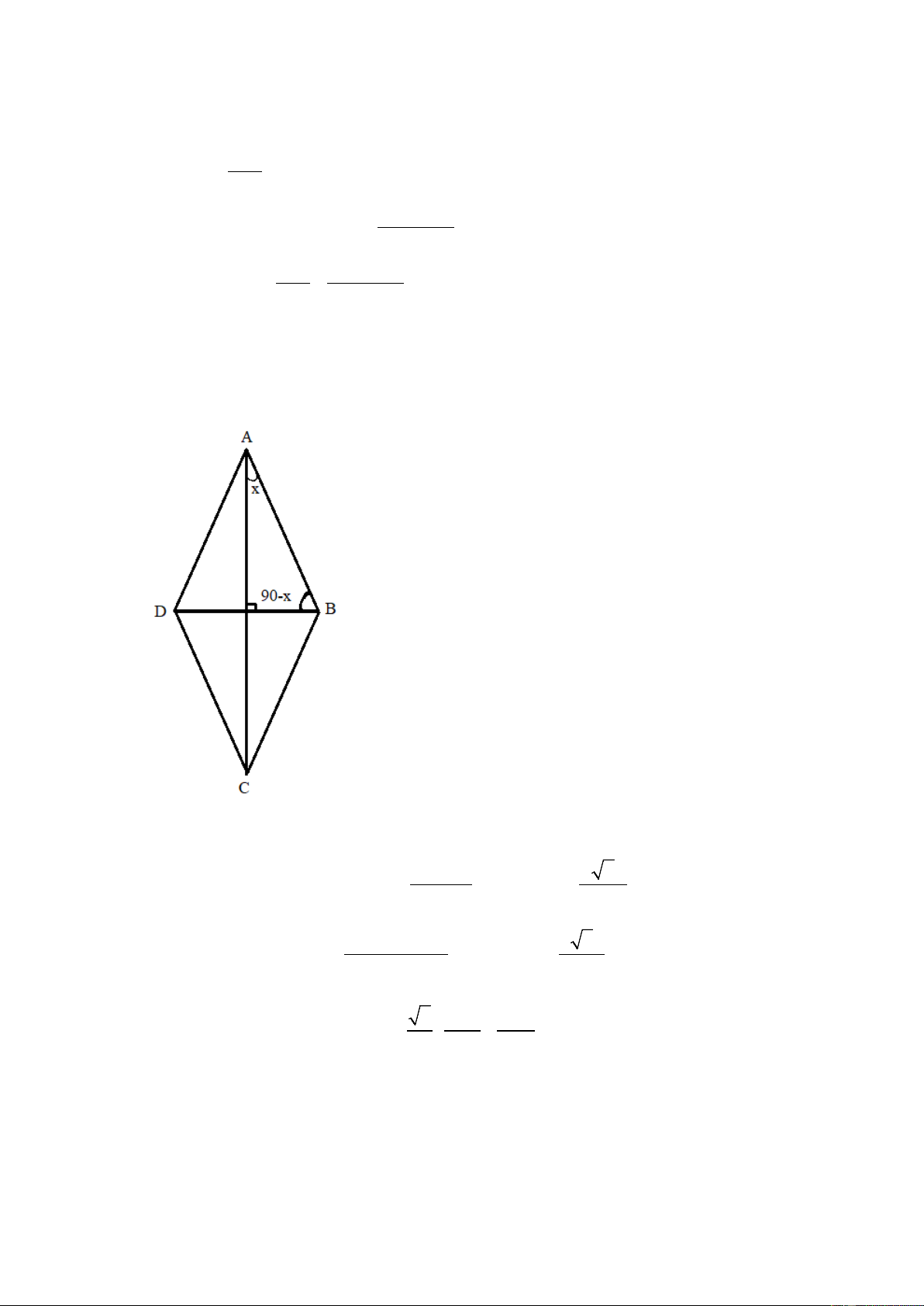
2. Cho hình thoi ABCD có AB = 2 . Gọi R1, R2 lần lượt là bán kính đường tròn ngoại tiếp các
tam giác ABC và ABD. Chứng minh rằng R + R ≥ 2 . 1 2
Câu 5 (1,0 điểm). Cho a,b,c là các số thực dương thỏa mãn 2 2
a + 4b + c = 6ab . Tìm giá trị nhỏ 3 3 nhất của biểu thức a 2b a + 8b P = + + .
2b + c a + c 16c
………… HẾT ………. Lời giải Câu 1 x ≥ 0
a. ĐKXĐ: x ≠ 4 x ≠  9    + + +  x x 2 x 3 x 2 A=1−  :  + +  
x 1  x 5 x 6 x 2 3 x  + − + − −     x +1− x  x + 2 x − 9 x − 4    ⇔ A=  :  + −    x +1  
 ( x − 2)( x −3) ( x − 2)( x −3) ( x − 2)( x −3) 1 x − 3 x − 2 ⇔ A = : =
x +1 ( x − 2)( x −3) x +1 2 5 2 5 ( x −2)+5( x x + − )1 Ta có : 7 x +1 A + = + = = 2 x +1 2 2( x + )1 2( x + )1 Vì 5 5
x ≥ 0 ⇒ A + > 0 ⇒ A > − 2 2 Vậy 5 A > − . 2 b. Vì 1 3 3 1 x − = − = nên 3 1 x − =
là nghiệm của đa thức 2 2x + 2x −1 2 3 − 2 2 3 + 2 2 2 2023 2 Do đó:
2x (2x + 2x −1) + 2x +1 2x +1 B = = = 3− 3 . 2
(2x + 2x −1) + x +1 x +1 Câu 2.  x > 0  a. ĐKXĐ:  1 x ≥ −  3
Phương trình đã cho đương đương với :
4x(3x −1) + x −1 = 4x 3x +1 2
⇔ 12x − (3x +1) = 4x 3x +1  b = a
Đặt a = 2x,b = 3x +1 ta có phương trình 2 2
3a − b = 2ab ⇔ (b − a)(b + 3a) = 0 ⇔  b = 3 − a  3x +1 = 2x Khi đó   3x +1 = 6 − x
+) Với 3x +1 = 2x , điều kiện x > 0 , ta có  x =1 2 2
3x +1 = 2x ⇔ 3x +1 = 4x ⇔ 4x − 3x −1 = 0  ⇔ 1
x = − (KTM )  4 +) Với 3x +1 = 6
− x , điều kiện 1
− ≤ x < 0 , ta có 3  3− 153  x = 2 3x +1 = 6
− x ⇔ 36x − 3x −1 = 0 72 ⇔   3+ 153 x = (KTM )  72
Vậy phương trinh có hai nghiệm là x =1, 3 153 x − = . 72 
x + y + xy = 8  (x +1)(y +1) = 9   b. Ta có  1 1 1 ⇔  1 1 1 + =  + = 2 2 2 2
 x + 2x y + 2y 4  ( x + ) 1 −1 ( y + ) 1 −1 4
Đặt u = x +1,v = y +1  uv = 9 u  ≠ 1 ±
Hệ đã cho trở thành  1 1 1 , điều kiện:  (∗) + =  v ≠ 1 ± 2 2
u −1 v −1 4  uv = 9 ⇔  2 2 2 2 2 2
4(u + v − 2) = u v − u − v +1  uv = 9  uv = 9  u = v = 3 ⇔  ⇔  ⇔  (TM ( )) ∗ 2 2 u  + v = 18 u  + v = 6 ± u  = v = 3 −
x = 2 x = 4 −
Từ đó suy ra nghiệm của hệ phương trình là  ; . y 2  = y = 4 − Câu 3. a. Ta có: 2 2 2
y − 5y + 62 = (y − 2)x + (y − 6y + 8)x 2 2
⇔ (y − 5y + 6) + 56 = (y − 2)x + (y − 2)(y − 4)x 2
⇔ (y − 2)(y − 3) + 56 = (y − 2)x + (y − 2)(y − 4)x 2
⇔ (y − 2)(x + yx − 4x − y + 3) = 56
⇔ (x −1)(y − 2)(x + y − 3) = 56
Nhận thấy (y − 2) + (x −1) = x + y − 3, nên ta phải phân tích số 56 thành tích của 3 số nguyên
mà tổng 2 số đầu bằng 2 số còn lại. Như vậy, ta có: 56 =1.7.8 ⇒ ( ; x y) = (2;9) 56 = 7.1.8 ⇒ ( ; x y) = (8;3) 56 = ( 8 − ).1.( 7 − ) ⇒ ( ; x y) = ( 7 − ;3) 56 =1.( 8 − ).( 7 − ) ⇒ ( ; x y) = (2; 6 − ) 56 = ( 8 − ).7.(− ) 1 ⇒ ( ; x y) = ( 7 − ;9) 56 = 7.( 8 − ).(− ) 1 ⇒ ( ; x y) = (8; 6 − )
Vậy phương trình có 6 nghiệm trên.
b. Giả sử đa thức P(x) có 1 nghiệm nguyên là a.
Ta có: P(a) − 2024 = (x − a)Q(x) , (Q(x) là đa thức có hệ số nguyên) Ta có: P( )
2021 − 2024 = (2021− a)Q( ) 2021
P(2022) − 2024 = (2022 − a)Q(2022) Mà P( )
2021 .P(2022) = 2023 là số lẻ ⇒ P( )
2021 , P(2022) là số lẻ
Do đó 2021− a , 2022 − a là các số lẻ
⇒ (2021− a) − (2022 − a) là số chẵn ⇒ 1
− là số chẵn (điều này vô lí)
⇒ P(x) − 2024 không có nghiệm nguyên. Câu 4. 1. a. Chứng minh MB.BD = MD.BC Ta có:  1 =  MBC sdAM 2  1 =  MDB sdMB 2 Mà:  = 
AM MB ( vì M là điểm chính giữa cung  AB ) ⇒  =  MBC MDB
Xét MBC và MDB có  BMC góc chung  =  MBC MDB (cmt) Do đó, MBC 
∽ MDB(g.g) MB BC ⇒ = hay M . B BD = M . D BC (dpcm). MD BD
b. Chứng minh rằng MB là tiếp tuyến của đường tròn ngoại tiếp tam giác BCD và khi điểm D
thay đổi thì tâm đường tròn ngoại tiếp tam giác BCD nằm trên một đường thẳng cố định.
Gọi (I) là đường tròn ngoại tiếp BCD . ⇒  =  = 
BIC 2BDC 2MBC ( 
BIC là góc ở tâm chắn  BC , 
BDC là góc nội tiếp chắn  BC trong (I)) ⇒   BIC MBC = 2 Ta có BIC BIC cân tại I   180 IBC − ⇒ = 2     BIC 180 BIC MBC IBC − ⇒ + = + = 90o 2 2
⇒ MB ⊥ BI ⇒ MB là tiếp tuyến của (I), và I ∈ đường thẳng vuông góc với MB.
Vì M, B cố định, nên đường thẳng vuông góc với MB cố định. Do đó, khi điểm D thay đổi
thì tâm I của đường tròn ngoại tiếp tam giác BCD nằm trên một đường thẳng cố định. 2. Đặt  = ⇒  0 CAB x ABD = 90 − x Xét BC 2
ABC , theo định lý sin, ta có: = ⇒ =  2R R 1 1 sin CAB 2sin x Tương tự, xét AB 2 ABD , có: = R ⇒ R = 2sin ( 2 0 90 − x) 2 2 2 os c x 2  1 1  ⇒ + = + 0 < ≤   90o R R x 1 2 ( ) 2  sinx cosx 
Đặt sinx = t (0 < t < ) 1 2 1 1  ⇒ R + R =  + 1 2  2 2  t 1− t  1 1 ' 1 2 ( ) = + ⇒ ( ) t f t f t = − − 2 2 2 2 t 1− t t
2(1− t ) 1− t ' 2
⇒ f (t) = 0 ⇔ t = 2 2  2 2 R R  ⇒ + ≥ + =   2(dpcm) . 1 2 2  2 2  Câu 5. 3 3 Ta có: a 2b a + 8b P = + +
2b + c a + c 16c 3 3 a 2b a + 8 ⇔ = +1+ +1 b P + − 2 2b + c a + c 16c 3 3 ⇔ = ( + + ) 1 1  a + 8 2 b P a b c + + −   2
 2b + c a + c  16c Ta có: 2
(x − y) ≥ 0 nên 2 2
x + y ≥ 2xy 2 + 4 ⇒ ( + ) ≥ 4 x y x y xy ⇒ ≥ với ; x y > 0 xy x + y 1 1 4 ⇒ + ≥ x y x + y Lại có: 2 2
x + y − xy ≥ xy nên x + y ( 2 2 (
) x + y − xy) ≥ xy(x + y) 3 3
⇒ x + y ≥ xy(x + y)
⇒ P ≥ (a + b + c) 4 .
a 2b(a + 2b) 2 + − 2
2b + c + a + c 16c 2(a + 2b)
2ab(a + 2b) ⇔ P ≥ +
a + 2b + 2c 16c Mặc khác: 2 2
a + 4b + c = 6ab nên 2
(a − 2b) + c = 2ab 2 (a 2b) c 2ab 4 .2 a b 4c c + ⇒ ≤ ⇔ = ⇒ ≤ 4
Đặt t = a + 2b , ta có: 2t 2t 4 t 4 t + 2 2 P ≥ + = + = + − 2 t
16 t + 2 16 t + 2 16 16 + t 2 4 t 1 7 ⇒ P ≥ 2 . − = t + 2 16 8 8 7 4 t + 2 P = khi = ⇔ t = 6 min 8 t + 2 16 a = 3 a + 2b = 6    3
⇔  a = 2b ⇔ b  = 2  c 2ab  =  c = 9  Vậy GTNN của 7 3
P = khi a = 3,b = ,c = 9 . 8 2
Document Outline

• de-vao-lop-10-mon-toan-chuyen-2022-2023-truong-chuyen-nguyen-trai-hai-duong
• 26. HẢI DƯƠNG.FULL