Đề vào lớp 10 môn Toán (chuyên) năm 2022 – 2023 trường chuyên Lê Hồng Phong – Nam Định

HƯỚNG DẪN GIẢI Câu 1. (2,0 điểm)
1. Cho f  x 2
 2x  2x  7 có 2 nghiệm phân biệt là x , x . Đặt g x 2
 x 1. Tính giá trị 1 2
của biểu thức T  g  x .g x . 1   2
2. Cho các số thực , a ,
b c bất kì thoả mãn 2 2 2
a  b  c  2022 . Chứng minh rằng
 a  bc2  b c a2  c  a b2 2 2 2 2 2 2 18198. Lời giải
1. Vì f  x 2
 2x  2x  7 có 2 nghiệm phân biệt là x , x nên f x  2x  x x  x 1   2  1 2
Ta có T  g  x .g  x    2 x   1  2
x 1  x 1 x 1 x 1 x 1 1 2 1 2
  1  2  1  2    
 T    x   x   x   x  f   1 f   1  7. 3 21 1 1 1 1  .   . 1 2 1 2 2 2 4 4 1 15 1 15
Cách khác: Học sinh có thể tìm hai nghiệm của f  x là x  , x  1 2 2 2 2 2     1 15  1 15  21
Từ đó tính T  g  x .g x    1   1  . 1   2      2   2  4        
2. Đặt t  a  b  c . Khi đó ta có
 a  bc2  b c a2  c  a b2   t  a2  t  b2  t  c2 2 2 2 2 2 2 2 3 2 3 2 3 2
 t  t a b  c   2 2 2
a  b  c  2 2
 t  t   2 2 2
a  b  c    2 2 2 12 12 9 12 12 9
9 a  b  c 
Do đó  a  b  c2   b  c  a2   c  a b2 2 2 2 2 2 2  9.2022 18198.
Cách khác: Học sinh có thể khai triển bình phương từng biểu thức rồi rút gọn và cũng được kết quả cần chứng minh. Câu 2.
(2,0 điểm) Giải các phương trình và hệ phương trình:
1. x   x  3 2 1  3x  4 .  y 3 7
 42x  y  2x  4 y  7  4
2. 2 2x1 2y14  x4.  Lời giải
1. Điều kiện xác định x  1  . x  
Phương trình cho tương đương với  x  x   x   1 1 4
1  0   x1  4 x  x  4 4  x  0  x  4  9  21
Ta có x 1  4  x        x    9 21 x 1   4 x2 2
x  9x 15  0 x  2  2   
Đối chiếu điều kiện có tập nghiệm của phương trình là 9 21  1  ;  .  2   1
2. Điều kiện xác định x   , y  7 2 Ta có     
 y   y   x     x   y    y    y  x   y 7 4 1 7 7 2 8 4 2 1 0 7 4 2
1  0  y  2x1
Trường hợp 1: y  7  4  y  9 , thay vào (2) ta được 1
x    x  
x   x    x   2 2 2 1 2 4 2 2 1 2 4 2
1  x  4x  4 (do x    2  ) 2 x  0 2
 x  4x  0  
(thoả mãn điều kiện). x  4
Trường hợp 2: y  2x 1, thay vào (2) ta được x   x 
 x    x   x     x  2  x 2 2 2 1 4 12 4 2 2 1 3 2 1 3 (*)
Do 2x 1 và x  3 không đồng thời bằng 0 nên 2x 1  x  3  0 Khi đó  
*  2  2x 1  x  3  2x 1  2  x  3  x   
x    x    x   x  x  2 2 1 4 4 3 3 4 3 16
3  x (do y  2x 1  7  x  3) x  4 2
 x 16x  48  0  x 12
Với x  4 thì y  9
Với x  12 thì y  25
Kết hợp các điều kiện ta có tập nghiệm của hệ phương trình là 
 0; 9, 4; 9, 12; 25. Câu 3.
(3,0 điểm) Cho đường tròn  ,
O R và điểm M nằm ngoài đường tròn. Từ điểm M kẻ hai tiếp tuyến M ,
A MB với đường tròn O ( ,
A B là các tiếp điểm). Gọi D là điểm trên cung lớn AB của đường tròn  ,
O R sao cho AD // MB và C là giao điểm thứ hai của đường thẳng MD với đường tròn  , O R .
1. Gọi H là giao điểm của các đường thẳng OM và AB . Chứng minh rằng
MH.MO  M .
C MD và tứ giác OHCD nội tiếp.
2. Gọi G là trọng tâm tam giác MA .
B Chứng minh rằng ba điểm ,
A C, G thẳng hàng.
3. Giả sử OM  3 .
R Kẻ đường kính BK của đường tròn  ,
O R . Gọi I là giao điểm của các 2 2  đườ IM IA IA
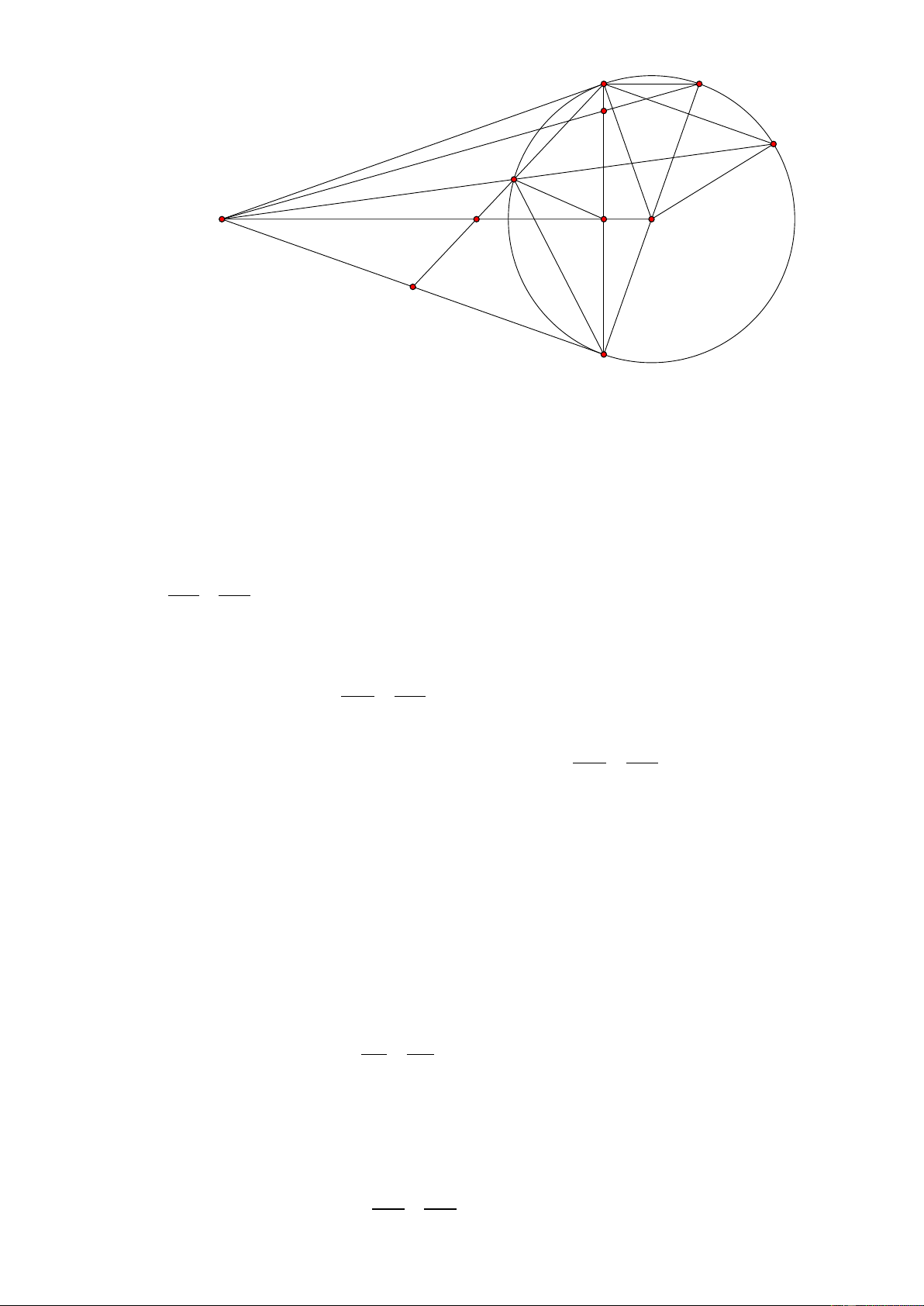
ng thẳng MK và AB . Tính giá trị biểu thức T  8  5 . 2 2 IK  IH AB Lời giải A K I D C M G H O E B 1. Vì M ,
A MB là các tiếp tuyến tại ,
A B của đường tròn  , O R  
Nên ta suy ra OM  AB ; MA  OA và MAC  MDA
Xét tam giác OAM vuông tại A và có đường cao AH ta có 2 MA  M . O MH (1)    Mặt khác xét M  AC và M
 DA có MAC  MDA và M chung nên M  AC ∽ M  DA gg MC MA 2  
 MA  MC.MD (2) MA MD
Từ (1) và (2) suy ra MH.MO  M . C MD MH MC
Vì MH.MO  MC.MD   MD MO MH MC  Xét hai tam giác M  CH và M  OD có  và M chung nên MD MO M  CH ∽ M  OD cgc         0
 MHC  MDO  CHO  CDO  CHO  MDO  CHO  MHC 180
Do hai đỉnh H, D ở hai vị trí đối diện nên tứ giác OHCD nội tiếp.
2. Gọi E là giao điểm của AC và MB    Xét EBC  và EAB 
có E chung và EBC  EAB (góc giữa tiếp tuyến và một dây cung và
góc nội tiếp cùng chắn một cung)  E  BC ∽ E  AB gg EB EC 2    EB  E . A EC (3) EA EB   
Mặt khác, vì AD // MB nên EMC  MDA  MAE    Xét E  MC và EAM 
có E chung và EMC  MAE  E  MC ∽ E  AM gg EM EC 2    EM  E . A EC (4) EA EM Từ (3) và (4) suy ra 2 2
EB  EM  EB  EM hay E là trung điểm của MB
Tam giác MAB có AE là đường trung tuyến nên AE đi qua trọng tâm G của M  AB hay ba điểm ,
A C, G thẳng hàng. 3. Tam giác OAM vuông tại A và có đường cao AH nên 2 2 OA R R 2
OA  OH.OM  OH    OM 3R 3 2 R 8R   R  4 2
MH  OM  OH  3R   và 2 2 2
AB  2AH  2 OA  OH  2 R   R   3 3  3  3
Mà BK là đường kính của đường tròn  , O R nên ABK 
vuông tại A và BK  2R 2        R AK BK AB 2R2 4 2 2 2 2   R     3 3   Tính đượ 2 2R 8 2R 8 3R 2 3R c IA  , IH  , IM  , IK  15 15 5 5 7003 Vậy T  . 118 Câu 4. (1,5 điểm)
1. Chứng minh rằng Pn 4 3 2
 n 14n  71n 154n 120 chia hết cho 24 với mọi số tự nhiên . n
2. Cho p là số nguyên tố có dạng 4k  3, k  . Chứng minh rằng nếu , a b   thoả mãn 2 2
a  b chia hết cho p thì a  p và b  p . Từ đó suy ra phương trình 2 2
x  4x  9y  58 không có nghiệm nguyên. Lời giải
1. Ta có Pn 4 3 2
 n 14n  71n 154n 120  n  2n  
3 n  4n  5
Ta thấy với mọi số tự nhiên n , thì P n là tích của 4 số nguyên liên tiếp nên P
 n  3, n    P
 n  8, n  
Mà 3, 8  1 nên Pn  24, n   .
2. Giả sử a không chia hết cho p thì từ giả thiết 2 2
a  b chia hết cho p ta suy ra b cũng không chia hết cho p p 1 a  1  mod p Do đó  , a p   ,
b p 1. Áp dụng định lý Fermat ta có  p 1 b   1  mod p p 1  p 1
 a  b    p 4k2 4k2 2 mod  a  b  2mod p (*) 2k 1  2k 1 
Mặt khác ta có 4k2 4k 2 a  b   2 a    2 b  chia hết cho 2 2 a  b Kết hợp 2 2
a  b chia hết cho  
p ta suy ra 4k 2 4k 2 a  b
chia hết cho p (**)
Từ (*) và (**) suy ra 2  p  p  2 (mâu thuẫn với giả thiết là số nguyên tố có dạng 4k  3).
Do đó điều giả sử là sai.
Suy ra a  p . Kết hợp giả thiết suy ra b  p . Vậy ta có điều phải chứng minh. Giả sử phương trình 2 2
x  4x  9y  58 có nghiệm nguyên
Khi đó phương trình đã cho tương đương vớ 2 2
i  x  2  3y  62 2 2
Suy ra  x  2  3y chia hết cho 31 và 31 là số nguyên tố có dạng 4k  3   x  2    31   x  2  2 2  31
Áp dụng chứng minh trên ta suy ra     3y    31   3y  2 2  31
 x  2  y2 2 2 2 3
 31  62  31 (vô lý).
Vậy phương trình đã cho không có nghiệm nguyên. Câu 5. (1,5 điểm)
1. Xét các số thực không âm ,
x y, z thoả mãn x  y  z  6. Tìm giá trị nhỏ nhất của biểu thức 2 2 2 x y z P    . 3 3 3 yz  1 x zx  1 y xy  1 z
2. Từ 2022 số nguyên dương đầu tiên là 1, 2, 3, …, 2022, người ta chọn ra n số phân biệt sao
cho cứ hai số bất kì được chọn ra đều có hiệu không là ước của tổng hai số đó. Chứng minh rằng n  674 . Lời giải 2 2
1 x  1 x  x x  2 1. Ta có 3
1 x  1 x 2
1 x  x        2 2 2 2 2 x x 2x    2 2 3   x  2 2 yz  x  2 yz 1 x yz  2 2 2 2 2 y 2 y z 2z
Chứng minh tương tự ta cũng có  ;  2 2 3 3   2zx  y  2   2xy  z  2 zx 1 y xy 1 z 2x 2 y 2z
x  y  z2 2 2 2 Suy ra P     2 2 2 2 2 yz  x  2 2zx  y  2 2xy  z  2
x  y  z2  6
x  y  z2 12
Kết hợp giả thiết ta có P  2 
x  y  z2 1
 x  y  z2 7 6 12
Với x  y  z  2 thì P  . 7 12
Vậy giá trị nhỏ nhất của biểu thức P là . 7 2. Với hai số ,
x y bất kì trong số n số lấy ra thì rõ ràng x  y  0 và x  y  1.
Nếu x  y  2 thì ,
x y cùng tính chẵn lẻ nên có  x  y x  y (mâu thuẫn giả thiết), do đó
x  y  2 . Vậy x  y  3.
Gọi n số lấy ra sắp thứ tự là a  a    a . Khi đó có: 1 2 n a  1 1
a  a  3  a  a  3 2 1 2 1
a  a  3  a  a  3  a  2.3 3 2 3 2 1
… Cứ tiếp tục quá trình trên, ta có a  a  n 1 .3. n 1   2024 2
Vậy có 2022  a  a  3 n 1  1 3n  3  n   674 . n 1   3 3
Từ đó dẫn đến n  674 , ta có điều phải chứng minh. ---Hết---
Document Outline

• de-vao-lop-10-mon-toan-chuyen-nam-2022-2023-truong-chuyen-le-hong-phong-nam-dinh
• 40-NAM DINH-TOAN CHUYEN