APPLIED STATISTICS COURSE CODE: ENEE1006IU Lecture 5:
Chapter 3: Descriptive statistics
(3 credits: 2 is for lecture, 1 is for lab-work)
Instructor: TRAN THANH TU Email: tttu@hcmiu.edu.vn tttu@hcmiu.edu.vn 1
3.3. MEASURES OF DISTRIBUTION SHAPE, RELATIVE LOCATION, AND DETECTING OUTLIERS •Distribution Shape •z-Scores •Chebyshev’s Theorem •Empirical Rule •Detecting Outliers
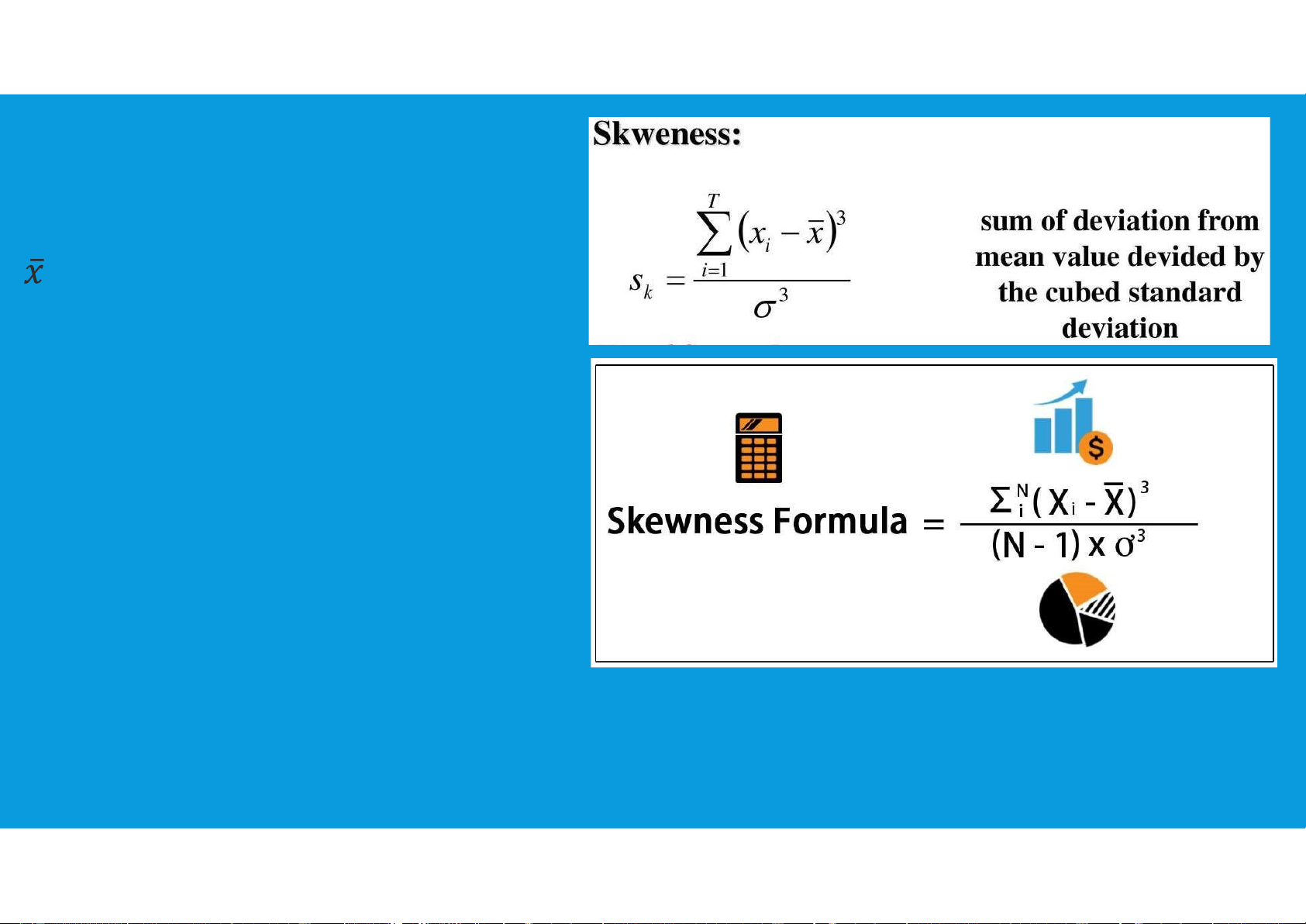
3.3. MEASURES OF DISTRIBUTION SHAPE, RELATIVE LOCATION, AND DETECTING OUTLIERS tttu@hcmiu.edu.vn 2 •Distribution Shape: •xi = ith Random Variable
• = Mean of the Distribution
•n = Number of Variables in the Distribution
•σ (or s) = Standard Distribution 3.3. MEASURES OF DISTRIBUTION SHAPE, RELATIVE LOCATION, AND DETECTING OUTLIERS tttu@hcmiu.edu.vn 3 •Distribution Shape:
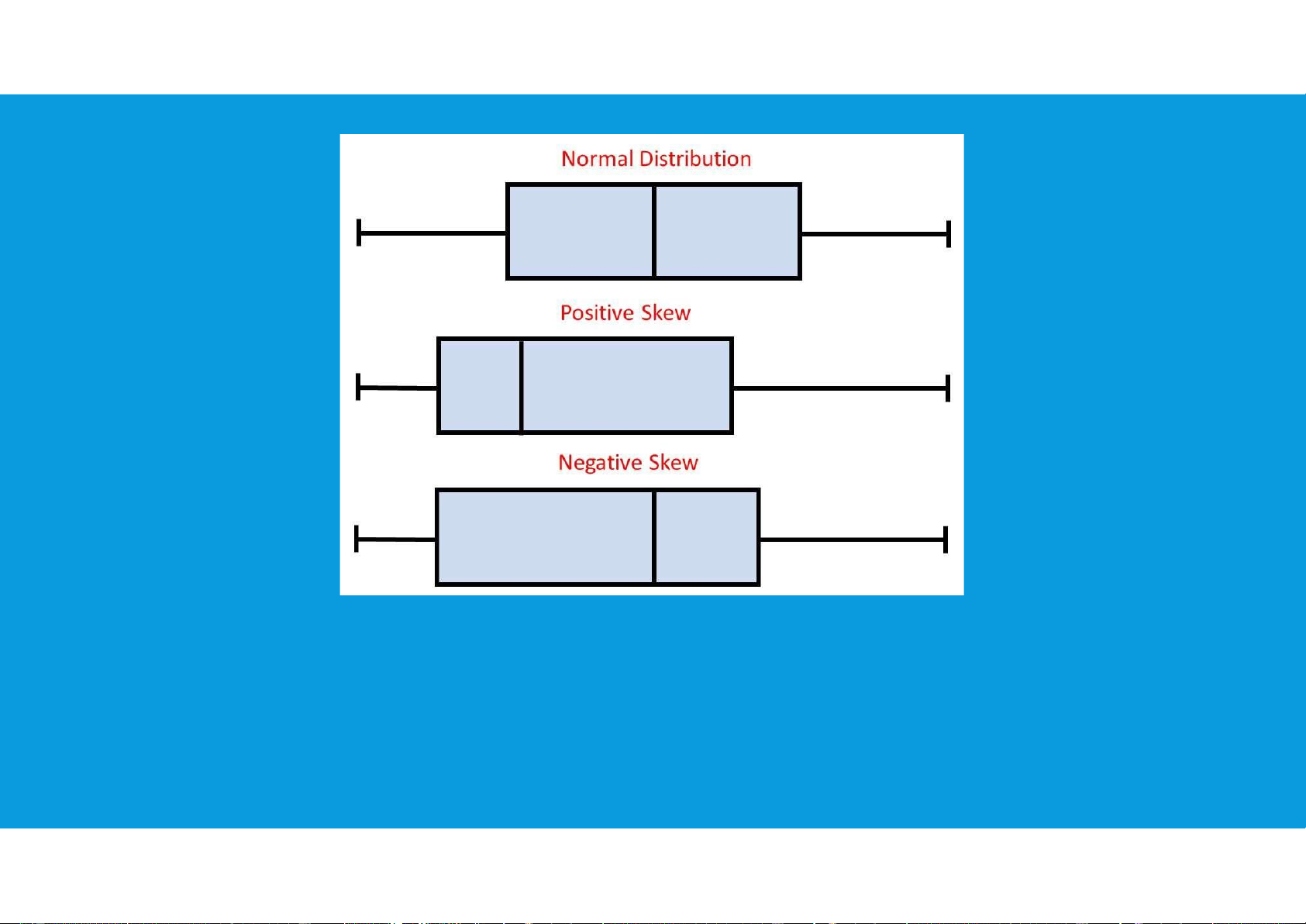
•For a symmetric distribution, the mean and the median are equal.
•When the data are positively skewed, the mean will usually be greater than the median.
•When the data are negatively skewed, the mean will usually be less than the median. 3.3. MEASURES OF DISTRIBUTION SHAPE, RELATIVE
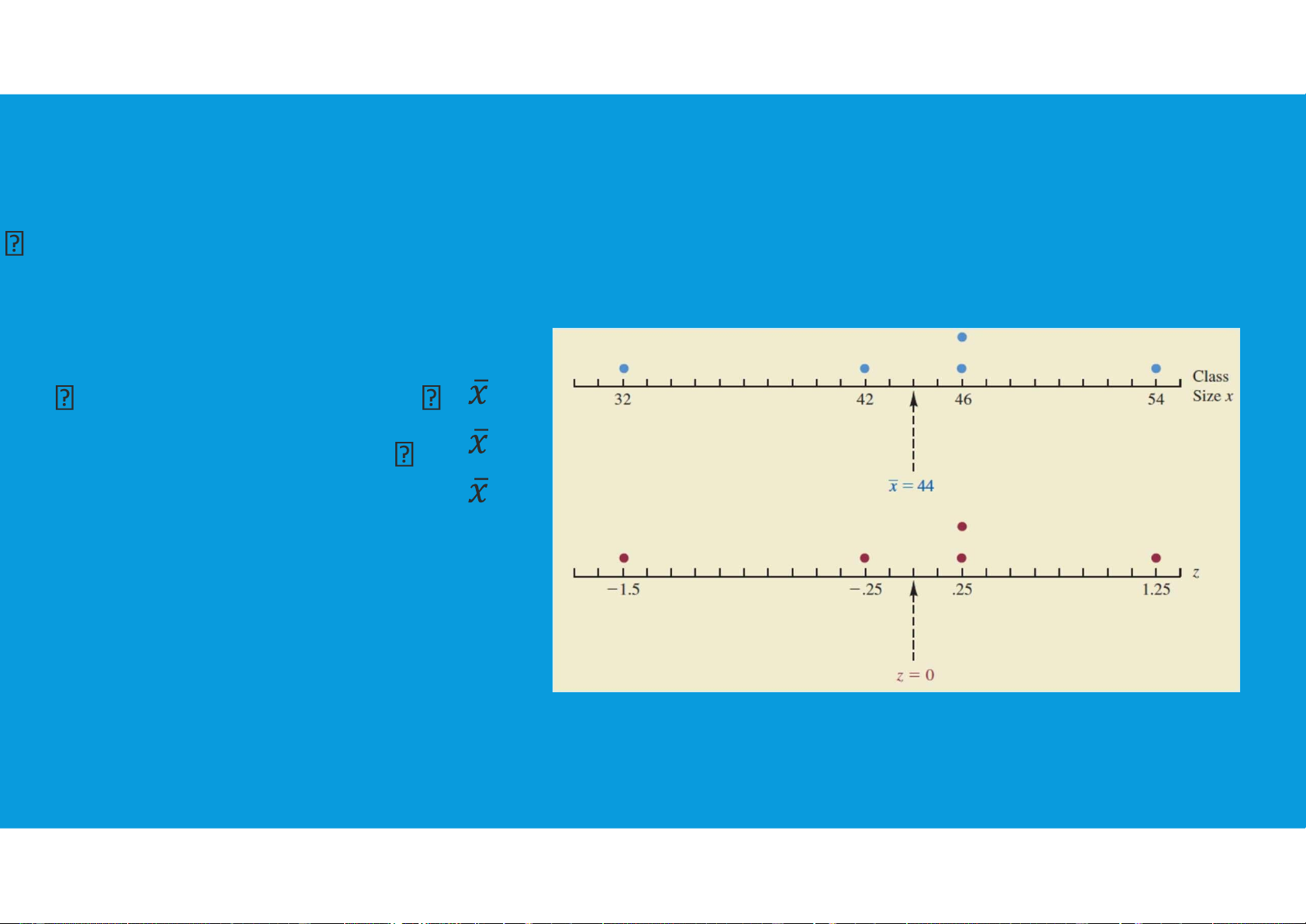
LOCATION, AND DETECTING OUTLIERS •z-Scores: By using both the tttu@hcmiu.edu.vn 4
mean and standard deviation, we can determine the relative location of any observation i.
The z-score is often called the standardized value.
•The z-score, zi, can be interpreted as the number of standard deviations xi is from the mean x. z-score > 0 means xi >
z-score < 0 means xi < z- score = 0 means xi = 3.3. MEASURES OF DISTRIBUTION SHAPE, RELATIVE LOCATION, AND DETECTING OUTLIERS
•Chebyshev’s Theorem: enables us to make statements about the tttu@hcmiu.edu.vn 5
proportion (%) of data values that must be within a specified number of standard
deviations of the mean (applied for all distribution shapes).
“At least (1 − 1/z2) of the data values must be within z standard deviations of the
mean, where z is any value greater than 1.”
(but z need not be an integer)
3.3. MEASURES OF DISTRIBUTION SHAPE, RELATIVE LOCATION, AND DETECTING OUTLIERS tttu@hcmiu.edu.vn 6
3.3. MEASURES OF DISTRIBUTION SHAPE, RELATIVE LOCATION, AND DETECTING OUTLIERS tttu@hcmiu.edu.vn 7 •Detecting Outliers:
•Sometimes a data set will have one or more observations with unusually large or
unusually small values. These extreme values are called outliers.
•An outlier may be a data value that has been incorrectly recorded that needed to
be corrected or removed before further analysis.
- Standardized values (z-scores) can be used to identify outliers
Treat any data value with a z-score less than −3 or greater than +3 as an outlier
3.3. MEASURES OF DISTRIBUTION SHAPE, RELATIVE LOCATION, AND DETECTING OUTLIERS •Detecting Outliers:
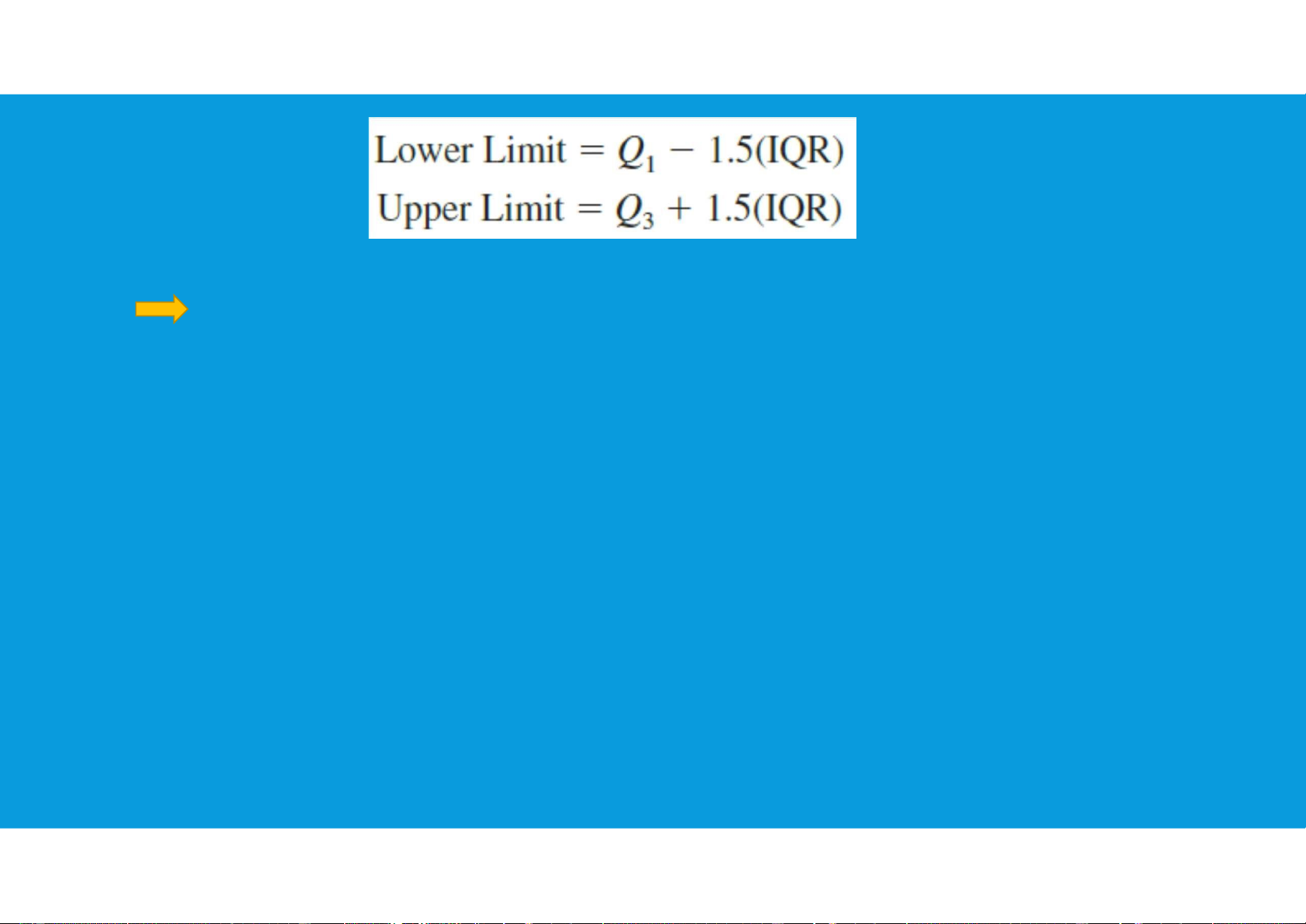
- Another approach to identifying outliers is based upon the values of the first and
third quartiles (Q1 and Q3) and the interquartile range (IQR). tttu@hcmiu.edu.vn 8
An observation is classified as an outlier if its value is less than
the lower limit or greater than the upper limit tttu@hcmiu.edu.vn 9 lOMoARcPSD|47231818 End of file 1. Any questions? tttu@hcmiu.edu.vn 10
3.4. FIVE NUMBERS SUMMARIES AND BOX PLOTS •Five-Number Summary •Box Plot
•Comparative Analysis Using Box Plots lOMoARcPSD|47231818
3.4. FIVE NUMBERS SUMMARIES AND BOX PLOTS
•Five-Number Summary: is especially useful in descriptive analyses or during
the preliminary investigation of a large data set.
A summary consists of five values: the most extreme values in the data set (the
maximum and minimum values), the lower and upper quartiles, and the median. tttu@hcmiu.edu.vn 11 lOMoARcPSD|47231818
3.4. FIVE NUMBERS SUMMARIES AND BOX PLOTS
•Box Plot: A box plot is a graphical display of data based on a fivenumber
summary. A key to the development of a box plot is the computation of the
interquartile range, IQR = Q3 − Q1. tttu@hcmiu.edu.vn 12 lOMoARcPSD|47231818 tttu@hcmiu.edu.vn 13 lOMoARcPSD|47231818
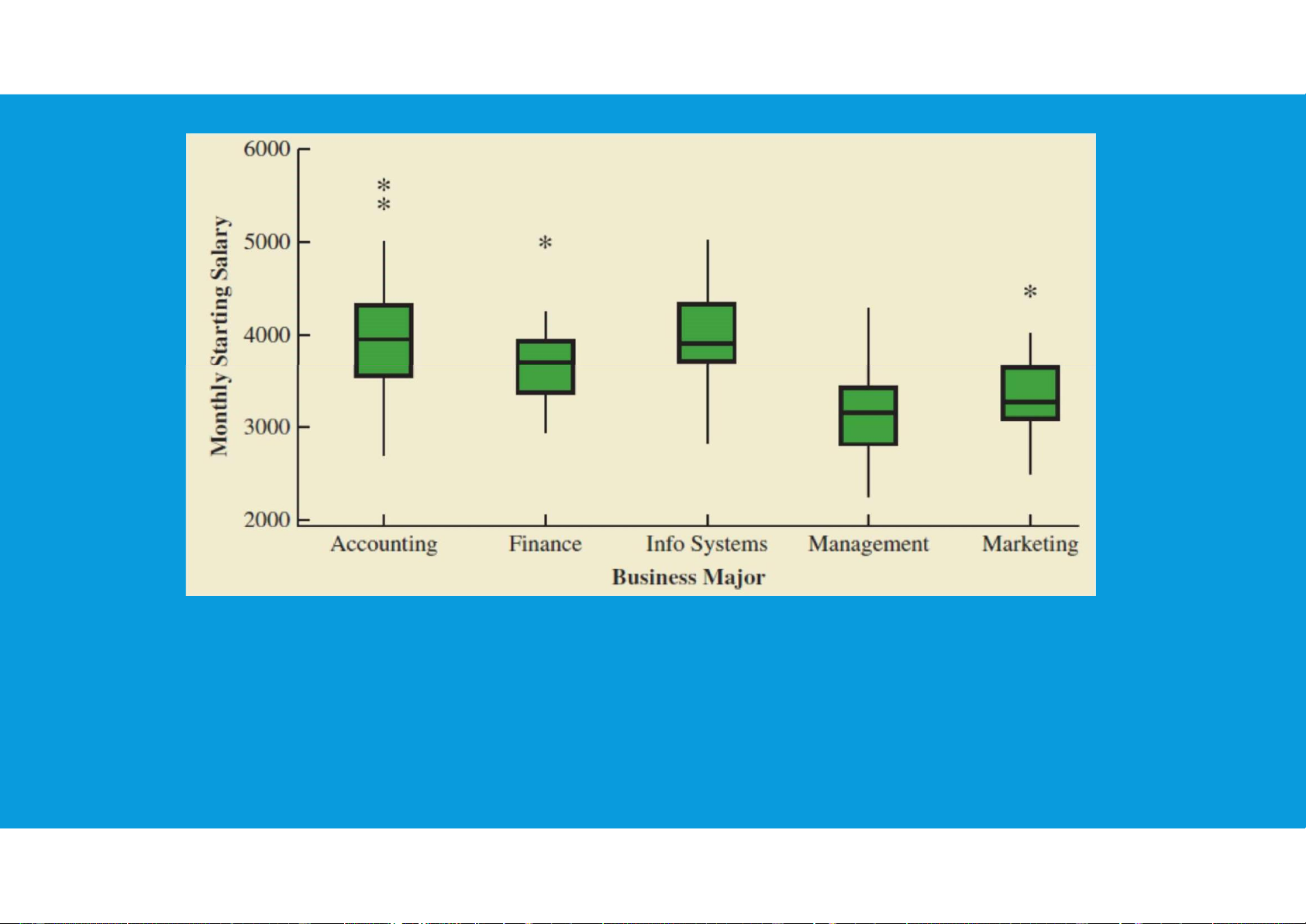
3.4. FIVE NUMBERS SUMMARIES AND BOX PLOTS
•Comparative Analysis Using Box Plots: Box plots can also be used to
provide a graphical summary of two or more groups and facilitate visual comparisons among the groups. tttu@hcmiu.edu.vn 14 lOMoARcPSD|47231818 tttu@hcmiu.edu.vn 15 lOMoARcPSD|47231818 End of file 2. Any questions? tttu@hcmiu.edu.vn 15
3.5. MEASURES OF ASSOCIATION BETWEEN TWO VARIABLES •Covariance
•Interpretation of the Covariance •Correlation Coefficient lOMoARcPSD|47231818
•Interpretation of the Correlation Coefficient
3.5. MEASURES OF ASSOCIATION BETWEEN TWO VARIABLES
•Covariance: For a sample of size n with the observations (x1, y1),
(x2, y2), and so on, the sample covariance and population covariance are defined as follows:
To measure the strength of the linear relationship between x and y tttu@hcmiu.edu.vn 17 lOMoARcPSD|47231818
3.5. MEASURES OF ASSOCIATION BETWEEN TWO VARIABLES
•Interpretation of the Covariance: The lines divide the graph into four quadrants:
Points in quadrant I correspond to xi greater than and yi greater than
Points in quadrant II correspond to xi less than and yi greater than tttu@hcmiu.edu.vn 18 lOMoARcPSD|47231818
Points in quadrant III correspond to xi less than and yi less than Points in
quadrant IV correspond to x greater i i than and y less than
value of (xi − )(yi − ) must be:
- positive for points in quadrant I
- negative for points in quadrant II
- positive for points in quadrant III
- negative for points in quadrant IV
3.5. MEASURES OF ASSOCIATION BETWEEN TWO VARIABLES
•Correlation Coefficient: Person product moment correlation coefficient: tttu@hcmiu.edu.vn 19 lOMoARcPSD|47231818
the sample correlation coefficient rxy is a point estimator of the
population correlation coefficient ρxy.
3.5. MEASURES OF ASSOCIATION BETWEEN TWO VARIABLES
•Interpretation of the Correlation Coefficient: tttu@hcmiu.edu.vn 20