Định Lí Brocard Và Một Số Thí Dụ Áp Dụng

ĐỊNH LÍ BROCARD VÀ MỘT SỐ THÍ DỤ ÁP DỤNG
Nguyễn Trường Sơn – THPT Chuyên Lương Văn Tụy, Ninh Bình.
I. Các kiến thức liên quan.
a. Định lí Brocard.
Cho tứ giác ABCD nội tiếp đường tròn (O) có M  AB  DC, N  AD  BC,
E  AC  BD . Khi đó:O là trực tâm tam giác MNE. Chứng minh:
Cách 1. Gọi P, Q tương ứng là giao điểm của NE với AB và CD.
Theo tính chất của hình tứ điểm toàn phần ta có:
(MPAB)  (MQDC)  1  .
Do đó M liên hợp với P, Q. Suy ra PQ là đường đối cực của điểm M.
Hay: OM  NE .
Tương tự ta cũng chứng minh được: ON  ME . N B A K E O C M D
Suy ra: O là trực tâm tam giác MNE. Cách 2.
Gọi K là giao điểm thứ hai của đường tròn ngoại tiếp các tam giác ABE,CDE .
Ta có: K, E,M cùng nằm trên trục đẳng phương của (ABE),(CDE) nên chúng thẳng hàng. Lại có: (K , B KC)  (K , B KE)  (K , E KC)  ( A , B AE)  (D ,
E DC)  (OB,OC)(mod ) nên
tứ giác OKBC nội tiếp.
Tương tự, tứ giác OKAD cũng nội tiếp. Suy ra K cũng chính là giao điểm thứ hai khác O
của hai đường tròn (OBC),(OA ) D nên các điểm ,
O K, N nằm trên trục đẳng phương của
hai đường tròn này. Suy ra: ,
O K, N thẳng hàng. Mặt khác:
(KM , KN )  (KM , KB)  (K ,
B KN )  ( AE, AB)  (C , B CO) 
 (DC, DB)  (CB,CO)  (mod ) 2
Do đó: ME  ON .
Chứng minh tương tự, ta có NE  OM hay
E là trực tâm của tam giác OMN và N OE  MN. X
Định lí được chứng minh. B
b. Một số nhận xét. A E O
Nhận xét 1. Bán kính đường tròn ngoại C
tiếp các tam giác OMN, ONE và OME M D bằng nhau. Chứng minh: Y
Theo định lí Brocard: O là trực tâm của tam giác MNE.
Suy ra bán kính đường tròn ngoại tiếp các
tam giác OMN, ONE và OME bằng nhau.
Nhận xét 2. Gọi X, Y lần lượt là tâm các đường tròn (OEN ) và (OEM ) . Khi đó: OX  OY .
Chứng minh: Theo định lí Brocard, ta có: E là trực tâm của tam giác OMN. Do đó:  
ONE  OME . OE OE Suy ra:        2.OX 2.OY OX OY sin ONE sin OME
Nhận xét 3. Cho tam giác ABC, M là trung điểm BC, H là trực tâm tam giác ABC. I là
giao điểm của AM với cung BC chứa H của (HBC). Khi đó: HI  AM .
Chứng minh: Gọi AD, BE, CF là ba đường cao của tam giác ABC. G là giao điểm của EF
với BC. GH giao với AM tại K. A E I F H C G B D M
Theo định lí Brocard, M là trực tâm tam giác AHG.
Do đó: GK  AM .
Khi đó: K thuộc đường tròn ngoại tiếp tứ giác AFHE.
Suy ra: GH.GK  G . E GF  G . B GC .
Vậy: K thuộc đường tròn ngoại tiếp tam giác HBC. Suy ra: K trùng với I.
Do đó: HI  AM .
Nhận xét 4. Gọi U, V lần lượt là hình chiếu của E lên BC và AD. K, J lần lượt là giao
điểm của MO với các đường BC và AD. Khi đó tứ giác JKUV nội tiếp. Chứng minh: N B U A E K V O J L C D M
Gọi L là giao điểm của NE với MO.
Theo định lí Brocard ta có: NE  OM .
Khi đó các tứ giác JLEV, LKUE nội tiếp. Suy ra:
NV.NJ  N .
E NL  NU.NK . Vậy tứ giác JKUV nội tiếp.
Nhận xét 5. Cho H là trực tâm tam giác ABC không cân, góc A nhọn. Hình chiếu vuông
góc của H lên các cạnh AB, AC theo thứ tự là E, F. D là trung điểm của BC. P, Q là giao
điểm của hai đường tròn đường kính AD,BC. Khi đó H, P, Q thẳng hàng và BC, EF, PQ đồng quy.
Chứng minh: Gọi S là chân đường vuông góc hạ từ A xuống BC. Vì H . A HS  H .
B HF nên H thuộc trục đẳng phương của hai đường tròn đường kính AD và
BC. Suy ra H, P, Q thẳng hàng.
Từ đó suy ra: PQ  AD . A Q F E P H B I S D C
Gọi I là giao điểm của EF với BC.
Theo định lí Brocard ta có: IH  AD .
Suy ra: I, P, H, Q thẳng hàng hay BC, EF, PQ đồng quy.
Nhận xét 6. Gọi V là giao điểm thứ hai của hai đường tròn ngoại tiếp các tam giác DCN
và BCM. Khi đó O, E, V thẳng hàng. N V B A E O C M D
Chứng minh: Các tứ giác CDVN, CBVM nội tiếp nên ta có:
(VM ,VN)  (VM ,VC)  (VC,VN)  (BM , BC)  (D . C DN)  0(mod ) Hay M, V, N thẳng hàng. Ta cũng có: (V , B V ) D  (V ,
B VN)  (VN,VM )  (VM ,V ) D  2(C , B C ) D  (O , B O ) D (mod )
Vậy tứ giác DOBV nội tiếp.    
Suy ra: DVO  DBO  ODB  OVB  OV  MN .
Theo định lí Brocard ta có: OE  MN . Điều này dẫn đến O, E, V thẳng hàng.
Từ điều này ta cũng dễ dàng chứng minh được các nhận xét sau:
+ Nếu V là hình chiếu của O lên MN thì OV sẽ là phân giác của  BVD .
+ V thuộc cả bốn đường tròn ngoại tiếp các tam giác (MAD), (MBC), (NAB), (NDC) .
Điểm V là một điểm Miquel của tứ giác toàn phần ABCDMN.
Nhận xét 7. Cho tam giác ABC không cân. D là chân đường cao hạ từ A xuống BC. E
nằm trên đoạn AD sao cho  
EBA  ECA . Khi đó E là trực tâm tam giác ABC. A F M E N C B D O
Chứng minh: Gọi F là giao điểm của BE với AC, M là giao điểm của CE với AB, N là
giao điểm của MF với BC. Vì  
EBA  ECA nên tứ giác BCFM nội tiếp đường tròn tâm O.
Theo định lí Brocard ta có: AE  ON  AD  ON .
Lại có: AD  BC  OBC .
Khi đó: OB  OC  O là trung điểm đoạn BC. Hay nói cách khác E là trực tâm tam giác ABC.
Sau đây ta sẽ đi vào một số thí dụ áp dụng của định lí Brocard.
II. Một số thí dụ áp dụng.
Thí dụ 1. Cho tam giác không cân ABC, A , B ,C lần lượt là hình chiếu của các điểm A, 1 1 1
B, C xuống các đường thẳng BC, CA, AB. A , B ,C lần lượt là giao điểm của các cặp 2 2 2
đường thẳng BC và B C , AC và AC , AB và A B . D, E, F lần lượt là trung điểm của các 1 1 1 1 1 1
cạnh BC, CA, AB. Chứng minh rằng các đường vuông góc hạ từ D, E, F lần lượt xuống
các đường thẳng AA ,BB ,CC đồng quy. 2 2 2 C2 B2 A B1 C1 H E F A B A 2 1 D C
Lời giải: Gọi H là trực tâm tam giác ABC.
Dễ thấy: D chính là tâm của đường tròn ngoại tiếp tứ giác BCB C 1 1
Theo định lí Brocard ta có: DH  AA . 2
Tương tự ta cũng có: EH  BB , FH  CC . 2 2
Vậy các đường vuông góc hạ từ D, E, F lần lượt xuống các đường thẳng AA ,B B ,CC 2 2 2 đồng quy.
Thí dụ 2. Cho tứ giác ABCD nội tiếp đường tròn. M, N lần lượt là trung điểm của các 2 đoạ PD BD
n CD, AB. P nằm trên đoạn thẳng CD sao cho 
. E là giao điểm của AC và 2 PC AC
BD. H là hình chiếu của E trên PN. Chứng minh rằng hai đường tròn ngoại tiếp các tam
giác HMP và EDC tiếp xúc với nhau. X A Z N O D B H E M P C Y Lời giải:
Bổ đề: Cho tam giác ABC không cân, AF là đường đối trung của tam giác ABC. E là
trung điểm của đoạn BC. Khi đó đường tròn ngoại tiếp các tam giác ABC và AEF tiếp
xúc với nhau.
Chứng minh bổ đề: A O D B F E C
Gọi D là giao điểm của tiếp tuyến tại A của đường tròn (ABC) với BC. Suy ra:   DAB  ACB .
Do AF là đường đối trung của tam giác ABC nên   BAF  CAE .
Khi đó:      
AEF  EAC  ACE  BAF  BAD  DAF . Do đó DA cũng là tiếp tuyến của
đường tròn (AEF). Khi đó đường tròn ngoại tiếp các tam giác ABC và AEF tiếp xúc với nhau.
Trở lại bài toán trên:
Gọi O là tâm đường tròn ngoại tiếp tam giác ABC.
Gọi X là giao điểm của AD và BC, Y là giao điểm của AB và CD, Z là giao điểm thứ hai
của hai đường tròn ngoại tiếp các tam giác ABE và CDE.
Dễ thấy: E, Y, Z thẳng hàng.
Vì (ZA,ZD)  (ZA,ZE)  (ZE,ZD)  (B , A B )
D  (CE,C ) D  (O , A O )
D (mod ) nên tứ giác
ADOZ nội tiếp đường tròn. Khi đó  (Z , O ZY )  (Z , O ZD)  (Z , D ZY )  ( A , O A ) D  (Z , D ZE)  ( A , O A ) D  (C , D CE)  (mod ) 2
Suy ra: O, M, N, Y, Z cùng nằm trên đường tròn đường kính OY.
Theo định lí Brocard, ta có: O là trực tâm tam giác EXY. Vì  0
OZY  90 nên ba điểm O, X, Z thẳng hàng. 2 2 Ta có: PD BD XD  
. Do đó: XP là đường đối trung của tam giác XCD. 2 2 PC AC XC Vì tam giác X  AB  X
 CD nên P nằm trên đường thẳng NX.
Vì E, H, X, Z nằm trên một đường tròn và H là trực tâm tam giác OXY nên    
XHZ  XEZ  YOZ  YMZ . Suy ra: Z thuộc đường tròn ngoại tiếp tam giác HMP. 2 2
Vì Z là tâm của phép quay biến AC thành BD nê PD BD ZD n   . Do đó ZP là đường 2 2 PC AC ZC
đối trung trong tam giác ZCD.
Áp dụng bổ đề trên ta có: đường tròn ngoại tiếp tứ giác HMPZ tiếp xúc với đường tròn
ngoại tiếp tứ giác EDCZ tại Z. Điều phải chứng minh.
Thí dụ 3. Tứ giác ABCD nội tiếp đường tròn (C), P  AB CD, Q  AD  BC ,
R  AC  BD . Gọi M là trung điểm của đoạn PQ, K là giao điểm của đoạn MR với đường
tròn (C). Chứng minh rằng đường tròn ngoại tiếp tam giác KPQ tiếp xúc với đường tròn (C). Lời giải: P N G B M K O R A C H D E F Q U
Cách 1. Gọi E là giao điểm thứ hai của MK với đường tròn (C).
U là giao điểm của hai tiếp tuyến tại K, E đối với đường tròn (C). Ta có KE là đường đối
cực của U đối với đường tròn (C).
Gọi H là giao điểm của UO với KE. Ta có: 2 2
OH.OU  OK  R
( trong đó R là bán kính đường tròn (C)).
Theo định lí Brocard ta có: RPQ 
là tam giác tự đối cực so với đường tròn (C). Do đó: PQ
là đường đối cực của R với đường tròn (C). Theo định lí La Hire, do R nằm trên KL nên U
nằm trên đường thẳng PQ.
Theo định lí Brocard, R là trực tâm của tam giác OPQ.
Gọi N là điểm đối xứng của R qua M. Khi đó ta có: NP  P , O NQ  QO .
Lại có: NH  HO . Do đó bốn điểm O, H, P, Q cùng nằm trên một đường tròn. Suy ra: U .
PUQ  UH.UO .
Gọi F, G là giao điểm của UO với đường tròn (C). Ta có: 2 2 2 2
OH.OU  R  UO(UO UH )  R  UO  R  U . O UH 2
 (UO  R)(UO  R) U .
O UH  U F.UG  U .
O UH  UK  U . O UH  U . P UQ
Suy ra UK tiếp xúc với đường tròn (KPQ).
Cách 2. Theo định lí Brocard, tam giác PQR tự đối cực. Gọi  là đường đối cực của R. S
là ảnh nghịch đảo của R qua đường tròn (C). Khi đó: R .
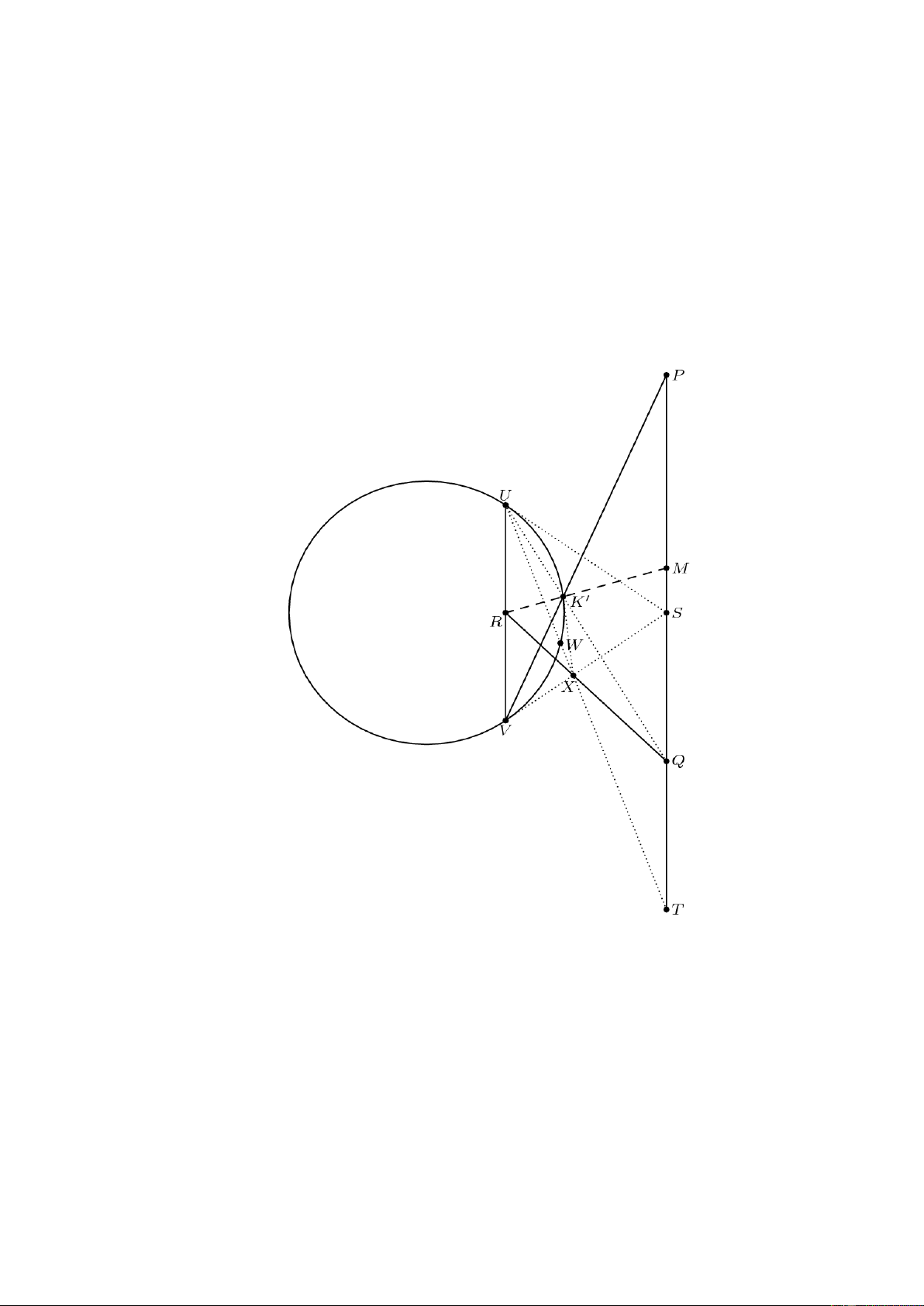
Gọi SU, SV là hai tiếp tuyến của đường tròn (C) ( U, V là hai tiếp điểm và U,P cùng phía
so với đường thẳng RS). K’ là giao điểm thứ hai của PV với đường tròn (C).
Gọi X là giao điểm của hai tiếp tuyến tại K’ và V. UX cắt đường tròn (C),  theo thứ tự tại W, T.
Ta có: X là cực của đường thẳng VK’, R là cực của đường thẳng  . Vì UK’ cắt  tại P và
P chính là cực của đường thẳng RX nên Q, R, X thẳng hàng.
Phép vị tự tâm X biến UV thành  . Do R là trung điểm của đoạn thẳng UV nên Q là trung
điểm của đoạn ST. Hơn nữa, UVWK’ là tứ giác điều hòa và ST UV nên U, K’ Q thẳng
hàng. Vì R là trung điểm của UV, M là trung điểm của đoạn PQ. Do đó R, K’, M thẳng
hàng. Vì vậy K trùng K’. Vì K là tâm của phép vị tự biến PQ thành VU nên hai đường tròn
(KPQ) và (KUV) tiếp xúc với nhau.
Thí dụ 4. Cho tam giác nhọn ABC, D là hình chiếu của A trên BC, G là trung điểm đoạn
AD. Hai điểm X, Y theo thứ tự thuộc GC, GB sao cho DX  GC, DY  G ,
B BX  CY  Z
Chứng minh rằng đường tròn ngoại tiếp tam giác XYZ và đường tròn đường kính AD tiếp xúc với nhau. A M G X Y Z C B T D E O
Lời giải: Dễ dàng chứng minh trong trường hợp tam giác ABC cân tại A. Ta xét trường
hợp tam giác ABC không cân tại A.
Ta có: DX  GC, DY  GB .  
Tứ giác GYDX nội tiếp đường tròn nên YDG  YXG . Lại có:  
GBD  GDY nên   GBD  GXY .
Do đó tứ giác BCXY nội tiếp đường tròn tâm O.
Gọi T là giao điểm của XY với BC, M là điểm đối xứng của D qua GT, E là giao điểm của
GZ với OT. Gọi (M,0) là đường tròn tâm M bán kính bằng 0.
Theo định lí Brocard ta có: O là trực tâm của tam giác GZT (1). Ta có: 2 2
GY.GB  GZ.GE  GX .GC  GD  GM . Khi đó: P  P . G/(M,0) G/(O)
Do TD tiếp xúc với đường tròn đường kính GD nên 2 2
TM  TD  TX .TY  P  P T/(M,0) T/(O)
Suy ra: TG chính là trục đẳng phương của hai đường tròn (M;0) và (O). Do đó: OM  GT (2).
Từ (1) và (2) suy ra O, D, Z, M thẳng hàng.
Phép nghịch đảo tâm G, tỷ số 2
GD biến đường tròn ngoại tiếp tam giác XYZ thành đường
tròn ngoại tiếp tam giác EBC, biến đường tròn đường kính AD thành đường tròn đường kính AD. Ta có: 2 2 2 2 2 2
GD  GY.GB  GO  OB  OB  GO  GD  P  O . D OM  O . E OT . O/(G,GD)
Khi đó: OB là tiếp tuyến của các đường tròn ngoại tiếp các tam giác TBE và MBD. Suy ra
các điểm O, E, B, C, M cùng thuộc một đường tròn.
Khi đó: MD là phân giác của góc  BMC .
Ta có: Đường tròn đường kính AD và đường tròn ngoại tiếp tam giác MBC tiếp xúc.
Suy ra: Đường tròn đường kính AD và đường tròn ngoại tiếp tam giác XYZ tiếp xúc.
Thí dụ 5. Cho nửa đường tròn tâm O đường kính AB, E là một điểm trên tia đối của tia
BA. Một cát tuyến qua E cắt nửa đường tròn tại C, D sao cho EC  ED . Gọi H là giao
điểm của hai đường tròn ngoại tiếp (AOD), (BOC). Chứng minh rằng EH vuông góc với OH.
Lời giải: Gọi I là giao điểm của AC với BD, F là giao điểm của AD với BC.
Dễ thấy: X chính là tâm đẳng phương của ba đường tròn (O), (AOD), (BOC) nên F, O, H thẳng hàng. Ta có:       
AHB  AHO  OHB  ADO  OCB  DAO  OCB       
 DAC  CAO  ACB  ACO  DAC  DAI  AIB
Vậy tứ giác AHIB nội tiếp.
Tương tự ta cũng chứng minh được tứ giác CKYD nội tiếp. Do E . A EB  E .
C ED nên E thuộc trục đẳng phương của hai đường tròn (AHIB) và
(CDHI). Suy ra: E, H, I thẳng hàng.
Theo định lí Brocard ta có: O là trực tâm tam giác EFI nên EI vuông góc với OF hay EH vuông góc với OK. F D H C I E A O B
Thí dụ 6. Cho tứ giác ABCD nội tiếp đường tròn (O), F  AB CD, E  AD  BC ,
I  AC  BD . Gọi Q là giao điểm thứ hai của hai đường tròn ngoại tiếp các tam giác FAD
và EAB. Chứng minh rằng O, Q, I thẳng hàng.
Đây chính là nội dung của nhận xét 6. Lời giải: AI IB AB A  IB  D
 IC(g.g)   
 AI.IC  I . B DI DI IC DC IB IA IC AB IC   .  . (1) ID ID ID CD ID J F Q D A I O C E B AQ QB AB Q  AB  Q
 DC(g.g)     A .
Q QC  Q . B DQ DQ QC DC QB QA QC AB QC   .  . (2) QD QD QD CD QD IC BC A  ID  B
 IC(g.g)   (3) ID AD QC BC Q  AD  Q
 BC(g.g)   (4) QD AD IB QB
Từ (1), (2), (3), (4) suy ra:  ID QD
Suy ra QI chính là phân giác của góc  BQD .
Gọi J là giao điểm của BD với EF. Ta có: ( Q D , B IS)  1
 và QI là phân giác của góc  BQD nên    QI QS QI EF .
Theo định lí Brocard ta có: O là trực tâm tam giác EFI. Suy ra OI  EF . Suy ra O, I, Q thẳng hàng.
Thí dụ 7. Cho tứ giác lồi ABCD nội tiếp đường tròn tâm O ( AC, BD không bằng nhau).
E là giao điểm của AC và BD. P là điểm nằm trong tứ giác ABCD sao cho     0
PAB  PCB  PBC  PDC  90 . Chứng minh rằng O, P, E thẳng hàng. G D R C E P O B A F Lời giải: Ta có:  0    
BPC 180  PBC  PCB  PAB  PDC .  
Dựng đường thẳng Px sao cho xPB  PAB . Khi đó:   CPx  PDC .
Suy ra: Px chính là tiếp tuyến chung của hai đường tròn (PAB), (PCD).
Vậy Px đi qua giao điểm F của hai đường thẳng AB và CD.   0     Lại có: 0
BAD  BCD 180 , PAB  PCB  PBC  PDC  90   0   0
 PAD  PCD  90 ,PDA  PBA  90 Ta có:  0    
DPC 180  PDC  PCD  PAD  PBC .  
Dựng đường thẳng Py sao cho yPD  PAD . Khi đó:   CPy  PBC .
Suy ra: Py chính là tiếp tuyến chung của hai đường tròn (PAD), (PCB).
Vậy Py đi qua giao điểm G của hai đường thẳng AD và CB.
Gọi R là hình chiếu của P lên đường thẳng FG. Ta có: 2 2 2 2 2 2 2 2 2 2
RF  RG  PF  PG  FO  r  (GO  r )  FO  GO .
( trong đó r là bán kính đường tròn (O)).
Suy ra: OP  GF .
Theo định lí Brocard ta có: O là trực tâm tam giác EFG. Suy ra: OE  GF . Vậy O, P, E thẳng hàng.
Thí dụ 8. Cho tứ giác ABCD nội tiếp đường tròn tâm O. E là giao điểm của AC với BD. P
là điểm bất kì nằm trong tứ giác ABCD, X, Y, Z, T lần lượt là tâm các đường tròn (ABP),
(BCP), (CDP), (DAP). Chứng minh rằng XZ, YT, OE đồng quy. Lời giải. Q C Z D G P E Y T H O F R A B X
Gọi F là giao điểm thứ hai của hai đường tròn (Y), (T).G là giao điểm thứ hai của hai đường tròn (X) và (Z).
Khi đó PF, PG lần lượt là trục đẳng phương của các cặp đường tròn ((Y), (T)) và ((X), (Z)).
Ta có: XZ, YT lần lượt là các đường trung trực của các đoạn PG,PF.
Gọi H là giao điểm của XZ và YT. Khi đó tam giác PFG nội tiếp đường tròn (H).
Gọi R, Q là giao điểm của các cặp đường thẳng (AB,DC) và (AD,BC).
Theo định lí Brocard: O là trực tâm tam giác ERQ. Khi đó: OE  R ( Q 1) . Vì R . A RB  R .
D RC nên R thuộc trục đẳng phương của (X), (Z). Suy ra: R, P, G thẳng hàng và R . A RB  R .
P RG . Vậy R thuộc trục đẳng phương của hai đường tròn (O) và (H).
Tương tự, ta cũng chứng minh được Q thuộc trục đẳng phương của hai đường tròn (O) và (H).
Do đó: QR chính là trục đẳng phương của hai đường tròn (O) và (H). Vậy OH  RQ(2) .
Từ (1), (2) ta có: O, H, E thẳng hàng. Tức là XZ, YT, OE đồng quy. Thí dụ 9. Cho tứ giác ABCD nội tiếp đường tròn tâm O,
X  AC  B ,
D Y  AD  BC,Z  DC  AB . M, N lần lượt là trung điểm của AB và CD.
 là đường thẳng qua M và vuông góc với DC, ' là đường thẳng qua N và vuông góc với
AB. Gọi H là giao điểm của ,
 ' . Chứng minh rằng X, Y, Z, H cùng nằm trên một đường tròn. Z D L A H N M X O C B K Y
Lời giải: Do M, N lần lượt là trung điểm của đoạn AB, CD nên OM  A , B ON  CD .
Ta có: H là trực tâm tam giác ZMN và ZO là đường kính đường tròn (ZMN). Suy ra:   AZO  DZH .
Gọi K, L lần lượt là trung điểm của BC và AD.Q là trực tâm tam giác YLK. Ta có:   AYO  BYQ
Ta có: OM  NH ( cùng vuông góc với đường thẳng AB)
MH  ON ( cùng vuông góc với đường thẳng CD)    
    
Suy ra: ONHM là hình bình hành. Vậ CB AD CD AB
y: OH  OM  ON   (1) . 2 2
Lại có: OK  LQ ( cùng vuông góc với đường thẳng BC)
KQ  OL ( cùng vuông góc với đường thẳng AD)  
   
Suy ra: OLQK là hình bình hành. Vậ CD AB
y: OQ  OL  OK  (2) . 2  
Từ (1), (2) suy ra: OQ  OH . Suy ra H, Q trùng nhau. Ta có:  0   0    
ZHY  180  ZHD  YHB  180  (BDC  HZD)  (DBC  HYB) 0    0    0
180  (BAD  AZO  AYO) 180  ZOY  ZHY  ZOY 180 (3)
Theo định lí Brocard ta có: O là trực tâm tam giác XYZ. Do đó:   0
ZXY  ZOY 180 (4) . Từ (3), (4) ta có:  
ZHY  ZXY tức là X, Y, Z, H cùng nằm trên một đường tròn.
Thí dụ 10. Cho đường tròn (O) và điểm P nằm ngoài đường tròn. Dựng hai cát tuyến
PXY, PX’Y’ sao cho X, X’ theo thứ tự nằm giữa PY và PY’. Chứng minh rằng đường
thẳng đi qua tâm của hai đường tròn (PX’Y) và (PXY’) luôn đi qua một điểm cố định. Lời giải : S I Y' Q X' L P O X Y J
Trường hợp XX ',YY ' không song song:
Gọi S, L lần lượt là giao điểm của các cặp đường thẳng (YY’,XX’) và (XY’,YX’), Q là
giao điểm thứ hai của hai đường tròn (OXX’) và (OYY’).
Dễ dàng suy ra S, Q, O thẳng hàng. Ta có:       
YQX '  OQY '  OQX  XQX '  OY 'Y  OX ' X  XOX ' 0  0   0   0 
 90 YX 'Y '  90  XY ' X '  2.XY ' X ' 180  (YX 'Y '  XY ' X ') 180  YPX '
Suy ra: Q nằm trên đường tròn (PYX’).
Chứng minh tương tự ta có: Q nằm trên đường tròn (PXY’).
Khi đó: PQ chính là trục đẳng phương của hai đường tròn (PYX’) và (PXY’).
Lại có: LX '.LY  LX .LY ' nên L nằm trên đường thẳng PQ.
Theo định lí Brocard ta có:  PL  OS 0 hay OQP  90 .
Gọi I, J lần lượt là tâm của hai đường tròn (PXY’), (PX’Y).
Khi đó: IJ  PQ  IJ  OQ.
Do IJ đi qua trung điểm của PQ nên IJ đi qua trung điểm của OP.
Điều này có nghĩa là IJ luôn đi qua một điểm cố định.
Trường hợp XX '  YY ' dễ dàng chứng minh được IJ cũng đi qua trung điểm OP.
Thí dụ 11. (IMO Shortlist 2005). Cho tam giác ABC nhọn không cân nội tiếp đường tròn
(O) có trực tâm H. M là trung điểm của BC. Gọi D, E nằm trên AB, AC sao cho AE  AD
và D, H, E thẳng hàng. Chứng minh rằng HM vuông góc với dây cung chung của hai
đường tròn (O) và (ADE). Lời giải:
Gọi F là giao điểm thứ hai của đường tròn (O) và đường tròn đường kính AH.
Dựng G  CH  A ,
B K  CH  AC .