












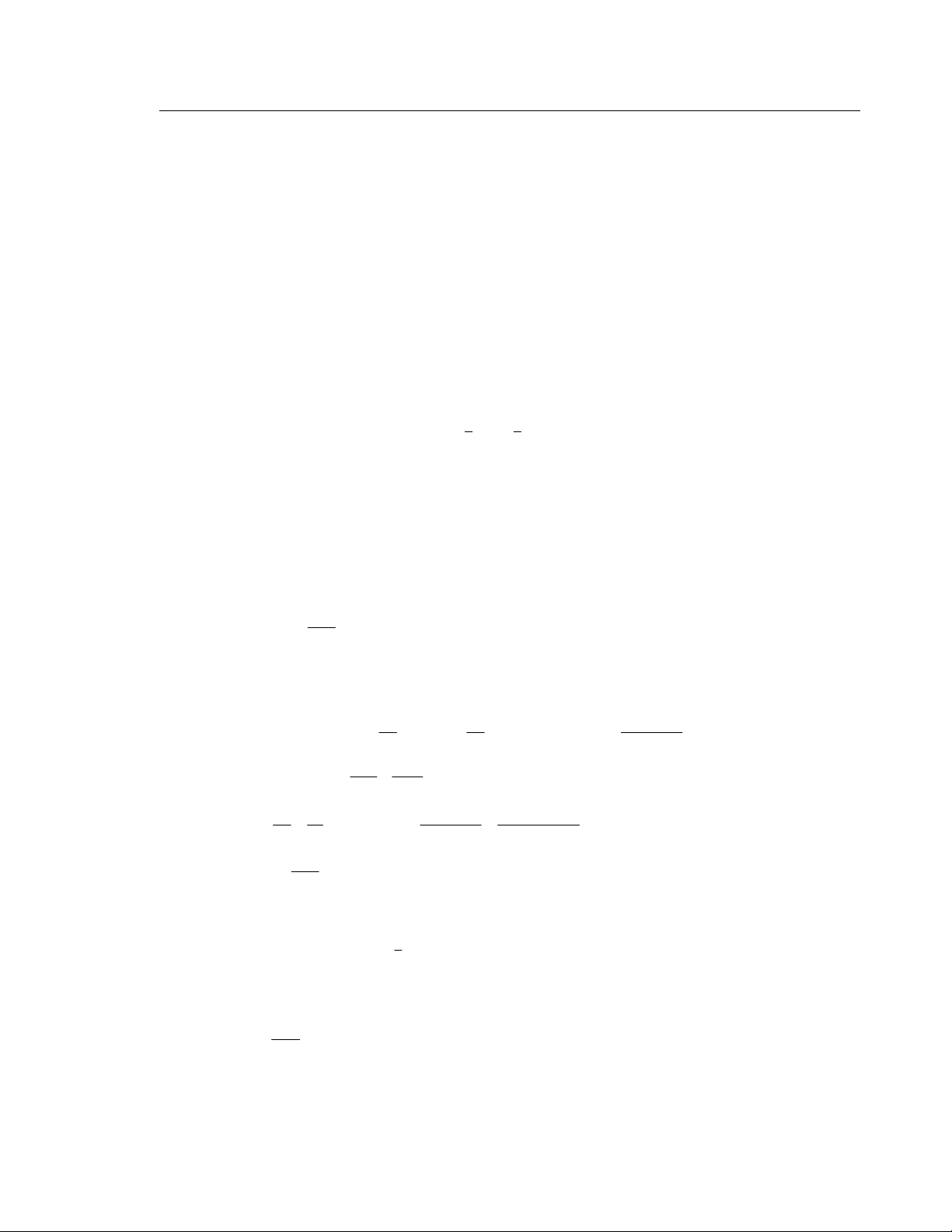
Preview text:
19
THE FIRST LAW OF THERMODYNAMICS
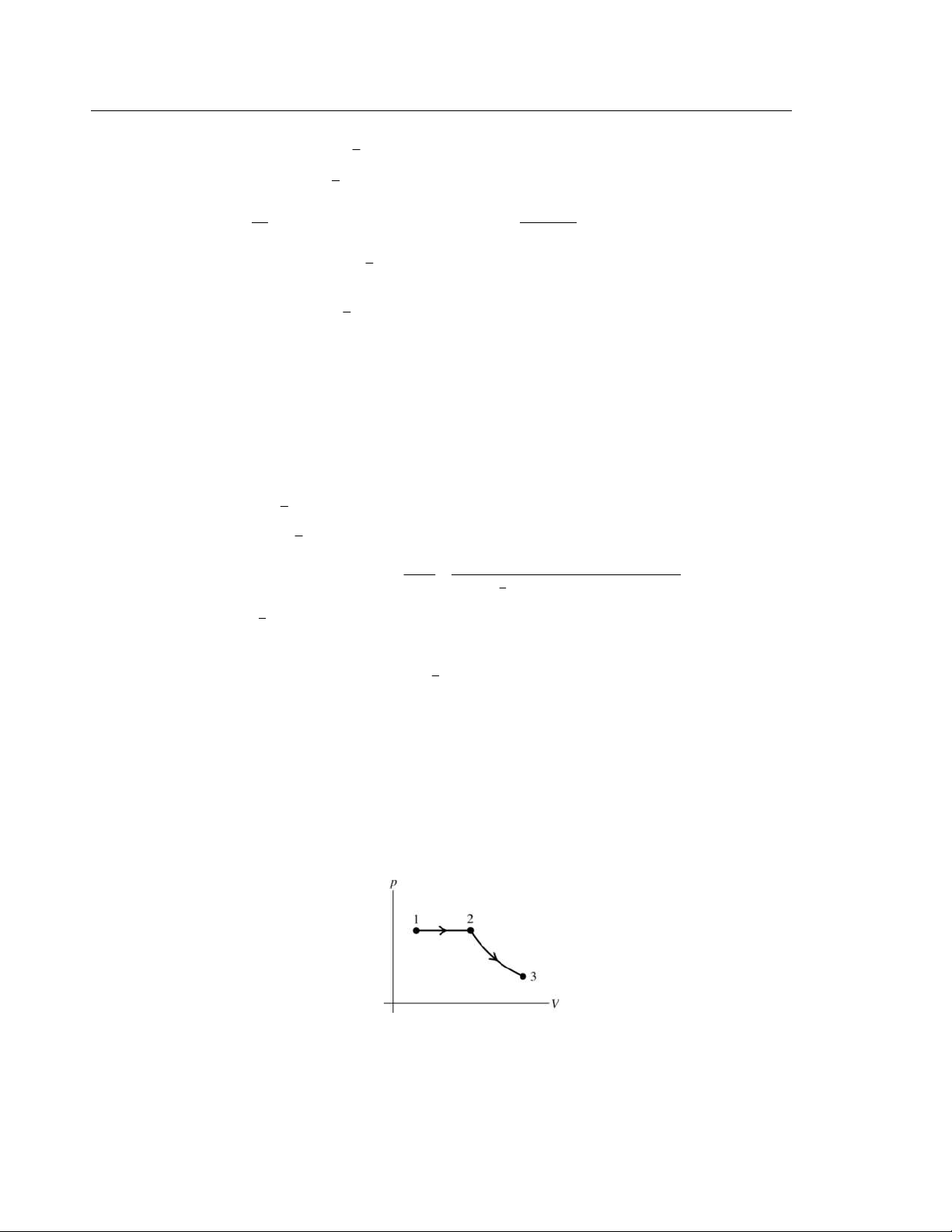
19.1. (a) IDENTIFY and SET UP: The pressure is constant and the volume increases. The pV-diagram is sketched in Figure 19.1. Figure 19.1 V (b) 2 W = Ñ p d V 1 V V Since p is constant, 2
W = pÑ dV = p( 2 V − 1 V ) 1 V
The problem gives T rather than p and V, so use the ideal gas law to rewrite the expression for W.
EXECUTE: pV = nRT so 1 p 1 V = nR 1 T , 2 p 2 V = nR 2
T ; subtracting the two equations gives p( 2 V − 1 V ) = nR( 2 T − 1 T ) Thus W = nR( 2 T − 1
T ) is an alternative expression for the work in a constant pressure process for an ideal gas. Then W = nR( 2 T − 1 T ) = (2 0
. 0 mol)(8.3145 J/mol ⋅ K)(107 C ° − 27 C ° ) = 1 + 330 J.
EVALUATE: The gas expands when heated and does positive work.
19.2. IDENTIFY: At constant pressure, W = pΔV = nR T
Δ . Since the gas is doing work, it must be expanding, so V
Δ is positive, which means that ΔT must also be positive.
SET UP: R = 8.3145 J/mol ⋅ K. ΔT has the same numerical value in kelvins and in C°. 3 W 2.40×10 J EXECUTE: ΔT = =
= 48.1 K. ΔT = ΔT and nR (6 mol) (8.3145 J/mol ⋅ K) K C 2
T = 27.0°C + 48.1 C° = 75.1°C. EVALUATE: When 0
W > the gas expands. When p is constant and V increases, T increases.
19.3. IDENTIFY: Example 19.1 shows that for an isothermal process W = nRT ln( 1 p / 2
p ). pV = nRT says V
decreases when p increases and T is constant.
SET UP: T = 65.0 + 273.15 = 338.15 K. 2 p = 3 1 p .
EXECUTE: (a) The pV-diagram is sketched in Figure 19.3. ⎛ p ⎞ (b) 1
W = (2.00 mol)(8.314 J/mol ⋅ K)(338.15 K)ln⎜ ⎟ = 6 − 180 J. 3 ⎝ 1 p ⎠
EVALUATE: Since V decreases, W is negative.
© Copyright 2012 Pearson Education, Inc. All rights reserved. This material is protected under all copyright laws as they currently exist.
No portion of this material may be reproduced, in any form or by any means, without permission in writing from the publisher. 19-1 19-2 Chapter 19 Figure 19.3
19.4. IDENTIFY: The work done in a cycle is the area enclosed by the cycle in a pV diagram.
SET UP: (a) 1 mm of Hg = 133.3 Pa. ga p uge = p − a
p ir. In calculating the enclosed area only changes in
pressure enter and you can use gauge pressure. −3 3 1 L = 10 m .
(b) Since pV = nRT and T is constant, the maximum number of moles of air in the lungs is when pV is a
maximum. In the ideal gas law the absolute pressure p = ga p uge + a p ir must be used. ai
p r = 760 mm of Hg. 1 mm of Hg = 1 torr.
EXECUTE: (a) By counting squares and noting that the area of 1 square is (1 mm of Hg)(0.1 L), we
estimate that the area enclosed by the cycle is about 7.5 (mm of Hg) ⋅ L = 1.00 N ⋅ m. The net work done is positive.
(b) The maximum pV is when 5
p = 11 torr + 760 torr = 771 torr = 1.028 ×10 Pa and 3 − 3
V = 1.4 L = 1.4 × 10 m . The maximum pV is ( pV )max = 144 N ⋅ m. pV = nRT so ( pV )max 1 44 N ⋅ m ma n x = = = 0.059 mol. RT (8.315 J/mol ⋅ K)(293 K)
EVALUATE: While inhaling the gas does positive work on the lungs, but while exhaling the lungs do work
on the gas, so the net work is positive.
19.5. IDENTIFY: Example 19.1 shows that for an isothermal process W = nRT ln( 1 p / 2 p ). Solve for 1 p .
SET UP: For a compression (V decreases) W is negative, so W = −468 J. 295 T = .15 K. W ⎛ p ⎞ p EXECUTE: (a) 1 = ln⎜ ⎟. 1 / W nRT = e . nRT ⎝ 2 p ⎠ 2 p W 46 − 8 J = = 0.6253 − . nRT
(0.305 mol)(8.314 J/mol ⋅ K)(295.15 K) / W nRT 0.6253 1 p 2 p e (1.76 atm)e− = = = 0.942 atm.
(b) In the process the pressure increases and the volume decreases. The pV-diagram is sketched in Figure 19.5.
EVALUATE: W is the work done by the gas, so when the surroundings do work on the gas, W is negative.
The gas was compressed at constant temperature, so its pressure must have increased, which means that
p1 < p2, which is what we found. Figure 19.5
© Copyright 2012 Pearson Education, Inc. All rights reserved. This material is protected under all copyright laws as they currently exist.
No portion of this material may be reproduced, in any form or by any means, without permission in writing from the publisher.
The First Law of Thermodynamics 19-3
19.6. (a) IDENTIFY and SET UP: The pV-diagram is sketched in Figure 19.6. Figure 19.6
(b) Calculate W for each process, using the expression for W that applies to the specific type of process.
EXECUTE: 1 → 2, V
Δ = 0, so W = 0 2 → 3 p is constant; so 5 3 3 4 W = p V Δ = (5 00 . ×10 Pa)(0.120 m − 0 20 . 0 m ) = 4
2 .00 ×10 J (W is negative since
the volume decreases in the process.) 4 tot W = 1 W 2 + 2 W → →3 = 4 − .00×10 J
EVALUATE: The volume decreases so the total work done is negative.
19.7. IDENTIFY: Calculate W for each step using the appropriate expression for each type of process.
SET UP: When p is constant, W = p V Δ . When V Δ = 0, W = 0. EXECUTE: (a) 13 W = 1 p ( 2 V − 1 V ), 3 W 2 = 0 , 2 W 4 = 2 p ( 1 V − 2 V ) and 4
W 1 = 0. The total work done by the system is 13 W + 3 W 2 + 24 W + 41 W = ( 1 p − 2 p )( 2 V − 1
V ), which is the area in the pV plane enclosed by the loop.
(b) For the process in reverse, the pressures are the same, but the volume changes are all the negatives of
those found in part (a), so the total work is negative of the work found in part (a). EVALUATE: When 0 V
Δ > , W > 0 and when V Δ < 0, W < 0.
19.8. IDENTIFY: The gas is undergoing an isobaric compression, so its temperature and internal energy must be decreasing.
SET UP: The pV diagram shows that in the process the volume decreases while the pressure is constant. 3 − 3 1 L = 10 m and 5 1 atm = 1.013 × 10 Pa. V nR V V
EXECUTE: (a) pV = nRT. n, R and p are constant so = = constant. a b = . T p a T b T ⎛ ⎞ ⎛ ⎞ b T a T /4 b V = a V ⎜ ⎟ = (0.500 L)⎜ ⎟ = 0.125 L. ⎝ a T ⎠ ⎝ a T ⎠
(b) For a constant pressure process, W = p ΔV = (1.50 atm)(0.125 L − 0.500 L) and 3 − 3 5 ⎛10 m ⎞⎛1.013×10 Pa ⎞ W = ( 0 − .5625 L ⋅atm)⎜ ⎟⎜ ⎟ = 5 − 7.0 J. ⎜
W is negative since the volume decreases. 1 L ⎟⎜ 1 atm ⎟ ⎝ ⎠⎝ ⎠
Since W is negative, work is done on the gas.
(c) For an ideal gas, U = nCT so U decreases when T decreases. The internal energy of the gas decreases
because the temperature decreases.
(d) For a constant pressure process, Q = nC ΔT. p
T decreases so ΔT is negative and Q is therefore
negative. Negative Q means heat leaves the gas.
EVALUATE: W = nR ΔT and Q = nC T Δ . p C > R, p
so more energy leaves as heat than is added by work
done on the gas, and the internal energy of the gas decreases.
19.9. IDENTIFY: ΔU = Q −W. For a constant pressure process, W = pΔV . SET UP: 5 Q = 1.15 +
×10 J, since heat enters the gas. EXECUTE: (a) 5 3 3 4
W = pΔV = (1.65×10 Pa)(0.320 m − 0.110 m ) = 3.47 ×10 J. (b) 5 4 4
ΔU = Q −W =1.15×10 J − 3.47 ×10 J = 8.04×10 J.
© Copyright 2012 Pearson Education, Inc. All rights reserved. This material is protected under all copyright laws as they currently exist.
No portion of this material may be reproduced, in any form or by any means, without permission in writing from the publisher. 19-4 Chapter 19
EVALUATE: (c) W = pΔV for a constant pressure process and ΔU = Q −W both apply to any material.
The ideal gas law wasn’t used and it doesn’t matter if the gas is ideal or not.
19.10. IDENTIFY: The type of process is not specified. We can use ΔU = Q −W because this applies to all
processes. Calculate ΔU and then from it calculate ΔT.
SET UP: Q is positive since heat goes into the gas; Q = 1200 1 J.
W positive since gas expands; W = 2100 1 J.
EXECUTE: ΔU =1200 J − 2100 J = 9 2 00 J
We can also use ΔU = n( 3 R ΔT since this is true for any process for an ideal gas. 2 ) 2 U Δ − 2( 900 J) ΔT = = = 14 2 .4C° 3nR 3(5 0 . 0 mol)(8.3145 J/mol⋅ K) 2 T = 1 T + T Δ =127 C ° −14.4C° =113 C °
EVALUATE: More energy leaves the gas in the expansion work than enters as heat. The internal energy
therefore decreases, and for an ideal gas this means the temperature decreases. We didn’t have to convert
ΔT to kelvins since ΔT is the same on the Kelvin and Celsius scales.
19.11. IDENTIFY: Part ab is isochoric, but bc is not any of the familiar processes.
SET UP: pV = nRT determines the Kelvin temperature of the gas. The work done in the process is the
area under the curve in the pV diagram. Q is positive since heat goes into the gas. 5 1 atm = 1.013 × 10 Pa. 3 − 3
1 L = 1× 10 m . ΔU = Q − W.
EXECUTE: (a) The lowest T occurs when pV has its smallest value. This is at point a, and 5 3 − 3 p V
(0.20 atm)(1.013 × 10 Pa/atm)(2.0 L)(1.0 × 10 m /L) a a T = = = 278 K. a nR
(0.0175 mol)(8.315 J/mol ⋅ K)
(b) a to b: ΔV = 0 so W = 0.
b to c: The work done by the gas is positive since the volume increases. The magnitude of the work is the area under the curve so 1
W = (0.50 atm + 0.30 atm)(6.0 L − 2.0 L) and 2 3 − 3 5
W =(1.6 L ⋅ atm)(1× 10 m /L)(1.013 × 10 Pa/atm) = 162 J. (c) For abc, 162 W =
J. ΔU = Q − W = 215 J − 162 J = 53 J.
EVALUATE: 215 J of heat energy went into the gas. 53 J of energy stayed in the gas as increased internal
energy and 162 J left the gas as work done by the gas on its surroundings.
19.12. IDENTIFY and SET UP: Calculate W using the equation for a constant pressure process. Then use
ΔU = Q −W to calculate Q. V (a) EXECUTE: 2 W =
p dV = p( 2 V − ∫ 1
V ) for this constant pressure process. 1 V 5 3 3 4
W = (1.80×10 Pa)(1.20 m −1.70 m ) = 9
− .00×10 J. (The volume decreases in the process, so W is negative.) (b) U Δ = Q −W. 5 4 5 Q = U
Δ +W = −1.40×10 J + (−9.00×10 J) = 2.30 −
×10 J. Negative Q means heat flows out of the gas. V (c) EVALUATE: 2 W =
p dV = p( 2 V − ∫ 1
V ) (constant pressure) and ΔU = Q −W apply to any system, 1 V
not just to an ideal gas. We did not use the ideal gas equation, either directly or indirectly, in any of the
calculations, so the results are the same whether the gas is ideal or not.
19.13. IDENTIFY: Calculate the total food energy value for one doughnut. 1 2 K = mv . 2
SET UP: 1 cal = 4.186 J
EXECUTE: (a) The energy is (2.0 g)(4.0 k
cal/g) + (17.0 g)(4.0 kcal/g) + (7.0 g)(9.0 kcal/g) =139 kcal.
The time required is (139 kcal)/(510 kcal/h) = 0.273 h = 16.4 min. (b) 3 v = 2 /
K m = 2(139×10 cal)(4.186 J/cal)/(60 kg) = 139 m/s = 501 km/h.
EVALUATE: When we set K = Q, we must express Q in J, so we can solve for v in m/s.
© Copyright 2012 Pearson Education, Inc. All rights reserved. This material is protected under all copyright laws as they currently exist.
No portion of this material may be reproduced, in any form or by any means, without permission in writing from the publisher.
The First Law of Thermodynamics 19-5
19.14. IDENTIFY: U
Δ = Q −W. For a constant pressure process, W = p V Δ . SET UP: 6 Q = 2
1 .20 ×10 J; Q > 0 since this amount of heat goes into the water. 5 p = 2 0 . 0 atm = 2.03×10 Pa. EXECUTE: (a) 5 3 3 2 3 5 W = p V Δ = (2 0 . 3×10 Pa)(0.824 m −1 00 . ×10 m ) =1.67×10 J (b) 6 5 6
ΔU = Q −W = 2.20×10 J −1.67×10 J = 2 0 . 3×10 J. EVALUATE: 6
2.20×10 J of energy enters the water. 5 1 6
. 7 ×10 J of energy leaves the materials through
expansion work and the remainder stays in the material as an increase in internal energy.
19.15. IDENTIFY: Apply ΔU = Q −W to the gas.
SET UP: For the process, V Δ = 0. 70 Q = + 0
J since heat goes into the gas.
EXECUTE: (a) Since V Δ = 0, W = 0. p nR
(b) pV = nRT says =
= constant. Since p doubles, T doubles. T = 2T . T V b a
(c) Since W = 0, 700 U Δ = Q = + J. 700 U = U + J b a .
EVALUATE: For an ideal gas, when T increases, U increases.
19.16. IDENTIFY: Apply ΔU = Q −W . |W | is the area under the path in the pV-plane.
SET UP: W > 0 when V increases.
EXECUTE: (a) The greatest work is done along the path that bounds the largest area above the V-axis in
the p-V plane, which is path 1. The least work is done along path 3.
(b) W > 0 in all three cases; Q = ΔU +W , so Q > 0 for all three, with the greatest Q for the greatest work,
that along path 1. When Q > 0, heat is absorbed.
EVALUATE: ΔU is path independent and depends only on the initial and final states. W and Q are path
dependent and can have different values for different paths between the same initial and final states.
19.17. IDENTIFY: ΔU = Q −W . W is the area under the path in the pV-diagram. When the volume increases, W > 0.
SET UP: For a complete cycle, ΔU = 0.
EXECUTE: (a) and (b) The clockwise loop (I) encloses a larger area in the p-V plane than the
counterclockwise loop (II). Clockwise loops represent positive work and counterclockwise loops negative work, so I W > 0 and I
W I < 0. Over one complete cycle, the net work I W + I
W I > 0, and the net work done by the system is positive.
(c) For the complete cycle, ΔU = 0 and so W = Q. From part (a), W > 0, so Q > 0, and heat flows into the system.
(d) Consider each loop as beginning and ending at the intersection point of the loops. Around each loop,
ΔU = 0, so Q =W; then, I Q = I W > 0 and II Q = II
W < 0. Heat flows into the system for loop I and out of the system for loop II.
EVALUATE: W and Q are path dependent and are in general not zero for a cycle.
19.18. IDENTIFY: ΔU = Q −W
SET UP: Q < 0 when heat leaves the gas.
EXECUTE: For an isothermal process, ΔU = 0, so W = Q = −335 J.
EVALUATE: In a compression the volume decreases and W < 0.
19.19. IDENTIFY: For a constant pressure process, W = p V Δ , Q = nCp T Δ and ΔU = n V C T
Δ . ΔU = Q −W and Cp = V
C + R. For an ideal gas, pΔV = nR T Δ .
SET UP: From Table 19.1, 28 46 J/mol K V C = . ⋅ .
EXECUTE: (a) The pV diagram is given in Figure 19.19.
(b) W = p 2 V − p 1 V = nR( 2 T − 1 T ) = (0 2
. 50 mol)(8.3145 J/mol ⋅ K)(100.0 K) = 208 J.
(c) The work is done on the piston.
(d) Since Eq. (19.13) holds for any process, ΔU = nC T Δ = (0 25 . 0 mol)( 28.46 J/mol ⋅ K)(100 0 . K) 712 = J V .
© Copyright 2012 Pearson Education, Inc. All rights reserved. This material is protected under all copyright laws as they currently exist.
No portion of this material may be reproduced, in any form or by any means, without permission in writing from the publisher. 19-6 Chapter 19
(e) Either Q = nC T Δ or Q = U Δ +W gives Q = 920 J p
to three significant figures.
(f) The lower pressure would mean a correspondingly larger volume, and the net result would be that the
work done would be the same as that found in part (b).
EVALUATE: W = nR T
Δ , so W, Q and ΔU all depend only on ΔT. When T increases at constant
pressure, V increases and W > 0. ΔU and Q are also positive when T increases. Figure 19.19
19.20. IDENTIFY: For constant volume Q = n V C T
Δ . For constant pressure, Q = nCp T Δ . For any process of an
ideal gas, ΔU = n V C T Δ .
SET UP: R = 8.315 J/mol ⋅ K. For helium, 12 47 J/mol K V C = .
⋅ and C = 20.78 J/mol ⋅ K p . EXECUTE: (a) (
Q = nC ΔT = 0 010 . 0 mol )(12 47 . J/mol ⋅ K)(40.0 C ) ° = 4 99 . J V . The pV-diagram is sketched in Figure 19.20a.
(b) Q = nC T Δ = (0 0
. 100 mol)(20.78 J/mol ⋅ K)(40 0 . C ) ° = 8 3 . 1 J p
. The pV-diagram is sketched in Figure 19.20b.
(c) More heat is required for the constant pressure process. ΔU is the same in both cases. For constant volume 0
W = and for constant pressure W > 0. The additional heat energy required for constant pressure goes into expansion work. (d) ΔU = nC T Δ = 4.99 J V
for both processes. ΔU is path independent and for an ideal gas depends only on ΔT.
EVALUATE: C = C + R, p V so Cp > V C . Figure 19.20
19.21. IDENTIFY: For constant volume, Q = n V C T
Δ . For constant pressure, Q = nCp T Δ .
SET UP: From Table 19.1, 20 76 J/mol K V C = . ⋅ and 29 C = .07 J/mol ⋅ K. p Q 645 J
EXECUTE: (a) Using Eq. (19.12), ΔT = = =167 9 . K and T = 948 K. nC (0.185 mol)(20 7 . 6 J/mol⋅ K) V
The pV-diagram is sketched in Figure 19.21a.
© Copyright 2012 Pearson Education, Inc. All rights reserved. This material is protected under all copyright laws as they currently exist.
No portion of this material may be reproduced, in any form or by any means, without permission in writing from the publisher.
The First Law of Thermodynamics 19-7 Q 645 J
(b) Using Eq. (19.14), ΔT = = =119.9 K and 900 T = K. nC (0 18 . 5 mol)(29 07 . J/mol ⋅ K) p
The pV-diagram is sketched in Figure 19.21b.
EVALUATE: At constant pressure some of the heat energy added to the gas leaves the gas as expansion
work and the internal energy change is less than if the same amount of heat energy is added at constant
volume. ΔT is proportional to ΔU. Figure 19.21
19.22. IDENTIFY: For an ideal gas, ΔU = C ΔT, V
and at constant pressure, pΔV = nR T Δ . SET UP: 3 V
C = R for a monatomic gas. 2 E − −
XECUTE: ΔU = n( 3 R ΔT = p V
Δ = (4.00×10 Pa)(8.00×10 m − 2.00×10 m ) = 360 J. 2 ) 3 3 4 3 3 3 3 2 2 EVALUATE: 2 W = nR T
Δ = ΔU = 240 J. Q = nC T Δ = n(5 R T Δ = U Δ = 600 J p . 600 J of heat energy 2 ) 5 3 3
flows into the gas. 240 J leaves as expansion work and 360 J remains in the gas as an increase in internal energy.
19.23. IDENTIFY: ΔU = Q −W . For an ideal gas, U Δ = V
C ΔT, and at constant pressure, W = p V Δ = nR T Δ . SET UP: 3 V
C = R for a monatomic gas. 2
EXECUTE: ΔU = n( 3 R) 3 3 T
Δ = pΔV = W. Then 5 2
Q = ΔU +W = W , so / W Q = . 2 2 2 2 5
EVALUATE: For diatomic or polyatomic gases, V
C is a different multiple of R and the fraction of Q that is
used for expansion work is different.
19.24. IDENTIFY: Apply pV = nRT to calculate T. For this constant pressure process, W = p V Δ . Q = nCp T Δ .
Use ΔU = Q −W to relate Q, W and ΔU. SET UP: 5
2.50 atm = 2.53×10 Pa. For a monatomic ideal gas, 12 47 J/mol K V C = . ⋅ and C = 20.78 J/mol ⋅ K p . 5 −2 3 pV (2 53 . ×10 Pa)(3 2 . 0×10 m ) EXECUTE: (a) 1 1 T = = = 325 K. nR (3.00 mol)(8.314 J/mol ⋅ K) 5 −2 3 2 pV (2.53×10 Pa)(4 5 . 0×10 m ) 2 T = = = 456 K. nR (3 0 . 0 mol)(8 3 . 14 J/mol ⋅ K) (b) 5 −2 3 −2 3 3
W = pΔV = (2 5
. 3×10 Pa)(4.50×10 m − 3 20 . ×10 m ) = 3 2 . 9×10 J (c) 3 Q = nC T
Δ = (3.00 mol)(20.78 J/mol⋅ K)(456 K − 325 K) = 8 1 . 7 ×10 J p (d) 3
ΔU = Q −W = 4 8 . 8×10 J
EVALUATE: We could also calculate ΔU as 3
ΔU = nC ΔT = (3.00 mol)(12.47 J/mol⋅ K)(456 K − 325 K) = 4.90×10 J, V
which agrees with the value we calculated in part (d).
© Copyright 2012 Pearson Education, Inc. All rights reserved. This material is protected under all copyright laws as they currently exist.
No portion of this material may be reproduced, in any form or by any means, without permission in writing from the publisher. 19-8 Chapter 19
19.25. IDENTIFY: For a constant volume process, Q = n V C T
Δ . For a constant pressure process, Q = nCp T Δ .
For any process of an ideal gas, ΔU = n V C T Δ .
SET UP: From Table 19.1, for N2, 20 76 J/mol K V C = . ⋅ and 29 C = .07 J/mol ⋅ K p
. Heat is added, so Q is positive and Q = 1557 1 J. Q 1557 J
EXECUTE: (a) ΔT = = = 25 1 .0 K nC (3.00 mol)(20 7 . 6 J/mol⋅ K) V Q 1557 J (b) ΔT = = = +17 9 . K nC (3 0 . 0 mol)(29 0 . 7 J/mol ⋅ K) p
(c) ΔU = n V
C ΔT for either process, so ΔU is larger when ΔT is larger. The final internal energy is larger
for the constant volume process in (a).
EVALUATE: For constant volume W = 0 and all the energy added as heat stays in the gas as internal
energy. For the constant pressure process the gas expands and W > 0. Part of the energy added as heat
leaves the gas as expansion work done by the gas. C
19.26. IDENTIFY: Cp = V C + R and p γ = . V C
SET UP: R = 8.315 J/mol ⋅ K C R R 8.315 J/mol ⋅ K E p
XECUTE: Cp = V C + R. γ = =1+ . C = = = 65 5 . J/mol ⋅ K V . Then V C V C γ −1 0 1 . 27
C = C + R = 73 8 . J/mol ⋅ K p V .
EVALUATE: The value of V
C is about twice the values for the polyatomic gases in Table 19.1. A propane
molecule has more atoms and hence more internal degrees of freedom than the polyatomic gases in the table. 19.27.
IDENTIFY: Calculate W and ΔU and then use the first law to calculate Q. V (a) SET UP: 2 W = Ñ p d V 1 V
pV = nRT so p = nRT/V 2 V 2 V W = Ñ
(nRT/V ) dV = nRT Ñ dV/V = nRT ln( 2 V / 1
V ) (work done during an isothermal process). 1 V 1 V
EXECUTE: W = (0.150 mol)(8 3
. 145 J/mol ⋅ K)(350 K)ln(0.25 1 V / 1
V ) = (436.5 J)ln(0.25) = −605 J.
EVALUATE: W for the gas is negative, since the volume decreases.
(b) EXECUTE: ΔU = n V
C ΔT for any ideal gas process.
ΔT = 0 (isothermal) so ΔU = 0. EVALUATE: U
Δ = 0 for any ideal gas process in which T doesn’t change.
(c) EXECUTE: ΔU = Q −W
ΔU = 0 so Q = W = −605 J. (Q is negative; the gas liberates 605 J of heat to the surroundings.)
EVALUATE: Q = n V C T
Δ is only for a constant volume process so doesn’t apply here. Q = nCp T
Δ is only for a constant pressure process so doesn’t apply here. 19.28.
IDENTIFY: ΔU = Q −W . Apply Q = nCp T
Δ to calculate Cp. Apply ΔU = n V
C ΔT to calculate V C . γ = C / p V C .
SET UP: ΔT = 15 0
. C° =15.0 K. Since heat is added, Q = 97 1 0 J.
EXECUTE: (a) ΔU = Q −W = 97 1 0 J − 223 J = 747 J Q 970 J U Δ 747 J (b) C = = = 37.0 J/mol ⋅ K p . C = = = 28.5 J/mol⋅ K. nΔT (1 7 . 5 mol)(15 0 . K) V n T Δ (1.75 mol)(15.0 K) Cp 37 0 J/mol K γ . ⋅ = = =1.30 C 28.5 J/mol ⋅ K V
EVALUATE: The value of γ we calculated is similar to the values given in Tables 19.1 for polyatomic gases.
© Copyright 2012 Pearson Education, Inc. All rights reserved. This material is protected under all copyright laws as they currently exist.
No portion of this material may be reproduced, in any form or by any means, without permission in writing from the publisher.
The First Law of Thermodynamics 19-9 1 19.29. I γ γ
DENTIFY: For an adiabatic process of an ideal gas, 1 p 1 V = p2 2 V , W = ( 1 p 1 V − 2 p 2 V ) and γ −1 γ 1 − γ 1 − 1 T 1 V = 2 T 2 V .
SET UP: For a monatomic ideal gas γ = 5/3. γ 5/3 3 ⎛ V ⎞ ⎛ 0 0 . 800 m ⎞ EXECUTE: (a) 1 5 5 2 p = 1 p ⎜ ⎟ = (1 5 . 0×10 Pa)⎜ ⎟ = 4.76×10 Pa. ⎜ 3 ⎟ ⎝ 2 V ⎠ 0 0 ⎝ . 400 m ⎠
(b) This result may be substituted into Eq. (19.26), or, substituting the above form for 2 p , 1 ⎛ ⎞ ⎛ . ⎞ W =
p V (1− (V /V )γ − ) 2/3 1 3 5 3 0 0800 4 = . × . ⎜ − ⎟ 1 1 1 2 (1 50 10 Pa)(0 0800 m ) 1 ⎜ ⎟ = 1 − .06×10 J. γ −1 2 ⎜ ⎝ 0.0400 ⎟ ⎠ ⎝ ⎠ (c) From Eq. (19.22), γ 1 − 2/3 ( 2 T / 1 T ) = ( 2 V / 1 V ) = (0 08 . 00/0 0 . 400)
=1.59, and since the final temperature is
higher than the initial temperature, the gas is heated.
EVALUATE: In an adiabatic compression W < 0 since 0
ΔV < . Q = 0 so ΔU = W − . U Δ > 0 and the temperature increases.
19.30. IDENTIFY and SET UP: For an ideal gas ΔU = n V C T
Δ . The sign of ΔU is the same as the sign of ΔT.
Combine Eq. (19.22) and the ideal gas law to obtain an equation relating T and p, and use it to determine the sign of ΔT. E γ − γ − γ −γ γ −γ γ γ γ − XECUTE: 1 1 1 T 1 V = 2 T 2 V
and V = nRT/p so, 1 1 1 T 1 p = 2 T p2 and 1 2 T = 1 T ( p2/ 1 p ) 2 p < 1
p and γ −1 is positive so 2 T < 1
T . ΔT is negative so ΔU is negative; the energy of the gas decreases.
EVALUATE: Eq. (19.24) shows that the volume increases for this process, so it is an adiabatic expansion.
In an adiabatic expansion the temperature decreases. 1 19.31. I γ γ
DENTIFY: For an adiabatic process of an ideal gas, W = ( 1 p 1 V − 2 p 2
V ) and p V = p V γ −1 1 1 2 2 . S − ET UP: γ = 1 4
. 0 for an ideal diatomic gas. 5 1 atm =1.013×10 Pa and 3 3 1 L = 10 m . 1
EXECUTE: Q = ΔU +W = 0 for an adiabatic process, so ΔU = W − = ( 2 p 2 V − 1 p 1 V ). γ −1 5 γ . 1 p =1.22×10 Pa. 5 1 4 5 2 p = 1 p ( 1 V / 2 V ) = (1 2 . 2×10 Pa)(3) = 5.68×10 Pa. 1 5 3 − 3 − 5 3 − 3 − 3 W =
([5.68×10 Pa][10×10 m ] −[1.22×10 Pa][30×10 m ]) = 5.05×10 J. The internal 0.40
energy increases because work is done on the gas ( U
Δ > 0) and Q = 0. The temperature increases because
the internal energy has increased.
EVALUATE: In an adiabatic compression W < 0 since 0
ΔV < . Q = 0 so ΔU = W − . U Δ > 0 and the temperature increases.
19.32. IDENTIFY and SET UP: (a) In the process the pressure increases and the volume decreases. The
pV-diagram is sketched in Figure 19.32. Figure 19.32
(b) For an adiabatic process for an ideal gas γ 1 − γ 1 − γ γ 1 T 1 V = 2 T 2 V , 1 p 1 V = 2 p 2
V , and pV = nRT.
© Copyright 2012 Pearson Education, Inc. All rights reserved. This material is protected under all copyright laws as they currently exist.
No portion of this material may be reproduced, in any form or by any means, without permission in writing from the publisher. 19-10 Chapter 19 E γ − . −
XECUTE: From the first equation, 1 1 4 1 2 T = 1 T ( 1 V / 2 V ) = (293 K)( 1 V /0.0900 1 V ) 0.4 2 T = (293 K)(11.11) = 768 K = 495 C ° (Note: In the equation γ 1 − γ 1 − 1 T 1 V = 2 T 2 V
the temperature must be in kelvins.) γ γ γ . 1 p 1 V = 2 p 2 V implies 1 4 2 p = 1 p ( 1 V / 2 V ) = (1.00 atm)( 1 V /0.0900 1 V ) 1 4 . 2 p = (1.00 atm)(11 1 . 1) = 29.1 atm
EVALUATE: Alternatively, we can use pV = nRT to calculate 2
p : n, R constant implies /
pV T = nR = constant so 1 p 1 V / 1 T = 2 p 2 V / 2 T . 2 p = 1 p ( 1 V / 2 V )( 2 T / 1 T ) = (1 00 . atm)( 1 V /0 0 . 900 1 V )(768 K/293 K) = 29 1 . atm, which checks.
19.33. (a) IDENTIFY and SET UP: In the expansion the pressure decreases and the volume increases. The
pV-diagram is sketched in Figure 19.33. Figure 19.33
(b) Adiabatic means Q = 0.
Then ΔU = Q −W gives W = − U
Δ = −nC ΔT = nC ( 1 T − 2 T ) V V (Eq. 19.25). 12 47 J/mol K V C = . ⋅ (Table 19.1)
EXECUTE: W = (0.450 mol)(12 4 . 7 J/mol ⋅ K)(50.0 C ° −10.0 C ° ) = +224 J
W positive for ΔV > 0 (expansion) (c) 22 ΔU = W − = − 4 J.
EVALUATE: There is no heat energy input. The energy for doing the expansion work comes from the
internal energy of the gas, which therefore decreases. For an ideal gas, when T decreases, U decreases. 19.34. I γ − γ −
DENTIFY: Assume the expansion is adiabatic. 1 1 1 T 1 V = 2 T 2 V
relates V and T. Assume the air behaves as
an ideal gas, so ΔU = n V C T
Δ . Use pV = nRT to calculate n. SET UP: For air, 29 76 J/mol K V C = . ⋅ and γ =1.40. 2 V = 0.800 1 V . 1 T = 293 1 . 5 K. 5 1 p = 2 026 . ×10 Pa. For a sphere, 4 3 V = π r . 3 γ 1 − 0.40 ⎛ V ⎞ ⎛ V ⎞ EXECUTE: (a) 1 1 2 T = 1 T ⎜ ⎟ = (293.15 K)⎜ ⎟ = 320.5 K = 47 4 . C ° . ⎝ 2 V 0 ⎠ ⎝ .800 1 V ⎠ 4π (b) 4 3 3 −3 3 1 V = π r = (0 1 . 195 m) = 7 1 . 5×10 m . 3 3 5 −3 3 1 p 1 V (2.026×10 Pa)(7 1 . 5×10 m ) n = = = 0.594 mol. 1 RT (8.314 J/mol ⋅ K)(293 1 . 5 K) U Δ = nC T
Δ = (0.594 mol)(20.76 J/mol ⋅ K)(321 K − 293 K) = 345 J V . 1
EVALUATE: We could also use U Δ = W = ( 1 p 1 V − 2 p 2
V ) to calculate U Δ , if we first found γ −1 2 p from pV = nRT. 19.35. I γ − γ − DENTIFY: Combine 1 1 1 T 1 V = 2 T 2 V
with pV = nRT to obtain an expression relating T and p for an
adiabatic process of an ideal gas. SET UP: 1 T = 299.15 K
© Copyright 2012 Pearson Education, Inc. All rights reserved. This material is protected under all copyright laws as they currently exist.
No portion of this material may be reproduced, in any form or by any means, without permission in writing from the publisher.
The First Law of Thermodynamics 19-11 γ 1 − γ 1 − nRT ⎛ nRT ⎞ ⎛ nRT ⎞ T γ T γ EXECUTE: V = so 1 2 T ⎜ ⎟ = T ⎜ ⎟ and 1 2 = . p 1 2 ⎝ γ 1 − γ 1 − 1 p ⎠ ⎝ 2 p ⎠ 1 p 2 p (γ 1 − )/γ 0.4/1 4 5 . ⎛ ⎞ ⎛ . × ⎞ 2 p 0 850 10 Pa 2 T = 1 T ⎜ ⎟ = (299 15 . K)⎜ ⎟ = 284.8 K =11.6 C ° ⎜ 5 ⎟ ⎝ 1 p ⎠ 1 ⎝ .01×10 Pa ⎠
EVALUATE: For an adiabatic process of an ideal gas, when the pressure decreases the temperature decreases. 19.36. I γ − γ −
DENTIFY: pV = nRT For an adiabatic process, 1 1 1 T 1 V = 2 T 2 V .
SET UP: For an ideal monatomic gas, γ = 5/3. 5 −3 3 pV (1.00×10 Pa)(2.50×10 m ) EXECUTE: (a) T = = = 301 K. nR (0.1 mol)(8.3145 J/mol ⋅ K)
(b) (i) Isothermal: If the expansion is isothermal, the process occurs at constant temperature and the final
temperature is the same as the initial temperature, namely 301 K. 1 4 2 p = 1 p ( 1 V / 2 V ) = 1 p = 5 0 . 0×10 Pa. 2 (ii) Isobaric: p Δ = 0 so 5 2 p =1 0 . 0×10 Pa. 2 T = 1 T ( 2 V / 1 V ) = 2 1 T = 60 2 K. γ 1 − 0.67 T V (301 K)(V ) 0.67
(iii) Adiabatic: Using Eq. (19.22), 1 1 1 T = = = (301 K) γ = . Then − . (1 2 189 K 1 0 67 2 ) 2 V (2 1 V ) pV = nRT gives 4 2 p = 3 1 . 4×10 Pa.
EVALUATE: In an isobaric expansion, T increases. In an adiabatic expansion, T decreases.
19.37. IDENTIFY: The compression does work on the gas, but the heat transferred and the internal energy change
depend on the process by which the compression occurs. The ideal gas law and the first law of
thermodynamics apply to the gas. SET UP: Q = U
Δ +W , pV = nRT, and C = C − . V p R
EXECUTE: (a) This is an isothermal process for an ideal gas, so U
Δ = 0 and Q = W. Since the volume
decreases (compression), W is negative and Q = 600 −
J. Since Q is negative, heat flows out of the gas. W 600 − J
(b) W = p V Δ = nR T Δ = −600 J. T Δ = = = 72 − .2 K. nR (1)(8.314 J/mol ⋅ K) 5R
C = C − R = = 20.78 J/mol ⋅ K. V p U Δ = nC T
Δ = (1)(20.78 J/mol ⋅ K)( 72.2 − K) = 1500 − J . Since 2 V U
Δ is negative, the internal energy decreases.
EVALUATE: In part (a) work is done on the gas, so heat must flow out of it for its temperature to remain
the same. In (b) gas is compressed, so the molecules must slow down if the pressure is to remain the same,
which means that the internal energy (and the temperature) must decrease.
19.38. IDENTIFY: Apply ΔU = Q −W. For any process of an ideal gas, U Δ = nC T Δ . V For an isothermal ⎛V ⎞ ⎛ p ⎞ expansion, 2 1 W = nRT ln⎜ ⎟ = nRT ln⎜ ⎟. ⎝ 1 V ⎠ ⎝ 2 p ⎠ p V
SET UP: T = 288 15 . K. 1 2 = = 2 0 . 0. 2 p 1 V EXECUTE: (a) U Δ = 0 since 0 T Δ = . (b) 3
W = (1.50 mol)(8.314 J/mol ⋅ K)(288 15
. K)ln(2.00) = 2.49×10 J. W > 0 and work is done by the gas. Since 0 U Δ = , 3
Q = W = +2.49×10 J. Q > 0 so heat flows into the gas.
EVALUATE: When the volume increases, W is positive.
19.39. IDENTIFY and SET UP: For an ideal gas, pV = nRT. The work done is the area under the path in the pV-diagram.
EXECUTE: (a) The product pV increases and this indicates a temperature increase.
© Copyright 2012 Pearson Education, Inc. All rights reserved. This material is protected under all copyright laws as they currently exist.
No portion of this material may be reproduced, in any form or by any means, without permission in writing from the publisher. 19-12 Chapter 19
(b) The work is the area in the pV plane bounded by the blue line representing the process and the verticals at V and 1 1 a b
V . The area of this trapezoid is 5 3
( p + p )(V −V ) = (2 4 . 0×10 Pa)(0 0 . 400 m ) = 4800 J. 2 b a b a 2
EVALUATE: The work done is the average pressure, 1 ( 1 p + 2
p ), times the volume increase. 2
19.40. IDENTIFY: Use pV = nRT to calculate T. W is the area under the process in the pV-diagram. Use U Δ = n V C T Δ and U
Δ = Q −W to calculate Q.
SET UP: In state c, 5 2 0 10 Pa c p = . × and 3 0 0040 m c V = . . In state a, 5 4 0 10 Pa a p = . × and 3 0 0020 m a V = . . 5 3 p V (2.0×10 Pa)(0.0040 m ) EXECUTE: (a) c c T = = =192 K c nR (0.500 mol)(8.314 J/mol ⋅ K) (b) 1 5 5 3 3 5 3 3 W = (4.0×10 Pa + 2 0
. ×10 Pa)(0.0030 m − 0.0020 m ) + (2 0 . ×10 Pa)(0 0 . 040 m − 0.0030 m ) 2 W = 50
+ 0 J. 500 J of work is done by the gas. 5 3 p V (4.0×10 Pa)(0 0 . 020 m ) (c) a a T = = =192 K a . For the process, T Δ = 0, so U Δ = 0 and nR (0.500 mol)(8.314 J/mol ⋅ K) Q = W = 500 +
J. 500 J of heat enters the system.
EVALUATE: The work done by the gas is positive since the volume increases. 19.41. IDENTIFY: Use U
Δ = Q −W and the fact that U Δ is path independent.
W > 0 when the volume increases, W < 0 when the volume decreases, and W = 0 when the volume is constant. 0
Q > if heat flows into the system.
SET UP: The paths are sketched in Figure 19.41. Q = 90 + .0 J acb
(positive since heat flows in) W = 60 + .0 J acb
(positive since ΔV > 0) Figure 19.41
EXECUTE: (a) ΔU = Q −W U
Δ is path independent; Q and W depend on the path. U Δ = Ub −Ua
This can be calculated for any path from a to b, in particular for path acb: U Δ = Q −W = 90.0 J − 60.0 J = 30 0 . J a→b acb acb .
Now apply ΔU = Q −W to path adb; 30 U Δ = .0 J for this path also. W = 15 + .0 J adb
(positive since ΔV > 0) U Δ a b = a Q db − adb W → so Q = U Δ +W = 30 0 . J +15.0 J = 4 + 5.0 J adb a→b adb
(b) Apply ΔU = Q −W to path ba: U Δ b a = b Q a − b W → a 35 0 J ba W = − .
(negative since ΔV < 0) U Δ
= U −U = − U ( −U ) = − U Δ = 30 − 0 . J b→a a b b a a→b Then Q = U Δ +W = 30 − 0 . J − 35.0 J = 6 − 5 0 . J ba b→a ba . ( 0; ba
Q < the system liberates heat.) (c) 0, Ua = U = 8 0 . J d U Δ = U −U = 30 + .0 J, a→b b a so U = 3 + 0 0 . J b .
© Copyright 2012 Pearson Education, Inc. All rights reserved. This material is protected under all copyright laws as they currently exist.
No portion of this material may be reproduced, in any form or by any means, without permission in writing from the publisher.
The First Law of Thermodynamics 19-13
process a → d U Δ a d = ad Q − ad W → U Δ =U −U = 8 + 0 . J a→d d a W = 15 + .0 J adb and ad W b = a W d + d
W b. But the work db
W for the process d → b is zero since V Δ = 0 for
that process. Therefore W = W = +15.0 J ad adb . Then Q = U Δ +W = 8 + 0 . J +15.0 J = 2 + 3.0 J ad a→d ad
(positive implies heat absorbed).
process d → b U Δ d b = db Q − db W → 0, db W = as already noted. U Δ =U −U = 30 0 J . − 8 0 . J = 2 + 2.0 J d →b b d . Then 22 Q = U Δ +W = + 0 . J db d →b db (positive; heat absorbed).
EVALUATE: The signs of our calculated ad Q and db
Q agree with the problem statement that heat is absorbed in these processes. 19.42.
IDENTIFY: ΔU = Q −W .
SET UP: W = 0 when V Δ = 0.
EXECUTE: For each process, Q = U
Δ +W. No work is done in the processes ab and dc, and so W = W = 450 J bc abc and W = W =120 J ad adc
. The heat flow for each process is: for ab, 90 Q = J. For bc,
Q = 440 J + 450 J = 890 J. For ad, Q =180 J +120 J = 300 J. For dc, Q = 350 J. Heat is absorbed in each
process. Note that the arrows representing the processes all point in the direction of increasing temperature (increasing U). EVALUATE: U
Δ is path independent so is the same for paths adc and abc. Q = 300 J + 350 J = 650 J adc . Q = 90 J + 890 J = 980 J abc
. Q and W are path dependent and are different for these two paths. 19.43.
IDENTIFY: Use pV = nRT to calculate T / c a T . Calculate U
Δ and W and use U
Δ = Q −W to obtain Q.
SET UP: For path ac, the work done is the area under the line representing the process in the pV-diagram. 5 3 T p V (1.0×10 J)(0.060 m ) EXECUTE: (a) c c c = = =1 0 . 0. T = T . 5 3 c a a T a p a V (3.0×10 J)(0 02 . 0 m )
(b) Since T = T , c a U
Δ = 0 for process abc. For ab, 0 V Δ = and 0 ab
W = . For bc, p is constant and 5 3 3 = Δ = (1 0 . ×10 Pa)(0.040 m ) = 4 0 . ×10 J bc W p V . Therefore, 3 W = 4 + .0×10 J abc . Since U Δ = 0, 3 Q = W = 4 + .0×10 J. 3
4.0×10 J of heat flows into the gas during process abc. (c) 1 5 5 3 3 W = (3 0 . ×10 Pa +1 0 . ×10 Pa)(0 0 . 40 m ) = 8 + .0×10 J. 3
Q = W = +8.0×10 J. 2 ac ac
EVALUATE: The work done is path dependent and is greater for process ac than for process abc, even
though the initial and final states are the same. 19.44.
IDENTIFY: For a cycle, U
Δ = 0 and Q = W. Calculate W.
SET UP: The magnitude of the work done by the gas during the cycle equals the area enclosed by the
cycle in the pV-diagram.
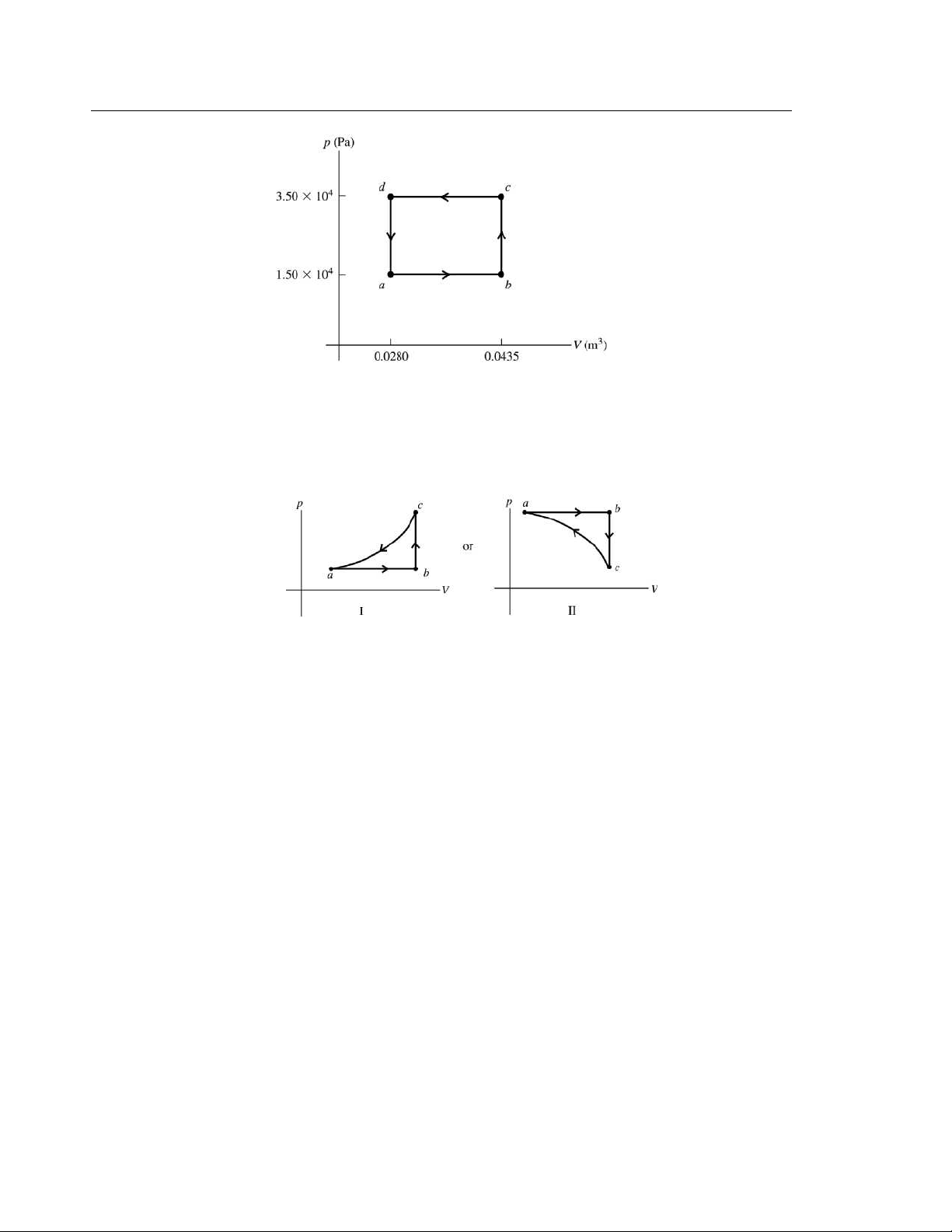
EXECUTE: (a) The cycle is sketched in Figure 19.44. (b) 4 4 3 3 |W | = (3 5
. 0×10 Pa −1.50×10 Pa)(0 043 .
5 m − 0.0280 m ) = +310 J. More negative work is done
for cd than positive work for ab and the net work is negative. W = −310 J. (c) 310 Q = W = −
J. Since Q < 0, the net heat flow is out of the gas.
EVALUATE: During each constant pressure process W = pΔV and during the constant volume process W = 0.
© Copyright 2012 Pearson Education, Inc. All rights reserved. This material is protected under all copyright laws as they currently exist.
No portion of this material may be reproduced, in any form or by any means, without permission in writing from the publisher. 19-14 Chapter 19 Figure 19.44 19.45.
IDENTIFY: Use the 1st law to relate to Q t to to W t for the cycle. Calculate ab W and bc
W and use what we know about tot W to deduce . ca W
(a) SET UP: We aren’t told whether the pressure increases or decreases in process bc. The two
possibilities for the cycle are sketched in Figure 19.45. Figure 19.45
In cycle I, the total work is negative and in cycle II the total work is positive. For a cycle, U Δ = 0, so to Q t = t W ot.
The net heat flow for the cycle is out of the gas, so heat to Q t < 0 and tot
W < 0. Sketch I is correct. (b) EXECUTE: tot W = t Q ot = 800 − J tot W = ab W + bc W + ca W 0 bc W = since V Δ = 0. ab W = p V
Δ since p is constant. But since it is an ideal gas, pΔV = nR T Δ .
W = nR(T − T ) =1660 J ab b a W = tot W −W = 800 − J −1660 J = −2460 J ca ab
EVALUATE: In process ca the volume decreases and the work W is negative. 19.46.
IDENTIFY: Apply the appropriate expression for W for each type of process. pV = nRT and Cp = V C + R.
SET UP: R = 8.315 J/mol ⋅ K
EXECUTE: Path ac has constant pressure, so = Δ = Δ , ac W p V nR T and 3
W = nR(T − T ) = (3 mol)(8.3145 J/mol ⋅ K)(492 K − 300 K) = 4.789×10 J ac c a .
Path cb is adiabatic (Q = 0), so W = Q − U Δ =2 U Δ = −nC T Δ , cb V
and using C = C − R, V p 3
W = −n(C − R)(T − T ) = −(3 mol)(29 1
. J/mol⋅ K − 8.3145 J/mol K ⋅ )(600 K − 492 K) 6 = − .735×10 J cb p b c .
Path ba has constant volume, so 0 ba
W = . So the total work done is 3 3 3
W = W +W +W = 4 7
. 89×10 J − 6.735×10 J + 0 = 1 2 9 . 5×10 J ac cb ba .
EVALUATE: W > 0 when V
Δ > 0, W < 0 when 0 V Δ < and 0 W = when 0 V Δ = .
© Copyright 2012 Pearson Education, Inc. All rights reserved. This material is protected under all copyright laws as they currently exist.
No portion of this material may be reproduced, in any form or by any means, without permission in writing from the publisher.
The First Law of Thermodynamics 19-15 19.47.
IDENTIFY: Segment ab is isochoric, bc is isothermal, and ca is isobaric.
SET UP: For bc, ΔT = 0, ΔU = 0, and Q = W = nRT ln(V /V ). c b For ideal H2 (diatomic), 5 V C = R and 2 7 C = . p R U Δ = nC T
Δ for any process of an ideal gas. 2 V
EXECUTE: (a) T = T . b
c For states b and c, pV = nRT = constant so b p b V = c p c V and ⎛ p ⎞ ⎛ 2.0 atm b ⎞ V = V ⎜ ⎟ = (0.20 L)⎜ ⎟ = 0.80 L. c b p ⎝ ⎠ ⎝ 0.50 atm c ⎠ 5 3 − 3 p V
(0.50 atm)(1.013×10 Pa/atm)(0.20×10 m ) (b) a a T = = = 305 K. a
V = V so for states a and b, nR
(0.0040 mol)(8.315 J/mol ⋅ K) a b T V ⎛ ⎞ = = T T p ⎛ 2.0 atm ⎞ constant so a b = . b
T = T = T ⎜ ⎟ = (305 K)⎜ ⎟ = 1220 K; 1220 K p nR b c a c T = . a p b p p ⎝ ⎠ ⎝ 0.50 atm a ⎠
(c) ab: Q = nC T
Δ = n(5 R T Δ , V which gives 2 )
Q = (0.0040 mol)( 5 (8.315 J/mol⋅K)(1220 K −305 K) = 76
+ J. Q is positive and heat goes into the gas. 2 )
ca: Q = nC T
Δ = n(7 R T Δ , p which gives 2 )
Q = (0.0040 mol)(7 (8.315 J/mol⋅K)(305 K −1220 K) = −107 J. Q is negative and heat comes out of 2 ) the gas. bc: l
Q = W = nRT n(V /V ), c b which gives
Q = (0.0040 mol)(8.315 J/mol ⋅ K)(1220 K)ln(0.80 L/0.20 L) = 56 J. Q is positive and heat goes into the gas.
(d) ab: ΔU = nC ΔT = n( 5 R T Δ , V which gives 2 ) U
Δ = (0.0040 mol)(5 (8.315 J/mol⋅K)(1220 K −305 K) = +76 J. The internal energy increased. 2 ) bc: 0 T Δ = so U
Δ = 0. The internal energy does not change.
ca: ΔU = nC T
Δ = n(5 R ΔT, V which gives 2 ) U
Δ = (0.0040 mol)(5 (8.315 J/mol⋅K)(305 K −1220 K) = −76 J. The internal energy decreased. 2 )
EVALUATE: The net internal energy change for the complete cycle a → b → c → a is U Δ tot = 76 + J + 0 + ( 7
− 6 J) = 0. For any complete cycle the final state is the same as the initial state and
the net internal energy change is zero. For the cycle the net heat flow is to Q t = 7 + 6 J + ( 10 − 7 J) + 56 J = 2 + 5 J. U Δ tot = 0 so to Q t = t
W ot. The net work done in the cycle is
positive and this agrees with our result that the net heat flow is positive. 19.48.
IDENTIFY: Segment ab is isobaric, bc is isochoric, and ca is isothermal.
SET UP: He is a monatomic gas so 3 V C = R and 5 C = .
R For any process of an ideal gas, 2 p 2 U Δ = nC T Δ . V
For an isothermal process of an ideal gas, U
Δ = 0 so Q = W = nRT ln( 2 V / 1 V ).
EXECUTE: (a) Apply pV = nRT to states a and c. a T = c
T so nRT is constant and p V = p V . a a c c 3 ⎛ ⎞ ⎛ ⎞ c V 5 0.040 m 5 p = p ⎜ ⎟ = (2.0 ×10 Pa)⎜ ⎟ = 8.0 × 10 Pa. a c ⎜ 3 ⎟ ⎝ a V ⎠ 0.010 m ⎝ ⎠ 5 3 p V (8.0 × 10 Pa)(0.010 m ) (b) a a T = = = 296 K; a nR (3.25 mol)(8.315 J/mol ⋅ K) 5 3 p V (8.0 × 10 Pa)(0.040 m ) b b T = = = 1184 K; b nR (3.25 mol)(8.315 J/mol ⋅ K) 5 3 p V (2.0 × 10 Pa)(0.040 m ) c c T = = = 296 K = T . c nR (3.25 mol)(8.315 J/mol ⋅ K) a
© Copyright 2012 Pearson Education, Inc. All rights reserved. This material is protected under all copyright laws as they currently exist.
No portion of this material may be reproduced, in any form or by any means, without permission in writing from the publisher. 19-16 Chapter 19
(c) ab: Q = nC T
Δ = (3.25 mol)(5 (8.315 J/mol⋅K)(1184 K − 296 K) = 6.00×10 J; p heat enters the gas. 2 ) 4
bc: Q = nC T
Δ = (3.25 mol)( 3 (8.315 J/mol⋅K)(296 K −1184 K) = −3.60×10 J; V heat leaves the gas. 2 ) 4 3 ⎛V ⎞ ⎛ 0.010 m ⎞ ca: a 4 Q = nRT ln⎜
⎟ = (3.25 mol)(8.315 J/mol⋅ K)(296 K)ln⎜ ⎟ = −1.11×10 J; ⎜ heat leaves the gas. 3 ⎟ ⎝ c V ⎠ 0.040 m ⎝ ⎠
(d) ab: ΔU = nC T
Δ = (3.25 mol)(3 (8.315 J/mol⋅K)(1184 K − 296 K) = 3.60×10 J; V the internal energy 2 ) 4 increased.
bc: ΔU = nC T
Δ = (3.25 mol)(3 (8.315 J/mol⋅K)(296 K −1184 K) = 3 − .60×10 J; V the internal energy 2 ) 4 decreased.
ca: ΔT = 0 so ΔU = 0.
EVALUATE: As we saw in (d), for any closed path on a pV diagram, U
Δ = 0 because we are back at the
same values of P, V, and T. 19.49.
IDENTIFY: The segments ab and bc are not any of the familiar ones, such as isothermal, isobaric or
isochoric, but ac is isobaric. SET UP: For helium, 12.47 J/mol K V C =
⋅ and C = 20.78 J/mol ⋅ K. p U
Δ = Q − W. W is the area under
the p versus V curve. U Δ = n V C T
Δ for any process of an ideal gas. EXECUTE: (a) 1 5 5 3 3
W = (1.0 × 10 Pa + 3.5 × 10 Pa)(0.0060 m − 0.0020 m ) 2 1 5 5 3 3
+ (1.0 ×10 Pa + 3.5 ×10 Pa)(0.0100 m − 0.0060 m ) = 1800 J. 2 5 3 3 p V Δ
(1.0 × 10 Pa)(0.0100 m − 0.0020 m ) Find . T Δ = c T − a
T p is constant so ΔT = = = Then nR ( 289 K. 1 mol (8.315 J/mol ⋅ K) 3 ) ΔU = nC T
Δ = (1 mol (12.47 J/mol⋅K)(289 K) =1.20 ×10 J. V 3 ) 3 3 3 Q = U
Δ + W = 1.20 ×10 J + 1800 J = 3.00 ×10 J. Q > 0, so this heat is transferred into the gas.
(b) This process is isobaric, so Q = nC ΔT = (1 mol (20.78 J/mol⋅K)(289 K) = 2.00 ×10 J. p Q > 0, so 3 ) 3
this heat is transferred into the gas.
(c) Q is larger in part (a).
EVALUATE: ΔU is the same in parts (a) and (b) because the initial and final states are the same, but in (a) more work is done. 19.50.
IDENTIFY: We have an isobaric expansion followed by an adiabatic expansion. SET UP: 1
T = 300 K. When the volume doubles at constant pressure the temperature doubles, so 2
T = 600 K. For helium, C = 20.78 J/mol ⋅ K p
and γ = 1.67. ΔU = n V C T
Δ for any process of an ideal
gas. ΔU = Q − W.
EXECUTE: (a) The process is sketched in Figure 19.50. Figure 19.50
(b) For the isobaric step, 4
Q = nC ΔT = (2.00 mol)(20.78 J/mol ⋅ K)(300 K) = 1.25 × 10 J. p For the
adiabatic process, Q = 0. The total heat is Q is 4 1.25 × 10 J.
© Copyright 2012 Pearson Education, Inc. All rights reserved. This material is protected under all copyright laws as they currently exist.
No portion of this material may be reproduced, in any form or by any means, without permission in writing from the publisher.
The First Law of Thermodynamics 19-17 (c) U Δ = 0 since ΔT = 0.
(d) Since ΔU = 0, 4
W = Q = 1.25 × 10 J. (e) γ − γ − 3 T = 300 K, 2 T = 600 K and 3 2 V = 0.0600 m . 1 1 2 T 2 V = 3 T 3 V . 1/(γ − 1) 1/0.67 ⎛ ⎞ 2 T 3 ⎛ 600 K ⎞ 3 3 V = 2 V ⎜ ⎟ = (0.0600 m )⎜ ⎟ = 0.169 m . ⎝ 3 T ⎠ ⎝ 300 K ⎠
EVALUATE: In both processes the internal energy changes. In the isobaric expansion the temperature
increases and the internal energy increases. In the adiabatic expansion the temperature decreases and ΔU < 0.
The magnitudes of the two temperature changes are equal and the net change in internal energy is zero. 19.51.
IDENTIFY: Use Q = n V C T
Δ to calculate the temperature change in the constant volume process and use
pV = nRT to calculate the temperature change in the constant pressure process. The work done in the
constant volume process is zero and the work done in the constant pressure process is W = p V Δ . Use Q = nCp T
Δ to calculate the heat flow in the constant pressure process. ΔU = nC T Δ , V
or ΔU = Q −W . SET UP: For N2, 20 76 J/mol K V C = .
⋅ and C = 29.07 J/mol⋅ K p . 4 Q 1.52×10 J
EXECUTE: (a) For process ab, ΔT = = = 293 K. 293 K, nC (2.50 mol)(20.76 J/mol ⋅ K) a T = so V 586 K b T =
. pV = nRT says T doubles when V doubles and p is constant, so 2(586 K) 1172 K 899 C c T = = = ° .
(b) For process ab, 0 ab
W = . For process bc, 4 = Δ =
Δ = (2.50 mol)(8.314 J/mol⋅ K)(1172 K − 586 K) =1.22×10 J bc W p V nR T . 4
W = W +W =1.22×10 J ab bc .
(c) For process bc, 4 Q = nC T Δ = (2 50 . mol)(29 0
. 7 J/mol⋅ K)(1172 K − 586 K) = 4.26×10 J p . (d) 4 ΔU = nC T Δ = (2 5
. 0 mol)(20.76 J/mol ⋅ K)(1172 K − 293 K) = 4.56×10 J V .
EVALUATE: The total Q is 4 4 4 1 5
. 2×10 J + 4.26×10 J = 5.78×10 J. 4 4 4
ΔU = Q −W = 5.78×10 J −1.22×10 J = 4 56
. ×10 J, which agrees with our results in part (d). 19.52.
IDENTIFY: For a constant pressure process, Q = nCp T Δ . U
Δ = Q −W. ΔU = n V
C ΔT for any ideal gas process. SET UP: For N2, 20 76 J/mol K V C = .
⋅ and C = 29.07 J/mol⋅ K p
. Q < 0 if heat comes out of the gas. 4 Q −2 5 . ×10 J EXECUTE: (a) n = = = 21.5 mol. C ΔT (29 0 . 7 J/mol⋅ K)(−40. 0 K) p (b) 4 4 ΔU = nC T
Δ = Q(C /C ) = (−2 5 . ×10 J)(20.76/29.07) = 1 − 79 . ×10 J V V p . (c) 3
W = Q − U Δ = 7 − .15×10 J.
(d) ΔU is the same for both processes, and if ΔV = 0, W = 0 and 4 Q = U Δ = 1 − 7 . 9×10 J.
EVALUATE: For a given T
Δ , Q is larger in magnitude when the pressure is constant than when the volume is constant. 19.53.
IDENTIFY and SET UP: Use the first law to calculate W and then use W = pΔV for the constant pressure
process to calculate ΔV .
EXECUTE: ΔU = Q −W 5 Q = 2
− .15×10 J (negative since heat energy goes out of the system) U Δ = 0 so 5 W = Q = 2 − .15×10 J V Constant pressure, so 2
W = Ñ pdV = p( 2 V − 1 V ) = p V Δ . 1 V
© Copyright 2012 Pearson Education, Inc. All rights reserved. This material is protected under all copyright laws as they currently exist.
No portion of this material may be reproduced, in any form or by any means, without permission in writing from the publisher. 19-18 Chapter 19 5 W 2 − .15×10 J Then 3 ΔV = = = −0 2 . 26 m . 5 p 9.50×10 Pa
EVALUATE: Positive work is done on the system by its surroundings; this inputs to the system the energy
that then leaves the system as heat. Both Eqs. (19.4) and (19.2) apply to all processes for any system, not just to an ideal gas. 19.54.
IDENTIFY: pV = nRT. For an isothermal process W = nRT ln( 2 V / 1
V ). For a constant pressure process, W = p V Δ . S − ET UP: 3 3 1 L =10 m .
EXECUTE: (a) The pV-diagram is sketched in Figure 19.54.
(b) At constant temperature, the product pV is constant, so 5 ⎛ 1 0 . 0 ×10 P a ⎞ 2 V = 1 V ( 1 p / 2 p ) = (1.5 L)⎜ ⎟ = 6.00 L. ⎜
The final pressure is given as being the same as 4 2 50 10 Pa ⎟ ⎝ . × ⎠ 4 3 p = 2
p = 2.5×10 Pa. The final volume is the same as the initial volume, so 3 T = 1 T ( 3 p / 1 p ) = 75.0 K.
(c) Treating the gas as ideal, the work done in the first process is W = nRT ln( 2 V / 1 V ) = 1 p 1 V ln( 1 p / 2 p ). 5 ⎛ . × ⎞ 5 3 − 3 1 00 10 Pa W = (1.00×10 Pa)(1 5 . ×10 m )ln⎜ ⎟ = 208 J. ⎜ 4 2 50 10 Pa ⎟ ⎝ . × ⎠
For the second process, W = 2 p ( 3 V − 2 V ) = 2 p ( 1 V − 2 V ) = 2 p 1 V (1− ( 1 p / 2 p )). 5 ⎛ . × ⎞ 4 3 − 3 1 00 10 Pa
W = (2.50×10 Pa)(1.5×10 m )⎜1− ⎟ = 113 J − . ⎜ 4 2 50 10 Pa ⎟ ⎝ . × ⎠
The total work done is 208 J −113 J = 95 J.
(d) Heat at constant volume. No work would be done by the gas or on the gas during this process.
EVALUATE: When the volume increases, W > 0. When the volume decreases, W < 0. Figure 19.54 19.55.
IDENTIFY: ΔV = 0 V β T Δ . W = p V
Δ since the force applied to the piston is constant. Q = mcpΔT.
ΔU = Q −W.
SET UP: m = V ρ
EXECUTE: (a) The change in volume is 2 − 3 3 − 1 − 4 − 3 ΔV = 0 V β T Δ = (1.20×10 m )(1 2 . 0×10 K )(30 0 . K) = 4 3 . 2×10 m . (b) 4 2 4 − 3 W = p V Δ = (F/ )
A ΔV = ((3.00×10 N)/(0.0200 m ))(4 3 . 2×10 m ) = 648 J. (c) 2 − 3 3 3 Q = mc T Δ = 0 V ρc T Δ = (1 20 . ×10 m )(791kg/m )(2 51 . ×10 J/kg ⋅ K)(30.0 K) p p . 5 Q = 7.15×10 J. (d) 5
ΔU = Q −W = 7.15×10 J to three figures.
(e) Under these conditions W is much less than Q and there is no substantial difference between c and V cp.
EVALUATE: ΔU = Q −W is valid for any material. For liquids the expansion work is much less than Q.
© Copyright 2012 Pearson Education, Inc. All rights reserved. This material is protected under all copyright laws as they currently exist.
No portion of this material may be reproduced, in any form or by any means, without permission in writing from the publisher.
The First Law of Thermodynamics 19-19 19.56.
IDENTIFY: ΔV = β 0
V ΔT. W = p V
Δ since the applied pressure (air pressure) is constant. Q = mcp T Δ .
ΔU = Q −W. S − − ET UP: For copper, 5 1 β = 5.1×10 (C ) ° , 390 c = J/kg ⋅ K p and 3 3 ρ = 8.90×10 kg/m . E − − − − XECUTE: (a) 5 1 2 3 8 3 ΔV = β T Δ 0 V = (5 1 . ×10 (C ) ° )(70 0 . C )
° (2.00×10 m) = 2.86×10 m . (b) 3 W = p V Δ = 2 8 . 8×102 J. (c) 3 3 6 3 Q mc T ρ − = Δ = 0 V c T Δ = (8 9 . ×10 kg/m
)(8.00×10 m )(390 J/kg ⋅ K)(70 0 . C ) ° =1944 J p p .
(d) To three figures, ΔU = Q = 1940 J.
(e) Under these conditions, the difference is not substantial, since W is much less than Q.
EVALUATE: ΔU = Q −W applies to any material. For solids the expansion work is much less than Q.
19.57. IDENTIFY and SET UP: The heat produced from the reaction is re Q action = m r L eaction, where r L eaction is the
heat of reaction of the chemicals. re
Q action =W + ΔUspray
EXECUTE: For a mass m of spray, 1 2 1 2
W = mv = m(19 m/s) = (180 5 . J/kg)m and 2 2 ΔUspray = s
Q pray = mcΔT = m(4190 J/kg ⋅ K)(100 C ° − 20 C
° ) = (335,200 J/kg)m. Then re
Q action = (180 J/kg + 335,200 J/kg)m = (335,380 J/kg)m and re Q action = m r L eaction implies re
mL action = (335,380 J/kg)m.
The mass m divides out and 5 r
L eaction = 3.4×10 J/kg.
EVALUATE: The amount of energy converted to work is negligible for the two significant figures to which the
answer should be expressed. Almost all of the energy produced in the reaction goes into heating the compound. 19.58. I γ γ
DENTIFY: The process is adiabatic. Apply 1 p 1 V = 2 p 2
V and pV = nRT. Q = 0 so 1 ΔU = W − = − ( 1 p 1 V − 2 p 2 V ). γ −1
SET UP: For helium, γ =1.67. 5 1
p =1.00 atm =1.013×10 Pa. 3 3 1 V = 2.00×10 m . 4 2 p = 0.900 atm = 9 1 . 17×10 Pa. 1 T = 288 1 . 5 K. 1/γ 1/1.67 γ γ ⎛ p ⎞ ⎛ p ⎞ ⎛ 1.00 atm ⎞ EXECUTE: (a) 1 1 3 3 3 3 2 V = 1 V ⎜ ⎟. 2 V = 1 V ⎜ ⎟ = (2.00×10 m )⎜ ⎟ = 2.13×10 m . ⎝ 2 p ⎠ ⎝ 2 p ⎠ ⎝ 0.900 atm ⎠ T T
(b) pV = nRT gives 1 2 = . 1 p 1 V 2 p 2 V 3 3 ⎛ ⎞⎛ ⎞ ⎛ . ⎛ ⎞ . × ⎞ 2 p 2 V 0 900 atm 2 13 10 m 2 T = 1 T ⎜ ⎟⎜ ⎟ = (288 15 . K)⎜ ⎟⎜ ⎟ = 276 2 . K = 3 0 . C ° . ⎜ 3 3 ⎟ ⎝ 1 p ⎠⎝ 1 V ⎠ ⎝ 1 0 . 0 atm ⎠ 2 ⎝ .00×10 m ⎠ 1 (c) 5 3 3 4 3 3 7 ΔU = −
([1.013×10 Pa)(2.00×10 m )] −[9 1
. 17×10 Pa)(2.13×10 m )] = −1.25×10 J. 0.67
EVALUATE: The internal energy decreases when the temperature decreases. 19.59. I γ − γ −
DENTIFY: For an adiabatic process of an ideal gas, 1 1 1 T 1 V = 2 T 2 V . pV = nRT. SET UP: For air, 7 γ =1.40 = . 5
EXECUTE: (a) As the air moves to lower altitude its density increases; under an adiabatic compression,
the temperature rises. If the wind is fast-moving, Q is not as likely to be significant, and modeling the
process as adiabatic (no heat loss to the surroundings) is more accurate. nRT (b) V = , so γ 1 − γ 1 T V T V − = gives γ 1−γ γ 1 T p
= T p −γ . The temperature at the higher pressure is p 1 1 2 2 1 1 2 2 ( 1 − )/ 4 4 2/7 2 T = 1 T ( 1 p /p γ γ 2 ) = (258 1 . 5 K)( 8 [ 12 . ×10 Pa /] 5 [ 60 . ×10 Pa )] = 287.1 K =13 9 . C ° so the
temperature would rise by 11.9 C°.
© Copyright 2012 Pearson Education, Inc. All rights reserved. This material is protected under all copyright laws as they currently exist.
No portion of this material may be reproduced, in any form or by any means, without permission in writing from the publisher. 19-20 Chapter 19
EVALUATE: In an adiabatic compression, Q = 0 but the temperature rises because of the work done on the gas. 19.60.
IDENTIFY: For constant pressure, W = p V
Δ . For an adiabatic process of an ideal gas, V C W = ( γ γ 1 p 1 V − 2 p 2
V ) and p V = p V . R 1 1 2 2 C C + C R S p p V ET UP: γ = = =1+ V C V C V C
EXECUTE: (a) The pV-diagram is sketched in Figure 19.60. (b) The work done is V C W = γ 0 p (2 0 V − 0 V ) + ( 0 p (2 0 V ) − 3 p (4 0
V )). p = p (2V /4V ) and so R 3 0 0 0 ⎡ V C 2 ⎤ W −γ = 0 p 0 V 1+ (2 − 2 ) . ⎢ Note that R ⎥ ⎣ ⎦ 0
p is the absolute pressure.
(c) The most direct way to find the temperature is to find the ratio of the final pressure and volume to the γ γ ⎛V ⎞ ⎛ V ⎞
original and treat the air as an ideal gas. 2 2 3 p = 2 p ⎜ ⎟ = 1 p ⎜ ⎟ , since 1 p = 2 p . Then ⎝ 3 V ⎠ ⎝ 3 V ⎠ γ γ ⎛ ⎞ ⎛ ⎞ 3 p 3 V 2 V 3 V ⎛ 1 ⎞ 2−γ 3 T = 0 T = 0 T ⎜ ⎟ ⎜ ⎟ = 0 T 4 ⎜ ⎟ = 0 T (2) . 1 p 1 V ⎝ 3 V ⎠ ⎝ 1 V ⎠ ⎝ 2 ⎠ p V p V ⎛ C ⎞ (d) Since 0 0 0 0 n = , Q = (C + R)(2 V V 0 T − 0 T ) = 0 p 0 V ⎜
+1⎟. This amount of heat flows into the gas, 0 RT 0 RT ⎝ R ⎠ since 0 Q > .
EVALUATE: In the isobaric expansion the temperature doubles and in the adiabatic expansion the
temperature decreases. If the gas is diatomic, with 7 γ = , 3
2 − γ = and T =1.52T , W = 2 2 . 1p V and 5 5 3 0 0 0 Q = 3 5 . 0 0 p 0 V . ΔU =1.29 0 p 0 V . U
Δ > 0 and this is consistent with an increase in temperature. Figure 19.60 19.61.
IDENTIFY: Assume that the gas is ideal and that the process is adiabatic. Apply Eqs. (19.22) and (19.24)
to relate pressure and volume and temperature and volume. The distance the piston moves is related to the
volume of the gas. Use Eq. (19.25) to calculate W.
(a) SET UP: γ = C /C = (C + R)/C =1+ / R C =1.40 p V V V V
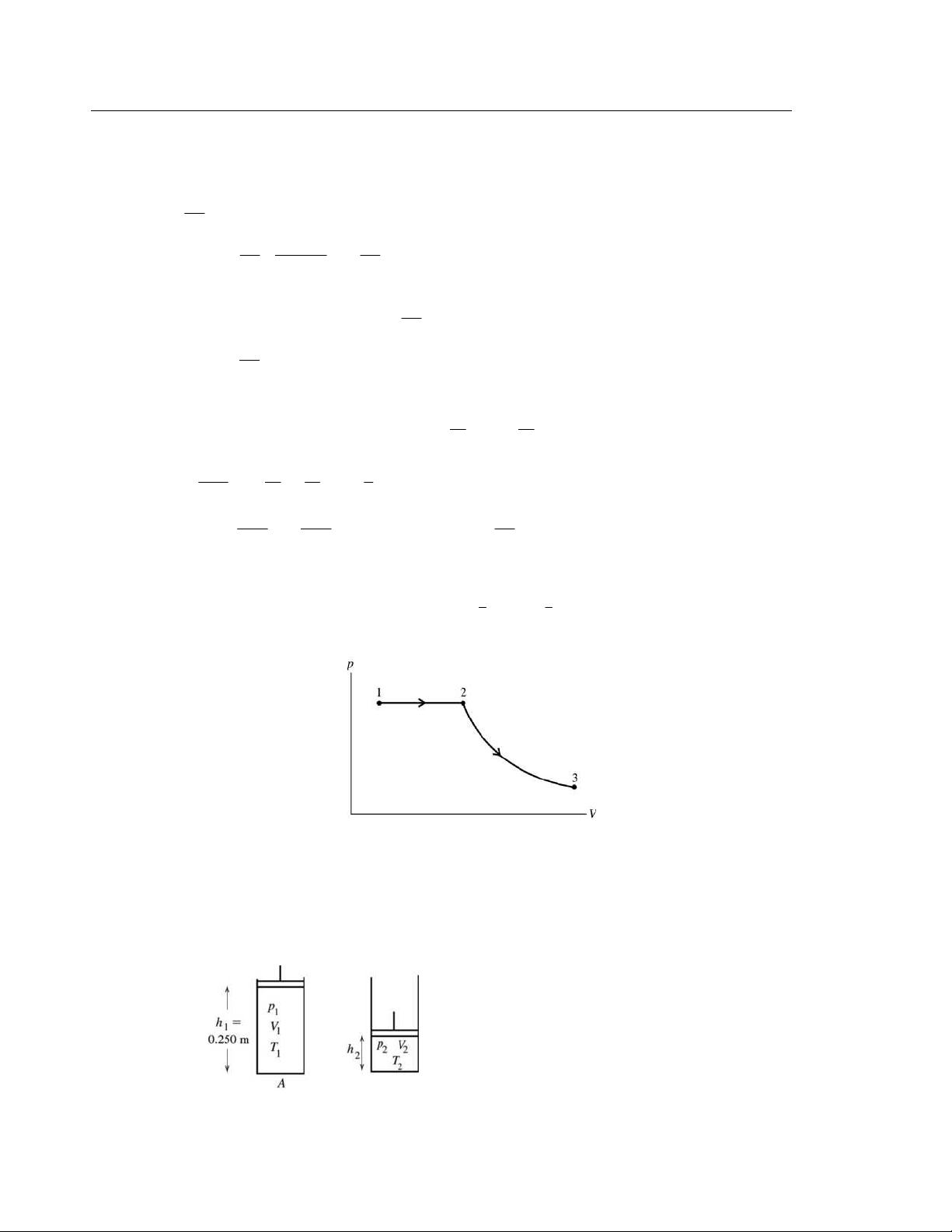
. The two positions of the piston are shown in Figure 19.61. 5 1 p =1.01×10 Pa 5 5 2 p = 4.20×10 Pa + a p ir = 5.21×10 Pa 1 V = 1 h A 2 V = 2 h A Figure 19.61
© Copyright 2012 Pearson Education, Inc. All rights reserved. This material is protected under all copyright laws as they currently exist.
No portion of this material may be reproduced, in any form or by any means, without permission in writing from the publisher.



