Đồ án môn Thiết kế hệ thống cơ điện tử | Trường Đại học Bách Khoa Hà Nội

MỤC LỤC
LỜI NÓI ĐẦU ............................................................................................................ 4
CHƯƠNG 1 MỞ ĐẦU ............................................................................................. 5
1.1.Tổng quan về hệ Cơ điện tử .............................................................................. 5
1.1.1. Định nghĩa .................................................................................................. 5
1.1.2 Các thành phần cơ bản của hệ Cơ điện tử ................................................... 5
1.2. Tổng quan về Robot công nghiệp ..................................................................... 6
1.2.1. Lịch sử phát triển ........................................................................................ 6
1.2.2. Các định nghĩa về Robot ............................................................................ 7
1.2.3. Tình hình phát triển Robot công nghiệp..................................................... 7
1.2.4. Cấu trúc và phân loại Robot công nghiệp .................................................. 8
1.2.5. Ứng dụng Robot công nghiệp trong sản xuất........................................... 10
1.3. Đặt vấn đề ....................................................................................................... 11
CHƯƠNG 2 TÍNH TOÁN ĐỘNG HỌC ROBOT................................................. 14
2.1. Đặt hệ trục tọa độ theo Denavit – Hartenberg ................................................ 14
2.2. Thiết lập bảng DH .......................................................................................... 15
2.3. Ma trận Denavit – Hartenberg ........................................................................ 16
2.4. Bài toán động học thuận Robot ...................................................................... 17
2.4.1. Tính các ma trận DH ................................................................................ 18
2.4.2. Xác định vị trí điểm tác động cuối ........................................................... 18
2.4.2. Xác định hướng khâu thao tác .................................................................. 18
2.5. Tính vận tốc, gia tốc điểm tác động cuối và vận tốc góc, gia tốc góc các khâu
............................................................................................................................... 20
2.5.1 Tính vận tốc góc, gia tốc góc các khâu ..................................................... 21
2.5.2. Tính vận tốc, gia tốc điểm tác động cuối ................................................. 23
2.6. Bài toán động học ngược Robot ..................................................................... 24
CHƯƠNG 3 THIẾT KẾ QUỸ ĐẠO CHUYỂN ĐỘNG CỦA ROBOT ................. 26
3.1. Khái niệm, nhiệm vụ của thiết kế quỹ đạo ..................................................... 26
3.2. Không gian làm việc của Robot ..................................................................... 27
3.3. Thiết kế quỹ đạo trong không gian khớp ........................................................ 28
3.3.1. Thiết kế quỹ đạo trong không gian khớp cho Robot RRR phẳng ............ 28
3.3.2. Ví dụ ......................................................................................................... 29
3.4. Thiết kế quỹ đạo trong không gian thao tác ................................................... 33
3.4.1. Thiết kế quỹ đạo trong không gian thao tác cho Robot RRR phẳng ....... 33
3.4.2. Ví dụ ......................................................................................................... 34
CHƯƠNG 4 TÍNH TOÁN ĐỘNG LỰC HỌC ROBOT ........................................ 36
4.1. Phương trình Lagrange dạng ma trận ............................................................. 36
4.2. Thiết lập phương trình động lực học cho Robot ............................................. 42
4.2.1. Phương trình động lực học tay máy ......................................................... 42
4.2.2. Phương trình động lực học của động cơ và bộ truyền ............................. 49
4.2.3. Phương trình động lực học cho toàn hệ (cơ-điện) .................................... 58
CHƯƠNG 5 THIẾT KẾ ĐIỀU KHIỂN ROBOT ............................................... 60
5.1.Điều khiển phản hồi và điều khiển vòng kín ................................................... 60
5.2. Hệ thống điều khiển mô men (τ) .................................................................... 61
5.2.1. Bộ điều khiển trong không gian khớp ...................................................... 61
5.2.2. Bộ điều khiển trong không gian thao tác ................................................. 74
5.3. Hệ thống điều khiển điện áp (u) ..................................................................... 80
KẾT LUẬN ............................................................................................................. 87
TÀI LIỆU THAM KHẢO ...................................................................................... 88 LỜI NÓI ĐẦU
Cơ điện tử là một trong 6 ngành công nghệ mũi nhọn của thế kỷ 21. Ở Việt Nam
trong vòng 10 năm trở lại đây, và đặc biệt là trong những năm tới, xuất hiện nhu cầu
lớn về đào tạo nhân lực Cơ điện tử. Cơ điện tử đóng vai trò vô cùng quan trọng trong
tự động hóa sản xuất, nâng cao năng suất, chất lượng sản phẩm.. Các sản phẩm Cơ
điện tử rất đa dạng, góp mặt trong hầu hết các lĩnh vực kinh tế xã hội như giao thông,
Robot, hệ thống sản xuất, năng lượng mới, thiết bị y tế, hàng không vũ trụ... Chính
vì thế việc nghiên cứu hệ thống Cơ điện tử đóng một vai trò quan trọng. Trong các
sản phẩm Cơ điện tử thì Robot công nghiệp là lĩnh vực tiêu biểu.
Môn học “ Đồ án thiết kế hệ thống Cơ điện tử” giúp em củng cố, ôn tập những
kiến thức đã học trong 3 năm qua, đồng thời bước đầu làm quen, tìm hiểu, tính toán,
mô phỏng một hệ Cơ điện tử điển hình, đó là Robot công nghiệp. Em xin chân
thành cảm ơn sự hướng dẫn tận tình của ThS. Nguyễn Thái Minh Tuấn, đã trực tiếp
hướng dẫn em hoàn thành đồ án này. Sự chỉ bảo của thầy giúp em tiếp cận, giải quyết
và trình bày vấn đề một cách khoa học, rõ ràng. Đó thực sự là những kinh nghiệm quý báu cho em sau này.
Dù đã cố gắng nhưng do khối lượng tính toán khá lớn đồng thời kiến thức còn
hạn chế nên không tránh khỏi thiếu sót, em rất mong nhận được sự đóng góp ý kiến
từ các thầy cô. Sinh viên thực hiện Lê Ngọc Linh CHƯƠNG 1 MỞ ĐẦU
1.1.Tổng quan về hệ Cơ điện tử
1.1.1. Định nghĩa [2]
Từ Cơ điện tử, tiếng Anh “Mechatronics” là viết tắt của từ ghép giữa Mechanics
và Electronics, được người Nhật sử dụng đầu tiên vào năm 1975 trong việc điều khiển
động cơ điện bằng máy tính. Thuật ngữ này sau đó trở nên phổ thông ở Nhật và nhanh
chóng được nhiều nước trên thế giới sử dụng khi các linh kiện điện tử và tiếp theo là
máy tính được sử dụng ngày càng nhiều trong điều khiển thiết bị, đặc biệt là trong
các hệ thống sản xuất.
Đã hơn 30 năm kể từ khi thuật ngữ Cơ điện tử ra đời, nhưng thuật ngữ này vẫn là
một khái niệm tiến triển không ngừng. Sau đây là một số định nghĩa về Cơ điện tử
của một số cơ quan tổ chức:
- Cơ điện tử là sự kết hợp của kỹ thuật cơ khí, điều khiển điện tử và kỹ thuật
hệ thống trong thiết kế sản phẩm và quá trình (theo Nanyang Politechnic Singapore).
- Cơ điện tử là sự kết hợp đồng vận của kỹ thuật cơ khí, điều khiển điện tử và tư
duy hệ thống trong thiết kế sản phẩm và các quá trình sản xuất (theo Ủy ban Tư
vấn Phát triển và Nghiên cứu Công nghiệp châu Âu, viết tắt là IRDAC).
- Cơ điện tử là sự kết hợp của 3 công nghệ then chốt: cơ khí, điện và điều khiển
(theo Louisian State University U.S.A).
Hiện nay, người ta vẫn đang cố gắng để định nghĩa Cơ điện tử, để phân loại các
sản phẩm Cơ điện tử và phát triển một chương trình giảng dạy Cơ điện tử chuẩn. Tuy
nhiên rất khó để miêu tả hoàn thiện “Cơ điện tử là gì”. Điều đó cho thấy lĩnh vực này
đang tồn tại, phát triển không ngừng và vẫn rất mới mẻ.
1.1.2 Các thành phần cơ bản của hệ Cơ điện tử [2]
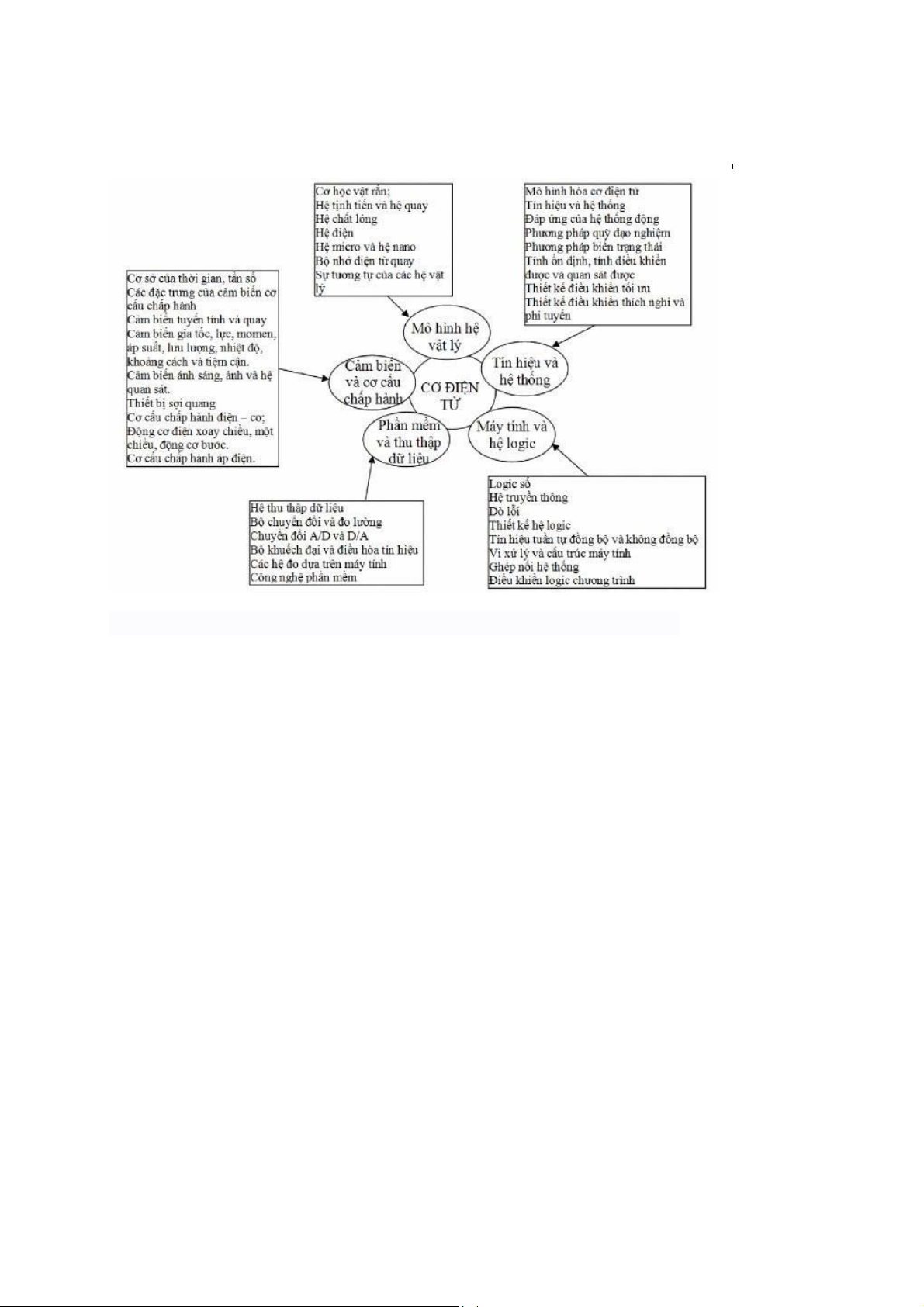
Lược đồ sau đây mô tả tương đối dễ hiểu và đầy đủ các thành phần chính của hệ
Cơ điện tử. Năm thành phần cơ bản trong sơ đồ này là đối tượng nghiên cứu của tất
cả các giáo trình Cơ điện tử.
Hình 1.1. Các thành phần cơ bản của hệ Cơ điện tử
Tại Hội nghị Khoa học toàn quốc về Cơ điện tử 2012 (VCM 2012) diễn ra tại
Trường ĐH Công nghệ, ĐH Quốc gia Hà Nội tháng 12/2012, GS.TSKH. Nguyễn
Khoa Sơn – Phó chủ tịch Hội Cơ điện tử Việt Nam đã khẳng định một trong những
lĩnh vực chuyên ngành cần quan tâm hàng đầu là Robotics, vì các hệ Robotic thường
tích hợp đầy đủ nhất các đặc thù của Cơ điện tử. Robot công nghiệp là một ứng dụng quan trọng của Robotics.
1.2. Tổng quan về Robot công nghiệp
1.2.1. Lịch sử phát triển [1]
Robot là một thuật ngữ chủ người lao động trong hệ ngôn ngữ Slaves. Từ khoảng
năm 1921, nhà viết kịch người Séc Karl Capek đã viết vở kịch mang tên Rossum’s
Universal Robots, trong đó từ Robot là tên của một loại máy tự động đã tiêu diệt ông
chủ và chiếm lĩnh thế giới. Năm 1926, thuật ngữ Robot lần đầu tiên lên phim ảnh tại
Đức, bộ phim mang tên Metropolis. Năm 1939, Robot đi bộ Elutoo và chú chó
Sporko được triển lãm tại một hội chợ tại New York, Mỹ, thu hút được nhiều sự quan
tâm của công chúng. Năm 1948, trước nhu cầu tự động hóa ngày một lớn của các dây
chuyền sản xuất và lắp ráp công nghiệp, một số loại tay máy đã được nghiên cứu và
chế tạo thử tại các phòng thí nghiệm ở Mỹ, châu Âu và một số nước khác. Các kỹ
thuật điều khiển động cơ điện và điều khiển từ xa đã được đưa vào lĩnh vực Robot
trong khoảng thời gian này. Cùng với sự phát triển nhanh chóng của cơ khí tự động
hóa và kỹ thuật điện tử, vào năm 1952, chiếc máy CNC đầu tiên trên thế giới đã ra
đời tại Viện Công nghệ Massachusett, Mỹ. Thành tựu này là cơ sở quan trọng cho sự
phát triển các bộ điều khiển Robot hiện đại như ngày nay.
1.2.2. Các định nghĩa về Robot [1]
Cho đến nay đã có một số định nghĩa về Robot như sau:
- McKerrow (1986) định nghĩa Robot là một loại máy móc cơ khí có thể lập
trình để thực hiện một số công việc nào đó, cũng tương tự như máy tính PC là
một thiết bị điện tử có thể lập trình để thực thi các nhiệm vụ cụ thể.
- Schulussel (1985) lại định nghĩa Robot là một tay máy đa chưc năng, khả trình
được thiết kế để vận chuyển nguyên nhiên vật liệu, phôi, chi tiết gia công; hoặc
Robot là thiết bị đặc thù được lập trình chuyển động đa dạng để thực hiện các nhiệm vụ nào đó.
1.2.3. Tình hình phát triển Robot công nghiệp [1]
Hiện nay nhu cầu sử dụng Robot trong công nghiệp nói chung ngày càng tăng,
các loại Robot được chế tạo ngày càng đa dạng, độ chính xác cao hơn, linh hoạt hơn,
giá cả phù hợp hơn, năng suất và tuổi thọ cao hơn. Mặc dù dải ứng dụng của Robot
ngày càng mở rộng (thay thế con người trong các hoạt động nặng nhọc, nhàm chán,
nguy hiểm, độc hại,…), nhưng theo thống kê vào năm 2000 tại Mỹ, lượng Robot hàn
và Robot xử lý phôi chiếm khoảng 78% tổng số lượng Robot công nghiệp đang sử
dụng tại thời điểm đó. Số lượng Robot lắp ráp chiếm khoảng 10% cũng trong thống
kê này. Phần còn lại là của các Robot công nghiệp khác.
Nhằm mục tiêu thiết kế, chế tạo các thế hệ Robot công nghiệp ngày càng thông
minh, linh hoạt, nhỏ gọn, rẻ, độ tin cậy cao,… một số bài toán sau đây đang là vấn
đề thời sự, được các nhà khoa học quan tâm giải quyết:
- Tối ưu cấu trúc cơ khí với nhiều chú ý tới việc sử dụng vật liệu nhé, độ bền
cao, lựa chọn các bộ truyền có tỷ số truyền và hiệu suất lớn, tuổi thọ cao,
độ chính xác cao để tăng độ chính xác điều khiển, tăng ổn định và tuổi thọ.
- Các bài toán cơ học: động học, động lực – điều khiển, cân bằng, dư dẫn
động, rung, tránh va chạm,.. cho các cấu trúc Robot công nghiệp truyền
thống và đặc biệt cho các cấu trúc động học song song, cấu trúc Robot công
nghiệp tích hợp trên Robot di động.
- Các cơ cấu dẫn động và cảm nhận tín hiệu cũng là vấn đề quan tâm lớn trong
kỹ thuật Robot. Đáp ứng yêu cầu về kết cấu và điều khiển Robot, các cơ cấu
dẫn động được nghiên cứu ứng dụng theo hướng tiết kiệm năng lượng, bền
lâu, đủ công suất, gọn, nhẹ.
- Điều khiển thông minh là hướng phát triển lớn của kỹ thuật Robot, thu hút sự
quan tâm của nhiều nhà khoa học trên thế giới. Cùng với sự phát triển và
thành tựu của các lĩnh vực Trí tuệ nhân tạo, Thị giác máy và xử lý ảnh, xử lý
âm thanh, tiếng nói,… lĩnh vực điều khiển thông minh trong kỹ thuật Robot
đang trên đà phát triển vô cùng mạnh mẽ.
Cho đến nay, hầu hết các trường đại học kỹ thuật ở Việt Nam đã đưa môn kỹ
thuật Robot vào chương trình chính khóa. Môn học này dành chủ yếu cho các chuyên
ngành cơ khí, song các khía cạnh riêng biệt của nó như kỹ thuật điều khiển, lập trình
mô phỏng cũng được các ngành khác quan tâm.
1.2.4. Cấu trúc và phân loại Robot công nghiệp
1.2.4.1. Cấu trúc chung của Robot công nghiệp [3]
Một Robot công nghiệp được cấu thành bởi các hệ thống sau:
- Tay máy: là cơ cấu cơ khí gồm các khâu, các khớp. Chúng hình thành cánh
tay để tạo chuyển động cơ bản, cổ tay tạo nên sự khéo léo linh hoạt và bàn tay
(End Effector) để trực tiếp hoàn thành các thao tác trên đối tượng.
- Hệ thống truyền dẫn động: có thể là cơ khí, thủy khí hoặc điện khí, là bộ
phận chủ yếu tạo nên sự chuyển dịch ở các khớp động.
- Hệ thống điều khiển: bảo đảm sự hoạt động của Robot theo các thông tin đặt
trước hoặc được nhận biết trong quá trình làm việc.
- Hệ thống cảm biến tín hiệu: thực hiện việc nhận biết và biến đổi thông tin về
hoạt động của bản thân Robot và của môi trường, đối tượng mà Robot phục vụ.
1.2.4.2. Bậc tự do của Robot [5]
Bậc tự do là khả năng chuyển động của một cơ cấu. Để dịch chuyển được một vật
thể trong không gian, cơ cấu chấp hành của Robot phải đạt được một số bậc tự do.
Nói chung cơ hệ Robot là một cơ cấu hở, do đó số bậc tự do của Robot có thể tính theo công thức (1.1): 5 w 6n ipi (1.1) i 1
trong đó: n – số khâu đông; pi – số khớp loại i (i=
1,2,…,5 : số bậc tự do bị hạn chế).
Đối với các cơ cấu có các khâu được nối với nhau bằng khớp quay hoặc tịnh tiến
(khớp động loại 5) thì số bậc tự do bằng với số khâu động. Đối với cơ cấu hở, số bậc
tự do bằng tổng số bậc tự do của các khớp động.
1.2.4.3. Hệ toạ độ [5]
Mỗi Robot thường bao gồm nhiều khâu liên kết với nhau qua các khớp, tạo thành
một chuỗi động học xuất phát từ một khâu cơ sở đứng yên. Hệ toạ độ gắn với khâu
cơ sở gọi là hệ toạ độ cơ sở (hay hệ toạ độ chuẩn). Các hệ toạ độ trung gian khác gắn
với các khâu động gọi là hệ toạ độ suy rộng. Trong từng thời điểm hoạt động, các toạ
độ suy rộng xác định cấu hình của Robot bằng các chuyển dịch dài hoặc các chuyển
dịch góc của các khớp tịnh tiến hoặc khớp quay. Các toạ độ suy rộng còn được gọi là biến khớp.
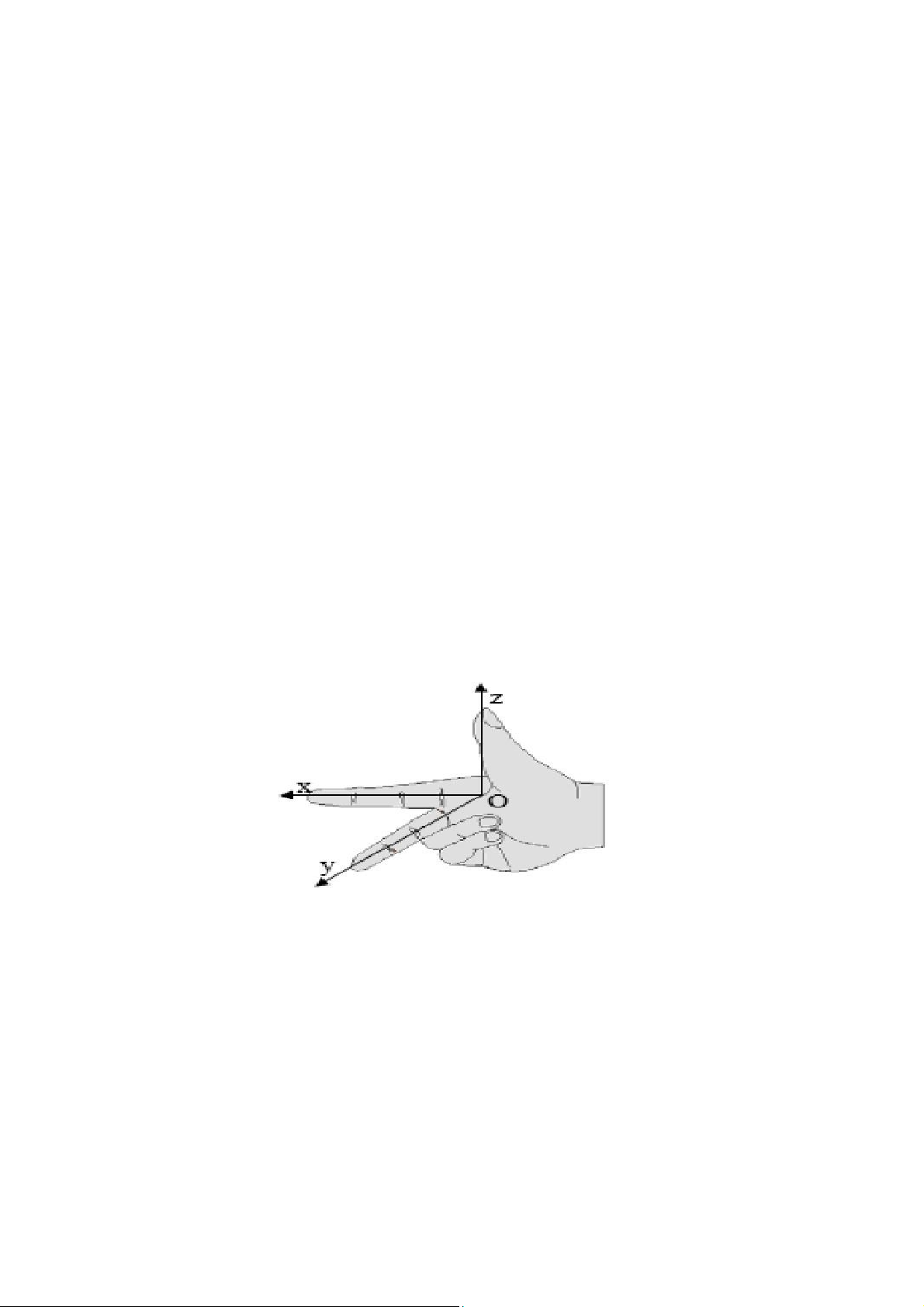
Các hệ toạ độ gắn trên các khâu của Robot phải tuân theo qui tắc bàn tay phải:
Dùng tay phải, nắm hai ngón tay út và áp út vào lòng bàn tay, xoè 3 ngón : cái, trỏ
và giữa theo 3 phương vuông góc nhau, nếu chọn ngón cái là phương và chiều của
trục z, thì ngón trỏ chỉ phương, chiều của trục x và ngón giữa sẽ biểu thị phương,
chiều của trục y (hình 1.2).
Hình 1.2. Quy tắc bàn tay phải
Trong Robot ta thường dùng chữ O và chỉ số i để chỉ hệ toạ độ gắn trên khâu thứ
i. Như vậy hệ toạ độ cơ sở (hệ toạ độ gắn với khâu cố định) sẽ được ký hiệu là
(Oxyz)0; hệ toạ độ gắn trên các khâu trung gian tương ứng sẽ là (Oxyz)1, (Oxyz)2,...,
(Oxyz)n-1, hệ toạ độ gắn trên khâu chấp hành cuối ký hiệu là (Oxyz)n, với i=
1,2,3,…,n, n là số khâu của Robot.
1.2.4.4. Phân loại Robot [4]
Thế giới Robot hiện nay rất phong phú và đa dạng, xuất hiện trong hầu hết các lĩnh
vực nên việc phân loại chúng chỉ mang tính tương đối, tùy thuộc quan điểm và mục
đích phân loại. Tuy nhiên, có 3 cách phân loại cơ bản: theo kết cấu, theo điều khiển
và theo phạm vi ứng dụng của Robot. a. Phân loại theo kết cấu
Theo kết cấu hình học của phạm vi làm việc Robot, người ta phân Robot thành
các loại: kiểu Đề-các, trụ, cầu, SCARA, kiểu tay người… b. Phân loại theo điều khiển
Có 2 kiểu điều khiển Robot: điều khiển hở và điều khiển kín.
Điều khiển hở: Dùng truyền động bước (động cơ điện hoặc động cơ thủy lực, khí
nén,…) mà quãng đường hoặc góc dịch chuyển tỷ lệ với số xung điều khiển. Điều khiển
kiểu này đơn giản nhưng đạt độ chính xác thấp.
Điều khiển kín: (điều khiển servo), sử dụng tín hiệu phản hồi vị trí để tăng độ chính
xác điều khiển, có 2 kiểu: điều khiển điểm-điểm và điều khiển theo đường (contour).
- Với điều khiển điểm-điểm, phần công tác dịch chuyển từ điểm này đến điểm
kia theo đường thẳng với tốc độ cao (trạng thái không làm việc). Nó chỉ làm
việc tại các điểm dừng. Kiểu điều khiển này dùng trên các Robot hàn điểm,
vận chuyển, tán đinh, bắn đinh…
- Điều khiển contour đảm bảo cho phần công tác dịch chuyển theo quỹ đạo bất
kì với tốc độ có thể điều khiển được. Có thể gặp kiểu điều khiển này trên các
Robot hàn hồ quang, phun sơn…
c. Phân loại theo ứng dụng
Dựa theo ứng dụng cụ thể của Robot: Robot dùng trong công nghiệp, Robot dùng
trong quân sự, trong kỹ thuật thám hiểm vũ trụ, trong nghiên cứu khoa học, y tế, giáo dục….
1.2.5. Ứng dụng Robot công nghiệp trong sản xuất
Từ khi mới ra đời Robot công nghiệp đã được áp dụng trong nhiều lĩnh vực khác
nhau để thay thế sức người. Nhờ vậy các dây chuyền sản xuất được tổ chức lại, năng
suất và hiệu quả tăng lên rõ rệt. Mục tiêu ứng dụng Robot công nghiệp nhằm góp
phần nâng cao năng suất dây chuyền công nghệ, giảm giá thành, nâng cao chất lượng
và khả năng cạnh tranh của sản phẩm đồng thời cải thiện điều kiện lao động. Đạt
được những mục tiêu trên là nhờ vào những khả năng to lớn của Robot như: làm việc
không biết mệt mỏi, rất dễ dàng chuyển nghề một cách thành thạo, chịu được phóng
xạ và các môi trường làm việc độc hại, nhiệt độ cao, cảm thấy được cả từ trường và
nghe được cả siêu âm… Robot được dùng thay thế con người trong các trường hợp
trên hoặc thực hiện các công việc tuy không nặng nhọc nhưng đơn điệu, dễ gây mệt mỏi, nhầm lẫn.
Trong ngành cơ khí, Robot được sử dụng nhiều trong công nghệ đúc, công nghệ
hàn, cắt kim loại, sơn, phun phủ kim loại, tháo lắp vận chuyển phôi, lắp ráp sản phẩm …
Ngày nay đã xuất hiện nhiều dây chuyền sản xuất tự động gồm các máy CNC
với Robot công nghiệp, các dây chuyền đó đạt mức tự động hoá cao, mức độ linh
hoạt cao... ở đây các máy và Robot được điều khiển bằng cùng một hệ thống chương trình.
Ngoài các phân xưởng, nhà máy, kỹ thuật Robot cũng được sử dụng trong việc
khai thác thềm lục địa và đại dương, trong y học, sử dụng trong quốc phòng, trong
chinh phục vũ trụ, trong công nghiệp nguyên tử, trong các lĩnh vực xã hội... Rõ
ràng là khả năng làm việc của Robot trong một số điều kiện vượt hơn khả năng của
con người, do đó nó là phương tiện hữu hiệu để tự động hoá, nâng cao năng suất lao
động, giảm nhẹ cho con người những công việc nặng nhọc và độc hại. Nhược điểm
lớn nhất của Robot là chưa linh hoạt như con người, trong dây chuyền tự động, nếu
có một Robot bị hỏng có thể làm ngừng hoạt động của cả dây chuyền, cho nên Robot
vẫn luôn hoạt động dưới sự giám sát của con người.
1.3. Đặt vấn đề
‐ Nhiệm vụ: Thiết kế điều khiển cho Robot hàn điểm, hoạt động trong một mặt
phẳng, hướng của khâu thao tác không đổi với là góc quay Cardan. 3
- Lựa chọn mô hình: vì Robot có nhiệm vụ hàn điểm và chỉ hoạt động trong mặt
phẳng nên ta lựa chọn mô hình Robot RRR 3 bậc tự do, gồm 3 khớp quay quanh trục
z (hình 1.3) với các thông số như sau: + Chiều dài các khâu: a1=0,6 m, a2=a3=0,4m
+ Giới hạn các góc khớp: q1 [min = 0 , max = ] (rad) 2 q2 [min = , max = ] (rad) 2 18 7 q3 [min = , max = ] (rad) 9 6
+ Khối lượng các khâu: m1=26,25 (kg); m2=18,5 (kg); m3 =19,5(kg) 3 q 2 q 1 q
Hình 1.3. Mô hình Robot RRR phẳng
Hình 1.4. Mô hình 3D đơn giản của Robot
Để thiết kế điều khiển Robot này, ta sẽ lần lượt giải các bài toán sau:
- Bài toán động học Robot
- Bài toán thiết kế quỹ đạo trong không gian khớp và không gian thao tác
- Bài toán động lực học Robot
- Bài toán điều khiển (gồm điều khiển momen và điều khiển điện áp u)
CHƯƠNG 2 TÍNH TOÁN ĐỘNG HỌC ROBOT
2.1. Đặt hệ trục tọa độ theo Denavit – Hartenberg
Đối với các Robot công nghiệp, Denavit – Hartenberg (1995) đã đưa ra cách chọn
các hệ trục tọa độ có gốc tại khớp thứ i như sau: [1]
- Trục zi-1 được chọn dọc theo trục của khớp động thứ i.
- Trục xi-1 được chọn dọc theo đường vuông góc chung của hai trục zi-2 và zi-1,
hướng đi từ trục zi-2 sang zi-1. Nếu trục zi-1 cắt trục zi-2 thì hướng của trục xi-1
được chọn tùy ý, miễn là vuông góc với zi-1. Khi hai trục zi-1 và zi-2 song song
với nhau, trục xi-1 chọn hướng theo pháp tuyến chung nào cũng được.
- Gốc tọa độ Oi-1 được chọn tại giao điểm của trục xi-1 và trục zi-1.
- Trục yi-1 được chọn sao cho hệ (Oxyz)i-1 là hệ quy chiếu thuận. Chú ý:
- Đối với hệ tọa độ (Oxyz)0 theo quy ước trên ta mới chỉ chọn được trục z0, còn
trục x0 chưa có trong quy ước trên. Ta có thể chọn trục x0 được chọn một cách
tùy ý, miễn là x0 vuông góc với z0.
- Đối với hệ tọa độ (Oxyz)n, do không có khớp n+1, nên theo quy ước ta không
xác định được trục zn. Trục zn không được xác định duy nhất, trong khi trục xn
lại được chọn theo pháp tuyến của trục zn-1. Trong trường hợp này, nếu khớp
là khớp quay ta có thể chọn trục zn song song với trục zn-1. Ngoài ra ta có thể
chọn tùy ý sao cho hợp lý.
- Khi khớp thứ i là khớp tịnh tiến, về nguyên tắc ta có thể chọn trục zi-1 một cách
tùy ý. Người ta thường chọn trục zi-1 dọc theo trục của khớp tịnh tiến này. Từ
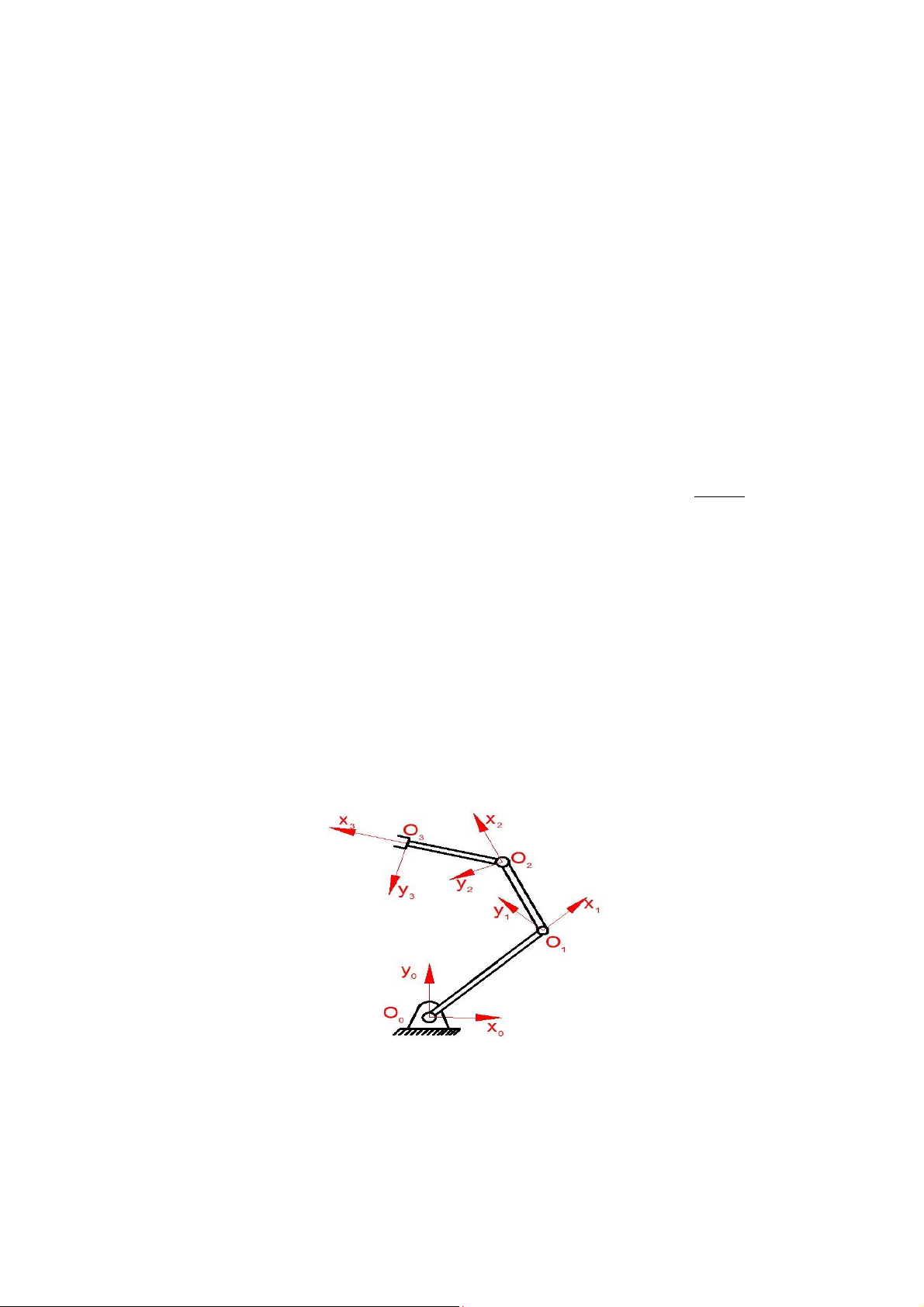
quy tắc trên ta xây dựng được các hệ tọa độ như hình 2.1:
Hình 2.1. Hệ trục tọa độ của Robot
Các trục O z , O z , O z , O z0 0 1 1 2 2 3 3 lần lượt đặt tại O , O , O , O0 1 2 3, phương vuông
góc với mặt giấy, chiều hướng từ trong ra ngoài.
2.2. Thiết lập bảng DH
Vị trí của hệ tọa độ khớp (Oxyz)i đối với hệ tọa độ khớp (Oxyz)i-1 được xác định
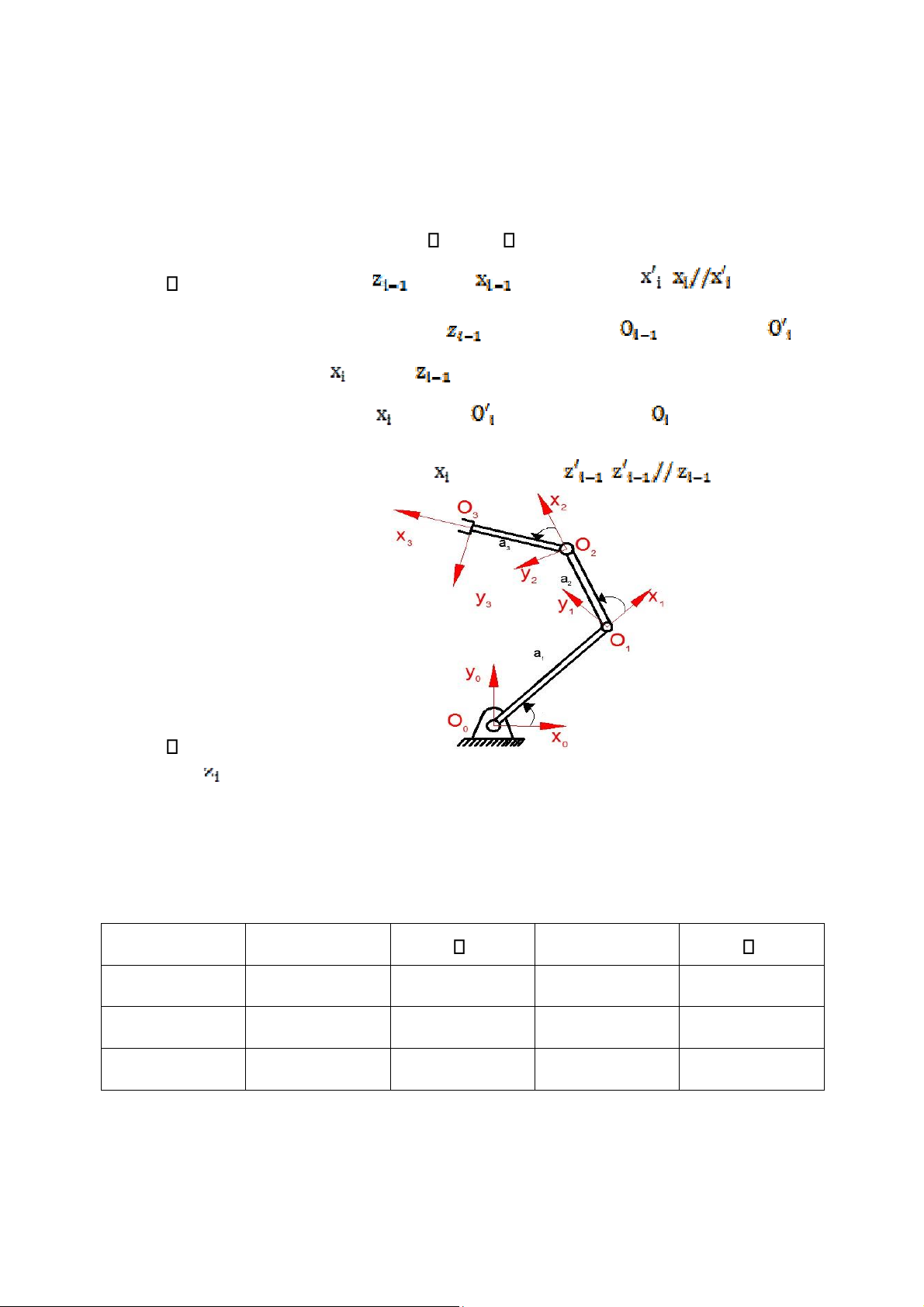
bởi bốn tham số Denavit- Hartenberg i , di , ai , i như sau: [1] - (
i : góc quay quanh trục để trục trùng với trục )
- di : dịch chuyển tịnh tiến dọc trục
để gốc tọa độ chuyển đến là giao điểm của trục và trục
- ai : dịch chuyển dọc trục để điểm chuyển đến điểm sao cho tr ụ c ( 3 q 2 q 1 q - i : góc quay quanh tr ục ) trùng với trục
Hình 2.2. Các tham số Denavit – Hartenberg
Như vậy từ các hệ tọa độ đã xây dựng ở trên, ta có các tham số DH như trong bảng 2.1.
Bảng 2.1. Các tham số Denavit – Hartenberg Khâu di i ai i 1 0 q1 a1 0 2 0 q2 a2 0 3 0 q3 a3 0
Trong đó q q1, 2,q3 là các biến khớp, còn a1, a2, a3 là hằng số
2.3. Ma trận Denavit – Hartenberg
Ta có thể chuyển hệ tọa độ khớp (Oxyz)i-1 sang hệ tọa độ (Oxyz)i bằng bốn phép biến
đổi cơ bản như sau: [1]
- Quay quanh trục zi-1 một góc i .
- Dịch chuyển tịnh tiến dọc trục zi-1 một đoạn di.
- Dịch chuyển tịnh tiến dọc trục xi một đoạn ai.
- Quay quanh trục xi một góc i .
Như vậy ma trận của phép biến đổi hệ tọa độ khớp (Oxyz)i-1 sang hệ tọa độ (Oxyz)i , kí
hiệu là i-1 Ai , là tích của 4 ma trận biến đổi cơ bản và có dạng như sau: cos 0 0 0 i sin i 0 0 1 0 0 0 1 0 ai 1 0 0 0 0 cos i sin 0 sin cos i 0 i i 0 0 1 0 0 0 1 1 A = 0 1 sin i cos i i-1 i 0 0 0 0 0 0 0 0 0 0 0 1 d 0 i 0 0 1 0 -cos isin i 1 0 1 0 0 cos 1 0 0 icos i cos i sin 0 sin a i icos i 2.1 sin 0 i isin i aisin i -sin icos i di 0 cos i 0 0 1
Ma trận được xác định bởi công thức (2.1) được gọi là ma trận Denavit – Hartenberg
địa phương. Nó cho ta biết thông tin về vị trí của khâu thứ i của Robot đối với hệ quy
chiếu (Oxyz)i-1. Ngoài ra còn có ma trận 0An, cho biết vị trí của điểm tác động cuối E
và hướng của khâu thao tác đối với hệ quy chiếu cố định (Oxyz)0. Ta tính ma trận 0
An bằng cách áp dụng liên tiếp các phép biến đổi (2.1) đối với Robot n khâu: 0 0 1 n 1
0 Rn rE
An A A1 2... An T (2.2) 0 1 trong đó: r T E xE ,y ,zE E
là véc tơ mô tả vị trí điểm tác động cuối trong hệ tọa độ (Oxyz)0.
0 Rn là ma trận cosin chỉ hướng của khâu thao tác đối với hệ tọa độ (Oxyz)0.
2.4. Bài toán động học thuận Robot
Vị trí mỗi khâu trong không gian được xác định bởi vị trí một điểm định vị và
hướng của khâu đó đối với một hệ quy chiếu đã chọn. Điểm định vị là một điểm xác
định nào đó của khâu, thường chọn là khối tâm của khâu. Hướng của khâu được xác
định bằng ma trận cosin chỉ hướng hoặc bằng các tọa độ suy rộng xác định vị trí của
vật rắn quay quanh một điểm. C 0 0 a C 2 S2 0 a C2 2 C3 S3
a C3 3 C1 S1 a S3 3 1 0 0 1 a 1 S2 C2 0 a S2 2 ; 2 A3 =
S3 C3 1 0 A1= S1 C1 1 S 0 0 1 1 A 2 0 0 1 0 0 0 0 0 0 (2.3) 1 0 0 0 0 0 0 1 0 0 1
C12 S12 0 C a1 1 C a12 2 0
S12 C12 1 S a1 1 S a122 0A2 0 A A11 2 0 0 0 0 2.4 0 0 1 C123 S123
C a1 1 C a122 C123a3 S123 C123 0
0 S a1 1 S a122 S123a3 0 A3 0 A A22 3 1 0 0 0 0 2.5 1 0 0
Nhiệm vụ của bài toán động học thuận là xác định vị trí của khâu thao tác, hay
nói cách khác là vị trí điểm tác động cuối và hướng của khâu thao tác đối với hệ tọa
độ cố định với điều kiện các biến khớp đã biết. Ở đây ta sẽ xác định từ ma trận Denavit
– Hartenberg của khâu thao tác 0 A3
2.4.1. Tính các ma trận DH
Đặt cosq1 = C1, sinq1 = S1, cosq2 = C2, sinq2 = S2, cosq3 = C3, sinq3 = S3, cos(q1
+ q2) = C12, cos(q2 + q3) = C23, cos(q1 + q3) = C13, cos(q1+q2+q3) = C123, sin(q1+q2+q3)
= S123 và thay các giá trị trong bảng tham số Denavit – Hartenberg vào công thức
(2.1) và ta được các ma trận biến đổi Denavit – Hartenberg giữa các hệ trục tọa độ như sau:
2.4.2. Xác định vị trí điểm tác động cuối Từ (2.2) và (2.5) suy ra: rE
C a1 1 C a122 C123a3 S a1 1 S a122 S123a3 0 T Mà r T E xE ,y ,zE E nên:
xE = C a1 1 C a12 2 C123a3
yE = S a1 1 S a122 S123a3 (2.6) zE =0
2.4.2. Xác định hướng khâu thao tác [6]
Theo (2.2) và (2.5) suy ra: C123 S123 0 0 S123 C123 0 R 3 0 1 0
Hướng của khâu thao tác so với hệ tọa độ (Oxyz)0 được xác định qua ma trận 0 R3
. Ngoài ra còn có thể xác định qua các gócα,β,η trong phép quay Cardan.
Chú thích: Phép quay Cardan là phép biến đổi hệ tọa độ cố định (Oxyz)i sang hệ tọa
độ động (Oxyz)i+3 bằng cách quay liên tiếp quanh các trục của hệ tọa độ động, cụ thể là:
- Quay (Oxyz)i góc α quanh trục xi. Biến đổi hệ tọa độ (Oxyz)i thành hệ tọa độ (Oxyz)i+1
- Quay (Oxyz)i+1 góc β quanh trục yi+1. Biến đổi hệ tọa độ (Oxyz)i+1 thành hệ tọa độ (Oxyz)i+2
- Quay (Oxyz)i+2 góc η quanh trục zi+2. Biến đổi hệ tọa độ (Oxyz)i+2 thành hệ tọa độ (Oxyz)i+3 i z 1 z i i z 2 , z i 3 y i 3
y i 1 , y i 2 y i O i x , ix 1 i x 2 i x 3
Hình 2.3. Các góc quay Cardan
Ma trận quay Cardan biểu diển hướng của hê tọa độ động (Oxyz)i+3 so với hệ tọa
độ cố định (Oxyz)i là tích của ba ma trận quay thành phần cơ bản, được tính theo công thức sau: 1 0 0 cos 0 sin cos sin 0 1 0 R cos CD 0 cos sin 0 0 0 sin 0 0 1 cos 0 sin cos sin sin -cos sin cos cos η
sin sin cos +cos sin -sin sin sin +cos cos -sin cos 2.7
-cos sin cos +si n sincos sin sin +sin cos cos cos
Như vậy bằng cách so sánh 2 ma trận quay RCD và 0 R3 , ta có thể tìm được các góc Cardan ,
, biểu diễn hướng của khâu thao tác đối với hệ tọa độ cố định (Oxyz)0.
0 R3 RCD hay: C123 -S123 0 cos cos η -cos sin sin S123 C1230
sin sin cos +cos sin -sin sin sin +cos cos -sin cos 0 0 1
-cos sin cos +sin sin cos sin sin +sin cos cos cos
So sánh các phần tử tương ứng của 2 ma trận ta có: sin 0, cos 1, sin 0, cos 1, sin S123, cos C123 2.8 Suy ra các góc Cardan 0,
0, q1 q2 q3 thỏa mãn (2.8).
Như vậy đối với cơ cấu Robot RRR phẳng này, để biến đổi hệ tọa độ cố định
(Oxyz)0 sang hệ tọa độ khâu thao tác, ta chỉ cần quay (Oxyz)0 quanh trục z0 một góc
q1 q2 q3 .
2.5. Tính vận tốc, gia tốc điểm tác động cuối và vận tốc góc, gia tốc góc các khâu [1]
Sau khi đã biết các biến khớp q , q , q1 2 3 và các vận tốc khớp, gia tốc khớp, ta sẽ
đi tính vận tốc góc, gia tốc góc các khâu cũng như vận tốc, gia tốc điểm tác động cuối.
- Vận tốc, gia tốc điểm thao tác cuối vE : v T E rE
xE yE zE (2.9)