Đồ án trí tuệ nhân tạo - Công nghệ thông tin | Trường đại học Điện Lực

I. GIỚI THIỆU BÀI TOÁN
1. Thuật giải heuristic
1.1.Khái niệm heuristic
 Là mở rộng khái niệm thuật toán . o
Thường tìm lời giải tốt nhưng không tốt nhất . o
Nhanh chóng tìm ra kết quả hơn so với giải thuật tối
ưu , vì vậy chi phí thấp hơn o
Thường thể hiện khá tự nhiên , gần gũi với cách suy
nghĩ và hành động của con người . o 
Là mở rộng khái niệm thuật toán.
o Thuờng tìm lời giải tốt nhưng không tốt nhất.
o Nhanh chóng tìm ra kết quả hơn so với giải thuật tối ưu, vì vậy chi phí thấp hơn.
o Thuờng thể hiện khá tự nhiên, gần gũi với cách suy nghĩ và
hành động của con nguời. c
Các nguyên lí của giải thuật heuristic Hàm heuristic Vét cạn thông minh Nguyên lí thứ tự Nguyên lí tham lam Hàm heuristic Kĩ thuật heuristic
2. Bài toán tô mầu đồ thị
Tô màu đồ thị và sự tổng quát của nó là công cụ hữu dụng trong việc mô hình hóa
rất nhiều bài toán khác nhau trong vấn đề xếp lịch, xây dựng chương trình và vấn
đề phân công công việc. Bài toán tô màu đồ thị bao gồm nhiều loại: tô màu đỉnh đồ
thị (vertex graph coloring) , tô màu cạnh đồ thị (edge graph coloring) ...
2.1. Bài toán tô mầu cạnh Bài toán
Cho G=(V,E) là đơn đồ thị vô hướng ( G không là đồ thị khuyên) ,
hãy tìm cách gán (tô màu) cho mỗi cạnh của đồ thị một màu sao
cho hai cạnh có cùng chung 1 đỉnh không bị tô bởi cùng một màu.
Một phép gán màu cho các cạnh như vậy gọi là một phép tô màu
cạnh đồ thị. Nói cách khác, phép tô cạnh đồ thị bởi k màu nói trên
có thể được hiểu là một phân hoạch của tập cạnh Ecủa G thành k
tập con (tương ứng với k màu) sao cho mỗi tập con ứng với một màu i nhất định.
Bài toán đặt ra là tìm cách tô màu nào sử dụng số màu ít nhất có thể. Ví dụ
Đồ thị trong hình trên có thể tô bởi 4 màu. Đồ thị G gọi là tô được
bởi k màu-cạnh nếu G có một phép tô k màu-cạnh phù hợp.Thông
thường hầu hết các đồ thị không là đồ thị khuyên đều tô được.Và
nếu G có tính chất như vậy thì G cũng có thể tô bởi l màu với l>k.
2.2. Bài toán tô mầu đỉnh
Một phép tô mầu sử dụng nhiều nhất k mầu gọi là một phép tô k
mầu. Số lượng mầu nhỏ nhất cần để tô các đỉnh của đồ thị G gọi
là sắc số đỉnh của đồ thị G, sao cho không có hai đỉnh kề nhau nào được tô cùng mầu.
Một đồ thị có thể tô được bằng k mầu, trong đó mỗi một tập các
đỉnh cùng mầu gọi là một lớp mầu.
Một đồ thị có thể được tô bằng k mầu nghĩa là có có k tập độc lập trong đồ thị
2.3. Các nguyên lý của thuật giải heuristic 1.Vét c n thông min 1.Vét cạn thông minh
 Hạn chế vùng không gian tìm kiếm và định hướng nahnh chóng để tìm đến mục tiêu.
 Tạo miền D’ rất nhỏ so với D  Vét cạn trên D’ 1. Nguyên lí tham lam
Lấy tiêu chuẩn tối ưu( trên phạm vi toàn cục) của bài toán làm tiêu chuẩn lựa
chọn hành động cho phạm vi cục bộ của từng bước.
a) Thuật giải GTS1: (Greedy-traveling saleman)
Xây dựng một lịch trình du lịch có chi phí cost tối thiểu cho bài toán
trong trường hợp phải qua n thành phố với ma trận chi phí C bắt đầu tại một đỉnh U nào đó.  Thu t gi iậ ả :
 B c 1ướ : {Kh i đâằu}ở  Đ t Tour := {};ặ  Cost := 0;
 V := U; {V là đ nh hi n t i
đang làm vi c}ỉ ệ ạ ệ
 B c 2ướ : {Thắm tâết c các thành phôế}ả  For k := 1 To n Do  qua b c 3;ướ
 B c 3ướ : {Ch n cung kêế tiêếp}ọ
 Đ t (V, W) là cung có chi phí
nh nhâết tnh t V đêến các đ
nh W ch a dùng:ặ ỏ ừ ỉ ư  Tour := Tour + {(V,W)};  Cost := Cost + Cost(V,W);
 Nhãn W đ c s d ngượ ử ụ
 Đ t V := W; {Gán đ xét b c kêế tiêếp}ặ ể ướ
 B c 4ướ : {Chuyêến đi hoàn thành}
 Đ t Tour := Tour + {(V,U)};ặ  Cost := Cost + Cost(V,U);  D ng.ừ  U = A  Tour = {}  Cost = 0  V = A  W ∈ {B, C, D, E}{Các đ
nh có th đêến t A}ỉ ể ừ
 → W = B{Vì qua B có giá thành bé nhâết}  Tour = {(A, B)}  Cost = 1  V = B W ∈ {C, D, E}→ W = EA  Tour = {(A, B),(B, E)}  Cost = 1 + 3 = 4  V = E W ∈ {C, D} → W = C  Thu t gi iậ ả :
 B c 1ướ : {Kh i đâằu}ở  Đ t Tour := {};ặ  Cost := 0;
 V := U; {V là đ nh hi n t i
đang làm vi c}ỉ ệ ạ ệ
 B c 2ướ : {Thắm tâết c các thành phôế}ả  For k := 1 To n Do  qua b c 3;ướ
 B c 3ướ : {Ch n cung kêế tiêếp}ọ
 Đ t (V, W) là cung có chi phí
nh nhâết tnh t V đêến các đ
nh W ch a dùng:ặ ỏ ừ ỉ ư  Tour := Tour + {(V,W)};  Cost := Cost + Cost(V,W);
 Nhãn W đ c s d ngượ ử ụ
 Đ t V := W; {Gán đ xét b c kêế tiêếp}ặ ể ướ
 B c 4ướ : {Chuyêến đi hoàn thành}
 Đ t Tour := Tour + {(V,U)};ặ  Cost := Cost + Cost(V,U);  D ng.ừ  U = A  Tour = {}  Cost = 0  V = A  W ∈ {B, C, D, E}{Các đ
nh có th đêến t A}ỉ ể ừ
 → W = B{Vì qua B có giá thành bé nhâết}  Tour = {(A, B)}  Cost = 1  V = B W ∈ {C, D, E}→ W = EA  Tour = {(A, B),(B, E)}  Cost = 1 + 3 = 4  V = E W ∈ {C, D} → W = C  Thu t gi iậ ả :
 B c 1ướ : {Kh i đâằu}ở  Đ t Tour := {};ặ  Cost := 0;
 V := U; {V là đ nh hi n t i
đang làm vi c}ỉ ệ ạ ệ
 B c 2ướ : {Thắm tâết c các thành phôế}ả  For k := 1 To n Do  qua b c 3;ướ
 B c 3ướ : {Ch n cung kêế tiêếp}ọ
 Đ t (V, W) là cung có chi phí
nh nhâết tnh t V đêến các đ
nh W ch a dùng:ặ ỏ ừ ỉ ư  Tour := Tour + {(V,W)};  Cost := Cost + Cost(V,W);
 Nhãn W đ c s d ngượ ử ụ
 Đ t V := W; {Gán đ xét b c kêế tiêếp}ặ ể ướ
 B c 4ướ : {Chuyêến đi hoàn thành}
 Đ t Tour := Tour + {(V,U)};ặ  Cost := Cost + Cost(V,U);  D ng.ừ  U = A  Tour = {}  Cost = 0  V = A  W ∈ {B, C, D, E}{Các đ
nh có th đêến t A}ỉ ể ừ
 → W = B{Vì qua B có giá thành bé nhâết}  Tour = {(A, B)}  Cost = 1  V = B W ∈ {C, D, E}→ W = EA  Tour = {(A, B),(B, E)}  Cost = 1 + 3 = 4  V = E W ∈ {C, D} → W = C  Thu t gi iậ ả :
 B c 1ướ : {Kh i đâằu} Thuật giải : Bước 1 : { Khởi đâu } Đặt Tour : = { } ;
Cost : = 0 ; V : = U ; { V là đỉnh hiện tại đang làm việc }
Bước 2 : { Thăm tất cả các thành phố } For k = 1 To n Do qua bước 3 ;
Bước 3 : { Chọn cung kê tiếp }
Đặt ( V , W ) là cung có chi phí nhỏ nhất tnh từ V đến các đỉnh W chưa dùng :
Tour : = Tour + { ( V , W ) } ;
Cost : = Cost + Cost ( V , W ) ; Nhãn W được sử dụng
Đặt V : = W ; { Gán để xét bước kê tiếp }
Bước 4 : { Chuyên đi hoàn thành }
Đặt Tour : = Tour + { ( V , U ) } ;
Cost : = Cost + Cost ( V , U ) ; Dừng . U = A Tour = { } Cost = 0 V = A
W € { B , C , D , E } { Các đỉnh có thể đến từ A }
= > W = B { Vì qua B có giá thành bé nhất } Tour = { ( A , B ) } Cost = 1 V = B
W € { C , D , E } → W = EA
Tour = { ( A , B ) , ( B , E ) } Cost = 1 + 3 = 4 V = E W € { C , D } -> W = C a) Thuật giải GTS2:
Tạo ra lịch trình từ p thành phố xuất phát riêng biệt. Tìm chu trình của
người bán hàng qua n thành phố (1

chỉ chu trình tốt nhất trong p chu trình được giữ lại mà thôi (giải thuật
này đòi hỏi phải nhập n,p và c) Thuật giải: Bước 1: {Khởi đầu}
k := 0; {Đếm số thành phố đi qua}
Tour = { ( A , B ) , ( B , E ) , ( E , C ) }
Bước 2 : { Bắt đầu chu trình mới }
Chuyển qua bước 3 khi k < p , ngược lại dừng .
Bước 3 : { Tạo chu trình mới } k: = k + 1 ;
Call ( GTS1 ( Vk ) ) : Trả về một chu trình T ( k ) ứng với chi phí C ( k ) .
Bước 4 : { Cập nhật chu trình tốt nhất } Nếu C(k) < Cost thì Best := T(k) Cost := C(k);
2.Bài toán đồ thị
- Bài toán lập lịch:
Ở đây nhóm xin đưa ra một ví dụ cụ thể là bài toán lập lịch thi: hãy lập lịch thi trong một trường
đại học sao cho không có sinh viên nào thi hai môn cùng một lúc Giải pháp:
Biểu diễn bằng đồ thị với: 
Mỗi môn học là một đỉnh 
Nếu hai môn học nào được dự thi bởi cùng 1 sinh viên thì sẽ nối bằng 1 cạnh
Mỗi môn học là một đỉnh
Nếu 2 môn học nào được dự thi bởi cùng 1 sinh viên thì sẽ nối bằng 1 cạnh
Các lập lịch sẽ tương ứng với bài toán tô màu của đồ thị này: số các màu
được tô là số các đợt thi
đợt thi, các đỉnh có cùng mầu sẽ thi cùng 1 đợt. Ví dụ: Có 7 môn như sau:
Môn 1: có các sinh viên A,B,C và D thi
Môn 2: có các sinh viên A,E,F,G và H thi
Môn 3: có các sinh viên B,E,J,I và K thi
Môn 4: có các sinh viên B,F,L và M thi
Môn 5: có các sinh viên G,L,N và O thi
Môn 6: có các sinh viên J,M,N và P thi
Môn 7: có các sinh viên D,H,K,Ovà P thi
Hãy xếp lịch thi thành các đợt sao cho các sinh viên đều có thể dự
thi tuần tự các môn mình đăng ký
Hình 02: Đồ thị G của bài toán lập lịch trên Đ t thi ợ Môn thi 1 1,5 2 2,6 3 3 4 4,7
Bài toán phân phối các thanh ghi chỉ số (register  allocation)
Trong lập trình các thanh ghi thường được dung để lưu trữ giá trị các biến
tạm thời. Bài toán yêu cầu tìm số thanh ghi ít nhất cần sử dụng trong một chương trình Giải pháp:
Biểu diễn bằng đồ thị với:
 Mỗi biến tương ứng là một đỉnh
 Hai đỉnh được nối với nhau nếu hai biến cùng được ghi xuống tại một thời điểm
Số thanh ghi ít nhất cần sử dụng sẽ là số mầu của đồ thị trên II. GIẢI THUẬT
1. Bài toán tô mầu đỉnh
1.1. Các định nghĩa sử dụng:
Để mô tả giải thuật nhóm bắt đầu với việc diễn giải các thuật ngữ,
định nghĩa mà giải thuật đề cập tới.
- ⌊x ⌋: biểu thị các chức năng
sàn tức là số nguyên lớn nhất không lớn hơn x
- ⌈ x⌉: biểu thị chức năng
trần nghĩa là số nguyên bé nhất là không bé hơn x
- ⌊x ⌋: biểu thị các chức năng sàn tức là số nguyên lớn nhất không lớn hơn x
- ⌈ x⌉: biểu thị chức năng trần nghĩa là số nguyên bé nhất là không bé hơn x
Một đồ thị đơn giản G với n đỉnh bao gồm một tập các đỉnh V,với | V |= n, và một bộ các
- Một đồ thị đơn giản G với n đỉnh bao gồm một tập các đỉnh V, với |V|=n,
và một cạnh E, sao cho mỗi cạnh là một cặp không có thứ tự của các đỉnh
khác nhau. Lưu ý rằng định nghĩa của G rõ ràng cấm các vòng lặp(cạnh nối
một đỉnh với chính nó) và các cạnh đa (nhiều cạnh tham gia một cặp đỉnh),
khi thiết lập E cũng phải được giới hạn. Chúng tôi cóthể gán nhãn các đỉnh
của G với 1 số nguyên, 2, ..., n.
- Nếu các cặp cạnh không có thứ tự của các đỉnh {u,v} là một cạnh trong G,
chúng ta nói u là một lân cận của v (hoặc u kề với v) và viết uv ∈ E. Lân
cận đối xứng rõ ràng là một mối quan hệ: uv ∈ E nếu và chỉ nếu vu ∈ E .
Bậc của một đỉnh v, ký hiệu là d (v), là số lân cận của v. Số bậc tối đa của tất cả các đỉnh
-Bậc của một đỉnh v, kí hiệu là d(v) là số lân cận của v. Số bậc tối đa của tất
cả các đỉnh của G được ký hiệu là Δ
- Các ma trận kề của G là một ma trận n × n với các mục
trong hàng u và cột v bằng 1 nếu uv ∈ E và bằng 0 nếu ngược lại.
- Cho đồ thị G và H, tích đề các G × H được định nghĩa là các đồ thị mà tập các đỉnh là V
(G) × V (H) với một cạnh đang kết nối đỉnh (u v 1, 1) với đỉnh (u v 2, 2)
nếu và chỉ nếu hoặc u = u 1 và {v 2
1, v 2} là một cạnh trong H hoặc v 1 = v 2 và {u 1, 2} u là một cạnh trong G.
- Đồ thị đầy đủ với m đỉnh được ký hiệu là K m.
- Tập độc lập S của đồ thị G là một tập các đỉnh như vậy mà không chứa cặp không có thứ tự
của các đỉnh trong S là một cạnh. Với một bộ độc lập S củaG và
một đỉnh v bên ngoài S, chúng ta nói v là có thể thêm vào nếu đặt S ∪ {v}
vẫn là một tập độc lập của G. Ký hiệu ρ (S) là số đỉnh có thể thêm vào của
một tập độc lập S của G. Một tập độc lập tối đa không có đỉnh có thể thêm
vào. Một tập độc lập tối đa là một tập độc lập với số lượng các đỉnh lớn nhất.
Lưu ý rằng một tập độc lập tối đa luôn luôn là tối đa, nhưng không nhất thiết phải ngược lại.
- Cho một tập m màu {1, 2, ..., m}, một tập m-màu của các đỉnh của đồ thị
G là sự phân một màu duy nhất cho mỗi đỉnh của G sao cho không có hai
đỉnh kề nhau có cùng màu. phân một
Số màu χ(G) của đồ thị G là giá trị nhỏ nhất của m mà tồn tại tương ứng một
một m-màu của các đỉnh của G.
- Thuật toán là một phương pháp giải quyết vấn đề thích hợp để thực hiện
như một chương trình máy tính. Trong khi thiết kế thuật toán chúng ta
thường phải đối mặt với một số phương pháp tiếp cận khác nhau chương
- Thuật toán thời gian - đa thức A có số lượng các bước tính toán luôn bị
chặn bởi một hàm đa thức của các kích thước của đầu vào. Do đó, một thuật
toán thời gian đa thức là một vấn đề thực sự hữu ích trong thực tế. Các lớp
của tất cả các vấn đề như vậy có thuật toán thời gian đa thức được ký hiệu là
P. Đối với một số vấn đề, không có thuật toán thời gian đa thứcđược biết
đến, nhưng những vấn đề này có thuật toán thời gian đa thức bất định: hãy
thử tất cả các ứng viên cho các giải pháp cùng một lúc và cho mỗi ứng viên
nhất định, xác minh xem đó là một giải pháp chính xác trong thời gian đa thức. 1.2. Thuật toán
Nhóm bắt đầu với tích Đề Các cho phép chúng ta chuyển đổi
các vấn đề của việc tìm kiếm một
tập m-màu của các đỉnh n của một đồ thị tương đương như việc
tìm kiếm một bộ độc lập kích
thước n trong tích đề các G × Km . - Tích Đề Các - Tích đề các:
Một đơn đồ thị G với n đỉnh là tô được bằng m mầu khi và chỉ khi
tích đề các G × K m có một tập độc lập kích thước n. Chứng minh.
Giả sử có một tập m-màu của các đỉnh của G. Xác định một tập
con S của các đỉnh của tích đề các G × K m như sau. Một đỉnh (u,
v) của G × Km thuộc S nếu và chỉ nếu đỉnh u của G được giao
màu v đối với tập m màu thích hợp. Vì mỗi đỉnh của G được giao
một màu duy nhất, | S | = n.
Bây giờ chúng ta sẽ chỉ ra rằng S là một tập độc lập. Cho (u 1, v
1) và (u 2, v 2) thuộc S, giả sử có một cạnh {(u 1, v 1), (u 2, v 2)}
trong G × K . Do đó, theo định nghĩa của tích đề các, có hai khả m năng.
 u1= u 2 và {v 1, v 2}là một cạnh trong K m. Nhưng u = u 1 với v 2 = v 1
từ mỗi đỉnh trong G được giao một màu 2,
duy nhất. Nhưng sau đó {v v
1, 1} không thể là một cạnh trong K m khi
K m là một đơn đồ thị (mâu thuẫn).
 {U 1, u 2} là một cạnh trong G, và v 1 = v 2. Nhưng điều này vi phạm các
định nghĩa của một tập m màu của G từ đỉnh kề phải được giao các màu khác nhau (mâu thuẫn). u
Vì vậy không thể có một cạnh giữa hai đỉnh trong S và S phải là một tập độc lập.
Ngược lại, giả sử có một tập độc lập S kích thước n trong tích đề các G × Km
Chúng ta sẽ chỉ ra rằng G có m màu riêng biệt. Nếu m lớn hơn hoặc bằng n thì G
có thể được m màu một cách tầm thường , do đó giả sử m nhỏ hơn n. Sự phân chia
các đỉnh của S vào nhiều nhất là m lớp tươngđương C 1, C ,..., C 2 m, nơi một
đỉnh (u, v) trong S thuộc về lớp tương đương C i khi và chỉ khi v = v i. Rõ
ràng , điều này đưa ra một định nghĩa phân chia tốt của các đỉnh trong S. Bây giờ
các đỉnh của G vào nhiều nhất là m lớp tương đương C '1, C' 2, ..., C'm, nơi một u
đỉnh của G thuộclớp tương đương C 'i nếu và chỉ nếu (u, v i) thuộc về lớp tương
đương C i. Để chứng tỏ điều đó ta đưa ra một định nghĩa phân chia tốt của các đỉnh
các đỉnh của G tuân theo:
Cho một đỉnh u của G, nếu u thuộc về cả hai C’i và C’j thì (u, vi) thuộc Ci và (u,v
j) thuộc C j. Khi K mđầy đủ, {v i, v k} là một cạnh trong K m, do đó, {(u, v i), (u,
v j)} là một cạnh trong tích đề các G ×K m. Điều này mâu thuẫn với
thực tế là S là một tập độc lập .Vì vậy, các bộ C’1, C’2 ,..., C’m là cặp phân chia
Danh sách các phần tử của S sắp xếp như sau: o
Danh sách các phần tử của S sắp xếp như sau: 1, 1 1
-(U 1 v 1), (u 2, v 1), ..., (u i (1), v 1) 2 2, 2
-(U 1, v 2), (u 2 v 2), ..., (u i (2), v 2) -... m m m
-(U 1, v m), (u 2, v m), ..., (u i (m), m v) i k
Nếu một số u j = l u trong danh sách thì khi Km đầy đủ, i k
{vi,vj} là một cạnh trong K m, do đó, {(u j, v i), (u l , v l)} là
một cạnh trong tích đề các
G × K m. Điều này mâu thuẫn với i
thực tế S là một tập độc lập. Vì vậy, tất cả các u j i xuất hiện i
trong danh sách là riêng biệt và từ | S | = n , có n u j i phân biệt
mọi đỉnh của G được chứa trong một số lớp tương đương 'C Do đó,...
Chỉ định màu i đến đỉnh u của G nếu u thuộc về các lớp tương
đương C i' . Điều này tạo ra một tập m-màu của các đỉnh của G.
Bây giờ chúng ta định nghĩa hai thủ tục để thực hiện với tập độc
lập trong tích đề các G × K m. -Thủ tục 1
Với một tập độc lập S của tích đề các G×Km nếu S không có đỉnh
có thể thêm, đầu ra S. Ngược lại, cho mỗi đỉnh có thể thêm (u, v)
của S, tìm số ρ (S∪ {(u, v)}) của đỉnh có thể thêm của tập độc lập
S ∪ {(u, v)}. Cho (u,v ) max biểu thị một đỉnh có thể thêm sao cho ρ (S ∪ {(u, v)
là lớn nhất và chứa tập độc lập S ∪ {(u, max})
v) max}. Lặp lại cho đến khi tập độc lập không có đỉnh có thể thêm vào. -Thủ tục2:
Cho một tập độc lập tối đa S của tích đề các G × K m, nếu không có đỉnh (u 1, v 1) bên ngoài S sao cho (u v
1, 1) có đúng một lân cận (u v 2, ) trong S, đầu ra 2
S.Ngược lại,tìm thấy một đỉnh (u v 1, 1) ngoài S sao cho (u v 1, 1) có đúng một lân (u , v ), (u , v )
cận (u 2, v 2) trong S Xác định S 1.
bằng cách thêm (u1, v1) vào 1 1 2 2 (u v (u v S và bỏ (u v
2, 2) từ S. Thực hiện thủ tục 3.1 trên S 1, và đầu ra 1), 2, 2)
các tập độc lập kết quả. Giải thuật
Với đầu vào là một đơn đồ thị G với n đỉnh, tìm kiếm một tập m-
màu của các đỉnh của G. Để {u 1, u 2, ..., u n} biểu thị các đỉnh
của G và để {v1, v 2, ..., v m} biểu thị các đỉnh của K m.. Chúng
ta tạo các tập độc lập tối đa trong tích đề các G×Km. Ở mỗi giai
đoạn, nếu tập độc lập thu được có kích thước n nhỏ nhất, thì đi đến phần III:
Phần I. Đối với i = 1, 2, ..., n và j = 1, 2, ..., n lần lượt Khởi tạo tập độc l
-Khởi tạo tập độc lập S i, j = {(u v i, j)}
-Thực hiện thủ tục 3.1 trên S i, j
-Đối với r = 1, 2, ..., n thực hiện thủ tục 3.2 lặp lại r
lần -Kết quả là một tập độc lập tối đa S i, j.
Phần II. Với mỗi cặp tập độc lập tối đa S i, j, S k, l tìm thấy trong phần I
-Khởi tạo S đặt độc lập i, j, k, l = S i, j ∩ S k, l.
-Thực hiện thủ tục 3,1 trên S i, j, k, l
-Đối với r = 1, 2, ..., n thực hiện thủ tục 3,2 lần r lặp đi lặp lại
-Kết quả là một tập độc lập tối đa S i, j, k, l.
Phần III. Nếu một tập độc lập S với kích thước n đã được
tìm thấy tại bất kỳ giai
Phần III. Nếu một tập độc lập S với kích thước n đã được
tìm thấy tại bất kỳ giai đoạn của phần I hoặc phần II, đầu
ra S như là một tập m-màu của các đỉnh của G theo Bổ đề
Đề các. Ngược lại, kết luận thuật toán không thể tìm thấy
bất kỳ tương ứng m-màu của các đỉnh của G. 1.3. Ví dụ
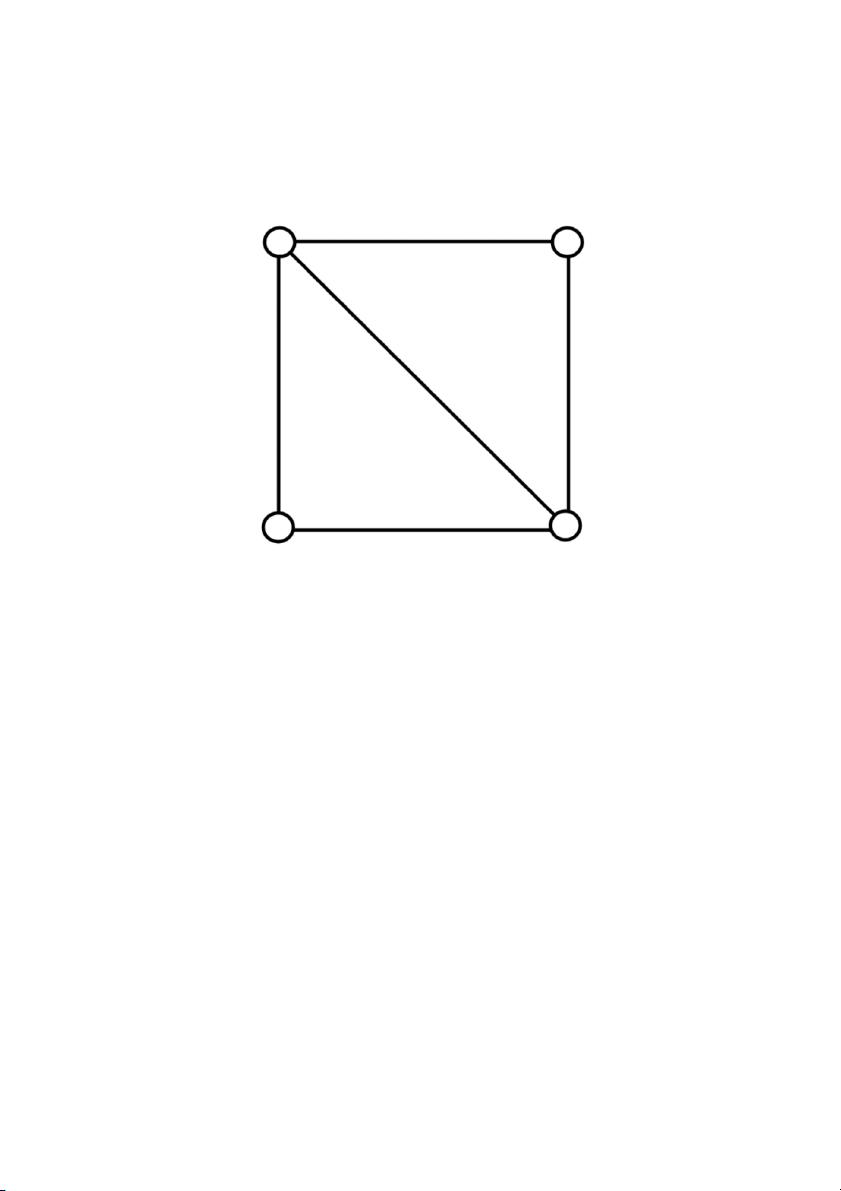
Chúng ta thể hiện các bước của thuật toán bằng một ví dụ
nhỏ. Đồ thị đầu vào được thể hiện dưới đây trong hình 3.1 với n =
4 đỉnh có nhãn V = {1, 2, 3, 4}. Các thuật toán tìm kiếm cho một
tương ứng 3- màu của các đỉnh bằng cách sử dụng các thiết lập
của các màu {1, 2, 3} đại diện bởi màu xanh lá cây, đỏ và màu xanh tương ứng.
Hình 03.Các đồ thị đầu vào G với 3- màu tương ứng của các
đỉnh của nó được tìm thấy bởi thuật toán
Thuật toán đầu tiên xây dựng tích đề các G × K hiển thị dưới đây trong các con 3
số 3,2 với 12 đỉnh {(1,1), (1,2), (1,3), (2,1), (2,2), (2,3), (3,1), (3,2), (3,3), (4,1),
(4,2), (4,3)}. Chúng ta tách các đỉnh {1, 2, 3} của thành phần thứ hai K như các 3
màu sắc xanh, đỏ và màu xanh tương ứng.
Hình 04: tích đề các G×K3với một tập độc lập với kích thước
4 được tìm thấy bằng thuật toán
Thuật toán bây giờ tìm kiếm một tập độc lập với kích thước 4 trong tích đề các
G × K . Phần I cho i = 1 và j = 1 khởi tạo tập độc lập như S 3 = {(1, 1)}. 1,1
Bây giờ chúng ta thực hiện các thủ tục 1. Sau đây là các kết quả dưới dạng bảng: Tập độc lập S
= {(1, 1)}. Kích thước: 1. 1,1
Đỉnh có thể thêm (u,v) của S1,1
Đỉnh có thể thêm của S1,1 ∪{(u,v)} ρ (1,1 S ∪ {(u,v)}) (2,2) (3,3), (4,2), (4,3) 3 (2,3) (3,2), (4,2), (4,3) 3 (3,2) (2,3), (4,3) 2 (3,3) (2,2), (4,2) 2 (4,2) (2,2), (2,3), (3,3) 3 (4,3) (2,2), (2,3), (3,2) 3 Tối đa ρ S ∪ (1,1
{(u, v)}) = 3 cho (v, u) = (2, 2). Thêm đỉnh (2, 2) vào S1,1.
Tập độc lập S1,1 = {(1, 1), (2, 2)}. Kích thước: 2.
Đỉnh có thể thêm (u,v) của S1,1
Đỉnh có thể thêm (u,v) của S1,1 ρ (1,1 S ∪ {(u,v)}) (3,3) (4,2) 1 (4,2) (3,3) 1 (4,3) Không có 0 Tối đa ρ S ∪ (1,1
{(u, v)}) = 1 cho (v, u) = (3, 3). Thêm đỉnh (3, 3) vào S1,1.
Tập độc lập S1,1 = {(1, 1), (2, 2), (3, 3)}:. Kích thước 3.
Đỉnh có thể thêm (u,v) của S1,1
Đỉnh có thể thêm (u,v) của S1,1 ρ (1,1 S ∪ {(u,v)}) (4,2) Không có 0 Tối đa ρ S ∪ (1,1
{(u, v)}) = 0 với (v, u) = (4, 2). Thêm đỉnh (4, 2) để S1,1.
Chúng ta có được một tập độc lập tối đa S1,1 = {(1, 1), (2, 2), (3,
3), (4, 2)} của kích thước yêu cầu n = 4. Bây giờ đầu ra phần III
S 1,1 được yêu cầu đúng 3-màu của đầu vào đồ thị G và thuật
toán kết thúc. Lưu ý rằng chúng ta giải thích kết quả như sau:
đỉnh 1 được tô với màu 1 (màu xanh), đỉnh 2 được tô với màu 2
(màu đỏ), đỉnh 3 được tô với màu 3 (màu xanh) và đỉnh 4 được tô với màu 2 ( màu đỏ). 1.4. Độ phức tạp:
Tiếp theo để đánh giá độ phức tạp của giải thuật, nhóm sẽ chỉ ra
rằng thuật toán kết thúc trong
thời gian đa thức, trong khi tìm kiếm một tập m-màu cho một đồ
thị với n đỉnh, bằng cách xác
định một đa thức của N=nm đó là một cận trên trên tổng số bước
tính toán thực hiện bởi thuật toán.Lưu ý rằng chúng ta xem xét.
 Kiểm tra xem một cặp của các đỉnh được kết nối bởi một cạnh trong G, và 
kiểm tra xem một cặp của các đỉnh được kết nối bởi một cạnh trong G, và 
so sánh xem một số nguyên cho trước nhỏ hơn một số
nguyên cho trước được tính toán các bước cơ bản.
so sánh xem một số nguyên cho trước nhỏ hơn một số nguyên
cho trước được tính toán các bước cơ bản. Mệnh Đề 1
Cho một đồ thị đơn giản G với n đỉnh và một tập độc lập S của
G×Km , thủ tục 1 mất ít nhất (nm)5 bước. Chứng minh
Kiểm tra việc một đỉnh riêng có thể thêm thì mất tối đa (nm)2
bước, từ đỉnh có ít hơn các lân cận nm và cho mỗi lân cận phải
mất ít hơn nm bước để kiểm tra xem nó là ở ngoài tập độc lập. Đối
với một tập độc lập riêng, việc tìm kiếm số ρ của các đỉnh có thể
thêm mất ít nhất (nm)3 = (nm)(nm)2 bước, khi nhiều nhất nm
đỉnh bên ngoài tập độc lập chúng ta phải kiểm tra xem nó có thể
thêm hay không. Đối với một tập độc lập riêng, việc tìm kiếm một
đỉnh sao cho ρ là tối đa thì mất ít nhất (nm)4 = (nm)(nm)3 bước,
khi có hầu hết nm đỉnh bên ngoài. Thủ tục 1 kết thúc khi hầu hết
nm đỉnh được thêm, do đó phải mất một tổng của hầu hết
(nm)5 = (nm)(nm)4 bước. Mệnh Đề 2
Cho một đơn đồ thị G với n đỉnh và một tập độc lập tối đa S của
G×Km , thủ tục 2 mất ít nhất (nm)5 + (nm)2 +1 bước. Chứng minh
Để tìm một đỉnh (u 1, v 1) bên ngoài S mà có đúng một lân cận
(u 2, v 2) bên trong S có tối đa (nm)2 bước, khi có ít hơn nm đỉnh
ngoài S và chúng ta phải tìm ra nếu ít nhất một trong các lân cận
bé hơn nm của bất kỳ đỉnh nào ở trong S. Nếu như một đỉnh (u 1,
v 1) đã được tìm thấy, phải mất một bước để hoán đổi (u 1, v 1) và
(u 2, v 2). Sau đó, bằng mệnh đề 4.1, phải mất ít nhất (nm)5
bước để thực hiện các thủ tục 1 vào tập độc lập kết quả. Như vậy,
thủ tục 2 mất ít nhất (nm)2 +1 + (nm)5 bước. Mệnh Đề 3
Cho một đơn đồ thị G với n đỉnh và m màu, phần I của thuật toán có tối đa
(nm)7 + (nm)6 + (nm)4 + (nm)2 bước. Chứng minh
Tại mỗi lượt, thủ tục 1 mất ít nhất (nm)5 bước bằng mệnh đề 1.
Sau đó, thủ tục 2 được thực hiện tối đa nm lần mà theo mệnh đề 2, mất tối đa
nm((nm)5 + (nm)5 +1) = (nm)6 + (nm)3 + nm bước .Vì vậy, tại mỗi
lượt, tối đa (nm)5 + (nm)6 + (nm)3 + nm bước được thực hiện. Có
nm lượt cho i = 1, 2, ..., n, và j = 1, 2, ..., m, do đó, một phần I
thực hiện tổng cộng tối đa là
nm((nm)5 + (nm)6 + (nm)3 + nm)= (nm)6 + (nm)7 + (nm)4 + (nm)2 bước. Mệnh Đề 4
Cho một đơn đồ thị G với n đỉnh và m màu, thuật toán mất ít
hơn (nm)6 + 2(nm)7 + (nm)6 + (nm)5 + (nm)4 + (nm)3 + (nm)2 bước để kết thúc. Chứng minh
Có ít hơn (nm)2 cặp riêng biệt của tập độc lập tối đa được tìm
thấy bởi phần I, mà được thực hiện lần lượt. Tương tự như các
thực nghiệm về mệnh đề 3, phần II có ít hơn (nm)2 nm((nm)5 +
(nm)6 + (nm)3 + nm) = (nm)7 + (nm)8 + (nm)5 + (nm)3
Do đó, phần I và phần II cùng nhau mất ít hơn tổng cộng của
((nm)6 + (nm)7 + (nm)4 + (nm)2) + ((nm)7 + (nm)8 + (nm)5 +
(nm)3) = 2(nm)7 + (nm)8 + (nm)6 + (nm)5 + (nm)4 + (nm)3 +
(nm)2 bước để kết thúc.
2. Bài toán tô mầu cạnh 2.1. Giải thuật
Về thuật toán giải quyết bài toán tô màu cạnh đồ thị hiện
nay trên thế giới có nhiều thuật toán được đề suất như
 Thuật toán thu gọn (Contraction algorthms) được đề xuất bởi Zykov
 Thuật toán tô màu theo dãy (sequential coloring).
Trong đó thuật toán tô màu theo dãy lại được ứng dụng theo nhiều cách khác nhau.
Ý tưởng của thuật toán này xoay quanh việc sắp xếp thứ tự
các cạnh của đồ thị theo một thứ tự nhất định. Đánh trọng số cho
các màu được dung để tô. Sau đó duyệt các cạnh theo thứ tự nêu
trên. Trong quá trình duyệt sẽ tô màu cho cạnh bằng màu có
trọng số nhỏ nhất mà chưa được sử dụng để tô cho các cạnh kề.
Đây là một vận dụng của sử dụng thuật toán tham lam. Kết quả
của bài toán khác nhau nếu chúng ta chọn được thứ tự của các
cạnh khác nhau. Do đó các cải tiến hay các thuật toán khác nhau
dựa trên thuật toán này hầu hết đều là cải tiến việc lựa chọn thứ
tự cho các cạnh ban đầu.
Trong chương trình ứng dụng của nhóm, giải thuật đưa ra ở
mức minh hoạ một cách tô màu cạnh của đồ thị vô hướng. Trong
đó, việc xếp thứ tự của đỉnh được đồng nghĩa với thứ tự các đỉnh
được sắp xếp của đầu vào. Do đó thuật toán được thu gọn như sau :
Thứ tự các cạnh được sắp xếp
trong quá trình nhập dữ liệu về
đồ thị. Các cạnh được đánh
 Thứ tự các cạnh được sắp xếp trong quá trình nhập dữ
liệu về đồ thị. Các cạnh được đánh số theo thứ tự E1, E2, ...,En.
 Tìm bậc lớn nhất của đồ thị (Δ)
 Chuẩn bị (Δ+1) màu để tô 
 Bước i: Tô màu cạnh Ei bởi màu có chỉ số nhỏ nhất trong
số các màu chưa được sử dụng để tô màu cạnh kề của
nó. Trong đó ở bước i tùy theo cách cài đặt sẽ có những cách đánh màu khác nhau.
Với thuật toán trên chúng ta có thể tìm được 1 cách tô màu
cho các cạnh của đồ thị với số màu không quá Δ+1 màu ( vấn đề
này sẽ thấy rõ hơn khi đi sâu vào phần cài dặt). Vậy đó đã là số
màu nhỏ nhất hay chưa. Theo định lý Vizing chúng ta phát biểu ở
trên, ta có Δ(G)≤ χ′(G) ≤ Δ(G) + 1. Vậy sắc số cạnh chỉ có thể
nằm ở 1 trong hai giá trị là Δ(G) và Δ(G) + 1. Với việc chọn số
màu lớn nhất có thể tô là Δ(G)+1, thuật toán đã kẹp được cận
trên của sắc số cạnh. Với việc lựa chọn màu có chỉ số nhỏ nhất
chưa được sử dụng để tô các cạnh kề cho một cạnh, số màu được
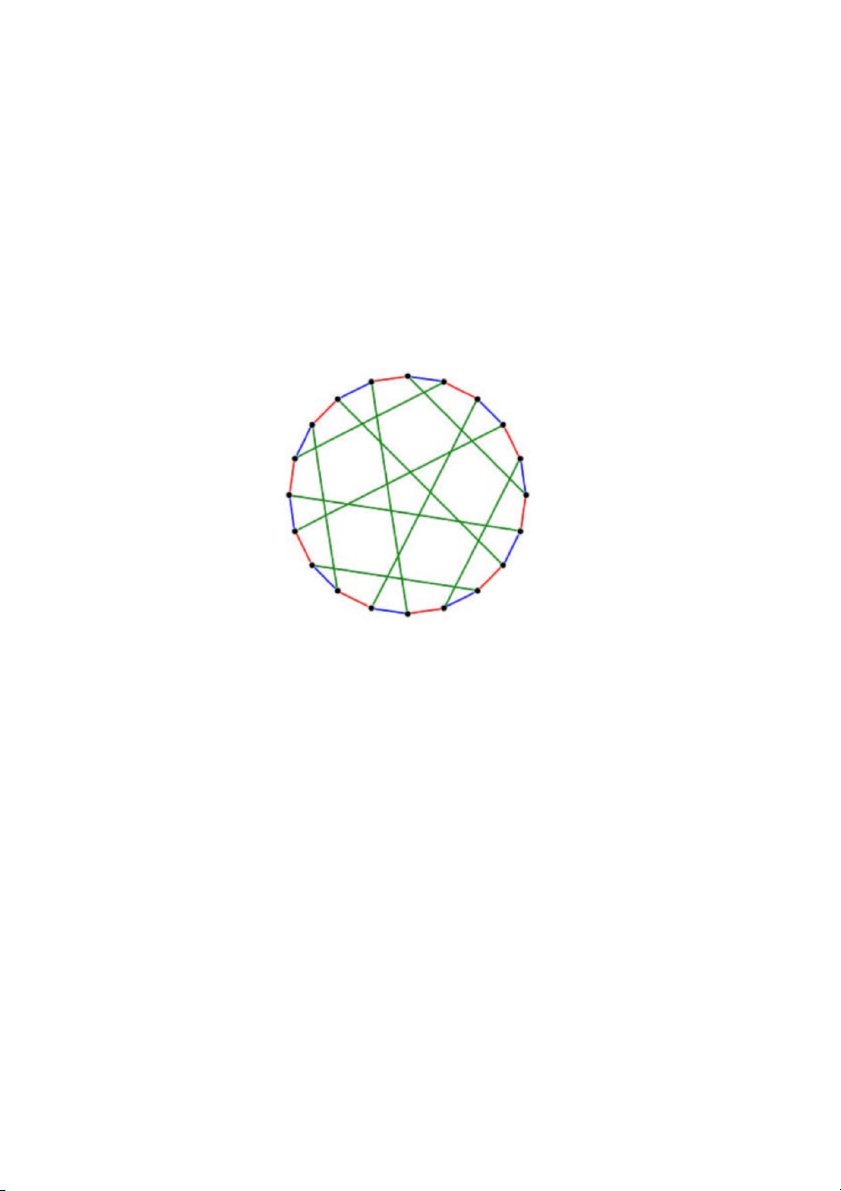
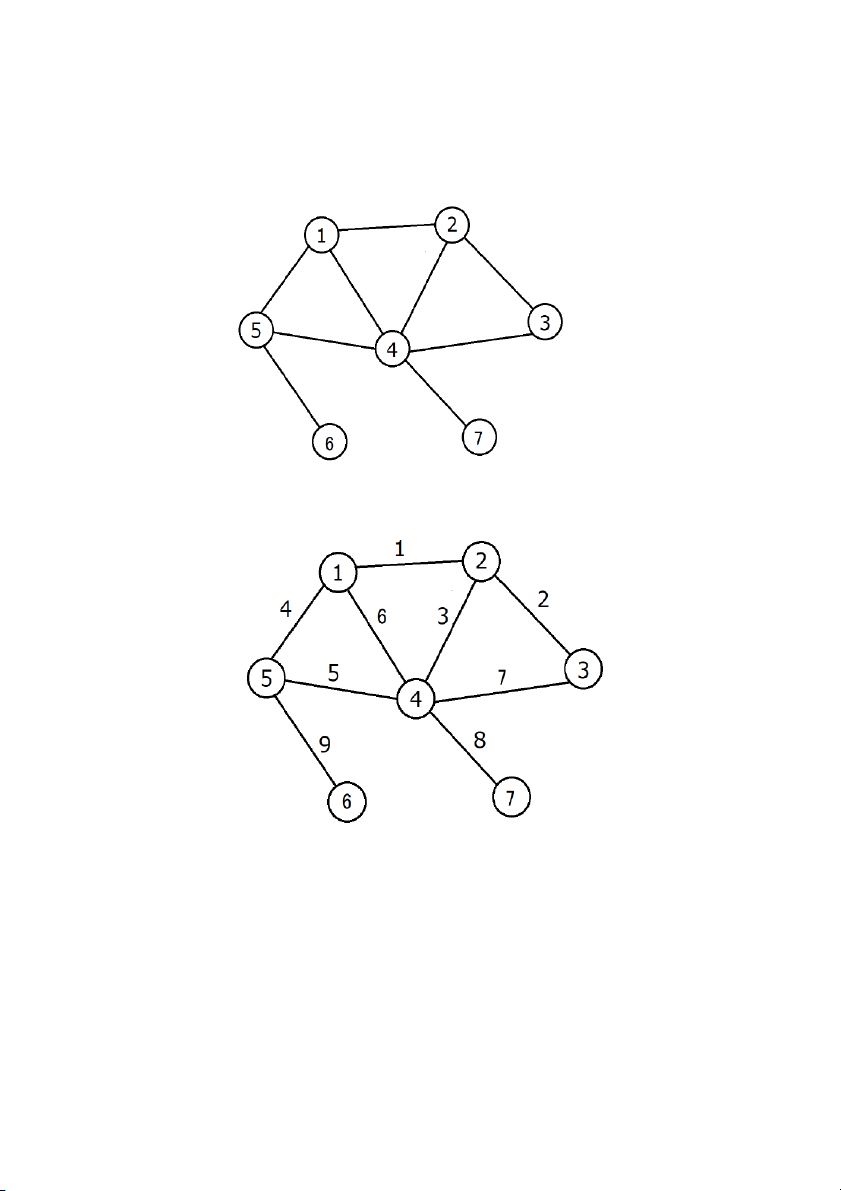
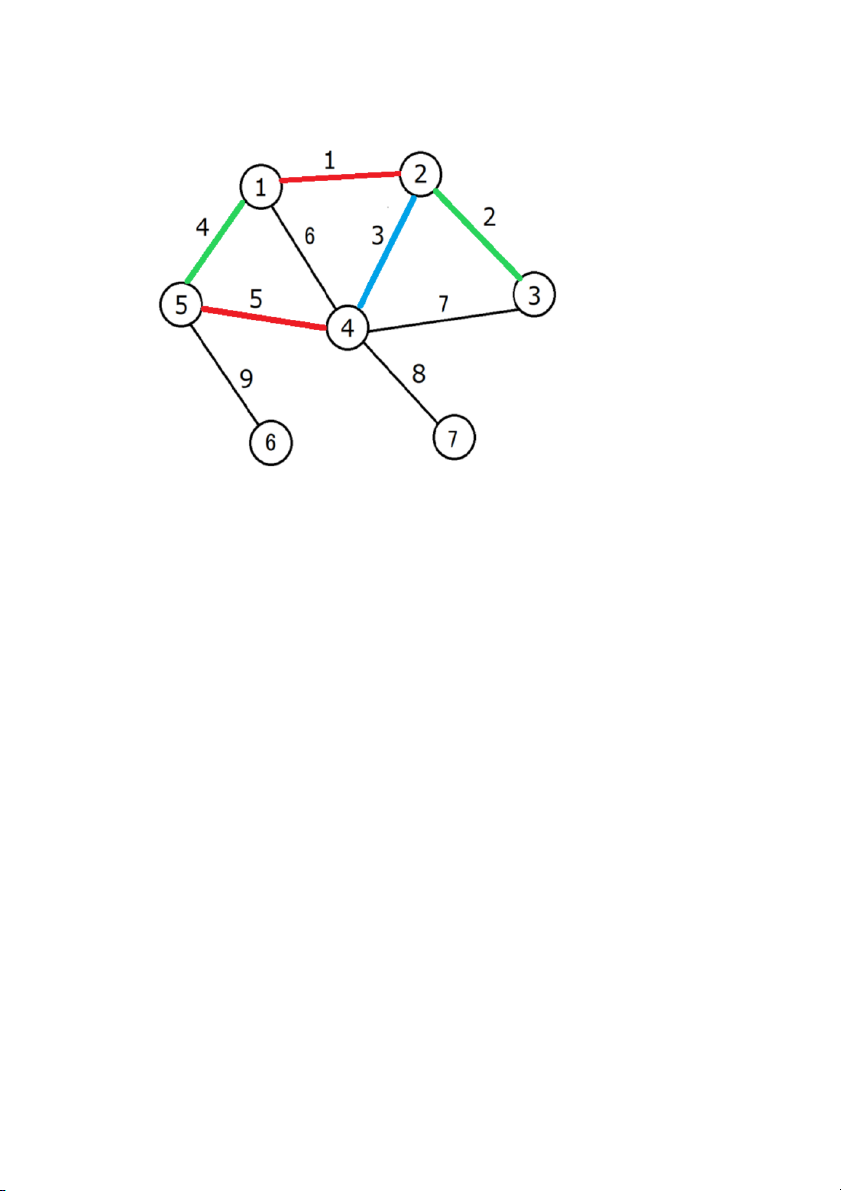
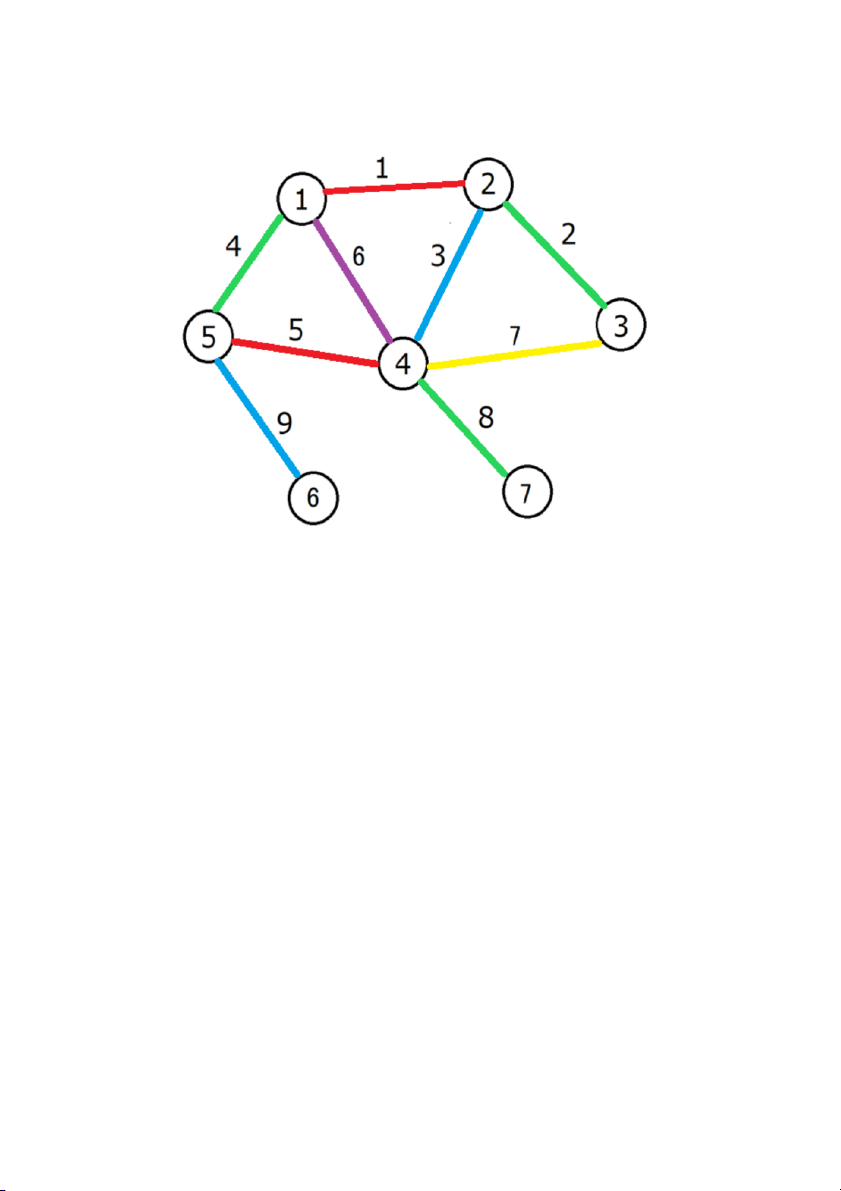
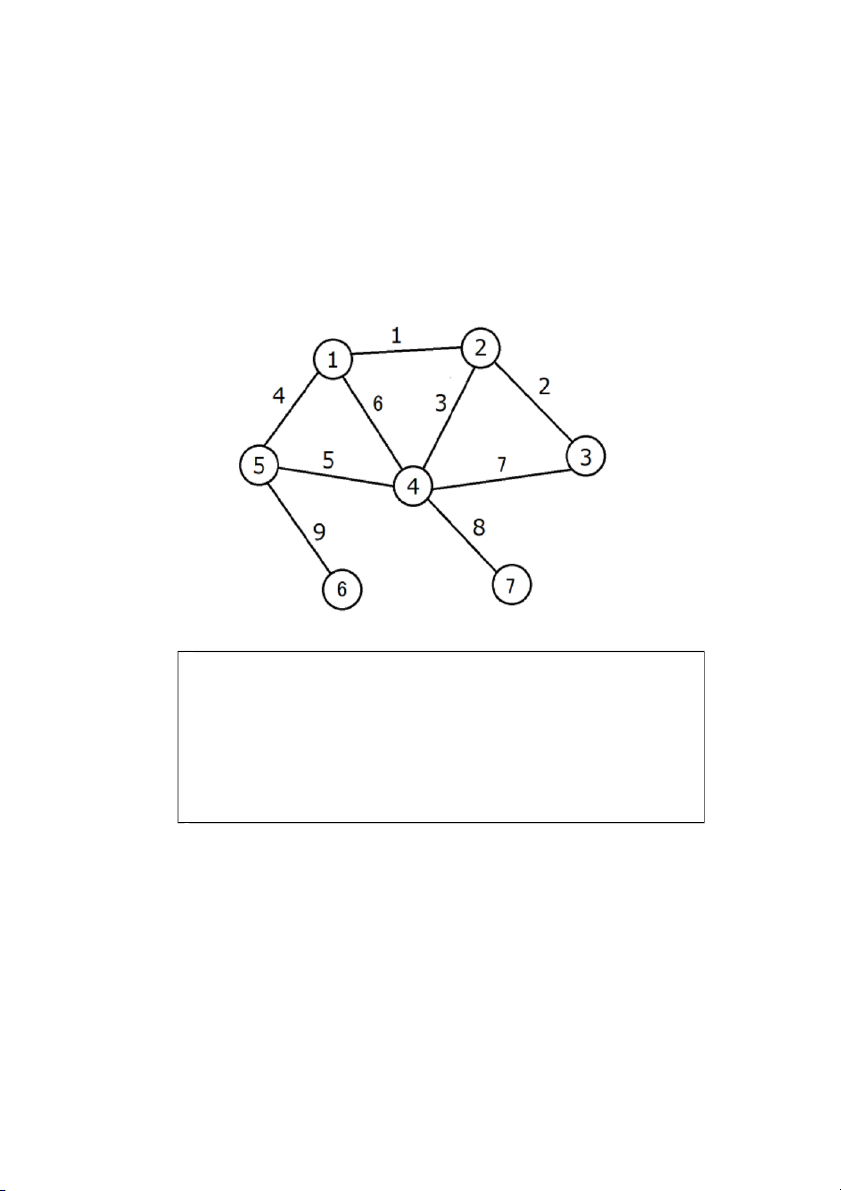
sử dụng là số màu nhỏ nhất. 2.2. Ví dụ Ta có đồ thị sau:
Ta sắp xếp các cạnh theo thứ tự như sau:
Bước 1: Tô màu cạnh thứ 1
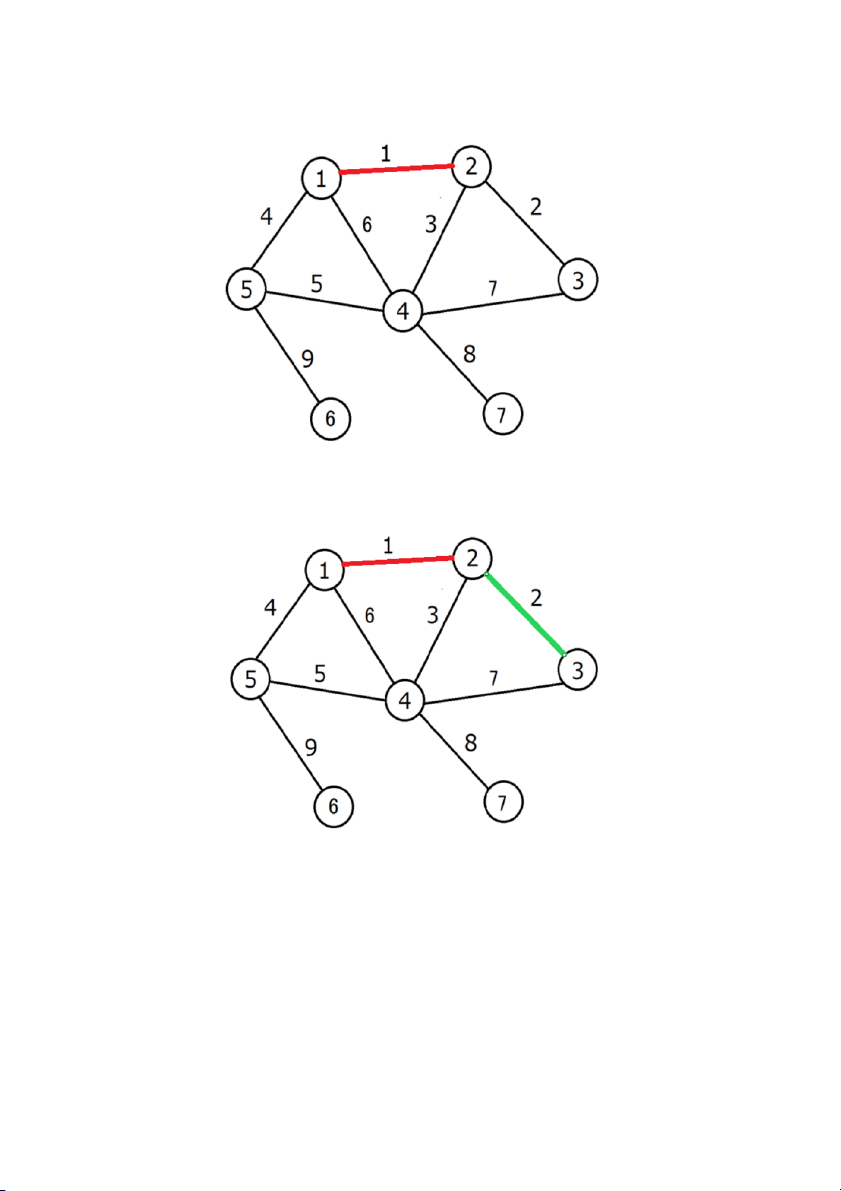
Cạnh này tô màu đỏ trước tiên Bước 2: tô màu cạnh 2.
Cạnh 2 kề với cạnh 1 (tô màu đỏ) do đó cạnh 2 sẽ tô màu xanh lá cây Bước 3: tô màu cạnh 3
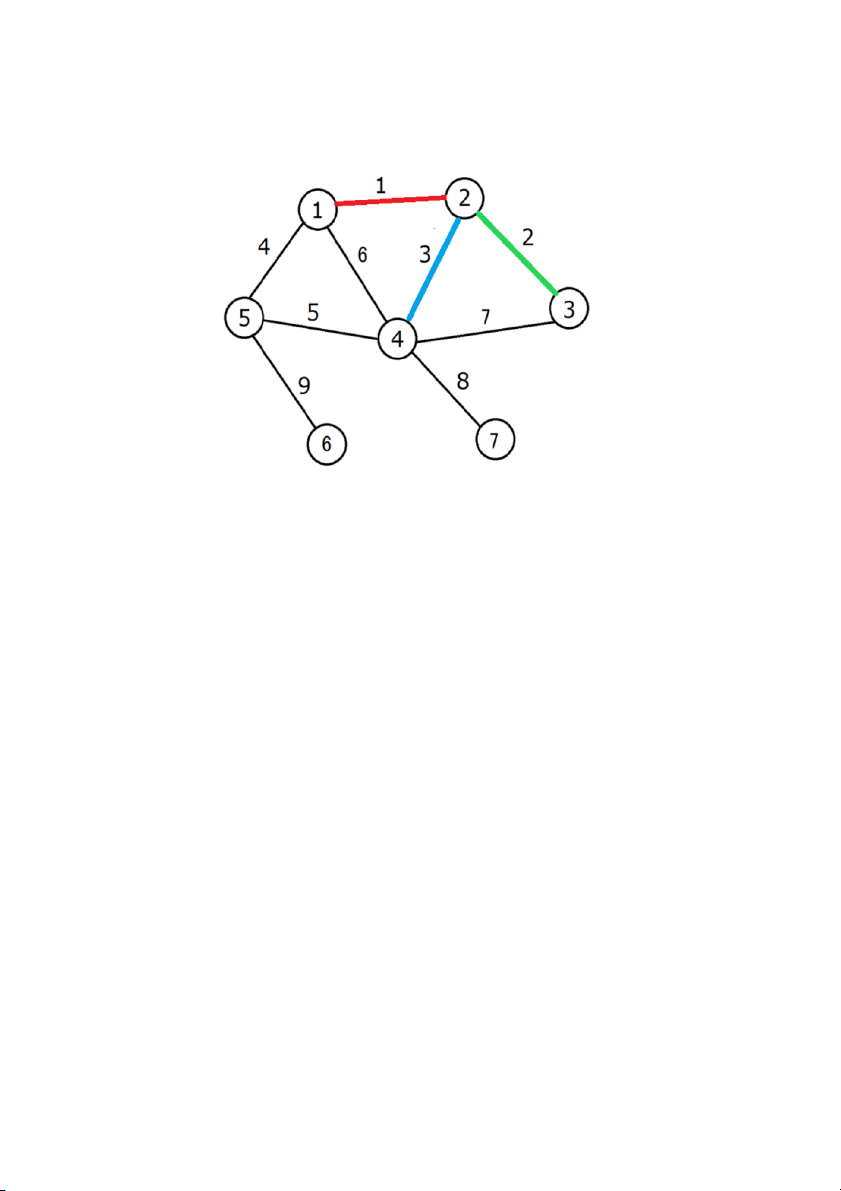
Cạnh 3 kề với cạnh 1 (tô màu đỏ), cạnh 2 (tô màu xanh lá cây) do đó
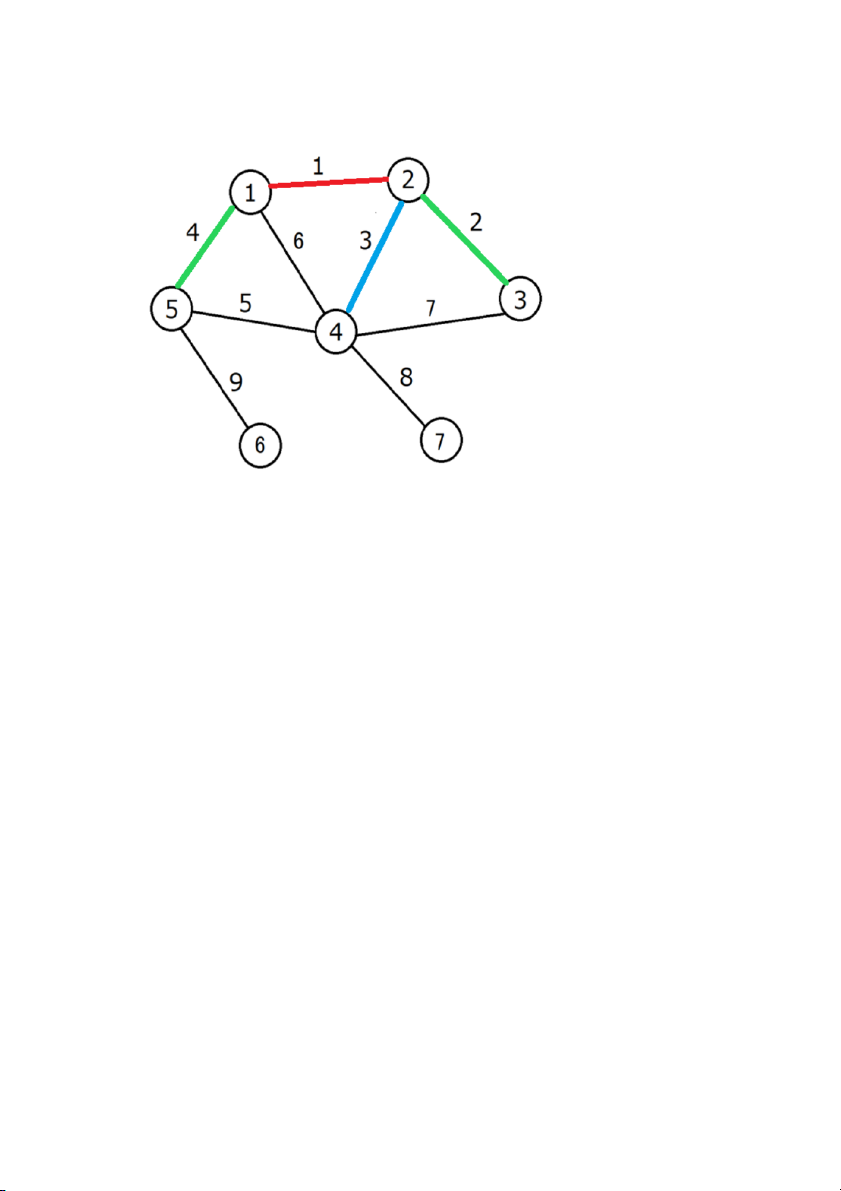
cạnh 3 phải tô màu xanh da trời Bước 4: tô màu cạnh 4
Cạnh 4 kề với cạnh 1 (tô màu đỏ) nên sẽ tô màu xanh lá cây Bước 5: tô màu cạnh 5
Cạnh 5 kề với cạnh 3 (tô màu xanh da trời), cạnh 4 (tô màu xanh lá cây) nên cạnh 5 tô màu đỏ Bước 6: tô màu cạnh 6
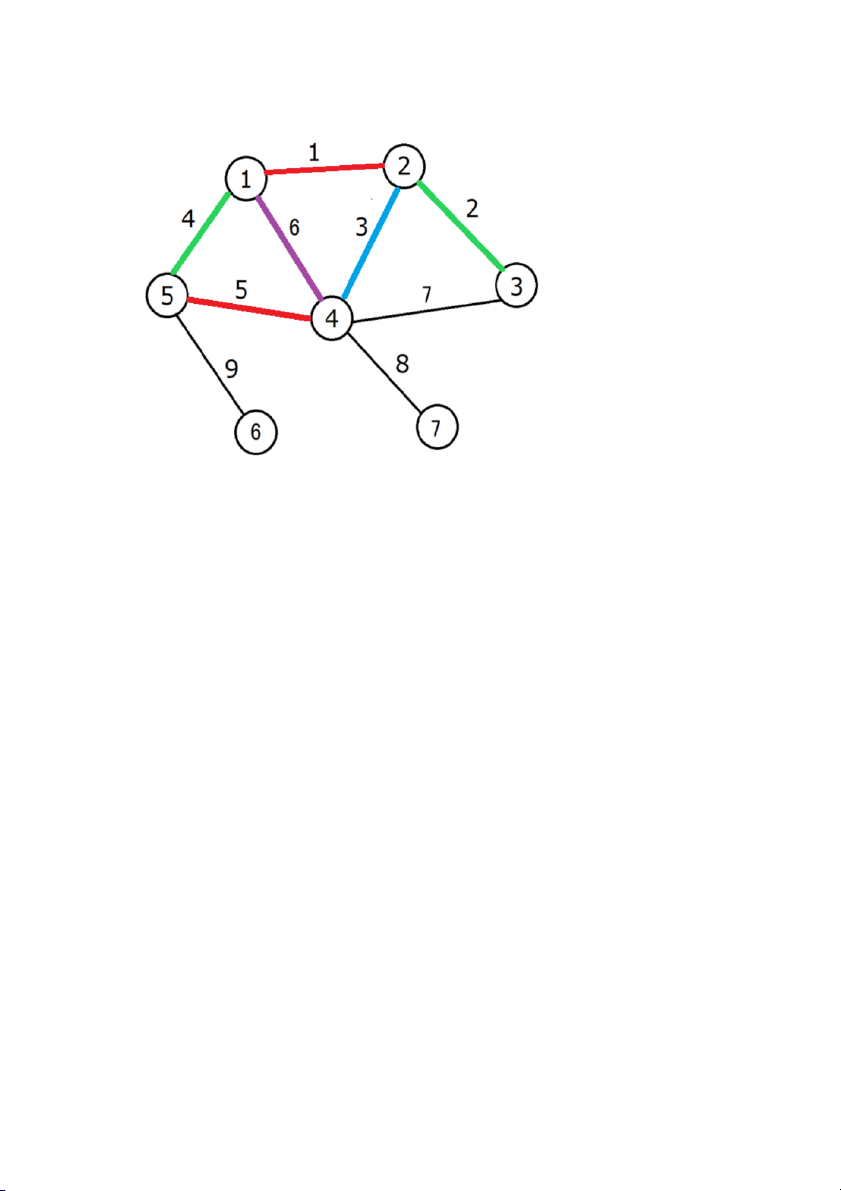
Cạnh 6 kề với cạnh 1,5 (tô màu đỏ), cạnh 3 (tô màu xanh da trời),
cạnh 4 (tô màu xanh lá cây) nên cạnh 6 phải tô màu tím Bước 7: tô màu cạnh 7
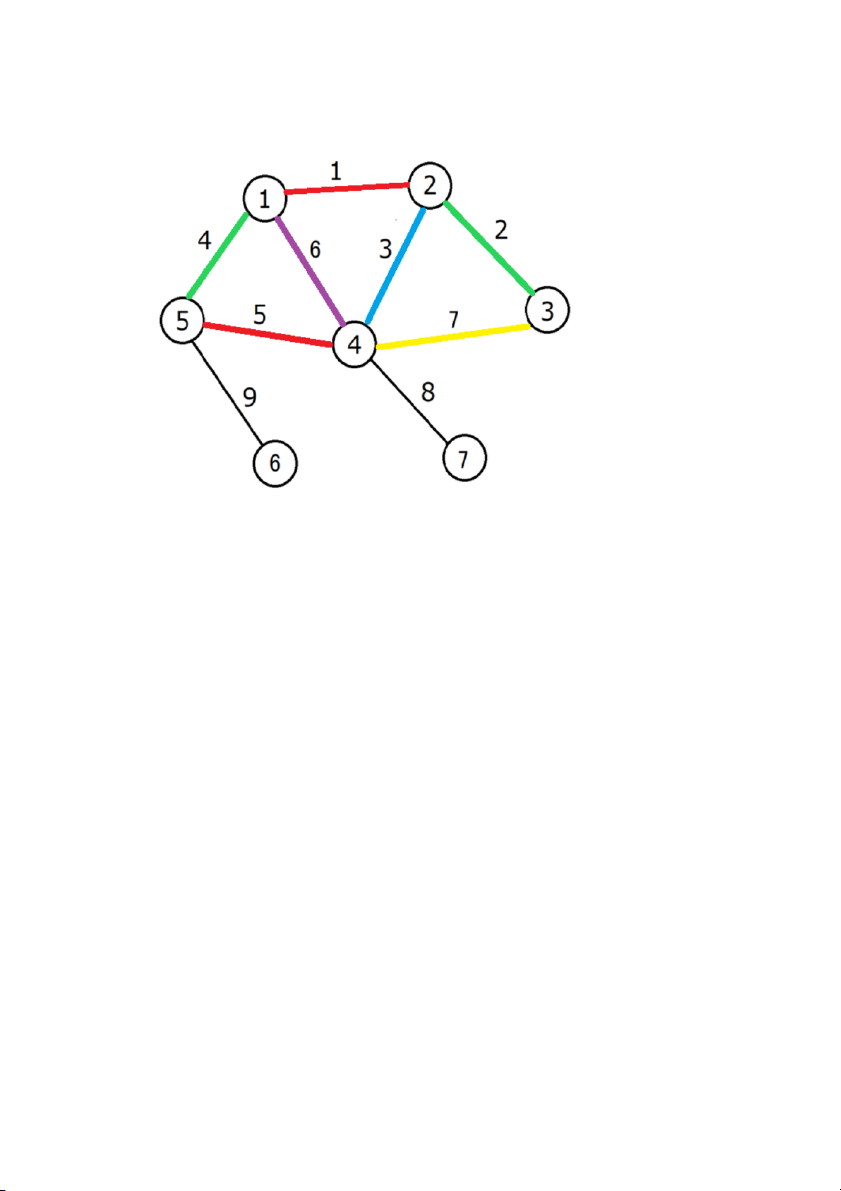
Cạnh 7 kề với cạnh 2 (tô màu xanh lá cây), cạnh 3 (tô màu xanh
da trời), cạnh 5 (tô màu đỏ), cạnh 6 (tô àu tím) do đó cạnh 7 tô màu vàng Bước 8: tô màu cạnh 8
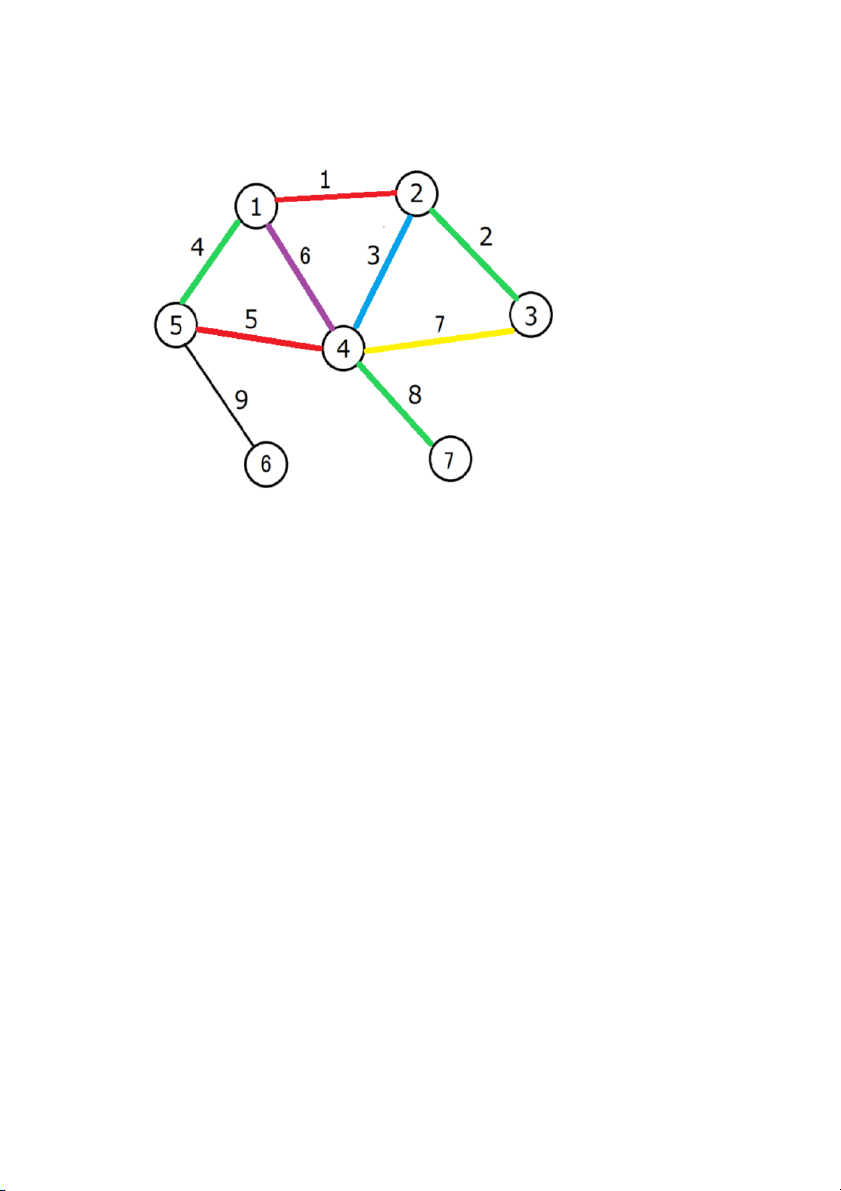
Cạnh 8 kề với cạnh 5 (tô màu đỏ), cạnh 7 (tô màu vàng) nên sẽ tô màu xanh lá cây Bước 9: tô màu cạnh 9
Cạnh 9 kề với cạnh 4 (tô màu xanh lá cây), cạnh 5 (tô màu đỏ)
nên sẽ tô màu xanh da trời
Kết luận: Đồ thị này có thể tô được với 5 màu. Mặt khác Δ = 5 nên
đây chính là số màu nhỏ nhất
có thể dùng để tô cạnh của đồ thị trong trường hợp này.
2.3. Độ phức tạp:
Độ phức tạp của giải thuật là: O (E+V2) III.CÀI ĐẶT THUẬT TOÁN
Trong phần cài đặt này bài toán tô mầu cạnh có 2 cách nhập dữ
liệu (bằng file và nhập từ bàn phím), bài toán tô mầu đỉnh cho
phép nhập dữ liệu từ file.
Menu chương trình hiển thị các lựa chọn nhập dữ liệu:
1. Bài toán tô mầu đỉnh - Cài đặt:
Đọc dữ liệu từ file: graph.txt
Kết quả sẽ trả ra ở file: coloring.txt - Mã nguồn chương trình
 Mã nguồn chương trình #include #include #include using namespace std; int n, a[7][7],sm=0,m[7]; void docfile()
{ //Dung de doc file, sau do gan vao mang a[][] int q,p;
ifstream dothi ("C:/data/dothi.txt"); if (dothi.is_open()) { dothi >> n;
while(!dothi.eof()) //Doc file den cuoi file { dothi >> q; dothi >> p; a[q][p]=9; a[p][q]=9; } dothi.close(); }
else cout << "Khong mo duoc file"; }
void xuly(){ //Xử lí để cho kết quả vào bảng màu
int kt;for(int i=1;i<=n;i++) if(!m[i]) { sm++; //Dem so mau m[i]=sm;
for(int j=i+1;j<=n;j++) //Kiểm tra xem còn đỉnh
nào gắn được bảng màu không
if((a[i][j]==0)&&(m[j]==0)){ kt=1;
for(int k=i+1;kif((a[k][j]==1)&&(m[i]==m[k])){ kt=0; break; } if(kt==1) m[j]=sm; } } }
void xuatkq(){ //In kết quả ra màn hình for(int i=1;i<=sm;i++){
cout << "Mau " << i << ": ";
for(int j=1;j<=n;j++) if(m[j]==i) cout << j << " "; cout << endl; } } int main(){ docfile(); cout << n << endl;
for(int i=1;i<=n;i++){ //In mang ra man hinh de theo doi
for(int j=1;j<=n;j++) cout << a[i][j] << " "; cout << endl; }cout << endl; xuly(); xuatkq(); return 0; }
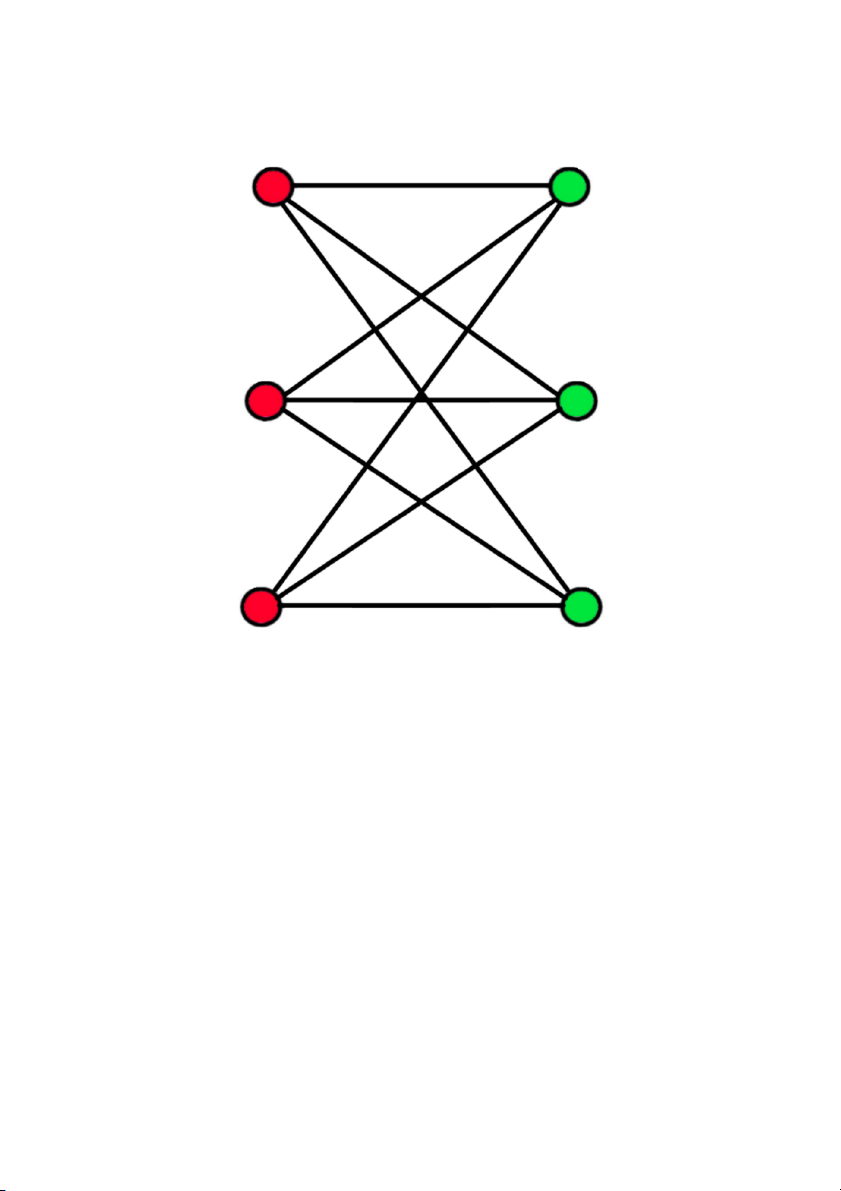
a. Đồ thị 2 phía K (3,3): b . Chúng ta chạy
chương trình trên đồ thị hai
phía Kuratowski K3, 3 với n = 6 đỉnh. Thuật toán
 Chúng ta chạy chương trình trên đồ thị hai phía Kuratowski K với n = 6 3,3
đỉnh. Thuật toán tìm được đúng m-màu của các đỉnh hh
Hình 5: đồ thị hai phía Kuratowski K3,3 với tập đúng m-màu
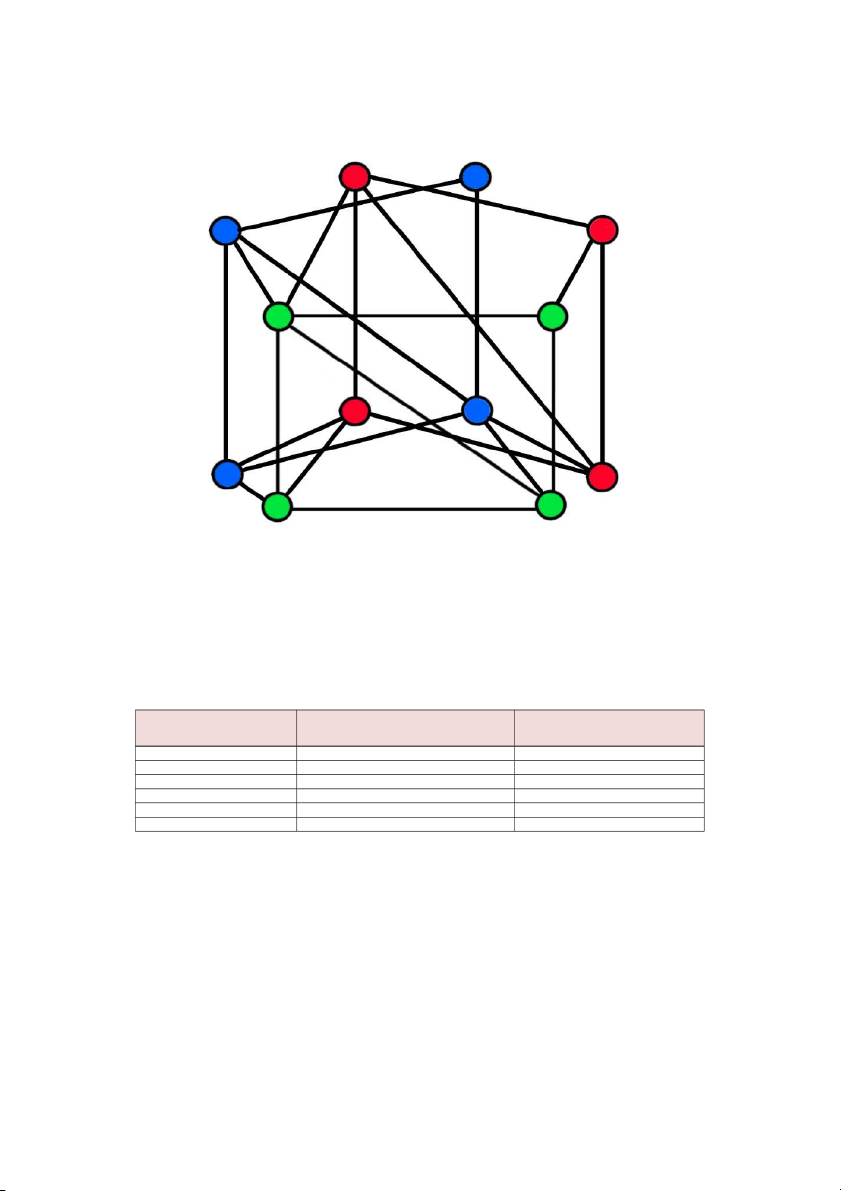
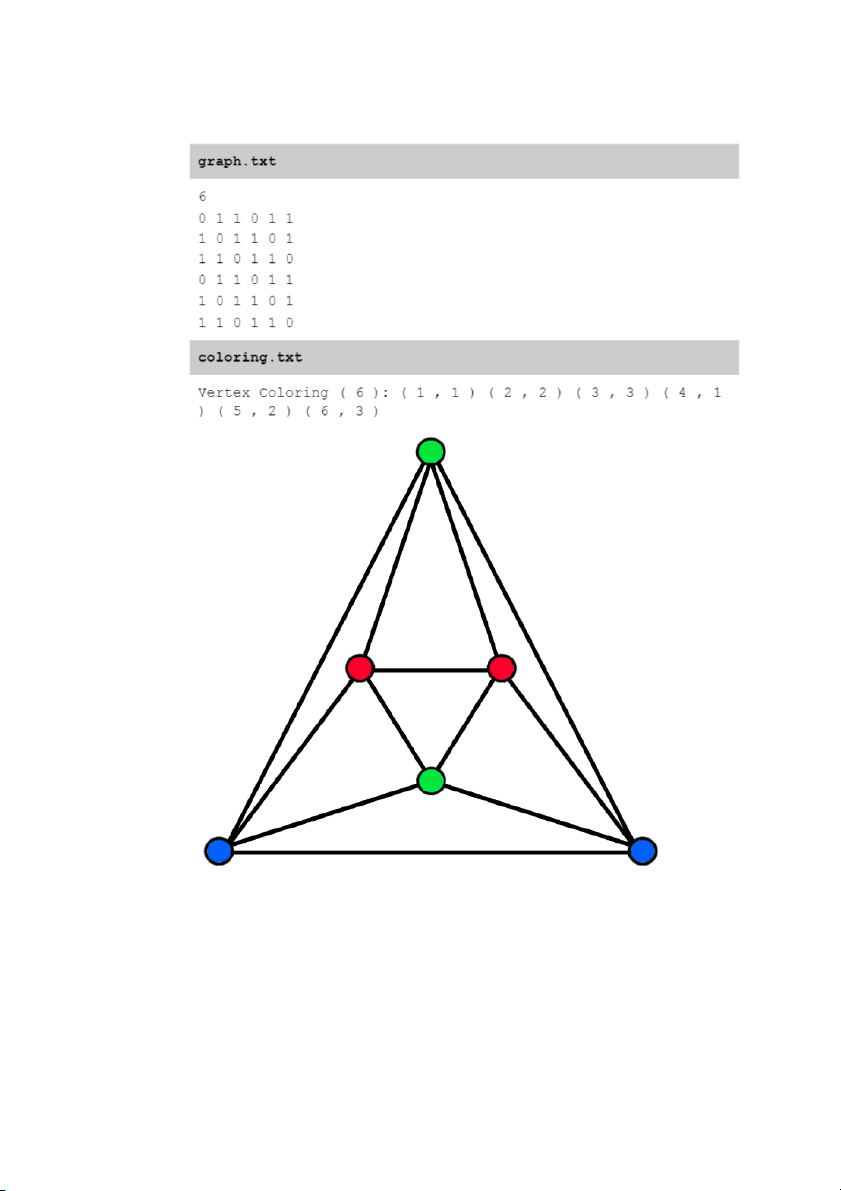
c. Đồ thị Octahedron
Chúng ta chạy chương trình trên đồ thị Octahedron với n=6 đỉnh
Hình 05: Đồ thị Octahedron với tập đúng m-màu (n= 6,m= χ(G) = 3 )
d. Đồ thị Bondy-Murty G1
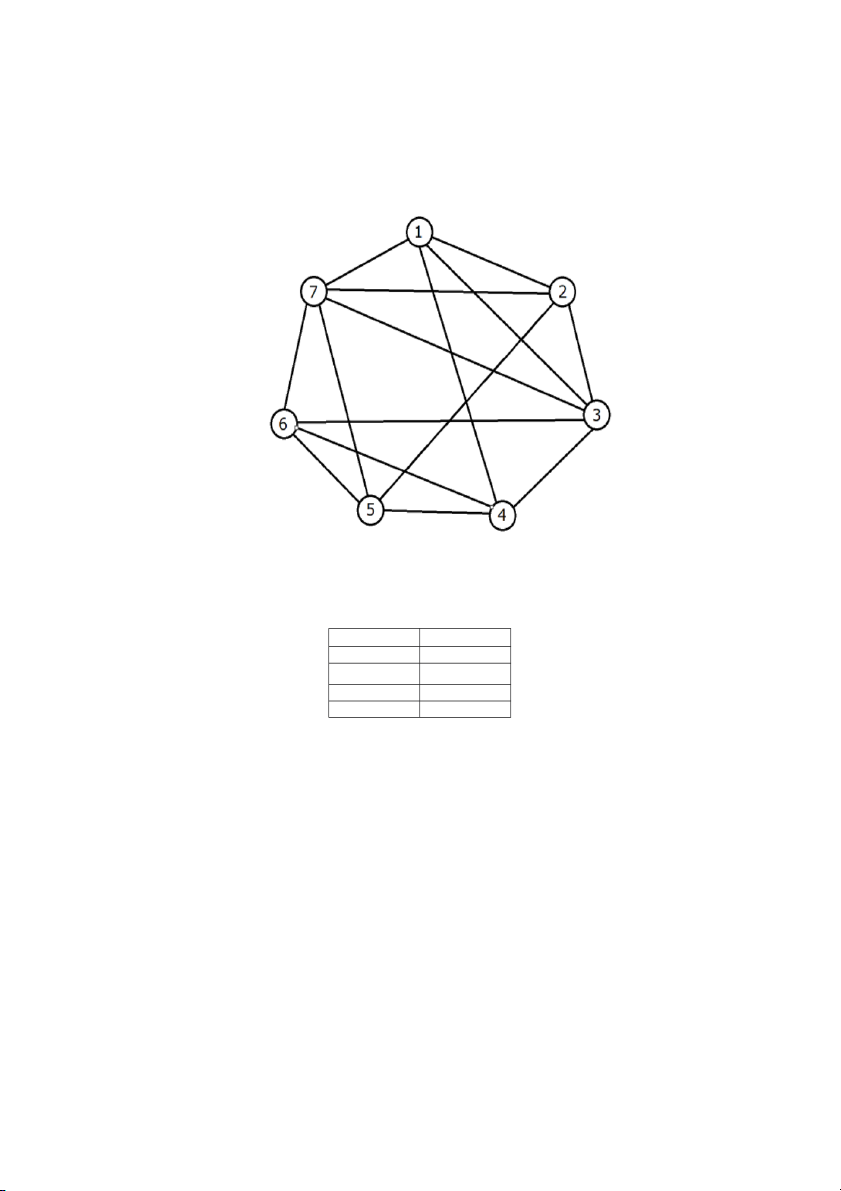
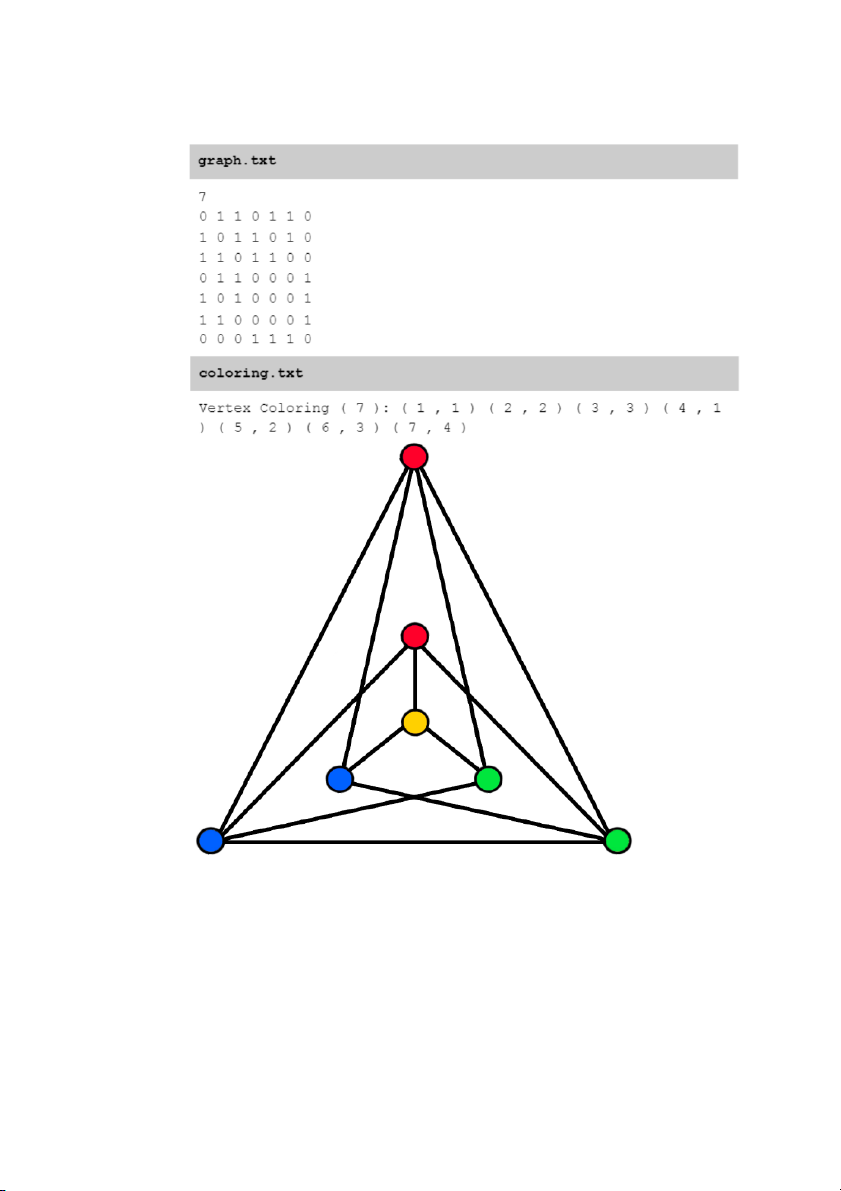
Chúng ta chạy chương trình trên đồ thị Bondy-Murty G 1 với n=7 đỉnh
Hình 06: Đồ thị Bondy-Murty G1 với tập đúng m-màu (n= 7,m= χ(G) = 4 )
2. Bài toán tô mầu cạnh
2.1. Đọc dữ liệu từ file - Cài đặt
 Đọc dữ liệu từ file văn bản .txt, file .txt có cấu tríc dạng
Đọc dữ liệu từ File văn bản .txt ,file .txt có cấu trúc dạng
Dòng đầu là số đỉnh, các dòng tiếp theo dòng thứ i là các đỉnh kể với đỉnh i.
Với ví dụ minh họa ở phần trước Ta sẽ có file .txt dạng 7 0 1 0 1 1 0 0 1 0 1 1 0 0 0 0 1 0 1 0 0 0 1 1 1 0 1 0 1 1 0 0 1 0 1 0 0 0 0 0 1 0 0 0 0 0 1 0 0 0
Dữ liệu đọc từ file được lưu vào mảng 2 chiều a.
 Khởi tạo các giá trị ban đầu cho màu với giá trị mã nhỏ nhất là 2
 Tìm bậc lớn nhất của đồ thị (Δ)
 Chuẩn bị (Δ+1) màu để tô  Tô màu các cạnh: Tại bước thứ i:
+) Với các đỉnh j kề với i trong danh sách đã xây dựng ở trên
+)A[i][j] = t (t>1) tức là cạnh [I,j] được tô bởi màu có mã là t
+)A[i][j] = 1 tức là có cạnh [i,j] và cạnh [I,j] chưa được tô
Khi tô cạnh i,j ta xét đỉnh i và đỉnh j
Ta tất cả các cạnh có 1 đầu cạnh là I hoặc j và đánh dấu các màu đã được tô
Sau đó ta tìm mã màu gần nhất chưa được tô bởi các cạnh có 1
đầu cạnh là i hoặc j và gắn mã màu cho a[i][j] Gán a[j][i] = a[i][j] Sdf dsf dsf
Kết quả là một tập độc lập tối đa S
i, j, k, l Kết quả là một tập độc lập tối
đa S i, j, k, l Nếu các cặp không có thứ tự của các đỉnh {u, v} là một cạnh
trong G, chúng ta nói u đó là 2 . 3 .
BuLâếy tiêu chu n tôếi u (trên
ph m vi toàn c c) c a bài toán đ làm tiêuẩ ư ạ ụ ủ ể
4. chu n ch n l a hành đ ng cho ph m vi c c b c a t ng b c. 5 .
Lâếy tiêu chu n tôếi u (trên ph
m vi toàn c c) c a bài toán đ làm tiêuẩ ư ạ ụ ủ ể
6. chu n ch n l a hành đ ng cho ph m vi c c b c a t ng b c.Hạn chế vùng Môn 1:
có các sinh viên A, B, C và D thikhông gian tìm kiếm và định hướng nahnh
Kết quả là một tập độc lập tối đa S i, j, k, l
chóng để lêitìm đến mục tiêu.