Đường thẳng và mặt phẳng trong không gian, quan hệ song song – Lư Sĩ Pháp

Giới thiệu đến quý thầy, cô giáo và các em học sinh tài liệu chuyên đề đường thẳng và mặt phẳng trong không gian, quan hệ song song do thầy Lư Sĩ Pháp biên soạn

78 39 lượt tải Tải xuống

Chia sẻ Báo cáo tài liệu

HÌNH HỌC 11

CHƯƠNG

ĐƯỜNG THẲNG

VÀ

MẶT PHẲNG

TRONG KHÔNG GIAN

QUAN HỆ SONG SONG

Giáo Viên Trư

ờ

ng THPT Tuy Phong

Quý đọc giả, quý thầy cô và các em học sinh thân mến!

Nhằm giúp các em học sinh có tài liệu tự học môn Toán,

tôi biên soạn cuốn giải toán trọng tâm HÌNH HỌC 11.

Nội dung của cuốn tài liệu bám sát chương trình chuẩn và

chương trình nâng cao về môn Toán đã được Bộ Giáo dục

và Đào tạo quy định.

Nội dung gồm 4 phần

Phần 1. Kiến thức cần nắm

Phần 2. Dạng bài tập có hướng dẫn giải và bài tập đề nghị

Phần 3. Phần trắc nghiệm có đáp án.

Phần 4. Một số đề ôn kiểm tra

Cuốn tài liệu được xây dựng sẽ còn có những khiếm

khuyết. Rất mong nhận được sự góp ý, đóng góp của quý

đồng nghiệp và các em học sinh.

Mọi góp ý xin gọi về số 0939989966 – 0916620899

Email: lsp02071980@gmail.com

Chân thành cảm ơn.

Lư Sĩ Pháp

Gv_Trường THPT Tuy Phong

LỜI NÓI ĐẦU

MỤC LỤC

CHƯƠNG I

ĐƯỜNG THẲNG VÀ MẶT PHẲNG TRONG KHÔNG GIAN

QUAN HỆ SONG SONG

§1. ĐẠI CƯƠNG VỀ ĐƯỜNG THẲNG VÀ MẶT PHẲNG ................ Trang 01 – 05

§2. HAI ĐƯỜNG THẲNG CHÉO NHAU

VÀ HAI ĐƯỜNG THẲNG SONG SONG ........................................ Trang 06 – 10

§3. ĐƯỜNG THẲNG VÀ MẶT PHẲNG SONG SONG ...................... Trang 11 – 16

§4. HAI MẶT PHẲNG SONG SONG .................................................. Trang 17 – 21

§5. PHÉP CHIẾU SONG SONG ............................................................ Trang 22 – 23

ÔN TẬP CHƯƠNG II ............................................................................ Trang 24 – 30

TRẮC NGHIỆM CHƯƠNG II .............................................................. Trang 31 – 43

MỘT SỐ ĐỀ ÔN KIỂM TRA MỘT TIẾT ........................................... Trang 44 – 49

ĐÁP ÁN ................................................................................................... Trang 50

Toán 11 GV. Lư Sĩ Pháp

HÌNH HỌC 11 Chương II. ĐT & MP Trong KG. QHSS

CHƯƠNG II

ĐƯỜNG THẲNG VÀ MẶT PHẲNG TRONG KHÔNG GIAN

QUAN HỆ SONG SONG

----------0o0----------

§1. ĐẠI CƯƠNG VỀ ĐƯỜNG THẲNG VÀ MẶT PHẲNG

A. KIẾN THỨC CẦN NẮM

I. Các tính chất thừa nhận

Tính chất 1. Có một và chỉ một đường thẳng đi qua hai điểm phân biệt .

Tính chất 2. Có một và chỉ một mặt phẳng đi qua ba điểm không thẳng hàng.

Tính chất 3. Nếu đường thẳng có hai điểm phân biệt thuộc một mặt phẳng thì mọi điểm của đường thẳng

đều thuộc mặt phẳng đó.

Lưu ý: Đường thẳng d nằm trong

( )

ta kí hiệu:

d hay d

( ) ( )

α α

⊂ ⊃

Tính chất 4. Tồn tại bốn điểm không cùng thuộc một mặt phẳng.

Tính chất 5. Nếu hai mặt phẳng phân biệt có một điểm chung thì chúng còn có một điểm chung khác nữa.

Như vậy: Nếu hai mặt phẳng phân biệt có một điểm chung thì chúng có một đường thẳng chung đi qua

điểm chung ấy và đường thẳng đó gọi là giao tuyến của hai mặt phẳng.

Tính chất 6. Trên mỗi mặt phẳng, các kết quả đã biết trong hình học phẳng đều đúng.

II. Cách xác định mặt phẳng.

Một mặt phẳng hoàn toàn xác định khi biết:

1. Nó đi qua ba điểm không thẳng hàng

(ABC) biểu thị mặt phẳng xác định bởi ba điểm phân biệt không thẳng

hàng A, B, C.

2. Nó đi qua một điểm và chứa một đường thẳng không đi qua điểm đó

(M, d) biểu thị mặt phẳng xác định bởi đường thẳng d và điểm M

không nằm trên d.

3. Nó chứa hai đường thẳng cắt nhau

(a, b) biểu thị mặt phẳng xác định bởi hai đường thẳng cắt nhau a và b.

a caét b taïi M

III. Hình chóp và hình tứ diện

1. Hình chóp : Trong mặt phẳng

( )

cho đa giác lồi

A A A

1 2

...

Điểm S nằm ngoài

( )

. Lần lượt nối S với các đỉnh

A A A

1 2

, ,...,

được n tam giác

SA A SA A SA A

1 2 2 3 1

, ,...,

. Hình gồm có đa giác

A A A

1 2

...

và n tam giác

SA A SA A SA A

1 2 2 3 1

, ,...,

được gọi là hình

chóp , kí hiệu

S A A A

1 2

. ...

maët beân

maët ñaùy

caïnh ñaùy

caïnh beân

ñænh

2. Hình tứ diện

Cho bốn điểm A, B, C, D không đồng phẳng. Hình gồm

bốn tam giác ABC, ABD, ACD và BCD được gọi là hình tứ

diện , kí hiệu ABCD.

Toán 11 GV. Lư Sĩ Pháp

HÌNH HỌC 11 Chương II. ĐT & MP Trong KG. QHSS

B. BÀI TẬP

ấn đề 1. Tìm giao tuyến của hai mặt phẳng

Phương pháp: Ta đi tìm hai điểm chung phân bệt của hai mặt phẳng đó. Giao tuyến của chúng là

đường thẳng đi qua hai điểm đó.

Nghĩa là:

N MN

M N

α β

α β α β



∩ =



∩ = ⇒ ∩ =





≡



Bài 1.1. Cho bốn điểm không đồng phẳng A, B, C và D. Trên đoạn AB và AC lấy hai điểm M và N sao

cho

AM AN

BM NC

1; 2

= =

. Hãy xác định giao tuyến của mặt phẳng (DMN) với các mặt (ABD), (ACD), (ABC)

và (BCD) .



Giải



DMN ADB

( ) ( ) ?

∩ =

Ta có

D DMN ADB

( ) ( )

∈ ∩



∈

⇒ ∈ ∩



∈ ⊂ ⇒ ∈



( )

( ) ( )

M DMN

M DMN ABD

M AB ABD M ABD

Vậy :

DM DMN ABD

( ) ( )

= ∩



DMN ACD DN

( ) ( )

∩ =



DMN ABC MN

( ) ( )

∩ =



DMN BCD

( ) ( ) ?

∩ =

Trong mp(ABC) có

AM AN

BM NC

≠

, nên

MN BC E

∩ =

Tương tự:

DMN BCD DE

( ) ( )

∩ =

Bài 1.2. Cho S là một điểm không thuộc mặt phẳng hình bình hành ABCD. Tìm giao tuyến của hai mặt

phẳng (SAC) và (SBD).



Giải

Gọi O là giao điểm của AC và BD. Ta có

S SAC SBD

( ) ( )

∈ ∩

O AC SAC

O SAC SBD

O BD SBD

( )

( ) ( )

( )



∈ ⊂

⇒

∈ ∩



∈ ⊂



nên

SO SAC SBD

( ) ( )

= ∩

Vậy giao tuyến hai mặt phẳng (SAC) và (SBD) là

đường thẳng SO

Bài 1.3. Cho S là một điểm không thuộc mặt phẳnh hình thang ABCD (AB // CD và AB > CD). Tìm giao

tuyến hai mặt phẳng (SAD) và (SBC).



Giải

Gọi I là giao điểm AD và BC. Ta có S và I là hai

điểm chung của (SAD) và (SBC), nên

SI SAD SBC

( ) ( )

= ∩

Vậy giao tuyến hai mặt phẳng (SAD) và (SBC) là

đường thẳng SI.

Toán 11 GV. Lư Sĩ Pháp

HÌNH HỌC 11 Chương II. ĐT & MP Trong KG. QHSS

Bài 1.4. Cho bốn điểm A,B,C,D không đồng phẳng. Gọi I, K lần lượt là trung điểm của hai đoạn thẳng AD

và BC.

a) Tìm giao tuyến của hai mặt phẳng (IBC) và (KAD)

b) Gọi M và N là hai điểm lần lượt trên hai đường thẳng AB và AC. Tìm giao tuyến của hai mặt phẳng

(IBC) và (DMN).



Giải

IBC KAD KI

( ) ( )

∩ =

. Vậy giao tuyến hai mặt phẳng (IBC) và (KAD) là đường thẳng KI.

b) Trong mp (ABD), g

ọi

E MD BI

= ∩

trong mp(ACD) , gọi

F ND CI

= ∩

Ta có:

IBC DMN EF

( ) ( )

∩ =

Vậy giao tuyến hai mặt phẳng (IBC) và (DMN)

là đường thẳng EF.

ấn đề 2. Tìm giao điểm của đường thẳng

và mặt phẳng

( )

Phương pháp: Để tìm giao điểm của một đường thẳng

và một mặt phẳng

( )

, ta có thể đưa về

việc tìm giao điểm của đường thẳng

với một đường thẳng

nằm trong mặt phẳng

( )

Nghĩa là:

mp phuï d

d d I

( )

( ) ( ) ( )

β α α



⊃



∩ = ⇒ ∩ =





∩ =



Bài 1.5. Cho tam giác BCD và điểm A không thuộc mặt phẳng (BCD). Gọi K là trung điểm của đoạn AD

và G là trọng tâm của tam giác ABC. Tìm giao điểm của đường thẳng GK với mặt phẳng (BCD).



Giải

Gọi J là giao điểm của AG và BC. Trong mặt

phẳng (AJD), ta có

AG AK

AJ AD

2 1

;

3 2

= =

nên GK và

JD cắt nhau. Gọi L là giao điểm của GK và JD.

Ta có

L GK

∈

L JD

L BCD

JD BCD

( )



∈

⇒

∈



⊂



Vậy L là giao điểm của GK và (BCD)

Bài 1.6. Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm các cạnh AB và CD, trên AD lấy điểm P

không trùng với trung điểm AD.

a) Gọi E là giao điểm của đường thẳng MP và BD. Tìm giao tuyến của hai mp (PMN) và (BCD)

b) Tìm giao điểm của hai mp (PMN) và BC.



Giải

a )

MNP BCD EN

( ) ( )

∩ =

b) Trong mp (BCD), gọi

Q EN BC

= ∩

Ta có :

BC MNP Q

( )

∩ =

Bài 1.7. Cho tứ diện ABCD. Gọi I, J là các điểm lần lượt nằm trên các cạnh AB, AD với

AI IB

và

Toán 11 GV. Lư Sĩ Pháp

HÌNH HỌC 11 Chương II. ĐT & MP Trong KG. QHSS

AJ JD

. Tìm giao điểm của đường thẳng IJ với mặt phẳng (BCD).



Giải

AI IB

AJ JD











nên IJ kéo dài cắt BD, gọi giao

điểm là K. Khi đó

K IJ BCD

( )

= ∩

Bài 1.8. Cho hình chóp S.ABCD có đáy là tứ giác ABCD có hai cạnh đối diện không song song. Lấy điểm

M thuôc miền trong của tam giác SCD. Tìm giao tuyến của hai mặt phẳng:

a) (SBM) và (SCD) b) (ABM) và(SCD) c) (ABM) và (SAC)



Giải

a) Ta có ngay:

SBM SCD SM

( ) ( )

∩ =

b) Ta có:

M ABM SCD

( ) ( )

∈ ∩

Trong mp (ABCD) gọi

I AB CD

= ∩

Suy ra :

MI ABM SCD

( ) ( )

= ∩

c) Ta có:

A ABM SAC

( ) ( )

∈ ∩

Trong mp (SCD), gọi

J IM SC

= ∩

Suy ra:

J ABM SAC

( ) ( )

∈ ∩

Vậy:

AJ ABM SAC

( ) ( )

= ∩

Bài 1.9. Cho hình chóp S.ABCD có đáy ABCD là tứ giác, M và N tương ứng là các điểm thuộc các cạnh

SC và BC. Tìm giao điểm của đường thẳng SD với mặt phẳng (AMN).



Giải

Gọi

O AC BD

= ∩

.Trong mp(SAC), gọi

K SO AM

= ∩

Trong mp(ABCD), gọi

L BD AN

= ∩

Chọn mặt phẳng phụ (SBD) chứa SD.

Và ta có:

LK SBD AMN

( ) ( )

= ∩

Mà trong mp (SBD), có

LK SD P

∩ =

Vậy:

P SD AMN

( )

= ∩

ấn đề 3. Chứng minh ba điểm thẳng hàng

Phương pháp: Để chứng ba điểm thẳng hàng, ta có thể chứng minh chúng cùng thuộc hai mặt

phẳng riêng biệt.

Bài 1.10. Cho tứ diện SABC. Trên SA, SB, SC lần lượt lấy các điểm D, E và F sao cho cắt AB tại I, EF cắt

BC tại J, FD cắt CA tại K. Chứng minh rằng ba điểm I, J, K thẳng hàng.



Giải

Ta có:

I DE

I DEF

DE DEF

( )



∈

⇒ ∈



⊂



và

I AB

I ABC

AB ABC

( )



∈

⇒ ∈



⊂



. Suy ra:

J MNK BCD

( ) ( )

∈ ∩

Lí luận tương tự ta có: J, K cũng là điểm chung của hai mặt phẳng

(DEF) và (ABC)

Vậy I, J, K thuộc về giao tuyến của hai

mặt phẳng (DEF) và (ABC) nên I, J, K thẳng

hàng.

Toán 11 GV. Lư Sĩ Pháp

HÌNH HỌC 11 Chương II. ĐT & MP Trong KG. QHSS

Bài 1.11. Cho ba điểm A, B, C không thuộc mặt phẳng (Q) và các đường thẳng BC, CA, AB cắt (Q) lần

lượt tại M, N, P. Chứng minh rằng M, N, P thẳng hàng.



Giải

Ta có

M, N, P

ần l

ợt thuộc về hai mặt phẳng (

)

và (ABC), nên M, N, P thuộc về giao tuyến của hai

mặt phẳng (Q) và (ABC). Vậy M, N, P thẳng hàng.

Bài 1.12. Cho hình chóp S.ABCD có AB và CD không song song. Gọi M là một điểm thuộc miền trong

của tam giác SCD.

a) Tìm giao điểm N của đường thẳng CD và mặt phẳng (SBM)

b) Tìm giao tuyến của hai mặt phẳng (SBM) và (SAC)

c) Tìm giao điểm I của đường thẳng BM và mp(SAC)

d) Tìm giao điểm P của SC và mp(ABM), từ đó suy ra giao tuyến của hai mặt phẳng (SCD) và (ABM).



Giải

a) Gọi

N SM CD

= ∩

. Ta có

N CD SBM

( )

= ∩

b) Gọi

O AC BN

= ∩

.Ta có:

SBM SAC SO

( ) ( )

∩ =

c) Gọi

I SO BM

= ∩

Ta có

I BM SAC

( )

= ∩

d) Gọi

R AB CD

= ∩

P MR SC

= ∩

Ta có

P SC ABM

( )

= ∩

PM SCD ABM

( ) ( )

⇒ = ∩

Bài 1.13. Cho hình chóp S.ABCD. Gọi M là một điểm nằm trong tam giác SCD.

a) Tìm giao tuyến của hai mặt phẳng (SBM) và (SAC)

b) Tìm giao điểm của đường thẳng BM và mp(SAC)

c) Xác định thiết diện của hình chóp khi cắt bởi mặt phẳng (ABM)



Giải

a) Gọi N = SM

∩

CD, O = AC

∩

BN. Khi đó SO = (SAC)

∩

(SBM).

b) Trong mp(SBM), đường thẳng BM cắt SO tại I. Ta có

I=BM

∩

(SAC).

c) Trong mp(SAC), đường thẳng AI cắt SC tại P. Ta có P và M là

hai điểm chung của mp(ABM) và mp(SCD).

vậy (ABM)

∩

(SCD) = PM. Đường thẳng PM cắt SD tại Q. thiết

diện của hình chóp khi cắt bởi mp(ABM) là tứ giác ABPQ.

Bài 1.14. Cho hình chóp S.ABCD có đáy là hình thang ABCD (AB//CD, AB > CD). Gọi

I, J theo thứ tự là trung điểm của các cạnh SB và SC.

a) Xác định giao tuyến của hai mặt phẳng (SAD) và (SBC), (SAC) và (SBD)

b) Tìm giao điểm của đường thẳng SD với mp(AIJ)

c) Xác định thiết diện của hình chóp S.ABCD cắt bởi mp(AIJ)



Giải

a) Gọi K là giao điểm của AD và BC, khi đó hai mặt phẳng

(SAD) và (SBC) có hai điểm ching là S và K. Vậy:

SAD ABC SK

( ) ( )

∩ =

Gọi O là giao điểm của AC và BD. Vậy

SAC ABD SO

( ) ( )

∩ =

b) Gọi M là giao điểm của SK và IJ. Khi đó

SAD AIJ AM

( ) ( )

∩ =

. Gọi E là giao điểm của AM và SD thì E

chính là giao điểm của SD với mp(AIJ).

c) Thiết diện của hình chóp khi cắt bởi mp(AIJ) là tứ giác AIJE.

Toán 11 GV. Lư Sĩ Pháp

HÌNH HỌC 11 Chương II. ĐT & MP Trong KG. QHSS

§2. HAI ĐƯỜNG THẲNG CHÉO NHAU

VÀ HAI ĐƯỜNG THẲNG SONG SONG

A. KIẾN THỪC CẦN NẮM

I. Vị trí tương đối của hai đường thẳng trong không gian

Cho hai đường thẳng a và b trong không gian. Có hai khả trường hợp sau đây xảy ra đối với a và b

TH1. Có một mặt phẳng chứa

và

1. a và b cắt nhau tại M, kí hiệu

a b M

∩ =

a caét b taïi M

2. a và b song song với nhau, kí hiệu a //

b hoặc b // a

a , b song song

3. a và b trùng nhau, kí

hiệu

a b

≡

a, b trùng nhau

TH2. Không có mặt phẳng nào chứa cả a và b. Khi đó ta nói a và b chéo nhau.

a, b chéo nhau

II. Các định lí và tính chất

1. Định lí 1. Trong không gian, qua một điểm không nằm trên đường

thẳng cho trước, có một và chỉ một đường thẳng song song với

đường thẳng đã cho.

Nhận xét: Hai đường thẳng song song a và b xác định một mặt

phẳng, kí hiệu mp(a, b) hay mp(b, a)

2. Định lí 2. (về giao tuyến ba mặt phẳng)

Nếu ba mặt phẳng phân biệt đôi một cắt nhau theo ba giao tuyến

phân biệt thì ba giao tuyến ấy hoặc đồng quy hoặc đôi một song song

với nhau.

Hệ quả

: Nếu hai mặt phẳng phân biệt lần lượt chứa hai đường thẳng song song thì giao tuyến của chúng

(nếu có) cũng song song với hai đường thẳng đó hoặc trùng với một trong hai đường thẳng đó.

Định lí 3

. Hai đường thẳng phân biệt cùng song song với đường

thẳng thứ ba thì song song với nhau.

4. Ba đoạn thẳng nối trung điểm các cạnh đối diện của một tứ diện

đồng quy tại trung điểm G của mỗi đoạn. Điểm G đó gọi là trọng tâm

của tứ diện.

5. Một mặt phẳng được xác định nếu nó đi qua hai đường thẳng song

song.

B. BÀI TẬP

ấn đề 1. Tìm giao tuyến hai mặt phẳng

Phương pháp: Nếu hai mặt phẳng

( )

và

( )

có điểm chung là S và lần lượt chứa hai đường thẳng

song song d và d’ thì giao tuyến của

( )

và

( )

là đường thẳng

∆

qua S và song song với d và d’.

Nghĩa là:

d d S d d

d d

( ) ( )

( ), ' ( ) ( ) ( ) ( , / / / / ')

/ / '

α β

α β α β



∈ ∩



⊂ ⊂

⇒

∩ = ∆ ∈∆ ∆







Toán 11 GV. Lư Sĩ Pháp

HÌNH HỌC 11 Chương II. ĐT & MP Trong KG. QHSS

Bài 2.1. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Tìm giao tuyến của

(SAD) và (SBC); (SAB) và (SCD); (SAC) và (SBD).



Giải

a) Ta có:

S SAC

S SAC SBD

S SBD

( )

( ) ( )

( )



∈

⇒

∈ ∩



∈



Gọi

O AC BD

= ∩

O SAC

O SAC SBD

O SBD

SO SAC SBD

( )

( ) ( )

( )

( ) ( )



∈

⇒ ∈ ∩



∈



⇒ = ∩

b) Ta có:

S SAB

S SAB SCD

S SCD

( )

( ) ( )

( )



∈

⇒ ∈ ∩



∈



Ta lại có:



⊂



⊂

⇒

∩ = ∆







( )

( ) ( ) ( ) / / / /

/ /

AB SAB

CD SCD SAB SCD AB CD

AB CD

(

∆

qua S và song song với AB, CD.

c) Lập luận tương tự câu b) ta có

∩ =

( ) ( ) / / / /

SAD SBC d AD BC

Bài 2.2. Cho tứ diện ABCD. Trên các cạnh AB và AC lần lượt lấy các điểm M và N sao

cho

AM AN

AB AC

. Tìm giao tuyến hai mặt phẳng (DBC) và (DMN).



Giải

Ta có:

M AB

MN ABC

N AC

( )



∈

⇒ ⊂



∈



Trong tam giác ABC ta có:

AM AN

MN BC

AB AC

/ /

⇒

Ta lại có:

D DBC DMN

( ) ( )

∈ ∩



⊂



⊂

⇒

∩ =







( )

( ) ( ) ( ) / / / /

/ /

BC DBC

MN DMN DBC DMN Dx BC MN

BC MN

Bài 2.3. Cho tứ diện ABCD. Cho I, J tương ứng là trung điểm của BC và AC, M là một điểm trên cạnh

AD sao cho không trùng với trung điểm của AD.

a) Tìm giao tuyến d của hai mặt phẳng (MIJ) và (ABD)

b) Gọi K là giao điểm của hai đường thẳng CD và JM. Tìm giao tuyến của hai mặt phẳng (ABK) và

(MIJ).



Giải

a) Ta có:

M MIJ

M AD ABD

( )



∈



∈ ⊂



M MIJ ABD

( ) ( )

⇒

∈ ∩

Ta cũng có





⊂

⇒

∩ =





⊂



/ /

( ) ( ) ( ) / / / /

( )

IJ AB

IJ MIJ MIJ ABD Mt IJ AB

AB ABD

b) Ta có

K ABK

K JM MIJ

( )



∈



∈ ⊂



K MIJ ABK

( ) ( )

⇒

∈ ∩

và





⊂





⊂



/ /

( )

IJ AB

IJ MIJ

AB ABK

⇒

∩ =

( ) ( ) / / / /

MIJ ABK Kx IJ AB

Bài 2.4. Cho tứ diện ABCD. Gọi M, N, P, Q, R và S lần lượt là trung điểm của AB, CD, BC, AD, AC và

BD. Chứng minh rằng tứ giác MPNQ là hình bình hành. Từ đó suy ra ba đoạn thẳng MN, PQ và RS cắt

nhau tại trung điểm mỗi đoạn, trung điểm đó gọi là trọng tâm của tứ diện.

Toán 11 GV. Lư Sĩ Pháp

HÌNH HỌC 11 Chương II. ĐT & MP Trong KG. QHSS



Giải

Trong tam giác ABC ta có: MP//AC và

Trong tam giác ACD ta có: QN//AC và

Từ đó suy ra:

MP QN

/ /







=> Tứ giác MPNQ là hình bình hành.

Do vậy hai đường chéo MN và PQ cắt nhau tại trung điểm G

của mỗi đường

Tương tự: PR//QS và

PR QS

= =

Do đó tứ giác PRQS là hình bình hành. Suy ra hai đường chéo

cắt nhau tại trung điểm G của PQ và OR = OS

Vậy ba đoạn thẳng MN, PQ, RS

cắt nhau tại trung điểm mỗi đoạn

và tại G.

Bài 2.5. Cho tứ diện ABCD có I, J lần lượt là trọng tâm của tam giác ABC và ABD.

Chứng minh rằng : IJ // CD.



Giải

Gọi K là trung điểm của AB

Vì I là trọng tâm của tam giác ABC nên

I KC

∈

và vì J là trọng tâm tam giác

ABD nên

I KD

∈

Từ đó suy ra:

KI KJ

KC KD

= =

IJ CD

/ /

⇒

Bài 2.6. Cho hình chóp S.ABCD đáy ABCD là hình bình hành. Trên đoạn SA lấy điểm M sao cho 2SM =

MA, trên đoạn SB lấy điểm N sao cho 2SN = NB.

a) Tìm giao tuyến của hai mặt phẳng (SAC) và (SBD); (SAD) và (SBC)

b) Chứng minh rẳng: MN//CD

c) Điểm P nằm trên cạnh SC không trùng với S, C. Tìm giao tuyến hai mp (MNP) và (SCD)



Giải

a) Ta có:

SAC SBD SO

( ) ( )

∩ =

Ta có:

S SAD

S SAD SBC

S SBC

( )

( ) ( )

( )



∈

⇒ ∈ ∩



∈



Mặt khác, ta có:

AD SAD

BC SBC

AD BC

( )

/ /



⊂



⊂







SAD SBC Sx AD BC

( ) ( ) / / / /

⇒ ∩ =

b) Từ giả thiết ta có:

SM SN

MA NB

= =

MN AB

/ /

⇒

và ABCD là

hình bình hành. Suy ra MN//AB//CD.



∈ ∈



⊂



⇒ ∩ =



⊂





( ), ( )

( )

( ) ( ) / / / /

( )

/ /

P MNP P SCD

MN MNP

MNP SCD Py MN CD

CD SCD

MN CD

Toán 11 GV. Lư Sĩ Pháp

HÌNH HỌC 11 Chương II. ĐT & MP Trong KG. QHSS

ấn đề 2. Tìm thiết điện của hình chóp khi cắt bởi một mặt phẳng

Phương pháp: Ta tìm giao tuyến của mặt phẳng đó với các mặt bên của hình chóp. Đoạn nối giữa

các giao tuyến cho ta một hình. Hình đó là thiết diện cần tìm.

Bài 2.7. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành.

a) Hãy xác định giao tuyến của các mặt phẳng (SAB) và (SCD); (SBC) và (SAD)

b) M là điểm thuộc cạnh SC, tìm thiết diện của hình chóp với mp(ABM). Thiết diện là hình gì?



Giải

a) i).

SAB SCD

( ) ( ) ?

∩ =

Ta có

S SAB SCD AB SAB

( ) ( ); ( );

∈ ∩ ⊂

CD SCD AB CD

( ), / /

⊂

Nên

SAB SCD Sx AB CD

( ) ( ) / / / /

∩ =

ii)

SBC SAD

( ) ( ) ?

∩ =

Ta có

S SBC SAD BC SBC AD SAD

( ) ( ); ( ); ( ),

∈ ∩ ⊂ ⊂

BC AD

/ /

. Nên

SBC SAD Sy BC AD

( ) ( ) / / / /

∩ =

b) Ta có:

ABM ABCD AB

( ) ( ) ;

∩ =

ABM SBC BM

( ) ( )

∩ =

;

ABM SDC MN AB DC N SD

( ) ( ) / / / / ,

∩ = ∈

ABM SAD AN

( ) ( )

∩ =

Vậy thiết diện cần tìm là tứ giác ABMN. Rõ ràng: ABMN là hình thang vì MN // AB.

Bài 2.8. Cho tứ diện ABCD. Gọi I, J lần lượt là trung điểm của BC và BD; E là một điểm thuộc cạnh AD

khác với A và D

a) Xác định thiết diện của hình tứ diện khi cắt bởi mp(IJE)

b) Tìm vị trí của điểm E trên AD sao cho thiết diện là hình bình hành

c) Tìm điều kiện của tứ diện và vị trí điểm E trên cạnh AD để thiết diện là hình thoi



Giải

a) Ta có IJ là đường trung bình trong tam giác BCD nên IJ //CD

Mặt khác

IJ IJE CD ACD

( ); ( )

⊂ ⊂

. Suy ra:

EIJ ACD Ex IJ CD

( ) ( ) / / / /

∩ =

. Gọi

F Ex AC

= ∩

Thiết diện là hình thang EFIJ

b) Để thiết diện EFIJ là hình bình hành điều kiện cần và đủ là IF //

JE. Điều này tương với JE //AB, tức là khi và chỉ khi E là trung

điểm của AD.

c) Thiết diện EFIJ là hình thoi khi và chỉ khi EFIJ là hình bình hành

và IF = IJ khi và chỉ khi E là trung điểm của AD và AB = CD (vì

IJ CD

và khi E là trung điểm của AD thì

IF AB

)

ấn đề 3. Chứng minh hai đường thẳng song song

Phương pháp:

1. Chứng minh chúng cùng thuộc một mặt phẳng và dùng phương pháp chứng minh hai đường thẳng

song song trong hình học phẳng( như tính chất đường trung bình của tam giác, định lí Talét đảo, tính chất

song song của hai đường thẳng cùng vuông góc với đường thẳng thứ ba, …)

2. Chứng minh chúng cùng song song với đường thẳng thứ ba.

3. Dùng tính chất: Hai mặt phẳng phân biệt lần lượt chứa hai đường thẳng song song thì giao tuyến của

chúng(nếu có) cũng song song với hai đường thẳng ấy. Tức là:

c a b

a b

( )

/ / / /

/ /

( ) ( )

α β



∈



∈



⇒





∩ =



Toán 11 GV. Lư Sĩ Pháp

HÌNH HỌC 11 Chương II. ĐT & MP Trong KG. QHSS

4. Dùng định lý về giao tuyến của ba mặt phẳng:

a b c

a b

/ / / /

, ñoàng quy

α γ

β γ

α β



∩ =





∩ = ⇒









∩ =



Bài 2.9. Cho hình chóp S.ABCD có đáy là một tứ giác lồi. Gọi M và N lần lượt là trọng tâm của tam giác

SAB và SAD; E là trung điểm của CB.

a) Chứng minh rằng: MN // BD

b) Xác định thiết diện hình chóp S.ABCD cắt bởi mp(MNE)

c) H và L lần lượt là giao điểm của mp(MNE) với các cạnh SB và SD. Chứng minh rằng: LH // BD



Giải

a) Gọi M’, N’ lầm lượt là trung điểm của AB và AD. Dễ thấy:

MN M N

MN BD

M N BD

/ / ' '

/ /

' '/ /



⇒





b)Ta có:

MN MNE

BD ABCD

MN BD

( )

/ /



⊂



⊂







MNE ABCD Ex MN BD

( ) ( ) / / / /

⇒ ∩ =

ậy từ E kẻ

đư

ờng thẳng song song với BD lần

lượt cắt CD, AB tại F và I. Nối IM lần lượt cắt

SB và SA tại H, K; nối KN cắt SD tại L. Thiết

diện cần tìm là ngũ giác KLFEH

c)Ta có:

MN MNE

BD SBD

MN BD

MNE SBD LH

( )

/ /

( ) ( )



⊂



⊂







∩ =



LH BD

/ /

⇒

Bài 2.11. Cho tứ diện ABCD. Có các điểm P, Q lần lượt là trung điểm của AB, CD; điểm R nằm trên

cạnh BC sao cho BR = 2RC. Gọi S là giao điểm của mp(PQR) và cạnh AD. Chứng minh rằng AS = 2SD.



Giải

Gọi

I RQ BD

= ∩

, E là trung điểm của BR. Khi đó EB = ER =

RC và RQ // ED.

Tam giác BRI có ED // RQ, suy ra

BD BE

DI ER

= =

Vậy DB = DI. Do đó AD và IP là hai đường trung tuyến của

tam giác ABI. Suy ra giao điểm S của AD và IP là trọng tâm

của tam giác ABI và ta có AS = 2DS

Toán 11 GV. Lư Sĩ Pháp

HÌNH HỌC 11 Chương II. ĐT & MP Trong KG. QHSS

§3. ĐƯỜNG THẲNG SONG SONG VỚI MẶT PHẲNG

A. KIẾN THỨC CẦN NẮM

I. Vị trí tương đối của đường thẳng và mặt phẳng

Giữa đường thẳng d và mặt phẳng

( )

ta có ba vị trí tương đối như sau:

1. d và

( )

cắt nhau tại

, kì hiệu

{

}

∩ =( )

a P A

d cắt mp(α) tại M

2. d

song song với

( )

, kí hiệu

d ||( )

hoặc

( ) || d

. Như vậy: Một

đường thẳng và một mặt phẳng gọi là song song với nhau nếu

chúng không có điểm chung.

d // (α)

nằm trong

( )

, kí hiệu

⊂

( )

d chứa trong (α)

II. Định lí và tính chất

1. Định lí 1. Nếu đường thẳng

không nằm trong mặt phẳng

( )

và

song song với đường thẳng

nằm trong thì

song song với

( )

; nghĩa là:



⊄ α



′

⇒ α





⊂ α



d ( )

d || d d || ( )

d' ( )

2. Định lí 2. Cho đường thẳng

song song với mặt phẳng

( )

. Nếu

mặt phẳng

( )

chứa

và cắt

( )

theo giao tuyến

thì

song song

với

; nghĩa là





β ⊃ ⇒





β ∩ α =



a/ /( )

( ) a b || a

( ) ( ) b

Hệ quả 1. Nếu một đường thẳng song song với một mặt phẳng thì

nó song song với một đường thẳng nào đó trong mặt phẳng.

Hệ quả2. Nếu hai mặt phẳng phân biệt cùng song song với một

đường thẳng thì giao tuyến của chúng (nếu có) cũng song song với

đường thẳng đó; nghĩa là

α β





′

⇒





′

∩ =



( )/ / d

( )/ / d d || d

( ) ( ) d

3. Định lí 3. Cho hai đường thẳng chéo nhau. Có duy nhất một mặt

phẳng chứa đường thẳng này và song song với đường thẳng kia.

Toán 11 GV. Lư Sĩ Pháp

HÌNH HỌC 11 Chương II. ĐT & MP Trong KG. QHSS

B. BÀI TẬP

ấn đề 1. Chứng minh đường thẳng song song với mặt phẳng

Phương pháp: Để chứng minh đường thẳng

song song với mặt phẳng

( )

ta chứng minh

không

nằm trong

( )

và song song với đường thẳng

chứa trong

( )

. Tức là

a d

d a

( )

( ) / /( )

/ /

α α



⊄



⊂ ⇒







Bài 3.1. Cho tứ diện ABCD. G là trọng tâm của tam giác ABD. Trên đoạn BC lấy điểm M sao cho MB =

2MC. Chứng minh rằng MG // (ACD).



Giải

Gọi I trung điểm của AD.

Trong tam giác CBI ta có,

BM BG

BC BI

= =

. Nên MG // CI

Mà CI nằm trong mặt phẳng (ACD)

Suy ra MG // (ACD).

Bài 3.2. Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm của các cạnh AB và AC.

a) Xét vị trí tương đối của đường thẳng MN và mp(BCD)

b) Gọi d là giao tuyến của hai mặt phẳng (DMN) và (DBC). Xét vị trí tương đối của d và mp(ABC)



Giải

a) MN là đường trung bình của tam giác ABC nên MN // BC.

Suy ra MN // (BCD)

b) Vì MN // (BCD) nên (DMN) đi qua MN cắt (BCD) theo

giao tuyến d // MN. Do đó d // (ABC).

Bài 3.3. Cho tứ diện ABCD. Gọi G

và G

lần lượt là trọng tậm của các tam giác ACD và BCD. Chứng

minh rằng G

song song với các mặt phẳng (ABC) và (ABD)



Giải

Gọi I là trung điểm CD

Vì G

là trọng tâm của tam giác ACD nên

G AI

∈

Vì G

là trọng tâm của tam giác BCD nên

G BI

∈

Ta có:

IG IG

G G AB

IA IB

1 2

/ /





⇒ = ⇒







AB ABC G G ABC

1 2

( ) / /( )

⊂

⇒

Và

AB ABD G G ABD

1 2

( ) / /( )

⊂ ⇒

Bài 3.4. Cho tứ hình chóp S.ABCD có đáy ABCD là hình bình hành ABCD. Gọi G là trọng tâm tam giác

SAB và I là trung điểm của AB. Lấy điểm M trên đoạn AD sao cho AD = 3AM.

a) Tìm giao tuyến của hai mặt phẳng (SAD) và (SBC)

b) Đường thẳng qua M và song song với AB cắt CI tại N. CMR: NG // (SCD)

c) Chứng minh rằng MG // (SCD).



Giải

Toán 11 GV. Lư Sĩ Pháp

HÌNH HỌC 11 Chương II. ĐT & MP Trong KG. QHSS

a) Dễ thấy S là điểm chung của hai mặt phẳng

(SAD) và (ABC)

Ta có:

AD SAD

BC SBC

AD BC

SAD SBC Sx AD BC

( )

/ /

( ) ( ) / / / /



⊂



⊂







⇒ ∩ =

b) Ta có: MN // IA //CD

AM IN

AD IC

⇒ = =

; mà

( G là trọng tâm

của tam giác SAB)

Nên

IG IN

GN SC

IS IC

/ /

⇒

= =

⇒

Mà

SC SCD GN SCD

( ) / /( )

⊂ ⇒

c) Gọi

K IM CD SK SCD

( )

= ∩ ⇒ ⊂

Mà

MN IN IM

MN CD

CK IC IK

1 1

/ /

3 3

⇒ = = ⇒ =

Ta có:

GM SK

GM SCD

/ /

I 1

/ /( )





⇒







⇒

Bài 3.5. Cho hình chóp S.ABCD có đáy ABCD là hình thang, đáy lớn AD và AD = 2BC. Gọi O là giao

điểm của AC và BD, G là trọng tâm của tam giác SCD.

a) Chứng minh rằng OG // (SBC)

c) Cho M là trung điểm của SD. Chứng minh rằng CM // (SAB)

d) Giả sử I nằm trên đoạn SC sao cho

SC SI

. Chứng minh rằng SA // (BID).



Giải

a) Gọi H là trung điểm của SC, ta có:

(1)

OD OA AD OD

BC AB OD OB

OB OC BC BD

/ / 2 2 (2)

⇒ = = = ⇒ = ⇒ =

Từ (1) và (2)

DG OD

OG BH

DH BD

(1) / /

⇒

= =

⇒

. Mà

BH SBC OG SBC

( ) / /( )

⊂ ⇒

b) Gọi M’ là trung điểm của SA

MM AD

'/ /





⇒







Mặt khác vì BC // AD và

BC AD

= (gt) và BC = MM’. Nên

tứ giác BCMM’ là hình bình hành

Suy ra CM //BM’, mà

BM SAB CM SAB

' ( ) / /( )

⊂ ⇒

c) Ta có:

nên

Mặt khác vì

SC SI

nên

CI OC

OI SA

CS CA

/ /

⇒ = ⇒ và

OI BID SA BID

( ) / /( )

⊂ ⇒

Bài 3.6. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N lần lượt là trung điểm của

AB và CD.

a) Chứng minh rằng MN song song với các mặt phẳng (SBC) và (SAD).

b) Gọi P là trung điểm của SA. Chứng minh rằng SB và SC đều song song với mp (MNP)



Giải

Toán 11 GV. Lư Sĩ Pháp

HÌNH HỌC 11 Chương II. ĐT & MP Trong KG. QHSS

a) Chứng minh MN //(SBC):

Ta có:

MN BC

MN SBC

BC SBC

/ /

/ /( )

( )



⇒



⊂



Chứng minh MN // (SAD):

Ta có:

MN AD

MN SAD

AD SAD

/ /

/ /( )

( )



⇒



⊂



b) Chứng minh SB // (MNP):

Ta có:

SB MP

SB MNP

MP MNP

/ /

/ /( )

( )



⇒



⊂



Chứng minh S // (MNP):

Gọi

Q AC MN

= ∩

. Khi đó Q là trung điểm của AC.

Do đó: SC // PQ (T/c đường trung bình trong tam giác SAC)

mà

PQ MNP

( )

⊂

. Vậy SC // (MNP)

Bài 3.7. Cho tứ diện ABCD. Gọi M, N lần lượt là trọng tâm của tam giác ABD và BCD.

a) Chứng minh rằng: MN // (ACD) và MN // (ABC)

b) Xác định giao tuyến của (DMN) và (ABC). Chứng minh giao tuyến này song song với MN. Tính



Giải

a) Gọi K là trung điểm của BD. Vì M, N là trọng

tâm của các tam giác ABD và BCD nên A, M, K

thẳng hàng và C, N, K thẳng hàng, tức là AM cắt

CN tại K

Ta có:

KM KN

KA KC

1 1

;

3 3

= =

KM KN

KA KC

⇒

MN AC

/ /

⇒

Tứ đó:

MN AC

MN ACD

AC ACD

/ /

/ /( )

( )



⇒



⊂



và

MN AC

MN ABC

AC ABC

/ /

/ /( )

( )



⇒



⊂



b) Trong mp (ABD): DM cắt AB tại I; trong

mp(BCD): DN cắt BC tại J. Khi đó I, J là hai

điểm chung của hai (DMN) và (ABC). Suy ra

DMN ABC IJ

( ) ( )

∩ =

I, J lấn lượt là trung điểm của AB và BC nên IJ

là đường trung bình trong tam giác ABC

IJ AC IJ AC

/ / ;

⇒

. Mà MN // AC (câu a)

nên MN // IJ.

Ta có

IJ AC

= ;

KM MN

MN AC

KA AC

1 1

3 3

= =

⇒

. Từ đó

ấn đề 2. Dựng thiết diện song song với một đường thẳng

Phương pháp: Cho đường thẳng

song song với mặt phẳng

( )

. Nếu mặt phẳng

( )

chứa

và cắt

( )

theo giao tuyến

d’

thì

d’

song song với

. Nghĩa là:

d d d

/ /( )

( ) / / '

( ) ( ) '

β α





⊃ ⇒





∩ =



Thiết diện cắt bởi một mặt phẳng chứa một đường thẳng song song với một đường thẳng cho trước được

xác định bằng cách phối hợp hai cách xác định giao tuyến đã biết.

Bài 3.9. Cho hình chóp S.ABCD có đáy là hình bình hành ABCD, O là giao điểm của AC và BD, M là

trung điểm của SA. Tìm thiết diện của mặt phẳng

( )

với hình chóp S.ABCD nếu

( )

qua M và đồng

Toán 11 GV. Lư Sĩ Pháp

HÌNH HỌC 11 Chương II. ĐT & MP Trong KG. QHSS

thời song song với SC và AD.



Giải

Vì

( )

song song với AD nên

( )

cắt hai mặt phẳng (SAD) và

(ABCD) theo hai giao tuyến song song với AD.

Tương tự

( )

song song với SC nên

( )

cắt hai mặt phẳng

(SAC) và (SCD) theo hai giao tuyến song song với SC.

Gọi

O AC BD

= ∩

, ta có SC//OM( đường trung bình trong tam

giác SAC)

Qua O kẻ đường thẳng song song với AD, cắt AB và CD tại Q

và P. Qua M, kẻ đường thẳng song song với AD cắt SD tại N.

Theo nhận xét trên, ta có MN // PQ // SC

Vậy thiết diện là hình thang MNPQ

Bài 3.10. Cho tứ diện ABCD. Trên AB lấy điểm M. Cho

( )

là mặt phẳng qua M, song song với hai

đường thẳng AC và BD.

a) Tìm giao tuyến của

( )

với các mặt của tứ diện

b) Thiết diên của tứ diện cắt bởi mặt phẳng

( )

là hình gì?



Giải

a) Giao tuyến của

( )

với các mặt của tứ diện là

các cạnh của tứ giác MNPQ có:

MN // PQ //AC và MQ // NP // BD

b) Thiết diện tạo bởi mặt phẳng

( )

với tứ diện là

hình bình hành MNPQ

Bài 3.11. Cho hình chóp S.ABCD có đáy ABCD là một tứ giác lồi. Gọi O là giao điểm của hai đường

chéo AC và BD. Xác định thiết diện của hình chóp cắt bởi mặt phẳng

( )

đi qua O, song song với AB và

SC. Thiết diện đó là hình gì?



Giải

Ta có:

AB ABCD MN AB

ABCD MN

( )/ /

( ) / /

( ) ( )





⊂ ⇒





∩ =



SC SBC MQ SC

SBC MQ

( )/ /

( ) / /

( ) ( )





⊂ ⇒





∩ =



SC SAB PQ AB

SAB PQ

( )/ /

( ) / /

( ) ( )





⊂ ⇒





∩ =



Vậy MN // PQ. Do đó tứ giác MNPQ là hình thang

Bài 3.12. Cho hình chóp S.ABCD có đáy là hình bình hành. Xác định thiết diện của hình chóp khi cắt bởi

mặt phẳng đi qua trung điểm M của cạnh AB, song song với BD và SA.



Giải

Qua M vẽ đường thẳng song song với BD cắt AD tại N và cắt AC tại I. Qua M, I, N vẽ các đường thẳng

song song với SA lần lượt cắt SB, SC, SD tại R, Q, P.

Thiết diện là ngũ giác MNPQR.

Toán 11 GV. Lư Sĩ Pháp

HÌNH HỌC 11 Chương II. ĐT & MP Trong KG. QHSS

Bài 3.13. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. M là một điểm di động trên đoạn AB.

Một mặt phẳng

( )

đi qua M và song song với SA và BC;

( )

cắt SB, SC và CD tại N, P, Q

a) Tứ giác MNPQ là hình gì?

b) Gọi I là giao điểm của MN và PQ. Chứng minh rằng I nằm trên một đường thẳng cố định.



Giải

a) Vì

M SAB

( )

∈

và

SA SAB

( )/ /

( )





⊂



nên

SAB MN

( ) ( )

∩ =

và MN // AB.

Tương tự

SBC NP

( ) ( )

∩ =

và NP // BC;

SCD PQ

( ) ( )

∩ =

;

ABCD MQ

( ) ( )

∩ =

và MQ

// BC. Từ đó suy ra, tứ giác ABCD là hình thang.

b) Ta có

S SAB SCD

AB SAB CD SCD

AB CD

( ) ( )

( ), ( )

/ /



∈ ∩



⊂ ⊂







SAB SCD Sx

( ) ( )

⇒ ∩ =

và Sx // AB // CD

MN PQ I

∩ =

I MN SAB

I PQ SCD

( )



∈ ⊂

⇒



∈ ⊂



I SAB SCD I Sx

( ) ( )

⇒ ∈ ∩ ⇒ ∈

(SAB) và (SCD) cố định nên Sx cố định.

Dó đó I thuộc đường thẳng Sx cố định.

Toán 11 GV. Lư Sĩ Pháp

HÌNH HỌC 11 Chương II. ĐT & MP Trong KG. QHSS

§4. HAI MẶT PHẲNG SONG SONG

A. KIẾN THỨC CẤN NẮM

Định nghĩa: Hai mặt phẳng

( )

và

( )

được gọi là song

song với nhau nếu chúng không có điểm chung. Kí hiệu:

( )/ /( )

α β

hoặc

( )/ /( )

β α

. Như vậy

( )/ /( ) ( ) ( )

α β α β

⇔ ∩ = Ο

II. Tính chất.

Định lí 1. Nếu mặt phẳng

( )

chứa hai đường thẳng cắt

nhau a, b và a, b cùng song với mặt phẳng

( )

thì

( )

song

song với

( )

; nghĩa là

a b

a b M

a b

( ), ( )

( )/ /( )

/ /( ), / /( )

α α

α β

β β



⊂ ⊂



∩ = ⇒







Hệ quả: Nếu mặt phẳng

( )

chứa hai đường thẳng cắt

nhau a và b, mặt phẳng

( )

chứa hai đường thẳng cắt nhau

a' và b' đồng thời a // a', b // b' thì mặt phẳng

( )

song song

với mặt phẳng

( )

Định lí 2. Qua một điểm nằm ngoài một mặt phẳng cho

trước có một và chỉ một mặt phẳng song song với mặt

phẳng đã cho.

Hệ quả 1. Nếu đường thẳng d song song với mặt phẳng

( )

thì trong

( )

có một đường thẳng song song với d và

qua d có duy nhất một mặt phẳng

( )

song song với

( )

Hệ quả 2. Hai mặt phẳng phân biệt cùng song song với mặt

phẳng thứ ba thì song song với nhau.

Hệ quả 3. Cho điểm A không nằm trên mặt phẳng

( )

Mọi đường thẳng đi qua A và song song với

( )

đều nằm

trong mặt phẳng đi qua A và song song với

( )

Định lí 3.

Cho hai mặt phẳng song. Nếu một mặt phẳng cắt

mặt phẳng này thì cũng cắt mặt phẳng kia và hai giao tuyến

song song với nhau.

Hệ quả

: Hai mặt phẳng song s

ong chắn trên hai cát tuyến

song song những đoạn thẳng bằng nhau.

Toán 11 GV. Lư Sĩ Pháp

HÌNH HỌC 11 Chương II. ĐT & MP Trong KG. QHSS

Định lí 4(Định lí Ta-lét). Ba mặt phẳng đôi một song song

chắn trên hai cát tuyến bất kì những đoạn thẳng tương ứng

tỉ lệ.

AB AC BC

A B A C B C

' ' ' ' ' '

= =

Định lí Ta-lét đảo.

Giả sử trên hai đường thẳng chéo nhau lần lượt lấy các

điểm A, B, C và A’, B’, C’ sao cho

AB BC CA

= =

A'B' B'C' C'A'

Khi đó AA’, BB’, CC’ lần lượt nằm trên ba mặt phẳng

song song, tức là chúng cùng song song với một mặt

phẳng.

III. Hình lăng trụ và hình chóp cụt

1. Hình lăng trụ

Hình lăng trụ là một hình đa diện có hai mặt nằm trong hai mặt phẳng song song (gọi là hai đáy) và tất cả

các cạnh không thuộc hai đáy đều song song với nhau (gọi là cạnh bên)

- Hai đáy của hình lăng trụ là các đa giác bằng nhau

- Các mặt khác hai đáy gọi là mặt bên: Mỗi mặt bên là một hình bình hành

- Các mặt tạo bởi hai cạnh bên không liên tiếp gọi là mặt chéo: Mỗi mặt chéo là một hình bình hành

- Đường chéo của các mặt chéo là đường chéo của hình lăng trụ

- Tùy theo đáy, ta gọi hình lăng trụ tam giác, hình lăng trụ tứ giác, hình lăng trụ lục giác, . . .

Lăng trụ ngũ giác

Lăng trụ tứ giác

Lăng trụ tam giác

2. Hình hộp

Hình hộp là hình lăng trụ có đáy là hình bình hành.

- 6 mặt của hình hộp chữ nhật đều là hình bình hành

- Các đường chéo của hình bình hành đồng qui tại một điểm là trung điểm của mỗi đường chéo

(điểm đó gọi là tâm của hình hộp)

- Hình hộp có tất cả các mặt bên và các mặt đáy đều là hình chữ nhật gọi là hình hộp chữ nhật

- Hình hộp có tất cả các mặt bên và các mặt đáy đều là hình vuông gọi là hình lập phương

3. Hình chóp cụt

Cho hình chóp S.A

...A

. Một mặt phẳng

không qua đỉnh, song song với mặt phẳng đáy

của hình chóp cắt các cạnh SA

, SA

, . . ., SA

lần lượt tại

A A A

' ' '

1 2

, ,...,

. Hình toạ bởi thiết

diện

A A A

' ' '

1 2

...

và đáy

A A A

1 2

...

của hình

Toán 11 GV. Lư Sĩ Pháp

HÌNH HỌC 11 Chương II. ĐT & MP Trong KG. QHSS

chóp cùng các từ giác

n n

A A A A A A A A A A A A

' ' ' ' ' '

1 2 2 1 2 3 3 2 1 1

, ,...,

được gọi là

hình chóp cụt, kí hiệu

n n

A A A A A A

' ' '

1 2 1 2

... . ..

Hình chóp cụt có:

- Hai đáy là hai da giác có cạnh tương ứng

song dong và tỉ số các cạnh tương ứng

bằng nhau

- Các mặt bên là những hình thang

- Các đường thẳng chứa các cạnh bên đồng

qui tại một điểm.

B. BÀI TẬP

ấn đề 1. Chứng minh hai mặt phẳng song song

Phương pháp:

1. Vận dụng định lí 1: Nếu mặt phẳng

( )

chứa hai đường thẳng cắt nhau

a, b

và

a, b

cùng song với mặt

phẳng

( )

thì

( )

song song với

( )

a b

a b M

a b

( ), ( )

( )/ /( )

/ /( ), / /( )

α α

α β

β β



⊂ ⊂



∩ = ⇒







2. Ta chứng minh hai mặt phẳng

( )

và

( )

cùng song song với mặt phẳng thứ ba

( )

Bài 4.1. Cho từ diện ABCD. Gọi G

, G

lần lượt là trọng tâm của các tam giác ABC, ACD, ABD.

Chứng minh mặt phẳng (G

) song song với mặt phẳng (BCD).



Giải

Gọi M, N, P lần lượt là trung điểm của BC, CD, DB. Ta có:

M AG

∈ và

N AG

∈

và

P AG

∈ và

Do đó

AG AG

G G MN

AM AN

1 2

/ /=

⇒

Vì MN nằm trong (BCD) nên

G G BCD

1 2

/ /( )

Tương tự

G G MP

AM AP

1 3

/ /=

⇒

Vì MP nằm trong (BCD) nên

G G BCD

1 3

/ /( )

Như vậy

G G G G G

G G G G G G G G BCD

G G BCD

1 2 1 2 3

1 3 1 2 3

1 2 1 3 1 1 2 3

1 2

1 3

( )

( )/ /( )

/ /( )



⊂



⊂



∩ = ⇒







Bài 4.2. Cho hai hình vuông ABCD và ABEF ở trong hai mặt phẳng phân biệt. Trên các đường chéo AC

và BF lần lượt lấy các điểm M và N sao cho AM = BN. Các đường thẳng song song với AB vẽ từ M và N

lần lượt cắt AD và AF tại M’ và N’. Chứng minh:

a) (ADF) // (BCE)

b) M’N’ // DF

c) (DEF) // (MM’N’N) và MN // (DEF).



Giải

Toán 11 GV. Lư Sĩ Pháp

HÌNH HỌC 11 Chương II. ĐT & MP Trong KG. QHSS

a) Ta c

ó:

AD BC

AD BCE

BC BCE

/ /

/ /( )

( )



⇒



⊂



AF BE

AF BCE

BE BCE

/ /

/ /( )

( )



⇒



⊂



mà

AD AF ADF

, ( )

⊂

Nên (ADF) // (BCE)

b) Vì ABCD và ABEF là các hình vuông nên AC = BF.

Ta có:

AM AM

MM CD

AD AC

'/ / (1)

⇒

AN BN

NN AB

AF BF

'/ / (2)

⇒ =

Từ (1) và (2):

AM AN

M N DF

AD AF

' '

' '/ /

⇒

c) Từ chứng minh trên suy ra: DF // (MM’N’N)

NN AB NN EF

NN MM N N

EF MM N N

'/ / '/ /

' ( ' ' )

/ /( ' ' )



⇒



⊂



⇒

Mà DF, EF chứa trong (MM’N’N)

Nên (DEF) // (MM’N’N)

Vì MN chứa trong (MM’N’N) và

(DEF)//(MM’N’N)

Nên MN // (DEF)

Bài 4.3. Cho hình lăng trụ tam giác ABC.A’B’C’. Gọi H là trung điểm của A’B’.

a) Chứng minh rẳng: CB’ // (AHC’)

b) Tìm giao tuyến d của (AB’C’) và (ABC).



Giải

a) Ta có tứ giác AA’C’C là hình bình hành suy ra

A’C cắt AC’ tại trung điểm I của mỗi đường.

Do đó IH // CB’(đường trung bình của tam giác

CB’A’)

Mà IH chứa trong (AHC’) nên CB’ // (AHC’)

b) Ta có

A AB C

A ABC

( ' ')

( )



∈



∈



A AB C ABC

( ' ') ( )

⇒ ∈ ∩

Mà

B C BC

B C AB C

BC ABC

' '/ /

' ' ( ' ')

( )





⊂





⊂



Nên

AB C ABC Ax BC B C

( ' ') ( ) / / / / ' '

∩ =

Bài 4.4. Cho hình lăng trụ tam giác ABC.A’B’C’. Gọi M, M’ lần lượt là trung điểm của các cạnh BC và

B’C’

a) Chứng minh rằng AM song song với A’M’

b) Tìm giao điểm của mặt phẳng (AB’C’) với đường thẳng A’M

c) Tìm giao tuyến d của hai mặt phẳng (AB’C’) và (BA’C’)

d) Tìm giao điểm G của đường thẳng d với mặt phẳng (AM’M). Chứng minh G là trọng tâm của tam giác

AB’C’.



Giải

a) MM’ // BB’ và MM’ = BB’ =>MM’ // AB và

MM’ = AB(hình lăng trụ)

Suy ra tứ giác AA’M’M là hình bình hành => AM

// A’M’

b) Gọi

I A M AM

' '

= ∩

Ta có:

I AM AB C

I A M AB C

I A M

' ( ' ')



∈ ⊂

⇒ = ∩



∈



C AB C

C AB C BA C

C BA C

' ( ' ')

' ( ' ') ( ' ')

' ( ' ')



∈

⇒ ∈ ∩



∈



Toán 11 GV. Lư Sĩ Pháp

HÌNH HỌC 11 Chương II. ĐT & MP Trong KG. QHSS

AB A B O

O AB C

O AB C BA C

O BA C

' '

( ' ')

( ' ') ( ' ')

( ' ')

∩ =



∈

⇒ ⇒ ∈ ∩



∈



d C O AB C BA C

' ( ' ') ( ' ')

⇒ ≡ = ∩

d AB C

d d AM G

AM AB C

( ' ')

) '

' ( ' ')



⊂

⇒ ∩ =



⊂



G d

G AM M

G AM

( ' )



∈

⇒ ⇒ ∈



∈



Ta có

OC AM G

' '

∩ =

Mà OC’, AM’ là trung tuyến tam giác AB’C’

Vậy G là trọng tâm của tam giác AB’C’

Toán 11 GV. Lư Sĩ Pháp

HÌNH HỌC 11 Chương II. ĐT & MP Trong KG. QHSS

§5. PHÉP CHIẾU SONG SONG

A. KIẾN THỨC CẦN NẮM

1. Phép chiếu song song

- Cho mặt phẳng

( )

và đường thẳng

∆

cắt

( )

. Với mỗi điểm M trong không gian, đường thẳng qua

M và song song hoặc trùng với

∆

cắt

( )

tại điểm M' xác định.

- Điểm M' gọi là hình chiếu song song của điểm M trên mặt phẳng

( )

theo phương

∆

- Mặt phẳng

( )

được gọi là mặt phẳng chiếu, phương của đường thẳng

∆

được gọi là phương chiếu.

- Phép đặt tương ứng mỗi điểm M trong không gian với hình chiếu M' của nó trên mặt phẳng

( )

được

gọi là phép chiếu song song lên

( )

theo phương

∆

2. Các tính chất của phép chiếu song song (với đường thẳng và đoạn thẳng không song song hoặc trùng

với phương chiếu)

- Phép chiều song song biến ba điểm thẳng hàng thành ba điểm thẳng hàng và không làm thay đổi thứ

tự ba điểm đó;

- Phép chiếu song song biến đường thẳng thành đường thẳng, biến tia thành tia, biến đoạn thẳng thành

đoạn thẳng;

- Phép chiếu song song biến hai đường thẳng song song thành hai đường thẳng song song hoặc trùng

nhau;

- Phép chiều song song không làm thay đổi tỉ số độ dài của hai đoạn thẳng nằm trên hai đường thẳng

song song hoặc cùng nằm trên một đường thẳng.

3. Hình biểu diễn của một số hình không gian trên mặt phẳng

- Một tam giác bất kì bao giờ cũng có thể là hình biểu diễn của một tam giác tuỳ ý cho trước ( có

thể là tam giác đều, tam giác cân, tam giác vuông, . . .);

- Một hình bình hành bất kì bao giờ cũng có thể coi là hình biểu diễn của một hình bình hành tuỳ ý

cho trước ( có thể là hình bình hành, hình vuông, hình chữ nhật, hình thoi, . . .).

- Một hình thang bất kì bao giờ cũng có thể coi là hình biểu diễn của một hình thang tuỳ ý cho

trước, miễn là tỉ số độ dài hai đáy của hình biểu diễn phải bằng tỉ số độ dài hai đáy của hình đã

cho.

- Người ta thường dùng hình elip để biểu diễn hình tròn.

B. BÀI TẬP

Bài 5.1. Tam giác ABC có hình chiếu song song là tam giác A'B'C'. Chứng minh rằng trọng tâm của tam

giác ABC có hình chiếu song song là trọng tâm của tam giác A'B'C'.



Giải

ọi G là trọng tâm của tam giác ABC G' là hình chiếu song song của

nó. Gọi M là trung điểm cùa BC thí A, G, M thẳng hàng.

Gọi M' là hình chiếu của M. Khi đó theo tính chất của phép chiếu

song song ta có:A', G' M' thẳng hàng và

A G AG

A M AM

' ' 2

(1)

' ' 3

= =

; B',

M', C' thằng hàng và

B M BM

M C MC

' ' 2

(2)

' ' 3

= =

Từ (1) và (2) suy ra G' là trọng tâm của tam giác A'B'C'.

Toán 11 GV. Lư Sĩ Pháp

HÌNH HỌC 11 Chương II. ĐT & MP Trong KG. QHSS

Bài 5.2.

a) Vẽ hình biểu diển của một tứ diện và trọng tâm của nó.

b) Vẽ hình biểu diễn của tam giác vuông nột tiếp trong đường tròn.



Giải

a) V

ẽ hình biểu diễn của tứ diện ABCD. Lấy M, N lần l

ợt là trung

điểm của AB và CD thì trung điểm G của MN sẽ biểu diễn cho trọng

tâm của tứ diện.

b) Vẽ elip tâm O là hình biểu diễn của đường tròn đã cho. Lấy hai

điểm A và B là hai điểm trên elip sao cho B, C, O thẳng hàng và một

điểm A thuộc elip sao cho A khác với B và C. Khi đó, tam giác ABC

là hình biểu diễn của một tâm giác vuông nội tiếp trong một đường

tròn.

Bài 5.3. Cho tam giác ABC. Hãy chọn mặt phẳng chiếu

( )

và phương chiếu của tam giác ABC trên

( )

là:

a) Một tam giác cân b) Một tam giác đều c) Một tam giác vuông



Giải

a) Qua BC dựng một mặt phẳng

( )

không đi qua

A. Trong mặt

( )

ta dựng tam giác cân BCA

(BA

= CA

). Khi đó, phép chiếu song song lên

( )

theo phương chiếu

∆

= AA

biến tam giác ABC

thành tam giác cân A

BC.

b) Trong

( )

ở câu a), ta dựng tam giác BCA

và

c) Chọn phương chiếu

∆

= AA

. Trong mặt phẳng

( )

câu a), ta dựng tam giác vuông BCA



(

)

BA C

và chọn phương

∆

= AA

Bài 5.4.

a) Vẽ hình biểu diễn của một hình vuông nội tiếp trong một đường tròn.

b) Vẽ hình biểu diễn của một lục giác đều.



Giải

a) Vẽ tam giác tam giác vuông nội tiếp trong một đường tròn . Qua O

ta kẻ hai dây ME và NF của elip lần lượt song song với AC và AB. Khi

đó, tứ giác MNEF là hình biểu diễn của một hình vuông nội tiếp trong

một đường tròn.

b) Xét hình l

ục giác

ều ABCDEF , ta nhận thấy:

- Tứ giác OABC là hình thoi

- Các điểm D, E, F lần lượt là các điểm đối xứng của các điểm A, B, C

qua tâm O

Từ đó, suy ra cách vẽ hình biểu diễn của lục giác đều ABCDEF như

- Vẽ hình bình hành O'A'B'C' biểu diễn cho hình thoi OABC.

- Lấy cá điểm D', E', F' lần lượt đối xứng với các điểm A', B' C' qua O',

ta được hình biểu diễn A' B'C'D'E'F' của hình lục giác đều ABCDEF.

Toán 11 GV. Lư Sĩ Pháp

HÌNH HỌC 11 Chương II. ĐT & MP Trong KG. QHSS

ÔN TẬP CHƯƠNG II

A. CÁC DẠNG TOÁN CƠ BẢN CỦA CHƯƠNG II

DẠNG 1. Tìm giao tuyến của hai mặt phẳng

Phương pháp 1. (áp dụng nội dung tính chất 5 của bài 1 sgk/47). Ta tìm hai điểm chung phân biệt của

hai mặt phẳng. Cụ thể:

(

)

(

)

( ) ( ) ( ) ( )

N MN

M N



∈ α ∩ β



∈ α ∩ β

⇒

= α ∩ β





≡





Phương pháp 2. (Áp dụng HQ của nội dung Định lí 2 của bài sgk/57)

Cụ thể:

(

)

(

)

( )

( ) ( )

/ /

, / / / /

a b



≡ β



⇒

α ∩ β = ∆ ∆



⊂ α



⊂ β



hoặc trùng với một trong hai đường thẳng

và

Phương pháp 3. (Áp dụng nội dung Định lí 2 của bài 3 sgk/61)

Cụ thể:

(

)

( )

( ) ( )

/ /

, / /

b b a





⇒ β ∩ α =



⊂ β





DẠNG 2. Tìm giao điểm của đường thẳng và mặt phẳng

Phương pháp: Tìm giao điểm của đường thẳng

và mặt phẳng

(

)

, phương pháp chung:

 

(

)

( )

I d

d d I



⊂ α



⇒ = ∩ α



∩ =





  Chọn mặt phẳng

(

)

chứa đường thẳng

sao cho dễ tìm giao tuyến với

(

)

là

Cụ thể:

(

)

( ) ( ) ( )

d I d

d d I



⊂ β



β ∩ α = ⇒ = ∩ α





∩ =





DẠNG 3. Chứng đường thẳng song song với mặt phẳng

Phương pháp: (áp dụng nội dung Định lí 1 của bài 3 sgk/61)

Cụ thể:

(

)

( )

/ / / /

d d d



⊂ α



⇒ α





⊂ α





DẠNG 4. Chứng minh hai mặt phẳng song song

Phương pháp: (Áp dụng nội dung Định lí 1 của bài 4 sgk/64)

Cụ thể:

(

)

( ) ( ) ( ) ( )

/ / , / / / /

a b

a b M



⊂ α



β β ⇒ α β





∩ =





DẠNG 5. Dựng thiết diện

Dựng thiết diện của hình (H) khi cắt bởi mặt phẳng

(

)

Phương pháp chung: Ta tìm các giao tuyến (nếu có) của

(

)

với mặt đáy và các mặt bên của hình (H).

Đoạn nối giữa các giao tuyến cho ta một hình, hình đó là thiết diện cần tìm.

Lưu ý:

Toán 11 GV. Lư Sĩ Pháp

HÌNH HỌC 11 Chương II. ĐT & MP Trong KG. QHSS



Dựng thiết diện song song với một đường thẳng:

(

)

đi qua một điểm và song song với hai đường

thẳng trong hình (H) hoặc qua hai điểm và song song với một đường thẳng trong hình (H).

Phương pháp: Cho đường thẳng

song song với mặt phẳng

(

)

. Nếu mặt phẳng

(

)

chứa

và cắt

(

)

theo giao tuyến

thì

song song với



Dựng thiết diện song song với một mặt phẳng trong hình (H):

(

)

song song với một mặt phẳng

nào đó trong hình (H).

Phương pháp:



ÁP d

ụ

: Khi

(

)

song song với một mặt phẳng

(

)

nào đó thì

(

)

sẽ song song với tất cả đường

thẳng trong

(

)

 Để xác định giao tuyến của

(

)

với các mặt của hình (H), ta làm như sau:

 Tìm đường thẳng

nằm trong

(

)

 Vì

(

)

(

)

/ /

α β

nên

(

)

cắt những mặt phẳng chứa

theo các giao tuyến song song với

DẠNG 6. Chứng minh hai đường thẳng song song

Phương pháp:

1. Chứng minh chúng cùng thuộc một mặt phẳng và dùng phương pháp chứng minh hai đường thẳng

song song trong hình học phẳng( như tính chất đường trung bình của tam giác, định lí Talét đảo, tính chất

song song của hai đường thẳng cùng vuông góc với đường thẳng thứ ba, …)

2. Chứng minh chúng cùng song song với đường thẳng thứ ba.

3. Dùng tính chất: Hai mặt phẳng phân biệt lần lượt chứa hai đường thẳng song song thì giao tuyến của

chúng(nếu có) cũng song song với hai đường thẳng ấy. Tức là:

c a b

a b

( )

/ / / /

/ /

( ) ( )

α β



∈



∈



⇒





∩ =



4. Dùng định lý về giao tuyến của ba mặt phẳng:

a b c

a b

/ / / /

, ñoàng quy

α γ

β γ

α β



∩ =





∩ = ⇒









∩ =



DẠNG 7. Chứng minh ba điểm thẳng hàng, ba đường thẳng đồng qui.

Phương pháp:

 Để chứng minh ba điểm thẳng hàng, ta chứng minh chúng cùng thuộc hai mặt phẳng phân biệt. Khi đó

chúng thuộc giao tuyến hai mặt phẳng đó.

 Để chứng minh ba đường thẳng đồng qui, ta chứng minh giao điểm của hai đường thẳng này là điểm

chung của hai mặt phẳng mà giao tuyến là đường thẳng thứ ba.

B. BÀI TẬP

Bài 1. Cho hình thang ABCD và ABEF có chung đáy lớn AB và không cùng nằm trong một mặt phẳng

a) Tìm giao tuyến của các mặt phẳng sau: (AEC) và (BFD); (BCE) và (ADF)

b) Lấy M là một điểm thuộc đoạn DF. Tìm giao tuyến của đường thẳng AM với mp(BCE)

c) Chứng minh hai đường thẳng AC và BF không cắt nhau.



Giải

a) Gọi

G AC BD H AE BF

;

= ∩ = ∩

Ta có

AEC BFD HG

( ) ( )

∩ =

Tương tự: Gọi

I AD BC K AF BE

;

= ∩ = ∩

Ta có:

BCE ADF IK

( ) ( )

∩ =

b) Gọi

N AM IK

= ∩

. Ta có:

N AM BCE

( )

= ∩

c) Nếu AC và BF cắt nhau thì hai hình thang đã cho cùng

nằm trên một mặt phẳng. Điểu này trái với giả thiết.

Toán 11 GV. Lư Sĩ Pháp

HÌNH HỌC 11 Chương II. ĐT & MP Trong KG. QHSS

Bài 2. Cho hình chóp S.ABCD, có đáy ABCD là hình thang và AB là đáy lớn. Gọi M, N theo thứ tự là

trung điểm của các cạnh SB và SC.

a) Tìm giao tuyến của hai mặt phẳng (SAD) và (SBC)

b) Tìm giao điểm của đường thẳng SD với mặt phẳng (AMN)

Tìm thiết diện của hình chóp S.ABCD cắt bởi mặt phẳng (AMN).



Giải

a) Gọi

E AD BC

= ∩

. Ta có

SAD SBC SE

( ) ( )

∩ =

b) Gọi

F SE MN P SD AF

= ∩ = ∩

Ta có:

P SD AMN

( )

= ∩

c) Thiết diện là tứ giác APNM

Bài 3. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi O là giao điểm hai đường chéo, M,

N, P, theo thứ tự là trung điểm các đoạn thẳng SA, BC, CD.

a) Tìm giao tuyến của hai mặt phẳng (SAC) và (SBD).

b) Tìm giao điểm của đường thẳng SO với mp(MNP).

c) Tìm thiết diện của hình chóp khi cắt bởi mp(MNP).



Giải

a) Ta có

∩ =

( ) ( )

SAC SBD SO

b) Gọi

= ∩ = ∩

;

H AC NP I SO MH

. Ta có:

= ∩

( )

I SO MNP

c) Gọi

= ∩ = ∩

;

E AB NP F AD NP

= ∩ = ∩

;

R SB ME Q SD MF

. Thiết diện cần tìm là

ngũ giác MQPNR

Bài 5. Cho tứ diện ABCD. Trên AD lấy trung điểm M, trên cạnh BC lấy một điểm N bất kì khác B và C.

Gọi (P) là mặt phẳng qua đường thẳng MN và song song với CD.

a) Xác định thiết diện của tứ diện ABCD khi cắt bởi mp(P).

b) Xác định vị trí N trên BC sau cho thiết diện là một hình bình hành.



Giải

a) T

a có

CD ACD CD P ACD P MJ

( ), / /( ) ( ) ( )

⊂ ⇒ ∩ =

. Sao

cho MJ // CD ( J thuôc trên AC)

Tương tự, ta có:

BCD P NI

( ) ( )

∩ =

, sao cho

NI//CD và I thuộc BD.

Vậy thiết diện là hình thang MINJ (MJ // NI)

b) Ta có:

. Vậy để hình thang MINJ là

hình bình hành

NI MJ CD

⇔ = =

Suy ra: N là trung điểm của BC

Toán 11 GV. Lư Sĩ Pháp

HÌNH HỌC 11 Chương II. ĐT & MP Trong KG. QHSS

Bài 6. Cho hình chóp S.ABCD đáy là hình bình hành. Gọi M là trung điểm của SC.

a) Tìm giao điểm I của AM với (SBD). Chứng minh: IA = 2IM

b) Tìm giao điểm F của SD với (ABM). Chứng minh F là trung điểm của SD

c) Gọi N là một điểm tùy ý trên AB. Tìm giao điểm của MN với (SBD).



Giải

a) Tìm giao điểm I của AM với (SBD):

Gọi

O AC BD

= ∩

. Trong mp (SAC), có

I SO AM

= ∩

khi đó

I AM

I SO SBD

I AM SBD

( )



∈



∈ ⊂



⇒ = ∩

Chứng minh IA = 2IM:

Trong tam giác

SAC

;

là trung tuyến và

I SO AM

= ∩

⇒

I là trọng tâm của tam giác SAC => IA =

2IM.

b) Tìm giao điểm F của SD với (ABM)

Trong (SBD), gọi

F SD BI

= ∩

khi đó:

F SD

F BI ABM

F SD ABM

( )



∈



∈ ⊂



⇒ = ∩

Chứng minh

là trung điểm của

là trọng

tâm tam giác

SAC

= 2

Trong tam giác

SBD

có:

là trung tuyến và

suy ra

là trọng tâm của tam giác SBD.

Từ đó suy ra:

là trung điểm của

c) Tìm giao điểm của

với (

SBD

Gọi

K MN BI

= ∩

,(Trong (

ABM

)), khi đó

K MN

K MN SBD

K BI SBD

( )



∈

⇒ = ∩



∈ ⊂



BÀI TẬP ĐỀ NGHỊ

Bài 1. Cho hình chóp

S.ABCD

có

và

không song song. Gọi

là một điểm thuộc miền trong của

tam giác

SCD

a) Tìm giao điểm

của đường thẳng

và mặt phẳng (

SBM

)

b) Tìm giao tuyến của hai mặt phẳng (

SBM

) và (

SAC

)

c) Tìm giao điểm

của đường thẳng

và mp(

SAC

)

d) Tìm giao điểm

của

và mp(

ABM

), từ đó suy ra giao tuyến của hai mặt phẳng (

SCD

) và (

ABM

)

Bài 2. Cho hình chóp

S.ABCD

. Gọi

M, N

lần lượt là trung điểm các cạnh

SA, SD

và

là trọng tâm của

tam giác

SCD

. Tìm giao điểm của:

và mp(

ABCD

) b)

và mp(

SAG

)

Bài 3. Cho hình chóp

S.ABCD

. Gọi

là một điểm nằm trong tam giác

SCD

a) Tìm giao tuyến của hai mặt phẳng (

SBM

) và (

SAC

)

b) Tìm giao điểm của đường thẳng

và mp(

SAC

)

c) Xác định thiết diện của hình chóp khi cắt bởi mặt phẳng (

ABM

)

Bài 4. Cho hình chóp

S.ABCD

có đáy là hình thang

ABCD

(

). Gọi

I, J

theo thứ tự là trung điểm của các cạnh

và

a) Xác định giao tuyến của hai mặt phẳng (

SAD

) và (

SBC

), (

SAC

) và (

SBD

)

b) Tìm giao điểm của đường thẳng

với mp(

AIJ

)

c) Xác định thiết diện của hình chóp

S.ABCD

cắt bởi mp(

AIJ

)

Bài 5. Cho hình chóp

S ABCD

có đáy

ABCD

là hình bình hành. Gọi

là điểm giữa

và

;

là điểm

nằm giữa

và

; giao điểm của hai đường thẳng

và

là

a) Tìm giao điểm của mặt phẳng (

CMN

) với đường thẳng

b) Xác định giao tuyến của hai mặt phẳng (

SAD

) và (

CMN

)

c) Xác định thiết diện của hình chóp khi cắt bởi mặt phẳng (

CMN

Bài 6. Cho hình thang

ABCD

và

ABEF

có chung đáy lớn

và không cùng nằm trong một mặt phẳng

Toán 11 GV. Lư Sĩ Pháp

HÌNH HỌC 11 Chương II. ĐT & MP Trong KG. QHSS

a) Tìm giao tuyến của các mặt phẳng sau: (

AEC

) và (

BFD

); (

BCE

) và (

ADF

)

b) Lấy

là một điểm thuộc đoạn

. Tìm giao tuyến của đường thẳng

với mp(

BCE

)

Bài 7. Cho hình chóp

S.ABCD

đáy

ABCD

là hình bình hành. Trên đoạn

lấy điểm

sao cho 2

, trên đoạn

lấy điểm

sao cho 2

a) Tìm giao tuyến của hai mặt phẳng (

SAC

) và (

SBD

); (

SAD

) và (

SBC

)

b) Chứng minh rẳng:

c) Điểm

nằm trên cạnh

không trùng với

. Tìm giao tuyến hai mp (

MNP

) và (

SCD

)

Bài 8. Cho hình chóp

S.ABCD

có đáy

ABCD

là hình bình hành.

a) Hãy xác định giao tuyến của các mặt phẳng (

SAB

) và (

SCD

); (

SBC

) và (

SAD

)

là điểm thuộc cạnh

, tìm thiết diện của hình chóp với mp(

ABM

). Thiết diện là hình gì?

Bài 9. Cho hình chóp

S.ABCD

, có đáy

ABCD

là hình thang và

là đáy lớn. Gọi

theo thứ tự là

trung điểm của các cạnh

và

a) Tìm giao tuyến của hai mặt phẳng (

SAD

) và (

SBC

)

b) Tìm giao điểm của đường thẳng

với mặt phẳng (

AMN

)

c) Tìm thiết diện của hình chóp

S.ABCD

cắt bởi mặt phẳng (

AMN

Bài 10. Cho hình chóp

S.ABCD

có đáy

ABCD

là hình bình hành. Gọi

là giao điểm hai đường chéo. Gọi

M, N, P

, theo thứ tự là trung điểm các đoạn thẳng

SA, BC, CD

a) Tìm giao tuyến của hai mặt phẳng (

SAC

) và (

SBD

b) Tìm giao điểm của đường thẳng

với mp(

MNP

c) Tìm thiết diện của hình chóp khi cắt bởi mp(

MNP

Bài 11. Cho hình chóp

S.ABCD

có đáy

ABCD

là hình bình hành. Gọi

lần lượt là trung điểm của

và

a) Chứng minh rằng

song song với các mặt phẳng (

SBC

) và (

SAD

b) Gọi

là trung điểm của

. Chứng minh rằng

và

đều song song với mp (

MNP

)

Bài 12. Cho hình chóp

S.ABCD

có đáy

ABCD

là hình thang, đáy lớn

và

= 2

. Gọi

là giao

điểm của

và

là trọng tâm của tam giác

SCD

a) Chứng minh rằng

// (

SBC

)

c) Cho

là trung điểm của

. Chứng minh rằng

// (

SAB

)

d) Giả sử

nằm trên đoạn

sao cho

SC SI

. Chứng minh rằng

// (

BID

Bài 13. Cho hình chóp

S.ABCD

có đáy là hình thang (

). Gọi

M, N, E

lần lượt là trung

điểm của

AB, CD, SA

a) Chứng minh rằng: (

MEN

) // (

SBC

)

b) Trong tam giác

SAD

vẽ

(

)

F SD

∈

. Chứng minh rằng

là giao điểm của mặt phẳng (

MNE

)

với

. Từ đó suy ra thiết diện của hình chóp khi cắt bởi mp(

MNE

) là hình gì?

Bài 14. Cho tứ diện

ABCD

. Gọi

lần lượt là trọng tâm của các tam giác

ABC, ACD, ABD

Chứng minh mặt phẳng (

) song song với mặt phẳng (

BCD

Bài 15. Cho hình chóp

S.ABCD

có đáy là hình bình hành

ABCD

là giao điểm của

và

là

trung điểm của

. Tìm thiết diện của mặt phẳng

( )

với hình chóp

S.ABCD

nếu

( )

qua

và đồng

thời song song với

và

Bài 16. Cho tứ diện

ABCD

. Trên

lấy điểm

. Cho

( )

là mặt phẳng qua

, song song với hai đường

thẳng

và

a) Tìm giao tuyến của

( )

với các mặt của tứ diện

b) Thiết diện của tứ diện cắt bởi mặt phẳng

( )

là hình gì?

Bài 17. Cho hình chóp

S.ABCD

có đáy

ABCD

là một tứ giác lồi. Gọi

là giao điểm của hai đường chéo

và

. Xác định thiết diện của hình chóp cắt bởi mặt phẳng

( )

đi qua

, song song với

và

Thiết diện đó là hình gì?

Bài 18. Cho hình chóp

S.ABCD

có đáy là hình bình hành. Xác định thiết diện của hình chóp khi cắt bởi

mặt phẳng đi qua trung điểm

của cạnh

, song song với

và

Bài 19. Cho hình chóp

S.ABCD

có đáy

ABCD

là hình bình hành. Gọi

là giao điểm của

và

. Gọi

, theo thứ tự là trung điểm các đoạn thẳng

Toán 11 GV. Lư Sĩ Pháp

HÌNH HỌC 11 Chương II. ĐT & MP Trong KG. QHSS

a) Tìm giao tuyến của mp(

SAC

) và mp(

MNP

). Từ đó suy ra giao điểm của đường thẳng

với

mp(

MNP

b) Xác định thiết diện của hình chóp khi cắt bởi mặt phẳng

(

)

qua

đồng thời song song với

và

Bài 20. Cho hình chóp

S.ABCD

có đáy

ABCD

là hình bình hành. Gọi

là giao điểm của

và

. Gọi

, theo thứ tự là trung điểm các đoạn thẳng

a) Tìm giao điểm của đường thẳng

với mp(

MNP

b) Xác định thiết diện của hình chóp khi cắt bởi mặt phẳng

(

)

qua

đồng thời song song với

và

Thiết diện là hình gì?

Bài 21. Cho hình chóp

S.ABCD

có đáy

ABCD

là hình bình hành tâm

. Gọi

M, N

lần lượt là trung điểm

SA, CD

a) Chứng minh rằng (

OMN

) // (

SBC

)

b) Xác định thiết diện của hình chóp với mặt phẳng (

OMN

)

Bài 22. Cho hình chóp

S.ABCD

có đáy

ABCD

là hình bình hành tâm

. Gọi

I, J

lần lượt là trung điểm

a) Chứng minh rằng:

//(

SAD

)

b) Gọi

(

)

là mặt phẳng qua

và song song với

. Xác định thiết diện của hình chóp

S.ABCD

khi cắt

bởi mp

(

)

Bài 23. Cho hình chóp

S.ABCD

có đáy

ABCD

là hình bình hành tâm

. Gọi

P, Q

lần lượt là trung điểm

a) Chứng minh rằng (

OPQ

) // (

SAD

)

b) Xác định thiết diện của hình chóp với mặt phẳng (

OPQ

)

Bài 24. Cho hình chóp

S.ABCD

có đáy

ABCD

là hình bình hành tâm

. Gọi

M, N

lần lượt là trung điểm

SD, BC

a) Chứng minh rằng:

//(

SAB

)

Gọi

(

)

là mặt phẳng qua

và song song với

. Xác định thiết diện của hình chóp

S.ABCD

khi cắt

bởi mp

(

)

Bài 25. Cho hình chóp

S.ABCD

có đáy

ABCD

là hình thang (

là đáy lớn). Gọi

M, N

lần lượt là trung

điểm của

và

a) Tìm giao điểm của đường thẳng

với mặt phẳng (

SBD

b) Gọi

( )

là mặt phẳng qua

và song song với

. Xác định thiết diện của hình chóp cắt bởi mặt

phẳng

( )

Bài 26. Cho hình chóp

S.ABCD

có đáy

ABCD

là hình bình hành. Lấy một điểm

trên cạnh

nhưng

không trùng với

và

a) Tìm giao điểm của đường thẳng

với mặt phẳng (

SBD

b) Gọi

( )

là mặt phẳng qua

và đồng thời song song với

AB, SC

. Xác định thiết diện của hình chóp cắt

bởi mặt phẳng

( )

Bài 27. Cho hình chóp

S.ABCD

, đáy

ABCD

hình bình hành tâm

. Gọi

M, N

lần lượt là trung điểm của

và

. Tìm giao điểm của

với mặt phẳng (

AMN

Bài 28. Cho hình chóp

S.ABCD

có đáy

ABCD

là một tứ giác lồi. Gọi

là giao điểm của hai đường chéo

và

;

là trung điểm của

. Xác định thiết diện của hình chóp khi cắt bởi mặt phẳng

(

)

qua

song song với

và

Bài 29. Cho hình chóp

S.ABCD

, đáy

ABCD

là hình thang với

là đáy lớn. Gọi

M, N

lần lượt là trung

điểm của

và

. Tìm giao điểm của

với mặt phẳng (

BMN

Bài 30. Cho hình chóp S

.ABCD

, đáy

ABCD

là hình bình hành. Xác định thiết diện của hình chóp khi cắt

bởi mặt phẳng

(

)

qua trung điểm

của

, song song với

và

Toán 11 GV. Lư Sĩ Pháp

HÌNH HỌC 11 Chương II. ĐT & MP Trong KG. QHSS

Bài 31. Cho hình chóp S.ABCD có đáy là một tứ giác lồi. Gọi O là giao điểm của hai đường chéo AC và

BD, M là trung điểm của cạnh SA.

a) Xác định thiết diện của hình chóp khi cắt bởi mặt phẳng (P) qua M, song song với SO và BC.

b) Xác định thiết diện của hình chóp khi cắt bởi mặt phẳng (Q) qua O, song song với BM và SD

Bài 32. Cho hình chóp S.ABCD có đáy ABCD là hình thang (AD // BC). Gọi M, N, G lần lượt là trung

điểm của AB, CD và trọng tâm tam giác SAD.

a) Xác định giao tuyến của mặt phẳng (SAB) và mặt phẳng (SCD)

b) Xác định thiết diện của hình chóp với mặt phẳng (MNG)

c) Gọi O là giao điểm của AC và BD. Giả sử đường thẳng SO cắt mặt phẳng (MNG) tại E. Hãy xác định

điểm E.

Bài 33. Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a, cạnh bên bằng b. Gọi M, N lần lượt là

trung điểm của AB và BC. Tính diện tích thiết diện của hình chóp với mặt phẳng đi qua M, N và song

song với SB.

Bài 34. CHo hình hộp ABCD.A'B'C'D'. Vẽ thiết diện của hình hộp tạo bởi mặt phẳng đi qua trung điểm

M, N của các cạnh AB, AD và tâm O của hình bình hành CDD'C'.

Bài 35. Cho hình lập phương ABCD.A'B'C'D' và các trung điểm E, F của các cạnh AB, DD'. Hãy xác

định các thiết diện của hình lập phương cắt bởi các mặt phẳng (EFB), (EFC), (EFC') và (EFK) với K là

trung điểm của cạnh B'C'.

Bài 36. Cho tứ diện đều ABCD có cạnh đáy bằng a, cạnh bên bằng b. Gọi M, N lần lượt là trung điểm của

AB và BC. Tính diện tích thiết diện của hình chóp với mặt phẳng (P) đi qua M, N và song song với SB.

Bài 37. Cho hình chóp S.ABCD có đáy là hình thang (AD//BC, AD > BC). Gọi M, N, E lần lượt là trung

điểm của AB, CD, SA.

a) Chứng minh rằng: (MEN) // (SBC)

b) Trong tam giác SAD vẽ EF // AD

(

)

F SD

∈

. Chứng minh rằng F là giao điểm của mặt phẳng (MNE)

với SD. Từ đó suy ra thiết diện của hình chóp khi cắt bởi mp(MNE) là hình gì?

Toán 11 GV. Lư Sĩ Pháp

HÌNH HỌC 11 Chương II. ĐT & MP Trong KG. QHSS

CHƯƠNG II

ĐƯỜNG THẲNG VÀ MẶT PHẲNG TRONG KHÔNG GIAN

QUAN HỆ SONG SONG

PHẦN TRẮC NGHIỆM

Câu 1: Cho hình chóp

S ABCD

có đáy

ABCD

là hình bình hành. Gọi

, ,

M N P

theo thứ tự là trung điểm

các đoạn thẳng

, ,

SA BC CD

. Gọi O là giao điểm của hai đường chéo của hình bình hành

ABCD

(như hình

vẽ). Xác định giao điểm I của đường thẳng SO với mặt phẳng

( ).

MNP

= ∩

I SO NP

= ∩

I SO MH

= ∩

I SO MP

= ∩

I SO MN

Câu 2: Cho tứ diện

ABCD

. Gọi

M N

lần lượt là trung điểm các cạnh AD và BC; G là trọng tâm của tam

giác

BCD

. Xác định giao điểm của đường thẳng

và mặt phẳng

(

)

ABC

A. Giao điểm của MG và đường thẳng

B. Đ

ể

C. Đ

ể

Giao

ể

m c

ủ

đườ

ng th

ẳ

ng MG và

đườ

ng th

ẳ

Câu 3:

ệ

đề

nào d

ướ

ây

úng ?

ế

u hai

đườ

ng th

ẳ

ng song song v

ớ

i nhau l

ầ

n l

ượ

t n

ằ

m trong hai m

ặ

t ph

ẳ

ng phân bi

ệ

( )

và

( )

thì

( )

và

( )

song song v

ớ

i nhau.

Qua m

ộ

ể

m n

ằ

m ngoài m

ặ

t ph

ẳ

ng cho tr

ướ

c ta v

ẽ

đượ

c m

ộ

t và ch

ỉ

ộ

đườ

ng th

ẳ

ng song song

ớ

i m

ặ

t ph

ẳ

ng cho tr

ướ

ế

u hai m

ặ

t ph

ẳ

( )

và

( )

song song v

ớ

i nhau thì m

ọ

đườ

ng th

ẳ

ng n

ằ

m trong

( )

đề

u song

song v

ớ

i m

ọ

đườ

ng th

ẳ

ng n

ằ

m trong m

ặ

t ph

ẳ

( )

ế

u hai m

ặ

t ph

ẳ

( )

và

( )

song song v

ớ

i nhau thì m

ọ

đườ

ng th

ẳ

ng n

ằ

m trong

( )

đề

u song

song v

ớ

( )

Câu 4:

Cho hình chóp

S ABCD

, có

áy

ABCD

là hình bình hành. Gi

ả

ử

M thu

ộ

ạ

n th

ẳ

ng SB . M

ặ

ẳ

ng (ADM) c

ắ

t hình chóp

S ABCD

theo m

ộ

t thi

ế

t di

ệ

n là hình gì?

Hình ch

ữ

ậ

Hình bình hành.

Hình tam giác.

Hình thang.

Câu 5:

ệ

đề

nào d

ướ

ây

úng ?

Hai

đườ

ng th

ẳ

ng phân bi

ệ

t cùng n

ằ

m trong m

ộ

t m

ặ

t ph

ẳ

ng thì không chéo nhau.

Hai

đườ

ng th

ẳ

ng phân bi

ệ

t không c

ắ

t nhau thì chéo nhau.

Hai

đườ

ng th

ẳ

ng phân bi

ệ

t không song song thì chéo nhau.

Hai

đườ

ng th

ẳ

ng phân bi

ệ

t l

ầ

n l

ượ

t thu

ộ

c hai m

ặ

t ph

ẳ

ng khác nhau thì chéo nhau.

Câu 6:

Cho tam giác

ABC

, l

ấ

ể

m I trên c

ạ

nh AC kéo dài. M

ệ

đề

nào d

ướ

ây sai ?

( ).

BI ABC

⊄

( ).

I ABC

∈

( ) ( ).

ABC BIC

≡

( ).

A ABC

∈

Câu 7:

Cho hai

đườ

ng th

ẳ

ng phân bi

ệ

t a và b trong không gian. Có bao nhiêu v

ị

trí t

ươ

đố

i gi

ữ

a a và b

cùng ch

ứ

a trong m

ộ

t m

ặ

t ph

ẳ

ng.

Câu 8:

Cho t

ứ

ệ

SABC

có

E F

ầ

n l

ượ

t là trung

ể

m c

ủ

a SB, AB . L

ấ

y G là m

ộ

ể

m trên

ạ

n th

ẳ

AC sao cho G không trùng v

ớ

i trung

ể

m AC . G

ọ

i I là giao

ể

m c

ủ

a GF và m

ặ

t ph

ẳ

ng (SBC). Thi

ế

ệ

n c

ủ

a t

ứ

ệ

n khi c

ắ

t b

ở

i m

ặ

t ph

ẳ

( )

EFG

là hình nào d

ướ

ây ?

Toán 11 GV. Lư Sĩ Pháp

HÌNH HỌC 11 Chương II. ĐT & MP Trong KG. QHSS

Hình bình hành.

Hình thang.

Tam giác.

Hình thoi.

Câu 9:

ệ

đề

nào d

ướ

ây sai ?

ế

u hai m

ặ

t ph

ẳ

ng phân bi

ệ

t cùng song song v

ớ

i m

ộ

đườ

ng th

ẳ

ng thì giao tuy

ế

n c

ủ

a chúng (n

ế

có) c

ng song song v

ớ

đườ

ng th

ẳ

ó.

ế

u m

ặ

t ph

ẳ

( )

ứ

a hai

đườ

ng th

ẳ

ng c

ắ

t nhau

a b

và

a b

cùng song song v

ớ

i m

ặ

t ph

ẳ

( )

thì

( )

song song v

ớ

( )

Qua m

ộ

ể

m n

ằ

m ngoài m

ặ

t ph

ẳ

ng cho tr

ướ

c có nhi

ề

u h

n m

ộ

t m

ặ

t ph

ẳ

ng song song v

ớ

i m

ặ

ẳ

ã cho.

ế

đườ

ng th

ẳ

ng d không n

ằ

m trong m

ặ

t ph

ẳ

( )

và d song song v

ớ

đườ

ằ

m trong

( )

thì d song song v

ớ

( )

Câu 10:

Cho hình chóp

S ABCD

có

áy là hình bình hành. G

ọ

I J

ầ

n l

ượ

t là trung

ể

m c

ủ

và

. Giao tuy

ế

n c

ủ

a hai m

ặ

t ph

ẳ

(

)

SAB

và

(

)

SCD

là

đườ

ng th

ẳ

ng song song

đườ

ng th

ẳ

ng nào d

ướ

ây ?

A. Đườ

ng th

ẳ

B. Đườ

ng th

ẳ

C. Đườ

ng th

ẳ

D. Đườ

ng th

ẳ

Câu 11:

Cho hai hình bình hành

ABCD

và

ABEF

ằ

m trong hai m

ặ

t ph

ẳ

ng phân bi

ệ

t. Kh

ẳ

đị

nh nào

ướ

ây

úng ?

(

)

(

)

|| .

ABD EFC

(

)

|| .

EC ABF

(

)

|| .

AD BEF

(

)

(

)

|| .

AFD BEC

Câu 12:

Trong các hình sau

ây, hình nào bi

ể

u di

ễ

n cho hình l

ậ

p ph

ươ

ng ?

Hình a)

Hình a) và c)

Hình b)

Hình c) và b)

Câu 13:

ệ

đề

nào d

ướ

ây

úng ?

Hình chi

ế

u song song c

ủ

a hai

đườ

ng th

ẳ

ng chéo nhau có th

ể

ắ

t nhau, trùng nhau, song song v

ớ

nhau.

Hình chi

ế

u song song c

ủ

a hai

đườ

ng th

ẳ

ng chéo nhau thì c

ắ

t nhau.

Hình chi

ế

u song song song c

ủ

a hai

đườ

ng th

ẳ

ng chéo nhau có th

ể

trùng nhau.

Hình chi

ế

u song song c

ủ

a hai

đườ

ng th

ẳ

ng chéo nhau có th

ể

song song v

ớ

i nhau.

Câu 14:

ệ

đề

nào d

ướ

ây

úng ?

ế

u hai m

ặ

t ph

ẳ

ng song song thì m

ỗ

đườ

ng th

ẳ

ng n

ằ

m trên m

ặ

t ph

ẳ

ng này

đề

u song song v

ớ

i m

ọ

đườ

ng th

ẳ

ng n

ằ

m trong m

ặ

t kia.

ộ

đườ

ng th

ẳ

ng c

ắ

t m

ộ

t trong hai

đườ

ng th

ẳ

ng song song thì c

ắ

đườ

ng th

ẳ

ng còn l

ạ

ế

u hai m

ặ

t ph

ẳ

ng song song thì m

ọ

đườ

ng th

ẳ

ng n

ằ

m trên m

ặ

t ph

ẳ

ng này

đề

u song song v

ớ

i m

ặ

ẳ

ng kia.

Hai m

ặ

t ph

ẳ

ng phân bi

ệ

t cùng song song v

ớ

i m

ộ

đườ

ng th

ẳ

ng thì song song v

ớ

i nhau.

Câu 15:

Cho hình l

ng tr

ụ

tam giác

/ / /

ABC A B C

. G

ọ

i I, J l

ầ

n l

ượ

t là tr

ọ

ng tâm c

ủ

a các tam giác

ABC

và

/ / /

A B C

. Thi

ế

t di

ệ

n t

ạ

o b

ở

i m

ặ

t ph

ẳ

( )

AIJ

ớ

i l

ng tr

ụ

ã cho là hình nào d

ướ

ây ? (tham kh

ả

o hình

ẽ

)

Toán 11 GV. Lư Sĩ Pháp

HÌNH HỌC 11 Chương II. ĐT & MP Trong KG. QHSS

Hình bình hành

Hình thang.

Tam giác cân.

Tam giác vuông.

Câu 16:

Cho t

ứ

ệ

ABCD

. G

ọ

i M, N l

ầ

n l

ượ

t là trung

ể

m c

ủ

a AB và AC , E là

ể

m trên c

ạ

nh CD v

ớ

ED EC

. Tìm thi

ế

t di

ệ

n t

ạ

o b

ở

i m

ặ

t ph

ẳ

(

)

MNE

và t

ứ

ệ

ABCD

. (tham kh

ả

o hình v

ẽ

)

Hình bình hành

MNEF

ớ

i F là

ể

m trên c

ạ

nh BD mà

|| .

EF BC

Hình thang

MNEF

ớ

i F là

ể

m trên c

ạ

nh BD mà

|| .

EF BC

Tam giác

MNE

ứ

giác

MNEF

ớ

i F là

ể

m b

ấ

t kì trên

Câu 17:

Cho hình chóp

S ABCD

ớ

áy là t

ứ

giác

ABCD

. Thi

ế

t di

ệ

n c

ủ

a m

ặ

t ph

ẳ

( )

tùy ý v

ớ

i hình

chóp không th

ể

là hình nào d

ướ

ây ?

Hình t

ứ

giác.

Hình ng

giác.

Hình tam giác.

Hình l

ụ

c giác.

Câu 18:

ế

u ba

đườ

ng th

ẳ

ng không cùng n

ằ

m trong m

ộ

t m

ặ

t ph

ẳ

ng và

ôi m

ộ

t c

ắ

t nhau thì ba

đườ

ẳ

ó nh

ế

nào ?

Cùng song song v

ớ

i m

ộ

t m

ặ

t ph

ẳ

ng.

Trùng nhau.

ạ

o thành m

ộ

t tam giác.

D. Đồ

ng quy.

Câu 19:

Cho hình chóp

S ABCD

có

áy là m

ộ

t hình bình hành. G

ọ

/ / / /

, , ,

A B C D

ầ

n l

ượ

t là trung

ể

ủ

a các c

ạ

, ,

SA SB SC

và

. Tìm m

ệ

đề

Đúng

trong các m

ệ

đề

sau ?

/ /

|| .

A C BD

(

)

/ /

A C SBD

(

)

/ /

A B SAD

(

)

(

)

/ / /

|| .

A C D ABC

Câu 20:

Cho t

ứ

ệ

SABC

có

E F

ầ

n l

ượ

t là trung

ể

m c

ủ

a SB, AB . L

ấ

y G là m

ộ

ể

m trên

ạ

ẳ

ng AC sao cho G không trùng v

ớ

i trung

ể

m AC . G

ọ

i I là giao

ể

m c

ủ

a GF và m

ặ

t ph

ẳ

ng (SBC).

ể

m I thu

ộ

đườ

ng th

ẳ

ng nào d

ướ

ây ?(tham kh

ả

o hình v

ẽ

)

Câu 21:

Cho t

ứ

ệ

n ABCD. G

ọ

i M,N l

ầ

n l

ượ

t là trung

ể

m các c

ạ

nh AB và AC . Xét v

ị

trí t

ươ

đố

i c

ủ

đườ

ng th

ẳ

ng MN và mp(BCD). Kh

ẳ

đị

nh nào d

ướ

ây

úng ?

MN n

ằ

m trong (BCD).

MN không song song (BCD).

MN // (BCD).

MN c

ắ

t (BCD).

Toán 11 GV. Lư Sĩ Pháp

HÌNH HỌC 11 Chương II. ĐT & MP Trong KG. QHSS

Câu 22:

ệ

đề

nào d

ướ

ây sai ?

Hai

đườ

ng th

ẳ

ng phân bi

ệ

t cùng song song v

ớ

i m

ộ

t m

ặ

t ph

ẳ

ng thì song song v

ớ

i nhau

ế

u m

ộ

đườ

ng th

ẳ

ng c

ắ

t m

ộ

t trong hai m

ặ

t ph

ẳ

ng song song thì c

ắ

t m

ặ

t ph

ẳ

ng còn l

ạ

Hai m

ặ

t ph

ẳ

ng phân bi

ệ

t cùng song song v

ớ

i m

ộ

t m

ặ

t ph

ẳ

ng thì song song v

ớ

i nhau

ế

u hai m

ặ

t ph

ẳ

ng song song thì m

ọ

đườ

ng th

ẳ

ng n

ằ

m trên m

ặ

t ph

ẳ

ng này

đề

u song song v

ớ

i m

ặ

ẳ

ng kia

Câu 23:

Cho hai

đườ

ng th

ẳ

ng a và b song song v

ớ

i m

ặ

t ph

ẳ

( )

. M

ệ

đề

nào d

ướ

ây

úng ?

a và b trùng nhau

a và b có th

ể

ắ

t nhau

a và b chéo nhau

a và b song song v

ớ

i nhau

Câu 24:

Cho hai

đườ

ng th

ẳ

ng a và b chéo nhau. Có bao nhiêu m

ặ

t ph

ẳ

ng ch

ứ

a a và song song v

ớ

i b?

Không có m

ặ

t ph

ẳ

ng nào

Ba m

ặ

t ph

ẳ

ộ

t m

ặ

t ph

ẳ

Hai m

ặ

t ph

ẳ

Câu 25:

ệ

đề

nào d

ướ

ây

úng ?

ế

/ /

a b

và

( ), ( )

a b

⊂ α ⊂ β

thì

( ) / /( )

α β

ế

( ) / /( )

α β

và

( ), ( )

a b

⊂ α ⊂ β

thì

/ /

a b

ế

( ) / /( )

α β

và

/ /( )

thì

/ /

a b

ế

( ) / /( )

α β

và

( )

⊂ α

thì

/ /( )

Câu 26:

ọ

n ph

ươ

ng án

Đúng

. N

ế

đườ

ng th

ẳ

song song v

ớ

i m

ặ

t ph

ẳ

( )

thì

có m

ọ

đườ

ng th

ẳ

không ch

ứ

a trong

( )

song song v

ớ

có duy nh

ấ

t m

ặ

t ph

ẳ

( )

ứ

và song song v

ớ

( )

C. đườ

ng th

ẳ

ứ

a trong m

ặ

t ph

ẳ

( )

có duy nh

ấ

t m

ặ

t ph

ẳ

( )

ứ

và

song song v

ớ

( )

Câu 27:

Cho t

ứ

ệ

ABCD

có các c

ạ

đề

u b

ằ

ng a . G

ọ

và

ầ

n l

ượ

t là tr

ọ

ng tâm các tam giác

BCD và ACD thì

ạ

1 2

G G

ằ

ng bao nhiêu?

Câu 28:

Trong các m

ệ

đề

sau, m

ệ

đề

nào

Đúng

Hai m

ặ

t ph

ẳ

ng phân bi

ệ

t cùng song song v

ớ

i m

ộ

t m

ặ

t ph

ẳ

ng thì song song v

ớ

i nhau

Hai m

ặ

t ph

ẳ

ng phân bi

ệ

t cùng song song v

ớ

i m

ộ

đườ

ng th

ẳ

ng thì song song v

ớ

i nhau

ế

u hai m

ặ

t ph

ẳ

ng phân bi

ệ

t l

ầ

n l

ượ

i qua hai

đườ

ng th

ẳ

ng song song thì song song v

ớ

i nhau

Hai

đườ

ng th

ẳ

ng phân bi

ệ

t cùng song song v

ớ

i m

ộ

t m

ặ

t ph

ẳ

ng thì song song v

ớ

i nhau

Câu 29:

Có bao nhiêu cách xác

đị

nh m

ộ

t m

ặ

t ph

ẳ

ng ?

Câu 30:

Tìm m

ệ

đề

Sai

trong các m

ệ

đề

ây:

ế

u hai m

ặ

t ph

ẳ

ng phân bi

ệ

t cùng song song v

ớ

i m

ặ

t ph

ẳ

ng th

ứ

ba thì chúng song song v

ớ

i nhau

ế

u m

ộ

đườ

ng th

ẳ

ng c

ắ

t m

ộ

t trong hai m

ặ

t ph

ẳ

ng song song v

ớ

i nhau thì s

ẽ

ắ

t m

ặ

t ph

ẳ

ng còn l

ạ

ế

u hai

đườ

ng th

ẳ

ng phân bi

ệ

t cùng song song v

ớ

i m

ộ

t m

ặ

t ph

ẳ

ng thì song song v

ớ

i nhau

ế

u hai m

ặ

t ph

ẳ

ng có m

ộ

ể

m chung thì chúng còn có vô s

ố

ể

m chung khác n

ữ

Câu 31:

Cho t

ứ

ệ

ABCD

có các c

ạ

đề

u b

ằ

. L

ấ

ể

m M trên AB v

ớ

. Di

ệ

n tích c

ủ

thi

ế

t di

ệ

n c

ủ

a hình t

ứ

ệ

n khi c

ắ

t b

ở

i m

ặ

t ph

ẳ

ng qua M và song song v

ớ

i mp(BCD) là :

Câu 32:

Cho hình chóp

S ABCD

. G

ọ

; ;

∩ = ∩ = ∩ =

AC BD I AB CD J AD BC K

Đẳ

ng th

ứ

c nào

Sai

trong các

đẳ

ng th

ứ

c sau

ây?

( ) ( )

∩ =

SAC SBD SI

( ) ( )

∩ =

SAC SAD AB

( ) ( )

∩ =

SAB SCD SJ

( ) ( )

∩ =

SAD SBC SK

Câu 33:

Cho t

ứ

ệ

ABCD

. G

ọ

, , , , ,

M N P Q R S

ầ

n l

ượ

t là trung

ể

m các c

ạ

, , , , ,

AC BD AB CD AD BC

. B

ố

ể

m nào sau

ây không

đồ

ng ph

ẳ

ng ?

, , ,

M P R S

, , ,

M R S N

, , ,

P Q R S

, , ,

M N P Q

Toán 11 GV. Lư Sĩ Pháp

HÌNH HỌC 11 Chương II. ĐT & MP Trong KG. QHSS

Câu 34:

Trong các m

ệ

đề

sau, m

ệ

đề

nào

Sai

ộ

t m

ặ

t ph

ẳ

ng c

ắ

t m

ộ

t trong hai

đườ

ng th

ẳ

ng song song thì c

ắ

đườ

ng th

ẳ

ng còn l

ạ

Hai

đườ

ng th

ẳ

ng chéo nhau thì không cùng thu

ộ

c m

ộ

t m

ặ

t ph

ẳ

Hai

đườ

ng th

ẳ

ng không song song thì chéo nhau

Hai m

ặ

t ph

ẳ

ng phân bi

ệ

t không song song thì c

ắ

t nhau

Câu 35:

Cho hai

đườ

ng th

ẳ

ng phân bi

ệ

t cùng n

ằ

m trong m

ộ

t m

ặ

t ph

ẳ

ng. Có bao nhiêu v

ị

trí t

ươ

đố

ữ

a hai

đườ

ng th

ẳ

ó ?

Câu 36:

Trong các m

ệ

đề

sau, m

ệ

đề

nào sai ?

Hình chi

ế

u song song c

ủ

a hai

đườ

ng th

ẳ

ng c

ắ

t nhau có th

ể

trùng nhau.

ộ

đườ

ng th

ẳ

ng luôn c

ắ

t hình chi

ế

u song song c

ủ

a nó.

Hình chi

ế

u song song c

ủ

a hai

đườ

ng th

ẳ

ng c

ắ

t nhau có th

ể

ắ

t nhau.

ộ

đườ

ng th

ẳ

ng có th

ể

song song ho

ặ

c trùng v

ớ

i hình chi

ế

u song song c

ủ

a nó.

Câu 37:

Trong không gian,cho hai m

ặ

t ph

ẳ

( )

và

( )

. Có bao nhiêu v

ị

trí t

ươ

đố

i gi

ữ

( )

và

( )

Câu 38:

Cho hình chóp

S ABCD

có

áy

ABCD

là hình thang và BA là

áy l

ớ

n. G

ọ

i M, N theo th

ứ

ự

là

trung

ể

m c

ủ

a c

ạ

nh SB và SC . Thi

ế

t di

ệ

n c

ủ

a hình chóp

S ABCD

ắ

t b

ở

i m

ặ

t ph

ẳ

( )

AMN

là hình nào

ướ

ây?(tham kh

ả

o hình v

ẽ

)

Hình ch

ữ

ậ

Hình thanh.

Hình bình hành.

Tam giác.

Câu 39:

Trong các m

ệ

đề

ướ

ây, m

ệ

đề

nào sai?

Hình h

ộ

p có các m

ặ

đố

i di

ệ

n b

ằ

ng nhau.

Hình l

ng tr

ụ

có t

ấ

t c

ả

các m

ặ

t bên b

ằ

ng nhau.

Hình h

ộ

p là m

ộ

t hình l

ng tr

ụ

Hình l

ng tr

ụ

có các m

ặ

t bên là hình bình hành.

Câu 40:

Ký hi

ệ

u nào d

ướ

ây sai ?

∈

( ).

A P

∈

( ).

A P

∈

( ).

d P

A d

∈

Câu 41:

Các y

ế

u t

ố

nào sau

ây xác

đị

nh m

ộ

t m

ặ

t ph

ẳ

ng duy nh

ấ

t ?

ố

ể

ộ

ể

m và m

ộ

đườ

ng th

ẳ

ng.

Hai

đườ

ng th

ẳ

ng c

ắ

t nhau.

Câu 42:

ữ

đườ

ng th

ẳ

ng và m

ặ

t ph

ẳ

ng có bao nhiêu v

ị

trí t

ươ

đố

i ?

Câu 43:

Cho hình chóp

S ABCD

, có

áy

ABCD

là hình bình hành. Giao tuy

ế

n c

ủ

a hai m

ặ

t ph

ẳ

ng (SAD)

và (SBC) là

đườ

ng th

ẳ

ng song song v

ớ

đườ

ng nào sau

ây?

SC.

AC.

AD.

BD.

Câu 44:

Cho hình chóp

S ABCD

có

áy

ABCD

là hình thang và BA là

áy l

ớ

n. G

ọ

i M, N theo th

ứ

ự

là

trung

ể

m c

ủ

a c

ạ

nh SB và SC . Tìm giao tuy

ế

n c

ủ

a hai m

ặ

t ph

ẳ

( )

SAD

và

( )

SBC

ớ

= ∩

E AD BC

B. Đườ

ng th

ẳ

(

)

∆ ∈∆ ∆

, , / / .

S AD

ớ

= ∩

O AC BD

D. Đườ

ng th

ẳ

(

)

∈

, , / / .

d S d d BC

Toán 11 GV. Lư Sĩ Pháp

HÌNH HỌC 11 Chương II. ĐT & MP Trong KG. QHSS

Câu 45:

Cho t

ứ

ệ

ABCD

có c

ạ

nh b

ằ

. G

ọ

G G

ầ

n l

ượ

t là tr

ọ

ng tâm c

ủ

ABC

và

ABD

. Tính

ệ

n tích S c

ủ

a thi

ế

t di

ệ

n c

ủ

a hình t

ứ

ệ

n khi c

ắ

t b

ở

i m

ặ

t ph

ẳ

(

)

BGG

Câu 46:

Cho hai

đườ

ng th

ẳ

ng a và b.

ề

u ki

ệ

n nào sau

ây

đủ

để

ế

t lu

ậ

n a và b chéo nhau ?

a và b là hai c

ạ

nh c

ủ

a m

ộ

t t

ứ

ệ

a và b không n

ằ

m trên b

ấ

t kì m

ặ

t ph

ẳ

ng nào.

a và b không có

ể

m chung.

a và b n

ằ

m trên hai m

ặ

t ph

ẳ

ng phân bi

ệ

Câu 47:

Trong các hình sau

ây, hình nào bi

ể

u di

ễ

n c

ủ

a m

ộ

t t

ứ

ệ

n ?

d)c)

Hình a) , b) và d).

Hình a) và c).

Hình b) và d).

ấ

t c

ả

Câu 48:

Cho m

ặ

t ph

ẳ

( )

và hai

đườ

ng th

ẳ

ng song song a, b. M

ệ

đề

nào d

ướ

ây

úng ?

ế

( )

song song v

ớ

i a thì

( )

song song v

ớ

i b ho

ặ

c ch

ứ

a b.

ế

( )

ắ

t a thì

( )

có th

ể

song song v

ớ

i b.

ế

( )

không ch

ứ

a a thì

( )

có th

ể

song song v

ớ

i b.

ế

( )

song song v

ớ

i a thì

( )

ng song song v

ớ

i b.

Câu 49:

Trong các m

ệ

đề

ướ

ây, m

ệ

đề

nào

úng?

Hai

đườ

ng th

ẳ

ng l

ầ

n l

ượ

t n

ằ

m trên hai m

ặ

t ph

ẳ

ng phân bi

ệ

t thì chéo nhau.

Hai

đườ

ng th

ẳ

ng phân bi

ệ

t không song song thì chéo nhau.

Hai

đườ

ng th

ẳ

ng chéo nhau thì không có

ể

m chung.

Hai

đườ

ng th

ẳ

ng không có

ể

m chung thì chéo nhau.

Câu 50:

Cho t

ứ

ệ

ABCD

và ba

ể

, ,

I J K

ầ

n l

ượ

t n

ằ

m trên các c

ạ

, ,

AB AC AD

mà không

trùng v

ớ

i các

đỉ

nh. Thi

ế

t di

ệ

n c

ủ

a t

ứ

ệ

ABCD

khi c

ắ

t b

ở

i mp

(

)

EFG

là hình nào d

ướ

ây ?

ộ

t tam giác.

ộ

t t

ứ

giác.

ộ

ạ

n th

ẳ

ng.

ộ

t ng

giác.

Câu 51:

Cho các gi

ả

thi

ế

t sau

ây. Gi

ả

thi

ế

t nào k

ế

t lu

ậ

đườ

ng th

ẳ

ng a song song v

ớ

i m

ặ

t ph

ẳ

( )

a b

thì

|| ( ).

∩ α = ∅

( ) .

|| ( )

thì

β α

( ) || ( ).

a b

thì

⊂ α

( ).

Câu 52:

Hãy ch

ọ

n ph

ươ

ng án

Đúng

ề

n vào ch

ỗ

ố

“N

ế

u ba m

ặ

t ph

ẳ

ng phân bi

ệ

ôi m

ộ

t c

ắ

t nhau theo ba giao tuy

ế

n phân bi

ệ

t thì . . . . . .”

ba giao tuy

ế

ấ

ôi m

ộ

t song song v

ớ

i nhau.

ba giao tuy

ế

ấ

y ho

ặ

c trùng nhau ho

ặ

ôi m

ộ

t song song v

ớ

i nhau.

ba giao tuy

ế

ấ

đồ

ng quy và

ôi m

ộ

t song song v

ớ

i nhau.

ba giao tuy

ế

ấ

y ho

ặ

đồ

ng quy ho

ặ

ôi m

ộ

t song song v

ớ

i nhau.

Câu 53:

Cho t

ứ

ệ

đề

SABC

có c

ạ

nh b

ằ

. G

ọ

i I là trung

ể

m c

ủ

a AB, M là

ể

m di

độ

ng trên

ạ

n AI. Qua M v

ẽ

ặ

t ph

ẳ

( )

song song v

ớ

( )

SCI

. Thi

ế

t di

ệ

n t

ạ

o b

ở

( )

và t

ứ

ệ

n là hình nào

ướ

ây ?

Hình thoi.

Tam giác

đề

Tam giác cân t

ạ

i M.

Hình bình hành.

Câu 54:

Cho t

ứ

ệ

ABCD

và ba

ể

, ,

P Q R

ầ

n l

ượ

t l

ấ

y trên ba c

ạ

, ,

AB CD BC

. Tìm giao

ể

m S

ủ

và m

ặ

t ph

ẳ

(

)

PQR

, bi

ế

t PR song song v

ớ

i AC .

Toán 11 GV. Lư Sĩ Pháp

HÌNH HỌC 11 Chương II. ĐT & MP Trong KG. QHSS

(

)

∩ =

AD PQR S

ớ

|| || .

QS PR AC

(

)

∩ =

AD PQR S

ớ

S AD PQ

= ∩

(

)

∩ =

AD PQR S

ớ

S AD PR

= ∩

(

)

∩ =

AD PQR S

ớ

|| || .

PS BD RQ

Câu 55:

Cho tam giác

ABC

. Có th

ể

xác

đị

đượ

c bao nhiêu m

ặ

t ph

ẳ

ng ch

ứ

a t

ấ

t c

ả

các

đỉ

nh tam giác

ABC

Câu 56:

Cho t

ứ

ệ

ABCD

. G

ọ

I J

và

ầ

n l

ượ

t là trung

ể

m c

ủ

AC BC

và

. Giao tuy

ế

n c

ủ

hai m

ặ

t ph

ẳ

(

)

ABD

và

(

)

IJK

là

IJ.

KI.

C. Đườ

ng th

ẳ

ng qua K và song song v

ớ

i AB.

KD.

Câu 57:

Cho t

ứ

ệ

ABCD

và ba

ể

, ,

P Q R

ầ

n l

ượ

t l

ấ

y trên ba c

ạ

, ,

AB CD BC

. Tìm giao

ể

m S

ủ

và m

ặ

t ph

ẳ

(

)

PQR

, bi

ế

t PR c

ắ

t AC t

ạ

i I .

(

)

∩ =

AD PQR S

ớ

S IQ AD

= ∩

(

)

∩ =

AD PQR S

ớ

S AC IQ

= ∩

(

)

∩ =

AD PQR S

ớ

S AD PQ

= ∩

(

)

∩ =

AD PQR S

ớ

S RQ AD

= ∩

Câu 58:

Cho t

ứ

ệ

đề

ABCD

có c

ạ

nh b

ằ

. G

ọ

i G là tr

ọ

ng tâm tam giác

ABC

. N

ế

u c

ắ

t t

ứ

ệ

n b

ở

ặ

t ph

ẳ

( )

GCD

thì di

ệ

n tích S c

ủ

a thi

ế

t di

ệ

n b

ằ

ng bao nhiêu ?

Câu 59:

Cho t

ứ

ệ

đề

SABC

có c

ạ

nh b

ằ

. G

ọ

i I là trung

ể

m c

ủ

a AB, M là

ể

m di

độ

ng trên

ạ

n AI và

AM x

. Qua M v

ẽ

ặ

t ph

ẳ

( )

song song v

ớ

( )

SCI

. Thi

ế

t di

ệ

n t

ạ

o b

ở

( )

và t

ứ

ệ

n là

tam giác cân t

ạ

i M. Tìm chu vi P c

ủ

a thi

ế

t di

ệ

(

)

= +

2 1 3 .

P x

(

)

= +

1 3 .

P x

(

)

= +

3 1 3 .

P x

(

)

= +

2 1 2 3 .

P x

Toán 11 GV. Lư Sĩ Pháp

HÌNH HỌC 11 Chương II. ĐT & MP Trong KG. QHSS

Câu 60:

Cho hình chóp

S ABCD

ớ

áy là t

ứ

giác

ABCD

có các c

ạ

đố

i di

ệ

n không song song. Gi

ả

ử

;

∩ = ∩ =

AC BD I AD BC O

. Tìm giao tuy

ế

n c

ủ

a hai m

ặ

t ph

ẳ

ng (SAC) và (SBD).

∩ =

( ) ( ) .

SAC SBD SB

∩ =

( ) ( ) .

SAC SBD SI

∩ =

( ) ( ) .

SAC SBD SO

∩ =

( ) ( ) .

SAC SBD SC

Câu 61:

Trong không gian cho b

ố

ể

m không

đồ

ng ph

ẳ

ng, có th

ể

xác

đị

nh nhi

ề

u nh

ấ

t bao nhiêu m

ặ

ẳ

ng phân bi

ệ

t t

ừ

các

ể

ó ?

Câu 62:

Cho t

ứ

ệ

ABCD

ể

m M thu

ộ

ạ

n AC . M

ặ

t ph

ẳ

( )

qua M song song v

ớ

i AB và AD .

Thi

ế

t di

ệ

n c

ủ

( )

ớ

i t

ứ

ệ

n ABCD là hình nào d

ướ

ây ?

Hình ch

ữ

ậ

Hình vuông.

Hình tam giác.

Hình bình hành.

Câu 63:

ệ

đề

nào d

ướ

ây

úng ?

Hai

đườ

ng th

ẳ

ng phân bi

ệ

t không c

ắ

t nhau thì chéo nhau

Hai

đườ

ng th

ẳ

ng phân bi

ệ

t không song song thì chéo nhau

Hai

đườ

ng th

ẳ

ng phân bi

ệ

t cùng n

ằ

m trong m

ộ

t m

ặ

t ph

ẳ

ng thì không chéo nhau

Hai

đườ

ng th

ẳ

ng phân bi

ệ

t l

ầ

n l

ượ

t thu

ộ

c hai m

ặ

t ph

ẳ

ng khác nhau thì chéo

Câu 64:

ệ

đề

nào d

ướ

ây

úng ?

ế

(

)

(

)

α β

và

(

)

⊂

thì

(

)

|| .

ế

(

)

và

(

)

thì

|| .

a b

ế

(

)

(

)

α β

và

(

)

(

)

α β

⊂ ⊂a b

thì

|| .

a b

ế

a b

và

(

)

(

)

α β

⊂ ⊂

a b

thì

Câu 65:

Cho t

ứ

ệ

ABCD G

là tr

ọ

ng tâm c

ủ

a tam giác

ABD

Trên

ấ

ể

sao cho

2 .

MB MC

ẳ

đị

nh nào d

ướ

ây

úng ?

|| ( ).

MG ACB

|| ( ).

MG ABD

|| (B ).

MG CD

|| ( ).

MG ACD

Câu 66:

Cho hai

đườ

ng th

ẳ

ng phân bi

ệ

t cùng n

ằ

m trong m

ộ

t m

ặ

t ph

ẳ

ng. Có bao nhiêu v

ị

trí t

ươ

đố

ữ

a hai

đườ

ng th

ẳ

ó?

Câu 67:

Cho hình l

ng tr

ụ

ABC A B C

′ ′ ′

. G

ọ

ầ

n l

ượ

t là tr

ọ

ng tâm c

ủ

a các tam giác

ABC

ACC

′

A B C

′ ′ ′

. M

ặ

t ph

ẳ

ng nào sau

ây song song v

ớ

i m

ặ

t ph

ẳ

(

)

IJK

?(tham kh

ả

o hình v

ẽ

)

(

)

ABC

(

)

BB C

′ ′

(

)

A BC

′ ′

(

)

AA C

′

Câu 68:

Cho l

ng tr

ụ

đứ

ABC A B C

′ ′ ′

có

′

ầ

n l

ượ

t là tr

ọ

ng tâm c

ủ

a hai tam giác

ABC

và

A B C

′ ′ ′

. Thi

ế

t di

ệ

n t

ạ

o b

ở

i m

ặ

t ph

ẳ

(

)

AGG

′

ớ

i hình l

ng tr

ụ

ã cho là hình nào d

ướ

ây ? (tham

ả

o hình v

ẽ

)

Hình ch

ữ

ậ

Tam giác cân.

Tam giác vuông.

Hình vuông.

Toán 11 GV. Lư Sĩ Pháp

HÌNH HỌC 11 Chương II. ĐT & MP Trong KG. QHSS

Câu 69:

Cho t

ứ

ệ

ABCD

ọ

và

ầ

n l

ượ

t là trung

ể

m c

ủ

AC BC

và

Xác

đị

nh giao

tuy

ế

n c

ủ

a hai m

ặ

t ph

ẳ

(

)

ABD

và

(

)

IKJ

(tham kh

ả

o hình v

ẽ

)

A. Đườ

ng th

ẳ

B. Đườ

ng th

ẳ

C. Đườ

ng th

ẳ

D. Đườ

ng th

ẳ

∆

qua K và song song v

ớ

Câu 70:

Cho t

ứ

ệ

ABCD

ể

thu

ộ

ạ

ặ

t ph

ẳ

(

)

qua

song song v

ớ

và

Thi

ế

t di

ệ

n c

ủ

(

)

ớ

i t

ứ

ệ

ABCD

là hình nào d

ướ

ây? (tham kh

ả

o hình v

ẽ

Hình thang.

Hình bình hành.

Hình ng

giác.

Hình tam giác.

Câu 71:

Trong các gi

ả

thi

ế

t d

ướ

ây. Gi

ả

thi

ế

t nào k

ế

t lu

ậ

đườ

ng th

ẳ

song song v

ớ

i m

ặ

t ph

ẳ

(

)

a b

và

(

)

⊂

(

)

và

(

)

(

)

|| .

β α

a b

và

(

)

|| .

(

)

∩ = ∅

Câu 72:

Cho hình chóp

S ABCD

có

áy

ABCD

là hình bình hành.

ể

ỏ

a mãn

3 .

MA MB

 

ặ

ẳ

(

)

qua

và song song v

ớ

. M

ệ

đề

nào sau

ây

úng?

(

)

ắ

t hình chóp theo thi

ế

t di

ệ

n là m

ộ

t ng

giác.

(

)

ắ

t hình chóp theo thi

ế

t di

ệ

n là m

ộ

t tam giác.

(

)

ắ

t hình chóp theo thi

ế

t di

ệ

n là m

ộ

t t

ứ

giác.

(

)

không c

ắ

t hình chóp.

Câu 73:

Cho hình chóp

S ABCD

có

áy

ABCD

là hình bình hành tâm

là trung

ể

m c

ạ

ẳ

đị

nh nào d

ướ

ây sai?(tham kh

ả

o hình v

ẽ

)

ặ

t ph

ẳ

(

)

IBD

ắ

t hình chóp

S ABCD

theo thi

ế

t di

ệ

n là m

ộ

ứ

giác.

B. Đườ

ng th

ẳ

song song v

ớ

i m

ặ

t ph

ẳ

(

)

SAD

C. Đườ

ng th

ẳ

song song v

ớ

i m

ặ

t ph

ẳ

(

)

SAB

Giao tuy

ế

n c

ủ

a hai m

ặ

t ph

ẳ

(

)

IBD

và

(

)

SAC

là

Câu 74:

Cho hai

đườ

ng th

ẳ

ng phân bi

ệ

và

trong không gian. Có bao nhiêu v

ị

trí t

ươ

đố

i gi

ữ

và

Câu 75:

Cho hai

đườ

ng th

ẳ

ng chéo nhau

và

. L

ấ

A B

thu

ộ

và

C D

thu

ộ

. Kh

ẳ

đị

nh nào

ướ

ây

úng khi nói v

ề

ị

trí t

ươ

đố

i gi

ữ

a hai

đườ

ng th

ẳ

và

Toán 11 GV. Lư Sĩ Pháp

HÌNH HỌC 11 Chương II. ĐT & MP Trong KG. QHSS

Chéo nhau.

ắ

t nhau.

Song song v

ớ

i nhau.

Có th

ể

song song ho

ặ

c c

ắ

t nhau.

Câu 76:

Cho hai

đườ

ng th

ẳ

ng phân bi

ệ

a b

và m

ặ

t ph

ẳ

(

)

. Gi

ả

ử

a b

(

)

. M

ệ

đề

nào d

ướ

ây

úng ?

(

)

ặ

(

)

⊂a

(

)

⊂a

ắ

(

)

(

)

|| .

Câu 77:

Trong không gian, kh

ẳ

đị

nh nào d

ướ

ây sai ?

ế

u ba m

ặ

t ph

ẳ

ng phân bi

ệ

t c

ắ

t nhau theo ba giao tuy

ế

n thì ba giao tuy

ế

ấ

y ho

ặ

đồ

ng quy ho

ặ

ôi m

ộ

t song song.

Cho hai

đườ

ng th

ẳ

ng chéo nhau. Có duy nh

ấ

t m

ộ

t m

ặ

t ph

ẳ

ng ch

ứ

đươ

ng th

ẳ

ng này và song song

ớ

đườ

ng th

ẳ

ng. kia.

Hai

đườ

ng th

ẳ

ng phân bi

ệ

t cùng vuông góc v

ớ

i m

ộ

đườ

ng th

ẳ

ng thì song song v

ớ

i nhau.

Hai m

ặ

t ph

ẳ

ng phân bi

ệ

t cùng vuông góc v

ớ

i m

ộ

đườ

ng th

ẳ

ng thì song song v

ớ

i nhau.

Câu 78:

Cho hình chóp

S ABCD

có

áy

ABCD

là hình bình hành tâm

. G

ọ

ầ

n l

ượ

t là trung

ể

m c

ủ

. Thi

ế

t di

ệ

n c

ủ

a hình chóp c

ắ

t b

ở

i m

ặ

t ph

ẳ

(

)

MNK

là m

ộ

a giác

(

)

. Kh

ẳ

đị

nh nào d

ướ

ây

úng ?

(

)

là m

ộ

t tam giác.

(

)

là m

ộ

t ng

giác.

(

)

là m

ộ

t hình bình hành.

(

)

là m

ộ

t hình thang.

Câu 79:

Cho hình chóp

S ABCD

có

áy là hình bình hành. Kh

ẳ

đị

nh nào d

ướ

ây

úng khi nói v

ề

giao tuy

ế

n c

ủ

(

)

SAB

và

(

)

SCD

A. Đườ

ng th

ẳ

ng qua

và song song v

ớ

B. Đườ

ớ

là tâm hình bình hành.

C. Đườ

ng th

ẳ

ng qua

và song song v

ớ

D. Đườ

ng th

ẳ

ng qua

và c

ắ

Câu 80:

Cho hai

đườ

ng th

ẳ

ng phân bi

ệ

a b

và m

ặ

t ph

ẳ

(

)

. Gi

ả

ử

(

)

và

(

)

. M

ệ

đề

nào

ây

úng?

và

không có

ể

m chung.

và

chéo nhau.

và

ặ

c song song ho

ặ

c chéo nhau.

và

ặ

c song song ho

ặ

c chéo nhau ho

ặ

c c

ắ

t nhau.

Câu 81:

ệ

đề

nào d

ướ

ây

úng ?

ế

u hai m

ặ

t ph

ẳ

ng song song thì m

ọ

đườ

ng th

ẳ

ng n

ằ

m trên m

ặ

t ph

ẳ

ng này

đề

u song song v

ớ

i m

ọ

đườ

ng th

ẳ

ng n

ằ

m trên m

ặ

t ph

ẳ

ng kia.

ế

u hai m

ặ

t ph

ẳ

ng cùng song song v

ớ

i m

ộ

đườ

ng th

ẳ

ng thì song song v

ớ

i nhau.

ế

u hai m

ặ

t ph

ẳ

(

)

và

(

)

ầ

n l

ượ

t ch

ứ

a hai

đườ

ng th

ẳ

ng song song thì song song v

ớ

i nhau.

ế

u hai m

ặ

t ph

ẳ

ng phân bi

ệ

t không song song thì c

ắ

t nhau.

Câu 82:

Các y

ế

u t

ố

nào sau

ây xác

đị

nh m

ộ

t m

ặ

t ph

ẳ

ng duy nh

ấ

ể

m phân bi

ệ

ố

ể

m phân bi

ệ

Hai

đườ

ng th

ẳ

ng c

ắ

t nhau.

ộ

ể

m và m

ộ

đườ

ng th

ẳ

ng.

Câu 83:

Cho hình l

ng tr

ụ

tam giác

. .

′ ′ ′

ABC A B C

ọ

I J

ầ

n l

ượ

t là tr

ọ

ng tâm c

ủ

a các tam giác

ABC

và

′ ′ ′

A B C

Xác

đị

nh hình d

ạ

ng thi

ế

t di

ệ

n t

ạ

o b

ở

i m

ặ

t ph

ẳ

(

)

AIJ

ớ

i hình l

ng tr

ụ

(tham kh

ả

o hình

bên)

Hình bình hành

Hình tam giác vuông.

Hình thang.

Hình tam giác cân

Toán 11 GV. Lư Sĩ Pháp

HÌNH HỌC 11 Chương II. ĐT & MP Trong KG. QHSS

Câu 84:

Cho hai

đườ

ng th

ẳ

và

chéo nhau. Có bao nhiêu m

ặ

t ph

ẳ

ng ch

ứ

và song song v

ớ

Câu 85:

Cho t

ứ

ệ

ABCD

. G

ọ

và

ầ

n l

ượ

t là tr

ọ

ng tâm c

ủ

a tam giác

ABD

và

ABC

. M

ệ

đề

nào d

ướ

ây

úng ?

ắ

// .

GE CD

và

chéo nhau.

ắ

Câu 86:

ệ

đề

nào d

ướ

ây

úng ?

ế

u hai

đườ

ng th

ẳ

ng song song v

ớ

i nhau l

ầ

n l

ượ

t n

ằ

m trong hai m

ặ

t ph

ẳ

ng phân bi

ệ

(

)

và

(

)

thì

(

)

và

(

)

song song v

ớ

i nhau

Qua m

ộ

ể

m n

ằ

m ngoài m

ặ

t ph

ẳ

ng cho tr

ướ

c ta v

ẽ

đượ

c m

ộ

t và ch

ỉ

ộ

đườ

ng th

ẳ

ng song song

ớ

i m

ặ

t ph

ẳ

ng cho tr

ướ

ế

u hai m

ặ

t ph

ẳ

(

)

và

(

)

song song v

ớ

i nhau thì m

ọ

đườ

ng th

ẳ

ng n

ằ

m trong

(

)

đề

u song

song v

ớ

(

)

ế

u hai m

ặ

t ph

ẳ

(

)

và

(

)

song song v

ớ

i nhau thì m

ọ

đườ

ng th

ẳ

ng n

ằ

m trong

(

)

đề

u song

song v

ớ

i m

ọ

đườ

ng th

ẳ

ng n

ằ

m trong

(

)

Câu 87:

Cho hai

đườ

ng th

ẳ

và

ề

u ki

ệ

n nào sau

ây

đủ

để

ế

t lu

ậ

và

chéo nhau?

và

không có

ể

m chung.

và

không cùng n

ằ

m trên b

ấ

t kì m

ặ

t ph

ẳ

ng nào.

và

ằ

m trên 2 m

ặ

t ph

ẳ

ng phân bi

ệ

và

là hai c

ạ

nh c

ủ

a m

ộ

t hình t

ứ

ệ

Câu 88:

Cho hình chóp

S ABCD

có

áy

ABCD

là hình bình hành. Gi

ả

ử

thu

ộ

ạ

n th

ẳ

ặ

ẳ

(

)

ADM

ắ

t hình chóp

S ABCD

theo thi

ế

t di

ệ

n là hình nào d

ướ

ây ? (tham kh

ả

o hình v

ẽ

)

Hình thang.

Hình tam giác.

Hình bình hành.

Hình ch

ữ

ậ

Câu 89:

Cho hình t

ứ

ệ

ABCD

có

ầ

n l

ượ

t là trung

ể

m c

ủ

. Các

ể

ầ

ượ

t trên c

ạ

sao cho

ắ

ạ

. Kh

ẳ

đị

nh nào d

ướ

ây

úng?

ẳ

ng hàng.

ẳ

ng hàng.

ẳ

ng hàng.

ẳ

ng hàng.

Câu 90:

Trong không gian, kh

ẳ

đị

nh nào d

ướ

ây sai ?

Hai m

ặ

t ph

ẳ

ng phân bi

ệ

t cùng vuông góc v

ớ

i m

ộ

đườ

ng th

ẳ

ng thi song song v

ớ

i nhau.

ế

u ba m

ặ

t ph

ẳ

ng c

ắ

t nhau theo ba giao tuy

ế

n phân bi

ệ

t thì bao giao tuy

ế

ấ

y ho

ặ

đồ

ng quy ho

ặ

ôi m

ộ

t song song v

ớ

i nhau.

Hai

đườ

ng th

ẳ

ng phân bi

ệ

t cùng vuông góc v

ớ

i m

ộ

đườ

ng th

ẳ

ng thì song song v

ớ

i nhau.

Cho hai

đườ

ng th

ẳ

ng chéo nhau. Có duy nh

ấ

t m

ộ

t m

ặ

t ph

ẳ

ng ch

ứ

đườ

ng th

ẳ

ng này và song song

ớ

đườ

ng th

ẳ

ng kia.

Câu 91:

Cho l

ng tr

ụ

đứ

ABC A B C

′ ′ ′

. G

ọ

ầ

n l

ượ

t là trung

ể

m c

ủ

A B

′ ′

và

′

ệ

đề

nào d

ướ

ây

úng ?

|| .

CB A N

′ ′

(

)

|| .

CB BC M

′ ′

(

)

|| .

CB AC M

′ ′

|| .

CB AM

′

Câu 92:

ắ

t hình chóp t

ứ

giác b

ở

i m

ặ

t ph

ẳ

ng vuông góc v

ớ

đườ

ng cao c

ủ

a hình chóp thi

ế

t di

ệ

n là hình

gì?

ộ

t hình bình hành.

ộ

t hình tam giác.

ộ

t ng

giác.

ộ

t hình t

ứ

giác.

Câu 93:

Trong không gian cho b

ố

ể

m không

đồ

ng ph

ẳ

ng, có th

ể

xác

đị

nh nhi

ề

u nh

ấ

t bao nhiêu m

ặ

ẳ

ng phân bi

ệ

t t

ừ

các

ể

ó?

Toán 11 GV. Lư Sĩ Pháp

HÌNH HỌC 11 Chương II. ĐT & MP Trong KG. QHSS

Câu 94:

Cho tam giác

ABC

ấ

ể

trên c

ạ

kéo dài. M

ệ

đề

nào d

ướ

ây là sai?

(

)

⊄

BI ABC

(

)

∈

I ABC

(

)

∈

A BIC

(

)

⊂

CI ABC

Câu 95:

ệ

đề

nào d

ướ

ây sai ?

Hai m

ặ

áy c

ủ

a hình l

ng tr

ụ

ằ

m trên hai m

ặ

t ph

ẳ

ng song song.

Hai

áy c

ủ

a l

ng tr

ụ

là hai

a giác

đề

Hình l

ng tr

ụ

có các c

ạ

nh bên song song và b

ằ

ng nhau.

Các m

ặ

t bên c

ủ

a l

ng tr

ụ

là các hình bình hành.

Câu 96:

Cho hình l

ậ

p ph

ươ

. .

′ ′ ′ ′

ABCD A B C D

Có bao nhiêu c

ạ

nh c

ủ

a hình l

ậ

p ph

ươ

ng chéo nhau v

ớ

đườ

ng chéo

′

ủ

a hình l

ậ

p ph

ươ

ng?(tham kh

ả

o hình v

ẽ

)

Câu 97:

ố

i chóp

đề

S ABCD

có m

ặ

áy

ABCD

là hình nào d

ướ

ây ?

Hình ch

ữ

ậ

Hình thoi.

Hình bình hành.

Hình vuông.

Câu 98:

Cho

đườ

ng th

ẳ

và m

ặ

t ph

ẳ

(

)

trong không gian. Có bao nhiêu v

ị

trí t

ươ

đố

i c

ủ

và

(

)

Câu 99:

Cho hình chóp t

ứ

giác

S ABCD

. G

ọ

và

ầ

n l

ượ

t là trung

ể

m c

ủ

và

ẳ

đị

nh nào d

ướ

ây

úng?

(

)

|| .

MN SCD

(

)

|| .

MN SAB

(

)

|| .

MN ABCD

(

)

|| .

MN SBC

Câu 100:

Cho hình l

ng tr

ụ

1 1 1

. .

ABC A B C

ẳ

đị

nh nào d

ướ

ây sai?

(

)

1 1

|| .

AA BCC

(

)

(

)

1 1 1

|| .

ABC A B C

(

)

1 1 1

|| .

AB A B C

1 1

AA B B

là hình ch

ữ

ậ

Câu 101:

Cho hình chóp

S ABCD

có

áy

ABCD

là hình bình hành tâm

ọ

là

ể

m thu

ộ

c c

ạ

(không trùng v

ớ

). G

ọ

(

)

là m

ặ

t ph

ẳ

ng qua

và song song v

ớ

Thi

ế

t di

ệ

n c

ủ

a hình

chóp khi c

ắ

t b

ở

i mp

(

)

là hình nào d

ướ

ây ? (tham kh

ả

o hình v

ẽ

)

Hình ch

ữ

ậ

Hình bình hành.

Hình thang.

Hình tam giác.

Câu 102:

Cho t

ứ

ệ

ABCD

ọ

I J

ầ

n l

ượ

t thu

ộ

c c

ạ

AD BC

sao cho

IA ID

và

2 .

JB JC

ọ

(

)

là m

ặ

t ph

ẳ

ng qua

và song song v

ớ

Thi

ế

t di

ệ

n c

ủ

a t

ứ

ệ

ABCD

khi c

ắ

t b

ở

(

)

hình

nào d

ướ

ây ? (tham kh

ả

o hình v

ẽ

)

Toán 11 GV. Lư Sĩ Pháp

HÌNH HỌC 11 Chương II. ĐT & MP Trong KG. QHSS

Hình tam giác.

Hình bình hành.

Hình thang.

Tam giác

đề

Câu 103:

Cho t

ứ

ệ

ABCD

ể

thu

ộ

ạ

ặ

t ph

ẳ

(

)

qua

song song v

ớ

và

Thi

ế

t di

ệ

n c

ủ

(

)

ớ

i t

ứ

ệ

ABCD

là hình nào d

ướ

ây? (tham kh

ả

o hình v

ẽ

Hình tam giác.

Hình ch

ữ

ậ

Hình ng

giác.

Hình bình hành.

Câu 104:

Cho hình l

ng tr

ụ

. .

′ ′ ′

ABC A B C

ọ

là trung

ể

m c

ủ

′ ′

A B

Đườ

ng th

ẳ

′

B C

song song

ớ

i m

ặ

t ph

ẳ

ng nào d

ướ

ây? (tham kh

ả

o hình v

ẽ

)

(

)

′

AHC

(

)

′

AA H

(

)

HAB

(

)

′

HA C

Câu 105:

Cho hình chóp

S ABCD

có

áy

ABCD

là hình bình hành,

và

là hai

ể

m trên

SA SB

sao cho

= =

SM SN

SA SB

ị

trí t

ươ

đố

i gi

ữ

và

(

)

ABCD

. Kh

ẳ

đị

nh nào d

ướ

ây

úng ?

song song

(

)

mp ABCD

ắ

(

)

mp ABCD

ằ

m trên

(

)

mp ABCD

và

(

)

mp ABCD

chéo nhau.

Toán 11 GV. Lư Sĩ Pháp

HÌNH HỌC 11 Chương II. ĐT & MP Trong KG. QHSS

MỘT SỐ ĐỀ ÔN KIỂM TRA MỘT TIẾT

ĐỀ 1

I. Phần trắc nghiệm

Câu 1:

Hãy ch

ọ

n ph

ươ

ng án

Đúng

ề

n vào ch

ỗ

ố

ng “....”.

“N

ế

u ba m

ặ

t ph

ẳ

ng phân bi

ệ

ôi m

ộ

t c

ắ

t nhau theo ba giao tuy

ế

n phân bi

ệ

t thì . . . . . .”

ba giao tuy

ế

ấ

đồ

ng quy và

ôi m

ộ

t song song v

ớ

i nhau.

ba giao tuy

ế

ấ

y ho

ặ

đồ

ng quy ho

ặ

ôi m

ộ

t song song v

ớ

i nhau.

ba giao tuy

ế

ấ

ôi m

ộ

t song song v

ớ

i nhau.

ba giao tuy

ế

ấ

y ho

ặ

c trùng nhau ho

ặ

ôi m

ộ

t song song v

ớ

i nhau.

Câu 2:

Cho t

ứ

ệ

n ABCD. G

ọ

i M, N l

ầ

n l

ượ

t là trung

ể

m các c

ạ

nh AB và AC . G

ọ

i d là giao tuy

ế

n c

ủ

hai m

ặ

t ph

ẳ

( )

DMN

và

( ).

DBC

ệ

đề

nào d

ướ

ây

úng ?

/ /( ).

d ACD

/ /( ).

d ABC

/ /( ).

d ABD

/ /( ).

d ABCD

Câu 3:

Cho hai

đườ

ng th

ẳ

ng a và b chéo nhau. Có bao nhiêu m

ặ

t ph

ẳ

ng ch

ứ

a a và song song v

ớ

i b?

Ba m

ặ

t ph

ẳ

ng.

Hai m

ặ

t ph

ẳ

ng.

ộ

t m

ặ

t ph

ẳ

ng.

Không có m

ặ

t ph

ẳ

ng nào.

Câu 4:

Trong các hình d

ướ

ây, hình nào là hình bi

ể

u di

ễ

n c

ủ

a m

ộ

t t

ứ

ệ

n ?

d)c)

Hình a) và c).

Hình b) và d).

Hình a).

Hình a) , b) và d).

Câu 5:

Cho t

ứ

ệ

ABCD

và ba

ể

, ,

P Q R

ầ

n l

ượ

t l

ấ

y trên ba c

ạ

, ,

AB CD BC

. Tìm giao

ể

m S

ủ

và m

ặ

t ph

ẳ

(

)

PQR

, bi

ế

ắ

ạ

(nh

hình v

ẽ

(

)

AD PQR S

∩ =

ớ

S IQ AD

= ∩

(

)

AD PQR S

∩ =

ớ

S AC IQ

= ∩

(

)

AD PQR S

∩ =

ớ

S AD PQ

= ∩

(

)

AD PQR S

∩ =

ớ

S RQ AD

= ∩

Câu 6:

Cho t

ứ

ệ

ABCD

. G

ọ

M, N

ầ

n l

ượ

t là trung

ể

m c

ủ

và

là

ể

m trên c

ạ

ớ

ED EC

(nh

hình v

ẽ

). Tìm thi

ế

t di

ệ

n c

ủ

a t

ứ

ệ

ABCD

khi c

ắ

t b

ở

i m

ặ

t ph

ẳ

(

)

MNE

ứ

giác

MNEF

ớ

là

ể

m b

ấ

t kì trên

Hình bình hành

MNEF

ớ

là

ể

m trên c

ạ

mà

/ / .

EF BC

Tam giác

MNE

Hình thang

MNEF

ớ

là

ể

m trên c

ạ

mà

/ / .

EF BC

Câu 7:

Cho tam giác

BCD

và

ể

không thu

ộ

c m

ặ

t ph

ẳ

ng (

BCD

). G

ọ

là trung

ể

m c

ủ

ạ

và

là tr

ọ

ng tâm c

ủ

a tam giác

ABC

(nh

hình v

ẽ

). Tìm giao

ể

m c

ủ

đườ

ng th

ẳ

ớ

i m

ặ

t ph

ẳ

(

BCD

Toán 11 GV. Lư Sĩ Pháp

HÌNH HỌC 11 Chương II. ĐT & MP Trong KG. QHSS

( ) .

GK BCD L

∩ =

( ) .

GK BCD B

∩ =

( ) .

GK BCD G

∩ =

( ) .

GK BCD I

∩ =

Câu 8:

Cho hai

đườ

ng th

ẳ

ng phân bi

ệ

t cùng n

ằ

m trong m

ộ

t m

ặ

t ph

ẳ

ng. Có bao nhiêu v

ị

trí t

ươ

đố

i gi

ữ

hai

đườ

ng th

ẳ

ó ?

Câu 9:

Cho t

ứ

ệ

ABCD

. G

ọ

M N

ầ

n l

ượ

t là trung

ể

m các c

ạ

và

;

là tr

ọ

ng tâm c

ủ

a tam

giác

BCD

. Tìm giao

ể

m c

ủ

đườ

ng th

ẳ

và m

ặ

t ph

ẳ

(

)

ABC

( ) .

MG ABC C

∩ =

( ) .

MG ABC N

∩ =

( )

MG ABC H

∩ =

ớ

H MG BC

= ∩

( )

MG ABC K

∩ =

ớ

K MG AN

= ∩

Câu 10:

Cho hình chóp

S ABCD

có

áy

ABCD

là hình thang và

là

áy l

ớ

n. Tìm giao tuy

ế

n c

ủ

a hai

ặ

t ph

ẳ

( )

SAD

và

( ).

SBC

( ) ( )

SAD SBC

∩ = ∆

ớ

, / / .

S AD

∈∆ ∆

( ) ( )

SAD SBC SE

∩ =

ớ

E AD BC

= ∩

( ) ( )

SAD SBC d

∩ =

ớ

, / / .

S d d AB

∈

( ) ( )

SAD SBC SO

∩ =

ớ

E AC BD

= ∩

II. Phần tự luận

Bài 1.

Cho hình chóp

S ABCD

có

áy là hình bình hành

ABCD

. G

ọ

là tr

ọ

ng tâm c

ủ

a tam giác

SAB

và

là trung

ể

m c

ủ

. L

ấ

trên

ạ

sao cho

AD AM

a/. Tìm giao tuy

ế

n c

ủ

a hai m

ặ

t ph

ẳ

ng (

SAD

) và (

SBC

b/.

Đườ

ng th

ẳ

ng qua

và song song v

ớ

ắ

ạ

. Ch

ứ

ng minh r

ằ

/ /( )

NG SCD

Bài 2.

Cho t

ứ

ệ

ABCD

. Trên

ấ

ể

. Cho

( )

là m

ặ

t ph

ẳ

ng qua

, song song v

ớ

i hai

đườ

ẳ

và

a/. Tìm giao

ể

m c

ủ

đườ

ng th

ẳ

và m

ặ

t ph

ẳ

( ).

b/ Xác

đị

nh thi

ế

t di

ệ

n c

ủ

a t

ứ

ệ

n c

ắ

t b

ở

i m

ặ

t ph

ẳ

( )

, thi

ế

t di

ệ

n là hình gì?

ĐỀ 2

I. Phần trắc nghiệm

Câu 1:

Trong không gian, có bao nhiêu cách xác

đị

nh m

ộ

t m

ặ

t ph

ẳ

ng ?

Câu 2:

Trong các hình sau

ây, hình nào bi

ể

u di

ễ

n cho hình l

ậ

p ph

ươ

ng ?

Hình a).

Hình a) và c).

Hình b).

Hình c) và b).

Câu 3:

Cho t

ứ

ệ

ABCD

. G

ọ

M, N

ầ

n l

ượ

t là trung

ể

m các c

ạ

và

. M

ệ

đề

nào d

ướ

ây

úng ?

ắ

t (

BCD

không song song (

BCD

Toán 11 GV. Lư Sĩ Pháp

HÌNH HỌC 11 Chương II. ĐT & MP Trong KG. QHSS

/ /( ).

MN BCD

ằ

m trong (

BCD

Câu 4:

Cho hình chóp

S ABCD

có

áy

ABCD

là hình thang và

là

áy l

ớ

n. G

ọ

M, N

theo th

ứ

ự

là

trung

ể

m c

ủ

a c

ạ

và

. Thi

ế

t di

ệ

n c

ủ

a hình chóp

S ABCD

ắ

t b

ở

i m

ặ

t ph

ẳ

( )

AMN

là hình gì ?

Hình thang.

Hình ch

ữ

ậ

Hình bình hành.

Hình tam giác.

Câu 5:

Cho t

ứ

ệ

ABCD

và ba

ể

, ,

P Q R

ầ

n l

ượ

t l

ấ

y trên ba c

ạ

, ,

AB CD BC

. Tìm giao

ể

ủ

và m

ặ

t ph

ẳ

(

)

PQR

, bi

ế

t PR song song v

ớ

i AC .

(

)

AD PQR S

∩ =

ớ

/ / / / .

QS PR AC

(

)

AD PQR S

∩ =

ớ

S AD PQ

= ∩

(

)

AD PQR S

∩ =

ớ

S AD PR

= ∩

(

)

AD PQR S

∩ =

ớ

/ / / / .

PS BD RQ

Câu 6:

Cho hình chóp

S ABCD

có

áy

ABCD

là hình bình hành. G

ọ

, ,

M N P

theo th

ứ

ự

là trung

ể

các

ạ

n th

ẳ

, ,

SA BC CD

. G

ọ

i O là giao

ể

m c

ủ

a hai

đườ

ng chéo c

ủ

a hình bình hành

ABCD

(nh

hình

ẽ

). Xác

đị

nh giao

ể

m I c

ủ

đườ

ng th

ẳ

ng SO v

ớ

i m

ặ

t ph

ẳ

( )

MNP

I SO NP

= ∩

I SO MH

= ∩

I SO MP

= ∩

I SO MN

= ∩

Câu 7:

Cho hình chóp .

S ABCD

có

áy là t

ứ

giác

ABCD

và các c

ạ

đố

i di

ệ

n không song song. Gi

ả

ử

;

AC BD I AD BC O

∩ = ∩ =

. Tìm giao tuy

ế

n c

ủ

a hai m

ặ

t ph

ẳ

ng (SAC) và (SBD).

( ) ( ) .

SAC SBD SB

∩ =

( ) ( ) .

SAC SBD SC

∩ =

( ) ( ) .

SAC SBD SO

∩ =

( ) ( ) .

SAC SBD SI

∩ =

Câu 8:

Cho hai

đườ

ng th

ẳ

ng a và b.

ề

u ki

ệ

n nào d

ướ

ây

đủ

để

ế

t lu

ậ

n a và b chéo nhau?

a và b không có

ể

m chung.

a và b n

ằ

m trên hai m

ặ

t ph

ẳ

ng phân bi

ệ

a và b không n

ằ

m trên b

ấ

t kì m

ặ

t ph

ẳ

ng nào.

a và b là hai c

ạ

nh c

ủ

a m

ộ

t t

ứ

ệ

Câu 9:

Cho hình chóp

S ABCD

có

áy là hình bình hành. G

ọ

I J

ầ

n l

ượ

t là trung

ể

m c

ủ

và

. Giao tuy

ế

n c

ủ

a hai m

ặ

t ph

ẳ

( )

SAB

và

( )

SCD

là

đườ

ng th

ẳ

ng song song v

ớ

đườ

ng th

ẳ

ng nào d

ướ

ây ?

A. Đườ

ng th

ẳ

B. Đườ

ng th

ẳ

C. Đườ

ng th

ẳ

D. Đườ

ng th

ẳ

Câu 10:

Trong các gi

ả

thi

ế

t d

ướ

ây, gi

ả

thi

ế

t nào k

ế

t lu

ậ

n v

ề

đườ

ng th

ẳ

ng a song song v

ớ

i m

ặ

t ph

ẳ

( )

( ) .

∩ = ∅

/ /

a b

và

/ /( ).

/ /

a b

và

( ).

⊂

/ /( )

và

( ) / /( ).

β α

Toán 11 GV. Lư Sĩ Pháp

HÌNH HỌC 11 Chương II. ĐT & MP Trong KG. QHSS

II. Phần tự luận

Bài 1.

Cho t

ứ

ệ

n ABCD. G

ọ

i M,N, P l

ầ

n l

ượ

t là trung

ể

m c

ủ

a các c

ạ

nh AB, CD, AN và G là trung

ể

m c

ủ

ạ

n MN.

a/ Tìm giao

ể

m c

ủ

đườ

ng th

ẳ

ng AG và m

ặ

t ph

ẳ

ng (BCD).

b/ Ch

ứ

ng minh r

ằ

ng MP song song v

ớ

i m

ặ

t ph

ẳ

ng (BCD).

Bài 2.

Cho hình chóp S.ABCD có

áy ABCD là hình thang (AB là

áy l

ớ

n). G

ọ

i M, N l

ầ

n l

ượ

t là trung

ể

m c

ủ

a SB và SC.

a/ Tìm giao

ể

m c

ủ

đườ

ng th

ẳ

ng AN v

ớ

i m

ặ

t ph

ẳ

ng (SBD).

b/ G

ọ

( )

là m

ặ

t ph

ẳ

ng qua MN và song song v

ớ

i CD. Xác

đị

nh thi

ế

t di

ệ

n c

ủ

a hình chóp c

ắ

t b

ở

i m

ặ

ẳ

( )

Đề 3

I. Phần trắc nghiệm

Câu 1:

ệ

đề

nào sau

ây

đúng?

Qua ba

ể

m xác

đị

nh m

ộ

t và ch

ỉ

ộ

t m

ặ

t ph

ẳ

ng.

Qua ba

ể

m phân bi

ệ

t không th

ẳ

ng hàng xác

đị

nh m

ộ

t và ch

ỉ

ộ

t m

ặ

t ph

ẳ

ng.

Qua ba

ể

m phân bi

ệ

t xác

đị

nh m

ộ

t và ch

ỉ

ộ

t m

ặ

t ph

ẳ

ng.

Qua ba

ể

m phân bi

ệ

t không th

ẳ

ng hàng xác

đị

nh hai m

ặ

t ph

ẳ

ng phân bi

ệ

Câu 2:

Cho hình chóp

S ABCD

có

áy là hình bình hành. G

ọ

E F

ầ

n l

ượ

t thu

ộ

SA SB

sao

cho

4 , 4 .

SA SE SB SF

= =

Khi

ó, v

ị

trí t

ươ

đố

i gi

ữ

và

(

)

ABCD

là:

EF ( D).

ABC

⊂

ắ

(

)

ABCD

chéo

(

)

// .

EF ABCD

Câu 3:

Cho hình chóp

. ,

S ABCD

áy là hình bình hành. G

ọ

M N

ầ

n l

ượ

t là trung

ể

m c

ủ

và

ẳ

đị

nh nào sau

ây

úng?

(

)

// .

MN ABCD

(

)

// .

MN SAB

(

)

// .

MN SCD

(

)

// .

MN SBC

Câu 4:

Cho hình chóp

S ABCD

có

áy

ABCD

là hình vuông. L

ấ

M SA N SB

∈ ∈

sao cho

SM SN

SA SB

= =

. Tìm m

ệ

đề

úng:

//CD.

(

)

// .

MN SAD

//AD.

(

)

// .

MN SBC

Câu 5:

Cho t

ứ

ệ

ABCD

. G

ọ

M N

ầ

n l

ượ

t là trung

ể

m c

ủ

a các c

ạ

AD BC

;

là tr

ọ

ng tâm tam

giác

BCD

. Giao

ể

m c

ủ

đườ

ng th

ẳ

và m

ặ

t ph

ẳ

(

)

ABC

là:

Giao

ể

m c

ủ

đườ

ng th

ẳ

và

đườ

ng th

ẳ

B. Đ

ể

Giao

ể

m c

ủ

đườ

ng th

ẳ

và

đườ

ng th

ẳ

D. Đ

ể

Câu 6:

Trong các m

ệ

đề

sau m

ệ

đề

nào

sai?

Hình bi

ể

u di

ễ

n c

ủ

a hai

đườ

ng c

ắ

t nhau có th

ể

là hai

đườ

ng song song.

Dùng nét

đứ

t bi

ể

u di

ễ

n cho

đườ

ng b

ị

che khu

ấ

Hình bi

ể

u di

ễ

n ph

ả

i gi

ữ

nguyên quan h

ệ

thu

ộ

c gi

ữ

ể

m và

đườ

ng th

ẳ

ng.

Hình bi

ể

u di

ễ

n c

ủ

đườ

ng th

ẳ

ng là

đườ

ng th

ẳ

ng.

Câu 7:

Cho t

ứ

ệ

ABCD

. G

ọ

, ,

I J K

ầ

n l

ượ

t là trung

ể

m c

ủ

, , .

AC BC BD

Giao tuy

ế

n c

ủ

a hai m

ặ

ẳ

(

)

ABD

và

(

)

KJI

là

B. Đườ

ng th

ẳ

ng qua

và song song v

ớ

Không có.

Câu 8:

Cho hình chóp

S ABCD

có

áy là hình thoi tâm

, g

ọ

là trung

ể

m c

ủ

, g

ọ

là trung

ể

m c

ủ

và

là giao

ể

m c

ủ

và

. Khi

ó giao tuy

ế

n c

ủ

a mp

(

)

SAD

và mp

(

)

MEB

là :

A. Đườ

ng th

ẳ

ng qua

và //

,//

B. Đườ

ng th

ẳ

C. Đườ

ng th

ẳ

D. Đườ

ng th

ẳ

ng qua

và //

, //

Câu 9:

Tìm m

ệ

đề

sai:

Hai

đườ

ng th

ẳ

ng cùng ch

ứ

a trong 1 m

ặ

t ph

ẳ

ng và không có

ể

m chung thì song song v

ớ

i nhau.

Hai

đườ

ng th

ẳ

ng phân bi

ệ

t không c

ắ

t nhau và không song song thì chéo nhau.

Toán 11 GV. Lư Sĩ Pháp

HÌNH HỌC 11 Chương II. ĐT & MP Trong KG. QHSS

Hai

đườ

ng th

ẳ

ng cùng ch

ứ

a trong 1 m

ặ

t ph

ẳ

ng n

ế

u không song song thì c

ắ

t nhau ho

ặ

c trùng nhau.

Hai

đườ

ng th

ẳ

ng chéo nhau cùng ch

ứ

a trong 1 m

ặ

t ph

ẳ

ng.

Câu 10:

Cho t

ứ

ệ

ABCD

. G

ọ

i M, N l

ầ

n l

ượ

t là trung

ể

m c

ủ

a AB và AC , E là

ể

m trên c

ạ

nh CD v

ớ

3 .

ED EC

Thi

ế

t di

ệ

n c

ủ

a t

ứ

ệ

ABCD

khi c

ắ

t b

ở

i m

ặ

t ph

ẳ

(

)

MNE

là hình gì?

Hình thang.

Hình bình hành.

Hình ng

giác.

Hình tam giác.

II. Phần tự luận

Bài 1:

Cho t

ứ

ệ

ABCD

có

và

ầ

n l

ượ

t là trung

ể

và

thu

ộ

sao cho

KD KB

a/ Ch

ứ

ng minh:

(

)

// DAB .

b/ Tìm giao

ể

m gi

ữ

đườ

ng th

ẳ

và m

ặ

t ph

ẳ

(

)

IJK

Bài 2:

Cho hình chóp

S ABCD

áy

ABCD

là hình thang cân có

không song song v

ớ

. G

ọ

là

trung

ể

m c

ủ

và

(

)

là m

ặ

t ph

ẳ

ng qua

, song song v

ớ

và

a/ Tìm giao tuy

ế

n gi

ữ

a 2 m

ặ

t ph

ẳ

(

)

SAB

và

(

)

SDC

b/ Xác

đị

nh thi

ế

t di

ệ

n c

ủ

a hình chóp

S ABCD

khi c

ắ

t b

ở

i m

ặ

t ph

ẳ

(

)

ĐỀ 4

I. Phần trắc nghiệm

Câu 1:

Các y

ế

u t

ố

nào sau

ây xác

đị

nh m

ộ

t m

ặ

t ph

ẳ

ng duy nh

ấ

ể

m phân bi

ệ

t không th

ẳ

ng hàng.

ố

ể

Hai

đườ

ng th

ẳ

ng chéo nhau.

ộ

ể

m và m

ộ

đườ

ng th

ẳ

ng.

Câu 2:

Cho

đườ

ng th

ẳ

ằ

m trong mp

(

)

và

đườ

ng th

ẳ

(

)

b mp

⊄

ệ

đề

nào sau

ây

úng ?

ế

ắ

(

)

thì

ắ

ế

b a

thì

(

)

// .

ế

ắ

(

)

thì

chéo

ế

(

)

thì

// .

b a

Câu 3:

Cho t

ứ

ệ

ABCD

ọ

M N

ầ

n l

ượ

t là trung

ể

m c

ủ

a c

ạ

, ;

AC AD

là tr

ọ

ng tâm

△

.Khi

ó giao tuy

ế

n c

ủ

(

)

BMN

và

(

)

GCD

là:

A. Đườ

ng th

ẳ

qua

và

// CD.

B. Đườ

ng th

ẳ

qua

và

// CD.

C. Đườ

ng th

ẳ

ớ

K MN C

= ∩

D. Đườ

ng th

ẳ

Câu 4:

Cho hai

đườ

ng th

ẳ

và

chéo nhau. Có bao nhiêu m

ặ

t ph

ẳ

ng ch

ứ

và song song v

ớ

Không có m

ặ

t ph

ẳ

ng nào.

Vô s

ố

Câu 5:

Cho hình chóp

S ABCD

áy là hình thoi tâm

ọ

là trung

ể

ệ

đề

nào

úng:

(

)

// .

PO SAC

(

)

// .

PO SBD

(

)

// .

PO SAB

(

)

// .

PO SCD

Câu 6:

Cho hình chóp

S ABCD

áy là hình bình hành. L

ấ

: .

M SB

∈ =

là tr

ọ

ng tâm

ABC

△

Tìm m

ệ

đề

úng:

(

)

// .

MG SAC

(

)

// .

MG SAD

// .

MG SC

// .

MG SA

Câu 7:

Cho hình chóp

S ABCD

áy

ABCD

là hình bình hành. Gi

ả

ử

thu

ộ

ạ

ặ

t ph

ẳ

(

)

ABM

ắ

t hình chóp

S ABCD

theo thi

ế

t di

ệ

n là hình gì?

Hình bình hành.

Tam giác

Hình ch

ữ

ậ

Hình thang.

Câu 8:

Cho t

ứ

ệ

ABCD

ọ

I J

ầ

n l

ượ

t là trung

ể

m c

ủ

, .

AD BC

Giao tuy

ế

n c

ủ

a hai m

ặ

ẳ

(

)

IBC

và

(

)

JAD

là

đườ

ng th

ẳ

ng nào sau

ây?

Toán 11 GV. Lư Sĩ Pháp

HÌNH HỌC 11 Chương II. ĐT & MP Trong KG. QHSS

Câu 9:

Cho hình chóp

S ABCD

có

áy là hình bình hành. G

ọ

, ,

M N K

ầ

n l

ượ

t là trung

ể

ủ

, , .

BC DC SB

Giao

ể

m c

ủ

và

(

)

SAK

là giao

ể

m c

ủ

ớ

đườ

ng th

ẳ

ng nào sau

ây?

Câu 10:

Cho hình chóp

S ABCD

có

áy

ABCD

là hình bình hành. Xác

inh giao tuy

ế

n c

ủ

a m

ặ

t ph

ẳ

(

)

SAD

và

(

)

SBC

A. Đ

ể

, .

SO O AC BD

= ∩

B. Đườ

ng th

ẳ

ng b

ấ

t k

ỳ

song song v

ớ

C. Đườ

ng th

ẳ

i qua S và song song v

ớ

D. Đườ

ng th

ẳ

ng b

ấ

t k

ỳ

song song v

ớ

II. Phần tự luận

Bài 1:

Cho t

ứ

ệ

ABCD

có

và

ầ

n l

ượ

t là trung

ể

và

thu

ộ

sao cho

KD KB

a/ Ch

ứ

ng minh:

(

)

// DAB .

b/ Tìm giao

ể

m gi

ữ

đườ

ng th

ẳ

và m

ặ

t ph

ẳ

(

)

IJK

Bài 2:

Cho hình chóp

S ABCD

có

áy

ABCD

là hình bình hành tâm

ọ

, ,

M N P

theo th

ứ

ự

là trung

ể

m c

ủ

a các

ạ

n th

ẳ

, , .

SA BC CD

a/ Tìm giao tuy

ế

n 2 m

ặ

t ph

ẳ

(

)

SAB

và

(

)

SCD

b/ Tìm thi

ế

t di

ệ

n hình chóp c

ắ

t b

ở

(

)

MNP

Toán 11 GV. Lư Sĩ Pháp

HÌNH HỌC 11 Chương II. ĐT & MP Trong KG. QHSS

ĐÁP ÁN

CHƯƠNG II. ĐƯỜNG THẲNG VÀ MẶT PHẲNG TRONG KHÔNG GIAN

QUAN HỆ SONG SONG

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20

21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40

41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60

61 62

63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82

94 95

100

101

102

103

104

105

Bấm Tải xuống để xem toàn bộ.

| 1/54

| | Tải xuống

Preview text:

Giáo Viên Trường THPT Tuy Phong HÌNH HỌC 11 CHƯƠNG II ĐƯỜNG THẲNG VÀ MẶT PHẲNG TRONG KHÔNG GIAN QUAN HỆ SONG SONG LỜI NÓI ĐẦU
Quý đọc giả, quý thầy cô và các em học sinh thân mến!
Nhằm giúp các em học sinh có tài liệu tự học môn Toán,
tôi biên soạn cuốn giải toán trọng tâm HÌNH HỌC 11.
Nội dung của cuốn tài liệu bám sát chương trình chuẩn và
chương trình nâng cao về môn Toán đã được Bộ Giáo dục và Đào tạo quy định. Nội dung gồm 4 phần
Phần 1. Kiến thức cần nắm
Phần 2. Dạng bài tập có hướng dẫn giải và bài tập đề nghị
Phần 3. Phần trắc nghiệm có đáp án.
Phần 4. Một số đề ôn kiểm tra
Cuốn tài liệu được xây dựng sẽ còn có những khiếm
khuyết. Rất mong nhận được sự góp ý, đóng góp của quý
đồng nghiệp và các em học sinh.
Mọi góp ý xin gọi về số 0939989966 – 0916620899 Email: lsp02071980@gmail.com Chân thành cảm ơn. Lư Sĩ Pháp Gv_Trường THPT Tuy Phong MỤC LỤC CHƯƠNG I
ĐƯỜNG THẲNG VÀ MẶT PHẲNG TRONG KHÔNG GIAN QUAN HỆ SONG SONG
§1. ĐẠI CƯƠNG VỀ ĐƯỜNG THẲNG VÀ MẶT PHẲNG ................ Trang 01 – 05
§2. HAI ĐƯỜNG THẲNG CHÉO NHAU
VÀ HAI ĐƯỜNG THẲNG SONG SONG ........................................ Trang 06 – 10
§3. ĐƯỜNG THẲNG VÀ MẶT PHẲNG SONG SONG ...................... Trang 11 – 16
§4. HAI MẶT PHẲNG SONG SONG .................................................. Trang 17 – 21
§5. PHÉP CHIẾU SONG SONG ............................................................ Trang 22 – 23
ÔN TẬP CHƯƠNG II ............................................................................ Trang 24 – 30
TRẮC NGHIỆM CHƯƠNG II .............................................................. Trang 31 – 43
MỘT SỐ ĐỀ ÔN KIỂM TRA MỘT TIẾT ........................................... Trang 44 – 49
ĐÁP ÁN ................................................................................................... Trang 50 Toán 11 GV. Lư Sĩ Pháp CHƯƠNG II
ĐƯỜNG THẲNG VÀ MẶT PHẲNG TRONG KHÔNG GIAN QUAN HỆ SONG SONG ----------0o0----------
§1. ĐẠI CƯƠNG VỀ ĐƯỜNG THẲNG VÀ MẶT PHẲNG
A. KIẾN THỨC CẦN NẮM
I. Các tính chất thừa nhận
Tính chất 1. Có một và chỉ một đường thẳng đi qua hai điểm phân biệt .
Tính chất 2. Có một và chỉ một mặt phẳng đi qua ba điểm không thẳng hàng.
Tính chất 3. Nếu đường thẳng có hai điểm phân biệt thuộc một mặt phẳng thì mọi điểm của đường thẳng
đều thuộc mặt phẳng đó.
Lưu ý: Đường thẳng d nằm trong mp(α ) ta kí hiệu: d ⊂ (α) hay (α) ⊃ d
Tính chất 4. Tồn tại bốn điểm không cùng thuộc một mặt phẳng.
Tính chất 5. Nếu hai mặt phẳng phân biệt có một điểm chung thì chúng còn có một điểm chung khác nữa.
Như vậy: Nếu hai mặt phẳng phân biệt có một điểm chung thì chúng có một đường thẳng chung đi qua
điểm chung ấy và đường thẳng đó gọi là giao tuyến của hai mặt phẳng.
Tính chất 6. Trên mỗi mặt phẳng, các kết quả đã biết trong hình học phẳng đều đúng.
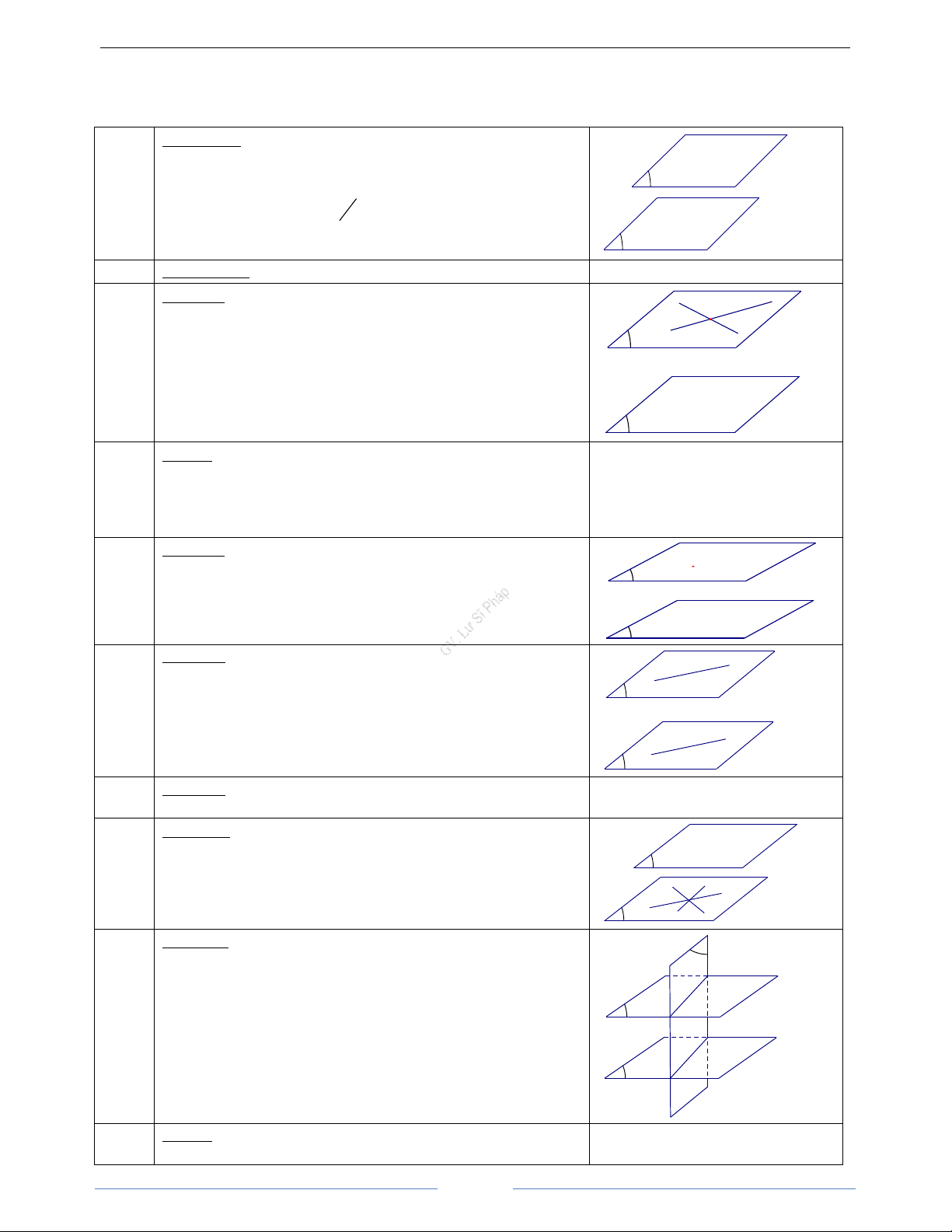
II. Cách xác định mặt phẳng.
Một mặt phẳng hoàn toàn xác định khi biết:
1. Nó đi qua ba điểm không thẳng hàng A C
(ABC) biểu thị mặt phẳng xác định bởi ba điểm phân biệt không thẳng
hàng A, B, C. α B
2. Nó đi qua một điểm và chứa một đường thẳng không đi qua điểm đó
(M, d) biểu thị mặt phẳng xác định bởi đường thẳng d và điểm M A không nằm trên d. d α
3. Nó chứa hai đường thẳng cắt nhau a
(a, b) biểu thị mặt phẳng xác định bởi hai đường thẳng cắt nhau a và b. M b α a caét b taïi M
III. Hình chóp và hình tứ diện
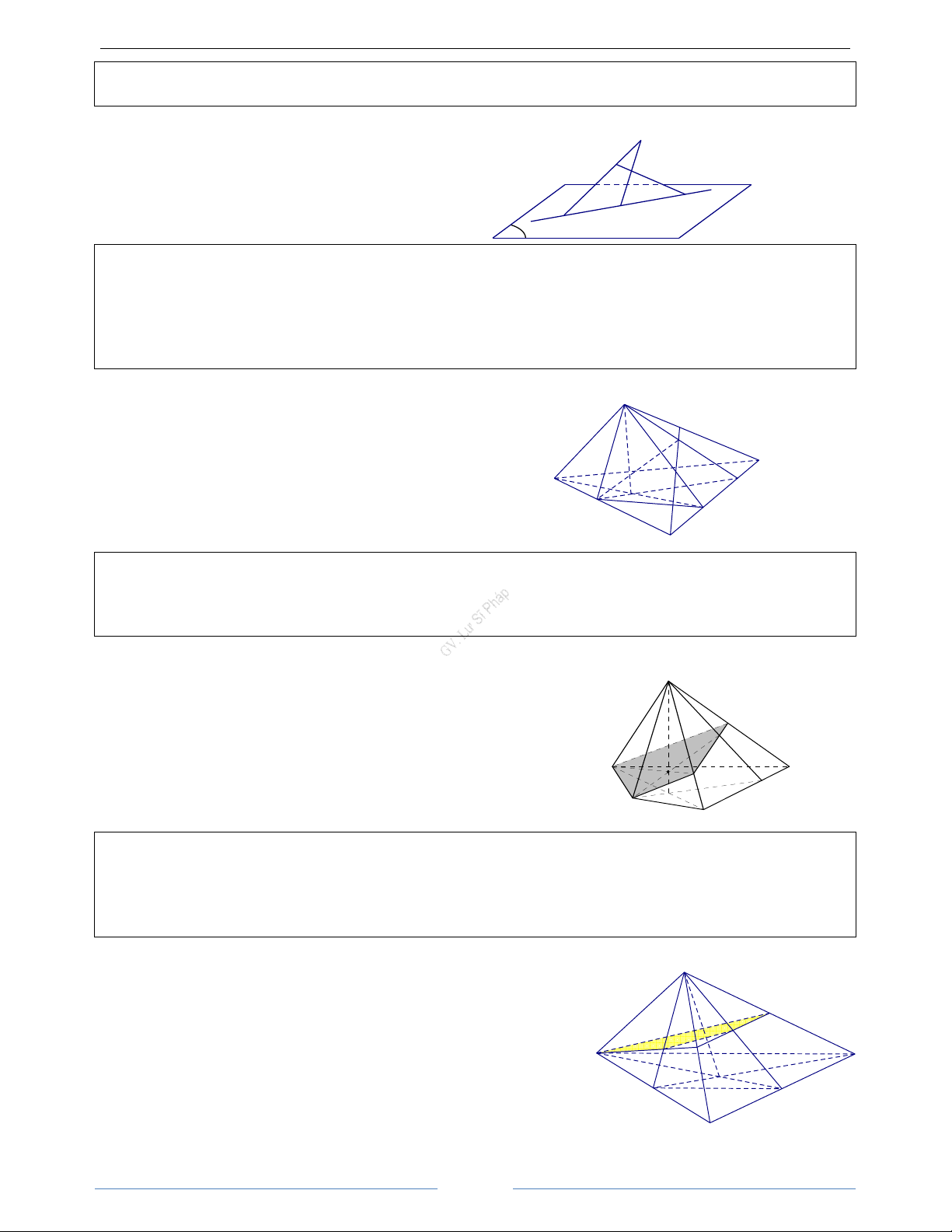
1. Hình chóp : Trong mặt phẳng (α) cho đa giác lồi A A ...A . S 1 2 ñænh n
Điểm S nằm ngoài (α) . Lần lượt nối S với các đỉnh A , A ,..., A ta 1 2 n caïnh beân maët be ân
được n tam giác SA A ,SA A ,...,SA A . Hình gồm có đa giác 1 2 2 3 n 1 A2
A A ...A và n tam giác SA A ,SA A ,...,SA A được gọi là hình A1 1 2 n 1 2 2 3 n 1 A3 caïnh ñaùy chóp , kí hiệu A
S.A A ...A 5 A 1 2 4 m aët ñaùy n 2. Hình tứ diện
Cho bốn điểm A, B, C, D không đồng phẳng. Hình gồm
bốn tam giác ABC, ABD, ACD và BCD được gọi là hình tứ
diện , kí hiệu ABCD. 1 HÌNH HỌC 11
Chương II. ĐT & MP Trong KG. QHSS Toán 11 GV. Lư Sĩ Pháp B. BÀI TẬP
ấn đề 1. Tìm giao tuyến của hai mặt phẳng
VPhương pháp: Ta đi tìm hai điểm chung phân bệt của hai mặt phẳng đó. Giao tuyến của chúng là
đường thẳng đi qua hai điểm đó. α  ∩ β = M  Nghĩa là: α
 ∩ β = N ⇒ α ∩ β = MN M  ≡ N
Bài 1.1. Cho bốn điểm không đồng phẳng A, B, C và D. Trên đoạn AB và AC lấy hai điểm M và N sao AM AN cho = 1;
= 2 . Hãy xác định giao tuyến của mặt phẳng (DMN) với các mặt (ABD), (ACD), (ABC) BM NC và (BCD) . HD Giải
(DMN ) ∩ (ADB) = ? . A
Ta có D ∈(DMN) ∩(ADB) M ∈(DMN) 
 ⇒ M ∈(DMN) ∩ (ABD)
M ∈ AB ⊂ (ABD) ⇒ M ∈(ABD) M
Vậy : DM = (DMN) ∩ (ABD) D
(DMN ) ∩ (ACD) = DN N
(DMN ) ∩ (ABC) = MN
(DMN ) ∩ (BCD) = ? B C AM AN E Trong mp(ABC) có ≠
, nên MN ∩ BC = E BM NC
Tương tự: (DMN ) ∩ (BCD) = DE
Bài 1.2. Cho S là một điểm không thuộc mặt phẳng hình bình hành ABCD. Tìm giao tuyến của hai mặt
phẳng (SAC) và (SBD). HD Giải
Gọi O là giao điểm của AC và BD. Ta có S
S ∈(SAC) ∩ (SBD)
O ∈ AC ⊂ (SAC) ⇒ O∈(SAC)∩(SBD)
O ∈ BD ⊂ (SBD)
nên SO = (SAC) ∩ (SBD) A D
Vậy giao tuyến hai mặt phẳng (SAC) và (SBD) là đường thẳng SO O B C
Bài 1.3. Cho S là một điểm không thuộc mặt phẳnh hình thang ABCD (AB // CD và AB > CD). Tìm giao
tuyến hai mặt phẳng (SAD) và (SBC). HD Giải
Gọi I là giao điểm AD và BC. Ta có S và I là hai S
điểm chung của (SAD) và (SBC), nên
SI = (SAD) ∩ (SBC)
Vậy giao tuyến hai mặt phẳng (SAD) và (SBC) là A D đường thẳng SI. I C B 2 HÌNH HỌC 11
Chương II. ĐT & MP Trong KG. QHSS Toán 11 GV. Lư Sĩ Pháp
Bài 1.4. Cho bốn điểm A,B,C,D không đồng phẳng. Gọi I, K lần lượt là trung điểm của hai đoạn thẳng AD và BC.
a) Tìm giao tuyến của hai mặt phẳng (IBC) và (KAD)
b) Gọi M và N là hai điểm lần lượt trên hai đường thẳng AB và AC. Tìm giao tuyến của hai mặt phẳng
(IBC) và (DMN). HD Giải
a) (IBC) ∩ (KAD) = KI . Vậy giao tuyến hai mặt phẳng (IBC) và (KAD) là đường thẳng KI.
b) Trong mp (ABD), gọi E = MD ∩ BI , A
trong mp(ACD) , gọi F = ND ∩CI Ta có:
(IBC) ∩(DMN) = EF I
Vậy giao tuyến hai mặt phẳng (IBC) và (DMN) M E là đường thẳng EF. N F D B K C
ấn đề 2. Tìm giao điểm của đường thẳng d và mặt phẳng (α)
VPhương pháp: Để tìm giao điểm của một đường thẳng dvà một mặt phẳng(α), ta có thể đưa về
việc tìm giao điểm của đường thẳng d với một đường thẳng d/ nằm trong mặt phẳng (α)
mp phuï(β ) ⊃ d 
Nghĩa là: (β ) ∩ (α) = d/  ⇒ d ∩(α) = I 
d / ∩ d = I 
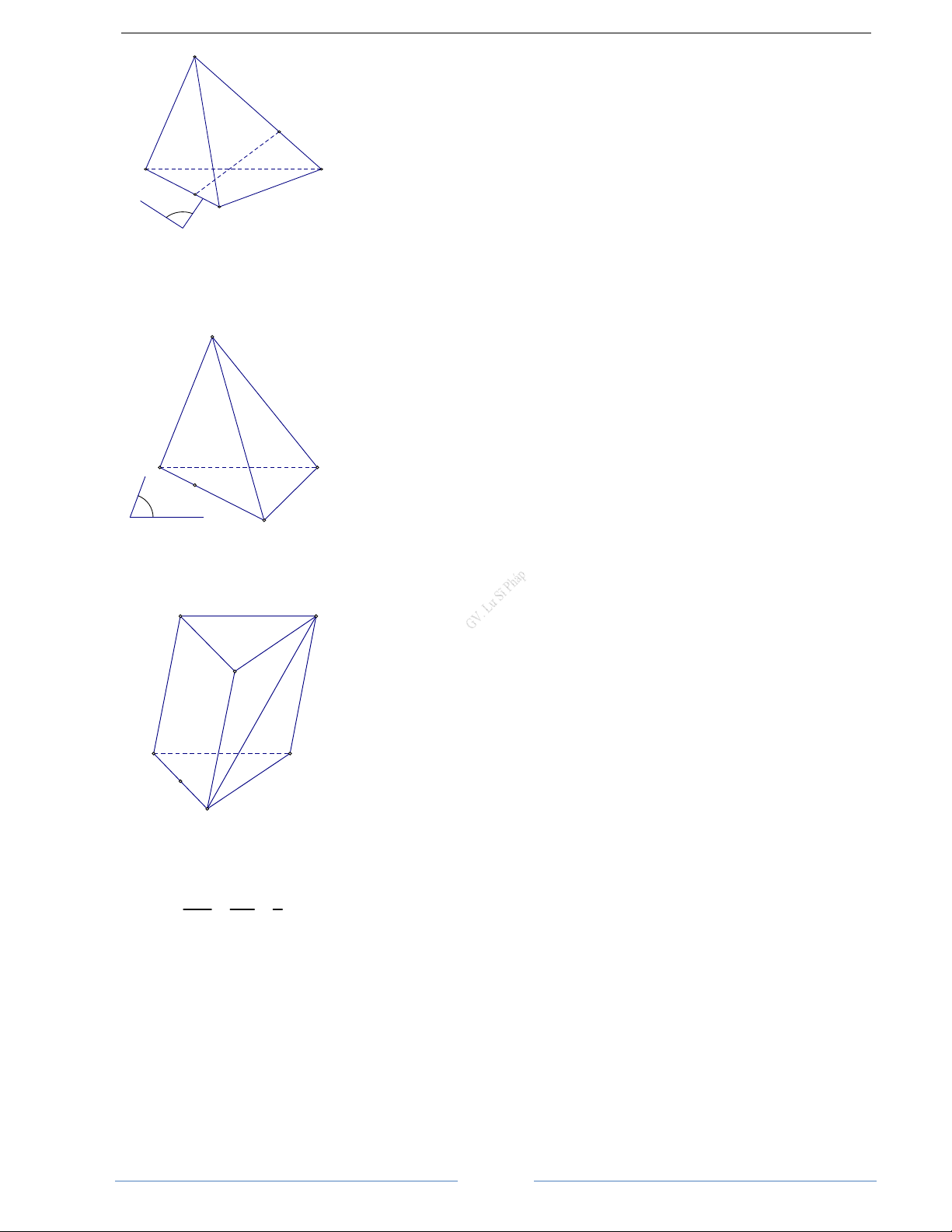
Bài 1.5. Cho tam giác BCD và điểm A không thuộc mặt phẳng (BCD). Gọi K là trung điểm của đoạn AD
và G là trọng tâm của tam giác ABC. Tìm giao điểm của đường thẳng GK với mặt phẳng (BCD). HD Giải
Gọi J là giao điểm của AG và BC. Trong mặt A AG 2 AK 1 phẳng (AJD), ta có = ; = nên GK và AJ 3 AD 2 K
JD cắt nhau. Gọi L là giao điểm của GK và JD. Ta có L ∈GK G  B D L ∈ JD  ⇒ L ∈(BCD) I JD ⊂ (BCD)
Vậy L là giao điểm của GK và (BCD) L C
Bài 1.6. Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm các cạnh AB và CD, trên AD lấy điểm P
không trùng với trung điểm AD.
a) Gọi E là giao điểm của đường thẳng MP và BD. Tìm giao tuyến của hai mp (PMN) và (BCD)
b) Tìm giao điểm của hai mp (PMN) và BC. HD Giải
a ) (MNP) ∩ (BCD) = EN A
b) Trong mp (BCD), gọi Q = EN ∩ BC P M
Ta có : BC ∩ (MNP) = Q E B D Q N C 1
Bài 1.7. Cho tứ diện ABCD. Gọi I, J là các điểm lần lượt nằm trên các cạnh AB, AD với AI = IB và 2 3 HÌNH HỌC 11
Chương II. ĐT & MP Trong KG. QHSS Toán 11 GV. Lư Sĩ Pháp 2
AJ = JD . Tìm giao điểm của đường thẳng IJ với mặt phẳng (BCD). 3 HD Giải  1 A AI = IB  Do 2 I 
nên IJ kéo dài cắt BD, gọi giao  2 J AJ = JD  3 K B D
điểm là K. Khi đó K = IJ ∩ (BCD) C
Bài 1.8. Cho hình chóp S.ABCD có đáy là tứ giác ABCD có hai cạnh đối diện không song song. Lấy điểm
M thuôc miền trong của tam giác SCD. Tìm giao tuyến của hai mặt phẳng:
a) (SBM) và (SCD)
b) (ABM) và(SCD)
c) (ABM) và (SAC) HD Giải
a) Ta có ngay: (SBM) ∩ (SCD) = SM S
b) Ta có: M ∈(ABM) ∩ (SCD)
Trong mp (ABCD) gọi I = AB ∩ CD M
Suy ra : MI = (ABM) ∩ (SCD) c) Ta có: A
A ∈(ABM) ∩ (SAC) . D J
Trong mp (SCD), gọi J = IM ∩ SC B
Suy ra: J ∈(ABM) ∩ (SAC) C
Vậy: AJ = (ABM) ∩ (SAC) I
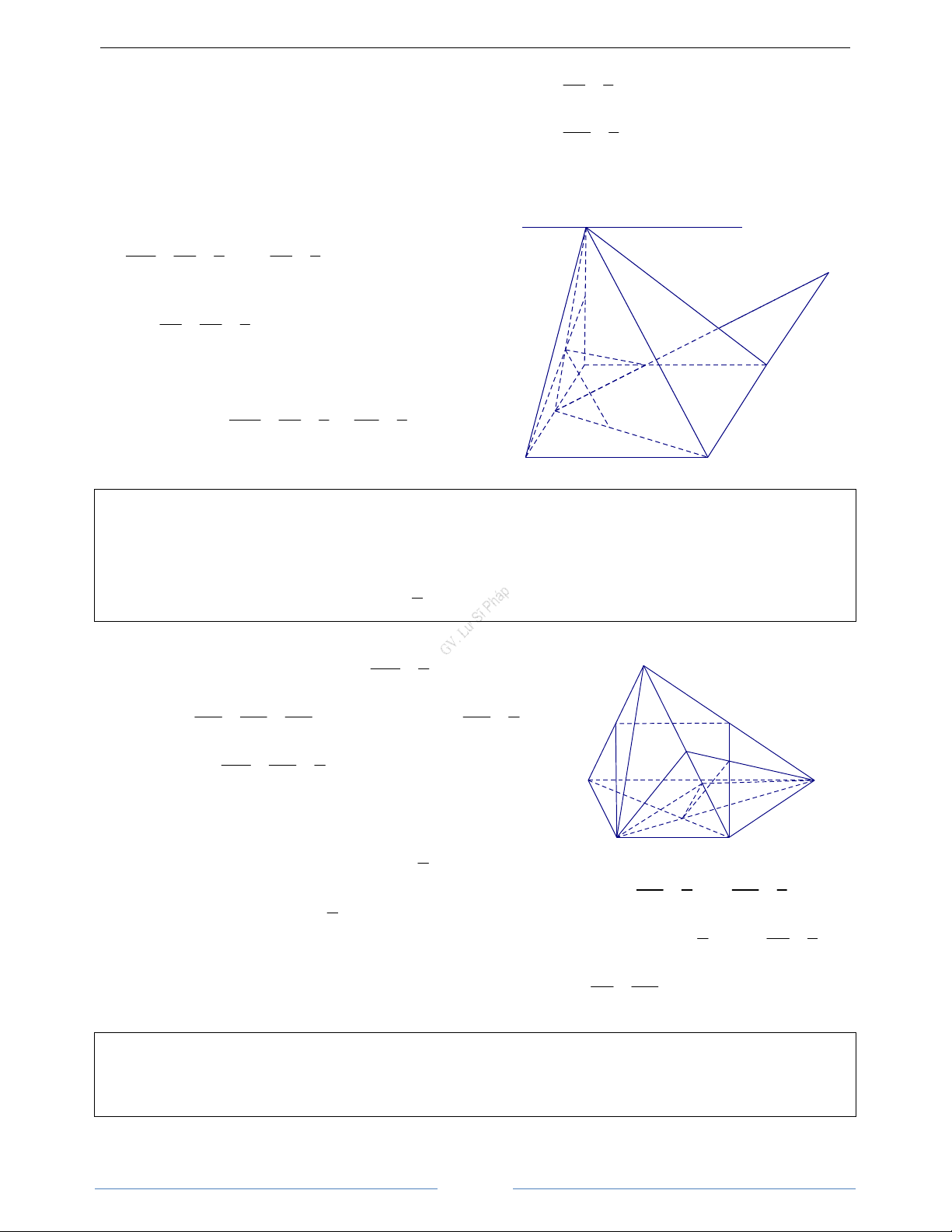
Bài 1.9. Cho hình chóp S.ABCD có đáy ABCD là tứ giác, M và N tương ứng là các điểm thuộc các cạnh
SC và BC. Tìm giao điểm của đường thẳng SD với mặt phẳng (AMN). HD Giải S
Gọi O = AC ∩ BD .Trong mp(SAC), gọi K = SO ∩ AM P
Trong mp(ABCD), gọi L = BD ∩ AN
Chọn mặt phẳng phụ (SBD) chứa SD. M
Và ta có: LK = (SBD) ∩ (AMN) K
Mà trong mp (SBD), có LK ∩ SD = P D
Vậy: P = SD ∩ (AMN) A O C B N
ấn đề 3. Chứng minh ba điểm thẳng hàng
VPhương pháp: Để chứng ba điểm thẳng hàng, ta có thể chứng minh chúng cùng thuộc hai mặt
phẳng riêng biệt.
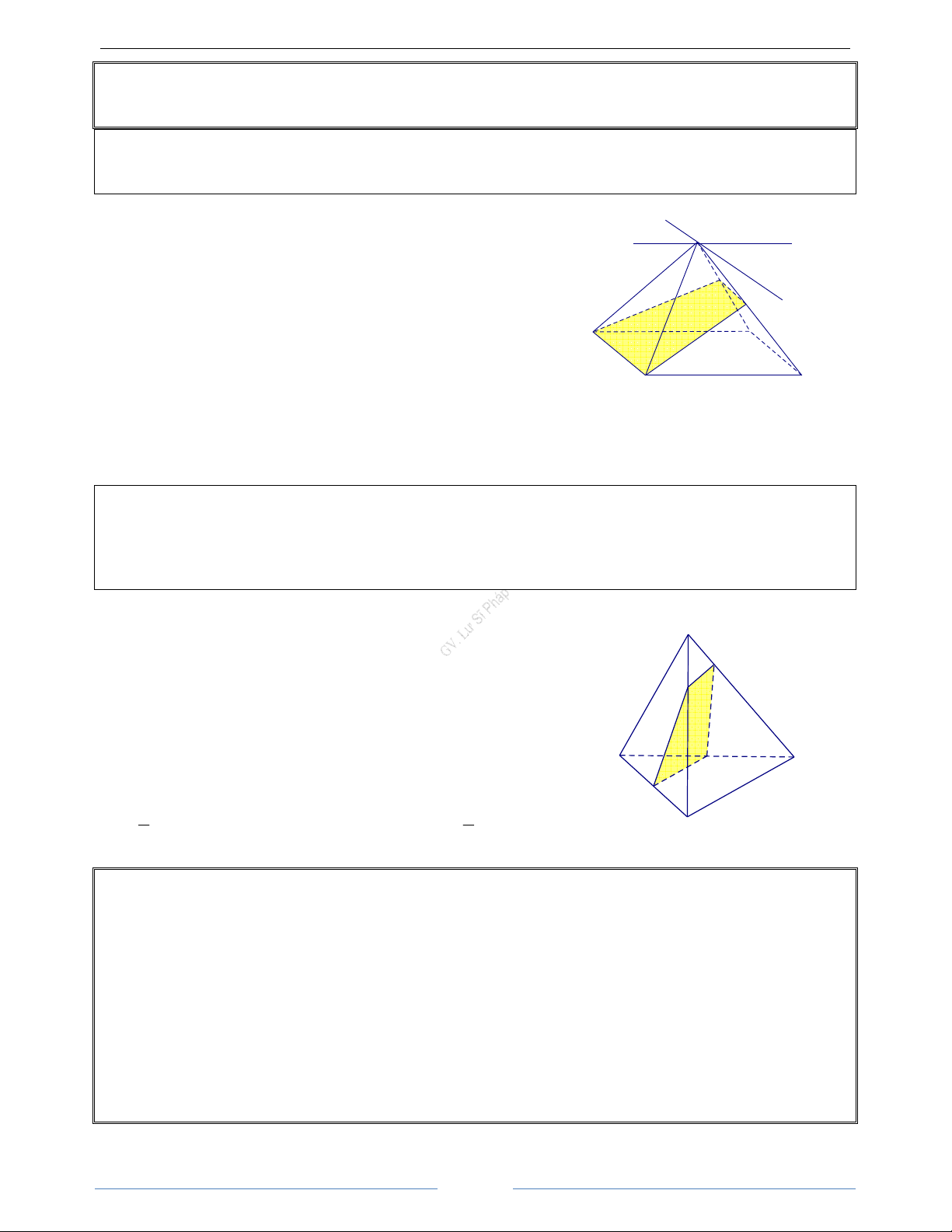
Bài 1.10. Cho tứ diện SABC. Trên SA, SB, SC lần lượt lấy các điểm D, E và F sao cho cắt AB tại I, EF cắt
BC tại J, FD cắt CA tại K. Chứng minh rằng ba điểm I, J, K thẳng hàng. HD Giải I ∈ DE  S Ta có:
 ⇒ I ∈(DEF) và F DE ⊂ (DEF) D I ∈AB  E
 ⇒ I ∈(ABC). Suy ra: J ∈(MNK) ∩ (BCD) AB ⊂ (ABC) K A C
Lí luận tương tự ta có: J, K cũng là điểm chung của hai mặt phẳng B (DEF) và (ABC) J
Vậy I, J, K thuộc về giao tuyến của hai
mặt phẳng (DEF) và (ABC) nên I, J, K thẳng I hàng. 4 HÌNH HỌC 11
Chương II. ĐT & MP Trong KG. QHSS Toán 11 GV. Lư Sĩ Pháp
Bài 1.11. Cho ba điểm A, B, C không thuộc mặt phẳng (Q) và các đường thẳng BC, CA, AB cắt (Q) lần
lượt tại M, N, P. Chứng minh rằng M, N, P thẳng hàng. HD Giải
Ta có M, N, P lần lượt thuộc về hai mặt phẳng (Q) A
và (ABC), nên M, N, P thuộc về giao tuyến của hai B
mặt phẳng (Q) và (ABC). Vậy M, N, P thẳng hàng. C M N P Q
Bài 1.12. Cho hình chóp S.ABCD có AB và CD không song song. Gọi M là một điểm thuộc miền trong
của tam giác SCD.
a) Tìm giao điểm N của đường thẳng CD và mặt phẳng (SBM)
b) Tìm giao tuyến của hai mặt phẳng (SBM) và (SAC)
c) Tìm giao điểm I của đường thẳng BM và mp(SAC)
d) Tìm giao điểm P của SC và mp(ABM), từ đó suy ra giao tuyến của hai mặt phẳng (SCD) và (ABM). HD Giải
a) Gọi N = SM ∩CD . Ta có N = CD ∩ (SBM) S
b) Gọi O = AC ∩ BN .Ta có:(SBM) ∩ (SAC) = SO
c) Gọi I = SO ∩ BM M
Ta có I = BM ∩(SAC) D P I A
d) Gọi R = AB ∩CD , P = MR ∩ SC N O
Ta có P = SC ∩ (ABM) ⇒ PM = (SCD) ∩ (ABM) B C R
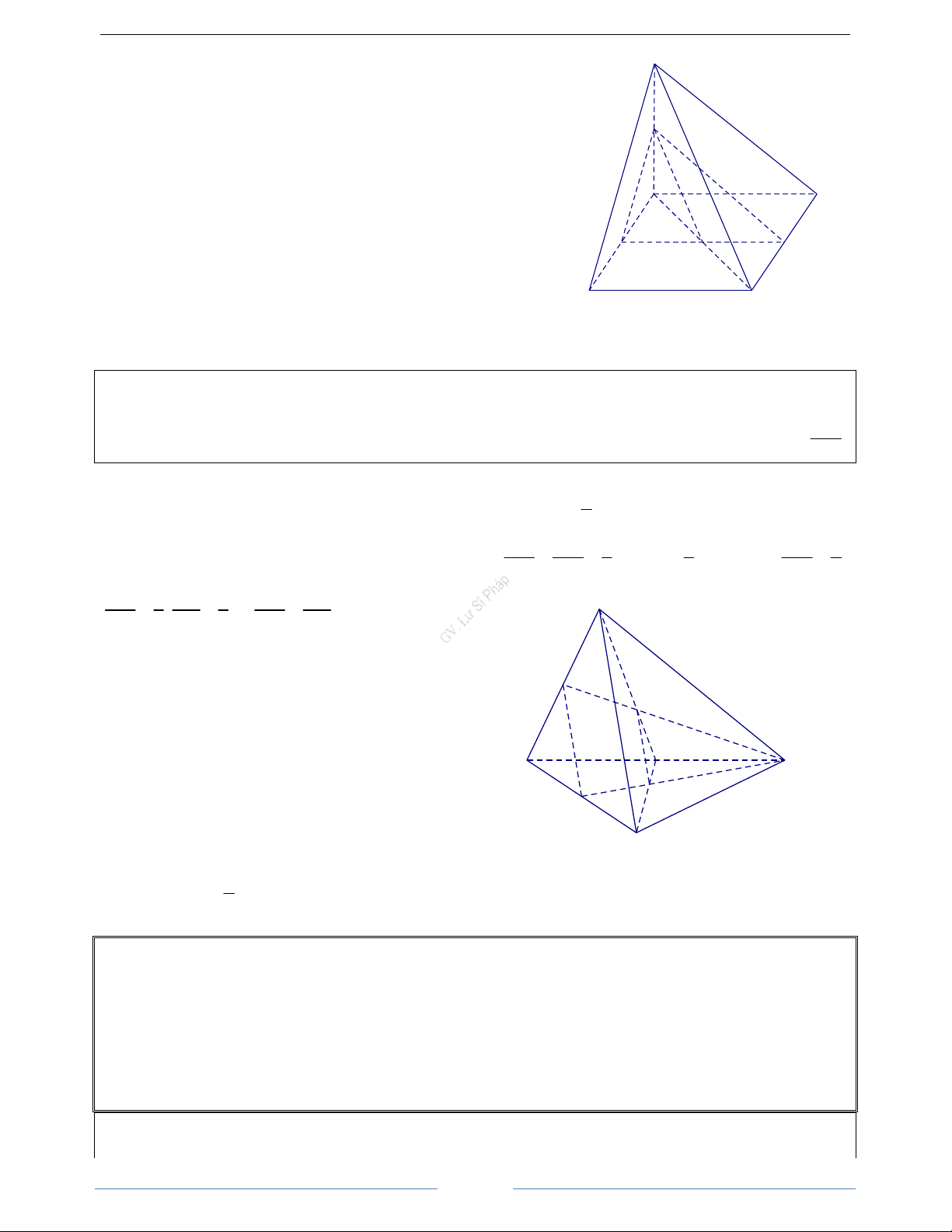
Bài 1.13. Cho hình chóp S.ABCD. Gọi M là một điểm nằm trong tam giác SCD.
a) Tìm giao tuyến của hai mặt phẳng (SBM) và (SAC)
b) Tìm giao điểm của đường thẳng BM và mp(SAC)
c) Xác định thiết diện của hình chóp khi cắt bởi mặt phẳng (ABM) HD Giải
a) Gọi N = SM∩CD, O = AC∩BN. Khi đó SO = (SAC) ∩ S (SBM).
b) Trong mp(SBM), đường thẳng BM cắt SO tại I. Ta có Q I=BM∩(SAC). M
c) Trong mp(SAC), đường thẳng AI cắt SC tại P. Ta có P và M là
hai điểm chung của mp(ABM) và mp(SCD). A D I P
vậy (ABM) ∩ (SCD) = PM. Đường thẳng PM cắt SD tại Q. thiết N O
diện của hình chóp khi cắt bởi mp(ABM) là tứ giác ABPQ. B C
Bài 1.14. Cho hình chóp S.ABCD có đáy là hình thang ABCD (AB//CD, AB > CD). Gọi
I, J theo thứ tự là trung điểm của các cạnh SB và SC.
a) Xác định giao tuyến của hai mặt phẳng (SAD) và (SBC), (SAC) và (SBD)
b) Tìm giao điểm của đường thẳng SD với mp(AIJ)
c) Xác định thiết diện của hình chóp S.ABCD cắt bởi mp(AIJ) HD Giải
a) Gọi K là giao điểm của AD và BC, khi đó hai mặt phẳng S
(SAD) và (SBC) có hai điểm ching là S và K. Vậy:
(SAD)∩(ABC) = SK I
Gọi O là giao điểm của AC và BD. Vậy (SAC) ∩ (ABD) = SO J
b) Gọi M là giao điểm của SK và IJ. Khi đó E M A B
(SAD)∩(AIJ) = AM . Gọi E là giao điểm của AM và SD thì E O
chính là giao điểm của SD với mp(AIJ). C D
c) Thiết diện của hình chóp khi cắt bởi mp(AIJ) là tứ giác AIJE. K 5 HÌNH HỌC 11
Chương II. ĐT & MP Trong KG. QHSS Toán 11 GV. Lư Sĩ Pháp
§2. HAI ĐƯỜNG THẲNG CHÉO NHAU
VÀ HAI ĐƯỜNG THẲNG SONG SONG
A. KIẾN THỪC CẦN NẮM
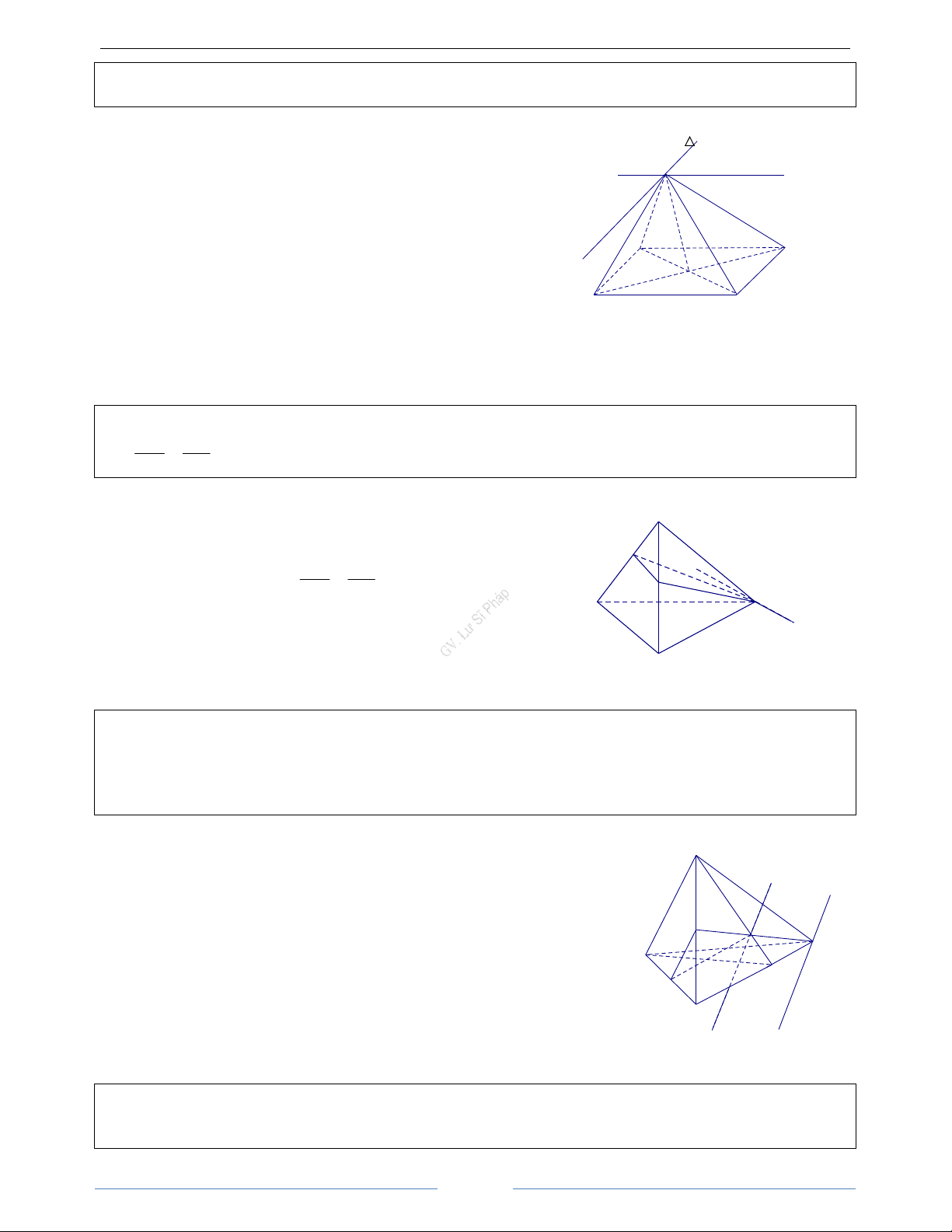
I. Vị trí tương đối của hai đường thẳng trong không gian
Cho hai đường thẳng a và b trong không gian. Có hai khả trường hợp sau đây xảy ra đối với a và b
TH1. Có một mặt phẳng chứa a và b
1. a và b cắt nhau tại M, kí hiệu
2. a và b song song với nhau, kí hiệu a //
3. a và b trùng nhau, kí
a ∩ b = M
b hoặc b // a hiệu a ≡ b M a a a b b α b α α a, b trùng nhau a caét b taïi M a , b song song
TH2. Không có mặt phẳng nào chứa cả a và b. Khi đó ta nói a và b chéo nhau. a b α a, b chéo nhau
II. Các định lí và tính chất
1. Định lí 1. Trong không gian, qua một điểm không nằm trên đường
thẳng cho trước, có một và chỉ một đường thẳng song song với M d đường thẳng đã cho. d'
Nhận xét: Hai đường thẳng song song a và b xác định một mặt α
phẳng, kí hiệu mp(a, b) hay mp(b, a)
2. Định lí 2. (về giao tuyến ba mặt phẳng)
Nếu ba mặt phẳng phân biệt đôi một cắt nhau theo ba giao tuyến I β γ
phân biệt thì ba giao tuyến ấy hoặc đồng quy hoặc đôi một song song α α a với nhau. a b c c b γ β
Hệ quả: Nếu hai mặt phẳng phân biệt lần lượt chứa hai đường thẳng song song thì giao tuyến của chúng
(nếu có) cũng song song với hai đường thẳng đó hoặc trùng với một trong hai đường thẳng đó. d d d α α b α a b a b a β β β
3. Định lí 3. Hai đường thẳng phân biệt cùng song song với đường
thẳng thứ ba thì song song với nhau. γ
4. Ba đoạn thẳng nối trung điểm các cạnh đối diện của một tứ diện α c b
đồng quy tại trung điểm G của mỗi đoạn. Điểm G đó gọi là trọng tâm a của tứ diện. β
5. Một mặt phẳng được xác định nếu nó đi qua hai đường thẳng song song. B. BÀI TẬP
ấn đề 1. Tìm giao tuyến hai mặt phẳng
VPhương pháp: Nếu hai mặt phẳng (α) và (β) có điểm chung là S và lần lượt chứa hai đường thẳng
song song d và d’ thì giao tuyến của (α) và (β ) là đường thẳng ∆ qua S và song song với d và d’. S ∈(α ) ∩ (β )  
Nghĩa là: d ⊂ (α),d ' ⊂ (β ) ⇒ (α) ∩ (β ) = ∆ (S ∈ ∆,∆ / /d / /d ') d / /d '   6 HÌNH HỌC 11
Chương II. ĐT & MP Trong KG. QHSS Toán 11 GV. Lư Sĩ Pháp
Bài 2.1. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Tìm giao tuyến của
(SAD) và (SBC); (SAB) và (SCD); (SAC) và (SBD). HD Giải S ∈(SAC) a) Ta có:
 ⇒ S ∈(SAC) ∩ (SBD) S ∈(SBD) S d
O ∈(SAC) ⇒ O∈(SAC)∩(SBD)
Gọi O = AC ∩ BD . O ∈(SBD)
⇒ SO = (SAC) ∩ (SBD) A D S ∈(SAB)  O b) Ta có:
 ⇒ S ∈(SAB) ∩ (SCD) S ∈(SCD) B C AB ⊂ (SAB) 
( ∆ qua S và song song với AB, CD. 
c) Lập luận tương tự câu b) ta có
Ta lại có: CD ⊂ (SCD) ⇒ (SAB) ∩ (SCD) = ∆ / / AB / /CD
(SAD)∩(SBC) = d / / AD / /BC  AB / /CD 
Bài 2.2. Cho tứ diện ABCD. Trên các cạnh AB và AC lần lượt lấy các điểm M và N sao AM AN cho =
. Tìm giao tuyến hai mặt phẳng (DBC) và (DMN). AB AC HD Giải M ∈ AB A Ta có:
 ⇒ MN ⊂ (ABC) N ∈ AC  M AM AN Trong tam giác ABC ta có: = ⇒ MN / /BC AB AC N D
Ta lại có: D ∈(DBC) ∩ (DMN) B x
BC ⊂ (DBC) 
MN ⊂ (DMN) ⇒ (DBC) ∩ (DMN) = Dx / / BC / / MN C  BC / / MN 
Bài 2.3. Cho tứ diện ABCD. Cho I, J tương ứng là trung điểm của BC và AC, M là một điểm trên cạnh
AD sao cho không trùng với trung điểm của AD.
a) Tìm giao tuyến d của hai mặt phẳng (MIJ) và (ABD)
b) Gọi K là giao điểm của hai đường thẳng CD và JM. Tìm giao tuyến của hai mặt phẳng (ABK) và (MIJ). HD Giải M ∈(MIJ)  A a) Ta có:
 ⇒ M ∈(MIJ) ∩ (ABD)
M ∈ AD ⊂ (ABD) t IJ / / AB x 
Ta cũng có IJ ⊂ (MIJ) ⇒ (MIJ) ∩ (ABD) = Mt / /IJ / / AB J M K  B AB ⊂ (ABD) D IJ / / AB I K ∈(ABK)   b) Ta có
 ⇒ K ∈(MIJ) ∩ (ABK) và IJ ⊂ (MIJ) C
K ∈ JM ⊂ (MIJ)  AB ⊂ (ABK)
⇒ (MIJ) ∩ (ABK) = Kx / /IJ / / AB
Bài 2.4. Cho tứ diện ABCD. Gọi M, N, P, Q, R và S lần lượt là trung điểm của AB, CD, BC, AD, AC và
BD. Chứng minh rằng tứ giác MPNQ là hình bình hành. Từ đó suy ra ba đoạn thẳng MN, PQ và RS cắt
nhau tại trung điểm mỗi đoạn, trung điểm đó gọi là trọng tâm của tứ diện. 7 HÌNH HỌC 11
Chương II. ĐT & MP Trong KG. QHSS Toán 11 GV. Lư Sĩ Pháp HD Giải AC A
Trong tam giác ABC ta có: MP//AC và MP = 2 AC
Trong tam giác ACD ta có: QN//AC và M QN = Q 2 MP / /QN G Từ đó suy ra: 
=> Tứ giác MPNQ là hình bình hành. D B MP = QN
Do vậy hai đường chéo MN và PQ cắt nhau tại trung điểm G P N của mỗi đường C AB
Tương tự: PR//QS và PR = QS = 2
Do đó tứ giác PRQS là hình bình hành. Suy ra hai đường chéo
Vậy ba đoạn thẳng MN, PQ, RS
cắt nhau tại trung điểm G của PQ và OR = OS
cắt nhau tại trung điểm mỗi đoạn và tại G.
Bài 2.5. Cho tứ diện ABCD có I, J lần lượt là trọng tâm của tam giác ABC và ABD.
Chứng minh rằng : IJ // CD. HD Giải
Gọi K là trung điểm của AB A
Vì I là trọng tâm của tam giác ABC nên
I ∈ KC và vì J là trọng tâm tam giác K
ABD nên I ∈ KD J KI KJ 1 I Từ đó suy ra: = = ⇒ IJ / /CD B N D KC KD 3 M C
Bài 2.6. Cho hình chóp S.ABCD đáy ABCD là hình bình hành. Trên đoạn SA lấy điểm M sao cho 2SM =
MA, trên đoạn SB lấy điểm N sao cho 2SN = NB.
a) Tìm giao tuyến của hai mặt phẳng (SAC) và (SBD); (SAD) và (SBC)
b) Chứng minh rẳng: MN//CD
c) Điểm P nằm trên cạnh SC không trùng với S, C. Tìm giao tuyến hai mp (MNP) và (SCD) HD Giải
a) Ta có: (SAC) ∩ (SBD) = SO S x S ∈(SAD) Ta có:
 ⇒ S ∈ (SAD) ∩ (SBC) S ∈(SBC) M y Mặt khác, ta có: N
AD ⊂ (SAD)
BC ⊂ (SBC) ⇒ (SAD) ∩ (SBC) = Sx / / AD / / BC A D AD / / BC   O P SM SN 1 b) Từ giả thiết ta có: =
= ⇒ MN / / AB và ABCD là B C MA NB 2
hình bình hành. Suy ra MN//AB//CD. c)
P ∈(MNP), P ∈(SCD) MN ⊂ (MNP) 
 ⇒ (MNP) ∩ (SCD) = Py / / MN / /CD CD ⊂ (SCD)   MN / /CD  8 HÌNH HỌC 11
Chương II. ĐT & MP Trong KG. QHSS Toán 11 GV. Lư Sĩ Pháp
ấn đề 2. Tìm thiết điện của hình chóp khi cắt bởi một mặt phẳng
VPhương pháp: Ta tìm giao tuyến của mặt phẳng đó với các mặt bên của hình chóp. Đoạn nối giữa
các giao tuyến cho ta một hình. Hình đó là thiết diện cần tìm.
Bài 2.7. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành.
a) Hãy xác định giao tuyến của các mặt phẳng (SAB) và (SCD); (SBC) và (SAD)
b) M là điểm thuộc cạnh SC, tìm thiết diện của hình chóp với mp(ABM). Thiết diện là hình gì? HD Giải
a) i). (SAB) ∩ (SCD) = ? S y
Ta có S ∈(SAB) ∩ (SCD); AB ⊂ (SAB); CD ⊂ (SCD), AB / /CD
Nên (SAB) ∩ (SCD) = Sx / / AB / /CD N
ii) (SBC) ∩ (SAD) = ? x M Ta có D
S ∈(SBC) ∩ (SAD); BC ⊂ (SBC); AD ⊂ (SAD), A
BC / / AD . Nên (SBC) ∩ (SAD) = Sy / / BC / / AD B C b) Ta có:
(ABM) ∩(ABCD) = AB; (ABM)∩(SBC) = BM ;(ABM)∩(SDC) = MN / / AB / /DC, N ∈SD
(ABM) ∩(SAD) = AN .
Vậy thiết diện cần tìm là tứ giác ABMN. Rõ ràng: ABMN là hình thang vì MN // AB.
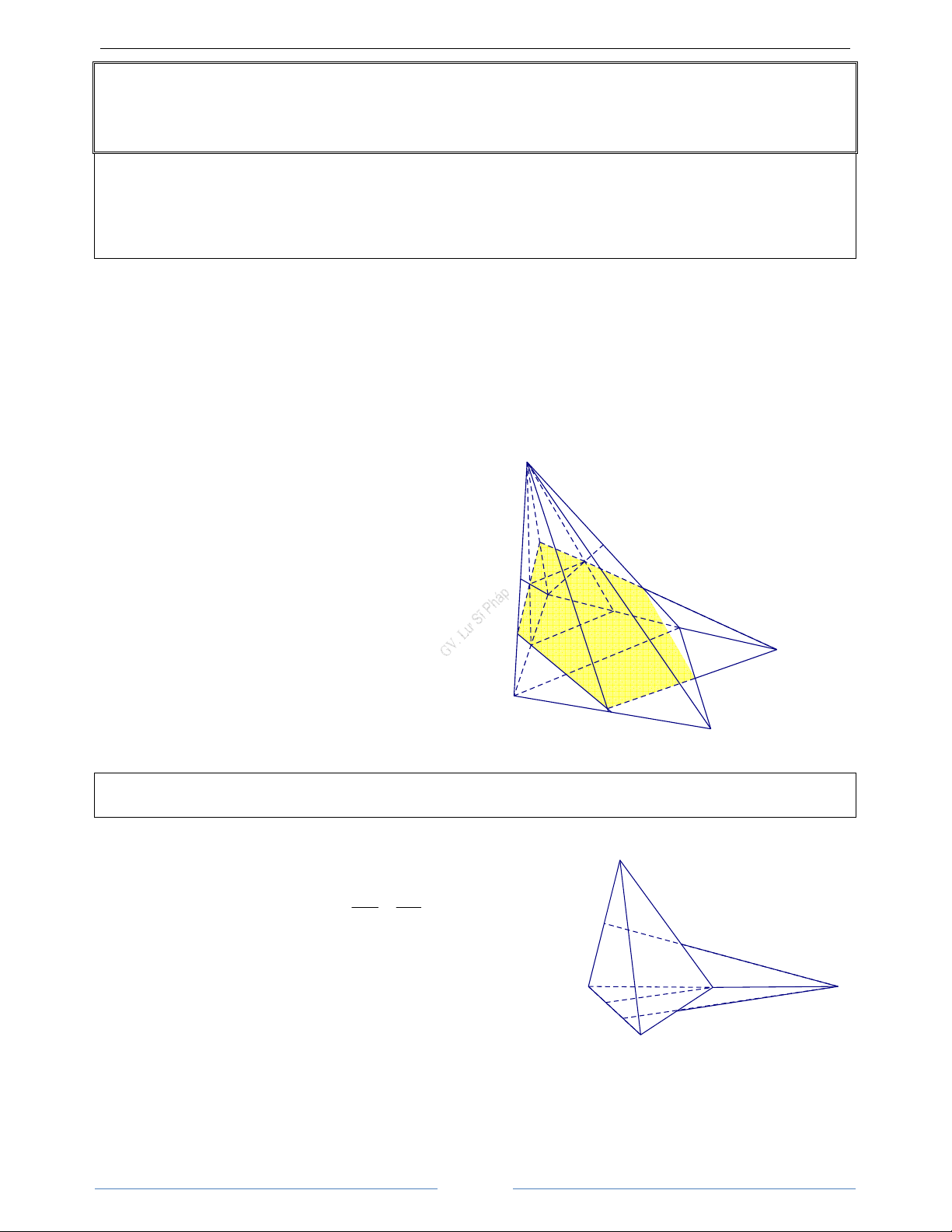
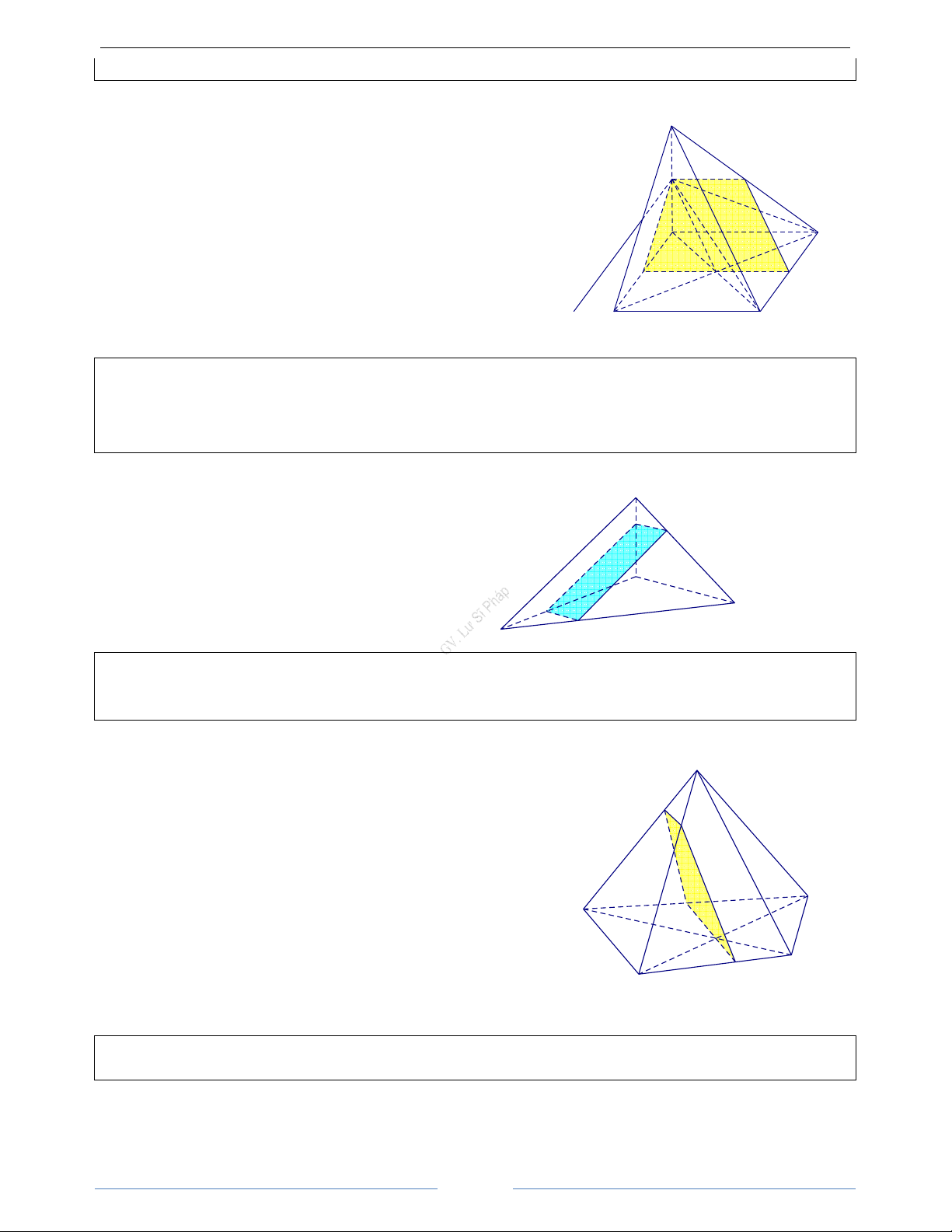
Bài 2.8. Cho tứ diện ABCD. Gọi I, J lần lượt là trung điểm của BC và BD; E là một điểm thuộc cạnh AD khác với A và D
a) Xác định thiết diện của hình tứ diện khi cắt bởi mp(IJE)
b) Tìm vị trí của điểm E trên AD sao cho thiết diện là hình bình hành
c) Tìm điều kiện của tứ diện và vị trí điểm E trên cạnh AD để thiết diện là hình thoi HD Giải
a) Ta có IJ là đường trung bình trong tam giác BCD nên IJ //CD A
Mặt khác IJ ⊂ (IJE);CD ⊂ (ACD). Suy ra:
(EIJ) ∩(ACD) = Ex / /IJ / /CD . Gọi F = Ex ∩ AC E
Thiết diện là hình thang EFIJ F
b) Để thiết diện EFIJ là hình bình hành điều kiện cần và đủ là IF //
JE. Điều này tương với JE //AB, tức là khi và chỉ khi E là trung điểm của AD.
c) Thiết diện EFIJ là hình thoi khi và chỉ khi EFIJ là hình bình hành B J D
và IF = IJ khi và chỉ khi E là trung điểm của AD và AB = CD (vì I 1 1
IJ = CD và khi E là trung điểm của AD thì IF = AB ) 2 2 C
ấn đề 3. Chứng minh hai đường thẳng song song
VPhương pháp:
1. Chứng minh chúng cùng thuộc một mặt phẳng và dùng phương pháp chứng minh hai đường thẳng
song song trong hình học phẳng( như tính chất đường trung bình của tam giác, định lí Talét đảo, tính chất
song song của hai đường thẳng cùng vuông góc với đường thẳng thứ ba, …)
2. Chứng minh chúng cùng song song với đường thẳng thứ ba.
3. Dùng tính chất: Hai mặt phẳng phân biệt lần lượt chứa hai đường thẳng song song thì giao tuyến của a ∈(α)  b ∈(β )
chúng(nếu có) cũng song song với hai đường thẳng ấy. Tức là: 
⇒ c / /a / /b a / /b (  α)∩(β) = c 9 HÌNH HỌC 11
Chương II. ĐT & MP Trong KG. QHSS Toán 11 GV. Lư Sĩ Pháp α  ∩γ = a 
a / /b / /c
4. Dùng định lý về giao tuyến của ba mặt phẳng: β ∩ γ = b ⇒  
a,b ñoàng quy α  ∩ β = c
Bài 2.9. Cho hình chóp S.ABCD có đáy là một tứ giác lồi. Gọi M và N lần lượt là trọng tâm của tam giác
SAB và SAD; E là trung điểm của CB.
a) Chứng minh rằng: MN // BD
b) Xác định thiết diện hình chóp S.ABCD cắt bởi mp(MNE)
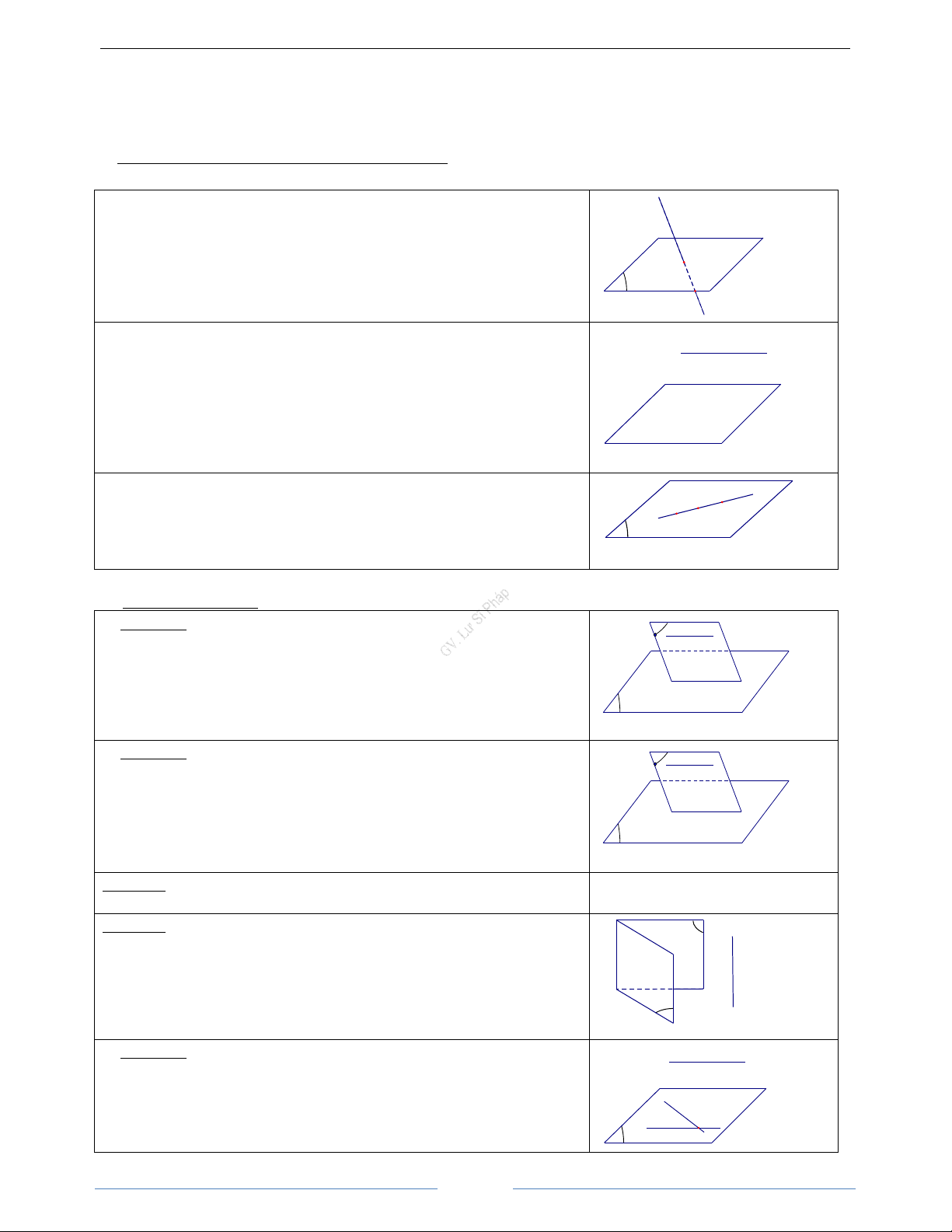
c) H và L lần lượt là giao điểm của mp(MNE) với các cạnh SB và SD. Chứng minh rằng: LH // BD HD Giải
MN / / M ' N '
a) Gọi M’, N’ lầm lượt là trung điểm của AB và AD. Dễ thấy:
 ⇒ MN / / BD
M ' N '/ / BD  b)Ta có:
MN ⊂ (MNE) 
BD ⊂ (ABCD) ⇒ (MNE) ∩ (ABCD) = Ex / / MN / / BD MN / / BD  
Vậy từ E kẻ đường thẳng song song với BD lần
lượt cắt CD, AB tại F và I. Nối IM lần lượt cắt S
SB và SA tại H, K; nối KN cắt SD tại L. Thiết
diện cần tìm là ngũ giác KLFEH c)Ta có: K MN ⊂ (MNE)   BD ⊂ (SBD)  N M H
 ⇒ LH / / BD MN / / BD  A ( M' B
MNE) (SBD) LH  ∩ =  L I N' E D F C
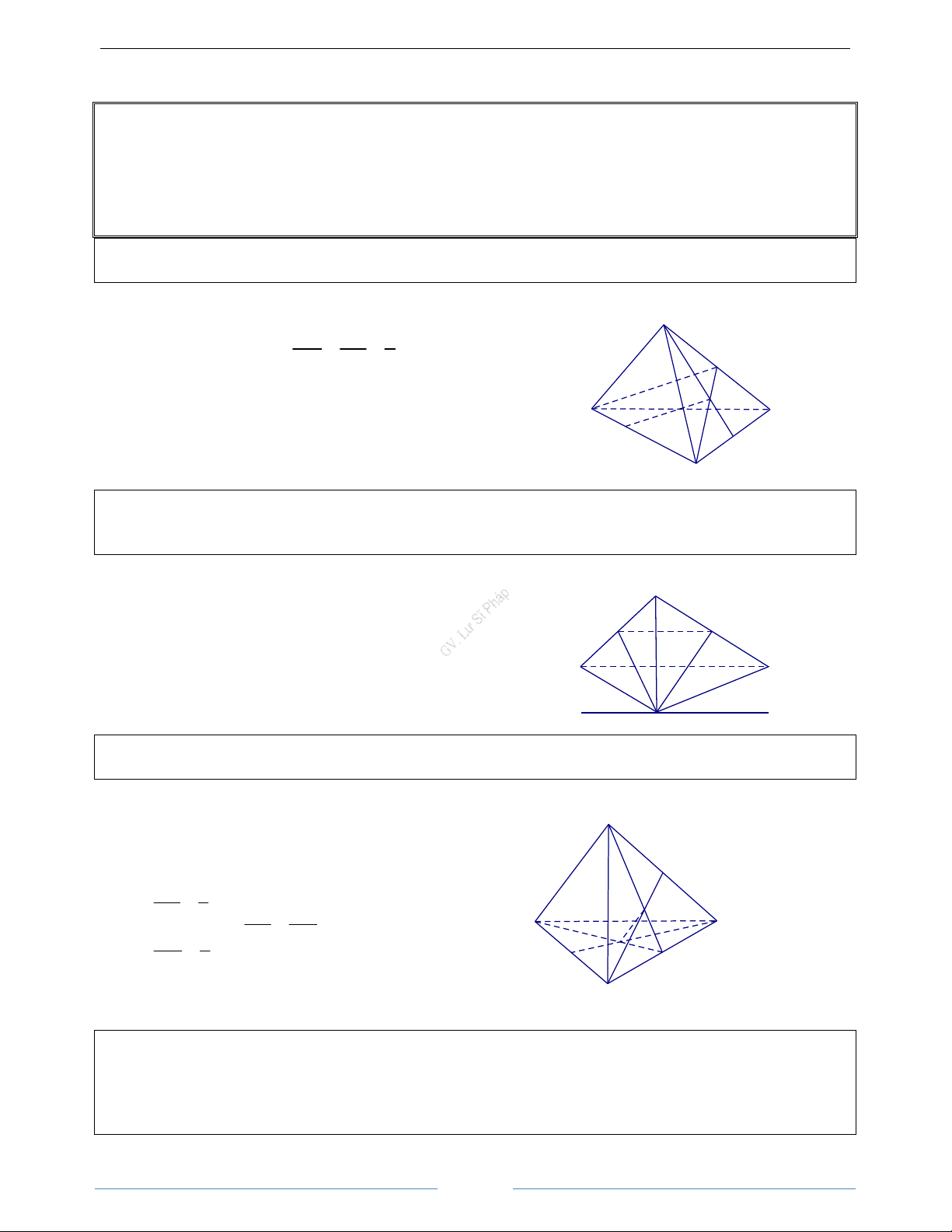
Bài 2.11. Cho tứ diện ABCD. Có các điểm P, Q lần lượt là trung điểm của AB, CD; điểm R nằm trên
cạnh BC sao cho BR = 2RC. Gọi S là giao điểm của mp(PQR) và cạnh AD. Chứng minh rằng AS = 2SD. HD Giải
Gọi I = RQ ∩ BD , E là trung điểm của BR. Khi đó EB = ER = A RC và RQ // ED. BD BE
Tam giác BRI có ED // RQ, suy ra = = 1 DI ER P
Vậy DB = DI. Do đó AD và IP là hai đường trung tuyến của S
tam giác ABI. Suy ra giao điểm S của AD và IP là trọng tâm
của tam giác ABI và ta có AS = 2DS D I B E Q R C 10 HÌNH HỌC 11
Chương II. ĐT & MP Trong KG. QHSS Toán 11 GV. Lư Sĩ Pháp
§3. ĐƯỜNG THẲNG SONG SONG VỚI MẶT PHẲNG
A. KIẾN THỨC CẦN NẮM
I. Vị trí tương đối của đường thẳng và mặt phẳng
Giữa đường thẳng d và mặt phẳng (α) ta có ba vị trí tương đối như sau:
1. d và (α) cắt nhau tại A, kì hiệu a ∩ (P) = { } A d M α d cắt mp(α) tại M
2. d song song với (α) , kí hiệu d | α ( ) hoặc α ( ) | d . Như vậy: Một d
đường thẳng và một mặt phẳng gọi là song song với nhau nếu
chúng không có điểm chung. α d // (α)
3. a nằm trong (P) , kí hiệu d ⊂ α ( ) d α d chứa trong (α)
II. Định lí và tính chất
1. Định lí 1. Nếu đường thẳng a không nằm trong mặt phẳng (P) β d
và a song song với đường thẳng d nằm trong thì a song song với d ⊄ α ( )  d' ( 
P) ; nghĩa là: d | d′  ⇒ d | (α) α  d ' ⊂ α ( ) 
2. Định lí 2. Cho đường thẳng a song song với mặt phẳng (P) . Nếu β a
mặt phẳng (Q) chứa a và cắt (P) theo giao tuyến d thì d song song a / / α ( )  b  với a; nghĩa là β ( ) ⊃ a  ⇒ b | a α  β ( ) ∩ α ( ) = b 
Hệ quả 1. Nếu một đường thẳng song song với một mặt phẳng thì
nó song song với một đường thẳng nào đó trong mặt phẳng.
Hệ quả2. Nếu hai mặt phẳng phân biệt cùng song song với một β
đường thẳng thì giao tuyến của chúng (nếu có) cũng song song với d' α ( ) / / d  d 
đường thẳng đó; nghĩa là (β ) / / d  ⇒ d′ | d α ( ) ∩(β  ) = d′ α 
3. Định lí 3. Cho hai đường thẳng chéo nhau. Có duy nhất một mặt b
phẳng chứa đường thẳng này và song song với đường thẳng kia. a b' α M 11 HÌNH HỌC 11
Chương II. ĐT & MP Trong KG. QHSS Toán 11 GV. Lư Sĩ Pháp B. BÀI TẬP
ấn đề 1. Chứng minh đường thẳng song song với mặt phẳng
VPhương pháp: Để chứng minh đường thẳng d song song với mặt phẳng (α) ta chứng minh d không d ⊄ (α) 
nằm trong (α) và song song với đường thẳng a chứa trong (α) . Tức là a ⊂ (α ) ⇒ d / /(α) d / /a 
Bài 3.1. Cho tứ diện ABCD. G là trọng tâm của tam giác ABD. Trên đoạn BC lấy điểm M sao cho MB =
2MC. Chứng minh rằng MG // (ACD). HD Giải
Gọi I trung điểm của AD. A BM BG 2 Trong tam giác CBI ta có, = = . Nên MG // CI BC BI 3 I
Mà CI nằm trong mặt phẳng (ACD) Suy ra MG // (ACD). G D C M B
Bài 3.2. Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm của các cạnh AB và AC.
a) Xét vị trí tương đối của đường thẳng MN và mp(BCD)
b) Gọi d là giao tuyến của hai mặt phẳng (DMN) và (DBC). Xét vị trí tương đối của d và mp(ABC) HD Giải
a) MN là đường trung bình của tam giác ABC nên MN // BC. A Suy ra MN // (BCD)
b) Vì MN // (BCD) nên (DMN) đi qua MN cắt (BCD) theo M N
giao tuyến d // MN. Do đó d // (ABC). B C d D
Bài 3.3. Cho tứ diện ABCD. Gọi G1 và G2 lần lượt là trọng tậm của các tam giác ACD và BCD. Chứng
minh rằng G1G2 song song với các mặt phẳng (ABC) và (ABD) HD Giải Gọi I là trung điểm CD A
Vì G1 là trọng tâm của tam giác ACD nên G ∈ AI 1
Vì G2 là trọng tâm của tam giác BCD nên G ∈ BI 2 IG 1  1 = 3 IG IG G1 Ta có: IA 1 2  ⇒ = ⇒ G G / / AB D B IG 1 IA IB 1 2 G2 2  = IB 3 I
AB ⊂ (ABC) ⇒ G G / /(ABC) 1 2 C
Và AB ⊂ (ABD) ⇒ G G / /(ABD) 1 2
Bài 3.4. Cho tứ hình chóp S.ABCD có đáy ABCD là hình bình hành ABCD. Gọi G là trọng tâm tam giác
SAB và I là trung điểm của AB. Lấy điểm M trên đoạn AD sao cho AD = 3AM.
a) Tìm giao tuyến của hai mặt phẳng (SAD) và (SBC)
b) Đường thẳng qua M và song song với AB cắt CI tại N. CMR: NG // (SCD)
c) Chứng minh rằng MG // (SCD). HD Giải 12 HÌNH HỌC 11
Chương II. ĐT & MP Trong KG. QHSS Toán 11 GV. Lư Sĩ Pháp
a) Dễ thấy S là điểm chung của hai mặt phẳng IG 1  (SAD) và (ABC) =  IS 3  ⇒ / / AD ⊂ (SAD) GM SK Ta có: I 1  M  = BC ⊂ (SBC)  Ta có: IK 3 AD / / BC   ⇒ GM / /(SCD)
⇒ (SAD) ∩ (SBC) = Sx / / AD / /BC b) Ta có: MN // IA //CD S x AM IN 1 IG 1 ⇒ = = ; mà = ( G là trọng tâm AD IC 3 IS 3 K của tam giác SAB) IG IN 1 Nên ⇒ = = ⇒ GN / /SC IS IC 3
Mà SC ⊂ (SCD) ⇒ GN / /(SCD) G c) Gọi A D
K = IM ∩CD ⇒ SK ⊂ (SCD) M MN IN 1 IM 1 Mà MN / /CD ⇒ = = ⇒ = . I CK IC 3 IK 3 B C
Bài 3.5. Cho hình chóp S.ABCD có đáy ABCD là hình thang, đáy lớn AD và AD = 2BC. Gọi O là giao
điểm của AC và BD, G là trọng tâm của tam giác SCD.
a) Chứng minh rằng OG // (SBC)
c) Cho M là trung điểm của SD. Chứng minh rằng CM // (SAB) 3
d) Giả sử I nằm trên đoạn SC sao cho SC = SI . Chứng minh rằng SA // (BID). 2 HD Giải DG 2
a) Gọi H là trung điểm của SC, ta có: = (1) S DH 3 OD OA AD OD 2 BC / / AB ⇒ = = = 2 ⇒ OD = O 2 B ⇒ = (2) M OB OC BC BD 3 M' DG OD 2 H Từ (1) và (2) ⇒ =
= (1) ⇒ OG / /BH . Mà G DH BD 3 A I D
BH ⊂ (SBC) ⇒ OG / /(SBC) MM '/ / AD O 
b) Gọi M’ là trung điểm của SA ⇒  1 . B C MM ' = AD  2 OC 1 OC 1 1 c) Ta có: = nên = . 2 3
Mặt khác vì BC // AD và BC = AD (gt) và BC = MM’. Nên OA CA 2 3 CI 1
tứ giác BCMM’ là hình bình hành
Mặt khác vì SC = SI nên = 2 CS 3
Suy ra CM //BM’, mà BM ' ⊂ (SAB) ⇒ CM / /(SAB) CI OC ⇒ =
⇒ OI / /SA và CS CA
OI ⊂ (BID) ⇒ SA / /(BID)
Bài 3.6. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N lần lượt là trung điểm của AB và CD.
a) Chứng minh rằng MN song song với các mặt phẳng (SBC) và (SAD).
b) Gọi P là trung điểm của SA. Chứng minh rằng SB và SC đều song song với mp (MNP) HD Giải 13 HÌNH HỌC 11
Chương II. ĐT & MP Trong KG. QHSS Toán 11 GV. Lư Sĩ Pháp a) Chứng minh MN //(SBC): S MN / /BC Ta có:  ⇒ MN / /(SBC) BC ⊂ (SBC) Chứng minh MN // (SAD): P MN / / AD Ta có:  ⇒ MN / /(SAD) AD ⊂ (SAD) b) Chứng minh SB // (MNP): A D SB / / MP Ta có:  ⇒ SB / /(MNP) M MP ⊂ (MNP) N Q Chứng minh S // (MNP):
Gọi Q = AC ∩ MN . Khi đó Q là trung điểm của AC. C B
Do đó: SC // PQ (T/c đường trung bình trong tam giác SAC)
mà PQ ⊂ (MNP). Vậy SC // (MNP)
Bài 3.7. Cho tứ diện ABCD. Gọi M, N lần lượt là trọng tâm của tam giác ABD và BCD.
a) Chứng minh rằng: MN // (ACD) và MN // (ABC) MN
b) Xác định giao tuyến của (DMN) và (ABC). Chứng minh giao tuyến này song song với MN. Tính IJ HD Giải
a) Gọi K là trung điểm của BD. Vì M, N là trọng 1
tâm của các tam giác ABD và BCD nên A, M, K
Ta có IJ = AC ; 2
thẳng hàng và C, N, K thẳng hàng, tức là AM cắt 1 1 2 CN tại K KM MN = = MN
⇒ MN = AC . Từ đó = Ta có: KA AC 3 3 IJ 3 KM 1 KN 1 = ; = KM KN ⇒ = ⇒ MN / / AC A KA 3 KC 3 KA KC MN / / AC  Tứ đó:
 ⇒ MN / /(ACD) và AC ⊂ (ACD) I MN / / AC  M
 ⇒ MN / /(ABC) AC ⊂ (ABC)
b) Trong mp (ABD): DM cắt AB tại I; trong K
mp(BCD): DN cắt BC tại J. Khi đó I, J là hai D B
điểm chung của hai (DMN) và (ABC). Suy ra N
(DMN)∩(ABC) = IJ J
I, J lấn lượt là trung điểm của AB và BC nên IJ C
là đường trung bình trong tam giác ABC 1
⇒ IJ / / AC; IJ = AC . Mà MN // AC (câu a) 2 nên MN // IJ.
ấn đề 2. Dựng thiết diện song song với một đường thẳng
VPhương pháp: Cho đường thẳng d song song với mặt phẳng (α). Nếu mặt phẳng (β)chứa d và cắt d / /(α )  (α) 
theo giao tuyến d’ thì d’ song song với d . Nghĩa là: (β ) ⊃ d
 ⇒ d / / d ' (β) (α) d ' ∩ = 
Thiết diện cắt bởi một mặt phẳng chứa một đường thẳng song song với một đường thẳng cho trước được
xác định bằng cách phối hợp hai cách xác định giao tuyến đã biết.
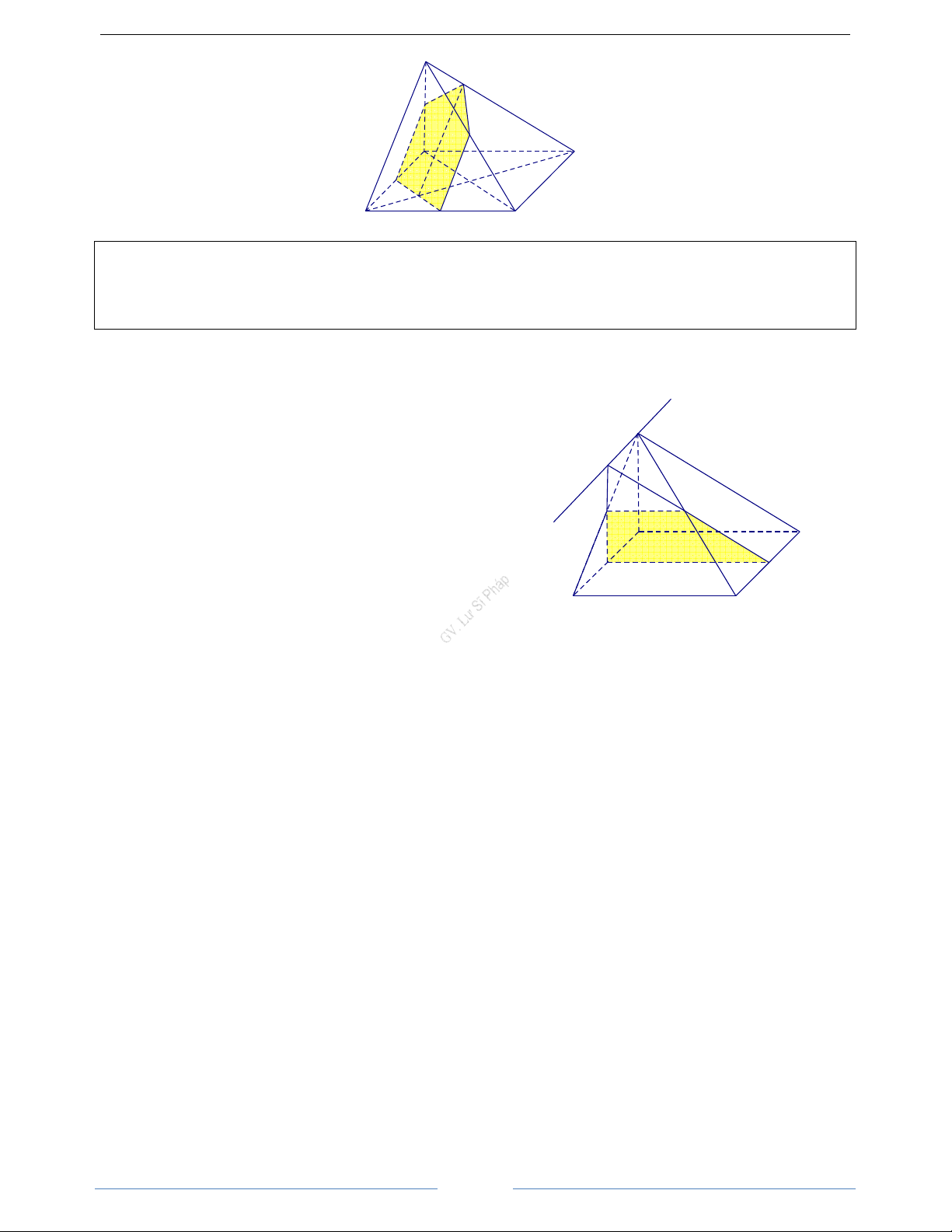
Bài 3.9. Cho hình chóp S.ABCD có đáy là hình bình hành ABCD, O là giao điểm của AC và BD, M là
trung điểm của SA. Tìm thiết diện của mặt phẳng (α) với hình chóp S.ABCD nếu (α) qua M và đồng 14 HÌNH HỌC 11
Chương II. ĐT & MP Trong KG. QHSS Toán 11 GV. Lư Sĩ Pháp
thời song song với SC và AD. HD Giải
Vì (α) song song với AD nên (α) cắt hai mặt phẳng (SAD) và S
(ABCD) theo hai giao tuyến song song với AD.
Tương tự (α) song song với SC nên (α) cắt hai mặt phẳng
(SAC) và (SCD) theo hai giao tuyến song song với SC. N M
Gọi O = AC ∩ BD , ta có SC//OM( đường trung bình trong tam giác SAC) I
Qua O kẻ đường thẳng song song với AD, cắt AB và CD tại Q A D
và P. Qua M, kẻ đường thẳng song song với AD cắt SD tại N. Q
Theo nhận xét trên, ta có MN // PQ // SC d P O
Vậy thiết diện là hình thang MNPQ B C
Bài 3.10. Cho tứ diện ABCD. Trên AB lấy điểm M. Cho (α) là mặt phẳng qua M, song song với hai đường thẳng AC và BD.
a) Tìm giao tuyến của (α) với các mặt của tứ diện
b) Thiết diên của tứ diện cắt bởi mặt phẳng (α) là hình gì? HD Giải
a) Giao tuyến của (α) với các mặt của tứ diện là A
các cạnh của tứ giác MNPQ có:
MN // PQ //AC và MQ // NP // BD M Q
b) Thiết diện tạo bởi mặt phẳng (α) với tứ diện là hình bình hành MNPQ B N P C
Bài 3.11. Cho hình chóp S.ABCD có đáy ABCD là một tứ giác lồi. Gọi O là giao điểm của hai đường
chéo AC và BD. Xác định thiết diện của hình chóp cắt bởi mặt phẳng (α) đi qua O, song song với AB và
SC. Thiết diện đó là hình gì? HD Giải (α) / / AB  S 
Ta có: AB ⊂ (ABCD)
 ⇒ MN / / AB
(α) (ABCD) MN ∩ =  P Q (α) / /SC   SC ⊂ (SBC)
 ⇒ MQ / /SC (α) (SBC) MQ ∩ =  D (α) / / A N AB   SC ⊂ (SAB)
 ⇒ PQ / / AB O (α) ( C SAB) PQ ∩ = M  B
Vậy MN // PQ. Do đó tứ giác MNPQ là hình thang
Bài 3.12. Cho hình chóp S.ABCD có đáy là hình bình hành. Xác định thiết diện của hình chóp khi cắt bởi
mặt phẳng đi qua trung điểm M của cạnh AB, song song với BD và SA. HD Giải
Qua M vẽ đường thẳng song song với BD cắt AD tại N và cắt AC tại I. Qua M, I, N vẽ các đường thẳng
song song với SA lần lượt cắt SB, SC, SD tại R, Q, P.
Thiết diện là ngũ giác MNPQR. 15 HÌNH HỌC 11
Chương II. ĐT & MP Trong KG. QHSS Toán 11 GV. Lư Sĩ Pháp S Q P R D C N I A M B
Bài 3.13. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. M là một điểm di động trên đoạn AB.
Một mặt phẳng (α) đi qua M và song song với SA và BC; (α) cắt SB, SC và CD tại N, P, Q
a) Tứ giác MNPQ là hình gì?
b) Gọi I là giao điểm của MN và PQ. Chứng minh rằng I nằm trên một đường thẳng cố định. HD Giải (  α) / / AB
(SAB) và (SCD) cố định nên Sx cố định.
a) Vì M ∈(SAB) và  nên
Dó đó I thuộc đường thẳng Sx cố định. SA ⊂ (SAB)
(α)∩(SAB) = MN và MN // AB. S
Tương tự (α) ∩ (SBC) = NP và NP // BC;
(α)∩(SCD) = PQ ; (α)∩(ABCD) = MQ và MQ I
// BC. Từ đó suy ra, tứ giác ABCD là hình thang.
S ∈(SAB) ∩ (SCD) x N P 
b) Ta có AB ⊂ (SAB),CD ⊂ (SCD) D  A AB / /CD  M Q
⇒ (SAB) ∩ (SCD) = Sx và Sx // AB // CD B C  ∈ ⊂ ( ) MN ∩ PQ = I MN SAB
I ⇒ I ∈PQ ⊂ (SCD)
⇒ I ∈(SAB) ∩ (SCD) ⇒ I ∈ Sx 16 HÌNH HỌC 11
Chương II. ĐT & MP Trong KG. QHSS Toán 11 GV. Lư Sĩ Pháp
§4. HAI MẶT PHẲNG SONG SONG
A. KIẾN THỨC CẤN NẮM I
Định nghĩa: Hai mặt phẳng (α) và (β ) được gọi là song
song với nhau nếu chúng không có điểm chung. Kí hiệu:
(α) / /(β ) hoặc(β) / /(α) . Như vậy α
(α) / /(β) ⇔ (α)∩(β) = Ο β II II. Tính chất. 1.
Định lí 1. Nếu mặt phẳng (α) chứa hai đường thẳng cắt b M
nhau a, b và a, b cùng song với mặt phẳng (β ) thì (α) song a
a ⊂ (α ),b ⊂ (α ) α 
song với (β ) ; nghĩa là a ∩ b = M  ⇒ (α ) / /(β )
a / /(β ),b / /(β )  β
Hệ quả: Nếu mặt phẳng (α) chứa hai đường thẳng cắt
nhau a và b, mặt phẳng (β ) chứa hai đường thẳng cắt nhau
a' và b' đồng thời a // a', b // b' thì mặt phẳng (α) song song với mặt phẳng(β ) . 2
Định lí 2. Qua một điểm nằm ngoài một mặt phẳng cho A
trước có một và chỉ một mặt phẳng song song với mặt α phẳng đã cho. β
Hệ quả 1. Nếu đường thẳng d song song với mặt phẳng (α) d
thì trong (α) có một đường thẳng song song với d và
qua d có duy nhất một mặt phẳng (β ) song song với (α) . β α
Hệ quả 2. Hai mặt phẳng phân biệt cùng song song với mặt
phẳng thứ ba thì song song với nhau.
Hệ quả 3. Cho điểm A không nằm trên mặt phẳng (α) .
Mọi đường thẳng đi qua A và song song với (α) đều nằm α
trong mặt phẳng đi qua A và song song với (α) . A β 3
Định lí 3. Cho hai mặt phẳng song. Nếu một mặt phẳng cắt γ
mặt phẳng này thì cũng cắt mặt phẳng kia và hai giao tuyến song song với nhau. a α b β
Hệ quả: Hai mặt phẳng song song chắn trên hai cát tuyến
song song những đoạn thẳng bằng nhau. 17 HÌNH HỌC 11
Chương II. ĐT & MP Trong KG. QHSS Toán 11 GV. Lư Sĩ Pháp 4
Định lí 4(Định lí Ta-lét). Ba mặt phẳng đôi một song song
chắn trên hai cát tuyến bất kì những đoạn thẳng tương ứng A' A AB AC BC tỉ lệ. = = P A ' B ' A 'C ' B 'C ' B B' Q C C' R 5 Định lí Ta-lét đảo.
Giả sử trên hai đường thẳng chéo nhau lần lượt lấy các AB BC CA
điểm A, B, C và A’, B’, C’ sao cho = = A'B' B'C' C'A'
Khi đó AA’, BB’, CC’ lần lượt nằm trên ba mặt phẳng
song song, tức là chúng cùng song song với một mặt phẳng.
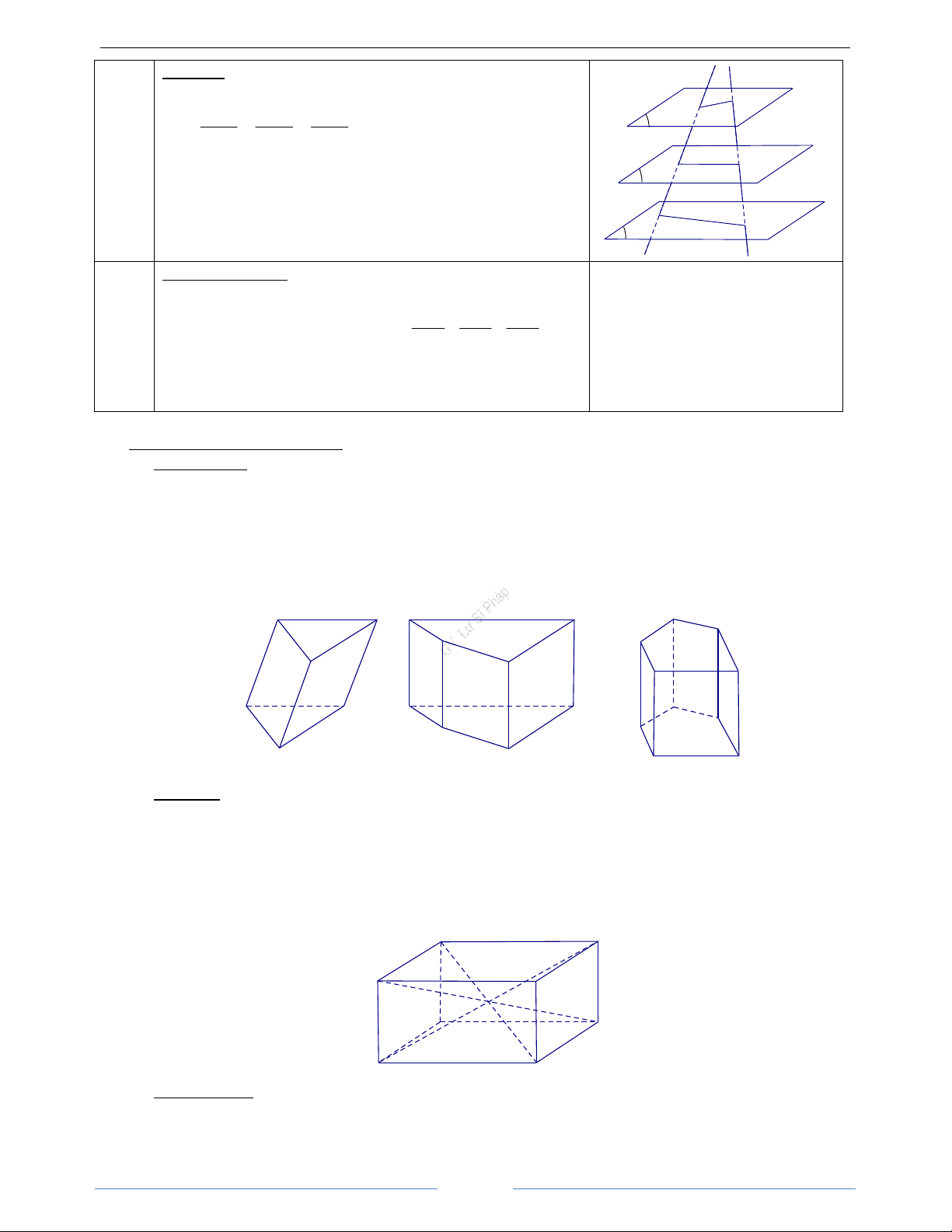
III. Hình lăng trụ và hình chóp cụt 1. Hình lăng trụ
Hình lăng trụ là một hình đa diện có hai mặt nằm trong hai mặt phẳng song song (gọi là hai đáy) và tất cả
các cạnh không thuộc hai đáy đều song song với nhau (gọi là cạnh bên)
- Hai đáy của hình lăng trụ là các đa giác bằng nhau
- Các mặt khác hai đáy gọi là mặt bên: Mỗi mặt bên là một hình bình hành
- Các mặt tạo bởi hai cạnh bên không liên tiếp gọi là mặt chéo: Mỗi mặt chéo là một hình bình hành
- Đường chéo của các mặt chéo là đường chéo của hình lăng trụ
- Tùy theo đáy, ta gọi hình lăng trụ tam giác, hình lăng trụ tứ giác, hình lăng trụ lục giác, . . . Lăng trụ tam giác Lăng trụ tứ giác Lăng trụ ngũ giác 2. Hình hộp
Hình hộp là hình lăng trụ có đáy là hình bình hành.
- 6 mặt của hình hộp chữ nhật đều là hình bình hành
- Các đường chéo của hình bình hành đồng qui tại một điểm là trung điểm của mỗi đường chéo
(điểm đó gọi là tâm của hình hộp)
- Hình hộp có tất cả các mặt bên và các mặt đáy đều là hình chữ nhật gọi là hình hộp chữ nhật
- Hình hộp có tất cả các mặt bên và các mặt đáy đều là hình vuông gọi là hình lập phương D' C' A' B' O D C A B 3. Hình chóp cụt
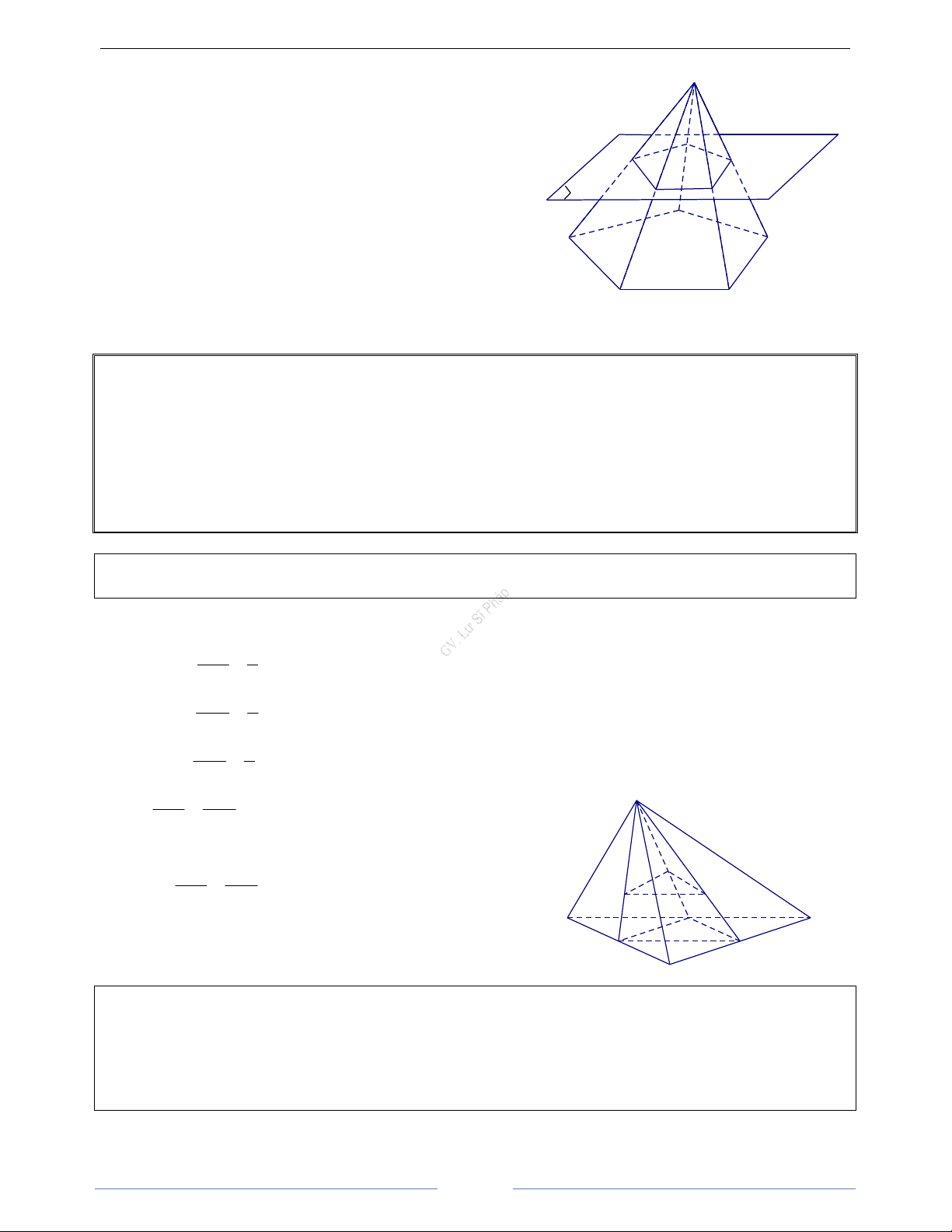
Cho hình chóp S.A1A2...An. Một mặt phẳng
lần lượt tại A' , A' ,..., A' . Hình toạ bởi thiết
không qua đỉnh, song song với mặt phẳng đáy 1 2 n ' ' '
của hình chóp cắt các cạnh SA
diện A A ...A và đáy A A ...A của hình 1, SA2, . . ., SAn 1 2 n 1 2 n 18 HÌNH HỌC 11
Chương II. ĐT & MP Trong KG. QHSS Toán 11 GV. Lư Sĩ Pháp chóp cùng các từ giác S
A' A' A A , A' A' A A ,..., A' A' A A được gọi là 1 2 2 1 2 3 3 2 n 1 1 n
hình chóp cụt, kí hiệu A' A' ...A' .A A ..A 1 2 n 1 2 n A' Hình chóp cụt có: 5 A'1 A'4
- Hai đáy là hai da giác có cạnh tương ứng
song dong và tỉ số các cạnh tương ứng A'2 A'3 P bằng nhau A5
- Các mặt bên là những hình thang A1 A
- Các đường thẳng chứa các cạnh bên đồng 4 qui tại một điểm. A2 A3 B. BÀI TẬP
ấn đề 1. Chứng minh hai mặt phẳng song song
VPhương pháp:
1. Vận dụng định lí 1: Nếu mặt phẳng (α) chứa hai đường thẳng cắt nhau a, b và a, b cùng song với mặt
a ⊂ (α ),b ⊂ (α )
phẳng (β ) thì (α) song song với (β ) : a ∩ b = M  ⇒ (α ) / /(β )
a / /(β ),b / /(β ) 
2. Ta chứng minh hai mặt phẳng (α) và (β ) cùng song song với mặt phẳng thứ ba (γ )
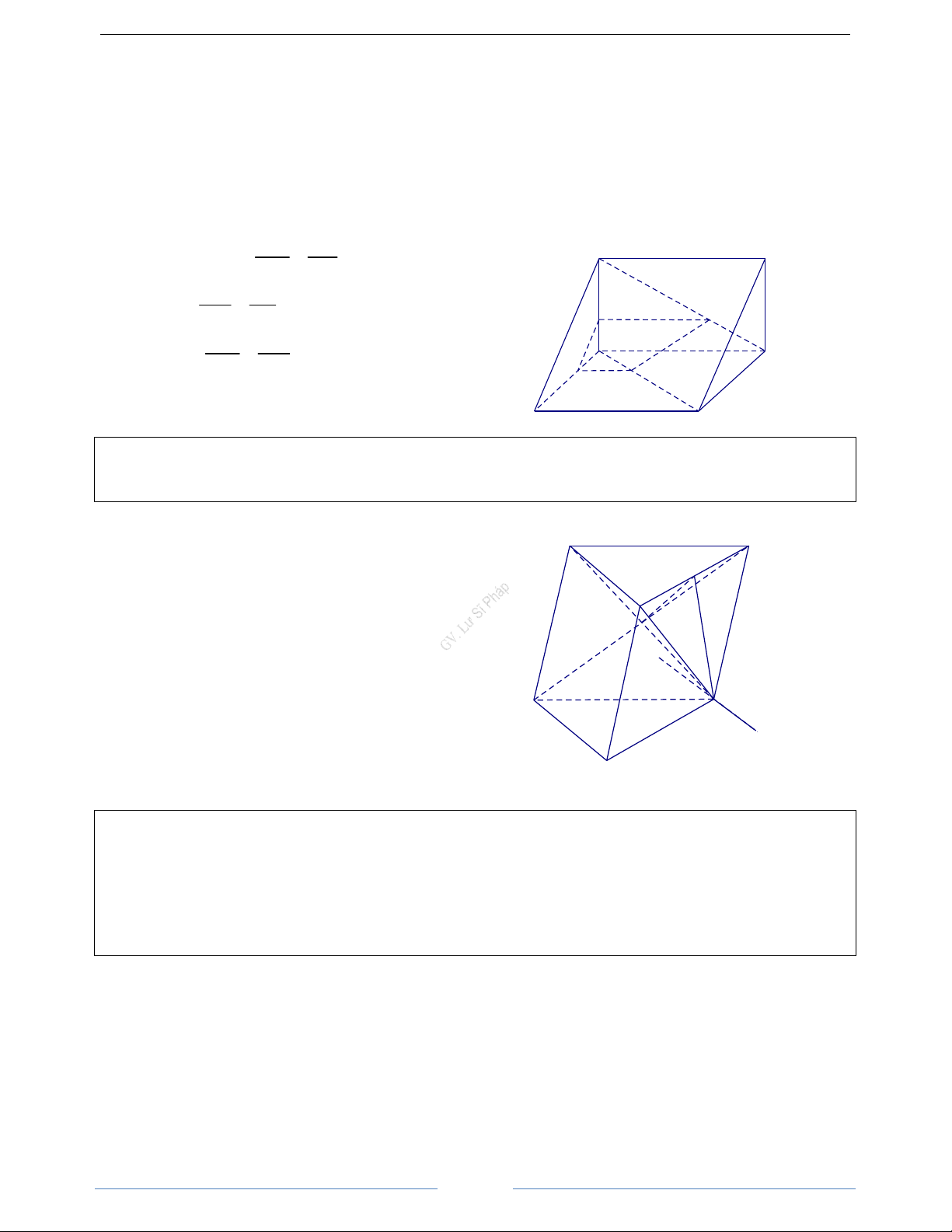
Bài 4.1. Cho từ diện ABCD. Gọi G1, G2, G3 lần lượt là trọng tâm của các tam giác ABC, ACD, ABD.
Chứng minh mặt phẳng (G1G2G3) song song với mặt phẳng (BCD). HD Giải
Gọi M, N, P lần lượt là trung điểm của BC, CD, DB. Ta có: Như vậy AG 2 G  G ⊂ G ( G G ) M ∈ AG và 1 = 1 2 1 2 3 1  AM 3 G  G ⊂ G ( G G ) 1 3 1 2 3 AG 2  N ∈ AG và 2 = G
 G ∩ G G = G ⇒ G
( G G ) / /(BCD) 2 1 2 1 3 1 1 2 3 AN 3 G G / /(BCD) AG 2  1 2 P ∈ AG và 3 = 3 G  G / /(BCD) AP 3  1 3 AG AG A Do đó 1 2 = ⇒ G G / / MN AM AN 1 2
Vì MN nằm trong (BCD) nên G G / /(BCD) 1 2 AG AG G3 Tương tự 1 3 = ⇒ G G / / MP AM AP 1 3 G1 G2
Vì MP nằm trong (BCD) nên G G / /(BCD) . P 1 3 B D M N C
Bài 4.2. Cho hai hình vuông ABCD và ABEF ở trong hai mặt phẳng phân biệt. Trên các đường chéo AC
và BF lần lượt lấy các điểm M và N sao cho AM = BN. Các đường thẳng song song với AB vẽ từ M và N
lần lượt cắt AD và AF tại M’ và N’. Chứng minh: a) (ADF) // (BCE) b) M’N’ // DF
c) (DEF) // (MM’N’N) và MN // (DEF). HD Giải 19 HÌNH HỌC 11
Chương II. ĐT & MP Trong KG. QHSS Toán 11 GV. Lư Sĩ Pháp a) Ta có:
c) Từ chứng minh trên suy ra: DF // (MM’N’N) AD / / BC 
NN '/ / AB ⇒ NN '/ / EF
 ⇒ AD / /(BCE)  BC ⊂ (BCE)
NN ' ⊂ (MM ' N ' N )  AF / / BE 
⇒ EF / /(MM ' N ' N)
 ⇒ AF / /(BCE) BE ⊂ (BCE)
Mà DF, EF chứa trong (MM’N’N) mà Nên (DEF) // (MM’N’N)
AD, AF ⊂ (ADF)
Vì MN chứa trong (MM’N’N) và Nên (ADF) // (BCE) (DEF)//(MM’N’N)
b) Vì ABCD và ABEF là các hình vuông nên AC = BF. Nên MN // (DEF) AM ' AM
Ta có: MM '/ /CD ⇒ = (1) F E AD AC AN ' BN NN '/ / AB ⇒ = (2) AF BF N' N AM ' AN ' Từ (1) và (2): =
⇒ M ' N '/ /DF A B AD AF M' M D C
Bài 4.3. Cho hình lăng trụ tam giác ABC.A’B’C’. Gọi H là trung điểm của A’B’.
a) Chứng minh rẳng: CB’ // (AHC’)
b) Tìm giao tuyến d của (AB’C’) và (ABC). HD Giải
a) Ta có tứ giác AA’C’C là hình bình hành suy ra C'
A’C cắt AC’ tại trung điểm I của mỗi đường. A'
Do đó IH // CB’(đường trung bình của tam giác H CB’A’) B'
Mà IH chứa trong (AHC’) nên CB’ // (AHC’)
A ∈(AB'C ') I b) Ta có  A ∈ (ABC)
⇒ A ∈(AB 'C ') ∩(ABC)
B 'C '/ /BC C A x 
Mà B 'C ' ⊂ (AB 'C ') BC B  ⊂ (ABC)
Nên (AB 'C ') ∩(ABC) = Ax / /BC / /B 'C '
Bài 4.4. Cho hình lăng trụ tam giác ABC.A’B’C’. Gọi M, M’ lần lượt là trung điểm của các cạnh BC và B’C’
a) Chứng minh rằng AM song song với A’M’
b) Tìm giao điểm của mặt phẳng (AB’C’) với đường thẳng A’M
c) Tìm giao tuyến d của hai mặt phẳng (AB’C’) và (BA’C’)
d) Tìm giao điểm G của đường thẳng d với mặt phẳng (AM’M). Chứng minh G là trọng tâm của tam giác AB’C’. HD Giải
a) MM’ // BB’ và MM’ = BB’ =>MM’ // AB và
I ∈ AM ' ⊂ (AB'C ') MM’ = AB(hình lăng trụ) 
⇒ I = A' M ∩ (AB'C ') c)  ∈ '
Suy ra tứ giác AA’M’M là hình bình hành => AM I A M // A’M’ C  '∈(AB'C ')  ⇒ '∈( ' ')∩( ' ') b) Gọi
I = A' M ∩ AM ' C AB C BA C C
 '∈(BA 'C ') Ta có: 20 HÌNH HỌC 11
Chương II. ĐT & MP Trong KG. QHSS Toán 11 GV. Lư Sĩ Pháp
AB '∩ A' B = O A' C' O  ∈(AB'C ') ⇒ 
⇒ O ∈(AB 'C ') ∩ (BA'C ') M' O  ∈(BA 'C ')
⇒ d ≡ C 'O = (AB 'C ') ∩ (BA'C ') B'
d ⊂ (AB'C ') G d) 
⇒ d ∩ AM ' = G
AM ' ⊂ (AB 'C ') O I G  ∈ d ⇒ 
⇒ G ∈(AM ' M) G  ∈ AM ' A C
Ta có OC '∩ AM ' = G
Mà OC’, AM’ là trung tuyến tam giác AB’C’ M
Vậy G là trọng tâm của tam giác AB’C’ B 21 HÌNH HỌC 11
Chương II. ĐT & MP Trong KG. QHSS Toán 11 GV. Lư Sĩ Pháp
§5. PHÉP CHIẾU SONG SONG
A. KIẾN THỨC CẦN NẮM 1. Phép chiếu song song
- Cho mặt phẳng (α) và đường thẳng ∆ cắt (α) . Với mỗi điểm M trong không gian, đường thẳng qua
M và song song hoặc trùng với ∆ cắt (α) tại điểm M' xác định.
- Điểm M' gọi là hình chiếu song song của điểm M trên mặt phẳng (α) theo phương ∆ .
- Mặt phẳng (α) được gọi là mặt phẳng chiếu, phương của đường thẳng ∆ được gọi là phương chiếu.
- Phép đặt tương ứng mỗi điểm M trong không gian với hình chiếu M' của nó trên mặt phẳng (α) được
gọi là phép chiếu song song lên (α) theo phương ∆ M M' α
2. Các tính chất của phép chiếu song song (với đường thẳng và đoạn thẳng không song song hoặc trùng với phương chiếu)
- Phép chiều song song biến ba điểm thẳng hàng thành ba điểm thẳng hàng và không làm thay đổi thứ tự ba điểm đó;
- Phép chiếu song song biến đường thẳng thành đường thẳng, biến tia thành tia, biến đoạn thẳng thành đoạn thẳng;
- Phép chiếu song song biến hai đường thẳng song song thành hai đường thẳng song song hoặc trùng nhau;
- Phép chiều song song không làm thay đổi tỉ số độ dài của hai đoạn thẳng nằm trên hai đường thẳng
song song hoặc cùng nằm trên một đường thẳng.
3. Hình biểu diễn của một số hình không gian trên mặt phẳng
- Một tam giác bất kì bao giờ cũng có thể là hình biểu diễn của một tam giác tuỳ ý cho trước ( có
thể là tam giác đều, tam giác cân, tam giác vuông, . . .);
- Một hình bình hành bất kì bao giờ cũng có thể coi là hình biểu diễn của một hình bình hành tuỳ ý
cho trước ( có thể là hình bình hành, hình vuông, hình chữ nhật, hình thoi, . . .).
- Một hình thang bất kì bao giờ cũng có thể coi là hình biểu diễn của một hình thang tuỳ ý cho
trước, miễn là tỉ số độ dài hai đáy của hình biểu diễn phải bằng tỉ số độ dài hai đáy của hình đã cho.
- Người ta thường dùng hình elip để biểu diễn hình tròn. B. BÀI TẬP
Bài 5.1. Tam giác ABC có hình chiếu song song là tam giác A'B'C'. Chứng minh rằng trọng tâm của tam
giác ABC có hình chiếu song song là trọng tâm của tam giác A'B'C'. HD Giải
Gọi G là trọng tâm của tam giác ABC G' là hình chiếu song song của A
nó. Gọi M là trung điểm cùa BC thí A, G, M thẳng hàng. C G
Gọi M' là hình chiếu của M. Khi đó theo tính chất của phép chiếu M A 'G ' AG 2
song song ta có:A', G' M' thẳng hàng và = = (1); B', B A ' M ' AM 3 B ' M ' BM 2 M', C' thằng hàng và = = (2) M 'C ' MC 3
Từ (1) và (2) suy ra G' là trọng tâm của tam giác A'B'C'. A' C' G' M' B' 22 HÌNH HỌC 11
Chương II. ĐT & MP Trong KG. QHSS Toán 11 GV. Lư Sĩ Pháp Bài 5.2.
a) Vẽ hình biểu diển của một tứ diện và trọng tâm của nó.
b) Vẽ hình biểu diễn của tam giác vuông nột tiếp trong đường tròn. HD Giải
a) Vẽ hình biểu diễn của tứ diện ABCD. Lấy M, N lần lượt là trung A
điểm của AB và CD thì trung điểm G của MN sẽ biểu diễn cho trọng M tâm của tứ diện. / G B D / N C
b) Vẽ elip tâm O là hình biểu diễn của đường tròn đã cho. Lấy hai B A
điểm A và B là hai điểm trên elip sao cho B, C, O thẳng hàng và một
điểm A thuộc elip sao cho A khác với B và C. Khi đó, tam giác ABC O
là hình biểu diễn của một tâm giác vuông nội tiếp trong một đường tròn. C
Bài 5.3. Cho tam giác ABC. Hãy chọn mặt phẳng chiếu (α) và phương chiếu của tam giác ABC trên (α) là: a) Một tam giác cân b) Một tam giác đều c) Một tam giác vuông HD Giải
a) Qua BC dựng một mặt phẳng (α) không đi qua
A. Trong mặt (α) ta dựng tam giác cân BCA1(BA1 = CA A
1). Khi đó, phép chiếu song song lên (α )
theo phương chiếu ∆ = AA1 biến tam giác ABC thành tam giác cân A1BC.
b) Trong (α) ở câu a), ta dựng tam giác BCA α 2 và / A1 C /
c) Chọn phương chiếu ∆ = AA A3 2. Trong mặt phẳng A2
(α) câu a), ta dựng tam giác vuông BCA B 3 ( BA C ) 0
= 90 và chọn phương ∆ = AA 3 3. Bài 5.4.
a) Vẽ hình biểu diễn của một hình vuông nội tiếp trong một đường tròn.
b) Vẽ hình biểu diễn của một lục giác đều. HD Giải
a) Vẽ tam giác tam giác vuông nội tiếp trong một đường tròn . Qua O N E
ta kẻ hai dây ME và NF của elip lần lượt song song với AC và AB. Khi D
đó, tứ giác MNEF là hình biểu diễn của một hình vuông nội tiếp trong A một đường tròn. O M F B
b) Xét hình lục giác đều ABCDEF , ta nhận thấy: A B
- Tứ giác OABC là hình thoi
- Các điểm D, E, F lần lượt là các điểm đối xứng của các điểm A, B, C qua tâm O F C
Từ đó, suy ra cách vẽ hình biểu diễn của lục giác đều ABCDEF như O sau:
- Vẽ hình bình hành O'A'B'C' biểu diễn cho hình thoi OABC. E D
- Lấy cá điểm D', E', F' lần lượt đối xứng với các điểm A', B' C' qua O', A'
ta được hình biểu diễn A' B'C'D'E'F' của hình lục giác đều ABCDEF. B' F' O C' E' D' 23 HÌNH HỌC 11
Chương II. ĐT & MP Trong KG. QHSS Toán 11 GV. Lư Sĩ Pháp ÔN TẬP CHƯƠNG II
A. CÁC DẠNG TOÁN CƠ BẢN CỦA CHƯƠNG II
DẠNG 1. Tìm giao tuyến của hai mặt phẳng
Phương pháp 1. (áp dụng nội dung tính chất 5 của bài 1 sgk/47). Ta tìm hai điểm chung phân biệt của M ∈(α)∩(β) 
hai mặt phẳng. Cụ thể: N ∈(α)∩(β) ⇒ MN = (α)∩(β) M  ≡ N 
Phương pháp 2. (Áp dụng HQ của nội dung Định lí 2 của bài sgk/57) (a) ≡ (β)  a / /b Cụ thể: 
hoặc trùng với một trong hai đường thẳng a và b.
 ⊂ (α) ⇒ (α) ∩ (β) = ∆,∆ / /a / /b a b ⊂ (β  )
Phương pháp 3. (Áp dụng nội dung Định lí 2 của bài 3 sgk/61) a / / ( ) α  Cụ thể:
⊂ (β)  ⇒ (β)∩(α) = ,bb / /a a 
DẠNG 2. Tìm giao điểm của đường thẳng và mặt phẳng
Phương pháp: Tìm giao điểm của đường thẳng d và mặt phẳng (α) , phương pháp chung: / d ( )  ⊂ α 
 ⇒ I = d ∩ α / ( )
d ∩ d = I 
Chọn mặt phẳng (β) chứa đường thẳng d sao cho dễ tìm giao tuyến với (α) là / d d ( )  ⊂ β  Cụ thể: (β)∩(α) /
= d  ⇒ I = d ∩(α)  /
d ∩ d = I 
DẠNG 3. Chứng đường thẳng song song với mặt phẳng
Phương pháp: (áp dụng nội dung Định lí 1 của bài 3 sgk/61) d ( ) ⊂ α  Cụ thể: / d / /d  ⇒ d / / (α) /  d ⊂ (α)
DẠNG 4. Chứng minh hai mặt phẳng song song
Phương pháp: (Áp dụng nội dung Định lí 1 của bài 4 sgk/64) , a b ( )  ⊂ α 
Cụ thể: a / / (β),b / / (β) ⇒ (α) / / (β) 
a ∩ b = M 
DẠNG 5. Dựng thiết diện
Dựng thiết diện của hình (H) khi cắt bởi mặt phẳng (α) :
Phương pháp chung: Ta tìm các giao tuyến (nếu có) của (α) với mặt đáy và các mặt bên của hình (H).
Đoạn nối giữa các giao tuyến cho ta một hình, hình đó là thiết diện cần tìm. Lưu ý: 24 HÌNH HỌC 11
Chương II. ĐT & MP Trong KG. QHSS Toán 11 GV. Lư Sĩ Pháp
Dựng thiết diện song song với một đường thẳng: (α) đi qua một điểm và song song với hai đường
thẳng trong hình (H) hoặc qua hai điểm và song song với một đường thẳng trong hình (H).
Phương pháp: Cho đường thẳng d song song với mặt phẳng (α) . Nếu mặt phẳng (β) chứa d và cắt (α) theo giao tuyến / d thì /
d song song với d.
Dựng thiết diện song song với một mặt phẳng trong hình (H): (α) song song với một mặt phẳng nào đó trong hình (H). Phương pháp:
ÁP dụng: Khi (α) song song với một mặt phẳng (β) nào đó thì (α) sẽ song song với tất cả đường thẳng trong (β) .
Để xác định giao tuyến của (α) với các mặt của hình (H), ta làm như sau:
Tìm đường thẳng d nằm trong (β)
Vì (α) / / (β) nên (α) cắt những mặt phẳng chứa d theo các giao tuyến song song với d.
DẠNG 6. Chứng minh hai đường thẳng song song Phương pháp:
1. Chứng minh chúng cùng thuộc một mặt phẳng và dùng phương pháp chứng minh hai đường thẳng
song song trong hình học phẳng( như tính chất đường trung bình của tam giác, định lí Talét đảo, tính chất
song song của hai đường thẳng cùng vuông góc với đường thẳng thứ ba, …)
2. Chứng minh chúng cùng song song với đường thẳng thứ ba.
3. Dùng tính chất: Hai mặt phẳng phân biệt lần lượt chứa hai đường thẳng song song thì giao tuyến của a ∈(α)  b ∈(β )
chúng(nếu có) cũng song song với hai đường thẳng ấy. Tức là: 
⇒ c / /a / /b a / /b (  α)∩(β) = c α  ∩γ = a 
a / /b / /c
4. Dùng định lý về giao tuyến của ba mặt phẳng: β ∩γ = b ⇒  
a,b ñoàng quy α  ∩ β = c
DẠNG 7. Chứng minh ba điểm thẳng hàng, ba đường thẳng đồng qui. Phương pháp:
Để chứng minh ba điểm thẳng hàng, ta chứng minh chúng cùng thuộc hai mặt phẳng phân biệt. Khi đó
chúng thuộc giao tuyến hai mặt phẳng đó.
Để chứng minh ba đường thẳng đồng qui, ta chứng minh giao điểm của hai đường thẳng này là điểm
chung của hai mặt phẳng mà giao tuyến là đường thẳng thứ ba. B. BÀI TẬP
Bài 1. Cho hình thang ABCD và ABEF có chung đáy lớn AB và không cùng nằm trong một mặt phẳng
a) Tìm giao tuyến của các mặt phẳng sau: (AEC) và (BFD); (BCE) và (ADF)
b) Lấy M là một điểm thuộc đoạn DF. Tìm giao tuyến của đường thẳng AM với mp(BCE)
c) Chứng minh hai đường thẳng AC và BF không cắt nhau. HD Giải
a) Gọi G = AC ∩ BD; H = AE ∩ BF I
Ta có (AEC) ∩ (BFD) = HG
Tương tự: Gọi I = AD ∩ BC; K = AF ∩ BE N C
Ta có: (BCE) ∩ (ADF) = IK D G
b) Gọi N = AM ∩ IK . Ta có: N = AM ∩ (BCE) B
c) Nếu AC và BF cắt nhau thì hai hình thang đã cho cùng M E
nằm trên một mặt phẳng. Điểu này trái với giả thiết. H K A F 25 HÌNH HỌC 11
Chương II. ĐT & MP Trong KG. QHSS Toán 11 GV. Lư Sĩ Pháp
Bài 2. Cho hình chóp S.ABCD, có đáy ABCD là hình thang và AB là đáy lớn. Gọi M, N theo thứ tự là
trung điểm của các cạnh SB và SC.
a) Tìm giao tuyến của hai mặt phẳng (SAD) và (SBC)
b) Tìm giao điểm của đường thẳng SD với mặt phẳng (AMN)
Tìm thiết diện của hình chóp S.ABCD cắt bởi mặt phẳng (AMN). HD Giải
a) Gọi E = AD ∩ BC . Ta có (SAD) ∩ (SBC) = SE S
b) Gọi F = SE ∩ MN,P = SD ∩ AF Ta có: P = SD ∩ (AMN)
c) Thiết diện là tứ giác APNM M N A B P F D C E
Bài 3. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi O là giao điểm hai đường chéo, M,
N, P, theo thứ tự là trung điểm các đoạn thẳng SA, BC, CD.
a) Tìm giao tuyến của hai mặt phẳng (SAC) và (SBD).
b) Tìm giao điểm của đường thẳng SO với mp(MNP).
c) Tìm thiết diện của hình chóp khi cắt bởi mp(MNP). HD Giải
a) Ta có (SAC) ∩(SBD) = SO S
b) Gọi H = AC ∩ N ;
P I = SO ∩ MH . Ta có:
I = SO ∩ (MNP)
c) Gọi E = AB ∩ N ;
P F = AD ∩ NP . M
R = SB ∩ ME;Q = SD ∩ MF . Thiết diện cần tìm là Q ngũ giác MQPNR I F A R D H O P B N C E
Bài 5. Cho tứ diện ABCD. Trên AD lấy trung điểm M, trên cạnh BC lấy một điểm N bất kì khác B và C.
Gọi (P) là mặt phẳng qua đường thẳng MN và song song với CD.
a) Xác định thiết diện của tứ diện ABCD khi cắt bởi mp(P).
b) Xác định vị trí N trên BC sau cho thiết diện là một hình bình hành. HD Giải a) Ta có A
CD ⊂ (ACD),CD / /(P) ⇒ (ACD) ∩ (P) = MJ . Sao
cho MJ // CD ( J thuôc trên AC)
Tương tự, ta có: (BCD) ∩(P) = NI , sao cho M NI//CD và I thuộc BD.
Vậy thiết diện là hình thang MINJ (MJ // NI) J CD B D b) Ta có: MJ =
. Vậy để hình thang MINJ là I 2 1 N
hình bình hành ⇔ NI = MJ = CD 2 C
Suy ra: N là trung điểm của BC 26 HÌNH HỌC 11
Chương II. ĐT & MP Trong KG. QHSS Toán 11 GV. Lư Sĩ Pháp
Bài 6. Cho hình chóp S.ABCD đáy là hình bình hành. Gọi M là trung điểm của SC.
a) Tìm giao điểm I của AM với (SBD). Chứng minh: IA = 2IM
b) Tìm giao điểm F của SD với (ABM). Chứng minh F là trung điểm của SD
c) Gọi N là một điểm tùy ý trên AB. Tìm giao điểm của MN với (SBD). HD Giải
Từ đó suy ra: F là trung điểm của SD
a) Tìm giao điểm I của AM với (SBD):
c) Tìm giao điểm của MN với (SBD):
Gọi O = AC ∩ BD . Trong mp (SAC), có
Gọi K = MN ∩ BI ,(Trong (ABM)), khi đó
I = SO ∩ AM K ∈ MN   ⇒ = ∩( ) I ∈ AM K MN SBD  ∈ ⊂ ( )  K BI SBD
khi đó I ∈SO ⊂ (SBD) S
⇒ I = AM ∩(SBD) Chứng minh IA = 2IM:
Trong tam giác SAC: AM; SO là trung tuyến và
I = SO ∩ AM
⇒ I là trọng tâm của tam giác SAC => IA = 2IM. F I M
b) Tìm giao điểm F của SD với (ABM) A K N B
Trong (SBD), gọi F = SD ∩ BI , F ∈ SD  O
khi đó: F ∈ BI ⊂ (ABM) ⇒ D
F = SD ∩ (ABM) C
Chứng minh F là trung điểm của SD: I là trọng
tâm tam giác SAC => SI = 2IO
Trong tam giác SBD có: SO là trung tuyến và SI =
2IO suy ra I là trọng tâm của tam giác SBD.
BÀI TẬP ĐỀ NGHỊ
Bài 1. Cho hình chóp S.ABCD có AB và CD không song song. Gọi M là một điểm thuộc miền trong của tam giác SCD.
a) Tìm giao điểm N của đường thẳng CD và mặt phẳng (SBM)
b) Tìm giao tuyến của hai mặt phẳng (SBM) và (SAC)
c) Tìm giao điểm I của đường thẳng BM và mp(SAC)
d) Tìm giao điểm P của SC và mp(ABM), từ đó suy ra giao tuyến của hai mặt phẳng (SCD) và (ABM)
Bài 2. Cho hình chóp S.ABCD. Gọi M, N lần lượt là trung điểm các cạnh SA, SD và G là trọng tâm của
tam giác SCD. Tìm giao điểm của:
a) MG và mp(ABCD)
b) BN và mp(SAG)
Bài 3. Cho hình chóp S.ABCD. Gọi M là một điểm nằm trong tam giác SCD.
a) Tìm giao tuyến của hai mặt phẳng (SBM) và (SAC)
b) Tìm giao điểm của đường thẳng BM và mp(SAC)
c) Xác định thiết diện của hình chóp khi cắt bởi mặt phẳng (ABM)
Bài 4. Cho hình chóp S.ABCD có đáy là hình thang ABCD ( AB // CD, AB > CD). Gọi
I, J theo thứ tự là trung điểm của các cạnh SB và SC.
a) Xác định giao tuyến của hai mặt phẳng (SAD) và (SBC), (SAC) và (SBD)
b) Tìm giao điểm của đường thẳng SD với mp(AIJ)
c) Xác định thiết diện của hình chóp S.ABCD cắt bởi mp(AIJ)
Bài 5. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M là điểm giữa S và A; N là điểm
nằm giữa S và B; giao điểm của hai đường thẳng AC và BD là O.
a) Tìm giao điểm của mặt phẳng (CMN) với đường thẳng SO
b) Xác định giao tuyến của hai mặt phẳng (SAD) và (CMN)
c) Xác định thiết diện của hình chóp khi cắt bởi mặt phẳng (CMN).
Bài 6. Cho hình thang ABCD và ABEF có chung đáy lớn AB và không cùng nằm trong một mặt phẳng 27 HÌNH HỌC 11
Chương II. ĐT & MP Trong KG. QHSS Toán 11 GV. Lư Sĩ Pháp
a) Tìm giao tuyến của các mặt phẳng sau: (AEC) và (BFD); (BCE) và (ADF)
b) Lấy M là một điểm thuộc đoạn DF. Tìm giao tuyến của đường thẳng AM với mp(BCE)
Bài 7. Cho hình chóp S.ABCD đáy ABCD là hình bình hành. Trên đoạn SA lấy điểm M sao cho 2SM =
MA, trên đoạn SB lấy điểm N sao cho 2SN = NB.
a) Tìm giao tuyến của hai mặt phẳng (SAC) và (SBD); (SAD) và (SBC)
b) Chứng minh rẳng: MN // CD
c) Điểm P nằm trên cạnh SC không trùng với S, C. Tìm giao tuyến hai mp (MNP) và (SCD)
Bài 8. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành.
a) Hãy xác định giao tuyến của các mặt phẳng (SAB) và (SCD); (SBC) và (SAD)
b) M là điểm thuộc cạnh SC, tìm thiết diện của hình chóp với mp(ABM). Thiết diện là hình gì?
Bài 9. Cho hình chóp S.ABCD, có đáy ABCD là hình thang và AB là đáy lớn. Gọi M, N theo thứ tự là
trung điểm của các cạnh SB và SC.
a) Tìm giao tuyến của hai mặt phẳng (SAD) và (SBC)
b) Tìm giao điểm của đường thẳng SD với mặt phẳng (AMN)
c) Tìm thiết diện của hình chóp S.ABCD cắt bởi mặt phẳng (AMN).
Bài 10. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi O là giao điểm hai đường chéo. Gọi
M, N, P, theo thứ tự là trung điểm các đoạn thẳng SA, BC, CD.
a) Tìm giao tuyến của hai mặt phẳng (SAC) và (SBD).
b) Tìm giao điểm của đường thẳng SO với mp(MNP).
c) Tìm thiết diện của hình chóp khi cắt bởi mp(MNP).
Bài 11. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N lần lượt là trung điểm của AB và CD.
a) Chứng minh rằng MN song song với các mặt phẳng (SBC) và (SAD).
b) Gọi P là trung điểm của SA. Chứng minh rằng SB và SC đều song song với mp (MNP)
Bài 12. Cho hình chóp S.ABCD có đáy ABCD là hình thang, đáy lớn AD và AD = 2BC. Gọi O là giao
điểm của AC và BD, G là trọng tâm của tam giác SCD.
a) Chứng minh rằng OG // (SBC)
c) Cho M là trung điểm của SD. Chứng minh rằng CM // (SAB) 3
d) Giả sử I nằm trên đoạn SC sao cho SC = SI . Chứng minh rằng SA // (BID). 2
Bài 13. Cho hình chóp S.ABCD có đáy là hình thang (AD // BC, AD > BC). Gọi M, N, E lần lượt là trung
điểm của AB, CD, SA.
a) Chứng minh rằng: (MEN) // (SBC)
b) Trong tam giác SAD vẽ EF // AD (F ∈SD) . Chứng minh rằng F là giao điểm của mặt phẳng (MNE)
với SD. Từ đó suy ra thiết diện của hình chóp khi cắt bởi mp(MNE) là hình gì?
Bài 14. Cho tứ diện ABCD. Gọi G1, G2, G3 lần lượt là trọng tâm của các tam giác ABC, ACD, ABD.
Chứng minh mặt phẳng (G1G2G3) song song với mặt phẳng (BCD).
Bài 15. Cho hình chóp S.ABCD có đáy là hình bình hành ABCD, O là giao điểm của AC và BD, M là
trung điểm của SA. Tìm thiết diện của mặt phẳng (α) với hình chóp S.ABCD nếu (α) qua M và đồng
thời song song với SC và AD.
Bài 16. Cho tứ diện ABCD. Trên AB lấy điểm M. Cho (α) là mặt phẳng qua M, song song với hai đường
thẳng AC và BD.
a) Tìm giao tuyến của (α) với các mặt của tứ diện
b) Thiết diện của tứ diện cắt bởi mặt phẳng (α) là hình gì?
Bài 17. Cho hình chóp S.ABCD có đáy ABCD là một tứ giác lồi. Gọi O là giao điểm của hai đường chéo
AC và BD. Xác định thiết diện của hình chóp cắt bởi mặt phẳng (α) đi qua O, song song với AB và SC.
Thiết diện đó là hình gì?
Bài 18. Cho hình chóp S.ABCD có đáy là hình bình hành. Xác định thiết diện của hình chóp khi cắt bởi
mặt phẳng đi qua trung điểm M của cạnh AB, song song với BD và SA.
Bài 19. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi O là giao điểm của AC và BD. Gọi
M, N, P, theo thứ tự là trung điểm các đoạn thẳng SA, BC, CD. 28 HÌNH HỌC 11
Chương II. ĐT & MP Trong KG. QHSS Toán 11 GV. Lư Sĩ Pháp
a) Tìm giao tuyến của mp(SAC) và mp(MNP). Từ đó suy ra giao điểm của đường thẳng SO với mp(MNP).
b) Xác định thiết diện của hình chóp khi cắt bởi mặt phẳng (α ) qua M đồng thời song song với AB và SC.
Bài 20. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi O là giao điểm của AC và BD. Gọi
M, N, P, theo thứ tự là trung điểm các đoạn thẳng SA, BC, CD.
a) Tìm giao điểm của đường thẳng SO với mp(MNP).
b) Xác định thiết diện của hình chóp khi cắt bởi mặt phẳng (P) qua M đồng thời song song với AB và SC. Thiết diện là hình gì?
Bài 21. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Gọi M, N lần lượt là trung điểm SA, CD.
a) Chứng minh rằng (OMN) // (SBC)
b) Xác định thiết diện của hình chóp với mặt phẳng (OMN)
Bài 22. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Gọi I, J lần lượt là trung điểm SB, CD.
a) Chứng minh rằng: IJ //(SAD)
b) Gọi (α ) là mặt phẳng qua IO và song song với SC. Xác định thiết diện của hình chóp S.ABCD khi cắt bởi mp(α ) .
Bài 23. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Gọi P, Q lần lượt là trung điểm SC, AB.
a) Chứng minh rằng (OPQ) // (SAD)
b) Xác định thiết diện của hình chóp với mặt phẳng (OPQ)
Bài 24. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Gọi M, N lần lượt là trung điểm SD, BC.
a) Chứng minh rằng: MN //(SAB)
Gọi (α ) là mặt phẳng qua MO và song song với SA. Xác định thiết diện của hình chóp S.ABCD khi cắt bởi mp(α ) .
Bài 25. Cho hình chóp S.ABCD có đáy ABCD là hình thang (AB là đáy lớn). Gọi M, N lần lượt là trung
điểm của SB và SC.
a) Tìm giao điểm của đường thẳng AN với mặt phẳng (SBD).
b) Gọi (α) là mặt phẳng qua MN và song song với CD. Xác định thiết diện của hình chóp cắt bởi mặt phẳng (α) .
Bài 26. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Lấy một điểm M trên cạnh SA nhưng
không trùng với S và A.
a) Tìm giao điểm của đường thẳng CM với mặt phẳng (SBD).
b) Gọi (α) là mặt phẳng qua M và đồng thời song song với AB, SC. Xác định thiết diện của hình chóp cắt bởi mặt phẳng (α) .
Bài 27. Cho hình chóp S.ABCD, đáy ABCD hình bình hành tâm O. Gọi M, N lần lượt là trung điểm của
SC và OB. Tìm giao điểm của SD với mặt phẳng (AMN).
Bài 28. Cho hình chóp S.ABCD có đáy ABCD là một tứ giác lồi. Gọi O là giao điểm của hai đường chéo
AC và BD; M là trung điểm của SD. Xác định thiết diện của hình chóp khi cắt bởi mặt phẳng (α ) qua M,
song song với SO và BC.
Bài 29. Cho hình chóp S.ABCD, đáy ABCD là hình thang với AB là đáy lớn. Gọi M, N lần lượt là trung
điểm của SA và SD. Tìm giao điểm của SC với mặt phẳng (BMN).
Bài 30. Cho hình chóp S.ABCD, đáy ABCD là hình bình hành. Xác định thiết diện của hình chóp khi cắt
bởi mặt phẳng (α ) qua trung điểm M của CD, song song với AC và SD. 29 HÌNH HỌC 11
Chương II. ĐT & MP Trong KG. QHSS Toán 11 GV. Lư Sĩ Pháp
Bài 31. Cho hình chóp S.ABCD có đáy là một tứ giác lồi. Gọi O là giao điểm của hai đường chéo AC và
BD, M là trung điểm của cạnh SA.
a) Xác định thiết diện của hình chóp khi cắt bởi mặt phẳng (P) qua M, song song với SO và BC.
b) Xác định thiết diện của hình chóp khi cắt bởi mặt phẳng (Q) qua O, song song với BM và SD
Bài 32. Cho hình chóp S.ABCD có đáy ABCD là hình thang (AD // BC). Gọi M, N, G lần lượt là trung
điểm của AB, CD và trọng tâm tam giác SAD.
a) Xác định giao tuyến của mặt phẳng (SAB) và mặt phẳng (SCD)
b) Xác định thiết diện của hình chóp với mặt phẳng (MNG)
c) Gọi O là giao điểm của AC và BD. Giả sử đường thẳng SO cắt mặt phẳng (MNG) tại E. Hãy xác định điểm E.
Bài 33. Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a, cạnh bên bằng b. Gọi M, N lần lượt là
trung điểm của AB và BC. Tính diện tích thiết diện của hình chóp với mặt phẳng đi qua M, N và song song với SB.
Bài 34. CHo hình hộp ABCD.A'B'C'D'. Vẽ thiết diện của hình hộp tạo bởi mặt phẳng đi qua trung điểm
M, N của các cạnh AB, AD và tâm O của hình bình hành CDD'C'.
Bài 35. Cho hình lập phương ABCD.A'B'C'D' và các trung điểm E, F của các cạnh AB, DD'. Hãy xác
định các thiết diện của hình lập phương cắt bởi các mặt phẳng (EFB), (EFC), (EFC') và (EFK) với K là
trung điểm của cạnh B'C'.
Bài 36. Cho tứ diện đều ABCD có cạnh đáy bằng a, cạnh bên bằng b. Gọi M, N lần lượt là trung điểm của
AB và BC. Tính diện tích thiết diện của hình chóp với mặt phẳng (P) đi qua M, N và song song với SB.
Bài 37. Cho hình chóp S.ABCD có đáy là hình thang (AD//BC, AD > BC). Gọi M, N, E lần lượt là trung điểm của AB, CD, SA.
a) Chứng minh rằng: (MEN) // (SBC)
b) Trong tam giác SAD vẽ EF // AD (F ∈SD) . Chứng minh rằng F là giao điểm của mặt phẳng (MNE)
với SD. Từ đó suy ra thiết diện của hình chóp khi cắt bởi mp(MNE) là hình gì? 30 HÌNH HỌC 11
Chương II. ĐT & MP Trong KG. QHSS Toán 11 GV. Lư Sĩ Pháp CHƯƠNG II
ĐƯỜNG THẲNG VÀ MẶT PHẲNG TRONG KHÔNG GIAN QUAN HỆ SONG SONG PHẦN TRẮC NGHIỆM
Câu 1: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N, P theo thứ tự là trung điểm
các đoạn thẳng S ,
A BC,CD . Gọi O là giao điểm của hai đường chéo của hình bình hành ABCD (như hình
vẽ). Xác định giao điểm I của đường thẳng SO với mặt phẳng (MNP). S
A. I = SO ∩ NP.
B. I = SO ∩ MH. M
C. I = SO ∩ MP. A D
D. I = SO ∩ MN. O P H B N C
Câu 2: Cho tứ diện ABCD . Gọi M, N lần lượt là trung điểm các cạnh AD và BC; G là trọng tâm của tam
giác BCD . Xác định giao điểm của đường thẳng MG và mặt phẳng ( ABC) .
A. Giao điểm của MG và đường thẳng BC. B. Điểm N. C. Điểm C.
D. Giao điểm của đường thẳng MG và đường thẳng AN.
Câu 3: Mệnh đề nào dưới đây đúng ?
A. Nếu hai đường thẳng song song với nhau lần lượt nằm trong hai mặt phẳng phân biệt (α ) và (β ) thì
(α ) và (β ) song song với nhau.
B. Qua một điểm nằm ngoài mặt phẳng cho trước ta vẽ được một và chỉ một đường thẳng song song
với mặt phẳng cho trước.
C. Nếu hai mặt phẳng (α ) và (β ) song song với nhau thì mọi đường thẳng nằm trong (α ) đều song
song với mọi đường thẳng nằm trong mặt phẳng (β ) .
D. Nếu hai mặt phẳng (α ) và (β ) song song với nhau thì mọi đường thẳng nằm trong (α ) đều song song với (β ) .
Câu 4: Cho hình chóp S.ABCD , có đáy ABCD là hình bình hành. Giả sử M thuộc đoạn thẳng SB . Mặt
phẳng (ADM) cắt hình chóp S.ABCD theo một thiết diện là hình gì? A. Hình chữ nhật. B. Hình bình hành. C. Hình tam giác. D. Hình thang.
Câu 5: Mệnh đề nào dưới đây đúng ?
A. Hai đường thẳng phân biệt cùng nằm trong một mặt phẳng thì không chéo nhau.
B. Hai đường thẳng phân biệt không cắt nhau thì chéo nhau.
C. Hai đường thẳng phân biệt không song song thì chéo nhau.
D. Hai đường thẳng phân biệt lần lượt thuộc hai mặt phẳng khác nhau thì chéo nhau.
Câu 6: Cho tam giác ABC , lấy điểm I trên cạnh AC kéo dài. Mệnh đề nào dưới đây sai ?
A. BI ⊄ (ABC).
B. I ∈ (ABC).
C. (ABC) ≡ (BIC).
D. A∈(ABC).
Câu 7: Cho hai đường thẳng phân biệt a và b trong không gian. Có bao nhiêu vị trí tương đối giữa a và b
cùng chứa trong một mặt phẳng. A. 2. B. 1. C. 4. D. 3.
Câu 8: Cho tứ diện SABC có E, F lần lượt là trung điểm của SB, AB . Lấy G là một điểm trên đoạn thẳng
AC sao cho G không trùng với trung điểm AC . Gọi I là giao điểm của GF và mặt phẳng (SBC). Thiết
diện của tứ diện khi cắt bởi mặt phẳng (EFG) là hình nào dưới đây ? 31 HÌNH HỌC 11
Chương II. ĐT & MP Trong KG. QHSS Toán 11 GV. Lư Sĩ Pháp S A. Hình bình hành. B. Hình thang. E C. Tam giác. G A C D. Hình thoi. F B
Câu 9: Mệnh đề nào dưới đây sai ?
A. Nếu hai mặt phẳng phân biệt cùng song song với một đường thẳng thì giao tuyến của chúng (nếu
có) cũng song song với đường thẳng đó.
B. Nếu mặt phẳng (α)chứa hai đường thẳng cắt nhau a,b và a,b cùng song song với mặt phẳng
(β) thì (α) song song với (β) .
C. Qua một điểm nằm ngoài mặt phẳng cho trước có nhiều hơn một mặt phẳng song song với mặt phẳng đã cho. D. /
Nếu đường thẳng d không nằm trong mặt phẳng (α) và d song song với đường d nằm trong (α)
thì d song song với (α) .
Câu 10: Cho hình chóp S.ABCD có đáy là hình bình hành. Gọi I, J lần lượt là trung điểm của AB và
CB . Giao tuyến của hai mặt phẳng (SAB) và (SCD) là đường thẳng song song đường thẳng nào dưới đây ?
A. Đường thẳng AD.
B. Đường thẳng IJ.
C. Đường thẳng BI.
D. Đường thẳng BJ.
Câu 11: Cho hai hình bình hành ABCD và ABEF nằm trong hai mặt phẳng phân biệt. Khẳng định nào dưới đây đúng ?
A. ( ABD) | (EFC).
B. EC | (ABF).
C. AD | (BEF).
D. ( AFD) | (BEC).
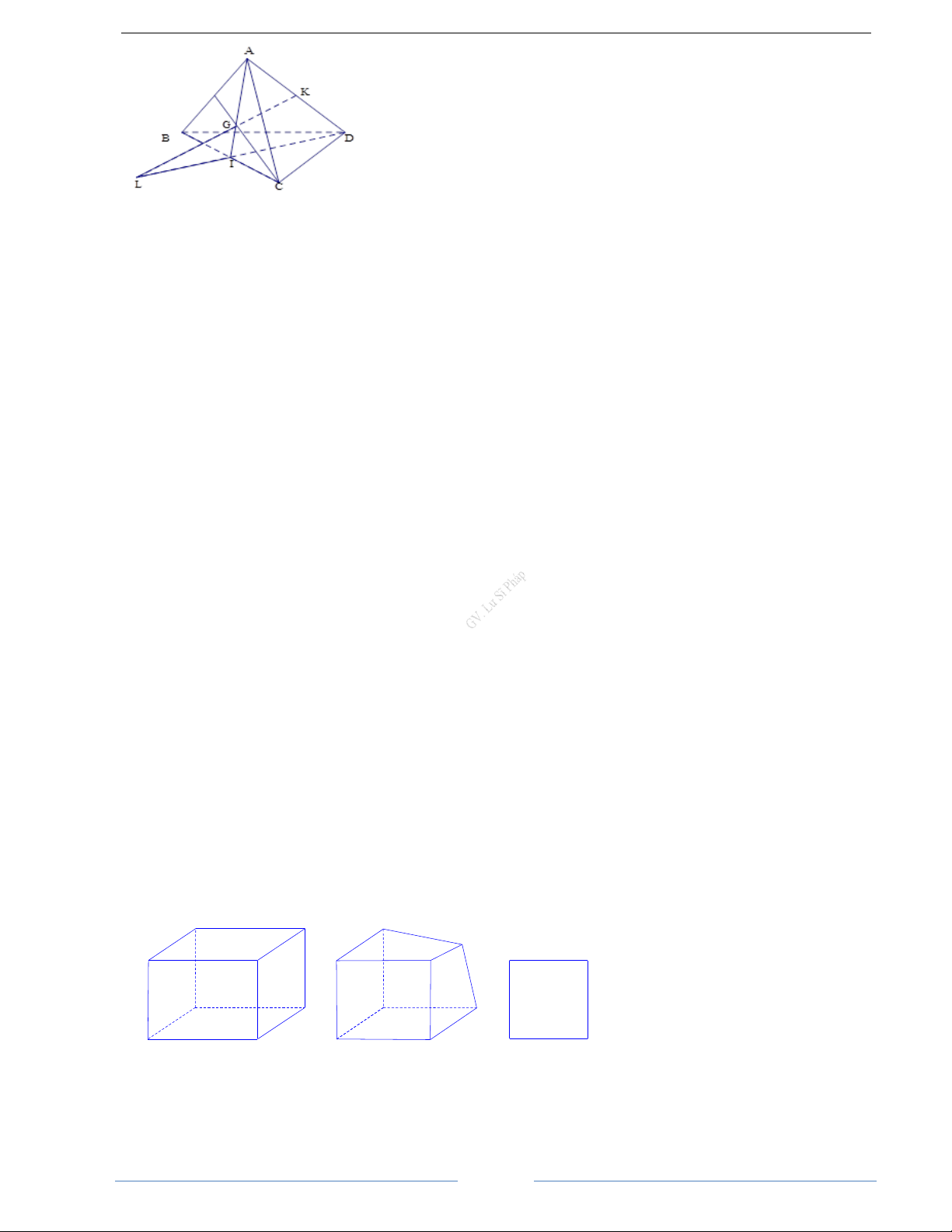
Câu 12: Trong các hình sau đây, hình nào biểu diễn cho hình lập phương ? a) b) c) A. Hình a) B. Hình a) và c) C. Hình b) D. Hình c) và b)
Câu 13: Mệnh đề nào dưới đây đúng ?
A. Hình chiếu song song của hai đường thẳng chéo nhau có thể cắt nhau, trùng nhau, song song với nhau.
B. Hình chiếu song song của hai đường thẳng chéo nhau thì cắt nhau.
C. Hình chiếu song song song của hai đường thẳng chéo nhau có thể trùng nhau.
D. Hình chiếu song song của hai đường thẳng chéo nhau có thể song song với nhau.
Câu 14: Mệnh đề nào dưới đây đúng ?
A. Nếu hai mặt phẳng song song thì mỗi đường thẳng nằm trên mặt phẳng này đều song song với mọi
đường thẳng nằm trong mặt kia.
B. Một đường thẳng cắt một trong hai đường thẳng song song thì cắt đường thẳng còn lại.
C. Nếu hai mặt phẳng song song thì mọi đường thẳng nằm trên mặt phẳng này đều song song với mặt phẳng kia.
D. Hai mặt phẳng phân biệt cùng song song với một đường thẳng thì song song với nhau. Câu 15: / / /
Cho hình lăng trụ tam giác ABC.A B C . Gọi I, J lần lượt là trọng tâm của các tam giác ABC và / / /
A B C . Thiết diện tạo bởi mặt phẳng (AIJ) với lăng trụ đã cho là hình nào dưới đây ? (tham khảo hình vẽ) 32 HÌNH HỌC 11
Chương II. ĐT & MP Trong KG. QHSS Toán 11 GV. Lư Sĩ Pháp A. A' Hình bình hành. C' J B. Hình thang. B' C. Tam giác cân. D. Tam giác vuông. A C I B
Câu 16: Cho tứ diện ABCD . Gọi M, N lần lượt là trung điểm của AB và AC , E là điểm trên cạnh CD với
ED = 3EC . Tìm thiết diện tạo bởi mặt phẳng (MNE) và tứ diện ABCD . (tham khảo hình vẽ) A
A. Hình bình hành MNEF với F là điểm trên cạnh BD mà EF || BC.
B. Hình thang MNEF với F là điểm trên cạnh BD mà EF || BC. M
C. Tam giác MNE. N B D
D. Tứ giác MNEF với F là điểm bất kì trên B . D E C
Câu 17: Cho hình chóp S.ABCD với đáy là tứ giác ABCD . Thiết diện của mặt phẳng (α ) tùy ý với hình
chóp không thể là hình nào dưới đây ? A. Hình tứ giác. B. Hình ngũ giác. C. Hình tam giác. D. Hình lục giác.
Câu 18: Nếu ba đường thẳng không cùng nằm trong một mặt phẳng và đôi một cắt nhau thì ba đường
thẳng đó như thế nào ?
A. Cùng song song với một mặt phẳng. B. Trùng nhau.
C. Tạo thành một tam giác. D. Đồng quy. Câu 19: / / / /
Cho hình chóp S.ABCD có đáy là một hình bình hành. Gọi A , B ,C , D lần lượt là trung điểm của các cạnh S ,
A SB, SC và SD . Tìm mệnh đề Đúng trong các mệnh đề sau ? A. / / A C | BD. / /
B. A C | (SBD). C. / / A B | (SAD). / / /
D. (A C D ) | (ABC).
Câu 20: Cho tứ diện SABC có E, F lần lượt là trung điểm của SB, AB . Lấy G là một điểm trên đoạn
thẳng AC sao cho G không trùng với trung điểm AC . Gọi I là giao điểm của GF và mặt phẳng (SBC).
Điểm I thuộc đường thẳng nào dưới đây ?(tham khảo hình vẽ) S A. BC. B. A . B E C. S . A G A C D. AC. F B
Câu 21: Cho tứ diện ABCD. Gọi M,N lần lượt là trung điểm các cạnh AB và AC . Xét vị trí tương đối của
đường thẳng MN và mp(BCD). Khẳng định nào dưới đây đúng ?
A. MN nằm trong (BCD).
B. MN không song song (BCD).
C. MN // (BCD).
D. MN cắt (BCD). 33 HÌNH HỌC 11
Chương II. ĐT & MP Trong KG. QHSS Toán 11 GV. Lư Sĩ Pháp
Câu 22: Mệnh đề nào dưới đây sai ?
A. Hai đường thẳng phân biệt cùng song song với một mặt phẳng thì song song với nhau
B. Nếu một đường thẳng cắt một trong hai mặt phẳng song song thì cắt mặt phẳng còn lại
C. Hai mặt phẳng phân biệt cùng song song với một mặt phẳng thì song song với nhau
D. Nếu hai mặt phẳng song song thì mọi đường thẳng nằm trên mặt phẳng này đều song song với mặt phẳng kia
Câu 23: Cho hai đường thẳng a và b song song với mặt phẳng (α ) . Mệnh đề nào dưới đây đúng ?
A. a và b trùng nhau
B. a và b có thể cắt nhau
C. a và b chéo nhau
D. a và b song song với nhau
Câu 24: Cho hai đường thẳng a và b chéo nhau. Có bao nhiêu mặt phẳng chứa a và song song với b?
A. Không có mặt phẳng nào B. Ba mặt phẳng C. Một mặt phẳng D. Hai mặt phẳng
Câu 25: Mệnh đề nào dưới đây đúng ?
A. Nếu a / /b và a ⊂ (α),b ⊂ (β) thì (α) / /(β) B. Nếu (α) / /(β) và a ⊂ (α),b ⊂ (β) thì a / /b
C. Nếu (α) / /(β) và b / /(β) thì a / /b
D. Nếu (α) / /(β) và a ⊂ (α) thì a / /(β)
Câu 26: Chọn phương án Đúng. Nếu đường thẳng a song song với mặt phẳng (α)thì
A. có mọi đường thẳng b không chứa trong (α) song song với a
B. có duy nhất mặt phẳng (β) chứa a và song song với (α)
C. đường thẳng a chứa trong mặt phẳng (α)
D. có duy nhất mặt phẳng (β) chứa b và b song song với (α)
Câu 27: Cho tứ diện ABCD có các cạnh đều bằng a . Gọi G G 1 và
2 lần lượt là trọng tâm các tam giác
BCD và ACD thì đoạn G G bằng bao nhiêu? 1 2 2a a a a 3 A. 3 B. C. D. 4 3 2
Câu 28: Trong các mệnh đề sau, mệnh đề nào Đúng ?
A. Hai mặt phẳng phân biệt cùng song song với một mặt phẳng thì song song với nhau
B. Hai mặt phẳng phân biệt cùng song song với một đường thẳng thì song song với nhau
C. Nếu hai mặt phẳng phân biệt lần lượt đi qua hai đường thẳng song song thì song song với nhau
D. Hai đường thẳng phân biệt cùng song song với một mặt phẳng thì song song với nhau
Câu 29: Có bao nhiêu cách xác định một mặt phẳng ? A. 1 B. 3 C. 2 D. 4
Câu 30: Tìm mệnh đề Sai trong các mệnh đề sau đây:
A. Nếu hai mặt phẳng phân biệt cùng song song với mặt phẳng thứ ba thì chúng song song với nhau
B. Nếu một đường thẳng cắt một trong hai mặt phẳng song song với nhau thì sẽ cắt mặt phẳng còn lại
C. Nếu hai đường thẳng phân biệt cùng song song với một mặt phẳng thì song song với nhau
D. Nếu hai mặt phẳng có một điểm chung thì chúng còn có vô số điểm chung khác nữa. a
Câu 31: Cho tứ diện ABCD có các cạnh đều bằng a . Lấy điểm M trên AB với AM = 3 . Diện tích của
thiết diện của hình tứ diện khi cắt bởi mặt phẳng qua M và song song với mp(BCD) là : 2 a 3 2 a 3 2 a 3 2 a 3 A. B. C. D. 12 24 18 36
Câu 32: Cho hình chóp S.ABCD . Gọi AC ∩ BD = I; AB ∩ CD = J; AD ∩ BC = K . Đẳng thức nào Sai
trong các đẳng thức sau đây?
A. (SAC) ∩ (SBD) = SI
B. (SAC) ∩ (SAD) = AB
C. (SAB) ∩ (SCD) = SJ
D. (SAD) ∩ (SBC) = SK
Câu 33: Cho tứ diện ABCD . Gọi M, N, P,Q, R,S lần lượt là trung điểm các cạnh
AC, BD, A ,
B CD, AD, BC . Bốn điểm nào sau đây không đồng phẳng ?
A. M, P, R, S
B. M, R, S, N
C. P, Q, R, S
D. M, N, P, Q 34 HÌNH HỌC 11
Chương II. ĐT & MP Trong KG. QHSS Toán 11 GV. Lư Sĩ Pháp
Câu 34: Trong các mệnh đề sau, mệnh đề nào Sai ?
A. Một mặt phẳng cắt một trong hai đường thẳng song song thì cắt đường thẳng còn lại
B. Hai đường thẳng chéo nhau thì không cùng thuộc một mặt phẳng
C. Hai đường thẳng không song song thì chéo nhau
D. Hai mặt phẳng phân biệt không song song thì cắt nhau
Câu 35: Cho hai đường thẳng phân biệt cùng nằm trong một mặt phẳng. Có bao nhiêu vị trí tương đối
giữa hai đường thẳng đó ? A. 3. B. 2. C. 1. D. 4
Câu 36: Trong các mệnh đề sau, mệnh đề nào sai ?
A. Hình chiếu song song của hai đường thẳng cắt nhau có thể trùng nhau.
B. Một đường thẳng luôn cắt hình chiếu song song của nó.
C. Hình chiếu song song của hai đường thẳng cắt nhau có thể cắt nhau.
D. Một đường thẳng có thể song song hoặc trùng với hình chiếu song song của nó.
Câu 37: Trong không gian,cho hai mặt phẳng (α ) và (β ) . Có bao nhiêu vị trí tương đối giữa (α ) và (β ) ? A. 3. B. 4. C. 2. D. 1.
Câu 38: Cho hình chóp S.ABCD có đáy ABCD là hình thang và BA là đáy lớn. Gọi M, N theo thứ tự là
trung điểm của cạnh SB và SC . Thiết diện của hình chóp S.ABCD cắt bởi mặt phẳng (AMN ) là hình nào
dưới đây?(tham khảo hình vẽ) S A. Hình chữ nhật. M N B. Hình thanh. A B C. Hình bình hành. D C D. Tam giác.
Câu 39: Trong các mệnh đề dưới đây, mệnh đề nào sai?
A. Hình hộp có các mặt đối diện bằng nhau.
B. Hình lăng trụ có tất cả các mặt bên bằng nhau.
C. Hình hộp là một hình lăng trụ.
D. Hình lăng trụ có các mặt bên là hình bình hành.
Câu 40: Ký hiệu nào dưới đây sai ?
A. A ∈ (P).
B. A ∈(P).
C. d ∈(P).
D. A∈ d.
Câu 41: Các yếu tố nào sau đây xác định một mặt phẳng duy nhất ? A. Bốn điểm. B. Ba điểm.
C. Một điểm và một đường thẳng.
D. Hai đường thẳng cắt nhau.
Câu 42: Giữa đường thẳng và mặt phẳng có bao nhiêu vị trí tương đối ? A. 2. B. 4. C. 3. D. 1.
Câu 43: Cho hình chóp S.ABCD , có đáy ABCD là hình bình hành. Giao tuyến của hai mặt phẳng (SAD)
và (SBC) là đường thẳng song song với đường nào sau đây? A. SC. B. AC. C. AD. D. BD.
Câu 44: Cho hình chóp S.ABCD có đáy ABCD là hình thang và BA là đáy lớn. Gọi M, N theo thứ tự là
trung điểm của cạnh SB và SC . Tìm giao tuyến của hai mặt phẳng (SAD) và (SBC) . S
A. SE với E = AD ∩ BC. B. Đườ
∆, S ∈ ∆,∆ / / AD . M ng thẳng ( ) N
C. SO với O = AC ∩ BD. A B
D. Đường thẳng d,(S∈d,d / /BC). D C 35 HÌNH HỌC 11
Chương II. ĐT & MP Trong KG. QHSS Toán 11 GV. Lư Sĩ Pháp Câu 45: /
Cho tứ diện ABCD có cạnh bằng a . Gọi G,G lần lượt là trọng tâm của ABC và ABD . Tính /
diện tích S của thiết diện của hình tứ diện khi cắt bởi mặt phẳng (BGG ) . 2 a 11 2 a 11 2 a 11 2 a 11 A. S = . S . S . S . 6 B. = 16 C. = 8 D. = 3
Câu 46: Cho hai đường thẳng a và b. Điều kiện nào sau đây đủ để kết luận a và b chéo nhau ?
A. a và b là hai cạnh của một tứ diện.
B. a và b không nằm trên bất kì mặt phẳng nào.
C. a và b không có điểm chung.
D. a và b nằm trên hai mặt phẳng phân biệt.
Câu 47: Trong các hình sau đây, hình nào biểu diễn của một tứ diện ? a) b) c) d)
A. Hình a) , b) và d). B. Hình a) và c). C. Hình b) và d). D. Tất cả.
Câu 48: Cho mặt phẳng (α ) và hai đường thẳng song song a, b. Mệnh đề nào dưới đây đúng ?
A. Nếu (α ) song song với a thì (α ) song song với b hoặc chứa b.
B. Nếu (α ) cắt a thì (α ) có thể song song với b.
C. Nếu (α ) không chứa a thì (α ) có thể song song với b.
D. Nếu (α ) song song với a thì (α ) cũng song song với b.
Câu 49: Trong các mệnh đề dưới đây, mệnh đề nào đúng?
A. Hai đường thẳng lần lượt nằm trên hai mặt phẳng phân biệt thì chéo nhau.
B. Hai đường thẳng phân biệt không song song thì chéo nhau.
C. Hai đường thẳng chéo nhau thì không có điểm chung.
D. Hai đường thẳng không có điểm chung thì chéo nhau.
Câu 50: Cho tứ diện ABCD và ba điểm I, J, K lần lượt nằm trên các cạnh AB, AC, AD mà không
trùng với các đỉnh. Thiết diện của tứ diện ABCD khi cắt bởi mp (EFG) là hình nào dưới đây ? A. Một tam giác. B. Một tứ giác.
C. Một đoạn thẳng. D. Một ngũ giác.
Câu 51: Cho các giả thiết sau đây. Giả thiết nào kết luận đường thẳng a song song với mặt phẳng (α )
A. a | b thì b | (α). B. a ∩ α ( ) = ∅. C. a | β ( ) thì β ( ) | α
( ). D. a | b thì b ⊂ α ( ).
Câu 52: Hãy chọn phương án Đúng điền vào chỗ trống
“Nếu ba mặt phẳng phân biệt đôi một cắt nhau theo ba giao tuyến phân biệt thì . . . . . .”
A. ba giao tuyến ấy đôi một song song với nhau.
B. ba giao tuyến ấy hoặc trùng nhau hoặc đôi một song song với nhau.
C. ba giao tuyến ấy đồng quy và đôi một song song với nhau.
D. ba giao tuyến ấy hoặc đồng quy hoặc đôi một song song với nhau.
Câu 53: Cho tứ diện đều SABC có cạnh bằng a . Gọi I là trung điểm của AB, M là điểm di động trên
đoạn AI. Qua M vẽ mặt phẳng (α) song song với (SCI) . Thiết diện tạo bởi (α) và tứ diện là hình nào dưới đây ? A. Hình thoi. B. Tam giác đều.
C. Tam giác cân tại M. D. Hình bình hành.
Câu 54: Cho tứ diện ABCD và ba điểm P,Q, R lần lượt lấy trên ba cạnh AB,CD,BC . Tìm giao điểm S
của AD và mặt phẳng (PQR) , biết PR song song với AC . 36 HÌNH HỌC 11
Chương II. ĐT & MP Trong KG. QHSS Toán 11 GV. Lư Sĩ Pháp A
A. AD ∩(PQR) = S với QS || PR || AC.
B. AD ∩(PQR) = S với S = AD ∩ P . Q P
C. AD ∩(PQR) = S với S = AD ∩ P . R B D Q
D. AD ∩(PQR) = S với PS || BD || R . Q R C
Câu 55: Cho tam giác ABC . Có thể xác định được bao nhiêu mặt phẳng chứa tất cả các đỉnh tam giác ABC ? A. 1. B. 3. C. 2. D. 4.
Câu 56: Cho tứ diện ABCD . Gọi I, J và K lần lượt là trung điểm của AC, BC và BD . Giao tuyến của
hai mặt phẳng ( ABD) và (IJK ) là A A. IJ. B. KI. I
C. Đường thẳng qua K và song song với AB. C D J D. K KD. B
Câu 57: Cho tứ diện ABCD và ba điểm P,Q, R lần lượt lấy trên ba cạnh AB,CD,BC . Tìm giao điểm S
của AD và mặt phẳng (PQR) , biết PR cắt AC tại I . A
A. AD ∩(PQR) = S với S = IQ ∩ A . D
B. AD ∩(PQR) = S với S = AC ∩ I . Q P B D
C. AD ∩(PQR) = S với S = AD ∩ P . Q Q R
D. AD ∩(PQR) = S với S = RQ ∩ A . D C I
Câu 58: Cho tứ diện đều ABCD có cạnh bằng a . Gọi G là trọng tâm tam giác ABC . Nếu cắt tứ diện bởi
mặt phẳng (GCD) thì diện tích S của thiết diện bằng bao nhiêu ? D 2 a 2 2 a 2 A. S = . S . 2 B. = 4 2 a 2 2 a 3 A C C. S = . S . 6 D. = 4 G B
Câu 59: Cho tứ diện đều SABC có cạnh bằng a . Gọi I là trung điểm của AB, M là điểm di động trên
đoạn AI và AM = x . Qua M vẽ mặt phẳng (α) song song với (SCI ) . Thiết diện tạo bởi (α) và tứ diện là
tam giác cân tại M. Tìm chu vi P của thiết diện.
A. P = 2x (1+ 3).
B. P = x (1+ 3).
C. P = 3x (1+ 3).
D. P = 2x (1+ 2 3). 37 HÌNH HỌC 11
Chương II. ĐT & MP Trong KG. QHSS Toán 11 GV. Lư Sĩ Pháp
Câu 60: Cho hình chóp S.ABCD với đáy là tứ giác ABCD có các cạnh đối diện không song song. Giả
sử AC ∩ BD = I; AD ∩ BC = O . Tìm giao tuyến của hai mặt phẳng (SAC) và (SBD).
A. (SAC) ∩(SBD) = S .
B B. (SAC) ∩ (SBD) = SI. C. (SAC) ∩ (SBD) = SO. D. (SAC) ∩ (SBD) = SC.
Câu 61: Trong không gian cho bốn điểm không đồng phẳng, có thể xác định nhiều nhất bao nhiêu mặt
phẳng phân biệt từ các điểm đó ? A. 6. B. 2. C. 3. D. 4.
Câu 62: Cho tứ diện ABCD . Điểm M thuộc đoạn AC . Mặt phẳng (α ) qua M song song với AB và AD .
Thiết diện của (α ) với tứ diện ABCD là hình nào dưới đây ? A. Hình chữ nhật. B. Hình vuông. C. Hình tam giác. D. Hình bình hành.
Câu 63: Mệnh đề nào dưới đây đúng ?
A. Hai đường thẳng phân biệt không cắt nhau thì chéo nhau.
B. Hai đường thẳng phân biệt không song song thì chéo nhau.
C. Hai đường thẳng phân biệt cùng nằm trong một mặt phẳng thì không chéo nhau.
D. Hai đường thẳng phân biệt lần lượt thuộc hai mặt phẳng khác nhau thì chéo
Câu 64: Mệnh đề nào dưới đây đúng ?
A. Nếu (α ) || (β ) và a ⊂ (α ) thì a || (β ).
B. Nếu a || (α ) và b || (β ) thì a || . b
C. Nếu (α ) || (β ) và a ⊂ (α ), b ⊂ (β ) thì a || . b
D. Nếu a || b và a ⊂ (α ), b ⊂ (β ) thì
Câu 65: Cho tứ diện ABCD,G là trọng tâm của tam giác AB .
D Trên BC lấy điểm M sao cho
MB = 2MC. Khẳng định nào dưới đây đúng ?
A. MG || (ACB).
B. MG || (ABD).
C. MG || (BCD).
D. MG || (ACD).
Câu 66: Cho hai đường thẳng phân biệt cùng nằm trong một mặt phẳng. Có bao nhiêu vị trí tương đối
giữa hai đường thẳng đó? A. 4. B. 3. C. 1. D. 2.
Câu 67: Cho hình lăng trụ ABC.A′B C
′ ′. Gọi I , J , K lần lượt là trọng tâm của các tam giác ABC , ACC′, A B ′ C
′ ′ . Mặt phẳng nào sau đây song song với mặt phẳng (IJK ) ?(tham khảo hình vẽ) A' C' A. ( ABC). B. (BB C ′ ′). K J B' C. ( A B ′ C′). D. ( AA C ′ ). A C I B
Câu 68: Cho lăng trụ đứng ABC.A′B C
′ ′ có G , G′ lần lượt là trọng tâm của hai tam giác ABC và A B ′ C
′ ′ . Thiết diện tạo bởi mặt phẳng ( AGG′) với hình lăng trụ đã cho là hình nào dưới đây ? (tham khảo hình vẽ) A' C' A. Hình chữ nhật. B. Tam giác cân. G' B' C. Tam giác vuông. D. Hình vuông. C A G B 38 HÌNH HỌC 11
Chương II. ĐT & MP Trong KG. QHSS Toán 11 GV. Lư Sĩ Pháp
Câu 69: Cho tứ diện ABC .
D Gọi I , J và K lần lượt là trung điểm của AC, BC và B . D Xác định giao
tuyến của hai mặt phẳng ( ABD) và ( IKJ ). (tham khảo hình vẽ) A
A. Đường thẳng KJ.
B. Đường thẳng KI. I
C. Đường thẳng IJ. B D K
D. Đường thẳng ∆ qua K và song song với A . B J C
Câu 70: Cho tứ diện ABC .
D Điểm M thuộc đoạn BC. Mặt phẳng (α ) qua M song song với AB và C .
D Thiết diện của (α ) với tứ diện ABCD là hình nào dưới đây? (tham khảo hình vẽ). A A. Hình thang. B. Hình bình hành.
C. Hình ngũ giác. D. Hình tam giác. B D M α C
Câu 71: Trong các giả thiết dưới đây. Giả thiết nào kết luận đường thẳng a song song với mặt phẳng (α)?
A. a || b và b ⊂ (α ).
B. a || (β ) và (β ) || (α ).
C. a || b và b || (α ).
D. a ∩(α ) = . ∅
Câu 72: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Điểm M thỏa mãn MA = 3M . B Mặt
phẳng ( P) qua M và song song với SC , BD . Mệnh đề nào sau đây đúng?
A. (P) cắt hình chóp theo thiết diện là một ngũ giác.
B. (P) cắt hình chóp theo thiết diện là một tam giác.
C. (P) cắt hình chóp theo thiết diện là một tứ giác.
D. (P) không cắt hình chóp.
Câu 73: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O , I là trung điểm cạnh SC .
Khẳng định nào dưới đây sai?(tham khảo hình vẽ)
A. Mặt phẳng (IBD) cắt hình chóp S.ABCD theo thiết diện là một S tứ giác.
B. Đường thẳng IO song song với mặt phẳng (SAD). I
C. Đường thẳng IO song song với mặt phẳng (SAB) . A D O
D. Giao tuyến của hai mặt phẳng (IBD) và (SAC) là IO . B C
Câu 74: Cho hai đường thẳng phân biệt a và b trong không gian. Có bao nhiêu vị trí tương đối giữa a và b ? A. 3. B. 4. C. 2. D. 1.
Câu 75: Cho hai đường thẳng chéo nhau a và b . Lấy ,
A B thuộc a và C, D thuộc b . Khẳng định nào
dưới đây đúng khi nói về vị trí tương đối giữa hai đường thẳng AD và BC ? 39 HÌNH HỌC 11
Chương II. ĐT & MP Trong KG. QHSS Toán 11 GV. Lư Sĩ Pháp A. Chéo nhau. B. Cắt nhau.
C. Song song với nhau.
D. Có thể song song hoặc cắt nhau.
Câu 76: Cho hai đường thẳng phân biệt a, b và mặt phẳng (α ) . Giả sử a||b , b||(α ) . Mệnh đề nào dưới đây đúng ?
A. a|| (α ) hoặc a ⊂ (α ). B. a ⊂ (α ).
C. a cắt (α ). D. a||(α ).
Câu 77: Trong không gian, khẳng định nào dưới đây sai ?
A. Nếu ba mặt phẳng phân biệt cắt nhau theo ba giao tuyến thì ba giao tuyến ấy hoặc đồng quy hoặc đôi một song song.
B. Cho hai đường thẳng chéo nhau. Có duy nhất một mặt phẳng chứa đương thẳng này và song song với đường thẳng. kia.
C. Hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thì song song với nhau.
D. Hai mặt phẳng phân biệt cùng vuông góc với một đường thẳng thì song song với nhau.
Câu 78: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâmO . Gọi M , N , K lần lượt là trung
điểm của CD , CB , SA . Thiết diện của hình chóp cắt bởi mặt phẳng (MNK ) là một đa giác (H ) . Khẳng
định nào dưới đây đúng ?
A. (H ) là một tam giác.
B. (H ) là một ngũ giác.
C. (H ) là một hình bình hành.
D. (H ) là một hình thang.
Câu 79: Cho hình chóp S.ABCD có đáy là hình bình hành. Khẳng định nào dưới đây đúng khi nói về
giao tuyến của (SAB) và (SCD) ?
A. Đường thẳng qua S và song song với AD .
B. Đường SO với O là tâm hình bình hành.
C. Đường thẳng qua S và song song với CD .
D. Đường thẳng qua S và cắt AB .
Câu 80: Cho hai đường thẳng phân biệt a, b và mặt phẳng (α ) . Giả sử a|| (α ) và b||(α ) . Mệnh đề nào sau đây đúng?
A. a và b không có điểm chung.
B. a và b chéo nhau.
C. a và b hoặc song song hoặc chéo nhau.
D. a và b hoặc song song hoặc chéo nhau hoặc cắt nhau.
Câu 81: Mệnh đề nào dưới đây đúng ?
A. Nếu hai mặt phẳng song song thì mọi đường thẳng nằm trên mặt phẳng này đều song song với mọi
đường thẳng nằm trên mặt phẳng kia.
B. Nếu hai mặt phẳng cùng song song với một đường thẳng thì song song với nhau.
C. Nếu hai mặt phẳng (P) và (Q) lần lượt chứa hai đường thẳng song song thì song song với nhau.
D. Nếu hai mặt phẳng phân biệt không song song thì cắt nhau.
Câu 82: Các yếu tố nào sau đây xác định một mặt phẳng duy nhất?
A. Ba điểm phân biệt.
B. Bốn điểm phân biệt.
C. Hai đường thẳng cắt nhau.
D. Một điểm và một đường thẳng.
Câu 83: Cho hình lăng trụ tam giác ABC. ′ A ′
B C .′ Gọi I , J lần lượt là trọng tâm của các tam giác ABC và ′
A B′C .′ Xác định hình dạng thiết diện tạo bởi mặt phẳng ( AIJ ) với hình lăng trụ (tham khảo hình bên) A. A' C' Hình bình hành J
B. Hình tam giác vuông. B' C. Hình thang. A C
D. Hình tam giác cân I B 40 HÌNH HỌC 11
Chương II. ĐT & MP Trong KG. QHSS Toán 11 GV. Lư Sĩ Pháp
Câu 84: Cho hai đường thẳng a và b chéo nhau. Có bao nhiêu mặt phẳng chứa a và song song với b ? A. 3. B. 1. C. 2. D. 0.
Câu 85: Cho tứ diện ABCD . Gọi G và E lần lượt là trọng tâm của tam giác ABD và ABC . Mệnh đề nào dưới đây đúng ?
A. GE cắt C . D
B. GE//C . D
C. GE và CD chéo nhau.
D. GE cắt A . D
Câu 86: Mệnh đề nào dưới đây đúng ?
A. Nếu hai đường thẳng song song với nhau lần lượt nằm trong hai mặt phẳng phân biệt (α ) và(β )
thì (α ) và (β ) song song với nhau.
B. Qua một điểm nằm ngoài mặt phẳng cho trước ta vẽ được một và chỉ một đường thẳng song song
với mặt phẳng cho trước đó .
C. Nếu hai mặt phẳng (α ) và(β ) song song với nhau thì mọi đường thẳng nằm trong (α ) đều song song với (β ).
D. Nếu hai mặt phẳng (α ) và (β ) song song với nhau thì mọi đường thẳng nằm trong (α ) đều song
song với mọi đường thẳng nằm trong (β ).
Câu 87: Cho hai đường thẳng a và b . Điều kiện nào sau đây đủ để kết luận a và b chéo nhau?
A. a và b không có điểm chung.
B. a và b không cùng nằm trên bất kì mặt phẳng nào.
C. a và b nằm trên 2 mặt phẳng phân biệt.
D. a và b là hai cạnh của một hình tứ diện.
Câu 88: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Giả sử M thuộc đoạn thẳng S . B Mặt
phẳng ( ADM ) cắt hình chóp S.ABCD theo thiết diện là hình nào dưới đây ? (tham khảo hình vẽ) S A. Hình thang. B. Hình tam giác. M
C. Hình bình hành. D. Hình chữ nhật. B C A D
Câu 89: Cho hình tứ diện ABCD có M , N lần lượt là trung điểm của AB , BD . Các điểm G , H lần
lượt trên cạnh AC , CD sao cho NH cắt MG tại I . Khẳng định nào dưới đây đúng?
A. B , G , H thẳng hàng.
B. A , C , I thẳng hàng.
C. N , G , H thẳng hàng.
D. B , C , I thẳng hàng.
Câu 90: Trong không gian, khẳng định nào dưới đây sai ?
A. Hai mặt phẳng phân biệt cùng vuông góc với một đường thẳng thi song song với nhau.
B. Nếu ba mặt phẳng cắt nhau theo ba giao tuyến phân biệt thì bao giao tuyến ấy hoặc đồng quy hoặc
đôi một song song với nhau.
C. Hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thì song song với nhau.
D. Cho hai đường thẳng chéo nhau. Có duy nhất một mặt phẳng chứa đường thẳng này và song song với đường thẳng kia.
Câu 91: Cho lăng trụ đứng ABC.A′B C
′ ′. Gọi M , N lần lượt là trung điểm của A′B′ và CC .′ Mệnh đề nào dưới đây đúng ?
A. CB′ || A′N.
B. CB′ || (BC M ′ ).
C. CB′ || ( AC M ′ ).
D. CB′ || AM .
Câu 92: Cắt hình chóp tứ giác bởi mặt phẳng vuông góc với đường cao của hình chóp thiết diện là hình gì?
A. Một hình bình hành. B. Một hình tam giác. C. Một ngũ giác.
D. Một hình tứ giác.
Câu 93: Trong không gian cho bốn điểm không đồng phẳng, có thể xác định nhiều nhất bao nhiêu mặt
phẳng phân biệt từ các điểm đó? 41 HÌNH HỌC 11
Chương II. ĐT & MP Trong KG. QHSS Toán 11 GV. Lư Sĩ Pháp A. 3. B. 6. C. 4. D. 5.
Câu 94: Cho tam giác ABC, lấy điểm I trên cạnh AC kéo dài. Mệnh đề nào dưới đây là sai?
A. BI ⊄ ( ABC).
B. I ∈( ABC).
C. A∈(BIC).
D. CI ⊂ ( ABC).
Câu 95: Mệnh đề nào dưới đây sai ?
A. Hai mặt đáy của hình lăng trụ nằm trên hai mặt phẳng song song.
B. Hai đáy của lăng trụ là hai đa giác đều.
C. Hình lăng trụ có các cạnh bên song song và bằng nhau.
D. Các mặt bên của lăng trụ là các hình bình hành.
Câu 96: Cho hình lập phương ABC . D ′
A B′C′D .′ Có bao nhiêu cạnh của hình lập phương chéo nhau với
đường chéo AC′ của hình lập phương?(tham khảo hình vẽ) A' B' A. 4. B. 6. C' D' C. 7. D. 9. A B D C
Câu 97: Khối chóp đều S.ABCD có mặt đáy ABCD là hình nào dưới đây ? A. Hình chữ nhật. B. Hình thoi. C. Hình bình hành. D. Hình vuông.
Câu 98: Cho đường thẳng a và mặt phẳng (P) trong không gian. Có bao nhiêu vị trí tương đối của a và (P)? A. 2. B. 3. C. 1. D. 4.
Câu 99: Cho hình chóp tứ giác S.ABCD . Gọi M và N lần lượt là trung điểm của SA và SC . Khẳng
định nào dưới đây đúng?
A. MN || (SCD).
B. MN || (SAB).
C. MN || ( ABCD).
D. MN ||(SBC).
Câu 100: Cho hình lăng trụ ABC.A B C . Khẳng định nào dưới đây sai? 1 1 1
A. AA || BCC .
B. ( ABC) || ( A B C . 1 1 1 ) 1 ( 1 )
C. AB || ( A B C .
D. AA B B là hình chữ nhật. 1 1 1 ) 1 1
Câu 101: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Gọi M là điểm thuộc cạnh
SA (không trùng với S , A ). Gọi ( P) là mặt phẳng qua OM và song song với AD. Thiết diện của hình
chóp khi cắt bởi mp ( P) là hình nào dưới đây ? (tham khảo hình vẽ) S
A. Hình chữ nhật. B. Hình bình hành. C. Hình thang. D. Hình tam giác. M A D O B C P
Câu 102: Cho tứ diện ABCD. Gọi I, J lần lượt thuộc cạnh AD, BC sao cho IA = 2 ID và JB = 2 JC .
Gọi ( P) là mặt phẳng qua IJ và song song với AB. Thiết diện của tứ diện ABCD khi cắt bởi ( P) hình
nào dưới đây ? (tham khảo hình vẽ) 42 HÌNH HỌC 11
Chương II. ĐT & MP Trong KG. QHSS Toán 11 GV. Lư Sĩ Pháp A
A. Hình tam giác. B. Hình bình hành. C. Hình thang. D. Tam giác đều. I B D J C P
Câu 103: Cho tứ diện ABC .
D Điểm M thuộc đoạn BC. Mặt phẳng (α ) qua M song song với AB và C .
D Thiết diện của (α ) với tứ diện ABCD là hình nào dưới đây? (tham khảo hình vẽ). A
A. Hình tam giác. B. Hình chữ nhật.
C. Hình ngũ giác. D. Hình bình hành. B D M α C
Câu 104: Cho hình lăng trụ ABC. ′
A B′C .′ Gọi H là trung điểm của ′
A B .′ Đường thẳng B′C song song
với mặt phẳng nào dưới đây? (tham khảo hình vẽ) A C A. ( AHC′). B. ( A ′ A H ). B C. (HAB). D. (H ′ A C ). A' C' H B'
Câu 105: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành, M và N là hai điểm trên S , A SB SM SN 1 sao cho =
= . Vị trí tương đối giữa MN và ( ABCD) . Khẳng định nào dưới đây đúng ? SA SB 3
A. MN song song mp ( ABCD).
B. MN cắt mp ( ABCD).
C. MN nằm trên mp ( ABCD).
D. MN và mp ( ABCD) chéo nhau. 43 HÌNH HỌC 11
Chương II. ĐT & MP Trong KG. QHSS Toán 11 GV. Lư Sĩ Pháp
MỘT SỐ ĐỀ ÔN KIỂM TRA MỘT TIẾT ĐỀ 1
I. Phần trắc nghiệm
Câu 1: Hãy chọn phương án Đúng điền vào chỗ trống “....”.
“Nếu ba mặt phẳng phân biệt đôi một cắt nhau theo ba giao tuyến phân biệt thì . . . . . .”
A. ba giao tuyến ấy đồng quy và đôi một song song với nhau.
B. ba giao tuyến ấy hoặc đồng quy hoặc đôi một song song với nhau.
C. ba giao tuyến ấy đôi một song song với nhau.
D. ba giao tuyến ấy hoặc trùng nhau hoặc đôi một song song với nhau.
Câu 2: Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm các cạnh AB và AC . Gọi d là giao tuyến của
hai mặt phẳng (DMN ) và (DBC). Mệnh đề nào dưới đây đúng ?
A. d / /(ACD).
B. d / /(ABC).
C. d / /(ABD).
D. d / /(ABCD).
Câu 3: Cho hai đường thẳng a và b chéo nhau. Có bao nhiêu mặt phẳng chứa a và song song với b? A. Ba mặt phẳng. B. Hai mặt phẳng.
C. Một mặt phẳng.
D. Không có mặt phẳng nào.
Câu 4: Trong các hình dưới đây, hình nào là hình biểu diễn của một tứ diện ? a) b) c) d) A. Hình a) và c). B. Hình b) và d). C. Hình a).
D. Hình a) , b) và d).
Câu 5: Cho tứ diện ABCD và ba điểm P,Q, R lần lượt lấy trên ba cạnh AB,CD, BC . Tìm giao điểm S
của AD và mặt phẳng ( PQR) , biết PR cắt AC tại I (như hình vẽ). A
A. AD ∩ (PQR) = S với S = IQ ∩ A . D
B. AD ∩ (PQR) = S với S = AC ∩ I . Q P B D
C. AD ∩ (PQR) = S với S = AD ∩ P . Q Q R C
D. AD ∩ (PQR) = S với S = RQ ∩ A . D I
Câu 6: Cho tứ diện ABCD . Gọi M, N lần lượt là trung điểm của AB và AC , E là điểm trên cạnh CD với
ED = 3EC (như hình vẽ). Tìm thiết diện của tứ diện ABCD khi cắt bởi mặt phẳng (MNE). A
A. Tứ giác MNEF với F là điểm bất kì trên B . D
B. Hình bình hành MNEF với F là điểm trên cạnh BD mà M
EF / / BC. N B D
C. Tam giác MNE. E
D. Hình thang MNEF với F là điểm trên cạnh BD mà EF / /BC. C
Câu 7: Cho tam giác BCD và điểm A không thuộc mặt phẳng (BCD). Gọi K là trung điểm của đoạn AD
và G là trọng tâm của tam giác ABC (như hình vẽ). Tìm giao điểm của đường thẳng GK với mặt phẳng (BCD). 44 HÌNH HỌC 11
Chương II. ĐT & MP Trong KG. QHSS Toán 11 GV. Lư Sĩ Pháp
A. GK ∩ (BCD) = . L
B. GK ∩ (BCD) = . B
C. GK ∩ (BCD) = . G
D. GK ∩ (BCD) = I.
Câu 8: Cho hai đường thẳng phân biệt cùng nằm trong một mặt phẳng. Có bao nhiêu vị trí tương đối giữa hai đường thẳng đó ? A. 2. B. 4. C. 3. D. 1.
Câu 9: Cho tứ diện ABCD . Gọi M , N lần lượt là trung điểm các cạnh AD và BC; G là trọng tâm của tam
giác BCD . Tìm giao điểm của đường thẳng MG và mặt phẳng ( ABC ).
A. MG ∩ (ABC) = C.
B. MG ∩ (ABC) = N.
C. MG ∩ (ABC) = H với H = MG ∩ BC.
D. MG ∩ (ABC) = K với K = MG ∩ AN.
Câu 10: Cho hình chóp S.ABCD có đáy ABCD là hình thang và BA là đáy lớn. Tìm giao tuyến của hai
mặt phẳng (SAD) và (SBC).
A. (SAD) ∩ (SBC) = ∆ với S ∈ ∆, ∆ / / A . D
B. (SAD) ∩ (SBC) = SE với E = AD ∩ BC.
C. (SAD) ∩ (SBC) = d với S ∈ d, d / / A . B
D. (SAD) ∩ (SBC) = SO với E = AC ∩ B . D II. Phần tự luận
Bài 1. Cho hình chóp S.ABCD có đáy là hình bình hànhABCD. Gọi G là trọng tâm của tam giác SAB và I
là trung điểm của AB. Lấy M trên đoạn AD sao cho AD = 3AM .
a/. Tìm giao tuyến của hai mặt phẳng (SAD) và (SBC).
b/. Đường thẳng qua M và song song với AB cắt CI tại N. Chứng minh rằng NG / /(SCD) .
Bài 2. Cho tứ diện ABCD. Trên AB lấy điểm M. Cho (α ) là mặt phẳng qua M, song song với hai đường
thẳng AC và BD.
a/. Tìm giao điểm của đường thẳng SD và mặt phẳng (α ).
b/ Xác định thiết diện của tứ diện cắt bởi mặt phẳng (α ) , thiết diện là hình gì? ĐỀ 2 I. Phần trắc nghiệm
Câu 1: Trong không gian, có bao nhiêu cách xác định một mặt phẳng ? A. 1. B. 4. C. 3. D. 2.
Câu 2: Trong các hình sau đây, hình nào biểu diễn cho hình lập phương ? a) b) c) A. Hình a). B. Hình a) và c). C. Hình b). D. Hình c) và b).
Câu 3: Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm các cạnh AB và AC . Mệnh đề nào dưới đây đúng ?
A. MN cắt (BCD).
B. MN không song song (BCD). 45 HÌNH HỌC 11
Chương II. ĐT & MP Trong KG. QHSS Toán 11 GV. Lư Sĩ Pháp
C. MN / /(BCD).
D. MN nằm trong (BCD).
Câu 4: Cho hình chóp S.ABCD có đáy ABCD là hình thang và BA là đáy lớn. Gọi M, N theo thứ tự là
trung điểm của cạnh SB và SC . Thiết diện của hình chóp S.ABCD cắt bởi mặt phẳng ( AMN ) là hình gì ? S A. Hình thang. B. Hình chữ nhật. M C. N Hình bình hành. D. Hình tam giác. A B D C
Câu 5: Cho tứ diện ABCD và ba điểm P,Q, R lần lượt lấy trên ba cạnh AB,CD, BC . Tìm giao điểm S
của AD và mặt phẳng ( PQR) , biết PR song song với AC . A
A. AD ∩ (PQR) = S với QS / /PR / / AC.
B. AD ∩ (PQR) = S với S = AD ∩ P . Q P
C. AD ∩ (PQR) = S với S = AD ∩ P . R B D
D. AD ∩ (PQR) = S với PS / /BD / /R . Q Q R C
Câu 6: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M , N, P theo thứ tự là trung điểm
các đoạn thẳng S ,
A BC, CD . Gọi O là giao điểm của hai đường chéo của hình bình hành ABCD (như hình
vẽ). Xác định giao điểm I của đường thẳng SO với mặt phẳng (MNP) . S
A. I = SO ∩ N . P
B. I = SO ∩ MH. M
C. I = SO ∩ M . P
D. I = SO ∩ MN. A D O P H B N C
Câu 7: Cho hình chóp S.ABCD có đáy là tứ giác ABCD và các cạnh đối diện không song song. Giả sử
AC ∩ BD = I; AD ∩ BC = O . Tìm giao tuyến của hai mặt phẳng (SAC) và (SBD).
A. (SAC) ∩ (SBD) = S . B
B. (SAC) ∩ (SBD) = SC.
C. (SAC) ∩ (SBD) = S . O
D. (SAC) ∩ (SBD) = SI.
Câu 8: Cho hai đường thẳng a và b. Điều kiện nào dưới đây đủ để kết luận a và b chéo nhau?
A. a và b không có điểm chung.
B. a và b nằm trên hai mặt phẳng phân biệt.
C. a và b không nằm trên bất kì mặt phẳng nào. D. a và b là hai cạnh của một tứ diện.
Câu 9: Cho hình chóp S.ABCD có đáy là hình bình hành. Gọi I, J lần lượt là trung điểm của AB và
CB . Giao tuyến của hai mặt phẳng (SAB) và (SCD) là đường thẳng song song với đường thẳng nào dưới đây ?
A. Đường thẳng IJ.
B. Đường thẳng BJ.
C. Đường thẳng A . D
D. Đường thẳng BI.
Câu 10: Trong các giả thiết dưới đây, giả thiết nào kết luận về đường thẳng a song song với mặt phẳng (α ) ?
A. a ∩ (α) = . ∅
B. a / /b và b / /(α).
C. a / /b và b ⊂ (α).
D. a / /(β ) và (β ) / /(α ). 46 HÌNH HỌC 11
Chương II. ĐT & MP Trong KG. QHSS Toán 11 GV. Lư Sĩ Pháp II. Phần tự luận
Bài 1. Cho tứ diện ABCD. Gọi M,N, P lần lượt là trung điểm của các cạnh AB, CD, AN và G là trung
điểm của đoạn MN.
a/ Tìm giao điểm của đường thẳng AG và mặt phẳng (BCD).
b/ Chứng minh rằng MP song song với mặt phẳng (BCD).
Bài 2. Cho hình chóp S.ABCD có đáy ABCD là hình thang (AB là đáy lớn). Gọi M, N lần lượt là trung
điểm của SB và SC.
a/ Tìm giao điểm của đường thẳng AN với mặt phẳng (SBD).
b/ Gọi (α ) là mặt phẳng qua MN và song song với CD. Xác định thiết diện của hình chóp cắt bởi mặt phẳng (α ) . Đề 3 I. Phần trắc nghiệm
Câu 1: Mệnh đề nào sau đây đúng?
A. Qua ba điểm xác định một và chỉ một mặt phẳng.
B. Qua ba điểm phân biệt không thẳng hàng xác định một và chỉ một mặt phẳng.
C. Qua ba điểm phân biệt xác định một và chỉ một mặt phẳng.
D. Qua ba điểm phân biệt không thẳng hàng xác định hai mặt phẳng phân biệt.
Câu 2: Cho hình chóp S.ABCD có đáy là hình bình hành. Gọi E, F lần lượt thuộc S , A SB sao
cho SA = 4SE, SB = 4SF. Khi đó, vị trí tương đối giữa EF và (ABCD) là:
A. EF ⊂ (ABCD).
B. EF cắt(ABCD).
C. EF chéo C . D
D. EF// (ABCD).
Câu 3: Cho hình chóp S.ABC ,
D đáy là hình bình hành. Gọi M, N lần lượt là trung điểm của SA và S . C
Khẳng định nào sau đây đúng?
A. MN//(ABCD).
B. MN//(SAB).
C. MN// (SCD).
D. MN// (SBC).
Câu 4: Cho hình chóp S.ABCD có đáy ABCD là hình vuông. Lấy M ∈ S ,
A N ∈ SB sao cho SM SN 2 = = . Tìm mệnh đề đúng: SA SB 3 A. MN//CD.
B. MN//(SAD). C. MN//AD.
D. MN// (SBC).
Câu 5: Cho tứ diện ABCD . Gọi M, N lần lượt là trung điểm của các cạnh AD, BC ; G là trọng tâm tam
giác BCD . Giao điểm của đường thẳng MG và mặt phẳng (ABC) là:
A. Giao điểm của đường thẳng MG và đường thẳng B . C B. Điểm . C
C. Giao điểm của đường thẳng MG và đường thẳng AN. D. Điểm . N
Câu 6: Trong các mệnh đề sau mệnh đề nào sai?
A. Hình biểu diễn của hai đường cắt nhau có thể là hai đường song song.
B. Dùng nét đứt biểu diễn cho đường bị che khuất.
C. Hình biểu diễn phải giữ nguyên quan hệ thuộc giữa điểm và đường thẳng.
D. Hình biểu diễn của đường thẳng là đường thẳng.
Câu 7: Cho tứ diện ABCD . Gọi I, J, K lần lượt là trung điểm của AC, BC, BD. Giao tuyến của hai mặt
phẳng (ABD) và (KJI) là A. K . D
B. Đường thẳng qua K và song song với AB C. Không có. D. KI.
Câu 8: Cho hình chóp S.ABCD có đáy là hình thoi tâm O , gọi M là trung điểm của SA , gọi E là trung
điểm của CD và I là giao điểm của AD và BE . Khi đó giao tuyến của mp(SAD) và mp(MEB)là :
A. Đường thẳng qua S và // AD ,// B . C
B. Đường thẳng SI.
C. Đường thẳng MI.
D. Đường thẳng qua M và // AB , // B . C
Câu 9: Tìm mệnh đề sai:
A. Hai đường thẳng cùng chứa trong 1 mặt phẳng và không có điểm chung thì song song với nhau.
B. Hai đường thẳng phân biệt không cắt nhau và không song song thì chéo nhau. 47 HÌNH HỌC 11
Chương II. ĐT & MP Trong KG. QHSS Toán 11 GV. Lư Sĩ Pháp
C. Hai đường thẳng cùng chứa trong 1 mặt phẳng nếu không song song thì cắt nhau hoặc trùng nhau.
D. Hai đường thẳng chéo nhau cùng chứa trong 1 mặt phẳng.
Câu 10: Cho tứ diện ABCD . Gọi M, N lần lượt là trung điểm của AB và AC , E là điểm trên cạnh CD với ED = 3E .
C Thiết diện của tứ diện ABCD khi cắt bởi mặt phẳng (MNE)là hình gì? A. Hình thang. B. Hình bình hành. C. Hình ngũ giác. D. Hình tam giác. II. Phần tự luận
Bài 1: Cho tứ diện ABCD có I và J lần lượt là trung điểm AC và BC. K thuộc BD sao cho KD < KB.
a/ Chứng minh: IJ // (DAB).
b/ Tìm giao điểm giữa đường thẳng AD và mặt phẳng(IJK).
Bài 2: Cho hình chóp S.ABCD , đáy ABCD là hình thang cân có AD không song song với BC . Gọi M là
trung điểm của AD và (α)là mặt phẳng qua M , song song với SA và BD.
a/ Tìm giao tuyến giữa 2 mặt phẳng (SAB) và(SDC).
b/ Xác định thiết diện của hình chóp S.ABCD khi cắt bởi mặt phẳng (α). ĐỀ 4 I. Phần trắc nghiệm
Câu 1: Các yếu tố nào sau đây xác định một mặt phẳng duy nhất?
A. Ba điểm phân biệt không thẳng hàng. B. Bốn điểm.
C. Hai đường thẳng chéo nhau.
D. Một điểm và một đường thẳng.
Câu 2: Cho đường thẳng a nằm trong mp( )
α và đường thẳng b mp(α ⊄
).Mệnh đề nào sau đây đúng ?
A. Nếu b cắt (α) thì b cắt . a
B. Nếu b//a thì b//(α).
C. Nếu b cắt (α) thì b chéo . a
D. Nếu b// (α) thì b// . a
Câu 3: Cho tứ diện ABC .
D Gọi M, N lần lượt là trung điểm của cạnh A , C A ;
D G là trọng tâm △B D C .Khi
đó giao tuyến của(BMN) và(GCD) là:
A. Đường thẳng d qua G và d // CD.
B. Đường thẳng d qua B và d// CD.
C. Đường thẳng BK với K = MN ∩ D C .
D. Đường thẳng BG.
Câu 4: Cho hai đường thẳng a và b chéo nhau. Có bao nhiêu mặt phẳng chứa a và song song với b ? A. 2.
B. Không có mặt phẳng nào. C. 1. D. Vô số.
Câu 5: Cho hình chóp S.ABCD đáy là hình thoi tâm .
O Gọi P là trung điểm S .
C Mệnh đề nào đúng:
A. PO// (SAC).
B. PO//(SBD).
C. PO//(SAB).
D. PO//(SCD). Câu 6: BM 2
Cho hình chóp S.ABCD đáy là hình bình hành. Lấy M ∈ SB :
= . G là trọng tâm △ABC . BS 3 Tìm mệnh đề đúng:
A. MG// (SAC).
B. MG// (SAD).
C. MG//SC.
D. MG //S . A
Câu 7: Cho hình chóp S.ABCD . Đáy ABCD là hình bình hành. Giả sử M thuộc đoạn SC .Mặt phẳng
(ABM)cắt hình chóp S.ABCD theo thiết diện là hình gì? A. Hình bình hành. B. Tam giác C. Hình chữ nhật. D. Hình thang.
Câu 8: Cho tứ diện ABCD Gọi I, J lần lượt là trung điểm của A , D B .
C Giao tuyến của hai mặt
phẳng(IBC)và(JAD) là đường thẳng nào sau đây? 48 HÌNH HỌC 11
Chương II. ĐT & MP Trong KG. QHSS Toán 11 GV. Lư Sĩ Pháp A. IJ. B. AB. C. IB. D. J . D
Câu 9: Cho hình chóp S.ABCD có đáy là hình bình hành. Gọi M, N, K lần lượt là trung điểm
của BC, DC, SB. Giao điểm của MN và(SAK) là giao điểm của MN với đường thẳng nào sau đây? A. A . D B. SK. C. AK. D. AB.
Câu 10: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Xác đinh giao tuyến của mặt phẳng
(SAD) và (SBC) .
A. Điểm SO,O = AC ∩ B . D
B. Đường thẳng bất kỳ song song với B . C
C. Đường thẳng đi qua S và song song với AD , B . C
D. Đường thẳng bất kỳ song song với A . D II. Phần tự luận
Bài 1: Cho tứ diện ABCD có I và J lần lượt là trung điểm AC và C .
D K thuộc BD sao cho KD > KB.
a/ Chứng minh: IJ // (DAB).
b/ Tìm giao điểm giữa đường thẳng AB và mặt phẳng(IJK).
Bài 2: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm .
O Gọi M, N, P theo thứ tự là trung
điểm của các đoạn thẳng S , A B , C C . D
a/ Tìm giao tuyến 2 mặt phẳng(SAB) và (SCD).
b/ Tìm thiết diện hình chóp cắt bởi (MNP). 49 HÌNH HỌC 11
Chương II. ĐT & MP Trong KG. QHSS Toán 11 GV. Lư Sĩ Pháp ĐÁP ÁN
CHƯƠNG II. ĐƯỜNG THẲNG VÀ MẶT PHẲNG TRONG KHÔNG GIAN QUAN HỆ SONG SONG 1 2 3 4 5 6 7 8
9 10 11 12 13 14 15 16 17 18 19 20 A B C D
21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 A B C D
41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 A B C D 61 62 A B C D
63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 A B C D
83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 A B C D 103 104 105 A B C D 50 HÌNH HỌC 11
Chương II. ĐT & MP Trong KG. QHSS

Đường thẳng và mặt phẳng trong không gian, quan hệ song song – Lư Sĩ Pháp

Thông tin :

Tài liệu liên quan:

Bộ đề đánh giá chất lượng Toán 11 chủ đề quan hệ song song trong không gian

Chuyên đề toán thực tế quan hệ song song trong không gian Toán 11

Quan hệ song song trong không gian Toán 11 KNTTVCS – Phan Nhật Linh

Toán 11 Bài tập cuối chương IX - sách Kết Nối Tri Thức

Toán 11 Bài 10: Đường thẳng và mặt phẳng trong không gian - sách Kết Nối Tri Thức