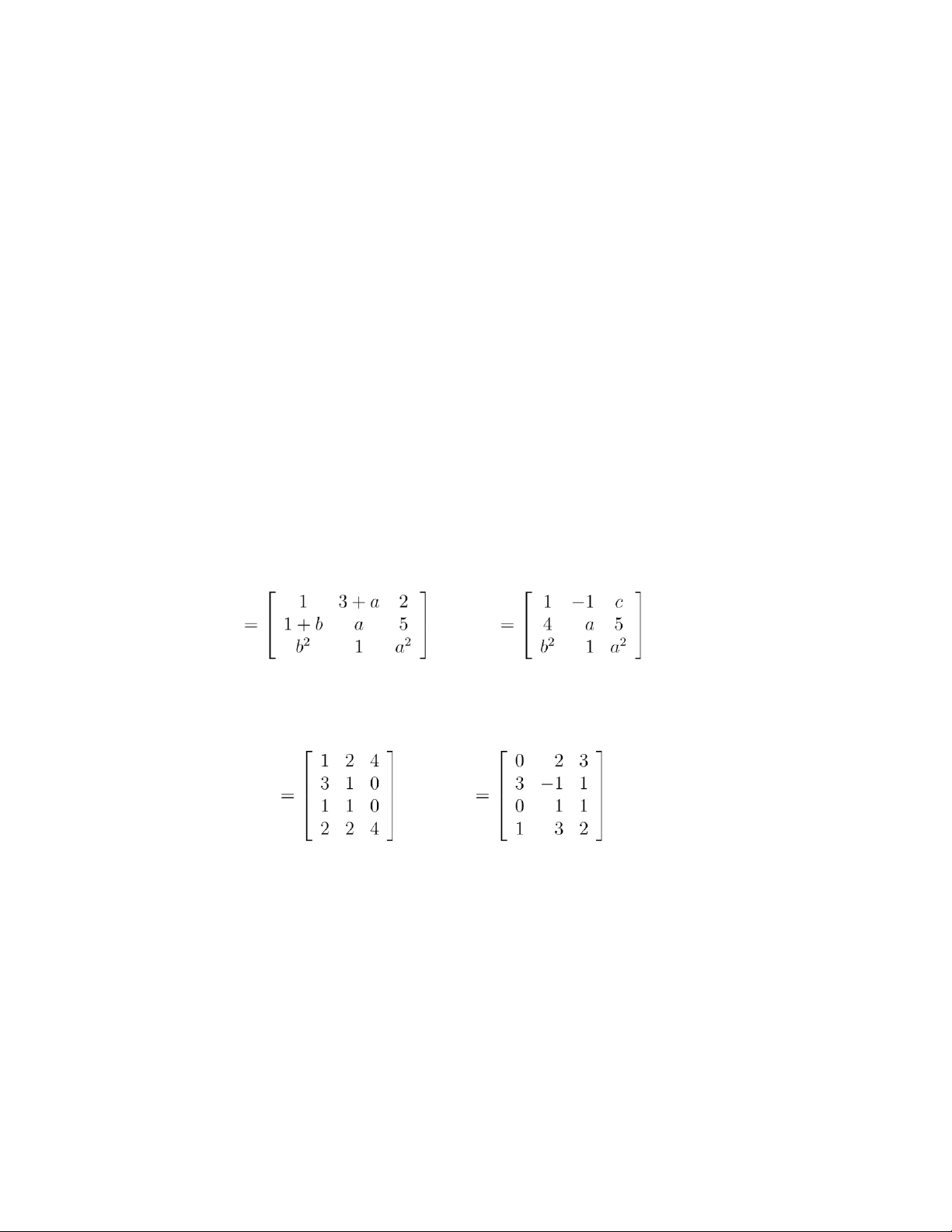






Preview text:
lOMoAR cPSD| 59085392 EXERCISES FOR CHAPTER 1:
MATRICES AND SYSTEMS OF LINEAR EQUATIONS
A. Non-assessed Exercises (corrected in class):
0.1.3(a), 0.1.4, 0.2.2, 0.2.4, 0.3.1(c), 0.3.4, 0.3.5, 0.3.10, 0.3.12, 0.4.1,
0.4.3, 0.4.5(a), 0.4.7, 0.4.8.
B. Assessed Assignments (to be submitted):
0.1.2, 0.1.3(b), 0.1.5, 0.1.6, 0.2.1, 0.2.3, 0.2.5, 0.3.1(a), (b), 0.3.2,
0.3.3, 0.3.6, 0.3.7, 0.3.9, 0.4.2, 0.4.4, 0.4.5(b), 0.4.6. 0.1
Matrices and Matrix Operations
Exercise 0.1.1. Find the values of the constants a, b, and c in order that A = B: A , B .
Exercise 0.1.2. Find 2A + 3B and 3A − 4B, where A and B .
Exercise 0.1.3. Find the products AB and, when it exists, the product BA. lOMoAR cPSD| 59085392 and B . and B .
Exercise 0.1.4. Show that for any matrix A, AAT is a symmetric matrix. Exercise 0.1.5. Let A
. Find all the 2 × 2 matrices B such that AB = BA. Exercise 0.1.6. If A , B and X , solve for X given that
3X + A = ATB − X + 3B. ANS. X .
Exercise 0.1.7. Given the matrices a , b , and C ,
determine the elements of X where
(ab)I + C2 = CT + X,
where I is the identity matrix. lOMoAR cPSD| 59085392 0.2 Systems of Linear Equations
Exercise 0.2.1. Reduce the given matrices to their row-reduced echelon form. 3 2 1 1 2 2 4 1 4 2 5 1 2 1 1 3 2 1 A = 3 1 1 3 , B = 3 2 5 1 4 0 1 3 4 1 0 3 1 2 2 1 3 1
Solve the linear system given explicitly or by its augmented matrix. Show details. Exercise 0.2.2. 1 −3 2 0 1 −1
ANS. The system is inconsistent.
In Exercises 0.2.3–0.2.5, solve the given systems of linear equations by Gaussian elimination. Exercise 0.2.3.
x2 + x3 = 1 x1 + 3x3 + 2x4 = 3
2x1 + x2 + 5x3 + 4x4 = 7 x1 − 2x2 + 2x4 = 2.
ANS. The system is inconsistent. lOMoAR cPSD| 59085392 2 −2 4 00 −3 3 −6 515 1 −1 2 00 ANS.
The system has the general solution
x1 = s − 2t, x2 = s, x3 = t, x4 = 3. Exercise 0.2.4. Exercise 0.2.5.
10x + 4y − 2z = −4
−3w − 17x + y + 2z = 2 w + x + y = 6
8w − 34x + 16y − 10z = 4. 0.3 Determinants Exercise 0.3.1. Evaluate (a) . (b) . (c) .
Exercise 0.3.2. Show that the value of the following determinant is independent of θ: . lOMoAR cPSD| 59085392
Exercise 0.3.3. Show that det(A) = det(B) = 0 without directly evaluating the determinant and B −4 1 1 1 1 −4 1 1 1 1 −4 1 1 1 1 −4 = 1 1 . A 1 1 1 1 1 −4 Exercise 0.3.4. Show that 1 Exercise 0.3.5. Evaluate .
Exercise 0.3.6. Evaluate the determinants of the following square matrices 5 4 1 1 A = 41 51 14 12 , B. 1 1 2 4 ANS. |A| = 100, |B| = −240
Exercise 0.3.7. Use row reduction to show that . lOMoAR cPSD| 59085392 Exercise 0.3.8. Show that .
In Exercises 0.3.9–0.3.10 confirm the identities without evaluating the determinants directly. Exercise 0.3.9. . Exercise 0.3.10. .
Exercise 0.3.11. Find the determinant of the following matrix. a b b b b a b b b b a b . b b b a
Exercise 0.3.12. Use Cramer’s rule to solve for y without solving for the
unknowns x,z, and w.
4x + y + z + w = 6
3x + 7y − z + w = 1
7x + 3y − 5z + 8w = −3 x + y
+ z + 2w = 3. lOMoAR cPSD| 59085392 ANS. y = 0. 0.4 The Inverse of a Matrix
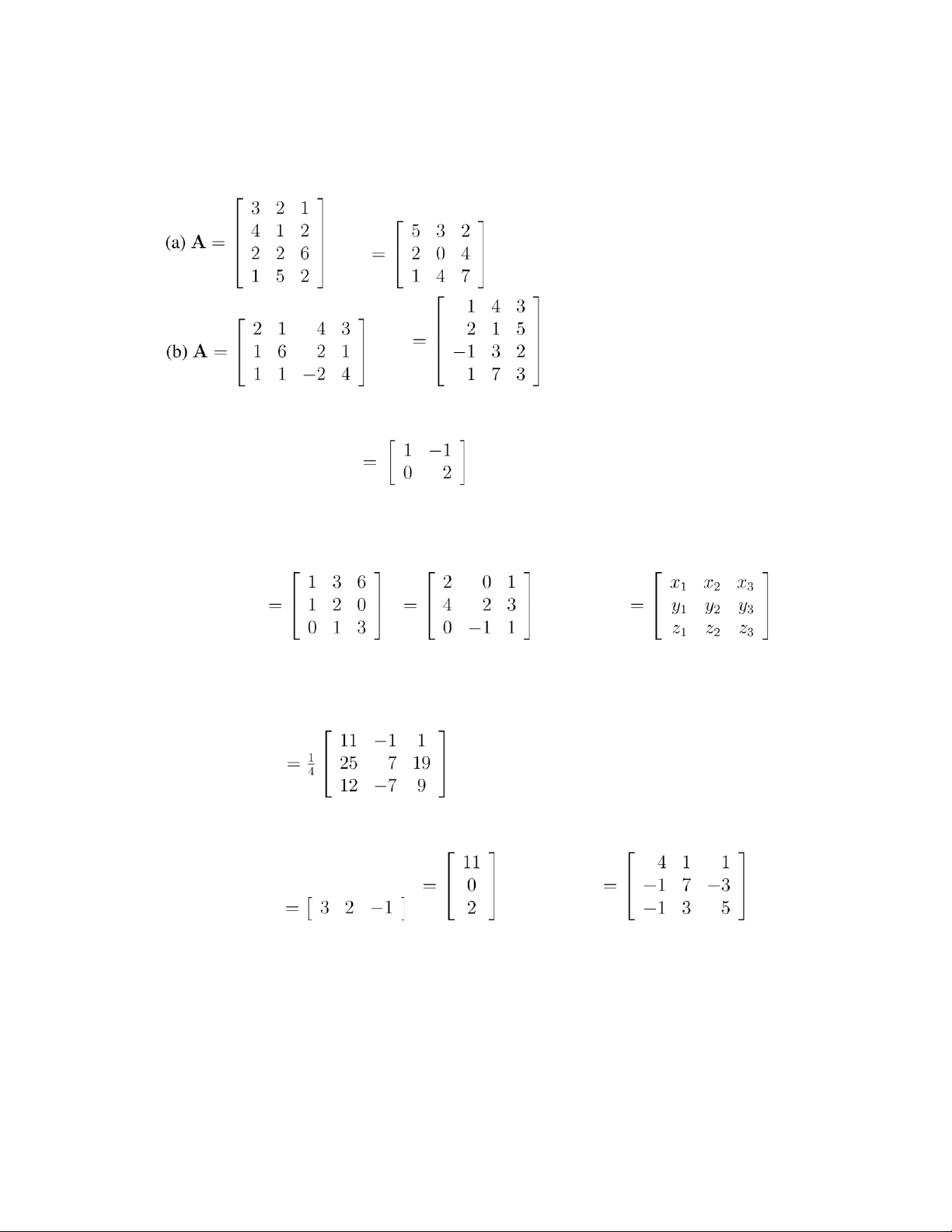
In Exercises 0.4.1–0.4.4, find the inverse of the matrix (if it exists). Exercise 0.4.1. . Exercise 0.4.2. . Exercise 0.4.3. 1 −2 3 0 1 −1 1 . 0 −2 2 2 −3 −2 4 0 1 Exercise 0.4.4. . ANS. The matrix is singular.
Exercise 0.4.5. Find all values of x, if any, for which the given matrix is invertible. , ( b) . lOMoAR cPSD| 59085392
Exercise 0.4.6. Prove the following statement.
(a) A triangular matrix is invertible if and only if its diagonal entries are all nonzero.
(b) The inverse of an invertible lower triangular matrix is lower triangular, and the
inverse of an invertible upper triangular matrix is upper triangular.
Exercise 0.4.7. Show that if A is an invertible symmetric matrix, then A−1 is symmetric.
Exercise 0.4.8. Use an inverse matrix to solve each system of linear equations
Ax = b, Ax = c where A , x , b , c .



