lOMoARcPSD|46958826 lOMoARcPSD|46958826 HCMUT CNCP GIẢI TÍCH 1
NGUYỄN QUỐC VƯƠNG
TRƯỜNG ĐẠI HỌC QUỐC GIA HỒ CHÍ MINH
TRƯỜNG BÁCH KHOA HỒ CHÍNH MINH
HCMUT-CNCP & CÔNG THỨC CUỐI KÌ
MÔN GIẢI TÍCH 1 HK231
(Bản lưu hành nội bộ của học viên lớp giải tích 1)
Biên soạn: Nguyễn Quốc Vương
Chủ sở hữu:……………
XEM TÀI LIỆU TẠI BACHKHOACNCP.COM
KHÓA HỌC ONLINE GIẢI TÍCH 1 1 lOMoARcPSD|46958826 HCMUT CNCP GIẢI TÍCH 1
NGUYỄN QUỐC VƯƠNG MụC LụC 1. Đ ạ o
hàm hay quên ..................................................................................................................................4 1.
1 M ộ t s ố đạ o
hàm hay quên .................................................................................................................4 1. 2
Ý nghĩa trong bài toán kinh tế ........................................................................................................4 2. P
hương trình tiế p
tuy ế n .........................................................................................................................4 3 . T i ệ m c ậ n c ủ
a phương trình tham số .....................................................................................................4 3. 1, Ti ệ m c ậ n
ngang ................................................................................................................................4 3. 2, Ti ệ m c ận đứ ng
.................................................................................................................................5 3. 3, Ti ệ m c ậ n
xiên ...................................................................................................................................5 4.
Nguyên hàm (tích phân b ất
định) và tích phân xác đị nh
.......................................................................5 4.
1 Phương pháp đổ i bi ế n ......................................................................................................................5 4.
2 Phương pháp đổ i bi ế n ( đặ t ẩ n ph ụ
) ...............................................................................................5 4.
3 M ộ t s ố tìm nguyên hàm hay g ặ p .......................................................................................................6 4.
4 Nguyên hàm hàm h ữ u
t ỉ ....................................................................................................................6 5. Đ ạ o hàm c ủ
a tích phân ............................................................................................................................7 6. Ứ ng d ụ ng c ủ
a nguyên hàm, tích phân trong hình h ọ c ( ) .................................................................................................................................................................................................................................................................... 7
6 .1 Trườ n g h ợ
p di ệ n tích mi ền D đượ c gi ớ i h ạ n b ở i ( ) và tr ụ c
hoàng ................................................................................................................................................................................................................................................................................................ 7
6 .2 Trườ n g h ợ
p di ệ n tích mi ề n D đượ c gi ớ i h ạ n b ở i ( ) và tr ( ) ụ
c tung ......................................................................................................................................................................................................... 7 6. 3 Trườ ng h ợ p di ệ n
tích mi ề n D đượ c gi ớ i h ạ n b ở i
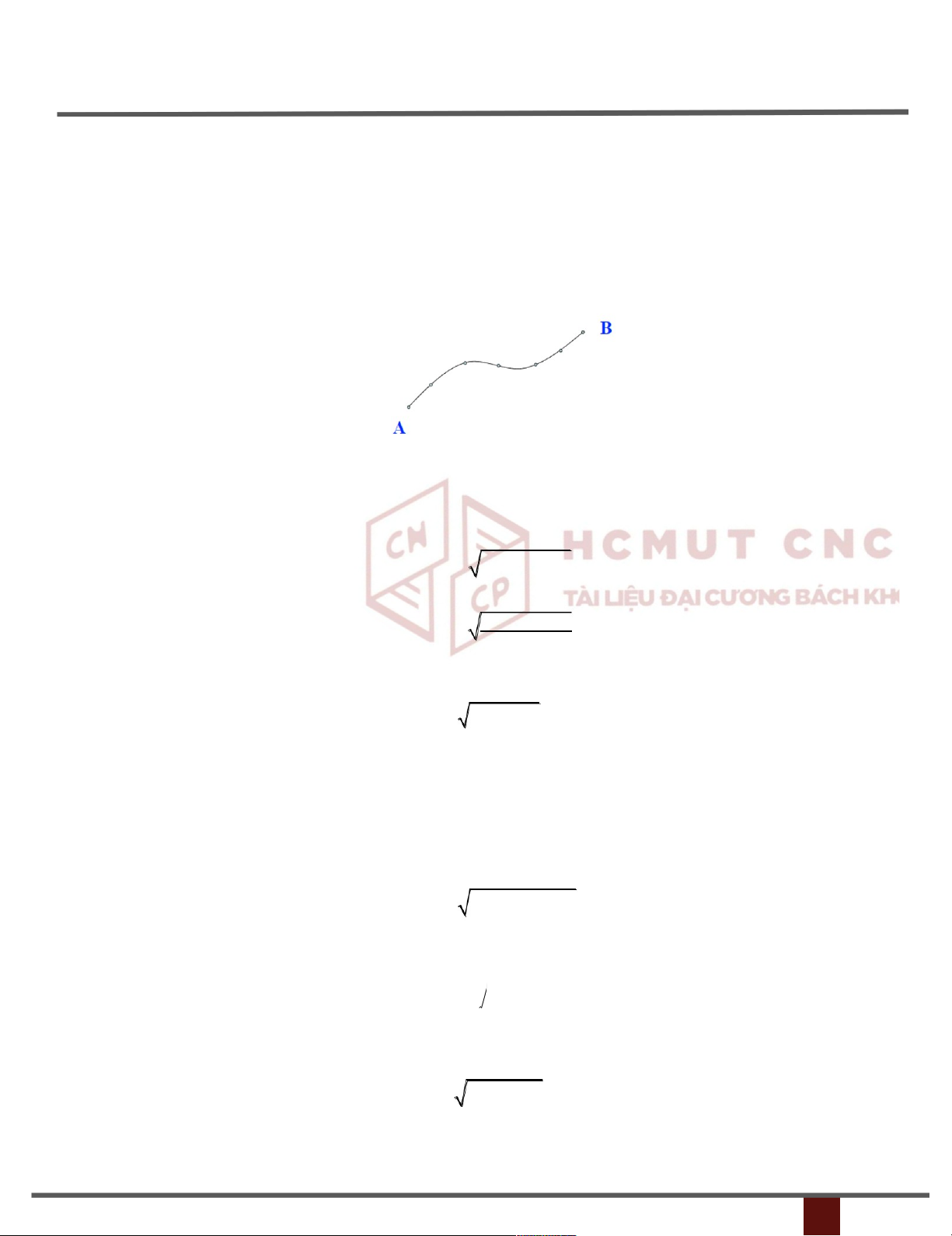
và..................................................................7 6. 4 Tính chi ề u dài s ợ
dây ........................................................................................................................8
a/ Phương trình f(x) là y = f(x)..........................................................................................................8
b/ Phương trình f(x) là phương trình tham số như sau..................................................................8 6.
5 Tính th ể tích hình tròn xoay ......................... ( ).................................................................................8
a /Th ể tích v ậ t th ể khi quay mi ề n D ho ặ c hàm ( ) quanh 0x ......................................................................................................................................................................................................................... 9 b/
Th ể tích v ậ t th ể khi quay mi ề n D ho ặ c hàm
quang oy.............................................................9
c /Th ể tích c ủ
a v ậ t th ể t ạ o b ở
i khi quay hình thang cong quanh tr ụ
c Oy ...........................................10 6. 6 Di ệ n tích xung quanh c ủ
a v ậ t th ể tròn xoay ....................................................................................10
a/ Phương trình f(x).........................................................................................................................10
b/ Phương trình f(x) là phương trình tham số...............................................................................10 7 . Ứ ng d ụ ng c ủ
a nguyên hàm, tích phân trong các bài toán khác .............................................................10 7.
1 Bài toán tính công l ự
c F ..................................................................................................................10 7.
2 Bài toán tính quãng đườ ng
............................................................................................................11 8 . Đị nh
lý giá tr ị trung bình .......................................................................................................................11
XEM TÀI LIỆU TẠI BACHKHOACNCP.COM
KHÓA HỌC ONLINE GIẢI TÍCH 1 2 lOMoARcPSD|46958826 HCMUT CNCP GIẢI TÍCH 1
NGUYỄN QUỐC VƯƠNG 9 . T ổ ng
Reiman .........................................................................................................................................11
9.1 Định nghĩa......................................................................................................................................11 a , T ổ ng
Riemann trái .........................................................................................................................12 b, T ổ ng
Riemann ph ả i .......................................................................................................................12 c , T ổ ng
Riemann trung tâm v ớ
i phân ho ạ c h là 2.dx ..........................................................................12 9. 2 Các d ạ ng
toán hay g ặ p ....................................................................................................................12 a / D ạn
g ướ c tính tích phân ( Ch ỉ b ấ m
máy tính v ề bài toán Reimann) ...............................................12 b/ D ạ ng cho b ả ng
giá tr ị ....................................................................................................................13 c / D ạ ng
cho hình v ẽ (ướ c tích di ệ n
tích, th ể tích) ..............................................................................13 10
. Tích phân suy r ộ ng
..............................................................................................................................14 10.
1 Tích phân suy r ộ ng
lo ạ i 1 ..............................................................................................................14 10.
2 Tích phân suy r ộ ng
lo ạ i 2 ..............................................................................................................14 11 . Kh ả o xác s ự h ộ i t ụ c ủ
a tích phân suy r ộ ng
(Vi ệ t Pháp) ......................................................................15 11.
1 Tích phân suy r ộ ng
lo ạ i 1 ..............................................................................................................15 11.
2 Tích phân suy r ộ ng
lo ạ i 2 ..............................................................................................................15 11.
3 Tích phân suy r ộ ng h ộ i t ụ
tuy ệ t đố i ...............................................................................................16 12 P
hương pháp giải phương trình vi phân cấ p
1 .................................................................................17 12.
1, Phương trình vi phân tách biế n .............................................................................................17 12.
2, Phương trình vi phân tuyế n
tính ............................................................................................17 12.
3, Phương trình đẳ ng
c ấ p ...........................................................................................................17
12.4, Phương trình vi phân Bernoully............................................................................................18 12. 5, D ạn
g phương trình vi phân đưa về tách bi ế n ........................................................................18 12. 6, D ạn
g phương trình vi phân toàn phầ n (Vi ệ t Pháp) ...............................................................18 13 . Ứ ng d ụ
ng phương trình vi phân cấ p
1 .............................................................................................19 13. 1 D ạ ng
toán 1: Bài toán h ỗ n h ợ p
hòa tan .........................................................................................19 13. 2 D ạ ng
toán 2: Bài toán d ẫ n
v ề phương trình vi phân ...................................................................20 13. 3 D ạ ng toán 3: Cho s ẵn
phương trình ............................................................................................20 13. 4 D ạn
g toán 4: Bài toán tăng trưở ng
.............................................................................................20 14
. Phương pháp giải phương trình vi phân cấ p
2 ................................................................................21 15
. H ệ phương trình vi phân tuyế n tính c ấ p
1 ........................................................................................22
XEM TÀI LIỆU TẠI BACHKHOACNCP.COM
KHÓA HỌC ONLINE GIẢI TÍCH 1 3 lOMoARcPSD|46958826 . Phần Giữa Kì HCMUT CNCP GIẢI TÍCH 1
NGUYỄN QUỐC VƯƠNG 1. Đạo hàm hay quên
1.1 Một số đạo hàm hay quên (arcsin( x)) 1
(arccos( x)) ' 1 ' 1 x2 1 x2 1 1 (ln( x)) '  (arctan( x)) x '  1  x 2
1.2 Ý nghĩa trong bài toán kinh tế
Chi phí cố định là chi phí mà không có sản xuất vẫn phải trả  Hàm doanh thu R(x)  Hàm chi phí C(x)
 Hàm lợi nhuận P(x) Ta có P(x) = R(x) – C(x)
 Hàm doanh thu cận biên là R’(x)
 Hàm chi phí cận biên là C’(x)  Hàml i ợnhu n ậ c n
ậ biênlàP’(x)
Phương trình tiếp tuyến tại = ’( ) 2
Phương trình tiếp tuyến =
Hệ số phương trình tiếp tuyến tại là =
Lưu ý, cho 2 đường thẳng ’( )( − ) + ( ) + + = 0 + +=0 1 1 1 2 2 2 khi = 1 1 2 ≠ 2  1 2 1 và 2 ệ 1 ô ó 2 = −1  khi
3 Ti m cận của phương trình tham số
3.1, Tiệm cận ngang
Bước 1: Xác định các giá trị a bất kì ( có thể là ) sao cho
lim x (t) ta Bước 2: Tính
XEM TÀI LIỆU TẠI BACHKHOACNCP.COM
KHÓA HỌC ONLINE GIẢI TÍCH 1 4 lOMoARcPSD|46958826 HCMUT CNCP GIẢI TÍCH 1
NGUYỄN QUỐC VƯƠNG
lim y (t ) k ta
Nếu k là số thực thì ta nói hàm số có 1 tiệm cận ngang y = k
3.2, Tiệm cận đứng 
Bước 1: Xác định các giá trị a bất kì ( có thể là  ) sao cho
lim y (t) ta Bước 2: Tính
lim x (t ) k ta
Nếu k là số thực thì ta nói hàm số có 1 tiệm cận đứng x = k
3.3, Tiệm cận xiên
Phương trình tiệm cận xiên có dạng y = ax + b
Bước 1: Tìm các giá trị a sao cho
lim x (t) ta lim ( )
ta y t
Bước 2: Tìm a, b ( a, b là số thực )  y (t) . Phần Cuối Kì a   lim 
ta x (t)
b lim y (t ) ax (t)  ta
4 Nguyên hàm (tích phân bất định) và tích phân xác
định 4.1 Phương pháp đổi biến 
u(x).v'(x)dxu(x).v(
x)u'(x).v(x)dx
4.2 Phương pháp đổi biến ( đặt ẩn phụ ) ( )
XEM TÀI LIỆU TẠI BACHKHOACNCP.COM ∫
KHÓA HỌC ONLINE GIẢI TÍCH 1 5 Tìm nguyên hàm lOMoARcPSD|46958826 HCMUT CNCP GIẢI TÍCH 1
NGUYỄN QUỐC VƯƠNG  u ( Đặt t x) biến đổi
Thay vào ( ), ta được: = ′( ) → = ′( )
Ta đạ o hàm 2 vế: ∫ ( ) = ∫
4.3 Một số tìm nguyên hàm hay gặp ( ) 1/
dx 2 arctan x  C 1 x 2 / dx 1 x  2  arctan  C  x 2 a a a 3 / dx  arcsin  x  C 1 x 2 4 / dx  x  arcsin  C a 2  x 2 a 5 / dx  k 2  ln C  x x x 2  k 6 / 2 x a 2 x 2 dx 2 2
 a  x  a  x  arcsin  C 2 2 a 7 / x k x 2
x x 2 k  kdx  x 2  k  ln C 2 2
8 /cosh x dx sinh x C
9 /sinh x dx cosh x C
10 / dx tanh x C cosh 2 x 11/ dx
 coth x C sinh2 x
12 / dx  ln(| x a |) C x a
4.4 Nguyên hàm hàm hữu tỉ
Cách làm: Tìm các hệ số A,B,C,… g ( x ) dx A B Z    ... ( x dx
( x a )( x b )....( x z )
( x a ) ( x b ) Z ) Skill casio: g ( x) g ( x)
A= ( x b ). . ( x z) tại x =a; B= ( x a )( x c ). . ( x z) tại x = b; ……… Dạng toán
XEM TÀI LIỆU TẠI BACHKHOACNCP.COM
KHÓA HỌC ONLINE GIẢI TÍCH 1 6 826 lOMoARcPSD|46958 HCMUT CNCP ( ) T i x = =a ∫ GIẢI TÍCH 1 2 +
NGUYỄN QUỐC VƯƠNG ∫ 2 1  + 2 + ( − ) ( − )( ạ− ) ( − ) ( − ) ( − ) ( − )  Tại x = a 2 = − )( − ) ( ) = )′ạ (( − )( − ) 1 ( )  Tại x = c = ( − )2( − )  ( ) T i x = b ( ) = ( − )2( − ) 4
Đạo hàm của tích phân ( ) = ∫ℎ( ) ( ) => ′( ) = ℎ′( ). (ℎ( )) + ′( ). ( ( )) ( ) 5
Ứng dụng của nguyên hàm, tích phân trong hình học
6.1 Trường hợp diện tích miền D được giới hạn bởi ( ) và trục hoàng = ∫ | ( )|
6.2 Trường hợp diện tích miền D được giới hạn bởi ( ) và trục tung = ∫ | ( )|
6.3 Trường hợp diện tích miền D được giới hạn bởi ( ) và ( )
XEM TÀI LIỆU TẠI BACHKHOACNCP.COM
KHÓA HỌC ONLINE GIẢI TÍCH 1 7 lOMoARcPSD|46958826 HCMUT CNCP GIẢI TÍCH 1
NGUYỄN QUỐC VƯƠNG
Có 2 phương pháp giải như sau:
S xb | f ( x ) g ( x ) |dx a d
S yc | f ( y ) g ( y ) |dy
6.4 Tính chiều dài sợ dây
a/ Phương trình f(x) là y = f(x)
Có 2 phương pháp giải như sau: b x  1 ( f '( 2 L  x )) dx a d L  y 
1 ( f '( y ))2 dy c
Khối lượng sợ dây khi biết mật độ khối lượng là p ( x) b
L 1 f '( 2 p ( x)dx  x ) a
b/ Phương trình f(x) là phương trình tham số như sau x x  (t) , a  t b  y y (t)
Lb x '(t ) 2 y '(t )2 dt a
Khối lượng sợ dây khi biết mật độ khối lượng là p ( x) b
L 1 f '( x ) 2 p (x )dx    a
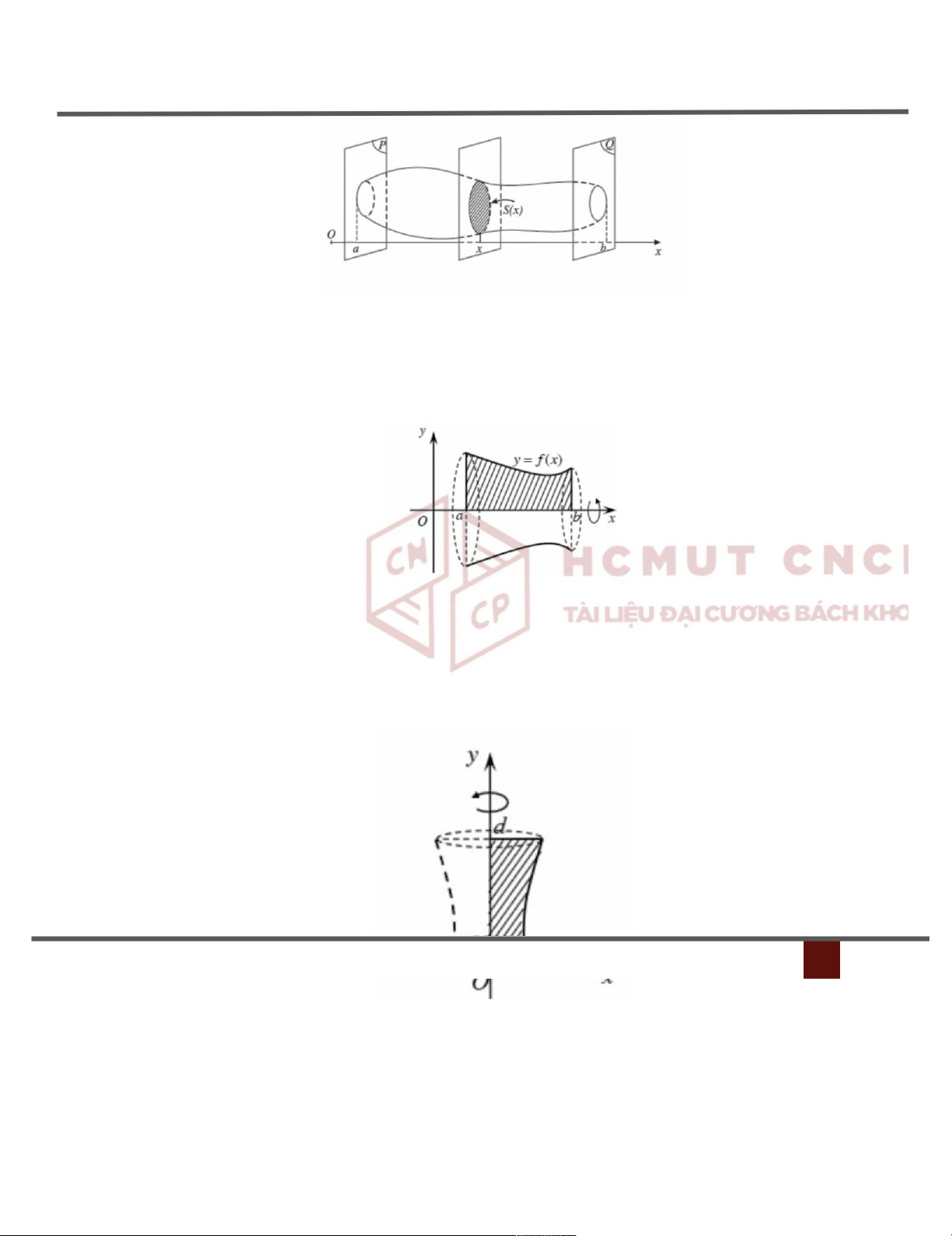
6.5 Tính thể tích hình tròn xoay
Nguồn gốc từ một công thức cấp 3:
XEM TÀI LIỆU TẠI BACHKHOACNCP.COM
KHÓA HỌC ONLINE GIẢI TÍCH 1 8 lOMoARcPSD|46958826 HCMUT CNCP GIẢI TÍCH 1
NGUYỄN QUỐC VƯƠNG
Vb S ( x )dx
a/Thể tích vật thể khi quay miền D hoặc hàm ( )a quanh 0x b ox   2 V  f ( x )dx
b/Thể tích vật thể khi quay miền D hoặc hàm ( )a quang oy
Voyb f 2 ( y )dy a
XEM TÀI LIỆU TẠI BACHKHOACNCP.COM
KHÓA HỌC ONLINE GIẢI TÍCH 1 9 lOMoARcPSD|46958826 HCMUT CNCP GIẢI TÍCH 1
NGUYỄN QUỐC VƯƠNG
c/Thể tích của vật thể tạo bởi khi quay hình thang cong quanh trục Oy b oy   V 2
| xf ( x ) | dx a
6.6 Diện tích xung quanh của vật thể tròn xoay a/ Phương trình f(x)
y f ( x ), a x b
Khi xoay f(x) quanh trục ox ta được 1 vật thể thì diện tích xung quanh vật thể đó là b S   1 f '( 2 vx
Khi xoay≤ f(x)≤ quanh trục oy ta 2
f ( x ) x ) dx là ( ) a
được 1 vật thể thì diện tích xung quanh vật thể đó d vy   1 f '( 2 S 2
f ( y ) y ) dy c
b/ Phương trình f(x) là phương trình tham số x x  (t) , a  t b y y  (t)
Khi xoay f(x) quanh trục ox ta được 1 vật thể thì diện tích xung quanh vật thể đó là b vx   2 2 S 2
y (t ) x '(t )  y '(t ) dt a
7 Ứng dụng của nguyên hàm, tích phân trong các bài toán khác
7.1 Bài toán tính công lực F Công để ể ộ ậ
ừ ị trí a sang vi trí b được tính như sau: d i ch uy n m t v∫t t ( ) v ( ) : Với là lực tác động
XEM TÀI LIỆU TẠI BACHKHOACNCP.COM
KHÓA HỌC ONLINE GIẢI TÍCH 1 10 HCMUT CNCP
7.2 Bài toán tính quãng đường ∫ | ( )|
chất điểm cách vị trí ban đầu là bao nhiêu thì ∫ ( ) lOMoARcPSD|46958826 GIẢI TÍCH 1
NGUYỄN QUỐC VƯƠNG
Cho 1 chất điểm với hàm vận tốc ( ). Quãng đường từ = đến = chất điểm đi được là:
Lưu ý: Nếu hỏi từ = đến = dung công thức
Một số bài toán khác sẽ gặp khi chúng ta vào các buổi ôn tập cuối kì
K23 8 Định lý giá trị trung bình 1
Nếu khả tích trên [a,b], giá trị trung bình của f trên [a, b] được định nghĩa là: − ∫ ( )
Nếu f liên tục trên [a,b], khi đó tồn tại c[a,b]1 sao cho ( ) = − ∫ ( ) 9 Tổng Reiman 9.1 Định nghĩa
XEM TÀI LIỆU TẠI BACHKHOACNCP.COM
KHÓA HỌC ONLINE GIẢI TÍCH 1 11 lOMoARcPSD|46958826 HCMUT CNCP GIẢI TÍCH 1
NGUYỄN QUỐC VƯƠNG b
Ước tính f (
bằng tổng Riemann với phân hoạch là dx x )dx a a, Tổng Riemann trái b
 f ( x ) dx f ( a ).dx f ( x1).dx f ( x 2) dx ... f ( x 5)dx a
b, Tổng Riemann phải
b f ( x ) dx f ( x1).dx f ( x 2) dx ... f ( x 5) dx f (b )dx a
c, Tổng Riemann trung tâm với phân hoạch là 2.dx
 f ( x ) dx f ( x1).2.dx f ( x 3).2 dx f ( x b 5).2.dx a
9.2 Các dạng toán hay gặp ∫
a/ Dạng ước tính tích phân (Chỉ bấm máy tính về bài toán Reimann) Bài giải ( )
Ước tính giá trị của
dx với phân hoạch n đoạn
Ta có khoảng phân hoạch: − ( ) ( ) ( ) ( (− 1 ) ∗ ∆ ) ∫ −1 ≈ ∆ . +∆ ∗+∆ +⋯+∆ ∗+  Dùng Reiman trái ∆ = ≈ ∑ =0 ∆ ∗ ( + ∆ ∗ ) (Dùng để casio) ∫ ≈ ∆ .+ ∆ +⋯+∆ ∗ dx
 Dùng Reiman ph ải )(Dùng để ( ) ( ) ( ) ( ớ ≈ ∑ =1 ∆ ∗ ( + ∆ ∗ ) ả ạ dx casio) 2. ∆ ( ) ( ) ( ) ( ) ∫ ≈ 2∆ .+ ∆ + ∆ ∗+ 3∆ +⋯+∆ ∗−∆ 
Dùng Reiman trung tâm v i kho ng phân ho ch ≈ = /2 ∆ ∗ ( + ∆ ∗ (2 − 1)) Ví c tính v i
∑d =1:Dùng t ng Riemann trái và ph (Dùng để casio) chia ∫1 sin( 2) ụ ổ ải ướ 4
ớ với 6 khoảng cách ∆ = 4−1 = 0,5
Ta có khoảng phân hoạch: 6
Riemann∫4sin(2 trái:) = 0,5. sin(12) + 0,5 ∗ sin((1 + 0.5)2) + sin((1 + 2 ∗ 0.5)2) + sin1((1 + 3 ∗ 0.5)2) +
sin((1 + 4 ∗ 0.5)2) + ∆ ∗ sin((1 + 5 ∗ 0.5)2)
XEM TÀI LIỆU TẠI BACHKHOACNCP.COM
KHÓA HỌC ONLINE GIẢI TÍCH 1 12 lOMoARcPSD|46958826 HCMUT CNCP GIẢI TÍCH 1
NGUYỄN QUỐC VƯƠNG = −1
≈ ∑ 0.5 ∗ (1 + 0.5 ∗ ) ≈ 0,46528 =0 1 ( 2) (( )2) (( )2) (( = 0,5 ∗ sin + 0,5 ∗ sin + 0,5 ∗ sin ∫ sin 1+0.5 1+2∗0.5 1+3∗ Riemann phải: 4
+ 0,5 ∗ sin((1 + 4 ∗ 0.5) 2) + 0,5 ∗ sin((1 + 5 ∗ 0.5) 2) + 0,5 ∗ sin((1 + 6 ∗ 0.5)2) 0.5)2) =
≈ ∑ 0.5 ∗ (1 + 0.5 ∗ ) ≈ −0,09941
b/ Dạng cho bảng giá trị =1 c f 1 2 3 4 5 6 7 Mỗ ( )i ị ủa x các đề a b d e k
Với phân hoạch ∫ 7 1 ( ) giá tr c u nhau ∆
Dùng tổng Riemann để ước 7 Tổng ∆ tính 2 +. . +∆ + ∆ 6 ∫ 7 ( ) = ∆ 1 ) 1 ( ) ( ) (
Với phân ho ạch ∫ ( ) = ∆ 2 + ∆ 3 +. . +∆ 7  Tổng Riemann trái: 7 
Tổng Riemann phải: 1 ( ) ( ) ( ) 1 ( ) ( ) ( )  Riemann trung tâm: ∫ ( ) = 2∆ 2 + 2∆ 4 + ∆ 6
c/ Dạng cho hình vẽ (ước tích diện tích, thể tích)
a/Ước diện tích một mặt phẳng bằng tổng Riemann
XEM TÀI LIỆU TẠI BACHKHOACNCP.COM
KHÓA HỌC ONLINE GIẢI TÍCH 1 13 lOMoARcPSD|46958826 HCMUT CNCP GIẢI TÍCH 1
NGUYỄN QUỐC VƯƠNG + ℎ2+ ℎ3 
Dùng tổng Riemann phải: á = (ℎ1 +⋯+ℎ11)
Với phân hoạch là a á = (ℎ 2 + ℎ 3 + ℎ 4 +⋯+ℎ12) 
Dùng tổng Riemann trái:
Với phân hoạch là 2a  ổ
Dùng t ng Riemann â trung= 2 (ℎtâm:2 + ℎ4 + ℎ6 + ⋯ +
ℎ11) b/Ước tính thể tích vật thể bằng tổng Riemann
Dùng tổng Riemann phải: á = ( 1 + 2 + 3 + ⋯ +  4 ) ổ á = ( 2 + 3 + 4 + ⋯ + 5 ) 
Dùng tổng Riemann trái:
10 Tích phân suy rộng â = 2 ( 2 + 4 ) 
Dùng t ng Riemann trung tâm: (V ới phân hoạch là 2a)
10.1 Tích phân suy rộng loại 1
a, Nhận biết tích phân suy rộng loại 1
Tích phân có 1 cận là hoặc cả 2 cận là thì đó là tích phân suy rộng
loại 1 b, Cách giải tích phân suy rộng loại 1
Giải sử F ( x) là nguyên hàm của f(x). Ta có:
 f ( x ) dx F ( x ) | lim F ( x ) F ( a) a x a
10.2 Tích phân suy rộng loại 2
a, Nhận biết tích phân suy rộng loại 2
Tích phân có chứa điểm không xác định của của hàm f(x) Ví dụ:  5ln( x 5 ch h ộ g ại cậ chứađiể x 5  x
dlàtí p ânsu5r n lo 5vì n  mx=5 0 5 ex v  x (
dx là tích phân suy rộng loại 2 vì cận chứa điểm x = 0, x = -1 x1) 2
b, Cách giải tích phân suy rộng loại 2
Với a,b là điểm không xác định của hàm số
XEM TÀI LIỆU TẠI BACHKHOACNCP.COM
KHÓA HỌC ONLINE GIẢI TÍCH 1 14