























































































































Preview text:
Bài tp Xác sut thng kê Dip Hoàng Ân BÀI TP
XÁC SUT THNG KÊ 1
Bài tp Xác sut thng kê Dip Hoàng Ân CHƯƠNG 1: XÁC SUT 1.1.
Mt hp có 100 tm th như nhau ñưc ghi các s t 1 ñn 100, Rút ngu
nhiên hai th ri ñt theo th t t trái qua phi. Tính xác sut ñn
a/ Rút ñưc hai th lp nên mt s có hai ch s.
b/ Rút ñưc hai th lp nên mt s chia ht cho 5. Gii
a/ A :“Hai th rút ñưc lp nên mt s có hai ch s” 2 A 9.8 P ( A) 9 = = ≈ 0,0073 2 A 100.99 100
b/ B : “Hai th rút ñưc lp nên mt s chia ht cho 5”
S chia ht cho 5 tn cùng phi là 0 hoc 5. Đ có bin c B thích hp vi ta rút
th th hai mt cách tùy ý trong 20 th mang các s 5;10;15;20;…;95;100, và rút 1
trong 99 th còn li ñt vào v trí ñâu. Do ñó s trưng hp thun li cho là 99.20 99.20 P (B) = = 0, 20 2 A100 1.2.
Mt hp có cha 7 qu cu trng và 3 qu cu ñen cùng kích thưc. Rút
ngu nhiên cùng mt lúc 4 qu cu. Tính xác sut ñ trong 4 qu cu rút ñưc có a/ Hai qu cu ñen. b/ Ít nht 2 cu ñen c/ Toàn cu trng Gii
Rút ngu nhiên cùng 1 lúc 4 trong 10 qu cu nên s trưng hp ñng kh năng là 4 C 10
a/ A :”trong 4 qu cu rút có 2 qu cu ñen” 2 2 C .C P ( A) 3 7 = = 0,30 4 C10
b/ B :”trong 4 qu cu ñưc rút có ít nht 2 qu cu ñen” 2 2 3 1
C .C +C .C 1 P (B) 3 7 3 7 = = 4 C 3 10
c/ C:”trong 4 qu cu ñưc chn có toàn cu trng” 2
Bài tp Xác sut th ng kê Dip Hoàng Ân 4 C 1 P (C ) 7 = = 4 C 6 10 1.3.
Mt hp thuc có 5 ng thuc tt và 3 ng kém cht lưng. Chn ngu
nhiên ln lưt không tr li 2 ng. Tính xác sut ñ:
a/ C hai ng ñưc chn ñu tt.
b/ Ch ng ñưc chn ra ñu tiên là tt.
c/ trong hai ng có ít nht mt ng thuc tt. Gii
Chn ngu nhiên ln lưt không tr li 2 trong 8 ng nên các trưng hp ñng kh năng là 2 A . 8 2 A
a/ A :” C hai ng ñưc chn ñu tt” P( ) 5 A = ≈ 0,357 2 A8 1 1 C C b/ .
B :” Ch ng ñưc chn ra ñu tiên là tt” P (B) 3 5 = ≈ 0,268 2 A8 2 A
c/ C:” trong hai ng có ít nht mt ng thuc tt” P(C) 3 = 1− ≈ 0,893 2 A8 1.4.
Mt hp ñng 15 qu bóng bàn trong ñó có 9 qu mi. Ln ñu ngưi ta ly
ngu nhiên 3 qu ñ thi ñu, sau ñó li tr vào hp. Ln th hai ly ngu nhiên 3
qu. Tính xác sut ñ c 3 qu ly ra ln sau ñu mi. Gii
Đt A :” c 3 qu ly ra ln sau ñu mi”
B :” Trong 3 qu ly ra ñ thi ñu có i qu mi” i ∈{0;1;2; } 3 i
Ta thy các {B ; B ; B ; B lp thành nhóm ñy ñ các bin c, theo công thc xác 0 1 2 3} sut toàn phn ( ) =
+
+
+
= ( + + + ) ≈ 1.5.
T mt lp có 8 n sinh viên và 12 nam sinh viên, ngưi ta chn ngu nhiên
5 sinh viên ñ lp Ban cán b lp (BCB). Tính xác sut ñ 3
Bài tp Xác sut th ng kê Dip Hoàng Ân
a/ BCB gm 3 n và 2 nam,
b/ BCB có ít nht mt n,
c/ BCB có ít nht hai nam và hai n. Gii
Đt A : “BCB có k nam sinh viên” ( k ∈ 0,1,2,3,4,5 ), k { } chúng ta có: k 5 k C . C − 12 8 P (A ) k = 5 2 C 0
a/ BCB gm 3 n và 2 nam. Xác sut phi tính: 2 3 C12. C 8 77 P( 2 A ) = = 5 323 C20
b/ Đt N: “BCB có ít nht mt n”, thì N = 5 A . Do ñó,
P(N ) = P( 5 A ) = 1 − P( 5 A ) 5 0 C 12. C 8 33 613 = − = 1 − = 5 646 646 C20
c/ Đt H: “BCB có ít nht hai nam và hai n”. Do ñó,
P (H ) = P( A + P A 2) ( 3) = + = 1.6.
T mt hp cha 8 viên bi ñ và 5 viên bi trng ngưi ta ly ngu nhiên 2
ln, m i ln 1 viên bi, không hoàn li. Tính xác sut ñ ly ñưc a/ 2 viên bi ñ; b/ hai viên bi khác màu;
c/ viên bi th hai là bi trng. Gii Vi i ∈{1, } 2 , ñăt:
T : “viên bi ly ra ln th i là bi trng”, i
D : “viên bi ly ra ln th i là bi ñ”. i
a/ Đt A :“ly ñưc 2 viên bi ñ”, chúng ta có:
P (A) = P ( 8 7 14 1 D D2 )= P ( 1
D ).P (D2 / 1 D )= . = 13 12 39
b/ Đt B : “ly ñưc hai viên bi khác màu”, chúng ta có: 4
Bài tp Xác sut thng kê Dip Hoàng Ân P (B ) =P (T D + D T = P T D + P D T 1 2 1 2 ) ( 1 2 ) ( 1 2 )
= P (T .P D / T + P D .P T / D 1 ) ( 2 1 ) ( 1 ) ( 2 1 ) Suy ra: 5 8 8 5 20
P(B) = 1312 + 1312 = 39
c/ T = TT + D T , nên xác sut phi tính là: 2 1 2 1 2
P (T = P TT + P D T 2 ) ( 1 2 ) ( 1 2 ) = P (T P T T + P D P D T 1 ). ( 2 / 1 ) ( 1 ). ( 2 / 1 ) suy ra P (T2) 5 4 8 5 5 = 13 12 + 13 12 = 13 1.7.
Mt công ty cn tuyn 4 nhân viên. Có 8 ngưi, gm 5 nam và 3 n np
ñơn xin d tuyn, và m i ngưi ñu có cơ hi ñưc tuyn như nhau. Tính xác sut
ñ trong 4 ngưi ñưc tuyn, a) có duy nht mt nam;
b) có ít nht mt n. Gii
Đt : “Có nam ñưc tuyn trong 4 nhân viên” ∈ 1 3 Gi . 5
: “có duy nht 1 nam” () = ( ) 5 3 = = 1 4 70 8
a) Gi : “có ít nht 1 n” 4 13 () 5
= 1− ( ) = 1 4 − = 4 14 8 1.8.
Mt công ty cn tuyn 4 nhân viên. Có 8 ngưi, gm 5 nam và 3 n np
ñơn xin d tuyn, và m i ngưi ñu có cơ hi ñưc tuyn như nhau. Tính xác sut
ñ trong 4 ngưi ñưc tuyn, a/ có không quá hai nam;
b/ có ba n, bit r"ng có ít nht mt n ñã ñưc tuyn. Gii
Đt : “Có nam ñưc tuyn trong 4 nhân viên” ∈
a/ Gi : “có không quá 2 nam” 1 3 2 2
. + . 1 ( ) 5 3 5 3
= ( ) + ( ) 1 2 = = 4 2 8
b/ Gi : “chn ra 3 n, bit r"ng có ít nht 1 n ñưc tuyn”.
Gi B : “Có ít nht mt n ñưc chn”. 5
Bài tp Xác sut thng kê Dip Hoàng Ân 4 Ta có 13 () 5 =1 − ( ) =1 − = 4 4 14 8 ( ) 1 () 1
= ( | ) = = 1 ( ) 13 1.9.
Mt c#a hàng sách ưc lưng r"ng: Trong t$ng s các khách hàng ñn c#a
hàng, có 30% khách cn hi nhân viên bán hàng, 20% khách mua sách và 15%
khách thc hi%n c hai ñiu trên. Gp ngu nhiên mt khách trong nhà sách. Tính
xác sut ñ ngưi này
a/ không thc hi%n c hai ñiu trên;
b/ không mua sách, bit r"ng ngưi này ñã hi nhân viên bán hàng. Gii
Đt : “khách hàng cn tư vn”
: “khách hàng cn mua sách”
Theo ñ ta có: () = 0,3; () = 0,2; ( )= 0,15
a/ Xác sut khách hàng không cn mua sách cũng không cn tư vn là:
( ) = ( )
+ ( )− ( ) 3 2 15 13 . = 1− + 1− − 1− = 10 10 100 20
b/ không mua sách, bit r"ng ngưi này ñã hi nhân viên bán hàng. 3 15 () − ( )
() − ( ) 1 10 100 / = = = = ( ) ( ) 3 2 10 1.10.
Mt cuc ñiu tra cho thy, ' mt thành ph, có 20,7% dân s dùng loi
sn ph(m , 50% dùng loi sn ph(m và trong s nhng ngưi dùng , có
36,5% dùng . Phng vn ngu nhiên mt ngưi dân trong thành ph ñó, tính xác sut ñ ngưi y
a/ Dùng c và ;
b/ Không dùng , cũng không dùng . Gii
Đt : “ ngưi dân trong thành ph dùng sn ph(m ”
: “ ngưi dân trong thành ph dùng sn ph(m ”
Theo ñ bài ta có: () = 0,207; ( ) = 0,5;(| ) = 0,365
a) Xác sut ngưi dân ñó dùng c và là
() = () . ( / ) = 0,5.0,365 = 0,1825
b) Xác sut ngưi dân ñó không dùng c và là ( .
) = (). + () − ( )= 0,4755 1.11. 6
Bài tp Xác sut thng kê Dip Hoàng Ân
Mt cuc ñiu tra cho thy, ' mt thành ph, có 20,7% dân s dùng loi
sn ph(m , 50% dùng loi sn ph(m và trong s nhng ngưi dùng , có
36,5% dùng . Phng vn ngu nhiên mt ngưi dân trong thành ph ñó, tính xác sut ñ ngưi y
a/ Dùng c và ;
b/ Dùng , bit r"ng ngưi y không dùng . Gii
Đt : “ ngưi dân trong thành ph dùng sn ph(m ”
: “ ngưi dân trong thành ph dùng sn ph(m ”
Theo ñ bài ta có: () = 0,207; ( )= 0,5; ( / ) = 0,365
a/ Xác sut ngưi dân ñó dùng c và là
() = () . ( / ) = 0,5.0,365 = 0,1825
b/ Xác sut ngưi dân ñó dùng , bit r"ng không dùng là
(. ) ( ) − ( ) ( ) 0,5 −0,1852 / = = = = 0,404 () ( ) 1 −0,207 1.12.
Theo mt cuc ñiu tra thì xác sut ñ mt h gia ñình có máy vi tính nu
thu nhp hàng năm trên 20 tri%u (VNĐ) là 0,75. Trong s các h ñưc ñiu tra thì
60% có thu nhp trên 20 tri%u và 52% có máy vi tính. Tính xác sut ñ mt h gia
ñình ñưc chn ngu nhiên
a/ có máy vi tính và có thu nhp hàng năm trên 20 tri%u;
b/ có máy vi tính, nhưng không có thu nhp trên 20 tri%u. Gii
Đt : “H gia ñình ñưc chn ngu nhiên có máy vi tính”
: “H gia ñình ñưc chn ngu nhiên có thu nhp hàng năm trên 20 tri%u”
Theo ñ bài ta có: () = 0,52; () = 0,6; ( / ) = 0,75
a/ Xác sut ñ h gia ñình ñưc chn có máy vi tính và có thu nhp hàng năm trên 20 tri%u là:
P ( AB) = P( B ).P ( A/ B) = 0,6.0,75 = 0, 45
b/ Xác sut ñ h gia ñình ñưc chn có máy vi tính nhưng thu nhp ít hơn 20 tri%u là:
() = ( )
− ( ) = 0,52 − 0,45 = 0, 07 1.13.
Theo mt cuc ñiu tra thì xác sut ñ mt h gia ñình có máy vi tính nu
thu nhp hàng năm trên 20 tri%u (VNĐ) là 0,75. Trong s các h ñưc ñiu tra thì
60% có thu nhp trên 20 tri%u và 52% có máy vi tính. Tính xác sut ñ mt h gia
ñình ñưc chn ngu nhiên
a/ Có máy vi tính và có thu nhp hàng năm trên 20 tri%u;
b/ Có thu nhp hàng năm trên 20 tri%u, bit r"ng h ñó không có máy vi tính. 7
Bài tp Xác sut th ng kê Dip Hoàng Ân Gii
Đt : “H gia ñình ñưc chn ngu nhiên có máy vi tính”
: “H gia ñình ñưc chn ngu nhiên có thu nhp hàng năm trên 20 tri%u”
Theo ñ bài ta có: () = 0,52; () = 0,6; ( / ) = 0,75
a/ Xác sut ñ h gia ñình ñưc chn có máy vi tính và có thu nhp hàng năm trên 20 tri%u là:
P ( AB) = P( )
B .P( A / B) = 0,6.0,75 = 0, 45
b/ Xác sut ñ h gia ñình ñưc chn có thu nhp hàng năm trên 20 tri%u nhưng không có máy vi tính là: () ( )
( ) − ( ) 0,6 −0, 45 / = = = = 0,3125 ( ) () 1 0 − ,52 1.14.
Trong mt ñi tuyn có hai vn ñng viên A và B thi ñu. A thi ñu trưc
và có hy vng 80% thng trn. Do nh hư'ng tinh thn, nu A thng trn thì có
60% kh năng B thng trn, còn nu A thua thì kh năng này ca B ch còn 30%.
Tính xác sut ca các bin c sau:
a/ Đi tuyn thng hai trn;
b/ Đi tuyn thng ít nht mt trn. Gii
Đt : “vn ñng viên thng” vi ∈{ , }
Theo ñ bài ta có: ( ) = 0,8; ( / ) = 0,6; ( / )= 0,3
a/ Xác sut ñi tuyn thng 2 trn là ( ) = ( ) . ( /
) = 0, 8.0, 6 = 0, 48
b/ Đi tuyn thng ít nht mt trn nghĩa là có ít nht mt trong hai vn ñng viên
A, hoc B thng. Xác sut cn tính là: P (M ∪M = P M + P M − P M M A B ) ( B ) ( A) ( . A B ) = 0,54 + 0,8 − 0,48 = 0,86 1.15.
Trong mt ñi tuyn có hai vn ñng viên A và B thi ñu. A thi ñu trưc
và có hy vng 80% thng trn. Do nh hư'ng tinh thn, nu A thng trn thì có
60% kh năng B thng trn, còn nu A thua thì kh năng này ca B ch còn 30%.
Tính xác sut ca các bin c sau: a/ B thng trn;
b/ Đi tuyn ch thng có mt trn. Gii
Đt : “vn ñng viên thng” vi ∈{ , }
Theo ñ bài ta có: ( ) = 0,8; ( / ) = 0,6; ( / )= 0,3
a/ Xác sut B thng trn là: P( M ) = (
P M ) P( M | M .) + P(M ).P (M | M ) = 0,54 B A B A A B A 8
Bài tp Xác sut th ng kê Dip Hoàng Ân
b/ Đt : “ñi tuyn ch thng 1 trn”
Xác sut ñi tuyn ch thng 1 trn là:
P (D) = P (M .M B + P M M = P M − P M M + P M − P M M A
) ( A. B ) ( A) ( .A B) ( B) ( .A B ) = P (M + P M − P M M A) ( B) 2. (
.A B)= 0,8 + 0,54 − 2.0,48 = 0,38 ` 1.16.
Đ thành lp ñi tuyn quc gia v mt môn hc, ngưi ta t$ chc mt cuc
thi tuyn gm 3 vòng. Vòng th nht ly 80% thí sinh; vòng th hai ly 70% thí
sinh ñã qua vòng th nht và vòng th ba ly 45% thí sinh ñã qua vòng th hai. Đ
vào ñưc ñi tuyn, thí sinh phi vưt qua ñưc c 3 vòng thi. Tính xác sut ñ mt thí sinh bt kỳ
a/ Đưc vào ñi tuyn;
b/ B loi ' vòng th ba. Gii
Đt : “thí sinh ñưc chn ' vòng ” vi { ∈ 1, 2, } 3 Theo ñ bài ta có:
( = 0,8; | = 0,7; | = 0, 45 1 ) ( 2 1) ( 3 1 2 )
a/ Xác sut ñ thí sinh ñó ñưc vào ñi tuyn là
( = . | . | = 0,8.0,7.0, 45 = 0,252 1 2 3 ) ( 1) ( 2 1 ) ( 3 1 2)
b/ Xác sut ñ thí sinh ñó b loi ' vòng th III là ( 3
) = ( ). ( / ). ( 3 / 1 2 1 2 1 1 2 )
= ( . | . 1− | = 0,8.0, 7.0,55 = 0,308 1 ) ( 2 1 ) ( ( 3 1 2 )) 1.17.
Đ thành lp ñi tuyn quc gia v mt môn hc, ngưi ta t$ chc mt cuc
thi tuyn gm 3 vòng. Vòng th nht ly 80% thí sinh; vòng th hai ly 70% thí
sinh ñã qua vòng th nht và vòng th ba ly 45% thí sinh ñã qua vòng th hai. Đ
vào ñưc ñi tuyn, thí sinh phi vưt qua ñưc c 3 vòng thi Tính xác sut ñ mt thí sinh bt kỳ
a/ Đưc vào ñi tuyn;
b/ B loi ' vòng th hai, bit r"ng thí sinh này b loi. Gii
Đt : “thí sinh ñưc chn ' vòng ” vi { ∈ 1, 2, } 3 Theo ñ bài ta có:
( = 0,8; | = 0,7; | = 0, 45 1 ) ( 2 1) ( 3 1 2 )
a/ Xác sut ñ thí sinh ñó ñưc vào ñi tuyn là
( = . | . | = 0,8.0,7.0, 45 = 0,252 1 2 3 ) ( 1) ( 2 1 ) ( 3 1 2)
b/ Đt K: “Thí sinh ñó b loi”
( ) = ( 1
) + ( 2
) + ( 3
) =1− () + ( ) − ( ) + ( 3 1 1 2 1 1 1 2 1 2 ) 9
Bài tp Xác sut th ng kê Dip Hoàng Ân
=1 − ( ). ( / ) + ( 3 =1 −0,8.0,7 +0,308 =0,748 1 2 1 1 2 )
Vy, xác sut ñ thí sinh ñó b loi ' vòng II, bit r"ng thí si nh ñó b loi là:
( 2. ) ( .2 ) ( ) . (2 | 1 1 1 ) ( 0,8 1− 0,7 2 | ) ( ) = = = = = 0,3209 ( ) ( ) ( ) 0,748 1.18.
Mt lô hàng có 9 sn ph(m ging nhau. M i ln kim tra, ngưi ta chn
ngu nhiên 3 sn ph(m; kim tra xong tr sn ph(m li lô hàng. Tính xác sut ñ
sau 3 ln kim tra, 9 sn ph(m ñu ñưc kim tra. Gii
Chia 9 sn ph(m thành 3 nhóm. Gi : “Kim tra nhóm ” { ∈ 1, 2, } 3
Đt :”Sau 3 ln kim tra, 9 sn ph(m ñu ñưc kim tra” ( )
= = = 1.19.
Mt lp hc ca Trưng Đi hc AG có 2/3 là nam sinh viên và 1/3 là n
sinh viên. S sinh viên quê ' An Giang chim t l% 40% trong n sinh viên, và
chim t l% 60% trong nam sinh viên.
a) Chn ngu nhiên mt sinh viên ca lp. Tính xác sut ñ chn ñưc mt
sinh viên quê ' An Giang. Nu bit r"ng sinh viên va chn quê ' An
Giang thì xác sut ñ sinh viên ñó là nam b"ng bao nhiêu?
b) Chn ngu nhiên không hoàn li hai sinh viên ca lp. Tính xác sut ñ
có ít nht mt sinh viên quê ' An Giang, bit r"ng lp hc có 60 sinh viên. Gii a) Đt : 2
: “Chn ñưc sinh viên nam” ()= 3 1
: “Chn ñưc sinh viên n” ( ) = 3
: “Chn ñưc sinh viên quê ' An Giang” 8
( ) = ( ) + ( ) = ( ) ( | ) + ( )
( | ) = 15 Do ñó, ( ) ( ) ( | ) 3
( | ) = = = ( ) ( ) 4
b) Lp có 60 sinh viên suy ra có 40 sinh viên nam và 20 sinh viên n
S sinh viên Nam quê ' An Giang: 24
S sinh viên N quê ' An Giang: 8
Nên t$ng s sinh viên quê ' An Giang là 32 sinh viên
: “ít nht mt sinh viên quê ' An Giang” 2 232 28
() = 1− () = 1− = 2 295 60 1.20. 10
Bài tp Xác sut th ng kê Dip Hoàng Ân
Có ba hp A, B và C ñng các l thuc. Hp A có 10 l tt và 5 l hng,
hp B có 6 l tt và 4 l hng, hp C có 5 l tt và 5 l hng
a/ Ly ngu nhiên t m i hp ra mt l thuc, tính xác sut ñ ñưc 3 l cùng loi.
b/ Ly ngu nhiên mt hp ri t hp ñó ly ra 3 l thuc thì ñưc 1 l tt
và 2 l hng. Tính xác sut ñ hp A ñã ñưc chn. Gii
a/ và :“l ly ra t hp th là tt” ∈ {}
Nên, xác sut ñ ñưc 3 l cùng loi +
=
+ = + =
b/ Đt :“Ly ñưc hp th ” ∈ {
} ; :“Ly ñưc 2 l hng và 1 l tt”
= ( ) + + ( ) ( ) ( ) ( ) ( ) = + + =
Khi ñó xác sut ñ hp A ñưc chn ( ) ( ) ( )
= = = = ( ) ( ) 1.21.
Có hai hp B và C ñng các l thuc. Hp B có 6 l tt và 4 l hng, hp C
có 5 l tt và 5 l hng. Ly ngu nhiên hai l thuc t hp B b vào hp C, ri
tip theo ly ngu nhiên mt l thuc t hp C thì ñưc l hng. Tính xác sut ñ
a/ L hng ñó là ca hp B b sang;
b/ Hai l thuc b t hp B vào hp C ñu là l hng. Gii
Gi : “Hai l thuc ly t hp B b vào hp C có l hng” ∈ {}
và ñt : “l thuc ly t hp C (sau khi ñã b 2 l t B b sang) b hng”
= ( ) ( ) + ( ) ( ) + ( ) ( = )
a/ l hng ñó là ca hp B b sang ( ) + ( ) ( ) ( )
= = () = + =
11
Bài tp Xác sut th ng kê Dip Hoàng Ân
b/ hai l thuc b t hp B vào hp C ñu là l hng
( )( ) = = = = ()
1.22.
Trong mt ñi tuyn có 3 vn ñng viên A, B và C thi ñu vi xác sut
chin thng ln lưt là 0,6; 0,7 và 0,8. Gi s# m i ngưi thi ñu mt trn ñc lp nhau.Tính xác sut ñ:
a/ ñi tuyn thng ít nht mt trn,
b/ ñi tuyn thng 2 trn. Gii Đt :
: “vn ñng viên A chin thng” ( ) = 0,6
: “vn ñng viên B chin thng” ( ) = 0,7
: “vn ñng viên C chin thng” ( ) = 0,8
a/ Gi : “ ñi tuyn thng ít nht 1 trn”
= − (
)= − =
b/ Gi : “ ñi tuyn thng 2 trn”
= (
)+ (
) + ( ) = 1.23.
Trong mt ñi tuyn có 3 vn ñng viên A, B và C thi ñu vi xác sut
chin thng ln lưt là 0,6; 0,7 và 0,8. Gi s# m i ngưi thi ñu mt trn ñc lp nhau.Tính xác sut ñ:
a/ Đi tuyn thng ít nht mt trn,
b/ A thua trong trưng hp ñi tuyn thng 2 trn. Gii Đt :
: “vn ñng viên A chin thng” ( ) = 0,6
: “vn ñng viên B chin thng” ( ) = 0,7
: “vn ñng viên C chin thng” ( ) = 0,8
a/ Gi : “ ñi tuyn thng ít nht 1 trn”
= − (
)= − =
b/ A thua trong trưng hp ñi tuyn thng 2 trn
Gi : “ ñi tuyn thng 2 trn”
= (
)+ (
) + ( ) = 12
Bài tp Xác sut th ng kê Dip Hoàng Ân
( ) = = = ≈ 1.24.
Trong năm hc va qua, ' trưng ñi hc XYZ, t l% sinh viên thi trưt
môn Toán là 34%, thi trưt môn Tâm lý là 20,5%, và trong s các sinh viên trưt
môn Toán, có 50% sinh viên trưt môn Tâm lý. Gp ngu nhiên mt sinh viên ca trưng XYZ.
a/ Tính xác sut ñ anh ta trưt c hai môn Toán và Tâm lý; ñu c hai môn Toán và Tâm lý.
b/ Nu bit r"ng sinh viên này trưt môn Tâm lý thì xác sut ñ anh ta ñu môn Toán là bao nhiêu? Gii
: “sinh viên thi trưt môn Toán” ( )= 0,34
và : “sinh viên thi trưt môn Tâm Lý” () = 0,205
khi ñó ( | ) = 0,5
a/ Xác sut sinh viên trut môn c môn Toán và Tâm Lý
= () ( ) = =
Xác sut sinh viên ñu c môn Toán và Tâm Lý ( )
= −
∪ = − () − ( )
+ ( ) =
b/ Xác sut sinh viên ñu môn Toán, bit r"ng trưt môn Tâm Lý: ()
() − ()
( ) = = = . ( ) () 1.25.
Trong năm hc va qua, ' trưng ñi hc XYZ, t l% sinh viên thi trưt
môn Toán là 34%, thi trưt môn Tâm lý là 20,5%, và trong s các sinh viên trưt
môn Toán, có 50% sinh viên trưt môn Tâm lý. Chn ngu nhiên 12 sinh viên ca
trưng XYZ. Nhiu kh năng nht là s+ có bao nhiêu sinh viên thi trưt c hai môn
Toán và Tâm lý. Tính xác sut tương ng. Đáp s
Gi : “sinh viên thi trưt môn Toán” ( ) = 0,34
và : “sinh viên thi trưt môn Tâm Lý” () = 0,205 khi ñó ( | )= 0,5
Xác sut sinh viên trut môn c môn Toán và Tâm Lý
= ()( ) = =
Nên, Sinh viên trưt c Toán và Tâm lý vi xác sut không ñ$i = . 13
Bài tp Xác sut th ng kê Dip Hoàng Ân
Do ñó, chn 12 sinh viên nghĩa là thc hi%n 12 phép th# Bernoulli vi xác
sut thành công (trưt c Toán và Tâm lý) không ñ$i = .s sinh viên nhiu
kh năng trưt c hai môn ( ) + = = .
Xác sut tương ng là (2 )= (0,17 )2 . (1 − 0,17 )10 2 = 0, 296 . 12 12 1.26.
Trong năm hc va qua, ' trưng ñi hc XYZ, t l% sinh viên thi trưt
môn Toán là 34%, thi trưt môn Tâm lý là 20,5%, và trong s các sinh viên trưt
môn Toán, có 50% sinh viên trưt môn Tâm lý. Phi chn bao nhiêu sinh viên
ca trưng XYZ sao cho, vi xác sut không bé hơn 99%, trong s ñó có ít nht
mt sinh viên ñu c hai môn Toán và Tâm lý. Gii
: “sinh viên thi trưt môn Toán” () = 0,34
và : “sinh viên thi trưt môn Tâm Lý” () = 0,205
khi ñó ( | ) = 0,5
Xác sut sinh viên ñu c môn Toán và Tâm Lý ( ) = −
∪ = − () − ()+ ( ) =
Gi n là s sinh viên cn chn. Xác sut ñ sinh viên ñu c hai môn Toán
và Tâm Lý không ñ$i = nên ta có quá trình Bernoulli B (n, p) .
Đt : “ ít nht mt sinh viên ñu c hai môn Toán và Tâm Lý ”.
Theo yêu cu bài toán ta ñưc
() = − ( ) = − − ≥ ( )
⇔ ≥ ( ) ⇔ ≥ ( ) ⇔ ≥
Vy, chn ít nht 5 sinh viên. 1.27.
Ba máy 1, 2 và 3 ca mt xí nghi%p sn xut, theo th t, 60%, 30% và
10% t$ng s sn ph(m ca mt xí nghi%p. T l% sn xut ra ph ph(m ca các máy
trên, theo th t, là 2%, 3% và 4%. Ly ngu nhiên mt sn ph(m t lô hàng ca
xí nghi%p, trong ñó ñ ln ln các sn ph(m do 3 máy sn xut.
a/ Tính xác sut ñ sn ph(m ly ra là sn ph(m tt. Ý nghĩa ca xác
sut ñó ñi vi lô hàng là gì?
b/ Nu sn ph(m ly ñưc là ph ph(m, thì nhiu kh năng nht là do máy nào sn xut? Gii
Đt : “sn ph(m ly ra do máy sn xut” vi ∈{1, 2, } 3
( = 0,6; = 0,3; = 0,1 1 ) ( 2) ( 3)
Và :“sn ph(m ly ra là ph ph(m”
( = = = ) ( ) ( ) 14
Bài tp Xác sut th ng kê Dip Hoàng Ân
a/ :”sn ph(m ly ra là sn ph(m tt”
( ) = ( ) ( ) + ( ) ( ) + ( ) ( = )
Ý nghĩa, xác sut th hi%n t l% sn ph(m tt ca lô hàng.
b/ Xác sut ly ra sn ph(m là ph ph(m
() = − () = Theo công thc Bayes (
) ( )( )
( = = = = ) ( ) ()
(
) ( ) ( ) ( = = = = ) ( ) ( ) (
) ()( )
( = = = = ) () ( )
Do ñó, sn ph(m do máy 1 sn xut ra ph ph(m nhiu nht. 1.28.
Chia ngu nhiên 9 tm vé s, trong ñó có 3 vé trúng thư'ng, ñu cho 3
ngưi (m i ngưi 3 tm). Tính xác sut ñ c 3 ngưi ñu ñưc trúng thư'ng. Gii
Đt : “Ngưi mua vé th ñưc vé trúng thư'ng” vi ∈{1, 2, } 3 ( ) = ( ) ( ) (
) = = 1.29.
Trong s các b%nh nhân ñang ñưc ñiu tr ti mt b%nh vi%n, có 50% ñiu
tr b%nh A, 30% ñiu tr b%nh B và 20% ñiu tr b%nh C. Ti b%nh vi%n này, xác
sut ñ cha khi các b%nh A, B và C, theo th t, là 0,7; 0,8 và 0,9. Hãy tính t
l% b%nh nhân ñưc cha khi b%nh A trong t$ng s b%nh nhân ñã ñưc cha khi b%nh trong b%nh vi%n. Gii
Đt : “b%nh nhân ñiu tr b%nh ” vi {
∈ , , }
: “b%nh nhân ñưc khi b%nh”
Theo ñ bài ta có: ( ) = 0,5; ( ) = 0,3; ( )= 0, 2
và ( / ) = 0,7; ( / ) = 0,8; ( / ) = 0,9
Xác sut ñ b%nh nhân khi b%nh là 15
Bài tp Xác sut th ng kê Dip Hoàng Ân
( ) = ∑ ( = + + = ).
( / ) 0,5.0,7 0,3.0,8 0,2.0,9 0,77 =
Xác sut ñ b%nh nhân tr khi b%nh A là ( ) . ( | ) 0,5.0,7
( | = = = ) 45, 45% ( ) 0,77 1.30.
Có hai bình như sau: Bình A cha 5 bi ñ, 3 bi trng và 8 bi xanh; bình B
cha 3 bi ñ và 5 bi trng. Gieo mt con xúc xc vô tư: Nu mt 3 hoc mt 5
xut hi%n thì chn ngu nhiên mt bi t bình B; các trưng hp khác thì chn ngu
nhiên mt bi t bình A. Tính xác sut ñ chn ñưc viên bi ñ. Nu viên bi trng
ñưc chn, tính xác sut ñ mt 5 ca con xúc xc xut hi%n. Gii Đt
: “Gieo con xúc xc ñưc mt 3 hoăc mt 5”, =
: “Ly t bình ra mt bi là bi ñ”. Ta có =
+
= + =
Gi : “mt viên bi ñưc chn là bi trng”
=
+ = + =
Đt : “gieo con xúc xc ñưc mt 5”.
Xác sut mt 5 xut hi%n, bit r"ng bi ñưc chn là bi trng là () ( ) = = = = ( ) () 1.31.
Có hai bình như sau: Bình A cha 5 bi ñ, 3 bi trng và 8 bi xanh; bình B
cha 3 bi ñ và 5 bi trng.
Ly ngu nhiên 3 viên bi t bình A b vào bình B, ri t bình B ly ngu
nhiên 1 viên bi thì ñưc bi ñ. Theo ý bn, viên bi ñó vn thuc bình nào? Gii
Gi : “ có k bi ñ trong 3 viên bi ly t bình A b vào bình B” vi ∈{0,1,2, } 3
Đt : “Ly mt bi t bình B ra là bi ñ”. =
= + + ∑ = + + =
Đt : “bi ñ sau cùng ly t bình B”. 16
Bài tp Xác sut th ng kê Dip Hoàng Ân = = () () Do ñó = = = = > . ( ) ()
Vy, bi ñ sau cùng nhiu kh năng nht là ca bình B. 1.32.
Có hai chung nuôi th. Chung th nht có 1 con th trng và 5 con th
nâu; chung th hai có 9 con th trng và 1 con th nâu. T m i chung bt ngu
nhiên ra mt con ñ nghiên cu. Các con th còn li ñưc dn vào mt chung th
ba. T chung th ba này li bt ngu nhiên ra mt con th. Tính xác sut ñ con
th bt ra sau cùng là mt con th nâu. Gii Đt
: “Th bt ' chung 1 ra nghiên cu là th nâu ” =
: “Th bt ' chung 2 ra nghiên cu là th nâu” =
Gi : “Th bt ' chung 3 ra nghiên cu là th nâu ”
= (
) + (
) + (
)+ ( ) = (
) (
) + (
) ( ) +
+ ( ) ( ) + ( ) ( ) = ( )
() (
) + ( )
( ) ( ) + + ( ) ( )
( )+ ( ) ( )
( ) = ( )
() + ( )
() + ( )
() + ( )
() = 1.33.
Ban giám ñc mt công ty liên doanh vi nưc ngoài ñang xem xét kh
năng ñình công ca công nhân ñ ñòi tăng lương ' hai nhà máy A và B. Kinh
nghi%m cho h bit cuc ñình công ' nhà máy A và B xy ra ln lưt vi xác sut
0,75 và 0,65. Ngoài ra, h cũng bit r"ng nu công nhân ' nhà máy B ñình công
thì có 90% kh năng ñ công nhân ' nhà máy A ñình công ng h.
a/ Tính xác sut ñ công nhân ' c hai nhà máy ñình công.
b/ Nu công nhân ' nhà máy A ñình công thì xác sut ñ công nhân ' nhà
máy B ñình công ñ ng h b"ng bao nhiêu? Gii
Đt : : “ Công nhân ñình công ' nhà máy A” = 17
Bài tp Xác sut th ng kê Dip Hoàng Ân
: “Công nhân ñình công ' nhà máy B”
= ( ) =
a/ Xác sut công nhân ñình công ' 2 nhà máy là
() = ( )
. ( | ) = , . , = ,
b/ Nu công nhân ' nhà máy A ñình công thì xác sut ñ công nhân ' nhà máy B ñình công là ( ) , ( | ) = = = , ( ) , 1.34.
Mt nhân viên kim toán nhn thy 15% các bn cân ñi thu chi cha các
sai lm. Trong các bn cha sai lm, 60% ñưc xem là các giá tr bt thưng so
vi các s xut phát t gc. Trong tt c các bn cân ñi thu chi thì 20% là nhng
giá tr bt thưng. Nu mt con s ' mt bng cân ñi t ra bt thưng thì xác sut
ñ s y là mt sai lm là bao nhiêu? Gii
Đt : “bn cân ñi thu chi cha sai lm” =
: “bn cân ñi thu chi cha giá tr bt thưng”
= ( ) =
Xác sut 1 con s ' 1 bng cân ñi t ra bt thưng là 1 sai lm: ( )
( ). ( |) , . ,
( | ) = = = = , ( ) ( ) , 1.35.
Mt hãng sn xut mt loi t lnh X ưc tính r"ng khong 80% s ngưi
dùng t lnh có ñc qung cáo t lnh do hãng y sn xut. Trong s nhng ngưi
ñc qung cáo, có 30% mua loi t lnh X; 10% không ñc qung cáo cũng mua
loi t lnh X. Tính xác sut ñ mt ngưi tiêu dùng ñã mua loi t lnh X mà có ñc qung cáo. Gii
Đt : “ngưi ñó ñc qung cáo” =
: “ngưi ñó mua t lnh X” ( / ) = , ;( / ) = ,
Trưc tiên tính xác sut ñ ngưi mua t lnh X
( ) = ( )
+ ( ) = ( )
. ( / ) + ( )
.( / ) = ,
Xác sut ñ 1 ngưi tiêu dùng ñã mua loi t lnh X mà có ñc qung cáo:
( ) (). ( | ) , . ,
(| ) = = = = () ( ) , 1.36.
Trên mt bng qung cáo, ngưi ta mc hai h% thng bóng ñèn ñc lp. H%
thng I gm 4 bóng mc ni tip, h% thng II gm 3 bóng mc song song. Kh
năng b hng ca m i bóng trong 18 gi thp sáng liên t,c là 0,1. Vi%c hng ca
m i bóng ca m i h% thng ñưc xem như ñc lp. Tính xác sut ñ a/ H% thng I b hng; 18
Bài tp Xác sut th ng kê Dip Hoàng Ân
b/ H% thng II không b hng. Gii
a/ Đt :”bóng ñèn th trong h% thng I bi hng” ∈ {}.
Xác sut h% thng I b hng =
+ + + = − ( )
= − =
b/ Đt :”bóng ñèn th trong h% thng II bi hng” ∈ {}.
Xác sut h% thng II không b hng
+ + = −
= − = 1.37.
Trên mt bng qung cáo, ngưi ta mc hai h% thng bóng ñèn ñc lp. H%
thng I gm 4 bóng mc ni tip, h% thng II gm 3 bóng mc song song. Kh
năng b hng ca m i bóng trong 18 gi thp sáng liên t,c là 0,1. Vi%c hng ca
m i bóng ca m i h% thng ñưc xem như ñc lp. Tính xác sut ñ
a/ C hai h% thng b hng;
b/ Ch có mt h% thng b hng. Gii
a/ Đt : “bóng ñèn th trong h% thng I bi hng” ∈ { } .
và :”bóng ñèn th trong h% thng II bi hng” ∈ {} .
Xác sut h% thng I b hng =
+ + + = − = − = ( )
Xác sut h% thng II b hng là: () = =
Nên, xác sut c hai h% thng b hng là =
= =
b/ Xác sut ch có mt h% thng b hng
+ = +
= 1.38.
Mt lô hàng gm rt nhiu bóng ñèn, trong ñó có 8% bóng ñèn xu. Mt
ngưi ñn mua hàng vi qui ñnh: Chn ngu nhiên 10 bóng ñèn ñem kim tra và
nu có nhiu hơn mt bóng ñèn xu thì không nhn lô hàng. Tính xác sut ñ lô hàng ñưc chp nhn. Gii
Vi%c kim tra 10 bóng ñèn, nghĩa là thc hi%n 10 phép th# Bernoulli, vi
xác sut “thành công” gp bóng xu = (không ñ$i).
Khi ñó ( ; , ) , . , − = , = , , ,...,
( :s ln thành công trong 10 phép th#)
Đt : “nhn lô hàng” 19
Bài tp Xác sut th ng kê Dip Hoàng Ân ( )
= ( ) + ( ) =( ) − ( ) = 1.39.
Mt nhóm nghiên cu ñang nghiên cu v nguy cơ mt s c ti mt nhà
máy ñi%n nguyên t# s+ gây ra s rò r phóng x. Nhóm nghiên cu nhn thy các
loi s c ch có th là: ho hon, s gãy ñ$ ca vt li%u hoc sai lm ca con
ngưi, và 2 hay nhiu hơn 2 s c không bao gi cùng xy ra.
Nu có ha hon thì s rò r phóng x xy ra khong 20% s ln. Nu có s
gãy ñ$ ca vt li%u thì s rò r phóng x xy ra khong 50% s ln, và nu có s
sai lm ca con ngưi thì s rò r s+ xy ra khong 10% s ln. Nhóm nghiên cu
cũng tìm ñưc xác sut ñ: Ho hon và s rò r phóng x cùng xy ra là 0,0010,
gãy ñ$ vt li%u và s rò r phóng x cùng xy ra là 0,0015, sai lm ca con ngưi
và s rò r phóng x cùng xy ra là 0,0012. Tìm xác sut ñ
a/ có ho hon; có gãy ñ$ vt li%u và có sai lm ca con ngưi;
b/ có mt s rò r phóng x;
c/ mt s rò r phóng x ñưc gây ra b'i s sai lm ca con ngưi. Gii
Đt : “xy ra ha hon”
: “xy ra gãy ñ$”
: “xy ra sai lm ca con ngưi”
: “s rò r phóng x” Ta có ( )
= ( )
= ( ) = ( )
= () = () =
a/ Xác sut có ho hon là ( ) ( ) = = ,
( |)
Xác sut có gãy ñ$ vt li%u là ( ) () = = ,
( | )
và xác sut sai lm ca con ngưi ( ) ( ) = = ,
( | )
b/ Xác sut có s rò r phóng x xy ra:
( ) = ( )+ ( ) + ( ) = , + , + , = ,
c/ Xác sut mt s rò r phóng x ñưc gây ra b'i s sai lm ca con ngưi là () = = = () 1.40. 20
Bài tp Xác sut th ng kê Dip Hoàng Ân
Mt ña phương có t l% ngưi dân nghi%n thuc lá là 30%. Bit r"ng t l%
ngưi b viêm hng trong s ngưi nghi%n thuc lá là 60%, còn t l% ñó trong s
ngưi không nghi%n thuc lá là 40%. Chn ngu nhiên mt ngưi t ña phương trên.
a/ Nu ngưi ñó b viêm hng, tính xác sut ñ ngưi ñó nghi%n thuc lá.
b/ Nu ngưi ñó không b viêm hng, tính xác sut ñ ngưi ñó nghi%n thuc lá. Gii
Đt : “ngưi dân nghi%n thuc lá” ( ) = ,
: “ngưi dân b viêm hng” ( | ) = , ; ( | ) = ,
a/ Trưc tiên ta tính xác sut ngưi này viêm hng
( ) = ( )+ () = (). ( |)+ (). ( | ) = ,
Xác sut ñ ngưi nghi%n thuc lá nu b viêm hng là ( )
(). ( | ) , . , ( | ) = = = = () () ,
b/ Xác sut ñ ngưi nghi%n thuc lá nu không b viêm hng là ( ) (
−
− | ) ( ) ( ) ( ) ( ). ( | ) = = = = ( ) ( ) − ( ) 1.41.
Mt nhà xut bn g#i bn gii thi%u sách mi ñn 80% ging viên ca mt
trưng ñi hc. Sau mt thi gian, nhà xut bn nhn thy: Có 30% ging viên
mua sách trong s nhng ngưi nhn ñưc bn gii thi%u, và trong s nhng ging
viên không nhn ñưc bn gii thi%u, có 10% mua sách . Tìm t l% nhng ging
viên nhn ñưc bn gii thi%u trong s nhng ngưi mua sách. Gii
Đt : “ging viên nhn ñưc bn gii thi%u sách mi” () = ,
: “ging viên mua sách” ( | )
= , ; ( | ) = ,
Trưc ht ta tính xác sut ñ ging viên mua sách
= ( )
+ ( ) = ( )
( ) + ( )
( ) =
Nên, xác sut ñ ging viên nhn ñưc bn gii thi%u trong s nhng ngưi mua sách: ( )
(). ( |) , . ,
(/ ) = = = = ( ) () , 1.42.
Nhà trưng mun chn mt s hc sinh t mt t$ gm 7 nam sinh và 6
n.sinh. Ln ñu chn ngu nhiên 2 hc sinh; sau ñó, chn tip 1 hc sinh na.
a/ Tính xác sut ñ hc sinh ñưc chn ln sau là nam sinh. 21
Bài tp Xác sut th ng kê Dip Hoàng Ân
b/ Bit r"ng hc sinh ñưc chn ln sau là n sinh, tính xác sut ñ c hai
hc sinh ñưc chn ln ñu ñu là nam sinh. Gii
a/ Gi : “chn hc sinh nam trong 2 hc sinh ln ñu” { ∈ } = = =
:”hc sinh ñưc chn sau cùng là nam” ( )
= +
+
= + + =
b/ Xác sut hc sinh chn ln sau cùng là n là = () =
nên xác sut ñ 2 hc sinh ñưc chn ln ñu là nam:
( ) = = = ( ) 1.43.
S li%u thng kê v b%nh lao ph$i ti mt ña phương cho bit: Có 15% s
ngưi làm ngh ñ,c ñá (LNĐĐ) và b lao ph$i; có 50% s ngưi không LNĐĐ và
không b lao ph$i; có 25% s ngưi LNĐĐ nhưng không b lao ph$i. Ngoài ra, t
l% nhng ngưi không LNĐĐ nhưng b lao ph$i là 10%. Chúng ta có th kt lun
gì v mi quan h% gia ngh ñ,c ñá và b%nh lao ph$i? Gii
Đt : “làm ngh ñ,c ñá”
: “b lao ph$i”
Theo s li%u ñ bài ta có: () =
= = = Khi ñó, =
+ () = + = và =
+ () = + =
D- thy ( )
= ≠ = ( )
do ñó b%nh lao ph$i có liên quan ñn ngh ñ,c ñá. Xét ( ) ( )
( ) =
= ( )= = ( ) () 22
Bài tp Xác sut th ng kê Dip Hoàng Ân
Ta thy ( ) ≈ ( )
. Chng t r"ng, xác sut ngưi b lao ph$i khi
ngưi ñó làm ngh ñ,c ñá cao gn gp hai ln xác sut ngưi b lao ph$i nhưng
ngưi ñó không làm ngh ñ,c ñá. 1.44.
Gi s# mt xét nghi%m X cho kt qu dương tính (+) ñi vi nhng ngưi
nhi-m HIV vi xác sut 95% và cho kt qu (+) ñi vi nhng ngưi không nhi-m
HIV vi xác sut 1%. Mt ngưi ñn t ña phương có t l% nhi-m HIV là 1%
ñưc làm xét nghi%m X và cho kt qu (+). Tính xác sut ñ ngưi này thc s nhi-m HIV. Gii
Đt : “Ngưi b nhi-m HIV ñn t ña phương” ( ) =
: “ngưi ñn t ña phương làm xét nghi%m X cho kt qu dương tính vi HIV” ( ) = ( )
( )
+ ()( )
= + =
Xác sut ñ ngưi ñn t ña phương có t l% 1% ñưc xét nghi%m và cho kt qu dương tính là = = = 1.45.
Mt hp cha 15 l thuc, trong ñó có 6 l hng. Ly ln lưt tng l
không hoàn li ñ kim tra, cho ñn khi gp 3 l hng thì dng.
a/ Tính xác sut ñ vi%c kim tra dng li ' l th ba; ' l th sáu
b/ Nu vi%c kim tra dng li ' l th sáu, tính xác sut ñ l ñưc kim
ra ñu tiên là l hng. Gii
Đt :” ln kim tra th ñưc l hng”
a/ Xác sut ñ vi%c kim tra dng li ' l th ba ( = = )
Đt :” kim tra liên tip 5 ln ñưc 2 l hng và 3 tt” = = = =
:”kim tra dng li ' l th sáu” = ( =
= )
b/ Vi%c kim tra dng li ' l th sáu, xác sut ñ l ñưc kim ra ñu tiên là l hng.
( ) ( ) ( ) ( ) ( )
( ) = = () () 23
Bài tp Xác sut th ng kê Dip Hoàng Ân = = ≈ 1.46.
T mt lô hàng có rt nhiu quyn v' vi t l% v' hng là 5%, ngưi ta
chn ngu nhiên tng quyn v' ñ kim tra.
a/ Hi phi kim tra ít nht bao nhiêu quyn v' ñ xác sut có ít nht mt
quyn v' hng không bé hơn 90% ?
b/ Gi s# vi%c kim tra s+ dng li khi phát hi%n 3 quyn v' hng. Tính
xác sut ñ vi%c kim tra dng li ' ln kim tra th 10, Gii
Gi là xác sut v' hng trong m i lô hàng. = và gi là s
quyn v' cn kim tra. Ta có dãy phép th# Bernoulli vi xác sut thành công (v'
hng) là 0,05. Do ñó, ( )
a/ Đt : “ít nht mt quyn v' hng”
= − = − ≥ ⇔ ≥
( ) ()
Nên phi kim tra ít nht 45 quyn v'.
b/ Vi%c kim tra phát hi%n 3 quyn v' hng suy ra 9 ln kim tra ñu phát hi%n 2
quyn v' hng và ln th 10 phi là v' hng.
Đt :”kim tra dng li ln th 10” ( )
= ( ) = (
= . ) 1.47.
Hp th nht có 8 sn ph(m loi và 2 sn ph(m loi ; hp th hai có 5
sn ph(m loi và 3 sn ph(m loi . Ly ngu nhiên t m i hp ra 2 sn ph(m.
a/ Tính xác sut ñ ñưc 3 sn ph(m loi ;
b/ Gi s# ly ñưc mt sn ph(m loi và 3 sn ph(m loi . Nhiu
kh năng là sn ph(m loi thuc hp nào? Ti sao? Gii
Ly ngu nhiên t m i hp ra 2 sp vi ∈ { }
và ∈ { }
Đt :” ly ñưc sp loi t hp th nht”
:” ly ñưc sp loi t hp th hai”
a/ : “ly ñưc 3 sp loi và 1 sp loi ”
( ) = ( ) + ( ) = + =
b/ Gi ( ln lưt là xác sut ñ sp loi thuc hp th nht và hp ) ( ) th hai 24
Bài tp Xác sut th ng kê Dip Hoàng Ân ( ) Ta có ( ) = = = ( ) ( ) ( ) = = = ( )
Ta thy ( < nên sp loi nhiu kh năng thuc hp th hai. ) ( ) 1.48.
Hp th nht có 8 sn ph(m loi và 2 sn ph(m loi ; hp th hai có 5
sn ph(m loi và 3 sn ph(m loi . Ly ngu nhiên mt hp, ri ly ngu
nhiên t ñó ra 4 sn ph(m.
a/ Tính xác sut ñ ñưc 3 sn ph(m loi ;
b/ Gi s# ly ñưc mt sn ph(m loi và 3 sn ph(m loi . Nhiu
kh năng là sn ph(m loi thuc hp nào? Ti sao? Gii
a/ Ly ngu nhiên ra 1 hp, ri ly ngu nhiên t ñó ra 4 sp Đt
:” ly ñưc hp th ”, ∈ {} suy ra ( = = ) ( )
gi :” ly ñưc 3 sp loi và 1 sp loi ”
() = ( + ) ( ) ( ) ( ) = + = + =
b/ Gi ( ln lưt là xác sut ñ sp loi thuc hp th nht và hp ) ( ) th hai (
) ( )
Ta có ( ) = = = () ( )
( ) ( ) = = = ( )
Thy ( ) > nên sp loi nhiu kh năng thuc hp th nht. ( ) 1.49. 25
Bài tp Xác sut th ng kê Dip Hoàng Ân
Mt nhà máy sn xut linh ki%n ñi%n t# vi 96% sn ph(m có cht lưng
cao. Mt qui trình kim tra cht lưng sn ph(m có ñc ñim: 2% sn ph(m có
cht lưng cao li không ñưc công nhn và 5% sn ph(m không có cht lưng
cao li ñưc công nhn. Hãy tính xác sut ñ sau khi kim tra, mt sn ph(m
ñưc công nhn có cht lưng cao ñúng là sn ph(m có cht lưng cao. Gii
Gi : “sp cht lưng cao” và : “sp ñưc công nhn” ( )
= , ( )
= và ( ) =
() ()− ()
Ta có ( )= = = ( ) ()
suy ra ()= . ()
()− ( )
Li có ( ) = = = () ( ) suy ra ( )
=
Xs ñ 1 sp ñó ñưc công nhn cht lưng cao ñúng là sp cht lưng cao là () ( ) = = = () 1.50.
Gi s# bn ñem giao mt lô hàng, rt nhiu sn ph(m, mà bn bit r"ng nó
có t l% ph ph(m là 10%. Ngưi nhn hàng ñ ngh ly ngu nhiên 6 sn ph(m ñ
kim tra, và nu có quá ph ph(m thì không nhn lô hàng. Bn ñ ngh b"ng
bao nhiêu ñ va thuyt ph,c ñưc ngưi nhn, va hy vng kh năng lô hàng
không b t chi ít nht là 95%? Gii
T l% ph ph(m là =
Vi%c ly ngu nhiên 6 sp ñ kim tra nghĩa là thc hi%n 6 phép th#
Bernoulli vi xs thành công (gp ph ph(m) = (không ñ$i). Ta ñưc ( )
− = Nhn xét:
+ < ( ) ( )
và + + = > ( ) ( ) ( )
nên theo yêu cu bài toán = . 1.51.
Mt khu dân cư A có t l% mc b%nh B là 30%.
a/ Trong mt ñt ñiu tra, ngưi ta chn ngu nhiên 10 ngưi. Tính xác sut
trong ñó có nhiu nht ba ngưi mc b%nh B. 26
Bài tp Xác sut th ng kê Dip Hoàng Ân
b/ Đưc bit trong khu vc ñó có 60% dân s có chích nga b%nh B. T. l%
ngưi kháng b%nh B ñi vi ngưi ñưc chích nga là 95%. Còn t. l% kháng b%nh
B ñi vi ngưi không chích nga là 20%. Chn ngu nhiên mt ngưi thy ngưi
này không mc b%nh B. Tính xác sut ngưi này có chích nga. Gii
Gi : “Ngưi ñưc chn mc b%nh B” ( ) = .
Chn ngu nhiên 10 ngưi là thc hi%n 10 phép th# Bernuolli vi xác sut thành
công (mc b%nh B) ()= (không ñ$i). Ta có ( ) − = .
a/ Xác sut trong ñó có nhiu nht ba ngưi mc b%nh B
+ + + = ( ) ( ) ( ) ( )
= + + + =
b/ :” chích nga b%nh B” ()= ( )
= và ( ) =
Xác sut chn ngu nhiên mt ngưi thy ngưi này không mc b%nh B: ( )
= () ( )
+ () ( ) =
xác sut ngưi này có chích nga: ( )
() ( ) ( ) = = = . () () 1.52.
T l% sn xut ra ph ph(m ca mt máy là 8%. Kho sát mt lô hàng gm 75
sn ph(m do máy ñó sn xut ra.
a/ Tính xác sut ñ trong lô hàng, có 10 ph ph(m
b/ Trong lô hàng, nhiu kh năng nht là có bao nhiêu ph ph(m? Tính xác sut tương ng. Gii
Nu xem vi%c máy sn xut ra mt sn ph(m là mt phép th# Bernoulli, vi
xác sut cho “thành công” là p = 0,08 , thì khi máy ñó sn xut 75 sn ph(m, nó ñã
thc hi%n quá trình P ; k 0,08 75 ( ) a/ Xác sut phi tính: 10 10 65 7
P 5 10 = C75 0 08 0 92 = 0 03941
b/ S ph ph(m nhiu kh năng nht trong lô hàng là: (75 +1).0,08 = 6
vi xác sut tương ng: 27
Bài tp Xác sut th ng kê Dip Hoàng Ân 6 6 69
P (6) = C (0,08) .(0,92) = 0,16745 75 75 1.53.
Ngưi ta mun ly ngu nhiên mt s ht ging t mt lô ht ging có t l%
ht lép là 3% ñ nghiên cu. Hi phi ly ít nht bao nhiêu ht sao cho xác sut
ñ có ít nht mt ht lép không bé hơn 95% ?. Gii
Gi n là s ht phi ly, chúng ta có P k
. Xác sut ñ có ít nht mt ht n ( ; 0, 03) lép là 1 1 ( 0,03) 1 (0,97 )n n − − = − .
Theo gi thit, chúng ta có: n n ln 0,05
1 − (0,97 ) ≥0,95 ⇔ (0,97 ) ≤ 0,05 ⇔ n ≥ = 98,3523 ln 0, 97
Vy, phi ly ít nht 99 ht ging. 28
Bài tp Xác sut th ng kê Dip Hoàng Ân
CHƯƠNG 2: BIN NGU NHIÊN 2.1. Có ba hp
và ñng các l thuc. Hp có 10 l tt và 5 l hng,
hp có 6 l tt và 4 l hng, hp có 5 l tt và 7 l hng. Ly ngu nhiên t
m i hp ra mt l thuc.
a/ Tìm lut phân phi xác sut cho s l thuc tt trong 3 l ly ra.
b/ Tìm xác sut ñ ñưc ít nht 2 l tt; ñưc 3 l cùng loi. Gii
Gi là bin ngu nhiên ch s l thuc tt trong 3 l ly ra
= { }
a) : “ l thuc ly ra t hp th là l tt”. ( = )
= = = ( ) ( ) ( ) ( = ) =
+ + = ( = ) =
+ + = ( = )
= = = ( ) ( ) ( )
Bng phân phi xác sut ca 0 1 2 3
( )
b) Xác sut ñ ñưc ít nht 2 l tt
( ≥ ) = ( = ) + ( = ) =
Xác sut ñưc 3 l cùng loi
( = ) + ( = ) = 2.2.
Trong mt ñi tuyn, 3 vn ñng viên
và thi ñu vi xác xut thng
trn ca m i ngưi ln lưt là 0,6; 0,7 và 0,8. Trong mt ñt thi ñu, m i vn ñng
viên thi ñu mt trn ñc lp nhau.
a/ Tìm lut phân phi xác sut cho s trân thng ca ñi tuyn.
b/ Tính xác sut ñ ñi tuyn thua nhiu nht mt trn. Tính xác sut ñ
ñi tuyn thng ít nht mt trn. Gii
a/ Gi là bin ngu nhiên ch s trn thng ca ñi tuyn. 29
Bài tp Xác sut th ng kê Dip Hoàng Ân
= { }
Gi : “Vn ñng viên thng”
: “Vn ñng viên thng”
: “Vn ñng viên thng” Ta có
( = ) =
= ( )
= = ( = ) = + +
=
( = )= + +
=
( = )=
= ( )
=
Bng phân phi xác sut : 0 1 2 3
( )
b/ Xác sut ñ ñi tuyn thua nhiu nht mt trn:
( ≥ ) = ( = )+ ( = ) =
Xác sut ñ ñi tuyn thng ít nht mt trn : ( ≥ )
= − ( = ) = 2.3.
Trong mt ñi tuyn, 3 vn ñng viên
và thi ñu vi xác xut thng
trn ca m i ngưi ln lưt là 0,6; 0,7 và 0,8. Trong mt ñt thi ñu, m i vn ñng
viên thi ñu mt trn ñc lp nhau.
a/ Tìm lut phân phi xác sut cho s trân thng ca ñi tuyn.
b/ Sau ñt thi ñu, ñi tuyn có hai trn thng; tính xác sut ñ A thua trn. Gii
a/ Gi là bin ngu nhiên ch s trn thng ca ñi tuyn.
= {}
Gi : “Vn ñng viên thng”;
: “Vn ñng viên thng”;
: “Vn ñng viên thng” Ta có
( = ) =
= ( )
= = ( = ) =
+
+
=
( = )= + +
=
( = )=
= ( )
=
Bng phân phi xác sut : 30
Bài tp Xác sut th ng kê Dip Hoàng Ân 0 1 2 3
( )
b/ Xác sut ñ thua trn, bit r"ng ñi tuyn có hai trn thng (
{ = }) ( ) ( = )
= = = = ( = ) ( = ) 2.4.
Trong mt ñi tuyn, 3 vn ñng viên
và thi ñu vi xác xut thng
trn ca m i ngưi ln lưt là 0,6; 0,7 và 0,8. Trong mt ñt thi ñu, m i vn ñng
viên thi ñu mt trn ñc lp nhau.
a/ Tìm lut phân phi xác sut cho s trân thng ca ñi tuyn.
b/ Tính s trn thng trung bình và phương sai ca s trn thng ca ñi tuyn. Gii
a/ Gi là bin ngu nhiên ch s trn thng ca ñi tuyn.
= { }
Gi : “Vn ñng viên thng”;
: “Vn ñng viên thng”;
: “Vn ñng viên thng” Ta có
( = ) =
= ( )
= = ( = ) = + +
=
( = )= + +
=
( = )=
= ( )
=
Bng phân phi xác sut : 0 1 2 3
( )
b/ S trn thng trung bình
= + + + =
và phương sai ca s trn thng ca ñi tuyn
() = ( ) − ( ) = Trong ñó, ( )
= + + + = . 2.5.
Mt cơ s' sn xut các bao k/o. S k/o trong m i bao là mt bin ngu
nhiên có phân phi xác sut như sau: 31
Bài tp Xác sut th ng kê Dip Hoàng Ân
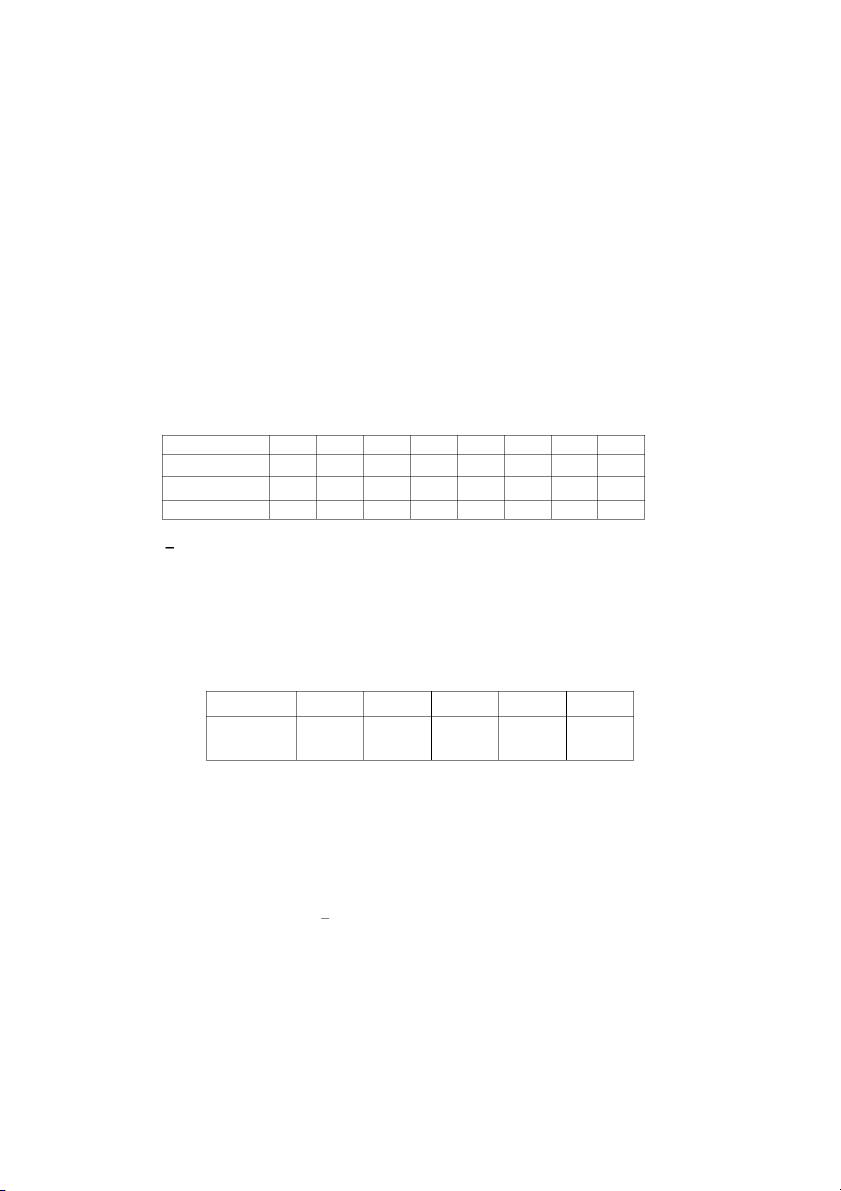
S k/o trong bao 18 19 20 21 22 Xác sut 0,14 0,24 0,32 0,21 0,09
a/ Tìm trung bình và phương sai ca s viên k/o trong m i bao.
b/ Chi phí sn xut ca m bao k/o là 3X + 16, trong ñó X là bin ngu
nhiên ch s k/o trong bao. Tin bán m i bao k/o là 100$. Không phân bi%t s k/o
trong bao. Tìm li nhun trung bình và ñ l%ch chu(n ca li nhun cho m i bao k/o. Gii
Gi là bin ngu nhiên ch s k/o trong bao.
a/ Trung bình và phương sai ca s viên k/o trong m i bao : () =
∑ ( = ) = =
và phương sai ca s viên k/o trong m i bao:
() = ( )− () =
b/ Gi là bin ngu nhiên ch li nhun cho m i bao k/o. Ta có:
= − li nhun trung bình
() = ( − )= − ( )=
và ñ l%ch chu(n ca li nhun cho m i bao k/o
σ ( )= ( )= (− ) = ( ) = 2.6.
Mt cơ s' sn xut các bao k/o. S k/o trong m i bao là mt bin ngu
nhiên có phân phi xác sut như sau:
S k/o trong bao 18 19 20 21 22 Xác sut 0,14 0,24 0,32 0,21 0,09
a/ Tìm xác sut ñ mt bao k/o ñưc chn ngu nhiên s+ cha t 19 ñn 21 viên k/o.
b/ Hai bao k/o ñưc chn ngu nhiên. Tính xác sut ñ ít nht mt trong
hai bao cha ít nht 20 viên k/o. Gii
Gi là bin ngu nhiên ch s k/o trong bao.
a/ Xác sut ñ bao ñưc chn ngu nhiên có t 19 ñn 21 viên k/o:
≤ ≤ = ( = ) + ( = )
+ ( = ) =
b/ Đt : “Bao cha ít nht 20 viên k/o” ( )
= + + =
Xác sut ñ ít nht mt trong hai bao cha ít nht 20 viên k/o: 32
Bài tp Xác sut th ng kê Dip Hoàng Ân
(+ ) = ( ) + ( )= ( ) + ( ) ( )
= 2.7.
Mt hp ñng 5 sn ph(m, trong ñó có hai ph ph(m. Ngưi ta ln lưt
kim tra tng sn ph(m (không hoàn li) cho ñn khi gp hai ph ph(m thì dng
li. Tìm lut phân phi xác sut cho s sn ph(m ñưc kim tra. Tính s ln kim tra trung bình. Gii
Goi là BNN ch s s sn ph(m kim tra.
= { }
:“ ln kim tra ln th ñưc ph ph(m”.( = )
( = ) = (
= = ) ( ) ( ) ( = )
= ( + ) ( ) = ( )
+ = ( ) ( )
( ) ( ) ( ) Tương t ( = ) = ( = ) =
Bng phân phi xác sut : 2 3 4 5
()
S ln kim tra trung bình: ()=
∑ ( = )= = 2.8.
Mt ngưi ñiu khin 3 máy t ñng hot ñông ñc lp vi nhau. Xác sut
b hng trong mt ca sn xut ca máy 1,2 và 3 ln lưt là 0,1; 0,2 và 0,3.
a/ Lp bng phân phi xác sut cho s máy hot ñng tt trong mt ca sn xut.
b/ Sau sn xut, ngưi ñiu khin báo r"ng sut ca ch có mt máy hot
ñng tt. Tính xác sut ñ máy hot ñng tt ñó là máy mt. Gii
a/ Gi là BNN ch s máy hot ñng tt trong 1 ca sn xut.
= { }
Đt “ máy th b hng trong 1 ca”. Suy ra,
( = = = ) ( ) ( )
( = ) = ( = = = ) ( ) ( ) ( ) 33
Bài tp Xác sut th ng kê Dip Hoàng Ân
( = )= ( + ) ( ) ( )
+ ( ) + = ( ) ( ) ( ) ( ) ( )
( = ) = ( + ) ( ) ( )
+ ( + = ) ( ) ( ) ( ) ( ) ( )
( = ) = ( = = ) ( ) ( ) ( )
Bng phân phi xác sut ca : 0 1 2 3
()
b/ Xác sut ñ máy hot ñng tt ñó là máy mt, bit r"ng sut ca ch có mt máy hot ñng tt.
( =
{ }) ( ) (
= = = = = ) ( = ) ( = ) 2.9.
Mt ngưi ñiu khin 3 máy t ñng hot ñông ñc lp vi nhau. Xác sut
b hng trong mt ca sn xut ca máy 1,2 và 3 ln lưt là 0,1; 0,2 và 0,3.
a/ Lp bng phân phi xác sut cho s máy hot ñng tt trong mt ca sn xut.
b/ Trung bình, trong mt ca, có bao nhiêu máy hot ñng tt? Tính ñ
l%ch chu(n ca s máy hot ñng tt trong mt ca sn xut. Gii
a/ Gi là BNN ch s máy hot ñng tt trong 1 ca sn xut.
= {}
Đt “ máy th b hng trong 1 ca”. Suy ra,
( = = = ) ( ) ( )
( = ) = ( = = = ) ( ) ( ) ( )
( = )= ( + ) ( ) ( )
+ ( ) + = ( ) ( ) ( ) ( ) ( )
( = ) = ( + ) ( ) ( )
+ ( + = ) ( ) ( ) ( ) ( ) ( )
( = ) = ( = = ) ( ) ( ) ( )
Bng phân phi xác sut ca : 0 1 2 3
() 34
Bài tp Xác sut th ng kê Dip Hoàng Ân
b/ Trung bình s máy hot ñng tt trong mt ca: ( )=
và ñ l%ch chu(n ca s máy hot ñng tt trong mt ca sn xut .
σ () = 2.10.
Mt công ty có 3 t$ng ñi lý. Gi và theo th t là khi lưng hàng
bán ñưc trong mt này ca 3 t$ng ñi lý trên (tính b"ng tn). Bit phân phi xác
sut ca các BNN và như sau: 5 6 7 8
( = 0,1 0,3 0,4 0,2 ) 4 5 6 7 8
( = 0,15 0,2 0,4 0,1 0,15 ) 7 8 9 10
( = 0,2 0,3 0,4 0,1 )
Tính khi lưng hàng hóa bán ñưc trung bình trong mt tháng (30 ngày) ca công ty trên. Gii
Trung bình khi lưng hàng hóa C bán ñưc trong 1 tháng. ( ) =
∑ = = ( ) =
Trung bình khi lưng hàng hóa bán ñưc trong 1 tháng.
() =
= = ∑ ( ) =
Trung bình khi lưng hàng hóa bán ñưc trong 1 tháng.
() =
∑ = = ( ) =
Nên khi lưng hàng hóa bán ñưc trung bình trong 1 tháng ca công ty là ( )
+ ( ) + ( ) = 2.11.
Tin hành kho sát s khách trên mt chuyn xe buýt (SK/1C) ti mt
chuyn giao thông, ngưi ta thu ñưc s liêu sau: SK/1C 25 30 35 40 45
Xác sut 0,15 0,2 0,3 0,25 0,1
a/ Tính kỳ vng và ñ l%ch chu(n ca SK/1C.
b/ Gi s# chi phí cho m i chuyn xe buýt là 200 ngàn ñng, không ph,
thuc vào s khách ñi trên xe, th2 công ty phi quy ñnh giá vé là bao nhiêu ñ có
th thu ñưc s tin li trung bình cho m i chuyn xe là 100 ngàn ñng? 35
Bài tp Xác sut th ng kê Dip Hoàng Ân Gii
Gi là BNN ch s khách trên mt chuyn xe. = {} a/ Kỳ vng ca SK/1C: (
) =
Đ l%ch chu(n ca SK/1C.: σ ( )= () = ( )− ( ) =
b/ Gi là BNN ch s tin li cho m i chuyn xe.
= −
trong ñó, (ñng) là s tin quy ñnh giá vé.
Yêu cu bài toán, ( ) = ( −) = ⇔ ( ) = ⇔ ≈ .
Vy, công ty phi quy ñnh giá vé là 8,6 ñng. 2.12.
Mt ngưi tham gia trò chơi gieo 3 ñng tin vô tư. Anh ta ñưc 500ñ nu
xut hi%n 3 mt sp, 300ñ nu xut hi%n 2 mt sp, và 100ñ nu ch có mt mt sp
xut hi%n. Mc khác, anh ta mt 900ñ nu xut hi%n 3 mt nga. Trò chơi này có
công băng vi ngưi này không? ( Trò chơi ñưc gi là công b"ng ñi vi ngưi
chơi nu tham gia chơi nhiu ln thì trung bình anh ta hòa vn). Gii
Gi là bin ngu nhiên ch s tin nhn ñưc khi tham gia trò chơi = {
− }
Đt :”Gieo ln th xut hi%n mt sp” ∈ {} ( = − ) = (
= = ) ( ) ( ) ( ) ( = ) = (
+ + = = ) ( ) ( )
Tương t, ( = )
= = =
Bng phân phi xác sut ca -900 100 300 500 ()
Và ( ) =
nên m i ln chơi anh ta thng ñưc 100ñ. Vy trò chơi không công b"ng. 2.13.
Mt ngưi tham gia trò chơi sau: Gieo mt con xúc xc vô tư ba ln ñc lp
nhau. Nu xut hiên “ mt 1” c 3 ln thì ñưc thư'ng 6 ngàn ñng; nu xut hi%n
“ mt 1” 2 ln thì ñưc thư'ng 4 ngàn ñng; xut hi%n “mt 1” 1 ln thì ñưc
thư'n 2 ngàn ñng; khi không có “mt 1” nào xut hi%n thì không ñưc thư'ng.
M i ln tham gia trò chơi, ngưi chơi phi ñóng ngàn ñng. Hãy ñnh ñ trò chơi công b"ng. 36
Bài tp Xác sut th ng kê Dip Hoàng Ân Gii
Gi là BNN ch s tin còn li sau m i ln tham gia trò chơi.
= { − − − } Ta có
= − = =
; = − = =
= − = = ;
= =
Bng phân phi xác sut ca
− − − ()
và ( ) = − . ( )
Trò chơi công b"ng ( ) = ⇔ − = ⇔ = .
Vy, m i ln chơi ngưi tham gia ñóng 1 ngàn ñng thì trò chơi công b"ng. 2.14.
Theo thng kê dân s, xác sut ñ mt ngưi ' ñ tu$i 40 s+ sng thêm 1
năm na là 0,995. Mt công ty bo him nhân th bán bo him mt năm cho
nhng ngưi ' ñ tu$i ñó là 10 ngàn, và trong trưng hp ngưi mua bo him b
cht thì s tin bi thưng là 1 tri%u. Hi li nhun trung bình ca công ty khi bán
m i th bo him là boa nhiêu? Gii
Gi là BNN ch li nhun ca công ty khi bán m i th bo him.
= {−}
Bng phân phi xác sut ca −
( )
và ( ) = .
Vy, trung bình công ty li 5 ngàn ñng khi bán 1 th bo him. 2.15.
S lưng xe ô tô mà mt ñi lý bán ñưc trong mt tun là mt BNN có
phân phi xác sut như sau: S xe bán ñưc 0 1 2 3 4 5 Xác sut tương ng 0,1 0,1 0,2 0,2 0,3 0,1
a/ Tính xác sut ñ ñi lý ñó bán ñưc nhiu nht 3 xe trong mt tun.
Tính kỳ vng và phương sai ca s xe mà ñi lý bán ñưc trong mt năm. 37
Bài tp Xác sut th ng kê Dip Hoàng Ân
b/ Gi s# chi phí cho hot ñng ca ñi lý b"ng căn bc hai ca s xe bán
ñưc vi 5 (tri%u ñng). Tìm chi phí cho hot ñng trung bình cho hot ñng ca
ñi lý trong mt tun.
Gi X là BNN s xe bán ra trong 1 tun.
a/ Xác sut ñ ñi lý ñó bán ñưc nhiu nht 3 xe trong mt tun P ( X ≤ )
3 = 1− P (X = 4)− P (X = 5) = 0,6
Kỳ vng và phương sai ca s xe mà ñi lý bán ñưc trong mt năm.
E ( X ) = 2,8;D (X )= 2,16
b/ Gi là chi phí cho hot ñng ca ñi lý trong 1 tun Y = X + 5
Nên chi phí cho hot ñng trung bình cho hot ñng ca ñi lý trong mt tun
E(Y) = E( X ) + 5= 6,55 2.16. 2x , x ∈ [0; ] 1 Cho hàm f (x) = 0 , x ∉ [0;1]
a/ Chng t f (x) là hàm mt ñ xác sut ca mt bin ngu nhiên liên t,c X .
b/ Tìm hàm phân phi xác sut F (x) ca X 1
c/ Tính xác sut P 0 < X < . 2 Gii +∞ 1 1
a/ f (x) ≥ 0,∀x∈ và 2
f (x)dx = 2xdx x = = 1 ∫ ∫ . Do ñó, f ( )
x là hàm mt ñ xác 0 −∞ 0
sut ca mt bin ngu nhiên liên t,c X . 0 , x ≤ 0 x b/ F ( ) 2
x = ∫ f (t)dt = x ,0 < x ≤1 −∞ 1 , x 1 > 1 2 1 1
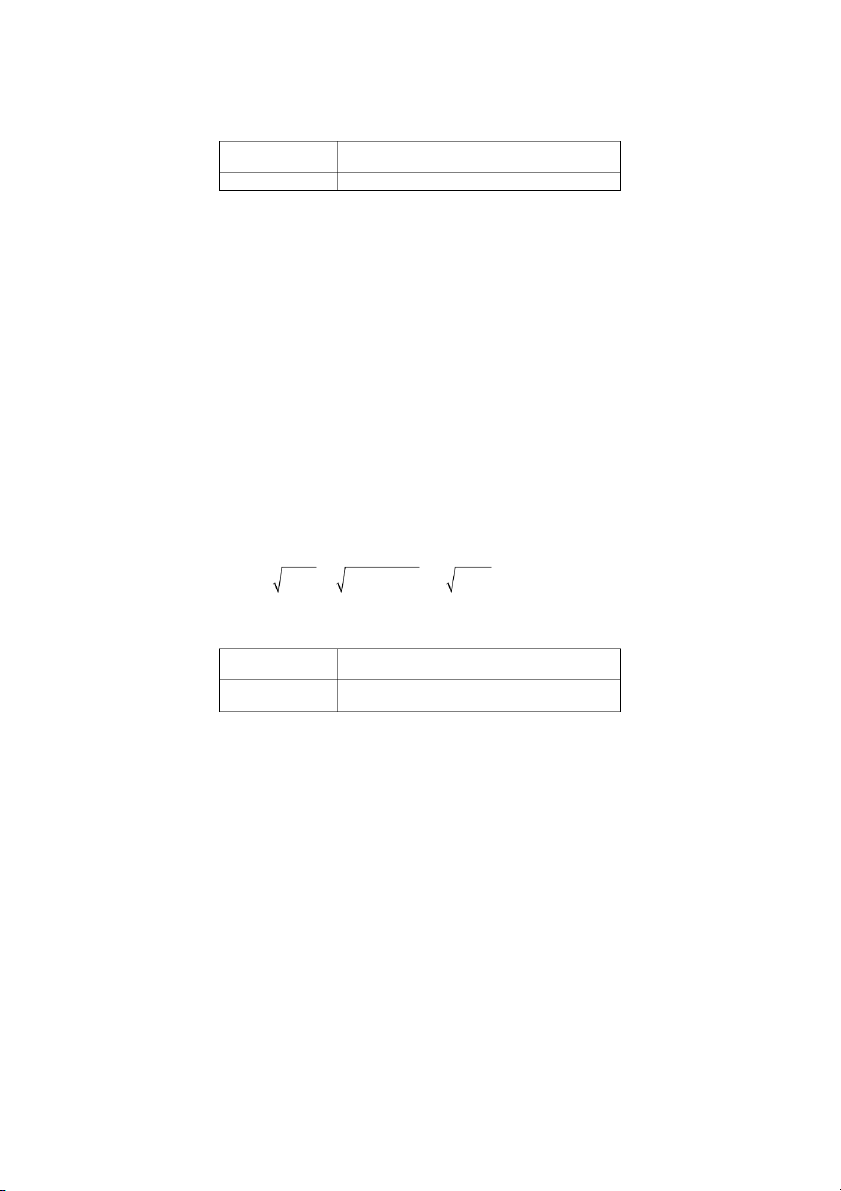
c/ P 0 < X < = 2 xdx = ∫ . 2 4 0 2.17. 2 , x >1 Cho hàm 3 f (x) = x 0 , x ≤1
a/ Chng t f (x) là hàm mt ñ xác sut ca mt bin ngu nhiên liên t,c X
b/ Tìm hàm phân phi xác sut F (x) ca X .
c/ Tính xác sut P(0 < X < ) 3 Gii 38
Bài tp Xác sut th ng kê Dip Hoàng Ân +∞ +∞ 2 1 b
a/ f (x) ≥ 0,∀x∈ và ∫ f (x)dx = ∫ dx = − 2 lim
= 1 . Do ñó, f (x) là 3 2 b x →+∞ 2x 1 −∞ 1
hàm mt ñ xác sut ca mt bin ngu nhiên liên t,c X . 0 , x ≤ 1 x 1 b/ F ( x) =
f (t )dt = 1− ,1< x < +∞ ∫ 2 x −∞ 1 , x = +∞ 3 8
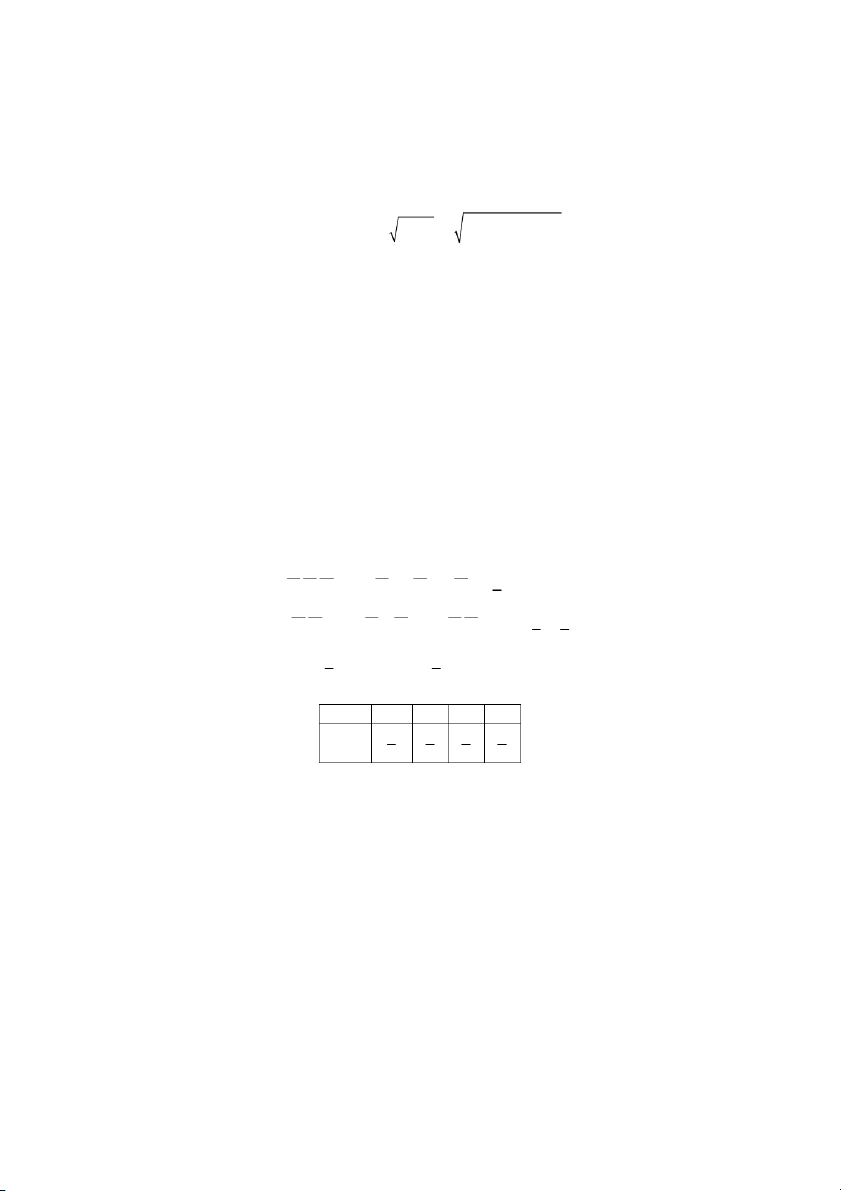
c/ P(0 < X < 3) = f ( ) x dx = ∫ . 9 0 2.18. a , x >1 Cho hàm 3 f (x) = x ( a là h"ng s) 0 , x ≤1
a/ Tìm a ñ f (x) là hàm mt ñ xác sut ca mt bin ngu nhiên liên t,c X
b/ Tìm hàm phân phi xác sut F (x) ca X . Gii a/ x ∀ R
∈ , f (x ) ≥ 0 ⇔a ≥ 0 và +∞ +∞ a 1 b a
∫ f (x)dx = ∫ dx = − a lim =
. Do ñó, f (x) là hàm mt ñ xác sut ca 3 2 b x →+∞ 2x 1 2 −∞ 1 a ≥ 0
mt bin ngu nhiên liên t,c X khi và ch khi ⇔ a a = 2 . 1 = 2 0 , x ≤ 1 x 1 b/ F ( x) =
f (t )dt = 1− ,1< x < +∞ ∫ 2 x −∞ 1 , x = +∞ 2.19.
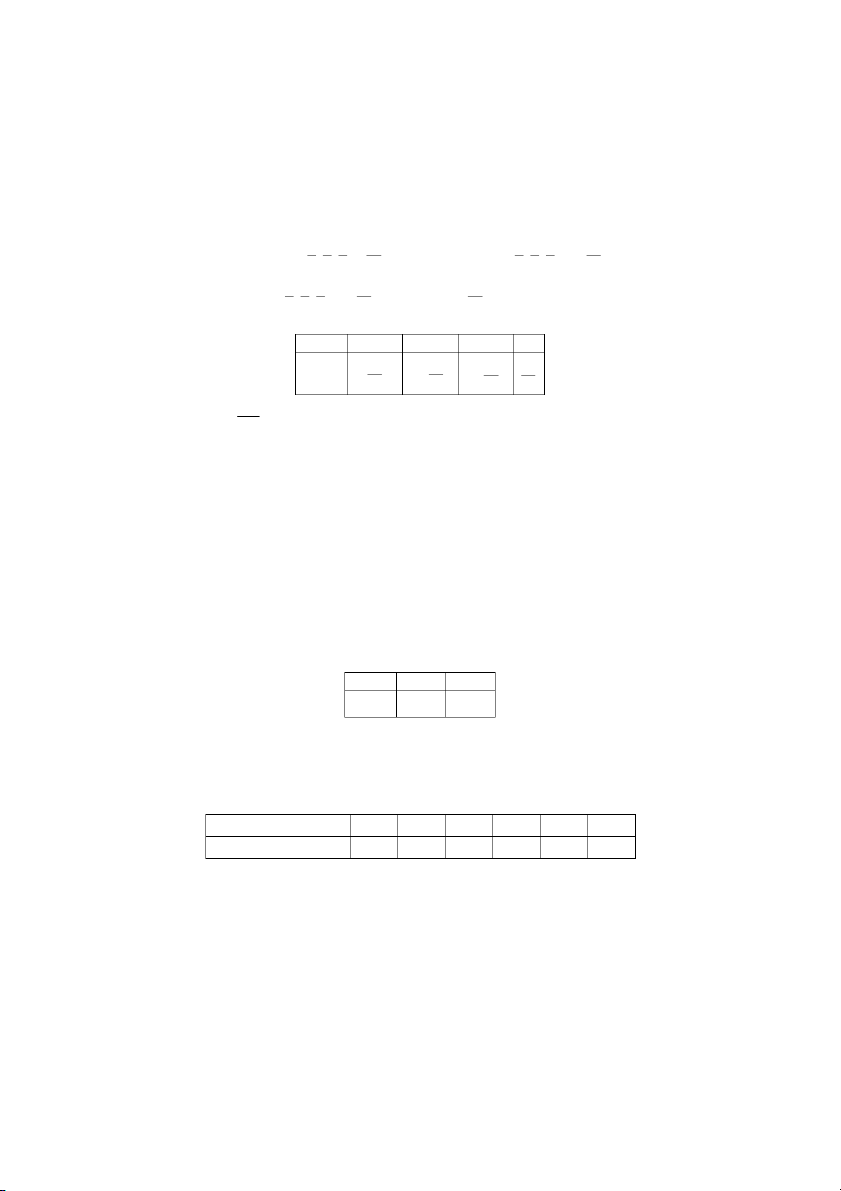
Cho X là bin ngu nhiên liên t,c có hàm mt ñ 2x , x [ ∈ 0;1] f (x) = 0 , x [ ∉ 0; ] 1
Tìm kỳ vng và phương sai ca X . Gii +∞ 1 2 E ( X ) 2 = xf ( ) x dx = 2 x dx = ∫ ∫ 3 −∞ 0 +∞ 1 E ( 1 2 X ) 2 3 =
x f (x)dx = 2x dx = ∫ ∫ 2 −∞ 0 do ñó, 39
Bài tp Xác sut th ng kê Dip Hoàng Ân 1 4 1
D( X) = E ( X ) − (E( X) )2 2 = − = 2 9 18 2.20.
Cho X là bin ngu nhiên liên t,c có hàm mt ñ 2 3x , x [ ∈ 0; ] 1 f (x) = 0 , x [ ∉ 0; ] 1
Tìm kỳ vng và phương sai ca X . Gii +∞ 1 3 E ( X ) 2 = xf ( ) x dx = 3x dx = ∫ ∫ 4 −∞ 0 +∞ 1 E ( 3 2 X ) 2 4 =
x f (x)dx = 3x dx = ∫ ∫ 5 −∞ 0 do ñó, 3 9 3
D( X ) = E ( X ) − (E( X ) )2 2 = − = . 5 16 80 40
Bài tp Xác sut th ng kê Dip Hoàng Ân
Chương 3: MT S PHÂN PHI THƯNG DÙNG 3.1.
Mt ki%n hàng có 10 sn ph(m, trong ñó có 8 sn ph(m loi A. Ly ngu
nhiên 2 sn ph(m. Đt X là bin ngu nhiên ch s sn ph(m loi A có trong các
sn ph(m ly ra. Tìm lut phân phi xác sut ca X . Tính E( X ) ,D( X ) . Gii
Gi X là BNN ch s sn ph(m loi A trong các sn ph(m ly ra ln th nht. Im X = {0;1; } 2 k k− 2 C .C M
Ta có X ~ H (10;8;2) ta có 8 2
P(X = k ) = ; p = = 0,8 2 C N 10 N − n 64
Nên E( X ) = np = 1,6; D( X ) = np(1− p) = . N 1 − 225 3.2.
Có 2 ki%n hàng, ki%n th nht và ki%n th 2. Bit r"ng, ki%n th hai có 8 sn
ph(m, trong ñó có 5 sn ph(m loi A. Ln ñu, ly ngu nhiên 2 sn ph(m ' ki%n
th nht b vào ki%n th hai, sau ñó ly ngu nhiên t ki%n th hai ra 2 sn ph(m.
Đt X và Y ln lưt là bin ngu nhiên ch s sn ph(m loi A có trong các sn
ph(m ly ra ' ln th nht và ln th hai. Bit r"ng bng phân phi xác sut ca 0 1 2
( )
Tìm lut phân phi xác sut ca Y ; tính E (Y ) và D (Y ) . Bài gii
Gi Y là BNN ch s sn ph(m loi A trong các sn ph(m ly ra ln th hai. ImY = {0;1; } 2 1 16 28
Ta thy P (X = 0) = ;P (X = 1) = ; P ( X = 2) = 45 45 45 Trong ñó, 0 2 C .C 10 6 3
P(Y = 0 | X = 0) 5 5 = =
; P Y = 0 | X =1 =
; P Y = 0 | X = 2 = 2 ( ) ( ) C 45 45 45 10 Mt khác 41
Bài tp Xác sut th ng kê Dip Hoàng Ân
P (Y = 0) = P (X =0).P (Y = 0 | X = 0) + P ( X = )
1 .P (Y = 0 | X =1) 190
+ P (X = 2 ).P (Y = 0 | X = 2 ) = 2025 997 838
Tương t P (Y = ) 1 = ; P (Y = 2) = . 2025 2025
Bng phân phi xác sut ca Y Y 0 1 2 190 997 838 P (Y ) 2025 2025 2025 2673 Nên E(Y) =
= 1,32; D( X ) = 0,40525. 2025 3.3.
Mt ki%n hàng cha 8 sn ph(m, trong ñó có 3 sn ph(m xu và 5 sn ph(m
tt. Ly ngu nhiên t ki%n hàng ra 4 sn ph(m (không hoàn li).
a/ Hãy lp bng phân phi xác sut cho s sn ph(m xu có trong 4 sn
ph(m ly ra, và tính xác sut ñ trong ñó có ít nht 2 sn ph(m tt.
b/ Đem 4 sn ph(m va ly ra ñi bán. Bit r"ng bán mt sn ph(m tt ñưc
li 50 ngàn ñng, và bán mt sn ph(m xu b l 15 ngàn ñng. Tính li nhun thu
ñưc trung bình và ñ l%ch chu(n ca li nhun khi bán 4 sn ph(m trên. Gii
a/ Gi X là BNN ch s sn ph(m xu có trong 4 sn ph(m ly ra. Im X = {0;1;2; } 3 0 4 1 3 2 2 C .C 1 C .C 6 C .C 6 P( X = 0) 3 5 = = ;P( X = ) 3 5 1 = = ; P( X = 2) 3 5 = = ; 4 4 4 C 14 C 14 C 14 8 8 8 3 1 C .C 1 P( X = ) 3 5 3 = = 4 C 14 8
Bng phân phi xác sut ca X X 0 1 2 3 1 6 6 1 P (X ) 14 14 14 14 13
Xác sut ñ có ít nht 2 sn ph(m tt: ( P X ≤ 2) =1− ( P X = ) 3 = . 14
b/ Gi Y là BNN ch li nhun thu ñưc khi bán 4 sn ph(m. Y = 200 − 65X 6 6 1 15
khi ñó E ( X ) = + 2. + 3.
= 1,5; D ( X ) = E ( X ) − E( X )2 2 = 14 14 14 28 42
Bài tp Xác sut th ng kê Dip Hoàng Ân
E(Y ) = E( 200 − 65X ) = 200 − 65E( X ) = 102,5 và
σ(Y ) = D(Y) = D(200 −65 X ) = 65 D( X ) = 47,5735 3.4.
Mt lô hàng có rt nhiu sn ph(m, vi t l% hàng gi là 30%.
a/ Ly ngu nhiên t lô hàng ra 10 sn ph(m, tính xác sut ñ có nhiu nht 2 sn ph(m gi.
b/ Ngưi ta ly ngu nhiên ra t ng sn ph(m mt ñ kim tra cho ñn khi
nào gp sn ph(m gi thì dng. Tìm lu t phân phi xác su t và tính kỳ v ng ca s
sn ph(m tht ñã kim tra Gii
Gi p là xác sut ch hàng gi trong 1 lô hàng nên p = 0,3.
a/ Gi X là BNN ch s sn ph(m gi. X B(10;0,3)
Xác sut ñ có nhiu nht 2 s n ph(m gi
P (X ≤ 2) = P( X = 0) + P( X = 1)+ P( X = 2) 10 9 2 8
= 0,7 + 0,3.0,7 + 0,3 .0,7 = 0,0455
b/ Gi Y là BNN ch s sn ph(m tht ñã kim tra. 1
Ta có Im Y = 0;1;2;... Ta thy P Y = 0 = 0,3;P Y = 1 = 0,7.0,3 theo quy np 1 { } ( 1 ) ( 1 ) ( = = 0,7n P Y n .0,3. 1 )
Nên kỳ vng c a s s n ph(m tht ñã kim tra: +∞ +∞ 1 7 E (Y ) = ∑ .
n P (Y = n) n− 1 = 0,7.0,3 ∑ . n 0,7 = 0,21. 1 1 = n= n= (1− 0,7)2 0 1 3 3.5.
Mt lô hàng có rt nhiu sn ph(m, vi t l% hàng gi là 30%.
a/ Ly ngu nhiên t lô hàng ra 10 sn ph(m, tính xác sut ñ có nhiu nht 2 sn ph(m gi.
b/ Ngưi ta ly ngu nhiên ra t ng sn ph(m mt ñ kim tra cho ñn khi
nào gp sn ph(m gi thì dng. Tìm lu t phân phi xác su t và tính kỳ v ng ca s sn ph(m ñã kim tra. Gii
Gi p là xác sut ch hàng gi trong 1 lô hàng nên p = 0,3.
a/ Gi X là BNN ch s sn ph(m gi. X B(10;0,3)
Xác sut ñ có nhiu nht 2 s n ph(m gi 43
Bài tp Xác sut th ng kê Dip Hoàng Ân
P (X ≤ 2) = P( X = 0) + P( X = 1)+ P( X = 2) 10 9 2 8
= 0,7 + 0,3.0,7 + 0,3 .0,7 = 0,0455
b/ Gi Y là BNN ch s sn ph(m ñã kim tra. 2
Ta có Im Y = 1;2;3;... 2 { }
P (Y = 1 = 0,3; P Y = 2 = 0,7.0,3 theo quy np ( 0,7n P Y n − = = .0,3 . 2 ) 1 2 ) ( 2 )
Nên kỳ vng c a s s n ph(m ñã kim tra: +∞ +∞ n − 1 10
E (Y ) = ∑n.P (Y = n) 1 = ∑ . n 0,7 .0,3 = 0,3. 2 2 = n = n = (1− 0, )2 1 1 7 3 3.6.
Mt khách hàng mua xe ti m t ñi lý, nu xe có s c k4 thut thì ñưc
quyn tr xe trong vòng 3 ngày sau khi mua và ñưc ly li nguyên s tin mau
xe. M i chic xe b tr li như th làm thi%t hi cho ñi lý 250 ngàn VNĐ. Có 50
xe ñưc bán ra. Xác sut ñ mt xe b tr li là 0,1.
a/ Tìm kỳ vong và phương sai c a s xe b tr . Tính xác xut ñ có nhiu nht 2 xe b tr li.
b/ Tìm kỳ vng và ñ l%ch chu(n ca t$ ng thi%t hi mà t$ng ñi lý phi chu do vi%c tr li xe. Gii
Gi p là xác sut ñ mt xe b tr li. Nên p = 0,1.
Gi X là BNN ch s xe b tr li. X B(50;0, ) 1
ta thy ( n = 50 > 30;n.p = 5 ≤ 5;npq = 4,5 ≤ 5 ) nên X Po (5)
Suy ra E (X ) = np = 5;D (X ) = np (1− p) = 4,5.
Xác sut nhiu nht 2 xe b tr li:
P (X ≤ 2) = Po (5) + Po (5) + Po (5) = 0,1246 (0 ) (1 ) (2 )
b/ Gi Y là BNN ch t$ng thi%t hi c a ñi lý phi chu do vi%c tr li xe. Y = 250X
suy ra E (Y ) = E (250X ) = 250E ( X ) =1250 và
σ(Y ) = D(Y) = D(250 X ) = 250 D( X ) = 530,330 3.7.
Mt thí sinh tên M tham d mt kỳ thi môn XSTK . M phi làm mt ñ thi
trc nghi%m khách quan gm 10 câu; m i câu có 4 li Gii khác nhau, trong ñó ch
có m t li Gii ñúng. M s+ ñưc chm ñu nu tr li ñúng ít nht 6 câu.
(a) Gi s# M không hc bài, mà ch chn ngu nhiên li Gii trong c 10
câu. Tính xác sut ñ M thi ñu.
(b) Gi s M chc ch n tr li ñúng ñưc 2 câu; còn các câu khác, M chn
ngu nhiên mt trong 4 li Gi i ca mi câu. Tính xác sut ñ M thi rt. 44
Bài tp Xác sut th ng kê Dip Hoàng Ân Gi i
Gi p là xác sut ñ M tr l i ñúng mt câu hi. Nên p = 0,25.
Gi X là BNN ch s câu tr li ñúng trong 10 câu. X B (10;0,25) .
Đt A :”M thi ñu”
P (A) = P (X ≥ 6)= P (X = 6) + P (X = 7)+
+ P( X = 8 ) + P( X = 9 ) + P( X =10 ) = 0,0197
b/ M chc chn tr li dung 2 câu, mà các câu ñưc ñc lp nhau và xác sut tr li dung m i câu là 0,25.
Do ñó, Xác sut ñ M rt trong trưng hp tr li ñúng 2 câu có ngh ĩa là ta tính xác sut ñ M rt tro
Gi Y là BNN ch s câu tr li ñúng trong 8 câu. Y B(8;0,25) .
Đt R :” M thi rt”
P (R) = P (Y ≤ )
3 = P (Y = 0 )+ P (Y = ) 1 + P (Y = ) 2 + P (Y = 3) 0 0 8 3 3 5
= C 0,25 0,75 + ... + C 0, 25 0,75 = 0,8862. 8 8 3.8.
Mt thí sinh M tham d mt kỳ . M phi làm mt ñ thi trc nghi% m khách
quan gm 10 câu; m i câu có 4 li Gii khác nhau, trong ñó ch có mt li Gii
ñúng. M s+ ñưc chm ñu nu tr li ñúng ít nht 6 câu.
a/ Gi s# M không hc bài, mà ch chn ngu nhiên li Gii trong c 10
câu. Tính xác sut ñ M thi ñu.
b/ Hi M phi d thi ít nht my l n ñ xác sut có ít nht mt ln thi ñu không nh hơn 97%? Gi i
a/ Gi p là xác sut ñ M tr li ñúng mt câu hi. Nên p = 0,25 .
Gi X là BNN ch s câu tr li ñúng trong 10 câu. X B (10;0,25) .
Đt A :”M thi ñu”
P (A) = P (X ≥ 6)= P (X = 6) + P (X = 7)+
+ P( X = 8 ) + P( X = 9 ) + P( X =10 ) = 0,0197
b/ Gi n là s ln d thi ca M. Và B:“ít nht mt ln ñu”
( ) =1− ( = 0 )=1− (1− 0,0197) n P B P X
≥ 0,97 ⇔ n ≥ 176,238
Vy, M phi thi th# 177 ln. 3.9.
Nhà máy d%t mun tuyn d,ng ngưi bit rành v mt loi si. Nhà máy
th# thách ngưi d tuyn 7 ln. M i ln nhà máy ñem ra 4 si ging nhau, trong
ñó ch có mt s i tht và yêu cu ngưi này chn ra si tht. Nu chn ñúng ít 45
Bài tp Xác sut th ng kê Dip Hoàng Ân
nht 6 ln thì ñưc tuyn d,ng. Mt ngưi ñn xin tuyn d,ng nói: "Ch cn nhìn
qua là có th phân bi%t si tht hay gi vi xác sut 80% ".
a/ Nu ngưi này nói ñúng kh năng ca mình thì xác sut ñưc tuyn d,ng là bao nhiêu?
b/ Tính xác sut ñ ñưc tuyn d,ng trong trưng hp, tht ra, ngưi
này không bit gì v s i c . Gii
a/ Gi B :” năng lc nhn ra si tht ca ngưi d tuyn” suy ra P( ) B = 0,8 .
Gi X là BNN ch s si tht trong 7 ln th. X B (7;0,8) .
Đt A :”Ngưi này ñưc chn”
P (A) = P ( X = 6)+ P( X = 7 ) 6 6 7 7
= C .0,8 .0, 2 + C .0,8 = 0,5767 7 7
b/ Gi p là xác su t chn ñưc si tht trong mt ln th# (không bit gì v si). p = 0,25 . Khi ñó X B(7;0,25)
Đt A :”Ngưi này ñưc chn”
P( A) = P( X = 6) + P( X = 7) 6 6 7 7
= C .0,25 .0,75 + C .0, 25 = 0,0014. 7 7 3.10.
T l% thuc h ng ' lô A là P = 0,1 ' lô B là P = 0,08 và ' lô C là A B
P = 0,15 . Gi s# m i lô có rt nhiu chai thuc. C
a/ Ly 3 chai ' lô A. Tìm lut phân ph i xác sut ca s chai hng có trong
3 chai. Tính xác sut ñ có 2 chai hng; có ít nht 1 chai hng.
b/ Phi ly bao nhiêu chai (' lô A) ñ xác sut có ít nht mt chai h ng không nh hơn 94% ? Gii
a/ Gi X là BNN ch s chai hng có trong 3 chai ly ra ' lô A. Im X = {0;1;2; } 3 Và X B(3;0, ) 1 vi ( ) k k 3 0,1 .0,9 k P X k C − = = (k ∈ 0,1,2,3 ) 3 { }
Bng phân phi xác sut c a X : X 0 1 2 3
P( X ) 0,729 0,243 0,027 0,001
Xác sut ñ có 2 chai hng: P( X = 2) = 0,027
và xác sut có ít nht 1 chai hng P( X ≥ )
1 = 1− P (X = 0) = 0,271.
b/ Gi n là s chai ly ra. Ta có X B( ; n 0,1)
1− ( = 0) ≥ 0,94 ⇔ 0,06 ≥ 0,9n P X ⇔ n ≥ 26,7 46
Bài tp Xác sut th ng kê Dip Hoàng Ân
Do ñó, ít nht ly 27 chai. 3.11.
T l% thuc h ng ' lô A là P = 0,1 ' lô B là P = 0,08 và ' lô C là A B
P = 0,15 . Gi s# m i lô có rt nhiu chai thuc. C
a/ Ly 3 chai ' lô A. Tìm lut phân ph i xác sut ca s chai hng có trong
3 chai. Tính xác sut ñ có 2 chai hng; có ít nht 1 chai hng.
b/ Chn ngu nhiên 1 trong 3 lô ri ly t lô ñó ra 3 chai. Tính xác sut ñ có ít nht 1 chai hng. Gii
a/ Gi X là BNN ch s chai hng có trong 3 chai ly ra ' lô A. Im X = {0;1;2; } 3
Và X ~ B(3;0,1) vi ( ) k k 3 0,1 .0,9 k P X k C − = = (k ∈ 0,1,2,3 ) 3 { }
Bng phân phi xác sut c a X : X 0 1 2 3
P( X ) 0,729 0,243 0,027 0,001
Xác sut ñ có 2 chai hng: P( X = 2) = 0,027
và xác sut có ít nht 1 chai hng P( X ≥ )
1 = 1− P (X = 0) = 0,271.
b/ Ta có X là BNN ch s chai hng có trong 3 chai ly ra ' lô i vi i ∈{1;2; } 3 i 1
Đt H :”lô i ñưc chn” i∈ {1;2; }
3 ⇒ P (H = . và i ) i 3
Đt H :” ít nh t 1 chai hng trong 3 chai ly ra” 3 1
P (H ) = ∑ P (H P H H = P X ≥ + P X ≥ + P X ≥ i ). ( | i ) ( 1 1 1 1 ) ( 2 ) ( 3 ) i= 1 3 1 =
3− P( X = 0 − P X = 0 + P X = 0 1 ) ( 2 ) ( 3 ) 3 1 =1 − ( 3 3 3 0,9 +0,92 + 0,85 ) = 0,2927 3 3.12.
T l% thuc h ng ' lô A là P = 0,1 ' lô B là P = 0,08 và ' lô C là A B
P = 0,15 . Gi s# m i lô có rt nhiu chai thuc. Ly ' m i lô mt chai. Tìm phân C
phi xác sut r i tính kỳ vng và phương sai ca s chai hng trong 3 chai ly ra. Gii
Gi Y là BNN ch s chai hng có trong 3 chai ly ra. 47
Bài tp Xác sut th ng kê Dip Hoàng Ân Im X ={0;1;2;3}
P(Y = 0) = P( X = 0 .P X = 0 .P X = 0 = 0,7038 1 ) ( 2 ) ( 3 ) P(Y = )
1 = P( X = 0 .P X = 0 .P X = 1 1 ) ( 2 ) ( 3 )+
+ P( X = 0 .P X = 1 .P X = 0 + P X = 1 .P X = 0 .P X = 0 = 0,2636 1 ) ( 2 ) ( 3 ) ( 1 ) ( 2 ) ( 3 )
Tương t P (Y = 2) = 0,0314; P (Y = ) 3 = 0,0012 Y 0 1 2 3
P (Y ) 0,7038 0,2636 0,0314 0,0012
Suy ra E (Y ) = 0,2636 + 2.0,0314 + 3.0,0012 = 0,33
và D(Y) = E(Y ) − E(Y)2 2 = ( + + ) 2
0,2636 4.0,0314 9.0,0012 − 0,33 = 0,2911. 3.13.
T l% thuc h ng ' lô A là P = 0,1 ' lô B là P = 0,08 và ' lô C là A B
P = 0,15 . Gi s# m i lô có rt nhiu chai thuc. C
a/ Ly ' m i lô mt chai. Tìm phân phi xác sut ca s chai hng trong 3 chai ly ra.
b/ Mt c #a hàng nhn v 500 chai ' lô A, 300 chai ' lô B và 200 chai '
lô C ri ñ ln l n. M t ngưi ñn mua 1 chai v dùng. Tính xác sut ñ ñưc chai tt. Gii
a/ G i Y là BNN ch s chai h ng có trong 3 chai ly ra. Im X ={0;1;2;3}
P(Y = 0) = P( X = 0 .P X = 0 .P X = 0 = 0,7038 1 ) ( 2 ) ( 3 ) P(Y = )
1 = P( X = 0 .P X = 0 .P X = 1 1 ) ( 2 ) ( 3 )+
+ P ( X = 0 .P X = 1 .P X = 0 + P X = 1 .P X = 0 .P X = 0 = 0,2636 1 ) ( 2 ) ( 3 ) ( 1 ) ( 2 ) ( 3 )
Tương t P (Y = 2) = 0,0314; P (Y = ) 3 = 0,0012 Y 0 1 2 3
P (Y ) 0,7038 0,2636 0,0314 0,0012
b/ Đt A :” Chn 1 chai hng” P( )
A = P( H P A | H + P H P A | H + P H P A| H 1) ( 1 ) ( 2) ( 2) ( 3) ( 3) = 500 300 200 1 499 1 299 1 199 = .C .0,1.0,9 + .C .0,08.0,92 + .C .0,15.0,85 = 0,104 500 300 200 1000 1000 1000
Do ñó xác sut ñưc 1 chai tt:
P (A) =1− P (A) = 0,896 48
Bài tp Xác sut th ng kê Dip Hoàng Ân 3.14.
T l% thuc h ng ' lô A là P = 0,1 ' lô B là P = 0,08 và ' lô C là A B
P = 0,15 . Gi s# m i lô có rt nhiu chai thuc. C
a/ Chn ngu nhiên 1 trong 3 lô ri ly t lô ñó ra 3 chai. Tính xác sut ñ có ít nht 1 chai hng.
b/ Mt c#a hàng nhn v 500 chai ' lô A, 300 chai ' lô B và 200 chai ' lô
C ri ñ ln ln. Mt ngưi ñn mua 1 chai v dùng. Tính xác sut ñ ñưc chai tt. Gii
a/ Đt H :”lô i ñưc ch n” i∈ ⇒ P H = . và i { } ( i ) 1 1;2;3 3
Đt H :” ít nh t 1 chai hng trong 3 chai ly ra” 3 1
P (H ) = ∑ P (H P H H = P X ≥ + P X ≥ + P X i ). ( | i ) ( 1 1 ≥1 1 ) ( 2 ) ( 3 ) i= 3 1 1 =
3− P( X = 0 − P X = 0 + P X = 0 1 ) ( 2 ) ( 3 ) 3 1 = 1− ( 3 3 3 0,9 + 0,92 + 0,85 )= 0,2927 3
Trong ñó X là BNN ch s chai hng có trong 3 chai ly ra ' lô i vi i∈ 1;2;3 i { }
b/ Đt A :” Chn 1 chai hng”
P (A) = P (H P A | H + P H P A | H + P H P A | H 1) ( 1 ) ( 2) ( 2) ( 3) ( 3 ) 500 1 499 300 1 299 200 1 199 = .C .0,1.0,9 + .C .0,08.0,92 + .C .0,15.0,85 500 300 200 1000 1000 1000 = 0,104
Do ñó xác sut ñưc 1 chai tt:
P (A) =1− P (A) = 0,896 3.15.
T l% thuc h ng ' lô A là P = 0,1 ' lô B là P = 0,08 và ' lô C là A B
P = 0,15 . Gi s# m i lô có rt nhiu chai thuc. C
a/ Ly 3 chai ' lô A. Tìm lu t phân phi xác sut ca s chai hng có trong 3
chai. Tính xác sut ñ có 2 chai hng; có ít nht 1 chai hng.
Phi ly bao nhiêu chai (' lô A) ñ xác su t có ít nht mt chai
hng không nh hơn 94% ?
b/ Mt c#a hàng nhn v 500 chai ' lô A, 300 chai ' lô B và 200 chai ' lô
C ri ñ ln ln. Mt ngưi ñn mua 1 chai v dùng. Tính xác sut ñ ñưc chai tt. 49
Bài tp Xác sut th ng kê Dip Hoàng Ân Gii
a/ Gi X là BNN ch s chai hng có trong 3 chai ly ra ' lô A. Im X = {0;1;2; } 3 Và X B(3;0,1) vi ( = ) k k 3 = 0,1 .0,9 −k P X k C (k ∈ 0,1, 2,3 ) 3 { }
Bng phân phi xác sut c a X : X 0 1 2 3
P( X ) 0,729 0,243 0,027 0,001
Xác sut ñ có 2 chai hng: P( X = 2) = 0,027
và xác sut có ít nht 1 chai hng P( X ≥ )
1 = 1− P ( X = 0) = 0,271.
Gi n là s chai l y ra. Ta có X B (n;0, ) 1
1− ( = 0) ≥ 0,94 ⇔ 0,06 ≥ 0,9n P X ⇔ n ≥ 26,7
Do ñó, ít nht ly 27 chai.
b/ Đt A :” Chn 1 chai hng”
P (A) = P (H P A | H + P H P A | H + P H P A | H 1) ( 1 ) ( 2) ( 2) ( 3) ( 3 ) 500 1 499 300 1 299 200 1 199 = .C .0,1.0,9 + .C .0,08.0,92 + .C .0,15.0,85 500 300 200 1000 1000 1000 = 0,104
Do ñó xác sut ñưc 1 chai tt:
P (A) =1− P (A) = 0,896 3.16.
T l% thuc h ng ' lô A là P = 0,1 ' lô B là P = 0,08 và ' lô C là A B
P = 0,15 . Gi s# m i lô có rt nhiu chai thuc. C
a/ Ly 3 chai ' lô A. Tìm lut phân phi xác sut c a s chai hng có trong
3 chai. Tính xác sut ñ có 2 chai hng; có ít nht 1 chai hng.
b/ Ly ' m i lô mt chai. Tìm phân ph i xác sut ca s chai hng trong 3 chai ly ra.
c/ M t c#a hàng nhn v 500 chai ' lô A, 300 chai ' lô B và 200 chai ' lô
C ri ñ ln ln. Mt ngưi ñn mua 1 chai v dùng. Tính xác sut ñ ñưc chai tt. Gii
a/ Gi X là BNN ch s chai hng có trong 3 chai ly ra ' lô A. Im X = {0;1;2; } 3
Và X ~ B(3;0,1) vi ( ) k k 3 0,1 .0,9 k P X k C − = = (k ∈ 0,1, 2,3 ) 3 { } 50
Bài tp Xác sut th ng kê Dip Hoàng Ân
Bng phân phi xác sut c a X : X 0 1 2 3
P( X ) 0,729 0,243 0,027 0,001
Xác sut ñ có 2 chai hng: P( X = 2) = 0,027
và xác sut có ít nht 1 chai hng P( X ≥ )
1 = 1− P ( X = 0) = 0,271.
b/ Gi Y là BNN ch s chai hng có trong 3 chai ly ra. Im X ={0;1;2;3}
P(Y = 0) = P( X = 0 .P X = 0 .P X = 0 = 0,7038 1 ) ( 2 ) ( 3 ) P(Y = )
1 = P( X = 0 .P X = 0 .P X = 1 1 ) ( 2 ) ( 3 )+
+ P ( X = 0 .P X =1 .P X = 0 + P X =1 .P X = 0 .P X = 0 = 0,2636 1 ) ( 2 ) ( 3 ) ( 1 ) ( 2 ) ( 3 )
Tương t P (Y = 2) = 0,0314; P (Y = ) 3 = 0,0012 Y 0 1 2 3
P (Y ) 0,7038 0,2636 0,0314 0,0012
c/ Đt A :” Chn 1 chai hng”
P (A) = P (H P A | H + P H P A | H + P H P A | H 1) ( 1 ) ( 2) ( 2) ( 3) ( 3 ) 500 300 200 1 499 1 299 1 199 = .C .0,1.0,9 + .C .0,08.0,92 + .C .0,15.0,85 500 300 200 1000 1000 1000 = 0,104
Do ñó xác sut ñưc 1 chai tt:
P (A) =1− P (A) = 0,896 3.17.
Gi s# ngày sinh ca ngưi dân trong mt thành ph ln có th rơi
ngu nhiên vào mt ngày b t kỳ trong m t năm (365) ngày. Chn ngu nhiên 1095
ngưi trong thành ph ñ ó. Tính xác sut ñ :
a/ Có hai ngưi có cùng ngày sinh ñã cho.
b/ Có không quá 7 ngưi có cùng ngày sinh ñã cho. Gii
Gi X là BNN ch s ngưi có cùng ngày sinh trong 1095 ngưi . 1 X ~ B 1095; 365
a/ Xác sut ñ có 2 ngưi có cùng ngày sinh ñã cho: 51
Bài tp Xác sut th ng kê Dip Hoàng Ân 2 1093 1 364 1 P (X = 2) 2 = C ≈ Po 1095. = Po 3 =0, 2565 1095 2 2 ( ) 365 365 365
b/ Xác sut ñ có không quá 7 ngưi có cùng ngày sinh ñã cho:
P (X ≤ 7 ) = Po 3 + Po 3 +Po 3 + Po 3 + Po 3 + Po 3 0 ( ) 1 ( ) 2 ( ) 3 ( ) 4 ( ) 5 ( )
+Po 3 + Po 3 = 0,988 6 ( ) 7 ( ) 3.18.
M t trm bưu ñi%n chuyn ñi%n trong khong thi gian 10 -5 giây.
Trong quá trình tránh ñi%n có các ting n ngu nhiên. S tín hi%u n ngu nhiên
trong 1 giây là 104 . nu trong thi gian truyn tín hi%u có dù cjir mt tín hi%u n
ngu nhiên thì trm s+ ngng làm vi%c. tính xác sut ñ cho vi%c truyn tính hi%u
b gián ñon. bit r"ng s tín hi%u n ngu nhiên rơi vào trong khong thi gian
truyn tín hi%u là bin ngu nhiên tuân theo lut phân phi poison. Gii
Gi X là BNN ch s các tín hi%u n trong khong thi gian 5 10− truyn tin. X P ( 4 −5
~ o 10 .10 )⇔ X ~ Po(0, ) 1 Trong ñó,
s tín hi%u n trong khong th i gian 5 10− giây truyn tin là 4 5 10 .10− = 0,1.
Do ñó, xác su t vi%c truyn tin b gián ñon 0,1 0,1 ( )0 P (X ) 1
1 P (X 0) 1 e− ≥ = − = = − = 0,0952 0! 3.19.
S l i trên 1 mét vuông vi là mt bin ngu nhiên tuân theo lu t phân
phi poison. Kim tra lô vi, ngưi ta thy 98% có l i. Vy trung bình m i mét
vuông vi có bao nhiêu l i? Gii
Gi X là BNN ch s l i trên 1mét vuông vi X P ( o λ) Lô vi thy có 98% l i P (X ) 1 0,98 1 P ( X 0 ) 0,98 e −λ ≥ = ⇔ − = = ⇔ = 0, 02 ⇔ λ ≈ 3,9 (1,5ñ)
Vy, trung bình m i mét vuông vi có 3,9 l i. 3.20.
Mt công nhân qun lý 12 máy d%t. Các máy d%t hot ñng ñc lp
nhau, và xác sut ñ m i máy, trong ca làm vi%c, cn s chăm sóc ca công nhân
(vit tt là CCN) là 0,3. 52
Bài tp Xác sut th ng kê Dip Hoàng Ân
a/ Tính xác sut ñ, trong ca làm vi%c, có a1/ 4 máy CCN a2/ t 3 ñn 7 máy CCN
b/ Trung bình, trong ca làm vi%c, có bao nhiêu máy CCN?
c/ Trong ca làm vi%c, tìm s máy CCN nhi u kh năng nht; tính xác sut tương ng. Gii.
a/ Gi X là BNN ch s máy CCN trong ca làm vi%c thì X ~ B (12;0,3) k k 12
P( X = k) = C (0,3) (0,7) − k , k∈ 0,1, 2,… ,12 , k 12 { } ∈ {0,1,2,…,12} a1/ Xác sut phi tính: 4 4 8
P(X = 4) = C (0,3) (0,7) = 0, 23 1 1 12 b2/ Xác sut phi tính: 7
P(3 ≤ X ≤ 7) = ∑P(X =k ) k = 3
= 0,2397 + 0,2311 + 0,1585 + 0,0792 + 0,0291 = 0,7376. b/ S máy CCN trung bình:
E (X ) =12 ×0,3 =3,6
c/ S máy CCN nhiu kh năng nht: Mod ( X ) = 1 [ 3 ×0,3] = . 3
Xác sut tương ng: P (X = ) 3 = 0,2397. 3.21.
Ngưi ta mun ly mt s ht lúa t mt kho lúa có t l% ht lép là
0,2 ñ kim tra. Bit r"ng kho lúa có rt nhiu ht.
a/ Phi ly ít nht bao nhiêu ht lúa ñ xác sut có ít nht mt ht lép không bé hơn 95% ?
b/ Ly ngu nhiên 100 ht lúa, tính xác sut ñ trong ñó có 25 ht lép; có t 10 ñn 40 ht lép. Gii.
a/ Gi n là s ht lúa cn ly. Vì s ht lúa trong kho rt ln, nên các ln ly xem
như ñc lp. Xác sut ñ trong n ht lúa ly ra, không có ht lép nào là (0,8)n. Theo gi thit: 53
Bài tp Xác sut th ng kê Dip Hoàng Ân n n ln (0,05) 1− (0, ) 8 ≥ 0,95 ⇔( 0, ) 8 ≤ 0, 05 ⇔ n≥ ln (0,8)
Vy, phi ly ít nht 14 ht lúa.
b/ Gi X là bin ngu nhiên ch s ht lép trong mu thì X ~ B (n, p ) , vi
n = 100 và p = 0,2 . Vì n > 30;n.p = 20 > 5 và . n (1 − )
p = 80 > 5 nên chúng ta có
th áp d,ng các công thc gn ñ úng DeMoivre − Laplace.
(i) Xác sut ñ có 25 ht lép: 25 25 75
P(X = 25) = C (0,2) (0,8) = 0,04388 100
(ii) Xác sut ñ có t 10 ñn 40 ht lép: 40 − 100× 0,2 10 − 100× 0,2 P(10 ≤ X ≤ 0 4 ) ≈ Φ − Φ 100 0 × ,2 0 × ,8 100 0 × , 2 0 × ,8 = ( Φ 5) − ( Φ 2 − ,5) =1 − (1 − ( Φ 2,5)) = ( Φ 2,5) ⇒ P 1
( 0≤ X ≤ 40 )≈ 0,9938 3.22.
Cn xét nghi%m máu cho 5000 ngưi ñ tìm du hi%u mt loi b%nh
B ti mt ña phương có t l% ng ưi mc b%nh B theo thng kê là 10%. Có 2 phương pháp:
a/ Xét nghi%m tng ngưi mt.
b/ M i ln ly máu mt nhóm 10 ngưi trn ln vào nhau r i xét nghi%m.
Nu kt qu âm tính thì thông qua, nu dương tính thì phi làm thêm 10 xét
nghi%m ñ xét nghi%m li tng ngưi mt trong nhóm.
Hi phương pháp nào có li hơn, bi t r"ng m i xét nghi%m ñu tn kém như
nhau và kh năng mc b%nh ca m i ngưi ñc l p nhau? Gii.
a/ Nu dùng phương pháp (1) thì phi thc hi%n 5000 xét nghi%m.
b/ Bây gi chúng ta xem ph ương pháp (2):
Đt X ch s nhóm có kt qu dương tính thì X B( −( 0, )10 ~ 500; 1 9 )
Đt Y ch s xét nghi%m theo phương pháp (2) thì Y = 500 + 10X
S xét nghi%m trung bình theo phương pháp (2) là: E(Y )= + E ( X )= + ( − ( )10 500 10 500 5000 1 0,9 )≈ 37 7 5 .
Vy, áp d,ng theo phương pháp (2) có li hơn. 54
Bài tp Xác sut th ng kê Dip Hoàng Ân 3.23.
Mt cơ s' sn xut, trung bình trong mt tun, nhn ñưc 4 ñơn ñt
hàng. Bit r"ng s ñơn ñt hàng X mà cơ s' nhn ñư c trong mt tun là mt
BNN có phân phi Poisson. Tính xác sut ñ cơ s' ñó
a/ Nhn ñưc h ơn 5 ñơn ñt hàng trong mt tun
b/ Nhn ñưc 6 ñơn ñt hàng trong hai tun liên tip Gii. a/ X ~ Po( ) 4 . Xác sut phi tính:
P( X > 5) =1 − P(X ≤ 5) 5 4k = − 4 1 − ∑ e =1 −0,7851 =0,2149 k = k ! 0
b/ Gi Y là BNN ch s ñơn ñt hàng ca cơ s' trong hai tun liên tip thì
Y ~ Po (8). Xác sut phi tính: 6 8 ( P Y = ) − 8 6 = e = 0,1221 6! 3.24.
Mt xe ti vn chuyn 1000 chai rưu vào kho. Xác sut ñ m i chai
b v5 trong khi vn chuyn là 0,0035. Tính xác sut ñ sau khi vn chuyn, có 6
chai rưu b v5; có t 2 ñn 8 chai rưu b v 5. (gi s# r"ng s ki%n các chai rưu
b v5 là ñc lp nhau, do ch t lưng riêng ca m i chai) Gii.
Gi X là BNN ch s chai rư u b v5 sau khi vn chuyn, thì
X ~ B (1000; 0,0035).
Xác sut ñ có 6 chai rưu b v5: 6 6 994 P( X = 6) = C (0,0035) (0,9965) = 0,07709 1000 Tính gn ñúng:
Vì n =1000 và n.p = 3,5 < 5 , nên có th xem: X ~ Po (3,5) . Do ñó: 6 (3,5) 3,5 P(X 6) e− = ≈ = 0,0771 6!
Xác sut ñ có t 2 ñn 8 chai rưu b v5 8 (3,5)k 3 − ,5
P(2 ≤ X ≤ 8) ≈ ∑ e = 0,8543 k = 2 k ! 55
Bài tp Xác sut th ng kê Dip Hoàng Ân 3.25.
Thi gian ñ sn xut m t sn ph(m loi A là mt BNN tuân theo lut
phân phi chu(n vi các tham s µ = 10 và σ = 1 (ñơn v là phút)
a/ Tính xác sut ñ m t sn ph(m loi A nào ñó ñưc sn xut trong khong
thi gian t 9 phút ñn 12 phút.
b/ Tính thi gian cn thit ñ sn xut m t sn ph(m loi A bt kỳ. Gii.
Gi X là BNN ch thi gian d sn xut mt sn ph(m loi A , X ~ N (10; ) 1 . a/ Xác sut phi tính: 12−10 9−10 P(9 ≤ X ≤12) = Φ − Φ 1 1 = Φ ( ) 2 – Φ(− ) 1 = Φ( 2) + Φ( ) 1 –1
= 0,9772 + 0,8413 – 1 = 0,88185.
b/ Theo qui tc 3σ, hu như ch c chn X ly giá tr trong khong: [10 −3 1 × ; 10 + 3 1 × ]= [7; 13]
Vy, thi gian cn thit ñ sn xut mt sn ph(m loi A bt kỳ là t 7 phút ñn
13 phút (hu như chc chn). 3.26.
Cho bin ngu nhiên X tuân theo lut phân phi 2 N ( , µ σ ) . Bit r"ng
X ly giá tr nh hơn 60 vi xác sut 0,1003 và ly giá tr ln hơn 90 vi xác sut 0,0516, hãy tính µ và σ. Gii. Theo gi thit, 60 − µ Φ = 0,1003 ( P X < 60) = 0,1003 σ ⇔ ( P X >90) = 0,0516 90 − µ 1 − Φ 0 = ,0516 σ µ 6 − 0 Φ = 0,8997 µ − 60 1 = ,28 σ σ ⇔ ⇔ 90 − µ 90 − µ Φ =0,9484 = 1,64 σ σ
Vy, µ = 73,15 và σ = 10,27 . 56
Bài tp Xác sut th ng kê Dip Hoàng Ân 3.27.
Đưng kính ca mt loi chi tit do mt máy sn xut có phân
phi chu(n, kỳ vng 20mm, phương sai ( )2
0,2 mm. Tính xác sut ly ngu nhiên mt chi tit
a/ Có ñư ng kính trong khong 19,9mm ñn 20,3mm.
b/ Có ñưng kính sai khác vi kỳ vng không quá 0,3mm. Gii
Gi X là BNN ch ñưng kính ca mt chi ti t, ta có X N( ( )2 ~ 20; 0,2 )
a/ Có ñư ng kính trong khong 19,9mm ñn 20,3mm 20,3 − 20 19,9 − 20
P (19,9 < X < 20,3) = Φ − Φ 0,2 0,2 = Φ(1, ) 5 + ( Φ 0, ) 5 = 0,6247
b/ Có ñưng kính sai khác vi k ỳ vng không quá 0,3mm P ( X − < ) 0,3 20 0,3 = 2Φ −1 = 0,8664 0,2 57
Bài tp Xác sut th ng kê Dip Hoàng Ân
CHƯƠNG 7: LÝ THUYT MU 4. 1.
Đ nghiên c u v s con trong m t gia ñình (SCTMGĐ) ' ña phương A,
ngưi ta ñiu tra s con c a m i gia ñ ình trong 30 gia ñình ñưc chn ngu nhiên
' ña phương A. Kt qu ñưc ghi li như sau: 0 2 5 3 7 4 3 3 1 4 2 4 3 1 6 1 0 2 4 1 1 2 3 2 0 5 5 1 3 2
a) Hãy lp bng phân phi tn s và tn sut tích lu4 cho d li%u trên mu.
b) Trên mu va nêu, tính SCTMGĐ trung bình ñ l%ch chu(n ca SCTMGĐ. Gii:
a) Gi X là BNN ch s con trong mt gia ñình. Bng phân b tn s, tn sut
và tn sut tích lũy cho X t d li%u trên. X 0 1 2 3 4 5 6 7 Tn s 3 6 6 6 4 3 1 1 Tn sut
0,100 0,200 0,200 0,200 0,133 0,100 0,033 0,033
Tn sut tích lũy 0,100 0,300 0,500 0,700 0,833 0,933 0,967 1,000
b) Giá tr trung bình mu là: = 2,67
Giá tr phương sai mu: 2 = 3,2644 Đ l%ch chu(n: 1 = ,81 . 4. 2.
Đ nghiên cu v thâm niên công tác (tính tròn năm) ca nhân viên ' mt
công ty ln, ngưi ta kho sát thâm niên ca 100 nhân viên ñưc chn ngu nhiên
trong công ty. Kt qu như sau: Thâm niên 5 - 7 8 - 10 11 - 13 14 - 16 17 -19 S nhân 8 21 36 25 10 viên
a) Hãy tính giá tr trung bình mu và giá tr ñ l%ch chu(n mu.
b) Gi s# thâm niên công tác ca nhân viên ca công ty trên là BNN X có kỳ
vng là 12 năm và ñ l %ch chu(n là 3 năm. Tính xác sut ñ trung bình mu
nhn giá tr ln hơn 12,5 năm. Gii
Gi X là BNN ch thâm niên công tác ca nhân viên ca công ty trên.
a) T d li%u ta tính ñưc:
- Giá tr trung bình mu: = 12.24 58
Bài tp Xác sut th ng kê Dip Hoàng Ân
- Giá tr ñ l%ch chu(n mu: = 3,27 .
b) Theo ñnh lý gii hn trung tâm ta có: − µ = ~ (0,1) σ
Do ñó xác sut ñ trung bình mu nhn giá tr ln h ơn 12,5 là: − µ − µ ( > ) 12,5 12,5 = >
= ( > 1,67) = 1− ( ≤ 1,67) = 0,0478 σ σ 4. 3.
Đ nghiên cu chiu cao ca thanh niên la
tu$i t 18 ñn 22 tu$i ' thành ph LX, ngưi ta Chiu cao S thanh
ño trên mt m u gm mt s thanh niên ñưc (cm) niên
ch n ngu nhiên ' thành ph LX. Kt qu như sau [154, 158) 10 (ñơ n v cm): [158, 162) 16
a) Tính giá tr trung bình mu và giá tr ñ l%ch chu(n mu. [162, 166) 29
b) Theo tài li%u kho sát trưc ñ ó chiu cao ca [166, 170) 37
nhng thanh niên la tu $i trên tuân theo lut phân [170, 174) 15
phi chu(n vi kỳ vng là µ = 166 cm và ñ l%ch chu(n là [174, 178) 10
σ = 7 cm. Hãy tính xác sut ñ trung
bình mu có giá tr ln 167 cm. [178, 182) 4 Gii:
Gi X là BNN ch chiu cao c a thanh niên la tu$i t 18 ñn 22 tu$i ' thành ph LX.
a) T d li%u ta tính ñưc:
- Giá tr trung bình mu: = 166,55 cm
- Giá tr ñ l%ch chu(n mu: = 5,865 cm.
b) Theo ñnh lý gii hn trung tâm ta có: − µ = ~ (0,1) σ
Do ñó xác sut ñ trung bình mu nhn giá tr ln h ơn 12,5 là: − µ − µ ( > ) 167 167 = >
= ( > 1,57 ) = 1− ( ≤ 1,57) = 0,058 σ σ . 4. 4.
Gi s# ñ tăng theo phn trăm lương hàng năm ca m i công nhân viên
chc trong công ty Alpha tuân theo lut phân phi chu(n vi trung bình 12,2% và 59
Bài tp Xác sut th ng kê Dip Hoàng Ân
ñ l%ch chu(n 3,6%. Mt mu ngu nhiên gm 9 phn t# ñưc chn t t$ng th y.
Tìm xác sut ñ trung bình mu nh hơn 10%. Gii:
Gi X là BNN ch ñ tăng lương theo phn trăm. Ta có ( 2 ~ 12,2; 3,6 ) và − µ = ~ (0,1) σ − − − ( < ) 12,2 10 12,2 10 12,2 10 = 9 < 9 = Φ 9 = 0,0334 . 3,6 3,6 3,6 4. 5.
Đ nghiên cu tu$i th ca m t loi bóng ñ èn, ngưi ta thp th # 100 bóng
ñèn trưc ci tin k4 thut. Sau khi ci tin k4 thu t, ngưi ta thp li 100 bóng.
S li%u có ñưc cho trong b ng sau:
Mu 1: Trưc ci tin Mu 2: Sau ci tin Tu$ i th (gi) S bóng Tu$i th S bóng ñèn (gi) ñèn < 1030 2 1150 10 [1030, 1050) 3 1160 15 [1050, 1070) 8 1170 20 [1070, 1090) 13 1180 30 [1090, 1110) 25 1190 15 [1110, 1130) 20 1200 10 [1130, 1150) 12 [1150, 1170) 10 [1170, 1200] 5 > 1200 2
a) Tính giá tr ñi di%n cho m i lp ' mu 1 và lp bng tn s, tn sut cho mu 1.
b) Hãy so sánh giá tr trung bình và giá tr ñ l%ch chu(n ca hai mu trên. 60
Bài tp Xác sut th ng kê Dip Hoàng Ân Gii: a) (1 ñ) Trưc ci tin Tu$i th Giá tr ñi di%n Tn s Tn sut (gi ) < 1030 1020 2 0,02 [1030, 1050) 1040 3 0,03 [1050, 1070) 1060 8 0,08 [1070, 1090) 1080 13 0,13 [1090, 1110) 1100 25 0,25 [1110, 1130) 1120 20 0,20 [1130, 1150) 1140 12 0,12 [1150, 1170) 1160 10 0,10 [1170, 1200] 1185 5 0,05 > 1200 1215 2 0,02 Tng s 100 1
b) Gi và ln lưt là các BNN ch tu$i th ca bóng ñèn trưc và sau
ci tin k4 thut. Ta có = 1112,15; = 1175,5 ; = 39,26 và = 14,38
Như vy, trung bình mu 1 bé hơn trung bình mu 2 và ñ l%ch chu(n mu 1
ln hơn ñ l%ch chu(n mu 2. 4. 6.
Theo Hi sinh viên ' thành ph LX thì có 60% sinh viên hi%n ñang theo hc
ñi hc mun tìm vi%c làm ngoài gi h c. M t mu g m 205 sinh viên ñưc chn
ngu nhiên. Tìm xác sut ñ trong s ñó có hơn 135 sinh viên mun tìm vi%c làm ngoài gi hc. Gii:
Gi là t l% sinh viên hi%n ñang theo hc ñi hc mun tìm vi%c làm ngoài gi hc, = 0,6 .
T l% sinh viên mun tìm vi%c làm ngoài gi trên mu là = . 205
Xác sut có hơn 135 sinh viên mun tìm vi%c làm ngoài gi: 61
Bài tp Xác sut th ng kê Dip Hoàng Ân 135 27
( > 13 ) 5 = > = > 205 205 41 − Vì 0 ~ ( 0, ) 1 1 − 0 ( 0 ) Do ñó 27 − 0 − ( > ) 0 41 135 = > 1 − 1 0 ( 0 ) 0 ( − 0 ) 27 27 − − 0,6 0 41 41 =1 − Φ =1 − Φ 205 1 − 0,6 1 −0,6 0 ( 0 ) ( ) =1 − Φ(1, ) 71 =1 −0,9564 = 0,0436 4. 7.
Mt mu kích thưc n ñưc thành lp t t$ng th tuân theo phân phi chu(n
vi kỳ vng µ và ñ l%ch chu(n là 8. Hãy xác ñnh n sao cho, v i xác su t b"ng
0,9524, trung bình mu n"m trong khong t µ - 4 ñn µ + 4. Gii: Ta có
( µ − 4 ≤ ≤ µ + 4) = 0,9524
⇔ ( − µ ≤4) =0,9524 (1 ñ) − µ 4 ⇔ ≤ = 0,9524 σ σ ⇔ 2Φ 1 − = 0,9524 2 ⇔ Φ = 0,9762 2 (1 ñ) ⇔ =1,98 2 ⇒ = 16 4. 8. 62
Bài tp Xác sut th ng kê Dip Hoàng Ân
S li%u thng kê cho bit có 40% các h gia ñình ' thành ph A có thu nhp
hàng năm n"m trong khng t 1200 USD ñn 2000 USD. Vy, phi ñiu tra mt
mu gm bao nhiêu h gia ñình ñ, vi xác sut 0,95, t l% các gia ñình có thu nhp
trong khong nói trên, sai l%ch so vi t l% chung ca thành ph không quá 4%? Gii:
Ta có t l% h gia ñình ' thành ph A có thu nhp hàng năm n "m trong khng t
1200 USD ñn 2000 USD là = 0,4 . Gi là t l% mu:
( − 0,4 < 0,0 ) 4 = 0,95 − 0,4 0,04 ⇔ < = 0,95 0, ( 4 1− 0, ) 4 0, ( 4 1− 0, ) 4 0,04 ⇔ 2Φ −1 = 0,95 0,4 (1− 0,4) 0,04 ⇔ Φ = 0,975 0,4(1 −0,4) 0,04 ⇔ =1,96 0,4(1− 0,4)
⇔ ≈ 576,24 ⇒ = 577 4. 9.
Mt lô hàng ñt tiêu chu(n xut kh(u nu t l% ph ph(m không quá 5%. Nu
kim tra ngu nhiên 100 sn ph(m thì vi t l% ph ph(m thc t ti ña là bao
nhiêu, chúng ta có th cho phép lô hàng ñưc xut kh(u mà kh n ăng không mc sai lm là 95%? Gii: Gi 0
là t. l% ph ph(m thc t ti ña.
Lô hàng ñưc phép xut kh(u mà không mc sai lm khi < . Theo ñ 0 bài:
( < = 0,95 0 ) −0,05 −0,05 0 ⇔ 100 < 100 = 0.95 0,05(1− 0,05) 0,05(1− 0,05) − 0,05 Vì 100 ~ (0, )
1 nên ñ6ng thc trên tương ñương: 0,05 (1− 0,05) 63
Bài tp Xác sut th ng kê Dip Hoàng Ân −0,05 0 Φ 100 = 0,95 0,05 (1 −0,05) − 0,05 0 ⇒ 100 = = 1,65 0,05 (1− 0,05 ) 0,95 1,65 0,05(1 −0,05) ⇔ = +0,05 ⇔ =0,086 0 0 100 4. 10.
Chiu cao (ñơn v cm) ca mt thanh niên ' thành ph ln A là BNN tuân theo
lut phân phi N(165; 100). Ngưi ta ño ngu nhiên chiu cao ca 100 thanh niên ' thành ph A (TP.A).
c) Xác sut ñ chiu cao trung bình ca 100 thanh niên ñó l%ch so v i chiu
cao trung bình ca thanh niên TP.A không vưt quá 2cm là bao nhiêu?
d) Nu mun chu cao trung bình ño ñưc sai l%ch so vi chiu cao trung bình
ca t$ng th không vưt quá 1cm vi xác sut không d ưi 99% thì chúng ta
phi tin hành ño chiu cao ca bao nhiêu thanh niên? Gii:
a) Gi là BNN ch chiu cao ca m i thanh niên ' thành ph A. Ta có
~ (165;100) .
Do ñó ~ (165; )
1 và −165 ~ ( 0, ) 1
⇒ ( −165 < 2)= 2Φ(2)−1= 0,9545 − 165
b) Gi là s thanh niên cn ño chi u cao. Khi ñó, ~ (0, ) 1 10
Theo ñ bài ta có: ( − 165 < ) 1 ≥ 0,99 − 165 ⇔ < ≥ 0,99 10 10 2 ⇔ Φ −1 ≥ 0,99 10 1,99 ⇔ Φ ≥ = 0,995 10 2 64
Bài tp Xác sut th ng kê Dip Hoàng Ân 1 − ⇒ ≥ Φ ( 0,99 ) 5 = 2,5758 10 ⇒ ≥ 663,47
CHƯƠNG 5: ƯC LƯNG THAM S 5. 1.
a) Hãy thit lp công thc tìm khong tin cy γ cho trung bình t$ng th
trong trưng hp t$ng th có phân phi chu(n ñã bit ñ l%ch chu(n.
b) Tìm khong tin cy 95% cho trung bình t$ng th X bit X ( 2 ~ µ ,σ ) vi
σ = 3 và mu ñc trưng X có kích thưc n = 25 trung bình mu x = 10 . Gii
a) Vi ñ tin cy γ cho trưc ta tìm khong (x − ;e x +e) sao cho
P ( X − e < µ < X + e) = γ
⇔ P (| X − µ |<e ) = γ | X − µ | n ⇔ P n < e = γ σ σ n
⇔ P |U |< e = γ σ n Vì U ~ N (0, )
1 nên ta có 2Φ (a ) 1 − = γ , a =e σ 1 ⇔ Φ (a) + γ = ⇒ a = u 1 2 + γ 2 n Suy ra: u = e ⇒ e = u . σ 1 γ + 1 γ σ + n 2 2 Vy, khong tin cy σ
γ cho µ là (x −e;x + e) vi e = u . . 1 γ + n 2
b) Áp d,ng công thc trên, khong tin cy 95% cho trung bình ca X là:
(x −e;x + e) σ 3 3 e = u . = u . = u . = 1,176 1+γ 1 0 + ,95 0,975 n 25 5 2 2 65
Bài tp Xác sut th ng kê Dip Hoàng Ân
Vy khong tin cy cn tìm là: (8,824;11,176). 5. 2.
a) Gi s # r"ng tu$i th ca mt loi bóng ñèn hình TV có ñ l% ch chu(n
b"ng 500, nhưng chưa bit trung bình. Ngoài ra, tu$i th ca loi bóng ñèn
ñó tuân theo lut phân phi chu(n. Kho sát trên mt mu ngu nhiên gm
15 bóng loi trên, ngưi ta tính ñưc tu$i th trung bình là 8900 gi. Hãy tìm
khong tin cy 95% cho tu$i th trung bình ca loi bóng ñ èn hình nói trên.
a) Mt t$ng th X có phân phi chu(n. Quan sát mt mu ngu nhiên kích
thưc 25 ngưi ta tính ñư c trung bình là 15 và ñ l%ch chu(n là 3. Hãy ưc
lưng kỳ vng ca X b"ng khong tin cy 95%. Gii
a) Khong tin cy 95% cho tu$i th trung bình ca bóng ñèn hình:
(x −e;x +e) σ 500 500
Vi x = 8900 , và e = u . = u . = 1,96. = 253 1+ γ 0,975 n 15 15 2 Do ñó ( )
b) Khong tin cy cho kỳ vng ca X là: (x -e;x +e ) vi x =15
Vì X có phân phi chu(n chưa bit ñ l%ch chu (n nên: s 3 3 (24 ) (24 ) e = t . = t . = 2,0639. = 1, 24 1+ γ 1+0 ,95 n 25 5 2 2
Vy, khong tin cy cn tìm là ( ) 5. 3.
Gi s# r"ng tu$i th ca mt loi bóng ñèn hình TV có ñ l%ch chu(n b"ng
500, nhưng chưa bit trung bình. Tuy nhiên, trung bình mu b"ng 8900 ñưc
tính trên mu c5 = 35 .
a) Hãy tìm khong tin cy 95% cho tu$i th trung bình ca loi bóng ñèn hình ñang kho sát.
b) Gi s# r"ng tu$i th ca mt loi bóng ñèn hình TV trên có phân phi
chu(n. Hãy tìm khong tin cy 90% cho trung bình t$ng th. Gii
a) Khong tin cy 95% cho tu$i th trung bình ca bóng ñèn hình: (x − ;
e x + e) , vi x = 8900 và σ 500 500 e = u . = u . =1,96. =165,65 1+γ 0,975 n 2 35 35
Vy, khong tin cy cn tìm là: (8734; 9066) (gi). 66
Bài tp Xác sut th ng kê Dip Hoàng Ân
b) Khong tin cy 90% cho tu$i th trung bình ca bóng ñèn hình:
(x −e;x + e) , vi x =8900 .
Do X có phân phi chu(n chưa bit ñ l%ch chu(n nên: − s n 500 500 ( ) 1 ( ) 34 e = t . = t . = 1, 6909. = 142,9 1+ γ 1+0 ,9 n 2 2 35 35
Vy, khong tin cy cn tìm: (8757; 9043) (gi). 5. 4.
a) Kim tra tu$i th ca mt loi bóng ñèn hình TV trên mt mu ngu nhiên
gm 100 bóng ñèn tính ñưc giá tr trung bình mu là 8900 gi và ñ l%ch
chu(n mu b"ng 500 gi. Hãy tìm khong tin cy 95% cho trung bình t $ng th.
b) Đ tin cy s+ là bao nhiêu nu cùng mu trên sai s ưc lưng b"ng 130 gi. Gii
a) Khong tin cy 95% cho tu$i th trung bình ca bóng ñèn hình:
(x −e;x + e) , vi x =8900 . s 500 500 e = u . = u . =1,96. = 98 1+ γ 1+0,95 2 n 2 100 100
Khong tin cy cn tìm: (8802; 8998) (gi).
b) Gi s# γ là ñ tin cy, khi sai s ưc lưng 500 100 = . = 130 ⇒ = 130. = 2, 6 1 γ + 1 100 γ + 500 2 2 1
Tra bng 4 ta tìm ñưc + γ = 0,9953⇔ γ = 0,9906. 2
(1+ γ = <
= < 2,6 v i ~ 0,1 ) 1 ( ) + γ ( ) 2 2
Vy, ñ tin cy γ = 99,06%. 5. 5.
Khi lưng X ca m t sn ph(m do m t nhà máy sn xut tuân theo lut phân
phi chu(n. Ly mt mu ngu nhiên (không hoàn li) gm 10% ca mt lô hàng
gm 300 sn ph(m ca nhà máy ñó, ngưi ta tính ñưc x = 148,50 gam và s = 35,75 gam.
a) Hãy xây dng công th c tìm khong tin cy γ cho trung bình t$ng th hu
hn trong trưng hp ly mu không hoàn li.
b) Tìm khong tin cy 95% cho khi lưng trung bình ca m i sn ph(m trong lô hàng nói trên. 67
Bài tp Xác sut th ng kê Dip Hoàng Ân Gii
a) Gi N là kích thưc t$ng th, n là kích thưc mu. σ N −n
Vì ly mu có hoàn li thì X σ = X n N −1 X − µ X − µ N −1
Theo ñnh lý gii hn trung tâm, U = = n ~ N (0, ) 1 σ σ N − n X X U X − µ N −1 Và T = = n ~ t (n 1 − ) / −1 S N −n Y n ( n 1 − ) 2 S 7 ñây 2 Y = ~ χ n −1 2 ( ) σX
Do ñó vi ñ tin cy γ cho trưc ta tìm e sao cho P ( X −µ < e) = γ e N −1
T ñó P( T < a) = γ vi a = n s N − n 1
Suy ra P (T <a) + γ =
vi T là BNN có phân phi student n− 1 bc t do. 2 Suy ra ( − ) 1 = n a t 1+ γ 2 s N n Vy ta tính ñưc (n − − ) 1 e = t 1+ γ n N − 1 2
b) Theo ñ bài ta có n = 30; s = 35,75; N = 300; x =148,5; γ = 0,95 35, 75 270 Ta tính ñưc (29 ) e = t . = 12,685 1+ 0,95 30 299 2
Khong tin cy 95% cho khi lưng trung bình là (135,815;161,185) 5. 6.
Mt lô bút bi ca xí nghi%p A sn xu t ra gm 1000 hp, m i hp 10 cây.
Kim tra ngu nhiên 50 hp, thy có 45 cây bút b hng.
a) Tìm khong tin cy 95% cho t l% bút b hng và s bút b hng ca lô hàng.
b) Vi mu trên, nu mun ư c lưng t l% bút hng vi ñ chính xác 1,5%
thì ñ tin cy ñt ñưc là bao nhiêu? Gii
a) Gi p là t l% bút hng ca lô bút. 68
Bài tp Xác sut th ng kê Dip Hoàng Ân 45
T. l% bút hng trên mu p = = 0,09 500
Khong tin cy 95% cho t. l% bút hng ca mu: p (1− p) 0, 09(1− 0,09) ( p− ; e p+ ) e vi e = 1 u + 0,95 = 1,96. = 0,025 n 500 2
Khong tin cy 95% cho t. l% bút h ng cn tìm là: (0,065;0,115) và cho s bút
hng là (650;1150 ) (cây).
b) Gi s# e = 0,015 , ta có p(1− p) n u1 = 0,015⇒ u +γ 1 = 0,015 = 1,172 n +γ p (1 − p) 2 2 1 + γ ⇒ = ⇒ γ = −1 = 0,7588 =75,88%. 2 5. 7.
Quan sát ' mt m u, ng ưi ta có kt qu v chiu cao X(m) ca loi cây công
nghi%p ' mt nông trưng như sau: xi 3 4 5 6 7 8 s cây 2 8 23 32 23 12
a) Hãy ưc lưng chiu cao trung bình ca loi cây ñó b"ng khong tin cy 90%.
b) Đ ưc lưng chiu cao trung bình ca loi cây ñó ' ñ tin cy 95%, vi
sai s không quá 2 dm thì cn phi quan sát thêm bao nhiêu cây na? Gii
a) T s li%u ñã cho ta tính ñưc x = 6,02 và ñ l%ch chu(n mu s = .
Khong tin cy 90% cho chiu cao trung bình ca loi cây ñó là: s 1, 206 1, 206 ( x − ;
e x + e) , e = u = u . = 1,65. 1+ γ 0,95 100 10 10 2 Do ñó ( )
b) Gi s# n là s cây cn quan sát vi ñ tin cy 95% và sai s không quá 1 0,2 (m) ta có: 1, 45 u ≤ 0, 2 0,975 n1 69
Bài tp Xác sut th ng kê Dip Hoàng Ân 2 1,206 1, 206 ⇔ n ≥ u ⇔ n ≥ 1, 96. =139,6 ⇒ n = 140 1 0,975 1 0,2 0, 2 1
Vy ta cn quan sát thêm ít nht 140 – 100 = 40 (cây) na. 5. 8.
Quan sát ' mt m u, ng ưi ta có kt qu v chiu cao X(m) ca loi cây công
nghi%p ' mt nông trưng như sau: xi 3 4 5 6 7 8 s cây 2 8 23 32 23 12
a) Hãy ưc lưng chiu cao trung bình ca loi cây ñó b"ng khong tin cy 90%.
b) Nhng cây cao t 7 m tr' lên gi là cây loi A. Hãy tìm khong tin cy
95,44% cho t l% cây loi A ca nông trưng. Gii
a) T s li%u ñã cho ta tính ñưc x = 6,02 và phương sai mu 2s =
Khong tin cy 90% cho chiu cao trung bình ca loi cây ñó là:
(x −e;x +e ), s 1, 2059 1, 2059 e = u = u . = 1,65. 1+ γ 0,95 100 10 10 2 Do ñó K = ( )
b) T. l% cây loi A trên mu là: 35 p = = 0,35 100
Khong tin cy 95,44% cho t. l% cây loi A ca nông trưng là: ( p − ; e p + e) p(1− p) vi 0,35.0,65 0,35.0,65 e = u = u = 2. = 0,0954 1 0 + ,9544 0,9772 n 100 10 2
Khong tin cy cn tìm là: (0,2546;0,4454). 5. 9.
Đ sâu ca bin ñưc xác ñnh b"ng mt máy ño có sai s h% thng b"ng 0,
còn sai s ngu nhiên ca nó tuân theo lut phân phi chu(n vi ñ l% ch chu(n 20m.
a) Cn phi tin hành bao nhiêu ln ño ñ xác ñnh ñưc ñ sâu ca bin vi
sai s cho phép không quá 15m ' ñ tin cy 90% ? 70
Bài tp Xác sut th ng kê Dip Hoàng Ân
b) Tìm khong tin cy 95% cho sai s ngu nhiên trung bình. Bit r"ng khi
tin hành ño ' m t ña ñim xác ñnh 25 ln ngưi ta tính ñưc sai s ngu
nhiên trung bình mu là 100m. Gii
a) Gi là s ln ño cn thit. 2 2 σ σ 20 Ta có 2 2 e =u ≤15 ⇔n ≥ u = .1, 65 = 4,84 1+γ 2 1 n 15 + γ 225 2 2
Vy cn ño ít nht 5 ln.
b) Khong tin cy 95% cho sai s trung bình ngu nhiên là: σ 20 20
( − ; + ) vi = . = . = 1,96. = 7,8 1+0,95 0,975 25 5 2
Vy khong tin cy cn tìm là: (92,2;107,8) . 5. 10.
Ngưi ta mun ưc lưng t l% viên thuc b st m trong mt lô thuc rt nhiu viên.
a) Nu mun sai s cho phép không quá 1% ' ñ tin cy 95% thì phi quan sát ít nht my viên?
b) Quan sát ngu nhiên 200 viên, thy có 20 viên b s t m. Hãy tìm khong
tin cy 95% cho t l% t$ng th. Nu mu n sai s cho phép không quá 1% ' ñ
tin cy 95% thì ph i quan sát ít nht my viên? Gii a) Theo ñ bài ta có: 2 2 u u 1+ γ 1+0,95 e≤ ε = 0,01; 2 2 ⇔ n ≥ = = 2.0,01 0,02
Vy, phi quan sát ít nht 9604 viên.
b) Gi p là t l% viên thuc b st m. Khong tin cy 95% cho p : ( p − ; e p +e) p (1 − p) 0,1 (0,9 ) 0,09 e = u = u =1,96. = 1 +γ 1 0 + ,95 n 200 200 2 2
Vy khong tin cy 95% cho t l% viên thuc b st m là: ( )
Nu sai s không quá 1% ' ñ tin cy 95% ta cn quan sát bao nhiêu: 71
Bài tp Xác sut th ng kê Dip Hoàng Ân 2 2 u u 1+ γ 1+0,95 2 n≥ p( − p) 2 . 1 = .0,1.0,9= ε 0,01
Vy, phi quan sát ít nht 3458. 5. 11.
Đ nghiên cu sn lưng sa hàng ngày (SLSHN) ca mt ñàn bò, ngưi ta
ñiu tra ngu nhiên trên 100 con bò ca nông trưng và có kt qu sau: SLSHN (kg) 9 10 12 14 15 S con bò 10 24 42 16 8
a) Ưc lưng sn lưng sa trung bình m i ngày ca mt con bò b"ng khong tin cy 97%.
b) Vi ñ tin cy 97%, có th nói sn lưng sa trung bình hàng ngày ca
mt con bò nhiu nht b"ng bao nhiêu? Gii
a) T s li%u ñã cho ta tính ñưc x = 11,78, s =1,79
Khong tin cy 97% cho SLSHN trung bình: (x −e;x +e) s 1,79 1, 79 Vi e = u . = u . = 2,1707. = 0,39 1+ 0,97 0,985 n 100 10 2
Vy, khong tin cy cn tìm là: (11,39; 12,17) (kg)
b) Ta tìm khong tin cy mt bên: (−∞;x +e) : s 1,79 1, 79 vi e =u =u =1,88. = 0,337 γ 0,97 n 100 10
T ñó suy ra s n lưng sa trung bình hàng ngày nhiu nht: 11,78 + 0,337 =12,117 (kg) 5. 12.
Đ nghiên cu sn lưng sa hàng ngày (SLSHN) ca mt ñàn bò, ngưi ta
ñiu tra ngu nhiên trên 100 con bò ca nông trưng và có kt qu sau: SLSHN (kg) 9 10 12 14 15 S con bò 10 24 42 16 8
a) Tìm khong tin cy 90% cho t l% bò cho SLSHN trên 11kg.
Mun sai s khi ưc lưng sn lưng sa trung bình m i ngày không
vưt quá 0,5kg và sai s khi ưc lưng t l% bò cho SLSHN trên 11kg không
vưt quá 12%, vi cùng ñ tin cy 98%, thì cn ñiu tra bao nhiêu con bò? Gii 72
Bài tp Xác sut th ng kê Dip Hoàng Ân
a) T s li%u ñã cho ta tính ñưc x = 11,78, s =1,79
Gi p là t l% bò cho SLSHN trên 11 kg. 66
T l% này trên mu kho sát là: p = = 0,66 100
Khong tin cy 90% cho p: ( p −e; p +e) Vi p (1− p) 0,66 (1− 0,66) 0,66 (1− 0,66) e = u = u . = 1,6449. = 0,0779 1+0,9 0,95 n 100 100 2
Vy, t l% bò cho SLSHN trên 11 kg t 58,21% ñn 73,79%.
b) Gi n là s bò cn ñiu tra. Ta phi có: 1 2 2 2 s 2 1, 79 n ≥ u . 1 1 0 + ,98 2 n ≥ 2,3263 . = 69, 4 1 2 0,5 2 0,5 ⇔ p 1− p 0,66.0,34 2 ( ) 2 n ≥ u . n 2, ≥ 3263 . 84, = 33 1 1 0 + ,98 1 2 2 0,12 0,12 2
Chn n = 85. Vy cn ñiu tra 85 con bò. 1 5. 13.
Đ dài ca mt loi chi tit máy ñưc ño 25 ln b"ng mt máy ño có sai s
h% thng b"ng 0. Bit r"ng sai s ngu nhiên ca vi%c ño có phân phi chu(n vi
phương sai 100cm2 và ñ dài trung bình trong 25 ln ño là 100cm.
a) Hãy tìm khong tin cy 99% cho ñ dài ca loi chi tit máy trên.
b) Phi tin hành bao nhiêu l n ño ñ b rng khong tin cy 99% cho ñ dài
c a loi chi tit máy trên không quá 8 cm. Gii
a) Khong tin cy 99% cho ñ dài chi tit máy nói trên: (x − ;e x +e) . σ 10 10 Vi e = u . = u . = 2,5758. = 5,15 1+γ 0,995 n 25 5 2 Đáp s: (94,85; 105,15).
b) Gi n là s ln ño. Ta cn có: 1
2e ≤ 8 ⇔ e ≤ 4 σ ⇔ u . ≤ 4 1+ γ n 2 1 2 2 2 σ σ 100 ⇔ n ≥ u . = u . = 2,5758 . = 41,47 +γ 2 ( )2 2 1 1 0,995 4 16 16 2 73
Bài tp Xác sut th ng kê Dip Hoàng Ân Suy ra, n = 42. 1
Vy, cn tin hành ño ít nht 42 ln. 5. 14.
Gi s# ñưng kính c a mt loi sn ph(m là bin ngu nhiên có phân phi
N(µ, σ2). Đo 10 sn ph(m, ngưi ta có bng s li%u:
4,1; 3,9; 4,7; 5,0; 4,4; 4,4; 4,2; 3,8; 4,4; 4,0
Tìm khong tin cy 95% cho µ và khong tin c y 99% cho µ và σ2. Gii
T s li%u ñã cho ta tính ñưc: x = s =
♣ Khong tin cy 95% cho ñưng kính trung bình: − s n 1 9 e = t = t = 1+0,95 0,975 10 10 2 (4,0257; 4,5543 )
♣ Khong tin cy 99% cho ñưng kính trung bình: ( 3,9102; 4,6698)
♣ Khong tin cy 99% cho phương sai là: 2 χ (n − = χ = χ = + γ ) 2 1 + (9) 2 9 23,589 1 1 0,99 0,995 ( ) 2 2 2 χ (n − = χ = χ = −γ ) 2 1 − (9) 2 9 1,735 1 1 0,99 0,005 ( ) 2 2 ( n − ) 2 1 s = 9. (n − ) 2 1 s ( n − ) 2 1 s ; 0, = 0521;0, 7084 2 2 ( ) χ n −1 χ n −1 1+γ ( ) 1−γ ( ) 2 2 5. 15.
Nghiên cu v ñ bn X (kg/mm2) ca mt loi thép, ngưi tin hành mt s
quan sát mt s tm thép trên mu và có kt qu cho trong bng sau: Đ bn (kg/mm2) S tm thép (95, 115] 15 (115,135] 19 (135,155] 23 (155,175] 31 74
Bài tp Xác sut th ng kê Dip Hoàng Ân (175,195] 29 (195,215] 21 > 215 6
a) Tìm khong tin cy 97% cho ñ bn trung bình ca loi thép trên.
b) S+ ñt ñ tin c y bao nhiêu nu mun ưc lưng ñ bn trung bình ca
loi thép trên b"ng khong tin cy có ñ dài b"ng 6? Gii
a) T s li%u trên ta tính ñưc: x =162,6389; s = 33,4076
Khong tin cy 97% cho trung bình ñ bn: ( x − ; e x + e) s e = u = u = = 6,0412 1+ γ 0,985 n 144 12 2 ( x − ;
e x + e) = (156,6;168,7)
b) Gi γ là ñ tin cy cn tìm s n 144 Ta có: e = u = 3 ⇒ u = 3. = 3. = 1,0814 1+γ 1 n + γ s 33,0476 2 2 1+ γ ⇒ = 0,86⇒ γ = 72% 2 5. 16.
Nghiên cu v ñ bn X (kg/mm2) ca mt loi thép, ngưi tin hành mt s
quan sát mt s tm thép trên mu và có kt qu cho trong bng sau: Đ bn (kg/mm2) S tm thép (95, 115] 15 (115,135] 19 (135,155] 23 (155,175] 31 (175,195] 29 (195,215] 21 > 215 6
a) Tìm khong tin cy 97% cho ñ bn trung bình ca loi thép trên. b) 2
Thép có ñ bn trên 195kg/mm ñư c gi là thép loi A. Tìm khong tin
cy 98% cho t l% thép loi A. Gii 75
Bài tp Xác sut th ng kê Dip Hoàng Ân
a) T s li%u trên ta tính ñưc: x =162,6389; s = 33,4076
Khong tin cy 97% cho trung bình ñ bn: s e = u = u = = 6,0412 1+ γ 0,985 n 144 12 2 ( x − ;
e x + e) = (156,6;168,7 )
b) Gi p là t. l% thép loi A. T l% mu: 27 p = = 0,1875 . 144
Khong tin cy 98% cho p: ( p − ; e p + ) e p (1− p ) 0,1875(1− 0,1875) e = u . = u . 1 0 + ,98 0,99 n 144 2 0,1875(1− 0,1875) = 2,3263. = 0,0106 144
Vy, khong tin cy cn tìm: (0,1769; 0,1981) . 5. 17.
Mc tiêu hao nguyên li%u cho mt ñơn v sn ph(m là mt bin ngu nhiên X
tuân theo qui lut chu (n. Quan sát 28 sn ph(m ñưc chn ngu nhiên, ngưi ta
thu ñưc k t qu cho trong b ng sau: x (gam) 19 19,5 20 20,5 s sn ph(m 5 6 14 3
Hãy xây dng khong tin c y 90% cho phương sai t$ng th trong hai trưng hp: a) bit E(X) = 20g; b) chưa bit E(X). Gii n n ∑(x − µ x k )2 ( ∑ − µ k )2
a) Khong tin cy γ cho phương sai t$ng th: =k1 = k 1 ; 2 χ n χ n γ + ( ) 2 1 1 γ − ( ) 2 2 2 χ ( n = χ = χ = + γ ) 2 + ( ) 2 28 28 41,337 1 1 0 ,9 0,95 ( ) 2 2 2 χ ( ) 2 n = χ = χ = −γ − (28) 2 28 16,928 1 1 0,9 0,05 ( ) 2 2 n ∑ (x −µ = k )2 7,25 k 1 =
Khong tin cy cn tìm: 76
Bài tp Xác sut th ng kê Dip Hoàng Ân 7, 25 7, 25 ; (0, = 175;0, 428) 41,337 16,928 (n−1) 2 s (n− ) 2 1 s
b) Khong tin cy γ cho phương sai t$ng th: ; 2 χ n − χ n − + γ ( ) 2 1 1 1 1− γ ( ) 2 2 2 χ ( n − = χ = χ = + γ ) 2 1 + (27) 2 27 40,113 1 1 0,9 0,95 ( ) 2 2 2 χ ( n− = χ = χ = −γ ) 2 1 − (27) 2 27 16,151 1 1 0,9 0,05 ( ) 2 2 ( n − ) 2 1 s = 5,74
Khong tin cy cn tìm: 5,74 5,74 ; (0, = 143;0,355) . 40,113 16,151 5. 18.
X (ñơn v tính b"ng %) là ch tiêu c a mt loi s n ph(m. Điu tra ' mt s
sn ph(m (s.ph), ngưi ta có s li%u: Xi S sn ph(m [5,7) 2 [7,9) 8 [9,11) 14 [11,13) 19 [13,15) 22 [15,17) 20 [17,19) 10 [19,21) 5
a) Đ ưc lưng trung bình ch tiêu X vi ñ tin cy 95% và ñ chính xác
0,3% thì cn ñiu tra thêm bao nhiêu sn ph(m na?
b) Ngưi ta xem các sn ph(m có ch tiêu X dưi mt mc qui ñ nh là loi 2.
T s li%u trên, b "ng phương pháp ưc lưng khong t l% (loi 2), ngưi ta
tính ñưc khong tin cy là (4%, 16%). Tìm ñ tin cy ca ưc lưng này. Gii
a) T s li%u ñã cho ta tính ñưc: x =13,52; s = 3,35.
Đ ưc lưng trung bình ch tiêu X vi ñ tin cy 95% và sai s 0,3 ta cn: 77
Bài tp Xác sut th ng kê Dip Hoàng Ân 2 u 2 1 + γ u 2 2 0,975 2 n ≥ .s = .s = ×11, 2420 = 1 0,3 0,3
Vy cn ñiu tra thêm 283 sn ph(m na.
b) Gi p là t l% sn ph(m loi 2 ' mu t khong tin cy γ c a t. l% sn ph(m loi 2 ta có: p −e =0,04 p =0,1 ⇔ p +e =0,16 e =0,06 Mt khác, p (1− p ) e = u1+γ n 2 p(1 − p) 0,06 0,06 ⇒ u = e / = 100 = 10= 2 1 +γ n 0,1×0,9 0,3 2 1+ γ = ⇔ γ 2 5. 19.
Vi%n thng kê mu n ưc lưng t l% p ngưi dân không ñng ý v m t ñiu
lut mi ñưc ñ ngh.
a) Nu mun sai s cho phép không quá 2% ' ñ tin cy 90% thì phi hi ý
kin ít nht my ngưi?
b) Trên mt mu ngu nhiên 344 ngưi ñưc hi ý kin, có 83 ngưi không
ñng ý. Hãy tìm khong tin cy 90% cho p . Da vào s li%u ca mu này, hãy gii l i câu a). Gii
a) Gi n là s ngưi cn h i ý kin. Ta phi có: 2 2 1 1 n ≥ u . = u . = 1691,1 1+0,9 1+0,9 2ε 2.0,02 2 2
Vy, phi hi ý kin ít nht 1692 ngưi. b) T l% mu: 83 p =
= 0,241. Kho ng tin cy 90% cho p : ( p− ; e p+ ) e 344 p (1− p) 0, 241(1− 0,241) e = u . = 1,6449. = 0,0379 1 0 + ,9 n 344 2
Vy, khong tin cy cn tìm là: (0,2031;0,2789) tc là t 20,31% ñn 27,89%. 78
Bài tp Xác sut th ng kê Dip Hoàng Ân
Gii li câu a), trên cơ s' có mu thăm dò, kích thưc mu cn tìm: p 1− p 0, 241 1− 0,241 2 ( ) 2 ( ) n ≥ u . = 1, 6449 . = 752, 2 1 1+0,9 2 2 ε 0,02 2
Vy, cn hi ý kin ít nht 753 ngưi. 5. 20.
Đ nghiên cu ñư ng kính X (mm) ca mt loi sn ph(m do m t xí nghi%p
sn xut, ngưi ta ño ngu nhiên 100 sn ph(m ca xí nghi%p và có kt qu cho trong bng sau: xi 9,85 9,90 9,95 10,00 10,05 10,10 10,15 Tn s 8 12 20 30 14 10 6
Theo qui ñnh, nhng sn ph(m có ñưng kính t 9,9 mm ñn 10,1 mm là
nhng sn ph(m ñt tiêu chu(n k4 thut. Tìm kho ng tin cy 95% cho t l% và
ñưng kính trung bình c a nhng s n ph(m ñt tiêu chu(n k4 thut. Gii
Bng s li%u cho các sn ph(m ñt tckt: xi 9,90 9,95 10,00 10,05 10,10 Tn s 12 20 30 14 10
♣ Gi p là t l% sn ph(m ñt tckt, t l% này trên mu là: 86 p = = 0,86 100
Khong tin cy 95% cho p : ( p− ; e p+ ) e p (1− p ) 0,86(1− 0,86) e = u . = 1,96. = 0,068 1 0 + ,95 n 100 2
Vy, khong tin c y cho p là: (0,792; 92,8) nghĩa là t 79,2% ñn 92,8%.
♣ Gi X là BNN ch ñưng kính ca nhng s n ph(m ñt tckt. T s 1 li%u ta có:
x = 9,994; s = 0,06. 1 1
Khong tin cy 95% cho ñưng kính trung bình nhng sn ph(m ñt tckt:
(x −e;x + e 1 1 ) s 0,06 1 e = u . = 1, 96. = 0,012 1+ 0,95 n 2 86 1
Khong tin cy cn tìm:(9,982;10,006) (mm). 79
Bài tp Xác sut th ng kê Dip Hoàng Ân 5. 21.
X (tính b"ng %) và Y (tính b"ng cm) là 2 ch tiêu ca mt loi sn ph(m.
Kim tra ngu nhiên ' mt s sn ph(m, ngưi ta có kt qu sau: x i 1 2 x x 3 4 yk (90, 95] 5 13 2 (95, 100] 19 23 15 8 (100, 105] 12 10 7 (105, 110] 5 2
a) Đ ưc lưng trung bình ca ch tiêu Y vi sai s cho phép 0,5 cm và ñ
tin cy 90% thì cn ñiu tra thêm bao nhiêu sn ph(m na?
b) Cho bit khong tin cy 96% ca ch tiêu X là (1,59%; 2,61%). Hãy tính
giá tr trung bình và ñ l%ch chu(n m u ca ch tiêu X. Gii
a) Bng phân b tn s ch tiêu Y: (100, y (90, 95] (95, 100] (105, k 105] 110] n 20 65 29 7 k
T ñó: y = 98,4504; s = 3,89 y
Gi n là s sn ph(m cn ñiu tra: 1 2 2 2 sY 2 3,89 n ≥ u . = 1, 6449 . = 163,8 1 1+ 0,9 2 2 ε 0,5 2 ⇒ n = 164 1
Vy, cn ñiu tra thêm 43 sn ph(m na. b) Theo ñ bài ta có: x −e = 1,59 x = 2,1 ⇔ x + e = 2,61 e = 0,51 s e n Mt khác, 0,51. 121 e = u . ⇒ s = = = 2,732 1+0,96 n u 2,0537 2 1+0,96 2 5. 22. 80




