













Preview text:
ThS. TRẮN THỊ THỤC LINH
Giải bài tập
liủ lý tin hiệu số và Matlab
NHÀ XUẤT BẢN THÔNG TIN VÀ TRUYỀN THÔNG Chương 1 TÍN HIỆU ■ VÀ HỆ T ■ HÓNG RỜI RẠC■
A. T Ó M T Ấ T LÝ T H U Y É T
1.1. Định lý ỉav mẫu
Ta chú ý rằng inột tín hiệu sẽ đưọc khỏi phục khi tần số lấy mẫu phải lón hơn hoặc bằng hai
lần bề rộng phơ của tín hiệu.
> 2B (B ĩmdx)
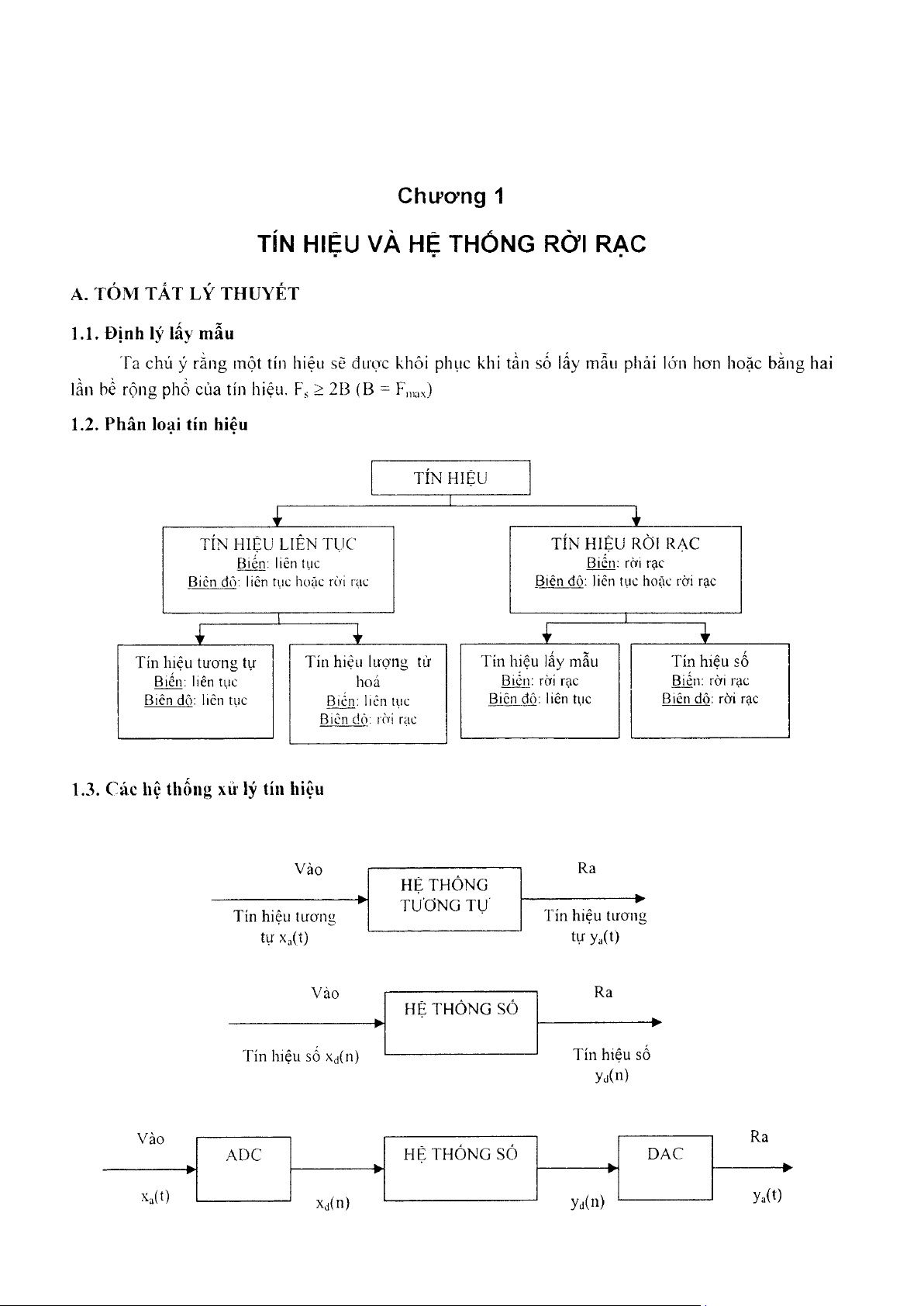
1.2. Phân loai tín hiêu T Í N H Ĩ Ệ U I
T Í N H I Ệ U L I Ê N T Ụ C
T Í N H I Ệ U R Ờ I R Ạ C Biển: liên tuc Biên: rời rac
Bi ên đỏ; liên ruc h o à c ròi rac
Bi ên đỏ: liên tuc h o ă c rời rac i ỉ £ ỉ
T í n h i ệ u t ư o n g t ự
T í n h i ệ u l i m n i í t ử
T í n h i ệ u l ấ y m ẫ u T í n h i ệ u s ố Biến; liên tuc h o á Biến: rời rac Biến: rời rac Bi ên dô: liên tuc Bicn: licn tuc Bi ên đô: liên tuc Bi ên dô: rời rac Bi ên dò: rờị rac
1.3. C ác hệ thống xử lý tín hiệu Vào Ra HỆ THÓNG
-----------------------------------^ TƯƠNG TỤ Tín hiệu tưonu Tín hiệu tưong Vào Ra HỆ THÓNG SỐ
---------------------------------- ^ rín hiêu số Tín hiêu số yj(n: Vào X a ( t )
Giải bà! tặp xưly tin hiéu só và Matlab
1.4. Tín hiệu ròi rạc
L 4 . L B iê u d iẽn tín lỉ ìệii n ) i rụ c
- Biẻu diẻn băniz liàm sò - Bicu diên băniì bảnụ - Biếu dicn bằniz dày se^
- Biêu diên bănii đỏ ihỊ
Clỉú ỷ ; m ộ t t í n h i ệ u b ấ t k ỳ x ( n ) d e u d i i ọ c b i ê u d i ễ n íhỏỊìLi q u a đ á p ử i m XUÌIU d ạ n u l ỏ n ^ q u á t như sau:
L 4 .2 M ộ ( sô (iãv c ơ h á n
a) D ã y x u n g cỉoiì vị:
Trong miền n, dăy xung đon vị đưọc dịnh nụhĩa như sau: ỉ n - 0 ỗ ( n ) = [0
h) D ã y n h a y clov vị:
TYong miền n, dày nhảy đon vị đu ọc định imliĩa như sau: 1 n > ( ) u ( n ) 0 n 7^ 0
c) D ã y c h ừ nlỉậl: 0 < n < N - 1
Tronu miôn n, dăy chiì nhật đượe dịnỉì nuhĩa nhu' sau: rccl^ ( n ) - n còn lại
(i) D â y dỏc d o n vị: n > 0
' ĩ ron g miền n, dày dốc đon vị được định nghĩa như sau: r ( n ) - n cò lì lại
e) D ã y hàỉìỉ ỉìỉũ:
Trong miền n, dãy hàm mũ được định nghĩa như sau: a" n > 0 e ( n ) = 0 n còn lại
L 4 3 , M ộ í sô đ ịn h n g h ĩa a. D ãy tuần hoàn:
Ta nói rằng một dãy x(n) là tuần hoàn với chu kỳ N nếu thỏa màn điều kiện sau đây:
x ( n ) X ( n + N)"= X ( n + f N ) Ký hiệu: x ( n ) ,.
Chương 7; Tín hiệu vá hệ thống rời rac 1
h. /)í/v có cỉììẻỉi dài hữu hạn:
Một dày đưọc xác dịnh với sô hữu ỉìạn N Iiìầu la gợi là day có chiều dài hữu hạn vói N là chiêu dài cua dãv. c.
ỉiíxrng c u a íỉàv:
N ả n u lưọnu cua mộl dàs' x(n) dưọ'c dịnh nuliĩa nliLi' sau:
d. Còìỉ<^ siíàl íriiỉỉ^ hình CỈÌU ìììộỉ líỉỉ Ììịựtí
( ' ỏ n g SLiàl truim bình cua một tín liiộu x ( n ) dưọ‘c clịnh nghĩa nhir saii: 1 p - ỉim z 2 N -i-1n - - N'
1.4.4. Các phép toán c ơ han
- Phép cộim. phép nhân liai líỉi hiệu.
- Phép nhàn mội tín hiệu vói liănu sỏ. - Plìcp tre íín hiộii.
ì. 4.5. H ộ th ô ìiịị tiiy Ề n íí n h h ã t h iê ỉĩ ( T T B B ) , Đ á p ín iịị x u n g h (ii)
- Cần lưu V hệ ihốim tuven líiih bat buộc pliai íhoà màn riíTuỵên Iv xếp chồim:
T [ a . X i ( n ) + b . X i ( n ) ] a . T [ x Ị ( n ) | b . T [ x 2 ( n ) ‘ .
- ỉ lệ thống luvến tính bất bien; ửnu vói kích ihích đầu vào x(n) ta có dủp ứnti ra là y(n) thì
iLixvim tự ửim vói kích thích đầu vào x(n-k) ta cỏ đáp ứnu ra là y(n-k).
- Khi ta có đầu vào hệ ihốnu lu>en linlì bất biến là xun ” đơn vỊ(S(n) thi đầu ra là dáp ứng
xLiim h(iì). Đ á p ứ n u XLum h( n) là d ặ c t r ư im h o à n t oàn c h o hệ t l iốnu l u y ế n tính hất biến.
ĩ . 4.6. Phép chập:
D â y là phép toán quan Irọn^ lìlìủí troiìiỊ xu lý lín hiệu dê xác địnlì đầu ra v(!ì) hệ l l ìống khi
bict đ â u v à o x(n) và d á p ứi m xLum h(n). y ( n ) ^ x ( n ) * h ( n ) ^ x ( k ) . h { n ~ k) ^ h ( k ) . x ( n - k) k~ - k^-■«
Phép chặp cỏ tínli chất: uiao hoán, phân phối, két họp.
L4, 7. Hộ thong TTBB nhãn (Ịiiảy tín hiệu ỉĩhâỉĩ quá
JIệ thống TT BB dược uợi là hệ tliốHii nhân quả khi đáp ứiiiỉ xuntí h(n) cua nó thoả mãn: h ( n ) ^ 0 v ó i Vn<{) .
Tin hiệu \ ( n ) đuxyc gọi tín hiệu nhân quả khi nó thoả mãn x(n) “ 0 vói V n < 0.
Lim ỷ: Các hệ íhônu nhân quả và tín hiệu nhân quả mói tồn tại troiiii thực tế
Hẹ ịIìôỉìọ^ TTBB ổn địn/ì
i ỉệ thốna ỏn định là hệ ihốiìíi BIBO. đáp ứni^ xinm h(n) của nó phái thoa màn điều kiện sau: s = z ll = - c c
Giải bài tập xử lỷ tín hiệu số và Matlab
L4.8. P h u ơ n g trình s a ip h ã n tuyến tinh h ệ số h ẵng (PTSPTTHSH )
Quan hệ vào ra cùa hệ tliốim tuyến tính bất biến sè đirọc mô tá ỉxVi phưoim trình sai phân
tuyến tính hệ số hằim có dạniĩ như sau:
^ a , ( n ) y ( n - k ) = 2 ] b , . ( n ) x ( n ^ r ) k=() r^O Trong đó: - X đầu vào. - y đầu ra.
Các hệ số ai,, br đặc trưiìii hoàn toàn cho hệ thốnổ, có vai trò tưong tự nlur đáp ứng xun" h(n).
Việc giải PTS PTTHS H đẻ tim ra đảu ra y(n) có hai phu'oníz pháp chính: - Phưoim pháp thế.
- Phưong pháp tim nghiệm riêng (yp(n)) và nghiệm thuần nhất (yo(n)). suy ra nghiệm tống quát y(n) - yo(n) + yp(n).
T ừ PTS PTTH SH trên ta sẽ có mộl sổ khái niệm về;
- H ệ thống không đệ quy khi N "= 0. Bản chất của hệ thốno này là khôn g có thành phần hồi tiếp.
- H ệ thốnỊỊ đ ệ quy khi N ^ 0. Bản chât của hệ thông này là có thành phân hôi tiẻp.
- H ệ thống đ ệ quy thuần tuỷ khi N
0. M “ 0. Hệ thốníí này chi gồm duy nhất các thành phần đệ quy.
Lim ỷ: N hư vậy đến đây ta có hai cách biểu diễn quan hệ vào ra hệ t hống rò'i rạc.
- Biểu diễn theo phép chập: v(n) x(n)*lì(n) M N
- Biểu diền theo phương trinh SPTTHSH: y ( n ) “ ^ b ^ x ( n ~ r) - ^ a ị ^ y ( n “ k) (thư('mg r = 0
p h a i chuàỉĩ hoá ŨQ ^ I)
1,4.9. Thực hiệỉt hệ thống
Các phần tử thực hiện hệ thống bao gồm: phần tử cộng, phần tử nhản, nhân với hằng số, phần từ trễ D.
Khi thực hiện hệ thống phải dựa vào PTSPTTHSH, luôn nhcT phải chuản hoá hệ số a,) = 1 để M N
CÓ y ( n ) - ^ b j . x ( n - r ) - ^ a | . y ( n “ k ) rồi m ó i vẽ SO' đồ hệ t h ố n g. T r ê n thụ-c tế ngưò'i ta sẽ d ù n g r-o k=!
r á c bộ xử lý toán học ALU, các thanh ghi dịch... để thực hiện hệ thống xử lý tín hiệu số theo SO' đồ.
L 4 J 0 . Tương quan tín hiệu
Phép tưong quan thường dùng để nhận biết các tín hiệu, phân biệt tín hiệu vói nhiều, phát
hiện vật thể... Có hai loại t ương quan: •fOO
- T ự tưo'ng quan: Tư ơ ng quan tín hiệiỉ x(n) vói chính n ó : R ^ ^ ( n ) = ^ x ( m ) . x ( m - n). ttl = -CC'
- Tư ơng quan chéo: Tưoìig quan tín hiệu x(n) vói y(n); R^y(n) = ^ x ( m ) . y ( m - n).
Chương 1: Tín hiệu và hệ thống rời rạc
B. BÀI T Ậ P C ơ B Ả N
L l . Cho tín hiệu x,^ ( t ) ^ 3cosl007Tt
a) Xác định tốc độ lay mẫu nhò nhấl cần thiết đế tránh sự chồng mẫu.
b) Giả sử tín hiệu đưọ'c lấy mẫu tại tốc độ
= 200 Hz. Tín hiệu rò'i rạc nào sẽ có đưọ'c sau lấy mẫu?
c) Giả sử tín hiệu đưọ'c lấy mầu tại tốc độ F. - 75 Hz. Tín hiệu ròi rạc nào đạt được sau lấy mẫu?
d) Tần số F < F^ / 2 của một hình sin có các mẫu đồng nhất với các mẫu trong phần c) là bao nhiêu ? L ờ i giái:
a) Tần số của tín hiệu tưong tự là F = 5 0 Hz. Vi thế, tốc độ lấy mẫu tối thiểu cần thiết để
tránh hiện tưọ‘niỉ chồng mẫu là - 100 Hz.
b) Neu tín hiệu đưọ'c lấy mẫu tại
- 200 H z thì tín hiệu rời rạc có dạng:
x ( n ) = 3 co s (l 0 0 7 ĩ / 2 0 0 ) n = 3 c o s ( 7ĩ / 2 ) n c) Nếu
- 75 Hz, tín hiệu rời rạc có dạng
x ( n ) = 3 c o s ( l 007i / 7 5 ) n ^ 3 c o s ( 47t / 3) n - 3 c o s ( 2 k - 27ĩ / 3 ) n := 3 c o s ( 2 Tc/3 ) n
d) Đối vói tốc độ lấy mẫu
= 75 Hz, ta có; F = fF^ =: 75f
Tần số của tín hiệu sin trong phần c) là f - 1/3 . Do đó: F = 25 Hz Tí n hiệu sin ià:
( t ) - 3cos27iFt - 3cos507tt được lấy mẫu tại R - 7 5 mẫu/s sinh ra các
mẫu đ ồ ng nhất. Vì thế F = 5 0 H z là bí danh (alias) của F - 2 5 H z ứng vói tốc độ lấy mẫu ĩ*: = 75 h I
1.2 . Xél tín hiệu tưon g tự
Xg ( t ) = 3 c o s 5 0 7 ĩ t + 1 0 s i n 3 0 0 7 il "CoslOƠTit
Hãy xác định tốc độ Nyquist đối với tín hiệu này?
L ờ i g iải: Tín hiệu trên có các tần số thành phần sau: F, = 2 5 H z , P . - I S O H z , F 3 - 5 0 H z N h ư vậy,
= 1 5 0 Hz và theo định lý lấy mẫu ta có: 300 Hz Tốc độ Nyquist là . Do đó, == 300 Hz.
Nhận xẻt: Ta nhận thấy rằng, khi lấy mẫu thành phần tín hiệu 10sin3007Tt vói tốc độ Nyq ui st
- 300 Hz sẽ tạo được các mẫu lOsinTin có giá trị luôn luôn bằng không. Nói khác đi, ta
đã lấy mẫu tín hiệu hình sin tại các điểm nó cắt trục hoành, vì thế thành phần của tín hiệu này bị
mất hoàn toàn. Hiện t ương này sẽ không xuất hiện, nếu dao động sin có một sự lệch pha 0 n ào đó.
Khĩ đó, ta có 10sin( 3007r í+ 0) và nếu lấy mẫu tại tốc độ Nyquist ta có:
10sin(Tcn + 0) - i o ( s i n 7m c o s 0 + cosTinsinG) = l O s i n 0 c o s 7ĩn - 10
Giải bài ỉàp xử lỳ tin hiệu số và Matlab Ncu 0
0 hoặc K thi các mầu S!1!, ỉô\ lại tỏc dộ N\tjiiisl sè kliác klìônii. Tu\ nhicn. biên dộ
cua các niầu \'ẫn chua xác định tlirợc niội cách chínli xác \ ì pha 0 \ẫii clura hict. Biện pliáp dơiì
ịXìàn dc tránh hiện Urọ‘n<’ này lủ nòn lắv mần tíii hiệu lirơng tụ' ơ tan số lỏn ho'iì laiì so Nyquisi.
1.3. C h o tín hi ệu í i roi m ÍỊI'
( t ) - 3 c o s 2 0 0 t)7ií -5sìn600()7ĩí + ỉOcosỊ20007ĨÍ
a) Xác địnlì lốc dộ Nyquisl cua ÍÌ11 hiệu'.^
b) Gia sư răim. tín hiệu duọc là\ màu lại lỏc dộ 1]. = 5 0 0 0 mau/s, !lày xác dịnli líii hiẹu lỜ!
rạc thu dưọc sau khi lấ\' mầu'!
c) ỉlày xác địnlì tín hiộii lưong tụ
( t ) . dưọc phục hồi lử cac mầu khi sư dụnu cònu thức nội suv lí tirònu?
Lửi ỵiái: a) Các tần sô cua tín hiệu tuơiìg tự' nav là: 1^ - 1 kHz. K - 3 kHz, 1% - 6 kỉ ỉz
Nlur vâv. r' ,, - 6 kHz và theo diỉilì lí lấv mẫu. có: F > 2P' ” 12 k\Ỉ7. * ^ M IU ' • > f U il \
Tốc đ ộ N y q u i s t là:F;, - 1 2 k ỉ l / . b) Vi la chọn
- 5 klỉz, nên lâii sỏ uập sè ià: F^/2 “ 2.5 kHz
dâv lủ tần số cực đại đưọc tíìi hiệu đà lấy mầu thê hiện ỉììột cácli duy Iihất. l'a cỏ: \ ( n ) (n r ) ^
( n / R ) = 3 c o s 2 n ( ỉ / 5 ) n + 5sin 27ĩ(3/5)n -t- l í)cos27r(6/5)n
3co s2 Tt (l /5) n -f 5sin 2 tĩ( ỉ - 2/5 )n f H)cos27ĩ(l --i-1/5) n
- 3 cos 2ti( 1/5) n + 5 sin 2 (-- 2/5) n -r Ị 0 cos 271 (1/5) n
C’ u ố i c ù n g , l a c ó : X ( n ) “ 1 3 c o s 2 t ĩ ( 1 / 5 ) n - 5 s i n 2 tt( 2 / 5 ) n
c) Vi chi có các thành phàn tnn sô 1 ki I/ và 2 k l ĩ / là hiện diện Iroim tín hiệu clă lây mau. ncn
tín hiệu tưonu tự có tlìẻ phục hỏi clirọc lủ ( t ) 13cos20()()7ĩt - 5sin 4000nt
Dây là kết quá khác đáng kè stì vói Ún liiệu I^ốc x,^ ( t ) . Việc Iiìéo tin hiệu lưo'im Xự lioc như llie
này là do ánh hưòng cua hiện tirọng chồnn mẫu Iiìà niTuvên nhân chính là vì lần số lay mẫu thấp.
1.4. Phân loại các tín hiệu sau theo cac íiẻu chí (1) tín hiệu một chiều hay nhièu chiều, (2) tín hiệu
đon kênh hay đa kênh, (3) tín hiệu liên íục hay rò'i rạc theo thời gian, và (4) tín hiệu lương tự hay số
(theo biên độ). Hàv đưa ra giải thích ngan min.
a) Giá ụần đủnu cua các chửim khoán trcn thị trưò'nu c hửn e khoán Việt Nam. b) Một bộ ph im màu
c) Vị trí của bánh lái của một xe hoi khi chuyến động đối vói vệt tham chiếu là ihàn xe.
d) Vị trí của bánh lái của mộl xe ho‘i khi chuyền độnu đối vói vạt Iham chiếu là mặt đất.
e) Các số đo trọng lưọ'ng và chiều cao cua một đứa trẻ hàng thánu. L ò i Ị*iãi: Gọi ý:
Chương 1: Tín hiệu và hệ ỉhống rời rạc 11
- Lá lín hiệu mộ t chiẻLL đa kênh, ròi l íic theo lliòi uian. và là tín hỉẹu sô.
' I .ủ lín hi ệu d a c h iều, d o n kên h, licn tục t h e o thòi g i a n , và là tín h i ệ u u u r n u tự.
- ỉ,à tin hiộu inột cliiều, đo‘n kênh, lièn lục theo Ihòi gian, và là tín hiệu tư'0‘ng tự.
- ỉ. à tín hiộti m ộ t c h iều, đ o n kê n h , liên lục t h e o t hò i g i an , và là tin hi ệu URTng tự.
- I.à lín hiệu một chiều, đa kènlì. ròi rạc llieo ihòi man, và là tín hiệu số.
1.5* Hày xác dịnh xem liệu các tín hiệu sau đây có phải là các tín hiệu tuầiì hoàn không. Tvoĩìịi
t r u ừ n u h ọ p là tín h iệ u tuân h o à n , h à y x ác dịnli c h u kì CO’ b a n c ủ a tín h i ệ u đó. a)
X,, ( t ) = cosỊ 5 t + “ ị J \ / Ị I V J b) x ( n ) = 2 c o s 5n-í--^ I \ ^ '
c) \ ( n ) =: 3exp Jị — - Tt V y nTT'' ( n ị d) X( n) = 2 cos — co s -- ! Á 1 ' 4 \ ^ y V ^ /' ' riTĩ ^ . ( ĨITT ì Ị nn n']
e) X ( n) ~ cos — __ " S in — i 4-■ 2c o s Ị ---------- 2 ; l 8 ; l 4 3 , Lời giải: - 2 7Ĩ
Tỉn hiôu tuân hoàn vói chu ki r - . 5 _ 5
tín hiệu khỏnụ tuần hoàn. 2 H
> tín hiện khỏnu tuần hoàn. 1 2 t ĩ / \ n
1'ưo‘ii^ tụ‘ la có; cos
là tín hiệu không tuần hoàn; cos ^ ] l à tín hiệu tuần hoàn, suy ra u V 4 ;
tích c ù a chúng là tín hiệu không luân hoàn. ^ 7ĨĨÌ cos
là tín hiệu tuần hoàn vói chu kì Tj,| - 4 Tĩn CCS
là tín hiêu tuân hoàn vó'i chu kì T - 1 6 8 y 7in 7Ĩ cos
là tín hỉệu tuần hoàn vói chu kì = 8 4 3
Do đó x(n) tuần hoàn vói chu kì Tp = 16 ( vì 16 là bội số chung nhò nhắt của 4,8,16). 1.6.
Chứnỵ minh rằng tần số CO' bán Np của các tín hiệu: s j n j - k - 0 , 1, 2, . . . 12
Giải bài tập xử lỳ tin hiệu số và Matlab
có dạnii Np = N/U SCI .N(k.N)
(U'SCLN(k,N) là ưóc số cliuiiẹ lỏn nhất của k và N)
b) Xác định chu ki cư baii cua tập họp này đối vói N =7
c) Câu hỏi n hư b) đối vói N = 16 r -. ■ 27rk k
L ờ i ơiai: a) co = ------ có nahĩa là t = — . N N
Đặt a = U'SCLN(k,N). có ntỉhĩa l à k = k a . N = N a
Do đó, f = ~ , có nghĩa là N = N = ^ (đpcm) N a b) N - 7 k = 0 1 2 3 4 5 6 7 ƯSCLN(k,N) = 7 1 1 1 1 1 1 7 Np = 1 7 7 7 7 7 7 1 c) N = 16
k = 0 1 2 3 4 5 6 7 8 9 10 11 1 2 . . . 16
ƯSCLN(k,N) = 16 ! 2 1 4 1 2 1 8 1 2 1 4 . . . 16
Np = 1 6 8 1 6 4 16 8 16 2 16 8 1 6 4 . . . 1
1.7. Xét tín hiệu tưoTig tự hình sin như sau: ( t ) = 3sin(1007:t) a) Vẽ tín Iiiệu
( t ) vói 0 < t < 30ms . b) Tí n hiệu
( t) đưọ' c lây máu vói tốc độ lấy mẫu
= 400 mẫu/s. Mãv xác định tẩn số của
tín hiệu ròi rạc x ( n ) =
(n']'),T = — và chứng minh rằng x(n) là tuần hoàn. ^ s
c) Tí nh giá trị của các mẫu troni> một chu kì của x(n). Vẽ x(n) trong cùng một hình vẽ vói
( t ) . Xác định chu kì của tín hiệu ròi rạc theo ms.
d) Có thể t im thấy một tốc độ lấy mẫu
sao cho lín hiệu x(n) đạt tói giá trị đỉnh của nó là 3? Giá ti'ị
nh ò nhất thoà màn điều kiện đó là bao nhiêu?
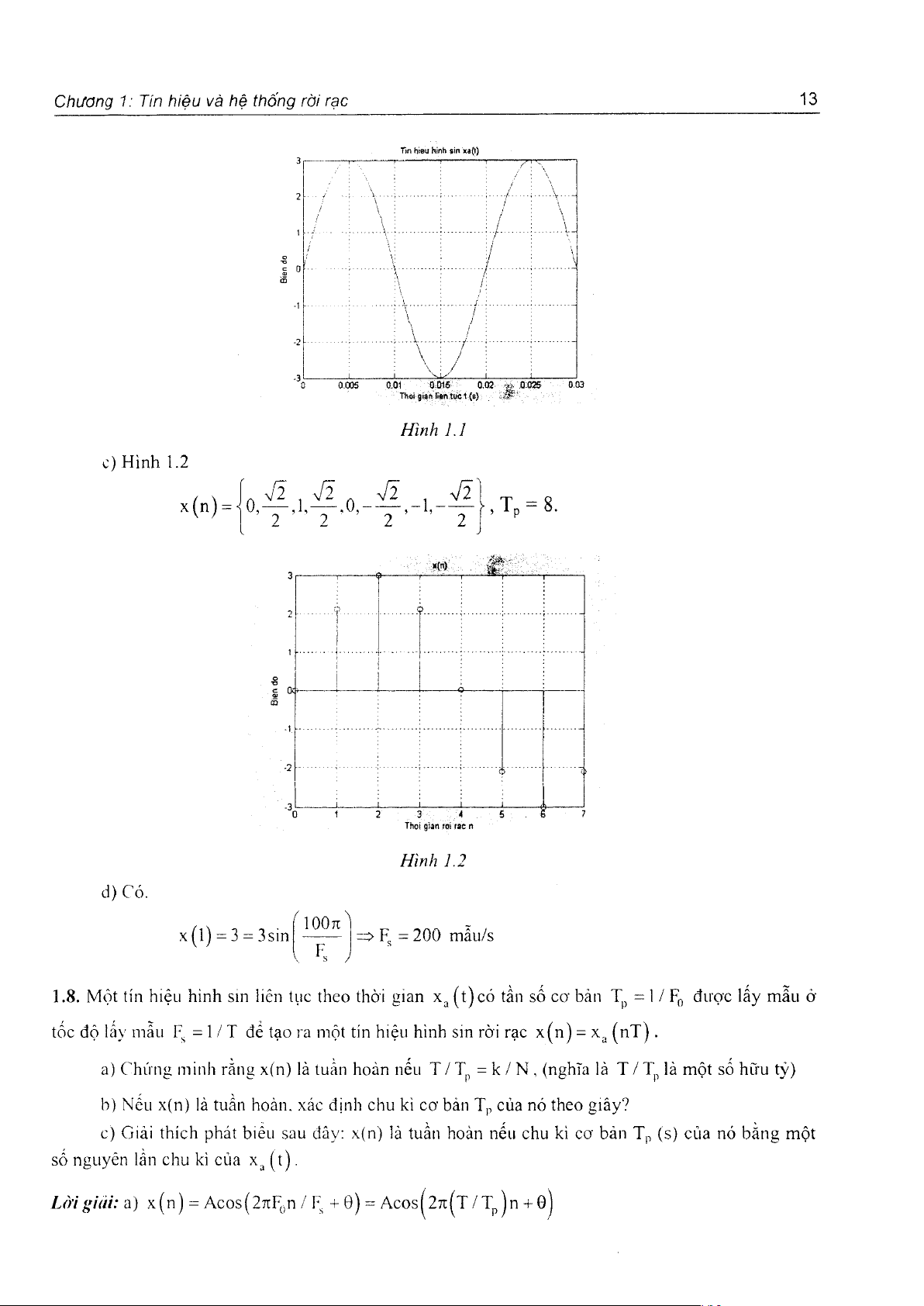
L ờ i giải: a) Hình 1.1 b) x ( n ) = X3 ( n T ) , T = ^ x ( n ) =
( n / F^) = 3 s i n ( l ( ) 07ĩn / = 3 s i n ( 7ĩ n / 4 ) / \ n f = - L 2n v 4 .
Chương 1: Tin hiệu và hệ thống rời rạc 13 Tin hieư hình sin xa(t) 0. 0)5 0.01 0.D16 0,02 -i. Q025 0.03 gitn l«n tuc t (c) ^ ' H ìn h L I c ) H i n h 1.2 (n) = 0 0 , T = 8. , . , o : :
. . . . . . . . . . . . . . . . . . . . . . 1 . . . . . . . . . . . . . . . . . . . . . . . i i
Ị . . . . . . . . . . . . . . . . . . . . . . . ' ! . . . . . . . . . . . . . . . . . . . . . • . . . . . . . . . . . . . . . . . . . . . . . . . . ■ . . . . . . . . . . . . . . . . . . . . . . . . i • • i ị : 1 : ỉ I ' ■ ‘ 1 1 i
. . . . . . . . . . . . . . . . . . . . . ■ . . . . . . . . . . . . . . . . . . . . . . . < : j . . . . . . . . . . . . . . . . . . . . . 7 > i.. _ _ _ _ _ _ _ L . . .
i.......... i ....... i......... Thoi gian roi rac rt H ìn h 1.2 d) Có. ' i OOtc' x ( l ) = 3 = 3sin =:> F = 200 mẫu/s
1.8. Một tín hiệu hinh sin licn tục theo thòi gian
( t ) c ó tần số CO' bàn - 1 / đưọ'c lấy mẫu ở tốc độ lấv mẫu
= 1 / T đe tạo ra một tín hiệu hình sin ròi rạc x ( n ) = ( n T ) .
a) Chứng minh r ằ n s x(n) là luần hoàn nếu T /
= k / N , (nghĩa là T / Tp là một số hiru tỷ)
b) Nếu x(n) là tuần hoàn, xác định chu kì cơ bản Tp của nó theo giây?
c) Giài t h í c h p h á t b i ê u s au đây; x (n ) là tuần h o à n nếu c h u ki CO' b à n Tp (s) của n ó b ằ n g m ộ t
số nguyên lằn chu ki của x,^ ( t ) .
LờiỊỊÍái: a) x ( n ) = Acos(27tF^)n / 1 ; + 0) Acos 1^271 ( T / T p ) n + 0^ 14
Giải bài tàp xử ly tín hiệu số và Matlab Mà T / T
là môt sổ hữu tv\ suy ra x(n) là iLiần hoàn. ' N
b) Neu x(n) là tuần hoàn thì f “ ky'N, troníí đó N là chu kì. Do đó. T, - ~ T = k d
nuhĩa là cần k chu ki Tp của tín hiệu tưo'ng tự đè tạo nên một chu kì cua Ún hiệu ròi rạc. c) Tị
kT,^ => N T = k T =:> í = ^
f là số hữu tv => X( n ) ỉà tLiầi! hoíxn. / a p p -^1 J - V ./
1.9. Một tín hiệu tưorm tự có các tần số lên đến 20 kllz.
a) X á c đ ị n h p h ạ m VI c u a l ần số l ấy m ẫ u đ ể c ó t hê kh ỏ i p h ụ c chi ìih x ac lin h ỉ ệ u n à y t ừ các mau cũa nó.
b) Giả thiết rằng c húnạ ta lấy mẫu tin hiệu này vcVi tan số lấv mau ^ 16k}Iz . Hày xác định
diều gì sẽ xảv ra đối vói tần so Fj = 10kHz
c) Lặp lại câu b) với F, ~ 18kHz L ở i giải:
a ) F _ = 2 0 k H z = i > F , > 2 F _ = 4 0 k H z b)
Đối vói \\ ^ 16kHz . F.âp(mid)
F, / 2 = 8 kHz, suy ra 10 kHz sẽ là aiìh (alias) của 61cHz.
c) F = 18 k l ỉ z sẽ là ảnh (alias) của 2 kHz
1.10. Một tín hiệu điện tâm đõ íỊÔm các tân sô hữu dụng lẽn đèn lOO Hz.
a) 'rằn số Nyquist cho tín hiệu này là bằim bao nhièu'.^
b) Giả ihiêl là la lâv mâu iín hiệu này ở lôc dộ 200 mâu/s. Hàv xác dịnlì tàn sò lỏn nlìâl mà
tín hiệu có thê được biêu diên duy nhât tại tôc độ lâv mâu này. L ò i gidi: a) =100kHz,l' > = 200kHz => = 200kMz
b) F,,p(,„id) = F, /2 = 1 0 0 H z
1.11. Một lín hiệu tuxTng tự X,, ( t ) = 2sin(240Ttt) + 3si n( 72 0ĩ i t) đuxrc lấv mầu 600 lần ,'s.
a) Xác địiili tôc độ lâv mâu Nyquist cho ( t ) ?
b) Xác dịnỉi tần sổ gấp (íblding tVequency)?
c) Xác địnli các tân sô theo radian trong tín hiệu ròi rạc x(n) thu đu'Ọ'c?
d) Nếu \ ( n ) đưọ'c cho qua một bộ biến đổi số/ tưoim tự, hăy xác định tin hiệu ^^^khỏi phục đưọc.
Lời Ịịiàì: a)
= 3 6 0 H z , F , „ = 2 F „ „ , = 7 2 0 H z
b) Ppìp = F, /2 = 600/2 = 300 Hz
Chương 1: Tín hiệu và hệ thống rời rạc 15
c ) x ( n ) = x,, ( n T ) = x , ( n / i g = 2 s i n (24()7m / 6 0 0 )
3s!n ( 72()7:n / 6 0 0 ) = 2 s i n (27TI1 / 5) - 3 s i n (ỎTtn / 5) 2 t : _ I n ' s " 5
d ) y ^ ( t ) = x ( l - ' t ) = 2 s i n (2407X1) 3 s m ( 7 2 0 T i t )
I .I 2 . Một cÌLrtrnLi truyen íhỏnii tin số nianu các ĩừ mà nhị phân hicii cỉiễn các mẫu cùa mộl tín hiệu vào:
( l ) “ 3cos(6007ĩt) r 2cos(l SOOĩit)
Diròiiu truyền hoạt dộim tại lOOOO bit/s và mỗi mầu đầu vào đưọ'c lirọiiu tử hoá thành 1024 niửc điện áp khác nhau.
a) 1 ỉày xác định tần so lấy mẫu \ à tần số lĩấp.
b) Màv xác định tán sô Nyquisl đỏi \ ỏ‘i lín hiệu (t)
c) l ỉ à v x á c đ ị n h c á c t ần số t ro nu Ún hi ệu ròi rạ c x (n ) t hu đirọc.
d) Fíàv xác định độ phân uiai A
Lời ịỉiiỉi: Số bil/mẫu log: {1024) ^ 10 Ị.;, ~ ^ -------- =: 1 OOOmai! s lObiĩ / mau
S u y r a : F,,:ip = Fs / 2 = 5 0 0 I I z ^ 0 .... ^ .
I ' , , = . 2 l - ; „ = 1 8 0 0 1 1 / .
Các tân sô trone tín hiệu ròi rạc x(n) thu dược: . ỎOOtĩÍ' ỉ = 0,3 = 0.9 2 tc i F Xct thầy f\ = 0,9 > 0,5
= 0.5) => i\ = 0,1 (tần số cua aiih_aliasing) Suy ra: X ( n )
. l cos Ị"2n(0. 3) nl + 2cos 2; i ( 0 . l)n m - 1 1023 1023
1.13. Xét một ỉiệ t h ố n u xư lÝ lín liiệu đơn liian nliu' t rên lìinh vè SÍUI đâ> . Các CỈÌLI kỳ lấy mẫu của
bộ biên đòi A/[) và D/A tuoiiu ửim là 1' = 5 ms và T' " 1 ms. Hãy xác địnỉì đâu ra Ya (t) cua hệ thôiiu, nêu dâu vào là: 16
Giải bài tập xử lỳ tin hiệu số và Matlab
X,, ( t ) - 2cos(l007it) + 3sin(2507it) t: tính theo giây
Bộ iọc phía sau (post tllter) lọc bỏ bất cứ thành phần tần số nào lớn hơn F, /2. X a ( t ) Hình 1.3
Lời giải: x ( n ) = x ^ ( n T ) = 2cos|^100Ttn,5.10'’ j + 3sinỊ2507m.5.10'^ j ^ nn ^ ^57m^ ^ 7rn ^ " 37in ' x ( n ) = ( n T ) = 2cos + 3sin = 2 cos - 3sin [ 2 J V 4 , V 2 , V 4 J
T ' = - ị - = > y a { t ) = x f t / T ' ì 1 n 1 n 00n 0 ’ \ ì ''TclOOOt'' 37tlOOOl = 2cos - 3sin
== 2cos(5007ĩt) - 3 s i n ( 7 5 0 T ĩ t )
y„ f t ) c ó các tằn số f, - - 250Hz,f-> - ~ 3 75Hz ■
Cả 2 tần số này đều nhò hoTi ^ ‘ 2 tĩ ' 2 7 1 rTtiooot ^ ^3Tcl000tì p / 2
- 500Hz nên đầu ra của hệ thống là; ( t ) = 2cos - 3sin l 2 y V 4 J
1.14. Xác định năng luxTiig của chuỗi x i n ) . ! * ' / - * * ' [ 3 ” n < 0
L ờ i giái: Theo định nghĩa ta có: co / 1 -1
E = ẳ M " ) i ' = Ẻ m l l = : - O C 1Ì = - ( ) V / n = - c o 1 16 1 6 9 , 143
_ ---------------- ---------- ị . \ — _
---------------- Ị---------------- = — + — - 1 : 1 = --- - < +C0 1 J _ £ í u j 15 5 8 120 16
Vì năng lượng E là hiÌLi hạn nên tín hiệu đang xét là tín hiệu năng lượnu.
1.15. Xác định năng lưọ’iig của tín hiệu nhảy bậc đo’n vị u (n)? Tín hiệu Li(n) có phải là m ột tín hiệu còng suất không? co 00
L ờ i giải: Theo định nghĩa ta có: E - ^ x ( n )
- ^ 11' (n ) - y ^ l I 1 = - C C i i = - c o 1 1 = 0
Chương 1: Tin hiệu và hệ thống rời rạc 17
Nănụ lưọnu của chuỗi là vò hạn. Do dỏ, tín hiệu nhay bậc đơn vị khôiìt’ phai là tín hiệu náng l i i ọ i m ,
( ' òn u suát truim binh cua tín liiệii là:
p - l i m ----------> i r n ^ l i m ---------— = l i m ------^----- = — n - - 2 N + 1; “ ■ V - ^ 2 N ^ 1 N - - 2 + 1 N 2
Do dó. tín hiệu nhảy bạc đưn vị là một tín hiệu côniĩ suấl.
1.16. Xác định Iiáns lượng cua dày:
Tronu dó. C0,J và A là các hànu số.
Dày x(n) có phải là dày cònu s u ẩ t '!
L ờ i <;iáì: Từ dịnlì ntihĩa ta có: E = Ì | A ' " " ! ’ = Ỉ A - ’ 1 = --/: n=— X
Nănu Urọim cùa dày là vô hạn. Bòi vàv. tín hiện hàm mù phức, biên độ là hằng số không
phái là lín hiệu nănií lưọng.
Còng suàl trung bình cùa tín hiệu này là p = l i m ^ ỳ Ae"^’" ' f = lim ỳ A" = lim — ( 2 N + 1) A" - A ' N - - 2 N + l „ f - ^ : ! N ^ 2 N + l „ f - ! , . N A - ' 2 N + r '
Bo'i vậv. d ã y x ( n ) - Ae'"''" là tín h i ệ u c ô n u SLiấí.
1.17. l l à y x ác d ị nh c ô n g s uả l t r u n g b ì n h và nủnti l ư ọ i m c u a d â y d ôc á a n vị n n > 0 x ( n ) = 0 n < 0
L ỏ i ịiiãi: Trên k h o á n u - N < < n < < N
] , tín hi ệu n ày c ó n ă i m lượnu. . N ( N + Ì ) ( 2 N + I) E n = 6 n=n
Rò rủng E == co . Công suât truniỊ bình là: 1 N Í N + l ) p - l i m — — ỉ u - l i m - - A : — ^ N-V-2N + 1 6
cũim là vó hạn. Dàv dốc đon vị có năno luợiìí’ vô hạii và công suất trung bình vô hạn. Do
đó. nó \'ừa khôim phai là tín hiỘLi nănii luọnu cũng khỏim phải ỉà tín hiệu cônu siiât.
1.18. ỉ l ã y d ù n u cá c loại SO' đồ kliối p h ù h ọ p đẽ bi êu d i ễ n hệ t h ố n g ròi r ạ c t h e o t hò i g i a n c ó q u a n hệ
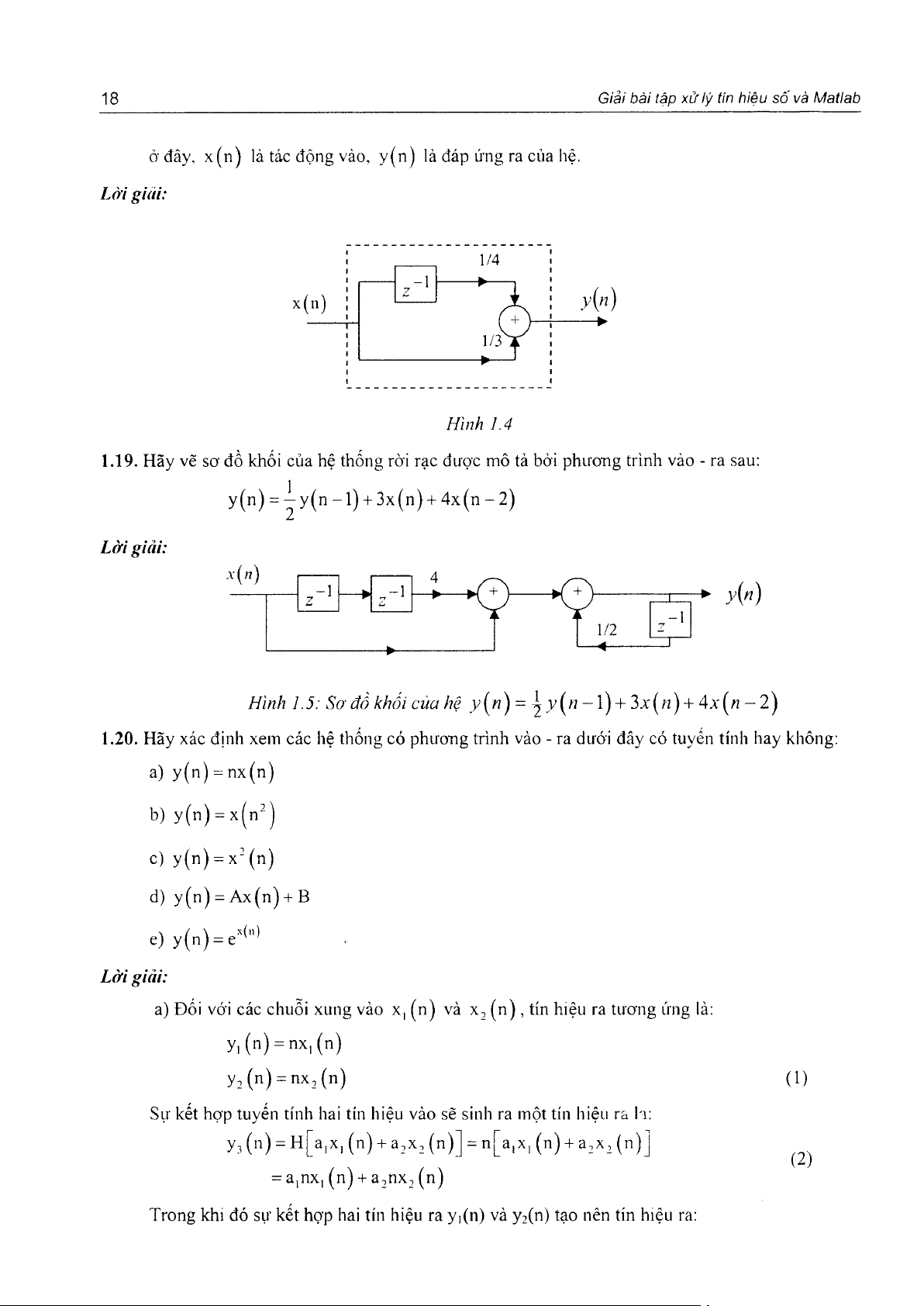
vào ra; y ( n ) = - X ( n ) + “ X( n - l) 3 4 18
Giải bài tập xử lý tín hiệu số và Matlab
ỏ'đâv. x ( n ) là tác động vào, y ( n ) là đáp ứng ra của hệ. Lời giải: Hình 1.4
1.19. Hãy vẽ sơ đồ khối của hệ thống rời rạc đượ'c mô tả bỏi phưoììg trình vào - ra sau:
y ( n ) = ^ y ( n - l ) + 3 x ( n ) + 4 x ( n - 2 ) L ờ i giải: y { n )
H ìn h 1.5: S ơ đ ồ kh ố i c ù a hệ
= Ậ v(/7 —1) + 3 x ( ; ỉ ) + 4a'(a2 - 2 )
1.20. Hãy xác định xem các hệ thốag có phưoTig trình vào - ra dưói đây có tuvén tính hay không: a) y ( n ) - n x ( n ) b) y ( n ) - x ( n ^ ) c) y ( n ) - x - ( n ) d) y ( n ) = A x ( n ) + B e) y ( n ) = e-<"' L ờ i giải:
a) Đối với các chuỗi xung vào X| ( n ) và
( n ) , tín hiệu ra t ương ứng là: y , ( n ) = n x , ( n ) y, ( n ) = n x , ( n ) (1)
Sự kết hợp tuyến tính hai tín hiệu vào sẽ sinh ra một tín hiệu ra i'ì: y 3 ( n ) = H a,Xj ( n ) + ( n ) a|X, ( n ) + ( n ) (2) - ajnx, ( n ) + a^nx, ( n )
Trong khi đó sự kết họp hai tín hiệu ra yi(n) và y2(n) tạo nên tín hiệư ra:
Chương 1: Tin hiệu va hệ thống rời rạc 19
a,y, ( n ) + a , y , {n) = a,nX| ( n ) + a , 0 X3 ( 0 ) (3)
So sánh (2) và (3), ta suy ra hệ thống là txiyển tính.
b) 'ĩirơng tự như ở phần a), ta tim đáp ứng của hệ đối vói hai tín hiệu riêng rẽ X, ( n ) và X, ( n ) . Ket quả là: y , ( n ) = x , ( n - ) y , ( n ) = x , ( n - ) (4)
Đầu ra của hệ khi tác động liên họp tuvến tính Xj ( n ) và ( n ) là:
y 3(n) = H[a, x, (n) + a , x , ( n ) ] = a,X| ( n - l + a^x, ( i r ) (5)
Liên họp tuyển tính của hai lối ra trong (2.2.36) có dạng:
a,y, ( n ) + a , y 2 {n) = a,x, [ n - ) + a , x , Ị n ' ) (6 )
So sánh (5) vói (6), ta suy ra hệ thốna là tuyến tính.
c) Đầu ra của hệ là bình p hưong của đầu vào, (Các thiết bị điện thường có qui luật như thế và
aọi là thiết bị bậc 2). Từ thảo luận trưóc đâv, ta thấv rõ rằng hệ là không nhớ. Bây giờ ta chỉ rõ hệ là tuyến tính hav không?
Đáp ứng của hệ đối vói hai tíii hiệu vào riêng rẽ là: y , ( n ) = x,-(n) y , ( n ) - x ^ n ) (7)
Đáp ứng của hệ với liên họp tuyen tính hai tín hiệu là:
y 3 ( n ) = H a, Xị ( n ) + a . X ; , ( n ) ~ a,X| ( n ) + a ^ x , ( n ) (8)
a;^x;^ ( n ) + -¥2'dị3.^Xị ( n ) x T ( n ) 4 - a 2 X ^ n )
Ngưọc lại. nếu hệ tuyến tính, nó sẽ lạo ra liên họp tuyến tính từ hai tín hiệu đã cho, tức là:
a i y i ( n ) + a 3 y , ( n ) = a,X| ( n ) + a , X 2 ( n ) (9)
Vì tín hiệu ra của hệ như đã cho trong (8) không bằng (9), nên hệ là không tuyến tính.
d) Giả thiết là hệ thống đưọ'c kích thích riêng rẽ bỏi X| ( n ) và X, ( n ) ta có; y , ( n ) = A X | ( n ) + B
Y2 ( n ) = A x , ( n ) + B (10)
Liên họp tuyến tính của X| ( n ) và X3 ( n ) cho tín hiệu ra là:
y, ( n ) = H 'a,X| ( n ) + (n) " = A a,X| ( n ) + a , X 2 ( n ) " + B (11)
= Aa,X| ( n ) + a, Ax , ( n ) + B
Nếu hệ tuyến tính, thì tín hiệu ra đối vói liên họp tuyến tính X| ( n ) , X, ( n ) sẽ là:
a,y, ( n ) + a . y , ( n ) = a, AX| ( n ) + a ^Ax, ( n ) + B (12) 20
Giải bài tàp xử lỵ tín hiệu số và Maĩlab
Rò rànu ( 11) và ( 12) khác nhau nen hệ kỉìòim ĩlioa niàn đicu kiện l u y ế n lính. Trên ihực tc. hệ
đu’Ọ‘c niô ta bãim plnroim trinh tuvẻn lính, tuy lìliièn cỏ mặt ihani sò B dà làni cho điẻu kiện tuvên
tính của hệ mât đi. Đáp ínm ra cua ỉìệ phụ lluíộc ca tác độnii \ ào và hệ sỏ B ^ í ) . Vì thẻ, nêu B 7^ 0,
hệ là khôn u triệí tiêu. Nmrọ‘c lại. nếu B - 0 hệ ỉà tnệt tiêu và thoa màn điều kiện tuyến tính. e)
C h ú ý r ầ i m , liệ đưọ'c m ò ta b ầ n u hiẻu i h ứ c và o ra: v ( n ) =
lã hệ g i ả m d ằn . N ế u
x ( n ) = 0 , ta có y ( n ) = 1 . Điều này nói lên rầim hệ là khònu íuven tínỉì.
1 .21. X á c đ ị n h x e m c á c hệ đ ư ợ c m ô la bài m nlì ìnm plìLiCim t ri nh dirói đ â y là n h à n q u à h a v khôníi:
a) y ( n ) = x ( n ) - x ( n - l ) ; b) y ( n ) = J x ( k ) ; c) y ( n ) = a x ( n ) ;
d) y ( n ) = x ( n ) + 3 x ( n + 4 ) ; e) y ( n ) - x Ị n “ ); 0 y ( n ) = x ( 2 n ) ; g) y ( n ) - x { - n ) ;
L ở i ịỊÌái: Các hộ thuộc phan a), b) và c) rò ràng là nhân qua vì đầu ra chí phụ llìLiộc hiện tại và quá
khứ cúa đầu vào. N g ưọ c lại các hệ ò' phần d). e) và í) là khỏng nhân quả vi dầu ra phụ thuộc cả vào
má Irị tirong lai cua đầu vào. Hệ g) cùníi kliôim nhân qua vi neu lựa chọn n ^ -1 thì y ( “ l) = x ( l ) .
Nh ư vậy đầu ra lại n - - 1 phụ thuộc vào đàu vào tại n = 1 cách nỏ hai đon vị thòi gian vẻ phía tircrnu lai.
1.22. Hăy xác định đầu ra y ( n ) đối vói liệ U 1 uiani dần, có dáp ửim xunii: h ( n ) ^ a " . u ( n )
| a | < l khi tín h i ệ u v à o là c h u ồ i n h â y b ậ c đ ơ n vị x ( n ) = u ( n )
L ờ i ỵiãi: Tr oi m triròiig lìọp này cá h ( n ) và x ( i ì ) là các chuỗi vô hạn. Ta dùng công thức chập
Các chuỗi h ( k ) , x ( k ) và x(--k) cỏ dạnii như ơ hình 1.6. Chuỗi tích v , , ( k ) , V | ( k ) và
v . ( k ) tLi0 'nu ứng x ( - k ) . h ( k ) , x ( l ~ k ) . h ( k ) . \ ( 2 - k ) . h ( k ) đirọc n i ô t a ỏ h i n h 1.6c,d v à e. N h ư
vậv ta có các uiá trị ra; y ( o ) - i y ( l ) = l + a y ( 2 ) = 1 + a + a '
R õ rànií. v ói n > 0 , tín hiệLi ra là:
Chương 1: Tin hiệu và hệ thống rời rạc 21 y ( n ) ~ 1 + a a “ -f ... -■ a" ( 1)
Ntíuxrc lại, v ói n < 0 , ch u ỏi luôn b ă n u 7.ero. Vì ihc: y ( n ) =^-0 n < 0
Dò thị cúa tín hiệu ra y ( n ) đirọc minh lìoạ O' hình l .6 f, với 0 < a < ỉ . Chú ý răntăng theo quy luậl hàm mù cua n . Vi
< I . nàn eiá trị cuối cùnu cua tín hiỘLi ra khi n xấp xi vô cùng là: y ( ^ ) = lim y(n) (2) It — - a
Tó m lại, còng thức chập cho chủim ta phưoiig tiện để tính đáp ứ n ” cúa niột hệ LTI giảm dần
đối vói tín hiệu vào tuỳ ý x ( n ) . h{k) a-(ả- ) 1 . f f f (/ 4 L u 2 3 4 k 0 1 2 3 4 ^ (■à) (b) '^'0 ) ---- ị► — •---- 0--- ------- -2 -1 0 1 A 0 1 2 ( c ) - v ( l - i ) ' ì (/’■) l ' <7 -2 - 1 0 1 2 -1 0 1 k (cl) x ị 2 - k ) V, (ả' ) T It Ỹ t 1' 1 1a 2 (:i <► 0 1 2 k -1 0 1 2 k y { n ) (e) 1 ----- Đưòìig tiệm cận - a [ -f í/ + a -f- a ' 1" ■2 -ỉ 0 1 2 3 4 5 (0
Hìnlì ỉ .6; Tuììì ĩoán lìinlì học cua phép chập Ịroĩì^ hùi iập ỉ. 22 22
Giải bài tập xử Ịỷ tín hiệu số và Matlab
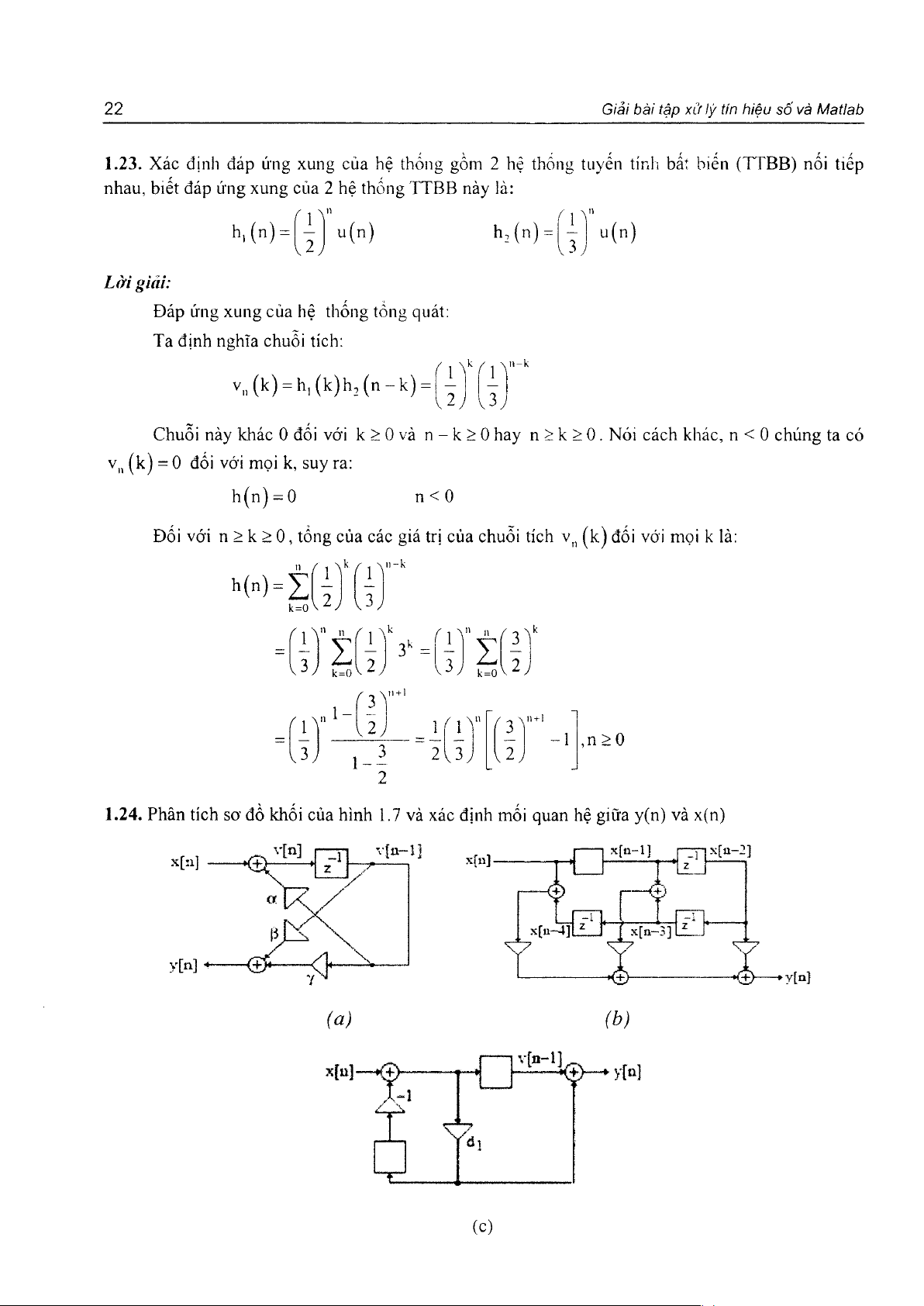
1.23. Xác định đáp ứng xung của hệ thống gồm 2 hệ thỏníi tuyến tính bất biến ( T Ĩ B B ) nối tiếp
nhau, biết đáp ứng xung của 2 hệ thống T T BB này là:
f 1 X h , ( n ) = u ( n ) V / L ờ i giải:
Đáp ứng xung của hệ thống tổng quát:
Ta định nghĩa chuỗi tích:
' „ ( k ) = h , ( k ) h , ( n - - k ) = v 2 . V y
Chuỗi này khác 0 đối với k > 0 và n - k > 0 hay n > k > 0 . Nói cách khác, n < 0 c h ú n g ta có
( k ) = 0 đối vói mọi k, suy ra: h ( n ) = 0 n < 0
Đối với n > k > 0 , tổng của các giá trị của chuỗi tích ( k ) đối vói mọi k là: Ii-k k=0 3 3 ' = k=0 v 2 . „ 1- , n > 0 v 3 . v 3 . 2
1.24. Phân tích sơ đồ khối của hỉnh 1.7 và xác định mối quan hệ giữa y(n) và x(n) (a) ( b ) v[n-l] m (c)