Giải chi tiết đề ôn tập HKI - Số 6 | môn Toán lớp 10

–
BẢNG ĐÁP ÁN TRẮC NGHIỆM 1.C 2.A 3.B 4.C 5.C 6.C 7.B 8.B 9.A 10.B 11.C 12.A 13.A 14.C 15.A 16.B 17.A 18.D 19.D 20.B 21.B 22.B/A
Câu 1:  Xét u là cấp số cộng với u  5  , d  3 n  1
 u  u  n 1 d  5  n 1 .3  3n  8  u  3.13  8  31. Chọn C. n 1     13 1  22u 11d 1  S 144   144 2u 11d  24 u  1
Câu 2:  Xét cấp số cộng có 12  1 1   2     . Chọn A. u  23  u 11d  23   d  2 12 1 u 11d  23  1 u  80000
Câu 3:  Nhận xét: giá của mỗi mét khoan tạo thành một cấp số cộng với 1  d  5000
 Biết cần phải khoan sâu 50m mới có nước  n  50
 Số tiền phải trả để khoan giếng là tổng của một cấp số cộng có 50 số hạng
 Áp dụng công thức tính tổng của một cấp số cộng 502u  49d 50 2.80000  49.5000 1     S    10125000 50 2 2
Vậy số tiền phải trả để khoan giếng là 10125000 đồng. Chọn B. 4 8 16
Câu 4:  Xét dãy số ở đáp án A có  
 2  Đây là một cấp số nhân với d  2 2 4 8 1  1
 Xét dãy số ở đáp án B có   1
  Đây là một cấp số nhân với d  1 1 1  2 2 2 3  9 
 Xét dãy số ở đáp án C có  4 
 Đây không phải là một cấp số nhân 2 2   1 2  4  3 5 7 a a a
 Xét dãy số ở đáp án D có 2  
 a a  0  Đây là một cấp số nhân với 2 d  a 3 5   a a a Chọn C. 2 u
Câu 5:  Áp dụng tính chất của cấp số nhân 2 2 u .u  u  u  1 3 2 3 u1  2 4x  2 1 2x  2 1 2x  2 1  u   u   u  2x   1  2 4x  4x   3 2
1  u  8x  4x  2x 1 3 3 3 3 2x 1 2x 1 Chọn C. u  20000
Câu 6:  Nhận xét: số tiền cược của du khách đó trong các lần tạo thành một cấp số nhân với 1  q  2 n 1 n 1 u u .q  20000.2     n 1
 Người đó thua 9 lần liên tiếp  Số tiền người đó thua là tổng của 9 số hạng đầu của cấp số nhân 9 9 1 q 1 2
 Áp dụng công thức tính tổng của cấp số nhân: S  u .  20000.  10220000 9 1 1 q 1 2
 Người đó đã thua 9 lần liên tiếp và thắng ở lần thứ 10
 Số tiền người đó thắng được là 9
u  S  20000.2 10220000  20000 . Chọn C. 10 9 1 5 2   n  n  5 1 2 Câu 7:  Xét L  lim   lim n n L 2 2n 1 1 2  2 n 1  Mà lim  1 0  L  . Chọn B. n 2 3 3 3  2 3 3  2n n Câu 8:  Xét lim  lim n  lim n   2 2 2n 1 n 1 2  2 n 3 2 2 2  2 2n  3 n 1 2  Xét lim  lim n  lim .  0 3 3 2n  4 n 4 n 2 2  3 n 2 3 3  3 2 2n  3n n 3   Xét lim  lim n  lim . n   2 2 2n 1 n 1 2 2   2 n 2 2 4  3 2 2n  3n 3  Xét lim  lim n  4 2 2n  n 1 2 2  2 n Chọn B. Câu 9:  Xét 2 2
L  lim 3x  7x 11  3.2  7.2 11  37 . Chọn A. x2 x  3  2 2 1  3 2 Câu 10:  Xét L  lim    2  . Chọn B. 3 x 1  x  2  3 1  2 1 x  8 x 2 2 3 x  2x  4 2 x  2x  4 Câu 11:  Xét I    2 x  4 x  2x  2 x  2 2 2 x  2x  4 2  2.2  4  Khi đó, lim I  lim   3 x2 x2 x  2 2  2 Chọn C. x    33 3   x  
x 3 2x  3x3 2 2 3 x  3x  3 2 6 3  Câu 12:  Xét I   2.  2.  2 2 3  x x  3 x 3x 3 x  3     x  x   2   32 2  3. 3  3 2 3 3    Khi đó, lim I lim     3 3 x 3 x 3 x  3  3  3 a  3 2 2    a  b  9 b   0 Chọn A. a b a b a  2 1 x  x  b Câu 13:  Xét I      3 1 x 1 x 1 x 1 x 2
1 x  x  1 x 2 1 x  x 
 Để lim I hữu tỷ, thì phương trình tử = 0 có nghiệm x  1 x 1  - Hay, a  2
111  b  0  3a  b 2 a 1 x  x  2 x  1x  2 x  2 - Mà a  b  4    I     b   3 1 x 2
1 x  x  1 x 2 1 x  x  2 1 x  x x  2 1 2
 Khi đó, limI   lim  1. Chọn A. 2 x 1  x 1  1 x  x 111
Câu 14:  Xét các đáp án:
- Đáp án A: Qua 2 điểm phân biệt có duy nhất một mặt phẳng.
- Đáp án B: Qua 3 điểm phân biệt bất kì có duy nhất một mặt phẳng.
- Đáp án D: Qua 4 điểm phân biệt bất kì có duy nhất một mặt phẳng.
 A, B, D sai vì 2 hoặc 3 hoặc 4 điểm này có thể nằm trên cùng một đường thẳng và có thể là giao
tuyến của hai hoặc nhiều mặt phẳng.
- Đáp án C: Qua 3 điểm không thẳng hàng có duy nhất một mặt phẳng.  Đúng. Chọn C. N  BC A
Câu 15:  Ta có: NP   BCD do  P  BD I BN 1 BP 2 BN BP  1 2  M - Do  và       BC 2 BD 3 BC BD  2 3  B D P
 NP không song song với CD N
 Gọi I  NP  CD  I  MNP  CD . C Chọn A.
Câu 16:  Gọi O là giao điểm của HF và IG . Ta cần chứng minh O  CD O   HF  A - Ta có:  HF  
 ACD H  AD và F  AC  O   ACD (1) E F O   IG  B - Ta có:  C I IG  
BCD I BC và GBD O  O BCD (2) G D
 Từ (1),(2), ta có: O  CD do CD   ACD  BCD Chọn B. H
Câu 17:  Ta có: d '      
 Khi đó, d và d ' cùng thuộc    d song song hoặc cắt d '
 Nếu d cắt d ' thì d cắt  
- Mà theo giả thuyết d ∥    Vậy d ∥ d ' Chọn A.
Câu 18:  Ta có: OO là đường trung bình tam giác AEC D M C 1
 OO ∥ EC  OO ∥ BEC  Loại A 1   1 O
 Ta có: OO là đường trung bình tam giác BFD 1 A B O  O ∥ AFD  1    OO ∥ FD  1 O  O ∥ CEFD  OO ∥ EFM M CD O  1 1   1      Loại B, D F E Chọn C. AD
Câu 19:  Dễ dàng chứng minh được MNOP là hình bình hành (do MN ∥ OP∥ AD và MN  OP  ) 2
 M , N,O, P đồng phẳng  Loại A, C S  Ta có:
MN là đường trung bình của tam giác SAD  MN ∥ AD∥ BC N M
ON là đường trung bình của tam giác SBD  ON ∥ SB 6 6 MN  NO  N D A 8
 MON ∥ SBC   B đúng P O
 Đáp án D sai vì N  MNP  SBD . Chọn B. B C
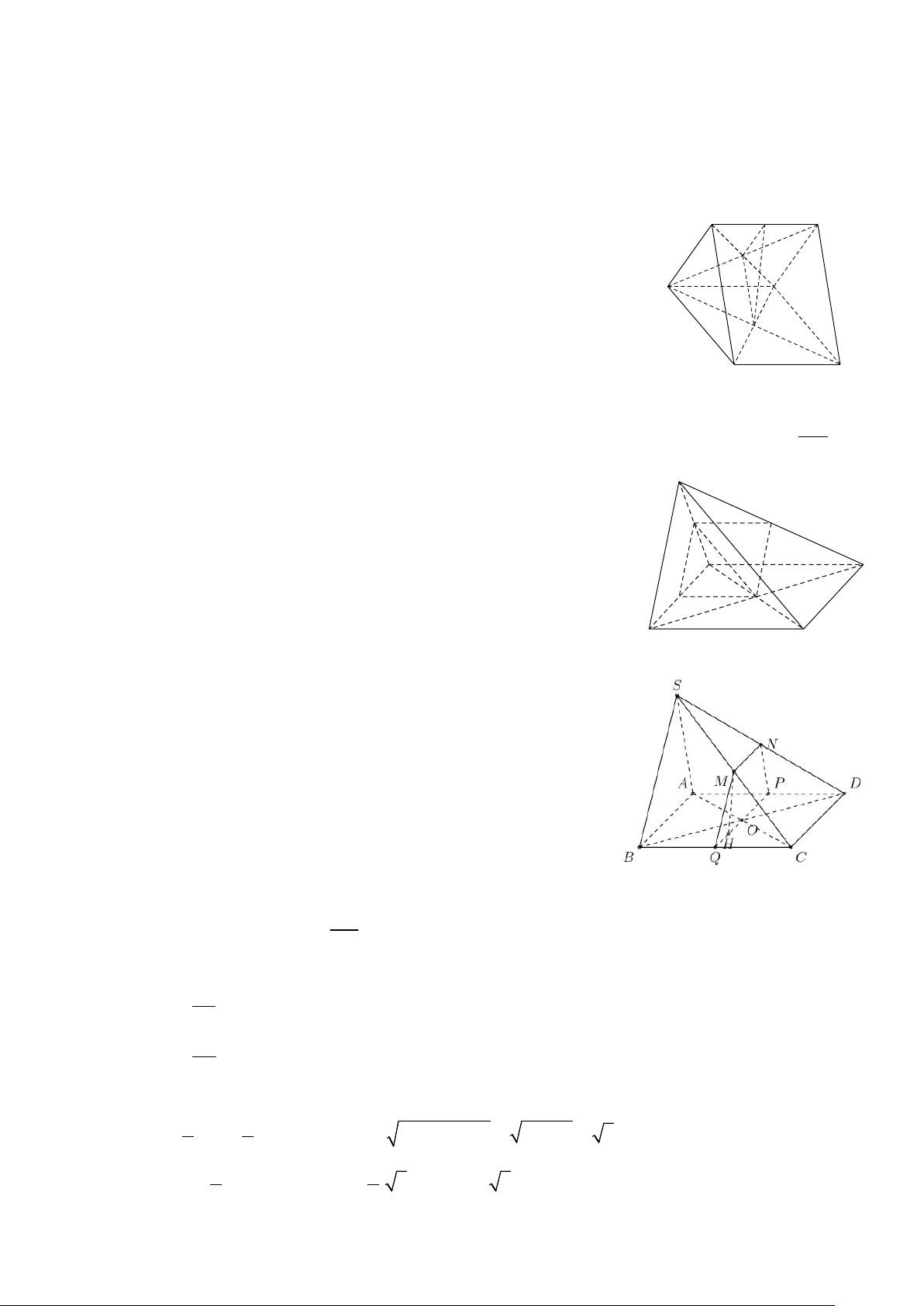
Câu 20:  Dựng thiết diện:
- Qua O dựng đường thẳng PQ∥ AB . Vậy P,Q lần lượt là
trung điểm của AD và BC.
- Tiếp tục, qua P dựng đường thẳng PN ∥ SA . Vậy N là trung điểm của S . D
- Qua Q dựng đường thẳng QM ∥ SB . Vậy M là trung điểm của SC. - Nối 2 điểm M , N
 Thiết diện của P và hình chóp S.ABCD là tứ giác MNP . Q
 MNPQ là hình thang do MN∥ PQ∥ AB∥ CD CD
 Có PQ  AB  8 và MN 
(do MN là đường trung bình tam giác SCD ) 2
 Ta có: MO và MQ lần lượt là đường trung bình tam giác SAC và SBC  SA MO   2  
 MO  MQ  3  Tam giác MOQ cân tại M SB MQ   2
 Kẻ MH  OQ H OQ  H là trung điểm OQ 1 1 2 2 2 2
 QH  OQ  PQ  2  MH  MQ  QH  3  2  5 2 4 1 1 Vậy S  MH. MN  PQ    . Chọn B. MNPQ   . 5.4 8 6 5 2 2
Câu 21:  Trong mỗi khoảng cân nặng, giá trị đại diện được thể hiện ở bảng sau: Cân nặng (kg) 43 48 53 58 63 68 Số học sinh 10 7 16 4 2 3
43.10  48.7  53.16  58.4  63.2  68.3
Cân nặng trung bình của học sinh lớp 11 là x   51,81
10  7 16  4  2  3 Chọn B.
Câu 22: a) Cỡ mẫu n  3 12 15  24  2  56
- Gọi a ; a ;...; a là thời gian vào internet của 56 học sinh và giả sử dãy này được sắp xếp theo thứ 1 2 56 a  a
tự tăng dần  trung vị là 28 29 2
- Do hai giá trị a ; a thuộc nhóm 15,5;18,5 nên nhóm này chứa trung vị 28 29 Chọn B. x  x
b) Tứ phân vị thứ nhất của mẫu gốc là 14 15 . 2
- Do x và x đều thuộc nhóm u ;u
 u ;u  12,5;15,5 nên nhóm này chứa Q i i 1    2 3   14 15 1 C   n  3 56 1   3 - Ta có u   u 12,5 4  Q 12,5  . 15,5 12,5  15, 25 1   i 2  12 n  n  12  1 2 Chọn A. PHẦN II: TỰ LUẬN
Câu 1: a) Ta có lim x  x  7   2 2 1    1  7  9 x 1  2 x  3x  2 x  1x  2 b) Ta có lim  lim
 limx  2 1 2  1  x 1  x 1  x 1 x 1 x 1      k2 4x  x   k2 x       
Câu 2: a) Ta có sin 4x  sin x  3 9 3     k      k     3    2 k2 4x    x   k2   x    3  15 5 x x
b) Ta có cot g x  30   cot g  x  30   k.180 k     x  6
 0  k.360 k    2 2
Câu 3: a) Trong mặt phẳng  ABCD : kẻ NP / / AC P  AD  NP   ABCD
- Mà NP / / AC  NP     NP là giao tuyến của   với S mặt phẳng  ABCD E Q
b) Trong mặt phẳng  ABCD : kéo dài NP cắt AB; BC lần lượt T tại E; F M D
- Trong mặt phẳng SBC  : kéo dài A MF cắt SB tại T P
 giao điểm của mặt phẳng SB và   là T N F
c) Ta có   SAB  TQ ;   SBC  TM ; C  B
SCD  MN ;    ABCD  NP ;   SDA  PQ
 thiết diện của hình chóp khi cắt bởi mặt phẳng   là MNPQT