Giải kì thi tuyển sinh vào lớp 10 THPT, năm 2023 tỉnh Bình Thuận môn Toán

GIẢI KÌ THI TUYỂN SINH VÀO 10 THPT, NĂM 2023 TỈNH BÌNH THUẬN
MÔN: TOÁN (chuyên Toán)
Bài 1. (2,0 điểm) Giải phương trình 2
9x  53x  2x 1  71. Lời giải. Đ 1 iều kiện: x   . 2 4 2  t  2t 1 2 x   Đặ 4
t t  2x 1(t  0) suy ra t  2x 1(t  0)  
khi đó phương đã cho trở thành: 2  t 1 x   2  t  3 (n) t  3  0   7 4 2 t  t  t 
  t   t   2 9 124 4 399 0 3 3
7 3t  2t 19  0  3t  7  0 
 t   (l)  3 2
3t  2t 19  0  2
3t  2t 19  0(4)
+ Với t = 3 suy ra 2x 1  3  2x 1  9  x  4(nha ) n  1   58 t  (nhan) 3 + 2
3t  2t 19  0    1   58 t  ( i loa )  3 1 58 1   58 59  2 58 25  58 +Với t  suy ra 2x 1   2x 1   x  3 3 9 9  25 58  Vậy S  4;  .  9  
Bài 2. (2,0 điểm)
a) Kí hiệu S (n) là tổng các chữ số của số nguyên dương n . Biết a và b là hai số nguyên dương thỏa
S (a)  S (b)  S (a  b) . Chứng minh rằng a và b chia hết cho 9 .
b) Tìm nghiệm nguyên của phương trình: 2 2 4 4
x  (x 1)  y  ( y 1) . Lời giải a) Theo giả thiết ta có: a  S  a 9  (1) (do ,
n S n có cùng số dư khi chia cho 9) b   S  b 9  (2) a b 
 S a b 9  (3) Từ (3) ta có : * a  
b S a b 9  a   
b S b 9  a 9  * b  
a  S a b 9  b  
a  S a 9  b 9 
b) Tìm nghiệm nguyên của phương trình: 2 2 4 4
x  (x 1)  y  ( y 1) . Ta có: Trang 1 2 2 4 4 2 4 3 2
x  (x 1)  y  ( y 1)  x  x  y  2 y  3y  2 y 2 4 3 2
 x  x 1  y  2y  3y  2y 1 2
 x  x 1   y  y  2 2 1 (*)
 xx  
1 1   y  y  2 2 1 (*) x  0 2 2
 y  y 1 1 + Nếu  thì từ (*) suy ra  2 y  y   1  1    y 0;  1 . x  1 2
 y  y 1  1 
Vậy trong trường hợp này phương trình (*) có 4 nghiệm là 0;0,0;   1 ,  1  ;0, 1  ;  1 . 2 + Nếu x  1
 thì do x   2
 x  x    2 x  x   2 2 1 2 1
1  x  x  x 1  x nên (*) không có nghiệm nguyên. 2
+ Nếu x  0 thì do  x   2
 x  x    2 x  x   2 2 1 2 1
1  x  x  x 1  x nên (*) không có nghiệm nguyên.
Vậy phương trình đã cho có 4 nghiệm nguyên là 0;0,0;   1 ,  1  ;0, 1  ;  1 .
Bài 3. (2,0 điểm) Cho các số dương a, b, c thỏa mãn ab  bc  ca  3abc . a b c 3 Chứng minh rằng    . 2 2 2 a  bc b  ca c  ab 2 Lời giải 1 1 1
*Ta có ab  bc  ca  3abc     3. a b c a 1 1 1 1 1  1 1  * Theo AM – GM ta có: 2 2
a  bc  2 a bc  2a bc    .2 .     . 2 a  bc 2 bc 4 b c 4  b c  b 1  1 1  c 1  1 1 
Chứng minh tương tự ta được:     và     . 2 b  ca 4  c a  2 c  ab 4  a b  a b c 1  1 1 1  3 Suy ra         (đpcm) 2 2 2 a  bc b  ca c  ab 2  a b c  2
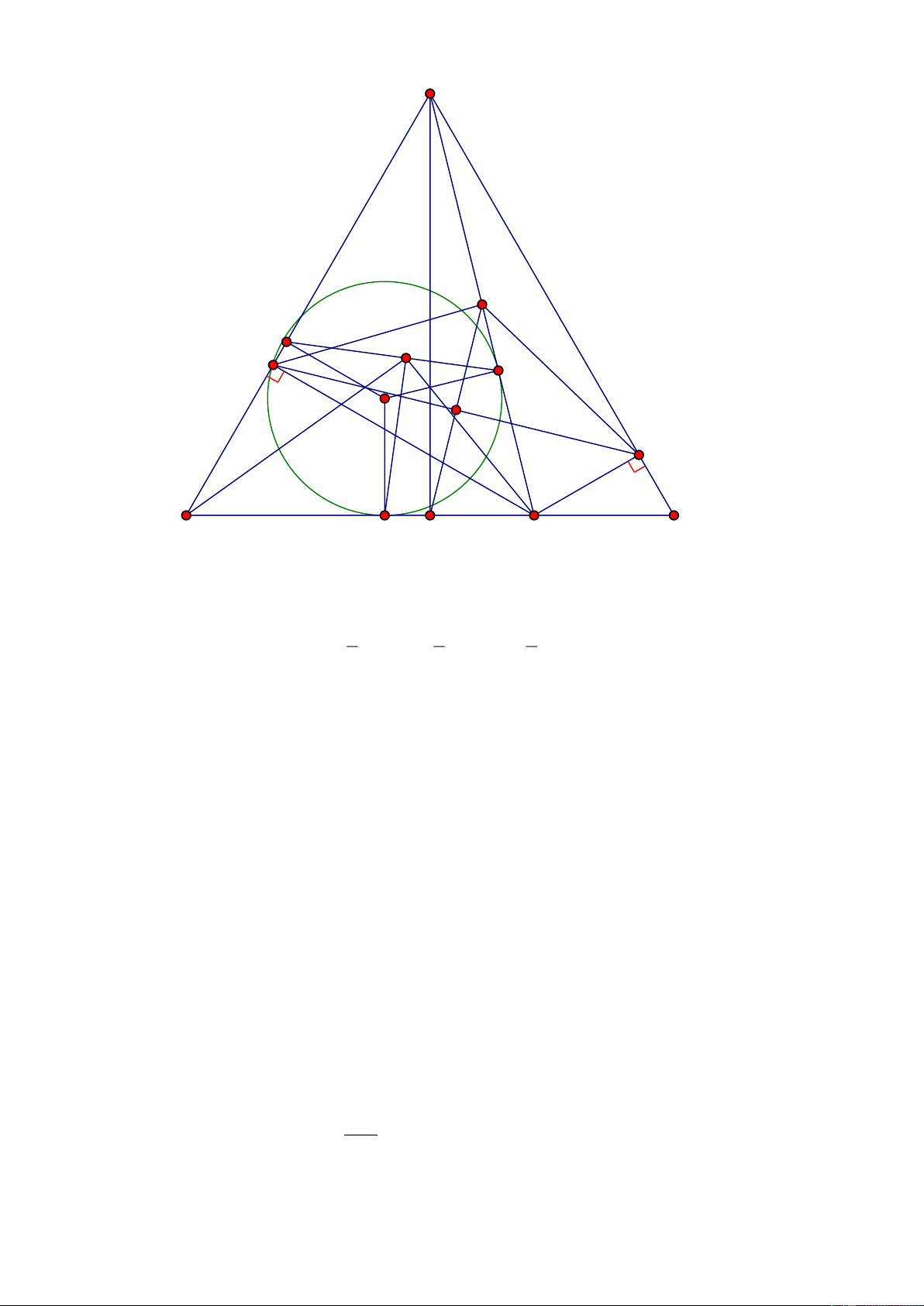
Bài 4. (3,0 điểm) Cho tam giác đều ABC có đường cao AH . Trên cạnh BC lấy điểm M tuỳ ý ( M không
trùng B, H , C) . Gọi P.Q lần lượt là chân đường vuông góc kẻ từ M đến AB, AC .
a) Chứng minh rằng MP  MQ  AH .
b) Gọi K là trung điểm của AM . Chứng minh KH  PQ .
c) Cho đường tròn (O) nội tiếp tam giác ABM . Gọi D, E, F theo thứ tự là tiếp điểm của (O) với các cạnh
BM , AB, AM . Vẽ DN vuông góc với EF tại N . Chứng minh BNE  MNF . Lời giải Trang 2 A K E N P F O Q H M C D B
a) Chứng minh rằng MP  MQ  AH . *Do ABC 
đều nên AB  AC  BC . 1 1 1 *Ta có S  S  S  M . P AB  M . Q AC 
AH .BC  MP  MQ  AH A  BM A  CM A  BC 2 2 2 Cách 2: M
 QC vuông tại Q  0
MQ  MC.sin 60 M
 PB vuông tại P  0 MP  M . B sin 60 Suy ra: MP + MQ = 0 0
MQ  MP  MC  MB
 MB  MC 0 0 .sin 60 .sin 60 sin 60  B . C sin 60 (1) A
 HC vuông tại H  0 0
AH  AC.sin 60  BC.sin 60 (do AC  BC) (2)
Từ (1) và (2) suy ra:MP+MQ = AH.
b) Gọi K là trung điểm của AM . Chứng minh KH  PQ . Ta có: 0
AHM  AQM  APM  90 suy ra năm điểm A, Q, M, H, P cùng thuộc một đường tròn
mà HAQ  HAP ( ABC 
đều có AH là cao đồng thời là phân giác) suy ra HP  HQ  HP  HQ (3). +Ta có: M  QC và M
 PB vuông lần lượt tại Q và P có QK và PK lần lượt là đường trung AM
tuyến(KA=KM(gt)). KP  KQ  (4). 2
Từ (3) và (4) suy ra: HK là đường trung trực của PQ suy ra: KH  PQ .
c) Cho đường tròn (O) nội tiếp tam giác ABM . Gọi D, E, F theo thứ tự là tiếp điểm của (O) với các
cạnh BM , AB, AM . Vẽ DN vuông góc với EF tại N . Chứng minh BNE  MNF . Trang 3 J F N E I O D M B
+Kẻ BI vuông góc với EF tại I, Kẻ MJ vuông góc với EF tại J,
Ta có : AEF  AFE (t/c hai tiếp tuyến cắt nhau) suy ra: IEB  JFC mà 0
BIE  CJF  90 IE BE BD IN Ta có: IBE  đồng dạng với J  MF suy ra:    (ta lét) IF MF MD JN IE BE BD IN IN  IE EN Suy ra:      IF MF MD JN JN  IF FN BE EN suy ra: 
(do t/c tiếp tuyến nên BD=BE và DM =MF) mà BEN  MFN (cùng kề bù với 2 góc MF FN
bằng nhau AEF  AFE ) suy ra: BEN  đồng dạng với M
 FN suy ra: ENB  MNF .
Cách 2: Theo tính chất tiếp tuyến ta có AEF 
cân tại A nên suy ra AEF  AFE , do đó BEI  MFJ . BI BE BD IN
Từ đây ta được hai tam giác B  IE, M
 JF đồng dạng với nhau (g.g), suy ra    MJ MF MD JN BI MJ    hai tam giác B  IN, M
 JN đồng dạng với nhau. Do đó ta được: BNI  MNJ hay IN JN
BNE  MNF (đpcm) Trang 4
Bài 5. (1,0 điểm) Chia bảng vuông có cạnh bằng 23 cm thành các ô vuông có cạnh bằng 1 cm . Ban đầu,
tất cả các ô vuông được điền bởi dấu "+". Sau đó, người ta thực hiện đổi dấu (mỗi lần đổi dấu là chuyển
"+" thành "-", "-" thành "+") trong các ô vuông ở các dòng và các cột của bảng theo qui tắc sau:
- Tất cả các ô của dòng thứ i được đổi dấu i lần (i  và 1  i  23) .
- Tất cả các ô của cột thứ j được đổi dấu 5 j 1 lần ( j  và 1  j  23) .
Hỏi sau khi thực hiện tất cả thao tác đổi dấu, trên bảng còn bao nhiêu dấu "+"? Lời giải
* Theo cách chia ta có bảng ô vuông 23x23; trong đó có 12 dòng mà i lẻ; 11 dòng mà i chẵn và 12
cột mà j lẻ; 11 cột mà j chẵn.
*Theo quy tắc đổi dấu thì ô vuông ở vị trí i  j (dòng thứ i và cột thứ j ) sẽ phải đổi dấu i  5j   1  i  5j 1 lần. *Do i  5j 
1  i  j  4j1 luôn là số lẻ nên hai số i  5j 
1 ; i  j không có cùng tính chẵn
lẻ. Do đó những ô vuông ở vị trí mà i  j lẻ sẽ đổi dấu một số chẵn lần (do i  5j 1 chẵn), nên
những ô này sau khi đổi dấu vẫn mang dấu (+); còn những ô vuông ở vị trí mà i  j chẵn sẽ đổi
dấu một số lẻ lần (do i  5 j 1 lẻ), nên những ô này sau khi đổi dấu sẽ mang dấu (-). *Ta có 11 1  212 1
 1 264 ô vuông mà i  j lẻ, tức là sau khi đổi dấu theo quy tắc trên thì trên
bảng còn lại 264 dấu (+) ----HẾT--- Trang 5