Giải Toán 10 Bài 3: Đường tròn trong mặt phẳng tọa độ CTST
Giải Toán 10 Bài 3: Đường tròn trong mặt phẳng tọa độ CTST được VnDoc.com sưu tầm và xin gửi tới bạn đọc cùng tham khảo.
Chủ đề: Chương 9: Phương pháp toạ độ trong mặt phẳng (CTST)
Môn: Toán 10
Sách: Chân trời sáng tạo
Thông tin:
Tác giả:
Thông tin :
Chủ đề:
Chương 9: Phương pháp toạ độ trong mặt phẳng (CTST)
Môn:
Sách:
Tác giả:
Tài liệu liên quan:
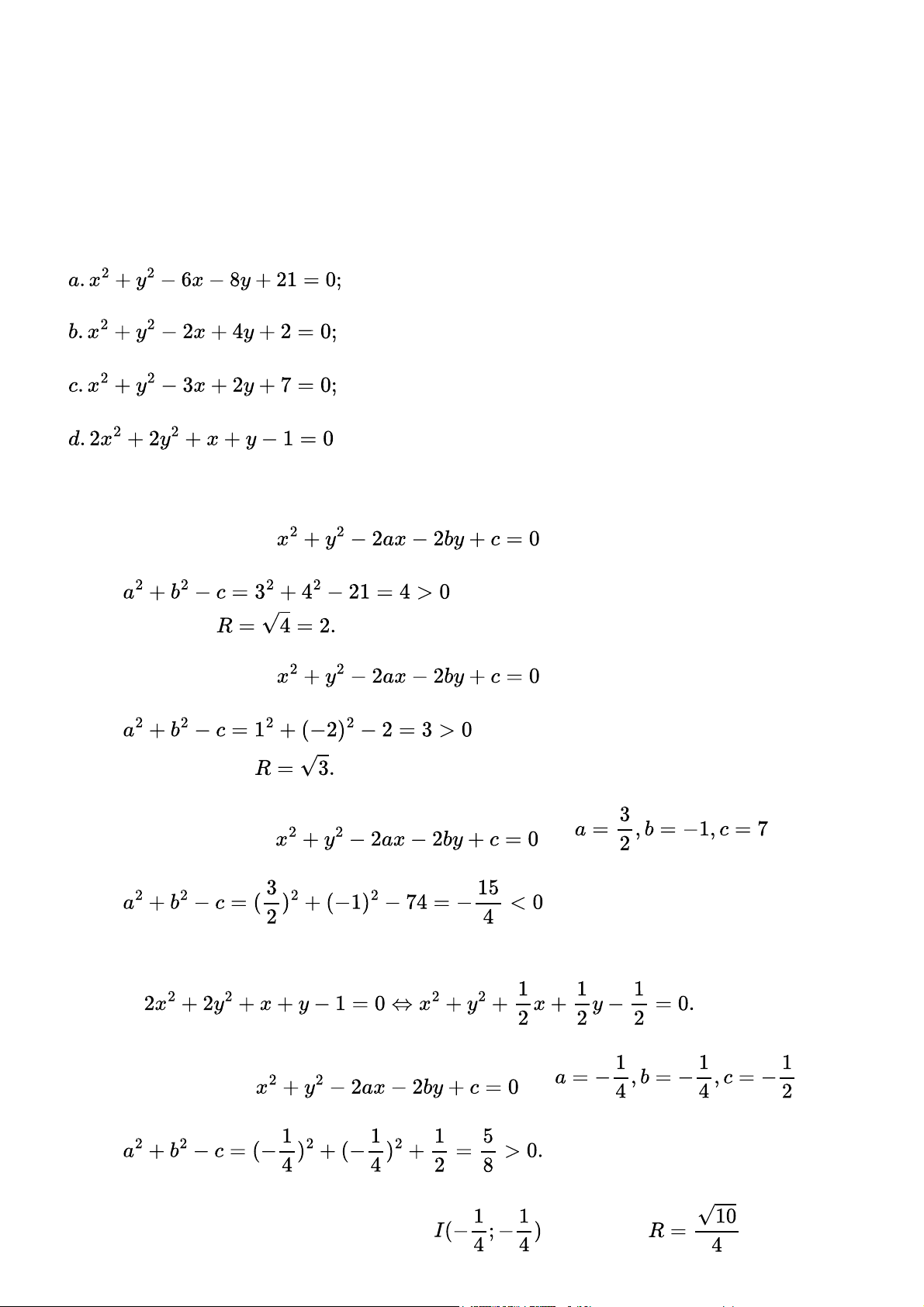
Preview text:
Giải Toán 10 trang 62, 63 Chân trời sáng tạo - Tập 2 Bài 1 trang 62
Phương trình nào trong các phương trình sau đây là phương trình đường tròn? Tìm tọa độ tâm
và bán kính của đường tròn đó. Gợi ý đáp án a. Phương trình có dạng với a = 3, b = 4, c = 21 Ta có:
. Vậy đây là phương trình đường tròn có tâm I(3; 4) và có bán kính b. Phương trình có dạng với a = 1, b = -2, c = 2 Ta có:
. Vậy đây là phương trình đường tròn có tâm I(1; -2) và có bán kính c. Phương trình có dạng với Ta có:
. Vậy đây không phải là phương trình đường tròn. d. Ta có: Phương trình có dạng với Ta có:
Vậy đây là phương trình đường tròn có tâm và bán kính Bài 2 trang 62
Lập phương trình đường tròn (C) trong các trường hợp sau:
a. (C) có tâm I(1; 5) và có bán kính r = 4;
b. (C) có đường kính MN với M(3; -1) và N(9; 3);
c. (C) có tâm I(2; 1) và tiếp xúc với đường thẳng 5x - 12y + 11 = 0;
d. (C) có tâm A(1; -2) và đi qua điểm B(4; -5). Gợi ý đáp án
a. Phương trình đường tròn (C) tâm I(1; 5) và bán kính r = 4 là:
b. Tâm I của đường tròn (C) là trung điểm của Ta có:
Phương trình đường tròn (C) tâm I(6; 1) và bán kính là: c. Ta có:
Phương tròn đường tròn (C) tâm I(2; 1) và bán kính là: d. Ta có
Phương trình đường tròn (C) tâm A(1; -2) và bán kính là: Bài 3 trang 62
Lập phương trình đường tròn ngoại tiếp tam giác có tọa độ các đỉnh là: a. M(2; 5), N(1; 2), P(5; 4); b. A(0; 6), B(7; 7), C(8; 0) Gợi ý đáp án
a. Phương trình đường tròn có dạng
Thay tọa độ các đỉnh M(2; 5), N(1; 2), P(5, 4) vào phương trình đường tròn, ta được hệ phương trình:
Vậy phương trình đường tròn ngoại tiếp tam giác MNP là:
b. Phương trình đường tròn có dạng
Thay tọa độ các đỉnh A(0; 6), B(7; 7), C(8; 0) vào phương trình đường tròn, ta được hệ phương trình:
Vậy phương trình đường tròn ngoại tiếp tam giác ABC là: Bài 4 trang 62
Lập phương trình đường tròn tiếp xúc với hai trục Ox, Oy và đi qua điểm A(4; 2). Gợi ý đáp án
Gọi I(a; b) là tâm đường tròn (C). Ta có:
có tâm I(a; a) và bán kính R = a.
Phương trình đường tròn (C) là: Ta có nên hoặc a = 2 Vậy ặ Bài 5 trang 62
Cho đường tròn (C) có phương trình
a. Chứng tỏ rằng điểm M(4; 6) thuộc đường tròn (C).
b. Viết phương trình tiếp tuyến của (C) tại điểm M(4; 6).
c. Viết phương trình tiếp tuyến của (C) song song với đường thẳng 4x + 3y + 2022 = 0 Gợi ý đáp án a. Ta có:
Vậy điểm M(4; 6) thuộc đường tròn (C).
b. Đường tròn (C) có tâm I(1; 2) và bán kính
Phương trình tiếp tuyến của (C) tại M(4; 6) là:
c. Tiếp tuyến của (C) song song với đường thẳng 4x + 3y + 2022 = 0 có dạng Ta có: ặ Vậy hoặc Bài 6 trang 62
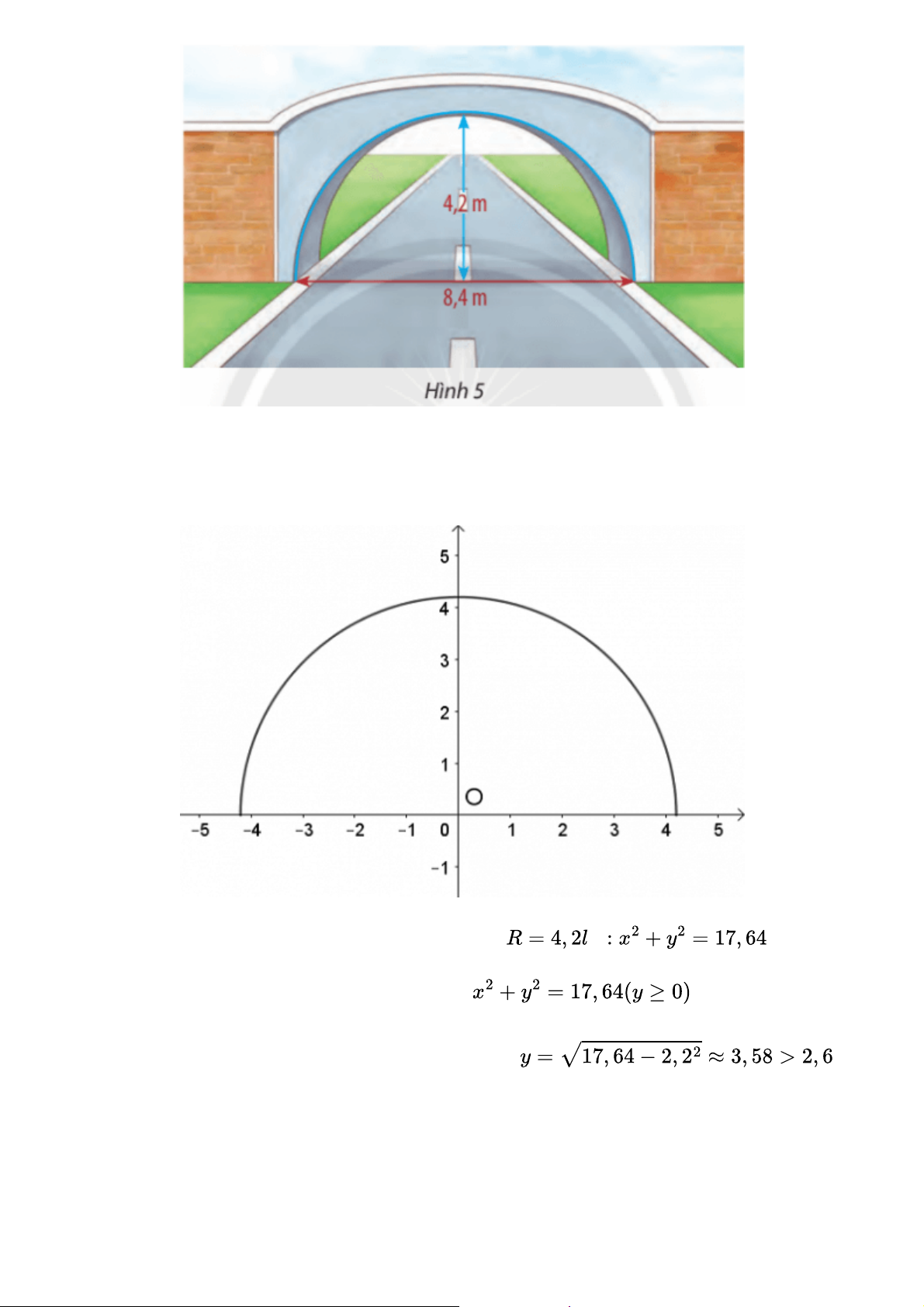
Một cái cổng hình bán nguyệt rộng 8,4m, cao 4,2m như Hình 5. Mặt đường dưới cổng được
chia thành hai làn xe ra vào.
a. Viết phương trình mô phỏng cái cổng.
b. Một chiếc xe tải rộng 2,2 m và cao 2,6m đi đúng làn đường quy định có thể đi qua cổng mà
không làm hư hỏng cổng hay không? Gợi ý đáp án
a. Chọn hệ tọa độ Oxy như hình vẽ.
Ta có phương trình đường tròn tâm O(0; 0) bán kính à
\Rightarrow Phương trình mô phỏng cái cổng là:
b. Thay x = 2,2 vào phương trình đường tròn, ta được
Vậy xe tải rộng 2,2m và cao 2,6m đi đúng làn đường quy định có thể đi qua cổng mà không làm hư hỏng cổng.