Giải Toán 11 Bài 1: Góc lượng giác. Giá trị lượng giác của góc lượng giác | Cánh diều
Giải Toán 11 Bài 1: Góc lượng giác. Giá trị lượng giác của góc lượng giác | Cánh diều được trình bày khoa học, chi tiếtgiúp cho các bạn học sinh chuẩn bị bài một cách nhanh chóng và đầy đủ đồng thời giúp quý thầy cô tham khảo để soạn giáo án cho học sinh của mình. Thầy cô và các bạn xem, tải về ở bên dưới.
Chủ đề: Chương 1: Hàm số lượng giác và phương trình lượng giác (CD)
Môn: Toán 11
Sách: Cánh diều
Thông tin:
Tác giả:
Thông tin :
Chủ đề:
Chương 1: Hàm số lượng giác và phương trình lượng giác (CD)
Môn:
Sách:
Tác giả:
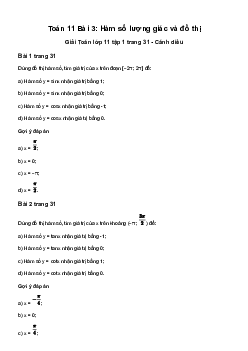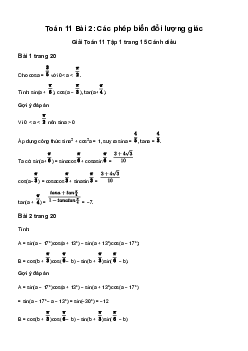
Preview text:
Toán 11 Bài 1: Góc lượng giác - Giá trị lượng giác của góc lượng giác
I. Giải Toán 11 Tập 1 trang 15 Cánh diều Bài 1 trang 15
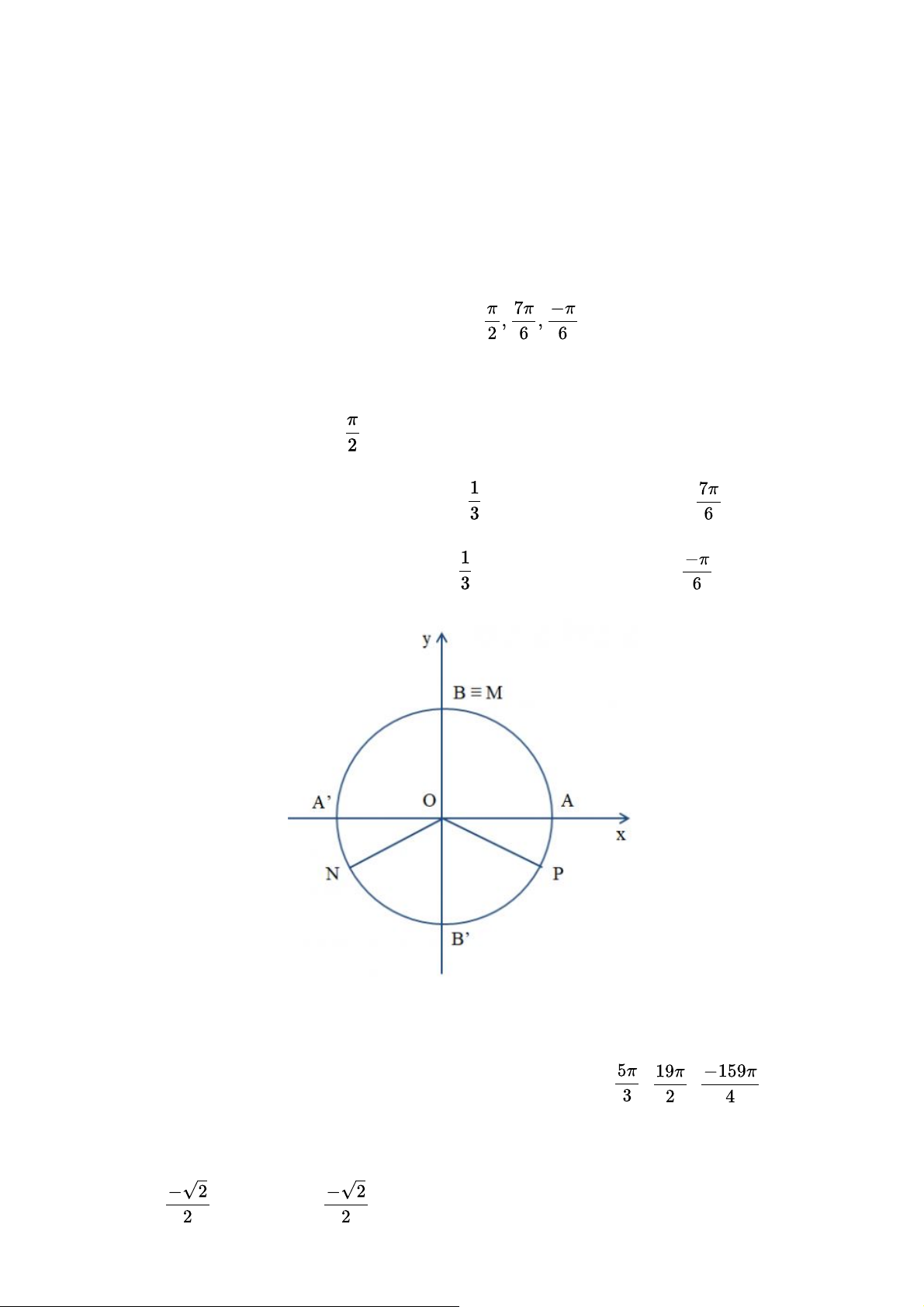
Xác định vị trí các điểm M, N, P trên đường tròn lượng giác sao cho số đo của các góc lượng
giác (OA, OM), (OA, ON), (OA, OP) lần lượt bằng . Gợi ý đáp án
Điểm M ≡ điểm B thì (OA, OM) = .
Điểm N nằm trên cung A'B', sao cho cung A'N = cung A'B' thì (OA, ON) = .
Điểm P nằm trên cung AB', sao cho cung AP = cung AB' thì (OA, OP) = . Bài 2 trang 15
Tính các giá trị lượng giác của mỗi góc sau: 225∘, −225∘, −1035∘, , , . Gợi ý đáp án sin(225∘) = , cos(225∘) =
, tan(225∘) = 1, cot(225∘) = 1 sin(−225∘) = , cos(−225∘) =
, tan(225∘) = −1, cot(225∘) = −1 sin (−1035∘) = , cos(−1035∘) =
, tan(−1035∘) = 1, cot(−1035∘) = 1 sin( ) = , cos( ) = 12, tan( ) = , cot( ) = sin( ) = −1, cos( ) = 0, cot( ) = 0 sin( ) = , cos( ) = , tan( ) =−1, cot( ) = −1 Bài 3 trang 15
Tính các giá trị lượng giác (nếu có) của mỗi góc sau: a) + k2π (k∈Z); b) kπ (k∈Z); c) + kπ (k∈Z); d) + kπ (k∈Z). Gợi ý đáp án a) sin( + k2π) =
; cos ( + k2π)= ; tan( + k2π) = ; cot( + k2π) = .
b) sin(kπ) = 0; cos(kπ) = −1 nếu k lẻ hoặc =1 nếu k chẵn; tan(kπ) = 0.
c) sin( + kπ) = −1 nếu k lẻ hoặc =1 nếu k chẵn; cos( +kπ) = 0; cot( +kπ) = 0. d) sin( + kπ) = nếu k lẻ hoặc =
nếu k chẵn; cos( + kπ) = nếu k lẻ hoặc =
nếu k chẵn; tan( +kπ) = 1; cot( +kπ) = 1. Bài 4 trang 15
Tính các giá trị lượng giác của góc α trong mỗi trường hợp sau: a) sinα = với < α < π; b) cosα = với −π < α < 0;
c) tanα = 3 với −π < α < 0;
d) cotα = −2 với 0 < α < π. Gợi ý đáp án a) sinα =
với < α < π ⇒ α ≈ 1.318 b) cosα =
với −π < α < 0⇒ α ≈ 2.3
c) tanα = 3 với −π < α < 0⇒ α ≈ 1.249
d) cotα =− 2 với 0 < α < π ⇒ α ≈ −0.464 Bài 5 trang 15 Tính:
a) A = sin25∘ + sin210∘ + sin215∘ +...+ sin285∘ (17 số hạng).
b) B = cos5∘ + cos10∘ + cos15∘ +...+ cos175∘ (35 số hạng). Gợi ý đáp án
a) A = cos285∘ + cos280∘ + cos275∘ +...+ sin245∘ +...+ sin285∘ =
b) B = −cos175∘ − cos170∘ − cos165∘ −...+ cos175∘ = 0 Bài 6 trang 15
Một vệ tinh được định vị tại vị trí A trong không gian. Từ vị trí A, vệ tinh bắt đầu chuyển động
quanh Trái Đất theo quỹ đạo là đường tròn với tâm là tâm O của Trái Đất, bán kính 9000 km.
Biết rằng vệ tinh chuyển động hết một vòng của quỹ đạo trong 2h.
a) Hãy tính quãng đường vệ tinh đã chuyển động được sau 1h; 3h; 5h.
b) Vệ tinh chuyển động được quãng đường 200 000 km sau bao nhiêu giờ (làm tròn kết quả đến hàng đơn vị)? Gợi ý đáp án
Ta có công thức độ dài của một cung tròn là: l = R.α
a) Sau 1h, vệ tinh chuyển động được một cung α = π
Như vậy, quãng đường vệ tinh đã chuyển động được sau 1h là: l = 9000π (km).
Sau 3h, vệ tinh chuyển động được một cung α = 3π
Như vậy, quãng đường vệ tinh đã chuyển động được sau 3h là: l = 27000π (km).
Sau 5h, vệ tinh chuyển động được một cung α = 5π
Như vậy, quãng đường vệ tinh đã chuyển động được sau 5h là: l = 45000π (km).
b) Vệ tinh chuyển động được quãng đường 200 000 km sau: ≈ 22h.
II. Lý thuyết Toán 11 Cánh diều Bài 1 1. Góc lượng giác
a, Khái niệm góc lượng giác và số đo của góc lượng giác
Trong mặt phẳng, cho 2 tia Ou, Ov. Xét tia Om cùng nằm tròn mặt phẳng này. Nếu tia Om quay
quanh điểm O, theo một chiều nhất định từ Ou đến Ov, thì ta nói nó quét một góc lượng giác
với tia đầu Ou và tia cuối Ov. Kí hiệu: (Ou, Ov).
Số đo của góc lượng giác có tia đầu Ou và tia cuối Ov kí hiệu là sđ(Ou, Ov). b, Hệ thức Chasles
Với 3 tia Ou, Ov, Ow bất kì ta có:
Sđ(Ou,Ov) + sđ(Ov, Ow) = sđ(Ou,Ow) +k360o.