Giải Toán 11 Bài 3: Hàm số lượng giác và đồ thị | Cánh diều
Giải Toán 11 Bài 3: Hàm số lượng giác và đồ thị | Cánh diều được trình bày khoa học, chi tiếtgiúp cho các bạn học sinh chuẩn bị bài một cách nhanh chóng và đầy đủ đồng thời giúp quý thầy cô tham khảo để soạn giáo án cho học sinh của mình. Thầy cô và các bạn xem, tải về ở bên dưới.
Chủ đề: Chương 1: Hàm số lượng giác và phương trình lượng giác (CD)
Môn: Toán 11
Sách: Cánh diều
Thông tin:
Tác giả:
Thông tin :
Chủ đề:
Chương 1: Hàm số lượng giác và phương trình lượng giác (CD)
Môn:
Sách:
Tác giả:
Tài liệu liên quan:
Preview text:
Toán 11 Bài 3: Hàm số lượng giác và đồ thị
Giải Toán lớp 11 tập 1 trang 31 - Cánh diều Bài 1 trang 31
Dùng đồ thị hàm số, tìm giá trị của x trên đoạn [−2π; 2π] để:
a) Hàm số y = sinx nhận giá trị bằng 1;
b) Hàm số y = sinx nhận giá trị bằng 0;
c) Hàm số y = cosx nhận giá trị bằng -1;
d) Hàm số y = cosx nhận giá trị bằng 0. Gợi ý đáp án a) x = ; b) x = 0; c) x = −π; d) x = . Bài 2 trang 31
Dùng đồ thị hàm số, tìm giá trị của x trên khoảng (−π; ) để:
a) Hàm số y = tanx nhận giá trị bằng -1;
b) Hàm số y = tanx nhận giá trị bằng 0;
c) Hàm số y = cotx nhận giá trị bằng 1;
d) Hàm số y = cotx nhận giá trị bằng 0. Gợi ý đáp án a) x = ; b) x = 0; c) x = ; d) x = . Bài 3 trang 31
Xét sự biến thiên của mỗi hàm số sau trên các khoảng tương ứng: a) y = sinx trên khoảng , ;
b) y = cosx trên khoảng (−20π;−19π),(−9π;−8π). Gợi ý đáp án a) = (
− 4π; − 4π) nên y = sinx đồng biến trên khoảng . = ( + 10π;
+ 10π) nên y = sinx nghịch biến trên khoảng .
b) (−20π; −19π) = (−π − 19π; −19π) nên y = cosx đồng biến trên khoảng (−20π; −19π).
(−9π; −8π) =(−9π; π−9π) nên y = cosx nghịch biến trên khoảng (−9π; −8π). Bài 4 trang 31
Dùng đồ thị hàm số, hãy cho biết:
a) Với mỗi m∈[−1;1], có bao nhiêu giá trị α∈[ ; ] sao cho sinα = m;
b) Với mỗi m∈[−1;1], có bao nhiêu giá trị α∈[0,π] sao cho cosα = m;
c) Với mỗi m∈R, có bao nhiêu giá trị α∈[ ; ] sao cho tanα = m;
d) Với mỗi m∈R, có bao nhiêu giá trị α∈[0,π] sao cho cotα = m. Gợi ý đáp án
a) Dựa vào hình 23, 24, ta thấy:
Với mỗi m∈[−1;1], có một giá trị α∈[ ; ] sao cho sinα = m;
b) Dựa vào hình 26, 27, ta thấy:
Với mỗi m∈[−1;1], có một giá trị α∈[0,π] sao cho cosα = m;
c) Dựa vào hình 28, 29, ta thấy:
Với mỗi m∈R, có một giá trị α∈[ ; ] sao cho tanα = m;
d) Dựa vào hình 30, 31, ta thấy:
Với mỗi m∈R, có một giá trị α∈[0,π] sao cho cotα = m. Bài 5 trang 31
Xét tính chẵn, lẻ của các hàm số: a) y = sinxcosx; b) y = tanx + cotx; c) y = sin2x. Gợi ý đáp án
a) f(−x) = sin(−x)cos(−x) = −sinxcosx = −f(x) nên hàm số y = sinxcosx là hàm số lẻ;
b) f(−x) = tan(−x) + cot(−x) = −tanx − cotx = −f(x) nên hàm số y = tanx + cotx là hàm số lẻ;
c) f(−x) = sin2(−x) = sin2x = f(x) nên hàm số y = sin2x là hàm số chẵn. Bài 6 trang 31 :
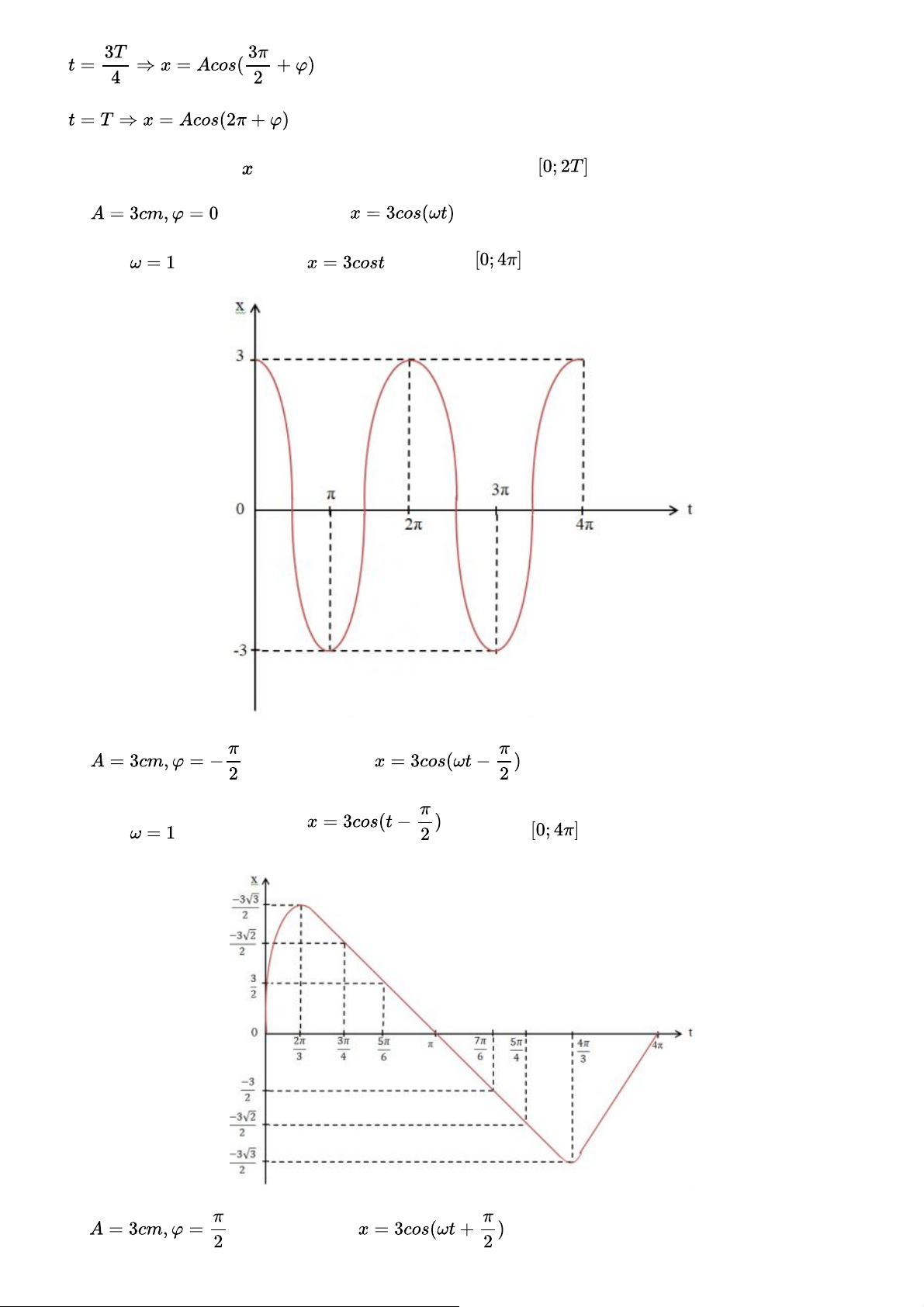
Một dao động điều hòa có phương trình li độ dao động là: x = Acos(ωt+φ), trong đó t là thời
gian tính bằng giây, A là biên độ dao động và x là li độ dao động đều được tính bằng cm. Khi
đó, chu kì T của dao động là T=2πω. Xác định giá trị của li độ khi t=0,t=T4,t=T2,t=3T4,t=T và
vẽ đồ thị biểu diễn li độ của dao động điều hòa trên đoạn [0;2T] trong trường hợp: a) A = 3cm, φ = 0; b) A = 3cm, φ = ; c) A = 3cm, φ = . Gợi ý đáp án Giá trị của li độ khi: ; ; ; ; .
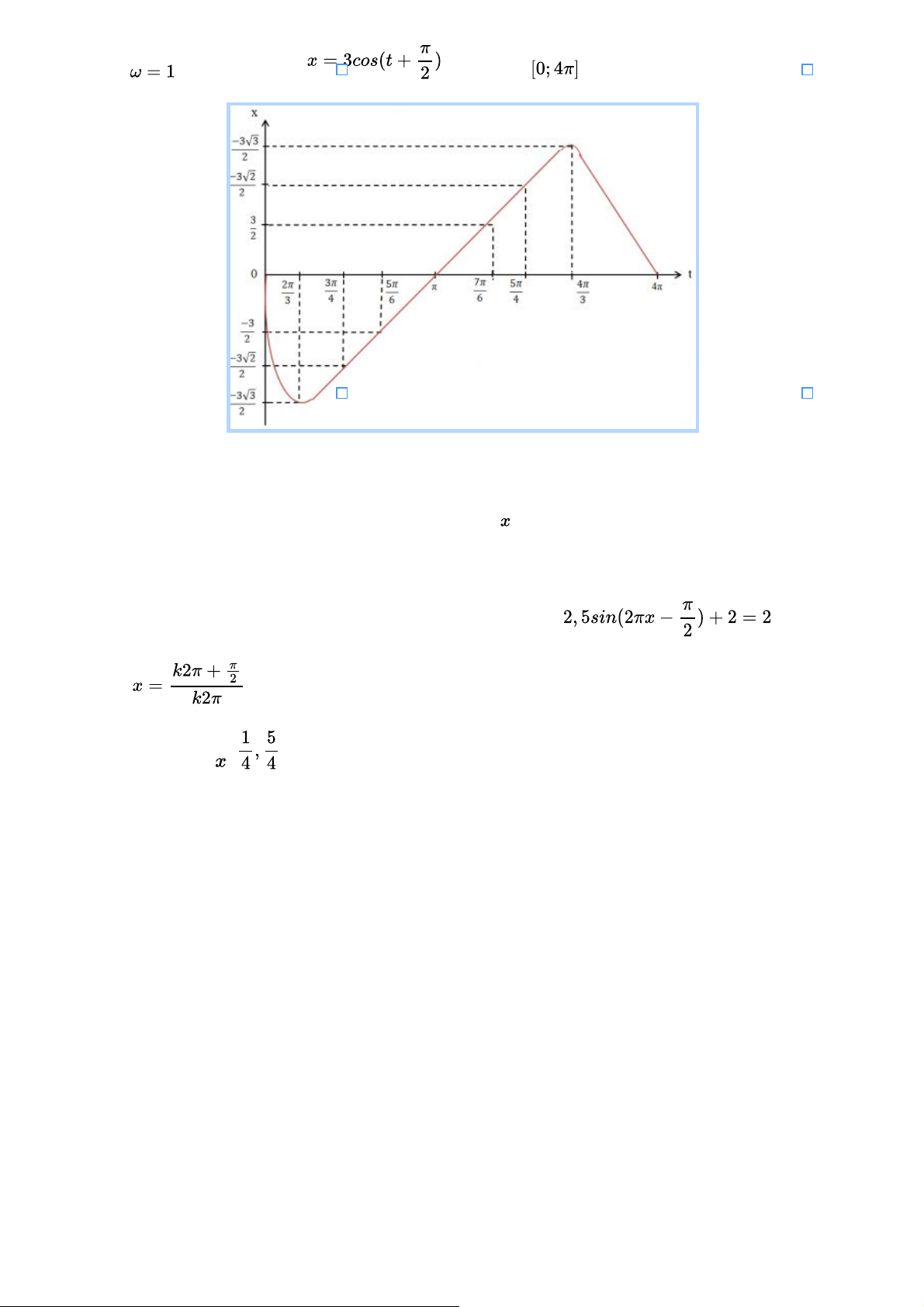
Đồ thị biểu diễn li độ của dao động điều hòa trên đoạn trong trường hợp: a) . Ta có hàm số: . Giả sử . Ta có hàm số: trên đoạn . b) . Ta có hàm số: . Giả sử . Ta có hàm số: trên đoạn . c) . Ta có hàm số: . Giả sử . Ta có hàm số: trên đoạn . Bài 7 trang 31
Trong bài toán mở đầu, hãy chỉ ra một số giá trị của để ống đựng nước cách mặt nước 2m. Gợi ý đáp án
Để ống đựng nước cách mặt nước 2m, ta có phương trình: Suy ra: Một số giá trị của : .