Giải Toán 6 Bài tập cuối chương III | Cánh diều

Giải Toán 6 trang 117, 118 tập 1 Bài 1
Tạo ra hình hộp có nắp.
Vẽ các hình chữ nhật trên một miếng bìa. sau đó cắt, gấp lại và dán miếng bìa để tạo ra một hình có nắp Gợi ý đáp án:
Kẻ các nét đứt và nét liền như hình vẽ.
Cắt miếng bìa theo mép ngoài cùng như hình vẽ.
Gấp miếng bìa theo các nét đứt về hướng miếng bìa hình chữ nhật lớn ở bên phải ta được một hình hộp có nắp Bài 2
Cho các hình sau đây: (1) Đoạn thẳng AB (2) Tam giác đều ABC (3) Hình tròn tâm O
(4) Hình thang cân ABCD ( có đáy lớn CD) (5) Hình thoi ABCD Trong các hình nói trên:
a) Hình nào có trục đối xứng? Chỉ ra trục đối xứng của hình đó
b) Hình nào có tâm đối xứng? Chỉ ra tâm đối xứng của hình đó Gợi ý đáp án: a) Hướng dẫn giải
- Tìm hình có trục đối xứng.
- Tìm trục đối xứng của mỗi hình.
Trong các hình trên, hình có trục đối xứng là:
(1) Đoạn thẳng AB: Trục đối xứng là đường thẳng đi qua và vuông góc với trung điểm
(2) Tam giác đều ABC: Trục đối xứng là đường thẳng đi qua trọng tâm
(3) Hình tròn tâm O: Trục đối xứng là đường thẳng đi qua tâm O
(4) Hình thang cân ABCD ( có đáy lớn CD): Trục đối xứng là đường thẳng đi qua và
vuông góc với trung điểm của hai cạnh đáy b) Hướng dẫn giải
- Tìm hình có tâm đối xứng
- Tìm tâm đối xứng của mỗi hình.
Hình nào có tâm đối xứng:
(1) Đoạn thẳng AB: Tâm đối xứng là trung điểm của đoạn thẳng
(2) Tam giác đều ABC: Tâm đối xứng là trọng tâm của tam giác
(3) Hình tròn tâm O: Tâm đối xứng là điểm O
(5) Hình thoi ABCD: Tâm đối xứng là giao điểm của hai đường chéo Bài 3
Hãy quan sát xung quanh và chỉ ra những hình a) Có trục đối xứng b) Có tâm đối xứng Gợi ý đáp án:
a) Quan sát xung quanh và chỉ ra những hình có trục đối xứng Hình chiếc lá: Hình chiếc lá: Hình con chuồn chuồn:
Trên thực tế, có nhiều hình khác có trục đối xứng, các em có thể tự tìm thêm.
b) Quan sát xung quanh và chỉ ra những hình có tâm đối xứng Hình gạch hoa Hình bông hoa Hình biển báo giao thông Bài 4
Hãy tìm và kể ra một số ứng dụng của tính đối xứng trong thực tiễn mà em biết Gợi ý đáp án:
Trong nghệ thuật trang trí
Trong thiết kế kiến trúc: Tháp Eiffel ở Paris, Pháp Bài 5
a) Một hình thoi có cạnh 4cm thì chu vi của nó bằng bao nhiêu?
b) Một hình vuông có chu vi 40cm thì cạnh của nó bằng bao nhiêu?
c) Một hình chữ nhật có chu vi 30 cm và chiều rộng là 7cm thì chiều dài của nó bằng bao nhiêu?
d) Một hình chữ nhật có chu vi 36 cm và chiều dài gấp đôi chiều rộng thì mỗi cạnh của nó bằng bao nhiêu? Phương pháp giải:
Chu vi của hình thoi cạnh a: C = 4. a. Gợi ý đáp án:
a) Một hình thoi có cạnh 4cm thì chu vi của nó bằng: 4 x 4 = 16cm
b) Một hình vuông có chu vi 40cm thì cạnh của nó bằng: 40 : 4 = 10 cm
c) Một hình chữ nhật có chu vi 30 cm và chiều rộng là 7cm thì chiều dài của nó bằng: 8 cm
d) Một hình chữ nhật có chu vi 36 cm và chiều dài gấp đôi chiều rộng thì chiều dài bằng 12cm, chiều rộng bằng 6cm Bài 6
Sử dụng thước, hãy đo và cho biết chu vi của một số đồ vật có dạng hình chữ nhật trong thực
tiễn. Chẳng hạn: đo chu vi mặt bàn học của em; đo chu vi bìa một quyển sách mà em có;... Phương pháp giải
Sử dụng thước đo dây đo chiều dài và chiều rộng của vật. Gợi ý đáp án
Chẳng hạn: chiều dài bàn học của em bằng 80 cm, chiều rộng bằng 50 cm.
Khi đó chu vi mặt bàn là: C=2.(80+50)=260cm Bài 7
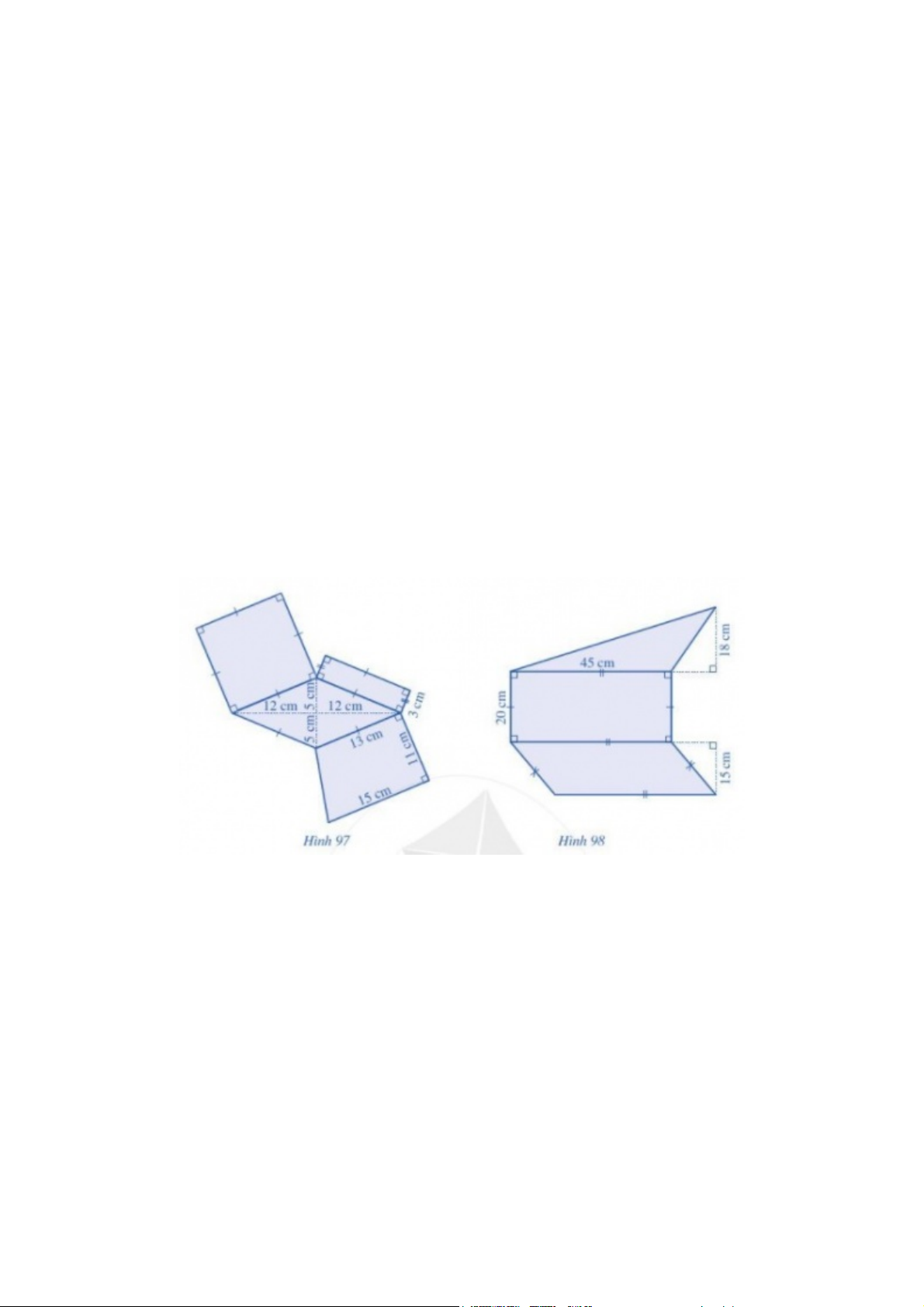
Quan sát Hình 97, Hình 98 và tính diện tích của phần tô xanh ở mỗi hình đó. Phương pháp giải - Quan sát.
- Tìm và xác định các hình nhỏ ghép thành hình 97 và 98.
- Diện tích hình vuông cạnh a: S=a.a
- Diện tích hình chữ nhật cạnh a và b: S=a.b Gợi ý đáp án:
Diện tích phần tô xanh hình 97 là tổng diện tích của một hình vuông, một hình thoi, một hình
chữ nhật và một hình thang
S = ( 13 x 4 ) + (3 x 13) + (5 x 12) + ( 13 + 15) x 11 : 2 = 305 ( cm2)
Diện tích phần tô xanh hình 98 là tổng diện tích của một hình bình hành, một hình chữ nhật và một tam giác
S = (15 x 45 ) + (20 x 45) + (18 x 45 ) : 2 = 1980 ( cm2) Bài 8
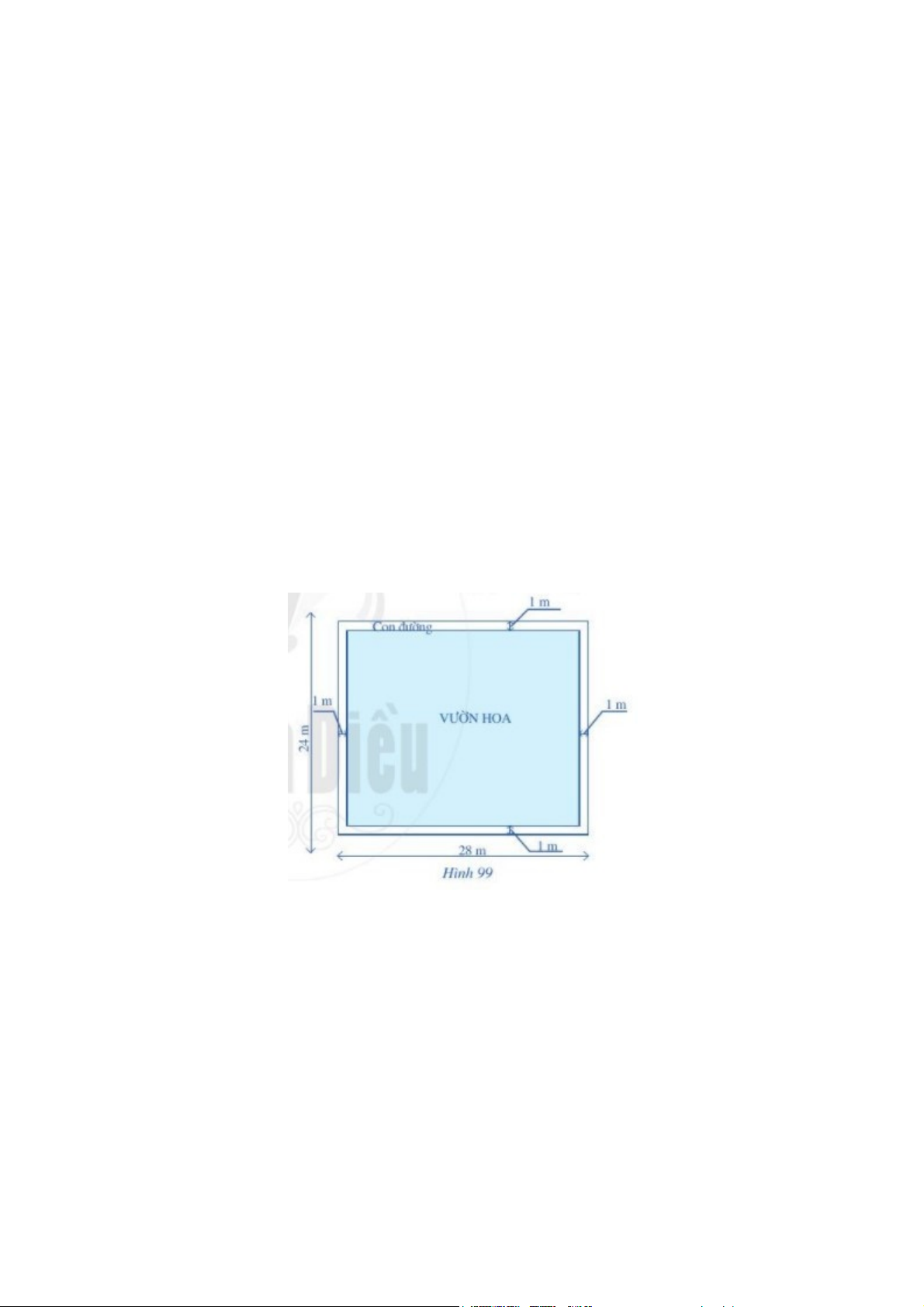
Trên mảnh đất có dạng hình chữ nhật với chiều dài là 28m và chiều rộng là 24 m, người ta định
xây dựng một vườn hoa hình chữ nhật và bớt ra một phần đường đi như ở Hình 99
a) Tính diện tích mảnh đất có dạng hình chữ nhật đó.
b) Tính diện tích vườn hoa
c) Người ta định dùng những viên gạch chống trượt có dạng hình vuông có cạnh là 50 cm để
lát đường đi. Cần dùng bao nhiêu viên gạch như thế? Biết rằng diện tích các mối nối và sự hao hụt không đáng kể
d)Người ta làm hàng rào xung quanh vườn hoa. Tính chiều dài hàng rào đó Gợi ý đáp án:
áp dụng công thức: Diện tích hình chữ nhật cạnh a và b: S=a.b.
a) Diện tích mảnh đất có dạng hình chữ nhật đó là: 24 x 28 = 672 m2
b) Diện tích vườn hoa là: 23 x 27 = 621 (m2)
c) Người ta định dùng những viên gạch chống trượt có dạng hình vuông có cạnh là 50 cm để
lát đường đi. Cần dùng bao nhiêu viên gạch như thế? Biết rằng diện tích các mối nối và sự hao hụt không đáng kể
Diện tích phần đường đi là: 672 - 621 = 51 (m2) = 510 000 cm2
Cần dùng số viên gạch để lát đường đi là: 510 000 : 50 = 10.200 ( viên gạch )
d) Chiều dài hàng rào là: ( 23 + 27) x 2 = 100 m Bài 9
Bạn Thảo muốn cắt miếng bìa màu xanh có diện tích là
28 cm2 như Hình 100. Biết chu vi hình vuông ABCD là
16cm. Tính giúp bạn Thảo độ dài cạnh EG Hướng dẫn giải - Tính cạnh hình vuông.
- Tính diện tích hình vuông
- Tính diện tích 1 hình thang cân.
- Độ dài cạnh hình thang chưa biết:
a= 2S:h-b, với b là cạnh đã biết. Gợi ý đáp án:
Diện tích của hình vuông ABCD là: 4 x 4 = 16 ( cm2)
Diện tích phần còn lại của miếng bìa là: 28 - 16 = 12 ( cm2)
Diện tích phần còn lại của miếng bìa là tổng diện tích của 4 hình thang cân. Do vậy, diện tích
của hình thang cân chứa cạnh EG là: 12 : 4 = 3 ( cm2)
Độ dài cạnh EG là: 3 x 2 - 4 = 2 (cm)
Lý thuyết Hình học trực quan 1. Tam giác đều
1.1 Nhận biết tam giác đều Tam giác đều ABC có
+ Ba cạnh bằng nhau: AB = BC = CA
+ Ba góc ở các đỉnh A, B, C bằng nhau.
Chú ý: Trong hình học nói chung, tam giác nói riêng, các cạnh bằng nhau (hay các góc bằng
nhau) thường được chỉ rõ ràng bằng cùng một ký hiệu (xem hình vẽ trên).
1.2 Vẽ tam giác đều
Vẽ tam giác đều bằng thước và compa khi biết độ dài cạnh.
Bước 1. Dùng thước vẽ đoạn thẳng AB = 3 cm
Bước 2. Lấy A làm tâm, dùng compa vẽ một phần đường tròn có bán kính AB.
Bước 3. Lấy B làm tâm, dùng compa vẽ một phần đường tròn có bán kính BA; gọi C là giao
điểm của hai phần đường tròn vừa vẽ.
Bước 4. Dùng thước vẽ các đoạn thẳng AC và BC
Khi đó ta được tam giác đều ABC có cạnh bằng 3 cm. 2. Hình vuông
2.1 Nhận biết hình vuông Hình vuông ABCD có:
+ Bốn cạnh bằng nhau: AB = BC = CD = DA
+ Hai cạnh đối AB và CD; AD và BC song song với nhau.
+ Hai đường chéo bằng nhau: AC = BD
+ Bốn góc ở các đỉnh A, B, C, D là góc vuông. 2.2 Vẽ hình vuông
Dùng ê ke vẽ hình vuông khi biết độ dài cạn