Giải Toán 6 Luyện tập chung trang 43 | Kết nối tri thức
Giải Toán lớp 6 Luyện tập chung trang 43 bao gồm đáp án chi tiết cho từng phần, từng bài tập trong SGK Toán 6 Tập 1 Kết nối tri thức với cuộc sống. Với lời giải chi tiết, trình bày khoa học, được biên soạn dễ hiểu, giúp các em nâng cao kỹ năng giải Toán 6, từ đó học tốt môn Toán lớp 6 hơn.
Chủ đề: Chương 2: Tính chia hết trong tập hợp các số tự nhiên (KNTT)
Môn: Toán 6
Sách: Kết nối tri thức
Thông tin:
Tác giả:
Thông tin :
Chủ đề:
Chương 2: Tính chia hết trong tập hợp các số tự nhiên (KNTT)
Môn:
Sách:
Tác giả:
Tài liệu liên quan:
Preview text:
Giải Toán 6 Luyện tập chung trang 43 sách Kết nối tri thức với cuộc sống
Đáp án Toán 6 trang 43 Kết nối tri thức với cuộc sống Bài 2.25:
a) 130; 135; 105; 150; 310; 315; 350; 305; 510; 530
b) 135; 153; 351; 315; 513; 531; 105; 150; 510; 501
Bài 2.26: A = 27.33; B = 36.52 Bài 2.27: a) x ∈ {0; 4; 8; 12; 16; 20} b) x ∈ {0; 9; 18}
Bài 2.28: Mỗi nhóm có thể có 4 người; 5 người; 8 người; 10 người; 20 người hoặc 40 người. Bài 2.29: 3 và 5 5 và 7 7 và 9 11 và 13 17 và 19 29 và 31
Hướng dẫn giải Toán 6 Kết nối tri thức với cuộc sống trang 43 tập 1 Bài 2.25
Từ các số 5, 0, 1, 3, viết các số tự nhiên có ba chữ số khác nhau thỏa mãn điều kiện:
a. Các số đó chia hết cho 5
b. Các số đó chia hết cho 3 Hướng dẫn giải:
Dấu hiệu chia hết cho 5: Các số có chữ số tận cùng là 0; 5 thì chia hết cho 5 và chỉ những
số đó mới chia hết cho 5.
Dấu hiệu chia hết cho 3: Các số có tổng các chữ số chia hết cho 3 thì chia hết cho 3 và
chỉ những số đó mới chia hết cho 3. Gợi ý đáp án:
a) Các số tự nhiên có ba chữ số khác nhau chia hết cho 5 được viết từ các chữ số đã cho: 130;
135; 105; 150; 310; 315; 350; 305; 510; 530
b) Các số tự nhiên có ba chữ số khác nhau chia hết cho 3 được viết từ các chữ số đã cho: 135;
153; 351; 315; 513; 531; 105; 150; 510; 501 Bài 2.26
Hãy phân tích các số A, B ra thừa số nguyên tố: A = 42.63 B = 92.152 Hướng dẫn giải
Muốn phân tích một số tự nhiên a lớn hơn 1 ra thừa số nguyên tố ta có thể làm như sau:
Kiểm tra xem 2 có phải là ước của a hay không. Nếu không ta xét số nguyên tố 3 và cứ
như thế đối với các số nguyên tố lớn dần.
Giả sử x là ước nguyên tố nhỏ nhất của a, ta chia a cho x được thương b.
Tiếp tục thực hiện quy trình trên đối với b. Cứ tiếp tục quá trình trên kéo dài cho đến khi ta
được thương là một số nguyên tố. Gợi ý đáp án:
A =42.63 =4.4.6.6.6=22.22.2.3.2.3.2.3 = 27.33
B = 92.152 =9.9.15.15 = 32.32.3.5.3.5=36.52 Bài 2.27
Tìm số tự nhiên x không vượt quá 22 sao cho: a. 100 - x chia hết cho 4
b. 18 + 90 + x chia hết cho 9 Hướng dẫn giải
Dấu hiệu chia hết cho 2: Các số có chữ số tận cùng là 0; 2; 4; 8 thì chia hết cho 2 và chỉ
những số đó mới chia hết cho 2.
Dấu hiệu chia hết cho 9: Các số có tổng các chữ số chia hết cho 9 thì chia hết cho 9 và
chỉ những số đó mới chia hết cho 9. Gợi ý đáp án:
a) 100 - x chia hết cho 4. Mà 100 chia hết cho 4 nên x chia hết cho 4
Do đó x là bội của 4 và không vượt quá 22
Vậy x ∈ {0; 4; 8; 12; 16; 20}
b) 18 + 90 + x chia hết cho 9. Mà 18 và 90 chia hết cho 9 nên x chia hết cho 9
Do đó x là bội của 9 và không vượt quá 22 Vậy x ∈ {0; 9; 18} Bài 2.28
Lớp 6B có 40 học sinh. Để thực hiện dự án học tập nhỏ, cô giáo muốn chia lớp thành các nhóm
có số người như nhau, mỗi nhóm có nhiều hơn 3 người. Hỏi mỗi nhóm có thể có bao nhiêu người? Hướng dẫn giải
Muốn tìm ước của a (a > 1) ta lần lượt chia a cho các số tự nhiên từ 1 đến a để xem a
chia hết cho những số nào thì các số đó là ước của a.
Ta có thể tìm các bội của một số khác bằng cách nhân số đó lần lượt với 0, 1, 2, 3, … Gợi ý đáp án:
Gọi số nhóm là x (nhóm, x ∈ N)
Vì cô giáo muốn chia lớp có 40 học sinh thành nhiều nhóm có số người như nhau nên 40 ⁝ x hay X ∈ Ư(40)
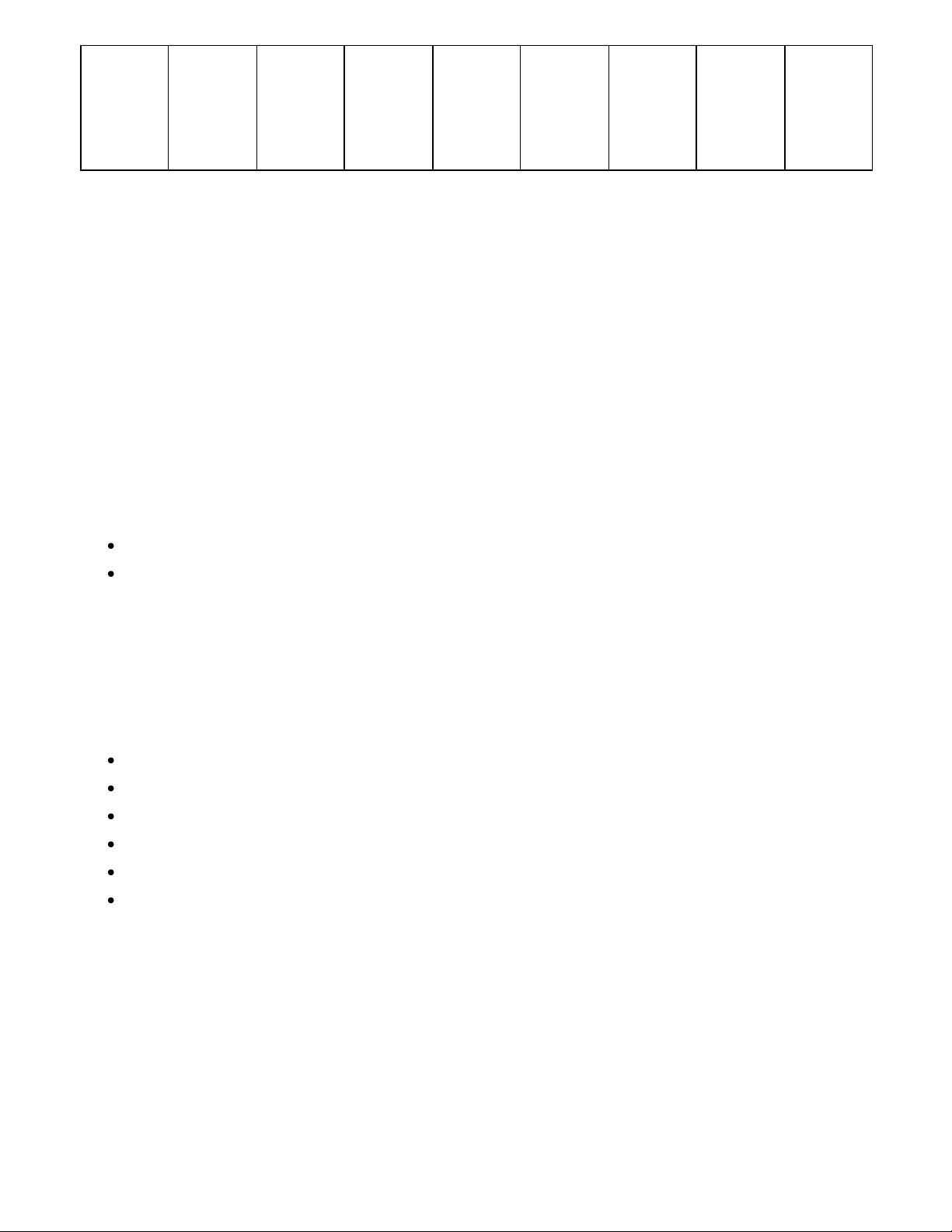
Ư(40) = {1; 2; 4; 5; 8; 10; 20; 40} Ta có bảng sau: Số nhóm 1 2 4 5 8 10 20 40 Số 40 20 10 8 5 4 2 1 người mỗi nhóm
Vì mỗi nhóm có nhiều hơn 3 người nên mỗi nhóm có thể có 4 người; 5 người; 8 người; 10
người; 20 người hoặc 40 người.
Vậy mỗi nhóm có thể có 4 người; 5 người; 8 người; 10 người; 20 người hoặc 40 người. Bài 2.29
Hai số nguyên tố được gọi là sinh đôi nếu chúng hơn kém nhau hai đơn vị. Ví dụ 17 và 19 là
hai số nguyên tố sinh đôi. Em hãy liệt kê các cặp số nguyên tố sinh đôi nhỏ hơn 40. Hướng dẫn giải
- Số nguyên tố là số tự nhiên lớn hơn 1, chỉ có hai ước là 1 và chính nó
Số 0 và số 1 không là số nguyên tố.
Số 2 là số nguyên tố nhỏ nhất và là số nguyên tố chẵn duy nhất
- Hợp số là số tự nhiên có nhiều hơn hai ước. Gợi ý đáp án:
Các cặp số nguyên tố sinh đôi nhỏ hơn 40: 3 và 5 5 và 7 7 và 9 11 và 13 17 và 19 29 và 31
Lý thuyết Luyện tập chung trang 43
1. Dấu hiệu chia hết cho 2, cho 5
Các số có chữ số tận cùng là 0, 2, 4, 6, 8 thì chia hết cho 2 và chỉ những số đó mới chia hết cho 2.
Các số có chữ số tận cùng là 0 hoặc 5 thì chia hết cho 5 và chỉ những số đó mới chia hết cho 5.
Ví dụ 1. Cho các số sau: 242; 102; 255; 76; 8 090; 260; 145. a) Các số chia hết cho 2; b) Các số chia hết cho 5;
c) Các số chia hết cho cả 2 và 5. Lời giải
a) Các số chia hết cho 2 là các số có chữ số tận cùng là .
Do đó trong các số trên các số chia hết cho 2 là: 242; 102; 76; 8 090; 260.
b) Các số chia hết cho 5 là các số có chữ số tận cùng là 0 hoặc 5.
Do đó trong các số trên số chia hết cho 5 là: 255; 8 090; 260; 145.
c) Các số chia hết cho cả 2 và 5 là: 8 090; 260.
2. Dấu hiệu chia hết cho 9, cho 3
Các số có tổng các chữ số chia hết cho 9 thì chia hết cho 9 và chỉ những số đó mới chia hết cho 9.
Các số có tổng các chữ số chia hết cho 3 thì chia hết cho 3 và chỉ những số đó mới chia hết cho 3.
Chú ý: Các số chia hết cho 9 thì chia hết cho 3 nhưng chia hết cho 3 chưa chắc chia hết cho 9.
Ví dụ 2. Trong các số sau: 1 954; 264; 315; 705; 2 231; 3 771 số nào chia hết cho 3, số nào chia hết cho 9. Lời giải
+) Ta có: 1 + 9 + 5 + 4 = 19 không chia hết cho 9 cũng không chia hết cho 3 nên 1954 không chia hết cho 3 và 9.
+) Ta có: 2 + 6 + 4 = 12 chia hết cho 3 nhưng không chia hết cho 9 nên 264 chia hết cho 3 và không chia hết cho 9.
+) Ta có: 3 + 1 + 5 = 9 vừa chia hết cho 3 vừa chia hết cho 9 nên 315 vừa chia hết cho 3 vừa chia hết cho 9.
+) Ta có 7 + 0 + 5 = 12 chia hết cho 3 nhưng không chia hết cho 9 nên 705 chia hết cho 3 và không chia hết cho 9.
+) Ta có 2 + 2 + 3 + 1 = 8 không chia hết cho 3 cũng không chia hết cho 9 nên 2 231 không chia
hết cho 3 cũng không chia hết cho 9.
+) Ta có: 3 + 7 + 7 + 1 = 18 vừa chia hết cho 3 vừa chia hết cho 9 nên 3771 vừa chia hết cho 3 vừa chia hết cho 9.
Vậy các số chia hết cho 3 là 264; 315; 705; 3 771; các số chia hết cho 9 là 315; 3 771.
3. Số nguyên tố và hợp số
- Số nguyên tố là số tự nhiên lớn hơn 1, chỉ có hai ước là 1 và chính nó.
- Hợp số là số tự nhiên lơn hơn 1, có nhiều hơn hai ước.
Ví dụ 1. Trong các số đã cho dưới đây, số nào là số nguyên tố, số nào là hợp số? Vì sao? 190; 11; 132; 23; 43; 17; 21. Lời giải
Ta thấy 190 có các ước là 1, 2, 5, 190 nhiều hơn hai ước nên 190 là hợp số;
11 chỉ có ước là 1 và 11 nên 11 là số nguyên tố;
132 có các ước là 1; 2; 132 nhiều hơn hai ước nên 132 là hợp số;
23 chỉ có ước là 1 và 23 nên 23 là số nguyên tố;
43 chỉ có ước là 1 và 43 nên 43 là số nguyên tố;
17 chỉ có ước là 1 và 17 nên 17 là số nguyên tố;
21 có các ước là 1; 3; 7; 21 nhiều hơn hai ước nên 21 là hợp số.