Giải Toán 7 Bài 2: Tam giác bằng nhau | Chân trời sáng tạo
Giải bài tập SGK Toán 7 Tập 2 trang 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58 sách Chân trời sáng tạo giúp các em học sinh lớp 7 xem gợi ý giải các bài tập của Bài 2: Tam giác bằng nhau.
Chủ đề: Chương 8: Tam giác (CTST)
Môn: Toán 7
Sách: Chân trời sáng tạo
Thông tin:
Tác giả:
Preview text:
Giải Toán 7 bài 1: Góc và cạnh của một tam giác Chân trời sáng tạo
Giải Toán 7 Chân trời sáng tạo trang 57, 58 tập 2 Bài 1
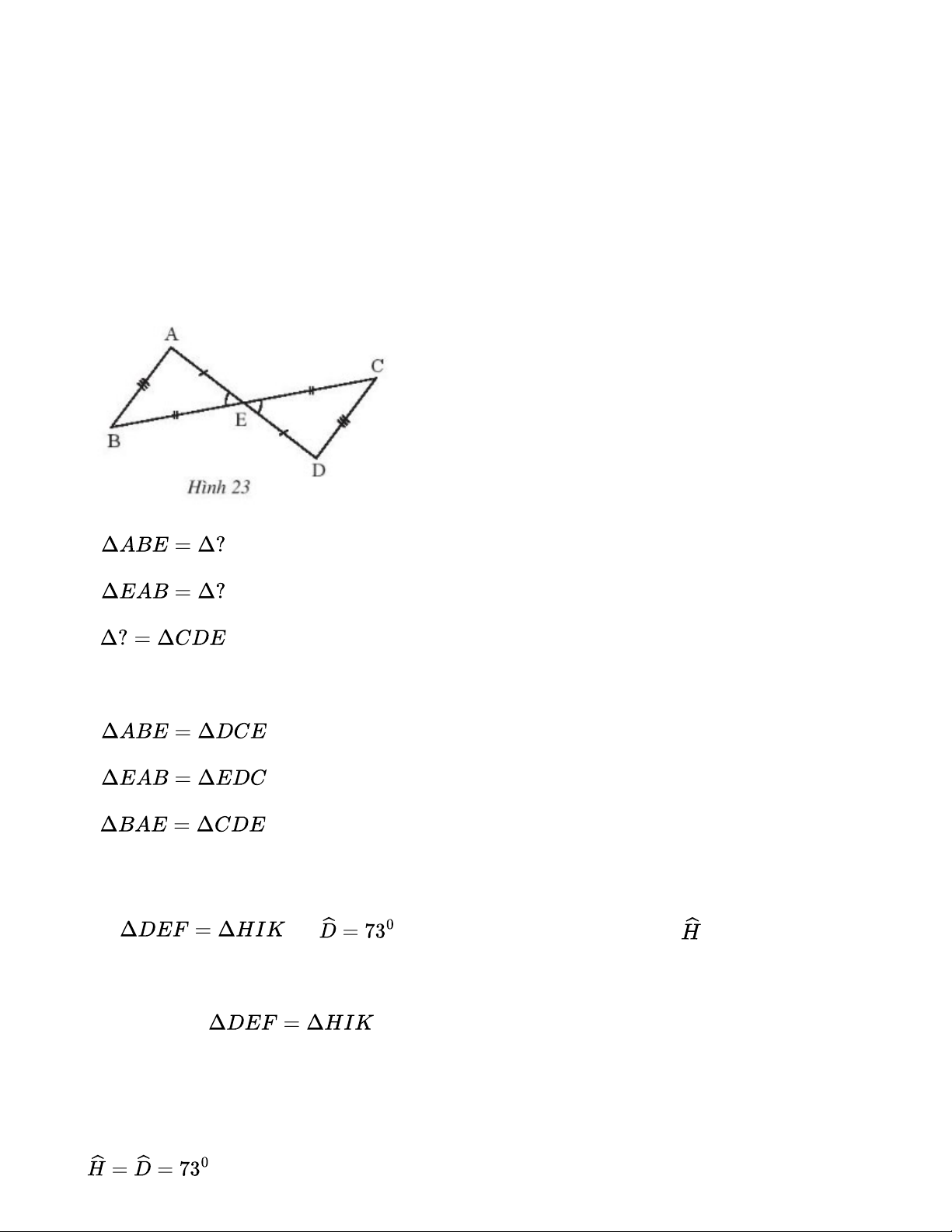
Quan sát Hình 23 rồi thay dấu ? bằng tên tam giác thích hợp. a. b. c. Gợi ý đáp án: a. b. c. Bài 2 Cho và
, DE = 5cm, IK = 7cm. Tính số đo và độ dài HI, EF. Gợi ý đáp án: Theo đề bài có , nên ta có: HI = DE = 5cm EF = IK = 7cm Bài 3
Cho hai tam giác bằng nhau ABC và DEF (các đỉnh viết chưa tương ứng), trong đó
. Tìm các cặp cạnh bằng nhau, cặp góc tương ứng bằng nhau còn lại. Gợi ý đáp án:
Xếp theo thứ tự tương ứng các đỉnh có: .
Các cặp góc tương ứng bằng nhau: .
Các cặp cạnh bằng nhau là: AB = EF, BC = FD, AC = ED. Bài 4 Cho biết
và MN = 4cm, MP = 5cm, EF = 6cm. Tính chu vi tam giác MNP Gợi ý đáp án: Vì nên NP = EF = 6cm.
Chu vi tam giác MNP là: MN + MP + NP = 4 + 5 + 6 = 15 (cm) Bài 5
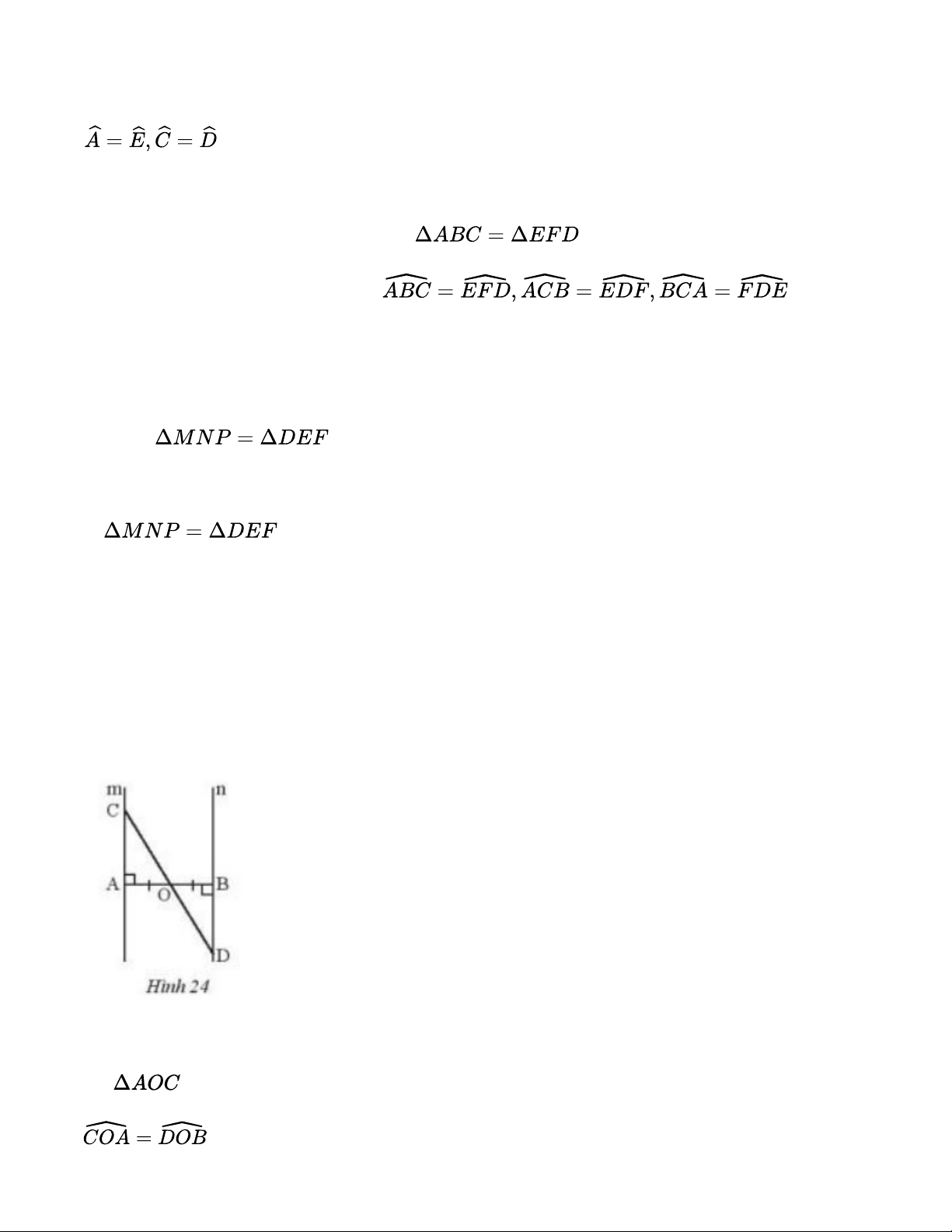
Cho đoạn thẳng AB có O là trung điểm. Vẽ hai đường thẳng m và n lần lượt vuông góc với AB
tại A và B. Lấy điểm C trên m, CO cắt n tại D (hình 24). Chứng minh rằng O là trung điểm của CD. Gợi ý đáp án: Xét
vuông tại A và \Delta BOD vuông tại B có: (2 góc đối đỉnh). AO = OB Suy ra
(cạnh góc vuông và góc nhọn).
mà 3 điểm O, C, D thẳng hàng là trung điểm của CD. Bài 6
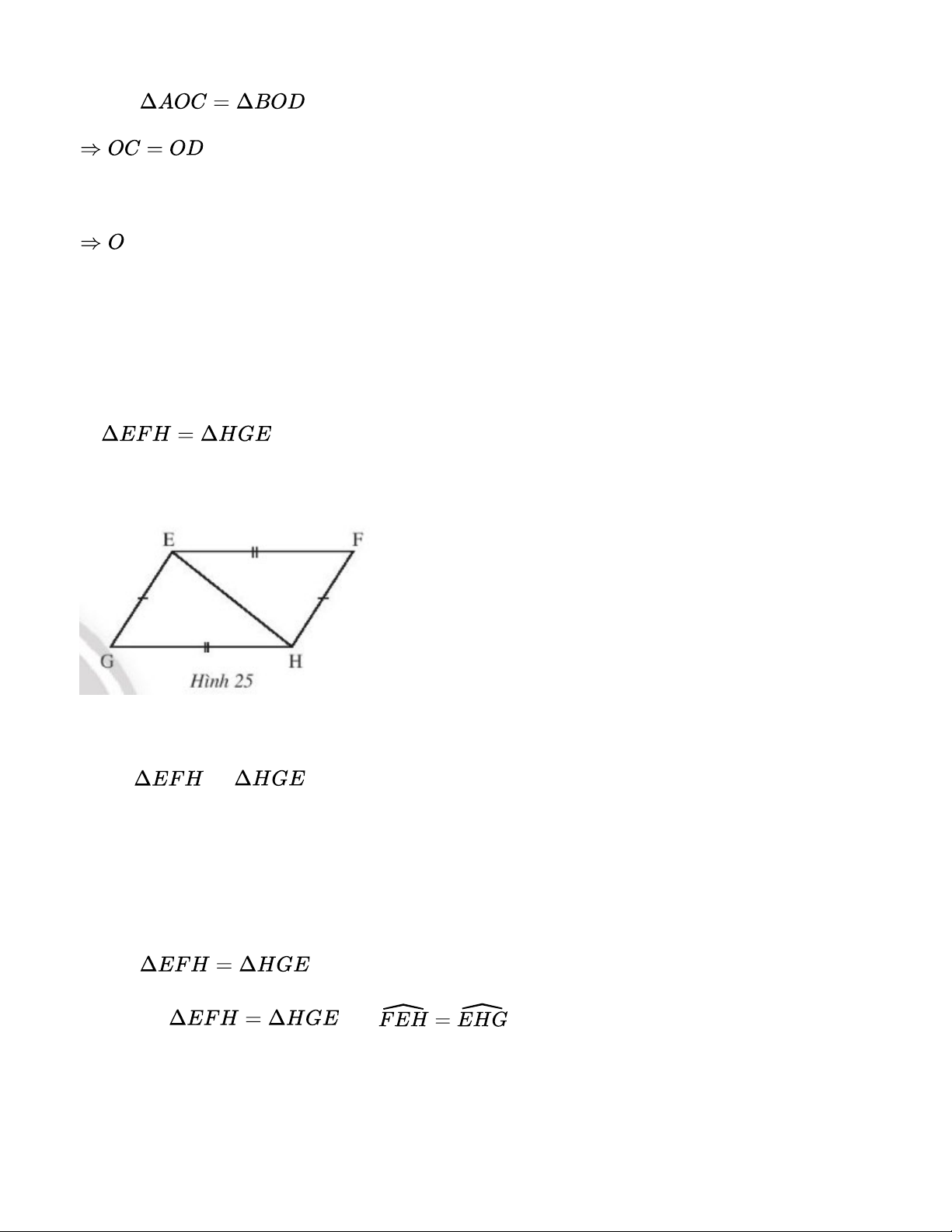
Cho hình 25 có EF = HG, EG = HF. Chứng minh rằng: a. b. EF // HG Gợi ý đáp án: a. Xét và có: EH chung GH = EF GE = HF Suy ra (c.c.c) b. Theo a: nên
Mà 2 góc này ở vị trí so le trong Suy ra EF // HG. Bài 7
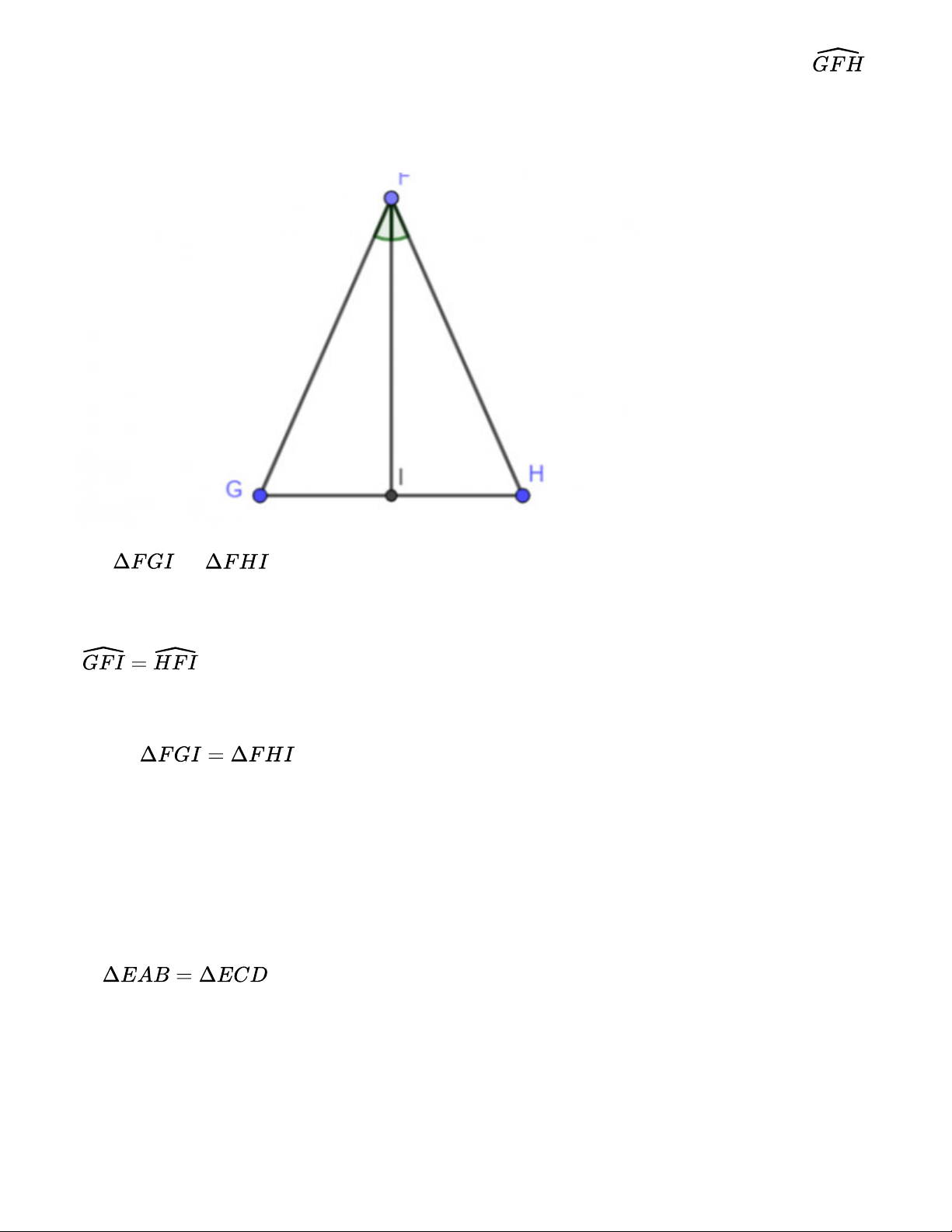
Cho tam giác FGH có FG = FH. Lấy điểm I trên cạnh GH sao cho FI là tia phân giác của .
Chứng minh rằng hai tam giác FIG và FIH bằng nhau Gợi ý đáp án: Xét và có: FI chung FG = FH Suy ra (c.g.c). Bài 8
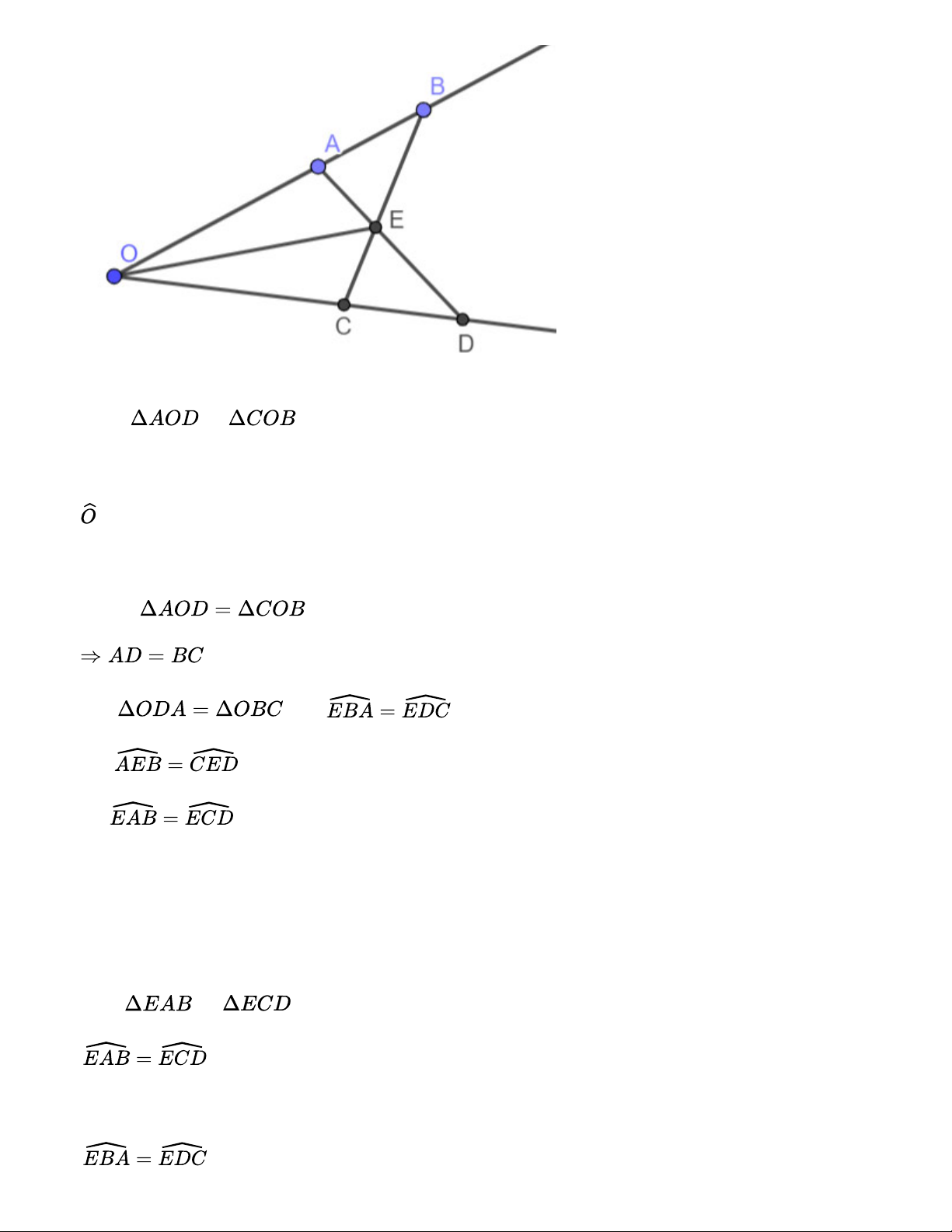
Cho góc xOy. Lấy hai điểm A, B thuộc tia Ox sao cho OA < OB. Lấy hai điểm C, D thuộc tia Oy
sao cho OC = OA, OD = OB. Gọi E là giao điểm AD và BC. Chứng minh rằng: a) AD = BC. b) .
c) OE là tia phân giác của góc xOy. Gợi ý đáp án: a) Xét và có: AO = CO chung OD = OB Suy ra (c.g.c). b. + nên Mà =>
Ta lại có: OA = OC và OB = OD => OB - OA = OD - OC => AB = CD + Xét và ta có: (chứng minh trên) AB = CD (chứng minh trên) (chứng minh trên). Suy ra (g.c.g) c. Xét và có: OE chung OB = OD EB = ED (vì ) Suy ra nên .
Suy ra OE là tia phân giác góc xOy. Bài 9
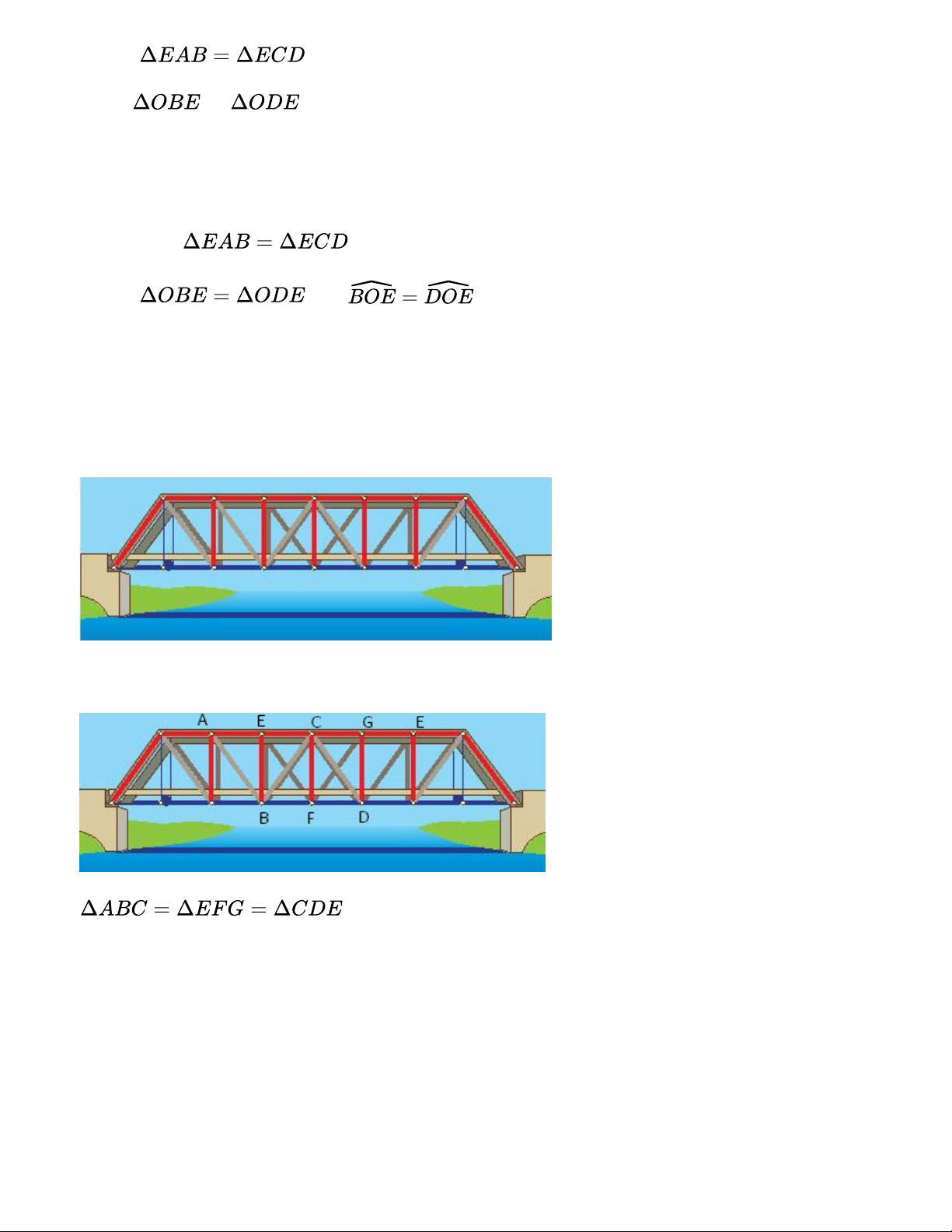
Đặt tên cho một số điểm có trong Hình 26 và chỉ ra ba cặp tam giác bằng nhau trong hình đó. Gợi ý đáp án: