Giải Toán 7 Bài 5: Đường trung trực của một đoạn thẳng | Chân trời sáng tạo
Giải bài tập SGK Toán 7 Tập 2 trang 67, 68, 69, 70 sách Chân trời sáng tạo giúp các em học sinh lớp 7 xem gợi ý giải các bài tập của Bài 5: Đường trung trực của một đoạn thẳng.
Chủ đề: Chương 8: Tam giác (CTST)
Môn: Toán 7
Sách: Chân trời sáng tạo
Thông tin:
Tác giả:
Preview text:
Giải Toán 7 bài 5: Đường trung trực của một đoạn thẳng
Chân trời sáng tạo
Giải Toán 7 Chân trời sáng tạo trang 70 tập 2 Bài 1
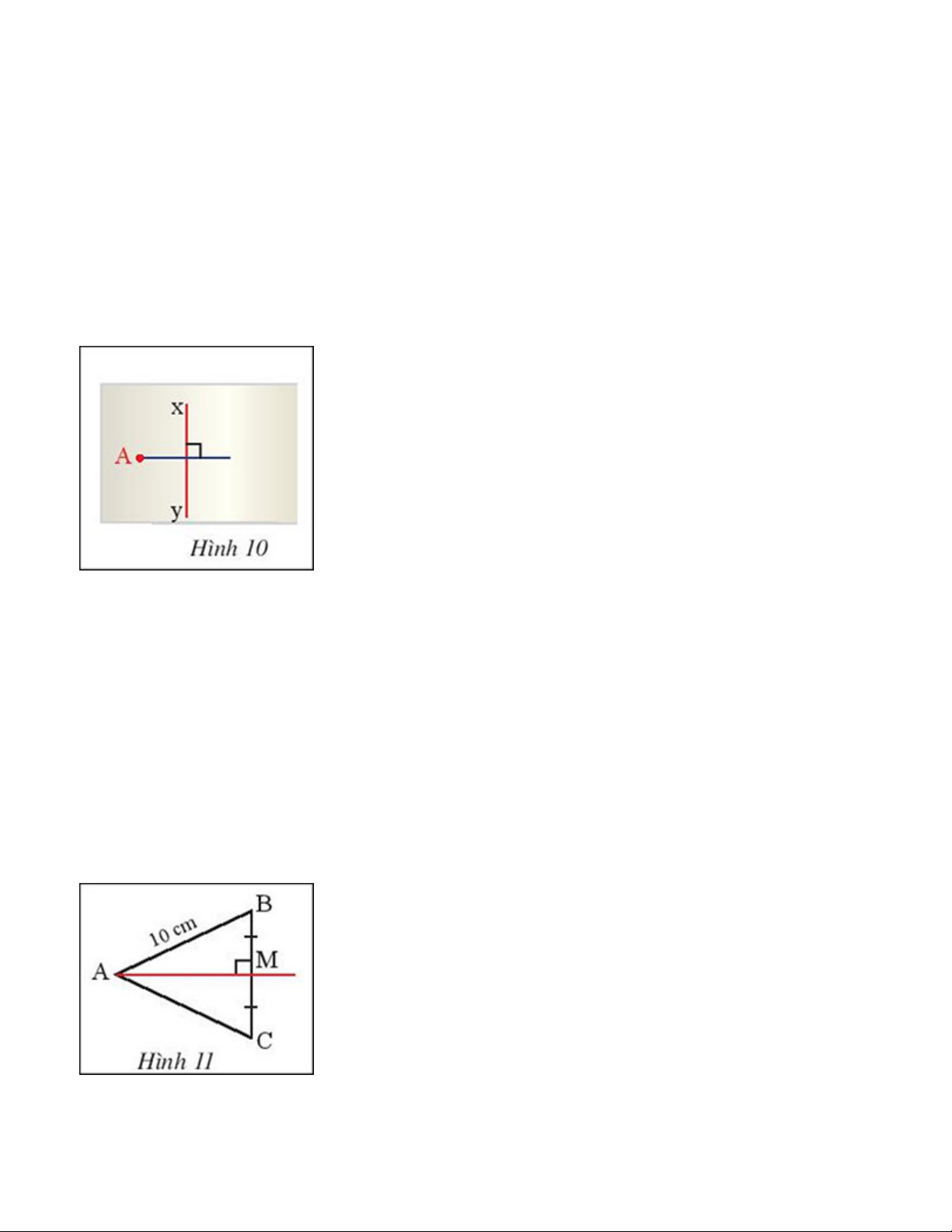
Hình 10 minh họa một tờ giấy có hình vẽ đường trung trực xy của đoạn thẳng AB mà hình ảnh
điểm B bị nhòe mất. Hãy nêu cách xác định điểm B Gợi ý đáp án:
Gọi O là giao điểm của đường trung trực xy với đoạn thẳng AB
=> O là trung điểm của AB
Lấy điểm B thuộc đường thẳng OA sao cho O là trung điểm AB. Bài 2
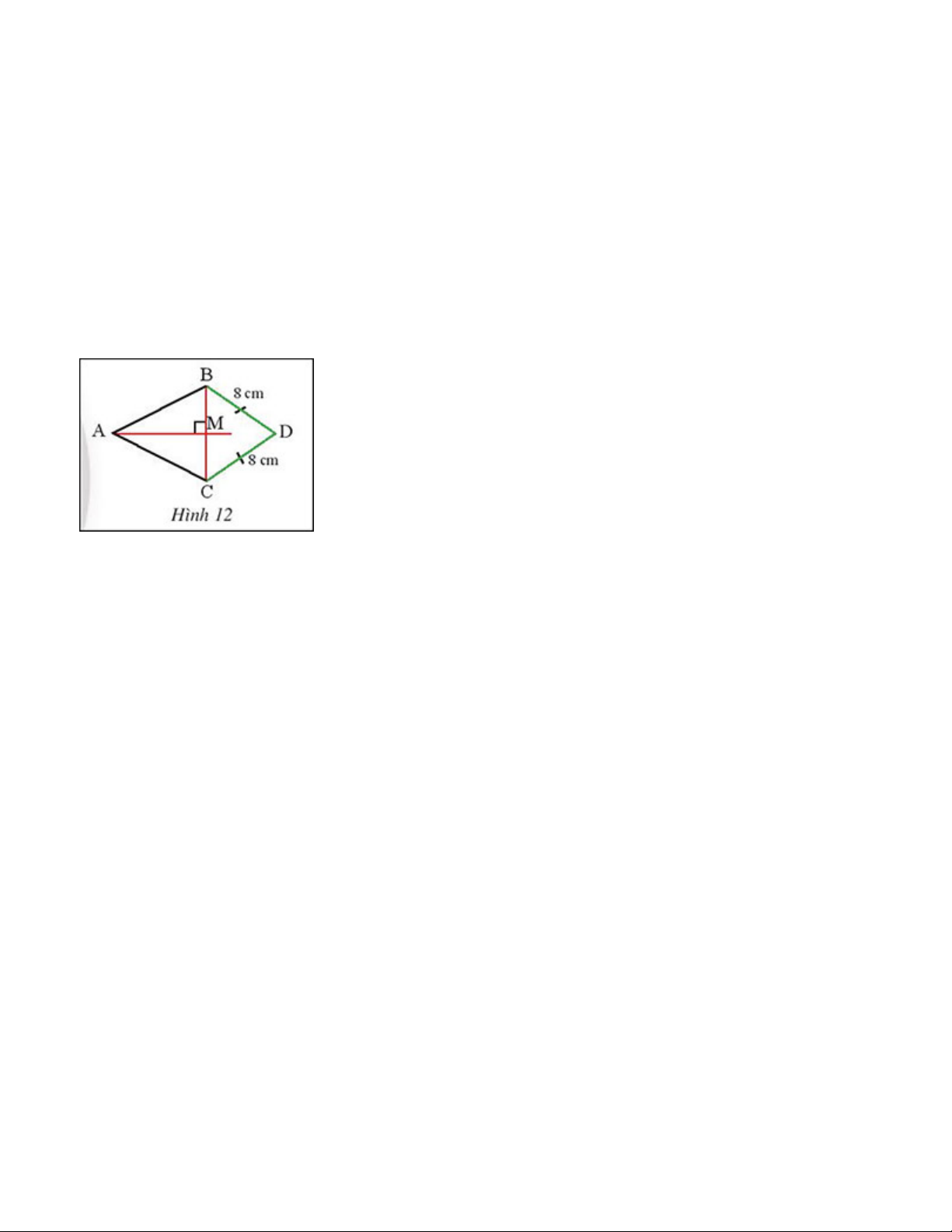
Quan sát hình 11, cho biết M là trung điểm BC, AM vuông góc với BC và AB = 10 cm. Tính AC. Gợi ý đáp án: M là trung điểm của BC AM ⊥ BC
=> AM là đường trung trực của BC => AB = AC => AC =10 cm. Bài 3
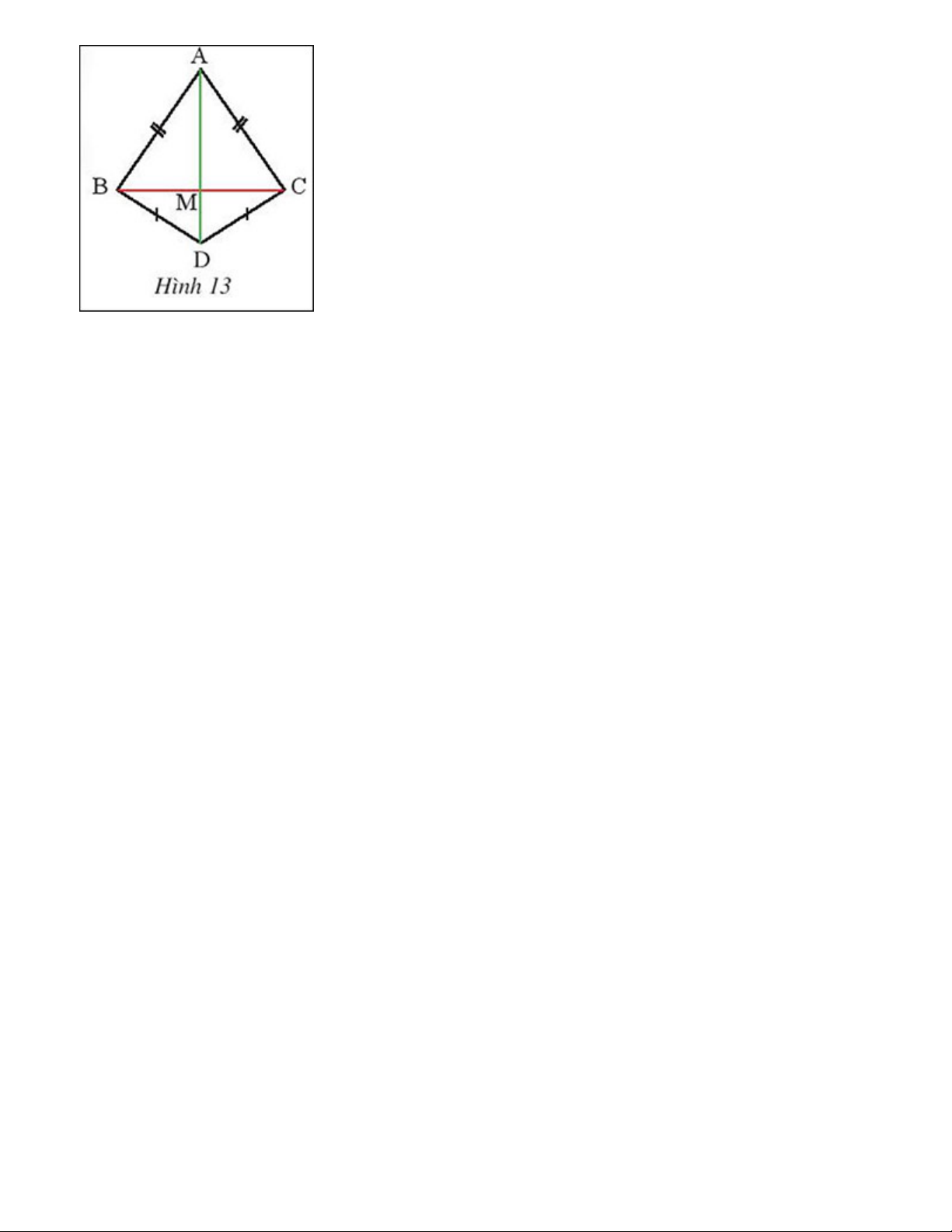
Quan sát hình 12, cho biết AM là đường trung trực của đoạn thẳng BC và DB = DC = 8 cm.
Chứng minh rằng 3 điểm A, M, D thẳng hàng. Gợi ý đáp án:
AM là đường trung trực của đoạn thẳng BC => AB = AC, MB = MC Ta có DB = DC = 8 cm
=> D cách đều 2 đầu mút của đoạn thẳng AB
=> D thuộc đường trung trực của AB
=> A, M, D cùng thuộc đường trung trực của AB => A, M, D thẳng hàng. Bài 4
Quan sát hình 13, biết AB = AC, DB = DC. Chứng minh rằng M là trung điểm của BC Gợi ý đáp án:
AB = AC => A thuộc đường trung trực của BC
DB= DC => D thuộc đường trung trực của BC
=> AD là đường trung trực của BC Mà AD cắt BC tại M
=> M cũng thuộc đường trung trực AD => MB = MC mà M thuộc BC
=> M là trung điểm của BC. Bài 5
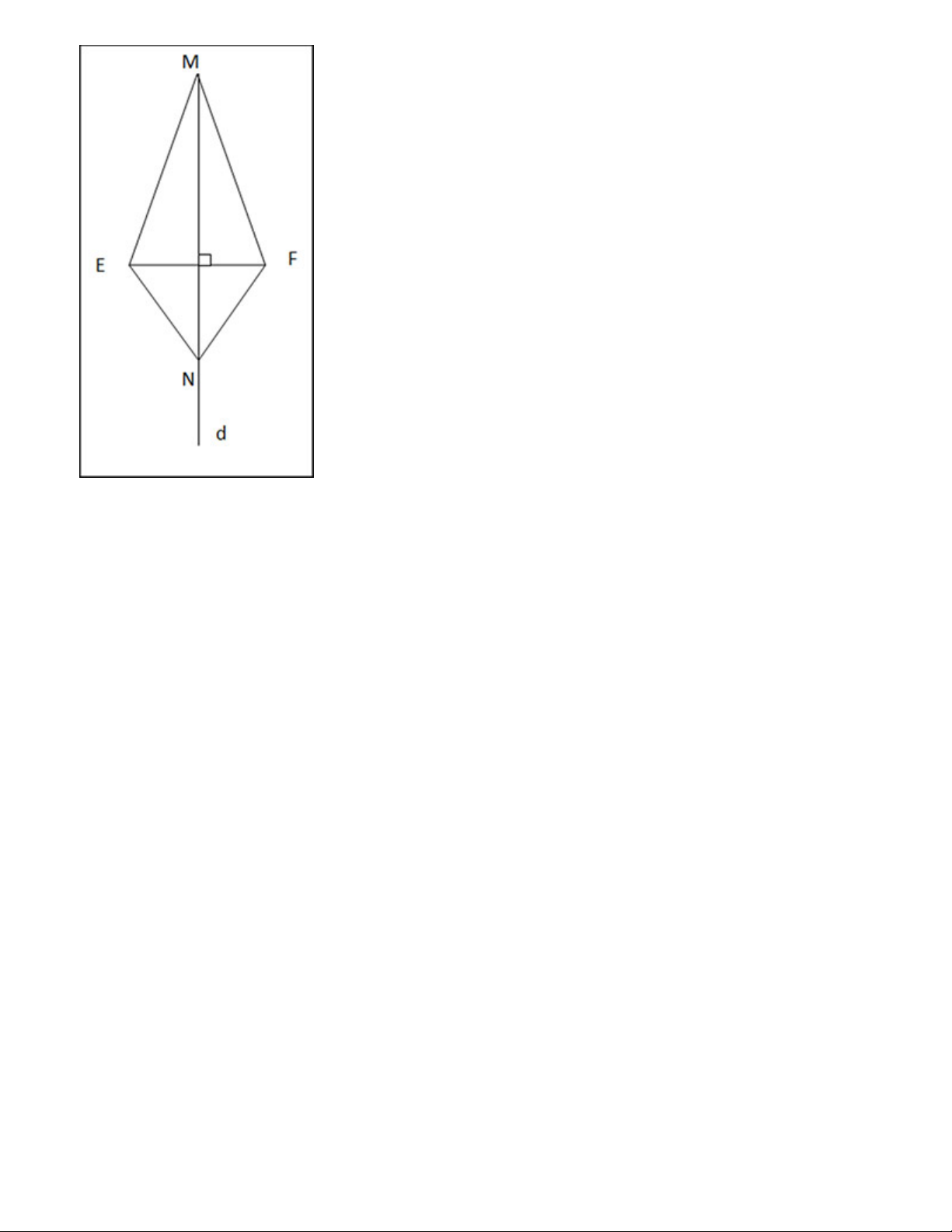
Cho hai điểm M và N nằm trên đường trung trực d của đoạn thẳng EF
Chứng minh rằng ∆EMN = ∆FMN. Gợi ý đáp án:
M, N thuộc đường trung trực d của đoạn thẳng EF => ME = MF, NE= NF Xét ∆EMN và ∆FMN ta có: ME = MF NE = NF MN chung => ∆EMN = ∆FMN (c.c.c) Bài 6
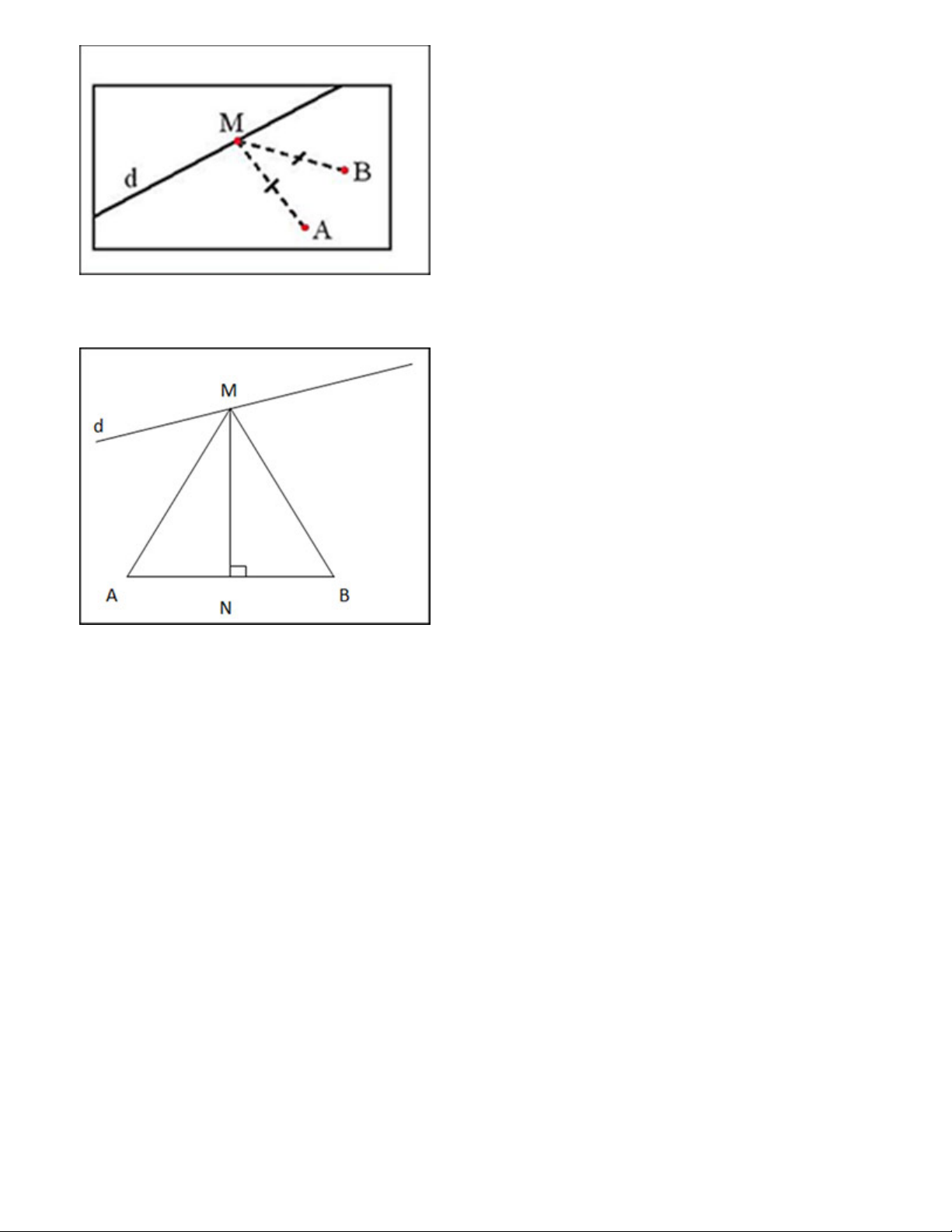
Trên bản đồ quy hoạch một khu dân cư có một con đường d và hai điểm dân cư A và B (Hình
14). Hãy tìm bên đường một địa điểm M để xây dựng một trạm y tế sao cho trạm y tế cách đều hai điểm dân cư. Gợi ý đáp án:
Gọi N là trung điểm của AB.
Qua N kẻ đường trung trực của đoạn thẳng AB, cắt đường thẳng d tại 1 điểm M.
=> M thuộc đường trung trực của AB => MA = MB
Vậy vị trí điểm M là nằm trên đường trung trực của đoạn thẳng AB.