Giải Toán 8 Bài 6: Hình thoi | Cánh diều

Toán 8 Bài 6: Hình thoi Cánh diều
Giải Toán 8 Cánh diều Tập 1 trang 115 Bài 1
Cho hình bình hành ABCD có tia AC là tia phân giác của góc DAB. Chứng minh ABCD là hình thoi. Lời giải:
ABCD là hình bình hành nên: AD = BC; AB = DC (1)
Xét 2 tam giác ADC và CBA có: AC chung Kết hợp với (1)
=> 2 tam giác ADC và CBA bằng nhau (c-c-c)=> 2 góc tương ứng (2)
Mà AC là tia phân giác của góc DAB => . Kết hợp với (2) =>
=> Tam giác DAC cân tại D => DA = DC. Kết hợp với (1) => AD = BC = AB = DC => ABCD có 4
cạnh bằng nhau nên là hình thoi. Bài 2
Cho hình thoi ABCD có hai đường chéo AC và BD cắt nhau tại O. Chứng minh: Lời giải:
ABCD là hình thoi nên 2 đường chéo AC và BD vuông góc với nhau và cắt nhau tại trung điểm
của mỗi đường => OA = OC, OB = OD. = (1)
Xét tam giác vuông OAB vuông tại O có: (2) Từ (1) và (2) => (đpcm) Bài 3 Cho hình thoi ABCD có
. Tính số đo mỗi góc của hình thoi ABCD. Bài giải:
ABCD là hình thoi nên DB là tia phân giác của góc D => =
ABCD là hình thoi nên nó cũng là một hình bình hành. Suy ra: (2 góc đối nhau) (2 góc đối nhau) Bài 4
Hình 62 mô tả một ô lưới mắt cáo có dạng hình thoi với độ dài của hai đường chéo là 45 mm và
90 mm. Độ dài cạnh của ô lưới mắt cáo đó là bao nhiêu milimét (làm tròn kết quả đến hàng đơn vị)? Bài giải:
Độ dài cạnh của ô lưới mắt cáo đó là: (mm) Bài 5
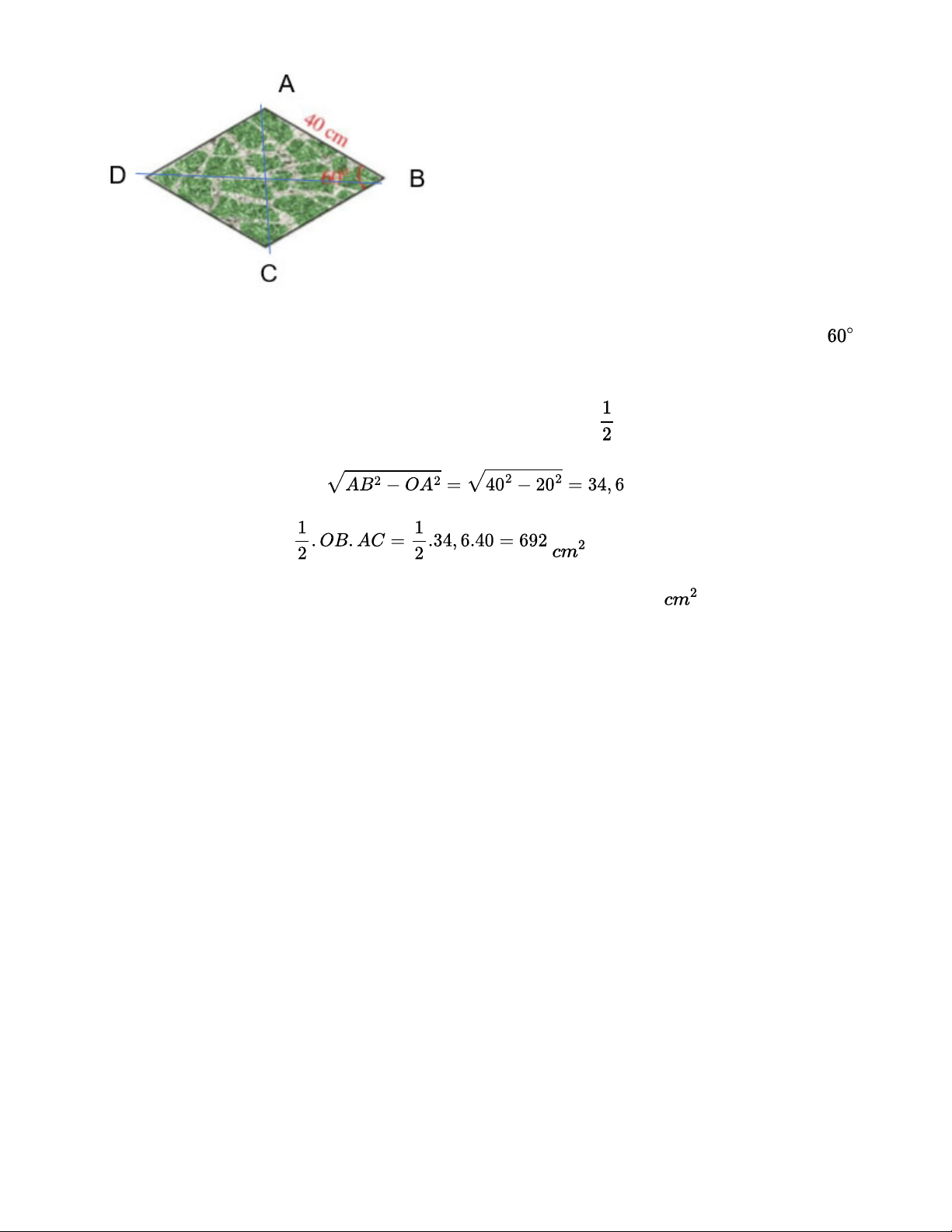
Một viên gạch trang trí có dạng hình thoi với độ dài cạnh là 40 cm và số đo một góc là 60°
(Hình 63). Diện tích của viên gạch đó là bao nhiêu centimét vuông (làm tròn kết quả đến hàng phần trăm)? Bài giải:
Tam giác ABC có AB = BC (2 cạnh của hình thoi) nên là tam giác cân tại B. Lại có góc B =
nên ABC là tam giác đều => AC = 40cm.
Gọi O là giao điểm của 2 đường chéo AC và BD. Khi đó: OA = AC = 20cm. Trong tam giác AOB có OB = cm Diện tích tam giác ABC =
=> Diện tích viên gạch có dạng hình thoi như trên sẽ là: 2. 692 = 1 384