Giải Toán 7 bài 3: Tam giác cân Chân trời sáng tạo
Giải Toán 7 Chân trời sáng tạo tập 2 Bài 3 - Thực hành Thực hành 1
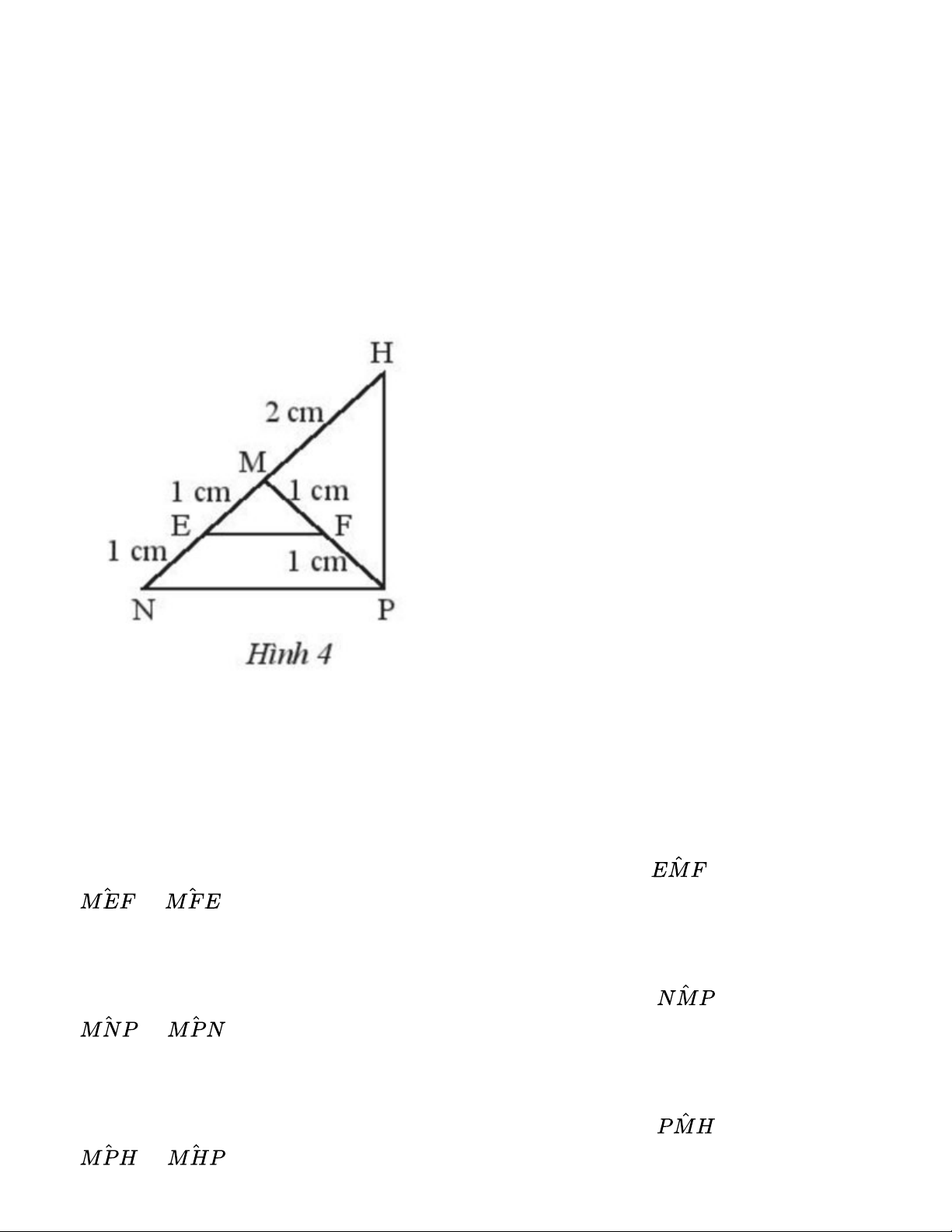
Tìm các tam giác cân trong Hình 4. Kể tên các cạnh bên, cạnh đáy, góc ở đỉnh, góc ở đáy của mỗi tam giác cân đó. Lời giải:
Ta có MN = ME + EN = 1 + 1 = 2 cm; MP = MF + FP = 1 + 1 = 2 cm.
Tam giác MEF có ME = MF = 1 cm nên tam giác MEF cân tại M.
Tam giác MEF cân tại M nên ME và MF là cạnh bên, EF là cạnh đáy, là góc ở đỉnh, và là góc ở đáy.
Tam giác MNP có MN = MP = 2 cm nên tam giác MNP cân tại M.
Tam giác MNP cân tại M nên MN và MP là cạnh bên, NP là cạnh đáy, là góc ở đỉnh, và là góc ở đáy.
Tam giác MPH có MP = MH = 2 cm nên tam giác MPH cân tại M.
Tam giác MPH cân tại M nên MP và MH là cạnh bên, PH là cạnh đáy, là góc ở đỉnh, và là góc ở đáy. Thực hành 2
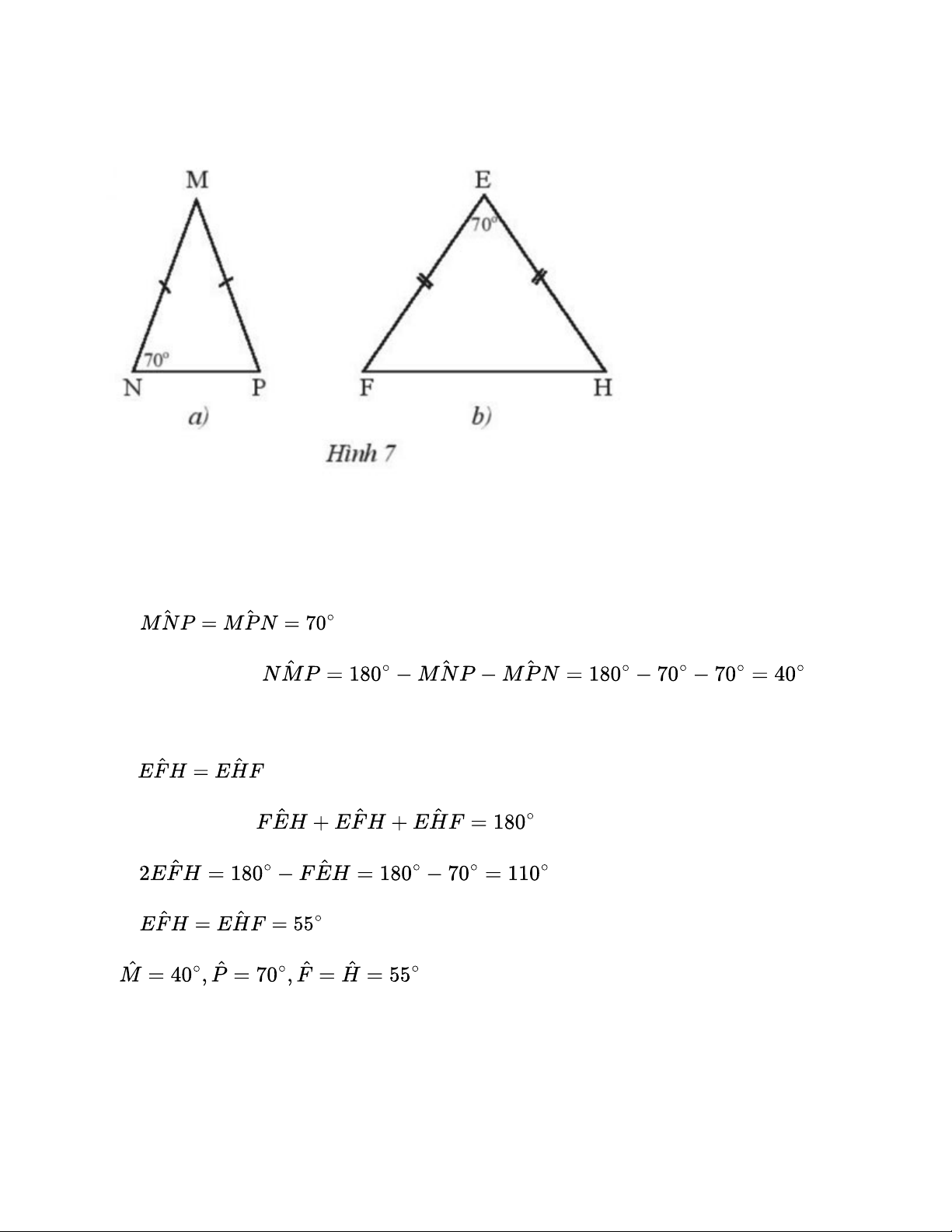
Tìm số đo các góc chưa biết của mỗi tam giác trong Hình 7. Lời giải:
Tam giác MNP có MN = MP nên tam giác MNP cân tại M. Do đó Trong tam giác MNP:
Tam giác EFH có EF = EH nên tam giác EFH cân tại E. Do đó Trong tam giác EFH: Suy ra Do đó Vậy Thực hành 3
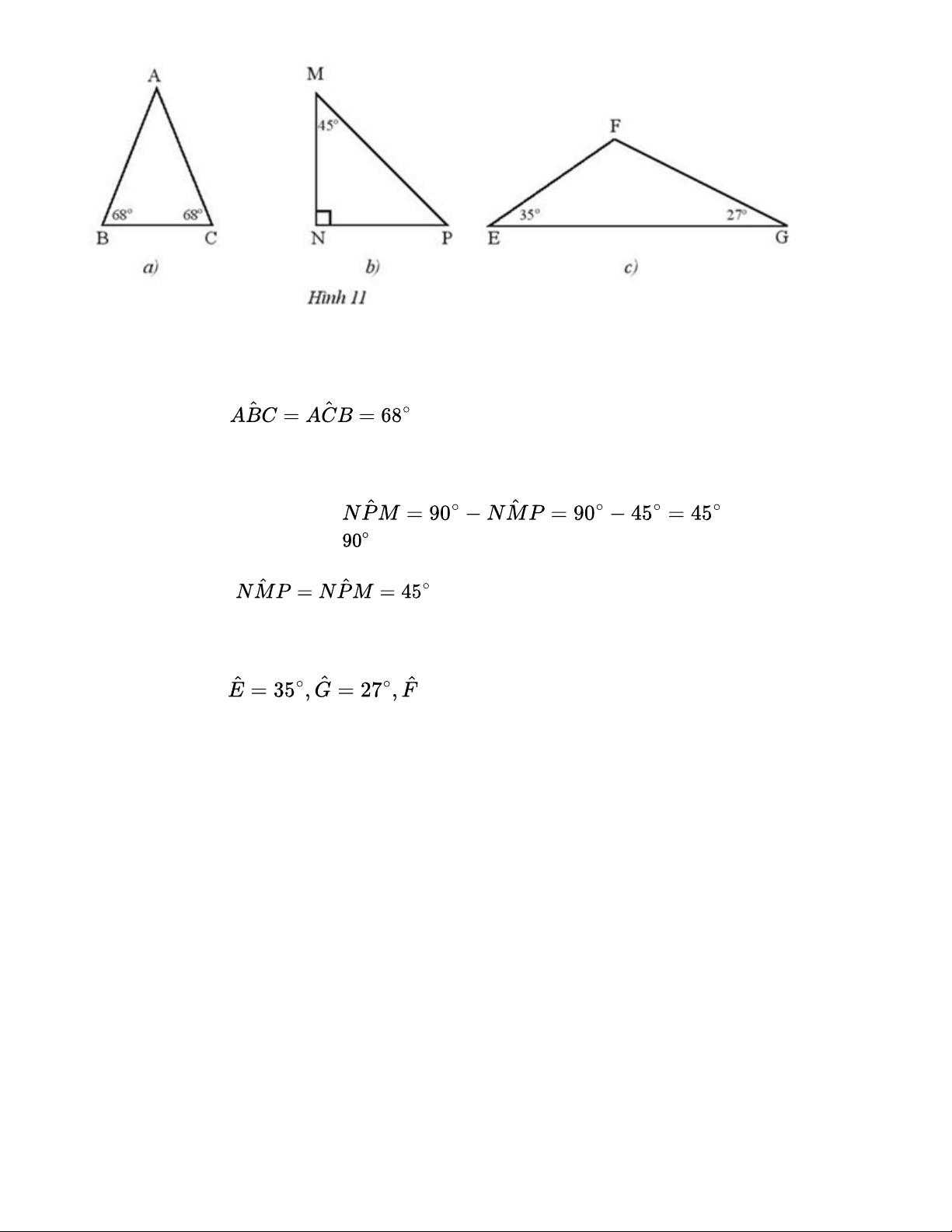
Tìm các tam giác cân trong Hình 11 và đánh dấu các cạnh bằng nhau. Lời giải: Tam giác ABC có
nên tam giác ABC cân tại A. Do đó AB = AC.
Tam giác MNP vuông tại N nên (trong tam giác
vuông, tổng hai góc nhọn bằng ) Tam giác MNP có
nên tam giác MNP cân tại N. Do đó NM = NP. Tam giác EFG có
là góc tù nên tam giác EFG không có hai góc nào bằng nhau.
Do đó tam giác EFG không phải tam giác cân. Ta có hình vẽ sau:
Giải Toán 7 Chân trời sáng tạo trang 62, 63 tập 2 Bài 1
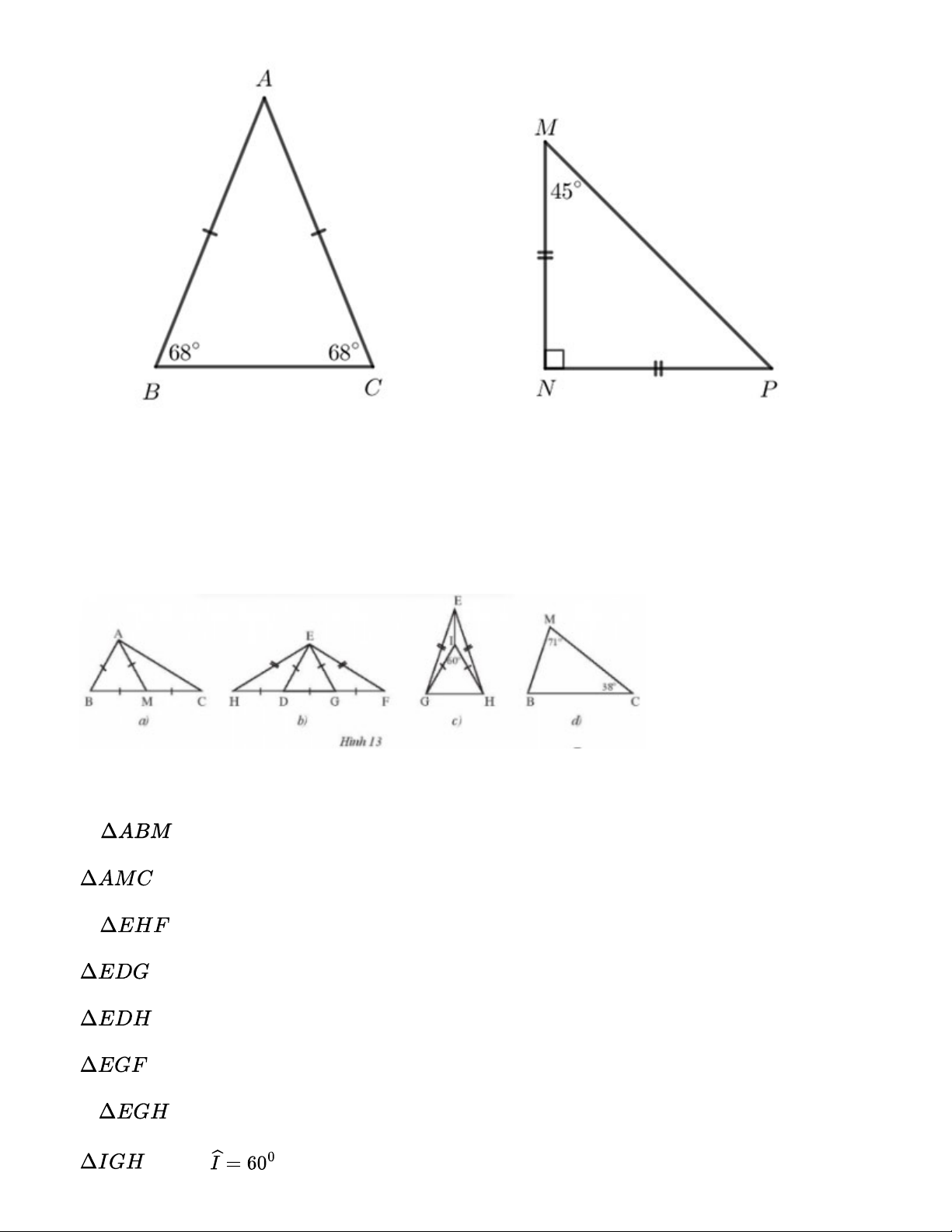
Tìm các tam giác cân và tam giác đều trong mỗi hình sau (Hình 13). Giải thích. Gợi ý đáp án: a. đều vì AB = AM = BM cân tại M vì AM= MC b. cân tại E vì EH = EF đều vì: ED = EG = DG cân tại D vì DE = DH cân tại G vì GE = GF c. cân tại E vì EG = EH đều vì , IG = IH d. cân tại C vì . . Bài 2
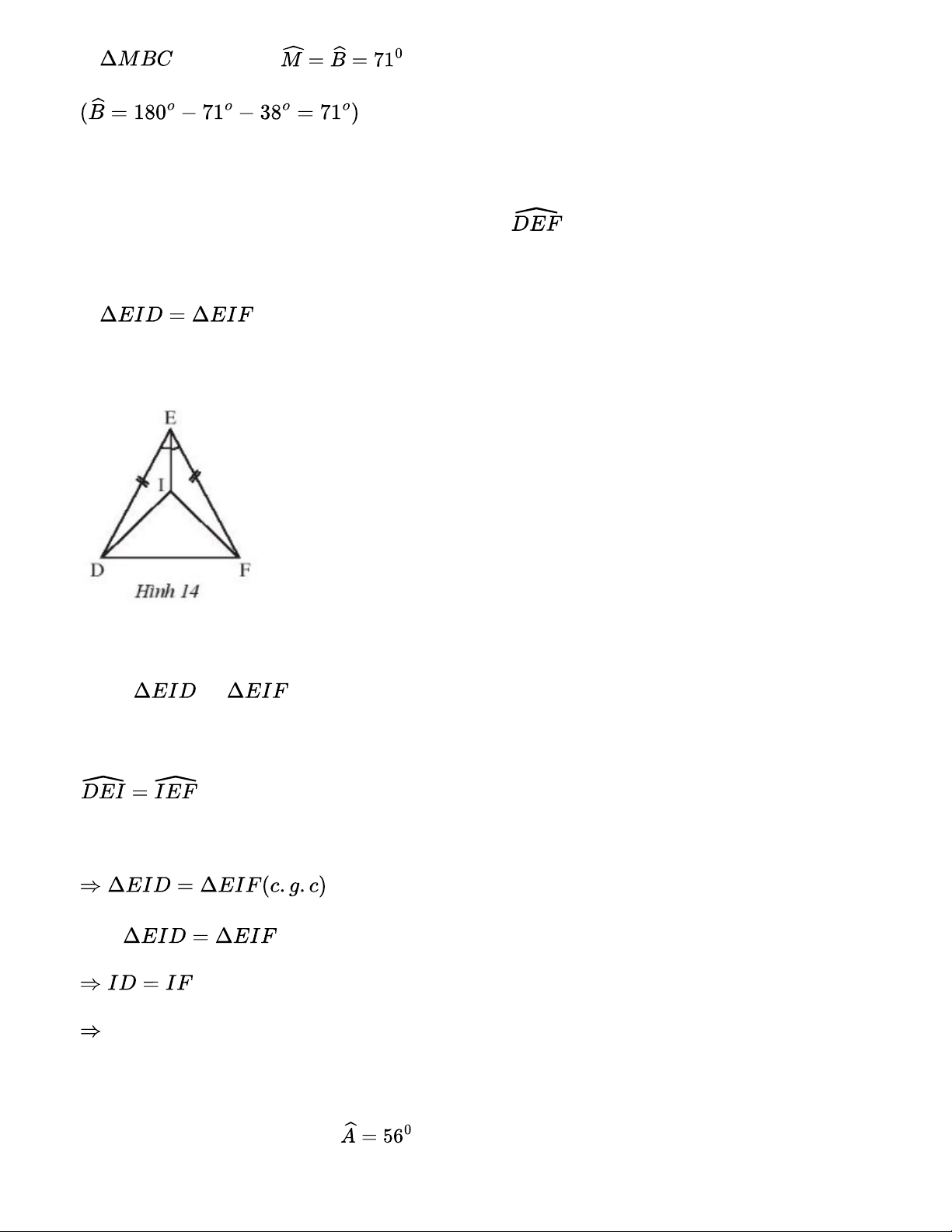
Cho hình 14, biết ED = EF và EI là tia phân giác của . Chứng minh rằng: a. b. Tam giác DIF cân. Gợi ý đáp án: a. Xét và có: EI chung DE = EF. b. Vì (chứng minh trên) Tam giác DIF cân tại I. Bài 3
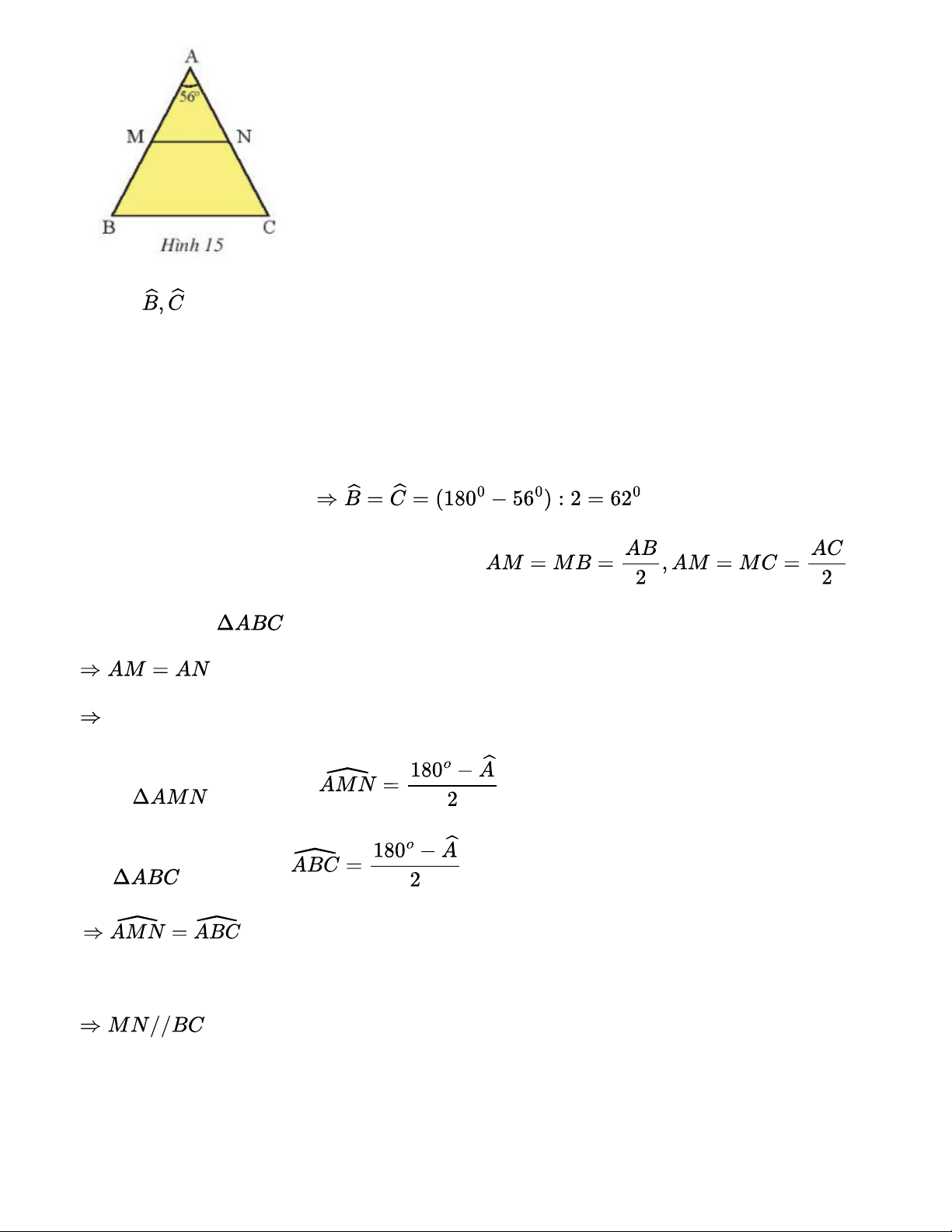
Cho tam giác ABC cân tại A có a. Tính .
b. Gọi M, N lần lượt là trung điểm của AB, AC. Chứng minh tam giác AMN cân.
c. Chứng minh rằng MN // BC. Gợi ý đáp án:
a. Vì tam giác ABC cân tại A
b. Vì M, N lần lượt là trung điểm của AB, AC nên mà AB = AC ( vì cân) Tam giác AMN cân tại A. c. Xét cân tại A có: Xét cân tại A có:
Mà 2 góc này ở vị trí đồng vị . Bài 4
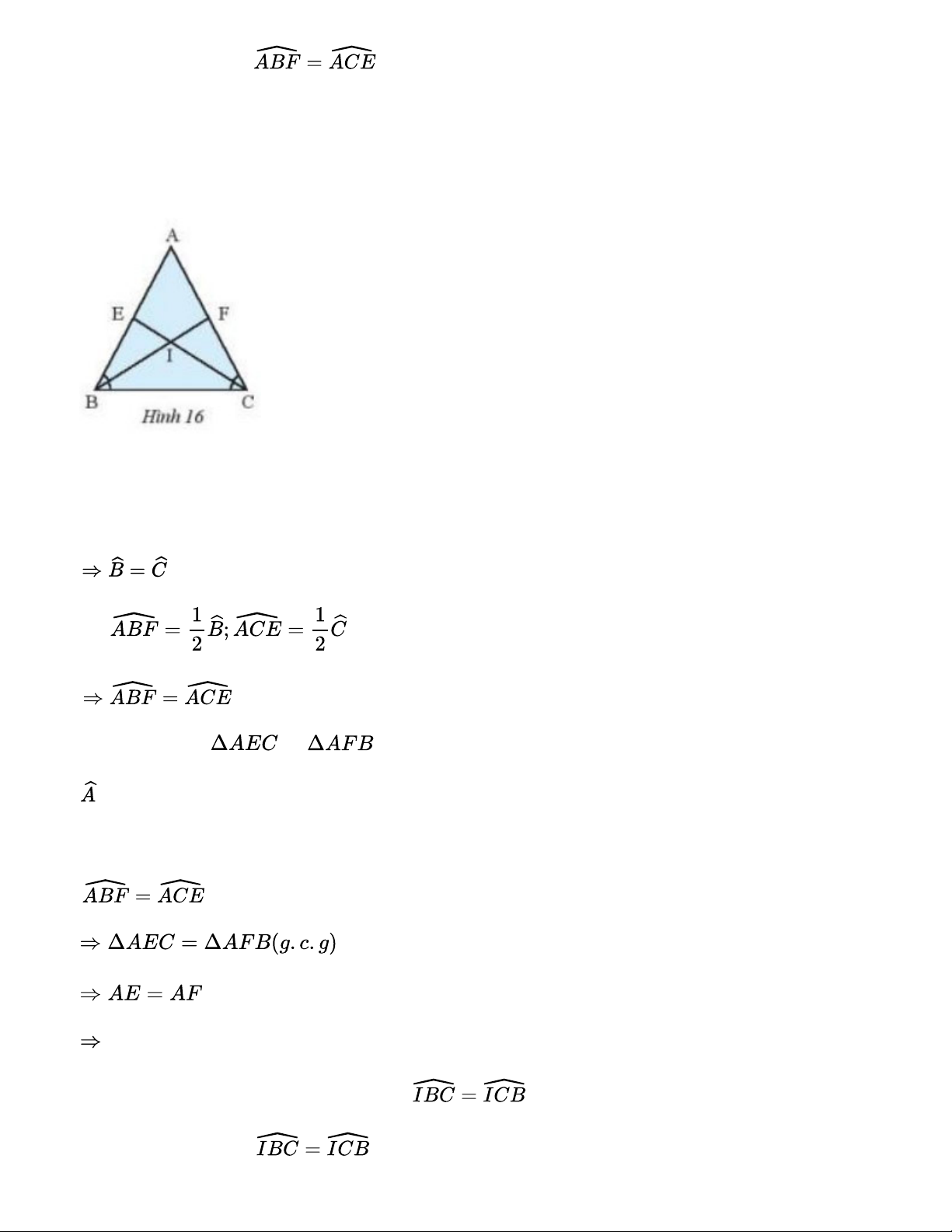
Cho tam giác ABC cân tại A (hình 16). Tia phân giác của góc B cắt AC tại F, tia phân giác của góc C cắt AB tại E. a) Chứng minh rằng
b) Chứng minh rằng tam giác AEF cân.
c) Gọi I là giao điểm của BF và CE. Chứng minh rằng tam giác IBC và tam giác IEF là những tam giác cân. Gợi ý đáp án:
a) Vì tam giác ABC cân tại A Mà b) Xét tam giác và có: chung AB = AC Tam giác AEF cân tại A.
c) +) Chứng minh tương tự câu a ta có: . Xét tam giác IBC có: cân tại I. +) cân tại I nên IB = IC nên BF = CE
Ta có: IE = CE - IC; IF = BF - BI cân tại I. Bài 5
Phần thân của một móc treo quần áo có dạng hình tam giác cân (Hình 17a) được vẽ lại như
Hình 17b. Cho biết AB = 20cm; BC = 28cm và
. Tìm số đo các góc còn lại và chu vi của tam giác ABC. Gợi ý đáp án: Vì tam giác ABC cân tại A
Chu vi tam giác ABC = AB + AC + BC = 20 + 20 + 28 = 68 (cm). Bài 6
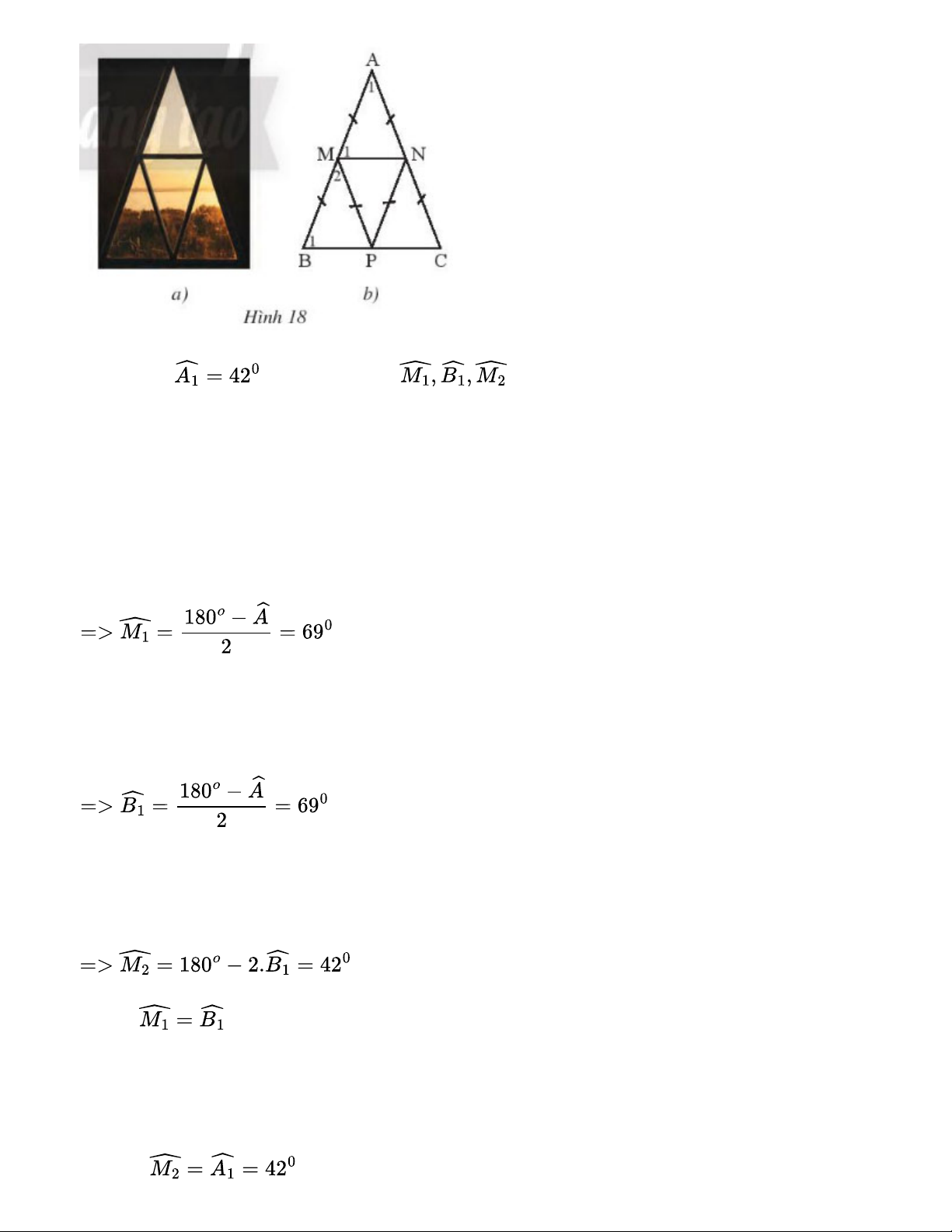
Một khung cửa sổ hình tam giác có thiết kế như Hình 18a được vẽ lại như Hình 18b a. Cho biết . Tính số đo của
b. Chứng minh MN // BC, MP // AC.
c. Chứng minh bốn tam giác cân AMN, MBP, PMN, NPC bằng nhau. Gợi ý đáp án:
a. Vì AM = AN => Tam giác AMN cân tại A .
+ Trong tam giác ABC có AB = BC (vì AM = AN = BM = CN; AB = AM + MB; AC = AN + NC)
=> Tam giác ABC cân tại A .
+ Trong tam giác MBP có MB = MP
=> Tam giác MBP cân tại M b. + Vì
Mà 2 góc này ở vị trí đồng vị => MN // BC + Ta có:
mà hai góc ở vị trí đồng vị => MP // AC. c. + Xét và có: AM = MB AN = MP . + Xét và có: PM = NP
(vì MP // AC, hai góc ở vị trí so le trong). PN = NC + Xét và có: MN chung PM = AM PN = AN .
Vậy bốn tam giác cân AMN, MBP, PMN, NPC bằng nhau.