Giáo án Đại số 10 cơ bản – Nguyễn Đình Khương

Giới thiệu đến quý thầy, cô. Xin lưu ý bộ giáo án Đại số 10 cơ bản của thầy Nguyễn Đình Khương dạng file word sử dụng font VNI – Times, nếu tải về bị lỗi font, thầy cô có thể tải 4 font VNI – Times cài vào máy để sửa lỗ

110 55 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Giáo án Toán 10

Môn: Toán 10

Thông tin:

118 trang 8 tháng trước

Tác giả:

Profile Thanh Tâm
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn
1
Ngaøy soaïn: 20/8/2012 Chöông I: MEÄNH ÑEÀ – TAÄP HÔÏP
Tieát daïy: 01 Baøøi 1: MEÄNH ÑEÀ
I. MUÏC TIEÂU:
Kieán thöùc:
– Naém vöõng caùc khaùi nieäm meänh ñeà, MÑ phuû ñònh, keùo theo, hai MÑ töông ñöông, caùc
ñieàu kieän caàn, ñuû, caàn vaø ñuû.
– Bieát khaùi nieäm MÑ chöùa bieán.
Kó naêng:
– Bieát laäp MÑ phuû ñònh cuûa 1 MÑ, MÑ keùo theo vaø MÑ töông ñöông.
– Bieát söû duïng caùc kí hieäu , trong caùc suy luaän toaùn hoïc.
Thaùi ñoä:
– Reøn luyeän tính töï giaùc, tích cöïc trong hoïc taäp.
– Tö duy caùc vaán ñeà cuûa toaùn hoïc moät caùch loâgic vaø heä thoáng.
II. CHUAÅN BÒ:
Giaùo vieân: Giaùo aùn, phieáu hoïc taäp. Moät soá kieán thöùc maø HS ñaõ hoïc ôû lôùp döôùi.
Hoïc sinh: SGK, vôû ghi. OÂn taäp moät soá kieán thöùc ñaõ hoïc ôû lôùp döôùi.
III. HOAÏT ÑOÄNG DAÏY HOÏC:
1. OÅn ñònh toå chöùc: Kieåm tra só soá lôùp.
2. Giaûng baøi môùi:
TL
Hoaït ñoäng cuûa Giaùo vieân
Hoaït ñoäng cuûa Hoïc sinh
Noäi dung
Hoaït ñoäng 1: Tìm hieåu khaùi nieäm Meänh ñeà, Meänh ñeà chöùa bieán
25’
GV ñöa ra moät soá caâu vaø cho
HS xeùt tính Ñ–S cuûa caùc caâu
ñoù.
a) “Phan–xi–paêng laø ngoïn nuùi
cao nhaát Vieät Nam.”
b) “
2
< 9,86”
c) “Hoâm nay trôøi ñeïp quaù!”
Cho caùc nhoùm neâu moät soá
caâu. Xeùt xem caâu naøo laø meänh
ñeà vaø tính Ñ–S cuûa caùc meänh
ñeà.
Xeùt tính Ñ–S cuûa caùc caâu:
d) “n chia heát cho 3”
e) “2 + n = 5”
–> meänh ñeà chöùa bieán.
Cho caùc nhoùm neâu moät soá
meänh ñeà chöùa bieán (haèng ñaúng
thöùc, …).
HS thöïc hieän yeâu caàu.
a) Ñ
b) S
c) khoâng bieát
Caùc nhoùm thöïc hieän yeâu
caàu.
Tính Ñ–S phuï thuoäc vaøo
giaù trò cuûa n.
Caùc nhoùm thöïc hieän yeâu
caàu.
I. Meänh ñeà. Meänh ñeà chöùa
bieán.
1. Meänh ñeà.
– Moät meänh ñeà laø moät caâu
khaúng ñònh ñuùng hoaëc sai.
– Moät meänh ñeà khoâng theå vöøa
ñuùng vöøa sai.
2. Meänh ñeà chöùa bieán.
Meänh ñeà chöùa bieán laø moät caâu
chöùa bieán, vôùi moãi giaù trò cuûa
bieán thuoäc moät taäp naøo ñoù, ta
ñöôïc moät meänh ñeà.
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn
2
Hoaït ñoäng 2: Tìm hieåu meänh ñeà phuû ñònh cuûa moät meänh ñeà
20’
P
Q
HS traû lôøi tính Ñ–S cuûa
caùc meänh ñeà.
Caùc nhoùm thöïc hieän yeâu
caàu.
II. Phuû ñònh cuûa 1 meänh ñeà.
Kí hieäu meänh ñeà phuû ñònh cuûa
meänh ñeà P laø
P
.
P
ñuùng khi P sai
P
sai khi P ñuùng
3. BAØI TAÄP VEÀ NHAØ:
Baøi 1, 2, 3 SGK
Ngaøy soaïn: 20/8/2012
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn
3
Tieát daïy: 02 Baøøi 1: MEÄNH ÑEÀ(TT)
I. MUÏC TIEÂU:
Kieán thöùc:
– Naém vöõng caùc khaùi nieäm meänh ñeà, MÑ phuû ñònh, keùo theo, hai MÑ töông ñöông, caùc
ñieàu kieän caàn, ñuû, caàn vaø ñuû.
– Bieát khaùi nieäm MÑ chöùa bieán.
Kó naêng:
– Bieát laäp MÑ phuû ñònh cuûa 1 MÑ, MÑ keùo theo vaø MÑ töông ñöông.
– Bieát söû duïng caùc kí hieäu , trong caùc suy luaän toaùn hoïc.
Thaùi ñoä:
– Reøn luyeän tính töï giaùc, tích cöïc trong hoïc taäp.
– Tö duy caùc vaán ñeà cuûa toaùn hoïc moät caùch loâgic vaø heä thoáng.
II. CHUAÅN BÒ:
Giaùo vieân: Giaùo aùn, phieáu hoïc taäp. Moät soá kieán thöùc maø HS ñaõ hoïc ôû lôùp döôùi.
Hoïc sinh: SGK, vôû ghi. OÂn taäp moät soá kieán thöùc ñaõ hoïc ôû lôùp döôùi.
III. HOAÏT ÑOÄNG DAÏY HOÏC:
1. OÅn ñònh toå chöùc: Kieåm tra só soá lôùp.
2. Kieåm tra baøi cuõ:
3. Giaûng baøi môùi:
TL
Hoaït ñoäng cuûa Giaùo vieân
Hoaït ñoäng cuûa Hoïc sinh
Noäi dung
Hoaït ñoäng 1: Tìm hieåu khaùi nieäm meänh ñeà keùo theo
15’
GV ñöa ra moät soá meänh ñeà
ñöôïc phaùt bieåu döôùi daïng “Neáu
P thì Q”.
a) “Neáu n laø soá chaün thì n chia
heát cho 2.”
b) “Neáu töù giaùc ABCD laø hbh
thì noù coù caùc caëp caïnh ñoái song
song.”
Cho caùc nhoùm neâu moät soá
VD veà meänh ñeà keùo theo.
+ Cho P, Q. Laäp P Q.
+ Cho P Q. Tìm P, Q.
Cho caùc nhoùm phaùt bieåu moät
soá ñònh lí döôùi daïng ñieàu kieän
caàn, ñieàu kieän ñuû.
Caùc nhoùm thöïc hieän yeâu
caàu.
Caùc nhoùm thöïc hieän yeâu
caàu.
III. Meänh ñeà keùo theo.
Cho 2 meänh ñeà P vaø Q. Meänh
ñeà “Neáu P thì Q” ñgl meänh ñeà
keùo theo, vaø kí hieäu P
Q.
Meänh ñeà P
Q chæ sai khi P
ñuùng vaø Q sai.
Caùc ñònh lí toaùn hoïc laø nhöõng
meänh ñeà ñuùng vaø thöôøng coù
daïng P
Q. Khi ñoù, ta noùi:
P laø giaû thieát, Q laø keát luaän.
P laø ñieàu kieän ñuû ñeå coù Q.
Q laø ñieàu kieän caàn ñeå coù P.
Hoaït ñoäng 2: Tìm hieåu khaùi nieäm meänh ñeà ñaûo – hai meänh ñeà töông ñöông
10’
Daãn daét töø KTBC, QP ñgl
meänh ñeà ñaûo cuûa PQ.
Cho caùc nhoùm neâu moät soá
meänh ñeà vaø laäp meänh ñeà ñaûo
cuûa chuùng, roài xeùt tính Ñ–S cuûa
Caùc nhoùm thöïc hieän yeâu
caàu.
IV. Meänh ñeà ñaûo – hai meänh
ñeà töông ñöông.
Meänh ñeà Q
P ñgl meänh ñeà
ñaûo cuûa meänh ñeà P
Q.
Neáu caû hai meänh ñeà P
Q vaø
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn
4
caùc meänh ñeà ñoù.
Trong caùc meänh ñeà vöøa laäp,
tìm caùc caëp PQ, QP ñeàu
ñuùng. Töø ñoù daãn ñeán khaùi nieäm
hai meänh ñeà töông ñöông.
Cho caùc nhoùm tìm caùc caëp
meänh ñeà töông ñöông vaø phaùt
bieåu chuùng baèng nhieàu caùch
khaùc nhau.
Caùc nhoùm thöïc hieän yeâu
caàu.
Q
P ñeàu ñuùng ta noùi P vaø Q
laø hai meänh ñeà töông ñöông.
Kí hieäu: P
Q
Ñoïc laø: P töông ñöông Q
hoaëc P laø ñk caàn vaø ñuû ñeå coù
Q
hoaëc P khi vaø chæ khi Q.
Hoaït ñoäng 3: Tìm hieåu caùc kí hieäu vaø
10’
GV ñöa ra moät soá meänh ñeà coù
söû duïng caùc löôïng hoaù: , .
a) “Bình phöông cuûa moïi soá
thöïc ñeàu lôùn hôn hoaëc baèng 0”.
–> xR: x
2
≥ 0
b) “Coù moät soá nguyeân nhoû hôn
0”.
–> n Z: n < 0.
Cho caùc nhoùm phaùt bieåu caùc
meänh ñeà coù söû duïng caùc löôïng
hoaù: , . (Phaùt bieåu baèng lôøi
vaø vieát baèng kí hieäu)
Caùc nhoùm thöïc hieän yeâu
caàu.
V. Kí hieäu vaø .
: vôùi moïi.
: toàn taïi, coù moät.
Hoaït ñoäng 4: Meänh ñeà phuû ñònh cuûa caùc meänh ñeà coù chöùa kí hieäu ,
7'
A
B
Caùc nhoùm thöïc hieän yeâu
caàu.
x X,P(x) x X,P(x)
x X,P(x) x X,P(x)
Hoaït ñoäng 5: Cuûng coá
3’
Nhaán maïnh caùc khaùi nieäm:
– Meänh ñeà, MÑ phuû ñònh.
– Meänh ñeà keùo theo.
– Hai meänh ñeà töông ñöông.
– MÑ coù chöùa kí hieäu , .
Cho caùc nhoùm neâu VD veà meänh ñeà, khoâng phaûi mñ, phuû ñònh moät mñ, meänh ñeà keùo theo.
Ngaøy soaïn: 20/8/2012 Chöông I: MEÄNH ÑEÀ – TAÄP HÔÏP
Tieát daïy: 03 Baøøi 1: LUYEÄN TAÄP MEÄNH ÑEÀ
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn
5
I. MUÏC TIEÂU:
Kieán thöùc:
Cuûng coá caùc khaùi nieäm: meänh ñeà, meänh ñeà phuû ñònh, meänh ñeà keùo theo, hai meänh ñeà
töông ñöông.
Kó naêng:
Bieát caùch xeùt tính Ñ–S cuûa moät meänh ñeà, laäp meänh ñeà phuû ñònh.
Bieát söû duïng caùc ñieàu kieän caàn, ñuû, caàn vaø ñuû.
Bieát söû duïng caùc kí hieäu , .
Thaùi ñoä:
Hình thaønh cho HS khaû naêng suy luaän coù lí, khaû naêng tieáp nhaän, bieåu ñaït caùc vaán ñeà moät
caùch chính xaùc.
II. CHUAÅN BÒ:
Giaùo vieân: Giaùo aùn, phieáu hoïc taäp.
Hoïc sinh: SGK, vôû ghi. Laøm baøi taäp veà nhaø.
III. HOAÏT ÑOÄNG DAÏY HOÏC:
1. OÅn ñònh toå chöùc: Kieåm tra só soá lôùp.
2. Kieåm tra baøi cuõ: (Loàng vaøo quaù trình luyeän taäp)
3. Giaûng baøi môùi:
TL
Hoaït ñoäng cuûa Giaùo vieân
Hoaït ñoäng cuûa Hoïc sinh
Noäi dung
Hoaït ñoäng 1: Xeùt tính Ñ–S cuûa moät meänh ñeà, laäp meänh ñeà phuû ñònh
10’
H1. Theá naøo laø meänh ñeà,
meänh ñeà chöùa bieán?
H2. Neâu caùch laäp meänh ñeà
phuû ñònh cuûa moät meänh ñeà P?
Ñ1.
– meänh ñeà: a, d.
– meänh ñeà chöùa bieán: b, c.
Ñ2. Töø P, phaùt bieåu “khoâng
P”
a) 1794 khoâng chia heát cho 3
b)
2
laø moät soá voâ tæ
c) ≥ 3,15
d)
125
> 0
1. Trong caùc caâu sau, caâu naøo
laø meänh ñeà, meänh ñeà chöùa
bieán?
a) 3 + 2 = 7
b) 4 + x = 3
c) x + y > 1
d) 2 –
5
< 0
2. Xeùt tính Ñ–S cuûa moãi
meänh ñeà sau vaø phaùt bieåu
meänh ñeà phuû ñònh cuûa noù?
a) 1794 chia heát cho 3
b)
2
laø moät soá höõu tæ
c) < 3,15
d)
125
≤ 0
Hoaït ñoäng 2: Luyeän kó naêng phaùt bieåu meänh ñeà baèng caùch söû duïng ñieàu kieän caàn, ñuû
15’
H1. Neâu caùch xeùt tính Ñ–S
cuûa meänh ñeà PQ?
H2. Chæ ra “ñieàu kieän caàn”,
“ñieàu kieän ñuû” trong meänh ñeà
P Q?
Ñ1. Chæ xeùt P ñuùng. Khi ñoù:
– Q ñuùng thì P Q ñuùng.
– Q sai thì P Q sai.
Ñ2.
– P laø ñieàu kieän ñuû ñeå coù Q.
– Q laø ñieàu kieän caàn ñeå coù P.
3. Cho caùc meänh ñeà keùo theo:
A: Neáu a vaø b cuøng chia heát
cho c thì a + b chia heát cho c
(a, b, c Z).
B: Caùc soá nguyeân coù taän cuøng
baèng 0 ñeàu chia heát cho 5.
C: Tam giaùc caân coù hai trung
tuyeán baèng nhau.
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn
6
H3. Khi naøo hai meänh ñeà P vaø
Q töông ñöông?
Ñ3. Caû hai meänh ñeà P Q
vaø Q P ñeàu ñuùng.
D: Hai tam giaùc baèng nhau coù
dieän tích baèng nhau.
a) Haõy phaùt bieåu meänh ñeà
ñaûo cuûa caùc meänh ñeà treân.
b) Phaùt bieåu caùc meänh ñeà
treân, baèng caùch söû duïng khaùi
nieäm “ñieàu kieän ñuû”.
c) Phaùt bieåu caùc meänh ñeà
treân, baèng caùch söû duïng khaùi
nieäm “ñieàu kieän caàn”.
4. Phaùt bieåu caùc meänh ñeà sau,
baèng caùch söû duïng khaùi nieäm
“ñieàu kieän caàn vaø ñuû”
a) Moät soá coù toång caùc chöõ soá
chia heát cho 9 thì chia heát cho
9 vaø ngöôïc laïi.
b) Moät hình bình haønh coù caùc
ñöôøng cheùo vuoâng goùc laø moät
hình thoi vaø ngöôïc laïi.
c) Phöông trình baäc hai coù hai
nghieäm phaân bieät khi vaø chæ
khi bieät thöùc cuûa noù döông.
Hoaït ñoäng 3: Luyeän kó naêng söû duïng caùc kí hieäu ,
13’
H. Haõy cho bieát khi naøo duøng
kí hieäu , khi naøo duøng kí
hieäu ?
Ñ.
– : moïi, taát caû.
– : toàn taïi, coù moät.
a) x R: x.1 = 1.
b) x R: x + x = 0.
c) x R: x + (–x) = 0.
5. Duøng kí hieäu , ñeå vieát
caùc meänh ñeà sau:
a) Moïi soá nhaân vôùi 1 ñeàu
baèng chính noù.
b) Coù moät soá coäng vôùi chính
noù baèng 0.
c) Moïi soá coäng vôùi soá ñoái cuûa
noù ñeàu baèng 0.
Laäp meänh ñeà phuû ñònh?
Hoaït ñoäng 4: Cuûng coá
5’
Nhaán maïnh:
– Caùch vaän duïng caùc khaùi
nieäm veà meänh ñeà.
– Coù nhieàu caùch phaùt bieåu
meänh ñeà khaùc nhau.
4. BAØI TAÄP VEÀ NHAØ:
Laøm caùc baøi taäp coøn laïi. Ñoïc tröôùc baøi “Taäp hôïp”
Ngaøy soaïn: 3/9/2012 Chöông I: MEÄNH ÑEÀ – TAÄP HÔÏP
Tieát daïy: 04 Baøøi 2: TAÄP HÔÏP
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn
7
I. MUÏC TIEÂU:
Kieán thöùc:
Naém vöõng caùc khaùi nieäm taäp hôïp, phaàn töû, taäp con, hai taäp hôïp baèng nhau.
Kó naêng:
Bieát caùch dieãn ñaït caùc khaùi nieäm baèng ngoân ngöõ meänh ñeà.
Bieát caùch xaùc ñònh moät taäp hôïp baèng caùch lieät keâ caùc phaàn töû hoaëc chæ ra tính chaát ñaëc
tröng.
Thaùi ñoä:
Luyeän tö duy loâgic, dieãn ñaït caùc vaán ñeà moät caùch chính xaùc.
II. CHUAÅN BÒ:
Giaùo vieân: Giaùo aùn, phieáu hoïc taäp.
Hoïc sinh: SGK, vôû ghi. OÂn taäp caùc kieán thöùc veà taäp hôïp ñaõ hoïc ôû lôùp döôùi.
III. HOAÏT ÑOÄNG DAÏY HOÏC:
1. OÅn ñònh toå chöùc: Kieåm tra só soá lôùp.
2. Kieåm tra baøi cuõ: (3’)
H. Haõy chæ ra caùc soá töï nhieân laø öôùc cuûa 24?
Ñ. 1, 2, 3, 4, 6, 8, 12, 24.
3. Giaûng baøi môùi:
TL
Hoaït ñoäng cuûa Giaùo vieân
Hoaït ñoäng cuûa Hoïc sinh
Noäi dung
Hoaït ñoäng 1: Tìm hieåu veà taäp hôïp vaø phaàn töû
15’
H1. Nhaéc laïi caùch söû duïng
caùc kí hieäu , ?
Haõy ñieàn caùc kí hieäu ,
vaøo nhöõng choã troáng sau
ñaây:
a) 3 … Z b) 3 … Q
c)
2
… Q d)
2
… R
H2. Haõy lieät keâ caùc öôùc
nguyeân döông cuûa 30?
H3. Haõy lieät keâ caùc soá thöïc
lôùn hôn 2 vaø nhoû hôn 4?
–> Bieåu dieãn taäp B goàm caùc
soá thöïc lôùn hôn 2 vaø nhoû hôn
4
B = {x R/ 2 < x < 4}
H4. Cho taäp B caùc nghieäm
cuûa pt: x
2
+ 3x – 4 = 0. Haõy:
a) Bieåu dieãn taäp B baèng caùch
söû duïng kí hieäu taäp hôïp.
b) Lieät keâ caùc phaàn töû cuûa B.
H5. Lieät keâ caùc phaàn töû cuûa
taäp hôïp A ={xR/x
2
+x+1 =
Ñ1.
a), c) ñieàn
b), d) ñieàn
Ñ2. {1, 2, 3, 5, 6, 10, 15, 30}
Ñ3. Khoâng lieät keâ ñöôïc.
Ñ4.
a) B = {x R/ x
2
+ 3x – 4 =
0}
b) B = {1, – 4}
Ñ5. Khoâng coù phaàn töû naøo.
I. Khaùi nieäm taäp hôïp
1. Taäp hôïp vaø phaàn töû
Taäp hôïp laø moät khaùi nieäm cô
baûn cuûa toaùn hoïc, khoâng ñònh
nghóa.
a
A; a
A.
2. Caùch xaùc ñònh taäp hôïp
– Lieät keâ caùc phaàn töû cuûa noù.
– Chæ ra tính chaát ñaëc tröng
cuûa caùc phaàn töû cuûa noù.
Bieåu ñoà Ven
B
3. Taäp hôïp roãng
Taäp hôïp roãng, kí hieäu laø
,
laø taäp hôïp khoâng chöùa phaàn töû
naøo.
A ≠
x: x
A.
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn
8
0}
Hoaït ñoäng 2: Tìm hieåu taäp hôïp con
10’
H1. Xeùt caùc taäp hôïp Z vaø Q.
a) Cho a Z thì a Q ?
b) Cho a Q thì a Z ?
Höôùng daãn HS nhaän xeùt caùc
tính chaát cuûa taäp con.
H2. Cho caùc taäp hôïp:
A ={xR/ x
2
– 3x + 2 = 0}
B = {nN/ n laø öôùc soá cuûa 6}
C = {nN/ n laø öôùc soá cuûa 9}
Taäp naøo laø con cuûa taäp naøo?
Ñ1.
a) a Z thì a Q
b) Chöa chaéc.
Z
Q
A
C
B
Ñ2.
A B
II. Taäp hôïp con
A
B
x (x
A
x
B)
Neáu A khoâng laø taäp con cuûa
B, ta vieát A
B.
Tính chaát:
a) A
A,
A.
b) Neáu A
B vaø B
C
thì A
C.
c)
A,
A.
Hoaït ñoäng 3: Tìm hieåu taäp hôïp baèng nhau
10’
H. Cho caùc taäp hôïp:
A = {nN/n laø boäi cuûa 2 vaø
3}
B = {nN/ n laø boäi cuûa 6}
Haõy kieåm tra caùc keát luaän:
a) A B b) B A
Ñ.
+ n A n 2 vaø n 3
n 6 n B
+ n B n 6
n 2 vaø n 3 n B
III. Taäp hôïp baèng nhau
A = B
x (x
A
x
B)
Hoaït ñoäng 4: Cuûng coá
5’
Nhaán maïnh caùc caùch cho
taäp hôïp, taäp con, taäp hôïp baèng
nhau.
Caâu hoûi: Cho taäp A = {1, 2,
3}. Haõy tìm taát caû caùc taäp con
cuûa A?
, {1}, {2}, {3}, {1, 2}, {1,
3}, {2, 3}, A.
4. BAØI TAÄP VEÀ NHAØ:
Baøi 1, 2, 3 SGK.
Ñoïc tröôùc baøi “Caùc pheùp toaùn taäp hôïp”
Ngaøy soaïn: 3/9/2012 Chöông I: MEÄNH ÑEÀ – TAÄP HÔÏP
Tieát daïy: 05 Baøøi 3: CAÙC PHEÙP TOAÙN TAÄP HÔÏP
I. MUÏC TIEÂU:
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn
9
Kieán thöùc:
Naém vöõng caùc khaùi nieäm hôïp, giao, hieäu, phaàn buø cuûa hai taäp hôïp.
Kó naêng:
Bieát caùch xaùc ñònh hôïp, giao, hieäu, phaàn buø cuûa hai taäp hôïp.
Thaùi ñoä:
Bieát vaän duïng kieán thöùc ñaõ hoïc vaøo thöïc teá.
II. CHUAÅN BÒ:
Giaùo vieân: Giaùo aùn, phieáu hoïc taäp. Hình veõ bieåu ñoà Ven.
Hoïc sinh: SGK, vôû ghi. OÂn laïi moät soá kieán thöùc ñaõ hoïc veà taäp hôïp.
III. HOAÏT ÑOÄNG DAÏY HOÏC:
1. OÅn ñònh toå chöùc: Kieåm tra só soá lôùp.
2. Kieåm tra baøi cuõ: (3’)
H. Neâu caùc caùch cho taäp hôïp? Cho ví duï minh hoaï.
Ñ. 2 caùch: lieät keâ caùc phaàn töû vaø chæ ra tính chaát ñaïc tröng cuûa caùc phaàn töû.
3. Giaûng baøi môùi:
TL
Hoaït ñoäng cuûa Giaùo vieân
Hoaït ñoäng cuûa Hoïc sinh
Noäi dung
Hoaït ñoäng 1: Tìm hieåu Giao cuûa hai taäp hôïp
12’
H1. Cho caùc taäp hôïp:
A = {nN/ n laø öôùc cuûa 12}
B = {nN/ n laø öôùc cuûa 18}
a) Lieät keâ caùc phaàn töû cuûa A,
B.
b) Lieät keâ caùc phaàn töû cuûa C
goàm caùc öôùc chung cuûa 12 vaø
18.
H2. Cho caùc taäp hôïp:
A = {1, 2, 3}, B ={3, 4, 7, 8},
C = {3, 4}. Tìm:
a) A B
b) A C
c) B C
d) A B C
Ñ1.
a) A = {1, 2, 3, 4, 6, 12}
B = {1, 2, 3, 6, 9, 18}
b) C = {1, 2, 3, 6}
A
B
C
AB
Ñ2.
A B = {3}
A C = {3}
B C = {3, 4}
A B C = {3}
I. Giao cuûa hai taäp hôïp
A
B = {x/ x
A vaø x
B}
x
A
B
xA
xB
Môû roäng cho giao cuûa nhieàu
taäp hôïp.
Hoaït ñoäng 2: Tìm hieåu Hôïp cuûa hai taäp hôïp
10’
H1. Cho caùc taäp hôïp:
A = {nN/ n laø öôùc cuûa 12}
B = {nN/ n laø öôùc cuûa 18}
Lieät keâ caùc phaàn töû cuûa C
goàm caùc öôùc chung cuûa 12
hoaëc 18.
H2. Nhaän xeùt moái quan heä
giöõa caùc phaàn töû cuûa A, B, C?
Ñ1.C = {1, 2, 3, 4, 6, 9,12, 18}
A
B
C=AB
Ñ2. Moät phaàn töû cuûa C thì
hoaëc thuoäc A hoaëc thuoäc B.
II. Hôïp cuûa hai taäp hôïp
A
B = {x/ x
A hoaëc x
B}
x
A
B
xA
xB
Môû roäng cho hôïp cuûa nhieàu
taäp hôïp.
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn
10
H3. Cho caùc taäp hôïp:
A = {1, 2, 3}, B ={3, 4, 7, 8},
C = {3, 4}. Tìm ABC ?
Ñ3. ABC ={1, 2, 3, 4, 7,
8}
Hoaït ñoäng 3: Tìm hieåu Hieäu vaø phaàn buø cuûa hai taäp hôïp
10’
H1. Cho caùc taäp hôïp:
A = {nN/ n laø öôùc cuûa 12}
B = {nN/ n laø öôùc cuûa 18}
a) Lieät keâ caùc phaàn töû cuûa C
goàm caùc öôùc chung cuûa 12
nhöng khoâng laø öôùc cuûa 18.
H2. Cho caùc taäp hôïp:
B ={3, 4, 7, 8}, C = {3, 4}.
a) Xeùt quan heä giöõa B vaø C?
b) Tìm C
B
C ?
Ñ1. C = {4, 12}
C=A\B
A
B
C
A
B
A
B
Ñ2.
a) C B
b) C
B
C = {7, 8}
III. Hieäu vaø phaàn buø cuûa hai
taäp hôïp
A \ B = {x/ x
A vaø x
B}
x
A \ B
xA
xB
Khi B
A thì A \ B ñgl phaàn
buø cuûa B trong A, kí hieäu C
A
B.
Hoaït ñoäng 4: Cuûng coá
8’
Nhaán maïnh caùc khaùi nieäm
giao, hôïp, hieäu, phaàn buø caùc
taäp hôïp.
Caâu hoûi: Goïi:
T: taäp caùc tam giaùc
T
C
: taäp caùc tam giaùc caân
T
Ñ
: taäp caùc tam giaùc ñeàu
T
v
: taäp caùc tam giaùc vuoâng
T
vc
: taäp caùc tam giaùc vuoâng
caân
Veõ bieåu ñoà Ven bieåu dieãn
moái quan heä giöõa caùc taäp hôïp
treân?
Cho caùc nhoùm thöïc hieän yeâu
caàu.
T
T
C
T
Ñ
T
VC
T
V
4. BAØI TAÄP VEÀ NHAØ:
Baøi 1, 2, 3, 4, 5 SGK.
Ñoïc tröôùc baøi “Caùc taäp hôïp soá”
Ngaøy soaïn: 3/9/2012 Chöông I: MEÄNH ÑEÀ – TAÄP HÔÏP
Tieát daïy: 06 Baøøi 3: BAØI TAÄP CAÙC PHEÙP TOAÙN TAÄP HÔÏP
I. MUÏC TIEÂU:
Kieán thöùc:
Cuûng coá caùc khaùi nieäm taäp hôïp, taäp hôïp con, taäp hôïp baèng nhau, taäp hôïp roãng.
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn
11
Cuûng coá caùc khaùi nieäm hôïp, giao, hieäu, phaàn buø cuûa hai taäp hôïp.
Kó naêng:
Bieát caùch xaùc ñònh taäp hôïp, hôïp, giao, hieäu, phaàn buø cuûa hai taäp hôïp.
Thaùi ñoä:
Bieát vaän duïng kieán thöùc ñaõ hoïc vaøo thöïc teá.
II. CHUAÅN BÒ:
Giaùo vieân: Giaùo aùn. Heä thoáng baøi taäp.
Hoïc sinh: SGK, vôû ghi. OÂn laïi moät soá kieán thöùc ñaõ hoïc veà taäp hôïp. Laøm baøi taäp veà nhaø.
III. HOAÏT ÑOÄNG DAÏY HOÏC:
1. OÅn ñònh toå chöùc: Kieåm tra só soá lôùp.
2. Kieåm tra baøi cuõ: (Loàng vaøo quaù trình luyeän taäp)
H.
Ñ.
3. Giaûng baøi môùi:
TL
Hoaït ñoäng cuûa Giaùo vieân
Hoaït ñoäng cuûa Hoïc sinh
Noäi dung
Hoaït ñoäng 1: Luyeän taäp xaùc ñònh taäp hôïp
10'
H1. Neâu caùc caùch xaùc ñònh
taäp hôïp?
Ñ1.
– Lieät keâ phaàn töû
– Chæ ra tính chaát ñaëc tröng
A = {0, 3, 6, 9, 12, 15, 18}
B = {xN/ x = n(n+1),
1≤n≤5}
1. Cho A = {xN/ x<20 vaø x
chia heát cho 3}. Haõy lieät keâ
caùc phaàn töû cuûa A.
2. Cho B = {2, 6, 12, 20, 30}.
Haõy xaùc ñònh B baèng caùch chæ
ra moät tính chaát ñaëc tröng cho
caùc phaàn töû cuûa coù.
Hoaït ñoäng 2: Luyeän taäp caùch xaùc ñònh taäp con
20'
H1. Nhaéc laïi khaùi nieäm taäp
con?
H2. Hình vuoâng coù phaûi laø
hình thoi khoâng?
H3. Tìm öôùc chung lôùn nhaát
cuûa 24 vaø 30?
Höôùng daãn caùch tìm taát caû
caùc taäp con cuûa moät taäp hôïp.
Höôùng daãn caùch tìm soá taäp
con goàm 2 phaàn töû
Ñ1. A B (xA xB)
Ñ2. Phaûi. A B.
Ñ3. Öôùc chung lôùn nhaát cuûa
24 vaø 30 laø 6 A = B.
Ñ4.
a) , {a}, {b}, A.
b) , {0}, {1}, {2}, {0, 1},
{0, 2}, {1, 2}, B.
a)
n(n 1)
2
= 6
b) 2
n – 1
= 8
3. Trong hai taäp hôïp A, B döôùi
ñaây, taäp naøo laø con cuûa taäp
naøo?
a) A laø taäp caùc hình vuoâng.
B laø taäp caùc hình thoi.
b) A = {nN/ n laø öôùc chung
cuûa 24 vaø 30}
B = {nN/ n laø öôùc cuûa 6}
4. Tìm taát caû caùc taäp con cuûa
taäp hôïp sau:
A = {a, b}, B = {0, 1, 2}
5. Cho A = {1, 2, 3, 4}.
a) Taäp A coù bao nhieâu taäp con
goàm 2 phaàn töû?
b) Taäp A coù bao nhieâu taäp con
coù chöùa soá 1.
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn
12
Hoaït ñoäng 3: Luyeän taäp caùc pheùp toaùn taäp hôïp
10'
H1. Veõ bieåu ñoà Ven bieåu dieãn
caùc taäp HS gioûi caùc moân cuûa
lôùp 10A?
H2. Nhaéc laïi ñònh nghóa giao,
hôïp, hieäu caùc taäp hôïp?
H
L
T
Ñ2. AB = {1, 5}
AB = {1, 3, 5}
A\B =
B\A = {3}
5. Lôùp 10A coù 7 HS gioûi
Toaùn, 5 HS gioûi Lyù, 6 HS gioûi
Hoaù, 3 HS gioûi caû Toaùn vaø
Lyù, 4 HS gioûi caû Toaùn vaø
Hoaù, 2 HS gioûi caû Lyù vaø Hoaù,
1 HS gioûi caû 3 moân Toaùn, Lyù,
Hoaù. Soá HS gioûi ít nhaát moät
moân (Toaùn, Lyù, Hoaù) cuûa lôùp
10A laø bao nhieâu?
6. Cho
A = {1, 5}, B = {1, 3, 5}
Tìm AB, AB, A\B, B\A
7. Cho taäp hôïp A. Haõy xaùc
ñònh caùc taäp hôïp sau:
AA, AA, A, A,
C
A
A, C
A
.
Hoaït ñoäng 4: Cuûng coá
3'
Nhaán maïnh caùch xaùc ñònh taäp
hôïp, caùc pheùp toaùn taäp hôïp
4. BAØI TAÄP VEÀ NHAØ:
Laøm caùc baøi taäp coøn laïi.
Ñoïc tröôùc baøi “Caùc taäp hôïp soá”
Ngaøy soaïn: 8/9/2012 Chöông I: MEÄNH ÑEÀ – TAÄP HÔÏP
Tieát daïy: 07 Baøøi 5: SOÁ GAÀN ÑUÙNG. SAI SOÁ
I. MUÏC TIEÂU:
Kieán thöùc:
Bieát khaùi nieäm soá gaàn ñuùng.
Kó naêng:
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn
13
Vieát ñöôïc soá qui troøn cuûa moät soá caên cöù vaøo ñoä chính xaùc cho tröôùc.
Bieát söû duïng MTBT ñeå tính toaùn vôùi caùc soá gaàn ñuùng.
Thaùi ñoä:
Reøn luyeän tính caån thaän, chính xaùc.
Bieát ñöôïc moái lieân quan giöõa toaùn hoïc vaø thöïc tieãn.
II. CHUAÅN BÒ:
Giaùo vieân: Giaùo aùn, phieáu hoïc taäp. MTBT.
Hoïc sinh: SGK, vôû ghi. OÂn taäp kieán thöùc ñaõ hoïc veà laøm troøn soá. MTBT.
III. HOAÏT ÑOÄNG DAÏY HOÏC:
1. OÅn ñònh toå chöùc: Kieåm tra só soá lôùp.
2. Kieåm tra baøi cuõ: (3’)
H. Vieát = 3,14. Ñuùng hay sai? Vì sao?
Ñ. Sai.
3. Giaûng baøi môùi:
TL
Hoaït ñoäng cuûa Giaùo vieân
Hoaït ñoäng cuûa Hoïc sinh
Noäi dung
Hoaït ñoäng 1: Tìm hieåu veà Soá gaàn ñuùng
7’
H1. Cho HS tieán haønh ño
chieàu daøi moät caùi baøn HS.
Cho keát quaû vaø nhaän xeùt
chung caùc keát quaû ño ñöôïc.
H2. Trong toaùn hoïc, ta ñaõ gaëp
nhöõng soá gaàn ñuùng naøo?
Ñ1. Caùc nhoùm thöïc hieän yeâu
caàu vaø cho keát quaû.
Ñ2. ,
2
, …
I. Soá gaàn ñuùng
Trong ño ñaïc, tính toaùn ta
thöôøng chæ nhaän ñöôïc caùc soá
gaàn ñuùng.
Hoaït ñoäng 2: Tìm hieåu veà Sai soá tuyeät ñoái
15’
Trong caùc keát quaû ño ñaït ôû
treân, cho HS nhaän xeùt keát quaû
naøo chính xaùc hôn. Töø ñoù daãn
ñeán khaùi nieäm sai soá tuyeät ñoái
H1. Ta coù theå tính ñöôïc caùc
sai soá tuyeät ñoái khoâng?
GV neâu moät soá VD veà sai soá
töông ñoái ñeå HS nhaän xeùt veà
ñoä chính xaùc cuûa soá gaàn ñuùng.
– Ñeám soá daân trong thaønh
phoá
– Ñeám soá HS trong moät lôùp
Caùc nhoùm thöïc hieän yeâu caàu
Ñ1. Khoâng. Vì khoâng bieát
ñöôïc soá ñuùng.
Caùc nhoùm thöïc hieän yeâu caàu
II. Sai soá tuyeät ñoái
1. Sai soá tuyeät ñoái cuûa moät
soá gaàn ñuùng
Neáu a laø soá gaàn ñuùng cuûa
a
thì
a
=
aa
ñgl sai soá tuyeät
ñoái cuûa soá gaàn ñuùng a.
2. Ñoä chính xaùc cuûa moät soá
gaàn ñuùng
Neáu
a
=
aa
≤ d
thì –d ≤
a
– a ≤ d hay
a – d ≤
a
≤ a + d.
Ta noùi a laø soá gaàn ñuùng cuûa
a
vôùi ñoä chính xaùc d, vaø qui öôùc
vieát goïn laø:
a
= a
d.
Chuù yù: Sai soá tuyeät ñoái cuûa soá
gaàn ñuùng nhaän ñöôïc trong moät
pheùp ño ñaïc ñoâi khi khoâng
phaûn aùnh ñaày ñuû tính chính
xaùc cuûa pheùp ño ñaïc ñoù.
Vì theá ngoaøi sai soá tuyeät ñoái
a
cuûa soá gaàn ñuùng a, ngöôøi ta
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn
14
coøn vieát tæ soá
a
=
a
a
, goïi laø
sai soá töông ñoái cuûa soá gaàn
ñuùng a.
Hoaït ñoäng 3: Tìm hieåu caùch vieát soá qui troøn cuûa soá gaàn ñuùng
15’
H1. Cho HS nhaéc laïi qui taéc
laøm troøn soá. Cho VD.
GV höôùng daãn caùch xaùc
ñònh chöõ soá chaéc vaø caùch vieát
chuaån soá gaàn ñuùng.
Ñ1. Caùc nhoùm nhaéc laïi vaø cho
VD.
(Coù theå cho nhoùm naøy ñaët yeâu
caàu, nhoùm kia thöïc hieän)
x
= 2841675300
x 2842000
y
= 3,14630,001
y 3,15
III. Qui troøn soá gaàn ñuùng
1. OÂn taäp qui taéc laøm troøn soá
Neáu chöõ soá sau haøng qui troøn
nhoû hôn 5 thì ta thay noù vaø caùc
chöõ soá beân phaûi noù bôûi soá 0.
Neáu chöõ soá sau haøng qui troøn
lôùn hôn hoaëc baèng 5 thì ta
cuõng laøm nhö treân, nhöng
coäng theâm 1 vaøo chöõ soá cuûa
haøng qui troøn.
2. Caùch vieát soá qui troøn cuûa
soá gaàn ñuùng caên cöù vaøo ñoä
chính xaùc cho tröôùc
Cho soá gaàn ñuùng a cuûa soá
a
. Trong soá a, moät chöõ soá ñgl
chöõ soá chaéc (hay ñaùng tin) neáu
sai soá tuyeät ñoái cuûa soá a khoâng
vöôït quaù moät nöûa ñôn vò cuûa
haøng coù chöõ soá ñoù.
Caùch vieát chuaån soá gaàn ñuùng
döôùi daïng thaäp phaân laø caùch
vieát trong ñoù moïi chöõ soá ñeàu
laø chöõ soá chaéc. Neáu ngoaøi caùc
chöõ soá chaéc coøn coù nhöõng chöõ
soá khaùc thì phaûi qui troøn ñeán
haøng thaáp nhaát coù chöõ soá chaéc
Hoaït ñoäng 4: Cuûng coá
3’
Nhaéc laïi caùch xaùc ñònh sai soá
tuyeät ñoái vaø vieát soá qui troøn
4. BAØI TAÄP VEÀ NHAØ:
Baøi 1, 2, 3, 4, 5, 6 SGK.
Ngaøy soaïn: 8/9/2012 Chöông I: MEÄNH ÑEÀ – TAÄP HÔÏP
Tieát daïy: 08 Baøøi daïy: OÂN TAÄP CHÖÔNG I
I. MUÏC TIEÂU:
Kieán thöùc:
Cuûng coá caùc kieán thöùc veà meänh ñeà, taäp hôïp, soá gaàn ñuùng.
Kó naêng:
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn
15
Nhaän bieát ñöôïc ñk caàn, ñk ñuû, ñk caàn vaø ñuû, giaû thieát, keát luaän trong moät ñònh lí Toaùn
hoïc.
Bieát söû duïng caùc kí hieäu , .
Xaùc ñònh ñöôïc giao, hôïp, hieäu cuûa hai taäp hôïp, ñaëc bieät khoaûng ñoaïn.
Bieát qui troøn soá gaàn ñuùng vaø vieát soá gaàn ñuùng döôùi daïng chuaån.
Thaùi ñoä:
Reøn luyeän tính caån thaän, chính xaùc.
Vaän duïng kieán thöùc ñaõ hoïc vaøo thöïc teá.
II. CHUAÅN BÒ:
Giaùo vieân: Giaùo aùn, phieáu hoïc taäp
Hoïc sinh: SGK, vôû ghi.
III. HOAÏT ÑOÄNG DAÏY HOÏC:
1. OÅn ñònh toå chöùc: Kieåm tra só soá lôùp.
2. Kieåm tra baøi cuõ: (Loàng vaøo quaù trình luyeän taäp)
H.
Ñ.
3. Giaûng baøi môùi:
TL
Hoaït ñoäng cuûa Giaùo vieân
Hoaït ñoäng cuûa Hoïc sinh
Noäi dung
Hoaït ñoäng 1: Cuûng coá khaùi nieäm meänh ñeà vaø caùc pheùp toaùn veà meänh ñeà
15’
H1. Xaùc ñònh tính ñuùng sai
cuûa meänh ñeà P Q?
H2. Xaùc ñònh tính ñuùng sai
cuûa meänh ñeà P Q?
Ñ1. P Q ñuùng khi P ñuùng
vaø Q ñuùng.
1. a) S b) Ñ
c) Ñ d) S
2.
a) P Q: Ñuùng
Q P: Sai
b) P Q: Sai
Q P: Sai
Ñ2. P Q ñuùng khi P Q
ñuùng vaø Q P ñuùng
2. a) S b) S
c) Ñ d) Ñ
1. Trong caùc meänh ñeà sau, tìm
meänh ñeà ñuùng ?
a) Neáu a ≥ b thì a
2
≥ b
2
b) Neáu a chia heát cho 9 thì a
chia heát cho 3
b) Neáu em coá gaéng hoïc taäp thì
em seõ thaønh coâng
c) Neáu moät tam giaùc coù moät
goùc baèng 60
0
thì tam giaùc ñoù
laø tam giaùc ñeàu
2. Cho töù giaùc ABCD. Xeùt
tính Ñ–S cuûa meänh ñeà P Q
vaø Q P vôùi:
a) P:”ABCD laø moät h.vuoâng”
Q:”ABCD laø moät hbh”
b) P:”ABCD laø moät hình thoi”
Q:”ABCD laø moät hcn”
3. Trong caùc meänh ñeà sau, tìm
meänh ñeà sai ?
a) – < – 2 <=>
2
< 4
b) < 4 <=>
2
< 16
c)
23
< 5 => 2
23
< 2.5
d)
23
< 5 => (–2)
23
>(–
2).5
Hoaït ñoäng 2: Cuûng coá khaùi nieäm taäp hôïp vaø caùc pheùp toaùn veà taäp hôïp
H1. Neâu caùc caùch xaùc ñònh
Ñ1.
4. Leät keâ caùc phaàn töû cuûa moãi
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn
16
15’
taäp hôïp?
H2. Nhaéc laïi khaùi nieäm taäp
hôïp con?
H3. Nhaéc laïi caùc pheùp toaùn
veà taäp hôïp?
Nhaán maïnh caùch tìm giao,
hôïp, hieäu cuûa caùc khoaûng,
ñoaïn.
– Lieät keâ .
– Chæ ra tính chaát ñaëc tröng.
A = {–2, 1, 4, 7, 10, 13}
B = {0, 1, 2, 3, 4, …, 12}
C = {–1, 1}
Ñ2.
A B x (x A xB)
E
A
B
D
G
C
Ñ3. Bieåu dieãn leân truïc soá.
A= (0; 7);B= (2; 5);C = [3;
+)
taäp hôïp sau:
A = {3k–2/ k = 0, 1, 2, 3, 4, 5}
B = {x N/ x ≤ 12}
C = {(–1)
n
/ n N}
5. Xeùt moái quan heä bao haøm
giöõa caùc taäp hôïp sau:
A laø taäp hôïp caùc töù giaùc
B laø taäp hôïp caùc hbh
C laø taäp hôïp caùc hình thang
D laø taäp hôïp caùc hcn
E laø taäp hôïp caùc hình vuoâng
G laø taäp hôïp caùc hình thoi
6. Xaùc ñònh caùc taäp hôïp sau:
A = (–3; 7) (0; 10)
B = (–; 5) (2; +)
C = R \ (–; 3)
Hoaït ñoäng 3: Cuûng coá khaùi nieäm soá gaàn ñuùng vaø sai soá
10’
H1. Nhaéc laïi ñoä chính xaùc cuûa
soá gaàn ñuùng?
H2. Nhaéc laïi caùch vieát soá qui
troøn cuûa soá gaàn ñuùng?
Ñ1.
a
=
aa
≤ d
a = 2,289;
a
< 0,001
Ñ3. Vì ñoä chính xaùc ñeán haøng
phaàn möôøi, neân ta qui troøn
ñeán haøng ñôn vò:
Soá qui troøn cuûa 347,13 laø 347
7. Duøng MTBT tính giaù trò
gaàn ñuùng a cuûa
3
12
(keát quaû
laøm troøn ñeán chöõ soá thaäp
phaân thöù ba). Öôùc löôïng sai
soá tuyeät ñoái cuûa a.
8. Chieàu cao cuûa moät ngoïn
ñoài laø h = 347,13m 0,2m.
Haõy vieát soá qui troøn cuûa soá
gaàn ñuùng 347,13.
Hoaït ñoäng 4: Cuûng coá
3’
Nhaán maïnh laïi caùc vaán ñeà cô
baûn ñaõ hoïc trong chöông I.
4. BAØI TAÄP VEÀ NHAØ:
Laøm caùc baøi taäp coøn laïi.
Ñoïc tröôùc baøi “Haøm soá”.
Ngaøy soaïn: 15/9/2012 Chöông II: HAØM SOÁ BAÄC NHAÁT VAØ BAÄC HAI
Tieát daïy: 09 Baøøi 1: HAØM SOÁ
I. MUÏC TIEÂU:
Kieán thöùc:
Hieåu khaùi nieäm haøm soá, taäp xaùc ñònh, ñoà thò cuûa haøm soá.
Hieåu caùc tính chaát haøm soá ñoàng bieán, nghòch bieán, haøm soá chaün, leû.
Bieát ñöôïc tính chaát ñoái xöùng cuûa ñoà thò haøm soá chaün, leû.
Kó naêng:
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn
17
Bieát tìm MXÑ cuûa caùc haøm soá ñôn giaûn.
Bieát caùch chöùng minh tính ñoàng bieán, nghòch bieán cuûa moät haøm soá treân moät khoaûng cho tröôùc.
Bieát xeùt tính chaün leû cuûa moät haøm soá ñôn giaûn.
Thaùi ñoä:
Reøn luyeän tính caån thaän, chính xaùc.
Bieát vaän duïng kieán thöùc ñaõ hoïc ñeå xaùc ñònh moái quan heä giöõa caùc ñoái töôïng thöïc teá.
II. CHUAÅN BÒ:
Giaùo vieân: Giaùo aùn. Hình veõ minh hoaï.
Hoïc sinh: SGK, vôû ghi. Duïng cuï veõ hình. OÂn taäp caùc kieán thöùc ñaõ hoïc veà haøm soá.
III. HOAÏT ÑOÄNG DAÏY HOÏC:
1. OÅn ñònh toå chöùc: Kieåm tra só soá lôùp.
2. Kieåm tra baøi cuõ: (3’)
H. Neâu moät vaøi loaïi haøm soá ñaõ hoïc?
Ñ. Haøm soá y = ax+b, y = ax
2
.
3. Giaûng baøi môùi:
TL
Hoaït ñoäng cuûa Giaùo vieân
Hoaït ñoäng cuûa Hoïc sinh
Noäi dung
200
282
295
311
339
363
375
394
564
0
200
400
600
USD
Thu nhaäp bình quaân ñaàu ngöôøi
Thu nhaäp
200
282
295
311
339
363
375
394
564
1995
1996
1997
1998
1999
2000
2001
2002
2004
Hoaït ñoäng 1: OÂn taäp caùc kieán thöùc ñaõ hoïc veà haøm soá
10’
Xeùt baûng soá lieäu veà thu
nhaäp bình quaân ñaøu ngöôøi töø
1995 ñeán 2004: (SGK)
H1. Neâu taäp xaùc ñònh cuûa h.soá
H2. Neâu caùc giaù trò töông öùng
y cuûa x vaø ngöôïc laïi?
Taäp caùc giaù trò cuûa y ñgl taäp
giaù trò cuûa haøm soá.
H3. Cho moät soá VD thöïc teá
veà h.soá, chæ ra taäp xaùc ñònh
cuûa h.soá ñoù
HS quan saùt baûng soá lieäu.
Caùc nhoùm thaûo luaän thöïc hieän
yeâu caàu.
Ñ1. D={1995, 1996, …, 2004}
Ñ2. Caùc nhoùm ñaët yeâu caàu vaø
traû lôøi.
Ñ3. Caùc nhoùm thaûo luaän vaø
traû lôøi.
I. OÂn taäp veà haøm soá
Neáu vôùi moãi giaù trò cuûa x
D
coù moät vaø chæ moät giaù trò
töông öùng cuûa y
R thì ta coù
moät haøm soá.
Ta goïi x laø bieán soá, y laø haøm
soá cuûa x.
Taäp hôïp D ñgl taäp xaùc ñònh
cuûa haøm soá.
Hoaït ñoäng 2: Tìm hieåu caùch cho haøm soá
15’
GV giôùi thieäu caùch cho haøm
soá baèng baûng vaø baèng bieåu
ñoà. Sau ñoù cho HS tìm theâm
VD.
Caùc nhoùm thaûo luaän
– Baûng thoáng keâ chaát löôïng
HS.
– Bieåu ñoà theo doõi nhieät ñoä.
2. Caùch cho haøm soá
a) Haøm soá cho baèng baûng
b) Haøm soá cho baèng bieåu ñoà
c) Haøm soá cho baèng coâng
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn
18
GV giôùi thieäu qui öôùc veà taäp
xaùc ñònh cuûa haøm soá cho baèng
coâng thöùc.
H1. Tìm taäp xaùc ñònh cuûa haøm
soá: a) f(x) =
x3
b) f(x) =
3
x2
GV giôùi thieäu theâm veà haøm
soá cho bôûi 2, 3.. coâng thöùc.
y = f(x) = /x/ =
x vôùix 0
x vôùix 0

Ñ1.
a) D = [3; +)
b) D = R \ {–2}
thöùc
Taäp xaùc ñònh cuûa haøm soá y =
f(x) laø taäp hôïp taát caû caùc soá
thöïc x sao cho bieåu thöùc f(x)
coù nghóa.
D = {x
R/ f(x) coù nghóa}
Chuù yù: Moät haøm soá coù theå xaùc
ñònh bôûi hai, ba, … coâng thöùc.
Hoaït ñoäng 3: Tìm hieåu veà ñoà thò cuûa haøm soá
10’
H1. Veõ ñoà thò cuûa caùc haøm soá:
a) y = f(x) = x + 1
b) y = g(x) = x
2
H2. Döïa vaøo caùc ñoà thò treân,
tính f(–2), f(0), g(0), g(2)?
-3 -2 -1 1 2 3
-2
2
4
6
8
x
y
f(x) = x + 1
f(x) = x
2
Ñ2. f(–2) = –1, f(0) = 1
g(0) = 0, g(2) = 4
3. Ñoà thò cuûa haøm soá
Ñoà thò cuûa haøm soá y=f(x) xaùc
ñònh treân taäp D laø taäp hôïp caùc
ñieåm M(x;f(x)) treân maët phaúng
toaï ñoä vôùi moïi x
D.
Ta thöôøng gaëp ñoà thò cuûa
haøm soá y = f(x) laø moät ñöôøng.
Khi ñoù ta noùi y = f(x) laø
phöông trình cuûa ñöôøng ñoù.
Hoaït ñoäng 4: Cuûng coá
5’
Nhaán maïnh caùc khaùi nieäm
taäp xaùc ñònh, ñoà thò cuûa haøm
soá.
Caâu hoûi: Tìm taäp xaùc ñònh
cuûa haøm soá: f(x) =
2
2x
x1
,
g(x) =
2
2x
x1
?
D
f
= R, D
g
= R \ {–1, 1}
4. BAØI TAÄP VEÀ NHAØ:
Baøi 1, 2, 3 SGK.
Ñoïc tieáp baøi “Haøm soá”
Ngaøy soaïn: 15/9/2012 Chöông II: HAØM SOÁ BAÄC NHAÁT VAØ BAÄC HAI
Tieát daïy: 10 Baøøi 1: HAØM SOÁ (tt)
I. MUÏC TIEÂU:
Kieán thöùc:
Hieåu khaùi nieäm haøm soá, taäp xaùc ñònh, ñoà thò cuûa haøm soá.
Hieåu caùc tính chaát haøm soá ñoàng bieán, nghòch bieán, haøm soá chaün, leû.
Bieát ñöôïc tính chaát ñoái xöùng cuûa ñoà thò haøm soá chaün, leû.
Kó naêng:
Bieát tìm MXÑ cuûa caùc haøm soá ñôn giaûn.
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn
19
Bieát caùch chöùng minh tính ñoàng bieán, nghòch bieán cuûa moät haøm soá treân moät khoaûng cho tröôùc.
Bieát xeùt tính chaün leû cuûa moät haøm soá ñôn giaûn.
Thaùi ñoä:
Reøn luyeän tính caån thaän, chính xaùc.
Bieát vaän duïng kieán thöùc ñaõ hoïc ñeå xaùc ñònh moái quan heä giöõa caùc ñoái töôïng thöïc teá.
II. CHUAÅN BÒ:
Giaùo vieân: Giaùo aùn. Hình veõ minh hoaï.
Hoïc sinh: SGK, vôû ghi. Duïng cuï veõ hình. OÂn taäp caùc kieán thöùc ñaõ hoïc veà haøm soá.
III. HOAÏT ÑOÄNG DAÏY HOÏC:
1. OÅn ñònh toå chöùc: Kieåm tra só soá lôùp.
2. Kieåm tra baøi cuõ: (3’)
H. Tìm taäp xaùc ñònh cuûa haøm soá: f(x) =
x1
2x 3
?
Ñ. D = (
3
2
; + )
3. Giaûng baøi môùi:
TL
Hoaït ñoäng cuûa Giaùo vieân
Hoaït ñoäng cuûa Hoïc sinh
Noäi dung
Hoaït ñoäng 1: Tìm hieåu veà Söï bieán thieân cuûa haøm soá
15’
Cho HS nhaän xeùt hình daùng
ñoà thò cuûa haøm soá: y = f(x) =
x
2
treân caùc khoaûng (–; 0) vaø
(0; + ).
GV höôùng daãn HS laäp baûng
bieán thieân.
Treân (–; 0) ñoà thò ñi xuoáng,
Treân (0; + ) ñoà thò ñi leân.
-3 -2 -1 1 2 3
-2
2
4
6
8
x
y
f(x) = x
2
0
II. Söï bieán thieân cuûa haøm soá
1. OÂn taäp
Haøm soá y=f(x) ñgl ñoàng bieán
(taêng) treân khoaûng (a;b) neáu:
x
1
, x
2
(a;b): x
1
<x
2
f(x
1
)<f(x
2
)
Haøm soá y=f(x) ñgl nghòch bieán
(giaûm) treân khoaûng (a;b) neáu:
x
1
, x
2
(a;b): x
1
<x
2
f(x
1
)>f(x
2
)
2. Baûng bieán thieân
x
y
a
b
ñoàng bieán
x
y
a
b
nghòch bieán
Hoaït ñoäng 2: Tìm hieåu tính chaün, leû cuûa haøm soá
15’
Cho HS nhaän xeùt veà tính ñoái
xöùng cuûa ñoà thò cuûa 2 haøm soá:
y = f(x) = x
2
vaø y = g(x) = x
Caùc nhoùm thaûo luaän.
– Ñoà thò y = x
2
coù truïc ñoái
xöùng laø Oy.
– Ñoà thò y = x coù taâm ñoái
xöùng laø O.
III. Tính chaün leû cuûa haøm soá
1. Haøm soá chaün, haøm soá leû
Haøm soá y = f(x) vôùi taäp xaùc
ñònh D goïi laø haøm soá chaün neáu
vôùi
x
D
thì –x
D vaø f(–x)=f(x).
Haøm soá y = f(x) vôùi taäp xaùc
ñònh D goïi laø haøm soá leû neáu
vôùi
x
D
thì –x
D vaø f(–x)=– f(x).
Chuù yù: Moät haøm soá khoâng
nhaát thieát phaûi laø haøm soá chaün
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn
20
-3 -2 -1 1 2 3
-1
1
2
3
4
5
6
7
x
y
O
y=x
2
H1. Xeùt tính chaün leû cuûa h.soá:
a) y = 3x
2
– 2
b) y =
1
x
-3 -2 -1 1 2 3
-3
-2
-1
1
2
3
x
y
O
Ñ1. a) chaün b) leû
hoaëc laø haøm soá leû.
2. Ñoà thò cuûa haøm soá chaün,
haøm soá leû
Ñoà thò cuûa haøm soá chaün nhaän
truïc tung laøm truïc ñoái xöùng.
Ñoà thò cuûa haøm soá leû nhaän goác
toaï ñoä laøm taâm ñoái xöùng.
Hoaït ñoäng 3: Cuûng coá
* Caùch chöùng minh haøm soá ñoàng bieán, nghòch bieán treân moät khoaûng:
f(x) ñoàng bieán treân (a;b) x (a;b) vaø x
1
≠ x
2
:
21
21
f(x ) f(x )
xx
> 0
f(x) nghòch bieán treân (a;b) x (a;b) vaø x
1
≠ x
2
:
21
21
f(x ) f(x )
xx
< 0
* Caùch veõ ñoà thò haøm soá chaün, haøm soá leû:
Ñeå veõ ñoà thò haøm soá chaün ta chæ caàn veõ phaàn ñoà thò naèm beân phaûi truïc tung, roài laáy ñoái xöùng
phaàn naøy qua truïc tung. Hôïp cuûa hai phaàn naøy laø ñoà thò cuûa haøm soá chaün ñaõ cho.
Ñeå veõ ñoà thò haøm soá chaün ta chæ caàn veõ phaàn ñoà thò naèm beân phaûi truïc tung, roài laáy ñoái xöùng
phaàn naøy qua goác toaï ñoä. Hôïp cuûa hai phaàn naøy laø ñoà thò cuûa haøm soá leû ñaõ cho.
10’
Caâu hoûi:
1) Chöùng toû haøm soá y =
1
x
luoân nghòch bieán vôùi moïi x ≠
0
2) Xeùt tính chaün leû vaø veõ ñoà
thò cuûa haøm soá y = f(x) = x
3
.
1) Xeùt 2 khoaûng (–;0) vaø
(0;+)
2) Haøm soá leû.
4. BAØI TAÄP VEÀ NHAØ:
Baøi 4 SGK.
Ñoïc tröôùc baøi “Haøm soá y = ax + b”.
Ngaøy soaïn: 22/9/2012 Chöông II: HAØM SOÁ BAÄC NHAÁT VAØ BAÄC HAI
Tieát daïy: 11 Baøøi 2: HAØM SOÁ Y = AX + B
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn
21
I. MUÏC TIEÂU:
Kieán thöùc:
Hieåu ñöôïc söï bieán thieân vaø ñoà thò cuûa haøm soá baäc nhaát.
Hieåu caùch veõ ñoà thò haøm soá baäc nhaát vaø haøm soá y = /x/.
Bieát ñöôïc ñoà thò haøm soá y = /x/ nhaän truïc Oy laøm truïc ñoái xöùng.
Kó naêng:
Thaønh thaïo vieäc xaùc ñònh chieàu bieán thieân vaø veõ ñoà thò cuûa haøm soá baäc nhaát.
Veõ ñöôïc ñoà thò haøm soá y = b, y = /x/.
Bieát tìm toaï ñoä giao ñieåm cuûa hai ñöôøng thaúng coù phöông trình cho tröôùc.
Thaùi ñoä:
Reøn luyeän tính caån thaän, chính xaùc.
II. CHUAÅN BÒ:
Giaùo vieân: Giaùo aùn. Hình veõ minh hoaï.
Hoïc sinh: SGK, vôû ghi, duïng cuï veõ hình.
Ñoïc baøi tröôùc. OÂn taäp kieán thöùc ñaõ hoïc veà haøm soá baäc nhaát.
III. HOAÏT ÑOÄNG DAÏY HOÏC:
1. OÅn ñònh toå chöùc: Kieåm tra só soá lôùp.
2. Kieåm tra baøi cuõ: (5’)
H. Tìm taäp xaùc ñònh cuûa haøm soá: y = f(x) =
2
1
x 3x 2
. Tính f(0), f(–1)?
Ñ. D = R \ {1, 2}. f(0) =
1
2
, f(–1) =
1
6
.
3. Giaûng baøi môùi:
TL
Hoaït ñoäng cuûa Giaùo vieân
Hoaït ñoäng cuûa Hoïc sinh
Noäi dung
Hoaït ñoäng 1: Tìm hieåu haøm soá y = /x/
10’
H1. Nhaéc laïi ñònh nghóa veà
GTTÑ?
H2. Nhaän xeùt veà chieàu bieán
Ñ1.
y=
x nÕu x 0
x
x nÕu x<0
Ñ2.
III. Haøm soá y = /x/
Taäp xaùc ñònh: D = R.
Chieàu bieán thieân:
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn
22
thieân cuûa haøm soá?
H3. Nhaän xeùt veà tính chaát
chaün leû cuûa haøm soá?
+ ñoàng bieán trong (0; +)
+ nghòch bieán trong (–; 0)
Ñ3. Haøm soá chaün ñoà thò
nhaän truïc tung laøm truïc ñoái
xöùng.
Ñoà thò
-2.5 -2 -1.5 -1 -0.5 0.5 1 1.5 2 2.5
-0.5
0.5
1
1.5
2
2.5
x
y
Hoaït ñoäng 2: Cuûng coá
7’
Nhaán maïnh tính chaát cuûa
ñöôøng thaúng y = ax + b (cho
HS nhaéc laïi):
– Heä soá goùc
– VTTÑ cuûa 2 ñöôøng thaúng
– Tìm giao ñieåm cuûa 2 ñt
Caùc nhoùm thaûo luaän, trình
baøy.
4. BAØI TAÄP VEÀ NHAØ:
Baøi 1, 2, 3, 4 SGK.
Ngaøy soaïn: 1/10/2012 Chöông II: HAØM SOÁ BAÄC NHAÁT VAØ BAÄC HAI
Tieát daïy: 12 Baøøi daïy: LUYEÄN TAÄP HAØM SOÁ Y = AX + B
I. MUÏC TIEÂU:
Kieán thöùc:
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn
23
Cuûng coá caùc kieán thöùc ñaõ hoïc veà haøm soá baäc nhaát, haøm soá haèng, haøm soá y = /x/: taäp xaùc
ñònh, chieàu bieán thieân, ñoà thò.
Kó naêng:
Bieát caùch tìm taäp xaùc ñònh, xaùc ñònh chieàu bieán thieân, veõ ñoà thò cuûa caùc haøm soá ñaõ hoïc.
Bieát caùch xaùc ñònh phöông trình cuûa ñöôøng thaúng thoaû maõn caùc ñieàu kieän cho tröôùc.
Thaùi ñoä:
Reøn luyeän tính caån thaän, chính xaùc.
II. CHUAÅN BÒ:
Giaùo vieân: Giaùo aùn.
Hoïc sinh: SGK, vôû ghi. Laøm baøi taäp ôû nhaø. OÂn taäp kieán thöùc ñaõ hoïc veà haøm soá baäc nhaát.
III. HOAÏT ÑOÄNG DAÏY HOÏC:
1. OÅn ñònh toå chöùc: Kieåm tra só soá lôùp.
2. Kieåm tra baøi cuõ: (Loàng vaøo quaù trình luyeän taäp)
3. Giaûng baøi môùi:
TL
Hoaït ñoäng cuûa Giaùo vieân
Hoaït ñoäng cuûa Hoïc sinh
Noäi dung
Hoaït ñoäng 1: Luyeän kó naêng khaûo saùt haøm soá baäc nhaát
15’
H1. Neâu caùc böôùc tieán haønh?
Cho HS nhaéc laïi caùc tính
chaát cuûa haøm soá.
Ñ1.
– Tìm taäp xaùc ñònh
– Laäp baûng bieán thieân
– Veõ ñoà thò
-8 -6 -4 -2 2 4 6 8
-8
-6
-4
-2
2
4
6
8
x
y
y = 2x - 3
y = - x + 7
3
2
1. Veõ ñoà thò cuûa haøm soá:
a) y = 2x – 3
b) y = –
3
2
+ 7
Hoaït ñoäng 2: Luyeän kó naêng xaùc ñònh phöông trình cuûa ñöôøng thaúng
15’
H1. Neâu ñieàu kieän ñeå moät
ñieåm thuoäc ñoà thò cuûa haøm
soá?
Cho HS nhaéc laïi caùch giaûi
heä phöông trình baäc nhaát hai
aån.
H2. Neâu ñieàu kieän ñeå moät
ñieåm thuoäc ñöôøng thaúng ?
Ñ1. Toaï ñoä thoaû maõn phöông
trình cuûa haøm soá.
a) a = –5, b = 3
b) a = –1, b = 3
c) a = 0, b = –3
Ñ2. Toaï ñoä thoaû maõn phöông
trình cuûa ñöôøng thaúng .
a) y = 2x – 5
b) y = –1
2. Xaùc ñònh a, b ñeå ñoà thò cuûa
haøm soá y = ax + b ñi qua caùc
ñieåm:
a) A(0; –3), B(
3
5
; 0)
b) A(1; 2), B(2; 1)
c) A(15; –3), B(21; –3)
3. Vieát phöông trình y = ax +
b cuûa caùc ñöôøng thaúng:
a) Ñi qua A(4;3), B(2;–1)
b) Ñi qua A(1;–1) vaø song
song vôùi Ox.
Hoaït ñoäng 3: Luyeän taäp kó naêng veõ ñoà thò cuûa caùc haøm soá lieân quan
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn
24
10’
H1. Neâu caùch tieán haønh?
Ñ1. Veõ töøng nhaùnh.
-8 -6 -4 -2 2 4 6 8
-8
-6
-4
-2
2
4
6
8
x
y
-3 -2 -1 1 2 3 4 5
-1
1
2
3
4
5
6
7
8
9
x
y
4. Veõ ñoà thò cuûa caùc haøm soá:
a) y = /2x – 4/
b) y=
x 1 vôùi x 1
2x 4 vôùi x 1

Hoaït ñoäng 4: Cuûng coá
3’
Nhaéc laïi caùch giaûi caùc daïng
toaùn.
4. BAØI TAÄP VEÀ NHAØ:
Laøm tieáp caùc baøi taäp coøn laïi.
Ñoïc tröôùc baøi “Haøm soá baäc hai”
Ngaøy soaïn: 1/10/2012 Chöông II: HAØM SOÁ BAÄC NHAÁT VAØ BAÄC HAI
Tieát daïy: 13 Baøøi 3: HAØM SOÁ BAÄC HAI
I. MUÏC TIEÂU:
Kieán thöùc:
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn
25
Hieåu quan heä giöõa ñoà thò cuûa caùc haøm soá y = ax
2
+ bx + c vaø y = ax
2
.
Hieåu vaø ghi nhôù caùc tính chaát cuûa haøm soá y = ax
2
+ bx + c.
Kó naêng:
Laäp ñöôïc baûng bieán thieân cuûa haøm soá baäc hai, xaùc ñònh toaï ñoä ñænh, truïc ñoái xöùng,
veõ ñöôïc ñoà thò haøm soá baäc hai.
Ñoïc ñöôïc ñoà thò cuûa haøm soá baäc hai, töø ñoà thò xaùc ñònh ñöôïc: truïc ñoái xöùng, caùc
giaù trò x ñeå y> 0, y < 0.
Tìm ñöôïc phöông trình cuûa parabol khi bieát moät trong caùc heä soá vaø ñoà thò ñi qua
hai ñieåm cho tröôùc.
Thaùi ñoä:
Reøn luyeän tính caån thaän, chính xaùc khi veõ ñoà thò.
II. CHUAÅN BÒ:
Giaùo vieân: Giaùo aùn. Hình veõ minh hoaï.
Hoïc sinh: SGK, vôû ghi. Ñoïc baøi tröôùc.
OÂn laïi kieán thöùc ñaõ hoïc veà haøm soá y = ax
2
. Duïng cuï veõ ñoà thò.
III. HOAÏT ÑOÄNG DAÏY HOÏC:
1. OÅn ñònh toå chöùc: Kieåm tra só soá lôùp.
2. Kieåm tra baøi cuõ: (3’)
H. Cho haøm soá y = x
2
. Tìm taäp xaùc ñònh vaø xeùt tính chaün leû cuûa haøm soá?
Ñ. D = R. Haøm soá chaün.
3. Giaûng baøi môùi:
TL
Hoaït ñoäng cuûa Giaùo vieân
Hoaït ñoäng cuûa Hoïc sinh
Noäi dung
Hoaït ñoäng 1: Nhaéc laïi caùc keát quaû ñaõ bieát veà haøm soá y = ax
2
15’
Cho HS nhaéc laïi caùc kieán
thöùc ñaõ hoïc veà haøm soá y = ax
2
(Minh hoaï bôûi haøm soá y = x
2
)
– Taäp xaùc ñònh
– Ñoà thò: Toaï ñoä ñænh, Hình
daùng, truïc ñoái xöùng.
H1. Bieán ñoåi bieåu thöùc:
ax
2
+ bx + c
H2. Nhaän xeùt vai troø ñieåm I ?
Caùc nhoùm thaûo luaän, traû lôøi
theo töøng yeâu caàu.
-4 -3 -2 -1 1 2 3 4
-9
-8
-7
-6
-5
-4
-3
-2
-1
1
2
3
4
5
6
7
8
9
x
y
O
y = x
2
y = -x
2
Ñ1. y = ax
2
+ bx + c
= a
2
b
x
2a



+
4a

Ñ2. Gioáng ñieåm O trong ñoà
thò cuûa y = ax
2
I. Ñoà thò cuûa haøm soá baäc hai
y = ax
2
+ bx + c (a ≠ 0)
1. Nhaän xeùt:
a) Haøm soá y = ax
2
:
– Ñoà thò laø moät parabol.
– a>0 (a<0): O(0;0) laø ñieåm
thaáp nhaát (cao nhaát).
b) Haøm soá y = ax
2
+ bx + c
(a≠0)
y = ax
2
+ bx + c
= a
2
b
x
2a



+
4a

I( –
b
2a
;
4a

) thuoäc ñoà thò.
a>0
I laø ñieåm thaáp nhaát
a<0
I laø ñieåm cao nhaát
Hoaït ñoäng 2: Tìm hieåu quan heä giöõa caùc ñoà thò cuûa caùc haøm soá y = ax
2
+ bx + c vaø y = ax
2
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn
26
10’
H2. Neáu ñaët
b
Xx
2a
Yy
4a


thì haøm soá coù daïng nhö theá
naøo?
Minh hoaï ñoà thò haøm soá:
y = x
2
– 4x – 2
Ñ1. Y = aX
2
-2 -1 1 2 3 4 5 6 7
-9
-8
-7
-6
-5
-4
-3
-2
-1
1
2
3
4
5
6
7
8
9
x
y
O
a > 0
I
2. Ñoà thò:
Ñoà thò cuûa haøm soá y = ax
2
+
bx + c (a≠0) laø moät ñöôøng
parabol coù ñænh I( –
b
2a
;
4a

),
coù truïc ñoái xöùng laø ñöôøng
thaúng x = –
b
2a
.
Parabol naøy quay beà loõm leân
treân neáu a>0, xuoáng döôùi neáu
a<0.
Hoaït ñoäng 3: Tìm hieåu caùch veõ ñoà thò haøm soá baäc hai
10’
GV gôïi yù, höôùng daãn HS
thöïc hieän caùc böôùc veõ ñoà thò
haøm soá baäc hai.
H1. Veõ ñoà thò haøm soá:
a) y = x
2
– 4x –3
b) y = –x
2
+ 4x +3
-2 -1 1 2 3 4 5 6 7
-9
-8
-7
-6
-5
-4
-3
-2
-1
1
2
3
4
5
6
7
8
9
x
y
O
a > 0
a < 0
I
I
3. Caùch veõ
1) Xaùc ñònh toaï ñoä ñænh
I( –
b
2a
;
4a

)
2) Veõ truïc ñoái xöùng x =–
b
2a
3) Xaùc ñònh caùc giao ñieåm cuûa
paranol vôùi caùc truïc toaï ñoä.
4) Veõ parabol
Hoaït ñoäng 3: Cuûng coá
5’
Nhaán maïnh caùc tính chaát veà
ñoà thò cuûa haøm soá baäc hai.
Caâu hoûi traéc nghieäm:
Cho haøm soá y = 2x
2
+ 3x + 1.
1) Toaï ñoä ñænh I cuûa ñoà thò (P)
a)
31
;
48




b)
31
;
48



c)
31
;
48



d)
31
;
48



2) Truïc ñoái xöùng cuûa ñoà thò
a) x =
3
2
b) x = –
3
2
c) x =
3
4
d) x = –
3
4
Caùc nhoùm thaûo luaän, traû lôøi
caùc caâu hoûi.
1 a)
2 b)
3) a)
3) Tìm giao ñieåm cuûa ñoà thò
vôùi truïc hoaønh
a) (–1; 0),
1
;0
2



b) (–1; 0),
1
;0
2



c) (1; 0),
1
;0
2



d) ) (1; 0),
1
;0
2



4. BAØI TAÄP VEÀ NHAØ:
Baøi 1 SGK
Ñoïc tieáp baøi “Haøm soá baäc hai”
Ngaøy soaïn: 1/10/2012 Chöông II: HAØM SOÁ BAÄC NHAÁT VAØ BAÄC HAI
Tieát daïy: 14 Baøøi 3: HAØM SOÁ BAÄC HAI (tt)
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn
27
I. MUÏC TIEÂU:
Kieán thöùc:
Hieåu quan heä giöõa ñoà thò cuûa caùc haøm soá y = ax
2
+ bx + c vaø y = ax
2
.
Hieåu vaø ghi nhôù caùc tính chaát cuûa haøm soá y = ax
2
+ bx + c.
Kó naêng:
Laäp ñöôïc baûng bieán thieân cuûa haøm soá baäc hai, xaùc ñònh toaï ñoä ñænh, truïc ñoái xöùng,
veõ ñöôïc ñoà thò haøm soá baäc hai.
Ñoïc ñöôïc ñoà thò cuûa haøm soá baäc hai, töø ñoà thò xaùc ñònh ñöôïc: truïc ñoái xöùng, caùc
giaù trò x ñeå y> 0, y < 0.
Tìm ñöôïc phöông trình cuûa parabol khi bieát moät trong caùc heä soá vaø ñoà thò ñi qua
hai ñieåm cho tröôùc.
Thaùi ñoä:
Reøn luyeän tính caån thaän, chính xaùc khi veõ ñoà thò. Luyeän tö duy khaùi quaùt, toång hôïp.
II. CHUAÅN BÒ:
Giaùo vieân: Giaùo aùn. Hình veõ minh hoaï.
Hoïc sinh: SGK, vôû ghi. Ñoïc baøi tröôùc.
OÂn laïi kieán thöùc ñaõ hoïc veà haøm soá y = ax
2
. Duïng cuï veõ ñoà thò.
III. HOAÏT ÑOÄNG DAÏY HOÏC:
1. OÅn ñònh toå chöùc: Kieåm tra só soá lôùp.
2. Kieåm tra baøi cuõ: (3’)
H. Cho haøm soá y = –x
2
+ 4. Tìm toaï ñoä ñænh, truïc ñoái xöùng cuûa ñoà thò haøm soá?
Ñ. I(0; 4). (): x = 0.
3. Giaûng baøi môùi:
TL
Hoaït ñoäng cuûa Giaùo vieân
Hoaït ñoäng cuûa Hoïc sinh
Noäi dung
Hoaït ñoäng 1: Tìm hieåu chieàu bieán thieân cuûa haøm soá baäc hai
10'
GV höôùng daãn HS nhaän xeùt
chieàu bieán thieân cuûa haøm soá
baäc hai döïa vaøo ñoà thò caùc
haøm soá minh hoaï.
-2 -1 1 2 3 4 5 6 7
-9
-8
-7
-6
-5
-4
-3
-2
-1
1
2
3
4
5
6
7
8
9
x
y
O
a > 0
a < 0
I
I
Neáu a > 0 thì haøm soá
+ Nghòch bieán treân
b
;
2a




+ Ñoàng bieán treân
b
;
2a




Neáu a < 0 thì haøm soá
+ Ñoàng bieán treân
b
;
2a




+ Nghòch bieán treân
b
;
2a




II. Chieàu bieán thieân cuûa
haøm soá baäc hai
Hoaït ñoäng 2: Luyeän taäp xaùc ñònh chieàu bieán thieân cuûa haøm soá baäc hai
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn
28
10'
Cho moãi nhoùm xeùt chieàu
bieán thieân cuûa moät haøm soá.
H1. Ñeå xaùc ñònh chieàu bieán
thieân cuûa haøm soá baäc hai, ta
döïa vaøo caùc yeáu toá naøo?
Caùc nhoùm thöïc hieän yeâu caàu
Ñ1. Heä soá a vaø toaï ñoä ñænh
Ñoàng bieán
Nghòch bieán
a
(–; –1)
(–1; +)
b
(0; +)
(–; 0)
c
(–; 2)
(2; +)
d
(1; +)
(–; 1)
Ví duï:
Xaùc ñònh chieàu bieán thieân cuûa
haøm soá:
a) y = –x
2
– 2x + 3
b) y = x
2
+ 1
c) y = –2x
2
+ 4x – 3
d) y = x
2
– 2x
Hoaït ñoäng 3: Luyeän taäp khaûo saùt haøm soá baäc hai
15'
Cho moãi nhoùm thöïc hieän
moät yeâu caàu:
– Tìm taäp xaùc ñònh
– Tìm toaï ñoä ñænh
– Xaùc ñònh chieàu bieán thieân
– Xaùc ñònh truïc ñoái xöùng
– Tìm toaï ñoä giao ñieåm cuûa
ñoà thò vôùi caùc truïc toaï ñoä.
– Veõ ñoà thò
– Döïa vaøo ñoà thò, xaùc ñònh x
ñeå y < 0, y > 0
Caùc nhoùm thöïc hieän
-4 -3 -2 -1 1 2 3 4 5 6 7 8 9
-9
-8
-7
-6
-5
-4
-3
-2
-1
1
2
x
y
O
I
y = - x
2
+ 4x - 3
Ví duï:
Khaûo saùt haøm soá vaø veõ ñoà thò
haøm soá:
y = –x
2
+ 4x – 3
Hoaït ñoäng 3: Cuûng coá
5'
Nhaéc laïi caùc tính chaát cuûa
haøm soá baäc hai.
Nhaán maïnh moái quan heä
giöõa tính chaát vaø ñoà thò cuûa
haøm soá.
4. BAØI TAÄP VEÀ NHAØ:
Baøi 2, 3 SGK
Laøm baøi taäp oân chöông II
Ngaøy soaïn: 1/10/2012 Chöông II: HAØM SOÁ BAÄC NHAÁT VAØ BAÄC HAI
Tieát daïy: 15 Baøøi daïy: OÂN TAÄP CHÖÔNG II
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn
29
I. MUÏC TIEÂU:
Kieán thöùc:
Hieåu vaø naém ñöôïc tính chaát cuûa haøm soá, mieàn xaùc ñònh, chieàu bieán thieân.
Hieåu vaø ghi nhôù caùc tính chaát cuûa haøm soá baäc nhaát, baäc hai. Xaùc ñònh ñöôïc chieàu bieán
thieân vaø veõ ñoà thò cuûa chuùng.
Kó naêng:
Veõ thaønh thaïo caùc ñöôøng thaúng daïng y = ax+b baèng caùch xaùc ñònh caùc giao ñieåm vôùi caùc
truïc toaï ñoä vaø caùc parabol y = ax
2
+bx+c baèng caùch xaùc ñònh ñænh, truïc ñoái xöùng vaø moät
soá ñieåm khaùc.
Bieát caùch giaûi moät soá baøi toaùn ñôn giaûn veà ñöôøng thaúng vaø parabol.
Thaùi ñoä:
Reøn luyeän tính tæ mæ, chính xaùc khi xaùc ñònh chieàu bieán thieân, veõ ñoà thò caùc haøm soá.
II. CHUAÅN BÒ:
Giaùo vieân: Giaùo aùn. Heä thoáng baøi taäp oân taäp.
Hoïc sinh: SGK, vôû ghi. OÂn taäp keán thöùc chöông II.
III. HOAÏT ÑOÄNG DAÏY HOÏC:
1. OÅn ñònh toå chöùc: Kieåm tra só soá lôùp.
2. Kieåm tra baøi cuõ: (Loàng vaøo quaù trình oân taäp)
H.
Ñ.
3. Giaûng baøi môùi:
TL
Hoaït ñoäng cuûa Giaùo vieân
Hoaït ñoäng cuûa Hoïc sinh
Noäi dung
Hoaït ñoäng 1: Luyeän taäp tìm taäp xaùc ñònh cuûa haøm soá
10'
H1. Nhaéc laïi ñònh nghóa taäp
xaùc ñònh cuûa haøm soá? Neâu
ñieàu kieän xaùc ñònh cuûa moãi
haøm soá?
Cho moãi nhoùm tìm taäp xaùc
ñònh cuûa moät haøm soá.
Ñ1. D = {xR/ f(x) coù nghóa}
a) D = [–3; +) \ {–1}
b) D =
1
;
2




c) D = R
1. Tìm taäp xaùc ñònh cuûa haøm
soá
a)
2
3
1
yx
x
b
b
)
)
1
23
12
yx
x
c
c
)
)
2 , 1
1
,1
3

xx
y
x
x
Hoaït ñoäng 2: Luyeän taäp khaûo saùt söï bieán thieân cuûa haøm soá
10'
H1. Nhaéc laïi söï bieán thieân
cuûa haøm soá baäc nhaát vaø baäc
hai?
Cho moãi nhoùm xeùt chieàu
bieán thieân cuûa moät haøm soá.
Ñ1.
a) nghòch bieán treân R
b) y =
2
x
= /x/
+ x ≥ 0: ñoàng bieán
+ x < 0: nghòch bieán
c) + x ≥ 1: ñoàng bieán
+ x < 1: nghòch bieán
d) + x ≥
3
2
: nghòch bieán
2. Xeùt chieàu bieán thieân cuûa
haøm soá
a) y = 4 – 2x
b) y =
2
x
c) y = x
2
– 2x –1
d) y = –x
2
+ 3x + 2
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn
30
+ x <
3
2
: ñoàng bieán
Hoaït ñoäng 3: Luyeän taäp veõ ñoà thò cuûa haøm soá
10'
H1. Nhaéc laïi daïng ñoà thò cuûa
haøm soá baäc nhaát vaø baäc hai?
Cho moãi nhoùm veõ ñoà thò cuûa
moät haøm soá.
Ñ1.
-9 -8 -7 -6 -5 -4 -3 -2 -1 1 2 3 4 5 6 7 8 9
-3
-2
-1
1
2
3
4
5
6
7
8
9
x
y
O
y = 4 - 2x
y = /x/
-4 -2 2 4 6 8
-8
-6
-4
-2
2
4
6
8
x
y
O
y = x
2
- 2x - 1
y = -x
2
+ 3x + 2
3. Veõ ñoà thò cuûa caùc haøm soá ôû
caâu 2
Hoaït ñoäng 4: Luyeän taäp xaùc ñònh haøm soá
10'
H1. Neâu ñieàu kieän ñeå moät
ñieåm thuoäc ñoà thò haøm soá?
H2. Neâu coâng thöùc xaùc ñònh
toaï ñoä ñænh cuûa parabol?
Ñ1. Toaï ñoä thoaû maõn phöông
trình haøm soá.
4)
a b 3
a b 5

a = –1; b = 4
Ñ2. I
b
;
2a 4a




5a)
a b c 1
a b c 1
c1

a1
b1
c1


b)
b 2a
a b c 4
9a 3b c 0

a1
b2
c3

4. Xaùc ñònh a, b bieát ñöôøng
thaúng y = ax + b qua hai ñieåm
A(1; 3), B(–1; 5)
5. Xaùc ñònh
a
a
,
,
b
b
,
,
c
c
,
,
b
b
i
i
e
e
á
á
t
t
p
p
a
a
r
r
a
a
b
b
o
o
l
l
y
y
=
=
a
a
x
x
2
2
+
+
b
b
x
x
+
+
c
c
:
:
a
a
)
)
Ñ
Ñ
i
i
q
q
u
u
a
a
b
b
a
a
ñ
ñ
i
i
e
e
å
å
m
m
A
A
(
(
0
0
;
;
–
–
1
1
)
)
,
,
B
B
(
(
1
1
;
;
–
–
1
1
)
)
,
,
C
C
(
(
3
3
;
;
0
0
)
)
.
.
b
b
)
)
C
C
o
o
ù
ù
ñ
ñ
æ
æ
n
n
h
h
I
I
(
(
1
1
;
;
4
4
)
)
v
v
a
a
ø
ø
ñ
ñ
i
i
q
q
u
u
a
a
ñ
ñ
i
i
e
e
å
å
m
m
D
D
(
(
3
3
;
;
0
0
)
)
Hoaït ñoäng 5: Cuûng coá
3'
Nhaán maïnh caùch giaûi caùc
daïng toaùn
4. BAØI TAÄP VEÀ NHAØ:
Laøm tieáp caùc baøi taäp coøn laïi
Chuaån bò kieåm tra 1 tieát chöông I, II.
Ngaøy soaïn: 10/10/2012 Chöông II: HAØM SOÁ BAÄC NHAÁT VAØ BAÄC HAI
Tieát daïy: 16 Baøøi daïy: KIEÅM TRA VIEÁT CHÖÔNG I, II
I. MUÏC TIEÂU:
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn
31
Kieán thöùc:
Cuûng coá caùc kieán thöùc veà meänh ñeà, taäp hôïp, sai soá.
Cuûng coá caùc kieán thöùc veà haøm soá: taäp xaùc ñònh, chieàu bieán thieân, ñoà thò cuûa haøm soá baäc
nhaát vaø baäc hai.
Kó naêng:
Thöïc hieän caùc pheùp toaùn veà meänh ñeà, taäp hôïp.
Tìm taäp xaùc ñònh, xeùt chieàu bieán thieân, veõ ñoà thò cuûa haøm soá baäc nhaát vaø baäc hai.
Thaùi ñoä:
Reøn luyeän tính caån thaän, chính xaùc.
II. CHUAÅN BÒ:
Giaùo vieân: Giaùo aùn. Ñeà kieåm tra.
Hoïc sinh: OÂn taäp kieán thöùc chöông I, II.
III. MA TRAÄN ÑEÀ:
Chuû ñeà
Nhaän bieát
Thoâng hieåu
Vaän duïng
Toång
TNKQ
TL
TNKQ
TL
TNKQ
TL
Meänh ñeà
2
0,5
1
0,5
1,5
Taäp hôïp
2
0,5
1
2,0
3
Sai soá
1
0,5
0,5
Haøm soá
2
0,5
1
2,0
1
2,0
5
Toång
3,5
0,5
4,0
2,0
10
IV. NOÄI DUNG ÑEÀ KIEÅM TRA:
A. Phaàn traéc nghieäm:
Caâu 1: Meänh ñeà naøo sau ñaây laø sai?
a) x Nx
2
chia heát cho 3 x chia heát cho 3 b) x Nx chia heát cho 3 x
2
chia heát
cho 3
c) x Nx
2
chia heát cho 6 x chia heát cho 6 d) x Nx
2
chia heát cho 9 x chia heát
cho 9
Câu 2: Cho meänh ñeà chöùa bieán : “xR, x
2
+2 > 0” , khi ñoù meänh ñeà phuû ñònh cuûa meänh ñeà treân
laø :
a) “xR, x
2
+2 ≤ 0” b) “xR, x
2
+2 < 0” c) “xR, x
2
+2 ≤ 0” d) “xR, x
2
+2 <
0”
Caâu 3: Cho meänh ñeà chöùa bieán P(n) : “ n laø soá chính phöông”, meänh ñeà ñuùng laø:
a) P(5) b) P(16) c) P(10) d) P(20)
Caâu 4: Haõy lieät keâ caùc phaàn töû cuûa taäp hôïp: X =
2
/ 1 0 x x x
a) X = 0 b) X =
0
c) X =
d) X =
Caâu 5: Cho tập X =
2,3,4
. Tập X có bao nhiêu tập hợp con?
a) 3 b) 6 c) 8 d) 9
Caâu 6: Khi söû duïng maùy tính boû tuùi vôùi 10 chöõ soá thaäp phaân ta ñöôïc:
8 2,828427125
. Giaù trò gaàn
ñuùng cuûa
8
chính xaùc ñeán haøng phaàn traêm laø :
a) 2,80 b) 2,81 c) 2,82 d) 2,83
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn
32
Caâu 7:
H
H
a
a
ø
ø
m
m
s
s
o
o
á
á
xxy
3
2
laø:
a) Haøm soá chaün b) Haøm soá leû c) Haøm haèng d) Haøm soá khoâng chaün khoâng leû
Caâu 8:
Điểm nào sau đây thuộc đồ thị hàm số y = 2|x–1| + 3|x| – 2 ?
a) (2; 6); b) (1; –1); c) (–2; –10); d) Cả ba điểm trên.
B. Phaàn töï luaän:
Caâu 1: (2 ñieåm) Cho hai tập hợp A[1 ; 5) và B(3 ; 6].
Xác định các tập hợp sau :A B, A B, B\A, C
R
A
Caâu 2: (2 ñieåm) Tìm miền xác định và xét tính chẵn lẻ của hàm số sau :
2
y
x 1 x 1
Caâu 3: a) (1 ñieåm ) Tìm parabol y = ax
2
+ bx + 2 bieát raèng parabol ñoù ñi qua ñieåm A(3 ; –4) vaø
coù truïc ñoái xöùng
3
x
2

.
b) ( 1 ñieåm ) Veõ ñoà thò haøm soá vöøa tìm ñöôïc ôû caâu a).
V. ÑAÙP AÙN VAØ BIEÅU ÑIEÅM:
A. Phaàn traéc nghieäm:
1d) 2c) 3b) 4c) 5c) 6d) 7b) 8a)
B. Töï luaän:
Caâu 1: A B = (3; 5), A B = [1; 6], B\A = [5; 6], C
R
A = (–; 1)[3; +)
Caâu 2: D = R \ {–1; 1}; Haøm soá chaün
Caâu 3: a)
9a 3b 2 4
b3
2a 2
1
a
3
b1


b)
-6 -5 -4 -3 -2 -1 1 2 3 4 5
-5
-4
-3
-2
-1
1
2
3
4
5
x
y
O
VI. KEÁT QUAÛ KIEÅM TRA:
Lôùp
Só soá
0 – 3,4
3,5 – 4,9
5,0 – 6,4
6,5 – 7,9
8,0 – 10
SL
%
SL
%
SL
%
SL
%
SL
%
10A3
44
10A5
42
10A7
44
10A10
42
10A11
38
Ngaøy soaïn: 20/10/2012 Chöông III: PHÖÔNG TRÌNH. HEÄ PHÖÔNG TRÌNH
Tieát daïy: 17 Baøøi 1: ÑAÏI CÖÔNG VEÀ PHÖÔNG TRÌNH
I. MUÏC TIEÂU:
Kieán thöùc:
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn
33
Hieåu khaùi nieäm phöông trình, nghieäm cuûa phöông trình.
Hieåu ñònh nghóa hai phöông trình töông ñöông vaø caùc pheùp bieån ñoåi töông ñöông.
Bieát khaùi nieäm phöông trình heä quaû.
Kó naêng:
Nhaän bieát moät soá cho tröôùc laø nghieäm cuûa pt ñaõ cho, nhaän bieát ñöôïc hai pt töông ñöông.
Neâu ñöôïc ñieàu kieän xaùc ñònh cuûa phöông trình.
Bieát bieán ñoåi töông ñöông phöông trình.
Thaùi ñoä:
Reøn luyeän tính caån thaän, chính xaùc.
II. CHUAÅN BÒ:
Giaùo vieân: Giaùo aùn.
Hoïc sinh: SGK, vôû ghi. OÂn taäp kieán thöùc veà phöông trình ñaõ hoïc.
III. HOAÏT ÑOÄNG DAÏY HOÏC:
1. OÅn ñònh toå chöùc: Kieåm tra só soá lôùp.
2. Kieåm tra baøi cuõ: (3')
H. Tìm taäp xaùc ñònh cuûa haøm soá: y = f(x) =
x1
; y = g(x) =
x
x1
Ñ. D
f
= [1; +); D
g
= R \ {–1}
3. Giaûng baøi môùi:
TL
Hoaït ñoäng cuûa Giaùo vieân
Hoaït ñoäng cuûa Hoïc sinh
Noäi dung
Hoaït ñoäng 1: Tìm hieåu khaùi nieäm phöông trình moät aån
10'
Cho HS nhaéc laïi caùc kieán
thöùc ñaõ bieát veà phöông trình.
H1. Cho ví duï veà phöông trình
moät aån, hai aån ñaõ bieát?
H2. Cho ví duï veà phöông trình
moät aån coù moät nghieäm, hai
nghieäm, voâ soá nghieäm, voâ
nghieäm?
Caùc nhoùm thaûo luaän, traû lôøi
Ñ1. 2x + 3 = 0; x
2
– 3x + 2 =
0;
x – y = 1
Ñ2.
a) 2x + 3 = 0 –> S =
3
2
b) x
2
– 3x + 2 = 0 –> S =
{1,2}
c) x
2
– x + 2 = 0 –> S =
d)
x 1 x 1 2
–>S=[–
1;1]
I. Khaùi nieäm phöông trình
1. Phöông trình moät aån
Phöông trình aån x laø meänh
ñeà chöùa bieán coù daïng:
f(x) = g(x) (1)
trong ñoù f(x), g(x) laø nhöõng
bieåu thöùc cuûa x.
x
0
R ñgl nghieäm cuûa (1)
neáu f(x
0
) = g(x
0
) ñuùng.
Giaûi (1) laø tìm taäp nghieäm S
cuûa (1).
Neáu (1) voâ nghieäm thì S =
.
Hoaït ñoäng 2: Tìm hieåu ñieàu kieän xaùc ñònh cuûa phöông trình
10'
H1. Tìm ñieàu kieän cuûa caùc
phöông trình sau:
a) 3 – x
2
=
x
2x
b)
2
1
x3
x1

(Neâu ñk xaùc ñònh cuûa töøng
Ñ1.
a) 2 – x > 0 x < 2
b)
2
x 1 0
x 3 0


x3
x1


2. Ñieàu kieän cuûa moät phöông
trình
Ñieàu kieän xaùc ñònh cuûa (1) laø
ñieàu kieän cuûa aån x ñeå f(x) vaø
g(x) coù nghóa.
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn
34
bieåu thöùc)
Hoaït ñoäng 3: Tìm hieåu khaùi nieäm phöông trình nhieàu aån
7'
H1. Cho ví duï veà phöông trình
nhieàu aån?
H2. Chæ ra moät soá nghieäm cuûa
caùc phöông trình ñoù?
H3. Nhaän xeùt veà nghieäm vaø
soá nghieäm cuûa caùc phöông
trình treân?
Ñ1. a) 2x + y = 5
b) x + y – z = 7
Ñ2. a) (2; 1), (1; 3), …
b) (3; 4; 0), (2; 4; –1), …
Ñ3. Moãi nghieäm laø moät boä soá
cuûa caùc aån.
Thoâng thöôøng phöông trình coù
voâ soá nghieäm.
3. Phöông trình nhieàu aån
Daïng f(x,y) = g(x,y), …
Hoaït ñoäng 4: Tìm hieåu khaùi nieäm phöông trình chöùa tham soá
10'
H1. Cho ví duï phöông trình
chöùa tham soá?
H2. Khi naøo phöông trình ñoù
voâ nghieäm, coù nghieäm?
Ñ1. a) (m + 1)x – 3 = 0
b) x
2
– 2x + m = 0
Ñ2.
a) coù nghieäm khi m ≠ –1
–> nghieäm x =
3
m1
b) coù nghieäm khi  = 1–m ≥0
m ≤ 1
–> nghieäm x = 1
1m
4. Phöông trình chöùa tham
soá
Trong moät phöông trình, ngoaøi
caùc chöõ ñoùng vai troø aån soá coøn
coù theå coù caùc chöõ khaùc ñöôïc
xem nhö nhöõng haèng soá vaø
ñöôïc goïi laø tham soá.
Giaûi vaø bieän luaän phöông
trình chöùa tham soá nghóa laø
xeùt xem vôùi giaù trò naøo cuûa
tham soá thì phöông trình voâ
nghieäm, coù nghieäm vaø tìm caùc
nghieäm ñoù.
Hoaït ñoäng 5: Cuûng coá
3'
Nhaán maïnh caùc khaùi nieäm veà
phöông trình ñaõ hoïc.
4. BAØI TAÄP VEÀ NHAØ:
Tìm ñieàu kieän xaùc ñònh cuûa caùc phöông trình trong baøi 3, 4 SGK.
Ñoïc tieáp baøi "Ñaïi cöông veà phöông trình"
Ngaøy soaïn: 20/10/2012 Chöông III: PHÖÔNG TRÌNH. HEÄ PHÖÔNG TRÌNH
Tieát daïy: 18 Baøøi 1: ÑAÏI CÖÔNG VEÀ PHÖÔNG TRÌNH (tt)
I. MUÏC TIEÂU:
Kieán thöùc:
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn
35
Hieåu khaùi nieäm phöông trình, nghieäm cuûa phöông trình.
Hieåu ñònh nghóa hai phöông trình töông ñöông vaø caùc pheùp bieån ñoåi töông ñöông.
Bieát khaùi nieäm phöông trình heä quaû.
Kó naêng:
Nhaän bieát moät soá cho tröôùc laø nghieäm cuûa pt ñaõ cho, nhaän bieát ñöôïc hai pt töông ñöông.
Neâu ñöôïc ñieàu kieän xaùc ñònh cuûa phöông trình.
Bieát bieán ñoåi töông ñöông phöông trình.
Thaùi ñoä:
Reøn luyeän tính caån thaän, chính xaùc.
II. CHUAÅN BÒ:
Giaùo vieân: Giaùo aùn.
Hoïc sinh: SGK, vôû ghi. OÂn taäp kieán thöùc veà phöông trình ñaõ hoïc.
III. HOAÏT ÑOÄNG DAÏY HOÏC:
1. OÅn ñònh toå chöùc: Kieåm tra só soá lôùp.
2. Kieåm tra baøi cuõ: (3')
H. Tìm ñieàu kieän xaùc ñònh cuûa phöông trình
2
x9
x 1 x 1

Ñ. x > 1
3. Giaûng baøi môùi:
TL
Hoaït ñoäng cuûa Giaùo vieân
Hoaït ñoäng cuûa Hoïc sinh
Noäi dung
Hoaït ñoäng 1: Tìm hieåu khaùi nieäm phöông trình töông ñöông
10'
H1. Hai pt:
2
x9
x 1 x 1

vaø 2x = 6 coù töông ñöông
khoâng?
H2. Hai phöông trình voâ
nghieäm coù töông ñöông
khoâng?
Ñ1. Töông ñöông, vì cuøng taäp
nghieäm S = {3}
Ñ2. Coù, vì cuøng taäp nghieäm
II. Phöông trình töông
ñöông vaø phöông trình heä
quaû
1. Phöông trình töông ñöông
Hai phöông trình ñgl töông
ñöông khi chuùng coù cuøng taäp
nghieäm
Chuù yù: Hai phöông trình voâ
nghieäm thì töông ñöông.
Hoaït ñoäng 2: Tìm hieåu caùc pheùp bieán ñoåi töông ñöông
15'
Xeùt caùc pheùp bieán ñoåi sau:
a) x +
1
x1
=
1
x1
+ 1
x +
1
x1
–
1
x1
=
1
x1
+ 1
–
1
x1
x = 1
b) x(x – 3) = 2x x – 3 = 2
x = 5
H1. Tìm sai laàm trong caùc
pheùp bieán ñoåi treân?
Ñ1.
a) sai vì ÑKXÑ cuûa pt laø x ≠ 1
b) sai vì ñaõ chia 2 veá cho x =
0
2. Pheùp bieán ñoåi töông
ñöông
Ñònh lí: Neáu thöïc hieän caùc
pheùp bieán ñoåi sau ñaây treân
moät phöông trình maø khoâng
laøm thay ñoåi ñieàu kieän cuûa noù
thì ta ñöôïc moät phöông trình
môùi töông ñöông:
a) Coäng hay tröø hai veá vôùi
cuøng moät soá hoaëc cuøng moät
bieåu thöùc;
b) Nhaân hoaëc chia hai veá vôùi
cuøng moät soá khaùc 0 hoaïc vôùi
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn
36
cuøng moät bieåu thöùc luoân coù
giaù trò khaùc 0.
Kí hieäu: Ta duøng kí hieäu
ñeå
chæ söï töông ñöông cuûa caùc
phöông trình.
Hoaït ñoäng 3: Tìm hieåu khaùi nieäm phöông trình heä quaû
10'
Xeùt pheùp bieán ñoåi:
8x
= x – 2 (1)
8 – x = (x–2)
2
x
2
–3x – 4 = 0
(2)
( x = –1; x = 4)
H1. Caùc nghieäm cuûa (2) coù
ñeàu laø nghieäm cuûa (1) khoâng?
Ñ1. x = –1 khoâng laø nghieäm
cuûa (1)
3. Phöông trình heä quaû
Neáu moïi nghieäm cuûa pt f(x) =
g(x) ñeàu laø nghieäm cuûa pt f
1
(x)
=g
1
(x) thì pt f
1
(x) =g
1
(x) ñgl pt
heä quaû cuûa pt f(x) = g(x).
Ta vieát f(x)=g(x)
f
1
(x)=g
1
(x)
Chuù yù: Pt heä quaû coù theå theâm
nghieäm khoâng phaûi laø nghieäm
cuûa pt ban ñaàu. Ta goïi ñoù laø
nghieäm ngoaïi lai.
Hoaït ñoäng 4: Cuûng coá
5'
Nhaán maïnh caùc pheùp bieán ñoåi
phöông trình.
Ñeå giaûi moät pt ta thöôøng
thöïc hieän caùc pheùp bieán ñoåi
töông ñöông.
Pheùp bình phöông hai veá,
nhaân hai veá cuûa pt vôùi moät ña
thöùc coù theå daãn tôùi pt heä quaû.
Khi ñoù ñeå loaïi nghieäm ngoaïi
lai ta phaûi thöû laïi caùc nghieäm
tìm ñöôïc hoaëc ñaët ñieàu kieän
phuï ñeå ñöôïc pheùp bieán ñoåi
töông ñöông.
4. BAØI TAÄP VEÀ NHAØ:
Baøi 1, 2, 3, 4 SGK.
Ñoïc tröôùc baøi "Phöông trình qui veà phöông trình baäc nhaát, baäc hai"
Ngaøy soaïn: 30/10/2012 Chöông III: PHÖÔNG TRÌNH. HEÄ PHÖÔNG TRÌNH
Tieát daïy: 19 Baøøi 2: PHÖÔNG TRÌNH QUI VEÀ
PHÖÔNG TRÌNH BAÄC NHAÁT, BAÄC HAI
I. MUÏC TIEÂU:
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn
37
Kieán thöùc:
Cuûng coá caùch giaûi phöông trình baäc nhaát, baäc hai moät aån.
Hieåu caùch giaûi vaø bieän luaän caùc phöông trình ax + b = 0, ax
2
+ bx + c = 0.
Kó naêng:
Giaûi vaø bieän luaän thaønh thaïo caùc phöông trình ax+ b=0, ax
2
+ bx + c = 0.
Thaùi ñoä:
Reøn luyeän tính caån thaän, chính xaùc.
II. CHUAÅN BÒ:
Giaùo vieân: Giaùo aùn. Baûng toùm taét caùch giaûi vaø bieän luaän phöông trình baäc nhaát, baäc hai.
Hoïc sinh: SGK, vôû ghi. OÂn taäp kieán thöùc ñaõ hoïc veà phöông trình baäc nhaát, baäc hai.
III. HOAÏT ÑOÄNG DAÏY HOÏC:
1. OÅn ñònh toå chöùc: Kieåm tra só soá lôùp.
2. Kieåm tra baøi cuõ: (3')
H. Theá naøo laø hai phöông trình töông ñöông? Taäp nghieäm vaø taäp xaùc ñònh cuûa phöông
trình khaùc nhau ôû ñieåm naøo?
Ñ. ((1) (2)) S
1
= S
2
; S D.
3. Giaûng baøi môùi:
TL
Hoaït ñoäng cuûa Giaùo vieân
Hoaït ñoäng cuûa Hoïc sinh
Noäi dung
Hoaït ñoäng 1: OÂn taäp veà phöông trình baäc nhaát
10'
Höôùng daãn caùch giaûi vaø
bieän luaän phöông trình ax + b
= 0 thoâng qua ví duï.
VD1. Cho pt:
m(x – 4) = 5x – 2 (1)
a) Giaûi pt (1) khi m = 1
b) Giaûi vaø bieän luaän pt (1)
H1. Goïi 1 HS giaûi caâu a)
H2. Bieán ñoåi (1) ñöa veà daïng
ax + b = 0
Xaùc ñònh a, b?
H3. Xeùt (2) vôùi a ≠ 0; a = 0?
HS theo doõi thöïc hieän laàn
löôït caùc yeâu caàu.
Ñ1. 4x = – 2 x = –
1
2
Ñ2. (m – 5)x + 2 – 4m = 0 (2)
a = m – 5; b = 2 – 4m
Ñ3. m ≠ 5: (2) x =
4m 2
m5
m = 5: (2) 0x – 18 = 0
(2) voâ nghieäm
I. OÂn taäp veà phöông trình
baäc nhaát, baäc hai
1. Phöông trình baäc nhaát
ax + b = 0 (1)
Heä soá
Keát luaän
a ≠ 0
(1) coù nghieäm
x = –
b
a
a = 0
b ≠ 0
(1) voâ nghieäm
b = 0
(1) nghieäm
ñuùng vôùi moïi x
Khi a ≠ 0 pt (1) ñgl phöông
trình baäc nhaát moät aån.
Hoaït ñoäng 2: OÂn taäp veà phöông trình baäc hai
15'
Höôùng daãn caùch giaûi vaø
bieän luaän ph.trình ax
2
+ bx + c
= 0 thoâng qua ví duï.
VD2. Cho pt:
x
2
– 2mx + m
2
– m + 1 = 0
(2)
a) Giaûi (2) khi m = 2
HS theo doõi thöïc hieän laàn
löôït caùc yeâu caàu.
2. Phöông trình baäc hai
ax
2
+ bx + c = 0 (a ≠ 0) (2)
= b
2
– 4ac
Keát luaän
> 0
(2) coù 2
nghieäm phaân
bieät
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn
38
b) Giaûi vaø bieän luaän (2)
H1. Goïi 1 HS giaûi caâu a)
H2. Tính ?
H3. Xeùt caùc tröôøng hôïp > 0,
= 0, < 0?
Ñ1. (2) x
2
– 4x + 3 = 0
x = 1; x = 3
Ñ2. = 4(m – 1)
Ñ3. m > 1: > 0 (2) coù 2
nghieäm x
1,2
= m
m1
m = 1: = 0 (2) coù
nghieäm keùp x = m = 1
m < 1: < 0 (2) voâ
nghieäm
x
1,2
=
b
2a
= 0
(2) coù nghieäm
keùp x = –
b
2a
< 0
(2) voâ nghieäm
Hoaït ñoäng 3: OÂn taäp veà ñònh lí Viet
10'
Luyeän taäp vaän duïng ñònh lí
Viet.
VD3. Chöùng toû pt sau coù 2
nghieäm x
1
, x
2
vaø tính x
1
+ x
2
,
x
1
x
2
: x
2
– 3x + 1 = 0
VD4. Pt 2x
2
– 3x – 1 = 0 coù 2
nghieäm x
1
, x
2
. Tính x
1
2
+ x
2
2
?
Ñ. = 5 > 0 pt coù 2
nghieäm phaân bieät
x
1
+ x
2
= 3, x
1
x
2
= 1
Ñ. x
1
+ x
2
=
3
2
, x
1
x
2
= –
1
2
x
1
2
+ x
2
2
= (x
1
+ x
2
)
2
–2x
1
x
2
=
7
4
3. Ñònh lí Viet
Neáu phöông trình baäc hai:
ax
2
+ bx + c = 0 (a≠0)
coù hai nghieäm x
1
, x
2
thì:
x
1
+ x
2
= –
b
a
, x
1
x
2
=
c
a
Ngöôïc laïi, neáu hai soá u, v coù
toång u + v = S vaø tích uv = P
thì u vaø v laø caùc nghieäm cuûa
phöông trình x
2
– Sx + P = 0
Hoaït ñoäng 4: Cuûng coá
5'
Nhaán maïnh caùc böôùc giaûi vaø
bieän luaän pt ax + b = 0, pt baäc
hai.
Caùc tính chaát veà nghieäm soá
cuûa phöông trình baäc hai:
– Caùch nhaåm nghieäm
– Bieåu thöùc ñoái xöùng cuûa caùc
nghieäm
– Daáu cuûa nghieäm soá
HS töï oân taäp laïi caùc vaán ñeà
4. BAØI TAÄP VEÀ NHAØ:
Baøi 2, 3, 5, 8 SGK.
Ñoïc tieáp baøi "Phöông trình qui veà phöông trình baäc nhaát, baäc hai"
Ngaøy soaïn: 30/10/2012 Chöông III: PHÖÔNG TRÌNH. HEÄ PHÖÔNG TRÌNH
Tieát daïy: 20 Baøøi 2: PHÖÔNG TRÌNH QUI VEÀ
PHÖÔNG TRÌNH BAÄC NHAÁT, BAÄC HAI (tt)
I. MUÏC TIEÂU:
Kieán thöùc:
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn
39
Hieåu caùch giaûi caùc pt qui veà daïng baäc nhaát, baäc hai, pt chöùa aån ôû maãu, pt coù chöùa daáu
GTTÑ, pt chöùa caên ñôn giaûn, pt tích.
Kó naêng:
Giaûi thaønh thaïo pt ax+ b=0, pt baäc hai.
Giaûi ñöôïc caùc pt qui veà baäc nhaát, baäc hai.
Bieát giaûi pt baäc hai baèng MTBT.
Thaùi ñoä:
Reøn luyeän tính caån thaän, chính xaùc.
Luyeän tö duy linh hoaït qua vieäc bieán ñoåi phöông trình.
II. CHUAÅN BÒ:
Giaùo vieân: Giaùo aùn. Heä thoáng caùch giaûi caùc daïng phöông trình.
Hoïc sinh: SGK, vôû ghi. OÂn taäp caùc kieán thöùc veà GTTÑ, caên thöùc baäc hai.
III. HOAÏT ÑOÄNG DAÏY HOÏC:
1. OÅn ñònh toå chöùc: Kieåm tra só soá lôùp.
2. Kieåm tra baøi cuõ: (3')
H. Neâu ñieàu kieän xaùc ñònh cuûa bieåu thöùc chöùa bieán ôû maãu?
AÙp duïng: Tìm ñkxñ cuûa f(x) =
2
x 3x 2
2x 3

Ñ. f(x) =
P(x)
Q(x)
–> Q(x) ≠ 0; f(x) xaùc ñònh khi x ≠ –
3
2
3. Giaûng baøi môùi:
TL
Hoaït ñoäng cuûa Giaùo vieân
Hoaït ñoäng cuûa Hoïc sinh
Noäi dung
Hoaït ñoäng 1: OÂn taäp phöông trình chöùa aån ôû maãu
10'
Cho HS nhaéc laïi caùc böôùc
giaûi phöông trình chöùa aån ôû
maãu thöùc.
VD1. Giaûi phöông trình:
2
x 3x 2 2x 5
2x 3 4
(1)
H1. Neâu ñkxñ cuûa (1)
H2. Bieán ñoåi phöông trình (1)
HS phaùt bieåu
Ñ1. 2x + 3 ≠ 0 x ≠ –
3
2
(*)
Ñ2. (1) 16x + 23 = 0
x = –
23
16
(thoaû ñk (*))
II. Phöông trình qui veà
phöông trình baäc nhaát, baäc
hai
1. Phöông trình chöùa aån ôû
maãu
Daïng
P(x)
Q(x)
B1: ÑKXÑ: Q(x) ≠ 0
B2: Giaûi phöông trình
B3: Ñoái chieáu nghieäm tìm
ñöôïc vôùi ÑKXÑ ñeå choïn
nghieäm thích hôïp.
Hoaït ñoäng 2: OÂn taäp veà phöông trình chöùa giaù trò tuyeät ñoái
15'
H1. Nhaéc laïi ñònh nghóa
GTTÑ ?
VD2. Giaûi phöông trình:
x 3 2x 1
(2)
Ñ1.
A neáu A 0
A
A neáu A 0

Ñ.
C1:
2. Phöông trình chöùa GTTÑ
Ñeå giaûi phöông trình chöùa
GTTÑ ta tìm caùch khöû daáu
GTTÑ:
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn
40
Höôùng daãn HS laøm theo 2
caùch. Töø ñoù ruùt ra nhaän xeùt.
VD3. Giaûi phöông trình:
2x 1 x 2
(3)
H1. Ta neân duøng caùch giaûi
naøo?
Chuù yù a
2
– b
2
= (a – b)(a +
b)
+ Neáu x ≥ 3 thì (2) trôû thaønh:
x – 3 = 2x + 1 x = –4 (loaïi)
+ Neáu x < 3 thì (2) trôû thaønh:
–x + 3 = 2x + 1 x=
2
3
(thoaû)
C2:
(2) (x – 3)
2
= (2x + 1)
2
3x
2
+ 10x – 8 = 0
x = –4; x =
2
3
Thöû laïi: x = –4 (loaïi),
x =
2
3
(thoaû)
Ñ1. Bình phöông 2 veá:
(3) (2x – 1)
2
= (x + 2)
2
(x – 3)(3x + 1) = 0
x = 3; x = –
1
3
– Duøng ñònh nghóa;
– Bình phöông 2 veá.
Chuù yù: Khi bình phöông 2 veá
cuûa phöông trình ñeå ñöôïc pt
töông ñöông thì caû 2 veá ñeàu
phaûi khoâng aâm.
f(x) 0
f(x) g(x)
f(x) g(x)
f(x) 0
f(x) g(x)


g(x) 0
f(x) g(x)
f(x) g(x)

f(x) g(x)
f(x) g(x)
f(x) g(x)


Hoaït ñoäng 3: AÙp duïng
10'
VD4. Giaûi caùc phöông trình:
a)
2
2x 3 4 24
2
x 3 x 3
x9

b)
2
2x 5 x 5x 1
c)
2x 1 5x 2
Ñ.
a) ÑKXÑ: x ≠ 3
S =
b) S = {–6, 1}
c) S = {–1, –
1
7
}
Hoaït ñoäng 4: Cuûng coá
5'
Nhaán maïnh caùch giaûi caùc
daïng phöông trình
4. BAØI TAÄP VEÀ NHAØ:
Baøi 1, 6 SGK.
Ñoïc tieáp baøi "Phöông trình qui veà phöông trình baäc nhaát, baäc hai"
Ngaøy soaïn: 1/11/2012 Chöông III: PHÖÔNG TRÌNH. HEÄ PHÖÔNG TRÌNH
Tieát daïy: 21 Baøøi 3: PHÖÔNG TRÌNH VAØ HEÄ PHÖÔNG TRÌNH
BAÄC NHAÁT NHIEÀU AÅN
I. MUÏC TIEÂU:
Kieán thöùc:
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn
41
Naém vöõng khaùi nieäm pt baäc nhaát hai aån, heä pt baäc nhaát hai aån vaø taäp nghieäm cuûa chuùng.
Hieåu roõ phöông phaùp coäng ñaïi soá vaø phöông phaùp theá.
Kó naêng:
Giaûi ñöôïc vaø bieåu dieãn ñöôïc taäp nghieäm cuûa pt baäc nhaát hai aån.
Giaûi thaønh thaïo heä pt baäc nhaát hai aån baèng phöông phaùp coäng vaø phöông phaùp theá.
Giaûi ñöôïc heä pt baäc nhaát ba aån ñôn giaûn.
Giaûi ñöôïc moät soá baøi toaùn thöïc teá ñöa veà vieäc laäp vaø giaûi heä pt baäc nhaát hai, ba aån.
Bieát duøng MTBT ñeå giaûi heä pt baäc nhaát hai, ba aån.
Thaùi ñoä:
Reøn luyeän tính caån thaän, chính xaùc.
Luyeän tö duy linh hoaït thoâng qua vieäc bieán ñoåi heä phöông trình.
II. CHUAÅN BÒ:
Giaùo vieân: Giaùo aùn. Hình veõ minh hoaï.
Hoïc sinh: SGK, vôû ghi. OÂn taäp kieán thöùc ñaõ hoïc veà heä pt baäc nhaát hai aån.
III. HOAÏT ÑOÄNG DAÏY HOÏC:
1. OÅn ñònh toå chöùc: Kieåm tra só soá lôùp.
2. Kieåm tra baøi cuõ: (3')
H. Neâu daïng cuûa heä phöông trình baäc nhaát hai aån vaø phöông phaùp giaûi?
Ñ. Phöông phaùp theá, phöông phaùp coäng ñaïi soá.
3. Giaûng baøi môùi:
TL
Hoaït ñoäng cuûa Giaùo vieân
Hoaït ñoäng cuûa Hoïc sinh
Noäi dung
Hoaït ñoäng 1: OÂn taäp phöông trình baäc nhaát hai aån
10'
H1. Theá naøo laø moät nghieäm
cuûa (1)?
H2. Tìm caùc nghieäm cuûa pt:
3x – 2y = 7
(Moãi nhoùm chæ ra moät soá
nghieäm)
H3. Xaùc ñònh caùc ñieåm (1; –
2), (–1; –5), (3; 1), … treân mp
Oxy?
Nhaän xeùt?
Ñ1. Nghieäm laø caëp (x
0
; y
0
)
thoaû ax
0
+ by
0
= c.
Ñ2.
(1; –2), (–1; –5), (3; 1), …
-9 -8 -7 -6 -5 -4 -3 -2 -1 1 2 3 4 5 6 7 8 9 10
-11
-10
-9
-8
-7
-6
-5
-4
-3
-2
-1
1
2
3
4
5
6
7
8
x
y
Caùc ñieåm naèm treân ñöôøng
thaúng y =
3x 7
2
1. Phöông trình baäc nhaát hai
aån
Daïng: ax + by = c (1)
trong ñoù a
2
+ b
2
≠ 0
Chuù yù:
a b 0
c0

(1) voâ nghieäm
a b 0
c0

moïi caëp
(x
0
;y
0
) ñeàu laø nghieäm
b ≠ 0: (1)
y =
ac
x
bb

Toång quaùt:
Phöông trình (1) luoân coù voâ
soá nghieäm.
Bieåu dieãn hình hoïc taäp
nghieäm cuûa (1) laø moät ñöôøng
thaúng trong mp Oxy.
Hoaït ñoäng 2: OÂn taäp Heä hai phöông trình baäc nhaát hai aån
17'
H1. Nhaéc laïi caùc caùch giaûi (2)
AÙp duïng: Giaûi heä:
Ñ1. Moãi nhoùm giaûi theo moät
caùch.
2. Heä hai phöông trình baäc
nhaát hai aån
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn
42
4x 3y 9
2x y 5


HD hoïc sinh nhaän xeùt yù
nghóa hình hoïc cuûa taäp
nghieäm cuûa (2).
4
2
-2
-5
5
d
2
d
1
12 1
x ;y
55




(d
1
): a
1
x + b
1
y = c
1
(d
2
): a
2
x + b
2
y = c
2
+ (d
1
), (d
2
) caét nhau (2) coù
1 nghieäm
+ (d
1
)//(d
2
) (2) voâ nghieäm
+ (d
1
)(d
2
) (2) voâ soá
nghieäm
4
2
-2
-5
5
d
2
d
1
Daïng:
1 1 1
2 2 2
a x b y c
a x b y c


(2)
Caëp soá (x
0
; y
0
) laø nghieäm
cuûa (2) neáu noù laø nghieäm cuûa
caû 2 phöông trình cuûa (2).
Giaûi (2) laø tìm taäp nghieäm
cuûa (2).
4
2
-2
-5
5
d
1
d
2
Hoaït ñoäng 3: Giôùi thieäu caùch giaûi heä phöông trình baèng ñònh thöùc
10'
H1. Giaûi caùc heä pt baèng ñònh
thöùc:
a)
5x 2y 9
4x 3y 2

b)
2x 3y 13
7x 4y 2


Ñ1.
a) D = 23, D
x
= –23, D
y
= 46
Nghieäm (x; y) = (–1; 2)
b) D = 29, D
x
= 58, D
y
= –87
Nghieäm (x; y) = (2; –3)
D =
11
22
ab
ab
D
x
=
11
22
cb
cb
, D
y
=
11
22
ac
ac
D ≠ 0: (2) coù nghieäm duy
nhaát
y
x
D
D
x ;y
DD




D = 0 vaø (D
x
≠ 0 hoaëc D
y
≠0)
(2) voâ nghieäm
D = D
x
= D
y
= 0: (2) voâ soá
nghieäm
Hoaït ñoäng 4: Cuûng coá
3'
Nhaéc laïi caùc caùch giaûi heä
phöông trình baäc nhaát hai aån
4. BAØI TAÄP VEÀ NHAØ:
1, 2, 3, 4 SGK.
Ñoïc tieáp baøi "Phöông trình vaø heä phöông trình baäc nhaát nhieàu aån"
Ngaøy soaïn: 1/11/2012 Chöông III: PHÖÔNG TRÌNH. HEÄ PHÖÔNG TRÌNH
Tieát daïy: 22 Baøøi 3: PHÖÔNG TRÌNH VAØ HEÄ PHÖÔNG TRÌNH
BAÄC NHAÁT NHIEÀU AÅN (tt)
I. MUÏC TIEÂU:
Kieán thöùc:
Naém vöõng khaùi nieäm pt baäc nhaát hai aån, heä pt baäc nhaát hai aån vaø taäp nghieäm cuûa chuùng.
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn
43
Hieåu roõ phöông phaùp coäng ñaïi soá vaø phöông phaùp theá.
Kó naêng:
Giaûi ñöôïc vaø bieåu dieãn ñöôïc taäp nghieäm cuûa pt baäc nhaát hai aån.
Giaûi thaønh thaïo heä pt baäc nhaát hai aån baèng phöông phaùp coäng vaø phöông phaùp theá.
Giaûi ñöôïc heä pt baäc nhaát ba aån ñôn giaûn.
Giaûi ñöôïc moät soá baøi toaùn thöïc teá ñöa veà vieäc laäp vaø giaûi heä pt baäc nhaát hai, ba aån.
Bieát duøng MTBT ñeå giaûi heä pt baäc nhaát hai, ba aån.
Thaùi ñoä:
Reøn luyeän tính caån thaän, chính xaùc.
Luyeän tö duy linh hoaït thoâng qua vieäc bieán ñoåi heä phöông trình.
II. CHUAÅN BÒ:
Giaùo vieân: Giaùo aùn. Hình veõ minh hoaï.
Hoïc sinh: SGK, vôû ghi. OÂn taäp kieán thöùc ñaõ hoïc veà heä pt baäc nhaát hai aån.
III. HOAÏT ÑOÄNG DAÏY HOÏC:
1. OÅn ñònh toå chöùc: Kieåm tra só soá lôùp.
2. Kieåm tra baøi cuõ: (3')
H. Giaûi heä phöông trình sau baèng ñònh thöùc:
3x 5y 6
4x 7y 8

Ñ. D = 41, D
x
= 2, D
y
= –48 Nghieäm (x; y) = (
2 48
;
41 41
)
3. Giaûng baøi môùi:
TL
Hoaït ñoäng cuûa Giaùo vieân
Hoaït ñoäng cuûa Hoïc sinh
Noäi dung
Hoaït ñoäng 1: Tìm hieåu caùch giaûi Heä phöông trình baäc nhaát 3 aån
10'
GV höôùng daãn tìm nghieäm
cuûa heä phöông trình:
x 3y 2z 1 (1)
3
4y 3z (2)
2
2z 3 (3)

–> Heä phöông trình treân coù
daïng tam giaùc.
(3) z =
3
2
(2) y =
3
4
(1) x =
17
4
II. Heä phöông trình baäc nhaát
3 aån
Phöông trình baäc nhaát 3 aån:
ax + by + cz = d
trong ñoù a
2
+ b
2
+ c
2
≠ 0
Heä 3 pt baäc nhaát 3 aån:
1 1 1 1
2 2 2 2
3 3 3 3
a x b y c y d
a x b y c y d
a x b y c y d
(4)
Moãi boä soá (x
0
; y
0
; z
0
) nghieäm
ñuùng caû 3 pt cuûa heä ñgl
nghieäm cuûa heä (4).
Phöông phaùp Gauss: Moïi heä
phöông trình baäc nhaát 3 aån
ñeàu bieán ñoåi ñöôïc veà daïng tam
giaùc baèng phöông phaùp khöû
daàn aån soá.
Hoaït ñoäng 2: Luyeän taäp giaûi heä phöông trình baäc nhaát 3 aån
10'
GV höôùng daãn caùch vaän
duïng phöông phaùp Gauss.
VD1: Giaûi heä phöông trình:
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn
44
(*)
1
x 2y 2z
2
y z 3
10z 5

7
x
2
5
y
2
1
z
2


1
x 2y 2z (1)
2
2x 3y 5z 2 (2)
4x 7y z 4 (3)
(*)
Hoaït ñoäng 3: Luyeän taäp giaûi toaùn baèng caùch laäp heä phöông trình
10'
H1. Nhaéc laïi caùc böôùc giaûi
toaùn baèng caùch laäp phöông
trình ?
Ñ1.
1) Choïn aån, ñk cuûa aån.
2) Bieåu dieãn caùc ñaïi löôïng
lieân quan theo aån.
3) Laäp pt, heä pt.
4) Giaûi pt, heä pt
5) Ñoái chieáu ñk ñeå choïn
nghieäm thích hôïp.
x (ñ): giaù tieàn moät quaû quyùt
y (ñ): giaù tieàn moät quaû cam
10x 7y 17800
12x 6y 18000


x = 800, y = 1400
VD2: Hai baïn Vaân vaø Lan
ñeán cöûa haøng mua traùi caây.
Baïn Vaân mua 10 quaû quyùt, 7
quaû cam vôùi giaù tieàn 17800 ñ.
Baïn Lan mua 12 quaû quyùt, 6
quaû cam heát 18000 ñ. Hoûi giaù
tieàn moãi quaû quyùt vaø moãi quaû
cam laø bao nhieâu?
Hoaït ñoäng 4: Höôùng daãn söû duïng MTBT ñeå giaûi heä phöông trình
7'
Höôùng daãn HS söû duïng
MTBT ñeå giaûi heä pt.
a)
x 0.048780487
y 1.170731707

b)
x 0.217821782
y 1.297029703
z 0.386138613

VD3: Giaûi caùc heä ph.trình:
a)
3x 5y 6
4x 7y 8

b)
2x 3y 4z 5
4x 5y z 6
3x 4y 3z 7
Hoaït ñoäng 5: Cuûng coá
3'
Nhaán maïnh caùch giaûi baèng
phöông phaùp Gauss.
4. BAØI TAÄP VEÀ NHAØ:
5, 6, 7 SGK.
Ngaøy soaïn: 10/11/2012 Chöông III: PHÖÔNG TRÌNH. HEÄ PHÖÔNG TRÌNH
Tieát daïy: 23 Baøøi 3: BAØI TAÄP PHÖÔNG TRÌNH
VAØ HEÄ PHÖÔNG TRÌNH BAÄC NHAÁT NHIEÀU AÅN
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn
45
I. MUÏC TIEÂU:
Kieán thöùc:
Cuûng coá caùch giaûi phöông trình, heä phöông trình baäc nhaát nhieàu aån.
Kó naêng:
Giaûi thaønh thaïo heä phöông trình baäc nhaát 2 aån.
Bieát giaûi heä phöông trình baäc nhaát 3 aån.
Vaän duïng thaønh thaïo vieäc giaûi toaùn baèng caùch laäp heä phöông trình.
Thaùi ñoä:
Reøn luyeän tính caån thaän, chính xaùc.
Luyeän tö duy linh hoaït thoâng qua vieäc giaûi heä phöông trình.
II. CHUAÅN BÒ:
Giaùo vieân: Giaùo aùn. Heä thoáng baøi taäp.
Hoïc sinh: SGK, vôû ghi. OÂn taäp caùch giaûi heä phöông trình baäc nhaát nhieàu aån.
III. HOAÏT ÑOÄNG DAÏY HOÏC:
1. OÅn ñònh toå chöùc: Kieåm tra só soá lôùp.
2. Kieåm tra baøi cuõ: (Loàng vaøo quaù trình luyeän taäp)
H.
Ñ.
3. Giaûng baøi môùi:
TL
Hoaït ñoäng cuûa Giaùo vieân
Hoaït ñoäng cuûa Hoïc sinh
Noäi dung
Hoaït ñoäng 1: Luyeän kyõ naêng giaûi heä phöông trình baäc nhaát 2 aån
15'
H1. Neân duøng phöông phaùp
naøo ñeå giaûi?
H2. Neân thöïc hieän pheùp bieán
ñoåi naøo?
Höôùng daãn theâm phöông
phaùp ñònh thöùc.
Ñ1. Coù theå duøng phöông phaùp
theá hoaëc coäng ñaïi soá.
a)
11 5
;
77



b)
97
;
11 11



Ñ2.
c) Qui ñoàng, khöû maãu
91
;
86



d) Nhaân 2 veá vôùi 10
(2; 0,5)
1. Giaûi caùc phöông trình:
a)
2x 3y 1
x 2y 3


b)
3x 4y 5
4x 2y 2


c)
2 1 2
xy
3 2 3
1 3 1
xy
3 4 2


d)
0,3x 0,2y 0,5
0,5x 0,4y 1,2


Hoaït ñoäng 2: Luyeän kyõ naêng giaûi heä phöông trình baäc nhaát 3 aån
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn
46
10'
Höôùng daãn HS vaän duïng
phöông phaùp Gauss.
(Cho HS nhaän xeùt vaø töï ruùt ra
caùch bieán ñoåi thích hôïp)
a)
11
x
14
5
y
2
1
z
7

b)
x1
y1
z2
2. Giaûi caùc phöông trình sau:
a)
x 3y 2z 7
2x 4y 3z 8
3x y z 5
b)
x 3y 2z 8
2x 2y z 6
3x y z 6
Hoaït ñoäng 3: Luyeän kyõ naêng giaûi toaùn baèng caùch laäp heä phöông trình
15'
H1. Neâu caùc böôùc giaûi toaùn
baèng caùch laäp heä phöông
trình?
Ñ1.
3. Goïi x laø soá aùo do daây
chuyeàn thöù nhaát may ñöôïc.
y laø soá aùo do daây chuyeàn thöù
hai may ñöôïc.
ÑK: x, y nguyeân döông
Ta coù heä phöông trình:
x y 930
1,18x 1,15y 1083


x 450
y 480
4. Goïi x (ngaøn ñoàng) laø giaù
baùn moät aùo.
y (ngaøn ñoàng) laø giaù baùn moät
quaàn.
z (ngaøn ñoàng) laø giaù baùn moät
vaùy.
ÑK: x, y, z > 0
Ta coù heä phöông trình:
12x 21y 18z 5349
16x 24y 12z 5600
24x 15y 12z 5259
x 86
y 125
z 98
3. Coù hai daây chuyeàn may aùo
sô mi. Ngaøy thöù nhaát caû hai
daây chuyeàn may ñöôïc 930 aùo.
Ngaøy thöù hai do daây chuyeàn
thöù nhaát taêng naêng suaát 18%,
daây chuyeàn thöù hai taêng naêng
suaát 15% neân caû hai daây
chuyeàn may ñöôïc 1083 aùo.
Hoûi trong ngaøy thöù nhaát moãi
daây chuyeàn may ñöôïc bao
nhieâu aùo sô mi?
4. Moät cöûa haøng baùn aùo sô mi,
quaàn aâu nam vaø vaùy nöõ. Ngaøy
thöù nhaát baùn ñöôïc 12 aùo, 21
quaàn vaø 18 vaùy, doanh thu laø
5349000 ñoàng. Ngaøy thöù hai
baùn ñöôïc 16 aùo, 24 quaàn vaø
12 vaùy, doanh thu laø 5600000
ñoàng. Ngaøy thöù ba baùn ñöôïc
24 aùo, 15 quaàn vaø 12 vaùy,
doanh thu laø 5259000 ñoàng.
Hoûi giaù baùn moãi aùo, moãi quaàn
vaø noãi vaùy laø bao nhieâu?
Hoaït ñoäng 4: Cuûng coá
3'
Nhaán maïnh caùc caùch giaûi heä
phöông trình baäc nhaát hai aån,
baäc nhaát ba aån.
4. BAØI TAÄP VEÀ NHAØ:
Söû duïng MTBT ñeå giaûi caùc heä phöông trình.
Ngaøy soaïn: 10/11/2012 Chöông III: PHÖÔNG TRÌNH. HEÄ PHÖÔNG TRÌNH
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn
47
Tieát daïy: 24 THÖÏC HAØNH GIAÛI TOAÙN TREÂN MAÙY TÍNH CAÀM TAY
I. MUÏC TIEÂU:
Kieán thöùc:
Cuûng coá caùch giaûi phöông trình, heä phöông trình baäc nhaát nhieàu aån.
Kó naêng:
Söû duïng MTBT thaønh thaïo ñeå giaûi heä phöông trình baäc nhaát 2 aån.
Bieát söû duïng MTBT ñeå giaûi heä phöông trình baäc nhaát 3 aån.
Thaùi ñoä:
Reøn luyeän tính caån thaän, chính xaùc.
II. CHUAÅN BÒ:
Giaùo vieân: Giaùo aùn. Heä thoáng baøi taäp.
Hoïc sinh: SGK, vôû ghi. Maùy tính boû tuùi.
III. HOAÏT ÑOÄNG DAÏY HOÏC:
1. OÅn ñònh toå chöùc: Kieåm tra só soá lôùp.
2. Kieåm tra baøi cuõ: (Loàng vaøo quaù trình luyeän taäp)
H.
Ñ.
3. Giaûng baøi môùi:
TL
Hoaït ñoäng cuûa Giaùo vieân
Hoaït ñoäng cuûa Hoïc sinh
Noäi dung
Hoaït ñoäng 1: Söû duïng MTBT giaûi heä phöông trình baäc nhaát 2 aån
15'
Chia nhoùm söû duïng MTBT
ñeå giaûi heä phöông trình baäc
nhaát hai aån.
Cho 4 HS giaûi baèng tay ñeå
ñoái chieáu.
a)
12
x
11
24
y
11

–>
x 1,0244
y 0,5854

b)
2
x
19
33
y
19
–>
x 0,1053
y 1,7368
c)
34
x
13
1
y
13
–>
x 2,6154
y 0,0763
d)
93
x
37
30
y
37
–>
x 2,5135
y 0,8108
1. Giaûi caùc phöông trình:
a)
3x 5y 6
4x 7y 8

b)
2x 3y 5
5x 2y 4

c)
2x 3y 5
3x 2y 8


d)
5x 3y 15
4x 5y 6


Hoaït ñoäng 2: Söû duïng MTBT giaûi heä phöông trình baäc nhaát 3 aån
10'
Chia nhoùm söû duïng MTBT
ñeå giaûi heä phöông trình baäc
nhaát ba aån.
Cho 2 HS giaûi baèng tay ñeå
ñoái chieáu.
a)
22
x
101
131
y
101
39
z
101

–>
x 0,2178
y 1,2970
z 0,3861

2. Giaûi caùc phöông trình sau:
a)
2x 3y 4z 5
4x 5y z 6
3x 4y 3z 7
b)
x 2y 3z 2
2x y 2z 3
2x 3y z 5
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn
48
b)
x4
11
y
7
12
z
7

–>
x4
y 1,5714
z 1,7143

Hoaït ñoäng 3: Luyeän kyõ naêng söû duïng MTBT ñeå giaûi heä phöông trình
15'
Cho HS söû duïng MTBT ñeå
giaûi vaø baùo keát quaû.
a)
x 1,5417
29
y
12
b)
x2
3
y
2
c)
x 1,8235
19
y
17
39
z
17


d)
x 4,2093
7
y
43
z 1,9302
3. Giaûi caùc heä phöông trình:
a)
2x 5y 9
4x 2y 11

b)
3x 4y 12
5x 2y 7


c)
2x 3y z 7
4x 5y 3z 6
x 2y 2z 5
d)
x 4y 2z 1
2x 3y z 6
3x 8y z 12
Hoaït ñoäng 4: Cuûng coá
3'
Nhaán maïnh:
– Khi söû duïng MTBT ñeå giaûi
heä phöông trình, thöôøng chæ
cho nghieäm gaàn ñuùng.
– Chuù yù thöù töï caùc heä soá x –>
y –> z
4. BAØI TAÄP VEÀ NHAØ:
Laøm baøi taäp oân chöông III.
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn
49
Ngaøy soaïn: 15/11/2012 Chöông III: PHÖÔNG TRÌNH. HEÄ PHÖÔNG TRÌNH
Tieát daïy: 25 Baøøi daïy: OÂN TAÄP CHÖÔNG III
I. MUÏC TIEÂU:
Kieán thöùc:
Cuûng coá caùc khaùi nieäm ñkxñ, pt töông ñöông, pt heä quaû, heä hai pt baäc nhaát hai aån.
Naém vöõng caùch giaûi phöông trình qui veà phöông trình baäc nhaát, baäc hai.
Naém ñöôïc caùch giaûi heä pt baäc nhaát hai aån.
Kó naêng:
Giaûi thaønh thaïo phöông trình qui veà phöông trình baäc nhaát, baäc hai.
Bieát vaän duïng ñònh lí Viet ñeå giaûi toaùn.
Giaûi thaønh thaïo heä phöông trình baäc nhaát hai aån.
Bieát giaûi heä pt baäc nhaát ba aån baèng pp Gause.
Thaùi ñoä:
Reøn luyeän tính caån thaän, chính xaùc.
Luyeän tö duy linh hoaït thoâng qua vieäc bieán ñoåi phöông trình.
II. CHUAÅN BÒ:
Giaùo vieân: Giaùo aùn. Heä thoáng baøi taäp.
Hoïc sinh: SGK, vôû ghi. OÂn taäp caùc kieán thöùc ñaõ hoïc veà phöông trình, heä phöông trình.
III. HOAÏT ÑOÄNG DAÏY HOÏC:
1. OÅn ñònh toå chöùc: Kieåm tra só soá lôùp.
2. Kieåm tra baøi cuõ: (Loàng vaøo quaù trình oân taäp)
H.
Ñ.
3. Giaûng baøi môùi:
TL
Hoaït ñoäng cuûa Giaùo vieân
Hoaït ñoäng cuûa Hoïc sinh
Noäi dung
Hoaït ñoäng 1: Cuûng coá caùch tìm ñkxñ, xeùt pt töông ñöông
10'
H1. Neâu ÑKXÑ cuûa caùc pt.
Töø ñoù thöïc hieän caùc pheùp
bieán ñoåi pt?
Ñ1.
a) ÑKXÑ: x ≥ 5 –> S = {6}
b) ÑKXÑ: x = 1 –> S =
c) ÑKXÑ: x > 2
–> S = {2
2
}
d) ÑKXÑ: x –> S =
1. Giaûi caùc phöông trình sau:
a)
x 5 x x 5 6
b)
1 x x x 1 2
c)
2
x8
x 2 x 2

d) 3 +
2x
= 4x
2
– x +
x3
Hoaït ñoäng 2: Luyeän kyõ naêng giaûi pt qui veà pt baäc nhaát, baäc hai
10'
H1. Neâu caùch bieán ñoåi? Caàn
chuù yù caùc ñieàu kieän gì?
Ñ1.
a) Qui ñoàng maãu.
ÑK: 2x – 1 ≠ 0 –> S =
1
9



b) Bình phöông 2 veá.
ÑK: x – 1 ≥ 0 –> S =
5
2



2. Giaûi caùc phöông trình sau:
a)
2
3x 2x 3 3x 5
2x 1 2
b)
2
x4
= x– 1
c)
4x 9
= 3 – 2x
d)
2x 1 3x 5
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn
50
c) Duøng ñònh nghóa GTTÑ.
–> S = {2, 3}
d) S =
6
4,
5




Hoaït ñoäng 3: Luyeän kyõ naêng giaûi heä pt baäc nhaát hai aån, ba aån
10'
H1. Neâu caùch giaûi?
Cho moãi nhoùm giaûi 1 heä pt
Ñ1.
a)
37
x
24
29
y
12
b)
x2
3
y
2
c)
3 3 13
x ;y ;z
5 2 10
d)
181 7 83
x ;y ;z
43 43 43
3. Giaûi caùc heä phöông trình:
a)
2x 5y 9
4x 2y 11

b)
3x 4y 12
5x 2y 7


c)
2x 3y z 7
4x 5y 3z 6
x 2y 2z 5
d)
x 4y 2z 1
2x 3y z 6
3x 8y z 12
Hoaït ñoäng 4: Luyeän kyõ naêng giaûi toaùn baèng caùch laäp heä phöông trình
10'
H1. Neâu caùc böôùc giaûi?
Ñ1.
Goïi t
1
(giôø) laø thôøi gian ngöôøi
thöù nhaát sôn xong böùc töôøng.
t
2
(giôø) laø thôøi gian ngöôøi thöù
hai sôn xong böùc töôøng.
ÑK: t
1
, t
2
> 0
12
12
7 4 5
t t 9
4 4 7
t t 18


1
2
t 18
t 24
4. Hai coâng nhaân cuøng sôn
moät böùc töôøng. Sau khi ngöôøi
thöù nhaát laøm ñöôïc 7 giôø vaø
ngöôøi thöù hai laøm ñöôïc 4 giôø
thì hoï sôn ñöôïc
5
9
böùc töôøng.
Sau ñoù hoï cuøng laøm vieäc vôùi
nhau tröông 4 giôø nöõa thì chæ
coøn laïi
1
18
böùc töôøng chöa
sôn. Hoûi neáu moãi ngöôøi laøm
rieâng thì sau bao nhieâu giôø
moãi ngöôøi môùi sôn xong böùc
töôøng?
Hoaït ñoäng 5: Cuûng coá
3'
Nhaán maïnh:
– Caùch giaûi caùc daïng toaùn.
– Caùch xeùt caùc ñieàu kieän khi
thöïc hieän caùc pheùp bieán ñoåi pt
4. BAØI TAÄP VEÀ NHAØ:
Laøm caùc baøi taäp coøn laïi.
Ñoïc tröôùc baøi "Baát ñaúng thöùc"
Ngaøy soaïn: 22/11/2012 Chöông IV: BAÁT ÑAÚNG THÖÙC. BAÁT PHÖÔNG TRÌNH
Tieát daïy: 26 Baøøi 1: BAÁT ÑAÚNG THÖÙC
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn
51
I. MUÏC TIEÂU:
Kieán thöùc:
Hieåu ñöôïc caùc khaùi nieäm veà BÑT.
Naém ñöôïc caùc tính chaát cuûa BÑT.
Naém ñöôïc caùc BÑT cô baûn vaø tính chaát cuûa chuùng.
Kó naêng:
Chöùng minh ñöôïc caùc BÑT ñôn giaûn.
Vaän duïng thaønh thaïo caùc tính chaát cô baûn cuûa BÑT ñeå bieán ñoåi, töø ñoù giaûi ñöôïc caùc baøi
toaùn veà chöùng minh BÑT.
Vaän duïng caùc BÑT Coâ–si, BÑT chöùa GTTÑ ñeå giaûi caùc baøi toaùn lieân quan.
Thaùi ñoä:
Töï giaùc, tích cöïc trong hoïc taäp.
Bieát phaân bieät roõ caùc khaùi nieäm cô baûn, caùc tính chaát vaø vaän duïng trong töøng tröôøng hôïp
cuï theå.
Tö duy caùc vaán ñeà cuûa toaùn hoïc moät caùch loâgic vaø heä thoáng.
II. CHUAÅN BÒ:
Giaùo vieân: Giaùo aùn. Heä thoáng caùc kieán thöùc ñaõ hoïc veà Baát ñaúng thöùc.
Hoïc sinh: SGK, vôû ghi. OÂn taäp caùc kieán thöùc ñaõ hoïc veà Baát ñaúng thöùc.
III. HOAÏT ÑOÄNG DAÏY HOÏC:
1. OÅn ñònh toå chöùc: Kieåm tra só soá lôùp.
2. Kieåm tra baøi cuõ:
H.
Ñ.
3. Giaûng baøi môùi:
TL
Hoaït ñoäng cuûa Giaùo vieân
Hoaït ñoäng cuûa Hoïc sinh
Noäi dung
Hoaït ñoäng 1: OÂn taäp khaùi nieäm Baát ñaúng thöùc
10'
H1. Ñeå so saùnh 2 soá a vaø b, ta
thöôøng xeùt bieåu thöùc naøo?
H2. Trong caùc meänh ñeà,
meänh ñeà naøo ñuùng?
a) 3,25 < 4 b) –5 > –4
1
4
c) –
2
≤ 3
H3. Ñieàn daáu thích hôïp (=, <,
>) vaøo oâ troáng?
a) 2
2
3
b)
4
3
2
3
c) 3 + 2
2
(1 +
2
)
2
d) a
2
+ 1 0 (vôùi a R)
Ñ1. a < b a – b < 0
a > b a – b > 0
Ñ2.
a) Ñ b) S c) Ñ
Ñ3.
a) <
b) >
c) =
d) >
I. OÂn taäp baát ñaúng thöùc
1. Khaùi nieäm baát ñaúng thöùc
Caùc meänh ñeà daïng "a < b"
hoaëc "a > b" ñgl BÑT.
Hoaït ñoäng 2: OÂn taäp Baát ñaúng thöùc heä quaû, töông ñöông
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn
52
10'
GV neâu caùc ñònh nghóa veà
BÑT heä quaû, töông ñöông.
H1. Xeùt quan heä heä quaû,
töông ñöông cuûa caùc caëp BÑT
sau:
a) x > 2 ; x
2
> 2
2
b) /x/ > 2 ; x > 2
c) x > 0 ; x
2
> 0
d) x > 0 ; x + 2 > 2
Ñ1.
a) x > 2 x
2
> 2
2
b) x > 2 /x/ > 2
c) x > 0 x
2
> 0
d) x > 0 x + 2 > 2
2. BÑT heä quaû, töông ñöông
Neáu meänh ñeà "a < b
c <
d" ñuùng thì ta nôùi BÑT c < d
laø BÑT heä quaû cuûa a < b. Ta
vieát: a < b
c < d.
Neáu a < b laø heä quaû cuûa c <
d vaø ngöôïc laïi thì hai BÑT
töông ñöông nhau. Ta vieát:
a < b
c < d.
a < b
a – b < 0
Hoaït ñoäng 3: OÂn taäp tính chaát cuûa Baát ñaúng thöùc
15'
GV giôùi thieäu gôïi yù cho HS
nhaéc laïi moät soá tính chaát cuûa
BÑT.
Caùc nhoùm ñoïc SGK, thaûo
luaän vaø thöïc hieän yeâu caàu cuûa
GV.
3. Tính chaát cuûa BÑT
Ñieàu kieän
Noäi dung
Teân goïi
a < b
a + c < b + c (1)
Coäng hai veá cuûa BÑT vôùi moät soá
c > 0
a < b
ac < bc (2a)
Nhaân hai veá cuûa BÑT vôùi moät soá
c < 0
a < b
ac > bc (2b)
a < b vaø c < d
a + c < b + d (3)
Coäng hai veá BÑT cuøng chieàu
a > 0, c > 0
a < b vaø c < d
ac < bd (4)
Nhaân hai veá BÑT cuøng chieàu vôùi caùc soá döông
n nguyeân
döông
a < b
a
2n+1
< b
2n+1
(5a)
Naâng hai veá cuûa BÑT leân moät luyõ thöøa
0 < a < b
a
2n
< b
2n
(5b)
a > 0
a < b
ab
(6a)
Khai caên hai veá cuûa moät BÑT
a < b
33
ab
(6b)
GV cho HS neâu VD minh
hoaï baèng caùc BÑT soá.
Ta coøn gaëp caùc BÑT khoâng
ngaët: a ≤ b hoaëc a ≥ b.
Hoaït ñoäng 4: AÙp duïng chöùng minh BÑT
5'
VD: Chöùng minh BÑT:
a
2
+ b
2
≥ 2ab
Daáu "=" xaûy ra khi naøo?
(Höôùng daãn HS caùch chöùng
minh)
Ñ.
Xeùt a
2
+ b
2
– 2ab = (a – b)
2
≥
0
ñpcm.
Daáu "=" xaûy ra a = b.
Hoaït ñoäng 5: Cuûng coá
5'
Nhaán maïnh:
– Caùc tính chaát cuûa BÑT
– Caùc tröôøng hôïp deã phaïm sai
laàm khi söû duïng caùc tính chaát.
4. BAØI TAÄP VEÀ NHAØ:
Baøi 1, 2 SGK.
Ñoïc tieáp baøi "Baát ñaúng thöùc"
Ngaøy soaïn: 22/11/2012 Chöông IV: BAÁT ÑAÚNG THÖÙC. BAÁT PHÖÔNG TRÌNH
Tieát daïy: 27 Baøøi 1: BAÁT ÑAÚNG THÖÙC (tt)
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn
53
I. MUÏC TIEÂU:
Kieán thöùc:
Hieåu ñöôïc caùc khaùi nieäm veà BÑT.
Naém ñöôïc caùc tính chaát cuûa BÑT.
Naém ñöôïc caùc BÑT cô baûn vaø tính chaát cuûa chuùng.
Kó naêng:
Chöùng minh ñöôïc caùc BÑT ñôn giaûn.
Vaän duïng thaønh thaïo caùc tính chaát cô baûn cuûa BÑT ñeå bieán ñoåi, töø ñoù giaûi ñöôïc caùc baøi
toaùn veà chöùng minh BÑT.
Vaän duïng caùc BÑT Coâ–si, BÑT chöùa GTTÑ ñeå giaûi caùc baøi toaùn lieân quan.
Thaùi ñoä:
Töï giaùc, tích cöïc trong hoïc taäp.
Bieát phaân bieät roõ caùc khaùi nieäm cô baûn, caùc tính chaát vaø vaän duïng trong töøng tröôøng hôïp
cuï theå.
Tö duy caùc vaán ñeà cuûa toaùn hoïc moät caùch loâgic vaø heä thoáng.
II. CHUAÅN BÒ:
Giaùo vieân: Giaùo aùn. Heä thoáng caùc kieán thöùc ñaõ hoïc veà Baát ñaúng thöùc.
Hoïc sinh: SGK, vôû ghi. OÂn taäp caùc kieán thöùc ñaõ hoïc veà Baát ñaúng thöùc.
III. HOAÏT ÑOÄNG DAÏY HOÏC:
1. OÅn ñònh toå chöùc: Kieåm tra só soá lôùp.
2. Kieåm tra baøi cuõ: (3')
H. Neâu moät soá tính chaát cuûa BÑT?
Ñ.
3. Giaûng baøi môùi:
TL
Hoaït ñoäng cuûa Giaùo vieân
Hoaït ñoäng cuûa Hoïc sinh
Noäi dung
Hoaït ñoäng 1: Tìm hieåu baát ñaúng thöùc Coâsi
10'
GV cho moät soá caëp soá a, b
0. Cho HS tính
ab
vaø
2
ab
,
roài so saùnh.
Höôùng daãn HS chöùng minh.
H. Khi naøo A
2
= 0 ?
Caùc nhoùm thöïc hieän yeâu
caàu, töø ñoù ruùt ra nhaän xeùt:
2
ab
ab
1
( 2 )
22
ab
ab a b ab
=
2
1
()
2
ab
0
Ñ. A
2
= 0 A = 0
II. Baát ñaúng thöùc Coâsi
1. Baát ñaúng thöùc Coâsi
2
ab
ab
,
a, b
0
Daáu "=" xaûy ra
a = b.
Hoaït ñoäng 2: Tìm hieåu caùc öùng duïng cuûa BÑT Coâsi
15'
H1. Vaän duïng BÑT Coâsi,
chöùng minh BÑT a +
1
a
2 ?
GV cho 1 giaù trò S, yeâu caàu
HS xeùt caùc caëp soá x, y sao cho
x + y = S. Nhaän xeùt caùc tích
xy ?
Höôùng daãn HS chöùng minh.
Ñ1.
1
1
.1
2
a
a
a
a

Tích xy lôùn nhaát khi x = y.
22
x y S
xy

2. Caùc heä quaû
HQ1: a +
1
a
2,
a > 0
HQ2: Neáu x, y cuøng döông vaø
coù toång x + y khoâng ñoåi thì
tích x.y lôùn nhaát khi vaø chæ khi
x = y.
YÙ nghóa hình hoïc: Trong taát caû
caùc hình chöõ nhaät coù cuøng chu
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn
54
Höôùng daãn HS nhaän xeùt yù
nghóa hình hoïc.
x + y chu vi hcn
x.y dieän tích hcn
x = y hình vuoâng
vi thì hình vuoâng coù dieän tích
lôùn nhaát.
HQ3: Neáu x, y cuøng döông vaø
coù tích x.y khoâng ñoåi thì toång x
+ y nhoû nhaát khi vaø chæ khi x =
y.
YÙ nghóa hình hoïc: Trong taát caû
caùc hình chöõ nhaät coù cuøng
dieän tích thì hình vuoâng coù chu
vi nhoû nhaát.
Hoaït ñoäng 3: Tìm hieåu baát ñaúng thöùc chöùa daáu GTTÑ
III. BÑT chöùa daáu GTTÑ
10'
H1. Nhaéc laïi ñònh nghóa veà
GTTÑ ?
H2. Nhaéc laïi caùc tính chaát veà
GTTÑ ñaõ bieát ?
Ñieàu kieän
Noäi dung
/x/
0, /x/
x, /x/
–x
a> 0
/x/
a
–a
x
a
/x/
a
x
–a hoaëc x
a
/a/ – /b/
/a + b/
/a/ + /b/
VD: Cho x [–2; 0]. Chöùng
minh: /x + 1/ 1
H3. Nhaéc laïi ñònh nghóa
khoaûng, ñoaïn ?
x [–2; 0] –2 x 0
–2 + 1 x + 1 0 + 1
–1 x + 1 1
/x + 1/ 1
Hoaït ñoäng 4: Cuûng coá
5'
Nhaán maïnh:
+ BÑT Coâsi vaø caùc öùng duïng
+ Caùc tính chaát veà BÑT chöùa
GTTÑ.
Caâu hoûi:
1) Tìm x:
a) x
2
> 4 b) x
2
< 3
2) Cho a, b > 0. Chöùng minh:
ab
ba
2
1) a) x
2
> 4
2
2
x
x

b) x
2
< 3 –
33x
4. BAØI TAÄP VEÀ NHAØ:
Baøi 3, 4, 5, 6 SGK.
OÂn taäp kieán thöùc HK1
Ngaøy soaïn: 1/12/2012 Chöông IV: BAÁT ÑAÚNG THÖÙC. BAÁT PHÖÔNG TRÌNH
Tieát daïy: 28 Baøøi 1: BAÁT ÑAÚNG THÖÙC –BÀI TẬP
I. MUÏC TIEÂU:
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn
55
Kieán thöùc:
Hieåu ñöôïc caùc khaùi nieäm veà BÑT.
Naém ñöôïc caùc tính chaát cuûa BÑT.
Naém ñöôïc caùc BÑT cô baûn vaø tính chaát cuûa chuùng.
Kó naêng:
Chöùng minh ñöôïc caùc BÑT ñôn giaûn.
Vaän duïng thaønh thaïo caùc tính chaát cô baûn cuûa BÑT ñeå bieán ñoåi, töø ñoù giaûi ñöôïc caùc baøi
toaùn veà chöùng minh BÑT.
Vaän duïng caùc BÑT Coâ–si, BÑT chöùa GTTÑ ñeå giaûi caùc baøi toaùn lieân quan.
Thaùi ñoä:
Töï giaùc, tích cöïc trong hoïc taäp.
Bieát phaân bieät roõ caùc khaùi nieäm cô baûn, caùc tính chaát vaø vaän duïng trong töøng tröôøng hôïp
cuï theå.
Tö duy caùc vaán ñeà cuûa toaùn hoïc moät caùch loâgic vaø heä thoáng.
II. CHUAÅN BÒ:
Giaùo vieân: Giaùo aùn. Heä thoáng caùc kieán thöùc ñaõ hoïc veà Baát ñaúng thöùc.
Hoïc sinh: SGK, vôû ghi. OÂn taäp caùc kieán thöùc ñaõ hoïc veà Baát ñaúng thöùc.
III. HOAÏT ÑOÄNG DAÏY HOÏC:
1. OÅn ñònh toå chöùc: Kieåm tra só soá lôùp.
Hoaït ñoäng 1: Kieåm tra baøi cuõ .Thôøi gian:10p
Hoaït ñoäng cuûa HS
Hoaït ñoäng cuûa GV
Noäi dung caàn
ghi
Nghe hieåu nhieäm vuï
Laøm baøi taäp aùp duïng
Nhaän xeùt vaø hoaøn chænh
lôøi giaûi
Goïi 1 hs kieåm tra laïi kieán thöùc cuõ:
Neâu ñònh lyù veà baát ñaúng thöùc coâ-si?
Ad:cho 2 soá a vaø b döông .Chöùng minh raèng :
(a+b)
11
ab



4
Caùc hs khaùc nhaän xeùt vaø laøm baøi taäp aùp duïng vaøo
vôû
Choïn 3 vôû coù keát quaû nhanh nhaát
Hoaït ñoäng 2: baøi taäp 1,2 sgk tr79 .Thôøi gian:10p
Hoaït ñoäng cuûa HS
Hoaït ñoäng cuûa GV
Noäi dung caàn ghi
1/ d.
2/
5
x
-1
Giaûi thích:vì x>5
0<
5
x
<1 ;1<
5
x
+1
5
x
-1< 0 ;
5
x
>1
Chia 4 nhoùm hoïc taäp vaø laøm vieäc theo nhoùm
Mñ1:Caû 4 nhoùm cho keát quaû vaø giaûi thích ôû
caùch choïn cuûa mình
Mñ2:traû lôøi caâu hoûi sau:
Caâu a sai vì sao?
Vôùi x>5 ,haõy so saùnh
5
x
vaø
5
x
Baøi taäp 1
Baøi taäp 2
Hoaït ñoäng 3: Baøi taäp 3 sgk tr79 .Thôøi gian:10p
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn
56
Hoaït ñoäng cuûa hs
Hoaït ñoäng cuûa GV
Noäi dung caàn
ghi
Nghe hieåu nhieäm vuï vaø
thöïc hieän tuøy töøng möùc ñoä
Tìm caùch giaûi ,trình baøy
caùch giaûi
Chænh söõa hoaøn thieän
( b-c)
2
<a
2
<=>(b-c-a)(b-c+a) < 0
a ,b,c laøñoä daøi 3 caïnh
tam giaùc neân :
a+c>b => b-c-a < 0
a+b>c => b-c+a>0
=>(b-c-a)(b-c+a) < 0
(ñuùng)
3a/
Mñ1:hs töï giaûi quyeát
Mñ2 :hs traû lôøi caâu hoûi gôïi yù sau:
Khi naøo thì 3 soá a ,b, c laø ñoä daøi 3 caïnh cuûa 1
tam giaùc?
Mñ3 :( b-c)
2
<a
2
<=>(b-c-a)(b-c+a) < 0
Khoâng maát tính toång quaùt ta cuõng coù
(a-b)
2
<c
2
;(c-a)
2
<b
2
3b/suy ra töø keát quaû caâu a
Coäng veá vôùi veá 3 keát quaû treân ta suy ra ñpcm
Baøi taäp 3
Hoaït ñoäng 4: Baøi taäp 4,5,6 sgk tr79 .Thôøi gian:10p
Hoaït ñoäng cuûa hs
Hoaït ñoäng cuûa GV
Noäi dung caàn ghi
Nghe hieåu nhieäm vuï
Tìm phöông aùn thaéng
Trình baøy keát quaû
Chænh söõa hoaøn thieän
4/hd:ta duøng pheùp bieán ñoåi töông ñöông
Xeùt hieäu:x
3
+y
3
-(x
2
y+xy
2
)=
Hs bieán ñoåi ñeå ñöa ñöôïc veà keát quaû
=(x+y)(x
2
+y
2
-xy) –xy(x+y)
=(x+y)(x
2
-2xy+y
2
)
=(x+y)(x-y)
2
Nhaän xeùt keát quaû sau khi ñaõ bieán ñoåi
5/höôùng daãn hs tìm caùch giaûi baøi toaùn,khoâng trình
baøy baøi giaûi
Ñaët
x
=t
Xeùt 2 tröôøng hôïp :
*
0 x
<1
* x
1
6/Hd:Goïi H laø tieáp ñieåm cuûa ñöôøng thaúng AB vôùi
ñöôøng troøn .Ta aùp duõng baát ñaúng thöùc coâ-si:
AB=HA+HB
2.HA HB
AB ngaén nhaát khi ñaúng thöùc xaûy ra <=>?
Baøi taäp 4
Baøi taäp 5
Baøi taäp 6
Hoaït ñoäng 5: Cuõng coá daën doø .Thôøi gian:5p
Ngaøy soaïn: 28/11/2012
Tieát daïy: 29 Baøøi daïy: OÂN TAÄP HOÏC KÌ I
I. MUÏC TIEÂU:
Kieán thöùc: Cuûng coá caùc kieán thöùc veà:
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn
57
Meänh ñeà – Taäp hôïp.
Haøm soá – Haøm soá baäc nhaát – Haøm soá baäc hai.
Phöông trình – Phöông trình baäc nhaát – Phöông trình baäc hai.
Heä phöông trình baäc nhaát nhieàu aån.
Baát ñaúng thöùc.
Kó naêng: Thaønh thaïo vieäc giaûi caùc baøi toaùn veà:
Meänh ñeà – Caùc pheùp toaùn taäp hôïp hôïp.
Tìm taäp xaùc ñònh, xeùt söï bieán thieân, xeùt tính chaün leû, veõ ñoà thò cuûa haøm soá baäc nhaát, baäc
hai.
Giaûi vaø bieän luaän phöông trình baäc nhaát, baäc hai.
Giaûi vaø bieän luaän heä phöông trình baäc nhaát hai aån.
Chöùng minh baát ñaúng thöùc.
Thaùi ñoä:
Reøn luyeän tính caån thaän, chính xaùc.
Luyeän tö duy toång hôïp, suy luaän linh hoaït.
II. CHUAÅN BÒ:
Giaùo vieân: Giaùo aùn. Heä thoáng baøi taäp.
Hoïc sinh: SGK, vôû ghi. OÂn taäp toaøn boä kieán thöùc hoïc kì 1.
III. HOAÏT ÑOÄNG DAÏY HOÏC:
1. OÅn ñònh toå chöùc: Kieåm tra só soá lôùp.
2. Kieåm tra baøi cuõ: (Loàng vaøo quaù trình oân taäp)
H.
Ñ.
3. Giaûng baøi môùi:
TL
Hoaït ñoäng cuûa Giaùo vieân
Hoaït ñoäng cuûa Hoïc sinh
Noäi dung
Hoaït ñoäng 1: Cuûng coá kieán thöùc veà Meänh ñeà – Taäp hôïp
10'
H1. Nhaéc laïi caùch laäp meänh
ñeà phuû ñònh ?
H2. Neâu caùch xaùc ñònh giao,
hôïp, hieäu cuûa caùc taäp con cuûa
taäp R ?
Ñ1.
a) xR: x + 3 5
b) xN: x khoâng chia heát 3
c) xR: x > 10
Ñ2. Bieåu dieãn leân truïc soá.
a) X Y = (–; 5]
X Y = [–3; 2]
X \ Y = (2; 5]
1. Laäp meänh ñeà phuû ñònh cuûa
caùc meänh ñeà sau:
a) xR: x + 3 = 5
b) xN: x laø boäi cuûa 3
c) xR: x 10
2. Xaùc ñònh X Y, X Y,
X \ Y neáu:
a) X = [–3; 5], Y = (–; 2]
b) X = (–; 5), Y = [0; +)
c) X = (–; 3), Y = (3; +)
Hoaït ñoäng 2: Cuûng coá caùc kieán thöùc veà haøm soá
20'
H1. Neâu ñieàu kieän xaùc ñònh
cuûa haøm soá ?
Ñ1.
a)
20
10
x
x


D = [1; 2]
b)
2
2
40
30
4 3 0
x
x
xx

x 2
3. Tìm taäp xaùc ñònh cuûa caùc
haøm soá:
a) y =
21xx
b) y =
2
43
x
xx
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn
58
H2. Neâu ñieàu kieän haøm soá
ñoàng bieán, nghòch bieán ?
H3. Neâu ñieàu kieän A, B, C
(P) ?
Ñ2.
+ m > 1: ñoàng bieán
+ m < 1: nghòch bieán
Ñ3.
a)
1
4 2 3
3
a b c
a b c
abc
1
1
3
a
b
c

4. Cho haøm soá :
y = (m–1)x + 2m – 3
a) Vôùi giaù trò naøo cuûa m, haøm
soá ñoàng bieán, nghòch bieán.
b) Ñònh m ñeå ñoà thò haøm soá ñi
qua ñieåm A(1; –2).
5. Cho (P): y = ax
2
+ bx + c.
a) Tìm a, b, c bieát (P) ñi qua
A(1; –1), B(2; 3), C(–1; –3).
b) Xeùt söï bieán thieân vaø veõ (P)
vöøa tìm ñöôïc.
Hoaït ñoäng 3: Cuûng coá vieäc giaûi phöông trình, heä phöông trình
10'
H1. Nhaéc laïi caùch giaûi caùc
daïng phöông trình ?
Ñ1.
a)
1
21
2
21
1
12
2
x neáu x
x
x neáu x



b)
2
4 4 2x x x
c) (m
2
+ 1)x = m + 1
d) Ñaët aån phuï:
1
2
u
x
37
2 5 3
uy
uy

6. Giaûi caùc phöông trình:
a)
2 1 3xx
b)
2
4 1 2x x x
c) m
2
x – 1 = m – x
d)
3
7
2
2
53
2
y
x
y
x


Hoaït ñoäng 4: Cuûng coá
5'
Nhaán maïnh caùch giaûi caùc
daïng toaùn
4. BAØI TAÄP VEÀ NHAØ:
Baøi taäp oân taäp Hoïc kì 1
Ngaøy soaïn: 10/12/2012
Tieát daïy: 30 Baøøi daïy: KIEÅM TRA HOÏC KÌ I
I. MUÏC TIEÂU:
Kieán thöùc: Cuûng coá caùc kieán thöùc ñaõ hoïc trong hoïc kì 1.
Meänh ñeà – Taäp hôïp.
Haøm soá – Haøm soá baäc nhaát – Haøm soá baäc hai.
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn
59
Phöông trình – Phöông trình baäc nhaát – baäc hai. Heä phöông trình baäc nhaát nhieàu aån.
Baát ñaúng thöùc.
Kó naêng: Thaønh thaïo vieäc giaûi caùc daïng toaùn:
Caùc pheùp toaùn veà meänh ñeà – taäp hôïp.
Tìm taäp xaùc ñònh, xeùt söï bieán thieân, tính chaün leû cuûa haøm soá.
Khaûo saùt haøm soá baäc nhaát, baäc hai.
Giaûi vaø bieän luaän phöông trình baäc nhaát, baäc hai, phöông trình qui veà baäc nhaát, baäc hai.
Giaûi heä phöông trình baäc nhaát nhieàu aån.
Thaùi ñoä:
Reøn luyeän tính caån thaän, chính xaùc. Luyeän tö duy linh hoaït, saùng taïo.
II. CHUAÅN BÒ:
Giaùo vieân: Ñeà kieåm tra.
Hoïc sinh: OÂn taäp kieán thöùc ñaõ hoïc trong hoïc kì 1.
III. MA TRAÄN ÑEÀ:
Chuû ñeà
Nhaän bieát
Thoâng hieåu
Vaän duïng
Toång
TNKQ
TL
TNKQ
TL
TNKQ
TL
Meänh ñeà – Taäp hôïp
1
0,25
1
0,25
0,5
Haøm soá
2
0,25
2
0,25
2
1,0
3,0
Phöông trình
2
0,25
2
0,25
2
1,0
3,0
Toång
0,75
1,25
2,0
0,5
2,0
6,5
IV. NOÄI DUNG ÑEÀ KIEÅM TRA:
A. Phaàn traéc nghieäm:
Caâu 1: Meänh ñeà "x R: x
2
+ 3x – 4 < 0" coù meänh ñeà phuû ñònh laø:
A. "x R: x
2
+ 3x – 4 0" B. "x R: x
2
+ 3x – 4 > 0"
C. "x R: x
2
+ 3x – 4 0" D. "x R: x
2
+ 3x – 4 = 0"
Caâu 2: Soá caùc taäp con cuûa taäp hôïp A = {0, 1, 2, 3} laø:
A. 16 B. 8 C. 12 D. 6
Caâu 3: Taäp xaùc ñònh cuûa haøm soá y =
1
1
1
x
x

laø:
A. [–1; +) \ {1} B. [1; +) \ {–1} C. R \ {1} D. [–1; +)
Caâu 4: Haøm soá y = 2x – m + 1
A. Luoân ñoàng bieán treân R B. Ñoàng bieán treân R vôùi m < 1
C. Luoân nghòch bieán treân R D. Nghòch bieán treân R vôùi m > 1
Caâu 5: Haøm soá y = x
2
– 2x + 3
A. Ñoàng bieán treân khoaûng (1; +) B. Ñoàng bieán treân khoaûng (0; +)
C. Nghòch bieán treân khoaûng (0; +) D. Nghòch bieán treân khoaûng (1; +)
Caâu 6: Ñoà thò cuûa haøm soá y = –x
2
+ 2x + 1 ñi qua ñieåm
A. A(–1; –2) B. B(–1; 0) C. C(1; 3) D. D(2; 9)
Caâu 7: Ñieàu kieän xaùc ñònh cuûa phöông trình: x + 3 –
2
3
x
x
= 0 laø:
A. x > – 3 B. x –3 C. x – 3 D. x 2
Caâu 8: Vôùi giaù trò naøo cuûa m thì phöông trình: (m
2
– 4)x = m(m + 2) voâ nghieäm:
A. m = 2 B. m = –2 C. m 2 D. m = 2
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn
60
Caâu 9: Vôùi giaù trò naøo cuûa m thì phöông trình: x
2
– mx + 1 = 0 coù 1 nghieäm:
A. m = 2 B. m = 4 C. m 2 D. m 2
Caâu 10: Caëp soá (2; –1) laø nghieäm cuûa phöông trình naøo döôùi ñaây:
A. 3x + 2y = 4 B. 3x + 2y = 8 C. 2x + 3y = 7 D. 2x + 3y = –1
B. Phaàn töï luaän:
Baøi 1: Cho haøm soá y = x
2
– 4x + 3 (1).
a) Tìm toaï ñoä ñænh vaø truïc ñoái xöùng cuûa ñoà thò haøm soá (1).
b) Vôùi giaù trò naøo cuûa m thì ñ.thaúng (d): y = mx + m – 1 caét ñoà thò cuûa haøm soá (1) taïi hai ñieåm phaân bieät.
Baøi 2: Cho phöông trình: (m – 1)x
2
+ 2x – 1 = 0 (2)
a) Tìm m ñeå phöông trình (2) coù nghieäm x = –1. Khi ñoù tìm nghieäm coøn laïi cuûa phöông trình (2).
b) Tìm m ñeå phöông trình (2) coù 2 nghieäm cuøng daáu.
V. ÑAÙP AÙN VAØ BIEÅU ÑIEÅM:
A. Phaàn traéc nghieäm: 1a) 2a) 3a) 4a) 5a) 6a) 7a) 8a) 9a) 10a)
B. Töï luaän:
Baøi 1: (2 ñieåm) Cho haøm soá y = x
2
– 4x + 3 (1).
a) Toaï ñoä ñænh I:
2
2
1
4
b
x
a
y
a
(0,5 ñieåm) Truïc ñoái xöùng: (): x =
2
2
b
a

(0,5
ñieåm)
b) (1 ñieåm) Phöông trình hoaønh ñoä giao ñieåm cuûa (1) vaø (d):
x
2
– 4x + 3 = mx + m – 1 x
2
– (m + 4)x + m – 4 = 0 (0,5 ñieåm)
+ (d) caét (1) taïi 2 ñieåm phaân bieät = (m + 4)
2
–4(m – 4) > 0 (0,5 ñieåm)
m
2
+ 4m + 32 > 0 (m + 2)
2
+ 28 > 0 m R (0,5 ñieåm)
Baøi 2: (2 ñieåm) Cho phöông trình: (m – 1)x
2
+ 2x – 1 = 0 (2)
a) + x = –1 laø nghieäm cuûa (2) m = 4 (0,5 ñieåm)
+ (2) 3x
2
+ 2x – 1 = 0
1
1
3
x
x

nghieäm coøn laïi laø x =
1
3
(0,5 ñieåm)
b) (2) coù 2 nghieäm cuøng daáu
1
'0
1
0
1
m
m
P
m
(0,5 ñieåm)
1
0
1
m
m
m
0 m < 1 (0,5 ñieåm)
VI. KEÁT QUAÛ KIEÅM TRA:
Lôùp
Só soá
0 – 3,4
3,5 – 4,9
5,0 – 6,4
6,5 – 7,9
8,0 – 10
SL
%
SL
%
SL
%
SL
%
SL
%
10A3
44
10A5
42
10A7
44
10A10
42
10A11
38
Ngaøy soaïn: 25/12/2012
Tieát daïy: 31 Baøøi daïy: TRAÛ BAØI KIEÅM TRA HOÏC KÌ I
I. MUÏC TIEÂU:
Kieán thöùc: Nhaéc nhôû hoïc sinh nhöõng sai laàm veà:
Meänh ñeà – Taäp hôïp.
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn
61
Haøm soá – Haøm soá baäc nhaát – Haøm soá baäc hai.
Phöông trình – Phöông trình baäc nhaát – baäc hai. Heä phöông trình baäc nhaát nhieàu aån.
Kó naêng: Nhaéc nhôû hoïc sinh nhöõng sai laàm veà:
Caùc pheùp toaùn veà meänh ñeà – taäp hôïp.
Tìm taäp xaùc ñònh, xeùt söï bieán thieân, tính chaün leû cuûa haøm soá.
Khaûo saùt haøm soá baäc nhaát, baäc hai.
Giaûi vaø bieän luaän phöông trình baäc nhaát, baäc hai, phöông trình qui veà baäc nhaát, baäc hai.
Giaûi heä phöông trình baäc nhaát nhieàu aån.
Thaùi ñoä:
Reøn luyeän tính caån thaän, chính xaùc. Luyeän tö duy linh hoaït, saùng taïo.
II. CHUAÅN BÒ:
Giaùo vieân: Ñeà kieåm tra vaø ñaùp aùn. Heä thoáng caùc sai laàm cuûa HS maéc phaûi.
Hoïc sinh: Vôû ghi.
III. HOAÏT ÑOÄNG DAÏY HOÏC:
1. OÅn ñònh toå chöùc: Kieåm tra só soá lôùp.
2. Kieåm tra baøi cuõ:
3. Giaûng baøi môùi:
Noäi dung ñeà kieåm tra
Sai laàm cuûa HS
A. Phaàn traéc nghieäm:
Caâu 1: Meänh ñeà "x R: x
2
+ 3x – 4 < 0" coù meänh ñeà phuû
ñònh laø:
A. "x R: x
2
+ 3x – 4 0" B. "x R: x
2
+ 3x – 4 > 0"
C. "x R: x
2
+ 3x – 4 0" D. "x R: x
2
+ 3x – 4 = 0"
Chöa naém vöõng moái lieân heä giöõa 2
meänh ñeà vaø .
Chöa naém vöõng pheùp so saùnh caùc soá :
=, , >, < ,
Caâu 2: Soá caùc taäp con cuûa taäp hôïp A = {0, 1, 2, 3} laø:
A. 16 B. 8 C. 12 D. 6
Chöa naém vöõng caùch laäp caùc taäp con
Caâu 3: Taäp xaùc ñònh cuûa haøm soá y =
1
1
1
x
x

laø:
A. [–1; +) \ {1} B. [1; +) \ {–1} C. R \ {1} D. [–1; +)
Chöa thaønh thaïo caùc pheùp toaùn taäp hôïp
treân caùc taäp con cuûa R.
Caâu 4: Haøm soá y = 2x – m + 1
A. Luoân ñoàng bieán treân R B. Ñoàng bieán treân R vôùi m < 1
C. Luoân nghòch bieán treân R D. Nghòch bieán treân R vôùi m > 1
Caâu 5: Haøm soá y = x
2
– 2x + 3
A. Ñoàng bieán treân khoaûng (1; +)
B. Ñoàng bieán treân khoaûng (0; +)
C. Nghòch bieán treân khoaûng (0; +)
D. Nghòch bieán treân khoaûng (1; +)
Caâu 6: Ñoà thò cuûa haøm soá y = –x
2
+ 2x + 1 ñi qua ñieåm
A. A(–1; –2) B. B(–1; 0) C. C(1; 3) D. D(2; 9)
Caâu 7: Ñieàu kieän xaùc ñònh cuûa ph.trình: x + 3 –
2
3
x
x
= 0
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn
62
laø:
A. x > – 3 B. x –3 C. x – 3 D. x 2
Caâu 8: Vôùi giaù trò naøo cuûa m thì phöông trình: (m
2
– 4)x = m(m
+ 2) voâ nghieäm:
A. m = 2 B. m = –2 C. m 2 D. m = 2
Caâu 9: Vôùi giaù trò naøo cuûa m thì phöông trình: x
2
– mx + 1 = 0
coù 1 nghieäm:
A. m = 2 B. m = 4 C. m 2 D. m 2
Caâu 10: Caëp soá (2; –1) laø nghieäm cuûa ph.trình naøo döôùi ñaây:
A. 3x + 2y = 4 B. 3x + 2y = 8
C. 2x + 3y = 7 D. 2x + 3y = –1
B. Phaàn töï luaän:
Baøi 1: Cho haøm soá y = x
2
– 4x + 3 (1).
a) Tìm toaï ñoä ñænh vaø truïc ñoái xöùng cuûa ñoà thò haøm soá (1).
b) Vôùi giaù trò naøo cuûa m thì ñ.thaúng (d): y = mx + m – 1 caét ñoà
thò cuûa haøm soá (1) taïi hai ñieåm phaân bieät.
Baøi 2: Cho phöông trình: (m – 1)x
2
+ 2x – 1 = 0
(2)
a) Tìm m ñeå phöông trình (2) coù nghieäm x = –1. Khi ñoù tìm
nghieäm coøn laïi cuûa phöông trình (2).
b) Tìm m ñeå phöông trình (2) coù 2 nghieäm cuøng daáu.
4. BAØI TAÄP VEÀ NHAØ:
– OÂn laïi kieán thöùc hoïc kì 1.
– Ñoïc tröôùc baøi "Baát phöông trình vaø heä baát phöông trình moät aån"
Ngaøy soaïn: 01/01/2013 Chöông IV: BAÁT ÑAÚNG THÖÙC. BAÁT PHÖÔNG TRÌNH
Tieát daïy: 32 Baøøi 2: BAÁT PHÖÔNG TRÌNH
vaø HEÄ BAÁT PHÖÔNG TRÌNH MOÄT AÅN
I. MUÏC TIEÂU:
Kieán thöùc:
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn
63
Naém ñöôïc caùc khaùi nieäm veà BPT, heä BPT moät aån; nghieäm vaø taäp nghieäm cuûa BPT, heä
BPT; ñieàu kieän cuûa BPT; giaûi BPT.
Naém ñöôïc caùc pheùp bieán ñoåi töông ñöông.
Kó naêng:
Giaûi ñöôïc caùc BPT ñôn giaûn.
Bieát caùch tìm nghieäm vaø lieân heä giöõa nghieäm cuûa PT vaø nghieäm cuûa BPT.
Xaùc ñònh nhanh taäp nghieäm cuûa caùc BPT vaø heä BPT ñôn giaûn döa vaøo bieán ñoåi vaø laáy
nghieäm treân truïc soá.
Thaùi ñoä:
Bieát vaän duïng kieán thöùc veà BPT trong suy luaän loâgic.
Dieãn ñaït caùc vaán ñeà toaùn hoïc maïch laïc, phaùt trieån tö duy vaø saùng taïo.
II. CHUAÅN BÒ:
Giaùo vieân: Giaùo aùn.
Hoïc sinh: SGK, vôû ghi. OÂn taäp caùc kieán thöùc ñaõ hoïc veà Baát ñaúng thöùc, Baát phöông trình.
III. HOAÏT ÑOÄNG DAÏY HOÏC:
1. OÅn ñònh toå chöùc: Kieåm tra só soá lôùp.
2. Kieåm tra baøi cuõ: (3')
H. Neâu moät soá tính chaát cuûa BÑT?
Ñ.
3. Giaûng baøi môùi:
TL
Hoaït ñoäng cuûa Giaùo vieân
Hoaït ñoäng cuûa Hoïc sinh
Noäi dung
Hoaït ñoäng 1: Tìm hieåu khaùi nieäm baát phöông trình moät aån
13'
Cho HS neâu moät soá bpt moät
aån. Chæ ra veá traùi, veá phaûi cuûa
baát phöông trình.
H1. Trong caùc soá –2;
1
2
2
; ;
10
, soá naøo laø nghieäm cuûa
bpt: 2x 3.
H2. Giaûi bpt ñoù ?
H3. Bieåu dieãn taäp nghieäm
treân truïc soá ?
Caùc nhoùm thöïc hieän yeâu
caàu.
a) 2x + 1 > x + 2
b) 3 – 2x x
2
+ 4
c) 2x > 3
Ñ1. –2 laø nghieäm.
Ñ2. x
3
2
Ñ3.
I. Khaùi nieäm baát phöông
trình moät aån
1. Baát phöông trình moät aån
Baát phöông trình aån x laø
meänh ñeà chöùa bieán coù daïng:
f(x) < (g(x) (f(x)
g(x)) (*)
trong ñoù f(x), g(x) laø nhöõng
bieåu thöùc cuûa x.
Soá x
0
R thoaû f(x
0
) < g(x
0
)
ñgl moät nghieäm cuûa (*).
Giaûi bpt laø tìm taäp nghieäm
cuûa noù.
Neáu taäp nghieäm cuûa bpt laø
taäp roãng ta noùi bpt voâ nghieäm.
Hoaït ñoäng 2: Tìm hieåu ñieàu kieän xaùc ñònh cuûa baát phöông trình
7'
H1. Nhaéc laïi ñieàu kieän xaùc
ñònh cuûa phöông trình ?
H2. Tìm ñkxñ cuûa caùc bpt sau:
a)
2
31x x x
b)
1
x
> x + 1
Ñ1. Ñieàu kieän cuûa x ñeå f(x)
vaø g(x) coù nghóa.
Ñ2.
a) –1 x 3
b) x 0
c) x > 0
d) x R
2. Ñieàu kieän cuûa moät baát
phöông trình
Ñieàu kieän xaùc ñònh cuûa (*) laø
ñieàu kieän cuûa x ñeå f(x) vaø g(x)
coù nghóa.
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn
64
c)
1
x
> x + 1
d) x >
2
1x
Hoaït ñoäng 3: Tìm hieåu baát phöông trình chöùa tham soá
7'
H1. Haõy neâu moät bpt moät aån
chöùa 1, 2, 3 tham soá ?
Ñ1. HS ñöa ra VD.
a) 2x – m > 0 (tham soá m)
b) 2ax – 3 > x – b (th.soá a, b)
3. Baát phöông trình chöùa
tham soá
Trong moät bpt, ngoaøi caùc
chöõ ñoùng vai troø aån soá coøn coù
theå coù caùc chöõ khaùc ñöôïc xem
nhö nhöõng haèng soá, ñgl tham
soá.
Giaûi vaø bieän luaän bpt chöùa
tham soá laø tìm taäp nghieäm cuûa
bpt töông öùng vôùi caùc giaù trò
cuûa tham soá.
Hoaït ñoäng 4: Tìm hieåu Heä baát phöông trình moät aån
10'
H1. Giaûi caùc bpt sau:
a) 3x + 2 > 5 – x
b) 2x + 2 5 – x
H2. Giaûi heä bpt:
3 2 5
2 2 5
xx
xx
Ñ1.
a) S
1
=
3
;
4




b) S
2
= (–; 1]
Ñ2.
S = S
1
S
2
=
3
;1
4


II. Heä BPT moät aån
Heä bpt aån x goàm moät soá bpt
aån x maø ta phaûi tìm caùc
nghieäm chung cuûa chuùng.
Moãi giaù trò cuûa x ñoàng thôøi
laø nghieäm cuûa taát caû caùc bpt
cuûa heä ñgl moät nghieäm cuûa heä.
Giaûi heä bpt laø tìm taäp
nghieäm cuûa noù.
Ñeå giaûi moät heä bpt ta giaûi
töøng bpt roài laáy giao caùc taäp
nghieäm.
Hoaït ñoäng 5: Cuûng coá
3'
Nhaán maïnh:
Caùch vaän duïng caùc tính chaát
cuûa BÑT.
Caùch bieåu dieãn taäp nghieäm
treân truïc soá.
4. BAØI TAÄP VEÀ NHAØ:
Baøi 1, 2 SGK.
Ñoïc tieáp baøi "Baát phöông trình vaø heä baát phöông trình moät aån"
Ngaøy soaïn: 01/01/2013 Chöông IV: BAÁT ÑAÚNG THÖÙC. BAÁT PHÖÔNG TRÌNH
Tieát daïy: 33 Baøøi 2: BAÁT PHÖÔNG TRÌNH
vaø HEÄ BAÁT PHÖÔNG TRÌNH MOÄT AÅN (tt)
I. MUÏC TIEÂU:
Kieán thöùc:
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn
65
Naém ñöôïc caùc khaùi nieäm veà BPT, heä BPT moät aån; nghieäm vaø taäp nghieäm cuûa BPT, heä
BPT; ñieàu kieän cuûa BPT; giaûi BPT.
Naém ñöôïc caùc pheùp bieán ñoåi töông ñöông.
Kó naêng:
Giaûi ñöôïc caùc BPT ñôn giaûn.
Bieát caùch tìm nghieäm vaø lieân heä giöõa nghieäm cuûa PT vaø nghieäm cuûa BPT.
Xaùc ñònh nhanh taäp nghieäm cuûa caùc BPT vaø heä BPT ñôn giaûn döa vaøo bieán ñoåi vaø laáy
nghieäm treân truïc soá.
Thaùi ñoä:
Bieát vaän duïng kieán thöùc veà BPT trong suy luaän loâgic.
Dieãn ñaït caùc vaán ñeà toaùn hoïc maïch laïc, phaùt trieån tö duy vaø saùng taïo.
II. CHUAÅN BÒ:
Giaùo vieân: Giaùo aùn.
Hoïc sinh: SGK, vôû ghi. OÂn taäp caùc kieán thöùc ñaõ hoïc veà Baát ñaúng thöùc, Baát phöông trình.
III. HOAÏT ÑOÄNG DAÏY HOÏC:
1. OÅn ñònh toå chöùc: Kieåm tra só soá lôùp.
2. Kieåm tra baøi cuõ: (3')
H. Giaûi caùc bpt: a) 3 – x 0 b) x + 1 0 ?
Ñ. a) S
1
= (–; 3] b) S
2
= [1; + )
3. Giaûng baøi môùi:
TL
Hoaït ñoäng cuûa Giaùo vieân
Hoaït ñoäng cuûa Hoïc sinh
Noäi dung
Hoaït ñoäng 1: Tìm hieåu khaùi nieäm baát phöông trình töông ñöông
10'
H1. Hai bpt sau coù töông
ñöông khoâng ?
a) 3 – x 0 b) x + 1
0
H2. Heä bpt:
10
10
x
x


töông
ñöông vôùi heä bpt naøo sau ñaây:
a)
10
10
x
x


b)
10
10
x
x


c)
10
10
x
x


d)
1x
Ñ1. khoâng vì S
1
S
2
Ñ2.
10
10
x
x


1x
III. Moät soá pheùp bieán ñoåi bpt
1. BPT töông ñöông
Hai bpt (heä bpt) coù cuøng taäp
nghieäm ñgl hai bpt (heä bpt) töông
ñöông.
Hoaït ñoäng 2: Tìm hieåu caùc pheùp bieán ñoåi baát phöông trình
5'
GV giaûi thích thoâng qua ví
duï minh hoaï.
10
10
x
x


1
1
x
x

–1 x 1
2. Pheùp bieán ñoåi töông ñöông
Ñeå giaûi moät bpt (heä bpt) ta bieán
ñoåi noù thaønh nhöõng bpt (heä bpt)
töông ñöông cho ñeán khi ñöôïc bpt
(heä bpt) ñôn giaûn maø ta coù theå
vieát ngay taäp nghieäm. Caùc pheùp
bieán ñoåi nhö vaäy ñgl caùc pheùp
bieán ñoåi töông ñöông.
Hoaït ñoäng 3: Tìm hieåu moät soá pheùp bieán ñoåi baát phöông trình
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn
66
20'
H1. Giaûi bpt sau vaø nhaän xeùt
caùc pheùp bieán ñoåi ?
(x+2)(2x–1) – 2
x
2
+ (x–1)(x+3)
H2. Giaûi bpt sau vaø nhaän xeùt
caùc pheùp bieán ñoåi ?
22
22
1
21
x x x x
xx

H3. Giaûi bpt sau vaø nhaän xeùt
caùc pheùp bieán ñoåi ?
22
2 2 2 3x x x x
Ñ1. (x+2)(2x–1) – 2
x
2
+ (x–1)(x+3)
x 1
Ñ2.
22
22
1
21
x x x x
xx

x<1
Ñ3.
22
2 2 2 3x x x x
x >
1
4
a) Coäng (tröø)
Coäng (tröø) hai veá cuûa bpt vôùi
cuøng moät bieåu thöùc maø khoâng
laøm thay ñoåi ñieàu kieän cuûa bpt ta
ñöôïc moät bpt töông ñöông.
b) Nhaân (chia)
Nhaân (chia) hai veá cuûa bpt vôùi
cuøng moät bieåu thöùc luoân nhaän giaù
trò döông (maø khoâng laøm thay ñoåi
ñieàu kieän cuûa bpt) ta ñöôïc moät
bpt töông ñöông.
Nhaân (chia) hai veá cuûa bpt vôùi
cuøng moät bieåu thöùc luoân nhaän giaù
trò aâm (maø khoâng laøm thay ñoåi
ñieàu kieän cuûa bpt) vaø ñoåi chieàu
bpt ta ñöôïc moät bpt töông ñöông.
c) Bình phöông
Bình phöông hai veá cuûa moät bpt
coù hai veá khoâng aâm maø khoâng
laøm thay ñoåi ñieàu kieän cuûa noù ta
ñöôïc moät bpt töông ñöông.
Hoaït ñoäng 4: Cuûng coá
5'
Nhaán maïnh caùc ñieåm caàn
löu yù khi thöïc hieän bieán ñoåi
baát phöông trình.
Chuù yù:
+ Khi bieán ñoåi caùc bieåu thöùc ôû 2
veá cuûa moät bpt thì ñk cuûa bpt coù
theå bò thay ñoåi. Neân ñeå tìm
nghieäm cuûa bpt ta phaûi tìm caùc
giaù trò cuûa x thoaû maõn ñk cuûa bpt
ñoù.
+ Khi nhaân (chia) hai veá cuûa bpt
vôùi moät bieåu thöùc f(x) ta caàn löu
yù ñeán ñk veà daáu cuûa f(x).
+ Khi bình phöông 2 veá cuûa moät
bpt ta caàn löu yù ñeán ñk caû 2 veá
ñeàu khoâng aâm.
4. BAØI TAÄP VEÀ NHAØ:
Baøi 3, 4, 5 SGK.
Ngaøy soaïn: 01/01/2013 Chöông IV: BAÁT ÑAÚNG THÖÙC. BAÁT PHÖÔNG TRÌNH
Tieát daïy: 34 Baøøi 3: DAÁU CUÛA NHÒ THÖÙC BAÄC NHAÁT
I. MUÏC TIEÂU:
Kieán thöùc:
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn
67
Bieát xeùt daáu moät nhò thöùc baäc nhaát, xeùt daáu moät tích, thöông cuûa nhieàu nhò thöùc baäc nhaát.
Khaéc saâu phöông phaùp baûng, phöông phaùp khoaûng.
Kó naêng:
Xeùt ñöôïc daáu cuûa nhò thöùc baäc nhaát.
Söû duïng thaønh thaïo pp baûng vaø pp khoaûng.
Vaän duïng moät caùch linh hoaït vieäc xeùt daáu ñeå giaûi caùc BPT vaø xeùt daáu caùc bieåu thöùc ñaïi
soá khaùc.
Thaùi ñoä:
Dieãn ñaït vaán ñeà roõ raøng, trong saùng.
Tö duy naêng ñoäng, saùng taïo.
II. CHUAÅN BÒ:
Giaùo vieân: Giaùo aùn. Heä thoáng baøi taäp.
Hoïc sinh: SGK, vôû ghi. OÂn taäp caùc kieán thöùc ñaõ hoïc veà Baát phöông trình baäc nhaát moät aån.
III. HOAÏT ÑOÄNG DAÏY HOÏC:
1. OÅn ñònh toå chöùc: Kieåm tra só soá lôùp.
2. Kieåm tra baøi cuõ: (3')
H. Cho f(x) = 3x + 5. Tìm x ñeå f(x) > 0; f(x) < 0 ?
Ñ. f(x) > 0 x >
5
3
; f(x) < 0 x <
5
3
.
3. Giaûng baøi môùi:
TL
Hoaït ñoäng cuûa Giaùo vieân
Hoaït ñoäng cuûa Hoïc sinh
Noäi dung
Hoaït ñoäng 1: Tìm hieåu Ñònh lí veà daáu cuûa nhò thöùc baäc nhaát
5'
H1. Cho VD veà nhò thöùc baäc
nhaát ? Chæ ra caùc heä soá a, b ?
Ñ1.
f(x) = 2x + 3;
g(x) = –2x + 3
I. Ñònh lí veà daáu cuûa nhò thöùc
baäc nhaát
1 Nhò thöùc baäc nhaát
Nhò thöùc baäc nhaát ñoái vôùi x laø bieåu
thöùc daïng f(x) = ax + b vôùi a
0.
15'
H2. Xeùt f(x) = 2x + 3
a) Giaûi BPT f(x) > 0 vaø bieåu
dieãn taäp nghieäm treân truïc soá.
b) Chæ ra caùc khoaûng maø
trong ñoù f(x) cuøng daáu (traùi
daáu) vôùi a ?
H3. Caàn chuù yù ñeán caùc yeáu
toá naøo ?
Ñ2.
2x + 3 > 0 x >
3
2
3
2
Ñ3. heä soá a vaø giaù trò
b
a
2. Daáu cuûa nhò thöùc baäc nhaát
Ñònh lí: Cho nhò thöùc f(x) = ax + b
a.f(x) > 0
x
;
b
a




a.f(x) < 0
x
;
b
a




x
f(x) = ax = b
-
b
a

0
traùi daáu
vôùi a
cuøng daáu
vôùi a
Ví duï: Xeùt daáu nhò thöùc:
a) f(x) = 3x + 2 b) g(x) = –2x + 5
Hoaït ñoäng 2: AÙp duïng xeùt daáu tích, thöông caùc nhò thöùc baäc nhaát
20'
II. Xeùt daáu tích, thöông caùc nhò
thöùc baäc nhaát
Giaû söû f(x) laø moät tích (thöông)
cuûa nhöõng nhò thöùc baäc nhaát. AÙp
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn
68
Höôùng daãn HS caùch laäp
baûng xeùt daáu baèng caùch cho
HS ñieàn vaøo choã troáng.
Moãi nhoùm thöïc hieän moät
yeâu caàu.
x
4x-1
x+2
-3x+5
f(x)
-
-2
1
4
5
3

0
0
0
0
0
–
–
–
–
–
–
+
+ +
++
+
+
+
+
duïng ñònh lí veà daáu cuûa nhò thöùc
baäc nhaát coù theå xeùt daáu töøng nhaân
töû. Laäp baûng xeùt daáu chung cho taát
caû caùc nhò thöùc baäc nhaát coù maët
trong f(x) ta suy ra ñöôïc daáu cuûa
f(x).
Ví duï: Xeùt daáu bieåu thöùc:
f(x) =
(4 1)( 2)
35
xx
x


Hoaït ñoäng 3: Cuûng coá
3'
Nhaán maïnh:
– Caùch xeùt daáu nhò thöùc
– Caùch vaän duïng vieäc xeùt
daáu nhò thöùc ñeå giaûi BPT
4. BAØI TAÄP VEÀ NHAØ:
Laøm baøi taäp 1, 2, 3 SGK.
Ñoïc tröôùc baøi "Baát phöông trình baäc nhaát hai aån".
Ngaøy soaïn: 01/01/2013 Chöông IV: BAÁT ÑAÚNG THÖÙC. BAÁT PHÖÔNG TRÌNH
Tieát daïy: 35 Baøøi 3: DAÁU CUÛA NHÒ THÖÙC BAÄC NHAÁT
I. MUÏC TIEÂU:
Kieán thöùc:
Bieát xeùt daáu moät nhò thöùc baäc nhaát, xeùt daáu moät tích, thöông cuûa nhieàu nhò thöùc baäc nhaát.
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn
69
Khaéc saâu phöông phaùp baûng, phöông phaùp khoaûng.
Kó naêng:
Xeùt ñöôïc daáu cuûa nhò thöùc baäc nhaát.
Söû duïng thaønh thaïo pp baûng vaø pp khoaûng.
Vaän duïng moät caùch linh hoaït vieäc xeùt daáu ñeå giaûi caùc BPT vaø xeùt daáu caùc bieåu thöùc ñaïi
soá khaùc.
Thaùi ñoä:
Dieãn ñaït vaán ñeà roõ raøng, trong saùng.
Tö duy naêng ñoäng, saùng taïo.
II. CHUAÅN BÒ:
Giaùo vieân: Giaùo aùn. Heä thoáng baøi taäp.
Hoïc sinh: SGK, vôû ghi. OÂn taäp caùc kieán thöùc ñaõ hoïc veà Baát phöông trình baäc nhaát moät aån.
III. HOAÏT ÑOÄNG DAÏY HOÏC:
1. OÅn ñònh toå chöùc: Kieåm tra só soá lôùp.
2. Kieåm tra baøi cuõ: (3')
H. Cho f(x) = 3x + 5. Tìm x ñeå f(x) > 0; f(x) < 0 ?
Ñ. f(x) > 0 x >
5
3
; f(x) < 0 x <
5
3
.
3. Giaûng baøi môùi:
TL
Hoaït ñoäng cuûa Giaùo vieân
Hoaït ñoäng cuûa Hoïc sinh
Noäi dung
Hoaït ñoäng 1: Tìm hieåu Ñònh lí veà daáu cuûa nhò thöùc baäc nhaát
5'
H1. Cho VD veà nhò thöùc baäc
nhaát ? Chæ ra caùc heä soá a, b ?
Ñ1.
f(x) = 2x + 3;
g(x) = –2x + 3
I. Ñònh lí veà daáu cuûa nhò thöùc
baäc nhaát
1 Nhò thöùc baäc nhaát
Nhò thöùc baäc nhaát ñoái vôùi x laø bieåu
thöùc daïng f(x) = ax + b vôùi a
0.
10'
H2. Xeùt f(x) = 2x + 3
a) Giaûi BPT f(x) > 0 vaø bieåu
dieãn taäp nghieäm treân truïc soá.
b) Chæ ra caùc khoaûng maø
trong ñoù f(x) cuøng daáu (traùi
daáu) vôùi a ?
H3. Caàn chuù yù ñeán caùc yeáu
toá naøo ?
Ñ2.
2x + 3 > 0 x >
3
2
3
2
Ñ3. heä soá a vaø giaù trò
b
a
2. Daáu cuûa nhò thöùc baäc nhaát
Ñònh lí: Cho nhò thöùc f(x) = ax + b
a.f(x) > 0
x
;
b
a




a.f(x) < 0
x
;
b
a




x
f(x) = ax = b
-
b
a

0
traùi daáu
vôùi a
cuøng daáu
vôùi a
Ví duï: Xeùt daáu nhò thöùc:
a) f(x) = 3x + 2 b) g(x) = –2x + 5
Hoaït ñoäng 2: AÙp duïng xeùt daáu tích, thöông caùc nhò thöùc baäc nhaát
10'
II. Xeùt daáu tích, thöông caùc nhò
thöùc baäc nhaát
Giaû söû f(x) laø moät tích (thöông)
cuûa nhöõng nhò thöùc baäc nhaát. AÙp
duïng ñònh lí veà daáu cuûa nhò thöùc
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn
70
Höôùng daãn HS caùch laäp
baûng xeùt daáu baèng caùch cho
HS ñieàn vaøo choã troáng.
Moãi nhoùm thöïc hieän moät
yeâu caàu.
x
4x-1
x+2
-3x+5
f(x)
-
-2
1
4
5
3

0
0
0
0
0
–
–
–
–
–
–
+
+ +
++
+
+
+
+
baäc nhaát coù theå xeùt daáu töøng nhaân
töû. Laäp baûng xeùt daáu chung cho taát
caû caùc nhò thöùc baäc nhaát coù maët
trong f(x) ta suy ra ñöôïc daáu cuûa
f(x).
Ví duï: Xeùt daáu bieåu thöùc:
f(x) =
(4 1)( 2)
35
xx
x


Hoaït ñoäng 3: AÙp duïng giaûi BPT
7'
H1. Bieán ñoåi BPT ?
H2. Xeùt daáu f(x) ?
Ñ1.
1
1
1 x
0
1
x
x
Ñ2.
x
x
1– x
f(x)
-
0 
0
0
0
–
+
+
+
–
+
–+
–
1
S = [0; 1)
III. AÙp duïng vaøo giaûi BPT
1. BPT tích, BPT chöùa aån ôû maãu
Ví duï: Giaûi BPT
1
1
1 x
7'
H3. Xeùt daáu, khöû daáu GTTÑ
Höôùng daãn pp khoaûng
Ñ3.
21x
=
=
2x 1 neáu 2x 1 0
2x 1 neáu 2x 1 0
(*)
1
2
7
1
2
3
x
x
x
x

–7<x
<3
2. BPT chöùa aån trong daáu GTTÑ
Ví duï: Giaûi BPT
21x
+ x – 3 < 5 (*)
Hoaït ñoäng 5: Cuûng coá
3'
Nhaán maïnh:
– Caùch xeùt daáu nhò thöùc
– Caùch vaän duïng vieäc xeùt
daáu nhò thöùc ñeå giaûi BPT
Vôùi a > 0 ta coù:
()f x a
–a f(x) a
()f x a
()
()
f x a
f x a

4. BAØI TAÄP VEÀ NHAØ:
Laøm baøi taäp 1, 2, 3 SGK.
Ñoïc tröôùc baøi "Baát phöông trình baäc nhaát hai aån".
Ngaøy soaïn: 8/01/2013 Chöông IV: BAÁT ÑAÚNG THÖÙC. BAÁT PHÖÔNG TRÌNH
Tieát daïy: 36 Baøøi 4: BAÁT PHÖÔNG TRÌNH BAÄC NHAÁT HAI AÅN
I. MUÏC TIEÂU:
Kieán thöùc:
Hieåu ñöôïc khaùi nieäm BPT, heä BPT baäc nhaát hai aån; taäp nghieäm cuûa BPT, heä BPT baäc
nhaát hai aån.
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn
71
Kó naêng:
Bieát xaùc ñònh mieàn nghieäm cuûa BPT, heä BPT baäc nhaát hai aån.
AÙp duïng ñöôïc vaøo baøi toaùn thöïc teá.
Thaùi ñoä:
Lieän heä kieán thöùc ñaõ hoïc vôùi thöïc tieãn.
Tö duy saùng taïo, lí luaän chaët cheõ.
II. CHUAÅN BÒ:
Giaùo vieân: Giaùo aùn. Moät soá baøi toaùn thöïc teá. Hình veõ minh hoaï.
Hoïc sinh: SGK, vôû ghi. OÂn taäp caùc kieán thöùc ñaõ hoïc veà Haøm soá baäc nhaát.
III. HOAÏT ÑOÄNG DAÏY HOÏC:
1. OÅn ñònh toå chöùc: Kieåm tra só soá lôùp.
2. Kieåm tra baøi cuõ: (3')
H. Ñoà thò cuûa haøm soá baäc nhaát? Veõ ñoà thò cuûa haøm soá y = 3 – 2x?
Ñ.
3. Giaûng baøi môùi:
TL
Hoaït ñoäng cuûa Giaùo vieân
Hoaït ñoäng cuûa Hoïc sinh
Noäi dung
Hoaït ñoäng 1: Tìm hieåu khaùi nieäm Baát phöông trình baäc nhaát hai aån
5'
Cho HS neâu moät soá pt baäc
nhaát hai aån. Töø ñoù chuyeån
sang bpt baäc nhaát hai aån.
Caùc nhoùm thöïc hieän yeâu
caàu.
3x + 2y < 1; x + 2y 2
I. Baát phöông trình baäc nhaát hai
aån
BPT baäc nhaát hai aån x, y coù daïng
toång quaùt laø: ax + by
c (1)
(<,
, >)
trong a
2
+ b
2
0).
Hoaït ñoäng 2: Tìm hieåu caùch bieåu dieãn taäp nghieäm cuûa BPT baäc nhaát hai aån
15'
GV bieåu dieãn mieàn
nghieäm cuûa moät soá bpt baäc
nhaát hai aån ñaëc bieät. Töø ñoù
giôùi thieäu caùch bieåu dieãn
mieàn nghieäm.
VD: Bieåu dieãn hình hoïc taäp
nghieäm cuûa bpt:
2x + y 3
GV höôùng daãn HS thöïc
hieän laàn löôït caùc böôùc.
O
x
y
1
Phaàn khoâng gaïch laø mieàn
nghieäm cuûa bpt y
1
O
x
y
1
Phaàn khoâng gaïch laø mieàn
nghieäm cuûa bpt x
1
II. Bieåu dieãn taäp nghieäm cuûa
BPT baäc nhaát hai aån
Trong mp Oxy, taäp hôïp caùc ñieåm
coù toaï ñoä laø nghieäm cuûa (1) ñgl
mieàn nghieäm cuûa noù.
Ñöôøng thaúng ax + by = c chia
maët phaúng thaønh hai nöûa mp, moät
trong hai nöûa mp ñoù (keå caû bôø) laø
mieàn nghieäm cuûa bpt ax + by
c,
nöûa mp kia (keå caû bôø) laø mieàn
nghieäm cuûa bpt ax + by
c.
Qui taéc thöïc haønh bieåu dieãn mieàn
nghieäm cuûa bpt ax + by
c (1):
B1: Veõ ñöôøng thaúng
: ax + by = c
B2: Laáy moät ñieåm M
0
(x
0
; y
0
) khoâng
thuoäc
(thöôøng laáy goác toaï doä O).
B3: Tính ax
0
+ by
0
vaø so saùnh côùi c
B4: Keát luaän:
+ Neáu ax
0
+ by
0
< c thì nöûa mp bôø
chöùa M
0
laø mieàn nghieäm cuûa (1).
+ Neáu ax
0
+ by
0
> c thì nöûa mp bôø
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn
72
Mieàn nghieäm laø mieàn
khoâng bò gaïch cheùo
khoâng chöùa M
0
laø mieàn nghieäm
cuûa (1).
Chuù yù: Mieàn nghieäm cuûa (1) boû ñi
ñöôøng thaúng
laø mieàn nghieäm cuûa
bpt ax + by < c.
Hoaït ñoäng 3: AÙp duïng bieåu dieãn taäp nghieäm cuûa BPT baäc nhaát hai aån
15'
Cho caùc nhoùm thöïc hieän
laàn löôït caùc böôùc. Moãi nhoùm
duøng baûng con ñeå veõ.
Ví duï: Bieåu dieãn hình hoïc taäp
nghieäm caùc BPT:
a) –3x + 2y > 0
b) 3x + y 6
c) 2x – y 3
d) x + y < 4
a) b) c) d)
Hoaït ñoäng 4: Cuûng coá
3'
Nhaán maïnh caùc böôùc bieåu
dieãn hình hoïc taäp nghieäm
cuûa BPT baäc nhaát hai aån.
4. BAØI TAÄP VEÀ NHAØ:
Laøm baøi taäp 1, 2 SGK.
Ñoïc tieáp baøi "Baát phöông trình baäc nhaát hai aån".
Ngaøy soaïn: 05/01/2013 Chöông IV: BAÁT ÑAÚNG THÖÙC. BAÁT PHÖÔNG TRÌNH
Tieát daïy: 37 Baøøi 4: BAØI TAÄP BPT BAÄC NHAÁT HAI AÅN
I. MUÏC TIEÂU:
Kieán thöùc:
Cuûng coá khaùi nieäm BPT, heä BPT baäc nhaát hai aån; taäp nghieäm cuûa BPT, heä BPT baäc nhaát
hai aån.
Kó naêng:
Bieát xaùc ñònh mieàn nghieäm cuûa BPT, heä BPT baäc nhaát hai aån.
AÙp duïng ñöôïc vaøo baøi toaùn thöïc teá.
Thaùi ñoä:
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn
73
Lieän heä kieán thöùc ñaõ hoïc vôùi thöïc tieãn.
Tö duy saùng taïo, lí luaän chaët cheõ.
II. CHUAÅN BÒ:
Giaùo vieân: Giaùo aùn. Heä thoáng baøi taäp. Hình veõ minh hoaï.
Hoïc sinh: SGK, vôû ghi. OÂn taäp caùc kieán thöùc ñaõ hoïc veà BPT baäc nhaát hai aån.
III. HOAÏT ÑOÄNG DAÏY HOÏC:
1. OÅn ñònh toå chöùc: Kieåm tra só soá lôùp.
2. Kieåm tra baøi cuõ: (Loàng vaøo quaù trình luyeän taäp)
3. Giaûng baøi môùi:
TL
Hoaït ñoäng cuûa Giaùo vieân
Hoaït ñoäng cuûa Hoïc sinh
Noäi dung
Hoaït ñoäng 1: Luyeän kyõ naêng bieåu dieãn mieàn nghieäm cuûa BPT baäc nhaát hai aån
7'
H1. Bieán ñoåi BPT?
H2. Neâu caùc böôùc bieåu dieãn
taäp nghieäm cuûa BPT baäc
nhaát hai aån?
Caùc mieàn nghieäm cuûa caùc
BPT a), b) laø caùc nöûa mp
khoâng keå bôø.
Ñ1.
a) x + 2y < 4
O
y
x
4
2
1. Bieåu dieãn hình hoïc taäp nghieäm
cuûa BPT:
a) –x + 2 +2(y – 2) < 2(1 – x)
b) 3(x – 1) + 4(y – 2) < 5x – 3
b) –x + 2y < 4
O
y
x
– 4
2
Hoaït ñoäng 2: Luyeän kyõ naêng bieåu dieãn mieàn nghieäm cuûa heä BPT baäc nhaát hai aån
13'
H1. Neâu caùc böôùc bieåu dieãn
taäp nghieäm cuûa caùc heä BPT?
Ñ1. a)
O
y
x
–2–3
3
x
–
2
y
=
0
–
x
+
y
=
3
x
+
3y
=
–2
b)
O
y
x
3
2
3
2
2. Bieåu dieãn hình hoïc taäp nghieäm
cuûa heä BPT:
a)
20
32
3
xy
xy
yx


b)
10
32
13
2
22
0
xy
y
x
x
Hoaït ñoäng 3: Luyeän kyõ naêng vaän duïng vaøo baøi toaùn thöïc teá
15'
Cho caùc nhoùm thaûo luaän,
phaân tích baøi toaùn, laäp ra caùc
heä thöùc.
Caùc nhoùm thaûo luaän,
trình baøy keát quaû.
Goïi x SP loaïi I, y SP loaïi II
2 2 10
24
2 4 12
0
0
xy
y
xy
x
y


L = 3x + 5y ñaït lôùn nhaát.
3. Coù 3 nhoùm maùy A, B, C duøng
ñeå saûn xuaát ra 2 loaïi saûn phaåm I
vaø II. Ñeå saûn xuaát moät ñôn vò saûn
phaåm moãi loaïi phaûi laàn löôït duøng
caùc maùy thuoäc caùc nhoùm maùy
khaùc nhau. Soá maùy trong moät
nhoùm vaø soá maùy cuûa töøng nhoùm
caàn thieát ñeå saûn xuaát ra moät ñôn
vò saûn phaåm thuoäc moãi loaïi ñöôïc
cho trong baûng sau:
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn
74
Nhoùm
Soá maùy trong
moãi nhoùm
Soá maùy trong töøng nhoùm ñeå saûn
xuaát moät ñôn vò SP
Loaïi I
Loaïi II
A
10
2
2
B
4
0
2
C
12
2
4
Cho caùc nhoùm laàn löôït bieåu dieãn caùc mieàn nghieäm cuûa
caùc BPT.
O
y
x
5
6
2
3
5
C B
D
A
(x;y)
B(2;2)
C(0;2)
O(0;0)
A(4;1)
D(5;0)
L=3x+5y
16
10
0
17
15
maxL = 17 khi x = 4; y = 1
Moät ñôn vò saûn phaåm I laõi 3000 ñ,
moät ñôn vò saûn phaåm II laõi 5000 ñ.
Haõy laäp phöông aùn saûn xuaát hai
loaïi saûn phaåm treân sao cho coù laõi
cao nhaát.
Hoaït ñoäng 4: Cuûng coá
5'
Nhaán maïnh:
+ Caùc böôùc bieåu dieãn taäp
nghieäm cuûa heä BPT baäc
nhaát hai aån.
+ Caùch phaân tích, tìm caùc heä
thöùc trong baøi toaùn kinh teá.
4. BAØI TAÄP VEÀ NHAØ:
Ñoïc tröôùc baøi " Daáu cuûa tam thöùc baäc hai".
Ngaøy soaïn: 08/01/2013 Chöông IV: BAÁT ÑAÚNG THÖÙC. BAÁT PHÖÔNG TRÌNH
Tieát daïy: 38 Baøøi 5: DAÁU CUÛA TAM THÖÙC BAÄC HAI
I. MUÏC TIEÂU:
Kieán thöùc:
Naém ñöôïc ñònh lí veà daáu cuûa tam thöùc baäc hai.
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn
75
Bieát vaø vaän duïng ñöôïc ñònh lí trong vieäc giaûi caùc baøi toaùn veà xeùt daáu tam thöùc baäc hai.
Bieát söû duïng pp baûng, pp khoaûng trong vieäc giaûi toaùn.
Bieát lieân heä giöõa baøi toaùn xeùt daáu vaø baøi toaùn veà giaûi BPT vaø heä BPT.
Kó naêng:
Phaùt hieän vaø giaûi caùc baøi toaùn veà xeùt daáu cuûa tam thöùc baäc hai.
Vaän duïng ñöôïc ñònh lí trong vieäc giaûi BPT baäc hai vaø moät soá BPT khaùc.
Thaùi ñoä:
Bieát lieân heä giöõa thöïc tieãn vôùi toaùn hoïc.
Tích cöïc, chuû ñoäng, töï giaùc trong hoïc taäp.
II. CHUAÅN BÒ:
Giaùo vieân: Giaùo aùn. Hình veõ minh hoaï.
Hoïc sinh: SGK, vôû ghi. OÂn taäp kieán thöùc xeùt daáu nhò thöùc baäc nhaát.
III. HOAÏT ÑOÄNG DAÏY HOÏC:
1. OÅn ñònh toå chöùc: Kieåm tra só soá lôùp.
2. Kieåm tra baøi cuõ: (3')
H. Xeùt daáu bieåu thöùc: f(x) = (x – 2)(2x – 3)
Ñ. f(x) > 0 vôùi x (–;
3
2
) (2; +); f(x) < 0 vôùi x (
3
2
; 2)
3. Giaûng baøi môùi:
TL
Hoaït ñoäng cuûa Giaùo vieân
Hoaït ñoäng cuûa Hoïc sinh
Noäi dung
Hoaït ñoäng 1: Tìm hieåu khaùi nieäm Tam thöùc baäc hai
15'
GV giôùi thieäu khaùi nieäm
tam thöùc baäc hai.
H1. Cho VD veà tam thöùc baäc
hai?
H2. Tính f(4), f(–2), f(–1),
f(0) vaø nhaän xeùt daáu cuûa
chuùng ?
H3. Quan saùt ñoà thò cuûa haøm
soá y = x
2
– 5x + 4 vaø chæ ra
caùc khoaûng treân ñoà thò ôû phía
treân, phía döôùi truïc hoaønh ?
H4. Quan saùt caùc ñoà thò trong
hình 32 vaø ruùt ra moái lieân heä
veà daáu cuûa giaù trò f(x) = ax
2
+
bx + c öùng vôùi x tuyø theo daáu
cuûa = b
2
– 4ac ?
Ñ1. Moãi nhoùm cho moät VD.
f(x) = x
2
– 5x + 4
g(x) = x
2
– 4x + 4
h(x) = x
2
– 4x + 5
Ñ2.
f(4) = 0; f(2) = –2 < 0
f(–1) = 10 > 0; f(0) = 4 > 0
Ñ3.
y > 0, x (–; 1) (4; +)
y < 0, x (1; 4)
Ñ4. Caùc nhoùm thaûo luaän
< 0 f(x) cuøng daáu vôùi a
= 0 f(x) cuøng daáu vôùi a,
tröø x = –
2
b
a
> 0 ….
I. Ñònh lí veà daáu cuûa tam
thöùc baäc hai
1. Tam thöùc baäc hai
Tam thöùc baäc hai ñoái vôùi x laø
bieåu thöùc coù daïng:
f(x) = ax
2
+ bx + c (a
0)
Hoaït ñoäng 2: Tìm hieåu ñònh lí veà daáu cuûa tam thöùc baäc hai
12'
GV neâu ñònh lí veà daáu cuûa
tam thöùc baäc hai.
2. Daáu cuûa tam thöùc baäc hai
Cho f(x) = ax
2
+ bx + c
(a
0),
= b
2
– 4ac.
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn
76
+
< 0
a.f(x) > 0, x
R
+
= 0
a.f(x) > 0, x
2
b
a
+
> 0
12
12
( ) 0,
( ) 0,
af x x x x x
af x x x x
Minh hoaï hình hoïc
< 0
= 0
> 0
a>0
x
y
O
+
+
+
+
+
+
+
+
+
+
+
+
+
x
y
O
+
+
+
+
+
+
+
+
+
+
+
+
+
2
b
a
x
y
O
+
+
+
+
+
+
+
+
+
+
-
-
-
-
-
-
-
x
1
x
2
a<0
x
y
O
-
-
-
-
-
-
-
-
-
x
y
O
2
b
a
-
-
-
-
-
-
-
-
x
y
O
+
+
+
+
+
-
-
-
-
-
-
x
1
x
2
Hoaït ñoäng 3: AÙp duïng xeùt daáu tam thöùc baäc hai
10'
H1. Xaùc ñònh a, ?
GV höôùng daãn caùch laäp
baûng xeùt daáu.
Ñ1.
a) a = –1 < 0; = –11 < 0
f(x) < 0, x
b) a = 2 > 0, = 9 > 0
f(x) > 0, x(–
;
1
2
)(2;+)
f(x) < 0, x (
1
2
;2)
3. AÙp duïng
VD1:
a) Xeùt daáu tam thöùc
f(x) = –x
2
+ 3x – 5
b) Laäp baûng xeùt daáu tam thöùc
f(x) = 2x
2
– 5x + 2
Hoaït ñoäng 4: Cuûng coá
3'
Nhaán maïnh:
Ñònh lí veà daáu cuûa tam thöùc
baäc hai.
4. BAØI TAÄP VEÀ NHAØ:
Baøi 1, 2 SGK.
Ñoïc tieáp baøi "Daáu cuûa tam thöùc baäc hai"
Ngaøy soaïn: 27/01/2013 Chöông IV: BAÁT ÑAÚNG THÖÙC. BAÁT PHÖÔNG TRÌNH
Tieát daïy: 39 Baøøi 5: BAØI TAÄP DAÁU CUÛA TAM THÖÙC BAÄC HAI
I. MUÏC TIEÂU:
Kieán thöùc:
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn
77
Cuûng coá ñònh lí veà daáu cuûa tam thöùc baäc hai.
Cuûng coá caùch söû duïng pp baûng, pp khoaûng trong vieäc giaûi toaùn.
Bieát lieân heä giöõa baøi toaùn xeùt daáu vaø baøi toaùn veà giaûi BPT vaø heä BPT.
Kó naêng:
Vaän duïng ñöôïc ñònh lí trong vieäc giaûi caùc baøi toaùn veà xeùt daáu tam thöùc baäc hai.
Vaän duïng ñöôïc ñònh lí trong vieäc giaûi BPT baäc hai vaø moät soá BPT khaùc.
Thaùi ñoä:
Reøn luyeän tính caån thaän, chính xaùc.
Tích cöïc, chuû ñoäng, töï giaùc trong hoïc taäp.
II. CHUAÅN BÒ:
Giaùo vieân: Giaùo aùn. Heä thoáng baøi taäp.
Hoïc sinh: SGK, vôû ghi. OÂn taäp kieán thöùc xeùt daáu tam thöùc baäc hai ñaõ hoïc.
III. HOAÏT ÑOÄNG DAÏY HOÏC:
1. OÅn ñònh toå chöùc: Kieåm tra só soá lôùp.
2. Kieåm tra baøi cuõ: (Loàng vaøo quaù trình luyeän taäp)
3. Giaûng baøi môùi:
TL
Hoaït ñoäng cuûa Giaùo vieân
Hoaït ñoäng cuûa Hoïc sinh
Noäi dung
Hoaït ñoäng 1: Luyeän kyõ naêng xeùt daáu tam thöùc baäc hai
20'
H1. Ta caàn xeùt caùc yeáu toá
naøo ?
Moãi nhoùm xeùt moät tam
thöùc
Ñ1. a vaø .
a) a = 5 > 0; = –11 < 0
f(x) > 0, x
b) a = –2 < 0; = 49 > 0
f(x) < 0, x
5
1;
2



f(x) >0,x(–;–
1. Xeùt daáu tam thöùc baäc hai
a) 5x
2
– 3x + 1
b) –2x
2
+ 3x + 5
c) x
2
+ 12x + 36
d) (2x – 3)(x + 5)
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn
78
20'
Höôùng daãn HS caùch laäp
baûng xeùt daáu. (Cho HS ñieàn
vaøo baûng xeùt daáu)
H2. Tìm taát caû caùc nghieäm
cuûa f(x) ? Saép xeáp caùc
nghieäm
H3. Tìm taát caû caùc nghieäm
cuûa töû vaø maãu ? Saép xeáp
caùc nghieäm ?
1)
5
;
2




c) a = 1 > 0; = 0
f(x) 0, x
d) f(x) < 0, x
3
5;
2



f(x)>0, x(–;–
5)
3
;
2




Ñ2. a) f(x) = 0 x = 3; x =
1
3
; x =
5
4
Ñ3.
Nghieäm cuûa töû:
x = 0; x =
1
3
; x =
3
Nghieäm cuûa maãu:
x = –1; x =
3
4
2. Laäp baûng xeùt daáu caùc
bieåu thöùc sau
a) f(x) = (3x
2
– 10x + 3)(4x
– 5)
b) g(x) =
22
2
(3 )(3 )
43
x x x
xx


Hoaït ñoäng 2: Cuûng coá
5'
Nhaán maïnh:
Caùch vaän duïng ñònh lí veà
daáu cuûa tam thöùc baäc hai
ñeå giaûi BPT baäc hai.
4. BAØI TAÄP VEÀ NHAØ: Ñoïc tröôùc baøi " Daáu cuûa tam thöùc baäc hai".
Ngaøy soaïn: 27/01/2013 Chöông IV: BAÁT ÑAÚNG THÖÙC. BAÁT PHÖÔNG TRÌNH
Tieát daïy: 40 Baøøi 5: DAÁU CUÛA TAM THÖÙC BAÄC HAI (tt)
I. MUÏC TIEÂU:
Kieán thöùc:
Naém ñöôïc ñònh lí veà daáu cuûa tam thöùc baäc hai.
Bieát vaø vaän duïng ñöôïc ñònh lí trong vieäc giaûi caùc baøi toaùn veà xeùt daáu tam thöùc baäc hai.
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn
79
Bieát söû duïng pp baûng, pp khoaûng trong vieäc giaûi toaùn.
Bieát lieân heä giöõa baøi toaùn xeùt daáu vaø baøi toaùn veà giaûi BPT vaø heä BPT.
Kó naêng:
Phaùt hieän vaø giaûi caùc baøi toaùn veà xeùt daáu cuûa tam thöùc baäc hai.
Vaän duïng ñöôïc ñònh lí trong vieäc giaûi BPT baäc hai vaø moät soá BPT khaùc.
Thaùi ñoä:
Bieát lieân heä giöõa thöïc tieãn vôùi toaùn hoïc.
Tích cöïc, chuû ñoäng, töï giaùc trong hoïc taäp.
II. CHUAÅN BÒ:
Giaùo vieân: Giaùo aùn.
Hoïc sinh: SGK, vôû ghi. OÂn taäp kieán thöùc xeùt daáu tam thöùc baäc hai ñaõ hoïc.
III. HOAÏT ÑOÄNG DAÏY HOÏC:
1. OÅn ñònh toå chöùc: Kieåm tra só soá lôùp.
2. Kieåm tra baøi cuõ: (3')
H. Neâu ñònh lí veà daáu cuûa tam thöùc baäc hai.
Ñ.
3. Giaûng baøi môùi:
TL
Hoaït ñoäng cuûa Giaùo vieân
Hoaït ñoäng cuûa Hoïc sinh
Noäi dung
Hoaït ñoäng 1: Tìm hieåu khaùi nieäm baát phöông trình baäc hai
7'
H1. Cho VD veà BPT baäc hai
moät aån ?
Ñ1. Moãi nhoùm cho moät VD.
–2x
2
+ 3x + 5 > 0
–3x
2
+ 7x – 4 < 0
II. Baát phöông trình baäc hai
moät aån
1. Baát phöông trình baäc hai
BPT baäc hai aån x laø BPT daïng
ax
2
+ bx + c < 0 (> 0;
0;
0)
(a
0)
Hoaït ñoäng 2: Tìm hieåu caùch giaûi baát phöông trình baäc hai
15'
H1. Cho moãi nhoùm giaûi moät
BPT.
Ñ1.
a) a = 3 > 0;  = –14 < 0
S = R
b) a = –2 < 0; f(x) coù 2
nghieäm
x
1
= –1; x
2
=
5
2
S =
5
1;
2



c) a = –3 < 0; f(x) coù 2
nghieäm
x
1
= 1; x
2
=
4
3
S = (–; 1)
4
;
3




d) a = 9 > 0; f(x) coù nghieäm
2. Giaûi BPT baäc hai
Ñeå giaûi BPT baäc hai ta döïa
vaøo vieäc xeùt daáu tam thöùc baäc
hai.
VD1: Giaûi caùc BPT sau:
a) 3x
2
+ 2x + 5 > 0
b) –2x
2
+ 3x + 5 > 0
c) –3x
2
+ 7x – 4 < 0
d) 9x
2
– 24x + 16 0
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn
80
keùp x =
4
3
S = R
Hoaït ñoäng 3: Vaän duïng vieäc giaûi BPT baäc hai
15'
GV höôùng daãn HS thöïc hieän
caùc böôùc.
H1. Neâu ñk ñeå pt (*) coù 2
nghieäm traùi daáu ?
H2. Giaûi bpt (1)
H3. Neâu ñk ñeå (*) nghieäm
ñuùng vôùi moïi x ?
H4. Giaûi BPT (2)
Ñ1. ac < 0
2(2m
2
– 3m – 5) < 0
2m
2
– 3m – 5 < 0 (1)
Ñ2. S =
5
1;
2



Ñ3.  < 0 m
2
+ 3m – 1 < 0
(2)
Ñ4. S =
3 13 3 13
;
22



VD2: Tìm caùc trò cuûa tham soá
m ñeå phöông trình sau coù 2
nghieäm traùi daáu:
2x
2
– (m
2
– m + 1)x + 2m
2
–
3m – 5 = 0 (*)
VD3: Tìm m ñeå BPT sau
nghieäm ñuùng vôùi moïi x:
–x
2
+ 2mx + 3m – 1 < 0 (*)
Hoaït ñoäng 4: Cuûng coá
3'
Nhaán maïnh:
Caùch vaän duïng ñònh lí veà daáu
cuûa tam thöùc baäc hai ñeå giaûi
BPT baäc hai.
4. BAØI TAÄP VEÀ NHAØ:
Baøi 3, 4 SGK.
Ngaøy soaïn: 27/01/2012 Chöông IV: BAÁT ÑAÚNG THÖÙC. BAÁT PHÖÔNG TRÌNH
Tieát daïy: 41 Baøøi 5: BAØI TAÄP DAÁU CUÛA TAM THÖÙC BAÄC HAI
I. MUÏC TIEÂU:
Kieán thöùc:
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn
81
Cuûng coá ñònh lí veà daáu cuûa tam thöùc baäc hai.
Cuûng coá caùch söû duïng pp baûng, pp khoaûng trong vieäc giaûi toaùn.
Bieát lieân heä giöõa baøi toaùn xeùt daáu vaø baøi toaùn veà giaûi BPT vaø heä BPT.
Kó naêng:
Vaän duïng ñöôïc ñònh lí trong vieäc giaûi caùc baøi toaùn veà xeùt daáu tam thöùc baäc hai.
Vaän duïng ñöôïc ñònh lí trong vieäc giaûi BPT baäc hai vaø moät soá BPT khaùc.
Thaùi ñoä:
Reøn luyeän tính caån thaän, chính xaùc.
Tích cöïc, chuû ñoäng, töï giaùc trong hoïc taäp.
II. CHUAÅN BÒ:
Giaùo vieân: Giaùo aùn. Heä thoáng baøi taäp.
Hoïc sinh: SGK, vôû ghi. OÂn taäp kieán thöùc xeùt daáu tam thöùc baäc hai ñaõ hoïc.
III. HOAÏT ÑOÄNG DAÏY HOÏC:
1. OÅn ñònh toå chöùc: Kieåm tra só soá lôùp.
2. Kieåm tra baøi cuõ: (Loàng vaøo quaù trình luyeän taäp)
3. Giaûng baøi môùi:
Hoaït ñoäng 1: Vaän duïng xeùt daáu tam thöùc ñeå giaûi baát phöông trình
20'
H1. Neâu caùch giaûi ?
Ñ1.
+ Ñöa veà daïng f(x) < 0
+ Xeùt daáu bieåu thöùc f(x)
+ Keát luaän nghieäm cuûa bpt.
a) S =
b) S =
4
1;
3



c)
S = (–;–
8)
4
2;
3




(1;2)
3. Giaûi caùc baát phöông trình
a) 4x
2
– x + 1 < 0
b) –3x
2
+ x + 4 0
c)
22
13
4 3 4x x x
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn
82
Hoaït ñoäng 2: Vaän duïng vieäc giaûi BPT baäc hai
20'
Höôùng daãn HS phaân tích
yeâu caàu baøi toaùn.
H1. Xaùc ñònh caùc tröôøng
hôïp coù theå xaûy ra cuûa ña
thöùc?
H2. Neâu ñk ñeå pt voâ
nghieäm ?
Ñ1. Xeùt a = 0; a 0
Ñ2.
a) m < 1; m > 3
b)
3
2
< m < –1
4. Tìm caùc giaù trò cuûa m ñeå
caùc phöông trình sau voâ
nghieäm
a) (m–2)x
2
+2(2m–3)x
+5m–6=0
b) (3–m)x
2
–2(m+3)x +m+2
=0
Hoaït ñoäng 3: Cuûng coá
3'
Nhaán maïnh:
Caùch vaän duïng ñònh lí veà
daáu cuûa tam thöùc baäc hai
ñeå giaûi BPT baäc hai.
4. BAØI TAÄP VEÀ NHAØ:
Baøi taäp oân chöông IV.
Ngaøy soaïn: 10/02/2013 Chöông IV: BAÁT ÑAÚNG THÖÙC. BAÁT PHÖÔNG TRÌNH
Tieát daïy: 42 Baøøi daïy: OÂN TAÄP CHÖÔNG IV
I. MUÏC TIEÂU:
Kieán thöùc:
OÂn taäp toaøn boä kieán thöùc trong chöông IV.
Kó naêng:
Vaän duïng caùc kieán thöùc moät caùch toång hôïp.
Thaùi ñoä:
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn
83
Taïo höùng thuù trong hoïc taäp, lieân heä ñöôïc caùc kieán thöùc ñaõ hoïc vaøo thöïc teá.
II. CHUAÅN BÒ:
Giaùo vieân: Giaùo aùn. Heä thoáng baøi taäp.
Hoïc sinh: SGK, vôû ghi. OÂn taäp kieán thöùc ñaõ hoïc trong chöông IV.
III. HOAÏT ÑOÄNG DAÏY HOÏC:
1. OÅn ñònh toå chöùc: Kieåm tra só soá lôùp.
2. Kieåm tra baøi cuõ: (Loàng vaøo quaù trình oân taäp)
H.
Ñ.
3. Giaûng baøi môùi:
TL
Hoaït ñoäng cuûa Giaùo vieân
Hoaït ñoäng cuûa Hoïc sinh
Noäi dung
Hoaït ñoäng 1: OÂn taäp veà Baát ñaúng thöùc
10'
Nhaéc laïi caùc tính chaát vaø
caùch chöùng minh BÑT.
H1. Neâu caùch chöùng minh ?
Ñ1.
a) Vaän duïng BÑT Coâsi
2 . 2
a b a b
b a b a
b) Bieán ñoåi töông ñöông
2
0ab
1. Cho a, b, c > 0. CMR:
a)
6
a b b c c a
c a b
b)
ab
ab
ba
Hoaït ñoäng 2: OÂn taäp giaûi BPT baäc nhaát, baäc hai moät aån
15'
Moãi nhoùm giaûi 1 heä BPT
H1. Neâu caùch giaûi ?
Ñ1. Giaûi töøng BPT trong heä,
roài laáy giao caùc taäp nghieäm.
a)
02
1
x
x


0 x 2
b)
2
2
2
1
x
x
x
x



2
2
x
x

c)
5 17 5 17
22
4 15 4 15
x
x


x
d)
13
21
x
x
–1 x 1
2. Giaûi caùc heä BPT sau:
a)
2
20
2 1 3 2
xx
xx

b)
2
40
11
21
x
xx


c)
2
2
5 2 0
8 1 0
xx
xx
d)
12
2 1 3
x
x


Hoaït ñoäng 3: OÂn taäp bieåu dieãn mieàn nghieäm cuûa heä BPT baäc nhaát hai aån
7'
H1. Neâu caùc böôùc thöïc hieän ?
Ñ1.
+ Veõ caùc ñöôøng thaúng treân
cuøng heä truïc toaï ñoä:
3x + y = 9; x – y = –3;
x + 2y = 8; y = 6
+ Xaùc ñònh mieàn nghieäm cuûa
3. Bieåu dieãn hình hoïc taäp
nghieäm cuûa heä BPT:
39
3
28
6
xy
xy
yx
y



Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn
84
moãi BPT.
+ Laáy giao caùc mieàn nghieäm.
Hoaït ñoäng 4: Vaän duïng vieäc xeùt daáu tam thöùc baäc hai
8'
Höôùng daãn caùch xeùt.
H1. Xeùt daáu x
2
– x + 3;
x
2
– 2x + 2 ?
Ñ1. x
2
– x + 3 > 0, x
a) f(x) = x
4
– (x – 3)
2
= (x
2
– x + 3)(x
2
+ x – 3)
g(x) =
=
22
2
( 2 2)( 2 2)
2
x x x x
xx
b)
(x
2
– x + 3)(x
2
+ x – 3) < 0
x
2
+ x – 3 < 0
1 13 1 13
22
x

x {–2; –1; 0; 1}
4. a) Baèng caùch söû duïng haèng
ñaúng thöùc a
2
–b
2
=(a + b)(a –
b) haõy xeùt daáu caùc bieåu thöùc:
f(x) = x
4
– x
2
+ 6x – 9
g(x) = x
2
– 2x –
2
4
2xx
b) Haõy tìm nghieäm nguyeân
cuûa BPT:
x(x
3
– x + 6) < 9
Hoaït ñoäng 4: Cuûng coá
3'
Nhaán maïnh:
– Caùch chöùng minh BÑT.
– Caùch giaûi BPT, heä BPT moät
aån.
4. BAØI TAÄP VEÀ NHAØ:
Chuaån bò kieåm tra 1 tieát chöông IV.
Ngaøy soaïn: 15/02/2013 Chöông IV: BAÁT ÑAÚNG THÖÙC. BAÁT PHÖÔNG TRÌNH
Tieát daïy: 43 Baøøi daïy: KIEÅM TRA 1 TIEÁT CHÖÔNG IV
I. MUÏC TIEÂU:
Kieán thöùc:
OÂn taäp toaøn boä kieán thöùc trong chöông IV.
Kó naêng:
Vaän duïng caùc kieán thöùc moät caùch toång hôïp.
Thaùi ñoä:
Reøn luyeän tính caån thaän, chính xaùc.
II. CHUAÅN BÒ:
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn
85
Giaùo vieân: Giaùo aùn. Ñeà kieåm tra.
Hoïc sinh: OÂn taäp kieán thöùc ñaõ hoïc trong chöông IV.
III. MA TRAÄN ÑEÀ:
Chuû ñeà
Nhaän bieát
Thoâng hieåu
Vaän duïng
Toång
TNKQ
TL
TNKQ
TL
TNKQ
TL
BPT baäc nhaát
2
0,5
1,0
BPT baäc hai
2
0,5
4
0,5
1
3,0
1
3,0
9,0
Toång
2,0
2,0
3,0
3,0
10
IV. NOÄI DUNG ÑEÀ KIEÅM TRA:
A. Phaàn traéc nghieäm: (4 ñieåm)
Caâu 1: Taäp nghieäm cuûa baát phöông trình:
11x 
laø:
A) (–2; 2) B) (0; 1) C) (0; 2) D) (–; 2)
Caâu 2: Taäp nghieäm cuûa heä baát phöông trình:
3 1 0
50
x
x


laø:
A)
1
;5
3


B)
1
;5
3



C) (5; + ) D)
1
;
3



Caâu 3: Taäp nghieäm cuûa baát phöông trình: x
2
– 2x – 3 < 0 laø:
A) (–3; 1) B) (–1; 3) C) (–;–1)(3;+) D) (–;–3)(1;+)
Caâu 4: Taäp nghieäm cuûa baát phöông trình: x
2
– 9 0 laø:
A) (–; 3] B) (–; –3] C) (–;–3][3;+) D) [–3; 3]
Caâu 5: Taäp xaùc ñònh cuûa haøm soá f(x) =
2
54xx
laø:
A) [1; 4] B) (–; 1][4;+) C) (–; 1)(4;+) D) (1; 4)
Caâu 6: Phöông trình: x
2
+ (2m – 3)x + m
2
– 6 = 0 voâ nghieäm khi:
A) m =
33
12
B) m <
33
12
C) m
33
12
D) m >
33
12
Caâu 7: Tam thöùc naøo sau ñaây luoân luoân döông vôùi moïi x:
A) 4x
2
– x + 1 B) x
2
– 4x + 1 C) x
2
– 4x + 4 D) 4x
2
– x – 1
Caâu 8: Giaù trò lôùn nhaát cuûa bieåu thöùc f(x) = – x
2
+ 5x + 1 laø:
A)
29
4
B) 1 C) –
29
4
D)
5
2
B. Phaàn töï luaän: (6 ñieåm)
Caâu 9: Giaûi baát phöông trình:
2
2
32
0
2 3 5
xx
xx


Caâu 10: Cho tam thöùc baäc hai: f(x) = –x
2
+ (m + 2)x – 4. Tìm caùc giaù trò cuûa tham soá m ñeå:
a) Phöông trình f(x) = 0 coù hai nghieäm phaân bieät.
b) Tam thöùc f(x) < 0 vôùi moïi x.
V. ÑAÙP AÙN VAØ BIEÅU ÑIEÅM:
A. Traéc nghieäm: (Moãi caâu 0,5 ñieåm)
Caâu 1
Caâu 2
Caâu 3
Caâu 4
Caâu 5
Caâu 6
Caâu 7
Caâu 8
C
A
B
D
B
D
A
A
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn
86
x
3 + 2x – x
2
2x
2
+ 3x – 5
VT
– 5/2 –1 1 3
0
0 0
0
0 0
+
+ +
+ +
– –
–
–
–
– –
–+ +


B. Töï luaän:
Caâu 9: (3 ñieåm) Tìm nghieäm cuûa töû vaø maãu: 3 + 2x – x
2
= 0 x = –1; x = 3 (0,5 ñieåm)
2x
2
+ 3x – 5 = 0 x = 1; x = –
5
2
(0,5 ñieåm)
Laäp baûng xeùt daáu:
(0,5 ñieåm)
(0,5 ñieåm)
(0,5 ñieåm)
Keát luaän: Taäp nghieäm cuûa BPT S =
5
; 1 (1;3)
2



(0,5 ñieåm)
Caâu 10: (3 ñieåm)
a) (1,5 ñieåm) PT coù 2 nghieäm phaân bieät = (m + 2)
2
– 16 > 0 (0,5 ñieåm)
6
2
m
m

(1 ñieåm)
b) (1,5 ñieåm) Vì a = –1 < 0 neân f(x) < 0, x = (m + 2)
2
– 16 < 0 (0,5 ñieåm)
– 6 < m < 2 (1 ñieåm)
VI. KEÁT QUAÛ KIEÅM TRA:
Lôùp
Só soá
0 – 3,4
3,5 – 4,9
5,0 – 6,4
6,5 – 7,9
8,0 – 10
SL
%
SL
%
SL
%
SL
%
SL
%
10A3
44
10A5
42
10A7
44
10A10
42
10A11
38
Ngaøy soaïn: 20/02/2013 Chöông V: THOÁNG KEÂ
Tieát daïy: 44 Baøøi 4: PHÖÔNG SAI VAØ ÑOÄ LEÄCH CHUAÅN
I. MUÏC TIEÂU:
Kieán thöùc:
Hieåu ñöôïc phöông sai vaø ñoä leäch chuaån.
Bieát ñöôïc yù nghóa cuûa phöông sai vaø ñoä leäch chuaån.
Kó naêng:
Giaûi thaønh thaïo caùc baøi toaùn veà phöông sai vaø ñoä leäch chuaån.
Bieát vaän duïng caùc kieán thöùc ñoù trong vieäc giaûi caùc baøi toaùn kinh teá.
Thaùi ñoä:
Thaáy ñöôïc söï gaàn guõi cuûa toaùn hoïc vaø ñôøi soáng.
II. CHUAÅN BÒ:
Giaùo vieân: Giaùo aùn. Maùy tính caàm tay.
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn
87
Hoïc sinh: SGK, vôû ghi. OÂn taäp caùch tính soá trung bình coäng.
III. HOAÏT ÑOÄNG DAÏY HOÏC:
1. OÅn ñònh toå chöùc: Kieåm tra só soá lôùp.
2. Kieåm tra baøi cuõ: (3')
H. Tính soá trung bình coäng cuûa caùc daõy soá sau:
a) 180; 190; 190; 200; 210; 210; 220 b) 150; 170; 170; 200; 230; 230; 250
Ñ. a)
X
= 200 b)
X
= 200
3. Giaûng baøi môùi:
TL
Hoaït ñoäng cuûa Giaùo vieân
Hoaït ñoäng cuûa Hoïc sinh
Noäi dung
Hoaït ñoäng 1: Tìm hieåu khaùi nieäm Phöông sai
20'
GV daãn daét töø KTBC. Nhaän
xeùt caùc soá lieäu ôû daõy a) gaàn
vôùi soá TBC hôn.
GV giôùi thieäu caùc khaùi nieäm
ñoä leäch, ñoä phaân taùn.
H1. Tính ñoä leäch cuûa caùc soá
lieäu ôû daõy a) so vôùi soá TBC ?
H2. Tính bình phöông caùc ñoä
leäch vaø TBC cuûa chuùng ?
GV giôùi thieäu khaùi nieäm
phöông sai.
Xeùt baûng soá lieäu
H3. Tính soá TBC, phöông sai
?
Xeùt baûng phaân boá taàn suaát
gheùp lôùp.
H4. Tính soá TBC, phöông sai
?
Ñ1. 180 –200; 190–200; 190–
200; 200–200; 210–200; 210–
200; 220–200
Ñ2.
2
x
s
1,74
Lôùp soá
ño
Taàn soá
Taàn suaát
%
[150;156
)
[156;162
)
[162;168
)
[168;174
]
6
12
13
5
16,7
33,3
36,1
13,9
Coäng
36
100 (%)
Ñ3.
x
= 162
2
x
s
31
Lôùp
Taàn suaát
[15; 17)
[17; 19)
[19; 21)
[21; 23]
16,7
43,3
36,7
3,3
Coäng
100 (%)
Ñ4.
x
18,5(
0
C)
2
x
s
2,38
I. Phöông sai
a) Tröôøng hôïp baûng phaân boá
taàn soá, taàn suaát (rôøi raïc)
22
1
2
1
1
()
()
k
x i i
i
k
ii
i
s n x x
n
f x x


(n
1
+ n
2
+ … + n
k
= n)
b) Tröôøng hôïp baûng phaân boá
taàn soá, taàn suaát gheùp lôùp
22
1
2
1
1
()
()
k
x i i
i
k
ii
i
s n c x
n
f c x


Chuù yù:
– Khi hai daõy soá lieäu coù cuøng
ñôn vò vaø coù soá TBC baèng
nhau hay xaáp xæ nhau, neáu
phöông sai caøng nhoû thì ñoä
phaân taùn cuûa caùc soá lieäu thoáng
keâ caøng beù.
– Coù theå tính phöông sai theo
coâng thöùc:
2 2 2
()
x
s x x
trong ñoù:
2 2 2
11
1
kk
i i i i
ii
x n x f x
n



hoaëc
2 2 2
11
1
kk
i i i i
ii
x n c f c
n



Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn
88
Hoaït ñoäng 2: Tìm hieåu khaùi nieäm Ñoä leäch chuaån
7'
GV giôùi thieäu khaùi nieäm ñoä
leäch chuaån.
H1. Tính ñoä leäch chuaån trong
caùc VD treân ?
Ñ1.
a)
2
x
s
31 s
x
31
5,57
b)
2
x
s
2,38
s
x
2,38
1,54 (
0
C)
II. Ñoä leäch chuaån
Ñoä leäch chuaån
s
x
=
2
x
s
Phöông sai vaø ñoï leäch chuaån
s
x
ñeàu ñöôïc duøng ñeå ñaùnh giaù
möùc ñoä phaân taùn cuûa caùc soá
lieäu thoáng keâ (so vôùi soá TBC).
Nhöng khi caàn chuù yù ñeán ñôn
vò ño thì ta duøng s
x
vì s
x
coù
cuøng ñôn vò ño vôùi daáu hieäu
ñöôïc nghieân cöùu.
Hoaït ñoäng 3: AÙp duïng tính phöông sai vaø ñoä leäch chuaån
10'
Tuoåi
18
19
20
21
22
Coäng
Taàn
soá
10
50
70
29
10
169
VD: Xeùt baûng soá lieäu "Tuoåi
cuûa 169 ñoaøn vieân"
H1. Tính soá TBC ?
H2. Tính phöpöng sai vaø ñoä
leäch chuaån ?
Ñ1.
10.18 50.19 70.20
29.21 10.22
x
169

19,9
Ñ2.
2
x
s
0,93
s
x
0,93
0,96
a) Tính soá TBC.
b) Tính phöông sai vaø ñoä leäch
chuaån.
Hoaït ñoäng 4: Cuûng coá
3'
Nhaán maïnh:
– Caùch tính phöông sai vaø ñoä
leäch chuaån
– YÙ nghóa cuûa phöông sai vaø
ñoä leäch chuaån.
4. BAØI TAÄP VEÀ NHAØ:
Baøi 1, 2, 3 SGK.
Ngaøy soaïn: 26/2/2013
Tieát daïy: 45 BAØI TAÄP PHÖÔNG SAI – ÑOÄ LEÄCH CHUAÅN
I. MUÏC TIEÂU:
Kieán thöùc:
Cuûng coá khaùi nieäm phöông sai vaø ñoä leäch chuaån.
Bieát ñöôïc yù nghóa cuûa phöông sai vaø ñoä leäch chuaån.
Kó naêng:
Giaûi thaønh thaïo caùc baøi toaùn veà phöông sai vaø ñoä leäch chuaån.
Bieát vaän duïng caùc kieán thöùc ñoù trong vieäc giaûi caùc baøi toaùn kinh teá.
Thaùi ñoä:
Thaáy ñöôïc söï gaàn guõi cuûa toaùn hoïc vaø ñôøi soáng.
II. CHUAÅN BÒ:
Giaùo vieân: Giaùo aùn. Maùy tính caàm tay.
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn
89
Hoïc sinh: SGK, vôû ghi. Maùy tính caàm tay.
III. HOAÏT ÑOÄNG DAÏY HOÏC:
1. OÅn ñònh toå chöùc: Kieåm tra só soá lôùp.
2. Kieåm tra baøi cuõ:
Kieåm tra khaùi nieäm vaø coâng thöùc veà taàn soá, taàn suaát vaø soá trung bình, phöông sai, ñoä leäch
chuaån thoâng qua caâu hoûi daïng traéc nghieäm(trong giaùo aùn power point)
3. Giaûng baøi môùi:
Hoaït ñoäng 1: Tính soá trung bình, phöông sai, ñoä leäch chuaån trong baûng phaân boá taàn soá
Phieáu hoïc taäp soá 1
Ñieàu tra soá con cuûa moãi gia ñình trong moät vuøng ta ñöôïc maãu soá lieäu
3
3
2
2
1
1
1
1
1
1
0
0
2
2
4
4
0
0
3
3
1
1
3
3
0
0
2
2
2
2
2
2
1
1
3
3
2
2
2
2
3
3
1
1
2
2
2
2
4
4
0
0
1
1
1
1
2
2
2
2
TL
Hoaït ñoäng cuûa Giaùo vieân
Hoaït ñoäng cuûa Hoïc sinh
Noäi dung
20'
GV: yeâu caàu hoïc sinh hoaøn
thaønh baûng phaân boá taàn soá taàn
suaát.
Bảng phân bố tần số, tần suất
Số
Con
Tần
số
Taàn
suất
Coäng
Cho caùc nhoùm tính vaø nhaän
xeùt.
Höôùng daãn hoïc sinh tính -
toaùn baèng maùy tính caàm tay.
Bảng phân bố tần số, tần suất
Số
Con
Tần
số
Taàn
suất
0
1
2
3
4
4
8
11
5
2
13,3
26,7
36,7
16,7
6,6
Coäng
30
100
x
1,77
2
x
s 1,18
;
x
s 1,09
- hs tính toaùn baèng maùy tính
caàm tay.
a) laäp baûng phaân boá taàn soá taàn
suaát
b) Tính caùc soá trung bình ,
phöông sai, ñoä leäch chuaån cuûa
maãu soá lieäu treân.
Hoaït ñoäng 2: Tính soá trung bình, phöông sai, ñoä leäch chuaån trong baûng phaân boá taàn soá gheùp
lôùp.
Phieáu hoïc taäp soá 2
Ñieåm thi toaùn cuûa hai lôùp 10A vaø 10B Cho daïng baûng sau:
Lôùp A Lôùp B
5
5
6
6
7
7
7
7
7
7
4
4
2
2
9
9
8
8
7
7
7
7
1
1
8
8
4
4
5
5
7
7
5
5
6
6
8
8
9
9
3
3
5
5
9
9
8
8
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn
90
6
6
7
7
8
8
6
6
5
5
6
6
8
8
8
8
7
7
2
2
2
2
9
9
7
7
4
4
8
8
7
7
6
6
5
5
9
9
7
7
2
2
9
9
8
8
9
9
TL
Hoaït ñoäng cuûa Giaùo vieân
Hoaït ñoäng cuûa Hoïc sinh
Noäi dung
20'
Ñieåm thi lôùp 10A
Ñieåm thi
Taàn soá
[4;6)
[6;8)
[8;10]
8
13
3
Coäng
24
Cho caùc nhoùm tính laàn löôït
caùc soá ôû 2 baûng.
Vaø tính toaùn
- caùc nhoùm leân trình baøy
lôøi giaûi
- höôùng daãn hoïc sinh
tìm keát quaû baèng maùy
tính caàm tay.
Ñieåm thi lôùp 10B
Ñieåm thi
Taàn soá
[1;3)
[3;5)
[5;7)
[7;9]
5
1
1
17
Coäng
24
A
X
= 6,58;
B
X
= 6,5
2
A
s
1,66;
2
B
s
6,08
S
A
1,28; s
B
2,47
Lôùp 10A hoïc ñoàng ñeàu hôn
Ñieåm thi toaùn hai lôùp 10A vaø
10B cuûa moät tröôøng THPT.
Keát quaû cho ôû hai baûng sau:
a) Laäp baûng phaân boá taàn soá
taàn suaát gheùp lôùp.
b) Tính caùc soá
2
xx
X,s ,s
?
c) Nhaän xeùt keát quaû baøi thi
cuûa 2 lôùp ?
Hoaït ñoäng 4: Cuûng coá
3'
Nhaán maïnh:
– Caùch tính phöông sai vaø ñoä
leäch chuaån
– YÙ nghóa cuûa phöông sai vaø
ñoä leäch chuaån.
- Cho hoïc sinh laøm moät soá baøi
taäp traéc nghieäm.
Ngaøy soaïn: 20/02/2013 Chöông V: THOÁNG KEÂ
Tieát daïy: 47 Baøøi daïy: OÂN TAÄP CHÖÔNG V
I. MUÏC TIEÂU:
Kieán thöùc: Cuûng coá caùc kieán thöùc ñaõ hoïc trong chöông:
Daõy soá lieäu thoáng keâ, taàn soá, taàn suaát.
Baûng phaân boá taàn soá, taàn suaát.
Bieåu ñoà taàn soá, taàn suaát hình coät, ñöôøng gaáp khuùc, hình quaït.
Soá trung bình, soá trung vò, moát, phöông sai, ñoä leäch chuaån.
Kó naêng: Hình thaønh caùc kó naêng:
Tính toaùn treân caùc soá lieäu thoáng keâ.
Kó naêng phaân lôùp.
Veõ vaø ñoïc caùc bieåu ñoà.
Thaùi ñoä:
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn
91
Reøn luyeän tính caån thaän, tæ mæ, chính xaùc.
Thaáy ñöôïc moái lieän heä vôùi thöïc tieãn.
II. CHUAÅN BÒ:
Giaùo vieân: Giaùo aùn. Maùy tính caàm tay. Heä thoáng baøi taäp.
Hoïc sinh: SGK, vôû ghi. Maùy tính caàm tay. OÂn taäp toaøn boä kieán thöùc chöông V.
III. HOAÏT ÑOÄNG DAÏY HOÏC:
1. OÅn ñònh toå chöùc: Kieåm tra só soá lôùp.
2. Kieåm tra baøi cuõ: (Loàng vaøo quaù trình luyeän taäp)
H.
Ñ.
3. Giaûng baøi môùi:
TL
Hoaït ñoäng cuûa Giaùo vieân
Hoaït ñoäng cuûa Hoïc sinh
Noäi dung
Hoaït ñoäng 1: Luyeän taäp tính toaùn treân caùc soá lieäu thoáng keâ
10'
Soá con cuûa 59 gia ñình
3
2
1
1
1
1
0
2
4
0
3
0
1
3
0
2
2
2
1
3
2
2
3
3
2
2
4
3
2
2
4
3
2
4
1
3
0
1
3
2
3
1
4
3
0
2
2
1
2
1
2
0
4
2
3
1
1
2
0
1. Keát quaû ñieàu tra 59 hoä gia
ñình ôû moät vuøng daân cö veà soá
con cuûa moãi hoä ñöôïc ghi trong
baûng sau:
a) Laäp baûng phaân boá taàn soá
vaø taàn suaát.
b) Neâu nhaän xeùt veà soá con
cuûa
H1. Neâu caùc böôùc laäp baûng
phaân boá taàn soá, taàn suaát ?
H2. Tính soá TBC, trung vò vaø
moát ?
Ñ1.
Soá con
Taàn soá
Taàn
suaát
0
1
2
3
4
8
15
17
13
6
13,6
25,4
28,8
22,0
10,2
Coäng
59
100 (%)
Ñ2.
x
2; M
e
= 2; M
O
= 2
59 gia ñình ñöôïc ñieàu tra.
c) Tính soá TBC, soá trung vò,
moát cuûa caùc soá lieäu thoáng keâ.
15'
Khoái löôïng cuûa nhoùm 1
645
650
645
644
650
635
650
654
650
650
643
650
630
647
650
645
650
645
642
652
635
647
652
650
Khoái löôïng cuûa nhoùm 2
640
650
645
650
643
645
650
650
642
640
650
645
650
641
650
650
649
645
640
645
650
650
644
650
650
Baûng phaân boá taàn soá, taàn suaát
cuûa nhoùm 1
Lôùp
Taàn soá
Taàn
suaát
[630; 635)
[635; 640)
[640; 645)
[645; 650)
[650; 655]
1
2
3
6
12
4,2
8,3
12,5
25,0
50,0
Coäng
24
100
(%)
Baûng phaân boá taàn soá, taàn suaát
2. Cho caùc soá lieäu thoáng keâ
ñöôïc ghi trong 2 baûng sau:
a) Laäp baûng phaân boá taàn soá
vaø taàn suaát gheùp lôùp theo
nhoùm caù thöù 1 vôùi caùc lôùp:
[630; 635); [635; 640); [640;
645); [645; 650); [650; 655].
b) Laäp baûng phaân boá taàn soá
vaø taàn suaát gheùp lôùp theo
nhoùm caù thöù 2 vôùi caùc lôùp:
[638; 642); [642; 646); [646;
650); [650; 654].
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn
92
645
640
H1. Neâu caùc böôùc laäp baûng
phaân boá taàn soá, taàn suaát ?
H2. Tính soá TBC, phöông sai,
ñoä leäch chuaån ?
cuûa nhoùm 2
Lôùp
Taàn soá
Taàn
suaát
[638; 642)
[642; 646)
[646; 650)
[650; 654]
5
9
1
12
18,5
33,3
3,7
44,5
Coäng
27
100 (%)
Ñ2.
x
648;
2
x
s
33,2; s
x
5,76
y
647;
2
y
s
23,4; s
y
4,81
c) Tính soá TBC, phöông sai,
ñoä leäch chuaån cuûa caùc baûng
phaân boá ôû treân.
Hoaït ñoäng 2: Luyeän taäp veõ bieåu ñoà
15'
H1. Neâu caùc böôùc veõ bieåu ñoà
taàn suaát hình coät vaø ñöôøng
gaáp khuùc taàn suaát ?
O
KL
tần
suất
630
635 640 645 650 655
632,5 637,5 642,5 647,5 652,5
4,2
8,3
12,5
25
50
3. Moâ taû baûng phaân boá taàn
suaát gheùp lôùp ôû caâu 2a) baèng
caùch veõ bieåu ñoà taàn suaát hình
coät vaø ñöôøng gaáp khuùc taàn
suaát.
Hoaït ñoäng 4: Cuûng coá
3'
Nhaán maïnh:
– Caùch tính toaùn treân caùc soá
lieäu thoáng keâ.
– YÙ nghóa cuûa caùc soá lieäu.
4. BAØI TAÄP VEÀ NHAØ:
Laøm caùc baøi taäp coøn laïi.
Ñoïc tröôùc baøi "Cung vaø goùc löôïng giaùc".
Ngaøy soaïn: 29/02/2013 Chöông VI: CUNG VAØ GOÙC LÖÔÏNG GIAÙC. COÂNG THÖÙC LÖÔÏNG GIAÙC
Tieát daïy: 48 Baøøi 1: CUNG VAØ GOÙC LÖÔÏNG GIAÙC
I. MUÏC TIEÂU:
Kieán thöùc:
Naém ñöôïc khaùi nieäm ñöôøng troøn ñònh höôùng, ñöôøng troøn löôïng giaùc, cung vaø goùc löôïng
giaùc.
Naém ñöôïc khaùi nieäm ñôn vò ñoä vaø rañian vaø moái quan heä giöõa caùc ñôn vò naøy.
Naém ñöôïc soá ño cung vaø goùc löôïng giaùc.
Kó naêng:
Bieåu dieãn ñöôïc cung löôïng giaùc treân ñöôøng troøn löôïng giaùc.
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn
93
Tính vaø chuyeån ñoåi thaønh thaïo hai ñôn vò ño.
Tính thaønh thaïo soá ño cuûa moät cung löôïng giaùc.
Thaùi ñoä:
Luyeän tính nghieâm tuùc, saùng taïo.
Luyeän oùc tö duy thöïc teá.
II. CHUAÅN BÒ:
Giaùo vieân: Giaùo aùn. Hình veõ minh hoaï.
Hoïc sinh: SGK, vôû ghi. OÂn taäp phaàn Giaù trò löôïng giaùc cuûa goùc (0
0
180
0
).
III. HOAÏT ÑOÄNG DAÏY HOÏC:
1. OÅn ñònh toå chöùc: Kieåm tra só soá lôùp.
2. Kieåm tra baøi cuõ: (5')
H. Nhaéc laïi ñònh nghóa GTLG cuûa goùc (0
0
180
0
) ?
Ñ. sin = y
0
; cos = x
0
; tan =
0
0
y
x
; cot =
0
0
x
y
.
3. Giaûng baøi môùi:
TL
Hoaït ñoäng cuûa Giaùo vieân
Hoaït ñoäng cuûa Hoïc sinh
Noäi dung
Hoaït ñoäng 1: Tìm hieåu khaùi nieäm Cung löôïng giaùc
20'
GV döïa vaøo hình veõ, daãn daét ñi
ñeán khaùi nieäm ñöôøng troøn ñònh
höôùng.
H1. Moãi ñieåm treân truïc soá ñöôïc
ñaët töông öùng vôùi maáy ñieåm treân
ñöôøng troøn ?
H2. Moãi ñieåm treân ñöôøng troøn
öùng vôùi maáy ñieåm treân truïc soá
A
+
–
A
M
1
M
2
A’
O
1
2
–1
–2
t
t’
N
1
Ñ1. Moät ñieåm treân truïc soá öùng
vôùi moät ñieåm treân ñöôøng troøn.
Ñ2. Moät ñieåm treân ñöôøng troøn
öùng vôùi voâ soá ñieåm treân truïc soá.
I. Khaùi nieäm cung vaø goùc löôïng
giaùc
1. Ñöôøng troøn ñònh höôùng vaø
cuøng löôïng giaùc
Ñöôøng troøn ñònh höôùng laø moät
ñöôøng troøn treân ñoù ñaõ choïn moät
chieàu chuyeån ñoäng goïi laø chieàu
döông, chieàu ngöôïc laïi laø chieàu
aâm. Qui öôùc choïn chieàu ngöôïc
vôùi chieàu quay cuûa kim ñoàng hoà
laøm chieàu döông.
Treân ñöôøng troøn ñònh höôùng
cho 2 ñieåm A, B. Moät ñieåm M di
ñoäng treân ñöôøng troøn luoân theo
moät chieàu töø A ñeán B taïo neân moät
cung löôïng giaùc coù ñieåm ñaàu A
vaø ñieåm cuoái B.
A
B
O
B
O
A
O
A
B
A
B
O
a) b) c) d)
Vôùi 2 ñieåm A, B ñaõ cho treân ñ.
troøn ñònh höôùng ta coù voâ soá cung
löôïng giaùc coù ñieåm ñaàu A, ñieåm
cuoái B. moãi cung nhö vaäy ñeàu
ñöôïc kí hieäu .
H3. Xaùc ñònh chieàu chuyeån
ñoäng cuûa ñieåm M vaø soá voøng
quay?
Ñ3.
a) chieàu döông, 0 voøng.
b) chieàu döông, 1 voøng.
c) chieàu döông, 2 voøng.
d) chieàu aâm, 0 voøng.
Treân moät ñ. troøn ñònh höôùng,
laáy 2 ñieåm A, B thì:
– Kí hieäu
AB
chæ moät cung hình
hoïc (lôùn hoaëc beù) hoaøn toaøn xaùc
ñònh.
– Kí hieäu chæ moät cung
O x
y
1–1
M
x
0
y
0
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn
94
löôïng giaùc ñieåm ñaàu A, ñieåm cuoái
B.
Hoaït ñoäng 2: Tìm hieåu khaùi nieäm goùc löôïng giaùc
7'
GV giôùi thieäu khaùi nieäm goùc
löôïng giaùc.
H1. Vôùi moãi cung löôïng giaùc coù
bao nhieâu cung löôïng giaùc vaø
ngöôïc laïi ?
M
C
D
O
Ñ1. Moät moät.
2. Goùc löôïng giaùc
Moät ñieåm M chuyeån ñoäng treân
ñöôøng troøn töø C ñeán D taïo neân
cung löôïng giaùc . Khi ñoù tia
OM quay xung quanh goác O töø vò
trí OD ñeán OD. Ta noùi tia OM
taïo neân goùc löôïng giaùc, coù tia
ñaàu OC vaø tia cuoái OD. Kí hieäu
(OC, OD).
Hoaït ñoäng 3: Tìm hieåu khaùi nieäm Ñöôøng troøn löôïng giaùc
8'
GV giôùi thieäu ñöôøng troøn löôïng
giaùc.
Nhaán maïnh caùc ñieåm ñaëc bieät
cuûa ñöôøng troøn:
– Ñieåm goác A(1; 0).
– Caùc ñieåm A(–1; 0), B(0; 1),
B(0; –1).
O
AA’
B’
B
x
y
1–1
1
–1
+
3. Ñöôøng troøn löôïng giaùc
Trong mp Oxy, veõ ñöôøng troøn ñôn
vò ñònh höôùng. Ñöôøng troøn naøy
caét hai truïc toaï ñoä taïi 4 ñieåm
A(1; 0), A
(–1; 0), B(0; 1), B
(0; –
1). Ta laáy ñieåm A(1; 0) laøm ñieåm
goác cuûa ñöôøng troøn ñoù.
Ñöôøng troøn xaùc ñònh nhö treân ñgl
ñöôøng troøn löôïng giaùc (goác A).
Hoaït ñoäng 4: Cuûng coá
3'
Nhaán maïnh caùc khaùi nieäm:
– Cung löôïng giaùc, goùc löôïng
giaùc.
– Ñöôøng troøn löôïng giaùc.
4. BAØI TAÄP VEÀ NHAØ:
Ñoïc tieáp baøi "Cung vaø goùc löôïng giaùc".
Ngaøy soaïn: 20/03/2013 Chöông VI: CUNG VAØ GOÙC LÖÔÏNG GIAÙC. COÂNG THÖÙC LÖÔÏNG GIAÙC
Tieát daïy: 54 Baøøi 1: CUNG VAØ GOÙC LÖÔÏNG GIAÙC (tt)
I. MUÏC TIEÂU:
Kieán thöùc:
Naém ñöôïc khaùi nieäm ñöôøng troøn ñònh höôùng, ñöôøng troøn löôïng giaùc, cung vaø goùc löôïng
giaùc.
Naém ñöôïc khaùi nieäm ñôn vò ñoä vaø rañian vaø moái quan heä giöõa caùc ñôn vò naøy.
Naém ñöôïc soá ño cung vaø goùc löôïng giaùc.
Kó naêng:
Bieåu dieãn ñöôïc cung löôïng giaùc treân ñöôøng troøn löôïng giaùc.
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn
95
Tính vaø chuyeån ñoåi thaønh thaïo hai ñôn vò ño.
Tính thaønh thaïo soá ño cuûa moät cung löôïng giaùc.
Thaùi ñoä:
Luyeän tính nghieâm tuùc, saùng taïo.
Luyeän oùc tö duy thöïc teá.
II. CHUAÅN BÒ:
Giaùo vieân: Giaùo aùn. Hình veõ minh hoaï.
Hoïc sinh: SGK, vôû ghi. OÂn taäp phaàn Giaù trò löôïng giaùc cuûa goùc (0
0
180
0
).
III. HOAÏT ÑOÄNG DAÏY HOÏC:
1. OÅn ñònh toå chöùc: Kieåm tra só soá lôùp.
2. Kieåm tra baøi cuõ: (3')
H. Neâu ñònh nghóa cung löôïng giaùc, goùc löôïng giaùc ?
Ñ.
3. Giaûng baøi môùi:
TL
Hoaït ñoäng cuûa Giaùo vieân
Hoaït ñoäng cuûa Hoïc sinh
Noäi dung
Hoaït ñoäng 1: Tìm hieåu Ñôn vò Radian
15'
GV giôùi thieäu ñôn vò radian.
H1. Cho bieát ñoä daøi cung nöûa
ñöôøng troøn ?
H2. Cung nöûa ñöôøng troøn coù soá
ño bao nhieâu ñoä, rad ?
Ñ1. R.
Ñ2. 180
0
, rad.
II. Soá ño cuûa cung vaø goùc löôïng
giaùc
1. Ñoä vaø radian
a) Ñôn vò radian
Treân ñöôøng troøn tuyø yù, cung coù ñoä
daøi baèng baùn kính ñgl cung coù soá
ño 1 rad.
b) Quan heä giöõa ñoä vaø radian
1
0
=
180
rad; 1 rad =
0
180



Cho caùc soá ño theo ñoä, yeâu caàu
HS ñieàn soá ño theo radian vaøo
baûng.
Baûng chuyeån ñoåi thoâng duïng
Ñoä
0
0
30
0
45
0
60
0
90
0
120
0
135
0
180
0
Rad
0
6
4
3
2
2
3
3
4
H3. Cung coù soá ño rad thì coù
ñoä daøi bao nhieâu ?
Ñ3. R.
Chuù yù: Khi vieát soá ño cuûa moät goùc
(cung) theo ñôn vò radian, ta khoâng
vieát chöõ rad sau soá ño.
c) Ñoä daøi cung troøn
Cung coù soá ño
rad cuûa ñöôøng
troøn baùn kính R coù ñoä daøi: l = R
Hoaït ñoäng 2: Tìm hieåu soá ño cung löôïng giaùc – goùc löôïng giaùc
10'
A
B
O
B
O
A
O
A
B
A
B
O
a) b) c) d)
2. Soá ño cuûa cung löôïng giaùc
Soá ño cuûa moät cung löôïng giaùc
(A
M) laø moät soá thöïc aâm hay
döông. Kí hieäu sñ .
H4. Xaùc ñònh soá ño cuûa caùc cung
löôïng giaùc nhö hình veõ ?
Ñ4.
a)
2
b)
5
2
c)
9
2
Ghi nhôù: Soá ño cuûa caùc cung
löôïng giaùc coù cuøng ñieåm ñaàu vaø
ñieåm cuoái sai khaùc nhau moät boäi
cuûa 2
hoaëc 360
0
.
sñ =
+ k2
(k
Z)
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn
96
H5. Xaùc ñònh soá ño caùc goùc
löôïng giaùc (OA, OC), (OA, OD),
(OA, OB) ?
d)
3
2
x
y
AA’
B’
B
O
C
D
Ñ5.
sñ(OA,OC) =
6
;
sñ(OA,OD) =
3
sñ = a
0
+ k360
0
(k
Z)
trong ñoù
(hay a
0
) laø soá ño cuûa
moät löôïng giaùc tuyø yù coù ñieåm ñaàu
A vaø ñieåm cuoái M.
3. Soá ño cuûa goùc löôïng giaùc
Soá ño cuûa goùc löôïng giaùc (OA,
OM) laø soá ño cuûa cung löôïng giaùc
töông öùng.
Chuù yù:
cung LG
11
goùc LG
Hoaït ñoäng 3: Tìm hieåu caùch bieåu dieãn cung löôïng giaùc treân ñöôøng troøn löôïng giaùc
10'
H1. Bieåu dieãn treân ñöôøng troøn
löôïng giaùc caùc cung coù soá ño:
a)
25
4
b) –765
0
Ñ1.
a)
25
4
=
4
+ 3.2 M laø
ñieåm giöõa cung
AB
.
b) –765
0
= –45
0
+ (–2).360
0
M ñieåm giöõa cung
'AB
4. Bieåu dieãn cung löôïng giaùc
treân ñöôøng troøn löôïng giaùc
Giaû söû sñ =
.
Ñieåm ñaàu A(1; 0)
Ñieåm cuoái M ñöôïc xaùc ñònh bôûi
sñ =
.
Hoaït ñoäng 4: Cuûng coá
5'
Nhaán maïnh:
– Ñôn vò radian
– Soá ño cuûa cung vaø goùc LG.
– Caùch bieåu dieãn cung LG treân
ñöôøng troøn LG.
Caâu hoûi: Chia lôùp thaønh 4
nhoùm, 2 nhoùm cho soá ño goùc theo
ñoä, 2 nhoùm ñoåi sang radian vaø
ngöôïc laïi
Caùc nhoùm thöïc hieän.
4. BAØI TAÄP VEÀ NHAØ:
Baøi 1, 2, 3, 4, 5, 6, 7 SGK.
Ñoïc tröôùc baøi "Giaù trò löôïng giaùc cuûa moät cung".
Ngaøy soaïn: 1/03/20113 Chöông VI: CUNG VAØ GOÙC LÖÔÏNG GIAÙC. COÂNG THÖÙC LÖÔÏNG GIAÙC
Tieát daïy: 50 Baøøi 2: GIAÙ TRÒ LÖÔÏNG GIAÙC CUÛA MOÄT CUNG
I. MUÏC TIEÂU:
Kieán thöùc:
Naém vöõng ñònh nghóa caùc giaù trò löôïng giaùc cuûa cung .
Naém vöõng caùc haèng ñaúng thöùc löôïng giaùc cô baûn.
Naém vöõng moái quan heä giöõa caùc giaù trò löôïng giaùc cuûa caùc goùc coù lieân quan ñaëc bieät.
Kó naêng:
Tính ñöôïc caùc giaù trò löôïng giaùc cuûa caùc goùc.
Vaän duïng linh hoaït caùc haèng ñaúng thöùc löôïng giaùc.
Bieát aùp duïng caùc coâng thöùc trong vieäc giaûi caùc baøi taäp.
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn
97
Thaùi ñoä:
Luyeän tính caån thaän, tö duy linh hoaït.
II. CHUAÅN BÒ:
Giaùo vieân: Giaùo aùn. Hình veõ minh hoaï.
Hoïc sinh: SGK, vôû ghi. OÂn taäp phaàn Giaù trò löôïng giaùc cuûa goùc (0
0
180
0
).
III. HOAÏT ÑOÄNG DAÏY HOÏC:
1. OÅn ñònh toå chöùc: Kieåm tra só soá lôùp.
2. Kieåm tra baøi cuõ: (3')
H. Nhaéc laïi ñònh nghóa GTLG cuûa goùc (0
0
180
0
) ?
Ñ. sin = y
0
; cos = x
0
; tan =
0
0
y
x
; cot =
0
0
x
y
.
3. Giaûng baøi môùi:
TL
Hoaït ñoäng cuûa Giaùo vieân
Hoaït ñoäng cuûa Hoïc sinh
Noäi dung
Hoaït ñoäng 1: Tìm hieåu Ñònh nghóa caùc giaù trò löôïng giaùc cuûa moät cung
10'
Töø KTBC, GV neâu ñònh nghóa
caùc GTLG cuûa cung .
H1. So saùnh sin, cos vôùi 1 vaø
–1 ?
H2. Neâu moái quan heä giöõa tan
vaø cot ?
H3. Tính sin
25
4
, cos(–240
0
),
tan(–405
0
) ?
M
x
y
H
K
O
A
A’
B
B’
Ñ1. –1 sin 1
–1 cos 1
Ñ2. tan.cot = 1
Ñ3.
25
3.2
44

sin
25
4
= sin
2
42
I. Giaù trò löôïng giaùc cuûa cung
1. Ñònh nghóa
Cho cung coù sñ =
.
sin
=
OK
; cos
=
OH
;
tan
=
sin
cos
(cos
0)
cot
=
cos
sin
(sin
0)
Caùc giaù trò sin
, cos
, tan
, cot
ñgl caùc GTLG cuûa cung
.
Truïc tung: truïc sin,
Truïc hoaønh: truïc cosin.
Chuù yù:
– Caùc ñònh nghóa treân cuõng aùp duïng
cho caùc goùc löôïng giaùc.
– Neáu 0
0
180
0
thì caùc GTLG
cuûa
cuõng chính laø caùc GTLG cuûa
goùc ñoù ñaõ hoïc.
Hoaït ñoäng 2: Nhaän xeùt moät soá keát quaû ruùt ra töø ñònh nghóa
15'
Höôùng daãn HS töø ñònh nghía
caùc GTLG ruùt ra caùc nhaän xeùt.
H1. Khi naøo tan khoâng xaùc
ñònh ?
H2. Döïa vaøo ñaâu ñeå xaùc ñònh
daáu cuûa caùc GTLG cuûa ?
Ñ1. Khi cos = 0 M ôû B
hoaëc B =
2
+ k
Ñ2. Döïa vaøo vò trí ñieåm cuoái
M cuûa cung =
.
2. Heä quaû
a) sin
vaø cos
xaùcñònh vôùi

R.
sin( k2 ) sin
cos( k2 ) cos
(
k
Z)
b) –1
sin
1; –1
cos
1
c) Vôùi
m
R maø –1
m
1 ñeàu
toàn taïi
vaø
sao cho:
sin
= m; cos
= m
d) tan
xaùc ñònh vôùi
2
+ k
e) cot
xaùc ñònh vôùi
k
f) Daáu cuûa caùc GTLG cuûa
I
II
III
IV
cos
+
–
–
+
sin
+
+
–
–
O x
y
1–1
M
x
0
y
0
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn
98
tan
+
–
+
–
cot
+
–
+
–
Hoaït ñoäng 3: Tìm hieåu caùch bieåu dieãn cung löôïng giaùc treân ñöôøng troøn löôïng giaùc
5'
Cho HS nhaéc laïi vaø ñieàn vaøo
baûng.
HS thöïc hieän yeâu caàu.
3. GTLG cuûa caùc cung ñaëc bieät
0
6
4
3
2
sin
0
1
2
2
2
3
2
1
cos
1
3
2
2
2
1
2
0
tan
0
3
3
1
3
//
cot
//
3
1
3
3
0
Hoaït ñoäng 4: Tìm hieåu yù nghóa hình hoïc cuûa tang vaø coâtang
8'
H1. Tính tan , cot ?
O
x
y
t’
t
A
s
B
s’
x’
M
H
K
T
S
Ñ1.
tan =
sin
cos
=
HM AT
OH OH
=
AT
cot =
cos KM BS
sin
OK OB

=
BS
II. YÙ nghóa hình hoïc cuûa tang vaø
coâtang
1. YÙ nghóa hình hoïc cuûa tan
tan
ñöôïc bieåu dieãn bôûi
AT
treân
truïc t'At. Truïc t
At ñgl truïc tang.
2. YÙ nghóa hình hoïc cuûa cot
cot
ñöôïc bieåu dieãn bôûi
BS
treân
truïc s
Bs. Truïc s
Bs ñgl truïc coâtang.
tan(
+ k
) = tan
cot(
+ k
) = cot
Hoaït ñoäng 5: Cuûng coá
3'
Nhaán maïnh
– Ñònh nghóa caùc GTLG cuûa .
– YÙ nghóa hình hoïc cuûa caùc
GTLG cuûa .
4. BAØI TAÄP VEÀ NHAØ:
Baøi 1, 2, 3 SGK.
Ñoïc tieáp baøi "Giaù trò löôïng giaùc cuûa moät cung".
Ngaøy soaïn: 25/03/2013 Chöông VI: CUNG VAØ GOÙC LÖÔÏNG GIAÙC. COÂNG THÖÙC LÖÔÏNG GIAÙC
Tieát daïy: 51 Baøøi 2: GIAÙ TRÒ LÖÔÏNG GIAÙC CUÛA MOÄT CUNG (tt)
I. MUÏC TIEÂU:
Kieán thöùc:
Naém vöõng caùc haèng ñaúng thöùc löôïng giaùc cô baûn.
Naém vöõng moái quan heä giöõa caùc giaù trò löôïng giaùc cuûa caùc goùc coù lieân quan ñaëc bieät.
Kó naêng:
Tính ñöôïc caùc giaù trò löôïng giaùc cuûa caùc goùc.
Vaän duïng linh hoaït caùc haèng ñaúng thöùc löôïng giaùc.
Bieát aùp duïng caùc coâng thöùc trong vieäc giaûi caùc baøi taäp.
Thaùi ñoä:
Luyeän tính caån thaän, tö duy linh hoaït.
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn
99
II. CHUAÅN BÒ:
Giaùo vieân: Giaùo aùn. Hình veõ minh hoaï.
Hoïc sinh: SGK, vôû ghi. OÂn taäp phaàn Giaù trò löôïng giaùc cuûa goùc .
III. HOAÏT ÑOÄNG DAÏY HOÏC:
1. OÅn ñònh toå chöùc: Kieåm tra só soá lôùp.
2. Kieåm tra baøi cuõ: (3')
H. Nhaéc laïi ñònh nghóa GTLG cuûa cung ?
Ñ. sin =
OK
; cos =
OH
; tan =
sin
cos
; cot =
cos
sin
.
3. Giaûng baøi môùi:
TL
Hoaït ñoäng cuûa Giaùo vieân
Hoaït ñoäng cuûa Hoïc sinh
Noäi dung
Hoaït ñoäng 1: Tìm hieåu caùc coâng thöùc löôïng giaùc cô baûn
15'
Höôùng daãn HS chöùng minh
caùc coâng thöùc.
H1. Neâu coâng thöùc quan heä
giöõa sin
vaø cos
?
H2. Haõy xaùc ñònh daáu cuûa
cos
?
H3. Neâu coâng thöùc quan heä
giöõa tan
vaø cos
?
H4. Haõy xaùc ñònh daáu cuûa
cos
?
1 + tan
2
= 1 +
2
2
sin
cos
=
=
22
22
cos sin 1
cos cos

Ñ1. sin
2
+ cos
2
= 1
Ñ2. Vì
2
<
<
neân cos
< 0
cos
= –
4
5
Ñ3. 1 + tan
2
=
2
1
cos
Ñ4. Vì
3
2
<
<2
neân cos
> 0
cos
=
5
41
III. Quan heä giöõa caùc GTLG
1. Coâng thöùc löôïng giaùc cô baûn
sin
2
+ cos
2
= 1
1 + tan
2
=
2
1
cos
(
2
+ k
)
1 + cot
2
=
2
1
sin
(
k
)
tan
.cot
= 1 (
k
2
)
2. Ví duï aùp duïng
VD1: Cho sin
=
3
5
vôùi
2
<
<
.
Tính cos
.
VD2: Cho tan
= –
4
5
vôùi
3
2
<
<
2
. Tính sin
vaø cos
.
Hoaït ñoäng 2: Tìm hieåu caùc GTLG cuûa caùc cung coù lieân quan ñaëc bieät
17'
GV treo caùc hình veõ vaø
höôùng daãn HS nhaän xeùt vò trí
cuûa caùc ñieåm cuoái cuûa caùc
cung lieân quan.
Moãi nhoùm nhaän xeùt moät hình.
a) M vaø M ñoái xöùng nhau qua
truïc hoaønh.
b) M vaø M ñoái xöùng nhau qua
truïc tung.
c) M vaø M ñoái xöùng nhau qua
ñöôøng phaân giaùc thöù I.
3. GTLG cuûa caùc cung coù lieân
quan ñaëc bieät
a) Cung ñoái nhau:
vaø –
cos(–
) = cos
; sin(–
) = –sin
tan(–
) = –tan
; cot(–
) = –cot
b) Cung buø nhau:
vaø
–
cos(
–
)=–cos
; sin(
–
) = sin
tan(
–
)=–tan
; cot(
–
) = –cot
c) Cung phuï nhau:
vaø
2




M
x
y
H
K
O
A
A’
B
B’
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn
100
d) M vaø M ñoái xöùng nhau qua
goác toaï ñoä O.
cos
2




=sin
; sin
2




=cos
tan
2




=cot
; cot
2




=tan
d) Cung hôn keùm
:
vaø (
+
)
cos(
+
)=–cos
; sin(
+
)=–sin
tan(
+
)=tan
; cot(
+
)=cot

O
x
y
M
M’
H

O
x
y
M
M’
H
O
x
y
M
M’
H
O
x
y
M
M’
H
ñoái nhau phuï nhau buø nhau hôn keùm
Hoaït ñoäng 3: AÙp duïng tính GTLG cuûa caùc cung coù lieân quan ñaëc bieät
5'
H. Tính vaø ñieàn vaøo baûng.
Ñ.
VD3: Tính GTLG cuûa caùc cung sau:
–
6
, 120
0
, 135
0
,
5
6
–
6
120
0
135
0
5
6
sin
–
1
2
3
2
2
2
1
2
cos
3
2
–
1
2
2
2
3
2
Hoaït ñoäng 4: Cuûng coá
3'
Nhaán maïnh:
– Caùc coâng thöùc löôïng giaùc.
– Caùch vaän duïng caùc coâng
thöùc.
4. BAØI TAÄP VEÀ NHAØ:
Baøi 4, 5 SGK.
Ngaøy soaïn: 25/03/2013 Chöông VI: CUNG VAØ GOÙC LÖÔÏNG GIAÙC. COÂNG THÖÙC LÖÔÏNG GIAÙC
Tieát daïy: 53 Baøøi 2: BAØI TAÄP GIAÙ TRÒ LÖÔÏNG GIAÙC CUÛA MOÄT CUNG
I. MUÏC TIEÂU:
Kieán thöùc: Cuûng coá caùc kieán thöùc veà:
Caùc haèng ñaúng thöùc löôïng giaùc cô baûn.
Moái quan heä giöõa caùc giaù trò löôïng giaùc cuûa caùc goùc coù lieân quan ñaëc bieät.
Kó naêng:
Tính ñöôïc caùc giaù trò löôïng giaùc cuûa caùc goùc.
Vaän duïng linh hoaït caùc haèng ñaúng thöùc löôïng giaùc.
Bieát aùp duïng caùc coâng thöùc trong vieäc giaûi caùc baøi taäp.
Thaùi ñoä:
Luyeän tính caån thaän, tö duy linh hoaït.
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn
101
II. CHUAÅN BÒ:
Giaùo vieân: Giaùo aùn. Heä thoáng baøi taäp.
Hoïc sinh: SGK, vôû ghi. OÂn taäp phaàn Giaù trò löôïng giaùc cuûa moät cung .
III. HOAÏT ÑOÄNG DAÏY HOÏC:
1. OÅn ñònh toå chöùc: Kieåm tra só soá lôùp.
2. Kieåm tra baøi cuõ: (Loàng vaøo quaù trình luyeän taäp)
H.
Ñ.
3. Giaûng baøi môùi:
TL
Hoaït ñoäng cuûa Giaùo vieân
Hoaït ñoäng cuûa Hoïc sinh
Noäi dung
Hoaït ñoäng 1: Luyeän taäp caùc coâng thöùc löôïng giaùc cô baûn
5'
H1. Neâu heä thöùc lieân quan
giöõa sinx vaø cosx ?
Ñ1. sin
2
x + cos
2
x = 1
a) khoâng
b) coù
c) khoâng
1. Caùc ñaúng thöùc sau coù theå ñoàng
thôøi xaûy ra khoâng ?
a) sinx =
2
3
vaø cosx =
3
3
b) sinx =
4
5
vaø cosx =
3
5
c) sinx = 0,7 vaø cosx = 0,3
Hoaït ñoäng 2: Luyeän taäp xeùt daáu caùc GTLG
10'
H1. Neâu caùch xaùc ñònh daáu
caùc GTLG ?
Ñ1. Xaùc ñònh vò trí ñieåm cuoái
cuûa cung thuoäc goùc phaàn tö
naøo.
a) sin(x – ) = –sin( – x)
= –sinx < 0
b) cos
3
x
2



vì
2
<
3
x
2
<
c) tan(x + ) = tanx > 0
d) cot
x
2



vì
x
22

2. Cho 0 < x <
2
. Xaùc ñònh daáu
cuûa caùc GTLG:
a) sin(x – )
b) cos
3
x
2



c) tan(x + )
d) cot
x
2



Hoaït ñoäng 3: AÙp duïng tính GTLG cuûa moät cung
15'
H1. Neâu caùc böôùc tính ?
H2. Neâu coâng thöùc caàn söû
duïng ?
Ñ1. + Xeùt daáu GTLG caàn tính
+ Tính theo coâng thöùc
Ñ2.
a) sinx > 0; sin
2
x + cos
2
x = 1
sinx =
3 17
13
; tanx =
3 17
4
;
cotx =
4
3 17
b) cosx < 0; sin
2
x + cos
2
x = 1
cosx = –
0,51
; tanx
1,01;
cotx 0,99
c) cosx < 0; 1 + tan
2
x =
2
1
cos x
3. Tính caùc GTLG cuûa x, neáu:
a) cosx =
4
vaø 0 x
13 2

b) sinx = – 0,7 vaø < x <
3
2
c) tanx =
5
vaø x
17 2
d) cotx = –3 vaø
3
x2
2
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn
102
cosx =
7
274
;
sinx =
15
274
; cotx =
7
15
d) sinx < 0; 1 + cot
2
x =
2
1
sin x
sinx =
1
10
; cosx =
3
10
;
tanx =
1
3
Hoaït ñoäng 4: Luyeän taäp bieán ñoåi bieåu thöùc löôïng giaùc
10'
Höôùng daãn HS caùch bieán
ñoåi.
a) VT = cos
2
x + cos
2
x.cot
2
x
= cos
2
x(1 + cot
2
x)
= cos
2
x.
2
1
sin x
= cot
2
x
b) cos
2
x – sin
2
x =
= (cosx – sinx).(cosx + sinx)
c) tanx.cotx = 1
d) Söû duïng haèng ñaúng thöùc:
sin
3
x + cos
3
x = (sinx + cosx).
.(sin
2
x – sinx.cosx+cos
2
x)
4. Chöùng minh caùc heä thöùc:
a) cos
2
x + cos
2
x.cot
2
x = cot
2
x
b)
2
2cos x 1
cosx sinx
= cosx – sinx
c)
2
2
tanx cot x 1
.1
cotx
1 tan x
d)
33
sin x cos x
1 sinx.cosx
sinx cosx

Hoaït ñoäng 5: Cuûng coá
3'
Nhaán maïnh:
– Caùc coâng thöùc löôïng
giaùc.
– Caùch vaän duïng caùc coâng
thöùc.
4. BAØI TAÄP VEÀ NHAØ:
Laøm tieáp caùc baøi coøn laïi.
Ñoïc tröôùc baøi " Coâng thöùc löôïng giaùc"
Ngaøy soaïn: 30/03/2013 Chöông VI: CUNG VAØ GOÙC LÖÔÏNG GIAÙC. COÂNG THÖÙC LÖÔÏNG GIAÙC
Tieát daïy: 54 Baøøi 3: COÂNG THÖÙC LÖÔÏNG GIAÙC
I. MUÏC TIEÂU:
Kieán thöùc:
Naém ñöôïc caùc coâng thöùc löôïng giaùc: coâng thöùc coäng, coâng thöùc nhaân ñoâi, coâng thöùc bieán
ñoåi toång thaønh tích, coâng thöùc bieán ñoåi tích thaønh toång.
Töø caùc coâng thöùc treân coù theå suy ra moät soá coâng thöùc khaùc.
Kó naêng:
Bieán ñoåi thaønh thaïo caùc coâng thöùc löôïng giaùc.
Vaän duïng caùc coâng thöùc treân ñeå giaûi baøi taäp.
Thaùi ñoä:
Luyeän tính caån thaän, tö duy linh hoaït.
II. CHUAÅN BÒ:
Giaùo vieân: Giaùo aùn. Caùc baûng coâng thöùc löôïng giaùc.
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn
103
Hoïc sinh: SGK, vôû ghi. OÂn taäp phaàn Giaù trò löôïng giaùc cuûa moät cung .
III. HOAÏT ÑOÄNG DAÏY HOÏC:
1. OÅn ñònh toå chöùc: Kieåm tra só soá lôùp.
2. Kieåm tra baøi cuõ: (3')
H. Neâu caùc coâng thöùc löôïng giaùc cô baûn ?
Ñ. sin
2
x + cos
2
x = 1; 1 + tan
2
x =
2
1
cos x
; 1 + cot
2
x =
2
1
sin x
; tanx.cotx = 1.
3. Giaûng baøi môùi:
TG
Hoạt động của HS
Hoạt động của GV
Nội dung
10’
15’
*Học sinh nhận nhiệm vụ
,thảoluận theo nhóm.
A
N
M
y
x
*Họcsinh phải xây dựng được .
).cos(...
sin.sincos.cos.
)sin;(cos
)sin;(cos
OMONONONOMON
OMON
OM
ON
Đại diện nhóm trình bày kết quả,
các nhóm khác tham gia thảo
luận, góp ý bổ sung để xây dựng
công thức.
Cos (
-
) = cos
.cos
+
sin
sin
(1)
Chốt công thức cộng đối cos(
-
)
thảo luận.
Nhóm 1 thay được
bởi (-
)
Nhóm 2 thay được sin(
+
)
bởi cos (
2
)
Đại diện nhóm trình bày kết qủa
của nhóm mình. Đại diện các
nhóm khác góp ý trao đổi bổ
HĐ1: (kiểm tra bài cũ)
Cho cung
NA
MA
;
.Hãy
biểu diễn cáccung đó
trên đường trònlương
giác .Tìm tọa độ của các
véc tơ
.; NOMO
Tính
tích vô hướng của hai
véc tơ theo hai phương
pháp .So sánh hai kết quả
đó rồi đưa ra công thức.
(cho học sinh hoạt động
theo nhóm).gv theo dõi
hướng dẫn học sinh thảo
luận ,giúp đỡ học sinh
khi cần thiết.
Cho 1 học sinh đại diện
nhóm mình trình bày kết
quả .
Các học sinh của nhóm
khác nhận xét ,góp ý, bổ
sung đưa ra công
thức.Công thức đó được
gọi là công thức cộng.Đó
là bài học hôm nay.
HĐ2: (chia lớp thành 2
nhóm)
HĐTP1: Từ công
thức(1) . Hãy tính
cos(
+
)?(nhóm 1
Từ công thức (1).Hãy
tinh sin(
-
)?(nhóm 2)
.GV theo dõi các nhóm
thảo luận và giúp đỡ khi
cần thiết.
Cho đại diện nhóm trình
bày kết quả của nhóm
I/ Công thức cộng:
1/Công tức cộng đối với
sin và cosin:
*cos(
)=cos
cos
sin
sin
*sin(
)=sin
cos
sin
cos
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn
104
15’
sung. -> Đưa ra công thức
HS nhận nhiệm vụ và thực hiện -
> hình thành ra công thức.
Học sinh làm bài tập theo yêu
cầu của GV
tan(
+
) =
)cos(
)sin(
=
sin.sincos.cos
cos.sincos.sin
=
coscos
sin.sincossin
coscos
cos.sincos.sin
=
tan.tan1
tantan
Tương tự ta có:
Tan(
-
) =
tan.tan1
tantan
HS giải:
mình . các nhóm còn lại
tham gia góp ý bổ sung
.Giáo viên tổng hợp công
thức.
HĐTP2: Tương tự tính
Sin(
+
)?
HĐTP 3: Hãy kiểm
nghiệm lại các công thức
nói trên với
tuỳ ý và
=
;
=
2
HĐ3: .
HĐTP1: Tính:
tan(
+
)
tan(
-
) theo tan
,
tan
Cho 2 nhóm hoạt động
GV theo dõi các nhóm
hoạt động và giúp đỡ các
em khi cần thiết. Cho đại
diện của nhóm lên trình
bày bài giải của mình.
Để các công thức trên
có nghĩa tìm điều kiện
của
và
; (
-
);
(
+
).
HĐTP 3:Ví dụ: Tính tan
15
o
= ?
2/ Công thức cộng đối
tan
*tan(
+
) =
=
tan.tan1
tantan
*Tan(
-
) =
tan.tan1
tantan
Để các công thức trên có
nghĩa thì:
;
;
(
+
); (
-
) không có
dạng
k
2
(k
z)
Ví dụ: Tính tan 15
o
3-
3
=
3 +
3
Hoaït ñoäng 4: Cuûng coá
5'
Nhaán maïnh caùc coâng thöùc löôïng
giaùc.
Ngaøy soaïn: 30/03/2013 Chöông VI: CUNG VAØ GOÙC LÖÔÏNG GIAÙC. COÂNG THÖÙC LÖÔÏNG GIAÙC
Tieát daïy: 55 Baøøi 3: COÂNG THÖÙC LÖÔÏNG GIAÙC
I. MUÏC TIEÂU:
Qua bài học sinh cần nắm được:
+ Về kiến thức: Công thức cộng, công tức nhân đôi.
+ Về kĩ năng: Học sinh áp dụng công thức vào giải toán,( chứng minh,rút gọn biểu
thức,tính toán …)
+ Về tư duy: Từ công thức cộng, công thức nhân đôi biến đổi thêm một số công thức
khác.
+ Về thái độ: Có thái độ học tập đúng đắn,chịu khó, kiên nhẫn.
II/ Chẩn bị:
- Học sinh: Dụng cụ học tập và máy tính bỏ túi.
-Giáo viên:đồ dùng giảng dạy,phiếu học tập, đường tròn lượng giác.
III/Tiến trình bài học:
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn
105
*Ổn định lớp, giới thiệu: Chia lớp thành 6 nhóm.
*Kiểm tra bài cũ:
- Viết các công thức lượng giác cơ bản;...
*Bài mới:
TG
Hoạt động của HS
Hoạt động của GV
Nội dung
40’
5’
HS trả lời:
cos(
+
) = cos2
= cos
2
-
cos
2
= 1- 2sin
2
= 2cos
2
-1
sin 2
= 2sin
cos
tan2
=
2
tan1
tan2
*Học sinh nhận nhiệm
vụ,thảo luận đưa ra kết
quả đúng..Đại diện nhóm
trình bày kết quả cuả
nhóm mình. Các nhóm
khácđại diện thảo
luận,góp ý bổ sung , đưa
ra kết quả đúng.
HĐ 1
HĐTP 1: từ công thức cộng
đối với sin và cos nếu thay
=
thì công thức thay đổi
ra sao ?
GV gọi HS đứng tại chỗ tính
toán
HĐTP2: GV hỏi: tan 2
cần
điều kiện gì ?
HĐTP3: TínhCos
2
;sin
2
;
tan
2
; Theo cos2
?
Cho học sinh thảo luận nhóm
rồi đưa ra công thức.
GV cho học trò trình bày thảo
luận vàsửa sai đưa ra công
thức đúng.
HĐTP4:(phát phiếu học tập)
,cho các nhóm.
1/Hãy tính cos4
theo cos
.
2/Tính cos
8
.
3/Đơn giản biểu thức :
sin
cos
cos2
Hoaït ñoäng 2: Cuûng coá
Nhaán maïnh caùc coâng thöùc
löôïng giaùc.
II. Công thức nhân đôi
cos2
= cos
2
-sin
2
=2cos
2
-1.
=1 - 2sin
2
sin2
= 2sin
cos
tan2
=
2
tan1
tan2
(Với tan2
; tan
) có
nghĩa.
Chú ý công thức hạ bậc
Sin
2
=
2
2cos1
Cos
2
=
2
2cos1
tan
2
=
2cos1
2cos1
Kết quả:1/ cos4
=
8cos
4
-8cos
2
+1
2/ cos
2
22
8
3/sin
.sin
cos2
=
1/4sin 4
4. BAØI TAÄP VEÀ NHAØ:
Baøi 1, 2, 3, 4, 5, 6, 7, 8 SGK.
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn
106
Ngaøy soaïn: 30/03/2013 Chöông VI: CUNG VAØ GOÙC LÖÔÏNG GIAÙC. COÂNG THÖÙC LÖÔÏNG GIAÙC
Tieát daïy: 56 Baøøi 3: COÂNG THÖÙC LÖÔÏNG GIAÙC
I. MUÏC TIEÂU:
Qua bài học sinh cần nắm được:
+ Về kiến thức: Công thức cộng, công tức nhân đôi.
+ Về kĩ năng: Học sinh áp dụng công thức vào giải toán,( chứng minh,rút gọn biểu
thức,tính toán …)
+ Về tư duy: Từ công thức cộng, công thức nhân đôi biến đổi thêm một số công thức
khác.
+ Về thái độ: Có thái độ học tập đúng đắn,chịu khó, kiên nhẫn.
II/ Chẩn bị:
- Học sinh: Dụng cụ học tập và máy tính bỏ túi.
-Giáo viên:đồ dùng giảng dạy,phiếu học tập, đường tròn lượng giác.
III/Tiến trình bài học:
*Ổn định lớp, giới thiệu: Chia lớp thành 6 nhóm.
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn
107
*Kiểm tra bài cũ:
- Viết các công thức lượng giác cơ bản;...
*Bài mới:
TG
Hoạt động của HS
Hoạt động của GV
Nội dung
40’
5’
HS trả lời:
cos(
+
) = cos2
= cos
2
-
cos
2
= 1- 2sin
2
= 2cos
2
-1
sin 2
= 2sin
cos
tan2
=
2
tan1
tan2
*Học sinh nhận nhiệm
vụ,thảo luận đưa ra kết
quả đúng..Đại diện nhóm
trình bày kết quả cuả
nhóm mình. Các nhóm
khácđại diện thảo
luận,góp ý bổ sung , đưa
ra kết quả đúng.
HĐ 1
HĐTP 1: từ công thức cộng
đối với sin và cos nếu thay
=
thì công thức thay đổi
ra sao ?
GV gọi HS đứng tại chỗ tính
toán
HĐTP2: GV hỏi: tan 2
cần
điều kiện gì ?
HĐTP3: TínhCos
2
;sin
2
;
tan
2
; Theo cos2
?
Cho học sinh thảo luận nhóm
rồi đưa ra công thức.
GV cho học trò trình bày thảo
luận vàsửa sai đưa ra công
thức đúng.
HĐTP4:(phát phiếu học tập)
,cho các nhóm.
1/Hãy tính cos4
theo cos
.
2/Tính cos
8
.
3/Đơn giản biểu thức :
sin
cos
cos2
Hoaït ñoäng 2: Cuûng coá
Nhaán maïnh caùc coâng thöùc
löôïng giaùc.
II. Công thức nhân đôi
cos2
= cos
2
-sin
2
=2cos
2
-1.
=1 - 2sin
2
sin2
= 2sin
cos
tan2
=
2
tan1
tan2
(Với tan2
; tan
) có
nghĩa.
Chú ý công thức hạ bậc
Sin
2
=
2
2cos1
Cos
2
=
2
2cos1
tan
2
=
2cos1
2cos1
Kết quả:1/ cos4
=
8cos
4
-8cos
2
+1
2/ cos
2
22
8
3/sin
.sin
cos2
=
1/4sin 4
4. BAØI TAÄP VEÀ NHAØ:
Baøi 1, 2, 3, 4, 5, 6, 7, 8 SGK.
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn
108
Ngaøy soaïn: 5/04/2013 Chöông VI: CUNG VAØ GOÙC LÖÔÏNG GIAÙC. COÂNG THÖÙC LÖÔÏNG GIAÙC
Tieát daïy: 57 Baøøi 3: COÂNG THÖÙC LÖÔÏNG GIAÙC
I/ Mục tiêu:
Qua bài học sinh cần nắm được:
+ Về kiến thức: Công thức cộng, công tức nhân đôi.
+ Về kĩ năng: Học sinh áp dụng công thức vào giải toán,( chứng minh,rút gọn biểu
thức,tính toán …)
+ Về tư duy: Từ công thức cộng, công thức nhân đôi biến đổi thêm một số công thức
khác.
+ Về thái độ: Có thái độ học tập đúng đắn,chịu khó, kiên nhẫn.
II/ Chẩn bị:
- Học sinh: Dụng cụ học tập và máy tính bỏ túi.
-Giáo viên:đồ dùng giảng dạy,phiếu học tập, đường tròn lượng giác.
III/Tiến trình bài học:
*Ổn định lớp, giới thiệu: Chia lớp thành 6 nhóm.
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn
109
*Kiểm tra bài cũ:
- Viết các công thức lượng giác cơ bản;...
*Bài mới:
TG
Hoạt động của HS
Hoạt động của GV
Nội dung
40’
Các nhóm nhận nhiệm vụ
thảo luận dể tìm ra lời
giải.
Đại diện nhóm trình bày
kết quả của nhóm
mình.Đại diện các nhóm
khác trao đổi đưa về công
thức đúng.
Các nhóm nhận nhiệm vụ
cùng nhau thảo luận tìm
ra kết quả.Đại diện các
nhóm trình bày kết quả
của nhóm mình,các nhóm
khác cùng trao đổi góp ý
đưa ra kết quả đúng.
Các nhóm nhận nhiệm vụ
cùng nhau thảo luận để
đưa ra công thức.Đại diện
nhóm trình bày kết quả
của nhóm mình. Các
nhóm khác cùng tham gia
ý kiến sửa sai hoặc bổ
sung để đưa về công thức
đúng.
Phát phiếu học tập cho các
nhóm. Theo dõi hoạt động của
các nhóm,giúp đỡ học sinh khi
cần thiết.
Đại diện của nhóm trình bày
kết quả của nhóm mình.Đại
diện các nhóm khác trao đổi
góp ý, bổ sung để đưa ra công
thức đúng.
HĐTP2: (khắc sâu), phát
phiếu học tập số 2 cho các
nhóm(chia ra 4 nhóm ,2 nhóm
làm 1 câu).
1/tính:
24
sin.
24
5
sin
2/tính:
12
5
sin
12
7
cos
Giáo viên hướng dẫn cho các
nhóm làm bài .cho đại diện
các nhóm trình bày kết quả
của nhóm mình.cho cả lớp
cùng kiểm tra đánh giá bổ
sungđưa về kết quả đúng.
HĐ2:
HĐTP1:(phiếu học tập
số3),phát cho các nhóm. Từ
các công thức biến đổi tích
thành tổng ở trên .Nếu
đặt
y
x
tứclà (
2
;
2
yxyx
)thì
ta được các công thức nào?
Cho các nhóm thảo luận .Đại
diện nhóm trình bày kết quả
,sửa sai ,bổ sung đưa ra kết
quả đúng.
Đưa ra công thức
HĐTP2(khắc sâu công
thức).Phát phiếu học tập cho
các nhóm ,mỗi nhóm làm 1
bài tập nhỏ sau :
III/ Công thức biến đổi
tích thành tổng và tổng
thành tích :
1/ công thức biến đổi tích
thanh tổng:
*cos
.cos
coscos
2
1
*Sin
sin
=
coscos
2
1
* sin
cos
=
sinsin
2
1
Ví dụ :Tính:
1.
24
sin.
24
5
sin
kq:
23
4
1
2/
12
5
sin
12
7
cos
kq:
4
1
2/Công thức biến đổi tổng
thành tích:
*cos x + cos y
=
2
cos
2
cos2
yxyx
.
* cos x - cos y
=
2
sin
2
sin2
yxyx
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn
110
5’
Các nhóm nhận nhiệm vụ
,tiến hành tìm ra phương
án của mình . Đại diện
nhóm trình bày kết quả
của nhóm mình. Cùng
tham gia thảo luận với các
nhóm khác để đưa ra kết
quả đúng.
Chứng minh
rằng
4
sin2cossin/3
4
sin2cossin/2
2
10
3
sin
1
10
sin
1
/1
Các nhóm thảo luận tìm ra
phương án của bài toán.đại
diện các nhóm trình bày kết
quả của nhóm mình .cùng
thảo luận ,góp ý với các nhóm
khác để được lời giải đúng.
Hoaït ñoäng 2: Cuûng coá
Nhaán maïnh caùc coâng thöùc
löôïng giaùc.
*sin x + siny
=
2
cos
2
sin2
yxyx
.
*sin x - siny
=
2
sin
2
cos2
yxyx
Ngaøy soaïn: 05/04/2013 Chöông VI: CUNG VAØ GOÙC LÖÔÏNG GIAÙC. COÂNG THÖÙC LÖÔÏNG GIAÙC
Tiết PP: 58 BAØI TẬP
I. Mục tiêu:
+ Kieán thöùc: - Cuûng coá caùc coâng thöùc löôïng giaùc ñaõ hoïc ôû tieát tröôùc
+ Kyõ naêng: - Reøn kó naêng aùp duïng caùc coâng thöùc löôïng giaùc ñaõ hoïc vaøo giaûi toaùn
+ Thaùi ñoä: - Reøn tính caån thaän trong giaûi toaùn
II. Chuẩn bị:
+ Giáo viên: soạn giáo án, chuẩn bị các bài tập cho học sinh thực hiện.
+ Học sinh: nắm vững lý thuyết và chuẩn bị trước các bài tập sách giáo khoa.
III. Nội dung và tiến trình lên lớp:
TG
Hoạt động của thầy
Hoạt động của trò
Nội dung ghi bảng
2’
+ Ổn định lớp
+ Giới thiệu nội dung bài
tập.
+ Ồn định trật tự
+ Chú ý theo dõi
15’
Vieát caùc coâng thöùc cuûa
coâng thöùc coäng
HS vieát coâng thöùc coäng
2 HS leân baûng laøm baøi
1. Tính:
a) cos225
0
= cos(180
0
+ 45
0
) = -
2
/2
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn
111
HS1: Laøm baøi 1, caâu a)
HS 2: Laøm baøi 1, caâu b)
Yeâu caàu daõy 1: laøm baøi 1,
caâu a); daõy 2: laøm baøi 1,
caâu b)
Goïi HS khaùc nhaän xeùt
Gv nhaän xeùt, cho ñieåm
Caùc HS cuøng laøm döôùi
lôùp
HS khaùc nhaän xeùt
sin240
0
= sin (180
0
+ 60
0
) = -
3
/2
cot(-15
0
) = cot(30
0
– 45
0
) =
32
)4530tan(
1
00
tan(75
0
) = tan(45
0
+ 30
0
) =
321
3
31
b)
4
312
34
sin
12
7
sin
4
312
34
cos
12
cos
32
43
tan
12
tan
12
tan
12
13
tan
15’
Baøi 2/ 154: GV neâu ñeà baøi
Yeâu caàu HS hoaït ñoäng
nhoùm
Môøi ñaïi dieän 3 nhoùm leân
treo baûng nhoùm vaø trình
baøy baøi laøm cuûa nhoùm
mình
Caùc nhoùm khaùc goùp yù, boå
sung
GV nhaän xeùt, cho ñieåm
baøi laøm töøng nhoùm
Yeâu caàu HS söûa baøi vaøo
vôû
HS hoaït ñoäng nhoùm 5
phuùt
Nhoùm 1,2: caâu a);
Nhoùm 3, 4: caâu b)
Nhoùm 5, 5: caâu c)
Ñaïi dieän 3 nhoùm leân
treo baûng nhoùm vaø
trình baøy baøi laøm cuûa
nhoùm mình
Caùc nhoùm khaùc nhaän
xeùt
HS söûa baøi vaøo vôû
2. Tính:
a)
1
3
6
2
1
3
cos
6
cos
b) /2 < < tan < 0
7
249
122
221
4
tan
22tan
cos
1
tan1
2
2
c) 0
0
< a <90
0
cosa > 0, 90
0
< b <
180
0
cosb < 0
15
546
sincoscossin)sin(
15
853
sinsincoscos)cos(
3
5
9
4
1cos;
5
3
25
16
1cos
bababa
bababa
ba
10’
Baøi 3/ 154: GV neâu ñeà baøi
Yeâu caàu HS hoaït ñoäng
nhoùm ruùt goïn caùc bieåu
thöùc
Môøi ñaïi dieän 3 nhoùm leân
treo baûng nhoùm vaø trình
baøy baøi laøm cuûa nhoùm
mình
Caùc nhoùm khaùc goùp yù, boå
sung
GV nhaän xeùt, cho ñieåm
baøi laøm töøng nhoùm
HS hoaït ñoäng nhoùm 6
phuùt
Nhoùm 1, 2: caâu a)
Nhoùm 3, 4: caâu b);
Nhoùm 5, 6: caâu c)
Ñaïi dieän 3 nhoùm leân
treo baûng nhoùm vaø
trình baøy baøi laøm cuûa
nhoùm mình
Caùc nhoùm khaùc nhaän
xeùt
3. Rút gọn biểu thức:
a)
cossin)sin(
2
sin)sin( bababa
b)
a
aaa
2
2
2
cos
2
1
asin
2
1
sinacosa
2
2
sina-cosa
2
2
sin
2
1
4
cos
4
cos
c)
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn
112
Yeâu caàu HS söûa baøi vaøo
vôû
HS söûa baøi vaøo vôû
bababa sincos)sin(
2
sin
2
cos
IV.Củng cố và dặn dò(3’):
- Nhắc lại cách giải các bài toán
-HS về học thuộc công thức.
Ngaøy soaïn: 15/04/2013 Chöông VI: CUNG VAØ GOÙC LÖÔÏNG GIAÙC. COÂNG THÖÙC LÖÔÏNG GIAÙC
Tieát daïy: 59 Baøøi daïy: OÂN TAÄP CHÖÔNG VI
I. MUÏC TIEÂU:
Kieán thöùc:
OÂn taäp toaøn boä kieán thöùc chöông VI.
Kó naêng:
Bieán ñoåi thaønh thaïo caùc coâng thöùc löôïng giaùc.
Vaän duïng caùc coâng thöùc treân ñeå giaûi baøi taäp.
Thaùi ñoä:
Luyeän tính caån thaän, tö duy linh hoaït.
II. CHUAÅN BÒ:
Giaùo vieân: Giaùo aùn. Heä thoáng baøi taäp.
Hoïc sinh: SGK, vôû ghi. OÂn taäp toaøn boä kieán thöùc chöông VI.
III. HOAÏT ÑOÄNG DAÏY HOÏC:
1. OÅn ñònh toå chöùc: Kieåm tra só soá lôùp.
2. Kieåm tra baøi cuõ: (Loàng vaøo quaù trình oân taäp)
H.
Ñ.
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn
113
3. Giaûng baøi môùi:
TL
Hoaït ñoäng cuûa Giaùo vieân
Hoaït ñoäng cuûa Hoïc sinh
Noäi dung
Hoaït ñoäng 1: Luyeän taäp tính GTLG cuûa moät cung
10'
H1. Neâu caùc böôùc tính vaø
coâng thöùc caàn söû duïng?
Ñ1. + Xeùt daáu caùc GTLG.
+ Vaän duïng coâng thöùc
phuø hôïp ñeå tính.
a) sin =
7
3
b) cos =
1
3
c) cos =
5
3
d) sin =
15
4
1. Tính caùc GTLG cuûa cung
neáu:
a) cos =
2
3
vaø
2
b) tan = 2
2
vaø
3
2
c) sin =
2
3
vaø
3
2
2
d) cos =
1
4
vaø
2
Hoaït ñoäng 2: Luyeän taäp bieán ñoåi bieåu thöùc löôïng giaùc
20'
GV höôùng daãn HS vaän
duïng caùc coâng thöùc ñeå bieán
ñoåi.
H1. Neâu caùch bieán ñoåi ?
H2. Xeùt quan heä caùc caëp
goùc ?
a) A = tan
2
b) B = 2cos
c)
sin cos 2 cos
44
sin cos 2sin
44


C = –cot
d) D = sin
Ñ1. Bieán ñoåi toång thaønh tích.
Ñ2.
4
+ x vaø
4
– x: phuï nhau
6
– x vaø
6
+ x: phuï
nhau
A = 0
B = 0
C =
1
4
2. Ruùt goïn bieåu thöùc
a) A =
2sin2 sin4
2sin2 sin4
b) B = tan
2
1 cos
sin
sin



c) C =
sin cos
44
sin cos
44


d) D =
sin5 sin3
2cos4
3. Chöùng minh ñoàng nhaát thöùc
a)
1 cosx cos2x
cotx
sin2x sinx

b)
x
sinx sin
x
2
tan
x
2
1 cosx cos
2

c)
2
2cos2x sin4x
tan x
2cos2x sin4x 4




d) tanx – tany =
sin(x y)
cosx.cosy
4. Chöùng minh caùc bieåu thöùc sau
khoâng phuï thuoäc vaøo x:
A =
sin x cos x
44

B =
cos x sin x
63

C = sin
2
x +
cos x cos x
33


D =
1 cos2x sin2x
.cotx
1 cos2x sin2x


Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn
114
D = 1
Hoaït ñoäng 3: Luyeän taäp tính giaù trò bieåu thöùc löôïng giaùc
10'
H1. Bieán ñoåi caùc goùc lieân
quan ?
Ñ1.
a) 75
0
= 45
0
+ 30
0
b) 267
0
= 360
0
– 93
0
c) 65
0
= 60
0
+ 5
0
;
55
0
= 60
0
– 5
0
d) 12
0
= 30
0
– 18
0
48
0
= 30
0
+ 18
0
5. Khoâng söû duïng maùy tính, haõy
chöùng minh:
a) sin75
0
+ cos75
0
=
6
2
b) tan267
0
+ tan93
0
= 0
c) sin65
0
+ sin55
0
=
3
cos5
0
d) cos12
0
– cos48
0
= sin18
0
Hoaït ñoäng 4: Cuûng coá
3'
Nhaán maïnh caùch vaän
duïng caùc coâng thöùc löôïng
giaùc.
4. BAØI TAÄP VEÀ NHAØ:
Baøi taäp oân cuoái naêm.
Ngaøy soaïn: 20/04/2013
Tieát daïy: 60 Baøøi daïy: OÂN TAÄP CUOÁI NAÊM
I. MUÏC TIEÂU:
Kieán thöùc:
OÂn taäp toaøn boä kieán thöùc chöông IV, V, VI.
Kó naêng:
Vaän duïng caùc coâng thöùc treân ñeå giaûi baøi taäp.
Thaùi ñoä:
Luyeän tính caån thaän, tö duy linh hoaït.
II. CHUAÅN BÒ:
Giaùo vieân: Giaùo aùn. Heä thoáng baøi taäp.
Hoïc sinh: SGK, vôû ghi. OÂn taäp toaøn boä kieán thöùc chöông IV, V, VI.
III. HOAÏT ÑOÄNG DAÏY HOÏC:
1. OÅn ñònh toå chöùc: Kieåm tra só soá lôùp.
2. Kieåm tra baøi cuõ: (Loàng vaøo quaù trình oân taäp)
H.
Ñ.
3. Giaûng baøi môùi:
TL
Hoaït ñoäng cuûa Giaùo vieân
Hoaït ñoäng cuûa Hoïc sinh
Noäi dung
Hoaït ñoäng 1: Cuûng coá vieäc giaûi baát phöông trình moät aån, xeùt daáu tam thöùc baäc hai
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn
115
10'
H1. Neâu caùch giaûi ?
H2. Neâu ñieàu kieän baøi toaùn
?
Ñ1.
a) Laäp baûng xeùt daáu.
S = (–; –3) (–1; 1]
b) Qui ñoàng, laäp baûng xeùt daáu
S = (–; –2)
1
;1
2


c) Giaûi töøng bpt, laáy giao caùc
taäp nghieäm.
S = (1; 2)
Ñ2.
a)  < 0 1 < m < 3
b) < 0 m <
1
4
1. Giaûi caùc baát phöông trình:
a)
2
x1
0
x 4x 3

b)
x 1 x 2
x 2 x 1


c)
2
x 7x 6 0
2x 1 3

2. Tìm m ñeå:
a) f(x) = x
2
– 2(2m – 3)x + 4m –
3 luoân luoân döông vôùi moïi x.
b) Bpt: x
2
– x + m 0 voâ nghieäm
Hoaït ñoäng 2: Cuûng coá vieäc tính toaùn caùc soá lieäu thoáng keâ
10'
H1. Neâu caùch tính taàn soá,
taàn suaát, soá trung bình, moát
?
Ñ1.
a) * = 12; ** = 20
b)
X
= 1170 (giôø)
c) M
O
= 1170
3. Tuoåi thoï cuûa 30 boùng ñeøn thaép
thöû ñöôïc cho bôûi baûng sau:
Tuoåi thoï
(giôø)
Taàn soá
Taàn suaát
(%)
1150
3
10
1160
6
20
1170
*
40
1180
6
**
1190
3
10
Coäng
30
100 (%)
a) Ñieàn soá thích hôïp vaøo caùc daáu
* vaø **.
b) Tính tuoåi thoï trung bình cuûa
30 boùng ñeøn.
c) Tìm moát cuûa baûng soá lieäu.
Hoaït ñoäng 3: Cuûng coá vieäc vaän duïng caùc coâng thöùc löôïng giaùc
20'
H1. Neâu coâng thöùc caàn söû
duïng ?
Ñ1.
a) Bieán ñoåi toång tích
A = tan3a
b) Söû duïng haèng ñaúng thöùc
B =
2
a
cos
2
c) Nhaân C vôùi
x
2sin
5
C =
16x
sin
5
x
16sin
5
d) Bieán ñoåi toång tích
4. Ruùt goïn caùc bieåu thöùc sau:
a)
sina sin3a sin5a
cosa cos3a cos5a


b)
4 4 2
sin a cos a cos a
2(1 cosa)

c)
x 2x 4x 8x
cos .cos .cos .cos
5 5 5 5
d)
x 3x 5x
sin sin sin
7 7 7

5. Tính:
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn
116
H2. Neâu caùch bieán ñoåi ?
H3. Neâu tính chaát veà goùc
trong tam giaùc ?
D =
2
3x x
4sin cos
77
Ñ2.
a) Bieán ñoåi toång tích
Nhaân töû vaø maãu vôùi cos18
0
A = 2
b) Coâng thöùc nhaân ñoâi
B = 9
Ñ3. A + B + C = 180
0
a) tan(A + B) = – tanC
b) sin(A + B) = sinC
a) 4(cos24
0
+ cos48
0
– cos84
0
–
cos12
0
)
b)
96 3sin cos cos cos cos
48 48 24 12 6
6. Chöùng minh raèng trong moät
ABC ta coù:
a) tanA + tanB + tanC =
= tanA.tanB.tanC (A, B, C
2
)
b) sin2A + sin2B + sin2C =
= 4sinA.sinB.sinC.
Hoaït ñoäng 4: Cuûng coá
3'
Nhaán maïnh:
– Caùc kieán thöùc cô baûn
trong caùc chöông IV, V, VI.
– Caùch giaûi caùc daïng toaùn.
4. BAØI TAÄP VEÀ NHAØ:
Chuaån bò kieåm tra Hoïc kì 2.
Ngaøy soaïn: 25/04/2013
Tieát daïy: 62 Baøøi daïy: KIEÅM TRA HOÏC KÌ II
I. MUÏC TIEÂU:
Kieán thöùc: Cuûng coá caùc kieán thöùc ñaõ hoïc trong hoïc kì 2.
Daáu nhò thöùc baäc nhaát. Daáu tam thöùc baäc hai.
Baát phöông trình, heä baát phöông trình baäc nhaát, baäc hai moät aån.
Thoáng keâ soá lieäu.
Giaù trò löôïng giaùc cuûa moät cung.
Coâng thöùc löôïng giaùc.
Kó naêng: Thaønh thaïo vieäc giaûi caùc daïng toaùn:
Giaûi baát phöông trình, heä baát phöông trình baäc nhaát, baäc hai moät aån.
Tính toaùn caùc soá lieäu thoáng keâ.
Tính GTLG cuûa moät cung, giaù trò moät bieåu thöùc löôïng giaùc.
Bieán ñoåi bieåu thöùc löôïng giaùc.
Thaùi ñoä:
Reøn luyeän tính caån thaän, chính xaùc. Luyeän tö duy linh hoaït, saùng taïo.
II. CHUAÅN BÒ:
Giaùo vieân: Ñeà kieåm tra.
Hoïc sinh: OÂn taäp kieán thöùc ñaõ hoïc trong hoïc kì 2.
III. MA TRAÄN ÑEÀ:
Chuû ñeà
Nhaän bieát
Thoâng hieåu
Vaän duïng
Toång
TNKQ
TL
TNKQ
TL
TNKQ
TL
Baát phöông trình
2
0,25
2
0,25
1
1,0
2,0
Thoáng keâ
2
0,25
1
0,25
2
1,0
2,75
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn
117
Löôïng giaùc
2
0,25
1
0,25
1
1,0
1,75
Toång
1,5
1,0
2,0
2,0
6,5
IV. NOÄI DUNG ÑEÀ KIEÅM TRA:
A. Phaàn traéc nghieäm:
001: Taäp nghieäm cuûa baát phöông trình:
2x 3 1
laø:
A. [1; 2] B. [1; 3] C. [–1; 1] D. [–1; 2]
002: Taäp nghieäm cuûa baát phöông trình: x
2
– 6x + 9 > 0 laø:
A. R \ {3} B. R C. (3; +) D. (–; 3)
003: Taäp nghieäm cuûa baát phöông trình:
2
x1
0
x 2x 3

laø:
A. (–; 1] B. [1; 2] C. [1; +) D. [–1; 2]
004: Tam thöùc f(x) = x
2
+ 4x + m – 5 luoân luoân döông vôùi moïi x khi:
A. m > 9 B. m < 9 C. m > –1 D. m < –1
005: Ñieàu tra thôøi gian hoaøn thaønh moät saûn phaåm cuûa 20 coâng nhaân, ngöôøi ta thu ñöôïc maãu soá lieäu sau (thôøi gian tính
baèng phuùt):
10 12 13 15 11 13 16 18 19 21 23 21 15 17 16 15 20 13 16 11
Haõy xaùc ñònh coù bao nhieâu giaù trò khaùc nhau trong maãu soá lieäu treân ?
A. 12 B. 10 C. 20 D. 23
006: Thoáng keâ ñieåm moân Toaùn trong moät kì thi cuûa 400 hoïc sinh thaáy coù 72 baøi ñöôïc ñieåm 5. Hoûi giaù trò taàn suaát cuûa
giaù trò x
i
= 5 laø:
A. 18% B. 10% C. 36% D. 72%
007: Keát quaû kieåm tra chaát löôïng cuûa 41 hoïc sinh ñöôïc cho bôûi baûng sau:
Ñieåm
1
2
3
4
5
6
7
8
9
10
Soá löôïng HS
3
6
4
4
6
7
3
4
2
2
Moát cuûa maãu soá lieäu treân laø:
A. 6 B. 3 C. 2 D. 10
008: Giaù trò cuûa bieåu thöùc A = m.sin90
0
+ n.cos90
0
+ p.cos180
0
baèng:
A. m – p B. m + p C. m + n + p D. m + n – p
009: Cho sinx =
1
2
vaø
x
2
. Khi ñoù cosx baèng:
A.
3
2
B.
3
2
C.
1
2
D.
1
2
010: Giaù trò cuûa bieåu thöùc B =
22
6
cos cos
14 14

baèng:
A. 1 B. 0 C.
2
2.cos
14
D.
2
6
2.cos
14
B. Phaàn töï luaän:
Baøi 1: Giaûi baát phöông trình: (2x – 1)(x + 3) x
2
– 9.
Baøi 2: Saûn löôïng luùa (ñôn vò laø taï) cuûa 40 thöûa ruoäng coù cuøng dieän tích ñöôïc trình baøy trong baûng soá lieäu sau:
Saûn löôïng (taï)
20
21
22
23
24
Taàn soá (soá thöûa)
5
8
11
10
6
N = 40
a) Laäp baûng phaân boá taàn soá, taàn suaát.
b) Tính saûn löôïng trung bình cuûa 40 thöûa ruoäng neâu treân.
Baøi 3: Ñôn giaûn bieåu thöùc A =
22
22
22
cos x sin y
cot x.cot y
sin x.sin y
.
V. ÑAÙP AÙN VAØ BIEÅU ÑIEÅM:
A. Phaàn traéc nghieäm: Taát caû ñaùp aùn laø A.
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn
118
B. Phaàn töï luaän:
Baøi 1: ( 1 ñieåm) (2x – 1)(x + 3) x
2
– 9 x
2
+ 5x + 6 0 (0,5 ñieåm)
x3
x2


(0,5 ñieåm)
Baøi 2: (2 ñieåm)
a) Baûng phaân boá taàn soá, taàn suaát: (1 ñieåm)
(Tính ñuùng moãi giaù trò taàn suaát ñöôïc 0,2 ñieåm)
b)
5.20 8.21 11.22 10.23 6.24
X
40
(0,5 ñieåm)
= 22,1 (taï) (0,5 ñieåm)
Baøi 3: (1 ñieåm) A =
22
22
22
cos x sin y
cot x.cot y
sin x.sin y
=
2 2 2 2
22
cos x sin y cos x.cos y
sin x.sin y

(0,5 ñieåm)
= – 1 (0,5 ñieåm)
VI. KEÁT QUAÛ KIEÅM TRA:
Lôùp
Só soá
0 – 3,4
3,5 – 4,9
5,0 – 6,4
6,5 – 7,9
8,0 – 10
SL
%
SL
%
SL
%
SL
%
SL
%
10A3
44
10A5
42
10A7
44
10A10
42
10A11
38
Saûn löôïng (taï)
Taàn soá
Taàn suaát (%)
20
5
12,5
21
8
20,0
22
11
27,5
23
10
25,0
24
6
15,0
Coäng
40
100 (%)
| 1/118
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn
Ngaøy soaïn: 20/8/2012
Chöông I: MEÄNH ÑEÀ – TAÄP HÔÏP Tieát daïy: 01
Baøøi 1: MEÄNH ÑEÀ I. MUÏC TIEÂU: Kieán thöùc:
– Naém vöõng caùc khaùi nieäm meänh ñeà, MÑ phuû ñònh, keùo theo, hai MÑ töông ñöông, caùc
ñieàu kieän caàn, ñuû, caàn vaø ñuû.
– Bieát khaùi nieäm MÑ chöùa bieán. Kó naêng:
– Bieát laäp MÑ phuû ñònh cuûa 1 MÑ, MÑ keùo theo vaø MÑ töông ñöông.
– Bieát söû duïng caùc kí hieäu ,  trong caùc suy luaän toaùn hoïc. Thaùi ñoä:
– Reøn luyeän tính töï giaùc, tích cöïc trong hoïc taäp.
– Tö duy caùc vaán ñeà cuûa toaùn hoïc moät caùch loâgic vaø heä thoáng. II. CHUAÅN BÒ:
Giaùo vieân: Giaùo aùn, phieáu hoïc taäp. Moät soá kieán thöùc maø HS ñaõ hoïc ôû lôùp döôùi.
Hoïc sinh: SGK, vôû ghi. OÂn taäp moät soá kieán thöùc ñaõ hoïc ôû lôùp döôùi.
III. HOAÏT ÑOÄNG DAÏY HOÏC:
1. OÅn ñònh toå chöùc: Kieåm tra só soá lôùp. 2. Giaûng baøi môùi: TL
Hoaït ñoäng cuûa Giaùo vieân
Hoaït ñoäng cuûa Hoïc sinh Noäi dung
Hoaït ñoäng 1: Tìm hieåu khaùi nieäm Meänh ñeà, Meänh ñeà chöùa bieán
 GV ñöa ra moät soá caâu vaø cho  HS thöïc hieän yeâu caàu.
I. Meänh ñeà. Meänh ñeà chöùa
25’ HS xeùt tính Ñ–S cuûa caùc caâu bieán. ñoù. 1. Meänh ñeà.
a) “Phan–xi–paêng laø ngoïn nuùi a) Ñ
– Moät meänh ñeà laø moät caâu
cao nhaát Vieät Nam.”
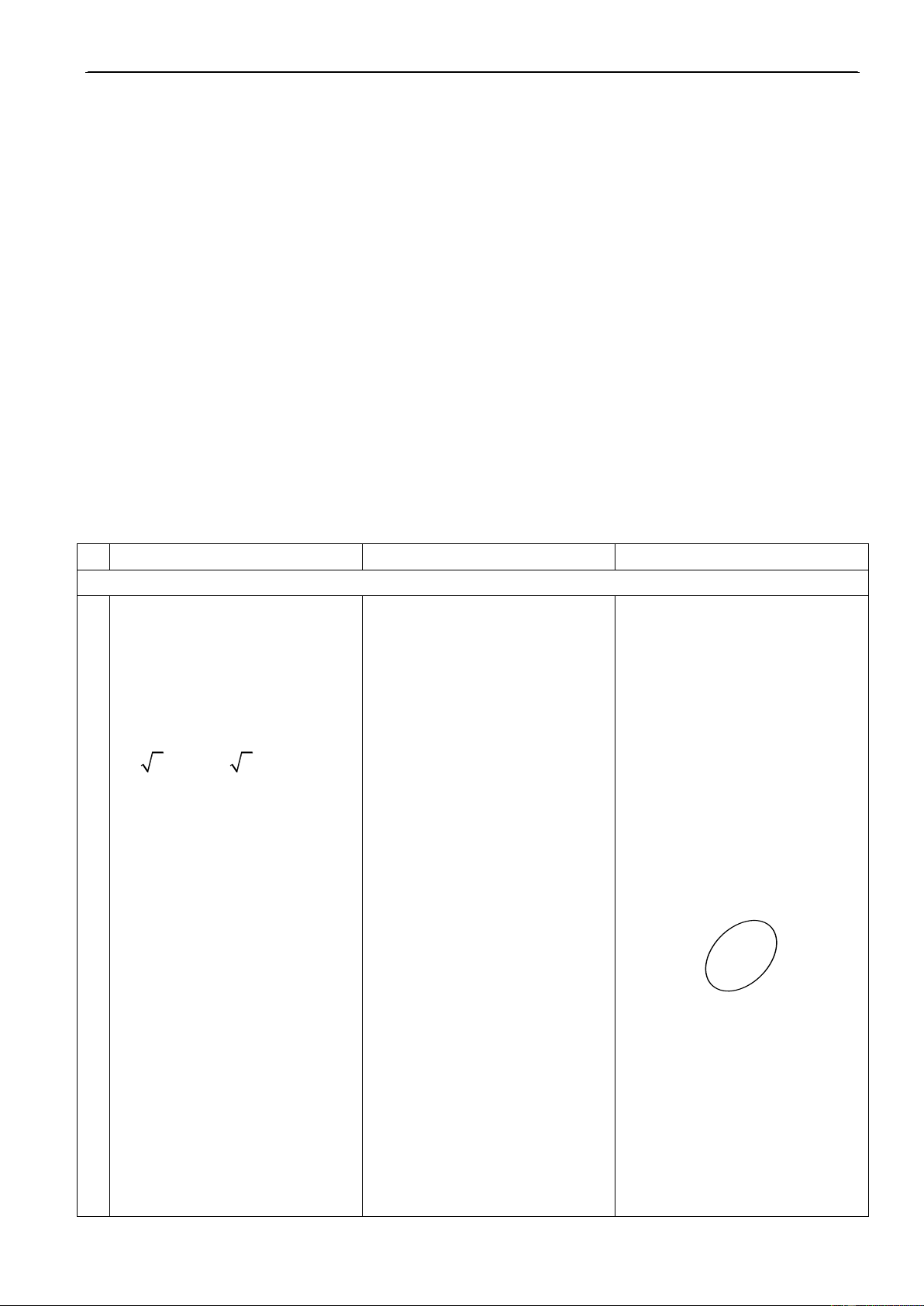
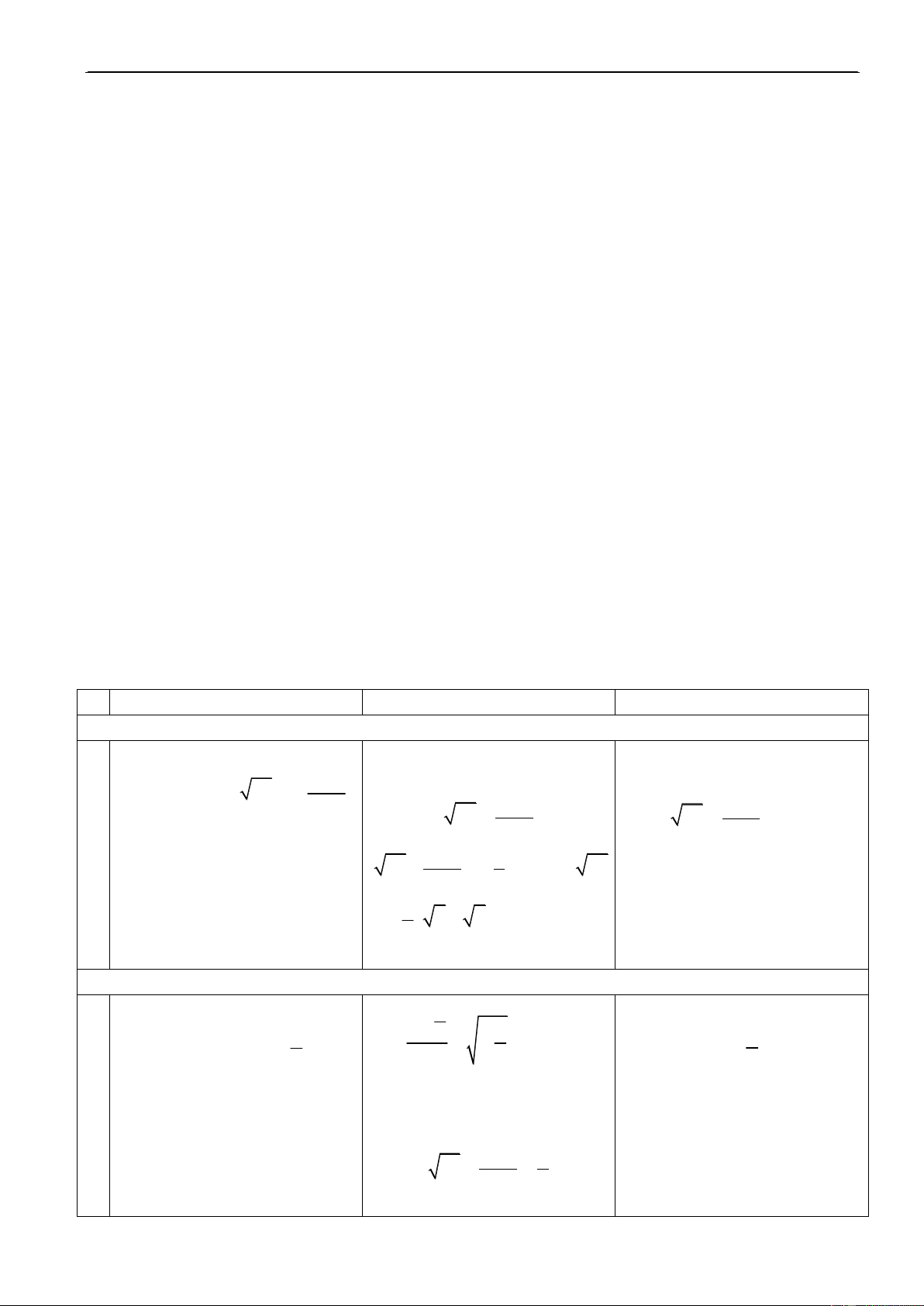
khaúng ñònh ñuùng hoaëc sai. b) “ 2  < 9,86” b) S
– Moät meänh ñeà khoâng theå vöøa
c) “Hoâm nay trôøi ñeïp quaù!” c) khoâng bieát ñuùng vöøa sai.
 Cho caùc nhoùm neâu moät soá  Caùc nhoùm thöïc hieän yeâu
caâu. Xeùt xem caâu naøo laø meänh caàu.
ñeà vaø tính Ñ–S cuûa caùc meänh ñeà.
2. Meänh ñeà chöùa bieán.
 Xeùt tính Ñ–S cuûa caùc caâu:
 Tính Ñ–S phuï thuoäc vaøo Meänh ñeà chöùa bieán laø moät caâu
d) “n chia heát cho 3” giaù trò cuûa n.
chöùa bieán, vôùi moãi giaù trò cuûa e) “2 + n = 5”
bieán thuoäc moät taäp naøo ñoù, ta
–> meänh ñeà chöùa bieán.
ñöôïc moät meänh ñeà.
 Cho caùc nhoùm neâu moät soá  Caùc nhoùm thöïc hieän yeâu
meänh ñeà chöùa bieán (haèng ñaúng caàu. thöùc, …). 1
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn
Hoaït ñoäng 2: Tìm hieåu meänh ñeà phuû ñònh cuûa moät meänh ñeà
 GV ñöa ra moät soá caëp meänh  HS traû lôøi tính Ñ–S cuûa II. Phuû ñònh cuûa 1 meänh ñeà.
20’ ñeà phuû ñònh nhau ñeå cho HS caùc meänh ñeà.
Kí hieäu meänh ñeà phuû ñònh cuûa
nhaän xeùt veà tính Ñ–S.
meänh ñeà P laø P .
a) P: “3 laø moät soá nguyeân toá” P ñuùng khi P sai
P : “3 khoâng phaûi laø soá ngtoá” P sai khi P ñuùng
b) Q: “7 khoâng chia heát cho 5”
Q : “7 chia heát cho 5”
 Cho caùc nhoùm neâu moät soá  Caùc nhoùm thöïc hieän yeâu
meänh ñeà vaø laäp meänh ñeà phuû caàu. ñònh.
3. BAØI TAÄP VEÀ NHAØ:  Baøi 1, 2, 3 SGK Ngaøy soaïn: 20/8/2012 2
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn
Tieát daïy: 02
Baøøi 1: MEÄNH ÑEÀ(TT) I. MUÏC TIEÂU: Kieán thöùc:
– Naém vöõng caùc khaùi nieäm meänh ñeà, MÑ phuû ñònh, keùo theo, hai MÑ töông ñöông, caùc
ñieàu kieän caàn, ñuû, caàn vaø ñuû.
– Bieát khaùi nieäm MÑ chöùa bieán. Kó naêng:
– Bieát laäp MÑ phuû ñònh cuûa 1 MÑ, MÑ keùo theo vaø MÑ töông ñöông.
– Bieát söû duïng caùc kí hieäu ,  trong caùc suy luaän toaùn hoïc. Thaùi ñoä:
– Reøn luyeän tính töï giaùc, tích cöïc trong hoïc taäp.
– Tö duy caùc vaán ñeà cuûa toaùn hoïc moät caùch loâgic vaø heä thoáng. II. CHUAÅN BÒ:
Giaùo vieân: Giaùo aùn, phieáu hoïc taäp. Moät soá kieán thöùc maø HS ñaõ hoïc ôû lôùp döôùi.
Hoïc sinh: SGK, vôû ghi. OÂn taäp moät soá kieán thöùc ñaõ hoïc ôû lôùp döôùi.
III. HOAÏT ÑOÄNG DAÏY HOÏC:
1. OÅn ñònh toå chöùc: Kieåm tra só soá lôùp.
2. Kieåm tra baøi cuõ: 3. Giaûng baøi môùi: TL
Hoaït ñoäng cuûa Giaùo vieân
Hoaït ñoäng cuûa Hoïc sinh Noäi dung
Hoaït ñoäng 1: Tìm hieåu khaùi nieäm meänh ñeà keùo theo
 GV ñöa ra moät soá meänh ñeà
III. Meänh ñeà keùo theo.
15’ ñöôïc phaùt bieåu döôùi daïng “Neáu
Cho 2 meänh ñeà P vaø Q. Meänh P thì Q”.
ñeà “Neáu P thì Q” ñgl meänh ñeà
a) “Neáu n laø soá chaün thì n chia
keùo theo, vaø kí hieäu P Q. heát cho 2.”
b) “Neáu töù giaùc ABCD laø hbh
Meänh ñeà P Q chæ sai khi P
thì noù coù caùc caëp caïnh ñoái song ñuùng vaø Q sai. song.”
 Cho caùc nhoùm neâu moät soá  Caùc nhoùm thöïc hieän yeâu Caùc ñònh lí toaùn hoïc laø nhöõng
VD veà meänh ñeà keùo theo. caàu.
meänh ñeà ñuùng vaø thöôøng coù + Cho P, Q. Laäp P  Q.
daïng P Q. Khi ñoù, ta noùi: + Cho P  Q. Tìm P, Q.
P laø giaû thieát, Q laø keát luaän.
P laø ñieàu kieän ñuû ñeå coù Q.
 Cho caùc nhoùm phaùt bieåu moät  Caùc nhoùm thöïc hieän yeâu Q laø ñieàu kieän caàn ñeå coù P.
soá ñònh lí döôùi daïng ñieàu kieän caàu. caàn, ñieàu kieän ñuû.
Hoaït ñoäng 2: Tìm hieåu khaùi nieäm meänh ñeà ñaûo – hai meänh ñeà töông ñöông
 Daãn daét töø KTBC, QP ñgl
IV. Meänh ñeà ñaûo – hai meänh
10’ meänh ñeà ñaûo cuûa PQ.
ñeà töông ñöông.
 Cho caùc nhoùm neâu moät soá  Caùc nhoùm thöïc hieän yeâu  Meänh ñeà QP ñgl meänh ñeà
meänh ñeà vaø laäp meänh ñeà ñaûo caàu.
ñaûo cuûa meänh ñeà PQ.
cuûa chuùng, roài xeùt tính Ñ–S cuûa
Neáu caû hai meänh ñeà PQ vaø 3
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn caùc meänh ñeà ñoù.
QP ñeàu ñuùng ta noùi P vaø Q
laø hai meänh ñeà töông ñöông.
 Trong caùc meänh ñeà vöøa laäp,
Kí hieäu: PQ
tìm caùc caëp PQ, QP ñeàu
Ñoïc laø: P töông ñöông Q
ñuùng. Töø ñoù daãn ñeán khaùi nieäm
hoaëc P laø ñk caàn vaø ñuû ñeå coù
hai meänh ñeà töông ñöông. Q
 Cho caùc nhoùm tìm caùc caëp  Caùc nhoùm thöïc hieän yeâu hoaëc P khi vaø chæ khi Q.
meänh ñeà töông ñöông vaø phaùt caàu.
bieåu chuùng baèng nhieàu caùch khaùc nhau.
Hoaït ñoäng 3: Tìm hieåu caùc kí hieäu vaø
 GV ñöa ra moät soá meänh ñeà coù
V. Kí hieäu vaø .
10’ söû duïng caùc löôïng hoaù: , . : vôùi moïi.
a) “Bình phöông cuûa moïi soá
: toàn taïi, coù moät.
thöïc ñeàu lôùn hôn hoaëc baèng 0”. –> xR: x2 ≥ 0
b) “Coù moät soá nguyeân nhoû hôn 0”. –> n  Z: n < 0.
 Cho caùc nhoùm phaùt bieåu caùc  Caùc nhoùm thöïc hieän yeâu
meänh ñeà coù söû duïng caùc löôïng caàu.
hoaù: , . (Phaùt bieåu baèng lôøi
vaø vieát baèng kí hieäu)
Hoaït ñoäng 4: Meänh ñeà phuû ñònh cuûa caùc meänh ñeà coù chöùa kí hieäu ,
 GV ñöa ra caùc meänh ñeà coù  x  X,P(x)  x  X,P(x)
7' chöùa caùc kí hieäu , . Höôùng  x  X,P(x)  x  X,P(x)
daãn HS laäp caùc meänh ñeà phuû ñònh.
a) A: “xR: x2 ≥ 0”
–> A : “x  R: x2 < 0”.
b) B: “n  Z: n < 0”
–> B: “n  Z: n ≥ 0”.
 Cho caùc nhoùm phaùt bieåu caùc  Caùc nhoùm thöïc hieän yeâu
meänh ñeà coù chöùa caùc kí hieäu , caàu.
, roài laäp caùc meänh ñeà phuû ñònh cuûa chuùng.
Hoaït ñoäng 5: Cuûng coá
 Nhaán maïnh caùc khaùi nieäm:
3’ – Meänh ñeà, MÑ phuû ñònh. – Meänh ñeà keùo theo.
– Hai meänh ñeà töông ñöông.
– MÑ coù chöùa kí hieäu , .
 Cho caùc nhoùm neâu VD veà meänh ñeà, khoâng phaûi mñ, phuû ñònh moät mñ, meänh ñeà keùo theo. Ngaøy soaïn: 20/8/2012
Chöông I: MEÄNH ÑEÀ – TAÄP HÔÏP Tieát daïy: 03
Baøøi 1: LUYEÄN TAÄP MEÄNH ÑEÀ 4
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn I. MUÏC TIEÂU: Kieán thöùc:
 Cuûng coá caùc khaùi nieäm: meänh ñeà, meänh ñeà phuû ñònh, meänh ñeà keùo theo, hai meänh ñeà töông ñöông. Kó naêng:
 Bieát caùch xeùt tính Ñ–S cuûa moät meänh ñeà, laäp meänh ñeà phuû ñònh.
 Bieát söû duïng caùc ñieàu kieän caàn, ñuû, caàn vaø ñuû.
 Bieát söû duïng caùc kí hieäu , . Thaùi ñoä:
 Hình thaønh cho HS khaû naêng suy luaän coù lí, khaû naêng tieáp nhaän, bieåu ñaït caùc vaán ñeà moät caùch chính xaùc. II. CHUAÅN BÒ:
Giaùo vieân: Giaùo aùn, phieáu hoïc taäp.
Hoïc sinh: SGK, vôû ghi. Laøm baøi taäp veà nhaø.
III. HOAÏT ÑOÄNG DAÏY HOÏC:
1. OÅn ñònh toå chöùc: Kieåm tra só soá lôùp.
2. Kieåm tra baøi cuõ: (Loàng vaøo quaù trình luyeän taäp)
3. Giaûng baøi môùi: TL
Hoaït ñoäng cuûa Giaùo vieân
Hoaït ñoäng cuûa Hoïc sinh Noäi dung
Hoaït ñoäng 1: Xeùt tính Ñ–S cuûa moät meänh ñeà, laäp meänh ñeà phuû ñònh
H1. Theá naøo laø meänh ñeà, Ñ1.
1. Trong caùc caâu sau, caâu naøo meänh ñeà chöùa bieán? – meänh ñeà: a, d.
laø meänh ñeà, meänh ñeà chöùa 10’
– meänh ñeà chöùa bieán: b, c. bieán? a) 3 + 2 = 7 b) 4 + x = 3 c) x + y > 1 d) 2 – 5 < 0
H2. Neâu caùch laäp meänh ñeà Ñ2. Töø P, phaùt bieåu “khoâng 2. Xeùt tính Ñ–S cuûa moãi
phuû ñònh cuûa moät meänh ñeà P? P”
meänh ñeà sau vaø phaùt bieåu
a) 1794 khoâng chia heát cho 3
meänh ñeà phuû ñònh cuûa noù? b) 2 laø moät soá voâ tæ a) 1794 chia heát cho 3 c)  ≥ 3,15
b) 2 laø moät soá höõu tæ d) 125  > 0 c)  < 3,15 d) 125  ≤ 0
Hoaït ñoäng 2: Luyeän kó naêng phaùt bieåu meänh ñeà baèng caùch söû duïng ñieàu kieän caàn, ñuû
H1. Neâu caùch xeùt tính Ñ–S Ñ1. Chæ xeùt P ñuùng. Khi ñoù:
3. Cho caùc meänh ñeà keùo theo: cuûa meänh ñeà PQ?
– Q ñuùng thì P  Q ñuùng.
A: Neáu a vaø b cuøng chia heát 15’ – Q sai thì P  Q sai.
cho c thì a + b chia heát cho c (a, b, c  Z).
H2. Chæ ra “ñieàu kieän caàn”, Ñ2.
B: Caùc soá nguyeân coù taän cuøng
“ñieàu kieän ñuû” trong meänh ñeà – P laø ñieàu kieän ñuû ñeå coù Q.
baèng 0 ñeàu chia heát cho 5. P  Q?
– Q laø ñieàu kieän caàn ñeå coù P. C: Tam giaùc caân coù hai trung tuyeán baèng nhau. 5
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn
D: Hai tam giaùc baèng nhau coù dieän tích baèng nhau.
a) Haõy phaùt bieåu meänh ñeà
ñaûo cuûa caùc meänh ñeà treân.
b) Phaùt bieåu caùc meänh ñeà
treân, baèng caùch söû duïng khaùi
nieäm “ñieàu kieän ñuû”.
c) Phaùt bieåu caùc meänh ñeà
treân, baèng caùch söû duïng khaùi
nieäm “ñieàu kieän caàn”.
H3. Khi naøo hai meänh ñeà P vaø Ñ3. Caû hai meänh ñeà P  Q 4. Phaùt bieåu caùc meänh ñeà sau, Q töông ñöông? vaø Q  P ñeàu ñuùng.
baèng caùch söû duïng khaùi nieäm
“ñieàu kieän caàn vaø ñuû”
a) Moät soá coù toång caùc chöõ soá
chia heát cho 9 thì chia heát cho 9 vaø ngöôïc laïi.
b) Moät hình bình haønh coù caùc
ñöôøng cheùo vuoâng goùc laø moät
hình thoi vaø ngöôïc laïi.
c) Phöông trình baäc hai coù hai
nghieäm phaân bieät khi vaø chæ
khi bieät thöùc cuûa noù döông.
Hoaït ñoäng 3: Luyeän kó naêng söû duïng caùc kí hieäu ,
H. Haõy cho bieát khi naøo duøng Ñ.
5. Duøng kí hieäu ,  ñeå vieát
13’ kí hieäu , khi naøo duøng kí – : moïi, taát caû. caùc meänh ñeà sau: hieäu ?
– : toàn taïi, coù moät.
a) Moïi soá nhaân vôùi 1 ñeàu a) x  R: x.1 = 1. baèng chính noù. b) x  R: x + x = 0.
b) Coù moät soá coäng vôùi chính
c) x  R: x + (–x) = 0. noù baèng 0.
c) Moïi soá coäng vôùi soá ñoái cuûa noù ñeàu baèng 0.
Laäp meänh ñeà phuû ñònh?
Hoaït ñoäng 4: Cuûng coá Nhaán maïnh:
5’ – Caùch vaän duïng caùc khaùi nieäm veà meänh ñeà.
– Coù nhieàu caùch phaùt bieåu meänh ñeà khaùc nhau.
4. BAØI TAÄP VEÀ NHAØ:
 Laøm caùc baøi taäp coøn laïi. Ñoïc tröôùc baøi “Taäp hôïp” Ngaøy soaïn: 3/9/2012
Chöông I: MEÄNH ÑEÀ – TAÄP HÔÏP Tieát daïy: 04
Baøøi 2: TAÄP HÔÏP 6
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn
I. MUÏC TIEÂU: Kieán thöùc:
 Naém vöõng caùc khaùi nieäm taäp hôïp, phaàn töû, taäp con, hai taäp hôïp baèng nhau. Kó naêng:
 Bieát caùch dieãn ñaït caùc khaùi nieäm baèng ngoân ngöõ meänh ñeà.
 Bieát caùch xaùc ñònh moät taäp hôïp baèng caùch lieät keâ caùc phaàn töû hoaëc chæ ra tính chaát ñaëc tröng. Thaùi ñoä:
 Luyeän tö duy loâgic, dieãn ñaït caùc vaán ñeà moät caùch chính xaùc. II. CHUAÅN BÒ:
Giaùo vieân: Giaùo aùn, phieáu hoïc taäp.
Hoïc sinh: SGK, vôû ghi. OÂn taäp caùc kieán thöùc veà taäp hôïp ñaõ hoïc ôû lôùp döôùi.
III. HOAÏT ÑOÄNG DAÏY HOÏC:
1. OÅn ñònh toå chöùc: Kieåm tra só soá lôùp.
2. Kieåm tra baøi cuõ: (3’)
H. Haõy chæ ra caùc soá töï nhieân laø öôùc cuûa 24?
Ñ. 1, 2, 3, 4, 6, 8, 12, 24.
3. Giaûng baøi môùi: TL
Hoaït ñoäng cuûa Giaùo vieân
Hoaït ñoäng cuûa Hoïc sinh Noäi dung
Hoaït ñoäng 1: Tìm hieåu veà taäp hôïp vaø phaàn töû
H1. Nhaéc laïi caùch söû duïng Ñ1.
I. Khaùi nieäm taäp hôïp caùc kí hieäu , ? a), c) ñieàn 
1. Taäp hôïp vaø phaàn töû
15’ Haõy ñieàn caùc kí hieäu  , b), d) ñieàn 
Taäp hôïp laø moät khaùi nieäm cô
vaøo nhöõng choã troáng sau
baûn cuûa toaùn hoïc, khoâng ñònh ñaây: nghóa. a) 3 … Z b) 3 … Q
a A; a A. c) 2 … Q d) 2 … R
2. Caùch xaùc ñònh taäp hôïp
H2. Haõy lieät keâ caùc öôùc Ñ2. {1, 2, 3, 5, 6, 10, 15, 30}
– Lieät keâ caùc phaàn töû cuûa noù. nguyeân döông cuûa 30?
– Chæ ra tính chaát ñaëc tröng
cuûa caùc phaàn töû cuûa noù.
H3. Haõy lieät keâ caùc soá thöïc Ñ3. Khoâng lieät keâ ñöôïc.  Bieåu ñoà Ven
lôùn hôn 2 vaø nhoû hôn 4?
–> Bieåu dieãn taäp B goàm caùc B
soá thöïc lôùn hôn 2 vaø nhoû hôn 4 B = {x  R/ 2 < x < 4} 3. Taäp hôïp roãng
H4. Cho taäp B caùc nghieäm Ñ4.
Taäp hôïp roãng, kí hieäu laø ,
cuûa pt: x2 + 3x – 4 = 0. Haõy:
a) B = {x  R/ x2 + 3x – 4 = laø taäp hôïp khoâng chöùa phaàn töû
a) Bieåu dieãn taäp B baèng caùch 0} naøo.
söû duïng kí hieäu taäp hôïp. b) B = {1, – 4}
A ≠ x: x A.
b) Lieät keâ caùc phaàn töû cuûa B.
H5. Lieät keâ caùc phaàn töû cuûa
taäp hôïp A ={xR/x2+x+1 = Ñ5. Khoâng coù phaàn töû naøo. 7
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn 0}
Hoaït ñoäng 2: Tìm hieåu taäp hôïp con
H1. Xeùt caùc taäp hôïp Z vaø Q. Ñ1. II. Taäp hôïp con a) Cho a  Z thì a  Q ? a) a  Z thì a  Q
A B x (x A x B)
10’ b) Cho a  Q thì a  Z ? b) Chöa chaéc.
Neáu A khoâng laø taäp con cuûa
B, ta vieát A B. Q
 Höôùng daãn HS nhaän xeùt caùc C  Tính chaát: B tính chaát cuûa taäp con.
a) A A, A. Z A
b) Neáu A B vaø B C
H2. Cho caùc taäp hôïp: thì A C. A ={xR/ x2 – 3x + 2 = 0} Ñ2.
c) A, A.
B = {nN/ n laø öôùc soá cuûa 6} A  B
C = {nN/ n laø öôùc soá cuûa 9}
Taäp naøo laø con cuûa taäp naøo?
Hoaït ñoäng 3: Tìm hieåu taäp hôïp baèng nhau
H. Cho caùc taäp hôïp: Ñ.
III. Taäp hôïp baèng nhau
10’ A = {nN/n laø boäi cuûa 2 vaø + n  A  n 2 vaø n 3
A = B x (x A x B) 3}  n 6  n  B
B = {nN/ n laø boäi cuûa 6} + n  B  n 6
Haõy kieåm tra caùc keát luaän:  n 2 vaø n 3  n  B a) A  B b) B  A
Hoaït ñoäng 4: Cuûng coá
 Nhaán maïnh caùc caùch cho
5’ taäp hôïp, taäp con, taäp hôïp baèng nhau.
 Caâu hoûi: Cho taäp A = {1, 2, , {1}, {2}, {3}, {1, 2}, {1,
3}. Haõy tìm taát caû caùc taäp con 3}, {2, 3}, A. cuûa A?
4. BAØI TAÄP VEÀ NHAØ:  Baøi 1, 2, 3 SGK.
 Ñoïc tröôùc baøi “Caùc pheùp toaùn taäp hôïp” Ngaøy soaïn: 3/9/2012
Chöông I: MEÄNH ÑEÀ – TAÄP HÔÏP Tieát daïy: 05
Baøøi 3: CAÙC PHEÙP TOAÙN TAÄP HÔÏP I. MUÏC TIEÂU: 8
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn Kieán thöùc:
 Naém vöõng caùc khaùi nieäm hôïp, giao, hieäu, phaàn buø cuûa hai taäp hôïp. Kó naêng:
 Bieát caùch xaùc ñònh hôïp, giao, hieäu, phaàn buø cuûa hai taäp hôïp. Thaùi ñoä:
 Bieát vaän duïng kieán thöùc ñaõ hoïc vaøo thöïc teá. II. CHUAÅN BÒ:
Giaùo vieân: Giaùo aùn, phieáu hoïc taäp. Hình veõ bieåu ñoà Ven.
Hoïc sinh: SGK, vôû ghi. OÂn laïi moät soá kieán thöùc ñaõ hoïc veà taäp hôïp.
III. HOAÏT ÑOÄNG DAÏY HOÏC:
1. OÅn ñònh toå chöùc: Kieåm tra só soá lôùp.
2. Kieåm tra baøi cuõ: (3’)
H. Neâu caùc caùch cho taäp hôïp? Cho ví duï minh hoaï.
Ñ. 2 caùch: lieät keâ caùc phaàn töû vaø chæ ra tính chaát ñaïc tröng cuûa caùc phaàn töû.
3. Giaûng baøi môùi: TL
Hoaït ñoäng cuûa Giaùo vieân
Hoaït ñoäng cuûa Hoïc sinh Noäi dung
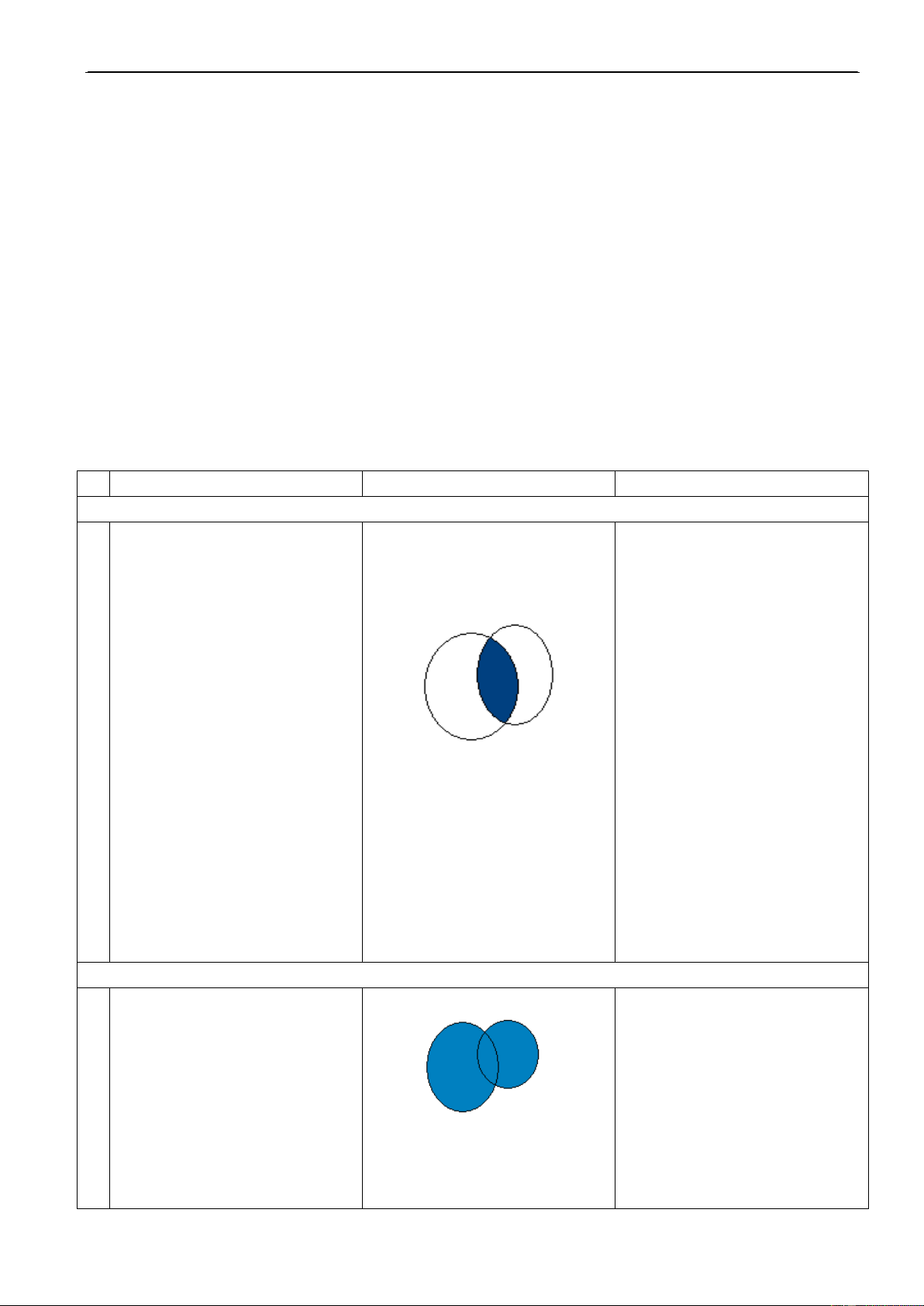
Hoaït ñoäng 1: Tìm hieåu Giao cuûa hai taäp hôïp
H1. Cho caùc taäp hôïp: Ñ1.
I. Giao cuûa hai taäp hôïp
12’ A = {nN/ n laø öôùc cuûa 12} a) A = {1, 2, 3, 4, 6, 12}
A B = {x/ x A vaø x B}
B = {nN/ n laø öôùc cuûa 18} B = {1, 2, 3, 6, 9, 18}
x A B xA
a) Lieät keâ caùc phaàn töû cuûa A, b) C = {1, 2, 3, 6} x  B B.
 Môû roäng cho giao cuûa nhieàu
b) Lieät keâ caùc phaàn töû cuûa C B taäp hôïp.
goàm caùc öôùc chung cuûa 12 vaø A C 18. AB
H2. Cho caùc taäp hôïp: Ñ2.
A = {1, 2, 3}, B ={3, 4, 7, 8}, A  B = {3} C = {3, 4}. Tìm: A  C = {3} a) A  B B  C = {3, 4} b) A  C A  B  C = {3} c) B  C d) A  B  C
Hoaït ñoäng 2: Tìm hieåu Hôïp cuûa hai taäp hôïp
H1. Cho caùc taäp hôïp:
Ñ1.C = {1, 2, 3, 4, 6, 9,12, 18} II. Hôïp cuûa hai taäp hôïp
10’ A = {nN/ n laø öôùc cuûa 12}
A B = {x/ x A hoaëc x B}
B = {nN/ n laø öôùc cuûa 18} B A
x A B x  A
Lieät keâ caùc phaàn töû cuûa C xB
goàm caùc öôùc chung cuûa 12 C=AB hoaëc 18.
 Môû roäng cho hôïp cuûa nhieàu
H2. Nhaän xeùt moái quan heä Ñ2. Moät phaàn töû cuûa C thì taäp hôïp.
giöõa caùc phaàn töû cuûa A, B, C? hoaëc thuoäc A hoaëc thuoäc B. 9
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn
H3. Cho caùc taäp hôïp:
Ñ3. ABC ={1, 2, 3, 4, 7,
A = {1, 2, 3}, B ={3, 4, 7, 8}, 8} C = {3, 4}. Tìm ABC ?
Hoaït ñoäng 3: Tìm hieåu Hieäu vaø phaàn buø cuûa hai taäp hôïp
H1. Cho caùc taäp hôïp: Ñ1. C = {4, 12}
III. Hieäu vaø phaàn buø cuûa hai
10’ A = {nN/ n laø öôùc cuûa 12} taäp hôïp B
B = {nN/ n laø öôùc cuûa 18} A A
A \ B = {x/ x A vaø x B}
a) Lieät keâ caùc phaàn töû cuûa C B
x A \ B xA
goàm caùc öôùc chung cuûa 12 x  B
nhöng khoâng laø öôùc cuûa 18. C=A\B CAB
Khi B A thì A \ B ñgl phaàn
buø cuûa B trong A, kí hieäu CAB.
H2. Cho caùc taäp hôïp: Ñ2. B ={3, 4, 7, 8}, C = {3, 4}. a) C  B
a) Xeùt quan heä giöõa B vaø C? b) C b) Tìm C BC = {7, 8} BC ?
Hoaït ñoäng 4: Cuûng coá
 Nhaán maïnh caùc khaùi nieäm
8’ giao, hôïp, hieäu, phaàn buø caùc taäp hôïp.  Caâu hoûi: Goïi:
 Cho caùc nhoùm thöïc hieän yeâu T: taäp caùc tam giaùc caàu.
TC: taäp caùc tam giaùc caân T T
Ñ: taäp caùc tam giaùc ñeàu
Tv: taäp caùc tam giaùc vuoâng T TÑ
vc: taäp caùc tam giaùc vuoâng caân
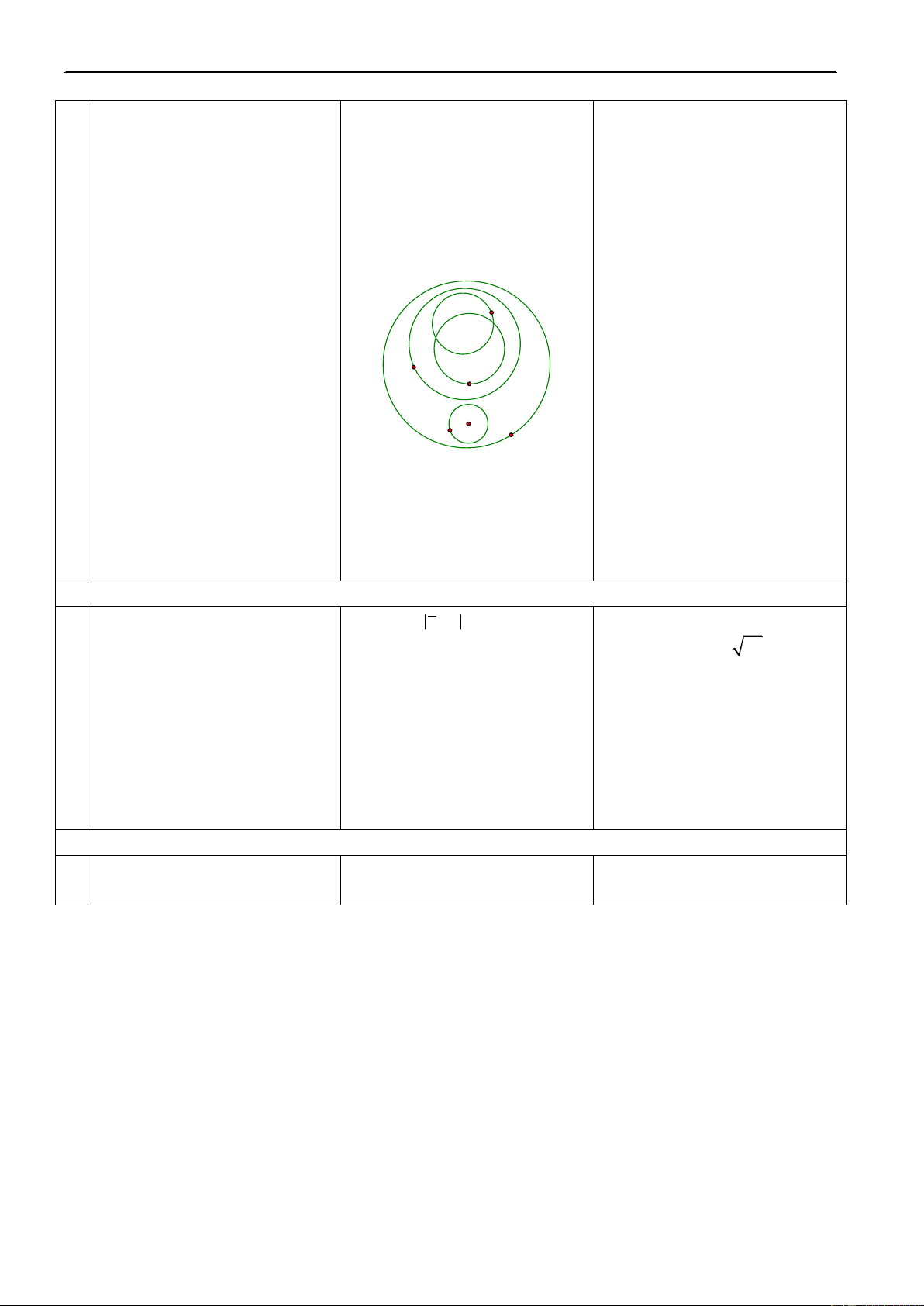
Veõ bieåu ñoà Ven bieåu dieãn TVC TC T
moái quan heä giöõa caùc taäp hôïp V treân?
4. BAØI TAÄP VEÀ NHAØ:  Baøi 1, 2, 3, 4, 5 SGK.
 Ñoïc tröôùc baøi “Caùc taäp hôïp soá” Ngaøy soaïn: 3/9/2012
Chöông I: MEÄNH ÑEÀ – TAÄP HÔÏP Tieát daïy: 06
Baøøi 3: BAØI TAÄP CAÙC PHEÙP TOAÙN TAÄP HÔÏP I. MUÏC TIEÂU: Kieán thöùc:
 Cuûng coá caùc khaùi nieäm taäp hôïp, taäp hôïp con, taäp hôïp baèng nhau, taäp hôïp roãng. 10
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn
 Cuûng coá caùc khaùi nieäm hôïp, giao, hieäu, phaàn buø cuûa hai taäp hôïp. Kó naêng:
 Bieát caùch xaùc ñònh taäp hôïp, hôïp, giao, hieäu, phaàn buø cuûa hai taäp hôïp. Thaùi ñoä:
 Bieát vaän duïng kieán thöùc ñaõ hoïc vaøo thöïc teá. II. CHUAÅN BÒ:
Giaùo vieân: Giaùo aùn. Heä thoáng baøi taäp.
Hoïc sinh: SGK, vôû ghi. OÂn laïi moät soá kieán thöùc ñaõ hoïc veà taäp hôïp. Laøm baøi taäp veà nhaø.
III. HOAÏT ÑOÄNG DAÏY HOÏC:
1. OÅn ñònh toå chöùc: Kieåm tra só soá lôùp.
2. Kieåm tra baøi cuõ: (Loàng vaøo quaù trình luyeän taäp) H. Ñ.
3. Giaûng baøi môùi: TL
Hoaït ñoäng cuûa Giaùo vieân
Hoaït ñoäng cuûa Hoïc sinh Noäi dung
Hoaït ñoäng 1: Luyeän taäp xaùc ñònh taäp hôïp
H1. Neâu caùc caùch xaùc ñònh Ñ1.
1. Cho A = {xN/ x<20 vaø x 10' taäp hôïp? – Lieät keâ phaàn töû
chia heát cho 3}. Haõy lieät keâ
– Chæ ra tính chaát ñaëc tröng caùc phaàn töû cuûa A. A = {0, 3, 6, 9, 12, 15, 18}
2. Cho B = {2, 6, 12, 20, 30}.
Haõy xaùc ñònh B baèng caùch chæ
B = {xN/ x = n(n+1), ra moät tính chaát ñaëc tröng cho 1≤n≤5}
caùc phaàn töû cuûa coù.
Hoaït ñoäng 2: Luyeän taäp caùch xaùc ñònh taäp con
H1. Nhaéc laïi khaùi nieäm taäp Ñ1. A  B  (xA  xB) 3. Trong hai taäp hôïp A, B döôùi 20' con?
ñaây, taäp naøo laø con cuûa taäp naøo?
H2. Hình vuoâng coù phaûi laø Ñ2. Phaûi. A  B.
a) A laø taäp caùc hình vuoâng. hình thoi khoâng?
B laø taäp caùc hình thoi.
b) A = {nN/ n laø öôùc chung
H3. Tìm öôùc chung lôùn nhaát Ñ3. Öôùc chung lôùn nhaát cuûa cuûa 24 vaø 30} cuûa 24 vaø 30? 24 vaø 30 laø 6  A = B.
B = {nN/ n laø öôùc cuûa 6}
 Höôùng daãn caùch tìm taát caû Ñ4.
4. Tìm taát caû caùc taäp con cuûa
caùc taäp con cuûa moät taäp hôïp. a) , {a}, {b}, A. taäp hôïp sau:
b) , {0}, {1}, {2}, {0, 1}, A = {a, b}, B = {0, 1, 2} {0, 2}, {1, 2}, B.
5. Cho A = {1, 2, 3, 4}.
 Höôùng daãn caùch tìm soá taäp 
a) Taäp A coù bao nhieâu taäp con con goàm 2 phaàn töû a) n(n 1) = 6 2 goàm 2 phaàn töû? b) 2n – 1 = 8
b) Taäp A coù bao nhieâu taäp con coù chöùa soá 1. 11
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn
Hoaït ñoäng 3: Luyeän taäp caùc pheùp toaùn taäp hôïp
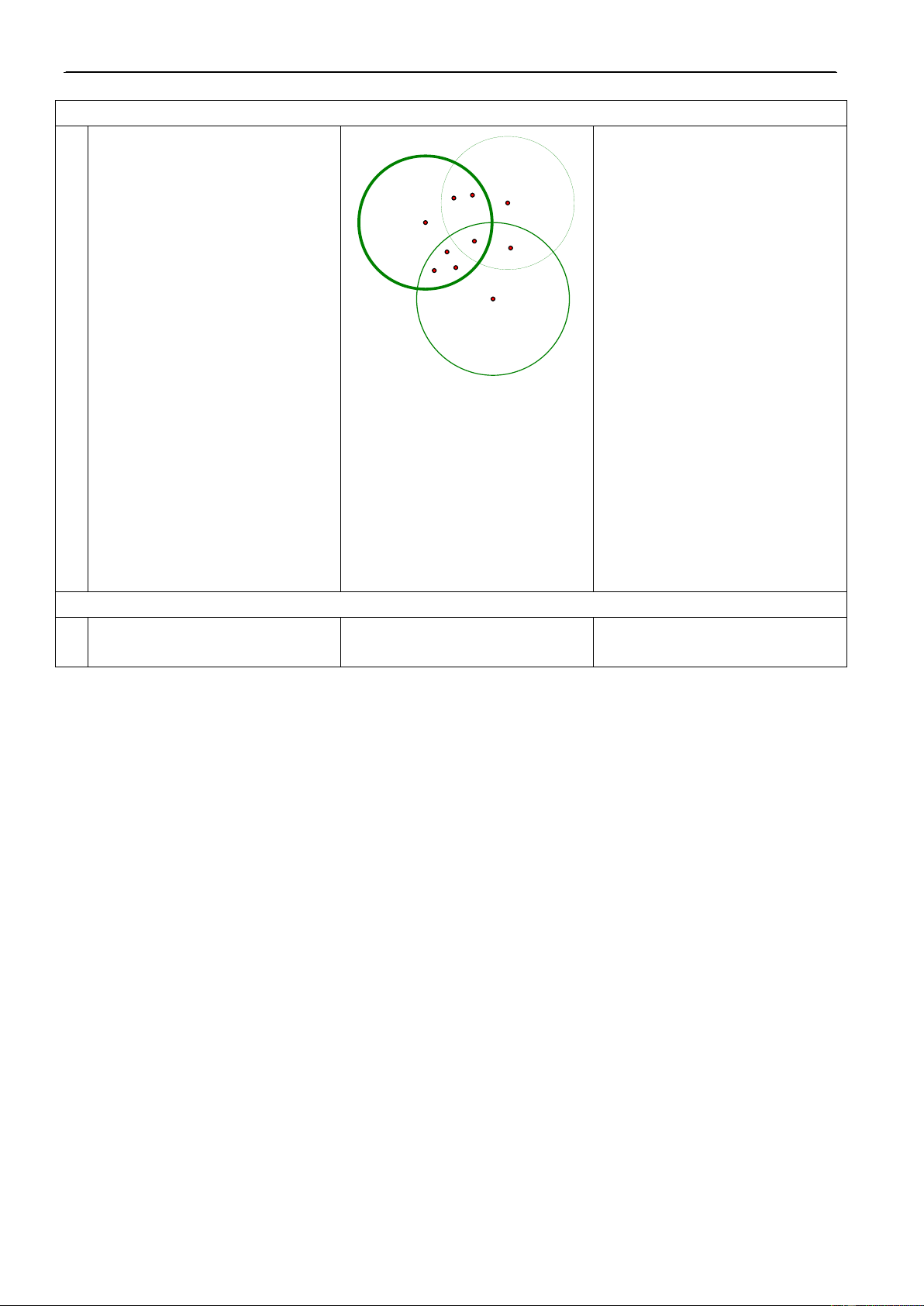
H1. Veõ bieåu ñoà Ven bieåu dieãn
5. Lôùp 10A coù 7 HS gioûi
10' caùc taäp HS gioûi caùc moân cuûa
Toaùn, 5 HS gioûi Lyù, 6 HS gioûi L lôùp 10A?
Hoaù, 3 HS gioûi caû Toaùn vaø T
Lyù, 4 HS gioûi caû Toaùn vaø
Hoaù, 2 HS gioûi caû Lyù vaø Hoaù,
1 HS gioûi caû 3 moân Toaùn, Lyù,
Hoaù. Soá HS gioûi ít nhaát moät H
moân (Toaùn, Lyù, Hoaù) cuûa lôùp 10A laø bao nhieâu?
H2. Nhaéc laïi ñònh nghóa giao, 6. Cho
hôïp, hieäu caùc taäp hôïp? Ñ2. AB = {1, 5} A = {1, 5}, B = {1, 3, 5} AB = {1, 3, 5} Tìm AB, AB, A\B, B\A A\B =  B\A = {3}
7. Cho taäp hôïp A. Haõy xaùc
ñònh caùc taäp hôïp sau:
AA, AA, A, A, CAA, CA.
Hoaït ñoäng 4: Cuûng coá
3' Nhaán maïnh caùch xaùc ñònh taäp
hôïp, caùc pheùp toaùn taäp hôïp
4. BAØI TAÄP VEÀ NHAØ:
 Laøm caùc baøi taäp coøn laïi.
 Ñoïc tröôùc baøi “Caùc taäp hôïp soá” Ngaøy soaïn: 8/9/2012
Chöông I: MEÄNH ÑEÀ – TAÄP HÔÏP Tieát daïy: 07
Baøøi 5: SOÁ GAÀN ÑUÙNG. SAI SOÁ I. MUÏC TIEÂU: Kieán thöùc:
 Bieát khaùi nieäm soá gaàn ñuùng. Kó naêng: 12
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn
 Vieát ñöôïc soá qui troøn cuûa moät soá caên cöù vaøo ñoä chính xaùc cho tröôùc.
 Bieát söû duïng MTBT ñeå tính toaùn vôùi caùc soá gaàn ñuùng. Thaùi ñoä:
 Reøn luyeän tính caån thaän, chính xaùc.
 Bieát ñöôïc moái lieân quan giöõa toaùn hoïc vaø thöïc tieãn. II. CHUAÅN BÒ:
Giaùo vieân: Giaùo aùn, phieáu hoïc taäp. MTBT.
Hoïc sinh: SGK, vôû ghi. OÂn taäp kieán thöùc ñaõ hoïc veà laøm troøn soá. MTBT.
III. HOAÏT ÑOÄNG DAÏY HOÏC:
1. OÅn ñònh toå chöùc: Kieåm tra só soá lôùp.
2. Kieåm tra baøi cuõ: (3’)
H. Vieát  = 3,14. Ñuùng hay sai? Vì sao? Ñ. Sai.
3. Giaûng baøi môùi: TL
Hoaït ñoäng cuûa Giaùo vieân
Hoaït ñoäng cuûa Hoïc sinh Noäi dung
Hoaït ñoäng 1: Tìm hieåu veà Soá gaàn ñuùng
H1. Cho HS tieán haønh ño Ñ1. Caùc nhoùm thöïc hieän yeâu I. Soá gaàn ñuùng
7’ chieàu daøi moät caùi baøn HS. caàu vaø cho keát quaû.
Trong ño ñaïc, tính toaùn ta
Cho keát quaû vaø nhaän xeùt
thöôøng chæ nhaän ñöôïc caùc soá
chung caùc keát quaû ño ñöôïc. gaàn ñuùng.
H2. Trong toaùn hoïc, ta ñaõ gaëp Ñ2. , 2 , …
nhöõng soá gaàn ñuùng naøo?
Hoaït ñoäng 2: Tìm hieåu veà Sai soá tuyeät ñoái
 Trong caùc keát quaû ño ñaït ôû  Caùc nhoùm thöïc hieän yeâu caàu II. Sai soá tuyeät ñoái
15’ treân, cho HS nhaän xeùt keát quaû
1. Sai soá tuyeät ñoái cuûa moät
naøo chính xaùc hôn. Töø ñoù daãn soá gaàn ñuùng
ñeán khaùi nieäm sai soá tuyeät ñoái
Neáu a laø soá gaàn ñuùng cuûa a
thì a = a a ñgl sai soá tuyeät
ñoái cuûa soá gaàn ñuùng a.
2. Ñoä chính xaùc cuûa moät soá gaàn ñuùng
H1. Ta coù theå tính ñöôïc caùc Ñ1. Khoâng. Vì khoâng bieát Neáu a = a a ≤ d
sai soá tuyeät ñoái khoâng? ñöôïc soá ñuùng.
thì –d ≤ a – a ≤ d hay
a – d ≤ a ≤ a + d.
Ta noùi a laø soá gaàn ñuùng cuûa a
vôùi ñoä chính xaùc d, vaø qui öôùc
 GV neâu moät soá VD veà sai soá  Caùc nhoùm thöïc hieän yeâu caàu vieát goïn laø: a = a d.
töông ñoái ñeå HS nhaän xeùt veà
Chuù yù: Sai soá tuyeät ñoái cuûa soá
ñoä chính xaùc cuûa soá gaàn ñuùng.
gaàn ñuùng nhaän ñöôïc trong moät
– Ñeám soá daân trong thaønh
pheùp ño ñaïc ñoâi khi khoâng phoá
phaûn aùnh ñaày ñuû tính chính
– Ñeám soá HS trong moät lôùp
xaùc cuûa pheùp ño ñaïc ñoù.
Vì theá ngoaøi sai soá tuyeät ñoái
a cuûa soá gaàn ñuùng a, ngöôøi ta 13
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn
coøn vieát tæ soá   a = a , goïi laø a
sai soá töông ñoái cuûa soá gaàn ñuùng a.
Hoaït ñoäng 3: Tìm hieåu caùch vieát soá qui troøn cuûa soá gaàn ñuùng
H1. Cho HS nhaéc laïi qui taéc Ñ1. Caùc nhoùm nhaéc laïi vaø cho III. Qui troøn soá gaàn ñuùng
15’ laøm troøn soá. Cho VD. VD.
1. OÂn taäp qui taéc laøm troøn soá
(Coù theå cho nhoùm naøy ñaët yeâu Neáu chöõ soá sau haøng qui troøn
caàu, nhoùm kia thöïc hieän)
nhoû hôn 5 thì ta thay noù vaø caùc
chöõ soá beân phaûi noù bôûi soá 0.
Neáu chöõ soá sau haøng qui troøn
lôùn hôn hoaëc baèng 5 thì ta
cuõng laøm nhö treân, nhöng
coäng theâm 1 vaøo chöõ soá cuûa haøng qui troøn.
2. Caùch vieát soá qui troøn cuûa
soá gaàn ñuùng caên cöù vaøo ñoä
 GV höôùng daãn caùch xaùc  x = 2841675300
chính xaùc cho tröôùc
ñònh chöõ soá chaéc vaø caùch vieát  x  2842000
Cho soá gaàn ñuùng a cuûa soá chuaån soá gaàn ñuùng.
y = 3,14630,001
a . Trong soá a, moät chöõ soá ñgl  y  3,15
chöõ soá chaéc (hay ñaùng tin) neáu
sai soá tuyeät ñoái cuûa soá a khoâng
vöôït quaù moät nöûa ñôn vò cuûa
haøng coù chöõ soá ñoù.
Caùch vieát chuaån soá gaàn ñuùng
döôùi daïng thaäp phaân laø caùch
vieát trong ñoù moïi chöõ soá ñeàu
laø chöõ soá chaéc. Neáu ngoaøi caùc
chöõ soá chaéc coøn coù nhöõng chöõ
soá khaùc thì phaûi qui troøn ñeán
haøng thaáp nhaát coù chöõ soá chaéc
Hoaït ñoäng 4: Cuûng coá
Nhaéc laïi caùch xaùc ñònh sai soá
3’ tuyeät ñoái vaø vieát soá qui troøn
4. BAØI TAÄP VEÀ NHAØ:
 Baøi 1, 2, 3, 4, 5, 6 SGK. Ngaøy soaïn: 8/9/2012
Chöông I: MEÄNH ÑEÀ – TAÄP HÔÏP Tieát daïy: 08
Baøøi daïy: OÂN TAÄP CHÖÔNG I I. MUÏC TIEÂU: Kieán thöùc:
 Cuûng coá caùc kieán thöùc veà meänh ñeà, taäp hôïp, soá gaàn ñuùng. Kó naêng: 14
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn
 Nhaän bieát ñöôïc ñk caàn, ñk ñuû, ñk caàn vaø ñuû, giaû thieát, keát luaän trong moät ñònh lí Toaùn hoïc.
 Bieát söû duïng caùc kí hieäu , .
 Xaùc ñònh ñöôïc giao, hôïp, hieäu cuûa hai taäp hôïp, ñaëc bieät khoaûng ñoaïn.
 Bieát qui troøn soá gaàn ñuùng vaø vieát soá gaàn ñuùng döôùi daïng chuaån. Thaùi ñoä:
 Reøn luyeän tính caån thaän, chính xaùc.
 Vaän duïng kieán thöùc ñaõ hoïc vaøo thöïc teá. II. CHUAÅN BÒ:
Giaùo vieân: Giaùo aùn, phieáu hoïc taäp
Hoïc sinh: SGK, vôû ghi.
III. HOAÏT ÑOÄNG DAÏY HOÏC:
1. OÅn ñònh toå chöùc: Kieåm tra só soá lôùp.
2. Kieåm tra baøi cuõ: (Loàng vaøo quaù trình luyeän taäp) H. Ñ.
3. Giaûng baøi môùi: TL
Hoaït ñoäng cuûa Giaùo vieân
Hoaït ñoäng cuûa Hoïc sinh Noäi dung
Hoaït ñoäng 1: Cuûng coá khaùi nieäm meänh ñeà vaø caùc pheùp toaùn veà meänh ñeà
H1. Xaùc ñònh tính ñuùng sai Ñ1. P  Q ñuùng khi P ñuùng 1. Trong caùc meänh ñeà sau, tìm
15’ cuûa meänh ñeà P  Q? vaø Q ñuùng. meänh ñeà ñuùng ? 1. a) S b) Ñ
a) Neáu a ≥ b thì a2 ≥ b2 c) Ñ d) S
b) Neáu a chia heát cho 9 thì a chia heát cho 3
b) Neáu em coá gaéng hoïc taäp thì em seõ thaønh coâng
c) Neáu moät tam giaùc coù moät
goùc baèng 600 thì tam giaùc ñoù laø tam giaùc ñeàu 2.
2. Cho töù giaùc ABCD. Xeùt a) P  Q: Ñuùng
tính Ñ–S cuûa meänh ñeà P  Q Q  P: Sai vaø Q  P vôùi: b) P  Q: Sai
a) P:”ABCD laø moät h.vuoâng” Q  P: Sai Q:”ABCD laø moät hbh”
b) P:”ABCD laø moät hình thoi” Q:”ABCD laø moät hcn”
H2. Xaùc ñònh tính ñuùng sai Ñ2. P  Q ñuùng khi P  Q 3. Trong caùc meänh ñeà sau, tìm cuûa meänh ñeà P  Q? ñuùng vaø Q  P ñuùng meänh ñeà sai ? 2. a) S b) S
a) –  < – 2 <=> 2 < 4 c) Ñ d) Ñ
b)  < 4 <=> 2 < 16
c) 23 < 5 => 2 23 < 2.5
d) 23 < 5 => (–2) 23 >(– 2).5
Hoaït ñoäng 2: Cuûng coá khaùi nieäm taäp hôïp vaø caùc pheùp toaùn veà taäp hôïp
H1. Neâu caùc caùch xaùc ñònh Ñ1.
4. Leät keâ caùc phaàn töû cuûa moãi 15
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn taäp hôïp? – Lieät keâ . taäp hôïp sau: 15’
– Chæ ra tính chaát ñaëc tröng.
A = {3k–2/ k = 0, 1, 2, 3, 4, 5} A = {–2, 1, 4, 7, 10, 13} B = {x  N/ x ≤ 12} B = {0, 1, 2, 3, 4, …, 12} C = {(–1)n/ n  N} C = {–1, 1}
H2. Nhaéc laïi khaùi nieäm taäp Ñ2.
5. Xeùt moái quan heä bao haøm hôïp con?
A  B  x (x A  xB)
giöõa caùc taäp hôïp sau:
A laø taäp hôïp caùc töù giaùc D B laø taäp hôïp caùc hbh E
C laø taäp hôïp caùc hình thang D laø taäp hôïp caùc hcn B
E laø taäp hôïp caùc hình vuoâng G
G laø taäp hôïp caùc hình thoi
H3. Nhaéc laïi caùc pheùp toaùn C
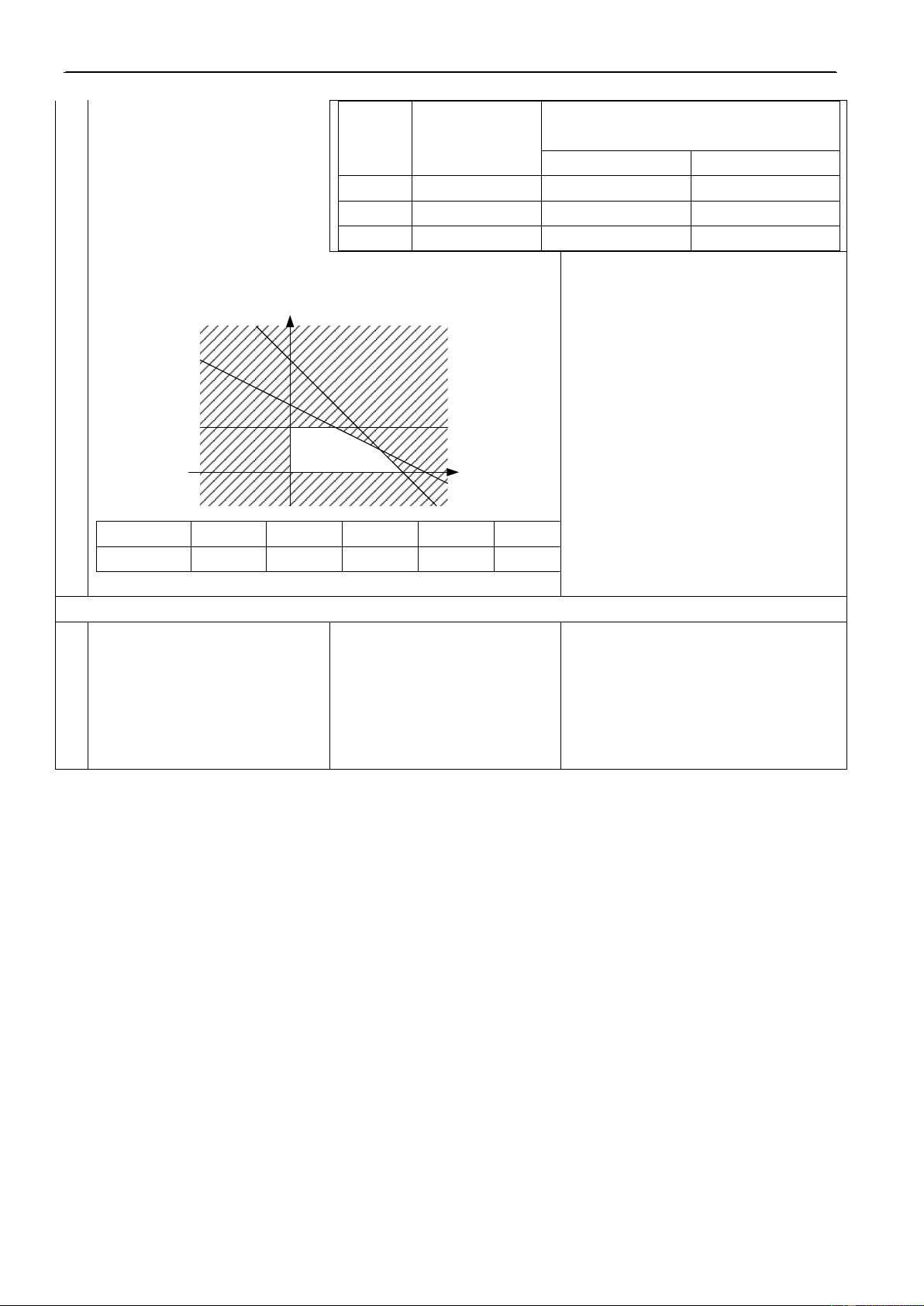
6. Xaùc ñònh caùc taäp hôïp sau: A veà taäp hôïp? A = (–3; 7)  (0; 10)
 Nhaán maïnh caùch tìm giao, Ñ3. Bieåu dieãn leân truïc soá. B = (–; 5)  (2; +)
hôïp, hieäu cuûa caùc khoaûng, A= (0; 7);B= (2; 5);C = [3; C = R \ (–; 3) ñoaïn. +)
Hoaït ñoäng 3: Cuûng coá khaùi nieäm soá gaàn ñuùng vaø sai soá
H1. Nhaéc laïi ñoä chính xaùc cuûa Ñ1.a = a a ≤ d
7. Duøng MTBT tính giaù trò 10’ soá gaàn ñuùng? a = 2,289; a < 0,001
gaàn ñuùng a cuûa 3 12 (keát quaû
laøm troøn ñeán chöõ soá thaäp
phaân thöù ba). Öôùc löôïng sai soá tuyeät ñoái cuûa a.
H2. Nhaéc laïi caùch vieát soá qui Ñ3. Vì ñoä chính xaùc ñeán haøng 8. Chieàu cao cuûa moät ngoïn
troøn cuûa soá gaàn ñuùng?
phaàn möôøi, neân ta qui troøn ñoài laø h = 347,13m  0,2m. ñeán haøng ñôn vò:
Haõy vieát soá qui troøn cuûa soá
Soá qui troøn cuûa 347,13 laø 347 gaàn ñuùng 347,13.
Hoaït ñoäng 4: Cuûng coá
3’ Nhaán maïnh laïi caùc vaán ñeà cô
baûn ñaõ hoïc trong chöông I.
4. BAØI TAÄP VEÀ NHAØ:
 Laøm caùc baøi taäp coøn laïi.
 Ñoïc tröôùc baøi “Haøm soá”. Ngaøy soaïn: 15/9/2012
Chöông II: HAØM SOÁ BAÄC NHAÁT VAØ BAÄC HAI Tieát daïy: 09 Baøøi 1: HAØM SOÁ I. MUÏC TIEÂU: Kieán thöùc:
 Hieåu khaùi nieäm haøm soá, taäp xaùc ñònh, ñoà thò cuûa haøm soá.
 Hieåu caùc tính chaát haøm soá ñoàng bieán, nghòch bieán, haøm soá chaün, leû.
 Bieát ñöôïc tính chaát ñoái xöùng cuûa ñoà thò haøm soá chaün, leû. Kó naêng: 16
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn
 Bieát tìm MXÑ cuûa caùc haøm soá ñôn giaûn.
 Bieát caùch chöùng minh tính ñoàng bieán, nghòch bieán cuûa moät haøm soá treân moät khoaûng cho tröôùc.
 Bieát xeùt tính chaün leû cuûa moät haøm soá ñôn giaûn. Thaùi ñoä:
 Reøn luyeän tính caån thaän, chính xaùc.
 Bieát vaän duïng kieán thöùc ñaõ hoïc ñeå xaùc ñònh moái quan heä giöõa caùc ñoái töôïng thöïc teá. II. CHUAÅN BÒ:
Giaùo vieân: Giaùo aùn. Hình veõ minh hoaï.
Hoïc sinh: SGK, vôû ghi. Duïng cuï veõ hình. OÂn taäp caùc kieán thöùc ñaõ hoïc veà haøm soá.
III. HOAÏT ÑOÄNG DAÏY HOÏC:
1. OÅn ñònh toå chöùc: Kieåm tra só soá lôùp.
2. Kieåm tra baøi cuõ: (3’)
H. Neâu moät vaøi loaïi haøm soá ñaõ hoïc?
Ñ. Haøm soá y = ax+b, y = ax2 .
3. Giaûng baøi môùi: TL
Hoaït ñoäng cuûa Giaùo vieân
Hoaït ñoäng cuûa Hoïc sinh Noäi dung
Thu nhaäp bình quaân ñaàu ngöôøi USD 564 600 400 282 295 311 339 363 375 394 200 200
0 1995 1996 1997 1998 1999 2000 2001 2002 2004 Thu nhaäp 200 282 295 311 339 363 375 394 564
Hoaït ñoäng 1: OÂn taäp caùc kieán thöùc ñaõ hoïc veà haøm soá
 Xeùt baûng soá lieäu veà thu  HS quan saùt baûng soá lieäu. I. OÂn taäp veà haøm soá
10’ nhaäp bình quaân ñaøu ngöôøi töø Caùc nhoùm thaûo luaän thöïc hieän Neáu vôùi moãi giaù trò cuûa x D 1995 ñeán 2004: (SGK) yeâu caàu.
coù moät vaø chæ moät giaù trò
H1. Neâu taäp xaùc ñònh cuûa h.soá Ñ1. D={1995, 1996, …, 2004} töông öùng cuûa y R thì ta coù moät haøm soá.
H2. Neâu caùc giaù trò töông öùng Ñ2. Caùc nhoùm ñaët yeâu caàu vaø Ta goïi x laø bieán soá, y laø haøm
y cuûa x vaø ngöôïc laïi? traû lôøi. soá cuûa x.
Taäp hôïp D ñgl taäp xaùc ñònh
Taäp caùc giaù trò cuûa y ñgl taäp cuûa haøm soá.
giaù trò cuûa haøm soá.
H3. Cho moät soá VD thöïc teá Ñ3. Caùc nhoùm thaûo luaän vaø
veà h.soá, chæ ra taäp xaùc ñònh traû lôøi. cuûa h.soá ñoù
Hoaït ñoäng 2: Tìm hieåu caùch cho haøm soá
 GV giôùi thieäu caùch cho haøm  Caùc nhoùm thaûo luaän
2. Caùch cho haøm soá
15’ soá baèng baûng vaø baèng bieåu – Baûng thoáng keâ chaát löôïng a) Haøm soá cho baèng baûng
ñoà. Sau ñoù cho HS tìm theâm HS.
b) Haøm soá cho baèng bieåu ñoà VD.
– Bieåu ñoà theo doõi nhieät ñoä.
c) Haøm soá cho baèng coâng 17
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn
 GV giôùi thieäu qui öôùc veà taäp thöùc
xaùc ñònh cuûa haøm soá cho baèng
Taäp xaùc ñònh cuûa haøm soá y = coâng thöùc.
f(x) laø taäp hôïp taát caû caùc soá
H1. Tìm taäp xaùc ñònh cuûa haøm Ñ1.
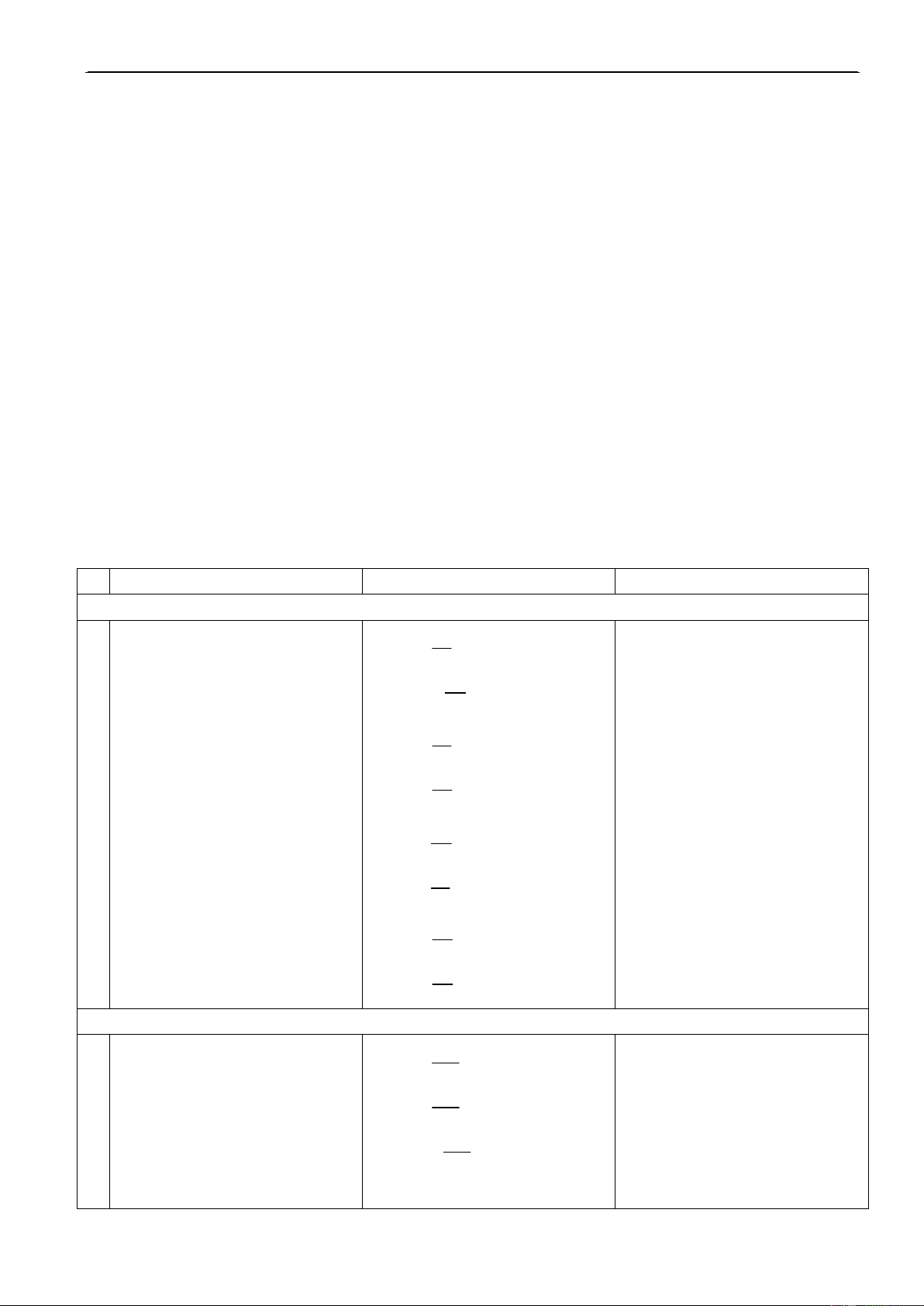
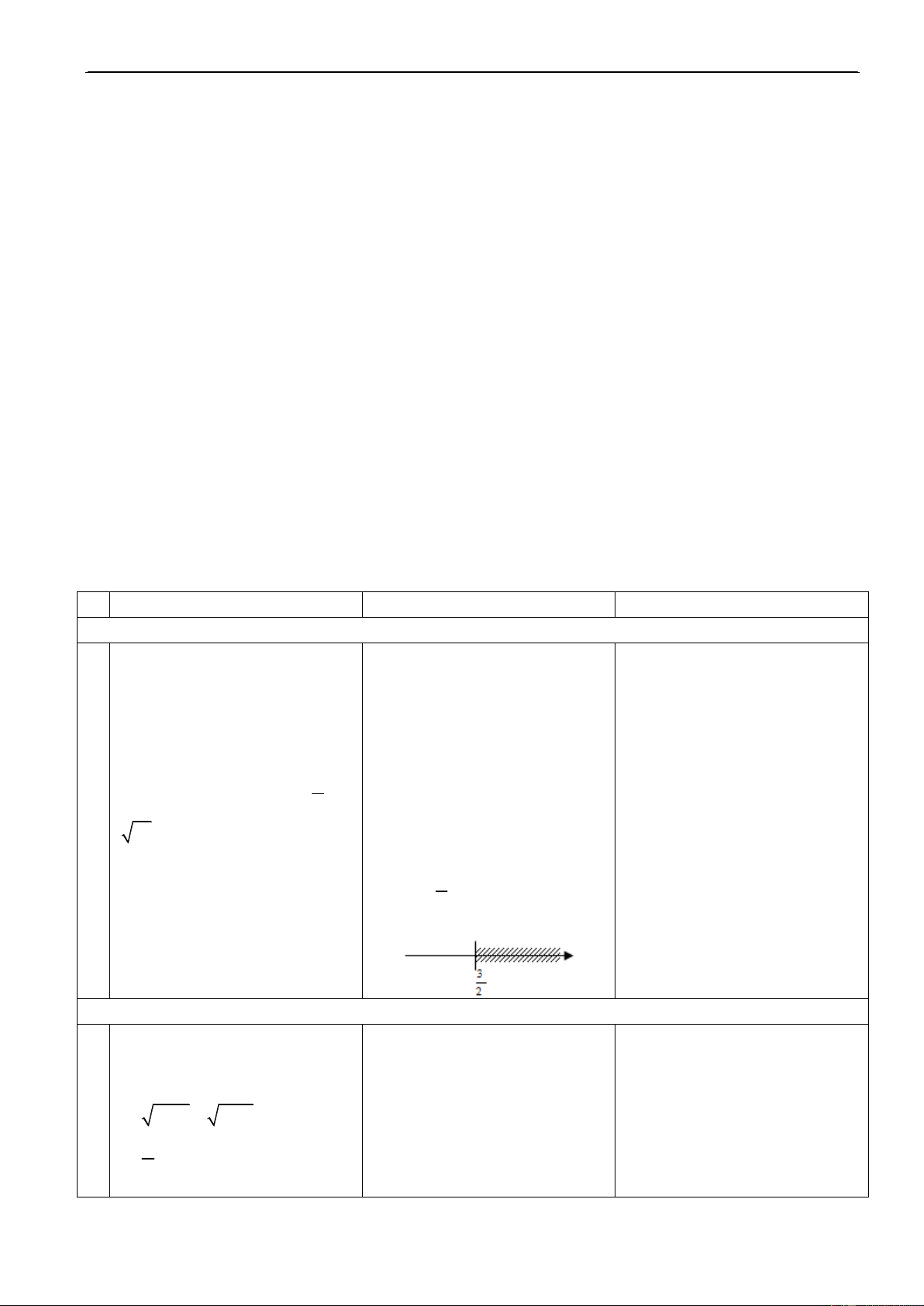
thöïc x sao cho bieåu thöùc f(x) soá: a) f(x) = x 3 a) D = [3; +) coù nghóa.
D = {xR/ f(x) coù nghóa} b) f(x) = 3 b) D = R \ {–2} x  2
Chuù yù: Moät haøm soá coù theå xaùc
 GV giôùi thieäu theâm veà haøm
ñònh bôûi hai, ba, … coâng thöùc.
soá cho bôûi 2, 3.. coâng thöùc.
y = f(x) = /x/ = x vôùix  0 x vôùi x  0
Hoaït ñoäng 3: Tìm hieåu veà ñoà thò cuûa haøm soá
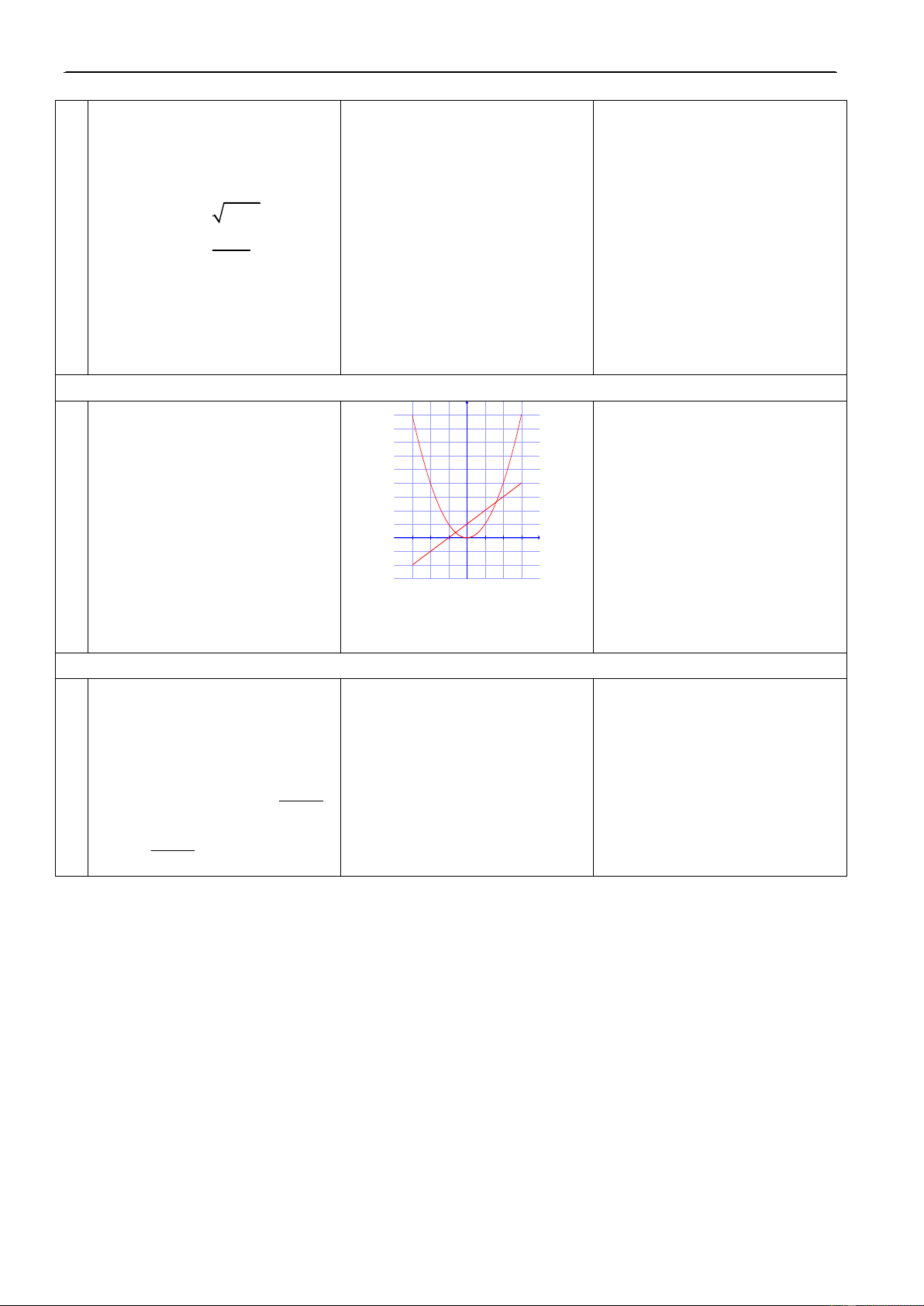
H1. Veõ ñoà thò cuûa caùc haøm soá: y
3. Ñoà thò cuûa haøm soá 10’ a) y = f(x) = x + 1 8
Ñoà thò cuûa haøm soá y=f(x) xaùc b) y = g(x) = x2 6
ñònh treân taäp D laø taäp hôïp caùc f(x) = x2 4
ñieåm M(x;f(x)) treân maët phaúng
toaï ñoä vôùi moïi xD. 2 x -3 -2 -1 1 2 3 f(x) = x + 1
Ta thöôøng gaëp ñoà thò cuûa -2
haøm soá y = f(x) laø moät ñöôøng.
H2. Döïa vaøo caùc ñoà thò treân,
Khi ñoù ta noùi y = f(x) laø
Ñ2. f(–2) = –1, f(0) = 1
tính f(–2), f(0), g(0), g(2)?
phöông trình cuûa ñöôøng ñoù. g(0) = 0, g(2) = 4
Hoaït ñoäng 4: Cuûng coá
 Nhaán maïnh caùc khaùi nieäm
5’ taäp xaùc ñònh, ñoà thò cuûa haøm soá.
 Caâu hoûi: Tìm taäp xaùc ñònh 
cuûa haøm soá: f(x) = 2x , Df = R, Dg = R \ {–1, 1} 2 x 1 g(x) = 2x ? 2 x 1
4. BAØI TAÄP VEÀ NHAØ:  Baøi 1, 2, 3 SGK.
 Ñoïc tieáp baøi “Haøm soá” Ngaøy soaïn: 15/9/2012
Chöông II: HAØM SOÁ BAÄC NHAÁT VAØ BAÄC HAI Tieát daïy: 10
Baøøi 1: HAØM SOÁ (tt) I. MUÏC TIEÂU: Kieán thöùc:
 Hieåu khaùi nieäm haøm soá, taäp xaùc ñònh, ñoà thò cuûa haøm soá.
 Hieåu caùc tính chaát haøm soá ñoàng bieán, nghòch bieán, haøm soá chaün, leû.
 Bieát ñöôïc tính chaát ñoái xöùng cuûa ñoà thò haøm soá chaün, leû. Kó naêng:
 Bieát tìm MXÑ cuûa caùc haøm soá ñôn giaûn. 18
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn
 Bieát caùch chöùng minh tính ñoàng bieán, nghòch bieán cuûa moät haøm soá treân moät khoaûng cho tröôùc.
 Bieát xeùt tính chaün leû cuûa moät haøm soá ñôn giaûn. Thaùi ñoä:
 Reøn luyeän tính caån thaän, chính xaùc.
 Bieát vaän duïng kieán thöùc ñaõ hoïc ñeå xaùc ñònh moái quan heä giöõa caùc ñoái töôïng thöïc teá. II. CHUAÅN BÒ:
Giaùo vieân: Giaùo aùn. Hình veõ minh hoaï.
Hoïc sinh: SGK, vôû ghi. Duïng cuï veõ hình. OÂn taäp caùc kieán thöùc ñaõ hoïc veà haøm soá.
III. HOAÏT ÑOÄNG DAÏY HOÏC:
1. OÅn ñònh toå chöùc: Kieåm tra só soá lôùp.
2. Kieåm tra baøi cuõ: (3’)
H. Tìm taäp xaùc ñònh cuûa haøm soá: f(x) = x 1 ? 2x  3 Ñ. D = ( 3  ; + ) 2
3. Giaûng baøi môùi: TL
Hoaït ñoäng cuûa Giaùo vieân
Hoaït ñoäng cuûa Hoïc sinh Noäi dung
Hoaït ñoäng 1: Tìm hieåu veà Söï bieán thieân cuûa haøm soá
 Cho HS nhaän xeùt hình daùng 
II. Söï bieán thieân cuûa haøm soá
15’ ñoà thò cuûa haøm soá: y = f(x) = Treân (–; 0) ñoà thò ñi xuoáng, 1. OÂn taäp
x2 treân caùc khoaûng (–; 0) vaø Treân (0; + ) ñoà thò ñi leân.
Haøm soá y=f(x) ñgl ñoàng bieán (0; + ).
(taêng) treân khoaûng (a;b) neáu: y
x1, x2(a;b): x1 8 f(x1) 6
Haøm soá y=f(x) ñgl nghòch bieán f(x) = x2
(giaûm) treân khoaûng (a;b) neáu: 4
x1, x2(a;b): x1 2 x f(x1)>f(x2) -3 -2 -1 1 2 3
 GV höôùng daãn HS laäp baûng 0
2. Baûng bieán thieân -2 bieán thieân. x a b x a b y y ñoàng bieán nghòch bieán
Hoaït ñoäng 2: Tìm hieåu tính chaün, leû cuûa haøm soá
 Cho HS nhaän xeùt veà tính ñoái  Caùc nhoùm thaûo luaän.
III. Tính chaün leû cuûa haøm soá
15’ xöùng cuûa ñoà thò cuûa 2 haøm soá: – Ñoà thò y = x2 coù truïc ñoái 1. Haøm soá chaün, haøm soá leû
y = f(x) = x2 vaø y = g(x) = x xöùng laø Oy.
Haøm soá y = f(x) vôùi taäp xaùc
– Ñoà thò y = x coù taâm ñoái ñònh D goïi laø haøm soá chaün neáu xöùng laø O.
vôùi xD
thì –xD vaø f(–x)=f(x).
Haøm soá y = f(x) vôùi taäp xaùc
ñònh D goïi laø haøm soá leû neáu vôùi xD
thì –xD vaø f(–x)=– f(x).
Chuù yù: Moät haøm soá khoâng
nhaát thieát phaûi laø haøm soá chaün 19
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn y y
hoaëc laø haøm soá leû. 7 3 6 y=x2 2 5
2. Ñoà thò cuûa haøm soá chaün, 1 4 x 3 haøm soá leû -3 -2 -1 O 1 2 3 2 -1
Ñoà thò cuûa haøm soá chaün nhaän 1 x -2
truïc tung laøm truïc ñoái xöùng. -3 -2 -1 O 1 2 3 -3 -1
Ñoà thò cuûa haøm soá leû nhaän goác
toaï ñoä laøm taâm ñoái xöùng.
H1. Xeùt tính chaün leû cuûa h.soá: Ñ1. a) chaün b) leû a) y = 3x2 – 2 b) y = 1 x
Hoaït ñoäng 3: Cuûng coá
* Caùch chöùng minh haøm soá ñoàng bieán, nghòch bieán treân moät khoaûng: f(x )  f(x )
 f(x) ñoàng bieán treân (a;b)  x (a;b) vaø x1 ≠ x2 : 2 1 > 0 x2  1 x f(x )  f(x )
 f(x) nghòch bieán treân (a;b)  x (a;b) vaø x1 ≠ x2 : 2 1 < 0 x2  1 x
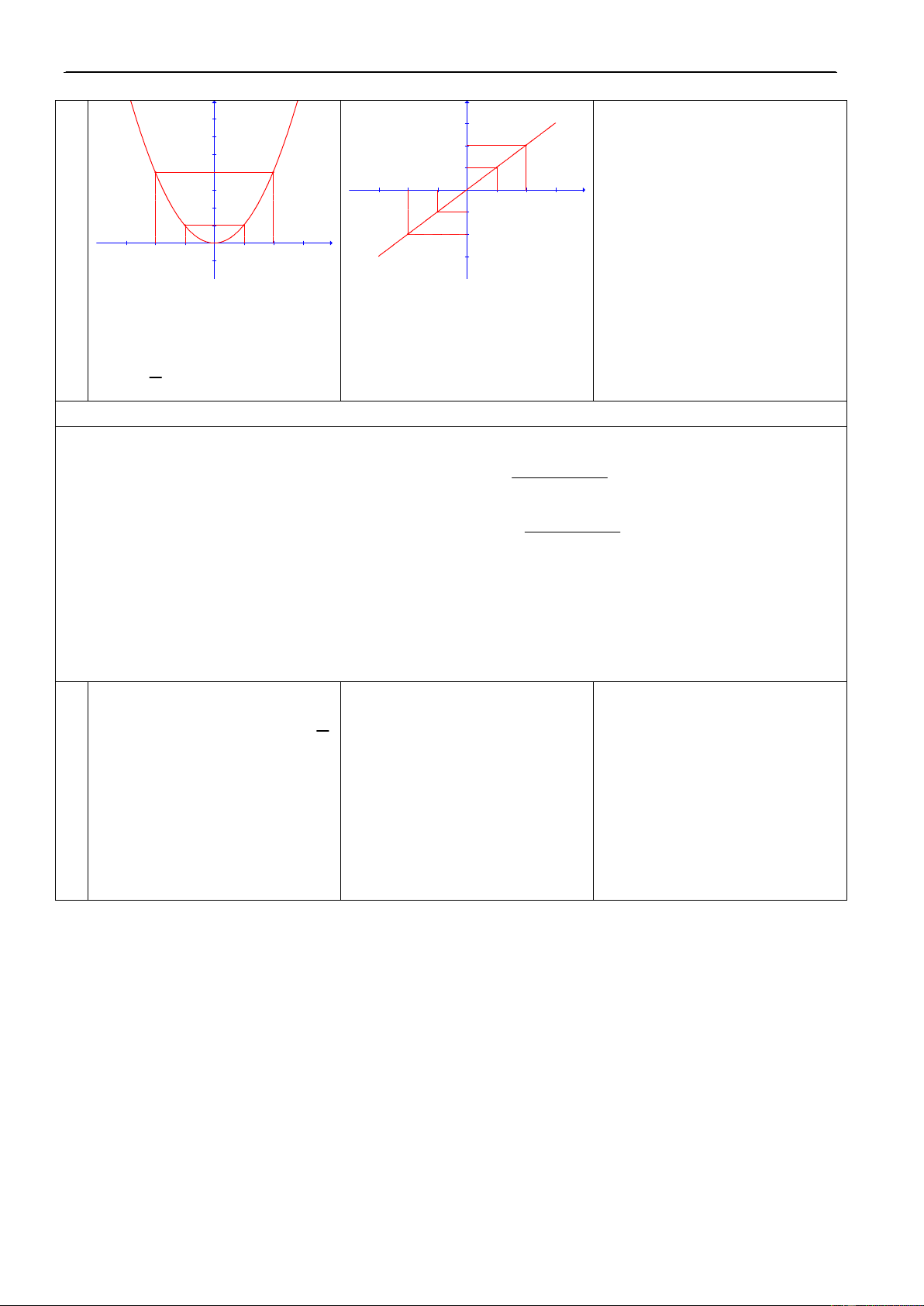
* Caùch veõ ñoà thò haøm soá chaün, haøm soá leû:
 Ñeå veõ ñoà thò haøm soá chaün ta chæ caàn veõ phaàn ñoà thò naèm beân phaûi truïc tung, roài laáy ñoái xöùng
phaàn naøy qua truïc tung. Hôïp cuûa hai phaàn naøy laø ñoà thò cuûa haøm soá chaün ñaõ cho.
 Ñeå veõ ñoà thò haøm soá chaün ta chæ caàn veõ phaàn ñoà thò naèm beân phaûi truïc tung, roài laáy ñoái xöùng
phaàn naøy qua goác toaï ñoä. Hôïp cuûa hai phaàn naøy laø ñoà thò cuûa haøm soá leû ñaõ cho. Caâu hoûi:
1) Xeùt 2 khoaûng (–;0) vaø
10’ 1) Chöùng toû haøm soá y = 1 (0;+) x
luoân nghòch bieán vôùi moïi x ≠ 0 2) Haøm soá leû.
2) Xeùt tính chaün leû vaø veõ ñoà
thò cuûa haøm soá y = f(x) = x3.
4. BAØI TAÄP VEÀ NHAØ:  Baøi 4 SGK.
Ñoïc tröôùc baøi “Haøm soá y = ax + b”. Ngaøy soaïn: 22/9/2012
Chöông II: HAØM SOÁ BAÄC NHAÁT VAØ BAÄC HAI Tieát daïy: 11
Baøøi 2: HAØM SOÁ Y = AX + B 20
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn
I. MUÏC TIEÂU: Kieán thöùc:
 Hieåu ñöôïc söï bieán thieân vaø ñoà thò cuûa haøm soá baäc nhaát.
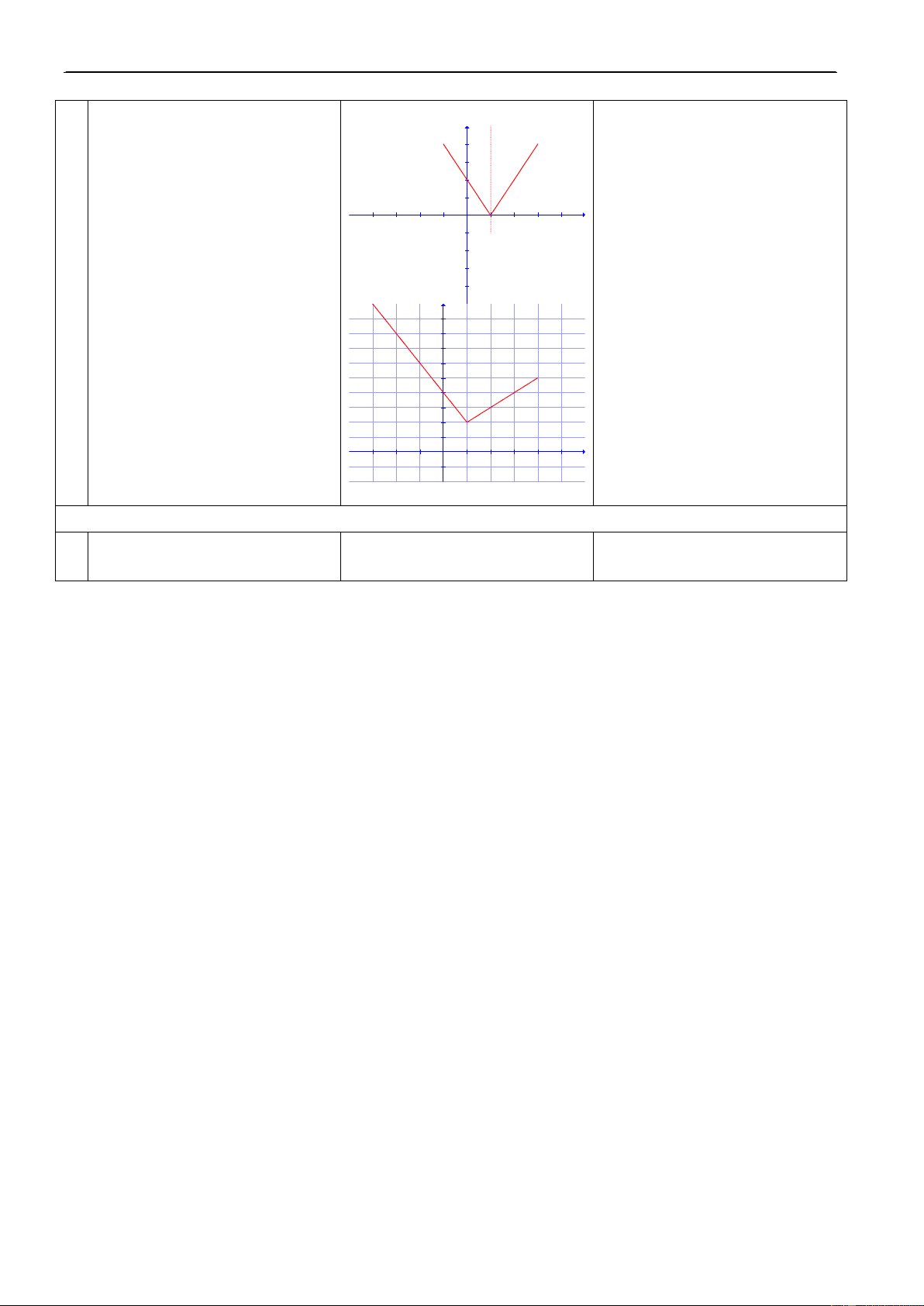
 Hieåu caùch veõ ñoà thò haøm soá baäc nhaát vaø haøm soá y = /x/.
 Bieát ñöôïc ñoà thò haøm soá y = /x/ nhaän truïc Oy laøm truïc ñoái xöùng. Kó naêng:
 Thaønh thaïo vieäc xaùc ñònh chieàu bieán thieân vaø veõ ñoà thò cuûa haøm soá baäc nhaát.
 Veõ ñöôïc ñoà thò haøm soá y = b, y = /x/.
 Bieát tìm toaï ñoä giao ñieåm cuûa hai ñöôøng thaúng coù phöông trình cho tröôùc. Thaùi ñoä:
 Reøn luyeän tính caån thaän, chính xaùc. II. CHUAÅN BÒ:
Giaùo vieân: Giaùo aùn. Hình veõ minh hoaï.
Hoïc sinh: SGK, vôû ghi, duïng cuï veõ hình.
Ñoïc baøi tröôùc. OÂn taäp kieán thöùc ñaõ hoïc veà haøm soá baäc nhaát.
III. HOAÏT ÑOÄNG DAÏY HOÏC:
1. OÅn ñònh toå chöùc: Kieåm tra só soá lôùp.
2. Kieåm tra baøi cuõ: (5’)
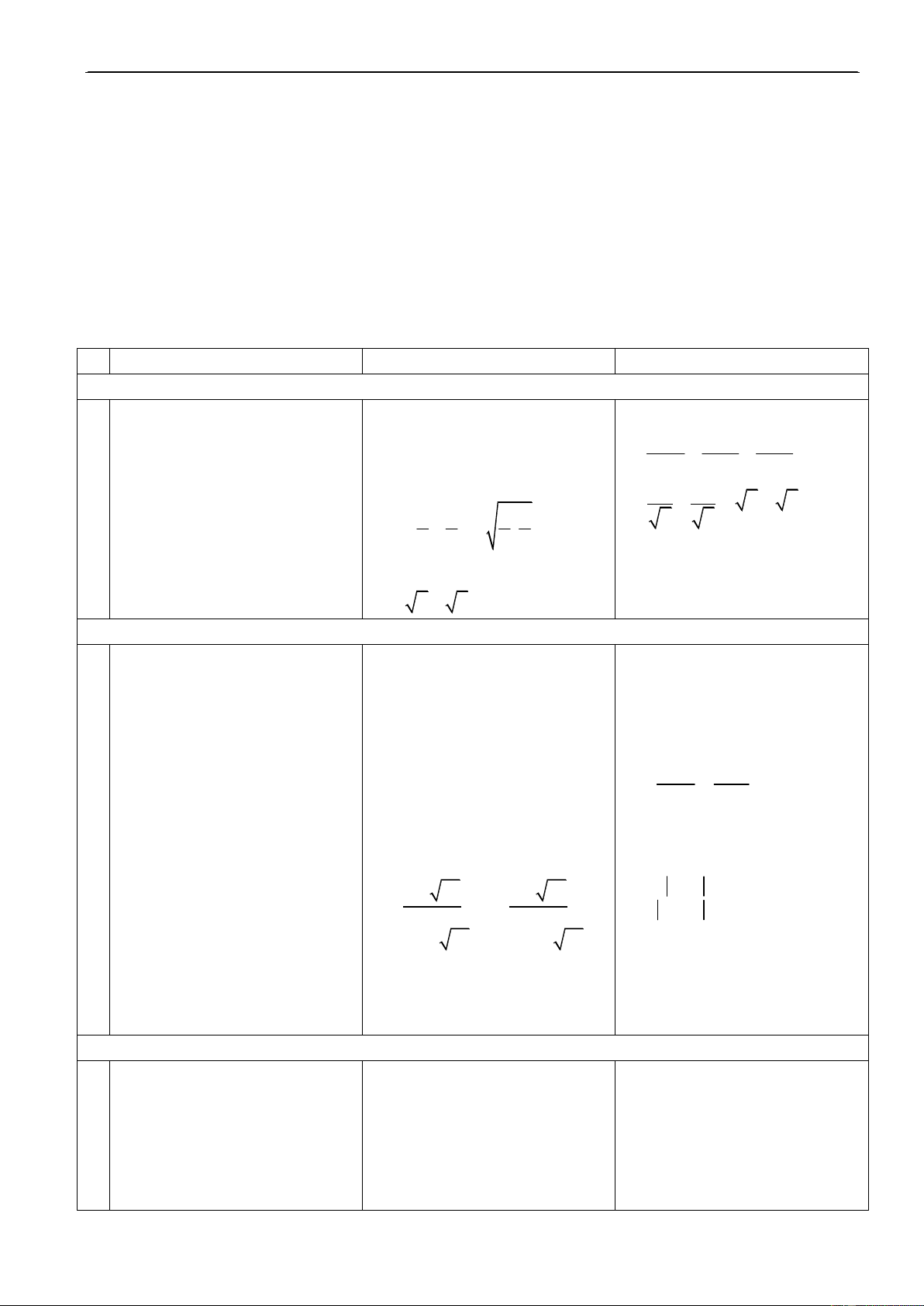
H. Tìm taäp xaùc ñònh cuûa haøm soá: y = f(x) = 1 . Tính f(0), f(–1)? 2 x  3x  2
Ñ. D = R \ {1, 2}. f(0) = 1 , f(–1) = 1 . 2 6
3. Giaûng baøi môùi: TL
Hoaït ñoäng cuûa Giaùo vieân
Hoaït ñoäng cuûa Hoïc sinh Noäi dung
Hoaït ñoäng 1: Tìm hieåu haøm soá y = /x/
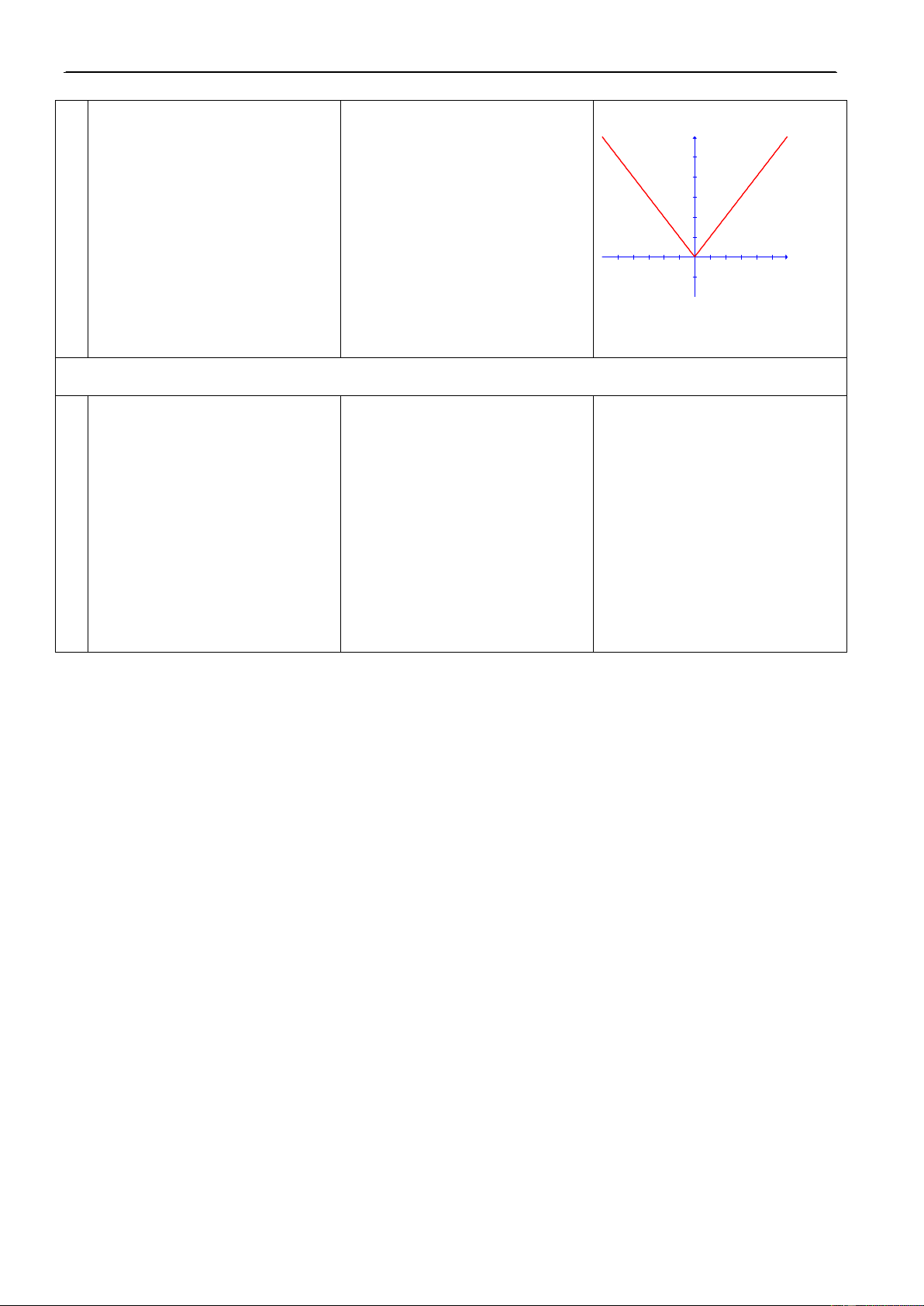
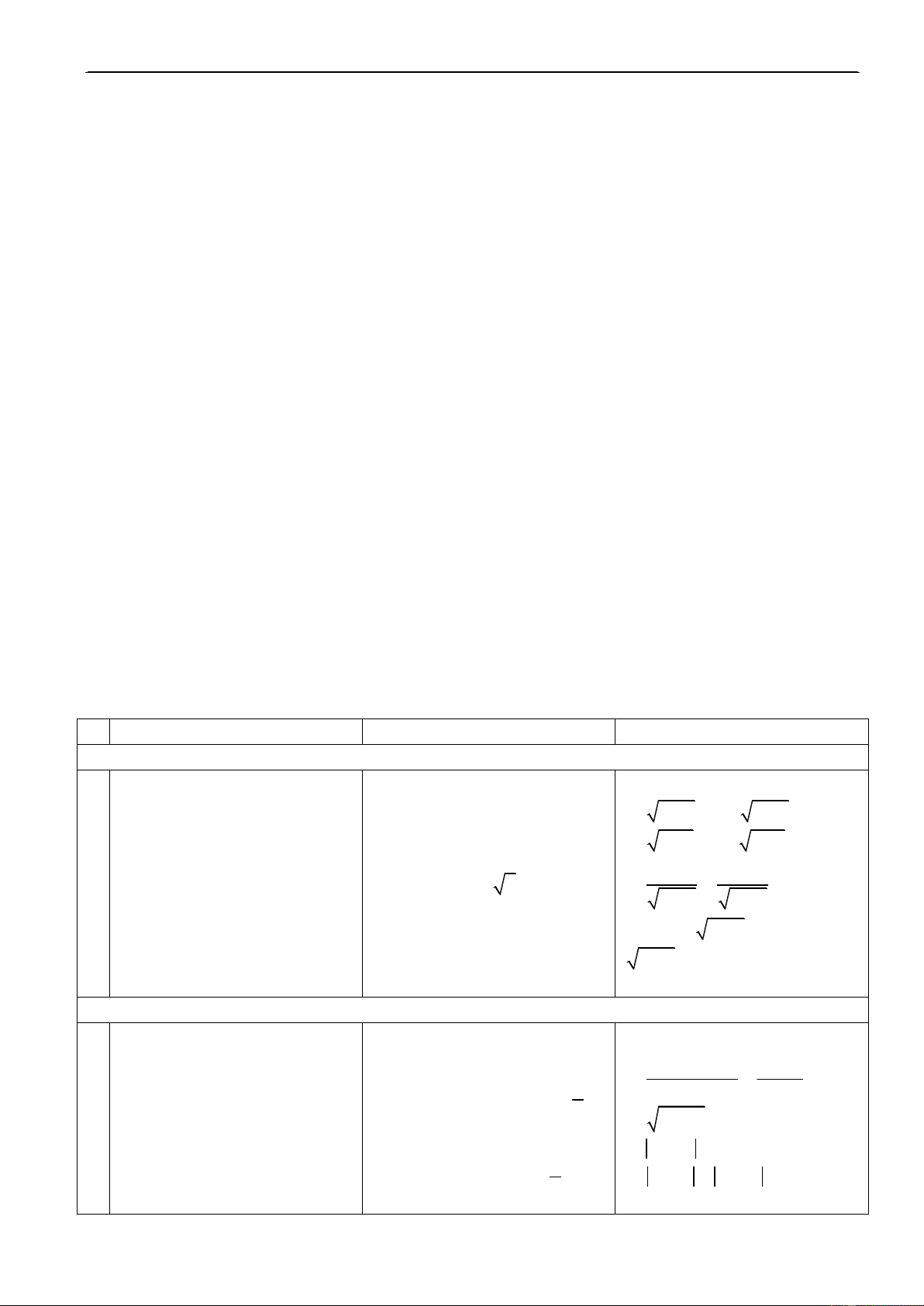
H1. Nhaéc laïi ñònh nghóa veà Ñ1.
III. Haøm soá y = /x/ 10’ GTTÑ?
Taäp xaùc ñònh: D = R. y= x nÕu x  0 x   x nÕu x<0
Chieàu bieán thieân:
H2. Nhaän xeùt veà chieàu bieán Ñ2. 21
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn thieân cuûa haøm soá?
+ ñoàng bieán trong (0; +) Ñoà thò
+ nghòch bieán trong (–; 0) y 2.5 2 1.5
H3. Nhaän xeùt veà tính chaát Ñ3. Haøm soá chaün  ñoà thò 1 0.5 chaün leû cuûa haøm soá?
nhaän truïc tung laøm truïc ñoái x -2.5 -2 -1.5 -1 -0.5 0.5 1 1.5 2 2.5 -0.5 xöùng.
Hoaït ñoäng 2: Cuûng coá
 Nhaán maïnh tính chaát cuûa  Caùc nhoùm thaûo luaän, trình
7’ ñöôøng thaúng y = ax + b (cho baøy. HS nhaéc laïi): – Heä soá goùc
– VTTÑ cuûa 2 ñöôøng thaúng
– Tìm giao ñieåm cuûa 2 ñt
4. BAØI TAÄP VEÀ NHAØ:  Baøi 1, 2, 3, 4 SGK. Ngaøy soaïn: 1/10/2012
Chöông II: HAØM SOÁ BAÄC NHAÁT VAØ BAÄC HAI Tieát daïy: 12
Baøøi daïy: LUYEÄN TAÄP HAØM SOÁ Y = AX + B I. MUÏC TIEÂU: Kieán thöùc: 22
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn
 Cuûng coá caùc kieán thöùc ñaõ hoïc veà haøm soá baäc nhaát, haøm soá haèng, haøm soá y = /x/: taäp xaùc
ñònh, chieàu bieán thieân, ñoà thò. Kó naêng:
 Bieát caùch tìm taäp xaùc ñònh, xaùc ñònh chieàu bieán thieân, veõ ñoà thò cuûa caùc haøm soá ñaõ hoïc.
 Bieát caùch xaùc ñònh phöông trình cuûa ñöôøng thaúng thoaû maõn caùc ñieàu kieän cho tröôùc. Thaùi ñoä:
 Reøn luyeän tính caån thaän, chính xaùc. II. CHUAÅN BÒ:
Giaùo vieân: Giaùo aùn.
Hoïc sinh: SGK, vôû ghi. Laøm baøi taäp ôû nhaø. OÂn taäp kieán thöùc ñaõ hoïc veà haøm soá baäc nhaát.
III. HOAÏT ÑOÄNG DAÏY HOÏC:
1. OÅn ñònh toå chöùc: Kieåm tra só soá lôùp.
2. Kieåm tra baøi cuõ: (Loàng vaøo quaù trình luyeän taäp) 3. Giaûng baøi môùi: TL
Hoaït ñoäng cuûa Giaùo vieân
Hoaït ñoäng cuûa Hoïc sinh Noäi dung
Hoaït ñoäng 1: Luyeän kó naêng khaûo saùt haøm soá baäc nhaát
H1. Neâu caùc böôùc tieán haønh? Ñ1.
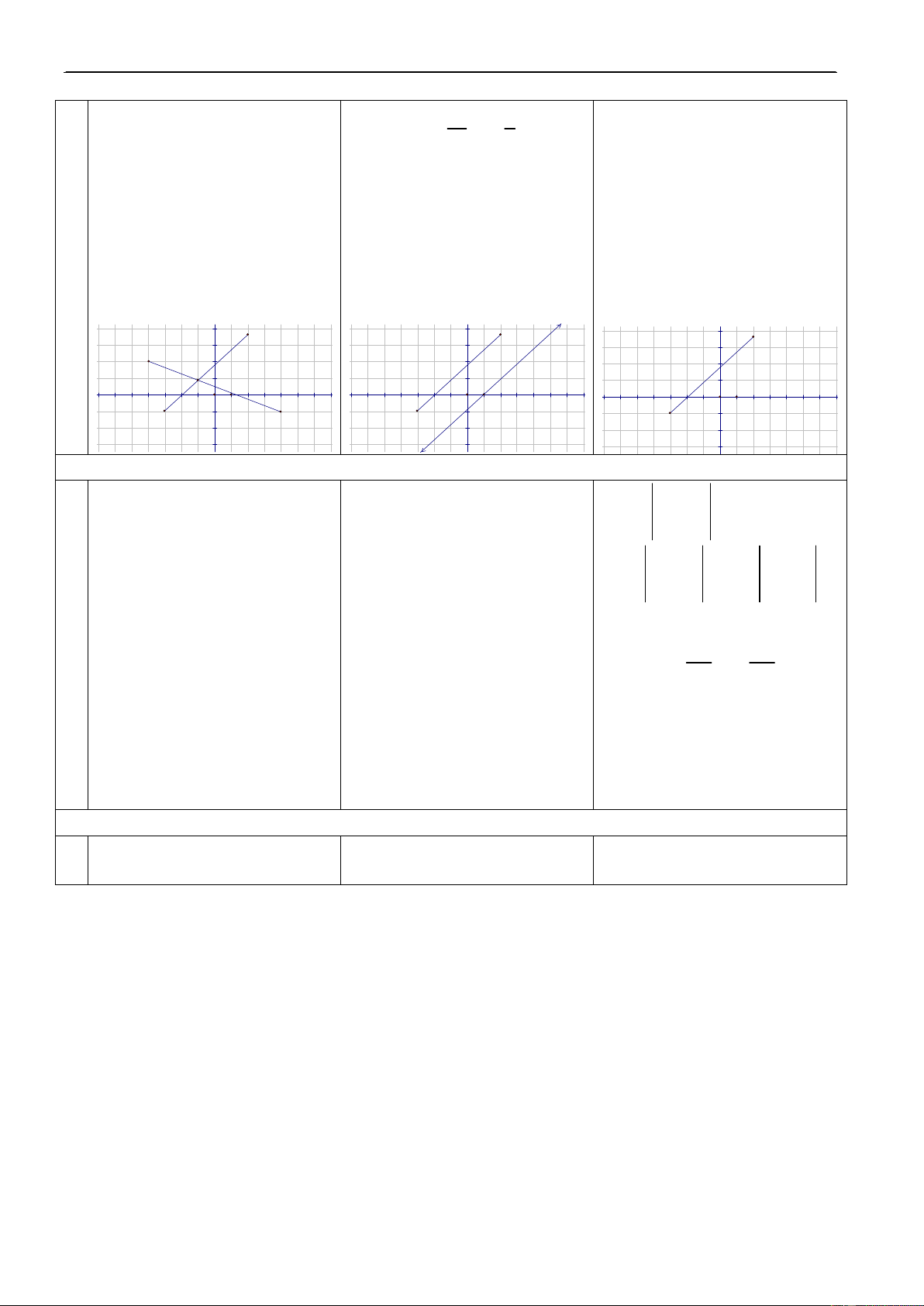
1. Veõ ñoà thò cuûa haøm soá: 15’ – Tìm taäp xaùc ñònh a) y = 2x – 3
 Cho HS nhaéc laïi caùc tính – Laäp baûng bieán thieân b) y = – 3 + 7 chaát cuûa haøm soá. – Veõ ñoà thò 2 y 8 3 y = - x + 7 6 2 4 2 x -8 -6 -4 -2 2 4 6 8 -2 -4 y = 2x - 3 -6 -8
Hoaït ñoäng 2: Luyeän kó naêng xaùc ñònh phöông trình cuûa ñöôøng thaúng
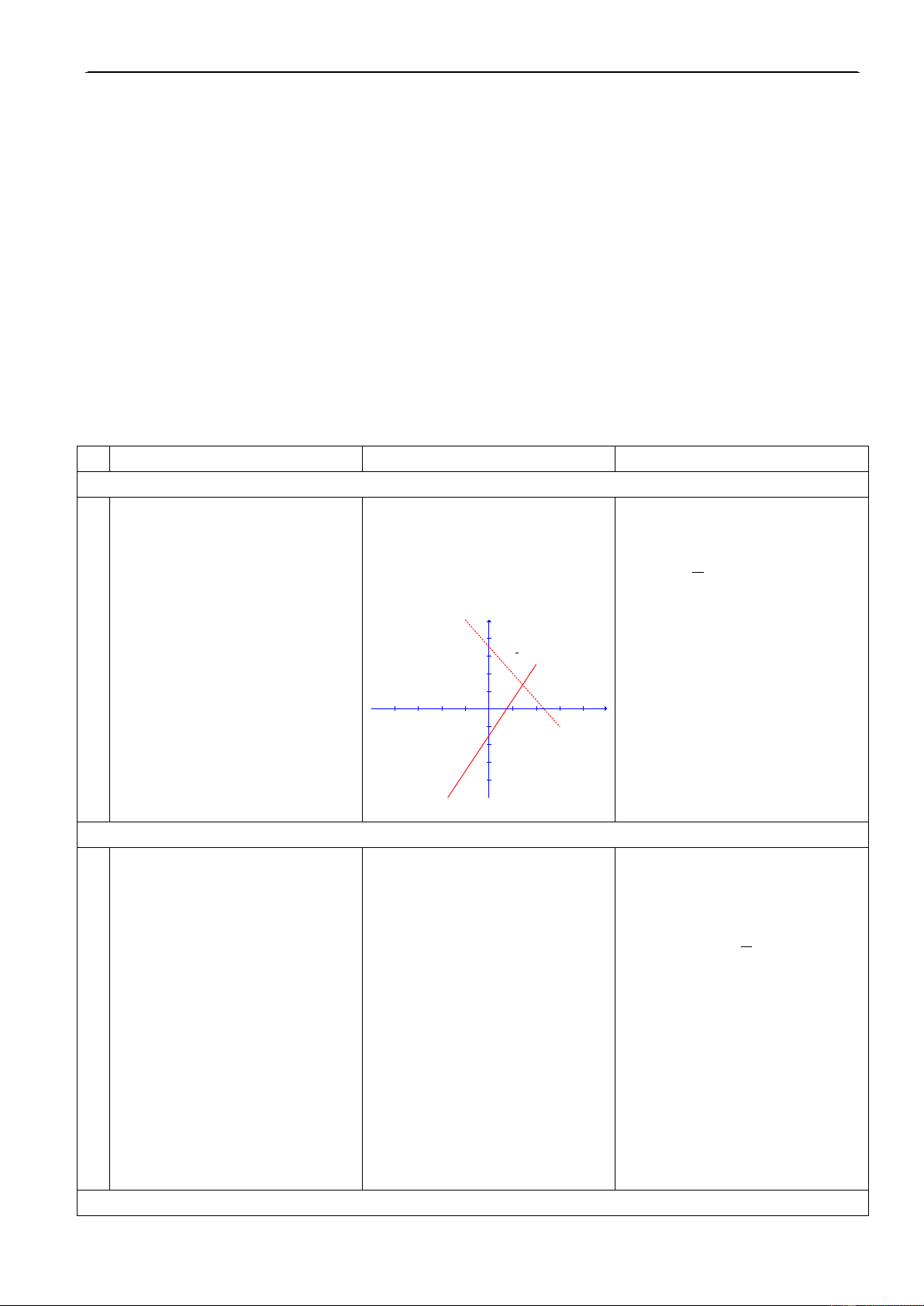
H1. Neâu ñieàu kieän ñeå moät Ñ1. Toaï ñoä thoaû maõn phöông 2. Xaùc ñònh a, b ñeå ñoà thò cuûa
15’ ñieåm thuoäc ñoà thò cuûa haøm trình cuûa haøm soá.
haøm soá y = ax + b ñi qua caùc soá? ñieåm: a) a = –5, b = 3 a) A(0; –3), B( 3 ; 0)
 Cho HS nhaéc laïi caùch giaûi b) a = –1, b = 3 5
heä phöông trình baäc nhaát hai c) a = 0, b = –3 b) A(1; 2), B(2; 1) aån. c) A(15; –3), B(21; –3)
H2. Neâu ñieàu kieän ñeå moät Ñ2. Toaï ñoä thoaû maõn phöông 3. Vieát phöông trình y = ax +
ñieåm thuoäc ñöôøng thaúng ?
trình cuûa ñöôøng thaúng .
b cuûa caùc ñöôøng thaúng: a) y = 2x – 5 a) Ñi qua A(4;3), B(2;–1) b) y = –1
b) Ñi qua A(1;–1) vaø song song vôùi Ox.
Hoaït ñoäng 3: Luyeän taäp kó naêng veõ ñoà thò cuûa caùc haøm soá lieân quan 23
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn
H1. Neâu caùch tieán haønh?
Ñ1. Veõ töøng nhaùnh.
4. Veõ ñoà thò cuûa caùc haøm soá: 10’ y a) y = /2x – 4/ 8 6 b) y= x1 vôùi x 1 4 2  x  4 vôùi x  1 2 x -8 -6 -4 -2 2 4 6 8 -2 -4 -6 -8 y 9 8 7 6 5 4 3 2 1 x -3 -2 -1 1 2 3 4 5 -1
Hoaït ñoäng 4: Cuûng coá
 Nhaéc laïi caùch giaûi caùc daïng 3’ toaùn.
4. BAØI TAÄP VEÀ NHAØ:
 Laøm tieáp caùc baøi taäp coøn laïi.
 Ñoïc tröôùc baøi “Haøm soá baäc hai” Ngaøy soaïn: 1/10/2012
Chöông II: HAØM SOÁ BAÄC NHAÁT VAØ BAÄC HAI Tieát daïy: 13
Baøøi 3: HAØM SOÁ BAÄC HAI I. MUÏC TIEÂU: Kieán thöùc: 24
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn
 Hieåu quan heä giöõa ñoà thò cuûa caùc haøm soá y = ax2 + bx + c vaø y = ax2.
 Hieåu vaø ghi nhôù caùc tính chaát cuûa haøm soá y = ax2 + bx + c. Kó naêng:
 Laäp ñöôïc baûng bieán thieân cuûa haøm soá baäc hai, xaùc ñònh toaï ñoä ñænh, truïc ñoái xöùng,
veõ ñöôïc ñoà thò haøm soá baäc hai.
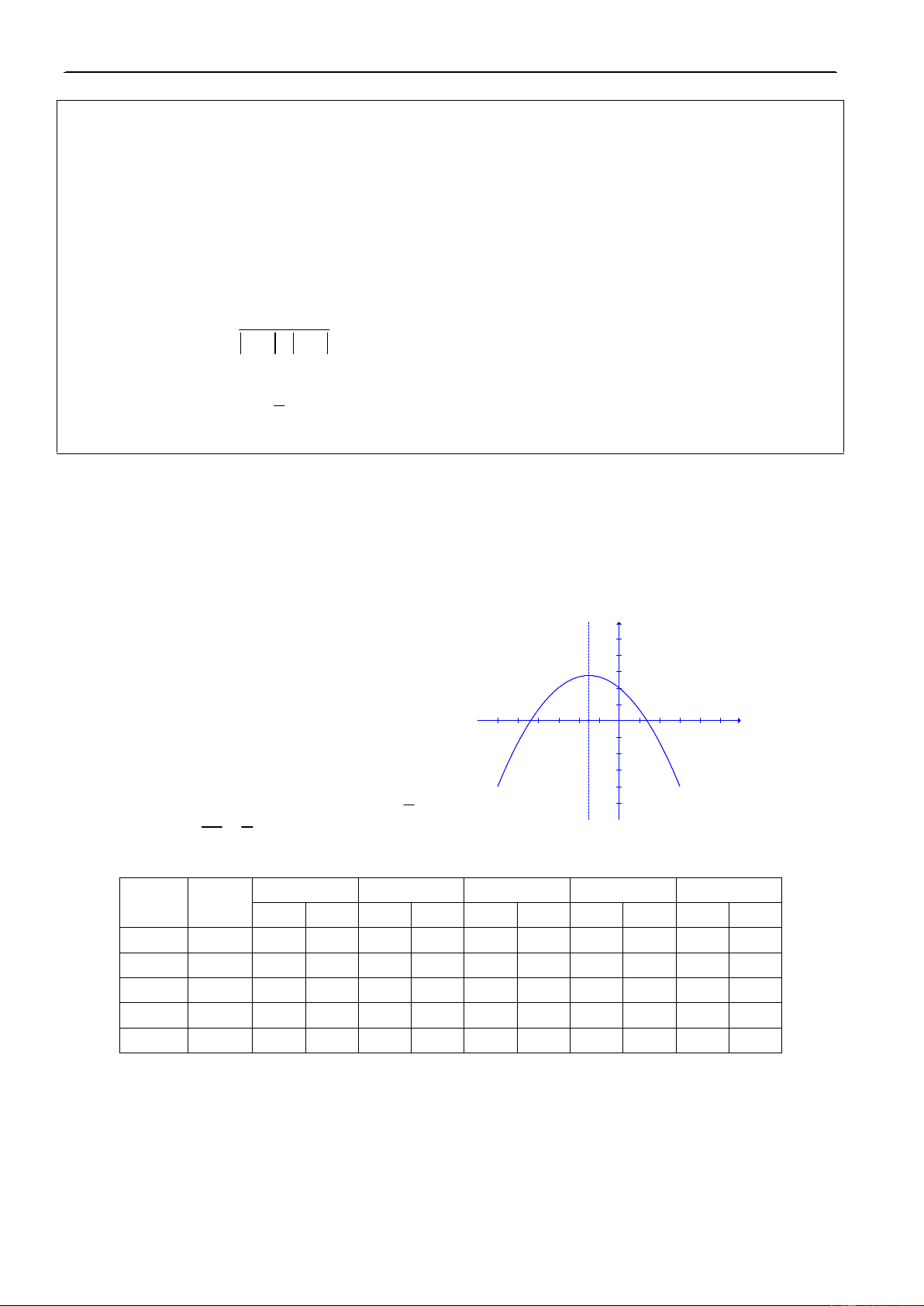
 Ñoïc ñöôïc ñoà thò cuûa haøm soá baäc hai, töø ñoà thò xaùc ñònh ñöôïc: truïc ñoái xöùng, caùc
giaù trò x ñeå y> 0, y < 0.
 Tìm ñöôïc phöông trình cuûa parabol khi bieát moät trong caùc heä soá vaø ñoà thò ñi qua hai ñieåm cho tröôùc. Thaùi ñoä:
 Reøn luyeän tính caån thaän, chính xaùc khi veõ ñoà thò. II. CHUAÅN BÒ:
Giaùo vieân: Giaùo aùn. Hình veõ minh hoaï.
Hoïc sinh: SGK, vôû ghi. Ñoïc baøi tröôùc.
OÂn laïi kieán thöùc ñaõ hoïc veà haøm soá y = ax2. Duïng cuï veõ ñoà thò.
III. HOAÏT ÑOÄNG DAÏY HOÏC:
1. OÅn ñònh toå chöùc: Kieåm tra só soá lôùp.
2. Kieåm tra baøi cuõ: (3’)
H. Cho haøm soá y = x2. Tìm taäp xaùc ñònh vaø xeùt tính chaün leû cuûa haøm soá?
Ñ. D = R. Haøm soá chaün.
3. Giaûng baøi môùi: TL
Hoaït ñoäng cuûa Giaùo vieân
Hoaït ñoäng cuûa Hoïc sinh Noäi dung
Hoaït ñoäng 1: Nhaéc laïi caùc keát quaû ñaõ bieát veà haøm soá y = ax2
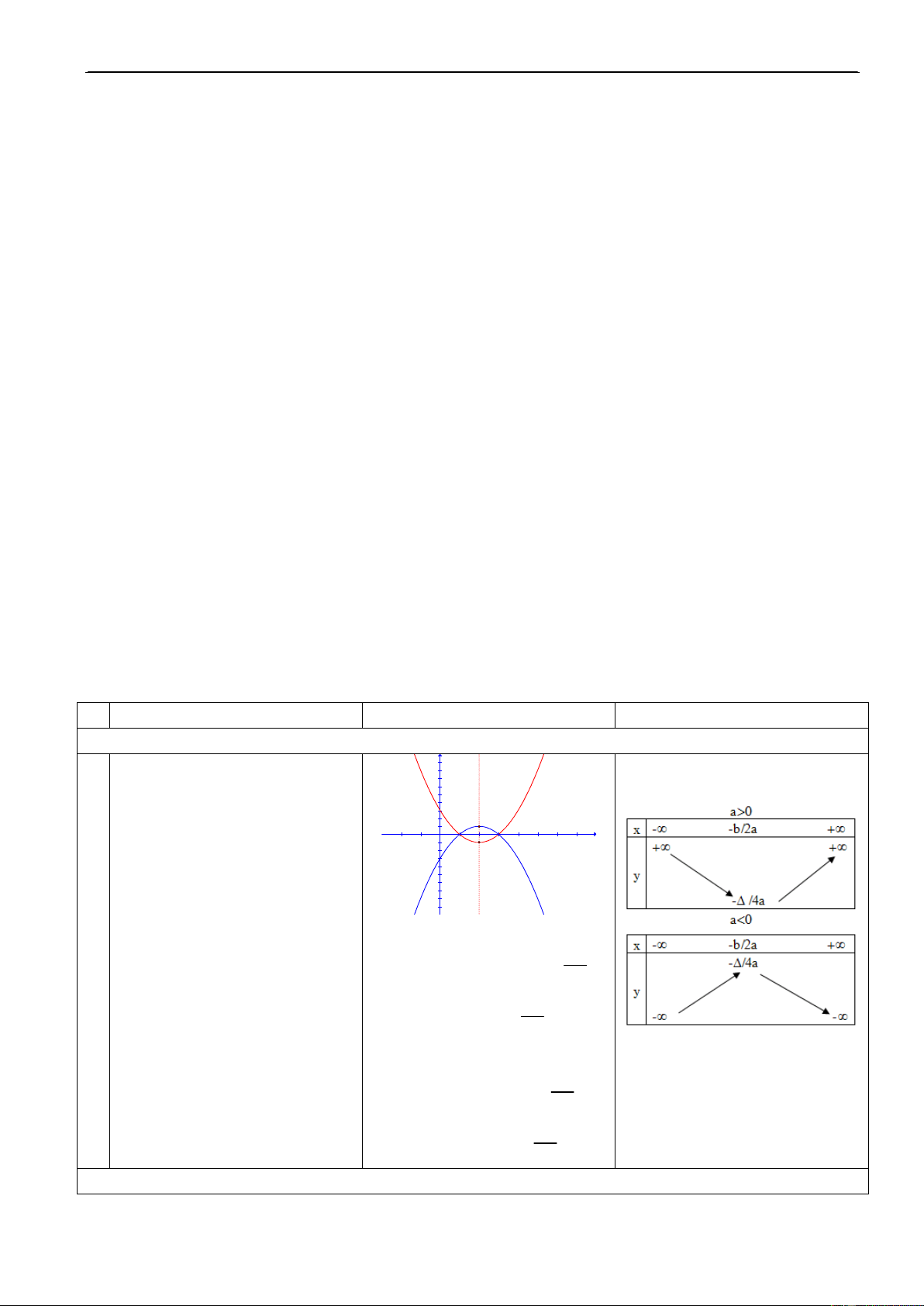
 Cho HS nhaéc laïi caùc kieán  Caùc nhoùm thaûo luaän, traû lôøi I. Ñoà thò cuûa haøm soá baäc hai
15’ thöùc ñaõ hoïc veà haøm soá y = ax2 theo töøng yeâu caàu.
y = ax2 + bx + c (a ≠ 0)
(Minh hoaï bôûi haøm soá y = x2) 1. Nhaän xeùt: – Taäp xaùc ñònh y 9 a) Haøm soá y = ax2: 8
– Ñoà thò: Toaï ñoä ñænh, Hình 7 y = x 6
– Ñoà thò laø moät parabol. 2 5
daùng, truïc ñoái xöùng. 4
– a>0 (a<0): O(0;0) laø ñieåm 3 2 1 x
thaáp nhaát (cao nhaát). -4 -3 -2 -1 1 2 3 4 O -1 -2
b) Haøm soá y = ax2 + bx + c -3 2 -4 (a≠0) -5 y = -x -6 -7  y = ax2 + bx + c -8 -9 2
Ñ1. y = ax2 + bx + c  b  
H1. Bieán ñoåi bieåu thöùc: = ax   + 2  2a  4a ax2 + bx + c  b = a   x    + b   2a  4a  I( – ; ) thuoäc ñoà thò. 2a 4a
a>0 I laø ñieåm thaáp nhaát
H2. Nhaän xeùt vai troø ñieåm I ? Ñ2. Gioáng ñieåm O trong ñoà  a<0 I laø ñieåm cao nhaát thò cuûa y = ax2
Hoaït ñoäng 2: Tìm hieåu quan heä giöõa caùc ñoà thò cuûa caùc haøm soá y = ax2 + bx + c vaø y = ax2 25
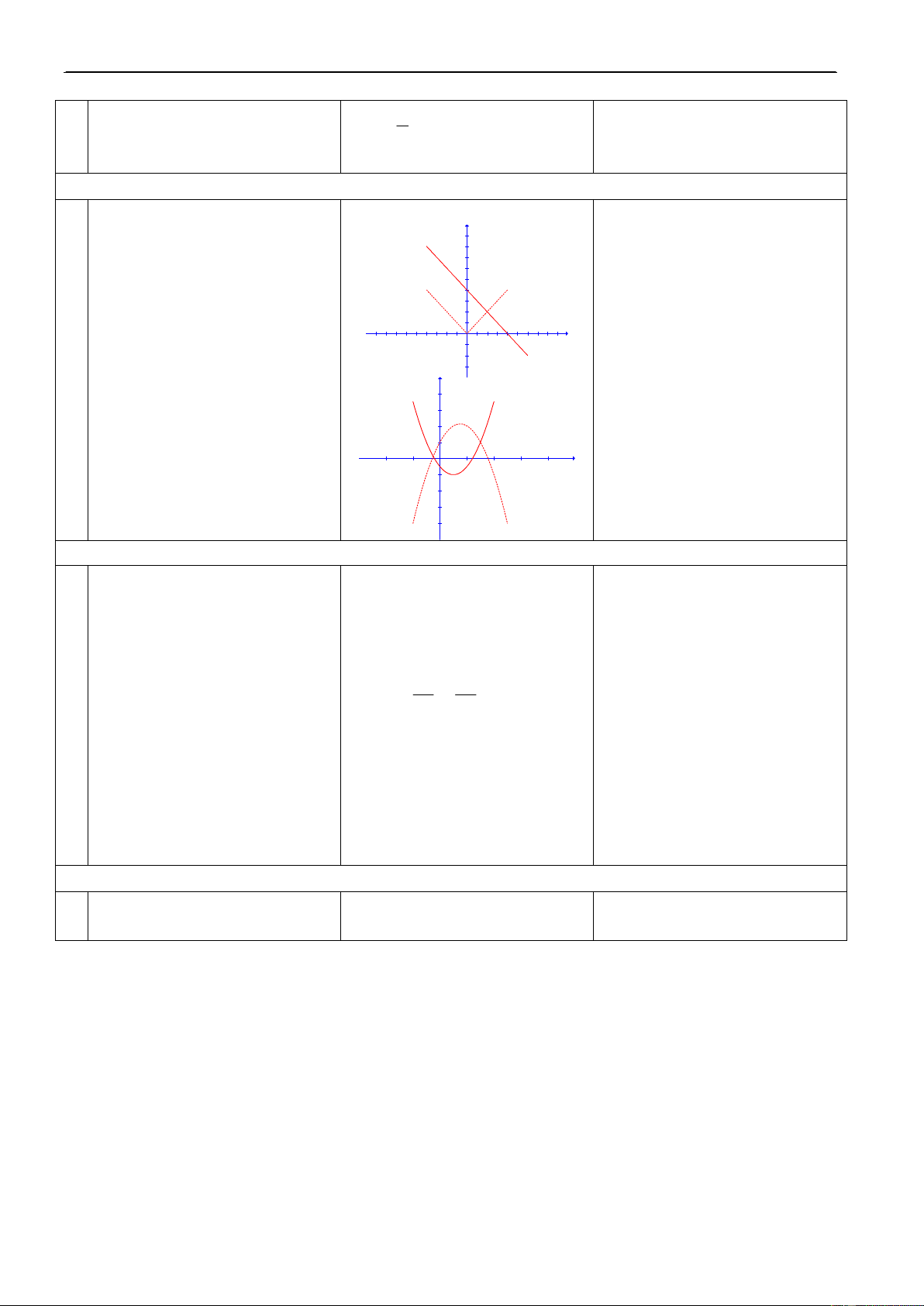
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn  b Ñ1. Y = aX2 2. Ñoà thò: 10’ X  x   H2. Neáu ñaët 2a
Ñoà thò cuûa haøm soá y = ax2 + y Y y     9
bx + c (a≠0) laø moät ñöôøng 8  4a 7  6 5
parabol coù ñænh I( – b ; ),
thì haøm soá coù daïng nhö theá a > 0 4 2a 4a 3 naøo? 2 1 x
coù truïc ñoái xöùng laø ñöôøng -2 -1 1 2 3 4 5 6 7 O -1 -2 -3
thaúng x = – b .
 Minh hoaï ñoà thò haøm soá: -4 2a -5 -6 y = x2 – 4x – 2 I -7
Parabol naøy quay beà loõm leân -8 -9
treân neáu a>0, xuoáng döôùi neáu a<0.
Hoaït ñoäng 3: Tìm hieåu caùch veõ ñoà thò haøm soá baäc hai
 GV gôïi yù, höôùng daãn HS y 9 3. Caùch veõ 8
10’ thöïc hieän caùc böôùc veõ ñoà thò 7 6
1) Xaùc ñònh toaï ñoä ñænh 5 haøm soá baäc hai. 4 a > 0  3 2 I( – b ; ) I 1 x 2a 4a -2 -1 1 2 3 4 5 6 7 O -1
H1. Veõ ñoà thò haøm soá: I -2 b -3 a < 0
2) Veõ truïc ñoái xöùng x =– a) y = x2 – 4x –3 -4 -5 2a -6 b) y = –x2 + 4x +3 -7
3) Xaùc ñònh caùc giao ñieåm cuûa -8 -9
paranol vôùi caùc truïc toaï ñoä. 4) Veõ parabol
Hoaït ñoäng 3: Cuûng coá
 Nhaán maïnh caùc tính chaát veà
5’ ñoà thò cuûa haøm soá baäc hai.
Caâu hoûi traéc nghieäm:
 Caùc nhoùm thaûo luaän, traû lôøi
Cho haøm soá y = 2x2 + 3x + 1. caùc caâu hoûi.
3) Tìm giao ñieåm cuûa ñoà thò
1) Toaï ñoä ñænh I cuûa ñoà thò (P) 1 a) vôùi truïc hoaønh a)  3 1   2 b)    ;    b) 3 1  ; a) (–1; 0), 1   ;0 4 8      4 8  3) a) 2    c)  3 1      ;   d) 3 1  ; b) (–1; 0), 1  ;0 4 8      4 8  2   
2) Truïc ñoái xöùng cuûa ñoà thò c) (1; 0),  1  ;0   a) x = 3 b) x = – 3  2  2 2
d) ) (1; 0),  1 ;0   c) x = 3 d) x = – 3  2  4 4
4. BAØI TAÄP VEÀ NHAØ:  Baøi 1 SGK
 Ñoïc tieáp baøi “Haøm soá baäc hai” Ngaøy soaïn: 1/10/2012
Chöông II: HAØM SOÁ BAÄC NHAÁT VAØ BAÄC HAI Tieát daïy: 14
Baøøi 3: HAØM SOÁ BAÄC HAI (tt) 26
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn I. MUÏC TIEÂU: Kieán thöùc:
 Hieåu quan heä giöõa ñoà thò cuûa caùc haøm soá y = ax2 + bx + c vaø y = ax2.
 Hieåu vaø ghi nhôù caùc tính chaát cuûa haøm soá y = ax2 + bx + c. Kó naêng:
 Laäp ñöôïc baûng bieán thieân cuûa haøm soá baäc hai, xaùc ñònh toaï ñoä ñænh, truïc ñoái xöùng,
veõ ñöôïc ñoà thò haøm soá baäc hai.
 Ñoïc ñöôïc ñoà thò cuûa haøm soá baäc hai, töø ñoà thò xaùc ñònh ñöôïc: truïc ñoái xöùng, caùc
giaù trò x ñeå y> 0, y < 0.
 Tìm ñöôïc phöông trình cuûa parabol khi bieát moät trong caùc heä soá vaø ñoà thò ñi qua hai ñieåm cho tröôùc. Thaùi ñoä:
 Reøn luyeän tính caån thaän, chính xaùc khi veõ ñoà thò. Luyeän tö duy khaùi quaùt, toång hôïp. II. CHUAÅN BÒ:
Giaùo vieân: Giaùo aùn. Hình veõ minh hoaï.
Hoïc sinh: SGK, vôû ghi. Ñoïc baøi tröôùc.
OÂn laïi kieán thöùc ñaõ hoïc veà haøm soá y = ax2. Duïng cuï veõ ñoà thò.
III. HOAÏT ÑOÄNG DAÏY HOÏC:
1. OÅn ñònh toå chöùc: Kieåm tra só soá lôùp.
2. Kieåm tra baøi cuõ: (3’)
H. Cho haøm soá y = –x2 + 4. Tìm toaï ñoä ñænh, truïc ñoái xöùng cuûa ñoà thò haøm soá?
Ñ. I(0; 4). (): x = 0.
3. Giaûng baøi môùi: TL
Hoaït ñoäng cuûa Giaùo vieân
Hoaït ñoäng cuûa Hoïc sinh Noäi dung
Hoaït ñoäng 1: Tìm hieåu chieàu bieán thieân cuûa haøm soá baäc hai
 GV höôùng daãn HS nhaän xeùt y 9
II. Chieàu bieán thieân cuûa 8
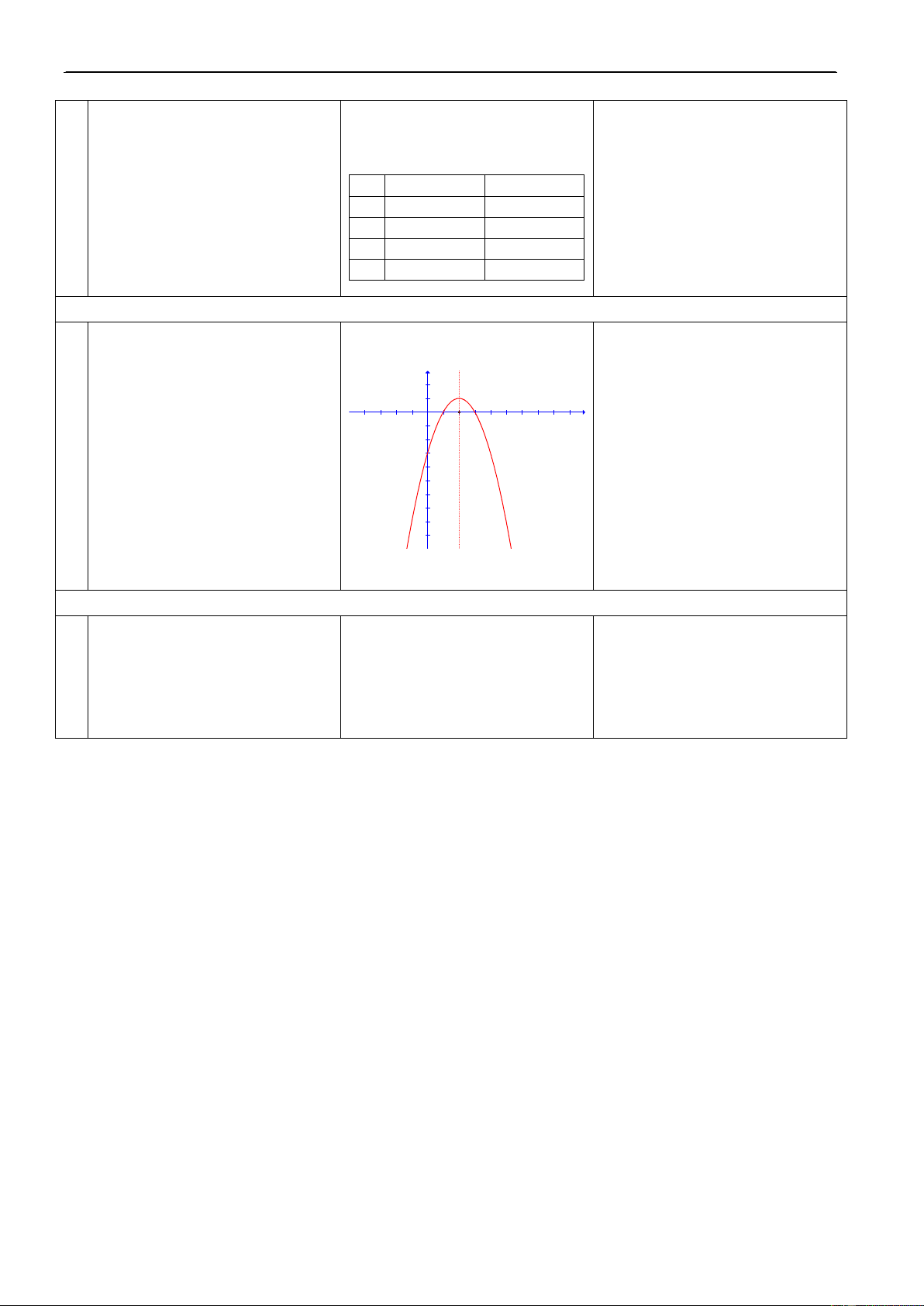
10' chieàu bieán thieân cuûa haøm soá 7 6 haøm soá baäc hai 5 4 a > 0
baäc hai döïa vaøo ñoà thò caùc 3 2 I 1 haøm soá minh hoaï. x -2 -1 1 2 3 4 5 6 7 O -1 I -2 -3 a < 0 -4 -5 -6 -7 -8 -9
 Neáu a > 0 thì haøm soá + Nghòch bieán treân  b  ;   2a   
+ Ñoàng bieán treân  b  ;   2a   
 Neáu a < 0 thì haøm soá  b + Ñoàng bieán treân  ;   2a     b + Nghòch bieán treân  ;   2a   
Hoaït ñoäng 2: Luyeän taäp xaùc ñònh chieàu bieán thieân cuûa haøm soá baäc hai 27
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn
 Cho moãi nhoùm xeùt chieàu  Caùc nhoùm thöïc hieän yeâu caàu Ví duï:
10' bieán thieân cuûa moät haøm soá.
Ñ1. Heä soá a vaø toaï ñoä ñænh
Xaùc ñònh chieàu bieán thieân cuûa
H1. Ñeå xaùc ñònh chieàu bieán haøm soá:
thieân cuûa haøm soá baäc hai, ta Ñoàng bieán Nghòch bieán a) y = –x2 – 2x + 3
döïa vaøo caùc yeáu toá naøo? a (–; –1) (–1; +) b) y = x2 + 1 b (0; +) (–; 0) c) y = –2x2 + 4x – 3 c (–; 2) (2; +) d) y = x2 – 2x d (1; +) (–; 1)
Hoaït ñoäng 3: Luyeän taäp khaûo saùt haøm soá baäc hai
 Cho moãi nhoùm thöïc hieän  Caùc nhoùm thöïc hieän Ví duï: 15' moät yeâu caàu:
Khaûo saùt haøm soá vaø veõ ñoà thò – Tìm taäp xaùc ñònh y 2 haøm soá: – Tìm toaï ñoä ñænh 1 y = - x2 + 4x - 3 I x y = –x2 + 4x – 3 -4 -3 -2 -1 1 2 3 4 5 6 7 8 9 O
– Xaùc ñònh chieàu bieán thieân -1 -2
– Xaùc ñònh truïc ñoái xöùng -3 -4
– Tìm toaï ñoä giao ñieåm cuûa -5
ñoà thò vôùi caùc truïc toaï ñoä. -6 -7 – Veõ ñoà thò -8 -9
– Döïa vaøo ñoà thò, xaùc ñònh x ñeå y < 0, y > 0
Hoaït ñoäng 3: Cuûng coá
 Nhaéc laïi caùc tính chaát cuûa 5' haøm soá baäc hai.
 Nhaán maïnh moái quan heä
giöõa tính chaát vaø ñoà thò cuûa haøm soá.
4. BAØI TAÄP VEÀ NHAØ:  Baøi 2, 3 SGK
 Laøm baøi taäp oân chöông II Ngaøy soaïn: 1/10/2012
Chöông II: HAØM SOÁ BAÄC NHAÁT VAØ BAÄC HAI Tieát daïy: 15
Baøøi daïy: OÂN TAÄP CHÖÔNG II 28
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn I. MUÏC TIEÂU: Kieán thöùc:
 Hieåu vaø naém ñöôïc tính chaát cuûa haøm soá, mieàn xaùc ñònh, chieàu bieán thieân.
 Hieåu vaø ghi nhôù caùc tính chaát cuûa haøm soá baäc nhaát, baäc hai. Xaùc ñònh ñöôïc chieàu bieán
thieân vaø veõ ñoà thò cuûa chuùng. Kó naêng:
 Veõ thaønh thaïo caùc ñöôøng thaúng daïng y = ax+b baèng caùch xaùc ñònh caùc giao ñieåm vôùi caùc
truïc toaï ñoä vaø caùc parabol y = ax2+bx+c baèng caùch xaùc ñònh ñænh, truïc ñoái xöùng vaø moät soá ñieåm khaùc.
 Bieát caùch giaûi moät soá baøi toaùn ñôn giaûn veà ñöôøng thaúng vaø parabol. Thaùi ñoä:
 Reøn luyeän tính tæ mæ, chính xaùc khi xaùc ñònh chieàu bieán thieân, veõ ñoà thò caùc haøm soá. II. CHUAÅN BÒ:
Giaùo vieân: Giaùo aùn. Heä thoáng baøi taäp oân taäp.
Hoïc sinh: SGK, vôû ghi. OÂn taäp keán thöùc chöông II.
III. HOAÏT ÑOÄNG DAÏY HOÏC:
1. OÅn ñònh toå chöùc: Kieåm tra só soá lôùp.
2. Kieåm tra baøi cuõ: (Loàng vaøo quaù trình oân taäp) H. Ñ.
3. Giaûng baøi môùi: TL
Hoaït ñoäng cuûa Giaùo vieân
Hoaït ñoäng cuûa Hoïc sinh Noäi dung
Hoaït ñoäng 1: Luyeän taäp tìm taäp xaùc ñònh cuûa haøm soá
H1. Nhaéc laïi ñònh nghóa taäp Ñ1. D = {xR/ f(x) coù nghóa} 1. Tìm taäp xaùc ñònh cuûa haøm
10' xaùc ñònh cuûa haøm soá? Neâu a) D = [–3; +) \ {–1} soá
ñieàu kieän xaùc ñònh cuûa moãi b) D =  1  ;   a) 2    haøm soá? y x 3 2    x 1
 Cho moãi nhoùm tìm taäp xaùc c) D = R b) 1   
ñònh cuûa moät haøm soá. y 2 3x 1 2x
 2  x, x 1 c)  y   1  , x  1  x  3
Hoaït ñoäng 2: Luyeän taäp khaûo saùt söï bieán thieân cuûa haøm soá
H1. Nhaéc laïi söï bieán thieân Ñ1.
2. Xeùt chieàu bieán thieân cuûa
10' cuûa haøm soá baäc nhaát vaø baäc a) nghòch bieán treân R haøm soá hai? b) y = 2 x = /x/ a) y = 4 – 2x
 Cho moãi nhoùm xeùt chieàu + x ≥ 0: ñoàng bieán b) y = 2 x
bieán thieân cuûa moät haøm soá. + x < 0: nghòch bieán c) y = x2 – 2x –1 c) + x ≥ 1: ñoàng bieán d) y = –x2 + 3x + 2 + x < 1: nghòch bieán d) + x ≥ 3 : nghòch bieán 2 29
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn + x < 3 : ñoàng bieán 2
Hoaït ñoäng 3: Luyeän taäp veõ ñoà thò cuûa haøm soá
H1. Nhaéc laïi daïng ñoà thò cuûa Ñ1.
3. Veõ ñoà thò cuûa caùc haøm soá ôû
10' haøm soá baäc nhaát vaø baäc hai? y 9 y = 4 - 2x caâu 2 8
 Cho moãi nhoùm veõ ñoà thò cuûa 7 6 moät haøm soá. 5 y = /x/ 4 3 2 1 x -9 -8 -7 -6 -5 -4 -3 -2 -1 1 2 3 4 5 6 7 8 9 O -1 -2 -3 y 8 6 y = x2 - 2x - 1 4 2 x -4 -2 2 4 6 8 O -2 y = -x2 + 3x + 2 -4 -6 -8
Hoaït ñoäng 4: Luyeän taäp xaùc ñònh haøm soá
H1. Neâu ñieàu kieän ñeå moät Ñ1. Toaï ñoä thoaû maõn phöông 4. Xaùc ñònh a, b bieát ñöôøng
10' ñieåm thuoäc ñoà thò haøm soá? trình haøm soá.
thaúng y = ax + b qua hai ñieåm 4) a b  3 A(1; 3), B(–1; 5)  a = –1; b = 4 a  b  5
H2. Neâu coâng thöùc xaùc ñònh   
toaï ñoä ñænh cuûa parabol? Ñ2. I b   ; 2a 4a   
5. Xaùc ñònh a,b,c, bieát parabol a   b  c  1  a   1 y = ax2+bx + c: 5a) a  
  b  c  1  b  1
 a) Ñi qua ba ñieåm A(0;–1), c  1  c  1  B(1;–1), C(3;0). b  2  a a  1 
b) Coù ñænh I(1; 4) vaø ñi qua b)  
a  b  c  4  b  2 ñieåm D(3; 0) 9a3b  c  0 c  3
Hoaït ñoäng 5: Cuûng coá
 Nhaán maïnh caùch giaûi caùc 3' daïng toaùn
4. BAØI TAÄP VEÀ NHAØ:
 Laøm tieáp caùc baøi taäp coøn laïi
 Chuaån bò kieåm tra 1 tieát chöông I, II. Ngaøy soaïn: 10/10/2012
Chöông II: HAØM SOÁ BAÄC NHAÁT VAØ BAÄC HAI Tieát daïy: 16
Baøøi daïy: KIEÅM TRA VIEÁT CHÖÔNG I, II I. MUÏC TIEÂU: 30
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn Kieán thöùc:
 Cuûng coá caùc kieán thöùc veà meänh ñeà, taäp hôïp, sai soá.
 Cuûng coá caùc kieán thöùc veà haøm soá: taäp xaùc ñònh, chieàu bieán thieân, ñoà thò cuûa haøm soá baäc nhaát vaø baäc hai. Kó naêng:
 Thöïc hieän caùc pheùp toaùn veà meänh ñeà, taäp hôïp.
 Tìm taäp xaùc ñònh, xeùt chieàu bieán thieân, veõ ñoà thò cuûa haøm soá baäc nhaát vaø baäc hai. Thaùi ñoä:
 Reøn luyeän tính caån thaän, chính xaùc. II. CHUAÅN BÒ:
Giaùo vieân: Giaùo aùn. Ñeà kieåm tra.
Hoïc sinh: OÂn taäp kieán thöùc chöông I, II. III. MA TRAÄN ÑEÀ: Nhaän bieát Thoâng hieåu Vaän duïng Chuû ñeà Toång TNKQ TL TNKQ TL TNKQ TL Meänh ñeà 2 1 1,5 0,5 0,5 Taäp hôïp 2 1 3 0,5 2,0 Sai soá 1 0,5 0,5 Haøm soá 2 1 1 5 0,5 2,0 2,0 Toång 3,5 0,5 4,0 2,0 10
IV. NOÄI DUNG ÑEÀ KIEÅM TRA: A. Phaàn traéc nghieäm:
Caâu 1: Meänh ñeà naøo sau ñaây laø sai?
a) x  Nx2 chia heát cho 3  x chia heát cho 3
b) x  Nx chia heát cho 3  x2 chia heát cho 3
c) x  Nx2 chia heát cho 6  x chia heát cho 6
d) x  Nx2 chia heát cho 9  x chia heát cho 9
Câu 2: Cho meänh ñeà chöùa bieán : “xR, x2 +2 > 0” , khi ñoù meänh ñeà phuû ñònh cuûa meänh ñeà treân laø :
a) “xR, x2 +2 ≤ 0” b) “xR, x2 +2 < 0” c) “xR, x2 +2 ≤ 0” d) “xR, x2 +2 < 0”
Caâu 3: Cho meänh ñeà chöùa bieán P(n) : “ n laø soá chính phöông”, meänh ñeà ñuùng laø: a) P(5) b) P(16) c) P(10) d) P(20)
Caâu 4: Haõy lieät keâ caùc phaàn töû cuûa taäp hôïp: X =  2 x
/ x x 1   0 a) X = 0 b) X =   0 c) X =  d) X =   
Caâu 5: Cho tập X = 2,3, 
4 . Tập X có bao nhiêu tập hợp con? a) 3 b) 6 c) 8 d) 9
Caâu 6: Khi söû duïng maùy tính boû tuùi vôùi 10 chöõ soá thaäp phaân ta ñöôïc: 8  2,828427125 . Giaù trò gaàn
ñuùng cuûa 8 chính xaùc ñeán haøng phaàn traêm laø : a) 2,80 b) 2,81 c) 2,82 d) 2,83 31
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn
Caâu 7: Haøm soá y x3 2  x laø:
a) Haøm soá chaün b) Haøm soá leû c) Haøm haèng d) Haøm soá khoâng chaün khoâng leû
Caâu 8: Điểm nào sau đây thuộc đồ thị hàm số y = 2|x–1| + 3|x| – 2 ? a) (2; 6); b) (1; –1); c) (–2; –10); d) Cả ba điểm trên. B. Phaàn töï luaän:
Caâu 1: (2 ñieåm) Cho hai tập hợp A[1 ; 5) và B(3 ; 6].
Xác định các tập hợp sau :A  B, A  B, B\A, CRA
Caâu 2: (2 ñieåm) Tìm miền xác định và xét tính chẵn lẻ của hàm số sau : 2 y  x 1  x 1
Caâu 3: a) (1 ñieåm ) Tìm parabol y = ax2 + bx + 2 bieát raèng parabol ñoù ñi qua ñieåm A(3 ; –4) vaø coù truïc ñoái xöùng 3 x   . 2
b) ( 1 ñieåm ) Veõ ñoà thò haøm soá vöøa tìm ñöôïc ôû caâu a).
V. ÑAÙP AÙN VAØ BIEÅU ÑIEÅM:
A. Phaàn traéc nghieäm:
1d) 2c) 3b) 4c) 5c) 6d) 7b) 8a) B. Töï luaän:
Caâu 1: A  B = (3; 5), A  B = [1; 6], B\A = [5; 6], CRA = (–; 1)[3; +)
Caâu 2: D = R \ {–1; 1}; Haøm soá chaün y 5 4 3 2 1 x -6 -5 -4 -3 -2 -1 1 2 3 4 5 O -1 -2 -3 9a  3b  2  4   1 -4 Caâu 3: a)  a    b 3  b) -5   3 2a 2 b  1 
VI. KEÁT QUAÛ KIEÅM TRA: 0 – 3,4 3,5 – 4,9 5,0 – 6,4 6,5 – 7,9 8,0 – 10 Lôùp Só soá SL % SL % SL % SL % SL % 10A3 44 10A5 42 10A7 44 10A10 42 10A11 38 Ngaøy soaïn: 20/10/2012
Chöông III: PHÖÔNG TRÌNH. HEÄ PHÖÔNG TRÌNH Tieát daïy: 17
Baøøi 1: ÑAÏI CÖÔNG VEÀ PHÖÔNG TRÌNH I. MUÏC TIEÂU: Kieán thöùc: 32
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn
 Hieåu khaùi nieäm phöông trình, nghieäm cuûa phöông trình.
 Hieåu ñònh nghóa hai phöông trình töông ñöông vaø caùc pheùp bieån ñoåi töông ñöông.
 Bieát khaùi nieäm phöông trình heä quaû. Kó naêng:
 Nhaän bieát moät soá cho tröôùc laø nghieäm cuûa pt ñaõ cho, nhaän bieát ñöôïc hai pt töông ñöông.
 Neâu ñöôïc ñieàu kieän xaùc ñònh cuûa phöông trình.
 Bieát bieán ñoåi töông ñöông phöông trình. Thaùi ñoä:
 Reøn luyeän tính caån thaän, chính xaùc. II. CHUAÅN BÒ:
Giaùo vieân: Giaùo aùn.
Hoïc sinh: SGK, vôû ghi. OÂn taäp kieán thöùc veà phöông trình ñaõ hoïc.
III. HOAÏT ÑOÄNG DAÏY HOÏC:
1. OÅn ñònh toå chöùc: Kieåm tra só soá lôùp.
2. Kieåm tra baøi cuõ: (3')
H. Tìm taäp xaùc ñònh cuûa haøm soá: y = f(x) = x 1 ; y = g(x) = x x 1
Ñ. Df = [1; +); Dg = R \ {–1}
3. Giaûng baøi môùi: TL
Hoaït ñoäng cuûa Giaùo vieân
Hoaït ñoäng cuûa Hoïc sinh Noäi dung
Hoaït ñoäng 1: Tìm hieåu khaùi nieäm phöông trình moät aån
 Cho HS nhaéc laïi caùc kieán  Caùc nhoùm thaûo luaän, traû lôøi I. Khaùi nieäm phöông trình
10' thöùc ñaõ bieát veà phöông trình.
1. Phöông trình moät aån
H1. Cho ví duï veà phöông trình Ñ1. 2x + 3 = 0; x2 – 3x + 2 =  Phöông trình aån x laø meänh
moät aån, hai aån ñaõ bieát? 0;
ñeà chöùa bieán coù daïng: x – y = 1 f(x) = g(x) (1)
H2. Cho ví duï veà phöông trình
trong ñoù f(x), g(x) laø nhöõng
moät aån coù moät nghieäm, hai Ñ2.
bieåu thöùc cuûa x.
nghieäm, voâ soá nghieäm, voâ  x
a) 2x + 3 = 0 –> S = 3
0 R ñgl nghieäm cuûa (1) 2 nghieäm?
neáu f(x0) = g(x0) ñuùng.
b) x2 – 3x + 2 = 0 –> S =  Giaûi (1) laø tìm taäp nghieäm S {1,2} cuûa (1).
c) x2 – x + 2 = 0 –> S = 
Neáu (1) voâ nghieäm thì S = . d)
x 1  x 1  2–>S=[– 1;1]
Hoaït ñoäng 2: Tìm hieåu ñieàu kieän xaùc ñònh cuûa phöông trình
H1. Tìm ñieàu kieän cuûa caùc Ñ1.
2. Ñieàu kieän cuûa moät phöông 10' phöông trình sau:
a) 2 – x > 0  x < 2 trình a) 3 – x2 = x
Ñieàu kieän xaùc ñònh cuûa (1) laø 2  x 2
ñieàu kieän cuûa aån x ñeå f(x) vaø b) x 1  0   1   x 3 x  1  g(x) coù nghóa. b)  x  3 x  3  0 2 x 1
(Neâu ñk xaùc ñònh cuûa töøng 33
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn bieåu thöùc)
Hoaït ñoäng 3: Tìm hieåu khaùi nieäm phöông trình nhieàu aån
H1. Cho ví duï veà phöông trình Ñ1. a) 2x + y = 5
3. Phöông trình nhieàu aån 7' nhieàu aån? b) x + y – z = 7
Daïng f(x,y) = g(x,y), …
H2. Chæ ra moät soá nghieäm cuûa Ñ2. a) (2; 1), (1; 3), … caùc phöông trình ñoù?
b) (3; 4; 0), (2; 4; –1), …
H3. Nhaän xeùt veà nghieäm vaø Ñ3. Moãi nghieäm laø moät boä soá
soá nghieäm cuûa caùc phöông cuûa caùc aån. trình treân?
Thoâng thöôøng phöông trình coù voâ soá nghieäm.
Hoaït ñoäng 4: Tìm hieåu khaùi nieäm phöông trình chöùa tham soá
H1. Cho ví duï phöông trình Ñ1. a) (m + 1)x – 3 = 0
4. Phöông trình chöùa tham 10' chöùa tham soá? b) x2 – 2x + m = 0 soá
Trong moät phöông trình, ngoaøi
H2. Khi naøo phöông trình ñoù Ñ2.
caùc chöõ ñoùng vai troø aån soá coøn voâ nghieäm, coù nghieäm?
a) coù nghieäm khi m ≠ –1
coù theå coù caùc chöõ khaùc ñöôïc
xem nhö nhöõng haèng soá vaø –> nghieäm x = 3 m 1
ñöôïc goïi laø tham soá.
b) coù nghieäm khi  = 1–m ≥0 Giaûi vaø bieän luaän phöông  m ≤ 1
trình chöùa tham soá nghóa laø
–> nghieäm x = 1  1 m
xeùt xem vôùi giaù trò naøo cuûa
tham soá thì phöông trình voâ
nghieäm, coù nghieäm vaø tìm caùc nghieäm ñoù.
Hoaït ñoäng 5: Cuûng coá
Nhaán maïnh caùc khaùi nieäm veà
3' phöông trình ñaõ hoïc.
4. BAØI TAÄP VEÀ NHAØ:
 Tìm ñieàu kieän xaùc ñònh cuûa caùc phöông trình trong baøi 3, 4 SGK.
 Ñoïc tieáp baøi "Ñaïi cöông veà phöông trình" Ngaøy soaïn: 20/10/2012
Chöông III: PHÖÔNG TRÌNH. HEÄ PHÖÔNG TRÌNH Tieát daïy: 18
Baøøi 1: ÑAÏI CÖÔNG VEÀ PHÖÔNG TRÌNH (tt) I. MUÏC TIEÂU: Kieán thöùc: 34
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn
 Hieåu khaùi nieäm phöông trình, nghieäm cuûa phöông trình.
 Hieåu ñònh nghóa hai phöông trình töông ñöông vaø caùc pheùp bieån ñoåi töông ñöông.
 Bieát khaùi nieäm phöông trình heä quaû. Kó naêng:
 Nhaän bieát moät soá cho tröôùc laø nghieäm cuûa pt ñaõ cho, nhaän bieát ñöôïc hai pt töông ñöông.
 Neâu ñöôïc ñieàu kieän xaùc ñònh cuûa phöông trình.
 Bieát bieán ñoåi töông ñöông phöông trình. Thaùi ñoä:
 Reøn luyeän tính caån thaän, chính xaùc. II. CHUAÅN BÒ:
Giaùo vieân: Giaùo aùn.
Hoïc sinh: SGK, vôû ghi. OÂn taäp kieán thöùc veà phöông trình ñaõ hoïc.
III. HOAÏT ÑOÄNG DAÏY HOÏC:
1. OÅn ñònh toå chöùc: Kieåm tra só soá lôùp.
2. Kieåm tra baøi cuõ: (3') 2 x 9
H. Tìm ñieàu kieän xaùc ñònh cuûa phöông trình  x 1 x 1 Ñ. x > 1
3. Giaûng baøi môùi: TL
Hoaït ñoäng cuûa Giaùo vieân
Hoaït ñoäng cuûa Hoïc sinh Noäi dung
Hoaït ñoäng 1: Tìm hieåu khaùi nieäm phöông trình töông ñöông 2 x 9
Ñ1. Töông ñöông, vì cuøng taäp II. Phöông trình töông 10' H1. Hai pt:  x 1 x 1 nghieäm S = {3}
ñöông vaø phöông trình heä
vaø 2x = 6 coù töông ñöông quaû khoâng?
1. Phöông trình töông ñöông
Hai phöông trình ñgl töông
H2. Hai phöông trình voâ Ñ2. Coù, vì cuøng taäp nghieäm
ñöông khi chuùng coù cuøng taäp
nghieäm coù töông ñöông nghieäm khoâng?
Chuù yù: Hai phöông trình voâ
nghieäm thì töông ñöông.
Hoaït ñoäng 2: Tìm hieåu caùc pheùp bieán ñoåi töông ñöông
 Xeùt caùc pheùp bieán ñoåi sau:
2. Pheùp bieán ñoåi töông 15' a) x + 1 = 1 + 1 ñöông x 1 x 1
Ñònh lí: Neáu thöïc hieän caùc
 x + 1 – 1 = 1 + 1
pheùp bieán ñoåi sau ñaây treân x 1 x 1 x 1
moät phöông trình maø khoâng – 1  x = 1
laøm thay ñoåi ñieàu kieän cuûa noù x 1
thì ta ñöôïc moät phöông trình
b) x(x – 3) = 2x  x – 3 = 2
môùi töông ñöông:  x = 5
a) Coäng hay tröø hai veá vôùi
H1. Tìm sai laàm trong caùc Ñ1.
cuøng moät soá hoaëc cuøng moät pheùp bieán ñoåi treân?
a) sai vì ÑKXÑ cuûa pt laø x ≠ 1 bieåu thöùc;
b) sai vì ñaõ chia 2 veá cho x = b) Nhaân hoaëc chia hai veá vôùi 0
cuøng moät soá khaùc 0 hoaïc vôùi 35
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn
cuøng moät bieåu thöùc luoân coù giaù trò khaùc 0.
Kí hieäu: Ta duøng kí hieäu ñeå
chæ söï töông ñöông cuûa caùc phöông trình.
Hoaït ñoäng 3: Tìm hieåu khaùi nieäm phöông trình heä quaû
 Xeùt pheùp bieán ñoåi:
3. Phöông trình heä quaû 10' 8 x = x – 2 (1)
Neáu moïi nghieäm cuûa pt f(x) =  8 – x = (x–2)2
g(x) ñeàu laø nghieäm cuûa pt f1(x)  x2 –3x – 4 = 0
=g1(x) thì pt f1(x) =g1(x) ñgl pt (2)
heä quaû cuûa pt f(x) = g(x). ( x = –1; x = 4)
Ñ1. x = –1 khoâng laø nghieäm Ta vieát f(x)=g(x)f1(x)=g1(x)
H1. Caùc nghieäm cuûa (2) coù cuûa (1)
Chuù yù: Pt heä quaû coù theå theâm
ñeàu laø nghieäm cuûa (1) khoâng?
nghieäm khoâng phaûi laø nghieäm
cuûa pt ban ñaàu. Ta goïi ñoù laø
nghieäm ngoaïi lai.
Hoaït ñoäng 4: Cuûng coá
Nhaán maïnh caùc pheùp bieán ñoåi
Ñeå giaûi moät pt ta thöôøng 5' phöông trình.
thöïc hieän caùc pheùp bieán ñoåi töông ñöông.
Pheùp bình phöông hai veá,
nhaân hai veá cuûa pt vôùi moät ña
thöùc coù theå daãn tôùi pt heä quaû.
Khi ñoù ñeå loaïi nghieäm ngoaïi
lai ta phaûi thöû laïi caùc nghieäm
tìm ñöôïc hoaëc ñaët ñieàu kieän
phuï ñeå ñöôïc pheùp bieán ñoåi töông ñöông.
4. BAØI TAÄP VEÀ NHAØ:  Baøi 1, 2, 3, 4 SGK.
 Ñoïc tröôùc baøi "Phöông trình qui veà phöông trình baäc nhaát, baäc hai" Ngaøy soaïn: 30/10/2012
Chöông III: PHÖÔNG TRÌNH. HEÄ PHÖÔNG TRÌNH Tieát daïy: 19
Baøøi 2: PHÖÔNG TRÌNH QUI VEÀ
PHÖÔNG TRÌNH BAÄC NHAÁT, BAÄC HAI I. MUÏC TIEÂU: 36
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn Kieán thöùc:
 Cuûng coá caùch giaûi phöông trình baäc nhaát, baäc hai moät aån.
 Hieåu caùch giaûi vaø bieän luaän caùc phöông trình ax + b = 0, ax2 + bx + c = 0. Kó naêng:
 Giaûi vaø bieän luaän thaønh thaïo caùc phöông trình ax+ b=0, ax2 + bx + c = 0. Thaùi ñoä:
 Reøn luyeän tính caån thaän, chính xaùc. II. CHUAÅN BÒ:
Giaùo vieân: Giaùo aùn. Baûng toùm taét caùch giaûi vaø bieän luaän phöông trình baäc nhaát, baäc hai.
Hoïc sinh: SGK, vôû ghi. OÂn taäp kieán thöùc ñaõ hoïc veà phöông trình baäc nhaát, baäc hai.
III. HOAÏT ÑOÄNG DAÏY HOÏC:
1. OÅn ñònh toå chöùc: Kieåm tra só soá lôùp.
2. Kieåm tra baøi cuõ: (3')
H. Theá naøo laø hai phöông trình töông ñöông? Taäp nghieäm vaø taäp xaùc ñònh cuûa phöông
trình khaùc nhau ôû ñieåm naøo?
Ñ. ((1)  (2))  S1 = S2; S  D.
3. Giaûng baøi môùi: TL
Hoaït ñoäng cuûa Giaùo vieân
Hoaït ñoäng cuûa Hoïc sinh Noäi dung
Hoaït ñoäng 1: OÂn taäp veà phöông trình baäc nhaát
 Höôùng daãn caùch giaûi vaø  HS theo doõi thöïc hieän laàn I. OÂn taäp veà phöông trình
10' bieän luaän phöông trình ax + b löôït caùc yeâu caàu.
baäc nhaát, baäc hai = 0 thoâng qua ví duï.
1. Phöông trình baäc nhaát VD1. Cho pt: m(x – 4) = 5x – 2 (1) ax + b = 0 (1) a) Giaûi pt (1) khi m = 1 Heä soá Keát luaän
b) Giaûi vaø bieän luaän pt (1) (1) coù nghieäm a ≠ 0 b x = – a
H1. Goïi 1 HS giaûi caâu a)
Ñ1. 4x = – 2  x = – 1 b ≠ 0 (1) voâ nghieäm 2 a = 0 (1) nghieäm
H2. Bieán ñoåi (1) ñöa veà daïng Ñ2. (m – 5)x + 2 – 4m = 0 (2) b = 0 ñuùng vôùi moïi x ax + b = 0 a = m – 5; b = 2 – 4m Xaùc ñònh a, b?
Khi a ≠ 0 pt (1) ñgl phöông
trình baäc nhaát moät aån.
H3. Xeùt (2) vôùi a ≠ 0; a = 0? Ñ3.  m ≠ 5: (2)  x = 4m 2 m  5 m = 5: (2)  0x – 18 = 0  (2) voâ nghieäm
Hoaït ñoäng 2: OÂn taäp veà phöông trình baäc hai
 Höôùng daãn caùch giaûi vaø  HS theo doõi thöïc hieän laàn 2. Phöông trình baäc hai
15' bieän luaän ph.trình ax2 + bx + c löôït caùc yeâu caàu. = 0 thoâng qua ví duï.
ax2 + bx + c = 0 (a ≠ 0) (2) VD2. Cho pt:  = b2 – 4ac Keát luaän
x2 – 2mx + m2 – m + 1 = 0 (2) coù 2 (2)  > 0 nghieäm phaân bieät a) Giaûi (2) khi m = 2 37
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn
b) Giaûi vaø bieän luaän (2)
Ñ1. (2)  x2 – 4x + 3 = 0 b x  
H1. Goïi 1 HS giaûi caâu a)  x = 1; x = 3 1,2 = 2a Ñ2.  = 4(m – 1) (2) coù nghieäm H2. Tính ?  = 0 b keùp x = –
Ñ3. m > 1:  > 0  (2) coù 2 2a  < 0 (2) voâ nghieäm
H3. Xeùt caùc tröôøng hôïp  > 0, nghieäm x1,2 = m  m 1  = 0,  < 0?
m = 1:  = 0  (2) coù nghieäm keùp x = m = 1
m < 1:  < 0  (2) voâ nghieäm
Hoaït ñoäng 3: OÂn taäp veà ñònh lí Viet
 Luyeän taäp vaän duïng ñònh lí 3. Ñònh lí Viet 10' Viet.
Neáu phöông trình baäc hai:
VD3. Chöùng toû pt sau coù 2 Ñ.  = 5 > 0  pt coù 2
ax2 + bx + c = 0 (a≠0)
nghieäm x1, x2 vaø tính x1 + x2, nghieäm phaân bieät
coù hai nghieäm x1, x2 thì: x1x2 : x2 – 3x + 1 = 0 x1 + x2 = 3, x1x2 = 1 x , x 1 + x2 = – b a 1x2 = ca
VD4. Pt 2x2 – 3x – 1 = 0 coù 2
Ngöôïc laïi, neáu hai soá u, v coù Ñ. x , x nghieäm x 2 2 1 + x2 = 3 1x2 = – 1 1, x2 . Tính x1 + x2 2 2
toång u + v = S vaø tích uv = P ? x 2 2
thì u vaø v laø caùc nghieäm cuûa 1 + x2 = (x1 + x2)2 –2x1x2
phöông trình x2 – Sx + P = 0 = 7 4
Hoaït ñoäng 4: Cuûng coá
 Nhaán maïnh caùc böôùc giaûi vaø
5' bieän luaän pt ax + b = 0, pt baäc hai.
 Caùc tính chaát veà nghieäm soá  HS töï oân taäp laïi caùc vaán ñeà
cuûa phöông trình baäc hai: – Caùch nhaåm nghieäm
– Bieåu thöùc ñoái xöùng cuûa caùc nghieäm – Daáu cuûa nghieäm soá
4. BAØI TAÄP VEÀ NHAØ:  Baøi 2, 3, 5, 8 SGK.
 Ñoïc tieáp baøi "Phöông trình qui veà phöông trình baäc nhaát, baäc hai" Ngaøy soaïn: 30/10/2012
Chöông III: PHÖÔNG TRÌNH. HEÄ PHÖÔNG TRÌNH Tieát daïy: 20
Baøøi 2: PHÖÔNG TRÌNH QUI VEÀ
PHÖÔNG TRÌNH BAÄC NHAÁT, BAÄC HAI (tt) I. MUÏC TIEÂU: Kieán thöùc: 38
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn
 Hieåu caùch giaûi caùc pt qui veà daïng baäc nhaát, baäc hai, pt chöùa aån ôû maãu, pt coù chöùa daáu
GTTÑ, pt chöùa caên ñôn giaûn, pt tích. Kó naêng:
 Giaûi thaønh thaïo pt ax+ b=0, pt baäc hai.
 Giaûi ñöôïc caùc pt qui veà baäc nhaát, baäc hai.
 Bieát giaûi pt baäc hai baèng MTBT. Thaùi ñoä:
 Reøn luyeän tính caån thaän, chính xaùc.
 Luyeän tö duy linh hoaït qua vieäc bieán ñoåi phöông trình. II. CHUAÅN BÒ:
Giaùo vieân: Giaùo aùn. Heä thoáng caùch giaûi caùc daïng phöông trình.
Hoïc sinh: SGK, vôû ghi. OÂn taäp caùc kieán thöùc veà GTTÑ, caên thöùc baäc hai.
III. HOAÏT ÑOÄNG DAÏY HOÏC:
1. OÅn ñònh toå chöùc: Kieåm tra só soá lôùp.
2. Kieåm tra baøi cuõ: (3')
H. Neâu ñieàu kieän xaùc ñònh cuûa bieåu thöùc chöùa bieán ôû maãu? 2
AÙp duïng: Tìm ñkxñ cuûa f(x) = x  3x  2 2x  3
Ñ. f(x) = P(x) –> Q(x) ≠ 0;
f(x) xaùc ñònh khi x ≠ – 3 Q(x) 2
3. Giaûng baøi môùi: TL
Hoaït ñoäng cuûa Giaùo vieân
Hoaït ñoäng cuûa Hoïc sinh Noäi dung
Hoaït ñoäng 1: OÂn taäp phöông trình chöùa aån ôû maãu
 Cho HS nhaéc laïi caùc böôùc  HS phaùt bieåu
II. Phöông trình qui veà
10' giaûi phöông trình chöùa aån ôû
phöông trình baäc nhaát, baäc maãu thöùc. hai
VD1. Giaûi phöông trình:
1. Phöông trình chöùa aån ôû 2 x  3x  2 2x  5 maãu  (1) 2x  3 4 Daïng P(x) Q(x)
H1. Neâu ñkxñ cuûa (1)
Ñ1. 2x + 3 ≠ 0  x ≠ – 3 (*) B1: ÑKXÑ: Q(x) ≠ 0 2
B2: Giaûi phöông trình
H2. Bieán ñoåi phöông trình (1) Ñ2. (1)  16x + 23 = 0
B3: Ñoái chieáu nghieäm tìm
 x = – 23 (thoaû ñk (*)) ñöôïc vôùi ÑKXÑ ñeå choïn 16
nghieäm thích hôïp.
Hoaït ñoäng 2: OÂn taäp veà phöông trình chöùa giaù trò tuyeät ñoái
H1. Nhaéc laïi ñònh nghóa Ñ1. A neáu A  0 A 
2. Phöông trình chöùa GTTÑ 15' GTTÑ ?  A neáu A  0
Ñeå giaûi phöông trình chöùa
VD2. Giaûi phöông trình: Ñ.
GTTÑ ta tìm caùch khöû daáu x 3  2x 1 (2) C1: GTTÑ: 39
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn
 Höôùng daãn HS laøm theo 2 + Neáu x ≥ 3 thì (2) trôû thaønh:
– Duøng ñònh nghóa;
caùch. Töø ñoù ruùt ra nhaän xeùt.
x – 3 = 2x + 1  x = –4 (loaïi) – Bình phöông 2 veá.
+ Neáu x < 3 thì (2) trôû thaønh:
Chuù yù: Khi bình phöông 2 veá
–x + 3 = 2x + 1  x= cuûa phöông trình ñeå ñöôïc pt 2
töông ñöông thì caû 2 veá ñeàu (thoaû) 3 phaûi khoâng aâm. C2:
(2)  (x – 3)2 = (2x + 1)2 f(x)  0   3x2 + 10x – 8 = 0 f(x)  g(x) f(x)  g(x)   f(x)  0   x = –4; x = 2 3 f(x)  g(x)
Thöû laïi: x = –4 (loaïi), g(x)  0
f(x)  g(x)
VD3. Giaûi phöông trình: x = 2 (thoaû)  3 f(x)  g(x) 2x 1  x 2 (3) f(x)  g(x)
H1. Ta neân duøng caùch giaûi f(x)  g(x)  f(x)  g(x) naøo?
Ñ1. Bình phöông 2 veá:
 Chuù yù a2 – b2 = (a – b)(a + (3)  (2x – 1)2 = (x + 2)2 b)  (x – 3)(3x + 1) = 0  x = 3; x = – 1 3
Hoaït ñoäng 3: AÙp duïng
VD4. Giaûi caùc phöông trình: Ñ. 10' a) ÑKXÑ: x a) 2x  3 4 24 ≠ 3    2 2 x 3 x  3 x 9 S =  b) 2 2x  5  x  5x 1 b) S = {–6, 1} c) 2x 1  5  x 2 c) S = {–1, – 1 } 7
Hoaït ñoäng 4: Cuûng coá
5'  Nhaán maïnh caùch giaûi caùc daïng phöông trình
4. BAØI TAÄP VEÀ NHAØ:  Baøi 1, 6 SGK.
Ñoïc tieáp baøi "Phöông trình qui veà phöông trình baäc nhaát, baäc hai" Ngaøy soaïn: 1/11/2012
Chöông III: PHÖÔNG TRÌNH. HEÄ PHÖÔNG TRÌNH Tieát daïy: 21
Baøøi 3: PHÖÔNG TRÌNH VAØ HEÄ PHÖÔNG TRÌNH
BAÄC NHAÁT NHIEÀU AÅN I. MUÏC TIEÂU: Kieán thöùc: 40
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn
 Naém vöõng khaùi nieäm pt baäc nhaát hai aån, heä pt baäc nhaát hai aån vaø taäp nghieäm cuûa chuùng.
 Hieåu roõ phöông phaùp coäng ñaïi soá vaø phöông phaùp theá. Kó naêng:
 Giaûi ñöôïc vaø bieåu dieãn ñöôïc taäp nghieäm cuûa pt baäc nhaát hai aån.
 Giaûi thaønh thaïo heä pt baäc nhaát hai aån baèng phöông phaùp coäng vaø phöông phaùp theá.
 Giaûi ñöôïc heä pt baäc nhaát ba aån ñôn giaûn.
 Giaûi ñöôïc moät soá baøi toaùn thöïc teá ñöa veà vieäc laäp vaø giaûi heä pt baäc nhaát hai, ba aån.
 Bieát duøng MTBT ñeå giaûi heä pt baäc nhaát hai, ba aån. Thaùi ñoä:
 Reøn luyeän tính caån thaän, chính xaùc.
 Luyeän tö duy linh hoaït thoâng qua vieäc bieán ñoåi heä phöông trình. II. CHUAÅN BÒ:
Giaùo vieân: Giaùo aùn. Hình veõ minh hoaï.
Hoïc sinh: SGK, vôû ghi. OÂn taäp kieán thöùc ñaõ hoïc veà heä pt baäc nhaát hai aån.
III. HOAÏT ÑOÄNG DAÏY HOÏC:
1. OÅn ñònh toå chöùc: Kieåm tra só soá lôùp.
2. Kieåm tra baøi cuõ: (3')
H. Neâu daïng cuûa heä phöông trình baäc nhaát hai aån vaø phöông phaùp giaûi?
Ñ. Phöông phaùp theá, phöông phaùp coäng ñaïi soá.
3. Giaûng baøi môùi: TL
Hoaït ñoäng cuûa Giaùo vieân
Hoaït ñoäng cuûa Hoïc sinh Noäi dung
Hoaït ñoäng 1: OÂn taäp phöông trình baäc nhaát hai aån
H1. Theá naøo laø moät nghieäm Ñ1. Nghieäm laø caëp (x0; y0) 1. Phöông trình baäc nhaát hai 10' cuûa (1)? thoaû ax0 + by0 = c. aån
Daïng: ax + by = c (1)
H2. Tìm caùc nghieäm cuûa pt: Ñ2.
trong ñoù a2 + b2 ≠ 0 3x – 2y = 7
(1; –2), (–1; –5), (3; 1), …
(Moãi nhoùm chæ ra moät soá Chuù yù: nghieäm)  a  b  0   (1) voâ nghieäm y 8 c  0 7 6
H3. Xaùc ñònh caùc ñieåm (1; – 5    4  a b 0  moïi caëp
2), (–1; –5), (3; 1), … treân mp 3  2 c  0 1 x Oxy? -9 -8 -7 -6 -5 -4 -3 -2 -1 1 2 3 4 5 6 7 8 9 10 -1 (x -2
0;y0) ñeàu laø nghieäm Nhaän xeùt? -3 -4 -5
b ≠ 0: (1) y = a c  x  -6 -7 b b -8 -9 -10 Toång quaùt: -11
Caùc ñieåm naèm treân ñöôøng  Phöông trình (1) luoân coù voâ soá nghieäm. thaúng y = 3x  7 2
Bieåu dieãn hình hoïc taäp
nghieäm cuûa (1) laø moät ñöôøng thaúng trong mp Oxy.
Hoaït ñoäng 2: OÂn taäp Heä hai phöông trình baäc nhaát hai aån
H1. Nhaéc laïi caùc caùch giaûi (2) Ñ1. Moãi nhoùm giaûi theo moät 2. Heä hai phöông trình baäc 17' AÙp duïng: Giaûi heä: caùch. nhaát hai aån 41
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn 4x  3y  9  12 1  a x  b y  c   x  ;y    Daïng: 1 1 1 (2) 2x  y  5  5 5  a  2x  b2y  c2
 HD hoïc sinh nhaän xeùt yù  (d1): a1x + b1y = c1
Caëp soá (x0; y0) laø nghieäm
nghóa hình hoïc cuûa taäp (d2): a2x + b2y = c2
cuûa (2) neáu noù laø nghieäm cuûa nghieäm cuûa (2).
+ (d1), (d2) caét nhau  (2) coù caû 2 phöông trình cuûa (2). 1 nghieäm
Giaûi (2) laø tìm taäp nghieäm
+ (d1)//(d2)  (2) voâ nghieäm cuûa (2).
+ (d1)(d2)  (2) voâ soá nghieäm 4 4 4 d1 2 d 2 2 2 d2 d d 1 1 d2 -5 5 -5 5 -5 5 -2 -2 -2
Hoaït ñoäng 3: Giôùi thieäu caùch giaûi heä phöông trình baèng ñònh thöùc
H1. Giaûi caùc heä pt baèng ñònh Ñ1. a b 10' thöùc: a) D = 23, D  D = 1 1 x = –23, Dy = 46 2 a b2 a) 5x  2y  9 
 Nghieäm (x; y) = (–1; 2)  c b a c 4x  3y  2
b) D = 29, Dx = 58, Dy = –87 Dx = 1 1 , Dy = 1 1
 Nghieäm (x; y) = (2; –3) c b a c b) 2x  3y  13 2 2 2 2  7x  4y  2
 D ≠ 0: (2) coù nghieäm duy  D D  nhaát x y  x  ;y    D D 
 D = 0 vaø (Dx ≠ 0 hoaëc Dy ≠0) (2) voâ nghieäm
 D = Dx = Dy = 0: (2) voâ soá nghieäm
Hoaït ñoäng 4: Cuûng coá
3'  Nhaéc laïi caùc caùch giaûi heä
phöông trình baäc nhaát hai aån
4. BAØI TAÄP VEÀ NHAØ:  1, 2, 3, 4 SGK.
Ñoïc tieáp baøi "Phöông trình vaø heä phöông trình baäc nhaát nhieàu aån" Ngaøy soaïn: 1/11/2012
Chöông III: PHÖÔNG TRÌNH. HEÄ PHÖÔNG TRÌNH Tieát daïy: 22
Baøøi 3: PHÖÔNG TRÌNH VAØ HEÄ PHÖÔNG TRÌNH
BAÄC NHAÁT NHIEÀU AÅN (tt) I. MUÏC TIEÂU: Kieán thöùc:
 Naém vöõng khaùi nieäm pt baäc nhaát hai aån, heä pt baäc nhaát hai aån vaø taäp nghieäm cuûa chuùng. 42
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn
 Hieåu roõ phöông phaùp coäng ñaïi soá vaø phöông phaùp theá. Kó naêng:
 Giaûi ñöôïc vaø bieåu dieãn ñöôïc taäp nghieäm cuûa pt baäc nhaát hai aån.
 Giaûi thaønh thaïo heä pt baäc nhaát hai aån baèng phöông phaùp coäng vaø phöông phaùp theá.
 Giaûi ñöôïc heä pt baäc nhaát ba aån ñôn giaûn.
 Giaûi ñöôïc moät soá baøi toaùn thöïc teá ñöa veà vieäc laäp vaø giaûi heä pt baäc nhaát hai, ba aån.
 Bieát duøng MTBT ñeå giaûi heä pt baäc nhaát hai, ba aån. Thaùi ñoä:
 Reøn luyeän tính caån thaän, chính xaùc.
 Luyeän tö duy linh hoaït thoâng qua vieäc bieán ñoåi heä phöông trình. II. CHUAÅN BÒ:
Giaùo vieân: Giaùo aùn. Hình veõ minh hoaï.
Hoïc sinh: SGK, vôû ghi. OÂn taäp kieán thöùc ñaõ hoïc veà heä pt baäc nhaát hai aån.
III. HOAÏT ÑOÄNG DAÏY HOÏC:
1. OÅn ñònh toå chöùc: Kieåm tra só soá lôùp.
2. Kieåm tra baøi cuõ: (3')
H. Giaûi heä phöông trình sau baèng ñònh thöùc: 3  x  5y  6  4x  7y  8 
Ñ. D = 41, Dx = 2, Dy = –48  Nghieäm (x; y) = ( 2 48 ; ) 41 41
3. Giaûng baøi môùi: TL
Hoaït ñoäng cuûa Giaùo vieân
Hoaït ñoäng cuûa Hoïc sinh Noäi dung
Hoaït ñoäng 1: Tìm hieåu caùch giaûi Heä phöông trình baäc nhaát 3 aån
 GV höôùng daãn tìm nghieäm 
II. Heä phöông trình baäc nhaát
10' cuûa heä phöông trình: (3)  z = 3 3 aån  x  3y  2z  1  (1) 2
Phöông trình baäc nhaát 3 aån:  3 ax + by + cz = d  4y  3z  (2) (2)  y = 3   2 4
trong ñoù a2 + b2 + c2 ≠ 0  2z  3 (3)
Heä 3 pt baäc nhaát 3 aån:
–> Heä phöông trình treân coù (1)  x = 17 4  1 a x  1 b y  1cy  1 d daïng tam giaùc.   2 a x  b2y  2 c y  d2 (4)  3ax 3 b y  3 c y  d3
Moãi boä soá (x0; y0; z0) nghieäm
ñuùng caû 3 pt cuûa heä ñgl nghieäm cuûa heä (4).
Phöông phaùp Gauss: Moïi heä
phöông trình baäc nhaát 3 aån
ñeàu bieán ñoåi ñöôïc veà daïng tam
giaùc baèng phöông phaùp khöû daàn aån soá.
Hoaït ñoäng 2: Luyeän taäp giaûi heä phöông trình baäc nhaát 3 aån
 GV höôùng daãn caùch vaän 
VD1: Giaûi heä phöông trình:
10' duïng phöông phaùp Gauss. 43
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn  1  x 1  2y  2z   x  2y  2z  (1) 2  2 (*)   y  z  3    2x  3y  5z  2  (2)  (*)  10z  5   4  x  7y  z  4  (3)  7 x    2  5  y   2  1 z    2
Hoaït ñoäng 3: Luyeän taäp giaûi toaùn baèng caùch laäp heä phöông trình
H1. Nhaéc laïi caùc böôùc giaûi Ñ1.
VD2: Hai baïn Vaân vaø Lan
10' toaùn baèng caùch laäp phöông 1) Choïn aån, ñk cuûa aån.
ñeán cöûa haøng mua traùi caây. trình ?
2) Bieåu dieãn caùc ñaïi löôïng Baïn Vaân mua 10 quaû quyùt, 7 lieân quan theo aån.
quaû cam vôùi giaù tieàn 17800 ñ. 3) Laäp pt, heä pt.
Baïn Lan mua 12 quaû quyùt, 6 4) Giaûi pt, heä pt
quaû cam heát 18000 ñ. Hoûi giaù
5) Ñoái chieáu ñk ñeå choïn tieàn moãi quaû quyùt vaø moãi quaû nghieäm thích hôïp. cam laø bao nhieâu?
 x (ñ): giaù tieàn moät quaû quyùt
y (ñ): giaù tieàn moät quaû cam 1  0x  7y  17800 1   2x  6y  18000  x = 800, y = 1400
Hoaït ñoäng 4: Höôùng daãn söû duïng MTBT ñeå giaûi heä phöông trình
 Höôùng daãn HS söû duïng a) x  0.048780487
VD3: Giaûi caùc heä ph.trình: 7' MTBT ñeå giaûi heä pt.  y  1  .170731707 a) 3  x  5y  6  x  0.217821782 4x  7y  8   b) y 1.297029703 2x  3y  4z  5    z  0  .386138613 b)  4  x  5y  z  6 3x  4y 3z  7
Hoaït ñoäng 5: Cuûng coá
3'  Nhaán maïnh caùch giaûi baèng phöông phaùp Gauss.
4. BAØI TAÄP VEÀ NHAØ:  5, 6, 7 SGK. Ngaøy soaïn: 10/11/2012
Chöông III: PHÖÔNG TRÌNH. HEÄ PHÖÔNG TRÌNH Tieát daïy: 23
Baøøi 3: BAØI TAÄP PHÖÔNG TRÌNH
VAØ HEÄ PHÖÔNG TRÌNH BAÄC NHAÁT NHIEÀU AÅN 44
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn
I. MUÏC TIEÂU: Kieán thöùc:
 Cuûng coá caùch giaûi phöông trình, heä phöông trình baäc nhaát nhieàu aån. Kó naêng:
 Giaûi thaønh thaïo heä phöông trình baäc nhaát 2 aån.
 Bieát giaûi heä phöông trình baäc nhaát 3 aån.
 Vaän duïng thaønh thaïo vieäc giaûi toaùn baèng caùch laäp heä phöông trình. Thaùi ñoä:
 Reøn luyeän tính caån thaän, chính xaùc.
 Luyeän tö duy linh hoaït thoâng qua vieäc giaûi heä phöông trình. II. CHUAÅN BÒ:
Giaùo vieân: Giaùo aùn. Heä thoáng baøi taäp.
Hoïc sinh: SGK, vôû ghi. OÂn taäp caùch giaûi heä phöông trình baäc nhaát nhieàu aån.
III. HOAÏT ÑOÄNG DAÏY HOÏC:
1. OÅn ñònh toå chöùc: Kieåm tra só soá lôùp.
2. Kieåm tra baøi cuõ: (Loàng vaøo quaù trình luyeän taäp) H. Ñ.
3. Giaûng baøi môùi: TL
Hoaït ñoäng cuûa Giaùo vieân
Hoaït ñoäng cuûa Hoïc sinh Noäi dung
Hoaït ñoäng 1: Luyeän kyõ naêng giaûi heä phöông trình baäc nhaát 2 aån
H1. Neân duøng phöông phaùp Ñ1. Coù theå duøng phöông phaùp 1. Giaûi caùc phöông trình: 15' naøo ñeå giaûi?
theá hoaëc coäng ñaïi soá. a) 2x  3y  1  11 5    x  2y  3  ; a) 7 7       b) 3x 4y 5  9 7   4x  2y  2 b)  ; 11 11   2 1 2
H2. Neân thöïc hieän pheùp bieán x  y  Ñ2. 3 2 3 ñoåi naøo? c)  c) Qui ñoàng, khöû maãu 1 3 1  x  y   9 1  3 4 2  ; 8 6       d) 0,3x 0,2y 0,5  d) Nhaân 2 veá vôùi 10 0,5x  0,4y  1,2
 Höôùng daãn theâm phöông (2; 0,5) phaùp ñònh thöùc.
Hoaït ñoäng 2: Luyeän kyõ naêng giaûi heä phöông trình baäc nhaát 3 aån 45
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn
 Höôùng daãn HS vaän duïng  11
2. Giaûi caùc phöông trình sau: 10' phöông phaùp Gauss. x   14   x  3y  2z  7 
(Cho HS nhaän xeùt vaø töï ruùt ra   a) 5 y  a)  2  x  4y  3z  8
caùch bieán ñoåi thích hôïp)  2  3x  y  z  5  1 z     x  3y  2z  8  7
b) 2x  2y  z  6 x  1  3x  y  z  6 b) y 1  z  2
Hoaït ñoäng 3: Luyeän kyõ naêng giaûi toaùn baèng caùch laäp heä phöông trình
H1. Neâu caùc böôùc giaûi toaùn Ñ1.
3. Coù hai daây chuyeàn may aùo
15' baèng caùch laäp heä phöông 3. Goïi x laø soá aùo do daây sô mi. Ngaøy thöù nhaát caû hai trình?
chuyeàn thöù nhaát may ñöôïc.
daây chuyeàn may ñöôïc 930 aùo.
y laø soá aùo do daây chuyeàn thöù Ngaøy thöù hai do daây chuyeàn hai may ñöôïc.
thöù nhaát taêng naêng suaát 18%, ÑK: x, y nguyeân döông
daây chuyeàn thöù hai taêng naêng Ta coù heä phöông trình:
suaát 15% neân caû hai daây  x  y  930
chuyeàn may ñöôïc 1083 aùo. 1   ,18x 1,15y  1083
Hoûi trong ngaøy thöù nhaát moãi
daây chuyeàn may ñöôïc bao  x  450  y  480 nhieâu aùo sô mi?
4. Goïi x (ngaøn ñoàng) laø giaù 4. Moät cöûa haøng baùn aùo sô mi, baùn moät aùo.
quaàn aâu nam vaø vaùy nöõ. Ngaøy
y (ngaøn ñoàng) laø giaù baùn moät thöù nhaát baùn ñöôïc 12 aùo, 21 quaàn.
quaàn vaø 18 vaùy, doanh thu laø
z (ngaøn ñoàng) laø giaù baùn moät 5349000 ñoàng. Ngaøy thöù hai vaùy.
baùn ñöôïc 16 aùo, 24 quaàn vaø ÑK: x, y, z > 0
12 vaùy, doanh thu laø 5600000 Ta coù heä phöông trình:
ñoàng. Ngaøy thöù ba baùn ñöôïc 1  2x 2  1y 1  8z  5349
24 aùo, 15 quaàn vaø 12 vaùy, 1   6x 2  4y 1  2z  5600
doanh thu laø 5259000 ñoàng. 24x 1  5y 1  2z  5259
Hoûi giaù baùn moãi aùo, moãi quaàn x  86
vaø noãi vaùy laø bao nhieâu?   y  125 z  98
Hoaït ñoäng 4: Cuûng coá
 Nhaán maïnh caùc caùch giaûi heä
3' phöông trình baäc nhaát hai aån, baäc nhaát ba aån.
4. BAØI TAÄP VEÀ NHAØ:
Söû duïng MTBT ñeå giaûi caùc heä phöông trình. Ngaøy soaïn: 10/11/2012
Chöông III: PHÖÔNG TRÌNH. HEÄ PHÖÔNG TRÌNH 46
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn
Tieát daïy: 24
THÖÏC HAØNH GIAÛI TOAÙN TREÂN MAÙY TÍNH CAÀM TAY I. MUÏC TIEÂU: Kieán thöùc:
 Cuûng coá caùch giaûi phöông trình, heä phöông trình baäc nhaát nhieàu aån. Kó naêng:
 Söû duïng MTBT thaønh thaïo ñeå giaûi heä phöông trình baäc nhaát 2 aån.
 Bieát söû duïng MTBT ñeå giaûi heä phöông trình baäc nhaát 3 aån. Thaùi ñoä:
 Reøn luyeän tính caån thaän, chính xaùc. II. CHUAÅN BÒ:
Giaùo vieân: Giaùo aùn. Heä thoáng baøi taäp.
Hoïc sinh: SGK, vôû ghi. Maùy tính boû tuùi.
III. HOAÏT ÑOÄNG DAÏY HOÏC:
1. OÅn ñònh toå chöùc: Kieåm tra só soá lôùp.
2. Kieåm tra baøi cuõ: (Loàng vaøo quaù trình luyeän taäp) H. Ñ.
3. Giaûng baøi môùi: TL
Hoaït ñoäng cuûa Giaùo vieân
Hoaït ñoäng cuûa Hoïc sinh Noäi dung
Hoaït ñoäng 1: Söû duïng MTBT giaûi heä phöông trình baäc nhaát 2 aån
 Chia nhoùm söû duïng MTBT  12
1. Giaûi caùc phöông trình:
15' ñeå giaûi heä phöông trình baäc x   a) 11    –> x 1,0244  a) 3x  5y  6 nhaát hai aån. 24  y y  0  ,5854   4x  7y  8 
 Cho 4 HS giaûi baèng tay ñeå  11    ñoái chieáu.  2 b) 2x 3y 5   5x  2y  4 x   b) 19    –> x 0,1053 33      c) 2x 3y 5 y y  1,7368  3   x  2y  8  19   34 d) 5x  3y  15 x    4x  5y  6 c) 13    –> x 2,6154 1  y y  0,0763   13  93 x   d) 37    –> x 2,5135 30  y y  0,8108   37
Hoaït ñoäng 2: Söû duïng MTBT giaûi heä phöông trình baäc nhaát 3 aån
 Chia nhoùm söû duïng MTBT  22
2. Giaûi caùc phöông trình sau:
10' ñeå giaûi heä phöông trình baäc x   101 x  0,2178 2x  3y  4z  5   nhaát ba aån.   a) 131 y 
–> y 1,2970 a)  4  x  5y  z  6
 Cho 2 HS giaûi baèng tay ñeå  101  3x  4y 3z  7 z  0  ,3861 ñoái chieáu.  39 z   x  2y  3z  2  101  b)  2x  y  2z  3   2  x  3y  z  5 47
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn x  4   x  4  b) 11   y  –> y 1,5714  7   12 z  1,7143 z   7
Hoaït ñoäng 3: Luyeän kyõ naêng söû duïng MTBT ñeå giaûi heä phöông trình
 Cho HS söû duïng MTBT ñeå x  1,5417
3. Giaûi caùc heä phöông trình: 15' 
giaûi vaø baùo keát quaû. a)  29 y  a)  2  x  5y  9  12   4x  2y  11 x  2    b)  3 b) 3x 4y 12  y  5x  2y  7  2  2x  3y  z  7  x  1  ,8235  c)  4  x  5y  3z  6  c) 19 y   x  2y 2z  5  17  39  x  4y  2z  1  z   d)  2  x  3y  z  6   17  3x 8y  z 12 x  4,2093   d) 7 y   43 z 1,9302
Hoaït ñoäng 4: Cuûng coá  Nhaán maïnh:
3' – Khi söû duïng MTBT ñeå giaûi
heä phöông trình, thöôøng chæ cho nghieäm gaàn ñuùng.
– Chuù yù thöù töï caùc heä soá x –> y –> z
4. BAØI TAÄP VEÀ NHAØ:
 Laøm baøi taäp oân chöông III. 48
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn
Ngaøy soaïn: 15/11/2012
Chöông III: PHÖÔNG TRÌNH. HEÄ PHÖÔNG TRÌNH Tieát daïy: 25
Baøøi daïy: OÂN TAÄP CHÖÔNG III I. MUÏC TIEÂU: Kieán thöùc:
 Cuûng coá caùc khaùi nieäm ñkxñ, pt töông ñöông, pt heä quaû, heä hai pt baäc nhaát hai aån.
 Naém vöõng caùch giaûi phöông trình qui veà phöông trình baäc nhaát, baäc hai.
 Naém ñöôïc caùch giaûi heä pt baäc nhaát hai aån. Kó naêng:
 Giaûi thaønh thaïo phöông trình qui veà phöông trình baäc nhaát, baäc hai.
 Bieát vaän duïng ñònh lí Viet ñeå giaûi toaùn.
 Giaûi thaønh thaïo heä phöông trình baäc nhaát hai aån.
 Bieát giaûi heä pt baäc nhaát ba aån baèng pp Gause. Thaùi ñoä:
 Reøn luyeän tính caån thaän, chính xaùc.
 Luyeän tö duy linh hoaït thoâng qua vieäc bieán ñoåi phöông trình. II. CHUAÅN BÒ:
Giaùo vieân: Giaùo aùn. Heä thoáng baøi taäp.
Hoïc sinh: SGK, vôû ghi. OÂn taäp caùc kieán thöùc ñaõ hoïc veà phöông trình, heä phöông trình.
III. HOAÏT ÑOÄNG DAÏY HOÏC:
1. OÅn ñònh toå chöùc: Kieåm tra só soá lôùp.
2. Kieåm tra baøi cuõ: (Loàng vaøo quaù trình oân taäp) H. Ñ.
3. Giaûng baøi môùi: TL
Hoaït ñoäng cuûa Giaùo vieân
Hoaït ñoäng cuûa Hoïc sinh Noäi dung
Hoaït ñoäng 1: Cuûng coá caùch tìm ñkxñ, xeùt pt töông ñöông
H1. Neâu ÑKXÑ cuûa caùc pt. Ñ1.
1. Giaûi caùc phöông trình sau:
10' Töø ñoù thöïc hieän caùc pheùp a) ÑKXÑ: x ≥ 5 –> S = {6}
a) x 5  x  x 5  6 bieán ñoåi pt?
b) ÑKXÑ: x = 1 –> S = 
b) 1 x  x  x 1  2 c) ÑKXÑ: x > 2 2 x 8 –> S = {2 2 } c) 
d) ÑKXÑ: x   –> S =  x  2 x  2 d) 3 + 2  x = 4x2 – x + x 3
Hoaït ñoäng 2: Luyeän kyõ naêng giaûi pt qui veà pt baäc nhaát, baäc hai
H1. Neâu caùch bieán ñoåi? Caàn Ñ1.
2. Giaûi caùc phöông trình sau:
10' chuù yù caùc ñieàu kieän gì? a) Qui ñoàng maãu. 2 3x  2x  3 3x  5  1 a) 
ÑK: 2x – 1 ≠ 0 –> S =   2x 1 2  9 b) 2 x  4 = x– 1 b) Bình phöông 2 veá. c) 4x  9 = 3 – 2x 5
ÑK: x – 1 ≥ 0 –> S =   d) 2x 1  3x  5 2 49
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn
c) Duøng ñònh nghóa GTTÑ. –> S = {2, 3}   d) S = 6  4,     5
Hoaït ñoäng 3: Luyeän kyõ naêng giaûi heä pt baäc nhaát hai aån, ba aån
H1. Neâu caùch giaûi? Ñ1.
3. Giaûi caùc heä phöông trình:
10'  Cho moãi nhoùm giaûi 1 heä pt  37 x a)  2  x  5y  9    a) 24  4x  2y  11  29 y      12 b) 3x 4y 12  5x  2y  7 x  2 b)   2x  3y  z  7   3  y   c)  4  x  5y  3z  6  2  x  2y 2z  5  c) 3 3 13 x   ;y  ;z    x  4y  2z  1  5 2 10 d)  2  x  3y  z  6   181 7 83  d) x  ;y  ;z   3x  8y  z  12  43 43 43
Hoaït ñoäng 4: Luyeän kyõ naêng giaûi toaùn baèng caùch laäp heä phöông trình
H1. Neâu caùc böôùc giaûi? Ñ1.
4. Hai coâng nhaân cuøng sôn 10'
Goïi t1 (giôø) laø thôøi gian ngöôøi moät böùc töôøng. Sau khi ngöôøi
thöù nhaát sôn xong böùc töôøng.
thöù nhaát laøm ñöôïc 7 giôø vaø
t2 (giôø) laø thôøi gian ngöôøi thöù ngöôøi thöù hai laøm ñöôïc 4 giôø
hai sôn xong böùc töôøng. ÑK: t
thì hoï sôn ñöôïc 5 böùc töôøng. 1, t2 > 0 9
Sau ñoù hoï cuøng laøm vieäc vôùi  7 4 5
nhau tröông 4 giôø nöõa thì chæ    1t t2 9 t  18   1
coøn laïi 1 böùc töôøng chöa 4 4 7   t  24    2 18 
sôn. Hoûi neáu moãi ngöôøi laøm 1 t t2 18
rieâng thì sau bao nhieâu giôø
moãi ngöôøi môùi sôn xong böùc töôøng?
Hoaït ñoäng 5: Cuûng coá  Nhaán maïnh:
3' – Caùch giaûi caùc daïng toaùn.
– Caùch xeùt caùc ñieàu kieän khi
thöïc hieän caùc pheùp bieán ñoåi pt
4. BAØI TAÄP VEÀ NHAØ:
 Laøm caùc baøi taäp coøn laïi.
 Ñoïc tröôùc baøi "Baát ñaúng thöùc" Ngaøy soaïn: 22/11/2012
Chöông IV: BAÁT ÑAÚNG THÖÙC. BAÁT PHÖÔNG TRÌNH Tieát daïy: 26
Baøøi 1: BAÁT ÑAÚNG THÖÙC 50
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn I. MUÏC TIEÂU: Kieán thöùc:
 Hieåu ñöôïc caùc khaùi nieäm veà BÑT.
 Naém ñöôïc caùc tính chaát cuûa BÑT.
 Naém ñöôïc caùc BÑT cô baûn vaø tính chaát cuûa chuùng. Kó naêng:
 Chöùng minh ñöôïc caùc BÑT ñôn giaûn.
 Vaän duïng thaønh thaïo caùc tính chaát cô baûn cuûa BÑT ñeå bieán ñoåi, töø ñoù giaûi ñöôïc caùc baøi
toaùn veà chöùng minh BÑT.
 Vaän duïng caùc BÑT Coâ–si, BÑT chöùa GTTÑ ñeå giaûi caùc baøi toaùn lieân quan. Thaùi ñoä:
 Töï giaùc, tích cöïc trong hoïc taäp.
 Bieát phaân bieät roõ caùc khaùi nieäm cô baûn, caùc tính chaát vaø vaän duïng trong töøng tröôøng hôïp cuï theå.
 Tö duy caùc vaán ñeà cuûa toaùn hoïc moät caùch loâgic vaø heä thoáng. II. CHUAÅN BÒ:
Giaùo vieân: Giaùo aùn. Heä thoáng caùc kieán thöùc ñaõ hoïc veà Baát ñaúng thöùc.
Hoïc sinh: SGK, vôû ghi. OÂn taäp caùc kieán thöùc ñaõ hoïc veà Baát ñaúng thöùc.
III. HOAÏT ÑOÄNG DAÏY HOÏC:
1. OÅn ñònh toå chöùc: Kieåm tra só soá lôùp.
2. Kieåm tra baøi cuõ: H. Ñ.
3. Giaûng baøi môùi: TL
Hoaït ñoäng cuûa Giaùo vieân
Hoaït ñoäng cuûa Hoïc sinh Noäi dung
Hoaït ñoäng 1: OÂn taäp khaùi nieäm Baát ñaúng thöùc
H1. Ñeå so saùnh 2 soá a vaø b, ta Ñ1. a < b  a – b < 0
I. OÂn taäp baát ñaúng thöùc
10' thöôøng xeùt bieåu thöùc naøo? a > b  a – b > 0
1. Khaùi nieäm baát ñaúng thöùc
Caùc meänh ñeà daïng "a < b"
H2. Trong caùc meänh ñeà, Ñ2.
hoaëc "a > b" ñgl BÑT. meänh ñeà naøo ñuùng? a) Ñ b) S c) Ñ a) 3,25 < 4 b) –5 > –4 1 4 c) – 2 ≤ 3
H3. Ñieàn daáu thích hôïp (=, <, >) vaøo oâ troáng? Ñ3. a) < a) 2 2  3 b) > b) 4  2 c) = 3 3 d) > c) 3 + 2 2  (1 + 2 )2
d) a2 + 1  0 (vôùi a  R)
Hoaït ñoäng 2: OÂn taäp Baát ñaúng thöùc heä quaû, töông ñöông 51
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn
 GV neâu caùc ñònh nghóa veà
2. BÑT heä quaû, töông ñöông
10' BÑT heä quaû, töông ñöông.
Neáu meänh ñeà "a < b c <
H1. Xeùt quan heä heä quaû, Ñ1.
d" ñuùng thì ta nôùi BÑT c < d
töông ñöông cuûa caùc caëp BÑT a) x > 2  x2 > 22
laø BÑT heä quaû cuûa a < b. Ta sau: b) x > 2  /x/ > 2
vieát: a < b c < d. a) x > 2 ; x2 > 22 c) x > 0  x2 > 0
Neáu a < b laø heä quaû cuûa c < b) /x/ > 2 ; x > 2 d) x > 0  x + 2 > 2
d vaø ngöôïc laïi thì hai BÑT c) x > 0 ; x2 > 0
töông ñöông nhau. Ta vieát: d) x > 0 ; x + 2 > 2
a < b c < d.
a < b a – b < 0
Hoaït ñoäng 3: OÂn taäp tính chaát cuûa Baát ñaúng thöùc
 GV giôùi thieäu gôïi yù cho HS  Caùc nhoùm ñoïc SGK, thaûo 3. Tính chaát cuûa BÑT
15' nhaéc laïi moät soá tính chaát cuûa luaän vaø thöïc hieän yeâu caàu cuûa BÑT. GV. Ñieàu kieän Noäi dung Teân goïi
a < b a + c < b + c (1)
Coäng hai veá cuûa BÑT vôùi moät soá c > 0
a < b ac < bc (2a)
Nhaân hai veá cuûa BÑT vôùi moät soá c < 0
a < b ac > bc (2b)
a < b vaø c < d a + c < b + d (3) Coäng hai veá BÑT cuøng chieàu a > 0, c > 0
a < b vaø c < d ac < bd (4)
Nhaân hai veá BÑT cuøng chieàu vôùi caùc soá döông n nguyeân
a < b a2n+1 < b2n+1 (5a)
Naâng hai veá cuûa BÑT leân moät luyõ thöøa döông
0 < a < b a2n < b2n (5b) a > 0
a < b a b (6a)
Khai caên hai veá cuûa moät BÑT a < b 3 3 a b (6b)  GV cho HS neâu VD minh
Ta coøn gaëp caùc BÑT khoâng hoaï baèng caùc BÑT soá.
ngaët: a ≤ b hoaëc a ≥ b.
Hoaït ñoäng 4: AÙp duïng chöùng minh BÑT
VD: Chöùng minh BÑT: Ñ. 5' a2 + b2 ≥ 2ab
Xeùt a2 + b2 – 2ab = (a – b)2 ≥ Daáu "=" xaûy ra khi naøo? 0
(Höôùng daãn HS caùch chöùng  ñpcm. minh) Daáu "=" xaûy ra  a = b.
Hoaït ñoäng 5: Cuûng coá  Nhaán maïnh:
5' – Caùc tính chaát cuûa BÑT
– Caùc tröôøng hôïp deã phaïm sai
laàm khi söû duïng caùc tính chaát.
4. BAØI TAÄP VEÀ NHAØ:  Baøi 1, 2 SGK.
 Ñoïc tieáp baøi "Baát ñaúng thöùc" Ngaøy soaïn: 22/11/2012
Chöông IV: BAÁT ÑAÚNG THÖÙC. BAÁT PHÖÔNG TRÌNH Tieát daïy: 27
Baøøi 1: BAÁT ÑAÚNG THÖÙC (tt) 52
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn I. MUÏC TIEÂU: Kieán thöùc:
 Hieåu ñöôïc caùc khaùi nieäm veà BÑT.
 Naém ñöôïc caùc tính chaát cuûa BÑT.
 Naém ñöôïc caùc BÑT cô baûn vaø tính chaát cuûa chuùng. Kó naêng:
 Chöùng minh ñöôïc caùc BÑT ñôn giaûn.
 Vaän duïng thaønh thaïo caùc tính chaát cô baûn cuûa BÑT ñeå bieán ñoåi, töø ñoù giaûi ñöôïc caùc baøi
toaùn veà chöùng minh BÑT.
 Vaän duïng caùc BÑT Coâ–si, BÑT chöùa GTTÑ ñeå giaûi caùc baøi toaùn lieân quan. Thaùi ñoä:
 Töï giaùc, tích cöïc trong hoïc taäp.
 Bieát phaân bieät roõ caùc khaùi nieäm cô baûn, caùc tính chaát vaø vaän duïng trong töøng tröôøng hôïp cuï theå.
 Tö duy caùc vaán ñeà cuûa toaùn hoïc moät caùch loâgic vaø heä thoáng. II. CHUAÅN BÒ:
Giaùo vieân: Giaùo aùn. Heä thoáng caùc kieán thöùc ñaõ hoïc veà Baát ñaúng thöùc.
Hoïc sinh: SGK, vôû ghi. OÂn taäp caùc kieán thöùc ñaõ hoïc veà Baát ñaúng thöùc.
III. HOAÏT ÑOÄNG DAÏY HOÏC:
1. OÅn ñònh toå chöùc: Kieåm tra só soá lôùp.
2. Kieåm tra baøi cuõ: (3')
H. Neâu moät soá tính chaát cuûa BÑT? Ñ.
3. Giaûng baøi môùi: TL
Hoaït ñoäng cuûa Giaùo vieân
Hoaït ñoäng cuûa Hoïc sinh Noäi dung
Hoaït ñoäng 1: Tìm hieåu baát ñaúng thöùc Coâsi
 GV cho moät soá caëp soá a, b   Caùc nhoùm thöïc hieän yeâu II. Baát ñaúng thöùc Coâsi 10'
caàu, töø ñoù ruùt ra nhaän xeùt:
0. Cho HS tính ab vaø a b ,
1. Baát ñaúng thöùc Coâsi 2 a b ab   a b ab  
, a, b 0 roài so saùnh. 2 2
 Höôùng daãn HS chöùng minh. a b 1
Daáu "=" xaûy ra a = b. ab
  (a b  2 ab) 2 2 1 = 2
 ( a b)  0 2 H. Khi naøo A2 = 0 ? Ñ. A2 = 0  A = 0
Hoaït ñoäng 2: Tìm hieåu caùc öùng duïng cuûa BÑT Coâsi
H1. Vaän duïng BÑT Coâsi, 1 a 2. Caùc heä quaû 15'  a 1
chöùng minh BÑT a + 1 2 ? Ñ1.  . a  1 HQ1:
a + 1 2, a > 0 a 2 a a
 GV cho 1 giaù trò S, yeâu caàu  Tích xy lôùn nhaát khi x = y.
HQ2: Neáu x, y cuøng döông vaø
HS xeùt caùc caëp soá x, y sao cho
coù toång x + y khoâng ñoåi thì
x + y = S. Nhaän xeùt caùc tích
tích x.y lôùn nhaát khi vaø chæ khi xy ? x y S xyx = y.  
 Höôùng daãn HS chöùng minh. 2 2
YÙ nghóa hình hoïc: Trong taát caû
caùc hình chöõ nhaät coù cuøng chu 53
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn  x + y  chu vi hcn
vi thì hình vuoâng coù dieän tích
 Höôùng daãn HS nhaän xeùt yù x.y  dieän tích hcn lôùn nhaát. nghóa hình hoïc. x = y  hình vuoâng
HQ3: Neáu x, y cuøng döông vaø
coù tích x.y khoâng ñoåi thì toång x
+ y nhoû nhaát khi vaø chæ khi x = y.
YÙ nghóa hình hoïc: Trong taát caû
caùc hình chöõ nhaät coù cuøng
dieän tích thì hình vuoâng coù chu vi nhoû nhaát.
Hoaït ñoäng 3: Tìm hieåu baát ñaúng thöùc chöùa daáu GTTÑ
III. BÑT chöùa daáu GTTÑ
10' H1. Nhaéc laïi ñònh nghóa veà Ñieàu kieän Noäi dung GTTÑ ? /x/ 0, /x/ x, /x/ –x
/x/ a –a x a a> 0
H2. Nhaéc laïi caùc tính chaát veà
/x/ a x –a hoaëc x a GTTÑ ñaõ bieát ?
/a/ – /b/ /a + b/ /a/ + /b/
VD: Cho x  [–2; 0]. Chöùng minh: /x + 1/  1
H3. Nhaéc laïi ñònh nghóa x  [–2; 0]  –2  x  0 khoaûng, ñoaïn ?
 –2 + 1  x + 1  0 + 1  –1  x + 1  1  /x + 1/  1
Hoaït ñoäng 4: Cuûng coá  Nhaán maïnh:
5' + BÑT Coâsi vaø caùc öùng duïng
+ Caùc tính chaát veà BÑT chöùa GTTÑ. Caâu hoûi: 1) Tìm x: 1) a) x2 > 4 x   a) x2 > 4 b) x2 < 3  2 x  2
2) Cho a, b > 0. Chöùng minh:
b) x2 < 3  – 3  x  3 a b   2 b a
4. BAØI TAÄP VEÀ NHAØ:  Baøi 3, 4, 5, 6 SGK.
 OÂn taäp kieán thöùc HK1 Ngaøy soaïn: 1/12/2012
Chöông IV: BAÁT ÑAÚNG THÖÙC. BAÁT PHÖÔNG TRÌNH Tieát daïy: 28
Baøøi 1: BAÁT ÑAÚNG THÖÙC –BÀI TẬP I. MUÏC TIEÂU: 54
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn Kieán thöùc:
 Hieåu ñöôïc caùc khaùi nieäm veà BÑT.
 Naém ñöôïc caùc tính chaát cuûa BÑT.
 Naém ñöôïc caùc BÑT cô baûn vaø tính chaát cuûa chuùng. Kó naêng:
 Chöùng minh ñöôïc caùc BÑT ñôn giaûn.
 Vaän duïng thaønh thaïo caùc tính chaát cô baûn cuûa BÑT ñeå bieán ñoåi, töø ñoù giaûi ñöôïc caùc baøi
toaùn veà chöùng minh BÑT.
 Vaän duïng caùc BÑT Coâ–si, BÑT chöùa GTTÑ ñeå giaûi caùc baøi toaùn lieân quan. Thaùi ñoä:
 Töï giaùc, tích cöïc trong hoïc taäp.
 Bieát phaân bieät roõ caùc khaùi nieäm cô baûn, caùc tính chaát vaø vaän duïng trong töøng tröôøng hôïp cuï theå.
 Tö duy caùc vaán ñeà cuûa toaùn hoïc moät caùch loâgic vaø heä thoáng. II. CHUAÅN BÒ:
Giaùo vieân: Giaùo aùn. Heä thoáng caùc kieán thöùc ñaõ hoïc veà Baát ñaúng thöùc.
Hoïc sinh: SGK, vôû ghi. OÂn taäp caùc kieán thöùc ñaõ hoïc veà Baát ñaúng thöùc.
III. HOAÏT ÑOÄNG DAÏY HOÏC:
1. OÅn ñònh toå chöùc: Kieåm tra só soá lôùp.
Hoaït ñoäng 1: Kieåm tra baøi cuõ .Thôøi gian:10p Hoaït ñoäng cuûa HS Hoaït ñoäng cuûa GV Noäi dung caàn ghi Nghe hieåu nhieäm vuï
Goïi 1 hs kieåm tra laïi kieán thöùc cuõ: Laøm baøi taäp aùp duïng
Neâu ñònh lyù veà baát ñaúng thöùc coâ-si?
Nhaän xeùt vaø hoaøn chænh Ad:cho 2 soá a vaø b döông .Chöùng minh raèng : lôøi giaûi (a+b) 1 1      4  a b
Caùc hs khaùc nhaän xeùt vaø laøm baøi taäp aùp duïng vaøo vôû
Choïn 3 vôû coù keát quaû nhanh nhaát
Hoaït ñoäng 2: baøi taäp 1,2 sgk tr79 .Thôøi gian:10p Hoaït ñoäng cuûa HS Hoaït ñoäng cuûa GV Noäi dung caàn ghi 1/ d.
Chia 4 nhoùm hoïc taäp vaø laøm vieäc theo nhoùm Baøi taäp 1 2/ 5 -1
Mñ1:Caû 4 nhoùm cho keát quaû vaø giaûi thích ôû Baøi taäp 2 x caùch choïn cuûa mình Giaûi thích:vì x>5
Mñ2:traû lôøi caâu hoûi sau: 0< 5 <1 ;1< 5 +1 Caâu a sai vì sao? x x
Vôùi x>5 ,haõy so saùnh 5 vaø x 5 -1< 0 ; x >1 x 5 x 5
Hoaït ñoäng 3: Baøi taäp 3 sgk tr79 .Thôøi gian:10p 55
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn Hoaït ñoäng cuûa hs Hoaït ñoäng cuûa GV Noäi dung caàn ghi Nghe hieåu nhieäm vuï vaø 3a/ Baøi taäp 3
thöïc hieän tuøy töøng möùc ñoä Mñ1:hs töï giaûi quyeát
Tìm caùch giaûi ,trình baøy
Mñ2 :hs traû lôøi caâu hoûi gôïi yù sau: caùch giaûi
Khi naøo thì 3 soá a ,b, c laø ñoä daøi 3 caïnh cuûa 1 Chænh söõa hoaøn thieän tam giaùc?
( b-c)2Mñ3 :( b-c)2(b-c-a)(b-c+a) < 0
<=>(b-c-a)(b-c+a) < 0
Khoâng maát tính toång quaùt ta cuõng coù
a ,b,c laøñoä daøi 3 caïnh (a-b)2 tam giaùc neân : a+c>b => b-c-a < 0 a+b>c => b-c+a>0 =>(b-c-a)(b-c+a) < 0
3b/suy ra töø keát quaû caâu a (ñuùng)
Coäng veá vôùi veá 3 keát quaû treân ta suy ra ñpcm
Hoaït ñoäng 4: Baøi taäp 4,5,6 sgk tr79 .Thôøi gian:10p Hoaït ñoäng cuûa hs Hoaït ñoäng cuûa GV Noäi dung caàn ghi
Nghe hieåu nhieäm vuï 4/hd:ta duøng pheùp bieán ñoåi töông ñöông Baøi taäp 4
Tìm phöông aùn thaéng Xeùt hieäu:x3+y3-(x2y+xy2)= Baøi taäp 5 Trình baøy keát quaû
Hs bieán ñoåi ñeå ñöa ñöôïc veà keát quaû Baøi taäp 6
Chænh söõa hoaøn thieän =(x+y)(x2+y2-xy) –xy(x+y) =(x+y)(x2-2xy+y2) =(x+y)(x-y)2
Nhaän xeùt keát quaû sau khi ñaõ bieán ñoåi
5/höôùng daãn hs tìm caùch giaûi baøi toaùn,khoâng trình baøy baøi giaûi Ñaët x =t Xeùt 2 tröôøng hôïp : * 0  x <1 * x 1
6/Hd:Goïi H laø tieáp ñieåm cuûa ñöôøng thaúng AB vôùi
ñöôøng troøn .Ta aùp duõng baát ñaúng thöùc coâ-si: AB=HA+HB  2 H . A HB
AB ngaén nhaát khi ñaúng thöùc xaûy ra <=>?
Hoaït ñoäng 5: Cuõng coá daën doø .Thôøi gian:5p Ngaøy soaïn: 28/11/2012 Tieát daïy: 29
Baøøi daïy: OÂN TAÄP HOÏC KÌ I I. MUÏC TIEÂU:
Kieán thöùc: Cuûng coá caùc kieán thöùc veà: 56
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn
 Meänh ñeà – Taäp hôïp.
 Haøm soá – Haøm soá baäc nhaát – Haøm soá baäc hai.
 Phöông trình – Phöông trình baäc nhaát – Phöông trình baäc hai.
 Heä phöông trình baäc nhaát nhieàu aån.  Baát ñaúng thöùc.
Kó naêng: Thaønh thaïo vieäc giaûi caùc baøi toaùn veà:
 Meänh ñeà – Caùc pheùp toaùn taäp hôïp hôïp.
 Tìm taäp xaùc ñònh, xeùt söï bieán thieân, xeùt tính chaün leû, veõ ñoà thò cuûa haøm soá baäc nhaát, baäc hai.
 Giaûi vaø bieän luaän phöông trình baäc nhaát, baäc hai.
 Giaûi vaø bieän luaän heä phöông trình baäc nhaát hai aån.
 Chöùng minh baát ñaúng thöùc. Thaùi ñoä:
 Reøn luyeän tính caån thaän, chính xaùc.
 Luyeän tö duy toång hôïp, suy luaän linh hoaït. II. CHUAÅN BÒ:
Giaùo vieân: Giaùo aùn. Heä thoáng baøi taäp.
Hoïc sinh: SGK, vôû ghi. OÂn taäp toaøn boä kieán thöùc hoïc kì 1.
III. HOAÏT ÑOÄNG DAÏY HOÏC:
1. OÅn ñònh toå chöùc: Kieåm tra só soá lôùp.
2. Kieåm tra baøi cuõ: (Loàng vaøo quaù trình oân taäp) H. Ñ.
3. Giaûng baøi môùi: TL
Hoaït ñoäng cuûa Giaùo vieân
Hoaït ñoäng cuûa Hoïc sinh Noäi dung
Hoaït ñoäng 1: Cuûng coá kieán thöùc veà Meänh ñeà – Taäp hôïp
H1. Nhaéc laïi caùch laäp meänh Ñ1.
1. Laäp meänh ñeà phuû ñònh cuûa 10' ñeà phuû ñònh ? a) xR: x + 3  5 caùc meänh ñeà sau:
b) xN: x khoâng chia heát 3 a) xR: x + 3 = 5 c) xR: x > 10
b) xN: x laø boäi cuûa 3 c) xR: x  10
H2. Neâu caùch xaùc ñònh giao, Ñ2. Bieåu dieãn leân truïc soá.
2. Xaùc ñònh X  Y, X  Y,
hôïp, hieäu cuûa caùc taäp con cuûa a) X  Y = (–; 5] X \ Y neáu: taäp R ? X  Y = [–3; 2]
a) X = [–3; 5], Y = (–; 2] X \ Y = (2; 5]
b) X = (–; 5), Y = [0; +)
c) X = (–; 3), Y = (3; +)
Hoaït ñoäng 2: Cuûng coá caùc kieán thöùc veà haøm soá
H1. Neâu ñieàu kieän xaùc ñònh Ñ1.
3. Tìm taäp xaùc ñònh cuûa caùc 20' cuûa haøm soá ?
a) 2  x  0  D = [1; 2] haøm soá:  x 1  0
a) y = 2  x x 1  2 x  4  0 x b) y = b) 3   x  0  x  2 2  x  4  3x 2
x  4  3x  0 57
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn 4. Cho haøm soá : Ñ2. y = (m–1)x + 2m – 3
H2. Neâu ñieàu kieän haøm soá + m > 1: ñoàng bieán
a) Vôùi giaù trò naøo cuûa m, haøm
ñoàng bieán, nghòch bieán ? + m < 1: nghòch bieán
soá ñoàng bieán, nghòch bieán.
b) Ñònh m ñeå ñoà thò haøm soá ñi qua ñieåm A(1; –2). Ñ3.
a b c  1  
5. Cho (P): y = ax2 + bx + c.
H3. Neâu ñieàu kieän A, B, C  a) 4a  2b c  3
a) Tìm a, b, c bieát (P) ñi qua (P) ?
 a b c  3 
A(1; –1), B(2; 3), C(–1; –3). a  1
b) Xeùt söï bieán thieân vaø veõ (P)   b  1 vöøa tìm ñöôïc. c  3 
Hoaït ñoäng 3: Cuûng coá vieäc giaûi phöông trình, heä phöông trình
H1. Nhaéc laïi caùch giaûi caùc Ñ1.
6. Giaûi caùc phöông trình: 10' daïng phöông trình ?  1 2x 1 neáu x
a) 2x 1  x  3   a) 2 2x 1   1 b) 2
x  4x 1  x  2 1   2x neáu x   2 c) m2x – 1 = m – x  3 b) 2
x  4x  4  x  2  y  7  x 2 c) (m2 + 1)x = m + 1 d)  2    5y  3 d) Ñaët aån phuï: 1 u   x  2 x  2
  3u y  7 
2u  5y  3
Hoaït ñoäng 4: Cuûng coá
5'  Nhaán maïnh caùch giaûi caùc daïng toaùn
4. BAØI TAÄP VEÀ NHAØ:
 Baøi taäp oân taäp Hoïc kì 1 Ngaøy soaïn: 10/12/2012 Tieát daïy: 30
Baøøi daïy: KIEÅM TRA HOÏC KÌ I I. MUÏC TIEÂU:
Kieán thöùc: Cuûng coá caùc kieán thöùc ñaõ hoïc trong hoïc kì 1.
 Meänh ñeà – Taäp hôïp.
 Haøm soá – Haøm soá baäc nhaát – Haøm soá baäc hai. 58
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn
 Phöông trình – Phöông trình baäc nhaát – baäc hai. Heä phöông trình baäc nhaát nhieàu aån.  Baát ñaúng thöùc.
Kó naêng: Thaønh thaïo vieäc giaûi caùc daïng toaùn:
 Caùc pheùp toaùn veà meänh ñeà – taäp hôïp.
 Tìm taäp xaùc ñònh, xeùt söï bieán thieân, tính chaün leû cuûa haøm soá.
 Khaûo saùt haøm soá baäc nhaát, baäc hai.
 Giaûi vaø bieän luaän phöông trình baäc nhaát, baäc hai, phöông trình qui veà baäc nhaát, baäc hai.
 Giaûi heä phöông trình baäc nhaát nhieàu aån. Thaùi ñoä:
 Reøn luyeän tính caån thaän, chính xaùc. Luyeän tö duy linh hoaït, saùng taïo. II. CHUAÅN BÒ:
Giaùo vieân: Ñeà kieåm tra.
Hoïc sinh: OÂn taäp kieán thöùc ñaõ hoïc trong hoïc kì 1. III. MA TRAÄN ÑEÀ: Nhaän bieát Thoâng hieåu Vaän duïng Chuû ñeà Toång TNKQ TL TNKQ TL TNKQ TL 1 1 Meänh ñeà – Taäp hôïp 0,5 0,25 0,25 2 2 2 Haøm soá 3,0 0,25 0,25 1,0 2 2 2 Phöông trình 3,0 0,25 0,25 1,0 Toång 0,75 1,25 2,0 0,5 2,0 6,5
IV. NOÄI DUNG ÑEÀ KIEÅM TRA: A. Phaàn traéc nghieäm:
Caâu 1: Meänh ñeà "x  R: x2 + 3x – 4 < 0" coù meänh ñeà phuû ñònh laø:
A. "x  R: x2 + 3x – 4  0"
B. "x  R: x2 + 3x – 4 > 0"
C. "x  R: x2 + 3x – 4  0"
D. "x  R: x2 + 3x – 4 = 0"
Caâu 2: Soá caùc taäp con cuûa taäp hôïp A = {0, 1, 2, 3} laø: A. 16 B. 8 C. 12 D. 6 1
Caâu 3: Taäp xaùc ñònh cuûa haøm soá y = x 1  laø: x 1 A. [–1; +) \ {1} B. [1; +) \ {–1} C. R \ {1} D. [–1; +)
Caâu 4: Haøm soá y = 2x – m + 1
A. Luoân ñoàng bieán treân R
B. Ñoàng bieán treân R vôùi m < 1
C. Luoân nghòch bieán treân R
D. Nghòch bieán treân R vôùi m > 1
Caâu 5: Haøm soá y = x2 – 2x + 3
A. Ñoàng bieán treân khoaûng (1; +)
B. Ñoàng bieán treân khoaûng (0; +)
C. Nghòch bieán treân khoaûng (0; +)
D. Nghòch bieán treân khoaûng (1; +)
Caâu 6: Ñoà thò cuûa haøm soá y = –x2 + 2x + 1 ñi qua ñieåm A. A(–1; –2) B. B(–1; 0) C. C(1; 3) D. D(2; 9) x  2
Caâu 7: Ñieàu kieän xaùc ñònh cuûa phöông trình: x + 3 – = 0 laø: x  3 A. x > – 3 B. x  –3 C. x  – 3 D. x  2
Caâu 8: Vôùi giaù trò naøo cuûa m thì phöông trình: (m2 – 4)x = m(m + 2) voâ nghieäm: A. m = 2 B. m = –2 C. m  2 D. m = 2 59
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn
Caâu 9: Vôùi giaù trò naøo cuûa m thì phöông trình: x2 – mx + 1 = 0 coù 1 nghieäm: A. m = 2 B. m = 4 C. m  2 D. m  2
Caâu 10: Caëp soá (2; –1) laø nghieäm cuûa phöông trình naøo döôùi ñaây: A. 3x + 2y = 4 B. 3x + 2y = 8 C. 2x + 3y = 7 D. 2x + 3y = –1 B. Phaàn töï luaän:
Baøi 1: Cho haøm soá y = x2 – 4x + 3 (1).
a) Tìm toaï ñoä ñænh vaø truïc ñoái xöùng cuûa ñoà thò haøm soá (1).
b) Vôùi giaù trò naøo cuûa m thì ñ.thaúng (d): y = mx + m – 1 caét ñoà thò cuûa haøm soá (1) taïi hai ñieåm phaân bieät.
Baøi 2: Cho phöông trình: (m – 1)x2 + 2x – 1 = 0 (2)
a) Tìm m ñeå phöông trình (2) coù nghieäm x = –1. Khi ñoù tìm nghieäm coøn laïi cuûa phöông trình (2).
b) Tìm m ñeå phöông trình (2) coù 2 nghieäm cuøng daáu.
V. ÑAÙP AÙN VAØ BIEÅU ÑIEÅM:
A. Phaàn traéc nghieäm:
1a) 2a) 3a) 4a) 5a) 6a) 7a) 8a) 9a) 10a) B. Töï luaän:
Baøi 1: (2 ñieåm) Cho haøm soá y = x2 – 4x + 3 (1).  b x    2  b a) Toaï ñoä ñænh I: 2a
(0,5 ñieåm) Truïc ñoái xöùng: (): x =   2 (0,5 y      1 2a  4a ñieåm)
b) (1 ñieåm) Phöông trình hoaønh ñoä giao ñieåm cuûa (1) vaø (d):
x2 – 4x + 3 = mx + m – 1  x2 – (m + 4)x + m – 4 = 0 (0,5 ñieåm)
+ (d) caét (1) taïi 2 ñieåm phaân bieät   = (m + 4)2 –4(m – 4) > 0 (0,5 ñieåm)
 m2 + 4m + 32 > 0  (m + 2)2 + 28 > 0  m  R (0,5 ñieåm)
Baøi 2: (2 ñieåm) Cho phöông trình: (m – 1)x2 + 2x – 1 = 0 (2) a)
+ x = –1 laø nghieäm cuûa (2)  m = 4 (0,5 ñieåm) x  1 1
+ (2)  3x2 + 2x – 1 = 0  
1  nghieäm coøn laïi laø x = (0,5 ñieåm) x  3  3 m  1 m  1 
b) (2) coù 2 nghieäm cuøng daáu   '  m  0
(0,5 ñieåm)  m  0  0  m < 1 (0,5 ñieåm)  1   m  1 P    0  m 1
VI. KEÁT QUAÛ KIEÅM TRA: 0 – 3,4 3,5 – 4,9 5,0 – 6,4 6,5 – 7,9 8,0 – 10 Lôùp Só soá SL % SL % SL % SL % SL % 10A3 44 10A5 42 10A7 44 10A10 42 10A11 38 Ngaøy soaïn: 25/12/2012 Tieát daïy: 31
Baøøi daïy: TRAÛ BAØI KIEÅM TRA HOÏC KÌ I I. MUÏC TIEÂU:
Kieán thöùc: Nhaéc nhôû hoïc sinh nhöõng sai laàm veà:
 Meänh ñeà – Taäp hôïp. 60
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn
 Haøm soá – Haøm soá baäc nhaát – Haøm soá baäc hai.
 Phöông trình – Phöông trình baäc nhaát – baäc hai. Heä phöông trình baäc nhaát nhieàu aån.
Kó naêng: Nhaéc nhôû hoïc sinh nhöõng sai laàm veà:
 Caùc pheùp toaùn veà meänh ñeà – taäp hôïp.
 Tìm taäp xaùc ñònh, xeùt söï bieán thieân, tính chaün leû cuûa haøm soá.
 Khaûo saùt haøm soá baäc nhaát, baäc hai.
 Giaûi vaø bieän luaän phöông trình baäc nhaát, baäc hai, phöông trình qui veà baäc nhaát, baäc hai.
 Giaûi heä phöông trình baäc nhaát nhieàu aån. Thaùi ñoä:
 Reøn luyeän tính caån thaän, chính xaùc. Luyeän tö duy linh hoaït, saùng taïo. II. CHUAÅN BÒ:
Giaùo vieân: Ñeà kieåm tra vaø ñaùp aùn. Heä thoáng caùc sai laàm cuûa HS maéc phaûi.
Hoïc sinh: Vôû ghi.
III. HOAÏT ÑOÄNG DAÏY HOÏC:
1. OÅn ñònh toå chöùc: Kieåm tra só soá lôùp.
2. Kieåm tra baøi cuõ:
3. Giaûng baøi môùi:
Noäi dung ñeà kieåm tra Sai laàm cuûa HS A. Phaàn traéc nghieäm:
Caâu 1: Meänh ñeà "x  R: x2 + 3x – 4 < 0" coù meänh ñeà phuû  Chöa naém vöõng moái lieân heä giöõa 2 ñònh laø: meänh ñeà  vaø .
A. "x  R: x2 + 3x – 4  0" B. "x  R: x2 + 3x – 4 > 0"
 Chöa naém vöõng pheùp so saùnh caùc soá :
C. "x  R: x2 + 3x – 4  0" D. "x  R: x2 + 3x – 4 = 0" =,  , >, < , 
Caâu 2: Soá caùc taäp con cuûa taäp hôïp A = {0, 1, 2, 3} laø:
 Chöa naém vöõng caùch laäp caùc taäp con A. 16 B. 8 C. 12 D. 6 1
 Chöa thaønh thaïo caùc pheùp toaùn taäp hôïp
Caâu 3: Taäp xaùc ñònh cuûa haøm soá y = x 1  laø: x 1
treân caùc taäp con cuûa R.
A. [–1; +) \ {1} B. [1; +) \ {–1} C. R \ {1} D. [–1; +)
Caâu 4: Haøm soá y = 2x – m + 1
A. Luoân ñoàng bieán treân R
B. Ñoàng bieán treân R vôùi m < 1
C. Luoân nghòch bieán treân R D. Nghòch bieán treân R vôùi m > 1
Caâu 5: Haøm soá y = x2 – 2x + 3
A. Ñoàng bieán treân khoaûng (1; +)
B. Ñoàng bieán treân khoaûng (0; +)
C. Nghòch bieán treân khoaûng (0; +)
D. Nghòch bieán treân khoaûng (1; +)
Caâu 6: Ñoà thò cuûa haøm soá y = –x2 + 2x + 1 ñi qua ñieåm A. A(–1; –2)
B. B(–1; 0) C. C(1; 3) D. D(2; 9) x  2
Caâu 7: Ñieàu kieän xaùc ñònh cuûa ph.trình: x + 3 – = 0 x  3 61
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn laø:
A. x > – 3 B. x  –3 C. x  – 3 D. x  2
Caâu 8: Vôùi giaù trò naøo cuûa m thì phöông trình: (m2 – 4)x = m(m + 2) voâ nghieäm: A. m = 2
B. m = –2 C. m  2 D. m = 2
Caâu 9: Vôùi giaù trò naøo cuûa m thì phöông trình: x2 – mx + 1 = 0 coù 1 nghieäm:
A. m = 2 B. m = 4 C. m  2 D. m  2
Caâu 10: Caëp soá (2; –1) laø nghieäm cuûa ph.trình naøo döôùi ñaây: A. 3x + 2y = 4 B. 3x + 2y = 8 C. 2x + 3y = 7 D. 2x + 3y = –1 B. Phaàn töï luaän:
Baøi 1: Cho haøm soá y = x2 – 4x + 3 (1).
a) Tìm toaï ñoä ñænh vaø truïc ñoái xöùng cuûa ñoà thò haøm soá (1).
b) Vôùi giaù trò naøo cuûa m thì ñ.thaúng (d): y = mx + m – 1 caét ñoà
thò cuûa haøm soá (1) taïi hai ñieåm phaân bieät.
Baøi 2: Cho phöông trình: (m – 1)x2 + 2x – 1 = 0 (2)
a) Tìm m ñeå phöông trình (2) coù nghieäm x = –1. Khi ñoù tìm
nghieäm coøn laïi cuûa phöông trình (2).
b) Tìm m ñeå phöông trình (2) coù 2 nghieäm cuøng daáu.
4. BAØI TAÄP VEÀ NHAØ:
– OÂn laïi kieán thöùc hoïc kì 1.
– Ñoïc tröôùc baøi "Baát phöông trình vaø heä baát phöông trình moät aån" Ngaøy soaïn: 01/01/2013
Chöông IV: BAÁT ÑAÚNG THÖÙC. BAÁT PHÖÔNG TRÌNH Tieát daïy: 32
Baøøi 2: BAÁT PHÖÔNG TRÌNH
vaø HEÄ BAÁT PHÖÔNG TRÌNH MOÄT AÅN I. MUÏC TIEÂU: Kieán thöùc: 62
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn
 Naém ñöôïc caùc khaùi nieäm veà BPT, heä BPT moät aån; nghieäm vaø taäp nghieäm cuûa BPT, heä
BPT; ñieàu kieän cuûa BPT; giaûi BPT.
 Naém ñöôïc caùc pheùp bieán ñoåi töông ñöông. Kó naêng:
 Giaûi ñöôïc caùc BPT ñôn giaûn.
 Bieát caùch tìm nghieäm vaø lieân heä giöõa nghieäm cuûa PT vaø nghieäm cuûa BPT.
 Xaùc ñònh nhanh taäp nghieäm cuûa caùc BPT vaø heä BPT ñôn giaûn döa vaøo bieán ñoåi vaø laáy nghieäm treân truïc soá. Thaùi ñoä:
 Bieát vaän duïng kieán thöùc veà BPT trong suy luaän loâgic.
 Dieãn ñaït caùc vaán ñeà toaùn hoïc maïch laïc, phaùt trieån tö duy vaø saùng taïo. II. CHUAÅN BÒ:
Giaùo vieân: Giaùo aùn.
Hoïc sinh: SGK, vôû ghi. OÂn taäp caùc kieán thöùc ñaõ hoïc veà Baát ñaúng thöùc, Baát phöông trình.
III. HOAÏT ÑOÄNG DAÏY HOÏC:
1. OÅn ñònh toå chöùc: Kieåm tra só soá lôùp.
2. Kieåm tra baøi cuõ: (3')
H. Neâu moät soá tính chaát cuûa BÑT? Ñ.
3. Giaûng baøi môùi: TL
Hoaït ñoäng cuûa Giaùo vieân
Hoaït ñoäng cuûa Hoïc sinh Noäi dung
Hoaït ñoäng 1: Tìm hieåu khaùi nieäm baát phöông trình moät aån
 Cho HS neâu moät soá bpt moät  Caùc nhoùm thöïc hieän yeâu I. Khaùi nieäm baát phöông
13' aån. Chæ ra veá traùi, veá phaûi cuûa caàu. trình moät aån baát phöông trình. a) 2x + 1 > x + 2
1. Baát phöông trình moät aån b) 3 – 2x  x2 + 4
Baát phöông trình aån x laø c) 2x > 3
meänh ñeà chöùa bieán coù daïng:
f(x) < (g(x) (f(x) g(x)) (*)
H1. Trong caùc soá –2; 1 2 ; ; 2
Ñ1. –2 laø nghieäm.
trong ñoù f(x), g(x) laø nhöõng
10 , soá naøo laø nghieäm cuûa
bieåu thöùc cuûa x. bpt: 2x  3.
Soá x0 R thoaû f(x0) < g(x0) H2. Giaûi bpt ñoù ?
ñgl moät nghieäm cuûa (*). Ñ2. x  3 2
Giaûi bpt laø tìm taäp nghieäm cuûa noù.
H3. Bieåu dieãn taäp nghieäm Ñ3.
Neáu taäp nghieäm cuûa bpt laø treân truïc soá ?
taäp roãng ta noùi bpt voâ nghieäm.
Hoaït ñoäng 2: Tìm hieåu ñieàu kieän xaùc ñònh cuûa baát phöông trình
H1. Nhaéc laïi ñieàu kieän xaùc Ñ1. Ñieàu kieän cuûa x ñeå f(x) 2. Ñieàu kieän cuûa moät baát
7' ñònh cuûa phöông trình ? vaø g(x) coù nghóa. phöông trình
H2. Tìm ñkxñ cuûa caùc bpt sau: Ñ2.
Ñieàu kieän xaùc ñònh cuûa (*) laø a) 2
3  x x 1  x a) –1  x  3
ñieàu kieän cuûa x ñeå f(x) vaø g(x) b) x  0 coù nghóa. b) 1 > x + 1 x c) x > 0 d) x  R 63
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn c) 1 > x + 1 x d) x > 2 x 1
Hoaït ñoäng 3: Tìm hieåu baát phöông trình chöùa tham soá
H1. Haõy neâu moät bpt moät aån Ñ1. HS ñöa ra VD.
3. Baát phöông trình chöùa
7' chöùa 1, 2, 3 tham soá ?
a) 2x – m > 0 (tham soá m) tham soá
b) 2ax – 3 > x – b (th.soá a, b)
Trong moät bpt, ngoaøi caùc
chöõ ñoùng vai troø aån soá coøn coù
theå coù caùc chöõ khaùc ñöôïc xem
nhö nhöõng haèng soá, ñgl tham soá.
Giaûi vaø bieän luaän bpt chöùa
tham soá laø tìm taäp nghieäm cuûa
bpt töông öùng vôùi caùc giaù trò cuûa tham soá.
Hoaït ñoäng 4: Tìm hieåu Heä baát phöông trình moät aån
H1. Giaûi caùc bpt sau: Ñ1.
II. Heä BPT moät aån 10' a) 3x + 2 > 5 – x  3 
Heä bpt aån x goàm moät soá bpt a) S  ; b) 2x + 2  5 – x 1 = 4   
aån x maø ta phaûi tìm caùc b) S
nghieäm chung cuûa chuùng. 2 = (–; 1]
Moãi giaù trò cuûa x ñoàng thôøi H2. Giaûi heä bpt: Ñ2.
laø nghieäm cuûa taát caû caùc bpt
cuûa heä ñgl moät nghieäm cuûa heä. 3
x  2  5  x   3  S = S ;1
2x  2  5  x
1 S2 =  4 
Giaûi heä bpt laø tìm taäp   nghieäm cuûa noù.
Ñeå giaûi moät heä bpt ta giaûi
töøng bpt roài laáy giao caùc taäp nghieäm.
Hoaït ñoäng 5: Cuûng coá Nhaán maïnh:
3'  Caùch vaän duïng caùc tính chaát cuûa BÑT.
 Caùch bieåu dieãn taäp nghieäm treân truïc soá.
4. BAØI TAÄP VEÀ NHAØ:  Baøi 1, 2 SGK.
 Ñoïc tieáp baøi "Baát phöông trình vaø heä baát phöông trình moät aån" Ngaøy soaïn: 01/01/2013
Chöông IV: BAÁT ÑAÚNG THÖÙC. BAÁT PHÖÔNG TRÌNH Tieát daïy: 33
Baøøi 2: BAÁT PHÖÔNG TRÌNH
vaø HEÄ BAÁT PHÖÔNG TRÌNH MOÄT AÅN (tt) I. MUÏC TIEÂU: Kieán thöùc: 64
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn
 Naém ñöôïc caùc khaùi nieäm veà BPT, heä BPT moät aån; nghieäm vaø taäp nghieäm cuûa BPT, heä
BPT; ñieàu kieän cuûa BPT; giaûi BPT.
 Naém ñöôïc caùc pheùp bieán ñoåi töông ñöông. Kó naêng:
 Giaûi ñöôïc caùc BPT ñôn giaûn.
 Bieát caùch tìm nghieäm vaø lieân heä giöõa nghieäm cuûa PT vaø nghieäm cuûa BPT.
 Xaùc ñònh nhanh taäp nghieäm cuûa caùc BPT vaø heä BPT ñôn giaûn döa vaøo bieán ñoåi vaø laáy nghieäm treân truïc soá. Thaùi ñoä:
 Bieát vaän duïng kieán thöùc veà BPT trong suy luaän loâgic.
 Dieãn ñaït caùc vaán ñeà toaùn hoïc maïch laïc, phaùt trieån tö duy vaø saùng taïo. II. CHUAÅN BÒ:
Giaùo vieân: Giaùo aùn.
Hoïc sinh: SGK, vôû ghi. OÂn taäp caùc kieán thöùc ñaõ hoïc veà Baát ñaúng thöùc, Baát phöông trình.
III. HOAÏT ÑOÄNG DAÏY HOÏC:
1. OÅn ñònh toå chöùc: Kieåm tra só soá lôùp.
2. Kieåm tra baøi cuõ: (3') H. Giaûi caùc bpt: a) 3 – x  0 b) x + 1  0 ?
Ñ. a) S1 = (–; 3] b) S2 = [1; + )
3. Giaûng baøi môùi: TL
Hoaït ñoäng cuûa Giaùo vieân
Hoaït ñoäng cuûa Hoïc sinh Noäi dung
Hoaït ñoäng 1: Tìm hieåu khaùi nieäm baát phöông trình töông ñöông
H1. Hai bpt sau coù töông Ñ1. khoâng vì S1  S2
III. Moät soá pheùp bieán ñoåi bpt 10' ñöông khoâng ?
1. BPT töông ñöông a) 3 – x  0 b) x + 1
Hai bpt (heä bpt) coù cuøng taäp  0
nghieäm ñgl hai bpt (heä bpt) töông ñöông. H2. Heä bpt: 1
  x  0 töông Ñ2. 1    x  0 1   x  0   x  1
ñöông vôùi heä bpt naøo sau ñaây: 1   x  0 a) 1   x  0 b) 1   x  0 1     x  0 1   x  0 c) 1
  x  0 d) x 1 1    x  0
Hoaït ñoäng 2: Tìm hieåu caùc pheùp bieán ñoåi baát phöông trình
 GV giaûi thích thoâng qua ví
2. Pheùp bieán ñoåi töông ñöông 5' duï minh hoaï.
Ñeå giaûi moät bpt (heä bpt) ta bieán 1   x  0
ñoåi noù thaønh nhöõng bpt (heä bpt)  x  1 1     x  0 x  1 
töông ñöông cho ñeán khi ñöôïc bpt  –1  x  1
(heä bpt) ñôn giaûn maø ta coù theå
vieát ngay taäp nghieäm. Caùc pheùp
bieán ñoåi nhö vaäy ñgl caùc pheùp
bieán ñoåi töông ñöông.
Hoaït ñoäng 3: Tìm hieåu moät soá pheùp bieán ñoåi baát phöông trình 65
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn
H1. Giaûi bpt sau vaø nhaän xeùt Ñ1. (x+2)(2x–1) – 2  a) Coäng (tröø)
20' caùc pheùp bieán ñoåi ?  x2 + (x–1)(x+3)
Coäng (tröø) hai veá cuûa bpt vôùi (x+2)(2x–1) – 2   x  1
cuøng moät bieåu thöùc maø khoâng  x2 + (x–1)(x+3)
laøm thay ñoåi ñieàu kieän cuûa bpt ta
ñöôïc moät bpt töông ñöông.
H2. Giaûi bpt sau vaø nhaän xeùt Ñ2. b) Nhaân (chia) caùc pheùp bieán ñoåi ? 2 2
x x 1 x x
Nhaân (chia) hai veá cuûa bpt vôùi 2 2   x<1
x x 1 x x 2 2
cuøng moät bieåu thöùc luoân nhaän giaù x  2 x 1 2 2
trò döông (maø khoâng laøm thay ñoåi x  2 x 1
ñieàu kieän cuûa bpt) ta ñöôïc moät bpt töông ñöông.
Nhaân (chia) hai veá cuûa bpt vôùi
cuøng moät bieåu thöùc luoân nhaän giaù
trò aâm (maø khoâng laøm thay ñoåi
ñieàu kieän cuûa bpt) vaø ñoåi chieàu
bpt ta ñöôïc moät bpt töông ñöông.
H3. Giaûi bpt sau vaø nhaän xeùt Ñ3. c) Bình phöông caùc pheùp bieán ñoåi ? 2 2
x  2x  2  x  2x  3 Bình phöông hai veá cuûa moät bpt 2 2
x  2x  2  x  2x  3
coù hai veá khoâng aâm maø khoâng  x > 1 4
laøm thay ñoåi ñieàu kieän cuûa noù ta
ñöôïc moät bpt töông ñöông.
Hoaït ñoäng 4: Cuûng coá
 Nhaán maïnh caùc ñieåm caàn  Chuù yù:
5' löu yù khi thöïc hieän bieán ñoåi
+ Khi bieán ñoåi caùc bieåu thöùc ôû 2 baát phöông trình.
veá cuûa moät bpt thì ñk cuûa bpt coù
theå bò thay ñoåi. Neân ñeå tìm
nghieäm cuûa bpt ta phaûi tìm caùc
giaù trò cuûa x thoaû maõn ñk cuûa bpt ñoù.
+ Khi nhaân (chia) hai veá cuûa bpt
vôùi moät bieåu thöùc f(x) ta caàn löu
yù ñeán ñk veà daáu cuûa f(x).
+ Khi bình phöông 2 veá cuûa moät
bpt ta caàn löu yù ñeán ñk caû 2 veá ñeàu khoâng aâm.
4. BAØI TAÄP VEÀ NHAØ: Baøi 3, 4, 5 SGK. Ngaøy soaïn: 01/01/2013
Chöông IV: BAÁT ÑAÚNG THÖÙC. BAÁT PHÖÔNG TRÌNH Tieát daïy: 34
Baøøi 3: DAÁU CUÛA NHÒ THÖÙC BAÄC NHAÁT I. MUÏC TIEÂU: Kieán thöùc: 66
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn
 Bieát xeùt daáu moät nhò thöùc baäc nhaát, xeùt daáu moät tích, thöông cuûa nhieàu nhò thöùc baäc nhaát.
 Khaéc saâu phöông phaùp baûng, phöông phaùp khoaûng. Kó naêng:
 Xeùt ñöôïc daáu cuûa nhò thöùc baäc nhaát.
 Söû duïng thaønh thaïo pp baûng vaø pp khoaûng.
 Vaän duïng moät caùch linh hoaït vieäc xeùt daáu ñeå giaûi caùc BPT vaø xeùt daáu caùc bieåu thöùc ñaïi soá khaùc. Thaùi ñoä:
 Dieãn ñaït vaán ñeà roõ raøng, trong saùng.
 Tö duy naêng ñoäng, saùng taïo. II. CHUAÅN BÒ:
Giaùo vieân: Giaùo aùn. Heä thoáng baøi taäp.
Hoïc sinh: SGK, vôû ghi. OÂn taäp caùc kieán thöùc ñaõ hoïc veà Baát phöông trình baäc nhaát moät aån.
III. HOAÏT ÑOÄNG DAÏY HOÏC:
1. OÅn ñònh toå chöùc: Kieåm tra só soá lôùp.
2. Kieåm tra baøi cuõ: (3')
H. Cho f(x) = 3x + 5. Tìm x ñeå f(x) > 0; f(x) < 0 ?
Ñ. f(x) > 0  x > 5  ; f(x) < 0  x < 5  . 3 3
3. Giaûng baøi môùi:
TL Hoaït ñoäng cuûa Giaùo vieân
Hoaït ñoäng cuûa Hoïc sinh Noäi dung
Hoaït ñoäng 1: Tìm hieåu Ñònh lí veà daáu cuûa nhò thöùc baäc nhaát
H1. Cho VD veà nhò thöùc baäc Ñ1.
I. Ñònh lí veà daáu cuûa nhò thöùc
5' nhaát ? Chæ ra caùc heä soá a, b ? f(x) = 2x + 3; baäc nhaát g(x) = –2x + 3
1 Nhò thöùc baäc nhaát
Nhò thöùc baäc nhaát ñoái vôùi x laø bieåu
thöùc daïng f(x) = ax + b vôùi a 0.
H2. Xeùt f(x) = 2x + 3 Ñ2.
2. Daáu cuûa nhò thöùc baäc nhaát
15' a) Giaûi BPT f(x) > 0 vaø bieåu
Ñònh lí: Cho nhò thöùc f(x) = ax + b 2x + 3 > 0
dieãn taäp nghieäm treân truïc soá.  x > 3  2  b
b) Chæ ra caùc khoaûng maø
a.f(x) > 0 x  ; 3  a
trong ñoù f(x) cuøng daáu (traùi  2   daáu) vôùi a ?
a.f(x) < 0 x  ; b   a    b  x - a  traùi daáu cuøng daáu f(x) = ax = b 0 vôùi a vôùi a b
H3. Caàn chuù yù ñeán caùc yeáu Ñ3. heä soá a vaø giaù trò  a
Ví duï: Xeùt daáu nhò thöùc: toá naøo ?
a) f(x) = 3x + 2 b) g(x) = –2x + 5
Hoaït ñoäng 2: AÙp duïng xeùt daáu tích, thöông caùc nhò thöùc baäc nhaát
II. Xeùt daáu tích, thöông caùc nhò thöùc baäc nhaát 20'
Giaû söû f(x) laø moät tích (thöông)
cuûa nhöõng nhò thöùc baäc nhaát. AÙp 67
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn
duïng ñònh lí veà daáu cuûa nhò thöùc
baäc nhaát coù theå xeùt daáu töøng nhaân
 Höôùng daãn HS caùch laäp  Moãi nhoùm thöïc hieän moät töû. Laäp baûng xeùt daáu chung cho taát
baûng xeùt daáu baèng caùch cho yeâu caàu.
caû caùc nhò thöùc baäc nhaát coù maët
HS ñieàn vaøo choã troáng. 1 5
trong f(x) ta suy ra ñöôïc daáu cuûa x - -2  4 3 f(x). 4x-1 – – 0 + + x+2 – 0 + +
Ví duï: Xeùt daáu bieåu thöùc: -3x+5 + + + 0 – f(x) + 0 – 0 + –
f(x) = (4x 1)(x  2) 3  x  5
Hoaït ñoäng 3: Cuûng coá  Nhaán maïnh:
3' – Caùch xeùt daáu nhò thöùc
– Caùch vaän duïng vieäc xeùt
daáu nhò thöùc ñeå giaûi BPT
4. BAØI TAÄP VEÀ NHAØ:
 Laøm baøi taäp 1, 2, 3 SGK.
 Ñoïc tröôùc baøi "Baát phöông trình baäc nhaát hai aån". Ngaøy soaïn: 01/01/2013
Chöông IV: BAÁT ÑAÚNG THÖÙC. BAÁT PHÖÔNG TRÌNH Tieát daïy: 35
Baøøi 3: DAÁU CUÛA NHÒ THÖÙC BAÄC NHAÁT I. MUÏC TIEÂU: Kieán thöùc:
 Bieát xeùt daáu moät nhò thöùc baäc nhaát, xeùt daáu moät tích, thöông cuûa nhieàu nhò thöùc baäc nhaát. 68
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn
 Khaéc saâu phöông phaùp baûng, phöông phaùp khoaûng. Kó naêng:
 Xeùt ñöôïc daáu cuûa nhò thöùc baäc nhaát.
 Söû duïng thaønh thaïo pp baûng vaø pp khoaûng.
 Vaän duïng moät caùch linh hoaït vieäc xeùt daáu ñeå giaûi caùc BPT vaø xeùt daáu caùc bieåu thöùc ñaïi soá khaùc. Thaùi ñoä:
 Dieãn ñaït vaán ñeà roõ raøng, trong saùng.
 Tö duy naêng ñoäng, saùng taïo. II. CHUAÅN BÒ:
Giaùo vieân: Giaùo aùn. Heä thoáng baøi taäp.
Hoïc sinh: SGK, vôû ghi. OÂn taäp caùc kieán thöùc ñaõ hoïc veà Baát phöông trình baäc nhaát moät aån.
III. HOAÏT ÑOÄNG DAÏY HOÏC:
1. OÅn ñònh toå chöùc: Kieåm tra só soá lôùp.
2. Kieåm tra baøi cuõ: (3')
H. Cho f(x) = 3x + 5. Tìm x ñeå f(x) > 0; f(x) < 0 ?
Ñ. f(x) > 0  x > 5  ; f(x) < 0  x < 5  . 3 3
3. Giaûng baøi môùi:
TL Hoaït ñoäng cuûa Giaùo vieân
Hoaït ñoäng cuûa Hoïc sinh Noäi dung
Hoaït ñoäng 1: Tìm hieåu Ñònh lí veà daáu cuûa nhò thöùc baäc nhaát
H1. Cho VD veà nhò thöùc baäc Ñ1.
I. Ñònh lí veà daáu cuûa nhò thöùc
5' nhaát ? Chæ ra caùc heä soá a, b ? f(x) = 2x + 3; baäc nhaát g(x) = –2x + 3
1 Nhò thöùc baäc nhaát
Nhò thöùc baäc nhaát ñoái vôùi x laø bieåu
thöùc daïng f(x) = ax + b vôùi a 0.
H2. Xeùt f(x) = 2x + 3 Ñ2.
2. Daáu cuûa nhò thöùc baäc nhaát
10' a) Giaûi BPT f(x) > 0 vaø bieåu
Ñònh lí: Cho nhò thöùc f(x) = ax + b 2x + 3 > 0
dieãn taäp nghieäm treân truïc soá.  x > 3  2  b
b) Chæ ra caùc khoaûng maø
a.f(x) > 0 x  ; 3  a
trong ñoù f(x) cuøng daáu (traùi  2   daáu) vôùi a ?
a.f(x) < 0 x  ; b   a    b  x - a  traùi daáu cuøng daáu f(x) = ax = b 0 vôùi a vôùi a b
H3. Caàn chuù yù ñeán caùc yeáu Ñ3. heä soá a vaø giaù trò  a
Ví duï: Xeùt daáu nhò thöùc: toá naøo ?
a) f(x) = 3x + 2 b) g(x) = –2x + 5
Hoaït ñoäng 2: AÙp duïng xeùt daáu tích, thöông caùc nhò thöùc baäc nhaát
II. Xeùt daáu tích, thöông caùc nhò thöùc baäc nhaát 10'
Giaû söû f(x) laø moät tích (thöông)
cuûa nhöõng nhò thöùc baäc nhaát. AÙp
duïng ñònh lí veà daáu cuûa nhò thöùc 69
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn
baäc nhaát coù theå xeùt daáu töøng nhaân
 Höôùng daãn HS caùch laäp  Moãi nhoùm thöïc hieän moät töû. Laäp baûng xeùt daáu chung cho taát
baûng xeùt daáu baèng caùch cho yeâu caàu.
caû caùc nhò thöùc baäc nhaát coù maët
HS ñieàn vaøo choã troáng. 1 5 x - -2 
trong f(x) ta suy ra ñöôïc daáu cuûa 4 3 f(x). 4x-1 – – 0 + + x+2 – 0 + +
Ví duï: Xeùt daáu bieåu thöùc: -3x+5 + + + 0 – f(x) + 0 – 0 + –
f(x) = (4x 1)(x  2) 3  x  5
Hoaït ñoäng 3: AÙp duïng giaûi BPT
H1. Bieán ñoåi BPT ? x
III. AÙp duïng vaøo giaûi BPT 7' Ñ1. 1 1   0 1 x 1 x
1. BPT tích, BPT chöùa aån ôû maãu Ñ2. Ví duï: Giaûi BPT H2. Xeùt daáu f(x) ? x - 0 1  1 1 x – + 0 + 1 x 1– x + 0 + – f(x) – 0 + –  S = [0; 1)
H3. Xeùt daáu, khöû daáu GTTÑ Ñ3.
2. BPT chöùa aån trong daáu GTTÑ 2  x 1 = Ví duï: Giaûi BPT 7' =  2  x 1 neáu  2x 1 0 2
x 1 + x – 3 < 5 (*)
 Höôùng daãn pp khoaûng  2x 1 neáu  2x 1 0  1   x   2  (*) x  7   –7 1 x   2  x  3 <3
Hoaït ñoäng 5: Cuûng coá  Nhaán maïnh:
Vôùi a > 0 ta coù:
3' – Caùch xeùt daáu nhò thöùc
f (x)  a  –a  f(x)  a
– Caùch vaän duïng vieäc xeùt  f x  a
daáu nhò thöùc ñeå giaûi BPT
f (x)  a  ( ) 
f (x)  a
4. BAØI TAÄP VEÀ NHAØ:
 Laøm baøi taäp 1, 2, 3 SGK.
 Ñoïc tröôùc baøi "Baát phöông trình baäc nhaát hai aån". Ngaøy soaïn: 8/01/2013
Chöông IV: BAÁT ÑAÚNG THÖÙC. BAÁT PHÖÔNG TRÌNH Tieát daïy: 36
Baøøi 4: BAÁT PHÖÔNG TRÌNH BAÄC NHAÁT HAI AÅN I. MUÏC TIEÂU: Kieán thöùc:
 Hieåu ñöôïc khaùi nieäm BPT, heä BPT baäc nhaát hai aån; taäp nghieäm cuûa BPT, heä BPT baäc nhaát hai aån. 70
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn Kó naêng:
 Bieát xaùc ñònh mieàn nghieäm cuûa BPT, heä BPT baäc nhaát hai aån.
 AÙp duïng ñöôïc vaøo baøi toaùn thöïc teá. Thaùi ñoä:
 Lieän heä kieán thöùc ñaõ hoïc vôùi thöïc tieãn.
 Tö duy saùng taïo, lí luaän chaët cheõ. II. CHUAÅN BÒ:
Giaùo vieân: Giaùo aùn. Moät soá baøi toaùn thöïc teá. Hình veõ minh hoaï.
Hoïc sinh: SGK, vôû ghi. OÂn taäp caùc kieán thöùc ñaõ hoïc veà Haøm soá baäc nhaát.
III. HOAÏT ÑOÄNG DAÏY HOÏC:
1. OÅn ñònh toå chöùc: Kieåm tra só soá lôùp.
2. Kieåm tra baøi cuõ: (3')
H. Ñoà thò cuûa haøm soá baäc nhaát? Veõ ñoà thò cuûa haøm soá y = 3 – 2x? Ñ.
3. Giaûng baøi môùi:
TL Hoaït ñoäng cuûa Giaùo vieân
Hoaït ñoäng cuûa Hoïc sinh Noäi dung
Hoaït ñoäng 1: Tìm hieåu khaùi nieäm Baát phöông trình baäc nhaát hai aån
 Cho HS neâu moät soá pt baäc  Caùc nhoùm thöïc hieän yeâu I. Baát phöông trình baäc nhaát hai
5' nhaát hai aån. Töø ñoù chuyeån caàu. aån
sang bpt baäc nhaát hai aån. 3x + 2y < 1; x + 2y  2
BPT baäc nhaát hai aån x, y coù daïng toång quaùt laø:
ax + by c (1)
(<, , >)
trong a2 + b2 0).
Hoaït ñoäng 2: Tìm hieåu caùch bieåu dieãn taäp nghieäm cuûa BPT baäc nhaát hai aån  GV bieåu dieãn mieàn y
II. Bieåu dieãn taäp nghieäm cuûa
15' nghieäm cuûa moät soá bpt baäc
BPT baäc nhaát hai aån
nhaát hai aån ñaëc bieät. Töø ñoù 1
Trong mp Oxy, taäp hôïp caùc ñieåm
giôùi thieäu caùch bieåu dieãn O x
coù toaï ñoä laø nghieäm cuûa (1) ñgl mieàn nghieäm.
mieàn nghieäm cuûa noù.
Phaàn khoâng gaïch laø mieàn Ñöôøng thaúng ax + by = c chia
nghieäm cuûa bpt y 1
maët phaúng thaønh hai nöûa mp, moät y
trong hai nöûa mp ñoù (keå caû bôø) laø
mieàn nghieäm cuûa bpt ax + by c,
nöûa mp kia (keå caû bôø) laø mieàn O 1 x
nghieäm cuûa bpt ax + by c.
Phaàn khoâng gaïch laø mieàn Qui taéc thöïc haønh bieåu dieãn mieàn
nghieäm cuûa bpt x 1
nghieäm cuûa bpt ax + by c (1):
B1: Veõ ñöôøng thaúng : ax + by = c
B2: Laáy moät ñieåm M0(x0; y0) khoâng
thuoäc (thöôøng laáy goác toaï doä O).
VD: Bieåu dieãn hình hoïc taäp
B3: Tính ax0 + by0 vaø so saùnh côùi c nghieäm cuûa bpt: B4: Keát luaän: 2x + y  3
+ Neáu ax0 + by0 < c thì nöûa mp bôø
 GV höôùng daãn HS thöïc
chöùa M0 laø mieàn nghieäm cuûa (1).
hieän laàn löôït caùc böôùc.
+ Neáu ax0 + by0 > c thì nöûa mp bôø 71
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn
khoâng chöùa M0 laø mieàn nghieäm cuûa (1).
Chuù yù: Mieàn nghieäm cuûa (1) boû ñi
ñöôøng thaúng laø mieàn nghieäm cuûa bpt ax + by < c. Mieàn nghieäm laø mieàn khoâng bò gaïch cheùo
Hoaït ñoäng 3: AÙp duïng bieåu dieãn taäp nghieäm cuûa BPT baäc nhaát hai aån
 Cho caùc nhoùm thöïc hieän
Ví duï: Bieåu dieãn hình hoïc taäp
15' laàn löôït caùc böôùc. Moãi nhoùm nghieäm caùc BPT: duøng baûng con ñeå veõ. a) –3x + 2y > 0 b) 3x + y  6 c) 2x – y  3 d) x + y < 4 a) b) c) d)
Hoaït ñoäng 4: Cuûng coá
 Nhaán maïnh caùc böôùc bieåu
3' dieãn hình hoïc taäp nghieäm
cuûa BPT baäc nhaát hai aån.
4. BAØI TAÄP VEÀ NHAØ:
 Laøm baøi taäp 1, 2 SGK.
 Ñoïc tieáp baøi "Baát phöông trình baäc nhaát hai aån". Ngaøy soaïn: 05/01/2013
Chöông IV: BAÁT ÑAÚNG THÖÙC. BAÁT PHÖÔNG TRÌNH Tieát daïy: 37
Baøøi 4: BAØI TAÄP BPT BAÄC NHAÁT HAI AÅN I. MUÏC TIEÂU: Kieán thöùc:
 Cuûng coá khaùi nieäm BPT, heä BPT baäc nhaát hai aån; taäp nghieäm cuûa BPT, heä BPT baäc nhaát hai aån. Kó naêng:
 Bieát xaùc ñònh mieàn nghieäm cuûa BPT, heä BPT baäc nhaát hai aån.
 AÙp duïng ñöôïc vaøo baøi toaùn thöïc teá. Thaùi ñoä: 72
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn
 Lieän heä kieán thöùc ñaõ hoïc vôùi thöïc tieãn.
 Tö duy saùng taïo, lí luaän chaët cheõ. II. CHUAÅN BÒ:
Giaùo vieân: Giaùo aùn. Heä thoáng baøi taäp. Hình veõ minh hoaï.
Hoïc sinh: SGK, vôû ghi. OÂn taäp caùc kieán thöùc ñaõ hoïc veà BPT baäc nhaát hai aån.
III. HOAÏT ÑOÄNG DAÏY HOÏC:
1. OÅn ñònh toå chöùc: Kieåm tra só soá lôùp.
2. Kieåm tra baøi cuõ: (Loàng vaøo quaù trình luyeän taäp)
3. Giaûng baøi môùi:
TL Hoaït ñoäng cuûa Giaùo vieân
Hoaït ñoäng cuûa Hoïc sinh Noäi dung
Hoaït ñoäng 1: Luyeän kyõ naêng bieåu dieãn mieàn nghieäm cuûa BPT baäc nhaát hai aån H1. Bieán ñoåi BPT? Ñ1.
1. Bieåu dieãn hình hoïc taäp nghieäm 7' a)  x + 2y < 4 cuûa BPT: y
a) –x + 2 +2(y – 2) < 2(1 – x)
H2. Neâu caùc böôùc bieåu dieãn
b) 3(x – 1) + 4(y – 2) < 5x – 3
taäp nghieäm cuûa BPT baäc 2 b)  –x + 2y < 4 nhaát hai aån? y O x 4
 Caùc mieàn nghieäm cuûa caùc 2
BPT a), b) laø caùc nöûa mp – 4 O x khoâng keå bôø.
Hoaït ñoäng 2: Luyeän kyõ naêng bieåu dieãn mieàn nghieäm cuûa heä BPT baäc nhaát hai aån
H1. Neâu caùc böôùc bieåu dieãn Ñ1. a)
2. Bieåu dieãn hình hoïc taäp nghieäm
13' taäp nghieäm cuûa caùc heä BPT? y cuûa heä BPT: 3x y  1  0  x–2y=0 –x+y=3
x  2y  0 3 2  O   1 3y –3 –2 x
a) x  3y  2 b) x    2  x+3 2 2 y=–
 y x  3 2  x  0 y 2 O 3 3 x 2 b)
Hoaït ñoäng 3: Luyeän kyõ naêng vaän duïng vaøo baøi toaùn thöïc teá
 Cho caùc nhoùm thaûo luaän,  Caùc nhoùm thaûo luaän, 3. Coù 3 nhoùm maùy A, B, C duøng
15' phaân tích baøi toaùn, laäp ra caùc trình baøy keát quaû.
ñeå saûn xuaát ra 2 loaïi saûn phaåm I heä thöùc.
Goïi x SP loaïi I, y SP loaïi II vaø II. Ñeå saûn xuaát moät ñôn vò saûn
2x  2y  10
phaåm moãi loaïi phaûi laàn löôït duøng  2y  4 
caùc maùy thuoäc caùc nhoùm maùy
2x  4y  12
khaùc nhau. Soá maùy trong moät  x  0 
nhoùm vaø soá maùy cuûa töøng nhoùm  y  0
caàn thieát ñeå saûn xuaát ra moät ñôn
L = 3x + 5y ñaït lôùn nhaát.
vò saûn phaåm thuoäc moãi loaïi ñöôïc cho trong baûng sau: 73
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn
Soá maùy trong töøng nhoùm ñeå saûn Soá maùy trong Nhoùm xuaát moät ñôn vò SP moãi nhoùm Loaïi I Loaïi II A 10 2 2 B 4 0 2 C 12 2 4
 Cho caùc nhoùm laàn löôït bieåu dieãn caùc mieàn nghieäm cuûa Moät ñôn vò saûn phaåm I laõi 3000 ñ, caùc BPT.
moät ñôn vò saûn phaåm II laõi 5000 ñ.
Haõy laäp phöông aùn saûn xuaát hai y
loaïi saûn phaåm treân sao cho coù laõi 5 cao nhaát. 3 2 C B A O D5 6 x (x;y)
B(2;2) C(0;2) O(0;0) A(4;1) D(5;0) L=3x+5y 16 10 0 17 15
 maxL = 17 khi x = 4; y = 1
Hoaït ñoäng 4: Cuûng coá Nhaán maïnh:
5' + Caùc böôùc bieåu dieãn taäp nghieäm cuûa heä BPT baäc nhaát hai aån.
+ Caùch phaân tích, tìm caùc heä
thöùc trong baøi toaùn kinh teá.
4. BAØI TAÄP VEÀ NHAØ:
 Ñoïc tröôùc baøi " Daáu cuûa tam thöùc baäc hai". Ngaøy soaïn: 08/01/2013
Chöông IV: BAÁT ÑAÚNG THÖÙC. BAÁT PHÖÔNG TRÌNH Tieát daïy: 38
Baøøi 5: DAÁU CUÛA TAM THÖÙC BAÄC HAI I. MUÏC TIEÂU: Kieán thöùc:
 Naém ñöôïc ñònh lí veà daáu cuûa tam thöùc baäc hai. 74
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn
 Bieát vaø vaän duïng ñöôïc ñònh lí trong vieäc giaûi caùc baøi toaùn veà xeùt daáu tam thöùc baäc hai.
 Bieát söû duïng pp baûng, pp khoaûng trong vieäc giaûi toaùn.
 Bieát lieân heä giöõa baøi toaùn xeùt daáu vaø baøi toaùn veà giaûi BPT vaø heä BPT. Kó naêng:
 Phaùt hieän vaø giaûi caùc baøi toaùn veà xeùt daáu cuûa tam thöùc baäc hai.
 Vaän duïng ñöôïc ñònh lí trong vieäc giaûi BPT baäc hai vaø moät soá BPT khaùc. Thaùi ñoä:
 Bieát lieân heä giöõa thöïc tieãn vôùi toaùn hoïc.
 Tích cöïc, chuû ñoäng, töï giaùc trong hoïc taäp. II. CHUAÅN BÒ:
Giaùo vieân: Giaùo aùn. Hình veõ minh hoaï.
Hoïc sinh: SGK, vôû ghi. OÂn taäp kieán thöùc xeùt daáu nhò thöùc baäc nhaát.
III. HOAÏT ÑOÄNG DAÏY HOÏC:
1. OÅn ñònh toå chöùc: Kieåm tra só soá lôùp.
2. Kieåm tra baøi cuõ: (3')
H. Xeùt daáu bieåu thöùc: f(x) = (x – 2)(2x – 3)
Ñ. f(x) > 0 vôùi x  (–; 3 )  (2; +); f(x) < 0 vôùi x  ( 3 ; 2) 2 2
3. Giaûng baøi môùi: TL
Hoaït ñoäng cuûa Giaùo vieân
Hoaït ñoäng cuûa Hoïc sinh Noäi dung
Hoaït ñoäng 1: Tìm hieåu khaùi nieäm Tam thöùc baäc hai
 GV giôùi thieäu khaùi nieäm
I. Ñònh lí veà daáu cuûa tam 15' tam thöùc baäc hai. thöùc baäc hai
H1. Cho VD veà tam thöùc baäc Ñ1. Moãi nhoùm cho moät VD.
1. Tam thöùc baäc hai hai? f(x) = x2 – 5x + 4
Tam thöùc baäc hai ñoái vôùi x laø g(x) = x2 – 4x + 4
bieåu thöùc coù daïng: h(x) = x2 – 4x + 5
f(x) = ax2 + bx + c (a0)
H2. Tính f(4), f(–2), f(–1), Ñ2.
f(0) vaø nhaän xeùt daáu cuûa f(4) = 0; f(2) = –2 < 0 chuùng ?
f(–1) = 10 > 0; f(0) = 4 > 0 Ñ3.
H3. Quan saùt ñoà thò cuûa haøm y > 0, x  (–; 1)  (4; +)
soá y = x2 – 5x + 4 vaø chæ ra y < 0, x  (1; 4)
caùc khoaûng treân ñoà thò ôû phía Ñ4. Caùc nhoùm thaûo luaän
treân, phía döôùi truïc hoaønh ?
 < 0  f(x) cuøng daáu vôùi a
H4. Quan saùt caùc ñoà thò trong  = 0  f(x) cuøng daáu vôùi a,
hình 32 vaø ruùt ra moái lieân heä b
veà daáu cuûa giaù trò f(x) = ax2 + tröø x = – 2a
bx + c öùng vôùi x tuyø theo daáu  > 0  …. cuûa  = b2 – 4ac ?
Hoaït ñoäng 2: Tìm hieåu ñònh lí veà daáu cuûa tam thöùc baäc hai
 GV neâu ñònh lí veà daáu cuûa
2. Daáu cuûa tam thöùc baäc hai 12' tam thöùc baäc hai.
Cho f(x) = ax2 + bx + c
(a0), = b2 – 4ac. 75
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn
+ < 0 a.f(x) > 0, x R
+ = 0 a.f(x) > 0, x b 2a + > 0
af (x)  0, x x x x 1 2  af (x)  0,  1
x x x2
Minh hoaï hình hoïc  < 0  = 0  > 0 + y y y + + + + + + + + + + + + + + + + a>0 + + + + + + + + + x x + 1 x2 + + + O - + + - + + + + - - x x + O O b -- 2a - y y y x O x - O b + +  2a - - - - + + - - x a<0 - - O x1 x2 - - - - - - - - - - - - - -
Hoaït ñoäng 3: AÙp duïng xeùt daáu tam thöùc baäc hai
H1. Xaùc ñònh a,  ? Ñ1. 3. AÙp duïng
a) a = –1 < 0;  = –11 < 0 VD1:  f(x) < 0, x a) Xeùt daáu tam thöùc
b) a = 2 > 0,  = 9 > 0 f(x) = –x2 + 3x – 5 10'  f(x) > 0,
x(– b) Laäp baûng xeùt daáu tam thöùc
 GV höôùng daãn caùch laäp f(x) = 2x2 – 5x + 2 ; 1 )(2;+) baûng xeùt daáu. 2 f(x) < 0, x  ( 1 ;2) 2
Hoaït ñoäng 4: Cuûng coá Nhaán maïnh:
3' Ñònh lí veà daáu cuûa tam thöùc baäc hai.
4. BAØI TAÄP VEÀ NHAØ:  Baøi 1, 2 SGK.
 Ñoïc tieáp baøi "Daáu cuûa tam thöùc baäc hai" Ngaøy soaïn: 27/01/2013
Chöông IV: BAÁT ÑAÚNG THÖÙC. BAÁT PHÖÔNG TRÌNH Tieát daïy: 39
Baøøi 5: BAØI TAÄP DAÁU CUÛA TAM THÖÙC BAÄC HAI I. MUÏC TIEÂU: Kieán thöùc: 76
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn
 Cuûng coá ñònh lí veà daáu cuûa tam thöùc baäc hai.
 Cuûng coá caùch söû duïng pp baûng, pp khoaûng trong vieäc giaûi toaùn.
 Bieát lieân heä giöõa baøi toaùn xeùt daáu vaø baøi toaùn veà giaûi BPT vaø heä BPT. Kó naêng:
 Vaän duïng ñöôïc ñònh lí trong vieäc giaûi caùc baøi toaùn veà xeùt daáu tam thöùc baäc hai.
 Vaän duïng ñöôïc ñònh lí trong vieäc giaûi BPT baäc hai vaø moät soá BPT khaùc. Thaùi ñoä:
 Reøn luyeän tính caån thaän, chính xaùc.
 Tích cöïc, chuû ñoäng, töï giaùc trong hoïc taäp. II. CHUAÅN BÒ:
Giaùo vieân: Giaùo aùn. Heä thoáng baøi taäp.
Hoïc sinh: SGK, vôû ghi. OÂn taäp kieán thöùc xeùt daáu tam thöùc baäc hai ñaõ hoïc.
III. HOAÏT ÑOÄNG DAÏY HOÏC:
1. OÅn ñònh toå chöùc: Kieåm tra só soá lôùp.
2. Kieåm tra baøi cuõ: (Loàng vaøo quaù trình luyeän taäp)
3. Giaûng baøi môùi:
TL Hoaït ñoäng cuûa Giaùo vieân
Hoaït ñoäng cuûa Hoïc sinh Noäi dung
Hoaït ñoäng 1: Luyeän kyõ naêng xeùt daáu tam thöùc baäc hai
 Moãi nhoùm xeùt moät tam 1. Xeùt daáu tam thöùc baäc hai
20' H1. Ta caàn xeùt caùc yeáu toá thöùc a) 5x2 – 3x + 1 naøo ? Ñ1. a vaø . b) –2x2 + 3x + 5
a) a = 5 > 0;  = –11 < 0 c) x2 + 12x + 36  f(x) > 0, x d) (2x – 3)(x + 5)
b) a = –2 < 0;  = 49 > 0  f(x) < 0, x   5   1;   2  f(x) >0,x(–;– 77
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn 1) 5   ; 2    c) a = 1 > 0;  = 0  f(x)  0, x   d) f(x) < 0, x  3  5;  2    f(x)>0, x(–;–
 Höôùng daãn HS caùch laäp
2. Laäp baûng xeùt daáu caùc 5) 3   ;
20' baûng xeùt daáu. (Cho HS ñieàn 2    bieåu thöùc sau vaøo baûng xeùt daáu)
Ñ2. a) f(x) = 0  x = 3; x = a) f(x) = (3x2 – 10x + 3)(4x
H2. Tìm taát caû caùc nghieäm 1 ; x = 5 – 5) 3 4
cuûa f(x) ? Saép xeáp caùc 2 2
(3x x)(3  x ) Ñ3. b) g(x) = 2 nghieäm 4x x  3  Nghieäm cuûa töû:
H3. Tìm taát caû caùc nghieäm x = 0; x = 1 ; x =  3 3
cuûa töû vaø maãu ? Saép xeáp  Nghieäm cuûa maãu: caùc nghieäm ? x = –1; x = 3 4
Hoaït ñoäng 2: Cuûng coá Nhaán maïnh:
5' Caùch vaän duïng ñònh lí veà
daáu cuûa tam thöùc baäc hai ñeå giaûi BPT baäc hai.
4. BAØI TAÄP VEÀ NHAØ: Ñoïc tröôùc baøi " Daáu cuûa tam thöùc baäc hai". Ngaøy soaïn: 27/01/2013
Chöông IV: BAÁT ÑAÚNG THÖÙC. BAÁT PHÖÔNG TRÌNH Tieát daïy: 40
Baøøi 5: DAÁU CUÛA TAM THÖÙC BAÄC HAI (tt) I. MUÏC TIEÂU: Kieán thöùc:
 Naém ñöôïc ñònh lí veà daáu cuûa tam thöùc baäc hai.
 Bieát vaø vaän duïng ñöôïc ñònh lí trong vieäc giaûi caùc baøi toaùn veà xeùt daáu tam thöùc baäc hai. 78
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn
 Bieát söû duïng pp baûng, pp khoaûng trong vieäc giaûi toaùn.
 Bieát lieân heä giöõa baøi toaùn xeùt daáu vaø baøi toaùn veà giaûi BPT vaø heä BPT. Kó naêng:
 Phaùt hieän vaø giaûi caùc baøi toaùn veà xeùt daáu cuûa tam thöùc baäc hai.
 Vaän duïng ñöôïc ñònh lí trong vieäc giaûi BPT baäc hai vaø moät soá BPT khaùc. Thaùi ñoä:
 Bieát lieân heä giöõa thöïc tieãn vôùi toaùn hoïc.
 Tích cöïc, chuû ñoäng, töï giaùc trong hoïc taäp. II. CHUAÅN BÒ:
Giaùo vieân: Giaùo aùn.
Hoïc sinh: SGK, vôû ghi. OÂn taäp kieán thöùc xeùt daáu tam thöùc baäc hai ñaõ hoïc.
III. HOAÏT ÑOÄNG DAÏY HOÏC:
1. OÅn ñònh toå chöùc: Kieåm tra só soá lôùp.
2. Kieåm tra baøi cuõ: (3')
H. Neâu ñònh lí veà daáu cuûa tam thöùc baäc hai. Ñ.
3. Giaûng baøi môùi: TL
Hoaït ñoäng cuûa Giaùo vieân
Hoaït ñoäng cuûa Hoïc sinh Noäi dung
Hoaït ñoäng 1: Tìm hieåu khaùi nieäm baát phöông trình baäc hai
H1. Cho VD veà BPT baäc hai Ñ1. Moãi nhoùm cho moät VD.
II. Baát phöông trình baäc hai 7' moät aån ? –2x2 + 3x + 5 > 0 moät aån –3x2 + 7x – 4 < 0
1. Baát phöông trình baäc hai
BPT baäc hai aån x laø BPT daïng
ax2 + bx + c < 0 (> 0; 0; 0) (a 0)
Hoaït ñoäng 2: Tìm hieåu caùch giaûi baát phöông trình baäc hai
H1. Cho moãi nhoùm giaûi moät Ñ1.
2. Giaûi BPT baäc hai 15' BPT.
a) a = 3 > 0;  = –14 < 0
Ñeå giaûi BPT baäc hai ta döïa  S = R
vaøo vieäc xeùt daáu tam thöùc baäc
b) a = –2 < 0; f(x) coù 2 hai. nghieäm
VD1: Giaûi caùc BPT sau: x1 = –1; x2 = 5 2 a) 3x2 + 2x + 5 > 0  5  b) –2x2 + 3x + 5 > 0  S =  1; 2    c) –3x2 + 7x – 4 < 0
c) a = –3 < 0; f(x) coù 2 d) 9x2 – 24x + 16  0 nghieäm x1 = 1; x2 = 4 3  4 
 S = (–; 1)   ; 3   
d) a = 9 > 0; f(x) coù nghieäm 79
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn keùp x = 4 3  S = R
Hoaït ñoäng 3: Vaän duïng vieäc giaûi BPT baäc hai
 GV höôùng daãn HS thöïc hieän
VD2: Tìm caùc trò cuûa tham soá 15' caùc böôùc.
m ñeå phöông trình sau coù 2
H1. Neâu ñk ñeå pt (*) coù 2 Ñ1. ac < 0 nghieäm traùi daáu: nghieäm traùi daáu ?
 2(2m2 – 3m – 5) < 0
2x2 – (m2 – m + 1)x + 2m2 –
 2m2 – 3m – 5 < 0 (1) 3m – 5 = 0 (*) H2. Giaûi bpt (1)   Ñ2. S = 5  1; 2   
H3. Neâu ñk ñeå (*) nghieäm Ñ3.  < 0  m2 + 3m – 1 < 0 VD3: Tìm m ñeå BPT sau ñuùng vôùi moïi x ? (2)
nghieäm ñuùng vôùi moïi x:
–x2 + 2mx + 3m – 1 < 0 (*) H4. Giaûi BPT (2)       Ñ4. S = 3 13 3 13  ;   2 2 
Hoaït ñoäng 4: Cuûng coá Nhaán maïnh:
3' Caùch vaän duïng ñònh lí veà daáu
cuûa tam thöùc baäc hai ñeå giaûi BPT baäc hai.
4. BAØI TAÄP VEÀ NHAØ:  Baøi 3, 4 SGK. Ngaøy soaïn: 27/01/2012
Chöông IV: BAÁT ÑAÚNG THÖÙC. BAÁT PHÖÔNG TRÌNH Tieát daïy: 41
Baøøi 5: BAØI TAÄP DAÁU CUÛA TAM THÖÙC BAÄC HAI I. MUÏC TIEÂU: Kieán thöùc: 80
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn
 Cuûng coá ñònh lí veà daáu cuûa tam thöùc baäc hai.
 Cuûng coá caùch söû duïng pp baûng, pp khoaûng trong vieäc giaûi toaùn.
 Bieát lieân heä giöõa baøi toaùn xeùt daáu vaø baøi toaùn veà giaûi BPT vaø heä BPT. Kó naêng:
 Vaän duïng ñöôïc ñònh lí trong vieäc giaûi caùc baøi toaùn veà xeùt daáu tam thöùc baäc hai.
 Vaän duïng ñöôïc ñònh lí trong vieäc giaûi BPT baäc hai vaø moät soá BPT khaùc. Thaùi ñoä:
 Reøn luyeän tính caån thaän, chính xaùc.
 Tích cöïc, chuû ñoäng, töï giaùc trong hoïc taäp. II. CHUAÅN BÒ:
Giaùo vieân: Giaùo aùn. Heä thoáng baøi taäp.
Hoïc sinh: SGK, vôû ghi. OÂn taäp kieán thöùc xeùt daáu tam thöùc baäc hai ñaõ hoïc.
III. HOAÏT ÑOÄNG DAÏY HOÏC:
1. OÅn ñònh toå chöùc: Kieåm tra só soá lôùp.
2. Kieåm tra baøi cuõ: (Loàng vaøo quaù trình luyeän taäp)
3. Giaûng baøi môùi:
Hoaït ñoäng 1: Vaän duïng xeùt daáu tam thöùc ñeå giaûi baát phöông trình
H1. Neâu caùch giaûi ? Ñ1.
3. Giaûi caùc baát phöông trình 20'
+ Ñöa veà daïng f(x) < 0 a) 4x2 – x + 1 < 0
+ Xeùt daáu bieåu thöùc f(x) b) –3x2 + x + 4  0
+ Keát luaän nghieäm cuûa bpt. c) 1 3  2 2 a) S = 
x  4 3x x  4 b) S =  4 1;  3   c) S = (–;– 8) 4   2;   (1;2) 3    81
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn
Hoaït ñoäng 2: Vaän duïng vieäc giaûi BPT baäc hai
 Höôùng daãn HS phaân tích
4. Tìm caùc giaù trò cuûa m ñeå 20' yeâu caàu baøi toaùn.
caùc phöông trình sau voâ
H1. Xaùc ñònh caùc tröôøng Ñ1. Xeùt a = 0; a  0 nghieäm
hôïp coù theå xaûy ra cuûa ña a) (m–2)x2 +2(2m–3)x thöùc? +5m–6=0 Ñ2. b) (3–m)x2 –2(m+3)x +m+2
H2. Neâu ñk ñeå pt voâ a) m < 1; m > 3 =0 nghieäm ? b) 3  < m < –1 2
Hoaït ñoäng 3: Cuûng coá Nhaán maïnh:
3' Caùch vaän duïng ñònh lí veà
daáu cuûa tam thöùc baäc hai ñeå giaûi BPT baäc hai.
4. BAØI TAÄP VEÀ NHAØ:
 Baøi taäp oân chöông IV. Ngaøy soaïn: 10/02/2013
Chöông IV: BAÁT ÑAÚNG THÖÙC. BAÁT PHÖÔNG TRÌNH Tieát daïy: 42
Baøøi daïy: OÂN TAÄP CHÖÔNG IV I. MUÏC TIEÂU: Kieán thöùc:
 OÂn taäp toaøn boä kieán thöùc trong chöông IV. Kó naêng:
 Vaän duïng caùc kieán thöùc moät caùch toång hôïp. Thaùi ñoä: 82
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn
 Taïo höùng thuù trong hoïc taäp, lieân heä ñöôïc caùc kieán thöùc ñaõ hoïc vaøo thöïc teá. II. CHUAÅN BÒ:
Giaùo vieân: Giaùo aùn. Heä thoáng baøi taäp.
Hoïc sinh: SGK, vôû ghi. OÂn taäp kieán thöùc ñaõ hoïc trong chöông IV.
III. HOAÏT ÑOÄNG DAÏY HOÏC:
1. OÅn ñònh toå chöùc: Kieåm tra só soá lôùp.
2. Kieåm tra baøi cuõ: (Loàng vaøo quaù trình oân taäp) H. Ñ.
3. Giaûng baøi môùi: TL
Hoaït ñoäng cuûa Giaùo vieân
Hoaït ñoäng cuûa Hoïc sinh Noäi dung
Hoaït ñoäng 1: OÂn taäp veà Baát ñaúng thöùc
 Nhaéc laïi caùc tính chaát vaø
1. Cho a, b, c > 0. CMR:
10' caùch chöùng minh BÑT.
a b b c c a
H1. Neâu caùch chöùng minh ? Ñ1. a)    6 c a b a) Vaän duïng BÑT Coâsi a b b)   a b a b
  2 a . b  2 b a b a b a
b) Bieán ñoåi töông ñöông
  a b 2  0
Hoaït ñoäng 2: OÂn taäp giaûi BPT baäc nhaát, baäc hai moät aån
 Moãi nhoùm giaûi 1 heä BPT
2. Giaûi caùc heä BPT sau:
15' H1. Neâu caùch giaûi ?
Ñ1. Giaûi töøng BPT trong heä,  2 x  2x  0
roài laáy giao caùc taäp nghieäm. a) 
 2x 1  3x  2 a)  0  x  2   0  x  2  2 xx  1   4  0 b)  1 1 x  2   
x  2 x 1 b) x  2 x     2  2 x  2 
x  5x  2  0  x  2 c)    2 x  1
x  8x 1 0 5 17 5 17 d)  x 1  2  c)   x   2 2  2x 1  3  4   15  x  4   15  x   d)  1   x  3   –1  x  1  2   x  1
Hoaït ñoäng 3: OÂn taäp bieåu dieãn mieàn nghieäm cuûa heä BPT baäc nhaát hai aån
H1. Neâu caùc böôùc thöïc hieän ? Ñ1.
3. Bieåu dieãn hình hoïc taäp 7'
+ Veõ caùc ñöôøng thaúng treân nghieäm cuûa heä BPT:
cuøng heä truïc toaï ñoä: 3
x y  9 3x + y = 9; x – y = –3;  x y  3 x + 2y = 8; y = 6  2y  8  x
+ Xaùc ñònh mieàn nghieäm cuûa  y  6 83
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn moãi BPT.
+ Laáy giao caùc mieàn nghieäm.
Hoaït ñoäng 4: Vaän duïng vieäc xeùt daáu tam thöùc baäc hai
 Höôùng daãn caùch xeùt.
4. a) Baèng caùch söû duïng haèng
8' H1. Xeùt daáu x2 – x + 3;
Ñ1. x2 – x + 3 > 0, x
ñaúng thöùc a2–b2=(a + b)(a – x2 – 2x + 2 ? a) f(x) = x4 – (x – 3)2
b) haõy xeùt daáu caùc bieåu thöùc:
= (x2 – x + 3)(x2 + x – 3) f(x) = x4 – x2 + 6x – 9 g(x) = g(x) = x2 – 2x – 4 2 2 2
= (x  2x  2)(x  2x  2) x  2x 2 x  2x
b) Haõy tìm nghieäm nguyeân b) cuûa BPT:
 (x2 – x + 3)(x2 + x – 3) < 0 x(x3 – x + 6) < 9  x2 + x – 3 < 0      1 13 1 13  x  2 2  x  {–2; –1; 0; 1}
Hoaït ñoäng 4: Cuûng coá  Nhaán maïnh:
3' – Caùch chöùng minh BÑT.
– Caùch giaûi BPT, heä BPT moät aån.
4. BAØI TAÄP VEÀ NHAØ:
 Chuaån bò kieåm tra 1 tieát chöông IV. Ngaøy soaïn: 15/02/2013
Chöông IV: BAÁT ÑAÚNG THÖÙC. BAÁT PHÖÔNG TRÌNH Tieát daïy: 43
Baøøi daïy: KIEÅM TRA 1 TIEÁT CHÖÔNG IV I. MUÏC TIEÂU: Kieán thöùc:
 OÂn taäp toaøn boä kieán thöùc trong chöông IV. Kó naêng:
 Vaän duïng caùc kieán thöùc moät caùch toång hôïp. Thaùi ñoä:
 Reøn luyeän tính caån thaän, chính xaùc. II. CHUAÅN BÒ: 84
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn
Giaùo vieân: Giaùo aùn. Ñeà kieåm tra.
Hoïc sinh: OÂn taäp kieán thöùc ñaõ hoïc trong chöông IV. III. MA TRAÄN ÑEÀ: Nhaän bieát Thoâng hieåu Vaän duïng Chuû ñeà Toång TNKQ TL TNKQ TL TNKQ TL BPT baäc nhaát 2 1,0 0,5 BPT baäc hai 2 4 1 1 9,0 0,5 0,5 3,0 3,0 Toång 2,0 2,0 3,0 3,0 10
IV. NOÄI DUNG ÑEÀ KIEÅM TRA:
A. Phaàn traéc nghieäm: (4 ñieåm)
Caâu 1: Taäp nghieäm cuûa baát phöông trình: x 1  1 laø: A) (–2; 2) B) (0; 1) C) (0; 2) D) (–; 2)
Caâu 2: Taäp nghieäm cuûa heä baát phöông trình: 3  x 1  0  laø: 5  x  0 1   1  1  A) ;5  B)  ;5 C) (5; + ) D) ;   3   3  3 
Caâu 3: Taäp nghieäm cuûa baát phöông trình: x2 – 2x – 3 < 0 laø: A) (–3; 1) B) (–1; 3)
C) (–;–1)(3;+) D) (–;–3)(1;+)
Caâu 4: Taäp nghieäm cuûa baát phöông trình: x2 – 9  0 laø: A) (–; 3] B) (–; –3]
C) (–;–3][3;+) D) [–3; 3]
Caâu 5: Taäp xaùc ñònh cuûa haøm soá f(x) = 2
x  5x  4 laø: A) [1; 4] B) (–; 1][4;+) C) (–; 1)(4;+) D) (1; 4)
Caâu 6: Phöông trình: x2 + (2m – 3)x + m2 – 6 = 0 voâ nghieäm khi: A) m = 33 B) m < 33 C) m  33 D) m > 33 12 12 12 12
Caâu 7: Tam thöùc naøo sau ñaây luoân luoân döông vôùi moïi x: A) 4x2 – x + 1 B) x2 – 4x + 1 C) x2 – 4x + 4 D) 4x2 – x – 1
Caâu 8: Giaù trò lôùn nhaát cuûa bieåu thöùc f(x) = – x2 + 5x + 1 laø: A) 29 B) 1 C) – 29 D) 5 4 4 2
B. Phaàn töï luaän: (6 ñieåm) 2
Caâu 9: Giaûi baát phöông trình:
3 2x x  0 2 2x  3x  5
Caâu 10: Cho tam thöùc baäc hai: f(x) = –x2 + (m + 2)x – 4. Tìm caùc giaù trò cuûa tham soá m ñeå:
a) Phöông trình f(x) = 0 coù hai nghieäm phaân bieät.
b) Tam thöùc f(x) < 0 vôùi moïi x.
V. ÑAÙP AÙN VAØ BIEÅU ÑIEÅM:
A. Traéc nghieäm: (Moãi caâu 0,5 ñieåm)
Caâu 1 Caâu 2 Caâu 3 Caâu 4 Caâu 5 Caâu 6 Caâu 7 Caâu 8 C A B D B D A A 85
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn B. Töï luaän:
Caâu 9: (3 ñieåm)  Tìm nghieäm cuûa töû vaø maãu: 3 + 2x – x2 = 0  x = –1; x = 3 (0,5 ñieåm)
2x2 + 3x – 5 = 0  x = 1; x = – 5 (0,5 ñieåm) 2  Laäp baûng xeùt daáu: x  – 5/2 –1 1 3  3 + 2x – x2 – – 0 + + 0 – (0,5 ñieåm) 2x2 + 3x – 5 + 0 – – 0 + + (0,5 ñieåm) VT – + 0 – + 0 – (0,5 ñieåm)  5 
 Keát luaän: Taäp nghieäm cuûa BPT S =  ; 1   (1;3) (0,5 ñieåm)  2  Caâu 10: (3 ñieåm) a) (1,5 ñieåm)
 PT coù 2 nghieäm phaân bieät   = (m + 2)2 – 16 > 0 (0,5 ñieåm)  m  6   (1 ñieåm) m  2 b) (1,5 ñieåm)
 Vì a = –1 < 0 neân f(x) < 0, x   = (m + 2)2 – 16 < 0 (0,5 ñieåm)  – 6 < m < 2 (1 ñieåm)
VI. KEÁT QUAÛ KIEÅM TRA: 0 – 3,4 3,5 – 4,9 5,0 – 6,4 6,5 – 7,9 8,0 – 10 Lôùp Só soá SL % SL % SL % SL % SL % 10A3 44 10A5 42 10A7 44 10A10 42 10A11 38 Ngaøy soaïn: 20/02/2013
Chöông V: THOÁNG KEÂ Tieát daïy: 44
Baøøi 4: PHÖÔNG SAI VAØ ÑOÄ LEÄCH CHUAÅN I. MUÏC TIEÂU: Kieán thöùc:
 Hieåu ñöôïc phöông sai vaø ñoä leäch chuaån.
 Bieát ñöôïc yù nghóa cuûa phöông sai vaø ñoä leäch chuaån. Kó naêng:
 Giaûi thaønh thaïo caùc baøi toaùn veà phöông sai vaø ñoä leäch chuaån.
 Bieát vaän duïng caùc kieán thöùc ñoù trong vieäc giaûi caùc baøi toaùn kinh teá. Thaùi ñoä:
 Thaáy ñöôïc söï gaàn guõi cuûa toaùn hoïc vaø ñôøi soáng. II. CHUAÅN BÒ:
Giaùo vieân: Giaùo aùn. Maùy tính caàm tay. 86
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn
Hoïc sinh: SGK, vôû ghi. OÂn taäp caùch tính soá trung bình coäng.
III. HOAÏT ÑOÄNG DAÏY HOÏC:
1. OÅn ñònh toå chöùc: Kieåm tra só soá lôùp.
2. Kieåm tra baøi cuõ: (3')
H. Tính soá trung bình coäng cuûa caùc daõy soá sau:
a) 180; 190; 190; 200; 210; 210; 220
b) 150; 170; 170; 200; 230; 230; 250
Ñ. a) X = 200 b) X = 200
3. Giaûng baøi môùi: TL
Hoaït ñoäng cuûa Giaùo vieân
Hoaït ñoäng cuûa Hoïc sinh Noäi dung
Hoaït ñoäng 1: Tìm hieåu khaùi nieäm Phöông sai
 GV daãn daét töø KTBC. Nhaän I. Phöông sai
xeùt caùc soá lieäu ôû daõy a) gaàn
a) Tröôøng hôïp baûng phaân boá 20' vôùi soá TBC hôn.
taàn soá, taàn suaát (rôøi raïc)
 GV giôùi thieäu caùc khaùi nieäm k 2 1 2
ñoä leäch, ñoä phaân taùn.
s  n (x x) x i i n i
H1. Tính ñoä leäch cuûa caùc soá Ñ1. 180 –200; 190–200; 190– 1  k
lieäu ôû daõy a) so vôùi soá TBC ? 200; 200–200; 210–200; 210– 2
  f (x x) i i 200; 220–200 i 1 
H2. Tính bình phöông caùc ñoä (n Ñ2. 2 s 1 + n2 + … + nk = n) x  1,74
leäch vaø TBC cuûa chuùng ?
b) Tröôøng hôïp baûng phaân boá
 GV giôùi thieäu khaùi nieäm
taàn soá, taàn suaát gheùp lôùp
Lôùp soá Taàn soá Taàn suaát phöông sai. 1 k ño % 2 2
s  n (c x) x i i n [150;156 6 16,7 i 1  ) 12 33,3 k 2
  f (c x) [156;162 13 36,1 i i i 1  ) 5 13,9  Chuù yù: [162;168 )
– Khi hai daõy soá lieäu coù cuøng  Xeùt baûng soá lieäu [168;174
ñôn vò vaø coù soá TBC baèng
H3. Tính soá TBC, phöông sai ]
nhau hay xaáp xæ nhau, neáu ? Coäng 36 100 (%)
phöông sai caøng nhoû thì ñoä
phaân taùn cuûa caùc soá lieäu thoáng Ñ3. x = 162 keâ caøng beù.  2 s
– Coù theå tính phöông sai theo x  31 coâng thöùc: 2 2 2
s x  (x)
 Xeùt baûng phaân boá taàn suaát x Lôùp Taàn suaát gheùp lôùp. trong ñoù: [15; 17) 16,7 1 k k [17; 19) 43,3 2 2 2
x  n x   f x i i i i [19; 21) 36,7 n i 1  i 1  [21; 23] 3,3 1 k k
H4. Tính soá TBC, phöông sai Coäng 100 (%) hoaëc 2 2 2
x   in ic   if ic n i 1  i 1  ?
Ñ4. x  18,5(0C)  2 sx  2,38 87
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn
Hoaït ñoäng 2: Tìm hieåu khaùi nieäm Ñoä leäch chuaån
 GV giôùi thieäu khaùi nieäm ñoä
II. Ñoä leäch chuaån 7' leäch chuaån.
Ñoä leäch chuaån s
H1. Tính ñoä leäch chuaån trong Ñ1. x = 2 x s caùc VD treân ?
Phöông sai vaø ñoï leäch chuaån a) 2
s  31  sx  31  5,57 x
sx ñeàu ñöôïc duøng ñeå ñaùnh giaù b) 2 s
möùc ñoä phaân taùn cuûa caùc soá x  2,38
lieäu thoáng keâ (so vôùi soá TBC).
 sx  2,38  1,54 (0C)
Nhöng khi caàn chuù yù ñeán ñôn
vò ño thì ta duøng sx vì sx coù
cuøng ñôn vò ño vôùi daáu hieäu
ñöôïc nghieân cöùu.
Hoaït ñoäng 3: AÙp duïng tính phöông sai vaø ñoä leäch chuaån Tuoåi 18 19 20 21 22 Coäng
VD: Xeùt baûng soá lieäu "Tuoåi 10' Taàn 10 50 70 29 10 169
cuûa 169 ñoaøn vieân" soá H1. Tính soá TBC ? 10.18  50.19  70.20  a) Tính soá TBC. Ñ1. 2  9.2110.22 x 
b) Tính phöông sai vaø ñoä leäch 169 chuaån.  19,9
H2. Tính phöpöng sai vaø ñoä Ñ2. 2 sx  0,93 leäch chuaån ?  sx  0,93  0,96
Hoaït ñoäng 4: Cuûng coá  Nhaán maïnh:
3' – Caùch tính phöông sai vaø ñoä leäch chuaån
– YÙ nghóa cuûa phöông sai vaø ñoä leäch chuaån.
4. BAØI TAÄP VEÀ NHAØ:  Baøi 1, 2, 3 SGK. Ngaøy soaïn: 26/2/2013
Tieát daïy: 45 BAØI TAÄP PHÖÔNG SAI – ÑOÄ LEÄCH CHUAÅN I. MUÏC TIEÂU: Kieán thöùc:
 Cuûng coá khaùi nieäm phöông sai vaø ñoä leäch chuaån.
 Bieát ñöôïc yù nghóa cuûa phöông sai vaø ñoä leäch chuaån. Kó naêng:
 Giaûi thaønh thaïo caùc baøi toaùn veà phöông sai vaø ñoä leäch chuaån.
 Bieát vaän duïng caùc kieán thöùc ñoù trong vieäc giaûi caùc baøi toaùn kinh teá. Thaùi ñoä:
 Thaáy ñöôïc söï gaàn guõi cuûa toaùn hoïc vaø ñôøi soáng. II. CHUAÅN BÒ:
Giaùo vieân: Giaùo aùn. Maùy tính caàm tay. 88
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn
Hoïc sinh: SGK, vôû ghi. Maùy tính caàm tay.
III. HOAÏT ÑOÄNG DAÏY HOÏC:
1. OÅn ñònh toå chöùc: Kieåm tra só soá lôùp.
2. Kieåm tra baøi cuõ:
Kieåm tra khaùi nieäm vaø coâng thöùc veà taàn soá, taàn suaát vaø soá trung bình, phöông sai, ñoä leäch
chuaån thoâng qua caâu hoûi daïng traéc nghieäm(trong giaùo aùn power point)
3. Giaûng baøi môùi:
Hoaït ñoäng 1: Tính soá trung bình, phöông sai, ñoä leäch chuaån trong baûng phaân boá taàn soá Phieáu hoïc taäp soá 1
Ñieàu tra soá con cuûa moãi gia ñình trong moät vuøng ta ñöôïc maãu soá lieäu 3 2 1 1 1 0 2 4 0 3 1 3 0 2 2 2 1 3 2 2 3 1 2 2 4 0 1 1 2 2 TL
Hoaït ñoäng cuûa Giaùo vieân
Hoaït ñoäng cuûa Hoïc sinh Noäi dung
GV: yeâu caàu hoïc sinh hoaøn
Bảng phân bố tần số, tần suất a) laäp baûng phaân boá taàn soá taàn
thaønh baûng phaân boá taàn soá taàn Số Tần Taàn suaát 20' suaát. Con số suất
b) Tính caùc soá trung bình ,
Bảng phân bố tần số, tần suất 0 4 13,3
phöông sai, ñoä leäch chuaån cuûa Số Tần Taàn 1 8 26,7 maãu soá lieäu treân. Con số suất 2 11 36,7 3 5 16,7 4 2 6,6 Coäng 30 100 x   1,77 Coäng 2  x s 1,18 ;  x s 1,09
 Cho caùc nhoùm tính vaø nhaän xeùt.
Höôùng daãn hoïc sinh tính - - hs tính toaùn baèng maùy tính
toaùn baèng maùy tính caàm tay. caàm tay.
Hoaït ñoäng 2: Tính soá trung bình, phöông sai, ñoä leäch chuaån trong baûng phaân boá taàn soá gheùp lôùp. Phieáu hoïc taäp soá 2
Ñieåm thi toaùn cuûa hai lôùp 10A vaø 10B Cho daïng baûng sau: Lôùp A Lôùp B 5 6 7 7 7 4 2 9 8 7 7 1 8 4 5 7 5 6 8 9 3 5 9 8 89
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn 6 7 8 6 5 6 8 8 7 2 2 9 7 4 8 7 6 5 9 7 2 9 8 9 TL
Hoaït ñoäng cuûa Giaùo vieân
Hoaït ñoäng cuûa Hoïc sinh Noäi dung Ñieåm thi lôùp 10A Ñieåm thi lôùp 10B
Ñieåm thi toaùn hai lôùp 10A vaø Ñieåm thi Taàn soá Ñieåm thi Taàn soá
10B cuûa moät tröôøng THPT. 20' [4;6) 8 [1;3) 5
Keát quaû cho ôû hai baûng sau: [6;8) 13 [3;5) 1 [8;10] 3 [5;7) 1
a) Laäp baûng phaân boá taàn soá Coäng 24 [7;9] 17 taàn suaát gheùp lôùp.
 Cho caùc nhoùm tính laàn löôït Coäng 24 b) Tính caùc soá 2 X,sx,s ? x caùc soá ôû 2 baûng.
c) Nhaän xeùt keát quaû baøi thi Vaø tính toaùn cuûa 2 lôùp ?  A X = 6,58; B X = 6,5
- caùc nhoùm leân trình baøy 2 s  1,66; 2 lôøi giaûi A B s  6,08 S - A  1,28; sB  2,47
höôùng daãn hoïc sinh  Lôùp 10A hoïc ñoàng ñeàu hôn tìm keát quaû baèng maùy tính caàm tay.
Hoaït ñoäng 4: Cuûng coá  Nhaán maïnh:
- Cho hoïc sinh laøm moät soá baøi
3' – Caùch tính phöông sai vaø ñoä taäp traéc nghieäm. leäch chuaån
– YÙ nghóa cuûa phöông sai vaø ñoä leäch chuaån. Ngaøy soaïn: 20/02/2013
Chöông V: THOÁNG KEÂ Tieát daïy: 47
Baøøi daïy: OÂN TAÄP CHÖÔNG V I. MUÏC TIEÂU:
Kieán thöùc: Cuûng coá caùc kieán thöùc ñaõ hoïc trong chöông:
 Daõy soá lieäu thoáng keâ, taàn soá, taàn suaát.
 Baûng phaân boá taàn soá, taàn suaát.
 Bieåu ñoà taàn soá, taàn suaát hình coät, ñöôøng gaáp khuùc, hình quaït.
 Soá trung bình, soá trung vò, moát, phöông sai, ñoä leäch chuaån.
Kó naêng: Hình thaønh caùc kó naêng:
 Tính toaùn treân caùc soá lieäu thoáng keâ.  Kó naêng phaân lôùp.
 Veõ vaø ñoïc caùc bieåu ñoà. Thaùi ñoä: 90
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn
 Reøn luyeän tính caån thaän, tæ mæ, chính xaùc.
 Thaáy ñöôïc moái lieän heä vôùi thöïc tieãn. II. CHUAÅN BÒ:
Giaùo vieân: Giaùo aùn. Maùy tính caàm tay. Heä thoáng baøi taäp.
Hoïc sinh: SGK, vôû ghi. Maùy tính caàm tay. OÂn taäp toaøn boä kieán thöùc chöông V.
III. HOAÏT ÑOÄNG DAÏY HOÏC:
1. OÅn ñònh toå chöùc: Kieåm tra só soá lôùp.
2. Kieåm tra baøi cuõ: (Loàng vaøo quaù trình luyeän taäp) H. Ñ.
3. Giaûng baøi môùi: TL
Hoaït ñoäng cuûa Giaùo vieân
Hoaït ñoäng cuûa Hoïc sinh Noäi dung
Hoaït ñoäng 1: Luyeän taäp tính toaùn treân caùc soá lieäu thoáng keâ
Soá con cuûa 59 gia ñình
1. Keát quaû ñieàu tra 59 hoä gia 3 2 1 1 1 1 0 2 4 0 3 0
ñình ôû moät vuøng daân cö veà soá 10' 1 3 0 2 2 2 1 3 2 2 3 3
con cuûa moãi hoä ñöôïc ghi trong 2 2 4 3 2 2 4 3 2 4 1 3 baûng sau: 0 1 3 2 3 1 4 3 0 2 2 1
a) Laäp baûng phaân boá taàn soá 2 1 2 0 4 2 3 1 1 2 0 vaø taàn suaát.
b) Neâu nhaän xeùt veà soá con cuûa
59 gia ñình ñöôïc ñieàu tra.
H1. Neâu caùc böôùc laäp baûng Ñ1.
c) Tính soá TBC, soá trung vò,
phaân boá taàn soá, taàn suaát ? Soá con Taàn soá Taàn
moát cuûa caùc soá lieäu thoáng keâ. suaát 0 8 13,6 1 15 25,4 2 17 28,8 3 13 22,0 4 6 10,2 Coäng 59 100 (%)
H2. Tính soá TBC, trung vò vaø moát ? Ñ2. x  2; M e = 2; MO = 2
Khoái löôïng cuûa nhoùm 1
Baûng phaân boá taàn soá, taàn suaát 2. Cho caùc soá lieäu thoáng keâ 645 650 645 644 650 cuûa nhoùm 1
ñöôïc ghi trong 2 baûng sau: 15' 635 650 654 650 650 Lôùp Taàn soá Taàn
a) Laäp baûng phaân boá taàn soá 643 650 630 647 650 suaát
vaø taàn suaát gheùp lôùp theo 645 650 645 642 652 [630; 635) 1 4,2
nhoùm caù thöù 1 vôùi caùc lôùp: 635 647 652 650 [635; 640) 2 8,3 [630; 635); [635; 640); [640; [640; 645) 3 12,5
Khoái löôïng cuûa nhoùm 2 645); [645; 650); [650; 655]. [645; 650) 6 25,0 640 650 645 650 643 [650; 655] 12 50,0
b) Laäp baûng phaân boá taàn soá 645 650 650 642 640 Coäng 24 100
vaø taàn suaát gheùp lôùp theo 650 645 650 641 650 (%)
nhoùm caù thöù 2 vôùi caùc lôùp: 650 649 645 640 645
Baûng phaân boá taàn soá, taàn suaát [638; 642); [642; 646); [646; 650 650 644 650 650 650); [650; 654]. 91
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn 645 640 cuûa nhoùm 2
c) Tính soá TBC, phöông sai, Lôùp Taàn soá Taàn
ñoä leäch chuaån cuûa caùc baûng
H1. Neâu caùc böôùc laäp baûng suaát phaân boá ôû treân.
phaân boá taàn soá, taàn suaát ? [638; 642) 5 18,5 [642; 646) 9 33,3 [646; 650) 1 3,7
H2. Tính soá TBC, phöông sai, [650; 654] 12 44,5 ñoä leäch chuaån ? Coäng 27 100 (%) Ñ2. x  648; 2
sx  33,2; sx  5,76 y  647; 2 y
s  23,4; sy  4,81
Hoaït ñoäng 2: Luyeän taäp veõ bieåu ñoà
H1. Neâu caùc böôùc veõ bieåu ñoà tần
3. Moâ taû baûng phaân boá taàn suất
15' taàn suaát hình coät vaø ñöôøng 50
suaát gheùp lôùp ôû caâu 2a) baèng gaáp khuùc taàn suaát ?
caùch veõ bieåu ñoà taàn suaát hình
coät vaø ñöôøng gaáp khuùc taàn suaát. 25 12,5 8,3 4,2 O 630 635 640 645 650 655 KL 632,5 637,5 642,5 647,5 652,5
Hoaït ñoäng 4: Cuûng coá  Nhaán maïnh:
3' – Caùch tính toaùn treân caùc soá lieäu thoáng keâ.
– YÙ nghóa cuûa caùc soá lieäu.
4. BAØI TAÄP VEÀ NHAØ:
 Laøm caùc baøi taäp coøn laïi.
 Ñoïc tröôùc baøi "Cung vaø goùc löôïng giaùc". Ngaøy soaïn: 29/02/2013
Chöông VI: CUNG VAØ GOÙC LÖÔÏNG GIAÙC. COÂNG THÖÙC LÖÔÏNG GIAÙC Tieát daïy: 48
Baøøi 1: CUNG VAØ GOÙC LÖÔÏNG GIAÙC I. MUÏC TIEÂU: Kieán thöùc:
 Naém ñöôïc khaùi nieäm ñöôøng troøn ñònh höôùng, ñöôøng troøn löôïng giaùc, cung vaø goùc löôïng giaùc.
 Naém ñöôïc khaùi nieäm ñôn vò ñoä vaø rañian vaø moái quan heä giöõa caùc ñôn vò naøy.
 Naém ñöôïc soá ño cung vaø goùc löôïng giaùc. Kó naêng:
 Bieåu dieãn ñöôïc cung löôïng giaùc treân ñöôøng troøn löôïng giaùc. 92
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn
 Tính vaø chuyeån ñoåi thaønh thaïo hai ñôn vò ño.
 Tính thaønh thaïo soá ño cuûa moät cung löôïng giaùc. Thaùi ñoä:
 Luyeän tính nghieâm tuùc, saùng taïo.
 Luyeän oùc tö duy thöïc teá. II. CHUAÅN BÒ:
Giaùo vieân: Giaùo aùn. Hình veõ minh hoaï.
Hoïc sinh: SGK, vôû ghi. OÂn taäp phaàn Giaù trò löôïng giaùc cuûa goùc  (00    1800).
III. HOAÏT ÑOÄNG DAÏY HOÏC:
1. OÅn ñònh toå chöùc: Kieåm tra só soá lôùp. y
2. Kieåm tra baøi cuõ: (5')
H. Nhaéc laïi ñònh nghóa GTLG cuûa goùc  (00    1800) ? y M 0 y x
Ñ. sin = y0; cos = x0; tan = 0 ; cot = 0 . x x O 0 x –1 1 0 y0
3. Giaûng baøi môùi: TL
Hoaït ñoäng cuûa Giaùo vieân
Hoaït ñoäng cuûa Hoïc sinh Noäi dung
Hoaït ñoäng 1: Tìm hieåu khaùi nieäm Cung löôïng giaùc
 GV döïa vaøo hình veõ, daãn daét ñi
I. Khaùi nieäm cung vaø goùc löôïng
ñeán khaùi nieäm ñöôøng troøn ñònh t 2 giaùc 20' höôùng.
1. Ñöôøng troøn ñònh höôùng vaø M 2 M1 1 +
cuøng löôïng giaùc A’ A A
Ñöôøng troøn ñònh höôùng laø moät O –
ñöôøng troøn treân ñoù ñaõ choïn moät N –1 1
chieàu chuyeån ñoäng goïi laø chieàu –2
döông, chieàu ngöôïc laïi laø chieàu t’
H1. Moãi ñieåm treân truïc soá ñöôïc
aâm. Qui öôùc choïn chieàu ngöôïc
ñaët töông öùng vôùi maáy ñieåm treân
Ñ1. Moät ñieåm treân truïc soá öùng
vôùi chieàu quay cuûa kim ñoàng hoà ñöôøng troøn ?
vôùi moät ñieåm treân ñöôøng troøn. laøm chieàu döông.
Treân ñöôøng troøn ñònh höôùng
H2. Moãi ñieåm treân ñöôøng troøn
cho 2 ñieåm A, B. Moät ñieåm M di
öùng vôùi maáy ñieåm treân truïc soá
Ñ2. Moät ñieåm treân ñöôøng troøn ñoäng treân ñöôøng troøn luoân theo
öùng vôùi voâ soá ñieåm treân truïc soá. moät chieàu töø A ñeán B taïo neân moät
cung löôïng giaùc coù ñieåm ñaàu A vaø ñieåm cuoái B.
Vôùi 2 ñieåm A, B ñaõ cho treân ñ. B B B B
troøn ñònh höôùng ta coù voâ soá cung A
löôïng giaùc coù ñieåm ñaàu A, ñieåm O O A O A A O
cuoái B. moãi cung nhö vaäy ñeàu ñöôïc kí hieäu . a) b) c) d)
H3. Xaùc ñònh chieàu chuyeån Ñ3.
Treân moät ñ. troøn ñònh höôùng,
ñoäng cuûa ñieåm M vaø soá voøng a) chieàu döông, 0 voøng.
laáy 2 ñieåm A, B thì: quay? b) chieàu döông, 1 voøng.
– Kí hieäu AB chæ moät cung hình c) chieàu döông, 2 voøng.
hoïc (lôùn hoaëc beù) hoaøn toaøn xaùc d) chieàu aâm, 0 voøng. ñònh. – Kí hieäu chæ moät cung 93
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn
löôïng giaùc ñieåm ñaàu A, ñieåm cuoái B.
Hoaït ñoäng 2: Tìm hieåu khaùi nieäm goùc löôïng giaùc
 GV giôùi thieäu khaùi nieäm goùc D
2. Goùc löôïng giaùc 7' löôïng giaùc.
Moät ñieåm M chuyeån ñoäng treân M O
ñöôøng troøn töø C ñeán D taïo neân C cung löôïng giaùc . Khi ñoù tia
H1. Vôùi moãi cung löôïng giaùc coù
OM quay xung quanh goác O töø vò
bao nhieâu cung löôïng giaùc vaø Ñ1. Moät  moät.
trí OD ñeán OD. Ta noùi tia OM ngöôïc laïi ?
taïo neân goùc löôïng giaùc, coù tia
ñaàu OC vaø tia cuoái OD. Kí hieäu (OC, OD).
Hoaït ñoäng 3: Tìm hieåu khaùi nieäm Ñöôøng troøn löôïng giaùc
 GV giôùi thieäu ñöôøng troøn löôïng
3. Ñöôøng troøn löôïng giaùc y 8' giaùc.
Trong mp Oxy, veõ ñöôøng troøn ñôn 1 B
vò ñònh höôùng. Ñöôøng troøn naøy +
 Nhaán maïnh caùc ñieåm ñaëc bieät
caét hai truïc toaï ñoä taïi 4 ñieåm cuûa ñöôøng troøn: A’ A A(1; 0), A –
(–1; 0), B(0; 1), B(0; – 1 O 1 x – Ñieåm goác A(1; 0).
1). Ta laáy ñieåm A(1; 0) laøm ñieåm
– Caùc ñieåm A(–1; 0), B(0; 1),
goác cuûa ñöôøng troøn ñoù. –1 B’ B(0; –1).
Ñöôøng troøn xaùc ñònh nhö treân ñgl
ñöôøng troøn löôïng giaùc (goác A).
Hoaït ñoäng 4: Cuûng coá
 Nhaán maïnh caùc khaùi nieäm:
3' – Cung löôïng giaùc, goùc löôïng giaùc.
– Ñöôøng troøn löôïng giaùc.
4. BAØI TAÄP VEÀ NHAØ:
 Ñoïc tieáp baøi "Cung vaø goùc löôïng giaùc". Ngaøy soaïn: 20/03/2013
Chöông VI: CUNG VAØ GOÙC LÖÔÏNG GIAÙC. COÂNG THÖÙC LÖÔÏNG GIAÙC Tieát daïy: 54
Baøøi 1: CUNG VAØ GOÙC LÖÔÏNG GIAÙC (tt) I. MUÏC TIEÂU: Kieán thöùc:
 Naém ñöôïc khaùi nieäm ñöôøng troøn ñònh höôùng, ñöôøng troøn löôïng giaùc, cung vaø goùc löôïng giaùc.
 Naém ñöôïc khaùi nieäm ñôn vò ñoä vaø rañian vaø moái quan heä giöõa caùc ñôn vò naøy.
 Naém ñöôïc soá ño cung vaø goùc löôïng giaùc. Kó naêng:
 Bieåu dieãn ñöôïc cung löôïng giaùc treân ñöôøng troøn löôïng giaùc. 94
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn
 Tính vaø chuyeån ñoåi thaønh thaïo hai ñôn vò ño.
 Tính thaønh thaïo soá ño cuûa moät cung löôïng giaùc. Thaùi ñoä:
 Luyeän tính nghieâm tuùc, saùng taïo.
 Luyeän oùc tö duy thöïc teá. II. CHUAÅN BÒ:
Giaùo vieân: Giaùo aùn. Hình veõ minh hoaï.
Hoïc sinh: SGK, vôû ghi. OÂn taäp phaàn Giaù trò löôïng giaùc cuûa goùc  (00    1800).
III. HOAÏT ÑOÄNG DAÏY HOÏC:
1. OÅn ñònh toå chöùc: Kieåm tra só soá lôùp.
2. Kieåm tra baøi cuõ: (3')
H. Neâu ñònh nghóa cung löôïng giaùc, goùc löôïng giaùc ? Ñ.
3. Giaûng baøi môùi: TL
Hoaït ñoäng cuûa Giaùo vieân
Hoaït ñoäng cuûa Hoïc sinh Noäi dung
Hoaït ñoäng 1: Tìm hieåu Ñôn vò Radian
II. Soá ño cuûa cung vaø goùc löôïng
15'  GV giôùi thieäu ñôn vò radian. giaùc 1. Ñoä vaø radian a) Ñôn vò radian
Treân ñöôøng troøn tuyø yù, cung coù ñoä
H1. Cho bieát ñoä daøi cung nöûa Ñ1. R.
daøi baèng baùn kính ñgl cung coù soá ñöôøng troøn ? ño 1 rad.
b) Quan heä giöõa ñoä vaø radian
H2. Cung nöûa ñöôøng troøn coù soá Ñ2. 1800,  rad.  0 180  ño bao nhieâu ñoä, rad ? 10 = rad; 1 rad = 180     
 Cho caùc soá ño theo ñoä, yeâu caàu Baûng chuyeån ñoåi thoâng duïng
HS ñieàn soá ño theo radian vaøo Ñoä 00 300 450 600 900 1200 1350 1800 baûng. Rad 0     2 3  6 4 3 2 3 4
Chuù yù: Khi vieát soá ño cuûa moät goùc
(cung) theo ñôn vò radian, ta khoâng
vieát chöõ rad sau soá ño.
c) Ñoä daøi cung troøn
H3. Cung coù soá ño  rad thì coù Ñ3. R.
Cung coù soá ño rad cuûa ñöôøng ñoä daøi bao nhieâu ?
troøn baùn kính R coù ñoä daøi: l = R
Hoaït ñoäng 2: Tìm hieåu soá ño cung löôïng giaùc – goùc löôïng giaùc B
2. Soá ño cuûa cung löôïng giaùc B B B
Soá ño cuûa moät cung löôïng giaùc 10' A (A O
M) laø moät soá thöïc aâm hay O A O A A O döông. Kí hieäu sñ . a) b) c) d)
H4. Xaùc ñònh soá ño cuûa caùc cung Ñ4.
Ghi nhôù: Soá ño cuûa caùc cung löôïng giaùc nhö hình veõ ?  5 9
löôïng giaùc coù cuøng ñieåm ñaàu vaø a) b) c) 2 2 2
ñieåm cuoái sai khaùc nhau moät boäi
cuûa 2 hoaëc 3600. sñ
= + k2 (k Z) 95
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn 3 sñ
= a0 + k3600 (k Z) d)  2
trong ñoù (hay a0) laø soá ño cuûa
moät löôïng giaùc tuyø yù coù ñieåm ñaàu y B
A vaø ñieåm cuoái M. D C
3. Soá ño cuûa goùc löôïng giaùc A’ A
H5. Xaùc ñònh soá ño caùc goùc O x
Soá ño cuûa goùc löôïng giaùc (OA,
löôïng giaùc (OA, OC), (OA, OD), B’
OM) laø soá ño cuûa cung löôïng giaùc (OA, OB) ? töông öùng. Ñ5. Chuù yù:  sñ(OA,OC) = ; cung LG 1 1    goùc LG 6  sñ(OA,OD) = 3
Hoaït ñoäng 3: Tìm hieåu caùch bieåu dieãn cung löôïng giaùc treân ñöôøng troøn löôïng giaùc
H1. Bieåu dieãn treân ñöôøng troøn Ñ1.
4. Bieåu dieãn cung löôïng giaùc
10' löôïng giaùc caùc cung coù soá ño: 25 
treân ñöôøng troøn löôïng giaùc 25 a) = + 3.2  M laø a) b) –7650 4 4 Giaû söû sñ = . 4
ñieåm giöõa cung AB .
Ñieåm ñaàu A(1; 0)
b) –7650 = –450 + (–2).3600
Ñieåm cuoái M ñöôïc xaùc ñònh bôûi sñ = .
 M ñieåm giöõa cung AB'
Hoaït ñoäng 4: Cuûng coá  Nhaán maïnh: 5' – Ñôn vò radian
– Soá ño cuûa cung vaø goùc LG.
– Caùch bieåu dieãn cung LG treân ñöôøng troøn LG.
Caâu hoûi: Chia lôùp thaønh 4  Caùc nhoùm thöïc hieän.
nhoùm, 2 nhoùm cho soá ño goùc theo
ñoä, 2 nhoùm ñoåi sang radian vaø ngöôïc laïi
4. BAØI TAÄP VEÀ NHAØ:
 Baøi 1, 2, 3, 4, 5, 6, 7 SGK.
 Ñoïc tröôùc baøi "Giaù trò löôïng giaùc cuûa moät cung". Ngaøy soaïn: 1/03/20113
Chöông VI: CUNG VAØ GOÙC LÖÔÏNG GIAÙC. COÂNG THÖÙC LÖÔÏNG GIAÙC Tieát daïy: 50
Baøøi 2: GIAÙ TRÒ LÖÔÏNG GIAÙC CUÛA MOÄT CUNG I. MUÏC TIEÂU: Kieán thöùc:
 Naém vöõng ñònh nghóa caùc giaù trò löôïng giaùc cuûa cung .
 Naém vöõng caùc haèng ñaúng thöùc löôïng giaùc cô baûn.
 Naém vöõng moái quan heä giöõa caùc giaù trò löôïng giaùc cuûa caùc goùc coù lieân quan ñaëc bieät. Kó naêng:
 Tính ñöôïc caùc giaù trò löôïng giaùc cuûa caùc goùc.
 Vaän duïng linh hoaït caùc haèng ñaúng thöùc löôïng giaùc.
 Bieát aùp duïng caùc coâng thöùc trong vieäc giaûi caùc baøi taäp. 96
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn Thaùi ñoä:
 Luyeän tính caån thaän, tö duy linh hoaït. II. CHUAÅN BÒ:
Giaùo vieân: Giaùo aùn. Hình veõ minh hoaï.
Hoïc sinh: SGK, vôû ghi. OÂn taäp phaàn Giaù trò löôïng giaùc cuûa goùc  (00    1800).
III. HOAÏT ÑOÄNG DAÏY HOÏC:
1. OÅn ñònh toå chöùc: Kieåm tra só soá lôùp. y
2. Kieåm tra baøi cuõ: (3')
H. Nhaéc laïi ñònh nghóa GTLG cuûa goùc  (00    1800) ? y M Ñ. sin y x  = y 0
0; cos = x0; tan = 0 ; cot = 0 . x  0 y0 O x0 x –1 1
3. Giaûng baøi môùi: TL
Hoaït ñoäng cuûa Giaùo vieân
Hoaït ñoäng cuûa Hoïc sinh Noäi dung
Hoaït ñoäng 1: Tìm hieåu Ñònh nghóa caùc giaù trò löôïng giaùc cuûa moät cung
 Töø KTBC, GV neâu ñònh nghóa
I. Giaù trò löôïng giaùc cuûa cung caùc GTLG cuûa cung . y 1. Ñònh nghóa B 10' M K Cho cung coù sñ = . A’  A
sin = OK ;
cos = OH ; O H x 
tan = sin (cos 0) B’ cos 
H1. So saùnh sin, cos vôùi 1 vaø
cot = cos (sin 0)
Ñ1. –1  sin  1 sin  –1 ? –1  cos  1
Caùc giaù trò sin, cos, tan, cot
ñgl caùc GTLG cuûa cung .
H2. Neâu moái quan heä giöõa tan Ñ2. tan.cot = 1
Truïc tung: truïc sin, vaø cot ?
Truïc hoaønh: truïc cosin. Chuù yù:
H3. Tính sin 25 , cos(–2400),
– Caùc ñònh nghóa treân cuõng aùp duïng 4
cho caùc goùc löôïng giaùc. tan(–4050) ? Ñ3. 25    3.2 4 4
– Neáu 00 1800 thì caùc GTLG
cuûa cuõng chính laø caùc GTLG cuûa sin 25 = sin  2 
goùc ñoù ñaõ hoïc. 4 4 2
Hoaït ñoäng 2: Nhaän xeùt moät soá keát quaû ruùt ra töø ñònh nghóa
 Höôùng daãn HS töø ñònh nghía 2. Heä quaû
15' caùc GTLG ruùt ra caùc nhaän xeùt.
a) sin vaø cos xaùcñònh vôùi  R. sin(  k2 )
  sin (k Z) cos(  k2 )   cos
b) –1 sin 1; –1 cos 1
c) Vôùi m R maø –1 m 1 ñeàu
toàn taïi vaø sao cho:
H1. Khi naøo tan khoâng xaùc Ñ1. Khi cos = 0  M ôû B
sin = m; cos = m ñònh ? 
hoaëc B   =  + k
d) tan xaùc ñònh vôùi + k 2 2
e) cot xaùc ñònh vôùi k
f) Daáu cuûa caùc GTLG cuûa
H2. Döïa vaøo ñaâu ñeå xaùc ñònh Ñ2. Döïa vaøo vò trí ñieåm cuoái I II III IV
daáu cuûa caùc GTLG cuûa  ? M cuûa cung = . cos + – – + sin + + – – 97
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn tan + – + – cot + – + –
Hoaït ñoäng 3: Tìm hieåu caùch bieåu dieãn cung löôïng giaùc treân ñöôøng troøn löôïng giaùc
 Cho HS nhaéc laïi vaø ñieàn vaøo  HS thöïc hieän yeâu caàu.
3. GTLG cuûa caùc cung ñaëc bieät 5' baûng.     0 6 4 3 2 sin 0 1 2 3 1 2 2 2 cos 1 3 2 1 0 2 2 2 tan 0 3 1 3 // 3 cot // 3 1 3 0 3 
Hoaït ñoäng 4: Tìm hieåu yù nghóa hình hoïc cuûa tang vaø coâtang
H1. Tính tan , cot ? Ñ1.
II. YÙ nghóa hình hoïc cuûa tang vaø 8' coâtang y  t tan = sin = HM AT  s’ B S s cos OH OH
1. YÙ nghóa hình hoïc cuûa tan M K T = AT
tan ñöôïc bieåu dieãn bôûi AT treân  A
truïc t'At. Truïc tAt ñgl truïc tang. x’  O H x cot = cos KM BS   sin  OK OB
2. YÙ nghóa hình hoïc cuûa cot = BS
cot ñöôïc bieåu dieãn bôûi BS treân t’
truïc sBs. Truïc sBs ñgl truïc coâtang.
tan( + k) = tan
cot( + k) = cot
Hoaït ñoäng 5: Cuûng coá  Nhaán maïnh
3' – Ñònh nghóa caùc GTLG cuûa .
– YÙ nghóa hình hoïc cuûa caùc GTLG cuûa .
4. BAØI TAÄP VEÀ NHAØ:  Baøi 1, 2, 3 SGK.
Ñoïc tieáp baøi "Giaù trò löôïng giaùc cuûa moät cung". Ngaøy soaïn: 25/03/2013
Chöông VI: CUNG VAØ GOÙC LÖÔÏNG GIAÙC. COÂNG THÖÙC LÖÔÏNG GIAÙC Tieát daïy: 51
Baøøi 2: GIAÙ TRÒ LÖÔÏNG GIAÙC CUÛA MOÄT CUNG (tt) I. MUÏC TIEÂU: Kieán thöùc:
 Naém vöõng caùc haèng ñaúng thöùc löôïng giaùc cô baûn.
 Naém vöõng moái quan heä giöõa caùc giaù trò löôïng giaùc cuûa caùc goùc coù lieân quan ñaëc bieät. Kó naêng:
 Tính ñöôïc caùc giaù trò löôïng giaùc cuûa caùc goùc.
 Vaän duïng linh hoaït caùc haèng ñaúng thöùc löôïng giaùc.
 Bieát aùp duïng caùc coâng thöùc trong vieäc giaûi caùc baøi taäp. Thaùi ñoä:
 Luyeän tính caån thaän, tö duy linh hoaït. 98
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn II. CHUAÅN BÒ:
Giaùo vieân: Giaùo aùn. Hình veõ minh hoaï.
Hoïc sinh: SGK, vôû ghi. OÂn taäp phaàn Giaù trò löôïng giaùc cuûa goùc  .
III. HOAÏT ÑOÄNG DAÏY HOÏC: y
1. OÅn ñònh toå chöùc: Kieåm tra só soá lôùp. B M
2. Kieåm tra baøi cuõ: (3') K A’  A
H. Nhaéc laïi ñònh nghóa GTLG cuûa cung  ? O H x
Ñ. sin = OK ; cos = OH ; tan = sin  ; cot = cos . B’ cos sin 
3. Giaûng baøi môùi: TL
Hoaït ñoäng cuûa Giaùo vieân
Hoaït ñoäng cuûa Hoïc sinh Noäi dung
Hoaït ñoäng 1: Tìm hieåu caùc coâng thöùc löôïng giaùc cô baûn
 Höôùng daãn HS chöùng minh 
III. Quan heä giöõa caùc GTLG caùc coâng thöùc. 2 sin 
1. Coâng thöùc löôïng giaùc cô baûn 15' 1 + tan2 = 1 + = 2 cos 
sin2 + cos2 = 1 2 2 cos   sin  1
1 + tan2 = 1 ( + k) =  2 2 2 cos  2 cos  cos  1 1 + cot2 =
( k) 2 sin  
tan.cot = 1
( k ) 2
2. Ví duï aùp duïng
H1. Neâu coâng thöùc quan heä 
giöõa sin vaø cos ?
Ñ1. sin2 + cos2 = 1
VD1: Cho sin = 3 vôùi <  < . 5 2 Tính cos.
H2. Haõy xaùc ñònh daáu cuûa Ñ2. Vì  <  <  neân cos < 0 2 cos ?  cos = – 4 5 
VD2: Cho tan = – 4 vôùi 3 <  < 5 2 1
2. Tính sin vaø cos.
H3. Neâu coâng thöùc quan heä Ñ3. 1 + tan2 = 2 cos 
giöõa tan vaø cos ?
H4. Haõy xaùc ñònh daáu cuûa Ñ4. Vì 3 <  <2 neân cos > 0 2 cos ? cos = 5 41
Hoaït ñoäng 2: Tìm hieåu caùc GTLG cuûa caùc cung coù lieân quan ñaëc bieät
 GV treo caùc hình veõ vaø  Moãi nhoùm nhaän xeùt moät hình.
3. GTLG cuûa caùc cung coù lieân
17' höôùng daãn HS nhaän xeùt vò trí quan ñaëc bieät
cuûa caùc ñieåm cuoái cuûa caùc a) M vaø M ñoái xöùng nhau qua a) Cung ñoái nhau: vaø – cung lieân quan. truïc hoaønh.
cos(–) = cos; sin(–) = –sin
tan(–) = –tan; cot(–) = –cot
b) M vaø M ñoái xöùng nhau qua b) Cung buø nhau: vaø – truïc tung.
cos(–)=–cos; sin(–) = sin
tan(–)=–tan; cot(–) = –cot
c) M vaø M ñoái xöùng nhau qua c) Cung phuï nhau: vaø      
ñöôøng phaân giaùc thöù I. 2    99
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn cos      
   =sin; sin    =cos 2      2  tan      
   =cot; cot    =tan
d) M vaø M ñoái xöùng nhau qua 2      2  goác toaï ñoä O.
d) Cung hôn keùm : vaø ( + )
cos(+)=–cos; sin( + )=–sin
tan(+)=tan; cot( + )=cot y y y y M M’ M M’ M        M H    O  x O H x O H x O H x M’ M’ ñoái nhau phuï nhau buø nhau
hôn keùm
Hoaït ñoäng 3: AÙp duïng tính GTLG cuûa caùc cung coù lieân quan ñaëc bieät
H. Tính vaø ñieàn vaøo baûng. Ñ.
VD3: Tính GTLG cuûa caùc cung sau: 5' –  , 1200, 1350, 5 6 6 –  1200 1350 5 6 6 sin – 1 3 1 2 2 2 2 2 cos 3 – 1  2  3 2 2 2 2
Hoaït ñoäng 4: Cuûng coá  Nhaán maïnh:
3' – Caùc coâng thöùc löôïng giaùc.
– Caùch vaän duïng caùc coâng thöùc.
4. BAØI TAÄP VEÀ NHAØ:  Baøi 4, 5 SGK. Ngaøy soaïn: 25/03/2013
Chöông VI: CUNG VAØ GOÙC LÖÔÏNG GIAÙC. COÂNG THÖÙC LÖÔÏNG GIAÙC Tieát daïy: 53
Baøøi 2: BAØI TAÄP GIAÙ TRÒ LÖÔÏNG GIAÙC CUÛA MOÄT CUNG I. MUÏC TIEÂU:
Kieán thöùc: Cuûng coá caùc kieán thöùc veà:
 Caùc haèng ñaúng thöùc löôïng giaùc cô baûn.
 Moái quan heä giöõa caùc giaù trò löôïng giaùc cuûa caùc goùc coù lieân quan ñaëc bieät. Kó naêng:
 Tính ñöôïc caùc giaù trò löôïng giaùc cuûa caùc goùc.
 Vaän duïng linh hoaït caùc haèng ñaúng thöùc löôïng giaùc.
 Bieát aùp duïng caùc coâng thöùc trong vieäc giaûi caùc baøi taäp. Thaùi ñoä:
 Luyeän tính caån thaän, tö duy linh hoaït. 100
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn II. CHUAÅN BÒ:
Giaùo vieân: Giaùo aùn. Heä thoáng baøi taäp.
Hoïc sinh: SGK, vôû ghi. OÂn taäp phaàn Giaù trò löôïng giaùc cuûa moät cung .
III. HOAÏT ÑOÄNG DAÏY HOÏC:
1. OÅn ñònh toå chöùc: Kieåm tra só soá lôùp.
2. Kieåm tra baøi cuõ: (Loàng vaøo quaù trình luyeän taäp) H. Ñ.
3. Giaûng baøi môùi:
TL Hoaït ñoäng cuûa Giaùo vieân
Hoaït ñoäng cuûa Hoïc sinh Noäi dung
Hoaït ñoäng 1: Luyeän taäp caùc coâng thöùc löôïng giaùc cô baûn
H1. Neâu heä thöùc lieân quan Ñ1. sin2x + cos2x = 1
1. Caùc ñaúng thöùc sau coù theå ñoàng 5' giöõa sinx vaø cosx ? a) khoâng thôøi xaûy ra khoâng ? b) coù a) sinx = 2 vaø cosx = 3 c) khoâng 3 3 b) sinx = 4  vaø cosx = 3  5 5 c) sinx = 0,7 vaø cosx = 0,3
Hoaït ñoäng 2: Luyeän taäp xeùt daáu caùc GTLG
H1. Neâu caùch xaùc ñònh daáu Ñ1. Xaùc ñònh vò trí ñieåm cuoái 2. Cho 0 < x <  . Xaùc ñònh daáu 10' caùc GTLG ?
cuûa cung thuoäc goùc phaàn tö 2 naøo. cuûa caùc GTLG:
a) sin(x – ) = –sin( – x) a) sin(x – ) = –sinx < 0 b) cos  3    x 2    b) cos  3      x vì < 3  x < 2    2 2 c) tan(x + )  d) cot     x   c) tan(x + ) = tanx > 0  2  d) cot       x  vì  x    2    2 2
Hoaït ñoäng 3: AÙp duïng tính GTLG cuûa moät cung
H1. Neâu caùc böôùc tính ?
Ñ1. + Xeùt daáu GTLG caàn tính 3. Tính caùc GTLG cuûa x, neáu: 15' + Tính theo coâng thöùc a) cosx = 4 vaø 0 x   
H2. Neâu coâng thöùc caàn söû Ñ2. 13 2 duïng ?
a) sinx > 0; sin2x + cos2x = 1
b) sinx = – 0,7 vaø  < x < 3 2
 sinx = 3 17 ; tanx = 3 17 ;  13 4 c) tanx = 5  vaø  x   17 2 cotx = 4  3 17
d) cotx = –3 vaø 3  x  2 2
b) cosx < 0; sin2x + cos2x = 1
 cosx = – 0,51 ; tanx  1,01; cotx  0,99 c) cosx < 0; 1 + tan2x = 1 2 cos x 101
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn  cosx = 7  ; 274 sinx = 15 ; cotx = 7  274 15 d) sinx < 0; 1 + cot2x = 1 2 sin x  sinx = 1  ; cosx = 3 ; 10 10 tanx = 1  3
Hoaït ñoäng 4: Luyeän taäp bieán ñoåi bieåu thöùc löôïng giaùc
 Höôùng daãn HS caùch bieán 
4. Chöùng minh caùc heä thöùc: 10' ñoåi. a) VT = cos2x + cos2x.cot2x
a) cos2x + cos2x.cot2x = cot2x = cos2x(1 + cot2x) 2
b) 2cos x 1 = cosx – sinx = cos2x. 1 = cot2x cosx  sin x 2 sin x 2 c) tanx cot x 1 b) cos2x – sin2x = .  1 2 1 tan x cot x
= (cosx – sinx).(cosx + sinx) 3 3 sin x  cos x c) tanx.cotx = 1 d)  1 sin x.cosx sin x  cosx
d) Söû duïng haèng ñaúng thöùc:
sin3x + cos3x = (sinx + cosx). .(sin2x – sinx.cosx+cos2x)
Hoaït ñoäng 5: Cuûng coá  Nhaán maïnh:
3' – Caùc coâng thöùc löôïng giaùc.
– Caùch vaän duïng caùc coâng thöùc.
4. BAØI TAÄP VEÀ NHAØ:
 Laøm tieáp caùc baøi coøn laïi.
 Ñoïc tröôùc baøi " Coâng thöùc löôïng giaùc" Ngaøy soaïn: 30/03/2013
Chöông VI: CUNG VAØ GOÙC LÖÔÏNG GIAÙC. COÂNG THÖÙC LÖÔÏNG GIAÙC Tieát daïy: 54
Baøøi 3: COÂNG THÖÙC LÖÔÏNG GIAÙC I. MUÏC TIEÂU: Kieán thöùc:
 Naém ñöôïc caùc coâng thöùc löôïng giaùc: coâng thöùc coäng, coâng thöùc nhaân ñoâi, coâng thöùc bieán
ñoåi toång thaønh tích, coâng thöùc bieán ñoåi tích thaønh toång.
 Töø caùc coâng thöùc treân coù theå suy ra moät soá coâng thöùc khaùc. Kó naêng:
 Bieán ñoåi thaønh thaïo caùc coâng thöùc löôïng giaùc.
 Vaän duïng caùc coâng thöùc treân ñeå giaûi baøi taäp. Thaùi ñoä:
 Luyeän tính caån thaän, tö duy linh hoaït. II. CHUAÅN BÒ:
Giaùo vieân: Giaùo aùn. Caùc baûng coâng thöùc löôïng giaùc. 102
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn
Hoïc sinh: SGK, vôû ghi. OÂn taäp phaàn Giaù trò löôïng giaùc cuûa moät cung .
III. HOAÏT ÑOÄNG DAÏY HOÏC:
1. OÅn ñònh toå chöùc: Kieåm tra só soá lôùp.
2. Kieåm tra baøi cuõ: (3')
H. Neâu caùc coâng thöùc löôïng giaùc cô baûn ?
Ñ. sin2x + cos2x = 1; 1 + tan2x = 1 ; 1 + cot2x = 1 ; tanx.cotx = 1. 2 cos x 2 sin x
3. Giaûng baøi môùi: TG
Hoạt động của HS
Hoạt động của GV Nội dung
10’ *Học sinh nhận nhiệm vụ
HĐ1: (kiểm tra bài cũ)
I/ Công thức cộng:  ,thảoluận theo nhóm. AM   ;
1/Công tức cộng đối với Cho cung  .Hãy sin và cosin: y AN     biểu diễn cáccung đó *cos(  )=cos cos   sin sin  M trên đường trònlương N
giác .Tìm tọa độ của các *sin(   )=sin cos     A véc tơ sin  cos  x M O ; N O . Tính tích vô hướng của hai véc tơ theo hai phương
pháp .So sánh hai kết quả
đó rồi đưa ra công thức.
(cho học sinh hoạt động theo nhóm).gv theo dõi
*Họcsinh phải xây dựng được .
hướng dẫn học sinh thảo
ON  (cos;sin  )
luận ,giúp đỡ học sinh khi cần thiết.
OM  (cos ;sin  )
Cho 1 học sinh đại diện
ON.OM  cos.cos  sin .sin  nhóm mình trình bày kết quả .
ON.OM ON .ON .cos(ON.OM ) Các học sinh của nhóm Đại diện nhóm trình
bày kết quả, khác nhận xét ,góp ý, bổ
các nhóm khác tham gia thảo sung đưa ra công
luận, góp ý bổ sung để xây dựng thức.Công thức đó được công thức.
gọi là công thức cộng.Đó
Cos ( -  ) = cos .cos  + là bài học hôm nay.
HĐ2: (chia lớp thành 2 sin sin  (1) 15’ nhóm)
Chốt công thức cộng đối cos( - HĐTP1:  Từ công ) thức(1) . Hãy tính thảo luận. cos( +  )?(nhóm 1
Nhóm 1 thay được  bởi (-  ) Từ công thức (1).Hãy Nhóm 2 thay được sin( +  )
tinh sin( -  )?(nhóm 2)  .GV theo dõi các nhóm bởi cos (      ) 2
thảo luận và giúp đỡ khi
Đại diện nhóm trình bày kết qủa cần thiết.
của nhóm mình. Đại diện các
Cho đại diện nhóm trình
nhóm khác góp ý trao đổi bổ bày kết quả của nhóm 103
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn
sung. -> Đưa ra công thức mình . các nhóm còn lại tham gia góp ý bổ sung
HS nhận nhiệm vụ và thực hiện - .Giáo viên tổng hợp công
> hình thành ra công thức. thức.
Học sinh làm bài tập theo yêu
HĐTP2: Tương tự tính cầu của GV Sin( +  )? HĐTP 3: Hãy kiểm
2/ Công thức cộng đối sin(   )
nghiệm lại các công thức tan tan( +  ) =   
nói trên với  tuỳ ý và *tan( +  ) = cos( )   tan  tan  =  ;  =
sin.cos  sin .co  s 2 = 1  tan .tan  = co  s .cos  sin.sin  HĐ3: . 15’ HĐTP1: Tính: *Tan( -  ) = tan( +  )
sin .cos  sin  .co  s tan   tan  tan( -  ) theo tan , co  s cos 1 tan . tan  tan 
= sin cos  sin.sin  Cho 2 nhóm hoạt động co  s cos GV theo dõi các nhóm
Để các công thức trên có nghĩa thì:  tan  tan 
hoạt động và giúp đỡ các ;  ; =
em khi cần thiết. Cho đại ( +  ); ( -  ) không có 1  tan .tan 
diện của nhóm lên trình Tương tự ta có:  bày bài giải của mình. dạng   k (k z) tan   tan  2 Tan( -  ) =
Để các công thức trên 1 tan . tan 
có nghĩa tìm điều kiện HS giải:
Ví dụ: Tính tan 15o
của  và  ; ( -  ); 3- 3 ( +  ).
HĐTP 3:Ví dụ: Tính tan = 15o = ? 3 + 3
Hoaït ñoäng 4: Cuûng coá
 Nhaán maïnh caùc coâng thöùc löôïng 5' giaùc. Ngaøy soaïn: 30/03/2013
Chöông VI: CUNG VAØ GOÙC LÖÔÏNG GIAÙC. COÂNG THÖÙC LÖÔÏNG GIAÙC Tieát daïy: 55
Baøøi 3: COÂNG THÖÙC LÖÔÏNG GIAÙC I. MUÏC TIEÂU:
Qua bài học sinh cần nắm được:
+ Về kiến thức: Công thức cộng, công tức nhân đôi.
+ Về kĩ năng: Học sinh áp dụng công thức vào giải toán,( chứng minh,rút gọn biểu thức,tính toán …)
+ Về tư duy: Từ công thức cộng, công thức nhân đôi biến đổi thêm một số công thức khác.
+ Về thái độ: Có thái độ học tập đúng đắn,chịu khó, kiên nhẫn. II/ Chẩn bị:
- Học sinh: Dụng cụ học tập và máy tính bỏ túi.
-Giáo viên:đồ dùng giảng dạy,phiếu học tập, đường tròn lượng giác.
III/Tiến trình bài học: 104
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn
*Ổn định lớp, giới thiệu: Chia lớp thành 6 nhóm. *Kiểm tra bài cũ:
- Viết các công thức lượng giác cơ bản;... *Bài mới: TG
Hoạt động của HS
Hoạt động của GV Nội dung HĐ 1
II. Công thức nhân đôi HS trả lời:
HĐTP 1: từ công thức cộng cos( +  ) = cos2
đối với sin và cos nếu thay cos2 = cos2 -sin2  = cos2 -
=  thì công thức thay đổi =2cos2 -1. 40’ cos2 ra sao ? =1 - 2sin2
= 1- 2sin2  GV gọi HS đứng tại chỗ tính sin2 = 2sin cos = 2cos2 -1 toán 2 tan sin 2 = 2sin cos
HĐTP2: GV hỏi: tan 2 cần tan2 = 2 1  tan  2 tan điều kiện gì ?
(Với tan2 ; tan ) có tan2 = HĐTP3 2 : TínhCos2 ;sin2 ; 1  tan  nghĩa. tan2 ; Theo cos2 ?
Chú ý công thức hạ bậc
Cho học sinh thảo luận nhóm   rồi đưa ra công thức. 1 cos2 Sin2 =
*Học sinh nhận nhiệm GV cho học trò trình bày thảo 2
luận vàsửa sai đưa ra công
vụ,thảo luận đưa ra kết 1  cos2 thức đúng.
quả đúng..Đại diện nhóm Cos2 = 2 trình bày kết quả cuả 1  cos  2 nhóm mình. Các nhóm tan2 = khácđại diện thảo 1  cos  2
luận,góp ý bổ sung , đưa ra kết quả đúng.
HĐTP4:(phát phiếu học tập) Kết quả:1/ cos4 ,cho các nhóm. = 8cos4  -8cos2  +1
1/Hãy tính cos4 theo cos   . 2  2 2/ cos   8 2 2/Tính cos . 8 3/sin .sin cos2 =
3/Đơn giản biểu thức : 1/4sin 4 sin cos cos2
Hoaït ñoäng 2: Cuûng coá
Nhaán maïnh caùc coâng thöùc 5’ löôïng giaùc.
4. BAØI TAÄP VEÀ NHAØ:
 Baøi 1, 2, 3, 4, 5, 6, 7, 8 SGK. 105
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn Ngaøy soaïn: 30/03/2013
Chöông VI: CUNG VAØ GOÙC LÖÔÏNG GIAÙC. COÂNG THÖÙC LÖÔÏNG GIAÙC Tieát daïy: 56
Baøøi 3: COÂNG THÖÙC LÖÔÏNG GIAÙC I. MUÏC TIEÂU:
Qua bài học sinh cần nắm được:
+ Về kiến thức: Công thức cộng, công tức nhân đôi.
+ Về kĩ năng: Học sinh áp dụng công thức vào giải toán,( chứng minh,rút gọn biểu thức,tính toán …)
+ Về tư duy: Từ công thức cộng, công thức nhân đôi biến đổi thêm một số công thức khác.
+ Về thái độ: Có thái độ học tập đúng đắn,chịu khó, kiên nhẫn. II/ Chẩn bị:
- Học sinh: Dụng cụ học tập và máy tính bỏ túi.
-Giáo viên:đồ dùng giảng dạy,phiếu học tập, đường tròn lượng giác.
III/Tiến trình bài học:
*Ổn định lớp, giới thiệu: Chia lớp thành 6 nhóm. 106
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn
*Kiểm tra bài cũ:
- Viết các công thức lượng giác cơ bản;... *Bài mới: TG
Hoạt động của HS
Hoạt động của GV Nội dung HĐ 1
II. Công thức nhân đôi HS trả lời:
HĐTP 1: từ công thức cộng cos( +  ) = cos2
đối với sin và cos nếu thay cos2 = cos2 -sin2  = cos2 -
=  thì công thức thay đổi =2cos2 -1. 40’ cos2 ra sao ? =1 - 2sin2
= 1- 2sin2  GV gọi HS đứng tại chỗ tính sin2 = 2sin cos = 2cos2 -1 toán 2 tan sin 2 = 2sin cos
HĐTP2: GV hỏi: tan 2 cần tan2 = 2 1  tan  2 tan điều kiện gì ?
(Với tan2 ; tan ) có tan2 = HĐTP3 2 : TínhCos2 ;sin2 ; 1  tan  nghĩa. tan2 ; Theo cos2 ?
Chú ý công thức hạ bậc
Cho học sinh thảo luận nhóm   rồi đưa ra công thức. 1 cos2 Sin2 =
*Học sinh nhận nhiệm GV cho học trò trình bày thảo 2
luận vàsửa sai đưa ra công
vụ,thảo luận đưa ra kết 1  cos2 thức đúng.
quả đúng..Đại diện nhóm Cos2 = 2 trình bày kết quả cuả 1  cos  2 nhóm mình. Các nhóm tan2 = khácđại diện thảo 1  cos  2
luận,góp ý bổ sung , đưa ra kết quả đúng.
HĐTP4:(phát phiếu học tập) Kết quả:1/ cos4 ,cho các nhóm. = 8cos4  -8cos2  +1
1/Hãy tính cos4 theo cos   . 2  2 2/ cos   8 2 2/Tính cos . 8 3/sin .sin cos2 =
3/Đơn giản biểu thức : 1/4sin 4 sin cos cos2
Hoaït ñoäng 2: Cuûng coá
Nhaán maïnh caùc coâng thöùc 5’ löôïng giaùc.
4. BAØI TAÄP VEÀ NHAØ:
 Baøi 1, 2, 3, 4, 5, 6, 7, 8 SGK. 107
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn Ngaøy soaïn: 5/04/2013
Chöông VI: CUNG VAØ GOÙC LÖÔÏNG GIAÙC. COÂNG THÖÙC LÖÔÏNG GIAÙC Tieát daïy: 57
Baøøi 3: COÂNG THÖÙC LÖÔÏNG GIAÙC I/ Mục tiêu:
Qua bài học sinh cần nắm được:
+ Về kiến thức: Công thức cộng, công tức nhân đôi.
+ Về kĩ năng: Học sinh áp dụng công thức vào giải toán,( chứng minh,rút gọn biểu thức,tính toán …)
+ Về tư duy: Từ công thức cộng, công thức nhân đôi biến đổi thêm một số công thức khác.
+ Về thái độ: Có thái độ học tập đúng đắn,chịu khó, kiên nhẫn. II/ Chẩn bị:
- Học sinh: Dụng cụ học tập và máy tính bỏ túi.
-Giáo viên:đồ dùng giảng dạy,phiếu học tập, đường tròn lượng giác.
III/Tiến trình bài học:
*Ổn định lớp, giới thiệu: Chia lớp thành 6 nhóm. 108
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn
*Kiểm tra bài cũ:
- Viết các công thức lượng giác cơ bản;... *Bài mới: TG
Hoạt động của HS
Hoạt động của GV Nội dung 40’
Các nhóm nhận nhiệm vụ Phát phiếu học tập cho các III/ Công thức biến đổi
thảo luận dể tìm ra lời nhóm. Theo dõi hoạt động của tích thành tổng và tổng giải.
các nhóm,giúp đỡ học sinh khi thành tích :
Đại diện nhóm trình bày cần thiết.
1/ công thức biến đổi tích kết quả của
nhóm Đại diện của nhóm trình bày thanh tổng:
mình.Đại diện các nhóm kết quả của nhóm mình.Đại *cos .cos 
khác trao đổi đưa về công diện các nhóm khác trao đổi 1
co s   co s   thức đúng.
góp ý, bổ sung để đưa ra công 2 thức đúng. *Sin sin  = HĐTP2: (khắc sâu), phát 1
phiếu học tập số 2 cho các
co s  co s   2
nhóm(chia ra 4 nhóm ,2 nhóm
Các nhóm nhận nhiệm vụ làm 1 câu). * sin cùng nhau thảo luận tìm   cos  = 1/tính: 5 sin .sin
ra kết quả.Đại diện các 24 24
1 sin  sin   nhóm trình bày kết quả   2/tính: 7 5 2 cos sin của nhóm mình,các nhóm 12 12 Ví dụ :Tính:
khác cùng trao đổi góp ý Giáo viên hướng dẫn cho các 5  1. sin .sin đưa ra kết quả đúng.
nhóm làm bài .cho đại diện 24 24
các nhóm trình bày kết quả 1 kq:  3  2
của nhóm mình.cho cả lớp 4  
cùng kiểm tra đánh giá bổ 7 5 2/ cos sin
sungđưa về kết quả đúng. 12 12 HĐ2: 1 kq: HĐTP1:(phiếu học tập 4
số3),phát cho các nhóm. Từ
các công thức biến đổi tích
thành tổng ở trên .Nếu
Các nhóm nhận nhiệm vụ     x đặt
cùng nhau thảo luận để      y
đưa ra công thức.Đại diện x y x y
nhóm trình bày kết quả tứclà (  ;   )thì 2 2
của nhóm mình. Các ta được các công thức nào?
nhóm khác cùng tham gia Cho các nhóm thảo luận .Đại 2/Công thức biến đổi tổng
ý kiến sửa sai hoặc bổ diện nhóm trình bày kết quả thành tích:
sung để đưa về công thức ,sửa sai ,bổ sung đưa ra kết *cos x + cos y đúng. quả đúng.   x y x y Đưa ra công thức 2cos cos = . 2 2 HĐTP2(khắc sâu công * cos x - cos y
thức).Phát phiếu học tập cho  
các nhóm ,mỗi nhóm làm 1 x y x y  2sin sin = bài tập nhỏ sau : 2 2 109
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn
Các nhóm nhận nhiệm vụ Chứng minh *sin x + siny
,tiến hành tìm ra phương rằng x y x y
án của mình . Đại diện 1 = 2sin cos . 1/  1  nhóm trình bày kết quả 2  2 2 3 của nhóm mình. Cùng sin sin *sin x - siny 10 10
tham gia thảo luận với các x y x y  = 2cos sin
nhóm khác để đưa ra kết  
2 / sin  cos  2 sin   2 2 quả đúng.  4    
3/ sin  cos  2 sin    4 
Các nhóm thảo luận tìm ra
phương án của bài toán.đại
diện các nhóm trình bày kết
quả của nhóm mình .cùng
thảo luận ,góp ý với các nhóm
khác để được lời giải đúng.
Hoaït ñoäng 2: Cuûng coá 5’
Nhaán maïnh caùc coâng thöùc löôïng giaùc. Ngaøy soaïn: 05/04/2013
Chöông VI: CUNG VAØ GOÙC LÖÔÏNG GIAÙC. COÂNG THÖÙC LÖÔÏNG GIAÙC Tiết PP: 58 BAØI TẬP I. Mục tiêu:
+ Kieán thöùc: - Cuûng coá caùc coâng thöùc löôïng giaùc ñaõ hoïc ôû tieát tröôùc
+ Kyõ naêng: - Reøn kó naêng aùp duïng caùc coâng thöùc löôïng giaùc ñaõ hoïc vaøo giaûi toaùn + Thaùi ñoä:
- Reøn tính caån thaän trong giaûi toaùn II. Chuẩn bị:
+ Giáo viên: soạn giáo án, chuẩn bị các bài tập cho học sinh thực hiện.
+ Học sinh: nắm vững lý thuyết và chuẩn bị trước các bài tập sách giáo khoa.
III. Nội dung và tiến trình lên lớp: TG
Hoạt động của thầy
Hoạt động của trò Nội dung ghi bảng 2’ + Ổn định lớp
+ Ồn định trật tự
+ Giới thiệu nội dung bài + Chú ý theo dõi tập.
15’ Vieát caùc coâng thöùc cuûa HS vieát coâng thöùc coäng 1. Tính: coâng thöùc coäng
2 HS leân baûng laøm baøi
a) cos2250 = cos(1800 + 450) = - /2 2 110
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn
HS1: Laøm baøi 1, caâu a)
sin2400 = sin (1800 + 600) = - /2 3
HS 2: Laøm baøi 1, caâu b)
cot(-150) = cot(300 – 450) =
Yeâu caàu daõy 1: laøm baøi 1, Caùc HS cuøng laøm döôùi 1
caâu a); daõy 2: laøm baøi 1, lôùp  2   3 tan(300  450 ) caâu b)
tan(750) = tan(450 + 300) =
Goïi HS khaùc nhaän xeùt
1  3 1  2  3
Gv nhaän xeùt, cho ñieåm HS khaùc nhaän xeùt 3 7     21  3 b) sin  sin    12  4 3  4        21  3 cos    cos     12   4 3  4 13         tan  tan    tan  tan    2  3 12  12  12  3 4 
15’ Baøi 2/ 154: GV neâu ñeà baøi HS hoaït ñoäng nhoùm 5 2. Tính:
Yeâu caàu HS hoaït ñoäng phuùt a)     1  6  cos   co  s        1 nhoùm Nhoùm 1,2: caâu a);   6  3  2  3  Nhoùm 3, 4: caâu b)
b) /2 < < tan < 0 Nhoùm 5, 5: caâu c) 2 1 1  tan    tan  2  2 2
Môøi ñaïi dieän 3 nhoùm leân Ñaïi dieän 3 nhoùm leân cos      
treo baûng nhoùm vaø trình treo baûng nhoùm vaø 1 2 2 9 4 2  tan      4  2 2  1 7
baøy baøi laøm cuûa nhoùm trình baøy baøi laøm cuûa c) 00 < a <900 cosa > 0, 900 < b < mình nhoùm mình
1800 cosb < 0
Caùc nhoùm khaùc goùp yù, boå Caùc nhoùm khaùc nhaän 16 3 4  5 sung xeùt cosa  1   ; cosb   1  25 5 9 3
GV nhaän xeùt, cho ñieåm 3 5  8 a b a b a b  
baøi laøm töøng nhoùm cos( ) cos cos sin sin 15
Yeâu caàu HS söûa baøi vaøo 6  4 5
sin(a b)  sin a cosb  cosa sin b   vôû
HS söûa baøi vaøo vôû 15
10’ Baøi 3/ 154: GV neâu ñeà baøi HS hoaït ñoäng nhoùm 6 3. Rút gọn biểu thức:
Yeâu caàu HS hoaït ñoäng phuùt a)
nhoùm ruùt goïn caùc bieåu Nhoùm 1, 2: caâu a)   
sin(a b)  sin  asin( b  )  sin acos b thöùc Nhoùm 3, 4: caâu b);  2  Nhoùm 5, 6: caâu c)
Ñaïi dieän 3 nhoùm leân b)
Môøi ñaïi dieän 3 nhoùm leân treo baûng nhoùm vaø       1 cos
acos  a 2   sin a
treo baûng nhoùm vaø trình trình baøy baøi laøm cuûa  4   4  2
baøy baøi laøm cuûa nhoùm nhoùm mình 2  cosa-  2 sina cosa sina 1 2  mình
Caùc nhoùm khaùc nhaän sin a 2 2 2
Caùc nhoùm khaùc goùp yù, boå xeùt 1 2  cos a sung 2
GV nhaän xeùt, cho ñieåm
baøi laøm töøng nhoùm c) 111
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn
Yeâu caàu HS söûa baøi vaøo HS söûa baøi vaøo vôû       c os
asin  b  sin(a b)  cosasin b vôû  2   2 
IV.Củng cố và dặn dò(3’):
- Nhắc lại cách giải các bài toán
-HS về học thuộc công thức. Ngaøy soaïn: 15/04/2013
Chöông VI: CUNG VAØ GOÙC LÖÔÏNG GIAÙC. COÂNG THÖÙC LÖÔÏNG GIAÙC Tieát daïy: 59
Baøøi daïy: OÂN TAÄP CHÖÔNG VI I. MUÏC TIEÂU: Kieán thöùc:
 OÂn taäp toaøn boä kieán thöùc chöông VI. Kó naêng:
 Bieán ñoåi thaønh thaïo caùc coâng thöùc löôïng giaùc.
 Vaän duïng caùc coâng thöùc treân ñeå giaûi baøi taäp. Thaùi ñoä:
 Luyeän tính caån thaän, tö duy linh hoaït. II. CHUAÅN BÒ:
Giaùo vieân: Giaùo aùn. Heä thoáng baøi taäp.
Hoïc sinh: SGK, vôû ghi. OÂn taäp toaøn boä kieán thöùc chöông VI.
III. HOAÏT ÑOÄNG DAÏY HOÏC:
1. OÅn ñònh toå chöùc: Kieåm tra só soá lôùp.
2. Kieåm tra baøi cuõ: (Loàng vaøo quaù trình oân taäp) H. Ñ. 112
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn
3. Giaûng baøi môùi:
TL Hoaït ñoäng cuûa Giaùo vieân
Hoaït ñoäng cuûa Hoïc sinh Noäi dung
Hoaït ñoäng 1: Luyeän taäp tính GTLG cuûa moät cung
H1. Neâu caùc böôùc tính vaø Ñ1. + Xeùt daáu caùc GTLG.
1. Tính caùc GTLG cuûa cung 
10' coâng thöùc caàn söû duïng?
+ Vaän duïng coâng thöùc neáu: phuø hôïp ñeå tính. a) cos = 2   vaø     a) sin = 7 3 2 3 b) tan = 2 2 vaø 3     b) cos = 1 2  3 c) sin = 2   vaø 3    2 3 2 c) cos = 5 3 d) cos = 1   vaø     4 2 d) sin = 15 4
Hoaït ñoäng 2: Luyeän taäp bieán ñoåi bieåu thöùc löôïng giaùc
 GV höôùng daãn HS vaän a) A = tan2
2. Ruùt goïn bieåu thöùc
duïng caùc coâng thöùc ñeå bieán b) B = 2cos a) A = 2sin2 sin4 20' ñoåi. c) 2sin2  sin 4        2  sin 1 cos 
    cos    2 cos b) B = tan  sin   4   4   sin        
sin    cos     2 sin sin       cos       4   4  c) C =  4   4   C = –cot       d) D = sin
sin    cos     4   4  d) D = sin5 sin3 2 cos4
3. Chöùng minh ñoàng nhaát thöùc  
H1. Neâu caùch bieán ñoåi ? a) 1 cosx cos2x  cot x
Ñ1. Bieán ñoåi toång thaønh tích. sin2x sin x x sin x  sin 2 x b)  tan x 2 1 cosx  cos 2 c) 2cos2x sin4x 2     tan   x 2 cos2x sin 4x 4      d) tanx – tany = sin(x y) cosx.cosy
4. Chöùng minh caùc bieåu thöùc sau
khoâng phuï thuoäc vaøo x:
H2. Xeùt quan heä caùc caëp         goùc ?
Ñ2. + x vaø – x: phuï nhau A = sin  x  cos  x 4 4  4   4 
 – x vaø  + x: phuï B =      
cos  x  sin  x 6 6  6   3  nhau C = sin2x +       cos  xcos  x A = 0 3 3      B = 0
D = 1 cos2x sin2x .cot x 1 cos2x  sin2x C = 1 4 113
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn D = 1
Hoaït ñoäng 3: Luyeän taäp tính giaù trò bieåu thöùc löôïng giaùc
H1. Bieán ñoåi caùc goùc lieân Ñ1.
5. Khoâng söû duïng maùy tính, haõy 10' quan ? a) 750 = 450 + 300 chöùng minh: b) 2670 = 3600 – 930 a) sin750 + cos750 = 6 c) 650 = 600 + 50; 2 550 = 600 – 50 b) tan2670 + tan930 = 0 d) 120 = 300 – 180 c) sin650 + sin550 = 3 cos50 480 = 300 + 180 d) cos120 – cos480 = sin180
Hoaït ñoäng 4: Cuûng coá
 Nhaán maïnh caùch vaän
3' duïng caùc coâng thöùc löôïng giaùc.
4. BAØI TAÄP VEÀ NHAØ:
 Baøi taäp oân cuoái naêm. Ngaøy soaïn: 20/04/2013 Tieát daïy: 60
Baøøi daïy: OÂN TAÄP CUOÁI NAÊM I. MUÏC TIEÂU: Kieán thöùc:
 OÂn taäp toaøn boä kieán thöùc chöông IV, V, VI. Kó naêng:
 Vaän duïng caùc coâng thöùc treân ñeå giaûi baøi taäp. Thaùi ñoä:
 Luyeän tính caån thaän, tö duy linh hoaït. II. CHUAÅN BÒ:
Giaùo vieân: Giaùo aùn. Heä thoáng baøi taäp.
Hoïc sinh: SGK, vôû ghi. OÂn taäp toaøn boä kieán thöùc chöông IV, V, VI.
III. HOAÏT ÑOÄNG DAÏY HOÏC:
1. OÅn ñònh toå chöùc: Kieåm tra só soá lôùp.
2. Kieåm tra baøi cuõ: (Loàng vaøo quaù trình oân taäp) H. Ñ.
3. Giaûng baøi môùi:
TL Hoaït ñoäng cuûa Giaùo vieân
Hoaït ñoäng cuûa Hoïc sinh Noäi dung
Hoaït ñoäng 1: Cuûng coá vieäc giaûi baát phöông trình moät aån, xeùt daáu tam thöùc baäc hai 114
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn
H1. Neâu caùch giaûi ? Ñ1.
1. Giaûi caùc baát phöông trình: a) Laäp baûng xeùt daáu. a) x 1  0 10'
S = (–; –3)  (–1; 1] 2 x  4x  3
b) Qui ñoàng, laäp baûng xeùt daáu b) x1 x2 
S = (–; –2)   1  x  2 x 1  ;1   2  c)  2 x  7x  6  0 
c) Giaûi töøng bpt, laáy giao caùc  2x 1  3 taäp nghieäm. S = (1; 2) 2. Tìm m ñeå:
H2. Neâu ñieàu kieän baøi toaùn Ñ2.
a) f(x) = x2 – 2(2m – 3)x + 4m – ?
a)  < 0  1 < m < 3
3 luoân luoân döông vôùi moïi x. b)  < 0  m < 1
b) Bpt: x2 – x + m  0 voâ nghieäm 4
Hoaït ñoäng 2: Cuûng coá vieäc tính toaùn caùc soá lieäu thoáng keâ
H1. Neâu caùch tính taàn soá, Ñ1.
3. Tuoåi thoï cuûa 30 boùng ñeøn thaép
10' taàn suaát, soá trung bình, moát a) * = 12; ** = 20
thöû ñöôïc cho bôûi baûng sau: ? b) X = 1170 (giôø)
Tuoåi thoï Taàn soá Taàn suaát c) MO = 1170 (giôø) (%) 1150 3 10 1160 6 20 1170 * 40 1180 6 ** 1190 3 10 Coäng 30 100 (%)
a) Ñieàn soá thích hôïp vaøo caùc daáu * vaø **.
b) Tính tuoåi thoï trung bình cuûa 30 boùng ñeøn.
c) Tìm moát cuûa baûng soá lieäu.
Hoaït ñoäng 3: Cuûng coá vieäc vaän duïng caùc coâng thöùc löôïng giaùc
H1. Neâu coâng thöùc caàn söû Ñ1.
4. Ruùt goïn caùc bieåu thöùc sau: duïng ?
a) Bieán ñoåi toång  tích a) sinasin3asin5a 20' A = tan3a cosa  cos3a  cos5a
b) Söû duïng haèng ñaúng thöùc 4 4 2 b) sin a  cos a  cos a 2(1 cosa) B = 2 a cos 2 c) x 2x 4x 8x cos .cos .cos .cos c) Nhaân C vôùi x 5 5 5 5 2sin 5 d) x 3x 5x sin  sin  sin 16x 7 7 7 sin 5  C = x 16sin 5
d) Bieán ñoåi toång  tích 5. Tính: 115
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn
H2. Neâu caùch bieán ñoåi ? D = 3x 2 x 4sin cos
a) 4(cos240 + cos480 – cos840 – 7 7 cos120) Ñ2. b)
a) Bieán ñoåi toång  tích
96 3 sin  cos  cos  cos  cos 
Nhaân töû vaø maãu vôùi cos180 48 48 24 12 6 A = 2
b) Coâng thöùc nhaân ñoâi
6. Chöùng minh raèng trong moät
H3. Neâu tính chaát veà goùc B = 9 ABC ta coù: trong tam giaùc ? Ñ3. A + B + C = 1800 a) tanA + tanB + tanC = a) tan(A + B) = – tanC
= tanA.tanB.tanC (A, B, C   ) 2 b) sin(A + B) = sinC b) sin2A + sin2B + sin2C = = 4sinA.sinB.sinC.
Hoaït ñoäng 4: Cuûng coá  Nhaán maïnh:
3' – Caùc kieán thöùc cô baûn
trong caùc chöông IV, V, VI.
– Caùch giaûi caùc daïng toaùn.
4. BAØI TAÄP VEÀ NHAØ:
 Chuaån bò kieåm tra Hoïc kì 2. Ngaøy soaïn: 25/04/2013 Tieát daïy: 62
Baøøi daïy: KIEÅM TRA HOÏC KÌ II I. MUÏC TIEÂU:
Kieán thöùc: Cuûng coá caùc kieán thöùc ñaõ hoïc trong hoïc kì 2.
 Daáu nhò thöùc baäc nhaát. Daáu tam thöùc baäc hai.
 Baát phöông trình, heä baát phöông trình baäc nhaát, baäc hai moät aån.  Thoáng keâ soá lieäu.
 Giaù trò löôïng giaùc cuûa moät cung.
 Coâng thöùc löôïng giaùc.
Kó naêng: Thaønh thaïo vieäc giaûi caùc daïng toaùn:
 Giaûi baát phöông trình, heä baát phöông trình baäc nhaát, baäc hai moät aån.
 Tính toaùn caùc soá lieäu thoáng keâ.
 Tính GTLG cuûa moät cung, giaù trò moät bieåu thöùc löôïng giaùc.
 Bieán ñoåi bieåu thöùc löôïng giaùc. Thaùi ñoä:
 Reøn luyeän tính caån thaän, chính xaùc. Luyeän tö duy linh hoaït, saùng taïo. II. CHUAÅN BÒ:
Giaùo vieân: Ñeà kieåm tra.
Hoïc sinh: OÂn taäp kieán thöùc ñaõ hoïc trong hoïc kì 2. III. MA TRAÄN ÑEÀ: Nhaän bieát Thoâng hieåu Vaän duïng Chuû ñeà Toång TNKQ TL TNKQ TL TNKQ TL 2 2 1 Baát phöông trình 2,0 0,25 0,25 1,0 2 1 2 Thoáng keâ 2,75 0,25 0,25 1,0 116
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn 2 1 1 Löôïng giaùc 1,75 0,25 0,25 1,0 Toång 1,5 1,0 2,0 2,0 6,5
IV. NOÄI DUNG ÑEÀ KIEÅM TRA:
A. Phaàn traéc nghieäm:
001: Taäp nghieäm cuûa baát phöông trình: 2x  3  1 laø: A. [1; 2] B. [1; 3] C. [–1; 1] D. [–1; 2]
002: Taäp nghieäm cuûa baát phöông trình: x2 – 6x + 9 > 0 laø: A. R \ {3} B. R C. (3; +) D. (–; 3) x 1
003: Taäp nghieäm cuûa baát phöông trình:  0 laø: 2 x  2x  3 A. (–; 1] B. [1; 2] C. [1; +) D. [–1; 2]
004: Tam thöùc f(x) = x2 + 4x + m – 5 luoân luoân döông vôùi moïi x khi: A. m > 9 B. m < 9 C. m > –1 D. m < –1
005: Ñieàu tra thôøi gian hoaøn thaønh moät saûn phaåm cuûa 20 coâng nhaân, ngöôøi ta thu ñöôïc maãu soá lieäu sau (thôøi gian tính baèng phuùt):
10 12 13 15 11 13 16 18 19 21 23 21 15 17 16 15 20 13 16 11
Haõy xaùc ñònh coù bao nhieâu giaù trò khaùc nhau trong maãu soá lieäu treân ? A. 12 B. 10 C. 20 D. 23
006: Thoáng keâ ñieåm moân Toaùn trong moät kì thi cuûa 400 hoïc sinh thaáy coù 72 baøi ñöôïc ñieåm 5. Hoûi giaù trò taàn suaát cuûa giaù trò xi = 5 laø: A. 18% B. 10% C. 36% D. 72%
007: Keát quaû kieåm tra chaát löôïng cuûa 41 hoïc sinh ñöôïc cho bôûi baûng sau: Ñieåm 1 2 3 4 5 6 7 8 9 10 Soá löôïng HS 3 6 4 4 6 7 3 4 2 2
Moát cuûa maãu soá lieäu treân laø: A. 6 B. 3 C. 2 D. 10
008: Giaù trò cuûa bieåu thöùc A = m.sin900 + n.cos900 + p.cos1800 baèng: A. m – p B. m + p C. m + n + p D. m + n – p 1
009: Cho sinx = vaø   x   . Khi ñoù cosx baèng: 2 2 3 3 1 1 A. B. C. D.  2 2 2 2
010: Giaù trò cuûa bieåu thöùc B = 2  2 6 cos cos   baèng: 14 14 A. 1 B. 0 C. 2 2.cos  D. 2 6 2.cos  14 14
B. Phaàn töï luaän:
Baøi 1: Giaûi baát phöông trình:
(2x – 1)(x + 3)  x2 – 9.
Baøi 2: Saûn löôïng luùa (ñôn vò laø taï) cuûa 40 thöûa ruoäng coù cuøng dieän tích ñöôïc trình baøy trong baûng soá lieäu sau: Saûn löôïng (taï) 20 21 22 23 24 Taàn soá (soá thöûa) 5 8 11 10 6 N = 40
a) Laäp baûng phaân boá taàn soá, taàn suaát.
b) Tính saûn löôïng trung bình cuûa 40 thöûa ruoäng neâu treân. 2 2 cos x sin y
Baøi 3: Ñôn giaûn bieåu thöùc A = 2 2  cot x.cot y . 2 2 sin x.sin y
V. ÑAÙP AÙN VAØ BIEÅU ÑIEÅM:
A. Phaàn traéc nghieäm: Taát caû ñaùp aùn laø A. 117
Nguyễn Đình Khương Giaùo aùn Đại Số 10 chuẩn
B. Phaàn töï luaän: Baøi 1: ( 1 ñieåm)
(2x – 1)(x + 3)  x2 – 9  x2 + 5x + 6  0 (0,5 ñieåm)  x  3  (0,5 ñieåm) x  2 Baøi 2: (2 ñieåm)
a) Baûng phaân boá taàn soá, taàn suaát: (1 ñieåm) Saûn löôïng (taï) Taàn soá Taàn suaát (%)
(Tính ñuùng moãi giaù trò taàn suaát ñöôïc 0,2 ñieåm) 20 5 12,5
5.20  8.2111.22 10.23  6.24 21 8 20,0 b) X  40 22 11 27,5 (0,5 ñieåm) 23 10 25,0 = 22,1 (taï) (0,5 ñieåm) 24 6 15,0 Coäng 40 100 (%) 2 2 cos x sin y 2 2 2 2
cos x  sin y  cos x.cos y
Baøi 3: (1 ñieåm) A = 2 2  cot x.cot y = (0,5 ñieåm) 2 2 sin x.sin y 2 2 sin x.sin y = – 1 (0,5 ñieåm)
VI. KEÁT QUAÛ KIEÅM TRA: 0 – 3,4 3,5 – 4,9 5,0 – 6,4 6,5 – 7,9 8,0 – 10 Lôùp Só soá SL % SL % SL % SL % SL % 10A3 44 10A5 42 10A7 44 10A10 42 10A11 38 118