





































































































































Preview text:
Chöông trình ñaïi soá lôùp 10 ban A_ Naâng cao Moân toaùn naâng cao
Caùc loaïi baøi kieåm tra trong 1 hoïc kyø:
(Aùp duïng töø naêm hoïc 2006-2007)
Kieåm tra mieäng :1 laàn /1 hoïc sinh.
Caû naêm : 35 tuaàn x 4 tieát/tuaàn = 140 tieát .
Kieåm tra 15’ : Ñs 2 baøi, Hh 2 baøi. T/haønh toaùn 1 baøi
Hoïc kyø I : 18 tuaàn x 4 tieát/tuaàn = 72 tieát .
Kieåm tra 45’ : Ñaïi soá 2 baøi, Hình hoïc 1 baøi.
Hoïc kyø II : 17 tuaàn x 4 tieát/tuaàn = 68 tieát .
Kieåm tra 90’ : 1 baøi (Ñs,Hh) cuoái HK I, cuoái naêm .
I. Phaân chia theo hoïc kyø vaø tuaàn hoïc : Caû naêm Ñaïi soá 90 tieát Hình hoïc 50 tieát 140 tieát Hoïc kyø I 46 tieát 26 tieát 18 tuaàn
10 tuaàn ñaàu x 3 tieát = 30 tieát
10 tuaàn ñaàu x 1 tieát = 10 tieát 72 tieát
8 tuaàn cuoái x 2 tieát = 16 tieát
8 tuaàn cuoái x 2 tieát = 16 tieát Hoïc kyø II 44 tieát 24 tieát 17 tuaàn
10 tuaàn ñaàu x 3 tieát = 30 tieát
10 tuaàn ñaàu x 1 tieát = 10 tieát 68 tieát
7 tuaàn cuoái x 2 tieát = 14 tieát
7 tuaàn cuoái x 2 tieát = 14 tieát
II. Phaân phoái chöông trình :Ñaïi soá Chöông Muïc Tieát thöù
I). Meänh ñeà-Taäp hôïp(13 tieát) 1) Meänh ñeà vaø meänh ñeà chöùa bieán 1-2
2) Aùp duïng meänh ñeà vaøo suy luaän toaùn hoïc 3-4 Luyeän taäp 5-6
3) Taäp hôïp vaø caùc pheùp toaùn treân taäp hôïp 7 Luyeän taäp 8-9
4) Soá gaàn ñuùng vaø sai soá 10-11
Caâu hoûi vaø baøi taäp oân taäp chöông 12
Kieåm tra 45 phuùt (tuaàn thöù 5) 13
II) Haøm soá baäc nhaát vaø baäc
1) Ñaïi cöông veà haøm soá 14-15-16 hai (10 tieát) Luyeän taäp 17
2) Haøm soá baäc nhaát tuaàn 6 18 Luyeän taäp 19 3) Haøm soá baäc hai 20-21 Luyeän taäp 22
Caâu hoûi vaø baøi taäp oân taäp chöông 23
III) Phöông trình vaø heä
1) Ñaïi cöông veà phöông trình 24-25 phöông trình (17 tieát)
2) Phöông trình baäc nhaát vaø baäc hai 1 aån 26-27 Luyeän taäp 28-29
3)Moät soá ptrình quy veà pt baäc nhaát hoaëc baäc hai t10,11 30-31
Ltaäp ( thhaønh gtoaùn treân mtính #500MS, 570MS) t11,12 32-33 1 Kieåm tra . t12 34
4) Heä phöông trình baäc nhaát nhieàu aån t13 35-36
Luyeän taäp(thhaønh gtoaùn treân mtính #500MS,570MS)t14 37
5) Moät soá ví duï veà heä phöông trình baäc hai 2 aån t14 38
Caâu hoûi vaø baøi taäp oân taäp chöông t15 39
IV) Baát ñaúng thöùc vaø baát
1) Baát ñaúng thöùc vaø chöùng minh baát ñaúng thöùc t15,16 40-41 phöông trình (26 tieát)
Kieåm tra cuoái hoïc kyø I t16 42
1) Baát ñaúng thöùc vaø chminh bñthöùc(tieáp) Luyeän taäp t17 43-44
OÂn taäp cuoái hoïc kyø I t18 45
Traû baøi kieåm tra cuoái hoïc kyø I t18 46
2) Ñaïi cöông veà baát phöông trình t19 47
3) Baát phöông trình vaø heä baát ph trình baâïc nhaát moät aån t19 48-49 Luyeän taäp t20 50
4) Daáu cuûa nhò thöùc baäc nhaát t20 51 Luyeän taäp t20 52
5) Baát phöông trình vaø heä baát ptrình baäc nhaát hai aån t21 53-54 Luyeän taäp t21 55
6) Daáu cuûa tam thöùc baäc hai t22 56
7) Baát phöông trình baäc hai t22 57-58 Luyeän taäp t23 59-60
8)Moät soá Phöông trình vaø bpt quy veà baäc hai t23,24 61-62 Luyeän taäp t24 63
Caâu hoûi vaø baøi taäp oân taäp chöông t24 64
Kieåm tra 45 phuùt (tuaàn thöù 7) t25 65 V) Thoáng keâ (9 tieát)
1) Moät vaøi khaùi nieäm môû ñaàu t25 66
2) Trình baøy moät maãu soá lieäu t25,26 67-68 Luyeän taäp t26 69
3) Caùc soá ñaëc tröng cuûa maãu soá lieäu t26,27 70-71 Luyeän taäp t27 72
C/hoûi &bt oân chöông(th gt / mtính #500MS, 570MS)t28 73
Kieåm tra t28 74
VI) Goùc löôïng giaùc vaø coâng
1) Goùc vaø cung löôïng giaùc t29 75-76
thöùc löôïng giaùc (15 tieát) Luyeän taäp t30 77
2) Giaù trò löôïng giaùc cuûa goùc (cung) löôïng giaùc t30,31 78-79 Luyeän taäp t31 80
3) Giaù trò lgiaùc cuûa goùc (cung) coù lieân quan ñaëc bieät t32 81 Luyeän taäp t32 82
4) Moät soá coâng thöùc löôïng giaùc t33 83-84 Luyeän taäp t34 85
Kieåm tra cuoái naêm t34 86
Caâu hoûi vaø baøi taäp oân taäp chöông t35 87
Caâu hoûi vaø baøi taäp oân taäp cuoái naêm t35,36 88-89
Traû baøi kieåm tra cuoái naêm t36 90 2
TRÖÔØNG THPT TX CAO LAÕNH ******
GIAÙO AÙN ÑAÏI SOÁ 10A
Naêm hoïc : 2006-2007 3
Chöông 1 Meänh ñeà – Taäp hôïp ******
Tieát 1,2 §1. MEÄNH ÑEÀ I).Muïc tieâu:
- Hs naém ñöôïc khaùi nieäm meänh ñeà , nhaän bieát ñöôïc moät caâu coù phaûi laø meänh ñeà hay khoâng
- Hs naém ñöôïc caùc khaùi nieäm meänh ñeà phuû ñònh , keùo theo , töông ñöông .
- Hs bieát laäp meänh ñeà phuû ñònh cuûa moät meänh ñeà , laäp meänh ñeà keùo theo vaø meänh ñeà töông ñöông
töø hai meänh ñeà ñaõ cho vaø xaùc ñònh ñöôïc tính ñuùng sai cuûa caùc meänh ñeà naøy
- Hs hieåu ñöôïc meänh ñeà chöùa bieán laø moät khaúng ñònh chöùa moät hay moät soá bieán, nhöng chöa phaûi laø moät meänh ñeà
Bieát bieán meänh ñeà chöùa bieán thaønh meänh ñeà baèng caùch : hoaëc gaùn cho bieán giaù trò cuï theå treân
mieàn xaùc ñònh cuûa chuùng , hoaëc gaùn caùc kí hieäu vaø vaøo phía tröôùc noù
Bieát söû duïng caùc kí hieäu vaø trong caùc suy luaän toaùn hoïc
Bieát phuû ñònh moät meänh ñeà coù chöùa kí hieäu vaø
II).Ñoà duøng daïy hoïc: Giaùo aùn , sgk
III).Caùc hoaït ñoäng treân lôùp: 1).Kieåm tra baøi cuû:
2).Baøi môùi:Döï kieán t1:1,2,3,4 vaø t2 :5,6,7 Tg Noäi dung
Hoaït ñoäng cuûa thaày
Hoaït ñoäng cuûa troø
Ví duï 1 (sgk) Goïi hs cho theâm ví duï
a) Haø noäi laø thuû ñoâ nöôùc Vieät Nam
b) Thöôïng Haûi laø moät thaønh phoá cuûa Aán Ñoä c) 1+1=2 d) Soá 27 chia heát cho 5
Ta goïi caùc caâu treân laø caùc meänh
ñeà loâ gíc goïi taét laø meänh ñeà.
1).Meänh ñeà laø gì?
Meänh ñeà laø moät caâu
khaúng ñònh ñuùng hoaëc moät
caâu khaúng ñònh sai
Moät caâu khaúng ñònh ñuùng
goïi laø moät meänh ñeà ñuùng
Moät caâu khaúng ñòng sai
goïi laø moät meänhn ñeà sai 4 Chuù yù :
Caâu khoâng phaûi laø caâu khaúng ñònh
hoaëc caâu khaúng ñònh maø khoâng coù tính
ñuùng sai thì khoâng laø meänh ñeà .(caùc
caâu hoûi, caâu caûm thaùn khoâng phaûi laø 1
2).Meänh ñeà phuû ñònh mñeà ) Cho meänh ñeà P. Meänh
ñeà “Khoâng phaûi P” ñöôïc goïi
laø meänh ñeà phuû ñònh cuûa P Kyù hieäu : P .
Neáu P ñuùng thì P sai Neáu P sai thì P ñuùng
Ví duï 2 (sgk) Goïi hs cho theâm ví duï
Hai baïn An vaø Bình ñang tranh luaän vôùi nhau .
Bình noùi:“2003 laø soá nguyeân toá“.
An khaúng ñònh:” 2003 khoâng phaûi laø soá nguyeân toá“. Chuù yù :
Meänh ñeà phuû ñònh cuûa P coù theå Chaúng haïn
dieãn ñaït theo nhieàu caùch khaùc
P:” 2 laø soá höõu tæ” nhau. P
:” 2 khoâng phaûi laø soá höõu tæ” hoaëc
P :” 2 laø soá voâ tæ” TL1
a) “Pa-ri khoâng laø thuû ñoâ nöôùc Anh”. Meänh ñeà phuû ñònh Ñ
HÑ1: Goïi hs traû lôøi
b) “2002 khoâng chia heát cho 4” Meänh ñeà phuû ñònh Ñ Ví duï3: Sgk
3).Meänh ñeà keùo theo:
Cho hai meänh ñeà P&Q.
Meänh ñeà “Neáu P thì Q” ñöôïc
goïi laø meänh ñeà keùo theo, kyù
hieäu laø PQ
Coøn noùi “P keùo theo Q” hay “P
suy ra Q” hay “Vì P neân Q “ …
Ta thöôøng gaëp caùc tình huoáng :
P ñuùng&Qñuùng:PQñuùng 5
P ñuùng & Q sai :PQ sai
Ví duï4 Sgk . Gv giaûi thích HÑ2
PQ: “Neáu töù giaùc ABCD laø hình chöõ
nhaät thì noù coù hai ñöôøng cheùo baèng
Cho meänh ñeà keùo theo PQ nhau” . meänh ñeà Q P
ñöôïc goïi laø meänh ñeà ñaûo cuûa meänh ñeà PQ
Ví duï 5 Sgk . Gv giaûi thích
4).Meänh ñeà töông ñöông:
Cho hai meänh ñeà P&Q.
Ví duï6: Goïi hs ñoïc
Meänh ñeà coù daïng “P neáu vaø
chæ neáu Q” ñöôïc goïi laø meänh ñeà töông ñöông. “P khi vaø chæ khi Q” HÑ3
Kyù hieäu : P Q
a) Ñaây laø meänh ñeà töông ñöông ñuùng vì
*Meänh ñeà P Q ñuùng khi
HÑ3 Goïi hs traû lôøi PQ vaø QP ñeàu PQ ñuùng & QP ñuùng
ñuùng vaø sai trong caùc tröôøng
b)i) P Q:”Vì 36 chia heát cho 4 vaø chia hôïp coøn laïi
heát cho 3 neân 36 chia heát cho 12 “;
*Meänh ñeà P Qñuùng neáu
QP:”Vì 36 chia heát cho 12 neân 36
P&Q cuøng ñuùng hoaëc cuøng
chia heát cho 4 vaø chia heát cho 3 “; sai
P Q:”36 chia heát cho 4 vaø chia heát
cho 3 neáu vaø chæ neáu 36 chia heát cho 12 “ .
ii)P ñuùng ,Q ñuùng ; P Q laø Ñ
5) Kn meänh ñeà chöùa bieán:
Giaûi thích :Caâu khaúng ñònh chöùa
Ví duï 7:Xeùt caùc caâu khaúng
1 hay nhieàu bieán nhaän giaù trò ñònh
trong 1 taäp hôïp X naøo ñoù.
P(n):“Soá n chia heát cho 3” ,
Tuøy theo giaù trò cuûa caùc bieán
P(6):”6 chia heát cho 3” Ñ
vôùi n laø soá töï nhieân
ta ñöôïc moät meänh ñeà Ñ hoaëc S Q(1;2):”2>1+3” S
Q(x;y):“ y x+3” vôùi x vaø y
Caùc khaúng ñònh treân goïi laø laø hai soá thöïc . meänh ñeà chöùa bieán
Ñaây laø nhöõng meänh ñeà chöùa H4 (sgk) H4 : bieán
P(2) : “2 > 4” laø meänh ñeà sai P 1 : “ 1 1
” laø meänh ñeà 2 2 4 ñuùng 6
6) Caùc kí hieäu ,
Cho mñ chöùa bieán P(x) vôùi xX.
a) Kí hieäu (moïi,vôùi moïi,tuyø Khi ñoù khaúng ñònh yù…)
“Vôùi moïi x thuoäc X, P(x) ñuùng”
laø 1 mñeà ñöôïc kyù hieäu
“ xX,P(x)” hoaëc
“ xX:P(x)” Ví duï 8:
Vì baát kyø xR ta ñeàu coù
a)“ xR, x2-2x+2 >0” . Ñaây x2-2x+2=(x-1)2+1>0 laø meänh ñeà ñuùng
“23+1 laø soá nguyeân toá ” laø meänh
b)“ nN, 2n+1 laø soá nguyeân ñeà sai
H5 : Meänh ñeà “ nN, n(n+1)
toá ” laø meänh ñeà sai H5 :(sgk)
laø soá leû” laø meänh ñeà sai
Vì 2(2+1) laø soá leû laø mñeà sai
Cho mñ chöùa bieán P(x) vôùi xX.
b) Kí hieäu (toàn taïi,coù,coù ít
Khi ñoù khaúng ñònh nhaát,…..)
“Toàn taïi x thuoäc X ñeå P(x) ñuùng”
laø 1 mñeà ñöôïc kyù hieäu
“ xX,P(x)” hoaëc
“ xX:P(x)” Giaûi thích:
a)n=3 thì 23+1=9 chia heát cho 3 Ví duï 9:
b) xoR,ta ñeàu coù (xo-1)2 0
a)“ nN,2n+1 chia heát cho H6:sgk
n”. Ñaây laø meänh ñeà ñuùng H6:
b)”xR,(x-1)2<0” laø mñeà sai
Meänh ñeà “Toàn taïi soá
7). Meänh ñeà phuû ñònh cuûa
nguyeân döông n ñeå 2n-1 laø soá
meänh ñeà coù chöùa kí hieäu , Ví duï 10: nguyeân toá” n
Cho meänh ñeà chöùabieán Meänh ñeà : “nN, 2 2 laø soá
Laø meänh ñeà Ñ, vì vôùi n=3 thì P(x) vôùi xX. nguyeân toá”
23-1 = 7 laø soá nguyeân toá
Meänh ñeà phuû ñònh cuûa Meänh ñeà phuû ñònh :
meänh ñeà “xX,P(x)” laø Ví duï 11ï: “ n
xX, P(x)”
“ nN,2 2 +1 khoâng phaûi laø soá " nN, 2n+1 chia heát cho n”
coù meänh ñeà phuû ñònh laø :
Cho meänh ñeà chöùa nguyeân toá” bieán P(x) vôùi xX.
“ nN, 2n+1 khoâng chia heát
Meänh ñeà phuû ñònh cuûa cho n”
meänh ñeà “ xX,P(x)” laø H7:(sgk)
“xX, P (x) ” H7:
“Coù ít nhaát moät baïn trong lôùp em
khoâng coù maùy tính” 7
3)Cuûng coá: Mñeà,mñeà phuû ñònh, mñeà keùo theo, mñeà töông ñöông, mñeà chöùa bieán , kyù hieäu , .
3)Daën doø :bt 1,2,3,4,5 sgk trang 9, bt 6-11 trang 12 sgk .
HD:1.a) Khoâng laø meänh ñeà (caâu meänh leänh );b) Meänh ñeà sai ;c) Meänh ñeà sai .
2.a) “Phöông trình x2-3x+2 = 0 voâ nghieäm” . Meänh ñeà phuû ñònh sai .
b) “210 -1 khoâng chia heát cho 11 “ . Meänh ñeà phuû ñònh sai;
c) “Coù höõu haïn soá nguyeân toá “ . Meänh ñeà phuû ñònh sai .
3) Meänh ñeà P Q :” Töù giaùc ABCD laø hình vuoâng neáu vaø chæ neáu töù giaùc ñoù laø hình chöõ nhaät coù
2 ñöôøng cheùo vuoâng goùc “ vaø ” Töù giaùc ABCD laø hình vuoâng khi vaø chæ khi töù giaùc ñoù laø hình chöõ nhaät
coù 2 ñöôøng cheùo vuoâng goùc “ laø meänh ñeà ñuùng .
4) Meänh ñeà P(5): “52-1 chia heát cho 4”laø meänh ñeà ñuùng . P(2): “22-1 chia heát cho 4” laø mñeà sai
5) a) P(n) : “ nN*, n2-1 laø boäi soá cuûa 3” laø sai vì n = 3 thì 32-1 khoâng chia heát cho 3
P(n): “ nN, n2-1 khoâng laø boäi soá cuûa 3”
b) Meänh ñeà Ñ ; Meänh ñeà phuû ñònh :“ xR, x2-x+1 0”
c) Meänh ñeà sai;Meänh ñeà phuû ñònh :“ xQ, x2 3”
d) Meänh ñeà Ñ ;Meänh ñeà phuû ñònh : “ nN, 2n+1 laø hôïp soá”
e) Meänh ñeà S ;Meänh ñeà phuû ñònh : “ nN, 2n< n+2 8
Tieát 3,4 §2. AÙP DUÏNG MEÄNH ÑEÀ VAØO SUY LUAÄN TOAÙN HOÏC .
I . Muïc tieâu :Giuùp học sinh Veà kieán thöùc:
- Hieåu roõ 1 soá pp suy luaän toaùn hoïc .
- Naém vöõng caùc pp cm tröïc tieáp vaø cm baèng phaûn chöùng .
- Bieát phaân bieät ñöôïc giaû thieát vaø keát luaän cuûa ñònh lyù .
- Bieát phaùt bieåu meänh ñeà ñaûo , ñònh lyù ñaûo , bieát söû duïng caùc thuaät ngöõ : “ñieàu kieän caàn” ,
“ñieàu kieän ñuû” , “ñieàu kieän caàn vaø ñuû” trong caùc phaùt bieåu toaùn hoïc. Veà kyõ naêng :
Chöùng minh ñöôïc 1 soá meänh ñeà baèng pp phaûn chöùng .
II . Ñoà duøng daïy hoïc :
Giaùo aùn , saùch giaùo khoa
III.Caùc hoaït ñoäng treân lôùp 1).Kieåm tra baøi cuû
Caâu hoûi : Cho ví duï moät meänh ñeà coù chöùa vaø neâu meänh ñeà phuû ñònh ,moät meänh ñeà coù
chöùa vaø neâu meänh ñeà phuû ñònh 2).Baøi môùi Tg Noäi dung
Hoaït ñoäng cuûa thaày
Hoaït ñoäng cuûa troø
1)Ñònh lyù vaø ch/minh ñlyù : Giaûi thích : Ví duï 1:
Xeùt ñ lyù “Neáu n laø soá töï nhieân leû
Ñònh lyù laø nhöõng meänh ñeà ñuùng ,
thì n2-1 chia heát cho 4” . thöôøng coù daïng :
hay “Vôùi moïi soá töï nhieân n, neáu n " x
X , P(x) (
Q x)" (1)
leû thì n2-1 chia heát cho 4”
Trong ñoù P(x) vaø Q(x) laø caùc meänh
ñeà chöùa bieán, X laø moät taäp hôïp naøo ñoù.
Coù theå chöùng minh ñònh lyù (1) tröïc tieáp hay giaùn tieáp :
a)Chöùng minh ñònh lyù tröïc tieáp :
-Laáy tuyø yù xX vaø P(x) ñuùng
Ví duï2 : Gv phaùt vaán hs Giaûi :
-Duøng suy luaän va ønhöõng
Chöùng minh ñònh lyù
Giaû söû nN , n leû
kieán thöùc toaùn hoïc ñaõ bieát ñeå chæ ra “Neáu n laø soá töï nhieân leû thì n2-1 Khi ñoù n = 2k+1 , k N raèng Q(x) ñuùng . chia heát cho 4” . Suy ra : n2-1 = 4k2+4k+1-1=4k(k+1) 9 chia heát cho 4
b)Chöùng minh ñònh lyù baèng phaûn
chöùng goàm caùc böôùc sau :
- Giaû söû toàn taïi x0X sao cho P(x0) ñuùng vaø Q(x0) sai.
-Duøng suy luaän vaø nhöõng kieán thöùc Ví duï 3 : Chöùng minh baèng phaûn
toaùn hoïc ñaõ bieát ñeå ñi ñeán maâu
chöùng ñònh lyù “ Trong maët phaúng, Chöùng minh : thuaãn.
neáu 2 ñöôøng thaúng a vaø b song
Giaû söû toàn taïi ñöôøng
song vôùi nhau .Khi ñoù, moïi ñöôøng thaúng c caét a nhöng song
thaúng caét a thì phaûi caét b”. song vôùi b. Goïi M laø
giao ñieåm cuûa a vaø c. Khi
ñoù qua M coù hai ñöôøng
thaúng a vaø c phaân bieät cuøng
song song vôùi b. Ñieàu naøy
m thuaãn vôùi tieân ñeà Ô-clít. HÑ1 :
Ñònh lyù ñöôïc chöùng minh.
Chöùng minh baèng phaûn HÑ1 :
chöùng ñònh lyù “vôùi moïi soá töï nhieân Giaû söû 3n+2 leû vaø n
n, neáu 3n+2 laø soá leû thì n laø soá leû” . chaún n=2k (kN). Khi ñoù: 3n+2 = 6k+2 = 2(3k+1) chaún
2)Ñieàu kieän caàn,ñ kieän ñuû: Maâu thuaãn .
Cho ñònh lyù döôùi daïng “ x
X , P(x) ( Q x) ” (1) P(x) : giaû thieát Q(x): keát luaän Ví du4ï:
ÑL(1) coøn ñöôïc phaùt bieåu:
“Vôùi moïi soá töï nhieân n, neáu n chia Hoaëc cuõng noùi
P(x) laø ñ k ñuû ñeå coù Q(x)
heát cho 24 thì noù chia heát cho 8”
“n chia heát cho 8 laø ñk caàn
Q(x) laø ñk caàn ñeå coù P(x) ñeå n HÑ2 chia heát cho 24”
Tìm meänh ñeà P(n) , Q(n) cuûa ñlyù HÑ2 trong ví duï 4
P(n) :“nchia heát cho 24”
Q(n) : “n chia heát cho 8”
Goïi hs phaùt bieåu döôùi daïng ñk caàn , Giaûi : ñk ñuû
“n chia heát cho 24 laø ñk
ñuû ñeå n chia heát cho 8”
“n chia heát cho 8 laø ñk
caàn ñeå n chia heát cho 24” 10
3) Ñònh lyù ñaûo . Ñkieän caàn vaø ñuû Cho ñònh lyù :
“ xX,P(x)Q(x)” (1)
Neáu meänh ñaûo :
“ xX,Q(x)P(x)” (2) laø
ñuùng thì noù ñgoïi laø ñònh lyù ñaûo cuûa
ñònh lyù (1). Ñlyù (1) ñgoïi laø ñlyù
“P(x) neáu vaø chæ neáu Q(x)”
thuaän. Ñlyù thuaän vaø ñaûo coù theå goäp “P(x) khi vaø chæ khi Q(x)” thaønh 1 ñlyù
“Ñk caàn vaø ñuû ñeå coù P(x) laø coù
“ xX,P(x) Q(x)”. Khi ñoù ta Q(x)” noùi HÑ3 (sgk) HÑ3 :
P(x) laø ñk caàn vaø ñuû ñeåcoùQ(x)
“Vôùi moïi soá nguyeân döông
n, ñkieän caàn vaø ñuû ñeå n
khoâng chia heát cho 3 laø n2 chia cho 3 dö 1”
3). Cuûng coá : Ñlyù ,cm ñlyù; ñk caàn, ñk ñuû; Ñlyù ñaûo, ñk caàn vaø ñuû
4) Daën doø: Caâu hoûi vaø baøi taäp sgk
6/.Meänh ñeà ñaûo “Neáu tam giaùc coù hai ñöôøng cao baèng nhau thì tam giaùc ñoù caân”. Meänh ñeà ñaûo Ñ
7/.Giaû söû a+b < 2 ab .Khi ñoù a+b -2 ab =( a - b )2< 0. Ta coù maâu thuaãn
8/.Ñk ñuû ñeå toång a+b laø soá höõu tyû laøcaû 2 soá a vaø b ñeàu laø soá höõu tyû
Chuù yù : Ñk naøy khoâng laø ñk caàn .Chaúng haïn vôùi a= 2 +1 , b = 1- 2 thì a+b = 2 laø soá höuõ tæ nhöng
a , b ñeàu laø soá voâ tæ
9/.Ñk caàn ñeå moät soá chia heát cho 15 laø noù chia heát cho 5
Chuù yù : Ñk naøy khoâng laø ñk ñuû . Chaúng haïn 10 chia heát cho 5 nhöng khoâng chia heát cho 15 .
10/.Ñk caàn vaø ñuû ñeå töù giaùc noäi tieáp ñöôïc trong 1 ñtroøn laø toång 2 goùc ñoái dieän cuûa noù baèng 180o .
11/. Giaû söû n2 chia heát cho 5 vaø n khoâng chia heát cho 5
Neáu n = 5k 1 (kN) Thì n2 = 25k2 10k+1 = 5(5k2 2k)+1 khoâng chia heát cho 5
Neáu n = 5k 2 (kN) Thì n2 = 25k2 20k+4 = 5(5k2 4k)+4 khoâng chia heát cho 5
Maâu thuaãn vôùi giaû thieát n2 chia heát cho 5. 11
Tieát 5,6 LUYEÄN TAÄP I). Muïc tieâu :
Giuùp hoïc sinh oân taäp kieán thöùc , cuûng coá vaø reøn luyeän kyõ naêng ñaõ hoïc .
Sau khi oân taäp cho hs caùc kieán thöùc ñaõ hoïc gv goïi hs leân baûng trình baøy lôøi giaûi caùc bt neâu trong
tieát luyeän taäp . Ñoái vôùi moãi bt, gv caàn phaân tích caùch giaûi vaø chæ ra caùc choã sai neáu coù cuûa hs
II).Ñoà duøng daïy hoïc : Giaùo aùn , sgk
III). Caùc hoaït ñoäng treân lôùp :
1).Kieåm tra baøi cuõ :
Kieåm tra caâu hoûi vaø baøi taäp 2).Baøi môùi : Tg
Hoaït ñoäng cuûa thaày
Hoaït ñoäng cuûa troø
Höôùng daãn hs giaûi caùc 12).a) Ñ ;
baøi taäp saùch giaùo khoa trang b) S ; 13-14
c) Khoâng laø mñeà ;
d) Khoâng laø mñeà;
13).a) Töù giaùc ABCD ñaõ cho khoâng laø hình chöõ nhaät
b) 9801 khoâng phaûi laø soá chính phöông .
14) Mñeà PQ:”Neáu töù giaùc ABCD coù toång hai goùc ñoái laø 1800 thì töù
giaùc ñoù noäi tieáp trong moät ñöôøng troøn “. Mñeà ñuùng .
15).PQ:”Neáu 4686 chia heát cho 6 thì 4686 chia heát cho 4”.
16).Mñeà P:”Tam giaùc ABC laø tam giaùc vuoâng taïi A“
vaø mñeà Q:” Tam giaùc ABC coù AB2+AC2=BC2”.
17) a) Ñuùng b) Ñuùng c) Sai
d) Sai e) Ñuùng g) Sai
18) a) Coù moät hs trong lôùp em khoâng thích moân toaùn
b) Caùc hs trong lôùp em ñeàu bieát söû duïng maùy tính
c) Coù moät hs trong lôùp em khoâng bieát chôi ñaù boùng
d) Caùc hs trong lôùp em ñeàu ñaõ ñöôïc taém bieån
19) a) Ñuùng . Meänh ñeà phuû ñònh : “ xR, x2 1” .
b) Ñuùng,vì vôùi n = 0 thì n(n+1) = 0 laø soá chính phöông Meänh ñeà phuû ñònh :
“ nN , n(n+1) khoâng laø soá chính phöông” .
c) Sai. Meänh ñeà phuû ñònh :
“ xR, (x-1)2 = x-1” .
d) Ñuùng . Thaät vaäy :
Neáu n laø soá töï nhieân chaún : n =2k (kN) 12
n2+1 = 4k2+1 khoâng chia heát cho 4
Neáu n laø soá töï nhieân le û: n = 2k+1 (kN)
n2+1 = 4(k2+k)+2 khoâng chia heát cho 4 Meänh ñeà phuû ñònh :
“ nN , n2+1 chia heát cho 4” . 20)B)Ñ 21)A)Ñ 13
Tieát 7 §3. TAÄP HÔÏP VAØ
CAÙC PHEÙP TOAÙN TREÂN TAÄP HÔÏP I). Muïc tieâu :
Kieán thöùc: Laøm cho hoïc sinh :
-Hieåu ñöôïc khaùi nieäm taäp con, hai taäp hôïp baèng nhau.
-Naém ñöôïc ñn caùc ptoaùn treân taäp hôïp : pheùp hôïp , pheùp giao , pheùp laáy phaàn buø vaøpheùp laáy hieäu
-Bieát caùch cho 1 taäp hôïp baèng hai caùch
-Bieát tö duy linh hoaït khi duøng caùc caùch khaùc nhau ñeå cho moät taäp hôïp
-Bieát duøng caùc kyù hieäu, ngoân ngöõ taäp hôïp ñeå dieãn taû caùc ñk baèng lôøi cuûa moät btoaùn vaø ngöôïc laïi
-Bieát caùch tìm hôïp,giao,phaàn buø,hieäu cuûa caùc taäp hôïp ñaõ cho vaø moâ taû taäp hôïp taïo ñöôïc sau khi
ñaõ thöïc hieän xong pheùp toaùn
-Bieát söû duïng caùc kyù hieäu vaø pheùp toaùn taäp hôïp ñeå phaùt bieåu caùc baøi toaùn vaø dieãn ñaït suy luaän
toaùn hoïc moät caùch saùng suûa , maïch laïc
-Bieát söû duïng bieåu ñoà Ven ñeå bieåu dieãn quan heä giöõa caùc taäp hôïp vaø caùc pheùp toaùn treân taäp hôïp
II).Ñoà duøng daïy hoïc : Giaùo aùn , sgk
III). Caùc hoaït ñoäng treân lôùp :
1).Kieåm tra baøi cuõ :
Kieåm tra caâu hoûi vaø baøi taäp 2).Baøi môùi : Tg Noäi dung
Hoaït ñoäng cuûa thaày
Hoaït ñoäng cuûa troø 1/.Taäp hôïp Gv thuyeát trình
1) Taäp hôïp laø gì ?
Taäp hôïp laø moät khaùi nieäm cô baûn cuûa toaùn hoïc
Thoâng thöôøng, moãi taäp Ví duï :
hôïp goàm caùc pt cuøng coù
-Taäp hôïp taát caû caùc hs lôùp 10 cuûa tröôøng
chung 1 hay 1 vaøi tc naøo ñoù. em .
X =a,b, c
-Taäp hôïp caùc soá nguyeân toá
a laø phaàn töû cuûa X : aX.
Ñoïc laø a thuoäc taäp X , d
d khoâng laø phaàn töû cuûa khoâng thuoäc taäp X X:dX.
2) Caùch cho moät taäp hôïp Giaûi thích :
HÑ1:A={k;h;oâ;n;g;c;où;ì;q;u;yù;
a) Lieät keâ caùc pt cuûa taäp Khi cho taäp hôïp baèng
ô;ñ;oä; l;aä;p;t;öï;d;o} hôïp
caùch lieät keâ caùc phaàn töû, ta qui öôùc : Khoâng caàn quan taâm
tôùi thöù töï caùc phaàn töû ñöôïc lieät keâ 14
Moãi phaàn töû cuûa taäp
hôïp chæ lieät keâ moät laàn
b). Chæ roõ caùc tính chaát ñaëc
Neáu qui luaät lieät keâ roõ
tröng cho caùc pt cuûa taäp hôïp raøng , ta coù theå lieät keâ moät soá
phaàn töû ñaàu tieân sau ñoù seõ
HÑ2: a)A={3;4;5;6;7;8…;20} . duøng daáu “…”
b)B={nZ;n15,n chia heát cho 5} HÑ2 :
Cho B = {0; 5; 10; 15}
*Taäp roãng laø taäp khoâng
Vieát taäp B baèng caùch chæ roõ
chöùa phaàn töû naøo, kyù hieäu laø caùc tính chaát ñaëc tröng cho . caùc phaàn töû cuûa noù
2/.Taäp con vaø t/h baèng nhau a)Taäp con :
Taäp A ñöôïc goïi laø taäp
con cuûa taäp B vaø kyù hieäu laø
AB neáu moïi phaàn töû cuûa Hoaëc B A
taäp A ñeàu laø phaàn töû cuûa taäp B. A B ( x, xA HÑ3: B A xB)
AB :A bò chöùa trong B, A HÑ3 :
naèm trong B , B chöùa A
A = {nNn chia heát cho 6} Tính chaát :
B = {nNn chia heát cho 12}
*(A B vaø B C)A C A B hay B A?
* A ; A
*A A ; A
HÑ4: Ñaây laø baøi toaùn c/m 2 taäp hôïp
b).Taäp hôïp baèng nhau : HÑ4 :(sgk)
ñieåm baèng nhau. Taäp hôïp thöù nhaát laø taäp
Hai taäp hôïp A vaø B ñöôïc
hôïp caùc ñieåm caùch ñeàu 2 muùt cuûa ñoaïn
goïi laø baèng nhau vaø kyù hieäu
thaúng ñaõ cho. Taäp hôïp thöù hai laø t/h caùc
laø A = B neáu moãi phaàn töû
ñieåm naèm treân ñöôøng trung tröïc cuûa
cuûa A laø 1 pt cuûa B vaø moãi ñoaïn thaúng ñaõ cho .
phaàn töû cuûa B cuõng laø 1 pt cuûa A .
A = B (A B vaø B A) c).Bieåu ñoà ven:
Taäp hôïp ñöôïc minh hoïa
tröïc quan baèng hình veõ, giôùi Gv veõ bieåu ñoà
haïn bôûi 1 ñöôøng kheùp kín. Ví duï1: •
N* N Z Q R B Aa A 15 B A B
3/Moät soá caùc taäp con cuûa HÑ6:
taäp hôïp soá thöïc: sgk a4;b1;c3;d2 HÑ6:sgk
Gv veõ bieåu ñoà Ven vaø giaûi
4/Caùc pheùp toaùn treân taäp thích hôïp a).Pheùp hôïp :
Hôïp cuûa hai taäp hôïp A A B
vaø B , kyù hieäu A B, laø taäp Ví duï 2: sgk Giaûi :
bao goàm taát caû caùc phaàn töû A B =[-2;3) thuoäc A hoaëc thuoäc B
A B = {xxA hoaëc
Gv veõ bieåu ñoà Ven vaø giaûi xB} thích b).Pheùp giao : Ví duï3 :sgk A B
Giao cuûa hai taäp hôïp Giaûi :AB=[1;2]
A vaø B, kyù hieäu laø A B, laø HÑ7:
taäp hôïp bao goàm taát caû caùc
A B laø taäp hôïp caùc hs gioûi Toaùn hoaëc
phaàn töû thuoäc caû A vaø B Vaên
A B = {x xA vaø xB}
A B laø taäp hôïp caùc hs gioûi caû toaùn vaø vaên.
Gv veõ bieåu ñoà Ven vaø giaûi thích Ví du4ï:
CZN laø taäp caùc soá nguyeân aâm;
c).Pheùp laáy phaàn buø :
Phaàn buø cuûa taäp caùc soá leû CEA
Cho A E . Phaàn buø cuûa trong taäp caùc soá nguyeân laø HÑ8:
A trong E , kyù hieäu :C taäp caùc soá chaún . EA laø
a) CRQ laø taäp hôïp caùc soá voâ tyû
taäp hôïp taát caû caùc phaàn töû HÑ8:
b) CBA laø taäp hôïp caùc hs nöõ trong lôùp
cuûa E maø khoâng laø pt cuûa A
em; CDA laø taäp hôïp caùc hs nam trong .
tröôøng em maø khoâng laø hs lôùp em. C
EA = {x xE vaø xA} Ví duï 5:
Chuù yù : Hieäu cuûa 2 taäp hôïp A =(1;3];B=[2;4]
A vaø B, kyù hieäu : A\B , laø
Goïi hs tìm A\B=(1;2) A\B
taäp hôïp bao goàm taát caû caùc
Nhaän xeùt : CEA = E\A
ptöû thuoäc A nhöng khoâng thuoäc B. 16
A\B = {x xA vaø xB}
3).Cuûng coá : Taäp hôïp, taäp con, giao, hôïp, hieäu vaø phaàn buø.
4)Daën doø: Caùc caâu hoûi vaø baøi taäp sgk
Caâu hoûi vaø baøi taäp trang 17 sgk 22/ a) A = 1 0 ; 2 ; b) B = 2 3 ; 4 ; 5 ; 2
23/ a) A laø taäp hôïp caùc soá nguyeân toá nhoû hôn 10; b)B = {xz x 3 };
c) C = {nZ -5 n 15 vaø n chia heát cho 5 }
24/. Khoâng baèng nhau .vì A = {1 ;2 ;3} , B ={1;3;5}
25/. B A , C A , C D
26/. a) A B laø taäp hôïp caùc hs lôùp 10 hoïc moân tieáng Anh cuûa tröôøng em;
b) A\B laø taäp hôïp caùc hs lôùp 10 nhöng khoâng hoïc moân tieáng Anh cuûa tröôøng em;
c) AB laø taäp hôïp caùc hs hoaëc hoïc lôùp 10 hoaëc hoïc moân tieáng Anh cuûa tröôøng em;
d) B\A laø taäp hôïp caùc hs hoïc moân tieáng Anh nhöng khoâng hoïc lôùp 10 cuûa tröôøng em .
27) F E C B A; F D C B A ; D E = F . 28) (A\B) = 5 , (B\A) =
2 , (A\B) (B\A) = 5 ; 2 , AB = 5 ; 3 ; 2 ; 1
, A B = 3 ; 1
, (A B)\(AB) = 5 ; 2
Hai taäp hôïp nhaän ñöôïc baèng nhau .
29) a)Sai ; b)Ñuùng ; c) Sai ; d) Ñuùng.
30) A B=[-5;2) ; A B=(-3;1 ] 17
Tieát 8,9 LUYEÄN TAÄP I).Muïc tieâu :
Cuûng coá kieán thöùc veà caùc pheùp toaùn giao , hôïp , hieäu vaø laáy phaàn buø caùc taäp hôïp
II).Ñoà duøng daïy hoïc : Giaùo aùn , sgk III). Baøi môùi :
Tg Hoaït ñoäng cuûa thaày
Hoaït ñoäng cuûa troø
Goïi hs giaûi caùc baøi taäp 30,31,32,33 sgk 31) trang 20
A = (A B) (A\B);B = (A B) (B\A) HD : Suy ra :
30) Duøng bieåu ñoà Ven A = 9 ; 6 ; 3 ; 8 ; 7 ; 5 ; 1 ;B = 9 ; 6 ; 3 ; 10 ; 2 32) 32)
Ta coù theå chöùng minh ñaúng thöùc A B = 9 ; 6 ; 4 ; 2 ; B\C = 9 ; 8 ; 2 ; 0
A (B\C) = (A B)\C ñuùng cho ba taäp A (B\C) = A,B,C baát kyø nhö sau : 9 ; 2 ; (A B)\C = 9 ; 2 Giaû söû x
Vaäy hai taäp hôïp nhaän ñöôïc baèng nhau A (B\C). Khi ñoù xA, x(B\C)
33) a)(A\B) A;b)A (B\A)=;c)A(B\A)=A B. Vaäy xA, xB, xC 34)a)A ; b) 10 ; 8 ; 3 ; 2 ; 1 ; 0 .
Töùc laø x A B, xC 35)a)Sai ; b)Ñuùng . Vaäy x (A B)\C
36)a){a;b;c},{a;b;d},{b;c;d},{a;c;d},
b) {a;b},{a;c},{a;d},{b;c},{b;d},{c;d}, 40)Cm:A=B.
c) {a},{b},{c},{d},.
Giaû söû nA,n=2k,kZ. n coù chöõ soá 37)Ñk ñeå AB= laø a+2taän cuøng {0;2;4;6;8} neân nB.
a>b+1.Vaäy ñk ñeå A B laø b-2 a b+1.
Ngöôïc laïi, giaû söû nB,n=10h+r,
38)(D) laø khaúng ñònh sai. Bôûi vì N N*=N.
r{0;2;4;6;8}.Vaäy r=2t, t{0;1;2;3;4}.
39)AB=(-1;1);A B={0};CRA=(- ;-1] (0;+ ).
Khi ñoù n=10h+2t=2(5h+t)=2k,
40) Gv höôùng daãn k=5h+tZ, do ñoù nA.
Cm:A=C. Giaû söû nA,n=2k,kZ.
Ñaët k’=k+1Z.Khi ñoù, n=2(k’-1)=2k’-2
neân nC.
Ngöôïc laïi, giaû söû nC,
n=2k-2=2(k-1), Ñaët k’=k-1Z. Khi
ñoù n=2k’, k’Z, do ñoù nA.
41) AB=(0;4);suy ra CR(A B)=(- ;0] [4;+)
Ta cm:A D. Ta coù 2A, nhöng 2D
A B=[1;2]; suy ra CR(A B)=(- ;1] (2;+)
vì neáu 2D thì ta phaûi co’=3k+1,kZ,
42) A(B C)={a,b,c};(A B) C={b,c}; nhöng k=1/3Z, vaäy 2D
(A B) (A C)={a,b,c};(A B)C={b,c;e};Vaäy(B)Ñ 18
Tieát 10-11 §4. SOÁ GAÀN ÑUÙNG VAØ SAI SOÁ I).Muïc tieâu : Laøm cho hs :
- Nhaän thöùc ñöôïc taàm quan troïng cuûa soá gaàn ñuùng , yù nghóa cuûa soá gaàn ñuùng .
- Naém ñöôïc theá naøo laø sai soá tuyeät ñoái , caän treân cuûa sai soá tuyeät ñoái , sai soá töông ñoái .
- Bieát quy troøn soá vaø xaùc ñònh caùc chöõ soá chaéc cuûa soá gaàn ñuùng , caùch vieát chuaån soá gaàn ñuùng.
- Bieát xaùc ñònh sai soá khi tính toaùn treân caùc soá gaàn ñuùng .
II). Ñoà duøng daïy hoïc : Giaùo aùn , sgk
III). Caùc hoaït ñoäng treân lôùp : 1). Kieåm tra baøi cuû : Caâu hoûi : 2). Baøi môùi : Tg Noäi dung
Hoaït ñoäng cuûa thaày
Hoaït ñoäng cuûa troø
1). Soá gaàn ñuùng :
Trong nhieàu tröôøng hôïp ta HÑ1 (sgk) HÑ1:
khoâng bieát ñöôïc giaù trò ñuùng
Caùc soá lieäu noùi treân laø soá gaàn
cuûa ñaïi löôïng maø chæ bieát giaù
ñuùng (ñöôïc quy troøn tôùi chöõ soá trò gaàn ñuùng cuûa noù haøng traêm) .
2).Sai soá tuyeät ñoái vaø sai soá töông ñoái:
a) Sai soá tuyeät ñoái :
a laø giaù trò ñuùng , a laø giaù trò gaàn ñuùng cuûa
a . Ñaïi löôïng a =
Treân thöïc teá nhieàu khi ta khoâng
a -a ñöôïc goïi laø sai soá
tuyeät ñoái cuûa soá gaàn ñuùng a .
bieát a neân khoâng theå tính ñöôïc chính xaùc a. Tuy nhieân ta coù
theå ñaùnh giaù ñöôïc a khoâng
vöôït quaù 1 soá döông d naøo ñoù. Ví duï 1:
Gv giaûi thích ví duï 1 sgk Neáu
a -a d hay a-d
a a+d thì d ñöôïc goïi HÑ2:
laø ñoä chính xaùc cuûa soá gaàn HÑ2:(sgk)
Chieàu daøi ñuùng cuûa caây caàu (kyù ñuùng a.
hieäu laø C) laø moät soá naèm trong 19
khoaûng töø 151,8m ñeán 152,2m, töùc
b).Sai soá töông ñoái : laø 151,8 C 152,2. Ví duï 2:
Ño chieàu cao moät ngoâi nhaø
ñöôïc ghi laø 15,2m 0,1m
Ta thöôøng vieát sai soá töông ñoái
döôùi daïng phaàn traêm : a a
Sai soá töông ñoái khoâng vöôït Tyû soá a= a = goïi laø 1 , 0 a a quaù 0,6579% , 15 2
sai soá töông ñoái cuûa soá gaàn
ñuùng a (thöôøng ñöôïc nhaân vôùi
100% ñeå vieát döôùi daïng phaàn traêm) . HÑ3: Soá HÑ3:
a ñöôïc cho bôûi giaù trò gaàn
ñuùng a=5,7824 vôùi sai soá töông Sai soá tuyeät ñoái khoâng vöôït quaù 3).Soá quy troøn:
ñoái khoâng vöôït quaù 0,5%. Haõy
a -a = a. a = 5,7824.0,005
Khi thay soá ñuùng bôûi soá quy =0,028912
troøn, thì sai soá tuyeät ñoái khoâng ñaùnh giaù sai soá tuyeät ñoái cuûa a .
vöôït quaù nöõa ñôn vò cuûa haøng quy troøn . hs ñoïc sgk *Neáu chöõ soá ngay sau
haøng quy troøn nhoû hôn 5 thì ta chæ
vieäc thay theá chöõ soá ñoù vaø caùc chöõ
soá beân phaûi noù bôûi 0 . *Neáu chöõ soá ngay sau Ví duï3 :
haøng quy troøn lôùn hôn hay baèng
Gv giaûi thích ví duï 3 sgk
5thì ta thay heá chöõ soá ñoù vaø caùc Ví duï4 :
chöõ soá beân phaûi noù bôûi 0 vaø coäng
Gv giaûi thích ví duï 4 sgk
theâm moät ñôn vò vaøo chöõ soá ôû haøng
Nhaän xeùt: Ñoä chính xaùc cuûa soá quy troøn
quy troøn baèng nöõa ñôn vò cuûa haøng quy troøn . HÑ4: *Quy troøn soá 7216,4
ñeán haøng ñôn vò cho ta soá 7216.
Sai soá tuyeät ñoái laø : 7216,4 7216 , 0 4 *Quy troøn soá 2,654 ñeán 20
haøng phaàn chuïc ta ñöôïc soá 2,7.
4).Chöõ soá chaéc vaø caùch vieát
Sai soá tuyeät ñoái laø :
chuaån soá gaàn ñuùng: 7 , 2 6 , 2 54 0 , 0 46
a).Chöõ soá chaéc:
Trong soá gaàn ñuùng a vôùi ñoä
chính xaùc d, moät chöõ soá cuûa a
goïi laø chöõ soá chaéc (hay ñaùng
tin) neáu d khoâng vöôït quaù nöõa
ñôn vò cuûa haøng coù chöõ soá ñoù . Ví duï5:
Gvgiaûi thích ví duï 5 sgk
Nhaän xeùt:Taát caû caùc chöõ soá ñöùng
beân traùi chöõ soá chaéc ñeàu laø chöõ soá
chaéc. Taát caû caùc chöõ soá ñöùng beân
b).Daïng chuaån cuûa soá gaàn
phaûi chöõ soá khoâng chaéc ñeàu laø chöõ ñuùng: soá khoâng chaéc.
*Daïng chuaån cuûa soá gaàn ñuùng Ví duï6:
döôùi daïng soá thaäp phaân laødaïng Gvgiaûi thích ví duï 6 sgk
maø moïi chöõ soá cuûa noù ñeàu laø chöõ soá chaéc .
*Neáu soá gaàn ñuùng laøsoá nguyeân
thì daïng chuaån cuûa noù laø A.10k
trong ñoù A laø soá nguyeân , k laø Ví duï7:
haøng thaáp nhaát coù chöõ soá chaéc
Gvgiaûi thích ví duï 7 sgk (kN)
(Töø ñoù moïi chöõ soá cuûa A ñeàu laø chöõ soá chaéc)
Chuù yù :Caùc soá gaàn ñuùng cho trong
“baûng soá vôùi 4 chöõ soá thaäp phaân “ Ví du8:
hoaëc maùy tính boû tuùi ñeàu ñöôïc cho
Gvgiaûi thích ví duï 8 sgk döôùi daïng chuaån.
5).Kyù hieäu khoa hoïc cuûa 1 soá: Chuù yù :
Moãi soá thaäp phaân khaùc 0 ñeàu
Ngöôøi ta thöôøng duøng kyù hieäu
Vôùi quy öôùc veà daïng chuaån soá gaàn
vieát ñöôïc döôùi daïng .10n,
khoa hoïc ñeå ghi nhöõng soá raát
ñuùng thì 2 soá gaàn ñuùng 0,14 vaø
trong ñoù 1 10,nZ.
lôùn hoaëc raát beù. Soá muõ n cuûa 10 0,140 vieát vôùi daïng chuaån coù yù
(Quy öôùc neáu n= -m, vôùi m laø
trong kyù hieäu khoa hoïc cuûa 1 soá nghóa khaùc nhau. Soá gaàn ñuùng 0,14 soá nguyeân döông thì
cho ta thaáy ñoä lôùn (beù) cuûa soá
coù sai soá tuyeät ñoái khoâng vöôït quaù
10-m=1/10m ). Daïng nhö theá goïi ñoù .
0,005 coøn soá gaàn ñuùng 0,140 coù
laø Kyù hieäu khoa hoïc cuûa soá ñoù. Ví duï 9:
sai soá tuyeät ñoái khoâng vöôït quaù
Gv giaûi thích ví duï 9 sgk 0,0005 21
3).Cuûng coá:Soá gaàn ñuùng,sai soá tuyeät ñoái vaø töông ñoái,soá quy troøn,chöõ soá chaéc,kyù hieäu khoa hoïc cuûa 1 soá
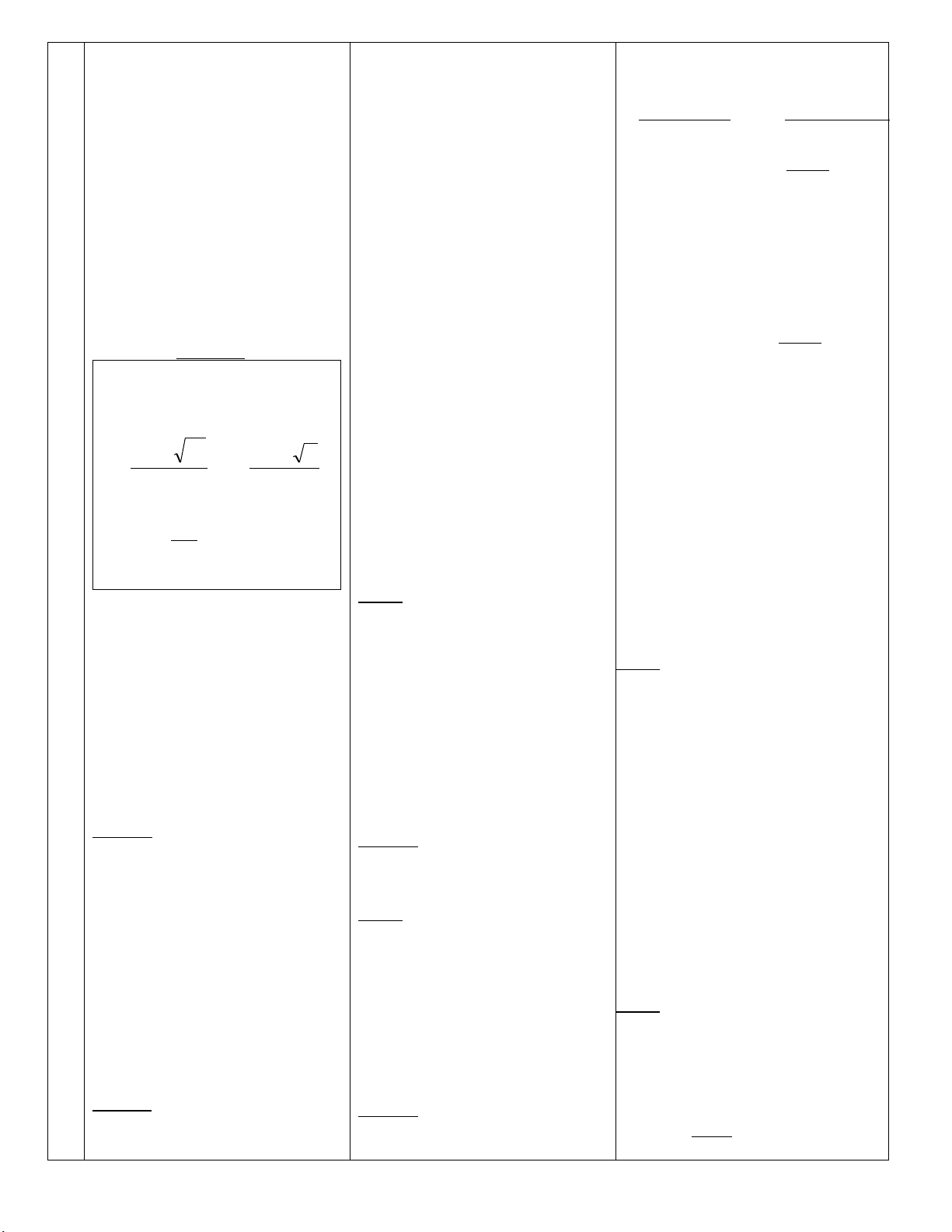
4)Daën doø: Caâu hoûi baøi taäp 43-49 sgk trang 29. 43/ = 22
= 22 - < 3,1429 – 3,1415 = 0,0014 7 7
44/ Giaû söû a=6,3+u, b=10+v, c=15+t.
Chu vi cuûa tam giaùc laø P=a+b+c= 31,3+u+v+t. Theo giaû thieát -0,1 u 0,1; -0,2 v 0,2; -0,2 t 0,2;
Do ñoù -0,5 u+v+t 0,5, thaønh thöû P=31,3cm 0,5cm
45/ Giaû söû x=2,56+u, y=4,2+v laø giaù trò ñuùng cuûa chieàu roäng vaø chieàu daøi cuûa saân.
Chu vi cuûa saân laø P=2(x+y)=13,52+2(u+v). Theo giaû thieát -0,01 u 0,01; -0,01 v 0,01;
Do ñoù -0,04 2(u+v) 0,04, thaønh thöû P=13,52m 0,04m
46/ a) 3 2 1,26 (chính xaùc ñeán haøng phaàn traêm) , 3 2 1,260 (chính xaùc ñeán haøng phaàn nghìn)
b) 3 100 4,64 (chính xaùc ñeán haøng phaàn traêm), 3 100 4,642 (chính xaùc ñeán haøng phaàn nghìn)
47/ 3.105.365.24.60.60 = 9,4608.1012 (km)
48/ 1,496.108 (km) =1,496.1011 (m)
Thôøi gian traïm ñôn vò vuõ truï ñi ñöôïc moät ñôn vò thieân vaên laø : 11 , 1 469 10 . 9773 , 9 10 . 6 (s) 10 . 5 , 1 4 49/ 5,475.1012 ngaøy. 22
Tieát 12 OÂN TAÄP I).Muïc tieâu: Hs bieát :
- Phuû ñònh moät meänh ñeà
- Phaùt bieåu moät ñònh lyù döôùi daïng ñk caàn, ñk ñuû, ñk caàn vaø ñuû
- Bieát bieåu dieãn moät taäp con cuûa R treân truïc soá
- Bieát laáy giao, hôïp, hieäu caùc taäp hôïp
- Bieát quy troøn soá, bieát xaùc ñònh sai soá khi tính toaùn treân caùc soá gaàn ñuùng
II).Ñoà duøng daïy hoïc: Giaùo aùn , sgk
III).Caùc hoaït ñoäng treân lôùp:
1).Kieåm tra baøi cuû : Söûa caùc baøi taäp sgk
Hoaït ñoäng cuûa thaày
Hoaït ñoäng cuûa troø
Goïi hs laøm caùc baøi taäp sgk 50) HD:
50).D) xR, x2 0
Phuû ñònh cuûa meänh ñeà :
“ xX, x coù tính chaát P”
51) Ñònh lyù : “ P(x) Q(x)” 51).a)
“P(x) laø ñieàu kieän ñuû ñeå coù Q(x)”
Ñeå töù giaùc MNPQ coù hai ñöôøng cheùo MP vaø NQ baèng
“Ñeå coù Q(x) ñieàu kieän ñuû laø P(x)”
nhau ñieàu kieän ñuû laø töù giaùc ñoù laø hình vuoâng b)
“Q(x) laø ñieàu kieän caàn ñeå coù P(x)”
Ñeå hai ñöôøng thaúng trong maët phaúng song song vôùi
“Ñeå coù P(x) ñieàu kieän caàn laø Q(x)” nhau ñieàu kieän ñuû laøhai ñöôøng thaúng ñoù cuøng vuoâng goùc vôùi ñöôøng thaúng thöù ba c)
Ñeå hai tam giaùc coù dieän tích baèng nhau ñieàu kieän ñuû laø chuùng baèng nhau 52) a)
Ñeå hai tam giaùc baèng nhau ñieàu kieän caàn laø hai tam
giaùc coù caùc ñöôøng trung tuyeán baèng nhau b)
Ñeå moät töù giaùc laø hình thoi ñieàu kieän caàn laø töù giaùc ñoù
coù hai ñöôøng cheùo vuoâng goùc vôùi nhau 53) a)
Vôùi moïi soá nguyeân döông n , 5n+6 laø soá leû khi vaø chæ khi 23 n laø soá leû b)
Vôùi moïi soá nguyeân döông n , 7n+4 laø soá chaün khi vaø chæ khi n laø soá chaün
54) a) Giaûsöû traùi laïi a 1 , b 1. Suy ra a+b 2. Maâu thuaãn
b) Giaû söû n laø soá töï nhieân chaün , n = 2k (kN).
Khi ñoù 5n+4 = 10k+4 = 2(5k+2) laø moät soá chaün. Maâu thuaãu 55) a) A B b) A \ B
c) CE(AB) = CEACEB 56) b) x[1;5] 1 x 5 x 3 2 x[1;7] 1 x 7 x 4 3
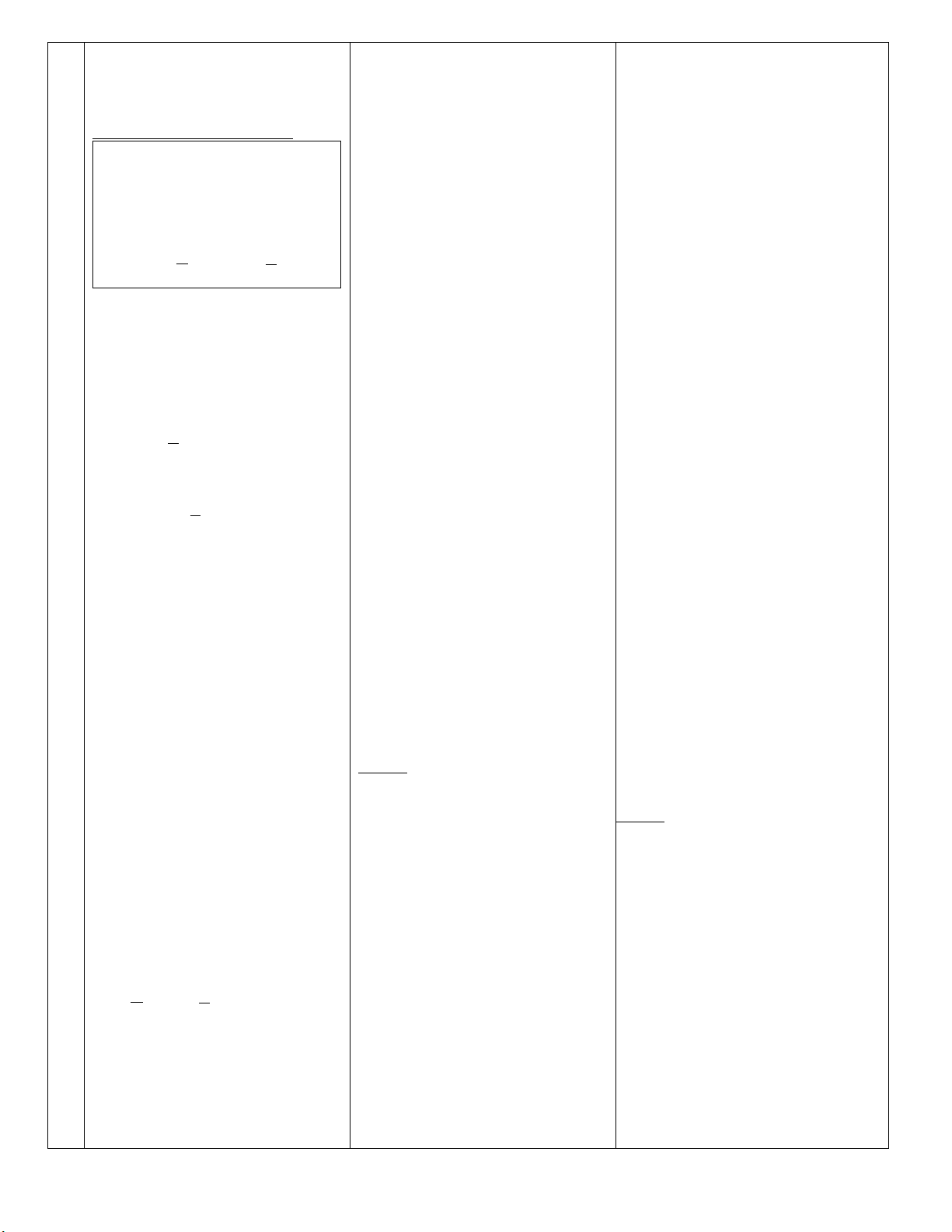
x[2,9 ; 3,1] 2,9 x 3,1 x 3 1 , 0 57) 2 x 5 x 5 ; 2 -3 x 2 x[-3;2] -1 x 5 x[-1;5] x 1 x(- ;1] -5 x(-5;+ ) 58) a) 14 , 3 14 , 3 0 , 0 02. b) 1 , 3 416 1 , 3 416 1 , 3 416 1 , 3 415 0 , 0 001.
59)Vì 0,01 < 0,05 < 0,1 neân V chæ coù 4 chöõ soá chaéc .Caùch vieát chuaån laø V 180 6 , cm3 .
60) Ta coù A B 5 neáu m 5 .
A B neáu m . 5
A B ;
5 m neáu m 5 Chuù yù:Coù theå giaûi 61)
A B laø 1 khoaûng A B .
Neáu m 2 thì mTa coù A B= Neáu 2Neáu 3khi m+1
4 thì 3 3 hoaëc 5 m Neáu 4töùc laø m B=(3;m+1). 2 hoaëc 5 m.
Neáu 5 m thì 3<5 mVaäy neáu 2B laø 2 khoaûng rôøi nhau .
B laø 1 khoaûng Vaäy neáu 262)a)15.104.8.107=1,2.1013. b)1,6.1022.
c)3.1013. Chuù yù raèng 1l=1dm3=106mm3 . 24
TIEÁT13 KIEÅM TRA VIEÁT (1 tiÕt)
A- Môc tiªu : KiÓm tra kÜ n¨ng gi¶i to¸n vµ kiÕn thøc c¬ b¶n cña ch-¬ng 1 . cñng cè kiÕn thøc c¬ b¶n .
B- Néi dung vµ møc ®é : KiÓm tra vÒ ¸p dông ph-¬ng ph¸p c/m ph¶n chøng . T×m hîp, giao cña c¸c tËp hîp sè .
TÝnh to¸n víi c¸c sè gÇn ®óng ( Cã thÓ sö dông m¸y tÝnh bá tói ®Ó tÝnh to¸n c¸c sè gÇn ®óng )
C- ChuÈn bÞ cña thÇy vµ trß : GiÊy viÕt , m¸y tÝnh bá tói , giÊy nh¸p.
D- Néi dung kiÓm tra : ÑEÀ 1
I. TRAÉC NGHIEÄM KHAÙCH QUAN ( 4 ñ)
Ñaùnh daáu x vaøo oâ vuoâng cuûa caâu traû lôøi ñuùng trong caùc caâu hoûi sau ñaây:
1. Trong caùc caâu sau coù bao nhieâu caâu laø meänh ñeà :
Caâu 1: Haõy coá gaéng hoïc thaät toát !
Caâu 2: Soá 20 chia heát cho 6.
Caâu 3: Soá 7 laø soá nguyeân toá
Caâu 4: Soá x laø moät soá chaún. A. 1 caâu B. 2 caâu C. 3 caâu D. 4 caâu.
2. Hai taäp hôïp A = [2;) , B = ( ;
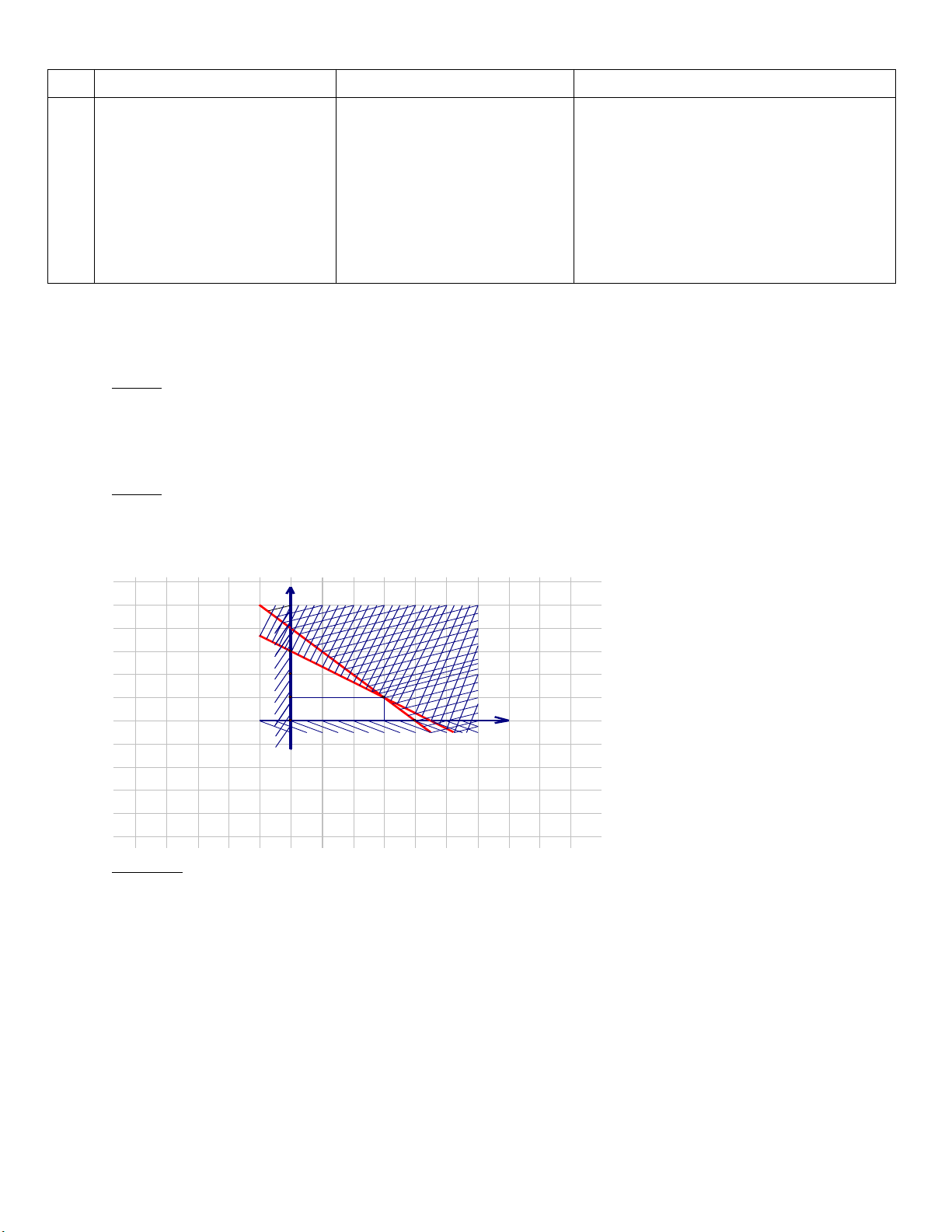
3) , hình veõ naøo sau ñaây bieãu dieãn taäp hôïp A \ B ? A. 2 3 )/////////////( B. 2 3 ////////[ )///////// C. 2 ////////[ 3 B. 2 3 //////////////////////[
3. Cho hai taäp hôïp A = 2
x R / x 4x 3
0 ; B = x N / 6 x
Trong caùc khaúng ñònh sau :
(I) A B B (II) A B (III) C A
6 . Khaúng ñònh naøo sai ? B A. (I) B. (II) C. (III) D. (II) vaø (III).
4. Phaàn gaïch soïc trong hình veõ bieåu thò taäp hôïp naøo ? A B A. A \ B B. A B C. A B D. B \ A. 5. Cho meänh ñeà x [0; )
, x 1 0 . Meänh ñeà phuû ñònh laø : A. x [0; ) , x 1 0 B. x [0; ) , x 1 0 C. x ( ; 0], x 1 0 D. x ( ; 0], x 1 0 6. Cho taäp hôïp X = 3
x R / (x 1)(x 2)(x 4x)
0 coù bao nhieâu phaàn töû ?
A. 1 phaàn töû, B. 2 phaàn töû, C. 3 phaàn töû, D. 5 phaàn töû 7. Cho meänh ñeà P(x) = 2
" x 2x 0", vôùi x R .
Meänh ñeà naøo sau ñaây ñuùng ? 25 A. P(-2) B. P(4) C. P(1) D. P 5
8. Meänh ñeà chöùa bieán naøo sau ñaây ñuùng ? A. 2 x
R, x 0 B. x ( ;
0), x x C. x (0; ) , x 1 0 D. 1 x , R x x
II. BAØI TOAÙN TÖÏ LUAÄN (6 ñ)
1. Phaùt bieåu vaø chöùng minh meänh ñeà sau ñaây : 2 " n
N,n 2 n 2". 2. Cho A ( ; 3 ]; B [4; )
;C (0;5) . Tính taäp hôïp A B C vaø A B \ C 3. Cho meänh ñeà P(x) = 2 " x
R / x 2x 1 0"
a. Laäp meänh ñeà phuû ñònh meänh ñeà P(x)
b. Meänh ñeà phuû ñònh cuûa P(x) ñuùng hay sai ? Taïi sao ? ÑEÀ 2
I. TRAÉC NGHIEÄM KHAÙCH QUAN ( 4 ñ)
Ñaùnh daáu x vaøo oâ vuoâng cuûa caâu traû lôøi ñuùng trong caùc caâu hoûi sau ñaây:
1. Meänh ñeà naøo sau ñaây sai ? A. 2 x , R x 1 0 B. x [0; )
, x 1 x 1
C. Neáu töù giaùc ABCD laø hình bình haønh thì AC = BD.
D. Soá 2007 chia heát cho 9.
2. Hình veõ sau ñaây (phaàn khoâng bò gaïch) bieåu dieãn hình hoïc cho taäp hôïp naøo ? 1 4 ]//////////////////( A. ( ; 1 ) [4; ) B. ( ; 1 ](4; ) C. ( ; 1 ][4; ) D. ( ; 1 ) (4; )
3. Cho hai taäp hôïp A = n N / n laø soá nguyeân toá vaø n <
9 ; B = nZ / nlaø öôùc cuûa 6
Taäp B \ A coù bao nhieâu phaàn töû ? A. 1 phaàn töû B. 2 phaàn töû C. 6 phaàn töû D. 8 phaàn töû .
4. Cho ba taäp hôïp A = (-1;2], B(0;4], C[2;3].
Xaùc ñònh taäp hôïp A BC , ta ñöôïc taäp hôïp : A. (-1;3] B. [2;4] C. (0;2] D. (0;3]
5. Cho hai taäp hôïp: A = 2
x N / 2x 3x
0 , B = x Z / x 1 .
Trong caùc khaúng ñònh sau ñaây : (I) A B (II) C A [ 1 ;1]
(III) A B A
(IV) A B B . B
Coù bao nhieâu khaúng ñònh ñuùng ? A. 1 B. 2 C. 3 D. 4 6. Cho meänh ñeà P(x) = 2 " x
R, x 2 x 4".
Meänh ñeà naøo sau ñaây sai ? A. P(3) B. P 5 C. P(1) D. P(4)
7. Soá phaàn töû cuûa taäp A = 2
x N * / x 4 laø : 26 A. 1 phaàn töû B. 2 phaàn töû C. 4 phaàn töû D. 5 phaàn töû.
II. BAØI TOAÙN TÖÏ LUAÄN ( 6 ñ)
1. Phaùt bieåu vaø chöùng minh meänh ñeà sau ñaây : 2 " n
N,n 3 n 3" . 2. Cho A ( ; 2
]; B [3;);C (0;4) . Tính taäp hôïp A B C vaø A B \ C 3. Cho meänh ñeà P(x) = 2 " x
N / x x 2 0"
a. Laäp meänh ñeà phuû ñònh meänh ñeà P(x)
b. Meänh ñeà phuû ñònh cuûa P(x) ñuùng hay sai ? Taïi sao ? 27
Chöông II Haøm soá baäc nhaát vaø baäc hai ******
Tieát 14-16 §1. ÑAÏI CÖÔNG VEÀ HAØM SOÁ I).Muïc tieâu: Kieán thöùc :
- Chính xaùc hoùa khaùi nieäm haøm soá vaø ñoà thò cuûa haøm soá maø hs ñaõ hoïc
- Naém vöõng khaùi nieäm haøm soá ñoàng bieán , nghòch bieán treân moät khoaûng ( nöõa khoaûng hoaëc ñoaïn );
khaùi nieäm haøm soá chaün , haøm soá leû vaø söï theå hieän caùc tính chaát aáy qua ñoà thò .
- Hieåu 2 pp cminh tính ñbieán, nghòch bieán cuûa hs treân moät khoaûng ( nöõa khoaûng hoaëc ñoaïn ): pp duøng
ñnghóa vaø pp laäp tyû soá f (x ) f (x ) 2 1
(tyû soá naøy coøn goïi laø tyû soá bieán thieân ) x x 2 1
- Hieåu caùc pheùp tònh tieán ñthò ssong vôùi caùc truïc toaï ñoä . Kó naêng :
- Khi cho haøm soá baèng bieåu thöùc , hs caàn :
+ Bieát caùch tìm taäp xaùc ñònh cuûa haøm soá
+ Bieát caùch tìm giaù trò cuûa haøm soá taïi moät ñieåm cho tröôùc thuoäc taäp xaùc ñònh
+ Bieát caùch kieåm tra moät ñieåm coù toïa ñoä cho tröôùc coù thuoäc ñoà thò haøm soá ñaõ cho hay khoâng
+ Bieát chöùng minh tính ñoàng bieán , nghòch bieán cuûa moät soá haøm soá ñôn giaûn treân moät khoaûng
( nöõa khoaûng hoaëc ñoaïn ) cho tröùôc baèng caùch xeùt tyû soá bieán thieân.
+ Bieát caùch cm haøm soá chaün , haøm soá leû baèng ñònh nghóa
- Khi cho haøm soá baèng ñoà thò , hs caàn :
+ Bieát caùch tìm giaù trò cuûa haøm soá taïi moät ñieåm cho tröôùc thuoäc taäp xaùc ñònh vaø ngöôïc laïi , tìm caùc giaù
trò cuûa x ñeå haøm soá nhaän moät giaù trò cho tröôùc
+ Nhaän bieát ñöôïc söï bieán thieân vaø bieát laäp baûng bieán thieân cuûa moät haøm soá thoâng qua ñoà thò cuûa noù
+ Böôùc ñaàu nhaän bieát moät vaøi tính chaát cuûa haøm soá nhö : giaù trò lôùn nhaát hay nhoû nhaát cuûa haøm soá (neáu
coù ), daáu cuûa haøm soá taïi moät ñieåm hoaëc treân moät khoaûng
+ Nhaän bieát ñöôïc tính chaün - leû cuûa hs qua ñoà thò
II) Ñoà duøng daïy hoïc: Giaùo aùn , sgk
III) Caùc hoaït ñoäng treân lôùp : 1) Kieåm tra baøi cuû:
2) Baøi môùi:T1:Knhs,hs ñb,hs ngb;T2:Ks söï bt cuûa hs,hs chaún,hs leû,T3:Slöôïc veà ttieán ñthò ss vôùi truïc TÑ Tg Noäi dung
Hoaït ñoäng cuûa thaày
Hoaït ñoäng cuûa troø
1) Khaùi nieäm veà haøm soá a) Haøm soá Ñònh nghóa Cho D R, D
Gv cho hs ghi ñònh nghóa sgk Haøm soá f xaùc ñònh 28
treân D laø moät quy taéc ñaët töông öùng
moãi soá xD vôùi 1 vaø chæ 1, kyù hieäu
laø f(x); soá f(x) ñoù goïi laø gtrò cuûa haøm soá f taïi x.
D goïi laø taäp xaùc ñònh
(hay mieàn xaùc ñònh), x goïi laø bieán soá
hay ñoái soá cuûa haøm soá f . Haøm soá f:D R x y= f(x)
goïi taét hs y= f(x) hay hs f(x) . Ví duï:sgk
b)Hsoá cho baèng bieåu thöùc:
Caùc hs daïng y=f(x), trong ñoù
f(x) laø moät bieåu thöùc cuûa bieán soá x.
Quy öôùc:Neáu khoâng coù giaûi thích
gì theâm thì taäp xñ cuûa hs y = f(x) laø
taäp hôïp taát caû caùc soá thöïc x sao
cho bieåu thöùc f(x) coù nghóa.
HÑ1: goïi hs thöïc hieän HÑ1: a)Choïn (C) x 0 x 0 Txñ cuûa hsoá a) Ñk:
x 1 0 x 1
Chuù yù:Trong kyù hieäu hs y=f(x) x h(x) = laø R x 2 0 x 2 x:bieán soá ñoäc laäp. (x -1)(x- 2) +\{1;2} b) (Haøm daáu) y:bieán soá phuï thuoäc. y - n 1 eáu x 0
Bieán soá ñlaäp vaø bieán soá phuï thuoäc d(x)= n 0 eáu x 0
cuûa 1 hsoá coù theå ñöôïc kyù hieäu bôûi 2
chöõ caùi tuyø yù khaùc nhau. t A + n 1 eáu x 0 1
Choïn (B)TXÑ: D=R=(-;). t O x -
c)Ñoà thò cuûa haøm soá: -1 B
Cho hsoá y = f(x) xñ treân taäp D. .
Trong maët phaúng toaï ñoä Oxy,
taäp hôïp (G) caùc ñieåm coù toaï ñoä
(x;f(x)) vôùi xD, goïi laø ñoà thò cuûa haøm soá f. M(x 0;y0)(G)x0D vaø y 0 = f(x0) .
Qua ñthò cuûa 1 hs ,ta coù theå Ví duï 2:
nhaän bieátñöôï nhieàu tính chaát
Hsoá y=f(x) xñ treân [-3;8] ñöôïc cho cuûa hs ñoù.
baèng ñthò nhö trong hình veõ 29 y -3 -1 2 4 8 x O Ví duï3 : Goïi hs
f(-3)= -2;f(1)=0;GTNN cuûa hs treân Xeùt hs f(x)=x2
[-3;8] laø -2; f(x)<0 neáu 1TH1:khi x1 vaø x2 [0;+ ) 0 x1x < 2 x 1 2
2) Söï bieán thieân cuûa haøm soá f(x
1)HÑ2:Giaù trò cuûa hs taêng trong
a) Haøm soá ñoàng bieán,nghòch bieán : TH2:khi x1 vaø x2 (-;0] TH1, giaûm trong TH2. Ví duï3 : sgk x1x < x 2 x > 2 x 1 2 1 2 f(x 1)>f(x2) HÑ2: sgk
Goïi hs thöïc hieän Giaûi thích :
f(x1) goïi laø giaù trò cuûa
haøm soá taïi x1, f(x2) goïi laø giaù
trò cuûa haøm soá taïi x2
K:1 khoaûng (nöõa khoaûng hay ñoaïn ); Ñònh nghóa:
Cho haøm soá f xaùc ñònh treân K .
*Hsoá f goïi laø ñoàng bieán (hay
taêng) treân K neáu x1,x2K : x1< x2f(x1) < f(x2)
*Hsoá f goïi laø ngh bieán (hay giaõm)
treân K neáu x1,x2K : x1< x2f(x1) > f(x2) HÑ3:
b) Ñoà thò haøm soá ñoàng bieán ,
Hsoá y=x2 nghòch bieán treân
Hs ñbieán treân caùc khoaûng
nghòch bieán treân moät khoaûng:
(- ;0] vaø ñbieán treân [0;+ ) (-3;-1) vaø (2;8) , nghòch bieán
*Neáu moät haøm soá ñoàng bieán HÑ3:sgk treân khoaûng (-1;2)
treân K thì treân ñoù ñoà thò cuûa noù ñi
leân (keå töø traùi sang phaûi)
*Neáu moät haøm soá nghòch bieán treân
K thì treân ñoù ñoà thò cuûa noù ñi xuoáng
(keå töø traùi sang phaûi)
Ngöøôi ta thöøông ghi laïi keát
b)Khaûo saùt söï bieán thieân cuûa hsoá:
quaû ks söï bthieân cuûa 1 hs
baèng caùch laäp baûng b thieân 30 Ta coù theå : cuûa noù . 1) Döïa vaøo ñònh nghóa
Trong BBT muõi teân ñi leân theå
2) Döïa vaøo nhaän xeùt sau :
hieän tính ñbieán, muõi teân ñi
hsoá fñoàng bieán treân (a;b)
xuoáng theå hieän tính nghòch x , x ( ; a )
b vaø x1 x2 bieán cuûa hsoá . Ví duï4: 1 2 f(x ) f(x Hs xem sgk . 2 1 ) > 0 x x
Gv cho hs ñoïc sgk höôùng daãn HÑ4: 2 1
Hsoá fàngh bieán treân (a;b) hs laøm ví duï 4 Vôùi x1 x2 , ta coù HÑ4:sgk f(x x -a 2 x x , x ( ; a ) b vaø x1 x2 2) - f(x1)=a 22 1 1 2 f(x =a(x ) f(x 2-x1)( x2+x1) . 2 1 ) < 0 x x Suy ra 2 1 f(x ) f(x Ví du4ï : 2 1 ) = a(x x x 2+x1)
Khaûo saùt söï bieán thieân cuûa haøm soá 2 1
f(x) = ax2 (vôùi a > 0) treân moãi Do a<0 neân BBT
khoaûng (- ;0) vaø (0;+ )
-Neáu x1<0,x2<0 thì a(x2+x1)>0 x - 0 + hs ñbieán treân (- ;0) x - 0 + 0 f(x)=ax2 -Neáu x + +
1>0,x2>0 thì a(x2+x1)<0 - - f(x)=a x2 (a<0)
hs nghbieán treân (0;+ ) (a>0) 0
3)Haøm soá chaün , haøm soá leû:
a) Khaùi nieäm haøm soá chaün, hsoá leû: Ñònh nghóa:
Cho haøm soá y = f(x) vôùi taäp xaùc Giaûi:Txñ D=[-1;1]. ñònh D
x,x[-1;1]-x[-1;1] vaø
Gv höùông daãn hs giaûi ví duï 5
*Hsoá f goïi laø haøm soá chaün f(-x) = 1- x - 1 x =
neáu xD, ta coù -xD = -( 1 x - 1- x )= -f(x) vaø f(-x) = f(x) Vaäy f laø hsoá leû .
*Hs f goïi laø haøm soá leû neáu
xD, ta coù -xD HÑ5: Txñ D=R. vaø f(-x) = - f(x) x,xR
HÑ5:Goïi hs phaùt bieåu -xR vaø Ví du5ï :Cmr hsoá f(-x) =a(-x)2=ax2=f(x) Vaäy f laø hsoá chaún .
f(x)= 1 x - 1- x laø hsoá leû. 31 y y
b) Ñoà thò haøm soá chaün vaø hsoá leû: Ñònh lyù:
Ñoà thò cuûa haøm soá chaün nhaän
truïc tung laøm truïc ñoái xöùng . O O x x
Ñoà thò cuûa haøm soá leû nhaän goác
toïa ñoä laøm taâm ñoái xöùng . y
HÑ6: 1a; 2c; 3d . y O x -2 0 2 x
2).Sô löôïc veà tònh tieán ñoà thò ssong
vôùi truïc toïa ñoä:
a)Tònh tieán moät ñieåm : Trong mp Oxy cho M0(x0;y0) .
Vôùi soá k > 0 ñaõ cho ta coù theå dòch chuyeån ñieåm M0 :
-Leân treân hoaëc xuoáng döôùi (theo
phöông truïc tung) k ñôn vò .
-Sang traùi hoaëc sang phaûi (theo
phöông truïc hoaønh) k ñôn vò. Gv höôùng daãn laøm hñ7 HÑ7:
Khi ñoù ta noùi raèng ñaõ ttieán ñieåm M0 Gôïi yù : Khi ttieán ñieåm M leân M1(xo;yo+2), M2(xo;yo-2),
ssong vôùi truïc toïa ñoä.
treân 2 ñôn vò thì hñoä cuûa noù M3(xo+2;yo), M1(xo-2;yo), HÑ7:sgk
khoâng thay ñoåi, nhöng tñoä
ñöôïc taêng theâm 2 ñvò
b).Tònh tieán moät ñoà thò: Ñònh lyù:
Trong maët phaúng toaïñoä Oxy, cho
(G) laø ñoà thò cuûa haøm soá y = f(x) ,
p vaø q laø hai soá döông tuyø yù. Khi ñoù:
1)Tònh tieán (G) leân treân q ñôn vò
thì ñöôïc ñoà thò cuûa haøm soá y= f(x) + q
2)Tònh tieán (G) xuoáng döôùi q ñôn 32
vò thì ñöôïc ñoà thò cuûa haøm soá y= f(x) - q
3) Tònh tieán (G) sang traùi p ñôn vò
thì ñöôïc ñoà thò cuûa haøm soá y= f(x+p)
4) Tònh tieán (G) sang phaûi p ñôn
vò thì ñöôïc ñoà thò cuûa haøm soá y=
Giaûi : Kyù hieäu f(x)=2x-1 . Khi f(x-p)
ttieán (d) sang phaûi 3 ñvò, ta
Ví duï 6:Neáu ttieán ñthaúng (d):y=2x-1 ñöôïc
sang phaûi 3 ñvò thì ta ñöôïc ñthò cuûa
Gv höôùng daãn hs laøm ví duï 6 (d1):y=f(x-3)=2(x-3)-1=2x-7 hs naøo ?
Ví duï 7:Cho ñthò (H) cuûa hs y= 1 .
Gv höôùng daãn hs laøm ví duï 7 x Giaûi: Kyù hieäu g(x)= 1 .
Hoûi muoán coù ñthò cuûa hs x - 2x 1 1
y= - 2x 1 thì ta phaûi ttieán (H) nhö Ta coù = -2+ = g(x)-2 x x x theá naøo ?
Vaäy muoán coù ñthò cuûa hs
y= - 2x 1 thì ta phaûi ttieán (H) x
HÑ 8:Choïn phöông aùn A) xuoáng döôùi 2 ñvò.
3)Cuûng coá: Hsoá, hs ñbieán, hs nghbieán, hs chaún, hs leû.
4)Daën doø : Bt 1-16 sgk trang 44-47
HD:1.a)R; b)R\{1;2} ;c)[1;2) (2;+ ) ; d) (-1;+ ).
2)Txñ {2000;2001;2002;2003;2004;2005}.Kyù hieäu hs laø f(x), ta coù f(2000)=3,48; f(2001)=3,72 ; f(2002)=3,24 ;
f(2003)=3,82 ; f(2004)=4,05 ; f(2005)=5,20 ; f(x ) f(x 3.a) Vôùi x 2 1 )
1 x2 , ta coù f(x2) - f(x1)=( 2 x +2x x +2x =x 2 2-2)-( 21 1-2)=(x2+x1+2)( x2-x1) x x 1+x2+2 2 1
Treân (- ;-1),hs nghbieán vì x1(- ;-1),x2(- ;-1), x1<-1,x2<-1 thì x2+x1+2<0
Treân (-1;+ ),hs ñbieán vì x1(-1;+ ),x2(-1;+ ),x1> -1,x2> -1 thì x2+x1+2>0 f(x )f(x b) Vôùi x 2 1 ) 1 x2,f(x2) - f(x1)=(-2 2 x +4x x +4x = -2(x 2 2+1)-(-2 21 1+1)= -2(x2+x1-2)( x2-x1) x x 1+x2-2) 2 1
Treân (- ;1),hs ñbieán vì x1(- ;1),x2(- ;1), x1<1,x2<1 thì -2(x2+x1-2)>0
Treân (1;+ ),hs nghbieán vì x1(1;+ ),x2(1;+ ),x1>1,x2>1 thì -2(x2+x1-2)<0 2 2 2 f(x ) f(x 2 c) Vôùi x 2 1 )
1 x2 , ta coù f(x2) - f(x1)= - = ( x =
x 3 x 3 (x 3)(x 3) 2-x1) x x (x 3)(x 3) 2 1 2 1 2 1 2 1 2
Treân (- ;3),hs nghbieán vì x1(- ;3),x2(- ;3), x1<3,x2<3 thì <0 (x 3)(x 3) 2 1 2
Treân (3;+ ),hs nghbieán vì x1(3;+ ),x2(3;+ ),x1>3,x2>3 thì <0 (x 3)(x 3) 2 1
5.a)Hs chaún;b)Hs leû;c)Hs leû gôïi yù f(-x)=-x+2--x-2=-(x-2)--(x+2)=x-2-x+2= -f(x);d)Hs chaún.
6.a) (d1):y=0,5x+3; b) (d2):y=0,5x-1; c) (d3):y=0,5(x-2); d) (d4):y=0,5(x +6). Nhaän xeùt: d1 d4, d2 d3 . 33
Tieát 17 LUYEÄN TAÄP I).Muïc tieâu:
- Cuûng coá caùc kieán thöùc ñaõ hoïc veà hsoá .
- Reøn luyeän caùc kyõ naêng : Tìm taäp xaùc ñònh cuûa hsoá , söû duïng tyû soá bieán thieân ñeå ks söï bthieân cuûa hsoá
treân 1 khoaûng ñaõ cho vaø laäp bbthieân cuûa noù , xaùc ñònh ñöôïc moái quan heä giöõa 2 hsoá (cho bôûi bthöùc )
khi bieát hsoá naøy laø do ttieán ñthò cuuûa hs kia ssong vôùi truïc toaï ñoä.
*Cho hs chuaån bò laøm baøi taäp ôû nhaø. Ñeán lôùp gv chöûa baøi, troïng taâm laø caùc baøi 12 ñeán 16. caùc baøi khaùc
coù theå cho hs traû lôøi mieäng.
II).Ñoà duøng daïy hoïc: Giaùo aùn , sgk
III).Caùc hoaït ñoäng treân lôùp:
1).Kieåm tra baøi cuû : Söûa caùc baøi taäp sgk
Hoaït ñoäng cuûa thaày
Hoaït ñoäng cuûa troø
Goïi hs laøm caùc baøi taäp sgk
7) HD:vì moãi soá thöïc döông coù tôùi 2
7).Quy taéc ñaõ cho khoâng xaùc ñònh 1 hsoá
caên baäc hai(vi phaïm ñk duy nhaát).
8).a)(d) vaø (G) coù ñieåm chung khi aD vaø khoâng coù ñieåm chung khi a(d)
b)(d) vaø (G) coù khoâng quaù 1 ñieåm chung vì neáu traùi laïi , goïi
M1 vaø M2 laø 2 ñieåm chung phaân bieät thì öùng vôùi a coù tôùi 2 giaù
trò cuûa hs ( caùc tung ñoä cuûa M1 vaø M2), traùi vôùi ñn cuûa hs.
c)Ñöôøng troøn khoâng theå laø ñthò cuûa hs naøo caû vì 1 ñthaúng coù
theå caét ñtroøn taïi 2 ñieåm phaân bieät .
9.a)x 3; b) -1 x 0; c)(-2;2] ; d)[1;2) (2;3) (3;4] 10) a)[-1;+ ); 2 2 b)f(-1)=6;f( )= -2( -2)=4- 2 ;f(1)=0;f(2)= 3 2 2
11) Caùc ñieåm A,B,C khoâng thuoäc ñthò ; ñieåm D thuoäc ñthò vì f(5)=25+ 2 . 1 12) a)Hs y=
nghbieán treân (- ;2) vaø (2;+ ) x 2
b)Hs y=x2-6x+5 nghbieán treân (- ;3)vaø ñbieán treân (3;+ )
c)Hs y=x2005+1 ñbieán treân (- ;+ )
vì vôùi x1,x2(- ;+ ), x1x < 2005 x 1 2 2005 x +1< 2005 x +1 f(x 1 2
1)13) a)Baûng bieán thieân 34 x - 0 +
b)Treân moãi khoaûng (- ;0) vaø (0;+ ), x1 vaø x2 luoân cuøng 0 + 1
daáu . Do ñoù vôùi x1 x2 y= x 1 1 1 0 f(x - = ( x - 2) - f(x1)= 2-x1) x x x x 2 1 2 1 f(x ) f(x 2 1 ) 1 = <0. x x x x 2 1 2 1 1
Vaäy hs f(x)= nghbieán treân moãi khoaûng (- ;0) vaø (0;+ ) x
14)Neáu 1 hs laø chaún hoaëc leû thì txñ cuûa noù laø ñxöùng . Txñ cuûa
hs y= x laø [0;+ ), khoâng phaûi laø taäp ñxöùng neân hs naøy
khoâng phaûi laø hs chaún, khoâng phaûi laø hs leû.
15.a)Goïi f(x)=2x. Khi ñoù 2x-3=f(x)-3. Do ñoù muoán coù (d’) ta
ttieán (d) xuoáng döôùi 3 ñôn vò .
b)Coù theå vieát 2x-3=2(x-1,5)=f(x-1,5). Do ñoù muoán coù (d’)
ta ttieán (d) sang phaûi 1,5 ñôn vò . 2
16.a)Ñaët f(x)= . Khi ttieán ñoà thò (H) leân treân 1 ñôn vò ta x - 2 x
ñöôïc ñthò cuûa hs f(x)+1=
.Goïi ñthò môùi naøy laø (H1). x b)(H’)
b) Khi ttieán ñoà thò (H) sang traùi 3 ñôn vò ta ñöôïc ñthò cuûa hs 2
c) Khi ttieán ñoà thò (H) leân treân 1 ñôn f(x+3)= .
vò roài sang traùi 3 ñôn vò, coù nghóa laø x 3
ttieán (H’) leân treân 1 ñôn vò. Do ñoù ta
c) Khi ttieán ñoà thò (H) leân treân 1 ñôn vò roài sang traùi 3 ñôn ñöôïc ñthò cuûa hs
vò, coù nghóa laø ttieán (H1) sang traùi 3 ñôn vò. Do ñoù ta ñöôïc ñthò 2 x 1 f(x+3)+1= 2 x 1 +1= cuûa hs f(x+3)+1= +1= x 3 x 3 x 3 x 3 35
Tieát 18 §2. HAØM SOÁ BAÄC NHAÁT
I).Muïc tieâu:Giu1p ho5c sinh *Kieán thöùc :
- Taùi hieän vaø cuûng coá caùc tính chaát vaø ñoà thò cuûa haøm soá baäc nhaát (ñaëc bieät laø khaùi nieäm heä soá goùc vaø ñk
ñeå hai ñöôøng thaúng song song)
- Hieåu caáu taïo vaø caùch veõ ñt cuûa caùc hs b nhaát treân töøng khoaûng maø hs daïng y = ax b laø moät trhôïp rieâng *Kyõ naêng :
- Khaûo saùt thaønh thaïo haøm soá baäc nhaát vaø veõ ñt cuûa chuùng .
- Bieát vaän duïng caùc tính chaát cuûa haøm soá baäc nhaát ñeå khaûo saùt söï bieán thieân vaø laäp baûng bieán
thieân cuûa caùc haøm soá baäc nhaát treân töøng khoaûng ñaëc bieät laø ñoái vôùi caùc hs daïng y = ax b . II).Chuaån bò: Giaùo aùn , sgk
III).Caùc hoaït ñoäng treân lôùp:
1). Kieåm tra baøi cuû: 2).Baøi môùi: Tg Noäi dung
Hoaït ñoäng cuûa thaày
Hoaït ñoäng cuûa troø
1).Söï bieán thieân vaø ñoà thò cuûa Ghi ñònh nghóa
haøm soá baäc nhaát: Ñònh nghóa:
Hsoá baäc nhaát laø hs ñöôïc cho baèng bthöùc coù daïng :
y = ax+b (a,b laø caùc haèng soá , a 0)
a). Söï bieán thieân:
Gv giaûi thích tính ñoàng bieán vaø Taäp xaùc ñònh : R
nghòch bieán cuûa haøm soá
a > 0 : hsoá ñoàng bieán /R
a < 0 : hsoá nghòch bieán /R Baûng bieán thieân :
Goïi hs laäp baûng bieán thieân (a< 0) x - + x - + + + y=ax+b y=ax+b (a>0) - - (a<0) Goïi hs phaùt bieåu b).Ñoà thò:
Ñoà thò cuûa hs y=ax+b (a 0) laø1
ñöôøng thaúng coù heä soá goùc baèng a
vaø coù ñaëc ñieåm sau : - Khoâng songsong vaøkhoâng
truøng vôùi caùc truïc toïa ñoä -
Caét truïc tung taïiB(0;b) vaø 36
caét truïc hoaønh taïi A(- b ) 0 ; a
Ví duï1: Goïi hs thöïc hieän
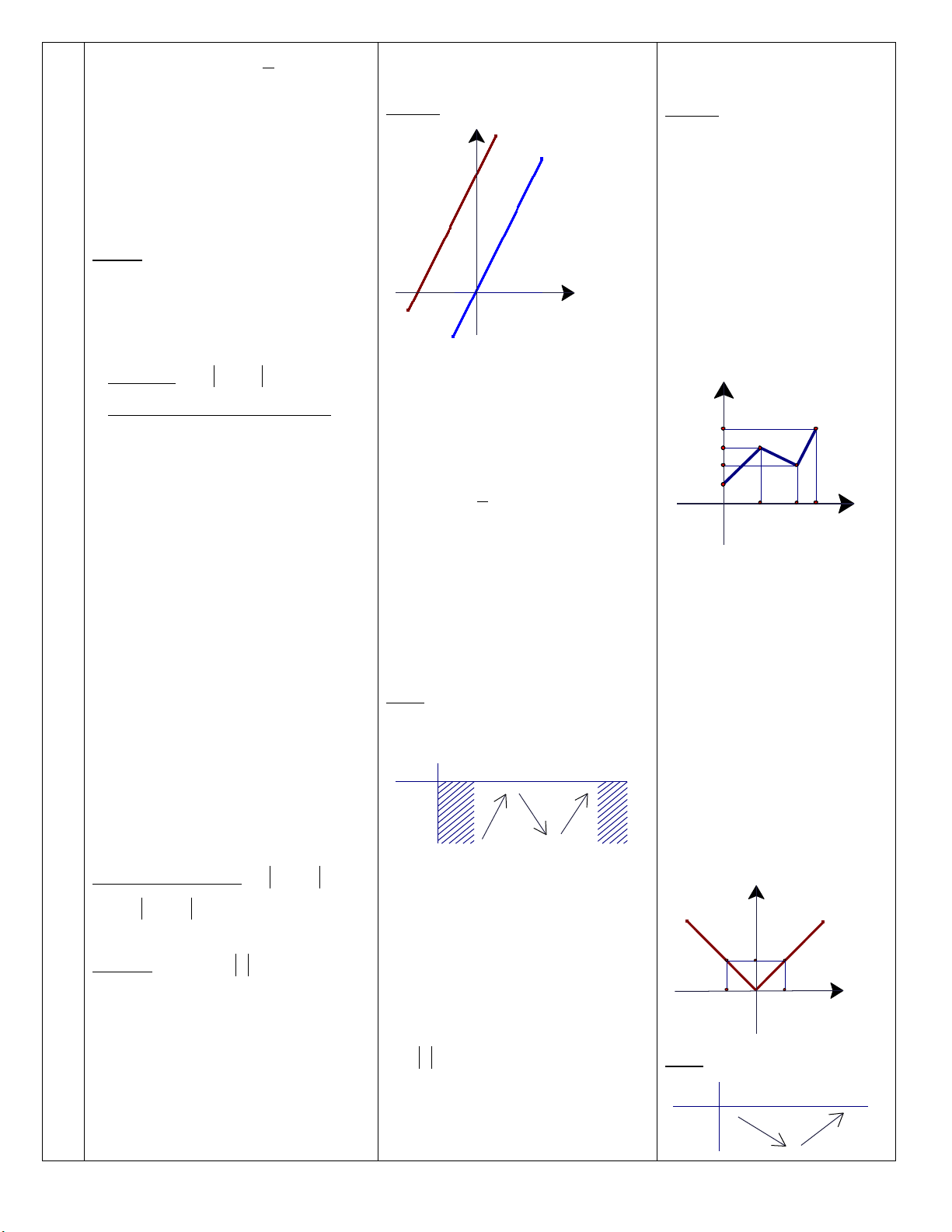
Ví duï1: Ñoà thò haøm soá y
y =2x+4 laø ñthaúng ñi qua 2
ñieåm A(-2;0) vaø B(0;4).
Töø ñaúng thöùc 2x+4=2(x+2)
Suy ra ñt y=2x+4 coù theå thu
ñöôïc töø ñt (d):y=2x baèng 1 Chuù yù: trong 2 caùch sau : (d) : y = ax+b O
-Tònh tieán (d) leân treân 4 ñvò (d’) :y = a’x+b’
-Tònh tieán sang traùi 2 ñôn vò x
1)(d)//(d’) a= a’vaøb b’
2) (d) caét (d’) a a’
2).Haøm soá: y = ax b y
a)Hs bnhaát treân töøng khoaûng Xeùt haøm soá B D x 1 n eá u 0 x 2 C 1 y=f(x)= x n 4 eá u 2 x 4 A 2 O x 2x 6 n eá u 4 x 5
hs khoâng phaûi laø hs bnhaát, ñaây laø
hs baäc nhaát treân töøng khoaûng .
Muoán veõ ñthò cuûa hs naøy , ta veõ
ñthò cuûa töøng hs taïo thaønh . Ñthò
cuûa hs naøy laø ñöøông gaáp khuùc
HÑ1: Goïi hs thöïc hieän *Txñ [0;5] *BBT x - 0 2 4 5 + 3 4 y 1 2
b)Ñt vaø söï bt of hs y= ax b ,a 0 *ymax=f(5)=4 y
Hs y= ax b veà thöïc chaát cuõng laø
hsb nhaát treân töøng khoaûng 1
Ví duï2: Xeùt hs y= x *Txñ R -1 O 1 x *Hs chaún n x eáu x 0 *y= x =
HÑ2: Goïi hs thöïc hieän n x eáu x 0 x - 0 +
Ñoù laø 2 tia phaân giaùc cuûa hai goùc + +
phaàn tö I vaø II ñx vôùi nhau qua y= x 0 Oy 37 ymin=f(0)=0
Ví duï3: Xeùt hs y= 2x - 4 2x - n 4 eáu x y= 2x - 4 = 2
HÑ3: Goïi hs thöïc hieän 2x n 4 eáu x 2 y HÑ3:
*Caùch veõ: Veõ 2 ñthaúng 4
y= (2x-4) roài xoaù phaàn ôû
phiaù döôùi truïc hoaønh . *BBT
Chuù yù : Coù theå veõ ñthò cuûa hs
y= ax b baèng caùch : veõ 2 ñthaúng x - 2 + + +
y=ax+b vaø y=-ax-b roài xoaù phaàn O 2 4 x y = 2x- 4
ñthaúng naèm ôû phiaù döôùi truïc hoaønh 0
3)Cuûng coá: Kn vaø ñthò cuûa hsb nhaát, hsb nhaát treân töøng khoaûng, hs y= ax b
4)Daën doø: Caâu hoûi vaø bt 17-19; Luyeän taäp 20-26 sgk trang 51,52,53,54. HD: y
17) Coù 3 caëp ñöôøng thaúng ssong laø a) y= 1 x+1 vaø y= 1 x-1 ; 2 2 2 b) y= 2 x+2 vaø y= 2 x-2 ; 2 -2 -1 O 1 3 x
c) y= - 1 x+3 vaø y= -( 2 x-1) 2 -2 2 18.a)Txñ [-2;3] . Ñthò x - -2 1 3 + -1 2 0
b)Hs nghòch bieán treân (-1;1), y y
ñoàng bieán treân moãi khoaûng (-2;-1) 0 -2 vaø (1;3) . BBT 19.a)Ñthò
b)Ta coù f2(x)= 2x+5=2x+2,5=f1(x+2,5).
Vaäy ñthò cuûa hs f2 coù ñöôïc khi tònh tieán ñthò cuûa hs f1 sang traùi 2,5 ñôn vò . -2,5 O x 38
Tieát 19 LUYEÄN TAÄP I).Muïc tieâu:
-Cuûng coá caùc kieán thöùc ñaõ hoïc veà hs baäc nhaát vaø hs baäc nhaát treân töøng khoaûng .
-Cuûng coá kieán thöùc vaø kyõ naêng veà tònh tieán ñoà thò .
-Reøn luyeän caùc kyõ naêng : Veõ ñthò hs bnhaát, hs baäc nhaát treân töøng khoaûng, ñaëc bieät laø hs y= ax b ,
töø ñoù neâu ñöôïc caùc tính chaát cuûa hsoá .
II).Ñoà duøng daïy hoïc: Giaùo aùn vaø sgk.
III).Caùc hoaït ñoäng treân lôùp:
1).Kieåm tra baøi cuû:Kn hs baäc nhaát, hs baäc nhaát treân töøng khoaûng?
2).Baøi môùi: Troïng taâm laø caùc baøi 21,23,24,26. Caùc baøi khaùc coù theå cho hs traû lôøi mieäng hoaëc töï kt laån nhau.
Tg Hoaït ñoäng cuûa thaày
Hoaït ñoäng cuûa troø
Höôùng daãn hs laøm caùc baøi taäp :
20)Khoâng, vì caùc ñthaúng ssong vôùi truïc tung khoâng laø ñthò 21) cuûa hs naøo caû . y
21) a)Haøm soá laø y= -1,5x+2; b)Ñoà thò 5
22) y=x 3 vaø y= -x 3. y
Gôïi yù: Ñoà thò laø 4 ñthaúng
chöùa 4 caïnh cuûa hình vuoâng
taâm O vaø 1 trong caùc ñænh laø A. y= -x+3 y=x+3 23) a)y=2 y= -1,5x+2 x+3; b)y=2x+1 ; O x c)y=2x-2-1 -2 O x y= -x-3 y y=x-3 y=2 x +3 y=2 x y=2 x-2 -1 y=2 x+1 O x y y= x y= x-2
24) a) Haøm soá y =x-2 ; b) Hs y=x-3
Nhaän xeùt : Tònh tieán ñthò (G) cuûa O
hs y=x-2sang traùi 2 ñôn vò x
( ñöôïc ñthò hs y=x) roài tònh tieán
tieáp xuoáng döôùi 3 ñôn vò thì y= x -3
ñöôïc ñoà thò haøm soá y=x-3. 39 y
25.a)Khi 0 x 10 töùc laø quaûng ñöôøng ñi naèm trong 10km
ñaàu tieân , soá tieàn phaûi traû laø f(x)=6x (nghìn ñoàng). Khi
x>10, töùc laø quaûng ñöôøng ñi treân 10km thì soá tieàn phaûi traû 60
goàm 2 khoaûn : 10km ñaàu phaûi traû vôùi giaù 6nghìn ñoàng/km
vaø (x-10)km tieáp theo phaûi traû vôùi giaù 2,5nghìn ñoàng /km.
Do ñoù, f(x)=60+2,5(x-10)=2,5x+35. Vaäy hs phaûi tìm laø 6x n eáu 0 x 10 f(x)= x 5 , 2 35 n eáu x 10
b)Töø coâng thöùc treân suy ra f(8) = 6.8 =48 ; O 10 f(10)=6.10=60; x f(18)=2,5.18+35=80
c)Ñoà thò neân laáy ñôn vò treân truïc tung vaø treân truïc y
hoaønh theo tæ leä 10:2chæ quan taâm ñeán ñoà thò hs maø thoâi . - x 5 neáu x 1 26.a)y= x 5 1 neáu - 1 x 1 x 5 neáu x 1 y=3 x -1 - 2x +2
b)Ñoà thò vaø baûng bieán thieân x - -1 1 + O + + x y 6 -4 40
Tieát 20-21 §3. HAØM SOÁ BAÄC HAI I).Muïc tieâu: *Kieán thöùc :
- Hieåu quan heä giöõa ñoà thò cuûa hs y = ax2+bx+c vaø ñoà thò cuûa haøm soá y = ax2 .
- Hieåu vaø ghi nhôù caùc tính chaát cuûa hs y = ax2+bx+c *Kyõ naêng : -
Khi cho moät hsb hai, bieát caùch xaùc ñònh toïa ñoä ñænh , phöông trình cuûa truïc ñoái xöùng vaø höôùng beà loõm cuûa
Parabol (ñoà thò hs baäc hai aáy)
- Veõ thaønh thaïo caùc parabol daïng y = ax2+bx+c baèng caùch xaùc ñònh ñænh , truïc ñoái xöùng vaø moät soá ñieåm khaùc
Qua ñoù suy ra ñöôïc söï bieán thieân , laäp baûng bieán thieân cuûa haøm soá vaø neâu ñöôïc 1 soá tính chaát khaùc cuûa hs
(xaùc ñònh caùc giao ñieåm cuûa parabol vôùi caùc truïc toaï ñoä,xaùc ñònh daáu cuûa hs treân 1 khoaûng ñaõ cho, tìm GTLN hay GTNN cuûa hs)
- Bieát caùch giaûi moät soá baøi toaùn ñôn giaûn veà ñoà thò cuûa hs baäc hai. II) Chuaån bò : Giaùo aùn, sgk
III).Caùc hoaït ñoäng treân lôùp: 1) Kieåm tra baøi cuû: 2) Baøi môùi: Tg Noäi dung
Hoaït ñoäng cuûa thaày
Hoaït ñoäng cuûa troø 1).Ñònh nghóa:
Haøm soá baäc hai laø haøm soá
ñöôïc cho baèng bieåu thöùc coù Cho hs ghi ñònh nghóa daïng y = ax2+bx+c
(a, b, c laø caùc haèng soá , a 0)
Taäp xñònh cuûa hsb hai laø R.
2) Ñoà thò cuûa hsoá baäc hai:
a)Nhaéc laïi veà ñthò hsoá
y = ax2 (a 0)
Goïi hs nhaéc laïi ñoà thò haøm soá
Ñoà thò hs y=ax2 (a 0) laø y = ax2(a 0)
parabol(Po) coù caùc ñaëc ñieåm sau
①Ñænh cuûa parabol(Po) laø goác toaï ñoä O;
②Parabol (Po) coù truïc ñxöùng laø truïc tung ; ③Parabol (P o) höôùng beà loõm
leân treân khi a>0 vaø xuoáng döôùi khi a<0. 41
b) Ñoà thò haøm soá
y = ax2+bx+c (a 0) ax2+bx+c= b b2 2 b2 =a x 2 x c 2a 4a2 4a2 2 2 =a b b ac x 4 2 2a 4a Ñaët b =b2-4ac, p= - , q= - 2a 4a
Thì hs y= ax2+bx+c coù daïng y=a(x-p)2+q
Gv giaûi thích bieán ñoåi ñöa ñeán b p - y = a(x-p)2+q vôùi 2a q - 4a
Phaùt vaán hs traû lôøi ñöôïc :
Ñoà thò haøm soá coù ñöôïc baèng caùch
-Laàn1 : tònh tieán (P0) sang tònh tieán ñoà thò
phaûi p ñôn vò neáu p > 0, sang (P0) : y = ax2 hai laàn:
traùi p ñôn vò neáu p < 0 ta ñöôïc (P1)
-Laàn2 : tònh tieán (P1) leân
treân q ñôn vò neáu q > 0,
xuoáng döôùi q ñôn vò neáu
HÑ1 , HÑ2: Goïi hs thöïc hieän q < 0 HÑ1: -Ñænh I1(p;0)
-P trình truïc ñoái xöùng :x = p HÑ2: -Ñænh I(p;q)
-P trình truïc ñoái xöùng :x = p
Gv phaùt vaán hs ñöa ñeán keát luaän Keát luaän:
Ñt hs y = ax2+bx+c (a 0) laø
moät parabol coù ñænh I b ;
, nhaän ñöôøng 2a a 4
thaúng x = - b laøm truïc ñoái 2a
xöùng vaø höôùng beà loõm leân
treân khi a > 0, xuoáng döôùi 42 khi a < 0
*Caùch veõ ñoà thò: - Xñ ñænh : I b ; 2a a 4
-Xaùc ñònh truïc ñoái xöùng vaø
höôùng beà loõm cuûa parabol
-Xaùc ñònh caùc ñieåm ñaëc bieät
(thöôøng laø giao ñieåm cuûa
parabol vôùi caùc truïc toïa ñoä vaø
caùc ñieåm ñx vôùi chuùng qua truïc ñx)
-Caên cöù vaøo tính ñx , beà loõm
vaø hình daùng parabol ñeå noái
caùc ñieåm ñoù laïi
3).Söï bthieân cuûa hs baäc hai:
Gv laäp baûng bieán thieân cuûa haøm b
Töø ñt hs baâc hai, suy ra BBT _ - x - 2 a +
soá vôùi a > 0. Goïi hs laäp baûngbieán b _ - f(x)=ax2+bx+c - x - 2a +
thieân haømsoá vôùi a < 0 (a<0) - 4a - + y=ax2+bx+c +
Gv goïi hs neâu keát luaän Nhö vaäy: (a>0) _ - 4a *Khi a>0,hs nb treân (- b ;- ), 2a
ñb treân (- b ;+ ) vaø coù GTNN 2a laø - khi x= - b .
Ví duï: Khaûo saùt söï bieán thieân 4a 2a
vaø veõ ñoà thò haøm soá : * Khi a<0,hs ñb treân (- b ;- ), y = -x2+4x-3 2a b y nb treân (- ;+ ) vaø coù GTLN 2a - b 1 laø khi x= - . 4a 2a O A 2 Gv giaûi thích x
Höôùng daãn hs laøm ví duï y= -x2+4x-3 *Taäp xaùc ñònh : R Ví duï Môû roäng: *Ñænh :I(-1;-4)
Veõ ñthò hs y=-x2+4x-3
*Truïc ñoái xöùng :x = -1 Giaûi: *Baûng bieán thieân :
*Veõ parabol (P1):y= -x2+4x-3 x - 2 + *Veõ parabol 1
(P2):y= -(-x2+4x-3) baèng caùch y= -x2+4x-3 - - laáy ñx (P1) qua Ox. *Ñieåm ñaëc bieät :
*Xoaù ñi caùc ñieåm cuûa (P1) vaø x = 0 y = -3
(P2) naèm ôû phía döôùi truïc y = 0 x = 1 hoaëc x = -3 hoaønh . 43
HÑ3: Goïi hs thöïc hieän y
Cho haøm soá y = x2+2x-3 coù ñthò Hs giaûi HÑ3: laø parabol (P) a)
a) Tìm toaï ñoä ñænh, phöông trình *Ñænh :I(-1;-4)
truïc ñx vaø höôùng beà loõm cuûa (P). *Truïc ñoái xöùng :x = -1 y= -x2+4x-3
Töø ñoù suy ra söï bieán thieân cuûa hs *a=1>0 neân beà loõm höôùng leân y = x2+2x-3. treân O b)Veõ parabol (P). Baûng bieán thieân : x
c)Veõ ñoà thò haøm soá : x - -1 + y = x2 + + 2x 3 y=x2+2x-3 -4
Gv höôùng daãn hs baèng ñoà thò : b) *Tìm x ñeå x2+2x-3 0
*Ñieåm ñaëc bieät :Ñænh I(-1;-4) *Tìm x ñeå x2+2x-3 0 x = 0 y = -3 Suy ra : y ? y = 0 x = 1 hoaëc x = -3 y y y= x2+2x-3 -1 -3 O 1 x O -3 1 x -3 -4 I
Gv giaûi thích vaø veõ ñoà thò haøm soá c)Muoán veõ ñthò hs
y= x2 2x 3 , ta veõ ñthò 2 hs
y= x2+2x-3 vaø y= -( x2+2x-3)
roài xoaù ñi phaàn phía döôùi truïc hoaønh.
3) Cuûng coá: Ñthi haøm soá baäc hai, söï bieán thieân cuûa hs baäc hai y
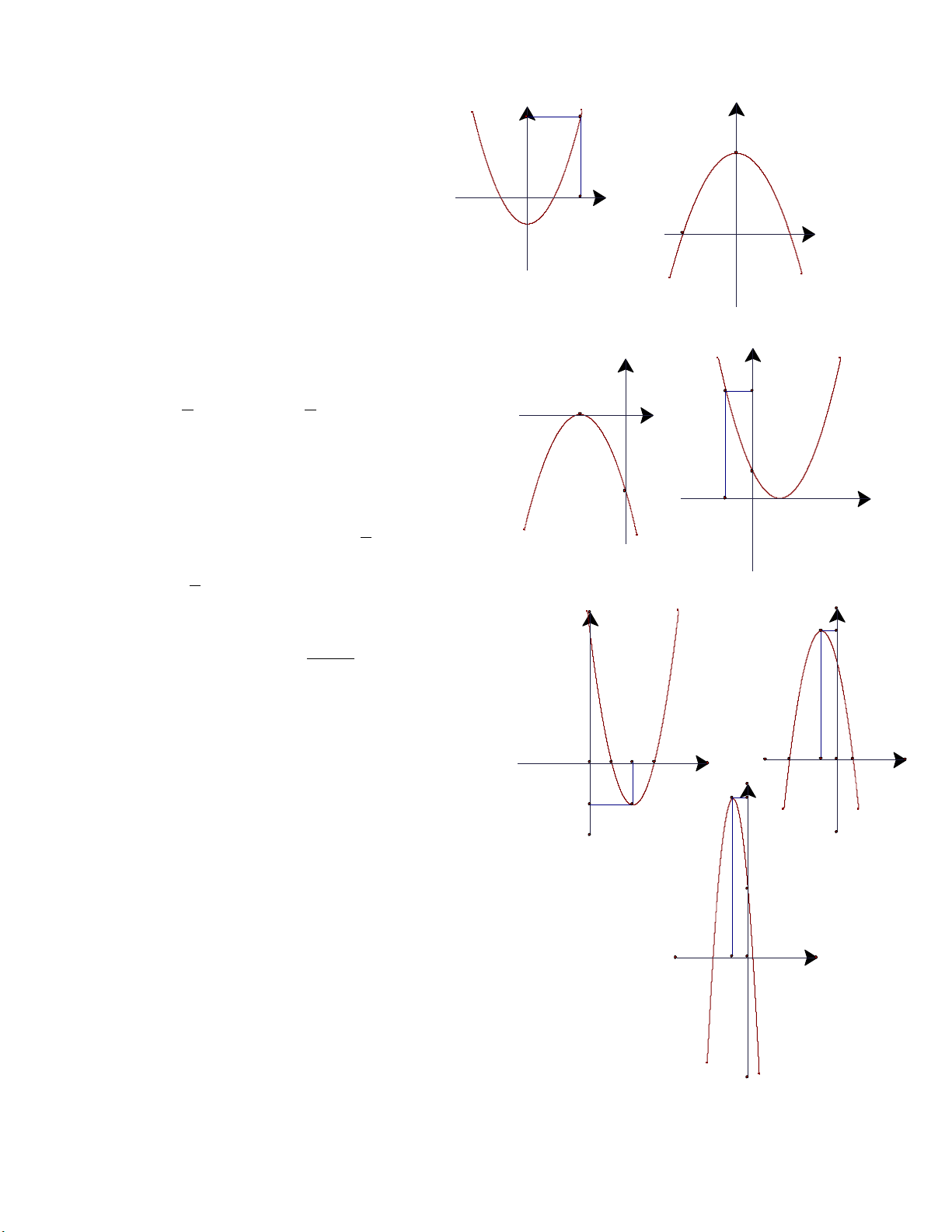
4)Daën doø: Caâu hoûi vaø baøi taäp: 27-31, luyeän taäp: 32-36, Caâu hoûi vaø bt oân taäp chöông II : 39-45 HD: y y y= - 2 x+12 27) O O c) Parabol y = y x 2 x2+1 coù ñöôïc laø do x M2 M
tònh tieán parabol y = 2 x2 theo
truïc tung leân treân 1 ñôn vò . Do ñoù : y=x-32 y= 2 x2+1 - Ñænh I(0;1) -3
- Truïc ñoái xöùng : x = 0 O 3 x
- Beà loõm höôùng leân treân
d) Parabol y = - 2 (x+1)2 laø do tònh tieán
parabol y = - 2 x2 sang traùi 1 ñôn vò . y= -x O 2-3 A x 44 Do ñoù: - Ñænh I(-1;0)
- Truïc ñoái xöùng : x = -1 y y 3
- Beà loõm höôùng xuoáng döôùi 3
28.a) Kyù hieäu haøm soá : y = f(x) = ax2+c, y=x2-1 ta coù f(2)=3.
*Haøm soá coù GTNN baèng c khi a > 0. O 2 x Do ñoù ta coù a > 0 -1 -2 O
*f(2) = 4a+c = 3 vaø c = -1 . Töø ñoù a = 1. x 3
Ta coù haøm soá : y = x2-1 y= - x2+3 4
b) Kyù hieäu haøm soá : y = f(x) = ax2+c,
*Do ñænh parabol laø I(0;3) neân c = 3
*Parabol caét truïc hoaønh taïi (-2;0) y y neân f(-2)=0, hay 4a+c=0. 4 3 3 -3
Töø ñoù : a= vaø hs laø y= x2+3 4 4 O x
29) Kyù hieäu haøm soá laø f(x) = a(x-m)2 y=(x-1) 2
a) Ñænh cuûa (P) laø I(-3;0) m = -3 5 y= - (x+3) 2 9 -5
(P) caét truïc tung taïi M(0;-5) f(0) = -5 -1 O 1 x
a(0-m)2 = -5 9a = -5 a = - 5 9 Vaäy : f(x) = - 5 (x+3)2 9 y y
b) Ñöôøng thaúng x = m laø truïc ñoái xöùng cuûa (P) 12 8
neân töø giaû thieát suy ra : m = 1 3 1 2 y=x2-8x+12
Ngoaøi ra ta coù f(-1) = 4 neân a(-1-m)2 = 4 a = 1 y= -2x2-4x+6 Vaäy f(x)=(x-1)2
30) a) y = x2-8x+12 = (x-4)2-4 . Ñoà thò coù ñöôïc baèng -3 -1
caùch tònh tieán (P) : y = x2 sang phaûi 4 ñôn vò , 2 4 6 O 1 O x y x
roài xuoáng döôùi 4 ñôn vò. 21 -4
b) y = -3x2-12x+9 = -3(x+2)2+21 . Ñoà thò coù ñöôïc
baèng caùch tònh tieán (P) : y = -3x2 sang traùi 2 ñôn vò ,
roài leân treân 21 ñôn vò 9
31.a)Ñænh laø I(-1;8); b)Ñoà thò y= -3x2-12x+9
c)Töø ñoà thò ta coù y 0 -3 x 1 -2 O x 45
Tieát 22 LUYEÄN TAÄP I). Muïc tieâu :
-Cuûng coá caùc kieán thöùc ñaõ hoïc veà hs baäc hai
-Cuûng coá kieán thöùc vaø kyõ naêng veà tònh tieán ñoà thò ñaõ hoïc
- Reøn luyeän caùc kyõ naêng : Veõ dthò hs baäc hai vaø hs y= ax2 bx c ,
töø ñoù laäp ñöôïc baûng bieán thieân vaø neâu ñöôïc caùc tính chaát cuûa hs naøy
II) Ñoà duøng daïy hoïc : Giaùo aùn, sgk
III).Caùc hoaït ñoäng treân lôùp: 1). Kieåm tra baøi cuû:
Caâu hoûi : Toïa ñoä ñænh cuûa Parabol ? Caùc tính chaát cuûa Parabol ? Caùch veõ Parabol
2) Baøi môùi: Troïng taâm laø caùc baøi 32,33,34,35. Caùc baøi khaùc coù theå cho hs traû lôøi mieäng hoaëc töï kt laån nhau
döôùi söï höôùng daãn cuûa gv.
Tg Hoaït ñoäng cuûa thaày
Hoaït ñoäng cuûa troø
Goïi hs giaûi caùc baøi taäp32, 33, 34, 32.a)Ñthò;Ñaët f(x)= -x2+2x+3 vaø g(x)=0,5x2+x-4.Töø ñt suy ra 35, 36
b)f(x)>0 -10 x<-4 hoaëc x>2.
c)f(x)<0 x<-1 hoaëc x>3 ; g(x)<0 -4 33). Haøm soá Hs coù GTLN / GTLN GTNN GTNN khi x= y=3x2-6x+7 x=1 4 y y= -5x2-5x+3 x= -0,5 4,25 y=x2-6x+9 x=3 0 3 y= -4x2+4x-1 x=0,5 0
34)a)a>0 vaø <0; b) a<0 vaø <0; c) a<0 vaø >0;
35) a) Veõ parabol y=x2+
2 x vaø parabol y= -(x2+ 2 x)
(chuùng ñx nhau qua truïc hoaønh ). Sau ñoù xoaù ñi phaàn naèm ôû y= - x2 +2 x +3
phía döùôi truïc hoaønh cuûa caû 2 parabol aáy. -3 -1 O 1 3 x BBT 2 x 2x 3 x vôùi 0
b)Thöïc chaát laø veõ ñthò hs y= x2 2x 3 x vôùi 0 x2 5 , 0 x 2 x vôùi 1
c)Thöïc chaát laø veõ ñthò hs y= x2 5 , 0 x x vôùi 1 x 1 1 n eáu x -1 (x ) 3 2 n eáu x -1 36.a) y= b) y= 2 x2 n 3 eáu x 1 2 n eáu x 1 46
Tieát 23 CAÂU HOÛI VAØ BAØI TAÄP OÂN TAÄP CHÖÔNG II I). Muïc tieâu :
-Cuûng coá caùc kieán thöùc ñaõ hoïc veà hs baäc hai
-Cuûng coá kieán thöùc vaø kyõ naêng veà tònh tieán ñoà thò ñaõ hoïc
- Reøn luyeän caùc kyõ naêng : Veõ dthò hs baäc hai vaø hs y= ax2 bx c ,
töø ñoù laäp ñöôïc baûng bieán thieân vaø neâu ñöôïc caùc tính chaát cuûa hs naøy
II) Ñoà duøng daïy hoïc : Giaùo aùn, sgk
III).Caùc hoaït ñoäng treân lôùp: 1). Kieåm tra baøi cuû:
Caâu hoûi : Caùch veõ ñöôøng thaúng ? Caùch veõ Parabol ? 2) Baøi môùi:
Tg Hoaït ñoäng cuûa thaày
Hoaït ñoäng cuûa troø
39.a)Choïn B:nghòch bieán;b)Choïn A:ñoàng bieán c)Choïn C
Ñaët f(x)= -x2+2x+3 vaø g(x)=0,5x2+x-4. Töø ñoà thò suy ra
Goïi hs giaûi caùc baøi taäp39,…,44
40.a)b=0,a 0 tuøy yù; b)b=0, a 0 tuøy yù; c tuøy yù;
41.a) (P) höôùng beà loõm xuoáng döôùi neân a<0, caét phaàn döông
cuûa truïc tung neân c>0, coù truïc ñx laø ñthaúng x= - b <0 ,(maø 2a a<0), neân b<0 .
b) (P) höôùng beà loõm leân treân neân a>0, caét phaàn döông cuûa
truïc tung neân c>0, coù truïc ñx laø ñthaúng x= - b >0 ,(maø a>0), 2a neân b<0.
c) (P) höôùng beà loõm leân treân neân a>0, ñi qua goác toaï ñoä O b
neân c=0, coù truïc ñx laø ñthaúng x= -
<0 ,(maø a>0), neân b>0. 2a
d) (P) höôùng beà loõm xuoáng döôùi neân a<0, caét phaàn aâm b
cuûa truïc tung neân c<0, coù truïc ñx laø ñthaúng x= - >0 ,(maø 2a a<0), neân b>0 .
42)a)Giao ñieåm (0;-1) vaø (3;2); b)Giao ñieåm (-1;4) vaø (-2;5);
c)Giao ñieåm (3- 5 ;1-2 5 ) vaø (3+ 5 ;1+2 5 )
43) Ñaët f(x) = ax2+bx+c Ta coù f(1) = a+b+c = 1 1 1 1 3 f = a+ b+c = 2 4 2 4
Maët khaùc vì haøm soá ñaït giaù trò nhoûnhaát taïi x = 1 neân - b = 1 2 2a 2
Hay b = -a . Töø ñoù suy ra a = 1, b = -1, c = 1
Ta coù haøm soá : y = x2-x+1 47 y 2 x n eáu x 0 44) b) y = x2 n x eáu x 0 2 O -2 -1 1 2 x c) y = 1 2 3 x x 2 2 y 2 y O -3 -1 1 A x -2 2 1 3 y= x x-2x-1 y= x2+x- 2 2 O -2 -1 1 A 3 x -1 x2 - 2x - 1 n eáu x 0 d)y= x x-2x-1= -(x 1)2 n eáux 0 48
Chöông 3 Phöông trình vaø heä phöông trình ******
Tieát 24-25 §1. ÑAÏI CÖÔNG VEÀ PHÖÔNG TRÌNH I). Muïc tieâu : *Kieán thöùc :
- Hieåu khaùi nieäm phöông trình , TXÑ (ñieàu kieän xaùc ñònh) vaø taäp nghieäm cuûa phöông trình
- Hieåu khaùi nieäm phöông trình töông ñöông vaø caùc pheùp bieán ñoåi töông ñöông *Kyõ naêng :
- Bieát caùch thöû xem moät soá cho tröôùc coù phaûi laø nghieäm cuûa phöông trình khoâng
- Bieát söû duïng caùc pheùp bieán ñoåi töông ñöông thöôøng duøng.
*Thaùi ñoä:Reøn luyeän tính nghieâm tuùc khoa hoïc.
II). Ñoà duøng daïy hoïc: Giaùo aùn , sgk
III).Caùc hoaït ñoäng treân lôùp: 1).Kieåm tra baøi cuû:
Haøm soá , txñ cuûa hs ? 2). Baøi môùi : Tg Noäi dung
Hoaït ñoäng cuûa thaày
Hoaït ñoäng cuûa troø
T1 1). Khaùi nieäm phöông trình moät aån : Cho hs ghi ñònh nghóa Ghi ñònh nghóa Ñònh nghóa :
Cho 2 hsoá y=f(x) vaø y=g(x) coù txñ laàn
löôït laø Df vaø Dg. Ñaët D= Df Dg.
*Mñeà chöùa bieán “f(x) = g(x)”ñöôïc
goïi laø phtrình moät aån , x goïi laø aån soá
vaø D goïi laø txñ cuûa phöông trình.
*Soá x0D laø moät nghieäm cuûa
phöông trình f(x) = g(x) neáu
“ f(x0) = g(x0)” laø mñeà ñuùng Chuù yù: *Giaûi phöông trình laø
Ñieàu kieän xaùc ñònh cuûa
tìm taäp nghieäm cuûa phöông trình ñoù
phöông trình :laø ñieàu kieän cuûa
x ñeå giaù trò cuûa f(x) vaø g(x)
cuøng ñöôïc xñ (x thuoäc D ) vaø
caùc ñk khaùc cuûa aån (neáu coù yeâu caàu ) Giaûi:
Ví du1ï: Hd hs xem vd1 ,goïi 1) Ñk : x2 -2x -3 0
hs tìm Ñk xaùc ñònh cuûa pt x 1 1) 2x 1 = 0 x 3 2 x 2x 3 49 2) x 1 + x 0 x = 0 2) Ñk : x x 0 Chuù yù: Chaúng haïn
-Taäp nghieäm kyù hieäu : S 1 S = :pt voâ nghieäm Khi giaûi pt 1 0 vôùi 2 x
S = R : pt nghieäm ñuùng vôùi
x < 1 ta hieåu Ñkxñ pt laø moïi x
x 0vaø x <1 . Do ñoù x = 1
- Nghieäm gaàn ñuùng cuûa pt : khoâng laø nghieäm cuûa pt
ví duï : x3= 7 x= 3 7 9 , 1 13 S=
( nghieäm chính xaùc ñeán haøng phaàn nghìn)
2) Ph trình töông ñöông:
a) K nieäm pt töôngñöông: Ñònh nghóa :
f1(x) = g1(x) f2(x) = g2(x) neáu hai
phöông trình coù cuøng taäp nghieäm.
Cho hs ghi ñònh nghóa
HÑ1: goïi hs thöïc hieän HÑ1: a) Ñuùng.
Chuù yù:Khi muoán nhaán maïnh 2 pt coù
b) Sai (thöû laïi thaáy x=1
cuøng txñ D vaø töông ñöông vôùi nhau,
khoâng laø nghieäm cuûa pt ta noùi : ñaàu).
-2 pt t ñöông vôùi nhau treân D, hoaëc c) Sai (pt ñaàu coøn coù
-Vôùi ñk D, 2 pt laø t ñöông vôùi nhau.
nghieäm khaùc nöõa laø x= -1.
b)Bieán ñoåi t ñöông caùc pt: Chaúng haïn x2=1 x = 1 trong ñk x > 0. Gv giaûi thích :
Caùc pheùp bñ khoâng laøm thay
ñoåi taäp nghieäm cuûa pt goïi laø Ñònh lyù1:
caùc pheùp bñ t ñöông :bieán 1 pt
Cho pt f(x)=g(x) coù txñ D; thaønh pt tñ vôùi noù.
Chaúng haïn pheùp bñ ñoàng nhaát
y=h(x) laø 1 hs xñ treân D (h(x) coù theå
ôû moãi veá cuûa 1 pt vaø khoâng
laø 1 haèng soá ). Khi ñoù treân D, pt
thay ñoåi txñ cuûa noù laø 1 pheùp
f(x)=g(x) t ñöông vôùi moãi pt sau: bñtñ ①f(x)+h(x)=g(x)+h(x);
Cho hs ghi ñònh lyù1
HÑ2: goïi hs thöïc hieän HÑ2:
②f(x)h(x)=g(x)h(x) neáu h(x)≠0 vôùi ∀x a)Ñuùng D. b)Sai (pbñ laøm thay ñoåi Heä quaû:
ñkxñ thöû laïi x = 0 khoâng
1) Qui taéc chuyeån veá:
thoûa phöông trình ñaàu) f(x)+g(x) = h(x) f(x)=h(x)-g(x) 50
2) Qui taéc ruùt goïn: f(x)+h(x)=g(x)+h(x)
Cho hs ghi ñònh nghóa f(x)=g(x)
(neáu h(x) khoâng laøm thay ñoåi txñ)
3) Phöông trình heä quaû:
Ví du2ï: Gv giaûi thích ví duï2 Ñònh nghóa: sgk Cho pt:
f1(x)=g1(x)(1) coù taäp ngh S1
f2(x)=g2(x)(2) coù taäp ngh S2
Pt(2) laø heä quaû pt(1) neáu S2 S1 Ta vieát :
f1(x) = g1(x) f2(x) = g2(x)
Neáu 2 pt tñ thì moãi pt ñeàu laø hq cuûa pt coøn laïi.
HÑ3: Goïi hs thöïc hieän HÑ3:
a)Ñuùng (coù theå thay daáu bôûi daáu )
b)Ñuùng vì taäp nghieäm cuûa Ñònh lyù2: pt thöù nhaát laø
Khi bình phöông 2 veá cuûa moät
phöông trình ta ñöôïc phöông trình heä quaû
f1(x) = g1(x)[f(x)]2 =[g(x)]2 Chuù yù:
1) Neáu hai veá cuûa moät
phöông trình luoân cuøng daáu vôùi moïi x
thoûa ñkxñ cuûa pt thì khi bình phöông
hai veá cuûa noù ta ñöôïc pt töông ñöông
2) Neáu pheùp bieán ñoåi
daãn ñeán pt heä quaû thì sau khi giaûi pt
heä quaû, ta phaûi thöû laïi caùc nghieäm tìm
ñöôïc vaøo pt ñaõ cho ñeå phaùt hieän vaø
Ví duï3: Gv giaûi thích ví duï
loaïi boû nghieäm ngoaïi lai Giaûi: sgk x = 2x -1
Goïi hs laøm ví duï töông töï: 2 Gpt: (x-2)2=(2x-1)2 x = 2x -1 2 x2-4x+4 = 4x2-4x+1 3x2=3 x2=1 x=1 hoaëc x= -1
Thöû laïi ta thaáy x= -1 khoâng 51 thoûa pt ñaõ cho
4) Phöông trình nhieàu aån: Vaäy pt coù nghieäm x=1
Trong thöïc teá , coøn coù nhöõng pt coù
nhieàu hôn moät aån. Ñoù laø caùc pt daïng
F=G, trong ñoù F vaø G laø nhöõng bieåu
thöùc cuûa nhieàu bieán . Ví duï: Gv giaûi thích :
2x+3y-5= 0 (1) laø pt hai aån x vaø y
Nghieäm cuûa pt 2 aån laø moät 5x2-2xy+1= -x+3y-2 (2)
boä soá (x0;y0) thoûa maõn pt
(1;1) laø moät nghieäm cuûa (1)
x+y+z=3xyz (3) laø pt ba aån x,y vaø z.
Nghieäm cuûa pt 3 aån laø moät boä (0;1) laø moät nghieäm cuûa (2)
soá (x0;y0;z0) thoûa maõn pt
(1;1;1) laø 1 nghieäm cuûa (3)
5) Phöông trình chöùa tham soá:
Laø phöông trình ,trong ñoù ngoaøi caùc aån
coøn coù nhöõng chöõ khaùc ñöôïc goïi laø tham soá . Ví duï:
Pt : m(x+2)= 3mx-1 vôùi aån x laø pt chöùa tham soá m .
HÑ4: Goïi hs thöïc hieän HÑ4: Cho pt :
a)Neáu m = 0 thì pt coù taäp
mx+2 = 1-m (m laø tham soá) nghieäm laø S = ∅ Tìm taäp nghieäm cuûa pt
b)Neáu m 0 thì pt coù taäp
nghieäm laøS = 1 m m
3)Cuûng coá:pt,txñ,nghieäm cuûa pt,giaûi pt, pttñ, pthq,pt nhieàu bieán, pt chöùa tham soá.
4)Daën doø:bt1-4 sgk trang 71. x HD:1)a) Ñkxñ : 0
x 0 thoûa pt .Vaäy taäp nghieäm S = 0 x 0 x x b) 3x- 2 0 2 x 2
2 x + 6 Ñkxñ :
x 2 thoûa pt.Vaäy taäp ngh S= 2 2 x 0 x 2 3 x 0 x c) 3 x 3 x
x 3 Ñkxñ :
x ∅. Vaäy pt voâ nghieäm x 3 x 3 0 x 3 x 1 0 x d)x+ 1 x 1
x Ñkxñ :
x ∅.Vaäy pt voâ nghieäm x 0 x 0
2) a) x = 2;b) Ñk x 1 Ta coù : x+ x 1 = 0,5+ x 1 x = 0,5 (loaïi) Vaäy pt voâ nghieäm
c)x = 6 ; d)Voâ nghieäm
3)a) x = 2 ; b) Voâ nghieäm ; c) x = 3 ; d) x = -1 hoaëc x = 2
4) a) x = 4 ; b) x = 5 ; c) x = 0 hoaëc x = 4 ; d) x = 1 52
Tieát 26-27 §2. PHÖÔNG TRÌNH BAÄC NHAÁT
VAØ BAÄC HAI MOÄT AÅN I) Muïc tieâu: *Kieán thöùc :
-Cuûng coá theâm moät böôùc vaán ñeà bieán ñoåi töông ñöông caùc phöông trình
-Hieåu theá naøo laøgiaûi vaø bieän luaän phöông trình
-Naém ñöôïc caùc öùng duïng cuûa ñlí Vieùt . *Kyõ naêng :
-Naém vöõng caùch giaûi vaø bieän luaän phöông trình daïng ax+b = 0 vaø ax2+bx+c=0.
-Bieát caùch bluaän soá gñieåm cuûa 1 ñthaúng vaø 1 parabolvaø kieåm nghieäm laïi baèng ñoà thò .
-Bieát aùp duïng ñlí Vieùt ñeå xeùt daáu caùc nghieäm cuûa 1 pt baäc hai vaø bluaän soá nghieäm cuûa 1 pt truøng phöông . II) Chuaån bò : Giaùo aùn , sgk
III) Caùc hoaït ñoäng treân lôùp:
1)Kieåm tra baøi cuû:
Hai phtrình tñöông ? phöông trình heä quaû ? Giaûi phöông trình : x+2 x 1 = 1- x 1
2)Baøi môùi: Tieát 1 : muïc 1 vaø 2 ; tieát 2 : muïc 3. Tg Noäi dung
Hoaït ñoäng cuûa thaày
Hoaït ñoäng cuûa troø
T1 -Pt baäc nhaát (aån x) laø pt coù daïng ax+b = 0 (a 0)
-Pt baäc hai (aån x) laø pt coù daïng ax+b = 0 (a 0)
Coù bieät thöùc =b2-4ac hoaëc
’=b’2-ac (vôùi b=2b’) goïi laø bieät thöùc thu goïn .
1) Giaûi vaø bl pt daïng ax+ b = 0
*a 0:pt coù nghieäm duy nhaát x= - b a
*a= 0 vaø b 0 :pt voâ nghieäm
*a= 0 vaø b= 0 : pt nghieäm ñuùng vôùi moïi xR
Ví du1ï: Giaûi vaø bieän luaän pt : m2(x-1)+m = x(3m-2) (1)
Ví du1ï: Gv giaûi thích ví duï sgk
vaø höôùng daãn hs thöïc hieän ví duï m2(x-1)+m = x(3m-2) (1) Giaûi: (1) m2x-m2+m=3mx-2x (m2-3m+2)x= m2-m Vôùi m2-3m+2 0 53 m 1vaøm 2 Pt (1) coù ngh duynhaát 2 x= m m m m x= ( ) 1 2 m 3m 2 (m )( 1 m ) 2 x= m m 2
Vôùi m2-3m+2= 0 m=1hoaëc m=2
* m=1, pt(1) 0x= 0:ngh tuøy yù
* m= 2, pt(1) 0x= 2:pt voâ ngh Keát luaän:
m 1 vaø m 2. S= m
2) G vaø bl Pt daïng ax2+bx+c = 0 m 2
*a=0: Trôû veà gbl pt bx+c=0. m=1 . S= R *a 0:Tính =b2-4ac m= 2 . S= ∅
+ >0:pt coù 2 ngh (pbieät)
x b Δ ; x b Δ ; 1= 4a 2= 4a
+ =0:pt coù 1 ngh (keùp) x= b ; 2a
+ <0:pt voâ nghieäm . HÑ1:
Gv giaûi thích vaø höôùng daãn hs thöïc hieän hñ1 HÑ1: Pt ax2+bx+c = 0 T2
a)Coù nghieäm duy nhaát trong moãi tröôøng hôïp sau : *a=0 vaø b 0; *a 0 vaø =b2-4ac =0
b)Pt voâ nghieäm trong moãi tröôøng
Ví duï2: Giaûi vaø bieän luaän pt sau Ví du2ï: Gv giaûi thích vaø höôùng hôïp sau : theo tham soá m:
daãn hs thöïc hieän ví duï2 sgk. *a=b=0 vaø c 0; mx2-2(m-2)x+m-3=0 (1)
*a 0 vaø =b2-4ac <0 HÑ2:
Gv giaûi thích vaø höôùng daãn hs thöïc hieän hñ2 HÑ2: (1-m)x2+(1+m)x-2=0
*m=1,pt coù nghieäm duy nhaát x=1.
*m=3, pt coù 1 ngh (keùp) x=1 ; Ví du3: Cho pt
Ví du3ï: Gv giaûi thích vaø höôùng *m 1 vaø m 3,pt coù 2 nghieäm 3x+2= -x2+x+a (1)
daãn hs thöïc hieän ví duï3 sgk. x 2 1=1 ;x2= . m 1 54
Baèng ñthò haõy bl soá nghieäm cuûa
pt tuøy theo caùc gtrò cuûa tham soá a
3)ÖÙng duïng cuûa ñlí Vieùt:
Hai soá x1 vaø x2 laø caùc nghieäm ÔÛ lôùp döôùi cuûa pt baäc hai ax2+bx+c=0
khi vaø chæ khi chuùng thoûa maõn caùc heä thöùc x b c 1+x2= vaø x a 1x2= a
Ñònh lí Vieùt coù nhieàu öùng duïng quan troïng chaúng haïn
①Nhaåm nghieäm cuûa ptbhai ax2+bx+c=0 (1)
Neáu a+b+c=0 thì (1) coù nghieäm x c 1=1; x2= a
Neáu a-b+c=0 thì (1) coù nghieäm x c 1= -1; x2= - a
②Phaân tích ña thöùc thaønh nhaân töû :
Neáu ña thöùc f(x)= ax2+bx+c coù 2
nghieäm x1 vaø x2 thì noù coù theå
phaân tích thaønh nhaân töû f(x)= a(x- x1)(x- x2)
③Tìm 2 soá bieát toång vaø tích cuûa chuùng :
Neáu 2 soá coù toång laø S vaø tích laø P HÑ 3: Gv giaûi thích vaø höôùng
thì chuùng laø caùc nghieäm cuûa pt daãn hs thöïc hieän hñ 4 sgk. x2-Sx+P=0. ÔÛ lôùp 10 HÑ 3:
④Xeùt daáu caùc nghieäm cuûa a) x1=9 vaø x2=11 b) x1=10 vaø x2=10
ptb2 maø khoâng caàn tìm caùc
c) x2-20x+101=0 vn vaäy khoâng coù nghieäm ñoù.
hcnhaät naøo thoaû maõn yeâu caàu ñeà Cho ptbhai ax2+bx+c=0 coù 2 baøi nghieäm x 1 vaø x2 (x1 x2).Ñaët b S= c vaø P= . Khi ñoù a a -Neáu P<0 thì x 1<0daáu).
-Neáu P>0, 0 thì 2 ngh cuøng daáu.
-Neáu P>0, 0,S>0 thì 55
0< x1 x2 (2 ngh cuøng döông).
-Neáu P>0, 0,S<0 thì Ví duï 4: Gv giaûi thích vaø höôùng
x1 x2<0 (2 ngh cuøng aâm).
daãn hs thöïc hieän ví duï4 sgk.
Ví duï 5: Gv giaûi thích vaø höôùng
daãn hs thöïc hieän ví duï5 sgk.
HÑ 4: Gv giaûi thích vaø höôùng
daãn hs thöïc hieän hñ 4 sgk. HÑ 4: a)Choïn phöông aùn A)
⑤Vieäc xeùt daáu caùc nghieäm cuûa HÑ 5: Gv giaûi thích vaø höôùng b)Choïn phöông aùn B)
pt baäc hai giuùp ta xñ ñöôïc soá daãn hs thöïc hieän hñ 5 sgk
nghieäm cuûa pt truøng phöông HÑ 5: ax4+bx2+c=0 (1) a)Ñuùng .
Ñaët y=x2 (y 0) thì ta ñi ñeán pt Ví duï 6: Gv giaûi thích vaø höôùng b)Sai vì khi pt (2) chæ coù nghieäm baäc hai ñvôùi y
daãn hs thöïc hieän ví duï6 sgk.
aâm (hoaëc 1 nghieäm keùp aâm hoaëc 2 ay2+by+c=0 (2)
nghieäm aâm phaân bieät) thì pt(1)vn
3) cuûng coá:Giaûi vaø bl pt baäc nhaát, baäc hai, ñlí Vieùt, öùng duïng ñlí Vieùt, pt truøng phöông.
4)Daën doø: Bt 5-11, 12-21 trang 78-81.
HD:5.a)Sai vì x=1 khoâng thoûa maõn ñkxñ.b)Sai vì khi bình phöông 2 veá ta chæ ñöôïc pthquaû .
6.a)x= 2m -3 ( m);b)m=1:S=R;m 1:S={m+2}; m2 1
c)pt daïng 0x=(m-2)(m-3) BL: *m 2 vaø m 3:ptvn; *m=2 hoaëc m=3:S=R
d)pt daïng (m2-3m+2)x=m(m-1) BL: *m 1 vaø m 2: S= m
;*m=1 : S= R; *m= 2 : S= ∅ m 2
7) x2+2x+2-a=0 coù nghieäm döông a>2. Khi ñoù pt coù 2 nghieäm vaø nghieäm döông laø x= -1 a 1
3 4m 5
8.a)*m=1,S={1/3};*m -5/4 vaø m 1:S=
;*M<-5/4:S=∅;b)*m 7:x=2 7 m ;*m>7:S=ptvn. ( 2 m ) 1
9.a) ax2+bx+c=a(x2+ b x+ c )=a[x2+( x a a
1+x2)x+ x1x2]=a(x- x1)(x- x2);b)f(x)= -2(x+4)(x-1/2)=(x+4)(1-2x); g(x)=(x- 2 )[( 2 +1)x- 2 ] 10)x 2 2 3 3 4 4
1+x2=2; x1x2= -15. a) x1 +x2 =34; x1 +x2 =98; x1 +x2 =706 11)Choïn phöông aùn B) 56
Tieát 28,29 LUYEÄN TAÄP I) Muïc tieâu:
- Cuûng coá caùc kthöùc ñaõ hoïc veà pt baäc nhaát vaø baäc hai.
- Reøn luyeän caùc kyõ naêng :giaûi vaø bieän luaän phöông trình baäc nhaát hay baäc hai 1 aån coù chöùa tham soá ; bieän
luaän soá gñieåm cuûa ñöôøng thaúng vaø parabol; caùc öùng duïng cuûa ñlí Vieùt, nhaát laø trong vieäc xeùt daáu caùc nghieäm
cuûa pt baäc hai vaø bl soá nghieäm cuûa pt truøng phöông. II) Chuaån bò: Giaùo aùn, sgk
III) Caùc hoaït ñoäng treân lôùp:
Cho hs chuaån bò laøm bt ôû nhaø . Ñeán lôùp, gv chöûa baøi, troïng taâm laø baøi 12 vaø töø caùc baøi 16 ñeán 20.
Tg Hoaït ñoäng cuûa thaày
Hoaït ñoäng cuûa troø 12. a)*m m 3 -2, x= ;*m= -2, ptvn;
Goïi hs laøm caùc baøi taäp 12,16- m 2 20 trang 80,81 b) *m m 1, x=
1 ;*m= 1, pt nghieäm ñuùng x 3 c) *Neáu m 5m 1 - 1 , x=
; *Neáu m = - 1 , pt voâ nghieäm 3 3m 1 3 d)*Neáu m 3 2 ,x=
;*Neáu m = -2,pt voâ nghieäm; m 2
*Neáu m = 2 , pt nghieäm ñuùng x
13) a) p = 0 b) p = 2;14) a) x 4,00; x 1,60; b) x 0,38 ; x -5,28. 12 1 - 7 1 48m 16) a)*Vôùi m=1,x= ;*Vôùi - m 1:x= ; 7 48 2(m -1) 1 *Vôùi m< - : pt vn 48
b) *Neáu m=0,x= 1 ; *Neáu - 9 m 3 5m 9 m 0:x= ;*m<- 9 :ptvn 6 5 m 5 1
c)Vôùi k -1 : pt coù 2 nghieäm x=1 vaø x=
; Vôùi k= -1(hoaëc k=0):x=1 k 1
d)m(2m-1)x2-(3m-2)x-2=0 .BL:*m=0:x=1;*m=1/2:x=4; *m 2 -1 0 vaø m 1/2: x1= vaø x (m=2/5, x m 2= 2m -1 1=x2=5)
17)Soá gñieåm 2 parabolbaèng soá nghieäm pt 2x2+2x-m-3=0, ’=2m+7
*m<-3,5,ptvn,2 parabol khoâng coù ñieåm chung
*m= -3,5,pt coù nghieäm keùp ,2 parabol coù 1 ñieåm chung
*m>-3,5,pt coù 2 nghieäm pbieät ,2 parabol coù 2 ñieåm chung 18)Ñk m 5;x 3 3
1 +x2 =40 76-12m=40 m=3 (thoaû maõn ñk)
19)Gs x1>x2. x1-x2=17( x1+x2)2-4x1x2=28916m2+33=289m= 4
20)a)vn(pttgian coù 2 ngh aâm);b)2nghieäm ñoái nhau;c)4 nghieäm;d)3 ngh. 57
21)a)k>-1;b)Ñaët x=y+1.pt ky2-2y-1=0 pt coù 2 ngh traùi daáu khi k>0.
Tieát 30-31 §3. MOÄT SOÁ PHÖÔNG TRÌNH QUY VEÀ
PHÖÔNG TRÌNH BAÄC NHAÁT HOAËC BAÄC HAI I) Muïc tieâu: Giuùp hoïc sinh
-Naém ñöôïc nhöõng pp chuû yeáu giaûi vaø bl caùc daïng pt neâu trong baøi hoïc.
-Cuûng coá vaø naâng cao kyõ naêng giaûi vaø bieän luaän phöông trình coù chöùa tham soá quy ñöôïc veà pt baäc nhaát hoaëc baäc hai
-Phaùt trieån tö duy trong quaù trình giaûi vaø bieän luaän phöông trình.
II) Ñoà duøng daïy hoïc: Giaùo aùn , sgk
III) Caùc hoaït ñoäng treân lôùp:
1)Kieåm tra baøi cuû:
Giaûi bl pt ax+b=0 ? Giaûi bl pt ax2+bx+c=0 ?
2)Baøi môùi: Tieát 1 : muïc 1 vaø 2 ; tieát 2 : muïc 3. Tg Noäi dung
Hoaït ñoäng cuûa thaày
Hoaït ñoäng cuûa troø
T1 1) Pt daïng: ax b cx d a)Caùch giaûi 1:
ax b cx d (1)
X Y X= Y vôùi X vaø Y laø ax+b= (cx+d) hai soá tuøy yù
ax b cx d ( 1a) ax b -(cx d) ( 1b)
Giaûi 2 pt roài laáy taát caû caùc nghieäm Ví duï 1: gv giaûi thích vaø höôùng thu ñöôïc.
daãn hs laøm ví duï 1 sgk. +1a) (m-1)x = m+2
Ví duï 1: Giaûi bieän luaän pt : mx - 2 x m ( 1a) * Vôùi m m 2 1 , (1a) coù ngh x=
1) mx - 2 x m (1) Pt(1) m 1 mx - 2 -(x ( m) 1b)
* Vôùi m= 1, (1a) 0x= 3:vngh
Goïi hai hs bieän luaän pt(1a), +1b) (m+1)x= -m+2 pt(1b) m 2
* Vôùi m -1,(1b)coù ngh x= m 1
* Vôùi m= -1,(1b) 0x= 3:vngh HÑ1
HÑ1 Goïi hs ñieàn vaøo baûng keát 1 luaän nghieäm
m =1 nghieäm cuûa (1) laø x= Coät cuoái 2 1 x=1/2
m = -1:ngh cuûa (1) laø x= - x= -1/2 2 m 2 m 2 m 2
m 1:ngh cuûa (1) laøx1= vaø m 1 m 1 m 1 m 2 vaø x2= m 1 58 b)Caùch giaûi 2: (1) (mx-2)2=(x+m)2 HÑ2: HÑ2: (m2-1)x2-6mx+4-m2=0
gv giaûi thích vaø höôùng
*Khi m= -1,pt trôû thaønh 6x+3=0 coù
daãn hs laøm hñ 2 sgk. nghieäm x= -1/2.
*Khi m=1,pt trôû thaønh -6x+3=0 coù nghieäm x=1/2.
*Khi m 1 pt coù =(m2+2)2>0
Neân noù luoân coù 2 ngh pbieät x m 2 m 2 1= vaø x2= m 1 m 1 T2
2) Pt chöùa aån ôû maãu thöùc:
Khi giaûi pt chöùa aån ôû maãu thöùc ta
phaûi chuù yù ñkxñ cuûa pt.
Gv giaûi thích vaø höôùng daãn hs Ví duï2:
Ví duï2: Giaûi vaø bieän luaän pt thöïc hieän ÑK : x 1 mx 1 2 (1) Chuù yù ÑK :x 1 Pt (1) mx+1 = 2x-2 x 1 (m-2)x= -3 (2) *Vôùi m-2 0 m 2
Pt(2) coù ngh duy nhaát x= - 3 m 2
Ngh treân laø ngh cuûa (1) neáu x 1 3 - 1 m 2 -3 m-2 m -1 *Vôùi m-2= 0 m= 2
Pt(1) 0x= -3:pt voâ nghieäm Keát luaän: Khi m -1 vaø m 2 Taäp nghieäm S= 3 m 2 Khi m= -1 hoaëc m= 2. S= ∅
Ví duï 3: Giaûi vaø bl pt
Ví duï 3: Gv giaûi thích vaø höôùng HÑ3: Choïn phöông aùn B) x2 2(m 1)x 6m 2
daãn hs thöïc hieän ví duï 3 sgk. = x 2
Vì pt coù nghieäm laø x=a hoaëc x= -3 x 2
HÑ3: gv giaûi thích vaø höôùng
hoaëc x= -1. pt coù 2 ngh -3 a<-1 daãn hs laøm hñ 3 sgk.
3)Cuûng coá: Pt daïng ax b cx d , pt chöùa aån ôû maãu thöùc .
4)Daën doø: Bt 22-29 trang 84,85 sgk. HD:22.
a)Ñk:x -1/2.pt(1) 2(x2-1)=2(2x+1)-(x+2) 2x2-3x-2=0 x=2 hoaëc x= -1/2(loaïi)
b)Ñk: x 1 vaø x -5/3.pt(1) (2x-5)(3x+5)=(5x-3)(x-1) x2+3x-28=0 x=4 hoaëc x= -7. 23.Ñk:x 4.
a)Khi m=3, deã thaáy pt nghieäm ñuùng vôùi moïi x 4. 59 b)Khi m 1
3, vôùi ñk treân, pt(1) =m+2 (*) x 1
Töø ñoù , neáu m= -2 thì pt(*)vn ,keùo theo pt(1)vn; Neáu m 1 4m 9
-2 thì pt(*) coù nghieäm laø x= +4= . m 2 m 2 Xeùt ñk x 4m 9 4, ta coù 4 m -2 m 2 Keát luaän: m= -2:ptvn.
m=3:pt nghieäm ñuùng vôùi moïi x 4 m 4m 9
-2 vaø m 3:pt ñaõ cho coù nghieäm x= m 2
24.a) 2ax 3 =5 2ax+3= 5 2ax=2 hoaëc 2ax= -8 BL:Khi a=0, ptvn. Khi a 1 4
0, pt coù 2 nghieäm x1= vaø x . a 2= - a
b)Ñk:x 1. Khi ñoù pt ñaõ cho tñ vôùi pt f(x)=0 trong ñoù f(x)=x2-2mx+m2-m+1=0 (*)
’=m-1. Do ñoù vôùi m 1, noù coù 2 nghieäm x1=m- m 1 vaø x2=m+ m 1
Pt(*) nhaän x=1 laø nghieäm neáu f(1)=m2-3m+2=0, töùc laø m{1;2}. Ta xeùt cuï theå hôn
+Neáu m=1 thì pt(*) coù nghieäm keùp x=1, nhöng khoâng laø nghieäm pt ñaõ cho do khoâng thoaû ñk x 1.
+Neáu m=2 thì pt(*) coù 2 nghieäm x1=3 vaø x2=1 (loaïi)
Pt(*) khoâng bao giôø nhaän -1 laø nghieäm vì f(-1)=m2+m+2 0 vôùi moïi m . Keát luaän: Vôùi m 1 ptvn.
Vôùi m=2, pt coù nghieäm duy nhaát x=3. Vôùi 1 60
Tieát 32,33,34 LUYEÄN TAÄP I) Muïc tieâu:
- Bieát giaûi vaø bieän luaän phöông trình baäc nhaát vaø baäc hai, moät soá phöông trình ñöa veà pt baäc nhaát vaø b2
- Tìm tham soá ñeå pt baäc nhaát vaø baäc hai voâ nghieäm, voâ soá nghieäm hoaëc coù nghieäm duy nhaát II) Chuaån bò: Giaùo aùn, sgk
III) Caùc hoaït ñoäng treân lôùp:
Goïi hs laøm caùc baøi taäp chuaån bò veà nhaø
Tg Hoaït ñoäng cuûa thaày
Hoaït ñoäng cuûa troø (m 2)x 1
25) a) mx x 1 x 2
Goïi hs laøm caùc baøi taäp 25-29 mx 3 trang 85 1 1 +Khi m=0,pt coù 1 nghieäm x= = - . m 2 2 -3 3
+Khi m=2, pt coù 1 nghieäm x= = - . m 2 1 -3
+Khi m 0 vaø m 2, pt coù 2 nghieäm x1= vaø x m 2 2= m
b) Ñk:x 2 vaø x 2a, ta coù pt tñ x2-3(a+1)x+2(a+1)2=0 (*)
pt (*) luoân coù 2 nghieäm x1=2(a+1) vaø x2=a+1. Xeùt caùc ñk
x1 2 2a+2 2 a 0 ; x2 2 a+1 2 a 1;
x1 2a 2a+2 2a(vôùi moïi a); x2 2a a+1 2a a 1; Keát luaän:
+Vôùi a=0, pt coù nghieäm x=a+1=1.
+Vôùi a=1, pt coù nghieäm x=2(a+1)=4.
+Vôùi a 0 vaø a 1, pt coù 2 nghieäm laø x1=2(a+1) vaø x2=a+1
c) Ñk:x -1. ta coù pt tñ (m-1)x=m+4 (1) Vôùi m=1, pt (1)vn. m 4 Vôùi m 1, pt(1) x= .Xeùt ñk:x -1. ta coù m 1 m 4 m 4
= -1 m+4= -m+1 m= -3/2. Do ñoù neáu m= -3/2 thì x= bò m 1 m 1 loaïi vaø ptvn. m 4
Keát luaän: +m 1 vaø m -3/2, pt coù nghieäm x= . m 1 +m=1 hoaëc m= -3/2, ptvn.
d) Ñk:x 3, ta coù pt tñ x2+(k+6)x=0 (1)
pt coù 2 nghieäm laø x1=0 vaø x2= -(k+6). Tuy nhieân ñk seõ loaïi boû nghieäm
thöù 2 khi k{-3;-9}
KL:+k= -3 hoaëc k= -9, pt coù nghieäm x=0;
+k -3 vaø k -9, pt coù 2 nghieäm x 1=0 vaø x2= -(k+6). 61 2x m 4 0 ( 1) 26) a) Ta coù (*) 2mx x m 0 ( 2) 1 (1) x= (4-m) , m 2 m
(2) (2m-1)x= -m,Pt (2) vn khi m=1/2, coù nghieäm x= khi m 1/2, 1- 2m 1 m
Keát luaän:+m=1/2, x=7/4, + m 1/2, x1= (4-m) ;x 2 2= 1-2m 1 m
b)+m -1 vaø m -3, x1= (4-m) ;x . 2 2= 1-2m
+m= -1, x=1/2 ;+m= -3, x= -1/2.
c)S={ 1;-1/m} neáu -1{ 1} neáu m -1 hoaëc m 0;
d) Ñk :x 2, (*) (a-2)x=4a-5 (1).
Khi a=2, (1)vn neân pt ñaõ cho vn. 4a-5
Khi a 2, (1) coù 1 nghieäm x=
. Do ñk , nghieäm naøy seõ bò loaïi neáu a -2 4a-5 =2 a=1/2. a -2 x a 29) ÑK 1 4a-5
KL:+Khi a=2 hoaëc a=1/2, ptvn ;+Khi a 2 vaø a 1 :pt coù ngh x=
x a 2 2 a -2 Ta coù pt(1)
e)Ñk:x -3, (*) x=2m+2.
(x+1)(x+a+2) = x(x-a+1) Keát luaän: +Neáu m - 5 : pt coù nghieäm x = 2m+2;+Neáu m= - 5 : pt vngh. 2(a+1)x = - 2 2 (a+2) (2)
f) Vôùi a<0 thì ptvn.
*Neáu a= -1 : pt(2) voâ nghieäm 0.x a 1 0 ( 1)
Vôùi a 0, ñk: x 1, (*) neân pt(1) voâ nghieäm
2axa1 0 ( 2)
*Neáu a -1 : pt(2) coù nghieäm Pt (1)vn do a0;
x = - a 2 nghieäm naøy bò a -1
Pt (2) vn khi a=0 , coù nghieäm x=
khi a>0, do ñk , nghieäm naøy seõ bò ( 2 a ) 1 2a loaïi neáu : a -1 a -1 loaïi neáu
=1 a= -1. KL:+a 0, ptvn ;+a>0, x= .
- a 2 = a-1 a= 0 2a 2a ( 2 a ) 1
27)a)Ñaët y= 4x2 12x 11 0, ta coù pt y2-5y+4=0.KL:x= 3 14 hoaëc a = - 1 2 2
b) Ñaët y= x 2 0, ta coù pt y2-3y=0.KL:x1= -5;x2= -2;x3=1.
- a 2 = -a-2 a= -2 1 ( 2 a ) 1 c)Ñaët y= 2x -
0, ta coù pt y2+y-2=0.KL:x x 1= -1;x2= -1/2;x3=1/2;x4=1. hoaëc a= - 1 (m -1)x 6 ( 1) 2 28)(*)
pt (*) coù nghieäm duy nhaát trong 3 (m 1)x 2 ( 2)
Keát luaän :pt voâ nghieäm neáu
tröôøng hôïp:+(1) coù ngh duy nhaát,(2)vn;+(2) coù ngh duy nhaát,(1)vn; a 1 ; 2 ; 1 0 ;
+(1) vaø (2) ñeàu coù nghieäm duy nhaát vaø truøng nhau. 2
KL:m{ -1;1/2;1} 62
Tieát 35-36,§4. HỆ PHƢƠNG TRÌNH BAÄC NHAÁT NHIEÀU AÅN I) Muïc tieâu: Kieán thöùc :
- Naém vöõng khaùi nieäm pt baäc nhaát hai aån , heä hai pt baäc nhaát hai aån , taäp nghieäm vaø yù nghóa hình hoïc cuûa chuùng
- Hieåu roõ phöông phaùp coäng ñaïi soá vaø phöông phaùp theá trong vieäc giaûi hpt
- Naém ñöôïc coâng thöùc giaûi heä hai pt baäc nhaát hai aån baèng ñònh thöùc caáâp hai Kyõ naêng :
- Giaûi thaønh thaïo pt baäc nhaát hai aån vaø caùc hpt baäc nhaát hai aån , ba aån vôùi heä soá baèng soá
- Bieát caùch laäp vaø tính thành thạo caùc ñònh thöùc caáp hai D, Dx vaø Dy töø moät heä hai pt baäc nhaát hai aån soá cho tröôùc
- Bieát caùch giaûi vaø bieän luaän heä hai pt baäc nhaát hai aån coù chöùa tham soá II) Chuaån bò: Giaùo aùn , sgk
III) Caùc hoaït ñoäng treân lôùp: 1) Kieåm tra baøi cuû:
Caâu hoûi : Caùch giaûi vaø bieän luaän pt baäc nhaát moät aån
Aùp duïng : Giaûi vaø bl pt : m(x-2)-2x = -m2x+4
2) Baøi môùi : T1:mục1(oân taäp kieán thöùc cuû) ,T2:mục 2a,b ( troïng taâm) ,T3:thực haønh . Tg Noäi dung
Hoaït ñoäng cuûa thaày
Hoaït ñoäng cuûa troø
Goïi hs nhaéc laïi Pt baäc nhaát hai aån
Nhaéc laïi Pt baäc nhaát hai aån Daïng : ax+by = c (1) - Veà nghieäm ?
(x,y laø aån soá , a2+b2 0).
- Bieåu dieãn taäp nghieäm pt (1) trong mp toïa ñoä ?
- Pt (1) coù voâ soá nghieäm
- Taäp nghieäm pt(1) ñöôïc bieåu
1) Heä hai pt baäc nhaát hai aån:
dieãn bôûi 1 ñöôøng thaúng : Daïng :
Giôùi thieäu ñònh nghóa ax+by=c. ax by c
Goïi hs neâu caùc pp giaûi hpt ñaõ hoïc Neâu caùch giaûi : pp theá , pp (I) (x,y laø aån) coäng ñaïi soá ,…….. / a x / b y / c ôû lôùp döôùi a2+b2 0 , a/2+b/2 0 Moãi caëp soá (x o;yo) ñoàng thôøi laø
nghieäm cuûa caû 2 pt trong heä
ñöôïc goïi laø 1 nghieäm cuûa heä .
Giaûi hpt laø tìm taát caû caùc nghieäm cuûa noù . 63
Hñ1:Giaûi caùc hpt sau : Goïi hs giaûi Hñ1: 2x 5y 1 - 2x 6y a)(x;y)=(2;1) ; a) 2 ; b) ; x 3y 5 x - 3y 2 b)Voâ nghieäm ; 3x y 1
c)(x;y)=(x;3x-1) vôùi xR. c) 1 1 ; x - y 3 3
YÙ nghóa hình hoïc:
Höôùng daãn hs neâu yù nghóa hh Goïi (d):ax+by=c (d’):a’x+b’y=c’.
* Heä (I) coù nghieäm duy nhaát (d) & (d/) caét nhau
* Heä (I) voâ nghieäm (d) // (d/)
* Heä (I) coù voâ soá nghieäm (d) truøng (d/)
2) Giaûi _ bl heä 2 pt baäc nhaát 2 aån:
Gv phaùt vaán hs xaây döïng coâng
thöùc trong sgk ñöa ñeán keát quaû
Xeùt hpt baäc nhaát hai aån ax by c ( 1) (I) / / / a x b y c ( 2) *(1).b’+(2).(-b)
(ab’-a’b)x= cb’-c’b *(1).(-a’)+(2).a (3)
(ab’-a’b)y= ac’-a’c (4)
*Trong (3) vaø (4), ñaët D= ab’-a’b, (nhaân 2 veá cuûa caùc pt vôùi 1 soá
Dx= cb’-c’b,Dy= ac’-a’c. Ta coù hpt maø khoâng coù gt caùc soá naøy heä quaû khaùc 0) D.x D (II) x D.y D y
Ñoái vôùi heä (II) ta xeùt caùc tröôøng hôïp sau: D Dy HÑ2: (x;y)=( x ; ) ngh
1)D 0,heä (II) coù 1 nghieäm duy I D D D D ñuùng pt ax+by=c
(x;y)=( x ; y ) cuõng laø ngh heä(I) D D aD x+bDy=cD. Thaät vaäy 0.x D aD 2)D=0, heä (II) x+bDy=a(cb’-c’b)+b(ac’- x 0.y D a’c)=c(ab’-a’b)=cD y
+Neáu Dx 0 hoaëc Dy 0 thì heä (II)vn neân heä (I)vn.
+Neáu Dx=Dy=0 thì heä (II) coù vsn.
Trôû veà heä (I) ñeå tìm ngh cuûa hpt
Giaû söû a 0 (töông töï b 0)
D= ab’-a’b=0 b’=a’b/a D
y= ac’-a’c c’=a’c/a. Bôûi vaäy 64 heä (I) vieát thaønh ax by c a' a' Taäp ngh heä (ax by) c a a
(I) truøng taäp ngh pt ax+by=c c - by (x;y)=( ;y) a
-Giôùi thieäu ñònh thöùc vaø caùch tính HÑ3:
Gv höôùng daãn hs laøm hñ3. HÑ3:
a)Trong ñònh thöùc D, coät thöù
nhaát goàm caùc heä soá cuûa x, coät
thöù hai goàm caùc heä soá cuûa y.
b)Trong ñònh thöùc Dx, coät thöù Toùm taét
Laäp baûng toùm taét
nhaát goàm caùc heä soá töï do, coät
thöù hai goàm caùc heä soá cuûa y. Trong ñònh thöùc D ax by c a ( y, coät thöù 2 b2 0)
nhaát goàm caùc heä soá cuûa x, coät
a/x b/y c/ ( a'2 b'2 ) 0
thöù hai goàm caùc heä soá töï do. laäp ñthöùc Ñs : (x;y)=(-1;2). b a D = = ab/-a/b / / a b c b D x= = cb/-c/b / / c b a c D y= = ac/-a/c / / a c Bieän luaän :
+Neáu D 0. Hpt coù ngh duy nhaát x Dx D Dy y D +Neáu D = 0
* Khi Dx 0 hoaëc Dy 0:hpt vn
* Khi Dx= Dy = 0:hpt coù vsoá ng
(Taäp nghieäm cuûa heä laø taäp ngh cuûa pt ax+by= c)
5x 2y Ví duï 1:Giaûi hpt 9
gv höôùng daãn hs laøm ví duï 1.
4x 3y 2 Hñ4: Ta coù :
Hñ4: Baèng ñònh thöùc, giaûi hpt
Goïi hs thöïc hieän HÑ4 2 - 3 D = =2.4-7.(-3)=29 7 4 65 2x 3y - 13 3 13 Dx = =13.4-2.(-3)=58
7x 4y 2 2 4 13 2 Dy = = 2.2-7.13= -87 2 7 Dx 58 x 2 D Do ñoù 29 D y 87 y 3 D 29
Hpt ñaõ cho coù ng (x;y)=(2;-3)
Goïi hs laäp ñònh thöùc Vd2: Ta coù :
Ví duï 2: Giaûi bieän luaän hpt :
Phaùt vaán hs bieän luaän m 1 D= 2 m 1 mx y m 1 1 m x my 2 =(m-1)(m+1) m 1 1 Dx = = m2+m-2 2 m = (m-1)(m+2) m m 1 D = m-1 y = 1 2 Bieän luaän :
1) Neáu D 0 m = 1
Hpt coù nghieäm duy nhaát : Dx m 2 x D m 1 Dy 1 y D m 1 m 1 2) Neáu D = 0 m 1 *Khi m=1 thì D = D x = Dy = 0
Hpt coù voâ soá ngh (x;y) tính theo coâng thöùc x R . Daïng nghieäm : y 2 x (x ; y) = (x ; 2-x) , xR *Khi m = -1 .Ta coù D = 0,
Dx 0 neân hpt voâ nghieäm KL:
+Vôùi m 1, heä coù nghieäm m 2 1 duy nhaát (x;y)= ; ; m 1 m 1
+Vôùi m= -1, heä voâ nghieäm; +Vôùi m=1 66 Hpt trôû thaønh x y 2 x+y=2 x y 2
Heä coù voâ soá nghieäm (x;y) tính x R theo coâng thöùc y 2 x
3) Ví duï veà giaûi hpt bnhaát ba aån : Daïng : a x b y c z d 1 1 1 1
a x b y c z d 2 2 2 2 a x b y c z d 3 3 3 3
trong ñoù caùc heä soá cuûa 3 aån x,y,z
trong moãi pt cuûa heä khoâng ñoàng thôøi baèng 0.
Giaûi hpt treân laø tìm taát caû caùc boä ba
(x;y;z)ñoàng thôøi nghieäm ñuùng caû
Giaûi: (1)z=2-x-y theá vaøo 2 pt ba pt cuûa heä .
Gv giaûi thích ví duï sgk, gv höôùng coøn laïi ta ñöôïc hpt Ví duï 3: Giaûi hpt daãn hs laøm ví duï3 2x y 5 x y z 2 x 2y 7 x 2y 3z 1
HÑ5:D=3;Dx=3;Dy=9, töø ñoù 2x y 3z 1
gv höôùng daãn hs laøm hñ 5.
x=1;y=3. Suy ra nghieäm cuûa hpt laø (x;y;z)=(1;3;-2) HÑ6: HÑ6:
(3) x = 2y+4z+1 theá vaøo (1) HÑ6: Giaûi hpt:
gv höôùng daãn hs laøm hñ 6. &(2) ta ñöôïc hpt : 2x 3y 5z 13
Ruùt x töø pt (3) theá vaøo pt (1) & (2) 2(2y 4z 1) 3y 5z 13 4x 2y 3z 3
seõ ñöôïc hpt baäc nhaát hai aån
4(2y 4z 1) 2y 3z 3
x 2y 4z 1 7y 3z 11 y 2 6y 13z 1 z 1 Do ñoù hpt coù ngh (x;y;z)=(1; 2; -1)
3)Cuûng coá : Caùch giaûi bieän luaän heä pt baäc nhaát hai aån , yù nghóa hh
4)Daën doø : Baøi taäp 30,31 , 32 ,33,34 , 39 ,40 ,41 42
HD:30)Phöông aùn (C):Taäp nghieäm hpttruøng vôùi taäp nghieäm cuûa pt thöù nhaát.
31.a)D= -17;Dx=5;Dy=19; (x;y)=(-5/17;-19/17); b)D= -1; Dx= 3 ;Dy= 2 2 ; (x;y)=( 3 ;- 2 2 ) 2X Y 3
32.a) Ñaët 2 =X; 1 =Y, ta coù hpt
(X;Y)=(2;-1) (x;y)=(1;0) x y -1 X 2Y 4 b)Ñk: x≠y . x R 3(x y) -7(x- y) 10x - 4y Hpt 0 5
. Ñk: x≠y thoaõ maûn khi vaø chæ khi x≠0. 3(5x- y) 5(y - x) 20x -8y 0 y x 2 33.a)D=m2-1;Dx=m(m+1);Dy=m+1; 67 -Neáu m m 1
≠±1 thì hpt coù nghieäm ; ; m 1 m 1 -Neáu m=1 thì hpt vn; x R
- Neáu m= -1 thì hpt coù voâ soá nghieäm tính theo coâng thöùc ; y x
b)D= -(a+3); Dx=5 ;Dy= -5(a+1); - Neáu a - 5 5(a 1)
≠ -3 thì hpt coù 1 nghieäm ; ; a 3 a 3 - Neáu a= -3 thì hpt vn; 34)(x;y;z)=(4;5;2) 68
Tieát 37 LUYEÄN TAÄP I) Muïc tieâu:
- Cuûng coá caùc kieán thöùc ñaõ hoïc trong baøi veà hpt baäc nhaát hai aån vaø ba aån .
- Reøn luyeän caùc kyõ naêng : giaûi vaø bl hpt baäc nhaát 2 aån coù chöùa tham soá baèng pp tính ñònh thöùc caáp 2;
Giaûi heä 3 pt baäc nhaát 3 aån (khoâng chöùa tham soá )
II) Chuaån bò:Cho hs chuaån bò laøm bt ôû nhaø . Ñeán lôùp, gv chöûa baøi, troïng taâm 39 ñeán 43. Thaûo luaän taïi lôùp vaø
tìm phöông aùn traû lôøi cho caâu hoûi traéc nghieäm 36. Giaùo aùn, sgk
III) Caùc hoaït ñoäng treân lôùp:
Goïi hs laøm caùc baøi taäp chuaån bò veà nhaø
Tg Hoaït ñoäng cuûa thaày
Hoaït ñoäng cuûa troø
36)Phöông aùn (B):hpt vn.
Goïi hs laøm caùc baøi taäp 36-43 2 3 2 trang 96,97 37)a)x= , 0 42 ; y= , 0 27 ; 5 6 5 6 b)x= 8 5 3 19 3 07 , 0 ; y= 73 , 1 10 10
38)Goïi 2 kích thöôùc (tính baèng meùt) cuûa hcn laø x vaø y (x>0,y>0). x y p x 3p - 240 Giaûi hpt vôùi 80
(x 3)(y 2) xy 246 y 240 2p
39) a)D= -m(m+3); Dx= -2m(m+3);Dy=m+3; +Neáu m 1
0 vaø m -3, thì D 0 neân hpt coù 1 nghieäm (2;- );
41)Neáu hpt vn thì D=ab-6. m
Coù 8 caëp soá nguyeân thoõa maûn +Neáu m=0, thì hpt voâ nghieäm ;
ñk naøy laø (1;6), (-1;-6), (6;1), x 3y x 3y
+Neáu m= -3, thì hpt trôû thaønh 1 1
(-6;-1) , (2;3) , (-2;-3) , (3;2), - 3x 9y 3 y R (-3;-2).
b) D= (m+1)(m-2); Dx= -(m-2)2;Dy=(m+4)(m-2); Trong ñoù chæ coù caëp - m 2 m 4
(a;b)=(3;2) laø khoâng thoõa maûn +Vôùi m -1 vaø m 2, thì D 0 neân hpt coù 1 nghieäm ; m 1 m 1
ñk cuûa btoaùn .Vaäy chæ coù 7
+Vôùi m= -1, thì hpt voâ nghieäm ;
caëp thoõa maûn yeâu caàu cuûa ñeà x R baøi.
+Vôùi m= 2, thì hpt coù vsn tính theo coâng thöùc y 1 ( 2 - x) x my 42)xeùt hpt 3 40.a) D=a2. mx 4y 6
*Hpt coù nghieäm duy nhaát , töùc laø D 0 (xaûy ra khi vaø chæ khi a 0)
D=4-m2;Dx=12-6m;Dy=6-3m *Hpt coù vsn, töùc laø D=D a)caét x=Dy=0 (khoâng xaûy ra) D 0 m≠±2 KL: a 0.
b)// D=0 vaø Dx 0 (hoaëc b)D=(a+1)(a+5). Heä coù nghieäm trong 2 tröôøng hôïp sau : Dy 0) m= -2.
*Hpt coù nghieäm duy nhaát , töùc laø D 0 (xaûy ra khi vaø chæ khi a -1 vaø
c)truøng nhau D=Dx=Dy=0 a -5) m=2
*Hpt coù vsn, töùc laø D=Dx=Dy=0 (xeùt cuï theå vôùi a= -1 vaø a= -5)
43)(x;y;z)=(4;2;5). KL: a= -5. 69
Tieát 38-39. §5. MOÄT SOÁ VÍ DUÏ VEÀ
HEÄ PHÖÔNG TRÌNH BAÄC HAI HAI AÅN
I) Muïc tieâu:Giuùp hs:
Kieán thöùc : Naém ñöôïc caùc phöông phaùp chuû yeáu giaûi heä phöông trình baäc hai hai aån , nhaát laø heä phöông trình ñoái xöùng.
Kyõ naêng : Bieát caùch giaûi moät soá daïng heä phöông trình baäc hai hai aån , ñaëc bieät laø caùc heä goàm moät phöông
trình baäc nhaát vaø moät phöông trình baäc hai , heä phöông trình ñoái xöùng II) Chuaån bò: Giaùo aùn , sgk
III) Caùc hoaït ñoäng treân lôùp :
Tg Noäi dung Hoaït ñoäng cuûa Hoaït ñoäng cuûa troø thaày
I)Heä goàm moät phöông trình
baäc nhaát vaø moät
Giaûi baèng phöông phaùp
phöông trình baäc hai theá Giaûi : hai aån x 2y 5 ( 1)
Ví duï 1: Giaûi heä pt
Goïi hs laøm ví duï x2 2y2 2xy 5 ( 2) x 2y 5 (I) x 5 2y
(1) x = 5-2y theá vaøo (2) x2 2y2 2xy 5 (Ia)
(2) (5-2y)2+2y2-2y(5-2y)=5 2
10y 30y 20 0 10y2-30y+20 = 0
HÑ1:Giaûi tieáp hpt roài y 1 x 3
suy ra nghieäm cuûa heä (I) y 2 x 1
Vaäy heä phöông trình coù hai nghieäm (3;1) , (1;2)
2) Heä phöông trình ñoái xöùng: Ví duï: Giaûi heä phöông trình
x2 xy y2 4 Nhaän xeùt: (II) xy x y 2
-Ñaëc ñieåm hpt ñoái xöùng
laø moãi pt trong heä khoâng
ñoåi khi ta ñoàng thôøi thay
x bôûi y vaø thay y bôûi x Caùch giaûi : 70 x y S (x y)2 xy 4 Ñaët aån phuï: Hpt xy P xy x y 2
Goïi hs bieán ñoåi hpt ñöa S2 P 4 ( 1) veà heä theo S vaø P S P 2 ( 2) (1)+(2) : S2+S-6 = 0 S 2 P 0 S 3 P 5 S 2 x y 2 * (IIa) P 0 xy 0
x,y laø 2 nghieäm pt : X2-2X=0 X 0 X 2
Hpt coù nghieäm (0;2) vaø (2;0)
HÑ2: Giaûi tieáp hpt roài S 3 x y 3
suy ra nghieäm cuûa heä * (IIb) P 5 xy 5 (II) x , y laø hai nghieäm pt : X2+3X+5 = 0 voâ nghieäm
Vaäy hpt coù hai nghieäm(0;2) vaø(2;0) Giaûi : (1) – (2) ta ñöôïc : x2-y2-2x+2y = y-x Ví duï: Giaûi hpt x2-y2-(x-y) = 0 x2 2x ( y 1) (x-y)(x+y-1) = 0 (III) x y y2 2y ( x 2) 0
Nhaän xeùt ñaëc ñieåm cuûa
x y 1 0 hpt
x-y = 0 x = y thay vaøo (1)
Khi thay ñoåi vai troø (1) x2-2x = x
cuûa x vaø y thì pt thöù nhaát x2-3x = 0
bieán thaønh pt thöù hai vaø
x 0 y 0 ngöôïc laïi
x 3 y 3 Caùch giaûi :
x+y-1 = 0 y = 1-x thay
Tröø töøng veá hai pt vaøo (1) ta ñöôïc : Goïi hs giaûi (1) x2-2x = 1-x x2-x-1 = 0
HÑ3: Giaûi tieáp hpt roài 1 5 1 5 suy ra nghieäm cuûa heä x y 2 2 (III) 1 5 1 5 x y 2 2 71 HÑ 4:
Deã thaáy (0;0) laø nghieäm thöù ba cuûa hpt. Ngoaøi ra, do tính ñx,töø nghieäm ñaõ cho
3 3 3 3 ,suy ra nghieäm thöù tö cuûa hpt laø ; 2 2 3 3 3 3 ; 2 2 Chuù yù: Heä phöông trình ñoái HÑ 4:Cho hpt
xöùng neáu coù nghieäm laø
(a;b) thì cuõng coù nghieäm 2x2 y 5x Bieát laø (b;a) 2y2 x 5y raèng hpt ñaõ cho coù 4 nghieäm vaø 2 trong 4
nghieäm ñoù laø (2;2) vaø 3 3 3 3 ; . 2 2 Tìm caùc nghieäm coøn
laïi maø khoâng caàn bñoåi hpt. Haõy neâu roõ caùch tìm .
3)Cuûng coá:Pp theá, coäng ñaïi soá , ñaët aån phuï.
4)Daën doø:Caâu hoûi vaø bt 45-49 sgk trang 100
HD:45.a)(10;8) vaø (-8;-10);b)(1;-1) vaø (-2/5;9/5)
46.a)Ñaët S=x+y vaø P=xy.Ñs: (1;2) vaø (2;1).b)Ñaët t= -x ñeå ñöa veà heä ñx .Ñs : (0;1) vaø (-1;0). x2 x 3 2y x2 -3x 2y c)hpt (I) hoaëc (II) x - y 0 x y -1 0 x(x - 5) (I) 0 x=y=0 hoaëc x=y=5. x y x x 2 (II) 1 hoaëc y 2 y 1
KL:hpt coù 4 nghieäm (0;0),(5;5),(-1;2),(2;-1). 47)S2-4P≥0. x y 20 x y - 20 48.a)Hpt hoaëc
.KL : (-8;-12),(-12;-8),(8;12),(12;8). xy 96 xy 96 x2 y2 55 u - v
b)Ta coù hpt heä quaû : 55
Ñaët u=x2,v=y2 ta coù hpt
;u≥0;v≥0, ta ñöôïc u=64; v=9. x2y2 57 6 uv 576 72
Trong 4 caëp (8;3),(8;-3),(-8;3),(-8;-3) , thöû laïi chæ coù 2 caëp (8;3) vaø (-8;-3) laø thoõa maûn .KL:hpt coù 2 nghieäm (8;3) vaø (-8;-3).
49)(P):y=f(x)=ax2+bx-4 (a≠0). Goïi x1 vaø x2 laø nghieäm pt f(x)=0.
Töø gt ta coù (x1 - x2 )2=25 (x1 + x2 )2-4x1x2=25(-b/a)2+16/a=25. Töø ñoù cuøng vôùi ñk f(2)=6 ta coù hpt 4a 2b - 4 6 2a b 5 b2 16
.Hpt coù 2 nghieäm (a;b)=(1;3) vaø (a;b)=(-25/21;155/21). KL: 2 2 2 5 b 16a 25a a2 a f 25 155 1(x)=x2+3x-4 vaø f2(x)= x2+ x-4 21 21
ChöôngIV Baát ñaúng thöùc vaø baát phöông trình ******
Tieát 40-42. §1. BAÁT DAÚNG THÖÙC VAØ
CHÖÙNG MINH BAÁT ÑAÚNG THÖÙC I) Muïc tieâu :
Kieán thöùc :
- Hieåu khaùi nieäm baát ñaúng thöùc
- Naém vöõng caùc tính chaát cuûa baát ñaúng thöùc Kyõ naêng :
Chöùng minh ñöôïc moät soá baát ñaúng thöùc ñôn giaûn . II) Chuaån bò : Giaùo aùn , sgk
III) Caùc hoaït ñoäng treân lôùp : Tg Noäi dung
Hoaït ñoäng cuûa thaày
Hoaït ñoäng cuûa troø
1)Oân taäp vaø boå sung tc cuûa bñt: Gv giaûi thích
Ghi caùc ñònh nghóa vaø tính chaát
a) So saùnh caùc soá thöïc : a
,b R luoân xaûy ra moät trong ba khaû naêng : *a = b a-b = 0 *a > b a-b > 0 *a < b a-b < 0 Neáu a b a-b 0 (a-b khoâng aâm)
Meänh ñeà phuû ñònh cuûa meänh ñeà
“a>b” laø meänh ñeà “a b” Tính chaát:
*Toång cuûa hai soá döông laø moät soá döông
*Tích hoaëc thöông cuûa hai soá 73
cuøng daáu laø moät soá döông
*Bình phöông moät soá thöïc laø moät soá khoâng aâm
b) Khaùi nieäm baát ñaúng thöùc: Caùc meänh ñeà :
“a >b”, “a < b”, “a b”, “a b” goïi laø caùc bñt
a laø veá traùi, b laø veá phaûi
c) Tính chaát cô baûn cuûa bñt : Tính chaát 1:
a > b vaø b > ca > c Khoâng CM: a > ba-b > 0 b > cb-c > 0 Tính chaát 2: a-c = (a-b)+(b-c) > 0 a > b a+c > b+c Vaäy a > c
Heä quaû: (quy taéc chuyeån veá) a+c > b a > b-c Tính chaát 3: ac bc n eáu c 0
Phaùt bieåu baèng lôøi : a > b
Neáu nhaân 2 veá cuûa moät baát ac bc n eáu c 0
ñaúng thöùc vôùi cuøng moät bieåu thöùc
döông thì ta ñöôïc moät bñt cuøng chieàu vaø töông ñöông
Neáu nhaân 2 veá cuûa moät bñt
vôùi cuøng moät bieåu thöùc aäm thì ta
ñöôïc moät bñt ngöôïc chieàu vaø töông ñöông
d) Bñt vôùi caùc pheùp toaùn:
Heä quaû 1: (pheùp coäng)
Neáu coäng caùc veá töông öùng cuûa hai Khoâng ñuùng vôùi pheùp toaùn tröø a b
bñt cuøng chieàu thì ñöôïc moät bñt a + c > b + d c d cuøng chieàu
Heä quaû 2: (pheùp nhaân) a b 0
Neáu nhaân caùc veá töông öùng cuûa2 Khoâng ñuùng vôùi pheùp toaùn chia a.c > b.d
bñt cuøng chieàu coù caùc veá döông thì c d 0
ñöôïc moät bñt cuøng chieàu
Heä quaû 3 : (pheùp naâng leân luõy thöøa)
a > b ≥ 0, nN*an>bn 74
Heä quaû 4: (pheùp khai caên) a > b ≥ 0 a b a > b 3 3 a b
Ví duï 1: (höôùng daãn hs giaûi) Giaûi:
Khoâng duøng baûng soá hoaëc maùy Neáu 2 3 3
tính haõy so saùnh hai soá 2 3 vaø Bình phöông hai veá : soá 3 2 3 3 ( 2 3)2 9
5 2 6 9 6 2 6 4 voâ lyù Vaäy : 2 3 3 Giaûi : Ví duï 2:
x2 > 2(x-1) x2 >2x-2
CMR: x2 > 2(x-1) vôùi xR x2-2x+2 > 0 (x2 -2x +1)+1 > 0 (x – 1)2+1 > 0 luoân luoân ñuùng Ví duï 3: Giaûi:
Chöùng minh raèng neáu a,b,c laø ñoä Ta coù :
daøi 3 caïnh cuûa moät tam giaùc thì :
a2 a2-(b-c)2= (a-b+c)(a+b-c) >0 (b+c-a)(c+a-b)(a+b-c) abc
b2 b2-(c-a)2= (b-c+a)(b+c-a) >0
Cho hs ñoïc lôøi giaûi sgk
c2 c2-(a-b)2= (c-a+b)(c+a-b) >0
Nhaân caùc veá töông öùng cuûa ba
baát ñaúng thöùc treân, ta ñöôïc :
a2b2c2 (b+c-a)2(c+a-b)2(a+b- c)2
(b+c-a)(c+a-b)(a+b-c) abc
3) Cuûng coá : Caùc ñn vaø tc cuûa bñt.
4) Daën doø : Caùc baøi taäp sgk 1-9 trang 109,110 Baøi taäp: b a 1 1
1) CMR neáu a > b vaø ab > 0 thì 1 1
1) b < a vaø ab > 0 a b ab ab a b 75
2) CMR nöûa chu vi cuûa moät tam giaùc lôùn hôn moãi
2) p-a = a b c 2a b c a 0vì b+c > a caïnh cuûa tam giaùc ñoù 2 2 Do ñoù : p > a
Töông töï : p > b, p > c
3) CMR a2+b2+c2 ab+bc+ca a, b, cR. Ñaúng thöùc 3)
xaûy ra khi vaø chæ khi a = b = c
a2+b2+c2 ab+bc+ca 2a2+2b2+2c2-2ab-2bc-2ca 0
(a-b)2+(b-c)2+(c-a)2 0
Ñaúng thöùc xaûy ra a-b = b-c = c-a = 0 a = b = c
6) CMR neáu a 0 vaø b 0 thì a3+b3 ab(a+b). Khi naøo 6) Ta coù : ñaúng thöùc xaûy ra ?
a3+b3 ab(a+b) (a+b)(a2-ab+b2) -ab(a+b) 0 (a+b)(a2 -2ab +b2) 0
(a+b)(a-b)2 0 luoân luoân ñuùng 2 b 3 2 b
7.a) CMR a2+ab+b2 0 a, bR
7.a) a2+ab+b2 = a 0 2 4
8) CMR neáu a,b,c laø ba caïnh cuûa một tam giaùc thì :
8) Giaû thieát raèng : a b c . Khi ñoù : a2+b2+c2<2(ab+bc+ca)
0 a-b < c neân (a-b)2< c2 a2+b2< c2+2ab (1)
0 b-c < a neân (b-c)2< a2 b2+c2< a2+2bc (2)
0 a-c < b neân (a-c)2< b2 a2+c2< b2+2ac (3)
Coäng (1),(2) vaø (3) ta ñöôïc :
2(a2+b2+c2) < a2+b2+c2+2(ab+bc+ca) a2+b2+c2 < 2(ab+bc+ca) Caùch khaùc: a0 neân a2 b0 neân b2 c0 neân c2
neân a2+b2+c2 < 2(ab+bc+ca)
9) CMR neáu a 0 vaø b 0 thì : 2 2 3 3
9) a b a b a b . a3+ab2+a2b+b3 2a3+2b3 2 2 3 3
a b a b a b . 2 2 2 2 2 2 a3-ab2-a2b+b3 0 (a-b)(a2-b2) 0 (a-b)2(a+b) 0 76
Tieát43-46. §1. BAÁT DAÚNG THÖÙC VAØ
CHÖÙNG MINH BAÁT ÑAÚNG THÖÙC I) Muïc tieâu: * Kieán thöùc:
- Naém ñöôïc caùc baát ñaúng thöùc veà giaù trò tuyeät ñoái .
- Naém vöõng baát ñaúng thöùc giöõa trung bình coäng vaø trung bình nhaân cuûa hai soá khoâng aâm.
- Naém ñöôïc baát ñaúng thöùc giöõa trung bình coäng vaø trung bình nhaân cuûa ba soá khoâng aâm * Kyõ naêng :
- Chöùng minh ñöôïc moät soá baát ñaúng thöùc ñôn giaûn baèng caùch aùp duïng caùc bñt neâu trong baøi hoïc .
- Bieát caùch tìm giaù trò lôùn nhaát vaø giaù trò nhoû nhaát cuûa moät haøm soá hoaëc moät bieåu thöùc chöùa bieán II) Chuaån bò:
Giaùo aùn , saùch giaùo khoa
III) Caùc hoaït ñoäng treân lôùp: Tg Noäi dung
Hoaït ñoäng cuûa thaày Hoaït ñoäng cuûa troø
T43 2) Baát ñaúng thöùc veà giaù trò tuyeät ñoái Tính chaát 1: a a a v ôùi mo ïi a R . x a a x ( a vôùi a 0) . x a x x or a a ( a 0) .
HD: Cminh ñònh lyù baèng * a b a b Tính chaát 2:
caùch bình phöông hai veá (a+b)2a2+2 ab +b2
a b a b a b ( a,bR) a2+2ab+b2 a2+2 ab +b2
Caùc ñaúng thöùc xaûy ra khi vaø chæ khi Töông töï a b a b ab 0
ab ab luoân luoân ñuùng
HÑ1:Cho hs laøm hñ 1
* a = a b (-b) a b b a b a b
3) Bñt giöõa trbình coäng vaø tb nhaân: 77
a) Ñoái vôùi hai soá khoâng aâm:
Giaûi thích:Trung bình
Chöùng minh ñònh lyù: Ñònh lyù :
coäng cuûa hai soá khoâng aâm a b 1 ab (a+b-2 ab )
Vôùi moïi a 0, b 0 ta coù
lôùn hôn hoaëc baèng trung 2 2 a b ab bình nhaân cuûa chuùng. = 1 ( a b)2 0 luoân 2 Trung bình coäng cuûa hai 2
Ñaúng thöùc xaûy ra khi vaø chæ khi
soá khoâng aâm baèng trung luoân ñuùng. Ñaúng thöùc xaûy ra khi vaø chæ a=b
bình nhaân cuûa chuùng khi khi ( a )2 b 0 a = b
vaø chæ khi 2 soá ñoù baèng HÑ2: nhau OD = a b , HC = ab
Goïi hs chöùng minh ñònh 2 lyù Vì OD a b HC neân ab HÑ2: 2
Goïi hs thöïc hieän h ñoäng 2 Giaûi : Ta coù : a b a b (1) Ví duï 4: b a 2 b . a
Cho a, b, c > 0. Chöùng minh raèng : HD: b c b c a b b c c a
Aùp duïng bñt tbc & tbn cho 2 . (2) 6 c b c b c a b 3 caëp soá : c a c a a b b c c a 2 . (3) & , & , & b a c b a c a c a c (1)+(2)+(3) ta ñöôïc : a b b c c a
2 2 2 b a c b a c a b b c c a 6 c a b Heä quaû 1:
Neáu hai soá döông thay ñoåi nhöng CM:sgk
YÙ nghóa hình hoïc:
coù toång khoâng ñoåi thì tích cuûa chuùng
Trong taát caû caùc hình chöõ nhaät coù
lôùn nhaát khi hai soá ñoù baèng nhau .
cuøng chu vi , hình vuoâng coù dieän tích
YÙ nghóa hình hoïc: lôùn nhaát
Trong taát caû caùc hình chöõ nhaät coù Goïi hs phaùt bieåu yù nghóa
cuøng chu vi , hình vuoâng coù dieän tích hình hoïc lôùn nhaát Heä quaû 2:
YÙ nghóa hình hoïc:
Neáu hai soá döông thay ñoåi nhöng CM:sgk
Trong taát caû caùc hình chöõ nhaät coù
coù tích khoâng ñoåi thì toång cuûa chuùng
cuøng dieän tích , hình vuoâng coù chu vi
nhoû nhaát khi hai soá ñoù baèng nhau nhoû nhaát.
YÙ nghóa hình hoïc:
Goïi hs phaùt bieåu yù nghóa
Trong taát caû caùc hình chöõ nhaät coù hình hoïc Giaûi:
cuøng dieän tích , hình vuoâng coù chu vi x -1 nhoû nhaát.
Ta coù : -1 x 7 x 7 Ví duï 5:
Tìm giaù trò lôùn nhaát & giaù trò nhoû HD: x 1 0 nhaát cuûa haøm soá :
Aùp duïng bñt tbc & tbn cho 7 - x 0 78
y = (x+1)(7-x) vôùi -1 x 7
hai soá x+1 &7-x ñeå tìm
(x+1)+(7-x) 2 (x 1)(7- x) gtln 8 2 (x 1)(7- x) (x+1)(7-x) 16
Neân gtln cuûa f(x) = 16 khi vaø chæ khi : x+1 = 7-x 2x = 6 x = 3 Ta coù f(x) = (x+1)(7-x) 0
Daáu baèng xaûy ra khi x = -1 hoaëc x = 7 neân gtnn cuûa f(x) laø : f(-1) = f(7) = 0
b) Ñoái vôùi ba soá khoâng aâm : Ñònh lyù 3:
Giaûi thích:Trung bình
Vôùi moïi a 0, b 0, c 0 , ta coù
coäng cuûa ba soá khoâng aâm a b c
lôùn hôn hoaëc baèng trung 3 abc 3 bình nhaân cuûa chuùng.
Ñthöùc xaûy ra khi vaø chæ khi a = b = Trung bình coäng cuûa ba soá c
khoâng aâm baèng trung bình HÑ3:
nhaân cuûa chuùng khi vaø chæ Neáu ba soá döông thay ñoåi Ví duï 6: khi 3 soá ñoù baèng nhau
nhöng coù toång khoâng ñoåi thì tích cuûa
Cmr neáu a,b,c laø 3 soá döông thì
Goïi hs laøm ví duï 6
chuùng lôùn nhaát khi ba soá ñoù baèng nhau (a+b+c)(1/a+1/b+1/c) ≥9 .
Khi naøo xaûy ra ñaúng thöùc ?
Neáu ba soá döông thay ñoåi
Goïi hs thöïc hieän hñoäng 3 nhöng coù tích khoâng ñoåi thì toång cuûa
chuùng nhoû nhaát khi ba soá ñoù baèng nhau .
3)Cuûng coá: Bñt veà gttñ vaø bñt giöõa tb coäng vaø tb nhaân.
4)Daën doø : Baøi taäp coøn laïi cuûa sgk.
Höôùng daãn hs laøm caùc baøi taäp
10.a) Vôùi x≥y≥0 ta coù 10,11,12,13,14,17,18,19,20,21 x y
x(1+y)≥y(1+x) x≥y (ñuùng)
10.a) CMR: neáu x≥y≥0 thì 1 x 1 y x y
b) a b a b 1 x 1 y a b a b a b
b) CMR a, b ta coù: = 1 a b 1 a b 1 a b 1 a b a b a b a b 1 a b 1 a 1 b ≤ 1 a 1 b 11) CMR:
a) Neáu a, b laø hai soá cuøng daáu thì : 79 a b a b 2
11. a) Neáu a, b laø hai soá cuøng daáu thì b a
b & laø hai soá döông neân a
b) Neáu a, b laø hai soá traùi daáu thì : a b a b 2 . 2 a b b a b a 2 b a a b
b) Neáu a, b laø hai soá traùi daáu thì - 2 vaø vì vaäy b a a b 2 b a
12) Tìm gtln & gtnn cuûa haøm soá : 12) Keát quaû :
f(x) = (x+3)(5-x) vôùi -3 x 5
Gtln cuûa f(x) = 16 khi vaø chæ khi x = 1
13) Tìm gtnn cuûa haøm soá :
Gtnn cuûa f(x) = 0 khi vaø chæ khi x = -3 hoaëc x = 5 f(x) = x 2 vôùi x > 1 13) x -1
Gtnn cuûa f(x) = 1+2 2 khi vaø chæ khi x = 1+ 2
14) CMR neáu a, b, c laø ba soá döông thì a4 b4 c4 a4 b4 c4 4 4 4 14) 33 a 3 bc a b c a 3 bc b c a b c a b c a
16) CMR vôùi moïi soá nguyeân döông n , ta coù : 16) a) 1 1 1 1 ... 1 1 1 1 1 2 . 1 3 . 2 4 . 3 n(n ) 1 a) ... 2 . 1 3 . 2 4 . 3 n(n ) 1 b) 1 1 1 1 ... 2 1 1 1 1 1 1 1 1 12 22 32 2 n
= ... 1 2 2 3 3 4 n n 1 = 1 - 1 1 n 1 b) Ta coù : 1 + 1 1 1 1 1 1 ... <1 ... 2 2 2 2 n n 1 2 3 n 1 . 2 2 . 3 ( ) 1 < 1+1 1 1 1 1 1 ...
17) Tìm gtln & gtnn cuûa bieåu thöùc : 1 2 2 3 n 1 n 1 A = x -1 4 - x = 2 - < 2 n 17) A2= x -1 4 - 2 x
= 3+2 (x -1)(4- x) 3 x -1 4 - x 6 A 6
Daáu baèng xaûy ra khi vaø chæ khi x-1 = 4-x x = 5 2 Vaäy gtln cuûa A laø 6
A2 = 3+2 (x -1)(4 - x) 3 maø A 0 neân A 3
A2= 3 khi x =1 hoaëc x= 4 neân A =
18) CMR vôùi moïi soá thöïc a, b, c ta 3 khi x =1 hoaëc x =4 Vaäy gtnn cuûa A laø 3 80 coù:
(a + b + c)2 3(a2 + b2 + c2).
18) (a+ b + c)2 3(a2 + b2 + c2)
a2 + b2 + c2 + 2ab + 2bc + 2ca 3(a2 + b2 + c2)
2ab + 2bc + 2ca 2(a2+ b2 + c2)
(a - b)2 + (b - c)2 + (c - a)2 0
19) CMR neáu a, b, c & d laø 4 soá 4
khoâng aâm thì a b c d abcd 4 19) a b 2 ab v aø c d 2 cd a b c d ( 2 ab cd) a b c d 2 ab cd2 ab cd 2 abcd 4 abcd 2 a b c d 2 a b c d 4 abcd a bcd. 4 4
20) CMR vôùi moïi soá thöïc a, b, c & d
ta coù : (ab + cd)2 (a2+ c2)(b2+ d2) 20)
Aùp duïng , chöùng minh raèng :
(ab + cd)2 = a2b2 + 2abcd + c2d2 a2b2 + a2d2 + b2c2 +c2d2
a)Neáu x2+ y2 = 1 thì x y 2 = (a2 + c2)(b2 + d2)
b)Neáu 4x-3y = 15 thì x2+ y2 9
a)(x + y)2 = (x.1 + y.1)2 (x2 + y2)(12 + 12) = 1.2 = 2 x y 2
Caùch khaùc: (x + y)2 = x 2+y2 +2xy≤2(x 2+y2)=2 neân x y 2
b)152 = (4x -3y)2 (x2 + y2)[ 42 + (-3)2] = 25(x2 + y2) x2 + y2 9
Caùch khaùc : Vì 4x-3y=15 neân y= 4x/3-5. Do ñoù
x2 + y2= x2 + (4x/3-5)2= x2 + 16x2/9-40x/3+25
= 25x2/9 – 40x/3+25= (5x/3-4)2 + 9 9. 81
Tieát 47 §2. ÑAÏI CÖÔNG VEÀ BAÁT PHÖÔNG TRÌNH
I). Muïc tieâu :Giuùp hoïc sinh: *Kieán thöùc :
- Hieåu khaùi nieämbaát phöông trình , 2 b phöông trình töông ñöông.
- Naém ñöôïc caùc pheùp bieán ñoåi töông ñöông caùc bpt. *Kyõ naêng :
- Neâu ñöôïc ñieàu kieän xñ cuûa 1 baát phöông trình ñaõ cho .
- Bieát caùch xeùt xem 2 baát phöông trình cho tröôùc coù töông ñöông vôùi nhau hay khoâng.
II). Ñoà duøng daïy hoïc: Giaùo aùn , sgk
III).Caùc hoaït ñoäng treân lôùp: 1).Kieåm tra baøi cuû: Bñt? Tính chaát bñt? 2). Baøi môùi : Tg Noäi dung
Hoaït ñoäng cuûa thaày
Hoaït ñoäng cuûa troø
1).Khaùi nieäm bptrình moät aån :
Cho hs ghi ñònh nghóa Ghi ñònh nghóa Ñònh nghóa :
Cho 2 hsoá y=f(x) vaø y=g(x) coù txñ laàn
löôït laø Df vaø Dg. Ñaët D= Df Dg.
*Mñeà chöùa bieán coù 1 trong caùc daïng
f(x) < g(x) , f(x) > g(x) , f(x) < g(x) ,
f(x) < g(x), ñöôïc goïi laø bphtrình moät
aån , x goïi laø aån soá vaø D goïi laø txñ cuûa bphöông trình ñoù .
*Soá x0D laø moät nghieäm cuûa bpt
f(x) < g(x) neáu f(x0) = g(x0) laø mñeà ñuùng.
*Giaûi 1 bpt laø tìm taát caû caùc nghieäm
(hay tìm taäp nghieäm) cuûa bpt ñoù
Ttöï cho 3 daïng bpt coøn laïi.
Chuù yù: Trong thöïc haønh, ta
khoâng caàn vieát roõ txñ cuûa bpt
maø chæ caàn neâu ñk ñeå xD 82
goïi laø ñieàu kieän xaùc ñònh cuûa
bpt,goïi taét laø ñkieän cuûa bpt
Hñ 1ï: Cho hs thöïc hieän. Hñ 1: a)S=(-∞;-4);b)S=[-1;1].
2)BPtrình töông ñöông: Ñònh nghóa :
f1(x) = g1(x) f2(x) = g2(x) neáu hai
bpt coù cuøng taäp nghieäm.
Hñ 2ï: Cho hs thöïc hieän.
Hñ2:a)Sai vì 1S2 , 1 S1 b)Sai vì 0S2 , 0 S1
Chuù yù : Khi muoán nhaán maïnh
2 bpt coù cuøng ñkxñ (hay cuøng
txñ D) vaø töông ñöông vôùi
nhau, ta noùi vôùi ñkxñ 2 bpt laø tñ vôùi nhau.
Ví duï 1:Vôùi ñk x>2, ta coù 1 11 x2 x 2
3)Bieán ñoåi töông ñöông caùc bpt: Gv giaûi thích :
Caùc pheùp bñ khoâng laøm thay
ñoåi taäp nghieäm cuûa bpt goïi laø
Pheùp bieán ñoåi töông ñöông bieán 1 bpt
caùc pheùp bñ t ñöông :bieán 1
thaønh 1 bpt töông ñöông vôùi noù.
bpt thaønh bpt tñ vôùi noù.
Chaúng haïn pheùp bñ ñoàng nhaát
ôû moãi veá cuûa 1 bpt vaø khoâng
thay ñoåi txñ cuûa noù laø 1 pheùp bñtñ Ñònh lyù: Cho hs ghi ñònh lyù Cho bpt f(x)D;
y=h(x) laø 1 hs xñ treân D.
Khi ñoù treân D, bpt f(x) vôùi moãi pt sau: ①f(x)+h(x) ②f(x)h(x) h(x)>0,∀x D. CM: ③∀x ③f(x)h(x)>g(x)h(x) neáu
0D thì caùc gtrò xñ h(x)<0,∀x f(x D.
0)R,g(x0)R,h(x0)R,vaø h(x
0)<0 neân f(x0)< g(x0) f(x 0)h(x0)>g(x0)h(x0)
Töø ñoù suy ra 2 bpt coù cuøng
taäp nghieäm nghóa laø chuùng töông ñöông vôùi nhau. Ví duï 2: a) x 2 x x 2 - x 83 b)x> -2⇎x- x > -2- x
HÑ3: goïi hs thöïc hieän HÑ3:
a)Bpt(1) coù txñ D=[0;+∞),
- x xñ treân D. Do ñoù chuùng laø tñ.
HÑ4: goïi hs thöïc hieän b)-1S1 , -1 S2 HÑ4: a)Sai vì 0S2 , 0 S1 b)Sai vì 1S2 , 1 S1 Heä quaû: Cho hs ghi heä quaû Cho bpt f(x)D;
1)f(x) < g(x) [f(x)]3 < [g(x)]3
2)Neáu f(x) vaøg(x) khoâng aâm vôùi ∀xD thì f(x) < g(x) [f(x)]2 < [g(x)]2
HÑ5: goïi hs thöïc hieän HÑ5: (1) x2+2x+1≤ x2 2x≤-1x≤-1/2
3)Cuûng coá:bpt,txñ,nghieäm cuûa bpt,giaûi bpt, 2 bpttñ.
4)Daën doø:bt 21-24 sgk trang 116. HD:
21)Khoâng tñ vì 0S2 , 0 S1 22.a)Ñk:x=0;S=. b)Ñk:x≥3;S=[3;+∞).
c)Ñk:x≠3;S=[2;3)∪(3;+∞). d)Ñk:x>2;S=. 23)2x-1- 1 1 . x 3 x 3 24)x-2≤0 vaø x2(x-2) ≤0 84
Tieát 48-49 §3. BAÁT PHÖÔNG TRÌNH VAØ
HEÄ BAÁT PHÖÔNG TRÌNH BAÄC NHAÁT MOÄT AÅN
I) Muïc tieâu:Giuùp hoïc sinh
*Kieán thöùc : Hieåu khaùi nieäm bpt baäc nhaát moät aån . *Kyõ naêng :
-Bieát caùch giaûi vaø bieän luaän bpt daïng ax+b < 0 .
-Coù kyõ naêng thaønh thaïo trong vieäc bieåu dieãn taäp nghieäm cuûa bpt baäc nhaát 1 aån treân truïc soá vaø giaûi heä bpt Baäc nhaát moät aån . II) Chuaån bò : Giaùo aùn , sgk
III) Caùc hoaït ñoäng treân lôùp:
1)Kieåm tra baøi cuû:
Hai bpt tñöông ? Caùc pheùp bñ töông ñöông ?
2)Baøi môùi: Tieát 1 : muïc 1 ; tieát 2 : muïc 2. Tg Noäi dung
Hoaït ñoäng cuûa thaày
Hoaït ñoäng cuûa troø
T1 Bpt baäc nhaát moät aån laø bpt coù 1
trong caùc daïng ax+b<0,ax+b ≤ 0,
ax+b > 0, ax+b ≥ 0, a 0,x laø aån. Hñ 1:Goïi hoïc sinh thöïc hieän Hñ 1: a)m=2, S=(-∞;3] b)m= - 2 , S=[1- 2 ;+∞)
1) Giaûi vaø bl bpt daïng ax+ b < 0
Keát quaû giaûi vaø bieän luaän bpt ax+b < 0 (1) b
*Neáu a>0 thì (1)x < . a b S=(-∞; ). a b
*Neáu a< 0 thì (1)x > . a b S=( ;+∞). a
*Neáu a=0 thì (1)0x <-b.
+Bpt (1) vn,S= neáu b≥0;
+Bpt (1) nghieäm ñuùng vôùi 85 moïi x, S=R neáu b < 0.
Ví du1ï: Giaûi vaø bieän luaän bpt : mx+1 > x+ m2 (1)
Ví du1ï: Gv giaûi thích ví duï sgk Giaûi:(1) (m-1)x > m2-1 (2)
vaø höôùng daãn hs thöïc hieän ví duï1 *Neáu m>1 thì m-1>0 neân (2) x > m+1
* Neáu m<1 thì m-1<0 neân (2) x < m+1
* Neáu m=1 thì bpt (2) 0x > 0 neân noù voâ nghieäm. Keát luaän: m>1 thì S=(m+1;+∞). m<1 thì S=(-∞;m+1). m= 1 thì S= ∅ HÑ2: HÑ2:
Gv giaûi thích vaø höôùng daãn hs m>1 thì S=[m+1;+∞). thöïc hieän hñ2. m<1 thì S=(-∞;m+1]. m= 1 thì S=R.
Ví duï 2:Giaûi vaø bieän luaän bpt
Ví duï 2: Gv giaûi thích vaø höôùng Ví duï 2: 2mx≥x+4m-3
daãn hs thöïc hieän ví duï 2 sgk. KL:
m> 1 , S= 4m 3; . 2 2m 1 1 4m 3 m< , S=(-∞; . 2 2m 1 1 m= , S=R. 2
2)Giaûi heä bpt baäc nhaát moät aån: T2
Muoán giaûi heä bpt moät aån , ta giaûi
töøng bpt cuûa heä roài laáy giao cuûa
caùc taäp nghieäm thu ñöôïc.
Ví du3ï:Giaûi heä bpt
Ví du3ï: Gv giaûi thích vaø höôùng Giaûi : (1)x 3x 5 0 ( 1)
daãn hs thöïc hieän ví duï3 sgk. ≤5/3 , S1=(-∞;5/3]. (2)x≥- (I) 3/2, S 2x 3 0 ( 2) 2=[-3/2;+∞).
(3)x> -1 , S3=(-1;+∞). x 1 0 ( 3) S= S ∩S ∩S 1 2 3=(-1;5/3]. Caùch khaùc x 5 3 3 5
(I) x -1< x ≤ 2 3 x 1 5 KL: S=(-1; ]. 3 86
Hñ 3: Cho hoïc sinh thöïc hieän 3x 2 0 Hñ 3:Giaûi heä bpt
Ví duï 4: Gv giaûi thích vaø höôùng 5 2x 0
daãn hs thöïc hieän ví duï4 sgk. KL: S=[-2/3;5/2]
3) cuûng coá:Giaûi vaø bl bpt baäc nhaát, heä bpt baäc nhaát moät aån .
4)Daën doø: Bt 25-27, 28-31 trang 121. HD:25.a)x<-4/5 b)x≤-5
c)Ta coù 3-2 2 =1-2 2 +2=(1- 2 )2 vaø 1- 2 < 0, neân (1- 2 )x<3-2 2 (1- 2 )x<(1- 2 )2x>1- 2
d)(x+ 3 )2≥(x- 3 )2+2 (x+ 3 )2-(x- 3 )2≥2 4 3 x≥2 x 3 /6
Tieát 50 LUYEÄN TAÄP I). Muïc tieâu : - kieán thöùc :
Naém vöõng veà bpt ,hbpt baäc nhaát moät aån - kyõ naêng :
Giaûi vaø bieän luaän thaønh thaïo bpt daïng ax+b > 0 coù kyû naêng trong vieäc bieåu dieãn nghieäm cuûa baát pt baäc nhaát moät aån II). Chuaån bò:
- Giaùo vieân : Baûng phuï
- Hoïc sinh : hoïc thuoäc baøi , laøm caùc baøi taäp sgk.
III). Tieán trình baøi daïy
1) Kieåm tra baøi cuõ:Heä bpt baäc nhaát 1 aån . 2) Baøi môùi : TG HÑ cuûa troø HÑ cuûa thaày Noäi dung
Neâu laïi pp giaûi vaø bieän luaän
HÑ1 :Oân taäp lyù thuyeát giaûi vaø 28) Gaûi vaø bl caùc baát pt sau: Bpt ax + b 0
bieän luaän bpt daïng ax + b 0 a) m (x-m) > 2 (4 –x) 28) a) m(x-m) > 2(4-x)
Goïi hs neâu pp giaûi bpt treân c) k(x-1) +4x 5 (m+2)x > m 2 - 8
HÑ2 : Giaûi bt veà bl pt goïi 4 29) Giaûi caùc baát hpt
+ m>-2 : (1) coù hs leân baûng giaûi bt 28a,b 30
5x 2 4 x 2 m 8 a,b 3 S= ( ; ) a) m 2 .
- Giao nhieäm vuï cho hoïc sinh 6 5x
-ktra baøi cuû cuûa caùc hs khaùc 3x 1 13 + m<-2 : (1)
coù gôïi yù baøi taäp 29a,b 2 2
(1 x) 5 3x x 2 ñöa veà daïng ax > -b b) S= m 8 3 3 2 ; .
xeùt caùc tröôøng hôïp :
(x 2) x 6x 7x 5 m 2 a > 0 ; a < 0 ; a = 0 + m = -2 ; S= R. 28 c) k(x-1) +4x 5 (2) (k+4)x k+5 + k > -4 : (2) co S= k 5 ; ù k 4 Gôïi yù baøi taäp 30 +k < -4 :(2) coù S= k 5 ; k 4 87 + k = -4 :(2) coù S= x 1 3 x 2 4 x 5 Giaûi m 1 x 3
x m 2 0 3
30) Tìm caùc giaù trò cuûa m ñeå moãi Heä coù daïng :A < B ; 7x 7 hbpt sau coù nghieäm 30 a) B < C m 2 x Heä coù nghieäm khi: 2x 7 8x 1 3 a) A < B
x m 5 0 m 5
Bt 30 b ) giaûi töông töï 2 2 x 2 0 (x 3) x 7x 1 b) b)
m x 1 2m 5x 8 x 1 31) a)
2x 7 8x 1 2
x m 5 0
Gôïi yù:31a) S = S S 1 2 4
Neân bieåu dieãn taäp nghieäm x 3 treân truïc soá. m 5 31 b) heä coù daïng : x 2 A > B ;B > C.
Heä coù nghieäm khi :C > A 4 m 5 S ; ; 3 2
29 )Giaûi caùc heä pt sau :
hbpt voâ nghieäm khi vaø chæ khi:
x x c) 4 5 7 2 m 5 4 3x 8 8x 20 2 3 x x a) 5 2 12 3 7 m
6 5x 39x 13 3 5
x 2 12 3x
6 5x 39x 13 5 x 29a) 4
+Goïi 2 hs leân baûng giaûi caùc bt 7 29a,b x 44 +Caùc hs khaùc theo doõi 5
+ Goïi nhaän xeùt ñuùng sai, söõa x sai. 4
+ Gv nhaän xeùt ñuùng sai , suõa
4x 5 7x 2
sai , uoán naén caùch trình baøi 29 c) 3
x 8 8x 20 11 5 x 5 2 3). Cuûng coá
+ Giaûi vaø bieän luaän pt ax+b > 0 (<0 ; 0; 0) +Giaûi heä bpt
4) . Daën doø : Giaûi caùc baøi taäp coøn laïi. 88
Tieát 51 §4. DAÁU CUÛA NHÒ THÖÙC BAÄC NHAÁT 1/ Muïc tieâu:
1. Kieán thöùc cô baûn: Naém vöõng ñònh lí veà daáu cuûa nhò thöùc baäc nhaát vaø yù nghóa hình hoïc cuûa noù.
2. Kyõ naêng, kyõ xaûo: Bieát caùch laäp baûng xeùt daáu ñeå giaûi baát phöông trình tích vaø baát phöông trình
chöùa aån ôû maãu thöùc. Bieát caùch laäp baûng xeùt daáu ñeå giaûi caùc phöông trình, baát phöông trình moät aån
chöùa daáu giaù trò tuyeät ñoái.
3. Thaùi ñoä nhaän thöùc: Tích cöïc trong hoïc taäp, reøn luyeän vaø phaùt trieån tö duy thuaät toaùn, tö duy saùng taïo.
2/ Chuaån bò phöông tieän daïy hoïc: a) Thöïc tieãn:
b) Phöông tieän daïy hoïc: Baûng phuï, maùy tính boû tuùi.
3/ Tieán trình tieát daïy:
a)Kieåm tra baøi cuõ: (5') Giaûi vaø bieän luaän caùc bpt : (a+1).x + a + 3 4x + 1. b) Giaûng baøi môùi: TG
Hoaït ñoäng cuûa g v
Hoaït ñoäng cuûa hoïc sinh Noäi dung 5'
-Cần chú ý nói rõ cho -Ghi nhận
I. Nhị thức bậc nhất và dấu của nó học sinh sự khác nhau
a.Đn :Nhị thức bậc nhất (đối với x) giữa pt bậc nhất , bpt
là biểu thức có dạng ax + b, trong đó
bậc nhất và nhị thức bậc
a và b là hai số cho trước với a ≠ 0 nhất
.f(x) = ax + b (a,b:số cho trước , a ≠ 0) .ax + b = 0 có nghiệm x b = cũng 0 a
là nghiệm của f(x) = ax + b
b.Dấu của nhị thức bậc nhất -Ghi nhận
.Định lí : Nhị thức bậc nhất f(x) =
10’ -Hướng dẫn học sinh
ax + b cùng dấu với hệ số a khi x lớn biết cách chứng minh
hơn nghiệm và trái dấu với a khi nhỏ
định lí và đưa ra định lí hơn nghiệm của nó .Bảng xét dấu: Vd: xét dấu biểu thức f(x) = -x + 1,5 3’ x 1,5 + - f(x) + - 0 .f(x) 0 x ≤ 1,5
Hãy giải thích bằng đồ .f(x) ≤ 0 x 1,5
II. Một số ứng dụng: 89
thị các kết của định lí
a)Giải bất phƣơng trình tích : trên. VD: x(x-2) 2 (3-x) ≤ 0
.Đặt P(x) = x(x-2) 2 (3-x) x 0 - Cần chú ý cách xác Giải P(x) = 0 x 2 định x và y -Ghi nhận và biến đổi x
5’ - Chia nhóm hoạt động 3 -Gọi 2 nhóm lên trình Bxd: bày
-Xét dấu trên cùng một bảng
5’ -Nhận xét và sữa chữa
-Chú ý cần xác định rõ các bước làm
Vậy S = (-∞;0] [3;+ ∞) + Giải pt P(x) = 0 tìm
b)Giải bpt chứa ẩn ở mẫu: nghiệm 3 5 Vd:
+Lập bảng xét dấu cần 1 x 2x 1 ghi thứ tự các nghiệm x 7 cho đúng 0 (x ) 2 .(2x ) 1 + Chọn đúng giá trị x Bxd: theo dấu bpt -Chuyển bpt về dạng P(x) 5’ 0 Q(x) -Xét dấu P(x) và Q(x) Vậy S = ( cùng bảng -∞;7] (2;+ ∞)
c) Giải phƣơng trình, bất phƣơng
-Lấy kết quả ở những giá trị mà mẫu không
trình chứa ẩn trong dấu giá trị tuyệt xác định đối: VD1:Giải bpt: 2x 1 x 3 5 4 S = (– ;+ ) 5 VD2: Bài tập c) bài 34 5’ -Ghi nhận 2x 2 2 x x 3 2 -Hướng dẫn học sinh cách giải bpt chứa ẩn trong dấu gttđ
c) Củng cố: Gọi một học sinh nêu lại các bước xét dấu nhị thức bậc nhất.
d) Bài tập về nhà: Bài tập SGK trang 126, 127. 90
Tieát 53,54 §5 BAÁT PHÖÔNG TRÌNH VAØ
HEÄ BAÁT PHÖÔNG TRÌNH BAÄC NHAÁT HAI AÅN. 1/ Muïc tieâu:
1. Kieán thöùc cô baûn: Hieåu khaùi nieäm baát phöông trình, heä baát phöông trình baäc nhaát hai aån,
nghieäm vaø mieàn nghieäm cuûa noù.
2. Kyõ naêng, kyõ xaûo: Bieát caùch xaùc ñònh mieàn nghieäm cuûa baát phöông trình vaø heä baát phöông trình
baäc nhaát hai aån. Bieát caùch giaûi baøi toaùn quy hoaïch tuyeán tính ñôn giaûn.
3. Thaùi ñoä nhaän thöùc: Phaùt trieån tö duy lí luaän chaët cheõ vaø tö duy saùng taïo. Töø vieäc giaûi caùc baøi
toaùn hoïc sinh lieân heä ñöôïc vôùi thöïc tieãn.
2/ Chuaån bò phöông tieän daïy hoïc: a) Thöïc tieãn:
b) Phöông tieän daïy hoïc: Baûng phuï, maùy tính boû tuùi.
3/ Tieán trình tieát daïy: a)Kieåm tra baøi cuõ: b) Giaûng baøi môùi:
Hoaït ñoäng 1:Ñònh nghóa baát phöông trình baäc nhaát hai aån vaø mieàn nghieäm cuûa noù. TG
Hoaït ñoäng cuûa giaùo vieân
Hoaït ñoäng cuûa hoïc sinh Noäi dung
_Töø vieäc kieåm tra baøi cuõ giaùo
I.Bpt baäc nhaát 2 aån
vieân daãn daét vaøo baøi môùi
1.Bpt baäc nhaát hai aån vaø
_Goïi hai hoïc sinh phaùt bieåu HS1:Phaùt bieåu ñònh nghóa. mieàn nghieäm.
ñònh nghóa baát phöông trình baäc HS2:Phaùt bieåu laïi ñònh nghóa.
Ñònh nghóa: Baát phöông nhaát hai aån.
trình baäc nhaát hai aån coù
_Chính xaùc laïi noäi dung vaø daïng: chieáu leân baûng. ax + by + c > 0 (1)
_Laáy ñieåm O(0;0) thay vaøo baát HS3:Phaùt bieåu ñònh nghóa ax + by + c < 0 (2)
phöông trình 2x-y+1 > 0.Ta coù nghieäm cuûa baát phöông trình ax + by + c 0 (3)
5’ O(0;0)laø moät nghieäm cuûa baát baäc nhaát hai aån. ax + by + c ≤ 0 (4)
phöông trình 2x-y+1 > 0 .
HS4:Phaùt bieåu laïi ñònh nghóa Trong ñoù x,y laø aån soá, a, b, c
_Nhö vaäy trong maët phaúng toaï nghieäm cuûa baát phöông trình laø nhöõng soá thöïc sao cho a2
ñoä,moãi moät nghieäm cuûa baát baäc nhaát hai aån. +b2 ≠0
phöông trình baäc nhaát hai aån
Moãi caëp soá(x0;y0) sao
ñöôïc bieåu dieãn bôûi moät ñieåm,
cho ax0+by0+c >0 laø moät
taäp nghieäm cuûa noù ñöôïc bieåu
nghieäm cuûa baát phöông trình
dieãn bôûi moät taäp hôïp ñieåm vaø (1)
taäp hôïp ñieåm ñoù laø mieàn
nghieäm cuûa baát phöông trình. 91
Hoaït ñoäng 2:Caùch xaùc ñònh mieàn nghieäm cuûa baát phöông trình baäc nhaát hai aån. TG
Hoaït ñoäng cuûa giaùo vieân
Hoaït ñoäng cuûa hoïc sinh Noäi dung
_Goïi hoïc sinh nhaän xeùt HS5:O(0;0);M(1;0)ñeàu
laø 2.Caùch xaùc ñònh mieàn
O(0;0) ; M(1;0) coù laø nghieäm nghieäm
nghieäm cuûa baát phöông
cuûa baát phöông trình 2x-y+1 cuûa baát phöông trình 2x-y+1 trình baäc nhaát hai aån. > 0. =0.
a.Ñònh lyù:Trong maët
_Vaán ñeà ñaët ra laø”Nöõa maët
phaúng toaï ñoä,ñöôøng thaúng
phaúng chöùa ñieåm O,M (d):ax+by+c = 0 chia maët
(khoâng keå bôø (d)) coù laø mieàn
phaúng thaønh hai nöõa maët
nghieäm cuûa baát phöông trình
phaúng.Moät trong hai nöõa
2x-y+1>0 khoâng”?Daãn ñeán
maët phaúng aáy (khoâng keå bô ñònh lyù
ø(d)) goàm caùc ñieåm coù toaï
_Giaùo vieân khaúng ñònh”Nöõa
ñoä thoaû maõn baát phöông
maët phaúng chöùa ñieåm O,M
trình ax+by+c > 0 ,nöõa maët
(khoâng keå bôø (d)) laø mieàn
phaúng coøn laïi (khoâng keå bô
nghieäm cuûa baát phöông trình
ø(d)) goàm caùc ñieåm coù toaï 2x-y+1 > 0.
ñoä thoaû maõn baát phöông
_Goïi hoïc sinh phaùt bieåu ñònh HS6:Phaùt bieåu ñònh lyù. trình ax+by+c < 0 ly.ù
HS7:Phaùt bieåu laïi ñònh lyù.
* Töø ñònh lyù,ta coù
_ Chieáu noäi dung ñònh lyù Neáu M(x0;y0) laø moät
HS8: Neáu M(x0;y0) laø moät nghieäm cuûa baát phöông
9’ _Töø ñònh lyù,neáu M(x0;y0) laø nghieäm cuûa baát phöông trình trình ax+by+c >0 (hay
moät nghieäm cuûa baát phöông ax+by+c >0 (hay ax+by+c <0) ax+by+c <0) thì nöõa maët
trình (1) thì mieàn nghieäm cuûa thì nöõa maët phaúng (khoâng keå phaúng (khoâng keå bôø (d))
baát phöông trình (1) xaùc ñònh bôø (d)) chöùa ñieåm M(x0;y0) laø chöùa ñieåm M(x0;y0) laø mieàn nhö theá naøo?
mieàn nghieäm cuûa baát phöônh nghieäm cuûa baát phöônh trình aáy. trình aáy.
b.Caùch xaùc ñònh mieàn
nghieäm cuûa baát phöông trình ax+by+c > 0
Veõ ñöôøng thaúng (d): ax
_Höôùng daãn hoïc sinh xaùc + by + c = 0.
ñònh mieàn nghieäm cuûa baát
Xeùt moät ñieåm M(x0;y0) phöông trình 2x-y+1 > 0 khoâng naèm treân (d).
_Goïi hoïc sinh ñöa ra caùch HS9:Ñöa ra caùch xaùc ñònh _ Neáu ax0+by0+c >0 thì
xaùc ñònh mieàn nghieäm cuûa mieàn nghieäm cuûa baát phöông nöûa maët phaúng (khoâng keå
baát phöông trình ax+by+c > 0 trình ax+by+c > 0
bôø (d)) chöùa ñieåm M laø
_Chieáu caùch xaùc ñònh mieàn HS10: Nhaéc laïi caùch xaùc ñònh mieàn nghieäm cuûa baát
nghieäm cuûa baát phöông trình mieàn nghieäm cuûa baát phöông phöông trình ax+by+c > 0 ax+by+c > 0 trình ax+by+c > 0
_ Neáu ax0+by0+c < 0 thì
_Ñoái vôùi baát phöông trình HS11: Ñoái vôùi baát phöông nöûa maët phaúng (khoâng keå
(3),(4) thì mieàn nghieäm cuûa 92
noù xaùc ñònh nhö theá naøo?
trình (3),(4) thì mieàn nghieäm bôø (d)) khoâng chöùa ñieåm M
_Cho hoïc sinh ghi chuù yù : cuûa noù laø nöõa maët phaúng keå caû laø mieàn nghieäm cuûa baát
Ñoái vôùi baát phöông trình bôø.
phöông trình ax+by+c > 0
(3),(4) thì mieàn nghieäm cuûa
noù laø nöõa maët phaúng keå caû bôø.
Hoaït ñoäng 3:Ví duï nhaèm khaéc saâu caùch xaùc ñònh mieàn nghieäm baát phöông trình baäc nhaát hai aån. TG
Hoaït ñoäng cuûa giaùo vieân
Hoaït ñoäng cuûa hoïc sinh Noäi dung
_Chieáu ñeà cuûa ví duï leân
Ví duï 1 : Xaùc ñònh mieàn baûng.
_Hoïc sinh hoaït ñoäng theo nhoùm nghieäm cuûa caùc baát phöong
_Phaân coâng:Nhoùm I ;II caâu giaûi ví duï trình sau : a) a) 3x-y+3 > 0. (1) Nhoùm
III;IV _Hoïc sinh ñaïi dieän nhoùm leân b) -2x+3y-6 < 0. (2) caâu b
daùn keát quaû vaø thuyeát trình lôøi c) 2x+y+4 > 0. (3) 10' Nhoùm V;VI caâu giaûi. c).
_Goïi ñaïi dieän nhoùm leân
daùn keát quaû vaø thuyeát trình lôøi giaûi.
_Giaùo vieân chieáu keát quaû
chính xaùc cuûa baøi toaùn.
Hoaït ñoäng 4:Heä baát phöông trình baäc nhaát hai aån. TG
Hoaït ñoäng cuûa giaùo vieân
Hoaït ñoäng cuûa hoïc sinh Noäi dung
_Töø ví duï 1 lieân heä ñöa ra
II. HEÄ BAÁT PHÖÔNG
ñònh nghóa heä baát phöông
TRÌNH BAÄC NHAÁT HAI trình baäc nhaát hai aån. AÅN.
_Goïi hoïc sinh neâu ñònh HS12 :Neâu ñònh nghóa heä baát Ñònh nghóa: Heä baát
nghóa heä baát phöông trình phöông trình baäc nhaát hai aån.
phöông trình baäc nhaát hai aån baäc nhaát hai aån.
laø moät taäp hôïp goàm nhieàu
_Chieáu noäi dung ñònh nghóa HS13 :Neâu laïi ñònh nghóa heä baát phöông trình baäc nhaát hai 4'
baát phöông trình baäc nhaát hai aån.
_Goïi hoïc sinh nhaéc laïi caùch aån. Caùch giaûi:
giaûi heä baát phöông trình HS14 :Neâu laïi caùch giaûi heä baát +Vôùi moãi baát phöông trình
baäc nhaát moät aån, lieân heä phöông trình baäc nhaát moät aån. cuûa heä,ta xaùc ñònh mieàn
ñöa ra caùch giaûi heä baát
nghieäm cuûa chuùng treân cuøng
phöông trình baäc nhaát hai
moät heä truïc toaï ñoä. aån.
+ Mieàn coøn laïi khoâng bò
_Chieáu caùch giaûi heä bpt
gaïch chính laø mieàn nghieäm 93 baäc nhaát hai aån. cuûa heä ñaõ cho.
Hoaït ñoäng 5:Ví duï. TG
Hoaït ñoäng cuûa giaùo vieân
Hoaït ñoäng cuûa hoïc sinh Noäi dung
_Chieáu ñeà cuûa ví duï leân y
Ví duï 2:Xaùc ñònh mieàn d d baûng. 1 3
nghieäm cuûa heä baát phöông
_Cho hoïc sinh hoaït ñoäng d 3 2 trình theo nhoùm. 2
3x y 3 0 -3 x
_ Goïi ñaïi dieän nhoùm leân -1 -2 O
2x 3y 6 0
daùn keát quaû vaø thuyeát trình
2x y 4 0 lôøi giaûi. -4
_Giaùo vieân chieáu keát quaû
chính xaùc cuûa baøi toaùn.
_Hoïc sinh hoaït ñoäng theo nhoùm giaûi ví duï
Ví duï 3: Xaùc ñònh mieàn 7’ Hoïc sinh töï giaûi
nghieäm cuûa heä baát phöông
_Chieáu ñeà cuûa ví duï leân trình. baûng. y 3x 0
_Höôùng daãn hoïc sinh veà
x 2y 5 nhaø töï giaûi 0
5x 2y 10 0
Caâu hoûi traéc nghieäm
HS15: Hoïc sinh traû lôøi caâu hoûi traéc nghieäm.
_Chieáu caâu hoûi traéc nghieäm
_Goïi hoïc sinh traû lôøi caâu 94 hoûi traéc nghieäm.
Hoaït ñoäng 6:Cuûng coá. TG
Hoaït ñoäng cuûa giaùo vieân
Hoaït ñoäng cuûa hoïc sinh Noäi dung
_Chieáu caùch xaùc ñònh mieàn
nghieäm cuûa baát phöông trình baäc nhaát hai aån.
HS16: Phaùt bieåu laïi caùch xaùc
_Goïi hoïc sinh phaùt bieåu laïi ñònh mieàn nghieäm cuûa baát
caùch xaùc ñònh mieàn nghieäm phöông trình baäc nhaát hai aån.
cuûa baát phöông trình baäc nhaát hai aån.
d) Baøi taäp veà nhaø:Laøm caùc bt 42,43,45,46,47 trang 132,135 saùch giaùo khoa Ñai Soá 10 naâng cao. 95
(15') 1.Kieåm tra baøi cuõ: 0 x 4
Baøi taäp: Cho heä baát phöông trình : 0 y 3 2x y 3 x 3y 4
1.Xaùc ñònh mieàn nghieäm cuûa heä baát phöông trình
2.Tính giaù trò cuûa bieåu thöùc F(x;y)= 2x – 4y
a. Taïi caùc ñænh cuûa mieàn nghieäm
b. Taïi caùc ñieåm (1;2) ; (2;1) ; (3;1) ; (4;0) ; (5;0)
2.Giaûng baøi môùi :Qua baøi taäp treân daãn hoïc sinh vaøo baøi toaùn kinh teá
Hoaït ñoäng 1:Giôùi thieäu öùng duïng cuûa vieäc tìm mieàn nghieäm cuûa heä baát phöông trình baäc nhaát hai
aån vaøo baøi toaùn kinh teá :
TG Hoaït ñoäng cuûa giaùo vieân Hoaït ñoäng cuûa hoïc sinh Noäi dung Theo doõi ñeà baøi Chieáu ñeà baøi toaùn
3.Moät ví duï aùp duïng vaøo baøi toaùn kinh teá Baøi toaùn :
Ngöôøi ta döï ñònh duøng hai loaïi
nguyeân lieäu ñeå chieát xuaát ít nhaát 12
kg chaát A vaø 1 kg chaát B. Töø moãi taán
nguyeân lieäu loaïi I giaù 4 trieäu ñoàng,
coù theå chieát xuaát ñöôïc 8 kg chaát A
vaø 0,25 kg chaát B. Töø moãi taán 5'
nguyeân lieäu loaïi II giaù 3 trieäu ñoàng,
coù theå chieát xuaát ñöôïc 4 kg chaát A
vaø 0,75 kg chaát B. Hoûi phaûi duøng bao
nhieâu taán nguyeân lieäu moãi loaïi ñeå chi
phí mua nguyeân lieäu laø ít nhaát, bieát
raèng cô sôû cung caáp nguyeân lieäu chæ
coù theå cung caáp khoâng quaù 4 taán
nguyeân lieäu loaïi I vaø khoâng quaù 3 taán
nguyeân lieäu loaïi II ?
Hoaït ñoäng 2: Phaân tích baøi toaùn
TG Hoaït ñoäng cuûa giaùo vieân Hoaït ñoäng cuûa hoïc sinh Noäi dung
- Phaân tích giaû thuyeát baøi -Yeâu caàu toùm taét giaû Goïi x, y laø soá taán nguyeân lieäu loaïi I vaø
toaùn Töø hai loaïi nguyeân thuyeát II caàn söû duïng
lieäu chieát xuaát ít nhaát
- Theo giaû thuyeát ta coù :
10' 12kg chaát A vaø 1 kg chaát B 96
Moãi taán nguyeân lieäu loaïi I 0 x 4 giaù 4 trieäu ñoàng 0 y 3 2x y 3 x 3y 4
sao cho T(x;y) = 4x + 3y coù giaù trò nhoû nhaát 8 kg chaát A 0,25 kg chaát B
Moãi taán nguyeân lieäu loaïi II giaù 3 trieäu ñoàng
4 kg chaát A 0,75 kg chaát B
- Tìm caùc raøng buoäc cuûa aån x vaø y
Tìm x taán nguyeân lieäu loaïi
I vaø y taán nguyeân lieäu loaïi
II thoûa yeâu caàu baøi toaùn - Tìm x vaø y thoûa 0 x 4 0 y 3 2x y 3
- Giaùo vieân chæ ra cho hoïc x 3y 4
sao cho T(x;y) = 4x + 3y sinh thaáy baøi toaùn treân coù giaù trò nhoû nhaát
daãn ñeán hai baøi toaùn nhoû
1.Xaùc ñònh taäp hôïp (S)
caùc ñieåm coù toïa ñoä (x;y) thoûa maõn : 0 x 4 0 y 3 2x y 3 x 3y 4 2.Trong taäp hôïp (S), tìm ñieåm (x;y) sao cho T(x;y) = 4x + 3y coù giaù trò nhoû nhaát 97
Hoaït ñoäng 3: Giaûi baøi toaùn
TG Hoaït ñoäng cuûa giaùo vieân Hoaït ñoäng cuûa hoïc sinh Noäi dung
- Chia hs thaønh caùc nhoùm hoaït ñoäng - Caùc nhoùm giaûi
-Yeâu caàu caùc nhoùm giaûi
10' - Ñaïi dieän nhoùm leân trình - Goïi ñaïi dieän nhoùm leân baøy
trình baøy vaø nhaän xeùt
- Hieåu ñöôïc yù nhóa baøi toaùn
(5’) Hoaït ñoäng 4: Cuõng coá tieát hoïc Phieáu hoïc taäp:
Haõy khoanh troøn vaøo phöông aùn ñuùng .
Caâu 1: Khaúng ñònh sau ñuùng hay sai?
Hình veõ beân bieåu dieãn giaù trò nhoû nhaát cuûa bieåu thöùc F(x;y)= x – 3y
treân mieàn nghieäm baèng 4. a. Ñ b. S
Caâu 2: Hình veõ beân bieåu dieãn giaù
trò lôùn nhaát cuûa bieåu thöùc F(x;y) = – x + 4y
treân mieàn nghieäm ñaït ñöôïc taïi ñieåm a.O b.A c.B d.C y A 3 2 1 B C O 3 4 x
Cuõng coá :Thaáy ñöôïc öùng duïng cuûa vieäc tìm mieàn nghieäm cuûa heä baát
phöông trình vaøo vieäc giaûi baøi toaùn thöïc teá ñôøi soáng 0 x 0 y x 3 y 9
Baøi taäp veà nhaø : Cho heä baát phöông trình : x 2y 8 x 6y 2
a.Xaùc ñònh mieàn nghieäm cuûa heä baát phöông trình
b.Tìm giaù trò nhoû nhaát cuûa bieåu thöùc F(x;y) = 2x + 3
treân mieàn nghieäm cuûa heä baát phöôngtrình
Baøi taäp SGK : baøi taäp 44 trang 133 SGK, baøi taäp 48 trang 135 SGK 98
Tieát 55 LUYEÄN TAÄP
(5') 1.Kieåm tra baøi cuõ: OÅn ñònh lôùp
Trình baøy phöông phaùp xaùc ñònh mieàn nghieäm bpt baäc nhaát hai aån Laøm caâu a) baøi taäp 45 2.Giaûng baøi môùi : TG
Hoaït ñoäng cuûa gv
Hoaït ñoäng cuûa hs Noäi dung 2' -Goïi 2 hoïc sinh giaûi - Laøm nhieäm vuï
45.Xaùc ñònh mieàn nghieäm cuûa caùc bpt -Gv söõa sai neáu coù -Ghi baøi hai aån
a) x + 3+ 2(2y + 5) < 2(1–x) b) 1 ( 3 x ). 1 ( 3 y ). 2 10’
46. Xaùc ñònh mieàn nghieäm cuûa caùc heä bpt hai aån : x y 0 a) x 3y 3
-Caâu a) goïi hoïc sinh xaùc -Hoïc sinh thöïc hieän x y 5 ñònh mieàn nghieäm x 3 2y 6 0 b) 4x 3y 12 x 0 - Caâu b) do f(x;y) coù
47.Xaùc ñònh toïa ñoä caùc ñænh gtnn taïi moät trong caùc 2 2 7 8 ñænh cuûa mieàn nghieäm, ( ; );(4;1);( ; ) 3 3 3 3
goïi hoïc sinh tính giaù trò
cuûa f(x;y) taïi moät trong f( 2 2 4 ; ) =
10’ caùc ñænh cuûa mieàn 3 3 3 nghieäm f(4;1) = – 3 -Gv söõa sai neáu coù f( 7 8 1 ; ) = 3 3 3 Do ñoù : Min f(x;y) = –3 48. 99 0 x 600 0 y 500 15’ x y 1000 x y 1000 -Höôùng daãn hoïc sinh x y 400 x y 400 phaân tích baøi toaùn 1 y x 1 -Ñ/k cuûa x;y y 2 x 2
-Moái quan heä giöõa x vaø y x 3 y x 3 y thoâng qua hai ñieàu kieän gì ?
Cho hoïc sinh tìm ñaùp soá baèng caùch döïng hình -Chia laøm 6 nhoùm veõ hình vaø tìm ñaùp soá
-Goïi moät nhoùm trình baøy
-Nhaän xeùt vaø söõa sai neáu
Vaäy mieàn nghieäm laø ña giaùc (keå caû coù - Hoïc sinh thöïc hieän bieân)
5.Cuõng coá daën doø : 3’
-Xem laïi caùc baøi taäp vaø laøm theâm baøi taäp saùch baøi taäp
Tieát 56 §6. DAÁU CUÛA TAM THÖÙC BAÄC HAI. 1/ Muïc tieâu: 100
1. Kieán thöùc cô baûn: Naém vöõng ñònh lí veà daáu cuûa tam thöùc baäc hai thoâng qua vieäc khaûo saùt ñoà thò
haøm soá baäc hai trong caùc tröôøng hôïp khaùc nhau.
2. Kyõ naêng, kyõ xaûo: Vaän duïng thaønh thaïo ñònh lí veà daáu cuûa tam thöùc baäc hai ñeå xeùt daáu caùc tam
thöùc baäc hai vaø giaûi moät baøi toaùn ñôn giaûn coù tham soá.
3. Thaùi ñoä nhaän thöùc: Tích cöïc, chuû ñoäng vaø töï giaùc trong hoïc taäp, nhaän bieát söï gaàn guõi giöõa ñònh
lí veà daáu cuûa tam thöùc baäc hai vaø vieäc giaûi baát phöông trình. Bieát lieân heä giöõa thöïc tieãn ñôøi soáng vaø toaùn hoïc.
2/ Chuaån bò phöông tieän daïy hoïc: a) Thöïc tieãn:
b) Phöông tieän daïy hoïc: Baûng phuï, maùy tính boû tuùi.
3/ Tieán trình tieát daïy: a)Kieåm tra baøi cuõ: b) Giaûng baøi môùi:
1.Kieåm tra baøi cuõ: OÅn ñònh lôùp 2.Giaûng baøi môùi : TG
Hoaït ñoäng cuûa gv
Hoaït ñoäng cuûa hs Noäi dung
5' -Höôùng daãn hoïc sinh naém -Ghi nhaän
1. Tam thöùc baäc hai
ñònh nghóa tam thöùc baäc
Ñn:Tam thöùc baäc hai (ñoái vôùi x) laø hai
bieåu thöùc coù daïng ax² + bx + c, trong
ñoù a,b,c laø nhöõng soá cho tröôùc vôùi a 5’ 0
Chuù yù : Nghieäm cuûa pt baäc hai ax² + bx
+ c = 0 cuõng ñöôïc goïi laø nghieäm cuûa tam thöùc baäc hai 10’
2.Daáu cuûa tam thöùc baäc hai: y > 0 neáu a > 0
Ñònh lí : Cho ttbh f(x) = ax² + bx + c (a
-Höôùng daãn hoïc sinh xaùc y < 0 neáu a < 0 0)
ñònh daáu cuûa ttbh döïa vaøo y > 0 neáu a > 0 vôùi x Neáu < 0 thì f(x) cuøng daáu vôùi heä soá
ñoà thò haøm soá baäc hai b a vôùi moïi x R trong caùc tröôøng hôïp a 2
Neáu = 0 thì f(x) cuøng daáu vôùi heä soá
+ < 0 nhaän xeùt daáu cuûa y < 0 neáu a < 0 vôùi x a vôùi moïi x b ttbh vaø daáu cuûa a b a 2
+ = 0 nhaän xeùt daáu cuûa a 2
Neáu > 0 thì f(x) coù hai nghieäm x vaø 1 ttbh vaø daáu cuûa a
x ( x < x ) .Khi ñoù f(x) traùi daáu vôùi heá 2 1 2
+ > 0 nhaän xeùt daáu cuûa
soá a vôùi moïi x naèm trong khoaûng ( x ; 1 ttbh vaø daáu cuûa a
x ) vaø f(x) cuøng daáu vôùi heá soá a vôùi 2
moïi x naèm ngoaøi khoaûng [ x ; x ] 1 2 H1 Vd: Xeùt daáu ttbh sau : 1 10’ - Hoïc sinh thöïc hieän 101
-Höôùng daãn hoïc sinh laøm a)–2x² + 5x + 7
aùp duïng ñònh lí veà daáu cuûa b) –2x² + 5x – 7 ttbh c) 9x² –12x + 4 Giaûi
a) Ñaët f(x) = –2x² + 5x + 7
f(x) > 0 vôùi x (- ;-1) ( 7 ;+ ) 2
f(x) < 0 vôùi x (-1; 7 ) 2 b) f(x) < 0 vôùi x R c) f(x) > 0 vôùi x 2 3 Nhaän xeùt : a
x R,ax2 bx c 0 0 0 2’ - Phuï thuoäc daáu cuûa a a
x R,ax2 bx c 0 0
-Coù nhaän xeùt gì veà daáu - a > 0 0
cuûa ttbh trong tröôøng hôïp - a < 0
Vd3 : Vôùi nhöõng giaù trò naøo cuûa m thì < 0 ña thöùc
-x R,ax2 bx c 0 ? f(x) = (2–m) x2 2x 1 luoân döông ?
x R, ax 2 bx c 0 ? - Hoïc sinh giaûi 10’ Giaûi
-AÙp duïng nhaän xeùt treân - Chöa laø ttbh
.Vôùi m = 2 thì f(x) = – 2x + 1 khoâng giaûi vd 3 luoân döông vôùi moïi x - f(x) = (2–m)
. Vôùi m 2 , f(x) laø ttbh x 2 2x 1
coù phaûi laø ttbh khoâng ? Ta coù : ’ = m – 1 a Do ñoù : 0 x ,f(x) > 0 m < 1 ' 0
Vaäy m < 1 thì ña thöùc f(x) luoân döông
5).Cuõng coá daën doø : (3’)-Naém vöõng caùch xeùt daáu tam thöùc baäc hai; - Naém ñöôïc caùc daïng baøi taäp
6) Baøi taäp veà nhaø: 49-52 trang 140,141 102
Tieát 57,58 §7. BAÁT PHÖÔNG TRÌNH BAÄC HAI
I.MUÏC TIEÂU: Giuùp hoïc sinh: - Veà kieán thöùc:
+ Naém vöõng caùch giaûi baát phöông trìnhbaäc hai moät aån, baát phöông trình tích, baát phöông trình
chöùa aån ôû maãu thöùc vaø heä baát phöông trình baäc hai.
+ Vieát chính xaùc taäp nghieäm cuûa baát phöông trình daïng f(x) 0 hoaëc f(x) 0.
+ Khoâng ñöôïc ñôn giaûn caùc bieåu thöùc trong moät baát phöông trình moät caùch tuøy tieän.
- Veà kyõ naêng: Giaûi thaønh thaïo caùc baát phöông trình, heä baát phöông trình vaø giaûi moät soá baát phöông trình ñôn giaûn.
II. CHUAÅN BÒ CUÛA GIAÙO VIEÂN – HOÏC SINH:
- Giaùo vieân: Giaùo aùn, ñoà duøng daïy hoïc: thöôùc thaúng, baûng phuï.
- Hoïc sinh: Hoïc laïi baøi cuû, laøm baøi taäp veà nhaø vaø xem tröôùc baøi môùi.
III. TIEÁN TRÌNH BAØI DAÏY: Tg
HOAÏT ÑOÄNG CUÛA THAÀY
HOAÏT ÑOÄNG CUÛA TROØ NOÄI DUNG 103
5 Hoaït ñoäng1: -Gv kieåm tra só soá -Gv kieåm tra baøi cuû
Yeâu caàu: Xeùt daáu tam thöùc baäc hai
-Lôùp tröôûng baùo caùo só soá
sau: f(x) = 2x2 – 3x + 1 vaø goïi moät hoïc -Caû lôùp chuù yù. sinh leân baûng.
-Hoïc sinh leân baûng (coù theå
thöïc hieännhö sau) * Ta coù:
Tam thöùc baäc hai 2x2 – 3x + 1 coù hai nghieäm: x 1 1=1 vaø x2 = 2 Vì a = 2 > 0 neân 1
f(x) > 0 khi x ; ; 1 2 1
f(x) < 0 khi x 1 ; 2 1 f(x) = 0 khi x =1 hoaëc x = 2
-Gv goïi moät hoïc sinh nhaän xeùt baïn
-Gv söõa baøi laøm cuûa hoïc sinh vaø ñaùnh
- Hoïc sinh nhaän xeùt baïn giaù ñieåm. 104
15 Hoaït ñoäng2: -Caû lôùp chuù yù.
Gv chuyeån sang baøi môùi:”Neáu
yeâu caàu cuûa baøi toaùn laø: tìm
nhöõng giaù trò cuûa x maø sao cho f(x)
> 0 , f(x) < 0, hoaëc f(x) 0 hay
f(x) 0 thì ta seõ giaûi nhö theá naøo?
Ñoù laø noäi dung cuûa tieát hoïc
naøy”.Gv giôùi thieäu baøi môùi. §7. BAÁT PHÖÔNG -Gv giôùi thieäu muïc 1
-Gv: “Neáu ta coù f(x) > 0 , f(x) < 0, TRÌNH BAÄC HAI
hoaëc f(x) 0 hay f(x) 0 thì ta goïi -Hoïc sinh phaùt bieåu: “Baát
1.Ñònh nghóa vaø caùch giaûi.
ñoù laø baát phöông trình baäc hai vôùi phöông trình baäc hai (aån x) laø
f(x) laø tam thöùc baäc hai” Gv goïi
baát phöông trình coù moät a) Ñònh nghóa:
moät hoïc sinh phaùt bieåu.
trong caùc daïng f(x) > 0 , f(x) “Baát phöông trình baäc hai (aån
-Gv khaúng ñònh laïi ñònh nghóa vaø < 0, f(x)
x) laø baát phöông trình coù moät 0, f(x) 0 trong
ñöa noäi dung ñònh nghóa leân baûng.
trong caùc daïng f(x) > 0 , f(x)
ñoù f(x) laø moät tam thöùc baäc
-Gv giôùi thieäu caùch giaûi: “ AÙp < 0, f(x) hai”
0, f(x) 0 trong ñoù
duïng ñònh lí veà daáu cuûa tam thöùc
f(x) laø moät tam thöùc baäc hai” baäc hai”
-Gv ñöa ra Ví duï1 Giaûi baát
phöông trình: 2x2 – 3x + 1 > 0
b) Caùch giaûi: AÙp duïng ñònh lí
veà daáu cuûa tam thöùc baäc hai
Ví duï1: Giaûi baát phöông trình: 2x2 – 3x + 1 > 0 Giaûi:
Tam thöùc baäc hai 2x2 – 3x +
1 coù hai nghieäm: x1=1 vaø x2 = 1 2 Vaø coù a = 2 > 0 neân 1
2x2 – 3x + 1 > 0 khi x < 2 hoaëc x >1
Vaäy taäp nghieâm cuûa BPT 1
laø x ; ; 1 2
-Gv yeâu caàu thöïc hieän H1.
Bieåu dieãn taäp nghieäm BPT
-Gv goïi hoïc sinh ñoïc yeâu caàu cuûa
H1 sau ñoù Gv höôùng daãn hoïc sinh 1
-Hoïc sinh ñoïc ñeà baøi ) ( 2 1 thöïc hieän.
-Gv goïi 1 hoïc sinh ñöùng taïi choã
-Hoïc sinh ñöùng taïi choã traû H1.Tìm taäp nghieäm caûu caùc 105 thöïc hieän caâu a)
lôøi coù theå traû lôøi nhö sau baát phöông trình sau:
baát phöông trình coù taäp a) x2 + 5x + 4 < 0
nghieäm laø: x ; 4 1 b) -3x2 +2 3 x < 1
- Sau ñoùù Gv goïi hai hoïc sinh leân -Hai hoïc sinh leân baûng c) 4x – 5 7 2 x
baûng thöïc hieän caâu b) vaø c) thöïc hieän: 3
+HS1: taäp nghieäm cuûa baát phöông trình laø 1 x R \ 3
+HS2: taäp nghieäm cuûa baát
-Gv goïi hoïc sinh nhaän xeùt baïn vaø phöông trình laø x R
sau ñoù Gv söõa baøi taäp H1.
10 Hoaït ñoäng3:
2.Baát phöông trình tích vaø
Sau ñoù GV: “Töông töï nhö
baát phöông trình chöùa aån ôû
phöông trình thì ta cuõng coù baát maãu.
phöông trình tích vaø baát phöông
Ví duï2: Giaûi baát phöông
trình chöùa aån ôû maãu” 2
trình 2x 3x 2
chuyeån sang muïc 2 cuûa baøi hoïc. 0 2 x 5x 6
-Gv ñöa ra ví duï2 vaø Gv höôùng Giaûi:
daãn cho hoïc sinh caùch giaûi vaø tieán -Caû lôùp chuù yù
Ta xeùt daáu bieåu thöùc sau:
haønh caùch giaûi maãu cho caû lôùp 2 2 x 3x 2 f x hieåu. ( ) 2 x 5x 6
Töû thöùc laø tam thöùc baäc hai
-Gv höôùng daãn kyõ cho hoïc sinh
coù hai nghieäm laø: -2 vaø 1
caùch laáy nghieäm cuûa baát phöông 2 trình treân.
Maãu thöùc laø tam thöùc baäc
hai coù hai nghieäm laø: 2 vaø 3 Hoaït ñoäng4: * Gv laäp baûng xeùt daáu
15 -Gv cho caû lôùp thöïc hieän H2. -Hoïc sinh ñoïc H2.
* Keát luaän nghieäm cuûa baát
-Gv goïi moät hoïc sinh ñoïc yeâu caàu phöông trình laø H2. 1 -Caû lôùp chuù yù S ; 2 2 ; ; 3
-Gv höôùng daãn cho caû lôùp caùch 2 giaûi H2.
-Gv goïi moät hoïc sinh leân baûng
thöïc hieän H2 caû lôùp theo doõi caùch -Hoïc sinh leân baûng thöïc laøm cuûa baïn
hieän caùc baïn khaùc chuù yù
(hoïc sinh coù theå thöïc hieän nhö sau) Tacoù: 106
Xeùt f(x) = (4 -2x)(x2 +7x+ 12) H2 Giaûi baát phöông -Gv goïi hoïc
Nhò thöùc 4 -2x coù nghieäm x = 2 trình: sinh nhaän xeùt
Tam thöùc baäc hai x2 +7x+ 12 coù 2 nghieäm laø -3 vaø - (4 -2x)(x2 +7x+ 12) baøi laøm cuûa baïn 4. < 0
-Gv söõa BT vaø Xeùt daáu f(x) coù theå cho ñieåm hoïc sinh neáu x -4 -3 2 hoïc sinh thöïc 4 – 2x + + + 0 - hieän toát. x2+7x+1 + 0 - 0 + + - Gv ñöa ra ví 2 duï 3 vaø ñoàng f(x) + - + -
thôøi höôùng daãn Töø baûng xeùt daáu ta ñöôïc taäp nghieäm cuûa baát phöông cho hoïc sinh
trình laø: S ; 4 3 ; 2 caùch bieán ñoåi
- Moät hoïc sinh nhaän xeùt baïn cuûa baát phöông trình vaø nhaán maïnh laø chuùng ta khoâng ñöôïc - Caû lôùp chuù yù boû maãu thöùc. - Sau ñoù nhaän xeùt lôùp, ñaùnh giaù giôø hoïc vaø cho caû lôùp nghæ 15 Hoaït ñoäng1:
-Lôùp tröôûng baùo caùo só soá -Gv kieåm tra só soá -Caû lôùp chuù yù
3.Heä baát phöông baäc hai
Gv daãn vaøo baøi môùi: “Töông töï
Ví duï4: Giaûi heä baát phöông
nhö heä PT thì ta cuõng coù heä baát trình phöông trình” 3 2
x 7x 2 0 ) 1 ( -Gv giôùi thieäu muïc 3
(I ) 2 2x x 3 0 (2)
-Gv ñöa ra ví duï4 vaø höôùng daãn -HS1: BPT (1) coù taäp Giaûi caùch giaûi cho hoïc sinh. nghieäm BPT (1) coù taäp nghieäm
-Gv goïi töøng hoïc sinh giaûi töøng baát 1 S ; 1 1 ; 2
phöông trình (ñöùng taïi choã) S ; 1 ; 2 3 3 -HS2: BPT (2) coù taäp BPT (2) coù taäp nghieäm 8 nghieäm 3 S ; 1 3 2 S ;1 2 2 2 S 1 1 2 ) ( 3 S 2 3 -1 ( ) 2
Töø hai truïc soá ta deã daøng 107
suy ra taäp nghieäm cuûa heä
-Sau ñoù Gv höôùng daãn caùch laáy
baát phöông trình (I) laø:
nghieäm cuûa heä baát phöông trình S = 1 S S 1 ; 1 2 3
Bieåu dieãn taäp nghieäm
cuûa heä baát phöông trình treân
-Gv noùi theâm trong thöïc haønh giaûi ta 1 3 (-1 ) ) ( 2
coù theå laøm goïn laïi nhöng caàn kieåm 3 2
tra laïi baèng veõ nhaùp truïc soá. 15 Trong thöïc haønh Giaûi: Tacoù Hoaït ñoäng2: 1 x hoaëc x > 2
Gv cho hoïc sinh leân baûng thöïc (I) 3 hieän H3
-Hoïc sinh leân baûng (coù theå x 3 1
- Gv goïi moät hoïc sinh leân baûng thöïc thöïc hieän nhö sau) 2 1
hieän H3 caû lôùp chuù yù theo doõi baïn. Ta coù 2x 1 5 1 x 3 2 2
x 9x 7 0 Taäp nghieäm cuûa heä BPT x 2 ( 2 1 7 (I) laø: ;1 1 x 3 2 7 1 [ ] 2 H3 Giaûi heä baát phöông trình
Do ñoù heä coù taäp nghieäm laø 2x 1 5 7 2 2
x 9x 7 0
-Gv goïi hoïc sinh nhaän xeùt baïn S ; 2 2
-Gv söõa BT H3 vaø khaúng ñònh laïi keát quaû
- Hoïc sinh nhaän xeùt baïn Hoaït ñoäng3:
Gv giôùi thieäu baát phöông trình
coù chöùa tham soá vaø ñöa ra Ví duï 5
-Gv höôùng daãn cho hoïc sinh vì ñaây -Caû lôùp chuù yù
laø moät daïng toaùn ñoøi hoûi phaûi coù suy nghó.
-Gv hoûi: “Ñaây coù phaûi laø baát phöông
trình baäc hai ( aån x) hay khoâng? ”
-Gv:ñoái vôùi daïng toaùn naøy neáu heä soá
Ví duï 5. Tìm caùc giaù trò
a coù chöùa tham soá ta caàn xeùt tröôøng cuûa m ñeå baát phöông
-Hoïc sinh ñöùng taïi choã traû lôøi trình sau voâ nghieäm 108
7 Hoaït ñoäng4: (Neáu thôøi gian
coøn dö thì GV cho hoïc sinh söõa BT 56a-SGK trang 145)
-Gv cho hoïc sinh söõaBT 56a.
-Gv goïi moät hoïc sinh leân baûng thöïc hieän
-Hoïc sinh leân baûng thöïc hieän BT 56a
(hoïc sinh coù theå thöïc hieän nhö sau) 2
56a) 2x 9x 7 0 (*) 2
x x 6 0 Ta coù 7 hoaëc x > -1 (*) x 2 3 x 2
-Gv goïi moät hoïc sinh nhaän xeùt (*) -1 < x < 2 baïn.
Vaäy taäp nghieäm cuûa heä BPT (*) laø (-1;2)
-Gv söõa BT khaúng ñònh laïi vaø
coù theå cho ñieåm hoïc sinh neáu laøm toát BT.
- Sau ñoù nhaän xeùt lôùp, ñaùnh
giaù giôø hoïc vaø cho caû lôùp nghæ.
hôïp a = 0 vaø a 0
(coù theå traû lôøi nhö sau): Ñaây (m-2) x2+ 2(m+1)x + 2m
chöa phaûi laø baát phöông trình > 0
baäc hai. Vì neáu m = 2 thì baát
phöông trình khoâng coøn baäc hai.
(GV trình baøy baøi giaûi vaø
höôùng daãn töøng böùôc cho hoïc sinh hieåu)
Daën doø: (1phuùt)
Caùc em veà nhaø xem laïi baøi cuû
Laøm caùc baøi taäp trong saùch giaùo khoa: BT53 ; 54; 55; 56
vaø chuaån bò BT cho tieát luyeän taäp 109
Tieát 59-60 LUYEÄN TAÄP A . Muïc tieâu : 1/ Kieán thöùc :
Naém vöõng caùch giaûi baát phöông trình baäc hai moät aån, baát phöông trình tích , baát phöông trình chöùa aån ôû maãu
2/ Kyõ naêng : Giaûi thaønh thaïo caùc baát phöông trình.
3/ Tö duy- thaùi ñoä : Caån thaän , chính xaùc. B . Chuaån bò :
C . Tieán trình baøi daïy :
Baøi taäp 57. Tìm caùc giaù trò cuûa m ñeå pt sau coù nghieäm : x2 + (m-2)x- 2m + 3 = 0. TG Noäi dung HÑ cuûa Thaày HÑ cuûa Troø
Pt : x2 + (m-2)x - 2m+ 3 = 0 Laäp b2 ac 4 (m ) 2 2 ( 4 2 m ) 3 0 Pt coù nghieäm ? 2
m 4m 8 0 m 2 2 3 m 2 2 3
Baøi taäp 58. CMR: caùc pt sau voâ nghieäm duø m laáy baát kyø giaù trò naøo.
a) x2 – 2(m+1)x + 2m2 m + 3 = 0.
b) (m2+1)x2 + 2(m+2)x + 6 = 0 TG Noâi dung HÑ cuûa Thaày HÑ cuûa Troø
a)x2-2(m+1)x+2m2+m+3=0 CM : 0 m
döïa vaøo keát * ' (m+1)2 -2m2 –m -3 = -m2+m-2 quaû : Vì 1
0 vaø a = -1 < 0 m
a 0 ' 0 m x : 2
ax bx c 0 0 Vaäy Pt treân voâ nghieäm vôùi moïi m.
b)(m2+1)x2+2(m+2)x+6 = 0
a 0 * ' (m+2)2-(m2+1)6= -4m2+4m-2 x : 2
ax bx c 0
0 Vì = -4< 0 vaø a = -4 < 0 m ' 0 m
Vaäy Pt treân voâ nghieäm vôùi moïi m.
Baøi taäp 59. Tìm caùc giaù trò cuûa m ñeå BPT : (m-1)x2-2(m+1)x+3(m-2) > 0 nghieäm ñuùng x R TG Noäi dung HÑ cuûa Thaày HÑ cuûa Troø
(m-1)x2-2(m+1)x+3(m-2) >0 Ñaët veá traùi BPT baèng f(x) .m= 1 f(x)= - 4x-3 > 0 3 x 4
Khoâng thoûa maõn ñieàu kieän. .m 1 a f(x) > 0 x 0 ' 0 1
m m 5 2 m 5 m 1 110
Baøi taäp 60. Giaûi caùc baát phöông trình. 4 2
a) x x 0 2 x 5x 6 b) 1 1 0 2 x 7x 10 2 x 5x 6 TG Noäi dung HÑ cuûa Thaày HÑ cuûa Troø 4 2
a) x x
Goïi hs leân baûng giaûi baøi taäp a) 0 2 x 5x 6
Uoán naén caùch dieãn ñaït , 2 x ( 2 x )
1 0 x 0 x 1
Trình baøy baøi giaûi cuûa hoïcx 2 5x 6 0 x 3 x 2 sinh.
Laäp baûng xeùt daáu b) 1 1 0
Ta ñöôïc keát quaû :S=(-3;-2) ( ) 1 ; 1 2 x 7x 10 2 x 5x 6 b)
HD hs giaûi nhö caâu a) 1 1
HS leân baûng thöïc hieän baøi 0 2 x 7x 10 2 x 5x 6 giaûi 2x 4 0 ( 2
x 7x 10)( 2 x 5x ) 6 Laäp baûng xeùt daáu.
Ta ñöôïc keát quaû: S=(2;3) ; 5 ( )
Baøi taäp 61.Tìm taäp xaùc ñònh cuûa caùc haøm soá. a) y = (2x 1 )( 5 2x) . 2 b) x 5x 4 y = 2 2 x 3x 1 TG Noäi dung HÑ cuûa Thaày HÑ cuûa Troø a) y = (2x 1 )( 5 2x)
* A coù nghóa khi naøo ? * A coù nghóa khi A 0
HSXÑ (2x+5)(1-2x) 0 5 1
x 2 2 2
b) y = x 5x 4
* Caùch giaûi nhö caâu a) 2 x 5x 4 2 2 x 3x 1 HSXÑ 0 2 2 x 3x 1 x (x )( 1 x ) 4 1 0 x (x )( 1 2x 4 ) 1 0 2x 1 1 x 4
x 2
D. Cuûng coá: Höôùng daãn giaûi caùc baøi taäp coøn laïi.
E. Daën doø: veà nhaø laøm caùc baøi taäp coøn laïi vaø xem tröôùc baøi môùi. 111
Tieát 61 §8. MOÄT SOÁ PHÖÔNG TRÌNH VAØ
BAÁT PHÖÔNG TRÌNH QUY VEÀ BAÄC HAI
I.MUÏC TIEÂU: Giuùp hoïc sinh:
* Veà kieán thöùc: Naém vöõng caùch giaûi caùc phöông trình vaø baát phöông trình (quy veà baäc hai) chöùa aån
trong daáu giaù trò tuyeät ñoái vaø moät soá phöông trình vaø baát phöông trình chöùa aån trong daáu caên baäc hai
* Veà kyõ naêng: Giaûi thaønh thaïo caùc phöông trình vaø baát phöông trình coù daïng ñaõ neâu ôû treân.
II. CHUAÅN BÒ CUÛA GIAÙO VIEÂN – HOÏC SINH:
- Giaùo vieân: Giaùo aùn, ñoà duøng daïy hoïc: thöôùc thaúng, baûng phuï.
- Hoïc sinh: Hoïc laïi baøi cuû, xem tröôùc baøi môùi
III. TIEÁN TRÌNH BAØI DAÏY: tg
HOAÏT ÑOÄNG CUÛA THAÀY
HOAÏT ÑOÄNG CUÛA TROØ NOÄI DUNG BAØI HOÏC 20
§8. MOÄT SOÁ PHÖÔNG
TRÌNH VAØ BAÁT PHÖÔNG
TRÌNH QUY VEÀ BAÄC HAI
1.Phöông trình vaø baát
-Gv höôùng daãn töøng böôùc caùch
phöông trình chöùa aån trong giaûi cuûa Ví duï1
-Caû lôùp chuù yù caùch giaûi
daáu giaù trò tuyeät ñoái. cuûa phöông trình
Ví duï1: Giaûi baát phöông trình 2
x x x 3 2 0 Giaûi: +Neáu 3x – 2 0 thì 2
x x 3x 2 2 x 2x 2 +Neáu 3x – 2 < 0 thì 2
x x 3x 2 2 x 4x 2
Do ñoù ta coùbaát phöông trình töông ñöông vôùi: 3x 2 0 (I) 2
x 2x 2 0
-Gv goïi hai hoïc sinh leân baûng 3x 2 0
thöïc hieän giaûi heä (I) vaø heä (II) (II) 2
x 4x 2 0 112
-Hai hoïc sinh leân baûng thöïc hieän +HS1: x 2 Heä (I) 3
x 1 3 hoaëc x 1 3 x 1 3 +HS2: x 2
-Gv höôùng daãn caùch laáy taäp Heä (I) 3
nghieäm cuûa baát phöông trình
x 2 2 hoaëc x 2 2
Taäp nghieäm cuûa baát phöông x 2 2
trình: ;2 2 1 ; 3
H1 Giaûi phöông trình Hoaït ñoäng1: 2
x 8x 15 x 3
-Gv cho hoïc sinh thöïc hieän H1
-Gv höôùng daãn cho hoïc sinh caùch -Hoïc sinh leân baûng thöïc hieän H1 giaûi H1 Giaûi PT: 2
x 8x 15 x 3
-Gv goïi hoïc sinh leân baûng 2
x 8x 15 0 (I) 2
x 9x 18 0 2
x 8x 15 0 (II) 2
x 7x 12 0 x hoaëc x (I) 3 5 x ; 3 x 6 3 x (II) 5
-Gv goïi hoïc sinh nhaän xeùt baïn x ; 3 x 4
2.Phöông trình vaø baát 15 -Gv söõa BT H1 Vaäy S = 6 ; 4 ; 3
phöông trình chöùa aån
-Hoïc sinh nhaän xeùt baïn
trong daáu caên baäc hai -Gv giôùi thieäu muïc2
-Gv ñöa ra chuù yù ñoái vôùi vieäc giaûi PT coù chöùa caên -Gv giôùi thieäu Ví duï2 Ví duï2: Giaûi PT 3 2
x 24x 22 2x 1(*)
-Gv höôùng daãn caùch giaûi VD2 -Gv hoûi:
+ PT naøy coù ñieàu kieän gì?
+ Nghieäm cuûa noù phaûi thoûa ñieàu -Hoïc sinh traû lôøi kieän gì? + Bieåu thöùc 3 2
x 24x 22 0
+Nghieäm cuûa noù phaûi thoûa 113
+Nhaän xeùt VT vaø VP cuûa PT(*) 2x 1 0
+ VT vaø VP cuûa PT(*) laø nhöõng bieåu thöùc khoâng aâm.
-Gv khaúng ñònh laïi ta coù theå “Bình -Hoïc sinh leân baûng thöïc hieän
phöông hai veá cuûa PT (*)” Giaûi:
-Sau ñoù GV goïi hoïc sinh leân baûng (*) 2x 1 0
a) Ví duï2: Giaûi phöông trình
trình baøy baøi giaûi cuûa VD2 2
3x 24x 22 2x 2 1 3 2
x 24x 22 2x 1(*) x 1 2 2
x 20x 21 0 x 1 Hoaït ñoäng2: 2 x 21
-Gv goïi hoïc sinh nhaän xeùt baïn
x ;1 x 21
10 -Gv khaúng ñònh laïi vaø cho hoïc sinh Vaäy PT(*) coù nghieäm x = 21 thöïc hieän tieáp H2 -Gv höôùng daãn H2
-Gv goïi hoïc sinh leân baûng thöïc hieän
-Hoïc sinh leân baûng thöïc hieän Giaûi PT 2
x 56x 80 x 20 (I) x 20 (I) 0 2
x 56x 80 x 202 x 20 x 20 x 20
-Gv goïi hoïc sinh nhaän xeùt baïn
Vaäy PT(I) coù 1 nghieäm x = 20
-Gv khaúng ñònh laïi vaø cho ñieåm
-Hoïc sinh nhaän xeùt baïn
hoïc sinh (neáu laøm ñuùng) vaø cho lôùp nghó.
-Neáu coøn thôøi gian GV cho hoïc sinh giaûi BT 65 a)
Daën doø: (1phuùt)
Caùc em veà nhaø xem laïi baøi cuû
Laøm caùc baøi taäp trong saùch giaùo khoa: BT 65; 66 (trang 151)
vaø xem tröôùc baøi môùi 114
Tieát 62 §8. MOÄT SOÁ PHÖÔNG TRÌNH VAØ
BAÁT PHÖÔNG TRÌNH QUY VEÀ BAÄC HAI (tieáp theo)
I.MUÏC TIEÂU: Giuùp hoïc sinh:
* Veà kieán thöùc: Naém vöõng caùch giaûi caùc phöông trình vaø baát phöông trình (quy veà baäc hai) chöùa aån
trong daáu giaù trò tuyeät ñoái vaø moät soá phöông trình vaø baát phöông trình chöùa aån trong daáu caên baäc hai
* Veà kyõ naêng: Giaûi thaønh thaïo caùc phöông trình vaø baát phöông trình coù daïng ñaõ neâu ôû treân.
II. CHUAÅN BÒ CUÛA GIAÙO VIEÂN – HOÏC SINH:
- Giaùo vieân: Giaùo aùn, ñoà duøng daïy hoïc: thöôùc thaúng, baûng phuï.
- Hoïc sinh: Hoïc laïi baøi cuû, xem tröôùc baøi môùi
III. TIEÁN TRÌNH BAØI DAÏY: tg
HOAÏT ÑOÄNG CUÛA THAÀY
HOAÏT ÑOÄNG CUÛA TROØ NOÄI DUNG BAØI HOÏC 10
2.Phöông trình vaø baát phöông
trình chöùa aån trong daáu caên baäc hai
Ví duï3: Giaûi baát phöông trình 2
x 3x 10 x 2 (A) Giaûi:
-Gv giôùi thieäu Ví duï 3
BPT (*) töông ñöông vôùi:
Ví duï3: Giaûi baát phöông trình
-Caû lôùp chuù yù caùch giaûi 2
x 3x 10 0 2
x 3x 10 x 2 cuûa baát phöông trình (A) x 2 0
-Gv höôùng daãn töøng böôùc caùch giaûi 2
x 3x 10 x 22 cuûa Ví duï3
x hoaëc x
-Gv giôùi thieäu daïng cuûa BPT 2 5 x Daïng: 2 5 x 14 A B (*) x 14 A 0 (*)
Vaäy taäp nghieäm cuûa baát phöông B 0 trình laø: 14 ; 5 A 2 B
-Sau ñoù Gv trình baøy caùch giaûi cho
hoïc sinh hieåu caùch laøm baøi 115
10 Hoaït ñoäng3:
-Hoïc sinh leân baûng thöïc hieän
-Gv goïi hai hoïc sinh leân baûng thöïc H3
H3 Giaûi baát phöông trình :
hieän H3 vôùi caùch laøm töông töï nhö 2
x 2x 15 x 3 (I) 2
x 2x 15 x 3 VD3 2
x 2x 15 0 (I) x 3 0 2
x 2x 15 x 2 3 hoaëc x 3 x 5 x 3 x 6 5 x 6
Vaäy taäp nghieäm cuûa baát phöông trình laø: 6 ; 5
-Hoïc sinh nhaän xeùt baïn
-Gv goïi hoïc sinh nhaän xeùt baïn
Ví duï4: Giaûi baát phöông trình 10 2
x x x
-Caû lôùp chuù yù caùch giaûi cuûa 4 3
Ví duï4: Giaûi baát phöông
-Gv höôùng daãn töøng böôùc caùch giaûi baát phöông trình trình cuûa Ví duï4 2
x 4x x 3 (B)
-Sau ñoù Gv trình baøy caùch giaûi cho -Hai hoïc sinh leân baûng thöïc x 3 0
hoïc sinh hieåu caùch laøm baøi cuûa Ví hieän (I) 2 x 4x 0 duï4 +HS1 (B) x 3 0
-Gv giôùi thieäu daïng cuûa BPT x 3 0 (II) (I) 2
x 4x x 2 3 (II) Daïng: (**) 2 x 4x 0 A B hoaëc B B 0 x 3 x (**) 0 hoaëc 4 A A 2 x 0 0 B
-Gv ñöa ra hai heä baát phöông trình x 0
vaø goïi hai hoïc sinh leân baûng thöïc +HS2 hieän x 3 (II) 0
-Gv höôùng daãn caùch laáy nghieäm 2
x 4x x 2 3
cuûa (**) laø ta Hôïp mieàn nghieäm x 3 9 cuûa hai heä treân. 9 x x 2 2
Vaäy nghieäm cuûa bpt laø: 9 x 0 v x 2
-Gv goïi hoïc sinh nhaän xeùt baïn x 2 x 2 (A) 0 hoaëc B) 0 Hoaït ñoäng4: 2 x 1 0 2
x 1 x 22
-Gv cho hoïc sinh thöïc hieän H4 x 2 H4 Giaûi baát phöông Vôùi (A) x
-Gv höôùng daãn caùch giaûi H4 töông 2 x 1 x 1 trình
töï nhö VD4 vaø goïi hoïc sinh leân x 2 5 2
x 1 x 2 Vôùi (B) baûng thöïc hieän. 2 x 4x 5 4 Giaûi: Bpt töông 15 5 5 ñöông vôùi hai heä sau: S= ;2 ; 2 = ; 4 4 116
-Hoïc sinh nhaän xeùt baïn
Daën doø: (1phuùt)
Caùc em veà nhaø xem laïi baøi cuû
Laøm caùc baøi taäp trong saùch giaùo khoa: BT 67; 68 (trang 151)
vaø chuaån bò baøi taäp cho tieát luyeän taäp 117
Tieát 63 LUYEÄN TAÄP A. Muïc tieâu:
1/ Kieán thöùc :Naém vöõng caùch giaûi caùc phöông trình vaø baát phöông trình ( quy veà baäc hai ), chöùa aån trong daáu
giaù trò tuyeät ñoái vaø moät soá phöông trình , baát phöông trình chöùa aån trong daáu caên baäc hai.
2/ Kyõ naêng : Giaûi thaønh thaïo caùc phöông trình , baát phöông trình ñaõ neâu.
3/ Tö duy thaùi ñoä : Chính xaùc , caån thaän. B . Chuaån bò: 1/ Giaùo vieân :
2/ Hoïc sinh : Thuoäc baøi vaø laøm baøi taäp ñaày ñuû . C.Tieán trình baøi daïy:
1/ Baøi taäp 68. Tìm taäp xaùc ñònh cuûa caùc haøm soá a) y = 2
x 3x 4 x 8 . 2 b) x x 1
2x 1 x 2 TG Noäi dung HÑ cuûa thaày HÑ cuûa troø a) y = 2
x 3x 4 x 8 HÑ1:KTBC
HS neâu laïi caùc coâng thöùc theo söï höôùng
HS neâu coâng thöùc. daãn cuûa GV.
f (x) g(x) 0 ( ) 0 2 * HSXÑ
* HSXÑ x x x ? 3 4 8 0
* Ta ñöa veà C thöùc naøo ? 2
x 3x 4 0 hoaëc 2
x 3x 4 x 8 0 2
x 3x 4 0 2
x 3x 4 x 8 0 x , 4 x 4 x 1 1 hoaëc x R 6 x 2 x , 4
x 1 hoaëc -4< x < 1 Taäp n0 S = (- ; ) 4 ; 1 [ ) ( ) 1 ; 4 . 2 2 x x b) y = x x 1 * 1
0 2x 1 x 2 0
2x 1 x 2
2x 1 x 2 * HSXÑ ?
( x 2 x 1 0 x )
* Xeùt daáu x2+x+1 > 0 2x 1 0 hoaëc
2x 1 x 2 0 2x 1 0 1
x 3 x
2x 1 x 2 0 3 118 S = (- 1 ; ) ; 3 ( ) 3
2/ Baøi taäp 69. Giaûi caùc phöông trình vaø baát phöông trình. 2
a) x 2 2 x 1
b) 3x 4 3 . x 2 TG Noäi dung HÑ cuûa Thaày HÑ cuûa Troø 2 ( ) 0 2 2 2 a) x 2 x x x x a a x a 2 2 2 2 2 2 2 x 1
Döïa vaøo ct treân giaûi pt. x 1 x 1 x 1 x 1 x 1 2
x 2x 4 0 2
x 2x 0
x 1 5 x 0 x 2 b) 3x 4 3 3x 4 3x 4 x 2 x a (a )
0 a x a 3 3 3 x 2 x 2
3x 4 3 0 1 x
x x 2 2 3 3x 4 3 0 x 2 x 2 1 x 3
3/ Baøi taäp 70 a). Giaûi baát phöông trình : 2 x 5x 4 2
x 6x 5 . TG Noäi dung HÑ cuûa Thaày HÑ cuûa Troø 2
x 5x 4 x2+ 6x +5 Baát phöông trình thuoäc daïng 2
x 5x 4 2 x 6x 5
CT naøo ? trình baøy caùch giaûi 2x 5x 4 0 2
x 5x 4 2 x 6x 5 2
x 5x 4 0 2
x 5x 4 2 x 6x 5
x 1 x 4 1 x 4 1 x x R 11
x 4 1 x 4 x 1
4/ Baøi taäp 72 b) Giaûi baát phöông trình : 2x 4 1 2 x 3x 10 119 TG Noäi duïng HÑ cuûa Thaày HÑ cuûa Troø * 2x 4 2x 4 1
* Ñ K cuûa baát phöông trình 1 2 x 3x 10 2 x 3x 10 2
x 3x 10 0 2
x 3x 10 2x 4
x2 3x 10 0
x 2 x 5 2x 4 0 x 2 2 2
x 3x 10 (2x ) 4 x R x 5
D. Cuûng coá : * Höôùng daãn giaûi baøi taäp.
E. Daën doø veà nhaø laøm heát caùc baøi taäp coøn laïi. 120
Tieát 64 OÂN TAÄP CHÖÔNG IV A .Muïc tieâu :
1/ Veà kieán thöùc :Naém vöõng caùc tính chaát veà BÑT , BÑT coù chöùa giaù trò tuyeät ñoái, BÑT Coâsi, BPT
thöông , BPT vaø HBPT baäc nhaát hai aån.
2/ Veà kyõ naêng : Giaûi thaønh thaïo caùc baøi taäp PT, BPT, moät soá PT vaø BPT quy veà baäc hai.
3/ Veà tö duy thaùi ñoä : Caån thaän , chính xaùc. B . Chuaån bò :
GV : baûng phuï; phieáu hoïc taäp
HS : hoïc thuoäc baøi , laøm tröôùc baøi taäp oân chöông .
C .Tieán trình baøi daïy : I. Lyù thuyeát:
1/ Baát ñaúng thöùc .
a) Moät soá tính chaát cuûa BÑT: Giaû söû a, b, c, d laø nhöõng soá thöïc . Khi ñoù:
a> b vaø b > c a > c ;
a > b a + c > b + c ;
a+c > b a > b – c ;
Neáu c > 0 thì a > b ac bc
Neáu c < 0 thì a > b ac bc a b a b
a c b d ;
a c b d ; c d c d a b 0
ac bd ; c d 0 a > b n n *
0 a b n N ;
a b 0 a b ; 3 3 a b a b ;
b) Baát ñaúng thöùc veà giaù trò tuyeät ñoái. * a
R, a a x * a a
0 ; x a a x a ; x a x a
* a b a b a
,b R . Coù ñaúng thöùc ab 0 .
* a b a b a
,b R .
c) Baát ñaúng thöùc Coâsi.
* a b ab vôùi moïi a,b khoâng aâm. Coù ñaúng thöùc khi vaø chæ khi a = b. 2 121
* a b c 3
abc vôùi a, b, c khoâng aâm. Coù ñaúng thöùc khi vaø chæ khi a = b = c . 3
2/ Caùc ñònh lyù veà daáu cuûa nhò thöùc baäc nhaát vaø tam thöùc baäc hai.
a) Cho nhò thöùc f(x) = ax + b . Khi ñoù : x -
b + a af(x) - 0 +
b) Cho tam thöùc baäc hai f(x) = ax2 + bx +c .
Neáu 0 thì f(x) coù hai nghieäm phaân bieät x1< x2. Khi ñoù,
x - x1 x2 + af(x) + 0 - 0 + b
Neáu 0 thì f(x) coù nghieäm keùp x0 = - . Khi ñoù, 2a
x - x0 + af(x) + 0 +
* Neáu 0 thì f(x) voâ nghieäm. Khi ñoù ,
x. - + af(x) +
3/ Baát phöông trình .
a) Baát phöông trình töông ñöông.
Hai baát phöông trình goïi laø töông ñöông vôùi nhau neáu chuùng coù cuøng moät taäp nghieäm.
Moät baát phöông trình goïi laø töông ñöông vôùi moät heä baát phöông trình neáu BPT vaø HBPT coù cuøng moät taäp nghieäm.
b) Baát phöông trình ax + b < 0
- Neáu a > 0 , S = (- ; - b) a
- Neáu a < 0 , S = (- b ;) a
c) Baát phöông trình baäc hai, baát phöông trình tích vaø baát phöông trình chöùa aån ôû maãu thöùc.
d) Baát phöông trình vaø phöông trình chöùa aån trong daáu giaù trò tuyeät ñoái vaø trong daáu caên baäc hai. f (x) 0 f (x)
* Baát phöông trình
f (x) g(x) 0 0
f (x) g(x) 0 f (x) g(x) 0 122 g(x) * Phöông trình 0
f (x) g(x) f (x) 2 g (x) f (x) 0 Baát phöông trình
f (x) g(x) g(x) 0 f (x) 2 g (x)
f (x) 0 g(x) 0 Baát phöông trình
f (x) g(x)
g(x) 0 f (x) 2 g (x)
c) Baát phöông trình vaø heä baát phöông trình baäc nhaát hai aån.
Daïng ax + by + c > 0 ( hoaëc ax + by + c < 0 )
Mieàn nghieäm cuûa BPT laø moät nöõa maët phaúng.
Mieàn nghieäm cuûa heä BPT laø giao caùc mieàn nghieäm cuûa caùc baát phöông trình. II. Baøi taäp.
Baøi taäp 77.CM caùc baát ñaúng thöùc sau :
a) a+b+c ab bc ac vôùi a , 0 b , 0 c .
0 Khi naøo coù ñaúng thöùc? b) 2 2 2 2 2 2
a b b c a c (
abc a b c) vôùi a, b, c R . Khi naøo coù ñaúng thöùc? TG Noäi dung HÑ cuûa Thaày HÑ cuûa Troø
a) a+b+c ab bc ac * a+b 2 ab
* a+b 2 ab
* a+b = 2 ab a b
b+c 2 bc
a+c 2 ac
Coäng töøng veá ba BÑT ta coù
ñieàu caàn chöùng minh.
Coù ñaúng thöùc khi a = b = c b) 2 2 a b 2 2 b c 2 2 c a
* ( x – y)2 0 ?
* x2 y2 2xy abc(a+b+c) 2 2 2 2 2
a c b c 2abc 2 2 2 2 2
a b c b 2acb 2 2 2 2 2
b a c a 2bca
Coäng töøng veá ba BÑT ta coù ñieàu caàn chöùng minh
Coù ñaúng thöùc khi a = b = c
Baøi taäp 78. Tìm giaù trò nhoû nhaát cuûa caùc haøm soá. 2 a) f(x) = 1 x 2 x b) g(x) = x 2 x 1 TG Noäi dung HÑ cuûa Thaày HÑ cuûa Troø a) 1 1 f(x) = x
Vì x 0 neân x vaø cuøng daáu x x .f(x)= 1 1 x 2 x
2 x 0 x x Daáu baèng xaûy ra 1 x x 1 x 123 Vaäy minf(x) = 2 2
b) g(x) = x 2 * x R , 2 2 x 1 .g(x) = x 1 1 2 x 1 2 x 1 2 = x 2 1 1 x 1 2 2 2 x 1 2 x 1 .g(x) = 2 2 1 x 1 2 x 1 2
x 1 1 x 0 Ming(x) = 2
Baøi taäp 79. Tìm caùc giaù trò cuûa tham soá m sao cho heä BPT sau coù nghieäm.
7 x 1 3 x 13 ) 1 ( 6 2 2 3 2 m x 1 4 m x ( ) 2 TG Noäi dung HÑ cuûa Thaày HÑ cuûa Troø 7 1 3 13 23 Tìm S x x 1 vaø S2 S1 = (- ; ) 6 2 2 3
HeäBPT coù nghieäm 2
m2x 1 m4 x 2
S S
S2 = [ m ;1) 1 2 2 23
Heä BPT coù nghieäm m 1 2 2 25 5 2 m m 2 2
3)Cuûng coá: Xem laïi nhöõng kieán thöùc ñaõ hoïc .
4)Daën doø: Giaûi nhöõng bt coøn laïi 124
Chöông V Thoáng keâ ******
Tieát 66 §1. MOÄT SOÁ KHAÙI NIEÄM MÔÛ ÑAÀU. 1/ Muïc tieâu:
1. Kieán thöùc cô baûn: Khaùi nieäm thoáng keâ, maãu soá lieäu vaø kích thöôùc maãu.
2. Kyõ naêng, kyõ xaûo: Reøn luyeän kó naêng nhaän bieát khaùi nieäm thoáng keâ, kyõ naêng tìm kích thöôùc maãu.
3. Thaùi ñoä nhaän thöùc: Thoâng qua khaùi nieäm thoáng keâ, maãu soá lieäu vaø kích thöôùc maãu hoïc sinh lieân
heä vôùi thöïc teá vaø töø thöïc teá coù theå thieát laäp moät baøi toaùn thoáng keâ. Hieåu roõ hôn vai troø cuûa thoáng keâ trong ñôøi soáng.
2/ Chuaån bò phöông tieän daïy hoïc:
a) Thöïc tieãn: Học sinh đã biết khái niệm về thống kê.
b) Phöông tieän daïy hoïc: Baûng phuï, maùy tính boû tuùi.
3/ Tieán trình tieát daïy: a)Kieåm tra baøi cuõ: b) Giaûng baøi môùi:
Hoaït ñoäng 1:Khaùi nieäm thoáng keâ. TG
Hoaït ñoäng cuûa giaùo vieân
Hoaït ñoäng cuûa hoïc sinh Noäi dung
_GV neâu moät soá VD veà +Neâu VD veà thoáng keâ maø em 1.Thoáng keâ laø gì ? thoáng keâ. bieát. Thoáng keâ laø khoa hoïc
Thoáng keâ daân soá cuûa ñòa +Neâu ñoái töôïng ñieàu tra trong veà caùc phöông phaùp thu
5' phöông,T.keâ keát quaû hoïc thoáng keâ em vöøa neâu. thaäp, toå chöùc,trình taäp cuûa HS,T.keâ taêng
baøy,phaân tích vaø xöû lyù
tröôûng kinh teá cuûa moät ñôn soá lieäu. vò saûn xuaát…..
Hoaït ñoäng 2: Khaùi nieäm maãu soá lieäu. TG
Hoaït ñoäng cuûa giaùo vieân
Hoaït ñoäng cuûa hoïc sinh Noäi dung Treo baûng phuï trang 2.Maãu soá lieäu. 160(sgk) +Soá löôïng HS Moät taäp con höõu haïn
+Daáu hieäu ñieàu tra laø gì?
+Moät lôùp hoïc caáp THPT
caùc ñôn vò ñieàu tra ñgl
10' +Ñôn vò ñieàu tra laø gì ?
moät maãu.Soá phaàn töû
+Töø ñoù neâu khaùi nieäm kích
cuûa moät maãu ñgl kích thöôùc maãu.
+ Kích thöôùc maãu laø 10.
thöôùc maãu.Daõy caùc giaù
+Haõy neâu kích thöôùc maãu trò cuûa daáu hieäu thu 125 trong VD treân.
ñöôïc treân maãu ñgl moät
+Ta chæ ñieàu tra maãu maø maãu soá lieäu. thoâi
* Neáu thöïc hieän ñieàu
tra treân moïi ñôn vò ñieàu
tra thì ñoù laø ñieàu tra
toaøn boä.Neáu chæ ñieàu tra
treân moät maãu thì ñoù laø ñieàu tra maãu. +HS ñoïc vaø thaûo luaän * Thöïc hieän H1
+ Nhaø maùy saûn xuaát söõa vôùi soá _Neâu BT H1
löôïng hoäp söõa raát nhieàu.
+Moät nhaø maùy saûn xuaát
söõa vôùi soá löôïng hoäp söõa +Khoâng theå ñieàu tra ñöôïc toaøn nhieàu hay ít? boä
+ Coù theå ñieàu tra ñöôïc toaøn boä khoâng ? _GV neâu caùc khaû naêng ñieàu tra.
Hoaït ñoäng 3:Caâu hoûi traéc nghieäm. TG
Hoaït ñoäng cuûa giaùo vieân
Hoaït ñoäng cuûa hoïc sinh Noäi dung
Goïi HS nhaéc laïi khaùi nieäm Daõy caùc giaù trò cuûa daáu hieäu thu Caâu 1:Khi ñieàu tra maãu soá lieäu.
ñöôïc treân maãu ñgl moät maãu soá chieàu cao cuûa HS moät lieäu
khoái lôùp taïi moät tröôøng
Maãu soá lieäu ôû ñaây laø gì? MSL laø 30 HS phoå thoâng.Ngöôøi ta
Khaúng ñònh naøo ñuùng ? Khaúng ñònh d).Ñuùng choïn 30 HS cuûa khoái
Caâu 2:Töø gt caâu 1.Haõy
ñoù.Haõy choïn khaúng ñònh
choïn khaúng ñònh ñuùng. ñuùng : a. a. 15'' Kích thöôùc maãu laø Maãu soá lieäu laø taát 30 Khaúng ñònh a).Ñuùng caû HS cuûa khoái ñoù.
b. Kích thöôùc maãu laø 1
b. Maãu soá lieäu laø taát c. Kích thöôùc maãu laø caû HS cuûa tröôøng moät khoái lôùp ñoù. d. Kích thöôùc maãu
c. Maãu soá lieäu laø moät khoâng xaùc ñònh HS cuûa khoái ñoù. d. Maãu soá lieäu laø 30 HS cuûa khoái ñoù.
Hoaït ñoäng 4:Höôùng daãn caâu hoûi vaø baøi taäp. TG
Hoaït ñoäng cuûa giaùo vieân
Hoaït ñoäng cuûa hoïc sinh Noäi dung Daáu hieäu laø gì?
soá con trong moät gia ñình Baøi 1:
Ñôn vò ñieàu tra laø gì?
moät gia ñình ôû huyeän A a). Daáu hieäu : soá con
10' Kích thöôùc maãu laøbao laø 80 trong moät gia ñình.Ñôn nhieâu?
vò ñieàu tra:moät gia ñình 126
ôû huyeän A .Kích thöôùc Baøi 2 töông töï HS giaûi maãu laø 80. Goïi HS giaûi b). Coù 8 giaù trò khaùc nhau trong maãu soá lieäu
treân laø :0,1,2,3,4,5,6,7 .
c). Cuûng coá: (5') Goïi HS nhaéc laïi khaùi nieäm thoáng keâ, maãu soá lieäu, kích thöôùc maãu.
d) Baøi taäp veà nhaø: Chuaån bò baøi taäp 2 trang 161 sgk. 127
Tieát 67,68 §2. TRÌNH BAØY MOÄT MAÃU SOÁ LIEÄU. 1/ Muïc tieâu:
1. Kieán thöùc cô baûn: Ñoïc vaø hieåu ñöôïc noäi dung moät baûng phaân boá taàn soá - taàn suaát, baûng phaân boá
taàn soá - taàn suaát gheùp lôùp.
2. Kyõ naêng, kyõ xaûo: Bieát laäp baûng phaân boá taàn soá - taàn suaát töø maãu soá lieäu ban ñaàu. Bieát veõ bieåu
ñoà taàn soá, taàn suaát hình coät; bieåu ñoà taàn suaát hình quaït; ñöôøng gaáp khuùc taàn soá, taàn suaát ñeå theå hieän
baûng phaân boá taàn soá - taàn suaát gheùp lôùp.
3. Thaùi ñoä nhaän thöùc: Thoâng qua khaùi nieäm thoáng keâ, maãu soá lieäu vaø kích thöôùc maãu hoïc sinh lieân
heä vôùi thöïc teá vaø töø thöïc teá coù theå thieát laäp moät baøi toaùn thoáng keâ. Hieåu roõ hôn vai troø cuûa thoáng keâ trong ñôøi soáng.
2/ Chuaån bò phöông tieän daïy hoïc:
a) Thöïc tieãn: Học sinh đã biết một số khái niệm liên quan đến thống kê.
b) Phöông tieän daïy hoïc: Baûng phuï, maùy tính boû tuùi.
3/ Tieán trình tieát daïy:
a) Kieåm tra baøi cuõ: (5') Khi ñieàu tra soá hoïc sinh trong moät lôùp hoïc cuûa tröôøng THPT Traàn Quoác
Toaûn, ngöôøi ta thu ñöôïc nhö sau:
10A1 10A2 10A3 10A4 10A5 10C 10CBA 10CBB 10CBD 44 44 40 40 34 40 44 42 34
Haõy chæ ra: maãu, kích thöôùc maãu vaø maãu soá lieäu? b) Giaûng baøi môùi:
Hoaït ñoäng 1: Baûng phaân boá taàn soá - taàn suaát. TG
Hoaït ñoäng cuûa giaùo vieân
Hoaït ñoäng cuûa hoïc sinh Noäi dung
?: " Treân maãu soá lieäu treân coù TL: Coù 4 loaïi soá lieäu 1/ Baûng phaân boá taàn soá - taàn
bao nhieâu loaïi soá lieäu khaùc khaùc nhau vaø x1 = 34 suaát:
nhau? Moãi loaïi xuaát hieän bao xuaát hieän 2 laàn, x2 = 40 Soá laàn xuaát hieän cuûa moãi nhieâu laàn?"
xuaát hieän 3 laàn, x3 = 42 giaù trò trong maãu soá lieäu ñöôïc
xuaát hieän 1 laàn, x4 = 44 goïi laø taàn soá cuûa cuûa giaù trò
xuaát hieän 3 laàn. ñoù.
15' Soá n1 = 2 goïi laø taàn soá cuûa Chuù yù nghe, hieåu.
Coù theå trình baøy goïn baûng giaù trò x1.
soá lieäu vaø taàn soá thaønh moät
Yeâu caàu hoïc sinh tính caùc Hoïc sinh tính. baûng:
taàn soá cuûa caùc giaù trò coøn laïi. Giaù trò (x) x1 ... xm
?: "Ñeå bieát ñöôïc tæ leä xuaát TL: Ta laáy 2 chia cho 9. Taàn soá n1 ... nm N
hieän lôùp coù 34 hoïc sinh trong (n)
9 lôùp ta tính nhö theá naøo? 128
* Ngöôøi ta thöôøng vieát taàn
goïi laø baûng phaân boá taàn soá.
suaát döôùi daïng %.
Taàn suaát fi cuûa giaù trò xi laø
Yeâu caàu hoïc sinh tính caùc Tính vaø ghi keát quaû tæ soá giöõa taàn soá ni vaø kích
taàn suaát cuûa caùc giaù trò coøn leân baûng phaân soá taàn soá thöôùc maãu N: f ni laïi. - taàn suaát. i = N
Yeâu caáu thöïc hieän hoaït Thöïc hieän hoaït ñoäng Boå sung theâm moät haøng ñoäng H1. theo nhoùm.
taàn suaát vaøo baûng phaân boá
Chuù yù Coù theå laäp baûng phaân
taàn soá ta ñöôïc baûng phaân boá
soá taàn soá - taàn suaát theo coät taàn soá - taàn suaát. doïc.
* Chuù yù: Kích thöôùc maãu baèng toång caùc taàn soá.
Hoaït ñoäng 2: Baûng phaân boá taàn soá vaø taàn suaát gheùp lôùp. TG
Hoaït ñoäng cuûa g v
Hoaït ñoäng cuûa h s Noäi dung
2/ Baûng phaân boá taàn soá vaø taàn suaát gheùp lôùp:
Giôùi thieäu veà baøi Nghe vaø hieåu vaán Ví duï: Ñeå chuaån bò may ñoàng phuïc
toaùn ví duï: Ñeå may ñoà ñeà.
cho hoïc sinh trong moät lôùp hoïc, ngöôøi cho hoïc sinh cuûa moät
ta ño chieàu cao cuûa 36 hoïc sinh vaø thu
lôùp, ngöôøi thôï may ño
ñöôïc:(Chieàu cao cuûa hoïc sinh (ñvò:
chieàu cao cuûa töøng hoïc cm) sinh. Nhöng khoâng theå 158 152 156 168 160 may theo töøng soá ño 170 neân thôï may phaân chia 166 161 160 172 173 caùc hoïc sinh thaønh 150 töøng nhoùm coù chieàu 167 165 163 158 162 cao gaàn nhau ñeå may 169 chung moät kích thöôùc. 159 163 164 161 160
15' Yeâu caàu hoïc sinh 164
ñeám vaø thoáng keâ laïi soá Thoáng keâ soá lieäu. 159 163 155 163 154 lieäu töùng "lôùp". 161 Xeùt baûng:
Lôùp soá ño chieàu cao Taàn Taàn Neâu öùng duïng cuûa (cm) soá suaát baûng phaân boá treân.
Nghe vaø lieân heä vôùi (%) thöïc teá. [150; 156) 6 16,7 [156; 162) 12 33,3 [162; 168) 13 36,1 [168; 174] 5 13,9 Yeâu caàu hoïc sinh Coäng 36 100%
thöïc hieän hoaït ñoäng Thöïc hieän hoaït Baûng treân ñöôïc goïi laø baûng phaân boá H2. ñoäng theo nhoùm.
taàn soá vaø taàn suaát gheùp lôùp. Neáu trong
baûng 4 boû coät taàn soá thì seõ coù baûng 129
phaân boá taàn suaát gheùp lôùp, boû coät taàn
suaát thì seõ coù phaân boá taàn soá gheùp lôùp.
Hoaït ñoäng 3: Bieåu ñoà. TG
Hoaït ñoäng cuûa giaùo vieân
H ñ cuûa hoïc sinh Noäi dung 3/ Bieåu ñoà :
Treo baûng phaân boá taàn soá - Quan saùt, hình thaønh a) Bieåu ñoà taàn soá taàn suaát taàn suaát gheùp lôùp: vaán ñeà. hình coät: Lôùp Taàn soá 14 [160; 162] 6 12 10 [163; 165] 12 8 [166; 168] 10 6 [169; 171] 5 4 2 [172; 174] 3 0 160 162 163 165 166 168 169 171 172 174 N = 36
Neâu yù nghóa cuûa baûng phaân Chuù yù nghe ñeå thaáy
boá taàn soá - taàn suaát gheùp lôùp.
ñöôïc vai troø cuûa bieåu
Treo baûng phaân boá taàn soá - ñoà. taàn suaát gheùp lôùp:
Lôùp soá ño chieàu Taàn suaát
b) Ñöôøng gaáp khuùc taàn soá cao (%) taàn suaát: (cm) _Veõ caùc ñoaïn M1M2, M2M3,M3M4,M4M5 ta ñöôïc [150; 156) 16,7
moät ñöôøng gaáp khuùc. 30' [156; 162) 33,3
_Neáu ñoä daøi ñoaïn AiMi laáy [162; 168) 36,1
baèng taàn suaát cuûa lôùp thöù I thì [168; 174] 13,9 khi veõ caùc ñoaïn M1M2, Coäng 100% M2M3,M3M4,M4M5 ta ñöôïc
?: "Hai bieåu ñoà hình coät treân TL: Moät bieåu ñoà coù ñöôøng gaáp khuùc taàn suaát
coù ñaëc ñieåm naøo khaùc nhau?". khe hôû ôû giöõa, moät c).Bieåu ñoà hình quaït Baûng
bieåu ñoá khoâng.
Bieåu ñoà hình quaït raát thích Neâu VD3 treo hình 5.1
hôïp cho vieäc theå hieän baûng
?: "Ñoä roäng cuûa moãi coät so vôùi
phaân boá taàn suaát gheùp lôùp.
moãi lôùp nhö theá naøo?" 5 lôùp (5 coät )
Hình troøn ñöôïc chia thaønh
?: "Ñoä cao cuûa moãi coät so vôùi Chieàu cao töông öùng nhöõng hình quaït .Moãi lôùp
taàn soá cuûa moãi lôùp nhö theá vôùi taàn suaát.
ñöôïc töông öùng vôùi moät hình naøo?
quaït maø dieän tích cuûa noù tæ leä
Yeâu caàu hoïc sinh so saùnh soá 161,164,167,170,173
vôùi taàn suaát cuûa lôùp ñoù. lôùp vaø soá coät.
Yeâu caàu hoïc sinh neâu caùc
böôùc veõ bieãu ñoà hình coät.
Yeâu caàu hoïc sinh thöïc hieän HS quan saùt hoaït ñoäng H1. 130
+Trong baûbg coù maáy lôùp?
+Chieàu cao cuûa moãi coät nhö HS phaân nhoùm töï laøm theá naøo? H4
_Haõy xaùc ñònh giaù trò trung
ñieåm cuûa moãi lôùp ôû baûng 5
+Neâu caùc giaù trò trung ñieåm ñoù _Treo hình 5.3
+Dieän tích tæ leä thuaän vôùi taàn suaát _Höôùng daãn HS laøm H4
+Taàn suaát tæ leä thuaän vôùi taàn soá
+Dieän tích tæ leä thuaän vôùi taàn soá
_Neâu yù nghóa vieäc veõ bieãu ñoà +Goùc ôû taâm cuûa lôùp I : hình quaït. 1 0 0 360 60 _Neâu VD5 6
+So saùnh dieän tích moãi hình quaït vôùi taàn suaát
+Tìm goùc ôû taâm cuûa moãi hình quaït Neâu chuù yù trong sgk
Hoaït ñoäng 4:Höôùng daãn caâu hoûi vaø baøi taäp.
TG Hoaït ñoäng cuûa giaùo vieân
Hoaït ñoäng cuûa hoïc sinh Noäi dung
Ta coù kích thöôùc maãu N = N = 30 Baøi 4: ?
[ 36 ;43] ; [ 44 ;51 ] ; [ 52 ;59 Lôùp Taàn Taàn Chia thaønh 6 lôùp ] ; soâ' suaát
[ 60 ; 67 ] ; [ 68 ;75 ]; [ 76 (%)
Tìm taàn soá cuûa moãi lôùp ;83 ] [ 36 ;43] 3 10
Tìm taàn suaát baèng coâng [ 44 ;51 6 20 thöùc 20' ] 6 20 n [ 52 ;59 8 26,7 f i i N ] 3 10 [60 ; 67 4 13,3 ] Goïi HS giaûi [ 68 ;75 HS giaûi ] [ 76 ;83 131 ] N=30 Baøi 5: Lôùp Taàn Taàn soâ' suaát (%) [ 1 ; 10 ] 5 6,25 [ 11 ;20 29 36,25 ] 21 26,25 [ 21 ;30 16 20 ] 7 8,75 [31 ; 40 2 2,5 ] [ 41 ;50 ] [ 51 ;60 ] N=80
c) Cuûng cố: Goïi HS nhaéc laïi caùc ñôn vò kthöùc :taàn soá,taàn suaát,kích thöôùc maãu,caùc daïng bieåu ñoà.
d) Baøi taäp veà nhaø: bt 3-5 trang 168 sgk . Laøm caùc baøi taäp 6,7,8 trang 169 132
Tieát 69 LUYEÄN TAÄP 1/ Muïc tieâu:
1. Kieán thöùc cô baûn:Thoâng qua baøi taäp giuùp HS naém :taàn soá,taàn suaát,baûng phaân boá taàn soá,taàn
suaát,bieåu ñoà,caùch veõ ñoïc bieåu ñoà.
2. Kyõ naêng, kyõ xaûo:Reøn luyeän kyõ naêng tính toaùn,veõ bieåu ñoà.
3. Thaùi ñoä nhaän thöùc:Lieân heä ñöôïc thöïc teá,hieåu ñöôïc yù nghóa thoáng keâ trong cuoäc soáng.
2/ Chuaån bò phöông tieän daïy hoïc:
Phöông tieän daïy hoïc: Baûng phuï, maùy tính boû tuùi.
3/ Tieán trình tieát daïy:
a)Kieåm tra baøi cuõ: Neâu caùc böôùc veõ bieåu ñoà, khaùi nieäm taàn soá ,taàn suaát. b) Giaûng baøi môùi:
Hoaït ñoäng 1: Baøi taäp 6.
TG Hoaït ñoäng cuûa
Hoaït ñoäng cuûa hoïc sinh Noäi dung giaùo vieân
_Daáu hieäu ñieàu _Laø doanh thu cuûa cöûa haøng trong 1 Baøi 6: tra laø gì? thaùng a).Daáu hieäu ñieàu tra _Ñôn vò ñieàu tra
laø:Doanh thu cuûa cöûa haøng laø gì? trong moät thaùng.
_Chia HS laøm 6 _Laø moät cöûa haøng
Ñôn vò ñieàu tralaø:1 cöûa nhoùm giaûi caâu haøng. b). b).
_Goïi HS veõ bieåu _HS giaûi theo nhoùm Lôùp Taàn Taàn ñoà hình coät soâ' suaát 20' (%) _HS veõ bieåu ñoà [26,5;48,5) 2 4 c). [48,5;70,5) 8 16 [70,5;92,5) 12 24 [92,5;114,5) 12 24 [114,5;136,5) 8 16 [136,5;158,5) 7 14 [158,5;180,5) 1 2 N=50 133
Hoaït ñoäng 2: Baøi taäp 7. TG
Hoaït ñoäng cuûa gv
Hoaït ñoäng cuûa hoïc sinh Noäi dung
_Daáu hieäu ñieàu tra _Soá cuoän phim maø moät nhaø nhieáp aûnh Baøi 7: laø gì?
duøng trong thaùng tröôùc. a).Daáu hieäu:soá cuoän
_Moät nhaø nhieáp aûnh nghieäp dö. phim moät nhaø nhieáp _Ñôn vò ñieàu tra laø aûnh duøng trong thaùng gì? tröôùc. _HS giaûi theo nhoùm Ñôn vò :moät nhaø nhieáp aûnh nghieäp dö. _HS veõ bieåu ñoà _Chia HS laøm 6 c). Lôùp Taàn nhoùm giaûi caâu b). soâ' _Goïi HS veõ bieåu ñoà [ ; 2 ] 10 hình coät 15' [ 3 ;5 ] 23 [ 6 ;8 ] 10 [9 ; 11 ] 3 [ 12 ;14 3 ] 1 [ 15 ;17 ] HS töï giaûi N=50 Baøi 8 goïi HS giaûi Baøi 8:(HS giaûi)
c) Cuûng coá: Qua baøi taäp caàn naém vöõng: daáu hieäu ñieàu tra, ñôn vò ñieàu tra, taàn soá, taàn suaàt, veõ bieãu ñoà.
d) Daën doø: xem tröôùc baøi 3, xem laïi kieán thöùc cuõ . 134
Tieát 70,71 §3. CAÙC SOÁ ÑAËC TRÖNG CUÛA MAÃU SOÁ LIEÄU. 1/ Muïc tieâu:
1. Kieán thöùc cô baûn: Bieát ñöôïc moät soá ñaëc tröng cuûa maãu soá lieäu nhö trung bình, soá trung vò, moát,
phöông sai, ñoä leäch chuaån vaø yù nghóa cuûa caùc soá ñaëc tröng naøy.
2. Kyõ naêng, kyõ xaûo: Bieát caùch tính caùc soá trung bình, soá trung vò, moát, phöông sai vaø ñoä leäch chuaån.
3. Thaùi ñoä nhaän thöùc: Thoâng qua khaùi nieäm trung bình coäng, soá trung vò vaø moát hoïc sinh thaáy ñöôïc
moái lieân heä giöõa toaùn hoïc vaø ñôøi soáng, töø ñoù yeâu thích boä moân.
2/ Chuaån bò phöông tieän daïy hoïc: a) Thöïc tieãn:
b) Phöông tieän daïy hoïc: Baûng phuï, maùy tính boû tuùi.
3/ Tieán trình tieát daïy: a)Kieåm tra baøi cuõ: b) Giaûng baøi môùi:
Hoaït ñoäng 1: Soá trung bình. TG
Hoaït ñoäng cuûa g v
Hoaït ñoäng cuûa h s Noäi dung 1/ Soá trung bình:
Giaû söû maãu soá lieäu ñöôïc cho döôùi Giaù trò Taàn soá
daïng baûng phaân boá taàn soá: x1 n1 x2 n2 ... ... Cho hs ñoïc baøi
Soá trung bình (soá trung bình coäng) xm nm
cuûa maãu soá lieäu naøy, kí hieäu laø x m N = n x
ñöôïc tính bôûi coâng thöùc: i i n x n x ... m n x 1 i 1 x 1 1 2 2 m m n x i i N N i1
Giaû söû maãu soá lieäu cho döôùi daïng
baûng phaân boá taàn soá gheùp lôùp: Lôùp G. trò ñaïi dieän Taàn soá Lôùp 1 x1 n1 Lôùp 2 x2 n2 ... ... ... Lôùp m xm nm m N = n x i i i1
Soá trung bình cuûa maãu soá lieäu ñöôïc
Ví duï 1: Gv höôùng daãn
tính xaáp xæ theo coâng thöùc: cho hs thöïc hieän Goïi hs 135 m 1 x n x i i N i1 Cho hs ñoïc baøi
* YÙ nghóa cuûa soá trung bình: Soá
trung bình cuûa maãu soá lieäu ñöôïc duøng
Ví duï 2: Gv höôùng daãn
laøm ñaïi dieän cho caùc soá lieäu cuûa maãu. cho hs thöïc hieän Goïi hs
Noù laø moät soá ñaëc tröng quan troïng cuûa maãu soá lieäu.
Hoaït ñoäng 2: Soá trung vò. TG
Hoaït ñoäng cuûa giaùo vieân
Hoaït ñoäng cuûa hoïc sinh Noäi dung 2/ Soá trung vò:
Giaû söû coù moät maãu goàm N Cho hs ñoïc baøi
soá lieäu ñöôïc saép xeáp theo
thöù töï khoâng giaûm. Neáu N laø
moät soá leû thì soá lieäu ñöùng
thöù N 1 (soá lieäu ñöùng
Ví duï 3: Gv höôùng daãn cho 2 hs thöïc hieän Goïi hs
chính giöõa) goïi laø soá trung Gv giaûi thích vò.
HÑ 1: Gv höôùng daãn cho hs HÑ 1: hs thöïc hieän
Trong tröôøng hôïp N laø moät thöïc hieän Chuùyù:
soá chaün, ta laáy trung bình
coäng cuûa hai soá lieäu ñöùng
HÑ 2: Gv höôùng daãn cho hs
thöù N vaø N + 1 laøm soá trung thöïc hieän
HÑ 2: hs thöïc hieän 2 2 vò.
Soá trung vò ñöôïc kí hieäu laø Me. Hoaït ñoäng 3: Moát. TG
Hoaït ñoäng cuûa giaùo vieân
Hoaït ñoäng cuûa hoïc sinh Noäi dung 3/ Moát:
Cho moät maãu soá lieäu döôùi
Ví duï 4: Gv höôùng daãn cho Goïi hs
daïng baûng phaân boá taàn soá. hs thöïc hieän
Giaù trò coù taàn soá lôùn nhaát a'
ñöôïc goïi laø moát cuûa maãu soá
lieäu vaø ñöôïc kí hieäu laø M0.
* Chuù yù: Moät maãu soá lieäu
Ví duï 5: Gv höôùng daãn cho Goïi hs
coù theå coù moät hay nhieàu hs thöïc hieän moát. 136
Hoaït ñoäng 4: Phöông sai vaø ñoä leäch chuaån. TG
Hoaït ñoäng cuûa g v
Hoaït ñoäng cuûa hoïc sinh Noäi dung
Ví duï 5: Gv höôùng daãn Goïi hs
4/ Phöông sai vaø ñoä leäch cho hs thöïc hieän chuaån:
Giaû söû ta coù moät maãu soá lieäu
kích thöôùc N laø {x1,..., xN}.
Phöông sai cuûa maãu soá lieäu
naøy, kí hieäu laø s2, ñöôïc tính bôûi coâng thöùc sau: N s2 = 1 2 (x x) (*)
HÑ 3: Gv höôùng daãn HÑ 3: hs thöïc hieän N i i 1 cho hs thöïc hieän
trong ñoù x laø soá trung bình cuûa maãu soá lieäu.
Caên baäc hai cuûa phöông sai
ñöôïc goïi laø ñoä leäch chuaån, kí hieäu laø s. N s = 1 2 (x x) i N i 1 a'
YÙ nghóa cuûa phöông sai vaø
ñoä leäch chuaån: Phöông sai vaø
ñoä leäch chuaån ño möùc ñoä phaân
taùn cuûa caùc soá lieäu trong maãu
quanh soá trung bình. Phöông
sai vaø ñoä leäch chuaån caøng lôùn
thì ñoä phaân taùn caøng lôùn.
* Chuù yù: Coù theå bieán ñoåi coâng thöùc (*) thaønh: 1 N 1 N 2 s2 = 2 x ( x i ) 2 i N N i 1 i 1
Ví duï 7: Gv höôùng daãn Goïi hs
Neáu soá lieäu ñöôïc cho döôùi cho hs thöïc hieän
daïng baûng phaân boá taàn soá thì
phöông sai ñöôïc tính bôûi coâng
Ví duï 8: Gv höôùng daãn Goïi hs thöùc: cho hs thöïc hieän N N s2 = 1 1 2 2 n x ( n x i i ) 2 i i N N i 1 i 1
c) Cuûng coá:Soá trung bình, soá trung vò , moát , phöông sai vaø ñoä leäch chuaån .
d) Baøi taäp veà nhaø:9-11 trang 177,178 sgk 137
Chöông VI Goùc luôïng giaùc vaø coâng thöùc löôïng giaùc. ******
Tieát 75,76 §1. GOÙC VAØ CUNG LÖÔÏNG GIAÙC. I/ Muïc tieâu:
1. Kieán thöùc cô baûn: Hieåu roõ soá ño ñoä, soá ño radian cuûa cung troøn vaø goùc, ñoä daøi cuûa cung troøn
(hình hoïc). Hieåu khaùi nieäm ñöôøng troøn löôïng giaùc, goùc vaø cung löôïng giaùc; soá ño cuûa cung vaø goùc löôïng giaùc.
2. Kyõ naêng, kyõ xaûo: Bieát ñoåi soá ño ñoä sang soá ño rañian vaø ngöôïc laïi. Bieát tính ñoä daøi cung troøn
(hình hoïc). Bieát moái lieân heä giöõa goùc hình hoïc vaø goùc löôïng giaùc. Bieát caùch xaùc ñònh ñieåm cuoái cuûa
moät cung löôïng giaùc vaø tia cuoái cuûa moät goùc löôïng giaùc hay moät hoï goùc löôïng giaùc treân ñöôøng troøn löôïng giaùc.
3. Thaùi ñoä nhaän thöùc: Reøn luyeän tính nghieâm tuùc, khoa hoïc, tính thöïc tieãn cao. Reøn luyeän oùc tö
duy thöïc teá vaø tính saùng taïo.
II/ Chuaån bò phöông tieän daïy hoïc: a) Thöïc tieãn:
b) Phöông tieän daïy hoïc: Baûng phuï, maùy tính boû tuùi.
III/ Tieán trình tieát daïy:
1)Kieåm tra baøi cuõ:Sñ goùc ôû taâm cuûa ñtroøn baùn kính R. 2) Giaûng baøi môùi: tg Noäi dung
Hoaït ñoäng cuûa giaùo vieân Hoaït ñoäng cuûa hoïc sinh
1/Ñôn vò ño goùc vaø cungtroøn,ñoä daøi cuûa -Goùc vaø cung löôïng giaùc cung troøn :
khaùc gì vôùi goùc vaø cung
a).Ñoä:Ta ñaõ bieát 1ñôn vò ñeå ño goùc laø hình hoïc? Ñieàu quan
ñoä:-Ñöôøng troøn baùn kính R coù ñoä daøi troïng laø moãi goùc vaø cung -Goùc beït coù soá ño: 180 0
baèng 2 R vaø coù soá ño baèng 3600
löôïng giaùc ñeàu töông öùng -Goùc 1 1 0 = goùc beït.
-Cung troøn baùn kính R coù soá ño a0 vôùi moät soá thöïc duy nhaát 180
(0≤a≤360) thì coù ñoä daøi
vaø vôùi moät ñieåm duy nhaát -1 ñoä baèng 60 phuùt: a .
treân ñöôøng troøn löôïng 0 ' 1 60 R . 180 giaùc.
-1 phuùt baèng 60 giaây:
Ví duï 1: Gv giaûi thich, höôùng daãn cho -Ta thöôøng duøng ñôn vò 1’=60”. hs thöïc hieän naøo ñeå ño goùc?
Hñ 1: cho hs thöïc hieän 138 b.Radian: Ñn: Sgk
-Ñeå thuaän tieän trong vieäc
*Xeùt caùc cung troøn baùn kính R (qh nghieân cöùu, tính toaùn
giöõa ñoä daøi cung troøn bk R vaø sñ ngöôøi ta söû duïng 1 ñôn vò
rañian).Vì cung troøn coù ñoä daøi baèng R khaùc laø radian.
Hñ 2: cho hs thöïc hieän
thì coù soá ño 1rad neân :
-Ñöôøng troøn baùn kính R coù ñoä daøi
baèng 2 R vaø coù soá ño rañian laø 2
-Cung troøn coù ñoä daøi l thì coù soá ño rañian laø l R
-Cung troøn baùn kính R coù soá ño α
rañian thì coù ñoä daøi l=αR
vaø khi R=1 (töùc laø treân ñtñv) thì ñoä daøi
cung troøn baèng soá ño rañian cuûa noù.
*Xeùt qh giöõa sñ rañian vaø sñ ñoä cuûa
cuøng 1 cung troøn.
Goïi α laø sñ rañian vaø a laø sñ ñoä cuûa cung ñoù, ta coù l= αR= a . R . , suy ra 180 a 180 -Ta coù: 180 0 1 rad 57 17 0 '45" π 0 π 1 rad 0,017 5rad 180
Chuù yù: Coù theå vieát hoaëc Ghi nhôù :
khoâng vieát chöõ radian sau
Baûng chuyeån ñoåi soá ño ñoä vaø soá ño soá ño goùc.
radian cuûa moät soá cung troøn:
Ñoä 300 450 600 900 1200 1350
2 3 5 Rad 6 4 3 2 3 4 6
2/GOÙC VAØ CUNG LÖÔÏNG GIAÙC:
a).Khaùi nieäm goùc lg vaø sñ cuûa chuùng : 139
- Quy öôùc:Chieàu ngöôïc chieàu kim ñoàng
hoà laø chieàu döông, chieàu cuøng chieàu
kim ñoàng hoà laø chieàu aâm. m
- Cho hai tia Ou vaø Ov trong 1 mp, xeùt
tia Om cuøng naèm trong mp naøy. Neáu v m -
Om quay quanh ñieåm O theo moät chieàu v
nhaát ñònh töø Ou ñeán Ov, ta noùi noù queùt +
moät goùc löôïng giaùc.Kyù hieäu :(Ou,Ov). O u
Ou goïi laø tia ñaàu, Ov goïi laø tia cuoái .
Vaäy ta coù voâ soá goùc löôïng giaùc vôùi hai O u
tia Ou, Ov cho tröôùc.
sñ(Ou,Ov)=a0+k3600,
k (1)
sñ(Ou,Ov)=
k2 , k , 0 2 (2)
Ví duï 2: Gv giaûi thich, höôùng daãn cho hs thöïc hieän
Ví duï 3: Gv giaûi thich, höôùng daãn cho hs thöïc hieän
Hñ 3: cho hs thöïc hieän
b)Khaùi nieäm cung lg vaø sñ cuûa chuùng :
*Ñöôøng troøn ñònh höôùng:
Ñöôøng troøn ñònh höôùng laø ñöôøng
troøn treân ñoù ñaõ choïn chieàu di ñoäng laø
chieàu döông hoaëc laø chieàu aâm v V
Quy öôùc: chieàu döông ngöôïc chieàu
kim ñoàng hoàø, chieàu aâm cuøng chieàu kim U v ñoàng hoà . O u + V
*Cung löôïng giaùc: M M m - m
-Cho goùc löôïng giaùc (Ou,Ov) vaø ñöôøng
troøn ñònh höôùng taâm O, caét Ou taïi U U O u
vaø caét Ov taïi V, caét tia Om taïi M.
-Khi Om quay töø Ou ñeán Ov taïo thaønh
goùc löôïng giaùc(Ou,Ov) thì ñieåm M di -Goùc löôïng giaùc (Ou,Ov)
ñoäng töø U ñeán V taïo thaønh moät cung coøn vieát laø (OU,OV), ñgl
löôïng giaùc.Kyù hieäu : UV
goùc töông öùng vôùi cung
U goïi laø ñieåm ñaàu, V goïi laø ñieåm cuoái . UV hay chaén cung UV.
-Vôùi hai ñieåm U, V treân
*Soá ño cuûa cung löôïng giaùc:
ñöôøng troøn ñònh höôùng thì
-Sñ cuûa cung löôïng giaùc UV
coù voâ soá cung löôïng giaùc
laø soá ño cuûa goùc lg (OU,OV).
coù ñieåm goác laø U, ñieåm
ngoïn laø V. Soá ño caùc cung 140 -Ta coù: naøy sai khaùc nhau moät
boäi nguyeân cuûa 2 hay
3)Heä thöùc Sa-lô :
Vôùi 3 tia tuøy yù Ou, Ov, Ow ta coù
sñ(Ou,Ov)+sñ(Ov,Ow)= sñ(Ou,Ow)+k2
(kZ).
Suy ra: Vôùi 3 tia tuøy yù Ox, Ou, Ov ta coù
sñ(Ou,Ov)+sñ(Ov,Ow)=sñ(Ou,Ow)+k2 .
(kZ).
Ví duï 4: Gv giaûi thich, höôùng daãn cho
hs thöïc hieän.
3.Cuûng coá:-Ñoåi caùc soá ño sau töø Ñoä sang rañian:200, 35010’, 70010’50”.
-Ñoái caùc soá ño sau töø rañian sang ñoä: 9 25 ; . 4 6
4.Daën doø: -Hoïc baøi vaø laøm caùc baøi taäp:1-7 trang 190,191 SGK.. 141
Tieát 78,79 §2. GIAÙ TRÒ LÖÔÏNG GIAÙC
CUÛA GOÙC (CUNG) LÖÔÏNG GIAÙC. I/ Muïc tieâu:
1. Kieán thöùc cô baûn: Hieåu theá naøo laø ñöôøng troøn löôïng giaùc vaø heä toïa ñoä vuoâng goùc gaén vôùi noù,
ñieåm M treân ñöôøng troøn löôïng giaùc xaùc ñònh bôûi soá (hay bôûi goùc , cung ). Bieát caùc ñònh nghóa
coâsin, sin, tang, co6tang cuûa goùc löôïng giaùc vaø y nghóa hình hoïc cuûa chuùng. Naém chaéc caùc coâng
thöùc löôïng giaùc cô baûn (sin2 + cos2 = 1, cot = 1 , 1 + tan2 = 1 , 1 + cot2 = 1 ). tan 2 cos 2 sin
2. Kyõ naêng, kyõ xaûo: Bieát tìm ñieåm M treân ñöôøng troøn löôïng giaùc xaùc ñònh bôûi soá thöïc . Bieát xaùc
ñònh daáu cuûa cos, sin, tan, cot khi bieát ; bieát caùc giaù trò coâsin, sin, tang, co6tang cuûa moät soá
goùc löôïng giaùc thöôøng gaëp. Söû duïng thaønh thaïo caùc coâng thöùc löôïng giaùc cô baûn.
3. Thaùi ñoä nhaän thöùc: Reøn luyeän tính caån thaän, oùc tö duy logic vaø tö duy hình hoïc.
II/ Chuaån bò phöông tieän daïy hoïc: a) Thöïc tieãn:
b) Phöông tieän daïy hoïc: Baûng phuï, maùy tính boû tuùi.
III/ Tieán trình tieát daïy:
1)Kieåm tra baøi cuõ: Theá naøo laø ñöôøng troøn ñònh höôùng? 2) Giaûng baøi môùi: tg Ghi Baûng
Hoaït ñoäng cuûa hoïc sinh
Hoaït ñoäng cuûa GV
1).Ñtroøn löôïng giaùc - Nghe, hieåu nhieäm vuï
1.Treân cô sôû ñöôøng troøn ñònh a).Ñònh nghóa: SGK
höôùng, phaùt bieåu ñ/n ñ.troøn l.giaùc?
b).Töông öùng giöõa - Phaùt bieåu ñ/n -Giaûi thích ñ/n
soá thöïc vaø ñieåm 2.Xem hình veõ
treân ñöôøng troøn löôïng giaùc (SGK) t
Hñ 1: cho hs thöïc hieän M2 3 - Giaûi quyeát: M - Trình baøy keát quaû: A A
a. Caùc ñieåm caàn tìm coù toaï ñoä k2 (k Z )
b. Caùc ñieåm caàn tìm coù toaï ñoä - 3 (2k + 1) (k Z )
Hình dung: At laø 1 sôïi daây vaø quaán
quanh ñtroøn löôïng giaùc. 142 - Veõ
a. Caùc ñieåm naøo treân truïc soá At ñeán
truøng vôùi A treân ñtroøn löôïng giaùc.
b. Caùc ñieåm naøo treân truïc At ñeán
c).Heä toaï ñoä vuoâng Hñ 2: cho hs thöïc hieän truøng vôùi A’
goùc gaén vôùi ñtroøn - NX, söûa chöõa l.giaùc (SGK) - Phaùt bieåu
3. Veõ toaï ñoä vuoâng goùc Oxy: Ox - Giaûi quyeát:
OA. (Ox, Oy) = K 2 ? 2 2 2 - Keát quaû: M ; 2 2
2).Giaù trò löôïng giaùc
Tìm toïa ñoä ñieåm M treân ñtroøn sao - Phaùt bieåu ñònh nghóa sin vaø cosin: cho cung coù soá ño ?
Ví duï 1: Gv giaûi thich, höôùng 3 4 AM
a).Ñònh nghóa: SGK daãn cho hs thöïc hieän 5. Xem hình veõ B M K y O x A' H A B' *Chuù yù:
- Ñoïc, nghieân cöùu, phaùt bieåu ñ/n. +Cos = - NX, ghi nhaän kieán thöùc SGK OH +Sin = OK
Hñ 3: cho hs thöïc hieän
- Giaûi quyeát: (Laøm theo nhoùm) 6/ a. Tìm ñeå sin = 0 - Trình baøy keát quaû
Khi ñoù cos baèng bao nhieâu?
b. Tìm ñeå cos = 0. khi ñoù sin baèng bao nhieâu? b).Tính chaát - NX söûa chöõa. (SGK)
- Töø ñ/n, kieán thöùc ñaõ bieát, ta coù - Giaûi quyeát: caùc tính chaát sau: (SGK) OH² + OK² = OM² = 1 7. C/m t/c (3): (h 2.1) cos² + sin² = 1 (ñpcm) - Giaûi, neâu keát quaû
8. Treân ñ.troøn l.gi aùc goác A xeùt cung
Hñ 4: cho hs thöïc hieän l.giaùc coù AM soá ño . Hoûi M
naèm trong nöûa mp naøo thì cos >
0, trong nöûa mp naøo thì cos < 0?
Veõ hình minh hoaï. Cuõng caâu hoûi ñoù cho sin . 143
2).Giaù trò löôïng giaùc tang vaø coâtang :
a).caùc ñònh nghóa: SGK
Ví duï 2: Gv giaûi thich, höôùng
b)YÙ nghóa hình hoïc: daãn cho hs thöïc hieän Sgk
Ví duï 3: Gv giaûi thich, höôùng daãn cho hs thöïc hieän
Hñ 5: cho hs thöïc hieän y I II III IV II B M I cos + - - + b).Tính chaát sin + + - - x (SGK) A' O A tan + - + - cot + - + - III IV B'
4)Tìm gtlg cuûa moät soá goùc: Sgk
Ví duï 4: Gv giaûi thich, höôùng daãn cho hs thöïc hieän Chuù yù: Sgk
Ví duï 5: Gv giaûi thich, höôùng daãn cho hs thöïc hieän 3/. Cuûng coá:
CH1:Phaùt bieåu ñ/n ñöôøng troøn löôïng giaùc;Neâu ñ/n giaù trò löôïng giaùc cuûa sin vaø cosin
CH2: Cuûng coá thoâng qua baøi taäp
Giaù trò löôïng giaùc cuûa sin 2250 laø: a. 2 b. - 2 c. 1 d. moät giaù trò khaùc 2 2 2
4/. Baøi taäp veà nhaø: 14, 15, 16 - SGK 144
Tieát 81 §3. GIAÙ TRÒ LÖÔÏNG GIAÙC CUÛA
CAÙC GOÙC (CUNG) COÙ LIEÂN QUAN ÑAËC BIEÄT. I) Muïc tieâu:
1. Kieán thöùc cô baûn: Bieát ñöôïc moái lieân heä giöõa caùc giaù trò löôïng giaùc cuûa caùc goùc coù lieân quan
ñaëc bieät vaø söû duïng ñöôïc chuùng.
2. Kyõ naêng, kyõ xaûo: Bieát duøng hình veõ ñeå tìm vaø nhôù ñöôïc caùc coâng thöùc veà giaù trò löôïng giaùc cuûa
caùc goùc (cung) coù lieân quan ñaëc bieät. Söû duïng caùc coâng thöùc ñeå tìm caùc giaù trò löôïng giaùc.
3. Thaùi ñoä nhaän thöùc: Phaùt trieån tö duy trong quaù trình giaûi baøi taäp löôïng giaùc.
II)/ Chuaån bò phöông tieän daïy hoïc: a) Thöïc tieãn:
b) Phöông tieän daïy hoïc: Baûng phuï, maùy tính boû tuùi.
III) Tieán trình tieát daïy: 1)Kieåm tra baøi cuõ: 2) Giaûng baøi môùi:
Hoaït ñoäng 1: Cho 2 cung 300 vaø (-300)
- Haõy bieån dieån 2 cung ñoù treân ñöôøng troøn löôïng giaùc.
- Tính giaù trò sin vaø cos cuûa 2 cung ñoù. TG
HOAÏT ÑOÄNG CUÛA HS
HOAÏT ÑOÄNG CUÛA GV NOÄI DUNG - Nghe, hieåu, nhieäm vuï.
- Giao nhieäm vuï, phieáu hoïc - Thöïc hieän theo nhoùm.
taäp coù veõ ñöôøng troøn löôïng
- Trình baøi keát quaû vaøo giaáy giaùc. trong.
- Phaân nhoùm, cho HS thöïc
- Trình chieáu vaø giaûi thích. hieän.
- Theo doõi, nhaän xeùt baøi laøm cuûa HS
Hoaït ñoäng 2:
Cho cung . Bieåu dieãn goùc (cung) giaù trò löôïng giaùc sin vaø cos cuûa (- ) leân ñöôøng troøn
löôïng giaùc vaø nhaän xeùt moái quan heä giöõa sin vaø sin(- ), cos vaø cos(- ). TG
HOAÏT ÑOÄNG CUÛA HS
HOAÏT ÑOÄNG CUÛA GV NOÄI DUNG - Nghe, hieåu, nhieäm vuï. - Giao nhieäm vuï cho HS.
1)Hai goùc ñoái nhau:
- Thaûo luaän vaø trình baøy lôøi giaûi - Chia nhoùm HS. sin(- ) = -sin
vaøo phieáu hoïc taäp theo nhoùm. - Quan saùt HS laøm baøi. cos(- ) = cos
- Cöû ñaïi dieän cuûa nhoùm trình - Cho HS trình chieáu lôøi giaûi. tan(- ) = -tan
chieáu vaø giaûi thích khi GV goïi. - Nhaän xeùt lôøi giaûi. cot(- ) = -cot
- Nhaän xeùt moái quan heä tan,
cot cuûa hai cung vaø (- ) 145
Hoaït ñoäng 3:
Cho cung Bieåu dieãn goùc (cung) giaù trò löôïng giaùc sin vaø cos cuûa leân ñöôøng troøn
löôïng giaùc vaø nhaän xeùt moái quan heä sin vaø sin( ), cos vaø cos( ). TG
HOAÏT ÑOÄNG CUÛA HS
HOAÏT ÑOÄNG CUÛA GV NOÄI DUNG -Nghe, hieåu, nhieäm vuï. - Giao nhieäm vuï cho HS. 2)Hai goùc hôn keùm
- Thaûo luaän vaø trình baøy lôøi giaûi - Chia nhoùm HS. nhau :
vaøo phieáu hoïc taäp theo nhoùm. - Quan saùt HS laøm baøi. sin( )= -sin( )
- Cöû ñaïi dieän cuûa nhoùm trình - Cho HS trình chieáu lôøi giaûi. cos( )= -cos( )
chieáu vaø giaûi thích khi GV goïi. - Nhaän xeùt lôøi giaûi. tan( )= tan( )
- Nhaän xeùt moái quan heä giöõa cot( )= cot( ) tan, cot cuaû hai cung vaø
Hoaït ñoäng 4:
Cho cung . Bieåu dieãn goùc (cung) giaù trò löôïng giaùc sin vaø cos cuûa - leân ñöôøng troøn
löôïng giaùc vaø nhaän xeùt moái quan heä sin vaø sin( - ), cos vaø cos( ). TG
HOAÏT ÑOÄNG CUÛA HS
HOAÏT ÑOÄNG CUÛA GV NOÄI DUNG - Nghe, hieåu, nhieäm vuï. - Giao nhieäm vuï cho HS. 3)Hai goùc buø nhau:
- Thaûo luaän vaø trình baøy lôøi giaûi - Chia nhoùm HS. sin( )= sin( )
vaøo phieáu hoïc taäp theo nhoùm. - Quan saùt HS laøm baøi. cos( )= -cos( )
- Cöû ñaïi dieän cuûa nhoùm trình
- Cho HS trình chieáu lôøi giaûi. tan( ) = -tan ( )
chieáu vaø giaûi thích khi GV goïi - Nhaän xeùt lôøi giaûi.
cot( ) = -cot ( )
- Nhaän xeùt moái quan heä giöõa
tan, cot cuaû hai cung vaø
Hoaït ñoäng 5:
Cho cung . Bieåu dieãn goùc (cung) giaù trò löôïng giaùc sin vaø cos cuûa leân ñöôøng troøn 2
löôïng giaùc vaø nhaän xeùt moái quan heä sin vaø sin(
), cos vaø cos( ). 2 2 TG
HOAÏT ÑOÄNG CUÛA HS
HOAÏT ÑOÄNG CUÛA GV NOÄI DUNG - Nghe, hieåu, nhieäm vuï. - Giao nhieäm vuï cho HS.
4)Hai goùc phuï nhau:
- Thaûo luaän vaø trình baøy lôøi giaûi - Chia nhoùm HS. sin( )= cos( )
vaøo phieáu hoïc taäp theo nhoùm. - Quan saùt HS laøm baøi. 2
- Cöû ñaïi dieän cuûa nhoùm trình - Cho HS trình chieáu lôøi giaûi. cos( )= sin( )
chieáu vaø giaûi thích khi GV goïi. - Nhaän xeùt lôøi giaûi. 2
- Nhaän xeùt moái quan heä giöõa tan( )= cot( )
tan, cot cuûa hai cung vaø 2 cot( )= tan( ) 2 2 146
Hoaït ñoäng 6:
Cho cos 10o=a, tính sin80o vaø sin(-100o) TG
HOAÏT ÑOÄNG CUÛA HS
HOAÏT ÑOÄNG CUÛA GV NOÄI DUNG - Nghe, hieåu, nhieäm vuï. - Giao nhieäm vuï cho HS. sin80o=sin(90o-10o)
- Thaûo luaän vaø trình baøy lôøi giaûi - Chia nhoùm HS. = cos10o= a
vaøo phieáu hoïc taäp theo nhoùm. - Quan saùt HS laøm baøi. sin(-100o)= -sin100o
- Cöû ñaïi dieän cuûa nhoùm trình - Cho HS trình chieáu lôøi giaûi. = -sin(180o-80o)
chieáu vaø giaûi thích khi GV goïi. - Nhaän xeùt lôøi giaûi. = -sin80o= -cos10o=-a - Cho HS ghi nhaän xeùt SGK
Hoaït ñoäng 7:
Baèng moái lieân quan giöõa caùc giaù trò löôïng giaùc, caùc goùc(cung) ñaëc bieät tính cos( ), 2 sin(
), tan( ), cot( ) theo sin , cos , tan , cot . 2 2 2 TG
HOAÏT ÑOÄNG CUÛA HS
HOAÏT ÑOÄNG CUÛA GV NOÄI DUNG - Nghe, hieåu, nhieäm vuï. - Giao nhieäm vuï cho HS. Ví duï :
- Thaûo luaän vaø trình baøy lôøi giaûi - Chia nhoùm HS. sin( )= -cos( )
vaøo phieáu hoïc taäp theo nhoùm. - Quan saùt HS laøm baøi. 2
- Cöû ñaïi dieän cuûa nhoùm trình - Cho HS trình chieáu lôøi giaûi. cos( )= sin( )
chieáu vaø giaûi thích khi GV goïi. - Nhaän xeùt lôøi giaûi. 2 tan( )= -cot( ) 2 cot( )= -tan( ) 2
Hoaït ñoäng 8: Tính cos( 13 ), 4 TG
HOAÏT ÑOÄNG CUÛA HS
HOAÏT ÑOÄNG CUÛA GV NOÄI DUNG - Nghe, hieåu, nhieäm vuï. - Giao nhieäm vuï cho HS. cos( 13 )
- Thaûo luaän vaø trình baøy lôøi giaûi - Chia nhoùm HS. 4
vaøo phieáu hoïc taäp theo nhoùm. - Quan saùt HS laøm baøi. =cos(13 )=cos( 3 )
- Cöû ñaïi dieän cuûa nhoùm trình - Cho HS trình chieáu lôøi giaûi. 4 4
chieáu vaø giaûi thích khi GV goïi. - Nhaän xeùt lôøi giaûi. =cos( )=-cos 4 4 =- 2 2
Hoaït ñoäng 9:
Haõy saép xeáp thöù töï cho hôïp lí roài ruùt goïn bieåu thöùc sau:
tan10otan20otan30otan40otan50otan60otan70otan80o TG
HOAÏT ÑOÄNG CUÛA HS
HOAÏT ÑOÄNG CUÛA GV NOÄI DUNG - Nghe, hieåu, nhieäm vuï. - Giao nhieäm vuï cho HS. tan10otan20otan30otan40o
- Thaûo luaän vaø trình baøy lôøi giaûi - Chia nhoùm HS. tan50otan60otan70otan80o
vaøo phieáu hoïc taäp theo nhoùm. - Quan saùt HS laøm baøi. =tan10otan80otan20otan70o 147
- Cöû ñaïi dieän cuûa nhoùm trình - Cho HS trình chieáu lôøi giaûi. tan30otan60otan40otan50o
chieáu vaø giaûi thích khi GV goïi. - Nhaän xeùt lôøi giaûi. =tan10ocot10otan20ocot20o tan30ocot30otan40ocot40o =1
Hoaït ñoäng 10:
Cho goùc uOv (0< < ), thì sñ(Ou,Ov)=?. Nhaän xeùt cos(uOv) vaø cos(Ou,Ov), sin(uOv) vaø sin(Ou,Ov). TG
HOAÏT ÑOÄNG CUÛA HS
HOAÏT ÑOÄNG CUÛA GV NOÄI DUNG - Nghe, hieåu, nhieäm vuï. - Giao nhieäm vuï cho HS. Chuù yù :
- Thaûo luaän vaø trình baøy lôøi giaûi - Chia nhoùm HS. sñ(Ou,Ov) baèng
vaøo phieáu hoïc taäp theo nhoùm. - Quan saùt HS laøm baøi. k 2 hoaëc
- Cöû ñaïi dieän cuûa nhoùm trình - Cho HS trình chieáu lôøi giaûi. k 2
chieáu vaø giaûi thích khi GV goïi. - Nhaän xeùt lôøi giaûi. cos(uOv)=cos(Ou,Ov) sin(uOv)= sin(Ou, Ov)
Hoaït ñoäng 11: (cuûng coá)
Haõy quan saùt moái quan heä cuûa 4 tröôøng hôïp ñaëc bieät: cung ñoái, cung hôn keùm , cung buø,
cung phuï. Neâu nhaän xeùt neùt ñaëc tröng nhaát ôû moãi tröôøng hôïp? TG
HOAÏT ÑOÄNG CUÛA HS
HOAÏT ÑOÄNG CUÛA GV NOÄI DUNG - Nghe, hieåu, nhieäm vuï. - Giao nhieäm vuï cho HS.
- Thaûo luaän vaø trình baøy lôøi giaûi - Chia nhoùm HS.
vaøo phieáu hoïc taäp theo nhoùm. - Quan saùt HS laøm baøi.
- Cöû ñaïi dieän cuûa nhoùm trình - Cho HS trình chieáu lôøi giaûi.
chieáu vaø giaûi thích khi GV goïi. - Nhaän xeùt lôøi giaûi. Daën doø:
- Hoïc thuoäc caùc tröôøng hôïp cuûa gtlg cuûa caùc goùc(cung) coù lieân quan ñaëc bieät.
- Laøm baøi taäp 24-29 SGK trang 205-206 148
Tieát 83,84 §4. MOÄT SOÁ COÂNG THÖÙC LÖÔÏNG GIAÙC. 1/ Muïc tieâu:
1. Kieán thöùc cô baûn: Giuùp hoïc sinh nhôù vaø söû duïng ñöôïc caùc coâng thöùc coäng, coâng thöùc nhaân ñoâi,
coâng thöùc haï baäc, bieán ñoåi toång thaønh tích vaø bieán ñoåi tích thaønh toång.
2. Kyõ naêng, kyõ xaûo: Bieán ñoåi thaønh thaïo caùc coâng thöùc treân, vaän duïng giaûi caùc baøi taäp veà löôïng giaùc.
3. Thaùi ñoä nhaän thöùc: Phaùt trieån tö duy trong quaù trình giaûi baøi taäp löôïng giaùc.
2/ Chuaån bò phöông tieän daïy hoïc: a) Thöïc tieãn:
b) Phöông tieän daïy hoïc: Baûng phuï, maùy tính boû tuùi.
3/ Tieán trình tieát daïy: a)Kieåm tra baøi cuõ: b) Giaûng baøi môùi: Tg Noäi dung
Hoaït ñoäng cuûa thaày Hoaït ñoäng cuûa troø
Caùc cthöùc lg cô baûn? sin 2 cos 2 1 si n
1)Coâng thöùc coäng : tan co s
a) Coâng thöùc coäng ñvôùi sin vaø coâsin : co s cos( co t α-β)=cosαcosβ -sinαsinβ si n
cos(α+β)=cosαcosβ+sinαsinβ tanco t 1
sin(α-β)=sinαcosβ+cosαsinβ 1 sin( 2 α+β)=sinαcosβ-cosαsinβ 1 tan cos 2 1 Ví du•1 :Gv giaûi 1 cot 2 2 sin thích, höôùng daãn vaø
(khi caùc b thöùc coù nghóa) cho hs thöïc hieän HÑ1: cho hs thöïc hieän
b) Coâng thöùc coäng ñvôùi tang : tan tan tan ( ) 1 tantan tan tan tan ( ) 1- tantan Ví du•2 :Gv giaûi thích, höôùng daãn vaø
(khi caùc bieåu thöùc coù nghóa) cho hs thöïc hieän 149
HÑ2: cho hs thöïc hieän Ñ
2)Coâng thöùc nhaân ñoâi : cos2α =cos2α -sin2α sin2α =2sinαcosα tan2 tan 2 α = . 1- 2 tan Ví du•3 :Gv giaûi thích, höôùng daãn vaø Ví du•3: cho hs thöïc hieän
a) cos2α =cos2α -sin2α =2cos2α - ( k , k , k Z ) 2 4 2 1=1-2sin2α
b) Vôùi ( k ,k Z) thì 4 2 cos2α ≠ 0 vaø ta coù 1 sin 2 cos 2 2 sin 2 cos 2sin co s = 2 cos 2 sin (sin cos )2 = (cos sin )(cos sin ) co s sin = co s sin
Chuù yù : caùc coâng thöùc haï baäc cos2x= 1 cos2x 2 sin2x= 1- cos2x tg2x ? 2 45 Ví du•4 :Gv giaûi thích, höôùng daãn vaø cho hs thöïc hieän HÑ3 : cos4 α=2cos2 2α -1= =2(2cos2 α -1)2-1 =8cos4 α -8 cos2α +1 HÑ4 : sin αcosαcos2αcos4α= 1 1 = sin2αcos2αcos4α= sin4αco 2 4 s4 α
3)Coâng thöùc b ñoåi tích thaønh toång vaø 1 = sin8α
bieán ñoåi toång thaønh tích : 8
a) coâng thöùc b ñoåi tích thaønh toång : 150 1
coscos [cos( ) cos( )] 2 1 sinsin
[cos( ) cos( )] 2 1 Ví du•5 :Gv giaûi
sincos [sin( ) sin( )] 2 thích, höôùng daãn vaø cho hs thöïc hieän HÑ5 : 7 5 1 cos sin sin sin
b) coâng thöùc b ñoåi toång thaønh tích : 12 12 2 6 x y x y 1 cosx cosy 2cos cos 2 2 4 x y x y cosx cosy 2 sin sin 2 2 x y x y sinx siny 2sin cos 2 2 45 x y x y sinx siny 2cos sin 2 2 Ví du•6 :Gv giaûi thích, höôùng daãn vaø cho hs thöïc hieän
3) Cuûng coá: Coâng thöùc coäng, coâng thöùc nhaân ñoâi, coâng thöùc haï baäc, coâng thöùc bieán ñoåi tích thaønh
toång vaø bieán ñoåi toång thaønh tích .
4) Baøi taäp veà nhaø:Caâu hoûi vaø bt 38-45 trang 213, 214 sgk.
Nguoàn: diendantoanhoc.net/upload (Sa Ñeùc), 26/08/2009
++++++++++++++++++++++++++++++++++++++++++++++++++
http://ngoclinhson.violet.vn, http://ngoclinhson.tk
- website ñang xaây döïng, caäp nhaät phaàn meàm, taøi lieäu caù nhaân coù trong quaù trình laøm vieäc, söû
duïng maùy tính vaø hoã trôï coäng ñoàng:
+ Quaûn lyù giaùo duïc, caùc hoaït ñoäng giaùo duïc;
+ Tin hoïc, coâng ngheä thoâng tin;
+ Giaùo trình, giaùo aùn; ñeà thi, kieåm tra; Vaø caùc noäi dung khaùc.
++++++++++++++++++++++++++++++++++++++++++++++++++ 151




