






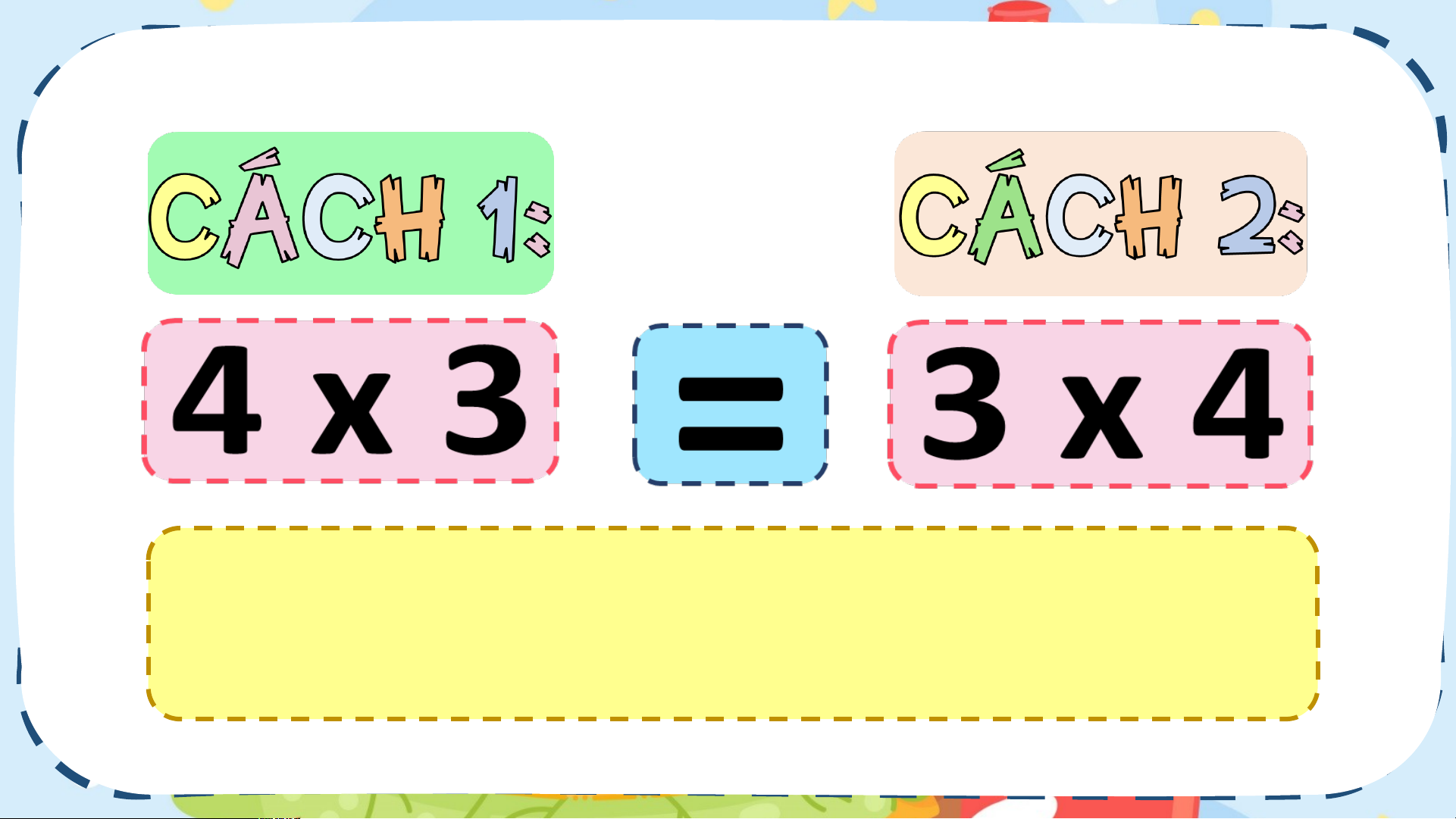











Preview text:
Thứ Tư, ngày 11 tháng 10 năm 2023 TOÁN O TÌN TÍ H N C H H C ẤT G HẤT IA GI O H A0 O H ÁN OÁ , N, TÍN TÍNH C CHẤT K ẤT KẾT H T HỢP C CỦA A PHÉP (Tiết 1) NHÂN ÂN
Các bạn đã làm cách nào để có thể tìm ra AI NH A đượI N c đá H p ánANH A N của ha HƠ H HƠ i bức ả N nh ! trên? Mỗi hàng có mấy Mỗi cột có mấy biển báo và có bao biển báo và có nhiêu hàng? bao nhiêu cột? Nhóm chẵn Nhóm lẻ THẢO LUẬN THẢO LUẬN
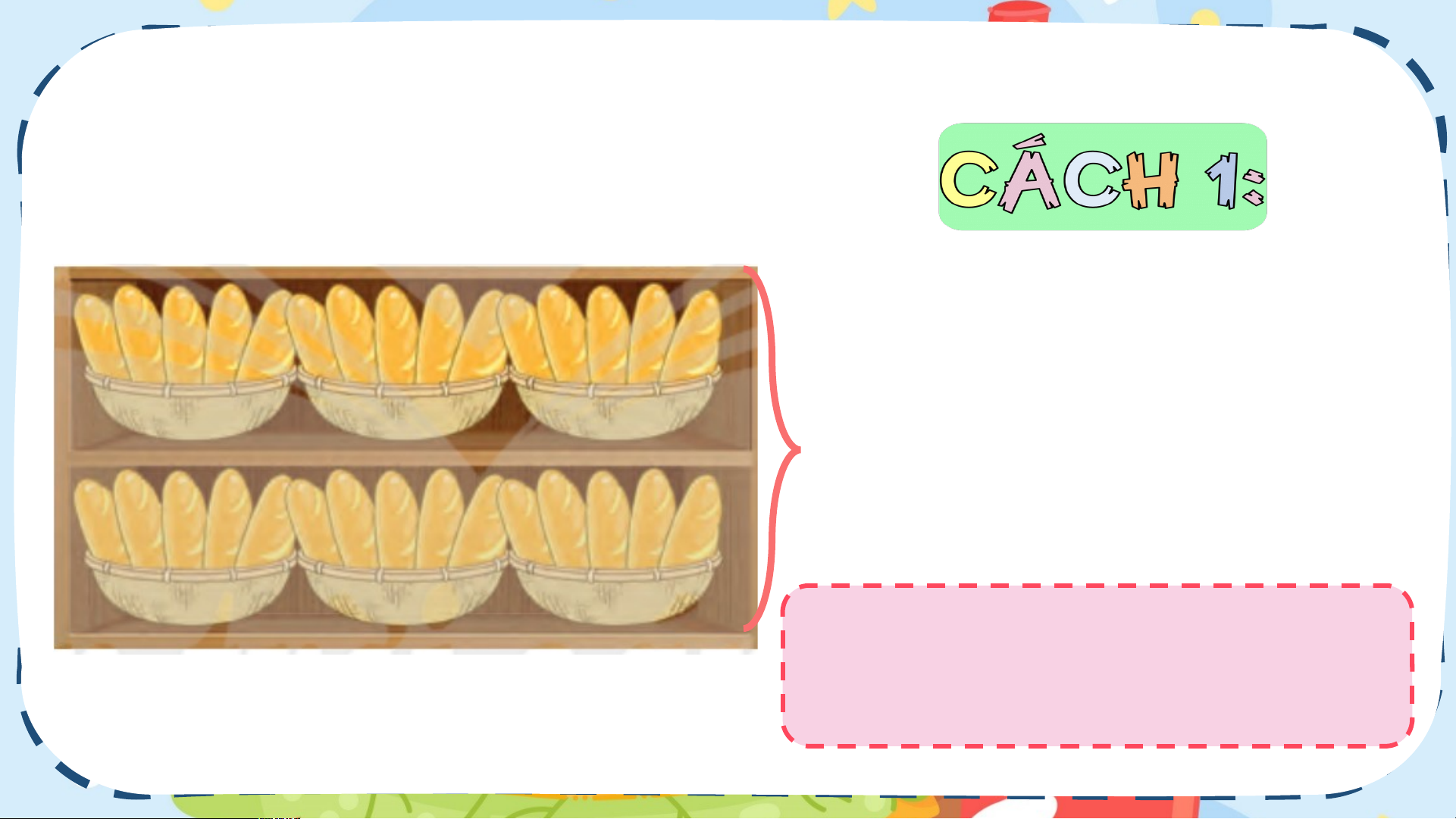
1. Tính chất giao hoán của phép nhân 1 2 3 4 - Mỗi hàng có 4 biển báo. 3 - Có 3 hàng, ta có: 4 x 3
1. Tính chất giao hoán của phép nhân 4 1 - Mỗi cột có 3 biển báo. 2 - Có 4 cột, ta có: 3 3 x 4
1. Tính chất giao hoán của phép nhân a x b = b x a KẾT LUẬ ẾT L N a x b = b x a
Khi đổi chỗ các thừa số
trong một tích thì tích không thay đổi. Mỗi hàng có Mỗi rổ có mấy cái bánh, mấy cái bánh, và có mấy có mấy rổ và hàng? mấy hàng? Nhóm chẵn Nhóm lẻ THẢO LUẬN THẢO LUẬN
1. Tính chất kết hợp của phép nhân 12 - Mỗi hàng 5 cái 345 1 2 3 bánh và 3 cái rổ. 2- Có 2 hàng, ta có: (5 x 3) x 2
1. Tính chất kết hợp của phép nhân 12 - Mỗi rổ có 5 cái 345 1 2 3 bánh.
2- Có 3 rổ và 2 hàng: 5 x (3 x 2)
1. Tính chất kết hợp của phép nhân = 15 x 2 = 5 x 6 = ( 3 a x 0b) x c = a = x (b 30 x c) KẾT LUẬ ẾT L N
a x b x c = (a x b) x c = a x (b x c)
Khi nhân một tích hai số với số
thứ ba, ta có thể nhân số thứ nhất
với tích của số thứ hai và số thứ ba.
1 Tính bằng cách thuận tiện. a) 5 x 3 x 4 b) 6 x 5 x 7 c) 20 x 9 x 5 d) 2 x 7 x 50
1 Tính bằng cách thuận tiện. Mẫu: 2 x 9 x 5 = (2 x 5) x 9 = 10 x 9 = 90
1 Tính bằng cách thuận tiện. a) 5 x 3 x 4 b) 6 x 5 x 7 c) 20 x 9 x 5 d) 2 x 7 x 50 LÀM BÀI VÀO VỞ NH N Ữ H N Ữ G N MI G M ẾNG G IẾNG À G GIÒN T IÒN AN TAN




