Giáo án Hình học 10 cơ bản thầy Nguyễn Đình Khương

Giới thiệu đến quý thầy, cô Giáo án Hình học 10 cơ bản thầy Nguyễn Đình Khương. Xin lưu ý bộ giáo án Hình học 10 cơ bản của thầy Nguyễn Đình Khương dạng file word sử dụng font VNI – Times, nếu tải về bị lỗi font, thầy cô có thể tải 4 font VNI – Times cài vào máy để sửa lỗi

45 23 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Giáo án Toán 10

Môn: Toán 10

Thông tin:

86 trang 8 tháng trước

Tác giả:

Profile Thanh Tâm
Nguyễn Đình Khương Hình Học 10 Cơ Bản
1
Ngaøy soaïn: 20/8/2012 Chöông I: VECTÔ
Tieát daïy: 01 Baøøi 1: CAÙC ÑÒNH NGHÓA
I. MUÏC TIEÂU:
Kieán thöùc:
Naém ñöôïc ñònh nghóa vectô vaø nhöõng khaùi nieäm quan troïng lieân quan ñeán vectô nhö: söï
cuøng phöông cuûa hai vectô, ñoä daøi cuûa vectô, hai vectô baèng nhau, …
Hieåu ñöôïc vectô
0
laø moät vectô ñaïc bieät vaø nhöõng qui öôùc veà vectô
0
.
Kó naêng:
Bieát chöùng minh hai vectô baèng nhau, bieát döïng moät vectô baèng vectô cho tröôùc vaø coù
ñieåm ñaàu cho tröôùc.
Thaùi ñoä:
Reøn luyeän oùc quan saùt, phaân bieät ñöôïc caùc ñoái töôïng.
II. CHUAÅN BÒ:
Giaùo vieân: Giaùo aùn, phieáu hoïc taäp.
Hoïc sinh: SGK, vôû ghi. Ñoïc tröôùc baøi hoïc.
III. HOAÏT ÑOÄNG DAÏY HOÏC:
1. OÅn ñònh toå chöùc: Kieåm tra só soá lôùp.
2. Kieåm tra baøi cuõ:
H.
Ñ.
3. Giaûng baøi môùi:
TL
Hoaït ñoäng cuûa Giaùo vieân
Hoaït ñoäng cuûa Hoïc sinh
Noäi dung
Hoaït ñoäng 1: Tìm hieåu khaùi nieäm vectô
15’
Cho HS quan saùt hình 1.1.
Nhaän xeùt veà höôùng chuyeån
ñoäng. Töø ñoù hình thaønh khaùi
nieäm vectô.
Giaûi thích kí hieäu, caùch veõ
vectô.
H1. Vôùi 2 ñieåm A, B phaân
bieät coù bao nhieâu vectô coù
ñieåm ñaàu vaø ñieåm cuoái laø A
hoaëc B?
H2. So saùnh ñoä daøi caùc vectô
AB vaø BA
?
HS quan saùt vaø cho nhaän xeùt
veà höôùng chuyeån ñoäng cuûa oâ
toâ vaø maùy bay.
a
Ñ.
AB vaø BA
.
Ñ2.
AB BA
I. Khaùi nieäm vectô
ÑN: Vectô laø moät ñoaïn thaúng
coù höôùng.
AB
coù ñieåm ñaàu laø A, ñieåm
cuoái laø B.
Ñoä daøi vectô
AB
ñöôïc kí
hieäu laø:
AB
= AB.
Vectô coù ñoä daøi baèng 1 ñgl
vectô ñôn vò.
Vectô coøn ñöôïc kí hieäu laø
a,b,x,y
, …
Hoaït ñoäng 2: Tìm hieåu khaùi nieäm vectô cuøng phöông, vectô cuøng höôùng
20’
Cho HS quan saùt hình 1.3.
Nhaän xeùt veà giaù cuûa caùc vectô
H1. Haõy chæ ra giaù cuûa caùc
Ñ1. Laø caùc ñöôøng thaúng AB,
Ñöôøng thaúng ñi qua ñieåm
ñaàu vaø ñieåm cuoái cuûa moät
vectô ñgl giaù cuûa vectô ñoù.
Nguyễn Đình Khương Hình Học 10 Cơ Bản
2
vectô:
AB,CD,PQ,RS
, …?
H2. Nhaän xeùt veà VTTÑ cuûa
caùc giaù cuûa caùc caëp vectô:
a)
AB vaø CD
b)
PQ vaø RS
c)
EF vaø PQ
?
GV giôùi thieäu khaùi nieäm hai
vectô cuøng höôùng, ngöôïc
höôùng.
H3. Cho hbh ABCD. Chæ ra
caùc caëp vectô cuøng phöông,
cuøng höôùng, ngöôïc höôùng?
H4. Neáu ba ñieåm phaân bieät A,
B, C thaúng haøng thì hai vectô
AB vaø BC
coù cuøng höôùng
hay khoâng?
CD, PQ, RS, …
Ñ2.
a) truøng nhau
b) song song
c) caét nhau
A B
C D
E
F
P
Q
R
S
Ñ3.
AB vaø AC
cuøng phöông
AD vaø BC
cuøng phöông
AB vaø DC
cuøng höôùng, …
Ñ4. Khoâng theå keát luaän.
ÑN: Hai vectô ñgl cuøng
phöông neáu giaù cuûa chuùng
song song hoaëc truøng nhau.
Hai vectô cuøng phöông thì
coù theå cuøng höôùng hoaëc ngöôïc
höôùng.
Ba ñieåm phaân bieät A, B, C
thaúng haøng
AB vaø AC
cuøng phöông.
Hoaït ñoäng 3: Cuûng coá
8’
Nhaán maïnh caùc khaùi nieäm:
vectô, hai vectô phöông, hai
vectô cuøng höôùng.
Caâu hoûi traéc nghieäm:
Cho hai vectô
AB vaø CD
cuøng phöông vôùi nhau. Haõy
choïn caâu traû lôøi ñuùng:
a)
AB
cuøng höôùng vôùi
CD
b) A, B, C, D thaúng haøng
c)
AC
cuøng phöông vôùi
BD
d)
BA
cuøng phöông vôùi
CD
Caùc nhoùm thöïc hieän yeâu caàu
vaø cho keát quaû d).
4. BAØI TAÄP VEÀ NHAØ:
Baøi 1, 2 SGK
Ñoïc tieáp baøi “Vectô”
Ngaøy soaïn: 20/8/2012 Chöông I: VECTÔ
Nguyễn Đình Khương Hình Học 10 Cơ Bản
3
Tieát daïy: 02 Baøøi 1: CAÙC ÑÒNH NGHÓA (tt)
I. MUÏC TIEÂU:
Kieán thöùc:
Naém ñöôïc ñònh nghóa vectô vaø nhöõng khaùi nieäm quan troïng lieân quan ñeán vectô nhö: söï
cuøng phöông cuûa hai vectô, ñoä daøi cuûa vectô, hai vectô baèng nhau, …
Hieåu ñöôïc vectô
0
laø moät vectô ñaïc bieät vaø nhöõng qui öôùc veà vectô
0
.
Kó naêng:
Bieát chöùng minh hai vectô baèng nhau, bieát döïng moät vectô baèng vectô cho tröôùc vaø coù
ñieåm ñaàu cho tröôùc.
Thaùi ñoä:
Reøn luyeän oùc quan saùt, phaân bieät ñöôïc caùc ñoái töôïng.
II. CHUAÅN BÒ:
Giaùo vieân: Giaùo aùn, phieáu hoïc taäp.
Hoïc sinh: SGK, vôû ghi. Ñoïc tröôùc baøi hoïc.
III. HOAÏT ÑOÄNG DAÏY HOÏC:
1. OÅn ñònh toå chöùc: Kieåm tra só soá lôùp.
2. Kieåm tra baøi cuõ: (5’)
H. Theá naøo laø hai vectô cuøng phöông? Cho hbh ABCD. Haõy chæ ra caùc caëp vectô cuøng
phöông, cuøng höôùng?
Ñ.
AB vaø DC
cuøng höôùng, …
3. Giaûng baøi môùi:
TL
Hoaït ñoäng cuûa Giaùo vieân
Hoaït ñoäng cuûa Hoïc sinh
Noäi dung
Hoaït ñoäng 1: Tìm hieåu khaùi nieäm hai vectô baèng nhau
20’
Töø KTBC, GV giôùi thieäu
khaùi nieäm hai vectô baèng
nhau.
H1. Cho hbh ABCD. Chæ ra
caùc caëp vectô baèng nhau?
H2. Cho ABC ñeàu.
AB BC
?
H3. Goïi O laø taâm cuûa hình luïc
giaùc ñeàu ABCDEF.
1) Haõy chæ ra caùc vectô baèng
OA
,
OB
, …?
2) Ñaúng thöùc naøo sau ñaây laø
ñuùng?
a)
AB CD
b)
AO DO
c)
BC FE
d)
OA OC
Ñ1.
AB DC
, …
Ñ2. Khoâng. Vì khoâng cuøng
höôùng.
Ñ3. Caùc nhoùm thöïc hieän
1)
OA CB DO EF
….
2) c) vaø d) ñuùng.
III. Hai vectô baèng nhau
Hai vectô
avaø b
ñgl baèng
nhau neáu chuùng cuøng höôùng
vaø coù cuøng ñoä daøi, kí hieäu
ab
.
Chuù yù: Cho
a
, O.
! A sao
cho
OA a
.
Nguyễn Đình Khương Hình Học 10 Cơ Bản
4
Hoaït ñoäng 2: Tìm hieåu khaùi nieäm vectô – khoâng
10’
GV giôùi thieäu khaùi nieäm
vectô – khoâng vaø caùc qui öôùc
veà vectô – khoâng.
H. Cho hai ñieåm A, B thoaû:
AB BA
. Meänh ñeà naøo sau
ñaây laø ñuùng?
a)
AB
khoâng cuøng höôùng vôùi
BA
.
b)
AB 0
.
c)
AB
> 0.
d) A khoâng truøng B.
Ñ. Caùc nhoùm thaûo luaän vaø
cho keát quaû b).
IV. Vectô – khoâng
Vectô – khoâng laø vectô coù
ñieåm ñaàu vaø ñieåm cuoái truøng
nhau, kí hieäu
0
.
0 AA
,
A.
0
cuøng phöông, cuøng höôùng
vôùi moïi vectô.
0
= 0.
A
B
AB 0
.
Hoaït ñoäng 3: Cuûng coá
8’
Nhaán maïnh caùc khaùi nieäm
hai vectô baèng nhau, vectô –
khoâng.
Caâu hoûi traéc nghieäm. Choïn
phöông aùn ñuùng:
1) Cho töù giaùc ABCD coù
AB DC
. Töù giaùc ABCD laø:
a) Hình bình haønh
b) Hình chöõ nhaät
c) Hình thoi
d) Hình vuoâng
2) Cho nguõ giaùc ABCDE. Soá
caùc vectô khaùc
0
coù ñieåm
ñaàu vaø ñieåm cuoái laø caùc ñænh
cuûa nguõ giaùc baèng:
a) 25 b) 20 c) 16 d) 10
Caùc nhoùm thaûo luaän vaø cho
keát quaû:
1) a
2) b
4. BAØI TAÄP VEÀ NHAØ:
Baøi 2, 3, 4 SGK
Ngaøy soaïn: 03/9/2012 Chöông I: VECTÔ
Nguyễn Đình Khương Hình Học 10 Cơ Bản
5
Tieát daïy: 03 Baøøi 2: TOÅNG VAØ HIEÄU CUÛA HAI VECTÔ
I. MUÏC TIEÂU:
Kieán thöùc:
Naém ñöôïc caùc tính chaát cuûa toång hai vectô, lieân heä vôùi toång hai soá thöïc, toång hai caïnh
cuûa tam giaùc.
Naém ñöôïc hieäu cuûa hai vectô.
Kó naêng:
Bieát döïng toång cuûa hai vectô theo ñònh nghóa hoaëc theo qui taéc hình bình haønh.
Bieát vaän duïng caùc coâng thöùc ñeå giaûi toaùn.
Thaùi ñoä:
Reøn luyeän tö duy tröøu töôïng, linh hoaït trong vieäc giaûi quyeát caùc vaán ñeà.
II. CHUAÅN BÒ:
Giaùo vieân: Giaùo aùn. Caùc hình veõ minh hoaï.
Hoïc sinh: SGK, vôû ghi. OÂn taäp kieán thöùc vectô ñaõ hoïc.
III. HOAÏT ÑOÄNG DAÏY HOÏC:
1. OÅn ñònh toå chöùc: Kieåm tra só soá lôùp.
2. Kieåm tra baøi cuõ: (5’)
H. Neâu ñònh nghóa hai vectô baèng nhau.
AÙp duïng: Cho ABC, döïng ñieåm M sao cho:
AM BC
.
Ñ. ABCM laø hình bình haønh.
3. Giaûng baøi môùi:
TL
Hoaït ñoäng cuûa Giaùo vieân
Hoaït ñoäng cuûa Hoïc sinh
Noäi dung
Hoaït ñoäng 1: Tìm hieåu veà Toång cuûa hai vectô
20’
H1. Cho HS quan saùt h.1.5.
Cho bieát löïc naøo laøm cho
thuyeàn chuyeån ñoäng?
GV höôùng daãn caùch döïng
vectô toång theo ñònh nghóa.
Chuù yù: Ñieåm cuoái cuûa
AB
truøng vôùi ñieåm ñaàu cuûa
BC
.
H2. Tính toång:
a)
AB BC CD DE
b)
AB BA
H3. Cho hình bình haønh
ABCD. Chöùng minh:
AB AD AC
Töø ñoù ruùt ra qui taéc hình
bình haønh.
Ñ1. Hôïp löïc
F
cuûa hai löïc
12
F vaø F
.
1
F
2
F
F
a
ab
b
A
B
C
Ñ2. Döïa vaøo qui taéc 3 ñieåm.
a)
AE
b)
0
Ñ3.
AB AD AB BC AC
A
B
C
D
I. Toång cuûa hai vectô
a) Ñònh nghóa: Cho hai vectô
avaø b
. Laáy moät ñieåm A tuyø yù,
veõ
AB a,BC b
. Vectô
AC
ñgl toång cuûa hai vectô
avaø b
.
Kí hieäu laø
ab
.
b) Caùc caùch tính toång hai
vectô:
+ Qui taéc 3 ñieåm:
AB BC AC
+ Qui taéc hình bình haønh:
AB AD AC
Nguyễn Đình Khương Hình Học 10 Cơ Bản
6
Hoaït ñoäng 2: Tìm hieåu tính chaát cuûa toång hai vectô
15’
H1. Döïng
a b,b a
. Nhaän
xeùt?
H2.
Döïng
a b,b c
,
a b c
,
a b c
. Nhaän xeùt?
Ñ1. 2 nhoùm thöïc hieän yeâu
caàu.
A
B
C
D
a
b
a
b
ab
ba
a
b
c
bc
ab
A
B
C
D
II. Tính chaát cuûa pheùp coäng
caùc vectô
Vôùi
a,b,c
, ta coù:
a)
a b b a
(giao hoaùn)
b)
a b c a b c
c)
a 0 0 a a
Hoaït ñoäng 3: Cuûng coá
Nhaán maïnh caùc caùch xaùc
ñònh vectô toång.
Môû roäng cho toång cuûa nhieàu
vectô.
So saùnh toång cuûa hai vectô
vôi toång hai soá thöïc vaø toång
ñoä daøi hai caïnh cuûa tam giaùc.
4. BAØI TAÄP VEÀ NHAØ:
Baøi 1, 2, 3, 4 SGK.
Ngaøy soaïn: 09/9/2012 Chöông I: VECTÔ
Nguyễn Đình Khương Hình Học 10 Cơ Bản
7
Tieát daïy: 04 Baøøi 2: TOÅNG VAØ HIEÄU CUÛA HAI VECTÔ (tt)
I. MUÏC TIEÂU:
Kieán thöùc:
Naém ñöôïc caùc tính chaát cuûa toång hai vectô, lieân heä vôùi toång hai soá thöïc, toång hai caïnh
cuûa tam giaùc.
Naém ñöôïc hieäu cuûa hai vectô.
Kó naêng:
Bieát döïng toång cuûa hai vectô theo ñònh nghóa hoaëc theo qui taéc hình bình haønh.
Bieát vaän duïng caùc coâng thöùc ñeå giaûi toaùn.
Thaùi ñoä:
Reøn luyeän tö duy tröøu töôïng, linh hoaït trong vieäc giaûi quyeát caùc vaán ñeà.
II. CHUAÅN BÒ:
Giaùo vieân: Giaùo aùn. Hình veõ minh hoaï.
Hoïc sinh: SGK, vôû ghi. OÂn taäp kieán thöùc vectô ñaõ hoïc.
III. HOAÏT ÑOÄNG DAÏY HOÏC:
1. OÅn ñònh toå chöùc: Kieåm tra só soá lôùp.
2. Kieåm tra baøi cuõ: (5’)
H. Neâu caùc caùch tính toång hai vectô? Cho ABC. So saùnh:
a)
AB AC vôùi BC
b)
AB AC vôùi BC
Ñ. a)
AB AC BC
b)
AB AC BC
3. Giaûng baøi môùi:
TL
Hoaït ñoäng cuûa Giaùo vieân
Hoaït ñoäng cuûa Hoïc sinh
Noäi dung
Hoaït ñoäng 1: Tìm hieåu Hieäu cuûa hai vectô
15’
H1. Cho ABC coù trung ñieåm
caùc caïnh BC, CA, AB laàn löôït
laø D, E, F. Tìm caùc vectô ñoái
cuûa:
a)
DE
b)
EF
Nhaán maïnh caùch döïng hieäu
cuûa hai vectô
Ñ1. Caùc nhoùm thöïc hieän yeâu
caàu
A
B
C
D
E
F
a)
ED,AF,FB
b)
FE,BD,DC
O
A
B
III. Hieäu cuûa hai vectô
a) Vectô ñoái
+ Vectô coù cuøng ñoä daøi vaø
ngöôïc höôùng vôùi
a
ñgl vectô
ñoái cuûa
a
, kí hieäu
a
.
+
AB BA
+ Vectô ñoái cuûa
0
laø
0
.
b) Hieäu cuûa hai vectô
+
a b a ( b)
+
AB OB OA
Hoaït ñoäng 2: Vaän duïng pheùp tính toång, hieäu caùc vectô
20’
H1. Cho I laø trung ñieåm cuûa
AB. CMR
IA IB 0
.
H2. Cho
IA IB 0
. CMR: I
laø trung ñieåm cuûa AB.
H3. Cho G laø troïng taâm
Ñ1. I laø trung ñieåm cuûa AB
IA IB
IA IB 0
Ñ2.
IA IB 0
IA IB
I naèm giöõa A, B vaø IA = IB
I laø trung ñieåm cuûa AB.
Ñ3. Veõ hbh BGCD.
IV. AÙp duïng
a) I laø trung ñieåm cuûa AB
IA IB 0
b) G laø troïng taâm cuûa
ABC
GA GB GC 0
Nguyễn Đình Khương Hình Học 10 Cơ Bản
8
ABC.
CMR:
GA GB GC 0
GB GC GD
,
GA GD
A
B
C
G
D
I
Hoaït ñoäng 3: Cuûng coá
5’
Nhaán maïnh:
+ Caùch xaùc ñònh toång, hieäu
hai vectô, qui taéc 3 ñieåm, qui
taéc hbh.
+ Tính chaát trung ñieåm ñoaïn
thaúng.
+ Tính chaát troïng taâm tam
giaùc.
+
a b a b
HS nhaéc laïi
4. BAØI TAÄP VEÀ NHAØ:
Baøi 5, 6, 7, 8, 9, 10.
Ngaøy soaïn: 09/9/2011 Chöông I: VECTÔ
Tieát daïy: 05 Baøøi 2: BAØI TAÄP TOÅNG VAØ HIEÄU HAI VECTÔ
Nguyễn Đình Khương Hình Học 10 Cơ Bản
9
I. MUÏC TIEÂU:
Kieán thöùc:
Cuûng coá caùc kieán thöùc ñaõ hoïc veà pheùp coäng vaø tröø caùc vectô.
Khaéc saâu caùch vaän duïng qui taéc 3 ñieåm vaø qui taêc hình bình haønh.
Kó naêng:
Bieát xaùc ñònh vectô toång, vectô hieäu theo ñònh nghóa vaø caùc qui taéc.
Vaän duïng linh hoaït caùc qui taéc xaùc ñònh vectô toång, vectô hieäu.
Thaùi ñoä:
Reøn luyeän tính caån thaän, chính xaùc.
Luyeän tö duy hình hoïc linh hoaït.
II. CHUAÅN BÒ:
Giaùo vieân: Giaùo aùn. Heä thoáng baøi taäp.
Hoïc sinh: SGK, vôû ghi. Laøm baøi taäp veà nhaø.
III. HOAÏT ÑOÄNG DAÏY HOÏC:
1. OÅn ñònh toå chöùc: Kieåm tra só soá lôùp.
2. Kieåm tra baøi cuõ: (3’)
H. Neâu caùc qui taéc xaùc ñònh vectô toång, vectô hieäu?
Ñ. Qui taéc 3 ñieåm, qui taéc hình bình haønh.
3. Giaûng baøi môùi:
TL
Hoaït ñoäng cuûa Giaùo vieân
Hoaït ñoäng cuûa Hoïc sinh
Noäi dung
Hoaït ñoäng 1: Luyeän kyõ naêng chöùng minh ñaúng thöùc vectô
H1. Neâu caùch chöùng minh
moät ñaúng thöùc vectô?
H2. Neâu qui taéc caàn söû duïng?
H3. Haõy phaân tích caùc vectô
theo caùc caïnh cuûa caùc hbh?
Ñ1. Bieán ñoåi veá naøy thaønh veá
kia.
A
D
B
C
M
Ñ2. Qui taéc 3 ñieåm.
Ñ3.
RJ RA IJ
IQ IB BQ
PS PC CS
A
B
C
R
S
J
I
Q
P
1. Cho hbh ABCD vaø ñieåm M
tuyø yù. CMR:
MA MC MB MD
2. CMR vôùi töù giaùc ABCD baát
kì ta coù:
a)
AB BC CD DA 0
b)
AB AD CB CD
3. Cho ABC. Beân ngoaøi tam
giaùc veõ caùc hbh ABIJ, BCPQ,
CARS. CMR:
RJ IQ PS 0
Hoaït ñoäng 2: Cuûng coá moái quan heä giöõa caùc yeáu toá cuûa vectô
H1. Xaùc ñònh caùc vectô
a)
AB BC
b)
AB BC
Ñ1.
a)
AB BC
=
AC
b)
AB BC
=
AD
4. Cho ABC ñeàu, caïnh a.
Tính ñoä daøi cuûa caùc vectô:
a)
AB BC
b)
AB BC
Nguyễn Đình Khương Hình Học 10 Cơ Bản
10
H2. Neâu baát ñaúng thöùc tam
giaùc?
Ñ2. AB + BC > AC
5. Cho
a,b 0
. Khi naøo coù
ñaúng thöùc:
a)
a b a b
b)
a b a b
6. Cho
ab
= 0. So saùnh ñoä
daøi, phöông, höôùng cuûa
a,b
?
Hoaït ñoäng 3: Luyeän kó naêng chöùng minh 2 ñieåm truøng nhau
H1. Neâu ñieàu kieän ñeå 2 ñieåm
I, J truøng nhau?
Ñ1.
IJ 0
7. CMR:
AB CD
trung
ñieåm cuûa AD vaø BC truøng
nhau.
Hoaït ñoäng 4: Cuûng coá
Nhaán maïnh caùch vaän duïng
caùc kieán thöùc ñaõ hoïc.
Caâu hoûi:
Choïn phöông aùn ñuùng.
1) Cho 3 ñieåm A,B,C.Ta coù:
A.
AB AC BC
B.
AB AC BC
C.
AB BC CB
D.
AB AC CB
2) Cho I laø trung ñieåm cuûa
AB, ta coù:
A.
IA IB 0
B. IA + IB=0
C.
AI BI
D.
AI IB
Caùc nhoùm thaûo luaän, traû lôøi
nhanh.
1C, 2A.
4. BAØI TAÄP VEÀ NHAØ:
Laøm tieáp caùc baøi taäp coøn laïi.
Ñoïc tröôùc baøi “Tích cuûa vectô vôùi moät soá”
Ngaøy soaïn: 20/9/2012 Chöông I: VECTÔ
Tieát daïy: 06 Baøøi 3: TÍCH CUÛA VECTÔ VÔÙI MOÄT SOÁ
Nguyễn Đình Khương Hình Học 10 Cơ Bản
11
I. MUÏC TIEÂU:
Kieán thöùc:
Naém ñöôïc ñònh nghóa vaø tính chaát cuûa pheùp nhaân moät vectô vôùi moät soá.
Naém ñöôïc ñieàu kieän ñeå hai vectô cuøng phöông.
Kó naêng:
Bieát döïng vectô
ka
khi bieát kR vaø
a
.
Söû duïng ñöôïc ñieàu kieän caàn vaø ñuû cuûa 2 vectô cuøng phöông ñeå chöùng minh 3 ñieåm thaúng haøng
hoaëc hai ñöôøng thaúng song song.
Bieát phaân tích moät vectô theo 2 vectô khoâng cuøng phöông cho tröôùc.
Thaùi ñoä:
Luyeän tö duy phaân tích linh hoaït, saùng taïo.
II. CHUAÅN BÒ:
Giaùo vieân: Giaùo aùn. Hình veõ minh hoaï.
Hoïc sinh: SGK, vôû ghi. Ñoïc baøi tröôùc. OÂn laïi kieán thöùc veà toång, hieäu cuûa hai vectô.
III. HOAÏT ÑOÄNG DAÏY HOÏC:
1. OÅn ñònh toå chöùc: Kieåm tra só soá lôùp.
2. Kieåm tra baøi cuõ: (3')
H. Cho ABCD laø hình bình haønh. Tính
AB AD
. Nhaän xeùt veà vectô toång vaø
AO
?
Ñ.
AB AD AC
.
AC,AOcuønghöôùngvaø AC 2 AO
.
3. Giaûng baøi môùi:
TL
Hoaït ñoäng cuûa Giaùo vieân
Hoaït ñoäng cuûa Hoïc sinh
Noäi dung
Hoaït ñoäng 1: Tìm hieåu khaùi nieäm Tích cuûa vectô vôùi moät soá
10'
GV giôùi thieäu khaùi nieäm tích
cuûa vectô vôùi moät soá.
H1. Cho
AB a
. Döïng 2
a
.
H2. Cho G laø troïng taâm cuûa
ABC. D vaø E laàn löôït laø
trung ñieåm cuûa BC vaø AC. So
saùnh caùc vectô:
a)
DEvôùi AB
b)
AG vôùi AD
c)
AG vôùi GD
Ñ1. Döïng
BC a
AC 2a
A B
C
Ñ2.
A
B
C
D
E
G
a)
1
DE AB
2

b)
2
AG AD
3
c)
AG 2 GD
I. Ñònh nghóa
Cho soá k ≠ 0 vaø vectô
a0
.
Tích cuûa
a
vôùi soá k laø moät
vectô, kí hieäu k
a
, ñöôïc xaùc
ñònh nhö sau:
+ cuøng höôùng vôùi
a
neáu k>0,
+ ngöôïc höôùng vôùi
a
neáu k<0
+ coù ñoä daøi baèng
ka
.
Qui öôùc: 0
a
=
0
, k
0
=
0
Hoaït ñoäng 2: Tìm hieåu tính chaát cuûa tích vectô vôùi moät soá
10'
GV ñöa ra caùc ví duï minh
hoaï, roài cho HS nhaän xeùt caùc
tính chaát.
H1. Cho ABC. M, N laø trung
ñieåm cuûa AB, AC. So saùnh
caùc vectô:
HS theo doõi vaø nhaän xeùt.
Ñ1.
MA AN
=
1
BA AC
2
II. Tính chaát
Vôùi hai vectô
a
vaø
b
baát kì,
vôùi moïi soá h, k ta coù:
k(
a
+
b
) = k
a
+ k
b
(h + k)
a
= h
a
+ k
a
h(k
a
) = (hk)
a
Nguyễn Đình Khương Hình Học 10 Cơ Bản
12
MA AN
vôùi
BA AC
11
BA AC
22
=
1
BA AC
2
1.
a
=
a
, (–1)
a
= –
a
Hoaït ñoäng 3: Tìm hieåu theâm veà tính chaát trung ñieåm ñoaïn thaúng vaø troïng taâm tam giaùc
10'
H1. Nhaéc laïi heä thöùc trung
ñieåm cuûa ñoaïn thaúng?
H2. Nhaéc laïi heä thöùc troïng
taâm tam giaùc?
Ñ1. I laø trung ñieåm cuûa AB
IA IB 0
Ñ2. G laø troïng taâm ABC
GA GB GC 0
III. Trung ñieåm cuûa ñoaïn
thaúng vaø troïng taâm cuûa tam
giaùc
a) I laø trung ñieåm cuûa AB
MA MB 2MI
b) G laø troïng taâm
ABC
MA MB MC 3MG
(vôùi M tuyø yù)
Hoaït ñoäng 4: Cuûng coá
10'
Nhaán maïnh khaùi nieäm tích
vectô vôùi moät soá.
Caâu hoûi:
1) Cho ñoaïn thaúng AB. Xaùc
ñònh caùc ñieåm M, N sao cho:
MA 2MB
,
NA 2NB
2) Cho 4 ñieåm A, B, E, F thaúng
haøng. Ñieåm M thuoäc ñoaïn AB
sao cho AE =
1
2
EB, ñieåm F
khoâng thuoäc ñoaïn AB sao cho
AF =
1
2
FB. So saùnh caùc caëp
vectô:
EA vaø EB
,
FA vaø FB
?
1)
2)
1
EA EB
2

,
1
FA FB
2
4. BAØI TAÄP VEÀ NHAØ:
Baøi 1, 4, 5, 6, 7, 8, 9 SGK.
Ñoïc tieáp baøi "Tích cuûa vectô vôùi moät soá"
Ngaøy soaïn: 01/10/2012 Chöông I: VECTÔ
Tieát daïy: 07 Baøøi 3: TÍCH CUÛA VECTÔ VÔÙI MOÄT SOÁ (tt)
Nguyễn Đình Khương Hình Học 10 Cơ Bản
13
I. MUÏC TIEÂU:
Kieán thöùc:
Naém ñöôïc ñònh nghóa vaø tính chaát cuûa pheùp nhaân moät vectô vôùi moät soá.
Naém ñöôïc ñieàu kieän ñeå hai vectô cuøng phöông.
Kó naêng:
Bieát döïng vectô
ka
khi bieát kR vaø
a
.
Söû duïng ñöôïc ñieàu kieän caàn vaø ñuû cuûa 2 vectô cuøng phöông ñeå chöùng minh 3 ñieåm thaúng haøng
hoaëc hai ñöôøng thaúng song song.
Bieát phaân tích moät vectô theo 2 vectô khoâng cuøng phöông cho tröôùc.
Thaùi ñoä:
Luyeän tö duy phaân tích linh hoaït, saùng taïo.
II. CHUAÅN BÒ:
Giaùo vieân: Giaùo aùn. Hình veõ minh hoaï.
Hoïc sinh: SGK, vôû ghi. Ñoïc baøi tröôùc. OÂn laïi kieán thöùc veà toång, hieäu cuûa hai vectô.
III. HOAÏT ÑOÄNG DAÏY HOÏC:
1. OÅn ñònh toå chöùc: Kieåm tra só soá lôùp.
2. Kieåm tra baøi cuõ: (3')
H. Neâu heä thöùc trung ñieåm cuûa ñoaïn thaúng, heä thöùc troïng taâm tam giaùc?
Ñ.
MA MB 2MI
;
MA MB MC 3MG
.
3. Giaûng baøi môùi:
TL
Hoaït ñoäng cuûa Giaùo vieân
Hoaït ñoäng cuûa Hoïc sinh
Noäi dung
Hoaït ñoäng 1: Tìm hieåu ñieàu kieän ñeå hai vectô cuøng phöông
10'
H1. Cho 4 ñieåm A, B, E, F
thaúng haøng. Ñieåm M thuoäc
ñoaïn AB sao cho AE =
1
2
EB,
ñieåm F khoâng thuoäc ñoaïn AB
sao cho AF =
1
2
FB. So saùnh
caùc caëp vectô:
EA vaø EB
,
FA vaø FB
?
H2. Nhaéc laïi caùch chöùng minh
3 ñieåm thaúng haøng?
Ñ1.
1
EA EB
2

,
1
FA FB
2
Ñ2. A, B, C thaúng haøng
ABvaø AC
cuøng phöông.
IV. Ñieàu kieän ñeå hai vectô
cuøng phöông
a
vaø
b
(
b
≠
0
) cuøng phöông
k
R:
a
= k
b
Nhaän xeùt: A, B, C thaúng
haøng
k
R:
AB kAC
Hoaït ñoäng 2: Tìm hieåu phaân tích moät vectô theo hai vectô khoâng cuøng phöông
7'
GV giôùi thieäu vieäc phaân tích
moät vectô theo hai vectô
khoâng cuøng phöông.
H1. Cho ABC, M laø trung
ñieåm cuûa BC. Phaân tích
AM
theo
AB,AC
?
A
B CM
Ñ1.
AM
=
1
AB AC
2
V. Phaân tích moät vectô theo
hai vectô khoâng cuøng
phöông
Cho
a
vaø
b
khoâng cuøng
phöông. Khi ñoù moïi vectô
x
ñeàu phaân tích ñöôïc moät caùch
duy nhaát theo hai vectô
a
,
b
,
nghóa laø coù duy nhaát caëp soá h,
k sao cho
x
= h
a
+ k
b
.
Nguyễn Đình Khương Hình Học 10 Cơ Bản
14
Hoaït ñoäng 3: Vaän duïng phaân tích vectô, chöùng minh 3 ñieåm thaúng haøng
20'
H1. Vaän duïng heä thöùc troïng
taâm tam giaùc, tính
CA CB
?
H2. Phaân tích
CI
theo
a
,
b
?
H3. Phaân tích
AK
theo
a
,
b
?
H4. Phaân tích giaû thieát: Phaân
tích
AI,CK
theo
a CA
,
b CB
?
A
B
C
M
I
K
G
a
b
Ñ1.
CA CB
= 3
CG
CG
=
1
ab
3
Ñ2.
CI
=
1
CA CG
2
=
21
ab
36
Ñ3.
AK
=
1
AB
5
=
1
ba
5
Ñ4.
AI CI CA
=
11
ba
63
CK CA AK
=
41
ab
55
Ví duï: Cho ABC vôùi troïng
taâm G. Goïi I laø trung ñieåm
cuûa AG vaø K laø ñieåm treân
caïnh AB sao cho AK =
1
5
AB.
a) Phaân tích caùc vectô
AI,AK
,CI,CK
theo
a CA
,
b CB
b) CMR C, I, K thaúng haøng.
Hoaït ñoäng 4: Cuûng coá
3'
Nhaán maïnh:
+ Caùc kieán thöùc caàn söû duïng:
heä thöùc trung ñieåm, troïng taâm
+ Caùch phaân tích: qui taéc 3
ñieåm
4. BAØI TAÄP VEÀ NHAØ:
Baøi 2, 3 SGK.
Ngaøy soaïn: 20/10/2012 Chöông I: VECTÔ
Tieát daïy: 08 Baøøi 3: BAØI TAÄP TÍCH CUÛA VECTÔ VÔÙI MOÄT SOÁ
I. MUÏC TIEÂU:
Nguyễn Đình Khương Hình Học 10 Cơ Bản
15
Kieán thöùc:
Cuûng coá ñònh nghóa vaø
c
c
a
a
ù
ù
c
c
t
t
í
í
n
n
h
h
c
c
h
h
a
a
á
á
t
t
c
c
u
u
û
û
a
a
p
p
h
h
e
e
ù
ù
p
p
n
n
h
h
a
a
â
â
n
n
v
v
e
e
c
c
t
t
ô
ô
v
v
ô
ô
ù
ù
i
i
m
m
o
o
ä
ä
t
t
s
s
o
o
á
á
.
.
S
S
ö
ö
û
û
d
d
u
u
ï
ï
n
n
g
g
ñ
ñ
i
i
e
e
à
à
u
u
k
k
i
i
e
e
ä
ä
n
n
c
c
a
a
à
à
n
n
v
v
a
a
ø
ø
ñ
ñ
u
u
û
û
ñ
ñ
e
e
å
å
h
h
a
a
i
i
v
v
e
e
c
c
t
t
ô
ô
c
c
u
u
ø
ø
n
n
g
g
p
p
h
h
ö
ö
ô
ô
n
n
g
g
.
.
Kó naêng:
B
B
i
i
e
e
á
á
t
t
v
v
a
a
ä
ä
n
n
d
d
u
u
ï
ï
n
n
g
g
t
t
í
í
c
c
h
h
v
v
e
e
c
c
t
t
ô
ô
v
v
ô
ô
ù
ù
i
i
m
m
o
o
ä
ä
t
t
s
s
o
o
á
á
ñ
ñ
e
e
å
å
c
c
h
h
ö
ö
ù
ù
n
n
g
g
m
m
i
i
n
n
h
h
ñ
ñ
a
a
ú
ú
n
n
g
g
t
t
h
h
ö
ö
ù
ù
c
c
v
v
e
e
c
c
t
t
ô
ô
.
.
.
.
B
B
i
i
e
e
á
á
t
t
v
v
a
a
ä
ä
n
n
d
d
u
u
ï
ï
n
n
g
g
ñ
ñ
i
i
e
e
à
à
u
u
k
k
i
i
e
e
ä
ä
n
n
h
h
a
a
i
i
v
v
e
e
c
c
t
t
ô
ô
c
c
u
u
ø
ø
n
n
g
g
p
p
h
h
ö
ö
ô
ô
n
n
g
g
ñ
ñ
e
e
å
å
c
c
h
h
ö
ö
ù
ù
n
n
g
g
m
m
i
i
n
n
h
h
3
3
ñ
ñ
i
i
e
e
å
å
m
m
t
t
h
h
a
a
ú
ú
n
n
g
g
h
h
a
a
ø
ø
n
n
g
g
.
.
B
B
i
i
e
e
á
á
t
t
v
v
a
a
ä
ä
n
n
d
d
u
u
ï
ï
n
n
g
g
c
c
a
a
ù
ù
c
c
p
p
h
h
e
e
ù
ù
p
p
t
t
o
o
a
a
ù
ù
n
n
v
v
e
e
c
c
t
t
ô
ô
ñ
ñ
e
e
å
å
p
p
h
h
a
a
â
â
n
n
t
t
í
í
c
c
h
h
m
m
o
o
ä
ä
t
t
v
v
e
e
c
c
t
t
ô
ô
t
t
h
h
e
e
o
o
h
h
a
a
i
i
v
v
e
e
c
c
t
t
ô
ô
k
k
h
h
o
o
â
â
n
n
g
g
c
c
u
u
ø
ø
n
n
g
g
p
p
h
h
ö
ö
ô
ô
n
n
g
g
.
.
Thaùi ñoä:
Reøn luyeän tính caån thaän, chính xaùc.
Luyeän tö duy linh hoaït qua vieäc phaân tích vectô.
II. CHUAÅN BÒ:
Giaùo vieân: Giaùo aùn. Heä thoáng baøi taäp.
Hoïc sinh: SGK, vôû ghi. OÂn taäp caùc kieán thöùc veà vectô.
III. HOAÏT ÑOÄNG DAÏY HOÏC:
1. OÅn ñònh toå chöùc: Kieåm tra só soá lôùp.
2. Kieåm tra baøi cuõ: (Loàng vaøo quaø trình luyeän taäp)
H.
Ñ.
3. Giaûng baøi môùi:
TL
Hoaït ñoäng cuûa Giaùo vieân
Hoaït ñoäng cuûa Hoïc sinh
Noäi dung
Hoaït ñoäng 1: Vaän duïng chöùng minh ñaúng thöùc vectô
10'
H1. Nhaéc laïi heä thöùc trung
ñieåm?
H2. Neâu caùch chöùng minh b)?
Höôùng daãn: Töø M veõ caùc
ñöôøng thaúng song song vôùi
caùc caïnh cuûa ABC.
H3. Nhaän xeùt caùc tam giaùc
MA
1
A
2
, MB
1
B
2
, MC
1
C
2
?
H4. Neâu heä thöùc troïng taâm
tam giaùc?
A
B CM
D
Ñ1.
DB DC 2DM
Ñ2. Töø a) söû duïng qui taéc 3
ñieåm.
A
B
C
O
M
D
E
F
A
1
A
2
B
1
B
2
C
1
C
2
Ñ3. Caùc tam giaùc ñeàu
Ñ4.
MA MB MC 3MO
1. Goïi AM laø trung tuyeán cuûa
ABC vaø D laø trung ñieåm cuûa
ñoaïn AM. CMR:
a)
2DA DB DC 0
b)
2OA OB OC 4OD
,
vôùi O tuyø yù.
2. Cho ABC ñeàu coù troïng
taâm O vaø M laø 1 ñieåm tuyø yù
trong tam giaùc. Goïi D, E, F
laàn löôït laø chaân ñöôøng vuoâng
goùc haï töø M ñeán BC, AC, AB.
CMR:
3
MD ME MF MO
2
Hoaït ñoäng 2: Vaän duïng xaùc ñònh ñieåm thoaû moät ñaúng thöùc vectô
10'
H1. Neâu caùch xaùc ñònh moät
ñieåm?
Ñ1. Chöùng toû:
OM a
(vôùi O
vaø
a
ñaõ bieát)
3. Cho hai ñieåm phaân bieät A,
B. Tìm ñieåm K sao cho:
3KA 2KB 0
Nguyễn Đình Khương Hình Học 10 Cơ Bản
16
H2. Tính
MA MB
?
Ñ2.
MA MB
= 2
MI
A
C
B
I
M
4. Cho ABC. Tìm ñieåm M
sao cho:
MA MB 2MC 0
Hoaït ñoäng 3: Vaän duïng chöùng minh 3 ñieåm thaúng haøng, hai ñieåm truøng nhau
10'
H1. Neâu caùch chöùng minh 3
ñieåm A, B, C thaúng haøng?
H2. Neâu caùch chöùng minh 2
ñieåm truøng nhau?
Ñ1. Chöùng minh
CA,CB
cuøng phöông.
CA 2CB 0
Ñ2.
GG 0
5. Cho boán ñieåm O, A, B, C
sao cho:
OA 2OB 3OC 0
CMR 3 ñieåm A, B, C thaúng
haøng.
6. Cho hai tam giaùc ABC vaø
ABC laàn löôït coù troïng taâm
laø G vaø G. CMR:
AA BB CC 3GG
Töø ñoù suy ra ñieàu kieän caàn vaø
ñuû ñeå hai tam giaùc coù cuøng
troïng taâm.
Hoaït ñoäng 4: Vaän duïng phaân tích vectô
10'
H1. Vaän duïng tính chaát naøo?
Ñ1. Heä thöùc trung ñieåm.
2
AB u v
3

,
24
BC u v
33

42
CA u v
33
Ñ2. Qui taéc 3 ñieåm
13
AM u v
22
7. Cho AK vaø BM laø hai trung
tuyeán cuûa ABC. Phaân tích
caùc vectô
AB,BC,CA
theo
u AK, v BM
8. Treân ñöôøng thaúng chöùa
caïnh BC cuûa ABC, laáy moät
ñieåm M sao cho:
MB 3MC
.
Phaân tích
AM
theo
u AB, v AC
.
Hoaït ñoäng 5: Cuûng coá
3'
Nhaán maïnh caùch giaûi caùc
daïng toaùn
4. BAØI TAÄP VEÀ NHAØ:
Laøm tieáp caùc baøi taäp coøn laïi.
Ñoïc tröôùc baøi "Heä truïc toaï ñoä"
Ngaøy soaïn: 20/10/2012 Chöông I: VECTÔ
Tieát daïy: 09 Baøøi 4: HEÄ TRUÏC TOAÏ ÑOÄ
I. MUÏC TIEÂU:
Kieán thöùc:
Naém ñöôïc ñònh nghóa vaø caùc tính chaát veà toaï ñoä cuûa vectô vaø cuûa ñieåm.
Nguyễn Đình Khương Hình Học 10 Cơ Bản
17
Kó naêng:
Bieát bieåu dieãn caùc ñieåm vaø caùc vectô baèng caùc caëp soá trong heä truïc toaï ñoä ñaõ cho.
Bieát tìm toaï ñoä caùc vectô toång, hieäu, tích moät soá vôùi moät vectô.
Bieát söû duïng coâng thöùc toaï ñoä trung ñieåm cuûa ñoaïn thaúng vaø toaï ñoä troïng taâm tam giaùc.
Thaùi ñoä:
Reøn luyeän tính caån thaän, chính xaùc.
Gaén kieán thöùc ñaõ hoïc vaøo thöïc teá.
II. CHUAÅN BÒ:
Giaùo vieân: Giaùo aùn. Hình veõ minh hoaï.
Hoïc sinh: SGK, vôû ghi. OÂn taäp kieán thöùc vectô ñaõ hoïc.
III. HOAÏT ÑOÄNG DAÏY HOÏC:
1. OÅn ñònh toå chöùc: Kieåm tra só soá lôùp.
2. Kieåm tra baøi cuõ: (3')
H. Cho ABC, ñieåm M thuoäc caïnh BC:
3
MB MC
2

. Haõy phaân tích
AM
theo
AB,AC
.
Ñ.
23
AM AB AC
55

.
3. Giaûng baøi môùi:
TL
Hoaït ñoäng cuûa Giaùo vieân
Hoaït ñoäng cuûa Hoïc sinh
Noäi dung
Hoaït ñoäng 1: Tìm hieåu veà Toaï ñoä cuûa ñieåm treân truïc
15'
GV giôùi thieäu truïc toaï ñoä,
toaï ñoä cuûa ñieåm treân truïc, ñoä
daøi ñaïi soá cuûa vectô treân truïc.
H1. Cho truïc (O;
e
) vaø caùc
ñieåm A, B, C nhö hình veõ.
Xaùc ñònh toaï ñoä caùc ñieåm A,
B, C, O.
H2. Cho truïc (O;
e
). Xaùc ñònh
caùc ñieåm M(–1), N(3), P(–3).
H3. Tính ñoä daøi ñoaïn thaúng
MN vaø neâu nhaän xeùt?
H4. Xaùc ñònh toaï ñoä trung
ñieåm I cuûa MN?
Ñ1.
Ñ3.
Ñ3. MN = 4 =
3 ( 1)
Ñ4. I(1)
I. Truïc vaø ñoä daøi ñaïi soá treân
truïc
a) Truïc toaï ñoä (O;
e
)
b) Toaï ñoä cuûa ñieåm treân truïc:
Cho M treân truïc (O;
e
).
k laø toaï ñoä cuûa M
OM ke
c) Ñoä daøi ñaïi soá cuûa vectô:
Cho A, B treân truïc (O;
e
).
a =
AB
AB ae
Nhaän xeùt:
+
AB
cuøng höôùng
e
AB
>0
+
AB
ngöôïc höôùng
e
AB
<0
+ Neáu A(a), B(b) thì
AB
=b–a
+ AB =
AB AB b a
+ Neáu A(a), B(b), I laø trung
ñieåm cuûa AB thì
ab
I
2



Hoaït ñoäng 2: Tìm hieåu veà Toaï ñoä cuûa vectô, cuûa ñieåm trong heä truïc toaï ñoä
Nguyễn Đình Khương Hình Học 10 Cơ Bản
18
22'
Cho HS nhaéc laïi kieán thöùc
ñaõ bieát veà heä truïc toaï ñoä. Sau
ñoù GV giôùi thieäu ñaày ñuû veà
heä truïc toaï ñoä.
H1. Nhaéc laïi ñònh lí phaân tích
vectô?
H2. Xaùc ñònh toaï ñoä cuûa
AB
nhö hình veõ?
H3. Xaùc ñònh toaï ñoä cuûa
i, j
?
GV giôùi thieäu khaùi nieäm toaï
ñoä cuûa ñieåm.
H4.
a) Xaùc ñònh toaï ñoä caùc ñieåm
A, B, C nhö hình veõ?
b) Veõ caùc ñieåm D(–2; 3),
E(0; –4), F(3; 0)?
c) Xaùc ñònh toaï ñoä
AB,BC,CA
?
Ñ1. ! x, yR:
u xi yj
Ñ2.
AB 3i 2 j
AB
= (3;2)
a) A(3; 2), B(–1;
3
2
), C(2; –1)
b)
AB
= (–3;
1
2
)
II. Heä truïc toaï ñoä
a) Ñònh nghóa:
Heä truïc toaï ñoä
O; i; j
O : goác toaï ñoä
Truïc
O; i
: truïc hoaønh Ox
Truïc
O; j
: truïc tung Oy
i, j
laø caùc vectô ñôn vò
Heä
O; i; j
coøn kí hieäu Oxy
Maët phaúng toaï ñoä Oxy.
b) Toaï ñoä cuûa vectô
u
= (x; y)
u xi yj
Cho
u
= (x; y),
u'
= (x
; y
)
u u'
x x'
y y'
Moãi vectô ñöôïc hoaøn toaøn
xaùc ñònh khi bieát toaï ñoä cuûa
noù
i (1;0), j (0;1)
c) Toaï ñoä cuûa ñieåm
M(x; y)
OM
= (x; y)
Neáu MM
1
Ox, MM
2
Oy
thì x =
1
OM
, y =
OM2
Neáu M
Ox thì y
M
= 0
M
Oy thì x
M
= 0
d) Lieân heä giöõa toaï ñoä cuûa
ñieåm vaø vectô trong maët
phaúng
Cho A(x
A
; y
A
), B(x
B
; y
B
).
AB
= (x
B
– x
A
; y
B
– y
A
)
Hoaït ñoäng 3: Cuûng coá
3'
Nhaán maïnh caùc khaùi nieäm
toaï ñoä cuûa vectô vaø cuûa ñieåm
4. BAØI TAÄP VEÀ NHAØ:
Baøi 1, 2, 3, 4, 5 SGK.
Ñoïc tieáp baøi "Heä truïc toaï ñoä"
Ngaøy soaïn: 1/11/2012 Chöông I: VECTÔ
Tieát daïy: 10 Baøøi 4: HEÄ TRUÏC TOAÏ ÑOÄ (tt)
Nguyễn Đình Khương Hình Học 10 Cơ Bản
19
I. MUÏC TIEÂU:
Kieán thöùc:
Naém ñöôïc ñònh nghóa vaø caùc tính chaát veà toaï ñoä cuûa vectô vaø cuûa ñieåm.
Kó naêng:
Bieát bieåu dieãn caùc ñieåm vaø caùc vectô baèng caùc caëp soá trong heä truïc toaï ñoä ñaõ cho.
Bieát tìm toaï ñoä caùc vectô toång, hieäu, tích moät soá vôùi moät vectô.
Bieát söû duïng coâng thöùc toaï ñoä trung ñieåm cuûa ñoaïn thaúng vaø toaï ñoä troïng taâm tam giaùc.
Thaùi ñoä:
Reøn luyeän tính caån thaän, chính xaùc.
Gaén kieán thöùc ñaõ hoïc vaøo thöïc teá.
II. CHUAÅN BÒ:
Giaùo vieân: Giaùo aùn. Hình veõ minh hoaï.
Hoïc sinh: SGK, vôû ghi. OÂn taäp kieán thöùc vectô ñaõ hoïc.
III. HOAÏT ÑOÄNG DAÏY HOÏC:
1. OÅn ñònh toå chöùc: Kieåm tra só soá lôùp.
2. Kieåm tra baøi cuõ: (3')
H. – Neâu ñònh nghóa toaï ñoä cuûa vectô trong mp Oxy?
– Lieân heä giöõa toaï ñoä cuûa ñieåm vaø cuûa vectô trong mp Oxy?
Ñ.
u
= (x; y)
u xi yj
.
AB
= (x
B
– x
A
; y
B
– y
A
)
3. Giaûng baøi môùi:
TL
Hoaït ñoäng cuûa Giaùo vieân
Hoaït ñoäng cuûa Hoïc sinh
Noäi dung
Hoaït ñoäng 1: Tìm hieåu veà Toaï ñoä cuûa caùc vectô
u v,u v,ku
15'
HD hoïc sinh chöùng minh
moät soá coâng thöùc.
VD1.
Cho
a
= (1; –2),
b
= (3; 4),
c
= (5; –1). Tìm toaï ñoä cuûa
caùc vectô:
a)
u 2a b c
b)
v a 2b c
c)
x a 2b 3c
d)
1
y 3a b c
2
VD2.
Cho
a
= (1; –1),
b
= (2; 1).
Haõy phaân tích caùc vectô sau
theo
a
vaø
b
:
a)
c
= (4; –1)
b)
d
= (–3; 2)
GV höôùng daãn caùch phaân
tích.
Ñ.
a)
u
= (0; 1)
b)
v
= (0; 11)
Ñ. Giaû söû
c ka hb
= (k + 2h; –k + h)
k 2h 4
k h 1

k2
h1
III. Toaï ñoä cuûa caùc vectô
u v,u v,ku
Cho
u
=(u
1
; u
2
),
v
=(v
1
; v
2
).
uv
= (u
1
+ v
1
; u
2
+v
2
)
uv
= (u
1
– v
1
; u
2
–v
2
)
k
u
= (ku
1
; ku
2
), k
R
Nhaän xeùt: Hai vectô
u
=(u
1
;
u
2
),
v
=(v
1
; v
2
) vôùi
v
≠
0
cuøng
phöông
k
R sao cho:
11
22
u kv
u kv
Hoaït ñoäng 2: Tìm hieåu veà Toaï ñoä cuûa trung ñieåm, cuûa troïng taâm
H1. Cho A(1;0), B(3; 0) vaø I
Ñ1. I(2;0)
IV. Toaï ñoä cuûa trung ñieåm
Nguyễn Đình Khương Hình Học 10 Cơ Bản
20
20'
laø trung ñieåm cuûa AB. Bieåu
dieãn 3 ñieåm A, B, I treân
mpOxy vaø suy ra toaï ñoä ñieåm
I?
GV höông daãn chöùng minh
coâng thöùc xaùc ñònh toaï ñoä
trung ñieåm vaø troïng taâm.
H2. Neâu heä thöùc trung ñieåm
cuûa ñoaïn thaúng vaø troïng taâm
cuûa tam giaùc?
VD: Cho tam giaùc ABC coù
A(–1;–2), B(3;2), C(4;–1).
a) Tìm toaï ñoä trung ñieåm I
cuûa BC.
b) Tìm toaï ñoä troïng taâm G
cuûa ABC.
c) Tìm toaï ñoä ñieåm M sao cho
MA 2MB
.
x
y
O
A
1
B
3
I
Ñ2.
a) I laø trung ñieåm cuûa AB
OA OB
OI
2
b) G laø troïng taâm cuûa ABC
OA OB OC
OG
3

Ñ.
a) I
71
;
22



b) G(2;
1
3
)
c)
OM 2OB OA
M(7;6)
ñoaïn thaúng, cuûa troïng taâm
tam giaùc
a) Cho A(x
A
; y
A
), B(x
B
; y
B
). I laø
trung ñieåm cuûa AB thì:
x
I
=
AA
xy
2
, y
I
=
AB
yy
2
b) Cho
ABC vôùi A(x
A
; y
A
),
B(x
B
; y
B
), C(x
C
; y
C
). G laø troïng
taâm cuûa
ABC thì:
A B C
G
A B C
G
x x x
x
3
y y y
y
3


Hoaït ñoäng 3: Cuûng coá
5'
Nhaán maïnh caùch xaùc ñònh
toaï ñoä cuûa vectô, cuûa ñieåm.
Caâu hoûi:
Cho
ABC coù A(1;2), B(–2;1)
vaø C(3;3). Tìm toaï ñoä:
a) Troïng taâm G cuûa
ABC.
b) Ñieåm D sao cho ABCD laø
hình bình haønh.
a) G
2
;2
3



b) D(6; 4)
4. BAØI TAÄP VEÀ NHAØ:
Baøi 6, 7, 8 SGK.
Ngaøy soaïn:5 /11/2012 Chöông I: VECTÔ
Tieát daïy: 11 Baøøi 4: BAØI TAÄP HEÄ TRUÏC TOAÏ ÑOÄ
I. MUÏC TIEÂU:
Nguyễn Đình Khương Hình Học 10 Cơ Bản
21
Kieán thöùc:
Cuûng coá caùc kieán thöùc veà vectô, toaï ñoä cuûa vectô vaø cuûa ñieåm.
Caùch xaùc ñònh toaï ñoä cuûa trung ñieåm ñoaïn thaúng, troïng taâm cuûa tam giaùc.
Kó naêng:
Thaønh thaïo vieäc xaùc ñònh toaï ñoä cuûa vectô, cuûa ñieåm.
Thaønh thaïo caùch xaùc ñònh toaï ñoä vectô toång, hieäu, tích moät vectô vôùi moät soá.
Vaän duïng vectô vaø toaï ñoä ñeå giaûi toaùn hình hoïc.
Thaùi ñoä:
Reøn luyeän tính caån thaän, chính xaùc.
II. CHUAÅN BÒ:
Giaùo vieân: Giaùo aùn. Heä thoáng baøi taäp.
Hoïc sinh: SGK, vôû ghi. OÂn taäp caùc kieán thöùc ñaõ hoïc veà vectô vaø toaï ñoä.
III. HOAÏT ÑOÄNG DAÏY HOÏC:
1. OÅn ñònh toå chöùc: Kieåm tra só soá lôùp.
2. Kieåm tra baøi cuõ: (Loàng vaøo quaù trình luyeän taäp)
H.
Ñ.
3. Giaûng baøi môùi:
TL
Hoaït ñoäng cuûa Giaùo vieân
Hoaït ñoäng cuûa Hoïc sinh
Noäi dung
Hoaït ñoäng 1: Söû duïng toaï ñoä ñeå xeùt quan heä phöông, höôùng cuûa caùc vectô
10'
H1. Nhaéc laïi ñieàu kieän ñeå hai
vectô cuøng phöông, cuøng
höôùng, baèng nhau, ñoái nhau?
Ñ1.
a)
a
vaø
i
ngöôïc höôùng
b)
a
vaø
b
ñoái nhau
c) khoâng coù quan heä gì
Ñ2.
a)
u
+
v
= (4; 4) vaø
a
khoâng
coù quan heä
b)
u
–
v
= (2; –8) vaø
b
cuøng
höôùng
c) 2
u
+
v
= (7; 2) vaø
v
khoâng
coù quan heä
Ñ3.
AB
= (–3; –3),
AC
= (6; 6)
AC
= –2
AB
A, B, C
thaúng haøng.
1. Xeùt quan heä phöông, höôùng
cuûa caùc vectô:
a)
a
= (–3; 0) vaø
i
= (1; 0)
b)
a
= (3; 4) vaø
b
= (–3; –4)
c)
a
= (5; 3) vaø
b
= (3; 5)
2. Cho
u
= (3; –2),
v
= (1; 6).
Xeùt quan heä phöông, höôùng
cuûa caùc vectô:
a)
u
+
v
vaø
a
= (–4; 4)
b)
u
–
v
vaø
b
= (6; –24)
c) 2
u
+
v
vaø
v
3. Cho A(1; 1), B(–2; –2),
C(7; 7). Xeùt quan heä giöõa 3
ñieåm A, B, C.
Hoaït ñoäng 2: Luyeän taäp caùc pheùp toaùn vectô döïa vaøo toaï ñoä
15'
H1. Nhaéc laïi caùch xaùc ñònh
toaï ñoä vectô toång, hieäu, tích
moät vectô vôùi moät soá?
Ñ1.
c
= 2
a
+ 3
b
= (2x – 15; 7)
c
= (x; 7) x = 15
Ñ2. Giaû söû
c
= h
a
+ k
b
3. Cho
a
= (x; 2),
b
= (–5; 1),
c
= (x; 7). Tìm x ñeå
c
= 2
a
+
3
b
.
4. Cho
a
= (2; –2),
b
= (1; 4).
Nguyễn Đình Khương Hình Học 10 Cơ Bản
22
2h k 5
2h 4k 0

h2
k1
c
= 2
a
+
b
Haõy phaân tích vectô
c
=(5; 0)
theo hai vectô
a
vaø
b
.
Hoaït ñoäng 3: Vaän duïng vectô–toaï ñoä ñeå giaûi toaùn hình hoïc
15'
H1. Nhaéc laïi caùch xaùc ñònh
toaï ñoä trung ñieåm ñoaïn thaúng
vaø troïng taâm tam giaùc?
M
N
P
A
B
C
D
a)
NA MP
A(8; 1)
MB NP
B(–4; 5)
MC PN
C(–4; 7)
b)
AD BC
D(8; 3)
c) G(0; 1)
5. Cho caùc ñieåm M(–4; 1),
N(2; 4), P(2; –2) laàn löôït laø
trung ñieåm cuûa caùc caïnh BC,
CA, AB cuûa ABC.
a) Tính toaï ñoä caùc ñænh cuûa
ABC.
b) Tìm toaï ñoä ñieåm D sao cho
ABCD laø hình bình haønh.
c) CMR troïng taâm cuûa caùc
tam giaùc MNP vaø ABC truøng
nhau.
Hoaït ñoäng 4: Cuûng coá
5'
Nhaán maïnh
– Caùc kieán thöùc cô baûn veà
vectô – toaï ñoä.
– Caùch vaän duïng vectô–toaï
ñoä ñeå giaûi toaùn.
4. BAØI TAÄP VEÀ NHAØ:
Laøm caùc baøi taäp coøn laïi.
Baøi taäp oân chöông I.
Ngaøy soaïn: 10/11/2012 Chöông I: VECTÔ
Tieát daïy: 12 Baøøi daïy: OÂN TAÄP CHÖÔNG I
I. MUÏC TIEÂU:
Kieán thöùc:
Nguyễn Đình Khương Hình Học 10 Cơ Bản
23
Naém laïi toaøn boä kieán thöùc ñaõ hoïc veà vectô vaø toaï ñoä.
Kó naêng:
Bieát vaän duïng caùc tính chaát cuûa vectô trong vieäc giaûi toaùn hình hoïc.
Vaän duïng moät soá coâng thöùc veà toaï ñoä ñeå giaûi moät soá baøi toaùn hình hoïc.
Thaùi ñoä:
Reøn luyeän tính caån thaän, chính xaùc.
II. CHUAÅN BÒ:
Giaùo vieân: Giaùo aùn. Heä thoáng baøi taäp.
Hoïc sinh: SGK, vôû ghi. OÂn taäp caùc kieán thöùc ñaõ hoïc veà vectô vaø toaï ñoä.
III. HOAÏT ÑOÄNG DAÏY HOÏC:
1. OÅn ñònh toå chöùc: Kieåm tra só soá lôùp.
2. Kieåm tra baøi cuõ: (Loàng vaøo quaù trình oân taäp)
H.
Ñ.
3. Giaûng baøi môùi:
TL
Hoaït ñoäng cuûa Giaùo vieân
Hoaït ñoäng cuûa Hoïc sinh
Noäi dung
Hoaït ñoäng 1: Luyeän kyõ naêng thöïc hieän caùc pheùp toaùn vectô
20'
H1. Döïa vaøo tính chaát naøo ?
H2. Nhaän xeùt tính chaát cuûa
tam giaùc ñeàu?
H3. Söû duïng caùch bieán ñoåi
naøo?
Ñ1. Tính chaát trung ñieåm.
Ñ2.
OM OA OB OC
M ñoái xöùng vôùi C qua O.
Ñ3. Qui taéc 3 ñieåm.
N
M
O
A
B
1
2
OM OA
1
2
AN OB OA
11
22
MN OB OA
1
2
MB OA OB
1. Cho tam giaùc ñeàu ABC noäi
tieáp trong ñöôøng troøn taâm O.
Haõy xaùc ñònh caùc ñieåm M, N,
P sao cho:
a)
OM OA OB
b)
ON OB OC
c)
OP OC OA
2. Cho 6 ñieåm M, N, P, Q, R,
S baát kì. Chöùng minh raèng:
MP NQ RS MS NP RQ
3. Cho OAB. Goïi M, N laàn
löôït laø trung ñieåm cuûa OA vaø
OB. Tìm caùc soá m, n sao cho:
a)
OM mOA nOB
b)
AN mOA nOB
c)
MN mOA nOB
d)
MB mOA nOB
Hoaït ñoäng 2: Luyeän kyõ naêng vaän duïng toaï ñoä ñeå giaûi toaùn
20'
H1. Neâu ñieàu kieän ñeå DABC
laø hình bình haønh?
H2. Neâu coâng thöùc xaùc ñònh
Ñ1.
DABC laø hbh
AD BC
Ñ2.
4. Cho ABC vôùi A(3; 1), B(–
1; 2), C(0; 4).
a) Tìm ñieåm D ñeå DABC laø
hình bình haønh.
Nguyễn Đình Khương Hình Học 10 Cơ Bản
24
toaï ñoä troïng taâm tam giaùc?
H3. Neâu ñieàu kieän xaùc ñònh
ñieåm C?
H4. Neâu ñieàu kieän ñeå 3 ñieåm
thaúng haøng?
H5. Neâu caùch phaân tích moät
vectô theo 2 vectô khoâng
cuøng phöông?
3
3
A B C
G
A B C
G
y y y
y
x x x
x


Ñ3. B laø trung ñieåm cuûa AC.
Ñ4.
,AB AC
cuøng phöông.
Ñ5. Tìm caùc soá k vaø h sao
cho:
c ka hb
b) Tìm troïng taâm G cuûa
ABC.
c) Tìm hai soá m n sao cho:
0mAB nAC
5.
a) Cho A(2; 3), B(–3; 4). Tìm
ñieåm C bieát C ñoái xöùng vôùi A
qua B.
b) Cho A(1; –2), B(4; 5),
C(3m; m–1). Xaùc ñònh m ñeå
A, B, C thaúng haøng.
6. Cho
a
=(2; 1),
b
= (3; –4),
c
= (–7; 2).
a) Tìm toaï ñoä cuûa:
3 2 4u a b c
b) Tìm toaï ñoä cuûa
x
:
x a b c
c) Phaân tích
c
theo
a vaø b
.
Hoaït ñoäng 3: Cuûng coá
3'
Nhaán maïnh caùch vaän duïng
caùc kieán thöùc veà vectô vaø toaï
ñoä ñeå giaûi toaùn.
4. BAØI TAÄP VEÀ NHAØ:
Chuaån bò kieåm tra 1 tieát chöông I
Ngaøy soaïn: 15/11/2012 Chöông I: VECTÔ
Tieát daïy: 13 Baøøi daïy: KIEÅM TRA VIEÁT CHÖÔNG I
I. MUÏC TIEÂU:
Kieán thöùc:
Cuûng coá caùc kieán thöùc veà vectô vaø toaï ñoä.
Kó naêng:
Nguyễn Đình Khương Hình Học 10 Cơ Bản
25
Thöïc hieän caùc pheùp toaùn veà vectô.
Vaän duïng toaï ñoä ñeå giaûi toaøn hình hoïc.
Thaùi ñoä:
Reøn luyeän tính caån thaän, chính xaùc.
II. CHUAÅN BÒ:
Giaùo vieân: Giaùo aùn. Ñeà kieåm tra.
Hoïc sinh: OÂn taäp kieán thöùc chöông I.
III. MA TRAÄN ÑEÀ:
Chuû ñeà
Nhaän bieát
Thoâng hieåu
Vaän duïng
Toång
TNKQ
TL
TNKQ
TL
TNKQ
TL
Vectô
2
0,5
2
0,5
1
1,5
1
1,5
5
Toaï ñoä
2
0,5
2
0,5
1
1,0
1
2,0
5
Toång
2
2
2,5
3,5
10
IV. NOÄI DUNG ÑEÀ KIEÅM TRA:
A. Phaàn traéc nghieäm: (4 ñieåm) Choïn caâu traû lôøi ñuùng nhaát.
Caâu 1. Cho töù giaùc ABCD. Soá caùc vectô khaùc vectô–khoâng coù ñieåm ñaàu vaø ñieåm cuoái laø caùc ñænh
cuûa töù giaùc baèng:
A) 20 B) 16 C) 12 D) 6
Caâu 2. Xaùc ñònh vò trí cuûa 3 ñieåm A, B, C thoaû heä thöùc:
AB CA
A) C truøng B B) ABC caân C) A truøng B D) A laø trung ñieåm cuûa BC.
Caâu 3. Cho hình bình haønh ABCD. Ñaúng thöùc naøo sau ñaây laø ñuùng:
A)
AB AD AC
B)
AB AC AD
C)
AB BC CA
D)
AB CD
Caâu 4. Cho ABC coù troïng taâm G. M laø moät ñieåm tuyø yù. Ñaúng thöùc naøo sau ñaây laø ñuùng:
A)
MA MB MC 0
B)
AM BM CM 3GM
C)
AB AC 2AG
D)
MA MB 2MG
Caâu 5. Cho 3 ñieåm A(1; 1), B(–1; –1), C(6; 6). Khaúng ñònh naøo sau ñaây laø ñuùng:
A) G(2; 2) laø troïng taâm cuûa ABC B) B laø trung ñieåm cuûa AC
C) C laø trung ñieåm cuûa AB. D)
ABvaø AC
ngöôïc höôùng.
Caâu 6. Cho hai ñieåm M(8; –1), N(3; 2). Toaï ñoä cuûa ñieåm P ñoái xöùng vôùi ñieåm M qua ñieåm N laø:
A) (–2; 5) B)
11 1
;
22



C) (13; –4) D) (11; –1)
Caâu 7. Cho hai ñieåm A(4; 0), B(0; –8). Toaï ñoä cuûa ñieåm C thoaû:
CA 3CB
laø:
A) (–3; 7) B) (1; –6) C) (–2; –12) D) (3; –1)
Caâu 8. Cho hai vectô
a
= (2; –4),
b
= (–5; 3). Toaï ñoä cuûa vectô
u 2a b
laø:
A) (7; –7) B) (9; –5) C) (9; –11) D) (–1; 5)
B. Phaàn töï luaän: (6 ñieåm)
Caâu 9. (3 ñieåm) Cho ABC vaø ñieåm M thoaû heä thöùc:
BM 2MC
.
a) Chöùng minh raèng:
12
AM AB AC
33

b) Goïi BN laø trung tuyeán cuûa ABC, I laø trung ñieåm cuûa BN.
Chöùng minh raèng:
MA 2MB MC 4MI
.
Caâu 10. (3 ñieåm) Cho ABC coù A(3; 1), B(–1; 2), C(0; 4).
Nguyễn Đình Khương Hình Học 10 Cơ Bản
26
a) Tìm ñieåm D ñeå töù giaùc ABCD laø hình bình haønh.
b) Tìm troïng taâm G cuûa ABC.
V. ÑAÙP AÙN VAØ BIEÅU ÑIEÅM:
A. Phaàn traéc nghieäm:
1 C
2 D
3 A
4 B
5 D
6 A
7 B
8 C
B. Töï luaän:
Caâu 9: a)
BM 2MC
AM AB 2(AC AM)
(0,5 ñieåm)
3AM AB 2AC
(0,5 ñieåm)
ñpcm. (0,5 ñieåm)
b)
MA MC 2MN
(0,5 ñieåm)
MB MN 2MI
(0,5 ñieåm)
MA 2MB MC 4MI
(0,5 ñieåm)
Caâu 10: a)
AD (x 3;y 1)
BC (1;2)
(0,5 ñieåm)
ABCD laø hình bình haønh
AD BC
(0,5 ñieåm)
x 3 1
y 1 2


(0,5 ñieåm)
x4
y3
D(4; 3) (0,5 ñieåm)
b)
A B C
G
A B C
G
x x x
x
3
y y y
y
3


G
G
3 1 0 2
x
33
1 2 4 7
y
33




G
27
;
33



(1 ñieåm)
Ngaøy soaïn: 20/11/2012 Chöông II: TÍCH VOÂ HÖÔÙNG CUÛA HAI VECTÔ & ÖÙNG DUÏNG
Tieát daïy: 14 Baøøi 1: GIAÙ TRÒ LÖÔÏNG GIAÙC CUÛA MOÄT GOÙC BAÁT KÌ
TÖØ 0
0
ÑEÁN 180
0
I. MUÏC TIEÂU:
Kieán thöùc:
Naém ñöôïc ñònh nghóa vaø tính chaát cuûa caùc GTLG cuûa caùc goùc töø 0
0
ñeán 180
0
vaø moái quan
heä giöõa chuùng.
A
B
C
M
N
I
Nguyễn Đình Khương Hình Học 10 Cơ Bản
27
Nhôù ñöôïc baûng caùc giaù trò löôïng giaùc cuûa caùc goùc ñaëc bieät.
Naém ñöôïc khaùi nieäm goùc giöõa hai vectô.
Kó naêng:
Vaän duïng ñöôïc baûng caùc giaù trò löôïng giaùc cuûa caùc goùc ñaëc bieät.
Xaùc ñònh ñöôïc goùc giöõa hai vectô.
Thaùi ñoä:
Reøn luyeän tính caån thaän, chính xaùc.
II. CHUAÅN BÒ:
Giaùo vieân: Giaùo aùn. Hình veõ minh hoaï.
Hoïc sinh: SGK, vôû ghi. OÂn taäp kieán thöùc ñaõ hoïc veà tæ soá löôïng giaùc cuûa goùc nhoïn.
III. HOAÏT ÑOÄNG DAÏY HOÏC:
1. OÅn ñònh toå chöùc: Kieåm tra só soá lôùp.
2. Kieåm tra baøi cuõ: (3')
H. Nhaéc laïi caùc tæ soá löôïng giaùc cuûa goùc nhoïn?
Ñ. sin =
ñoái
huyeàn
; cos =
keà
huyeàn
; tan =
ñoái
keà
; cot =
keà
ñoái
3. Giaûng baøi môùi:
TL
Hoaït ñoäng cuûa Giaùo vieân
Hoaït ñoäng cuûa Hoïc sinh
Noäi dung
Hoaït ñoäng 1: Tìm hieåu ñònh nghóa caùc giaù trò löôïng giaùc cuûa goùc (0
0
180
0
)
15'
Trong mpOxy, cho nöûa
ñöôøng troøn ñôn vò taâm O. Xeùt
goùc nhoïn =
xOM
. Giaû söû
M(x
0
, y
0
).
H1. Tính sin, cos, tan,
cot
Töø ñoù môû roäng ñònh nghóa
vôùi 0
0
180
0
.
H2. Nhaän xeùt tung ñoä, hoaønh
ñoä cuûa M khi = 0
0
; 90
0
; 180
0
VD. Tính sin180
0
, cos180
0
,
tan180
0
, cot180
0
.
O x
y
M
x
y
1
-1
Ñ1. sin =
y
OM
= y
cos =
x
OM
= x
Ñ2. = 0
0
x = 1; y = 0
= 180
0
x = –1; y =
0
= 90
0
x = 0; y = 1
sin180
0
= 0; cos180
0
= –1;
tan180
0
= 0; cot180
0
= //
I. Ñònh nghóa
sin
= y (tung ñoä)
cos
= x (hoaønh ñoä)
tan
=
y tungñoä
x hoaønhñoä



cot
=
x hoaønhñoä
y tungñoä



Chuù yù:
+ Neáu
tuø thì
cos
< 0, tan
< 0, cot
< 0
+ tan
xaùc ñònh khi
90
0
+ cot
xaùc ñònh khi
0
0
vaø
180
0
.
Hoaït ñoäng 2: Tìm hieåu GTLG cuûa caùc goùc coù lieân quan ñaëc bieät
20'
H1. Nhaéc laïi tæ soá löôïng giaùc
cuûa caùc goùc phuï nhau?
Cho
xOM
= ,
Ñ1. sin cuûa goùc naøy baèng cos
cuûa goùc kia.
O x
y
M
x
y
1
-1
N
-x
II. Tính chaát
1. Goùc phuï nhau
sin(90
0
– ) = cos
cos(90
0
– ) = sin
tan(90
0
– ) = cot
cot(90
0
– ) = tan
2. Goùc buø nhau
Nguyễn Đình Khương Hình Học 10 Cơ Bản
28
xON
= 180
0
–
H2. Nhaän xeùt hoaønh ñoä, tung
ñoä cuûa M, N ?
VD: Gheùp caëp caùc giaù trò ôû
coät A vôùi caùc giaù trò ôû coät B:
A
B
sin50
0
–tan45
0
cos42
0
cos40
0
tan120
0
sin30
0
sin150
0
sin48
0
tan135
0
–tan60
0
Ñ2. x
N
= –x
M
; y
N
= y
M
sin50
0
= cos40
0
cos42
0
= sin48
0
tan120
0
= –tan60
0
sin150
0
= sin30
0
tan135
0
= –tan45
0
sin(180
0
– ) = sin
cos(180
0
– ) = – cos
tan(180
0
– ) = – tan
cot(180
0
– ) = – cot
Hoaït ñoäng 3: Cuûng coá
5'
Nhaán maïnh
+ Ñònh nghóa caùc GTLG
+ GTLG caùc goùc lieân quan ñb
Caâu hoûi: Tính caùc GTLG cuûa
caùc goùc 120
0
, 135
0
, 150
0
.
Chia moãi nhoùm tính caùc
GTLG cuûa moät goùc.
4. BAØI TAÄP VEÀ NHAØ:
Baøi 1, 2, 3 SGK.
Ngaøy soaïn: 25/11/2012 Chöông II: TÍCH VOÂ HÖÔÙNG CUÛA HAI VECTÔ & ÖÙNG DUÏNG
Tieát daïy: 14 Baøøi 1: GIAÙ TRÒ LÖÔÏNG GIAÙC CUÛA MOÄT GOÙC BAÁT KÌ
TÖØ 0
0
ÑEÁN 180
0
(tt)
I. MUÏC TIEÂU:
Kieán thöùc:
Naém ñöôïc ñònh nghóa vaø tính chaát cuûa caùc GTLG cuûa caùc goùc töø 0
0
ñeán 180
0
vaø moái quan
heä giöõa chuùng.
Nhôù ñöôïc baûng caùc giaù trò löôïng giaùc cuûa caùc goùc ñaëc bieät.
Naém ñöôïc khaùi nieäm goùc giöõa hai vectô.
Nguyễn Đình Khương Hình Học 10 Cơ Bản
29
Kó naêng:
Vaän duïng ñöôïc baûng caùc giaù trò löôïng giaùc cuûa caùc goùc ñaëc bieät.
Xaùc ñònh ñöôïc goùc giöõa hai vectô.
Thaùi ñoä:
Reøn luyeän tính caån thaän, chính xaùc.
II. CHUAÅN BÒ:
Giaùo vieân: Giaùo aùn. Hình veõ minh hoaï.
Hoïc sinh: SGK, vôû ghi. OÂn taäp kieán thöùc ñaõ hoïc veà tæ soá löôïng giaùc cuûa goùc nhoïn.
III. HOAÏT ÑOÄNG DAÏY HOÏC:
1. OÅn ñònh toå chöùc: Kieåm tra só soá lôùp.
2. Kieåm tra baøi cuõ: (3')
H. Nhaéc laïi coâng thöùc löôïng giaùc cuûa caùc goùc buø nhau?
Ñ. sin(180
0
– ) = sin; cos(180
0
– ) = –cos;
tan(180
0
– ) = –tan; cot(180
0
–) =–cot
3. Giaûng baøi môùi:
TL
Hoaït ñoäng cuûa Giaùo vieân
Hoaït ñoäng cuûa Hoïc sinh
Noäi dung
Hoaït ñoäng 1: Tìm hieåu baûng GTLG cuûa caùc goùc ñaëc bieät
10'
Cho HS ñieàn vaøo baûng giaù
trò löôïng giaùc cuûa caùc goùc ñaëc
bieät.
GV höôùng daãn HS caùch laäp
baûng
III. Giaù trò löôïng giaùc cuûa caùc goùc ñaëc bieät
0
0
30
0
45
0
60
0
90
0
sin
0
1
2
2
2
3
2
1
cos
1
3
2
2
2
1
2
0
tan
0
3
3
1
3

cot

3
1
3
3
0
Hoaït ñoäng 2: Tìm hieåu khaùi nieäm goùc giöõa hai vectô
10'
GV giôùi thieäu ñònh nghóa
goùc giöõa hai vectô
a
,
b
.
VD. Cho ABC ñeàu. Xaùc
ñònh goùc giöõa caùc caëp vectô:
a)
AB,AC
b)
AB,BC
c)
AB,CA
.
O
A
B
a
b
a
b
A
B
C
60
0
120
0
120
0
a) 60
0
b) 120
0
c) 120
0
IV. Goùc giöõa hai vectô
1. Ñònh nghóa
Cho
a,b 0
.
OA a,OB b
.
a,b AOB
vôùi 0
0
AOB
180
0
.
+
a,b
= 90
0
ab
+
a,b
= 0
0
a,b
cuøng
höôùng
+
a,b
= 180
0
a,b
ngöôïc
höôùng
Hoaït ñoäng 3: Höôùng daãn söû duïng MTBT ñeå tính GTLG cuûa moät goùc
15'
GV höôùng daãn HS caùch söû
duïng MTBT döïa vaøo höôùng
daãn cuûa SGK vaø baûng höôùng
daãn cuûa MTBT.
HS veà nhaø thöïc haønh, ñoái
chieáu vôùi pheùp tính.
V. Söû duïng MTBT ñeå tính
GTLG cuûa moät goùc
1. Tính caùc GTLG cuûa goùc
Nguyễn Đình Khương Hình Học 10 Cơ Bản
30
VD1. Tính sin63
0
52'41''
VD2. Tìm x bieát sinx = 0,3502
Chia nhoùm thöïc haønh vôùi
MTBT.
sin63
0
52'41'' 0,8979
x 20
0
29'58''
Caùc nhoùm thöïc haønh vaø ñoái
chieáu keát quaû.
2. Xaùc ñònh ñoä lôùn cuûa goùc
khi bieát GTLG cuûa goùc ñoù
Hoaït ñoäng 4: Cuûng coá
5'
Nhaán maïnh
+ Baûng giaù trò ñaëc bieät
+ Caùch xaùc ñònh goùc giöõa hai
vectô
4. BAØI TAÄP VEÀ NHAØ:
Baøi 4, 5, 6 SGK.
Ngaøy soaïn: 25/11/2012 Chöông II: TÍCH VOÂ HÖÔÙNG CUÛA HAI VECTÔ & ÖÙNG DUÏNG
Tieát daïy: 15 Baøøi 1: BAØI TAÄP GIAÙ TRÒ LÖÔÏNG GIAÙC CUÛA
MOÄT GOÙC BAÁT KÌ TÖØ 0
0
ÑEÁN 180
0
I. MUÏC TIEÂU:
Kieán thöùc:
Cuûng coá caùc kieán thöùc veà GTLG cuûa moät goùc (0
0
180
0
), vaø moái lieân quan giöõa
chuùng.
Caùch xaùc ñònh goùc giöõa hai vectô.
Kó naêng:
Bieát söû duïng baûng giaù trò löôïng giaùc cuûa caùc goùc ñaëc bieät ñeå tính GTLG cuûa moät goùc.
Nguyễn Đình Khương Hình Học 10 Cơ Bản
31
Bieát xaùc ñònh goùc giöõa hai vectô.
Thaùi ñoä:
Reøn luyeän tính caån thaän, chính xaùc.
Luyeän tö duy linh hoaït thoâng qua vieäc xaùc ñònh goùc giöõa hai vectô.
II. CHUAÅN BÒ:
Giaùo vieân: Giaùo aùn. Heä thoáng baøi taäp.
Hoïc sinh: SGK, vôû ghi. OÂn taäp caùc kieán thöùc veà GTLG cuûa moät goùc.
III. HOAÏT ÑOÄNG DAÏY HOÏC:
1. OÅn ñònh toå chöùc: Kieåm tra só soá lôùp.
2. Kieåm tra baøi cuõ: (Loàng vaøo quaù trình luyeän taäp)
3. Giaûng baøi môùi:
TL
Hoaït ñoäng cuûa Giaùo vieân
Hoaït ñoäng cuûa Hoïc sinh
Noäi dung
Hoaït ñoäng 1: Tính giaù trò löôïng giaùc cuûa moät goùc
15'
H1. Cho bieát giaù trò löôïng
giaùc cuûa caùc goùc ñaëc bieät ?
H2. Neâu coâng thöùc GTLG cuûa
caùc goùc phuï nhau, buø nhau ?
H3. Chæ ra moái quan heä giöõa
caùc goùc trong tam giaùc ?
Ñ1.
a)
3
2
b) 1
c) 0 d) 1
e)
6
4
Ñ3.
+ A + (B + C) = 180
0
+
2
A
+
2
BC
= 90
0
1. Tính giaù trò cuûa caùc bieåu
thöùc sau:
a) cos30
0
cos60
0
+ sin30
0
sin60
0
b) sin30
0
cos60
0
+
cos30
0
sin60
0
c) cos0
0
+ cos20
0
+…+cos180
0
d) tan10
0
.tan80
0
e) sin120
0
.cos135
0
2. Chöùng minh raèng trong tam
giaùc ABC, ta coù:
a) sinA = sin(B + C)
b) cosA = – cos(B + C)
c) sin
2
A
= cos
2
BC
d) cos
2
A
= sin
2
BC
Hoaït ñoäng 2: Vaän duïng caùc coâng thöùc löôïng giaùc
10'
H1. Nhaéc laïi ñònh nghóa caùc
GTLG ?
H2. Neâu coâng thöùc lieân quan
giöõa sinx vaø cosx ?
Ñ1. sin = y, cos = x
a) sin
2
+ cos
2
= OM
2
= 1
b) 1 + tan
2
= 1 +
2
2
sin
cos
=
22
2
cos sin
cos
c) 1 + cot
2
= 1 +
2
2
cos
sin
Ñ2. sin
2
x + cos
2
x = 1
sin
2
x = 1 – cos
2
x =
8
9
3. Chöùng minh:
a) sin
2
+ cos
2
= 1
b) 1 + tan
2
=
2
1
cos
c) 1 + cot
2
=
2
1
sin
4. Cho cosx =
1
3
. Tính giaù trò
cuûa bieåu thöùc:
P = 3sin
2
x + cos
2
x.
Nguyễn Đình Khương Hình Học 10 Cơ Bản
32
P =
25
9
Hoaït ñoäng 3: Luyeän caùch xaùc ñònh goùc giöõa hai vectô
5'
H1. Xaùc ñònh goùc giöõa caùc
caëp vectô ?
A B
CD
Ñ1.
a)
,AC BA
= 135
0
b)
,AC BD
= 90
0
c)
,AB CD
= 180
0
4. Cho hình vuoâng ABCD.
Tính:
a) cos
,AC BA
b) sin
,AC BD
c) cos
,AB CD
Hoaït ñoäng 4: Vaän duïng löôïng giaùc ñeå giaûi toaùn hình hoïc
10'
Höôùng daãn HS vaän duïng caùc
tæ soá löôïng giaùc cuûa goùc nhoïn.
H1. Ñeå tính AK vaø OK ta caàn
xeùt tam giaùc vuoâng naøo ?
A
B
O
H
K
a
Ñ1. Xeùt tam giaùc vuoâng AOH
vôùi OA = a,
AOK
= 2.
AK = OA.sin
AOK
= a.sin2
OK = OA.cos
AOK
= a.cos2
5. Cho AOB caân taïi O vaø
OA = a. OH vaø AK laø caùc
ñöôøng cao. Giaû söû
AOH
= .
Tính AK vaø OK theo a vaø .
Hoaït ñoäng 5: Cuûng coá
3'
Nhaán maïnh caùch vaän duïng
caùc kieán thöùc ñaõ hoïc.
4. BAØI TAÄP VEÀ NHAØ:
Ñoïc tröôùc baøi "Tích voâ höôùng cuûa hai vectô"
Ngaøy soaïn: 5/12/2012 Chöông II: TÍCH VOÂ HÖÔÙNG CUÛA HAI VECTÔ & ÖÙNG DUÏNG
Tieát daïy: 19 Baøøi 2: TÍCH VOÂ HÖÔÙNG CUÛA HAI VECTÔ
I. MUÏC TIEÂU:
Kieán thöùc:
Naém ñöôïc ñònh nghóa vaø tính chaát cuûa tích voâ höôùng cuûa hai vectô cuøng vôùi yù nghóa vaät lí
cuûa tích voâ höôùng.
Kó naêng:
Bieát söû duïng bieåu thöùc toaï ñoä cuûa tích voâ höôùng ñeå tính ñoä daøi cuûa moät vectô, khoaûng
caùch giöõa hai ñieåm, goùc giöõa hai vectô vaø chöùng minh hai vectô vuoâng goùc.
Thaùi ñoä:
Nguyễn Đình Khương Hình Học 10 Cơ Bản
33
Reøn luyeän tính caån thaän, chính xaùc.
II. CHUAÅN BÒ:
Giaùo vieân: Giaùo aùn. Hình veõ minh hoaï.
Hoïc sinh: SGK, vôû ghi. OÂn taäp caùch xaùc ñònh goùc giöõa hai vectô.
III. HOAÏT ÑOÄNG DAÏY HOÏC:
1. OÅn ñònh toå chöùc: Kieåm tra só soá lôùp.
2. Kieåm tra baøi cuõ: (3')
H. Neâu caùch xaùc ñònh goùc giöõa hai vectô?
Ñ.
,a b AOB
, vôùi
,a OA b OB
.
3. Giaûng baøi môùi:
TL
Hoaït ñoäng cuûa Giaùo vieân
Hoaït ñoäng cuûa Hoïc sinh
Noäi dung
Hoaït ñoäng 1: Tìm hieåu ñònh nghóa tích voâ höôùng cuûa hai vectô
10'
Cho löïc
F
taùc ñoäng leân moät
vaät taïi ñieåm O vaø laøm cho vaät
ñoù di chuyeån moät quaõng
ñöôøng OO thì coâng A cuûa löïc
F
ñöôïc tính theo coâng thöùc:
A =
. .cosF OO
GV giôùi thieäu ñònh nghóa
VD. Cho ABC ñeàu caïnh
baèng a. Veõ ñöôøng cao AH.
Tính:
a)
.AB AC
b)
.AB BC
c)
.AH BC
O
O’
F
A
B
C
H
a)
.AB AC
= a.a.cos60
0
=
2
2
a
b)
.AB BC
= a.a.cos120
0
=–
2
2
a
c)
.AH BC
= 0
I. Ñònh nghóa
Cho
,0ab
.
. . cos ,a b a b a b
Neáu
0
0
a
b
thì
.ab
= 0
Chuù yù:
a) Vôùi
,0ab
, ta coù:
.0a b a b
b)
2
2
aa
Hoaït ñoäng 2: Tìm hieåu tính chaát cuûa tích voâ höôùng
15'
GV giaûi thích caùc tính chaát
cuûa tích voâ höôùng.
H. Daáu cuûa
.ab
phuï thuoäc vaø
yeáu toá naøo ?
a
b
,a b nhoïn
a
b
,a b tuø
a
b
,a b vuoâng
Ñ. Phuï thuoäc vaø cos
,ab
II. Caùc tính chaát cuûa tich voâ
höôùng
Vôùi
,,a b c
baát kì vaø
k
R:
+
..a b b a
+
..a b c a b a c
+
. . .ka b k a b a kb
+
22
0; 0 0a a a
2
22
2.a b a a b b
2
22
2.a b a a b b
22
a b a b a b
.ab
> 0
,ab
nhoïn
.ab
< 0
,ab
tuø
.ab
= 0
,ab
vuoâng
Nguyễn Đình Khương Hình Học 10 Cơ Bản
34
GV giaûi thích yù nghóa coâng
thöùc tính coâng cuûa moät löïc.
F
1
F
2
F
B
A
12
F F F
A =
.F AB
=
12
F F AB
=
2
.F AB
Hoaït ñoäng 3: AÙp duïng tính tích voâ höôùng cuûa hai vectô
12'
Chia nhoùm luyeän taäp.
H. Xaùc ñònh goùc cuûa caùc caëp
vectô ?
A
B
C
b
c
A
B C
a
Ñ.
1a) cos(
,BA BC
) =
22
c
bc
.BA BC
= c
2
2)
2
3
2
a
Ví duï:
1) Cho ABC vuoâng ôû A, AB
= c, AC = b. Tính:
a)
.BA BC
b)
.CA CB
c)
.BA AC
d)
.CA AB
2) Cho ABC ñeàu caïnh a.
Tính:
. . .AB BC BC CA CA AB
Hoaït ñoäng 4: Cuûng coá
3'
Nhaán maïnh:
– Caùch xaùc ñònh goùc giöõa hai
vectô.
– Caùch tính tích voâ höôùng
4. BAØI TAÄP VEÀ NHAØ:
Baøi 1, 2, 3 SGK
Ngaøy soaïn: 10/12/2012 Chöông II: TÍCH VOÂ HÖÔÙNG CUÛA HAI VECTÔ & ÖÙNG DUÏNG
Tieát daïy: 18 Baøøi 2: TÍCH VOÂ HÖÔÙNG CUÛA HAI VECTÔ (tt)
I. MUÏC TIEÂU:
Kieán thöùc:
Naém ñöôïc ñònh nghóa vaø tính chaát cuûa tích voâ höôùng cuûa hai vectô cuøng vôùi yù nghóa vaät lí
cuûa tích voâ höôùng.
Kó naêng:
Bieát söû duïng bieåu thöùc toaï ñoä cuûa tích voâ höôùng ñeå tính ñoä daøi cuûa moät vectô, khoaûng
caùch giöõa hai ñieåm, goùc giöõa hai vectô vaø chöùng minh hai vectô vuoâng goùc.
Nguyễn Đình Khương Hình Học 10 Cơ Bản
35
Thaùi ñoä:
Reøn luyeän tính caån thaän, chính xaùc.
II. CHUAÅN BÒ:
Giaùo vieân: Giaùo aùn.
Hoïc sinh: SGK, vôû ghi. OÂn taäp ñònh nghóa tích voâ höôùng cuûa hai vectô.
III. HOAÏT ÑOÄNG DAÏY HOÏC:
1. OÅn ñònh toå chöùc: Kieåm tra só soá lôùp.
2. Kieåm tra baøi cuõ: (3')
H. Neâu ñònh nghóa tích voâ höôùng cuûa hai vectô?
Ñ.
. . cos ,a b a b a b
.
3. Giaûng baøi môùi:
TL
Hoaït ñoäng cuûa Giaùo vieân
Hoaït ñoäng cuûa Hoïc sinh
Noäi dung
Hoaït ñoäng 1: Tìm hieåu bieåu thöùc toaï ñoä cuûa tích voâ höôùng
10'
H1. Tính
2
i
,
2
j
,
.ij
?
H2. Bieåu dieãn caùc vectô
a
,
b
theo
,ij
?
VD: Cho A(2; 4), B(1; 2),
C(6; 2). Chöùng minh
AB AC
?
H3. Tính toaï ñoä cuûa
,AB AC
?
Ñ1.
2
i
=
2
j
= 1
.ij
= 0
Ñ2.
12
a a i a j
,
12
b b i b j
Ñ3.
AB
= (–1; –2),
AC
= (4; –2)
.AB AC
= 0
AB AC
III. Bieåu thöùc toaï ñoä cuûa
tích voâ höôùng
Cho
a
= (a
1
, a
2
),
b
= (b
1
, b
2
)
.ab
= a
1
b
1
+ a
2
b
2
ab
a
1
b
1
+ a
2
b
2
= 0
Hoaït ñoäng 2: Tìm hieåu caùc öùng duïng cuûa tích voâ höôùng
20'
H1. Tính
2
a
?
VD: Cho
a
= (4; –5). Tính
a
H2. Töø ñònh nghóa tích voâ
höôùng, haõy suy ra coâng thöùc
tính cos
,ab
?
VD: Cho
OM
= (–2; –1),
ON
= (3; –1). Tính
MON
?
Ñ1.
2
a
= a
1
2
+ a
2
2
a
=
22
4 ( 5) 41
Ñ2. cos
.
,
.
ab
ab
ab
cos
MON
= cos
,OM ON
=
.
.
OM ON
OM ON
=
61
5. 10

2
2

MON
= 135
0
IV. ÖÙng duïng
1) Ñoä daøi cuûa vectô
Cho
a
= (a
1
, a
2
)
22
12
a a a
2) Goùc giöõa hai vectô
Cho
a
= (a
1
, a
2
),
b
= (b
1
, b
2
)
(
,0ab
)
cos
.
,
.
ab
ab
ab
=
1 1 2 2
2 2 2 2
1 2 1 2
.
a b a b
a a b b

3) Khoaûng caùch giöõa hai
Nguyễn Đình Khương Hình Học 10 Cơ Bản
36
H3. Nhaéc laïi coâng thöùc tính
toaï ñoä cuûa
AB
?
VD: Cho M(–2; 2), N(1; 1).
Tính MN ?
Ñ3.
AB
= (x
B
– x
A
; y
B
– y
A
)
MN =
22
(1 2) (1 2)
10
ñieåm
Cho A(x
A
; y
A
), B(x
B
; y
B
)
AB =
22
B A B A
(x x ) (y y )
Hoaït ñoäng 3: AÙp duïng tích voâ höôùng cuûa hai vectô
7'
H1. Neâu ñieàu kieän ñeå ABCD
laø hình bình haønh ?
H2. Tính AB, AD ?
H3. Neâu coâng thöùc tính goùc A
Ñ1.
AB DC
2
4
D
D
x
y


Ñ2. AB =
22
1 2 5
AD =
22
3 5 34
Ñ3. cosA = cos
,AB AD
=
.
.
AB AD
AB AD
=
3 10 13
5. 34 170


Ví duï: Cho A(1; 1), B(2; 3),
C(–1; –2).
a) Xaùc ñònh ñieåm D sao cho
ABCD laø hình bình haønh.
b) Tính chu vi hbh ABCD.
c) Tính goùc A.
Hoaït ñoäng 4: Cuûng coá
3'
Nhaán maïnh:
– Caùc öùng duïng cuûa tích voâ
höôùng
4. BAØI TAÄP VEÀ NHAØ:
Baøi 4, 5, 6, 7 SGK
Ngaøy soaïn: 20/12/2012 Chöông II: TÍCH VOÂ HÖÔÙNG CUÛA HAI VECTÔ & ÖÙNG DUÏNG
Tieát daïy: 21 Baøøi 2: BAØI TAÄP TÍCH VOÂ HÖÔÙNG CUÛA HAI VECTÔ
I. MUÏC TIEÂU:
Kieán thöùc:
Cuûng coá khaùi nieäm tích voâ höôùng cuûa hai vectô.
Kó naêng:
Bieát vaän duïng tích voâ höôùng ñeå giaûi toaùn hình hoïc: tính goùc giöõa hai vectô, khoaûng caùch
giöõa hai ñieåm.
Thaùi ñoä:
Reøn luyeän tính caån thaän, chính xaùc.
Nguyễn Đình Khương Hình Học 10 Cơ Bản
37
Luyeän tö duy linh hoaït.
II. CHUAÅN BÒ:
Giaùo vieân: Giaùo aùn. Heä thoáng baøi taäp.
Hoïc sinh: SGK, vôû ghi. OÂn taäp kieán thöùc veà tích voâ höôùng cuûa hai vectô.
III. HOAÏT ÑOÄNG DAÏY HOÏC:
1. OÅn ñònh toå chöùc: Kieåm tra só soá lôùp.
2. Kieåm tra baøi cuõ: (3')
H. Neâu coâng thöùc tính goùc giöõa hai vectô, khoaûng caùch giöõa hai ñieåm ?
Ñ. cos
.
,
.
ab
ab
ab
=
1 1 2 2
2 2 2 2
1 2 1 2
.
a b a b
a a b b

; AB =
22
B A B A
(x x ) (y y )
3. Giaûng baøi môùi:
TL
Hoaït ñoäng cuûa Giaùo vieân
Hoaït ñoäng cuûa Hoïc sinh
Noäi dung
10'
H3. Nhaéc laïi coâng thöùc tính
toaï ñoä cuûa
AB
?
VD: Cho M(–2; 2), N(1; 1).
Tính MN ?
Ñ3.
AB
= (x
B
– x
A
; y
B
– y
A
)
MN =
22
(1 2) (1 2)
10
IV. ÖÙng duïng
3) Khoaûng caùch giöõa hai
ñieåm
Cho A(x
A
; y
A
), B(x
B
; y
B
)
AB =
22
B A B A
(x x ) (y y )
Hoaït ñoäng2: AÙp duïng tích voâ höôùng cuûa hai vectô
10'
H1. Neâu ñieàu kieän ñeå ABCD
laø hình bình haønh ?
H2. Tính AB, AD ?
H3. Neâu coâng thöùc tính goùc A
Ñ1.
AB DC
2
4
D
D
x
y


Ñ2. AB =
22
1 2 5
AD =
22
3 5 34
Ñ3. cosA = cos
,AB AD
=
.
.
AB AD
AB AD
=
3 10 13
5. 34 170


Ví duï: Cho A(1; 1), B(2; 3),
C(–1; –2).
a) Xaùc ñònh ñieåm D sao cho
ABCD laø hình bình haønh.
b) Tính chu vi hbh ABCD.
c) Tính goùc A.
Hoaït ñoäng 3: Luyeän taäp tính tích voâ höôùng cuûa hai vectô
TL
Hoaït ñoäng cuûa Giaùo vieân
Hoaït ñoäng cuûa Hoïc sinh
Noäi dung
Hoaït ñoäng 1: Luyeän taäp tính tích voâ höôùng cuûa hai vectô
20'
H1. Xaùc ñònh goùc giöõa caùc
caëp vectô ?
A B
C
Ñ1. a)
,AB AC
= 90
0
.AB AC
= 0
b)
,AC CB
= 135
0
.AC CB
= –a
2
1. Cho tam giaùc vuoâng caân
ABC coù AB = AC = a. Tính
caùc tích voâ höôùng:
a)
.AB AC
b)
.AC CB
Nguyễn Đình Khương Hình Học 10 Cơ Bản
38
H2. Xaùc ñònh goùc cuûa
,OA OB
trong moãi tröôøng
hôïp ?
A BO
A BO
A BO
M
N
I
H3. Vieát bieåu thöùc tính
. , .AI AM AI AB
Höôùng daãn HS vaän duïng
tính chaát tích voâ höôùng cuûa
hai vectô vuoâng goùc
Ñ2.
a)
,OA OB
= 0
0
.OA OB
= ab
b)
,OA OB
= 180
0
.OA OB
= –ab
Ñ3.
. . .cos ,AI AM AI AM AI AM
= AI.AM
.AI AB
= AI.AB.cos
AI AB
=AI.AB.cos
IAB
=AI.AM
. .( )AI AM AI AB BM
=
.AI AB
..AI AM BI BN
=
.AB AB
= AB
2
= 4R
2
2. Cho 3 ñieåm O, A, B thaúng
haøng vaø bieát OA = a, OB = b.
Tính
.OA OB
khi:
a) O naèm ngoaøi ñoaïn AB.
b) O naèm trong ñoaïn AB.
3. Cho nöûa ñöôøng troøn taâm O
coù ñöôøng kính AB = 2R. Goïi
M vaø N laø hai ñieåm thuoäc nöûa
ñöôøng troøn sao cho hai daây
cung AM vaø BN caét nhau taïi
I.
a) CMR:
..AI AM AI AB
vaø
..BI BN BI BA
b) Haõy duøng keát quaû caâu a)
ñeå tính
..AI AM BI BN
theo
R.
Hoaït ñoäng 4: Cuûng coá
5'
Nhaán maïnh caùch vaän duïng
tích voâ höôùng ñeå giaûi toaùn
hình hoïc
Ngaøy soaïn: 30/12/2012
Tieát daïy: 16 Baøøi daïy: OÂN TAÄP HOÏC KÌ I
1. Muïc tieâu :
a. Kieán thöùc : Cuûng coá vaø khaéc saâu caùc kieán thöùc :
- Toång vaø hieäu caùc vtô, tích cuûa vtô vôùi moät soá, toïa ñoä cuûa vtô vaø cuûa ñieåm, caùc bieåu
thöùc toïa ñoä cuûa caùc pheùp toaùn vtô.
b. Kyõ naêng : Vaän duïng ñöôïc caùc kieán thöùc ñaõ hoïc ñeå giaûi caùc baøi taäp coù lieân quan.
c. Thaùi ñoä : Caån thaän chính xaùc.
2. Chuaån bò phöông tieän daïy hoïc :
a. Thöïc tieãn : Hs ñaõ hoïc caùc kieán thöùc veà : toång vaø hieäu caùc vtô, tích cuûa vtô vôùi moät soá,
toïa ñoä cuûa vtô vaø cuûa ñieåm, caùc bieåu thöùc toïa ñoä cuûa caùc pheùp toaùn vtô; giaù trò löôïng
giaùc cuûa caùc goùc töø 0
0
ñeán 180
0
, ñònh nghóa tích voâ höôùng hai vtô, ñònh lí cosin, ñònh lí
Nguyễn Đình Khương Hình Học 10 Cơ Bản
39
sin trong tam giaùc, coâng thöùc ñoä daøi ñöôøng trung tuyeánvaø caùc coâng thöùc tính dieän tích
tam giaùc ôû nhöõng baøi tröôùc.
b. GV :Soaïn giaùo aùn,saùch giaùo khoa, giaùo aùn, thöôùc keû, phaán maøu.
c. Phöông phaùp : cô baûn duøng phöông phaùp gôïi môû vaán ñaùp thoâng qua caùc HÑ ñieàu
khieån tö duy.
3. Tieán trình baøi hoïc vaø caùc HÑ :
HÑ 1 : Giaûi baøi toaùn :
Cho hai hbh ABCD vaø AB’C’D’ coù chung ñænh A. CMR :
a)
' ' 'CC BB DD
b) Hai tam giaùc BC’D vaø B’CD’ coù cuøng troïng taâm.
HÑ cuûa GV
HÑ cuûa HS
Noäi dung
- Nghe hieåu nhieäm vuï.
- Tìm phöông aùn thaéng
(töùc laø hoaøn thaønh
nhieäm vuï nhanh nhaát)
.
- Trình baøy keát quaû.
- Chænh söûa hoaøn
thieän.
- Giao nhieäm vuï cho hs.
- Nhaän xeùt keát quaû
cuûa hs vaø cho ñieåm
Ta coù :
''
' ' ( )
''
''
CC AC AC
AB AD AB AD
AB AB AD AD
BB DD


b) Töø
' ' 'CC BB DD
suy ra vôùi moïi ñieåm G
ta coù :
' ' '
'''
' 0 ' ' 0
GC GC GB GB GD GD
GB GD GC GB GD GC
GB GD GC GB GD GC
Suy ra
Vaäy neáu G laø troïng taâm cuûa tam giaùc BC’D thì
G cuõng laø troïng taâm tam giaùc B’CD’.
HÑ 2 : Giaûi baøi toaùn :
Trong mp Oxy cho hai ñieåm A(1;4), B(2;2). Ñöôøng thaúng ñi qua A vaø B caét truïc Ox taïi
M vaø caét truïc Oy taïi N. Tính dieän tích tam giaùc OMN.
HÑ cuûa GV
HÑ cuûa HS
Noäi dung
- Nghe hieåu nhieäm vuï.
- Tìm phöông aùn thaéng
(töùc laø hoaøn thaønh
nhieäm vuï nhanh nhaát)
.
- Trình baøy keát quaû.
- Chænh söûa hoaøn
- Giao nhieäm vuï cho hs.
- Nhaän xeùt keát quaû
cuûa hs vaø cho ñieåm.
Giaû söû M(x;0), N(0;y). Khi ñoù
(1; 2)AB 
,
( 1; 4)AM x
,
( 1; 4)AN y
. Vì
AB
vaø
AM
cuøng phöông neân
14
12
x
hay x = 3.
Vaäy M(3;0). Vì
AB
vaø
AM
cuøng phöông neân
14
12
y
hay y = 6. Vaäy N(0;6).
Nguyễn Đình Khương Hình Học 10 Cơ Bản
40
thieän.
Dieän tích tam giaùc OMN laø :
11
. . 9
22
S OM ON OM ON
4. Cuûng coá : Nhaán maïnh laïi caùc kieán thöùc caàn nhôù.
Ngaøy soaïn: 30/12/2012
Tieát daïy: 17 Baøøi daïy: OÂN TAÄP HOÏC KÌ I
I. MUÏC TIEÂU:
Kieán thöùc: Cuûng coá caùc kieán thöùc veà:
Vectô – Caùc pheùp toaùn cuûa vectô.
Toaï ñoä cuûa vectô vaø cuûa ñieåm. Caùc tính chaát veà toaï ñoä cuûa vectô vaø cuûa ñieåm.
GTLG cuûa moät goùc 0
0
180
0
.
Tích voâ höôùng cuûa hai vectô.
Kó naêng: Thaønh thaïo trong vieäc giaûi caùc baøi toaùn veà:
Chöùng minh ñaúng thöùc vectô. Phaân tích moät vectô theo hai vectô khoâng cuøng phöông.
Nguyễn Đình Khương Hình Học 10 Cơ Bản
41
Vaän duïng vectô – toaï ñoä ñeå giaûi toaùn hình hoïc.
Thaùi ñoä:
Reøn luyeän tính caån thaän, chính xaùc.
Luyeän tö duy linh hoaït, saùng taïo.
II. CHUAÅN BÒ:
Giaùo vieân: Giaùo aùn. Heä thoáng baøi taäp.
Hoïc sinh: SGK, vôû ghi. OÂn taäp caùc kieán thöùc ñaõ hoïc trong HK 1.
III. HOAÏT ÑOÄNG DAÏY HOÏC:
1. OÅn ñònh toå chöùc: Kieåm tra só soá lôùp.
2. Kieåm tra baøi cuõ: (Loàng vaøo quaù trình oân taäp)
H.
Ñ.
3. Giaûng baøi môùi:
TL
Hoaït ñoäng cuûa Giaùo vieân
Hoaït ñoäng cuûa Hoïc sinh
Noäi dung
Hoaït ñoäng 1: Cuûng coá caùc pheùp toaùn vectô
10'
A
B C
M
NP
H1. Nhaéc laïi heä thöùc trung
ñieåm ?
A
B
C
M
N
D
K
H2. Phaân tích vectô
KD
?
Ñ1.
2
AB AC
AM
Ñ2. a)
2
AM AN
AK
11
46
AK AB AC
b)
KD AD AK
1. Cho ABC. Goïi M, N, P
laàn löôït laø trung ñieåm cuûa BC,
CA, AB. Chöùng minh:
0AM BN CP
2. Cho ABC. Goïi M laø trung
ñieåm cuûa AB, N laø ñieåm treân
ñoaïn AC sao cho NC = 2NA.
Goïi K laø trung ñieåm cuûa MN.
a) Chöùng minh:
11
46
AK AB AC
b) Goïi D laø trung ñieåm BC.
Chöùng minh:
11
43
KD AB AC
Hoaït ñoäng 2: Cuûng coá caùc pheùp toaùn veà toaï ñoä
15'
A
B
C
M
N
P
H1. Neâu caùch xaùc ñònh caùc
dieåm M, N, P ?
H2. Nhaéc laïi coâng thöùc xaùc
ñònh toaï ñoä vectô ?
Ñ1.
AM BC
;
AN CB
;
BP AC
Ñ2.
AB
= (x
B
– x
A
; y
B
– y
A
)
3. Cho ABC vôùi A(2; 0),
B(5; 3), C(–2; 4).
a) Tìm caùc ñieåm M, N, P sao
cho A, B, C laàn löôït laø trung
ñieåm cuûa MN, NP, PM.
b) Tìm caùc ñieåm I, J, K sao
cho
2IA IB
,
3JB JC
,
5KC KA
.
4. Cho A(2; 3), B(4; 2).
Nguyễn Đình Khương Hình Học 10 Cơ Bản
42
H3. Neâu ñieàu kieän xaùc ñònh
ñieåm C ?
H4. Nhaéc laïi coâng thöùc tính
khoaûng caùch giöõa hai ñieåm ?
Ñ3.
0
C
x
CA CB
Ñ4.
AB =
2
2
B A B A
x – x y –y
a) Tìm treân Ox, ñieåm C caùch
ñeàu A vaø B.
b) Tính chu vi OAB.
Hoaït ñoäng 3: Vaän duïng vectô – toaï ñoä ñeå giaûi toaùn hình hoïc
15'
H1. Neâu caùch xaùc ñònh taâm I
cuûa ñöôøng troøn ngoaïi tieáp ?
A B
C
1
D
3
H2. Nhaéc laïi coâng thöùc tính
tích voâ höôùng hai vectô ?
H3. Phaân tích vectô
DB
theo
,AB AD
?
Ñ1.
IA IB
IA IC
Ñ2.
. . .cos ,AB AD AB AD AB AD
=
3
.1.cos60
0
=
3
2
Ñ3.
DB AB AD
DB
2
=
2
AB AD
= 3 + 1 – 2.
3
2
= 4 –
3
5. Cho A(1; –1), B(5; –3),
C(2; 0)
a) Tính chu vi vaø nhaän daïng
ABC.
b) Tìm taâm I vaø tính baùn kính
ñöôøng troøn ngoaïi tieáp ABC.
6. Cho hình bình haønh ABCD
vôùi AB =
3
, AD = 1,
BAD
= 60
0
.
a) Tính
.AB AD
,
.BA BC
.
b) Tính ñoä daøi hai ñöôøng cheùo
AC vaø BD.
Hoaït ñoäng 4: Cuûng coá
3'
Nhaán maïnh vieäc vaän duïng
caùc kieán thöùc vectô – toaï ñoä
ñeå giaûi toaùn.
4. BAØI TAÄP VEÀ NHAØ:
OÂn taäp chuaån bò kieåm tra HK1.
Ngaøy soaïn: 30/12/2012 Chöông :
Tieát daïy: 21 Baøøi daïy: KIEÅM TRA HOÏC KÌ I
I. MUÏC TIEÂU:
Kieán thöùc: Kieåm tra caùc kieán thöùc ñaõ hoïc trong hoïc kì 1:
Vectô – Caùc pheùp toaùn vectô.
Toaï ñoä cuûa vectô, cuûa ñieåm.
GTLG cuûa goùc 0
0
180
0
.
Tích voâ höôùng cuûa hai vectô.
Kó naêng: Thaønh thaïo caùch giaûi caùc daïng toaùn:
Thöïc hieän caùc pheùp toaùn vectô. Phaân tích moät vectô theo hai vectô khoâng cuøng phöông.
Vaän duïng vectô – toaï ñoä ñeå giaûi toaùn hình hoïc.
Thaùi ñoä:
Nguyễn Đình Khương Hình Học 10 Cơ Bản
43
Reøn luyeän tính caån thaän, chính xaùc.
Luyeän tö duy linh hoaït saùng taïo.
II. CHUAÅN BÒ:
Giaùo vieân: Ñeà kieåm tra.
Hoïc sinh: OÂn taäp kieán thöùc ñaõ hoïc trong hoïc kì 1.
III. MA TRAÄN ÑEÀ:
Chuû ñeà
Nhaän bieát
Thoâng hieåu
Vaän duïng
Toång
TNKQ
TL
TNKQ
TL
TNKQ
TL
Vectô
1
0,25
2
0,25
0,75
Toaï ñoä
2
0,25
1
1,0
1
1,0
2,5
Tích voâ höôùng
1
0,25
0,25
Toång
0,5
1,0
1,0
1,0
3,5
IV. NOÄI DUNG ÑEÀ KIEÅM TRA:
A. Phaàn traéc nghieäm:
Caâu 11: Cho boán ñieåm A, B, C, D. Meänh ñeà naøo sau ñaây laø ñuùng:
A.
AB CD AD CB
B.
AB BC CD DA
C.
AB BC CD DA
D.
AB AD CD CB
Caâu 12: Cho ABC coù troïng taâm G. Meänh ñeà naøo sau ñaây laø ñuùng:
A.
3BA BC BG
B.
2
3
AB AC AG
C.
CA CB CG
D.
0AB AC BC
Caâu 13: Cho ABC ñeàu. Meänh ñeà naøo sau ñaây laø ñuùng:
A.
AB BC CA
B.
AB BC CA
C.
CA AB
D.
CA BC
Caâu 14: Trong maët phaúng Oxy, cho A(3; 0), B(0; –3) vaø ñieåm C sao cho
2CA CB
. Toaï ñoä ñieåm
C laø:
A. C(1; –2) B. C(–1; 2) C. C
33
;
22



D. C(2; –1)
Caâu 15: Trong maët phaúng Oxy, cho A(–1; 2), B(–3; 4). Toaï ñoä cuûa ñieåm C ñoái xöùng vôùi ñieåm B
qua ñieåm A laø:
A. C(1; 0) B. C(–5; 6) C. C(–1; 3) D. C(0; 1)
Caâu 16: Cho ABC ñeàu coù caïnh baèng 1. Tích voâ höôùng
.AB AC
baèng:
A.
1
2
B. 2 C.
3
2
D.
3
4
B. Phaàn töï luaän:
Baøi 3: Trong maët phaúng Oxy, cho ABC vôùi A(1; 3), B(–3; 0), C(5; –3). Treân ñöôøng thaúng BC laáy
ñieåm M sao cho:
2MB MC
.
a) Tìm toaï ñoä ñieåm M
b) Phaân tích vectô
AM
theo caùc vectô
,AB AC
.
V. ÑAÙP AÙN VAØ BIEÅU ÑIEÅM:
A. Phaàn traéc nghieäm: 11a) 12a) 13a) 14a) 15a) 16a)
Nguyễn Đình Khương Hình Học 10 Cơ Bản
44
B. Töï luaän:
Baøi 3: (2 ñieåm) Cho A(1; 3), B(–3; 0), C(5; –3).
2MB MC
a)
2MB MC
(–3 – x; –y) = –2(5 – x; –3 – y)
3 10 2
62
xx
yy
(0,5 ñieåm)
7
3
2
x
y

M
7
;2
3



(0,5 ñieåm)
b)
2MB MC
2( )AB AM AC AM
(0,5 ñieåm)
3AM AB AC
12
33
AM AB AC
(0,5 ñieåm)
VI. KEÁT QUAÛ KIEÅM TRA:
Lôùp
Só soá
0 – 3,4
3,5 – 4,9
5,0 – 6,4
6,5 – 7,9
8,0 – 10
SL
%
SL
%
SL
%
SL
%
SL
%
10A3
44
10A5
42
10A7
44
10A10
42
10A11
38
Ngaøy soaïn: 10/01/2013 Chöông :
Tieát daïy: 22 Baøøi daïy: TRAÛ BAØI KIEÅM TRA HOÏC KÌ I
I. MUÏC TIEÂU:
Kieán thöùc: Nhaéc nhôû hoïc sinh nhöõng sai laàm veà:
Caùc pheùp toaùn vectô.
Vaän duïng vectô – toaï ñoä.
Kó naêng: Nhaéc nhôû hoïc sinh nhöõng sai laàm veà:
Kyõ naêng thöïc hieän caùc pheùp toaùn veà vectô – toaï ñoä.
Thaùi ñoä:
Reøn luyeän tính caån thaän, chính xaùc.
II. CHUAÅN BÒ:
Giaùo vieân: Ñeà kieåm tra vaø ñaùp aùn. Heä thoáng caùc sai laàm cuûa HS maéc phaûi.
Hoïc sinh: Vôû ghi.
Nguyễn Đình Khương Hình Học 10 Cơ Bản
45
III. HOAÏT ÑOÄNG DAÏY HOÏC:
1. OÅn ñònh toå chöùc: Kieåm tra só soá lôùp.
2. Kieåm tra baøi cuõ:
H.
Ñ.
3. Giaûng baøi môùi:
Noäi dung ñeà kieåm tra
Sai laàm cuûa hoïc sinh
A. Phaàn traéc nghieäm:
Caâu 11: Cho boán ñieåm A, B, C, D. Meänh ñeà naøo
sau ñaây laø ñuùng:
A.
AB CD AD CB
B.
AB BC CD DA
C.
AB BC CD DA
D.
AB AD CD CB
Caâu 12: Cho ABC coù troïng taâm G. Meänh ñeà
naøo sau ñaây laø ñuùng:
A.
3BA BC BG
B.
2
3
AB AC AG
C.
CA CB CG
D.
0AB AC BC
Caâu 13: Cho ABC ñeàu. Meänh ñeà naøo sau ñaây
laø ñuùng:
A.
AB BC CA
B.
AB BC CA
C.
CA AB
D.
CA BC
Caâu 14: Trong maët phaúng Oxy, cho A(3; 0), B(0;
–3) vaø ñieåm C sao cho
2CA CB
. Toaï ñoä ñieåm
C laø:
A. C(1; –2) B. C(–1; 2)
C. C
33
;
22



D. C(2; –1)
Caâu 15: Trong maët phaúng Oxy, cho A(–1; 2),
B(–3; 4). Toaï ñoä cuûa ñieåm C ñoái xöùng vôùi ñieåm
B qua ñieåm A laø:
A. C(1; 0) B. C(–5; 6)
C. C(–1; 3) D. C(0; 1)
Caâu 16: Cho ABC ñeàu coù caïnh baèng 1. Tích voâ
höôùng
.AB AC
baèng:
A.
1
2
B. 2 C.
3
2
D.
3
4
Nguyễn Đình Khương Hình Học 10 Cơ Bản
46
B. Phaàn töï luaän:
Baøi 3: Trong maët phaúng Oxy, cho ABC vôùi
A(1; 3), B(–3; 0), C(5; –3). Treân ñöôøng thaúng
BC laáy ñieåm M sao cho:
2MB MC
.
a) Tìm toaï ñoä ñieåm M
b) Phaân tích vectô
AM
theo caùc vectô
AB,AC
.
4. BAØI TAÄP VEÀ NHAØ:
OÂn laïi kieán thöùc trong hoïc kì 1.
Ñoïc tröôùc baøi "Caùc heä thöùc löôïng trong tam giaùc vaø giaûi tam giaùc"
Ngaøy soaïn: 05/01/2013 Chöông II: TÍCH VOÂ HÖÔÙNG CUÛA HAI VECTÔ & ÖÙNG DUÏNG
Tieát daïy: 23 Baøøi 3: CAÙC HEÄ THÖÙC LÖÔÏNG TRONG TAM GIAÙC
vaø GIAÛI TAM GIAÙC
I. MUÏC TIEÂU:
Kieán thöùc:
Naém ñöôïc caùc ñònh lí coâsin, ñònh lí sin trong tam giaùc.
Naém ñöôïc caùc coâng thöùc tính ñoä daøi trung tuyeán, dieän tích tam giaùc.
Kó naêng:
Bieát vaän duïng caùc ñònh lí coâsin, ñònh lí sin ñeå tính caïnh hoaëc goùc cuûa moät tam giaùc.
Bieát söû duïng coâng thöùc tính ñoä daøi trung tuyeán vaø tính dieän tích tam giaùc.
Bieát giaûi tam giaùc vaø bieát thöïc haønh vieäc ño ñaïc trong thöïc teá.
Thaùi ñoä:
Reøn luyeän tính caån thaän, chính xaùc. Vaän duïng kieán thöùc ñaõ hoïc vaøo thöïc teá.
II. CHUAÅN BÒ:
Nguyễn Đình Khương Hình Học 10 Cơ Bản
47
Giaùo vieân: Giaùo aùn. Hình veõ minh hoaï.
Hoïc sinh: SGK, vôû ghi. OÂn taäp kieán thöùc veà tích voâ höôùng cuûa hai vectô.
III. HOAÏT ÑOÄNG DAÏY HOÏC:
1. OÅn ñònh toå chöùc: Kieåm tra só soá lôùp.
2. Kieåm tra baøi cuõ: (3')
H. Nhaéc laïi ñònh nghóa tích voâ höôùng cuûa hai vectô ?
Ñ.
. . .cos ,a b a b a b
3. Giaûng baøi môùi:
TL
Hoaït ñoäng cuûa Giaùo vieân
Hoaït ñoäng cuûa Hoïc sinh
Noäi dung
Hoaït ñoäng 1: OÂn taäp heä thöùc löôïng trong tam giaùc vuoâng
8'
Cho HS nhaéc laïi caùc heä
thöùc löôïng trong tam giaùc
vuoâng.
Caùc nhoùm laàn löôït thöïc hieän
yeâu caàu.
B
A
C
H
b
c
a
b’c’
h
I. Heä thöùc löôïng trong tam
giaùc vuoâng
a
2
= b
2
+ c
2
b
2
= a.b c
2
= a.c
h
2
= b.c ah = bc
2 2 2
1 1 1
h b c

sinB = cosC =
b
a
sinC = cosB =
c
a
tanB = cotC =
b
c
Hoaït ñoäng 2: Tìm hieåu ñònh lí coâsin
20'
H1. Phaân tích vectô
BC
theo caùc vectô
,AB AC
?
H2. Tính BC
2
?
H3. Phaùt bieåu ñònh lí coâsin
baèng lôøi ?
B
A
C
b
c
a
Ñ1.
BC
=
AC AB
Ñ2. BC
2
=
2
BC
= (
AC AB
)
2
=
22
2.AC AB AC AB
= AC
2
+ AB
2
– 2AC.AB.cosA
Ñ3. Trong moät tam giaùc, bình
phöông moät caïnh baèng toång hai
caïnh kia tröø ñi hai laàn tích cuûa
hai caïnh ñoù vôùi coâsin cuûa goùc
giöõa chuùng.
II. Ñònh lí coâsin
a) Baøi toaùn: Trong ABC,
cho bieát hai caïnh AB, AC vaø
goùc A. Tính caïnh BC.
b) Ñònh lí coâsin
a
2
= b
2
+ c
2
– 2bc.cosA
b
2
= a
2
+ c
2
– 2ac.cosB
c
2
= a
2
+ b
2
– 2ab.cosC
Heä quaû:
2 2 2
2 2 2
2 2 2
cos
2
cos
2
cos
2
b c a
A
bc
a c b
B
ac
a b c
C
ab



Nguyễn Đình Khương Hình Học 10 Cơ Bản
48
Höôùng daãn HS aùp duïng
ñònh lí coâsin ñeå tính ñoä daøi
ñöôøng trung tuyeán trong tam
giaùc
B
A
C
b
c
a
M
m
a
c) Ñoä daøi trung tuyeán tam
giaùc
2 2 2
2
2 2 2
2
2 2 2
2
2( )
4
2( )
4
2( )
4
a
b
c
b c a
m
a c b
m
a b c
m



Hoaït ñoäng 3: AÙp duïng
10'
H1. Vieát coâng thöùc tính AB,
cosA ?
Ñ1.
AB
2
= c
2
= a
2
+ b
2
– 2ab.cosC
465,44
AB
21,6 (cm)
2 2 2
cos
2
b c a
A
bc

0,7188
A
44
0
2
B
25
0
58
d) Ví duï
Cho ABC coù caùc caïnh AC =
10 cm, BC = 16 cm,
C
= 110
0
.
a) Tính caïnh AB vaø caùc goùc
A, B cuûa ABC.
b) Tính ñoä daøi ñöôøng trung
tuyeán AM.
Hoaït ñoäng 4: Cuûng coá
3'
Nhaán maïnh ñònh lí coâsin vaø
caùc öùng duïng tính goùc trong
tam giaùc, tính ñoä daøi trung
tuyeán.
4. BAØI TAÄP VEÀ NHAØ:
Baøi 1, 2, 3 SGK.
Ñoïc tieáp baøi "Caùc heä thöùc löôïng trong tam giaùc vaø giaûi tam giaùc"
Ngaøy soaïn: 05/01/2013 Chöông II: TÍCH VOÂ HÖÔÙNG CUÛA HAI VECTÔ & ÖÙNG DUÏNG
Tieát daïy: 24 Baøøi 3: CAÙC HEÄ THÖÙC LÖÔÏNG TRONG TAM GIAÙC
vaø GIAÛI TAM GIAÙC (tt)
I. MUÏC TIEÂU:
Kieán thöùc:
Naém ñöôïc caùc ñònh lí coâsin, ñònh lí sin trong tam giaùc.
Naém ñöôïc caùc coâng thöùc tính ñoä daøi trung tuyeán, dieän tích tam giaùc.
Kó naêng:
Bieát vaän duïng caùc ñònh lí coâsin, ñònh lí sin ñeå tính caïnh hoaëc goùc cuûa moät tam giaùc.
Bieát söû duïng coâng thöùc tính ñoä daøi trung tuyeán vaø tính dieän tích tam giaùc.
Bieát giaûi tam giaùc vaø bieát thöïc haønh vieäc ño ñaïc trong thöïc teá.
Thaùi ñoä:
Reøn luyeän tính caån thaän, chính xaùc. Vaän duïng kieán thöùc ñaõ hoïc vaøo thöïc teá.
II. CHUAÅN BÒ:
Nguyễn Đình Khương Hình Học 10 Cơ Bản
49
Giaùo vieân: Giaùo aùn. Hình veõ minh hoaï.
Hoïc sinh: SGK, vôû ghi. Ñoïc baøi tröôùc.
III. HOAÏT ÑOÄNG DAÏY HOÏC:
1. OÅn ñònh toå chöùc: Kieåm tra só soá lôùp.
2. Kieåm tra baøi cuõ: (3')
H. Neâu ñònh lí coâsin ? AÙp duïng: Cho ABC vôùi a = 7, b = 8, c = 6. Tính soá ño goùc A?
Ñ. a
2
= b
2
+ c
2
– 2bc.cosA
3. Giaûng baøi môùi:
TL
Hoaït ñoäng cuûa Giaùo vieân
Hoaït ñoäng cuûa Hoïc sinh
Noäi dung
Hoaït ñoäng 1: Tìm hieåu ñònh lí sin
12'
GV höôùng daãn HS chöùng
minh ñònh lí.
H1. Cho ABC vuoâng taïi A.
Tính
;;
sin sin sin
a b c
A B C
?
Neáu A 90
0
thì veõ ñöôøng
kính BD.
H2. Tính a theo R ?
Ñ1. ABC vuoâng taïi A
BC = 2R
2
sin sin sin
a b c
R
A B C
Ñ2. BC = BD.sinA
a = 2R.sinA
III. Ñònh lí sin
a) Ñònh lí sin
2
sin sin sin
a b c
R
A B C
A
B C
D
a
O
A
B
C
D
a
O
Hoaït ñoäng 2: AÙp duïng
5'
H1. Tính sinA ?
Ñ1. sinA = sin60
0
=
3
2
2
sin
a
R
A
R =
3
3
b) AÙp duïng
Ví duï 1: Cho ABC ñeàu coù
caïnh baèng a. Tính baùn kính
ñöôøng troøn ngoaïi tieáp ABC.
10'
Cho moãi nhoùm tính giaù trò
moät ñaïi löôïng.
H2. Neâu caùch tính hoaëc
coâng thöùc caàn duøng ?
Ñ2.
A
= 129
0
a =
0
0
.sin 210.sin129
sin
sin20
bA
B
477,2 (cm)
b =
0
0
.sin 210.sin31
sin
sin20
bC
B
316,2 (cm)
R =
0
477,2
2sin
2.sin129
a
A
307,02 (cm)
Ví duï 2: Cho ABC coù
B
=20
0
C
= 31
0
vaø AC = 210 cm. Tính
goùc A, caùc caïnh coøn laïi vaø
baùn kính R cuûa ñöôøng troøn
ngoaïi tieáp tam giaùc ñoù.
5'
H3. Neâu caùch tính hoaëc
coâng thöùc caàn duøng ?
Ñ3.
a)
AB
AC
=
sin
2
sin
C
B
b)
AB
AC
=
sin 2
sin
3
C
B
Ví duï 3: Cho ABC. Tính tæ
soá
AB
AC
trong caùc tröôøng hôïp
sau:
a)
00
30 , 45BC
b)
00
60 , 90BC
Nguyễn Đình Khương Hình Học 10 Cơ Bản
50
5'
H4. Neâu caùch tính hoaëc
coâng thöùc caàn duøng ?
Ñ4.
a)
A
= 45
0
2
sin
a
R
A
R =
2
2
a
b)
A
= 120
0
2
sin
a
R
A
R =
3
a
Ví duï 4: Cho ABC. Tìm baùn
kính ñöôøng troøn ngoaïi tieáp
tam giaùc trong caùc tröôøng hôïp
sau:
a)
BC
= 135
0
vaø BC = a.
b)
BC
= 60
0
vaø BC = a.
Hoaït ñoäng 3: Cuûng coá
3'
Nhaán maïnh caùch vaän duïng
ñònh lí sin
4. BAØI TAÄP VEÀ NHAØ:
Baøi 5, 6, 7, 8 SGK.
Ñoïc tieáp baøi "Caùc heä thöùc löôïng trong tam giaùc vaø giaûi tam giaùc"
Ngaøy soaïn: 15/01/2013 Chöông II: TÍCH VOÂ HÖÔÙNG CUÛA HAI VECTÔ & ÖÙNG DUÏNG
Tieát daïy: 25 Baøøi 3: CAÙC HEÄ THÖÙC LÖÔÏNG TRONG TAM GIAÙC
vaø GIAÛI TAM GIAÙC (tt)
I. MUÏC TIEÂU:
Kieán thöùc:
Naém ñöôïc caùc ñònh lí coâsin, ñònh lí sin trong tam giaùc.
Naém ñöôïc caùc coâng thöùc tính ñoä daøi trung tuyeán, dieän tích tam giaùc.
Kó naêng:
Bieát vaän duïng caùc ñònh lí coâsin, ñònh lí sin ñeå tính caïnh hoaëc goùc cuûa moät tam giaùc.
Bieát söû duïng coâng thöùc tính ñoä daøi trung tuyeán vaø tính dieän tích tam giaùc.
Bieát giaûi tam giaùc vaø bieát thöïc haønh vieäc ño ñaïc trong thöïc teá.
Thaùi ñoä:
Reøn luyeän tính caån thaän, chính xaùc. Vaän duïng kieán thöùc ñaõ hoïc vaøo thöïc teá.
II. CHUAÅN BÒ:
Giaùo vieân: Giaùo aùn. Hình veõ minh hoaï.
Nguyễn Đình Khương Hình Học 10 Cơ Bản
51
Hoïc sinh: SGK, vôû ghi. Ñoïc baøi tröôùc.
III. HOAÏT ÑOÄNG DAÏY HOÏC:
1. OÅn ñònh toå chöùc: Kieåm tra só soá lôùp.
2. Kieåm tra baøi cuõ: (5')
H. Neâu ñònh lí sin ? AÙp duïng: Cho ABC coù
B
= 60
0
,
C
= 45
0
, tæ soá
AB
AC
baèng bao nhieâu?
Ñ.
AB
AC
=
sin 6
sin 3
C
B
3. Giaûng baøi môùi:
TL
Hoaït ñoäng cuûa Giaùo vieân
Hoaït ñoäng cuûa Hoïc sinh
Noäi dung
Hoaït ñoäng 1: Tìm hieåu caùc coâng thöùc tính dieän tích tam giaùc
15'
A
B H
C
a
h
a
H1. Neâu coâng thöùc (1)?
Höôùng daãn HS chöùng minh
caùc coâng thöùc 2, 3, 4.
H2. Tính h
a
?
H3. Töø ñl sin, tính sinC ?
H4. Taâm O ñöôøng troøn noäi
tieáp tam giaùc laø ?
H5. Tính dieän tích caùc tam
giaùc OBC, OCA, OAB ?
A
B HC
a
h
a
Ñ1. S =
1
2
BC.AH =
1
2
a.h
a
Caùc nhoùm thaûo luaän.
Ñ2.
h
a
= AH = AC.sinC = bsinC
S =
1
2
ab.sinC
Ñ3. sinC =
2
c
R
S =
4
abc
R
Ñ4. Giao ñieåm caùc ñöôøng
phaân giaùc.
Ñ5. S
OBC
=
1
2
ra,
S
OCA
=
1
2
rb, S
OAB
=
1
2
rc
III. Coâng thöùc tính dieän tích
tam giaùc
S =
2 2 2
a b c
ah bh ch

(1)
11
sin sin
22
1
sin
2
ab C bc A
ca B

(2)
=
4
abc
R
(3)
= pr (4)
=
( )( )( )p p a p b p c
(5)
Hoaït ñoäng 2: AÙp duïng
10'
H1. Neâu coâng thöùc caàn duøng
Ñ1.
Coâng thöùc Heâ–roâng
p = 21 S = 84 (m
2
)
S = pr r =
S
p
= 4
S =
4 S
abc
= 8,125
VD1: Tam giaùc ABC coù caùc
caïnh a = 13m, b = 14m, c =
15m
a) Tính dieän tích ABC.
b) Tính baùn kính caùc ñöôøng
troøn noäi tieáp, ngoaïi tieáp ABC.
10'
H2. Neâu coâng thöùc caàn duøng
Ñ2.
c
2
= a
2
+ b
2
–2ab.cosC = 4
VD2: Tam giaùc ABC coù a =
2
3
, b = 2,
C
= 30
0
. Tính c,
Nguyễn Đình Khương Hình Học 10 Cơ Bản
52
c = 2
b = c = 2
BC
= 30
0
A
= 120
0
S =
1
2
ca.sinB =
3
A
, S
ABC
.
Hoaït ñoäng 3: Cuûng coá
3'
Nhaán maïnh caùch vaän duïng
caùc coâng thöùc tính dieän tích
4. BAØI TAÄP VEÀ NHAØ:
Laøm tieáp caùc baøi taäp SGK.
Ñoïc tieáp baøi "Caùc heä thöùc löôïng trong tam giaùc vaø giaûi tam giaùc"
Ngaøy soaïn: 25/01/2013 Chöông II: TÍCH VOÂ HÖÔÙNG CUÛA HAI VECTÔ & ÖÙNG DUÏNG
Tieát daïy: 26 Baøøi 3: CAÙC HEÄ THÖÙC LÖÔÏNG TRONG TAM GIAÙC
vaø GIAÛI TAM GIAÙC (tt)
I. MUÏC TIEÂU:
Kieán thöùc:
Naém ñöôïc caùc ñònh lí coâsin, ñònh lí sin trong tam giaùc.
Naém ñöôïc caùc coâng thöùc tính ñoä daøi trung tuyeán, dieän tích tam giaùc.
Kó naêng:
Bieát vaän duïng caùc ñònh lí coâsin, ñònh lí sin ñeå tính caïnh hoaëc goùc cuûa moät tam giaùc.
Bieát söû duïng coâng thöùc tính ñoä daøi trung tuyeán vaø tính dieän tích tam giaùc.
Bieát giaûi tam giaùc vaø bieát thöïc haønh vieäc ño ñaïc trong thöïc teá.
Thaùi ñoä:
Reøn luyeän tính caån thaän, chính xaùc. Vaän duïng kieán thöùc ñaõ hoïc vaøo thöïc teá.
II. CHUAÅN BÒ:
Giaùo vieân: Giaùo aùn. Hình veõ minh hoaï.
Hoïc sinh: SGK, vôû ghi. Ñoïc baøi tröôùc.
Nguyễn Đình Khương Hình Học 10 Cơ Bản
53
III. HOAÏT ÑOÄNG DAÏY HOÏC:
1. OÅn ñònh toå chöùc: Kieåm tra só soá lôùp.
2. Kieåm tra baøi cuõ: (3')
H. Tam giaùc coù 3 caïnh laàn löôït laø: 9, 12, 13. Dieän tích cuûa tam giaùc ñoù baèng bao nhieâu?
Ñ. S = 4
170
3. Giaûng baøi môùi:
TL
Hoaït ñoäng cuûa Giaùo vieân
Hoaït ñoäng cuûa Hoïc sinh
Noäi dung
Hoaït ñoäng 1: Tìm hieåu baøi toaùn giaûi tam giaùc
8'
Cho caùc nhoùm thaûo luaän,
neâu coâng thöùc caàn duøng.
A
B
C
a
bc
0
180 ( )A B C
= 71
0
30
b =
sin
sin
aB
A
12,9
c =
sin
sin
aC
A
16,5
IV. Giaûi tam giaùc vaø öùng duïng
vaøo vieäc ño ñaïc
1. Giaûi tam giaùc
Giaûi tam giaùc laø tìm moät soá yeáu
toá cuûa tam giaùc khi bieát ñöôïc
caùc yeáu toá khaùc.
VD1: Cho ABC coù a = 17,4,
B
= 44
0
30,
C
= 64
0
. Tính
A
,
b, c ?
7'
c
2
= a
2
+ b
2
– 2ab.cosC
1369,66
c 37
cosA =
2 2 2
2
b c a
bc

– 0,191
A
101
0
0
180 ( )B A C
31
0
40
VD2: Cho ABC coù a = 49,4, b
= 26,4,
C
= 47
0
20. Tính c,
A vaø B
.
Hoaït ñoäng 2: AÙp duïng giaûi baøi toaùn thöïc teá
12'
Höôùng daãn HS phaân tích
caùch ño ñaïc vaø tính toaùn.
h
A
B
C
D
b
g
Xeùt tröôøng hôïp ñaëc bieät:
coù theå ñeán ñöôïc chaân thaùp.
Xeùt tam giaùc ABD
g = – b
AD =
.sin
sin( )
AB b
b
Xeùt tam giaùc vuoâng ACD
h = CD = AD.sin
2. ÖÙng duïng vaøo vieäc ño ñaïc
Baøi toaùn 1: Ño chieàu cao cuûa
moät caùi thaùp maø khoâng theå ñeán
ñöôïc chaân thaùp.
Choïn 2 ñieåm A, B treân maët
ñaát sao cho A, B, C thaúng haøng.
Ño AB,
,CAD CBD
.
Tính chieàu cao h = CD cuûa
thaùp.
Nguyễn Đình Khương Hình Học 10 Cơ Bản
54
10'
C
A
B
b
Cho caùc nhoùm thaûo luaän
tìm caùch ño khaùc.
Xeùt tam giaùc ABC
AC =
.sin
sin( )
AB b
b
Baøi toaùn 2: Tính khoaûng caùch
giöõa 2 ñieåm maø khoâng theå ño
tröïc tieáp ñöôïc.
Ñeå ño khoaûng caùch töø ñieåm A
treân bôø soâng ñeán goác caây C
treân cuø lao giöõa soâng, ngöôøi ta
choïn moät ñieåm B cuøng ôû treân
bôø vôùi A sao cho töø A vaø B coù
theå nhìn thaáy C. Ño AB,
,CAB CBA
.
Tính khoaûng caùch AC.
Hoaït ñoäng 3: Cuûng coá
3'
Nhaán maïnh caùch vaän duïng
caùc coâng thöùc trong tam giaùc
ñaõ hoïc.
4. BAØI TAÄP VEÀ NHAØ:
Baøi 10, 11 SGK.
Ngaøy soaïn: 25/01/2013 Chöông II: TÍCH VOÂ HÖÔÙNG CUÛA HAI VECTÔ & ÖÙNG DUÏNG
Tieát daïy: 27 Baøøi 3: BAØI TAÄP CAÙC HEÄ THÖÙC LÖÔÏNG
TRONG TAM GIAÙC vaø GIAÛI TAM GIAÙC
I. MUÏC TIEÂU:
Kieán thöùc:
Naém ñöôïc caùc ñònh lí coâsin, ñònh lí sin trong tam giaùc.
Naém ñöôïc caùc coâng thöùc tính ñoä daøi trung tuyeán, dieän tích tam giaùc.
Kó naêng:
Bieát vaän duïng caùc ñònh lí coâsin, ñònh lí sin ñeå tính caïnh hoaëc goùc cuûa moät tam giaùc.
Bieát söû duïng coâng thöùc tính ñoä daøi trung tuyeán vaø tính dieän tích tam giaùc.
Bieát giaûi tam giaùc vaø bieát thöïc haønh vieäc ño ñaïc trong thöïc teá.
Thaùi ñoä:
Reøn luyeän tính caån thaän, chính xaùc. Vaän duïng kieán thöùc ñaõ hoïc vaøo thöïc teá.
Nguyễn Đình Khương Hình Học 10 Cơ Bản
55
II. CHUAÅN BÒ:
Giaùo vieân: Giaùo aùn. Heä thoáng baøi taäp.
Hoïc sinh: SGK, vôû ghi. OÂn taäp kieán thöùc ñaõ hoïc veà Heä thöùc löôïng trong tam giaùc.
III. HOAÏT ÑOÄNG DAÏY HOÏC:
1. OÅn ñònh toå chöùc: Kieåm tra só soá lôùp.
2. Kieåm tra baøi cuõ: (Loàng vaøo quaù trình luyeän taäp)
H.
Ñ.
3. Giaûng baøi môùi:
TL
Hoaït ñoäng cuûa Giaùo vieân
Hoaït ñoäng cuûa Hoïc sinh
Noäi dung
Hoaït ñoäng 1: Cuûng coá caùc heä thöùc löôïng trong tam giaùc
8'
H1. Neâu coâng thöùc caàn söû
duïng ?
Ñ1.
C
= 90
0
–
B
= 42
0
b = a.sinB 61,06 (cm)
c = a.sinC 38,15 (cm)
h
a
=
bc
a
32,36 (cm)
1. Cho ABC vuoâng taïi A,
B
=58
0
vaø caïnh a = 72 cm. Tính
C
, caïnh b, caïnh c vaø ñöôøng
cao h
a
.
A
B CH a
b
c
h
a
7'
H2. Neâu coâng thöùc caàn söû
duïng ?
Ñ2.
a
2
= b
2
+ c
2
– 2bc.cosA =
129
a 11,36 (cm)
cosB =
2 2 2
2
a c b
ac

0,79
B
37
0
48
C
= 180
0
– (
AB
) 22
0
12
2. Cho ABC coù
A
= 120
0
,
caïnh b = 8 cm, c = 5 cm. Tính
caïnh a vaø caùc goùc
B
,
C
.
A
B
Ca
b
c
7'
H3. Goùc naøo coù theå laø goùc tuø
?
H4. Neâu coâng thöùc tính MA
?
Ñ3. Goùc ñoái dieän vôùi caïnh lôùn
nhaát.
cosC =
2 2 2
2
a b c
ab

= –
5
160
C
tuø.
Ñ4. MA
2
=
2 2 2
2( )
4
b c a
= 118,5
MA 10,89 (cm)
3. Cho ABC coù caùc caïnh a = 8
cm, b = 10 cm, c = 13 cm.
a) Tam giaùc ñoù coù goùc tuø
khoâng?
b) Tính ñoä daøi trung tuyeán MA
cuûa ABC.
A
B
C
a
b
c
M
8'
H5. Neâu coâng thöùc caàn söû
duïng ?
Ñ5.
A
= 180
0
– (
BC
) = 40
0
R =
2sin
a
A
107 (cm)
b = 2RsinB 212,31 (cm)
4. Cho ABC coù caïnh a = 137,5
cm,
B
= 83
0
,
C
= 57
0
. Tính
A
,
baùn kính R cuûa ñöôøng troøn
ngoaïi tieáp, caùc caïnh b, c.
Nguyễn Đình Khương Hình Học 10 Cơ Bản
56
c = 2RsinC 179,40 (cm)
A B
C
a
b
c
O
R
Hoaït ñoäng 2: AÙp duïng giaûi baøi toaùn thöïc teá
10'
H1. Neâu caùc böôùc tính?
A
B
Q P
h
Ñ1. Xeùt BPQ
PBQ
= 48
0
– 35
0
= 13
0
BQ =
.sin
sin
PQ P
B
=
0
0
300.sin35
sin13
764,94
AB = BQ.sinQ 568,46 (m)
5. Hai chieác taøu thuyû P vaø Q
caùch nhau 300 m. Töø P vaø Q
thaúng haøng vôùi chaân A cuûa thaùp
haûi ñaêng AB ôû treân bôø bieån
ngöôøi ta nhìn chieàu cao AB cuûa
thaùp döôùi caùc goùc
BPA
= 35
0
vaø
BQA
= 48
0
. Tính chieàu cao cuûa
thaùp.
Hoaït ñoäng 3: Cuûng coá
3'
Nhaán maïnh caùch vaän duïng
caùc heä thöùc löôïng trong tam
giaùc ñaõ hoïc.
4. BAØI TAÄP VEÀ NHAØ:
Baøi taäp oân chöông II.
Ngaøy soaïn: 30/01/2013 Chöông II: TÍCH VOÂ HÖÔÙNG CUÛA HAI VECTÔ & ÖÙNG DUÏNG
Tieát daïy: 28 Baøøi daïy: OÂN TAÄP CHÖÔNG II
I. MUÏC TIEÂU:
Kieán thöùc:
OÂn taäp toaøn boä kieán thöùc chöông II.
Kó naêng:
Bieát söû duïng caùc kieán thöùc ñaõ hoïc ñeå giaûi toaùn.
Thaùi ñoä:
Reøn luyeän tính caån thaän, chính xaùc. Vaän duïng kieán thöùc ñaõ hoïc vaøo thöïc teá.
II. CHUAÅN BÒ:
Giaùo vieân: Giaùo aùn. Heä thoáng baøi taäp.
Nguyễn Đình Khương Hình Học 10 Cơ Bản
57
Hoïc sinh: SGK, vôû ghi. OÂn taäp kieán thöùc chöông II.
III. HOAÏT ÑOÄNG DAÏY HOÏC:
1. OÅn ñònh toå chöùc: Kieåm tra só soá lôùp.
2. Kieåm tra baøi cuõ: (Loàng vaøo quaù trình oân taäp)
H.
Ñ.
3. Giaûng baøi môùi:
TL
Hoaït ñoäng cuûa Giaùo vieân
Hoaït ñoäng cuûa Hoïc sinh
Noäi dung
Hoaït ñoäng 1: Cuûng coá GTLG cuûa goùc
10'
Cho HS nhaéc laïi: ñn, caùc
tính chaát cuûa GTLG ñaõ hoïc.
Caùc nhoùm thöïc hieän, giaûi
thích roõ caên cöù ñeå xeùt.
a) S b) Ñ c) Ñ
1. Cho hai goùc nhoïn , b ( <
b). Xeùt tính Ñ–S ?
a) cos < cosb b)sin < sinb
c) cos = sinb + b = 90
0
Cuûng coá baûng GTLG caùc
goùc ñaëc bieät.
a) S b) Ñ c) Ñ d) Ñ
2. Tam giaùc ABC vuoâng ôû A,
coù
B
= 30
0
. Xeùt tính Ñ–S ?
a) cosB =
1
3
b)sinC =
3
2
c) cosC =
1
2
d) sinB =
1
2
Cuûng coá ñn, GTLG caùc
goùc buø nhau, baûng giaù trò
ñaëc bieät.
a) S b) S c) Ñ
3. Xeùt tính Ñ–S ?
a) sin150
0
= –
3
2
b) cos150
0
=
3
2
c) tan150
0
= –
1
3
Hoaït ñoäng 2: Cuûng coá tích voâ höôùng cuûa hai vectô
15'
H1. Neâu caùch xaùc ñònh goùc
cuûa hai vectô ?
Ñ1. Tònh tieán caùc vectô sao cho
chuùng coù ñieåm ñaàu truøng nhau.
a) Ñ b) Ñ c) Ñ d) S
4. ABC vuoâng ôû A vaø
B
=
50
0
. Xeùt tính Ñ–S ?
a)
,AB BC
= 130
0
b)
,BC AC
= 40
0
c)
,AB CB
= 50
0
d)
,AC CB
= 120
0
H2. Nhaéc laïi ñònh nghóa tích
voâ höôùng cuûa hai vectô ?
Ñ2.
a) Ñ b) Ñ c) Ñ d) S
5. ABC vuoâng ôû A. Xeùt tính
Ñ–S ?
a)
..AB AC BA BC
b)
..AC CB AC BC
c)
..AB BC CA CB
d)
..AC BC BC AB
H3. Nhaéc laïi coâng thöùc tính
ñoä daøi ñoaïn thaúng, goùc giöõa
hai caïnh ?
Ñ3. AB = AC =
8
, BC = 4
a) S b) S c) S d) Ñ
6. ABC coù A(–1; 1), B(1; 3),
C(1; –1). Xeùt tính Ñ–S ?
a) ABC ñeàu.
Nguyễn Đình Khương Hình Học 10 Cơ Bản
58
b) ABC coù 3 goùc nhoïn.
c) ABC caân taïi B.
d) ABC vuoâng caân taïi A.
Hoaït ñoäng 3: Cuûng coá heä thöùc löôïng trong tam giaùc
15'
H1. Neâu coâng thöùc caàn söû
duïng ?
Ñ1. p =
1
2
(12 + 16 + 20) = 24
S =
( )( )( )p p a p b p c
= 96
h
a
=
2S
a
= 16; R =
4
abc
R
=10
r =
S
p
= 4
m
a
2
=
2 2 2
2( )
4
b c a
= 292
7. Cho ABC coù a = 12, b =
16, c = 20. Tính S, h
a
, R, r, m
a
?
Höôùng daãn HS phaân tích
baøi toaùn, tìm caùch tính.
+ Veõ GH AC
+ Tính GH =
1
3
AB = 10
+ S
CFG
=
1
2
CF.GH = 75
8. Cho ABC vuoâng caân taïi A
coù AB = AC = 30. Hai ñöôøng
trung tuyeán BF, CE caét nhau
taïi G. Tính dieän tích CFG.
A
B C
FE
G
H
Hoaït ñoäng 4: Cuûng coá
3'
Nhaán maïnh caùch vaän duïng
caùc kieán thöùc ñaõ hoïc.
4. BAØI TAÄP VEÀ NHAØ:
Ñoïc tröôùc baøi "Phöông trình ñöôøng thaúng".
Ngaøy soaïn: 01/02/2013 Chöông III: PHÖÔNG PHAÙP TOAÏ ÑOÄ TRONG MAËT PHAÚNG
Tieát daïy: 29 Baøøi 1: PHÖÔNG TRÌNH ÑÖÔØNG THAÚNG
I. MUÏC TIEÂU:
Kieán thöùc:
Naém ñöôïc caùc khaùi nieäm vectô chæ phöông cuûa ñöôøng thaúng.
Naém ñöôïc phöông trình tham soá cuûa ñöôøng thaúng.
Naém ñöôïc moái lieân heä giöõa vectô chæ phöông vaø heä soá goùc cuûa ñöôøng thaúng.
Kó naêng:
Bieát caùch laäp phöông trình tham soá cuûa ñöôøng thaúng.
Naém vöõng caùch veõ ñöôøng thaúng trong maët phaúng toaï ñoä khi bieát phöông trình cuûa noù.
Thaùi ñoä:
Reøn luyeän tính caån thaän, chính xaùc.
Laøm quen vieäc chuyeån tö duy hình hoïc sang tö duy ñaïi soá.
Nguyễn Đình Khương Hình Học 10 Cơ Bản
59
II. CHUAÅN BÒ:
Giaùo vieân: Giaùo aùn. Hình veõ minh hoaï.
Hoïc sinh: SGK, vôû ghi. OÂn taäp kieán thöùc veà ñöôøng thaúng ñaõ hoïc. Duïng cuï veõ hình.
III. HOAÏT ÑOÄNG DAÏY HOÏC:
1. OÅn ñònh toå chöùc: Kieåm tra só soá lôùp.
2. Kieåm tra baøi cuõ: (3')
H. Cho ñöôøng thaúng (d): y = 2x + 3. Giaûi thích yù nghóa caùc heä soá? Xaùc ñònh toaï ñoä moät
ñieåm thuoäc ñöôøng thaúng ?
Ñ. Heä soá goùc a = 2; tung ñoä goác b = 3. A(0; 3), B(1; 5) (d).
3. Giaûng baøi môùi:
TL
Hoaït ñoäng cuûa Giaùo vieân
Hoaït ñoäng cuûa Hoïc sinh
Noäi dung
Hoaït ñoäng 1: Tìm hieåu khaùi nieäm vectô chæ phöông cuûa ñöôøng thaúng
15'
Töø kieåm tra baøi cuõ, daãn
daét hình thaønh khaùi nieäm
vectô chæ phöông cuûa ñöôøng
thaúng.
H1. Chöùng toû
AB
cuøng
phöông vôùi
u
= (1; 2) ?
H2. Vectô naøo trong caùc
vectô sau cuõng laø vectô chæ
phöông cuûa ?
(0;0)v
,
( 2; 4)a
,
(2;1)b
,
(1; 2)c 
H3. Cho d coù VTCP
u
= (2;
1) vaø M(1; 1) d. Ñieåm
naøo sau ñaây cuõng thuoäc d ?
A(3; 2), B(–5; –2), C(0; 2)
x
y
O
3
1
5
A
B
u
Ñ1.
AB
= (1; 2)
Ñ2.
( 2; 4)a
= –2
u
a
cuõng laø vectô chæ phöông
Ñ3. A, B d
vì
MA
= (2; 1) =
u
MB
= (–6; –3) = –2
u
1. Vectô chæ phöông cuûa
ñöôøng thaúng
Vectô
u
ñgl vectô chæ phöông
cuûa ñöôøng thaúng
neáu
u
0
vaø giaù cuûa
u
song song hoaëc
truøng vôùi
.
Nhaän xeùt:
Moät ñöôøng thaúng coù voâ soá
vectô chæ phöông.
Moät ñöôøng thaúng hoaøn toaøn
ñöôïc xaùc ñònh neáu bieát moät
ñieåm vaø moät vectô chæ phöông
cuûa noù.
Cho
coù VTCP
u
vaø ñi qua
M. Khi ñoù:
N
MN
cuøng phöông
u
Hoaït ñoäng 2: Tìm hieåu phöông trình tham soá cuûa ñöôøng thaúng
10'
GV höôùng daãn tìm phöông
trình tham soá cuûa ñöôøng
thaúng.
H1. Neâu ñieàu kieän ñeå
M(x;y) naèm treân ?
H2. Ta caàn xaùc ñònh yeáu toá
naøo ?
Ñ1.
M
0
M M cuøng phöôngu
0
M M tu
01
02
x x tu
y y tu


Ñ2. Vectô chæ phöông
2. Phöông trình tham soá cuûa
ñöôøng thaúng
a) Ñònh nghóa
Trong mp Oxy, cho
ñi qua
M
0
(x
0
; y
0
) vaø coù VTCP
12
( ; )u u u
. Phöông trình
tham soá cuûa
:
01
02
x x tu
y y tu


(1)
Cho t moät giaù trò cuï theå thì ta
xaùc ñònh ñöôïc moät ñieåm treân
Nguyễn Đình Khương Hình Học 10 Cơ Bản
60
H3. Choïn giaù trò t ?
(Moãi nhoùm choïn moät giaù
trò)
AB
= (1; –2)
:
2
32
xt
yt


Ñ3. t = 2 M(4; –1)
t = –1 N(1; 5)
VD1: Cho A(2; 3), B(3; 1).
a) Vieát pt tham soá cuûa ñöôøng
thaúng AB.
b) Haõy xaùc ñònh toaï ñoä ñieåm
M thuoäc ñt AB (khaùc A vaø B).
Hoaït ñoäng 3: Tìm hieåu moái lieân heä giöõa VTCP vaø heä soá goùc cuûa ñöôøng thaúng
10'
Cho HS nhaéc laïi nhöõng
ñieàu ñaõ bieát veà heä soá goùc
cuûa ñöôøng thaúng.
* : y = ax + b k = a
*
xAv
= k =
2
1
u
u
= tan
H1. Tính heä soá goùc cuûa
ñöôøng thaúng AB ?
Caùc nhoùm thaûo luaän vaø trình
baøy.
O
x
y
A
v
u
u
1
u
2
Ñ1. k =
2
1
= –2
b) Lieân heä giöõa VTCP vaø heä
soá goùc cuûa ñöôøng thaúng
Cho
coù VTCP
12
( ; )u u u
vôùi u
1
0 thì
coù heä soá goùc
k =
2
1
u
u
Phöông trình
ñi qua M
0
(x
0
;
y
0
) vaø coù heä soá goùc k:
y – y
0
= k(x – x
0
)
Hoaït ñoäng 4: Cuûng coá
5'
Nhaán maïnh:
– VTCP, PT tham soá, heä soá
goùc cuûa ñöôøng thaúng.
– Caùch laäp phöông trình
tham soá cuûa ñt.
– Caùch xaùc ñònh toaï ñoä 1
ñieåm treân ñöôøng thaúng
Cho caùc nhoùm tính heä soá goùc
cuûa ñöôøng thaúng döïa vaøo toaï ñoä
cuûa VTCP.
4. BAØI TAÄP VEÀ NHAØ:
Baøi 1 SGK.
Ñoïc tieáp baøi "Phöông trình ñöôøng thaúng".
Ngaøy soaïn: 10/02/2013 Chöông III: PHÖÔNG PHAÙP TOAÏ ÑOÄ TRONG MAËT PHAÚNG
Tieát daïy: 30 Baøøi 1: PHÖÔNG TRÌNH ÑÖÔØNG THAÚNG (tt)
I. MUÏC TIEÂU:
Kieán thöùc:
Naém ñöôïc caùc khaùi nieäm vectô phaùp tuyeán cuûa ñöôøng thaúng.
Naém ñöôïc phöông trình toång quaùt cuûa ñöôøng thaúng.
Naém ñöôïc moái lieân heä giöõa vectô chæ phöông vaø vectô phaùp tuyeán cuûa ñöôøng thaúng.
Kó naêng:
Bieát caùch laäp phöông trình toång quaùt cuûa ñöôøng thaúng.
Naém vöõng caùch veõ ñöôøng thaúng trong maët phaúng toaï ñoä khi bieát phöông trình cuûa noù.
Thaùi ñoä:
Reøn luyeän tính caån thaän, chính xaùc.
Laøm quen vieäc chuyeån tö duy hình hoïc sang tö duy ñaïi soá.
II. CHUAÅN BÒ:
Giaùo vieân: Giaùo aùn. Hình veõ minh hoaï.
Hoïc sinh: SGK, vôû ghi. OÂn taäp kieán thöùc veà ñöôøng thaúng ñaõ hoïc. Duïng cuï veõ hình.
Nguyễn Đình Khương Hình Học 10 Cơ Bản
61
III. HOAÏT ÑOÄNG DAÏY HOÏC:
1. OÅn ñònh toå chöùc: Kieåm tra só soá lôùp.
2. Kieåm tra baøi cuõ: (3')
H. Laäp phöông trình tham soá cuûa ñöôøng thaúng d ñi qua M(2; 1) vaø coù VTCP
u
= (3; 4).
Xeùt quan heä giöõa vectô
u
vôùi
n
= (4; –3) ?
Ñ. d:
x 2 3t
y 1 4t


;
u
n
.
3. Giaûng baøi môùi:
TL
Hoaït ñoäng cuûa Giaùo vieân
Hoaït ñoäng cuûa Hoïc sinh
Noäi dung
Hoaït ñoäng 1: Tìm hieåu khaùi nieäm vectô phaùp tuyeán cuûa ñöôøng thaúng
7'
Daãn daét töø KTBC, GV giôùi
thieäu khaùi nieäm VTPT cuûa
ñöôøng thaúng.
H1. Neáu
n
laø moät VTPT cuûa
thì coù nhaän xeùt gì veà vectô
k
n
(k
0) ?
H2. Coù bao nhieâu ñt ñi qua
moät ñieåm vaø vuoâng goùc vôùi
moät ñt cho tröôùc ?
Ñ1. k
n
cuõng laø VTPT vì k
n
u
Ñ2. Coù moät vaø chæ moät.
III. Vectô phaùp tuyeán cuûa
ñöôøng thaúng
Vectô
n
ñgl vectô phaùp tuyeán
cuûa ñöôøng thaúng
neáu
n
0
vaø
n
vuoâng goùc vôùi VTCP
u
cuûa
.
Nhaän xeùt:
– Moät ñöôøng thaúng coù voâ soá
vectô phaùp tuyeán.
– Moät ñöôøng thaúng ñöôïc hoaøn
toaøn xaùc ñònh neáu bieát moät ñieåm
vaø moät vectô phaùp tuyeán.
Hoaït ñoäng 2: Tìm hieåu phöông trình toång quaùt cuûa ñöôøng thaúng
15'
H1. Cho ñi qua M
0
(x
0
; y
0
) vaø
coù VTPT
n
= (a; b). Tìm ñk
ñeå M(x; y) ?
GV höôùng daãn HS ruùt ra
nhaän xeùt.
H2. Xaùc ñònh VTCP, VTPT
cuûa ñt AB ?
H3. Xaùc ñònh VTPT cuûa d ?
Ñ1. M(x; y)
0
M M u
a(x – x
0
) + b(y – y
0
) = 0
ax + by + c = 0 (c=–ax
0
–by
0
)
O
x
y
x
0
y
0
M
0
M
u
n
Laáy M, N . Ch.minh:
MN n
Ñ2.
u AB
= (2; 1)
n
= (1; –2)
: x – 2 + (–2)(y – 2) = 0
x – 2y + 2 = 0
Ñ3.
d
n AB
= (2; 1)
d: 2(x – 2) + (y – 2) = 0
2x + y – 6 = 0
IV. Phöông trình toång quaùt cuûa
ñöôøng thaúng
1. Ñònh nghóa: Phöông trình ax
+ by + c = 0 vôùi a
2
+ b
2
0 ñgl
phöông trình toång quaùt cuûa
ñöôøng thaúng.
Nhaän xeùt:
+ Pt ñt ñi qua M(x
0
; y
0
) vaø coù
VTPT
n
= (a; b):
a(x – x
0
) + b(y – y
0
) = 0
+ Neáu
: ax + by + c = 0 thì
coù: VTPT
n
= (a; b)
VTCP
u
= (b; –a)
VD: Cho hai ñieåm A(2; 2), B(4;
3).
a) Laäp pt ñt ñi qua A vaø B.
b) Laäp pt ñt d ñi qua A vaø vuoâng
goùc vôùi ñt AB.
Hoaït ñoäng 3: Tìm hieåu caùc tröôøng hôïp ñaëc bieät cuûa phöông trình toång quaùt cuûa ñöôøng thaúng
Nguyễn Đình Khương Hình Học 10 Cơ Bản
62
15'
GV höôùng daãn HS nhaän xeùt
caùc tröôøng hôïp ñaëc bieät. Minh
hoaï baèng hình veõ.
H1. Caùc ñöôøng thaúng coù ñaëc
ñieåm gì ?
O
x
y
c
b
O
x
y
c
a
O
x
y
O
x
y
c
a
c
b
M
N
Ñ1.
d
1
ñi qua O; d
2
Ox; d
3
Oy
d
4
caét caùc truïc toaï ñoä taïi (8; 0),
(0; 4)
2. Caùc tröôøng hôïp ñaëc bieät
Cho
: ax + by + c = 0 (1)
Neáu a = 0 thì (1): y =
c
b
Oy taïi
c
0;
b



Neáu b = 0 thì (1): x =
c
a
Ox taïi
c
;0
a



Neáu c = 0 thì (1) trôû thaønh:
ax + by = 0
ñi qua goác toaï ñoä O.
Neáu a, b, c
0 thì
(1)
00
xy
1
ab

(2)
vôùi a
0
=
c
a
, b
0
=
c
b
.
(2) ñgl pt ñt theo ñoaïn chaén
VD: Veõ caùc ñöôøng thaúng sau:
d
1
: x – 2y = 0
d
2
: x = 2
d
3
: y + 1 = 0
d
4
:
1
84
xy

Hoaït ñoäng 4: Cuûng coá
3'
Nhaán maïnh:
+ VTPT cuûa ñt
+ Caùch laäp pt toång quaùt cuûa ñt
4. BAØI TAÄP VEÀ NHAØ:
Baøi 1, 2, 3, 4 SGK.
Ñoïc tieáp baøi "Phöông trình ñöôøng thaúng".
Ngaøy soaïn: 20/02/2013 Chöông III: PHÖÔNG PHAÙP TOAÏ ÑOÄ TRONG MAËT PHAÚNG
Tieát daïy: 31 Baøøi 1: PHÖÔNG TRÌNH ÑÖÔØNG THAÚNG (tt)
I. MUÏC TIEÂU:
Kieán thöùc:
Naém ñöôïc caùc tröôøng hôïp veà VTTÑ cuûa hai ñöôøng thaúng.
Naém ñöôïc moái lieân heä giöõa VTCP, VTPT vôùi VTTÑ cuûa hai ñöôøng thaúng.
Kó naêng:
Bieát caùch xeùt VTTÑ cuûa hai ñöôøng thaúng.
Bieát caùch laäp phöông trình ñöôøng thaúng song song vôùi ñöôøng thaúng ñaõ cho.
Thaùi ñoä:
Reøn luyeän tính caån thaän, chính xaùc.
Nguyễn Đình Khương Hình Học 10 Cơ Bản
63
Laøm quen vieäc chuyeån tö duy hình hoïc sang tö duy ñaïi soá.
II. CHUAÅN BÒ:
Giaùo vieân: Giaùo aùn. Hình veõ minh hoaï.
Hoïc sinh: SGK, vôû ghi. OÂn taäp kieán thöùc veà ñöôøng thaúng ñaõ hoïc. Duïng cuï veõ hình.
III. HOAÏT ÑOÄNG DAÏY HOÏC:
1. OÅn ñònh toå chöùc: Kieåm tra só soá lôùp.
2. Kieåm tra baøi cuõ: (3')
H. Xaùc ñònh VTCP cuûa caùc ñöôøng thaúng: : x – y – 1 = 0 vaø d: 2x – 2y + 2 = 0.
Ñ.
u
= (1; 1),
d
u
= (2; 2)
3. Giaûng baøi môùi:
TL
Hoaït ñoäng cuûa Giaùo vieân
Hoaït ñoäng cuûa Hoïc sinh
Noäi dung
Hoaït ñoäng 1: Tìm hieåu caùch xeùt VTTÑ cuûa hai ñöôøng thaúng
15'
H1. Nhaéc laïi caùch tìm giao
ñieåm cuûa hai ñöôøng thaúng ?
Cho moãi nhoùm giaûi moät
heä pt. GV minh hoaï baèng
hình veõ.
Ñ1. Toaï ñoä giao ñieåm cuûa
1
vaø
2
laø nghieäm cuûa phöông trình:
1 1 1
2 2 2
0
()
0
a x b y c
I
a x b y c
a)
x y 1 0
2x y 4 0
coù nghieäm (1;
2)
d caét
1
taïi A(1; 2)
b)
x y 1 0
x y 1 0
voâ nghieäm
d //
2
c)
x y 1 0
2x 2y 2 0
coù VSN
d .
V. VTTÑ cuûa 2 ñöôøng thaúng
Xeùt 2 ñöôøng thaúng:
1
: a
1
x + b
1
y + c
1
= 0
vaø
2
: a
2
x + b
2
y + c
2
= 0
Toaï ñoä giao ñieåm cuûa
1
vaø
2
laø nghieäm cuûa phöông trình:
1 1 1
2 2 2
0
()
0
a x b y c
I
a x b y c
1
caét
2
(I) coù 1 nghieäm
1
//
2
(1) voâ nghieäm
1
2
(1) coù VSN
VD1: Cho d: x – y + 1 = 0.
Xeùt VTTÑ cuûa d vôùi moãi ñt
sau:
1
: 2x + y – 4 = 0
2
: x – y – 1 = 0
3
: 2x – 2y + 2 = 0.
O
1
2 M
x
y
d
1
a)
O
1
1
x
y
d
2
b)
–1
–1
O
1
–1
x
y
d
3
c)
Hoaït ñoäng 2: Tìm hieåu caùch xeùt VTTÑ cuûa hai ñt döïa vaøo caùc heä soá cuûa pt toång quaùt
10'
Höôùng daãn HS nhaän xeùt
qua vieäc giaûi heä pt ôû treân.
H1. Khi naøo heä (I):
+ coù 1 nghieäm
+ voâ nghieäm
Ñ1.
Nhaän xeùt:
Giaû söû a
2
, b
2
, c
2
0.
+
11
22
ab
ab
1
caét
2
Nguyễn Đình Khương Hình Học 10 Cơ Bản
64
+ coù voâ soá nghieäm
H2. Xeùt VTTÑ cuûa vôùi d
1
,
d
2
, d
3
?
+ (I) coù 1 nghieäm khi
11
22
ab
ab
+ (I) voâ nghieäm khi
1 1 1
2 2 2
a b c
a b c

+ (I) coù VSN khi
1 1 1
2 2 2
a b c
a b c

Ñ2.
+
1 2 1
3 6 3


d
1
+
12
21
caét d
2
+
1 2 1
2 4 5

// d
3
+
1 1 1
2 2 2
a b c
a b c

1
//
2
+
1 1 1
2 2 2
a b c
a b c

1
2
VD2: Xeùt VTTÑ cuûa : x –
2y + 1 = 0 vôùi moãi ñt sau:
d
1
: –3x + 6y – 3 = 0
d
2
: y = –2x
d
3
: 2x + 5 = 4y
Hoaït ñoäng 3: Vaän duïng VTTÑ cuûa hai ñöôøng thaúng ñeå laäp pt ñöôøng thaúng
10'
Höôùng daãn HS caùc caùch
laäp ph.trình ñöôøng thaúng d.
H1. Xaùc ñònh VTCP cuûa BC
H2. Xaùc ñònh daïng pt cuûa d
Ñ1.
u BC
= (3; 3)
BC: 3(x – 3) –3(y + 1) = 0
x – y – 4 = 0
Ñ2. d: x – y + m = 0
A(1; 4) d m = 3
d: x – y + 3 = 0
VD3: Cho ABC vôùi A(1; 4),
B(3; –1), C(6; 2).
a) Laäp pt ñöôøng thaúng BC.
b) Laäp pt ñt d ñi qua A vaø
song song vôùi BC.
Hoaït ñoäng 4: Cuûng coá
5'
Nhaán maïnh
– Caùch xeùt VTTÑ cuûa 2
ñöôøng thaúng.
– Caùch vaän duïng VTTÑ cuûa
2 ñöôøng thaúng ñeå laäp pt ñt.
Gôïi yù cho HS tìm caùc caùch
khaùc nhau ñeå giaûi VD3.
4. BAØI TAÄP VEÀ NHAØ:
Baøi 5 SGK.
Ñoïc tieáp baøi "Phöông trình ñöôøng thaúng".
Ngaøy soaïn: 5/03/2013 Chöông III: PHÖÔNG PHAÙP TOAÏ ÑOÄ TRONG MAËT PHAÚNG
Tieát daïy: 32 Baøøi 1: PHÖÔNG TRÌNH ÑÖÔØNG THAÚNG (tt)
I. MUÏC TIEÂU:
Kieán thöùc:
Naém ñöôïc khaùi nieäm goùc giöõa hai ñöôøng thaúng.
Naém ñöôïc caùch tính goùc giöõa hai ñöôøng thaúng, khoaûng caùch töø moät ñieåm ñeán moät ñöôøng
thaúng .
Naém ñöôïc moái lieân heä giöõa VTCP, VTPT vôùi goùc giöõa hai ñöôøng thaúng.
Kó naêng:
Bieát caùch tính goùc giöõa hai ñöôøng thaúng, khoaûng caùch töø moät ñieåm ñeán moät ñöôøng thaúng.
Nguyễn Đình Khương Hình Học 10 Cơ Bản
65
Thaùi ñoä:
Reøn luyeän tính caån thaän, chính xaùc.
Laøm quen vieäc chuyeån tö duy hình hoïc sang tö duy ñaïi soá.
II. CHUAÅN BÒ:
Giaùo vieân: Giaùo aùn. Hình veõ minh hoaï.
Hoïc sinh: SGK, vôû ghi. OÂn taäp kieán thöùc veà ñöôøng thaúng ñaõ hoïc. Duïng cuï veõ hình.
III. HOAÏT ÑOÄNG DAÏY HOÏC:
1. OÅn ñònh toå chöùc: Kieåm tra só soá lôùp.
2. Kieåm tra baøi cuõ: (3')
H. Cho ABC vôùi A(1; 4), B(3; –1), C(6; 2). Tính goùc A.
Ñ. cosA = cos
AB,AC
=
AB.AC
AB.AC
=
20
29
3. Giaûng baøi môùi:
TL
Hoaït ñoäng cuûa Giaùo vieân
Hoaït ñoäng cuûa Hoïc sinh
Noäi dung
Hoaït ñoäng 1: Tìm hieåu caùch tính goùc giöõa hai ñöôøng thaúng
15'
GV giôùi thieäu khaùi nieäm
goùc giöõa hai ñöôøng thaúng.
H1. Cho ABC coù
A
=
120
0
. Tính goùc (AB, AC) ?
H2. So saùnh goùc (
1
,
2
) vôùi
goùc
12
n ,n
?
H3. Nhaéc laïi coâng thöùc tính
goùc giöõa 2 vectô ?
H4. Tính goùc giöõa 2 ñt:
d
1
: 4x – 10y + 1 = 0
d
2
: x + y + 2 = 0
H5. Cho
1
2
. Nhaän xeùt
veà caùc vectô
12
n vaø n
?
1
2
A
B
C
120
0
Ñ1. (AB, AC)=180
0
– 120
0
=
60
0
1
2
1
n
2
n
Ñ2.
12
12
0
12
n ,n
,
180 n ,n
Ñ3.
12
12
12
n .n
cos n ,n
n . n
Ñ4. cos(d
1
, d
2
) =
=
2 2 2 2
4.1 ( 10).1
4 ( 10) . 1 1

=
3
58
Ñ5.
1
2
12
nn
VI. Goùc giöõa 2 ñöôøng thaúng
Hai ñt
1
,
2
caét nhau taïo
thaønh 4 goùc (
1
2
). Goùc
nhoïn trong 4 goùc ñoù ñgl goùc
giöõa
1
vaø
2
. Kí hieäu (
1
,
2
)
hoaëc
12
,
.
+
1
2
(
1
,
2
) = 90
0
+
1
//
2
(
1
,
2
) = 0
0
0
0
(
1
,
2
)
90
0
Cho
1
: a
1
x + b
1
y + c
1
= 0
2
: a
2
x + b
2
y + c
2
= 0
Ñaët
= (
1
,
2
).
cos
=
12
cos(n ,n )
=
12
12
n .n
n . n
cos
=
1 2 1 2
2 2 2 2
1 1 2 2
a a b b
a b . a b

Chuù yù:
1
2
a
1
a
2
+ b
1
b
2
= 0
1
: y = k
1
x + m
1
2
: y = k
2
x + m
2
1
2
k
1
.k
2
= –1
Hoaït ñoäng 2: Tìm hieåu caùch tính khoaûng caùch töø moät ñieåm ñeán moät ñöôøng thaúng
Nguyễn Đình Khương Hình Học 10 Cơ Bản
66
12'
GV höôùng daãn HS chöùng
minh coâng thöùc tính khoaûng
caùch töø moät ñieåm ñeán moät
ñöôøng thaúng.
H1. Vieát pt tham soá cuûa ñt
m ñi qua M
0
vaø vuoâng goùc
vôùi ?
H2. Tìm toaï ñoä giao ñieåm H
cuûa vaø m ?
H3. Tính M
0
H ?
H4. Tính d(M, ) ?
O
x
y
H
m
M
0
n
Ñ1. m:
0
0
x x ta
y y tb


Ñ2. H(x
0
+ t
H
a; y
0
+ t
H
b)
vôùi t
H
=
00
22
ax by c
ab

Ñ3. M
0
H=
22
H 0 H 0
(x x ) (y y )
Ñ4.
d(M, ) =
22
3.( 2) 2.1 1
3 ( 2)

=
9
13
VII. Khoaûng caùch töø moät
ñieåm ñeán moät ñöôøng thaúng
Cho
: ax + by + c = 0
vaø ñieåm M
0
(x
0
; y
0
).
d(M
0
,
) =
00
22
ax by c
ab

VD: Tính khoaûng caùch töø
ñieåm M(–2; 1) ñeán ñöôøng
thaúng : 3x – 2y – 1 = 0.
Hoaït ñoäng 3: AÙp duïng tính goùc vaø khoaûng caùch
10'
H1. Vieát pt caùc ñt AB, BC ?
H2. Tính goùc (AB, BC) ?
H3. Tính baùn kính R ?
Ñ1. AB: 5x + 2y – 13 = 0
BC: x – y – 4 = 0
Ñ2. cos(AB, BC) =
=
2 2 2 2
5.1 2( 1)
3
58
5 2 . 1 ( 1)

Ñ3. R = d(C, AB) =
=
22
5.6 2.2 13 21
29
52

VD: Cho ABC vôùi A(1; 4),
B(3; –1), C(6; 2).
a) Tính goùc giöõa hai ñt AB,
BC ?
b) Tính baùn kính ñöôøng troøn
taâm C vaø tieáp xuùc vôùi ñt AB ?
Hoaït ñoäng 4: Cuûng coá
3'
Nhaán maïnh:
– Caùch tính goùc giöõa 2 ñt.
– Caùch tính khoaûng caùch töø
moät ñieåm ñeán moät ñt.
4. BAØI TAÄP VEÀ NHAØ:
Baøi 6, 7, 8, 9 SGK.
Ngaøy soaïn: 05/03/2013 Chöông III: PHÖÔNG PHAÙP TOAÏ ÑOÄ TRONG MAËT PHAÚNG
Tieát daïy: 33 Baøøi 1: BAØI TAÄP PHÖÔNG TRÌNH ÑÖÔØNG THAÚNG
I. MUÏC TIEÂU:
Kieán thöùc: Cuûng coá caùc kieán thöùc veà:
Phöông trình tham soá, phöông trình toång quaùt cuûa ñöôøng thaúng.
Nguyễn Đình Khương Hình Học 10 Cơ Bản
67
Vò trí töông ñoái cuûa hai ñöôøng thaúng.
Goùc giöõa hai ñöôøng thaúng, khoaûng caùch töø moät ñieåm ñeán moät ñöôøng thaúng.
Kó naêng:
Bieát laäp phöông trình tham soá, phöông trình toång quaùt cuûa ñöôøng thaúng.
Bieát xeùt VTTÑ cuûa hai ñöôøng thaúng.
Bieát caùch tính goùc giöõa hai ñöôøng thaúng, khoaûng caùch töø moät ñieåm ñeán moät ñöôøng thaúng.
Thaùi ñoä:
Reøn luyeän tính caån thaän, chính xaùc.
Laøm quen vieäc chuyeån tö duy hình hoïc sang tö duy ñaïi soá.
II. CHUAÅN BÒ:
Giaùo vieân: Giaùo aùn. Hình veõ minh hoaï.
Hoïc sinh: SGK, vôû ghi. OÂn taäp kieán thöùc veà ñöôøng thaúng ñaõ hoïc. Duïng cuï veõ hình.
III. HOAÏT ÑOÄNG DAÏY HOÏC:
1. OÅn ñònh toå chöùc: Kieåm tra só soá lôùp.
2. Kieåm tra baøi cuõ: (Loàng vaøo quaù trình luyeän taäp)
H.
Ñ.
3. Giaûng baøi môùi:
TL
Hoaït ñoäng cuûa Giaùo vieân
Hoaït ñoäng cuûa Hoïc sinh
Noäi dung
Hoaït ñoäng 1: Luyeän taäp laäp phöông trình ñöôøng thaúng
15'
Cho HS nhaéc laïi caùch laäp
pt tham soá, pt toång quaùt cuûa
ñöôøng thaúng.
H1. Xaùc ñònh caùc VTCP,
VTPT cuûa caùc ñöôøng thaúng
AB, BC, AC ?
H2. Xaùc ñònh VTPT cuûa AH
H3. Xaùc ñònh toaï ñoä ñieåm
M ?
Moãi nhoùm laäp phöông trình
moät ñöôøng thaúng.
Ñ1.
AB
u
= (2; –5);
BC
u
= (3; 3);
AC
u
= (5; –2)
AB:
12
45
xt
yt


5x+2y–13= 0
BC:
33
13
xt
yt

x – y – 4 = 0
AC:
65
22
xt
yt


2x+5y–22= 0
Ñ2.
AH
n BC
= (3; 3)
AH: x + y – 5 = 0
Ñ3.
9
22
1
22
BC
M
BC
M
xx
x
yy
y


1. Cho ABC vôùi A(1; 4),
B(3; –1), C(6; 2). Laäp phöông
trình tham soá, phöông trình
toång quaùt cuûa caùc ñöôøng
thaúng:
a) Chöùa caùc caïnh AB, BC,
AC.
b) Ñöôøng cao AH vaø trung
tuyeán AM.
Hoaït ñoäng 2: Luyeän taäp xeùt VTTÑ cuûa hai ñöôøng thaúng
10'
H1. Neâu caùch xeùt VTTÑ
cuûa hai ñöôøng thaúng ?
Ñ1.
C1: Döïa vaøo caùc VTCP cuûa 2 ñt
C2: Döïa vaøo caùc heä soá cuûa 2 pt
a) d
1
caét d
2
b) d
1
// d
2
2. Xeùt VTTÑ cuûa caùc caëp ñt:
a) d
1
: 4x – 10y + 1
d
2
: x + y + 2 = 0
b) d
1
: 12x – 6y + 10 = 0
Nguyễn Đình Khương Hình Học 10 Cơ Bản
68
c) d
1
d
2
d
2
:
5
32
xt
yt


c) d
1
: 8x + 10y – 12 = 0
d
2
:
65
64
xt
yt

Hoaït ñoäng 3: Luyeän taäp tính goùc vaø khoaûng caùch
10'
H1. Neâu coâng thöùc tính goùc
giöõa 2 ñöôøng thaúng ?
H2. Neâu coâng thöùc tính
khoaûng caùch töø moät ñieåm
ñeán moät ñöôøng thaúng ?
Ñ1.
cos(d
1
, d
2
) =
1 2 1 2
2 2 2 2
1 1 2 2
.
a a b b
a b a b

=
2
2
(d
1
, d
2
) = 45
0
Ñ2. d(M
0
, ) =
00
22
ax by c
ab

a) d(A, d) =
28
5
b) d(B, d) = 3
3. Tính goùc giöõa 2 ñt:
d
1
: 4x – 2y + 6 = 0
d
2
: x – 3y + 1 = 0
4. Tính khoaûng caùch töø moät
ñieåm ñeán ñöôøng thaúng:
a) A(3; 5); d: 4x + 3y + 1 = 0
b) B(1; –2); d: 3x – 4y – 26
=0
Hoaït ñoäng 4: Cuûng coá
5'
Nhaán maïnh :
– Caùch giaûi caùc daïng toaùn.
– Caùch chuyeån ñoåi caùc daïng
phöông trình ñöôøng thaúng.
pt tham soá <–> pt toång quaùt
4. BAØI TAÄP VEÀ NHAØ:
Laøm baøi taäp oân chöông II vaø ñöôøng thaúng.
Chuaån bò kieåm tra 1 tieát phaàn Heä thöùc löôïng trong tam giaùc vaø Phöông trình ñöôøng thaúng.
Ngaøy soaïn: 20/03/2013 Chöông III: PHÖÔNG PHAÙP TOAÏ ÑOÄ TRONG MAËT PHAÚNG
Tieát daïy: 35 Baøøi daïy: KIEÅM TRA 1 TIEÁT CHÖÔNG II – III
I. MUÏC TIEÂU:
Kieán thöùc: Cuûng coá caùc kieán thöùc veà:
Heä thöùc löôïng trong tam giaùc.
Phöông trình cuûa ñöôøng thaúng. Vò trí töông ñoái cuûa hai ñöôøng thaúng.
Goùc giöõa hai ñöôøng thaúng, khoaûng caùch töø moät ñieåm ñeán moät ñöôøng thaúng.
Kó naêng:
Nguyễn Đình Khương Hình Học 10 Cơ Bản
69
Vaän duïng heä thöùc löôïng trong tam giaùc ñeå giaûi tam giaùc.
Bieát laäp phöông trình cuûa ñöôøng thaúng. Bieát xeùt VTTÑ cuûa hai ñöôøng thaúng.
Bieát caùch tính goùc giöõa hai ñöôøng thaúng, khoaûng caùch töø moät ñieåm ñeán moät ñöôøng thaúng.
Thaùi ñoä:
Reøn luyeän tính caån thaän, chính xaùc.
Laøm quen vieäc chuyeån tö duy hình hoïc sang tö duy ñaïi soá.
II. CHUAÅN BÒ:
Giaùo vieân: Giaùo aùn. Ñeà kieåm tra.
Hoïc sinh: OÂn taäp kieán thöùc veà heä thöùc löôïng trong tam giaùc, phöông trình ñöôøng thaúng.
III. MA TRAÄN ÑEÀ:
Chuû ñeà
Nhaän bieát
Thoâng hieåu
Vaän duïng
Toång
TNKQ
TL
TNKQ
TL
TNKQ
TL
Heä thöùc löôïng trong
tam giaùc
4
0,5
2
1,0
4,0
Phöông trình ñöôøng
thaúng
2
0,5
2
0,5
1
2,0
2
1,0
6,0
Toång
3,0
2,0
1,0
2,0
2,0
10,0
IV. NOÄI DUNG ÑEÀ KIEÅM TRA:
A. Phaàn traéc nghieäm: (4 ñieåm) Choïn caâu traû lôøi ñuùng nhaát.
Caâu 1: Cho ABC coù AB = 5, AC = 8,
BAC
= 60
0
. Dieän tích cuûa ABC baèng:
A) 10 B) 40
3
C) 20
3
D) 10
3
Caâu 2: Cho ABC coù AB = 8, AC = 7, BC = 3. Ñoä daøi trung tuyeán CM baèng:
A)
35
B)
52
4
C)
52
2
D)
52
4
Caâu 3: Cho ABC coù AB = 5, AC = 8,
BAC
= 60
0
. Ñoä daøi caïnh BC baèng:
A) 7 B)
89 40 3
C)
89 40 3
D)
129
Caâu 4: Cho ABC vôùi A(–1; 2), B(3; 0), C(5; 4). Khi ñoù soá ño goùc A baèng:
A) 30
0
B) 60
0
C) 45
0
D) 90
0
Caâu 5: Cho ñ.thaúng d coù ph.trình tham soá:
23
12
xt
yt

. Moät VTPT cuûa d coù toaï ñoä laø:
A) (–2; 3) B) (2; 3) C) (–3; 2) D) (3; 2)
Caâu 6: Ñöôøng thaúng ñi qua 2 ñieåm M(2; 0), N(0; 3) coù phöông trình laø:
A) 3x + 2y – 6 = 0 B) 3x + 2y + 6 = 0 C) 3x – 2y – 6 = 0 D) 3x + 2y = 0
Caâu 7: Cho hai ñöôøng thaúng d: 3x – 2y – 6 = 0 vaø : 3x + 2y – 4 = 0. Khi ñoù:
A) d B) d // C) d D) d caét
Caâu 8: Soá ño goùc giöõa hai ñöôøng thaúng d: x – 2y + 1 = 0 vaø : 3x – y – 2 = 0 baèng:
A) 30
0
B) 45
0
C) 60
0
D) 90
0
B. Phaàn töï luaän: (6 ñieåm)
Caâu 9: Cho ABC coù AB = 2, AC = 4, BC = 2
3
.
a) Tính soá ño goùc A cuûa ABC. b) Tính dieän tích cuûa ABC.
Caâu 10: Trong mp Oxy, cho caùc ñieåm A(–2; 1), B(6; –3), C(8; 4).
a) Vieát phöông trình caùc ñöôøng thaúng chöùa caïnh BC vaø ñöôøng cao AH.
b) Vieát phöông trình ñöôøng thaúng d ñi qua A vaø song song vôùi BC.
c) Tính dieän tích cuûa ABC.
Nguyễn Đình Khương Hình Học 10 Cơ Bản
70
V. ÑAÙP AÙN VAØ BIEÅU ÑIEÅM:
A. Phaàn traéc nghieäm:
1 D
2 C
3 A
4 C
5 B
6 A
7 D
8 B
B. Töï luaän:
Caâu 9: a) cosA =
2 2 2 2 2 2
AB AC BC 2 4 (2 3) 1
2AB.AC 2.2.4 2

(0,5 ñieåm)
A = 60
0
. (0,5 ñieåm)
b) S =
0
11
AB.AC.sinA .2.4.sin60
22
(0,5 ñieåm)
= 2
3
(0,5 ñieåm)
Caâu 10:
a)
BC (2;7)
BC
n
= (7; –2) (0,5 ñieåm)
Phöông trình BC: 7(x – 6) – 2(y + 3) = 0 7x – 2y – 48 = 0 (0,5 ñieåm)
AH
n BC
= (2; 7) (0,5 ñieåm)
Phöông trình AH: 2(x + 2) + 7(y – 1) = 0 2x + 7y – 3 = 0 (0,5 ñieåm)
b) Phöông trình ñöôøng thaúng d // BC coù daïng: 7x – 2y + c = 0 (0,5 ñieåm)
d ñi qua A(–2; 1) 7(–2) – 2.1 + c = 0 c = 16
Phöông trình ñöôøng thaúng d: 7x – 2y + 16 = 0 (0,5 ñieåm)
c) BC =
53
; AH = d(A, BC) =
64
53
(0,5 ñieåm)
S
ABC
=
1
B C.AH
2
= 32 (0,5 ñieåm)
VI. KEÁT QUAÛ KIEÅM TRA:
Lôùp
Só soá
0 – 3,4
3,5 – 4,9
5,0 – 6,4
6,5 – 7,9
8,0 – 10
SL
%
SL
%
SL
%
SL
%
SL
%
10A3
44
10A5
42
10A7
44
10A10
42
10A11
38
Ngaøy soaïn: 05/04/2013 Chöông III: PHÖÔNG PHAÙP TOAÏ ÑOÄ TRONG MAËT PHAÚNG
Tieát daïy: 35 Baøøi 2: PHÖÔNG TRÌNH ÑÖÔØNG TROØN
I. MUÏC TIEÂU:
Kieán thöùc:
Naém ñöôïc phöông trình ñöôøng troøn.
Naém ñöôïc phöông trình tieáp tuyeán cuûa ñöôøng troøn.
Kó naêng:
Laäp ñöôïc phöông trình ñöôøng troøn khi bieát taâm vaø baùn kính.
Nhaän daïng ñöôïc phöông trình ñöôøng troøn vaø tìm ñöôïc toaï ñoä taâm vaø baùn kính cuûa noù.
Nguyễn Đình Khương Hình Học 10 Cơ Bản
71
Laäp ñöôïc phöông trình tieáp tuyeán cuûa ñöôøng troøn.
Thaùi ñoä:
Reøn luyeän tính caån thaän, chính xaùc.
Laøm quen vieäc chuyeån tö duy hình hoïc sang tö duy ñaïi soá.
II. CHUAÅN BÒ:
Giaùo vieân: Giaùo aùn. Hình veõ minh hoaï.
Hoïc sinh: SGK, vôû ghi. OÂn taäp kieán thöùc veà ñöôøng troøn ñaõ hoïc. Duïng cuï veõ hình.
III. HOAÏT ÑOÄNG DAÏY HOÏC:
1. OÅn ñònh toå chöùc: Kieåm tra só soá lôùp.
2. Kieåm tra baøi cuõ: (3')
H. Neâu khaùi nieäm veà ñöôøng troøn. Moät ñöôøng troøn ñöôïc xaùc ñònh bôûi nhöõng yeáu toá naøo?
Ñ. (O, R) = {M / OM = R}.
3. Giaûng baøi môùi:
TL
Hoaït ñoäng cuûa Giaùo vieân
Hoaït ñoäng cuûa Hoïc sinh
Noäi dung
Hoaït ñoäng 1: Tìm hieåu veà Phöông trình ñöôøng troøn
15'
GV höôùng daãn HS tìm
hieåu phöông trình ñöôøng
troøn döïa vaøo hình veõ.
H1. Neâu ñieàu kieän ñeå M
(C) ?
H2. Ta caàn xaùc ñònh caùc
yeáu toá naøo ?
O
x
y
M
I
R
a
b
Ñ1. M(x; y) (C) IM = R
22
( ) ( )x a y b
= R
Ñ2.
+ Taâm I laø trung ñieåm cuûa AB
+ Baùn kính R =
5
22
AB
(C): x
2
+ y
2
=
25
4
I. Phöông trình ñöôøng troøn
coù taâm vaø baùn kính cho
tröôùc
Phöông trình ñöôøng troøn (C)
taâm I(a; b), baùn kính R:
(x – a)
2
+ (y – b)
2
= R
2
(1)
Phöông trình ñöôøng troøn (C)
taâm O(0; 0), baùn kính R:
x
2
+ y
2
= R
2
(2)
VD: Cho hai ñieåm (A(3; –4),
B(–3; 4). Vieát pt ñöôøng troøn
(C) nhaän AB laøm ñöôøng kính
?
Hoaït ñoäng 2: Tìm hieåu daïng khaùc cuûa phöông trình ñöôøng troøn
10'
Höôùng daãn HS nhaän xeùt
ñaëc ñieåm cuûa phöông trình
(3).
H1. Kieåm tra ñieàu kieän ñeå
pt laø pt ñöôøng troøn ?
+ Pt baäc hai ñoái vôùi x, y.
+ Caùc heä soá cuûa x
2
, y
2
baèng
nhau.
+ Khoâng chöùa soá haïng tích xy.
Ñ1.
a) Khoâng, vì caùc heä soá cuûa x
2
,
y
2
khoâng baèng nhau.
b) Coù, vì a
2
+ b
2
– c > 0
c) Khoâng, vì a
2
+ b
2
– c < 0
II. Nhaän xeùt
Phöông trình:
x
2
+ y
2
– 2ax – 2by + c = 0 (3)
vôùi a
2
+ b
2
– c > 0 laø pt ñöôøng
troøn coù taâm I(a; b), baùn kính R
=
22
a b c
.
VD: Trong caùc pt sau, pt naøo
laø pt ñöôøng troøn?
a) 2x
2
+ y
2
– 8x + 2y – 1 = 0
b) x
2
+ y
2
+ 2x – 4y – 4 = 0
c) x
2
+ y
2
– 2x – 6y + 20 = 0
Hoaït ñoäng 3: Tìm hieåu phöông trình tieáp tuyeán cuûa ñöôøng troøn
Nguyễn Đình Khương Hình Học 10 Cơ Bản
72
10'
H1. Xaùc ñònh VTPT cuûa ?
H2. Xaùc ñònh taâm ñöôøng
troøn ?
I
M
0
M
Ñ1.
0
n IM
= (x
0
–a; y
0
– b)
Ñ2. I(1; 2)
: (3–1)(x–3)+(4–2)(y–4) =
0
x + y – 7 = 0
III. Phöông trình tieáp tuyeán
cuûa ñöôøng troøn
Cho (C) coù taâm I(a; b),
M(x
0
; y
0
)
(C). Phöông trình
tieáp tuyeán cuûa (C) taïi M
0
(x
0
;
y
0
):
(x
0
–a)(x–x
0
) + (y
0
–b)(y–y
0
)=0
Nhaän xeùt:
laø tieáp tuyeán cuûa (C)
d(I,
) = R
VD: Vieát phöông trình tieáp
tuyeán taïi ñieåm M(3; 4) thuoäc
ñöôøng troøn:
(x – 1)
2
+ (y – 2)
2
= 8
Hoaït ñoäng 4: Cuûng coá
5'
Nhaán maïnh:
– Daïng phöông trình ñöôøng
troøn.
– Xaùc ñònh taâm, baùn kính
ñöôøng troøn.
– Pt tieáp tuyeán ñöôøng troøn.
Caâu hoûi:
a) Xaùc ñònh taâm vaø baùn kính
ñöôøng troøn (C):
x
2
+ y
2
– 2y – 1 = 0
b) Vieát pttt cuûa (C) taïi M(1;
2).
a) I(0; 1), R =
2
b) x + y – 3 = 0
4. BAØI TAÄP VEÀ NHAØ:
Baøi 1, 2, 3, 4, 5, 6 SGK.
Ngaøy soaïn: 05/04/2013 Chöông III: PHÖÔNG PHAÙP TOAÏ ÑOÄ TRONG MAËT PHAÚNG
Tieát daïy: 37 Baøøi 2: BAØI TAÄP PHÖÔNG TRÌNH ÑÖÔØNG TROØN
I. MUÏC TIEÂU:
Kieán thöùc: Cuûng coá caùc kieán thöùc veà:
Phöông trình ñöôøng troøn.
Phöông trình tieáp tuyeán cuûa ñöôøng troøn.
Kó naêng:
Laäp ñöôïc phöông trình ñöôøng troøn khi bieát taâm vaø baùn kính.
Nhaän daïng ñöôïc phöông trình ñöôøng troøn vaø tìm ñöôïc toaï ñoä taâm vaø baùn kính cuûa noù.
Laäp ñöôïc phöông trình tieáp tuyeán cuûa ñöôøng troøn.
Nguyễn Đình Khương Hình Học 10 Cơ Bản
73
Thaùi ñoä:
Reøn luyeän tính caån thaän, chính xaùc.
Laøm quen vieäc chuyeån tö duy hình hoïc sang tö duy ñaïi soá.
II. CHUAÅN BÒ:
Giaùo vieân: Giaùo aùn. Heä thoáng baøi taäp.
Hoïc sinh: SGK, vôû ghi. OÂn taäp kieán thöùc veà ñöôøng troøn ñaõ hoïc.
III. HOAÏT ÑOÄNG DAÏY HOÏC:
1. OÅn ñònh toå chöùc: Kieåm tra só soá lôùp.
2. Kieåm tra baøi cuõ: (Loàng vaøo quaù trình luyeän taäp)
H.
Ñ.
3. Giaûng baøi môùi:
TL
Hoaït ñoäng cuûa Giaùo vieân
Hoaït ñoäng cuûa Hoïc sinh
Noäi dung
Hoaït ñoäng 1: Luyeän taäp xaùc ñònh taâm vaø baùn kính ñöôøng troøn
10'
H1. Neâu caùch xaùc ñònh taâm
vaø baùn kính ñöôøng troøn ?
Ñ1.
C1: Ñöa veà daïng:
(x – a)
2
+ (y – b)
2
= R
2
C2: Kieåm tra ñk: a
2
+ b
2
– c > 0
a) I(1; 1), R = 2
b) Chia 2 veá cho 16.
I
11
;
24



; R = 1
c) I(2; –3); R = 4
1. Tìm taâm vaø baùn kính cuûa
caùc ñöôøng troøn:
a) x
2
+ y
2
– 2x – 2y – 2 = 0
b) 16x
2
+16y
2
+16x–8y–11 = 0
c) x
2
+ y
2
– 4x + 6y – 3 = 0
Hoaït ñoäng 2: Luyeän taäp vieát phöông trình ñöôøng troøn
15'
H1. Ta caàn xaùc ñònh caùc
yeáu toá naøo ?
GV höôùng daãn caùch vieát
phöông trình ñöôøng troøn ñi
qua 3 ñieåm.
Ñ1.
a) R = IM =
52
(C): (x + 2)
2
+(y – 3)
2
= 52.
b) R = d(I, ) =
2
5
(C): (x + 1)
2
– (y – 2)
2
=
4
5
c) I(4; 3), R =
13
(C): (x – 4)
2
+ (y – 3
2
= 13
Pt ñöôøng troøn (C) coù daïng:
x
2
+ y
2
– 2ax – 2by + c = 0 (*)
Thay toaï ñoä caùc ñieåm A, B, C
vaøo (*) ta ñöôïc heä pt:
1 4 2 4 0
25 4 10 4 0
1 9 2 6 0
a b c
a b c
a b c
a = 3; b =
1
2
; c = – 1
(C): x
2
+ y
2
– 6x + y – 1 = 0
2. Laäp pt ñöôøng troøn (C) trong
caùc tröôøng hôïp sau:
a) (C) coù taâm I(–2; 3) vaø ñi
qua M(2; –3).
b) (C) coù taâm I(–1; 2) vaø tieáp
xuùc vôùt ñt : x – 2y + 7 = 0.
c) (C) coù ñöôøng kính AB vôùi
A(1; 1), B(7; 5).
3. Laäp pt ñöôøng troøn (C) ñi
qua 3 ñieåm A(1; 2), B(5; 2),
C(1; –3)
Hoaït ñoäng 3: Luyeän taäp vieát phöông trình tieáp tuyeán cuûa ñöôøng troøn
Nguyễn Đình Khương Hình Học 10 Cơ Bản
74
12'
H1. Xaùc ñònh taâm vaø baùn
kính ?
H2. Kieåm tra A (C) ?
H3. Xaùc ñònh daïng pt cuûa
tieáp tuyeán () ?
H4. Ñieàu kieän tieáp xuùc
vôùi (C) ?
Ñ1. I(2; –4); R = 5
Ñ2. Toaï ñoä cuûa A thoaû (C) A
(C) Pttt ():
(–1–2)(x+1) + (0+4)(y–0) = 0
3x – 4y + 3 = 0
Ñ3. d : 4x + 3y + c = 0
Ñ4. d(I, ) = R
8 12
5
c
29
21
c
c

1
: 4x + 3y + 29 = 0
2
: 4x + 3y – 21 = 0
4. Cho ñöôøng troøn (C) coù pt:
x
2
+ y
2
– 4x + 8y – 5 = 0
a) Tìm toaï ñoä taâm vaø baùn kính
b) Vieát pttt () vôùi (C) ñi qua
ñieåm A(–1; 0).
c) Vieát pttt () vôùi (C) vuoâng
goùc vôùi ñt d: 3x – 4y + 5 = 0.
Hoaït ñoäng 4: Cuûng coá
3'
Nhaán maïnh:
– Caùch xaùc ñònh taâm vaø baùn
kính cuûa ñöôøng troøn.
– Caùch laäp pt ñöôøng troøn.
– Caùch vieát pttt cuûa ñöôøng
troøn.
4. BAØI TAÄP VEÀ NHAØ:
Laøm caùc baøi taäp coøn laïi.
Ñoïc tröôùc baøi "Phöông trình ñöôøng elip".
Ngaøy soaïn: 5/04/2013 Chöông III: PHÖÔNG PHAÙP TOAÏ ÑOÄ TRONG MAËT PHAÚNG
Tieát daïy: 38 Baøøi 3: PHÖÔNG TRÌNH ÑÖÔØNG ELIP
I. MUÏC TIEÂU:
Kieán thöùc:
Hieåu ñöôïc ñònh nghóa, phöông trình chính taéc, caùc yeáu toá cuûa elip.
Kó naêng:
Laäp ñöôïc phöông trình chính taéc cuûa elip.
Töø pt chính taéc cuûa elip, xaùc ñònh ñöôïc truïc lôùn, truïc nhoû, tieâu cöï, tieâu ñieåm, caùc ñænh, …
Thoâng qua pt chính taéc cuûa elip ñeå tìm hieåu tính chaát hình hoïc vaø giaûi moät soá baøi toaùn cô
baûn veà elip.
Nguyễn Đình Khương Hình Học 10 Cơ Bản
75
Thaùi ñoä:
Reøn luyeän tính caån thaän, chính xaùc.
II. CHUAÅN BÒ:
Giaùo vieân: Giaùo aùn. Hình veõ minh hoaï.
Hoïc sinh: SGK, vôû ghi. Taám bìa cöùng, 2 ñinh ghim, sôïi daây.
III. HOAÏT ÑOÄNG DAÏY HOÏC:
1. OÅn ñònh toå chöùc: Kieåm tra só soá lôùp.
2. Kieåm tra baøi cuõ: (5')
H. Vieát caùc daïng phöông trình ñöôøng troøn? Neâu phöông trình tieáp tuyeán cuûa ñöôøng troøn taïi
moät ñieåm thuoäc ñöôøng troøn ?
Ñ.
3. Giaûng baøi môùi:
TL
Hoaït ñoäng cuûa Giaùo vieân
Hoaït ñoäng cuûa Hoïc sinh
Noäi dung
Hoaït ñoäng 1: Tìm hieåu ñöôøng elip
10'
Cho HS quan saùt:
– Maët nöôùc trong coác nöôùc
caàm nghieâng.
– Boùng cuûa moät ñöôøng troøn
treân moät maët phaúng.
H1. Caùc hình treân coù phaûi laø
ñöôøng troøn khoâng ?
Cho HS thöïc hieän thao taùc
veõ ñöôøng elip treân taám bìa.
HS quan saùt vaø cho nhaän xeùt.
Ñ1. Khoâng.
F
1
F
2
M
I. Ñònh nghóa ñöôøng elip
Cho 2 ñieåm coá ñònh F
1
, F
2
vaø
moät ñoä daøi khoâng ñoåi 2a lôùn
hôn F
1
F
2
.
M
(E)
F
1
M + F
2
M = 2a
F
1
, F
2
: caùc tieâu ñieåm
F
1
F
2
= 2c: tieâu cöï.
Hoaït ñoäng 2: Tìm hieåu phöông trình chính taéc cuûa elip
15'
GV giôùi thieäu phöông
trình chính taéc cuûa elip.
H1. Xaùc ñònh toaï ñoä caùc
ñieåm B
1
, B
2
?
H2. Tính B
2
F
1
, B
2
F
2
?
H3. Tính B
2
F
1
+ B
2
F
2
?
F
1
F
2
M(x; y)
x
y
O
A
2
A
1
B
1
B
2
Ñ1. B
1
(0; –b); B
2
(0; b)
Ñ2. B
2
F
1
= B
2
F
2
=
22
bc
Ñ3. B
2
F
1
+ B
2
F
2
= 2a
2
22
bc
= 2a b
2
= a
2
–
c
2
II. Phöông trình chính taéc
cuûa elip
22
22
1
xy
ab

(b
2
= a
2
– c
2
)
Nguyễn Đình Khương Hình Học 10 Cơ Bản
76
15'
GV höôùng daãn HS nhaän
xeùt.
H1. Cho M(x; y) (E). Caùc
ñieåm M
1
(–x; y), M
2
(x; –y),
M
3
(–x; –y) coù thuoäc (E)
khoâng ?
H2. Tìm toaï ñoä caùc giao
ñieåm cuûa (E) côùi caùc truïc
toaï ñoä ?
H3. So saùnh a vaø b ?
H4. Töø ptct cuûa (E), chæ ra
a
2
, b
2
?
F
1
F
2
M(x; y)
x
y
O
A
2
A
1
B
1
B
2
–a a
– b
b
– c c
Ñ1. Coù, vì toaï ñoä ñeàu thoaû maõn
(*).
Ñ2.
y = 0 x = a (E) caét Ox
taïi 2 ñieåm A
1
(–a; 0), A
2
(a; 0)
x = 0 y = b (E) caét Oy
taïi 2 ñieåm B
1
(0; –b), B
2
(0; b)
Ñ3. a > b.
Ñ4. a
2
= 9, b
2
= 1 c
2
= 8
a = 3, b = 1, c = 2
2
Ñoä daøi truïc lôùn: 2a = 6
Ñoä daøi truïc nhoû: 2b = 2
Tieâu cöï: 2c = 4
2
Toaï ñoä caùc tieâu ñieåm:
F
1,2
(2
2
; 0)
Toaï ñoä caùc ñænh: A
1;2
(3; 0),
B
1,2
(0; 1)
III. Hình daïng cuûa elip
Cho (E):
22
22
1
xy
ab

(*)
a) (E) coù caùc truïc ñoái xöùng laø
Ox, Oy vaø coù taâm ñoái xöùng laø
O.
b) Caùc ñænh A
1
(–a; 0), A
2
(a; 0)
B
1
(0; –b), B
2
(0; b)
A
1
A
2
= 2a : truïc lôùn
B
1
B
2
= 2b : truïc nhoû
VD: Cho (E):
22
1
91
xy

.
Tìm ñoä daøi caùc truïc, tieâu cöï,
toaï ñoä caùc tieâu ñieåm, toaï ñoä
caùc ñænh cuûa (E).
Hoaït ñoäng 3: Cuûng coá
3'
Nhaán maïnh:
– Caùc hình coù daïng ñöôøng
elip.
– Phöông trình chính taéc cuûa
elip.
4. BAØI TAÄP VEÀ NHAØ:
Ñoïc tieáp baøi "Phöông trình ñöôøng elip".
Tìm theâm caùc hình coù daïng ñöôøng elip.
Ngaøy soaïn: 10/04/2013 Chöông III: PHÖÔNG PHAÙP TOAÏ ÑOÄ TRONG MAËT PHAÚNG
Tieát daïy: 38 Baøøi 3: PHÖÔNG TRÌNH ÑÖÔØNG ELIP (tt)
I. MUÏC TIEÂU:
Kieán thöùc:
Hieåu ñöôïc ñònh nghóa, phöông trình chính taéc, caùc yeáu toá cuûa elip.
Kó naêng:
Nguyễn Đình Khương Hình Học 10 Cơ Bản
77
Laäp ñöôïc phöông trình chính taéc cuûa elip.
Töø pt chính taéc cuûa elip, xaùc ñònh ñöôïc truïc lôùn, truïc nhoû, tieâu cöï, tieâu ñieåm, caùc ñænh, …
Thoâng qua pt chính taéc cuûa elip ñeå tìm hieåu tính chaát hình hoïc vaø giaûi moät soá baøi toaùn cô
baûn veà elip.
Thaùi ñoä:
Reøn luyeän tính caån thaän, chính xaùc.
II. CHUAÅN BÒ:
Giaùo vieân: Giaùo aùn. Hình veõ minh hoaï.
Hoïc sinh: SGK, vôû ghi. Duïng cuï veõ hình.
III. HOAÏT ÑOÄNG DAÏY HOÏC:
1. OÅn ñònh toå chöùc: Kieåm tra só soá lôùp.
2. Kieåm tra baøi cuõ: (3')
H. Neâu phöông trình chính taéc cuûa elip ?
Ñ.
22
22
1
xy
ab

(b
2
= a
2
– c
2
)
3. Giaûng baøi môùi:
TL
Hoaït ñoäng cuûa Giaùo vieân
Hoaït ñoäng cuûa Hoïc sinh
Noäi dung
Hoaït ñoäng 1: Tìm hieåu hình daïng cuûa elip
20'
GV höôùng daãn HS nhaän
xeùt.
H1. Cho M(x; y) (E). Caùc
ñieåm M
1
(–x; y), M
2
(x; –y),
M
3
(–x; –y) coù thuoäc (E)
khoâng ?
H2. Tìm toaï ñoä caùc giao
ñieåm cuûa (E) côùi caùc truïc
toaï ñoä ?
H3. So saùnh a vaø b ?
H4. Töø ptct cuûa (E), chæ ra
a
2
, b
2
?
F
1
F
2
M(x; y)
x
y
O
A
2
A
1
B
1
B
2
–a a
– b
b
– c c
Ñ1. Coù, vì toaï ñoä ñeàu thoaû maõn
(*).
Ñ2.
y = 0 x = a (E) caét Ox
taïi 2 ñieåm A
1
(–a; 0), A
2
(a; 0)
x = 0 y = b (E) caét Oy
taïi 2 ñieåm B
1
(0; –b), B
2
(0; b)
Ñ3. a > b.
Ñ4. a
2
= 9, b
2
= 1 c
2
= 8
a = 3, b = 1, c = 2
2
Ñoä daøi truïc lôùn: 2a = 6
Ñoä daøi truïc nhoû: 2b = 2
Tieâu cöï: 2c = 4
2
Toaï ñoä caùc tieâu ñieåm:
F
1,2
(2
2
; 0)
Toaï ñoä caùc ñænh: A
1;2
(3; 0),
B
1,2
(0; 1)
III. Hình daïng cuûa elip
Cho (E):
22
22
1
xy
ab

(*)
a) (E) coù caùc truïc ñoái xöùng laø
Ox, Oy vaø coù taâm ñoái xöùng laø
O.
b) Caùc ñænh A
1
(–a; 0), A
2
(a; 0)
B
1
(0; –b), B
2
(0; b)
A
1
A
2
= 2a : truïc lôùn
B
1
B
2
= 2b : truïc nhoû
VD: Cho (E):
22
1
91
xy

.
Tìm ñoä daøi caùc truïc, tieâu cöï,
toaï ñoä caùc tieâu ñieåm, toaï ñoä
caùc ñænh cuûa (E).
Nguyễn Đình Khương Hình Học 10 Cơ Bản
78
Hoaït ñoäng 2: Tìm hieåu moái lieân heä giöõa ñöôøng troøn vaø ñöôøng elip
10'
GV höôùng daãn HS nhaän
xeùt.
x
x
O
H
M(x;y)
M’(x’;y’)
M(x; y) (C) x
2
+ y
2
= a
2
x
2
+
2
2
'
a
y
b
= a
2
22
22
''
1
xy
ab

M
(E)
IV. Lieân heä giöõa ñöôøng troøn
vaø ñöôøng elip
a) Töø b
2
= a
2
– c
2
c caøng
nhoû thì b caøng gaàn baèng a
(E) coù daïng gaàn nhö ñtroøn.
b) Cho ñöôøng troøn (C):
x
2
+ y
2
= a
2
Xeùt pheùp bieán ñoåi:
M(x; y)
M
(x
; y
)
vôùi:
'
'
xx
b
yy
a
(0 < b < a)
Khi ñoù,
22
22
''
1
xy
ab

laø (E)
Ta noùi (C) co thaønh (E).
Hoaït ñoäng 3: Cuûng coá
10'
Nhaán maïnh:
– Caùc yeáu toá cuûa (E).
– Moái lieân heä giöõa ñöôøng
troøn vaø elip.
Caâu hoûi: Xaùc ñònh caùc yeáu
toá cuûa (E):
a)
22
1
62
xy

b)
22
1
18 8
xy

Chuù yù:
+ a, b, > 0.
+ Toaï ñoä ñænh vaø tieâu ñieåm.
a) a =
6
; b =
2
; c = 2
b) a =
32
; b =
22
; c =
10
4. BAØI TAÄP VEÀ NHAØ:
Baøi 1, 2, 3, 4, 5 SGK.
Ñoïc baøi ñoïc theâm "Ba ñöôøng coânic vaø quyõ ñaïo cuûa taøu vuõ truï"
Ngaøy soaïn: 15/04/2013 Chöông III: PHÖÔNG PHAÙP TOAÏ ÑOÄ TRONG MAËT PHAÚNG
Tieát daïy: 39 Baøøi 3: BAØI TAÄP PHÖÔNG TRÌNH ÑÖÔØNG ELIP
I. MUÏC TIEÂU:
Kieán thöùc:
Hieåu ñöôïc ñònh nghóa, phöông trình chính taéc, caùc yeáu toá cuûa elip.
Kó naêng:
Laäp ñöôïc phöông trình chính taéc cuûa elip.
Nguyễn Đình Khương Hình Học 10 Cơ Bản
79
Töø pt chính taéc cuûa elip, xaùc ñònh ñöôïc truïc lôùn, truïc nhoû, tieâu cöï, tieâu ñieåm, caùc ñænh, …
Thoâng qua pt chính taéc cuûa elip ñeå tìm hieåu tính chaát hình hoïc vaø giaûi moät soá baøi toaùn cô
baûn veà elip.
Thaùi ñoä:
Reøn luyeän tính caån thaän, chính xaùc.
II. CHUAÅN BÒ:
Giaùo vieân: Giaùo aùn. Heä thoáng baøi taäp.
Hoïc sinh: SGK, vôû ghi. OÂn taäp kieán thöùc veà ñöôøng elip.
III. HOAÏT ÑOÄNG DAÏY HOÏC:
1. OÅn ñònh toå chöùc: Kieåm tra só soá lôùp.
2. Kieåm tra baøi cuõ: (Loàng vaøo quaù trình luyeän taäp)
H.
Ñ
3. Giaûng baøi môùi:
TL
Hoaït ñoäng cuûa Giaùo vieân
Hoaït ñoäng cuûa Hoïc sinh
Noäi dung
Hoaït ñoäng 1: Luyeän taäp xaùc ñònh caùc yeáu toá cuûa elip
10'
H1. Xaùc ñònh a, b, c ?
Ñ1.
a) a = 5, b = 3, c = 4
b) 4x
2
+ 9y
2
= 1
22
1
11
49
xy

a =
1
2
, b =
1
3
, c =
5
6
c) 4x
2
+ 9y
2
= 36
22
1
94
xy

a = 3, b = 2, c =
5
1. Xaùc ñònh ñoä daøi caùc truïc,
tieâu cöï, toaï ñoä caùc tieâu ñieåm,
toaï ñoä caùc ñænh cuûa (E):
a)
22
1
25 9
xy

b) 4x
2
+ 9y
2
= 1
c) 4x
2
+ 9y
2
= 36
Hoaït ñoäng 2: Luyeän taäp laäp phöông trình chính taéc cuûa elip
20'
H1. Neâu yeáu toá caàn xaùc
ñònh ?
Ñ1. a, b.
a) a = 4, b = 3
(E):
22
1
16 9
xy

b) a = 5, b = 4
(E):
22
1
25 16
xy

c) M(0; 3) (E)
2
9
1
b
N
12
3;
5



(E)
22
9 144
1
25ab

a = 5, b = 3
(E):
22
1
25 9
xy

2. Laäp phöông trình chính taéc
cuûa (E) trong caùc tröôøng hôïp
sau:
a) Ñoä daøi truïc lôùn laø 8, ñoä daøi
truïc nhoû laø 6.
b) Ñoä daøi truïc lôùn laø 10, tieâu
cöï laø 6.
c) (E) ñi qua caùc ñieåm M(0; 3)
vaø N
12
3;
5



.
d) (E) coù 1 tieâu ñieåm laø
F
1
(
3
; 0) vaø ñi qua ñieåm
M
3
1;
2



.
Nguyễn Đình Khương Hình Học 10 Cơ Bản
80
d) F
1
(
3
; 0) c =
3
M
3
1;
2



(E)
22
13
1
4ab

a = 2, b= 1
(E):
22
1
41
xy

Hoaït ñoäng 3: Luyeän taäp giaûi toaùn lieân quan ñeán elip
10'
GV höôùng daãn HS chöùng
minh.
H1. Tính MF
1
, MF
2
?
H2. Tính MF
1
+ MF
2
?
F
1
F
2
M
(C
2
)
(C
1
)
(C)
Ñ1. MF
1
= R
1
+ R
MF
2
= R
2
– R
Ñ2. MF
1
+ MF
2
= R
1
+ R
2
M thuoäc (E) coù 2 tieâu ñieåm
laø F
1
, F
2
vaø truïc lôùn 2a = R
1
+
R
2
3. Cho 2 ñöôøng troøn C
1
(F
1
; R
1
)
vaø C
2
(F
2
; R
2
). (C
1
) naèm trong
(C
2
) vaø F
1
F
2
. Ñöôøng troøn
(C) thay ñoåi luoân tieáp xuùc
ngoaøi vôùi (C
1
) vaø tieáp xuùc
trong vôùi (C
2
). Haõy chöùng toû
raèng taâm M cuûa (C) di ñoäng
treân moät elip.
Hoaït ñoäng 4: Cuûng coá
3'
Nhaán maïnh:
– Caùch xaùc ñònh caùc yeáu toá
cuûa (E).
– Caùch laäp pt chính taéc cuûa
(E).
4. BAØI TAÄP VEÀ NHAØ:
Baøi taäp oân chöông III.
Ngaøy soaïn: 20/04/2013 Chöông III: PHÖÔNG PHAÙP TOAÏ ÑOÄ TRONG MAËT PHAÚNG
Tieát daïy: 40 Baøøi daïy: OÂN TAÄP CHÖÔNG III
I. MUÏC TIEÂU:
Kieán thöùc:
OÂn taäp toaøn boä kieán thöùc chöông III.
Kó naêng:
Vaän duïng kieán thöùc ñaõ hoïc ñeå giaûi toaùn.
Thaùi ñoä:
Nguyễn Đình Khương Hình Học 10 Cơ Bản
81
Reøn luyeän tính caån thaän, chính xaùc.
II. CHUAÅN BÒ:
Giaùo vieân: Giaùo aùn. Heä thoáng baøi taäp.
Hoïc sinh: SGK, vôû ghi. OÂn taäp kieán thöùc chöông III.
III. HOAÏT ÑOÄNG DAÏY HOÏC:
1. OÅn ñònh toå chöùc: Kieåm tra só soá lôùp.
2. Kieåm tra baøi cuõ: (Loàng vaøo quaù trình luyeän taäp)
H.
Ñ
3. Giaûng baøi môùi:
TL
Hoaït ñoäng cuûa Giaùo vieân
Hoaït ñoäng cuûa Hoïc sinh
Noäi dung
Hoaït ñoäng 1: Luyeän taäp giaûi toaùn veà ñöôøng thaúng
20'
H1. Nhaän xeùt veà caùc ñt AB,
BC, AD ?
GV höôùng daãn caùch xaùc
ñònh ñieåm A.
H2. Xaùc ñònh VTCP cuûa ?
H3. Neâu ñieàu kieän xaùc ñònh
ñieåm H ?
H4. Khi naøo OMA ngaén
nhaát ?
H5. Neâu tính chaát ñöôøng
phaân giaùc ?
A
B
C
D
Ñ1.
AB chöùa A vaø AB // CD
AB: x + 2y – 7 = 0
BC chöùa C vaø BC CD
BC: 2x – y + 6 = 0
AD chöùa A vaø AD CD
AD: 2x – y – 9 = 0
O
A’
A
M
H
Ñ2.
u
= (1; 1)
Ñ3.
OH u
H

A(–2; 2)
Ñ4. M laø giao ñieåm cuûa AA vôùi
. M(–2; 0)
Ñ5. M d(M,d
1
) =
d(M,d
2
)
3 4 12 12 5 7
5 13
x y x y

1. Cho hình chöõ nhaät ABCD.
Bieát caùc ñænh A(5; 1), C(0; 6)
vaø phöông trình CD: x + 2y –
12 = 0. Tìm phöông trình caùc
ñöôøng thaúng chöùa caùc caïnh
coøn laïi.
2. Cho ñöôøng thaúng : x – y +
2 = 0 vaø ñieåm A(2; 0).
a) Tìm ñieåm A ñoái xöùng cuûa
O qua .
b) Tìm ñieåm M sao cho
ñoä daøi ñöôøng gaáp khuùc OMA
ngaén nhaát.
3. Laäp phöông trình hai ñöôøng
phaân giaùc cuûa caùc goùc taïo bôûi
hai ñöôøng thaúng:
d
1
: 3x – 4y + 12 = 0
d
2
: 12x + 5y – 7 = 0
Hoaït ñoäng 2: Luyeän taäp giaûi toaùn veà ñöôøng troøn
10'
H1. Neâu caùch xaùc ñònh G, H
Ñ1.
G:
3
OA OB OC
OG

4. Cho 3 ñieåm A(4; 3), B(2;
7), C(–3; –8).
a) Tìm toaï ñoä troïng taâm G vaø
tröïc taâm H cuûa ABC.
b) Vieát phöông trình ñöôøng
troøn ngoaïi tieáp ABC.
Nguyễn Đình Khương Hình Học 10 Cơ Bản
82
GV höôùng daãn HS caùch
vieát phöông trình ñöôøng troøn
ñi qua 3 ñieåm.
H2. Neâu tính chaát taâm ñtroøn
ngoaïi tieáp tam giaùc ?
1
( ) 1
3
12
()
33
G A B C
G A B C
x x x x
y y y y
H:
.0
.0
AH BC
BH AC
3 13
7 11 91
xy
xy


13
0
x
y
Ñ2.
IA IB
IA IC
5
1
a
b

R = IA =
85
(C): (x + 5)
2
+ (y – 1)
2
= 85
C2:
(C): x
2
+ y
2
– 2ax – 2by + c = 0
Thay laàn löôït toaï ñoä 3 ñieåm A,
B, C vaøo pt (C), ta ñöôïc heä pt:
8 6 25
4 14 53
6 16 73
a b c
a b c
a b c
5
1
59
a
b
c


Hoaït ñoäng 3: Luyeän taäp giaûi toaùn veà ñöôøng elip
10'
H1. Neâu coâng thöùc xaùc ñònh
caùc yeáu toá cuûa (E) ?
Ñ1. a = 4, b = 3, c =
7
2a = 8, 2b = 6, 2c = 2
7
Tieâu ñieåm:F
1
(–
7
;0),
F
2
(
7
;0)
Ñænh: A
1
(–4; 0), A
2
(4; 0),
B
1
(0; –3), B
2
(0; 3)
5. Cho (E):
22
1
16 9
xy

. Tìm
caùc yeáu toá cuûa (E).
Hoaït ñoäng 4: Cuûng coá
3'
Nhaán maïnh caùch giaûi caùc
daïng toaùn.
4. BAØI TAÄP VEÀ NHAØ:
Baøi taäp cuoái naêm.
Ngaøy soaïn: 25/04/2013
Tieát daïy: 41 Baøøi daïy: OÂN TAÄP CUOÁI NAÊM
I. MUÏC TIEÂU:
Kieán thöùc: OÂn taäp theo töøng chuû ñeà:
Vectô – Toaï ñoä.
Heä thöùc löôïng trong tam giaùc. Giaûi tam giaùc.
Nguyễn Đình Khương Hình Học 10 Cơ Bản
83
Phöông trình ñöôøng thaúng.
Khoaûng caùch töø moät ñieåm ñeán ñöôøng thaúng, goùc giöõa hai ñöôøng thaúng.
Phöông trình ñöôøng troøn.
Phöông trình elip.
Kó naêng: Cuûng coá caùc kó naêng giaûi toaùn veà:
Vectô – Toaï ñoä.
Heä thöùc löôïng trong tam giaùc. Giaûi tam giaùc.
Caùc baøi toaùn veà ñöôøng thaúng, ñöôøng troøn, ñöôøng elip.
Thaùi ñoä:
Reøn luyeän tính caån thaän, chính xaùc.
II. CHUAÅN BÒ:
Giaùo vieân: Giaùo aùn. Heä thoáng baøi taäp.
Hoïc sinh: SGK, vôû ghi. OÂn taäp kieán thöùc hình hoïc lôùp 10 ñaõ hoïc.
III. HOAÏT ÑOÄNG DAÏY HOÏC:
1. OÅn ñònh toå chöùc: Kieåm tra só soá lôùp.
2. Kieåm tra baøi cuõ: (Loàng vaøo quaù trình luyeän taäp)
H.
Ñ
3. Giaûng baøi môùi:
TL
Hoaït ñoäng cuûa Giaùo vieân
Hoaït ñoäng cuûa Hoïc sinh
Noäi dung
Hoaït ñoäng 1: Cuûng coá vectô – toaï ñoä
7'
H1. Neâu ñieàu kieän ñeå
AMB vuoâng taïi M ?
H2. Neâu ñieàu kieän ñeå A, P,
B thaúng haøng ?
Ñ1.
MA MB
MA.MB 0
y0
y7
Ñ2.
AB,AP
cuøng phöông
x = –5
1. Cho caùc ñieåm A(2; 3), B(9;
4), M(5; y), P(x; 2).
a) Tìm y ñeå AMB vuoâng taïi
M.
b) Tìm x ñeå A, P, B thaúng
haøng.
Hoaït ñoäng 2: Cuûng coá heä thöùc löôïng trong tam giaùc
13'
A
B
CM
N6 6
2
4
Cho HS neâu laàn löôït caùc
coâng thöùc tính.
a)
AM
2
= AB
2
+ BM
2
–
2AB.BM.cosB
= 28
cos
BAM
=
2 2 2
AB AM BM
2AB.AM

=
57
14
b)
AM
2R
sinB
R =
2 21
3
c) CN
2
=
2 2 2
2(CA CM ) AM
4

= 19
d) S =
1
2
BA.BM.sinB = 3
3
2. Cho ABC ñeàu caïnh baèng
6 cm. Moät ñieåm M treân caïnh
BC sao cho BM = 2 cm.
a) Tính ñoä daøi ñoaïn thaúng AM
vaø tính cos
BAM
.
b) Tính baùn kính ñöôøng troøn
ngoaïi tieáp ABM.
c) Tính ñoä daøi trung tuyeán veõ
töø C cuûa ACM.
d) Tính dieän tích ABM.
Hoaït ñoäng 3: Cuûng coá ñöôøng thaúng, ñöôøng troøn, ñöôøng elip
Nguyễn Đình Khương Hình Học 10 Cơ Bản
84
20'
H1. Xaùc ñònh toaï ñoä caùc
ñieåm A, B, H ?
H2. Neâu caùch xaùc ñònh caùc
ñt AC, BC, CH ?
GV höôùng daãn HS phaân
tích caùc giaû thieát.
H3. Taâm I(a; b) cuûa ñöôøng
troøn coù tính chaát gì ?
H4. Nhaéc laïi caùc coâng thöùc
xaùc ñònh caùc yeáu toá cuûa (E)
H5. Vieát phöông trình ñt ñi
qua F
2
(8; 0) vaø // Oy ?
Ñ1. A = AB AH A
5
;2
2



B = AB BH B(3; 0)
H = BH AH H
11 5
;
36



Ñ2.
AC BH
A AC
AC: 4x+5y–20=0
BC AH
B BC
BC:x – y – 3 = 0
CH AB
H CH
CH:3x–12y–1=0
Ñ3.
12
I
d(I,d ) d(I,d ) R


a 2;b 2;R 2 2
a 4;b 6;R 3 2
Ñ4. a = 10, b = 6 , c = 8
Ñ5. : x = 8
3. Cho ABC côùi tröïc taâm H.
Bieát phöông trình caùc ñt:
AB: 4x + y – 12 = 0,
BH: 5x – 4y – 15 = 0,
AH: 2x + 2y – 9 = 0
Vieát pt caùc ñt chöùa caùc caïnh
coøn laïi vaø ñöôøng cao thöù ba.
4. Laäp pt ñöôøng troøn coù taâm
naèm treân ñt : 4x + 3y – 2 = 0
vaø tieáp xuùc vôùi 2 ñöôøng
thaúng:
d
1
: x + y + 4 = 0
d
2
: 7x – y + 4 = 0
5. Cho (E):
22
xy
1
100 36

.
a) Xaùc ñònh toaï ñoä caùc tieâu
ñieåm, caùc ñænh cuûa (E).
b) Qua tieâu ñieåm beân phaûi
cuûa (E) döïng ñt song song vôùi
Oy vaø caét (E) taïi 2 ñieåm M,
N. Tính MN.
Hoaït ñoäng 4: Cuûng coá
3'
Nhaán maïnh caùc noäi dung
ñaõ hoïc.
4. BAØI TAÄP VEÀ NHAØ:
Chuaån bò kieåm tra Hoïc kì 2.
Ngaøy soaïn: 30/04/2013 Chöông :
Tieát daïy: 42 Baøøi daïy: KIEÅM TRA HOÏC KÌ II
I. MUÏC TIEÂU:
Kieán thöùc: Kieåm tra caùc kieán thöùc ñaõ hoïc trong hoïc kì 2:
Heä thöùc löôïng trong tam giaùc. Giaûi tam giaùc.
Nguyễn Đình Khương Hình Học 10 Cơ Bản
85
Phöông trình ñöôøng thaúng. Khoaûng caùch töø moät ñieåm ñeán moät ñöôøng thaúng. Goùc giöõa hai
ñöôøng thaúng.
Phöông trình ñöôøng troøn.
Phöông trình ñöôøng elip.
Kó naêng: Thaønh thaïo caùch giaûi caùc daïng toaùn:
Giaûi tam giaùc.
Vieát phöông trình ñöôøng thaúng. Tính khoaûng caùch. Tính goùc.
Vieát phöông trình ñöôøng troøn.
Xaùc ñònh caùc yeáu toá cuûa elip.
Thaùi ñoä:
Reøn luyeän tính caån thaän, chính xaùc.
Luyeän tö duy linh hoaït saùng taïo.
II. CHUAÅN BÒ:
Giaùo vieân: Ñeà kieåm tra.
Hoïc sinh: OÂn taäp kieán thöùc ñaõ hoïc trong hoïc kì 2.
III. MA TRAÄN ÑEÀ:
Chuû ñeà
Nhaän bieát
Thoâng hieåu
Vaän duïng
Toång
TNKQ
TL
TNKQ
TL
TNKQ
TL
Heä thöùc löôïng trong
tam giaùc
2
0,25
0,5
Phöông trình ñöôøng
thaúng
2
0,25
1
1,0
1,5
Phöông trình ñöôøng
troøn
1
0,25
1
1,0
1,25
Phöông trình ñöôøng
elip
1
0,25
0,25
Toång
1,5
1,0
1,0
3,5
IV. NOÄI DUNG ÑEÀ KIEÅM TRA:
A. Phaàn traéc nghieäm:
011: Baùn kính cuûa ñöôøng troøn ngoaïi tieáp tam giaùc vôùi ba caïnh laø a = 6, b = 8, c = 10 baèng:
A. 5 B. 4
2
C. 5
2
D. 6
012: Dieän tích cuûa tam giaùc vôùi ba caïnh laø a = 6, b = 8, c = 10 baèng:
A. 24 B. 20
2
C. 48 D. 30
013: Moät vectô phaùp tuyeán cuûa ñöôøng thaúng ñi qua 2 ñieåm A(2; 0) vaø B(0; 3) laø:
A.
n
= (3; 2) B.
n
= (2; 3) C.
n
= (2; –3) D.
n
= (3; –2)
014: Heä soá goùc cuûa ñöôøng thaúng ñi qua 2 ñieåm A(2; 0) vaø B(0; 3) laø:
A.
3
2
B.
3
2
C.
2
3
D.
2
3
015: Baùn kính cuûa ñöôøng troøn coù phöông trình: x
2
+ y
2
– 10x – 2y – 12 = 0 baèng:
A. 6 B. 36 C.
12
D.
116
016: Ñoä daøi truïc lôùn cuûa elip:
22
1
25 16
xy

baèng:
A. 10 B. 8 C. 50 D. 16
Nguyễn Đình Khương Hình Học 10 Cơ Bản
86
B. Phaàn töï luaän:
Baøi 4: Trong maët phaúng Oxy, cho ABC vôùi A(3; 4), B(1; 3), C(5; 0).
a) Vieát phöông trình toång quaùt ñöôøng thaúng BC.
b) Vieát phöông trình ñöôøng troøn coù taâm A vaø tieáp xuùc vôùi ñöôøng thaúng BC.
V. ÑAÙP AÙN VAØ BIEÅU ÑIEÅM:
A. Phaàn traéc nghieäm: Taát caû ñeàu coù ñaùp aùn laø A.
B. Töï luaän:
Baøi 4: (2 ñieåm)
a)
(4; 3)BC 
(3;4)n
(0,5 ñieåm)
Phöông trình BC: 3(x – 1) + 4(y – 3) = 0 3x + 4y – 15 = 0 (0,5 ñieåm)
b) Baùn kính R = d(A, BC) =
32
3.3 4.4 15
34

= 2 (0,5 ñieåm)
Phöông trình ñöôøng troøn: (x – 3)
2
+ (y – 4)
2
= 4 (0,5 ñieåm)
VI. KEÁT QUAÛ KIEÅM TRA:
Lôùp
Só soá
0 – 3,4
3,5 – 4,9
5,0 – 6,4
6,5 – 7,9
8,0 – 10
SL
%
SL
%
SL
%
SL
%
SL
%
10A3
44
10A5
42
10A7
44
10A10
42
10A11
38
| 1/86
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

Nguyễn Đình Khương
Hình Học 10 Cơ Bản Ngaøy soaïn: 20/8/2012 Chöông I: VECTÔ Tieát daïy: 01
Baøøi 1: CAÙC ÑÒNH NGHÓA I. MUÏC TIEÂU: Kieán thöùc:
 Naém ñöôïc ñònh nghóa vectô vaø nhöõng khaùi nieäm quan troïng lieân quan ñeán vectô nhö: söï
cuøng phöông cuûa hai vectô, ñoä daøi cuûa vectô, hai vectô baèng nhau, …
 Hieåu ñöôïc vectô 0 laø moät vectô ñaïc bieät vaø nhöõng qui öôùc veà vectô 0 . Kó naêng:
 Bieát chöùng minh hai vectô baèng nhau, bieát döïng moät vectô baèng vectô cho tröôùc vaø coù ñieåm ñaàu cho tröôùc. Thaùi ñoä:
 Reøn luyeän oùc quan saùt, phaân bieät ñöôïc caùc ñoái töôïng. II. CHUAÅN BÒ:
Giaùo vieân: Giaùo aùn, phieáu hoïc taäp.
Hoïc sinh: SGK, vôû ghi. Ñoïc tröôùc baøi hoïc.
III. HOAÏT ÑOÄNG DAÏY HOÏC:
1. OÅn ñònh toå chöùc: Kieåm tra só soá lôùp.
2. Kieåm tra baøi cuõ: H. Ñ.
3. Giaûng baøi môùi: TL
Hoaït ñoäng cuûa Giaùo vieân
Hoaït ñoäng cuûa Hoïc sinh Noäi dung
Hoaït ñoäng 1: Tìm hieåu khaùi nieäm vectô
 Cho HS quan saùt hình 1.1.  HS quan saùt vaø cho nhaän xeùt I. Khaùi nieäm vectô
Nhaän xeùt veà höôùng chuyeån veà höôùng chuyeån ñoäng cuûa oâ ÑN: Vectô laø moät ñoaïn thaúng
15’ ñoäng. Töø ñoù hình thaønh khaùi toâ vaø maùy bay. coù höôùng. nieäm vectô.
AB coù ñieåm ñaàu laø A, ñieåm B cuoái laø B.
Ñoä daøi vectô ABñöôïc kí A a
hieäu laø: AB = AB.
 Giaûi thích kí hieäu, caùch veõ
Vectô coù ñoä daøi baèng 1 ñgl vectô. vectô ñôn vò.
Vectô coøn ñöôïc kí hieäu laø a,b,x,y , …
H1. Vôùi 2 ñieåm A, B phaân Ñ. AB vaø BA .
bieät coù bao nhieâu vectô coù
ñieåm ñaàu vaø ñieåm cuoái laø A hoaëc B?
H2. So saùnh ñoä daøi caùc vectô Ñ2. AB  BA AB vaø BA ?
Hoaït ñoäng 2: Tìm hieåu khaùi nieäm vectô cuøng phöông, vectô cuøng höôùng
 Cho HS quan saùt hình 1.3.
Ñöôøng thaúng ñi qua ñieåm
20’ Nhaän xeùt veà giaù cuûa caùc vectô
ñaàu vaø ñieåm cuoái cuûa moät
H1. Haõy chæ ra giaù cuûa caùc Ñ1. Laø caùc ñöôøng thaúng AB, vectô ñgl giaù cuûa vectô ñoù. 1
Nguyễn Đình Khương
Hình Học 10 Cơ Bản vectô: AB,CD,PQ,RS, …? CD, PQ, RS, …
ÑN: Hai vectô ñgl cuøng
H2. Nhaän xeùt veà VTTÑ cuûa Ñ2.
phöông neáu giaù cuûa chuùng
caùc giaù cuûa caùc caëp vectô: a) truøng nhau
song song hoaëc truøng nhau. a) AB vaø CD b) song song
Hai vectô cuøng phöông thì c) caét nhau
coù theå cuøng höôùng hoaëc ngöôïc b) PQ vaø RS A B C D höôùng. c) EF vaø PQ ?
Ba ñieåm phaân bieät A, B, C Q F R
thaúng haøng AB vaø AC
 GV giôùi thieäu khaùi nieäm hai P E cuøng phöông.
vectô cuøng höôùng, ngöôïc S höôùng.
H3. Cho hbh ABCD. Chæ ra Ñ3.
caùc caëp vectô cuøng phöông, AB vaø AC cuøng phöông
cuøng höôùng, ngöôïc höôùng? AD vaø BC cuøng phöông
AB vaø DC cuøng höôùng, …
H4. Neáu ba ñieåm phaân bieät A, Ñ4. Khoâng theå keát luaän.
B, C thaúng haøng thì hai vectô
AB vaø BC coù cuøng höôùng hay khoâng?
Hoaït ñoäng 3: Cuûng coá
 Nhaán maïnh caùc khaùi nieäm:
8’ vectô, hai vectô phöông, hai vectô cuøng höôùng.
 Caâu hoûi traéc nghieäm:
 Caùc nhoùm thöïc hieän yeâu caàu
Cho hai vectô AB vaø CD vaø cho keát quaû d).
cuøng phöông vôùi nhau. Haõy
choïn caâu traû lôøi ñuùng:
a) AB cuøng höôùng vôùi CD b) A, B, C, D thaúng haøng
c) AC cuøng phöông vôùi BD
d) BA cuøng phöông vôùi CD
4. BAØI TAÄP VEÀ NHAØ:  Baøi 1, 2 SGK
 Ñoïc tieáp baøi “Vectô” Ngaøy soaïn: 20/8/2012 Chöông I: VECTÔ 2
Nguyễn Đình Khương
Hình Học 10 Cơ Bản Tieát daïy: 02
Baøøi 1: CAÙC ÑÒNH NGHÓA (tt) I. MUÏC TIEÂU: Kieán thöùc:
 Naém ñöôïc ñònh nghóa vectô vaø nhöõng khaùi nieäm quan troïng lieân quan ñeán vectô nhö: söï
cuøng phöông cuûa hai vectô, ñoä daøi cuûa vectô, hai vectô baèng nhau, …
 Hieåu ñöôïc vectô 0 laø moät vectô ñaïc bieät vaø nhöõng qui öôùc veà vectô 0 . Kó naêng:
 Bieát chöùng minh hai vectô baèng nhau, bieát döïng moät vectô baèng vectô cho tröôùc vaø coù ñieåm ñaàu cho tröôùc. Thaùi ñoä:
 Reøn luyeän oùc quan saùt, phaân bieät ñöôïc caùc ñoái töôïng. II. CHUAÅN BÒ:
Giaùo vieân: Giaùo aùn, phieáu hoïc taäp.
Hoïc sinh: SGK, vôû ghi. Ñoïc tröôùc baøi hoïc.
III. HOAÏT ÑOÄNG DAÏY HOÏC:
1. OÅn ñònh toå chöùc: Kieåm tra só soá lôùp.
2. Kieåm tra baøi cuõ: (5’)
H. Theá naøo laø hai vectô cuøng phöông? Cho hbh ABCD. Haõy chæ ra caùc caëp vectô cuøng phöông, cuøng höôùng?
Ñ. AB vaø DC cuøng höôùng, …
3. Giaûng baøi môùi: TL
Hoaït ñoäng cuûa Giaùo vieân
Hoaït ñoäng cuûa Hoïc sinh Noäi dung
Hoaït ñoäng 1: Tìm hieåu khaùi nieäm hai vectô baèng nhau
 Töø KTBC, GV giôùi thieäu
III. Hai vectô baèng nhau
khaùi nieäm hai vectô baèng
Hai vectô avaø b ñgl baèng 20’ nhau.
nhau neáu chuùng cuøng höôùng
H1. Cho hbh ABCD. Chæ ra Ñ1. AB DC , …
vaø coù cuøng ñoä daøi, kí hieäu
caùc caëp vectô baèng nhau? a b.
Chuù yù: Cho a , O. ! A sao H2. Cho ABC
ñeàu. Ñ2. Khoâng. Vì khoâng cuøng cho OA  a. AB BC ? höôùng.
H3. Goïi O laø taâm cuûa hình luïc Ñ3. Caùc nhoùm thöïc hieän giaùc ñeàu ABCDEF. 1) OA  CB  DO  EF
1) Haõy chæ ra caùc vectô baèng …. OA , OB, …?
2) Ñaúng thöùc naøo sau ñaây laø ñuùng? a) AB  CD b) AO  DO c) BC  FE 2) c) vaø d) ñuùng. d) OA  OC 3
Nguyễn Đình Khương
Hình Học 10 Cơ Bản
Hoaït ñoäng 2: Tìm hieåu khaùi nieäm vectô – khoâng
 GV giôùi thieäu khaùi nieäm IV. Vectô – khoâng
10’ vectô – khoâng vaø caùc qui öôùc
Vectô – khoâng laø vectô coù veà vectô – khoâng.
ñieåm ñaàu vaø ñieåm cuoái truøng
nhau, kí hieäu 0 .
H. Cho hai ñieåm A, B thoaû: Ñ. Caùc nhoùm thaûo luaän vaø  0  AA , A.
AB  BA . Meänh ñeà naøo sau cho keát quaû b).
0 cuøng phöông, cuøng höôùng ñaây laø ñuùng? vôùi moïi vectô.
a) AB khoâng cuøng höôùng vôùi  0 = 0. BA .
A B AB  0 . b) AB  0 . c) AB > 0. d) A khoâng truøng B.
Hoaït ñoäng 3: Cuûng coá
 Nhaán maïnh caùc khaùi nieäm
8’ hai vectô baèng nhau, vectô – khoâng.
 Caâu hoûi traéc nghieäm. Choïn  Caùc nhoùm thaûo luaän vaø cho phöông aùn ñuùng: keát quaû:
1) Cho töù giaùc ABCD coù 1) a
AB  DC . Töù giaùc ABCD laø: 2) b a) Hình bình haønh b) Hình chöõ nhaät c) Hình thoi d) Hình vuoâng
2) Cho nguõ giaùc ABCDE. Soá
caùc vectô khaùc 0 coù ñieåm
ñaàu vaø ñieåm cuoái laø caùc ñænh cuûa nguõ giaùc baèng: a) 25 b) 20 c) 16 d) 10
4. BAØI TAÄP VEÀ NHAØ:  Baøi 2, 3, 4 SGK Ngaøy soaïn: 03/9/2012 Chöông I: VECTÔ 4
Nguyễn Đình Khương
Hình Học 10 Cơ Bản Tieát daïy: 03
Baøøi 2: TOÅNG VAØ HIEÄU CUÛA HAI VECTÔ I. MUÏC TIEÂU: Kieán thöùc:
 Naém ñöôïc caùc tính chaát cuûa toång hai vectô, lieân heä vôùi toång hai soá thöïc, toång hai caïnh cuûa tam giaùc.
 Naém ñöôïc hieäu cuûa hai vectô. Kó naêng:
 Bieát döïng toång cuûa hai vectô theo ñònh nghóa hoaëc theo qui taéc hình bình haønh.
 Bieát vaän duïng caùc coâng thöùc ñeå giaûi toaùn. Thaùi ñoä:
 Reøn luyeän tö duy tröøu töôïng, linh hoaït trong vieäc giaûi quyeát caùc vaán ñeà. II. CHUAÅN BÒ:
Giaùo vieân: Giaùo aùn. Caùc hình veõ minh hoaï.
Hoïc sinh: SGK, vôû ghi. OÂn taäp kieán thöùc vectô ñaõ hoïc.
III. HOAÏT ÑOÄNG DAÏY HOÏC:
1. OÅn ñònh toå chöùc: Kieåm tra só soá lôùp.
2. Kieåm tra baøi cuõ: (5’)
H. Neâu ñònh nghóa hai vectô baèng nhau.
AÙp duïng: Cho ABC, döïng ñieåm M sao cho: AM  BC .
Ñ. ABCM laø hình bình haønh.
3. Giaûng baøi môùi: TL
Hoaït ñoäng cuûa Giaùo vieân
Hoaït ñoäng cuûa Hoïc sinh Noäi dung
Hoaït ñoäng 1: Tìm hieåu veà Toång cuûa hai vectô
H1. Cho HS quan saùt h.1.5. Ñ1. Hôïp löïc F cuûa hai löïc I. Toång cuûa hai vectô
20’ Cho bieát löïc naøo laøm cho
a) Ñònh nghóa: Cho hai vectô 1 F vaø 2 F . thuyeàn chuyeån ñoäng?
avaø b . Laáy moät ñieåm A tuyø yù, 1 F
veõ AB  a,BC  b. Vectô AC F
ñgl toång cuûa hai vectô avaø b .
 GV höôùng daãn caùch döïng
vectô toång theo ñònh nghóa.
Kí hieäu laø a b . 2 F
Chuù yù: Ñieåm cuoái cuûa AB B a
truøng vôùi ñieåm ñaàu cuûa BC . b
b) Caùc caùch tính toång hai vectô: A a  b C H2. Tính toång:
Ñ2. Döïa vaøo qui taéc 3 ñieåm. + Qui taéc 3 ñieåm: a) AB BC  CD  DE a) AE b) 0
AB BC  AC
+ Qui taéc hình bình haønh: b) AB BA AB AD  AC
H3. Cho hình bình haønh Ñ3. ABCD. Chöùng minh: AB AD  AB BC  AC AB AD  AC B C
 Töø ñoù ruùt ra qui taéc hình bình haønh. A D 5
Nguyễn Đình Khương
Hình Học 10 Cơ Bản
Hoaït ñoäng 2: Tìm hieåu tính chaát cuûa toång hai vectô
H1. Döïng a  b,b  a. Nhaän Ñ1. 2 nhoùm thöïc hieän yeâu II. Tính chaát cuûa pheùp coäng 15’ xeùt? caàu. caùc vectô B b C
Vôùi  a,b,c , ta coù: a a  b a
a) a  b  b  a (giao hoaùn) b  a A D b
b) a  b  c  a  b  c H2. b
c) a  0  0  a  a
Döïng a  b,b  c, a  b  c , B C a c
a  b  c . Nhaän xeùt? b a  b  A c D
Hoaït ñoäng 3: Cuûng coá
 Nhaán maïnh caùc caùch xaùc ñònh vectô toång.
 Môû roäng cho toång cuûa nhieàu vectô.
 So saùnh toång cuûa hai vectô
vôi toång hai soá thöïc vaø toång
ñoä daøi hai caïnh cuûa tam giaùc.
4. BAØI TAÄP VEÀ NHAØ:  Baøi 1, 2, 3, 4 SGK. Ngaøy soaïn: 09/9/2012 Chöông I: VECTÔ 6
Nguyễn Đình Khương
Hình Học 10 Cơ Bản Tieát daïy: 04
Baøøi 2: TOÅNG VAØ HIEÄU CUÛA HAI VECTÔ (tt) I. MUÏC TIEÂU: Kieán thöùc:
 Naém ñöôïc caùc tính chaát cuûa toång hai vectô, lieân heä vôùi toång hai soá thöïc, toång hai caïnh cuûa tam giaùc.
 Naém ñöôïc hieäu cuûa hai vectô. Kó naêng:
 Bieát döïng toång cuûa hai vectô theo ñònh nghóa hoaëc theo qui taéc hình bình haønh.
 Bieát vaän duïng caùc coâng thöùc ñeå giaûi toaùn. Thaùi ñoä:
 Reøn luyeän tö duy tröøu töôïng, linh hoaït trong vieäc giaûi quyeát caùc vaán ñeà. II. CHUAÅN BÒ:
Giaùo vieân: Giaùo aùn. Hình veõ minh hoaï.
Hoïc sinh: SGK, vôû ghi. OÂn taäp kieán thöùc vectô ñaõ hoïc.
III. HOAÏT ÑOÄNG DAÏY HOÏC:
1. OÅn ñònh toå chöùc: Kieåm tra só soá lôùp.
2. Kieåm tra baøi cuõ: (5’)
H. Neâu caùc caùch tính toång hai vectô? Cho ABC. So saùnh: a) AB AC vôùi BC b) AB  AC vôùi BC
Ñ. a) AB AC  BC b) AB  AC  BC
3. Giaûng baøi môùi: TL
Hoaït ñoäng cuûa Giaùo vieân
Hoaït ñoäng cuûa Hoïc sinh Noäi dung
Hoaït ñoäng 1: Tìm hieåu Hieäu cuûa hai vectô
H1. Cho ABC coù trung ñieåm Ñ1. Caùc nhoùm thöïc hieän yeâu III. Hieäu cuûa hai vectô
15’ caùc caïnh BC, CA, AB laàn löôït caàu
a) Vectô ñoái
laø D, E, F. Tìm caùc vectô ñoái B
+ Vectô coù cuøng ñoä daøi vaø cuûa: E F
ngöôïc höôùng vôùi a ñgl vectô a) DE b) EF A C D
ñoái cuûa a , kí hieäu a . a) ED,AF,FB + AB  BA b) FE,BD,DC
+ Vectô ñoái cuûa 0 laø 0 .
 Nhaán maïnh caùch döïng hieäu
b) Hieäu cuûa hai vectô A cuûa hai vectô +
a  b  a  (b) O B + AB  OB OA
Hoaït ñoäng 2: Vaän duïng pheùp tính toång, hieäu caùc vectô
H1. Cho I laø trung ñieåm cuûa Ñ1. I laø trung ñieåm cuûa AB IV. AÙp duïng
20’ AB. CMR IA  IB  0.  IA  IB
a) I laø trung ñieåm cuûa AB  IA  IB  0 IA  IB  0
H2. Cho IA  IB  0 . CMR: I Ñ2. IA  IB  0  IA  IB laø trung ñieåm cuûa AB.
 I naèm giöõa A, B vaø IA = IB b) G laø troïng taâm cuûa ABC
 I laø trung ñieåm cuûa AB.
GA  GB GC  0
H3. Cho G laø troïng taâm Ñ3. Veõ hbh BGCD. 7
Nguyễn Đình Khương
Hình Học 10 Cơ Bản ABC.  GB GC  GD,
CMR: GA  GB GC  0 GA  G  D A G B I C D
Hoaït ñoäng 3: Cuûng coá  Nhaán maïnh:  HS nhaéc laïi
5’ + Caùch xaùc ñònh toång, hieäu
hai vectô, qui taéc 3 ñieåm, qui taéc hbh.
+ Tính chaát trung ñieåm ñoaïn thaúng.
+ Tính chaát troïng taâm tam giaùc. + a  b  a  b
4. BAØI TAÄP VEÀ NHAØ:  Baøi 5, 6, 7, 8, 9, 10. Ngaøy soaïn: 09/9/2011 Chöông I: VECTÔ Tieát daïy: 05
Baøøi 2: BAØI TAÄP TOÅNG VAØ HIEÄU HAI VECTÔ 8
Nguyễn Đình Khương
Hình Học 10 Cơ Bản I. MUÏC TIEÂU: Kieán thöùc:
 Cuûng coá caùc kieán thöùc ñaõ hoïc veà pheùp coäng vaø tröø caùc vectô.
 Khaéc saâu caùch vaän duïng qui taéc 3 ñieåm vaø qui taêc hình bình haønh. Kó naêng:
 Bieát xaùc ñònh vectô toång, vectô hieäu theo ñònh nghóa vaø caùc qui taéc.
 Vaän duïng linh hoaït caùc qui taéc xaùc ñònh vectô toång, vectô hieäu. Thaùi ñoä:
 Reøn luyeän tính caån thaän, chính xaùc.
 Luyeän tö duy hình hoïc linh hoaït. II. CHUAÅN BÒ:
Giaùo vieân: Giaùo aùn. Heä thoáng baøi taäp.
Hoïc sinh: SGK, vôû ghi. Laøm baøi taäp veà nhaø.
III. HOAÏT ÑOÄNG DAÏY HOÏC:
1. OÅn ñònh toå chöùc: Kieåm tra só soá lôùp.
2. Kieåm tra baøi cuõ: (3’)
H. Neâu caùc qui taéc xaùc ñònh vectô toång, vectô hieäu?
Ñ. Qui taéc 3 ñieåm, qui taéc hình bình haønh.
3. Giaûng baøi môùi: TL
Hoaït ñoäng cuûa Giaùo vieân
Hoaït ñoäng cuûa Hoïc sinh Noäi dung
Hoaït ñoäng 1: Luyeän kyõ naêng chöùng minh ñaúng thöùc vectô
H1. Neâu caùch chöùng minh Ñ1. Bieán ñoåi veá naøy thaønh veá 1. Cho hbh ABCD vaø ñieåm M moät ñaúng thöùc vectô? kia. tuyø yù. CMR: M MA  MC  MB MD A D
2. CMR vôùi töù giaùc ABCD baát kì ta coù: B C
a) AB BC  CD  DA  0
H2. Neâu qui taéc caàn söû duïng? Ñ2. Qui taéc 3 ñieåm. b) AB AD  CB CD
H3. Haõy phaân tích caùc vectô Ñ3. RJ  RA  IJ
3. Cho ABC. Beân ngoaøi tam
theo caùc caïnh cuûa caùc hbh? IQ  IB BQ
giaùc veõ caùc hbh ABIJ, BCPQ, PS  PC  CS CARS. CMR: R RJ  IQ  PS  0 A S J B I C Q P
Hoaït ñoäng 2: Cuûng coá moái quan heä giöõa caùc yeáu toá cuûa vectô
H1. Xaùc ñònh caùc vectô Ñ1.
4. Cho ABC ñeàu, caïnh a. a) AB BC b) AB BC a) AB BC = AC
Tính ñoä daøi cuûa caùc vectô: b) AB BC = AD a) AB BC b) AB BC 9
Nguyễn Đình Khương
Hình Học 10 Cơ Bản
5. Cho a,b  0 . Khi naøo coù ñaúng thöùc: a) a  b  a  b b) a  b  a  b
H2. Neâu baát ñaúng thöùc tam giaùc?
6. Cho a  b = 0. So saùnh ñoä Ñ2. AB + BC > AC
daøi, phöông, höôùng cuûa a,b ?
Hoaït ñoäng 3: Luyeän kó naêng chöùng minh 2 ñieåm truøng nhau
H1. Neâu ñieàu kieän ñeå 2 ñieåm Ñ1. IJ  0
7. CMR: AB  CD  trung I, J truøng nhau?
ñieåm cuûa AD vaø BC truøng nhau.
Hoaït ñoäng 4: Cuûng coá
 Nhaán maïnh caùch vaän duïng
caùc kieán thöùc ñaõ hoïc.  Caâu hoûi: Choïn phöông aùn ñuùng.
 Caùc nhoùm thaûo luaän, traû lôøi
1) Cho 3 ñieåm A,B,C.Ta coù: nhanh. A. AB  AC  BC B. 1C, 2A. AB  AC  BC C. AB  BC  CB D. AB  AC  CB
2) Cho I laø trung ñieåm cuûa AB, ta coù: A. IA  IB  0 B. IA + IB=0 C. AI  BI D. AI  I  B
4. BAØI TAÄP VEÀ NHAØ:
 Laøm tieáp caùc baøi taäp coøn laïi.
 Ñoïc tröôùc baøi “Tích cuûa vectô vôùi moät soá” Ngaøy soaïn: 20/9/2012 Chöông I: VECTÔ Tieát daïy: 06
Baøøi 3: TÍCH CUÛA VECTÔ VÔÙI MOÄT SOÁ 10
Nguyễn Đình Khương
Hình Học 10 Cơ Bản I. MUÏC TIEÂU: Kieán thöùc:
 Naém ñöôïc ñònh nghóa vaø tính chaát cuûa pheùp nhaân moät vectô vôùi moät soá.
 Naém ñöôïc ñieàu kieän ñeå hai vectô cuøng phöông. Kó naêng:
 Bieát döïng vectô ka khi bieát kR vaø a .
 Söû duïng ñöôïc ñieàu kieän caàn vaø ñuû cuûa 2 vectô cuøng phöông ñeå chöùng minh 3 ñieåm thaúng haøng
hoaëc hai ñöôøng thaúng song song.
 Bieát phaân tích moät vectô theo 2 vectô khoâng cuøng phöông cho tröôùc. Thaùi ñoä:
 Luyeän tö duy phaân tích linh hoaït, saùng taïo. II. CHUAÅN BÒ:
Giaùo vieân: Giaùo aùn. Hình veõ minh hoaï.
Hoïc sinh: SGK, vôû ghi. Ñoïc baøi tröôùc. OÂn laïi kieán thöùc veà toång, hieäu cuûa hai vectô.
III. HOAÏT ÑOÄNG DAÏY HOÏC:
1. OÅn ñònh toå chöùc: Kieåm tra só soá lôùp.
2. Kieåm tra baøi cuõ: (3')
H. Cho ABCD laø hình bình haønh. Tính AB AD . Nhaän xeùt veà vectô toång vaø AO ?
Ñ. AB AD  AC . AC,AOcuøng höôùngvaø AC  2 AO .
3. Giaûng baøi môùi: TL
Hoaït ñoäng cuûa Giaùo vieân
Hoaït ñoäng cuûa Hoïc sinh Noäi dung
Hoaït ñoäng 1: Tìm hieåu khaùi nieäm Tích cuûa vectô vôùi moät soá
 GV giôùi thieäu khaùi nieäm tích I. Ñònh nghóa
10' cuûa vectô vôùi moät soá.
Cho soá k ≠ 0 vaø vectô a  0 .
Tích cuûa a vôùi soá k laø moät
H1. Cho AB  a . Döïng 2 a .
Ñ1. Döïng BC  a  AC  2a vectô, kí hieäu ka , ñöôïc xaùc A B ñònh nhö sau: C
+ cuøng höôùng vôùi a neáu k>0,
H2. Cho G laø troïng taâm cuûa Ñ2.
+ ngöôïc höôùng vôùi a neáu k<0
ABC. D vaø E laàn löôït laø A
+ coù ñoä daøi baèng k a .
trung ñieåm cuûa BC vaø AC. So E
Qui öôùc: 0 a = 0 , k 0 = 0 saùnh caùc vectô: G  a) DEvôùi AB B D C b) AG vôùi AD a) 1 DE  AB 2 c) AG vôùi GD b) 2 AG  AD 3 c) AG  2 GD
Hoaït ñoäng 2: Tìm hieåu tính chaát cuûa tích vectô vôùi moät soá
 GV ñöa ra caùc ví duï minh  HS theo doõi vaø nhaän xeùt. II. Tính chaát
10' hoaï, roài cho HS nhaän xeùt caùc
Vôùi hai vectô a vaø b baát kì, tính chaát.
vôùi moïi soá h, k ta coù:
H1. Cho ABC. M, N laø trung Ñ1. MA 1
 AN = BA  AC  k( a + b ) = k a + k b
ñieåm cuûa AB, AC. So saùnh 2
(h + k)a = h a + k a caùc vectô: 
h(k a ) = (hk)a 11
Nguyễn Đình Khương
Hình Học 10 Cơ Bản MA  AN vôùi BA  AC 1 1 BA 1  AC = BA  AC
1. a = a , (–1) a = –a 2 2 2
Hoaït ñoäng 3: Tìm hieåu theâm veà tính chaát trung ñieåm ñoaïn thaúng vaø troïng taâm tam giaùc
H1. Nhaéc laïi heä thöùc trung Ñ1. I laø trung ñieåm cuûa AB
III. Trung ñieåm cuûa ñoaïn
10' ñieåm cuûa ñoaïn thaúng?
IA  IB  0
thaúng vaø troïng taâm cuûa tam giaùc
a) I laø trung ñieåm cuûa AB
H2. Nhaéc laïi heä thöùc troïng Ñ2. G laø troïng taâm ABC
MA  MB  2MI taâm tam giaùc?  GA  GB GC  0
b) G laø troïng taâm ABC
MA  MB MC  3MG (vôùi M tuyø yù)
Hoaït ñoäng 4: Cuûng coá
 Nhaán maïnh khaùi nieäm tích 10' vectô vôùi moät soá.  Caâu hoûi:
1) Cho ñoaïn thaúng AB. Xaùc
ñònh caùc ñieåm M, N sao cho: 1) MA  2M  B , NA  2NB
2) Cho 4 ñieåm A, B, E, F thaúng 2)
haøng. Ñieåm M thuoäc ñoaïn AB 1 EA   EB, 1 FA FB
sao cho AE = 1 EB, ñieåm F 2 2 2
khoâng thuoäc ñoaïn AB sao cho
AF = 1 FB. So saùnh caùc caëp 2
vectô: EA vaø EB, FA vaø FB?
4. BAØI TAÄP VEÀ NHAØ:
 Baøi 1, 4, 5, 6, 7, 8, 9 SGK.
 Ñoïc tieáp baøi "Tích cuûa vectô vôùi moät soá" Ngaøy soaïn: 01/10/2012 Chöông I: VECTÔ Tieát daïy: 07
Baøøi 3: TÍCH CUÛA VECTÔ VÔÙI MOÄT SOÁ (tt) 12
Nguyễn Đình Khương
Hình Học 10 Cơ Bản I. MUÏC TIEÂU: Kieán thöùc:
 Naém ñöôïc ñònh nghóa vaø tính chaát cuûa pheùp nhaân moät vectô vôùi moät soá.
 Naém ñöôïc ñieàu kieän ñeå hai vectô cuøng phöông. Kó naêng:
 Bieát döïng vectô ka khi bieát kR vaø a .
 Söû duïng ñöôïc ñieàu kieän caàn vaø ñuû cuûa 2 vectô cuøng phöông ñeå chöùng minh 3 ñieåm thaúng haøng
hoaëc hai ñöôøng thaúng song song.
 Bieát phaân tích moät vectô theo 2 vectô khoâng cuøng phöông cho tröôùc. Thaùi ñoä:
 Luyeän tö duy phaân tích linh hoaït, saùng taïo. II. CHUAÅN BÒ:
Giaùo vieân: Giaùo aùn. Hình veõ minh hoaï.
Hoïc sinh: SGK, vôû ghi. Ñoïc baøi tröôùc. OÂn laïi kieán thöùc veà toång, hieäu cuûa hai vectô.
III. HOAÏT ÑOÄNG DAÏY HOÏC:
1. OÅn ñònh toå chöùc: Kieåm tra só soá lôùp.
2. Kieåm tra baøi cuõ: (3')
H. Neâu heä thöùc trung ñieåm cuûa ñoaïn thaúng, heä thöùc troïng taâm tam giaùc?
Ñ. MA  MB  2MI ; MA  MB MC  3MG.
3. Giaûng baøi môùi: TL
Hoaït ñoäng cuûa Giaùo vieân
Hoaït ñoäng cuûa Hoïc sinh Noäi dung
Hoaït ñoäng 1: Tìm hieåu ñieàu kieän ñeå hai vectô cuøng phöông
H1. Cho 4 ñieåm A, B, E, F Ñ1.
IV. Ñieàu kieän ñeå hai vectô
10' thaúng haøng. Ñieåm M thuoäc cuøng phöông ñoaïn AB sao cho AE = 1 EB,
a vaø b ( b ≠ 0 ) cuøng phöông 2 1 EA   EB, 1 FA FB
kR: a = k b
ñieåm F khoâng thuoäc ñoaïn AB 2 2 sao cho AF = 1 FB. So saùnh 2
caùc caëp vectô: EA vaø EB, FA vaø FB?
H2. Nhaéc laïi caùch chöùng minh
Nhaän xeùt: A, B, C thaúng
Ñ2. A, B, C thaúng haøng 3 ñieåm thaúng haøng?
haøng kR: AB  kAC
 ABvaø AC cuøng phöông.
Hoaït ñoäng 2: Tìm hieåu phaân tích moät vectô theo hai vectô khoâng cuøng phöông
 GV giôùi thieäu vieäc phaân tích A
V. Phaân tích moät vectô theo
7' moät vectô theo hai vectô
hai vectô khoâng cuøng khoâng cuøng phöông. B M C phöông
H1. Cho ABC, M laø trung 1
Cho a vaø b khoâng cuøng
ñieåm cuûa BC. Phaân tích AM Ñ1. AM = AB AC 2
phöông. Khi ñoù moïi vectô x theo AB,AC ?
ñeàu phaân tích ñöôïc moät caùch
duy nhaát theo hai vectô a , b ,
nghóa laø coù duy nhaát caëp soá h,
k sao cho x = h a + k b . 13
Nguyễn Đình Khương
Hình Học 10 Cơ Bản
Hoaït ñoäng 3: Vaän duïng phaân tích vectô, chöùng minh 3 ñieåm thaúng haøng A
Ví duï: Cho ABC vôùi troïng 20' K 
taâm G. Goïi I laø trung ñieåm a I G 
cuûa AG vaø K laø ñieåm treân B b M C caïnh AB sao cho AK = 1 AB. 5
H1. Vaän duïng heä thöùc troïng Ñ1. CA  CB= 3 CG
a) Phaân tích caùc vectô AI,AK taâm tam giaùc, tính CA 1
 CB ?  CG = a  b
,CI,CK theo a  CA , b  CB 31
b) CMR C, I, K thaúng haøng.
H2. Phaân tích CI theo a , b ? Ñ2. CI = CA  CG 2 = 2 1 a  b 3 6
H3. Phaân tích AK theo a , 1 b ?
Ñ3. AK = 1 AB = b  a 5 5
H4. Phaân tích giaû thieát: Phaân tích AI,CK theo a
Ñ4. AI  CI  CA = 1 1  CA , b  a 6 3 b  CB ? CK  CA  AK = 4 1 a  b 5 5
Hoaït ñoäng 4: Cuûng coá  Nhaán maïnh:
3' + Caùc kieán thöùc caàn söû duïng:
heä thöùc trung ñieåm, troïng taâm
+ Caùch phaân tích: qui taéc 3 ñieåm
4. BAØI TAÄP VEÀ NHAØ:  Baøi 2, 3 SGK. Ngaøy soaïn: 20/10/2012 Chöông I: VECTÔ Tieát daïy: 08
Baøøi 3: BAØI TAÄP TÍCH CUÛA VECTÔ VÔÙI MOÄT SOÁ I. MUÏC TIEÂU: 14
Nguyễn Đình Khương
Hình Học 10 Cơ Bản Kieán thöùc:
 Cuûng coá ñònh nghóa vaø caùc tính chaát cuûa pheùp nhaân vectô vôùi moät soá.
 Söû duïng ñieàu kieän caàn vaø ñuû ñeå hai vectô cuøng phöông. Kó naêng:
 Bieát vaän duïng tích vectô vôùi moät soá ñeå chöùng minh ñaúng thöùc vectô..
 Bieát vaän duïng ñieàu kieän hai vectô cuøng phöông ñeå chöùng minh 3 ñieåm thaúng haøng.
 Bieát vaän duïng caùc pheùp toaùn vectô ñeå phaân tích moät vectô theo hai vectô khoâng cuøng phöông. Thaùi ñoä:
 Reøn luyeän tính caån thaän, chính xaùc.
 Luyeän tö duy linh hoaït qua vieäc phaân tích vectô. II. CHUAÅN BÒ:
Giaùo vieân: Giaùo aùn. Heä thoáng baøi taäp.
Hoïc sinh: SGK, vôû ghi. OÂn taäp caùc kieán thöùc veà vectô.
III. HOAÏT ÑOÄNG DAÏY HOÏC:
1. OÅn ñònh toå chöùc: Kieåm tra só soá lôùp.
2. Kieåm tra baøi cuõ: (Loàng vaøo quaø trình luyeän taäp) H. Ñ.
3. Giaûng baøi môùi: TL
Hoaït ñoäng cuûa Giaùo vieân
Hoaït ñoäng cuûa Hoïc sinh Noäi dung
Hoaït ñoäng 1: Vaän duïng chöùng minh ñaúng thöùc vectô A
1. Goïi AM laø trung tuyeán cuûa 10'
ABC vaø D laø trung ñieåm cuûa  D ñoaïn AM. CMR: B M C a) 2DA  DB DC  0
H1. Nhaéc laïi heä thöùc trung Ñ1. DBDC  2DM b) 2OA OBOC  4OD , ñieåm? vôùi O tuyø yù.
H2. Neâu caùch chöùng minh b)? Ñ2. Töø a) söû duïng qui taéc 3 ñieåm.
 Höôùng daãn: Töø M veõ caùc A
2. Cho ABC ñeàu coù troïng
ñöôøng thaúng song song vôùi
taâm O vaø M laø 1 ñieåm tuyø yù caùc caïnh cuûa ABC. B2 C1
trong tam giaùc. Goïi D, E, F O E F C
laàn löôït laø chaân ñöôøng vuoâng 2 B1
H3. Nhaän xeùt caùc tam giaùc M B A
goùc haï töø M ñeán BC, AC, AB. 1 D A2 C MA1A2, MB1B2, MC1C2 ?
Ñ3. Caùc tam giaùc ñeàu CMR:
H4. Neâu heä thöùc troïng taâm 3 MD  ME  MF  MO
Ñ4. MA  MB MC  3MO 2 tam giaùc?
Hoaït ñoäng 2: Vaän duïng xaùc ñònh ñieåm thoaû moät ñaúng thöùc vectô
H1. Neâu caùch xaùc ñònh moät Ñ1. Chöùng toû: OM  a (vôùi O 3. Cho hai ñieåm phaân bieät A, 10' ñieåm? vaø a ñaõ bieát) B. Tìm ñieåm K sao cho: 3KA  2KB  0 15
Nguyễn Đình Khương
Hình Học 10 Cơ Bản Ñ2. MA  MB = 2 MI H2. Tính MA  MB ? A
4. Cho ABC. Tìm ñieåm M
sao cho: MA  MB 2MC  0 I M  B C
Hoaït ñoäng 3: Vaän duïng chöùng minh 3 ñieåm thaúng haøng, hai ñieåm truøng nhau
H1. Neâu caùch chöùng minh 3 Ñ1. Chöùng minh CA,CB 5. Cho boán ñieåm O, A, B, C
10' ñieåm A, B, C thaúng haøng? cuøng phöông.
sao cho: OA 2OB3OC  0 CA  2CB  0 CMR 3 ñieåm A, B, C thaúng haøng.
6. Cho hai tam giaùc ABC vaø
H2. Neâu caùch chöùng minh 2 Ñ2. GG  0
ABC laàn löôït coù troïng taâm ñieåm truøng nhau? laø G vaø G. CMR:
AA BB CC  3GG
Töø ñoù suy ra ñieàu kieän caàn vaø
ñuû ñeå hai tam giaùc coù cuøng troïng taâm.
Hoaït ñoäng 4: Vaän duïng phaân tích vectô
H1. Vaän duïng tính chaát naøo?
Ñ1. Heä thöùc trung ñieåm.
7. Cho AK vaø BM laø hai trung 10' 2
tuyeán cuûa ABC. Phaân tích AB  u  v , 2 4 BC  u  v 3 3 3 caùc vectô AB,BC,CA theo 4 2 u  AK, v  BM CA   u  v 3 3
8. Treân ñöôøng thaúng chöùa
Ñ2. Qui taéc 3 ñieåm
caïnh BC cuûa ABC, laáy moät 1 3 AM   u  v
ñieåm M sao cho: MB  3MC. 2 2 Phaân tích AM theo u  AB, v  AC .
Hoaït ñoäng 5: Cuûng coá
3'  Nhaán maïnh caùch giaûi caùc daïng toaùn
4. BAØI TAÄP VEÀ NHAØ:
 Laøm tieáp caùc baøi taäp coøn laïi.
 Ñoïc tröôùc baøi "Heä truïc toaï ñoä" Ngaøy soaïn: 20/10/2012 Chöông I: VECTÔ Tieát daïy: 09
Baøøi 4: HEÄ TRUÏC TOAÏ ÑOÄ I. MUÏC TIEÂU: Kieán thöùc:
 Naém ñöôïc ñònh nghóa vaø caùc tính chaát veà toaï ñoä cuûa vectô vaø cuûa ñieåm. 16
Nguyễn Đình Khương
Hình Học 10 Cơ Bản Kó naêng:
 Bieát bieåu dieãn caùc ñieåm vaø caùc vectô baèng caùc caëp soá trong heä truïc toaï ñoä ñaõ cho.
 Bieát tìm toaï ñoä caùc vectô toång, hieäu, tích moät soá vôùi moät vectô.
 Bieát söû duïng coâng thöùc toaï ñoä trung ñieåm cuûa ñoaïn thaúng vaø toaï ñoä troïng taâm tam giaùc. Thaùi ñoä:
 Reøn luyeän tính caån thaän, chính xaùc.
 Gaén kieán thöùc ñaõ hoïc vaøo thöïc teá. II. CHUAÅN BÒ:
Giaùo vieân: Giaùo aùn. Hình veõ minh hoaï.
Hoïc sinh: SGK, vôû ghi. OÂn taäp kieán thöùc vectô ñaõ hoïc.
III. HOAÏT ÑOÄNG DAÏY HOÏC:
1. OÅn ñònh toå chöùc: Kieåm tra só soá lôùp.
2. Kieåm tra baøi cuõ: (3')
H. Cho ABC, ñieåm M thuoäc caïnh BC: 3
MB   MC. Haõy phaân tích AM theo AB,AC . 2 Ñ. 2 3 AM  AB AC. 5 5
3. Giaûng baøi môùi: TL
Hoaït ñoäng cuûa Giaùo vieân
Hoaït ñoäng cuûa Hoïc sinh Noäi dung
Hoaït ñoäng 1: Tìm hieåu veà Toaï ñoä cuûa ñieåm treân truïc
 GV giôùi thieäu truïc toaï ñoä,
I. Truïc vaø ñoä daøi ñaïi soá treân
toaï ñoä cuûa ñieåm treân truïc, ñoä truïc
15' daøi ñaïi soá cuûa vectô treân truïc.
a) Truïc toaï ñoä (O; e )
H1. Cho truïc (O; e ) vaø caùc Ñ1.
b) Toaï ñoä cuûa ñieåm treân truïc:
ñieåm A, B, C nhö hình veõ.
Cho M treân truïc (O; e ).
Xaùc ñònh toaï ñoä caùc ñieåm A,
k laø toaï ñoä cuûa M OM  ke B, C, O.
c) Ñoä daøi ñaïi soá cuûa vectô:
Cho A, B treân truïc (O; e ).
H2. Cho truïc (O; e ). Xaùc ñònh Ñ3.
a = AB AB  ae
caùc ñieåm M(–1), N(3), P(–3). Nhaän xeùt:
+ AB cuøng höôùng e  AB>0
H3. Tính ñoä daøi ñoaïn thaúng
+ ABngöôïc höôùng e  AB<0 MN vaø neâu nhaän xeùt? Ñ3. MN = 4 = 3  ( 1  )
+ Neáu A(a), B(b) thì AB=b–a
H4. Xaùc ñònh toaï ñoä trung Ñ4. I(1)
+ AB = AB  AB  b  a ñieåm I cuûa MN?
+ Neáu A(a), B(b), I laø trung  a  b 
ñieåm cuûa AB thì I 2   
Hoaït ñoäng 2: Tìm hieåu veà Toaï ñoä cuûa vectô, cuûa ñieåm trong heä truïc toaï ñoä 17
Nguyễn Đình Khương
Hình Học 10 Cơ Bản
 Cho HS nhaéc laïi kieán thöùc
II. Heä truïc toaï ñoä
ñaõ bieát veà heä truïc toaï ñoä. Sau
a) Ñònh nghóa:
22' ñoù GV giôùi thieäu ñaày ñuû veà
Heä truïc toaï ñoä O; i; j heä truïc toaï ñoä.
O : goác toaï ñoä
Truïc O; i  : truïc hoaønh Ox
Truïc O; j : truïc tung Oy
i, j laø caùc vectô ñôn vò
Heä O; i; j coøn kí hieäu Oxy
Maët phaúng toaï ñoä Oxy.
H1. Nhaéc laïi ñònh lí phaân tích
b) Toaï ñoä cuûa vectô vectô?
u = (x; y) u  xi  yj
Cho u = (x; y), u' = (x; y)
u  u' x  x' 
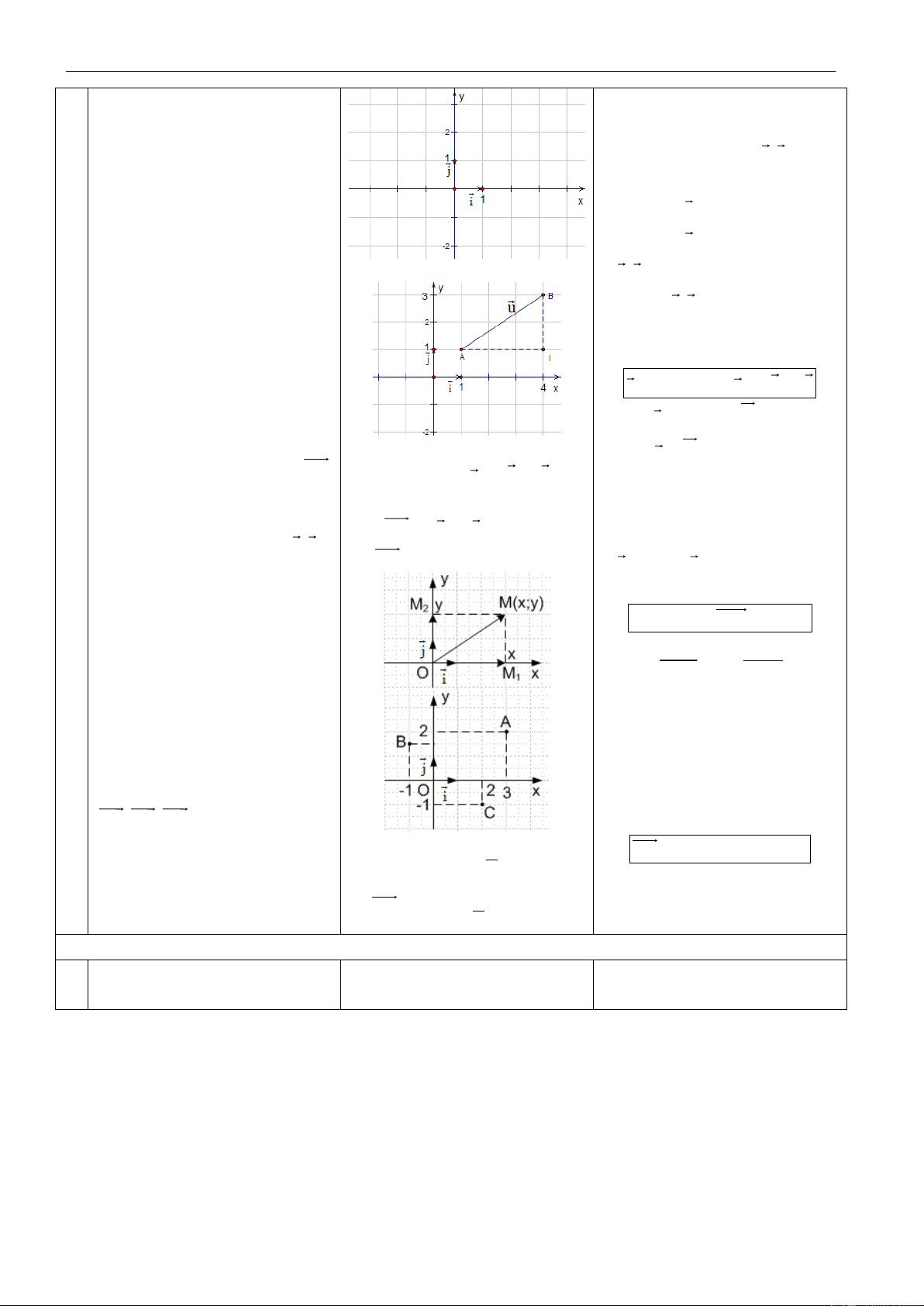
H2. Xaùc ñònh toaï ñoä cuûa AB Ñ1. y  y'
! x, yR: u  xi  yj nhö hình veõ?
Moãi vectô ñöôïc hoaøn toaøn
xaùc ñònh khi bieát toaï ñoä cuûa Ñ2. AB  3i  2 j
H3. Xaùc ñònh toaï ñoä cuûa i, j ? noù  AB = (3;2)
i  (1;0), j  (0;1)
 GV giôùi thieäu khaùi nieäm toaï
c) Toaï ñoä cuûa ñieåm ñoä cuûa ñieåm.
M(x; y) OM = (x; y)
Neáu MM1 Ox, MM2 Oy H4. thì x = 1 OM , y = OM2
a) Xaùc ñònh toaï ñoä caùc ñieåm
Neáu M Ox thì y A, B, C nhö hình veõ? M = 0
M Oy thì xM = 0
b) Veõ caùc ñieåm D(–2; 3),
d) Lieân heä giöõa toaï ñoä cuûa E(0; –4), F(3; 0)?
ñieåm vaø vectô trong maët c) Xaùc ñònh toaï ñoä phaúng AB,BC,CA ?
Cho A(xA; yA), B(xB; yB).
a) A(3; 2), B(–1; 3 ), C(2; –1)
AB = (xB – xA; yB – yA) 2 b) AB = (–3; 1  ) 2
Hoaït ñoäng 3: Cuûng coá
3'  Nhaán maïnh caùc khaùi nieäm
toaï ñoä cuûa vectô vaø cuûa ñieåm
4. BAØI TAÄP VEÀ NHAØ:  Baøi 1, 2, 3, 4, 5 SGK.
 Ñoïc tieáp baøi "Heä truïc toaï ñoä" Ngaøy soaïn: 1/11/2012 Chöông I: VECTÔ Tieát daïy: 10
Baøøi 4: HEÄ TRUÏC TOAÏ ÑOÄ (tt) 18
Nguyễn Đình Khương
Hình Học 10 Cơ Bản I. MUÏC TIEÂU: Kieán thöùc:
 Naém ñöôïc ñònh nghóa vaø caùc tính chaát veà toaï ñoä cuûa vectô vaø cuûa ñieåm. Kó naêng:
 Bieát bieåu dieãn caùc ñieåm vaø caùc vectô baèng caùc caëp soá trong heä truïc toaï ñoä ñaõ cho.
 Bieát tìm toaï ñoä caùc vectô toång, hieäu, tích moät soá vôùi moät vectô.
 Bieát söû duïng coâng thöùc toaï ñoä trung ñieåm cuûa ñoaïn thaúng vaø toaï ñoä troïng taâm tam giaùc. Thaùi ñoä:
 Reøn luyeän tính caån thaän, chính xaùc.
 Gaén kieán thöùc ñaõ hoïc vaøo thöïc teá. II. CHUAÅN BÒ:
Giaùo vieân: Giaùo aùn. Hình veõ minh hoaï.
Hoïc sinh: SGK, vôû ghi. OÂn taäp kieán thöùc vectô ñaõ hoïc.
III. HOAÏT ÑOÄNG DAÏY HOÏC:
1. OÅn ñònh toå chöùc: Kieåm tra só soá lôùp.
2. Kieåm tra baøi cuõ: (3')
H. – Neâu ñònh nghóa toaï ñoä cuûa vectô trong mp Oxy?
– Lieân heä giöõa toaï ñoä cuûa ñieåm vaø cuûa vectô trong mp Oxy?
Ñ. u = (x; y)  u  xi  yj . AB = (xB – xA; yB – yA)
3. Giaûng baøi môùi: TL
Hoaït ñoäng cuûa Giaùo vieân
Hoaït ñoäng cuûa Hoïc sinh Noäi dung
Hoaït ñoäng 1: Tìm hieåu veà Toaï ñoä cuûa caùc vectô u  v,u  v,ku
 HD hoïc sinh chöùng minh
III. Toaï ñoä cuûa caùc vectô
15' moät soá coâng thöùc. u  v,u  v,ku
Cho u =(u1; u2), v =(v1; v2). VD1.
u  v = (u1+ v1 ; u2+v2)
Cho a = (1; –2), b = (3; 4),
u  v = (u1– v1 ; u2–v2)
c = (5; –1). Tìm toaï ñoä cuûa
k u = (ku1; ku2), k R caùc vectô: Ñ. a) u  2a  b  c a) u = (0; 1)
Nhaän xeùt: Hai vectô u =(u1; b) v  a   2b  c b) v = (0; 11)
u2), v =(v1; v2) vôùi v ≠ 0 cuøng c) x  a  2b  3c
phöông k R sao cho: u  kv d) 1 y  3a  b  c 1 1  2 u  2  kv2 VD2.
Cho a = (1; –1), b = (2; 1). Ñ. Giaû söû c  ka  hb
Haõy phaân tích caùc vectô sau = (k + 2h; –k + h) theo a vaø b :  k  2h  4     k 2  a) c = (4; –1) k  h  1  h  1 b) d = (–3; 2)
 GV höôùng daãn caùch phaân tích.
Hoaït ñoäng 2: Tìm hieåu veà Toaï ñoä cuûa trung ñieåm, cuûa troïng taâm
H1. Cho A(1;0), B(3; 0) vaø I Ñ1. I(2;0)
IV. Toaï ñoä cuûa trung ñieåm 19
Nguyễn Đình Khương
Hình Học 10 Cơ Bản
laø trung ñieåm cuûa AB. Bieåu
ñoaïn thaúng, cuûa troïng taâm y
20' dieãn 3 ñieåm A, B, I treân tam giaùc
mpOxy vaø suy ra toaï ñoä ñieåm A I B a) Cho A(x O 1 3 x
A; yA), B(xB; yB). I laø I?
trung ñieåm cuûa AB thì:
 GV höông daãn chöùng minh x  y y  y
coâng thöùc xaùc ñònh toaï ñoä xI = A A , yI = A B Ñ2. 2 2
trung ñieåm vaø troïng taâm.
a) I laø trung ñieåm cuûa AB
b) Cho ABC vôùi A(xA; yA),
H2. Neâu heä thöùc trung ñieåm
B(xB; yB), C(xC; yC). G laø troïng
cuûa ñoaïn thaúng vaø troïng taâm   OA OB OI 
taâm cuûa ABC thì: cuûa tam giaùc? 2  x  x  x A B C x  G  3
b) G laø troïng taâm cuûa ABC  y  A  yB  yC   y   OA OB OC OG  G  3
VD: Cho tam giaùc ABC coù 3
A(–1;–2), B(3;2), C(4;–1). Ñ.
a) Tìm toaï ñoä trung ñieåm I  7 1  a) I  ; cuûa BC. 2 2   
b) Tìm toaï ñoä troïng taâm G cuûa ABC. b) G(2; 1  ) 3
c) Tìm toaï ñoä ñieåm M sao cho c) OM  2OBOA  M(7;6) MA  2MB.
Hoaït ñoäng 3: Cuûng coá
 Nhaán maïnh caùch xaùc ñònh
5' toaï ñoä cuûa vectô, cuûa ñieåm. Caâu hoûi:
Cho ABC coù A(1;2), B(–2;1)
vaø C(3;3). Tìm toaï ñoä:  2 
a) Troïng taâm G cuûa ABC. a) G ;2 3   
b) Ñieåm D sao cho ABCD laø b) D(6; 4) hình bình haønh.
4. BAØI TAÄP VEÀ NHAØ:  Baøi 6, 7, 8 SGK. Ngaøy soaïn:5 /11/2012 Chöông I: VECTÔ Tieát daïy: 11
Baøøi 4: BAØI TAÄP HEÄ TRUÏC TOAÏ ÑOÄ I. MUÏC TIEÂU: 20
Nguyễn Đình Khương
Hình Học 10 Cơ Bản Kieán thöùc:
 Cuûng coá caùc kieán thöùc veà vectô, toaï ñoä cuûa vectô vaø cuûa ñieåm.
 Caùch xaùc ñònh toaï ñoä cuûa trung ñieåm ñoaïn thaúng, troïng taâm cuûa tam giaùc. Kó naêng:
 Thaønh thaïo vieäc xaùc ñònh toaï ñoä cuûa vectô, cuûa ñieåm.
 Thaønh thaïo caùch xaùc ñònh toaï ñoä vectô toång, hieäu, tích moät vectô vôùi moät soá.
 Vaän duïng vectô vaø toaï ñoä ñeå giaûi toaùn hình hoïc. Thaùi ñoä:
 Reøn luyeän tính caån thaän, chính xaùc. II. CHUAÅN BÒ:
Giaùo vieân: Giaùo aùn. Heä thoáng baøi taäp.
Hoïc sinh: SGK, vôû ghi. OÂn taäp caùc kieán thöùc ñaõ hoïc veà vectô vaø toaï ñoä.
III. HOAÏT ÑOÄNG DAÏY HOÏC:
1. OÅn ñònh toå chöùc: Kieåm tra só soá lôùp.
2. Kieåm tra baøi cuõ: (Loàng vaøo quaù trình luyeän taäp) H. Ñ.
3. Giaûng baøi môùi: TL
Hoaït ñoäng cuûa Giaùo vieân
Hoaït ñoäng cuûa Hoïc sinh Noäi dung
Hoaït ñoäng 1: Söû duïng toaï ñoä ñeå xeùt quan heä phöông, höôùng cuûa caùc vectô
H1. Nhaéc laïi ñieàu kieän ñeå hai Ñ1.
1. Xeùt quan heä phöông, höôùng
10' vectô cuøng phöông, cuøng a) a vaø i ngöôïc höôùng cuûa caùc vectô:
höôùng, baèng nhau, ñoái nhau? b) a vaø b ñoái nhau
a) a = (–3; 0) vaø i = (1; 0) c) khoâng coù quan heä gì
b) a = (3; 4) vaø b = (–3; –4) c) a = (5; 3) vaø b = (3; 5) Ñ2.
2. Cho u = (3; –2), v = (1; 6).
a) u + v = (4; 4) vaø a khoâng Xeùt quan heä phöông, höôùng coù quan heä cuûa caùc vectô:
b) u – v = (2; –8) vaø b cuøng a) u + v vaø a = (–4; 4) höôùng
b) u – v vaø b = (6; –24)
c) 2 u + v = (7; 2) vaø v khoâng c) 2 u + v vaø v coù quan heä Ñ3.
3. Cho A(1; 1), B(–2; –2),
AB = (–3; –3), AC = (6; 6)
C(7; 7). Xeùt quan heä giöõa 3
 AC = –2 AB  A, B, C ñieåm A, B, C. thaúng haøng.
Hoaït ñoäng 2: Luyeän taäp caùc pheùp toaùn vectô döïa vaøo toaï ñoä
H1. Nhaéc laïi caùch xaùc ñònh Ñ1.
3. Cho a = (x; 2), b = (–5; 1),
15' toaï ñoä vectô toång, hieäu, tích c = 2a + 3 b = (2x – 15; 7)
c = (x; 7). Tìm x ñeå c = 2 a +
moät vectô vôùi moät soá? c = (x; 7)  x = 15 3 b .
Ñ2. Giaû söû c = h a + k b
4. Cho a = (2; –2), b = (1; 4). 21
Nguyễn Đình Khương
Hình Học 10 Cơ Bản
Haõy phaân tích vectô c =(5; 0)   2h  k  5     h 2   2  h  4k  0 k  1 theo hai vectô a vaø b .  c = 2 a + b
Hoaït ñoäng 3: Vaän duïng vectô–toaï ñoä ñeå giaûi toaùn hình hoïc
H1. Nhaéc laïi caùch xaùc ñònh
5. Cho caùc ñieåm M(–4; 1), A D
15' toaï ñoä trung ñieåm ñoaïn thaúng
N(2; 4), P(2; –2) laàn löôït laø
vaø troïng taâm tam giaùc? P N
trung ñieåm cuûa caùc caïnh BC, CA, AB cuûa ABC.
a) Tính toaï ñoä caùc ñænh cuûa B M C ABC. a) NA  MP  A(8; 1)
b) Tìm toaï ñoä ñieåm D sao cho MB  NP  B(–4; 5) ABCD laø hình bình haønh. MC  PN  C(–4; 7)
c) CMR troïng taâm cuûa caùc b) AD  BC  D(8; 3)
tam giaùc MNP vaø ABC truøng c) G(0; 1) nhau.
Hoaït ñoäng 4: Cuûng coá  Nhaán maïnh
5' – Caùc kieán thöùc cô baûn veà vectô – toaï ñoä.
– Caùch vaän duïng vectô–toaï ñoä ñeå giaûi toaùn.
4. BAØI TAÄP VEÀ NHAØ:
 Laøm caùc baøi taäp coøn laïi.
 Baøi taäp oân chöông I. Ngaøy soaïn: 10/11/2012 Chöông I: VECTÔ Tieát daïy: 12
Baøøi daïy: OÂN TAÄP CHÖÔNG I I. MUÏC TIEÂU: Kieán thöùc: 22
Nguyễn Đình Khương
Hình Học 10 Cơ Bản
 Naém laïi toaøn boä kieán thöùc ñaõ hoïc veà vectô vaø toaï ñoä. Kó naêng:
 Bieát vaän duïng caùc tính chaát cuûa vectô trong vieäc giaûi toaùn hình hoïc.
 Vaän duïng moät soá coâng thöùc veà toaï ñoä ñeå giaûi moät soá baøi toaùn hình hoïc. Thaùi ñoä:
 Reøn luyeän tính caån thaän, chính xaùc. II. CHUAÅN BÒ:
Giaùo vieân: Giaùo aùn. Heä thoáng baøi taäp.
Hoïc sinh: SGK, vôû ghi. OÂn taäp caùc kieán thöùc ñaõ hoïc veà vectô vaø toaï ñoä.
III. HOAÏT ÑOÄNG DAÏY HOÏC:
1. OÅn ñònh toå chöùc: Kieåm tra só soá lôùp.
2. Kieåm tra baøi cuõ: (Loàng vaøo quaù trình oân taäp) H. Ñ.
3. Giaûng baøi môùi: TL
Hoaït ñoäng cuûa Giaùo vieân
Hoaït ñoäng cuûa Hoïc sinh Noäi dung
Hoaït ñoäng 1: Luyeän kyõ naêng thöïc hieän caùc pheùp toaùn vectô
H1. Döïa vaøo tính chaát naøo ?
Ñ1. Tính chaát trung ñieåm.
1. Cho tam giaùc ñeàu ABC noäi 20'
tieáp trong ñöôøng troøn taâm O.
Haõy xaùc ñònh caùc ñieåm M, N,
H2. Nhaän xeùt tính chaát cuûa Ñ2. OM OA OB OC P sao cho: tam giaùc ñeàu?
 M ñoái xöùng vôùi C qua O.
a) OM OA OB
b) ON OB OC
c) OP OC OA
2. Cho 6 ñieåm M, N, P, Q, R,
H3. Söû duïng caùch bieán ñoåi Ñ3. Qui taéc 3 ñieåm.
S baát kì. Chöùng minh raèng: naøo? O
MP NQ RS MS NP RQ N M
3. Cho OAB. Goïi M, N laàn A B
löôït laø trung ñieåm cuûa OA vaø 1
OB. Tìm caùc soá m, n sao cho: OM OA 2
a) OM mOA nOB 1
b) AN mOA nOB
AN OB OA 2
c) MN mOA nOB 1 1
d) MB mOA nOB
MN OB OA 2 2 1
MB   OA OB 2
Hoaït ñoäng 2: Luyeän kyõ naêng vaän duïng toaï ñoä ñeå giaûi toaùn
H1. Neâu ñieàu kieän ñeå DABC Ñ1.
4. Cho ABC vôùi A(3; 1), B(– 20' laø hình bình haønh?
DABC laø hbh  AD BC 1; 2), C(0; 4).
a) Tìm ñieåm D ñeå DABC laø
H2. Neâu coâng thöùc xaùc ñònh Ñ2. hình bình haønh. 23
Nguyễn Đình Khương
Hình Học 10 Cơ Bản
toaï ñoä troïng taâm tam giaùc?  y b) Tìm troïng taâm G cuûa
A yB C y  G y  3 ABC.  xA xB   C x c) Tìm hai soá m n sao cho: G x   3
mAB nAC  0 5.
H3. Neâu ñieàu kieän xaùc ñònh Ñ3. B laø trung ñieåm cuûa AC. a) Cho A(2; 3), B(–3; 4). Tìm ñieåm C?
ñieåm C bieát C ñoái xöùng vôùi A qua B.
H4. Neâu ñieàu kieän ñeå 3 ñieåm Ñ4. A , B AC cuøng phöông. b) Cho A(1; –2), B(4; 5), thaúng haøng?
C(3m; m–1). Xaùc ñònh m ñeå A, B, C thaúng haøng.
6. Cho a =(2; 1), b = (3; –4), c = (–7; 2). a) Tìm toaï ñoä cuûa:
Ñ5. Tìm caùc soá k vaø h sao
u  3a  2b  4c
H5. Neâu caùch phaân tích moät cho:
b) Tìm toaï ñoä cuûa x : vectô theo 2 vectô khoâng
c ka hb
x a b c cuøng phöông?
c) Phaân tích c theo a vaø b .
Hoaït ñoäng 3: Cuûng coá
 Nhaán maïnh caùch vaän duïng
3' caùc kieán thöùc veà vectô vaø toaï ñoä ñeå giaûi toaùn.
4. BAØI TAÄP VEÀ NHAØ:
 Chuaån bò kieåm tra 1 tieát chöông I Ngaøy soaïn: 15/11/2012 Chöông I: VECTÔ Tieát daïy: 13
Baøøi daïy: KIEÅM TRA VIEÁT CHÖÔNG I I. MUÏC TIEÂU: Kieán thöùc:
 Cuûng coá caùc kieán thöùc veà vectô vaø toaï ñoä. Kó naêng: 24
Nguyễn Đình Khương
Hình Học 10 Cơ Bản
 Thöïc hieän caùc pheùp toaùn veà vectô.
 Vaän duïng toaï ñoä ñeå giaûi toaøn hình hoïc. Thaùi ñoä:
 Reøn luyeän tính caån thaän, chính xaùc. II. CHUAÅN BÒ:
Giaùo vieân: Giaùo aùn. Ñeà kieåm tra.
Hoïc sinh: OÂn taäp kieán thöùc chöông I. III. MA TRAÄN ÑEÀ: Nhaän bieát Thoâng hieåu Vaän duïng Chuû ñeà Toång TNKQ TL TNKQ TL TNKQ TL Vectô 2 2 1 1 5 0,5 0,5 1,5 1,5 Toaï ñoä 2 2 1 1 5 0,5 0,5 1,0 2,0 Toång 2 2 2,5 3,5 10
IV. NOÄI DUNG ÑEÀ KIEÅM TRA:
A. Phaàn traéc nghieäm: (4 ñieåm) Choïn caâu traû lôøi ñuùng nhaát.
Caâu 1. Cho töù giaùc ABCD. Soá caùc vectô khaùc vectô–khoâng coù ñieåm ñaàu vaø ñieåm cuoái laø caùc ñænh cuûa töù giaùc baèng: A) 20 B) 16 C) 12 D) 6
Caâu 2. Xaùc ñònh vò trí cuûa 3 ñieåm A, B, C thoaû heä thöùc: AB  CA A) C truøng B B) ABC caân C) A truøng B
D) A laø trung ñieåm cuûa BC.
Caâu 3. Cho hình bình haønh ABCD. Ñaúng thöùc naøo sau ñaây laø ñuùng: A) AB AD  AC B) AB AC  AD C) AB BC  CA D) AB  CD
Caâu 4. Cho ABC coù troïng taâm G. M laø moät ñieåm tuyø yù. Ñaúng thöùc naøo sau ñaây laø ñuùng: A) MA  MB MC  0 B) AM BMCM  3GM C) AB AC  2AG D) MA  MB  2MG
Caâu 5. Cho 3 ñieåm A(1; 1), B(–1; –1), C(6; 6). Khaúng ñònh naøo sau ñaây laø ñuùng:
A) G(2; 2) laø troïng taâm cuûa ABC
B) B laø trung ñieåm cuûa AC
C) C laø trung ñieåm cuûa AB.
D) ABvaø AC ngöôïc höôùng.
Caâu 6. Cho hai ñieåm M(8; –1), N(3; 2). Toaï ñoä cuûa ñieåm P ñoái xöùng vôùi ñieåm M qua ñieåm N laø:  11 1  A) (–2; 5) B)  ; C) (13; –4) D) (11; –1) 2 2   
Caâu 7. Cho hai ñieåm A(4; 0), B(0; –8). Toaï ñoä cuûa ñieåm C thoaû: CA  3  CB laø: A) (–3; 7) B) (1; –6) C) (–2; –12) D) (3; –1)
Caâu 8. Cho hai vectô a = (2; –4), b = (–5; 3). Toaï ñoä cuûa vectô u  2a  b laø: A) (7; –7) B) (9; –5) C) (9; –11) D) (–1; 5)
B. Phaàn töï luaän: (6 ñieåm)
Caâu 9. (3 ñieåm) Cho ABC vaø ñieåm M thoaû heä thöùc: BM  2MC . a) Chöùng minh raèng: 1 2 AM  AB AC 3 3
b) Goïi BN laø trung tuyeán cuûa ABC, I laø trung ñieåm cuûa BN.
Chöùng minh raèng: MA  2MB MC  4MI.
Caâu 10. (3 ñieåm) Cho ABC coù A(3; 1), B(–1; 2), C(0; 4). 25
Nguyễn Đình Khương
Hình Học 10 Cơ Bản
a) Tìm ñieåm D ñeå töù giaùc ABCD laø hình bình haønh.
b) Tìm troïng taâm G cuûa ABC.
V. ÑAÙP AÙN VAØ BIEÅU ÑIEÅM:
A. Phaàn traéc nghieäm: 1 C 2 D 3 A 4 B 5 D 6 A 7 B 8 C B. Töï luaän:
Caâu 9: a) BM  2MC  AM  AB  2(AC  AM) (0,5 ñieåm)  3AM  AB 2AC (0,5 ñieåm) A  ñpcm. (0,5 ñieåm) b) MA  MC  2MN (0,5 ñieåm) N I MB MN  2MI (0,5 ñieåm) B M C  MA  2MB MC  4MI (0,5 ñieåm) 
Caâu 10: a) AD  (x 3;y 1)  (0,5 ñieåm) BC  (1;2)
ABCD laø hình bình haønh  AD  BC (0,5 ñieåm)  x  3  1  (0,5 ñieåm) y 1  2  x  4   D(4; 3) (0,5 ñieåm) y  3  xA  xB  xC  3 1 0 2 x  G  xG      b) 3   3 3  G 2 7  ; (1 ñieåm) y    A  yB  yC 1 2  4 7 y y    3 3  G   3 G  3 3 Ngaøy soaïn: 20/11/2012
Chöông II: TÍCH VOÂ HÖÔÙNG CUÛA HAI VECTÔ & ÖÙNG DUÏNG Tieát daïy: 14
Baøøi 1: GIAÙ TRÒ LÖÔÏNG GIAÙC CUÛA MOÄT GOÙC BAÁT KÌ TÖØ 00 ÑEÁN 1800 I. MUÏC TIEÂU: Kieán thöùc:
 Naém ñöôïc ñònh nghóa vaø tính chaát cuûa caùc GTLG cuûa caùc goùc töø 00 ñeán 1800 vaø moái quan heä giöõa chuùng. 26
Nguyễn Đình Khương
Hình Học 10 Cơ Bản
 Nhôù ñöôïc baûng caùc giaù trò löôïng giaùc cuûa caùc goùc ñaëc bieät.
 Naém ñöôïc khaùi nieäm goùc giöõa hai vectô. Kó naêng:
 Vaän duïng ñöôïc baûng caùc giaù trò löôïng giaùc cuûa caùc goùc ñaëc bieät.
 Xaùc ñònh ñöôïc goùc giöõa hai vectô. Thaùi ñoä:
 Reøn luyeän tính caån thaän, chính xaùc. II. CHUAÅN BÒ:
Giaùo vieân: Giaùo aùn. Hình veõ minh hoaï.
Hoïc sinh: SGK, vôû ghi. OÂn taäp kieán thöùc ñaõ hoïc veà tæ soá löôïng giaùc cuûa goùc nhoïn.
III. HOAÏT ÑOÄNG DAÏY HOÏC:
1. OÅn ñònh toå chöùc: Kieåm tra só soá lôùp.
2. Kieåm tra baøi cuõ: (3')
H. Nhaéc laïi caùc tæ soá löôïng giaùc cuûa goùc nhoïn? Ñ. sin = ñoái ;
cos = keà ; tan = ñoái ; cot = keà huyeàn huyeàn keà ñoái
3. Giaûng baøi môùi: TL
Hoaït ñoäng cuûa Giaùo vieân
Hoaït ñoäng cuûa Hoïc sinh Noäi dung
Hoaït ñoäng 1: Tìm hieåu ñònh nghóa caùc giaù trò löôïng giaùc cuûa goùc (00 1800)  Trong mpOxy, cho nöûa y I. Ñònh nghóa
15' ñöôøng troøn ñôn vò taâm O. Xeùt
sin = y (tung ñoä) goùc nhoïn  = y M xOM . Giaû söû 
cos = x (hoaønh ñoä) M(x x   0, y0). O 1 -1 x
tan = y tungñoä   x  hoaønhñoä
H1. Tính sin, cos, tan,
cot = x  hoaønhñoä cot Ñ1. sin = y = y   OM y  tungñoä   Chuù yù:
 Töø ñoù môû roäng ñònh nghóa cos = x = x OM
+ Neáu tuø thì vôùi 00    1800.
cos < 0, tan < 0, cot < 0
+ tan xaùc ñònh khi 900
H2. Nhaän xeùt tung ñoä, hoaønh Ñ2.  = 00  x = 1; y = 0
+ cot xaùc ñònh khi 00 vaø
ñoä cuûa M khi  = 00; 900; 1800
 = 1800  x = –1; y =  1800. 0  = 900  x = 0; y = 1
VD. Tính sin1800, cos1800, tan1800, cot1800.
 sin1800 = 0; cos1800 = –1; tan1800 = 0; cot1800 = //
Hoaït ñoäng 2: Tìm hieåu GTLG cuûa caùc goùc coù lieân quan ñaëc bieät
H1. Nhaéc laïi tæ soá löôïng giaùc Ñ1. sin cuûa goùc naøy baèng cos II. Tính chaát
20' cuûa caùc goùc phuï nhau? cuûa goùc kia. 1. Goùc phuï nhau sin(900 – ) = cos y cos(900 – ) = sin tan(900 – ) = cot y N M  cot(900 – ) = tan  Cho xOM = , -x O x 1 -1 x 2. Goùc buø nhau 27
Nguyễn Đình Khương
Hình Học 10 Cơ Bản xON = 1800 –  sin(1800 – ) = sin
H2. Nhaän xeùt hoaønh ñoä, tung Ñ2. x
cos(1800 – ) = – cos N = –xM; yN = yM ñoä cuûa M, N ?
tan(1800 – ) = – tan
cot(1800 – ) = – cot
VD: Gheùp caëp caùc giaù trò ôû
coät A vôùi caùc giaù trò ôû coät B: A B sin500 = cos400 sin500 –tan450 cos420 = sin480 cos420 cos400 tan1200 = –tan600 tan1200 sin300 sin1500 = sin300 sin1500 sin480 tan1350 = –tan450 tan1350 –tan600
Hoaït ñoäng 3: Cuûng coá  Nhaán maïnh 5' + Ñònh nghóa caùc GTLG
+ GTLG caùc goùc lieân quan ñb
Caâu hoûi: Tính caùc GTLG cuûa  Chia moãi nhoùm tính caùc
caùc goùc 1200, 1350, 1500. GTLG cuûa moät goùc.
4. BAØI TAÄP VEÀ NHAØ:  Baøi 1, 2, 3 SGK. Ngaøy soaïn: 25/11/2012
Chöông II: TÍCH VOÂ HÖÔÙNG CUÛA HAI VECTÔ & ÖÙNG DUÏNG Tieát daïy: 14
Baøøi 1: GIAÙ TRÒ LÖÔÏNG GIAÙC CUÛA MOÄT GOÙC BAÁT KÌ
TÖØ 00 ÑEÁN 1800 (tt) I. MUÏC TIEÂU: Kieán thöùc:
 Naém ñöôïc ñònh nghóa vaø tính chaát cuûa caùc GTLG cuûa caùc goùc töø 00 ñeán 1800 vaø moái quan heä giöõa chuùng.
 Nhôù ñöôïc baûng caùc giaù trò löôïng giaùc cuûa caùc goùc ñaëc bieät.
 Naém ñöôïc khaùi nieäm goùc giöõa hai vectô. 28
Nguyễn Đình Khương
Hình Học 10 Cơ Bản Kó naêng:
 Vaän duïng ñöôïc baûng caùc giaù trò löôïng giaùc cuûa caùc goùc ñaëc bieät.
 Xaùc ñònh ñöôïc goùc giöõa hai vectô. Thaùi ñoä:
 Reøn luyeän tính caån thaän, chính xaùc. II. CHUAÅN BÒ:
Giaùo vieân: Giaùo aùn. Hình veõ minh hoaï.
Hoïc sinh: SGK, vôû ghi. OÂn taäp kieán thöùc ñaõ hoïc veà tæ soá löôïng giaùc cuûa goùc nhoïn.
III. HOAÏT ÑOÄNG DAÏY HOÏC:
1. OÅn ñònh toå chöùc: Kieåm tra só soá lôùp.
2. Kieåm tra baøi cuõ: (3')
H. Nhaéc laïi coâng thöùc löôïng giaùc cuûa caùc goùc buø nhau?
Ñ. sin(1800 – ) = sin; cos(1800 – ) = –cos;
tan(1800 – ) = –tan; cot(1800 –) =–cot
3. Giaûng baøi môùi: TL
Hoaït ñoäng cuûa Giaùo vieân
Hoaït ñoäng cuûa Hoïc sinh Noäi dung
Hoaït ñoäng 1: Tìm hieåu baûng GTLG cuûa caùc goùc ñaëc bieät
 Cho HS ñieàn vaøo baûng giaù III. Giaù trò löôïng giaùc cuûa caùc goùc ñaëc bieät
10' trò löôïng giaùc cuûa caùc goùc ñaëc 00 300 450 600 900 bieät. sin 0 1 2 3 1 2 2 2
 GV höôùng daãn HS caùch laäp baûng cos 1 3 2 1 0 2 2 2 tan 0 3 1 3  3 cot  3 1 3 0 3
Hoaït ñoäng 2: Tìm hieåu khaùi nieäm goùc giöõa hai vectô
 GV giôùi thieäu ñònh nghóa a b
IV. Goùc giöõa hai vectô
10' goùc giöõa hai vectô a , b . A a 1. Ñònh nghóa O
Cho a,b  0. OA  a,OB  b . b B a,b  AOB C
vôùi 00 AOB 1800. A 600
+ a,b = 900 a  b 1200 1200
+ a,b = 00 a,b cuøng B
VD. Cho ABC ñeàu. Xaùc höôùng
ñònh goùc giöõa caùc caëp vectô: a) 600 b) 1200
c) 1200 + a,b = 1800 a,b ngöôïc a) AB,AC b) AB,BC höôùng c) AB,CA .
Hoaït ñoäng 3: Höôùng daãn söû duïng MTBT ñeå tính GTLG cuûa moät goùc
 GV höôùng daãn HS caùch söû  HS veà nhaø thöïc haønh, ñoái V. Söû duïng MTBT ñeå tính
15' duïng MTBT döïa vaøo höôùng chieáu vôùi pheùp tính. GTLG cuûa moät goùc
daãn cuûa SGK vaø baûng höôùng
1. Tính caùc GTLG cuûa goùc daãn cuûa MTBT. 29
Nguyễn Đình Khương
Hình Học 10 Cơ Bản
VD1. Tính sin63052'41'' sin63052'41''  0,8979
VD2. Tìm x bieát sinx = 0,3502 x  20029'58''
2. Xaùc ñònh ñoä lôùn cuûa goùc
khi bieát GTLG cuûa goùc ñoù
 Chia nhoùm thöïc haønh vôùi  Caùc nhoùm thöïc haønh vaø ñoái MTBT. chieáu keát quaû.
Hoaït ñoäng 4: Cuûng coá  Nhaán maïnh
5' + Baûng giaù trò ñaëc bieät
+ Caùch xaùc ñònh goùc giöõa hai vectô
4. BAØI TAÄP VEÀ NHAØ:  Baøi 4, 5, 6 SGK. Ngaøy soaïn: 25/11/2012
Chöông II: TÍCH VOÂ HÖÔÙNG CUÛA HAI VECTÔ & ÖÙNG DUÏNG Tieát daïy: 15
Baøøi 1: BAØI TAÄP GIAÙ TRÒ LÖÔÏNG GIAÙC CUÛA
MOÄT GOÙC BAÁT KÌ TÖØ 00 ÑEÁN 1800 I. MUÏC TIEÂU: Kieán thöùc:
 Cuûng coá caùc kieán thöùc veà GTLG cuûa moät goùc  (00    1800), vaø moái lieân quan giöõa chuùng.
 Caùch xaùc ñònh goùc giöõa hai vectô. Kó naêng:
 Bieát söû duïng baûng giaù trò löôïng giaùc cuûa caùc goùc ñaëc bieät ñeå tính GTLG cuûa moät goùc. 30
Nguyễn Đình Khương
Hình Học 10 Cơ Bản
 Bieát xaùc ñònh goùc giöõa hai vectô. Thaùi ñoä:
 Reøn luyeän tính caån thaän, chính xaùc.
 Luyeän tö duy linh hoaït thoâng qua vieäc xaùc ñònh goùc giöõa hai vectô. II. CHUAÅN BÒ:
Giaùo vieân: Giaùo aùn. Heä thoáng baøi taäp.
Hoïc sinh: SGK, vôû ghi. OÂn taäp caùc kieán thöùc veà GTLG cuûa moät goùc.
III. HOAÏT ÑOÄNG DAÏY HOÏC:
1. OÅn ñònh toå chöùc: Kieåm tra só soá lôùp.
2. Kieåm tra baøi cuõ: (Loàng vaøo quaù trình luyeän taäp)
3. Giaûng baøi môùi: TL
Hoaït ñoäng cuûa Giaùo vieân
Hoaït ñoäng cuûa Hoïc sinh Noäi dung
Hoaït ñoäng 1: Tính giaù trò löôïng giaùc cuûa moät goùc
H1. Cho bieát giaù trò löôïng Ñ1.
1. Tính giaù trò cuûa caùc bieåu
giaùc cuûa caùc goùc ñaëc bieät ? thöùc sau: 15' a) 3 b) 1 2
a) cos300cos600 + sin300sin600 c) 0 d) 1 b) sin300cos600 +
H2. Neâu coâng thöùc GTLG cuûa cos300sin600
caùc goùc phuï nhau, buø nhau ? e) 6  4 c) cos00 + cos200+…+cos1800 d) tan100.tan800 e) sin1200.cos1350
H3. Chæ ra moái quan heä giöõa Ñ3.
caùc goùc trong tam giaùc ? + A + (B + C) = 1800
2. Chöùng minh raèng trong tam giaùc ABC, ta coù:
+ A + B C = 900 a) sinA = sin(B + C) 2 2 b) cosA = – cos(B + C)
c) sin A = cos B C 2 2
d) cos A = sin B C 2 2
Hoaït ñoäng 2: Vaän duïng caùc coâng thöùc löôïng giaùc
H1. Nhaéc laïi ñònh nghóa caùc Ñ1. sin = y, cos = x 3. Chöùng minh: 10' GTLG ?
a) sin2 + cos2 = OM2 = 1 a) sin2 + cos2 = 1 2 sin  1 b) 1 + tan2 = 1 + b) 1 + tan2 = 2 cos  2 cos  2 2 1 = cos   sin  c) 1 + cot2 = 2 2 sin cos   2 c) 1 + cot2 cos   = 1 + 2 sin 
H2. Neâu coâng thöùc lieân quan Ñ2. sin2x + cos2x = 1
4. Cho cosx = 1 . Tính giaù trò giöõa sinx vaø cosx ? 3  sin2x = 1 – cos2x = 8 cuûa bieåu thöùc: 9 P = 3sin2x + cos2x. 31
Nguyễn Đình Khương
Hình Học 10 Cơ Bản  P = 25 9
Hoaït ñoäng 3: Luyeän caùch xaùc ñònh goùc giöõa hai vectô A B
4. Cho hình vuoâng ABCD. 5' Tính: D C
a) cos AC,BA
H1. Xaùc ñònh goùc giöõa caùc Ñ1.
b) sin AC,BD caëp vectô ?
a)  AC,BA = 1350 c) cos A , B CD
b)  AC,BD = 900 c)  A , B CD = 1800
Hoaït ñoäng 4: Vaän duïng löôïng giaùc ñeå giaûi toaùn hình hoïc
 Höôùng daãn HS vaän duïng caùc O
5. Cho AOB caân taïi O vaø
10' tæ soá löôïng giaùc cuûa goùc nhoïn. K  OA = a. OH vaø AK laø caùc a
ñöôøng cao. Giaû söû AOH = . A H B
Tính AK vaø OK theo a vaø .
H1. Ñeå tính AK vaø OK ta caàn Ñ1. Xeùt tam giaùc vuoâng AOH
xeùt tam giaùc vuoâng naøo ?
vôùi OA = a, AOK = 2.  AK = OA.sin AOK = a.sin2
OK = OA.cos AOK = a.cos2
Hoaït ñoäng 5: Cuûng coá
3' Nhaán maïnh caùch vaän duïng
caùc kieán thöùc ñaõ hoïc.
4. BAØI TAÄP VEÀ NHAØ:
 Ñoïc tröôùc baøi "Tích voâ höôùng cuûa hai vectô" Ngaøy soaïn: 5/12/2012
Chöông II: TÍCH VOÂ HÖÔÙNG CUÛA HAI VECTÔ & ÖÙNG DUÏNG Tieát daïy: 19
Baøøi 2: TÍCH VOÂ HÖÔÙNG CUÛA HAI VECTÔ I. MUÏC TIEÂU: Kieán thöùc:
 Naém ñöôïc ñònh nghóa vaø tính chaát cuûa tích voâ höôùng cuûa hai vectô cuøng vôùi yù nghóa vaät lí cuûa tích voâ höôùng. Kó naêng:
 Bieát söû duïng bieåu thöùc toaï ñoä cuûa tích voâ höôùng ñeå tính ñoä daøi cuûa moät vectô, khoaûng
caùch giöõa hai ñieåm, goùc giöõa hai vectô vaø chöùng minh hai vectô vuoâng goùc. Thaùi ñoä: 32
Nguyễn Đình Khương
Hình Học 10 Cơ Bản
 Reøn luyeän tính caån thaän, chính xaùc. II. CHUAÅN BÒ:
Giaùo vieân: Giaùo aùn. Hình veõ minh hoaï.
Hoïc sinh: SGK, vôû ghi. OÂn taäp caùch xaùc ñònh goùc giöõa hai vectô.
III. HOAÏT ÑOÄNG DAÏY HOÏC:
1. OÅn ñònh toå chöùc: Kieåm tra só soá lôùp.
2. Kieåm tra baøi cuõ: (3')
H. Neâu caùch xaùc ñònh goùc giöõa hai vectô?
Ñ.a,b  AOB , vôùi a O , A b OB.
3. Giaûng baøi môùi: TL
Hoaït ñoäng cuûa Giaùo vieân
Hoaït ñoäng cuûa Hoïc sinh Noäi dung
Hoaït ñoäng 1: Tìm hieåu ñònh nghóa tích voâ höôùng cuûa hai vectô
 Cho löïc F taùc ñoäng leân moät I. Ñònh nghóa
10' vaät taïi ñieåm O vaø laøm cho vaät F
Cho a,b  0 .
ñoù di chuyeån moät quaõng  .
a b a . b cosa,b
ñöôøng OO thì coâng A cuûa löïc O O’ a
F ñöôïc tính theo coâng thöùc: Neáu 0  thì . a b = 0 b  0
A = F . OO .cos A Chuù yù:
GV giôùi thieäu ñònh nghóa
a) Vôùi a,b  0 , ta coù:
VD. Cho ABC ñeàu caïnh B H C .
a b  0  a b
baèng a. Veõ ñöôøng cao AH. 2 a Tính: a) A . B AC = a.a.cos600 = b) 2 2 a a 2 a) A . B AC b) A . B BC b) A . B BC = a.a.cos1200=– c) AH.BC 2 a 2 c) AH.BC = 0
Hoaït ñoäng 2: Tìm hieåu tính chaát cuûa tích voâ höôùng
II. Caùc tính chaát cuûa tich voâ
15'  GV giaûi thích caùc tính chaát höôùng cuûa tích voâ höôùng. b
Vôùi a,b,c baát kì vaø kR: a b + .
a b b.a a
a,bnhoïn
a,btuø
+ a b c   a.b a.c
+ ka.b k a.b  a.kb b + 2 2
a  0; a  0  a  0 a
a b2 2 2
a  2a.b b
a,bvuoâng
a b2 2 2
a  2a.b b 2 2
Ñ. Phuï thuoäc vaø cos a,b
a b  a ba b H. Daáu cuûa .
a b phuï thuoäc vaø  .
a b > 0 a,b nhoïn yeáu toá naøo ? .
a b < 0 a,b tuø .
a b = 0 a,b vuoâng 33
Nguyễn Đình Khương
Hình Học 10 Cơ Bản
 GV giaûi thích yù nghóa coâng F F 1
thöùc tính coâng cuûa moät löïc. A  F2 B  F  1 F  2 F A = F.AB =  1 F  2 F AB = 2 F .AB
Hoaït ñoäng 3: AÙp duïng tính tích voâ höôùng cuûa hai vectô
 Chia nhoùm luyeän taäp. Ví duï: 12' A
1) Cho ABC vuoâng ôû A, AB C = c, AC = b. Tính: b a) . BA BC
H. Xaùc ñònh goùc cuûa caùc caëp A c B B a C b) C . A CB vectô ? Ñ. c) B . A AC c 1a) cos( B , A BC ) = d) . CA AB 2 2 b c
2) Cho ABC ñeàu caïnh a.  . BA BC = c2 Tính: 2 2) 3aA .
B BC BC.CA C . A AB 2
Hoaït ñoäng 4: Cuûng coá  Nhaán maïnh:
3' – Caùch xaùc ñònh goùc giöõa hai vectô.
– Caùch tính tích voâ höôùng
4. BAØI TAÄP VEÀ NHAØ:  Baøi 1, 2, 3 SGK Ngaøy soaïn: 10/12/2012
Chöông II: TÍCH VOÂ HÖÔÙNG CUÛA HAI VECTÔ & ÖÙNG DUÏNG Tieát daïy: 18
Baøøi 2: TÍCH VOÂ HÖÔÙNG CUÛA HAI VECTÔ (tt) I. MUÏC TIEÂU: Kieán thöùc:
 Naém ñöôïc ñònh nghóa vaø tính chaát cuûa tích voâ höôùng cuûa hai vectô cuøng vôùi yù nghóa vaät lí cuûa tích voâ höôùng. Kó naêng:
 Bieát söû duïng bieåu thöùc toaï ñoä cuûa tích voâ höôùng ñeå tính ñoä daøi cuûa moät vectô, khoaûng
caùch giöõa hai ñieåm, goùc giöõa hai vectô vaø chöùng minh hai vectô vuoâng goùc. 34
Nguyễn Đình Khương
Hình Học 10 Cơ Bản Thaùi ñoä:
 Reøn luyeän tính caån thaän, chính xaùc. II. CHUAÅN BÒ:
Giaùo vieân: Giaùo aùn.
Hoïc sinh: SGK, vôû ghi. OÂn taäp ñònh nghóa tích voâ höôùng cuûa hai vectô.
III. HOAÏT ÑOÄNG DAÏY HOÏC:
1. OÅn ñònh toå chöùc: Kieåm tra só soá lôùp.
2. Kieåm tra baøi cuõ: (3')
H. Neâu ñònh nghóa tích voâ höôùng cuûa hai vectô? Ñ. .
a b a . b cosa,b.
3. Giaûng baøi môùi: TL
Hoaït ñoäng cuûa Giaùo vieân
Hoaït ñoäng cuûa Hoïc sinh Noäi dung
Hoaït ñoäng 1: Tìm hieåu bieåu thöùc toaï ñoä cuûa tích voâ höôùng H1. Tính 2 i , 2
j , i .j ? Ñ1. 2 i = 2 j = 1
III. Bieåu thöùc toaï ñoä cuûa 10' i .j = 0 tích voâ höôùng
H2. Bieåu dieãn caùc vectô a , b Ñ2. a
Cho a = (a1, a2), b = (b1, b2) 1 a i  2 a j , theo i , j ? . a b = a b 1b1 + a2b2
b i b j 1 2
VD: Cho A(2; 4), B(1; 2),
a b a1b1 + a2b2 = 0 C(6; 2). Chöùng minh AB AC ? Ñ3.
H3. Tính toaï ñoä cuûa A ,
B AC ? AB = (–1; –2), AC = (4; –2)  A .
B AC = 0  AB AC
Hoaït ñoäng 2: Tìm hieåu caùc öùng duïng cuûa tích voâ höôùng H1. Tính 2 a ? Ñ1. 2 a = a 2 2 IV. ÖÙng duïng 1 + a2 20'
1) Ñoä daøi cuûa vectô
VD: Cho a = (4; –5). Tính a
Cho a = (a a = 2 2 4  ( 5  )  41 1, a2) 2 2 a  1 a  2 a
2) Goùc giöõa hai vectô Cho a = (a 1, a2), b = (b1, b2)
( a,b  0 )
H2. Töø ñònh nghóa tích voâ a b
höôùng, haõy suy ra coâng thöùc Ñ2. cosa b . ,  a b a . b
cosa b . , 
tính cos a,b ? a . b a b a b
VD: Cho OM = (–2; –1), ON cosMON = cosOM,ON = 1 1 2 2 2 2 2 2
= (3; –1). Tính MON ?
a a . b b OM.ON 6 1 1 2 1 2 = = OM . ON 5. 10 2    MON = 1350 2
3) Khoaûng caùch giöõa hai 35
Nguyễn Đình Khương
Hình Học 10 Cơ Bản
H3. Nhaéc laïi coâng thöùc tính ñieåm
toaï ñoä cuûa AB ? Ñ3. AB = (x Cho A(x B – xA; yB – yA) A; yA), B(xB; yB) AB = 2 2 (x B  xA )  (yB  yA )
VD: Cho M(–2; 2), N(1; 1). Tính MN ? MN = 2 2 (1 2) (12)  10
Hoaït ñoäng 3: AÙp duïng tích voâ höôùng cuûa hai vectô
H1. Neâu ñieàu kieän ñeå ABCD x  2
Ví duï: Cho A(1; 1), B(2; 3), D  7' laø hình bình haønh ?
Ñ1. AB DC   y  4 C(–1; –2). D  
a) Xaùc ñònh ñieåm D sao cho ABCD laø hình bình haønh. H2. Tính AB, AD ? Ñ2. AB = 2 2 1  2  5 b) Tính chu vi hbh ABCD. AD = 2 2 3  5  34 c) Tính goùc A.
H3. Neâu coâng thöùc tính goùc A Ñ3. cosA = cosA , B ADA . B AD = AB . AD 3  10 13 =   5. 34 170
Hoaït ñoäng 4: Cuûng coá  Nhaán maïnh:
3' – Caùc öùng duïng cuûa tích voâ höôùng
4. BAØI TAÄP VEÀ NHAØ:  Baøi 4, 5, 6, 7 SGK Ngaøy soaïn: 20/12/2012
Chöông II: TÍCH VOÂ HÖÔÙNG CUÛA HAI VECTÔ & ÖÙNG DUÏNG Tieát daïy: 21
Baøøi 2: BAØI TAÄP TÍCH VOÂ HÖÔÙNG CUÛA HAI VECTÔ I. MUÏC TIEÂU: Kieán thöùc:
 Cuûng coá khaùi nieäm tích voâ höôùng cuûa hai vectô. Kó naêng:
 Bieát vaän duïng tích voâ höôùng ñeå giaûi toaùn hình hoïc: tính goùc giöõa hai vectô, khoaûng caùch giöõa hai ñieåm. Thaùi ñoä:
 Reøn luyeän tính caån thaän, chính xaùc. 36
Nguyễn Đình Khương
Hình Học 10 Cơ Bản
 Luyeän tö duy linh hoaït. II. CHUAÅN BÒ:
Giaùo vieân: Giaùo aùn. Heä thoáng baøi taäp.
Hoïc sinh: SGK, vôû ghi. OÂn taäp kieán thöùc veà tích voâ höôùng cuûa hai vectô.
III. HOAÏT ÑOÄNG DAÏY HOÏC:
1. OÅn ñònh toå chöùc: Kieåm tra só soá lôùp.
2. Kieåm tra baøi cuõ: (3')
H. Neâu coâng thöùc tính goùc giöõa hai vectô, khoaûng caùch giöõa hai ñieåm ? a b a b
Ñ. cos   . , a b a b = 1 1 2 2 ; AB = 2 2
(x  x )  (y  y ) a . b 2 2 2 2 B A B A 1 a  2 a . 1b  2 b
3. Giaûng baøi môùi:
TL Hoaït ñoäng cuûa Giaùo vieân
Hoaït ñoäng cuûa Hoïc sinh Noäi dung IV. ÖÙng duïng
10' H3. Nhaéc laïi coâng thöùc tính Ñ3. AB = (xB – xA; yB – yA)
toaï ñoä cuûa AB ?
3) Khoaûng caùch giöõa hai ñieåm
VD: Cho M(–2; 2), N(1; 1). MN = 2 2 (1 2) (12)
Cho A(xA; yA), B(xB; yB) Tính MN ? AB = 2 2 (x B  xA )  (yB  yA )  10
Hoaït ñoäng2: AÙp duïng tích voâ höôùng cuûa hai vectô
H1. Neâu ñieàu kieän ñeå ABCD x  2
Ví duï: Cho A(1; 1), B(2; 3), D  10' laø hình bình haønh ?
Ñ1. AB DC   y  4 C(–1; –2). D  
a) Xaùc ñònh ñieåm D sao cho ABCD laø hình bình haønh. H2. Tính AB, AD ? Ñ2. AB = 2 2 1  2  5 b) Tính chu vi hbh ABCD. AD = 2 2 3  5  34 c) Tính goùc A.
H3. Neâu coâng thöùc tính goùc A Ñ3. cosA = cosA , B ADA . B AD = AB . AD 3  10 13 =   5. 34 170
Hoaït ñoäng 3: Luyeän taäp tính tích voâ höôùng cuûa hai vectô
TL Hoaït ñoäng cuûa Giaùo vieân
Hoaït ñoäng cuûa Hoïc sinh Noäi dung
Hoaït ñoäng 1: Luyeän taäp tính tích voâ höôùng cuûa hai vectô
H1. Xaùc ñònh goùc giöõa caùc Ñ1. a) A , B AC = 900
1. Cho tam giaùc vuoâng caân 20' caëp vectô ?  A . B AC = 0 ABC coù AB = AC = a. Tính C caùc tích voâ höôùng:
b)  AC,CB = 1350 a) A . B AC b) AC.CB A B
AC.CB = –a2 37
Nguyễn Đình Khương
Hình Học 10 Cơ Bản
H2. Xaùc ñònh goùc cuûa Ñ2.
2. Cho 3 ñieåm O, A, B thaúng O ,
A OB trong moãi tröôøng a) O , A OB = 00
haøng vaø bieát OA = a, OB = b. hôïp ?  O . A OB = ab Tính O . A OB khi: O A B
a) O naèm ngoaøi ñoaïn AB. b) O , A OB = 1800 b) O naèm trong ñoaïn AB. A O B  O . A OB = –ab N M I
3. Cho nöûa ñöôøng troøn taâm O
coù ñöôøng kính AB = 2R. Goïi A O B Ñ3.
M vaø N laø hai ñieåm thuoäc nöûa
H3. Vieát bieåu thöùc tính
AI.AM AI.AM.cosAI, AM ñöôøng troøn sao cho hai daây
AI.AM, AI.AB = AI.AM
cung AM vaø BN caét nhau taïi
AI.AB = AI.AB.cosAI AB I.
a) CMR: AI.AM AI.AB
=AI.AB.cos IAB =AI.AM vaø BI.BN BI.BA
AI.AM AI.(AB BM)
b) Haõy duøng keát quaû caâu a)
 Höôùng daãn HS vaän duïng = AI.AB
tính chaát tích voâ höôùng cuûa
ñeå tính AI.AM BI.BN theo
AI.AM BI.BN = A . B AB hai vectô vuoâng goùc R. = AB2 = 4R2
Hoaït ñoäng 4: Cuûng coá
Nhaán maïnh caùch vaän duïng
5' tích voâ höôùng ñeå giaûi toaùn hình hoïc   Ngaøy soaïn: 30/12/2012 Tieát daïy: 16
Baøøi daïy: OÂN TAÄP HOÏC KÌ I
1. Muïc tieâu :
a. Kieán thöùc : Cuûng coá vaø khaéc saâu caùc kieán thöùc :
- Toång vaø hieäu caùc vtô, tích cuûa vtô vôùi moät soá, toïa ñoä cuûa vtô vaø cuûa ñieåm, caùc bieåu
thöùc toïa ñoä cuûa caùc pheùp toaùn vtô.
b. Kyõ naêng : Vaän duïng ñöôïc caùc kieán thöùc ñaõ hoïc ñeå giaûi caùc baøi taäp coù lieân quan.
c. Thaùi ñoä : Caån thaän chính xaùc.
2. Chuaån bò phöông tieän daïy hoïc :
a. Thöïc tieãn : Hs ñaõ hoïc caùc kieán thöùc veà : toång vaø hieäu caùc vtô, tích cuûa vtô vôùi moät soá,
toïa ñoä cuûa vtô vaø cuûa ñieåm, caùc bieåu thöùc toïa ñoä cuûa caùc pheùp toaùn vtô; giaù trò löôïng
giaùc cuûa caùc goùc töø 00 ñeán 1800, ñònh nghóa tích voâ höôùng hai vtô, ñònh lí cosin, ñònh lí 38
Nguyễn Đình Khương
Hình Học 10 Cơ Bản
sin trong tam giaùc, coâng thöùc ñoä daøi ñöôøng trung tuyeánvaø caùc coâng thöùc tính dieän tích
tam giaùc ôû nhöõng baøi tröôùc.
b. GV :Soaïn giaùo aùn,saùch giaùo khoa, giaùo aùn, thöôùc keû, phaán maøu.
c. Phöông phaùp : cô baûn duøng phöông phaùp gôïi môû vaán ñaùp thoâng qua caùc HÑ ñieàu khieån tö duy.
3. Tieán trình baøi hoïc vaø caùc HÑ :
HÑ 1 : Giaûi baøi toaùn :
Cho hai hbh ABCD vaø AB’C’D’ coù chung ñænh A. CMR :
a) CC'  BB' DD'
b) Hai tam giaùc BC’D vaø B’CD’ coù cuøng troïng taâm. HÑ cuûa GV HÑ cuûa HS Noäi dung
- Nghe hieåu nhieäm vuï. - Giao nhieäm vuï cho hs.
CC '  AC '  AC
- Tìm phöông aùn thaéng - Nhaän xeùt keát quaû
AB ' AD' (AB AD) (töùc laø hoaøn thaønh cuûa hs vaø cho ñieåm Ta coù :     nhieäm vuï nhanh nhaát) AB ' AB AD ' AD .  BB ' DD' - Trình baøy keát quaû.
b) Töø CC'  BB' DD' suy ra vôùi moïi ñieåm G - Chænh söûa hoaøn ta coù : thieän.
GC '  GC GB '  GB GD '  GD
GB GD GC '  GB '  GD '  GC Suy ra G
B GD GC '  0  GB '  GD '  GC  0
Vaäy neáu G laø troïng taâm cuûa tam giaùc BC’D thì
G cuõng laø troïng taâm tam giaùc B’CD’.
HÑ 2 : Giaûi baøi toaùn :
Trong mp Oxy cho hai ñieåm A(1;4), B(2;2). Ñöôøng thaúng ñi qua A vaø B caét truïc Ox taïi
M vaø caét truïc Oy taïi N. Tính dieän tích tam giaùc OMN. HÑ cuûa GV HÑ cuûa HS Noäi dung
- Nghe hieåu nhieäm vuï. - Giao nhieäm vuï cho hs. Giaû söû M(x;0), N(0;y). Khi ñoù AB  (1; 2  ),
- Tìm phöông aùn thaéng - Nhaän xeùt keát quaû
AM  (x 1; 4  ), AN  ( 1
 ; y  4) . Vì AB vaø (töùc laø hoaøn thaønh cuûa hs vaø cho ñieåm. x   nhieäm vuï nhanh nhaát)
AM cuøng phöông neân 1 4  hay x = 3. 1 2  .
Vaäy M(3;0). Vì AB vaø AM cuøng phöông neân - Trình baøy keát quaû. 1  y  4  hay y = 6. Vaäy N(0;6). - Chænh söûa hoaøn 1 2  39
Nguyễn Đình Khương
Hình Học 10 Cơ Bản thieän.
Dieän tích tam giaùc OMN laø : 1 1
S OM.ON OM . ON  9 2 2
4. Cuûng coá : Nhaán maïnh laïi caùc kieán thöùc caàn nhôù. Ngaøy soaïn: 30/12/2012 Tieát daïy: 17
Baøøi daïy: OÂN TAÄP HOÏC KÌ I I. MUÏC TIEÂU:
Kieán thöùc: Cuûng coá caùc kieán thöùc veà:
 Vectô – Caùc pheùp toaùn cuûa vectô.
 Toaï ñoä cuûa vectô vaø cuûa ñieåm. Caùc tính chaát veà toaï ñoä cuûa vectô vaø cuûa ñieåm.
 GTLG cuûa moät goùc 00    1800.
 Tích voâ höôùng cuûa hai vectô.
Kó naêng: Thaønh thaïo trong vieäc giaûi caùc baøi toaùn veà:
 Chöùng minh ñaúng thöùc vectô. Phaân tích moät vectô theo hai vectô khoâng cuøng phöông. 40
Nguyễn Đình Khương
Hình Học 10 Cơ Bản
 Vaän duïng vectô – toaï ñoä ñeå giaûi toaùn hình hoïc. Thaùi ñoä:
 Reøn luyeän tính caån thaän, chính xaùc.
 Luyeän tö duy linh hoaït, saùng taïo. II. CHUAÅN BÒ:
Giaùo vieân: Giaùo aùn. Heä thoáng baøi taäp.
Hoïc sinh: SGK, vôû ghi. OÂn taäp caùc kieán thöùc ñaõ hoïc trong HK 1.
III. HOAÏT ÑOÄNG DAÏY HOÏC:
1. OÅn ñònh toå chöùc: Kieåm tra só soá lôùp.
2. Kieåm tra baøi cuõ: (Loàng vaøo quaù trình oân taäp) H. Ñ.
3. Giaûng baøi môùi: TL
Hoaït ñoäng cuûa Giaùo vieân
Hoaït ñoäng cuûa Hoïc sinh Noäi dung
Hoaït ñoäng 1: Cuûng coá caùc pheùp toaùn vectô A
1. Cho ABC. Goïi M, N, P 10' P N
laàn löôït laø trung ñieåm cuûa BC, CA, AB. Chöùng minh: B M C
AM BN CP  0
H1. Nhaéc laïi heä thöùc trung AB AC ñieåm ? Ñ1. AM   2 A
2. Cho ABC. Goïi M laø trung N M
ñieåm cuûa AB, N laø ñieåm treân K ñoaïn AC sao cho NC = 2NA. B D C AM AN
Goïi K laø trung ñieåm cuûa MN. Ñ2. a) AK   2 a) Chöùng minh:
H2. Phaân tích vectô KD ? 1 1 1 1
AK AB AC
AK AB AC 4 6 4 6
b) KD AD AK
b) Goïi D laø trung ñieåm BC. Chöùng minh: 1 1
KD AB AC 4 3
Hoaït ñoäng 2: Cuûng coá caùc pheùp toaùn veà toaï ñoä P
3. Cho ABC vôùi A(2; 0), 15' C B B(5; 3), C(–2; 4).
a) Tìm caùc ñieåm M, N, P sao M A N
cho A, B, C laàn löôït laø trung
H1. Neâu caùch xaùc ñònh caùc Ñ1. AM BC ; ñieåm cuûa MN, NP, PM. dieåm M, N, P ?
AN CB ; BP AC
b) Tìm caùc ñieåm I, J, K sao
cho IA  2IB , JB  3  JC ,
H2. Nhaéc laïi coâng thöùc xaùc Ñ2. AB = (x KC  5  KA . ñònh toaï ñoä vectô ? B – xA; yB – yA)
4. Cho A(2; 3), B(4; 2). 41
Nguyễn Đình Khương
Hình Học 10 Cơ Bản
H3. Neâu ñieàu kieän xaùc ñònh
a) Tìm treân Ox, ñieåm C caùch Ñ3.   0 C x ñieåm C ? C   A CB ñeàu A vaø B. Ñ4. b) Tính chu vi OAB.
H4. Nhaéc laïi coâng thöùc tính 2 2
khoaûng caùch giöõa hai ñieåm ? AB = x
B – xA    yB – yA 
Hoaït ñoäng 3: Vaän duïng vectô – toaï ñoä ñeå giaûi toaùn hình hoïc
5. Cho A(1; –1), B(5; –3),
15' H1. Neâu caùch xaùc ñònh taâm I Ñ1.IA IB C(2; 0)
cuûa ñöôøng troøn ngoaïi tieáp ?  IA IC
a) Tính chu vi vaø nhaän daïng ABC. D C
b) Tìm taâm I vaø tính baùn kính 1
ñöôøng troøn ngoaïi tieáp ABC. A 3 B
6. Cho hình bình haønh ABCD
H2. Nhaéc laïi coâng thöùc tính Ñ2.
vôùi AB = 3 , AD = 1, BAD
tích voâ höôùng hai vectô ? A . B AD A . B A . D cos A , B AD = 600. a) Tính A . B AD , . BA BC . = 3 .1.cos600 = 3 2
b) Tính ñoä daøi hai ñöôøng cheùo
H3. Phaân tích vectô DB theo Ñ3. DB AC vaø BD.  AB AD A , B AD ?  DB2 =   2 AB AD = 3 + 1 – 2. 3 = 4 – 2 3
Hoaït ñoäng 4: Cuûng coá
Nhaán maïnh vieäc vaän duïng
3' caùc kieán thöùc vectô – toaï ñoä ñeå giaûi toaùn.
4. BAØI TAÄP VEÀ NHAØ:
 OÂn taäp chuaån bò kieåm tra HK1. Ngaøy soaïn: 30/12/2012 Chöông : Tieát daïy: 21
Baøøi daïy: KIEÅM TRA HOÏC KÌ I I. MUÏC TIEÂU:
Kieán thöùc: Kieåm tra caùc kieán thöùc ñaõ hoïc trong hoïc kì 1:
 Vectô – Caùc pheùp toaùn vectô.
 Toaï ñoä cuûa vectô, cuûa ñieåm.
 GTLG cuûa goùc 00    1800.
 Tích voâ höôùng cuûa hai vectô.
Kó naêng: Thaønh thaïo caùch giaûi caùc daïng toaùn:
 Thöïc hieän caùc pheùp toaùn vectô. Phaân tích moät vectô theo hai vectô khoâng cuøng phöông.
 Vaän duïng vectô – toaï ñoä ñeå giaûi toaùn hình hoïc. Thaùi ñoä: 42
Nguyễn Đình Khương
Hình Học 10 Cơ Bản
 Reøn luyeän tính caån thaän, chính xaùc.
 Luyeän tö duy linh hoaït saùng taïo. II. CHUAÅN BÒ:
Giaùo vieân: Ñeà kieåm tra.
Hoïc sinh: OÂn taäp kieán thöùc ñaõ hoïc trong hoïc kì 1. III. MA TRAÄN ÑEÀ: Nhaän bieát Thoâng hieåu Vaän duïng Chuû ñeà Toång TNKQ TL TNKQ TL TNKQ TL 1 2 Vectô 0,75 0,25 0,25 2 1 1 Toaï ñoä 2,5 0,25 1,0 1,0 1 Tích voâ höôùng 0,25 0,25 Toång 0,5 1,0 1,0 1,0 3,5
IV. NOÄI DUNG ÑEÀ KIEÅM TRA: A. Phaàn traéc nghieäm:
Caâu 11: Cho boán ñieåm A, B, C, D. Meänh ñeà naøo sau ñaây laø ñuùng:
A. AB CD AD CB
B. AB BC CD DA
C. AB BC CD DA
D. AB AD CD CB
Caâu 12: Cho ABC coù troïng taâm G. Meänh ñeà naøo sau ñaây laø ñuùng:
A. BA BC  3BG B. 2
AB AC AG C. CA CB CG
D. AB AC BC  0 3
Caâu 13: Cho ABC ñeàu. Meänh ñeà naøo sau ñaây laø ñuùng:
A. AB BC CA B. AB BC CA
C. CA  AB
D. CA  BC
Caâu 14: Trong maët phaúng Oxy, cho A(3; 0), B(0; –3) vaø ñieåm C sao choCA  2
CB . Toaï ñoä ñieåm C laø: A. C(1; –2) B. C(–1; 2) C. C 3 3   ; D. C(2; –1) 2 2   
Caâu 15: Trong maët phaúng Oxy, cho A(–1; 2), B(–3; 4). Toaï ñoä cuûa ñieåm C ñoái xöùng vôùi ñieåm B qua ñieåm A laø: A. C(1; 0) B. C(–5; 6) C. C(–1; 3) D. C(0; 1)
Caâu 16: Cho ABC ñeàu coù caïnh baèng 1. Tích voâ höôùng A . B AC baèng: 3 3 A. 1 B. 2 C. D. 2 2 4 B. Phaàn töï luaän:
Baøi 3: Trong maët phaúng Oxy, cho ABC vôùi A(1; 3), B(–3; 0), C(5; –3). Treân ñöôøng thaúng BC laáy
ñieåm M sao cho: MB  2  MC . a) Tìm toaï ñoä ñieåm M
b) Phaân tích vectô AM theo caùc vectô AB, AC .
V. ÑAÙP AÙN VAØ BIEÅU ÑIEÅM:
A. Phaàn traéc nghieäm: 11a) 12a) 13a) 14a) 15a) 16a) 43
Nguyễn Đình Khương
Hình Học 10 Cơ Bản B. Töï luaän:
Baøi 3: (2 ñieåm) Cho A(1; 3), B(–3; 0), C(5; –3). MB  2  MC a)
  x    x MB  2
MC  (–3 – x; –y) = –2(5 – x; –3 – y)  3 10 2  (0,5 ñieåm) 
y  6  2y  7   7   x   3  M ; 2   (0,5 ñieåm)   3  y  2 b) MB  2
MC AB AM  2  (AC AM) (0,5 ñieåm) 1 2
 3AM AB AC AM AB AC (0,5 ñieåm) 3 3
VI. KEÁT QUAÛ KIEÅM TRA: 0 – 3,4 3,5 – 4,9 5,0 – 6,4 6,5 – 7,9 8,0 – 10 Lôùp Só soá SL % SL % SL % SL % SL % 10A3 44 10A5 42 10A7 44 10A10 42 10A11 38 Ngaøy soaïn: 10/01/2013 Chöông : Tieát daïy: 22
Baøøi daïy: TRAÛ BAØI KIEÅM TRA HOÏC KÌ I I. MUÏC TIEÂU:
Kieán thöùc: Nhaéc nhôû hoïc sinh nhöõng sai laàm veà:
 Caùc pheùp toaùn vectô.
 Vaän duïng vectô – toaï ñoä.
Kó naêng: Nhaéc nhôû hoïc sinh nhöõng sai laàm veà:
 Kyõ naêng thöïc hieän caùc pheùp toaùn veà vectô – toaï ñoä. Thaùi ñoä:
 Reøn luyeän tính caån thaän, chính xaùc. II. CHUAÅN BÒ:
Giaùo vieân: Ñeà kieåm tra vaø ñaùp aùn. Heä thoáng caùc sai laàm cuûa HS maéc phaûi.
Hoïc sinh: Vôû ghi. 44
Nguyễn Đình Khương
Hình Học 10 Cơ Bản
III. HOAÏT ÑOÄNG DAÏY HOÏC:
1. OÅn ñònh toå chöùc: Kieåm tra só soá lôùp.
2. Kieåm tra baøi cuõ: H. Ñ.
3. Giaûng baøi môùi:
Noäi dung ñeà kieåm tra
Sai laàm cuûa hoïc sinh A. Phaàn traéc nghieäm:
Caâu 11: Cho boán ñieåm A, B, C, D. Meänh ñeà naøo sau ñaây laø ñuùng:
A. AB CD AD CB B. AB BC CD DA
C. AB BC CD DA D. AB AD CD CB
Caâu 12: Cho ABC coù troïng taâm G. Meänh ñeà
naøo sau ñaây laø ñuùng:
A. BA BC  3BG B. 2
AB AC AG 3
C. CA CB CG D. AB AC BC  0
Caâu 13: Cho ABC ñeàu. Meänh ñeà naøo sau ñaây laø ñuùng:
A. AB BC CA
B. AB BC CA
C. CA  AB
D. CA  BC
Caâu 14: Trong maët phaúng Oxy, cho A(3; 0), B(0;
–3) vaø ñieåm C sao choCA  2
CB . Toaï ñoä ñieåm C laø: A. C(1; –2) B. C(–1; 2)  3 3  C. C ; D. C(2; –1) 2 2   
Caâu 15: Trong maët phaúng Oxy, cho A(–1; 2),
B(–3; 4). Toaï ñoä cuûa ñieåm C ñoái xöùng vôùi ñieåm B qua ñieåm A laø: A. C(1; 0) B. C(–5; 6) C. C(–1; 3) D. C(0; 1)
Caâu 16: Cho ABC ñeàu coù caïnh baèng 1. Tích voâ höôùng A . B AC baèng: 3 3 A. 1 B. 2 C. D. 2 2 4 45
Nguyễn Đình Khương
Hình Học 10 Cơ Bản B. Phaàn töï luaän:
Baøi 3: Trong maët phaúng Oxy, cho ABC vôùi
A(1; 3), B(–3; 0), C(5; –3). Treân ñöôøng thaúng
BC laáy ñieåm M sao cho: MB  2  MC . a) Tìm toaï ñoä ñieåm M
b) Phaân tích vectô AM theo caùc vectô AB,AC .
4. BAØI TAÄP VEÀ NHAØ:
 OÂn laïi kieán thöùc trong hoïc kì 1.
 Ñoïc tröôùc baøi "Caùc heä thöùc löôïng trong tam giaùc vaø giaûi tam giaùc" Ngaøy soaïn: 05/01/2013
Chöông II: TÍCH VOÂ HÖÔÙNG CUÛA HAI VECTÔ & ÖÙNG DUÏNG Tieát daïy: 23
Baøøi 3: CAÙC HEÄ THÖÙC LÖÔÏNG TRONG TAM GIAÙC vaø GIAÛI TAM GIAÙC I. MUÏC TIEÂU: Kieán thöùc:
 Naém ñöôïc caùc ñònh lí coâsin, ñònh lí sin trong tam giaùc.
 Naém ñöôïc caùc coâng thöùc tính ñoä daøi trung tuyeán, dieän tích tam giaùc. Kó naêng:
 Bieát vaän duïng caùc ñònh lí coâsin, ñònh lí sin ñeå tính caïnh hoaëc goùc cuûa moät tam giaùc.
 Bieát söû duïng coâng thöùc tính ñoä daøi trung tuyeán vaø tính dieän tích tam giaùc.
 Bieát giaûi tam giaùc vaø bieát thöïc haønh vieäc ño ñaïc trong thöïc teá. Thaùi ñoä:
 Reøn luyeän tính caån thaän, chính xaùc. Vaän duïng kieán thöùc ñaõ hoïc vaøo thöïc teá. II. CHUAÅN BÒ: 46
Nguyễn Đình Khương
Hình Học 10 Cơ Bản
Giaùo vieân: Giaùo aùn. Hình veõ minh hoaï.
Hoïc sinh: SGK, vôû ghi. OÂn taäp kieán thöùc veà tích voâ höôùng cuûa hai vectô.
III. HOAÏT ÑOÄNG DAÏY HOÏC:
1. OÅn ñònh toå chöùc: Kieåm tra só soá lôùp.
2. Kieåm tra baøi cuõ: (3')
H. Nhaéc laïi ñònh nghóa tích voâ höôùng cuûa hai vectô ? Ñ. .
a b a . b .cosa,b
3. Giaûng baøi môùi:
TL Hoaït ñoäng cuûa Giaùo vieân
Hoaït ñoäng cuûa Hoïc sinh Noäi dung
Hoaït ñoäng 1: OÂn taäp heä thöùc löôïng trong tam giaùc vuoâng
 Cho HS nhaéc laïi caùc heä  Caùc nhoùm laàn löôït thöïc hieän
I. Heä thöùc löôïng trong tam
8' thöùc löôïng trong tam giaùc yeâu caàu. giaùc vuoâng vuoâng. A a2 = b2 + c2 b2 = a.b c2 = a.c c b h h2 = b.c ah = bc c’ b’ 1 1 1   B H a C 2 2 2 h b c sinB = cosC = b a sinC = cosB = c a tanB = cotC = b c
Hoaït ñoäng 2: Tìm hieåu ñònh lí coâsin A II. Ñònh lí coâsin c b
a) Baøi toaùn: Trong ABC, 20'
cho bieát hai caïnh AB, AC vaø B a C
H1. Phaân tích vectô BC goùc A. Tính caïnh BC.
Ñ1. BC = AC AB theo caùc vectô A , B AC ? H2. Tính BC2 ? 2
Ñ2. BC2 = BC = ( AC AB )2 2 2
= AC AB  2AC.AB = AC2 + AB2 – 2AC.AB.cosA
H3. Phaùt bieåu ñònh lí coâsin b) Ñònh lí coâsin
Ñ3. Trong moät tam giaùc, bình baèng lôøi ? a2 = b2 + c2 – 2bc.cosA
phöông moät caïnh baèng toång hai b2 = a2 + c2 – 2ac.cosB
caïnh kia tröø ñi hai laàn tích cuûa c2 = a2 + b2 – 2ab.cosC
hai caïnh ñoù vôùi coâsin cuûa goùc Heä quaû: giöõa chuùng. 2 2 2 cos
b c a A  2bc 2 2 2 cos
a c b B  2ac 2 2 2 cos
a b c C  2ab 47
Nguyễn Đình Khương
Hình Học 10 Cơ Bản A
c) Ñoä daøi trung tuyeán tam
 Höôùng daãn HS aùp duïng giaùc
ñònh lí coâsin ñeå tính ñoä daøi c b 2 2 2 m 2
2(b c )  a
ñöôøng trung tuyeán trong tam a a m  4 giaùc B M a C 2 2 2 2
2(a c )  b b m  4 2 2 2 2
2(a b )  c c m  4
Hoaït ñoäng 3: AÙp duïng
H1. Vieát coâng thöùc tính AB, Ñ1. d) Ví duï 10' cosA ?
AB2 = c2 = a2 + b2 – 2ab.cosC Cho ABC coù caùc caïnh AC =  465,44
10 cm, BC = 16 cm, C = 1100.  AB  21,6 (cm)
a) Tính caïnh AB vaø caùc goùc 2 2 2 cos
b c a A  0,7188 A, B cuûa ABC. 2bc
b) Tính ñoä daøi ñöôøng trung  A  4402 tuyeán AM. B  25058
Hoaït ñoäng 4: Cuûng coá
Nhaán maïnh ñònh lí coâsin vaø
3' caùc öùng duïng tính goùc trong
tam giaùc, tính ñoä daøi trung tuyeán.
4. BAØI TAÄP VEÀ NHAØ:  Baøi 1, 2, 3 SGK.
 Ñoïc tieáp baøi "Caùc heä thöùc löôïng trong tam giaùc vaø giaûi tam giaùc" Ngaøy soaïn: 05/01/2013
Chöông II: TÍCH VOÂ HÖÔÙNG CUÛA HAI VECTÔ & ÖÙNG DUÏNG Tieát daïy: 24
Baøøi 3: CAÙC HEÄ THÖÙC LÖÔÏNG TRONG TAM GIAÙC
vaø GIAÛI TAM GIAÙC (tt) I. MUÏC TIEÂU: Kieán thöùc:
 Naém ñöôïc caùc ñònh lí coâsin, ñònh lí sin trong tam giaùc.
 Naém ñöôïc caùc coâng thöùc tính ñoä daøi trung tuyeán, dieän tích tam giaùc. Kó naêng:
 Bieát vaän duïng caùc ñònh lí coâsin, ñònh lí sin ñeå tính caïnh hoaëc goùc cuûa moät tam giaùc.
 Bieát söû duïng coâng thöùc tính ñoä daøi trung tuyeán vaø tính dieän tích tam giaùc.
 Bieát giaûi tam giaùc vaø bieát thöïc haønh vieäc ño ñaïc trong thöïc teá. Thaùi ñoä:
 Reøn luyeän tính caån thaän, chính xaùc. Vaän duïng kieán thöùc ñaõ hoïc vaøo thöïc teá. II. CHUAÅN BÒ: 48
Nguyễn Đình Khương
Hình Học 10 Cơ Bản
Giaùo vieân: Giaùo aùn. Hình veõ minh hoaï.
Hoïc sinh: SGK, vôû ghi. Ñoïc baøi tröôùc.
III. HOAÏT ÑOÄNG DAÏY HOÏC:
1. OÅn ñònh toå chöùc: Kieåm tra só soá lôùp.
2. Kieåm tra baøi cuõ: (3')
H. Neâu ñònh lí coâsin ? AÙp duïng: Cho ABC vôùi a = 7, b = 8, c = 6. Tính soá ño goùc A?
Ñ. a2 = b2 + c2 – 2bc.cosA
3. Giaûng baøi môùi:
TL Hoaït ñoäng cuûa Giaùo vieân
Hoaït ñoäng cuûa Hoïc sinh Noäi dung
Hoaït ñoäng 1: Tìm hieåu ñònh lí sin
 GV höôùng daãn HS chöùng III. Ñònh lí sin 12' minh ñònh lí. a) Ñònh lí sin
H1. Cho ABC vuoâng taïi A. Ñ1. ABC vuoâng taïi A a b c    2R  BC = 2R
Tính a ; b ; c ?
sin A sin B sinC
sin A sin B sinC a b c     2R A A C a
sin A sin B sinC D
 Neáu A  900 thì veõ ñöôøng O B D O kính BD. B a C H2. Tính a theo R ? Ñ2. BC = BD.sinA  a = 2R.sinA
Hoaït ñoäng 2: AÙp duïng H1. Tính sinA ? b) AÙp duïng 5' Ñ1. sinA = sin600 = 3 2
Ví duï 1: Cho ABC ñeàu coù a
caïnh baèng a. Tính baùn kính   2R  R = 3 sin A 3
ñöôøng troøn ngoaïi tieáp ABC.
 Cho moãi nhoùm tính giaù trò Ñ2. A = 1290
Ví duï 2: Cho ABC coù 10' moät ñaïi löôïng. 0 .
b sin A 210.sin129 B =200
H2. Neâu caùch tính hoaëc a =  0 sin B
C = 310 vaø AC = 210 cm. Tính coâng thöùc caàn duøng ? sin20
goùc A, caùc caïnh coøn laïi vaø  477,2 (cm) 0
baùn kính R cuûa ñöôøng troøn b = . b sinC 210.sin31  0 sin B
ngoaïi tieáp tam giaùc ñoù. sin20  316,2 (cm) a R = 477,2  0 2sin A 2.sin129  307,02 (cm)
Ví duï 3: Cho ABC. Tính tæ
5' H3. Neâu caùch tính hoaëc Ñ3.
soá AB trong caùc tröôøng hôïp coâng thöùc caàn duøng ? AB C a) = sin  2 AC AC sin B sau: AB sinC 2 b) =  a) 0 0
B  30 ,C  45 AC sin B 3 b) 0 0
B  60 ,C  90 49
Nguyễn Đình Khương
Hình Học 10 Cơ Bản
H4. Neâu caùch tính hoaëc Ñ4.
Ví duï 4: Cho ABC. Tìm baùn
5' coâng thöùc caàn duøng ? a) A = 450
kính ñöôøng troøn ngoaïi tieáp a a
tam giaùc trong caùc tröôøng hôïp  2R  R = 2 sin A 2 sau: b) A = 1200
a) B C = 1350 vaø BC = a. a a
b) B C = 600 vaø BC = a.  2R  R = sin A 3
Hoaït ñoäng 3: Cuûng coá
 Nhaán maïnh caùch vaän duïng 3' ñònh lí sin
4. BAØI TAÄP VEÀ NHAØ:  Baøi 5, 6, 7, 8 SGK.
 Ñoïc tieáp baøi "Caùc heä thöùc löôïng trong tam giaùc vaø giaûi tam giaùc" Ngaøy soaïn: 15/01/2013
Chöông II: TÍCH VOÂ HÖÔÙNG CUÛA HAI VECTÔ & ÖÙNG DUÏNG Tieát daïy: 25
Baøøi 3: CAÙC HEÄ THÖÙC LÖÔÏNG TRONG TAM GIAÙC
vaø GIAÛI TAM GIAÙC (tt) I. MUÏC TIEÂU: Kieán thöùc:
 Naém ñöôïc caùc ñònh lí coâsin, ñònh lí sin trong tam giaùc.
 Naém ñöôïc caùc coâng thöùc tính ñoä daøi trung tuyeán, dieän tích tam giaùc. Kó naêng:
 Bieát vaän duïng caùc ñònh lí coâsin, ñònh lí sin ñeå tính caïnh hoaëc goùc cuûa moät tam giaùc.
 Bieát söû duïng coâng thöùc tính ñoä daøi trung tuyeán vaø tính dieän tích tam giaùc.
 Bieát giaûi tam giaùc vaø bieát thöïc haønh vieäc ño ñaïc trong thöïc teá. Thaùi ñoä:
 Reøn luyeän tính caån thaän, chính xaùc. Vaän duïng kieán thöùc ñaõ hoïc vaøo thöïc teá. II. CHUAÅN BÒ:
Giaùo vieân: Giaùo aùn. Hình veõ minh hoaï. 50
Nguyễn Đình Khương
Hình Học 10 Cơ Bản
Hoïc sinh: SGK, vôû ghi. Ñoïc baøi tröôùc.
III. HOAÏT ÑOÄNG DAÏY HOÏC:
1. OÅn ñònh toå chöùc: Kieåm tra só soá lôùp.
2. Kieåm tra baøi cuõ: (5')
H. Neâu ñònh lí sin ? AÙp duïng: Cho ABC coù B = 600, C = 450, tæ soá AB baèng bao nhieâu? AC
Ñ. AB = sinC 6  AC sin B 3
3. Giaûng baøi môùi:
TL Hoaït ñoäng cuûa Giaùo vieân
Hoaït ñoäng cuûa Hoïc sinh Noäi dung
Hoaït ñoäng 1: Tìm hieåu caùc coâng thöùc tính dieän tích tam giaùc A A
III. Coâng thöùc tính dieän tích 15' tam giaùc h h a a ah bh ch S = a b c   (1) B H a 2 2 2 C a B C H 1 1
H1. Neâu coâng thöùc (1)?
absinC bcsin A
Ñ1. S = 1 BC.AH = 1 a.h 2 2 2 2 a (2) 1
 Höôùng daãn HS chöùng minh  Caùc nhoùm thaûo luaän.  casin B 2 caùc coâng thöùc 2, 3, 4. abc H2. Tính h = (3) a ? Ñ2. 4R ha = AH = AC.sinC = bsinC = pr (4) = (
p p a)(p b)(p c) (5)  S = 1 ab.sinC 2
H3. Töø ñl sin, tính sinC ? c abc Ñ3. sinC =  S = 2R 4R
H4. Taâm O ñöôøng troøn noäi Ñ4. Giao ñieåm caùc ñöôøng tieáp tam giaùc laø ? phaân giaùc.
H5. Tính dieän tích caùc tam giaùc OBC, OCA, OAB ? Ñ5. SOBC = 1 ra, 2 SOCA = 1 rb, S rc 2 OAB = 1 2
Hoaït ñoäng 2: AÙp duïng
H1. Neâu coâng thöùc caàn duøng Ñ1.
VD1: Tam giaùc ABC coù caùc 10'
 Coâng thöùc Heâ–roâng caïnh a = 13m, b = 14m, c = p = 21  S = 84 (m2) 15m S a) Tính dieän tích ABC.  S = pr  r = = 4 p
b) Tính baùn kính caùc ñöôøng
troøn noäi tieáp, ngoaïi tieáp ABC.  S = 4S = 8,125 abc
H2. Neâu coâng thöùc caàn duøng Ñ2.
VD2: Tam giaùc ABC coù a = 10'
 c2 = a2 + b2 –2ab.cosC = 4
2 3 , b = 2, C = 300. Tính c, 51
Nguyễn Đình Khương
Hình Học 10 Cơ Bản  c = 2 A , SABC.
 b = c = 2  B C = 300  A = 1200  S = 1 ca.sinB = 3 2
Hoaït ñoäng 3: Cuûng coá
 Nhaán maïnh caùch vaän duïng
3' caùc coâng thöùc tính dieän tích
4. BAØI TAÄP VEÀ NHAØ:
 Laøm tieáp caùc baøi taäp SGK.
 Ñoïc tieáp baøi "Caùc heä thöùc löôïng trong tam giaùc vaø giaûi tam giaùc" Ngaøy soaïn: 25/01/2013
Chöông II: TÍCH VOÂ HÖÔÙNG CUÛA HAI VECTÔ & ÖÙNG DUÏNG Tieát daïy: 26
Baøøi 3: CAÙC HEÄ THÖÙC LÖÔÏNG TRONG TAM GIAÙC
vaø GIAÛI TAM GIAÙC (tt) I. MUÏC TIEÂU: Kieán thöùc:
 Naém ñöôïc caùc ñònh lí coâsin, ñònh lí sin trong tam giaùc.
 Naém ñöôïc caùc coâng thöùc tính ñoä daøi trung tuyeán, dieän tích tam giaùc. Kó naêng:
 Bieát vaän duïng caùc ñònh lí coâsin, ñònh lí sin ñeå tính caïnh hoaëc goùc cuûa moät tam giaùc.
 Bieát söû duïng coâng thöùc tính ñoä daøi trung tuyeán vaø tính dieän tích tam giaùc.
 Bieát giaûi tam giaùc vaø bieát thöïc haønh vieäc ño ñaïc trong thöïc teá. Thaùi ñoä:
 Reøn luyeän tính caån thaän, chính xaùc. Vaän duïng kieán thöùc ñaõ hoïc vaøo thöïc teá. II. CHUAÅN BÒ:
Giaùo vieân: Giaùo aùn. Hình veõ minh hoaï.
Hoïc sinh: SGK, vôû ghi. Ñoïc baøi tröôùc. 52
Nguyễn Đình Khương
Hình Học 10 Cơ Bản
III. HOAÏT ÑOÄNG DAÏY HOÏC:
1. OÅn ñònh toå chöùc: Kieåm tra só soá lôùp.
2. Kieåm tra baøi cuõ: (3')
H. Tam giaùc coù 3 caïnh laàn löôït laø: 9, 12, 13. Dieän tích cuûa tam giaùc ñoù baèng bao nhieâu? Ñ. S = 4 170
3. Giaûng baøi môùi:
TL Hoaït ñoäng cuûa Giaùo vieân
Hoaït ñoäng cuûa Hoïc sinh Noäi dung
Hoaït ñoäng 1: Tìm hieåu baøi toaùn giaûi tam giaùc A
IV. Giaûi tam giaùc vaø öùng duïng 8'
vaøo vieäc ño ñaïc c b 1. Giaûi tam giaùc B a C
Giaûi tam giaùc laø tìm moät soá yeáu
toá cuûa tam giaùc khi bieát ñöôïc
 Cho caùc nhoùm thaûo luaän,
caùc yeáu toá khaùc.  0
A 180 (B C) = 71030
neâu coâng thöùc caàn duøng. a B  b = sin  12,9
VD1: Cho ABC coù a = 17,4, sin A
B = 44030, C = 640. Tính A , a C  c = sin  16,5 b, c ? sin A  c2 = a2 + b2 – 2ab.cosC
VD2: Cho ABC coù a = 49,4, b 7'  1369,66
= 26,4, C = 47020. Tính c,  c  37 A vaø B . 2 2 2
b c a  cosA = 2bc
 – 0,191  A  1010  0
B 180 (A C)  31040
Hoaït ñoäng 2: AÙp duïng giaûi baøi toaùn thöïc teá
 Höôùng daãn HS phaân tích  Xeùt tam giaùc ABD
2. ÖÙng duïng vaøo vieäc ño ñaïc
12' caùch ño ñaïc vaø tính toaùn. g =  – b
Baøi toaùn 1: Ño chieàu cao cuûa D AB b
moät caùi thaùp maø khoâng theå ñeán  AD = .sin sin(  ) b ñöôïc chaân thaùp. g
 Xeùt tam giaùc vuoâng ACD
 Choïn 2 ñieåm A, B treân maët h h = CD = AD.sin
ñaát sao cho A, B, C thaúng haøng. Ño AB, CA , D CBD .
 Tính chieàu cao h = CD cuûa  b C thaùp. A B
 Xeùt tröôøng hôïp ñaëc bieät:
coù theå ñeán ñöôïc chaân thaùp. 53
Nguyễn Đình Khương
Hình Học 10 Cơ Bản  Xeùt tam giaùc ABC
Baøi toaùn 2: Tính khoaûng caùch 10' AC = . AB sinb
giöõa 2 ñieåm maø khoâng theå ño sin(  ) b tröïc tieáp ñöôïc. C
 Ñeå ño khoaûng caùch töø ñieåm A
treân bôø soâng ñeán goác caây C b 
treân cuø lao giöõa soâng, ngöôøi ta A B
choïn moät ñieåm B cuøng ôû treân
 Cho caùc nhoùm thaûo luaän
bôø vôùi A sao cho töø A vaø B coù tìm caùch ño khaùc. theå nhìn thaáy C. Ño AB, CA , B CBA .  Tính khoaûng caùch AC.
Hoaït ñoäng 3: Cuûng coá
 Nhaán maïnh caùch vaän duïng
3' caùc coâng thöùc trong tam giaùc ñaõ hoïc.
4. BAØI TAÄP VEÀ NHAØ:  Baøi 10, 11 SGK. Ngaøy soaïn: 25/01/2013
Chöông II: TÍCH VOÂ HÖÔÙNG CUÛA HAI VECTÔ & ÖÙNG DUÏNG Tieát daïy: 27
Baøøi 3: BAØI TAÄP CAÙC HEÄ THÖÙC LÖÔÏNG
TRONG TAM GIAÙC vaø GIAÛI TAM GIAÙC I. MUÏC TIEÂU: Kieán thöùc:
 Naém ñöôïc caùc ñònh lí coâsin, ñònh lí sin trong tam giaùc.
 Naém ñöôïc caùc coâng thöùc tính ñoä daøi trung tuyeán, dieän tích tam giaùc. Kó naêng:
 Bieát vaän duïng caùc ñònh lí coâsin, ñònh lí sin ñeå tính caïnh hoaëc goùc cuûa moät tam giaùc.
 Bieát söû duïng coâng thöùc tính ñoä daøi trung tuyeán vaø tính dieän tích tam giaùc.
 Bieát giaûi tam giaùc vaø bieát thöïc haønh vieäc ño ñaïc trong thöïc teá. Thaùi ñoä:
 Reøn luyeän tính caån thaän, chính xaùc. Vaän duïng kieán thöùc ñaõ hoïc vaøo thöïc teá. 54
Nguyễn Đình Khương
Hình Học 10 Cơ Bản II. CHUAÅN BÒ:
Giaùo vieân: Giaùo aùn. Heä thoáng baøi taäp.
Hoïc sinh: SGK, vôû ghi. OÂn taäp kieán thöùc ñaõ hoïc veà Heä thöùc löôïng trong tam giaùc.
III. HOAÏT ÑOÄNG DAÏY HOÏC:
1. OÅn ñònh toå chöùc: Kieåm tra só soá lôùp.
2. Kieåm tra baøi cuõ: (Loàng vaøo quaù trình luyeän taäp) H. Ñ.
3. Giaûng baøi môùi:
TL Hoaït ñoäng cuûa Giaùo vieân
Hoaït ñoäng cuûa Hoïc sinh Noäi dung
Hoaït ñoäng 1: Cuûng coá caùc heä thöùc löôïng trong tam giaùc
H1. Neâu coâng thöùc caàn söû Ñ1.
1. Cho ABC vuoâng taïi A, 8' duïng ?
C = 900 – B = 420
B =580 vaø caïnh a = 72 cm. Tính  b = a.sinB  61,06 (cm)
C , caïnh b, caïnh c vaø ñöôøng  c = a.sinC  38,15 (cm) cao ha.  h A a = bc  32,36 (cm) a c h b a B H a C
H2. Neâu coâng thöùc caàn söû Ñ2.
2. Cho ABC coù A = 1200, 7' duïng ?
 a2 = b2 + c2 – 2bc.cosA = caïnh b = 8 cm, c = 5 cm. Tính 129
caïnh a vaø caùc goùc B , C .  a  11,36 (cm) A 2 2 2
a c b  cosB =  0,79 2ac c b  B  37048 B a C
C = 1800 – ( A B )  22012
H3. Goùc naøo coù theå laø goùc tuø Ñ3. Goùc ñoái dieän vôùi caïnh lôùn 3. Cho ABC coù caùc caïnh a = 8 7' ? nhaát. cm, b = 10 cm, c = 13 cm. 2 2 2
a b c
a) Tam giaùc ñoù coù goùc tuø cosC = = – 5 2ab 160 khoâng?  C tuø.
b) Tính ñoä daøi trung tuyeán MA 2 2 2 cuûa ABC.
b c a Ñ4. MA2 = 2( ) C
H4. Neâu coâng thöùc tính MA 4 a b M ? = 118,5  MA  10,89 (cm) A c B
4. Cho ABC coù caïnh a = 137,5
8' H5. Neâu coâng thöùc caàn söû Ñ5.
cm, B = 830, C = 570. Tính A , duïng ?
A = 1800 – ( B C ) = 400
baùn kính R cuûa ñöôøng troøn a
ngoaïi tieáp, caùc caïnh b, c.  R =  107 (cm) 2sin A
 b = 2RsinB  212,31 (cm) 55
Nguyễn Đình Khương
Hình Học 10 Cơ Bản
 c = 2RsinC  179,40 (cm) C a b R O A c B
Hoaït ñoäng 2: AÙp duïng giaûi baøi toaùn thöïc teá B
5. Hai chieác taøu thuyû P vaø Q
caùch nhau 300 m. Töø P vaø Q 10' h
thaúng haøng vôùi chaân A cuûa thaùp
haûi ñaêng AB ôû treân bôø bieån A Q P
ngöôøi ta nhìn chieàu cao AB cuûa
H1. Neâu caùc böôùc tính? Ñ1. Xeùt BPQ
thaùp döôùi caùc goùc BPA = 350 vaø
PBQ = 480 – 350 = 130
BQA = 480. Tính chieàu cao cuûa PQ P  BQ = .sin thaùp. sin B 0 = 300.sin35  764,94 0 sin13
 AB = BQ.sinQ  568,46 (m)
Hoaït ñoäng 3: Cuûng coá
 Nhaán maïnh caùch vaän duïng
3' caùc heä thöùc löôïng trong tam giaùc ñaõ hoïc.
4. BAØI TAÄP VEÀ NHAØ:
 Baøi taäp oân chöông II. Ngaøy soaïn: 30/01/2013
Chöông II: TÍCH VOÂ HÖÔÙNG CUÛA HAI VECTÔ & ÖÙNG DUÏNG Tieát daïy: 28
Baøøi daïy: OÂN TAÄP CHÖÔNG II I. MUÏC TIEÂU: Kieán thöùc:
 OÂn taäp toaøn boä kieán thöùc chöông II. Kó naêng:
 Bieát söû duïng caùc kieán thöùc ñaõ hoïc ñeå giaûi toaùn. Thaùi ñoä:
 Reøn luyeän tính caån thaän, chính xaùc. Vaän duïng kieán thöùc ñaõ hoïc vaøo thöïc teá. II. CHUAÅN BÒ:
Giaùo vieân: Giaùo aùn. Heä thoáng baøi taäp. 56
Nguyễn Đình Khương
Hình Học 10 Cơ Bản
Hoïc sinh: SGK, vôû ghi. OÂn taäp kieán thöùc chöông II.
III. HOAÏT ÑOÄNG DAÏY HOÏC:
1. OÅn ñònh toå chöùc: Kieåm tra só soá lôùp.
2. Kieåm tra baøi cuõ: (Loàng vaøo quaù trình oân taäp) H. Ñ.
3. Giaûng baøi môùi:
TL Hoaït ñoäng cuûa Giaùo vieân
Hoaït ñoäng cuûa Hoïc sinh Noäi dung
Hoaït ñoäng 1: Cuûng coá GTLG cuûa goùc
 Cho HS nhaéc laïi: ñn, caùc  Caùc nhoùm thöïc hieän, giaûi 1. Cho hai goùc nhoïn , b ( <
tính chaát cuûa GTLG ñaõ hoïc. thích roõ caên cöù ñeå xeùt. b). Xeùt tính Ñ–S ? 10' a) S b) Ñ c) Ñ
a) cos < cosb b)sin < sinb
c) cos = sinb   + b = 900
 Cuûng coá baûng GTLG caùc
2. Tam giaùc ABC vuoâng ôû A, goùc ñaëc bieät.
coù B = 300. Xeùt tính Ñ–S ? 1 a) S b) Ñ c) Ñ d) Ñ a) cosB = b)sinC = 3 2 3 c) cosC = 1 d) sinB = 1 2 2
 Cuûng coá ñn, GTLG caùc
3. Xeùt tính Ñ–S ?
goùc buø nhau, baûng giaù trò ñaëc bieät. a) S b) S c) Ñ a) sin1500 = – 3 2 b) cos1500 = 3 2 1 c) tan1500 = – 3
Hoaït ñoäng 2: Cuûng coá tích voâ höôùng cuûa hai vectô
H1. Neâu caùch xaùc ñònh goùc Ñ1. Tònh tieán caùc vectô sao cho 4. ABC vuoâng ôû A vaø B = 15' cuûa hai vectô ?
chuùng coù ñieåm ñaàu truøng nhau. 500. Xeùt tính Ñ–S ? a) Ñ b) Ñ c) Ñ d) S a)  A , B BC = 1300
b) BC, AC = 400 c)  A , B CB = 500
d)  AC,CB = 1200
H2. Nhaéc laïi ñònh nghóa tích Ñ2.
5. ABC vuoâng ôû A. Xeùt tính
voâ höôùng cuûa hai vectô ? a) Ñ b) Ñ c) Ñ d) S Ñ–S ? a) A . B AC B . A BC
b) AC.CB AC.BC c) A . B BC C . A CB
d) AC.BC BC.AB
H3. Nhaéc laïi coâng thöùc tính Ñ3. AB = AC = 8 , BC = 4
6. ABC coù A(–1; 1), B(1; 3),
ñoä daøi ñoaïn thaúng, goùc giöõa a) S b) S c) S d) Ñ
C(1; –1). Xeùt tính Ñ–S ? hai caïnh ? a) ABC ñeàu. 57
Nguyễn Đình Khương
Hình Học 10 Cơ Bản
b) ABC coù 3 goùc nhoïn. c) ABC caân taïi B.
d) ABC vuoâng caân taïi A.
Hoaït ñoäng 3: Cuûng coá heä thöùc löôïng trong tam giaùc
H1. Neâu coâng thöùc caàn söû
7. Cho ABC coù a = 12, b = 15'
Ñ1. p = 1 (12 + 16 + 20) = 24 duïng ? 2
16, c = 20. Tính S, ha, R, r, ma S = (
p p a)(p b)(p c) = 96 ? h abc a = 2S = 16; R = =10 a 4R r = S = 4 p 2 2 2
b c a m 2 2( ) a = = 292 4
 Höôùng daãn HS phaân tích
8. Cho ABC vuoâng caân taïi A
baøi toaùn, tìm caùch tính. + Veõ GH  AC
coù AB = AC = 30. Hai ñöôøng
trung tuyeán BF, CE caét nhau + Tính GH = 1 AB = 10 3
taïi G. Tính dieän tích CFG. A
+ SCFG = 1 CF.GH = 75 H 2 E F G B C
Hoaït ñoäng 4: Cuûng coá
 Nhaán maïnh caùch vaän duïng
3' caùc kieán thöùc ñaõ hoïc.
4. BAØI TAÄP VEÀ NHAØ:
 Ñoïc tröôùc baøi "Phöông trình ñöôøng thaúng". Ngaøy soaïn: 01/02/2013
Chöông III: PHÖÔNG PHAÙP TOAÏ ÑOÄ TRONG MAËT PHAÚNG Tieát daïy: 29
Baøøi 1: PHÖÔNG TRÌNH ÑÖÔØNG THAÚNG I. MUÏC TIEÂU: Kieán thöùc:
 Naém ñöôïc caùc khaùi nieäm vectô chæ phöông cuûa ñöôøng thaúng.
 Naém ñöôïc phöông trình tham soá cuûa ñöôøng thaúng.
 Naém ñöôïc moái lieân heä giöõa vectô chæ phöông vaø heä soá goùc cuûa ñöôøng thaúng. Kó naêng:
 Bieát caùch laäp phöông trình tham soá cuûa ñöôøng thaúng.
 Naém vöõng caùch veõ ñöôøng thaúng trong maët phaúng toaï ñoä khi bieát phöông trình cuûa noù. Thaùi ñoä:
 Reøn luyeän tính caån thaän, chính xaùc.
 Laøm quen vieäc chuyeån tö duy hình hoïc sang tö duy ñaïi soá. 58
Nguyễn Đình Khương
Hình Học 10 Cơ Bản II. CHUAÅN BÒ:
Giaùo vieân: Giaùo aùn. Hình veõ minh hoaï.
Hoïc sinh: SGK, vôû ghi. OÂn taäp kieán thöùc veà ñöôøng thaúng ñaõ hoïc. Duïng cuï veõ hình.
III. HOAÏT ÑOÄNG DAÏY HOÏC:
1. OÅn ñònh toå chöùc: Kieåm tra só soá lôùp.
2. Kieåm tra baøi cuõ: (3')
H. Cho ñöôøng thaúng (d): y = 2x + 3. Giaûi thích yù nghóa caùc heä soá? Xaùc ñònh toaï ñoä moät
ñieåm thuoäc ñöôøng thaúng ?
Ñ. Heä soá goùc a = 2; tung ñoä goác b = 3. A(0; 3), B(1; 5)  (d).
3. Giaûng baøi môùi:
TL Hoaït ñoäng cuûa Giaùo vieân
Hoaït ñoäng cuûa Hoïc sinh Noäi dung
Hoaït ñoäng 1: Tìm hieåu khaùi nieäm vectô chæ phöông cuûa ñöôøng thaúng
 Töø kieåm tra baøi cuõ, daãn y
1. Vectô chæ phöông cuûa
daét hình thaønh khaùi nieäm B 5 u ñöôøng thaúng
15' vectô chæ phöông cuûa ñöôøng 3 A
Vectô u ñgl vectô chæ phöông thaúng. 
cuûa ñöôøng thaúng neáu u 0 O 1 x
vaø giaù cuûa u song song hoaëc
H1. Chöùng toû AB cuøng
truøng vôùi .
Ñ1. AB = (1; 2)
phöông vôùi u = (1; 2) ? Nhaän xeùt:
Moät ñöôøng thaúng coù voâ soá
H2. Vectô naøo trong caùc vectô chæ phöông. Ñ2. a  ( 2  ; 4  ) = –2 u
vectô sau cuõng laø vectô chæ
Moät ñöôøng thaúng hoaøn toaøn phöông cuûa  ?
a cuõng laø vectô chæ phöông
ñöôïc xaùc ñònh neáu bieát moät
v  (0;0), a  ( 2  ; 4  ) ,
ñieåm vaø moät vectô chæ phöông b cuûa noù.  (2;1) , c  (1; 2  )
Cho coù VTCP u vaø ñi qua M. Khi ñoù:
H3. Cho d coù VTCP u = (2; Ñ3. A, B  d
N MN cuøng phöông u
1) vaø M(1; 1)  d. Ñieåm vì MA = (2; 1) = u
naøo sau ñaây cuõng thuoäc d ?
A(3; 2), B(–5; –2), C(0; 2)
MB = (–6; –3) = –2 u
Hoaït ñoäng 2: Tìm hieåu phöông trình tham soá cuûa ñöôøng thaúng
 GV höôùng daãn tìm phöông
2. Phöông trình tham soá cuûa
trình tham soá cuûa ñöôøng ñöôøng thaúng 10' thaúng. a) Ñònh nghóa
H1. Neâu ñieàu kieän ñeå Ñ1.
Trong mp Oxy, cho ñi qua M(x;y) naèm treân  ? M    M M 0M cuøng phöông u 0(x0; y0) vaø coù VTCP
u  (u ;u ) . Phöông trình M M tu 1 2  0
tham soá cuûa :
x x tu  0 1 
x x tu y y 0 1 (1) 0  t 2 u
y y tu  0 2
Cho t moät giaù trò cuï theå thì ta
H2. Ta caàn xaùc ñònh yeáu toá
xaùc ñònh ñöôïc moät ñieåm treân
Ñ2. Vectô chæ phöông naøo ? 59
Nguyễn Đình Khương
Hình Học 10 Cơ Bản AB = (1; –2)
VD1: Cho A(2; 3), B(3; 1).
H3. Choïn giaù trò t ? x   t
a) Vieát pt tham soá cuûa ñöôøng
(Moãi nhoùm choïn moät giaù  : 2 
y  3  2t thaúng AB. trò)
Ñ3. t = 2  M(4; –1)
b) Haõy xaùc ñònh toaï ñoä ñieåm t = –1  N(1; 5)
M thuoäc ñt AB (khaùc A vaø B).
Hoaït ñoäng 3: Tìm hieåu moái lieân heä giöõa VTCP vaø heä soá goùc cuûa ñöôøng thaúng
 Cho HS nhaéc laïi nhöõng  Caùc nhoùm thaûo luaän vaø trình b) Lieân heä giöõa VTCP vaø heä
10' ñieàu ñaõ bieát veà heä soá goùc baøy.
soá goùc cuûa ñöôøng thaúng cuûa ñöôøng thaúng.
Cho coù VTCP u  (u ;u ) y 1 2 * : y = ax + b  k = a u
vôùi u1 0 thì coù heä soá goùc u v  u2
* xAv =   k = 2 = tan u u 1 k = 2 1 u  1 u O A x 
Phöông trình ñi qua M0(x0;
y0) vaø coù heä soá goùc k:
H1. Tính heä soá goùc cuûa Ñ1. k = 2  = –2 y – y0 = k(x – x0) ñöôøng thaúng AB ? 1
Hoaït ñoäng 4: Cuûng coá  Nhaán maïnh:
 Cho caùc nhoùm tính heä soá goùc
5' – VTCP, PT tham soá, heä soá cuûa ñöôøng thaúng döïa vaøo toaï ñoä
goùc cuûa ñöôøng thaúng. cuûa VTCP.
– Caùch laäp phöông trình tham soá cuûa ñt.
– Caùch xaùc ñònh toaï ñoä 1
ñieåm treân ñöôøng thaúng
4. BAØI TAÄP VEÀ NHAØ:  Baøi 1 SGK.
 Ñoïc tieáp baøi "Phöông trình ñöôøng thaúng". Ngaøy soaïn: 10/02/2013
Chöông III: PHÖÔNG PHAÙP TOAÏ ÑOÄ TRONG MAËT PHAÚNG Tieát daïy: 30
Baøøi 1: PHÖÔNG TRÌNH ÑÖÔØNG THAÚNG (tt) I. MUÏC TIEÂU: Kieán thöùc:
 Naém ñöôïc caùc khaùi nieäm vectô phaùp tuyeán cuûa ñöôøng thaúng.
 Naém ñöôïc phöông trình toång quaùt cuûa ñöôøng thaúng.
 Naém ñöôïc moái lieân heä giöõa vectô chæ phöông vaø vectô phaùp tuyeán cuûa ñöôøng thaúng. Kó naêng:
 Bieát caùch laäp phöông trình toång quaùt cuûa ñöôøng thaúng.
 Naém vöõng caùch veõ ñöôøng thaúng trong maët phaúng toaï ñoä khi bieát phöông trình cuûa noù. Thaùi ñoä:
 Reøn luyeän tính caån thaän, chính xaùc.
 Laøm quen vieäc chuyeån tö duy hình hoïc sang tö duy ñaïi soá. II. CHUAÅN BÒ:
Giaùo vieân: Giaùo aùn. Hình veõ minh hoaï.
Hoïc sinh: SGK, vôû ghi. OÂn taäp kieán thöùc veà ñöôøng thaúng ñaõ hoïc. Duïng cuï veõ hình. 60
Nguyễn Đình Khương
Hình Học 10 Cơ Bản
III. HOAÏT ÑOÄNG DAÏY HOÏC:
1. OÅn ñònh toå chöùc: Kieåm tra só soá lôùp.
2. Kieåm tra baøi cuõ: (3')
H. Laäp phöông trình tham soá cuûa ñöôøng thaúng d ñi qua M(2; 1) vaø coù VTCP u = (3; 4).
Xeùt quan heä giöõa vectô u vôùi n = (4; –3) ?
Ñ. d: x  2  3t  ; u  n . y 1 4t
3. Giaûng baøi môùi: TL
Hoaït ñoäng cuûa Giaùo vieân
Hoaït ñoäng cuûa Hoïc sinh Noäi dung
Hoaït ñoäng 1: Tìm hieåu khaùi nieäm vectô phaùp tuyeán cuûa ñöôøng thaúng
 Daãn daét töø KTBC, GV giôùi
III. Vectô phaùp tuyeán cuûa
thieäu khaùi nieäm VTPT cuûa ñöôøng thaúng 7' ñöôøng thaúng.
Vectô n ñgl vectô phaùp tuyeán
cuûa ñöôøng thaúng neáu n  0 vaø
n vuoâng goùc vôùi VTCP u cuûa . Nhaän xeùt:
H1. Neáu n laø moät VTPT cuûa Ñ1. k n cuõng laø VTPT vì k n  – Moät ñöôøng thaúng coù voâ soá
 thì coù nhaän xeùt gì veà vectô u vectô phaùp tuyeán.
k n (k 0) ?
– Moät ñöôøng thaúng ñöôïc hoaøn
H2. Coù bao nhieâu ñt ñi qua
toaøn xaùc ñònh neáu bieát moät ñieåm
moät ñieåm vaø vuoâng goùc vôùi Ñ2. Coù moät vaø chæ moät.
vaø moät vectô phaùp tuyeán. moät ñt cho tröôùc ?
Hoaït ñoäng 2: Tìm hieåu phöông trình toång quaùt cuûa ñöôøng thaúng
H1. Cho  ñi qua M0(x0; y0) vaø Ñ1. M(x; y)    M M  u
IV. Phöông trình toång quaùt cuûa 0
coù VTPT n = (a; b). Tìm ñk  a(x – x ñöôøng thaúng 15' ñeå M(x; y)   ? 0) + b(y – y0) = 0
 ax + by + c = 0 (c=–ax
1. Ñònh nghóa: Phöông trình ax 0–by0)
+ by + c = 0 vôùi a2 + b2 0 ñgl y n u
phöông trình toång quaùt cuûa ñöôøng thaúng. M  Nhaän xeùt: y0 M0
+ Pt ñt ñi qua M(x0; y0) vaø coù O x0 x
VTPT n = (a; b):
 GV höôùng daãn HS ruùt ra  Laáy M, N  . Ch.minh:
a(x – x0) + b(y – y0) = 0 nhaän xeùt. MN  n
+ Neáu : ax + by + c = 0 thì
coù: VTPT n = (a; b)
VTCP u = (b; –a)
H2. Xaùc ñònh VTCP, VTPT Ñ2. u AB
VD: Cho hai ñieåm A(2; 2), B(4; cuûa ñt AB ?   = (2; 1) 3).  n = (1; –2)
a) Laäp pt ñt  ñi qua A vaø B.
 : x – 2 + (–2)(y – 2) = 0
b) Laäp pt ñt d ñi qua A vaø vuoâng  x – 2y + 2 = 0 goùc vôùi ñt AB.
H3. Xaùc ñònh VTPT cuûa d ? Ñ3. n d  AB = (2; 1)
 d: 2(x – 2) + (y – 2) = 0  2x + y – 6 = 0
Hoaït ñoäng 3: Tìm hieåu caùc tröôøng hôïp ñaëc bieät cuûa phöông trình toång quaùt cuûa ñöôøng thaúng 61
Nguyễn Đình Khương
Hình Học 10 Cơ Bản
 GV höôùng daãn HS nhaän xeùt
2. Caùc tröôøng hôïp ñaëc bieät y
caùc tröôøng hôïp ñaëc bieät. Minh c
Cho : ax + by + c = 0 (1) 15' hoaï baèng hình veõ.   b
Neáu a = 0 thì (1): y = c  b O x  
Oy taïi c  0; b    y 
Neáu b = 0 thì (1): x = c  a   c O  x
Ox taïi c   ;0 a   a  y
Neáu c = 0 thì (1) trôû thaønh: ax + by = 0
ñi qua goác toaï ñoä O. O x
Neáu a, b, c 0 thì x y y (1)   1 (2) a b c N 0 0  b cvôùi a, b. a 0 = c a 0 = cb O M x 
(2) ñgl pt ñt theo ñoaïn chaén
H1. Caùc ñöôøng thaúng coù ñaëc Ñ1.
VD: Veõ caùc ñöôøng thaúng sau: ñieåm gì ? d d1: x – 2y = 0
1 ñi qua O; d2  Ox; d3  Oy d d 2: x = 2
4 caét caùc truïc toaï ñoä taïi (8; 0), d (0; 4) 3: y + 1 = 0 x y d4:   1 8 4
Hoaït ñoäng 4: Cuûng coá  Nhaán maïnh: 3' + VTPT cuûa ñt
+ Caùch laäp pt toång quaùt cuûa ñt
4. BAØI TAÄP VEÀ NHAØ:  Baøi 1, 2, 3, 4 SGK.
Ñoïc tieáp baøi "Phöông trình ñöôøng thaúng". Ngaøy soaïn: 20/02/2013
Chöông III: PHÖÔNG PHAÙP TOAÏ ÑOÄ TRONG MAËT PHAÚNG Tieát daïy: 31
Baøøi 1: PHÖÔNG TRÌNH ÑÖÔØNG THAÚNG (tt) I. MUÏC TIEÂU: Kieán thöùc:
 Naém ñöôïc caùc tröôøng hôïp veà VTTÑ cuûa hai ñöôøng thaúng.
 Naém ñöôïc moái lieân heä giöõa VTCP, VTPT vôùi VTTÑ cuûa hai ñöôøng thaúng. Kó naêng:
 Bieát caùch xeùt VTTÑ cuûa hai ñöôøng thaúng.
 Bieát caùch laäp phöông trình ñöôøng thaúng song song vôùi ñöôøng thaúng ñaõ cho. Thaùi ñoä:
 Reøn luyeän tính caån thaän, chính xaùc. 62
Nguyễn Đình Khương
Hình Học 10 Cơ Bản
 Laøm quen vieäc chuyeån tö duy hình hoïc sang tö duy ñaïi soá. II. CHUAÅN BÒ:
Giaùo vieân: Giaùo aùn. Hình veõ minh hoaï.
Hoïc sinh: SGK, vôû ghi. OÂn taäp kieán thöùc veà ñöôøng thaúng ñaõ hoïc. Duïng cuï veõ hình.
III. HOAÏT ÑOÄNG DAÏY HOÏC:
1. OÅn ñònh toå chöùc: Kieåm tra só soá lôùp.
2. Kieåm tra baøi cuõ: (3')
H. Xaùc ñònh VTCP cuûa caùc ñöôøng thaúng: : x – y – 1 = 0 vaø d: 2x – 2y + 2 = 0.
Ñ. u = (1; 1), d u = (2; 2)
3. Giaûng baøi môùi:
TL Hoaït ñoäng cuûa Giaùo vieân
Hoaït ñoäng cuûa Hoïc sinh Noäi dung
Hoaït ñoäng 1: Tìm hieåu caùch xeùt VTTÑ cuûa hai ñöôøng thaúng
H1. Nhaéc laïi caùch tìm giao Ñ1. Toaï ñoä giao ñieåm cuûa 1 vaø V. VTTÑ cuûa 2 ñöôøng thaúng
ñieåm cuûa hai ñöôøng thaúng ? 2 laø nghieäm cuûa phöông trình: Xeùt 2 ñöôøng thaúng: 15'   1
a x  1by  1c  0 1: a1x + b1y + c1 = 0  (I)  vaø  2 a x  2 b y  2 c  0 2: a2x + b2y + c2 = 0
Toaï ñoä giao ñieåm cuûa 1 vaø 2
laø nghieäm cuûa phöông trình:  1
a x  1by  1c  0  (I)  2 a x  2 b y  2 c  0
1 caét 2 (I) coù 1 nghieäm
1 // 2 (1) voâ nghieäm
1 2 (1) coù VSN
 Cho moãi nhoùm giaûi moät    
VD1: Cho d: x – y + 1 = 0.
heä pt. GV minh hoaï baèng a) x y 1 0  coù nghieäm (1; 2x  y  4  0
Xeùt VTTÑ cuûa d vôùi moãi ñt hình veõ. 2) sau: 1: 2x + y – 4 = 0
 d caét 1 taïi A(1; 2) 2: x – y – 1 = 0 b) x  y 1  0  voâ nghieäm 3: 2x – 2y + 2 = 0. x  y 1  0  d // 2 c)  x  y 1  0  coù VSN 2x  2y  2  0  d  . y y y d d d   2 3 2 M 1 1 –1 –1 O 1 1 x O 1 O x x –1 a) b) c)
Hoaït ñoäng 2: Tìm hieåu caùch xeùt VTTÑ cuûa hai ñt döïa vaøo caùc heä soá cuûa pt toång quaùt
 Höôùng daãn HS nhaän xeùt  Nhaän xeùt:
qua vieäc giaûi heä pt ôû treân.
Giaû söû a2, b2, c2 0.
10' H1. Khi naøo heä (I): Ñ1. + 1 a 1 b 
1 caét 2 + coù 1 nghieäm 2 a b2 + voâ nghieäm 63
Nguyễn Đình Khương
Hình Học 10 Cơ Bản + coù voâ soá nghieäm + (I) coù 1 nghieäm khi 1 a 1 b a b c  + 1 1 1   1 // 2 2 a b2 2 a b2 2 c + (I) voâ nghieäm khi 1 a 1 b 1 c + 1 a 1 b 1 c    
1 2 2 a b2 2 c 2 a b2 2 c a b c H2. Xeùt VTTÑ cuûa + (I) coù VSN khi 1 1 1  vôùi d   1, 2 a b2 2 c
VD2: Xeùt VTTÑ cuûa : x – d2, d3 ? Ñ2.
2y + 1 = 0 vôùi moãi ñt sau: + 1 2  1 d      d 1: –3x + 6y – 3 = 0 3  6 3  1 d2: y = –2x + 1 2     caét d d3: 2x + 5 = 4y 2 1 2 + 1 2  1     // d 2 4  5 3
Hoaït ñoäng 3: Vaän duïng VTTÑ cuûa hai ñöôøng thaúng ñeå laäp pt ñöôøng thaúng
 Höôùng daãn HS caùc caùch
VD3: Cho ABC vôùi A(1; 4),
10' laäp ph.trình ñöôøng thaúng d. B(3; –1), C(6; 2).
H1. Xaùc ñònh VTCP cuûa BC Ñ1. u  BC = (3; 3)
a) Laäp pt ñöôøng thaúng BC.
 BC: 3(x – 3) –3(y + 1) = 0
b) Laäp pt ñt d ñi qua A vaø  x – y – 4 = 0 song song vôùi BC.
H2. Xaùc ñònh daïng pt cuûa d Ñ2. d: x – y + m = 0 A(1; 4)  d  m = 3  d: x – y + 3 = 0
Hoaït ñoäng 4: Cuûng coá  Nhaán maïnh
5' – Caùch xeùt VTTÑ cuûa 2 ñöôøng thaúng.
– Caùch vaän duïng VTTÑ cuûa  Gôïi yù cho HS tìm caùc caùch
2 ñöôøng thaúng ñeå laäp pt ñt. khaùc nhau ñeå giaûi VD3.
4. BAØI TAÄP VEÀ NHAØ:  Baøi 5 SGK.
 Ñoïc tieáp baøi "Phöông trình ñöôøng thaúng". Ngaøy soaïn: 5/03/2013
Chöông III: PHÖÔNG PHAÙP TOAÏ ÑOÄ TRONG MAËT PHAÚNG Tieát daïy: 32
Baøøi 1: PHÖÔNG TRÌNH ÑÖÔØNG THAÚNG (tt) I. MUÏC TIEÂU: Kieán thöùc:
 Naém ñöôïc khaùi nieäm goùc giöõa hai ñöôøng thaúng.
 Naém ñöôïc caùch tính goùc giöõa hai ñöôøng thaúng, khoaûng caùch töø moät ñieåm ñeán moät ñöôøng thaúng .
 Naém ñöôïc moái lieân heä giöõa VTCP, VTPT vôùi goùc giöõa hai ñöôøng thaúng. Kó naêng:
 Bieát caùch tính goùc giöõa hai ñöôøng thaúng, khoaûng caùch töø moät ñieåm ñeán moät ñöôøng thaúng. 64
Nguyễn Đình Khương
Hình Học 10 Cơ Bản Thaùi ñoä:
 Reøn luyeän tính caån thaän, chính xaùc.
 Laøm quen vieäc chuyeån tö duy hình hoïc sang tö duy ñaïi soá. II. CHUAÅN BÒ:
Giaùo vieân: Giaùo aùn. Hình veõ minh hoaï.
Hoïc sinh: SGK, vôû ghi. OÂn taäp kieán thöùc veà ñöôøng thaúng ñaõ hoïc. Duïng cuï veõ hình.
III. HOAÏT ÑOÄNG DAÏY HOÏC:
1. OÅn ñònh toå chöùc: Kieåm tra só soá lôùp.
2. Kieåm tra baøi cuõ: (3')
H. Cho ABC vôùi A(1; 4), B(3; –1), C(6; 2). Tính goùc A.
Ñ. cosA = cos AB,AC = AB.AC = 20 AB.AC 29
3. Giaûng baøi môùi:
TL Hoaït ñoäng cuûa Giaùo vieân
Hoaït ñoäng cuûa Hoïc sinh Noäi dung
Hoaït ñoäng 1: Tìm hieåu caùch tính goùc giöõa hai ñöôøng thaúng
 GV giôùi thieäu khaùi nieäm 2
VI. Goùc giöõa 2 ñöôøng thaúng
goùc giöõa hai ñöôøng thaúng. A 
Hai ñt 1, 2 caét nhau taïo 15' 1200
thaønh 4 goùc (1  2). Goùc
H1. Cho ABC coù A = 1 B
C nhoïn trong 4 goùc ñoù ñgl goùc 1200. Tính goùc (AB, AC) ?
Ñ1. (AB, AC)=1800 – 1200 = giöõa 1 vaø 2. Kí hieäu (1, 2) 600 hoaëc  1  ,2  . n +   1
1 2 (1, 2) = 900 n +
1 // 2 (1, 2) = 00   2 1
00 (
1, 2) 900 2
H2. So saùnh goùc (1, 2) vôùi  1 n ,n2
Cho 1: a1x + b1y + c1 = 0 goùc  Ñ2.  1  ,2     1 n ,n2 ? 0 1  80     2: a2x + b2y + c2 = 0 1 n ,n2
Ñaët = (1, 2).
H3. Nhaéc laïi coâng thöùc tính n .n n .n
cos = cos(n ,n ) = 1 2 goùc giöõa 2 vectô ? Ñ3. cosn ,n  1 2 1 2 1 2  1 n . n2 1 n . n2 a a  b b
H4. Tính goùc giöõa 2 ñt:  cos = 1 2 1 2 d 2 2 2 2 1: 4x – 10y + 1 = 0 Ñ4. cos(d1, d2) = 1 a  1 b . a2  b2 d2: x + y + 2 = 0 4.1 ( 1  0).1 3 = = 2 2 2 2 4  ( 1  0) . 1 1 58 Chuù yù:
H5. Cho 1  2. Nhaän xeùt
1 2 a1a2 + b1b2 = 0 veà caùc vectô
Ñ5. 1  2  1 n  n2 1 n vaø n2 ?
1: y = k1x + m1
2: y = k2x + m2
1 2 k1.k2 = –1
Hoaït ñoäng 2: Tìm hieåu caùch tính khoaûng caùch töø moät ñieåm ñeán moät ñöôøng thaúng 65
Nguyễn Đình Khương
Hình Học 10 Cơ Bản
 GV höôùng daãn HS chöùng y
VII. Khoaûng caùch töø moät
minh coâng thöùc tính khoaûng m
ñieåm ñeán moät ñöôøng thaúng
12' caùch töø moät ñieåm ñeán moät n M0
Cho : ax + by + c = 0 ñöôøng thaúng. H
vaø ñieåm M0(x0; y0). O x ax  by  c
H1. Vieát pt tham soá cuûa ñt d(M x  x  ta 0, ) = 0 0 2 2 m ñi qua M Ñ1. m: 0  a  b 0 vaø vuoâng goùc y  y  0  tb vôùi  ? Ñ2. H(x
H2. Tìm toaï ñoä giao ñieåm H 0 + tHa; y0 + tHb) cuûa ax  by  c  vaø m ? vôùi t H = 0 0  2 2 a  b H3. Tính M 0H ? Ñ3. M0H= 2 2 (x H  x0 )  (yH  y0 ) H4. Tính d(M, ) ?
VD: Tính khoaûng caùch töø Ñ4.
ñieåm M(–2; 1) ñeán ñöôøng 3.( 2)   2.11 d(M, ) = = 9
thaúng : 3x – 2y – 1 = 0. 2 2 3  ( 2)  13
Hoaït ñoäng 3: AÙp duïng tính goùc vaø khoaûng caùch
H1. Vieát pt caùc ñt AB, BC ? Ñ1. AB: 5x + 2y – 13 = 0
VD: Cho ABC vôùi A(1; 4), 10' BC: x – y – 4 = 0 B(3; –1), C(6; 2).
H2. Tính goùc (AB, BC) ? Ñ2. cos(AB, BC) =
a) Tính goùc giöõa hai ñt AB, = 5.1 2( 1  ) 3 BC ?  2 2 2 2 5  2 . 1  ( 1  ) 58
b) Tính baùn kính ñöôøng troøn
H3. Tính baùn kính R ? Ñ3. R = d(C, AB) =
taâm C vaø tieáp xuùc vôùi ñt AB ? = 5.6  2.2 13 21  2 2 5  2 29
Hoaït ñoäng 4: Cuûng coá  Nhaán maïnh:
3' – Caùch tính goùc giöõa 2 ñt.
– Caùch tính khoaûng caùch töø
moät ñieåm ñeán moät ñt.
4. BAØI TAÄP VEÀ NHAØ:  Baøi 6, 7, 8, 9 SGK. Ngaøy soaïn: 05/03/2013
Chöông III: PHÖÔNG PHAÙP TOAÏ ÑOÄ TRONG MAËT PHAÚNG Tieát daïy: 33
Baøøi 1: BAØI TAÄP PHÖÔNG TRÌNH ÑÖÔØNG THAÚNG I. MUÏC TIEÂU:
Kieán thöùc: Cuûng coá caùc kieán thöùc veà:
 Phöông trình tham soá, phöông trình toång quaùt cuûa ñöôøng thaúng. 66
Nguyễn Đình Khương
Hình Học 10 Cơ Bản
 Vò trí töông ñoái cuûa hai ñöôøng thaúng.
 Goùc giöõa hai ñöôøng thaúng, khoaûng caùch töø moät ñieåm ñeán moät ñöôøng thaúng. Kó naêng:
 Bieát laäp phöông trình tham soá, phöông trình toång quaùt cuûa ñöôøng thaúng.
 Bieát xeùt VTTÑ cuûa hai ñöôøng thaúng.
 Bieát caùch tính goùc giöõa hai ñöôøng thaúng, khoaûng caùch töø moät ñieåm ñeán moät ñöôøng thaúng. Thaùi ñoä:
 Reøn luyeän tính caån thaän, chính xaùc.
 Laøm quen vieäc chuyeån tö duy hình hoïc sang tö duy ñaïi soá. II. CHUAÅN BÒ:
Giaùo vieân: Giaùo aùn. Hình veõ minh hoaï.
Hoïc sinh: SGK, vôû ghi. OÂn taäp kieán thöùc veà ñöôøng thaúng ñaõ hoïc. Duïng cuï veõ hình.
III. HOAÏT ÑOÄNG DAÏY HOÏC:
1. OÅn ñònh toå chöùc: Kieåm tra só soá lôùp.
2. Kieåm tra baøi cuõ: (Loàng vaøo quaù trình luyeän taäp) H. Ñ.
3. Giaûng baøi môùi:
TL Hoaït ñoäng cuûa Giaùo vieân
Hoaït ñoäng cuûa Hoïc sinh Noäi dung
Hoaït ñoäng 1: Luyeän taäp laäp phöông trình ñöôøng thaúng
 Cho HS nhaéc laïi caùch laäp  Moãi nhoùm laäp phöông trình 1. Cho ABC vôùi A(1; 4),
pt tham soá, pt toång quaùt cuûa moät ñöôøng thaúng.
B(3; –1), C(6; 2). Laäp phöông 15' ñöôøng thaúng.
trình tham soá, phöông trình
H1. Xaùc ñònh caùc VTCP, Ñ1. uAB = (2; –5); BC
u = (3; 3); toång quaùt cuûa caùc ñöôøng
VTPT cuûa caùc ñöôøng thaúng u = (5; –2) thaúng: AB, BC, AC ? AC
a) Chöùa caùc caïnh AB, BC,
AB: x  1 2t   5x+2y–13= 0 AC.
y  4  5t
b) Ñöôøng cao AH vaø trung
BC: x  3 3t
 x – y – 4 = 0 tuyeán AM. y  1   3t
AC: x  6  5t  2x+5y–22= 0
y  2  2t
H2. Xaùc ñònh VTPT cuûa AH Ñ2. nAH BC = (3; 3)  AH: x + y – 5 = 0
H3. Xaùc ñònh toaï ñoä ñieåm  x x M ? B C 9 xM   Ñ3. 2 2  yB   C y 1 yM    2 2
Hoaït ñoäng 2: Luyeän taäp xeùt VTTÑ cuûa hai ñöôøng thaúng
H1. Neâu caùch xeùt VTTÑ Ñ1.
2. Xeùt VTTÑ cuûa caùc caëp ñt:
10' cuûa hai ñöôøng thaúng ?
C1: Döïa vaøo caùc VTCP cuûa 2 ñt a) d1: 4x – 10y + 1
C2: Döïa vaøo caùc heä soá cuûa 2 pt d2: x + y + 2 = 0 a) d1 caét d2 b) d1: 12x – 6y + 10 = 0 b) d1 // d2 67
Nguyễn Đình Khương
Hình Học 10 Cơ Bản c) d1  d2
d x   t 2: 5 
y  3  2t c) d1: 8x + 10y – 12 = 0
d x    t 2: 6 5 
y  6  4t
Hoaït ñoäng 3: Luyeän taäp tính goùc vaø khoaûng caùch
H1. Neâu coâng thöùc tính goùc Ñ1.
3. Tính goùc giöõa 2 ñt:
10' giöõa 2 ñöôøng thaúng ? a a b b d1: 4x – 2y + 6 = 0 cos(d1, d2) = 1 2 1 2 2 2 2 2 d2: x – 3y + 1 = 0 1 a  1b . 2 a  2 b = 2 2  (d1, d2) = 450
4. Tính khoaûng caùch töø moät
H2. Neâu coâng thöùc tính ax  by  c
ñieåm ñeán ñöôøng thaúng:
khoaûng caùch töø moät ñieåm Ñ2. d(M0, ) = 0 0 2 2
a) A(3; 5); d: 4x + 3y + 1 = 0
ñeán moät ñöôøng thaúng ? a  b
b) B(1; –2); d: 3x – 4y – 26 a) d(A, d) = 28 =0 5 b) d(B, d) = 3
Hoaït ñoäng 4: Cuûng coá  Nhaán maïnh :
5' – Caùch giaûi caùc daïng toaùn.
– Caùch chuyeån ñoåi caùc daïng pt tham soá <–> pt toång quaùt
phöông trình ñöôøng thaúng.
4. BAØI TAÄP VEÀ NHAØ:
 Laøm baøi taäp oân chöông II vaø ñöôøng thaúng.
 Chuaån bò kieåm tra 1 tieát phaàn Heä thöùc löôïng trong tam giaùc vaø Phöông trình ñöôøng thaúng. Ngaøy soaïn: 20/03/2013
Chöông III: PHÖÔNG PHAÙP TOAÏ ÑOÄ TRONG MAËT PHAÚNG Tieát daïy: 35
Baøøi daïy: KIEÅM TRA 1 TIEÁT CHÖÔNG II – III I. MUÏC TIEÂU:
Kieán thöùc: Cuûng coá caùc kieán thöùc veà:
 Heä thöùc löôïng trong tam giaùc.
 Phöông trình cuûa ñöôøng thaúng. Vò trí töông ñoái cuûa hai ñöôøng thaúng.
 Goùc giöõa hai ñöôøng thaúng, khoaûng caùch töø moät ñieåm ñeán moät ñöôøng thaúng. Kó naêng: 68
Nguyễn Đình Khương
Hình Học 10 Cơ Bản
 Vaän duïng heä thöùc löôïng trong tam giaùc ñeå giaûi tam giaùc.
 Bieát laäp phöông trình cuûa ñöôøng thaúng. Bieát xeùt VTTÑ cuûa hai ñöôøng thaúng.
 Bieát caùch tính goùc giöõa hai ñöôøng thaúng, khoaûng caùch töø moät ñieåm ñeán moät ñöôøng thaúng. Thaùi ñoä:
 Reøn luyeän tính caån thaän, chính xaùc.
 Laøm quen vieäc chuyeån tö duy hình hoïc sang tö duy ñaïi soá. II. CHUAÅN BÒ:
Giaùo vieân: Giaùo aùn. Ñeà kieåm tra.
Hoïc sinh: OÂn taäp kieán thöùc veà heä thöùc löôïng trong tam giaùc, phöông trình ñöôøng thaúng. III. MA TRAÄN ÑEÀ: Nhaän bieát Thoâng hieåu Vaän duïng Chuû ñeà Toång TNKQ TL TNKQ TL TNKQ TL
Heä thöùc löôïng trong 4 2 4,0 tam giaùc 0,5 1,0 Phöông trình ñöôøng 2 2 1 2 6,0 thaúng 0,5 0,5 2,0 1,0 Toång 3,0 2,0 1,0 2,0 2,0 10,0
IV. NOÄI DUNG ÑEÀ KIEÅM TRA:
A. Phaàn traéc nghieäm: (4 ñieåm) Choïn caâu traû lôøi ñuùng nhaát.
Caâu 1: Cho ABC coù AB = 5, AC = 8, BAC = 600. Dieän tích cuûa ABC baèng: A) 10 B) 40 3 C) 20 3 D) 10 3
Caâu 2: Cho ABC coù AB = 8, AC = 7, BC = 3. Ñoä daøi trung tuyeán CM baèng: A) 3 5 B) 52 C) 52 D) 52 4 2 4
Caâu 3: Cho ABC coù AB = 5, AC = 8, BAC = 600. Ñoä daøi caïnh BC baèng: A) 7 B) 89  40 3 C) 89  40 3 D) 129
Caâu 4: Cho ABC vôùi A(–1; 2), B(3; 0), C(5; 4). Khi ñoù soá ño goùc A baèng: A) 300 B) 600 C) 450 D) 900
Caâu 5: Cho ñ.thaúng d coù ph.trình tham soá: x  2  3t
. Moät VTPT cuûa d coù toaï ñoä laø: y  1   2t A) (–2; 3) B) (2; 3) C) (–3; 2) D) (3; 2)
Caâu 6: Ñöôøng thaúng ñi qua 2 ñieåm M(2; 0), N(0; 3) coù phöông trình laø: A) 3x + 2y – 6 = 0 B) 3x + 2y + 6 = 0 C) 3x – 2y – 6 = 0 D) 3x + 2y = 0
Caâu 7: Cho hai ñöôøng thaúng d: 3x – 2y – 6 = 0 vaø : 3x + 2y – 4 = 0. Khi ñoù: A) d   B) d //  C) d   D) d caét 
Caâu 8: Soá ño goùc giöõa hai ñöôøng thaúng d: x – 2y + 1 = 0 vaø : 3x – y – 2 = 0 baèng: A) 300 B) 450 C) 600 D) 900
B. Phaàn töï luaän: (6 ñieåm)
Caâu 9: Cho ABC coù AB = 2, AC = 4, BC = 2 3 .
a) Tính soá ño goùc A cuûa ABC.
b) Tính dieän tích cuûa ABC.
Caâu 10: Trong mp Oxy, cho caùc ñieåm A(–2; 1), B(6; –3), C(8; 4).
a) Vieát phöông trình caùc ñöôøng thaúng chöùa caïnh BC vaø ñöôøng cao AH.
b) Vieát phöông trình ñöôøng thaúng d ñi qua A vaø song song vôùi BC.
c) Tính dieän tích cuûa ABC. 69
Nguyễn Đình Khương
Hình Học 10 Cơ Bản
V. ÑAÙP AÙN VAØ BIEÅU ÑIEÅM:
A. Phaàn traéc nghieäm: 1 D 2 C 3 A 4 C 5 B 6 A 7 D 8 B B. Töï luaän: 2 2 2 2 2 2 Caâu 9: AB  AC  BC 2  4  (2 3) 1 a) cosA =   (0,5 ñieåm) 2AB.AC 2.2.4 2  A = 600. (0,5 ñieåm) 1 1 b) S = 0 AB.AC.sin A  .2.4.sin60 (0,5 ñieåm) 2 2 = 2 3 (0,5 ñieåm) Caâu 10:
a)  BC  (2;7)  nBC = (7; –2) (0,5 ñieåm)
 Phöông trình BC: 7(x – 6) – 2(y + 3) = 0  7x – 2y – 48 = 0 (0,5 ñieåm)  nAH  BC = (2; 7) (0,5 ñieåm)
 Phöông trình AH: 2(x + 2) + 7(y – 1) = 0  2x + 7y – 3 = 0 (0,5 ñieåm)
b) Phöông trình ñöôøng thaúng d // BC coù daïng: 7x – 2y + c = 0 (0,5 ñieåm)
d ñi qua A(–2; 1)  7(–2) – 2.1 + c = 0  c = 16
 Phöông trình ñöôøng thaúng d: 7x – 2y + 16 = 0 (0,5 ñieåm) 64 c) BC = 53 ; AH = d(A, BC) = (0,5 ñieåm) 53 1  SABC = BC.AH = 32 (0,5 ñieåm) 2
VI. KEÁT QUAÛ KIEÅM TRA: 0 – 3,4 3,5 – 4,9 5,0 – 6,4 6,5 – 7,9 8,0 – 10 Lôùp Só soá SL % SL % SL % SL % SL % 10A3 44 10A5 42 10A7 44 10A10 42 10A11 38 Ngaøy soaïn: 05/04/2013
Chöông III: PHÖÔNG PHAÙP TOAÏ ÑOÄ TRONG MAËT PHAÚNG Tieát daïy: 35
Baøøi 2: PHÖÔNG TRÌNH ÑÖÔØNG TROØN I. MUÏC TIEÂU: Kieán thöùc:
 Naém ñöôïc phöông trình ñöôøng troøn.
 Naém ñöôïc phöông trình tieáp tuyeán cuûa ñöôøng troøn. Kó naêng:
 Laäp ñöôïc phöông trình ñöôøng troøn khi bieát taâm vaø baùn kính.
 Nhaän daïng ñöôïc phöông trình ñöôøng troøn vaø tìm ñöôïc toaï ñoä taâm vaø baùn kính cuûa noù. 70
Nguyễn Đình Khương
Hình Học 10 Cơ Bản
 Laäp ñöôïc phöông trình tieáp tuyeán cuûa ñöôøng troøn. Thaùi ñoä:
 Reøn luyeän tính caån thaän, chính xaùc.
 Laøm quen vieäc chuyeån tö duy hình hoïc sang tö duy ñaïi soá. II. CHUAÅN BÒ:
Giaùo vieân: Giaùo aùn. Hình veõ minh hoaï.
Hoïc sinh: SGK, vôû ghi. OÂn taäp kieán thöùc veà ñöôøng troøn ñaõ hoïc. Duïng cuï veõ hình.
III. HOAÏT ÑOÄNG DAÏY HOÏC:
1. OÅn ñònh toå chöùc: Kieåm tra só soá lôùp.
2. Kieåm tra baøi cuõ: (3')
H. Neâu khaùi nieäm veà ñöôøng troøn. Moät ñöôøng troøn ñöôïc xaùc ñònh bôûi nhöõng yeáu toá naøo?
Ñ. (O, R) = {M / OM = R}.
3. Giaûng baøi môùi:
TL Hoaït ñoäng cuûa Giaùo vieân
Hoaït ñoäng cuûa Hoïc sinh Noäi dung
Hoaït ñoäng 1: Tìm hieåu veà Phöông trình ñöôøng troøn
 GV höôùng daãn HS tìm y
I. Phöông trình ñöôøng troøn
15' hieåu phöông trình ñöôøng M
coù taâm vaø baùn kính cho
troøn döïa vaøo hình veõ. I R b tröôùc O a x
Phöông trình ñöôøng troøn (C)
H1. Neâu ñieàu kieän ñeå M 
taâm I(a; b), baùn kính R: Ñ1. M(x; y) (C) ?  (C)  IM = R
(x – a)2 + (y – b)2 = R2 (1)  2 2 (x  ) a (y  ) b = R
Phöông trình ñöôøng troøn (C)
taâm O(0; 0), baùn kính R: x2 + y 2 = R2 (2)
H2. Ta caàn xaùc ñònh caùc Ñ2.
VD: Cho hai ñieåm (A(3; –4), yeáu toá naøo ?
+ Taâm I laø trung ñieåm cuûa AB
B(–3; 4). Vieát pt ñöôøng troøn
(C) nhaän AB laøm ñöôøng kính + Baùn kính R = AB 5  2 2 ?  (C): x2 + y2 = 25 4
Hoaït ñoäng 2: Tìm hieåu daïng khaùc cuûa phöông trình ñöôøng troøn
 Höôùng daãn HS nhaän xeùt  + Pt baäc hai ñoái vôùi x, y. II. Nhaän xeùt
10' ñaëc ñieåm cuûa phöông trình + Caùc heä soá cuûa x2, y2 baèng Phöông trình: (3). nhau.
x2 + y2 – 2ax – 2by + c = 0 (3)
+ Khoâng chöùa soá haïng tích xy. vôùi a2 + b2 – c > 0 laø pt ñöôøng
troøn coù taâm I(a; b), baùn kính R = 2 2
a b c .
H1. Kieåm tra ñieàu kieän ñeå Ñ1.
VD: Trong caùc pt sau, pt naøo
pt laø pt ñöôøng troøn ?
a) Khoâng, vì caùc heä soá cuûa x2, laø pt ñöôøng troøn? y2 khoâng baèng nhau.
a) 2x2 + y2 – 8x + 2y – 1 = 0
b) Coù, vì a2 + b2 – c > 0
b) x2 + y2 + 2x – 4y – 4 = 0
c) Khoâng, vì a2 + b2 – c < 0
c) x2 + y2 – 2x – 6y + 20 = 0
Hoaït ñoäng 3: Tìm hieåu phöông trình tieáp tuyeán cuûa ñöôøng troøn 71
Nguyễn Đình Khương
Hình Học 10 Cơ Bản
III. Phöông trình tieáp tuyeán 10' M0
cuûa ñöôøng troøn M
Cho (C) coù taâm I(a; b), I
M(x0; y0) (C). Phöông trình
H1. Xaùc ñònh VTPT cuûa  ? Ñ1. n IM
tieáp tuyeán cuûa (C) taïi M0(x0; 0 = (x0 –a; y0 – b) y 0): (x
0–a)(x–x0) + (y0–b)(y–y0)=0 Nhaän xeùt:
laø tieáp tuyeán cuûa (C)
d(I, ) = R
H2. Xaùc ñònh taâm ñöôøng
VD: Vieát phöông trình tieáp Ñ2. I(1; 2) troøn ?
tuyeán taïi ñieåm M(3; 4) thuoäc
 : (3–1)(x–3)+(4–2)(y–4) = ñöôøng troøn: 0 (x – 1)2 + (y – 2)2 = 8  x + y – 7 = 0
Hoaït ñoäng 4: Cuûng coá  Nhaán maïnh:
– Daïng phöông trình ñöôøng 5' troøn.
– Xaùc ñònh taâm, baùn kính ñöôøng troøn.
– Pt tieáp tuyeán ñöôøng troøn.  Caâu hoûi:
a) Xaùc ñònh taâm vaø baùn kính a) I(0; 1), R = 2 ñöôøng troøn (C):
x2 + y2 – 2y – 1 = 0 b) x + y – 3 = 0
b) Vieát pttt cuûa (C) taïi M(1; 2).
4. BAØI TAÄP VEÀ NHAØ:
 Baøi 1, 2, 3, 4, 5, 6 SGK. Ngaøy soaïn: 05/04/2013
Chöông III: PHÖÔNG PHAÙP TOAÏ ÑOÄ TRONG MAËT PHAÚNG Tieát daïy: 37
Baøøi 2: BAØI TAÄP PHÖÔNG TRÌNH ÑÖÔØNG TROØN I. MUÏC TIEÂU:
Kieán thöùc: Cuûng coá caùc kieán thöùc veà:
 Phöông trình ñöôøng troøn.
 Phöông trình tieáp tuyeán cuûa ñöôøng troøn. Kó naêng:
 Laäp ñöôïc phöông trình ñöôøng troøn khi bieát taâm vaø baùn kính.
 Nhaän daïng ñöôïc phöông trình ñöôøng troøn vaø tìm ñöôïc toaï ñoä taâm vaø baùn kính cuûa noù.
 Laäp ñöôïc phöông trình tieáp tuyeán cuûa ñöôøng troøn. 72
Nguyễn Đình Khương
Hình Học 10 Cơ Bản Thaùi ñoä:
 Reøn luyeän tính caån thaän, chính xaùc.
 Laøm quen vieäc chuyeån tö duy hình hoïc sang tö duy ñaïi soá. II. CHUAÅN BÒ:
Giaùo vieân: Giaùo aùn. Heä thoáng baøi taäp.
Hoïc sinh: SGK, vôû ghi. OÂn taäp kieán thöùc veà ñöôøng troøn ñaõ hoïc.
III. HOAÏT ÑOÄNG DAÏY HOÏC:
1. OÅn ñònh toå chöùc: Kieåm tra só soá lôùp.
2. Kieåm tra baøi cuõ: (Loàng vaøo quaù trình luyeän taäp) H. Ñ.
3. Giaûng baøi môùi:
TL Hoaït ñoäng cuûa Giaùo vieân
Hoaït ñoäng cuûa Hoïc sinh Noäi dung
Hoaït ñoäng 1: Luyeän taäp xaùc ñònh taâm vaø baùn kính ñöôøng troøn
H1. Neâu caùch xaùc ñònh taâm Ñ1.
1. Tìm taâm vaø baùn kính cuûa
10' vaø baùn kính ñöôøng troøn ? C1: Ñöa veà daïng: caùc ñöôøng troøn: (x – a)2 + (y – b)2 = R2
a) x2 + y2 – 2x – 2y – 2 = 0
C2: Kieåm tra ñk: a2 + b2 – c > 0 b) 16x2 +16y2+16x–8y–11 = 0 a) I(1; 1), R = 2
c) x2 + y2 – 4x + 6y – 3 = 0 b) Chia 2 veá cho 16.   I 1 1   ; ; R = 1 2 4    c) I(2; –3); R = 4
Hoaït ñoäng 2: Luyeän taäp vieát phöông trình ñöôøng troøn
H1. Ta caàn xaùc ñònh caùc Ñ1.
2. Laäp pt ñöôøng troøn (C) trong 15' yeáu toá naøo ? a) R = IM = 52 caùc tröôøng hôïp sau:
 (C): (x + 2)2 +(y – 3)2 = 52.
a) (C) coù taâm I(–2; 3) vaø ñi 2 qua M(2; –3). b) R = d(I, ) = 5
b) (C) coù taâm I(–1; 2) vaø tieáp
xuùc vôùt ñt : x – 2y + 7 = 0.
 (C): (x + 1)2 – (y – 2)2 = 4
c) (C) coù ñöôøng kính AB vôùi 5 A(1; 1), B(7; 5). c) I(4; 3), R = 13
 (C): (x – 4)2 + (y – 32 = 13
 GV höôùng daãn caùch vieát  Pt ñöôøng troøn (C) coù daïng:
3. Laäp pt ñöôøng troøn (C) ñi
phöông trình ñöôøng troøn ñi x2 + y2 – 2ax – 2by + c = 0 (*) qua 3 ñieåm A(1; 2), B(5; 2), qua 3 ñieåm.
Thay toaï ñoä caùc ñieåm A, B, C C(1; –3)
vaøo (*) ta ñöôïc heä pt:
 1 4  2a  4b c  0 
25 4 10a  4b c  0
 1 92a  6b c  0  a = 3; b = 1  ; c = – 1 2
 (C): x2 + y2 – 6x + y – 1 = 0
Hoaït ñoäng 3: Luyeän taäp vieát phöông trình tieáp tuyeán cuûa ñöôøng troøn 73
Nguyễn Đình Khương
Hình Học 10 Cơ Bản
H1. Xaùc ñònh taâm vaø baùn Ñ1. I(2; –4); R = 5
4. Cho ñöôøng troøn (C) coù pt: kính ? x2 + y2 – 4x + 8y – 5 = 0 12'
a) Tìm toaï ñoä taâm vaø baùn kính
H2. Kieåm tra A  (C) ?
Ñ2. Toaï ñoä cuûa A thoaû (C)  A b) Vieát pttt () vôùi (C) ñi qua  (C)  Pttt (): ñieåm A(–1; 0).
(–1–2)(x+1) + (0+4)(y–0) = 0 c) Vieát pttt () vôùi (C) vuoâng  3x – 4y + 3 = 0
goùc vôùi ñt d: 3x – 4y + 5 = 0.
H3. Xaùc ñònh daïng pt cuûa Ñ3.   d  : 4x + 3y + c = 0 tieáp tuyeán () ?
H4. Ñieàu kieän  tieáp xuùc Ñ4. d(I, ) = R vôùi (C) ?   c c   8 12  29 5 c  21  1: 4x + 3y + 29 = 0 2: 4x + 3y – 21 = 0
Hoaït ñoäng 4: Cuûng coá  Nhaán maïnh:
3' – Caùch xaùc ñònh taâm vaø baùn
kính cuûa ñöôøng troøn.
– Caùch laäp pt ñöôøng troøn.
– Caùch vieát pttt cuûa ñöôøng troøn.
4. BAØI TAÄP VEÀ NHAØ:
 Laøm caùc baøi taäp coøn laïi.
 Ñoïc tröôùc baøi "Phöông trình ñöôøng elip". Ngaøy soaïn: 5/04/2013
Chöông III: PHÖÔNG PHAÙP TOAÏ ÑOÄ TRONG MAËT PHAÚNG Tieát daïy: 38
Baøøi 3: PHÖÔNG TRÌNH ÑÖÔØNG ELIP I. MUÏC TIEÂU: Kieán thöùc:
 Hieåu ñöôïc ñònh nghóa, phöông trình chính taéc, caùc yeáu toá cuûa elip. Kó naêng:
 Laäp ñöôïc phöông trình chính taéc cuûa elip.
 Töø pt chính taéc cuûa elip, xaùc ñònh ñöôïc truïc lôùn, truïc nhoû, tieâu cöï, tieâu ñieåm, caùc ñænh, …
 Thoâng qua pt chính taéc cuûa elip ñeå tìm hieåu tính chaát hình hoïc vaø giaûi moät soá baøi toaùn cô baûn veà elip. 74
Nguyễn Đình Khương
Hình Học 10 Cơ Bản Thaùi ñoä:
 Reøn luyeän tính caån thaän, chính xaùc. II. CHUAÅN BÒ:
Giaùo vieân: Giaùo aùn. Hình veõ minh hoaï.
Hoïc sinh: SGK, vôû ghi. Taám bìa cöùng, 2 ñinh ghim, sôïi daây.
III. HOAÏT ÑOÄNG DAÏY HOÏC:
1. OÅn ñònh toå chöùc: Kieåm tra só soá lôùp.
2. Kieåm tra baøi cuõ: (5')
H. Vieát caùc daïng phöông trình ñöôøng troøn? Neâu phöông trình tieáp tuyeán cuûa ñöôøng troøn taïi
moät ñieåm thuoäc ñöôøng troøn ? Ñ.
3. Giaûng baøi môùi:
TL Hoaït ñoäng cuûa Giaùo vieân
Hoaït ñoäng cuûa Hoïc sinh Noäi dung
Hoaït ñoäng 1: Tìm hieåu ñöôøng elip  Cho HS quan saùt:
 HS quan saùt vaø cho nhaän xeùt.
I. Ñònh nghóa ñöôøng elip
10' – Maët nöôùc trong coác nöôùc
Cho 2 ñieåm coá ñònh F1, F2 vaø caàm nghieâng.
moät ñoä daøi khoâng ñoåi 2a lôùn
– Boùng cuûa moät ñöôøng troøn hôn F1F2. treân moät maët phaúng.
M (E) F1M + F2M = 2a
H1. Caùc hình treân coù phaûi laø Ñ1. Khoâng.
F1, F2: caùc tieâu ñieåm ñöôøng troøn khoâng ?
F1F2 = 2c: tieâu cöï.
 Cho HS thöïc hieän thao taùc M
veõ ñöôøng elip treân taám bìa. F 1 F2
Hoaït ñoäng 2: Tìm hieåu phöông trình chính taéc cuûa elip
 GV giôùi thieäu phöông y
II. Phöông trình chính taéc
15' trình chính taéc cuûa elip. B2 M(x; y) cuûa elip 2 2 A x y 1 A 2   1 (b2 = a2 – c2) F O 1 F2 x 2 2 a b B1
H1. Xaùc ñònh toaï ñoä caùc Ñ1. B1(0; –b); B2(0; b) ñieåm B1, B2 ? Ñ2. B  H2. Tính B 2F1 = B2F2 = 2 2 b c 2F1, B2F2 ? Ñ3. B H3. Tính B 2F1 + B2F2 = 2a 2F1 + B2F2 ?  2 2 2
b c = 2a  b2 = a2 – c2 75
Nguyễn Đình Khương
Hình Học 10 Cơ Bản
 GV höôùng daãn HS nhaän y
III. Hình daïng cuûa elip xeùt. B b 2 2 2 M(x; y) x y 15' Cho (E):   1 (*) A 2 2 1 F A a b 1 F2 2 –a – c O c a x
a) (E) coù caùc truïc ñoái xöùng laø
H1. Cho M(x; y)  (E). Caùc – b
Ox, Oy vaø coù taâm ñoái xöùng laø ñieåm M B1 1(–x; y), M2(x; –y), O.
M3(–x; –y) coù thuoäc (E) Ñ1. Coù, vì toaï ñoä ñeàu thoaû maõn b) Caùc ñænh A1(–a; 0), A2(a; 0) khoâng ? (*). B1(0; –b), B2(0; b)
A1A2 = 2a : truïc lôùn
H2. Tìm toaï ñoä caùc giao Ñ2.
B1B2 = 2b : truïc nhoû
ñieåm cuûa (E) côùi caùc truïc y = 0  x =  a  (E) caét Ox toaï ñoä ?
taïi 2 ñieåm A1(–a; 0), A2(a; 0)
x = 0  y =  b  (E) caét Oy
taïi 2 ñieåm B1(0; –b), B2(0; b)
H3. So saùnh a vaø b ? Ñ3. a > b. 2 2 x y
H4. Töø ptct cuûa (E), chæ ra Ñ4. a2 = 9, b2 = 1  c2 = 8 VD: Cho (E):   1. 9 1 a2, b2 ?  a = 3, b = 1, c = 2 2
Tìm ñoä daøi caùc truïc, tieâu cöï,
Ñoä daøi truïc lôùn: 2a = 6
toaï ñoä caùc tieâu ñieåm, toaï ñoä
Ñoä daøi truïc nhoû: 2b = 2 caùc ñænh cuûa (E). Tieâu cöï: 2c = 4 2
Toaï ñoä caùc tieâu ñieåm: F1,2(2 2 ; 0)
Toaï ñoä caùc ñænh: A1;2(3; 0), B1,2(0; 1)
Hoaït ñoäng 3: Cuûng coá  Nhaán maïnh:
3' – Caùc hình coù daïng ñöôøng elip.
– Phöông trình chính taéc cuûa elip.
4. BAØI TAÄP VEÀ NHAØ:
 Ñoïc tieáp baøi "Phöông trình ñöôøng elip".
 Tìm theâm caùc hình coù daïng ñöôøng elip. Ngaøy soaïn: 10/04/2013
Chöông III: PHÖÔNG PHAÙP TOAÏ ÑOÄ TRONG MAËT PHAÚNG Tieát daïy: 38
Baøøi 3: PHÖÔNG TRÌNH ÑÖÔØNG ELIP (tt) I. MUÏC TIEÂU: Kieán thöùc:
 Hieåu ñöôïc ñònh nghóa, phöông trình chính taéc, caùc yeáu toá cuûa elip. Kó naêng: 76
Nguyễn Đình Khương
Hình Học 10 Cơ Bản
 Laäp ñöôïc phöông trình chính taéc cuûa elip.
 Töø pt chính taéc cuûa elip, xaùc ñònh ñöôïc truïc lôùn, truïc nhoû, tieâu cöï, tieâu ñieåm, caùc ñænh, …
 Thoâng qua pt chính taéc cuûa elip ñeå tìm hieåu tính chaát hình hoïc vaø giaûi moät soá baøi toaùn cô baûn veà elip. Thaùi ñoä:
 Reøn luyeän tính caån thaän, chính xaùc. II. CHUAÅN BÒ:
Giaùo vieân: Giaùo aùn. Hình veõ minh hoaï.
Hoïc sinh: SGK, vôû ghi. Duïng cuï veõ hình.
III. HOAÏT ÑOÄNG DAÏY HOÏC:
1. OÅn ñònh toå chöùc: Kieåm tra só soá lôùp.
2. Kieåm tra baøi cuõ: (3')
H. Neâu phöông trình chính taéc cuûa elip ? 2 2 Ñ. x y   1 (b2 = a2 – c2) 2 2 a b
3. Giaûng baøi môùi:
TL Hoaït ñoäng cuûa Giaùo vieân
Hoaït ñoäng cuûa Hoïc sinh Noäi dung
Hoaït ñoäng 1: Tìm hieåu hình daïng cuûa elip
 GV höôùng daãn HS nhaän y
III. Hình daïng cuûa elip xeùt. B b 2 2 2 M(x; y) x y 20' Cho (E):   1 (*) A 2 2 1 F A a b 1 F2 2 –a – c O c a x
a) (E) coù caùc truïc ñoái xöùng laø
H1. Cho M(x; y)  (E). Caùc – b
Ox, Oy vaø coù taâm ñoái xöùng laø ñieåm M B1 1(–x; y), M2(x; –y), O.
M3(–x; –y) coù thuoäc (E) Ñ1. Coù, vì toaï ñoä ñeàu thoaû maõn b) Caùc ñænh A1(–a; 0), A2(a; 0) khoâng ? (*). B1(0; –b), B2(0; b)
A1A2 = 2a : truïc lôùn
H2. Tìm toaï ñoä caùc giao Ñ2.
B1B2 = 2b : truïc nhoû
ñieåm cuûa (E) côùi caùc truïc y = 0  x =  a  (E) caét Ox toaï ñoä ?
taïi 2 ñieåm A1(–a; 0), A2(a; 0)
x = 0  y =  b  (E) caét Oy
taïi 2 ñieåm B1(0; –b), B2(0; b)
H3. So saùnh a vaø b ? Ñ3. a > b. 2 2 x y
H4. Töø ptct cuûa (E), chæ ra Ñ4. a2 = 9, b2 = 1  c2 = 8 VD: Cho (E):   1. 9 1 a2, b2 ?  a = 3, b = 1, c = 2 2
Tìm ñoä daøi caùc truïc, tieâu cöï,
Ñoä daøi truïc lôùn: 2a = 6
toaï ñoä caùc tieâu ñieåm, toaï ñoä
Ñoä daøi truïc nhoû: 2b = 2 caùc ñænh cuûa (E). Tieâu cöï: 2c = 4 2
Toaï ñoä caùc tieâu ñieåm: F1,2(2 2 ; 0)
Toaï ñoä caùc ñænh: A1;2(3; 0), B1,2(0; 1) 77
Nguyễn Đình Khương
Hình Học 10 Cơ Bản
Hoaït ñoäng 2: Tìm hieåu moái lieân heä giöõa ñöôøng troøn vaø ñöôøng elip
 GV höôùng daãn HS nhaän
IV. Lieân heä giöõa ñöôøng troøn x xeùt. vaø ñöôøng elip 10' M(x;y)
a) Töø b2 = a2 – c2 c caøng M’(x’;y’)
nhoû thì b caøng gaàn baèng a
(E) coù daïng gaàn nhö ñtroøn. O H x
b) Cho ñöôøng troøn (C): x2 + y2 = a2
Xeùt pheùp bieán ñoåi:
M(x; y) M(x; y)
 M(x; y)  (C)  x2 + y2 = a2 x '  x 2 
x 2 + a y' = a2 vôùi: b (0 < b < a) 2 y'  y b  a 2 2 2 2  x ' y' 
 1 M (E) Khi ñoù, x ' y'   1 laø (E) 2 2 a b 2 2 a b
Ta noùi (C) co thaønh (E).
Hoaït ñoäng 3: Cuûng coá  Nhaán maïnh:
– Caùc yeáu toá cuûa (E).  Chuù yù:
10' – Moái lieân heä giöõa ñöôøng + a, b, > 0. troøn vaø elip.
+ Toaï ñoä ñænh vaø tieâu ñieåm.
Caâu hoûi: Xaùc ñònh caùc yeáu toá cuûa (E): 2 2 x y a)   1 6 2 a) a = 6 ; b = 2 ; c = 2 2 2 b) x y   1 b) a = 3 2 ; b = 2 2 ; c = 10 18 8
4. BAØI TAÄP VEÀ NHAØ:  Baøi 1, 2, 3, 4, 5 SGK.
 Ñoïc baøi ñoïc theâm "Ba ñöôøng coânic vaø quyõ ñaïo cuûa taøu vuõ truï" Ngaøy soaïn: 15/04/2013
Chöông III: PHÖÔNG PHAÙP TOAÏ ÑOÄ TRONG MAËT PHAÚNG Tieát daïy: 39
Baøøi 3: BAØI TAÄP PHÖÔNG TRÌNH ÑÖÔØNG ELIP I. MUÏC TIEÂU: Kieán thöùc:
 Hieåu ñöôïc ñònh nghóa, phöông trình chính taéc, caùc yeáu toá cuûa elip. Kó naêng:
 Laäp ñöôïc phöông trình chính taéc cuûa elip. 78
Nguyễn Đình Khương
Hình Học 10 Cơ Bản
 Töø pt chính taéc cuûa elip, xaùc ñònh ñöôïc truïc lôùn, truïc nhoû, tieâu cöï, tieâu ñieåm, caùc ñænh, …
 Thoâng qua pt chính taéc cuûa elip ñeå tìm hieåu tính chaát hình hoïc vaø giaûi moät soá baøi toaùn cô baûn veà elip. Thaùi ñoä:
 Reøn luyeän tính caån thaän, chính xaùc. II. CHUAÅN BÒ:
Giaùo vieân: Giaùo aùn. Heä thoáng baøi taäp.
Hoïc sinh: SGK, vôû ghi. OÂn taäp kieán thöùc veà ñöôøng elip.
III. HOAÏT ÑOÄNG DAÏY HOÏC:
1. OÅn ñònh toå chöùc: Kieåm tra só soá lôùp.
2. Kieåm tra baøi cuõ: (Loàng vaøo quaù trình luyeän taäp) H. Ñ
3. Giaûng baøi môùi:
TL Hoaït ñoäng cuûa Giaùo vieân
Hoaït ñoäng cuûa Hoïc sinh Noäi dung
Hoaït ñoäng 1: Luyeän taäp xaùc ñònh caùc yeáu toá cuûa elip
H1. Xaùc ñònh a, b, c ? Ñ1.
1. Xaùc ñònh ñoä daøi caùc truïc, 10' a) a = 5, b = 3, c = 4
tieâu cöï, toaï ñoä caùc tieâu ñieåm, 2 2 x y
toaï ñoä caùc ñænh cuûa (E): b) 4x2 + 9y2 = 1    1 1 1 2 2 a) x y   1 4 9 25 9 b) 4x2 + 9y2 = 1  a = 1 , b = 1 , c = 5 2 3 6 c) 4x2 + 9y2 = 36 2 2 x y c) 4x2 + 9y2 = 36    1 9 4  a = 3, b = 2, c = 5
Hoaït ñoäng 2: Luyeän taäp laäp phöông trình chính taéc cuûa elip
H1. Neâu yeáu toá caàn xaùc Ñ1. a, b.
2. Laäp phöông trình chính taéc 20' ñònh ? a) a = 4, b = 3
cuûa (E) trong caùc tröôøng hôïp 2 2 sau: x y  (E):   1 16 9
a) Ñoä daøi truïc lôùn laø 8, ñoä daøi b) a = 5, b = 4 truïc nhoû laø 6. 2 2 x y
b) Ñoä daøi truïc lôùn laø 10, tieâu  (E):   1 25 16 cöï laø 6.
c) (E) ñi qua caùc ñieåm M(0; 3) c) M(0; 3) 9  (E)   1  12  2 b vaø N3; . 5     12  N3;  (E)
d) (E) coù 1 tieâu ñieåm laø 5   
F1(  3 ; 0) vaø ñi qua ñieåm 9 144    1   2 2 3 a 25b M1;  .  a = 5, b = 3  2  2 2 x y  (E):   1 25 9 79
Nguyễn Đình Khương
Hình Học 10 Cơ Bản d) F1(  3 ; 0)  c = 3   M 3 1;   (E)  2  1 3    1 2 2 a 4b  a = 2, b= 1 2 2 x y  (E):   1 4 1
Hoaït ñoäng 3: Luyeän taäp giaûi toaùn lieân quan ñeán elip
 GV höôùng daãn HS chöùng
3. Cho 2 ñöôøng troøn C1(F1; R1) 10' minh. M
vaø C2(F2; R2). (C1) naèm trong (C)
(C2) vaø F1  F2. Ñöôøng troøn F2 F
(C) thay ñoåi luoân tieáp xuùc 1 (C1)
ngoaøi vôùi (C1) vaø tieáp xuùc (C trong vôùi (C 2) 2). Haõy chöùng toû
raèng taâm M cuûa (C) di ñoäng treân moät elip. H1. Tính MF Ñ1. MF1 = R1 + R 1, MF2 ? MF2 = R2 – R H2. Tính MF Ñ2. MF 1 + MF2 ? 1 + MF2 = R1 + R2
 M thuoäc (E) coù 2 tieâu ñieåm
laø F1, F2 vaø truïc lôùn 2a = R1 + R2
Hoaït ñoäng 4: Cuûng coá  Nhaán maïnh:
3' – Caùch xaùc ñònh caùc yeáu toá cuûa (E).
– Caùch laäp pt chính taéc cuûa (E).
4. BAØI TAÄP VEÀ NHAØ:
 Baøi taäp oân chöông III. Ngaøy soaïn: 20/04/2013
Chöông III: PHÖÔNG PHAÙP TOAÏ ÑOÄ TRONG MAËT PHAÚNG Tieát daïy: 40
Baøøi daïy: OÂN TAÄP CHÖÔNG III I. MUÏC TIEÂU: Kieán thöùc:
 OÂn taäp toaøn boä kieán thöùc chöông III. Kó naêng:
 Vaän duïng kieán thöùc ñaõ hoïc ñeå giaûi toaùn. Thaùi ñoä: 80
Nguyễn Đình Khương
Hình Học 10 Cơ Bản
 Reøn luyeän tính caån thaän, chính xaùc. II. CHUAÅN BÒ:
Giaùo vieân: Giaùo aùn. Heä thoáng baøi taäp.
Hoïc sinh: SGK, vôû ghi. OÂn taäp kieán thöùc chöông III.
III. HOAÏT ÑOÄNG DAÏY HOÏC:
1. OÅn ñònh toå chöùc: Kieåm tra só soá lôùp.
2. Kieåm tra baøi cuõ: (Loàng vaøo quaù trình luyeän taäp) H. Ñ
3. Giaûng baøi môùi:
TL Hoaït ñoäng cuûa Giaùo vieân
Hoaït ñoäng cuûa Hoïc sinh Noäi dung
Hoaït ñoäng 1: Luyeän taäp giaûi toaùn veà ñöôøng thaúng A B
1. Cho hình chöõ nhaät ABCD.
Bieát caùc ñænh A(5; 1), C(0; 6) 20'
vaø phöông trình CD: x + 2y – D C
H1. Nhaän xeùt veà caùc ñt AB, Ñ1.
12 = 0. Tìm phöông trình caùc BC, AD ?
 AB chöùa A vaø AB // CD
ñöôøng thaúng chöùa caùc caïnh  AB: x + 2y – 7 = 0 coøn laïi.
 BC chöùa C vaø BC  CD  BC: 2x – y + 6 = 0
 AD chöùa A vaø AD  CD  AD: 2x – y – 9 = 0 A O
2. Cho ñöôøng thaúng : x – y +
 GV höôùng daãn caùch xaùc  2 = 0 vaø ñieåm A(2; 0). ñònh ñieåm A. H M
a) Tìm ñieåm A ñoái xöùng cuûa A’
H2. Xaùc ñònh VTCP cuûa  ? O qua . Ñ2. u = (1; 1)
b) Tìm ñieåm M   sao cho
H3. Neâu ñieàu kieän xaùc ñònh
ñoä daøi ñöôøng gaáp khuùc OMA ñieåm H ? 
Ñ3. OH u   A(–2; 2) ngaén nhaát. H  
H4. Khi naøo OMA ngaén Ñ4. M laø giao ñieåm cuûa AA vôùi nhaát ? .  M(–2; 0)
3. Laäp phöông trình hai ñöôøng
phaân giaùc cuûa caùc goùc taïo bôûi
H5. Neâu tính chaát ñöôøng Ñ5. M    d(M,d1) = hai ñöôøng thaúng: phaân giaùc ? d(M,d2) d1: 3x – 4y + 12 = 0 x y x y   3 4 12 12 5 7   d2: 12x + 5y – 7 = 0 5 13
Hoaït ñoäng 2: Luyeän taäp giaûi toaùn veà ñöôøng troøn
H1. Neâu caùch xaùc ñònh G, H Ñ1.
4. Cho 3 ñieåm A(4; 3), B(2; OA OB OC 7), C(–3; –8). 10'  G: OG    3
a) Tìm toaï ñoä troïng taâm G vaø tröïc taâm H cuûa ABC.
b) Vieát phöông trình ñöôøng troøn ngoaïi tieáp ABC. 81
Nguyễn Đình Khương
Hình Học 10 Cơ Bản  1 x
x x x ( )  1  G A B C  3  1 2
y  (y y y )  G  3 A B C 3
 GV höôùng daãn HS caùch AH BC
vieát phöông trình ñöôøng troøn  H: . 0 
BH.AC  0 ñi qua 3 ñieåm.  
H2. Neâu tính chaát taâm ñtroøn  x  3y  13 x    13 
7x 11y  91 y  0 ngoaïi tieáp tam giaùc ?
Ñ2.IA IBa     5  IA ICb  1 R = IA = 85
 (C): (x + 5)2 + (y – 1)2 = 85 C2:
(C): x2 + y2 – 2ax – 2by + c = 0
Thay laàn löôït toaï ñoä 3 ñieåm A,
B, C vaøo pt (C), ta ñöôïc heä pt:  8
a  6b c  2  5   4
a 14b c  5  3
6a 16b c  7  3 a  5   b  1 c  59
Hoaït ñoäng 3: Luyeän taäp giaûi toaùn veà ñöôøng elip
H1. Neâu coâng thöùc xaùc ñònh Ñ1. a = 4, b = 3, c = 7 2 2 x y
10' caùc yeáu toá cuûa (E) ? 5. Cho (E):   1. Tìm  2a = 8, 2b = 6, 2c = 2 7 16 9 Tieâu ñieåm:F caùc yeáu toá cuûa (E). 1(– 7 ;0), F2( 7 ;0)
Ñænh: A1(–4; 0), A2(4; 0), B1(0; –3), B2(0; 3)
Hoaït ñoäng 4: Cuûng coá
 Nhaán maïnh caùch giaûi caùc 3' daïng toaùn.
4. BAØI TAÄP VEÀ NHAØ:  Baøi taäp cuoái naêm. Ngaøy soaïn: 25/04/2013 Tieát daïy: 41
Baøøi daïy: OÂN TAÄP CUOÁI NAÊM I. MUÏC TIEÂU:
Kieán thöùc: OÂn taäp theo töøng chuû ñeà:  Vectô – Toaï ñoä.
 Heä thöùc löôïng trong tam giaùc. Giaûi tam giaùc. 82
Nguyễn Đình Khương
Hình Học 10 Cơ Bản
 Phöông trình ñöôøng thaúng.
 Khoaûng caùch töø moät ñieåm ñeán ñöôøng thaúng, goùc giöõa hai ñöôøng thaúng.
 Phöông trình ñöôøng troøn.  Phöông trình elip.
Kó naêng: Cuûng coá caùc kó naêng giaûi toaùn veà:  Vectô – Toaï ñoä.
 Heä thöùc löôïng trong tam giaùc. Giaûi tam giaùc.
 Caùc baøi toaùn veà ñöôøng thaúng, ñöôøng troøn, ñöôøng elip. Thaùi ñoä:
 Reøn luyeän tính caån thaän, chính xaùc. II. CHUAÅN BÒ:
Giaùo vieân: Giaùo aùn. Heä thoáng baøi taäp.
Hoïc sinh: SGK, vôû ghi. OÂn taäp kieán thöùc hình hoïc lôùp 10 ñaõ hoïc.
III. HOAÏT ÑOÄNG DAÏY HOÏC:
1. OÅn ñònh toå chöùc: Kieåm tra só soá lôùp.
2. Kieåm tra baøi cuõ: (Loàng vaøo quaù trình luyeän taäp) H. Ñ
3. Giaûng baøi môùi:
TL Hoaït ñoäng cuûa Giaùo vieân
Hoaït ñoäng cuûa Hoïc sinh Noäi dung
Hoaït ñoäng 1: Cuûng coá vectô – toaï ñoä
H1. Neâu ñieàu kieän ñeå Ñ1. MA  MB  MA.MB  0
1. Cho caùc ñieåm A(2; 3), B(9; 7' AMB vuoâng taïi M ?  y  0 4), M(5; y), P(x; 2). y  7
a) Tìm y ñeå AMB vuoâng taïi M.
H2. Neâu ñieàu kieän ñeå A, P, Ñ2. AB,AP cuøng phöông
b) Tìm x ñeå A, P, B thaúng B thaúng haøng ?  x = –5 haøng.
Hoaït ñoäng 2: Cuûng coá heä thöùc löôïng trong tam giaùc A
2. Cho ABC ñeàu caïnh baèng a)
6 cm. Moät ñieåm M treân caïnh 13' 6 N 6
AM2 = AB2 + BM2 – BC sao cho BM = 2 cm. 2 4 2AB.BM.cosB
a) Tính ñoä daøi ñoaïn thaúng AM B M C = 28 vaø tính cos BAM . 2 2 2 AB  AM  BM
b) Tính baùn kính ñöôøng troøn
 Cho HS neâu laàn löôït caùc cos BAM = 2AB.AM ngoaïi tieáp coâng thöùc tính. ABM.
c) Tính ñoä daøi trung tuyeán veõ = 5 7 14 töø C cuûa ACM. d) Tính dieän tích b) AM  2R  R = 2 21 ABM. sin B 3 2 2 2 c) CN2 = 2(CA  CM ) AM 4 = 19 d) S = 1 BA.BM.sinB = 3 3 2
Hoaït ñoäng 3: Cuûng coá ñöôøng thaúng, ñöôøng troøn, ñöôøng elip 83
Nguyễn Đình Khương
Hình Học 10 Cơ Bản
H1. Xaùc ñònh toaï ñoä caùc Ñ1. A = AB  AH  A 5 
3. Cho ABC côùi tröïc taâm H.  ;2  ñieåm A, B, H ?  2 
Bieát phöông trình caùc ñt: 20' B = AB  BH  B(3; 0) AB: 4x + y – 12 = 0,
H = BH  AH  H 11 5   ;  BH: 5x – 4y – 15 = 0,  3 6  AH: 2x + 2y – 9 = 0
H2. Neâu caùch xaùc ñònh caùc Ñ2.
Vieát pt caùc ñt chöùa caùc caïnh ñt AC, BC, CH ? AC  BH  AC: 4x+5y–20=0
coøn laïi vaø ñöôøng cao thöù ba. A  AC BC  AH   BC:x – y – 3 = 0 B BC CH  AB   CH:3x–12y–1=0 H  CH
4. Laäp pt ñöôøng troøn coù taâm
 GV höôùng daãn HS phaân I 
naèm treân ñt : 4x + 3y – 2 = 0 tích caùc giaû thieát. Ñ3.  d(I,  1 d )  d(I,d2)  R
vaø tieáp xuùc vôùi 2 ñöôøng
H3. Taâm I(a; b) cuûa ñöôøng     thaúng:
troøn coù tính chaát gì ?  a 2;b 2;R 2 2  a  4  ;b  6;R  3 2 d1: x + y + 4 = 0 d2: 7x – y + 4 = 0
H4. Nhaéc laïi caùc coâng thöùc Ñ4. a = 10, b = 6 , c = 8
xaùc ñònh caùc yeáu toá cuûa (E) 2 2 5. Cho (E): x y   1 . 100 36
H5. Vieát phöông trình ñt ñi Ñ5. : x = 8
a) Xaùc ñònh toaï ñoä caùc tieâu qua F
ñieåm, caùc ñænh cuûa (E). 2(8; 0) vaø // Oy ?
b) Qua tieâu ñieåm beân phaûi
cuûa (E) döïng ñt song song vôùi
Oy vaø caét (E) taïi 2 ñieåm M, N. Tính MN.
Hoaït ñoäng 4: Cuûng coá
3'  Nhaán maïnh caùc noäi dung ñaõ hoïc.
4. BAØI TAÄP VEÀ NHAØ:
Chuaån bò kieåm tra Hoïc kì 2. Ngaøy soaïn: 30/04/2013 Chöông : Tieát daïy: 42
Baøøi daïy: KIEÅM TRA HOÏC KÌ II I. MUÏC TIEÂU:
Kieán thöùc: Kieåm tra caùc kieán thöùc ñaõ hoïc trong hoïc kì 2:
 Heä thöùc löôïng trong tam giaùc. Giaûi tam giaùc. 84
Nguyễn Đình Khương
Hình Học 10 Cơ Bản
 Phöông trình ñöôøng thaúng. Khoaûng caùch töø moät ñieåm ñeán moät ñöôøng thaúng. Goùc giöõa hai ñöôøng thaúng.
 Phöông trình ñöôøng troøn.
 Phöông trình ñöôøng elip.
Kó naêng: Thaønh thaïo caùch giaûi caùc daïng toaùn:  Giaûi tam giaùc.
 Vieát phöông trình ñöôøng thaúng. Tính khoaûng caùch. Tính goùc.
 Vieát phöông trình ñöôøng troøn.
 Xaùc ñònh caùc yeáu toá cuûa elip. Thaùi ñoä:
 Reøn luyeän tính caån thaän, chính xaùc.
 Luyeän tö duy linh hoaït saùng taïo. II. CHUAÅN BÒ:
Giaùo vieân: Ñeà kieåm tra.
Hoïc sinh: OÂn taäp kieán thöùc ñaõ hoïc trong hoïc kì 2. III. MA TRAÄN ÑEÀ: Nhaän bieát Thoâng hieåu Vaän duïng Chuû ñeà Toång TNKQ TL TNKQ TL TNKQ TL
Heä thöùc löôïng trong 2 0,5 tam giaùc 0,25 Phöông trình ñöôøng 2 1 1,5 thaúng 0,25 1,0 Phöông trình ñöôøng 1 1 1,25 troøn 0,25 1,0 Phöông trình ñöôøng 1 0,25 elip 0,25 Toång 1,5 1,0 1,0 3,5
IV. NOÄI DUNG ÑEÀ KIEÅM TRA: A. Phaàn traéc nghieäm:
011: Baùn kính cuûa ñöôøng troøn ngoaïi tieáp tam giaùc vôùi ba caïnh laø a = 6, b = 8, c = 10 baèng: A. 5 B. 4 2 C. 5 2 D. 6
012: Dieän tích cuûa tam giaùc vôùi ba caïnh laø a = 6, b = 8, c = 10 baèng: A. 24 B. 20 2 C. 48 D. 30
013: Moät vectô phaùp tuyeán cuûa ñöôøng thaúng ñi qua 2 ñieåm A(2; 0) vaø B(0; 3) laø: A. n = (3; 2) B. n = (2; 3)
C. n = (2; –3)
D. n = (3; –2)
014: Heä soá goùc cuûa ñöôøng thaúng ñi qua 2 ñieåm A(2; 0) vaø B(0; 3) laø: A. 3  B. 3 C. 2 D. 2  2 2 3 3
015: Baùn kính cuûa ñöôøng troøn coù phöông trình: x2 + y2 – 10x – 2y – 12 = 0 baèng: A. 6 B. 36 C. 12 D. 116 2 2 x y
016: Ñoä daøi truïc lôùn cuûa elip:   1 baèng: 25 16 A. 10 B. 8 C. 50 D. 16 85
Nguyễn Đình Khương
Hình Học 10 Cơ Bản B. Phaàn töï luaän:
Baøi 4: Trong maët phaúng Oxy, cho ABC vôùi A(3; 4), B(1; 3), C(5; 0).
a) Vieát phöông trình toång quaùt ñöôøng thaúng BC.
b) Vieát phöông trình ñöôøng troøn coù taâm A vaø tieáp xuùc vôùi ñöôøng thaúng BC.
V. ÑAÙP AÙN VAØ BIEÅU ÑIEÅM:
A. Phaàn traéc nghieäm:
Taát caû ñeàu coù ñaùp aùn laø A. B. Töï luaän: Baøi 4: (2 ñieåm) a) BC  (4; 3  )  n  (3;4) (0,5 ñieåm)
 Phöông trình BC: 3(x – 1) + 4(y – 3) = 0  3x + 4y – 15 = 0 (0,5 ñieåm)
b) Baùn kính R = d(A, BC) = 3.3  4.4 15 = 2 (0,5 ñieåm) 3 2 3  4
 Phöông trình ñöôøng troøn: (x – 3)2 + (y – 4)2 = 4 (0,5 ñieåm)
VI. KEÁT QUAÛ KIEÅM TRA: 0 – 3,4 3,5 – 4,9 5,0 – 6,4 6,5 – 7,9 8,0 – 10 Lôùp Só soá SL % SL % SL % SL % SL % 10A3 44 10A5 42 10A7 44 10A10 42 10A11 38 86