lOMoARcPSD|36477180
Chương 2: ĐỘNG HỌC
Nội dung chương này làm rõ mối liên hệ giữa LỰC và CHUYỂN ĐỘNG của hạt, hệ hạt và vật rắn.
§1. NHỮNG KHÁI NIỆM CƠ BẢN ĐỘNG LỰC HỌC
I. Định luật cơ bản động lực học
Các định luật cơ bản động lực học gồm ba định luật của Newton, chúng là nền
tảng để xây dựng các ngành cơ học ứng dụng trong kỹ thuật.
1) Định luật I Newton
Một chất điểm không có lực hoặc có lực tổng hợp tác dụng bằng không sẽ ở một
trong hai trạng thái: Nếu đang đứng yên sẽ tiếp tục đứng yên, nếu đang chuyển động sẽ
chuyển động thẳng đều mãi mãi.
Tính chất các chất điểm duy trì trạng thái đứng yên hoặc chuyển động thẳng đều gọi là quán tính.
Định luật 1 đề cập đến chuyển động, có nghĩa là chất điểm được xem xét trong
một hệ qui chiếu nào đó. Hệ qui chiếu mà ở đó định luật I Newton được nghiệm đúng
gọi là hệ qui chiếu quán tính.
Ví dụ 1: Bạn hãy chỉ ra một hiện tượng mà định luật một vi phạm.
2) Định luật II Newton
Trong hệ qui chiếu quán tính, gia tốc của chất điểm tỉ lệ thuận với độ lớn của lực
tác dụng lên nó và tỉ lệ nghịch với khối lượng của nó. F a  k
, k phụ thuộc hệ đơn vị, trong hệ SI: k  1 , vậy ta có pt: m F  ma
Ta thấy với cùng một lực tác dụng, m càng lớn thì a càng nhỏ. Suy ra vật có khối
lượng lớn khó thay đổi vận tốc hơn vật có khối lượng nhỏ.
Nếu chất điểm chịu nhiều lực tác dụng F   F thì biểu thức trở thành: i i F  ma i i
3) Định luật III Newton
Thực ngiệm chúng tỏ rằng: khi hai chất điểm tương tác, chất điểm A tác dụng lên
chất điểm B một lực FA thì đồng thời chất điểm B cũng tác dụng ngược lại A một lực B F
(gọi là phản lực). Hai lực này cùng phương, ngược chiều và cùng cường độ. B A Biểu thức: F  F AB B A
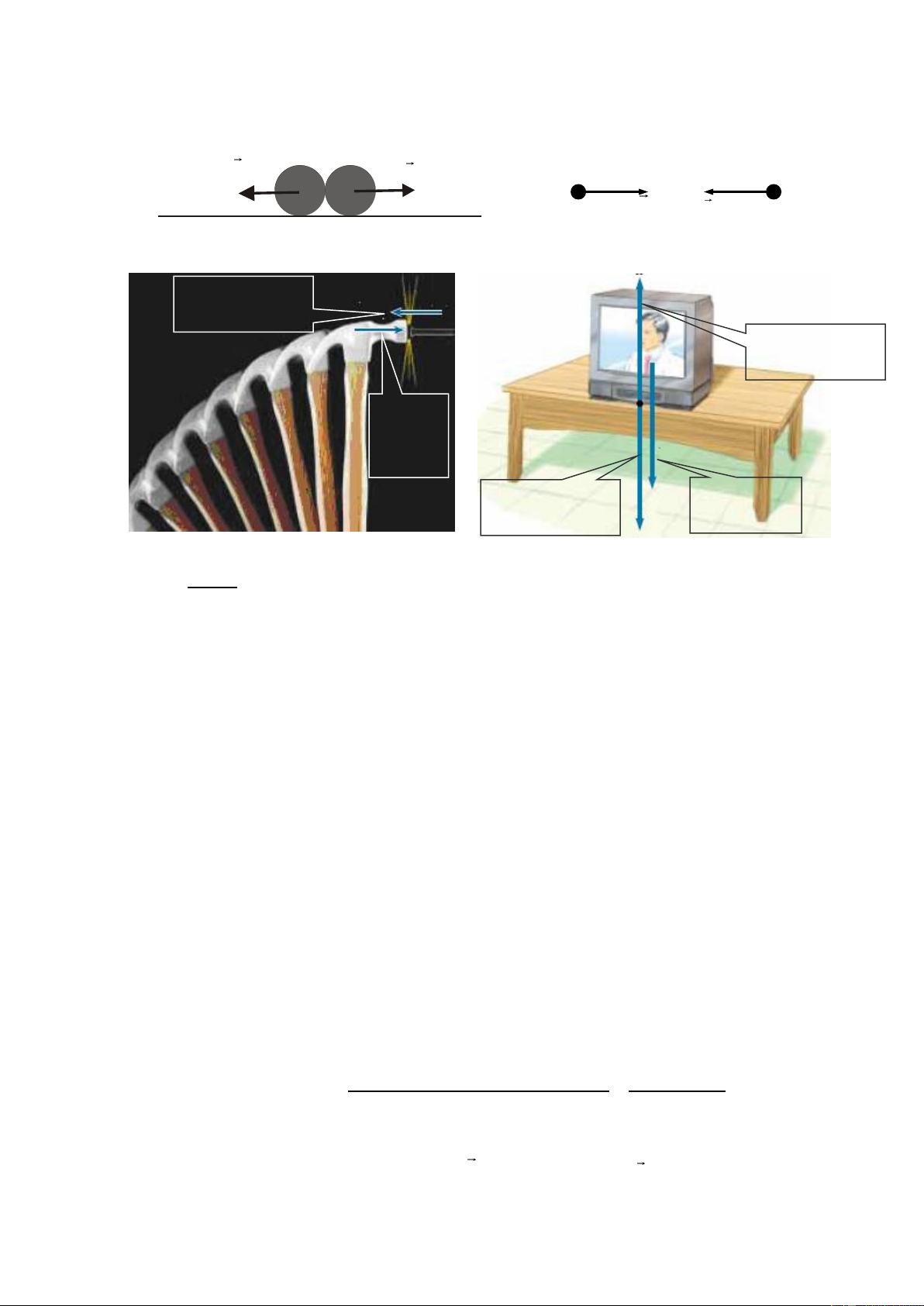
Ví dụ 2: Các trường hợp lực và phản lực minh họa định luật 3: 20
Downloaded by Ng?c Di?p ??ng (ngocdiep10012000@gmail.com) lOMoARcPSD|36477180 F A B A A B F B AB + _ FB A FA B Hai traùi bia va chaïm nhau Hai ñieän tích huùt nhau Phaûn löïc ñinh taùc duïng leân buùa Phaûn löïc maët baøn taùc duïng leân tivi
Hai quaû caàu va chaïm nhau Löïc buùa taùc duïng leân ñinh Löïc tivi taùc duïng Troïng löïc taùc leân maët baøn duïng leân tivi
Chú ý: Lực và phản lực không triệt tiêu nhau vì điểm đặt của chúng nằm trên hai vật khác nhau.
II. Khối tâm của cơ hệ
Tập hợp nhiều chất điểm gọi là hệ chất điểm. Nếu hệ chất điểm mà khoảng cách
giữa hai chất điểm bất kì luôn không đổi hoặc các chất điểm liên kết chặt với nhau, hệ
chất điểm đó gọi là vật rắn.
Hệ chất điểm cũng như vật rắn chứa quá nhiều chất điểm, khó có thể khảo sát từng
chất điểm một. Vì thế ta sẽ chỉ quan tâm đến một điểm đặc biệt, điểm này cho ta khá
nhiều thông tin về hệ đó là khối tâm.
Khối tâm mang ý nghĩa là vị trí trung tâm của phân bố khối lượng của hệ và mọi
lực tác dụng vào hệ có thể được đặt tại vị trí này.
1) Khối tâm hệ chất điểm
Định nghĩa: Các chất điểm có khối lượng m ,m ,...., m nằm tại các điểm tương 1 2 N
ứng M ,M ,.. M .
, chọn điểm O bất kỳ làm gốc, khối tâm của hệ là một điểm hình học G 1 2 N xác định bởi: N     (OM .m ) 
OM .m  OM .m  ...  OM N . i i m 1 2 1 2 N i 1 OG    m  m  ... N  m 1 2 N mi i 1   
Trong hệ tọa độ Descartes, kí hiệu: R (x , y , z )  OG; r (x , y , z )  OM i . G G G G i i i i 21
Downloaded by Ng?c Di?p ??ng (ngocdiep10012000@gmail.com) lOMoARcPSD|36477180 N m rii Viết lại: i 1 R   G N mi i 1 
Dưới dạng các thành phần tọa độ: N  N N m x m y m z i i i i i i i 1 x   ; i 1 y   ; i 1 z   G N  G N G N m m m i i i i 1  i 1  i 1  m 3
Ví dụ 1: Cho ba chất điểm khối lượng m  m  m và 1 2
m  2m đặt tại ba đỉnh của một tam giác đều có cạnh là a . 3
Hãy xác định khối tâm G của hệ. m m 1 2
2) Khối tâm vật rắn
Chia vật rắn thành vô số phần nhỏ, mỗi phần có khối lượng vô
cùng nhỏ, khi đó vật trở thành hệ chất điểm khối lượng các chất điểm
là dm , dm ,..., dm , với N   . 1 2 N dm
Áp dụng công thức tính vị trí khối tâm cho hệ chất điểm ở trên, ta có: N dm .rii i 1 R  lim  G N N  dmi i 1  N
dm là tổng toàn bộ khối lượng các phần nhỏ, chính là khối lượng vật rắn, ký i i 1  N
hiệu: M. Theo định lý Newton-Leibniz trong toán học lim dm .r  r.dm  i i N  i 1  (V ) Vậy 1 : R  r.dm  G M (V )
Dưới dạng các thành phần tọa độ: 1 1 1 x  . x d ; m y  . y d ; m z  z.dm    G G G M M M (V ) (V ) (V )
* Chú ý: Các vật đồng chất có đối xứng hình học thì khối tâm trùng với tâm hình học.
Vài hình ảnh của khối tâm: 22
Downloaded by Ng?c Di?p ??ng (ngocdiep10012000@gmail.com) lOMoARcPSD|36477180
III. Mô men quán tính của vật rắn
1) Momen quán tính chất điểm
Một chất điểm khối lượng 
m quay quanh trục  , đại lượng 2 I  .
m r được định nghĩa là momen quán tính của chất điểm đối với trục quay. r
2) Momen quán tính của vật rắn đối với một trục
Khối lượng của vật rắn thường phân bố một cách liên tục,
ta chia vật rắn thành những phần tử vô cùng nhỏ, vật rắn trở thành hệ chất điểm. Các chất
điểm lần lượt có khối lượng dm ,dm ,...dm và khoảng cách đến trục quay tương ứng là 1 2 N
r , r ,..., r , với N   . 1 2 N
Momen quán tính của vật rắn là tổng cộng momen quán tính của toàn bộ các chất điểm: I  lim  2 2 2
dm .r  dm .r ,...dm r  r dm  N N  2 . 1 1 2 2 N  (V )
Momen quán tính I là đại lượng đặc trưng cho quán tính quay của vật rắn trong
chuyển động quay, quán tính quay chính là tính chất duy trì trạng thái của chuyển động quay.
Căn cứ vào biểu thức của momen quán tính, thấy rằng I không những phụ thuộc
vào khối lượng mà còn phụ thuộc vào khoảng cách từ các chất điểm của vật đến trục
quay. Hai vật cùng khối lượng, nhưng khối lượng của vật nào được phân bố cách trục
quay càng xa thì quán tính quay của vật đó càng lớn.
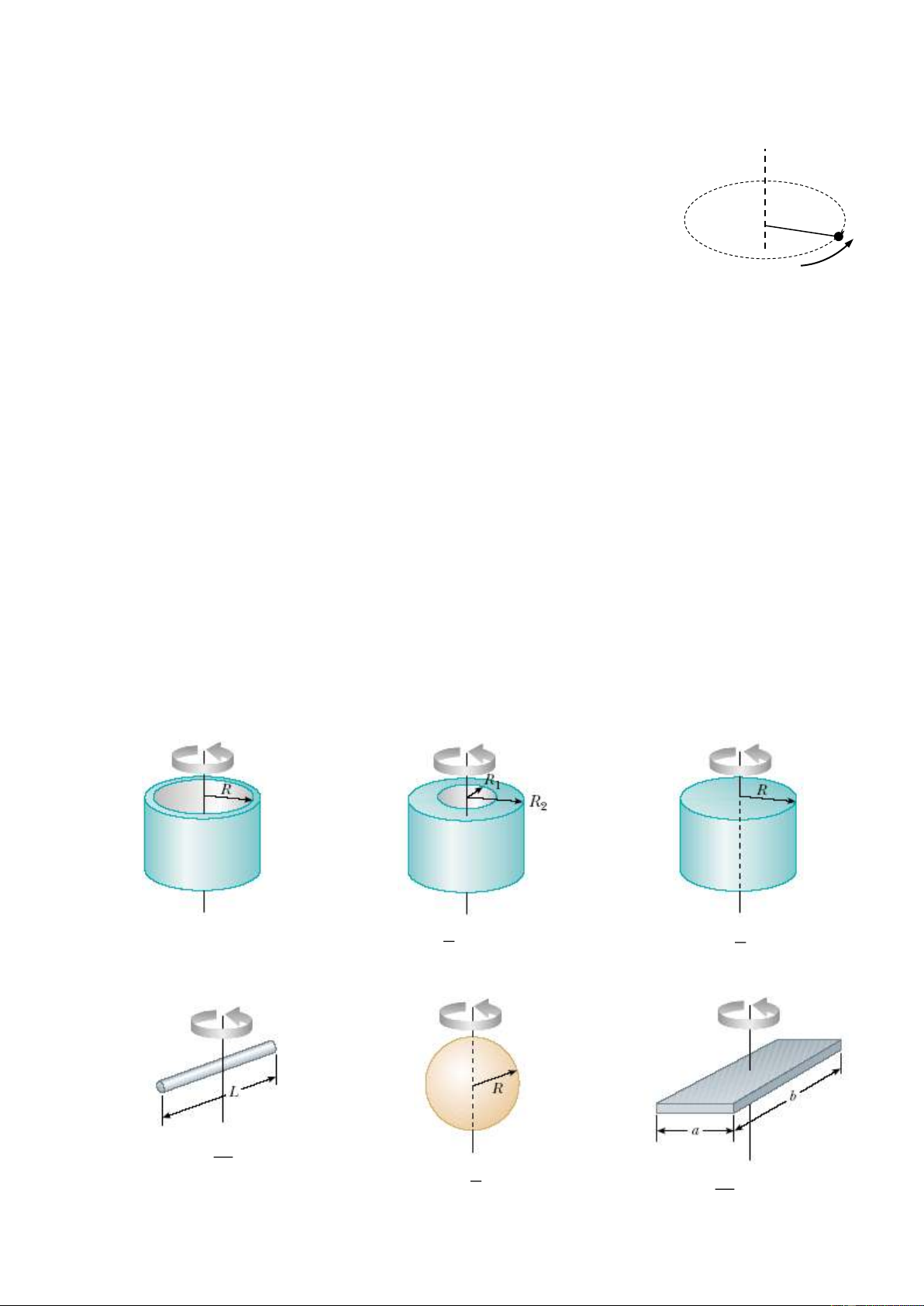
Sau đây là momen quán tính của một số vật đồng chất: 2 I  MR 1 1  2 2 2 G I
 M(R  R ) I  MR G 1 2 2 G 2 1 2 I  ML  G 12 2 2 I  MR 1  2 2 I 
M(a  b ) G 5 G 12 23
Downloaded by Ng?c Di?p ??ng (ngocdiep10012000@gmail.com) lOMoARcPSD|36477180
+ Định lý Stene-Huyghen: Mômen quán tính của một vật rắn đối với một trục  bất
kì bằng momen quán tính của vật đối với trục  (đi qua khối tâm của vật và song song G
với  ) cộng với tích khối lượng M của vật với bình phương khoảng cách d giữa hai trục. 2 I  I  M.d   G
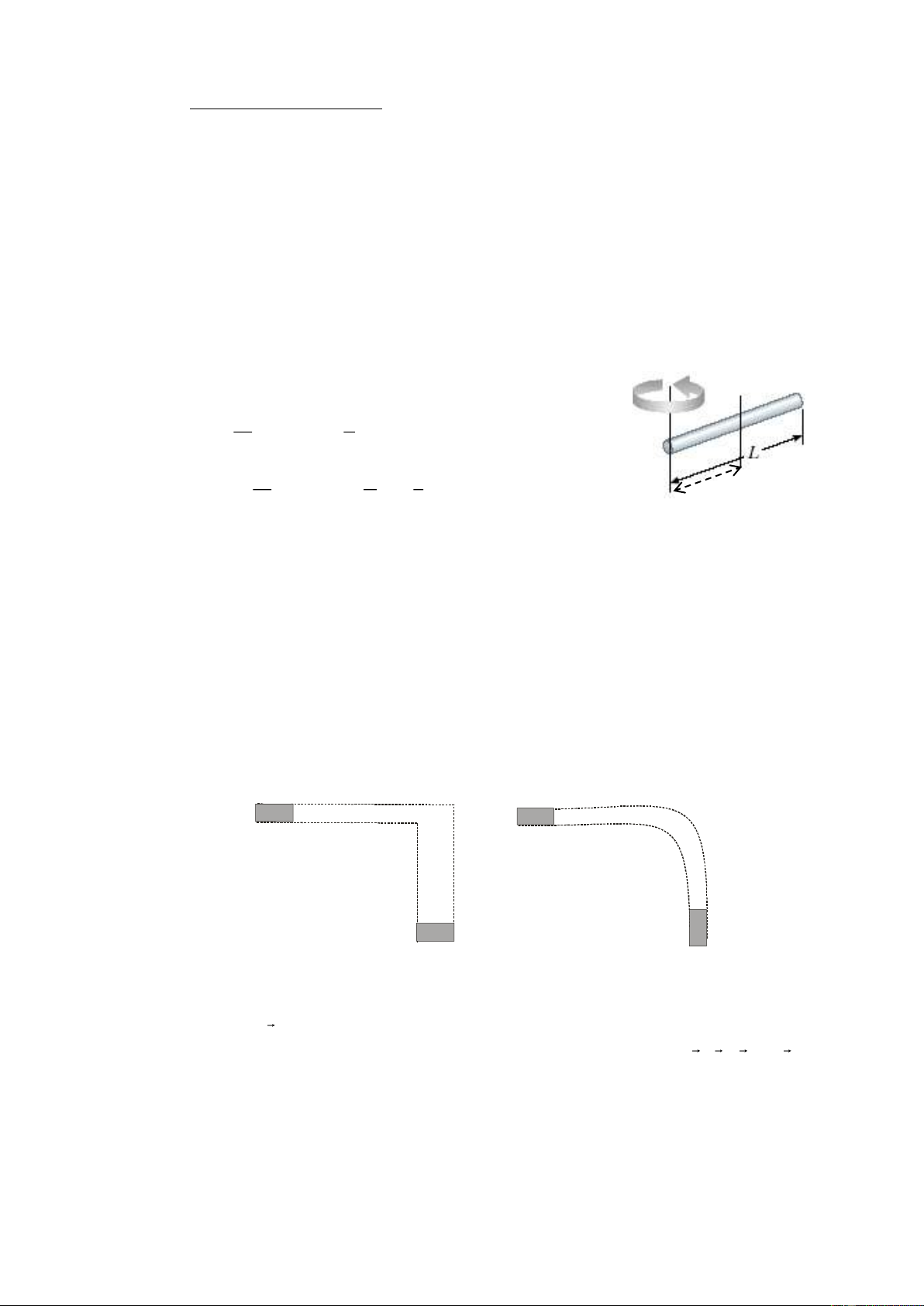
Ví dụ 3: Tính momen quán tính của một thanh đồng nhất có chiều dài L , có khối lượng
M đối với trục quay  đi qua một đầu của thanh và vuông góc với thanh. Giải
Gọi I là momen quán tính của thanh đối với trục  . Theo công thức chuyển trục: 2 I  I  M.d   G Với:  G 1 1  2 I  M .L   ; d L G 12 2 2 Ta được: 1  L  1 2 2 I 
M .L  M .  M.L    d 12  2  3
IV. Chuyển động tịnh tiến, chuyển động quay quanh trục cố định
Vật rắn là hệ chất điểm trong đó các chất diểm liên kết chặt với nhau và khoảng
cách giữa các chất điểm luôn luôn không đổi. Chuyển động của một vật nói chung phức
tạp nhưng người ta chứng minh được rằng: mọi chuyển động vật rắn bao giờ cũng có thể
phân tích thành hai loại thành phần: chuyển động tịnh tiến và quay quanh một trục.
1) Chuyển động tịnh tiến
Chuyển động của một vật rắn được gọi là chuyển động tịnh tiến khi mọi điểm
trên vật đều chuyển động giống nhau(quĩ đạo giống nhau, tại một thời điểm bất kỳ vận
tốc, gia tốc giống nhau). Chuyển động tịnh tiến
Không phải chuyển động tịnh tiến
* Phương trình Newton cho chuyển động tịnh tiến
Giả thiết a là vectơ gia tốc chung của các chất điểm chuyển động tịnh tiến có khối
lượng m ,m ,...,m ,... và lần lượt chịu tác dụng của ngoại lực F , F , F ,..., F ,...Theo 1 2 i 1 2 3 i
phương trình động lực học ta có: 24
Downloaded by Ng?c Di?p ??ng (ngocdiep10012000@gmail.com) lOMoARcPSD|36477180 m a  F 1 1 m a  F 2 2 ................ m a  F i i
Các phương trình đó chứng tỏ những ngoại lực tác dụng lên vật rắn
F , F , F ,..., F ,... song song và cùng chiều: đó là điều kiện cần để một vật rắn chuyển động 1 2 3 i
tịnh tiến. Cộng các vế phương trình trên ta được:
(m )a   F  M.a  F i i G i i
Với: M  m : khối lượng vật rắn; F   F : tổng hợp lực tác dụng vào vật rắn; i i i i
a  a : gia tốc của vật bằng gia tốc khối tâm vì chuyển đđộng tịnh tiến mọi điểm trên vật G chuyển động như nhau.
2) Chuyển động quay quanh một trục
Chuyển động quay của vật rắn là chuyển động trong đó mọi chất điểm của vật đều
vẽ lên một quĩ đạo tròn có tâm cùng nằm trên một đường thẳng(trục quay).
Khi một vật rắn quay quanh một trục  cố định thì:
- Trong cùng một khoảng thời gian, mọi điểm của vật rắn đều quay được cùng một góc  .
- Tại một thời điểm, mọi chất điểm của vật rắn đều có cùng vận tốc góc và gia tốc góc.
- Tại một thời điểm, véctơ vận tốc thẳng và vectơ gia tốc tiếp tuyến của một
điểm bất kỳ trong vật rắn cách trục quay một khoảng r xác định bởi: v    r a    r t
Đó là những tính chất động học của vật rắn chuyển động quay xung quanh một trục cố định. 25
Downloaded by Ng?c Di?p ??ng (ngocdiep10012000@gmail.com) lOMoARcPSD|36477180 TÓM TẮT NỘI DUNG 26
Downloaded by Ng?c Di?p ??ng (ngocdiep10012000@gmail.com) lOMoARcPSD|36477180
§2. CÁC ĐỊNH LÝ TỔNG QUÁT ĐỘNG LỰC HỌC
I. Định lý động lượng chất điểm
Xét chất điểm khối lượng m chuyển động với vận tốc v , đại lượng mv được định
nghĩa là vectơ động lượng của chất điểm. Kí hiệu: p  mv 1) Định lý 1
Theo định luật II Newton, nếu một chất điểm khối lượng m chịu tác dụng của lực
F thì sẽ có gia tốc: dv F  ma  . m dt
Giả thiết khối lượng m không đổi, đưa nó vào trong đạo hàm d (mv) dp F   dt dt
được gọi là phương trình động lực học, khi dẫn ra phương trình này ta giả thiết
khối lượng không đổi, nhưng phương trình lại đúng cả trong trường hợp khối lượng thay đổi.
+ Định lý 1: Đạo hàm động lượng của một chất điểm theo thời gian có giá trị
bằng lực tác dụng lên chất điểm đó. 2) Định lý 2 Từ dp F 
=> Fdt  dp . Tại thời điểm t động lượng của hạt là p , dưới tác dụng dt 1 1
của lực F , tại thời điểm t sau đó động lượng của hạt là p . Có nghĩa rằng trong khoảng 2 2 thời gian t
  t  t thì động lượng sẽ biến đổi một lượng p
  p  p . 2 1 2 1
Lấy tích phân hai vế phương trình vi phân Fdt  dp : p t t t 2 2 2 2 dp 
Fdt  p  p  Fdt  p   Fdt     2 1 p t t t 1 1 1 1 t2 Đại lượng Fdt
 : Xung lượng của lực F tác dụng trong khoảng thời gian t  t . 1 2 t1
+ Định lý 2: Độ biến thiên động lượng của một chất điểm trong một khoảng thời
gian nào đó có giá trị bằng xung lượng của lực tác dụng lên chất điểm trong khoảng thời gian đó.
Áp dụng định lý trung bình của tích phân cho xung lượng của lực: t2     dt F
 F t(  t )  F t   .
, thay vào biểu thức định lý 2, ta thu được lực trung bình: p F  2 1 t  t1
Ví dụ 1: Tính lực đẩy trung bình của hơi thuốc súng lên đầu đạn ở trong nòng một súng
bộ binh, biết rằng đầu đạn có khối lượng m  10g , thời gian chuyển động của đạn trong nòng là t  ,
0 001s , vận tốc của viên đạn ở đầu nòng là v  865m / s . 27
Downloaded by Ng?c Di?p ??ng (ngocdiep10012000@gmail.com) lOMoARcPSD|36477180
Ví dụ 2: Tại sao khi rơi từ nhà cao tầng xuống đất, lúc tiếp đất trên một túi không khí lại
tránh khỏi cho họ thương tích hoặc tử vong?.
II. Định lý động lượng hệ chất điểm
Xét hệ chất điểm có khối lượng m ,m ,...,m chuyển động với các vận tốc 1 2 N
v , v ,..., v , động lượng của chất điểm thứ i : p  m v . Đại lượng: 1 2 N i i i N
P   p i i 1 
gọi là động lượng của hệ.
Bây giờ ta tìm mối liên hệ giữa động lượng của hệ với vận tốc khối tâm, vì vận tốc khối tâm là: N mvii i 1 v   G n mi i 1  P
Mà m v   p  P , do đó: v  i i i G n mi i 1  Suy ra:
P  ( m )v i G
Vậy: Tổng động lượng của một hệ bằng động lượng của một chất điểm đặt tại
khối tâm của hệ, có khối lượng bằng tổng khối lượng của hệ và có vận tốc bằng vận tốc
khối tâm của hệ. 1) Định lý 1
Xét các chất điểm m , m ,..., m chịu tác dụng lần lượt của N ngoại lực tương ứng 1 2 N ng F , ng F ,..., ng F
. Khi đó một chất điểm trong hệ chịu tác dụng của hai loại lực: ngoại lực 1 2 N ng F
và nội lực f   f do các chất điểm còn lại tác dụng lên chất điểm thứ i . i i ij j i
Theo định lý về động lượng đối với chất điểm: dp i ng  F  f i i dt dp suy ra: i ng
  F  f
(  f  0: tổng nội lực trong hệ bằng 0) i i dt i i i i i Vậy ta có: dP ng  F i dt
Phát biểu: Đạo hàm động lượng của hệ chất điểm theo thời gian bằng tổng hợp
các ngoại lực tác dụng vào hệ. 2) Định lý 2 Từ biểu thức dP ng
 F suy ra: dP  ( ng
F )dt . Lấy tích phân hai vế trong i dt i i
khoảng thời gian từ t  t ứng với sự biến thiên động lượng của hệ từ P  P : 1 2 1 2 28
Downloaded by Ng?c Di?p ??ng (ngocdiep10012000@gmail.com) lOMoARcPSD|36477180 P t t 2 2 2 dK  ( ng 
 F )dt  P  P  ( ng  F )dt i 2 1 i i i P t t 1 1 1
Phát biểu: Độ biến thiên động lượng của hệ chất điểm trong khoảng thời gian có
giá trị bằng xung lượng của ngoại lực tác dụng lên hệ trong khoảng thời gian đó.
III. Định lý dịch chuyển khối tâm
Xét hệ chất điểm có khối lượng m ,m ,...,m chịu tác dụng lần lượt của ngoại lực 1 2 N ng F , ng F ,..., ng F
. Tổng hợp lực tác dụng lên chất điểm thứ i gồm nội lực và ngoại lực: 1 2 N N ng F  F
  f ; f : nội lực do chất điểm thứ j tác dụng lên chất điểm thứ i . i i ij ij i j
Theo định luật II Newton, ta có: N ng m a  F   f 1 1 1 1 j j 1  N ng m a  F   f 2 2 2 2 j j 2 ......................... N ng m a  F   f N N N Nj j  N
Vì tổng nội lực bằng không, cộng theo vế ta được: ng ma  F i i i i i N m aii
Mặt khác, gia tốc khối tâm là i 1 a  
, nên cuối cùng ta thu được phương G n mi i 1 
trình thể hiện mối liên quan giữa lực và chuyển động khối tâm hệ chất điểm:   ng a m  F G  i  i  i  i
Phát biểu: Khối tâm của hệ chuyển động như một chất điểm có khối lượng bằng
tổng khối lượng của hệ và chịu tác dụng của lực bằng tổng hợp ngoại lực tác dụng lên hệ.
Sau đây là vài hình ảnh chuyển động của khối tâm: 29
Downloaded by Ng?c Di?p ??ng (ngocdiep10012000@gmail.com) lOMoARcPSD|36477180
IV. Định lý mô men động lượng chất điểm
Xét chất điểm tại M trong hệ qui chiếu đã chọn, gọi r là vectơ vị trí của chất điểm
đối với một điểm 0 nào đó và p là vectơ động lượng của chất điểm. Vectơ:
l  r  p O
gọi là momen động lượng của chất điểm đối với điểm 0. l l O có: p - Gốc tại 0. (C)
- Có phương  với mặt phẳng xác định bởi 0 và p . 
- Có chiều xác định bằng qui tắc đinh ốc.
- Độ lớn:  l  =  r . p .sin, trong đó  là góc O 0 r m
giữa r và p .
Tương tự: M  r  F gọi là vectơ momen lực F O đối với điểm 0.
Mômen M đặc trưng cho khả năng của lực F làm quay chất điểm mà nó tác O
dụng quanh điểm O. Nếu chất điểm có thể quay quanh O một cách tuỳ ý thì mômen lực
sẽ làm chất điểm quay quanh trục qua O vuông góc với mặt phẳng chứa F và điểm O. Ta
thấy rằng khả năng quay này không những phụ thuộc vào lực F mà còn vào vị trí của
chất điểm đối với O và góc giữa r và F .
 Định lý về momen động lượng
Đạo hàm hai vế theo thời gian biểu thức l  r  p O dl dr dp O   p  r  dt dt dt dr dk Vì:
 v , v / / p nên suy ra số hạng thứ nhất bằng không. Thay F  vào, ta dt dt được: dl
O  r  F  M O dt
Định lý momen động lượng: Đạo hàm theo thời gian của momen động lượng đối
với điểm 0 của chất điểm chuyển động bằng momen lực đối với điểm 0 tác dụng lên chất điểm.
Trong trường hợp M  0, tức có thể F  0 hay F // r (lực xuyên tâm): O dl 
O  0  l  const O dt
Tức vector momen động lượng bảo toàn. Từ định nghĩa ta thấy l luôn vuông góc O
với p hay v , do đó nếu l không thay đổi theo thời gian, vectơ vận tốc luôn vuông góc O
với một trục cố định dẫn đến quĩ đạo chất điểm nằm trên một mặt phẳng.
Ví dụ 3: Giải thích tại sao người ta đưa ra kết luận các hành tinh trong hệ mặt trời có quĩ
đạo nằm trên mặt phẳng. 30
Downloaded by Ng?c Di?p ??ng (ngocdiep10012000@gmail.com) lOMoARcPSD|36477180
V. Định lý mô men động lượng hệ chất điểm
Mômen động lượng của hệ chất điểm đối với O được định nghĩa bằng tổng các
momen động lượng của các chất điểm trong hệ đối vớiO : L  l i i
 Định lý về mômen động lượng của hệ chất điểm
Như đã biết với chất điểm m , định lý về momen động lượng của nó đối với một i
gốc O chọn trước là: dl i  M Oi dt
Cộng các phương trình trên ta được: dl i   M Oi dt i i Vế đầu: dl d d i
  l  L là đạo hàm theo thời gian momen động lượng của i dt dt dt i i
hệ. Vế thứ hai biểu thị tổng momen lực của các chất điểm đối với gốc O . Các lực này
bao gồm ngoại lực tác dụng và nội lực tương tác của các chất điểm trong hệ.
Chú ý rằng các nội lực tương tác của chất điểm trong hệ từng đôi một đối nhau do
đó tổng mômen đối với O của những lực này bằng không. Vậy vế thứ hai của phương
trình trên chỉ còn là tổng momen đối với O của các ngoại lực tác dụng lên hệ. Kết quả ta có: dL  M Oi dt i
Định lý: Đạo hàm theo thời gian của momen động lượng của một hệ bằng tổng
mômen ngoại lực tác dụng lên hệ.
VI. Phương trình động lực học cho chuyển động quay quanh trục cố định
1. Tác dụng của lực trong chuyển động quay
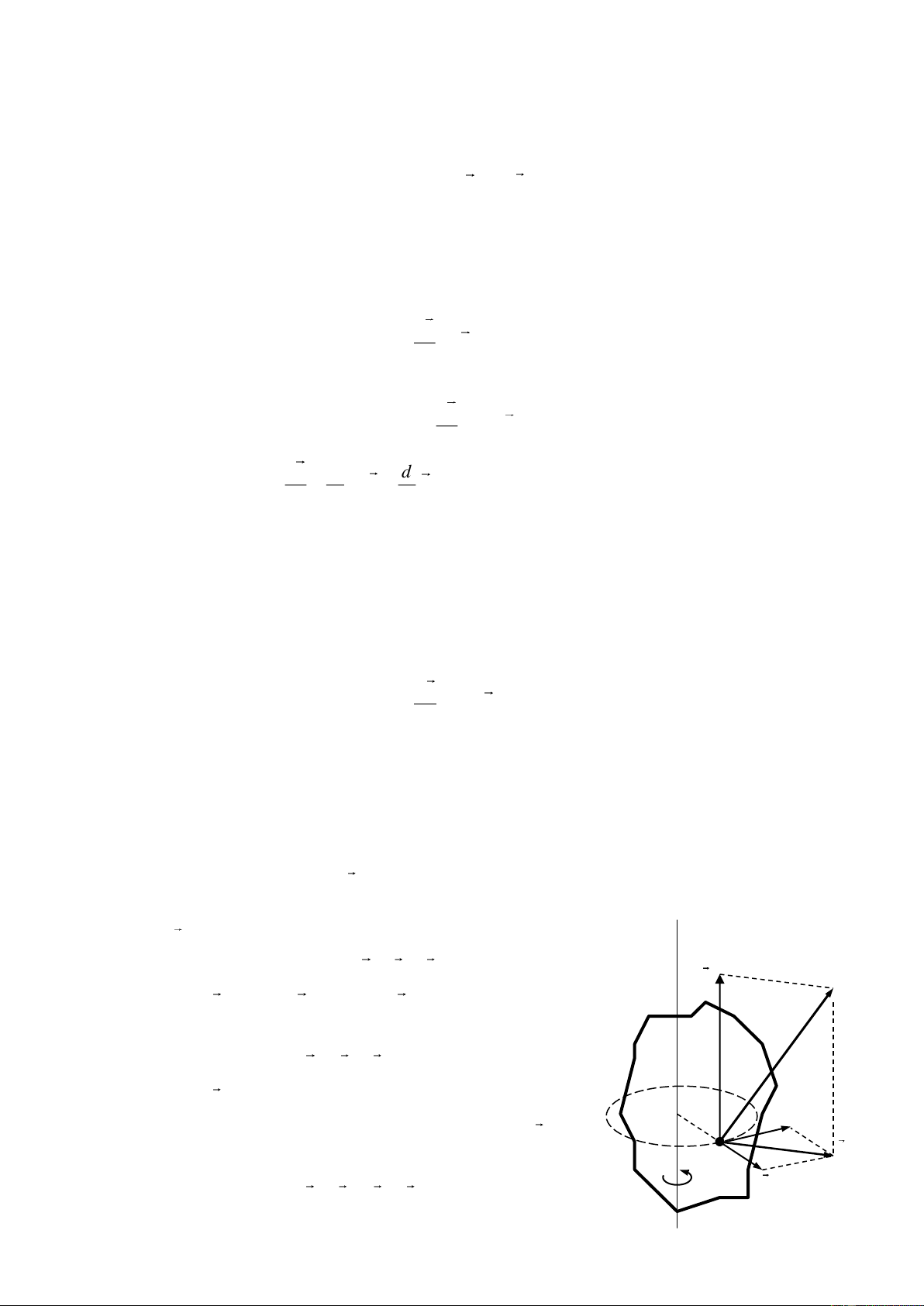
Giả sử có một lực F tác dụng lên vật rắn quay
quanh một trục  , đặt tại điểm M . Trước hết, ta phân  : trục quay
tích F ra hai thành phần:
F  F  F 1 2 F 2
trong đó F   và F //  . Lực F nằm trong mặt phẳng 1 2 1
  và đi qua M lại được phân tích ra hai thành phần:
F  F  F 1 t r
trong đó F  với bán kính OM , nghĩa là nằm theo tiếp t  O
tuyến của vòng tròn tâm F t
O , bán kính OM . Còn F nằm r > F 1
theo bán kính OM , kết quả ta có: M F r
F  F  F  F 2 t r 31
Downloaded by Ng?c Di?p ??ng (ngocdiep10012000@gmail.com) lOMoARcPSD|36477180 Ta thấy:
- Thành phần F không gây ra chuyển động quay của vật rắn quanh trục  , mà 2
chỉ có tác dụng làm vật rắn trượt dọc theo trục quay.
- Thành phần F cũng không gây ra chuyển động quay, chỉ có tác dụng làm vật r
rắn rời khỏi trục quay.
- Như vậy trong chuyển động quay, tác dụng của lực F tương đương với tác
dụng của thành phần F của nó. t
Ta kết luận: Khi vật rắn quay xung quanh một trục, chỉ những thành phần lực tiếp
tuyến với quĩ đạo của điểm đặt mới có tác dụng làm quay của vật rắn. Ngoài ra, tác dụng
này còn phụ thuộc vào vị trí điểm đặt của lực.
2. Mô men lực đối với trục quay
Để đặc trưng cho tác dụng của lực trong chuyển động quay, người ta đưa ra đại
lượng gọi là momen lực đối với trục quay.
Định nghĩa: Momen của lực F đối với trục quay  là một vectơ M xác định bởi:
M  r  F t
r : bán kính vectơ xác định vị trí điểm đặt của lực F và nằm vuông góc với trục quay  .
Theo định nghĩa này ta thấy: Vectơ M có phương  với mặt phẳng chứa r và F , t
nghĩa là M có phương trục quay, có chiều xác định bằng qui tắc bàn tay phải, có trị số:
M  rF sin(r , F )  M  rF t t t
Dễ dàng thấy rằng: Mômen của lực F đối với trục quay  sẽ bằng không khi lực
đó bằng không hoặc khi lực đó đồng phẳng với  .
3. Phương trình động lực học của chuyển động quay:
Gọi m là khối lượng một chất điểm bất kỳ của vật rắn cách trục quay một khoảng i
r chịu tác dụng của ngoại lực tiếp tuyến F . Phương trình động lực học của m : i ti i m a  F i ti ti
Nhân hữu hướng hai vế với vectơ bán kính r : m (r a )  r  F i i i i ti
Ở vế phải, đại lượng r  F chính là mômen M của lực F đối với trục quay  . i ti i ti Vế trái, đại lượng:
r  a  r  (  r )  r  (  r )  (r .r )  (r . ) .r i ti i i i i i i i i 2   0;do r r  i i Vậy ta viết lại : 2 m r   M i i i
Lấy tổng theo mọi chất điểm trong vật rắn ta được: 2
(m r )   M i i i i i 32
Downloaded by Ng?c Di?p ??ng (ngocdiep10012000@gmail.com) lOMoARcPSD|36477180
M  M : tổng hợp các mômen ngoại lực tác dụng lên vật rắn; (m r2)  I : i i i i i
gọi là mômen quán tính của vật rắn đối với trục quay  . Pt trên viết lại thành: I  M , hay: M   I
gọi là phương trình cơ bản chuyển động quay của vật rắn xung quanh một trục.
Phát biểu: Gia tốc góc trong chuyển động quay của vật rắn xung quanh một trục tỉ
lệ với tổng hợp momen các ngoại lực đối với trục và tỉ lệ nghịch với momen quán tính
của vật rắn đối với trục.
Ta thấy momen quán tính I là đại lượng đặc trưng cho quán tính của vật rắn trong
chuyển động quay. Căn cứ vào biểu thức của momen quán tính: I  ( 2
m r ), thấy rằng i i i
nó không những phụ thuộc vào khối lượng mà còn phụ thuộc vào khoảng cách từ các
chất điểm của vật đến trục quay. Hai vật cùng khối lượng, nhưng khối lượng của vật nào
được phân bố cách trục quay càng xa thì quán tính quay của vật đó càng lớn. 33
Downloaded by Ng?c Di?p ??ng (ngocdiep10012000@gmail.com) lOMoARcPSD|36477180 TÓM TẮT NỘI DUNG 34
Downloaded by Ng?c Di?p ??ng (ngocdiep10012000@gmail.com) lOMoARcPSD|36477180 BÀI TẬP CHƯƠNG 2
Bài 1: Cho hệ thống gồm 2 vật: Đĩa tròn đồng chất bán kính
R=20cm, khối lượng M=2kg gắn chặt vào đầu một thanh
dài đồng chất L=1m, khối lượng m=1kg. Hãy xác định: A a) Khối tâm của hệ.
b) Momen quán tính của hệ thống đối với trục quay đi qua A vuông góc với đĩa tròn.
Bài 2: Cho hệ như hình vẽ gồm: Thanh AB đồng chất khối lượng D
m  4kg dài L  40cm ;Thanh CD đồng chất khối 1 1 ( . m R)
lượng m  2kg dài L  20cm ; Vành tròn đồng chất khối 2 2 A O B
lượng m  1kg bán kính R  10cm có tâm O nằm tại trung C điểm AB.
a) Xác định khối tâm G của hệ.
b) Tính mômen quán tính đi qua A và vuông góc với mặt phẳng chứa hệ.
Bài 3: Quả cầu đồng chất được đặt trên đỉnh mặt phẳng nghiêng α sau đó thả cho lăn
không trượt, tìm gia tốc khối tâm.
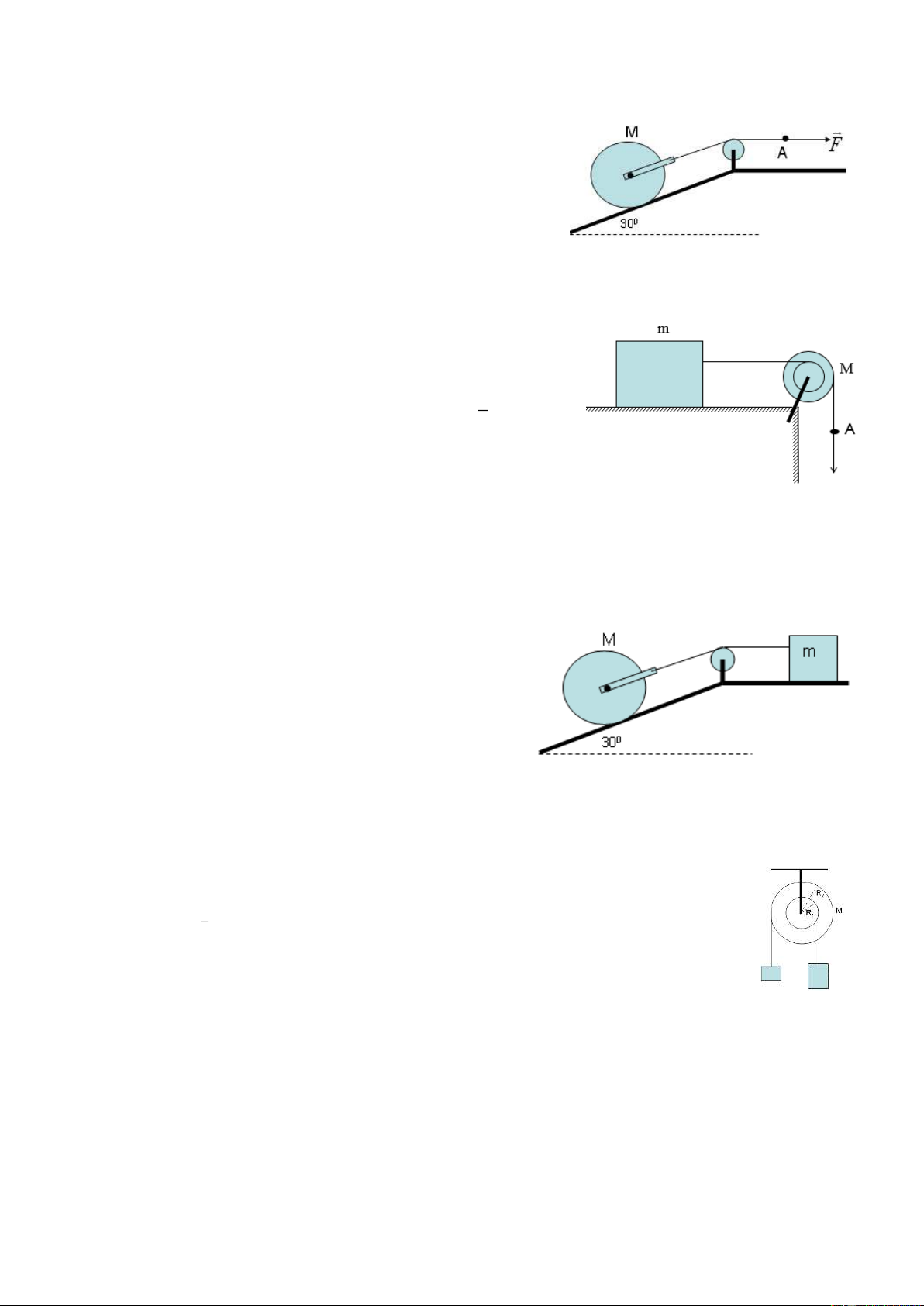
Bài 4: Ta dùng một lực F=121N tác dụng lên đầu dây A để kéo một xô
vữa lên cao. Xô vữa có khối lượng m=10kg. Ròng rọc là đĩa tròn đặc,
đồng chất có khối lượng M=1kg. Cho rằng sợi dây không co dãn, khối lượng không đáng kể.
Tính gia tốc của xô vữa và lực căng dây. Lấy g=10m/s2
Bài 5:. Cho cơ hệ như hình vẽ, các vật m1=2kg, m2=1kg.
Các ròng rọc là các đĩa tròn đặc, đồng chất có khối lượng
M=2kg. Hệ bắt đầu chuyển động từ trạng thái đứng yên.
Dây nối không co dãn, khối lượng không đáng kể.
a) Tính gia tốc của các vật m1 và lực căng dây ớ các nhánh dây.
b) Tính phản lực tác dụng lên trục ròng rọc A, biết 0   30 .
Bài 6: Cho cơ hệ như hình vẽ, vật m=2kg. Ròng rọc là
đĩa tròn đặc, đồng chất có khối lượng M=2kg. Tác dụng
lên đầu dây A một lực F=16N. Vật m bắt đầu chuyển động
từ trạng thái đứng yên từ chân của mặt phẳng nghiêng.
Dây nối không co dãn, khối lượng không đáng kể. Chiều 35
Downloaded by Ng?c Di?p ??ng (ngocdiep10012000@gmail.com) lOMoARcPSD|36477180
dài của mặt phẳng nghiêng là 50cm. Cho 0
  30 . Hệ số ma sát giữa vật và mặt nghiêng là 0,2. Tính:
a) Gia tốc của các vật m và lực căng dây.
b) Vận tốc của m tại đỉnh mặt phẳng nghiêng.
c) Phản lực tác dụng lên trục ròng rọc.
Bài 7: Cho cơ hệ như hình vẽ. Trong đó m1=1kg, m2=2kg.
Góc nghiêng của nêm là 300. Dây nối không co dãn, khối
lượng không đáng kể. Ròng rọc là một đĩa tròn đồng chất. Hệ m1
số ma sát trượt giữa vật m1 và mặt nêm là 0,2. Hệ bắt đầu m2
chuyển động từ trạng thái nghỉ. 
Khối lượng của ròng rọc là 1kg. Tính gia tốc của m2 và
lực căng trên các nhánh dây
Bài 8: Cho cơ hệ như hình vẽ, vật m1=0,5kg, m2=1kg. Ròng rọc
là đĩa tròn đặc, đồng chất có khối lượng M=0,4kg. Hệ bắt đầu
chuyển động từ trạng thái đứng yên. Dây nối không co dãn, khối
lượng không đáng kể. Hệ số ma sát giữa m2 và mặt phẳng nghiêng là 0,1. Cho 0   30 . Tính:
a) Gia tốc của vật m1 và lực căng dây trên các nhánh dây.
b) Vận tốc của m1 khi m2 đi được quãng đường 40cm.
c) Phản lực tác dụng lên trục ròng rọc.
Bài 9: Cho cơ hệ như hình vẽ. Trong đó vật m1 là khối
trụ đặc khối lượng 5kg, m2= 2kg. Thả cho cơ hệ chuyển
động từ trạng thái nghỉ, khối trụ lăn không trượt trên
mặt sàn. Cho rằng dây không co dãn, dây và ròng rọc
có khối lượng không đáng kể.
Tính gia tốc của vật m2 và lực căng dây
Bài 10: Cho cơ hệ như hình vẽ. Vật m0 là một khối trụ
đặc, đồng chất, được quấn vào cuộn dây. Thả cho hệ
chuyển động từ trạng thái nghỉ, vật m0 chuển động lăn
không trượt trên mặt ngang. Biết m0=2m. Dây không co
dãn, khối lượng dây và ròng rọc không đáng kể.
a) Tính gia tốc của m và khối tâm C của vật m0. b) Tính lực căng dây. 36
Downloaded by Ng?c Di?p ??ng (ngocdiep10012000@gmail.com) lOMoARcPSD|36477180
Bài 11: Cho cơ hệ như hình vẽ. Trong đó, vật M là
khối trụ đặc đồng chất khối lượng 40kg, ròng rọc là
đĩa tròn đặc đồng chất có khối lượng là m= 2kg. Tác
dụng vào A một lực F=215,5N kéo khối trụ lăn
không trượt lên dốc nghiêng. Cho rằng dây không
co dãn, có khối lượng không đáng kể.
Tính gia tốc của điểm C và lực căng dây.
Bài 12: Cho cơ hệ như hình vẽ. Trong đó, vật
m=20kg có thể trượt trên sàn với hệ số ma sát 0,1.
Ròng rọc hai bán kính R  2R , có khối lượng là M= 2 1 3
4kg, momen quán tính đối trục quay là 2 MR . Tác 2 8
dụng lực F lên điểm A, F  20N . Biết dây nhẹ và không co gãn. Tính: a) Gia tốc của m b) Lực căng dây.
c) Phản lực trục quay tác dụng lên ròng rọc.
Bài 13: Hệ cơ học như hình vẽ, trong đó vật M
là một khối trụ đặc, đồng chất, M= 5kg lăn
không trượt trên mặt phẳng nghiêng. Vật
m=2kg là một khối hộp trượt trên sàn nằm
ngang với hệ số ma sát 0,1. Cho rằng dây
không dãn, khối lượng dây và ròng rọc không đáng kể.
Tính gia tốc vật m và lực căng dây.
Bài 14: Cho hệ cơ học như hình vẽ, m1=2kg, m2=3kg. Ròng rọc 2 bán
kính R2=2R1, M=1kg. Momen qun tính của ròng rọc so với trục đối xứng là 3 2
MR . Tính gia tốc các vật và các lực căng dây. 8 2 m2 m 1 37
Downloaded by Ng?c Di?p ??ng (ngocdiep10012000@gmail.com)