Giáo Trình Cơ Học Kết Cấu năm 2019 | Môn Cơ học kết cấu - Đại học Cần Thơ

lOMoAR cPSD| 23136115 TRƯ
ỜNG ĐẠI HỌC CẦN THƠ KHOA CÔNG NGHỆ
BỘ MÔN KỸ THUẬT XÂY DỰNG
CƠ HỌC KẾT CẤU (STRUCTURAL MECHANICS) CAN THO- 2019 lOMoAR cPSD| 23136115 LỜI NÓI ĐẦU
Giáo trình “Cơ học kết cấu” ược biên soạn theo ề cương của môn học “Cơ học kết
cấu” của trường Đại học Cần Thơ. Trong giáo trình này có bổ sung một số kiến thức mới
và các ví dụ thực tế ể giúp sinh viên học tập thuận tiện hơn.
Giáo trình ược dùng làm tài liệu học tập cho sinh viên các ngành: Xây dựng dân dụng
và công nghiệp, xây dựng cầu ường, xây dựng công trình thuỷ…, hoặc có thể làm tài
liệu tham khảo cho các kỹ sư, các cán bộ kỹ thuật có liên quan ến tính toán kết cấu công trình.
Tuy ã cố gắng rất nhiều trong quá trình biên soạn với mong muốn cung cấp cho sinh
viên một giáo trình ngắn gọn, dễ hiểu và bổ ích cho nghề nghiệp, song khó tránh khỏi
những thiếu sót. Chúng tôi mong nhận ược những ý kiến óng góp của các bạn ồng
nghiệp, sinh viên và bạn ọc ể giáo trình ngày càng ược hoàn thiện hơn.
Xin chân thành cảm ơn trường Đại học Cần Thơ ã hỗ trợ và giúp ỡ chúng tôi hoàn thành giáo trình này. NHÓM TÁC GIẢ CHƯƠNG 1
CÁC KHÁI NIỆM CƠ BẢN
1.1. ĐỐI TƢỢNG NGHIÊN CỨU VÀ NHIỆM VỤ CỦA MÔN HỌC
1.1.1. Đối tƣợng và phạm vi nghiên cứu
a. Đối tƣợng nghiên cứu:
Là vật rắn biến dạng àn hồi, tức là có thể thay ổi hình dạng dưới tác dụng của các nguyên nhân bên ngoài.
b. Phạm vi nghiên cứu: lOMoAR cPSD| 23136115
Phạm vi nghiên cứu của môn Cơ học kết cấu là giống môn Sức bền vật liệu nhưng
gồm nhiều cấu kiện liên kết lại với nhau. Do vậy, trong kết cấu hay dùng tên gọi là hệ kết cấu.
1.1.2. Nhiệm vụ của môn học:
Nhiệm vụ chủ yếu của môn Cơ học kết cấu là i xác ịnh nội lực, biến dạng và chuyển
vị trong công trình nhằm xây dựng công trình thỏa mãn các yêu cầu:
- Điều kiện về ộ bền: Đảm bảo cho công trình không bị phá hoại dưới tác dụng của
các nguyên nhân bên ngoài.
- Điều kiện về ộ cứng: Đảm bảo cho công trình không có chuyển vị và biến dạng
vượt qúa giới hạn cho phép nhằm ảm bảo sự làm việc bình thường của công trình.
- Điều kiện về ổn ịnh: Đảm bảo cho công trình có khả năng bảo toàn vị trí và hình
dạng ban ầu của nó dưới dạng cân bằng trong trạng thái biến dạng.
Với yêu cầu về ộ bền, cần i xác ịnh nội lực; với yêu cầu về ộ cứng, cần i xác ịnh
chuyển vị; với yêu cầu về ổn ịnh, cần i xác ịnh lực tới hạn mà kết cấu có thể chịu ược.
1.1.3. Các bài toán môn học giải quyết a.
Bài toán kiểm tra: Ở bài toán này, ta ã biết trước hình dạng, kích thước cụ thể của
các cấu kiện trong công trình và các nguyên nhân tác dụng.
Yêu cầu: kiểm tra công trình theo ba iều kiện trên (ộ bền, ộ cứng và ổn ịnh) có ảm bảo
hay không? Và ngoài ra còn kiểm tra công trình thiết kế có tiết kiệm nguyên vật liệu hay không? b.
Bài toán thiết kế: Ở bài toán này, ta mới chỉ biết nguyên nhân tác dụng bên ngoài.
Yêu cầu: Xác ịnh hình dáng, kích thước của các cấu kiện trong công trình một cách hợp
lý mà vẫn ảm bảo ba iều kiện trên. Để giải quyết bài toán này, thông thường, dựa vào
kinh nghiệm hoặc dùng phương pháp thiết kế sơ bộ ể giả thiết trước hình dạng, kích
thước của các cấu kiện. Sau ó tiến hành giải bài toán kiểm tra như ở trên.
Và trên cơ sở ó người thiết kế iều chỉnh lại giả thiết ban ầu của mình, tức là i giải bài toán lặp.
1.1.4. Vị trí của môn học
Là môn học kỹ thuật cơ sở làm nền tảng cho các môn học chuyên ngành như: kết cấu
bê tông, kết cấu thép & gỗ, kỹ thuật thi công...
1.2. SƠ ĐỒ TÍNH KẾT CẤU
1.2.1. Khái niệm sơ ồ tính lOMoAR cPSD| 23136115
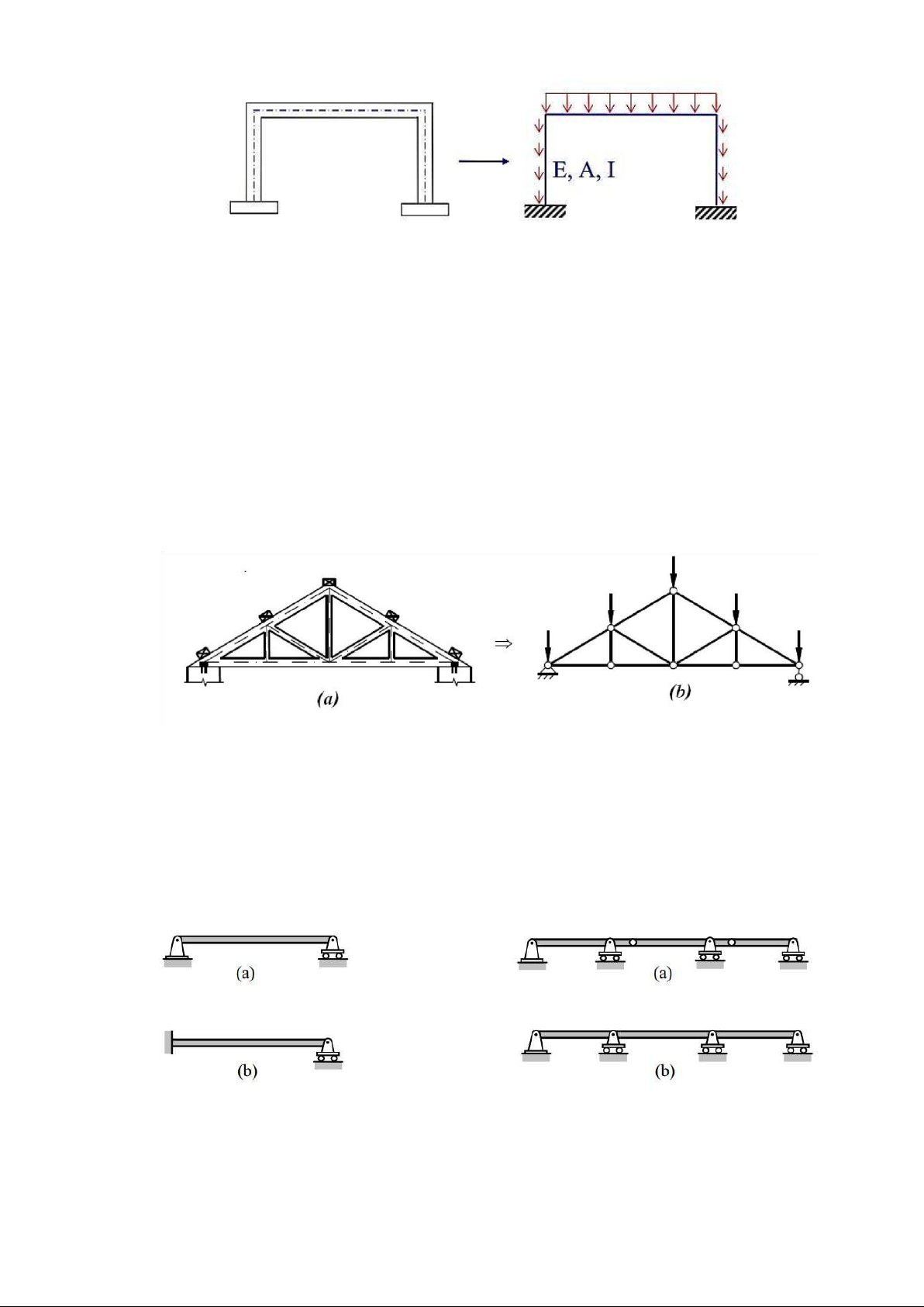
Sơ ồ tính là hình ảnh ơn giản hóa của công trình thực mà vẫn ảm bảo phản ánh ược
chính xác sự làm việc thực tế của các cấu kiện chịu lực chính trong công trình và phải dùng ể tính tóan ược. Hình 1.1
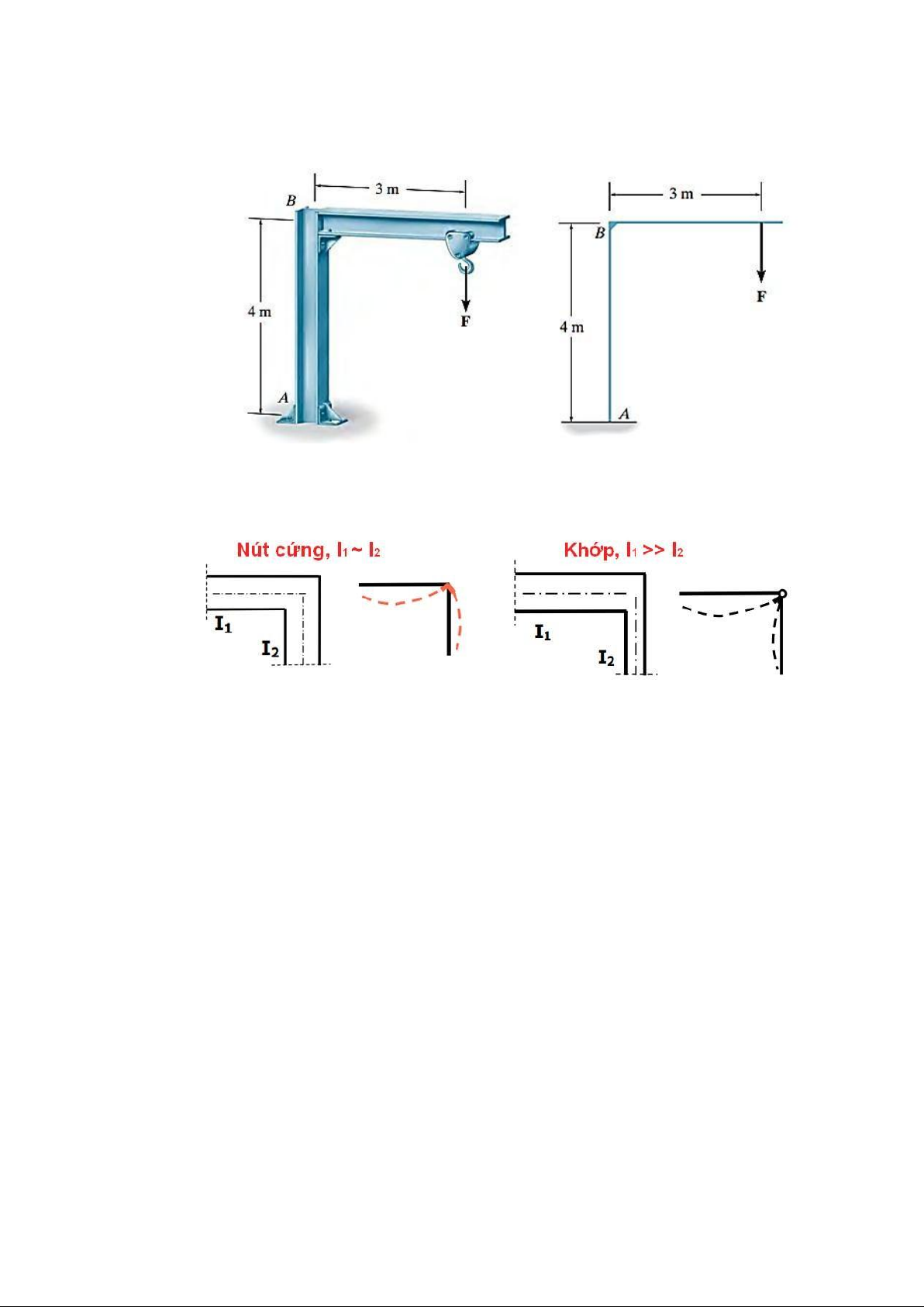
1.2.2. Các yếu tố ảnh hƣởng ến việc chọn sơ ồ tính
- Hình dáng, kích thước của công trình. - Tỷ lệ ộ cứng của các cấu kiện. Hình 1.2
- Tầm quan trọng của công trình.
- Khả năng tính toán của người thiết kế.
- Tải trọng và tính chất tác dụng của nó…
1.2.3. Các bƣớc xây dựng sơ ồ tính
Sơ ồ tính ược xây dựng từ sơ ồ công trình thông qua việc ơn giản hóa bằng các nguyên tắc sau:
- Thay các thanh bằng ường trục thanh, thay các bản và vỏ bằng các mặt trung gian.
- Thay tiết diện, vật liệu bằng các ại lượng ặc trưng: diện tích (A), momen quán
tính (I), modun àn hồi (E), hệ số dãn nở vì nhiệt (α) ...
- Thay thiết bị tựa bằng các liên kết lý tưởng (không ma sát, cứng tuyệt ối hoặc àn hồi…).
- Đưa tải trọng tác dụng trên mặt cấu kiện về trục cấu kiện.
- Thêm các giả thuyết phụ (nút khớp, tường xây…) lOMoAR cPSD| 23136115 Hình 1.3
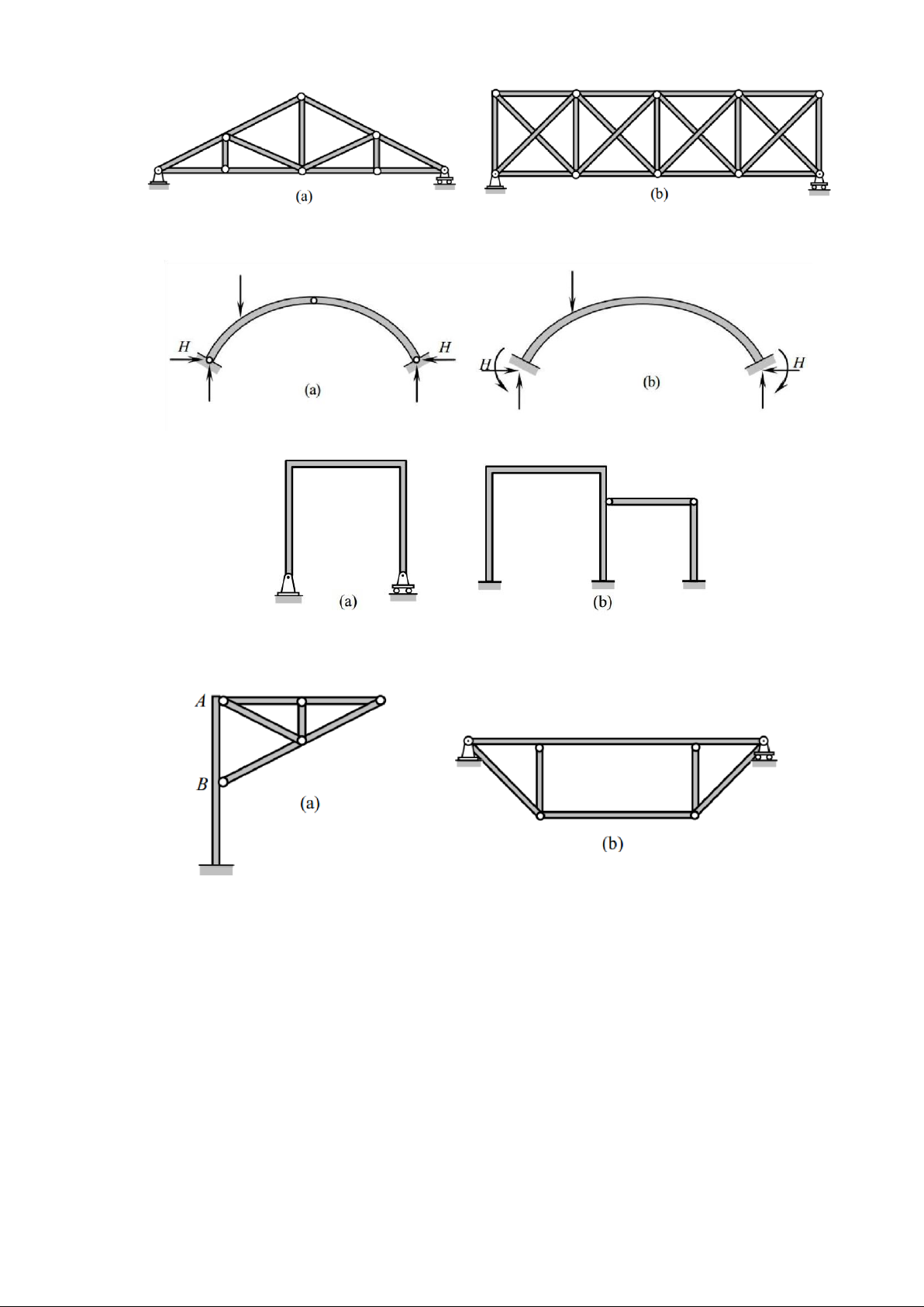
Ví dụ 1.1: Hãy ưa ra sơ ồ tính của một hệ dàn ược mô tả như hình 1.4a.
Để ưa ra sơ ồ tính của dàn chúng ta cần tiến hành các bước sau:
- Thay các thanh dàn bằng ường trục thanh của nó.
- Tải trọng mái tác dụng lên dàn thông qua các thanh xà gồ ược ưa về thành tải trọng tập trung.
- Các cột ở dàn ược thay bằng lý tưởng bằng một gối cố ịnh và một gối di ộng.
- Lý tưởng hóa các mối nối trong dàn bằng các liên kết khớp. Hình 1.4
1.3. PHÂN LOẠI KẾT CẤU
1.3.1. Phân loại theo sơ ồ tính
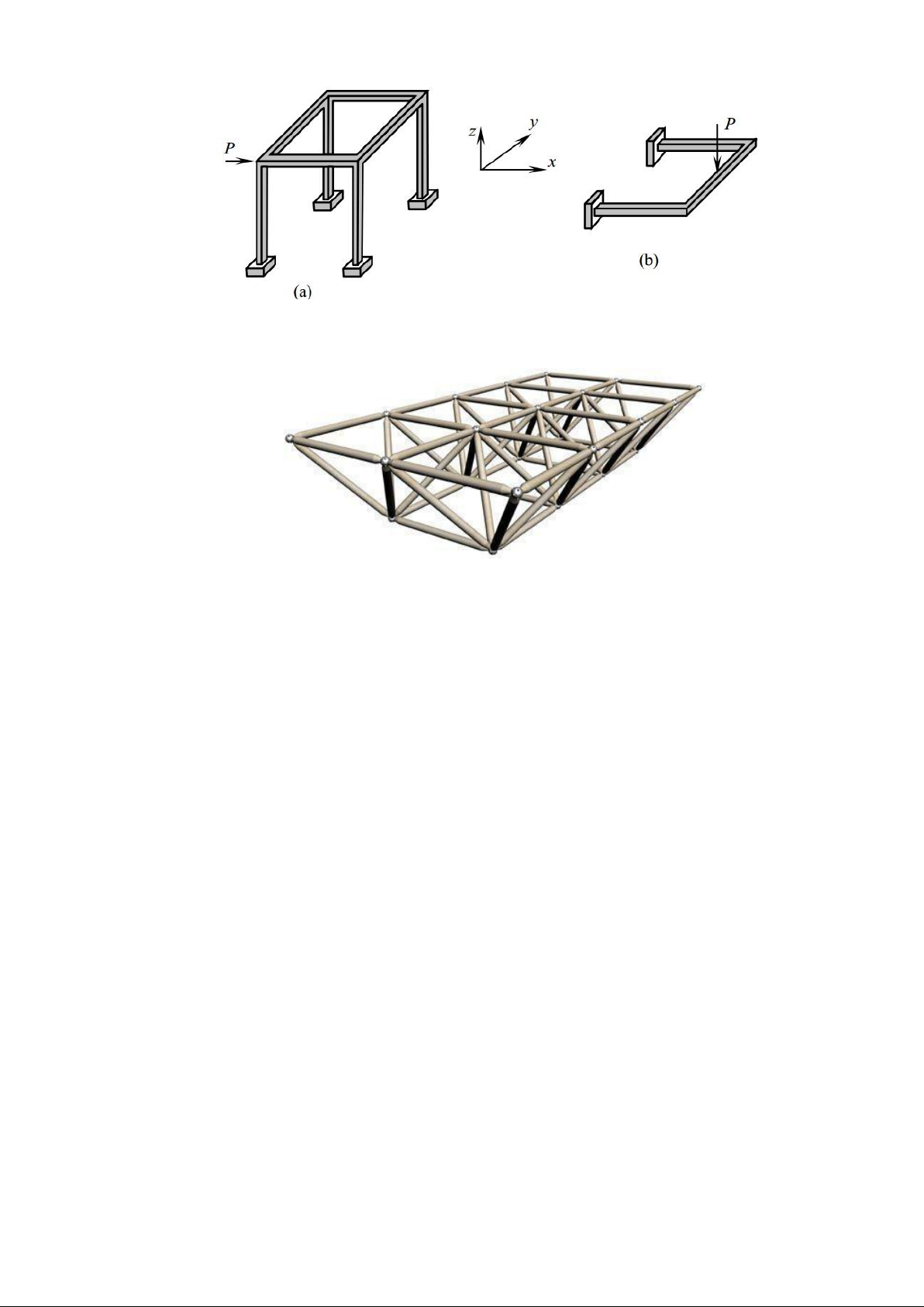
a. Hệ phẳng: khi tất cả các cấu kiện cùng thuộc một mặt phẳng và tải trọng tác dụng
cũng nằm trong mặt phẳng ó. Có các loại hệ phẳng sau: - Dầm Hình 1.5 Hình 1.6 - Dàn lOMoAR cPSD| 23136115 Hình 1.7 - Vòm Hình 1.8 - Khung Hình 1.9 - Hệ liên hợp Hình 1.10
b. Hệ không gian: khi các cấu kiện không cùng nằm trong một mặt phẳng, hoặc
cùng nằm trong một mặt phẳng nhưng tải trọng tác dụng ra ngoài mặt phẳng ó.
Một số loại hệ không gian: - Hệ thanh không gian lOMoAR cPSD| 23136115 Hình 1.11 - Dàn không gian Hình 1.12
1.3.2. Phân loại theo phƣơng pháp tính
Dựa vào sự cần thiết hay không phải sử dụng iều kiện ộng học khi xác ịnh toàn bộ các
phản lực và nội lực trong hệ, người ta chia ra hai loại hệ:
a. Hệ tĩnh ịnh: là loại hệ mà chỉ bằng các iều kiện tĩnh học có thể xác ịnh toàn
bộ các phản lực và nội lực trong hệ. Ví dụ các hệ trên hình a từ hình 1.5 ến hình 1.10.
b. Hệ siêu tĩnh: là loại hệ mà chỉ bằng các iều kiện tĩnh học thì chưa ủ ể xác ịnh toàn
bộ các phản lực và nội lực mà còn phải sử dụng thêm iều kiện ộng học và iều kiện vật
lý. Ví dụ các hệ trên hình b từ hình 1.5 ến hình 1.10.
Nếu dựa vào sự cần thiết hay không phải sử dụng iều kiện cân bằng tĩnh học khi xác
ịnh biến dạng trong hệ khi hệ chịu chuyển vị cưỡng bức, người ta chia ra hai loại hệ:
a. Hệ xác ịnh ộng: là loại hệ khi chịu chuyển vị cưỡng bức, có thể xác ịnh ược biến
dạng của hệ chỉ bằng các iều kiện ộng học (hình học).
b. Hệ siêu ộng: là loại hệ khi chịu chuyển vị cưỡng bức, nếu chỉ bằng các iều kiện
ộng học thì chưa thể xác ịnh ược biến dạng của hệ mà còn phải sử dụng thêm iều kiện tĩnh học. lOMoAR cPSD| 23136115
a. Hệ xác ịnh ộng
b. Hệ siêu ộng Hình 1.13
1.3.3. Phân loại theo kích thƣớc tƣơng ối của các cấu kiện
- Thanh: nếu kích thước một phương khá lớn hơn hai phương càn lại.
- Bản: nếu kích thước của hai phương khá lớn hơn phương còn lại.
- Khối: nếu kích thước của ba phương gần bằng nhau. 1.3.4. Phân loại theo khả năng
thay ổi hình dạng hình học - Hệ biến hình.
- Hệ biến hình tức thời. - Hệ bất biến hình.
1.4. NGUYÊN NHÂN GÂY RA NỘI LỰC, BIẾN DẠNG & CHUYỂN VỊ 1.4.1. Tải trọng
Tải trọng gây ra nội lực, biến dạng và chuyển vị trong tất cả các loại hệ. Thường
phân loại tải trọng như sau:
- Theo thời gian tác dụng: tải trọng lâu dài (như trọng lượng bản thân công trình...)
còn ược gọi là tĩnh tải và tải trọng tạm thời (như tải trọng do gió, do con người i lại khi
sử dụng..) còn ược gọi là hoạt tải.
- Theo sự thay ổi vị trí tác dụng: tải trọng bất ộng và tải trọng di ộng.
- Theo tính chất tác dụng có gây ra lực quán tính hay không: tải trọng tác dụng tĩnh
và tải trọng tác dụng ộng.
Ngoài ra, còn phân loại tải trọng theo hình thức tác dụng của tải trọng: tải trọng tập
trung, tải trọng phân bố...
1.4.2. Sự thay ổi nhiệt ộ
Sự thay ổi nhiệt ộ chính là sự thay ổi nhiệt ộ tác dụng lên công trình khi làm việc so
với lúc chế tạo ra nó.
Đối với hệ tĩnh ịnh, tác nhân này chỉ gây ra biến dạng và chuyển vị, không gây ra nội
lực, còn ối với hệ siêu tĩnh thì gây ra ồng thời cả ba yếu tố trên.
1.4.3. Chuyển vị cƣỡng bức của gối tựa và do cấu tạo lắp ráp không chính xác lOMoAR cPSD| 23136115
Đối với hệ tĩnh ịnh, tác nhân này chỉ gây ra chuyển vị, không gây ra biến dạng và nội
lực; còn ối với hệ siêu tĩnh thì gây ra ồng thời cả ba yếu tố trên.
1.5. CÁC GIẢ THIẾT TÍNH TOÁN - NGUYÊN LÝ CỘNG TÁC DỤNG
1.5.1. Điều kiện vật lý của bài toán:
Giả thiết rằng vật liệu là àn hồi tuyệt ối và tuân theo ịnh luật Hooke, nghĩa là quan
hệ giữa nội lực và biến dạng là quan hệ tuyến tính.
Chú ý: Nếu chấp nhận giả thiết này thì bài toán gọi là àn hồi tuyến tính (tuyến tính
vật lý). Nếu không chấp nhận giả thiết này thì bài toán gọi là àn hồi phi tuyến (phi tuyến vật lý).
1.5.2. Điều kiện hình học của bài toán:
Chuyển vị và biến dạng ược xem như là những ại lượng vô cùng bé. Do vậy khi tính
toán, xem công trình là không có biến dạng.
Chú ý: Nếu chấp nhận giả thiết này thì bài toán gọi là tuyến tính hình học. Nếu không
chấp nhận giả thiết này thì bài toán gọi là phi tuyến hình học. 1.5.3. Nguyên lý cộng tác
dụng (Principal of Superposition) Hình 1.14
Một ại lượng nghiên cứu S (nội lực, phản lực, chuyển vị...) do một số các nguyên
nhân ồng thời tác dụng gây ra sẽ bằng tổng ại số hay tổng hình học của ại lượng S do
từng nguyên nhân tác dụng riêng rẽ gây ra. (Lấy tổng ại số khi ại lượng S là ại lượng vô
hướng, lấy tổng hình học khi ại lượng S là ại lượng vec tơ).
Biểu thức giải tích của NLCTD:
S(P1, P2,...,Pn) = S(P1) + S(P2) +.....+ S(Pn) Trong ó:
- S(P1, P2,..... Pn): là ại lượng S do các nguyên nhân P1, P2,..... Pn ồng thời
tác dụng lên hệ gây ra.
- S(Pk): là ại lượng S do riêng Pk tác dụng lên hệ gây ra.
Gọi Sk là ại lượng S do riêng Pk = 1 gây ra. Tức là S(Pk) = Sk .Pk lOMoAR cPSD| 23136115
Vậy S(P1, P2,...,Pn) = S1.P1 + S2.P2 + ...Sn.Pn
Chú ý: Nguyên lý cộng tác dụng chỉ áp dụng cho hệ tuyến tính vật lý cũng như tuyến tính hình học. lOMoAR cPSD| 23136115 CHƢƠNG 2
CẤU TẠO HÌNH HỌC CỦA HỆ PHẲNG
Nội dung chính của chương này giúp người học nắm vững các nguyên tắc cơ bản cấu
tạo hệ kết cấu bền vững từ nhiều cấu kiện riêng lẽ, hệ kết cấu này phải có khả năng chịu
ược tất cả các tải trọng và tác ộng từ bên ngoài trong suốt quá trình làm việc của công trình. 2.1 CÁC KHÁI NIỆM
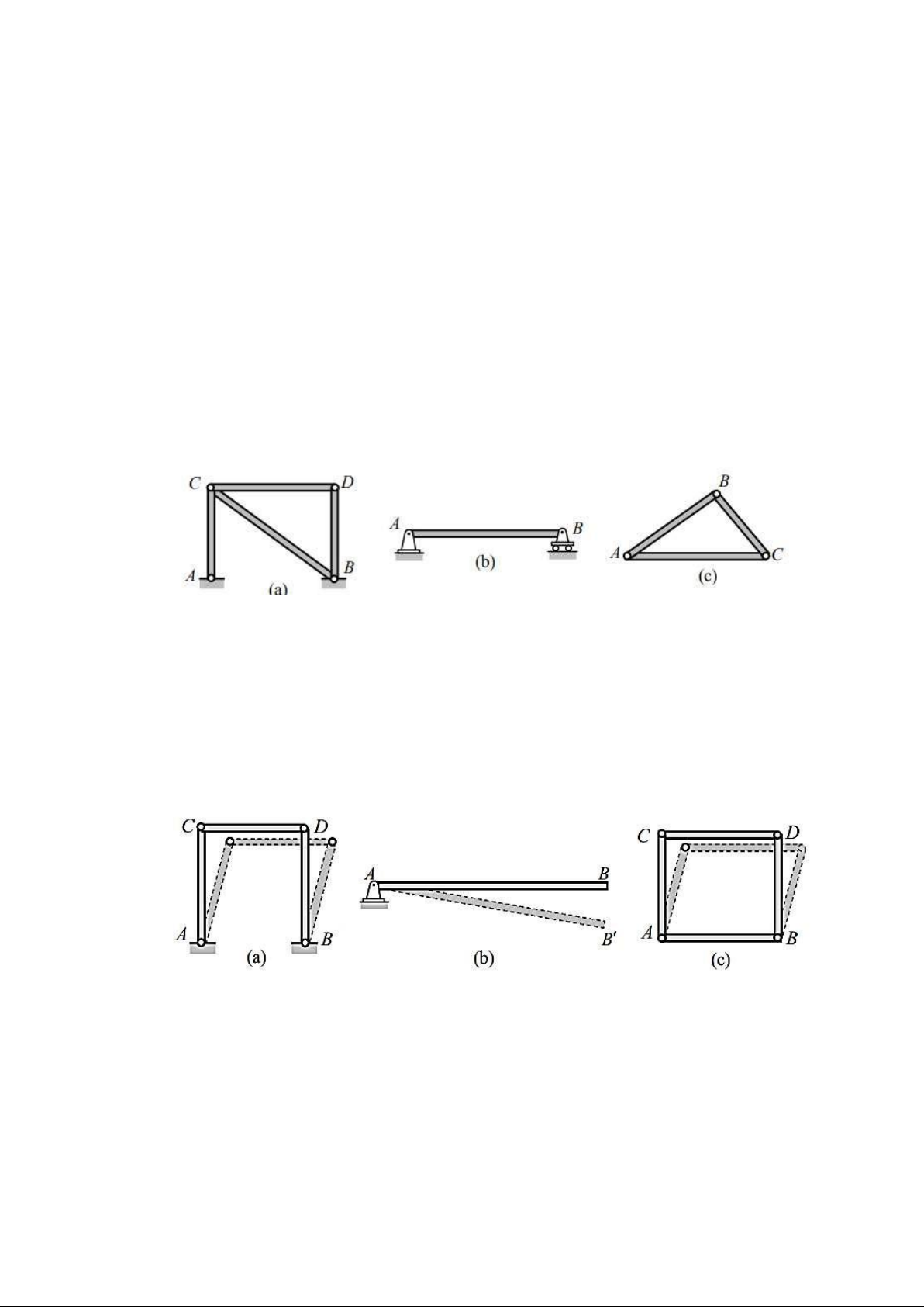
2.1.1. Hệ bất biến hình (Geometrically stable system):
Là hệ không có sự thay ổi hình dạng hình học dưới tác dụng của tải trọng nếu xem
các cấu kiện của hệ là tuyệt ối cứng. Hình 2.1
* Chú ý: Do hệ BBH có khả năng chịu lực tác dụng nên nó ược sử dụng làm các kết
cấu xây dựng và thực tế là chủ yếu sử dụng loại hệ này.
2.1.2. Hệ không bất biến hình (Geometrically unstable system)
a. Hệ biến hình (BH): là hệ có sự thay ổi hình dạng hình học một lượng hữu hạn dưới
tác dụng của tải trọng mặc dù xem các cấu kiện của hệ là tuyệt ối cứng. Hình 2.2
* Chú ý: Do hệ BH không có khả năng chịu tải trọng tác dụng nên các kết cấu xây
dựng không sử dụng loại hệ này.
b. Hệ biến hình tức thời (BHTT): là hệ có sự thay ổi hình dạng hình học một lượng
vô cùng bé dưới tác dụng của tải trọng mặc dù xem các cấu kiện của hệ là tuyệt ối cứng. lOMoAR cPSD| 23136115 Hình 2.3
Ví dụ: Hệ ABC có cấu tạo như trên hình 2.3a, khớp A có thể i xuống một oạn vô cùng
bé , nên hệ ã cho là hệ BHTT.
* Chú ý: Các kết cấu xây dựng không sử dụng hệ BHTT hay hệ gần BHTT (là hệ mà chỉ
cần thay ổi một lượng vô cùng bé hình dạng hình học sẽ trở thành hệ BHTT) vì nội lực
trong hệ gần BHTT rất lớn.
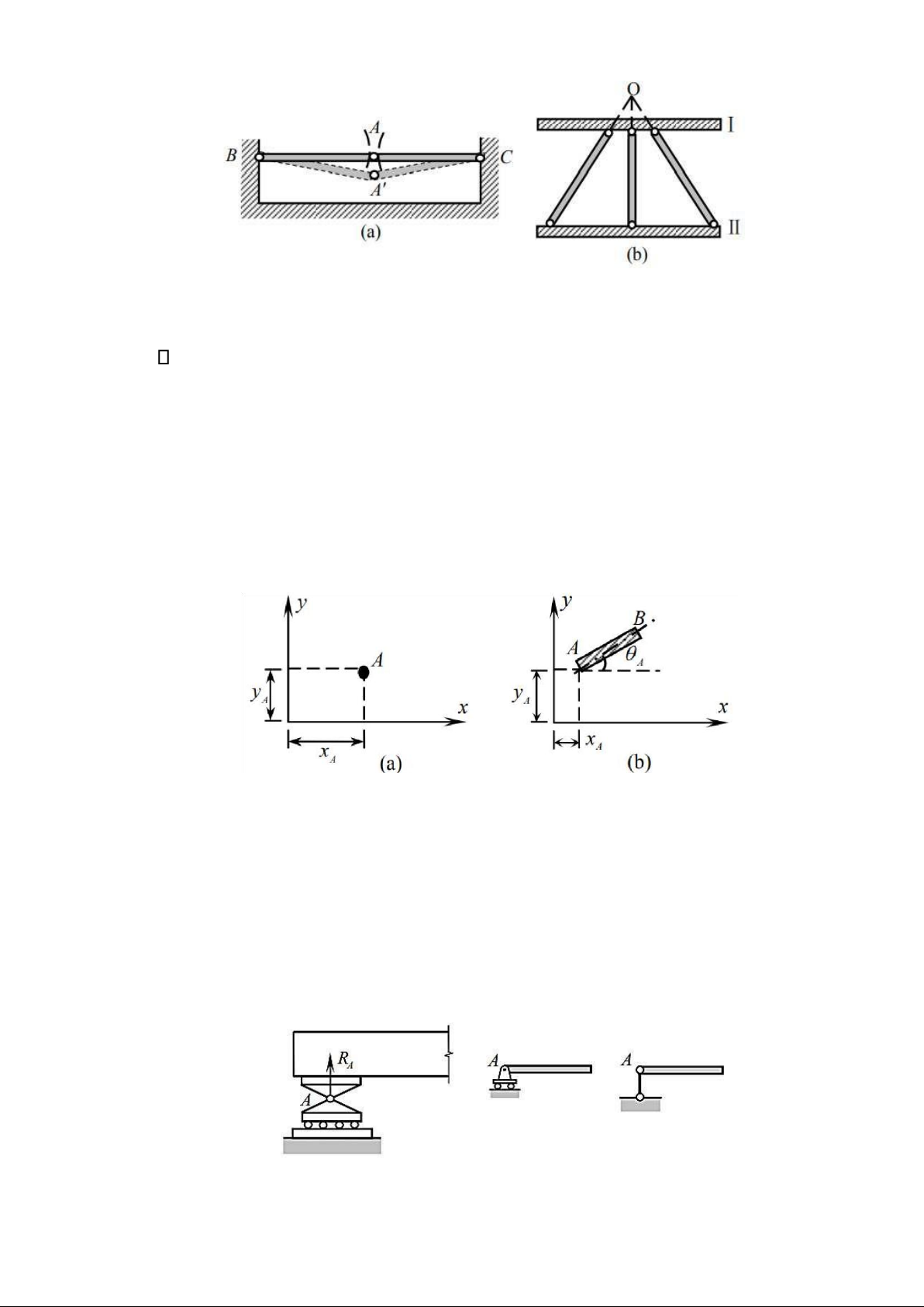
2.1.3. Bậc tự do (Degrees of Freedom)
Là số các thông số ộc lập ủ ể xác ịnh vị trí của một hệ so với một hệ cố ịnh.
Trong hệ phẳng, một chất iểm có bậc tự do bằng 2 (hình 2.4a); một miếng cứng có
bậc tự do bằng 3 (hình 2.4b). Hình 2.4
2.2. CÁC LOẠI LIÊN KẾT
2.2.1. Liên kết nối ất
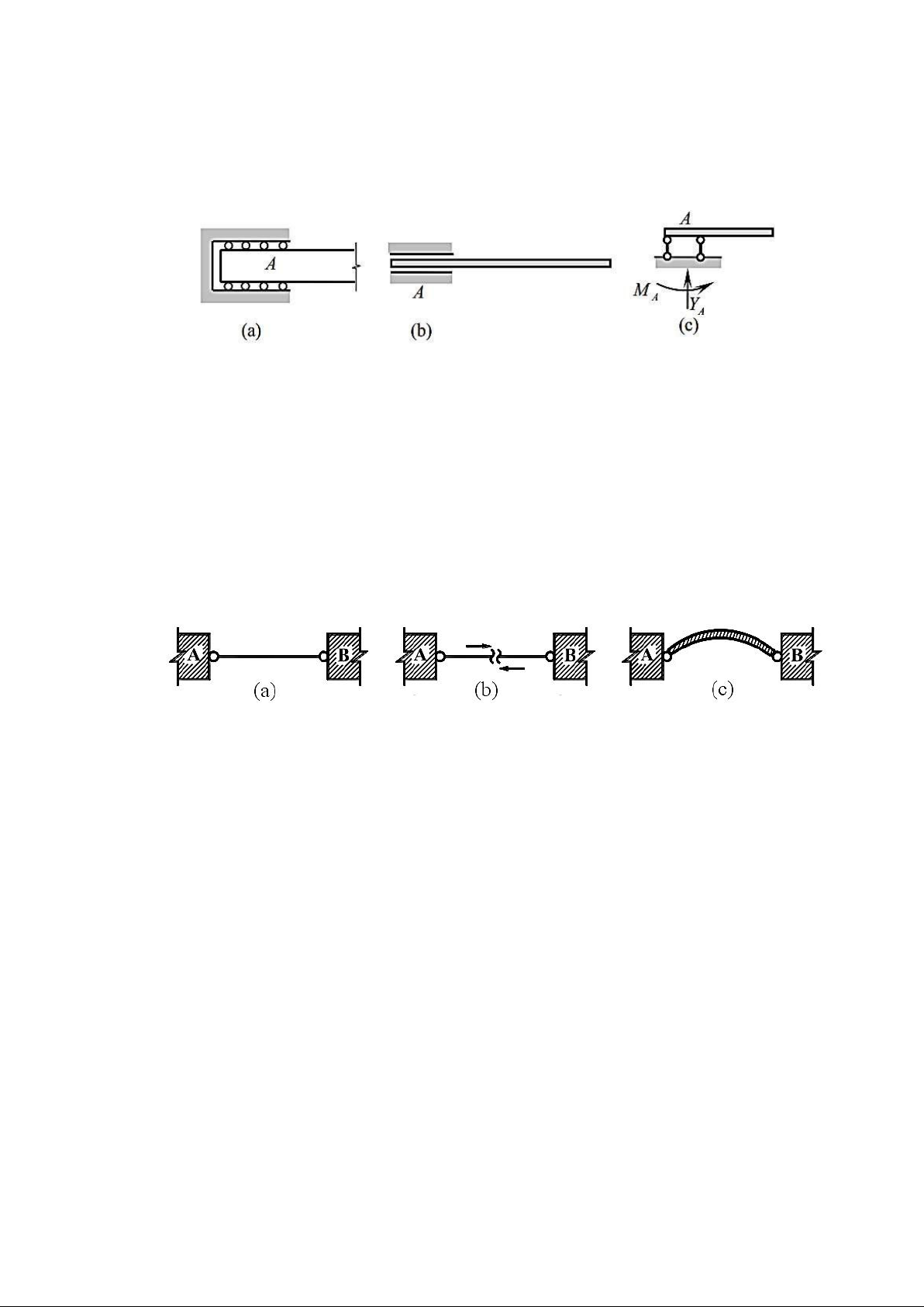
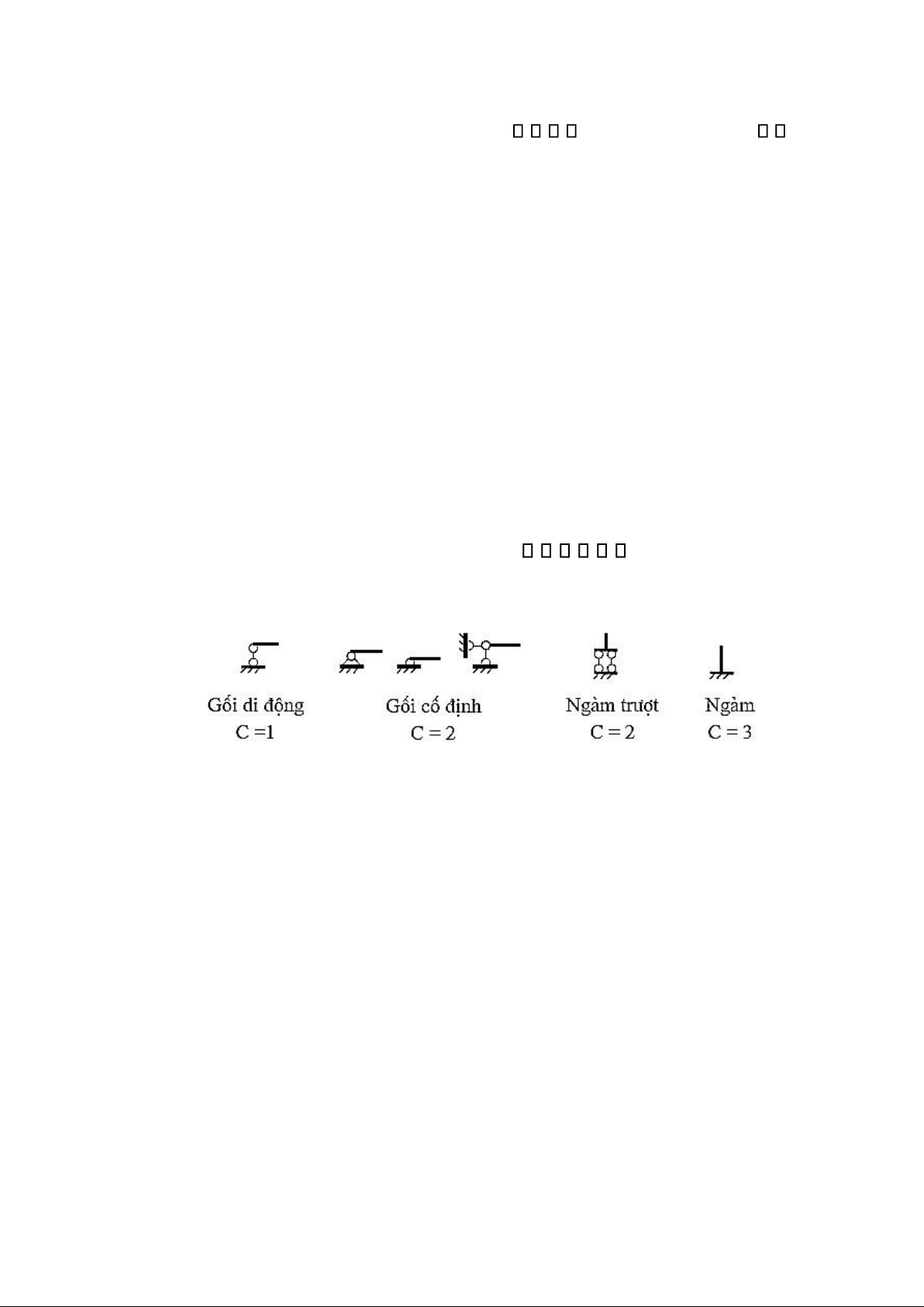
a. Liên kết gối tựa di ộng (Roller support)
Là liên kết ngăn cản một thành phần chuyển ộng thẳng theo phương liên kết của cấu
kiện (khử một bậc tự do) và phát sinh một phản lực thẳng dọc theo phương ngăn cản chuyển ộng. Hình 2.5 lOMoAR cPSD| 23136115
Hình 2.6. Hình ảnh gối di ộng trong thực tế
b. Liên kết gối tựa cố ịnh (Hinged support)
Là liên kết ngăn cản toàn bộ các chuyển ộng thẳng của cấu kiện (khử hai bậc tự do)
và phát sinh một phản lực có phương xiên i qua khớp.
Hình 2.7. Sơ ồ tính và h ình ảnh gối cố ịnh trong thực tế
c. Liên kết ngàm cứng (Fixed support)
Là liên kết ngăn cản toàn bộ các chuyển ộng của cấu kiện, gồm hai chuyển ộng thẳng
và một chuyển ộng xoay (khử ba bậc tự do), tại liên kết phát sinh ba thành phần phản lực.
Hình 2.8. Liên kết ngàm cứng lOMoAR cPSD| 23136115
d. Liên kết ngàm trƣợt (Sliders)
Là liên kết ngăn cản hai thành phần chuyển ộng của cấu kiện, gồm một chuyển ộng
thẳng theo phương liên kết và một chuyển ộng xoay (khử hai bậc tự do), tại liên kết phát
sinh hai thành phần phản lực.
Hình 2.9. Liên kết ngàm trượt
2.2.2. Liên kết giữa các miếng cứng
2.2.2.1 Liên kết ơn giản
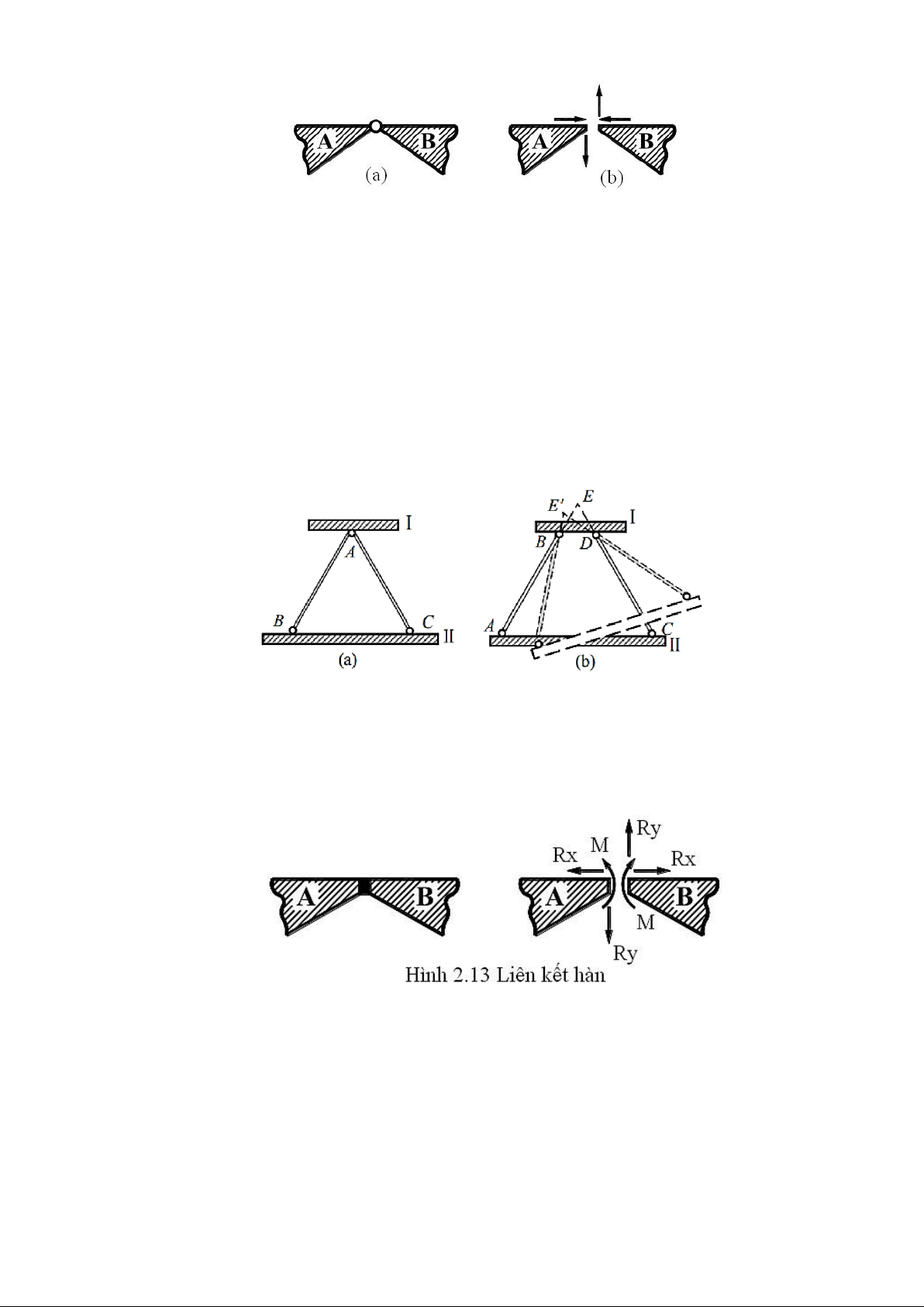
Liên kết ơn giản là liên kết nối hai miếng cứng với nhau. Có 3 loại: a.
Liên kết thanh (Link):
Cấu tạo: Gồm một thanh thẳng không chịu tải trọng có hai khớp lý tưởng ở hai ầu (hình 2.10).
Hình 2.10. Liên kết thanh
Tính chất của liên kết:
+ Về mặt ộng học: liên kết thanh không cho miếng cứng di chuyển theo phương dọc
trục thanh, tức là khử ược một bậc tự do, do ó liên kết thanh còn ược gọi là liên kết loại một.
+ Về mặt tĩnh học: tại liên kết chỉ có thể phát sinh một thành phần phản lực theo
phương dọc trục thanh (hình 2.10b).
* Trường hợp ặc biệt: một miếng cứng có hai ầu khớp và không chịu tải trọng thì có
thể như một liên kết thanh, có trục thanh là ường nối hai khớp (hình 2.10c).
b. Liên kết khớp ơn giản (Simple hinge):
Cấu tạo: Gồm hai miếng cứng nối với nhau bằng một khớp lý tưởng (hình 2.11). lOMoAR cPSD| 23136115
Hình 2.11. Liên kết khớp ơn giản
Tính chất của liên kết:
+ Về mặt ộng học: liên kết khớp không cho miếng cứng chuyển vị thẳng, nhưng không
ngăn cản chuyển vị xoay, tức là khử ược hai bậc tự do, do ó liên kết khớp còn ược gọi là liên kết loại hai.
+ Về mặt tĩnh học: tại liên kết có thể phát sinh một phản lực có phương chưa biết.
Phản lực này thường ược phân tích thành hai thành phần theo hai phương xác ịnh (hình 2.11b).
* Trường hợp ặc biệt: hai liên kết thanh có thể xem là một liên kết khớp (khớp giả
tạo), có vị trí tại giao iểm ường nối hai trục thanh (hình 2.12).
Hình 2.12. Liên kết khớp thực và khớp ảo
c. Liên kết hàn ơn giản (Simple rigid joint):
Cấu tạo: Gồm hai miếng cứng nối với nhau bằng một mối hàn (hình 2.13).
Tính chất của liên kết:
+ Về mặt ộng học: liên kết hàn không cho miếng cứng có chuyển vị, tức là khử ược
3 bậc tự do, do ó liên kết hàn còn ược gọi là liên kết loại ba.
+ Về mặt tĩnh học: liên kết có thể làm phát sinh một phản lực có phương và vị trí chưa
biết. Thường ưa phản lực này về tại vị trí liên kết và phân tích thành ba thành phần M, Rx , R y . lOMoAR cPSD| 23136115
* Chú ý: Liên kết hàn tương ương với ba liên kết thanh hoặc một liên kết thanh và một
liên kết khớp ược sắp xếp một cách hợp lý.
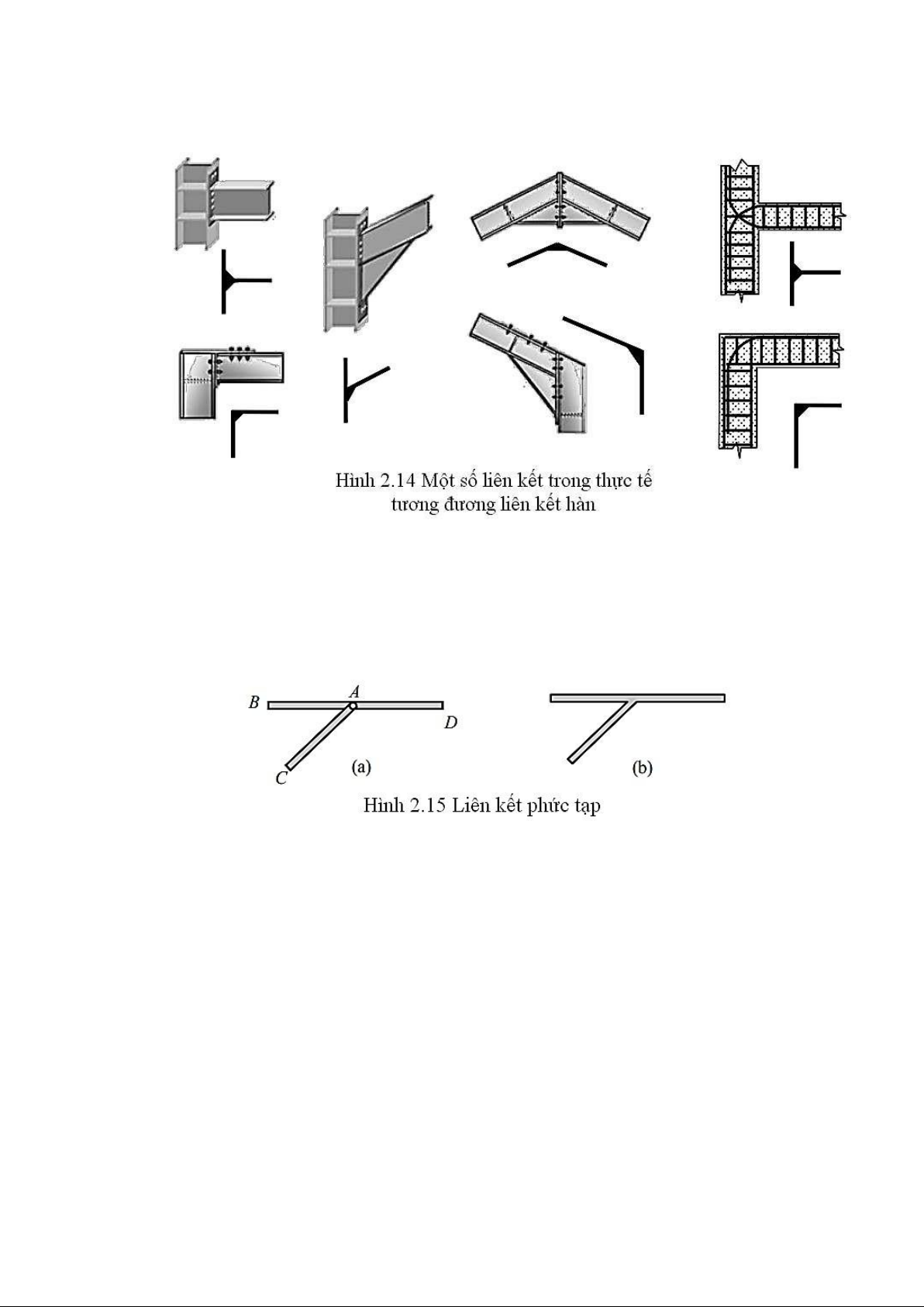
2.2.2. Liên kết phức tạp:
Liên kết phức tạp là liên kết nối nhiều miếng cứng với nhau, số miếng cứng lớn hơn hai.
Về mặt cấu tạo, chỉ có liên kết khớp phức tạp và hàn phức tạp (hình 2.15).
* Độ phức tạp của liên kết: là số liên kết ơn giản cùng loại, tương ương với liên kết ã cho. Ký hiệu p.
* Công thức xác ịnh: p = D -1
với p: ộ phức tạp của liên kết tương ương số liên kết ơn giản D: số
miếng cứng nối vào liên kết.
Do ó một liên kết khớp phức tạp có n miếng cứng thì tương ương n-1 liên kết khớp
ơn giản và khử ược 2(n-1) bậc tự do; với một liên kết hàn phức tạp có n miếng cứng thì
tương ương n-1 liên kết hàn ơn giản và khử ược 3(n-1) bậc tự do.
2.3. CÁCH NỐI CÁC MIẾNG CỨNG THÀNH HỆ BBH
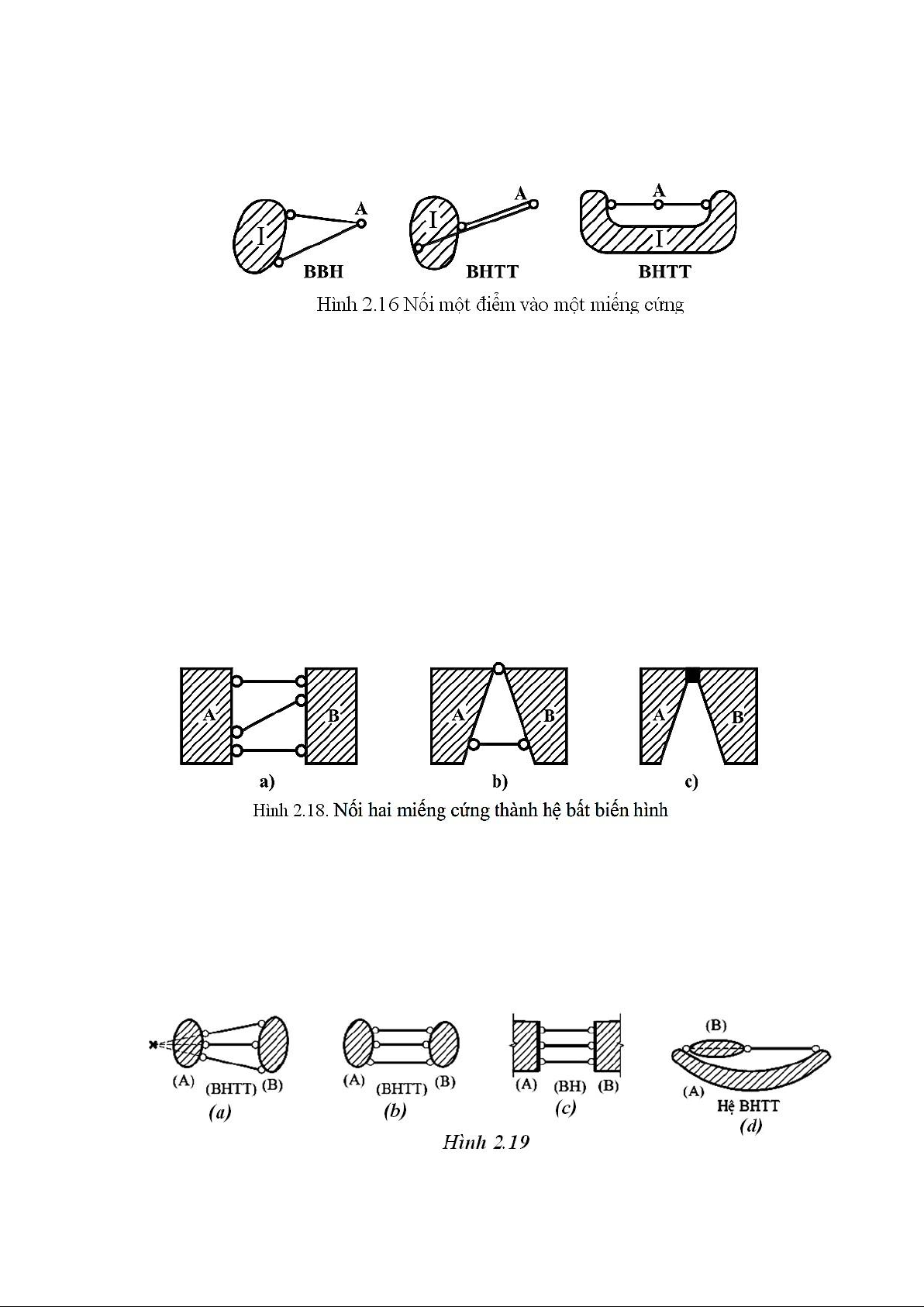
2.3.1. Nối một iểm vào một miếng cứng lOMoAR cPSD| 23136115
a. Điều kiện cần: ể nối một iểm vào miếng cứng cần phải khử hai bậc tự do của nó.
Nghĩa là cần dùng hai liên kết thanh (hình 2.16).
b. Điều kiện ủ: hai liên kết thanh không ược thẳng hàng.
Hai liên kết thanh không thẳng hàng nối một iểm vào miếng cứng gọi là bộ ôi.
* Tính chất của bộ ôi: khi thêm hay bớt lần lượt các bộ ôi thì tính chất ộng học của
hệ không thay ổi. Tính chất này ược sử dụng ể phân tích cấu tạo hình học của hệ.
2.3.2. Cách nối hai miếng cứng
a. Điều kiện cần: Xem một miếng cứng là cố ịnh. Để nối miếng cứng còn lại vào
miếng cứng cố ịnh cần khử ba bậc tự do của nó, nghĩa là cần sử dụng tổ hợp các liên kết:
+ Ba liên kết thanh (hình 2.18a).
+ Một liên kết thanh cộng một liên kết khớp (hình 2.18b).
+ Một liên kết hàn (hình 2.18c). b. Điều kiện ủ:
+ Nếu sử dụng ba liên kết thanh: yêu cầu ba thanh không ược ồng quy hoặc song song
(hình 2.19a, 2.19b, 2.19c).
+ Nếu sử dụng một liên kết thanh cộng một liên kết khớp: yêu cầu khớp không ược
nằm trên ường trục thanh (hình 2.19d).
+ Nếu sử dụng liên kết hàn: thì ó cũng là iều kiện ủ. lOMoAR cPSD| 23136115
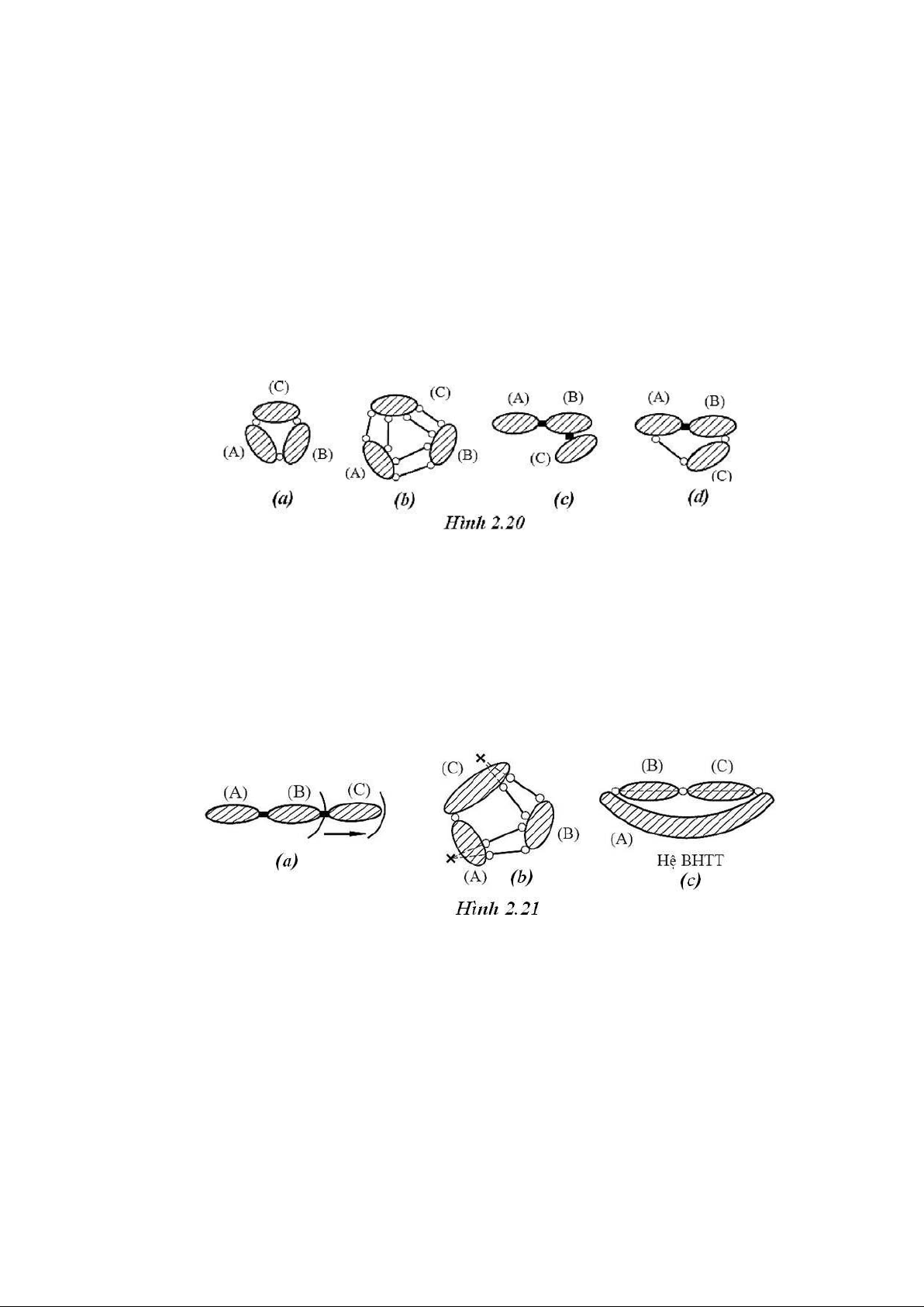
2.3.3. Cách nối ba miếng cứng
a. Điều kiện cần: xem một miếng cứng là cố ịnh. Để nối hai miếng cứng còn lại vào
miếng cứng cố ịnh cần phải khử sáu bậc tự do, nghĩa là cần phải sử dụng tổ hợp các liên kết:
+ Ba liên kết khớp (hình 2.20a).
+ Sáu liên kết thanh (hình 2.20b).
+ Hai liên kết hàn (hình 2.20c).
+ Một liên kết thanh cộng một liên kết khớp cộng một liên kết hàn (hình 2.20d) . v.v.v. b. Điều kiện ủ:
+ Nếu các miếng cứng nối lần lượt với nhau: trở về lại bài toán nối hai miếng cứng.
Ví dụ (hình 2.21a).
+ Nếu các miếng cứng nối ồng thời với nhau (nếu loại bỏ một miếng cứng bất kỳ, hệ
còn lại bị biến hình): lúc này hệ cần sử dụng ba liên kết khớp (thực hoặc giả tạo) tương
hỗ (hình 2.21b). Và yêu cầu các liên kết khớp không cùng nằm trên một ường thẳng (hình 2.21c).
2.3.4. Cách nối nhiều miếng cứng a. Điều kiện cần:
* Trường hợp hệ bất kỳ không nối ất:
Xét một hệ không nối ất gồm D miếng cứng. Các liên kết giữa các miếng cứng là: T
liên kết thanh, K liên kết khớp ã quy về khớp ơn giản và H liên kết hàn ã quy về hàn ơn giản.
Xem một miếng cứng là cố ịnh. Nối (D - 1) miếng cứng còn lại vào miếng cứng cố
ịnh, nghĩa là cần phải khử 3(D-1) bậc tự do. Đó là yêu cầu. lOMoAR cPSD| 23136115
Về khả năng: T , K, H khử ược T + 2K + 3H bậc tự do.
Như vậy, iều kiện cần ể hệ BBH là n T K H 2 3 3(D 1) 0 (1 - 2) Các trường hợp của n:
+ n = 0: hệ ủ liên kết và nếu hệ ã cho là hệ BBH thì hệ là hệ tĩnh ịnh.
+ n > 0: hệ dư liên kết và nếu hệ ã cho là hệ BBH thì hệ là hệ siêu tĩnh.
+ n < 0: hệ thiếu liên kết, hệ ã cho là hệ BH.
* Trường hợp hệ bất kỳ có nối ất:
Xét một hệ nối ất gồm D miếng cứng. Các liên kết giữa các miếng cứng là: T liên kết
thanh, K liên kết khớp ã quy về khớp ơn giản và H liên kết hàn ã quy về hàn ơn giản.
Liên kết giữa hệ và ất gồm C liên kết ã quy về liên kết loại một.
Xem trái ất là cố ịnh. Nối D miếng cứng còn lại vào trê ất, nghĩa là phải khử 3D bậc tự do. Đó là yêu cầu.
Về khả năng: T, K, H, C khử ược T + 2.K + 3H + C bậc tự do.
Vậy iều kiện cần ể hệ BBH là: n T K H C D 2 3 3 0 (1 - 3)
Các loại liên kết nối ất: Hình 2.22 b. Điều kiện ủ:
Thường sử dụng tính chất của bộ ôi, cách nối hai hoặc ba miếng cứng nhằm thu hẹp
hoặc phát triển hệ ến mức tối a cho phép. Nếu kết quả thu ược:
+ Một miếng cứng: hệ ã cho là BBH.
+ Hai hoặc ba miếng cứng: sử dụng iều kiện ủ của bài toán nối hai, ba miếng cứng ã
biết ể phân tích tiếp.
Ngoài ra còn sử dụng phương pháp tải trọng bằng không hoặc phương pháp ộng học ể khảo sát.
2.3.5. Trƣờng hợp ặc biệt: Hệ dàn.
Hệ dàn là hệ gồm những thanh thẳng liên kết với nhau chỉ bằng các khớp ở hai ầu mỗi thanh.
* Đối với hệ dàn cũng cho phép áp dụng công thức (1 - 2) hoặc (1 - 3) ể khảo sát iều
kiện cần. Tuy nhiên, trong hệ dàn, các liên kết khớp thường là khớp phức tạp cần quy ổi lOMoAR cPSD| 23136115
về khớp ơn giản. Cách làm như vậy thường dễ nhằm lẫn. Dưới ây sẽ trình bày một cách
khác thuận lợi hơn mà không phải quan tâm ến ộ phức tạp của các liên kết khớp.
a. Trường hợp hệ dàn không nối ất:
Xét hệ dàn không nối ất gồm D thanh dàn và M mắt.
Xem một thanh dàn là miếng cứng cố ịnh, còn lại (D - 1) thanh. Và i nối (M -2) mắt
còn lại vào miếng cứng cố ịnh, nghĩa là cần phải khử 2(M - 2) bậc tự do.
Xem các thanh dàn là các liên kết thanh. Như vậy, (D -1) thanh còn lại có khả năng
khử ược (D -1) bậc tự do.
Vậy iều kiện cần ể hệ BBH là: n D (1) 2(M 2) D M2 3 0 (1 - 4)
b. Trường hợp hệ dàn nối ất:
Xét hệ dàn gồm D thanh dàn và M mắt. Ngoài ra hệ dàn còn nối ất bằng số liên kết
tương ương C liên kết loại một. Nối M mắt vào miếng cứng cố ịnh. Nghĩa là cần khử 2M bậc tự do.
Xem các thanh dàn là các liên kết thanh. Như vậy, D thanh dàn có khả năng khử ược
D bậc tự do. Ngoài ra các liên kết nối ất khử ược C bậc tự do.
Vậy iều kiện cần ể hệ BBH là: n D C M 2 0 (1 - 5)
* Chú ý: - Các trường hợp của n và iều kiện ủ vẫn như trường hợp tổng quát.
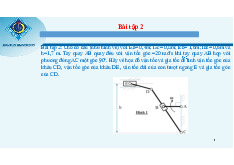
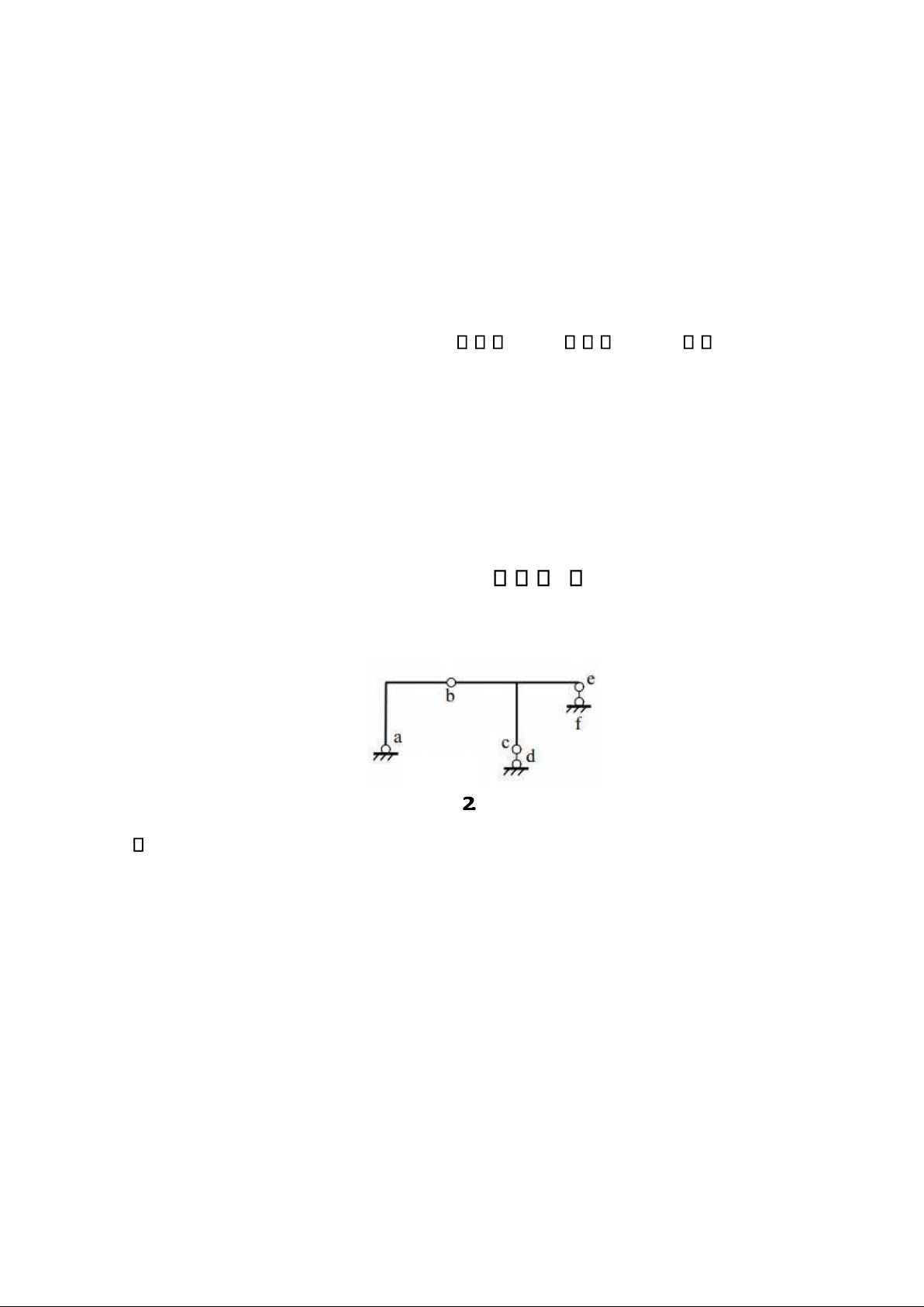
Ví dụ 1: Phân tích cấu tạo hình học của hệ cho trên hình 2.23
Hình 23
Điều kiện cần: Hệ ã cho thuộc hệ bất kỳ nối ất nên iều kiện cần sử dụng biểu thức (1-
3). Có thể giải bài toán theo nhiều quan niệm khác nhau:
a. Quan niệm mỗi oạn thanh thẳng là một miếng cứng:
Lúc này D = 5, T = 0, K = 1, H = 3, C = 4. Thay vào (1 - 3) n =
T + 2.K + 3.H + C - 3.D = 0 + 2.1 + 3.3 + 4 - 3.5 = 0 → Hệ ã cho có khả năng BBH.
b. Quan niệm mỗi thanh gãy khúc là một miếng cứng (quan niệm số miếng cứng tối thiểu):
Lúc này D = 2 (ab, bce), T = 0, K = 1, H = 0, C = 4. Thay vào (1 - 3) n
= 0 + 2.1 + 3.0 + 4 - 3.2 = 0 → Hệ ã cho có khả năng BBH.
c. Quan niệm trái ất là một miếng cứng: