NỘI DUNG Trang
MỤC LỤC ............................................................................................................. 1
LỜI NÓI ĐẦU ..................................................................................................... .5
CHƯƠNG 1: TỔNG QUAN VỀ HỆ THỐNG ĐIỀU KHIỂN TỰ ĐỘNG.......... 6
1.1. Các khái niệm cơ bản ..................................................................................... 6
1.2. Các phần tử cơ bản của hệ thống điều khiển tự động .................................... 6
1.3. Các nguyên tắc điều khiển cơ bản .................................................................. 7
1.3.1. Nguyên tắc điều khiển theo sai lệch ............................................................ 7
1.3.2. Nguyên tắc điều khiển bù nhiễu .................................................................. 8
1.3.3. Điều khiển phối hợp .................................................................................... 8
1.4. Phân loại hệ thống điều khiển tự động ........................................................... 8
1.4.1. Phân loại sơ đồ tổng quát ............................................................................ 8
1.4.2. Phân loại theo đặc điểm toán học .............................................................. 10
1.4.3. Phân loại theo số lượng ngõ vào/ra ........................................................... 10
1.5. Lịch sử phát triển lý thuyết điều khiển tự động ........................................... 11
1.5.1. Điều khiển kinh điển (classical control) .................................................. .11
1.5.2. Điều khiển hiện đại (modern control) ....................................................... 11
1.5.3. Điều khiển thông minh (intelligent control) ............................................. 12
1.6. Nhiệm vụ cơ bản của hệ thống điều khiển ................................................... 12
BÀI TẬP CHƯƠNG 1 ........................................................................................ 14
CHƯƠNG 2: MÔ TẢ TOÁN HỌC HỆ THỐNG ĐIỀU KHIỂN TỰ ĐỘNG ... 15
2.1. Mô hình phương trình vi phân ..................................................................... 16
2.2. Phép biến đổi Laplace .................................................................................. 18
2.2.1. Biến đổi Laplace thuận .............................................................................. 18
2.2.2. Biến đổi Laplace ngược ............................................................................ 21
2.2.3. Ứng dụng biến đổi Laplace giải phương trình vi phân. ............................ 28
2.3. Hàm truyền ................................................................................................... 31
2.3.1. Hàm truyền đạt của mạch điện. ................................................................. 32
2.3.2. Hàm truyền đạt của hệ thống cơ khí. ........................................................ 35 1
2.3.3. Sự tương đương giữa hệ cơ khí và các phần tử mạch điện. ...................... 37
2.3.4. Hàm truyền của các phần tử điện tử. ......................................................... 39
2.3.5. Động cơ điện DC. ...................................................................................... 40
2.4. Sơ đồ khối ................................................................................................... .44
2.4.1. Định nghĩa ................................................................................................. 44
2.4.2. Đại số sơ đồ khối ....................................................................................... 45 2.5. Graph tí
n hiệu ............................................................................................... 53
2.5.1.Định nghĩa .................................................................................................. 53
2.5.2.Đại số graph tín hiệu .................................................................................. 54
2.5.3. Công thức Mason ...................................................................................... 54
2.6. Phương pháp không gian trạng thái ............................................................. 57
2.6.1. Khái niệm .................................................................................................. 57
2.6.2. Trạng thái của hệ thống, hệ phương trình biến trạng thái ......................... 58
2.6.3. Hệ tuyến tính hệ số hằng ........................................................................... 59
2.6.4. Ứng dụng biểu diễn mô hình toán học trên không gian trạng thái ........... 59
2.6.5. Chuyển từ hàm truyền đạt sang phương trình trạng thái và ngược lại. ... .63
2.6.6. Tính điều khiển được và quan sát được. ................................................... 74
BÀI TẬP CHƯƠNG 2 ........................................................................................ 77
Phụ lục: Mô tả hệ thống tự động dùng Matlab .................................................. .82
CHƯƠNG 3: ĐẶC TÍNH ĐỘNG HỌC CỦA HỆ TUYẾN TÍNH .................... 89
3.1. Khái niệm về đặc tính động học ................................................................... 89
3.2. Đặc tính thời gian ......................................................................................... 89
3.2.1. Hàm quá độ ............................................................................................... 89
3.2.2. Hàm trọng lượng ....................................................................................... 90
3.3. Đặc tính tần số .............................................................................................. 92
3.3.1. Biểu đồ Bode ............................................................................................. 94
3.3.2. Biểu đồ Nyquist ......................................................................................... 95
3.4. Các khâu động học ....................................................................................... 96
3.4.1. Khâu tỷ lệ .................................................................................................. 96
3.4.2. Khâu tích phân lý tưởng ............................................................................ 98 2
3.4.3. Khâu vi phân lý tưởng ............................................................................... 99
3.4.4. Khâu quán tính bậc nhất .......................................................................... 100
3.4.5. Khâu vi phân bậc nhất ............................................................................. 103
3.4.6. Khâu dao động bậc hai ............................................................................ 104
3.4.7. Khâu trì hoãn(khâu trễ) ........................................................................... 107
3.5. Đặc tính tần số của hệ thống ...................................................................... 108
3.5.1. Đặc tính biên pha..................................................................................... 108 3.5.2. M
ô hình ZPK ........................................................................................... 109
3.5.3. Phương pháp vẽ biểu đồ Bode biên độ bằng các đường tiệm cận .......... 11 1
BÀI TẬP CHƯƠNG 3 ...................................................................................... 116
Phụ lục: Khảo sát đặc tính động học của hệ thống dùng Matlab ...................... 117
CHƯƠNG 4: KHẢO SÁT TÍNH ỔN ĐỊNH CỦA HỆ THỐNG ..................... 120
4.1. Khái niệm về ổn định hệ thống .................................................................. 120
4.2. Tiêu chuẩn ổn định đại số .......................................................................... 122
4.2.1. Điều kiện cần ........................................................................................... 122
4.2.2. Tiêu chuẩn Routh .................................................................................... 122
4.2.3 Tiêu chuẩn Hurwitz .................................................................................. 127
4.2.4 Xét ổn định cho hệ có mô tả toán học dưới dạng mô hình trạng thái. ..... 128
4.3. Tiêu chuẩn ổn định tần số .......................................................................... 129
4.3.1. Nguyên lý góc quay ............................................................................... .129
4.3.2. Tiêu chuẩn Mikhailov ............................................................................. 130
4.3.3. Tiêu chuẩn Nyquist ................................................................................. 133
4.4. Phương pháp quỹ đạo nghiệm số ............................................................... 136
4.4.1. Khái niệm ................................................................................................ 136
4.4.2. Quy tắc xây dựng quỹ đạo nghiệm số ..................................................... 137
BÀI TẬP CHƯƠNG 4 ...................................................................................... 143
CHƯƠNG 5: ĐÁNH GIÁ CHẤT LƯỢNG HỆ THỐNG ĐIỀU KHIỂN ........ 145
5.1. Các chỉ tiêu chất lượng ............................................................................... 145
5.2. Sai số xác lập(SSE) .................................................................................... 146
5.2.1. Tín hiệu vào là bậc thang đơn vị (loại 0) ................................................ 147 3
5.2.2. Tín hiệu vào là hàm dốc đơn vị (loại 1) ................................................ 147
5.2.3. Tín hiệu vào là hàm parabol (loại 2) ..................................................... 148
5.3. Đáp ứng quá độ .......................................................................................... 148
5.3.1. Hệ quán tính bậc một .............................................................................. 148
5.3.2. Hệ dao động bậc hai ................................................................................ 149
5.3.3. Hệ bậc cao ............................................................................................... 152
BÀI TẬP CHƯƠNG 5 ...................................................................................... 16 0
Phụ lục: Mô phỏng hệ thống tự động dùng Simulink ....................................... 16 2
CHƯƠNG 6: THIẾT KẾ VÀ HIỆU CHỈNH HỆ THỐNG ĐIỀU KHIỂN ...... 168
6.1. Khái niệm chung ........................................................................................ 168
6.2. Đặc tính động học của các bộ điều chỉnh ................................................... 168
6.2.1. Bộ điều chỉnh tỷ lệ (bộ P) ....................................................................... 169
6.2.2. Bộ điều chỉnh tích phân (bộ I)................................................................. 170
6.2.3. Bộ điều chỉnh vi phân (bộ D) .................................................................. 170
6.2.4. Bộ điều chỉnh tỷ lệ - tích phân (bộ PI) .................................................... 171
6.2.5. Bộ điều chỉnh tỷ lệ - vi phân (bộ PD) ..................................................... 17 2
6.2.6. Bộ điều chỉnh tỷ lệ - vi tích phân (bộ PID) ............................................. 17 3
6.3. Xác định thông số của bộ điều chỉnh ......................................................... 17 4
6.3.1. Phương pháp Ziegler - Nichols ............................................................... 174
6.3.2. Phương pháp Chien - Hrones - Reswick ................................................ 178
6.3.3. Phương pháp tổng T của Kuln ................................................................ 180
6.3.4. Phương pháp tối ưu hóa modul ............................................................... 181
6.3.5. Phương pháp tối ưu đối xứng .................................................................. 184
6.3.6. Phương pháp giải tích.............................................................................. 18 7
6.4. Thiết kế hệ thống phản hồi trạng thái bằng phương pháp gán điểm cực ... 18 8
6.4.1. Điều khiển hồi tiếp trạng thái .................................................................. 18 8
6.4.2. Phân bố cực bằng cách cân bằng các hệ số của phương trình đặc trưng 189
6.4.3. Phân bố cực dùng công thức Ackermann ............................................... 19 1
BÀI TẬP CHƯƠNG 6 ...................................................................................... 19 4 4 LỜI NÓI ĐẦU
Cuối thế kỷ 20, công nghệ thông tin bắt đầu được sử dụng rộng rãi trong
kỹ thuật điều khiển cho phép dễ dàng điều khiển với độ chính xác cao các đối
tượng khác nhau. Các phương pháp của Liapunov, Minorsky cũng như lý thuyết
điều khiển tối ưu hiện đại của L.S. Pontryagin (Liên Xô cũ), của R.Belman (Mỹ)
có ý nghĩa rất lớn. Các nguyên tắc điều khiển thích nghi, điều khiển bền vững,
điều khiển mờ, các “hệ thông minh” v.v… ra đời và được áp dụng có hiệu quả vào thực tiễn.
Nhiệm vụ cơ bản của lý thuyết điều khiển tự động là khảo sát các đặc tính
tĩnh (ở chế độ xác lập) và đặc tính động của các hệ tự động để phân tích, đánh
giá và tổng hợp hệ thống điều khiển kỹ thuật trong miền thời gian và miền tần số
bằng công cụ toán học. Nội dung giáo trình trình bày các vấn đề cơ bản nhất của
lý thuyết hệ thống điều khiển tự động từ điều khiển kinh điển đến điều khiển
hiện đại chẳng hạn như bộ điều khiển PID, phương pháp gán điểm cực...
Vì vậy với mong muốn đem lại cho sinh viên những kiến thức tổng quan
nhất về hệ thống điều khiển tự động trong thực tế, với những kiến thức sẵn có
thêm vào là những hiểu biết từ thực tế chúng tôi đã mạnh dạn biên soạn cuốn
giáo trình “Lý thuyết điều khiển tự động” dành cho sinh viên. Cuốn giáo trình gồm có 6 chương:
CHƯƠNG 1: TỔNG QUAN VỀ HỆ THỐNG ĐIỀU KHIỂN TỰ ĐỘNG.
CHƯƠNG 2: MÔ TẢ TOÁN HỌC HỆ THỐNG ĐIỀU KHIỂN TỰ ĐỘNG.
CHƯƠNG 3: ĐẶC TÍNH ĐỘNG HỌC CỦA HỆ TUYẾN TÍNH.
CHƯƠNG 4: KHẢO SÁT TÍNH ỔN ĐỊNH CỦA HỆ THỐNG.
CHƯƠNG 5: ĐÁNH GIÁ CHẤT LƯỢNG HỆ THỐNG ĐIỀU KHIỂN.
CHƯƠNG 6: THIẾT KẾ VÀ HIỆU CHỈNH HỆ THỐNG ĐIỀU KHIỂN.
Trong quá trình biên soạn không thể tránh khỏi những thiếu sót kính
mong quý độc giả có những đóng góp thiết thực để giáo trình hoàn thiện hơn.
Mọi ý kiến đóng góp hoặc trao đổi xin liên hệ N ó h m tác giả 5
CHƯƠNG 1: TỔNG QUAN VỀ HỆ THỐNG ĐIỀU KHIỂN TỰ ĐỘNG
1.1. CÁC KHÁI NIỆM CƠ BẢN
- Điều khiển: Điều khiển là quá trình can thiệp vào hệ thống có mục đích nhằm
đáp ứng yêu cầu của hệ theo quy luật định trước. Quá trình điều khiển bao gồm
các công đoạn: thu thập thông tin, xử lý thông tin và tác động lên hệ thống. Quá
trình điều khiển không có sự tham gia trực tiếp của con người gọi là điều khiển tự động.
Thí dụ: Xét quá trình điều khiển xe máy chạy với tốc độ ổn định là 50 km/h. Để
đạt được tốc độ theo yêu cầu, người lái xe phải quan sát đồng hồ đo tốc độ hiện
tại của xe (thu thập thông tin). Nếu tốc độ của xe chưa đạt như mong muốn thì
người lái xe phải ra quyết định tăng ga hay giảm ga (xử lý thông tin). Cuối cùng
người lái xe thực hiện việc điều chỉnh tăng hay giảm ga để xe đạt tốc độ ổn định
- Điều khiển học: là một ngành khoa học nghiên cứu các quá trình điều khiển
trong các hệ thống gọi là điều khiển học. Tùy theo đặc điểm của đối tượng
nghiên cứu, điều khiển học được chia thành: điều khiển học kỹ thuật, điều khiển
học kinh tế, điều khiển học quân sự…Trong các ngành kể trên, điều khiển học
kỹ thuật là ngành phát triển nhất hiện nay.
- Tín hiệu: Thông tin trong hệ thống điều khiển được thể hiện bằng các tín hiệu.
Các tín hiệu có thể là đại lượng điện(dòng điện, điện áp, công suất) hoặc đại
lượng không điện (lưu lượng, nhiệt độ, vận tốc, gia tốc …). Mỗi phần tử điều
khiển sẽ nhận tín hiệu vào từ một số phần tử của hệ thống và tạo nên tín hiệu ra
tác động vào đối tượng điều khiển. Thay vì sử dụng tín hiệu vào/ra người ta còn
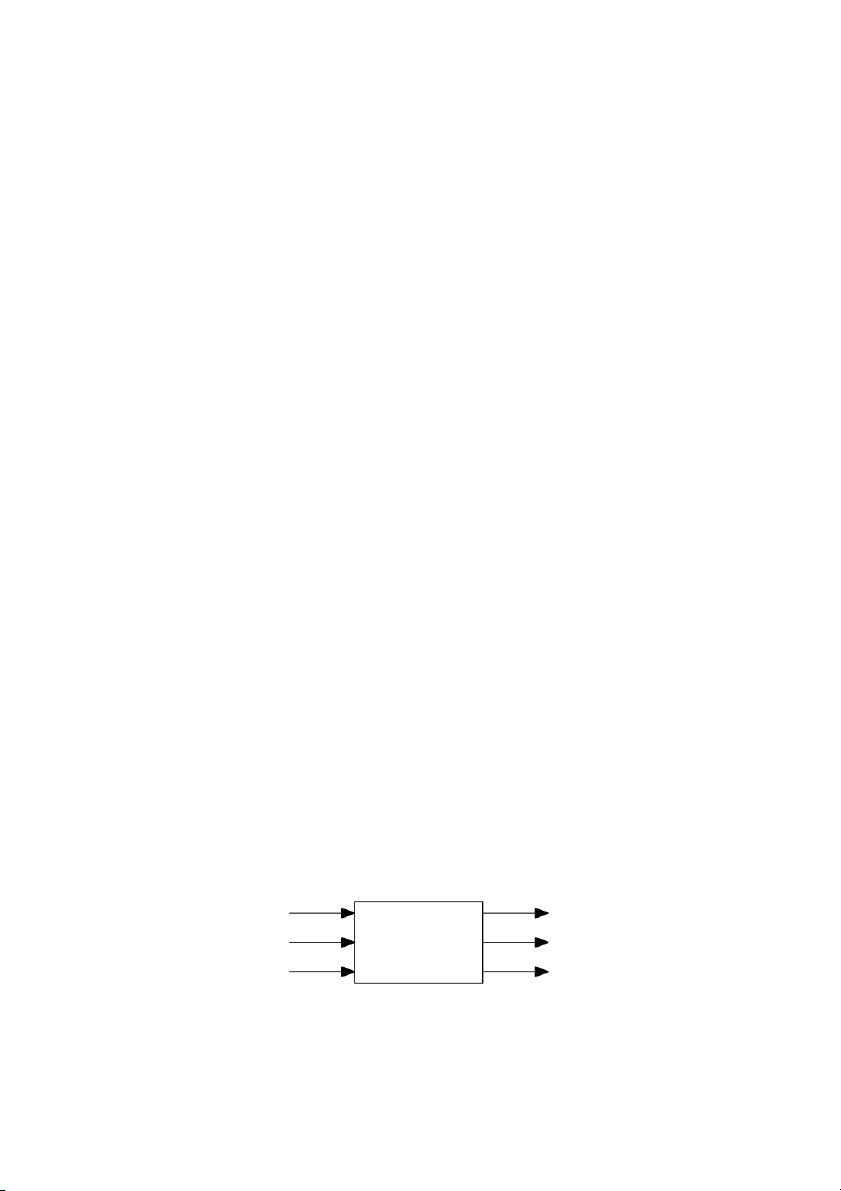
sử dụng khái niệm tác động và đáp ứng. TÝn hiÖu vµo PhÇn tö TÝn hiÖu ra (T¸c ®éng) hÖ thèng (§ ¸p øng)
Hình 1.1: Sơ đồ mô tả tín hiệu vào/ra
1.2. CÁC PHẦN TỬ CƠ BẢN CỦA HỆ THỐNG ĐIỀU KHIỂN TỰ ĐỘNG
Hệ thống điều khiển cơ bản gồm ba phần tử chủ yếu: 6
- Bộ điều khiển (Control er - C )
- Đối tượng điều khiển (Object - O )
- Thiết bị đo lường (Measurement - M)
Sơ đồ tổng quát của hệ thống điều khiển tự động có dạng như sau: r(t) e(t) x(t) y( C O z(t) M
Hình 1.2: Cấu trúc cơ bản của hệ thống điều khiển Trong đó:
r(t): Tín hiệu vào, tín hiệu chuẩn (reference input) hay giá trị đặt trước
y(t): Tín hiệu ra (output), đại lượng cần điều khiển, giá trị đặt trước e(t): Tín hiệu sai lệch
x(t): Tín hiệu điều khiển (control)
z(t): Tín hiệu phản hồi (feedback)
1.3. CÁC NGUYÊN TẮC ĐIỀU KHIỂN CƠ BẢN
Nguyên tắc điều khiển thể hiện đặc điểm lượng thông tin và phương thức
hình thành tác động điều khiển lên hệ thống. Có 3 nguyên tắc điều khiển cơ bản:
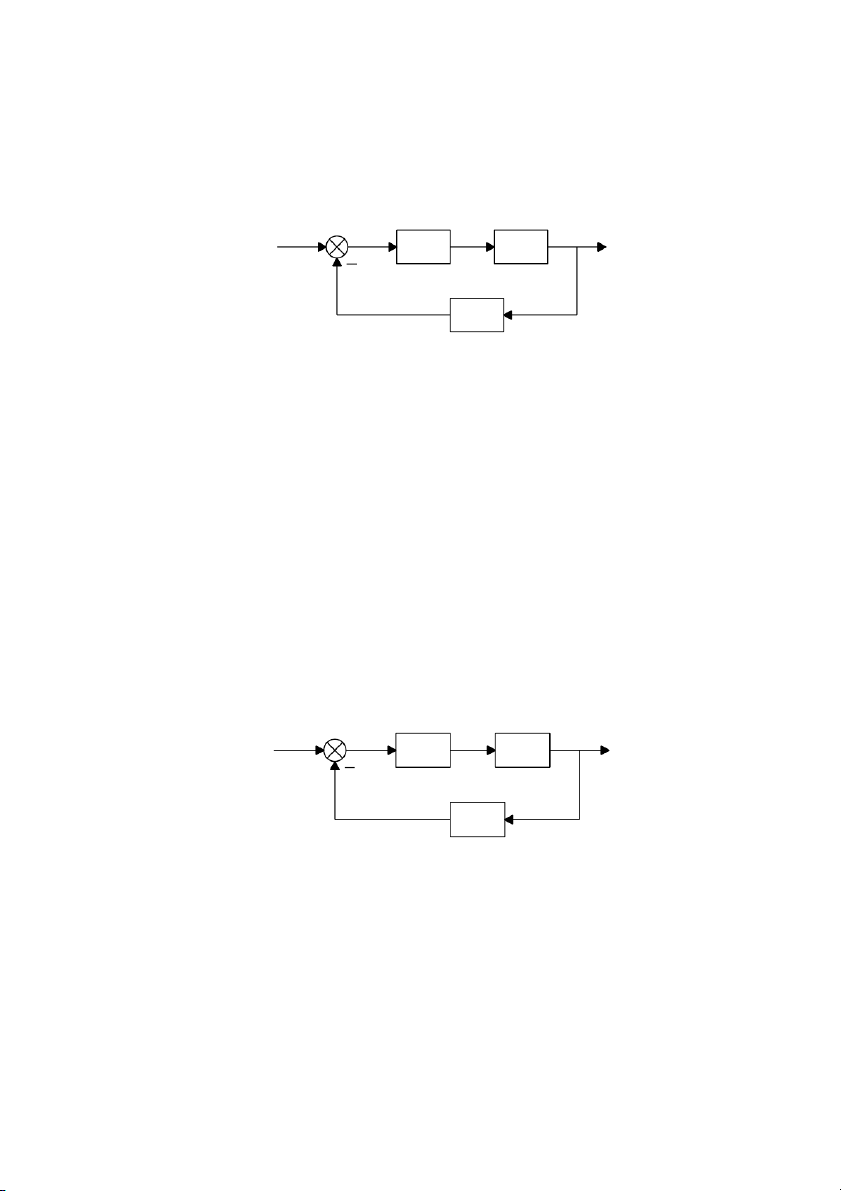
1.3.1. Nguyên tắc điều khiển theo sai lệch r(t) e(t) x(t) y(t C O z(t) M
Hình 1.3: Sơ đồ nguyên tắc điều khiển theo sai lệch
Nguyên tắc này được dùng khi các tác động bên ngoài không kiểm tra và
đo lường được còn đặc tính của đối tượng điều khiển chưa được xác định đầy đủ
Tín hiệu ra y(t) được đo và phản hồi về so sánh với tín hiệu vào r(t). Bộ
điều khiển sử dụng sai lệch vào/ra để tính toán tín hiệu điều khiển r(t) điều chỉnh
lại tín hiệu ra theo hướng làm triệt tiêu sai lệch. 7
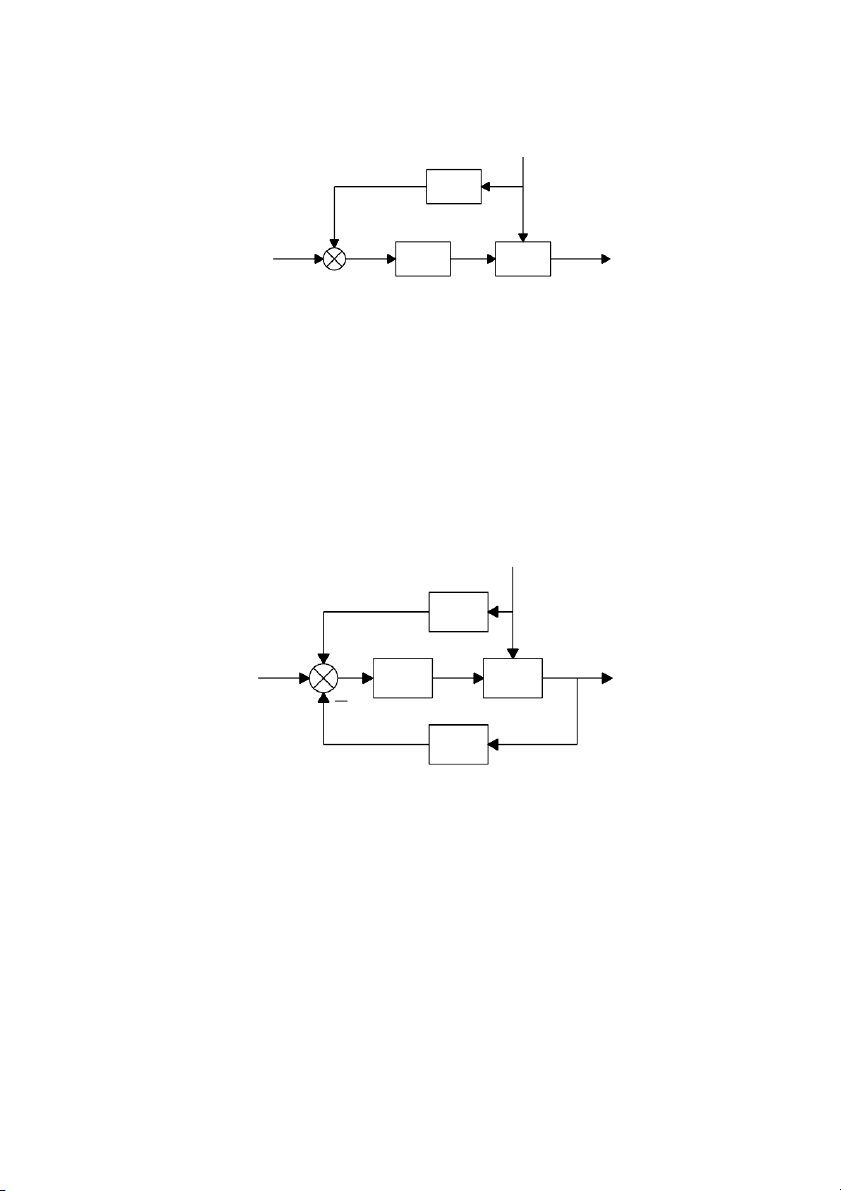
1.3.2. Nguyên tắc điều khiển bù nhiễu N(t) K r(t) e(t) x(t) y(t C O
Hình 1.4: Sơ đồ nguyên tắc điều khiển bù nhiễu
Nguyên tắc này được dùng khi các tác động bên ngoài kiểm tra và đo
lường được còn đặc tính của đối tượng điều khiển đã được xác định đầy đủ.
Nguyên tắc bù nhiễu là sử dụng thiết bị bù K để giảm ảnh hưởng của nhiễu là
nguyên nhân trực tiếp gây hậu quả cho hệ thống. Tuy nhiên trong thực tế không
thể dự đoán và kiểm tra hết mọi loại nhiễu nên với các hệ phức tạp thì điều
khiển bù nhiễu không cho chất lượng cao.
1.3.3. Điều khiển phối hợp N(t) K r(t) e(t) x(t) y(t C O z(t) M
Hình 1.5: Sơ đồ nguyên tắc điều khiển phối hợp
Để nâng cao chất lượng điều khiển, có thể kết hợp nguyên tắc điều khiển
bù nhiễu và nguyên tắc điều khiển bằng sai lệch. Mạch bù nhiễu sẽ tác động
nhanh để bù trừ sai số tạo ra bởi nhiễu đo được, còn mạch điều khiển phản hồi
sẽ hiệu chỉnh tiếp các sai số tạo ra bởi nhiễu không đo được.
1.4. PHÂN LOẠI HỆ THỐNG ĐIỀU KHIỂN TỰ ĐỘNG
1.4.1. Phân loại sơ đồ tổng quát
- Hệ thống điều khiển vòng hở: là hệ thống điều khiển mà tín hiệu điều khiển
r(t) không phụ thuộc vào tín hiệu đáp ứng đầu ra y(t) hay là hệ thống không có
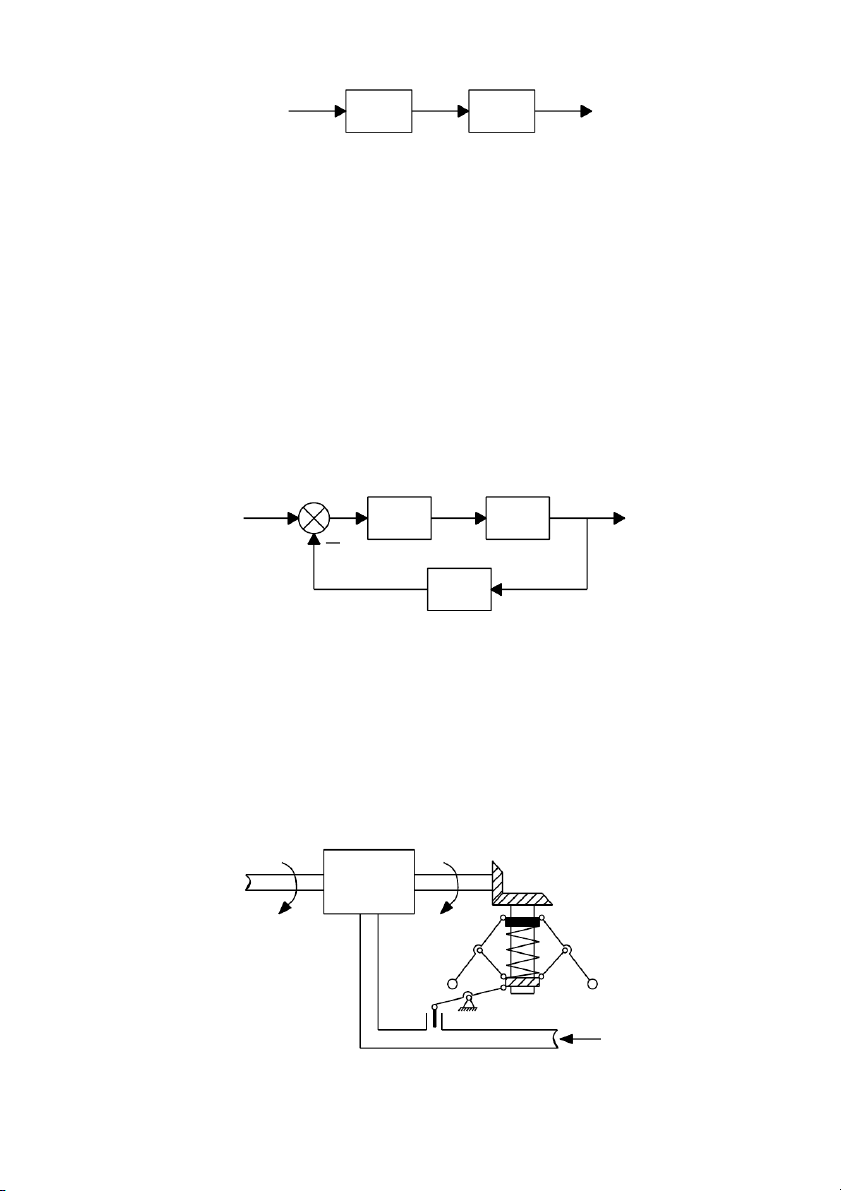
tín hiệu phản hồi từ ngõ ra về bộ điều khiển 8 r(t) x(t) y(t) C O
Hình 1.6: Hệ thống điều khiển vòng hở Thí dụ:
Xét hệ thống điều khiển máy giặt gia đình. Với các tín hiệu đặt được lập
trình sẵn trong bộ điều khiển như mức nước bơm vào, thời gian đặt, thời gian
vắt, tốc độ làm việc của động cơ trong sao cho chất lượng đầu ra là độ sạch của
quần áo. Trong quá trình giặt, thì độ sạch của quần áo là không đo được tự động
mà chất lượng của hệ thống hoàn toàn phụ thuộc vào thông số cài đặt sẵn của bộ điều khiển.
- Hệ thống điều khiển vòng kín: là hệ thống có tín hiệu phản hồi từ ngõ ra về bộ điều khiển r(t) y(t) C O M
Hình 1.7: Hệ thống điều khiển vòng kín Thí dụ:
Hệ thống điều khiển tự động tốc độ quay của tua bin nước + ĐTĐK: Cánh tua bin
+ TBĐK: Van điều chỉnh lượng hơi vào + TBĐL: cơ cấu ly tâm ù ù T¶i trôc Tua bin quay h¬i C¬ cÊu ly t©m Van H¬i vµo Hình 1.8: Sơ đồ đ ề
i u khiển tự động tốc độ ổn định của tua bin 9
1.4.2. Phân loại theo đặc điểm toán học
- Hệ liên tục: Các tín hiệu truyền trong hệ đều là hàm liên tục theo thời gian. Hệ
liên tục được mô tả bởi phương trình vi phân.
- Hệ rời rạc: Tín hiệu được mô tả ở dạng chuỗi xung không liên tục theo thời
gian. Hệ rời rạc được mô tả bởi phương trình sai phân.
- Hệ tuyến tính: Mọi phần tử của hệ đều có quan hệ vào/ra là hàm tuyến tính.
Hệ tuyến tính được mô tả bằng phương trình vi phân tuyến tính. Đặc trưng cơ
bản của hệ tuyến tính là áp dụng nguyên lý xếp chồng tức là hệ có nhiều tác
động vào đồng thời thì sẽ có đáp ứng đầu ra tương ứng do từng tác động tạo nên.
- Hệ phi tuyến: Hệ có ít nhất một phần tử có quan hệ vào/ra là hàm phi tuyến.
Các hệ thống điều khiển thực tế đều có tính phi tuyến. Ví dụ trong các bộ
khuếch đại điện, điện từ, thủy lực, khí nén luôn có sự bão hòa tín hiệu ra khi tín
hiệu vào đủ lớn; trong truyền động cơ khí, thủy lực, khí nén luôn tồn tại các
khâu khe hở, vùng không nhạy với tín hiệu vào nhỏ, các hệ thống điều khiển
ON/OFF là phi tuyến với mọi giá trị tín hiệu vào.
- Hệ bất biến theo thời gian: Các thông số của hệ không thay đổi trong suốt
thời gian hoạt động của hệ thống. Hệ bất biến được mô tả bởi phương trình vi
phân/sai phân hệ số hằng. Đáp ứng của hệ này không phụ thuộc vào thời điểm
mà tín hiệu vào được đưa vào hệ thống.
- Hệ biến đổi theo thời gian: Các thông số của hệ luôn thay đổi trong suốt thời
gian hoạt động để đáp ứng được yêu cầu của hệ thống. Phương trình mô tả hệ
biến đổi theo thời gian là phương trình vi phân/sai phân hệ số hàm. Đáp ứng của
hệ này phụ thuộc vào thời điểm mà tín hiệu vào đặt vào hệ thống.
1.4.3. Phân loại theo số lượng ngõ vào/ra.
- Hệ SISO (Single Input – Single Ouput): một ngõ vào – một ngõ ra
- Hệ MIMO (Multi Input – Multi Output): nhiều ngõ vào – nhiều ngõ ra
Trong khuôn khổ của chương trình môn học, tài liệu này chỉ tập trung đề
cập đến các vấn đề của hệ thống điều khiển tuyến tính, bất biến một ngõ vào – một ngõ ra. 10
1.5. LỊCH SỬ PHÁT TRIỂN LÝ THUYẾT ĐIỀU KHIỂN TỰ ĐỘNG
1.5.1. Điều khiển kinh điển (classical control)
Lý thuyết điều khiển kinh điển (trước 1960) mô tả hệ thống trong miền
tần số (phép biến đổi Fourier) và mặt phẳng s (phép biến đổi Laplace). Dựa trên
các phép biến đổi này, lý thuyết điều khiển kinh điển chủ yếu áp dụng cho hệ
tuyến tính bất biến theo thời gian, mặc dù có một vài mở rộng để áp dụng cho hệ
phi tuyến. Lý thuyết điều khiển kinh điển thích hợp để thiết kế hệ thống một ngõ
vào - một ngõ ra (SISO: Single Input/Single Input), rất khó áp dụng cho các hệ
thống có nhiều ngõ vào - nhiều ngõ ra (MIMO: Multi Input/Multi Output) và các
hệ thống biến đổi theo thời gian. Các phương pháp phân tích và thiết kế hệ thống
trong lý thuyết điều khiển kinh điển gồm có phương pháp Nyquist, giản đồ
Bode, phương pháp quỹ đạo nghiệm số.
Các khâu hiệu chỉnh đơn giản như hiệu chỉnh vi tích phân tỷ lệ PID
(Proportional Integrater Derivative), hiệu chỉnh sớm trễ pha,... thường được sử
dụng trong các hệ thống điều khiển kinh điển. Ảnh hưởng của các khâu hiệu
chỉnh này đến biểu đồ Bode, biểu đồ Nyquist và quỹ đạo nghiệm số có thể thấy
được dễ dàng nhờ đó dễ dàng lựa chọn các khâu hiệu chỉnh thích hợp.
1.5.2. Điều khiển hiện đại (modern control)
Kỹ thuật thiết kế hệ thống điều khiển hiện đại dựa trên miền thời gian. Mô
tả toán học dùng để phân tích và thiết kế hệ thống là phương trình trạng thái. Mô
hình không gian trạng thái có ưu điểm là mô tả được đặc tính động học bên
trong hệ thống (các biến trạng thái) và có thể dễ dàng áp dụng cho hệ MIMO và
hệ thống biến đổi theo thời gian. Lý thuyết điều khiển hiện đại ban đầu được
phát triển chủ yếu cho hệ tuyến tính sau đó được mở rộng cho hệ phi tuyến bằng
cách sử dụng lý thuyết của Lyapunov.
Bộ điều khiển được sử dụng chủ yếu trong thiết kế hệ thống điều khiển
hiện đại là bộ điều khiển phản hồi trạng thái. Tùy theo cách tính véctơr phản hồi
trạng thái mà có phương pháp phân bố cực, điều khiển tối ưu, điều khiển bền vững ... 11
Với sự phát triển của lý thuyết điều khiển số và hệ thống rời rạc, lý thuyết
điều khiển hiện đại rất thích hợp để thiết kế các bộ điều khiển chạy trên nền vi
xử lý và máy tính số. Điều này cho phép thực thi được các bộ điều khiển có đặc
tính động phức tạp hơn cũng như hiệu quả hơn so với các bộ điều khiển đơn
giản như PID hay sớm trễ pha trong lý thuyết kinh điển
1.5.3. Điều khiển thông minh (intelligent control)
Điều khiển kinh điển và điều khiển hiện đại gọi chung là điểu khiển thông
thường (conventional control) có khuyết điểm là để thiết kế được hệ thống điều
khiển cần phải biết mô hình toán học của đối tượng. Trong khi thực tế có những
đối tượng điều khiển rất phức tạp, rất khó hoặc không thể các định được mô
hình toán. Các phương pháp điều khiển thông minh như điều khiển mờ, mạng
thần kinh nhân tạo, thuật toán di truyền mô phỏng/ bắt chước các hệ thống thông
minh sinh học, về nguyên tắc không cần dùng mô hình toán học để thiết kế hệ
thống do đó có khả năng ứng dụng thực tế rất lớn. Khuyết điểm của điều khiển
mờ là quá trình thiết kế mang tính thử sai, dựa vào kinh nghiệm của chuyên gia.
Nhờ kết hợp logic mờ với mạng thần kinh nhân tạo hay thuật toán di truyền mà
thông số bộ điều khiển mờ có thể thay đổi thông qua quá trình học hay quá trình
tiến hóa, vì vậy khắc phục được khuyết điểm thử sai. Hiện nay các bộ điều khiển
thông thường kết hợp với các kỹ thuật điều khiển thông minh tạo nên các bộ
điều khiển lai điều khiển các hệ thống phức tạp với chất lượng rất tốt.
1.6. NHIỆM VỤ CƠ BẢN CỦA HỆ THỐNG ĐIỀU KHIỂN
Nhiệm vụ cơ bản của lý thuyết điều khiển tự động là khảo sát các đặc tính
tĩnh (ở chế độ xác lập) và đặc tính động của các hệ tự động nhằm thiết kế hệ
thống điều khiển thỏa mãn các yêu cầu cho trước
Lý thuyết điều khiển tự động nhằm giải quyết hai bài toán cơ bản:
- Phân tích hệ thống: nhằm tìm hiểu sự hoạt động của hệ thống, khảo sát các
đặc tính sẵn có của hệ, từ đó đánh giá hệ thống theo các chỉ tiêu đặt ra: sự ổn
định của hệ thống, sai số xác lập, độ quá điều chỉnh nhỏ…
- Thiết kế hệ thống: Cấu trúc và thông số của đối tượng điều khiển đã biết. Yêu
cầu thiết kế bộ điều khiển để hệ thống thỏa mãn các yêu cầu chất lượng đầu ra 12
Các bước thiết kế bao gồm:
- Xuất phát từ mục tiêu điều khiển, yêu cầu về chất lượng điều khiển và đặc
điểm của đối tượng điều khiển, xây dựng mô hình toán học của đối tượng
- Từ mô hình, mục tiêu điều khiển, yêu cầu chất lượng điều khiển lựa chọn
nguyên tắc điều khiển cụ thể. Khi đó lựa chọn thiết bị cụ thể để thực hiện nguyên tắc đề ra.
- Trên cơ sở nguyên lý điều khiển và thiết bị được chọn, kiểm tra tính hiệu quả
điều khiển trên các phương diện: khả năng đáp ứng mục tiêu, chất lượng, giá
thành, điều kiện sử dụng. Từ đó hiệu chỉnh phương án chọn thiết bị, chọn
nguyên tắc điều khiển và hoàn thiện mô hình
- Khi phương án đã chọn đạt yêu cầu tiến hành chế tạo, lắp ráp thiết bị từng
phần và hiệu chỉnh các sai sót hoàn thành toàn bộ hệ thống điều khiển. 13 BÀI TẬP CHƯƠNG 1
Bài 1. Trình bày các khái niệm cơ bản của hệ thống điều khiển tự động
Bài 2. Hệ thống điều khiển tự động có thể phân loại như thế nào?
Bài 3. Hệ thống điều khiển có mấy phần tử cơ bản?
Bài 4. Nêu các quy tắc điều khiển cơ bản để điều khiển một hệ thống điều khiển?
Bài 5. Nêu các bước thiết lập một hệ thống điều khiển? 14
CHƯƠNG 2: MÔ TẢ TOÁN HỌC HỆ THỐNG ĐIỀU KHIỂN TỰ ĐỘNG
Thiết kế bộ điều khiển cho một hệ thống điều khiển tự động là tìm cách
tác động vào hệ thống để hệ thống làm việc theo mong muốn. Ta không thể can
thiệp vào hệ thống khi mà không có những hiểu biết cần thiết về hệ thống đó.
Do đó, công việc đầu tiên khi thiết kế hệ thống là phải tìm cách mô tả hệ thống
hay xây dựng mô hình hệ thống
Mô tả hệ thống là sử dụng những hiểu biết của mình đề biểu diễn các đại
lượng vật lý về hệ thống một cách khoa học nhằm phục vụ cho mục đích mô
phỏng, phân tích và tổng hợp bộ điều khiển cho hệ thống. Việc xây dựng mô
hình cho hệ thống được gọi là mô hình hóa. Phương pháp mô hình hóa thường
được chia làm hai loại: - Phương pháp lý thuyết
- Phương pháp thực nghiệm
* Phương pháp lý thuyết: là phương pháp xây dựng mô hình dựa trên các định
luật có sẵn về quan hệ vật lý bên trong và quan hệ giao tiếp với môi trường bên
ngoài của hệ thống. Có ba phương pháp cơ bản thường được dùng để mô tả hệ thống điều khiển: - Phương trình vi phân - Hàm truyền
- Mô hình không gian trạng thái
* Phương pháp thực nghiệm: là phương pháp được sử dụng khi những hiểu
biết về đối tượng điều khiển không được đầy đủ để có thể xây dựng cho hệ
thống một cách hoàn chỉnh. Về cơ bản, phải được cung cấp đầy đủ lượng thông
tin ban đầu về dạng mô hình, khoanh vùng lớp các mô hình thích hợp cho hệ thống v
à áp dụng các phương pháp thực nghiệm để hoàn tất công việc. Việc xây
dựng mô hình hệ thống bằng cách tìm một mô hình trong lớp mô hình thích hợp
trên cơ sở quan sát các tín hiệu vào - ra sao cho sai lệch là bé nhất.
Trong cuốn sách này, tác giả sẽ giới thiệu chi tiết các phương pháp
thường được dùng trong hệ thống điều khiển là phương trình vi phân, hàm
truyền, phương pháp không gian trạng thái 15
2.1. MÔ HÌNH PHƯƠNG TRÌNH VI PHÂN.
Tổng quát, mối quan hệ giữa tín hiệu vào r(t) và tín hiệu ra y(t) của hệ
thống điều khiển tuyến tính bất biến liên tục có thể mô tả bởi phương trình vi phân: n n 1 m m 1 d y(t) d y(t) d r(t) d r(t) a  a  ... a y(t) b  b  ... b r( (2-1) n n n 1 n 1 0 m m m  1 m 1 0 dt dt dt dt i j n m d y d Hay: a   b  i i j j  dt  dt i 0 j 0
Trong đó: ai, bj là các hằng số được xác định từ thông số các phần tử
Số mũ m, n là bậc của hệ thống. Hệ thống có m ≤ n gọi là hệ thống hợp thức
Mô hình phương trình vi phân được xây dựng theo phương pháp lý
thuyết, tức là được thiết lập dựa trên các định luật vật lý biểu diễn các quá trình
động học xảy ra bên trong và các quan hệ giao tiếp với môi trường bên ngoài của hệ thống.
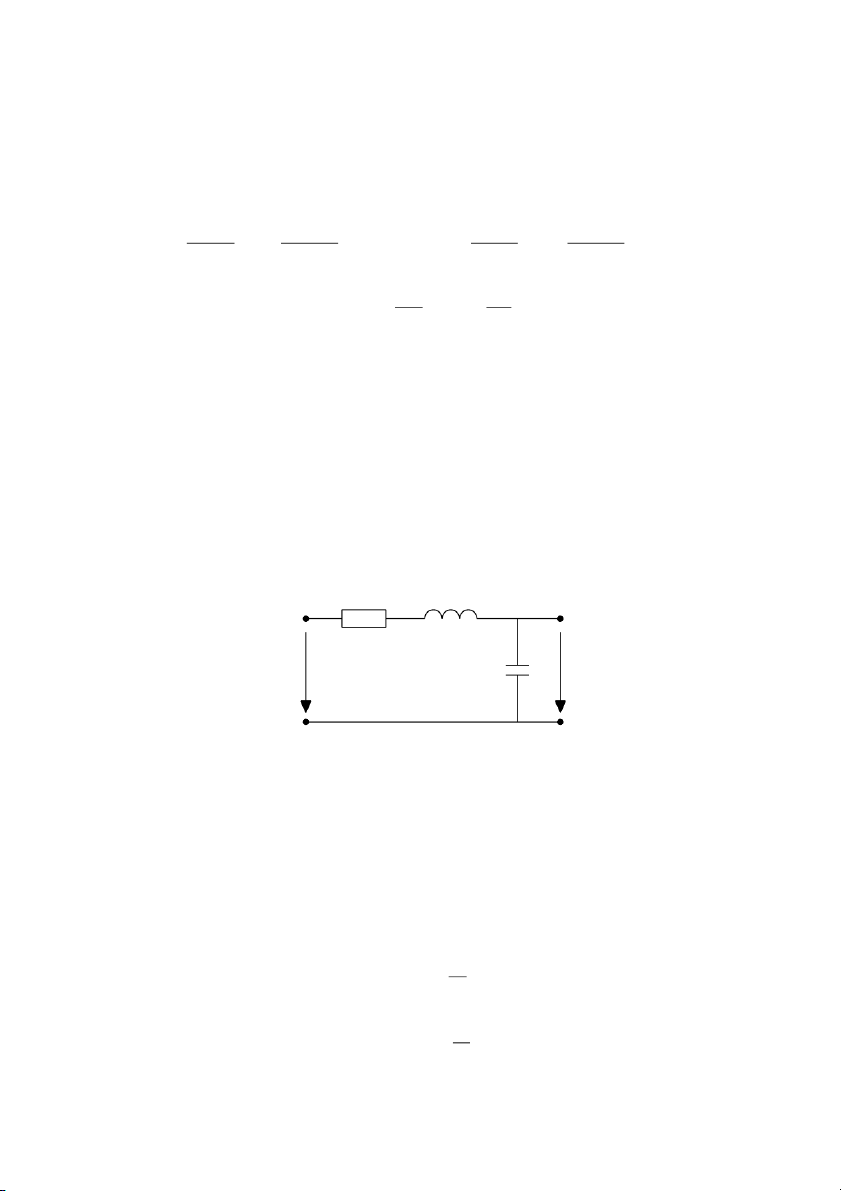
Ví dụ 2.1: Xác định phương trình vi phân của mạch R-L-C m ắc nối tiếp R L u C ur
Hình 2.1: Mạch điện R - L - C
- Tín hiệu vào: điện áp ngõ vào u [Volt]
- Tín hiệu ra: điện áp ngõ ra ur [Volt] chính là điện áp trên hai bản cực của tụ điện.
Theo định luật Kirchoff ta có u(t) u  (t)  u (t)  u (t) R L C di hay u(t)  R.i L u  (t) (2-2) r dt 1 m à u  u  idt r C C  16 du suy ra r i  C dt (2-3)
Thay giá trị (2-3) vào phương trình (2-2) thu được phương trình vi phân
bậc nhất mô tả quan hệ vào – ra : 2 d u du r r u  LC  RC  u (2-4) 2 r dt dt
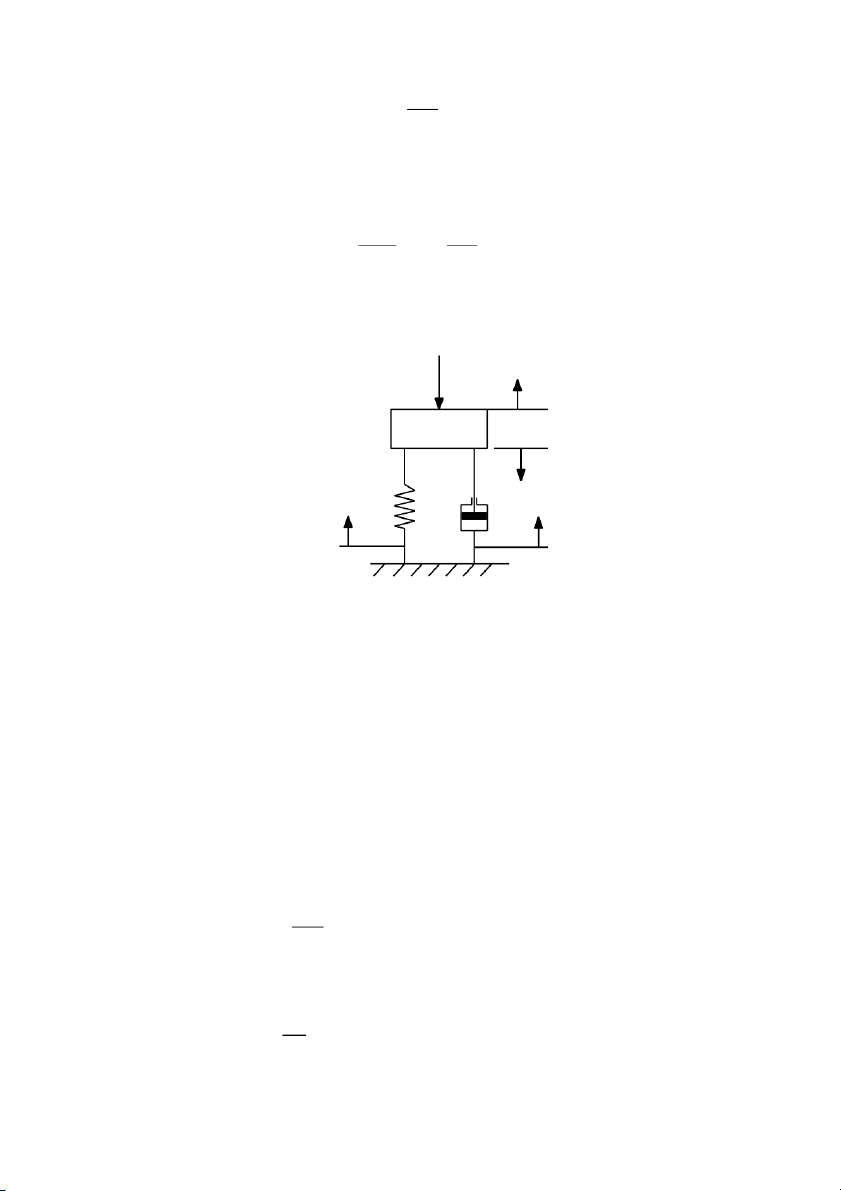
Ví dụ 2.2: Xác định phương trình vi phân mô tả thiết bị giảm chấn ô tô gồm lò
xo - khối lượng - giảm chấn có dạng như sau: F(t) FM M y(t) K FK B FB
Hình 2.2: Mô hình bộ giảm chấn
Trong đó: M: Khối lượng tác động lên bánh xe [kg]
B: Hệ số ma sát nhớt [N.s/m]
K: Độ cứng của lò xo [N/m]
F(t): Áp lực do xóc; tín hiệu vào [N]
y(t): Dịch chuyển của thân xe; tín hiệu ra [m]
Xây dựng phương trình vi phân mô tả quan hệ giữa tín hiệu đầu vào là lực
F(t) ép lên bộ giảm chấn và tín hiệu ra y(t) là độ lún của giảm chấn.
Trên cơ sở sơ đồ nguyên lý ta có các lực cản độ lún y(t) của bộ giảm chấn 2 d y F  M M
(tiên đề về lực của Newton) 2 dt
F  Ky(t) (lực cản của lò xo) K dy F  B B
dt (lực cản của bộ giảm tốc) F F 
F  F(t) (Định luật hai của Newton) M K B 17
Phương trình vi phân bậc hai mô tả quan hệ vào - ra của bộ giảm chấn: 2 d y dy M B Ky(t)  F(t) 2 dt dt
2.2. PHÉP ĐỔI BIẾN LAPLACE
- Phép đổi biến: là quá trình biến đổi tín hiệu hệ thống từ miền thời gian sang
miền khác để thuận tiện trong việc xử lý tín hiệu.
Trong hệ thống điều khiển liên tục người ta sử dụng phép biến đổi
Laplace để biến đổi từ miền thời gian sang miền tần số phức. Các phương trình
vi tích phân sẽ được chuyển đổi thành phương trình đại số thông thường
2.2.1. Biến đổi Laplace thuận
2.2.1.1. Định nghĩa
Cho hàm f(t) xác định với t ≥ 0, biến đổi Laplace của hàm f(t) là  st F(s) L [f(t)]= f (t)e dt  (2-2) o Trong đó:
s là biến phức gọi là biến Laplace với s = α + jβ
f(t) là hàm biểu diễn trên miền thời gian xác định trên R
F(s) là ảnh Laplace hay biến đổi Laplace của hàm f(t).
L là ký hiệu phép biến đổi Laplace.
Điều kiện để hàm f(t) có biến đổi Laplace là tích phân ở công thức định nghĩa (2-2) hội tụ.
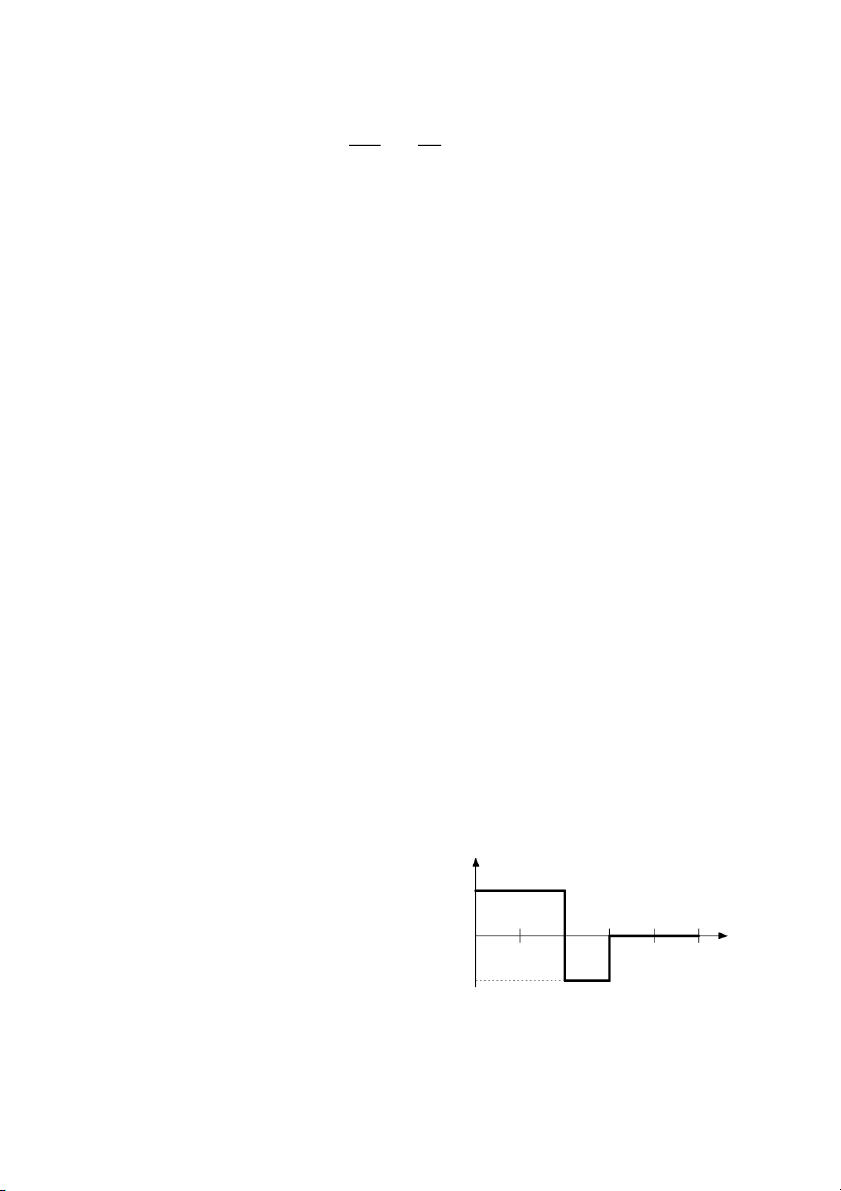
Ví dụ 2.3: Tìm ảnh của hàm gốc sau f(t) 1 khi 0  t  2  f (t)   1 khi 2  t 3 1 0  khi t 3 0 t  1 2 3 4 5 -1
Tìm biến đổi Laplace trên?
Áp dụng công thức biến đổi ta có 18  2 3 s  t st  st
F(s) L [f(t)]= f (t)e dt f (t)e dt f (t)e    o o 2 1 1 1 s  t 2  st 3 e e   2s 1 2e e        3s 0 2 s s s
Ví dụ 2.4: Tìm ảnh của hàm gốc sau f(t) khi 1 t  0 f (t)    0 khi 1 t  0  t 0
Tìm biến đổi Laplace trên?  s  t e 1 s  t F(s)= f (t)e dt      0 s s o 2
Ví du 2.5: Tìm ảnh Laplace của hàm f(t) = 4t
Từ bảng biến đổi Laplace ta có L  n! n t   n 1 s  2
Áp dụng biến đổi tìm ảnh Laplace của hàm f(t) = 4t L 4t  2! 8 2  4  2 1 3 s s 2.2.1.2. Tính chất
a. Tính chất tuyến tính
Nếu F(s), F1(s), F2(s) là ảnh Laplace của f(t), f1(t), f2(t) và K là hệ số hằng thì:
L [f (t) ± f (t)] = L [f (t)] ± L [f (t)] = F (s) ± F (s) (2-3) 1 2 1 2 1 2
L [a.f(t)]= a.L [f(t)] = a.F(s). (2-4)
b. Tính chất trễ
Nếu f(t) có ảnh là F(s), a là một số thực và f(t-a) =0 khi 0 < t < a thì: -as L [f(t- a)] = e F s ( ) ( 2-5)
c. Tính chất tích phân thực 19
Nếu F(s) là ảnh của f(t) thì : t   F(s) L f (t)dt    ( - 2 6) s 0 
d. Tính chất vi phân thực
Nếu f(t) có ảnh là F(s) thì : df (t)        s  t L  L f (t)  f (t).e d  dt         0  f st (t)e    s f (t)dt sF(s)  f (  (2-7) 0 0
Trong đó: f(0) là giá trị của hàm tại thời điểm t = 0
Từ kết quả trên, suy ra ảnh các đạo hàm bậc cao có dạng như sau:         2 L f (t)  sL f (t) f (0)  s F(s  ) sf ( 0) f              3 2
L f (t)  s F(s) s F(0) sf (0  ) f    
…….................................................. n n   n n k k 1 L f (t)  s F(s) s f (0      k 1
Nếu điều kiện đầu bằng 0 thì công thức được xác định như sau: n   n L f (t)  s F(s   (2-8)  
e. Tính chất giá trị cuối
Nếu biến đổi Laplace của f(t) là F(s) và nếu giới hạn f(t) tồn tại khi t → ∞ khi đó:
limsF(s) limf (t) f ( (2-9) s 0 t 0
f. Tính chất giá trị cuối
Nếu tồn tại limf (t)thì: f (0) limf (t) limsF(s (2-10) t 0  t 0 s 0 20