









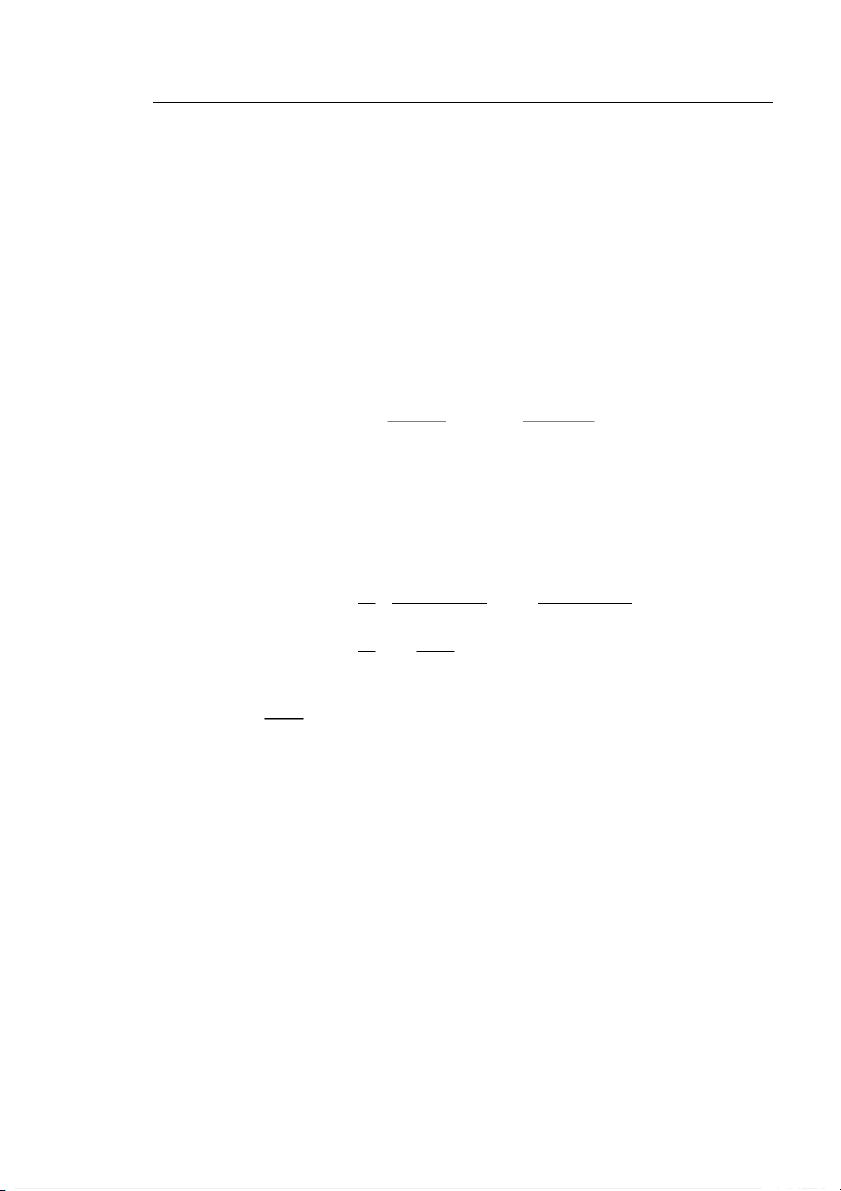























































































Preview text:
Mục lục
1 Phương trình vi phân thường cấp I 3 1.1
Mở đầu . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3 1.1.1
Vài mô hình đơn giản. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3 1.1.2
Các khái niệm. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 4 1.1.3
Ý nghĩa hình học của phương trình vi phân: . . . . . . . . . . . . . . 5 1.2
Định lý tồn tại và duy nhất nghiệm . . . . . . . . . . . . . . . . . . . . . . . . . . 7 1.2.1
Bài toán Cauchy . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 7 1.2.2
Phương pháp xấp xỉ Picard . . . . . . . . . . . . . . . . . . . . . . . . . . . 7 1.2.3
Sự tồn tại và duy nhất nghiệm . . . . . . . . . . . . . . . . . . . . . . . . 8 1.2.4
Phân loại nghiệm của phương trình vi phân . . . . . . . . . . . . . . 11 1.3
Phương pháp giải một số phương trình vi phân cấp I . . . . . . . . . . . . 12 1.3.1
Phương trình với biến số phân ly: . . . . . . . . . . . . . . . . . . . . . . 12 1.3.2
Phương trình vi phân thuần nhất: . . . . . . . . . . . . . . . . . . . . . . 14 1.3.3
Phương trình vi phân toàn phần: . . . . . . . . . . . . . . . . . . . . . . 16 1.3.4
Phương trình vi phân tuyến tính cấp I: . . . . . . . . . . . . . . . . . . 18 1.3.5
Phương trình Bernoully . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 20 1.3.6
Phương trình Darboux . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 21 1.3.7
Phương trình Riccati: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 22
1.4 Phương trình vi phân cấp I chưa giải ra đối với đạo hàm . . . . . . . . . . 23
1.4.1 Tích phân một số phương trình vi phân cấp I . . . . . . . . . . . . . 23 1.5
Phương trình Clairaut và phương trình Lagrange . . . . . . . . . . . . . . . 26
1.5.1 Phương trình Clairaut . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 26
1.5.2 Phương trình Lagrange . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 27 1.5.3
Tham số hoá tổng quát: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 28 1.6
Nghiệm kỳ dị của phương trình vi phân cấp I . . . . . . . . . . . . . . . . . . 29 1.6.1
Sự tồn tại nghiệm kỳ dị . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 29 1.6.2
Tìm nghiệm kỳ dị theo p−biệt tuyến . . . . . . . . . . . . . . . . . . . 30 1.6.3
Tìm nghiệm kỳ dị theo C −biệt tuyến . . . . . . . . . . . . . . . . . . . 31 ii MỤC LỤC
2 Phương trình vi phân cấp cao 35 2.1
Phương trình vi phân cấp cao . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 35 2.1.1
Các khái niệm: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 35 2.1.2
Sự tồn tại và duy nhất nghiệm: . . . . . . . . . . . . . . . . . . . . . . . . 36 2.1.3
Một số phương trình vi phân cấp cao giải được bằng cầu phương: 37 2.1.4
Một số phương trình vi phân cấp cao có thể hạ cấp: . . . . . . . . 39 2.1.5
Tích phân trung gian và tích phân đầu: . . . . . . . . . . . . . . . . . 42
2.2 Lý thuyết tổng quát về phương trình vi phân tuyến tính cấp cao. . . . . 43 2.2.1
Các khái niệm . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 43 2.2.2
Nghiệm tổng quát của phương trình thuần nhất . . . . . . . . . . . 44 2.2.3
Nghiệm của phương trình vi phân tuyến tính không thuần nhất 49
2.2.4 Phương pháp biến thiên hằng số tìm nghiệm riêng của phương
trình không thuần nhất . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 50
2.3 Phương trình vi phân tuyến tính cấp cao hệ số hằng . . . . . . . . . . . . . . 52 2.3.1
Nghiệm của phương trình thuần nhất hệ số hằng . . . . . . . . . . 53 2.3.2
Tìm nghiệm riêng của phương trình không thuần nhất: . . . . . 55
3 Hệ phương trình vi phân 59 3.1
Hệ phương trình vi phân cấp I tổng quát. . . . . . . . . . . . . . . . . . . . . . 59 3.1.1
Các định nghĩa: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 59 3.1.2
Liên hệ giữa hệ phương trình và phương trình vi phân cấp cao. 60 3.1.3
Sự tồn tại và duy nhất nghiệm . . . . . . . . . . . . . . . . . . . . . . . . 61 3.1.4
Các phương pháp giải hệ phương trình vi phân: . . . . . . . . . . . 62
3.2 Một số định lý cơ bản của phương trình vi phân . . . . . . . . . . . . . . . . 64 3.2.1
Sự tồn tại nghiệm: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 64 3.2.2
Thác triển nghiệm và sự tồn tại toàn cục: . . . . . . . . . . . . . . . . 66
3.3 Hệ phương trình vi phân tuyến tính . . . . . . . . . . . . . . . . . . . . . . . . . 67 3.3.1
Hệ tuyến tính thuần nhất: . . . . . . . . . . . . . . . . . . . . . . . . . . . . 68 3.3.2
Hệ tuyến tính không thuần nhất: . . . . . . . . . . . . . . . . . . . . . . 72
3.4 Hệ phương trình vi phân tuyến tính hệ số hằng. . . . . . . . . . . . . . . . . 73 3.4.1
Phương trình đặc trưng . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 74 3.4.2
Hệ nghiệm cơ bản . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 74
3.5 Sự ổn định nghiệm của hệ phương trình vi phân . . . . . . . . . . . . . . . . 78
3.5.1 Bài toán ổn định nghiệm . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 78
3.5.2 Ổn định hệ tuyến tính . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 80
3.5.3 Ổn định theo xấp xỉ thứ nhất . . . . . . . . . . . . . . . . . . . . . . . . . . 81
3.5.4 Ổn định theo phương pháp Liapunov thứ hai . . . . . . . . . . . . . 81 MỤC LỤC 1
4 Nhập môn lý thuyết định tính phương trình vi phân 85 4.1
Các định lý tồn tại nghiệm . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 85 4.1.1
Định lý tồn tại nghiệm Peano . . . . . . . . . . . . . . . . . . . . . . . . . 85 4.1.2
Thác triển nghiệm và sự tồn tại toàn cục: . . . . . . . . . . . . . . . . 87
4.2 Sự ổn định nghiệm . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 88
4.2.1 Bài toán ổn định nghiệm . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 88
4.2.2 Ổn định hệ tuyến tính . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 91
4.2.3 Ổn định theo xấp xỉ thứ nhất . . . . . . . . . . . . . . . . . . . . . . . . . . 92
4.2.4 Ổn định theo phương pháp trực tiếp Liapunov đối với hệ au-
tonomous . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 93
Tài liệu tham khảo . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 97 2 MỤC LỤC Chương 1
Phương trình vi phân thường cấp I 1.1 Mở đầu
Trong rất nhiều lĩnh vực ứng dụng, chuyển động của một hệ được mô hình hoá bởi
các phương trình vi phân, tức là phương trình có chứa các đạo hàm của ẩn hàm cần
tìm. Chẳng hạn, trong cơ học cổ điển (định luật Newton), trong thiên văn học (sự
chuyển động của các hành tinh), trong hoá học (các phản ứng hoá học), trong sinh
học (sự phát triển của dân số), trong điện tử. . Trong hầu hết các lĩnh vực như thế,
bài toán chung nhất là mô tả nghiệm của các phương trình này (cả về định tính lẫn về định lượng).
1.1.1 Vài mô hình đơn giản.
Sự rơi tự do. Xét một vật có khối lượng m được thả rơi tự do trong khí quyển gần
mặt đất. Theo định luật II Newton, chuyển động của vật đó có thể mô tả bởi phương trình F = m a (1.1)
trong đó F là hợp lực tác động lên vật và a là gia tốc chuyển động. Hợp lực F có
thể giả thiết chỉ bao gồm lực hấp dẫn (tỷ lệ với khối lượng của vật và hướng xuống)
và lực cản (tỷ lệ với vận tốc chuyển động và hướng lên trên). Ngoài ra, do gia tốc
chuyển động a = dv nên (1.1) có thể viết dưới dạng d t d v m = m g − γv (1.2) d t
trong đó g ≈ 9,8m/s2 là gia tốc trọng trường, còn γ là hệ số cản.
Vậy vận tốc v của vật rơi tự do thỏa mãn phương trình (1.2) với sự xuất hiện của
đạo hàm của v . Những phương trình như vậy ta sẽ gọi là phương trình vi phân.
Dung dịch hóa học. Giả sử tại thời điểm ban đầu t = t kg
0 một thùng chứa x0
muối hòa tan trong 1000 lít nước. Ta cho chảy vào thùng một loại nước muối nồng
độ a (kg/lít) với lưu lượng r (lít/phút) và khấy đều. Đồng thời, cho hỗn hợp đó chảy 4
Phương trình vi phân thường cấp I
ra khỏi thùng cũng với tốc độ như trên. Gọi x = x (t ) là lượng muối trong thùng
tại thời điểm bất kỳ. Rõ ràng tỉ lệ thay đổi lượng muối trong thùng dx bằng hiệu d t
của tỉ lệ muối chảy vào a r (kg/phút) trừ đi tỉ lệ muối chảy ra tại thời điểm đang xét
r x (kg/phút). Vậy ta có phương trình vi phân 1000 d x r x = a r − (1.3) d t 1000 với dữ kiện ban đầu
x (t0) = x0 1.1.2 Các khái niệm.
Phương trình vi phân là phương trình có dạng
F (x , y , y 0, y 00, . . . , y (n)) = 0 (1.4)
trong đó y = y (x ) là ẩn hàm cần tìm và nhất thiết phải có sự tham gia của đạo hàm
(đến cấp nào đó) của ẩn.
Trong trường hợp ẩn hàm cần tìm là hàm nhiều biến (xuất hiện các đạo hàm riêng)
thì phương trình vi phân còn gọi là phương trình đạo hàm riêng. Để phân biệt, người
ta thường gọi phương trình với ẩn hàm là hàm một biến là phương trình vi phân
thường và là đối tượng chính của giáo trình này.
Thông thường ta xét các phương trình với ẩn hàm là hàm số một biến thực y = y (x )
xác định trên khoảng mở I ⊂ R; khi đó hàm F trong đẳng thức trên xác định trong
một tập mở G của R × Rn+1. Trong truờng hợp ẩn hàm cần tìm là vector-hàm (hàm
với giá trị vector) y (x ) = (y1(x),..., y (
m x ))T ∈ Rm , F là một ánh xạ nhận giá trị trong
Rm và (1.4) được hiểu là hệ phương trình vi phân.
Ta nói một phương trình vi phân có cấp n nếu n là cấp lớn nhất của đạo hàm của
ẩn xuất hiện trong phương trình.
Phương trình vi phân thường cấp I có dạng tổng quát
F (x , y , y 0) = 0 (1.5)
trong đó F (x , y,z) được giả thiết liên tục cùng với các đạo hàm riêng của nó trên
miền G ⊂ R3. Với một số giả thiết thích hợp (xem định lý hàm ẩn), phương trình vi
phân cấp I có thể viết được dưới dạng sau (gọi là dạng giải ra được đối với đạo hàm)
y 0 = f (x , y ) (1.6)
với f liên tục trong một miền D ⊂ R2.
Ví dụ: Các phương trình
e y + y 02 cos x = 1
y 0002 − 2x y = ln x ∂ 2u ∂ 2u + = 0 ∂ x 2 ∂ y 2 1.1 Mở đầu 5
lần lượt là phương trình vi phân thường cấp I, cấp III và phương trình đạo hàm riêng cấp II.
Xét phương trình (1.4), hàm giá trị vector ϕ : I → Rn (với I = (a,b ) là khoảng nào
đó của R) là nghiệm của phương trình (1.4) nếu nó có các đạo hàm liên tục đến cấp
m trên I và thoả mãn
F (x , ϕ(x ), ϕ0(x ), ϕ00(x ), . . . , ϕ(m))(x ) = 0,
với mọi x ∈ I (1.7)
Trong trường hợp phương trình vi phân cấp I, nghiệm là một hàm thực một biến
y = ϕ(x ) mà khi thay vào (1.5) hoặc (1.6), ta được một đẳng thức đúng.
Ví dụ: Dễ kiểm tra rằng họ hàm (phụ thuộc vào hai tham số tuỳ ý)
y = C1 cos x + C2 sin x
là nghiệm của phương trình vi phân y 00 + y = 0 z X 3 2 1 1 2 3 4 y
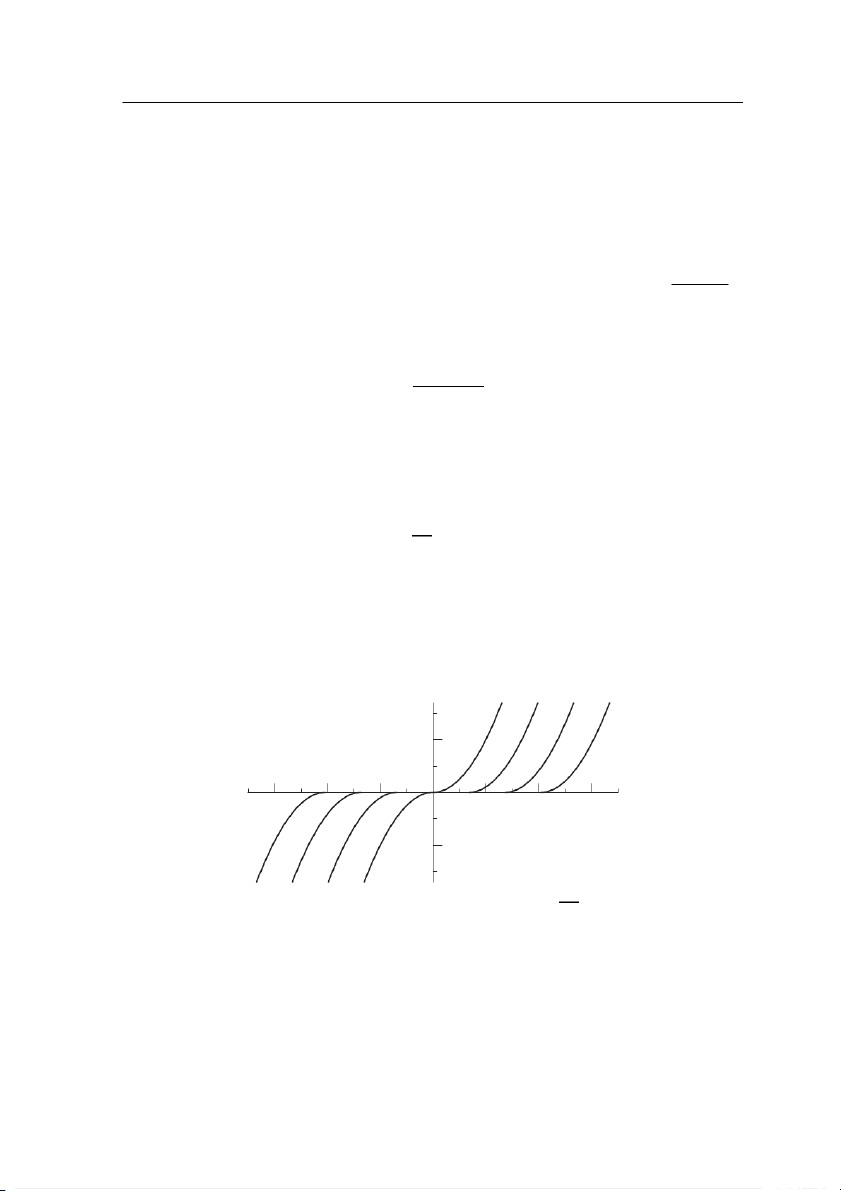
Hình 1.1: Nghiệm của phương trình Volterra-Lotka.
Ví dụ: (Săn mồi và mồi) Sự phát triển của hai quần thể sinh vật (chẳng hạn, x = x(t )
là số con mèo và y = y (t ) là số con chuột) theo thời gian được mô tả bởi (hệ) phương
trình Volterra−Lotka sau đây
y 0 = y (α − β x ),
x 0 = x (γy − δ) (1.8)
với α,β,γ và δ là những hằng số đặc trưng cho sự tăng trưởng của các quần thể.
Để tìm nghiệm của phương trình này ta có thể xem y như là hàm theo x , phương
trình có thể viết dưới dạng d y
y (α − β x ) (α − β x ) =
hay (γy − δ)d y = d x d x
x (γy − δ) y x
Nghiệm của phương trình này cho bởi
γy − δ ln y = αln x − β x + C
trong đó C là hằng số tuỳ ý. Hình 1.1 mô tả nghiệm của phương trình khi α = β = γ = 1,δ = 2. 6
Phương trình vi phân thường cấp I
1.1.3 Ý nghĩa hình học của phương trình vi phân:
Xét phương trình vi phân (1.6), với f (x , y ) liên tục trên miền mở trong R2. Tại mỗi
điểm M (x , y ) thuộc miền này, ta gán cho nó một hướng với hệ số góc là d y k =
= f (x , y ) (1.9) d x
Khi đó ta thu được một trường các hướng xác định bởi (1.9), và dĩ nhiên hướng của
tiếp tuyến của đường cong tại mỗi điểm trùng với hướng của trường tại điểm đó.
Giải phương trình vi phân dạng (1.6) về mặt hình học là tìm tất cả các đường cong
sao cho tại mỗi điểm của nó hướng của tiếp tuyến trùng với hướng của trường. Hình
1.2 cho ta trường hướng của phương trình y y 0 = − . x 2 y(x) 1 0 –2 –1 1 2 x –1 –2
Hình 1.2: Trường hướng của phương trình y y 0 = − x
Ngược lại, cho trước họ đường cong
φ(x , y , C ) = 0 (1.10)
phụ thuộc vào tham số C sao cho qua mỗi điểm chỉ có duy nhất một đường cong
của họ đi qua. Ta sẽ lập phương trình vi phân nhận họ đường cong này làm nghiệm
tổng quát như sau. Đạo hàm hai vế của phương trình trên theo x , ta được ∂ φ ∂ φ
(x , y , C ) + y 0
(x , y , C ) = 0 ∂ x ∂ y
Từ phương trình (1.10), với mỗi (x , y ) ta luôn tìm được duy nhất giá trị C = C (x , y ).
Thay C vào đẳng thức trên ta nhận được ∂ φ ∂ φ
(x , y , C (x , y )) + y 0
(x , y , C (x , y )) = 0 ∂ x ∂ y
1.2 Định lý tồn tại và duy nhất nghiệm 7
và đây là phương trình vi phân cần tìm.
Ví dụ: Tìm phương trình vi phân của họ đường cong sau: y = C x 2
Đạo hàm hai vế theo x ta được y 0 = 2C x . Khử C ta thu được phương trình vi phân: y y 0 = 2 x
1.2 Định lý tồn tại và duy nhất nghiệm 1.2.1 Bài toán Cauchy
Ta nhận xét rằng nghiệm của một phương trình vi phân nói chung phụ thuộc vào
một hay nhiều hằng số tuỳ ý nào đó. Để xác định một nghiệm cụ thể, ta cần thêm một
hay vài dữ kiện nào đó về nghiệm (tuỳ theo cấp của phương trình vi phân). Chẳng
hạn, y = x3 +C là nghiệm (tổng quát) của phương trình y 0 = x2. Dễ thấy y = x3 +1 là 3 3
nghiệm (duy nhất) thoả điều kiện y (0) = 1.
Ta xét bài toán sau đây đặt ra đối với phương trình (1.5), gọi là bài toán Cauchy
(hay bài toán giá trị ban đầu):
y 0 = f (x, y )
Bài toán: Tìm nghiệm y (x ) thỏa: (1.11)
y (x0) = y0
trong đó (x0, y0) ∈ D được gọi là điều kiện ban đầu.
Câu hỏi tự nhiên đặt ra là bài toán (1.11) có hay không và có bao nhiêu lời giải. Ta
lưu ý rằng không phải lúc nào bài toán Cauchy cũng có nghiệm, và khi có nghiệm
cũng không nhất thiết có duy nhất nghiệm. Chẳng hạn, phương trình y 0 = x 2, y (0) = 0
có duy nhất một nghiệm là y = x 3/3. Phương trình x y 0 = y , y (0) = 1 không có nghiệm
nào; còn phương trình y 0 = y 1/3, y (0) = 0 có ít nhất 2 nghiệm là là y ≡ 0 và y 2 = 8 x3. 27
Trong mục sau ta sẽ phát biểu và chứng minh một định lý giải quyết trọn vẹn bài
toán Cauchy cho phương trình vi phân cấp I.
1.2.2 Phương pháp xấp xỉ Picard
Ta xét bài toán Cauchy đối với phương trình cấp I dạng giải ra được đối với đạo hàm
(1.11), trong đó f xác định và liên tục trên miền mở D ⊂ R2.
Giả sử y (x ) là nghiệm của bài toán (1.11), tích phân hai vế của phương trình trong
(1.11) ta được phương trình tích phân đối với y (x ) là Z x
y (x ) = y +
f (t , y (t ))d t (1.12) 0 x0 8
Phương trình vi phân thường cấp I
Rõ ràng mỗi nghiệm của (1.11) cũng là nghiệm của (1.12) và ngược lại, mỗi nghiệm
của (1.12) đều khả vi liên tục (tức là thuộc lớp C 1) trên một khoảng I nào đó và thoả phương trình (1.11).
Phép lặp Picard-Lindelöf.
Về mặt toán tử, nghiệm của phương trình tích phân (1.12) chính là lời giải của bài
toán điểm bất động của các ánh xạ co trong không gian metric đầy đủ (ở đây ta xét
không gian các hàm khả vi liên tục trên I ) mà lời giải có thể cho bởi phương pháp
xấp xỉ liên tiếp Picard-Lindelöf sau đây.
Xét dãy các hàm xác định một cách đệ qui bởi y (hay một hàm nào đó) 0(x ) = y0 R x (1.13)
yk+1(x ) = y0 + f (t , y x
k (t ))d t , với k ∈ N 0
Bổ đề 1.1. Giả sử f liên tục trên hình chữ nhật
D = (x , y ) ∈ R2/|x − x0| ≤ a ,|y − y0| ≤ b Đặt b
M := max f (x , y ) và h := min a ,
. Khi đó với mọi x ∈ I := [x0 − h, x0 + h] ta
(x ,y )∈D M có y
k (x ) − y0 ≤ b , với mọi k
Nói cách khác, trong phép lặp (1.13) các hàm yk không đi ra khỏi phần hình chữ
nhật D , ứng với x ∈ I .
Chứng minh: Ta có, với x0 − h ≤ x ≤ x0 + h: Z Z x x y k − y0 = f (t , y ≤ f (t , y
d t ≤ M |x − x
k −1(t ))d t k −1(t )) 0| ≤ M h ≤ b x0 x0
Ví dụ: Xét phương trình y 0 = −y 2, với y (0) = 1. Nghiệm chính xác của nó là y = 1 . x +1
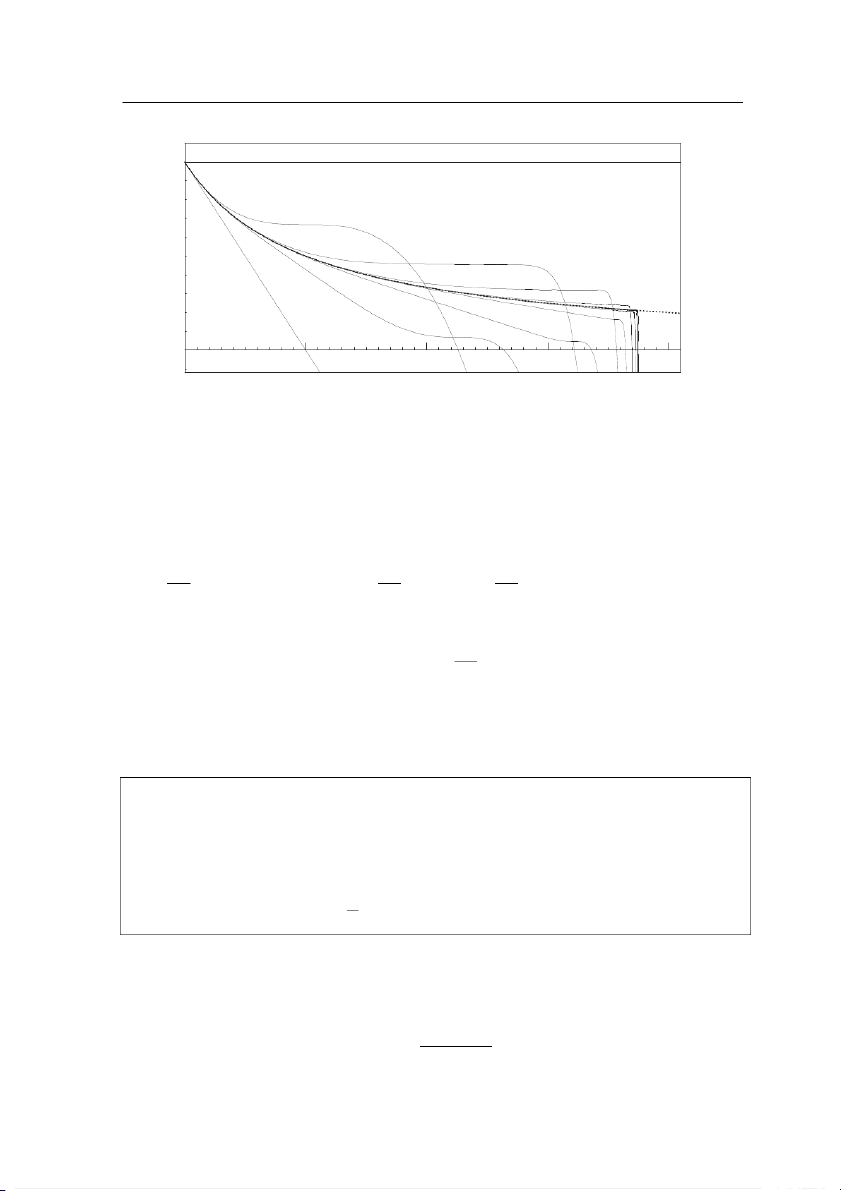
Vài xấp xỉ đầu tiên trong phép lặp Picard-Lindelöf là y0 = 1, y1 = 1 − x, y2 = 1 − x + x 3 x 2 −
,. .(xem Hình 1.3). Ta nhận thấy các xấp xỉ y hội tụ nhanh khi x bé, với các 3 k
giá trị x lớn phép lặp là phân kỳ.
1.2.3 Sự tồn tại và duy nhất nghiệm
Trong phần này ta sẽ phát biểu và chứng minh định lý cơ bản của lý thuyết phương
trình vi phân, khẳng định sự tồn tại và duy nhất nghiệm của bài toán Cauchy.
1.2 Định lý tồn tại và duy nhất nghiệm 9 Y (x) 0 Y (x) 2 Y (x) 4 Y (x) 1 Y (x) 3 1 2 3 4
Hình 1.3: Phép lặp Picard-Lindelöf cho phương trình y 0 = −y 2, với y (0) = 1
Định nghĩa 1.2. Cho hàm f (x, y ) xác định trên miền D ⊂ R2. Ta nói f thoả điều kiện
Lipschitz theo biến y trên D nếu tồn tại hằng số dương L (gọi là hằng số Lipschitz) sao cho:
f (x , y
1) − f (x , y2) ≤ L y1 − y2 ,
với mọi (x , y (
1), x , y2) ∈ D
Nhận xét: Điều kiện Lipschitz là yếu hơn so với điều kiện giới nội của đạo hàm riêng ∂ f trên ∂ f
D . Thật vậy, giả sử ∂ f liên tục và ∂ y ∂ y
∂ y ≤ L. Khi đó, áp dụng định lý
Lagrange cho hàm f (x , y ) theo biến y ta được ∂ f
f (x , y1) − f (x , y2) = (y1 − y2) x , y ∂ y
1 + θ ( y2 − y1)
Từ đó suy ra điều kiện Lipschitz.
Ví dụ: Hàm f (x, y ) = y 1/3 liên tục nhưng không thỏa điều kiện Lipschitz theo biến
y trong lân cận bất kỳ của (0,0).
Định lý 1.3 (Định lý tồn tại và duy nhất nghiệm). Giả sử hàm số f (x, y ) trong (1.11)
liên tục và thoả điều kiện Lipschitz theo biến y trên hình chữ nhật
D = (x , y ) ∈ R2/ |x − x
0| ≤ a , y − y0 ≤ b
Khi đó nghiệm của bài toán Cauchy (1.11) là tồn tại và duy nhất trong đoạn I := [x ) và M := max .
0 − h , x0 + h ], với h := min(a , b M
f (x , y )
(x ,y )∈D
Chứng minh: Chứng minh chia làm hai bước:
Sự tồn tại: Ta chứng minh rằng phép lặp Picard hội tụ đều trên I đến một nghiệm
của bài toán Cauchy. Trước tiên ta chứng minh bằng qui nạp rằng y
k +1(x ) − yk (x ) ≤ M L k |x − x0|k +1 ,
với mọi x ∈ I (k + 1)! 10
Phương trình vi phân thường cấp I R Với x
k = 0, bất đẳng thức trên chính là f (t , y
≤ M |x − x x 0(t ))d t 0|; bất đẳng thức 0 này đúng.
Giả sử ta có điều đó với k − 1, khi đó với x0 ≤ x ≤ x0 + h ta có Z x y
k +1(x ) − yk (x ) =
f (t , y t )) − f t , y d t k ( ( k −1(t )) x0 Z x Z x ≤
f (t , y (t )) − f ( ( k
t , yk−1 t )) d t ≤ L
yk (t ) − yk−1(t ) d t x0 x0 Z x ≤ L y
k (t ) − yk −1(t ) d t
x0 Z x |x −x0|k ≤ M Lk
d t = M L k |x − x0|k+1 k ! (k + 1)! x0 (với x ta đánh giá tương tự).
0 − h ≤ x ≤ x0 Xét dãy hàm y trên k (x ) I , ta có y + +
k +p (x ) − yk (x ) ≤ yk +p (x ) − yk +p −1(x ) yk+p y
−1(x ) − k +p −2(x ) ··· + y
k +1(x ) − yk (x ) M
(L |x − x
(L |x − x ≤
0|)k +p + ···+ 0|)k +1 L (k + p )! (k + 1)!
M X (L h )j ≤ L j ! j ≥k +1
Chuổi số P∞ (Lh)j là hội tụ, nên phần dư của nó (xuất hiện trong biểu thức cuối j =0 j !
cùng) có thể làm cho bé tuỳ ý khi
k đủ lớn. Theo tiêu chuẩn Cauchy, dãy yk (x ) hội
tụ đều trên I đến hàm y (x ). Để chứng minh y (x ) là nghiệm ta chỉ cần qua giới hạn trong đẳng thức Z x y ( +
k +1 x ) = y0
f (t , yk (t ))d t x0 Vì dãy hàm y
hội tụ đều, f liên tục đều trên hình chữ nhật k (x ) D nên dãy hàm f (t , y hội tụ đều trên k (t ))
I đến hàm f (t , y (t )). Do đó có thể chuyển giới hạn
qua dấu tích phân để được đẳng thức (1.12). Vậy y (x ) chính là nghiệm của bài toán Cauchy (1.11). Tính duy nhất:
Giả sử bài toán Cauchy (1.11) còn có nghiệm z (x ), khi đó ta có Z x
y (x ) − z (x ) =
f (t , y (t )) − f (t , z (t )) d t x0
1.2 Định lý tồn tại và duy nhất nghiệm 11 Suy ra Z x
y (x ) − z (x ) =
f (t , y (t )) − f (t , z (t )) d t ≤ 2M |x − x0| . x0 Từ đó Z Z x x |x − x
y (x ) − z (x ) =
f (t , y (t )) − f (t , z (t )) d t ≤ L
|y (t ) − z (t )|d t ≤ 2M L 0|2 2 x0 x0
Lặp lại quá trình trên, ta dễ dàng chứng minh được rằng với mọi số tự nhiên k:
y (x ) − z(x) ≤ 2M Lk |x − x0|k+1, với mọi x ∈ I (k + 1)!
Cho k −→ +∞ ta có y (x) − z(x) = 0 trên I . Như vậy, một cách địa phương, nghiệm
y (x ) là duy nhất.
Nhận xét: Điều kiện Lipschitz là quan trọng, ngay cả khi f (x, y ) liên tục trên R2.
Chẳng hạn xét phương trình Æ y 0 = 2 |y |, y (0) = 0
Ta thấy ngay y ≡ 0 là một nghiệm. Ngoài ra còn có vô số nghiệm khác (xem hình 1.4) là
(x − C )2 nếu x ≥ C 0 nếu x ≥ C y (x ) = và y (x ) = 0 nếu x ≤ C
−(x − C )2 nếu x ≤ C
trong đó C là hằng số tùy ý. Nói cách khác, tính duy nhất nghiệm bị vi phạm. 1 -3 -2 -1 1 2 3 -1
Hình 1.4: Nghiệm của bài toán Cauchy p y 0 = 2 |y |, y (0) = 0
Nhận xét: Thực chất chứng minh là dùng nguyên lý ánh xạ co trong các không gian
metric đủ. Giả sử E là không gian metric với metric d . Ta nói E là không gian metric
đủ nếu mọi dãy Cauchy trong E đều hội tụ đến một phần tử của E . Ánh xạ T : E → E
được gọi là ánh xạ co nếu tồn tại số α ∈ (0,1) sao cho với mọi cặp phần tử x, y ∈ E ta đều có
d (T x , T y ) ≤ αd (x , y ) 12
Phương trình vi phân thường cấp I
Định lý 1.4 (Nguyên lý ánh xạ co). 1 Mọi ánh xạ co T trong không gian metric đủ
đều có duy nhất một điểm bất động. Tức là điểm x ∗ ∈ E sao cho
T (x ∗) = x ∗
1.2.4 Phân loại nghiệm của phương trình vi phân
Về mặt hình học, bài toán Cauchy cho phương trình vi phân cấp I có thể hiểu là tìm
nghiệm y (x ) của (1.6) mà đồ thị của hàm số y = y (x ) (còn gọi là đường cong tích
phân của phương trình vi phân) đi qua điểm (x0, y0). Nói cách khác, bài toán Cauchy
là tìm đường cong tích phân của phương trình (1.6) đi qua điểm (x0, y0) ∈ D cho trước.
Định nghĩa 1.5. Giả sử D ⊂ R2 sao cho vế phải của phương trình (1.6) xác định và
liên tục trên D . Hàm số y = y (x ,C ) phụ thuộc liên tục vào hằng số C được gọi là
nghiệm tổng quát của (1.6) nếu:
a) Với mỗi điều kiện ban đầu (x0, y0) ∈ D ta luôn giải được C dưới dạng
C = φ(x0, y0) (∗)
trong đó φ là hàm liên tục.
b) Hàm y = y (x ,C ) thoả mãn phương trình (1.6) với mỗi giá trị của C cho bởi (∗)
khi (x0, y0) chạy khắp D .
Khi đó hệ thức φ(x , y ) = C (hoặc chính hàm φ(x , y )) được gọi là tích phân tổng quát của phương trình (1.6).
Ví dụ: Phương trình y 0 + y = 0 có nghiệm tổng quát là y (x) = C e −x với C là hằng số tuỳ ý.
Định nghĩa 1.6. Nghiệm của phương trình (1.6) mà tại mỗi điểm (x0, y0) của nó tính
chất duy nhất nghiệm của bài toán Cauchy (1.11) được thoả mãn được gọi là nghiệm
riêng. Ngược lại, nghiệm của phương trình (1.6) mà tại mỗi điểm của nó tính chất
duy nhất nghiệm của bài toán Cauchy bị vi phạm được gọi là nghiệm kỳ dị.
Nhận xét: Từ định nghĩa nghiệm tổng quát, ta suy ra rằng với mỗi điều kiện ban
đầu (x0, y0) ∈ D , ta luôn tìm được C0 = φ(x0, y0) sao cho y = y (x,C0) là nghiệm của
bài toán Cauchy tương ứng. Nói cách khác, bằng cách chọn các giá trị thích hợp cho
hằng số, ta có thể thu được các nghiệm riêng tuỳ ý của phương trình, không kể các nghiệm kỳ dị.
Giải (hay còn gọi là tích phân) một phương trình vi phân là tìm tất cả các nghiệm
(biểu thức nghiệm tổng quát) của phương trình đó hoặc nghiệm của bài toán Cauchy
với điều kiện ban đầu cho trước.
1Ý chứng minh: Lấy x0 ∈ E tùy ý, đặt xn = T (xn là ánh xạ co nên −1). Vì T
{xn } là dãy Cauchy. E
đầy đủ nên dãy đó hội tụ đến x ∗. Vì T liên tục nên x ∗ chính là điểm bất động.
1.3 Phương pháp giải một số phương trình vi phân cấp I 13
Ví dụ: Tìm nghiệm riêng y (x) của phương trình y 0 = 3y + x thoả điều kiện y (0) = 1.
Ta dễ kiểm tra rằng nghiệm tổng quát của phương trình đã cho là x 1
y = − − +C e 3x . 3 9
Để tìm nghiệm riêng thoả điều kiện như trên ta chỉ cần thay các giá trị ban đầu và tính C . 1
1 = y (0) = − + C e 0 9 Suy ra 10 x 1 10 C =
, nghiệm cần tìm là y = − − + e 3x. 9 3 9 9
1.3 Phương pháp giải một số phương trình vi phân cấp I
Trong bài này ta sẽ giới thiệu một số dạng phương trình vi phân cấp I mà có thể tích
phân được theo nghĩa có thể viết biểu thức của nghiệm tổng quát dưới dạng tường
minh hoặc phụ thuộc tham số. Ta nói một phương trình vi phân là cầu phương được
nếu có thể biễu diễn nghiệm của nó dưới dạng tổ hợp hữu hạn các phép toán trên
các hàm sơ cấp và tích phân của chúng. Lưu ý rằng ta không có phương pháp giải
tổng quát cho phương trình vi phân, thậm chí với những phương trình vi phân cấp I.
1.3.1 Phương trình với biến số phân ly:
Phương trình vi phân cấp I dạng
M (x )d x + N (y )d y = 0 (1.14)
được gọi là phương trình với biến số phân ly (hay còn gọi phương trình tách biến).
Cách giải: Các hàm M (x),N (y ) được giả thiết liên tục trên các khoảng nào đó. Khi
đó chỉ cần tích phân hai vế của (1.14) ta thu được tích phân tổng quát của nó là Z Z
M (x )d x +
N (y )d y = C
Ví dụ: Giải phương trình y 2y 0 = x(1 + x2).
Phương trình này có dạng tách biến
y 2d y − x (1 + x 2)d x = 0
Tích phân hai vế ta thu được nghiệm tổng quát là: y 3 x 2 x 4 − − = C 3 2 4 14
Phương trình vi phân thường cấp I
Nhận xét: Phương trình dạng
M1(x )N1(y )d x + M2(x )N2(y )d y = 0 (1.15)
cũng đưa được về dạng (1.14) với biến số phân ly, bằng cách chia hai vế cho M2(x)N1(y )
(với giả thiết biểu thức này khác 0) M1(x ) N d x + 2( y ) d y = 0 M N 2(x ) 1( y )
Do đó tích phân tổng quát là Z Z M N (y ) 1(x ) d x + 2 d y = C M2(x ) N1(y )
Ví dụ: Giải phương trình x(1 + y 2)d x + y (1 + x2)d y = 0
Chia hai vế cho (1 + x 2)(1 + y 2) ta được x d x y d y + = 0 1 + x 2 1 + y 2
Tích phân hai vế ta được Z Z x d x y d y + = C 1 + x 2 1 + y 2 tức là 1 1 1
ln(1 + x 2) + ln(1 + y 2) = C := ln C 2 2 2 1
Vậy tích phân tổng quát của phương trình đã cho là (1 + x 2)(1 + y 2) = C trong đó 1 C1
là hằng số dương tuỳ ý.
1.3.2 Phương trình vi phân thuần nhất:
Hàm số f (x , y ) được gọi là thuần nhất bậc d nếu với mọi t > 0 ta có
f (t x , t y ) = t d f (x , y )
Phương trình vi phân y 0 = f (x , y ) được gọi là thuần nhất (hay còn gọi đẳng cấp) nếu
hàm số ở vế phải là hàm thuần nhất bậc 0, tức là f (t x ,t y ) = f (x , y ) với mọi t > 0.
Nhận xét: Nếu đặt y y u :=
ta có f (x , y ) = f (±|x|,|x| ) = f (±1,±u) =: g (u). x |x | Cách giải: Đặt d u
y = x u , ta có d y = x + u . Từ đó d x d x d u x
+ u = g (u ) d x
1.3 Phương pháp giải một số phương trình vi phân cấp I 15
hoặc dưới dạng tách biến d u d x =
g (u ) − u x
Tích phân hai vế ta được Z d u x = ln
g (u ) − u C hay Z d u x = C exp với C 6= 0
g (u ) − u Thay y u =
vào biểu thức trên ta tìm được tích phân tổng quát của phương trình x thuần nhất.
Ví dụ: Giải phương trình (x2 + y 2)d x + x y d y = 0
Ta có thể viết phương trình đã cho dưới dạng d y y x = − − d x x y
Vế phải của phương trình này là hàm thuần nhất. Đặt d u 1
y = x u ta có x + u + u +
= 0, hay tương đương với d x u d x u d u = − x 1 + 2u 2
Tích phân phương trình này ta được x 1 ln = − ln(1 + 2u2) C 4 Thay y u =
vào đẳng thức này ta được nghiệm x C 4x 2
x 4 = x2 +2y 2 với C 6= 0.
Phương trình đưa về thuần nhất: Các phương trình dạng d y
a x + b y + c = f ( ) d x
a1x + b1 y + c1
có thể đưa về dạng thuần nhất bằng phép biến đổi
x = ξ+ x0
y = η + y0 16
Phương trình vi phân thường cấp I trong đó x và được chọn sao cho: 0 y0 ax0+b y + 0 c = 0
a1x0 + b1 y0 + c1 = 0 Khi đó d η a ξ + b η = f d ξ
a1ξ + b1η a + b η ξ η = f = g a η 1 + b1 ξ ξ
và đây chính là phương trình dạng thuần nhất.
Ví dụ: Giải phương trình (2x − 4y + 6)d x + (x + y − 3)d y = 0.
Trước hết ta xét hệ phương trình sau
2x0−4y0+6=0
x0 + y0 − 3 = 0
Hệ này có nghiệm là x0 = 1, y0 = 2. Tiếp đến ta thực hiện ph?p đổi biến x = ξ+1 y = η + 2
Khi đó phương trình đã cho được biến đổi thành phương trình thuần nhất:
(2ξ − 4η)d ξ + (ξ + η)d η = 0
Để giải phương trình này ta đặt η = uξ thì thu được
(2 − 3u + u2)d ξ + ξ(1 + u)d u = 0
Phương trình này chấp nhận nghiệm u = 1 và u = 2. Để tìm nghiệm tổng quát ta chia
2 vế cho 2 − 3u + u2: d ξ (1 + u )d u + = 0 ξ 2 − 3u + u2 d ξ 3 2 ⇔ + − d u = 0 ξ u − 2 u − 1 Tích phân 2 vế ta được |u − 2|3 ln |ξ| + ln = ln C (u − 1)2 1 hay (u − 2)3 ξ = C (u − 1)2
Trở lại biến x , y ban đầu ta có nghiệm tổng quát
(y − 2x )3 = C (y − x − 1)2
cùng với hai nghiệm y = x + 1 và y = 2x tương ứng với u = 1 và u = 2.
1.3 Phương pháp giải một số phương trình vi phân cấp I 17
1.3.3 Phương trình vi phân toàn phần:
Phương trình vi phân dạng
P (x , y )d x + Q (x , y )d y = 0 (1.16)
được gọi là phương trình vi phân toàn phần nếu vế trái của nó là vi phân toàn phần
của hàm nào đó, tức là tồn tại hàm U (x , y ) sao cho
d U (x , y ) = P (x , y )d x + Q (x , y )d y
Khi đó tích phân tổng quát của (1.16) cho bởi
U (x , y ) = C
Nhận xét: Điều kiện cần và đủ để phương trình (1.16) là phương trình vi phân toàn phân là ∂ P ∂ Q = ∂ y ∂ x
Và khi đó hàm U (x , y ) có thể tìm dưới dạng: Z x Z y
U (x , y ) =
P (x , y )d x +
Q (x0, y )d y x0 y0 Z (1.17) x Z y
hay U (x , y ) =
P (x , y )
Q (x , y )d y 0 d x + x0 y0
trong đó (x0, y0) là một điểm nào đó sao cho các tích phân trên tồn tại.
Ví dụ: Giải phương trình (x3 + x y 2)d x + (x2y + y 3)d y = 0.
Ta có P (x , y ) = x 3 + x y 2 và Q(x , y ) = x 2y + y 3 nên ∂ P ∂ Q = 2x y = ∂ y ∂ x
Hệ thức này chứng tỏ rằng phương trình đã cho là phương trình vi phân toàn phần
với hàm U (x , y ) có thể chọn là Z x Z y
U (x , y ) =
(x 3 + x y 2)d x +
(0.y + y 3)d y 0 0 hay x 4 x 2 y 2 y 4
U (x , y ) = + + 4 2 4
Vậy nghiệm của phương trình đã cho là
(x 2 + y 2)2 = 4C1 := C 2 hay
x 2 + y 2 = C với C ≥ 0 18
Phương trình vi phân thường cấp I
Thừa số tích phân:
Có những trường hợp phương trình (1.16) chua phải là phương trình vi phân toàn
phần, nhưng có thể tìm được hàm số µ(x , y ) sao cho phương trình sau trở thành
phương trình vi phân toàn phần:
µ(x , y ){P (x , y )d x +Q (x , y )d y } = 0
Hàm µ(x , y ) như thế được gọi là thừa số tích phân của phương trình (1.16). Điều kiện
để µ là thừa số tích phân là µ phải thoả mãn phương trình: ∂ ∂ (µP ) = (µQ ) ∂ y ∂ x Hay tương đương ∂ µ ∂ µ ∂ P ∂ Q Q − P = µ − (1.18) ∂ x ∂ y ∂ y ∂ x
Không có phương pháp tổng quát để giải phương trình đạo hàm riêng này. Tuy
nhiên trong một vài trường hợp đặc biệt ta có thể tìm được µ.
Trường hợp I: µ chỉ phụ thuộc vào x.
Giả sử µ > 0, khi đó chia hai vế của (1.18) cho µ, ta được ∂ P d ln µ ∂ − ∂ Q y ∂ x = =: φ d x Q
Vậy trường hợp này chỉ thoả mãn khi vế phải của đẳng thức trên không phụ thuộc
vào y . Với điều kiện này, thừa số tích phân cho bởi: Z µ(x ) = exp φ(x )d x
Trường hợp II: µ chỉ phụ thuộc vào y .
Làm tương tự như trên, thừa số tích phân cho bởi: Z µ(y ) = exp ψ(y )d y ∂ Q − ∂ P trong đó ∂ x ∂ y ψ(y ) :=
được giả thiết không phụ thuộc vào x . P
Ví dụ: Tìm thừa số tích phân rồi giải phương trình (2x y + x2y + y 3/3)d x + (x2 + y 2)d y = 0.
Ta có P (x , y ) = 2x y + x 2y + y 3/3 và Q(x , y ) = x 2 + y 2 nên ∂ P ∂ − ∂ Q y ∂ x
2x + x 2 + y 2 − 2x = = 1 Q x 2 + y 2
1.3 Phương pháp giải một số phương trình vi phân cấp I 19 Do đó có thể chọn R
µ(x ) = exp( d x ) = e x để cho phương trình
e x [(2x y + x 2 y + y 3/3)d x + (x 2 + y 2)d y ] = 0
là phương trình vi phân toàn phần. Tích phân phương trình này theo công thức (1.17)
ta được nghiệm tổng quát
y e x (x 2 + y 2/3) = C
1.3.4 Phương trình vi phân tuyến tính cấp I:
Trong mục này ta xđt lớp các phương trình vi phân mà biểu thức là tuyến tính đối
với ẩn và đạo hàm của nó. Các phương trình như thế được gọi là phương trình vi
phân tuyến tính. Dạng tổng quát của phương trình vi phân tuyến tính cấp I là
y 0 + p (x )y = q (x ) (1.19)
trong đó p(x ),q(x ) là các hàm xác định trên khoảng (a,b ) nào đó.
Nếu q(x ) ≡ 0, ta có phương trình vi phân tuyến tính thuần nhất:
y 0 + p (x )y = 0 (1.20)
Định lý 1.7. Giả sử p(x) và q(x) liên tục trên (a,b ) và x0 ∈ (a,b) thì với mọi giá trị y0,
phương trình (1.20) có một nghiệm duy nhất thỏa y (x0) = y0.
Chứng minh: Phương trình (1.20) có dạng y 0 = f (x , y ) trong đó
f (x , y ) = q (x ) − p (x )y
là hàm liên tục và có đạo hàm riêng ∂ f liên tục trong lân cận của (x ∂ y
0, y0). Vậy f thỏa
điều kiện Lipschitz theo biến y . Kết luận suy từ định lý 1.3.
Cách giải: Để giải phương trình (1.19) trước hết ta giải phương trình thuần nhất
tương ứng (1.20). Thực ra, đây là phương trình tách biến
d y +p(x)d x = 0 y
Nghiệm tổng quát của phương trình này là R
y (x ) = Ae − p(x)d x (1.21)
trong đó A là hằng số tùy ý.
Phương pháp biến thiên hằng số: Ta sẽ tìm nghiệm tổng quát của (1.19) dưới dạng tích R
y = A(x )e − p(x)d x , (1.22) 20
Phương trình vi phân thường cấp I
tức là xem hằng số A trong biểu thức nghiệm (1.21) như là hàm theo biến x (phương
pháp biến thiên hằng số). Thay vào phương trình (1.19) ta được R
A0e − p(x)d x = q (x ) (1.23) Từ đó, Z R A(x ) =
q (x )e p(x)d x d x + C .
Thay vào (1.22), ta thu được nghiệm tổng quát của (1.19) là Z R R
y = e − p(x)d x
q (x )e p(x)d x d x + C (1.24)
trong đó C là hằng số tuỳ ý.
Ví dụ: Tìm nghiệm của phương trình vi phân y 0 + 3x y = x đi qua điểm (0,4).
Ta có p(x ) = 3x nên R p(x )d x = 3x 2/2. Do đó nghiệm tổng quát là Z
y = e −3x2/2
x e 3x2/2d x + C 1 1
= e −3x2/2
e 3x2/2 + C =
+ C e −3x2/2 3 3 Thay 11
x = 0 và y = 4 vào đẳng thức trên, ta tìm được C = và nghiệm riêng cần tìm 3 là: 1 11 y = +
e −3x2/2 3 3
Hệ quả 1.8. Nghiệm của phương trình (1.19) với điều kiện y (x0) = y0 cho bởi công thức
R x q(t )µ(t )dt + y x 0 y (x ) = 0 , µ(x ) R trong đó x
µ(x ) := e p (t )d t x0 .
1.3.5 Phương trình Bernoully Phương trình có dạng
y 0 + p (x )y = y αg (x ) (1.25)
trong đó α là số thực nào đó, được gọi là phương trình Bernoully2.
Để giải phương trình này ta đưa về giải phương trình tuyến tính (1.19) đã xđt trong
mục trước. Rõ ràng với α = 0 hay α = 1 thì (1.25) đã có dạng phương trình tuyến tính.
2I.Bernoully (1667_1746) là nhà toán học Thụy si.
1.3 Phương pháp giải một số phương trình vi phân cấp I 21
Nếu α 6= 0 và α 6= 1 thì đặt
z = y 1−α Khi đó
z 0 = (1 − α)y −α y 0
Chia hai vế của (1.25) cho y α, rồi thay biểu thức của z và z 0 vào đẳng thức đó ta được
phương trình vi phân tuyến tính theo z :
z 0 + (1 − α)p (x )z = (1 − α)g (x ) (1.26)
Nhận xét: Chú ý rằng ta phải xét riêng trường hợp y = 0 trước khi chia hai vế cho
y α để tránh làm mất nghiệm này.
Ví dụ: Giải phương trình x y 0 − 4y = x2py
Rõ ràng đây là phương trình Bernoully với α = 1/2 và y = 0 là một nghiệm của
phương trình đã cho. Giả sử y 6= 0, chia hai vế cho x y 1/2 ta được 4 1
y −1/2 y 0 − y 2 = x x Đặt 1 1
z = y 2 ta có z 0 =
y −1/2 y 0. Khi đó phương trình đã cho trở thành phương trình 2
vi phân tuyến tính không thuần nhất 2 x z 0 − z = . x 2
Giải phương trình này, ta tìm được nghiệm 1 z = x 2 ln |x | + C 2
Do đó phương trình đã cho có nghiệm tổng quát là 1 2 y = x 4 ln |x | + C 2 và nghiệm y = 0.
1.3.6 Phương trình Darboux
Phương trình Darboux3 là phương trình vi phân dạng
A(x , y )d x + B (x , y )d y + H (x , y )(x d y − y d x ) = 0 (1.27)
trong đó A,B là các hàm thuần nhất bậc m và H là hàm thuần nhất bậc n.
3J.G.Darboux (1842−1917) là nhà toán học Pháp 22
Phương trình vi phân thường cấp I
Chú ý rằng nếu n = m −1 thì phương trình Darboux chính là phương trình thuần
nhất. Trong trường hợp tổng quát, ta luôn luôn đua phương trình Darboux về phương trình Bernoully.
Thật vậy, đặt y = x z , ta có y
d y = x d z + z d x ,
x d y − y d x = x 2d = x 2d z x
Do đó phương trình (1.27) có thể viết lại dạng y y y y x m A 1, d x + x m B 1, d y + x n H 1, x 2d = 0 x x x x
Hay, sau khi chia 2 vế cho x m và thu gọn, ta có
[A(1, z ) + z B (1, z )] d x + x B (1, z ) + H (1, z )x n+2−m d z = 0
Với giả thiết x B(1,z) + H (1,z )x n+2−m 6= 0, ta có thể viết phương trình cuối cùng dưới dạng d x B (1, z ) H (1, z ) + x = − x n+2−m d z
A(1, z ) + z B (1, z )
A(1, z ) + z B (1, z )
Đây là phương trình Bernoully của ẩn x = x (z ) xem như hàm theo z .
Ví dụ: Giải phương trình xd x + y d y + x2(xd y − y d x) = 0
Đây là phương trình Darboux, đặt y = x z ta được
x d x + x z (x d z + z d x ) + x 4d z = 0 hay
(1 + z 2)d x + (x z + x 3)d z = 0 Từ đó ta có d x z 1 + x = − x 3 d z 1 + z 2 1 + z 2
Đây là phương trình Bernoully, giải phương trình này (sau khi đưa về phương trình
tuyến tính bậc I) ta được nghiệm là
1 = C (1+ z2)+(1+ z2)arctanz + z x 2
Trở lại biến ban đầu, ta có nghiệm tổng quát cho bởi y
C (x 2 + y 2) + (x 2 + y 2) arctan + x y − 1 = 0 x
với C là hằng số tuỳ ý.
1.3 Phương pháp giải một số phương trình vi phân cấp I 23
1.3.7 Phương trình Riccati:
Phương trình Riccati4 tổng quát là phương trình vi phân dạng
y 0 = p (x )y 2 + q (x )y + r (x ) (1.28)
trong đó p(x ),q(x ) và r (x ) là các hàm liên tục trên khoảng (a,b ) nào đó.
Nhận xét: Phương trình Riccati không phải bao giờ cũng giải được bằng phép cầu
phương (tức là có thể biểu diễn nghiệm dưới dạng hữu hạn các phép lấy tích phân
của các hàm tường minh nào đó!). Trong vài trường hợp đặc biệt như p(x ) ≡ 0 hay
r (x ) ≡ 0 ta đưa về phương trình tuyến tính hoặc phương trình Bernoully. Tuy vậy,
kết quả sau cho phép ta tích phân phương trình Riccati nếu biết một nghiệm nào đó của nó.
Mệnh đề 1.3.1. Nếu biết một nghiệm của phương trình Riccati (1.28) thì có thể đưa
nó về phương trình Bernoully.
Chứng minh: Gọi một nghiệm của (1.28) là ˜y, tức là
˜y 0 = p (x ) ˜
y 2 + q (x ) ˜y + r (x )
Ta đặt y = ˜y + z, trong đó z là ẩn mới. Thay vào phương trình (1.28) ta được
˜y 0 + z 0 = p (x ) ˜y 2 + 2p (x ) ˜
y z + p (x )z 2 + q (x ) ˜
y + q (x )z + r (x ) Từ đó suy ra
z 0 − [2p (x ) ˜y + q (x )]z = p (x )z 2
và đây là phương trình Bernoully.
Ví dụ: Giải phương trình y 0 + 2y (y − x) = 1
Đây là phương trình Riccati. Dễ thấy y = x là một nghiệm của phương trình đã cho. Bây giờ, đặt y = x + z
ta đưa phương trình đã cho về dạng
z 0 + 2z (z + x ) = 0
Đây là phương trình Bernoully với α = 2. Đặt u = z −1 ta được u 0 − 2x u = 2
Nghiệm tổng quát của phương trình này theo (1.24) là Z u = e x2
2e −x2d x + C
Vậy nghiệm tổng quát của phương trình đã cho là e −x2 y = x + R , và y = x
C + 2 e −x2d x
4J.F.Riccati (1676−1754) là nhà toán học Ý 24
Phương trình vi phân thường cấp I
1.4 Phương trình vi phân cấp I chưa giải ra đối với đạo hàm
Trong mục này ta sẽ khảo sát các phương trình vi phân cấp một dạng tổng quát:
F (x , y , y 0) = 0 (1.29)
trong đó F là hàm ba biến liên tục trong một tập mở G ⊂ R3 cùng với các đạo hàm
riêng của nó, ngoài ra ∂ F không đồng nhất bằng không. ∂ y 0
1.4.1 Tích phân một số phương trình vi phân cấp I
Ta sẽ khảo sát một số dạng phương trình vi phân cấp I dạng chưa giải ra đạo hàm
đặc biệt mà có thể giải bằng cầu phương.
F chỉ phụ thuộc vào y 0 Xét phương trình dạng F (y 0) = 0 (1.30)
Giả sử F (xem như hàm của biến y 0) liên tục và có một số hữu hạn các không điểm
(chẳng hạn khi F là đa thức). Khi đó mỗi nghiệm của y = y (x ) của phương trình
(1.30) phải thoả y 0(x ) = k, với k là một không điểm của F .
Do đó y (x ) = k x + C với C là hằng số tuỳ ý; và ta có y − C F ( ) = 0 (1.31) x
Ngược lại, nếu có đẳng thức (1.31) với một giá trị y − C
C nào đó thì k := phải là x
nghiệm của F = 0. Khi đó
y = k x + C , y 0 = k
do đó F (y 0) = 0.
Nói cách khác, công thức (1.31) cho ta nghiệm tổng quát của phương trình đã cho.
Ví dụ: Giải phương trình y 02 − y 0 + 2 = 0. 2
Phương trình này có nghiệm là y − C y − C − + 2 = 0. x x
Dạng có thể giải ra đối với y hay x :
Giả sử (với những điều kiện nào đó) phương trình (1.29) có thể giải ra được y hay x
theo các biến còn lại. Chẳng hạn,
y = f (x , y 0) (1.32)
1.4 Phương trình vi phân cấp I chưa giải ra đối với đạo hàm 25 Khi đó, đặt d y p = y 0 =
và xem p như tham số, ta được d x
y = f (x , p )
Vi phân hai vế của đẳng thức này ta được
∂ f (x , p )
∂ f (x , p ) d y = d x + d p ∂ x ∂ p
Thay d y = pd x ta được phương trình vi phân dạng
M (x , p )d x + N (x , p )d p = 0
Xem x như là hàm của p và giả sử phương trình này có nghiệm tổng quát là x =
g (p , C ). Khi đó nghiệm tổng quát của phương trình (1.32) được cho dưới dạng tham số
x =g(p,C)
y = f (x , p )
Tương tự như thế, các phương trình dạng giải ra được đối với x
x = h (y , y 0)
cũng giải được bằng cách đưa vào tham số p như trên.
Ví dụ: Giải phương trình y = x(y 0)2
Đặt p = y 0, ta có y = xp2. Vi phân hai vế đẳng thức này, ta được
d y = p 2d x + 2p x d p
thay d y = pd x , ta được
p [(1 − p )d x − 2x d p ] = 0 .
Với p = 0, ta được nghiệm y = 0. Ngoài ra ta có phương trình
(1 − p )d x − 2x d p = 0.
Đây là phương trình tách biến có nghiệm tổng quát là C x = . (1 − p )2
Vậy ta thu được nghiệm tổng quát dưới dạng tham số y = xp2 x = C (1−p )2 26
Phương trình vi phân thường cấp I
Phương trình khuyết x hoặc y
Xét phương trình khuyết y
F (x , y 0) = 0 (1.33)
Nếu có thể giải ra được y 0 dạng
y 0 = f (x ) Z
Khi đó nghiệm tổng quát của (1.33) là y =
f (x )d x + C .
Trường hợp ta không giải ra được y 0 nhưng có thể tìm một phép tham số hoá phương trình (1.33) gồm
x = φ(t)
y 0 = ψ(t ) sao cho
F (φ(t ), ψ(t )) = 0 Khi đó d y
ψ(t ) = y 0 =
=⇒ d y = ψ(t ).φ0(t )d t d x
Vậy nghiệm tổng quát của phương trình (∗) cho bởi dạng tham số
x = φ(t) R y =
ψ(t )φ0(t )d t + C
Ví dụ: Giải phương trình ln y 0 + cos y 0 − x = 0
Tham số hoá y 0 = t , x = lnt + cost ta có 1 d y = t d x
và d x = ( −sint )d t t Suy ra Z y =
(1 − t sin t )d t = t − sin t + t cos t + C
Vậy nghiệm của phương trình đã cho là
x = lnt +cost
y = t − sin t + t cos t + C
Tương tự, ta có thể tìm nghiệm trong trường hợp khuyết x .
1.5 Phương trình Clairaut và phương trình Lagrange 27
1.5 Phương trình Clairaut và phương trình Lagrange
1.5.1 Phương trình Clairaut
Phương trình Clairaut5 là lớp các phương trình vi phân dạng
y = x y 0 + f (y 0) (1.34)
trong đó, nói chung, f là một hàm phi tuyến.
Ta sẽ tìm nghiệm tổng quát của phương trình này bằng cách đặt p = y 0. Khi đó
y = p x + f (p )
Vi phân hai vế đẳng thức này, với chú ý rằng d y = pd x ta được
p d x = p d x + x + f 0(p ) d p hay
x + f 0(p ) d p = 0
Từ đó ta suy ra d p = 0 hay x + f 0(p) = 0.
Nếu d p = 0 thì p = C , thay vào (1.34) ta được nghiệm tổng quát
y = C x + f (C ) (1.35)
và đây là một họ đường thẳng.
Nếu x + f 0(p) = 0, cùng với (1.34), ta thu được một nghiệm cho dưới dạng tham số
x = −f 0(p)
y = −p f 0(p ) + f (p )
Người ta chứng minh được rằng nếu f 00(p) liên tục và khác không thì nghiệm cho
dưới dạng tham số là bao hình của họ đường thẳng (1.35).
Ví dụ: Xét phương trình y = (x − 1)y 0 − y 02
Đây là phương trình Clairaut với f (t ) = −t 2 −t . Thay thế y 0 bởi C ta được nghiệm
tổng quát là họ đường thẳng
y = C (x − 1) − C 2
Để tìm nghiệm kỳ dị, tức là bao hình của họ đường thẳng trên ta xét hệ x = 2C +1
y = C (x − 1) − C 2 Khử (x − 1)2
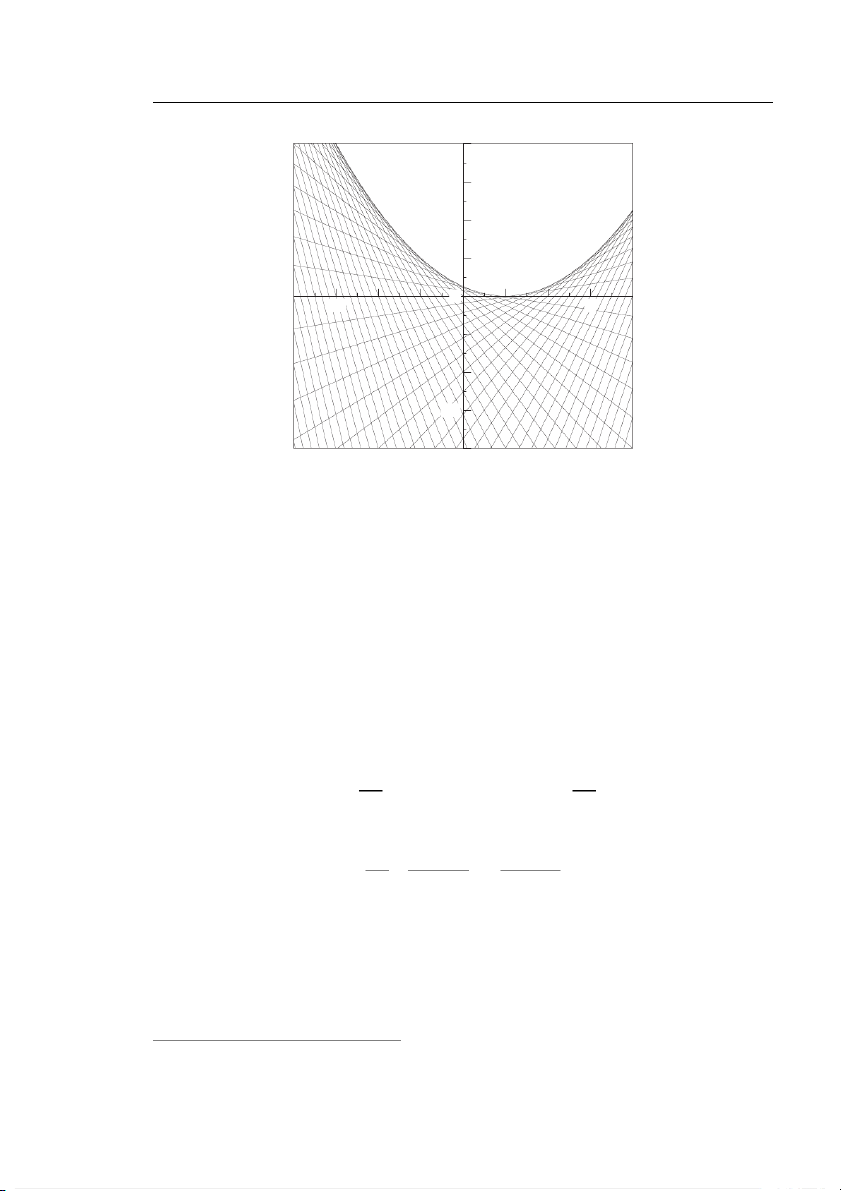
C từ hệ phương trình này ta được bao hình là parabol y = (xem Hình 4 1.5).
5Alexis Claude Clairaut (1713-1765) là nhà khoa học nổi tiếng người Pháp. 28
Phương trình vi phân thường cấp I 3 0 -3 3 -3
Hình 1.5: Nghiệm của phương trình Clairaut với f (t ) = −t 2 − t .
1.5.2 Phương trình Lagrange
Phương trình vi phân cấp I mà là tuyến tính đối với x và y dạng
y = φ(y 0)x + ψ(y 0) (1.36)
được gọi là phương trình Lagrange6.
Giả sử φ(y 0) 6= y 0, nếu không phương trình đã cho là phương trình Clairaut mà ta
đã xét trên đây. Cũng tương tự như trường hợp phương trình Clairaut, ta đặt p = y 0.
Khi đó phương trình (1.36) trở thành
y = φ(p )x + ψ(p ) (1.37)
Vi phân hai vế theo x ta được d y d p p =
= φ(p ) + φ0(p )x + ψ0(p ) d x d x
Xem p là biến số độc lập ta có phương trình tuyến tính mà ẩn là x = x (p) như sau: d x φ0(p ) φ0(p ) + x = d p
φ(p ) − p
p − φ(p )
Tích phân phương trình tuyến tính này theo phương pháp đã biết ta được nghiệm
tổng quát x = h(p,C ), với C là tham số tuỳ ý.
Kết hợp với (1.37) ta có nghiệm tổng quát của (1.36) cho dưới dạng tham số tham
số hoá theo tham số p:
y =φ(p)h(p,C)+ψ(p)
x = h (p , C )
6J.L.Lagrange (1736 - 1813) là nhà toán học nổi tiếng người Pháp.
1.5 Phương trình Clairaut và phương trình Lagrange 29
Nhận xét: Chú ý rằng ứng với các giá trị của tham số p = p (trong đó là nghiệm i pi
của phương trình φ(p) − p = 0) ta cũng nhận được các nghiệm của phương trình
(1.36). Tuỳ theo từng trường hợp nghiệm này có thể là nghiệm kỳ dị hoặc không.
Ví dụ: Giải phương trình y = x y 02 − y 0.
Đặt p = y 0, khi đó
y = x p 2 − p
Vi phân hai vế của đẳng thức này theo x với chú ý d y = pd x, sau khi thu gọn ta được
(p 2 − p )d x + (2p x − 1)d p = 0
Giả sử p2 − p 6= 0 ta có d x 2 1 + x = d p p − 1 p (p − 1)
Giải phương trình này ta được:
C + p − lnp x = (p − 1)2
Thay vào biểu thức của y ta được nghiệm tổng quát dạng tham số:
¨ x = C+p−lnp (p −1)2
y = (C +p−lnp)p2 (p −1)2 − p
Các nghiệm ứng với p = 0 và p = 1 là y = 0 và y = x − 1 tương ứng.
1.5.3 Tham số hoá tổng quát:
Trong tiểu mục này ta xét một số phương trình vi phân chưa giải ra đối với đạo hàm
F (x , y , y 0) = 0 (1.38)
nhưng có thể tham số hoá được dưới dạng
x = φ(u , v ), y = ψ(u , v ) và y 0 = χ(u, v ) sao cho
F [φ(u , v ), ψ(u , v ), χ(u , v )] = 0
Vi phân x và y theo u,v rồi thay vào đẳng thức d y = y 0d x ta có ∂ ψ ∂ ψ ∂ φ ∂ φ d u +
d v = χ(u , v ) d u + d v ∂ u ∂ v ∂ u ∂ v
Xem u như là hàm của v ta có phương trình ∂ φ ∂ ψ χ d u − ∂ v = ∂ v d v ∂ φ ∂ ψ − χ ∂ u ∂ u 30
Phương trình vi phân thường cấp I
Đây là dạng phương trình đã giải ra đối với đạo hàm, giả sử có nghiệm là
u = ϕ(v, C )
Ta thay vào biểu thức của x và y ta được nghiệm tổng quát dưới dạng tham số của phương trình (1.38) là
x = φ[ϕ(v,C),v]
y = ψ[ϕ(v, C ), v ]
Ví dụ: Giải phương trình x 2
y = y 02 − y 0x + 2
Ta có thể tham số hoá phương trình bằng cách đặt x 2
x = x , y 0 = p và y = p 2 −p x + 2
(xem x và p là hai tham số). Khi đó, vi phân đẳng thức cuối ta được
d y = (x − p )d x + (2p − x )d p
Để ý rằng d y = pd x, từ đẳng thức trên, nếu 2p −x 6= 0 ta có dp = 1, suy ra p = x +C . d x
Do đó nghiệm tổng quát của phương trình đã cho là x 2 y = + C x + C 2 2 Nếu x x 4
2p − x = 0 ta có p =
, thay vào biểu thức tham số hoá ta có nghiệm y = , 2 2
nghiệm này là nghiệm kỳ dị.
1.6 Nghiệm kỳ dị của phương trình vi phân cấp I
1.6.1 Sự tồn tại nghiệm kỳ dị
Trong chương trước ta đã đề cập đến sự tồn tại và duy nhất nghiệm đối với phương
trình vi phân cấp I dạng giải ra được đối với đạo hàm
d y = f (x, y ) d x
Trong mục này ta xét trường hợp phương trình vi phân cấp I dạng tổng quát
F (x , y , y 0) = 0 . (1.39)
Nói chung, không phải lúc nào ta cũng viết được phương trình này dưới dạng giải
ra đối với đạo hàm. Điều đó cho thấy rằng sự tồn tại và tính chất duy nhất nghiệm
của phương trình vi phân (1.39), với điều kiện ban đầu (x0, y0), không phải lúc nào
cũng được bảo đảm. Nói cách khác, với (x0, y0) ∈ R2 nào đó, có thể có nhiều nghiệm
của phương trình (1.39) đi qua điểm này.
1.6 Nghiệm kỳ dị của phương trình vi phân cấp I 31
Ví dụ: Phương trình Clairaut (1.34) với f (t ) = −t 2 − t có nghiệm kỳ dị là parabol
(x −1)2 (xem hình 1.5). Tại mỗi điểm dọc theo parabol này có tồn tại một nghiệm khác 4
mà đồ thị là đường thẳng tiếp xúc với parabol nói trên tại điểm đó.
Định lý sau đây khẳng định sự tồn tại và duy nhất nghiệm trong trường hợp tổng quát.
Định lý 1.9. Nếu hàm F (x, y,p) thoả các điều kiện sau:
i) F (x , y,p) liên tục cùng với các đạo hàm riêng của nó trong lân cận của (x0, y0,p0) ∈
R3 (tức là F thuộc lớp C 1 trong lân cận điểm này)
ii) F (x0, y0,p0) = 0 iii) ∂ F (x ∂ p 0, y0, p0) 6= 0
thì phương trình (1.39) có duy nhất một nghiệm y = y (x ) lớp C 1 trong lân cận của x0
thoả điều kiện ban đầu: y (x sao cho 0 0) = y0
y (x0) = p0
Chứng minh: Các giả thiết trong định lý trên chính là các giả thiết của định lý hàm
ẩn, do đó phương trình (1.39) xác định duy nhất hàm p = f (x , y ) lớp C 1 sao cho
p0 = f (x0, y0). Khi đó ta có phương trình vi phân dạng giải ra được đối với đạo hàm
d y = f (x, y ) d x
trong đó f khả vi liên tục. Tính chất này mạnh hon điều kiện Lipchitz nên theo định
lý tồn tại và duy nhất nghiệm (cho phương trình đã giải ra đối với đạo hàm), ta thấy
có tồn tại duy nhất một nghiệm y = y (x ) thoả điều kiện ban đầu y (x . 0) = y0
1.6.2 Tìm nghiệm kỳ dị theo p−biệt tuyến
Định lý trên cho thấy nghiệm kỳ dị có thể xảy ra khi các điều kiện của định lý không
thoả mãn. Rõ ràng với hàm F = F (x , y,p) khả vi liên tục, nghiệm kỳ dị chỉ có thể xảy ra nếu tại đó ∂ F = 0 ∂ p
Ta gọi M ⊂ R3 là siêu mặt cho bởi phương trình F (x, y,p) = 0 và giả sử π : M −→ R2,
π(x , y , p ) = (x , y ) là phép chiếu tự nhiên theo toạ độ p . Khi đó các điểm kỳ dị của
ánh xạ π cho bởi hệ phương trình
F (x , y , p ) = 0 ∂ F (1.40) = 0 ∂ p 32
Phương trình vi phân thường cấp I
Khử p từ hệ phương trình này ta thu được một phương trình dạng
Φ(x , y ) = 0 (1.41)
Phương trình này xác định một đường cong trong R2, được gọi là đường cong biệt
lập (discriminant) hay p−biệt tuyến của phương trình (1.39).
Vậy để tìm nghiệm kỳ dị theo p−biệt tuyến trước hết ta tìm p− biệt tuyến cho bởi
hệ (1.40), sau đó thử xem biệt tuyến có phải là nghiệm của phương trình (1.39) hay
không. Cuối cùng trong số các nghiệm này chọn ra các nghiệm mà dọc theo nó tính
duy nhất bị vi phạm; đó chính là nghiệm kỳ dị.
Ví dụ: Tìm nghiệm kỳ dị của phương trình y = 2x y 0 − y 02
Ta có biệt tuyến cho bởi
y = 2x p − p 2, 2x − 2p = 0
Từ đó biệt tuyến là parabol y = x 2 trong mặt phẳng (x , y ). Tuy nhiên, y = x 2 lại
không phải là nghiệm của phương trình đã cho, nên phương trình không có nghiệm kỳ dị.
Ví dụ: Tìm nghiệm kỳ dị của phương trình x 2
y = y 02 − x y 0 + 2
Ta có p−biệt tuyến cho bởi x 2
y = p 2 − x p + , 2p − x = 0 2
Từ đó ta có biệt tuyến là parabol x 2 y =
và cũng là nghiệm của phương trình đã cho. 4
Ngoài ra nghiệm tổng quát của nó là (xem ví dụ trang 29) x 2
y = C x + C 2 + 2 x 2
Do đó với mọi điểm (x
0 , ta xét phương trình theo C :
0, y0) trên parabol này, i.e. y0 = 4 x 2 y 0
0 = C x0 + C 2 + 2 hay tương đương x 2 C 2 + x 0 0C + = 0 4
Phương trình này luôn có nghiệm x0 C = −
, tức là luôn có nghiệm thứ hai đi qua 2 (x0, y0). Vậy x 2 y =
là nghiệm kỳ dị của phương trình đã cho. 4
1.6 Nghiệm kỳ dị của phương trình vi phân cấp I 33
1.6.3 Tìm nghiệm kỳ dị theo C −biệt tuyến
Đối với những phương trình mà tích phân tổng quát của nó cho bởi
Φ(x , y , C ) = 0 (1.42)
ta có thể tìm nghiệm kỳ dị của nó thông qua việc tìm các C − biệt tuyến, tức là đường
cong trong R2 xác định bằng cách khử C từ hệ
( Φ(x, y,C ) = 0 ∂ Φ (1.43)
(x , y , C ) = 0 ∂ C
Nhận xét: Có thể kiểm tra không khó (xem [1]) rằng nếu C − biệt tuyến là bao hình
của họ đường cong (1.42) thì nó là một nghiệm kỳ dị của phương trình (1.39). Do đó
để tìm nghiệm kỳ dị của (1.39) trước hết ta tìm C −biệt tuyến của nó. Biệt tuyến đó là
đường cong R(x , y ) = 0 nhận được bằng cách khử C từ hệ (1.43). Sau đó , thử xem có
nhánh nào của C − biệt tuyến là bao hình của họ đường cong (1.42) hay không; nếu
có, đó chính là nghiệm kỳ dị của phương trình.
Chú ý: Nếu hàm Φ trong (1.42) có các đạo hàm riêng cấp I theo x và y bị chặn và
không đồng thời bằng không thì C −biệt tuyến là bao hình của họ nghiệm tổng quát
(1.42); nói cách khác C −biệt tuyến là nghiệm kỳ dị.
Ví dụ: (xem [1]) Tìm nghiệm kỳ dị của phương trình Lagrange 4 8
x − y = y 02 − y 03 9 27
Phương trình Lagrange này có tích phân tổng quát là (y − C )2 = (x − C )3. Do đó biệt tuyến cho bởi hệ
(y −C)2 =(x −C)3
2(y − C ) = 3(x − C )2 Khử C ta được 4 y = x , y = x − 27 Chỉ có 4 y = x −
là bao hình nên nó là nghiệm kỳ dị. Còn đường thẳng y = x chứa 27
các điểm kỳ dị của nghiệm tổng quát (xem Hình 1.6). 34
Phương trình vi phân thường cấp I Y=x - 4/2 Y=x
Hình 1.6: Nghiệm kỳ dị của phương trình 4 8
x − y = y 02 − y 03 9 27 BÀI TẬP
1. Giải các phương trình vi phân tách biến:
(a) (x y 2 + 4x )d x + (y + x 2y )d y = 0 (b) p 2x
1 − y 2 + y y 0 = 0
(c) y 0 = e x+y (d)
x 2 y − y y 0 = y + 1
2. Tìm nghiệm tổng quát của các phương trình vi phân thuần nhất sau (a) y y 0 = − 1 x (b) 2x y
y 0 = x2 − y 2
(c) (y 2 − 3x2)d y + 2x y d x = 0 (d) y
x y 0 = y ln x
3. Tích phân các phương trình vi phân sau đây:
(a) (x − 2y + 9)d x = (3x − y + 2)d y 2 (b) y + 2
y 0 = 2 x + y −1
4. Kiểm tra các phương trình sau là phương trình vi phân toàn phần và giải chúng
1.6 Nghiệm kỳ dị của phương trình vi phân cấp I 35
(a) y d x + (y 3 + ln x )d y = 0 x
(b) e y d x + (x e y − 2y )d y = 0
(c) 2x y d x + (x 2 − y 2)d y = 0
(d) [(x + 1)e x − e y ]d x = xe y d y
5. Tìm thừa số tích phân rồi giải các phương trình vi phân sau
(a) (x + y 2)d x − 2x y d y = 0
(b) (y 2 − 6x y )d x + (3x y − 6x2)d y = 0
(c) y (1 + x y )d x − xd y = 0 (d) p
x y ln y d x + (x 2 + y 2 y 2 + 1)d y = 0
6. Tìm nghiệm tổng quát của các phương trình vi phân tuyến tính sau
(a) y 0 − 4y = x − 2x2
(b) x y 0 + y = e x (c) 1
y 0 − y tan x = cosx
(d) y 2d x − (2x y + 3)d y = 0
7. Tìm nghiệm tổng quát của các phương trình Bernoully sau
(a) 3y 0 + y = (1 − 2x)y 4
(b) y y 0 + y 2 = x (c) 2 p
y 0 + y = e 2 y
8. Giải các phương trình vi phân sau đây
(a) y 02 − (x + y )y 0 + x y = 0
(b) y 03 − y y 02 − x2y 0 + x2y = 0
(c) x y 03 = 1 + y 0
(d) y 03 + y 3 = 3y y 0
9. Tìm nghiệm tổng quát và nghiệm kỳ dị của các phương trình sau đây
(a) y = x y 0 + 12
(b) x y 0 − y = ln y 0 Æ
(c) y = x y 0 + y 02 + 1
(d) y y 0 = 2y 02x + 1 36
Phương trình vi phân thường cấp I Chương 2
Phương trình vi phân cấp cao
Chương này trình bày một số kiến thức tổng quan về phương trình vi phân cấp cao
và lý thuyết tổng quát về phương trình vi phân tuyến tính cấp cao.
2.1 Phương trình vi phân cấp cao
2.1.1 Các khái niệm:
Phương trình vi phân thường cấp n là phương trình có dạng
F (x , y , y 0, y 00, . . . , y (n)) = 0 (2.1)
trong đó F là một hàm xác định (liên tục) trên tập mở nào đó của Rn+2 và nhất thiết
phải có sự tham gia của đạo hàm cấp n của ẩn y (n).
Với một vài giả thiết thích hợp, định lý hàm ẩn cho phép viết phương trình (2.1)
dưới dạng sau đây, được gọi là dạng đã giải ra đối với đạo hàm:
y (n) = f (x , y , y 0, . . . , y (n−1)) (2.2)
Dưới dạng này ta có thể đưa việc nghiên cứu một phương trình cấp cao về nghiên
cứu (hệ) phương trình vi phân cấp I. Thật vậy, bằng cách đưa thêm vào các ẩn mới
y1 := y , yk := y (k−1), k = 1,n, ta thu được y 0 = y2 1 y 0 = y 2 3 ............... (2.3) y 0 = y n−1 n
y 0 = f (x , y n 1, . . . , yn ) Đặt Y := (y
là các vector-hàm ta có thể
1, . . . , yn )t , g (x , Y ) :=
y2, . . . , yn , f (x , y1, . . . , yn )t
viết lại (2.3) dưới dạng đơn giản
Y 0 = f (x , Y ) (2.4) 38
Phương trình vi phân cấp cao
2.1.2 Sự tồn tại và duy nhất nghiệm:
Tương tự như trường hợp phương trình vi phân cấp I, bài toán Cauchy đối với
phương trình vi phân cấp cao (2.1) đặt ra như sau:
Tìm nghiệm y (x ) của phương trình (2.1) thoả điều kiện ban đầu:
y (x0) = y0, y 0(x 0 0) = y , 0 (2.5) . . . . . . . . .
y (n−1)(x (n −1) 0) = y0
trong đó x0 ∈ I ⊂ R và Y0 := (y0, y 0,..., y (n−1)) ∈ Rn cố định, cho trước. 0 0
Để phát biểu định lý khẳng định sự tồn tại lời giải của bài toán Cauchy ta cần khái niệm sau:
Cho vector-hàm f (x ,Y ) xác định trên miền G ⊂ R × Rn. Ta nói f thoả điều kiện
Lipschitz trên G theo Y nếu tồn tại hằng số dương L (gọi là hằng số Lipschitz) sao cho:
||f (x , Y1) − f (x , Y2)|| ≤ L||Y1 − Y2||,
với mọi (x ,Y1),(x,Y2) ∈ G
Ta luu ý rằng điều kiện Lipschitz không phải là hệ quả của tính liên tục. Chẳng hạn hàm p
f (x , y ) =
y liên tục nhưng không thoả điều kiện Lipschitz trong lân cận của 0.
Hệ quả 2.1. Với các ký hiệu trong mục trước, nếu hàm f (x,Y ) thỏa điều kiện Lips-
chitz theo biến Y thì g (x ,Y ) cũng thỏa điều kiện Lipschitz theo biến Y .
Định lý 2.2 (Định lý tồn tại và duy nhất nghiệm cho PHươNG TRìNH VI PHâN cấp
cao). Giả sử vector-hàm g (x , y ) trong (2.4) liên tục và thoả điều kiện Lipschitz theo Y trên miền
G = {(x , Y ) ∈ R × Rn/ |x − x0| ≤ a ,||Y − Y0|| ≤ b }
Khi đó bài toán Cauchy với điều kiện ban đầu (2.5) có một nghiệm duy nhất trên đoạn I := [x
) và M := max(x,Y ) .
0 − h , x0 + h ], với h := min(a , b M
∈G ||g (x , Y )||
Chứng minh: Tương tự như trong trường hợp phương trình vi phân cấp I, chỉ cần
thay giá trị tuyệt đối bởi chuẩn trong Rn.
Hệ quả 2.3. Nếu hàm f trong (2.2) liên tục và có các đạo hàm riêng theo biến yk :=
y (k−1) cũng liên tục trong một lân cận nào của (x0, Y0) thì bài toán Cauchy với điều
kiện ban đầu (2.5) có một nghiệm duy nhất trong lân cận của điểm này.
Nhận xét: Tương tự như trong chương I, ta cũng định nghĩa các loại nghiệm của
phương trình vi phân cấp cao. Chẳng hạn, nghiệm kỳ dị của (2.2) là nghiệm mà tại
mỗi điểm của nó tính chất duy nhất nghiệm bị vi phạm. Ta gọi nghiệm tổng quát
của (2.2) là họ các hàm φ(x ,C1,...,Cn) phụ thuộc (một cách liên tục) vào n hằng số tuỳ ý C
. Với mỗi bộ giá trị của 1, . . . , Cn
n tham số này ta nhận được một nghiệm riêng của phương trình.
Ví dụ: Nghiệm tổng quát của phương trình y 00 = y là y (x) = C1e x + C2e −x. Nó phụ
thuộc vào hai hằng số tuỳ ý C và C2. 1
2.1 Phương trình vi phân cấp cao 39
2.1.3 Một số phương trình vi phân cấp cao giải được bằng cầu phương:
a) Phương trình F (x , y (n)) = 0
Phương trình này chỉ phụ thuộc vào biến độc lập và đạo hàm cấp cao nhất. Trong
trường hợp có thể giải ra đối với đạo hàm:
y (n) = f (x )
ta có thể tích phân liên tiếp theo x và thu được R x y (n−1) =
f (x )d x + C x 1 0 R x R x y (n−2) = d x
f (x )d x + C (x − x ) + C x 1 0 2 0 x0 .................... Z x Z x y = d x . . .
f (x )d x + C1 (x ( − x n −1)! 0)n −1+ x0 x0 | {z } n lần + C2 (x ( − x ··· C n −2)! 0)n −2 +
+ n−1(x − x0) + Cn
Ví dụ: Phương trình y (n) = 0 có nghiệm là đa thức tổng quát cấp n − 1
y (x ) = c1(x − x0)n−1 + c2(x − x0)n−2 + ··· + cn x c −1( − x0) + n
Trong trường hợp không giải ra được y (n) nhưng có thể tham số hoá
x = φ(t ),
y (n) = ψ(t ) khi đó ta có
d y (n−1) = y (n)d x = ψ(t )φ0(t )d t Vì vậy Z y (n−1) =
ψ(t )φ0(t )d t = ψ(t , C ) 1
Lặp lại quá trình trên sau n bước, ta thu được nghiệm tổng quát cho dưới dạng tham số
¨ x = φ(t ),
y = ψm (t , C1, . . . , Cn )
b) Phương trình F (y (n−1), y (n)) = 0:
Cách giải: Nếu có thể giải được
y (n) = f (y (n−1)) 40
Phương trình vi phân cấp cao
thì, bằng cách đặt z := y (n−1), có thể viết lại phương trình dưới dạng sau:
z 0 = f (z )
Đây là phương trình vi phân cấp I theo z, giả sử nghiệm là z = g (x ,C ), ta trở lại
trường hợp trên với phương trình
y (n−1) = g (x , C ) với C là tham số. Nếu có thể tham số hoá
y (n−1) = φ(t ),
y (n) = ψ(t )
thì từ d y (n−1) = y (n)d x ta suy ra d y (n−1)
φ0(t )d t d x = = y (n) ψ(t ) Do đó
Z φ0(t )dt x =
= φ (t , C ψ(t ) 1 1)
và ta trở lại trường hợp trên với
x = φ1(t , C1),
y (n−1) = φ(t )
Ví dụ: Giải phương trình y 000 = y 00 + 1
Đặt z = y 00 ta có phương trình z 0 −z = 1. Phương trình này có nghiệm tổng quát là
z = C1e x − 1
Do đó, ta được phương trình
y 00 = C1e x − 1
Vậy nghiệm tổng quát của phương trình đã cho là x 2
y (x ) = C1e x − + C 2 2 x + C3
c) Phương trình F (y (n−2), y (n)) = 0:
Đối với dạng phương trình này ta đặt z = y (n−2) và viết lại phương trình theo z
F (z , z 00) = 0
Nếu từ phương trình này có thể giải được z 00 = f (z ) thì ta có
2z 0z 00 = 2 f (z )z 0
2.1 Phương trình vi phân cấp cao 41 hay
d ((z 0)2) = 2 f (z )d z Từ đó ta tìm được v u Z t z 0 = ± 2
f (z )d z + C1
Đây là phương trình vi phân cấp I với ẩn là z = z (x ) với nghiệm tổng quát có dạng
Φ(x , z , C1, C2) = 0
Thay z = y (n−2) vào phương trình này ta trở lại trường hợp a).
Ví dụ: Giải phương trình y 000 = y 0.
Đặt z = y 0 ta thu được phương trình z 00 = z
Nhân hai vế phương trình này với 2z 0, ta được
d (z 0)2 = d z 2 và có nghiệm là p z 0 = z 2 + A .
Đây là phương trình tách biến, nghiệm tổng quát của nó là p z +
z 2 + A = B e x
Nhân với lượng liên hợp, ta thu được p A z −
z 2 + A = − e −x B Từ đó, ta có B A z = e x − e −x 2 2B
Trở lại ẩn y , ta được nghiệm tổng quát B A y = e x +
e −x + C 2 2B Hay
y = C1e x + C2e −x + C3
2.1.4 Một số phương trình vi phân cấp cao có thể hạ cấp:
Ta sẽ xét một số dạng phương trình cấp cao mà có thể đưa về phương trình cấp thấp
hơn bằng cách đổi biến. 42
Phương trình vi phân cấp cao
a) Phương trình dạng F (y, y 0,..., y (n)) = 0:
Phương trình này không chứa biến độc lập x . Ta đặt p = y 0. Khi đó d y
y 0 = p = d x d p d p y 00 = = p d x d y d d p d p d p d d p y 000 = p = + p d x d y d x d y d x d y d p 2 d 2p = p + p 2 d y d y 2 ............................. d p d n−1p
y (n) = g p , , . . . , d y d y n−1
Thay các biểu thức trên vào phương trình ban đầu ta thu được phương trình vi phân
cấp n − 1 theo ẩn p = p(y )
G (y , p , p 0, . . . , p (n−1)) = 0
Giả sử phương trình này có nghiệm tổng quát là
Φ(y , p, C1, . . . , Cn−1) = 0
ta thay p = y 0 thì thu được phương trình dạng F (y, y 0) = 0 mà là phương trình vi phân cấp I.
Ví dụ: Giải phương trình (1 + y 2)y y 00 = (3y 2 − 1)y 02
Đặt p = y 0 như đã trình bày, phương trình đưa về dạng d p (1 + y 2)y p
= (3y 2 − 1)p 2 d y
Chia 2 vế cho p (với giả thiết p 6= 0) và viết lại dưới dạng phương trình tách biến d p 3y 2 − 1 = d y p (1 + y 2)y
Nghiệm tổng quát của nó là p y = C (1 + y 2)2 1
Thay p = y 0, ta có phương trình y y 0 = C (1 + y 2)2 1
Nghiệm tổng quát của phương trình cuối cùng là 1 − = 2C 1 + y 2 1 x + C2
2.1 Phương trình vi phân cấp cao 43
b) Phương trình thuần nhất đối với ẩn hàm y và các đạo hàm của nó:
T a nói phương trình vi phân F (x , y, y 0,..., y (n)) = 0 là thuần nhất theo ẩn hàm y và các
đạo hàm của nó nếu F là hàm thuần nhất (bậc m nào đó) theo các biến y, y 0,..., y (n). Tức là
F (x , t y , t y 0, . . . , t y (n)) = t m F (x , y , y 0, . . . , y (n))
Đối với lớp các phương trình này ta có thể hạ cấp bằng cách đặt y 0 = u y Khi đó ta có y 0 = u y
y 00 = y 0u + u 0 y = y (u 0 + u 2)
y 000 = y (u 00 + 3u u 0 + u 3) .............................
y (n) = y .g (u , u 0, . . . , u (n−1))
Nhờ tính thuần nhất, phương trình đã cho có thể viết lại dạng
y m F (x , 1, u , u 0 + u 2, . . . , g (u , u 0, . . . , u (n−1))) = 0
Đây là phương trình cấp n − 1 của ẩn hàm u = u(x), giả sử có nghiệm tổng quát là
u = u (x , C1, . . . , Cn−1)
Khi đó từ y 0 = u y ta có nghiệm tổng quát của phương trình ban đầu là Z Z y = exp u (x , C )d x + ln |C = C u ( ) 1, . . . , Cn −1 n | n exp x , C C 1, . . . , n −1 d x
Ví dụ: Giải phương trình x2y y 00 = (y − x y 0)2.
Đây là phương trình thuần nhất (cấp 2) theo y và các đạo hàm của nó. Đặt y 0 = u y giống như trên, ta có
y 00 = y (u 0 + u 2)
Thay vào và rút gọn cho y 2 (giả sử y 6= 0) ta được phương trình tuyến tính bậc nhất:
x 2u 0 + 2x u − 1 = 0
với nghiệm tổng quát là x + C u = 1 x 2
Trở lại ẩn hàm y với u = y 0/y ta được nghiệm tổng quát là C1 y = C x 2 x e −
Dĩ nhiên nghiệm y = 0 cũng chứa trong nghiệm tổng quát này. 44
Phương trình vi phân cấp cao
2.1.5 Tích phân trung gian và tích phân đầu:
Xét phương trình vi phân cấp n (2.1). Giả sử có tồn tại hệ thức dạng
Φ(x , y , y 0, . . . , y (k), Ck+1, . . . , Cn ) = 0 (2.6)
sao cho Φ phụ thuộc vào n −k hằng số tuỳ ý Ck+1,...,Cn và không phụ thuộc vào các
đạo hàm cấp > k (nhưng nhất thiết phải có mặt y (k)).
Nếu từ hệ n −k phương trình nhận được bằng cách lấy vi phân hệ thức (2.6) theo
x n − k lần và chính hệ thức đó ta có thể nhận được phương trình đã cho (bằng cách
khử các tham số) thì hệ thức (2.6) được gọi là tích phân trung gian của phương trình (2.1).
Nếu k = n − 1, tức là hệ thức chỉ chứa một tham số C
Φ(x , y , y 0, . . . , y (n−1), C ) = 0
thì ta gọi là tích phân đầu.
Nhận xét: Tích phân trung gian thực chất là một phương trình vi phân cấp k đã
chứa sẵn n −k hằng số tuỳ ý Ck+1,...,Cn. Nghiệm tổng quát của nó còn chứa k hằng
số mới là C1,...,Ck (tức là chứa tất cả n hằng số), và đó cũng là nghiệm tổng quát của
phương trình ban đầu (2.1). Vậy tích phân trung gian cho phép đưa việc giải phương
trình vi phân cấp cao về giải phương trình cấp thấp hon.
Phương trình dạng F (x , y (k),..., y (n)) = 0
Bằng cách đổi ẩn z = y (k) ta có thể viết phương trình dưới dạng
F (x , z , z 0, . . . , z (n−k)) = 0
Giả sử đã tìm được tích phân tổng quát của phương trình này Φ(x,z,Ck+1,...,Cn) = 0.
Khi đó, ta có tích phân trung gian của phương trình đã cho là
Φ(x , y (k), Ck+1, . . . , Cn ) = 0
Đây là phương trình vi phân cấp k, nghiệm của nó cho ta tích phân tổng quát của phương trình ban đầu.
Ví dụ: Giải phương trình y 00 − x y 000 + y 000 = 0.
Đặt z = y 00 ta thu được phương trình
z − x z 0 + z 0 = 0
mà nghiệm tổng quát là z = C1(x − 1). Từ đó ta có tích phân đầu
y 00 = C1(x − 1)
Vậy nghiệm tổng quát của phương trình đã cho là C C y =
1 x 3 − 1 x2 + C2x + C3 3 2
2.2 Lý thuyết tổng quát về phương trình vi phân tuyến tính cấp cao. 45
2.2 Lý thuyết tổng quát về phương trình vi phân tuyến tính cấp cao. 2.2.1 Các khái niệm
Phương trình vi phân tuyến tính cấp n có dạng tổng quát
p0(x )y (n) + p1(x )y (n−1) + ··· + p (
n −1 x ) y 0 + pn (x ) y = g (x ) (2.7)
trong đó các pj(x) và g (x) là các hàm (thực) nào đó theo biến x.
Nếu g (x ) ≡ 0 thì phương trình (2.7) được gọi là phương trình vi phân tuyến tính thuần nhất.
Chú ý: Ta có thể xem p0(x) ≡ 1, vì nếu không ta chia hai vế của phương trình cho hệ
số này, và thu được phương trình mới cùng dạng.
Sự tồn tại nghiệm: Ta xét phương trình vi phân tuyến tính cấp cao (2.7), với điều kiện ban đầu (2.5).
Định lý 2.4. (Sự tồn tại và duy nhất nghiệm) Nếu các hàm pj(x) và g (x) là liên tục
trên khoảng (a,b ) và, ngoài ra, p0(x) 6= 0 với mọi x ∈ (a,b ) thì bài toán Cauchy cho
phương trình (2.7) có duy nhất nghiệm, với mọi dữ kiện ban đầu dạng (2.5) miễn là
x0 ∈ (a , b ).
Chứng minh: Phương trình (2.7) có thể viết lại dạng −1 y (n) =
p x )y (n−1) + ··· + p
x )y − g x ) p 1( (
n −1 x ) y 0 + pn ( ( 0(x )
Để ý rằng vế phải là hàm liên tục theo (x ,Y ) và khả vi liên tục theo biến Y :=
(y , y 0, . . . , y (n−1)) nên thỏa điều kiện Lipschitz theo biến này.
Dạng toán tử của phương trình vi phân tuyến tính:
Ký hiệu D là toán tử đạo hàm d và đặt: d x L = p (2.8)
0D n + p1D n −1 + · · · + pn−1D + pn
L được gọi là toán tử vi phân cấp n và khi đó (2.7) viết lại dưới dạng sau, gọi là dạng
toán tử của phương trình (2.7)
L (y ) = g (2.9)
Đặc biệt, khi g ≡ 0, phương trình vi phân tuyến tính thuần nhất tương ứng viết một cách đơn giản L (u ) = 0 (2.10)
Nhận xét: L là toán tử tuyến tính trên không gian các hàm (khả vi) vì L(αu + β v ) =
αL (u) + β L (v ), với u, v là hai hàm khả vi và α, β là hai số tuỳ ý. Do đó giải phương
trình vi phân tuyến tính thuần nhất là tìm không gian con ker(L). 46
Phương trình vi phân cấp cao
Mệnh đề 2.2.1. Giả sử u và 1
u2 là hai nghiệm tuỳ ý của phương trình vi phân tuyến
tính thuần nhất (2.10). Khi đó, với C1,C2 là hai hằng số bất kỳ, C1u1 + C2u2 cũng là nghiệm của (2.10).
Chứng minh: Ta có L(C1u1 + C2u2) = C1L(u1) + C2L(u2) = 0.
Hệ quả 2.5. Tập tất cả các nghiệm của phương trình (2.10) có cấu trúc không gian vector.
Hạ cấp phương trình tuyến tính thuần nhất:
Nếu biết một hay nhiều nghiệm của phương trình thuần nhất (2.10) thì có thể hạ cấp
phương trình đó như sau đây.
Giả sử φ(x ) là một nghiệm của (2.10), đặt u(x ) = v (x )φ(x ) rồi thay vào (2.10). Khi
đó v (x ) thỏa phương trình vi phân tuyến tính dạng e L (v ) = 0
Nhưng phương trình này có một nghiệm v ≡ 1, nên không chứa v. Vậy, nếu xem ẩn
mới w := v 0, thì w là nghiệm của một phương trình vi phân tuyến tính thuần nhất cấp n − 1 dạng Ln−1(w ) = 0
Ví dụ: Xét phương trình 2x2y 00 + 3x y 0 − y = 0 (x > 0), có nghiệm là φ(x) = x−1. Đặt
y = v (x )x −1, tính các đạo hàm và thay vào phương trình đã cho ta được
2x v 00 − v 0 = 0.
Với ẩn phụ w = v 0, ta tìm được w = C C . Cuối cùng
1 x 1/2. Do đó v = 2 3
1 x 3/2 + C2 2
y (x ) = C
3 1x 1/2 + C2x −1
2.2.2 Nghiệm tổng quát của phương trình thuần nhất
a) Định thức Wronski
Định nghĩa 2.6. Ta nói các hàm u1(x),u2(x),...,un(x) là phụ thuộc tuyến tính trên
(a , b ) nếu có tồn tại các hằng số C
không đồng thời bằng không, sao cho
1, C2, . . . , Cn
C1u1(x ) + ··· + Cn un(x ) = 0,
với mọi x ∈ (a,b )
Các hàm u1(x),u2(x),...,un(x) được gọi là độc lập tuyến tính trên (a,b ) nếu chúng
không phụ thuộc tuyến tính trên khoảng này.
2.2 Lý thuyết tổng quát về phương trình vi phân tuyến tính cấp cao. 47
Nói cách khác, {u1(x),u2(x),...,un(x)} độc lập tuyến tính nếu đẳng thức
C1u1(x ) + ··· + Cn un(x ) ≡ 0
chỉ xảy ra với C1 = 0, C2 = 0, … ,Cn = 0.
Nhận xét: Hệ chứa hàm đồng nhất bằng không phải là hệ phụ thuộc tuyến tính.
Mệnh đề 2.2.2. Cho u1(x),u2(x),...,un(x) là các hàm khả vi đến cấp n −1 trên (a,b).
Nếu chúng phụ thuộc tuyến tính trên (a,b ) thì định thức u1(x ) u2(x ) ··· u n (x ) u0(x ) u 0 (x ) ··· u 0 (x ) 1 2 n .. .. = 0,
với mọi x ∈ (a,b ) (2.11) . . ... ..
u(n−1)(x) u(n−1)(x) ··· u(n−1)(x) 1 2 n
Chứng minh: Theo giả thiết của mệnh đề, có tồn tại các hằng số Cj không đồng thời bằng không sao cho
C1u1(x ) + ··· + Cn un(x ) ≡ 0 trên (a , b )
Đạo hàm theo biến x đẳng thức này n − 1 lần, ta thấy các C thoả mãn hệ phương j
trình tuyến tính thuần nhất sau (với x cố định nào đó) C 1 u1(x ) + ···+ Cn un (x ) = 0 C ( 1 u 0 x ) + ···+ C (x ) = 0 1 n u 0n ··· ··· ··· ··· C (x ) + ( 1 u (n −1) x ) = 0 1
···+ Cn u(n−1) n
Vì hệ thuần nhất này có nghiệm không tầm thường nên định thức của ma trận của hệ phải bằng không.
Định nghĩa 2.7. Định thức ở vế trái của (2.11) được gọi là định thức Wronski của n
hàm u1(x),u2(x),...,un(x) và thường được ký hiệu là W (x) hay W [u1,...,un].
Hệ quả 2.8. Nếu W (x) 6= 0 tại x nào đó thuộc (a,b) thì hệ hàm {u1(x),u2(x),...,un(x)}
độc lập tuyến tính trên (a,b ).
Ví dụ: Hệ hàm {cos x,sin x} là độc lập tuyến tính trên khoảng bất kỳ.
Ví dụ: Hệ hàm {1, x, x2,··· , xn−1} là độc lập tuyến tính trên khoảng bất kỳ vì 1 x ··· x n−1
0 1 ··· (n − 1)x n−2 W (x ) =
= 1.1!2!. .. (n − 1)! = .. .. 6 0 với mọi x ∈ R . . ... ... 0 0 ··· (n − 1)!
Nhận xét: Hệ các hàm có định thức Wronski đồng nhất bằng 0 không nhất thiết phụ
thuộc tuyến tính. Nói cách khác, mệnh đề 2.2.2 chỉ là điều kiện cần để hệ hàm khả
vi phụ thuộc tuyến tính. Chẳng hạn xét {x3,|x|3} có W (x) ≡ 0, nhưng độc lập tuyến
tính trên (a,b ) tùy ý, miễn là a,b trái dấu. 48
Phương trình vi phân cấp cao
Định lý 2.9. Giả sử các hàm pj(x) là liên tục và p0(x) 6= 0 trên khoảng (a,b). Khi đó n
nghiệm u1(x),u2(x),...,un(x) của phương trình vi phân tuyến tính thuần nhất (2.10) là
độc lập tuyến tính nếu và chỉ nếu định thức Wronski W [u1,u2,...,un] 6= 0,∀x ∈ (a,b ).
Chứng minh: Nếu W [u1,u2,...,un] 6= 0,∀x ∈ (a,b ) thì theo hệ quả trên, các nghiệm
u1(x ), u2(x ), . . . , un (x ) là độc lập tuyến tính.
Ngược lại, giả sử có x0 ∈ (a,b ) mà W (x0) = 0. Khi đó hệ phương trình tuyến tính
thuần nhất sau (ẩn là C1,...,Cn) có nghiệm không tầm thường
C1u1(x0) + ···+ C n un (x0) = 0 C ( (x 1 u 0 x 1 0) + ···+ Cn u0n 0) = 0 ··· ··· ··· ···
C1u(n−1)(x (x 1 0)
+ ···+ Cn u(n−1) n 0) = 0
Gọi (C1,...,Cn) là một nghiệm như vậy và đặt
u (x ) = C1u1(x ) + ··· + Cn un(x ).
Rõ ràng u(x ) là một nghiệm của của (2.10) thoả điều kiện ban đầu u(x 0 0) = 0, u (x0) =
0, . . . , u (n−1)(x0) = 0. Mặt khác nghiệm tầm thường v ≡ 0 cũng thoả điều kiện này. Do
đó, theo định lý tồn tại và duy nhất nghiệm ta phải có
C1u1(x ) + ··· + Cn un(x ) ≡ 0
tức là các u1(x),u2(x),...,un(x) là phụ thuộc tuyến tính: trái giả thiết.
Định nghĩa 2.10. Hệ gồm n nghiệm u1(x),u2(x),...,un(x) độc lập tuyến tính trên
(a , b ) của phương trình vi phân tuyến tính thuần nhất cấp n được gọi là hệ nghiệm
cơ bản của phương trình đó.
Định lý 2.11. (Sự tồn tại hệ nghiệm cơ bản) Với các giả thiết như định lý 2.9, phương
trình vi phân tuyến tính thuần nhất (2.10) có ít nhất một hệ nghiệm cơ bản.
Chứng minh: Xét n bài toán Cauchy đối với phương trình (2.10) tương ứng với các dữ kiện ban đầu (u (x ( (
0), u 0 x0), . . . , u (n −1) x0)) = ek , k = 1, n trong đó e Rn
k := (0, . . . , 0, 1, 0, . . . , 0) là vector đơn vị thứ k trong không gian Euclide .
Với giả thiết của định lý, mỗi bài toán trên có một nghiệm duy nhất uk(x). Ta
chứng minh hệ {u1,...,un} độc lập tuyến tính. Thật vậy xét đẳng thức
C1u1(x ) + ··· + Cn un(x ) ≡ 0
Đạo hàm n −1 lần đẳng thức này ta thu được hệ phương trình đại số tuyến tính thuần
nhất (ẩn là các Ck) có định thức của ma trận hệ số tại x0 bằng
W [u1, . . . , un ] = det[e1, . . . , en ] = 1 6= 0
nên hệ này chỉ có nghiệm tầm thường C1 = 0,...,Cn = 0.
Nhận xét: Theo chứng minh trên, dễ thấy rằng phương trình đã cho có vô số nghiệm.
2.2 Lý thuyết tổng quát về phương trình vi phân tuyến tính cấp cao. 49
b) Nghiệm tổng quát của phương trình tuyến tính thuần nhất:
Định lý 2.12. Giả sử các hàm p ,
j (x ) là liên tục trên (a , b )
p0(x ) 6= 0,∀x ∈ (a , b ) và
{u1(x ), u2(x ),..., un(x )} là hệ nghiệm cơ bản của phương trình vi phân tuyến tính
thuần nhất (2.10) trên (a,b ). Khi đó nghiệm tổng quát của (2.10) có dạng
u (x ) = C1u1(x ) + ··· + Cn un(x ) (2.12) trong đó C là các hằng số tuỳ ý. 1, . . . , Cn
Chứng minh: Rõ ràng với C
là các hằng số bất kỳ, vế phải của (2.12) là nghiệm 1, . . . , Cn của (2.10).
Gọi v (x ) là nghiệm tùy ý của (2.10). Với x0 ∈ (a,b ) là giá trị nào đó ta đặt
v0 := v (x0), v 0 := v 0(x
:= v (n−1)(x 0
0), . . . , v (n −1) 0 0)
Xét hệ phương trình (ẩn là các Ck)
C1u1(x0) + ···+ C n un (x0) = v0 C ( ( 1 u 0 x x 1 0) + ···+ Cn u0n 0) = v 00 ··· ··· ··· ···
C1u(n−1)(x (x 1 0)
+ ···+ Cn u(n−1) n 0) = v (n−1) 0
Vì các u1(x),u2(x),...,un(x) lập thành hệ nghiệm cơ bản nên W (x0) 6= 0, tức là định
thức của ma trận hệ số của hệ phương trình trên khác không. Theo định lý Cramer,
hệ này có duy nhất nghiệm (C ). Đặt 1, . . . , Cn
u (x ) := C1u1(x ) + ··· + Cn un(x )
thì u(x ) cũng là nghiệm của (2.10) thoả cùng điều kiện ban đầu như v (x ). Do đó
u (x ) ≡ v (x ).
Tìm phương trình vi phân tuyến tính thuần nhất biết hệ nghiệm cơ bản của nó:
Để đơn giản, ta xét trường hợp phương trình vi phân tuyến tính cấp II. Cho trước hệ
hai hàm khả vi đến cấp II, độc lập tuyến tính {y1, y2}, ta sẽ tìm phương trình vi phân dạng
y 00 + p (x )y 0 + q (x )y = 0 nhận y làm nghiệm. 1, y2
Nếu y là nghiệm tổng quát của phương trình này thì y1 y2 y W [y y 0 y 0
1, y2, y ] = y 0 = 1 2 0
y 00 y 00 y 00 1 2 50
Phương trình vi phân cấp cao
Khai triển định thức này theo cột cuối ta được: y y y 0 y 0 y 00 1 y2 1 y2 1 2
y 0 y 0 − y 0 y 00 y 00 + y y 00 y 00 = 0 1 2 1 2 1 2
Đây chính là phương trình vi phân cần tìm.
Ví dụ: Tìm phương trình vi phân cấp II biết rằng nó nhận các hàm e x và e −2x làm nghiệm.
Dễ thấy hệ hai hàm đã cho độc lập tuyến tính. Theo kết quả trên, phương trình cần tìm có dạng e x e −2x e x e −2x
e x −2e −2x y 00
e x −2e −2x − y 0 e x 4e −2x + y e x 4e −2x = 0
Rút gọn ta được phương trình y 00 + y 0 − 2y = 0.
c) Đồng nhất thức Abel:
Ta sẽ chỉ ra sau đây biễu diễn đơn giản của định thức Wronski của hệ n nghiệm
{u1(x ), u2(x ),..., un(x )} của phương trình thuần nhất (2.10).
Định lý 2.13. (Đồng nhất thức Abel)1 Giả sử W (x) là định thức Wronski của n nghiệm
{u1(x ), u2(x ),..., un(x )} của phương trình thuần nhất (2.10). Khi đó ¨ Z « x p
W (x ) = W (x 1 (2.13) 0) exp − d t p x 0 0
Chứng minh: Đạo hàm W (x ) theo x ta có: u1(x ) u2(x ) ··· un (x ) u 0(x ) u 0(x ) ··· u 0 (x ) 1 2 n d W . . = .. .. ... ... (2.14) d x
u(n−2)(x ) u(n−2)(x ) ( 1 x ) 2 ··· u(n−2) n
u(n)(x ) u (n)(x ) ···
u (n) (x ) 1 2 n
(thực ra, vế phải là tổng của n định thức nhưng các định thức khác có hai hàng giống
nhau nên bằng không). Ngoài ra, do p 0 0 u (n ) = − p k
−p1u(n−1) − ··· − p k n −1uk n uk
nên hàng cuối trong định thức vế phải (2.14) có dạng tổ hợp tuyến tính của các hàng
trong định thức W (x ). Sau khi tách ra thành n định thức, (2.14) trở thành d W p = − 1 W d x p0
1Cũng được gọi là công thức Ostrogradski−Liouville.
2.2 Lý thuyết tổng quát về phương trình vi phân tuyến tính cấp cao. 51
Tích phân phương trình vi phân tách biến này ta thu được R x p1
W (x ) = W (x d t x p 0)e − 0 0
ở đây W (x0) là giá trị của định thức Wronski tại x0 ∈ (a,b ) nào đó.
Hệ quả 2.14. Nếu các pj(x) liên tục và p0(x) 6= 0 trên (a,b) thì W (x) hoặc luôn luôn
khác không, hoặc đồng nhất bằng không trên (a,b ). Ứng dụng:
Đồng nhất thức Abel cho phép ta tìm nghiệm thứ n, độc lập tuyến tính với n − 1
nghiệm độc lập tuyến tính đã biết của phương trình tuyến tính cấp n, bằng cách giải
phương trình vi phân cấp n−. Với n = 2, việc này hoàn toàn đơn giản. Thật vậy, giả
sử đã biết nghiệm y của phương trình 1
y 00 + p (x )y 0 + q (x )y = 0
Giả sử y là một nghiệm độc lập tuyến tính với sao cho 2 y1
W [y1, y2](x0) = 1. Khi đó y R
1 y 0 − y 0 y W (x ) 1 x 2 1 2 = = e − p (t )d t x0 y 2 y 2 y 2 1 1 1 Tức là y 0 1 R x 2 = e − p (t )d t x0 y1 y 21 Từ đó ta có Z 1 R y (
e − p(x)d x d x 2 x ) = y ( 1 x ) y1(x )2
Ví dụ: Tìm nghiệm tổng quát của phương trình
2x 2 y 00 + 3x y 0 − y = 0
trên (0,+∞) biết nó có một nghiệm là y1(x) = 1/x.
Giải: Theo công thức trên, nghiệm độc lập tuyến tính với y cho bởi 1 Z 1 R 3 y 2x d x 2(x ) = x 2e − d x x
Tính toán tích phân, ta thu được y 1/2
2(x ) = 2/3x
Vậy nghiệm tổng quát của phương trình đã cho trên (0,+∞) là C p y ( 1 x ) = + C x x 2 52
Phương trình vi phân cấp cao
2.2.3 Nghiệm của phương trình vi phân tuyến tính không thuần nhất
Ta lưu ý rằng, giống như các kết quả trong đại số tuyến tính, nghiệm của phương
trình vi phân tuyến tính không thuần nhất có quan hệ chặt chẽ với nghiệm của
phương trình thuần nhất tương ứng. Cụ thể, ta có thể kiểm tra dễ dàng các tính chất sau:
i) Hiệu hai nghiệm của phương trình vi phân tuyến tính không thuần nhất là một
nghiệm của phương trình thuần nhất tương ứng.
ii) Tổng của một nghiệm của phương trình không thuần nhất và một nghiệm của
phương trình thuần nhất tương ứng là nghiệm của phương trình không thuần nhất.
Hơn thế nữa, định lý sau mô tả cấu trúc nghiệm của phương trình không thuần nhất.
Định lý 2.15. Với các giả thiết như trong định lý 2.9, nghiệm tổng quát của phương
trình vi phân tuyến tính không thuần nhất (2.7) bằng tổng của một nghiệm riêng nào
đó của nó và nghiệm tổng quát của phương trình thuần nhất tương ứng.
Chứng minh: Giả sử yr (x) là một nghiệm riêng nào đó và y (x) là nghiệm tuỳ ý của
phương trình không thuần nhất L(y ) = g . Giả sử {u1(x),u2(x),...,un(x)} là hệ nghiệm
cơ bản của phương trình thuần nhất tương ứng. Theo giả thiết ta có L(y −yr ) = 0. Nói
cách khác, y (x )−yr (x) là nghiệm của phương trình thuần nhất tương ứng. Theo định
lý 2.12, tồn tại các hằng số C sao cho 1, . . . , Cn
y (x )−yr (x ) = C1u1(x )+···+Cn un(x ) =: u(x ).
Vì vậy, y (x ) = yr (x) + u(x).
Ví dụ: Cho phương trình y 00 + 4y = e x. Dễ thấy cos2x và sin2x là hai nghiệm độc
lập tuyến tính của phương trình thuần nhất tương ứng y 00 + 4y = 0. Một nghiệm
riêng của phương trình đã cho ban đầu là yr = 1e x. Do đó nghiệm tổng quát của 5 phương trình đã cho là 1
y = C1 cos2x + C2 sin2x + e x 5 trong đó C là hai hằng số tuỳ ý. 1, C2
Mệnh đề 2.2.3. Giả sử y
là nghiệm riêng của phương trình 1, y2
L (y ) = g1, L(y ) = g2 tương ứng. Khi đó
yr := y1 + y2
là nghiệm riêng của phương trình
L (y ) = g
với g := g1 + g2.
2.2 Lý thuyết tổng quát về phương trình vi phân tuyến tính cấp cao. 53
Nhận xét: Mệnh đề này giúp ta tìm nghiệm riêng của phương trình tuyến tính không
thuần nhất trong trường hợp hàm g (x ) ở vế phải có dạng tổng của các hàm đơn giản.
Ví dụ: Tìm nghiệm riêng của phương trình y 00 + y = x + cos3x.
Ta tìm các nghiệm riêng của các phương trình y 00 + y = x và y 00 + y = cos3x . Dễ
thấy phương trình thứ nhất có nghiệm riêng là y1 = x; còn phương trình thứ hai có
một nghiệm riêng (xem mục 2.3.2) là y
cos 3x . Do đó một nghiệm riêng của 2 = − 18 phương trình đã cho là 1
y = x − cos3x 8
2.2.4 Phương pháp biến thiên hằng số tìm nghiệm riêng của phương
trình không thuần nhất
Như đã biết, nghiệm tổng quát của phương trình vi phân tuyến tính không thuần
nhất bằng tổng của một nghiệm riêng của nó và nghiệm tổng quát của phương trình
thuần nhất tương ứng. Vấn đề đặt ra là tìm nghiệm riêng này.
Trong phần này ta sẽ giới thiệu một phương pháp thông dụng, gọi là phương pháp
biến thiên hằng số, để tìm nghiệm riêng của phương trình không thuần nhất dựa vào
nghiệm tổng quát của phương trình thuần nhất tương ứng.
Xét phương trình không thuần nhất
L (y ) = y (n) + p (n −1) 1(x ) y + ···+ pn y
−1(x ) 0 + pn (x )y = g (x ) (2.15)
trong đó các hàm pj(x) và g (x) liên tục trên (a,b ).
Giả sử u1(x),u2(x),...,un(x) là n nghiệm độc lập tuyến tính của phương trình
thuần nhất tương ứng và nghiệm tổng quát của nó là u(x ) = C1u1(x) + ··· + Cnun(x).
Xem các hằng số C1,C2,...,Cn như là các hàm theo biến x (biến thiên hằng số!), ta sẽ
nghiệm của (2.15) dưới dạng
y (x ) = C1(x )u1(x ) + ··· + Cn(x )un(x )
Một cách tự nhiên, ta thay y (x ) cùng với các đạo hàm của nó vào phương trình (2.15)
để tìm các hàm Cj(x). Vì ta chỉ có một phương trình vi phân trong khi có n ẩn là các
hàm Cj(x) nên ta có thể chọn thêm n − 1 hệ thức khác giữa các Cj(x) miễn là đủ để
giải các hàm này. Cụ thể, ta sẽ chọn các Cj(x) thoả n − 1 hệ thức sau: C 0u u 1
1(x ) + · · · + C 0 n n (x ) = 0
C 0u 0(x ) + · · · + C 0 u0 (x ) = 0 1 1 n n . (2.16) . .
C 0 u(n−2)(x)+···+C 0u(n−2)(x) = 0 1 1 n n
Và khi đó, các đạo hàm của y trở thành y 0 = C ( (x ),
1 u 0 x ) + · · · + C 1 n u 0n y 00 = C (
1 u 00 x ) + · · · + C (x ), 1 n u 00 n ...
y (n−1) = C ( (
1 u (n −1) x ) + x ) 1
··· + Cn u(n−1) n 54
Phương trình vi phân cấp cao Vì thế
y (n) = C1u(n)(x ) + ··· + C (x ) 1 n u (n ) n
+ C 0 u (n−1)(x ) + ··· + C 0 u(n−1)(x ) 1 1 n n
Như vậy, y sẽ thoả phương trình (2.15) miễn là
C 0u (n−1)(x ) + ··· + C 0 u(n−1)(x ) = g (x ) 1 1 n n
Kết hợp với (2.16), ta thu được hệ n phương trình cho C 0 là j C 0u u
1(x ) + · · · + C 0 n (x ) = 0 1 n
C 0u 0 (x ) + · · · + C 0u0 (x ) = 0 1 1 n n ... (2.17)
C 0 u(n−2)(x ) + ··· + C 0 u(n−2)(x ) = 0 1 1 n n
C 0 u(n−1)(x ) + ··· + C 0 u(n−1)(x ) = g (x ) 1 1 n n
Vì các hàm u1(x),u2(x),...,un(x) là độc lập tuyến tính nên hệ (2.17) xác định duy nhất
C 0(x ), . . . , C 0 (x ) theo u C ), . . . , C ) 1 n
1(x ), u2(x ), . . . , un (x ). Từ đó ta tìm được 1(x n (x .
Ví dụ: (n = 2) Cho phương trình
y 00 + p (x )y 0 + q (x )y = g (x ) Giả sử y
là hai nghiệm độc lập tuyến tính trên khoảng I của phương trình 1, y2 y 00 +
p (x )y 0 + q (x )y = 0. Tìm nghiệm riêng dưới dạng y = r
C1(x )y1(x ) + C2(x )y2(x ). Ta có
y 0 = C 0 y + C 0y . Ta chọn C sao cho trước hết: 1, C r 1 1 + C1 y 0 1 2 2 + C2 y 0 2 2 C 0 y y 1 1 + C 0 2 2 = 0
Khi đó y 00 = C 0y 0 + C 0y 0 + C + C
. Thay vào phương trình đã cho ta có: r 1 1 2 2 1 y 00 1 2 y 00 2
C 0y 0 + C 0 y 0 = g (x ) 1 1 2 2 Do đó ta có hệ C0y y 1 1 + C 0 2 2 = 0
C 0 y 0 + C 0y 0 = g (x ) 1 1 2 2
Giải hệ này với ẩn là C 0,C 0 ta được 1 2 y y C 0 = − 2g và C 0 = 1g 1 W [y 2 1, y2]
W [y1, y2] trong đó W [y
luôn khác không trên I .
1, y2] = y1 y 0 − y 0 y 2 1 2
Tích phân các phương trình này ta thu được nghiệm riêng Z Z y y
y (x ) = −y ( 2g 1g r 1 x )
d x + y (x ) d x W [y 2 W [y 1, y2] 1, y2]
2.3 Phương trình vi phân tuyến tính cấp cao hệ số hằng 55
Ví dụ: Tìm một nghiệm riêng của phương trình 1
y 00 + y = sinx Nghiệm riêng có dạng
yr = C1(x ) cos x + C2(x ) sin x
trong đó C 0,C 0 thỏa hệ phương trình 1 2
( C 0cosx +C 0 sinx = 0 1 2 1
−C 0sin x + C 0 cos x = 1 2 sin x Từ đó, cos x
C 0 = −1 và C 0 =
= (ln |sin x |)0. Vậy một nghiệm riêng thu được là 1 2 sin x
yr = −x cos x + ln| sin x |.sin x
2.3 Phương trình vi phân tuyến tính cấp cao hệ số hằng
Trong mục này ta xét các phương trình vi phân tuyến tính với hệ số là các hằng số.
Dạng tổng quát của chúng là y (n) + A (n −1) 0 1 y + ··· + An y −1
+ An y = g (x ) (2.18)
và dạng thuần nhất tương ứng y (n) + A (n −1) 0 1 y + ··· + An y −1 + An y = 0 (2.19)
2.3.1 Nghiệm của phương trình thuần nhất hệ số hằng
Ta viết lại phương trình (2.19) dưới dạng toán tử (D n + A + + 1D n −1 + · · ·
An−1D An)y = 0 (2.20)
với D như thường lệ ký hiệu cho toán tử tuyến tính d . Gọi λ , j = 1,n, là các d x j
nghiệm (có thể phức) của phương trình λn + A n −1 1λ
+ ··· + An−1λ + An = 0 (2.21)
mà được gọi là phương trình đặc trưng của (2.19). Khi đó, một cách hình thức có thể
viết (2.20) dưới dạng (do tính chất giao hoán của D và phép nhân với hằng số) (D − λ (
1)(D − λ2) . . . D − λn ) y = 0
Phương trình này được thoả mãn đối với mỗi nghiệm của các phương trình vi phân bậc nhất sau (D − λ ( 1) y = 0,
D − λ2)y = 0,..., (D − λn)y = 0
Nghiệm tổng quát của mỗi phương trình này là yj = Cj e λj x 56
Phương trình vi phân cấp cao
Bổ đề 2.16. Hệ các hàm e λ1x,e λ2x,...,e λnx là độc lập tuyến tính trên R nếu các λj khác nhau từng đôi một.
Chứng minh: Định thức Wronski của n hàm này là e λ1x e λ2x ··· e λn x
λ1e λ1x λ2e λ2x ··· λn e λn x W (x ) = .. .. . . ... ...
λn−1e λ1x λn−1 e λ2x ··· λn−1e λnx 1 2 n 1 1 ··· 1 λ1 λ2 ··· λn
= e (λ1+···+λn)x .. .. . . ... ...
λn−1 λn−1 ··· λn−1 1 2 n Y
= e (λ1+···+λn)x
(λi − λj ) 6= 0 i > j
(để ý định thức sau cùng chính là định thức Vandermon).
Trường hợp I: Phương trình đặc trưng có n nghiệm thực phân biệt.
Theo bổ đề trên, nếu phương trình đặc trưng (2.21) tương ứng với (2.19) có n nghiệm
thực λ khác nhau từng đôi một thì nghiệm tổng quát của (2.19) là j
y = C1e λ1x + ··· + Cn e λn x
trong đó C là các hằng số tùy ý. j
Ví dụ: Xét phương trình y 00 + 2y 0 − 3y = 0, phương trình đặc trưng tương ứng λ2 +
2λ − 3 = 0 có hai nghiệm thực phân biệt λ1 = 1 và λ2 = −3. Nghiệm tổng quát của phương trình đã cho là
y = C1e x + C2e −3x
Trường hợp II: Phương trình đặc trưng có nghiệm phức.
Giả sử các hệ số A
đều thực và phương trình đặc trưng (2.21) có nghiệm phức 1, . . . , An λ . Vì vậy, dùng hệ thức
r = α + i β . Khi đó nó cũng có nghiệm phức λs = α − i β = λr Euler, ta có C λr x λs x r e + Cs e
= e αx {Cr (cosβ x + i sin β x ) + Cs (cosβ x − i sin β x )} = e αx ( ˜ Cr cosβ x + ˜ Cs sinβ x )
Để ý rằng nếu các hệ số A là một nghiệm phức
j trong (2.19) là thực và y = y1 + i y2
của (2.19) thì phần thực và phần ảo cũng là nghiệm của nó. Vậy phần nghiệm tổng
quát tương ứng với λr và liên hợp phức với nó λs là
e αx (C1 cosβ x + C2 sin β x )
2.3 Phương trình vi phân tuyến tính cấp cao hệ số hằng 57 trong đó C và
là những hằng số thực tuỳ ý. 1 C2
Ví dụ: Xét phương trình y 00 −2y 0 +5y = 0, phương trình đặc trưng λ2 −2λ+5 = 0 có
hai nghiệm phức liên hợp là λ1,2 = 1±2i. Do đó nghiệm tổng quát là y = e x(C1 cos2x + C2 sin2x ).
Trường hợp III: Phương trình đặc trưng có nghiệm bội.
Nếu phương trình đặc trưng nhận λ là nghiệm (thực) bội m, khi đó vế trái của
phương trình (2.20) chứa nhân tử dạng (D −λ)m. Ta xét phương trình vi phân cấp m tương ứng
(D − λ)m y = 0
Nghiệm của phương trình này có thể tìm dưới dạng
y = e λx V (x )
trong đó V (x ) là hàm cần xác định. Ta có:
(D − λ)m e λx V (x ) = (D − λ)m−1e λx DV (x )
= (D − λ)m−2e λx D 2V (x )
= ··· = e λx D mV (x )
Do đó y = e λxV (x ) là nghiệm của (2.19) nếu D mV (x ) = 0. Vậy V (x ) phải là đa thức
bậc m − 1 theo x và nghiệm cần tìm là
y = (C1 + C2x + ··· + Cm x m−1)e λx
Trong trường hợp nghiệm bội λ = α + iβ là số phức thì phương trình đặc trưng (giả
sử các hệ số đều thực) cũng có nghiệm bội là α−iβ với cùng số bội như λ. Khi đó ta
khi đó vế trái của phương trình (2.20) chứa nhân tử dạng (D −α+iβ)m(D −α−iβ)m.
Lập luận tương tự ta cũng tìm được nghiệm là
y = (C1 + C2x + ··· + Cm x m−1)e λx cosβ x + (D1 + D2x + ··· + Dm x m−1)e λx sinβ x
với 2m hằng số C , tuỳ ý. j Dj
Ví dụ: Nghiệm tổng quát của phương trình y (4) +2y 00 + y = 0 là y = (C1 +C2x)cos x +
(C3 + C4x ) sin x .
2.3.2 Tìm nghiệm riêng của phương trình không thuần nhất:
Trong mục trước ta đã biết cách tìm nghiệm riêng của phương trình không thuần
nhất bằng phương pháp biến thiên hằng số từ các nghiệm của phương trình thuần
nhất tương ứng. Trong một số trường hợp mà hàm g (x ) ở vế phải của phương trình
(2.18) có dạng đặc biệt, ta có thể tìm được nghiệm riêng của nó theo phương pháp
sau đây (tạm gọi là phương pháp hệ số bất định). 58
Phương trình vi phân cấp cao
Trường hợp I: g (x ) = e αxPm(x)
(ở đây Pm(x) là đa thức bậc m)
a) Nếu α không phải là nghiệm của phương trình đặc trưng thì nghiệm riêng có thể tìm dưới dạng
yr = e αxQm (x )
b) Nếu α là nghiệm bội k của phương trình đặc trưng thì nghiệm riêng có thể tìm dưới dạng y k
r = x e αx Qm (x )
trong đó Qm(x) là đa thức tổng quát bậc m mà ta phải xác định các hệ số của nó.
Ví dụ: Tìm nghiệm riêng của phương trình
y 00 − 3y 0 + 2y = (3 − 4x )e x
Phương trình đặc trưng là
λ2 − 3λ + 2 = 0
có hai nghiệm là λ1 = 1 và λ2 = 2, trong đó α = 1 là nghiệm đơn của nó nên nghiệm riêng có dạng
yr = x e x (Ax + B )
Thay vào phương trình đã cho và cân bằng các hệ số ta thu được hệ −2A =4 2A − B = 1
Giải ra ta được A = 2 và B = 1, khi đó nghiệm riêng là yr = xe x(2x + 1). Cuối cùng,
nghiệm tổng quát của phương trình đã cho là y = C1e x + C2e 2x + xe x(2x + 1).
Trường hợp II: g (x ) = e αx{P (x)cosβ x +Q(x)sinβ x}
(ở đây P (x ),Q(x ) là hai đa thức nào đó)
a) Nếu α+iβ không phải là nghiệm của phương trình đặc trưng thì nghiệm riêng có thể tìm dưới dạng
yr = e αx {R (x ) cosβ x + S(x ) sinβ x }
b) Nếu α + iβ là nghiệm bội k của phương trình đặc trưng thì nghiệm riêng có thể tìm dưới dạng y k
r = x e αx {R (x ) cos β x + S (x ) sin β x }
2.3 Phương trình vi phân tuyến tính cấp cao hệ số hằng 59
trong đó R(x ),S(x ) là hai đa thức có bậc bằng max{deg(P ),deg(Q)} mà các hệ số của
chúng được tìm nhờ phương pháp hệ số bất định.
Ví dụ: Tìm nghiệm tổng quát của phương trình y 00 + y = 4x sin x
Phương trình đặc trưng có nghiệm là ±i và α + iβ = i là nghiệm đơn (bội 1) của
nó nên nghiệm riêng có dạng
yr = x [(A x + B ) cos x + (C x + D ) sin x ]
Thay vào phương trình đã cho và cân bằng các hệ số ta được −2A = 2 A = −1 C − B = 0 B = 0 ⇔ D + A = 0 C = 0 2C = 0 D = 1
Vì thế, nghiệm riêng là yr = x(−x cos x +sin x) và nghiệm tổng quát của phương trình đã cho là
y = C1 cos x + C2 sin x + x (sin x − x cos x )
Chú ý: Nếu g (x) không có các dạng đặc biệt trên nhưng có thể viết thành
g (x ) = g1(x ) + ··· + gm(x )
trong đó mỗi g có dạng đặc biệt như trên thì ta tìm nghiệm riêng dưới dạng j
yr = y1 + ··· + y2
trong đó y là nghiệm riêng của phương trình tương ứng với g j. j
Ví dụ: Tìm nghiệm tổng quát của phương trình y 00 − y 0 = 5e x − sin2x.
Ta lần lượt tìm nghiệm riêng của các phương trình y 00 − y 0 = 5e x và y 00 − y 0 =
−sin2x theo phương pháp trên. Kết quả ta được hai nghiệm riêng là y1 = 5x e x và 1 1 y2 = sin2x −
cos 2x . Do đó nghiệm riêng của phương trình đã cho là yr = y + y 5 10 1 2 = 1 1 5x e x + sin 2x − cos 2x . 5 10 BÀI TẬP
1. Giải các phương trình vi phân cấp cao sau đây:
(a) x − e y00 + y 00 = 0
(b) y 02 + 2y y 00 = 0 (c) y 0
y 00 = x − x
(d) y 002 + x 2 = 1 60
Phương trình vi phân cấp cao
(e) y 00 = a y 0(1 + y 02)
2. Giải các phương trình vi phân tuyến tính cấp II biết một nghiệm riêng của nó
(a) x 2(ln x −1)y 00−x y 0+y = 0, biết rằng nó có một nghiệm riêng dạng y (x) = xα
(b) (2x − x2)y 00 + (x2 − 2)y 0 + 2(1 − x)y = 0, y (1) = 0, y 0(1) = 1, biết rằng nó có
một nghiệm riêng dạng y (x ) = e x
(c) (2x − x2)y 00 + 2(x − 1)y 0 − 2y = −2, biết rằng nó có hai nghiệm riêng dạng
y1(x ) = 1 và y2(x ) = x
3. Giải các phương trình tuyến tính hệ số hằng sau đây
(a) y 00 − 7y 0 + 6y = sin x
(b) y 00 + 9y = 6e 3x
(c) y 00 − 9y 0 + 20y = x2e 4x
(d) y 00 − 3y 0 = e 3x − 18x
(e) y 00 + y = x 2 cos2 x − 18x
(f) y 00 − 4y 0 + 4y = e 2x cos2 x
4. Tìm nghiệm tổng quát của các phương trình vi phân sau đây: (a) e x
y 00 − y = e x +1
(b) y 00 + y = tan x (c) p
y 00 + 2y 0 + y = 3e −x x + 1 (d) 1
y 00 + 5y 0 + 6y = e2x +1
5. Tìm phương trình vi phân tuyến tính thuần nhất cấp II biết hệ nghiệm cơ bản: (a) {x3, x4} (b) {x, xe x}
6. Tìm nghiệm tổng quát của các phương trình vi phân sau đây:
(a) y 000 − 4y 00 − y 0 + 4y = 0
(b) y (4) − 5y 00 + 4y = 0
(c) y 000 − 2y 0 + 4y = 0
7. Giải các bài toán giá trị ban đầu
(a) y 00 − 4y = −7e 2x + x, với y (0) = 1, y 0(0) = 3
(b) y 00 + 4y = 34cos x + 8, với y (0) = 3, y 0(0) = 2
(c) y 00 + y = 5sin2 x , với y (0) = 2, y 0(0) = −4
2.3 Phương trình vi phân tuyến tính cấp cao hệ số hằng 61
8. Với các giá trị nào của các số thực a,b thì phương trình
y 00 + a y 0 + b y = 0
(a) có mọi nghiệm triệt tiêu tại ∞
(b) có mọi nghiệm giới nội trên (0,+∞)
(c) có mọi nghiệm tuần hoàn trên R
(d) mỗi nghiệm đều có vô số không điểm. R
9. Chứng tỏ rằng với phép đổi ẩn y = z e −12 p(x)dx có thể đưa phương trình y 00 +
p (x )y 0 + q (x )y = 0 về dạng z 00 +Q (x )z = 0.
Áp dụng vào giải phương trình y 00 − 2x y 0 + x2y = 0 62
Phương trình vi phân cấp cao Chương 3
Hệ phương trình vi phân
Trong chương này ta sẽ nghiên cứu các hệ phương trình vi phân cấp I, đặc biệt là các
hệ phương trình vi phân tuyến tính mà cấu trúc nghiệm của nó tương tự như trường
hợp phương trình vi phân tuyến tính cấp cao.
3.1 Hệ phương trình vi phân cấp I tổng quát.
3.1.1 Các định nghĩa:
Hệ phương trình vi phân tổng quát là hệ gồm các phương trình chứa biến độc lập,
các hàm (nghiệm) cần tìm và nhất thiết phải chứa các đạo hàm của chúng theo biến
độc lập. Nếu chỉ xuất hiện các đạo hàm cấp I của các ẩn, ta nói hệ đó là hệ phương trình vi phân cấp I.
Ta nói một hệ gồm n phương trình vi phân cấp I là có dạng chuẩn tắc (dạng giải
ra được đối với đạo hàm) nếu có thể viết dưới dạng: d y 1 = f (
1 x , y1, . . . , yn ) d x
d y2 = f (x , y d x 2 1, . . . , yn ) (3.1)
· · · · · · · · · · · · · · · · · · · · · d y n
= f (x , y d x n 1, . . . , yn )
trong đó x là biến độc lập, y1,..., yn là các ẩn cần tìm.
Hệ phương trình chuẩn tắc trên có thể viết lại dưới dạng thu gọn nhu sau
y 0 = f (x , y ) (3.2)
trong đó y = (y1,..., yn)T , y 0 = (y 0,..., y 0)T và f = (f1,..., fn)T . 1 n 64 Hệ phương trình vi phân
Định nghĩa 3.1. Mỗi nghiệm của hệ (3.1) là một bộ gồm n hàm y1 = φ1(x),..., yn =
φn(x ) khả vi liên tục trên khoảng I ⊂ R mà khi thay vào (3.1) thì được đẳng thức đúng.
3.1.2 Liên hệ giữa hệ phương trình và phương trình vi phân cấp cao.
Với một số giả thiết nào đó, việc giải hệ phương trình (3.1) có thể đưa về giải phương
trình vi phân cấp cao dựa trên phương pháp khử sau đây. Đạo hàm hai vế của
phương trình đầu tiên của hệ (3.1), ta được ∂ f ∂ f ∂ f y 00 = 1 + 1 y 0 + ···+ 1 y 0 1 ∂ x ∂ y 1 n 1 ∂ yn
Thay các y 0 bởi các biểu thức của nó, ta có thể viết y 00 như là hàm của x , y j 1 1, . . . , yn y 00 = F 1
1(x , y1, . . . , yn )
Lại lấy đạo hàm hai vế đẳng thức này theo x , ta có ∂ F ∂ F ∂ F y 000 = 1 + 1 y 0 + ···+ 1 y 0 1 ∂ x ∂ y 1 n 1 ∂ yn
=: F2(x , y1, . . . , yn )
Tiếp tục quá trình trên cho đến đạo hàm cấp n của y ta được hệ 1 y 0 = f 1
1(x , y1, . . . , yn ) y 00 = F 1
1(x , y1, . . . , yn )
· · · · · · · · · · · · · · · · · · · · ·
y (n) = F 1
n −1(x , y1, . . . , yn )
Trong hệ này ta xét n − 1 phương trình đầu tiên với n − 1 ẩn là y . Với một vài 2, . . . , yn
điều kiện nào đó (thoả mãn giả thiết của định lý hàm ngược) ta có thể giải được (duy nhất) các y . Thay biểu thức của
2, . . . , yn như là hàm theo các biến x , y1, y 0, . . . , y (n −1) 1 1
chúng vào phương trình cuối cùng của hệ, ta có y (n) = F
, . . . , y (n−1) ) 1
n (x , y1, y 0 1 1
Đây là phương trình vi phân cấp n dạng đã giải ra đối với đạo hàm. Giải phương
trình này để tìm y , rồi tính các đạo hàm
. Từ đó ta tính được các . 1
y 0 , . . . , y (n−1) y2, . . . , y 1 1 n
Ngược lại, cho trước phương trình vi phân cấp n dạng
y (n) = f (x , y , y 0, . . . , y (n−1))
3.1 Hệ phương trình vi phân cấp I tổng quát. 65
ta có thể đưa về một hệ phương trình vi phân dạng chuẩn tắc bằng cách đặt y1 = y ,
yk+1 = y 0k y 0 = y 1 2 y 0 = y 2 3
· · · · · · · · · · · · · · ·
y 0 = f (x, y n
1, y2, . . . , yn )
Ví dụ: Giải hệ sau d x d y = y , = x d t d t
Đạo hàm hai vế của phương trình đầu rồi kết hợp với phương trình sau ta được phương trình
d 2x − x = 0 d t 2
từ đó nghiệm tổng quát là
x = x (t ) = C1e −t + C2e t
Từ phương trình thứ nhất ta tính được
y = y (t ) = −C1e −t + C2e t
3.1.3 Sự tồn tại và duy nhất nghiệm
Đối với hệ phương trình vi phân cấp I, bài toán Cauchy được phát biểu một cách
tương tự nhu trường hợp một phương trình: Tìm nghiệm y1(x),..., yn(x) của hệ (3.1)
thoả điều kiện ban đầu
yj (x0) = y 0,
j = 1, 2, . . . , n (3.3) j
trong đó các giá trị x
cho trước, gọi là giá trị ban đầu.
0 ∈ I , y 0, . . . , y 0 1 n
Để ý rằng không phải bao giờ định lý Cauchy cũng có (duy nhất ) nghiệm. Định
lý sau đây giải quyết bài toán này đối với hệ chuẩn tắc.
Định lý 3.2 (Sự tồn tại và duy nhất nghiệm). Giả sử các hàm f1(x, y ),..., fn(x, y ) trong
(3.1) là liên tục trên một tập mở G ⊂ Rn+1 chứa (x
) và thoả điều kiện Lip-
0, y 0 , . . . , y 0 1 n
schitz theo biến y . Khi đó trong một lân cận nào đó của x có tồn tại một nghiệm 0
y1(x ), . . . , y (
n x ) thoả bài toán Cauchy với điều kiện ban đầu đã cho và nghiệm đó là duy nhất.
Chứng minh: : Viết lại hệ dưới dạng d y = f (x , y ), trong đó y := (y d x
1, . . . , yn )T và
f := ( f1, . . . , fn )T và lập lại các bước chứng minh nhu trong định lý tồn tại và duy nhất
cho phương trình vi phân cấp I.
Nhận xét: Thay cho điều kiện Lipschitz ta có thể yêu cầu (mạnh hơn rằng) hàm
f (x , y ) có các đạo hàm riêng theo biến y bị chặn. 66 Hệ phương trình vi phân
Định nghĩa 3.3. Giả sử tập G thoả mãn tất cả các giả thiết của định lý 3.2. Khi đó n hàm
yj = yj (x , C1, . . . , Cn )
j = 1, 2, . . . , n (∗)
phụ thuộc vào n tham số C
và có các đạo hàm riêng theo x được gọi là nghiệm 1, . . . , Cn
tổng quát của hệ (3.1) nếu: • Với mỗi (x
) trong G , từ hệ (∗) có thể giải được (duy nhất) các hằng số
0, y 0, . . . , y 0 1 n C . 1, . . . , Cn
• Tập hợp n hàm trong (∗) là nghiệm của hệ (3.1) với mỗi bộ giá trị của các tham số C giải ra đối với mỗi 1, . . . , Cn
(x , y1, . . . , yn ) ∈ G .
Định nghĩa 3.4. Nghiệm của hệ mà tại mỗi điểm của nó thoả mãn các điều kiện của
định lý 3.2 được gọi là nghiệm riêng của hệ. Ngược lại, nghiệm của hệ mà tính chất
duy nhất nghiệm bị vi phạm được gọi là nghiệm kỳ dị.
Ví dụ: Kiểm tra rằng hệ các hàm
y1(x)=C1e−x +C2e−3x
y2(x ) = C1e −x + 3C2e −3x + cos x
là nghiệm tổng quát của hệ
y0(x)=−y 1 2 + cos x
y 0(x ) = 3y 2
1 − 4 y2 + 4 cos x − sin x
Ta có f1(x, y1, y2) = −y2 + cos x và f2(x, y1, y2) = 3y1 − 4y2 + 4cos x − sin x, do đó chúng
có các đạo hàm riêng liên tục trên R3.
Với mỗi (x , y1, y2) ∈ R3, ta luôn có thể giải được (duy nhất) các C1,C , cụ thể 2
C1 = 1ex(3y 2
1 − y2 + cos x )
C2 = 1 e −3x (y 2
2 − y1 − cos x
Ngoài ra, từ các hàm đã cho, ta có
y0(x)=−C 1
1e −x − 3C2e −3x
y 0 (x ) = −C 2
1e −x − 9C2e −3x − sin x
nên chúng là nghiệm của hệ nói trên.
3.1.4 Các phương pháp giải hệ phương trình vi phân:
a) Đưa hệ về phương trình cấp cao:
Nhờ mối liên hệ chặt chẽ giữa hệ phương trình vi phân cấp I và phương trình vi
phân cấp cao, ta có thể đưa việc giải hệ phương trình vi phân về giải phương trình
vi phân cấp cao, như ví dụ trên. Ta xét một ví dụ khác
3.1 Hệ phương trình vi phân cấp I tổng quát. 67
Ví dụ: Tìm nghiệm của hệ chuẩn tắc y0 =−y 1 2 + cos x y 0 = 3y 2
1 − 4 y2 + 4 cos x − sin x
Ta đưa hệ phương trình đã cho về phương trình vi phân cấp II với ẩn là y . Đạo hàm 1
hai vế phương trình đầu tiên ta được y 00 = −y 0 1 − sin x 2
= −(3y1 − 4y2 + 4cos x − sin x )
= −3y1 + 4y2 − 4cos x
Thay y 0 từ phương trình thứ II ta được: 2
y 00 + 4y 0 − 3y 1 1 1 = 0
Phương trình thuần nhất này có nghiệm tổng quát là
y1 = C1e −x + C2e −3x
Từ phương trình thứ nhất ta tìm được
y2 = C1e −x + 3C2e −3x + cos x
b) Phương pháp lập tổ hợp tích phân:
Cho hệ phương trình vi phân cấp I
d yi = f (x, y d x i 1, . . . , yn ),
với i = 1,2,...,n
Để giải hệ này ta có thể tìm một phương trình hệ quả (chẳng hạn tổ hợp tuyến tính
của các phương trình trên) của hệ đã cho, dễ lấy tích phân hơn, và được gọi là tổ hợp
tích phân của hệ phương trình đã cho.
Ví dụ: Bằng cách lập tổ hợp tích phân, giải hệ sau d x d y = y , = x d t d t
Lấy hai phương trình đã cho cộng và trừ với nhau ta được
d (x + y ) = x + y và d(x − y ) = −(x − y ) d t d t
Giải từng phương trình, ta thu được hệ
x + y = C1e t
và x − y = C2e −t 68 Hệ phương trình vi phân
Và từ đây ta tìm được nghiệm x (t ), y (t ).
Nhận xét: Mỗi tổ hợp tích phân có thể viết dưới dạng
Φ(x , y1, . . . , yn ) = C
và phương trình này (hoặc vế trái của nó) được gọi là tích phân đầu của hệ.
Nếu tìm được k tổ hợp tích phân của hệ Φ
1(x , y1, . . . , yn ) = C1
Φ2(x , y1,..., yn) = C2
................................
Φk(x, y1,..., yn) = Ck
và nếu k tích phân đầu này độc lập, thì có thể đưa về giải hệ gồm n −k phương trình.
Trường hợp k = n, khi đó n tích phân đầu độc lập cho ta nghiệm tổng quát của hệ.
Ví dụ: Tích phân hệ phương trình sau đây d x d y d z = z − y , = x − z , = y − x d t d t d t
Cộng các phương trình với nhau ta được
d (x + y + z ) = 0 d t
Phương trình này cho một tích phân đầu là
φ1 = x + y + z = C1
Bây giờ nhân các phương trình với x , y,z lần lượt rồi cộng lại, ta được
d (x 2 + y 2 + z 2) = 0 d t
từ đây ta cung thu được tích phân đầu
φ2 = x 2 + y 2 + z 2 = C2
Ta dễ kiểm tra rằng φ
cũng là một tích phân đầu nhung bộ ba
3 = x y + y z + z x = C3
gồm các tích phân đầu φ1,φ2,φ3 không độc lập tuyến tính nên không thể cho nghiệm tổng quát của hệ.
Tuy nhiên, từ hai tích phân đầu đầu tiên, ta giải để tìm x , y : 1 q x = C 2C + 2C 2 1 − z − 2 − C 2 1 1 z − 3z 2 1 q y = C 2C + 2C 2 1 − z + 2 − C 2 1 1 z − 3z 2
3.2 Một số định lý cơ bản của phương trình vi phân 69
Thay các biểu thức này vào phương trình cuối d z q = 2C
+ 2C1z − 3z 2 d t 2 − C 2 1 ta tìm được nghiệm 3z − C p arcsin 1 Æ − 3t = C3 6C2 − 2C 21
Kết hợp với hai tích phân đầu φ1,φ2 ta tìm được nghiệm tổng quát của hệ.
3.2 Một số định lý cơ bản của phương trình vi phân
3.2.1 Sự tồn tại nghiệm:
Trong định lý tồn tại và duy nhất nghiệm của bài toán Cauchy, điều kiện Lipschitz
không thể bỏ được. Định lý sau đây khẳng định sự tồn tại (nhưng không duy nhất!)
của nghiệm, không đòi hỏi điều kiện Lipschitz.
Định lý 3.5 (Peano). Xét hình hộp A = {(x, y ) ∈ R×Rn/|x − x0| ≤ a,||y − y0|| ≤ b} và giả
sử f : A → Rn liên tục. Đặt M = maxA ||f (x, y )|| và α = min(a,b /M ). Khi đó bài toán
Cauchy y 0 = f (x , y ), y (x
có ít nhất một nghiệm trên [x0 − α, x0 + α]. 0) = y0
Nhận xét: Trước hết hãy lưu ý rằng ta không thể sử dụng phương pháp lặp Picard
vì không có đủ giả thiết bảo đảm dãy xấp xỉ Picard hội tụ. Thay vào đó, người ta xây
dựng các nghiệm xấp xỉ (địa phương) bởi tiếp tuyến của nó
y (x + h ) ∼
= y (x ) + h . f (x , y (x )) Với
h cho trước ta xây dựng dãy xn , yn xác định bởi: n ≥0
yn+1 = yn + h f (xn , yn ),
xn+1 = xn + h. (3.4)
Ta gọi yh(x) là hàm tuyến tính từng khúc qua các điểm (xn, yn); đồ thị của nó được gọi là đa giác Euler.
Bổ đề 3.6. Với các giả thiết trong định lý 4.1 và với h := α/N (N ∈ N), đa giác Euler thoả (x , y (
h x )) ∈ A với mọi x ∈ [x0, x0 + α]. Ngoài ra, ||y 0 0 0
h (x ) − yh (x )|| ≤ M |x − x |
với mọi x , x ∈ [x0, x0 + α]
Chứng minh: Qui nạp theo n. Giả sử điều đó đúng với n, i.e. kyn − y0k ≤ b , ta có
||yn+1 − yn|| ≤ hM
nên, với n + 1 ≤ N ta đều có
||yn+1 − y0|| ≤ (n + 1)hM ≤ αM ≤ b 70 Hệ phương trình vi phân
Điều này chứng tỏ (x , yh(x)) ∈ A với mọi x ∈ [x0, x0 + α].
Bất đẳng thức trong mệnh đề là hiển nhiên đúng vì yh(x) là tuyến tính từng khúc
và có “hệ số góc” bị chặn bởi M .
Để chứng minh định lý ta cần khái niệm sau:
Định nghĩa 3.7. Họ hàm fλ : I → Rn được gọi là đồng liên tục nếu với mọi ϵ > 0, có
tồn tại một δ > 0 (không phụ thuộc vào cả ϵ lẫn λ) sao cho
∀λ, ∀x , x 0 |x − x 0| < δ =⇒ ||fλ(x ) − fλ(x 0)|| < ϵ
Định lý 3.8 (Arzela-Ascoli). Cho họ các hàm fλ : [a,b ] → Rn đồng liên tục và bị chặn đều trên
[a , b ]. Khi đó họ hàm f có chứa một dãy con λ
{gn(x )} hội tụ đều đến một
hàm g (x ) liên tục trên [a,b ].
Chứng minh: Xem giáo trình giải tích hàm.
Chứng minh định lý Peano:
Xét đa giác Euler yh(x) với h = α/N , Dãy này bị chặn và đồng liên tục (theo Bổ đề
4.2) nên theo định lý Arzela−Ascoli, họ hàm yh(x) có chứa một dãy con hội tụ đều
về hàm liên tục y : [a,b ] → Rn
Ta chỉ ra rằng hàm giới hạn này chính là nghiệm của bài toán Cauchy. Ta xét
x ∈ [x0, x0 + α] (trên [x0 − α, x0] ta xét tương tự), ký hiệu k = k (h) là chỉ số sao cho
x ∈ [xk , xk+1], với xk = x0 + k h. Khi đó, trên đoạn con này ta có
yh (x ) − y0 = h f (x0, y0) + ··· + h f (xk−1, yk−1) + (x − xk )f (xk , yk )
với các cặp giá trị (xj, yj) là các xấp xỉ bằng phương pháp Euler (xem (4.1)).
Vì f liên tục nên khả tích, và có thể viết Z x
f (t , y (t ))d t = h f (x0, y (x0)) + ··· + h f (xk x y
−1, y ( k −1)) + (x − xk ) f (xk ,
(xk )) + r (h) x0
với r (h) → 0 khi h → 0.
Tính liên tục đều của f trên A và sự hội tụ đều của dãy con của {yh(x)} đến y (x) cho phép ta đánh giá
||f (x , yh(x )) − f (x , y (x ))|| < ϵ
với h đủ bé. Khi đó từ các đẳng thức trên ta có Z x y
f (t , y (t ))d t ≤ ϵ|x − x r (h )
εα + r (h)
h (x ) − y0 − 0| + || || ≤ || || x0
Cho h → 0 ta thấy hàm y (x) thoả mãn phương trình tích phân Z x
y (x ) = y +
f (t , y (t ))d t 0 x0
mà nghiệm của nó chính là lời giải của bài toán Cauchy.
Nhận xét: Định lý Peano hoàn toàn không chứa thông tin về sự duy nhất nghiệm.
3.2 Một số định lý cơ bản của phương trình vi phân 71
3.2.2 Thác triển nghiệm và sự tồn tại toàn cục:
Ta quan tâm đến bài toán kéo dài nghiệm của bài toán Cauchy y 0 = f (x , y ) với điều
kiện ban đầu y (x0) = y0.
Định nghĩa 3.9. Hàm f : U → Rn (với U là mở trong R × Rn) được gọi là thoả điều
kiện Lipschitz địa phương trên U nếu tại mỗi (x0, y0) ∈ U đều tồn tại lân cận V ⊂ U
sao cho f thoả điều kiện Lipschitz trên V .
Nhận xét: Nếu hàm f thuộc lớp C 1 trên U thì thoả điều kiện Lipschitz địa phương.
Bổ đề 3.10. Nếu f : U → Rn liên tục và thoả điều kiện Lipschitz địa phương trên U thì với mọi (x sao cho:
0, y0) ∈ U đều tồn tại một khoảng mở Imax = (ω_, ω+) 3 x0
• Bài toán Cauchy y 0 = f (x , y ) với y (x có nghiệm duy nhất trên 0) = y0 Imax
• Nếu z : I → Rn là một nghiệm nào đó của bài toán Cauchy này thì I ⊂ I và max z = y | . I
Chứng minh: Chỉ cần đặt I
và bài toán Cauchy có nghiệm trên
max = ∪ I /I mở chứa x0 I
Sau đó xác định hàm y : I ,
max → Rn theo cách sau: Với x ∈ Imax
x phải thuộc một I
nào đó, mà trên đó bài toán Cauchy có nghiệm. Khi đó, ta gán y (x ) bởi giá trị của
nghiệm đó tại x . Phần còn lại, ta cần chỉ ra nghiệm như thế là xác định tốt và duy
nhất. Chi tiết dành cho bạn đọc.
Định lý 3.11. Giả sử f :U → Rn liên tục và thoả điều kiện Lipschitz địa phương trên
U . Khi đó mỗi nghiệm của bài toán Cauchy đều có một thác triển đến biên của U .
Chính xác hơn, giả sử y : Imax → Rn là nghiệm qua (x0, y0) ∈ U , khi đó với mọi
compact K ⊂ U đều tồn tại x với sao cho 1, x2 ∈ Imax
x1 < x0 < x2 (x ( ( (
1, y x1)), x2, y x2)) / ∈ K .
Chứng minh: Giả sử Imax = (ω_,ω+). Nếu ω+ = ∞ thì hiển nhiên tồn tại x2 > x0 sao cho (x ( 2, y x2)) / ∈ K .
Xét trường hợp ω+ < ∞, giả sử có tồn tại compact K mà (x, y (x)) ∈ K với mọi
x ∈ (x0,ω+). Vì f bị chặn trên K nên Z x
||y (x ) − y (x 0)|| =
f (t , y (t ))d t ≤ M |x − x0| < ε x 0
nếu x , x 0 đủ gần ω+.
Điều này dẫn đến tồn tại lim ; và rõ ràng
x →ω y (x ) = y (ω + +
+, y+) ∈ K ⊂ U do K
compact. Theo định lý tồn tại và duy nhất nghiệm, có tồn tại nghiệm của bài toán
y 0 = f (x , y ), y trong lân cận của +(ω+) = y+
ω . Điều này vô lý vì Imax là cực đại. Chứng +
minh tương tự cho trường hợp x . 1 72 Hệ phương trình vi phân
3.3 Hệ phương trình vi phân tuyến tính
Trong mục này ta sẽ khảo sát các hệ phương trình vi phân tuyến tính dạng d x1
= a (t )x1 + a (t )x2 + ··· + a (t )yn + g1(t ) 11 12 1n d t
d x2 = a (t )x (t )x
··· a (t )y d t 21 1 + a22 2 + + 2n
n + g 2(t ) (3.5)
· · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · ·
d xn = a (t )x1 + an2(t )x ··· a (t )x d t n 1 2 + + nn
n + g n (t )
trong đó t là biến độc lập và x1(t ),..., xn(t ) là các ẩn hàm cần tìm, các hàm ai j(t ) và
gi (t ) lần lượt được gọi là các hệ số và hệ số tự do của hệ. Chúng được giả thiết liên
tục trên khoảng I = (a,b ) ⊂ R nào đó. Tên gọi hệ phương trình tuyến tính là do vế
phải là các hàm bậc nhất theo các ẩn hàm x1,..., xn.
Dùng ký hiệu ma trận, có thể viết hệ (3.5) dưới dạng thu gọn
x 0(t ) = A(t )x (t ) + g (t ) (3.6) trong đó
A(t ) = ai j (t ) là ma trận hàm cấp n × n, g (t ) = (g1(t ),...,gn(t ))T là vector cột.
Nếu g (t ) ≡ 0, ta nói hệ trên là hệ tuyến tính thuần nhất , nếu ngược lại, ta nói hệ
không thuần nhất. Định lý sau đây là một trường hợp riêng của định lý tồn tại và
duy nhất nghiệm tổng quát đối với bài toán Cauchy.
Định lý 3.12 (Tồn tại và duy nhất nghiệm). Giả sử các hệ số ai j(t ) và gi(t ) là các hàm
liên tục trên khoảng I 3 t0. Khi đó hệ phương trình (3.6) có duy nhất một nghiệm
x = x (t ) thoả điều kiện ban đầu
x (t0) = ξ (3.7)
trong đó, ξ ∈ Rn tùy ý.
3.3.1 Hệ tuyến tính thuần nhất:
Ta sẽ mô tả kỹ hơn không gian nghiệm của hệ thuần nhất mà, với ký hiệu ma trận,
có thể viết lại dưới dạng
x 0(t ) = A(t )x (t ) (3.8)
Trước hết hãy nhận xét rằng tập tất cả các nghiệm của một hệ thuần nhất có cấu
trúc không gian vector. Cụ thể ta có
Định lý 3.13. Giả sử ma trận A(t ) liên tục trên khoảng I ⊂ R. Khi đó tập nghiệm của
(3.8) là một không gian vector n chiều.
Chứng minh: Dễ kiểm tra tập nghiệm V của (3.8) là một không gian vector. Ta sẽ
chứng minh số chiều của nó là n. Thật vậy, giả sử {ξ1,...,ξn} là một cơ sở trong
3.3 Hệ phương trình vi phân tuyến tính 73
không gian n chiều. Theo định lý tồn tại và duy nhất nghiệm, với t0 ∈ I , có tồn tại n nghiệm ϕ của (3.8) sao cho 1, . . . , ϕn
ϕ1(t0) = ξ1, . . . , ϕn(t0) = ξn .
Ta chứng minh n nghiệm này độc lập tuyến tính. Thật vậy, nếu trái lại thì tồn tại các
hệ số α1,...,αn ∈ R không đồng thời bằng 0, sao cho n X αiϕi(t)=0,
với mọi t ∈ I . i =1
Với t = t , ta có 0 n X n X αi ϕi (t0) = αi ξi = 0. i =1 i =1
Nhưng do {ξ1,...,ξn} độc lập tuyến tính nên αi = 0,∀i = 1,n. Mâu thuẩn này chứng
tỏ n nghiệm ϕ độc lập tuyến tính. 1, . . . , ϕn
Bây giờ ta chứng minh các nghiệm ϕ1,...,ϕn lập thành cơ sở của không gian
nghiệm. Giả sử ϕ(t ) là một nghiệm tùy ý của (3.8) trên I . Đặt ξ = ϕ(t0), khi đó ta có biễu diễn n X ξ = Ci ξi . i =1 Đặt P ψ(t ) = n C ψ(t i =1
i ϕi (t ). Rõ ràng, ψ là nghiệm của (3.8) thỏa
0) = ξ; tức là cùng
điều kiện ban đầu với ϕ. Theo định lý tồn tại và duy nhất nghiệm, ta có n X
ϕ(t ) = ψ(t ) = Ci ϕi (t ) i =1
Do ϕ tùy ý, ta kết luận ϕ là cơ sở. 1, . . . , ϕn
Nhận xét: Để xây dựng nghiệm tổng quát của hệ (3.8), ta tìm n nghiệm độc lập tuyến
tính của nó. Nghiệm tổng quát sẽ là tổ hợp tuyến tính của n nghiệm này.
Định nghĩa 3.14. Tập gồm n nghiệm độc lập tuyến tính {ϕ1, ..., ϕn} của (3.8) được
gọi là tập nghiệm cơ bản của (3.8).
Ta ký hiệu Φ là ma trận vuông n × n mà các cột của nó là n nghiệm này
ϕ11 ϕ12 ··· ϕ1n
ϕ21 ϕ22 ··· ϕ
Φ(t ) = [ϕ 2n
1, . . . , ϕn ] = ··· ··· ··· ···
ϕn1 ϕn2 ··· ϕnn
Khi đó Φ được gọi là ma trận cơ bản của hệ. Định thức của nó cũng được gọi là định
thức Wronski của n nghiệm này.
Nếu gọi X (t ) = (x và thì hệ
i j (t ))n X 0(t ×n ) = (x 0 (t ))
n 2 phương trình sau đây được i j n ×n
gọi là phương trình vi phân ma trận.
X 0(t ) = A(t )X (t ) (3.9) 74 Hệ phương trình vi phân
Mệnh đề 3.3.1. Ma trận cơ bản của hệ (3.8) là một nghiệm của phương trình vi phân
ma trận (3.9) trên khoảng I.
Chứng minh: Kiểm tra trực tiếp.
Định lý 3.15 (Công thức Ostrogradski-Liouville). Giả sử A(t ) trong hệ (3.8) liên tục
trên một khoảng I nào đó và Φ(t ) là ma trận cơ bản của nó. Khi đó Z t
det Φ(t ) = det Φ(t0).exp trA(t)dt t0 trong đó trA(t) := a (
11 t) + · · · + ann(t) được gọi là vết của ma trận A(t ).
Chứng minh: Đặt Φ(t ) = (ϕ . Vì định thức i j (t )) det Φ( n ×n
t ) là tuyến tính theo mỗi hàng
của Φ(t ) nên ta có
ϕ11(t ) ··· ϕ1n(t ) ··· ··· ··· d n X (det Φ(t )) = det D
ϕ0 (t ) · · · ϕ0 (t ) d t i (t )
với Di(t ) = i1 i n i =1 ··· ··· ···
ϕn1(t ) ··· ϕnn(t )
trong đó ma trận Di(t ) suy từ ma trận Φ(t ) bằng cách thay dòng thứ i bởi các đạo hàm của nó.
Để ý rằng Φ(t ) là ma trận nghiệm của (3.9), tức là Φ0(t ) = A(t )Φ(t ), nên ta có ϕ0 (t ) = i j Pn a k =1
i k (t )ϕk j (t ). Từ đó
ϕ11(t ) ··· ϕ1n(t ) n X ··· ··· ··· det D a
ϕk1(t ) ··· ϕ i (t ) = i k (t ) det
←− hàng thứ i kn (t ) k =1 ··· ··· ···
ϕn1(t ) ··· ϕnn(t )
Nếu k 6= i thì định thức tương ứng ở vế phải bằng 0, do đó
det Di (t ) = aii (t ) detΦ(t ) Do đó d n X (det Φ(t )) = a
) det Φ( ) = trA(t).det Φ(t) d t i i (t t i =1
Tích phân phương trình vi phân này ta được điều phải chứng minh.
Nhận xét: Từ định lý trên ta thấy rằng hoặc detΦ(t ) 6= 0, ∀t ∈ I hoặc detΦ(t ) ≡ 0.
Định lý 3.16. Giả sử Φ(t ) là nghiệm của phương trình vi phân ma trận (3.9). Khi đó
Φ(t ) là ma trận nghiệm cơ bản của (3.8) khi và chỉ khi detΦ(t ) 6= 0.
3.3 Hệ phương trình vi phân tuyến tính 75
Chứng minh: Tương tự như chứng minh định lý (2.9).
Định lý 3.17. Nếu Φ(t ) là ma trận cơ bản của (3.8) và C là ma trận vuông không suy
biến (detC 6= 0) thì Φ(t )C cũng là ma trận cơ bản của (3.8). Ngoài ra, nếu Ψ(t ) là một
ma trận cơ bản khác của (3.8) thì có tồn tại ma trận hằng số không suy biến P sao
cho Ψ(t ) = Φ(t )C .
Chứng minh: Ta có (Φ(t )C )0 = Φ(t )0C = (A(t )Φ(t ))C = A(t )(Φ(t )C ). Vậy Φ(t )C là nghiệm
của (3.9). Hơn nữa, det(Φ(t )C ) 6= 0, nên Φ(t )C là ma trận cơ bản của (3.8).
Giả sử Ψ(t ) là ma trận cơ bản khác, ta xét Φ−1(t )Ψ(t ). Ta có
(Φ−1(t )Ψ(t ))0 = (Φ−1(t ))0Ψ(t ) + Φ−1(t )Ψ0(t )
= −[Φ−1(t )Φ0(t )Φ−1(t )]Ψ(t ) + Φ−1(t )A(t )Ψ(t )
= −[Φ−1(t )A(t )Φ(t )Φ−1(t )]Ψ(t ) + Φ−1(t )A(t )Ψ(t )
= −Φ−1(t )A(t )Ψ(t ) + Φ−1(t )A(t )Ψ(t ) = 0
Do đó Φ−1(t )Ψ(t ) = P , với P là ma trận hằng số.
Định nghĩa 3.18. Giả A(t ) liên tục trên I . Ma trận cơ bản của (3.8) gồm các nghiệm
thỏa điều kiện ban đầu
ϕk (t0) = ek
(trong đó ek là vector đơn vị thứ k trong Rn) được gọi là ma trận giải thức của hệ
(3.8), thường ký hiệu là R(t ,t0).
Mệnh đề 3.3.2. Giả sử Φ(t ) là ma trận cơ bản bất kỳ của (3.8). Khi đó
R (t , t0) = Φ(t )Φ−1(t0)
Chứng minh: Thật vậy, do tính chất tuyến tính của hệ (3.8), nghiệm ϕ(t ,t0,ξ) của hệ
này với điều kiện ban đầu ϕ(t0) = ξ ∈ Rn có thể viết dưới dạng
ϕ(t , t0, ξ) = R (t , t0)ξ
Mặt khác, Φ(t )Φ(t0)−1ξ cũng là một nghiệm của hệ này và thoả cùng điều kiện ban
đầu như ϕ(t ,t0,ξ). Do tính duy nhất nghiệm ta suy ra
R (t , t0)ξ = Φ(t )Φ(t0)−1ξ .
Điều này xảy ra với mọi ξ ∈ Rn, từ đó ta có kết luận.
Nhận xét: Cách biểu diễn R(t ,t0) = Φ(t )Φ−1(t0) không phụ thuộc vào ma trận cơ bản Φ.
Định lý sau cho ta vài tính chất đơn giản của ma trận giải thức:
Định lý 3.19. Giả sử A(t ) liên tục trên I 3 t0. Khi đó: 76 Hệ phương trình vi phân
a) R(t ,t0) là nghiệm duy nhất của phương trình vi phân ma trận (3.9) thỏa R(t0,t0) =
I (ma trận đơn vị cấp n n ).
b) R(t ,t0) = R(t ,t1)R(t1,t0)
c) R(t ,t0) khả nghịch ∀t ∈ I và R(t ,t0)−1 = R(t0,t )
d) Nghiệm duy nhất ϕ(t ,t0,ξ) thỏa điều kiện ban đầu ϕ(t0,t0,ξ) = ξ được cho bởi công thức
ϕ(t , t0, ξ) = R (t , t0)ξ
Chứng minh: Dành cho bạn đọc.
Nhận xét: Hệ n nghiệm của (3.8) lập thành hệ nghiệm cơ bản khi ma trận thành lập
bởi chúng có định thức khác không tại ít nhất một điểm t nào đó. Do đó để tìm 0
nghiệm tổng quát của hệ (3.8) ta tìm hệ n nghiệm cơ bản ϕi(t ) = (ϕi1(t ),...,ϕin(t )).
Khi đó nghiệm tổng quát của hệ là ϕ11(t ) ϕn1(t ) ϕ12(t ) ϕn2(t ) ϕ = C ( ( . .
1ϕ1 t ) + · · · + Cn ϕn t ) = C1
.. +···+Cn .. ϕ1n(t ) ϕnn(t ) trong đó C là các hằng số tuỳ ý. 1, . . . , Cn
3.3.2 Hệ tuyến tính không thuần nhất:
Trước hết ta để ý rằng nếu biết một nghiệm riêng nào đó của hệ không thuần nhất
(3.6) và nghiệm tổng quát của hệ thuần nhất tương ứng thì tổng của chúng cho ta
nghiệm tổng quát của hệ không thuần nhất.
Ngoài ra để xây dựng nghiệm riêng này, ta có thể dùng phương pháp biến thiên
hằng số khi biết n nghiệm độc lập tuyến tính của hệ thuần nhất tương ứng. Giả sử n
nghiệm như thế là ϕi(t ) = (ϕi1(t ),...,ϕin(t )), ta tìm nghiệm riêng của (3.6) dưới dạng ϕ11(t ) ϕn1(t ) ϕ12(t ) ϕn2(t ) ϕ = ( . . r
C1 t ) .. +···+Cn(t ) .. ϕ1n(t ) ϕnn (t )
Để ϕ là nghiệm của hệ (3.6), các hàm Ci(t ) phải thoả hệ phương trình vi phân sau: r ϕ11(t ) ϕn1(t ) g1(t ) ϕ12(t ) ϕn2(t ) g2(t ) C 0 (t )
. ··· C 0 (t ) . . 1
.. + + n .. = .. ϕ1n(t ) ϕnn(t ) gn (t )
3.3 Hệ phương trình vi phân tuyến tính 77
Vì định thức Wronski của hệ này luôn khác không, nên ta luôn giải được các C 0(t ) i
và từ đó tìm được Ci(t ).
Dùng ký hiệu ma trận, có thể diễn đạt phương pháp biến thiên hằng số như sau.
Gọi Φ(t ) là ma trận nghiệm cơ bản của hệ thuần nhất tương ứng với (3.6). Ta tìm
nghiệm của (3.6) dưới dạng x = Φ(t )u(t ), trong đó u là vector (cột) cần tìm. thay vào (3.6), ta có
Φ0(t )u(t ) + Φ(t )u0(t ) = A(t )Φ(t )u(t ) + g (t ). Từ đó,
u 0(t ) = Φ−1(t )g (t ) hay Z u (t ) =
Φ−1(t )g (t )d t + C , và ta có nghiệm là Z
x (t ) = Φ(t )C + Φ(t )
Φ−1(t )g (t )d t .
Với điều kiện ban đầu x (t0) = ξ, ta có chọn C = Φ−1(t0)ξ. Khi đó nghiệm của bài toán Cauchy là Z t x
= Φ(t )Φ−1(t )ξ + Φ(t ) 0
Φ−1(s )g (s )d s t0 Z t
= R (t , t ) 0 ξ +
R (t , s )g (s )d s t0
Định lý sau tổng kết những gì ta vừa trình bày
Định lý 3.20. Giả sử A(t ) và g (t ) liên tục trên I 3 t và 0
R (t , t0) là giải thức của phương
trình x 0 = A(t )x . Khi đó nghiệm duy nhất của phương trình x 0 = A(t )x + g (t ) thỏa
điều kiện x (t0) = ξ cho bởi công thức Z t
x (t ) = R (t , t ) 0 ξ +
R (t , s )g (s )d s (3.10) t0
Ví dụ: Tìm nghiệm tổng quát của phương trình −2 1 2e −t x 0 = x + . 1 −2 3t
Ma trận cơ bản của hệ thuần nhất tương tứng là e −3t e −t
Φ(t ) = −e−3t e−t
Nghiệm của hệ đã cho có dạng x = Φ(t )u(t ), với u(t ) thỏa hệ e −3t e −t u 0 2e −t 1 = .
−e −3t e −t u 0 3t 2 78 Hệ phương trình vi phân Hệ này có nghiệm là 3
u 0 = e 2t − t e 3t 1 2 3 u 0 = 1 + t e t 2 2 Vì vậy 1 1 1 u1 =
e 2t − t e 3t + e 3t + C1 2 2 6 3 3
u2 = t + t e t − e t + C 2 2 2
Thay vào biểu thức nghiệm ở trên, ta thu được nghiệm tổng quát của hệ phương trình đã cho là e −3t e −t t e −t 1 e −t t 12 x = C + + + + 1 C − −e −3t 2 e −t t e −t 2 −e −t 2t 15
3.4 Hệ phương trình vi phân tuyến tính hệ số hằng.
Trong tiết này ta xét hệ phương trình tuyến tính với các hệ số aij(t ) là hằng số d x 1 = a + a + ··· + a + 11 x1 12 y2 1n xn g1(t ) d t d x2 = a + a + ··· + a + g (t ) d t 21 x1 22 x2 2n xn 2 (3.11)
· · · · · · · · · · · · · · · · · · · · · · · · d x n = a + a + ··· + a + g (t ) d t n 1 x1 n 2 x2 nn xn n
Dưới dạng ma trận, hệ có thể viết một cách thu gọn:
x 0 = A x + g (t ) (3.12)
trong đó A = (ai j) là ma trận vuông cấp n.
Nếu g (t ) đồng nhất bằng không, ta có hệ tuyến tính thuần nhất hệ số hằng x 0 = A x (3.13)
3.4.1 Phương trình đặc trưng
Trước hết, ta tìm nghiệm của hệ thuần nhất (3.13). Giống như trong trường hợp
phương trình vi phân cấp cao hệ số hằng ta tìm nghiệm riêng khác không của hệ thuần nhất dưới dạng
x = (x1, . . . , xn ) với xj = γj e λt
3.4 Hệ phương trình vi phân tuyến tính hệ số hằng. 79
Thay x vào hệ (3.11) với chú ý j
g (t ) ≡ 0; sau khi rút gọn ta được hệ phương trình
tuyến tính cho λ và các γj là (a a 11 − λ)γ1 + + + 12γ2
··· a1nγn = 0
a21γ1 + (a22 − λ)γ2 + ··· + a2nγn = 0 (3.14)
· · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · ·
an1γ1 + an2γ2 + ··· + (ann − λ)γn = 0
Vì các γ không đồng thời bằng không nên định thức của hệ phải bằng không, tức j
là λ phải là nghiệm của phương trình: (a 11 − λ) a12 ··· a1n a21
(a22 − λ) ··· a 2n .. .. .. .. = 0 (3.15) . . . . a n 1 an2
··· (ann − λ)
Phương trình (3.15) (ẩn là λ) được gọi là phương trình đặc trưng của hệ (3.13). Đây
là một phương trình đa thức cấp n theo λ. Các nghiệm λk của phương trình này
chính là các giá trị đặc trưng của ma trận A. Vector nghiệm (không tầm thường) v của
k = (γ1k , . . . , γnk ) của hệ (3.14) ứng với giá trị riêng λk
A chính là các vector riêng của A.
3.4.2 Hệ nghiệm cơ bản
Để xây dựng nghiệm tổng quát của hệ thuần nhất ta cần tìm một hệ nghiệm cơ bản
của nó, tức là hệ gồm n nghiệm độc lập tuyến tính xét như hệ các vector hàm. Ta
nhận xét rằng nếu v = (γ1,...,γn) là vector riêng của A ứng với giá trị riêng λ thì vector
hàm y = v e λt là một nghiệm của hệ (3.13). Vậy vấn đề đưa về bài toán giá trị riêng của ma trận.
Trường hợp I (A chéo hoá được)
Trong trường hợp này có tồn tại n vector riêng độc lập tuyến tính v1,...,vn ứng với
các giá trị riêng λ1,...,λn của ma trận A. Xét ma trận nghiệm
Φ(t ) = e λ1t v1, . . . , e λn t vn
Ta có Φ(0) là khả nghịch, do đó theo định lý Ostrogradski-Liouville Φ(t ) luôn luôn khả
nghịch với mọi t . Khi đó giải thức của hệ (3.13) là R(t ,t −1
0) = Φ(t )Φ(t0)−1 = Φ(t − t0)Φ(0)
và nghiệm tổng quát là x = Φ(t )C , với C là ma trận cột các hằng số tuỳ ý C1,...,Cn.
Trường hợp I (A không chéo hoá được)
Mục đích là tìm cách đưa ma trận A về dạng đơn giản nhất có thể được, chẳng hạn
dạng tam giác hoặc dạng Jordan. Giả sử T là ma trận khả nghịch sao cho T −1AT = B 80 Hệ phương trình vi phân
với B có dạng như thế. Khi đó với phép đổi ẩn một cách tuyến tính x = T y , hệ thuần
nhất (3.13) trở thành y 0 = B y , trong đó B có dạng đơn giản. Đặc biệt, khi B có dạng tam giác, ta có d y 1 = b
11 y1 + b12 y2 + · · · + b1n yn d t d y2 = b d t
22 y2 + · · · + b2n yn · · · ············ d y n = b d t nn yn
Ta có thể giải hệ này bằng cách tích phân các phương trình tuyến tính bậc nhất
trước hết đối với y rồi đến
,v.v. . cuối cùng đến . Cuối cùng nghiệm của hệ n yn−1 y1
ban đầu cho bởi x (t ) = T y (t ).
Về mặt thực hành, trường hợp I tương đương với trường hợp phương trình đặc
trưng (3.15) có n nghiệm phân biệt. Khi các nghiệm này là phức (trong khi A là ma
trận thực) ta cũng tách phần thực và phần ảo để được các nghiệm độc lập tuyến tính
như đã làm đối với phương trình tuyến tính cấp cao hệ số hằng.
Trường hợp phương trình đặc trưng có nghiệm λ bội m, khi đó hệ (3.13) có m
nghiệm độc lập tuyến tính dạng P1(t ) P 2(t ) ... e λt Pn (t )
trong đó các P1(t ),...,Pn(t ) là các đa thức bậc m − 1.
Cuối cùng để tìm nghiệm của hệ tuyến tính không thuần nhất hệ số hằng ta tìm
một nghiệm riêng của nó bằng phương pháp biến thiên hằng số xuất phát từ hệ
nghiệm cơ bản của hệ thuần nhất tương ứng. Nghiệm tổng quát của hệ không thuần
nhất bằng tổng của nghiệm riêng này và nghiệm tổng quát của hệ thuần nhất tương ứng. Ví dụ: Giải hệ d x = −x − 2y d t
d y = 3x + 4y d t
Đây là hệ thuần nhất với ma trận −1 −2 A =
. Phương trình đặc trưng là 3 4 −1 − λ −2
λ2 − 3λ + 2 0 3 4 − λ = =
có các nghiệm là λ1 = 1, λ2 = 2.
3.4 Hệ phương trình vi phân tuyến tính hệ số hằng. 81
Ứng với λ1 = 1 ta có hệ
−2γ1−2γ2 =0 3γ1 + 3γ2 = 0
Chọn nghiệm γ1 = 1, γ2 = −1 ta được một nghiệm x1 = e t , y1 = −e t
Tương tự, với λ2 = 2 ta cũng tìm được nghiệm 3
x2 = e 2t ,
y2 = − e 2t 2
Vậy nghiệm tổng quát là
x = C1et +C2e2t
y = −C1e t − 3C 2 2e 2t trong đó C là các hằng số tuỳ ý. 1, C2
Ví dụ: Tìm nghiệm tổng quát của hệ
x 0 = x − z y 0 = x
z0 = x − y
Phương trình đặc trưng của hệ là 1 − λ 0 −1 1 −λ
0 = (1−λ)(1+λ2) = 0 1 −1 −λ
Phương trình này có các nghiệm là 1,±i.
Với λ = 1 ta có hệ −γ3 = 0 γ1 −γ2 = 0
γ1 −γ2 −γ3 = 0
Hệ này cho một vector riêng (1,1,0). Từ đó ta có nghiệm riêng tương ứng là
x = e t , y = e t , z = 0
Với λ = i ta có hệ (1 − i )γ tuỳ ý 1 −γ3 = 0 γ1 γ1 −i γ ⇔ γ 2 = 0 2 = −i γ1 γ 1 −γ2 −i γ3 = 0
γ3 = (1 − i )γ1
Chọn vector riêng (1,−i,1 − i) ta được nghiệm e i t
cos t + i sin t −i e it =
sin t − i cos t (1 − i )e it
(cos t + sin t ) + i (sin t − cos t ) 82 Hệ phương trình vi phân
Tách phần thực và phần ảo, ta được hai nghiệm độc lập tuyến tính cos t sin t sin t và −cos t cos t + sin t sin t − cos t
Vậy nghiệm tổng quát của hệ đã cho là
x = C1e t + C2 cos t + C3 sin t
y = C1e t + C2 sin t − C3 cos t
z = C2(cost +sint )+C3(sint −cost ) trong đó C là các hằng số tuỳ ý. 1, C2, C3 Ví dụ: Giải hệ
x0 = x − y
y 0 = x + 3y Phương trình đặc trưng 1 − λ −1 )2 = 1
3 − λ = (λ − 2 0
có nghiệm kép là λ = 2. Khi đó hệ đã cho có 2 nghiệm độc lập tuyến tính dạng
x =(C1t +C2)e2t
y = (D1t + D2)e 2t
Thay các biểu thức của x , y vào hệ đã cho, sau khi cân bằng hai vế, ta tìm được D1 =C1
D2 = −C1 − C2
vậy nghiệm tổng quát của hệ đã cho là
x =(C1t +C2)e2t
y = −(C1t + C1 + C2)e 2t trong đó C là hai hằng số tuỳ ý. 1, C2
3.5 Sự ổn định nghiệm của hệ phương trình vi phân 83
3.5 Sự ổn định nghiệm của hệ phương trình vi phân
3.5.1 Bài toán ổn định nghiệm
Xét hệ phương trình vi phân:
d x j = f (t ,x d t j 1, . . . , xn ), với j = 1,n (3.16)
Giả sử x (t ) := (x1(t ),...,xn(t )), f (t , x) := (f1(t , x),..., fn(t , x)). Khi đó, ta viết hệ dưới dạng thu gọn:
x 0 = f (t , x ) (3.17)
Nếu f (t , x ) không phụ thuộc vào t một cách trực tiếp, tức là:
x 0 = f (x ) (3.18)
thì hệ được gọi là hệ ôtônôm.
Ta nói hệ là T −tuần hoàn nếu f (t + T, x) = f (t , x), với mọi t .
Trong nhiều lĩnh vực ứng dụng người ta thường nghiên cứu dáng diệu của nghiệm
x (t ) với t ∈ [t0,+∞), đặc biệt là khi t → +∞. Gọi x (t , t0, x0) là nghiệm của hệ (4.2)
thỏa điều kiện ban đầu x (t0) = x0. Định nghĩa 3.21.
• Ta nói nghiệm x (t ) bị chặn trên t ∈ [t0,+∞) nếu ∃M > 0 sao
cho kx(t )k ≤ M , với mọi t ≥ t0.
• Nghiệm x (t ) = x (t ,t0, x0) được gọi là ổn định nếu: ∀ϵ > 0, tồn tại δ(ϵ) > 0 sao cho:
∀h ∈ Rn : khk < δ ⇒ ku(t , t0, x0 + h) − x (t , t0, x0)k < ϵ,∀t ≥ t0
Ngược lại, ta nói x (t ) không ổn định.
• Nghiệm x (t ) = x (t ,t0, x0) được gọi là ổn định tiệm cận nếu nó ổn định và: ∃δ0 > 0 sao cho
∀h ∈ Rn : khk < δ0 ⇒ lim ku(t , t0, x0 + h) − x (t , t0, x0)k = 0 t →+∞
Định nghĩa 3.22. Ta nói điểm x0 ∈ Rn là điểm cân bằng (hoặc điểm dừng, điểm tới
hạn) của hệ (4.2) tại thời điểm t ∗ ∈ R+ nếu:
f (t , x0) = 0, ∀t ≥ t ∗
Đối với hệ ôtônôm hoặc hệ tuần hoàn, điểm x là điểm cân bằng tại 0 t ∗ khi và chỉ
khi nó là điểm cân bằng tại mọi thời điểm. Sau đây, bằng cách đổi biến s := t − t ∗, có thể xem t ∗ = 0.
Nếu gọi ϕ(t ,t0;ξ) là nghiệm của hệ phương trình (4.2) thoả điều kiện ban đầu:
x (t0) = ξ 84 Hệ phương trình vi phân
và, nếu x là điểm cân bằng của hệ tại thì: 0 t0
ϕ(t , t0; x0) = x0
Ta nói x là điểm cân bằng cô lập nếu 0
∃r > 0 sao cho trong hình tâm x0, bán kính r
hệ không có điểm cô lập nào khác với x0.
Định nghĩa 3.23. Giả sử hệ (4.2) có điểm cân bằng cô lập là x0 = 0, tại t ∗ = 0. Ta nói điểm cân bằng 0 là: • ổn định nếu:
∀ϵ > 0,∀t0 ∈ R+,∃δ(ϵ,t
ξ ∈ Rn mà |ξ| < δ ⇒ |ϕ(t , t0,ξ)| < ϵ,∀t ≥ t 0) > 0 : ∀ 0 Nếu δ
không phụ thuộc vào , tức là δ(ϵ,t δ thì ta nói là ổn định (ϵ,t t 0) 0 0) = (ϵ) x0 = 0 đều.
• ổn định tiệm cận nếu nó ổn định và:
∃δ0(t0) > 0 : ∀ξ ∈ Rn mà |ξ| < δ0 ⇒ lim |ϕ(t , t0,ξ)| = 0 t →∞ • ổn định mũ nếu:
∀ϵ > 0,∃δ(ϵ) > 0, ∃α > 0 : ∀|ξ| < δ, t0 ≥ 0 ⇒ |ϕ(t , t0,ξ)| < ϵe −α(t −t0),∀t ≥ t0
Từ định nghĩa, ta thấy rằng điểm cân bằng x0 = 0 là không ổn định nếu tồn tại ϵ sao cho:
0 > 0, t0 ≥ 0 và các dãy {ξm } → 0, {tm } với tm ≥ t0
|ϕ(tm, t0,ξm)| ≥ ϵ0,∀m
Định nghĩa 3.24. Xét nghiệm ϕ(t ,t0,ξ) của hệ (4.2) với điểm cân bằng x0 = 0. Ta nói
• nghiệm ϕ(t ,t0,ξ) là bị chặn nếu tồn tại K > 0 sao cho:
|ϕ(t , t0,ξ)| < K ,∀t ≥ t0
• nghiệm ϕ(t ,t0,ξ) là bị chặn đều nếu với mọi α > 0 và t0 ∈ R+, có tồn tại K =
K (α) > 0 (không phụ thuộc vào t ) sao cho: 0
|ϕ(t , t0,ξ)| < K ,∀t ≥ t0
• Hệ (4.2) là ổn định theo Lagrange nếu với mọi ξ ∈ Rn và với mỗi t0 ∈ R+ thì
ϕ(t , t0, ξ) là bị chặn.
• điểm cân bằng x0 = 0 là ổn định tiệm cận toàn cục nếu nó ổn định và mọi
nghiệm của nó đều dần đến 0 khi t → +∞.
3.5 Sự ổn định nghiệm của hệ phương trình vi phân 85
Ví dụ: Phương trình x0 = 0.
Với điều kiện ban đầu x (0) = ξ có nghiệm ϕ(t ,0,ξ) = ξ. Mọi nghiệm đều là điểm
cân bằng. Nghiệm x = 0 là ổn định đều nhưng không ổn định tiệm cận.
Ví dụ: Phương trình x0 = a x, với a > 0.
Với điều kiện ban đầu x (0) = ξ có nghiệm ϕ(t ,0,ξ) = ξe at . Rõ ràng x = 0 là điểm
cân bằng của phương trình, nhưng không ổn định.
Ví dụ: Phương trình x0 = −a x, với a > 0.
Với điều kiện ban đầu x (0) = ξ có nghiệm ϕ(t ,0,ξ) = ξe −at . Rõ ràng x = 0 là điểm cân bằng ổn định mũ.
Ví dụ: Phương trình 1 x 0 = − x . 1 + t
Với điều kiện ban đầu 1 + t0
x (0) = ξ có nghiệm ϕ(t , 0,ξ) = ξ
. Khi đó x = 0 là điểm 1 + t
cân bằng ổn định đều và ổn định tiệm cận toàn cục.
Định nghĩa 3.25. Giả sử ϕ(t ) = (ϕ1,...,ϕn) là nghiệm thoả điều kiện ban đầu tại t0 của hệ (4.2). Ta nói:
• Nghiệm ϕ(t ) là ổn định (theo nghĩa Liapunov) nếu với mọi ϵ > 0, có tồn tại
δ(ϵ, t0) > 0 sao cho với mọi nghiệm x (t ) = (x1(t ), . . . , xn(t )) :
|xj (t0) − ϕj (t0)| < δ =⇒ |xj (t ) − ϕj (t )| < ϵ,∀t > t0, j = 1, n
• Nghiệm ϕ(t ) là ổn định tiệm cận (theo nghĩa Liapunov) nếu nó ổn định và:
lim |xj (t ) − ϕj (t )| = 0, j = 1, n t →+∞
Ví dụ: Phương trình x0 = −x + t + 1, điều kiện x(0) = 0.
Phương trình này có nghiệm ϕ(t ) = t là ổn định nhưng không bị chặn.
Ví dụ: Phương trình x0 = sin2 t .
Phương trình này có nghiệm x = kπ và nghiệm tổng quát là:
cotgx = C − t
Với điều kiện x (0) = x , nghiệm riêng bị chặn là 0
ϕ(t ) = arccotg(cotgx ) 0 − t . Cho x
, khi đó (so với nghiệm x ≡ 0) ta có 0 ∈ (0, π)
lim |ϕ(t ) − 0| = π t →∞
Vậy, bị chặn ; ổn định. 86 Hệ phương trình vi phân
3.5.2 Ổn định hệ tuyến tính
Xét hệ phương trình tuyến tính, hệ số hằng: x 0 = A x ,
A là ma trận vuông cấp n. (3.19)
Hiển nhiên, x = 0 là điểm cân bằng của hệ. Nghiệm thoả điều kiện x (t0) = ξ có dạng:
ϕ(t , t0, ξ) = Φ(t , t0)ξ = Φ(t − t0)ξ = e A(t −t0)ξ
Định lý 3.26 (Điều kiện cần và đủ). Điểm cân bằng x = 0 của hệ (4.4) là:
a) ổn định ⇔ tất cả các giá trị riêng của A có phần thực không dương và nếu phần
thực bằng không thì giá trị riêng đó phải là đơn (nghiệm đơn của đa thức đặc trưng của A).
b) ổn định tiệm cận ⇔ tất cả các giá trị riêng của A có phần thực âm.
Trường hợp n = 2: Giả sử A là ma trận vuông cấp hai, thực với hai giá trị riêng là λ . 1, λ2
λ1 ≥ λ2 > 0 không ổn định
λ1 ≤ λ2 < 0 ổn định tiệm cận λ không ổn định 1 ≤ 0 < λ2 λ ổn định 1 < 0 = λ2
Nếu λ1,2 = α ± iβ α > 0 không ổn định α = 0 ổn định α < 0 ổn định tiệm cận
3.5.3 Ổn định theo xấp xỉ thứ nhất
Trong phần này ta xét hệ phi tuyến:
x 0 = A x + g (x ) (3.20)
Giả sử rằng x = 0 là điểm cân bằng cô lập của hệ (khi đó g (x ) = 0).
Ta nói hệ (4.6) là hầu tuyến tính trong lân cận của 0 nếu: kg (x )k lim = 0 x →0 kx k
Để xét sự ổn định của hệ (4.6), ta có thể xét hệ xấp xỉ bằng cách xem g (x ) = 0. Phương
pháp như vậy gọi là ổn định theo xấp xỉ thứ nhất.
Tất cả các kết quả về ổn định đối với hệ tuyến tính đều đúng cho trường hợp hệ
hầu tuyến tính, trừ trường hợp α = 0 (xem bảng) mà tại đó ta chưa có kết luận.
3.5 Sự ổn định nghiệm của hệ phương trình vi phân 87
Xét hệ ôtônôm phi tuyến :
¨x0 = F (x,y) (3.21)
y 0 = G (x , y ) Giả sử (x
là điểm cân bằng của hệ mà trong lân cận điểm đó các hàm và 0, y0)
F (x , y )
G (x , y ) có các đạo hàm riêng đến cấp II liên tục. Khi đó, bằng cách khai triển Talor
tại điểm này, ta thấy ngay hệ là hầu tuyến tính.
3.5.4 Ổn định theo phương pháp Liapunov thứ hai
Giả sử hệ phi tuyến (4.7) có 0 là điểm cân bằng cô lập.
Ta nói một hàm V (x , y ) xác định trên D 3 (0,0) là
• xác định dương nếu:
V (x , y ) > 0 trên D , V (0, 0) = 0 • xác định âm nếu:
V (x , y ) < 0 trên D , V (0, 0) = 0
• nếu dấu = xảy ra thì ta nói bán xác định dương, bán xác định âm trương ứng.
Định lý 3.27. Giả sử hệ (4.7) có 0 là điểm cân bằng cô lập và tồn tại hàm V xác định
dương, liên tục cùng với các đạo hàm riêng trên D 3 (0,0). Ngoài ra, hàm:
VL (x , y ) := V 0F (x , y ) + V 0G (x , y ), đạo hàm của V theo hệ x y
xác định âm trên D thì điểm cân bằng 0 là ổn định tiệm cận.
Nếu V bán xác định âm thì điểm cân bằng L 0 là ổn định.
Định lý 3.28. Giả sử hệ (4.7) có 0 là điểm cân bằng cô lập và tồn tại hàm V liên tục
cùng với các đạo hàm riêng trên D 3 (0,0). Ngoài ra, V (0,0) = 0 và trong mỗi lân cận
của (0,0) đều tồn tại (x , y ) mà tại đó V xác định dương (âm). Khi đó nếu hàm V xác L
định dương (âm) trên lân cận D nào đó của (0,0) thì điểm cân bằng (0,0) là không ổn định.
Hàm V trong các định lý trên được gọi là hàm Liapunov.
Ví dụ: Hệ x0 = −x − x y 2, y 0 = −y − x2y
Hàm Liapunov có thể chọn dạng:
V = a x 2 + b x y + c y 2
Với phương trình này, ta cho b = 0, a,c > 0 tuỳ ý. Từ đó suy ra điểm 0 là ổn định tiệm cận. 88 Hệ phương trình vi phân BÀI TẬP
1. Giải các hệ phương trình vi phân sau và xây dựng ma trận nghiệm cơ bản d x d x = 3x − 2y = 2x − 5y (a) d t (b) d t d y d y = 2x − 2y = x − 2y d t d t
2. Giải các hệ phương trình vi phân sau d x d x = 2x − y
+ 2x + 4y = 1 + 4t (a) d t (c) d t d y d y = x + 2y
+ x − y = 3 t 2 d t d t 2 d x d x = x + 2y = y (b) d t (d) d t d y d y = 2x + y
= x + e t + e −t d t d t
3. Tìm nghiệm tổng quát của các hệ phương trình vi phân sau d x d x = 3x + 12y = − 4z
−4x + 2y + 5z d t d t (a) d y d y
= −x − 3y + z (c)
= 6x − y − 6z d t d t d x d x = −
x − 12y + 6z
= −8x + 3y + 9z d t d t d x = 2x − y − z d t (b)
d y = 12x −4y −12z d t d x
= −4x + y + 5z d t Chương 4
Nhập môn lý thuyết định tính phương trình vi phân
Trong chương này ta sẽ tìm hiểu một số vấn đề liên quan đến các nghiên cứu định
tính phương trình vi phân cấp I. Đặc biệt, vấn đề ổn định nghiệm của phương trình
vi phân cũng được đề cập.
4.1 Các định lý tồn tại nghiệm
4.1.1 Định lý tồn tại nghiệm Peano
Trong chương I, định lý tồn tại và duy nhất nghiệm được phát biểu và chứng minh
cho trường hợp f liên tục và thoả điều kiện Lipschitz trong lận cận của giá trị ban
đầu (x0, y0). Lưu ý rằng sự tồn tại và duy nhất có tính địa phương và giả thiết về
điều kiện Lipschitz là quan trọng. Nếu bỏ giả thiết về điều kiện Lipschitz, bài toán
Cauchy có thể không duy nhất nghiệm.
Trong mục này, ta tìm hiểu về sự tồn tại nghiệm của bài toán Cauchy trong trường
hợp vắng giả thiết ”thoả điều kiện Lipschitz”. Xét phương trình vi phân
x 0 = f (t , x ),
x (t0) = x0
trong đó f :U ⊂ Rn+1 → Rn liên tục trên
Định lý 4.1. (Peano) Xét hình hộp A = {(x, y ) ∈ R×Rn/|x − x0| ≤ a,||y − y0|| ≤ b} và giả
sử f : A → Rn liên tục. Đặt M = maxA ||f (x, y )|| và α = min(a,b /M ). Khi đó bài toán
Cauchy y 0 = f (x , y ), y (x
có ít nhất một nghiệm trên [x0 − α, x0 + α]. 0) = y0
Nhận xét: Trước hết hãy lưu ý rằng ta không thể sử dụng phương pháp lặp Picard
vì không có đủ giả thiết bảo đảm dãy xấp xỉ Picard hội tụ. Thay vào đó, người ta xây
dựng các nghiệm xấp xỉ (địa phương) bởi tiếp tuyến của nó
y (x + h ) ∼
= y (x ) + h . f (x , y (x )) 90
Nhập môn lý thuyết định tính phương trình vi phân Với
h cho trước ta xây dựng dãy x xác định bởi: n , yn n≥0
yn+1 = yn + h f (xn , yn ),
xn+1 = xn + h. (4.1)
Ta gọi yh(x) là hàm tuyến tính từng khúc qua các điểm (xn, yn); đồ thị của nó được gọi là đa giác Euler.
Bổ đề 4.2. Với các giả thiết trong định lý 4.1 và với h := α/N (N ∈ N), đa giác Euler thoả (x , y (
h x )) ∈ A với mọi x ∈ [x0, x0 + α]. Ngoài ra, ||y 0 0 0
h (x ) − yh (x )|| ≤ M |x − x |
với mọi x , x ∈ [x0, x0 + α]
Chứng minh: Qui nạp theo n. Giả sử điều đó đúng với n, i.e. kyn − y0k ≤ b , ta có
||yn+1 − yn|| ≤ hM
nên, với n + 1 ≤ N ta đều có
||yn+1 − y0|| ≤ (n + 1)hM ≤ αM ≤ b
Điều này chứng tỏ (x , yh(x)) ∈ A với mọi x ∈ [x0, x0 + α].
Bất đẳng thức trong mệnh đề là hiển nhiên đúng vì yh(x) là tuyến tính từng khúc
và có “hệ số góc” bị chặn bởi M .
Để chứng minh định lý ta cần khái niệm sau:
Định nghĩa 4.3. Họ hàm fλ : I → Rn được gọi là đồng liên tục nếu với mọi ϵ > 0, có
tồn tại một δ > 0 (không phụ thuộc vào cả ϵ lẫn λ) sao cho
∀λ, ∀x , x 0 |x − x 0| < δ =⇒ ||fλ(x ) − fλ(x 0)|| < ϵ
Định lý 4.4 (Arzela-Ascoli). Cho họ các hàm fλ : [a,b ] → Rn đồng liên tục và bị chặn đều trên
[a , b ]. Khi đó họ hàm f có chứa một dãy con λ
{gn(x )} hội tụ đều đến một
hàm g (x ) liên tục trên [a,b ].
Chứng minh: Xem giáo trình giải tích hàm.
Chứng minh định lý Peano:
Xét đa giác Euler yh(x) với h = α/N , Dãy này bị chặn và đồng liên tục (theo Bổ đề
4.2) nên theo định lý Arzela−Ascoli, họ hàm yh(x) có chứa một dãy con hội tụ đều
về hàm liên tục y : [a,b ] → Rn
Ta chỉ ra rằng hàm giới hạn này chính là nghiệm của bài toán Cauchy. Ta xét
x ∈ [x0, x0 + α] (trên [x0 − α, x0] ta xét tương tự), ký hiệu k = k (h) là chỉ số sao cho
x ∈ [xk , xk+1], với xk = x0 + k h. Khi đó, trên đoạn con này ta có
yh (x ) − y0 = h f (x0, y0) + ··· + h f (xk−1, yk−1) + (x − xk )f (xk , yk )
4.1 Các định lý tồn tại nghiệm 91
với các cặp giá trị (xj, yj) là các xấp xỉ bằng phương pháp Euler (xem (4.1)).
Vì f liên tục nên khả tích, và có thể viết Z x
f (t , y (t ))d t = h f (x0, y (x0)) + ··· + h f (xk x
−1, y ( k −1)) + (x − xk ) f (xk , y (xk )) + r (h ) x0
với r (h) → 0 khi h → 0.
Tính liên tục đều của f trên A và sự hội tụ đều của dãy con của {yh(x)} đến y (x) cho phép ta đánh giá
||f (x , yh(x )) − f (x , y (x ))|| < ϵ
với h đủ bé. Khi đó từ các đẳng thức trên ta có Z x y
f (t , y (t ))d t ≤ ϵ|x − x r (h )
εα + r (h)
h (x ) − y0 − 0| + || || ≤ || || x0
Cho h → 0 ta thấy hàm y (x) thoả mãn phương trình tích phân Z x
y (x ) = y +
f (t , y (t ))d t 0 x0
mà nghiệm của nó chính là lời giải của bài toán Cauchy.
Nhận xét: Định lý Peano hoàn toàn không chứa thông tin về sự duy nhất nghiệm.
4.1.2 Thác triển nghiệm và sự tồn tại toàn cục:
Ta quan tâm đến bài toán kéo dài nghiệm của bài toán Cauchy y 0 = f (x , y ) với điều
kiện ban đầu y (x0) = y0.
Định nghĩa 4.5. Hàm f : U → Rn (với U là mở trong R × Rn) được gọi là thoả điều
kiện Lipschitz địa phương trên U nếu tại mỗi (x0, y0) ∈ U đều tồn tại lân cận V ⊂ U
sao cho f thoả điều kiện Lipschitz trên V .
Nhận xét: Nếu hàm f thuộc lớp C 1 trên U thì thoả điều kiện Lipschitz địa phương.
Bổ đề 4.6. Nếu f :U → Rn liên tục và thoả điều kiện Lipschitz địa phương trên U thì với mọi (x sao cho:
0, y0) ∈ U đều tồn tại một khoảng mở Imax = (ω_, ω+) 3 x0
• Bài toán Cauchy y 0 = f (x , y ) với y (x có nghiệm duy nhất trên 0) = y0 Imax
• Nếu z : I → Rn là một nghiệm nào đó của bài toán Cauchy này thì I ⊂ I và max z = y | . I 92
Nhập môn lý thuyết định tính phương trình vi phân
Chứng minh: Chỉ cần đặt I
và bài toán Cauchy có nghiệm trên
max = ∪ I /I mở chứa x0 I
Sau đó xác định hàm y : I ,
max → Rn theo cách sau: Với x ∈ Imax
x phải thuộc một I
nào đó, mà trên đó bài toán Cauchy có nghiệm. Khi đó, ta gán y (x ) bởi giá trị của
nghiệm đó tại x . Phần còn lại, ta cần chỉ ra nghiệm như thế là xác định tốt và duy
nhất. Chi tiết dành cho bạn đọc.
Định lý 4.7. Giả sử f : U → Rn liên tục và thoả điều kiện Lipschitz địa phương trên
U . Khi đó mỗi nghiệm của bài toán Cauchy đều có một thác triển đến biên của U .
Chính xác hơn, giả sử y : Imax → Rn là nghiệm qua (x0, y0) ∈ U , khi đó với mọi
compact K ⊂ U đều tồn tại x với sao cho 1, x2 ∈ Imax
x1 < x0 < x2 (x ( ( (
1, y x1)), x2, y x2)) / ∈ K .
Chứng minh: Giả sử Imax = (ω_,ω+). Nếu ω+ = ∞ thì hiển nhiên tồn tại x2 > x0 sao cho (x ( 2, y x2)) / ∈ K .
Xét trường hợp ω+ < ∞, giả sử có tồn tại compact K mà (x, y (x)) ∈ K với mọi
x ∈ (x0,ω+). Vì f bị chặn trên K nên Z x
||y (x ) − y (x 0)|| =
f (t , y (t ))d t ≤ M |x − x0| < ε x 0
nếu x , x 0 đủ gần ω+.
Điều này dẫn đến tồn tại lim ; và rõ ràng
x →ω y (x ) = y (ω + +
+, y+) ∈ K ⊂ U do K
compact. Theo định lý tồn tại và duy nhất nghiệm, có tồn tại nghiệm của bài toán
y 0 = f (x , y ), y trong lân cận của +(ω+) = y+
ω . Điều này vô lý vì Imax là cực đại. Chứng +
minh tương tự cho trường hợp x . 1
4.2 Sự ổn định nghiệm
4.2.1 Bài toán ổn định nghiệm
Xét hệ phương trình vi phân
x 0 = f (t , x ) (4.2)
Nếu f (t , x ) không phụ thuộc vào t một cách trực tiếp, tức là
x 0 = f (x ) (4.3)
thì hệ được gọi là hệ ôtônôm.
Ta nói hệ là T −tuần hoàn nếu f (t + T, x) = f (t , x), với mọi t .
Trong nhiều lĩnh vực ứng dụng người ta cần nghiên cứu dáng diệu của nghiệm
x (t ) với t ∈ [t0,+∞), đặc biệt là khi t → +∞. Ta thường ký hiệu x (t ) = ϕ(t , t0, x0) là
nghiệm của hệ (4.2) thỏa điều kiện ban đầu x (t và, với 0) = x0 ∆x0 ∈ Rn
∆ϕ(t ) := ϕ(t , t0, x0 + ∆x0) − ϕ(t , t0, x0) 4.2 Sự ổn định nghiệm 93 Định nghĩa 4.8.
• Ta nói nghiệm x (t ) bị chặn trên [t0,+∞) nếu ∃M > 0 sao cho
kx (t )k ≤ M , với mọi t ≥ t0.
• Nghiệm x (t ) = ϕ(t ,t0, x0) được gọi là ổn định nếu: ∀ϵ > 0, tồn tại δ(ϵ,t0) > 0 sao cho:
∀∆x0 ∈ Rn : k∆x0k < δ ⇒ k∆ϕ(t )k < ϵ,∀t ≥ t0
Ngược lại, ta nói x (t ) không ổn định.
• Nghiệm ϕ(t ,t0, x0) được gọi là ổn định tiệm cận nếu nó ổn định và: ∃δ0 > 0 sao cho
∀∆x0 ∈ Rn : k∆x0k < δ0 ⇒ lim k∆ϕ(t )k = 0 t →+∞
Định nghĩa 4.9. Ta nói điểm x0 ∈ Rn là điểm cân bằng (hoặc điểm dừng, điểm tới
hạn) của hệ (4.2) tại thời điểm t0 ∈ R nếu:
f (t , x0) = 0, ∀t ≥ t0
Đối với hệ ôtônôm hoặc hệ tuần hoàn, điểm x là điểm cân bằng tại 0 t ∗ khi và chỉ
khi nó là điểm cân bằng tại mọi thời điểm. Ngoài ra, bằng cách đổi biến t 7→ t − t ∗,
có thể xem t ∗ = 0.
Nếu gọi ϕ(t ,t0;ξ) là nghiệm của hệ phương trình (4.2) thoả điều kiện ban đầu:
x (t0) = ξ
và, nếu x là điểm cân bằng của hệ tại thì: 0 t0
ϕ(t , t0; x0) = x0
Ta nói x0 là điểm cân bằng cô lập nếu ∃r > 0 sao cho trong hình cầu tâm x0, bán kính
r hệ không có điểm cô lập nào khác với x0.
Định nghĩa 4.10. Giả sử hệ (4.2) có điểm cân bằng cô lập là x0 = 0, tại t ∗ = 0. Ta nói điểm cân bằng 0 là: • ổn định nếu:
∀ϵ > 0,∀t0 ∈ R+,∃δ(ϵ,t
ξ ∈ Rn mà |ξ| < δ ⇒ |ϕ(t , t 0) > 0 : ∀
0, ξ)| < ϵ, ∀t ≥ t0 Nếu δ
không phụ thuộc vào , tức là δ(ϵ,t δ thì ta nói là ổn định (ϵ,t t 0) 0 0) = (ϵ) x0 = 0 đều.
• ổn định tiệm cận nếu nó ổn định và:
∃δ0(t0) > 0 : ∀ξ ∈ Rn mà |ξ| < δ0 ⇒ lim |ϕ(t , t0,ξ)| = 0 t →∞ • ổn định mũ nếu:
∀ϵ > 0,∃δ(ϵ) > 0, ∃α > 0 : ∀|ξ| < δ, t0 ≥ 0 ⇒ |ϕ(t , t0,ξ)| < ϵe −α(t −t0),∀t ≥ t0 94
Nhập môn lý thuyết định tính phương trình vi phân
Từ định nghĩa, ta thấy rằng điểm cân bằng x0 = 0 là không ổn định nếu tồn tại ϵ sao cho:
0 > 0, t0 ≥ 0 và các dãy {ξm } → 0, {tm } với tm ≥ t0
|ϕ(tm, t0,ξm)| ≥ ϵ0,∀m
Định nghĩa 4.11. Xét nghiệm ϕ(t ,t0,ξ) của hệ (4.2) với điểm cân bằng x0 = 0. Ta nói
• nghiệm ϕ(t ,t0,ξ) là bị chặn nếu tồn tại K > 0 sao cho:
|ϕ(t , t0,ξ)| < K ,∀t ≥ t0
• Hệ (4.2) là ổn định theo Lagrange nếu với mọi ξ ∈ Rn và với mỗi t0 ∈ R+ thì
ϕ(t , t0, ξ) là bị chặn.
• điểm cân bằng x0 = 0 là ổn định tiệm cận toàn cục nếu nó ổn định và mọi
nghiệm của nó đều dần đến 0 khi t → +∞.
Ví dụ: Phương trình x0 = 0.
Với điều kiện ban đầu x (0) = ξ có nghiệm ϕ(t ,0,ξ) = ξ. Mọi nghiệm đều là điểm
cân bằng. Nghiệm x = 0 là ổn định đều nhưng không ổn định tiệm cận.
Ví dụ: Phương trình x0 = a x , với a > 0.
Với điều kiện ban đầu x (0) = ξ có nghiệm ϕ(t ,0,ξ) = ξe at . Rõ ràng x = 0 là điểm
cân bằng của phương trình, nhưng không ổn định.
Ví dụ: Phương trình x0 = −a x, với a > 0.
Với điều kiện ban đầu x (0) = ξ có nghiệm ϕ(t ,0,ξ) = ξe −at . Rõ ràng x = 0 là điểm cân bằng ổn định mũ.
Ví dụ: Phương trình 1 x 0 = − x . 1 + t
Với điều kiện ban đầu 1 + t0
x (0) = ξ có nghiệm ϕ(t ,0, ξ) = ξ
. Khi đó x = 0 là điểm 1 + t
cân bằng ổn định đều và ổn định tiệm cận toàn cục.
Định nghĩa 4.12. Giả sử ϕ(t ) = (ϕ1,...,ϕn) là nghiệm thoả điều kiện ban đầu tại t0 của hệ (4.2). Ta nói:
• Nghiệm ϕ(t ) là ổn định (theo nghĩa Liapunov) nếu với mọi ϵ > 0, có tồn tại
δ(ϵ, t0) > 0 sao cho với mọi nghiệm x (t ) = (x1(t ), . . . , xn(t )) :
|xj (t0) − ϕj (t0)| < δ =⇒ |xj (t ) − ϕj (t )| < ϵ,∀t > t0, j = 1, n
• Nghiệm ϕ(t ) là ổn định tiệm cận (theo nghĩa Liapunov) nếu nó ổn định và:
lim |xj (t ) − ϕj (t )| = 0, j = 1, n t →+∞ 4.2 Sự ổn định nghiệm 95
Ví dụ: Phương trình x0 = −x + t + 1, điều kiện x(0) = 0.
Phương trình này có nghiệm ϕ(t ) = t là ổn định nhưng không bị chặn.
Ví dụ: Phương trình x0 = sin2 t .
Phương trình này có nghiệm x = kπ và nghiệm tổng quát là:
cotgx = C − t
Với điều kiện x (0) = x , nghiệm riêng bị chặn là 0
ϕ(t ) = arccotg(cotgx ) 0 − t .
Cho x0 ∈ (0,π), khi đó (so với nghiệm x ≡ 0) ta có
lim |ϕ(t ) − 0| = π t →∞
Vậy, bị chặn ; ổn định. Như sẽ thấy trong mục sau, đối với hệ tuyến tính thuần nhất
thì bị chặn ⇒ ổn định.
4.2.2 Ổn định hệ tuyến tính
Xét hệ phương trình tuyến tính thuần nhất
x 0 = A(t )x (4.4)
trong đó ma trận A(t ) liên tục trên [0,+∞).
Định lý 4.13. Tất cả các nghiệm của hệ (4.4) ổn định khi và chỉ khi chúng bị chặn.
Chứng minh: Giả sử tất cả các nghiệm của hệ đều bị chặn. Khi đó với mọi t0 ≥ 0, tồn
tại M > 0 sao cho kR(t ,t0)k ≤ M , với mọi t ≥ t0. Xét nghiệm x(t ) = ϕ(t ,t0, x0). Do tính
chất tuyến tính ∆ϕ(t ) = ϕ(t ,t0, x0 + ∆x0) − ϕ(t ,t0, x0) cũng là nghiệm thoả điều kiện
(t0, ∆x0). Do đó
k∆ϕ(t )k = kR (t , t0)(∆x0)k ≤ M k∆x0k
Có thể làm cho vế phải của bất đẳng thức trên bé hơn ϵ bằng cách chọn δ = ϵ/M .
Ngược lại, nếu tất cả các nghiệm đều ổn định thì nghiệm tầm thường cũng ổn
định. Tức là, với mọi ϵ > 0, ∃δ > 0 sao cho:
k∆x0k < δ ⇒ kϕ(t , t0,∆x0)k < ϵ
Từ đó kR(t ,t là các
0)(∆x0)k < ϵ, với mọi ∆x0 ∈ Rn thoả k∆x0k < δ. Lần lượt cho ∆x0
vector δe ta có đánh giá cho các vector cột r 2 j
j (t ) của R (t , t0) như sau 2 2ϵ
krj (t )k = kR (t , t0)ej k = kR (t , t0)( ∆x δ 0)k < δ
Vậy nếu x (t ) = x (t ,t0, x0) là một nghiệm bất kỳ của hệ (4.4) thì 2ϵ
kx (t )k = kR (t , t0)x0k ≤ kR (t , t0)k.kx0k ≤ max krj (t )k.kx0k = kx0k j δ
Điều đó đúng với mọi t ≥ t . 0 96
Nhập môn lý thuyết định tính phương trình vi phân
Định lý 4.14. Giả sử Φ(t ) là ma trận nghiệm cơ bản của hệ (4.4). Khi đó tất cả các
nghiệm của hệ (4.4) ổn định tiệm cận khi và chỉ khi lim kΦ(t )k = 0 t →+∞
Chứng minh: Từ điều kiện limt bị chặn. Khi đó với
→+∞ kΦ(t )k = 0 suy ra kΦ(t )k
nghiệm x (t ) = ϕ(t ,t0, x0) ta có
kx (t )k = kΦ(t )Φ−1(t0)x0k ≤ kΦ(t )kkΦ−1(t0)kkx0k
Từ đó suy ra x (t ) bị chặn. Theo định lý trên x (t ) ổn định.
Ngoài ra, cũng theo đánh giá trên ta có
k∆ϕ(t )k = kΦ(t )Φ−1(t0)∆x0k ≤ kΦ(t )kkΦ−1(t0)∆x0k → 0, t → +∞
Do đó x (t ) ổn định tiệm cận.
Ngược lại, nếu nghiệm tầm thường ổn định tiệm cận thì
kϕ(t , t0,∆x0)k = k∆ϕ(t )k = kΦ(t )Φ−1(t0)∆x0k → 0 Từ đó suy ra limt 0
Xét hệ tuyến tính thuần nhất với hệ số hằng
→+∞ kΦ(t )k = . x 0 = A x (4.5) Khi đó Hệ quả 4.15.
• Nếu phần thực của các giá trị riêng đơn không dương và phần
thực của các giá trị riêng bội đều âm thì tất cả các nghiệm của hệ (4.5) đều ổn định
• Nếu phần thực của tất cả các giá trị riêng đều âm thì tất cả các nghiệm của hệ
(4.5) đều ổn định tiệm cận.
Hiển nhiên, x = 0 là một điểm cân bằng của hệ (4.5). Nghiệm thoả điều kiện
x (t0) = ξ có dạng:
ϕ(t , t0, ξ) = Φ(t , t0)ξ = Φ(t − t0)ξ = e A(t −t0)ξ
Định lý 4.16 (Điều kiện cần và đủ). Điểm cân bằng x = 0 của hệ (4.4) là:
a) ổn định ⇔ tất cả các giá trị riêng của A có phần thực không dương và nếu phần
thực bằng không thì giá trị riêng đó phải là đơn (nghiệm đơn của đa thức đặc trưng của A).
b) ổn định tiệm cận ⇔ tất cả các giá trị riêng của A có phần thực âm. 4.2 Sự ổn định nghiệm 97
Trường hợp n = 2: Giả sử A là ma trận vuông cấp hai, thực với hai giá trị riêng là λ . 1, λ2
λ1 ≥ λ2 > 0 không ổn định
λ1 ≤ λ2 < 0 ổn định tiệm cận λ không ổn định 1 ≤ 0 < λ2 λ ổn định 1 < 0 = λ2
Nếu λ1,2 = α ± iβ α > 0 không ổn định α = 0 ổn định α < 0 ổn định tiệm cận
4.2.3 Ổn định theo xấp xỉ thứ nhất
Trong phần này ta xét hệ phi tuyến:
x 0 = A x + g (x ) (4.6)
Giả sử rằng x = 0 là điểm cân bằng cô lập của hệ (khi đó g (x ) = 0).
Ta nói hệ (4.6) là tựa tuyến tính trong lân cận của 0 nếu: kg (x )k lim = 0 x →0 kx k
Để xét sự ổn định của hệ (4.6), ta có thể xét hệ xấp xỉ bằng cách xem g (x ) = 0. Phương
pháp như vậy gọi là ổn định theo xấp xỉ thứ nhất.
Định lý 4.17. Giả sử hệ (4.6) là tựa tuyến tính. Khi đó
• Nếu tất cả các giá trị riêng của A đều có phần thực âm thì điểm cân bằng x0 = 0 ổn định tiệm cận.
• Nếu có ít nhất một giá trị riêng của A có phần thực dương thì điểm cân bằng
x0 = 0 là không ổn định.
4.2.4 Ổn định theo phương pháp trực tiếp Liapunov đối với hệ au- tonomous
Xét hệ ôtônôm phi tuyến :
¨x0 = F (x,y) (4.7)
y 0 = G (x , y ) Giả sử (x
là điểm cân bằng của hệ mà trong lân cận điểm đó các hàm và 0, y0)
F (x , y )
G (x , y ) có các đạo hàm riêng đến cấp II liên tục. Khi đó, bằng cách khai triển Talor
tại điểm này, ta thấy ngay hệ là tựa tuyến tính. Giả sử hệ phi tuyến (4.7) có 0 là điểm cân bằng cô lập. 98
Nhập môn lý thuyết định tính phương trình vi phân
Định nghĩa 4.18. Ta nói một hàm V (x, y ) xác định trên D 3 (0,0) là
• xác định dương nếu:
V (x , y ) > 0 trên D , V (0, 0) = 0 • xác định âm nếu:
V (x , y ) < 0 trên D , V (0, 0) = 0
• nếu dấu = xảy ra thì ta nói bán xác định dương, bán xác định âm trương ứng.
Định lý 4.19. Giả sử hệ (4.7) có 0 là điểm cân bằng cô lập và tồn tại hàm V xác định
dương, liên tục cùng với các đạo hàm riêng trên D 3 (0,0). Ngoài ra, hàm:
VL (x , y ) := V 0F (x , y ) + V 0G (x , y ), đạo hàm của V theo hệ x y
xác định âm trên D thì điểm cân bằng 0 là ổn định tiệm cận.
Nếu V bán xác định âm thì điểm cân bằng 0 là ổn định. L
Định lý 4.20. Giả sử hệ (4.7) có 0 là điểm cân bằng cô lập và tồn tại hàm V liên tục
cùng với các đạo hàm riêng trên D 3 (0,0). Ngoài ra, V (0,0) = 0 và trong mỗi lân cận
của (0,0) đều tồn tại (x , y ) mà tại đó V xác định dương (âm). Khi đó nếu hàm V xác L
định dương (âm) trên lân cận D nào đó của (0,0) thì điểm cân bằng (0,0) là không ổn định.
Hàm V trong các định lý trên được gọi là hàm Liapunov.
Ví dụ: Hệ x0 = −x − x y 2, y 0 = −y − x2y
Hàm Liapunov có thể chọn dạng:
V = a x 2 + b x y + c y 2
Với phương trình này, ta cho b = 0, a,c > 0 tuỳ ý. Từ đó suy ra điểm 0 là ổn định tiệm cận. 4.2 Sự ổn định nghiệm 99 BÀI TẬP
1. Xét tính ổn định của điểm can bằng (0,0) của các hệ: (a)
x 0 = −2x + y (c)
x 0 = 3x + y
y 0 = −5x − 6y
y 0 = −x + y (b)
x 0 = 4x + y (d)
x 0 = 7x + y
y 0 = 3x + 6x
y 0 = −3x + 4y
2. Xét tính ổn định của nghiệm tầm thường của các hệ: (a)
x 0 = −x + e 2t y
x 0 = ln(1 − z ) y 0 = −y (d)
y 0 = ln(1 − x )
z 0 = ln(1 − y )
x 0 = x + 2y (b)
x 0 = x − cos y − z + 1
y 0 = y + z (e) y 0 = y
z 0 = x + 3y + z
− cos z − x + 1
z0 = z −cos x − y +1
x 0 = −2x + y + 3z + 8x 2 + y 3
x 0 = 2x + y − x 2 − y 2 (c)
y 0 = −6y − 5z + 7z 3 (f)
y 0 = x + 3y − x 3 sin z
z0 = −z + x4 + y 2 + z3
z0 = y + 2z + x2 + y 2
3. Xét tính ổn định của nghiệm tầm thường của các phương trình:
(a) x 00 + µ(x 2 − 1)x0 + x = 0 (Phương trình Van der Pol)
(b) θ 00 + k θ 0 + g sinθ = 0 (Phương trình dao động con lắc đơn) m L
4. Tìm tất cả các điểm cân bằng của hệ và xét tính ổn định của chúng: (a)
x 0 = x + 4y (d)
x 0 = 4y 2 − x 2
y 0 = x + y − x 2
y 0 = 2x y − 4y − 8 (b)
x 0 = x − y + x 2 (e) x 0 = 1 − x y
y 0 = 12x − 6y + x y
y 0 = x − y 3 (c)
x 0 = 8x − y 2 (f) x 0 = x y
y 0 = y − x 2
y 0 = 4 − 4x − 2y
5. Với điều kiện nào của a,b,c thì hàm V (x , y ) = a x 2 + b x y + c y 2 (bán) xác định
dương, (bán) xác định âm, không xác định?
6. Trong các hệ sau, bằng cách xây dựng hàm Liapunov dạng V (x , y ) = a x 2 +b y 2
hãy xét tính ổn định của nghiệm tầm thường: 100
Nhập môn lý thuyết định tính phương trình vi phân (a)
x 0 = −x + y e x (d)
x 0 = x 3 − y
y 0 = −x e x − y
y 0 = x + y 3 (b)
x 0 = −x 3 − x 2 y (e) x 0 = −x y 4
y 0 = −x 3 + x 2 y y 0 = y x 4 2 (c)
x 0 = 2y − x (1 + 4y 2) (f)
x 0 = y + x (r 2 − x − y 2) y 0 = x 0 = ( 2)
2 − y + x 2 y y
−x + y r 2 − x 2 − y Tài liệu tham khảo
[1] Hoàng Hữu Đường, Lý thuyết phương trình vi phân. Nhà xuất bản ĐH và THCN (1977).
[2] Nguyễn Thế Hoàn, Trần Văn Nhung, Bài tập phương trình vi phân. Nhà xuất bản ĐH và THCN (1979).
[3] C.M. Bender, St.A. Orszag, Advanced mathematical methods for scientists and
engineers. Mc Graw-Hill Book Inc. Company (1978).
[4] W.E. Boyce, R.C. DiPrima, Elementary Differential Equations and Boundary
Value Problems. John Wiley & Sons Inc. (2001).
[5] E.A. Coddington, N.Levinson, Theory of ordinary differential equations. Newyork (1955).
[6] E.L. Ince, Ordinary differential equations. Dover Pub. (1956).



