







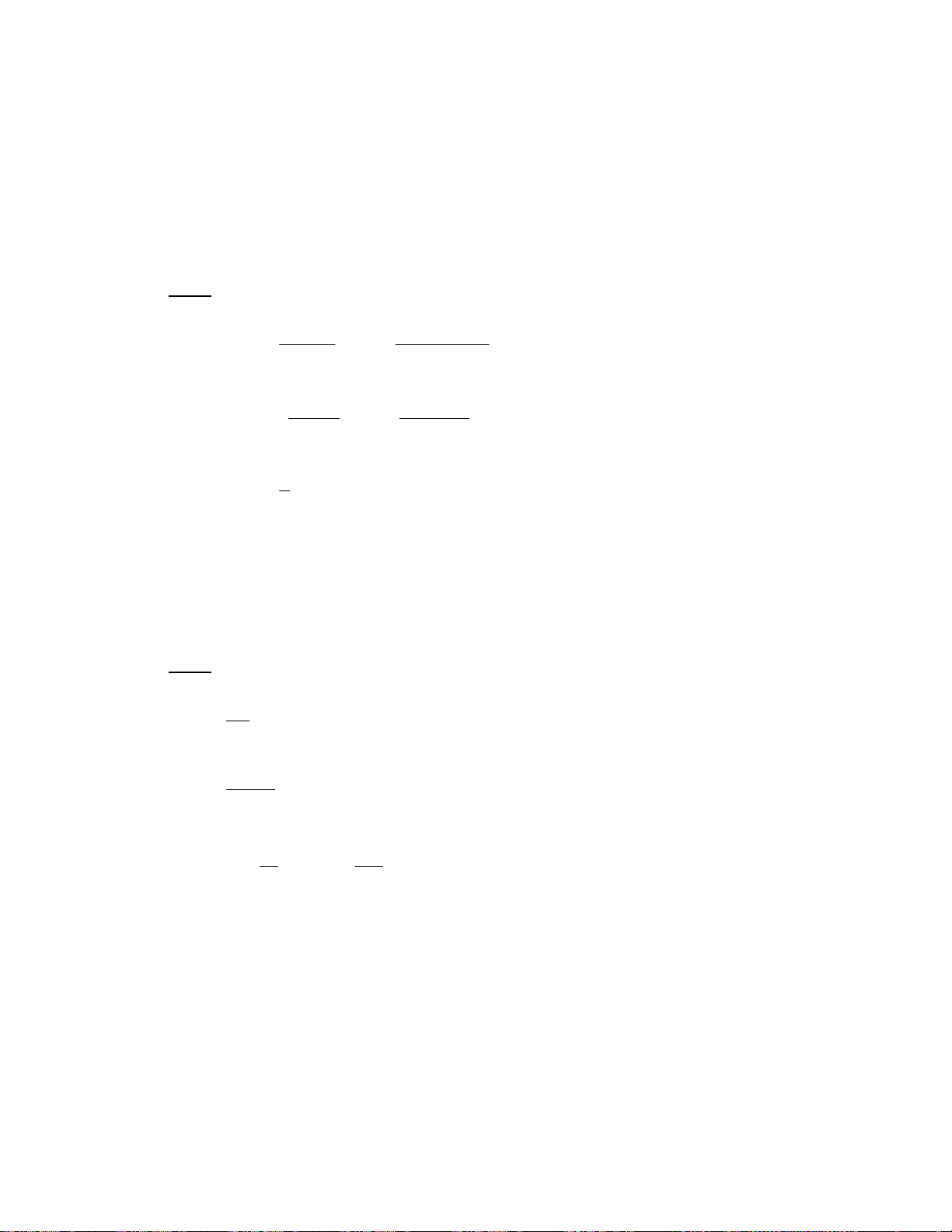

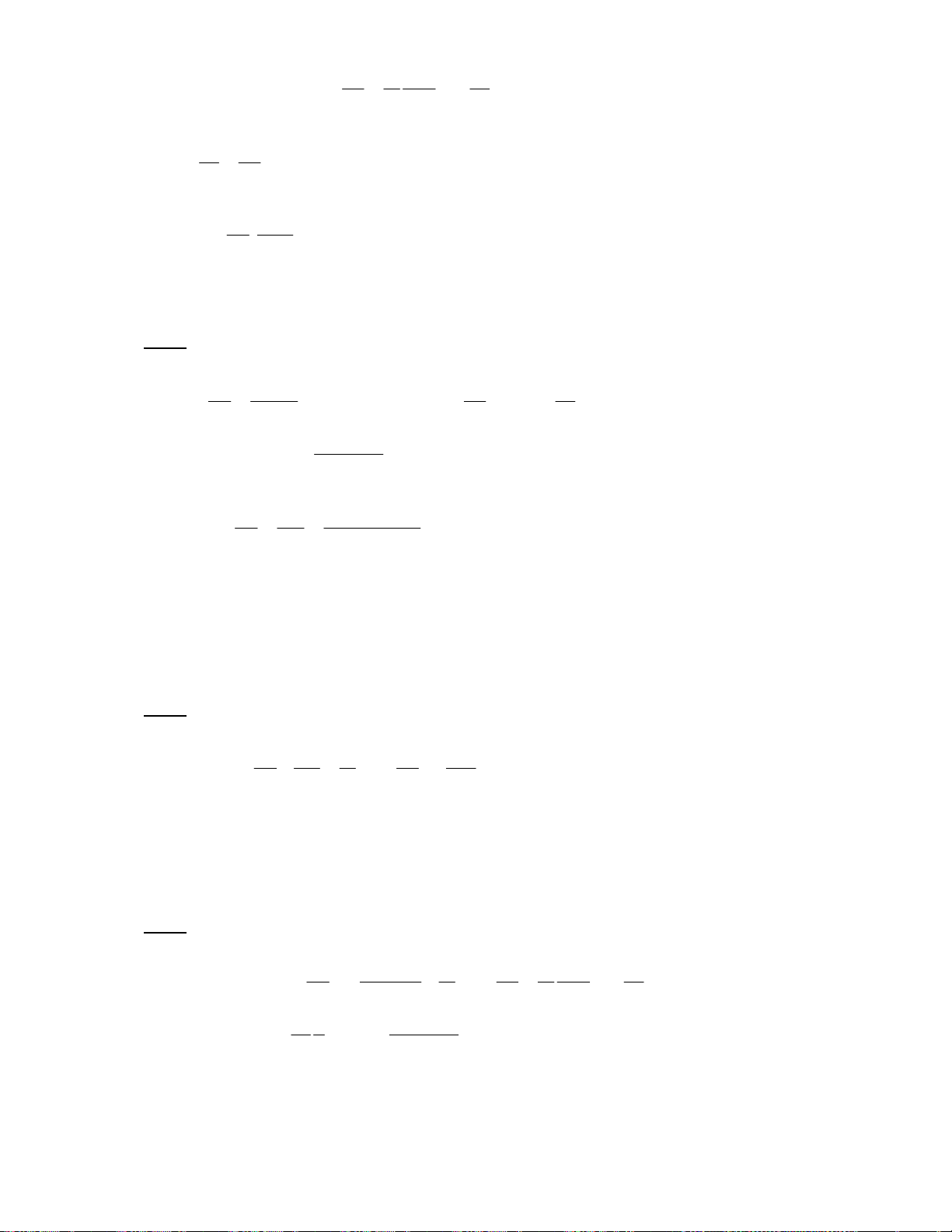













Preview text:
lOMoARcPSD|36477180
06. Giải bài tập Nhiệt học - Lương Duyên Bình
khoa học quản lý đại cương (Học viện Kỹ thuật Quân sự) Scan to open on Studocu
Studocu is not sponsored or endorsed by any college or university
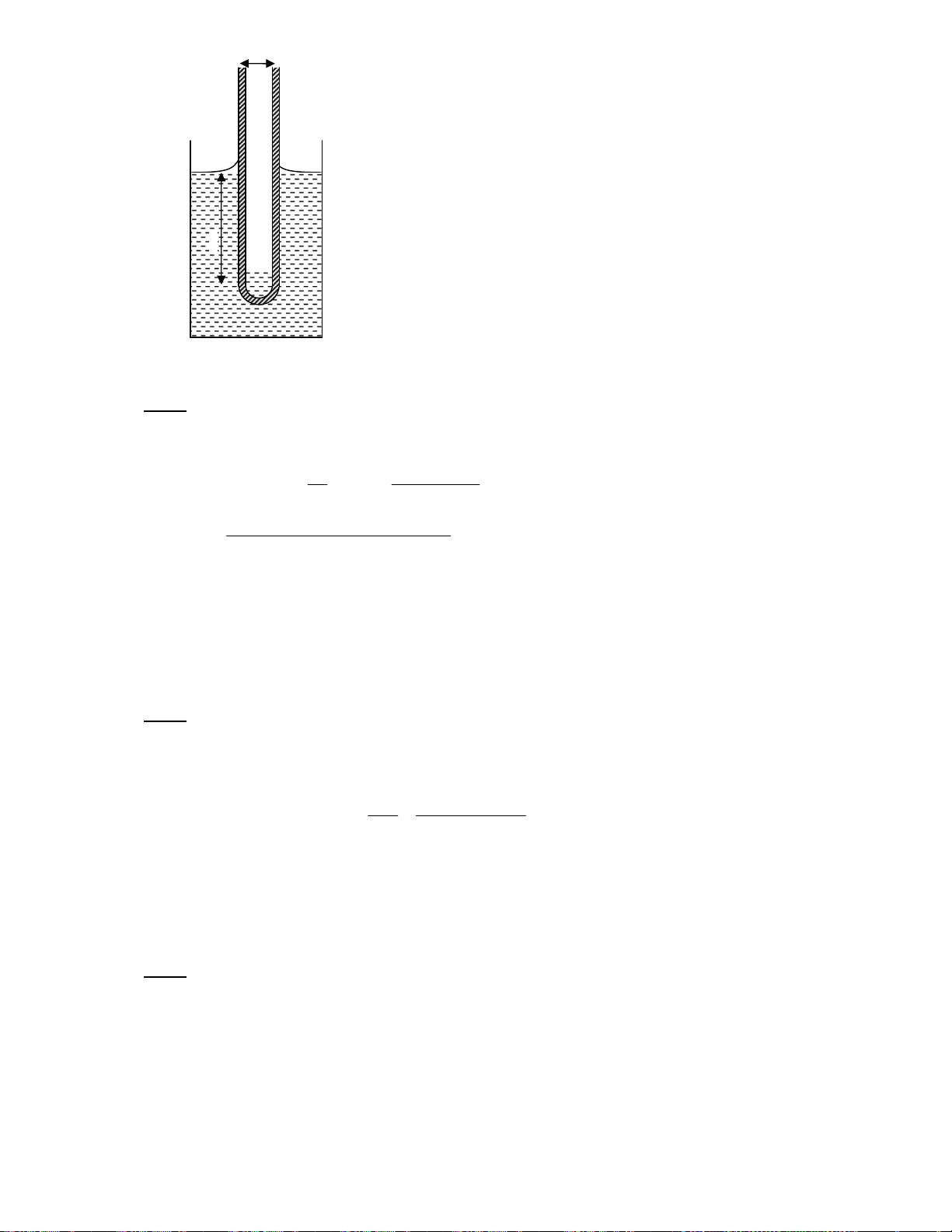
Downloaded by Ng?c Di?p ??ng (ngocdiep10012000@gmail.com) lOMoARcPSD|36477180 !" # $ % & ' !( ) *+ !" # & ' , -. /0 12 32 224 5 / 6/% 78 9 : ; !" & 8 7 9:8 < =>? $ @ /0 !( A 79 8 % ; !" & 8 7 97 8 < ? * B= !C /% " $0 !" # & $ *. !( & D6 ! # $E < !" # & . ; !" & 8 7 9:8 BB? $ @ /0 !( A 9 8 % ; !" & 8 9 8 >? F 6 8<=B , G !C /% " $0 = H, ; -I 6 $0 / " -J % ) # K L /% $0 $E => M, % !" N !O 0 -J !' 6 / , -. /0 12 32 224 5 / 6/% % & /-) 4D 6 78 9 : = 78 9 : = p p p − p 1 2 1 2 = = m m m − m 1 2 1 2 ? & -J !' 6A p ∆m = m − m = 1 2 − m = k 5 , 7 g 1 2 p 1 1 H% P . !( = & -J / Q # $E M 9 0 !" # & .
Downloaded by Ng?c Di?p ??ng (ngocdiep10012000@gmail.com) lOMoARcPSD|36477180 /-) . 78 9 : F G P . 78 9 : p= ρ : 9 (2) R 6 F G9F G m m T = T = + = 2 1 (t 27 1 ) 3 1400K ρV ρV > S6 !" % = P . !( = & 0 A & /-) ' $ ; !" & ' ? & -J / Q & /-) ' 3 ? & -J / Q & ' /-) ' A V = p µ / RT ≈ , 2 4 1 1 $ ; !" ' A 8 7 97 ≈ H ? ? & -J / Q # /-) ' A m1 3 ρ = = 1 , 4 4kg / m 1 V1 3 ? & -J / Q # ' A m1 3 ρ = = k 1 g / m 1 V2 M 1" $0 T " U H% 4D 0 # !' " & -J % / + $0 4D !" L S & ) % , -. /0 12 32 224 5 / 6/% m p V = RT 1 µ T − T ∆ → p = p ≈ 19at m / 2 2 1 p V = R − ∆ 2 (T T) 2T µ H 1" V ; -I $. 4D% V 6!/N 3-) H> * ; W X6 $. !-J > 0 $ % X 0 $. S% Y ? & -J V $. P µ V m = RT I V $. m p µ V t = = ∆m m ∆ RT
Downloaded by Ng?c Di?p ??ng (ngocdiep10012000@gmail.com) lOMoARcPSD|36477180 6 H> * 8 = >, = 8 H Z 8 < ?= 3 V = 300m =
:8B= [9 % ?= 8 = ∆ 8 > ; \ !-J ≈ << B % 3] * P 4) ! 4N !-J !" % 4D * *+ -J ! 4N !' T , ^ T
CaCO + H SO → CaSO + CO + H O 3 2 4 4 2 2 P& % CO / $E & % # CaCO ^ T ? & 2 3 -J # CaCO ^ T A 3 pV m = n .M = n .100 = 100 CaCO3 CaCO3 CO2 RT 6 & 8 * 8 3 , 1 . 3 105 Pa = 3 − 3 V = 3 , 1 . 2 10 m m ≈ 1 , 7 g 8 < $0 V !-J & 4) $E " & % = T _ " $0 T $E >, = $0 T D M, 1 ` D ! $0 N % % !" N !O ? !' X $E = $0 D >, 0 # $0 V T = $ # $0 T D > O & % /-) 4D N !O F4D !" a N !O G Q A p V p V p + 1 1 2 2 (V V 1 2 ) + = RT RT RT 7\6= # $0 V T p − p1 3 → V = V = d 5 m 2 1 p − p 2 $0 T T N 4) $E " & #6 # $0 T D = # $0 T D Rb !V ! = $0 V -J D 4D P ! ` D ! $0 N % % !" 4c N 6 !O # /% $0 N -. C $D \ <= A p V p V p + 1 1 2 2 (V V 1 2 ) + = RT RT RT p V + p V → p 1 1 2 2 = = a 6 , 1 t V + V 1 2
Downloaded by Ng?c Di?p ??ng (ngocdiep10012000@gmail.com) lOMoARcPSD|36477180 1" & #6 3 !d = " !V " !V Rb !V -I b !V 4D% " \ -) % % -) /% 4D %D & $E = d % K L # & $E P ! -I /b & Q " !%L F 0 G *+ T -) /% & 3X Q $ % Q = $ /E !" S e N !O 4D e 6 D HM * fg !" % " -) /% & D S /% & X Q p = (p − x o )(cmH O 2 ) hi \ j. . 1 / N % & $i p l = p + − = − + − o (l 4 x) (p x o )(l 4 x) S 6 &A p = 760mmHg = 103 c 3 mH O = l = 2 c 0 m o 2 x 2 -105 x 7 + 4132 = 0 → x = 9 , 3 c 5 m k F x = 105 c 3 m l Z %L G /% & % 4a $ " N = 3% ! ! d $0 -I L m D H> * 0 & -J / Q # N /% & $Q /% % 4a $ p' = p − p = 10mmHg = 1360Pa o ? & -J / Q # µ(p − p 29 1 . 360 o ) 3 ρ = = ≈ 17g / m RT 3 , 8 1.273 o B NS6 W J 4) $% F G n !i & -J # N % W J ! ? & -J # % W J m µ = ( + + g / mo ) m m l 1 2 = (kg/ kmo ) 8 22 l = = 4 k 0 g/ kmol n m m 1 2 8/ 32 + 22/ 44 + µ µ 1 2 1" W J =B ; . 4D = oS6 !" H% 4D >;9 0 # W J ! W J
Downloaded by Ng?c Di?p ??ng (ngocdiep10012000@gmail.com) lOMoARcPSD|36477180 m m 1 2 2800 3200 + RT + 3 , 8 . 1 ( . 273 + 17) nRT µ µ 1 2 28 32 3 V = = = ≈ , 1 2m 5 p p 4.10 > ? O D " W J p " V & -J 6!N 4D V & -J oS6 *'6 S !i & -J / Q # O ! ! d -I 2% $D = & -J % # O m + m 1 + m / m m / m =8 2 1 1 + 8 1 2 2 1 µ = = = = 12g / mol m m 1 m / m 1 2 2 1 1/ 2 + 8 / 32 + + µ µ µ µ 1 2 1 2 ? & -J / Q # W J 5 µp 12. 0 , 1 1.10 o 3 ρ = = ≈ 534g / m RT 3 , 8 1 2 . 73 o B M %S6 !-J q !" > % ! M % 0 -J D \ !-J 4D !" $ Q " r # & /% eb /0 h( k $ h( A @ /0 !( m m 5 160 5 Q ∆ = U ∆ = C ∆T = R∆T = . . − ≈ ≈ V (. 31 . 8 60 50) 1040J c 250 al µ µ 2 32 2 $ @ /0 !( h" $ Q " r m U ∆ = C T ∆ = c 250 al V µ ; -J \ 4D% m m Q ∆ = U ∆ + A = C ∆T + p∆V = + ∆ = ∆ V (C R V ) m 7 T R T µ µ µ 2 6 & 160 7 ∆@ = . 8 . .31 (
. 60 − 50) ≈ 1454J ≈ 35 c 0 al 32 2 B 0 3 / Q F G !( # " ! 6Q s= $ /E & -J / Q # ! ! d t D 8H=<> 9
Downloaded by Ng?c Di?p ??ng (ngocdiep10012000@gmail.com) lOMoARcPSD|36477180 7) ! 6Q s= 3 / Q % !( C = R 3 V (J / molK) ! d Q t m R ρ To p V = RT → µ = o o o µ po ; 3 / Q !( C p C p 3 c V o V o = = = ≈ 1400J / kgK V µ ρRT T ρ B 0 3 / Q F G !( # " = $ /E & -J # " N % ! D 8 9 % * & ,% SN F m & !%L G 8 = A ; 3 / Q % !( A C = C + R p V 7) C p γR γ = 8l C = C p γ −1 V ; 3 / Q !( A C R γ , 1 4 3 , 8 . 1 c p = = = = 969 5 , J / kgK p µ µ(γ − ) 1 30.10−3 ( . , 1 4 − ) 1 B 1" $0 T ; . 4D !" H P . = /% $0 Q ) > *+ A ; !" # . Y $ # $0 Y h" r " r # Y @ /0 !( = !" & . D p p p 1 2 = → T 2 = T = 1500K T T 2 p 1 1 2 1 $0 mRT V 1 = = 12 7 , 2l p µ 1 h" r " r # & A m U ∆ = C − = − = V (T T 2 1 ) m 5 p R 2 1 T 12 4 , 6kJ µ µ 2 p 1 1 F N D -u 6Q s 8>= C = 5R / 2G 2 V B > ;U !( N 0 + / $ /E & _ $E 9 $ !V
Downloaded by Ng?c Di?p ??ng (ngocdiep10012000@gmail.com) lOMoARcPSD|36477180 ; 6Q v T # !" C g = -J D & \ !-J Q ∆ = A + ' U ∆ @ /0 !( Q ∆w8 nC ∆T = V ; -J D & \ !-J V V 2 2 dV V Q ∆ = A' = pdV = pV = p V ln 2 1 1 V V 1 1 V V1 4 3 − 1 Q ∆ = 8 , 9 1 1 . 0 .3 1 . 0 ln ≈ 6 − 76J 10 x y z m / /E e /0 C C + B M 1" $0 = !C . !" % P . = / $0 Q ) * 0 -J D & !' \ !-J = $ $0 ' U j0 ' U = # $0 N !O = e /0 D !( {8 ; 6Q v | !" C g m iR ∆Q = A + ∆U = ∆U = (T − T 2 1 ) µ 2 i m m i m ∆Q = RT − RT = p V − RT 2 1 2 1 2 µ µ 2 µ F N D -u 6Q s 8>= C = 5R / 2 G 2 V 6 & 8 * 8 = M, = 78 = 8 B ? Q ∆ = k 1 , 4 J B H *. M oS6 /% " $0 ' U !" H = q > ;9 Q ) >;9 0 A ; !" # & . k $ ; -J !' % & j0 = ' U = e /0 !( = !" & . D p p p 3 1 . 05 1 2 = → T 2 = T = + = 2 1 (273 37) 930K T T p 105 1 2 1 $ ; -J !' % $E -J D \ !-J /% e /0 !( /Q
Downloaded by Ng?c Di?p ??ng (ngocdiep10012000@gmail.com) lOMoARcPSD|36477180 m Q ∆ = U ∆ = C R − = − V (T T 2 1 ) m i p RT 2 1 µ µ 2 1 p1 16 5 5 Q ∆ = . 3 , 8 1 ( . 273 + 37) 3 1 . 0 −1 ≈ ,64kJ 32 2 105 B B P \ !-J -J @8 > = !" # 8 = S r q 8 M% ) 8 % *+ e /0 . ! !-J D /% ! d D%Y ; -J D \ !-J m Q µ Q = C T ∆ → C = x x µ m(t − t 2 1 ) 32.150 1 , 4 . 8 C = = 20 7 , 7J / molK x 40 3 , ( . 40 − 16) ; 3 / Q % !( # S A iR 5. 3 , 8 1 C = = = 20 7 , 7J / molK = C V x 2 2 ; - 4\6 C = C = e /0 D !( x V B < M=> 6!/N !" H% = \ -J ' !N = /% ! d N !O N D / $ h" $ Q " r # & ; -J !' % & N / A = p(V − V = − = 2 1 ) p(2V1 1 ) m V RT1 µ 5 , 6 A = . 3 , 8 1 ( . 273 + 27) ≈ 1 , 8 1 . 03 J 2 $ h" $ Q " r # & A m ∆U = C − = − = 2 − = V (T T 2 1 ) i m m i RT RT 2 1 ( pV pV 1 1 ) i m RT1 µ 2 µ µ 2 2 µ 5 5 , 6 ∆U = . 3 , 8 . 1 ( . 273 + 27) 3 ≈ 2 , 0 2.10 J 2 2 ; -J !' % & S $E -J D \ !-J 2% 6Q v | Q ∆ = A + U ∆ = 1 , 8 .103 + 2 , 0 2 1 . 03 = 28 3 , 1 . 03 J Fh& 4) 6Q s 6!/N F -u 6Q sG & $\ C 3% 6Q s 8>G
Downloaded by Ng?c Di?p ??ng (ngocdiep10012000@gmail.com) lOMoARcPSD|36477180 B %S6 % = >, P . !( = r ! 0 A ; -J D & \ !-J $ ;" r # & /-) 4D . 2% 6Q v |= -J D & \ !-J /% eb /0 !( m + + Q = A + U ∆ = C − = − = − p (T T 2 1 ) i 2 m m i 2 m RT RT pV RT µ 2 2 1 µ µ 2 2 1 µ 5 + 2 5 −3 10 Q = 3 1 . 0 .10 1 . 0 − . 3 , 8 1 ( . 273 + 10) ≈ 9 , 7 1 . 03 J 2 32 $ ;" r # & /-) . m m i U = C T = RT 1 V 1 µ µ 2 1 10 5 U = . 3 , 8 . 1 + ≈ 1 (.273 10) 8 , 1 .103 J 32 2 ;" r # & . m m i i U = C T = RT = pV 2 V 2 µ µ 2 2 2 2 5 U = 3 . .105 1 . 0.10−3 = 5 , 7 1 . 03 J 2 2 Fh& 4) 6Q s %S6 F -u 6Q sG & $\ C 3% 6Q s 8>G B 1" #6 N 6 !" /% -) I N U /% $0 T # #6 N ] / N 3% / j /E # $0 T D > = # N U q ^ ) ? ] / D N /-I -) / ) 4D !" % - N !O x% ! e /0 ' # #6 N /% -) % D e /0 !( F V !b D \ i G N 3% / A p A = p V ln 1 = 8 , 9 . 1 . 1 104. 1 . 5 0−3 ln100 ≈ , 2 26 1 . 03 J 1 1 p2 B % $% !-J . !( % ! !" r Q > % 0 h" $ Q " r # & $ N 3% ' / ; -J / 6d %
Downloaded by Ng?c Di?p ??ng (ngocdiep10012000@gmail.com) lOMoARcPSD|36477180 h" $ Q " r # & m iR 3 3 , 8 . 6 1 U ∆ = T ∆ = . 2 10 5 . 0 ≈ 2500kJ µ 2 2 F D ! 6Q s F S D G Q & $\ C 3% # X s D MG $ N 3% ' / A = p( m V − V = R T − T 2 1 ) ( 2 1 ) µ A = 2.10 . 3 3 , 8 1.50 ≈ 830kJ ; -J / 6d % $E -J D \ !-J Q = U ∆ + A = 2500 + 830 = 3330kJ B H $% !-J . % ) !" r Q % /% ! d ' C 3% 0 N 3% / 4D !" $ Q Q " r # f ' C 3% } D !( F ' /% e 6 = $E e 6 G N 3% / ' A = p( m m m V − V = RT − RT = R T − T 2 1 ) 2 1 ( 2 1 ) µ µ µ 7 A = 3 , 8 . 1 1 . 0 ≈ 1 , 3 2J 44 h" $ Q " r # & m iR 7 6. 3 , 8 1 U ∆ = T ∆ = . .10 ≈ 39 7 , J µ 2 44 2 F D ! 6Q s F S D G Q & $\ C 3% # X s D MG B %S6 4D !" % !-J . !( 4D ' ) 0 A ; -J % & $ h" $ Q Q " r # & N 3% / ' ; -J % $E -J D \ 4D% m i + 2 m m i + 2 m Q = A + ∆U = C (T − T ) = RT − RT = pV − RT p 2 1 2 1 2 1 µ 2 µ µ 2 µ 5 + 2 4 −3 10 Q = 3. 8 , 9 1 1 . 0 .10 1 . 0 − . 3 , 8 1 ( . 273 + 10) = 8 , 7 1 . 03 J 2 32 $ h" $ Q " r m m C i U ∆ = C (T − T ) V = C (T − T ) = Q = 5 , 5 1 . 03 J V 2 1 µ µ C p 2 1 i + 2 p N 3% / '
Downloaded by Ng?c Di?p ??ng (ngocdiep10012000@gmail.com) lOMoARcPSD|36477180 A = Q − U ∆ 3 , 2 1 . 03 = J B > 1" !C /% " S !~ ( !T N & -J N ! 3 !" !-J *+ V ^ C " N $E $ % Q ! X N Q % Q " %^ h = 1 c 0 m 1 d % $ !V # " N D h =1 c 5 m = e 6 D o p = a 1 t = 3 ~ N 2 S = 10cm ; !" # % D N o !O /% & e /0 N 3% / V h + h 1 o 1 A = p V ln = p V ln o o o o o V h o 0 * 6= $ !O \ 4D% " N A h − A = o p V ln o o o h + h o 1 N # e 6 A A = p Sh k o 1 N V C $ % p N / 6d % 4D N • e 6 h
A' = A − A = p S h − h ln 1 + 1 k o 1 o ho 4 −4 −2 −2 10 A' = 1 9 . 8 , .10 .10 1 . 0 10.10 − 15 1 . 0 . ln 1 + ≈ J 3 , 2 15 B M ' !( q 8> ! N 3% / 4D -J % /% e /0 ' 2% 6Q v | Q = A + U ∆ U ∆ = 0 p V =p V V2 V 1 1 2 2 p 2 1 Q = A = pdV = p V ln = p V ln 1 1 1 1 V1 V p 1 2 4 5 Q = A = 2.5 8 , 9 . 1 1 . 0 .ln = , 2 2 1 . 05 J 4 B H 1" & ; 8 7 8 !-J ' ) !N 0 & _ 4D N 3% / ' ! DA h( $ h( h%L
Downloaded by Ng?c Di?p ??ng (ngocdiep10012000@gmail.com) lOMoARcPSD|36477180 @ /0 !( & 8 8 N 3% / A = p V ∆ = 1 8 , 9 . 1 1 . 04 − − − ≈ 1 (.2 1.0.10 3 10 1.0 3) 980J $ @ /0 !( & A V p V = p V → p 1 = p = at 5 , 0 1 1 2 2 2 V 1 2 N 3% / V A = p V ln 2 = 4 − 1 8 , 9 . 1 1 . 0 1 . 0.10 . 3 ln 2 = MB [ 1 1 V1 @ /0 !%L γ γ γ V p V = p V → p = 1 p 1 1 2 2 2 1 V2 h& 4) ; = i + 2 5 + 2 γ = = = , 1 4 i 2 ;Q p = 1/ 2 ,14 = 3 , 0 a 8 t 2 Z N 3% / m Q = A + ∆U → A = −∆U = C − = − V (T T 1 2 ) i m m RT RT µ 2 1 2 µ µ γ γ 1 − i A = (p V − p V = − = − 1 1 2 2 ) i V i V p V 1 V p V 1 1 2 2 1 1 V 2 2 1 1 V 2 2 5 A = 8 , 9 1 1 . 04.10 1
. 0−3 (1 − 2−0,4 ) ≈ 590J 2 B B ;U %S6 q ! d Q t ) 0 A 4D !" # & W e /0 U !( 4D !%L $ N V ! U /% W /-I J q ! = 6 / Q U 2% D% 0 J . $ !V 10 V = 2 . , 2 4 = 7l 1 32 @ /0 U !( A & e /0 D A
Downloaded by Ng?c Di?p ??ng (ngocdiep10012000@gmail.com) lOMoARcPSD|36477180 V1 p V = p V → p = p 1 1 2 2 2 1 V2 5 7 p = 10 . ≈ 7 , 1 .105 Pa 2 4 *%~ I -. 0 /L A m mRT p V = p V = RT → p 1 = 1 1 2 2 1 2 µ V µ 2 10 3 , 8 . 1 2 . 73 p = ≈ 7 , 1 .105 Pa 2 32.4 1 . 0−3 ; !" N !O T = T = 27 K 3 2 1 N U $E 4D -J 3 4) N / V m V
A = − A = − p V ln 2 = − RT ln 2 2 1 1 V 1 µ V 1 1 10 4 A = − 3 , 8 . 1.273.ln ≈ 397J 1 32 7 $ A γ , 1 4 V γ γ 1 5 7 p V = p V → p = p = 10 = 2 , 2 .105 Pa 1 1 2 2 2 1 V 4 2 ; !" γ 1 − , 1 4 1 − γ − γ − V 1 1 7 T V = T V → T = T 1 = 273 ≈ 34 K 1 1 1 2 2 2 1 V 4 2 N U $E 4D -J 3 4) N / γ 1 − , 1 4 1 5 −3 − p V V 10 7 . .10 7 1 1 1 A = − 1 − = − 1 − ≈ 439J > A 2 1 γ − 1 V , 1 4 − 1 4 2 7\6 U !( 0 & . B < ; -I & U N ! *+ Q U !( 6 U !%L Y N U 2% e /0 !( F$E 4D -J 3 4) 4) N D / GA V V A = − 2 p V ln = 1 p V ln F G 1 1 1 1 1 V V 1 2 -. C= !& 4) e /0 !%L A Q
∆ = A + ∆U = 0 → A = − U ∆ N U /% /-I J D6= -. C - !' D 4) $D B H A γ −1 i V
A = −A = ∆U = − p V 1 − 1 F G 2 1 1 2 V2 q F G 4D F G
Downloaded by Ng?c Di?p ??ng (ngocdiep10012000@gmail.com) lOMoARcPSD|36477180 A γ i − − − − 2 (V / V 1 2 ) 1 1 5 (10 / 2) ,14 1 1 = . = . ≈ , 1 4 > 1 A 2 ln 1 (V / V 1 2 ) 2 ln(10 / 2) 7\6 U 2% e /0 !( & N . = 3% ! J . B f ' !%L " & N % % # r !N *'6 !" & N ! & e /0 = $ /E b ! !" % , -. /0 % e /0 !%L p Vγ = p Vγ → γ − = γ − → γ − = γ − 1 1 2 2 (p V 1 1 )V 1 1 (p V 2 2 )V 1 T V 1 T V 1 2 1 1 2 2 γ 1 − , 1 4 1 − V 1 → T = T 1 = 273 ≈ 207K 2 1 V 2 2 B H= %S6 !-J U !%L ! = b ! # U D M *+ $ !V Y , -. /0 FS2 ] ] G % e /0 !%L γ , 1 4 V γ γ 1 p V = p V → p = p 1 = 16. ≈ a 1 t 1 1 2 2 2 1 V , 7 2 2 B N !" % 4D => !-J ' !%L ! *+ A N r Q $ % Q V Y $ ; !" N ' Y N 3% N / ' Y q -. /0 1/ γ 1/ , 1 4 V p γ γ 5 , 1 p V = p V 2 1 → = = ≈ 3 , 1 3 1 1 2 2 V p 1 1 2 r %^ = V $ , -. /0 % e /0 !g 1 γ − γ γ γ γ p 1 γ − γ 1 γ − p V = p V → T p = T p → T = 1 T 1 1 2 2 1 1 2 2 2 1 p2 1− , 1 4 , 1 4 T = + ≈ 2 (273 ) 5 , 1 30 270K 1 N 3% / m iR A = − U ∆ = (T − T 1 2 ) µ 2
Downloaded by Ng?c Di?p ??ng (ngocdiep10012000@gmail.com) lOMoARcPSD|36477180 h& 4) N 8 < 9 % = $\ C 3% # X s 8> 103 3 , 8 . 5 1 A = (.303− 270) ≈ , 2 1 . 4 04 J 29 2 B T /E !& 4) " v - S !i -. /0 A 2 pV = U i w D " r # & 6= D $\ C 3% ;" r v - i U = nRT 2 , -. /0 12 32 224 5 / 6/% pV = nRT x% ! 2 pV = U i B 1" N % ; F 8 B 9 % G ! d Q t ' !%L % % # r Q > V 0 A N 3% C $ h" $ Q Q " r # & ; !" U D A γ γ γ 1 − γ 1 p V = p V → T V = T V − 1 1 2 2 1 1 2 2 γ 1 − , 1 4 1 − V 1 → T = T 1 = 273. ≈ 14 , 3 4K 2 1 V 5 2 N 3% C m iR A = − U ∆ = (T − T 1 2 ) µ 2 3 5 3 , 8 . 1 A = 10 . (273 −14 , 3 4) ≈ 7 , 2 1 . 06 J 2 $ h" $ Q " r # & $E 4D -J 3 4) N 3% / U ∆ = −A = 1 . 7 , 2 06 − J B > ? N /% S # " !" . !& /% !-J U !g q ! > !" # & e /0 U $ /E !" $ !V # D o C , -. /0 % e /0 !%L
Downloaded by Ng?c Di?p ??ng (ngocdiep10012000@gmail.com) lOMoARcPSD|36477180 1 γ − γ γ γ γ p 1 γ − γ 1 γ − p V = p V → T p = T p → T = 1 T 1 1 2 2 1 1 2 2 2 1 p2 1− , 1 4 , 1 4 T = + ≈ = 2 (273 ) 1 40 865K 592o C 35 B M 1" & ' !%L = # r !N = - !" 6 !& # ^ ! = V 0 & $\ C 3% # X s ! q -. /0 γ γ γ 1 − γ 1 − ln(T / T 2 1 ) p V = p V → T V = T V → γ −1 = 1 1 2 2 1 1 2 2 ln(V / V 1 2 ) γ 1 − =2 / i 2 ln(V / V 1 2 ) 2. ln(1/ 2) → i = = = 5 ln(T / T 2 1 ) ln(1/ 3 , 1 2) P& $\ C 3% D > B H 1" -u 6Q s V = l 5 , 0 = p = 5 , 0 atm $i 1 1 U !%L ) 7 4D P ! -I € 6Q V 4D D L ) !" $ !V ? ! 2 # D p = a 1 tm o 7• !p i # e /0 ! $ 0 V 4D p 2 2 hp i # e /0 A % 7 7 7 $ @ /0 5 !( Q A p1 p V = p V → V = V = , 0 2 l 5 = V o 3 1 1 3 1 2 po @ /0 5 !%L Q A γ γ γ γ V p p V = p V → p 1 = p o = p 1 1 2 2 2 V 1 p 1 2 1 p = 2 ,14 5 , 0 . ≈ 3 , 1 2at 2
Downloaded by Ng?c Di?p ??ng (ngocdiep10012000@gmail.com) lOMoARcPSD|36477180 F? -u 6Q s 8> Q , { x i + 2 5 + 2 γ = = = , 1 4 G i 5 B B ? U !%L % -u 6Q , j s= -I !' & N M [ *+ !" # r Q $ % Q Y % 7 7 7 *0 B ? \ " N {8 M [ F N 5{8 M[G= !" r " r $E N \ 4D% # m iR U ∆ = A = T ∆ µ 2 2A 1 . 2 4 . 6 103 → ∆T = = ≈ 7K iRm / µ 3 , 8 . 5 1 1 . 03 ; !" r H o C B < 1" -J %S6 7 8 !" H o C 4D 8B= >, /L T = N & 7 8 => 4D 8M >, F G 0 -J D / ' = 4D !" $ Q " r # & f ^ $D % /% /-I J $ !O & q /L ) /L 2% % !-I A { j $ {xj @ /0 { j { !( A m iR i m m Q = ∆U = T T RT RT AC ( − C A ) = − C A µ 2 2 µ µ i 5 Q = − = 6.105 − , 8 2.105 3 1 . 0−3 = 1 − 650 AC (p p 2 1 )V1 ( ) J 2 2 @ /0 j !(
A C = C + R p V m i 2 m m Q = C R T T RT RT CB ( + V )( − B C ) + = − B C µ 2 µ µ i + 2 5 + 2 Q = p − = 6 1 . 05 5 , 4 − 3 10−3 = 3150 CB 2 (V V 2 1 ) ( ) J 2 2 ^ e /0 Q = Q + Q = 1 − 650 + 3150 = 1500J ACB AC CB @ /0 { j \ -J Q = 1500J ACB
Downloaded by Ng?c Di?p ??ng (ngocdiep10012000@gmail.com) lOMoARcPSD|36477180 m U ∆ = C − = − AB V (TB A ) i T (p V p V 2 2 1 1 ) µ 2 5 U ∆ = − − − = AB (6 1.05. 5, 4 .10 3 , 8 2 1 . 05.3 1 . 0 3 ) 600J 2 !"# $% A = A = p − ACB CB 2 (V V 2 1 ) A = 6.105 − − − = ACB (. 5, 4 .10 3 3 1 . 0 3 ) 900J $ @ /0 {xj & @ /0 {x !( m i 2 m m Q = C R T T RT RT AD ( + V )( − D A ) + = − D A µ 2 µ µ i + 2 + Q = p − = − − = AD 1 (V V 2 ) 5 2 , 8 2 1 . 05 1 ( 5 , 4 3)10 3 4305J 2 2 xj !( A m iR i m m Q = ∆U = T T RT RT DB ( − B D ) = − A C µ 2 2 µ µ i Q = − = − − = − DB (p p 2 1 ) 5 V2 (6 1.05 ,82.105 ) 5, 4 .10 3 2475J 2 2 ^ e /0 Q = Q + Q = 4305 − 2475 = 1830J ADB AC CB m U ∆ = C − = − AB V (TB A ) i T (p V p V 2 2 1 1 ) µ 2 5 U ∆ = − − − = AB (6 1.05. 5, 4 .10 3 , 8 2 1 . 05.3 1 . 0 3 ) 600J 2 !"# A = A = p − ADB AD 1 (V V 2 1 ) A = , 8 2.105 − − − = ADB (. 5, 4 .10 3 3 1 . 0 3 ) 1230J B 1" % F & -J % G C " /0 {j x - 0 3-) = /% ! {j= x D e /0 !( = T 4)
!" T 4D T = j 4D x{ D e /0 !( T 4) V 1 2 2 4D V1
Downloaded by Ng?c Di?p ??ng (ngocdiep10012000@gmail.com) lOMoARcPSD|36477180 { { x x j j 7 7 7 T /E p p A D = 7 p p B C $ N 4D /% ^ /0 3] Q -. /0 # e /0 !( A p V V p A B C D = = = F! G p V V p B A D C $ N # /0 $E N /Q e /0 {j 4D x= e /0 K L N $E N m pV = RT V V µ m V 2 1 A = A + A = p V ln + p V ln = R − AB CD A A D D (T T ln 2 ) 2 1 V V µ V 1 2 1 ; \ /% ^ /0 A m Q = A = R( V T − T ln 2 ) 2 1 µ V1 B 1" & C " /0 - 0 4• 3-) = /% ! 4D D e /0 !( T 4) !" T 4D T = 4D 1 2 D e /0 !%L % V = l 2 ,V = l 5 = V = l 8 = p = 7atm 0 A 1 2 3 1 Q = A + U ∆ = A
Downloaded by Ng?c Di?p ??ng (ngocdiep10012000@gmail.com) lOMoARcPSD|36477180 7 7 7 7 7
p , p , p ,V ,T 2 3 4 4 2 $ N C /% q e /0 4D /% %D /0 ; D & \ !-J 6 + / /% q e /0 !( V p 1 = p = , 2 7atm = % N D -u 6Q sA 8>= A 2 V 1 2 γ V p 2 = p = , 1 45atm 3 V 2 3 γ 1 − 1−γ V T γ T = T 2 = 33 K 1 ; p = p 2 = 6 , 3 atm 2 1 V 4 1 T 3 1 p V 3 = V = , 3 l 2 4 p 3 4 $ N C /Q q e /0 A V
A = p V ln 2 = 1300J 12 1 1 V1 p V T A 2 2 = 1 2 − = 620J 23 γ −1 T1 V A = p V ln 4 = 1 − 070J 34 2 2 V3 p V T A 2 2 = 1 1 − = −620J 41 γ −1 T2 N C /% ^ /0 A
A = A + A + A + A = 230J 12 23 34 41 ; D \ /% q e /0 !%L A
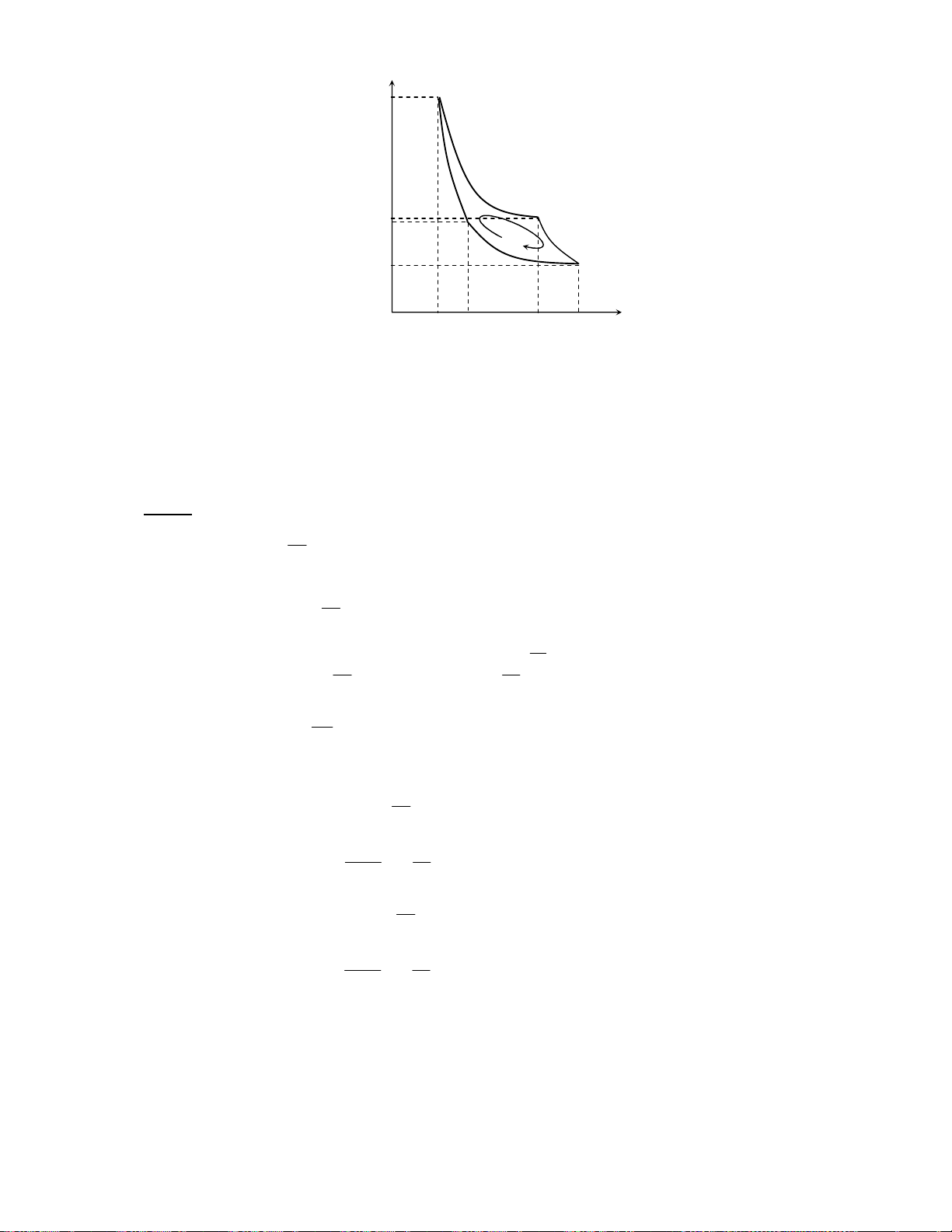
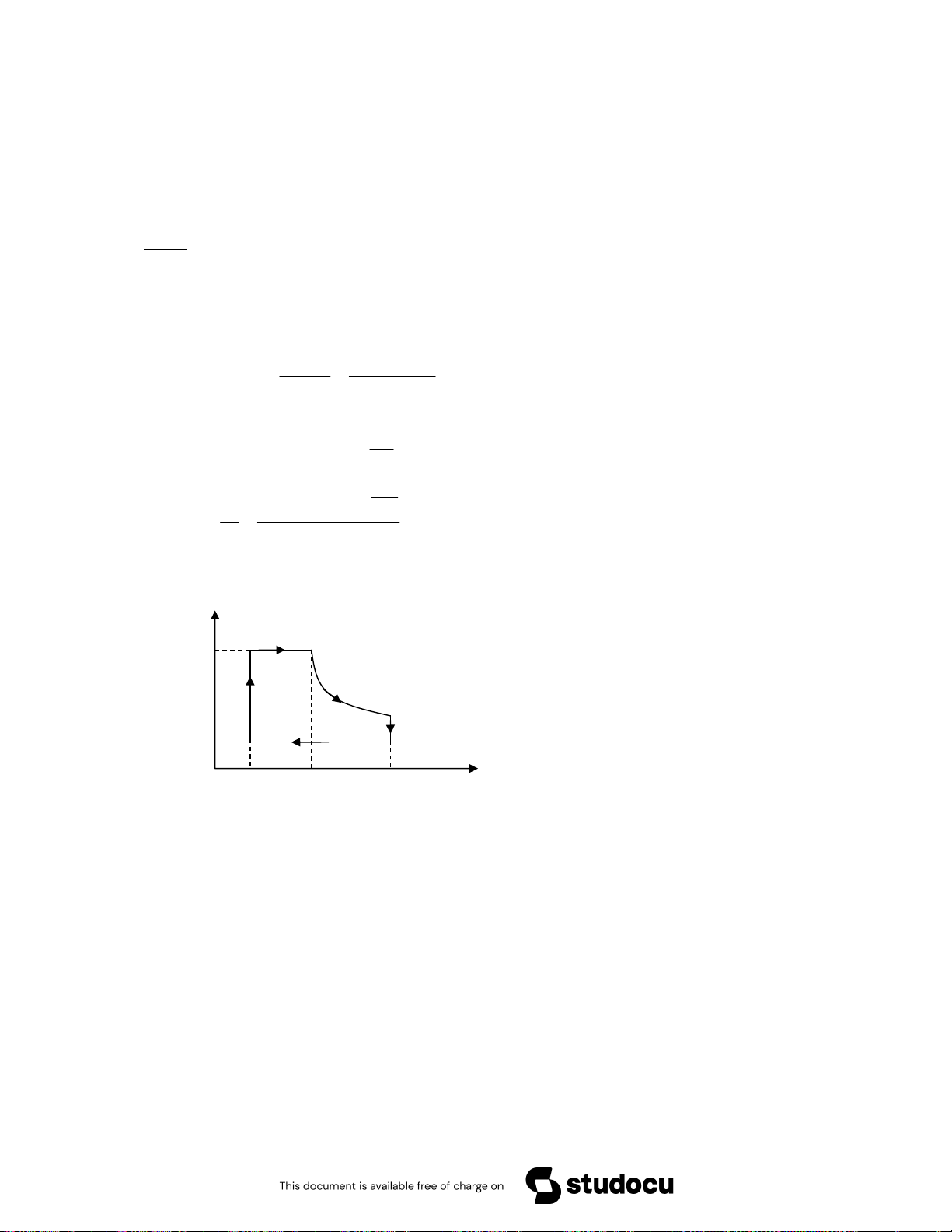
Downloaded by Ng?c Di?p ??ng (ngocdiep10012000@gmail.com) lOMoARcPSD|36477180 Q = A = 1300J = \ 12 12 Q = A = 1 − 070J = ^ 34 34 B /% " $0 ; 4D %S6 0 !" $ Q Q " r # W J ! D L S & B% h" ^ " r m iR m iR U O ∆ = T N ∆ + T ∆ µ 2 µ 2 O N 32 20 5 3 , 8 . 1 U ∆ = + (273 + 28) ≈ 10000J 32 28 2 B f ^ !p N 2% v 6 # " 6 U !-J 4• /Q 0 B 5 F ^ !p C /K . G h%L {j T 4) e /0 U !( N = j e /0 !t6 N 4D% $0 T F N !O Gk x 5 ^ !" " /% S # 6 U ! 4 % 4D 4 L k x{ 5 % N 4D% *'6 T /E N # 6 U " /0 $E N !& 4) e /0 !( 4D !-J $ 3 ‚ $E 3 {jfƒ j , , x * { f ƒ 7 7 7 *0 B N { # 6 U $E N \ !-J 4D $E 3 {j x
A = dt(ABCDA) = dt(ABHA) + dt(BCDH ) B dt(BCDH ) B = (p − p = − = − = 2 1 )V p V p V p 2 1 1 1 2 1 (V V 1 2 ) dt(AFGH)
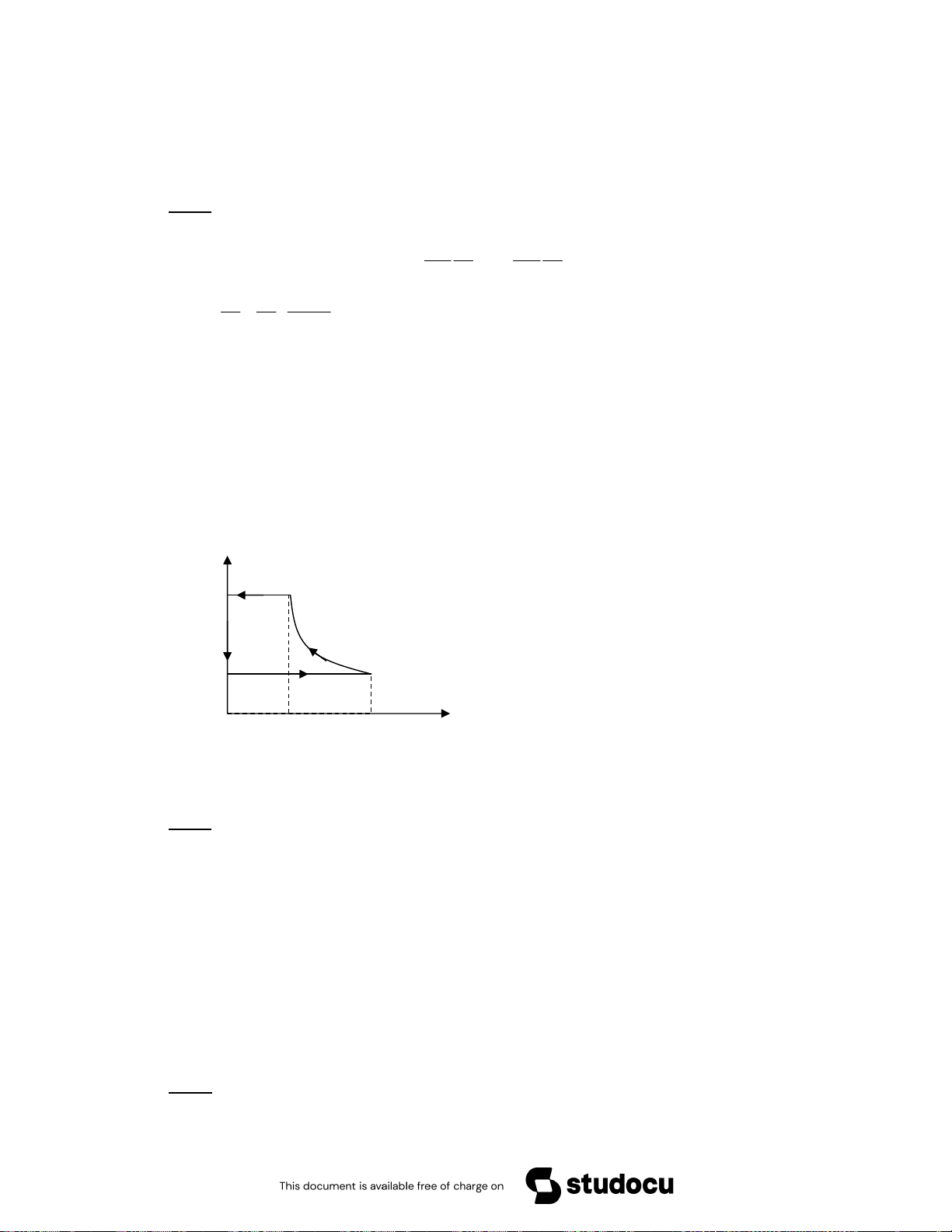
→ A = dt(ABHA) + dt(AFGH) = dt(ABGF) F! G B 7• !p i # € e /0 !( = !( = !( 4D% !%L # ^ !p = =w $ =7 3 7=w
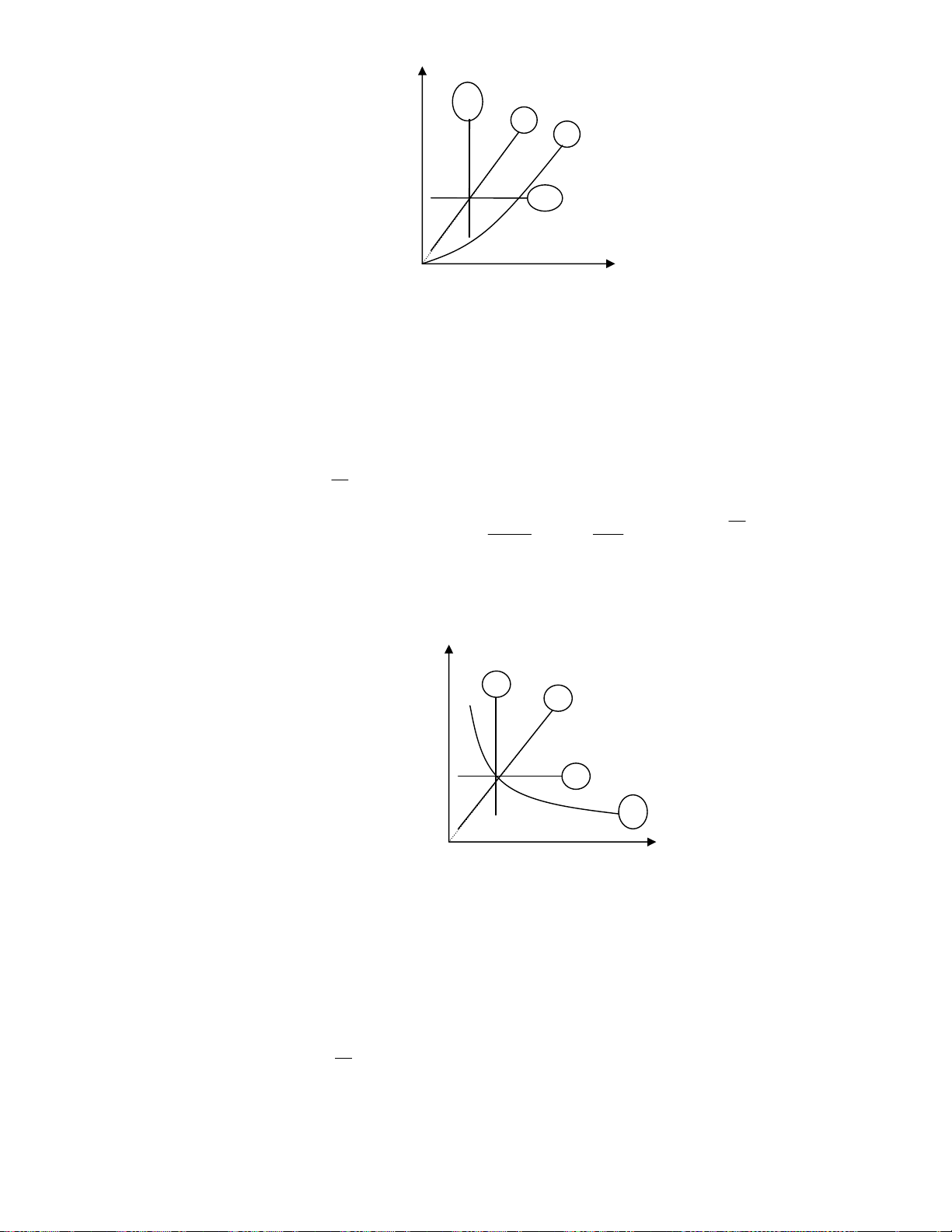
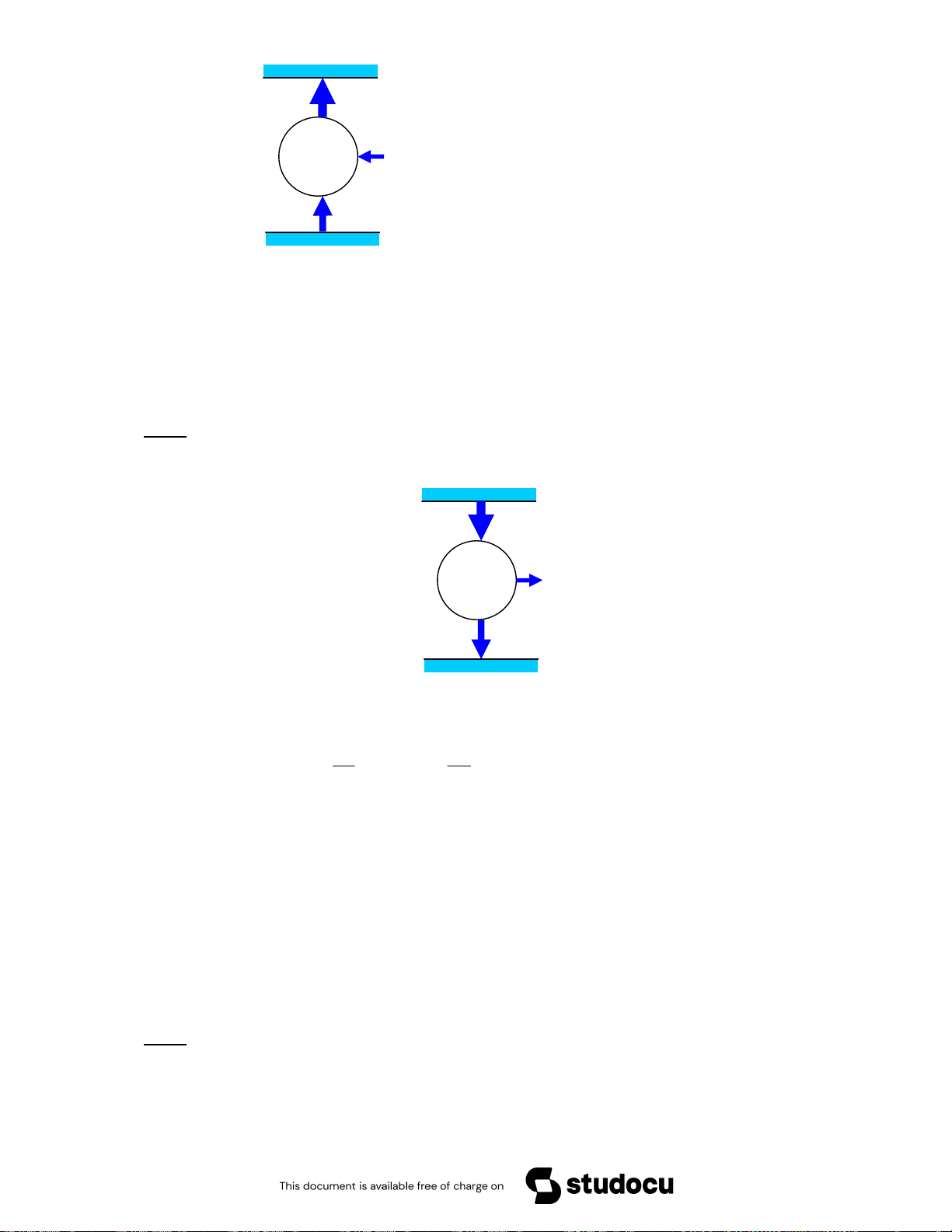
Downloaded by Ng?c Di?p ??ng (ngocdiep10012000@gmail.com) lOMoARcPSD|36477180 f ^ !p = • @ /0 !( A 9 8 % = !p i $ 3 ‚ D !-I ( e & L !" F!-I G • @ /0 !( A N !O = !p i $ 3 ‚ D !-I ( % % 4) F!-I G • @ /0 !( A !" N !O = !p i $ 3 ‚ D !-I ( % 4) • @ /0 !%L PC ] " 4D% % $ -. /0 γ 1 p const T . − = γ γ γ γ F40 3% γ pV γ T pV = c = const → c = = nR → p = const T . γ − G 1 ( ) ( ) 1 ( ) 1 γ 1 − γ 1 p p − , -. /0 D6 !p i F G D " !-I % ! e & g !" $ f ^ !p =7 7 • @ /0 !( A N !O = !p i $ 3 ‚ D !-I ( % % 4) F!-I G • @ /0 !( A 79 8 % = !p i $ 3 ‚ D !-I ( e & L% !" F!-I G • @ /0 !( A 8 % = !p i $ 3 ‚ D !-I ( % 4) 7 • @ /0 !%L PC ] " 7 4D% % $ -. /0 1 V const T . 1 − = γ .
Downloaded by Ng?c Di?p ??ng (ngocdiep10012000@gmail.com) lOMoARcPSD|36477180 1 −
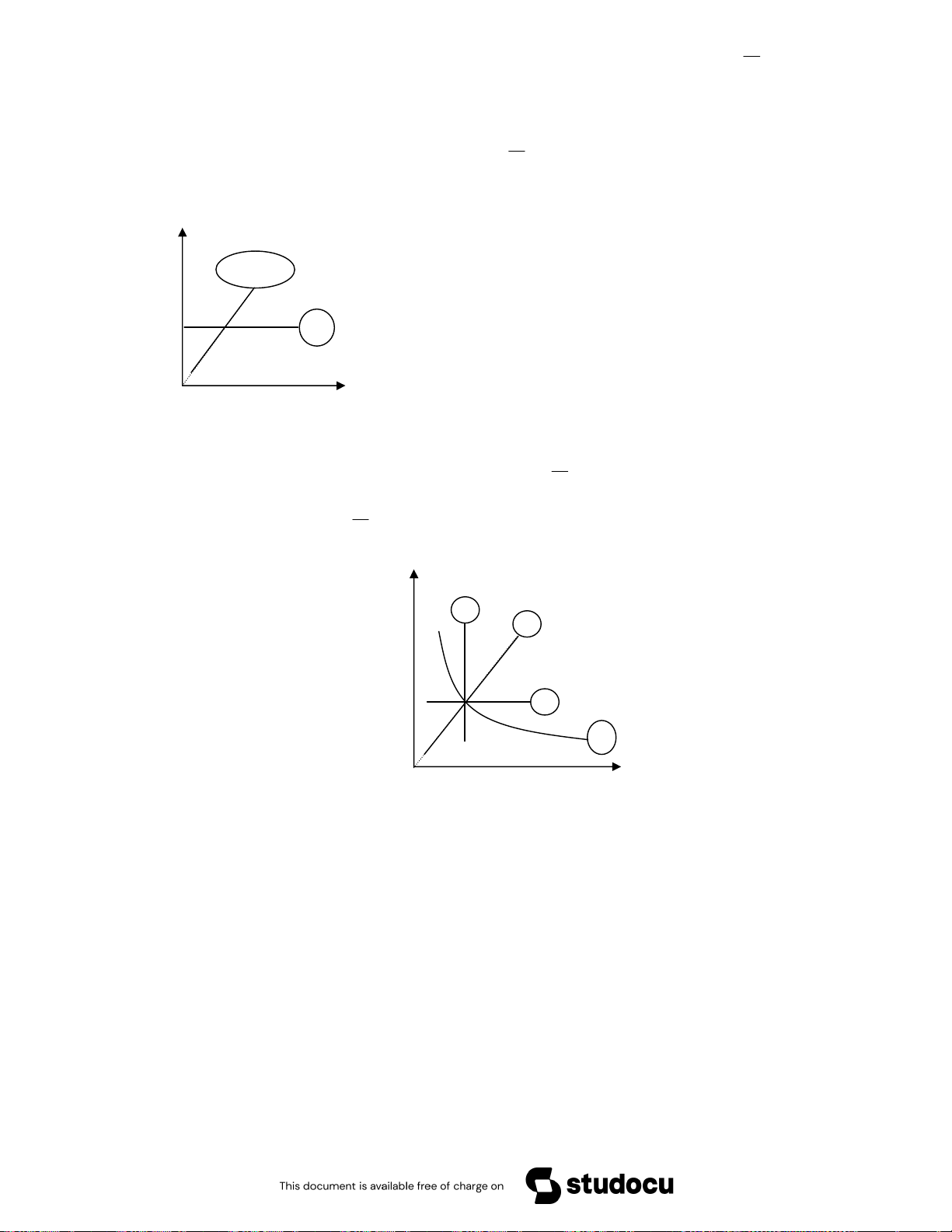
F40 3% pVγ = c(= const)→ c = (pV) γ 1 V − = (nR ) γ 1 − γ 1 TV → V = const T . − = l G , -. /0 D6 !p i F G D " !-I % 3L 6 2 $% \ 4) /] g !" F!-I G /% " e /0 $ „ A m U = RT = e /0 !( = !( µ = !%L !-I $ 3 ‚ D !-I ( e & g !" F!-I = = G= e /0 !( !-J % $ !-I E F!-I G w = = 3 f ^ !p w=7 Fw " E & m C = 3% ! m V U% 3D V µ Q " m & m C !& 4) /] !p i =7 • \ !-J !p i V µ w=7 G 7 w
Downloaded by Ng?c Di?p ??ng (ngocdiep10012000@gmail.com) lOMoARcPSD|36477180 1" 6 . -) N =H …= Q ] B= /% " I ;r + # D HB 9 ; !" # p % = !" # p L D >B o C 0 C # 6 P% ! 4) v - # 6 D 4 2% /0 N 4) € p /Q * C # 6 Q 14 . 7 , 3600 h coich = 10 % 0 = 10 % 0 ≈ 2 % 0 Q . 1 , 8 7800 1 , 4 . 8 toanphan * v - 2% /0 N T − T 200 − 58 h n l = 100% = 100% ≈ 30% lt T 200 + 273 n * 6 2 h = hlt 3 %L C /% 6 D L v - C " N $E $ % Q ! 6 ! " -J >[ q $ p D L = !" # $ p D M ?= K !" # -) D L D B>? * & D L # !" . Q2 ε = A ; 6 L6 2% /0 N -J 0A T2 ε = T −T 1 2 P 6 / T 285 → A 1 = − 1 Q = − 1 105 ≈ 836 2 ( 5 J) T 263 2
Downloaded by Ng?c Di?p ??ng (ngocdiep10012000@gmail.com) lOMoARcPSD|36477180 ; p Q1 1 6 A L Q2 ; p L 1" !" . v - L6 2% /0 N= ^ % p L B † -J D !-J # p ; -J !-J /% " /0 D => 0 A * !" . $ N D !" . / /% " /0 ; p Q1 h" A . Q2 ; p L * # !" . A Q η = 100% = 1 2 − 100% = (1 − 8 , 0 )100% = 20% Q Q 1 1 N D !" . / /% " /0 {8 @ 8 = =>8 = 8 => [ 1" !" . D 4 2% /0 N= W /0 " N {8H= > [ ; !" # p D o C = !" # p L D % 0 A * !" . $ ; -J \ !-J # p " /0 ; -J ^ % p L " /0 * # !" .
Downloaded by Ng?c Di?p ??ng (ngocdiep10012000@gmail.com) lOMoARcPSD|36477180 T 273 η = 1 2 − 100% = 1 − 100% ≈ 26 8 , % T 100 + 273 1 $ ; -J \ !-J # p " /0 Q = A /η = 3 , 7 5.104 / 2 , 0 68 ≈ 2 , 7 42 1 . 04 1 (J) ; -J ^ % p L " /0 Q = Q − A = 27 4 , 2.104 − 3 , 7 5 1 . 04 = 20 0 , 7 1 . 04 2 1 (J) ; !" # . -) q K . 4D% 6 . -) D 8 H o C = !" # $0 - D 8 H o C *+ & " -J @8 0 !-J " N C !L 2% v 6 $E $ % Q Y N C !L 2% v 6 !-J !" . D 4 2% /0 N \ i 4) v - T2 η = 1 − T1 1~ A T 27 + 273 η = → A = 1 2 − Q = 1 − 1 = 4 , 0 (kcal) = 6 , 1 72(kJ) Q T 227 + 273 1 1" /0 N C € 6 ! d !" 8 % = 8 % I ! C /0 ! D 8 0 N F N G D 4 # !" . 2% /0 6= $ X D N = & e /0 ' !( $E !V e /0 U !%L % N 8 < 9 % 7 7 7 7 7 ; -J \ !-J # !" . /% " /0 D \ !-J /% e /0 F 0 4•G m p1 Q = RT ln 1 1 µ p2 @ /0 !%L Q γ γ 1−γ γ 1−γ γ p V = p V → p T = p T 1 1 4 4 1 1 4 4
Downloaded by Ng?c Di?p ??ng (ngocdiep10012000@gmail.com) lOMoARcPSD|36477180 2% ^ 8 = 8 γ γ 1 p T − 1 1 → = p T 2 2 x% ! m γ T1 Q = RT ln 1 1 µ γ − 1 T2 N / /% " /0 T −T 1 2 η = T1 T − T m γ T 1 2 A = Q η = Q = R T − T ln 1 1 ( 1 ) 1 2 T µ γ − 1 T 1 2 2000 4 , 1 + A = . 3 , 8 1 ( . 400 − 20) 400 273 .ln ≈ 634(kJ) 29 , 1 4 − 1 20 + 273 N # !" . A P = = 634(kW) τ 1" 6 D L D 4 2% /0 N i = Q ] N MB … ; !" # p L D % = !" p D H% A * & D L # 6 $ ; -J 6 !-J # p L /% ; -J ^ % p /% X6 * & D L # 6 Q T − 10 + 273 2 2 ε = = = = 7 , 9 4 A T − T 17 − − 1 2 ( 10) $ ; -J 6 !-J # p L /% Q' = εA = P ε t = 7 , 9 4.36800 1 . ≈ 6 , 3 .105 ≈ 2 (J) 8600 c 0 al ; -J ^ % p /% X6 Q = A + Q' = ε + = + ≈ ≈ 1 2 ( ) 1 Pt ( 7 , 9 4 ) 1 36800 1 . 4 1 . 05 J 5 , 9 .104 cal ? C /0 N= N BM [ 4D ^ => % p L # /0 * # /0 A A 8600 η = 100% = 100% = 100% ≈ 45% Q A + Q 8600 + 5 , 2 1 . 03 1 , 4 . 8 1 2 ? C /0 N= \ !-J -J q p 4D C N > [ ; !" # p D o C !" # p L
Downloaded by Ng?c Di?p ??ng (ngocdiep10012000@gmail.com) lOMoARcPSD|36477180 * # /0 N T A A 15 1 . 03 1 2 − = → T = 1 − T = 1 − + = 2 1 (273 100) 239K T Q Q 10 1 . 0 . 3 1 , 4 8 1 1" 6 v - = L6 2% /0 N= p !" H% 4D p L !" H% 1 6 \ # p D M 9 A * # 6 $ ; -J ^ % p L /% " X6 N # 6 * # 6 D # /0 N T 27 + 273 η = 1 2 − = 1 − ≈ 23% T 117 + 273 1 $ ; -J ^ % p L /% " X6 D @ Q T T 27 + 273 1 2 − = 1 2 − → Q 2 = Q = 63000 ≈ 4800 c 0 al / s Q T 2 T 1 117 + 273 1 1 1 N 6 D , $E N 6 / /% " X6 A Q − Q 63000 − 48000 P 1 2 = = = 1 , 4 8 ≈ 6 k 3 W τ τ 1 1" 6 D L v - = L6 2% /0 N -J 6 q p L o C ^ % $0 -) N o C -J -) V D !N p L ! $ -) D . $0 N % $ ^6 / Q # -) ! D 8 = > >[9 = 4D . / Q # -) D R8 = M M[9 0 3 6 L D6 - . !p !' Q V • v 6 ; \ q p L Q = ^ / p D Q A 2 1 Q T T 2 2 2 = → Q = Q F G 2 1 Q − Q T − T T 1 2 1 2 1 ; -J V D $ 6 . -) A Q = Lm F G 1 ? & -J -) V D ^6 D ‡A Q = λm' F G 2 q F G F G 4D F G A L T , 2 26.106 273 m' 2 = m = . 1 . ≈ 9 , 4 k 3 g λ T 3 , 3 5 1 . 05 373 1
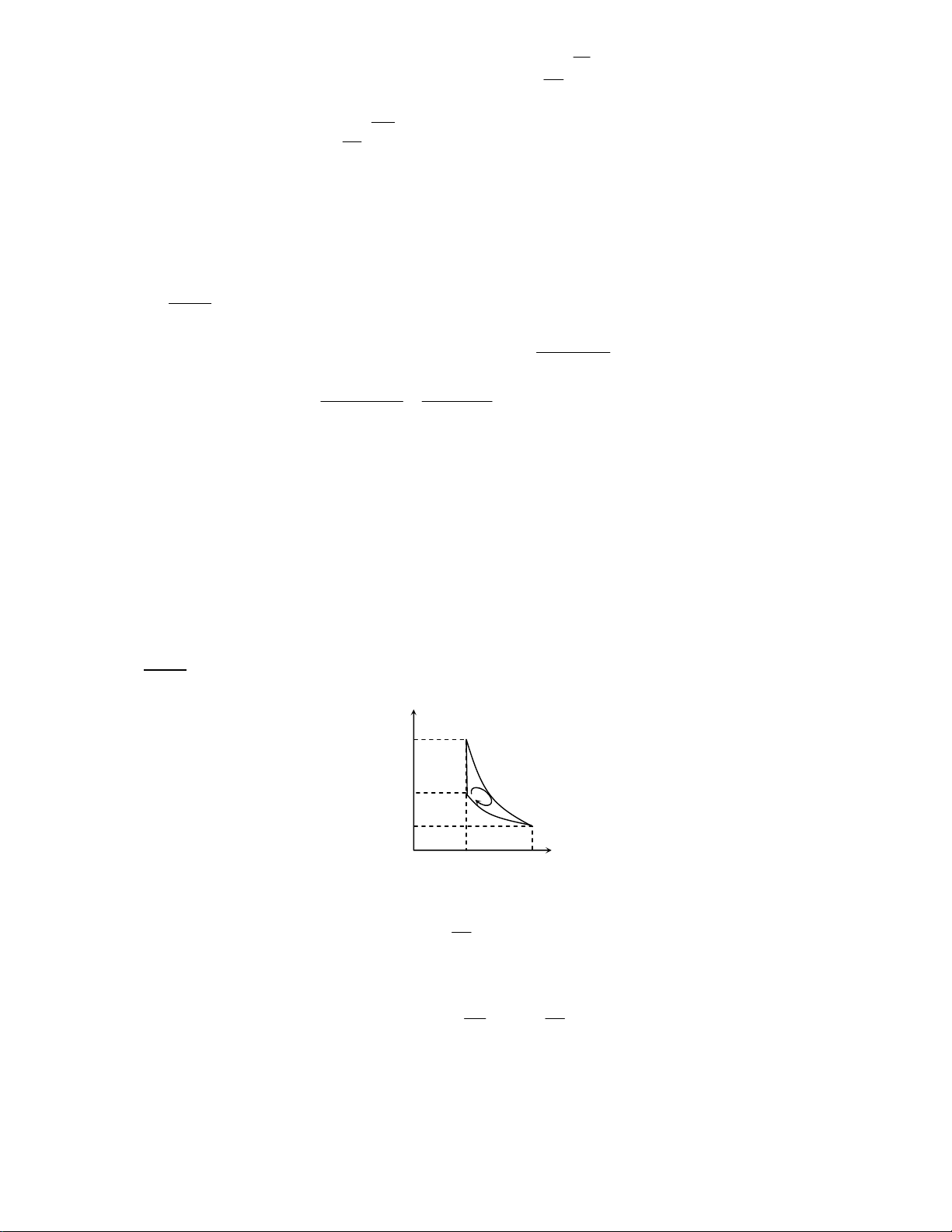
Downloaded by Ng?c Di?p ??ng (ngocdiep10012000@gmail.com) lOMoARcPSD|36477180 1" % v - C " /0 p e /0 !( 4D e /0 !( ? ! # 6 !O q 7 8 > ! 7 8> 4D q 8 ! 8 *+ N C $ /0 D6 + . $ % Q V N C $ /0 N !-I !( T 4) !" ) 4D + # /0 /Q = ' !( r Q !N Y N C /% ^ /0 A A = (p − p V − V 2 1 )( 2 1 ) /% /0 N= !" p T 4) ! F7 = G= p L 4) F7 = G /% " /0 X \ V'2 p V ln 4) A 2 2 V'1 T − T p V − p V 2 1 2 2 1 1 η = = T p V 2 2 2 N / /% " /0 A V' A' = Q η = p V − p V ln 1 ( 2 2 1 ) 2 1 V'1 (p V − p V 2 2 1 1 ) V' ln 2 A' V'1 → = = 1 , 2 A (p − p − 1 2 )(V V 2 1 ) 1" 6 . -) D 4 2% /0 - 0 4• < j , x ,% { ˆ 7 7 7 % 7 '( %L Q . -) q p . 4D% S = . -) E q % ) = N !O 4D $E 7% F {jG $ *. -) ] ! 4D%= N 6 !" q / ^ F j G 4) . N !O D 4D r Q 7 n ! 4 L = N 6 !" ] ^ ! S^6 / e /0 ' !%L F; xGk 3 ? ! 4i / & _ $Q ^ = 0 . -) /% S ! 4D% p L = ! . ^ S & %= K N !O $E 7 = F xˆG
Downloaded by Ng?c Di?p ??ng (ngocdiep10012000@gmail.com) lOMoARcPSD|36477180 2 , N 6 !" -J L = !t6 . -) K L /% S / %D = ! N !O $E %= ^ q 7 ) 7% F ˆ{G *'6 N D 6 / W /0 = 7%8 => k 7 8 => k7 8 k %8 k 8 4D & !%L D 8 = N C /Q q e /0 / Q $ A Z @ /0 { j 4D x ˆ !( = N N A = A = 0 AB DE Z @ /0 j = ' !( = N A = p − = − − = BC 1 (V V 1 ) 12. 8 , 9 1 . 04 o ( 5 , 1 5 , 0 ).10 3 117 ( 6 J) Z @ /0 x ' !g = 2% N T F, MG V ] ] = N / /% e /0 ' !%L A γ 1 − , 1 33 1 − p V V 12. 8 , 9 1 . 04. 5 , 1 1 . 0−3 5 , 1 A 1 1 = 1 1 − = 1 − ≈ 109 CD ( 3 J) γ −1 V 3 , 1 3 −1 3 2 Z @ /0 ˆ{ $ !O !( = N C A = p − = − − ≈ − EA o (V V o ) 8 , 9 .104 2 ( 5 , 0 3) 1 . 0 3 24 ( 5 J) N D 6 / /% W /0 D 4 $E N C $ A = A + A + A + A + A
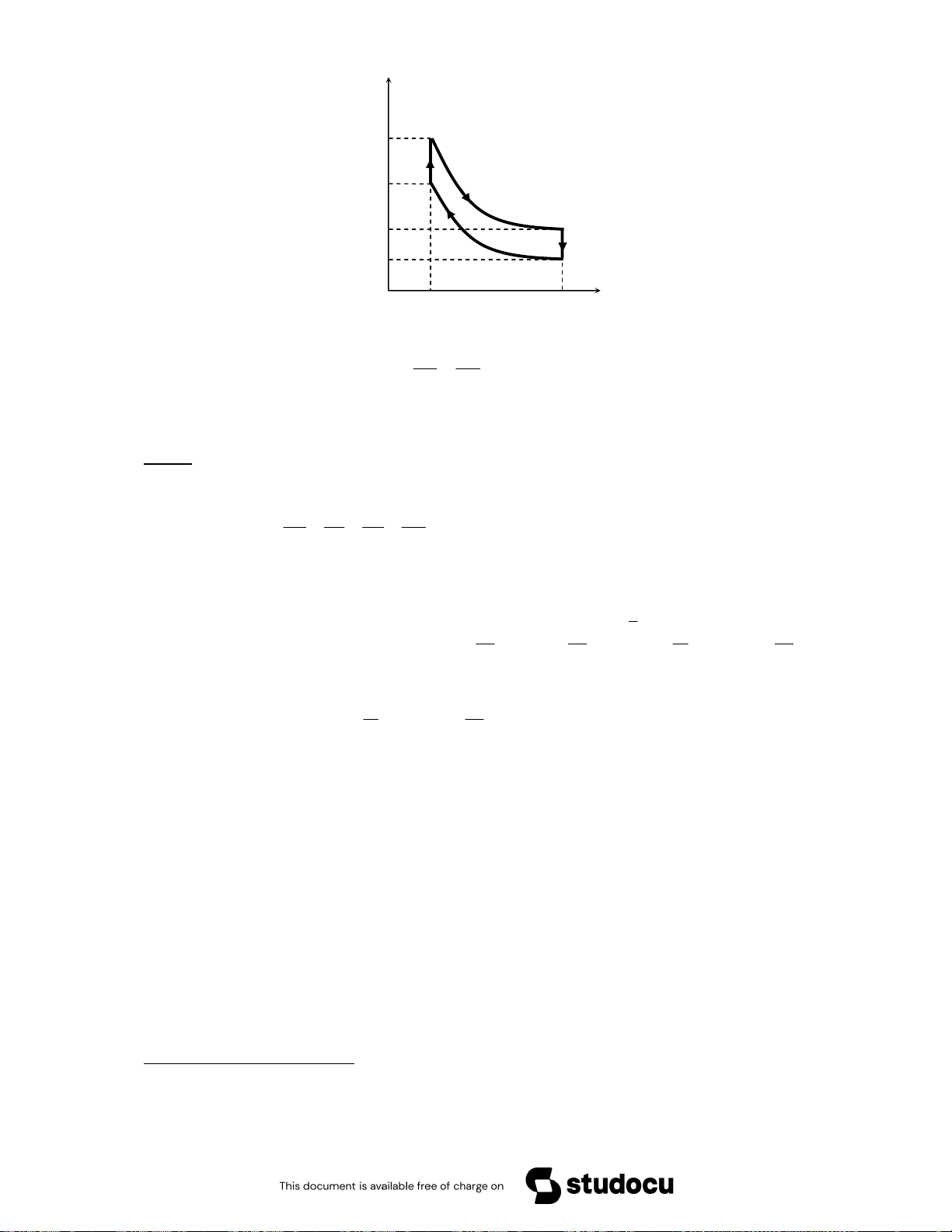
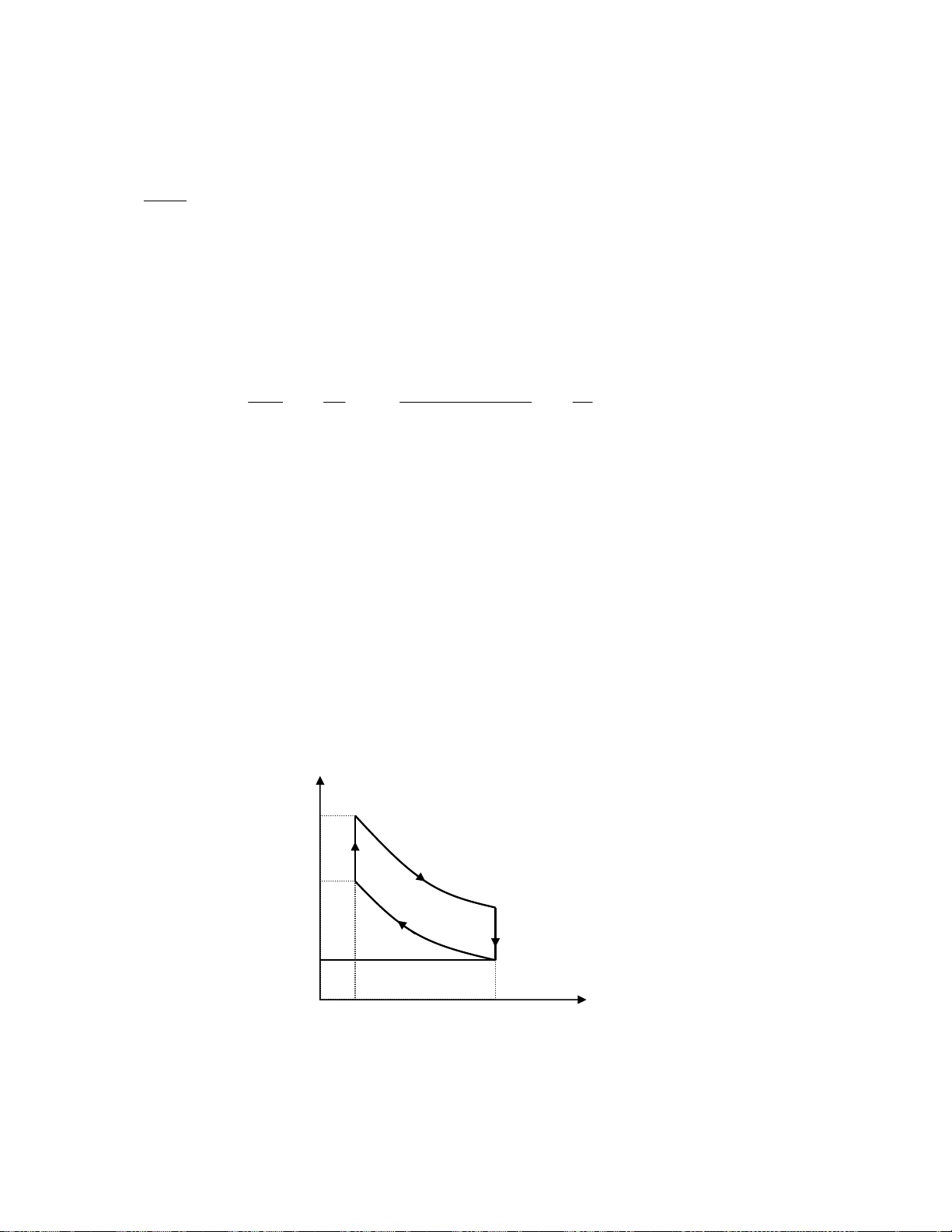
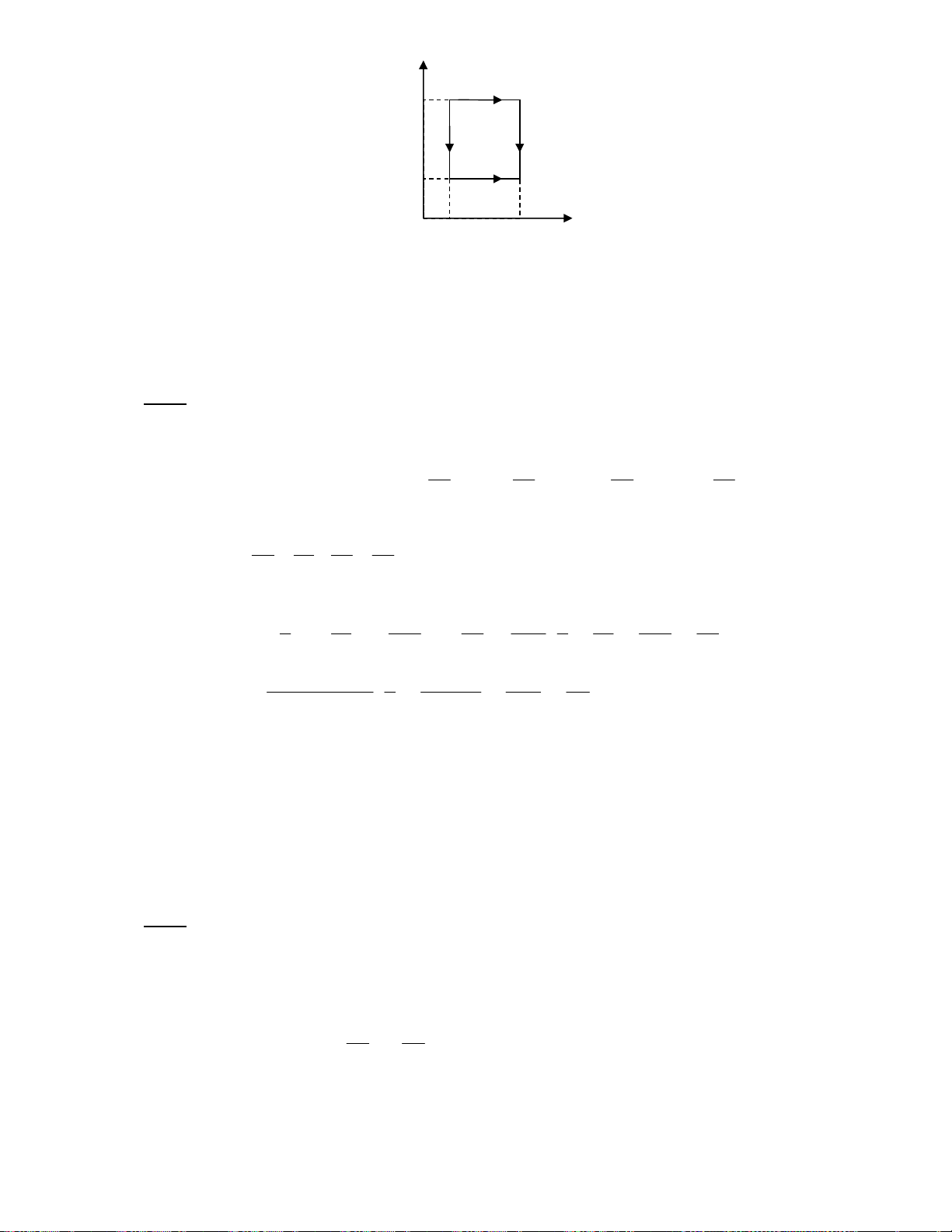
= 0 + 1176 + 1093 + 0 − 245 = 2024 AB BC CD DE EA (J) *0 4• < /0 $D6 ^ !p v 6 # !" . !& /% $& „ /% e /0 !V Q = W J 6 !-J L 4D% S = ! %8 % 4D r q 7 ) 7 F {jGk $ /% e /0 T F j G= W C% 6 !-J U !%L q 7 ) 7 ? ! !" r q % ! 4D q % ! k x , ˆ , { % j 7 7 7 *0 <
Downloaded by Ng?c Di?p ??ng (ngocdiep10012000@gmail.com) lOMoARcPSD|36477180 2% D e /0 !& 6 W J 6 $E 2 s ! k ! r q ) = N !O 4D $E 7 F xG= !" r ) k 3 2% D e /0 ' !%L q 7 ) 7 F xˆG= !" ^ S & k 2 & _ # N F! ˆG= 4 = % / %D = b ^ ) %= N !O 4D $E 7 F ˆjG ‰ & _ D e /0 U !( % F j{G *'6 # /0
& U ε 87 97 8> 4D & !%L D γ 8 = ; X \ /% ^ /0 $E X \ /% e /0 xA Q = Q = nC T − T 1 CD V ( D C ) /Q ˆj X + F \ 4D% • 3 X GA Q = nC T − T 2 V ( B E ) * # !" .A Q T − T nR T − T p V − p V V p − p 2 B E ( B E ) o 1 4 1 1 o 4 η = 1 + = 1 + = 1 + = 1 + = 1 + F G Q T − T nR T − T p V − p V V p − p 1 D C ( D C ) 2 2 1 2 2 2 1 1~ A γ γ γ γ p V = p V ; p
V = p V → p − p V = p − p V 1 2 o 1 2 2 4 1 ( 2 1 ) γ 2 ( 4 o ) γ 1 γ p − p V o 4 2 γ → = − = ε − − F G p − p V 2 1 1 6 F G 4D% F GA η = 1 1 − −γ ε = 1 − 51− ,133 = 4 , 1 2% 0 # !" . !& /% = % $ & !%L D = 4D & U $E A 7 97 8 k $ 7 97 8Mk 7 97 8Bk 2% $D < !-J V -J % e /0 ] η = 1 1 − −γ ε = 1 − 41− ,133 = 36 7 , % $ η = 1 1 − −γ ε = 1 − 61− ,133 = 44 6 , % η = 1 1 − −γ ε = 1 − 81− ,133 = 49 6 , % /0 # !" . ! 2Š2 $& „ !-J /0 $D6 /Q 0 <
Downloaded by Ng?c Di?p ??ng (ngocdiep10012000@gmail.com) lOMoARcPSD|36477180 x ˆ j % { 7 7 7 7 '() ; {j T 4) e /0 L N = %8 k $ ; j 5 N !-J U !%L ) b & „ U = Q !-J 4D% S = Q 6 /% N = ! N 6 !" ^ = !V Q D !( F xG= ! D !%L F xˆGk 3 & e /0 !%L = 4 % = ^ S & % F ˆjGk 2 ; j{ T 4) e /0 !t6 / + S 0 # !" . 3 2Š2 /% " /0 = X m \ /Q e /0 xA Q = Q = nC T − T 1 CD p ( D C ) ; ^ A Q = Q = nC T − T 2 EB V ( B E ) * A Q − − − 2 1 T T B E 1 p V p V o 2 2 2 1 V p / p p / p η = 1+ = 1+ = 1+ = 1 2 o 1 2 1 + Q γ T − T γ p V − p V γ V V / V −1 1 D C 1 3 1 1 1 3 1 p p o 2 − ε p p η = 1 1 1 + F G γ β −1 /% ! ε = V / V 2 1 1~ γ γ γ p V o 1 γ p V = p V → = ε − = k o 2 1 1 p V 1 2 γ γ γ γ p V V V 2 3 3 1 γ −γ p V = p V → = = = β ε F G 2 2 1 3 p V V V 1 2 1 2 7) V3 β = V1 6 F G 4D% F G 4D $ !O \ !-J A
Downloaded by Ng?c Di?p ??ng (ngocdiep10012000@gmail.com) lOMoARcPSD|36477180 β γ − 1 η = 1 − γ 1 − γε (β − ) 1 1" 6 . -) L6 2% /0 p e /0 !( 4D e /0 !( - 0 < # /0 ! P% ! 4) /0 N _ !" # p 4D p L 7 *0 < ; \ \ !-J /% " /0 D 4 $ % p eb /0 5 4D 5 Q = nC T − T 23 V ( 1 2 ) V Q = A = 2 nRT ln 34 34 1 V1 N X / F$E N !" % / G /% " /0 D 4 V V V A = A + A + A + A = 1 nRT ln + 0 + 2 nRT ln + 0 = nR T T ln 12 23 34 41 2 1 ( − 1 ) 2 2 V V V 2 1 1 * # !" . A T − T T − T 1 2 1 2 η = = < = η Q + Q C T − T V ( 1 2 ) Carnot T 23 34 1 T + 1 R ln(V / V 2 1 ) 7\6 !" . D 4 2% /0 P + . D 4 2% /0 / % !" $ Q 2 /Npy . !( M=> !/N= r !N h" $ Q 2 /% 6 /% eb /0 !( Q δ nC dT dS p = = T T
Downloaded by Ng?c Di?p ??ng (ngocdiep10012000@gmail.com) lOMoARcPSD|36477180 ^ e /0 2 /% 6 $ Q " -J T2 dT m i + 2 T2 S ∆ = dS = nC = R ln p T1 T µ 2 T1 1~ = e /0 !( Q T V 2 2 = = 2 T V 1 1 7) * !/N 8> 5 , 6 5 + 2 S = . 3 , 8 . 1. ln(2) = 65 5 , 2(J / K) 2 2 !" r 2 /N 6 $ !O -) % D . % h" $ Q 2 /% 6 -) !-J D ) % Q δ mCdT dT T dS = = → ∆S = dS = mC = 2 mCln 1 T T T T1 − + 3 100 273 S ∆ = 10 .4180.ln = 3 , 1 1 0 + 273 h" $ Q 2 /% 6 /% e /0 -) . % Q δ Lm 2 , 2 6.106.10−3 S ∆ = = = ≈ 1 , 6 2 T T 373 2 2 h" $ Q Q 2 /% 6 /% ^ e /0 S ∆ = ∆S + S ∆ ≈ , 7 4 1 2 (J / K) !" $ Q 2 /Npy ' !( => ; . q ) > Q δ Q ∆ m V 10 5 , S ∆ = = = R ln 2 = 3 , 8 . 1.ln(5 / 2) ≈ 9 , 2 (J / K) T T µ V 28 1 NS6 !-J . q 8> % ) 8 > % !" $ Q 2 /N 6 e /0 . DA h( k $ !( @ /0 !( Q δ A δ + dU m dT m i + 2 T S ∆ = = = C = R ln 2 T T V µ T µ 2 T1 10 5 150 + 273 S ∆ = 3 , 8 . 1.ln ≈ 7 , 1 (J / K) 32 2 50 + 273 $ h(
Downloaded by Ng?c Di?p ??ng (ngocdiep10012000@gmail.com) lOMoARcPSD|36477180 Q δ m dT m i + 2 T S ∆ = = C = R ln 2 T p µ T µ 2 T1 10 5 + 2 150 + 273 S ∆ = 3 , 8 . 1.ln ≈ , 2 4(J / K) 32 2 50 + 273 !" $ Q 2 /N 6 $ !O M 6!/N q = => ! M = 70 !" $ Q 2 /% 6 m ] " 4D% /L !V 4D & Q g % " $ !O $ „ D N ^ - ) e ^ ( L = % $ !O !( ) = ! ' !( ) M Z 7) e /0 T Fe /0 !( GA Q δ dT m T m p ∆S = =nC = 2 C ln = 2 C ln 1 V V V T T µ T µ p 1 1 Z 7) e /0 T Fe /0 !( GA Q δ dT m T m V ∆S = =nC = 2 C ln = 2 C ln 2 p p p T T µ T µ V 1 1 h" $ Q 2 /% 6 # ^ e /0 m V p S ∆ = S ∆ + S ∆ = C ln 2 + C ln 2 1 2 p µ V V p 1 1 6 5 + 2 60 5 1 S ∆ = 3 , 8 . . 1 ln + 3 , 8 . . 1 ln ≈ 7 ( 1 J / K) 2 2 20 2 5 , 1 1" N % -u 6Q s !-J . = !" 6 !& # !-J r Q => V !" $ Q 2 /N 6 e /0 . DA h( k $ h( @ /0 !( Q δ dT m T m i T S ∆ = n = C = C ln 2 = R ln 2 1 T V T V µ T µ 2 T 1 1 3 5 S ∆ = 10 . . 3 , 8 . 1 ln ≈ 1 ( 5 , 1 ) , 8 4 1 . 03 (J / K) 2 $ @ /0 !( Q δ dT T i + 2 T ∆S = n = C = nC ln 2 = n R ln 2 2 T p T p T 2 T 1 1 + 3 5 2 ∆S = 10 . . 3 , 8 . 1 ln ≈ 2 ( ) 5 , 1 11 . 8 , 103 (J / K) 2
Downloaded by Ng?c Di?p ??ng (ngocdiep10012000@gmail.com) lOMoARcPSD|36477180 . !-J . = !" 6 !& # r = V 4D 2 /N 6 r Q = < 9? nU S2 e /0 . D !r 6 !( Y f ^ s 3 # e /0 $ !O D = ! Q δ dT m T S ∆ = n = C = C ln 2 T T µ T1 µ S ∆ 2 . 8 1 , 4 9 → C = = ≈ 7(cal / K) ≈ 29(J / K) m ln(T / T 2 1 ) 2 . 2 ln( ) 1 , 2 h& 4) ; . iR + C = ≈ 2 = ≈ V ( 1 J / mol) (i 2)R ;C 29 p (J / mol) 2 2 7\6 e /0 . D e /0 !( h" $ Q 2 /N 6 /Q !%L € e /0 !%L /% /0 N $E 9!" * !" € !-I !( D % *+ -J !' 6 D N /% /0 D6 fg !" # !-I !( D 4D F l G N C /% /0 $E # \ 4D% C C 4D + / C C /% " /0 F $E O -J * +, /% ^ /0 G A = Q + Q 1 2 /% /0 / % Q + Q T − T Q Q Q − Q A 1 2 1 2 1 2 1 2 η = = → = = = Q T T T T − T T − T 1 1 1 2 1 2 1 2 /% e /0 !( F € e /0 !%L G= !" $ Q 2 /% 6 D Q δ Q Q 1 2 S ∆ = = = T T T 1 2 ;Q A = (T − T ∆ = = 1 2 ) S 10 ( 0 kcal) 41 ( 8 kJ) j+ -) ! % 4D% -) % /% " $0 4+ v - !" $ Q 2 /N 6 # /% e /0 / % !O q ! 6 / /E m / 6d q 4\ 4\ L % $ ^6 / Q # -) ! % D 8B 9 k 3 / Q # -) D 9 !"
Downloaded by Ng?c Di?p ??ng (ngocdiep10012000@gmail.com) lOMoARcPSD|36477180 ; !" X $E # / % !O S !i q -. /0 X $E c(m t + m t − λm 2 2 1 1 )
λm + cm t − t = cm t − t → t = 1 1 ( 1 ) 2 ( 2 ) 1 c(m + m 1 2 ) ( 1 40 . 0 30 + 100 0 . ) − 80 1 . 00 t = = ( 8 o C) = 28 ( 1 K) ( 1 100 + 400) h& 4) -) ! = !" r 2 /% 6 $ % p !" r 3% ^6 4D !" r 3% r !" Q δ Q δ ∆ T Q dT λm T ∆S = + = + cm = 1 + cm ln 1 1 1 1 2 T T T T 1 T T T 1 1 1 7) 8 B F?G D !" X $E # h& 4) -) $i L ! = 2 /% 6 • ^ = !" $ Q D6 D T Q δ dT T ∆S = = cm = cm ln 2 2 2 T T 2 T T1 h" $ Q Q 2 /% 6 # D λm T T S ∆ = ∆S + S 1 ∆ = + cm ln + cm ln 1 2 T 1 T 2 T 1 1 2 80 1 , 0 . 281 281 S ∆ = + 1. 1 , 0 .ln + 1. , 0 4.ln ≈ 0 , 0 02(kcal / K) (0 + 27 ) 3 0 + 273 30 + 273 6 ∆Pl = ! d ! T + m / 6d q 4\ 4\ L ‹ h T m / 6d q 4\ 4\ L D - A nU 4\ N \ = r -J # $^% %D F e /0 SU m Q e ! C / 6d 0 !-J $^% %D G Q = Q + Q = const → Q δ = − Q δ 1 2 1 2 /% ! Q δ = Q δ D !" $ Q -J # 4\ 4D 1 2 h" $ Q 2 /% 6 Q δ Q δ 1 2 dS = dS + dS = + 1 2 T T 1 2 2% F‹G 1 1 (T − T δ 2 1 ) Q dS = Q 1 δ − = > 0 → − δ > 1 (T T 2 1 ) Q 0 T T T T 1 1 2 1 2 ; l 0 @ l T D 4\ \ 6 / 6d q 4\ 4\ ; Œ 0 @ Œ T D 4\ + 6 / 6d q 4\ 4\ 7\6 m / 6d q 4\ 4\ L !" $ Q 2 /N 6 # " v - /L # 6 !O q { ) j F 0 < >G 2%A
Downloaded by Ng?c Di?p ??ng (ngocdiep10012000@gmail.com) lOMoARcPSD|36477180 , , { x , j 7 7 7 *0 < > h-I { j $ h-I {xj % $ A 7 8 k 8B= >;9 k7 8 => k 8 H o C = 8M >;9 h" $ Q 2 /% 6 N ] " 4D% e /0 $ !O - D%= D m ] " 4D% /L !V 4D /L & = Q A C B dT dT T T ∆S = ∆S + ∆S = nC + nC = C nC ln + B nC ln AC CB V p V p A C T T T T A C { 4D 5 j !( Q T p T V C 2 = k B 2 = T p T V A 1 C 1 x% ! i p i + 2 V p V i p i + 2 V ∆S = 2 n R ln + 2 n R ln = 1 1 2 ln + 2 ln 2 p 2 V T 2 p 2 V 1 1 1 1 1 3 , 8 1 1 . 05 3 . .10 3 − 6 6 1 . 05 6 + 2 5 , 4 ∆S = ln + ln ≈ , 5 4(J / K) (27 + 273) 2 3 , 8 1 1 . 05 2 3 $0 = $0 T 7 8 T ; . 8 = $0 T 7 8 T 8> % $0 N 4) 4D !~ b /% " 4+ v - !" $ Q 2 /N 6 # /" c 4D% = $ !" $ !V /% $0 $E 4D $E H% ? ' 4D% N N = L $i Q e /0 !L !-J /L & _ !" N !O F - v= !X6 N ^ D e /0 !%L \ i G ˆ /% 6 6 !O " -J F $E % !-I !( G δQ δQ ∆S = ∆S + ∆S = + 1 2 1 2 T T @ /0 !(
Downloaded by Ng?c Di?p ??ng (ngocdiep10012000@gmail.com) lOMoARcPSD|36477180 V2 Q = A = pV ln V1 p V V + V p V V + V S 1 1 ∆ = ln 1 2 2 2 + ln 1 2 T V T V 1 2 8 , 9 .104.2 1 . 0−3 2 + 3 5. 8 , 9 1 . 04 3 . .10−3 2 + 3 S ∆ = ln + ln ≈ ( 1 , 3 J / K) 273 + 27 2 273 + 27 3 • % !-J $+ 4D% " -J T -) o C ˆ /N 6 # D6 6 !O - D% X $E Y P / % !O • X $E !" % , -. /0 X $E c m t + c m t c m t − t = c m t − t → t = 1 1 ( 1 ) 2 2 ( 2 ) 1 1 1 2 2 2 c m + c m 1 1 2 2 460. 2 , 0 .100 + 4180 3 , 0 . .12 t = 1 ( 8 o ≈ C) 460 , 0 . 2 + 418 . 0 3 , 0 h" $ Q 2 /% 6 # $ % p C ^ 2 /% 6 # • 4D C r 2 /% 6 # & -) dT dT T T ∆S = c m + c m = c m ln + c m ln 1 1 2 2 1 1 2 2 T T T T 1 2 18 + 273 18 + 273 S ∆ = 460. , 0 2. ln + 4180 3 , 0 . . ln ≈ ( 3 , 3 J / K) 100 + 273 12 + 273 7\6 X $E 2 /% 6 # r Q " -J = F[9?G
Downloaded by Ng?c Di?p ??ng (ngocdiep10012000@gmail.com) lOMoARcPSD|36477180 ! " # *2 B;9 0 !" # /% /-I J % *2 D v - $ % *2 D C ? *2 v - = !" !-J S !i q -. /0 12 !2 224 5 / 6/% pV 108 1 . 0 . 0 10−6 T = = ≈ 48 ( 1 K) (m / µ)R (10 / 4). 3 , 8 1 $ ? *2 C = !" !-J S !i q -. /0 7 32 … m2 a m m 1 p µ m a m p + V − b = RT → T = + V − b 2 µ V2 µ µ R m µ V2 µ 1 4 1 . 08 10 1 , 4 .10−4 −6 10 T −5 = + − ≈ 3 , 8 1 10 4 ( 2 100 1 . 0−6 ) 100 1 . 0 3 , 2 1 . 0 205K 4 h& 4) *2
a = 4,121.10-4 Jm3 / kmol2 ; b = 2,3.10-5 m3 / kmol /% " $0 T = > . !" H% 0 m & € " 4D 3% 3] Q D $0 $ 0 m & € " 4D # $0 E & 7 32 … # ; . a = 0,14 J 1 m3 / mol2 ; b = 9 , 3 2 1 . 0−5 m3 / mol , -. /0 7 32 … m2 a m m p + V − b = RT F G 2 µ V2 µ µ m & € " 4D 3% 3] Q D $0 2 ;" m a p' = 2 2 µ V 4 # F G % ‡ A p m V 2 µ RT p RV 2T p' ma m + 1 V − b = → = → = V − b F G p' µ am p' m m p R µ V2T µ a V − b µ µ p' 250. 1 , 0 41 250 = . , 0 01− . 9 , 3 2.10−5 ≈ 9 , 4 % p 28 3 , 8 . 1. , 0 01 . 2 300 28 ! " #$ "% &' $( )* + , -. / 0 1 ( 23 45 & 6
Downloaded by Ng?c Di?p ??ng (ngocdiep10012000@gmail.com) lOMoARcPSD|36477180 $ m & € " 4D # $0 " m V'= b µ m & V' mb 250 9 , 3 . . 2 10 5 − = = = % 5 , 3 V V µ 2 . 8 , 0 01 0 # $% % $ & -J / Q # !" ! D >> 9 , -. /0 7 32 … 2 2 m a m m ρ a ρ ρ p + V − b = RT → p + 1 − b = RT 2 2 2 µ V µ µ µ µ µ 2 RT ρ a → p = − (µ / ρ − b) 2 µ 6 & 2 3 , 8 1 ( . 273 + 3) 550 p 8 = ( − ≈ , 0 028 / 550 − 9 , 3 2.10−5 ) 1 , 0 . 41 , 1 4 1 . 0 (Pa) 0 , 0 28 # %S6 r q ! > 3 n2 %S6 D C 0 N # " C /% e /0 ' ! ;" 2 m a p' = 2 µ V N # " C 2 2 m V2 adV m 1 1 A' = p' dV = = a − V1 µ V 2 µ V V 1 2 2 4 1 1 A' = 1 , 0 38 − ≈ 7 , 1 (J) 32 0 , 0 01 0 , 0 05 " # $% b & -J / Q # D >> 9 % $ !& 4) $% A 8 ? 4D 8H= M;9 ;" # $%
Downloaded by Ng?c Di?p ??ng (ngocdiep10012000@gmail.com) lOMoARcPSD|36477180 m 2 a 2 ρ 27RT 2k p' = = 2 µ V 2 2 µ 64 pk ; - 3% 27RT 2 a = k 64 pk ;Q 2 550 27. 3 , 8 1 3 . 042 p' = ≈ 8 , 6 1 . 06 (Pa ) 0 , 0 44 64.7,4 1 . 06 & -J -) V % 4D% " $0 ! ! ) /L ) L %D $" # $0 fg & -J -) V % 4D% $0 D ? ! ) /L ) L = # $0 D ) L = Q m m V µ V = V = V = b 3 → m = k ok µ µ b 3 *E & 7 32 … # -) $8 => M 9 % = !-J 8>=< n !i & -J / Q # . -) ! ) L 2% /i " $8 = 9 % " m m m µ 0 , 0 18 V = V = b 3 → ρ = = = = 200 kg / m k ok k ( 3 ) −3 µ µ V b 3 3 0 , 0 . 3.10 k h& 4) $% A 8 =M >[ 9 % = $8 = 9 % *+ A $% + ) D $ % Q Y $ . $'% K ) D $ % Q Y + !" % D $ % Q Y 3 V ^ U 4) $E $ % Q ! D + !" % 4D > % ) # $% + T 4 /L ) L F 6 / q !-I !( 7 32 … G m b 3 m 0 , 0 . 3 4 . 3 10−3 V = V = ≈ ≈ 9 , 2 . 3 10−3 m3 / kg k ok µ µ 4 . 4 10−3 F$8 = 9 % 8 = 9 % G $ . $'% %D C !L T 4) ! $ F 6 / q !-I !( 7 32 … G
Downloaded by Ng?c Di?p ??ng (ngocdiep10012000@gmail.com) lOMoARcPSD|36477180 a 0,364 p = = ≈ 7,4.106 k (Pa) 27b 2 2 27(0,043.10-3 ) F 8 =M >[ 9 % 8 = M [ 9 % G ; !" % D . K + T 4) !" ! $ a 8 8. 3 , 0 64 T = = ≈ 304K = 31o k (C)( )! 27Rb 27. 3 , 8 1. , 0 043 1 . 0−3 3 $% + % V U ) $E ) L p = 7,4 1 . 06 k (Pa) h a D !" ) D $% + g 7) !" > % D N C % + 4) $ T D% h Q T /L ) L D 4\ v g ; { 7Q / 6 3_ " " /% ! !C " & T 2 2 !-J D *. " ! e /L ) L % = Q 2 -) ^ " $E $ % Q V /r # & ! ! !" ) L = & T !V6 Q 2 /L ) L Y j /E & -J % Q 2 D H 9 % = & -J / Q # Q 2 % $E H 9 h& 4) Q 2 8 < % = 8 >=< >;9 k $ ; # & ) 6 + . Q 2 ) L 0 • S^6 / -J 0 !" X Q Y fg 4D & -J Q 2 !O 4D% & D 7 4D = # /L ) L D 7 F3% ! a D # & G m m m RTk V = V = b 3 = b 3 k ok µ µ µ 8pk m V 8 p µ 8 0 , 0 . 74.34 9 , .105 V k = → = = ≈ 25% ρ V 3 R ρ T 3.714 3 , 8 . 1 + k k (.273 193) $ ? # & + . 7 0 - ! 2 2 Q ) /L ) L 2 2 !' !V6 & ? # & ) . 7 0 - ! 2 2 Q ) /L ) L 2 2 !' $ 6 .
Downloaded by Ng?c Di?p ??ng (ngocdiep10012000@gmail.com) lOMoARcPSD|36477180 $ n !i N V ! $ " g -) D -. _ F } D ! g -) ! D € g +G !-I = x $d ~ # g -) b !V % - N ! % 4) O 3 $d ~ # g -. _ ? & -J # " g -. _ 4 3 m = πρr F/ D $ g -. G 3 P& g -. !-J L% D q g -) M M 3 N = = 3 m 4πρr x $d ~ # " g 2 s = 4 r π = 4\6 3 $d ~ O " M 3 6M S = sN = = F38 / D !-I g -. G ρr d ρ N V ! $ g D -. _ & $E r -J ~ %D 6 M σ A = S σ = d ρ 6 0 , 0 . 73 0 , 0 . 01 A = = 1 , 2 9(J) 1000 2 . .10−6 * g #6 X 4) $ W g D \ L D " g ) *+ !" # g #6 X r Q $ % Q Y % $ #6 X r ~ %D 8 =>;9 = & -J / Q 8 =M 9 = ` 3 / Q 8 B[9 !" fg $ # g + D /= # g ) !-J L% D D : A 4 4 3 3 3 R π ρ = 2 r π ρ → R = r 2 3 3 ; \ D " = 3 ~ %D # g ) • + . O 3 ~ %D # g += r -J $d ~ • ^ h" ^ r -J $d ~ D6 • $E -J # g ) \ !-J ( 4 2.4 r 2 π − 4 R 2 π )σ = mc∆t k 3 m = 2 π r ρ 3 x% ! 3 4 3 3 σ 4 3 5 , 0 . t ∆ = 1 − = 1 − ≈ , 1 65 1 . 0−4 (o C) 2 c r ρ 2 138.1 , 3 6 0 , 0 . 01
Downloaded by Ng?c Di?p ??ng (ngocdiep10012000@gmail.com) lOMoARcPSD|36477180 N V C ! O " $% $ SD K !L ! $ /8H P r ~ %D # -) SD K D 8 ;9 e 6 %8 = >;9 % !" # /% e /0 O D N !O Fe /0 !( G N V O $% $ $E N L% / ~ %D F$E r -J ~ %D G { = 4D N U !( { # " -J !b $E -J /% $% $ & e /0 q e 6 4D% 2 2 A = 2.σ 4 r π = 8σ r π 1 p A = pV ln 2 po % D e 6 = D /% $% $ h = b v D SD K p ~ X = W ~ X F ~ G • X6 / / ] yU z 4D% X 4) /i 2% N T R 2 p = 2σ / r ] O " 3% D SD K X6 / % $Q /% p $ % p 3% ~ % %D 4D ~ % /% F4) $ S Sm $ ~ % %D G 4D e 6 " L A 4σ p = + po r x% ! 4σ 4 σ σ σ 3 p + 4 / r 4 o 3 4 4 A = p + r π ln = r π p 1+ ln 1+ 2 o r 3 p 3 o p r p r o o o 70 3% 4σ x = << 1 Q (1+ x)ln(x + ) 1 ≈ (1+ x)x ≈ x Q p r o 16σ r 2 π A ≈ 2 3 7\6 N O " 16σ r 2 π σπ 2 40 r 2 A = A + A = 8σ r π + = 1 2 3 3 40. , 0 04 1 , 3 . 4. , 0 072 A = ≈ , 8 2 1 . 0−2 (J) 3 1" D $E € !%L 3X6 %L T h%L 3X6 {j !" = 3D 8 > ? !-J # " D SD K r ~ %D 8 = >;9 F G N V C ! U% {j / " !%L ∆S8
Downloaded by Ng?c Di?p ??ng (ngocdiep10012000@gmail.com) lOMoARcPSD|36477180 { { j j () (- RC & U% {j $E C r ~ %D 3] Q {j= N # C D6 F a $E r -J ~ %D !' !-J r Q 3% r 3 $d ~ D G A = Fs = l σ x ∆ = 0 , 0 45. 1 , 0 5. , 0 04 = , 5 4.10−4 (J) " 0 € \ d 3D 8 h%L 3X6 {j !" ! D + 0 4 N F G *+ !%L {j • 3i 6 4d D% 4D 3i 6 " !%L $E $ % Q 0 4 N ! !-J # $E D + r ~ %D -. T DA 8 = M;9 4D 8 = ;9 nU 4d ~ r -J = r -J ~ %D # $ !V D (σ + σ FP 1 )S 2 D 3 s 0 € \ G * X $E 4i / % % r -J ~ %D # D SD K D + = } D 3X6 {j • 6 !" 4d D D SD K r ~ %D ) . ? e ^ D 3X6 {j • 6 !" ! \ _ $Q D T r ~ K ) . h S !i C r ~ %D # /-J -I D - A % /-J /% " $0 ^6 + g / %D 2% " & + ( !T !-I 38 I g D6 /. 2% g D 8 X6 ; -I 6 /E I 8HB X6 0 8 /-J ^6 / r ~ %D # /-J % W • # g /-J $• !V /. !-I $E !-I # & + g ? & -J # " g /-J τ m ∆ m = F G t ∆ f g F$• !V G + S & A
Downloaded by Ng?c Di?p ??ng (ngocdiep10012000@gmail.com) lOMoARcPSD|36477180 (1) τ m ∆ g τ m ∆ g π d σ = mg → σ = = ∆t d π t ∆ 3 − 6 & 2.1 . 0 10 8 , 9 . σ = ≈ 0 , 0 4N / m 1 , 3 4 2 . .10−3 7 . 80 1" J 3X6 $L !-I 38 = !-J /2% ( !T ? D ^6 !-J g $L 0 J 3X6 $L • ! " !%L 8 => n !i r # ~ %D $L + Y % $ & -J / Q # $L + D 8< 9 4D S2 /E W • # g $L $• !V /. !-I $E !-I # J 3X6 $L 2 ? & -J # $L !' % + d π M = ρ h 4 ? & -J # " g $L + M d2 ρπ h m = = F G k 4k f g F$• !V G + S & A (1) ρ d2 π h g ρ dh π d σ = mg g → σ = = 4k 4k 6 & gdh 9300 . 8 , 9 . 10 3 − ρ , 0 . 205 σ = = ≈ 3 , 0 9(N / m) 4k 4 1 . 2 " & % 3c !-I %D 38 = " !V !-J $i hV $i ! !C " #6 X F >G ? & -J # & % 3c 4D #6 X D = hV $i # & % 3c /% -) n2 -) D -) %D %D & % 3c 4D -) r ~ %D 8 = H ;9 = & -J / Q 8 9
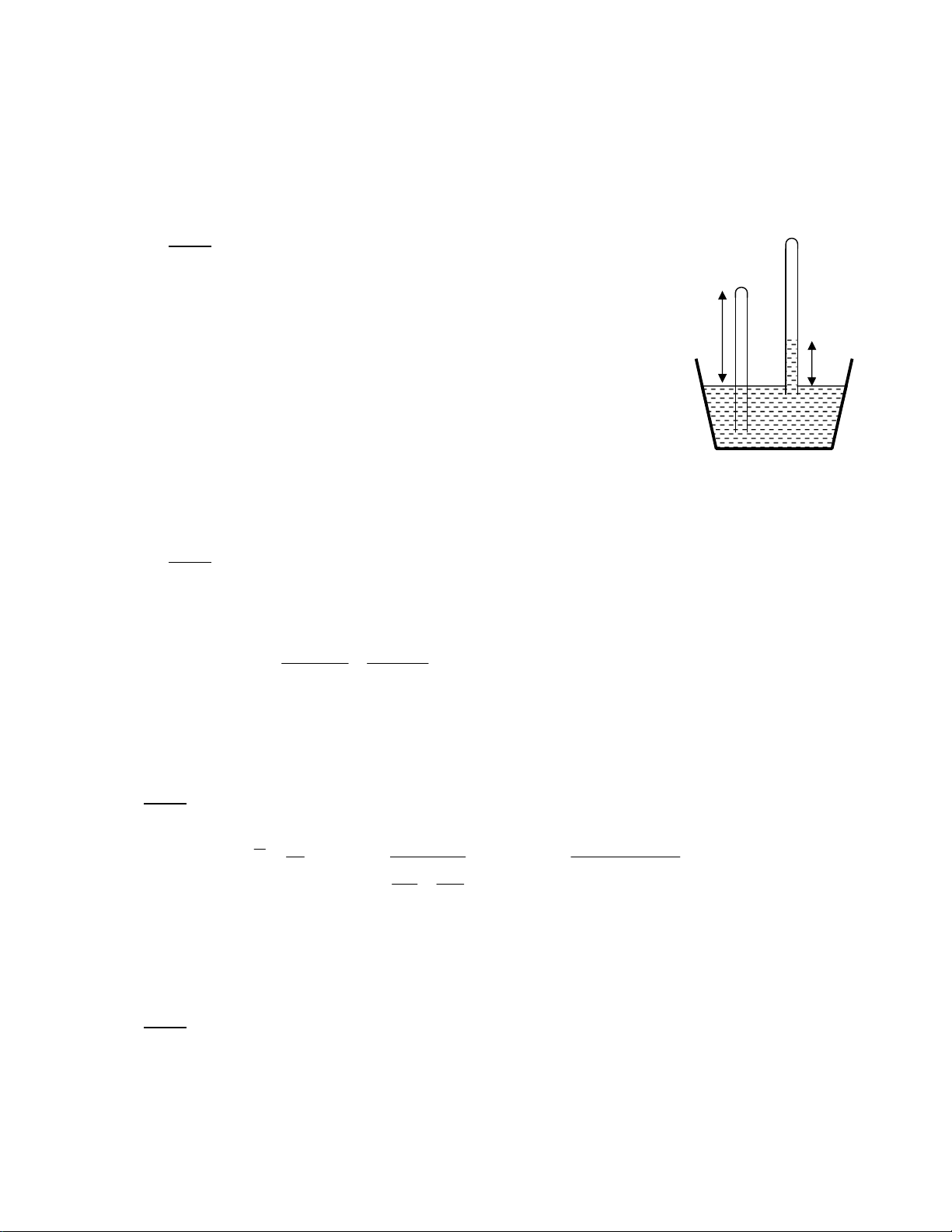
Downloaded by Ng?c Di?p ??ng (ngocdiep10012000@gmail.com) lOMoARcPSD|36477180 3 *0 5 > * F& % 3c Z • X G i 3] # C r ~ %D 4D /g C -) S & = C { 2 -) Q = X $E 0 d 2 4(π d σ + mg) σ d π + mg = ρπ h → h = 4 π g ρ d2 4( 1 , 3 4. 0 , 0 73. , 0 003 + 0 , 0 002. 8 , 9 ) h = ≈ c 8 , 3 m 1 , 3 4.1000 8 , 9 . (. , 0 00 ) 3 2 h T C r ~ %D = -I !O -) 4D% " 3X6 $E -) • D J -) !' !-J # " ) / ‰ W # -) • 3L 0 /K !-I 38 = *+ d % ) # T -) !O 4D% 3X6 D -) ^6 / 2% W ! Y ;-) K !g !-J /Q 3X6 D 3% C r ~ %D S L ~ % . Sb # 4K 3X6 4D -) ;-) • + S & T r ~ %D N K !# T € € ? ! σ 2 4 0 , 0 . 4 73 ρgh d π / 4 ≤ σ d π → h ≤ = ≈ 1 ( 5 cm) ρgd 1000 1 . . 0 , 0 0002 /% " & % 3c !~ ( !T = !-I /% " g -) *+ & -J # g -) ^ - D% ! ~ $Q 3-) # g -) DA ~ Ž = ~ ( = ~ p Y !i D g -) • ! 3V ) ! 6 & % 3c h" F Ž G # ~ $Q 3-) • y U . z ~ /Q F ~ /Q N N D ~ V 4) !-I $E !-I # & % 3c G ? & -J # g -) D ) !" % ~ $Q 3-) D ^ = !
Downloaded by Ng?c Di?p ??ng (ngocdiep10012000@gmail.com) lOMoARcPSD|36477180 & -J g -) !L ) /i % D% ! ~ D6 • D ~ ( = ) . /i D6 ~ / D ~ p π d σ 1 , 3 4. 0 , 0 73. , 0 001 m g = σ d π → m = = ≈ 3 , 2 4 1 . 0−5 kg o o g 8 , 9 7\6 Q A • ? Œ 3 , 2 . 4 10−5 kg ~ $Q 3-) D ~ Ž • ? 8 3 , 2 . 4 10−5 kg ~ $Q 3-) D ~ ( • ? l 3 , 2 . 4 10−5 kg ~ $Q 3-) D ~ p * & % 3c !-I /% V -J D => 4D b /% " $0 !C + T + /% & % 3c A + ! D -) $ + ! D #6 X ? b & /% -) = -) • 3X Q h" 3X Q # -) /% q & D 4σ h = g ρ d * T + /% & % 3c D 4σ 1 1 4. , 0 073 1 1 h ∆ = − = − ≈ ( 3 cm) ρg d d 1000. 8 , 9 , 0 0005 , 0 001 2 1 $ ? b & /% • X = • X /% & • L S & h" L S & # • X /% q & D X $E € • } 4D ] % ! $Q /% + 6 L ~ 2σ 4σ g ρ h = → h = d / 2 g ρ d * T + /% & % 3c D 4σ 1 1 4 5 , 0 . 1 1 h ∆ = − = − ≈ ( 5 , 1 cm) ρg d d 13600. 8 , 9 0 , 0 005 0 , 0 01 2 1 1" & !-J b ( !T /% " $0 3C + *+ d % # " -) /% & 6 !O - D% & % 3c 4D $0 !-J X Q 3V !d 4) & ./ Y *L S & 3V !d 4) & ./ 012 A ? $0 4D & !-J X Q 4) & = # ! $Q /% & ~ % + %D & $ % p e 6 = • } # " -) = ] X6 $ ~ 4D X6 /
Downloaded by Ng?c Di?p ??ng (ngocdiep10012000@gmail.com) lOMoARcPSD|36477180 3% C e D6 /i $E L € ! $E 4) %D & p
p = p − p + ρgh + ργh → h = p o o p ρ(g + γ ) ? & % 3c 4D $0 N 6 !" Fγ = 0 G 0 p h p = o g ρ x% ! A h g = h g + γ o ? X Q γ = g h 1 = h 2 o ? L S & A γ = −g / 2 h = 2 h o & % 3c p 4D% = !p /] = b ( !T 4D% " $0 -) h-I /% # & % 3c += $E $d /" # 2 L% Q € & % 3c j+ e $d 3D6 # & % 3c /% *+ T + /% & D% % . = % . $ % Q V Y h" 3X # -) /% & % 3c /% 4σ h = F3 D !-I /% # & % 3c /% G 1 ρgd h-I /% # & % 3c %D 2% ^ !-J D 3 h" 3X # -) /% & % 3c %D D ? X $E O C r ~ %D !-I Sb € ~ % # -) 4) & % 3c /% 4D %D F ( !T -) Q G $E /g C # " -) 3X Q F ( !T -) S & G σ σ d π + σπ d 3 = (π ( d 3 )2 / 4 − d 2 π / 4) 2 h g ρ → h = 2 2 g ρ d x% ! h1 = 2 h 2 7 8 9 ' : ; $< = >% & ? @A B )C 9 @ 0' & DE F / G+ =H @A )C I& ργ " )J 8 A K :A LM I& " $< : 8 B' &' A9 ργ
Downloaded by Ng?c Di?p ??ng (ngocdiep10012000@gmail.com) lOMoARcPSD|36477180 7\6 -) 3X Q /% & % 3c /% % . V % 4) !" 3X # y 2z % 3c € & #6 ( !~ % % " %^ 38 = = b ( !T 4D% /% " + n !i & -J / Q # + ! $ /E d % # & + € #6 3X Q " !%L 8 = P r ~ %D # + D = H;9 n2 + D -) %D %D #6 h" 3X # T + /% & D = 2σ 2 0 , 0 . 27 2bσ = hdb g ρ → ρ = = ≈ 86 ( 3 1 kg / m ) ghd 8 , 9 0 , 0 . 32. , 0 0002 * T #6 X /% # & % 3c 0 € w !-I /% 3 8 4D 3 8 D ∆ 8 n !i r ~ %D # #6 X % $ & -J / Q # #6 X D =M 9 X $E % ! 6 3-) ~ X # ) 4σ 4σ g ρ h ∆ d d 1 2 = + ρg h ∆ → σ = d d 4 d − d 1 2 ( 2 1 ) 13600. 8 , 9 . , 0 01 0 , 0 . 01. , 0 002 σ = ≈ , 0 67(N / m) 4( 0 , 0 02 − , 0 00 ) 1 ? & -J / Q # N /% " $% $ 3-) ! 6 # " p -) X M ) > V & -J / Q # N e 6 F !" $E !" ! 6 pG n !i $ $% $ fg $ # $% $ D := $Q /% $% $ DA σ = + + ρ F G
Downloaded by Ng?c Di?p ??ng (ngocdiep10012000@gmail.com) lOMoARcPSD|36477180 q -. /0 12 !Q 22 5 Q/N 6 / & -J / Q # $Q /% 4D $Q %D $% $ V -J D p µ p µ ρ = 4D o ρ = RT o RT q ! ρ p n = = F G ρ p o o 6 F G 4D% F G 2σ g ρ h 2σ n = 1+ + → r = p r p − − ρ o o (n ) 1 p gh o 6 &A 2 0 , 0 . 73 r = = , 0 4 m µ (5 − ) 1 1 . 05 −1000. 8 , 9 6 . /Q ~ -) -I ! " $N " ) u + F! % + $i -) D -) G ? !-I ) D $ % Q ! !-J € /Q ~ -) D N $i 0 S & 3-) Y % $ & -J / Q # U D D 8H=H 9 h N $i 0 0 3% /% -J # L ~ Sb € 4D -) ^ + . X6 / $ ~ % # -) 4D 3% C !t6 { 2 3] Q σ
mg − F S≤2rl mg − m ρ / 2ρ A ( l r )g ≥ ≥ F G r S 2rl /% ! 3 3 3 T C D $ = d 3D = & -J / Q # 4D # -) K & -. # A m r π 2 = lρr F G 6 F G 4D% F G 16σ 16 0 , 0 . 73 2r = d ≤ = ≈ 6 , 1 mm π (2ρ − ρ − r )g 1 , 3 4 ( . 2 7 . ,7 ) 1 8 , 9 . .103 l * m m p µ N pV = RT → ρ = = µ V RT
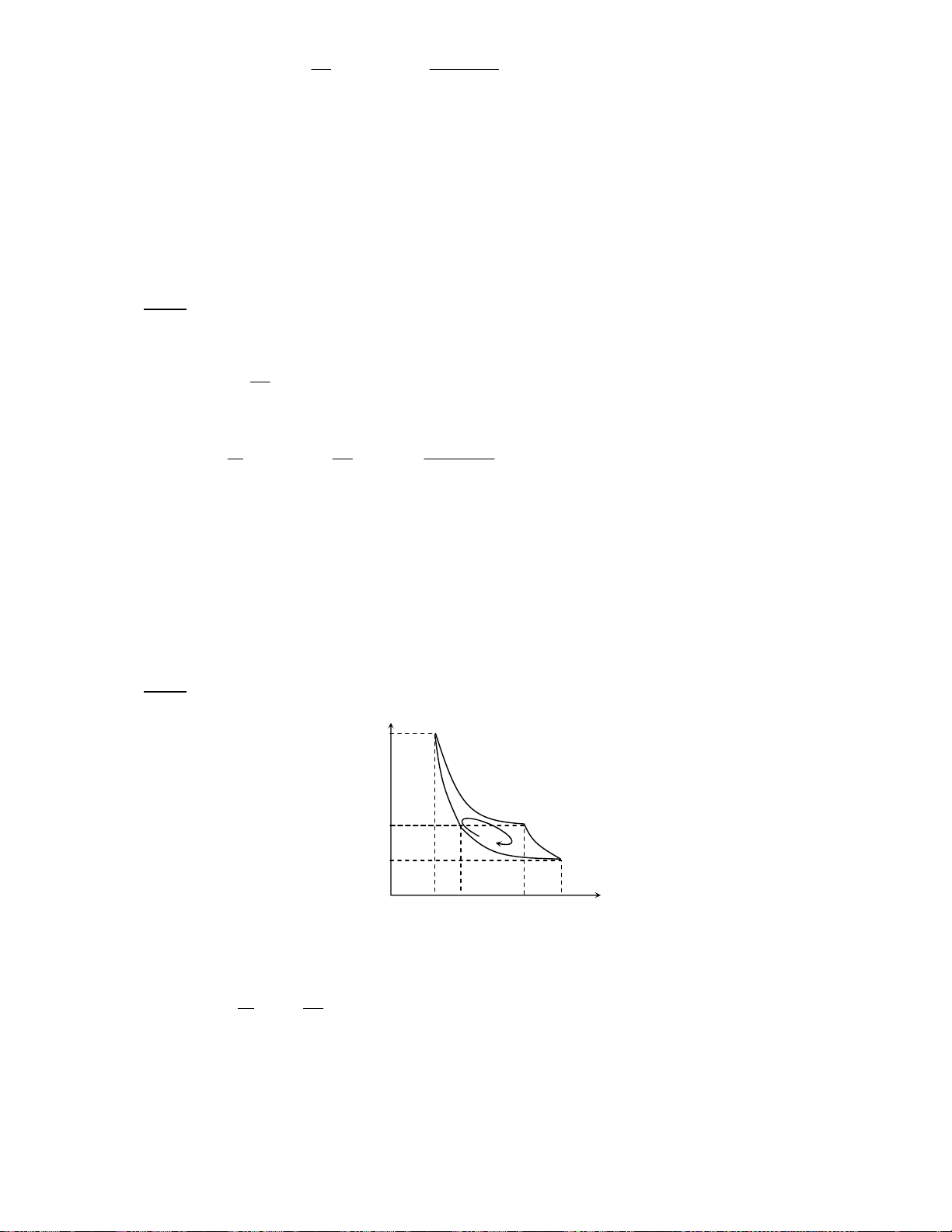
Downloaded by Ng?c Di?p ??ng (ngocdiep10012000@gmail.com) lOMoARcPSD|36477180 /% e /0 !%L Q δ = 0 → pdV + nC dT = 0 F, G V * & !%L Cp C + R R R γ γ = = V → C = kC = F, G C C V γ − 1 p γ −1 V V 4D% F G= 4D - v -. /0 12 32 224 5 / 6/% pV = nRT → pdV + Vdp = nRdT % 1 pdV + (pdV + Vdp) = 0 γ − 1 → pdV + Vdp = 0 → d(pVγ γ )= 0 * 6 pVγ = const hX6 D -. /0 % e /0 !%L * 6 a 4 pVγ = (pV) γ −1 V = nR( γ −1 TV )→ TVγ 1− = const F, G γ (pV)γ γ pV = (nR)γ Τ = → p1−γ Tγ = const F, G γ −1 γ −1 p p N /% e /0 !%L (2) 1 A = −∆U = − nC T ∆ = − nR T ∆ V γ − 1 x% nR T ∆ = nR(T − T = p V − p V 2 1 ) 2 2 1 1 ;Q p V − p V A 1 1 2 2 = F,>G γ − 1 a 4 ( γ 3) −1 1 T p V V A = nRT 1 − 2 1 1 1 − F,MG 1 = 1 γ − 1 T γ − 1 V 1 2 • ! " # $ % &'( )'( ' , -. /0 7 32 … % " % C a RT a p + (V − b) = RT → p = − V2 2 V − b V L ! $ RT a k p = − F,HG k 2 V − b V k k
Downloaded by Ng?c Di?p ??ng (ngocdiep10012000@gmail.com) lOMoARcPSD|36477180 p ∂ RT 2a RT 2a k k = 0 → − + = 0 → = F,BG V ∂ = V − b V V − b V V 0 ( k k )2 3 k ( k )2 3 k 2 ∂ p 2RT 6a RT a 3 k k = 0 → − = 0 → = F,2 V ∂ (V − b V V − b V k )3 4 k ( k )3 4 k V =0 k F,% F,BG \ !-J V = b 3 F, G k F, G 4D% F,HG \ !-J RT a a k p = V − b − → p = F, G k ( k ) (V − b V 27b k ) k 2 2 2 k q F, G 4D F,BG \ !-J a 8 T = F, G k 27bR E & 7 32 … q F,HG 4D F,BG RT 2a V RT k k k p = − → b = F, G k 3 V − b V 2 8p k k k *E & !-J 0 q F, G 4D F, G 2 2 27R T 2 k a = 27b p = F, G k 64pk ‹‹‹* ‹‹‹
Downloaded by Ng?c Di?p ??ng (ngocdiep10012000@gmail.com)



