






















































































































































































































































Preview text:
TRƯỜNG ĐẠI HỌC TÀI CHÍNH – MARKETING BỘ MÔN TOÁN THỐNG KÊ Giáo Trình TOÁN CAO CẤP Nhóm biên soạn:
Nguyễn Huy Hoàng (Chủ biên) Nguyễn Trung Đông
THÀNH PHỐ HỒ CHÍ MINH - 2020 MỤC LỤC Trang
Lời mở đầu..........................................................................................................................8
Một số ký hiệu...................................................................................................................10
Chương 1. Ma trận – Định thức……………………………………………….……………...12
1.1. Ma trận……………………………………………………………................12
1.1.1. Định nghĩa ma trận..............................................................................12
1.1.2. Ma trận bằng nhau...………………………………………………....12
1.1.3. Các ma trận đặc biệt...........................................................................13
1.1.4. Các phép toán trên ma trận……............................................................15
1.1.5. Các phép biến đổi sơ cấp trên hàng........................................................18
1.2. Định thức……………………………………….……………………….......20
1.2.1. Định nghĩa định thức ma trận vuông cấp n………….…………………...20
1.2.2. Định lý khai triển định thức theo một hàng hay một cột bất kỳ.................21
1.2.3. Các tính chất định thức………..............................................................23
1.2.4. Định lý sự thay đổi của định thức qua các phép biến đổi………………...24
1.2.5. Phần bù đại số và ma trận phụ hợp…………………….………………...25
1.3. Ma trận nghịch đảo……………….…………….……………………….......26
1.3.1. Định nghĩa ma trận nghịch đảo………….………………….…………...26
1.3.2. Giải thuật tìm ma trận nghịch đảo ..........................................................26
1.3.3. Định lý sự tồn tại của ma trận nghịch đảo...............................................28
1.3.4. Một số tính chất của ma trận nghịch đảo……………………………….. 28
1.4. Hạng ma trận…..……………….…………….………………………….......29
1.4.1. Định nghĩa tổng quát hạng của một ma trận….……………..…………...29
1.4.2. Tính chất.............................................................................................29
1.4.3. Phương pháp tìm hạng của ma trận........................................................29
1.4.4. Một số bất đẳng thức về hạng của ma trận............................................30
1.5. Bài tập……..…..……………….…………….………………………….......32
Chương 2. Hệ phương trình tuyến tính……………………………………………………….39 2
2.1. Khái niệm về hệ phương trình tuyến tính………………………………………....39
2.1.1. Định nghĩa hệ phương trình tuyến tính tổng quát………..………………39
2.1.2. Định nghĩa nghiệm của một hệ phương trình tuyến tính………….……..40
2.1.3. Hệ phương trình tuyến tính dạng tam giác…………….………….……..40
2.1.4. Hệ phương trình tuyến tính dạng hình thang………….………….……..41
2.1.5. Giải hệ phương trình tuyến tính bằng phương pháp khử ẩn Gauss.……..42
2.2. Hệ phương trình Cramer………………………………………………………….45
2.2.1. Định nghĩa hệ phương trình Cramer……………………….………..…..45
2.2.2. Các phương pháp giải hệ phương trình Cramer.......................................46
2.3. Hệ phương trình tuyến tính tổng quát.....................................................................47
2.3.1. Nhận xét về sự tồn tại nghiệm của hệ phương trình tuyến tính tổng quát...47
2.3.2. Định lý Kronecker – Capelli ..................................................................47
2.4. Hệ phương trình tuyến tính thuần nhất…………………….…………………….50
2.4.1. Định nghĩa hệ phương trình tuyến tính thuần nhất..................................50
2.4.2. Nghiệm của hệ phương trình tuyến tính thuần nhất….…….…………..50
2.5. Một số bài toán ứng dụng trong kinh tế……….……………………………….....51
2.5.1. Mô hình cân bằng thị trường..................................................................51
2.5.2. Mô hình cân bằng thu nhập quốc dân…………………………..……...54
2.5.3. Mô hình input – output của Leontief…………………………………..58
2.6. Bài tập…………………………………………………………………………....64
Chương 3. Không gian vectơ.…………………………………………………………….......71
3.1. Các khái niệm căn bản…………………………………………………………71
3.1.1. Định nghĩa không gian vectơ….……………………………..………….71
3.1.2. Định nghĩa tổ hợp tuyến tính của các vectơ…………………...…………71
3.1.3. Định nghĩa không gian vectơ con của một không gian vectơ……………72
3.1.4. Định nghĩa không gian con sinh bởi một tổ hợp tuyến tính……………...72
3.1.5. Định nghĩa độc lập tuyến tính – phụ thuộc tuyến tính…………………...73
3.2. Cơ sở và số chiều của không gian vectơ…………………………………………..74
3.2.1. Định nghĩa cơ sở của một không gian vectơ….…………………………74
3.2.2. Ma trận chuyển cơ sở................................................................................74
3.2.3. Tính chất...................................................................................................75
3.2.4. Mệnh đề....................................................................................................76 3
3.3. Bài tập…………………………………………………………………..…...79
Chương 4. Phép tính vi phân hàm một biến…………………………….…………………….84
4.1. Giới hạn của dãy số thực………………………….……………………………....84
4.1.1. Định nghĩa dãy, giới hạn của dãy số thực……………..…………………84
4.1.2. Các tính chất và các định lý về giới hạn của dãy số thực….…….………84
4.1.3. Một số dãy số thực đặc biệt….……………………………….….………86
4.2. Hàm số một biến số…………………………..…………………………………..89
4.2.1. Các khái niệm cơ bản về hàm số…..……………………….……….…..89
4.2.2. Hàm số hợp...............................................................................................89
4.2.3. Hàm số ngược….…….……………………………………………...…..90
4.2.4. Các hàm số sơ cấp cơ bản..........................................................................90
4.2.5. Dáng điệu hàm số .....................................................................................92
4.2.6. Một số hàm trong kinh tế..........................................................................93
4.3. Giới hạn hàm số.....................................................................................................95
4.3.1. Các định nghĩa giới hạn..........................................................................95
4.3.2. Giới hạn của các hàm sơ cấp cơ bản.......................................................97
4.3.3. Các dạng vô định....................................................................................97
4.3.4. Các giới hạn cơ bản................................................................................98
4.4. Vô cùng bé và vô cùng lớn......................................................................................99
4.4.1. Định nghĩa.............................................................................................99
4.4.2. Các tính chất........................................................................................100
4.5. Hàm số liên tục…………………….………………………………….………...101
4.5.1. Định nghĩa về hàm số liên tục...............................................................101
4.5.2. Tính chất liên tục của hàm sơ cấp…….………………………………...102
4.5.3. Các phép toán của hàm liên tục tại một điểm.........................................103
4.6. Đạo hàm………………………………………..................................................103
4.6.1. Khái niệm về đạo hàm..........................................................................103
4.6.2. Bảng công thức các đạo hàm cơ bản….……………………………….106
4.6.3. Các quy tắc tính đạo hàm…………….……………………………….106
4.6.4. Đạo hàm hàm hợp………………….………………………………...107
4.6.5. Đạo hàm của hàm ngược………….………………………………….108
4.6.6. Đạo hàm một phía……………….………………………………...…108 4
4.6.7. Đạo hàm cấp cao………………….………………………………….109
4.7. Vi phân…….…………………………………...................................................110
4.7.1. Định nghĩa vi phân...............................................................................110
4.7.2. Sự liên hệ giữa vi phân và đạo hàm……….………………...…..……110
4.7.3. Tính bất biến của biểu thức vi phân cấp 1….…………………………111
4.7.4. Các quy tắc tính vi phân…………….………………………………..111
4.7.5. Vi phân cấp cao…………………….………………………………...111
4.8. Các định lý cơ bản về hàm số khả vi.…...............................................................112
4.8.1. Định lý Fermat ....................................................................................112
4.8.2. Định lý Rolle …………………..…….………………………………112
4.8.3. Định lý Lagrange…………………………………………………….112
4.8.4. Định lý Cauchy………………….…………………………………...113
4.9. Một số ứng dụng của đạo hàm và vi phân.……………………………….……..113 0
4.9.1. Khử dạng vô định , …...................................................................113 0
4.9.2. Tính gần đúng………….………..…………………………………...115
4.9.3. Khảo sát tính tăng, giảm và cực trị của hàm số….……………………115
4.9.4. Khai triển Taylor – Maclaurin………………….…………………….116
4.9.5. Ứng dụng trong bài toán kinh tế………………….………………..…119
4.10. Bài tập…….……………………………………………………..……………122
Chương 5. Tích phân…………………………….…………………………..……………...129
5.1. Tích phân bất định……………………….…………………………….………..129
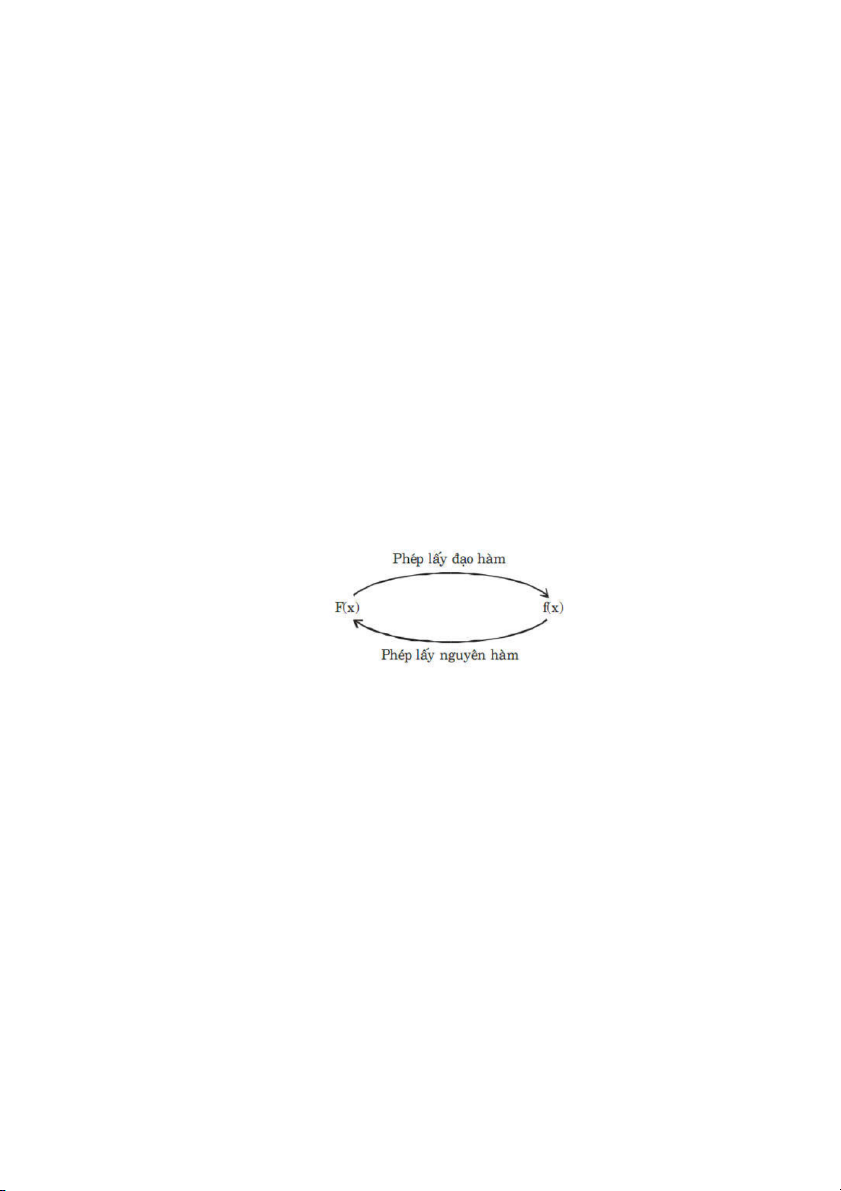
5.1.1. Nguyên hàm và tích phân bất định………….…..……………..……….129
5.1.2. Bảng công thức các tích phân cơ bản……….………………………….130
5.1.3. Các phương pháp tính tích phân bất định….……………….……..……130
5.2. Tích phân xác định………………..…………………………………………….137
5.2.1. Định nghĩa các tính chất của tích phân xác định….…….………...…...137
5.2.2. Các tính chất cơ bản của tích phân xác định..........................................140
5.2.3. Công thức NewTon – Leibnitz ………………….……………….....…140
5.2.4. Các phương pháp tính tích phân xác định..............................................141
5.2.5. Ứng dụng tích phân xác định..................................................................142
5.3. Tích phân suy rộng...................................................................................... ........144 5
5.3.1. Tích phân suy rộng loại 1: Định nghĩa và phương pháp tính.................144
5.3.2. Tích phân suy rộng loại 2: Định nghĩa và phương pháp tính................146
5.3.3. Khảo sát sự hội tụ của tích phân suy rộng.............................................148
5.4. Bài tập…………………………………………………………..……..……….151
Chương 6. Phép tính vi phân hàm nhiều biến………………………………………………..156
6.1. Các khái niệm…………...………….…………………………………………...156
6.1.1. Hàm số hai biến số.......………………………………………………...156
6.1.2. Định nghĩa hàm n biến số…...……….…………………………………157
6.1.3. Hàm số hợp………………………………………..………….….…….158
6.1.4. Một số hàm trong kinh tế……….….…………………………………..158
6.2. Giới hạn và liên tục của hàm số……...…………………………...……………..161
6.2.1. Giới hạn của hàm nhiều biến số….…..……………………………...…161
6.2.2. Hàm số liên tục.......................................................................................163
6.3. Đạo hàm riêng và vi phân toàn phần.............................................................164
6.3.1. Đạo hàm riêng……..……………………………….............................164
6.3.2. Vi phân và ứng dụng vi phân để tính gần đúng.....................................171
6.4. Cực trị hàm nhiều biến.........................................................................................175
6.4.1. Cực trị tự do.........................................................................................175
6.4.2. Cực trị có điều kiện..............................................................................183
6.4.3. Ứng dụng trong kinh tế.........................................................................188
6.5. Bài tập…………………………………………………………..………….196
Chương 7. Phương trình vi phân……………………………………………………………203
7.1. Phương trình vi phân cấp 1.………………………………………………….....203
7.1.1. Các khái niệm………..…..…………………………………………….203
7.1.2. Phương trình vi phân cấp 1 dạng tách biến….…………………………203
7.1.3. Phương trình vi phân cấp 1 dạng đẳng cấp….…….….……………..….204
7.1.4. Phương trình vi phân cấp 1 dạng tuyến tính……………………………206
7.1.5. Phương trình vi phân cấp 1 dạng Bernoulli…….………………………208
7.2. Phương trình vi phân cấp 2………….………………………………………….209
7.2.1. Các khái niệm chung……………….……………………………….…209
7.2.2. Phương trình vi phân cấp 2 có thể giảm cấp được...................................209
7.2.3. Phương trình vi phân tuyến tính cấp 2 hệ số hằng thuần nhất.................211 6
7.2.4. Phương trình vi phân tuyến tính cấp 2 hệ số hằng không thuần nhất.…..212
7.3. Một số ứng dụng trong kinh tế.............................................................................218
7.3.1. Tìm hàm y f(x) khi biết hệ số co dãn...............................................218
7.3.2. Mô hình cân bằng thị trường với kỳ vọng về giá…………..…………..218
7.4. Bài tập…………………………………………………………....…………….221
Một số đề tham khảo…………………………………………………………….…………..225
Phụ lục 1.Tập số, tổng, tích hữu hạn, hằng đẳng thức, bất đẳng thức, chứng minh bằng phương
pháp quy nạp…………………………………………..…………………………………....238
Phụ lục 2.Tập hợp và ánh xạ……………………….……………………………………......241
Phụ lục 3. Tính toán ma trận bằng máy tính cá nhân……………………………………......247
Tài liệu tham khảo…………………………………………………………………………..249 7 LỜI MỞ ĐẦU
Các bạn đang có trong tay cuốn “ Giáo trình Toán cao cấp” dành cho sinh viên hệ
đại trà, trường đại học Tài chính – Maketing. Đây là giáo trình dành cho sinh viên khối
ngành kinh tế và quản trị kinh doanh với thời lượng 4 tín chỉ (60 tiết giảng), được biên
soạn dựa trên cuốn sách cùng tên dành cho chương trình CLC; chính vì vậy chúng tôi cố
gắng lựa chọn các nội dung căn bản, trọng yếu và có nhiều ứng dụng trong kinh tế và quản
trị kinh doanh; nội dung giảng dạy không trùng lặp với nội dung sinh viên đã được trang
bị ở chương trình phổ thông; chú trọng ý nghĩa và khả năng áp dụng của kiến thức; giáo
trình được biên tập trên cơ sở tham khảo nhiều giáo trình quốc tế cũng như trong nước
(xem phần tài liệu tham khảo), cũng như kinh nghiệm giảng dạy nhiều năm của các tác giả;
Nội dung giáo trình, được thiết kế phù hợp với chương trình đào tạo đại học đại trà,
và trình độ của sinh viên khối ngành kinh tế và quản trị kinh doanh. Giáo trình bao gồm 7
chương, một số đề tự luyện và một số phụ lục cần thiết.
Chương 1. Trình bày về ma trận, phép toán trên ma trận, định thức, ma trận nghịch
đảo, hạng của ma trận, áp dụng vào giải mô hình cân đối liên ngành (Input – Output). Một
số ví dụ và bài tập rèn luyện.
Chương 2. Trình bày về hệ phương trình tuyến tính và ứng dụng giải mô hình cân
bằng thị trường n hàng hóa có liên quan. Một số ví dụ và bài tập rèn luyện
Chương 3. Trình bày về không gian vectơ; Một số ví dụ và bài tập rèn luyện.
Chương 4. Trình bày về phép tính vi phân hàm một biến : Giới hạn dãy số, giới hạn
hàm số, hàm số liên tục, đạo hàm và vi phân, ứng dụng trong toán học và kinh tế. Một số
ví dụ và bài tập rèn luyện.
Chương 5. Trình bày về nguyên hàm, tích phân bất định, tích phân xác định, tích
phân suy rộng và ứng dụng trong phân tích kinh tế. Một số ví dụ và bài tập rèn luyện.
Chương 6. Trình bày về phép tính vi phân hàm nhiều biến : Hàm số nhiều biến; đạo
hàm riêng, vi phân toàn phần và ứng dụng trong phân tích kinh tế. Bài toán cực trị tự do 8
và cực trị có điều kiện, phương pháp nhân tử Lagrange; Một số mô hình ứng dụng trong
kinh tế; Một số ví dụ và bài tập rèn luyện.
Chương 7. Trình bày về phương trình vi phân cấp 1 và phương trình vi phân cấp 2
hệ số hằng và ứng dụng trong phân tích kinh tế; Một số ví dụ và bài tập rèn luyện.
Phần cuối, chúng tôi biên soạn một số đề tham khảo để sinh viên có cơ hội thử sức,
tự rèn luyện và một số phụ lục khi cần có thể tự tra cứu.
Do đối tượng người đọc là sinh viên chuyên ngành kinh tế và quản trị kinh doanh
nên chúng tôi không quá đi sâu về lý thuyết mà chủ yếu quan tâm vào ý nghĩa và áp dụng
trong kinh tế quản trị kinh doanh của khái niệm và kết quả toán học, chúng tôi cũng sử
dụng nhiều ví dụ để người học dễ hiểu, dễ áp dụng, nhưng vẫn đảm bảo sự chặt chẽ và
logic của toán học. Giáo trình do Giảng viên cao cấp, TS. Nguyễn Huy Hoàng và ThS.
Nguyễn Trung Đông là các giảng viên của Bộ môn Toán – Thống kê, Khoa Kinh tế - Luật,
trường đại học Tài chính – Marketing, đã có nhiều năm kinh nghiệm giảng dạy toán dành
cho sinh viên khối ngành kinh tế và quản trị kinh doanh, cùng biên tập.
Lần đầu biên soạn, nên giáo trình này không tránh khỏi những thiếu sót. Rất mong
nhận được sự góp ý của các độc giả để lần sau giáo trình được hoàn thiện hơn.
Mọi ý kiến đóng góp xin gởi về địa chỉ email:
hoangtoancb@ufm.edu.vn và nguyendong@ufm.edu.vn.
Xin trân trọng cảm ơn Thư viện, Trường đại học Tài chính – Marketing đã hỗ trợ và
tạo điều kiện cho giáo trình sớm đến tay bạn đọc! Tp. HCM, Tháng 06 năm 2020 Các tác giả 9 MỘT SỐ KÝ HIỆU
1. : Tập số tự nhiên. 2. : Tập số nguyên.
3. : Tập số hữu tỉ. 4. : Tập số thực. 5. : Tập số phức. 6. M
Tập hợp các ma trận có kích thước cấp (cỡ) m n. : m n
7. M : Tập hợp các ma trận vuông cấp n. n 8. (i) : Dòng i (hàng i). 9. c : Cột j. j
10. : Phép gán (phép thay thế).
11. : Đổi chỗ (hoán vị).
12. Det(A) A : Định thức của ma trận A.
13. I hoặc E : Ma trận đơn vị.
14. r(A) rank(A): Hạng của ma trận A. 15. Dim : Số chiều. 16. lim : Giới hạn. f 17. / f
: Đạo hàm riêng của hàm f theo biến x . i x x i i
18. L : Sử dụng quy tắc L’hospital.
19. KGVT : Không gian vectơ.
20. Max : Giá trị lớn nhất.
21. Min : Giá trị nhỏ nhất. 10 22. Q : Sản lượng. 23. D : Demand (Cầu). 24. S : Supply (Cung). 25. Q : Lượng cầu. D 26. Q : Lượng cung. S 27. P : Giá bán.
28. L : Lao động (nhân công).
29. MPL: Hàm sản phẩm cận biên của lao động. 30. K : Vốn.
31. MPK : Hàm sản phẩm cận biên của vốn. 32. : Lợi nhuận. 33. TR : Tổng doanh thu.
34. MR : Doanh thu biên (doanh thu cận biên). 35. TC : Tổng chi phí.
36. FC : Chi phí cố định.
37. VC : Chi phí biến đổi (chi phí khả biến).
38. MC : Chi phí biên (chi phí cận biên).
39. AC : Chi phí trung bình.
40. TU : Tổng hữu dụng (Hàm lợi ích).
41. MU : Hàm hữu dụng biên (hàm lợi ích biên). 42. E
: Hệ số co dãn của Y theo X. Y X 11 Chương 1 MA TRẬN – ĐỊNH THỨC 1.1. Ma trận
1.1.1. Định nghĩa ma trận
Một bảng số hình chữ nhật gồm có m dòng (hàng) và n cột được gọi là ma trận có cấp (cỡ) m n. a a ü a 11 12 1n a a ü a Ký hiệu: 21 22 2n A øaijù (1.1) ü ü ü ü mn a a ü a m1 m2 mn với
i : gọi là chỉ số dòng (hàng).
j : gọi là chỉ số cột.
a ij : là phần tử nằm ở dòng i và cột j trong ma trận A.
Ví dụ 1. Cho các ma trận 1 2 3 A
là ma trận cấp ø2 3ù. 4 5 6 1 4 B 2 5
là ma trận cấp ø3 2ù. 3 6 1 3 2 C 0 1 3
là ma trận cấp ø3 3ù (ma trận vuông cấp 3). 2 4 5 1.1.2. Ma trận bằng nhau
Hai ma trận được gọi là bằng nhau nếu chúng cùng cấp và có tất cả các phần tử
tương ứng vị trí bằng nhau. Cho hai ma trận: A ø a B b ij ù và ø ijù mn m n a ü b ij ij A B ý (1.2) i 1,2,...,m; j 1, 2,...,n 12 1 2 1 b
Ví dụ 2. Cho hai ma trận: A ; B
. Tìm a, b để hai ma trận A, B bằng 3 4 a 4 nhau. Giải a ü 3
Ta có hai ma trận A và B đều có cấp là ø2 2ù . Do đó A B ý . b 2
1.1.3. Các ma trận đặc biệt 1.1.3.1. Ma trận không
Ma trận không là ma trận mà các phần tử đều là số không.
Ví dụ 3. Cho các ma trận không 0 0 0 0
là ma trân không cấp ø2 3ù 23 . 0 0 0 0 0 0 0 0
là ma trận không cấp ø3 2ù. 32 0 0 1.1.3.2. Ma trận vuông
Ma trận vuông là ma trận có số hàng và số cột bằng nhau. Ma trận vuông cấp n n
được gọi tắt là ma trận vuông cấp n. Tập hợp tất cả các ma trận vuông cấp n được ký hiệu là n
M . Với ma trận vuông A M n, các phần tử 11
a , a22,...,ann được gọi là thuộc
đường chéo (chính) của ma trận A. Các phần tử an1,an 1,2,..., 1 a
được gọi là thuộc đường n
chéo phụ của ma trận A. 1 2 3
Ví dụ 4. Cho ma trận vuông cấp 3: 4 5 6
có các phần tử a 1, a 5, a 9 11 22 33 7 8 9
thuộc đường chéo chính còn các phần tử a 7, a 5, a 3 thuộc đường chéo phụ. 31 22 13 1.1.3.3. Ma trận chéo
Ma trận chéo là ma trận vuông mà mọi phần tử không thuộc đường chéo chính đều là bằng 0. 1 0 0
Ví dụ 5. Cho ma trận chéo cấp 3 : 0 5 0. 0 0 9 13
1.1.3.4. Ma trận đơn vị cấp
Ma trận đơn vị là ma trận chéo mà mọi phần tử thuộc đường chéo chính đều bằng
1. Ký hiệu I là ma trận đơn vị cấp n. n
Ví dụ 6. Cho các ma trận đơn vị 1 0 ... 0 1 0 0 1 0 0 1 ... 0 I ; I 0 1 0 ;...;I 2 3 n . 0 1 ... ... ... ... 0 0 1 0 0 ... 1
1.1.3.5. Ma trận tam giác trên (dưới)
Ma trận tam giác trên (dưới) là ma trận vuông mà các phần tử ở phía dưới (hoặc ở
phía trên) đường chéo chính đều bằng 0.
Ví dụ 7. Cho các ma trận cấp 3 1 3 4 0 2 5
là ma trận tam giác trên. 0 0 3 1 0 0 3 2 0
là ma trận tam giác dưới. 5 4 3
1.1.3.6. Ma trận bậc thang (ma trận hình thang)
Ma trận bậc thang là ma trận ứng với hai dòng bất kỳ số hạng khác không đầu
tiên của hàng dưới phải nằm bên phải số hạng khác không đầu tiên của hàng trên. a a ü a ü a 11 12 1r 1n 0 a ü ü 22 a 2r a 2n ý ý ý ý ý 0 0 ü a ü a rr rn ý ý ý ý ý 0 0 ü 0 ü 0 với r n và 11
a , a22,...,arr gọi là các phần tử chéo. 1 2 3 4 5 0 2 4 3 7
Ví dụ 8. Cho ma trận bậc thang như sau: 0 0 3 5 4 0 0 0 5 8 14
Lưu ý: Ma trận tam giác trên là ma trận bậc thang đặc biệt.
1.1.3.7. Ma trận chuyển vị Cho A øa M , ij ù
m n chuyển vị của A , ký hiệu T
A , là ma trận cấp n m xác m n định bởi T A øa M . ji ù n m n m
Nhận xét : Ma trận chuyển vị của A là ma trận nhận được từ A bằng cách chuyển
hàng của A thành cột của T A . Tính chất (i) ø ùT T A A, (ii) ø ùT T T A B A B , (iii) ø ùT T T AB B A .
Định nghĩa: Ma trận vuông A được gọi là một ma trận đối xứng nếu T A A . Ví dụ 9. Cho ma trận 2 3 4 A
là ma trận cấp ø2 3ù. 4 5 6 Ta có 2 3 T A 3 5
là ma trận chuyển vị của ma trận A có cấp là ø 3 ù 2 . 4 6
1.1.4. Các phép toán trên ma trận
1.1.4.1. Nhân một số thực với ma trận
Nhân số thức với ma trận là nhân số đó với tất cả các phần tử của ma trận: Cho ma trận A ø aijù và k ta có: mn kA (k aij m ) n (1.3) Đặc biệt ( 1 )A A ø a . ij ù mn
1.1.4.2. Cộng hai ma trận cùng cấp
Cộng hai ma trận cùng cấp là cộng các phần tử tương ứng các vị trí với nhau: Cho hai ma trận : A ø a B b . ij ù và ø ijù Ta có m n m n 15 A B ø a b ij i ù j (1.4) m n
Ví dụ 10. Cho hai ma trận: 1 2 3 1 1 1 A , B . 4 5 6 1 1 1
Tính 2A, 4B, A B, 2A 4B. Giải Ta có 2 4 6 4 4 4 2A , 4 B 8 10 12 4 4 4 và 2 1 4 6 0 10 A B , 2A 4B . 3 6 5 4 14 8 1.1.4.3. Các tính chất
Cho ba ma trận A, B, C cùng cấp và ñ,ò . a) A B B A
b) (A B) C A (B C) c) A 0 A d) A (A) 0 e) 1 A A f) (ñ ) ò A ñA òA g) ñ(A B) A ñ B ñ h) (ñ ) ò A ( ñ A ò ) ( ò ñA).
1.1.4.4. Phép nhân hai ma trận
Cho hai ma trận A øa M , B b M
. Ta định nghĩa ma trận tích của ij ù m n ø ijù n p
hai ma trận A, B là ma trận cấp m p , ký hiệu AB ø c M , xác định bởi ij ù mp n
c a b a b a b a b , i 1 ,m, j 1 ,p (1.5) ij i1 1j i2 2 j in nj ik kj k 1 Tính chất
(i) Tính kết hợp : Cho A M , B M và C M , ta có m n n p pq 16 A øBCù øAB ùC .
(ii) Tính phân phối : Với mọi ma trận A,B M và C M , ta có m n np øA BùC AC BC ,
và với mọi ma trận C M và A,B M , ta có m n n p CøA Bù CA CB .
(iii) Với mọi ma trận A M và với mọi k , B M m n np , ta có kø A ù B ø kAù B Aø k ù B .
Hệ quả. Cho A là ma trận vuông cấp n. Ta có n A A A ü A (nhân n lần).
Ví dụ 11. Cho hai ma trận: 1 2 2 3 4 A 1 1 M , B M . 3x2 2x3 3 5 0 2 3 Tính AB và ø ù2 AB . Giải Ta có 1 2 8 7 4 2 3 4 AB 1 1 1 8 4 . 3 5 0 2 3 13 9 8 8 7 4 8 7 4 ø ù2 AB ø ù AB ø A ù B 1 8 4 1 8 4 13 9 8 13 9 8 123 148 36 36 35 60 . 217 235 123
Ví dụ 12. Cho hai ma trận vuông cấp 4: 1 0 3 4 3 2 2 4 2 3 1 2 2 1 1 3 A , B . 3 2 4 3 1 0 3 0 1 1 2 1 3 4 3 5 Tính AB và BA. 17 Giải Ta có 1 0 3 4 3 2 2 4 12 18 1 24 2 3 1 2 2 1 1 3 7 9 2 9 AB . 3 2 4 3 1 0 3 0 18 20 7 33 1 1 2 1 3 4 3 5 10 7 8 12 3 2 2 4 1 0 3 4 3 6 5 6 2 1 1 3 2 3 1 2 6 8 5 12 BA . 1 0 3 0 3 2 4 3 1 0 6 1 5 1 3 3 4 3 5 1 1 2 1 9 23 15 18
1.1.5. Các phép biến đổi sơ cấp trên hàng
1.1.5.1. Ba phép biến đổi sơ cấp trên hàng của ma trận
i) Phép biến đổi loại 1: Đổi chỗ 2 hàng của ma trận. / (i)(i ) A B
ii) Phép biến đổi loại 2: Nhân một số thực khác không với một hàng. (i):ñ (i) A B ñ 0
iii) Phép biến đổi loại 3: Thay 1 hàng bất kỳ bằng chính nó rồi cộng với một
số thực nhân cho hàng khác. / (i):(i)ñ (i ) A B.
Ví dụ 13. Cho ma trận vuông cấp 3 như sau: 1 2 3 A 2 2 4 3 2 5 1 2 3 1 2 3
Phép biến đổi loại 1: (2)(3) 2 2 4 3 2 5 . 3 2 5 2 2 4 1 2 3 1 2 3 1 Phép biến đổi loại 2: (2): (2) 2 2 2 4 1 1 2 . 3 2 5 3 2 5 1 2 3 1 2 3
Phép biến đổi loại 3: (2):(2)2(1) 2 2 4 0 2 2 . 3 2 5 3 2 5 18
1.1.5.2. Liên hệ giữa phép biến đổi sơ cấp trên hàng và phép nhân ma trận 1 0 ü 0 0 1 ü ý Cho ma trận A ø a I ijù
và ma trận đơn vị cấp m: mn m ý ý 0 0 ü 0 1 Định nghĩa: 1 0 1 doøng i I(i, j) 1 0 doøng j 1 1 I(i,ñ) ñ doøng i 1 1 1 ñ doøng i I(i, j, ) ñ 0 1 doøng j 1 Lưu ý:
+) Phép hoán vị hai hàng của ma trận A được coi là thực hiện phép nhân ma trận I(i, j) A.
+) Phép nhân một hàng của ma trận A với số thực ñ 0 được coi là phép nhân ma trận I(i,ñ) A.
+) Phép cộng vào hàng i hàng j đã nhân với ñ ( i j ) được coi là phép nhân ma trận I(i, j,ñ) A. 19 1.2. Định thức a a a 11 12 1n a a a
Xét ma trận vuông cấp n : 21 22 2n A ý ý ý a a a n1 n2 nn a
Với mỗi số hạng ij (số hạng nằm ở hàng i và cột j), ma trận nhận được từ A bằng a ,
cách bỏ đi hàng thứ i và cột thứ j được gọi là ma trận bù của A đối với số hạng ij ký A . hiệu là ij
Ví dụ 14. Cho ma trận vuông cấp 3 : 1 4 7 A 2 5 8 3 6 9
Ta có thể thành lập các ma trận bù cấp 2, chẳng hạn 5 8 1 4 1 4 A11 ; A 23 ; A 33 . 6 9 3 6 2 5
1.2.1. Định nghĩa định thức ma trận vuông cấp n
Định thức của ma trận vuông A Mn, ký hiệu det(A) hay A , là số thực được định
nghĩa bằng quy nạp theo n như sau :
Với n 1 , nghĩa là A øa11 ù, thì detøAù a11. Với n 2, A (a ) , thì : ij n n det øA ù 1 1 ( 1) a det øA ù 1 2 ( 1 ) a det øA ù 1 n 11 11 12 12 ü ( 1 ) a 1ndet øA1n ù n
det øAù ø1ù1 ja det A (1.6) 1j ø 1j ù j 1
Xét một số trường hợp đặc biệt: a a Với n 2, 11 12 A . Ta có a a 21 22
det(A) a11det (A11) a12 det 12 (A ) a11a22 a21a12 1 a a2 a3 b b b b b b 2 3 1 3 1 2 Với n 3, ta có: b b b a a a 1 2 3 1 2 3 c c c c c c 2 3 1 3 1 2 1 c c2 c3 20 1 a ø 2 b 3 c 3 b 2 c ù a2 ø 1 b 3 c 3 b 1 c ù 3 a ø 1 b 2 c 2 b 1 c ù 1 a 2 b 3 c a2 3 b 1 c a3 1 b 2 c 1 a 3 b 2 c a2 1 b 3 c a3 2 b 1 c .
Tính định thức của ma trận vuông cấp 3 bằng quy tắc 6 đường chéo (quy tắc Sarrus) a a a 11 12 13
Cho ma trận vuông cấp 3 : A a a a 21 22 23 a a a 31 32 33 a a a a a 11 12 13 11 12 Xây dựng ma trận / A a a a a a 3x3 21 22 23 21 22 a a a a a 31 32 33 31 32 Định thức của A detø ù
A ø a a a a a a a a a a a a a a a a a a 11 22 33 12 23 31 13 21 32ù
ø 31 22 13 32 23 11 33 21 12ù
3 số hạng mang dấu cộng trong định thức là tích các phần tử nằm trên ba đường song song với đường chéo chính.
3 số hạng mang dấu âm trong định thức là tích các phần tử nằm trên ba đường song song với đường chéo phụ.
Ví dụ 15. Tính các định thức 1 2 a)
1 4 3 2 2. 3 4 2 3 4 2 3 1 3 1 2 b) 1 2 3 2 3 4 1 . 4 2 5 2 5 4 5 4 2 2 3 4 c) 1 2 3 ø2 2 2 3 3 5 4 1 4 ù ø5 2 4 4 3 2 2 1 3 ù 1 . 5 4 2 3 0 5 5 1 2 1 2 5 d) 1 1 12 13 2 5 1 (1) 3 (1) 0 (1) (5) 31. 3 6 4 6 4 3 4 3 6
1.2.2. Định lý khai triển định thức theo một hàng hay một cột bất kỳ Cho ma trận A øa
, 1 i , j n . Khi đó: i jù nn 0 0 n det øAù i j 0 ( 1 ) a det A . (1.7) i0 j ø i0jù j 1 21 n det øAù i 0j ( 1 ) a det A . (1.8) ij 0 ø ij0ù i 1
Công thức (1.7) gọi là công thức khai triển theo hàng i và công thức (1.8) là công thức 0 khai triển theo cột j . 0
Ví dụ 16. Tính các định thức 1 2 3 4 2 3 4 1 a) A 3 4 1 2 4 1 2 3
Tính định thức của ma trận A. Chúng ta khai triển định thức này theo hàng 1 : 3 4 1 2 4 1 1 1 1 2 A ( 1 ) 1 4 1 2 ( 1 ) 2 3 1 2 1 2 3 4 2 3 2 3 1 2 3 4 1 3 1 4 ( 1 ) 3 3 4 2 ( 1 ) 4 3 4 1 4 1 3 4 1 2
36 8 12 176 160. 1 3 0 a 2 b 0 0 b) B 3 4 c 5 d 0 0 0
Tính định thức của ma trận B. Chúng ta khai triển định thức này theo hàng 4 : 3 0 a 3 a 4 1 32 B ( 1 ) d b 0 0 d( 1 ) c abcd. b 0 4 c 5 1 1 2 0 2 m 0 2 c) C 3 0 4 3 4 2 1 0
Tính định thức của ma trận C. Chúng ta khai triển định thức này theo cột 4 : 1 1 2 1 1 2 24 34 C ( 1 ) 2 3 0 4 ( 1 ) 3 2 m 0 4 8 9m. 4 2 1 4 2 1 22
1.2.3. Các tính chất định thức
i) Tính chất 1. Cho ma trận vuông A. Ta có ø ù ø T det A det A ù . Ví dụ 17. Cho ma trận: 1 3 4 A 2 5 1 3 1 2 Ta có: ø ù ø T det A det A ù 4 6.
ii) Tính chất 2. Cho A, B là hai ma trận vuông. Ta có
detø ABù det øBAù detø Aù detø ù B . 1 2 2 1
Ví dụ 18. Cho hai ma trận: A ; B 3 4 4 3 a) Tính AB và BA.
b) Tính det øA ù, det øBù, det øABù, det øBA ù Giải 10 7 5 8 a) Ta có: AB ; BA 22 15 13 20
b) Ta có: det øAù 2; detøBù 2; detøABù det øBAù 4.
iii) Tính chất 3. Cho I là ma trận đơn vị cấp n. Ta có detøIù 1.
iv) Tính chất 4. Cho ba ma trận A, B, C n M thỏa mãn: C A B và C A
B , i 2,3,..., n; j 1, 2,..., n. 1j 1j 1j ij ij ij
Ta có: det øCù detøAù detøBù. Ví dụ 19. Cho ba ma trận a b c b c a a b b c c a
A 1 2 3, B 1 2 3, C 1 2 3 2 3 4 2 3 4 2 3 4
Chứng minh rằng: det øCù det øA ù det øBù. Giải
Ta có: detøAù a 2b c; detøBù a b 2c; detøCù 2a b c
Vậy detøCù detøAù detøBù. 23
v) Tính chất 5. Cho số thực k và ma trận A n n
M . Ta có detøkAù k detøAù. 1 3 4
Ví dụ 20. Cho ma trận A 2 5 1 . 3 1 2 Ta có: ø ù ø ù 3 det A 46
det 2A 2 det øAù 368.
1.2.4. Định lý sự thay đổi của định thức qua các phép biến đổi / i) Nếu (i) ( i ) A B thì detø ù B detøAù. ii) Nếu (i):ñ(i) A B thì detø ù B ñ detø ù A (với ñ ≠ 0).
iii) Định thức của ma trận có 2 dòng hoặc hai cột tỉ lệ với nhau thì bằng 0. iv) Nếu / (i): ( i)ñ(i )
A B thì detøBù detø Aù.
v) Định thức của ma trận tam giác trên bằng tích các số hạng nằm trên đường. 1 2 3
Ví dụ 21. Cho ma trận: A 2 3 1 3 1 5
a) Thực hiện phép biến đổi loại 1. 1 2 3 2 3 1 A 2 3 1 1 2 3 B . (1)(2) 3 1 5 3 1 5 Ta có: det øA ù 2
1; det øBù 21; det øBù det øA ù
b) Thực hiện phép biến đổi loại 2 1 2 3 2 4 6 (1):2(1) A 2 3 1 2 3 1 B 3 1 5 3 1 5 Ta có: detøAù 2 1; detø ù B 4 2 2detøAù .
c) Thực hiện phép biến đổi loại 3 1 2 3 1 2 3 (2): (2) 2(1) A 2 3 1 0 1 5 B 3 1 5 3 1 5
Ta có: det øA ù det øBù 21 . 24
1.2.5. Phần bù đại số và ma trận phụ hợp
Cho ma trận vuông cấp n : A øaij ù n
+) Định thức cấp (n 1) thu được từ A bằng cách bỏ đi hàng i và cột j , lấy dấu
øù nếu øi jù chẵn, lấy dấu øù nếu øi jù lẻ, được gọi là phần bù đại số của phần tử i a j ø i
, j 1,2,...,nù , ký hiệu là * i j A . ij ( 1) Aij +) Ma trận ký hiệu *
A , được định nghĩa như sau : * * * 1 A 1 A21 n A 1 * * * * 1 A 2 A22 An2 A ý ý ý * * * A A A 1n 2n nn Trong đó : * A i , j 1,2,...,n a ij ø
ù là phần bù đại số của phần tử ij, được gọi là ma
trận phụ hợp của ma trận A.
Chú ý : Nếu A là ma trận vuông cấp n thì *
A cũng là ma trận vuông cấp n. 1 2 4
Ví dụ 22. Cho ma trận vuông cấp 3: A 4 5 6 7 8 9 * * * 11 A A21 31 A
Ta có ma trận phụ hợp cấp 3 như sau: * * * * A A 12 A 22 A32 * * * 13 A A23 33 A Với 5 6 4 6 4 5 * 1 1 1 A 1 (1) 3 ; * 1 2 A (1) 6; * 1 3 A ( 1 ) 3 8 9 12 7 9 13 7 8 2 4 1 4 1 2 * 21 A 21 (1) 14; * 2 2 A (1) 19 ; * 2 3 A (1) 6 8 9 22 7 9 23 7 8 2 4 1 4 1 2 * 3 1 A 31 ( 1) 8; * 3 2 A ( 1 ) 10; * 3 3 A ( 1 ) 3 5 6 32 4 6 33 4 5 3 14 8 Vậy: * A 6 19 10 . 3 6 3 25
1.3. Ma trận nghịch đảo
1.3.1. Định nghĩa ma trận nghịch đảo
Cho A, BM , ta nói A, B là hai ma trận nghịch đảo của nhau nếu n AB BA In.
Khi đó, ta nói A và B là các ma trận khả nghịch. Ký hiệu 1 B A hay 1 A B .
Tính chất: Ma trận A n
M khả nghịch khi và chỉ khi det( ) A 0.
Ví dụ 23. Định m để ma trận sau khả nghịch 1 2 m A 3 m 4 2 3 m Giải
Từ ma trận A ta biến đổi như sau 1 2 m 1 2 m (2):(2)3(1) A 3 m 4 0 m 6 4 3m (3):(3)2(1) 2 3 m 0 7 m Ta có m 6 4 3m 1 1 2 det(A) ( 1 ) 1 m 15m 28 7 m 15 113 15 113
Ma trận khả nghịch khi vào chỉ khi det(A) 0 m m . 2 2
Ví dụ 24. Cho ma trận A n M thỏa mãn 2
A 2A I 0. Chứng minh rằng ma trận A n khả nghịch. Giải Từ đẳng thức 2
A 2A I 0 , ta có I A 2I A (*) n n ø n ù
Lấy định thức hai vế của (*), ta có
1 det øI det A 2I A det A det 2I A . n ù ø n ù ø ù ø n ù
Suy ra det øAù 0. Vậy A khả nghịch.
1.3.2. Giải thuật tìm ma trận nghịch đảo Phương pháp 1. Tìm 1 A bằng định thức. +) Bước 1. Cho A n M , det A 0. 26
+) Bước 2. Tính các phần bù đại số của A đối với phần tử a * i j A ( 1 ) A . ij ø ij ij ù +) Bước 3. Đặt * A ø * A ji ù n M . Khi đó : n 1 1 * A A (1.9) det A
Phương pháp 2. Dùng phép biến đổi sơ cấp theo hàng.
+) Bước 1. Lập ma trận øA In ù là ma trận gồm n hàng và 2n cột, trong đó n cột đầu của øA chính là ma trận là ma trận đơn vị I . n I ù
A, n cột cuối của ø A nI ù n
+) Bước 2. Bằng các phép biến đổi sơ cấp theo hàng, ta có thể chuyển ma trận øA I n ù
về ma trận øIn Bù và khi đó 1 B A .
Nếu ma trận A không chuyển được về ma trận đơn vị thì ma trận A không khả nghịch.
Ví dụ 25. Tìm ma trận nghịch đảo của ma trận sau bằng phương pháp định thức 1 1 1 A 1 2 1 2 3 1
Giải. Ta có detø Aù 1, do đó A khả nghịch và 1
A được tính bởi công thức sau * * * 11 A A21 31 A 1 1 1 * * * * A A , 12 A A22 32 A det A det A * * * A A A 13 23 33 với * i j A ij ( 1) Aij , 2 1 1 1 1 2 * A ø1ù1 1 * 1, A ø1ù1 2 * 1, A 1 1, 11 12 13 ø ù1 3 3 1 2 1 2 3 * ø 1 ù2 1 1 1 * 4, A ø 1 ù22 1 1 * 1 1 A 21 22 3, A23 ø 1 ù2 3 1 , 3 1 2 1 2 3 1 1 1 1 1 1 * A ø1ù3 1 * 3 , A ø1ù3 2 * 2 , A 1 1. 31 32 33 ø ù3 3 2 1 1 1 1 2
Vậy ma trận nghịch đảo của ma trận A là 1 4 3 1 1 * A ø ù A 1 3 2 . det A 1 1 1 27
Ví dụ 26. Tìm ma trận nghịch đảo sau bằng phương pháp biến đổi sơ cấp trên hàng 1 1 1 A 1 2 1 2 3 1 Giải
Thực hiện các phéo biến đổi sơ cấp trên dòng như sau 1 1 1 1 0 0 1 1 1 1 0 0 øA I 1 2 1 0 1 0 0 1 2 1 1 0 3 ù ø2ù: ø2ù ø1ù ø ù 3 : ø ù 3 2 ø ù 1 2 3 1 0 0 1 0 1 3 2 0 1 1 1 1 1 0 0 1 0 3 2 1 0 ø3ù:ø3ùø2ù ø1ù:ø1ùø2ù 0 1 2 1 1 0 0 1 2 1 1 0 0 0 1 1 1 1 0 0 1 1 1 1 1 0 0 1 4 3 ø1ù: ø 1ù 3 ø3ù 0 1 0 1 3 2 ø 1 I3 A 2 : 2 2 3 ù ø ù ø ù ø ù 0 0 1 1 1 1
Vậy ma trận nghịch đảo của A là : 1 4 3 1 A 1 3 2 . 1 1 1
1.3.3. Định lý sự tồn tại của ma trận nghịch đảo
Nếu ma trận A khả nghịch thì ma trận nghịch đảo 1 A tồn tại duy nhất.
1.3.4. Một số tính chất của ma trận nghịch đảo
Nếu A, B là những ma trận vuông cấp n khả nghịch thì i) ø ù 1 1 A A, ii) ø ù1 1 1 AB B A , 1 T iii) ø Tù ø 1 A A ù . 1 iv) ø Aù 1 1 A ñ với ñ 0. ñ
Ví dụ 27. Giải phương trình ma trận XA B với 28 1 1 1 1 2 0 A 1 2 1 và B 4 5 1 2 3 1 0 1 3 Giải Theo ví dụ 26, ta có 1 4 3 1 A 1 3 2 1 1 1
Từ phương trình ma trận nhân bên phải hai vế cho 1 A , ta được 1 2 0 1 4 3 1 2 1 1 X BA 4 5 1 1 3 2 8 30 21 . 0 1 3 1 1 1 2 0 1 1.4. Hạng của ma trận
1.4.1. Định nghĩa tổng quát hạng của một ma trận Cho ma trận A m M n
, ta gọi hạng của ma trận A bằng r nếu
i) Mọi định thức con của A cấp lớn hơn r đều bằng 0.
ii) Trong A tồn tại một định thức con cấp r khác 0.
Ta ký hiệu hạng của ma trận A là rank ø Aù hay vắn tắt là rø Aù. Khi A là ma trận
0, ta quy ước røAù 0.
Lưu ý rằng : 0 r øA ù min m,n. 1.4.2. Tính chất
i) Hạng của ma trận không thay đổi qua các phép biến đổi sơ cấp trên hàng, nghĩa
là nếu B là ma trận nhận được từ A sau hữu hạn các phép biến đổi sơ cấp thì r ø ù A r øBù.
ii) Hạng của ma trận không thay đổi qua phép chuyển vị, nghĩa là ø ù ø T r A r A ù.
iii) Nếu A là ma trận bậc thang theo hàng thì hạng của A bằng số hàng khác không của nó.
1.4.3. Phương pháp tìm hạng của ma trận : Dùng các phép biến đổi sơ cấp trên hàng.
Dùng các phép biến đổi sơ cấp trên hàng để đưa ma trận A về dạng ma trận bậc
thang theo hàng B. Khi đó, r(A) bằng số hàng khác không của ma trận B. Ví dụ 28. Cho ma trận: 29 1 2 1 0 A 1 2 4 2 . 3 6 3 0
Tìm hạng của ma trận A. Giải.
Biến ma trận A về ma trận bậc thang theo hàng 1 2 1 0 ø ù 2 :ø ù 2 ø ù 1 1 2 1 0 (3):(3) 3 (1) 1 2 4
2 0 4 3 2 B 3 6 3 0 0 0 0 0
Ma trận B là ma trận bậc thang có hai dòng khác dòng không nên r(A) r(B) 2.
Ví dụ 29. Biện luận theo m hạng của ma trận sau: 1 3 2 A 2 1 m 3 8 5 Giải
Biến ma trận A về ma trận bậc thang theo dòng (hoặc ma trận tam giác trên) 1 3 2 1 3 2 (2): ( 2) 2 (1) A 2 1 m 0 5 m 4 (3): ( 3) 3 (1) 3 8 5 0 1 1 1 3 2 (3):5(3) (2) 0 5 m 4 B 0 0 1 m
Ma trận B là ma trận bậc thang theo dòng, ta có rank(A) rank(B). Biện luận Nếu m 1 thì rank(A) 2 . Nếu m 1 thì rank(A) 3 .
1.4.4. Một số bất đẳng thức về hạng của ma trận
a) Cho A và B là hai ma trận vuông cấp n. Khi đó
i) r(A B) r(A) r(B).
ii) r(A) r(B) n r(AB) minr(A), r(B ) .
iii) Nếu ma trận B khả nghịch thì r(AB) r(BA) r(A). 30 b) Cho ma trận A m
M n và ma trận B M . Khi đó r(AB) minr(A),r(B ) . n p
Ví dụ 30. Cho A là ma trận cấp 3 2 , B là ma trận cấp 2 3 sao cho 8 2 2 AB 2 5 4 2 4 5
a) Tìm hạng của ma trận AB.
b) Chứng minh ma trận BA khả nghịch và tìm BA. Giải
a) Tìm hạng của ma trận AB.
Thực hiện phép biến đổi sơ cấp trên hàng của ma trận AB, biến ma trận AB về ma trận bậc thang như sau. 8 2 2 8 2 2 (2): 4 (2) ( 1) (3): 4 (2) ( 1) AB 2 5 4 0 18 18 2 4 5 0 18 18 8 2 2 (3):(3)(2) 0 18 18 0 0 0
Vậy hạng của ma trận AB là r(AB) 2.
b) Chứng minh ma trận BA khả nghịch và tìm BA. Ta có 72 18 18 8 2 2
øABù2 18 45 36 9 2 5 4 9AB 18 36 45 2 4 5 Ta có : 2 2 r(AB) r (AB) r A
ø BAù B r(BA) 2
Vậy r(BA) 2 nên BA là ma trận khả nghịch. Ta có ø ù3 2 2 BA
(BA)(BA)(BA) B(AB) A 9B(AB)A 9(BA)
Nhân hai vế của đẳng thức cho ø ù 1 BA hai lần, ta được 9 0 BA 9I 2 . 0 9 31 1.5. Bài tập
Bài số 1. Thực hiện các phép tính trên các ma trận sau :
1. Tính 5A 3B 2C , biết : 1 2 1 3 2 5 A 1 0 , B 2 1 và C 0 3 . 2 1 3 2 4 2 2 1 1 2 5
2. Tính AB, BA biết : A 1 0 và B . 3 4 0 3 4 1 3 2 2 5 6
3. Tính AB, BA biết : A 3 4 1 và B 1 2 5 . 2 5 3 1 3 2 6 11
Đáp số: 1) 5A 3B 2C 11 3 . 27 15 1 8 10 1 5 19 2) AB 1 2 5 ; BA . 10 3 9 22 15 1 5 5 29 5 6 27 3) AB 3 10 0 ; BA 17 36 19 . 2 9 7 14 25 11 2 0 1 Bài số 2. Cho A 3 1 2
. Tính f ø Aù với ø ù 2 f x x – 5x 3. 0 1 0 3 1 3 Đáp số : f øAù 6 3 5 . 3 4 1 2 1 2 1 3 1 1
Bài số 3. Cho các ma trận : A , B 0 2 , C . 0 1 2 0 1 1 1
1. Có thể thành lập được tích của các ma trận nào trong các ma trận trên 2. Tính AB , ABC . 32 3. Tính ø ù3 n AB , C với n .
4. Tìm ma trận chuyển vị của A và tính ATC 1 3 1 4
Đáp số : 1) AB, BA, BC, CA; 2) AB , ABC ; 2 0 2 2 2 0 2 2 3) 3 11 15 (AB) , n 1 n C . 4) T A 1 1 , T A C 1 0 . 10 6 0 1 3 2 3 5 1 2 6
Bài số 4. Cho ma trận A 4 3 8
. Tìm ma trận X sao cho 3A 2X I . 3 2 2 5 1 3 9 Đáp số : X 6 4 12 . 3 3 7
Bài số 5. Tính các định thức sau : 2 0 1 1 0 0 1. 3 2 3 2. 3 2 4 1 3 5 4 1 3 1 2 3 4 1 0 2 a 2 3 4 1 2 0 b 0 3. 4. 3 4 1 2 3 c 4 5 4 1 2 3 d 0 0 0 x a b 0 c 2 1 1 1 1 0 y 0 0 d 1 3 1 1 1 5. 0 e z 0 f 6. 1 1 4 1 1 g h k u l 1 1 1 5 1 0 0 0 0 v 1 1 1 1 6 Đáp số : 1) 5
; 2) 10 ; 3) 160 ; 4) abcd ; 5) xyzuv ; 6) 394 .
Bài số 6. Chứng tỏ rằng các định thức sau bằng không a b c 1 x p ax bp 1. b c a 1 2. y q ay bq c a b 1 z r az br 33 2 2 ab a b øa b ù2 a b c 1 b c a 1 3. 2 2 bc b c øb cù2 4. c a b 1 ca c a øc aù2 2 2 c b b a a c 2
Hướng dẫn : 1) Lấy cột 1 cộng cột 2; 2) Từ cột 3, ta tách làm hai ma trận có cùng
cột 1 và 2 ; 3) Lấy cột 2 cộng 2 lần cột 1; 4) Lấy cột 1 cộng cột 2 và cột 3. 2 1 a a
Bài số 7. Chứng minh rằng : 2
1 b b øb a ùøc a ùøc bù 2 1 c c
Hướng dẫn : Biến đổi sơ cấp hoặc dùng qui tắc 6 đường chéo. Bài số 8. Tìm x sao cho : 2 3 1 x x x 1 2 4 8 = 0. 1 3 9 27 1 4 16 64
Đáp số : x 2 x 3 x 4 .
Bài số 9. Tính định thức cấp n sau: 1 2 3 ü n a 1 1 ü 1 1 0 3 ü n 1 a 1 ü 1 1. 1 2 0 ü n 2. 1 1 a ü 1 ü ü ü ü ü ü ü ü ü ü 1 2 3 ü 0 1 1 1 ü a 1 2 2 ... 2 a + 2b a + 2b ü a + 2b 2 2 2 ... 2 1 1 1 2 1 n a + 2b a + 2b ü a + 2b 3. 2 2 3 ... 2 4. 2 1 2 2 2 n ý ý ý ... ... ... ... ... a + 2b a + 2b ü a + 2b 2 2 2 ... n n 1 n 2 n n Đáp số : 1) n!; 2) ø ùø ùn 1 a n 1 a 1 ; 3) ; 4) 0 . 2 1 1 1
Bài số 10. Cho hai ma trận: A và B . 1 2 1 1 Tính ø ùn 1
B AB , n rồi suy ra n A . 34 3 0 1 3 1 3 1 Đáp số : øB ABù n n n n 1 n ; A . n n 0 1 2 3 1 3 1 5 4
Bài số 11. Cho ma trận A M 2. 4 3 Chứng minh rằng : 2 A 2A I 2 0. Suy ra 1 A .
Hướng dẫn : Tính trực tiếp ta có điều phải chứng minh rồi suy ra 1 A .
Bài số 12. Tìm a để ma trận sau khả nghịch và tính 1 A . 1 1 0 A 1 a 1 0 2 1 a 2 1 1 1 Đáp số : a 3 ; 1 A 1 1 1 . a 3 2 2 a 1
Bài số 13. Tìm m sao cho các ma trận sau khả nghịch 1 1 1 m 1 2 2 1 1 m 1 1. 2 m 2 m 5 2. 1 m 1 1 m 1 m 1 m 1 1 1
Đáp số : 1) m 1 m 3; 2) m 1 m 3 .
Bài số 14. Tìm x sao cho : 1 x x -1 x + 2 2 0 0 x 1 0 = 0. x 1 x x 2 5 100 0 0 x +1 x
Đáp số : x 0 x 1 x 1 .
Bài số 15. Tìm ma trận nghịch đảo của ma trận sau (nếu có ) : 1 1 1 1 2 3 1. 1 2 1 2. 2 1 2 2 3 1 2 1 0 35 0 0 1 1 1 1 1 1 0 3 1 4 1 1 1 1 3. 4. 1 1 0 0 1 1 1 1 0 0 1 1 1 1 1 1 3 1 1 1 4 3 2 2 Đáp số : 1) 1 A 1 3 2 ; 2) 1 A 2 3 2 ; 1 1 1 5 3 2 2 2 1 1 5 1 1 1 1 1 2 3 6 4 4 4 4 1 1 5 1 1 1 1 0 2 3 6 3) 1 A 4 4 4 4 ; 4) 1 A . 1 1 1 1 1 1 0 0 2 2 4 4 4 4 1 1 1 1 1 1 0 0 2 2 4 4 4 4 Bài số 16. Cho ma trận : 0,4 0,2 0,1 A = 0,1 0,3 0,4 0,2 0,2 0,3 Tìm ma trận: ø ù1 I A . 2,05 0,8 0,75
Đáp số: øI Aù1 0,75 2 1, 25 . 0,8 0,8 2
Bài số 17. Cho các ma trận : 3 4 6 1 1 2 A = 0 1 1 ; B = 0 1 2 2 3 4
Tìm ma trận X , sao cho : XA B . 7 4 11 Đáp số : X . 2 2 3
Bài số 18. Giải phương trình: AX B, Với 36 3 4 5 2 1 A = 2 3 1 ; B = 4 3 3 5 1 6 5 1 98 24 Đáp số: X 124 14 . 20 3
Bài số 19. Tìm A sao cho AB BA, với 1 3 B 2 0 2n m 3n Đáp số: A . 2n m
Bài số 20. Tính hạng của các ma trận sau : 1 5 4 3 1 3 1 1 2 1 2 1 2 1 0 1 1 2 4 5 1. 2. 5 3 8 1 1 1 1 3 6 9 4 9 10 5 2 12 2 1 2 1 0 1 5 4 3 1 0 1 3 4 5 2 1 2 1 0 1 0 2 3 4 3. 4. 5 3 8 1 1 3 2 0 5 12 4 9 10 5 2 4 3 5 0 5
Đáp số : 1) 3; 2) 2; 3) 2; 4) 4.
Bài số 21. Tùy theo m, tìm hạng của các ma trận sau 3 1 1 4 m 5m m m 4 10 1 1. 2m m 10m 2. 1 7 17 3 m 2m 3m 2 2 4 3 1 2 3 4 1 2 1 1 1 2 3 4 5 m 1 1 1 1 3. 4. 3 4 5 6 1 m 0 1 1 4 5 6 m 1 2 2 1 1
Đáp số : 1) m 0, rank 0; m 0,rank 2; 2)m 0, rank 02; m 0,rank 3;
3) m 7, rank 2; m 7,rank 3; 4) m 1, rank 3; m 1,rank 4. 37 Bài số 22*. Tính n A , biết rằng cos x sin x 1. A 3 1 1 sin x cos x 4. 2 A 2 1 1 3 1 2. A 2 2 1 2 4 1 3. A 0 3 cos nx sin nx n n 13 1 3 1 Đáp số : 1) n A ; 2) n A ; sin nx cos nx n n 2 3 1 3 1 n n n n n n 4 4 3 cos sin 2sin 3) n A ; 4) n 6 6 6 . A n 0 3 n n n sin cos sin 6 6 6 4 a b 3 1
Bài số 23*. Tìm a, b sao cho . b a 1 3 Đáp số : 4 4 a 2 cos k ; b 2 sin k . 24 2 24 2
Bài số 24*. Cho hai ma trận 2 0 0 2 1 0 A 1 1 0; B 0 1 0 0 0 2 0 0 2 Chứng minh rằng n n
det(A B ) chia hết cho n 1 2 . 1 0 0 1 0 0 1 0 0 1 1 0
Hướng dẫn : A 0 1 0 1 0 0 ;B 0 1 0 0 0 0 . 0 0 1 0 0 1 0 0 1 0 0 1
Bài số 25*. Cho A, B, C là ba ma trận vuông cấp 2 với các phần tử của ma trận là số thực. Chứng minh rằng: 2 2
øABBAù CCøAB BAù 0.
Hướng dẫn: Đặt A, B, C rồi đi tính trực tiếp ta có điều phải chứng minh. 38 Chương 2
HỆ PHƯƠNG TRÌNH TUYẾN TÍNH
2.1. Khái niệm về hệ phương trình tuyến tính
2.1.1. Định nghĩa hệ phương trình tuyến tính tổng quát
Hệ phương trình tuyến tính là một hệ thống gồm m phương trình bậc nhất theo n
ẩn số có dạng tổng quát như sau : a x a x ü a x b 11 1 12 2 1n n 1 a x a x ü a x b 21 1 22 2 2n n 2 ý (2.1) ý ý ý ý ý ý ý ý ý a x a x ü a x b þ m1 1 m2 2 mn n m trong đó x ,x , , x b 1 2
n là các ẩn cần tìm, a ij
(gọi là các hệ số) và i (gọi là các hệ
số tự do), i 1,m; j 1,n. Đặt ü 1 a 1 1 a 2 1 a n 1 x 1 b a a ü a x b 21 22 2n A , 2 X , 2 B , ü ü ü ü ý ý a ü m1 a m2 a mn x n b m a 11 a12 ... a1n b1 a a ... a b A øA Bù 21 22 2n 2 , (2.2) ... ... ... ... ... a m1 am2 ... amn bm
trong đó ta gọi A là ma trận các hệ số, A là ma trận bổ sung (ma trận các hệ số mở rộng),
X là ma trận ẩn và B là ma trận các hệ số tự do. Khi đó, hệ phương trình tuyến tính (2.1)
được viết lại dưới dạng phương trình ma trận là AX B.
Ví dụ 1. Cho hệ phương trình tuyến tính x 2x 3x 4x 10 1 2 3 4 ý2 1 x x2 3 x 2x4 9 (2.3) 3x 2x 4x 3x 7 þ 2 3 4 Đặt 39 x 1 2 3 4 1 10 x A 2 1 1 2 2 , X , B 9 , x 3 2 4 3 3 7 x 4 1 2 3 4 10 A ø A ù B A 2 1 1 2 9 , 3 2 4 3 7
Hệ phương trình tuyến tính (2.3) được dưới dạng ma trận là AX B.
2.1.2. Định nghĩa nghiệm của một hệ phương trình tuyến tính
i) Ta gọi bộ n số có thứ tự øc ,c ,,c ù n
là một nghiệm của hệ phương trình 1 2 n
tuyến tính (2.1) nếu ta thay 1 x 1 c , 2 x 2
c , ..., xn cn vào (2.1) thì tất cả các đẳng thức
trong (2.1) đều được thỏa.
ii) Hai hệ phương trình tuyến tính có cùng số ẩn được gọi là tương đương khi tập
nghiệm của chúng bằng nhau.
2.1.3. Hệ phương trình tuyến tính dạng tam giác
Cho hệ phương trình gồm n phương trình và n ẩn số có dạng: ü 1 a 1 1 x 1 a 2x2 1 a nxn 1 b a x ü a x b 22 2 2n n 2 ý (2.4) ý ý ý ý ý ý ý ý ý a nnxn þ bn
Trong đó a11,a 22,...,ann 0 .
Hệ phương trình (2.4) được gọi là hệ phương trình tuyến tính dạng tam giác.
Chú ý: Ma trận hệ số A là ma trận tam giác trên.
Ví dụ 2. Cho hệ phương trình tuyến tính dạng tam giác 1 x 4x2 3x3 5 ý 2x x 1 2 3 3x 9 þ 3
Chúng ta giải ngược từ dưới lên trên, tức là từ phương trình cuối cùng lên tới phương trình đầu tiên.
Hệ trên có nghiêm duy nhất là 1 x 22, x2 2 , x3 3.
Nhận xét: Hệ phương trình tuyến tính dạng tam giác luôn có nghiệm duy nhất. 40
2.1.4. Hệ phương trình tuyến tính dạng hình thang
Cho hệ phương trình gồm m phương trình và n ẩn số (với m n ) có dạng: ü ü 1 a 1 1 x 1 a 2x2 1 a mxm 1 a nxn 1 b a x ü a x ü a x b 22 2 2m m 2n n 2 ý (2.5) ý ý ý ý ý ý ý ý ý ý ý a x ü a x b þ mm m mn n m
Trong đó a11,a22,...,amm 0 .
Hệ phương trình (2.5) được gọi là hệ phương trình tuyến tính dạng hình thang.
Chú ý: Ma trận hệ số A là ma trận hình thang (bậc thang).
Để giải hệ phương trình tuyến tính dạng hình thang đầu tiên chúng ta giữ lại vế trái các ẩn x ,x ,...,x 1 2
m (gọi là các ẩn chính hay là các ẩn cơ sở) và chuyển sáng vế phải các ẩn xm 1,...,x
n (gọi là các ẩn tự do). Khi đó hệ phương trình (2.5) tương đương: a x a x ü a x b a x ü a x 11 1 12 2 1m m 1 1,m 1 m 1n n a x ü a x b a x ü a x 22 2 2m m 2 2,m 1 m 2n n ý (2.6) ý ý ý ý ý ý ý ý ý ý ý a x b a x ü a x þ mm m m m,m 1 m mn n
Các ẩn tự do nhận một giá trị tùy ý x c ,...,x c c ,...,c m1 m1 n n ø m 1 n ù
Khi đó hệ phương trình (2.6) có dạng hình thang, giải ra ta được:
x1 c1, x2 c2,...,xm cm
Tuy nhiên, cứ với mỗi bộ giá trị của các ẩn tự do chúng ta thu được một bộ giá trị
ẩn chính nên hệ có vô số nghiệm.
Ví dụ 3. Cho hệ phương trình tuyến tính dạng tam giác x 4x x 2x 10 1 2 3 4 ý x 3x x 8 þ 2 3 4
Hệ phương trình trên tương đượng với hệ phương trình sau x 4x x 2x 10 1 2 3 4 ý x 3 x x þ 8 2 3 4 Các ẩn chính ø 1
x ,x2 ù và các ẩn tự do là ø 3 x ,x4 ù.
Cho x ñ, x ò ñ,ò 3 4 ø
ù ta thu được hệ phương trình dạng tam giác: 41 x 4x ñ 2ò 10 1 2 ý x 3ñ ò þ 8 2 Suy ra x 13ñ 6ò 22 1 ý x 3ñ ò 8 þ 2
Vậy hê ban đầu có vô số nghiệm W ø 13ñ 6ò 22, 3 ñ ò 8, , ñ òù , ñ ò .
2.1.5. Giải hệ phương trình tuyến tính bằng phương pháp khử ẩn Gauss
Để giải một hệ phương trình tuyến tính chúng ta sẽ sử dụng các phép biến đổi tương
đương của hệ phương trình để đưa hệ ban đầu về hệ phương trình có dạng tam giác hoặc
hình thang (hay ma trận hệ số A có dạng tam giác hoặc hình thang) cụ thể đối với hệ
phương trình tuyến tính như sau: a x a x ü a x b 11 1 12 2 1n n 1 a x a x ü a x b 21 1 22 2 2n n 2 ý (2.7) ý ý ý ý ý ý ý ý ý a ü m1 1 x am2x2 amnxn þ bm
Không mất tính tổng quát, chúng ta luôn có giả thiết 1
a 1 0 (vì nếu chưa có ta có
thể đổi phương trình khác để có điều kiện đó).
Để ma trận hệ số A có dạng tam giác hoặc hình thang, đầu tiên, chúng ta làm cho
các phần tử ở cột thứ nhất, hàng thứ hai trở đi biến thành 0 bằng cách nhân hàng 1 với a i1
rồi cộng với hàng i (i 2,3,...) , sau øm ù
1 phép biến đổi như vậy ta thu được a 11
hệ phương trình tương đương. a x a x ü a x b 11 1 12 2 1n n 1 / / / a x ü a x b 22 2 2n n 2 ý (2.8) ý ý ý ý ý ý ý ý ý / / / a ü þ m2x2 amnxn bm a a Trong đó: / i1 / i1 a a a ; b b
b ; i 2,3,...,m, j 1,2,...,n. ij ij 1j i i 1 1 a 1 1 a 1
Ở đây, ta còn nói x2= từ phương trình thứ ba trở đi đối với hệ (2.8). Sau đó, lại 42
thứ tư trở đi (nếu có)…Quá trình hạn bước biến đổi quá trình sẽ dừng lại ở một trong các trường hợp sau đây:
Trường hợp 1. Hệ phương trình nhận được có dạng tam giác (hệ có nghiệm duy
nhất) hay ma trận hệ số A có dạng tam giác.
Trường hợp 2. Hệ phương trình nhận được có hình thang (hệ có vô số nghiệm) hay
ma trận hệ số A có dạng hình thang (bậc thang).
Trường hợp 3. Trong hệ xuất hệ phương trình có dạng 0x ü 1 0x2 0xn b, với b 0. Khi đó hệ vô nghiệm.
Chú ý: Trong qua trình biến đổi trong hệ có xuất hiện phương trình có dạng 0x ü 1 0x 2 0xn 0
Khi đó chúng ta có thể loại bỏ phương trình này ra khỏi hệ phương trình.
Về mặt thực hành, để giải hệ phương trình tuyến tính bằng phương pháp khử ẩn
liên tiếp Gauss ta làm như sau: Xác định ma trận hệ số mở rộng A øA Bù ; Tiếp theo, sử
dụng các phép biến đổi sơ cấp trên hàng để biến đổi ma trận hệ số A về ma trận tam giác
trên hoăc ma trận hình thang.
Ví dụ 4. Giải hệ phương trình tuyến tính sau bằng phương pháp Gauss x 3x 2x x 2 1 2 3 4 4 ý x1 x 2 3x 3 2x 4 1 2 x 7x x 1 þ 1 2 3 Giải
Thực hiện các phép biến đổi sơ cấp trên các hàng của ma trận các hệ số mở rộng của hệ 1 3 2 1 2 ø2ù: ø2ù 4ø1ù 1 3 2 1 2 ø3ù:ø3ù ø 2 ù 1 A 4 1 3
2 1 0 13 5 2 7 2 7 1 0 1 0 13 5 2 5 1 3 2 1 2 ø3ù: ø3ù ø2ù 0 13 5 2 7 0 0 0 0 2
ta nhận được hệ phương trình tương đương, trong đó hàng ø0 0 0 0 2ù cho ta phương
trình : 0x1 0x 2 0x3 0x4 2.
Phương trình này vô nghiệm, nên hệ đã cho vô nghiệm 43
Ví dụ 5. Giải hệ phương trình tuyến tính x 1 x 2 2x 4 5 2 x 1 4x 2 x 3 5x 4 1 ý x 3x 5x 3 1 2 4 3
x 7x 3x 9x 1 4 1 2 3 4 2þx 1 8x 2 4x 3 2x 4 22 Giải
Thực hiện các phép biến đổi sơ cấp trên các hàng của ma trận các hệ số mở rộng của hệ 1 1 0 2 5 1 1 0 2 5 2 4 1 5 1 ø2ù: ø 2ù 2 ø1ù 0 2 1 1 1 1 ø3ù: ø 3ù ø ù 1 A 1 3 0 5 3
0 2 0 3 8 ø 4ù: ø 4ù 3 ø1ù ø5ù: ø 5ù ø 2 ù 1 3 7 3 9 1 4 0 4 3 3 2 9 2 8 4 2 22 0 6 4 2 33 1 1 0 2 5 1 1 0 2 5 ø3ù:ø3ùø2ù 0 2 1 1 11 ø4ù:ø4ùø3ù 0 2 1 1 11 ø4ù: ø4ù 2ø2ù ø5ù: ø5ù ø3ù 0 0 1 2 3 0 0 1 2 3 ø5ù: ø 5ù ø 3 2ù 0 0 1 1 7 0 0 0 3 4 0 0 1 5 1 0 0 0 3 4 1 1 0 2 5 1 1 0 2 5 0 2 1 1 11 0 2 1 1 11 ø5ù: ø5ù ø4ù / 0 0 1 2 3 ; A 0 0 1 2 3 0 0 0 3 4 0 0 0 3 4 0 0 0 0 0
Hệ ban đầu tương đương với hệ phương trình x 1 x 2 2x 4 5 2x x x 11 2 3 4 ý x 2x 3 3 4 3x 4 þ 4 29 17 4
Giải từng phương trình của hệ này từ dưới lên, ta được nghiệm , 2, , . 3 3 3
Ví dụ 6. Giải hệ phương trình tuyến tính sau : 44 3x x x 2x 1 1 2 3 4 x x 2x 4x 5 1 2 3 4 ý x 1 x 2 3x 3 6x 4 9 12x þ 1 2x2 x3 2x4 1 0 Giải
Thực hiện các phép biến đổi sơ cấp trên các hàng của ma trận các hệ số mở rộng của hệ 3 1 1 2 1 1 1 2 4 5 1 1 2 4 5 3 1 1 2 1 ø2ù ø1ù A 1 1 3 6 9 1 1 3 6 9 1 2 2 1 2 10 1 2 2 1 2 10 1 1 2 4 5 1 1 2 4 5 ø ù 2 : ø ù 2 ø 3 ù 1 ø ù 3 : ø 3ù ø 2ù 0 2 5 1 0 1 4 0 2 5 1 0 1 4 ø ù 3 : ø ù 3 ø ù 1 ø4ù: ø4ù ø52ù ø ù 4 : ø 4ù 1 ø 2 ù 1 0 2 5 1 0 1 4 0 0 0 0 0 0 10 25 50 70 0 0 0 0 0
Bỏ hai hàng cuối, ta được ma trận bổ sung của hệ phương trình tương đương 1 1 2 4 5 0 2 5 1 0 1 4
Chọn x , x làm các ẩn cơ sở, x , x trở thành ẩn tự do. Cho ; 1 2 3 4 x 3 m, x 4 n m,n . Ta được 1 1 x 2 m n x x 5 2m 4n 1 2 2 ý 2x 14 5m 10n ý 5 þ 2 x 7 m 5n 2 þ 2
Hệ phương trình tuyến tính có vô số nghiệm với họ nghiệm ü 1 5 W
m n 2 , m 5n 7 , m , n / m,n ý ý . þ 2 2 þ
2.2. Hệ phương trình Cramer
2.2.1. Định nghĩa hệ phương trình Cramer
Hệ phương trình Cramer là hệ phương trình tuyến tính có số phương trình bằng số
ẩn số và định thức của ma trận các hệ số khác 0.
Ví dụ 7. Cho hệ phương trình 45 4 x1 3x2 2x3 7 x x ý 5 1 2 3 x þ 1 x 3 4 4 3 2
Hệ phương trình có 3 phương trình, 3 ẩn và det øAù 1 1 0 7 0 nên nó là 3 0 1 hệ phương trình Cramer.
2.2.2. Các phương pháp giải hệ phương trình Cramer
Ngoài phương pháp chung là phương pháp khử ẩn liên tiếp Gauss đã trình bày ở
phần trên, đối với hệ Cramer có thêm hai phương pháp như sau:
i) Phương pháp 1. Dùng ma trận nghịch đảo 1
A để giải phương trình ma trận : 1 AX B X A B.
ii) Phương pháp 2. Dùng định thức (công thức Cramer). Xét A , i 1, n là ma trận i
nhận được từ A bằng cách thay cột thứ i bằng cột các hệ số tự do. Khi đó, hệ Cramer có det A nghiệm duy nhất i xi , i 1,n . det A
Ví dụ 8. Cho hệ phương trình tuyến tính sau x 3x 7x 1 1 2 3 ý 2x x 2x 0 1 2 3 7 x x 4x 1 þ 1 2 3
1) Giải hệ bằng phương pháp ma trận nghịch đảo.
2) Giải hệ phương trình bằng phương pháp Cramer (định thức) Giải
1) Dùng ma trận nghịch đảo 1
A : Ma trận các hệ số 1 3 7 A 2 1 2 7 1 4
có định thức det(A) 0 nên khả nghịch, 2 5 1 1 A 22 53 12 9 22 5 46
và nghiệm duy nhất của hệ được xác định bởi x1 2 5 1 1 1 x1 1 1 X A B x 2 22 53 12 0 10 x ý 2 10 x 3 9 22 5 1 4 x þ 3 4 2) Dùng định thức. 1 3 7 1 3 7 detø Aù 2 1 2 1 , detø A 0 1 2 1 1ù , 7 1 4 1 1 4 1 1 7 1 3 1
detø A 2 0 2 10 , det øA 2 1 0 4 . 3 ù 2ù 7 1 4 7 1 1
Nghiệm của hệ phương trình là de øt A ù detø A detø A3ù 2ù 1 x 1 x 10 x 4 1 ; ; . det øAù 2 detøAù 3 det øAù
2.3. Hệ phương trình tuyến tính tổng quát
2.3.1. Nhận xét về sự tồn tại nghiệm của hệ phương trình tuyến tính tổng quát
Phương pháp Gauss là phương pháp dùng các phép biến đổi sơ cấp trên hàng để /
chuyển ma trận các hệ số mở rộng A øA Bù thành ma trận ø / / A A B ù sao cho / A là
ma trận bậc thang theo hàng. Khả năng 1. Ma trận /
A có một hàng 0 với hệ số tự do tương ứng khác 0, nghĩa là trong ma trận /
A có hàng dạng : ø0 0 ü 0 b ù, b 0 . Hàng này tương ứng với phương trình : 0x ü . 1 0x2 0xn b
Phương trình này vô nghiệm nên hệ vô nghiệm.
Khả năng 2. Mọi hàng 0 của /
A đều có hệ số tự do tương ứng bằng 0 nên ta có thể
bỏ đi mà không làm mất nghiệm của hệ. Khi đó hệ có nghiệm duy nhất hay vô số nghiệm.
2.3.2. Định lý Kronecker – Capelli
Cho hệ phương trình tuyến tính gồm m phương trình theo n ẩn số, AX B . Với A øA Bù, ta có 47 i) Nếu rankø ù
A rank øAù thì hệ vô nghiệm.
ii) Nếu rank øAù rankøAù n thì hệ có duy nhất nghiệm.
iii) Nếu rank øAù rankøAù n thì hệ có vô số nghiệm.
Ví dụ 9. Giải và biện hệ phương trình tuyến tính m x x mx 1 1 2 3 ý x mx mx 1 1 2 3 (*) 1 x x2 x3 þ 1 Giải
Thực hiện các phép biến đổi sơ cấp trên các hàng của ma trận các hệ số mở rộng của hệ m 1 m 1 1 1 1 1 ø ù1 ø ù 3 A 1 m m 1 1 m m 1 1 1 1 1 m 1 m 1 1 1 1 1 ø2ù: ø 2 ù ø 1ù
0 m 1 m 1 0 (3): (3) m(1) 0 1 m 0 1 m 1 1 1 1 0 m 1 m 1 0 (3): (3) (2) 0 0 m 11 m
Hệ phương trình (*) tương đương x x x 1 1 2 3 ý (m 1)x (m 1)x 0 2 3 (**) (m 1)x3 1 þ m
Ta giải và biện luận hệ phương trình (**) từ dưới lên trên
Trường hợp 1. Nếu m 1 0 m 1 thì hệ phương trình (**) tương đương x x x 1 x 1 1 2 3 1 ý x x 0 ýx 1 2 3 2 x 1 x 1 þ 3 þ 3
Trường hợp 2. Nếu m 1 0 m 1 thì hệ phương trình (**) tương đương
x x x 1 x 1 x x 1 2 3 1 2 3 48
Chọn x1 làm ẩn chính (ẩn cơ sở), x 2,x3 làm ẩn tự do.
Gán x2 a, x3 b với a,b . Suy ra x1 1a b .
Vậy hệ có vô số nghiệm vả tập nghiệm là W ø
1a b,a,bù a,b .
Ví dụ 10. Định m để hệ phương trình tuyến tính sau có nghiệm duy nhất x 2x mx 1 1 2 3 m ý x1 x 2 x 3 m m x x mx 1 þ 1 2 3 Giải
Hệ phương trình trên có ma trận hệ số 1 2 m 1 2 m (2): ( 2) m (1) 2
A m 1 1 0 1 2m 1 m (3): ( 3) m (1) 2 m 1 m 0 1 2m m m Ta có 2 1 2m 1 m detø Aù 1 1 ( 1 ) 1 (m 1)(1 2m) 2 1 2m m m
Hệ phương trình trên có nghiệm khi và chỉ khi ø ù 1
det A 0 m 1 m . 2
Ví dụ 10. Cho hệ phương trình tuyến tính sau : a x b x c 1 1 1 2 1 a ý 2 1 x 2 b x2 2 c a x b x c þ 3 1 3 2 3
Chứng minh rằng nếu hệ có nghiệm thì định thức của ma trận hệ số mở rộng luôn bằng 0. Giải
Ta có ma trận hệ số và ma trận hệ số mở rộng là 1 a 1 b 1 a 1 b 1 c A a b ; A a b c 2 3 2 2 2 a b a b c 3 3 3 3 3
Hệ phương trình có nghiệm khi và chỉ khi rankøAù rankøAù . 49
Ta lại có rankøAù Min3, 2 2 suy ra rankø ù
A 2 mà ma trận A là ma trận vuông cấp 3 nên det øAù 0.
2.4. Hệ phương trình tuyến tính thuần nhất
2.4.1. Định nghĩa hệ phương trình tuyến tính thuần nhất
Hệ phương trình tuyến tính được gọi là thuần nhất khi tất cả các hệ số tự do bằng 0, nghĩa là hệ có dạng a ü 11x 1 a 12x 2 a 1nx n 0 a x a x ü a x 0 21 1 22 2 2n n ý (2.9) ý ý ý ý ý ý ý ý ý a x a x ü a x 0 þ m1 1 m2 2 mn n
2.4.2. Nghiệm của hệ phương trình tuyến tính thuần nhất
Hệ phương trình tuyến tính thuần nhất (2.9) có ít nhất một nghiệm gồm toàn các số
0. Do đó, đối với hệ phương trình thuần nhất, ta chỉ có hai khả năng :
Hệ có duy nhất một nghiệm (nghiệm gồm toàn số 0) mà ta gọi là nghiệm tầm thường.
Hệ có ít nhất một nghiệm không tầm thường. Khi đó hệ có vô số nghiệm.
Để giải hệ phương trình tuyến tính thuần nhất bằng phương pháp Gauss, ta chỉ cần
thực hiện các phép biến đổi trên ma trận các hệ số.
Ví dụ 11. Giải hệ phương trình tuyến tính thuần nhất x1 2x 2 4x3 3x 4 0 3 x 5x 6x 4x 0 1 2 3 4 4 ý x 5x 2x 3x 0 1 2 3 4 3
x 1 8x 2 24x 3 19x 4 þ 0
Giải. Biến đổi sơ cấp trên dòng ma trận các hệ số 1 2 4 3 1 2 4 3 ø ù2: ø ù 2 ø 3 ù 1 3 5 6 4 0 1 6 5 ø ù3: ø ù3 ø4 ù1 A ø ù 4 : ø ù 4 ø 3 ù 1 4 5 2 3 0 3 1 8 15 3 8 24 1 9 0 2 12 1 0 1 2 4 3 ø3ù:ø3ù ø 3 2ù 0 1 6 5 1 2 4 3 ø4ù: ø4ù 2ø2ù ø2 ù: ø2 ù 0 0 0 0 0 1 6 5 0 0 0 0 50
Chọn x1, x2 làm các ẩn cơ sở, x3, x4 trở thành các ẩn tự do và ta được hệ phương trình tương đương x 2x 4x 3x 1 2 3 4 ý x 6x 5x þ 2 3 4
Cho x 3 a, x 4 b tùy ý, ta được x 8a 7b 1 ý x þ 6a 5b 2
Vậy hệ phương trình tuyến tính thuần nhất đã cho có vô số nghiệm và họ nghiệm: W ø
8a 7b , 6a 5b ,a , bù/ a,b .
2.5. Một số bài toán ứng dụng trong kinh tế
2.5.1. Mô hình cân bằng thị trường
Giả sử chúng ta nghiên cứu thị trường bao gồm n hàng hóa có liên quan: hàng
hóa 1, 2,..., n. Khái niệm này được hiểu là khi giá của một mặt hàng nào đó thay đổi
thì nó không những ảnh hưởng tới lượng cung øQ Q S và lượng cầu ø của bản thân i D ù i ù
mặt hàng đó, mà nó còn ảnh hưởng tới giá và lượng cung, lượng cầu của các mặt hàng
còn lại. Người ta thường biểu diễn sự phụ thuộc của lượng cung và lượng cầu vào giá
của các hàng hóa bởi hàm cung và hàm cầu như sau: QS i S ø 1 P , 2 P ,..., n P ù, i 1,2,...,n; i
Q D P , P ,...,P , i 1,2,...,n. D i ø 1 2 n ù i Trong đó 1 P , 2 P ,..., n
P là ký hiệu thứ tự là giá của hàng hóa 1, 2,..., n.
Mô hình cân bằng thị trường n hàng hóa có liên quan (cân bằng cung cầu) được xác định bởi: (2.10) S Q Q , i 1, 2,..., n i Di
Nếu giả thiết các Q và Q øi 1, 2,..., n ù có dạng tuyến tính, thì mô hình trên i S i D
chính là một hệ gồm có n phương trình và n ẩn P , P ,..., P . 1 2 n
Giải hệ phương trình chúng ta tìm được bộ giá cân bằng thị trường: P ø 1 P , 2 P ,..., n P ù
Thay vào Q (hoặc Q ) chúng ta thu được bộ lượng cân bằng thị trường: i S i D 51 Q øQ , Q ,..., Q 1 2 n ù
Ví dụ 12. Cho biết hàm cung, hàm cầu của thị trường hai loại hàng hóa như sau: Q 2 3P ; Q 8 2P P 1 S 1 1 D 1 2 Q 1 2P ; Q 11 P P 2 S 2 2 D 1 2 Với
Q , Q là lượng cung hàng hóa 1 và 2. 1 S S2 Q ,Q
là lượng cầu hàng hóa 1 và 2. 1 D D 2 1 P , 2
P là giá của hàng hóa 1 và 2.
Khi thị trường cân bằng hãy thiết lập hệ phương trình tuyến tính với ẩn số là 1 P và P2 .
Sử dụng quy tắc Cramer (phương pháp định thức) xác định giá và lượng cân bằng của hai mặt hàng. Giải
Áp dụng công thức (2.10), ta có hệ phương trình: Q Q 2 3P 8 2P P 5 P P 10 1 S 1 D 1 1 2 1 2 ý ý ý Q þ S Q 1 2P 11 P P P 3P þ þ 12 2 D2 2 1 2 1 2
Giải hệ bằng quy tắc Cramer: 5 1 10 1 5 10 D 14 ; D 42 ; D 70 1 3 1 P 12 3 2 P 1 12
Vậy bộ giá cân bằng là: D 42 D 70 1 P 2 P 1 P 3; 2 P 5 D 14 D 14 Lượng cân bằng là:
Q1 Q Q 2 3P 2 3.3 7 1 D 1 S 1 Q 2 Q D Q 1 2P 1 2.5 9 2 2 S 2
Ví dụ 13. Giả sử thị trường gồm hai loại hàng hóa: hàng hóa 1 và hàng hóa 2 có hàm cung và cầu như sau: Q 2 2P ; Q 1 P P 1 S 1 1 D 1 2 Q ; S 5 3P Q 2 5P P 2 1 D 2 1 2 52 trong đó:
Q (i 1, 2) : là lượng cung hàng hóa i. i S Q
(i 1, 2) : là lượng cầu hàng hóa i. i D i
P (i 1, 2) : là giá hàng hóa i.
Bằng phương pháp ma trận nghịch đảo, hãy xác định bộ giá và lượng cân bằng
thị trường của hai hàng hóa nói trên. Giải
Áp dụng công thức (2.10), ta có hệ phương trình: Q Q 2 2P 1 P P 1 S 1 D 1 1 2 ý ý Q Q 5 3P 2 5P P þ S þ 2 D 2 2 1 2 hay 3 P P 3 1 2 ý þ 5 P 4P2 7
Giải hệ phương trình trên bằng quy tắc Cramer Đặt các ma trận sau: 3 1 3 P 1 A ; B ; X 5 4 7 P 2 Ta có 3 1 1 4 1 A 7 ; 1 A 5 4 7 5 3
Hệ phương trình trên tương đương: AX B Suy ra 19 1 4 1 3 1 19 1 7 X A .B 7 5 3 7 7 36 36 7
Vậy bộ giá cân bằng là: 19 36 1 P ; P2 7 7
tương ứng với bộ lượng cân bằng là: 53 19 24 Q Q Q 2 2 1 1 D 1 S 7 7 36 73 Q Q Q 5 3 2 2 D 2 S 7 7
Ví dụ 14. Xét thị trường gồm ba loại hàng hóa gồm chè, cafe, cacao có hàm cung và
hàm cầu tương ứng như sau: Q 1 0 P ; Q 20 P P (chè) 1 S 1 1 D 1 3
QS 2P ; Q 40 2P P (café) 2 2 D 2 2 3 Q (ca cao) S 5 3P ; Q 10 P P P 3 3 D 3 1 2 3
Hãy thiết lập mô hình cân bằng thị trường của ba loại hàng hóa trên. Sử dụng
quy tắc Cramer xác định giá và lượng cafe ở trạng thái cân bằng thị trường. Giải
Áp dụng công thức (2.10), ta có hệ phương trình: Q Q 2 P P 30 1 S 1 D 1 3 Q ý ý S Q 4P P 40 2 D2 2 3 Q Q þ 1 P P2 4P3 15 þ S3 D3
Xác định giá và lượng cafe ở trạng thái cân bằng thị trường bằng quy tắc Cramer: 2 0 1 2 30 1 D 0
4 1 30 ; D 0 40 1 280 2 P 1 1 4 1 15 4
Vậy giá cafe ở trạng thái cân bằng thị trường là: D 280 28 2 P P2 D 30 3 và lượng cân bằng là: 28 56 2 Q S Q 2. . 2 3 3
2.5.2. Mô hình cân bằng thu nhập quốc dân
Xét mô hình cân bằng thu nhập quốc dân ở dạng đơn giản, với các ký hiệu: Y
là tổng thu nhập quốc dân, G là chi tiêu chính phủ, I là đầu tư hộ gia đình và C là
tiêu dùng của các hộ gia đình.
Chúng ta giả thiết rằng chi tiêu Chính phủ và đầu tư là cố định G G0 và 54
I 0I , còn chi tiêu hộ gia đình có dạng tuyến tính:
C aY b ø0 a 1, b 0 ù.
Mô hình cân bằng thu nhập quốc dân có dạng hệ phương trình tuyến tính gồm
hai phương trình, 2 ẩn Y và C: Y G I C Y C G I O O O O ý ý C aY b a Y C b þ þ
Giải hệ bằng quy tắc Cramer, chúng ta xác định được mức thu nhập cân bằng và
mức tiêu dùng cân bằng của nền kinh tế. 1 1 D
1 a 0 (do 0 a 1) a 1 G I 1 O O DY G I b ; O O b 1 1 G I O O DC b a øG I O O ù a b Vậy D G I b Y O O Y D 1 a D b aø G I O O ù C C D 1 a
Tiếp theo, xét mô hình trong trường hợp thu nhập chịu thuế với thuế suất t%
(thường biểu diễn dưới dạng thập phân). Khi đó, thu nhập sau thuế là: d
Y Y tY ø1 tù Y
và hàm chi tiêu khi đó có dạng: C a d
Y b aø1 tù Y b
Ngoài ra, chúng ta cũng xem xét mô hình với ảnh hưởng của yếu tố xuất khẩu
X và nhập khẩu M. Khi đó, mô hình có dạng: Y G I C X M O O ý C a þ ø1 tù.Y b Chú ý
Hai yếu tố xuất khẩu øXù và nhập khẩu øM ù có thể cho dưới dạng hàm của thu
nhập Y hoặc là giá trị cố định cho trước. 55
Chúng ta vẫn biến đổi đưa mô hình về hệ gồm 2 phương trình, 2 ẩn Y và C.
Ví dụ 15. Cho mô hình sau: C 0,8 d Y 250 ; I I ; G G ; 0 0 d
Y ø1 tù Y ( t là thuế suất thu nhập).
a) Sử dụng quy tắc Cramer, hãy xác định mức thu nhập quốc dân và chi tiêu ở trạng thái cân bằng.
b) Tính mức thu nhập quốc dân và chi tiêu ở trạng thái cân bằng với I0 150,
G 500 (đơn vị: tỉ VNĐ) và t 0,15 (15%). 0 Giải
Đầu tiên ta xác định mô hình cân bằng: Y G I C O O ý C þ 0,8Y 250 Hay Y C G I O O ý 0 ,8 þ ø1 t ùY C 250 Ta có 1 1 D ; 0 ,8ø1 tù 1 0,8ø1 tù 1 G I 1 O O D G I 250 Y ; O O 250 1 1 G I O O D
250 0,8 1 t G I . C 0,8ø1 tù ø ùø O O ù 250
a) Vậy thu nhập quốc dân và chi tiêu cân bằng là: D G I 250 Y O O Y D 1 0,8 ø1 t ù D 0,8 1 t G I 250 C ø ùø O O ù C D 1 0,8ø1 tù
Nhận xét: Y và C phụ thuộc vào I , G và 0 0 t.
b) Với 0I 150, G 0 500 , t 0,15 chúng ta có: 56 150 500 250 900 Y (tỉ VNĐ) ø ù 2812,5 1 0,8 1 0,15 0,32
0,8ø1 0,15ùø150 500ù 250 692 C 2162,5 (tỉ VNĐ). 1 0,8ø1 0,15ù 0,32
Ví dụ 16. Xét mô hình cân bằng:
Y C I0 G0 X0 M
Với C aø1 tù Y, ø0 a ù 1 , t là thuế suất
M bø1 tùY, ø0 b ù 1
a) Hãy xác định mức thu nhập và chi tiêu quốc dân ở trạng thái cân bằng Y , C bằng quy tắc Cramer.
b) Tính Y và C khi t 0,1; a 0,85; b 0,1; và . 0 I 250; G0 400 0 X 100 Đơn vị tính 0 I , G0, 0 X là tỉ VNĐ; t là %. Giải
a) Ta thiết lập hệ 2 phương trình 2 ẩn Y và C : Ta có Y
C I G X b 1 t Y O O O ø ù ý C a ø1 t ùY þ 1 b
ø1 t ùY C I G X O O O ý a þ ø1 t ùY C 0 Các định thức 1 b ø1 t ù 1 D
1 ø1 t ùøb a ù; a ø1 tù 1 I G X 1 O O O DY I G X ; O O O 0 1
1 bø1 tù I G X O O O DC
a ø1 tù øG I X . O O O ù a ø1 tù 0
Vậy thu nhập và chi tiêu quốc dân cân bằng là: D G I X Y O O O Y D 1 ø1 t ùøb a ù 57 D aø1 ù t G I X C ø O O Où C D 1ø1 ùtø b aù
b) Khi t 0,1; a 0,85; b 0,1; I và . 0 250; G 0 400 X0 100 Ta có: 250 400 100 750 Y (tỉ VNĐ) ø ùø ù 2307,6923 1 1 0,1 0,1 0,85 0,325 0,8 ø 5 1 0, ù 1 ø 250 400 10 ù 0 573,75 C 1765,3846 (tỉ VNĐ). 1 ø1 0, ù 1 ø0,1 0,85ù 0,325
2.5.3. Mô hình input – output của Leontief
Trong phần này, chúng tôi xin giới thiệu một mô hình kinh tế, công cụ chủ yếu
để giải mô hình này là các phép toán đối với ma trận và định thức.
2.5.3.1. Giới thiệu mô hình
Trong một nền kinh tế hiện đại, việc sản xuất một loại sản phẩm hàng hóa nào đó
(output) đòi hỏi phải sử dụng các loại hàng hóa khác nhau để làm nguyên liệu đầu vào
(input) của quá trình sản xuất và việc xác định tổng cầu đối với sản phẩm của mỗi ngành
sản xuất trong tổng thể nền kinh tế là quan trọng, nó bao gồm:
– Cầu trung gian từ phía các nhà sản xuất sử dụng loại sản phẩm đó cho quá trình sản xuất.
– Cầu cuối cùng từ phía những người sử dụng sản phẩm để tiêu dùng hoặc xuất
khẩu, bao gồm các hộ gia đình, Nhà nước, các tổ chức xuất khẩu,...
Xét một nền kinh tế có n ngành sản xuất, ngành 1,2,...,n. Để thuận tiện cho việc
tính chi phí cho các yếu tố sản xuất, ta phải biểu diễn lượng cầu của tất cả các loại
hàng hóa ở dạng giá trị, tức là đo bằng tiền. Tổng cầu về sản phẩm hàng hóa của
ngành i (i 1, 2,..., n) được ký hiệu, x và xác định bởi: i x ü i xi1 xi2
xin bi (i 1,2,...,n) (2.11) Trong đó: i
x k : là giá trị sản phẩm của ngành i mà ngành k cần sử dụng cho quá trình sản
xuất của mình (giá trị cầu trung gian).
bi : là giá trị sản phẩm của ngành i dành cho nhu cầu tiêu dùng và xuất khẩu
(giá trị cầu cuối cùng). 58
Tuy nhiên, trong thực tế, ta thường không có thông tin về giá trị cầu trung gian i
x k , nhưng người ta lại chủ động trong việc xác định tỉ phần chi phí đầu vào của sản xuất. Gọi
aik : là tỉ phần chi phí đầu vào của ngành k đối với sản phẩm của ngành i, nó
được tính bởi công thức: x ik aik øi 1, 2,..., nù xk Trong đó
+) 0 aik 1, và ở đây, giả thiết aik là cố định đối với mỗi ngành sản xuất i,
øk 1,2,...,nù. Người ta còn gọi aik là hệ số chi phí đầu vào và ma trận. +) A øa
được gọi là ma trận hệ số chi phí đầu vào (ma trận hệ số kỹ thuật). ik ùn
+) Giả sử aik 0,3 có nghĩa là để sản xuất ra 1 đồng giá trị sản phẩm của mình,
ngành k đã phải chi 0,3 đồng để mua sản phẩm của ngành i phục vụ cho quá trình sản xuất. Đặt b1 b 2 B ý bn
Ta gọi X là ma trận tổng cầu và B là ma trận cầu cuối cùng. Khi đó, từ đẳng
thức (2.11), thay x a x chúng ta có: ik ik k x ü
i a i1 x1 a i2 x 2
a in x n bi (i 1, 2,..., n)
Hay biểu diễn dưới dạng ma trận: 1 x 1 a 1 1 a 2 ... a1n 1 x 1 b x a a ... a x b 2 21 22 2n 2 2 ý ... ... ... ... ý ý n x an1 an2 ... n a n n x n b Tức là X AX B (2.12)
2.5.3.2. Phương pháp giải
Từ (2.12), ta có øI AùX B 59
Trong đó, I là ma trận đơn vị cấp n, nếu øI Aù không suy biến thì: ø ù 1 X I A B (2.13)
Công thức (2.13) được gọi là công thức tính ma trận tổng cầu.
+) Ma trận øI Aù được gọi là ma trận Leontief. Như vậy, nếu chúng ta biết ma
trận hệ số kỹ thuật A và ma trận cầu cuối cùng thì sẽ xác định được giá trị tổng cầu của các ngành sản xuất.
+) Ma trận C øI Aù 1 øc ù ij
, và gọi là ma trận hệ số chi phí toàn bộ. Hệ số c nn ij
cho biết: để sản xuất một đơn vị giá trị nhu cầu cuối cùng của ngành j, thì ngành i cần
phải sản xuất một lượng sản phẩm có giá trị là c . ij 2.5.3.3. Các ví dụ
Ví dụ 17. Giả sử trong một nền kinh tế có hai ngành sản xuất: ngành 1 và ngành 2 có
ma trận hệ số kỹ thuật là: 0,2 0,3 A 0,4 0,1
Cho biết giá trị cầu cuối cùng đối với sản phẩm của ngành 1 và ngành 2 thứ tự
là 10, 20 tỉ đồng. Hãy xác định giá trị tổng cầu đối với mỗi ngành. Giải Gọi x1 X là ma trận tổng cầu. x 2 Với 1
x là giá trị tổng cầu của ngành 1, x 2 là giá trị tổng cầu của ngành 2. 10
Theo giả thiết ma trận cầu cuối B có dạng: B 20 Ta có: 0,8 0, 3 I A 0,4 0,9
Ma trận phụ hợp tương ứng : ø ù 0,9 0,3 I A * 0, 4 0,8
Ma trận nghịch đảo của I A 60 øI A ù 1 1 0,9 0,3 0,6 0, 4 0,8
Áp dụng công thức (2.13) để tính ma trận tổng cầu: ø ù1 X I A B
Vậy ma trận tổng cầu là: 25 1 0,9 0,3 10 1 15 X 100
0,6 0,4 0,820 0,6 20 3 Hay:
Giá trị tổng cầu của ngành 1 là 1 x 25 tỉ đồng. 100
Giá trị tổng cầu của ngành 2 là x2 tỉ đồng. 3
Ví dụ 18. Giả sử trong một nền kinh tế có 3 ngành sản xuất: ngành 1, ngành 2 và
ngành 3. Biết ma trận hệ số kĩ thuật là: 0,4 0,1 0,2 A 0,2 0,3 0,2 0,1 0,4 0,3
và giá trị cầu cuối cùng đối với sản phẩm của từng ngành thứ tự là 40, 40 và 110 (đơn
vị tính: ngàn tỉ đồng). Hãy xác định giá trị tổng cầu của từng ngành sản xuất. Giải Gọi 1 x X x là ma trận tổng cầu. 2 x 3 Với 1
x là giá trị tổng cầu của ngành 1, x 2 là giá trị tổng cầu của ngành 2, x3 là
giá trị tổng cầu của ngành 3. 40
Theo giả thiết ma trận cầu cuối B có dạng: B 40 1 10 Ta có:
1 0 0 0,4 0,1 0,2 0,6 0 ,1 0 ,2
I A 0 1 0 0,2 0,3 0,2 0,2 0,7 0,2
0 0 1 0,1 0,4 0,3 0,1 0,4 0,7 61
Định thức của ma trận I A 0,6 0,1 0,2 I A 0 ,2 0,7 0 ,2 0,2 0,1 0,4 0,7
Ma trận phụ hợp tương ứng: 0,41 0,15 0,16
øI A ù* 0,16 0,40 0,16 0,15 0,25 0,40
Ma trận nghịch đảo của I A 0,41 0,15 0,16 1 1 (I A) 0,16 0,40 0,16 0,2 0,15 0,25 0,40
Áp dụng công thức (2.13) để tính ma trận tổng cầu:
0,41 0,15 0,16 40 200 ø ù1 1 X I A B
0,16 0,40 0,16 40 200 0,2
0,15 0,25 0,40110 300 Vậy
Giá trị tổng cầu của ngành 1 là x1 200 ngàn tỉ đồng.
Giá trị tổng cầu của ngành 2 là x ngàn tỉ đồng. 2 200
Giá trị tổng cầu của ngành 2 là x3 300 ngày tỉ đồng.
Ví dụ 19. Trong mô hình input – output mở biết ma trận kỹ thuật số như sau 0,2 m 0,3 A 0,3 0,1 0,2 0,2 0,3 0,2
a) Nêu ý nghĩa phần tử nằm ở hàng 2 cột 1 của ma trận A.
b) Tìm yêu cầu của ngành kinh tế mở khi m 0,2 biết sản lượng của 3 ngành là 300, 250, 220.
c) Tìm m biết rằng khi sản lượng của 3 ngành là 400, 400, 300 thì ngành kinh tế
thứ nhất cung cấp cho ngành kinh tế mở là 130.
d) Với m tìm được ở câu c). Tìm ma trận hệ số chi phí toàn bộ và nêu ý nghĩa phần
tử nằm ở hàng 3 cột 2 của ma trận này. 62 Giải
a) Ý nghĩa a21 0,3 : Hệ số này cho biết để sản xuất ra một đơn vị giá trị ngành 1
thì ngành 2 phải cung cấp trực tiếp cho ngành này một lượng sản phẩm có giá trị là 0,3.
b) Gọi X là ma trận giá trị sản lượng của 3 ngành.
Từ giả thiết đề cho, ta có 300 X 250 220
Giá trị sản lượng cầu cuối: 124 B øI A ùX 91 41
c) Gọi Y là ma trận giá trị sản lượng của 3 ngành 400 1 X Y 400 X 2 300 X 3
Từ giả thiết đề bài, ta có: 1 X 11 a 1 X 12 a 2 X 13 a 3 X 1 b hay
400 0,2400 400m 0,3300 130 m 0,25. d) Với m 0,25. Ta có 0,2 0,25 0,3 A 0,3 0,1 0,2 0,2 0,3 0,2
Ma trận hệ số chi phí toàn bộ: 1,751 0,769 0,849 C øI A ù 1 0,743 1,538 0,663 0,716 0,769 1,711 Hệ số
cho biết: để sản xuất một đơn vị giá trị nhu cầu cuối cùng của 32 c 0,769
ngành 2 thì ngành 3 cần phải sản xuất một lượng sản phẩm có giá trị là 0,769. 63 2.6. Bài tập
Bài số 1. Giải các hệ phương trình tuyến tính sau bằng quy tắc (phương pháp) Cramer x x 2x 6 1 2 3 1. ý2x 3x 7x 16 1 2 3
þ5 1x 2x2 x3 16 7 1 x 2 2 x 3 3 x 15 2. 5x 3x 2x ý 15 1 2 3 1 0 þ 1 x 11x2 5 3 x 36 x1 x 2 2x 3 1 3. ý2x x 2x 4 1 2 3 4x x 4x 2 þ 1 2 3 3x 2x x 5 1 2 3 4. ý2 1 x 3x2 3 x 1 2x x 3x 11 þ 1 2 3 2 1 x x2 5 3 x x4 5 x x 3x 4x 1 5. 1 2 3 4 ý 3x 6x 2x x 8 1 2 3 4 2 1 x 2x2 2x3 3x4 þ 2 x1 x 2 x3 x 4 5 x 2x 3x 4x 3 6. 1 2 3 4 ý 4x x 2x 3x 7 1 2 3 4 3 1 x 2x2 3x3 4x4 þ 2 2x x 3x 2x 4 1 2 3 4 3x 3x 3x 2x 6 7. 1 2 3 4 ý 3 1 x x2 x3 2x4 6 3 1 x x2 3x3 x4 þ 6
Đáp số : 1) ø3, 1, 1ù; 2) ø2,1, ù
1 ; 3) ø1, 2, 2ù ; 4) ø2, 2, 3ù ; 1 4 11 37 63 5) 2, , 0, ; 6) 5, , , ; 7) ø2, 0, 0, 0ù. 5 5 4 2 4
Bài số 2. Giải các hệ phương trình tuyến tính sau bằng phương pháp Gauss 64 2 1 x x2 2x3 10 1. 3x 2x 2x ý 1 1 2 3 5 þ 1 x 4x2 3x3 4 x 2x x 7 1 2 3 2. ý2x x 4x 17 1 2 3 3x 2x 2x 14 þ 1 2 3 x 2x x 3 1 2 3 3. ý2 1 x 5x2 4x3 5 3x 4x 2x 12 þ 1 2 3 2x x 3x 1 1 2 3 4. ý5x 2x 6x 5 1 2 3 þ3x x 4x 7 1 2 3 2x x 2x 8 1 2 3 5. ý3x 2x 4x 15 1 2 3 þ5 1x 4x2 3 x 1 1 x 2x2 2x3 1 6. 3x x 2x ý 7 1 2 3 5 þ 1 x 3x2 4x3 2 2 1 x 5x2 3 3 x 2x4 4 7. ý3x 7x 2x 4x 9 1 2 3 4
5x 10x 5x 7x 22 þ 1 2 3 4 1 x 2 x 7 x x x 5 8. 2 3 4 ý x x x x 6 1 2 3 4 x2 x4 þ 10
Đáp số : 1) ø1, 2, 3ù ; 2) ø2, 1, 3ù; 3) ø2, 1, 1ù ; 4) ø3, 2, 1ù ; 10 2 3 5) ø1, 2, 4ù ; 6) , ,
; 7) ø11m 11, 5m 4, m, 1ù ; 8) ø 1 7, 24, 33, 14ù . 7 7 2
Bài số 3. Giải các hệ phương trình tuyến tính thuần nhất sau x1 2x 2 x3 0 1. 2x 5x x ý 0 1 2 3 3 þ 1 x 2x2 x3 0 65 x1 x 2 2x 3 3x 4 0 2. 2x 3x 3x x ý 0 1 2 3 4 5 þ 1 x 7x2 4x3 x4 0 2x 2x x 0 1 2 3 3. ý3x x x 0 1 2 3 x 3x 2x 0 þ 1 2 3 3 1 x 2 2 x 5 3 x 4 x 0 2x 3x x 5x 0 4 1 2 3 4 ý x 2x 4x 0 1 2 4 þ 1 x x2 4 3 x 9 4 x 0 x 3x 2x x 0 1 2 3 4 x x x x 0 5. 1 2 3 4 ý 4 1 x x2 x3 x4 0 4 þ 1 x 3x2 4x3 x4 0 6x 5x 7x 8x 0 1 2 3 4 6x 11x 2x 4x 0 6. 1 2 3 4 ý 6 1 x 2x2 3x3 4x4 0 x þ 1 x 2 x 3 0 x 2x x 0 1 2 3 x 3x x 0 7. 2 3 4 ý 4 1 x 3 x x4 0 x x 5x 0 þ 1 2 4 3 1 x 4x2 5x3 7x4 0 2x 3x 3x 2x 0 8. 1 2 3 4 ý 4x 11x 13x 16x 0 1 2 3 4 7x 2x x 3x 0 þ 1 2 3 4
Đáp số : 1) ø0, 0, 0ù; 2) ø5a 4b, 7a 7b, a, bù ; 3) ø0, 0, 0ù;
4) ø0, 0, 0, 0 ù ; 5) ø6a, 15a, 20a, 11aù ; 6) ø0, 0, 0, 0 ù;
7) ø0, 0, 0, 0ù ; 8) ø3a 13b, 19a 20b, 17a, 17b ù .
Bài số 4. Giải và biện luận các hệ phương trình tuyến tính sau 66 m 1 x 2 x 3 x m 1. 2x m 1 x m 1 x m ý 1 1 ø ù 2 ø ù 3 þ 1 x x2 mx3 1 x 3x 2x 4x 1 1 2 3 4 x 4x 4x 3x 2 2. 1 2 3 4 ý x 1
5x 2 6x3 mx 4 3
2x1 5x2 2x3 9x4 þ 1 ø m ù 1 x1 x2 x3 1 3. ý x m 1 x x 1 1 ø ù 2 3 x x m 1 x 1 þ 1 2 ø ù 3 x 2x 4x 3x 0 1 2 3 4 3 x 5x 6x 4x 0 4. 1 2 3 4 ý 4x 5x 2x 3x 0 1 2 3 4 x x 2x mx 0 þ 1 2 3 4
Đáp số : 1) TH1: m 1 m 2: hệ có nghiệm duy nhất; TH2 : m 1 : hệ vô số
nghiệm; TH3 : m 2 : hệ vô nghiệm. 2) hệ vô số nghiệm với mọi m; 3) TH1: m 0 m 3
: hệ có nghiệm duy nhất; TH2 : m 0 : hệ vô số nghiệm; TH3 : m 3
: hệ vô nghiệm. 4) hệ vô số nghiệm với mọi m.
Bài số 5. Giải hệ phương trình sau bằng phương pháp ma trận nghịch đảo x x 3x 2 1 2 3 1. ý x 2x 3x 6 1 2 3
2 1x 4x2 5 3x þ 6 x x x x 1 1 2 3 4 x x x x 1 2. 1 2 3 4 ý 1 x 2 x 1 x x 1 þ 3 4 1 x 2 x 3 x 4 x 1 x x x x 1 3. 1 2 3 4 ý x x x x 1 1 2 3 4 x x x x 1 þ 1 2 3 4 1 1 Đáp số : 1) ø 6
4, 8, 18ù ; 2) 0, 1, , ; 3) ø0, 0, 1, 0 ù. 2 2
Bài số 6. Cho hệ phương trình 67 x1 x 2 x 3 1 2x 3x mx ý 3 1 2 3 x þ 1 mx 2 3x 3 2
Định m để hệ phương trình có nghiệm duy nhất Đáp số : m 3 m 2 .
Bài số 7. Cho hệ phương trình kx x x 1 1 2 3 ý x kx x 1 1 2 3 x1 x2 kx3 þ 1
Định k để hệ phương trình vô nghiệm. Đáp số : k 2 .
Bài số 8. Cho hệ phương trình 5 1 x 3x2 2x3 4x4 3 4x 2x 3x 7x 1 1 2 3 4 ý 8x 6x x 5x 9 1 2 3 4 7 1 x 3x2 7 3 x 17x4 þ k
Định k để hệ phương trình có vô số nghiệm Đáp số : k 0 .
Bài số 9. Cho hệ phương trình 3 1 x 2x2 5x3 4x4 3 2 1 x 3x2 6x3 8x4 5 ý x 6x 9x 20x 1 1 1 2 3 4 4x x 4x mx 2 þ 1 2 3 4
Định m để hệ phương trình vô nghiệm. Đáp số : m 0 .
Bài số 10. Cho A, B là hai ma trận vuông cấp n thỏa mãn 2019 A
0 và A 2019B AB .
Chứng minh rằng hệ phương trình thuần nhất có ma trận hệ số B có vô số nghiệm.
Hướng dẫn: Từ A 0 suy ra B 0.
Bài số 11. Cho A, B là hai ma trận vuông cấp n thỏa mãn 2019 A
0 và B ø3A 2I ù 5A .
Chứng minh rằng hệ phương trình thuần nhất có ma trận hệ số B có vô số nghiệm.
Hướng dẫn: Từ A 0 suy ra B 0. 68
Bài số 12. Cho A, B là hai ma trận vuông cấp n thỏa mãn 2019 A
0 và BøA Iù A 3I.
Chứng minh rằng hệ phương trình thuần nhất có ma trận hệ số B có nghiệm duy nhất.
Hướng dẫn: Từ A 0 suy ra B 0.
Bài số 13. Xét thị trường ba loại hàng hóa với hàm cung và hàm cầu như sau: Q 6
0 6P 2P ; Q 120 5P P 1 S 1 3 1 D 1 2 Q 3 0 P 9P P ; Q 160 P 6P P 2 S 1 2 3 2 D 1 2 3 Q 2 0 2P 8P ; Q 140 P 4P 3 S 1 3 3 D 2 3
Hãy xác định bộ giá trị và lượng cân bằng thị trường của ba hàng hóa đó bằng
phương pháp ma trận nghịch đảo. 19910 16760 17155 Đáp số: P1 ; P 2 ; P 3 ; 933 933 933 29170 28595 78760 Q 1 ; Q2 ; Q3 . 933 311 933
Bài số 14. Xét thị trường có 4 loại hàng hóa. Biết hàm cung và cầu của 4 loại hàng hóa trên là
Q 20P 3P P P 30; Q
11P P 2P 5P 115 1 S 1 2 3 4 1 D 1 2 3 4
Q 2P 18P 2P P 50; Q
P 9P P 2P 250 2 S 1 2 3 4 2 D 1 2 3 4
Q P 2P 12P 40; Q
P P 7P 3P 150 3 S 1 2 3 D3 1 2 3 4
Q 2P P 18P 15; Q P 2P 10P 180 4 S 2 3 4 4 D 1 3 4
Tìm điểm cân bằng thị trường. Đáp số : 1 P 10, 2 P 15, 3 P 15, 4 P 10 .
Bài số 15. Cho ma trận các hệ số chi phí trực tiếp dạng giá trị của năm t là: 0, 2 0 0,3 Aø tù 0,1 0,1 0,1 0,2 0,2 0,1
a) Tìm ma trận hệ số chi phí toàn bộ năm t.
b) Biết x(t) ø800,1500,700ù, tìm sản lượng mỗi ngành năm t. Hướng dẫn: a) 1 C I A(t) ; b) 1 X(t) I A(t) x(t) .
Bài số 16. Cho ma trận các hệ số chi phí trực tiếp dạng giá trị của năm t như sau: 69 0,3 0,2 0,3 A 0,1 0,3 0,2 0,3 0,3 0,2
a) Tìm ma trận hệ số chi phí toàn bộ dạng giá trị năm t. Giải thích ý nghĩa kinh tế của
phần tử ở dòng 2 cột 3 của ma trận này.
b) Năm (t 1) nhu cầu sản phẩm cuối cùng của các ngành là ø180,150,100ù (tỷ
VNĐ). Tính giá trị sản lượng của các ngành, biết rằng các hệ số chi phí năm (t 1) và năm t như nhau. Hướng dẫn: a) 1 C I A(t) ; b) 1 X(t 1) I A(t 1) x(t 1).
Bài số 17. Xét mô hình cân bằng thu nhập quốc dân: Y 0
G 0I C; C 0,4Y 30.
Hãy xác định mức thu nhập và chi tiêu quốc dân ở trạng thái cân bằng bằng quy tắc
Cramer, biết I0 200, G0 500 (triệu USD). 3650 3100 Đáp số: Y ; C . 3 6
Bài số 18. Xét mô hình: Y G ; d Y ø1 t ù 0 I0 C; C 0,8 d Y Y
Hãy xác định mức thu nhập và chi tiêu quốc dân ở trạng thái cân bằng bằng quy tắc Cramer, biết I
0 200, G 0 500 (triệu USD) và thuế suất thu nhập t 0,1.
Đáp số: Y 17500 / 3; C 4200.
Bài số 19. Cho mô hình thu nhập quốc dân: Y C I G0 C ý b b Y
(a , a , b , b 0; a b 1) 0 1 0 1 0 1 1 1 I a0 a1Y þ a2R0 trong đó: G R 0 là chi tiêu chính phủ;
0 là lãi suất; I là đầu tư; C : tiêu dùng; Y : thu nhập
1) Sử dụng quy tắc Cramer để xác định Y, C ở trạng thái cân bằng. 2) Với b ; ; ; ; ; ; 0 200 1 b 0,7 a0 100 1
a 0,2 a2 10 R0 7 G 0 500. Tính Y, C . a a R G b
b a b a b a b R b G Đáp số: 1) 0 2 0 0 0 0 1 0 0 1 2 1 0 1 0 Y ; C ; 1 1 a 1 b 1 1 a 1 b 2) Y 7300; C 5310. 70 Chương 3 KHÔNG GIAN VECTƠ
3.1. Các khái niệm căn bản
3.1.1. Định nghĩa không gian vectơ
Cho V là tập các phần tử khác rỗng trên đó có trang bị hai phép toán : Một phép
toán trong mà ta gọi là phép cộng hai phần tử của V và một phép toán ngoài mà ta gọi là
phép nhân số thực với một phần tử của V, : V V V : V V . (3.1) øu,vù u v øk,u ù ku
Tập V cùng với hai phép toán trên được gọi là một không gian vectơ trên nếu
các phép toán trên V thỏa các tính chất sau, với mọi u,v,w V; h,k , i) u v v u v) h øku ù øhkùu
ii) øu vù w u øv wù
vi) h øu vù hu hv iii) !0 V : u 0 u ,
vii) øh kùu hu ku
iv) u V : u ø ù u 0 viii) 1.u u
Khi đó, không gian vectơ V còn được ký hiệu là øV,,ù hay vắn tắt, V. a b Ví dụ 1. Cho V M 2 ø ù
/ a,b,c,d với hai phép toán: cộng hai ma trận c d
và nhân số thực cho ma trận. Ta chứng minh được V là một không gian vectơ. Ví dụ 2. Cho 3
øx, y,z ù/ x, y,z
với hai phép toán: cộng hai vectơ và nhân số thực cho vectơ như sau:
+) øx , y ,z x ,y ,z x x , y y ,z z 1 1 1 ù ø 2 2 2 ù ø 1 2 1 2 1 2 ù
+) kø x , y ,z kx ,ky ,kz 1 1 ù1 ø 1 1 ù1 Ta chứng minh được 3
là một không gian vectơ.
3.1.2. Định nghĩa tổ hợp tuyến tính của các vectơ
Cho øV, , ù là một không gian vectơ, với k ,k ,...,k 1 u ,u2,...,un V và 1 2 n , ta gọi k tổ hợp tuyến tính u ,u ,...,u .
1u1 k 2u 2 ... k nu n là một các vectơ 1 2 n 71 Nếu u V và u 1 k 1
u k2u2 ... knun thì u được gọi là biểu thị tuyến tính qua các vectơ u1,u 2,...,u n. Ví dụ 3. Trong không gian 3
cho các vectơ u ø1,1, 0ù, u ø0,1 ù ,1 , u ø1,0 ù 3 1 2 3 ,1
với k1,k 2,k3 , ta có tổ hợp tuyến tính của 1 u ,u2,u3 là
k u k u k u =øk k ,k k ,k k ù 3 1 1 2 2 3 3 1 3 1 2 2 3 .
3.1.3. Định nghĩa không gian vectơ con của một không gian vectơ
Cho V là một không gian vectơ, W V, W . Nếu với u ,v W , k mà
u v, ku W thì ta nói W là một không gian vectơ con hay vắn tắt là không gian con của V, ký hiệu W V.
Ví dụ 4. Trong không gian 2 , xét tập W ø
x, ù0 x. Ta dễ dàng chứng minh được W là không gian con của 2 .
Thật vậy, ta có ø0,0ù W nên W . (1) Lấy u øa, ù 0 , v ø b, ù
0 W với a,b và k Ta có:
u v øa b,0ù W vì a b (2) ku ø ka, ù 0 vì ka (3) Từ (1), (2), (3), ta có 2 W .
3.1.4. Định nghĩa không gian con sinh bởi một tổ hợp tuyến tính
Cho V là một không gian vectơ và S u ,u ,...,u V thì tập W các tổ hợp tuyến 1 2 n
tính của u , u ,..., u trở thành một không gian vectơ con của V , 1 2 n
W k u k u ü k u / k , k ,..., k V. (3.2) 1 1 2 2 n n 1 2 n
và ta nói W sinh bởi S hay S sinh ra W , ký hiệu
W S u , u ,..., u Span . S (3.3) 1 2 n Hệ quả
Tập hợp tất cả các nghiệm của một hệ phương trình tuyến tính thuần nhất theo n
ẩn số là một không gian vectơ con của n.
Ví dụ 5. Cho hệ phương trình tuyến tính 72 x 2x 4x 3x 0 1 2 3 4 3x 5x 6x 4x 0 1 2 3 4 4 1 x 5x2 2 3 x 3x4 0 3 1 x
8x2 24x3 19x4 0
Giải hệ phương trình trên ta có tập nghiệm W ø 8m 7n, 6
m 5n,m, nù, m,n
Biểu diễn tập nghiệm dưới dạng sau: W ø
8m,6m,m,0) (7n,5n,0,nù, m,n
mø8,6,1,0) n(7,5, ù 0,1 , m, n 1 u ø8, 6,1 ,0),u2 ( 7, 5, ù 0,1 .
Ta có tập nghiệm W được sinh bởi hai véctơ 1 u ,u2 nên 4 W .
3.1.5. Định nghĩa độc lập tuyến tính – phụ thuộc tuyến tính
Cho V là một không gian vectơ và S u , u ,...,u V. Hệ S 1 2 n độc lập tuyến tính nếu ü ü . 1 k ,k2,...,kn , 1 k 1
u k2u2 knun 0 thì 1 k k2 kn 0
Ngược lại, nếu S không độc lập tuyến tính, ta nói S phụ thuộc tuyến tính, nghĩa là k ü i 0 : 1 k 1
u k2u2 knun 0 .
Ví dụ 6. Các vectơ sau độc lập tuyến tính hay phụ thuộc tuyến tính.
a) u (0,1,1); u (1, 2,1); u (1,5,3) 1 2 3 b) u
1 (1,1, 2); u 2 (1, 2, 5); u 3 (0,1, 3) Giải
a) Xét hệ phương trình thuần nhất sau:
x1u1 x 2u 2 x 3u3 0 x2 x3 0 1 x 0 x 2x 5x 0 x 0 1 2 3 2 1 x x2 3 3 x 0 x 3 0
Vậy u , u , u độc lập tuyến tính. 1 2 3
b) Xét hệ phương trình nhất sau: x1u1 x 2u 2 x3u3 0 73 1 x 2 x 0 x 2x x 0 1 2 3 2 1 x 5x2 3x3 0
Giải hệ trên bằng phương pháp Gauss, ta có nghiệm tổng quát của hệ trên là 1
x m; x2 m; x3 m với m . Vậy 1
u , u2, u3 phụ thuộc tuyến tính.
3.2. Cơ sở và số chiều của không gian vectơ
3.2.1. Định nghĩa cơ sở của một không gian vectơ
Cho V là một không gian vectơ và S 1
u , u2 ,...,un V. S là một cơ sở của V nếu
S thỏa hai điều kiện sau : i) S V, và
ii) S độc lập tuyến tính. Tính chất
Cho V là một không gian vectơ và S 1
u , u2 ,...,un V. S là một cơ sở của V nếu Ma trận A ø u u ü u , với S 1 1 1
0 là một cơ sở chính tắc của V, có 0 S 0 S 0 S ù định thức khác 0.
Khi đó, ta nói V là một không gian vectơ hữu hạn chiều và người ta chứng minh
được rằng bất cứ một cơ sở nào khác của V cũng phải có đúng n vectơ và giá trị n này
được gọi là số chiều của V, ký hiệu dimV n. Hơn nữa, v V, ü 1 k ,k2,...,kn : v 1 k 1
u k2u2 knun . Khi đó,
k ,k ,...,k được gọi là tọa độ của 1 2 n
v đối với cơ sở S. Ký hiệu k1 k v 2 . (3.4) S ý k n
3.2.2. Ma trận chuyển cơ sở Giả sử 1 S 1
u , u2 ,...,un , S2 1
v , v2,..., vn là hai cơ sở của không gian vectơ
V . Khi đó, với mọi v V ta có v Av , trong đó S1 S 2 A øv v ü v 1 2 n . (3.5) 1 S 1 S S2 ù
Ma trận A được ký hiệu là Pø 1 S 2
S ù và được gọi là ma trận đổi cơ sở từ 1 S sang S2 . 74 3.2.3. Tính chất Cho S , S , S S 0 1
2 là 3 cơ sở của không gian vec tơ V, trong đó 0 là cơ sở chính tắc i)
PøS S ù PøS S ù 1 2 1 1 2 , (3.6) ii) Pø 1 S S2ù Pø 1 S S0ù PøS0 S2ù. (3.7)
Ví dụ 7. Trong không gian 3 cho hai cơ sở
S u 1,0,0 ,u 0,1,0 ,u 0,0,1 1 1 ø ù 2 ø ù 3 ø ù
S v 1,0,1 ,v 2,1,2 ,v 1,2,2 2 1 ø ù 2 ø ù 3 ø ù
a) Tìm ma trận chuyển cơ sở từ 1 S sang 2 S .
b) Tìm ma trận chuyển cơ sở từ S2 sang 1 S .
c) Tìm tọa độ của u (1,3,5) trong cơ sở S2 . Giải
a) Tìm ma trận chuyển cơ sở từ S sang S 1 2 1 2 1 Ta có PøS S [v ] [v ] [v ] 0 1 2 1 2 ù ø 1 1S 2 1S 3 1S ù 1 2 2
b) Tìm ma trận chuyển cơ sở từ 2 S sang 1 S 1 1 2 1 2 2 3 1 Ta có PøS S P S S 0 1 2 2 1 2 2 1 ù ø 1 2 ù 1 2 2 1 0 1
c) Tìm tọa độ của u (1,3,5) trong cơ sở S 2 k 1 Đặt u k 2 S 2 k 3
Xét hệ phương trình: u 1 k 1 v k2v2 k3v3 k 2k k 1 k 7 1 2 3 1 k 2k 3 k 5 2 3 2 1 k 2k2 2k3 5 k 3 4 7 Vậy u 5 . S 2 4 75 3.2.4. Mệnh đề
Cho một hệ vectơ S 1 v , v2 ,..., m v trong không gian n .
i) Nếu m n thì S không sinh ra n .
ii) Nếu m n thì S phụ thuộc tuyến tính.
Ví dụ 8. Hệ vectơ nào sau đây là cơ sở của 2 , 3
a) u1 (2,1); u 2 (3,0) . b) 1 u (1, 2,5); 2 u (1,3,2) .
c) u1 (1, 2,1); u 2 ( 1 ,1,2); u 3 (1, 2 ,3) . d) 1 u (1,6,4); 2 u (2,4, 1 ); 3 u ( 1 ,2,5); 4 u (2,0,5). Giải a) u (2,1); u (3,0) 1 2 Lập ma trận ø 2 3 A [u ] [u ] 1 0 S 2 0 S ù 1 0 Ta có 2 3 A 3 0 . 1 0
Vậy u1, u 2 là một cơ sở của 2 . b) 1 u (1,2,5); 2 u (1,3,2)
Ta thấy S gồm 2 vectơ u (1, 2,5); u (1,3,2) nên theo mệnh đề (3.2.4) ta có S 1 2 không sinh ra 3
. Vậy S không là cơ sở của 3 . c) u (1, 2,1); u ( 1 ,1,2); u (1, 2 ,3) 1 2 3 Lập ma trận 1 1 1 A øu u u 2 1 2 1 2 3 0 S 0 S 0 S ù 1 2 3 Ta có 1 1 1 A 2 1 2 18 0 . 1 2 3 76
Vậy u1, u 2, u3 là một cơ sở của 3 . d) 1 u (1,6,4); 2 u (2,4, 1 ); 3 u ( 1 ,2,5); 4 u (2,0,5) Ta thấy S gồm 4 vectơ 1 u (1,6,4); u2 (2,4, 1 ) ; u 3 (1,2,5); 4 u (2,0,5)
nên theo mệnh đề (3.2.4) ta có S không không độc lập tuyến tính.
Vậy S không là cơ sở của 3 .
Ví dụ 9. Trong không gian 3 , cho hệ vectơ
S u 1,1,1 ,u 1,1,2 ,u 1,2,3 1 ø ù 2 ø ù 3 ø ù
a) Chứng minh rằng S là cơ sở của 3 .
b) Tìm tọa độ của u (0,0,1) trong cơ sở 3 . Giải
a) Chứng minh rằng S là một cơ sở của 3 1 1 1 Lập ma trận : A øu 1 u2 u3 1 1 2 S 0 S0 S0 ù 1 2 3 1 1 1
Ta có : A 1 1 2 1 0 . 1 2 3
Vậy S là một cơ sở của 3 .
b) Tìm tọa độ của u (0,0,1) trong cơ sở 3 1 x Đặt u x 2 S x 3
Xét hệ phương trình sau: 1 x 1 u x2u2 x3u3 u 1 x 2 x 3 x 0 1 x 1 x x 2x 0 x 1 1 2 3 2 1 x 2 2 x 3 3 x 1 3 x 0 1 Vậy [u] 1 . S 0
Ví dụ 10. Xác định một cơ sở và số chiều của không gian nghiệm W của các hệ sau 77 x x x 0 a) 1 2 3 x 2x 3x 0 1 2 3 x1 2x 2 x 3 0 5 x 7x 4x 0 b) 1 2 3 2 x 7x 3x 0 1 1 2 3x1 9x2 4x3 0 Giải x x x 0 a) 1 2 3 x 2x 3x 0 1 2 3
Giải hệ trên bằng phương pháp Gauss, ta được 1 1 1 (2): (2) (1) 1 1 1 1 2 3 0 1 4
Chọn x ,x làm ẩn cơ sở x làm ẩn tự do, (với m tùy ý). 1 2 3 3 x m
Ta được nghiệm tổng quát của hệ là : W (5m,4m,m) m .
Vậy không gian nghiệm W m( 5,
4,1) m (5,4,1) được sinh ra bởi 1 vectơ
độc lập tuyến tính. Nên ta có dim W 1. x 2x x 0 1 2 3 5 x 7x 4x 0 b) 1 2 3 2 x 7x 3x 0 1 1 2 3x 9x 4x 0 1 2 3
Giải hệ trên bằng phương pháp Gauss, ta được 1 2 1 1 2 1 5 7 4 0 3 1 1 2 1 (2): ( 2) 5 (1) (3): ( 3) 2 (1) 2 7 3 0 3 1 0 3 1 (4): ( 4) 3 (1) 3 9 4 0 3 1
Chọn x1,x 2 làm ẩn cơ sở x3 làm ẩn tự do, 3 x m (với m tùy ý). 1 1
Ta được nghiệm tổng quát của hệ là W ( m, m, m) m . 3 3 1
Vậy không gian nghiệm W m(1,1, 3) m
(1,1,3) được sinh ra bởi 1 3
vectơ độc lập tuyến tính. Nên ta có dim W 1. 78 3.3. Bài tập
Bài số 1. Chứng minh các tập sau là không gian vectơ 1. n
øx ,x ,...,x / x , i 1,n với hai phép toán sau 1 2 n ù i
Phép cộng: øx , x ,..., x y , y ,..., y x y , x y ,..., x y 1 2 n ù ø 1 2 n ù ø 1 1 2 2 n n ù Phép nhân: k ø 1 x , x2 ,..., n x ù øk 1 x , kx2 ,...,k n x ù a b 2.
/ a,b,c,d ,với hai phép toán cộng hai ma trận và nhân một số 2 c d thực với một ma trận.
Hướng dẫn : Dùng định nghĩa.
Bài số 2. Hỏi các tập dưới đây là không gian con của 3 hay không?
1. Các vectơ có dạng øa,0,0 ù.
2. Các vectơ có dạng øa, 1, 1 ù.
Đáp số : 1) là không gian con; 2) không là không gian con.
Bài số 3. Cho không gian vectơ V trên trường số thưc , là một vectơ cố định thuộc
V. Chứng minh rằng tập hợp W r r R là một không gian con của V .
Hướng dẫn : Dùng định nghĩa về không gian con.
Bài số 4. Trong không gian 3 , cho các vectơ u 1
ø1, 2, 3ù,u 2 ø0, 1, 3ù . Xét xem vectơ u ø2, 3
, 3ù có phải là tổ hợp tuyến tính của u ,u hay không ? 1 2 Đáp số : u ø 2, 3 , ù
3 là tổ hợp tuyến tính của u , u 1 2
Bài số 5. Trong không gian 3
, xét xem vectơ u có phải là tổ hợp tuyến tính của u , u ,u 1 2 3 hay không 1. u 1 ø1,0, ù 1 , u2 ø1,1,0ù, u3 ø0,1, ù 1 , u ø1, 2, ù 1
2. u 2,1,0 ,u 3,1,1 ,u 2,0,2 ,u 1,3,1 . 1 ø ù 2 ø ù 3 ø ù ø ù
Đáp số : 1) u là tổ hợp tuyến tính của u ,u ,u ; 1 2 3
2) u là tổ hợp tuyến tính của 1 u ,u2,u3 .
Bài số 6. Hãy biểu diễn x thành tổ hợp tuyến tính của u, v, w. Trong đó 1. x ø 7, 2, 1 ù 5 , u ø 2, 3, ù 5 , v ø3, 7, ù 8 , w ø1, 6, ù 1 . 2. x ø1,4, 7, ù
7 , u ø 4,1,3, 2ù ,v ø1, 2, 3, ù 2 , w ø16,9,1, ù 3 . 79
Đáp số : 1) x 6u 2v w ; 2) x 3u 5v w .
Bài số 7. Trong không gian các ma trận thực vuông cấp hai M , cho bốn vectơ 2 ø ù 1 3 1 0 1 1 0 1 u ,u ,u ,u 1 2 3 . 2 2 1 0 0 0 1 1
Hỏi vectơ u có phải là tổ hợp tuyến tính của u ,u ,u hay không ? 1 2 3
Đáp số : u là tổ hợp tuyến tính của u ,u ,u . 1 2 3
Bài số 8. Trong không gian 3
, cho các vectơ u1 ø1,2, ù 3 , u2 ø 0,1, ù 3 . Tìm m để vectơ u ø1,m, 3
ù là tổ hợp tuyến tính của u1,u 2. Đáp số : m 0 .
Bài số 9. Hãy xác định m sao cho x là tổ hợp tuyến tính của u, v, w : 1. u ø 2, 3, ù 5 , v ø3, 7, ù 8 , w ø1, 6, ù 1 , x ø7, 2, ù m . 2. u ø3, 2, ù
5 , v ø 2, 4, 7ù, w ø5, 6, mù , x ø1, 3, ù 5 .
Đáp số : 1) m 15 ; 2) m 12.
Bài số 10. Trong không gian 3
, các hệ vectơ sau là độc lập tuyến tính hay phụ thuộc tuyến tính 1. u 1 ø1,1,0ù,u2 ø0,1, ù 1 , u3 ø1,0, ù 1 .
2. u1 ø1,1,0ù, u2 ø0,1,1ù, u3 ø2,3, ù 1 .
Đáp số : 1) độc lập; 2) phụ thuộc.
Bài số 11. Trong không gian 4
, các hệ véctơ sau là độc lập hay phụ thuộc tuyến tính 1. 1 u ( 1 , 2,0,1),u2 (1,2,3, 1 ),u3 (0,4,3,0). 2. 1 u (1, 2,3,2),u2 ( 1 ,2,1,2),u3 (1, 3 , 2 ,2). 3. 1 u (1,0,0, 1
),u2 (2,1,1,0),u3 (1,1,2,1).
Đáp số : 1) phụ thuộc; 2) phụ thuộc; 3) độc lập.
Bài số 12. Trong không gian các ma trận thực vuông cấp hai M 2 ø ù , cho hệ gồm 4 ma trận như sau: 1 0 1 1 1 1 1 1 e , e , e , e 1 2 3 4 . 0 0 0 0 1 0 1 1
Chứng minh rằng hệ trên độc lập tuyến tính.
Hướng dẫn : Xét hệ thuần nhất tương ứng và chứng minh nó có nghiệm duy nhất. 80 3 1
Bài số 13. Biểu thị ma trận E
dưới dạng tổ hợp tuyến tính của các ma trận sau 1 1 1 1 0 0 0 2 A , B , C . 1 0 1 1 0 1
Đáp số : E 3A 2B C .
Bài số 14. Mỗi hệ vectơ sau đây có sinh ra 3 không 1. v . 1 ø1,1 ù
,1 , v2 ø 2, 2,0ù, v3 ø3,0,0ù 2. v 2, 1
,3 , v 4,1, 2 , v 8, 1 ,8 . 1 ø ù 2 ø ù 3 ø ù Đáp số : 1) sinh ra 3 ; 2) không sinh ra 3 .
Bài số 15. Hệ vectơ nào trong các hệ vectơ sau đây là cơ sở của 3
1. S 1,2,3 , 0,2,3 . 1 ø ù 2 ø ù 2. S 1 ø1,2, ù 3 , 2 ø 0,2, ù 3 , 3 ø 0,0, ù 5 .
3. S 1,1,2 , 1,2,5 , 0,1,3 . 1 ø ù 2 ø ù 3 ø ù 4. S 1 ø 1 ,0, ù 1 , 2 ø 1 ,1, ù 0 , 3 ø1, 1 , ù 1 , 4 ø 2,0, ù 5 .
Đáp số : 1) không là cơ sở; 2) là cơ sở; 3) không là cơ sở; 4) không là cơ sở.
Bài số 16. Trong không gian 3 , xét hệ vectơ: S 1 ø1, 1, ù
1 ,2 ø1, 1, 2ù,3 ø1, 2, 3ù
1. Chứng minh rằng S là một cơ sở của 3 .
2. Tìm tọa độ của x ø6, 9, 14ù trong cơ sở S.
3. Tìm ma trận chuyển cơ sở từ S sang cơ sở chính tắc. 1 1 1 Đáp số : 1) A 1
; 2) x T ø1 2 3ù ; 3) PøS S 0 ù S 1 2 1 . S 1 1 0
Bài số 17. Trong không gian vector 3 , cho hệ vector
S u (1,6,9), u (1,4m,1), u ( 1 ,2, 5 ) . 1 2 3
1. Định m để hệ vector trên là một cơ sở của 3 . 2. m 1
, tìm tọa độ x ø1,2,3ù đối với cơ sở S. 81
3. Với m 0, tìm ma trận chuyển cơ sở từ S sang cơ sở chính tắc. 0 ,125 0 ,125 0,375 0 ,125
Đáp số: 1) m 1; 2) x 0,25 ; 3) P øS S 0,75 0, 25 0 ,25 . 0 ù S 0,875 0 ,375 0,625 0 ,375
Bài số 18. Tìm một cơ sở và số chiều của không gian nghiệm của các hệ phương trình thuần nhất sau: 3 x x x x 0 1. 1 2 3 4 5 1 x x2 x3 x4 0 3 x x 2x 0 1 2 3 2. x 1 3x 2 4x3 0 x1 2x 2 x3 0 2 x 4x x x 0 1 2 3 4 x 5x 2x 0 1 2 3 3. 2x 2 2x3 x4 0 x1 3x2 x 4 0 x 1 2x 2 x 3 x 4 0 x x x 0 1 2 3 3 1 x 2x2 x3 0 4. 2 1 x x2 2x3 0 4 1x 3x2 0
5 1x 3x2 3x3 0
Đáp số : 1) cơ sở W u ( 1 , 1 ,4,0), u (0, 1 ,0,1) 1 2 và số chiều dimW 2 . 2) cơ sở W ( 1
,1,1) và số chiều dim W 1.
3) W (0,0,0) và số chiều dim W 0. 4) cơ sở W (3, 4 ,
1 và số chiều dim W 1.
Bài số 19. Trong không gian 4 xét tập hợp :
W =øx ,x ,x ,x : x x x 2x 0 1 2 3 4ù 1 2 3 4
1. Chứng tỏ rằng W là một không gian con của 4 .
2. Tìm một cơ sở và số chiều cho W.
3. Kiểm tra xem các vectơ sau có nằm trong W không ? 82 u=ø1, 1, 0, ù 1 , v ø1, 0, 0, ù 1 , w ø1, 0, 1, ù 0 .
Đáp số : 1) Dùng định nghĩa; 2) cơ sở của Wø 1
,1,0,0ù ,ø1,0,1,0ù,ø 2, 0, ù 01 , dim W 3; 3) u W; v, w W .
Bài số 20. Trong không gian 4 cho hệ : S 1 ø0,1,1 ù ,1 , 2 ø1,0,1 ù ,1 , 3 ø1,1, ù 0,1 , 4 ø1,1,1,0ù
1. Chứng minh rằng S là một cơ sở của 4 .
2. Tìm tọa độ của vectơ x ø1,1,1, ù 1 trong S. 1 1 1 1 Đáp số : 1) A S 3 ; 2) xT . S 3 3 3 3
Bài số 21. Trong không gian 3 , cho hai cơ sở 1 S 1
u ø1,1,0ù,u2 ø0,1,1ù, 3 u ø1,0, ù 1
S v 2,1,1 ,v 1, 2,1 ,v 1,1, 2 2 1 ø ù 2 ø ù 3 ø ù
tìm ma trận đổi cơ sở từ cơ sở S S S S .
1 đến 2 và ma trận đổi cơ sở từ cơ sở 2 đến 1 1 1 0 1 / 2 1/ 2 1 / 2 Đáp số: PøS S 0 1 1, P S S 1/ 2 1/ 2 1 / 2 . 1 2 ù ø 2 1 ù 1 0 1 1/ 2 1/ 2 1/ 2
Bài số 22. Trong không gian 3 , cho các hệ vectơ S 1 u1 ø1,1 ù ,1 ,u 2 ø1,1, ù 2 ,u 3 ø1,2, ù 3
S v 2,1,1 ,v 3,2,5 ,v 1,1,m 2 1 ø ù 2 ø ù 3 ø ù
1. Chứng minh rằng S1 là cơ sở của 3 .
2. Tìm m để S là một cơ sở của 3 . 2
3. Với m 0 . Tìm ma trận chuyển Pø 1 S S2ù và PøS2 1 S ù. Đáp số : 1) AS 1 ; 2) m 20 . 4 0 0 1/ 4 0 0 3) PøS S 1 4 3 , P S S 1/ 4 2 / 5 3 / 5 . 1 2 ù ø 2 1ù 1 1 2 1/ 4 1/ 5 4 / 5 83 Chương 4
PHÉP TÍNH VI PHÂN HÀM MỘT BIẾN
4.1. Giới hạn của dãy số thực
4.1.1. Định nghĩa dãy, giới hạn của dãy số thực Cho hàm số f : n f (n) x n Ký hiệu: n x , n x , n x . n 1 n Định nghĩa: Cho a
, dãy xn có giới hạn là a 0, n0 , n n0 xn a (4.1) ký hiệu : lim xn a . n
Dãy có giới hạn được gọi là dãy hội tụ, ngược lại được gọi là dãy phân kỳ. 3n 1
Ví dụ 1. Dùng định nghĩa tính giới hạn của dãy số có số hạng tổng quát: x . n n Giải Ta có 1 1 x 3 x 3 n n n n
Theo định nghĩa giới hạn của dãy số (4.1), ta có 3n 1 1 1 1 0, 0 n , n 0 n , xét n x 3 3 0 n n n n0 Vậy lim x 3. n n
4.1.2. Các tính chất và các định lý về giới hạn của dãy số thực
4.1.2.1. Giới hạn duy nhất: Mọi dãy hội tụ đều có giới hạn duy nhất. 4.1.2.2. Định lý i) xn hội tụ thì n x bị chặn M 0, xn M .
ii) xn hội tụ thì x hội tụ tuyệt đối : lim x a lim x a . n n n n n 84 b arccosx
cosb a , với mọi 1 a 1, 0 b
c. Các hàm lượng giác: y tan x, y cot x tuần hòan với chu kỳ ü ü
Tập xác định của hàm số y tan x , D \ ý n n ý þ 2 þ
Tập xác định của hàm số y cot x , D \ n n
d. Các hàm lượng giác ngược: y arctan x, y arccot x
Hàm số y tan x thu hẹp trên miền ,
cho ta hàm lượng giác ngược 2 2
y arctan x. Tập xác định D b arctana tan b a , với mọi a , b . 2 2
Hàm số y cot x thu hẹp trên miền ø0, ù cho ta hàm lượng giác ngược
y arccot x. Tập xác định D b arccot a cot b a , với mọi a , 0 b .
4.2.5. Dáng điệu hàm số 4.2.5.1. Hàm đơn điệu
Hàm số f (x) được gọi là hàm tăng (đồng biến) trên khoảng øa,b ù nếu x ,x a,b , ta có : x x f x f x 1 2 ø 1 ù ø 1 2 ø ù 2
Hàm số f (x) được gọi là hàm giảm (nghịch biến) trên khoảng øa,b ù nếu x ,x a,b , ta có : x x f x f x 1 2 ø 1 ù ø 1 2 ø ù 2
Hàm số tăng (giảm) được gọi là hàm số đơn điệu.
Ví dụ 8. Cho hàm số f (x) ax b (a 0). Ta có x ,x , x x ta có f øx f x ax b ax b a(x x ) 1 ù ø2 ù ø 1 ù ø2 ù 1 2 1 2 1 2
Vậy hàm số đồng biến khi a 0 và nghịch biến khi a 0.
4.2.5.2. Hàm số chẵn và hàm số lẻ
Hàm số f (x) được gọi là hàm số chẵn trên miền xác định X nếu với mọi x X ta
luôn có x X và f ø x ù f øx ù .
Hàm số f (x) được gọi là hàm số lẻ trên miền xác định X nếu với mọi x X ta luôn có x X và f ø x ù f øx ù. 92
Ví dụ 9. Hàm số f (x) sin x là hàm lẻ trên
và hàm g(x) cos x là hàm chẵn trên .
4.2.5.3. Hàm số bị chặn
Hàm số f (x) được gọi là bị chặn dưới, (bị chặn trên) trên miền xác định X nếu tồn
tại số thực m, øM ù sao cho f øx ù m, øf øx ù M ù, x X.
Hàm số vừa bị chặn trên, vừa bị chặn dưới được gọi là hàm số bị chặn.
Ví dụ 10. Hàm số y sin x, y cosx bị chặn trên bởi 1 và bị chặn dưới bởi 1 trên .
4.2.5.4. Hàm số tuần hoàn
Hàm số f (x) xác định trên miền X được gọi là hàm số tuần hoàn nếu T \ 0
sao cho x X , ta luôn có x T X và f øx T ù f øx ù. Số T 0 nhỏ nhất thỏa mãn
định nghĩa được gọi là chu kỳ của hàm số f (x). Ví dụ 11.
Hàm số sin x và cos x là các hàm tuần toàn trên với chu kỳ T 2 vì:
sinøx k2 ù sin øx và cos øx k2 ù cos øx , x
Hàm số tan x và cot x là các hàm tuần toàn với chu kỳ T vì: tanøx k ù tan øx ù, x
k và cotøx k2 ù cot øx ù,x k . 2
4.2.6. Một số hàm trong kinh tế
4.2.6.1. Hàm sản xuất ngắn hạn
Để tiến hành sản xuất, đầu tiên chúng ta cần các yếu tố đầu vào là vốn øK ù và lao
động øL ù. Trong ngắn hạn, người ta giả thiết K là không thay đổi, khi đó sản lượng đầu
ra Q sẽ phụ thuộc hàm số vào yếu tố đầu vào L và gọi là hàm sản xuất ngắn hạn: Q f øL ù, L 0
Ví dụ 12. Cho hàm sản xuất ngắn hạn 2 3 Q 120.L ; Q a.L (a 0,0 1)
4.2.6.2. Hàm chi phí (tổng chi phí)
+) Chi phí TC phụ thuộc đầu ra Q : TC T ø C Q ù, Q 0
Ví dụ 13. Cho hàm chi phí phụ thuộc vào sản lượng Q ø ù 3 2 TC Q Q 6Q 140Q 1500, Q 0 93 ø ù 0,3Q TC Q 30.e 200 ø ù 2 TC Q 3Q 7Q 243
+) Chi phí TC phụ thuộc đầu vào L : TC p p L.L
TC øL ù, L 0 ( L giá thuê một đơn vị lao động).
Ví dụ 14. Cho hàm chi phí phụ thuộc vào lao động L
TCøL ù pL L 3.L øL 0, pL 3 .
4.2.6.3. Hàm doanh thu (tổng doanh thu)
Doanh thu TR phụ thuộc đầu ra Q:
TR P.Q TRøQ ù, Q 0 ( P ký hiệu là giá hàng hóa).
Ví dụ 15. Cho hàm doanh thu phụ thuộc vào sản lượng Q ø ù 2 TR Q 1200Q 3Q , Q 0
Doanh thu TR phụ thuộc đầu vào L :
TR P.Q P.f øL ù TR øL ,ùL 0 (P ký hiệu là giá hàng hóa)
Ví dụ 16. Cho hàm doanh thu phụ thuộc vào lao động L
TR øL ù 5.300 L 1500 L, L 0 (P 5; Q 300 L) .
4.2.6.4. Hàm lợi nhuận (tổng lợi nhuận)
Lợi nhuận được tính bằng hiệu giữa doanh thu TR và chi phí TC:
+) Lợi nhuận phụ thuộc đầu ra: øQ ù TR øQ ù TC ø Q
Ví dụ 17. Cho hàm doanh thu ø ù 2 TR Q
1200Q 3Q , Q 0 và hàm chi phí ø ù 3 2 TC Q Q 6Q 140Q 1500, Q 0
Suy ra hàm lợi nhuận phụ thuộc vào sản lượng Q ø ù ø ù ø ù 3 2 Q TR Q TC Q Q 3Q 1060Q 1500, Q 0
+) Lợi nhuận phụ thuộc đầu vào: øL ù TR øL ù TC ø L .
Ví dụ 18. Cho hàm sản xuất: Q 300 L, giá một đơn vị lao động là 3, giá sản phẩm là
5. Xác định hàm lợi nhuận. Ta có
+) Hàm doanh thu : TR øL ù PQ 5.300 L 1500 L
+) Hàm chi phí: TCøL ù p L 3L L 94
+) Suy ra hàm lợi nhuận phụ thuộc vào lao động L øL ù TR øL ù TC ø L ù1500 L 3.L, L 0 . 4.2.6.5. Hàm chi tiêu
Chi tiêu C phụ thuộc thu nhập Y : C CøY ù, Y 0.
Ví dụ 19. Cho hàm chi tiêu phụ thuộc vào mức thu nhập như sau:
CøY ù aY b (0 a 1, b 0), Y 0. 4.2.6.6. Hàm tiết kiệm
Tiết kiệm S phụ thuộc thu nhập Y : S ø S Yù, Y 0.
Ví dụ 20. Cho hàm tiết kiệm phụ thuộc vào mức thu nhập như sau: ø S Y ù 0,3Y 0,1. Y 100, Y 0 .
4.2.6.7. Hàm cung và hàm cầu một loại hàng hóa
Lượng cung và lượng cầu hàng hóa phụ thuộc vào giá hàng hóa: +) Hàm cung: Q S P , P 0 S ø ù .
+) Hàm cầu: QD DøP ù, P 0 .
Ví dụ 21. Cho hàm cung và hàm cầu dạng tuyến tính như sau: +) Hàm cung: ø S P ù aP b (a,b 0). +) Hàm cầu: DøP ù cP d (c,d 0) . 4.3. Giới hạn hàm số
4.3.1. Các định nghĩa giới hạn 4.3.1.1. Định nghĩa Cho hàm số f : D
. f có giới hạn là L khi x tiến tới a 0, 0, x D, x a f (x) L . (4.2) Ký hiệu : lim f (x) L. x a 4.3.1.2. Định lý Cho hàm số f : D . Ta có lim f (x) L (xn ) D \ x0 , xn x0 f (xn ) L. (4.3) x 0 x 1
Ví dụ 22. Chứng minh rằng không tồn tại lim sin . x 0 x 95 Giải 1 1 Lấy x khi x 0 khi n 0 n và / n 2n n 2n 2 Khi đó ta có f øx / n ù sin ø 2n ù 0 và f øx n ù sin 2n 1 2 Vậy khi x
0 thì hàm f øx ù không có giới hạn.
4.3.1.3. Các phép toán về giới hạn
Nếu lim f (x) A, lim g(x) B và k là hằng số, thì ta có x a x a i) lim f (x) g(x) A B , iv) lim kf (x) kA , x a x a ii) lim f (x) g(x) A B , f (x) A x a v) lim . x a g(x) B iii) lim f (x) g(x) A B , x a 0
với điều kiện vế phải không xuất hiện các dạng vô định ; ; 0 ; . 0
4.3.1.4. Định lý giới hạn kẹp Nếu f (x) g(x) h(x) khi x a và lim f (x) lim h(x) L. x a x a Vậy lim g(x) L. x a 1
Ví dụ 23. Tính giới hạn lim sin x. x 2 x 1 Giải Ta có 1 1 1 sin x 2 2 2 x 1 x 1 x 1 mà 1 1 lim lim 0. x 2 x 2 x 1 x 1 1
Theo tiêu chuẩn kẹp, ta có lim sin x 0. x 2 x 1 96
4.3.1.5. Giới hạn một phía Cho hàm số f : D
f có giới hạn là L khi x tiến tới a từ bên phải, ký hiệu lim f (x) L, ta có x a lim f(x) L 0, 0, x D, 0 x a f (x) L . x a
f có giới hạn là L khi x tiến tới a từ bên trái, ký hiệu lim f (x) L, ta có x a lim f (x) L 0, 0, x D, 0 a x f (x) L . x a
4.3.2. Giới hạn của các hàm sơ cấp cơ bản
4.3.2.1. Hàm số lũy thừa y x 0 ü khi 0 ü khi 0 lim x ý và lim x ý x 0 þ khi 0 x þ0 khi 0 4.3.2.2. Hàm số mũ 0 ü khi a 1 ü khi a 1 x lim a ý và x lim a ý x þ khi 0 a 1 x 0 þ khi 0 a 1 4.3.2.3. Hàm số logarit +) Với a 1 : lim log x ; lim log x . a a x 0 x +) Với 0 a 1 : lim log x ; lim log x . a a x 0 x
4.3.2.4. Các hàm lượng giác
Các hàm lượng giác sinx, cos x, tan x, cot x không có giới hạn khi x .
Hàm số tan x có giới hạn vô hạn khi x k øk ù. 2
Hàm số cot x có giới hạn vô hạn khi x k øk ù.
4.3.3. Các dạng vô định 0 f (x) Dạng và
xảy ra khi ta tính giới hạn của biểu thức , trong đó cả hai hàm 0 g(x)
f (x) và g(x) cùng có giới hạn là 0 hoặc cùng có giới hạn là . Dạng
xảy ra khi ta tính giới hạn của biểu thức f (x) g(x), trong đó cả hai
hàm f (x) và g(x) cùng dấu và cùng có giới hạn là . 97 Dạng 0
xảy ra khi ta tính giới hạn của biểu thức f (x) g(x) , trong đó hàm f (x)
có giới hạn là 0 và hàm g(x) có giới hạn là hoặc ngược lại. Dạng 0 0 1 , 0 ,
xảy ra khi ta tính giới hạn của biểu thức g(x) f (x) , trong đó hàm
f (x) là một hàm dương. Ta thường gặp: +) Dạng 1 nếu f (x) 1 và g(x) ; +) Dạng 0 0 nếu f (x) 0 và g(x) 0; +) Dạng 0 nếu f (x) và g(x) 0.
4.3.4. Các giới hạn cơ bản sin x arcsin x a) lim 1 f) lim 1 x 0 x x 0 x 1 cos x 1 arctan x b) lim g) lim 1 2 x 0 x 2 x 0 x tan x c) (1 x) 1 lim 1 h) lim x 0 x x 0 x x e 1 x d) lim 1 i) 1 lim 1 x 0 x x x ln(1 x) e) lim 1 1 k) lim ø1 x ùx e x 0 x x 0
Ví dụ 24. Tính các giới hạn sau a) lim ø 2 2 3x 4x 2 3x 4x 1 x ù ø x 1 e ùø1 cos3x ù b) lim 3 4 x 0 x sin 2x x x 1 c) lim x x 1 Giải 4x 3 a) lim 3x 4x 2 3x 4x 1 lim x ø 2 2 ù x 2 2 3x 4x 2 3x 4x 1 3 x 4 x lim x 4 2 4 1 x 3 3 2 2 x x x x 98 3 4 x 4 2 3 lim . x 4 2 4 1 2 3 3 3 3 2 2 x x x x ø x 1 e ùø1 cos3x ù b) lim 3 4 x 0 x sin 2x x e 1 1 cos3x 3 9x 2 x 9x lim 4 x 0 3 sin 2x x 1 16x 2x x e 1 1 cos 3x 9 2 x 9x 9 lim 4 x 0 sin 2x 2 1 16x 2x x e 1 1 cos x 1 tan x (vì lim 1; lim ; lim 1) 2 x 0 x 0 x 0 x x 2 x 2x x 1 x 1 2 x x x 1 2 1 c) 2 lim lim 1 lim 1 e . x x x x 1 x 1 x 1 2 û
4.4. Vô cùng bé và vô cùng lớn 4.4.1. Định nghĩa
Hàm số (x) được gọi là vô cùng bé khi x a nếu lim (x) 0. x a
Cho hai hàm số (x), (x) là hai vô cùng bé trong quá trình x a .
Giả sử tồn tại hữu hạn giới hạn: (x) lim k, øk ù x a (x)
+) Nếu k 0 thì ta nói (x) là vô cùng bé bậc cao hơn so với (x) và ký hiệu (x) o (x) .
+) Nếu k 0 thì ta nói (x), (x) là hai vô cùng bé cùng bậc. 99
+) Nếu k 1 thì ta nói (x), (x) là hai vô cùng bé tương đương và ký hiệu (x) (x).
Hàm số (x) được gọi là vô cùng lớn khi x a nếu lim (x) . x a 4.4.2. Các tính chất 1
a. Nếu (x) là một vô cùng lớn khi x a và (x) 0 thì là một vô cùng (x) bé khi x a và ngược lại.
b. Điều kiện cần và đủ để f (x) có giới hạn là b, (b ) khi và chỉ khi f(x) b
(x) trong đó (x) là một vô cùng bé khi x a. c. Giả sử khi x
a ta có các vô cùng bé tương đương: * (x) (x) và * (x) (x) * (x) * (x) (x)
khi đó, nếu tồn tại lim thì lim lim . * x a (x) * x a x a (x) (x)
Ví dụ 25. Áp dụng vô cùng bé tính giới hạn sin x e 1 a) lim x x 0 e cos x 1 2 2 sin 2x arcsin x arctan x b) lim 3 x 0 3x 4x Giải sin x e 1 a) lim x x 0 e cos x 1 Ta có: sin x x e 1 sin x; e cosx 1 x Vậy sin x e 1 sin x lim lim 1. x x 0 x 0 e cos x 1 x 2 2 sin 2x arcsin x arctan x b) lim 3 x 0 3x 4x Ta có: 2 2 2 2 sin 2x 2x; arcsin x x ; arctan x x ; 2 2 3 sin 2x arcsin x arctan x 2x; 3x 4x 3x 100 Vậy 2 2 sin 2x arcsin x arctan x 2x 2 2 lim lim lim . 3 x 0 x 0 x 0 3x 4x 3x 3 3 4.5. Hàm số liên tục
4.5.1. Các định nghĩa về hàm số liên tục 4.5.1.1. Định nghĩa Cho hàm số f : D , x0 D i) f liên tục tại x lim f (x) f (x ) 0 0 x x0 0, 0, x D, x x0 f (x) f (x0) . (4.4) ii) f liên tục trên D
f liên tục tại mọi điểm x D. 4.5.1.2. Định lý Cho hàm số f : D , x0 D f liên tục tại x (x ) D, x x f (x ) f (x ) . (4.5) 0 n n 0 n 0 4.5.1.3. Hệ quả f không liên tục tại x x D, x x f(x ) f (x ) . 0 ø n ù ø n 0 ù ø n 0 ù (4.6)
4.5.1.4. Liên tục một phía
i) f liên tục trái (phải) tại x
lim f (x) f (x ) ( lim f (x) f (x ) ). 0 0 0 x x 0 x x0
ii) f liên tục tại x0 khi và chỉ khi nó liên tục trái và liên tục phải tại 0 x .
Ví dụ 26. Xét tính liên tục của hàm số sau üsin x khi x 0 f (x) x ý 0 þ khi x 0 Giải
Hàm số f (x) liên tục tại mọi giá trị x 0 . Xét tại x 0 ta có sin x sin x lim f (x) lim lim 1 x 0 x 0 x x 0 x sin x sin x lim f (x) lim lim 1 x 0 x 0 x x 0 x
Hàm số trên không liên tục tại 0 (vì lim f (x) lim f (x) ). x 0 x 0 101
Ví dụ 27. Định m để hàm số sau liên tục trên 2 x ü 3x 1 khi x 1 f (x) ý 3 þ x m khi x 1 Giải
Hàm số f (x) liên tục tại mọi giá trị x 1. Xét tại x 1 ta có lim f (x) lim ø3x m ù 3 m x 1 x 1 2 lim f (x) lim (x 3x 1) 1 x 1 x 1
Hàm số liên tục tại x 1 khi và chỉ khi f (1) lim f (x) lim f (x) 3 m 1 m 4. x 1 x 1
4.5.2. Tính chất liên tục của hàm sơ cấp
4.5.2.1. Tính chất 1. Nếu hàm số f (x) liên tục trong khoảng đóng a,b và f (a) f (b)
thì nó nhận mọi giá trị trung gian giữa f (a) và f (b) , nghĩa là với mọi nằm giữa f (a)
và f (b) luôn tồn tại ít nhất số c øa,b ù sao cho f (c) .
4.5.2.2. Tính chất 2. Nếu hàm số f (x) liên tục trên khoảng đóng a,b và f (a) f (b) 0
thì tồn tại ít nhất một điểm c øa,b ù sao cho f (c) 0 ( hay c là nghiệm của phương trình f (x) 0).
4.5.2.3. Tính chất 3. Nếu hàm số f (x) liên tục trên đoạn a,b thì
+) f (x) bị chặn trên a,b ;
+) f (x) có giá trị lớn nhất và giá trị nhỏ nhất trên a,b , tức là tồn tại c,d a,b sao cho f (c) f (x) f (d), x a,b .
4.5.2.4. Tính chất 4. Nếu hàm số f (x) xác định, liên tục và đơn điệu tăng (đơn điệu giảm) trên khoảng X thì
+) Miền giá trị của hàm số y f (x) là một khoảng Y;
+) Hàm số y f (x) có hàm số ngược 1 x f (y); +) Hàm số ngược 1
x f (y) là hàm liên tục và đơn điệu tăng (đơn điệu giảm) trên Y. 102
Ví dụ 28. Chứng minh rằng phương trình 5 x
3x 1 0 có nghiệm trên đoạn 0,1 . Giải Đặt 5 f (x) x 3x 1
Ta nhận thấy hàm số f (x) liên tục trên đoạn 0,1 và đồng thời f (0) f (1) 1 0
Vậy phương trình f (x) 0 có ít nhất 1 nghiệm trong đoạn 0,1 .
4.5.3. Các phép toán của hàm liên tục tại một điểm 4.5.3.1. Định lý 1 Cho hai hàm số f, g : D , x0 D f
i) f, g liên tục tại x0 thì f g, fg, kf (k ), , øg(x x . 0) 0 ù đều liên tục tại g 0 f
ii) f ,g liên tục trên D thì f g, fg, kf (k ),
, øg(x 0) 0 ù đều liên tục trên g D. 4.5.3.2. Định lý Cho hàm số f / g D D
i) f liên tục tại x0 D và g liên tục tại / y x . 0 f (x0) D g f (x) liên tục tại 0
ii) f liên tục trên D và g liên tục trên / D g f (x) liên tục trên D. 4.6. Đạo hàm
4.6.1. Khái niệm về đạo hàm 4.6.1.1. Định nghĩa
Cho hàm số y f(x) xác định trong một lân cận của điểm x0 (một khoảng đủ nhỏ chứa x ). 0
Ký hiệu x x x0 gọi là số gia của đối số (với x đủ nhỏ), tương ứng y f ø 0 x x ù f ø 0
x ù được gọi là số gia của hàm số.
Nếu tồn tại giới hạn hữu hạn: f øx ù f øx0 ù y f (x x) f (x) lim lim lim . (4.7) x x0 x x x 0 x x 0 0 x 103
thì hàm số f øx ù được gọi là có đạo hàm tại điểm 0
x và kết quả của giới hạn này, được
gọi là đạo hàm của hàm số f øx ù tại điểm / / 0
x , ký hiệu là f øx hay y øx . 0 ù 0 ù
Ví dụ 29. Tính đạo hàm của hàm số sau bằng định nghĩa 3 f (x) x Giải
Tập xác định của hàm số: Df Với x , xét giới hạn 0 f øx ù f øx0 ù 3 3 x x 0 lim lim x x0 x x x x0 x x 0 0 2 2 (x x )(x xx x ) 0 0 0 lim x 0 x x x 0 2 2 2 lim (x xx x ) 3x 0 0 0 x x0 Vậy / f øx ù 2 0 3x0. Ví dụ 30. Cho hàm số: ü1 cos3x x 0, f (x) ý x 0 þ x 0.
Tính đạo hàm của hàm số tại điểm 0. Giải Xét giới hạn 1 cos3x f øx ù f ø0 ù 1 cos3x 1 cos 3x 9 x lim lim lim lim 9 . 2 2 x 0 x 0 x 0 x x 0 x 0 x 9x 2 9
Vậy hàm số có đạo hàm / f ø0 ù . 2
4.6.1.2. Ý nghĩa hình học của đạo hàm
Cho hàm số f (x) có đồ thị øC ù, một điểm M0 cố định thuộc øC ù có hoành độ x0.
Với mỗi điểm M thuộc øC ù khác M0, ta ký hiệu xM là hoành độ của nó và M k là hệ số góc của cát tuyến M M. 0
Giả sử tồn hạn hữu hạn k lim k . 0 M Khi đó đường thẳng xM x0 104 0 M T đi qua 0
M và có hệ số góc là k0 là vị trí giới hạn của cát tuyến M0M khi M di
chuyển dọc theo øC ù dần đến M . 0 Đường thẳng 0
M T được gọi là tiếp tuyến của øC ù tại điểm M0, còn 0 M còn gọi là tiếp điểm.
Đạo hàm của hàm số f (x) tại điểm x là hệ số góc của tiếp tuyến với đồ thị hàm 0
số y f (x) tại điểm M øx / 0, f (x 0) ù. Ta có f ø 0 x ù tan
Phương trình tiếp tuyến đó là: / y f (x0) f (x0)(x x0).
Ví dụ 31. Viết phương trình tiếp tuyến với đồ thị øC ù của hàm số 2 y f (x) x tại điểm có hoành độ x0 2. Giải Với 0 x 2 f (x0 ) f ø 2 ù 2 Hệ số góc: / / f (x ) f 2 2 2 0 ø ù
Phương trình tiếp tuyến với đồ thị øC ù của hàm số 2 y f (x) x có dạng: / y f (x0) f (x0)(x x0). Hay y 2 2 2 øx 2 ù y 2 2x 2.
4.6.1.3. Ý nghĩa của đạo hàm 105
Cho hàm số y f øx ù xác định trên một lân cận của điểm / / 0 x : f øx hay y øx 0 ù 0 ù
biểu thị tốc độ thay đổi của giá trị hàm số f øx ù tại điểm x0 , khi đối số x thay đổi một
lượng nhỏ. Nói cách khác, tại điểm x khi đối số 0
x thay đổi một lượng nhỏ thì giá trị hàm
số f øx ù sẽ thay đổi một lượng xấp xỉ bằng / f øx . 0 ù
4.6.2. Bảng công thức các đạo hàm cơ bản
Dưới đây là bảng công thức tính đạo hàm của một số hàm sơ cấp cơ bản 1. ø ù/ c 0 ( với c là hằng số) 9. ø ù/ cos x sin x 2. ø ù/ x 1 1 10. øtan x ù/ 2 1 tan x 2 cos x 3. ø ù/ 1 x x 1 11. øcot x ù/ ø 2 1 cot x ù 2 sin x 4. ø ù/ x x a a lna 1 12. øarcsin x ù/ 2 5. ø ù/ x x e e 1 x 1 13. øarccos x ù/ 6. ø ù/ 1 ln x 2 1 x x 1 1 14. øarctan x ù/ 7. ølog x ù/ 2 a 1 x x ln a 1 8. ø ù/ sin x cos x 15. øarccot x ù/ 2 1 x
4.6.3. Các quy tắc tính đạo hàm
Cho hai hàm số f , g :øa,b ù
khả vi tại x øa,b ù thì các hàm f f g, gf ,
, (g(x) 0) có đạo hàm x và g a) ø ù/ / / f g (x) f (x) g (x) . b) ø ù/ / / fg (x) f (x)g(x) f (x)g (x). / / / f f (x)g(x) f (x)g (x c) (x) ) . 2 g g (x)
Ví dụ 32. Tính đạo hàm của các hàm số sau: a) 5 3 2 y x 3x 4x x 2 106 1 3x b) y x 2 Giải a) 5 3 2 y x 3x 4x x 2
Đạo hàm của hàm số trên: / 4 2 y 5x 9x 8x 1 1 3x b) y x 2 / /
Đạo hàm của hàm số trên: / (1 3x) (x 2) (1 3x)(x 2) 7 y . 2 2 (x 2) (x 2) Lưu ý ax b ad bc Nếu hàm số y thì đạo hàm / y . cx d 2 (cx d) 4.6.4. Đạo hàm hàm hợp Cho hàm số ø ù f ø ù g a,b c,d
Nếu f có đạo tại x øa,b ù và g có đạo hàm tại y f (x) øc,d ù thì g f (x) có
đạo hàm tại x øa,b ù và ø ù/ / / g f (x) g f (x) f (x) .
Áp dụng quy tắc tính đạo hàm của hàm hợp, nếu u u(x) là một hàm có đạo hàm
thì ta có bảng các công thức như sau: / 1. ø ù/ 1 / u u u u 8. øtan u ù/ 2 cos u 2. ø ù/ u u / a a ln a u / u 9. øcot u ù/ 2 sin u 3. ø ù/ u u / e e u / u 10. øarcsin u ù/ / 2 1 u 4. ø ù/ u ln u u / u 11. øarccosu ù/ / u 2 5. ølog u ù/ 1 u a uln a / u 12. øarctan u ù/ 6. ø ù/ / sin u cos u u 2 1 u 7. ø ù/ / cos u sin u u / u 13. øarccot u ù/ 2 1 u 107
Ví dụ 33. Tính đạo hàm của các hàm số sau a) ø ù100 4 y x 6x 5 b) 2 y arctan(x 2x) Giải a) ø ù100 4 y x 6x 5
Đạo hàm của hàm số trên ø ù99 / 4 3 y 100 x 6x 5 (4x 6) b) 2 y arctan(x 2x)
Đạo hàm của hàm số trên x 2x / ø ù/ 2 2x 2 y 2 2 4 3 2 1 (x 2x) x 4x 4x 1
4.6.5. Đạo hàm của hàm ngược Cho hàm số f : øa,b ù
øc,d song ánh khả vi thì 1 f : øc,d ù øa,b khả vi và / 1 ø 1 f ù(y) , y øc,d ù. (4.8) / 1 f f (y) û Ví dụ 34. Cho hàm số x f (x) e
Hàm ngược của hàm f (x) là 1 f (x) ln x và / x f (x) e .
Áp dụng công thức đạo hàm của hàm ngược, ta có / 1 1 1 1 ø 1 f ù(x) . 1 / 1 ln x f (x ) f f (x) e e x û
4.6.6. Đạo hàm một phía
Cho hàm số y f (x) xác định trong lân cận phải tại x . Đạo hàm phải của f (x) 0
tại x0 là giới hạn (nếu có) của tỉ số y f ø 0 x x ù f ø0 x ù x x khi x
0 . Khi ấy đạo hàm phải tại x được ký hiệu / f (x). 0 Vậy 108 / f øx0 x ù f øx 0 f ( 0 x ) lim . x 0 x Tương tự / f øx0 x ù f øx 0 f ( 0 x ) lim . x 0 x
Hàm số có đạo hàm tại 0 khi và chỉ khi hàm số vừa có đạo hàm bên phải và hàm số
vừa có đạo hàm bên trái, nghĩa là / / f ( 0 x ) f ( 0 x ).
Ví dụ 35. Cho hàm số : f (x)
x . Hàm số có đạo hàm tại 0 hay không? Giải Ta có y f ø0 x ù f ø0 ù 0 x 0 x x x x x Đạo hàm bên phải: / f ø0 x ù f ø0 ù x x f (0) lim lim lim 1 x 0 x x 0 x x 0 x Đạo hàm bên trái: / fø0 x ù f ø0 ù x x f (0) lim lim lim 1 x 0 x x 0 x x 0 x
Tại điểm 0 hàm số f (x) x không có đạo hàm vì / / f (0) f (0). 4.6.7. Đạo hàm cấp cao Cho hàm số f : øa,b ù , khả vi tại trên (a,b) Ta có / f : øa,b ù / / x f (x) y Nếu /
f khả vi tại x, ta viết ø ù/ / // f (x) f (x) Qui nạp : (n) f :øa, b ù
, khả vi trên øa,b ù, ta viết ø ù/ (n) (n 1) f (x) f (x) . Qui ước : (0) f f.
Mệnh đề : Nếu u, v là hai hàm khả vi cấp n trên khoảng (a,b). Ta có 109 n øu v ù(n) k (k ) (n k) C u v (4.9) n k 0
Ví dụ 36. Tính đạo hàm cấp n của hàm số sau : 1 f (x) x 2 Giải Đạo hàm cấp 1 / 2 f (x) ( 1)(x 2) Đạo hàm cấp 2 // 3 f (x) ( 1)( 2)(x 2) Đạo hàm cấp 3 (3) 4 f (x) ( 1)( 2)( 3)(x 2)
Dự đoán đạo hàm cấp n (n) n (n 1) f (x) ( 1) n!(x 2) . 4.7. Vi phân của hàm số
4.7.1. Định nghĩa vi phân
Cho hàm số y f(x) xác định trên X. Giả sử f (x) liên tục tại x X. Nếu số gia 0
của hàm số f (x) tại x có thể biểu diễn được dưới dạng: 0 f(x) A x ( x) (4.10)
trong đó, A là một hằng số, ø x ù là một vô cùng bé bậc cao hơn x thì ta nói hàm số
f (x) khả vi tại x và giá trị A x được gọi là vi phân của hàm số f (x) tại điểm x , ký 0 0
hiệu là df øx . Như vậy, ta có 0 ù df (x ) A x (4.11) 0
4.7.2. Sự liên hệ giữa vi phân và đạo hàm
Hàm số f (x) khả vi tại x khi và chỉ khi hàm số f (x) có đạo hàm tại x và khi đó 0 0 / df(x ) f x x (4.12) 0 ø 0 ù
Nếu hàm số khả vi tại mọi điểm trong khoảng X thì ta nói hàm số khả vi trong X.
Khi đó, ta có một hàm số xác định trên X gọi là biểu thức vi phân của hàm số, ký hiệu: df (x) hay dy. 110 df (x) dy A x (4.13)
Đặc biệt nếu y x thì dx
x. Do đó, biểu thức vi phân của hàm số y f(x)
thường được viết dưới dạng: / df (x) f (x)dx (4.14)
4.7.3. Tính bất biến của biểu thức vi phân cấp 1
Xét hàm số hợp y f (x), x x(t) . Biểu thức vi phân của hàm số là / dy y dt ø / / y x ù / dt y dx (4.15) t x t x
Như vậy, biểu thức vi phân giữ nguyên dạng trong trường hợp x là biến độc lập,
cũng như x là biến trung gian.
4.7.4. Các quy tắc tính vi phân
Nếu các hàm số u u(x) và v v(x) khả vi tại điểm x thì tại điểm đó ta có: 0 a. d(u v) du dv b. d(u v) du dv
c. d(ku) kdu (k là hằng số) d. d(uv) vdu udv u vdu udv e. d , (v 0) 2 v v x
Ví dụ 37. Tính vi phân của hàm số y xcos tại x khi x 0,01. 2 0 2 Giải x x x Ta có: / y cos sin 2 2 2 1 Tại x , ta có / y 1 0 2 2 2 4 Vậy 4 / dy y x . 2 2 400 2 4.7.5. Vi phân cấp cao
Định nghĩa: Vi phân cấp n của hàm số y f(x) là vi phân của vi phân cấp (n 1)
của hàm số đó, ký hiệu là n d y hay n d f (x): 111 n ø n 1 d y d d y ù
Khi x là biến độc lập, ta có: ø ùn n (n) d y f (x) dx . (4.16)
Ví dụ 38. Tính vi phân cấp 2 của hàm số: 2x y e Giải Ta có ø ù/ 2x 2x dy e dx 2e dx. / ø ù ø ù ø ù2 ø ù 2 2 2x 2x d y d dy 2e dx 4e dx .
4.8. Các định lý cơ bản về hàm số khả vi 4.8.1. Định lý Fermat
Giả sử hàm số f (x) xác định trong lân cận điểm x x
0 và đạt cực trị tại 0 . Nếu tại / / 0
x tồn tại đạo hàm f øx thì f øx0 ù 0 ù 0. 4.8.2. Định lý Rolle
Giả sử hàm số f (x) xác định, liên tục trên đoạn a,b và khả vi trên khoảng øa,b ù.
Nếu f øa ù f øb thì tồn tại điểm c øa,b ù sao cho / f øc ù 0.
Ví dụ 39. Cho hàm số ø ù 5 4 3 2 f x x 3x x x 3x 2 .
Chứng minh rằng phương trình / f (x) 0 có nghiệm. Giải
Hàm số f (x) xác định và khả vi trên . Mặt khác, f (1) f (2) 0.
Theo kết quả của định lý Rolle, tồn tại c ø1,2ù thỏa mãn / f øc ù 0. Vậy phương trình /
f (x) 0 có nghiệm trong khoảng ø1,2 ù. 4.8.3. Định lý Lagrange
Nếu hàm số f (x) xác định, liên tục trên đoạn a,b và khả vi trên khoảng øa,b ù
thì tồn tại điểm c øa,b ù sao cho / f (b) f (a) f (c) øb a ù.
Ví dụ 40. Chứng minh rằng: lnø1 x ù x, x 0. Giải 112 Đặt f (x) lnø1 x ù x với x 0.
Ta có f liên tục và có đạo hàm: / 1 x f (x) 1 trên ø0, x ù 1 x 1 x
Áp dụng định lý Lagrange ta có /
f (x) f (0) (x 0)f (c), c ø0, x ù hay c ln(1 x) x x 0 1 c Vậy lnø1 x ù x, x 0 . 4.8.4. Định lý Cauchy
Nếu các hàm số f (x), gøx ù xác định, liên tục trên đoạn a,b và khả vi trên
khoảng øa,b ù và g(x) 0, x øa,b ù thì tồn tại điểm c øa,b ù sao cho / f (c) f (b) f (a) . (4.17) / g (c) g(b) g(a)
4.9. Một số ứng dụng của đạo hàm và vi phân 0
4.9.1. Quy tắc L’hospital khử dạng vô định , 0
Cho hai hàm số f , g :øa,bù
là hai hàm khả vi, với a, b , . / f (x) Nếu lim L
và lim f (x) lim g(x) 0 hay lim f (x) lim g(x) / x b g (x) x b x b x b x b f (x) thì lim L. x b g(x)
Ví dụ 41. Tính các giới hạn hàm số sau : 3x e 1 a) lim x 0 arctan 2x ln(2x 1) b) lim x x 113 c) lim xln x x 0 d) x lim x x 0 Giải 3x e 1 0 a) lim (có dạng ) x 0 arctan 2x 0 øe 1ù/ 3x 3x 3e 3 Xét lim lim øarctan 2x ù/ x 0 x 0 2 2 2 1 4x
Theo quy tắc L’Hospital, ta có 3x e 1 3 lim . x 0 arctan 2x 2 ln(2x 1) b) lim (có dạng ) x x / l n(2x 1) 2 Xét lim lim 0 / x x x 2x 1 ln(2x 1)
Theo quy tắc L’Hospital, ta có lim 0. x x c) lim xln x (có dạng 0 ) x 0 ln x Ta có lim x ln x lim (có dạng ) x 0 x 0 1 x 1 øln x ù/ Xét x lim lim lim øx ù 0. / x 0 x 0 1 x 0 1 2 x x
Theo quy tắc L’Hospital, ta có lim x ln x 0. x 0 d) x lim x (có dạng 0 0 ) x 0 Ta có x x ln x lim x lim e x 0 x 0 Theo câu c), ta có x 0 lim x e 1. x 0 114 4.9.2. Tính gần đúng
Chúng ta có kết quả là số gia hàm số tại điểm x0 xấp xỉ với vi phân của hàm số tại điểm đó: Ta có: f øx ù df øx ù f ø x x ùf ø x ù / 0 0 0 0 f x ø 0 ù x Vậy f øx x ù f øx ù / 0 0 f øx0 ùx. (4.18)
Ví dụ 42. Tính gần đúng biểu thức sau: A lnø1,005 ù Giải Đặt : / 1 f (x) ln x f (x) x Với x0 1, x 0,005 Ta có : / f (x) f (x ) f (x ) x 0 0 Suy ra ø ù 1 A ln 1,005 ln(1) 0,005 0,005 . 1
4.9.3. Khảo sát tính tăng, giảm và cực trị của hàm số Cho hàm số : y f(x)
+) Bước 1. Tìm tập xác định
+) Bước 2. Tính đạo hàm và tìm điểm dừng
+) Bước 3. Tính giới hạn tại các đầu mút
+) Bước 4. Kẻ bảng biến thiên +) Bước 5. Kết luận
Ví dụ 43. Khảo sát tính tăng, giảm và cực trị của hàm số sau : f (x) x ln x
Bước 1. Tập xác định : D ø0, ù Bước 2. Đạo hàm : / f (x) ln x 1 115 Cho / 1 f (x) 0 ln x 1 0 x e D Bước 3. Giới hạn lim x ln x ; lim x ln x 0 x x 0
Bước 4. Bảng biến thiên x 0 1 e / y 0 y 0 0 CT Bước 5. Kết luận
+) Hàm số giảm (nghịch biến) : ø 1 0, e ù
+) Hàm số tăng (đồng biến) : ø 1 e , ù
+) Hàm số đạt cực tiểu tại 1 x e với 1 f e . min
4.9.4. Khai triển Taylor – Maclaurin Cho hàm số f : øa,b ù
khả vi đến cấp n 1 . Khi ấy với x 0, x (a,b) ta có
công thức khai triển Taylor tại x của hàm số f (x) cóa dạng như sau : 0 / (n) f (x0) f (x0) n f (x) f ( 0 x ) (x 0 x ) (x 0 x ) n R 1 (x) (4.19) 1! n! với / (n) f (x ) f (x ) 0 0 n P(x) f (x ) (x x )
(x x ) gọi là đa thức Taylor. 0 0 0 1! n! (n 1) f (c) n 1 Rn 1(x) (x x0 ) , c x0 (x x0 ), 0 1 gọi là phần dư. (n 1)!
Tại x 0 0 thì công thức khai triển Taylor được gọi là công thức khai triển Maclaurin: / // (n) f (0) f (0) 2 f (0) n f (x) f (0) x x x n R 1 (x) (4.20) 1! 2! n! với phần dư 116 (n 1) f (c) n 1 R n 1(x) x , c x, 0 1. (n 1)!
Một số công thức khai triển Maclaurin cơ bản 2 n x n 1 x x x e x a) e 1 x 2! n! (n 1)! 2 3 n n 1 x x n 1 x n x b) ln(1 x) x ( 1) ( 1) n 1 2 3 n (n 1)(1 x) 3 5 2n 1 2n 1 x x n 1 x n x c) sin x x ( 1) ( 1) cos x 3! 5! (2n 1)! (2n 1)! 2 4 2n 2n 2 x x n x n 1 x d) cosx 1 ( 1) ( 1) sin x 2! 4! (2n)! (2n 2)! e) ø1 x ù ( 1) 2 ( 1) ( n 1) n 1 x x x 2! n! ( 1) ( n) x ø1 x ù n 1 n 1 (n 1)!
Ví dụ 44. Khai triển Taylor của hàm số sau tới lũy thừa bậc 3 f (x) arctan x tại x 0 1 Giải 2 4 Ta có : / 1 // 2x / / / 2(1 2x 3x ) f (x) ; f (x) ;f (x) 2 2 2 2 4 1 x (1 x ) (1 x ) 1 1 1 Với x0 1, ta có / // / // f (1) ; f (1) ; f (1) 2 2 2
Áp dụng công thức khai triển Taylor tại x0 1, ta có / // (3) f (1) f (1) 2 f (1) 3 f (x) f (1) (x 1) (x 1) (x 1) R4(x) 1! 2! 3! Vậy: 1 1 1 2 3 arctan x (x 1) (x 1) (x 1) R (x). 4 4 2 4 12
Ví dụ 45. Tính gần đúng số e với sai số không vượt quá 4 10 . Giải Đặt : x f (x) e Ta có : / x // x (n) x f (x) e ; f (x) e ;...;f (x) e 117 Suy ra (n) f (0) 1, n Vậy 2 n x n 1 x x x e x e 1 x 2! n! (n 1)! 1 1 e Với x 1, ta có e 1 1 2! n! (n 1)! Ta có sai số e e 3 4 10 (n 1)! (n 1)! (n 1)! Suy ra (n 1)! 30000 n 7 Do đó 1 1 1 1 1 1 e 1 1 2,718253968. 2! 3! 4! 5! 6! 7!
Ví dụ 46. Dùng công thức khai triển Maclorent tính giới hạn sau 2 4 2 2cos x x 2x a) lim x 0 x(x tan x) x 3 2 6e x 3x 6x 6 b) lim x 0 x sin x 3 4 3x 3arctan x x x c) lim x 0 x(x tan x) Giải 2 4 x x 2 4 2 2 1 x 2x 2 4 2 2cos x x 2x 2! 4! 23 23 a) lim lim lim . 3 x 0 x(x tan x) x 0 x 0 x 4 4 x x x 3 2 3 x x 3 2 6 1 x x 3x 6x 6 x 3 2 6e x 3x 6x 6 2! 3! b) lim lim 12. 3 x 0 x sin x x 0 x x x 3! 118 3 x 3 4 3x 3 x x x 3 4 3x 3arctan x x x 3 c) lim lim lim( 3) 3. 3 x 0 x(x tan x) x 0 x 0 x x x x 3
4.9.5. Ứng dụng trong bài toán kinh tế 4.9.5.1. Hàm cận biên
Hàm cận biên của đại lượng y f(x) theo đại lượng x tại x0 , ký hiệu là Mf øx0 ù,
là độ biến đổi của đại lượng y khi đại lượng x tăng lên 1 đơn vị tại x0 .
Biểu thức toán học của hàm cận biên f (x x) f (x ) y 0 0 / Mf (x0) lim lim f (x0 ) . (4.21) x 0 x x 0 x
Tổng quát ta có, hàm cận biên của đại lượng y f(x) theo đại lượng x , là / Mf (x) f (x) . (4.22)
Chú ý : Trong thực tế, lượng cận biên Mf ( x ) của y f( )
x theo x tại x xấp xỉ bằng độ 0 0
biến đổi của y khi x tăng 1 một đơn vị từ trạng thái x 0 x . 4.9.5.2. Hệ số co dãn
Hệ số co dãn của đại lượng y f(x) theo đại lượng x tại x0 , ký hiệu E , là độ y x
biến đổi của y khi x tăng lên một đơn vị (1%).
Biểu thức của hệ số co dãn / x E f (x) (%) y x . (4.23) y
4.9.5.3. Bài toán tối ưu trong kinh tế
Bài toán : Giả sử một xí nghiệp sản xuất độc quyền một loại sản phẩm. Biết hàm cầu là D Q
D(P) (P là đơn giá) và hàm tổng chi phí là TC TC(Q) (Q là sản lượng).
Hãy xác định mức sản lượng Q để xí nghiệp đạt lợi nhuận tối đa.
Giải quyết bài toán : Với một mức sản lượng Q, để bán hết sản phẩm, thì xí nghiệp
cần phải bán theo một đơn giá P sao cho D Q Q . Do đó, ta có 1 D(P) Q
P D (Q) , mặt khác doanh thu của xí nghiệp là 1
TR(Q) P Q D (Q) Q và lợi nhuận thu được của xí nghiệp là 119 1
(Q) TR(Q) TC(Q) D (Q) Q TC(Q) .
Vậy theo yêu cầu bài toán, ta cần tìm Q sao cho đạt giá trị lớn nhất.
Ví dụ 47. Cho hàm tổng chi phí 2 TC(Q) 0,1Q 0,3Q 100, (Q 0)
a) Tìm hàm chi phí biên MC(Q).
b) Tính chi phí biên tại mức sản lượng Q
120 và giải thích ý nghĩa kết quả nhận 0 được. Giải a) Hàm chi phí biên: / MC(Q) TC (Q) 0,2Q 0,3, (Q 0) .
b) Tại mức sản lượng Q 120 , ta có MC(120) 24,3. 0
Ý nghĩa: Tại mức sản lượng là 120 khi ta tăng Q lên một đơn vị thì chi phí tăng lên 24,3 đơn vị.
Ví dụ 48. Cho hàm cầu của một loại sản phẩm là Q
1000 5P. Tính hệ số co dãn của D
cầu theo giá tại mức giá là 120 đơn vị và nêu ý nghĩa. Giải
Đạo hàm của sản lượng Q theo mức giá P là / Q øP ù 5
Áp dụng công thức hệ số co dãn của cầu theo giá, ta có P 5P / E Q (P) D Q 1000 5P
Tại mức giá P 120, ta có E
1,5, nghĩa là khi đang bán với đơn giá P 120, D
nếu ta tăng giá lên 1%, thì lượng cầu sẽ giảm đi khoảng 1,5%.
Ví dụ 49. Cho hàm sản xuất 2 3 Q 120L
L , L 0. Hãy xác định mức sử dụng lao động
để sản lượng tối đa. Giải Đạo hàm cấp 1: / 2 Q (L) 240L 3L . Giải phương trình: / 2 Q (L) 240L 3L 0
L 80 (nhận) hay L 0 (loại).
Hàm số có điểm dừng: L 80 Đạo hàm cấp 2 : // Q (L) 240 6L, tại L 80. Xét tại L 80, ta có // Q (80) 240 0 120
Vậy khi lao động là L 80 thì sản lượng cực đại, với m Q ax 256000.
Ví dụ 50. Một xí nghiệp sản xuất độc quyền một loại sản phẩm. Biết hàm cầu của xí nghiệp 1 là Q và hàm tổng chi phí 3 2 D 656 P TC(Q) Q 77Q 1000Q 40000. Hãy xác 2
định mức sản lượng Q và giá bán tương ứng sao cho xí nghiệp đạt lợi nhuận tối đa. Giải
Với một mức sản lượng Q , để bán hết sản phẩm, thì xí nghiệp cần phải bán theo một đơn giá P sao cho Q Q . Do đó, ta có D 1 QD Q 656 P Q P 1312 2Q , 2
Mặt khác doanh thu của xí nghiệp là 2 TR(Q) P Q (1312 2Q) Q 2Q 1312Q
và lợi nhuận thu được của xí nghiệp là ø ù ø ù ø ù 2 3 2 Q TR Q TC Q 2Q 1312Q (Q 77Q 1000Q 40000 3 2 Q 75Q 312Q 40000
Bây giờ ta tìm Q 0 sao cho đạt giá giạ lớn nhất. Đạo hàm cấp 1: / 2 2 (Q) 3Q 150Q 312 Suy ra / 2 (Q) 0 3Q 150Q 312 0 Q 2 (loaï)i hay Q 52 Mặt khác, //(Q) 6Q 150 Xét tại Q 52, ta có //(52) 162 0 .
Vậy (Q) đạt cực đại tại Q 52 .
Khi đó, ta có các kết quả phù hợp sau : Lợi nhuận : 38416 , Đơn giá : P 1208, Tổng chi phí : TC 24400 . Kết luận:
Để đạt lợi nhuận cao nhất, xí nghiệp cần sản xuất với mức sản lượng Q 52. Khi
đó lợi nhuận tương ứng là 38416. 121 4.10. Bài tập
Bài số 1. Dùng định nghĩa để chứng minh rằng các dãy sau có giới hạn là 0 khi n n 1 ( 1) 1. xn n 2n 2. x n 3 n 1 3. x ( 1) ø0,999 ùn n n 1 2 Hướng dẫn : 1) xn ; 2) x ; 3) n x 0,999 . n n 2 n n
Bài số 2. Chứng minh rằng các dãy sau hội tụ 1 1 1 1. x 1 1 .... 1 n n 2 4 2 2. x 2, x 2 2 ,..., x 2 2 2 ( n căn) 1 2 n
Hướng dẫn : Chương minh dãy tăng bị chặn trên.
Bài số 3. Tính các giới hạn sau (n 1)(n 2)(n 3) 1 1 1 1. lim 1 3 2 n n 3n 5. 2 2 2 lim 1 1 1 ø n 1 n 1 2n ù2 2 2 n 3 3 3 2. lim 3 n 6 n 2 1 1 1 6. lim n 1 2 2 3 (n 1)n n 1 n 2 2 3 3. lim n n 1 n 2 3 1 1 1 7. lim 1 1 .... 1 2 2 2 n 2 3 n 1 2 n 1 4. lim 2 2 2 n n n n 8. n lim aq , q 1 n 1 1 4 1
Đáp số : 1) ; 2) 9; 3) 3; 4) ; 5) ; 6) 1; 7) ; 8) 0. 3 2 3 2
Bài số 4. Tính các giới hạn sau 1 2x 3 1 sin x 1 sin x 1. lim 10. lim x 4 x 2 x 0 x m x 1 ln cos x 2. lim 11. lim n 2 x 1 x 1 x 0 x 122 3 xosx cos x 3. lim x x x x 12. lim x 2 x 0 x ø1 x ùø 3 1 x ù ø n 1 x x 1 e 1 lim ln 4. lim 13. ø x x x 1 x ùn 1 x 1 2 2 2 x 1 x x 7 2x x 5. lim 14. lim 2 5 x 2 x 0 1 5x ø1 x ù x 2x x x 1 6. lim ø øx a x a x 15. lim 1 ù ø 2 ù ù x x 1 x ln x sin5x x x 5 4 7. lim 16. lim x 0 t an8x 2 x 0 x 2x 1 2 x 8. lim cot x 17. lim cos x x 0 sin x x 0 18. sin x lim cos x 1 cosx x 0 9. lim 2 x 0 x 19. x lim 1 sin 2x x 0 4 n 1 1 1 a a 5 1 Đáp số : 1) ; 2) ; 3) ; 4) ; 5) ; 6) 1
2 ; 7) ; 8) 0; 9) ; 10) 1; 11) 3 m 2 n! 2 2 8 4 1 1 7 1 5 1 ; 12) ; 13) 1; 14) ;15) 1; 16) ln ; 17) ; 18) 1; 19) 2 e . 2 12 4 2 4 e
Bài số 5. Xét tính liên tục các hàm số sau üsin x khi x 0 1. f (x) ý x 0 khi x 0 þ ü 2 1 x sin khi x 0 2. f (x) ý x 0 þ khi x 0
Đáp số: 1) Liên tục bên phải tại 0; 2) Liên tục tại 0.
Bài số 6. Định a để hàm số sau liên tục tại 0 x x üe e , x 0, f (x) ý sin 2x þa, x 0. Đáp số : a 1. 123
Bài số 7. Dùng định nghĩa, tính đạo hàm của hàm số sau : f (x) x x Đáp số : / f (x) 2 x
Bài số 8. Chứng minh hàm số : ø 2 ùøx y x 1 e
2 ù thỏa mãn phương trình 2xy / x y e ø 2 x 1 2 ù x 1
Hướng dẫn : Tính đạo hàm rồi thay vào đẳng thức ta có điều phải chứng minh. 2 cos x
Bài số 9. Cho hàm số f (x) . Chứng minh / f 3f 3 . 2 1 sin x 4 4
Hướng dẫn : Tính đạo hàm rồi thay vào đẳng thức ta có điều phải chứng minh. x n ( 1) n(n 1) Bài số 10. Cho hàm số 2 2 f (x) x e . Chứng minh (n) f (0) . n 2 2 n
Hướng dẫn : Sử dụng công thức tính đạo hàm øu v ù(n) k (n k ) (k) Cnu v . k 0 1 x
Bài số 11. Cho hàm số f (x) ln . Tính (2019) f ø0ù. 1 x
Hướng dẫn : Tính đạo hàm cấp 1,2,3,..,rồi dự đoán đạo hàm cấp n. Bài số 12. Cho hàm số m n f (x) 1 x (x 1) với m, n
. Chứng minh rằng phương trình /
f (x) 0 có ít nhất một nghiệm nằm trong khoảng (0, 1).
Hướng dẫn : Sử dụng định lý Rolle
Bài số 13. Ứng dụng đạo hàm chứng minh rằng với mọi x 0 ta có 2 x x ln ø1 x ù x 2 Hướng dẫn : xét 2
f (x) ln(1 x) x; g(x) ln(1 x) x x / 2, tính đạo hàm. ü 2 1 x sin khi x 0,
Bài số 14. Cho hàm số f (x) ý x 0 þ khi x 0. Chứng minh rằng : /
f øx ù xác định với mọi x .
Hướng dẫn : Dùng định nghĩa tính đạo hàm tại 0.
Bài số 15. Tính đạo hàm /
y øx ù của các hàm được xác định như sau 124 1. ø 2 x ln 1 t ù, y t arctan t 2. 3 2 y x ln y x e 0
Hướng dẫn : 1) Dùng công thức đạo hàm theo tham số;
2) Dùng công thức đạo hàm hàm ẩn. 0 ü khi x 0, Bài số 16. Cho hàm số x f (x) / ý khi x 0. . Tính f ø0 ù 1 x 1 þ e
Hướng dẫn : Dùng định nghĩa đạo hàm. a ü x b khi x 2,
Bài số 17. Cho hàm số f (x) ý 2 x þ khi x 2.
Tìm giá trị của a và b để hàm số f có đạo hàm tại mọi điểm. Đáp số : a 4, b 8. 2 x ü 2x 2 khi x 1,
Bài số 18. Cho hàm số f (x) ý 2 þ x khi x 1.
Hàm số f có đạo hàm tại điểm 1 không?
Đáp số : Hàm số không có đạo hàm tại 1. x üe 1
Bài số 19. Cho hàm số ø ù khi x 0 f x ý x . m þ khi x 0
Tìm m để hàm f liên tục tại x 0 . Với m tìm được hãy tính / f ø0 ù. 1 Đáp số: / m 1; f (0) . 2 2x ü3 1 , x 0,
Bài số 20. Cho hàm số : f (x) ý x 2l þ ø n mù, x 0.
1. Định m để hàm số sau liên tục tại 0
2. Với m vừa tìm được ở câu 1. Tính / f ø0 ù. Đáp số : / ø ù 2 1) m 3; 2) f 0 2ln 3.
Bài số 21. Tính vi phân của các hàm số sau 125 a x 1. y arctan x a 2. 2 2 y x x a 3. 5 2 y y x 1 4. y x y e
Hướng dẫn : Tính đạo hàm rồi thế vào biểu thức vi phân
Bài số 22. Tính gần đúng 1. 4 17
2. arctanø0,97 ù 3. tanø46 ù 4. 5 32,002
Đáp số : 1) 2,03125; 2) 0,7704; 3) 1,0349; 4) 2,000025.
Bài số 23. Tính đạo hàm cấp n của hàm số sau 1. f (x) sin x 1 x 2. f (x) 1 x 3. f(x) sin2x cos3x 1 4. f (x) 2 x 5x 6 2 n! Đáp số : 1) (n) f (x) sin x n ; 2) (n) f (x) 2 n 1 (1 x) 3) (n) n n f (x) 2 sin 2x n 3 cos 3x n . 2 2 n n 4) (n) ( 1) n! ( 1) n! f (x) . n 1 n 1 (x 3) (x 2)
Bài số 24. Khai triển Maclorent các hàm số sau tới lũy thừa bậc 5. 1 1. f (x) x 1 2x 2. f (x) 2 x 1 1 3. f (x) 2 x 3x 2 4. f (x) x x 1 Đáp số : 1) 2 3 4 5 1 x x x x x . 2) 3 5 2x 2x 2x . 126 1 3 7 15 31 63 3) 2 3 4 5 x x x x x . 2 4 8 16 32 64 3 1 1 5 7 4) 2 3 4 5 1 x x x x x . 2 8 16 128 256
Bài số 25. Khai triển Taylor của hàm số sau tại điểm x 2 tới lũy thừa bậc 4. 0 x f (x) x 1 Đáp số : 2 3 4 2 (x 2) (x 2) (x 2) (x 2) .
Bài số 26. Khảo sát tính tăng giảm và cực trị của hàm số sau 1. ø ù x f (x) x 5 e 2. 3 2 f (x) (2x 1) x ln x 3. f (x) 2 x 4. f (x) x ln x
Bài số 27. Giả sử giá thành để sản xuất x cặp quần jean được cho bởi hàm ø ù 2 3 C x 2000 3x 0,01x 0, 0002x
1. Xác định hàm chi phí biên. 2. Tìm /
C ø100 ù và giải thích ý nghĩa. Giá trị này dự báo điều gì?
3. So sánh giá Cø100 ù với giá thành để sản xuất sản phẩm thứ 101. Đáp số: 1) / ø ù 2 C x 3 0,02x 0,0006x ; 2) / C ø100 ù 11; 3) ø ù ø ù / C 101 C 100 11,0702 C ø 100 .
Bài số 28. Cho hàm sản xuất ngắn hạn Q 30 L ; L 0
1. Tìm hàm sản phẩm cận biên của lao động MPL. 2. Tại L
144, nếu L tăng thêm một đơn vị thì Q sẽ thay đổi bao nhiêu đơn vị? 0
3. Tại mức sử dụng lao động nào đó, nếu L tăng thêm 1%, hỏi sản lượng sẽ thay đổi bao nhiêu %? Hướng dẫn: 1) Tính / MPL Q ; 2) MPL(144) 1,25; 3) L Q/L 0,5.
Bài số 29. Cho hàm cầu của một loại hàng hoá là 2 Q
6P P . Tính hệ số co dãn tại D P
5 và giải thích ý nghĩa kết quả nhận được. 0 127 Đáp số : E 4. D
Bài số 30. Cho biết hàm sản xuất ngắn hạn 5 3
Q 100 L , L 0 và giá của sản phẩm là
P 5 USD , giá thuê lao động là P
3 USD . Hãy tìm mức sử dụng lao động để lợi nhuận L tối đa. Đáp số: L 100000 .
Bài số 31. Cho biết hàm tổng chi phí là 3 2 TC(Q) 4Q 5Q 500; Q 0 và hàm cầu
Q 11160 P . Hãy xác định mức sản lượng Q và giá bán tương ứng để lợi nhuận đạt cực đại. Đáp số: Q 30, P 11130.
Bài số 32. Cho biết hàm tổng chi phí là 3 2 TC(Q) Q Q 8 57Q 2; Q 0 và hàm cầu 1 đảo P 45
Q . Hãy xác định mức sản lượng Q và giá bán tương ứng để lợi nhuận đạt 2 cực đại. Đáp số: Q 4, P 43.
Bài số 33. Một công ty có hàm cầu về sản phẩm và hàm tổng chi phí là: 45 3 Q P 2750 Q ; TC øQ ù 2 15Q 2500Q 8 30
trong đó P là giá và Q là sản lượng.
1. Tính sản lượng và giá bán để tối đa hóa lợi nhuận.
2. Tính và nêu ý nghĩa hệ số co dãn của cầu sản phẩm tại mức giá và sản lượng tối ưu?
3. Tìm giá bán để tối đa hóa sản lượng bán ra mà công ty không bị lỗ? 13 Đáp số: 1) max ø200 ù 158333; 2) ; 3) 305,778. 9
Bài số 34. Cho biết hàm cầu ngược và hàm chi phí của một nhà độc quyền như sau: 2
P 200 Q, TC Q (trong đó P là giá, Q là sản lượng)
1. Tìm mức sản lượng và mức giá để lợi nhuận cực đại.
2. Tính hệ số co dãn của cầu tại mức tối đa hóa lợi nhuận.
Đáp số: 1) Q 50, P 150; 2) 3 . 128 Chương 5 TÍCH PHÂN
5.1. Tích phân bất định
5.1.1. Nguyên hàm và tích phân bất định
Hàm số F(x) được gọi là nguyên hàm của hàm số f (x) trên khoảng øa, b ù, nếu: / F (x) f (x), x (a, b) .
Nếu hàm số G øx ù là một nguyên hàm khác của hàm số f (x) trên khoảng øa, b ù thì
G(x) F(x) C , với C là hằng số.
Họ tất cả các nguyên hàm của của hàm số f (x) trên khoảng øa, b ù được gọi là tích
phân bất định của hàm số f (x) trên khoảng øa, b ù. Ký hiệu: f (x)dx. Vậy / f (x)dx F(x) C F (x) f (x) (5.1) Tính chất a) f (x) g(x) dx f (x)dx g(x)dx b) f (x) g(x) dx f (x)dx g(x)dx
c) kf (x)dx k f (x)dx với k là hằng số
d) Tính bất biến của biểu thức tích phân:
Nếu f (x)dx F(x) C thì f (u)du F(u) C trong đó u (x). 129 Ví dụ 1. Cho hàm số: ø 2 F(x) ln x x
k ù. Tính đạo hàm của hàm số trên rồi suy ra 1
nguyên hàm của tích phân sau: dx. 2 x k Giải Ta có x 1 2 / x k 1 F (x) f (x) 2 2 x x k x k Suy ra 1 2 dx ln x x k C. 2 x k
5.1.2. Bảng công thức các tích phân cơ bản 1 x 1 a) x dx C ( 1) g) dx cot x C 1 2 sin x 1 1 b) dx ln x C h) dx arcsin x C x 2 1 x x x c) e dx e C 1 i) dx arccos x C 2 1 x d) sin xdx cos x C 1 k) dx arctan x C e) cos xdx sin x C 2 1 x 1 1 f ) dx tan x C l) dx arc cot x C 2 2 cos x 1 x
5.1.3. Các phương pháp tính tích phân bất định
5.1.3.1. Sử dụng bảng tích phân cơ bản và phương pháp khai triển
Ta có thể tính tích phân của một hàm phức tạp bằng cách khai triển nó thành tổng
(hiệu) tích phân của các hàm đơn giản.
Ví dụ 2. Tính tích phân bất định 3 x x 1dx Giải
Nếu ta khai triển x x 1 1 , ta chuyển tích phân trên về tổng 2 tích phân sau: 3 ø ù3 x x 1dx x 1 1 x 1dx 130 ø ù3 3 x 1 x 1dx x 1dx ø ù4/3 ø ù1/3 x 1 dx x 1 dx 3 3 øx 1ù7/3 øx 1 ù4/3 C 7 4
5.1.3.2. Phương pháp đổi biến số
Xét tích phân bất định I
f øx ùdx , trong đó f (x) là một hàm số liên tục. Để tính
tích phân này ta có thể chuyển sang một tích phân khác bằng cách thay x øtù. Với giả thiết hàm x
øt ù đơn điệu có đạo hàm liên tục, ta có: / dx (t)dt Vậy ø ù / I f x dx f (t) (t)dt g(t)dt (5.2) với / g(t) f (t) (t)
Nếu ta tính được tích phân g(t)dt Gøt ù C thì 1 I g(t)dt G (x) C.
Công thức (5.2) được gọi là công thức đổi biến số. Ví dụ 3. Cho tích phân f øax bùdx Đặt t ax b dt adx Ta có 1 f øax b ùdx f øt ùdt a Hệ quả 1 1 (ax b) a) (ax b) dx C ( 1) a 1 1 1 b) dx ln ax b C ax b a ax b 1 ax b c) e dx e C a 1 d) sin(ax b)dx cos(ax b) C a 131 1 e) cos(ax b)dx sin(ax b) C a 1 1 f ) dx tan(ax b) C 2 cos (ax b) a 1 1 g) dx cot(ax b) C 2 sin (ax b) a 1 1 1 h) dx arcsin(ax b) C arccos(ax b) C 2 a a 1 (ax b) 1 1 1 i) dx arctan(ax b) C arccot(ax b) C 2 1 (ax b) a a
Ví dụ 4. Tính các tích phân sau: 1 a) I x ø dx 3 1 x ù 1 b) J dx 1 sin x Giải 1 a) I x ø dx 3 1 x ù
Ta có thể đổi biến như sau. Đặt 6 5 x t (t 0), dx 6t dt
Áp dụng công thức (5.2), ta có 5 2 6t t 1 I dt 6 dt 6 1 dt 3 t ø 2 1 t ù 2 2 1 t 1 t ø ù ø6 6 6 t arctan t C 6 x arctan x ù C. 1 b) J dx 1 sin x
Ta có thể đổi biến như sau. Đặt x 2 2t t tan , ta có x 2arctant, dx dt, sin x 2 2 2 1 t 1 t
Áp dụng công thức (5.2), ta có 132 1 1 1 J dx dt 2 1 sin x 2t 1 t 1 2 1 t 1 2 2 2 dt C C. 2 (t 1) t 1 x tan 1 2
5.1.3.3. Phương pháp tích phân từng phần
Giả sử u u(x) và v v(x) là các hàm số có đạo hàm liên tục. Ta có døuvù vdu udv udv d øuv ù vdu
Lấy tích phân 2 vế, ta có udv uv vdu (5.3) hay / / v(x)u (x)dx u(x)v(x) u(x)v (x)dx (5.4) với / / u u(x) du u (x)dx; v v(x) dv v (x)dx
Công thức (5.4) được gọi là công thức tích phân từng phần.
Ví dụ 5. Tính các tích phân bất định sau a) I x ln xdx b) x I xe dx c) I x sin xdx d) I x arctan xdx Giải a) I x ln xdx 1 1 Đặt 2 u ln x du dx; dv xdx v x x 2 Vậy 1 1 1 1 2 2 2 I x ln x xdx x ln x x C. 2 2 2 4 b) x I xe dx 133 Đặt x x u x du dx; dv e dx v e Vậy x x x x I xe e dx xe e C. c) I x sin xdx Đặt u x du dx; dv sin xdx v cos x Vậy I x cos x cos xdx x cos x sin x C. d) I x arctan xdx 1 1 Đặt 2 u arctan x du dx; dv xdx v x 2 1 x 2 Vậy 2 1 1 x 2 I x arctan x dx 2 2 2 1 x 1 1 1 2 x arctan x 1 dx 2 2 2 1 x 1 1 1 2 x arctan x x arctan x C. 2 2 2
5.1.3.4. Phương pháp tính tích phân của các hàm hữu tỉ
a. Tích phân của phân thức hữu tỉ với mẫu bậc nhất P(x) Xét tích phân
dx , với P(x) là một đa thức. Ta biểu diễn biểu thức dưới dấu ax b tích phân dưới dạng: P(x) c Q(x) ax b ax b
Trong đó: Q(x) là thương của phép chia đa thức và c là phần dư của phép chia. Tích phân
của đa thức Q(x) có thể tính dễ dàng, còn tích phân của phân thức thứ hai được tính theo công thức: c c dx ln ax b C. ax b a Ví dụ 6. Tính tích phân 134 3 2 x 3x I dx 1 2x Giải
Biểu thức dưới dấu tích phân ta lấy tử chia cho mẫu, ta được 1 7 7 7 1 2 I x x dx 2 4 8 8 1 2x 1 7 7 7 3 2 x x x x ln 1 2x C 6 8 8 16
b. Tích phân của phân thức hữu tỉ với mẫu bậc hai P(x) Xét tích phân
dx , với P(x) là một đa thức. Ta biểu diễn biểu thức 2 ax bx c
dưới dấu tích phân dưới dạng: P(x) Ax B Q(x) 2 2 ax bx c ax bx c
Trong đó: Q(x) là thương của phép chia đa thức và Ax B là phần dư của phép chia. Tích
phân của đa thức Q(x) có thể tính dễ dàng. Ax B Để tính tích phân I dx ta biến đổi như sau: 2 ax bx c Ax B A 2ax b Ap 1 B 2 2 2 ax bx c 2 ax bx c 2 ax bx c Khi đó ta được: Ax B A 2ax b Ap 1 I dx dx B dx 2 2 2 ax bx c 2 ax bx c 2 ax bx c A 2 Ap ln ax bx c B J 2 2 1 Tích phân: J dx được tính như sau: 2 ax bx c
Xét tam thức bậc 2 ở mẫu ta có 2 b 4ac
+) Trường hợp 1. Tam thức bậc 2 ở mẫu có hai nghiệm phân biệt x ,x : 1 2 1 1 1 J dx dx 2 ax bx c a (x x )(x x ) 1 2 1 1 1 1 1 1 x x 1 dx ln C. a x x x x x x a x x x x 1 2 1 2 1 2 2 135
+) Trường hợp 2. Tam thức bậc 2 ở mẫu có nghiệm kép x : 0 1 1 1 1 1 J dx dx C. 2 2 ax bx c a (x x ) a x x 0 0
+) Trường hợp 3. Tam thức bậc 2 ở mẫu vô nghiệm : 1 1 1 J dx dx 2 2 2 ax bx c a b x 2a 2a 1 2ax b arctan C. Ví dụ 7. Tính tích phân 1 a) I dx 2 x 3x 2 1 b) J dx 2 x 6x 9 1 c) K dx 2 x 2x 5 Giải 1 1 a) I dx dx 2 x 3x 2 (x 1)(x 2) 1 1 x 2 dx ln C. x 2 x 1 x 1 1 1 1 b) J dx dx C. 2 2 x 6x 9 (x 3) x 3 1 1 1 x 1 c) K dx dx arctan C. 2 2 2 x 2x 5 (x 1) 2 2 2
5.1.3.5. Phương pháp tính tích phân của các hàm lượng giác a. Tích phân có dạng: m n I sin xcos xdx
Nếu một trong hai số m, n là số lẻ thì tích phân loại này có thể đưa về tích phân
của đa thức bằng cách đổi biến số:
+) Nếu m là số lẻ thì ta đặt: t cos x , ta có d(cos x) sin xdx .
+) Nếu n là số lẻ thì ta đặt: t sin x , ta có d(sin x) cos xdx .
+) Nếu m, n là số chẵn thì ta sử dụng công thức hạ bậc: 136 1 cos 2x 1 cos 2x 1 2 2 sin x ; cos x ;sin x cos x sin 2x 2 2 2
Ví dụ 8. Tính tích phân: 4 5 I sin x cos xdx Giải
Đặt t sin x , dt cosxdx . Ta có I sin x cos x cos xdxdx t ø1 t ù2 4 4 4 2 dt ø8 6 4 t 2t t ùdt 1 9 2 7 1 5 1 9 2 7 1 5 t t t C sin x sin x sin x C 9 7 5 9 7 5
b. Nếu hàm dưới dấu tích phân không chẵn, không lẻ theo sin x, cosx x
Để tính tích phân loại này ta có thể đặt t tan , khi đó: 2 Ta có 2 1 2t 1 t 2t x 2 arctan t, dx dt, sin x , cos x , tan x 2 2 2 2 1 t 1 t 1 t 1 t Ví dụ 9. Tính tích phân 1 I
dx (a, b, c là hằng số cho trước) a sin x b cos x c Giải x Đặt t tan , khi đó: 2 2 1 2t 1 t x 2 arctan t, dx dt, sin x , cos x 2 2 2 1 t 1 t 1 t Ta có 1 2 1 I dt 2 dt 2 2 2 2t 1 t 1 t (c b)t 2at b c a b c 2 2 1 t 1 t
Đây là tích phân của phân thức hữu tỉ có mẫu là tam thức bậc 2. 5.2. Tích phân xác định
5.2.1. Định nghĩa các tính chất của tích phân xác định
Tính diện tích hình thang cong giới hạn bởi đường thẳng x a, x b và đường
cong (C) : y f (x) liên tục trên đoạn a, b . 137
Chia đoạn a, b thành n đoạn nhỏ đều nhau b a a a a a b với . 0 1 n i a i a 1 , i 1, 2,..., n n Trên mỗi đoạn a , a i 1 i lấy điểm xi tùy ý
Diện tích của n hình chữ nhật nhỏ n S f ( 1 x )( 1 a 0 a ) f ( 2 x )(a2 1 a ) f (xn )(an an 1) hay n n b a Sn f (xi)(ai ai 1) f (xi) i 1 n i 1
Diện tích hình thang cong S n b a S lim n S lim f ( i x ) n n n i 1 Đặt b n b a f (x)dx S lim S (5.5) n lim f (xi) n n n a i 1
Trong đó a là cận dưới, b là cận trên và f (x) là hàm lấy tích phân
Trường hợp đặc biệt a 0, b 1, xi ai , ta có 1 n 1 i f (x)dx S lim n S lim f (5.6) n n n n 0 i 1 138
Ví dụ 10. Dùng định nghĩa tính các tích phân xác định sau: 1 a) I xdx 0 1 b) 2 J x dx 0 1 c) 3 K x dx 0 Giải 1 a) I xdx 0
Dùng công thức (5.6), ta có 1 n 1 i 1 1 2 n I xdx lim lim n n n n i 1 n n 0 n(n 1) 1 1 1 lim lim 1 . 2 n 2n n 2 n 2 1 b) 2 J x dx 0
Dùng công thức (5.6), ta có 1 2 n 2 2 2 2 1 i 1 1 2 n J x dx lim lim 2 n n n n i 1 n n 0 n(n 1)(2n 1) 1 1 1 1 lim lim 1 2 . 3 n 6n n 6 n n 3 1 c) 3 K x dx 0
Dùng công thức (5.6), ta có 1 3 n 3 3 3 3 1 i 1 1 2 n K x dx lim lim 3 n n n n i 1 n n 0 2 2 n(n 1) 1 1 1 lim lim 1 . 2 n 2n n 4 n 4 139
5.2.2. Các tính chất cơ bản của tích phân xác định a a) f (x)dx 0 a b a b) f (x)dx f (x)dx a b b c b c) f (x)dx f (x)dx f (x)dx a a c b b b d) f (x) g(x) dx f (x)dx g(x)dx a a a b b b e) f (x) g(x) dx f (x)dx g(x)dx a a a b b
f) kf (x)dx k f (x)dx với k là hằng số a a b b g) Nếu a b và f (x) g(x), x [a,b] thì f (x)dx g(x)dx a a
5.2.3. Công thức NewTon – Leibnitz
Với Føx ù là một nguyên hàm bất kỳ của hàm số liên tục f øx ù, ta có công thức: b b f (x)dx F(b) F(a) F(x) (5.7) a a
Công thức (5.7) được gọi là công thức Newton – Leibnitz.
Ví dụ 11. Tính các tích phân xác định sau 5 dx a) I 2 0 x 4 2 1 b) J dx 2 x 4x 20 2 Giải 5 dx a) I . Ta có 2 0 x 4 5 5 dx 5 3 I ln ø 2 x x 4 ln 5 3 ln 2 ln . 2 ù ø ù 0 2 x 4 0 140 2 1 b) J dx . Ta có 2 x 4x 20 2 2 2 2 1 1 1 x 2 J dx dx arctan . 2 2 2 x 4x 20 (x 2) 4 4 4 16 2 2 2
5.2.4. Các phương pháp tính tích phân xác định
5.2.4.1. Phương pháp đổi biến
Giả sử ta cần tính tích phân: b I f (x)dx a Thay / x (t), dx
(t)dt với giả thiết hàm số (t) thỏa mãn các điều kiện sau:
+) Hàm số (t) xác định, liên tục và có đạo hàm liên tục trên đoạn ,
+) ø ù a, ø ù b, tức là cận x a tương ứng với cận t và cận x b tương ứng với cận t .
+) Khi t biến thiên trên đoạn , hàm số x
(t) nhận giá trị không vượt ra ngoài đoạn a,b . Khi đó, ta có b / I f (x)dx f (t) (t)dt g(t)dt (5.8) a Với / g(t) f (t) (t).
Ví dụ 12. Tính tích phân xác định sau e 3 (ln x 1) I dx x 1 Giải Đặt 1 t ln x 1 dt dx x Đổi cận
Với x 1 thì t 1 và x e thì t 2 Ta có 141 2 2 1 1 15 3 4 I t dt t ø 4 4 2 1 ù . 4 4 4 1 1
5.2.4.2. Phương pháp tích phân từng phần
Nếu các hàm uøxù, v øx ù khả vi liên tục trên đoạn a,b thì ta có b b b / / u(x)v (x)dx u(x)v(x) v(x)u (x)dx (5.9) a a a với / / u u(x) du u (x)dx; v v(x) dv v (x)dx
Ví dụ 13. Tính tích phân xác định sau e I x ln xdx 1 Giải 1 1 Đặt 2 u ln x du dx; dv xdx v x x 2 e e e 1 1 1 1 1 1 2 2 2 2 I x ln x xdx x ln x x e . 2 1 2 2 4 1 4 4 1
5.2.5. Ứng dụng tích phân
5.2.5.1. Ứng dụng tích phân bất định
Cho hai đại lượng kinh tế x, y và hàm cận biên Mf (x) với điều kiện đầu 0 y
f (x0). Tìm hàm y f (x) như sau y f (x) Mf (x)dx (5.10)
Ví dụ 14. Cho hàm sản phẩm biên của lao động 0,5
MPL 40L . Tìm hàm sản xuất ngắn
hạn Q f øLù, biết Qø100ù 4000 . Giải
Áp dụng công thức (5.10), ta có 80 0,5 1,5 Q(L) MPLdL 40 L dL L c 3 68000
Từ giả thiết : Q(100) 4000 c 3 Vậy 142 80 1,5 68000 Q(L) L . 3 3
Ví dụ 15. Cho hàm chi phí cận biên ở mỗi mức sản lượng Q là : ø ù 0,2Q MC Q 8e và chi
phí cố định FC 50 . Tìm hàm tổng chi phí. Giải
Áp dụng công thức (5.10), ta có 0,2Q 0,2Q TC(Q) MC(Q)dQ 8 e dQ 40e c
Từ chi phí cố định : FC 50 c 10 Vậy ø ù 0,2Q TC Q 40e 10.
5.2.5.2. Ứng dụng tích phân xác định Cho hàm cung Q S(P) và hàm cầu Q
D(P) . Tính thặng dư người tiêu dùng s D
và thặng dư nhà sản xuất như sau
Thặng dư của người tiêu dùng (Consumers’ Surplus) Q0 1 CS D (Q)dQ P Q 0 0 (5.11) 0
Thặng dư của nhà sản xuất (Producers’ Surplus) Q 0 1 PS P Q S (Q)dQ 0 0 (5.12) 0 Trong đó ø 0
P , Q0ù là điểm cân bằng của thị trường.
Ví dụ 16. Cho hàm cung và hàm cầu đối với một loại sản phẩm như sau: S Q P 1; D Q 113 P
Tính thặng dư của nhà sản xuất và thặng dư của người tiêu dùng. Giải
Tìm điểm cân bằng của thị trường ta giải phương trình sau Q D QS 113 P P 57 P 57 ý P 64 Q 7 2 P 113P 3136 0 þ
Ta có điểm cân bằng thị trường là 0 P 64, Q0 7 143
Tính thặng dư của người tiêu dùng ta áp dụng công thức (5.11) 0 Q 7 686 1 2 CS D (Q)dQ 0 P Q0 (113 Q )dQ 448 . 3 0 0
Tính thặng dư của nhà sản xuất ta áp dụng công thức (5.12) 0 Q 7 1 2 833 PS P Q S (Q)dQ 448 (Q 1) dQ . 0 0 3 0 0 5.3. Tích phân suy rộng
Khái niệm: Một tích phân được gọi là tích phân xác định nếu thỏa mãn hai điều kiện sau
i) Hàm lấy tích phân bị chặn
ii) Miền lấy tích phân bị chặn
Nếu một tích phân vi phạm một trong hai điều kiện trên được gọi là tích phân suy rộng
5.3.1. Tích phân suy rộng loại 1: Định nghĩa và phương pháp tính
Nếu một tích phân có miền lấy tích phân không bị chặn thì ta gọi tích phân đó là
tích phân suy rộng loại 1. 1 1 1 1
Ví dụ 17. Cho các tích phân suy rộng loại 1: dx; dx; dx 2 2 2 1 x 1 x 1 x 0 144 a) Cho f : a, ù
hàm số dương thì f øx ùdx là tích phân suy rộng loại 1. a Ta có : t f øxùdx lim f øx ùdx (5.13) t a a b b) Cho f :ø ,b
hàm số dương thì f øx ùdx là tích phân suy rộng loại 1. Ta có : b b f øx ùdx lim f øx ùdx (5.14) t t c) Cho f :ø , ù hàm số dương thì
f øxùdx là tích phân suy rộng loại 1. Ta có : 0 f øx ùdx f øx ùdx f øx ùdx 0 (5.15) 0 s lim f øx ùdx lim f øx ùdx t s t 0
Nếu các giới hạn này không tồn tại hay bằng
, ta nói tích phân suy rộng này phân
kỳ còn nếu giới hạn này bằng một hằng số ta nói tích phân suy rộng này hội tụ.
Ví dụ 18. Tính các tích phân suy rộng sau 1 a) I dx 2 x 2x 2 1 2 1 b) J dx 2 x 4x 5 1 c) K dx 2 x 4x 13 Giải 1 a) I dx 2 x 2x 2 1 145
Áp dụng công thức (5.13), ta có t 1 I lim dx lim ø t arctan(x 1) 2 1 ù t (x 1) 1 t 1 lim arctan(t 1) . t 2 2 1 b) J dx 2 x 4x 5
Áp dụng công thức (5.14), ta có 2 1 J lim dx lim ø 2 arctan(x 2) 2 t ù t t (x 2) 1 t lim arctan(t 2) . t 2 1 c) K dx 2 x 4x 13
Áp dụng công thức (5.15), ta có 0 1 1 K dx dx 2 2 x 4x 13 x 4x 13 0 0 s 1 1 lim dx lim dx 2 2 2 2 t s (x 2) 3 (x 2) 3 t 0 0 s 1 x 2 1 x 2 lim arctan lim arctan t 3 3 s 3 3 t 0 1 2 t 2 lim arctan arctan t 3 3 3 1 s 2 2 lim arctan arctan . s 3 3 3 3
5.3.2. Tích phân suy rộng loại 2: Định nghĩa và phương pháp tính
Nếu một tích phân có hàm lấy tích phân không bị chặn thì ta gọi tích phân đó là tích phân suy rộng loại 2. 1 1
Ví dụ 19. Cho tích phân suy rộng loại 2: 1 dx và lim 2 2 x x 0 x 0 146 b a) f : øa,b và lim f (x)
thì f øx ùdx là tích phân suy rộng loại 2. x a a Ta có : b b f øx ùdx lim f øx ùdx (5.16) t a a t b b) f : a,bù và lim f (x)
thì f øx ùdx là tích phân suy rộng loại 2. x b a Ta có : b t f øx ùdx lim f øx ùdx (5.17) t b a a
Ví dụ 20. Tính các tích phân suy rộng sau 2 1 a) I dx 4 2 x 1 e 1 b) J dx x ln x 1 Giải 2 1 a) I dx 4 2 x 1 1 Vì lim
, áp dụng công thức (5.17), ta có 2 x 2 2 x t t 1 4 4 3 I lim dx lim (2 x) 4 t 2 2 x t 2 3 1 1 4 4 3 4 lim 1 (2 t) . t 2 3 3 e 1 b) J dx x ln x 1 1 Vì lim
, áp dụng công thức (5.16), ta có x 1 x ln x e 1 J lim d(ln x)
lim ln øln x ù e lim ln øln e ù ln løn t ù . t t 1 ln x t 1 t 1 t 147
5.3.3. Khảo sát sự hội tụ của tích phân suy rộng 5.3.3.1. Mệnh đề i) Cho hàm số f : ø0,1 . Ta có
1 1 dx hội tụ khi và chỉ khi 1 x 0 ii) Cho hàm số f : 1, ù . Ta có 1 dx hội tụ và chỉ khi 1 x 1
5.3.3.2. Các tiêu chuẩn hội tụ
Hệ quả 1. Cho f , g : (a,b] là hai hàm số dương b b
i) Nếu f (x) g(x), x (a,b] và g(x)dx hội tụ thì f (x)dx hội tụ. a a f (x) b b ii) Nếu lim L (0,
) thì f (x)dx và g(x)dx cùng bản chất. x a g(x) a a Lưu ý: b b
+) Trường hợp: L 0: Nếu g(x)dx hội tụ thì f (x)dx hội tụ. a a b b +) Trường hợp: L
: Nếu g(x)dx phân kỳ thì f (x)dx phân kỳ. a a Hệ quả 2. Cho f , g : [a, ) là hai hàm số dương
i) Nếu f (x) g(x), x a và g(x)dx hội tụ thì f (x)dx hội tụ. a a f (x) ii) Nếu lim L (0,
) thì f (x)dx và g(x)dx cùng bản chất. x g(x) a a Lưu ý:
+) Trường hợp: L 0: Nếu
g(x)dx hội tụ thì f (x)dx hội tụ. a a +) Trường hợp: L : Nếu
g(x)dx phân kỳ thì f (x)dx phân kỳ. a a 148
Ví dụ 21. Khảo sát sự hội tụ của các tích phân suy rộng sau x 1 1 a) dx c) dx 3 x 1 x 1 0 e 1 x x 1 x b) dx d) dx 2 x 1 sin x e 1 1 0 Giải x a) dx 3 x 1 1
Sử dụng tiêu chuẩn bất đẳng thức để khảo sát sự hội tụ, ta có x 1 , x 1 3 2 x 1 x 1 x Ta có:
dx là tích phân hội tụ vì 2 1. Suy ra
dx là tích phân hội tụ. 2 x 3 x 1 1 1 x x b) dx 2 x 1 1 x x 1 Đặt : f (x) chọn g(x)
. Sử dụng tiêu chuẩn giới hạn để khảo sát sự 2 x 1 1/2 x hội tụ, ta có 2 f (x) x lim lim 1 (0, ) 2 x g(x) x x 1 1 x x Ta có: dx là tích phân kỳ vì 1 / 2 1. Suy ra
dx là tích phân phân kỳ. 1/ 2 x 2 x 1 1 1 1 1 c) dx x 0 e 1 1 1 Đặt f (x) chọn g(x)
. Sử dụng tiêu chuẩn giới hạn để khảo sát sự x e 1 1/2 x hội tụ, ta có f (x) x lim lim 1 (0, ) x x 0 g(x) x 0 e 1 149 1 1 1 1 Ta có:
dx là tích phân hội tụ vì 1/ 2 1. Suy ra
dx là tích phân hội tụ. 1/2 x x 0 0 e 1 1 x d) dx sin x e 1 0 1 Đặt x f (x) chọn g(x)
. Sử dụng tiêu chuẩn giới hạn để khảo sát sự sin x e 1 1/2 x hội tụ, ta có f (x) x lim lim 1 (0, ) sin x x 0 g(x) x 0 e 1 1 1 1 1 x Ta có:
dx là tích phân hội tụ vì 1. Suy ra
dx là tích phân hội tụ. 1/2 x 2 sin x e 1 0 0 5.3.3.3. Mệnh đề i) Nếu
f (x) dx hội tụ thì f (x)dx hội tụ và ta nói f (x)dx hội tụ tuyệt đối. 1 1 1 ii) Nếu f (x)dx hội tụ mà
f (x) dx phân kỳ thì ta nói f (x)dx bán hội tụ. 1 1 1
Ví dụ 22. Khảo sát sự hội tụ của tích phân 2 1 4sin 2x dx 3 2 1 x x 2x Giải Ta có 2 1 4sin 2x 5 5 , x 1. 5/3 3 2 3 2 x x x 2x x x 1 5 Ta có:
dx là tích phân hội tụ vì 1. Suy ra 5/3 x 3 1 2
1 4sin 2x dx là tích phân hội tụ. 3 2 1 x x 2x Vậy 2 1 4sin 2x
dx là tích phân hội tụ tuyệt đối. 3 2 1 x x 2x 150 5.4. Bài tập Bài số 1. Chứng minh F(x)
x ln ø1 x ù là một nguyên hàm của hàm số x f (x) . 1 x
Hướng dẫn : xét x 0 , x 0 , x 0 .
Bài số 2. Tìm a, b, c để hàm số ø 2 F(x) ax bx
ùc 3 2x là một nguyên hàm của hàm số f (x) x 3 2x. 2 1 3 Đáp số : a , b , c . 5 5 5
Bài số 3. Tích các tích phân bất định sau 2 (2x 1) 1 1) dx 8) dx x 2 4x 9 2 x 1 2) dx 9) dx 8 (1 x) 3 2 cos x sin x sin x 1 10) dx 3) dx 2 x 4 cos x 1 e x 2x e 11) dx 4) dx 2 x 5x 4 x e 1 1 5) 2 x x e dx 12) dx 2 x 4x 13 6) 2 x sin xdx 2 sin x 13) dx 2 cos x 7) 2 4 x dx 14) 5 x x e dx 1 1 1 Đáp số : 1) 2 1) 2x 4x ln x C; 2) C; 7 6 5 7(x 1) 3(x 1) 5(x 1) x 1 e 1 x x 2 x x x 3) ln C; 4) e 1 ln(e 1) C; 5) x e 2xe 2e C; x 1 e 1 2 1
6) x cos x 2xsin x 2cos x C; 7) sin ø2arccosx ù arccos x C; 2 151 x tan 1 1 2x 1 ø ù 2 8) arctan C; 9) sin 2arccos x arccos x C; 9) arctan C; 6 3 2 2 ø 2 ù 1 4 10) ln cosx 4 cos x C; 11) ln x 1 ln x 4 C; 3 3 x tan 1 x 2 4 2 12) arctan C; 13) arctan ln 2 cosx C; 3 3 3 3 5 x 4 x 3 x 2 x x x 14) x e 5x e 20x e 60x e 120xe 120e C.
Bài số 4. Tính các tích phân xác định sau bằng định nghĩa 1 /2 1) x I e dx 2) I cos xdx 0 0 Đáp số: 1) e 1; 2) 1.
Bài số 5. Tính các tích phân xác định sau 9 1 1) 3 x 1dx 7) x x e e dx 2 0 0 1 2) dx 2 4 2 sin x cos x 8) dx 4 4 sin x cos x 4 0 1 1 e 3) dx 9) 2 ln xdx 2 0 x 2x 2 1 e 1 4) 2 x ø dx 2 10) 2 x cos xdx 1 1 ln x ù 0 6 1 5) dx 2 1 1 3x 2 11) dx 1 3 2 cos x 0 ln8 1 6) dx 1 1 x 12) dx ln3 e 1 2 0 (2x 1) x 1 45 2 5 2 2 3 Đáp số : 1) ; 2) ; 3) ln ; 4) ; 5) 2 ln ; 6) ln ; 1 e 7) e e ; 4 4 1 2 4 3 5 2 152 2 2 tan1 1 6 3 5 8) ; 9) e 2; 10) 2; 11) arctan ; 12) ln . 4 4 5 5 5 10 1
Bài số 6. Chứng minh rằng: xf øsin xùdx f øsin x ùdx 2 0 0 Áp dụng: x x sin x 1) dx 2) dx 1 sin x 2 1 cos x 0 0 2 Hướng dẫn : Đặt t x ; 1) ; 2) . 4
Bài số 7*. Tính các tích phân xác định sau 1 1 1 lnø1 xù 1) dx 4) dx ø 2 1 x ù2 2 1 x 0 0 x sin x 5) dx 2 2 sin x cos x 4 9 4 cos x 2) dx 0 ø1 sin xù2 2 0 1 1 6) ø dx 2 1 x ùøx 1 e 1 ù 4 3) ln ø1 tan x ùdx 0 1 Đáp số : 1)
; 2) ; 3) ln 2; 4) ln 2 ; 5) ; 6) . 8 4 8 8 4
Bài số 8. Tính các tích phân suy rộng arctan x 1) dx 7) 2x xe dx 2 1 x 0 0 0 1 2x 1 2) dx 8) dx 2 4 x 3x e 0 1 3) 2x e dx 9) dx 2 x ln x 0 e 1 1 4) dx 10) dx 2 2 x 4x 8 1 x 4 x 153 2x 1 2 5 x 5) dx 11) dx 2 (x 2) 2 0 0 4 x 1 6) dx 2 2 x 6x 10 cos x 12) dx 3 sin x 0 2 1 1 5 2 Đáp số : 1) ; 2) ; 3) ; 4) ln ; 5) ; 8 2 2 4 5 2 1 1 256 6) ;7) ; 8) ; 9) 1; 10) ;11) ; 12) 2. 2 4 9 2 15
Bài số 9. Khảo sát sự hội tụ của tích phân suy rộng sau 1 n x 1) dx 6) dx 5 1 x x 1 e 0 0 x x arctan x 2) dx 7) dx 3 x 2x 1 2 2 x 0 0 1 arctan 3x 3) dx 8) dx x(x 1)(x 2) 2 x 3 0 1 4sin 3x x 1 4) dx 9) sin x ln dx 3 3 x x x 1 1 x 2 5) dx 10) 1 cos dx 2 2 1 x cos x x 0 1
Đáp số : 1) hội tụ; 2) hội tụ; 3) hội tụ; 4) hội tụ; 5) phân kỳ;
6) hội tụ; 7) phân kỳ; 8) phân kỳ; 9) hội tụ; 10) phân kỳ.
Bài số 10. Khảo sát sự hội tụ của tích phân suy rộng sau 1 1 1 ln x 1) dx 6) dx 2 2 1 x 0 x x 0 1 1 1 1 2) dx 7) dx x e cos x x x 0 3 0 xøe e ù 1 sin x ln x 3) dx 1 n x x 8) dx 0 4 0 1 x 154 1 x 3 2 lnøsin x ù 9) dx 4) dx 3 x x 0 3 ø1 x ùcos 0 2 1 sin 2x e 5) dx 1 10) dx 2 3 0 1 x x ln x 1
Đáp số : 1) hội tụ; 2) phân kỳ; 3) phân kỳ; 4) phân kỳ;
5) hội tụ; 6) hội tụ; 7) hội tụ; 8) hội tụ; 9) hội tụ; 10) phân kỳ.
Bài số 11. Cho hàm doanh thu biên ở mỗi mức sản lượng Q là ø ù 2 MR Q 50 2Q 3Q .
Hãy xác định hàm tổng doanh thu và hàm cầu đối với sản phẩm. Đáp số: ø ù 2 3 2 TR Q 50Q Q Q ; P 50 Q Q .
Bài số 12. Cho biết chi phí cận biên ở mỗi mức sản lượng Q là ø ù 2 MC Q 32 18Q 12Q .
và FC 43. Hãy tìm hàm tổng chi phí và chi phí khả biến. Đáp số: ø ù 2 3 ø ù 2 3 TC Q 43 32Q 9Q 4Q ; V Q 32Q 9Q 4Q .
Bài số 13. Cho biết chi phí cận biên ở mỗi mức sản lượng Q là ø ù 0,5Q MC Q 12e và
FC 36. Hãy tìm hàm tổng chi phí. Đáp số: ø ù 0,5Q TC Q 24e 12.
Bài số 14. Cho biết doanh thu cận biên ở mỗi mức sản lượng Q là ø ù 0,4Q MR Q 40Q 16e .
Hãy tìm hàm tổng doanh thu. Đáp số: ø ù 2 0,4Q TR Q 40 20Q 40e .
Bài số 15. Cho hàm cầu ngược đối với một loại sản phẩm như sau: 2 P 42 5Q Q
Giả sử sản phẩm được bán trên thị trường với giá P
6 . Hãy tính thặng dư của người tiêu 0 dùng. Đáp số : 248 / 3 .
Bài số 16. Cho hàm cung đối với một loại sản phẩm như sau: Q P 1 2 S
Giả sử sản phẩm được bán trên thị trường với giá P0 10 . Hãy tính thặng dư của nhà sản xuất. Đáp số : 100 / 3 . 155 Chương 6
PHÉP TÍNH VI PHÂN HÀM NHIỀU BIẾN
6.1. Các khái niệm cơ bản
6.1.1. Hàm số hai biến số
Định nghĩa: Cho x, y, w là các biến số, nếu có một quy luật f cho tương ứng với
mỗi cặp giá trị của hàm hai biến số øx, ù
y một giá trị xác định và duy nhất của biến số w
thì ta gọi f là một hàm số hai biến số. Coi øx, ù
y là tọa độ điểm M øx, ù
y trong mặt phẳng 2, thì f được coi là hàm với biến điểm M. Ký hiệu: w f øx, ù y hay w f ø ù M .
+) Khi x x và y y thì giá trị tương ứng của hàm số ký hiệu là f øx , y và 0 0ù 0 0
được gọi là giá trị của hàm số tại điểm øx , y . 0 0 ù
+) Miền D gồm tất cả các điểm M øx, yù mà tại đó biểu thức w f øx, yù có nghĩa,
được gọi là miền xác định của hàm số f, còn số thực w ứng với điểm M øx, yù được gọi
là giá trị của hàm số tại điểm M øx, yù và ký hiệu là f øx, ù y hay f ø ù M . Ví dụ 1. Cho hàm số : ø ù y f x, y xy
. Hãy tìm biểu thức của hàm số : ø ù 1 f y, x , f x, . x y Giải Tìm hàm số f øy, ù x Trong biểu thức ø ù y f x, y xy
thay x bởi y và y bởi x ta được: x ø ù x f y, x yx y 1 Tìm hàm số f x, y 1 Trong biểu thức ø ù y f x, y xy
thay x bởi x và y bởi ta được: x y 156 1 x 1 f x, y y xy
Ví dụ 2. Tìm miền xác định của các hàm số sau: a) f øx, ù y xy. b) ø ù ø 2 ù2 2 2 f x, y arcsin x y 2 x y . Giải
a) Điều kiện để hàm số f øx, ù y xy có nghĩa là x 0 x 0 xy 0 ý hoặc ý y þ 0 þy 0 Vậy miền xác định ø ù 2 D M x, y : xy 0 .
b) Điều kiện để hàm số ø ù ø 2 ù2 2 2 f x, y arcsin x y 2 x y có nghĩa là 2 2 x y 1 2 2 ý x y 1 2 2 2 x y 0 þ Vậy miền xác định ø ù 2 2 2 D M x, y : x y 1 .
6.1.2. Định nghĩa hàm n biến số
Một hàm số f của biến điểm Møx , x ,..., x (hàm số của n biến số x ,x ,...,x ), 1 2 ù n 1 2 n với miền biến thiên n D
, là một quy luật đặt tương ứng mội điểm M øx ,x ,..., x D 1 2 n ù
với một giá trị xác định và duy nhất của biến số w.
Ký hiệu: w f øx , x ,..., x hay w f ø ù M . 1 2 n ù
Miền D được gọi là miền xác định của hàm số f (nếu bài toán không cho biết trước
tập xác định thì miền D gồm tất cả các điểm M øx , x ,..., x mà tại đó biểu thức 1 2 nù
w f øx , x ,..., x có nghĩa), còn số thực w tương ứng với điểm M øx , x ,..., x được 1 2 nù 1 2 n ù
gọi là giá trị của hàm số tại điểm Møx , x ,..., x và ký hiệu f øx ,x ,..., x hay f ø ù M . 1 2 nù 1 2 nù 1 Ví dụ 3. Cho hàm số: ø ù 2 2 2 3 f x, y, z x y z 3 xyz . Tính f 2, ,1 . 3 Giải 2 1 1 1 28 2 Ta có : 2 2 3 3 f 2, ,1 2 1 3 2 1 3 3 3 3 3 3 157 6.1.3. Hàm số hợp
6.1.3.1. Hàm số hai biến số
Xét hàm số z f øu, v ù, øu, v ù Y Giả sử u u øx, ù y , v v øx, ù
y , M øx, yù X. Khi đó, hàm số z là hàm số của hai biến øx, ù y theo quy luật sau: ø ù u,v ø ù f x, y u, v z
Hàm số z f uøx, y ù, vøx, y ù được gọi là hàm số hợp của hàm số z f øu, ù v và hàm số u u øx, ù y , v v øx, ù y . Ví dụ 4. Hàm số ø ù2 xy z x 2y
2 là hàm hợp của hai hàm số 2 v z u 2 và các hàm hai biến số u x 2y, v xy.
6.1.3.2. Hàm số n biến số
Xét hàm số w f øu ,u ,...,u , u ,u ,...,u Y. 1 2 m ù ø 1 2 m ù Giả sử u u x , x ,..., x , u u x , x ,..., x ,..., 1 1 ø 1 2 2ù 2 2 ø 1 2 2 ù u u x ,x ,...,x , x ,x ,..., x X. m m ø 1 2 2 ù ø 1 2 2 ù
Khi đó, hàm số w là hàm số của n biến số theo quy luật sau:
øx ,x ,...,x ù uk øu ,u ,...,u ù f w 1 2 n 1 2 m
Hàm số w f u x ,x ,..., x ,u x ,x ,..., x ,...,u x , x ,..., x được gọi là 1 ø 1 2 2 ù 2 ø 1 2 2 ù m ø 1 2 2 ù
hàm số hợp của hàm số w f øu ,u ,...,u và hàm số u u x , x ,..., x . i i ø 1 2 ù 1 2 m ù n Ví dụ 5. Hàm số ø 2 2 2 ù ø 3 w ln x y 2z
sin x y ù là hàm hợp của hai hàm số
w ln u sin v và các hàm ba biến số 2 2 2 3 0 u x y 2z , v x yz .
6.1.4. Một số hàm trong kinh tế 6.1.4.1. Hàm sản suất
Khi phân tích hoạt động sản xuất, các nhà kinh tế quan tâm đến hai yếu tố đầu vào
quan trọng là vốn (capital) và lao động (labor) và chúng được ký hiệu là K và L. Do đó, hàm sản xuất có dạng: Q f øK, ù L . Ý nghĩa. 158
Hàm sản xuất biểu diễn sự phụ thuộc của sản lượng hàng hoá vào hai yếu tố đầu vào
vốn (tư bản) và lao động.
Một hàm sản xuất mà kinh tế học thường sử dụng là hàm sản xuất dạng Cobb –
Douglas có dạng: Q aKñ Lò
Trong đó: a,ñ ,ò là các hằng số dương.
6.1.4.2. Hàm doanh thu, chi phí, lợi nhuận a. Hàm chi phí
+) Hàm chi phí phụ thuộc đầu vào: TC TC øK, ù L .
Nếu tính theo các yếu tố sản xuất thì hàm chi phí là hàm số của các yếu tố sản xuất và có dạng: TCøK, ù L pKK pLL C0. Trong đó: K
p : Giá thuê một đơn vị vốn (tư bản). L
p : Giá thuê một đơn vị lao động. C : Chi phí cố định. 0
+) Hàm chi phí kết hợp: TC TCø 1 Q , 2 Q ù. Trong đó
Q1 : Số đơn vị hàng hóa 1;
Q2 : Số đơn vị hàng hóa 2.
b. Hàm doanh thu và hàm lợi nhuận
+) Nếu doanh nghiệp là doanh nghiệp cạnh tranh thì tổng doanh thu của doanh nghiệp
phụ thuộc vào K, L và có dạng: TR P f øK, ù L
TR øK, L ù ( P : là giá sản phẩm) +) Hàm doanh thu gộp: TR T 1 R TR2 1 P . 1 Q 2 P .Q2 TR ø 1 Q , 2 Q ù
Với P : là giá sản phẩm mặt hàng 1, P : là giá sản phẩm mặt hàng 2. 1 2 c. Hàm lợi nhuận Hàm lợi nhuận: TR TC
+) Hàm lợi nhuận phụ thuộc đầu vào 159 P.f øK, ù L øp K p L C K,L k L ù 0 ø ù
+) Hàm lợi nhuận phụ thuộc đầu ra ø 1 Q , Q2ù TR ø 1 Q , Q2ù TC ø 1 Q , Q2 ù. 6.1.4.3. Hàm lợi ích
Giả sử cơ cấu tiêu dùng của người tiêu dùng gồm có n mặt hàng. Mỗi giỏ hàng là
một bộ gồm n số thực X øx1, x2,..., x ù
n , trong đó x1 là lượng hàng hoá 1 T , x2 là lượng hàng hoá 2
T ,...,x là lượng hàng hoá n n
T . Hàm lợi ích là hàm số đặt tương ứng với mỗi túi hàng X ø 1 x , x2,...,x ù
n với một giá trị U nhất định theo quy tắc: Giỏ hàng nào được ưa
chuộng nhiều hơn thì gán giá trị lợi ích lớn hơn. Hàm lợi ích có dạng tổng quát như sau: U Uøx , x ,...,x 1 2 ù n
Hàm lợi ích hay được sử dụng là hàm Cobb – Douglas: ñ1 ñ 2 ñ n U ax x ...x (ñ ,ñ ,...,ñ
là các hằng số dương). 1 2 n 1 2 n
6.1.4.4. Hàm cung, cầu thị trường n hàng hóa liên quan
Mức cung và mức cầu đối với một loại hàng hoá trên thị trường không những chỉ phụ
thuộc vào giá hàng hoá đó mà còn bị chi phối bởi giá của các hàng hoá liên quan và thu
nhập của người tiêu dùng. Trên thị trường n hàng hoá liên quan hàm cung và hàm cầu đối
với hàng hoá i có dạng (giả thiết thu nhập không thay đổi): QS i S ø 1 P , 2 P ,..., n P ù i Q D P , P ,..., P D i ø 1 2 n ù i
Trong đó, Q là lượng cung hàng hoá i, Q là lượng cầu hàng hoá i, i S i D i P là giá của
hàng hoá i øi 1, 2, 3,..., ù n .
Ví dụ 6. Cho các hàm cầu: Q 40 P ; Q
30 0,5P . Hãy lập hàm doanh thu. 1 1 2 2 Giải
Từ hai hàm cầu thuận ta suy ra hai hàm cầu đảo như sau: 1 P 40 1 Q ; 2 P 60 2Q 2 Hàm doanh thu gộp TR ø 1 Q ,Q2ù P Q P Q 1 1 2 2 (40 1 Q ) 1 Q ( 60 2Q2)Q2 hay 160 TR øQ ,Q ù 2 2 1 2 1 Q 2 2Q 1 40Q 2 60Q
Ví dụ 7. Cho hàm sản xuất: ø ù 0,3 0,4 Q K, L
10K L . Giá thuê một đơn vị vốn K p 3 USD,
giá thuê một đơn vị lao động pL 2 USD và giá sản phẩm là P 4 USD. Hãy lập hàm lợi nhuận. Giải Hàm doanh thu: ø ù 0,3 0,4 TR K, L PQ 40K L Hàm chi phí : TCøK, ù L p KK p LL 3K 2L Hàm lợi nhuận: ø ù ø ù ø ù 0,3 0,4 K, L TR K, L TC K, L 40K L 3K 2L.
6.2. Giới hạn và liên tục của hàm số
6.2.1. Giới hạn của hàm nhiều biến số 6.2.1.1. Định nghĩa: Cho n f : D . Ta nói f ø ù X tiến về L øf ø ù X Lù khi X tiến về A øX ù A , ký hiệu lim f ø ù X L. X A
Khi đó các giá trị X D đủ gần A, các giá trị f ø ù
X tương ứng đủ gần L tùy ý.
Ta cũng có thể viết gọn định nghĩa trên theo mệnh đề sau:
6.2.1.2. Mệnh đề: ølim f ø ù X L X D,limX A limf X L . X A ù ø k k ø k ù k k ù
Giới hạn trên cũng được gọi là giới hạn kép. 2 2 x y
Ví dụ 8. Chứng minh rằng hàm số f øx, ù y
có giới hạn tại điểm A ø1, ù 2 . xy Giải
Dễ nhận thấy điểm Aø1, ù 2
D miền xác định của hàm số.
Xét một dãy điểm bất kỳ X x , y
D miền xác định của hàm số và dãy điểm k ø k k ù lim x 1 k
X x , y hội tụ đến điểm Aø1, ù 2 k
. Dãy điểm có giá trị hàm số tương k ø k k ù ý lim y 2 k k þ ứng là: 2 2 x y 2 2 2 2 x y 1 2 5 f øX ù k k và lim f øX lim K ù k k k x y k K x y 1 2 2 k k k k 161 5
Vậy hàm số luôn có giới hạn kép tại điểm Aø1, ù
2 và giới hạn đó bằng . 2 x y
Ví dụ 9. Tìm giới hạn của hàm số: lim . 2 2 x x xy y y Giải Ta có: x y x y x y 0 2 2 2 2 2 2 x xy y x xy y x y xy x y x y 1 1 2 xy xy xy x y 1 1 mà lim 0 x x y y x y
Theo nguyên lý kẹp ta được lim 0. 2 2 x x xy y y
6.2.1.3. Giới hạn lặp: Cho hàm hai biến số: z f øx, ù y
Trường hợp 1. Cố định y y . Ta có 0
lim f øx, y ù u øy ù và lim u ø ù y E x x y y 0 0 y y0 Ký hiệu: lim lim f øx, ù y E. y y0 x x0
Trường hợp 2. Cố định x x . Ta có 0
lim f øx, y ù v øx ù và lim v øxù F y y0 x x0 x 0 x Ký hiệu: lim lim f øx, ù y F. x x0 y 0 y
Các số E, F như trên được gọi là các giới hạn lặp của hàm số.
Lưu ý: Nói chung các giới hạn kép và giới hạn lặp là khác nhau. 3 2 x xy
Ví dụ 10. Xét giới hạn lặp và giới hạn kép của hàm số : f øx, yù tại điểm ø0,0ù. 3 3 x y Giải 162 Hàm số f øx, ù
y không có giới hạn kép tại điểm ø0,0ù. Thật vậy, lấy hai dãy điểm 1 1 1 2 X , ,Y ,
D, miền xác định của hàm số và đều hội tụ về điểm ø0,0ù nhưng k k k k k k
các giá trị của chúng khác nhau. Bây giờ, ta xét giới hạn lặp của hàm số tại điểm ø0,0ù Ta có 3 2 ø ù ø ù 0 0 y u y limf x, y 0, y 0. 3 x 0 0 y Suy ra
E lim lim f øx, y ù limu øy ù 0. y 0 x 0 y 0 Ta có 3 2 ø ù ø ù x x 0 v x lim f x, y 1, x 0. 3 3 y 0 x 0 Suy ra
F lim lim f øx, y ù lim v øx ù 1. yx 0 y 0 x 0
Cách làm tương tự cho hàm n biến số. 6.2.2. Hàm số liên tục Định nghĩa: Cho n f : D
và A D. Nếu giới hạn của hàm f tại điểm A
tồn tại và bằng giá trị của hàm số tại điểm đó, nghĩa là lim f ø ù X f ø ù A . Ta nói hàm f X A liên tục tại điểm A. Ví dụ 11. Cho hàm số x ø 2 y x y ù2 khi (x, y) (0,0) f øx, ù 2 2 y ý x y 0 þ khi (x, y) (0,0)
Chứng minh rằng hàm số f (x, y) liên tục tại điểm (0,0). Giải
Sử dụng bất đẳng thức tam giác, ta có xyø 2 2 x y ù 2 2 xy x y 2 2 0 x y x y 2 2 2 2 x y x y mà lim ø 2 x y ù 2 0 (x,y) (0,0) 163 nên suy ra ø 2 xy x y ù 2 lim 0. 2 2 (x,y) (0,0) x y Ta có
lim f øx, y ù f ø0,0 ù 0 . Vậy hàm số f (x, y) liên tục tại điểm (0,0). (x,y) (0,0)
6.3. Đạo hàm riêng và vi phân toàn phần 6.3.1. Đạo hàm riêng
6.3.1.1. Đạo hàm riêng cấp 1
a. Trường hợp hàm số hai biến số Cho hàm số z f øx, ù y , M x , y
D . Nếu giữ giá trị của biến y không đổi 0 ø 0 0 ù f
và cho giá trị của biến x thay đội một lượng x thì hàm số z f øx, ù y có số gia tương ứng là f øx x, y
f x , y , số gia này gọi là số gia riêng của hàm số z f øx, ù y theo 0 0 ù ø 0 0 ù biến x, tại M0 øx0 , 0 y ù, ký hiệu là x zø 0 M ù hay xf øM0ù.
Nếu tồn tại giới hạn f M f x x, y f x , y x ø 0 ù ø0 0 ù ø0 0 ù lim lim (6.1) x 0 x x 0 x
thì giới hạn đó được gọi là đạo hàm riêng của hàm số z f øx, ù y theo biến x tại điểm ø z f x , y , ký hiệu là / z / x øM ù hay øM ù hay fx øM ù hay øM 0 ù 0 0 ù 0 0 . x 0 x
Ý nghĩa: Đạo hàm riêng của hàm số z f øx, ù
y theo biến x tại điểm øx , y ù biểu 0 0
thị tốc độ biến thiên của giá trị hàm số z f øx, ù y tại điểm ø 0 x , 0 y ù khi x thay đổi một
lượng nhỏ, trong điều kiện giá trị của biến y không thay đổi.
Tương tự, ta cũng có định nghĩa đạo hàm riêng của hàm số z f øx, ù y theo biến y z f tại M / / 0 , ký hiệu là z M f M yø ù0 hay ø 0 M ù hay y ø ù hay øM0ù. y 0 y
Ví dụ 12. Sử dụng định nghĩa hãy tính đạo hàm riêng của các hàm số sau: a) 3 2 w x y tại điểm ø1, ù 2 . x b) f (x, y) x (y 1)arccos tại điểm øx, ù 1 . y Giải 164 a) 3 2 w x y tại điểm ø1, ù 2 . Ta có w ø1, ù 3 2 3 2 3 x 2 x .2 1 .2 4x 4 ; x x 1 Vậy 3 4x 4 / w ø1,2ù lim lim 4ø 2 x x x ù1 12. x 1 x 1 x 1 Tương tự: w ø1, ù 3 2 3 2 2 2 1 .y 1 .2 y 4 y ; y y 2 Vậy 2 y 4 / wy ø1,2ù lim lim øy 2 ù 4. y 2 y 2 y 2 x b) f (x, y) x (y 1)arccos tại điểm øx, ù 1 . y Ta có ø ù x x ø ù x x x 1 1 arccos x 1 1 arccos 1 1 / f x,1 lim 1 x ø ù x 0 x Tương tự: ø ù x ø ù x x 1 y 1 arccos x 1 1 arccos 1 y 1 / f x,1 lim y ø ù y 0 y x y.arccos y 1 lim arccos x. y 0 y
Nhận xét: Để tính đạo hàm riêng / fx của hàm số z f øx, ù y theo biến x ta xem y
như là hằng số và khi đó z f øx, ù
y là hàm số của một biến x , do đó ta áp dụng các công
thức đạo hàm cơ bản và quy tắc tính đạo hàm của hàm một biến. Tương tự, cho việc tính
đạo hàm riêng của z theo y. y sin
Ví dụ 13. Tính đạo hàm riêng của hàm số sau: x z e arctan(xy) Giải 165
Ta có đạo hàm riêng cấp 1 của hàm số y sin y y y / x z x e .cos . . 2 2 2 x x 1 x y y sin y 1 x / x z = e .cos . . y 2 2 x x 1 x y
b. Trường hợp hàm số n biến số
Đạo hàm riêng của hàm số n biến số w f øx , x ,..., x 1 2
nù theo một trong các biến
độc lập tại một điểm X øx1, x2,...,x n ù là giới hạn (nếu có) của tỷ số giữa số gia riêng hàm
số và số gia của biến độc lập tương ứng khi số gia của biến độc lập đó tiến tới 0. Ký hiệu: / w / f x ,x ,...,x wx fx ø 1 x ,x2,...,xnù ø 1 2 n ù i i xi xi f øx1,x2,...,xi
xi,...,xn ù f øx1,x 2,...,xi,...,x n ù lim x i 0 i x f ø 1 x , x2,..., i x ,...,xn ù f ø 1 x , x2,...,xi,...,xn ù lim . (6.2) i x i x xi xi
Chú ý: Đạo hàm riêng của hàm số w theo biến x tại điểm X øx1, x2,...,x n ù biểu i
thị tốc độ biến thiên của giá trị hàm số w f øx X x , x ,..., x
1, x 2,..., x n ù tại điểm ø 1 2 n ù khi i
x thay đổi một lượng nhỏ, trong điều kiện giá trị các biến còn lại không thay đổi. Khi tính đạo hàm / / w f x ,x ,...,x x x ø 1 2
nù (đạo hàm riêng theo biến i i i
x ) ta coi các biến còn lại
như hằng số và xem w như là một hàm của biến xi . Sau đó áp dụng các quy tắc tính đạo
hàm của hàm số một biến số.
Ví dụ 14. Tính các đạo hàm riêng cấp 1 của hàm số: a) 4 2 2 2 f (x, y) ln(x x y y ) 2 z x b) w y Giải
a) Đạo hàm riêng cấp 1 của f theo biến x, y 166 1 / f øx, ù y ø 3 4x 2xy ù 2 x 4 2 2 2 x x y y 1 / f øx, ù y ø 2 2x y 2y y 4 2 2 2 ù x x y y
b) Đạo hàm riêng cấp 1 của w theo biến x, y 2 z 1 x 1 / w øx, y, zù 2 z . x y y 2 z 1 2 z x x x / w øx, y,zù 2 2 y z . z 2 2 z 1 y y y 2 z x x / w x, y,z ln .2z z ø ù y y
6.3.1.2. Đạo hàm riêng của hàm hợp Nếu z f øu, ù
v và u u øxù, v v øxù thì đạo hàm của hàm số z theo biến x là dz z du z dv (6.3) dx u dx v dx Nếu w f øu u với øk = 1,2,..., ù 1, u 2,..., u và mỗi biến mù k
m lại là hàm của các biến 1
x ,x2,...,xn thì đạo hàm của hàm số w theo xi øi 1, 2,3..., ù
n được tính theo công thức: w w u w u w u 1 2 n (6.4) x u x u x u x i 1 i 2 i n i
(Nếu các đạo hàm ở vế phải tồn tại). Ví dụ 15. Cho hàm số 2 w u ln v với ø 2 u sin 2x y ù , 4 4 2 v x y cos x. Tính đạo hàm
riêng của hàm số theo biến x, y. Giải Ta có w w 1 u v 2u, ; 2cos ø 2 2x y ù 3 , 4x sin 2x u v v x x w 1 2sin ø 2 2x y ù2cos ø 2 2x y ù ø 3 4x sin 2x 4 4 2 ù x x y cos x u v 2ycosø 2 2x y ù 3 , 4y y y 167 w 1 2sin ø 2 2x y ù.2ycos ø 2 2x y ù . ø 3 4y . 4 4 2 ù y x y cos x Ví dụ 16. Cho hàm số ø ù ø 2 ù2 x z f x, y ln x y
arcco t . Tính đạo hàm riêng của hàm y 1 số f ø x, ù
y theo biến x và đạo hàm riêng của hàm số f x, theo biến y. y Giải Cách 1. Ta có: ø ù ø 2 ù2 x f x, y ln x y arccot gøx, ù y y 1 1 2 f x, ln x arccot øxyù h øx, y ù 2 y y
Đạo hàm riêng cấp 1 của hàm g theo biến x 2x 1 1 2x y / x g øx, ù y . . 2 2 2 2 2 x y x y x y 1 2 y
Đạo hàm riêng cấp 1 của hàm h theo biến y 1 2 x 2 xy / h y øx, ù y . . 3 2 2 2 2 2 1 y 1 x y (1 x y )y x 2 y Cách 2. Xem f ø x, ù
y là hàm hợp của hàm số f øu, ù v và các hàm số u x, v y sau
đó tính đạo hàm của hàm số f øu, ù
v theo biến x theo công thức đạo hàm của hàm hợp. 1 Tương tự, xem hàm f x,
là hàm hợp của hàm số f øu, ù v và các hàm số y 1 u x, v . y
6.3.1.3. Đạo hàm của hàm số ẩn
a. Khái niệm hàm số ẩn
Nếu giá trị của hai biến x, y quan hệ với nhau bởi hệ thức Føx, ù y 0 (*), trong đó Føx, ù
y là hàm hai biến xác định trên miền 2 D . 168
Nếu x X, tồn tại hàm số y f øxù thỏa mãn hệ thức (*), thì ta nói hệ thức này
xác định hàm ẩn y f øxù trên tập X.
Ví dụ 17. Xét hệ thức: ø ù 2 2 F x, y x y 1 0 (**) Với x 1,1 ta có ø ù 2 y x 1 x Vậy hàm 2 y 1 x với x 1,1 và hàm 2 y 1 x với x 1,1 là các
hàm ẩn xác định bởi hệ thức (**). b. Định lý hàm ẩn Cho hàm hai biến Føx, ù
y xác định trong một lân cận của điểm øx , y và 0 0 ù Føx , y
0, giả thiết rằng Føx, ù
y có các đạo hàm riêng liên tục và / Fyøx, ù y 0 tại mọi 0 0ù điểm øx, ù
y thuộc hàm lân cận của øx , y ù; Khi đó tồn tại duy nhất hàm liên tục y f ø ù x 0 0
xác định trong một lân cận của x0 thỏa mãn điều kiện: 0 y f øx0 ù, F x,f øxù 0 và / / Fxøx, ù y yx
(công thức đạo hàm của hàm ẩn) / F x, y y ø ù Ví dụ 18. Cho hàm số: ø ù 2 2 F x, y x y 1 0 (**)
Xác định hai hàm ẩn liên tục 2 y 1 x và 2 y 1 x với x 1,1 .
Tại điểm øx0, y0ù ø0, ù 1 ta có Fø0, ù 1
0. Khi đó chỉ có hàm ẩn 2 y 1 x thoả mãn điều kiện y ø ù 0 1.
Sử dụng công thức tính đạo hàm của hàm ẩn. Tính đạo hàm của y theo x.
Đạo hàm riêng của F theo x và theo y / F øx, ù / y 2x; F x, y 2y x yø ù / F x, y / x ø ù x Đạo hàm của y theo x: y . x / F x, y y y ø ù x x +) Nếu ø ù 2 y x 1 x thì / y . x 2 y 1 x x x +) Nếu ø ù 2 y x 1 x thì / y . x 2 y 1 x 169
6.3.1.4. Đạo hàm riêng cấp 2 z z Xét hàm số z f øx, ù
y . Tính các đạo hàm riêng lần thứ nhất ta được , gọi là x y
các đạo hàm cấp một của hàm z . Tính đạo hàm riêng của các đạo hàm riêng đó ta được
các đạo hàm riêng mới gọi là các đạo hàm riêng cấp hai của hàm số z ký hiệu là: 2 2 z z z z // f øx, yù // , f x, y . (6.5) 2 xx 2 yy ø ù x x x y y y 2 2 z z z z // f øx, ù // y , f x, y . xy yx ø ù (6.6) y x x y x y y x
Tương tự, đạo hàm riêng cấp hai của hàm số n biến số là đạo hàm riêng của đạo hàm riêng cấp một. Ký hiệu: // // w x f (6.7) ix j xixj Hàm số n biến số có 2
n đạo hàm riêng cấp hai và nếu i j thì các đạo hàm riêng
cấp 2 được gọi là đạo hàm hỗn hợp cấp 2.
Ví dụ 19. Tính các đạo hàm riêng cấp hai của hàm số sau: 3 2 w x y xy Giải
Tính các đạo hàm riêng cấp 1: / 2 2 / 3 w x 3x y y ; w y x 2xy.
Tính các đạo hàm riêng cấp 2: // // 2 // // w xx 6xy; w xy 3x 2y w yx; w yy 2x. x 2 2 z z
Ví dụ 20. Cho hàm số z arctan . Chứng minh rằng: 0. y 2 2 x y Giải
Tính các đạo hàm cấp 1: z 1 1 y z 1 x x . ; . 2 2 2 2 2 2 2 x x y x y y x y x y 1 1 2 2 y y Mặt khác: 170 2 2 z 2xy z 2xy ; 2 x ø ù2 2 y x y øx y ù2 2 2 2 2 Vậy: 2 2 z z 0. 2 2 x y Ví dụ 21. Cho ø ù
u là một hàm số có đạo hàm với u là hàm số của hai biến số x và y. 1 z 1 z z Đặt ø 2 2 z y. x y ù. Hãy chứng minh: . 2 x x y y y Giải
Đạo hàm riêng cấp 1 của hàm z theo biến x, y z z / .2x; ø ù / u y. . 2y u u ø ù x y Ta có 1 z 1 z 1 1 / .y. .2x . ø ù / u y . 2y u u ø ù x x y y x y ø ù y. ø 2 2 x y u ù z
(điều phải chứng minh) 2 2 y y y
Chú ý: Nói chung, hai đạo hàm hỗn hợp cấp hai theo cùng một cặp biến số nhưng sai
khác nhau ở trình tự lấy đạo hàm có thể không bằng nhau. Tuy nhiên, cả hai đạo hàm đó
cùng tồn tại và liên tục thì chúng bằng nhau. Trong chương trình của chúng ta chỉ xét
những đạo hàm hỗn hợp cấp hai tồn tại và liên tục.
6.3.2. Vi phân và ứng dụng vi phân để tính gần đúng 6.3.2.1. Vi phân cấp 1 Xét hàm số w f øx, ù
y . Khi đồng thời cho x số gia x và y số gia y thì hàm số w f øx, ù
y có số gia tương ứng là: w f f øx x, y y ù f øx, y ù.
Số gia này gọi là số gia toàn phần của hàm số w f øx, ù y tại điểm øx, ù y . Nếu hàm số w f øx, ù
y có các đạo hàm riêng / / x f øx, ù y và f y øx, ù y liên tục tại điểm
øx ,y thì số gia toàn phần f tại điểm øx ,y có thể viết dưới dạng: 0 0 ù 0 0 ù 171 / w f f øx , y ù / x f x , y y x ñ y ò . x 0 0 y ø 0 ù 0 (6.8) Trong đó, ñ ,ò 0 khi x và y 0.
Định nghĩa: Nếu hàm số w f øx, ù
y xác định trong miền D và có các đạo hàm riêng
liên tục tại điểm M x , y D thì biểu thức / f øx , y ù / x 0 0
x fy øx0, y0ù y được gọi là 0 ø 0 ù 0
vi phân toàn phần của hàm số w f øx, ù y tại điểm M0 øx0 , 0
y ù và được ký hiệu là dw hay df ø 0 x , 0 y ù .
Vậy vi phân toàn phần của hàm số hai biến số tại một điểm M x , y 0 ø 0 0 ù là: / dw f øx ,y ù / x f x , y y (6.9) x 0 0 y ø 0 0 ù Hay: df øx , y ù / f øx , y ù / x f x , y y . (6.10) 0 0 x 0 0 y ø 0 0ù
Với x, y là các biến độc lập, ta có dx x, dy
y và khi không nhấn mạnh vi
phân toàn phần tại một điểm nào đó thì biểu thức vi phân toàn phần của hàm số được viết: / / df f dx f dy x y (6.11)
Ví dụ 22. Tính vi phân toàn phần của hàm số : ø ù ø 2 2 w f x, y ln x xy y ù tại điểm M0 ø1, ù 2 biết x 0,1; y 0, 2 . Giải
Ta có đạo hàm riêng cấp 1 2x y x 2y / f x, y ; / f x, y x ø ù y ø ù 2 2 x xy y 2 2 x xy y Vậy 2.1 2 4 1 2.2 5 / f 1, 2 ; / f 1, 2 . y ø ù x ø ù 2 2 1 1.2 2 7 2 2 1 1.2 2 7
Vi phân toàn phần của hàm số tại điểm M0 ø1, ù 2 là: ø ù 4 5 df 1, 2 .0,1 0, 2 0, 2. 7 7
Tương tự, giả thiết hàm số n biến số w f øx1, x2,..., xnù có các đạo hàm riêng liên tục
theo tất cả các biến độc lập, biểu thức vi phân toàn phần là: dw 1 f 1 dx f2dx2 n f dxn (6.12) 172 f Với if . xi
Ví dụ 23. Viết biểu thức vi phân toàn phần của hàm số: 2 xy w tan z Giải
Ta có đạo hàm riêng cấp 1 2 1 y 1 2xy / w . ; / w . ; x 2 xy z y 2 xy z 2 cos 2 cos z z 2 1 xy / w . . z 2 2 2 xy z cos z
Biểu thức vi phân toàn phần của hàm số là: 2 2 1 y 1 2xy 1 xy dw . dx . dy . dz. 2 2 2 2 xy z xy z 2 2 2 xy z cos cos cos z z z
6.3.2.2. Ứng dụng vi phân toàn phần để tính gần đúng Từ (6.8) ta suy ra: f df ñ x y ò Trong đó, ñ ,ò 0 khi x và y
0. Do đó, trong trường hợp hàm số w f øx, ù y
có các đạo hàm riêng liên tục thì f khác df càng ít khi x, y càng nhỏ (về giá trị tuyệt
đối). Vì vậy, ta có thể tính đơn giản: f df với x, y đủ nhỏ.
Ví dụ 24. Tính gần đúng ø ù2,01 0,99 . Giải Ta xét hàm số ø ù y f x, y x thì số phải tính ø ù2,01 0,99 chính là f ø0,99;2,0 ù 1 . Mặt khác:
f ø0,99;2,01ù f ø1 0,01;2 0,01 ù f ø1; ù 2
f ø1 0,01;2 0,01ù f ø1,2 ù 173
Mà theo công thức gần đúng f df , tại x0 1, y0 2 với x 0,01, y 0,01. Suy ra:
f ø0,99;2,01ù f ø1, 2 ù df ø1,2 ù. Với ø ù 2 f 1, 2 1 1, / y 1 / y fx yx , fy x ln x ø ù y 1 y df 1, 2 yx . x x ln x. y 2. ø 1. 0, 01ù 1.ln1.0,01= 0,02 Vậy f ø0,99;2,0 ù 1 1 0,02 0,98. Nhận xét
Để tính gần đúng một số A nào đó ta phải tìm được biểu thức của hàm số f øx, ù y
(nếu chỉ cần hai biến độc lập) sao cho số A chính là giá trị của hàm số tại điểm øx1, y ù 1 nào đó A f øx1, y ù
1 . Sau đó viết f øx1, y ù 1 dưới dạng f øx , y f x x, y y , 1 ù1 ø 0 0 ù
trong đó x0, y0 được chọn sao cho giá trị của hàm f (x 0, y 0) được tính dễ dàng (chính xác), suy ra x 1 x x0, y 1 y 0
y rồi tính gần đúng số gia toàn phần f øx , y df x , y . 0 0ù ø 0 0ù
Cuối cùng sử dụng công thức: df øx , y ù / f øx , y ù / x f x , y y 0 0 x 0 0 y ø 0 0ù (6.13) Vậy A f øx , y f x , y df x , y . 1 ù1 ø 0 ù 0 ø 0 ù 0 (6.14) 6.3.2.3. Vi phân cấp 2
Định nghĩa: Vi phân toàn phần của vi phân toàn phần cấp một dw của hàm số
w f øx1, x2,..., xnù được gọi là vi phân toàn phần cấp hai của hàm số đó và được ký hiệu như sau: 2 2 d w, d f øx1,x2,..., xnù (6.15)
Đối với trường hợp hàm số hai biến số biểu thức vi phân toàn phần cấp hai là: d w w ødx ù2 2w ødxdy ù w ø dy ù 2 2 // // // xx xy yy . (6.16)
Ví dụ 25. Viết biểu thức vi phân toàn phần cấp hai của hàm số: 174 x 2y w e Giải
Tính đạo hàm riêng cấp 1: / x 2y / x 2y w e ; w 2e x y
Tính đạo hàm riêng cấp 2: // x 2y // x 2y // // x 2y w e ; w 2e w ; w 4e xx xy yx yy
Biểu thức vi phân toàn phần cấp 2: ø ù2 ø ù ø ù2 x 2y x 2y x 2y dw e dx 2.2e dxdy 4e dy .
6.4. Cực trị hàm nhiều biến 6.4.1. Cực trị tự do
6.4.1.1. Khái niệm cực trị địa phương Cho hàm n biến n f : D và X ø 0 0 x ,x ,...,x ù 0 D. 0 1 2 n Hàm f xác định và liên tục trong miền D X øx , x , ,x ù n | a x b ;i 1,2, ,n 1 2 n i i i (6.17)
+) Hàm f đạt cực đại tại điểm X f X f X ; X D. 0 , nếu ø ù ø 0ù
+) Hàm f đạt cực tiểu tại điểm X , nếu f ø ù X f ø 0 X ù; X D. 0 +) Hàm số f ø ù
X đạt cực đại hay cực tiểu tại điềm X0 được gọi là điểm cực trị của hàm số.
Bài toán 1: Tìm cực trị của hàm số w f øx X D 1, x 2, , x n ù f øX ù với 0 175
* Điều kiện cần: Giả sử hàm số w f øXù xác định, liên tục và có các đạo hàm riêng
theo tất cả các biến độc lập trong miền D. Để hàm số này đạt cực trị (cực đại hoặc cực tiểu) tại điểm X
D thì tại điểm đó tất cả các đạo hàm riêng cấp một triệt tiêu: 0 / / w f X 0; i 1,2, ,n x x ø ù (6.18) i i 0
Điểm X0 thoả mãn điều kiện trên được gọi là điểm dừng của hàm số f ø ù X .
* Điều kiện đủ: Giả sử X0 là một điểm dừng của hàm số w f øXù và tại điểm đó
hàm số có tất cả các đạo hàm riêng cấp hai liên tục.
• Định lý 1: Xét dạng toàn phương của n biến số dx ,dx , ,dx 1 2 n n n 2 d f i a jd i x dx (6.19) j i 1 j 1 trong đó // a ij fx x øX0ù. i j i) Nếu 2
d f là dạng toàn phương xác định dương thì điểm dừng X là điểm cực tiểu 0 của hàm số f ø ù X . ii) Nếu 2
d f là dạng toàn phương xác định âm thì điểm dừng X là điểm cực đại của 0 hàm số f ø ù X . iii) Nếu 2
d f là dạng toàn phương không xác định thì điểm dừng X0 không phải là
điểm cực trị của hàm số f ø ù X .
• Định lý 2: Xét ma trận của dạng toàn phương 2 d f (ma trận Hess): 1 a 1 1 a 2 1 a n a a a 21 22 2n H (6.20) a n1 a n2 a nn
có các định thức con chính cấp k øk 1,2, , ù n là: a a a 11 12 1k a a a 21 22 2k H (6.21) k a a a k1 k2 kk 176
i) Nếu Hk 0 với k 1,2, ,n (tức là ma trận H có tất cả các định thức con chính
dương) thì điểm dừng X0 là điểm cực tiểu của hàm số f ø ù X . ii) Nếu ø ùk 1 k H
0 với k 1,2, ,n (tức là ma trận H có các định thức con chính
cấp lẻ âm và cấp chẵn dương) thì điểm dừng X0 là điểm cực đại của hàm số f ø ù X .
Trong thực hành, ta thường gặp các bài toán tìm cực trị tự do của hàm hai biến và
hàm ba biến. Sau đây chúng tôi sẽ phát biểu các bước tìm cực trị cho các hàm trong những trường hợp này.
6.4.1.2. Trường hợp hàm hai biến
Với hàm hai biến z f øx, ù
y . Để khảo sát cực trị hàm này ta thực hiện các bước sau:
Bước 1: Giải hệ phương trình / / z f x, y 0 x x ø ù ý (6.22) / / z f x, y 0 þ y y ø ù
Các nghiệm của hệ là tọa độ các điểm dừng.
Bước 2: Kiểm tra điều kiện đủ tại các điểm dừng. Giả sử M øx0,y ù
0 là một điểm dừng của hàm số đã cho. Xét định thức a a 11 12 D 1 a 1 2 a 2 1 a 2 2 a 1 (6.23) a a 21 22 trong đó // a f øx , y ù // ; a f x ,y ; 11 xx 0 0 12 xy ø 0 0 ù // a f øx , y ù // ; a f x , y . 21 yx 0 0 22 yy ø 0 ù 0
Trường hợp 1 : Nếu D 0 thì điểm dừng M là điểm cực trị của hàm số w f øx, ù y : Møx0, 0
y ù là điểm cực đại nếu a 0. 11 Møx0, 0
y ù là điểm cực tiểu nếu 1 a 1 0.
Trường hợp 2 : Nếu D 0 thì điểm dừng M không phải là điểm cực trị của hàm số w f øx, ù y .
6.4.1.3. Trường hợp hàm ba biến
Với hàm ba biến w f øx, y, ù
z . Để khảo sát cực trị hàm này ta thực hiện các bước:
Bước 1: Giải hệ phương trình 177 / / w f x, y,z 0 x x ø ù / / w ý y f yøx, y, ù z 0 (6.24) / / w f x, y,z 0 þ z z ø ù
Các nghiệm của hệ là tọa độ các điểm dừng.
Bước 2: Kiểm tra điều kiện đủ tại các điểm dừng. Giả sử Møx0, y0,z ù
0 là một điểm dừng của hàm số đã cho. Xét các định thức con chính của ma trận: 1 a 1 1 a 2 1 a 3 H a (6.25) 21 a22 a23 a 31 a 32 a 33 a a Với 11 12 H a ; H ; H H , trong đó: 1 11 2 3 a21 a22 // a f øx , y ,z ù // ; a f øx , y ,z ù // ; a f x , y ,z ; 11 xx 0 0 0 12 xy 0 0 0 13 xz ø 0 0 0 ù // a f øx ,y ,z ù // ; a f øx ,y ,z ù // ; a f x , y ,z ; 21 yx 0 0 0 22 yy 0 0 0 23 yz ø 0 0 0 ù // a f øx , y ,z ù // ; a f øx ,y ,z ù // ; a f x , y ,z . 31 zx 0 0 0 32 zy 0 0 0 33 zz ø 0 0 0ù
Trường hợp 1: Nếu H1 0; H2 0; H3 0 thì M là điểm cực tiểu của hàm số w f øx, y, ù z . Trường hợp 2 : Nếu 1 H 0; 2 H 0; 3 H
0 thì M là điểm cực đại của hàm số w f øx, y, ù z .
Chú ý : Trong khuôn khổ chương trình, ta thường gặp những hàm số có các đạo hàm
riêng cấp hai liên tục, nên các đạo hàm chéo đều bằng nhau, do đó aij aji øi ùj.
Ví dụ 26. Tìm cực trị của hàm số 3 3 z x 2xy 8y . . Giải
Bước 1: Giải hệ phương trình: / 2 2 z 3x 2y 0 3x 2y x ý ý / 2 2 z 2x 24y 0 þ y 24y 2x þ
Lập tỉ số vế theo vế của hai phương trình trên, ta có x 2y
Thay vào phương trình thứ nhất của hệ, ta có 178 y 0 x 0 1 1 2y ø6y ù 1 0 1 1 y x 2 2 6 3 1 1
Vậy hàm số có hai điểm dừng M , 1 M ø0, ù 0 và 2 . 3 6
Bước 2: Kiểm tra điều kiện đủ // // // // zxx 6x; zyy 48y; zxy zyx 2 0 2 +) Tại điểm M1ø0, ù 0 , ta có: D 4 0 2 0
nên M1 không phải là điểm cực trị. 1 1 2 2 +) Tại điểm M , 2 , ta có: D 12 0 và a 2 0 3 6 2 8 11
nên M2 là điểm cực tiểu. Khi đó giá trị cực tiểu của hàm số là 3 3 1 1 1 1 1 z CT 2. . 8 . 3 3 6 6 27
Ví dụ 27. Tìm cực trị của hàm số: 2 2 z 3x 4y 2xy 2x 3y 1. Giải
Bước 1: Giải hệ phương trình 5 / x z 6x 2y 2 0 x 22 ý / ý z 8y 2x 3 0 7 þ y y þ 22 5 7
Vậy hàm số có một điểm dừng là M , . 22 22
Bước 2: Kiểm tra điều kiện đủ // // // 1 a 1 x z x 6;a22 y z y 8; 1 a 2 a21 zxy 2. a a 6 2 Ta có: 11 12 D 44 0 và a 6 0 a 11 21 a22 2 8
nên M là điểm cực đại của hàm số. Khi đó giá trị cực đại của hàm số là 5 7 825 z CD z , . 22 22 484 179
Ví dụ 28. Tìm cực trị của hàm số: 2 2 2 w x 2y 9z 4xz 2y 3z 4 . Giải
Bước 1: Giải hệ phương trình / 3 x wx 2x 4z 0 5 / 1 ýw 4y 2 0 ý y y 2 / w 18z 4x 3 0 3 þ z z þ 10 3 1 3
Vậy hàm số có một điểm dừng là M , , . 5 2 10
Bước 2: Kiểm tra điều kiện đủ // // // a w 2; a w 4; a w 18; 11 xx 22 yy 33 zz // // // 1 a 2 a21 wxy 0; 1 a 3 3 a 1 wxz 4; a23 a32 wyz 0. 2 0 4 Lập ma trận: H 0 4 0 4 0 18 2 0 4 2 0 Ta có: 1 H 2 0; H2 8 0; H3 0 4 0 80 0 0 4 4 0 18
nên M là điểm cực tiểu. Khi đó giá trị cực tiểu của hàm số là 3 1 3 61 z z , , . CT 5 2 10 20 10 5
Ví dụ 29. Tìm cực trị của hàm số z 20xy (điều kiện: x 0; y 0 ). x y Giải
Bước 1: Giải hệ phương trình / 10 1 z x 20y 0 2y 2 2 2 x x 2x y 1 ý 5 ý 1 ý 2 / 4xy 1 z 20x 0 4x þ y 2 2 þ y þ y
Theo giả thiết x 0; y 0 nên ta có thể xác định quan hệ giữa x, y như sau: 180 2 2x y 1 x 1 x 2y 2 4xy 1 2y
Thay vào phương trình thứ nhất của hệ, ta có 3 3 1 1 8y 1 y y x
1 (thoả mãn điều kiện) 8 2 1
Vậy hàm số có một điểm dừng M 1, . 2
Bước 2: Kiểm tra điều kiện đủ 20 1 // // zxx 1 a 1 zxx 1, 20; 3 x 2 10 1 // // z a z 1, 80; yy 22 yy 3 y 2 1 // // // z z 20 a a z 1, 20. xy yx 12 21 xy 2 Ta có: 20 20 D 1200 0 và a 20 0 20 80 11
nên M là điểm cực tiểu. Khi đó giá trị cực tiểu của hàm số là 1 10 5 z 20.ø ù 1 . 30 . CT 2 1 12
Ví dụ 30. Tìm cực trị của hàm số 4 4 2 2 z x y x 2xy y 2 . Giải
Bước 1: Giải hệ phương trình / 3 z 4x 2x 2y 0 x ý / 3 z 4y 2x 2y 0 þ y
Cộng phương trình thứ nhất với phương trình thứ hai của hệ, ta có quan hê giữa hai biến 3 3 4x 4y 0 x y
Thay vào phương trình thứ nhất của hệ, ta có 1 x 1 1 y 1 4x ø 2 x ù1 0 x2 1 2 y 1 x3 0 y3 0 181
Vậy hàm số có ba điểm dừng M ø1, 1 1 ù , M2 ø 1, ù 1 và M 3 ø0, ù 0 .
Bước 2: Kiểm tra điều kiện đủ // 2 // 2 // // z xx 12x 2; z yy 12y 2; z xy zyx 2 10 2 +) Tại điểm 1 M ø1, ù 1 , ta có D 96 0 và a 10 0 2 10 11
nên M1 là điểm cực đại. Khi đó giá trị cực đại của hàm số là z z 1, 1 0 CD ø ù 10 2 +) Tại điểm M 1,1 D 96 0 a 10 0 2 ø ù, ta có và 2 10 11
nên M là là điểm cực đại. Khi đó giá trị cực đại của hàm số là 2 z CD z ø1, ù 1 0 2 2 +) Tại điểm M3 ø0, ù 0 , ta có D 0 2 2
nên ta chưa thể kết luận được tính chất của điểm này. Ta cần xét điểm M thông qua định 3
nghĩa cực trị địa phương:
Xét những điểm M øx, yù có khoảng cách đến M 3ø0, ù
0 nhỏ hơn một số thực dương: 0 d øM, 3 M ù r . Xét hiệu : z ø ù M z øM ù 4 4 2 2 x y x 2xy y 3 øx ù2 y ø 4 4 x y ù
Tại những điểm M øx, yù thoả mãn x y 0 , ta có z ø ù M z øM ù ø 4x y ù4 0 z M z M 3 ø ù ø ù 3
Tại những điểm M øx, yù thoả mãn x 2y 0 , ta có ø ù ø ù 2 4 2 y 17y y ø1 17y ù 2 1 1 z M z M3 0 y 17 17 1 1
nên tại những điểm M ø2y, ù y mà y thì z ø ù M z ø 3 M ù. 17 17
Vậy theo định nghĩa, M không phải là điểm cực trị của hàm số. 3 182
6.4.2. Cực trị có điều kiện
6.4.2.1. Bài toán cực trị có điều kiện ràng buộc
Bài toán. Tìm cực trị của hàm số : w f øx ,x , ,x
f X với điều kiện : gøx , x , , x g X b . 1 2 n ù ø ù 1 2 n ù ø ù Lập hàm phụ Lagrange: L ø 1 x , x2 , , xn , ù f ø 1 x , x2 , , xn ù b g ø1 x , x2 , ,xn ù (6.26) với : nhân tử Lagrange.
Điều kiện cần: Giả sử các hàm f và g có các đạo hàm riêng liên tục trong một lân cận của điểm X ø 1
x , x2, , xn ù và tại điểm đó ít nhất một trong các đạo hàm riêng của g khác
0. Nếu hàm w f øXù với điều kiện gø ù X
b đạt cực trị tại X thì tồn tại một giá trị
của nhân tử Lagrange sao cho øx1,x 2, ,x n, ù là nghiệm của hệ phương trình: / L b gø ù X 0 ý øi 1,2, ,nù (6.27) / / / L f g 0 þ xi xi xi
Điều kiện đủ: Giả sử các hàm f và g có các đạo hàm riêng cấp hai liên tục tại điểm X và điểm øx ,x , ,x , 1 2 n
ù là một điểm dừng của hàm số Lagrange. Lập ma trận: g g g 0 1 2 n g L L L 1 11 12 1n H g L L L (6.28) 2 21 22 2n gn Ln1 Ln2 Lnn trong đó / g g øx ,x , , x ù // ; L L x , x , , x , ; i, j, k 1, 2, , n k x 1 2 n ij x x ø 1 2 n ù ø ù k i j
Các định thức con chính cấp k øk 2,3, , ù n là g g g 0 1 2 k g L L L 1 11 12 1k H k g L L L (6.29) 2 21 22 2k gk Lk1 Lk2 Lkk 183 i) Nếu ø ùk 1 k H
0 với k 2,3, ,n thì hàm w f øXù với điều kiện gø ù X b đạt
giá trị cực đại tại điểm X. ii) Nếu Hk
0 với k 2,3, ,n thì hàm w f øXù với điều kiện gø ù X b đạt giá
trị cực tiểu tại điểm X.
6.4.2.2. Trường hợp hàm hai biến
Xét hàm hai biến z f øx, ù
y với điều kiện gøx, ù y b .
Bước 1: Lập hàm Lagrange: L øx, y, ù f øx, y ù b g øx, y ù (6.30)
Bước 2: Giải hệ phương trình sau để tìm điểm dừng / / / Lx fx gx 0 / / / L ý f g 0 (6.31) y y y / L b g øx, yù 0 þ Bước 3: Giả sử Møx , y 0
0ù là một điểm dừng ứng với giá trị 0 , ta xét định thức 0 g g 1 2 H g L L (6.32) 1 11 12 g L L 2 21 22 trong đó: / g g øx ,y ù / ; g g øx , y ù // ; L L x , y , ; 1 x 0 0 2 y 0 0 11 xx ø 0 0 0 ù // L L øx , y , ù // 22 yy 0 0 0 ; 1 L 2 L21 Lxy øx0, y0, ù 0 . Trường hợp 1: Nếu H 0 thì hàm số z f øx, ù y với điều kiện ø g x, ù y b đạt giá
trị cực đại tại điểm M. Trường hợp 2: Nếu H 0 thì hàm số z f øx, ù
y với điều kiện gøx, ù y b đạt giá
trị cực tiểu tại điểm M.
6.4.2.3. Trường hợp hàm ba biến
Xét hàm ba biến w f øx, y, zù với điều kiện gøx, y, ù z b .
Bước 1: Lập hàm Lagrange L øx, y,z, ù f øx, y,z ù b g øx, y, z ù (6.33)
Bước 2: Giải hệ phương trình sau để tìm điểm dừng 184 / / / L f g 0 x x x / / / L f g 0 y y y ý (6.34) / / / Lz fz gz 0 / L b g øx, y, zù 0 þ
Bước 3: Giả sử M øx , y ,z 0 0
0ù là một điểm dừng ứng 0, ta có ma trận Hess 0 g g g 1 2 3 g L L L 1 11 12 13 H (6.35) g L L L 2 21 22 23 3 g 3 L 1 3 L 2 3 L 3
Xét các định thức con chính của ma trận Hess 0 g1 g2 H 2 g L L 1 11 12 và H 3 H , (6.36) g2 L21 L22 trong đó / g g øx , y ,z ù / ; g g øx , y ,z ù / ; g g x , y ,z ; 1 x 0 0 0 2 y 0 0 0 3 z ø 0 0 0ù // L L øx ,y ,z , ù // ; L L L x , y ,z , ; 11 xx 0 0 0 0 12 21 xy ø 0 0 0 ù 0 // L L øx ,y ,z , ù // ; L L L x , y ,z , ; 22 yy 0 0 0 0 23 32 yz ø 0 0 0 0ù // L L øx , y ,z , ù // 33 zz 0 0 0 0 ; 1 L 3 3 L 1 Lxz øx0 , 0 y , 0 z , 0ù.
Trường hợp 1: Nếu H2 0; H3 0 thì hàm số w f øx, y,zù với điều kiện gøx, y, ù z
b đạt giá trị cực đại tại điểm M.
Trường hợp 2: Nếu H2 0; H3 0 thì hàm số w f øx, y, zù với điều kiện ø g x, y, ù z
b đạt giá trị cực tiểu tại điểm M.
Ví dụ 31. Sử dụng phương pháp nhân tử Lagrange tìm cực trị của hàm số 2 2 z x 2y với điều kiện 3x 2y 22 . Giải
Bước 1: Lập hàm Lagrange 2 2 L(x, y, ) x 2y ø 22 3x 2 ù y
Bước 2: Giải hệ phương trình 185 / 3 x Lx 2x 3 0 2 x 6 / L ý y 4y 2 0 ýy ý y 2 2 / 4 L 22 3x 2y 0 3x 2y 22 þ þ þ
Vậy hàm số có một điểm dừng là M ø 6, ù 2 ứng với 2 .
Bước 3: Kiểm tra điều kiện đủ / / // g1 g x 3; g 2 g y 2; L11 Lxx 2; // // L L 4; L L L 0. 22 yy 12 21 xy Xét định thức : 0 3 2 H 3 2 0 44 0 2 0 4
Vậy điểm M là điểm cực đại. Khi đó giá trị cực đại của hàm số là z z ø 6,2 ù ø6 ù2 2 CD 2.2 44.
Ví dụ 32. Sử dụng phương pháp nhân tử Lagrange tìm cực trị của hàm số z 3x y với điều kiện 2 2 3x 4y 208. Giải
Bước 1: Lập hàm Lagrange: ø 2 2 L(x, y, ) 3x y 208 3x 4y ù
Bước 2: Giải hệ phương trình / L 3 6 x 0 x 2 x 1 (1) / L ý 1 8 y 0 ý 8 y 1 (2) y 2 2 / 2 2 L 208 3x 4y 0 3x þ 4y 208 (3) þ Từ (1) và (2), ta có x
4y ( x 0, y 0 , vì nếu x 0, y 0 là vô lý)
Thay vào phương trình thứ (3), ta có y 2 2 2 52y 208 y 4 y 2 Với y
2 kết hợp với (1) và (2), ta có : 186 2 x 1 x 8 8 ý y 1 ý y 2 y þ 2 1 þ 16
Với y 2 kết hợp với (1) và (2), ta có : 2 x 1 x 8 8 ý y 1 ý y 2 y 2 1 þ þ 16
Vậy hàm số có hai điểm dừng: 1 1 M1ø8, ù 2 ứng với ; M 2 ø 8,2ù ứng với . 1 16 2 16
Bước 3: Kiểm tra điều kiện đủ tại điểm M x , y ứng với i 1, 2 i ø ù i ø i iù / / // gx 6x; gy 8y; Lxx 6 ; // // // Lyy 8 ; Lxy Lyx 0. Suy ra g 6x ;g 8y ; L 6 ; L 8 ;L L 0. 1 i 2 i 11 i 22 i 12 21 Xét định thức: 0 6xi 8 i y H 6x 6 0 96 ø 2 2 3x 4y 19968. i i i i i ù i 8y 0 8 i i 1 1
+) Tại điểm M 8, 2 ứng với . Ta có 1ø ù H 19968 1248 0 16 16
nên M là điểm cực đại. Khi đó giá trị cực đại của hàm số là 1 z z 8, 2 3.8 2 26. CD ø ù 1 +) Tại điểm M 2 ø 8, ù 2 ứng với . 16 1 Ta có H 19968 1248 0. 16
nên M là điểm cực tiểu. Khi đó giá trị cực tiểu của hàm số là 2 z CT z ø 8,2 ù 3. ø8 ù 2 26. 187
6.4.3. Ứng dụng trong kinh tế
6.4.3.1. Hàm cận biên riêng
Hàm cận biên riêng của đại lượng y f ( 1
x , x2,..., xn ) theo đại lượng i x tại điểm ø 0 0 0 1
x , x2,...,xnù, ký hiệu là Mx f (x ,x ,..., x ), là độ biến đổi của đại lượng y khi đại i 1 2 n
lượng x tăng lên 1 đơn vị tại ø 0 0 0
x1,x 2,...,x ù trong điều kiện các yếu tố khác không đổi. i n
Biểu thức toán học của hàm cận biên riêng 0 0 0 f 0 0 0 M f x , x ,...,x x ,x ,...,x x . (6.37) i ø 1 2 n ù ø 1 2 n ù xi
Tổng quát ta có, hàm cận biên riêng của đại lượng y f ( x 1
x ,x2,...,xn ) theo đại lượng i : f M y x ,x ,...,x x ø 1 2 n ù . (6.38) i xi
Chú ý : Trong thực tế, lượng cận biên riêng 0 0 0 M y f (x ,x ,...,x ) x f x , x ,..., x của i ø 1 2 n ù 1 2 n theo x tại ø 0 0 0
x1,x 2,...,x ù xấp xỉ bằng độ biến đổi của
x tăng 1 một đơn vị từ trạng i n y khi i thái ø 0 0 0 1 x , x2,...,xnù.
Ví dụ 33. Giả sử hàm sản suất của một doanh nghiệp là: 1 3 ø ù 4 4 Q K,L 20K L
Trong đó: K, L, Q là mức sử dụng vốn, mức sử dụng lao động và sản lượng hàng ngày.
a) Giả sử doanh nghiệp đó đang sử dụng 16 đơn vị vốn và 81 đơn vị lao động trong một ngày tức K 16, L 81.
Sản lượng cận biên của vốn là: MPK ø16,8 ù / 1 f ø16,8 ù 1 5 ø 0,75 0,7 . 16 81 ù5 16,875 K
Sản lượng cận biên của lao động là: MP ø L 16,81ù / f ø16,81ù 15.ø 0,25 0,2 16 81 ù5 L 10
Nghĩa là, nếu doanh nghiệp tăng mức sử dụng vốn K từ 16 lên 17 đơn vị và giữ
nguyên mức sử dụng lao động L 81 trong một ngày, thì sản lượng tăng thêm xấp xỉ
16,875 đơn vị sản phẩm. Tương tự, nếu giữ nguyên mức sử dụng vốn K 16 và tăng mức 188
sử dụng lao động L từ 81 lên 82 trong một ngày thì sản lượng tăng thêm xấp xỉ 10 đơn vị sản phẩm. b) Tại K 16, L 81, nếu giảm vốn 0 0
K xuống 0,5 đơn vị và tăng lao động L lên
2 đơn vị thì Q sẽ thay đổi như thế nào?
Ta có biểu thức vi phân toàn phần của sản lượng Q theo vốn K và theo lao động L như sau: øQù / f øK ,L ù / K 0 0 K fL øK0,L0ù L hay ø ù 135 185 Q .( 0,5) 10 2 0 8 16
Vậy Q sẽ tăng xấp xỉ 185/16 đơn vị.
6.4.3.2. Hệ số co dãn riêng
Hệ số co dãn riêng của đại lượng y f ( x tại 1
x , x2,..., xn ) theo đại lượng i ø 0 0 0 x , x ,..., x E 1 2
n ù , ký hiệu y x , là (%) độ biến đổi của y khi x tăng lên một đơn vị (1%). i i
Biểu thức của hệ số co dãn riêng f xi E (%) . (6.39) y i x x y i
Ví dụ 34. Giả sử hàm cầu của hàng hoá 1 trên thị trường hai hàng hoá liên quan có dạng 5 sau: Q
. Trong đó, P , P tương ứng là giá của hàng hoá 1, D ø 1 P , 2 P ù 2 2 6300 2 1 P P 1 2 3 1 2
2. Tính hệ số co dãn của cầu theo giá tại điểm ø20,3 ù 0 . Giải
Hệ số co dãn của cầu theo giá 1
P đối với giá của hàng hoá đó tại thời điểm ø 1 P , 2 P ù Q P P 1 D 1 1 4P . 1 D Q 1 P 1 P Q 2 5 2 1 1 D 6300 2P P 1 2 3
Hệ số co dãn của cầu đối với hàng hoá thứ nhất theo giá hàng hoá thứ hai P tại thời 2 điểm ø 1 P , 2 P ù là: 10 P 2 P . 2 D Q 2 P 3 5 1 2 2 6300 2P P 1 2 3 189 Tại điểm ø20,3 ù 0 ta có: 0, 4; 0, 75. Q D P1 Q D P2 1 1
Điều này có nghĩa là khi hàng hoá 1 đang ở mức giá 20 và hàng hoá 2 ở mức giá
30 nếu tăng giá hàng hoá 1 lên 1% còn giá hàng hoá 2 không đổi thì cầu đối với hàng
hoá 1 sẽ giảm 0,4 %, tương tự, nếu giá của hàng hoá 1 không thay đổi nhưng giá của hàng
hoá hai tăng thêm 1% thì cầu đối với hàng hoá 1 cũng giảm 0,75%.
6.4.3.3. Một số bài toán cực trị hàm nhiều biến trong kinh tế
a. Xác định quỹ vốn và lao động để tối đa hóa doanh thu, lợi nhuận
Cho hàm sản xuất Q føK, ù
L và giá bán sản phẩm P. Biết giá thuê một đơn vị
vốn là p và giá thuê một đơn vị lao động là p . K L
Bài toán 1. Xác định mức sử dụng vốn K và lao động L để sản lượng Q cực đại/tối đa.
Bài toán được đưa về bài toán cực trị tự do của hàm sản xuất với hai biến K và L.
Bài toán 2. Hãy xác định mức sử dụng vốn K và lao động L để lợi nhuận cực đại /tối đa.
Chúng ta cần xác định hàm doanh thu, hàm chi phí và hàm lợi nhuận.
+) Hàm doanh thu : TR øK,Lù P.Q P.f øK, L ù +) Hàm chi phí : TCøK, ù L p K p L K L
+) Hàm lợi nhuận : øK, ù L TR TC P Q øK, ù L pK K pL L.
Bài toán được đưa về bài toán cực trị tự do của hàm lợi nhuận với hai biến K và L.
Ví dụ 35. Ước lượng hàm sản xuất của một doanh nghiệp có dạng: ø ù 3 3 Q K, L K 8L 3KL 200, øK 0,L 0 ù
Hãy xác định mức sử dụng vốn và lao động để sản lượng cực đại. Giải
+) Bước 1. Tính các đạo hàm riêng cấp 1 và cấp 2 Đạo hàm riêng cấp 1 / Q øK, ù 2 K L 3K 3L; / Q øK, ù 2 L 24L 3K. L Đạo hàm riêng cấp 2 190 // Q øK, ù / / KK L 6K; QLL øK, ù L 48L; // Q øK, ù // KL L QLKøK, ù L 3.
+) Bước 2. Giải hệ phương trình để tìm điểm dừng / Q øK, ù 2 K L 0 3K 3L 0 ý ý / Q þ øK, ù 2 L L 0 3K 24L 0 þ 1 2 K L K 2 K 0 ý ý hay ý (loại vì K 0,L 0 ) 4 1 þK 8K 0 þL 0 L þ 4 1 1
Hàm số có một điểm dừng M , 2 4 1 1
+) Bước 3. Kiểm tra điều kiện đủ tại M , 2 4 // 1 1 1 1 A Q , 3 0; C Q , 12 0; KK // 2 4 LL 2 4 // 1 1 // 1 1 B Q , Q , 3 0. KL LK 2 4 2 4 Xét định thức 3 3 D 27 0 và A 0 3 12 1 1 1 1 1601
Vậy hàm số đạt cực đại tại M , với Q Q , . 2 4 max 2 4 8
Ví dụ 36. Tìm K, L để hàm lợi nhuận sau đạt giá trị cực đại 2 1 ø ù 3 4 K, L 300K L 100K 150L Giải
+) Bước 1. Tính các đạo hàm riêng cấp 1 và cấp 2 Đạo hàm riêng cấp 1 1 1 / K, L 200K L 100; K ø ù 3 4 2 3 / øK, ù 3 4 L 75K L 150 L 191 Đạo hàm riêng cấp 2 4 1 2 7 // ø 225 K, ù 200 3 4 L K L ; // 3 4 K, L K L ; KK LLø ù 3 4 4 3 // øK, ù / / L øK, ù 3 4 L 50K L . KL LK
+) Bước 2. Giải hệ phương trình để tìm điểm dừng 1 1 / øK, Lù 3 4 K 0 200K L 100 0 ý ý / þ øK, ù 2 3 L 0 L 3 4 þ75K L 150 0 1 1 3 4 200K L 100 ø ù 1 ý 2 3 3 4 75K L 150 ø ù 2 þ
Lập tỷ số hai phương trình ta suy ra được: K 4L (3)
Thế (3) vào (2), ta được 3 1 2 2 75ø4 ù 4 12 3 L 3 L 150 L 2 4 L 16 (4)
Thay (4) vào (3), ta được: K 64
Hàm số có một điểm dừng Mø64,1 ù 6
+) Bước 3. Kiểm tra điều kiện đủ tại Mø64,1 ù 6 4 1 // A ø64,1 ù 200 25 3 4 KK 6 (64) (16) 0; 3 48 2 7 // C ø64,1 ù 225 225 3 4 LL 6 (64) (16) 0; 4 32 1 3 // B ø64,1 ù // 6 ø64,16 ù 25 3 4 KL LK 50(64) (16) 0. 16 Xét định thức 25 25 48 16 625 D và A 0 25 225 512 16 32
Vậy hàm số đạt cực đại tại M ø64,1 ù 6 với max (64,16) 800. 192
b. Xác định cơ cấu sản phẩm để tối thiểu hóa chi phí, tối đa hóa doanh thu, lợi nhuận
Bài toán 1. Hãng độc quyền sản xuất hai loại sản phẩm với giá bán/hàm cầu thứ tự
là P , P và hàm chi phí kết hợp TC TCø 1
Q , Q ù. Hãy xác định cơ cấu sản phẩm/sản 1 2 2
lượng của từng loại sản phẩm để hãng có doanh thu/ lợi nhuận tối đa.
Chúng ta cần xác định hàm doanh thu/ lợi nhuận +) Hàm doanh thu : TR ø 1 Q , 2 Q ù 1 P . 1 Q 2 P 2 Q . +) Hàm lợi nhuận: øQ , Q TR Q , Q TC Q , Q . 1 2ù ø 1 2ù ø 1 2ù
Bài toán được đưa về bài toán cực trị tự do của hàm doanh thu/hàm lợi nhuận với hai biến Q ;Q . 1 2
Bài toán 2. Hãng độc quyền sản xuất một loại sản phẩm nhưng tiêu thụ ở hai thị
trường phân biệt với hàm cầu ở từng thị trường thứ tự lần lượt là 1 P 1 P ( 1 Q ,Q2) ; P
P (Q ,Q ) và hàm chi phí kết hợp TC TCø 1
Q , Q ù. Hãy xác định lượng cung ở 2 2 1 2 2
từng thị trường để hãng có doanh thu/ lợi nhuận tối đa.
Chúng ta cần xác định hàm doanh thu/ lợi nhuận
+) Hàm doanh thu : TR øQ1, Q2 ù 1 P 1 Q 2 P Q2. +) Hàm lợi nhuận: ø 1 Q , Q2ù TR ø 1 Q , Q2ù TC ø 1 Q , Q2ù.
Bài toán được đưa về bài toán cực trị tự do của hàm doanh thu/hàm lợi nhuận với hai biến Q , Q . 1 2
Ví dụ 37. Một hãng độc quyền sản xuất hai loại sản phẩm. Cho biết hàm cầu đối với hai
loại sản phẩm đó như sau: Q 1300 P ; Q 675 0,5P 1 1 2 2
và hàm chi phí kết hợp là TCøQ , Q ù 2 2 1 2 1 Q 1 3Q 2 Q 2
Q . Hãy cho biết mức sản lượng
Q ,Q và các giá bán tương ứng để doanh nghiệp đó thu được lợi nhuận tối đa. 1 2 Giải
+) Bước 1. Lập hàm lợi nhuận
Từ các hàm cầu thuận ta suy ra hàm cầu đảo: 1 P 1300 1 Q ; 2 P 1350 2Q 2
Hàm lợi nhuận của doanh nghiệp ø 1 Q , Q ù 2 1 P 1 Q 2 P 2 Q T ø C 1 Q , Q ù 2 2 2 2 1 Q 3Q2 1300 1 Q 1350Q2 3 1 Q Q2 193
Vậy bài toán trở thành tìm điểm cực đại của hàm ø 1 Q , Q2ù .
+) Bước 2. Tính các đạo hàm riêng cấp 1 và cấp 2 / øQ ,Q ù / 4Q 3Q 1300; Q , Q 3Q 6Q 1350; Q 1 2 1 2 Q ø 1 2 ù 1 2 1 2 //Q ø 1 Q ,Q2ù // 4; Q Q ø 1 Q , 2 Q ù // Q 6; 3. 1 1 2 2 Q1Q 2
+) Bước 3. Giải hệ phương trình để tìm điểm dừng / Q ø 1 Q ,Q ù 2 0 4Q 3Q 1300 0 Q 250 1 1 2 1 ý ý ý / Q ,Q 0 þ 3Q 6Q 1350 0 Q þ 100 Q ø 1 ù 1 2 2 þ 2 2
Vậy hàm số có một điểm dừng là M ø250, 10 ù 0 .
Bước 4. Kiểm tra điều kiện đủ tại Mø250,10 ù 0 . // A ø250,10 ù // 0 4; C 250,100 6; Q Q Q Q ø ù 1 1 2 2 // B ø250,100 ù // 250,100 3. Q Q Q Q ø ù 1 2 2 1 4 3 Xét định thức: D 15 0 và A 4 0 3 6 nên M ø250, 10 ù
0 là điểm cực đại của hàm .
Bước 5. Kết luận: Doanh nghiệp cần bán hàng với mức sản lượng cho mỗi sản phẩm và
giá cả tương ứng là Q1 250; 1 P 1300 250 1050 ; 2 Q 100; 2 P 1350 200 1150
để thu được lợi nhuận tối đa là : max ø250, 10 ù 0 230000.
c. Tối đa hóa lợi ích trong điều kiện ràng buộc về ngân sách dành cho chi tiêu
Cho hàm lợi ích của chủ thể như sau: U U øX, ù
Y . Biết rằng giá mặt hàng hóa X là P , giá mặt hàng hóa
P và ngân sách dành cho chi tiêu của chủ thể là I. Hãy xác X Y là Y
định số lượng mặt hàng X, Y sao cho tối đa hóa lợi ích của chủ thể.
Mô hình bài toán. Tìm øX, ù
Y sao cho U(X, Y) đạt giá trị lớn nhất thỏa mãn điều kiện: X P Y P I. X Y
Ví dụ 38. Cho biết hàm lợi ích tiêu dùng: ø ù 0,4 0,6 U x, y
x y . Giả sử giá của các mặt hàng
tương ứng là 2 USD, 3 USD và thu nhập dành cho tiêu dùng là 130 USD. Hãy xác định
lượng cầu đối với mỗi mặt hàng để người tiêu dùng thu được lợi ích tối đa. Nếu thu nhập
người tiêu dùng tăng 1 USD thì lợi ích tối đa thay đổi như thế nào? 194 Giải
Gọi x là số lượng mặt hàng 1; y là số lượng mặt hàng 2.
+) Bước 1. Mô hình bài toán. Tìm (x, y) sao cho ø ù 0,4 0,6 U x, y x y đạt giá trị tối
đa thỏa mãn điều kiện g(x,y) 2x 3y 130 .
+) Bước 2. Lập hàm Lagrange: ø ù 0,4 0,6 L x, y, x y ø130 2x 3y ù
+) Bước 3. Giải hệ phương trình để tìm điểm dừng / L øx, y, ù 0,6 0,6 0,6 0,6 0,4x y 2 0 x x y 5 (1) / L ý øx,y, ù 0,4 0,4 0,4 0,4 0,6x y 3 0 ý x y 5 (2) y / ø ù 2x 3y 130 (3) L x, y, 130 2x 3y 0 þ þ
Từ (1) và (2) suy ra y x , thay vào phương trình thứ (3) ta có 2x 3.x 130 x 26 y 26; 0,2
Vậy hàm số có một điểm dừng M ø26,2 ù 6 ứng với 0,2.
+) Bước 4. Kiểm tra điều kiện đủ. Xét tại điểm dừng M ø26,2 ù 6 với 0,2. / g g ø26,2 ù / 1 x 6 2; g 2 g yø26,2 ù 6 3; // L L ø26;26;0, ù 1,6 0,6 11 xx 2 0, 24(26) (26) 3 / 325 0; // L L ø26;26;0, ù 0,4 1,4 22 yy 2 0,24(26) (26) 3 / 325 0; // L L L ø26;26;0, ù 0,6 0,4 12 21 xy 2 0,24(26) (26) 3 / 325 0. Xét định thức: 0 2 3 3 H 2 L11 L12 12 1 L 2 9 1 L 1 4L22 0 13 3 L L 21 22 nên Mø26,2 ù
6 là điểm cực đại của hàm số.
+) Bước 5. Kết luận. Người tiêu dùng cần mua mặt hàng 1 và mặt hàng 2 đều với
số lượng 26 đơn vị để thu được lợi ích tối đa là ø ù 0,4 0,6 U 26, 26 26 .26 26. U
Tại điểm tối ưu, ta có kết quả :
0, 2 (với M là thu nhập người tiêu dùng) M
Vậy tại điểm tối ưu, nếu thu nhập người tiêu dùng tăng 1 USD thì lợi ích tối đa tăng 0,2 đơn vị. 195 6.5. Bài tập
Bài số 1. Tính các giới hạn sau 2x 1. lim 2 2 (x,y) (0,0) 5 3x 2y 2 2. lim 2 2 (x,y) (1, 2)3x 2y 3. ø 2 2ù 1 lim x y sin (x ,y) (0,0) 2 2 x y 2 Đáp số : 1) 0 ; 2) ; 3) 0. 11
Bài số 2. Chứng minh hàm số sau liên tục tại (0,0) 2 2 xy(x y ) khi øx, y ù ø0,0 ù f øx, ù 2 2 y ý x y 0 khi þ øx,y ù ø0,0 ù Hướng dẫn : Kiểm tra lim f (x, y) f (0, 0) . (x,y) (0,0)
Bài số 3. Tính đạo hàm riêng cấp 1 của hàm số sau 1. ø ù 2 3 2 f x, y x y 2xy 3x 4y 10. 2. ø ù ø 2 2 f x, y ln x x y ù. 3. ø ù x f x, y arctan . y 4. ø ù 2 y f x, y x sin . x f (x, y) f (x, y) Đáp số : 1) 2 2 2x 2y 3, 3y 4xy 4 . x y f (x, y) 1 f (x, y) y 2) , . 2 2 x y x y ø 2 2 x x y ù 2 2 x y f (x, y) y f (x, y) x 3) , . 2 2 2 2 x x y y x y f (x, y) y y f (x, y) y 4) 2xsin ycos , x cos . x x x y x 196 z z
Bài số 4. Dùng quy tắc xích tìm và s t 1. 2 3 z x y , x scos t, y ssin t. 2. ø ù 2 2 z arcsin x y , x s t , y 1 2st 3. x 2y s t z e , x , y . t s 4. r 2 2 z e cos , r st, s t . z z Đáp số : 4 3 2 1) 5s sin t cos t; ø 2 3 4 3sin t cos t 2sin t cos ù 5 t s . s t z 2(t s) z 2(t s) 2) ; . 2 2 2 2 2 2 s t 1 (s t 1 2st) 1 (s t 1 2st) s 2t s 2t z 1 2t z 2 s t s t s 3) e ; e . 2 2 s t s t s t z ts 2 2 s 2 2 4) te cos s t sin s t , s 2 2 s t z ts 2 2 t 2 2 se cos s t sin s t . 2 2 t s t z z
Bài số 5. Dùng công thức đạo hàm hàm ẩn tìm x và y 1. 2 2 2 x y z 3xyz 2. yz ln øx ù z 3. x z arctan øy ù z 4. sin øxyzù x 2y 3z z 2x 3yz z 2y 3xz Đáp số : 1) ; . x 3xy 2z y 3xy 2z 2 z 1 z xz z 2) ; . x xy yz 1 y 1 xy yz 2 2 z 1 y z z z 3) ; . 2 2 2 2 x 1 y y z y 1 y y z z 1 yzcos(xyz) z 2 xzcos(xyz) 4) ; . x xycos(xyz) 3 y xycos(xyz) 3
Bài số 6. Tính vi phân toàn phần của hàm số sau 1. f øx, y ù arcsin øxy ù 197 2. ø ù x y f x, y arctan x y y x Đáp số : 1) df (x, y) dx dy . 2 2 2 2 1 x y 1 x y 2y 2x 2) df (x, y) dx dy. 2 2 (x y) (x y)
Bài số 7. Cho hàm số: y f (x) thỏa mãn đẳng thức 3 2 y x x e ln y 2019 . Tính đạo hàm của hàm số, / yx ( /x
y là đạo hàm của y theo x ). 2 y 3x y 2xye Đáp số : / y . x 2 y 1 x ye
Bài số 8. Tính đạo hàm riêng cấp 2 1. ø ù 3 2 2 3 f x, y 4x 3x y 3xy y 2019 2. ø ù 2 2 f x, y ln x y 2 2 2 f (x.y) f (x.y) f (x.y) Đáp số : 1) 24x 6y; 6x 6y; 6x 6y . 2 2 x y x y 2 2 2 2 2 2 2 f (x.y) y x f (x.y) x y f (x.y) 2xy 2) ; ; . 2 2 2 2 2 2 2 2 2 2 2 x (x y ) y (x y ) x y (x y )
Bài số 9. Tính vi phân toàn phần cấp 2 1. ø ù 2 2 f x, y x y 2. f øx, ù y arccos øx y ù 2 2 2 2 (y x ) 4xy (x y ) Đáp số : 2 2 2 1) d f (x, y) dx dxdy dy . 2 2 2 2 2 2 2 2 2 (x y ) (x y ) (x y ) 2 x y 2 x y x y 2 2) d f (x, y) dx 2 dxdy dy . 3 3 3 2 2 2 1 (x y) 1 (x y) 1 (x y)
Bài số 10. Chứng minh rằng 1 2 2 f f 1. Hàm số f øx, ù y ln thỏa 0. 2 2 2 2 x y x y 198 2 x x 1 1 3 f f x 2. Hàm số f øx, ù y thỏa 2 2 x y . 2y 2 x y x y y y 2 2 u u 3. Hàm số u arctan thỏa mãn 0. x 2 2 x y
Hướng dẫn : Tính đạo hàm riêng rồi thay vào đẳng thức ta có điều phải chứng minh.
Bài số 11. Tính gần đúng biểu thức sau : 1. 2 2 A (2,97) (4,05) 2. 3 2 B 2,03 (5,04) 3. ø ù2,01 C 0,99
Đáp số : 1) A 5,022 ; 2) B 3,013 ; C 0,98 .
Bài số 12. Khảo sát cực trị các hàm hai biến sau 1. ø ù 2 2 f x, y 2x y 4x 8. 2. ø ù 2 2 f x, y 10 4x 2y x y .
3. f øx, y ù øx y 9 ùø4x 3y ù 6xy. 4. ø ù 2 3 f x, y 3x y 3xy 1. 5. ø ù x f x, y x y ye 10. 6. ø ù 2x ø 2 f x, y e x y 2 ù y . 7. ø ù 3 2 f x, y x 3xy 15x 12y 6. 8. ø ù 3 3 f x, y x y 6xy 20. 1 9. f øx, ù y xy ø 3 x y ù 3 . 3 2 y 1 10. f øx, ù y x 2. 4x y 11. ø ù 10 5 f x, y 20xy với x, y 0. x y
Đáp số : 1) (1, 0) là cực tiểu; 2) (2, 1) là cực đại; 3) ø189 / 47,180 / 4 ù 7 là cực tiểu;
4) (0,0) không là cực trị, ø1/ 4,1/ ù
2 là cực tiểu; 5) (0,1) không là cực trị; 6) (1 / 2, 1)
là cực tiểu; 7) (1,2); ( 1, 2) không là cực trị; (2,1) là cực tiểu; ( 2, 1) là cực đại; 199
8) (0,0) không là cực trị; (2,2) là cực tiểu; 9) (0,0) không là cực trị; (1,1) là cực đại; 1 1 1 10) , 1 không là cực trị; ,1 là cực tiểu; 11) 1, là cực tiểu. 2 2 2
Bài số 13. Khảo sát cực trị các hàm ba biến sau 1. 2 2 2 f (x, y, z) x 5y 2z 4xy 6y 16z 100. 2. 2 2 2 f (x, y,z) x 2y 9z 4xz 2y 3z 4. y z 1 3. f (x, y,z) x 2015 . x y z 3 1 3
Đáp số: 1) M(6,3,4) cực tiểu; 2) , , là cực tiểu; 5 2 10 3) M (1,1,1) 1
cực tiểu, M2( 1,1, 1) cực đại.
Bài số 14. Tìm cực trị của hàm z z(x, y) cho bởi phương trình sau 2 2 2 x y z 2x 4y 6z 11 0
Đáp số : (1, 2) cực tiểu.
Bài số 15. Tìm cực trị của các hàm hai biến với ràng buộc sau 1. 2 2 f (x, y) 2x
6y , với ràng buộc x 2y 6 . 2. 2 2 f (x, y) x
3xy 5y , với ràng buộc 2x 3y 6. 3. 2 2 f (x, y) x
y , với ràng buộc 3x 2y 6 .
4. f (x,y) x y , với ràng buộc 2 2 x y 1.
5. f (x, y) xy, với ràng buộc x y 1.
6. f (x, y) xy, với ràng buộc 2 2 x y 1 . 2 2 x y
7. f (x, y) x y , với ràng buộc 1. 2 2 a b 1 1 1 1 1 8. f (x, y) , với ràng buộc . x y 2 2 x y 4 Đáp số : 1) ø 18, 1 ù
2 cực tiểu. 2) (3, 0) cực đại. 3) ø18 / 13, 12 /1 ù 3 cực tiểu. 2 2 2 2 1 1 4) , cực tiểu; , cực đại; 5) , cực đại. 2 2 2 2 2 2 200 2 2 2 2 6) , ; , cực tiểu; 2 2 2 2 , , , cực đại. 2 2 2 2 2 2 2 2 2 2 a b 2 2 a b 7) , cực tiểu; , cực đại. 2 2 2 2 a b a b 2 2 2 2 a b a b 8) ø 2 2, 2 ù 2 cực tiểu; ø2 2,2 ù 2 cực đại.
Bài số 16. Tìm giá trị nhỏ nhất và giá trị lớn nhất của f trên tập D. 1. 2 2 2 f (x, y) x y x y 4, D (x, y) / x 1, y 1 . 2. 4 4 f (x, y) x y 4xy 2, D (x, y) / 0 x 3, 0 y 2 . 3. 3 4 2 2 f (x, y) 2x y , D (x, y) / x y 1 . 4. 3 3 f (x, y) x 3x y
12y , D là tứ giác có 4 đỉnh: ( 2, 2), ( 2,3), (2, 2), (2,3).
Đáp số : 1) fmax f (0,1) 5 ; m f in f (0,0) 4. 2) fmin f ( 1, 1) f (1,1) 0 ; 3 3 m f ax f (3, 3) 83 9 3. 13 3) fmin f (0,0) 0 ; f f (1 / 2, 3 / 2) f (1/ 2, 3 / 2) . max 16
4) f max f ( 2,2) 30; fmin f ( 2, 2) f (2, 2) 18.
Bài số 17. Tìm cực trị của hàm ba biến với ràng buộc sau:
f (x, y, z) x y z , với ràng buộc 2 2 2 x y z 1. 1 1 1 1 1 1 Đáp số : 1) , , là cực đại; , , là cực tiểu. 3 3 3 3 3 3
Bài số 18. Cho hàm sản xuất của hãng 3 2 Q 120 K L øK,L 0ù
a) Tính MPK và MPL tại K 1000 và L 225. Nếu ý nghĩa. MPK b) Tính tỷ số MRTS øK 1000, L 225 0 0 ù MPL Đáp số: ø ù ø ù 3 a) MPK 1000, 225 120; MPL 1000, 225 400; b) MRTS . 10
Bài số 19. Tính hệ số co dãn của các hàm sau tại điểm cho trước 5 a) 2 2 Q( 1 P , 2 P ) 6300 2 1 P 2 P , tại (20,30). 3 b) 1/3 2/3 Q(K, L) 120K L 201 Đáp số: a) Q 1,15. b) Q 1. Bài số 20. Cho hàm cầu: 0,2 0,3 D 0,4Y P
với Y là thu nhập, P là giá. Hãy tính hệ số co
dãn của cầu theo giá và của cầu theo thu nhập. Đáp số: D/Y 0,2; D/P 0,3.
Bài số 21. Một hãng độc quyền sản xuất hai loại sản phẩm. Cho biết hàm cầu đối với hai loại sản phẩm là 1 Q 25 0, 1 5P ; Q2 30 2
P và hàm chi phí kết hợp là 2 2 TC 1 Q 2 1 Q 2 Q 2 Q
20. Hãy cho biết mức sản lượng 1 Q , 2
Q và giá bán tương ứng để
doanh nghiệp đạt lợi nhuận tối đa. Đáp số: Q 7, Q 4. 1 2
Bài số 22. Một hãng độc quyền sản xuất hai loại sản phẩm. Cho biết hàm cầu đối với hai loại sản phẩm là 1 Q 50 0,5 1 P ; Q2 76 2
P và hàm chi phí kết hợp là 2 2
TC=3Q +2Q Q +2Q +55. Hãy cho biết mức sản lượng Q ,Q và giá bán tương ứng để 1 1 2 2 1 2
doanh nghiệp đạt lợi nhuận tối đa. Đáp số: Q 8, Q 10. 1 2
Bài số 23. Cho hàm sản xuất của hãng 0,3 0,4
Q 10K L , biết giá thuê một đơn vị tư bản K
bằng 0,03, giá thuê một đơn vị lao động bằng 2, giá sản phẩm bằng 4. Hãy xác định mức
sử dụng K, L để hãng thu được lợi nhuận tối đa.
Đáp số: L 51200, K 2560000.
Bài số 24. Công ty M chuyên sản xuất một mặt hàng A, có hàm sản xuất phụ thuộc hai
yếu tố vốn K và lao động L như sau: 0,4 0,6
Q 40K L trong đó Q là sản lượng và
K 0, L 0 . Cho biết giỏ vốn và lao động lần lượt là K P
11 , PL 20 , với khả năng chi
phí tối đa cho vốn và lao động là C = 6600. Hãy sử dụng phương pháp nhân tử Lagrange
tìm K và L sao cho sản lượng Q đạt cực đại. Đáp án: K 240, L 198.
Bài số 25. Một công ty có hàm sản xuất: 3/4 1/2
Q K L (K – vốn, L – lao động). Biết giá
thuê một đơn vị vốn là 30 và giá thuê một đơn vị lao động 5. Công ty cần sản xuất 2048
sản phẩm, khi đó công ty nên sử dụng bao nhiêu đơn vị vốn và lao động để tối thiểu hóa chi phí Đáp án: K 256, L 1024 202 Chương 7 PHƯƠNG TRÌNH VI PHÂN
7.1. Phương trình vi phân cấp 1 7.1.1. Các khái niệm
Phương trình vi phân cấp 1 có dạng tổng quát: / / F(x, y,y ) 0 hay y f (x,y) (7.1) Hàm số y
(x) xác định và khả vi trên khoảng I
được gọi là nghiệm của phương trình (*) trên I , nếu (x, (x)) G, x I ý
với G là tập xác định của hàm f (x, y) / (x) f (x, (x)), x I þ
Bài toán Cauchy: Tìm hàm số y
(x) là nghiệm của phương trình (*) thỏa mãn điều kiện đầu 0 y (x0 ).
7.1.2. Phương trình vi phân cấp 1 dạng tách biến Có 3 dạng sau: / y f (x)g(y) (7.2) f (x)dx g(y)dy 0 (7.3) 1 f (x) 1 g (y)dx f2(x)g2(y)dy 0 (7.4) Phương pháp giải
Phân ly biến số x và dx về một vế; y và dy về một vế rồi lấy tích phân hai vế
Ví dụ 1. Giải phương trình vi phân sau 1) / x y e 2) ø ù 4 x sin x dx 5y dy 0 3) / 2 y xy 2xy Giải 1) / x x y e dy e dx (1)
Lấy tích phân 2 vế của phương trình (1) x y e C (C là hằng số) 203 2) ø ù 4 x sin x dx 5y dy 0 (2)
Lấy tích phân 2 vế của phương trình (2) ø ù 4 x sin x dx 5y dy C 1 2 5 x cos x y C (với C là hằng số) 2 3) / 2 y xy 2xy (3)
Phương trình (3) được viết lại như sau dy 2 xy 2xy xy(y 2) dy xy(y 2)dx (4) dx
Trường hợp 1: Nếu y 0, 2 là nghiệm của phương trình
Trường hợp 2: Nếu y 0, 2 , chia hai vế của phương trình (4) cho y(y 2), ta được dy xdx , y(y 2)
Lấy tích phân hai vế của phương trình trên, ta có dy 1 1 1 xdx C dy xdx C y(y 2) 2 y y 2 1øln y ln y 2 ù 1 2 x C 2 2 y 2 ln x C (với C là hằng số) y 2
7.1.3. Phương trình vi phân cấp 1 dạng đẳng cấp
Phương trình đẳng cấp có dạng: / y y f (7.5) x Phương pháp giải y Đặt / / u y ux y u x u x
Thay vào (7.5), ta được: ø ù/ F x,u,u 0 (7.6)
Giải (7.6) được u rồi suy ra y 204 a x b y c Nếu vế phải có dạng: 1 1 1 f , a x b y c 2 2 2 x u ñ Ta đặt ý y v ò þ Trong đó a x b y c 0 1 1 1 ý þa x b y c 0 2 2 2
Ví dụ 2. Giải phương trình vi phân sau 1) / y y 1 x 2) / 3x y 1 y x y 3 Giải 1) / y y 1 (1) x y Đặt / / u y ux y
u x u thế vào (1), ta được x / / 1 u x u 1 u u x 1 du dx x Suy ra u ln x C y x ln x Cx với C là hằng số 2) / 3x y 1 y (2) x y 3 Đặt x u ñ ý y v ò þ Trong đó 3ñ ò 1 0 ñ 1 ý 3 0 ý ñ ò ò 2 þ þ Từ (2) ta có / 3u v 3 v / u v (3) u v 1 v / u 205 v Đặt / / t v tu v
t u t thế vào (3), ta được u 2 / 3 t / 2 t t t u t t u 1 t 1 t 1 t 1 dt du 2 2 t t u
Lấy tích phân hai vế của phương trình trên, ta có 1 t 1 dt du C 2 2 t t u 1 2 1 dt ln u C 3 t 1 t 2 1 ø2ln t 1 ln t 2ù ln u C 3 Vậy y 2 y 2 2ln 1 ln 2 3ln x 1 C x 1 x 1
7.1.4. Phương trình vi phân cấp 1 dạng tuyến tính
Phương trình vi phân tuyến tính cấp 1 có dạng: / y a(x)y b(x) (7.7)
Trong đó a(x), b(x) là các hàm số liên tục. Phương pháp giải
Bước 1: Tìm một nguyên hàm của a(x) u(x) a(x)dx
Bước 2: Chọn thừa số tích phân u(x) v(x) e
Bước 3: Nhân hai vế của phương trình cho thừa số tích phân: v(x) (v(x) 0, x) thì ta có / v(x)y a(x)v(x)y v(x)b(x) ø ù/ v(x)y v(x)b(x) (*)
Bước 4: Lấy tích phân hai vế của (*), ta được 206 1 v(x)y v(x)b(x)dx y v(x)b(x)dx v(x)
Ví dụ 3. Giải phương trình vi phân sau / 1 1) y y 1 với x 0, y(1) 1. x 2 / x 2) y 2xy xe . Giải / 1 1) y y 1 với x 0, y(1) 1 x 1
Bước 1: có nguyên hàm là ln x ln x (vì x 0 ) x
Bước 2: Chọn thừa số tích phân: ln x e x
Bước 3: Nhân hai vế của phương trình cho x , thì ta có / xy y x øx ù/ y x (*)
Bước 4: Lấy tích phân hai vế của (*) 1 1 x C 2 xy xdx C y x C x 2 2 x 1 C 1
Với điều kiện đầu y(1) 1 1 C 2 1 2
Vậy nghiệm của phương trình: x 1 y . 2 2x 2 / x 2) y 2xy xe
Bước 1: 2x có nguyên hàm là 2 x 2
Bước 2: Chọn thừa số tích phân: x e 2
Bước 3: Nhân hai vế của phương trình cho x e , thì ta có 2 2 2 / x / x ø x e y 2xe y x e ùy x (*)
Bước 4: Lấy tích phân hai vế của (*) 2 2 1 x x 2 e y xdx C y e x C 2 207
7.1.5. Phương trình vi phân cấp 1 dạng Bernoulli
Phương trình Bernoulli có dạng: / y a(x)y b(x)y ñ, ø ñ 0, ñ ù 1 (7.8)
Trong đó a(x), b(x) là các hàm liên tục. Phương pháp giải
Bước 1: Chia hai vế của phương trình (6.8) cho yñ ta được / ñ 1 y y a(x)y ñ b(x) (7.9) Bước 2: Đặt 1 ñ / ñ / u y u (1 ) ñ y y
Phương trình (7.9) tương đương / u a1(x)u b1(x) (7.10)
Ví dụ 4. Giải phương trình vi phân sau a) / 3 2 y 2xy 4x y b) / 2 x 3 y y e y Giải a) / 3 2 y 2xy 4x y
Bước 1: Chia hai vế của phương trình cho 2 y ta được / 2 1 3 y y 2xy 4x (1) Bước 2: Đặt 1 / 2 / u y u y y
Phương trình (1) trên tương đương / 3 u 2xu 4x (2) Giải (2)
Bước 1: 2x có nguyên hàm là 2 x 2
Bước 2: Chọn thừa số tích phân: x e 2
Bước 3: Nhân hai vế của phương trình cho x e , thì ta có / 2 2 2 x / x 3 x ø 2x ù 2 3 x e u 2xe u 4x e e u 4x e (*)
Bước 4: Lấy tích phân hai vế của (*) 208 2 2 2 x 3 x x e u 4x e dx u 2e ø 2 2 2 x x x e e C ù 2 1 2 x 1 y 2x 2 Ce y 2 2 x 2x 2 Ce b) / 2 x 3 y y e y
Bước 1: Chia hai vế của phương trình cho 3 y ta được / 3 2 2x y y y e (2) Bước 2: Đặt 2 / 3 / u y u 2y y
Phương trình (2) trên tương đương / 2x u 2u 2e (3) Giải (3)
Bước 1: 2 có nguyên hàm là 2x
Bước 2: Chọn thừa số tích phân: 2x e
Bước 3: Nhân hai vế của phương trình cho 2x e , thì ta có ø ù/ 2x / 2x 4x 2x 4x e u e 2u 2e e u 2e (*)
Bước 4: Lấy tích phân hai vế của (*) 2x 4x 1 2x 2x e u 2e dx u e Ce 2 2 1 2x 2x 2 2 y e Ce y 2x 2x 2 e 2Ce
7.2. Phương trình vi phân cấp 2
7.2.1. Các khái niệm chung
Phương trình vi phân cấp hai có dạng ø / // F x, y,y , y ù 0 hay // ø / y f x, y, y ù (7.11)
Nghiệm tổng quát của phương trình vi phân cấp 2 chứa hai tham số 1 C , C2
Bài toán Cauchy: Tìm hàm số y
(x) thỏa điều kiện đầu // / (x) f x, (x), (x) ý þ øx ù / y , (x ) y 0 0 0 1
7.2.2. Phương trình vi phân cấp 2 có thể giảm cấp được Có dạng: 209 // F(x, y ) 0 (7.12) / // F(x, y , y ) 0 (7.13) / // F(y, y , y ) 0 (7.14) Phương pháp giải Đặt / / / / u y u
y thay vào phương trình đã cho, ta được phương trình vi phân cấp 1.
Giải phương trình vi phân cấp 1, ta được u rồi suy ra y.
Ví dụ 5. Giải phương trình vi phân sau: a) // y x cos x 2 b) // / 2 y y x x Giải a) // y x cos x (1) Đặt / / / / u y u
y thế vào phương trình (1) / u x cos x du x cos xdx
Lấy tích phân hai vế của phương trình trên, ta có du x cos xdx 1 C u x sin x cos x C1 Thay / u y , ta có / y xsin x cos x C1 dy øx sin x cos x C ù 1 dx
Lấy tích phân hai vế của phương trình trên, ta có dy øxsin x cosx C ùdx C 1 2 y x cos x 2sin x C1x C2 (với 1 C , 2 C là hai hằng số) 2 b) // / 2 y y x (2) x Đặt / / / / u y u
y thế vào phương trình (2) / 2 2 u
u x (Đây là dạng phương trình vi phân tuyến tính cấp 1) x 210 Ta giải được 3 2 u x 1 C x Thay / u y , ta có / 3 2 y x C1x hay dy ø 3 2 x C x dx 1 ù
Lấy tích phân hai vế của phương trình trên, ta có 1 4 1 3 y x C1x
C2 (với C , C là hai hằng số) 4 3 1 2
7.2.3. Phương trình vi phân tuyến tính cấp 2 hệ số hằng thuần nhất
Phương trình vi phân cấp 2 hệ số hằng thuần nhất có dạng // / ay by cy 0 (7.15)
Trong đó a, b, c là hằng số.
Phương trình đặc trưng ứng với (7.15) 2 ak bk c 0 (7.16) Ta có : 2 b 4ac Trường hợp 1: Nếu
0 Phương trình (7.16) có hai nghiệm thực phân biệt k ,k 1 2
Nghiệm tổng quát của (7.15) 1 k x k2x y 0(x) Ae Be , (A, B là hằng số) Trường hợp 2: Nếu
0 Phương trình (7.16) có nghiệm kép 1 k 2 k k
Nghiệm tổng quát của (7.15) y (x) øA ù kx Bx e , (A, B là hằng số) 0 Trường hợp 3: Nếu
0 Phương trình (7.16) có hai nghiệm phức liên hợp 1 k ,2 ñ iò b với ñ ;ò 2a 2a
Nghiệm tổng quát của (7.15) ñx y0(x) e øAsin x ò B cos ò ù x , (A, B là hằng số)
Ví dụ 6. Giải phương trình vi phân sau: a) // / y 4y 3y 0 b) // / y 4y 4y 0 c) // / y 2y 5y 0 Giải 211 a) // / y 4y 3y 0
Phương trình đặc trưng tương ứng k 1 2 k 4k 3 0 k 3
Nghiệm tổng quát của phương trình x 3x y (x) Ae Be 0
(Với A, B là hai hằng số) b) // / y 4y 4y 0
Phương trình đặc trưng tương ứng 2 k 4k 4 0 k 2
Nghiệm tổng quát của phương trình y (x) øA B ù 2x 0 x e
(Với A, B là hai hằng số) c) // / y 2y 5y 0
Phương trình đặc trưng tương ứng 2 k 2k 5 0 k 1 2i 1,2
Nghiệm tổng quát của phương trình x y 0(x) e øAsin 2x Bcos ù
2x (Với A, B là hai hằng số)
7.2.4. Phương trình vi phân tuyến tính cấp 2 hệ số hằng không thuần nhất
Phương trình vi phân cấp 2 hệ số hằng không thuần nhất có dạng // / ay by cy f (x) (7.17)
Trong đó a, b, c là hằng số.
Nghiệm tổng quát của phương trình (7.17) bằng nghiệm tổng quát của phương trình (7.15)
cộng cho nghiệm riêng của phương trình (7.17).
a) Tìm nghiệm riêng của (6.17) bằng phương pháp thừa số bất định Trương hợp 1: ñx f (x) e n P (x) ( với n
P (x) là đa thức bậc n của x )
i) Nếu ñ không là nghiệm của phương trình đặc trưng (7.16)
Ta tìm nghiệm riêng của (7.17) dưới dạng ñx
yr(x) e Qn(x) (Với Qn (x) là đa thức tổng quát của n P (x) )
ii) Nếu ñ là nghiệm đơn của phương trình đặc trưng (7.16)
Ta tìm nghiệm riêng của (7.17) dưới dạng 212 ñ x
yr(x) xe Qn(x) (Với Q (x) là đa thức tổng quát của P (x) ) n n
iii) Nếu ñ là nghiệm kép của phương trình đặc trưng (7.16)
Ta tìm nghiệm riêng của (7.17) dưới dạng 2 ñx
yr(x) x e Qn(x) (Với Q (x) là đa thức tổng quát của P (x) ) n n Trương hợp 2: ñx f (x) e P (x)sin x ò Q (x) cos x ò n n (với n
P (x), Qn (x) là hai đa thức bậc n của x)
i) Nếu ñ iò không là nghiệm của phương trình đặc trưng (6.16)
Ta tìm nghiệm riêng của (7.17) dưới dạng x y ñ r (x) e An(x)sin x ò Bn(x)cos x ò (Với An (x), n B (x) là hai đa thức tổng quát của n P (x), n Q (x) )
ii) Nếu ñ iò là nghiệm của phương trình đặc trưng (7.16)
Ta tìm nghiệm riêng của (7.17) dưới dạng ñ x yr(x) xe An(x)sin x ò Bn(x)cos x
ò (Với An(x), Bn(x) là hai đa thức tổng quát của n P (x), Qn (x)).
b) Tìm nghiệm riêng của phương trình (7.17) bằng phương pháp biến thiên hằng số
Từ nghiệm tổng quát của (7.15) ta thay A A(x), B B(x). Tìm nghiệm riêng của (7.17) dưới dạng y (x) A(x)y (x) B(x)y (x) r 1 2 thỏa điều kiện / / A (x)y (x) B (x)y (x) 0 1 2 ý / / / / A (x)y (x) B (x)y (x) f (x) þ 1 2
Nghiệm tổng quát của (7.17) y(x) y (x) y (x) 0 r
c) Nguyên lý chồng chất nghiệm
Nếu y1 là nghiệm riêng của phương trình vi phân // / ay by cy f (x) 1
Nếu y là nghiệm riêng của phương trình vi phân 2 // / ay by cy f2(x) 213 Thì r y 1 y
y2 là nghiệm riêng của phương trình // / ay by cy f (x) f (x) 1 2
Ví dụ 7. Giải phương trình vi phân sau: a) // / 2 y 4y 3y x b) // / y 2y 2x 3 c) // / x y 2y 5y e sin 2x Giải a) // / 2 y 4y 3y x (1)
Phương trình thuần nhất // / y 4y 3y 0 (2)
Phương trình đặc trưng tương ứng k 1 2 k 4k 3 0 k 3
Nghiệm tổng quát của phương trình (2) x 3x y 0(x) Ae
Be (Với A, B là hai hằng số)
Tìm nghiệm riêng của (1) dưới dạng øñ 0, n ù 2 2 y r(x) ax bx c Ta có / // y r(x) 2ax b; y r (x) 2a Thế / //
yr(x), yr(x), yr (x) vào (1), ta được 2 ø ù 2 3ax 3b 8a x 2a 4b 3c x Đồng nhất, ta có 1 a 3 3a 1 8 3 ý b 8a 0 ý b 9 2a 4b 3c 0 þ 26 c þ 27 Nghiệm riêng của (1) 214 1 8 26 2 yr(x) x x 3 9 27
Vậy nghiệm tổng quát của (1) 1 8 26 x 3x 2 y(x) 0 y (x) r y (x) Ae Be x x
(Với A, B là hai hằng số) 3 9 27 b) // / y 2y 2x 3 (1)
Phương trình thuần nhất // / y 2y 0 (2)
Phương trình đặc trưng tương ứng k 0 2 k 2k 0 k 2
Nghiệm tổng quát của phương trình (2) 2x
y 0(x) A Be (Với A, B là hai hằng số)
Tìm nghiệm riêng của (1) dưới dạng øñ 0, n ù 1 2 y r(x) ax bx Ta có / // y r(x) 2ax b; y r (x) 2a Thế / //
yr(x), yr(x), yr (x) vào (1), ta được 4ax 2a 2b 2x 3 Đồng nhất, ta có 1 4a 2 a ý ý 2 2 þ a 2b 3 b þ 2 Nghiệm riêng của (1) 1 2 y r(x) x 2x 2
Vậy nghiệm tổng quát của (1) 1 2x 2 y(x) y
(Với A, B là hai hằng số) 0(x) y r(x) A Be x 2x 2 c) // / x y 2y 5y e sin 2x (1)
Phương trình thuần nhất 215 // / y 2y 5y 0 (2)
Phương trình đặc trưng tương ứng 2 k 2k 5 0 k 1 2i 1,2
Nghiệm tổng quát của phương trình (2) x y0(x) e øAsin 2x Bcos2 ù
x (Với A, B là hai hằng số)
Tìm nghiệm riêng của (1) dưới dạng øñ 0, n ù 1 x yr(x) e ø 1 C sin 2x C2 cos 2xù Ta có / x yr(x) e ø 1 C 2C2 ùsin2x ø2 1 C C2 ùcos2x // x yr (x) e ø 3 1 C 4C2 ùsin 2x ø4 1 C 3C2 ùcos 2x Thế / //
yr(x), yr(x), yr (x) vào (1), ta được x e ø4C 8C ùsin 2x ø8C 4C ù x cos2x e sin 2x 1 2 1 2 Đồng nhất, ta có 1 C1 4C 8C 1 1 2 20 ý ý þ8 1 C 4 2 C 0 1 C2 þ 10 Nghiệm riêng của (1) 1 1 x yr(x) e sin 2x cos2x 20 10
Vậy nghiệm tổng quát của (1) 1 1 x
y(x) y (x) y (x) e øAsin 2x Bcos2 ù x x e sin 2x cos2x 0 r 20 10
(Với A, B là hai hằng số)
Ví dụ 8. Giải phương trình vi phân sau: // / y 3y 2y sin x (1) Giải
Bước 1: Giải phương trình thuần nhất: // / y 3y 2y 0 Phương trình đặc trưng 216 k 1 2 k 3k 2 0 k 2
Nghiệm tổng quát của phương trình thuần nhất x 2x y 0(x) Ae
Be ( với A, B là hai hằng số)
Bước 2 : Tìm nghiệm riêng dưới dạng x 2x y (x) A(x)e B(x)e r Thỏa điều kiện / x / 2x / 2x A (x)e B (x)e 0 B (x) e sin x ý ý / x / 2x / x A (x)e 2B (x)e sin x A (x) e sin x þ þ 1 2x B(x) e ø2sin x cos ù x 5 ý 1 x A(x) e øsin x cosxù þ 2 Nghiệm riêng của (1) 1 3 y (x) sin x cos x r 10 10
Nghiệm tổng quát của (1) x 2x 1 3 y(x) y0(x) yr(x) Ae Be sin x
cos x (Với A, B là hai hằng số) 10 10
Ví dụ 9. Giải phương trình vi phân sau // / x x y y xe 2e (1) Giải
Phương trình thuần nhất : // / y y 0
Nghiệm tổng quát của phương trình thuần nhất
y 0(x) Asin x Bcos x , (A, B là hằng số)
Nghiệm riêng của phương trình // / x 1 y y xe là x y (x) (x 1)e 1 2
Nghiệm riêng của phương trình // / x y y 2e là x y (x) e 2 Nghiệm riêng của (1) là 217 1 x x y r(x) y1(x) y 2(x) (x 1)e e 2
Nghiệm tổng quát của (1) 1 x x
y(x) y 0(x) yr(x) Asin x Bcos x (x 1)e e , (A, B là hằng số) 2
7.3. Một số ứng dụng trong kinh tế
7.3.1. Tìm hàm y f (x) khi biết hệ số co dãn
Giả sử x và y là hai đại lượng kinh tế có quan hệ với nhau bằng một hàm khả vi
y f (x) thì ta có hệ số co dãn E là một hàm của x được xác định bởi y x dy x Ey x (7.18) dx y
Vậy nếu ta biết hệ số co dãn E
là một hàm theo x ta có phương trình vi phân như sau : y x x dy E (7.19) y x y dx hay dy dx E (7.20) y x y x
Giải phương trình vi phân này, ta có E y x ln y dx (7.21) x
7.3.2. Mô hình cân bằng thị trường với kỳ vọng về giá
Xét hàm cung và hàm cầu tổng quát như sau / // Q (t) D P(t), P (t), P (t) D (7.22) / // Q (t) S P(t), P (t), P (t) S (7.23) Trong đó
+) P(t) : Xu thế giá tại thời điểm t +) / P (t) : Giá tăng / P (t) 0 hoặc /
P (t) 0 giá giảm tại thời điểm t. +) //
P (t) : Giá tăng ngày một nhanh //
P (t) 0 hoặc tốc độ tăng giá giảm dần / / P (t) 0 .
Mô hình cân bằng tại mọi thời điểm 218 / // / // Q (t) Q (t) D P(t), P (t), P (t) S P(t), P (t), P (t) D S (7.24)
Đây là phương trình vi phân cấp 2 của P.
Ví dụ 10. Cho hệ số co dãn của hàm cầu là 2P E D 2000 2P
Tìm hàm cầu QD biết rằng Q(0) 2000. Giải Từ hệ số co dãn ta có dQ P 2P dQ dP dP Q 2000 2P Q 1000 P Suy ra ln Q ln 1000 P C Q A(1000 P) mà Q(0) 2000 2000 1000A A 2 Vậy Q 2000 2P .
Ví dụ 11. Cho hàm cung và hàm cầu của một loại hàng / // Q (t)
6 8P(t); Q (t) 42 4P(t) 4P (t) P (t) S D
Với giá ban đầu P(0) 6 và /
P (0) 4 . Tìm sự biến động của giá P(t) theo thời gian và
giả thiết cung cầu thỏa mãn tại mọi thời điểm. Giải
Cho lượng cung bằng lượng cầu ta được / // S Q (t) QD(t)
6 8P(t) 42 4P(t) 4P (t) P (t) (1)
Ta được phương trình vi phân // / P (t) 4P (t) 12P(t) 48 Phương trình đặc trưng 2 k 4k 12 0 1 k 2 k2 6 Nghiệm riêng của (1) : r P (t) 4
Nghiệm tổng quát của (1) : 2t 6t P(t) 4 Ae Be (A, B là hai hằng số) 219
Từ điều kiện đầu giải ra ta được A B 1. Vậy 2t 6t P(t) 4 e e Ta có lim P(t)
. Do đó điểm cân bằng không ổn định. t
Ví dụ 12. Cho hàm cung và hàm cầu của một loại hàng / // S Q (t)
5 3P(t); QD(t) 40 2P(t) 2P (t) P (t)
Với giá ban đầu P(0) 12 và /
P (0) 1. Tìm sự biến động của giá P(t) theo thời gian và
giả thiết cung cầu thỏa mãn tại mọi thời điểm. Giải
Cho lượng cung bằng lượng cầu ta được / // S Q (t) QD(t) 5 3P(t) 40 2P(t) 2P (t) P (t)
Ta được phương trình vi phân // / P (t) 2P (t) 5P(t) 45 (1)
Phương trình thuần nhất // / P (t) 2P (t) 5P(t) 0 (2) Phương trình đặc trưng 2 k 2k 5 0 1 k 1 2i k2 1 2i
Nghiệm tổng quát của (2) t P0(t) e øAsin 2t Bcos 2 ù t
Tìm nghiệm dưới của (1) dưới dạng P (t) a thay vào (1) ta được nghiệm : t r P (t) 9
Nghiệm tổng quát của (1) t P(t) P (t) P (t) 9 e
A sin 2t Bcos 2t (A, B là hai hằng số) 0 r ø ù
Từ điều kiện đầu, ta có hệ phương trình P(0) 12 B 9 12 B 3 ý ý ý / þP (0) 1 2 þ A B 1 þA 2 Vậy t P(t) 9 e ø2sin 2t 3cos 2tù
Ta có lim P(t) 9. Do đó điểm cân bằng ổn định. t 220 7.4. Bài tập 1
Bài số 1. Chứng minh rằng hàm số 5 y ax
bx là nghiệm của phương trình 12x 2 // / 1 x y 5xy 5y x
Hướng dẫn: Tính đạo hàm rồi thay vào phương trình ta có điều phải chứng minh. 1
Bài số 2. Chứng minh rằng hàm số 3 2x y a bx x e
là nghiệm của phương trình 6 // / 2x y 4y 4y xe
Hướng dẫn: Tính đạo hàm rồi thay vào phương trình ta có điều phải chứng minh.
Bài số 3. Giải các phương trình vi phân cấp 1 1. / y 2y 4x 2 2. / x y 2xy xe 3. / y y cosx 4. (1 x)ydx (1 y)xdy 0 5. / x y 2 y x y 4 6. / y ysin x sin x cos x 7. / 2 y 1 x y arcsin x , y(0) 0 1 8. / y y x ln x , 2 y(e) e x ln x 2 2 9. / 2 5 2 3 y 9x y (x x )y , y(0) 0 10. / 1 y y tan x , y(0) 0 cos x y sin x 11. / 3 y y . 2x 2x Đáp số : 1 2 2 2x 2 x x 1 1) y(x) 2x 1 Ce ; 2) y(x) x e Ce ; 3) y(x) (sin x cos x) C; 2 2 221 y 1
4) ln xy x y C x 0 y 0; 5) arctan ln ø 2 2 (y 1) (x 3) ù C; x 3 cosx 1 2 6) y(x) cosx 1 Ce ; 7) y(x) arcsin x 1;8) y(x) x ln x; 2 3 1 3 x 6 3 x 2 9) y(x) e (x 2x ) ; 10) y(x) ;11) y øa cos ù x x hay y 0. 18 cos x
Bài số 4. Giải các phương trình vi phân cấp 2 thuần nhất sau 1. // / y y 2y 0 7. // / y y 6y 0 2. // y 9y 0 8. // y 4y 0 3. // / y 4y 0 9. // / y 6y 12y 0 4. // y y 0 10. // / y 2y 5y 0 5. // / y 6y 13y 0 11. // / y 2y y 0 6. // / y 10y 25y 0 12. // / 4y 20y 25y 0 Đáp số :1) x 2x y(x) Ae Be ; 2) 3x 3x y(x) Ae Be ; 3) 4x y(x) Ae B ; 4) y(x) Asin x Bcos x ; 5) 3x y(x) e øAsin 2x Bcos 2 ù x ; 6) x 5x y(x) Ae Be ; 7) 2x 3x y(x) Ae Be ; 8) y(x) Asin 2x Bcos2x; 9) 3x y(x) e øAsin 3x Bcos 3 ùx ; 10) x y(x) e øAsin 2x Bcos 2 ù x ; 5x 11) (1 2 )x (1 2) x y(x) Ae Be ; 12) ø ù 2 y(x) Ax B e .
Bài số 5. Giải các phương trình vi phân với điều kiện đầu sau: 1. // / / y 4y 3y 0, y(0) 6, y (0) 14 2. // / / 4y 4y y 0, y(0) 2, y (0) 0 3. // / / y 4y 29y 0, y(0) 0, y (0) 15 4. // x / y xe , y(0) 1, y (0) 1 5. // / 5x / y 4y 3y e , y(0) 3, y (0) 9 1 6. // / y 4y sin 2x 1, y(0) , y (0) 0 4 1 x Đáp số : x 3x 2x 2 1) y(x) 2e 4e ; 2) y(x) (x 2)e ; 3) y(x) 3e sin5x; 222 MỘT SỐ ĐỀ THAM KHẢO Đề số 01
Câu 1 (2 điểm). Cho hệ phương trình x1 2x 2 4x 3 3x 4 0 3x 5x 6x 4x 0 1 2 3 4 ý 4x 5x 2x 3x 0 1 2 3 4 3 þ x1 8x 2 24x3 19x 4 0
1) Giải hệ phương trình tuyến tính trên.
2) Tìm một cơ sở và số chiều cho không gian nghiệm của hệ phương trình trên. 1 3 7 1 1 3
Câu 2 (2 điểm). Cho hai ma trận: A 2 1 2 ; B 1 2 1 7 1 4 2 3 2
1) Tìm ma trận nghịch đảo của ma trận A(nếu có). AøX Yù B 2) Tìm X, Y sao cho ø ý X Y ùA B þ 3 x 2 x 20
Câu 3 (1 điểm). Tính giới hạn: lim . 4 x 7 x 9 2
Câu 4 (1 điểm). Khai triển Maclaurin của hàm số trên tới lũy thừa bậc 4 1 f øx ù 2 x 3x 2 dx
Câu 5 (1 điểm). Tính tích phân suy rộng: . 2 2x 8x 40
Câu 6 (1 điểm). Cho hàm số: 3 3 f (x, y) x 3xy y
2018. Tính vi phân toàn phần cấp
2 của hàm số trên tại điểm (1, 1).
Câu 7 (1 điểm). Khảo sát cực trị của hàm số: ø ù 3 2 2 f x, y 8x 2xy 3x y 2018.
Câu 8 (1 điểm). Giải phương trình vi phân: // / 2x y 5y 6y e . Đề số 02
Câu 1 (2 điểm). Cho hệ phương trình 225 x 2x 4x 3x 0 1 2 3 4 3x 5x 6x 4x 0 1 2 3 4 ý 4x1 5x 2 2x3 3x 4 0 7 þ x1 13x2 22x3 16x4 0
1) Giải hệ phương trình tuyến tính trên.
2) Tìm một cơ sở và số chiều cho không gian nghiệm của hệ phương trình trên. 1 3 7 1 1 3
Câu 2 (2 điểm). Cho hai ma trận: A 3 4 9 ; B 0 1 4 7 1 4 2 3 2
1) Tìm ma trận nghịch đảo của ma trận A(nếu có). AøX Yù B 2) Tìm X, Y sao cho ø ý X Y þ ùA B 3 cos2x cos x
Câu 3 (1 điểm). Tính giới hạn: lim . 2 x 0 x
Câu 4 (1 điểm). Khai triển Maclaurin của hàm số trên tới lũy thừa bậc 4 1 f øx ù 2 x 5x 4 dx
Câu 5 (1 điểm). Tính tích phân suy rộng: . 2 2x 4x 52
Câu 6 (1 điểm). Cho hàm số: 4 4 f (x, y) x 4xy y
2018. Tính vi phân toàn phần cấp
2 của hàm số trên tại điểm (1, 1).
Câu 7 (1 điểm). Khảo sát cực trị của hàm số: ø ù x 2y f x, y x 2ey e e 2018.
Câu 8 (1 điểm). Giải phương trình vi phân: // / x y 5y 4y e . Đề số 03
Câu 1 (2 điểm). Cho hệ phương trình x1 2x 2 4x3 3x 4 0 7x 10x 4x x 0 1 2 3 4 4 ý x 5x 2x 3x 0 1 2 3 4 7 þ x1 13x2 22x3 16x4 0
1) Giải hệ phương trình tuyến tính trên. 226
2) Tìm một cơ sở và số chiều cho không gian nghiệm của hệ phương trình trên. 1 3 7 1 1 3
Câu 2 (2 điểm). Cho hai ma trận: A 3 4 9 ; B 2 2 5 6 4 11 2 3 2
1) Tìm ma trận nghịch đảo của ma trận A(nếu có). AøX Yù B 2) Tìm X, Y sao cho ø ý X Y þ ùA B ø1 x ùø 3 1 x ù
Câu 3 (1 điểm). Tính giới hạn: lim . ø1 x ù2 x 1
Câu 4 (1 điểm). Khai triển Maclaurin của hàm số trên tới lũy thừa bậc 4: 1 f øx ù 2 x 5x 6 dx
Câu 5 (1 điểm). Tính tích phân suy rộng: .. 2 2x 12x 36
Câu 6 (1 điểm). Cho hàm số: 4 4 f (x, y) x 6xy y
2018. Tính vi phân toàn phần cấp
2 của hàm số trên tại điểm (1, 1).
Câu 7 (1 điểm). Khảo sát cực trị của hàm số: ø ù y x 2y f x, y x 2e e e 2018.
Câu 8 (1 điểm). Giải phương trình vi phân: // / 2x y 3y 2y e . Đề số 04
Câu 1 (2 điểm). Cho hệ phương trình x 2x 4x 3x 0 1 2 3 4 7x 10x 4x x 0 1 2 3 4 ý 4x 1 5x 2 2x 3 3x 4 0 11x 18x 20x 13x 0 þ 1 2 3 4
1) Giải hệ phương trình tuyến tính trên.
2) Tìm một cơ sở và số chiều cho không gian nghiệm của hệ phương trình trên. 1 3 7 1 1 3
Câu 2 (2 điểm). Cho hai ma trận: A 3 4 9 ; B 2 2 5 3 8 20 4 5 7
1) Tìm ma trận nghịch đảo của ma trận A(nếu có). 227 AøX Yù B 2) Tìm X, Y sao cho ø ý X Y þ ùA B 3 1 cos 2x
Câu 3 (1 điểm). Tính giới hạn: lim . 2 x 0 sin x
Câu 4 (1 điểm). Khai triển Maclaurin của hàm số trên tới lũy thừa bậc 4 1 f øx ù 2 x 9 dx
Câu 5 (1 điểm). Tính tích phân suy rộng: . 2 2x 8x 26
Câu 6 (1 điểm). Cho hàm số: 3 4 f (x, y) x 5xy y
2018. Tính vi phân toàn phần cấp
2 của hàm số trên tại điểm (1, 1).
Câu 7 (1 điểm). Khảo sát cực trị của hàm số: ø ù 3 3 f x, y x 3xy 8y 2018.
Câu 8 (1 điểm). Giải phương trình vi phân: // / 4x y 4y e . Đề số 05
Câu 1 (2 điểm). Cho hệ phương trình x 1 2x 2 4x 3 3x 4 0 3x1 4x 2 x 4 0 ý 4x 5x 2x 3x 0 1 2 3 4 11x 18x 20x 13x 0 þ 1 2 3 4
1) Giải hệ phương trình tuyến tính trên.
2) Tìm một cơ sở và số chiều cho không gian nghiệm của hệ phương trình trên. 1 3 7 1 1 3
Câu 2 (2 điểm). Cho hai ma trận: A 3 4 9 ; B 2 2 5 4 5 13 3 4 4
1) Tìm ma trận nghịch đảo của ma trận A(nếu có). AøX Yù B 2) Tìm X, Y sao cho ø ý X Y ùA B þ 2 x
Câu 3 (1 điểm). Tính giới hạn: lim . 5 x 0 1 5x 1 x 228 1
Câu 4 (1 điểm). Khai triển Maclaurin của hàm số trên tới lũy thừa bậc 4: f øxù 2 x 4 dx
Câu 5 (1 điểm). Tính tích phân suy rộng: . 2 2x 4x 10
Câu 6 (1 điểm). Cho hàm số: 4 2 f (x, y) x 7xy y
2018. Tính vi phân toàn phần cấp
2 của hàm số trên tại điểm (1, 1).
Câu 7 (1 điểm). Khảo sát cực trị của hàm số: ø ù 0,3 0,4 f x, y 40x y 0,03x 2y 2018
Câu 8 (1 điểm). Giải phương trình vi phân: // 3x y 9y e . Đề số 06 Câu 1 (2 điểm). x 2x 4x 3x 0 1 2 3 4 3x 5x 6x 4x 0
1) Giải hệ phương trình tuyến tính : 1 2 3 4 ý 4x1 5x2 2x3 3x 4 0 6x 13x 30x 23x 0 þ 1 2 3 4 2 3 4 1 1 3 2 1 2) Tính định thức sau : 3 2 1 3 4 3 5 2 1 3 7 1 1 3
Câu 2 (2 điểm). Cho hai ma trận: A 2 1 2 ; B 1 2 1 5 2 6 2 3 2
1) Tìm ma trận nghịch đảo của ma trận A(nếu có). AøX Yù B 2) Tìm X, Y sao cho ø ý X Y ùA B þ
Câu 3 (1 điểm). Tính giới hạn: x lim 1 sinø2018xù. x 0 1
Câu 4 (1 điểm). Khai triển Maclaurin của hàm số trên tới lũy thừa bậc 4: f øx ù 2 x 1 dx
Câu 5 (1 điểm). Tính tích phân suy rộng: . 2 x 2x 101 229
Câu 6 (1 điểm). Cho hàm số: 2 2 f (x, y) ln x
y . Tính vi phân toàn phần cấp 1 của hàm
số trên tại điểm (1, 1).
Câu 7 (1 điểm). Tìm cực trị của hàm f øx, yù 2x 3y, với ràng buộc 2 2 x 9y 180.
Câu 8 (1 điểm). Giải phương trình vi phân: / 2 y 3x y 0 với y(0) 5. Đề số 07 Câu 1 (2 điểm). x 2x 4x 3x 0 1 2 3 4 3x 5x 6x 4x 0
1) Giải hệ phương trình tuyến tính : 1 2 3 4 ý 4x1 5x 2 2x3 3x 4 0 þ5x1 9x 2 14x3 10x4 0 2 3 4 5 1 2 3 3 2) Tính định thức sau : 3 1 2 4 4 5 3 2 1 3 7 1 1 0
Câu 2 (2 điểm). Cho hai ma trận: A 1 2 5 ; B 1 2 1 5 2 6 2 1 2
1) Tìm ma trận nghịch đảo của ma trận A(nếu có). AøX Yù B 2) Tìm X, Y sao cho ø ý X Y ùA B þ
Câu 3 (1 điểm). Tính giới hạn: x lim 1 tanø2018xù. x 0
Câu 4 (1 điểm). Khai triển Maclaurin của hàm số trên tới lũy thừa bậc 5: f øxù ln(1 x) dx
Câu 5 (1 điểm). Tính tích phân suy rộng: . 2 x 4x 104 x y
Câu 6 (1 điểm). Cho hàm số: f (x, y) arctan
. Tính vi phân toàn phần cấp 1 của x y
hàm số trên tại điểm (1, 1).
Câu 7 (1 điểm). Tìm cực trị của hàm f øx, yù 3x y, với ràng buộc 2 2 9x y 162. 230
Câu 8 (1 điểm). Giải phương trình vi phân: / y y tan x 0 với y( ) 2. Đề số 08 Câu 1 (2 điểm). x 2x 4x 3x 0 1 2 3 4 3x 5x 6x 4x 0
1) Giải hệ phương trình tuyến tính : 1 2 3 4 ý 7x 10x 4x x 0 1 2 3 4 6x 13x 30x 23x 0 þ 1 2 3 4 2 3 4 5 1 4 2 3 2) Tính định thức sau : 3 2 1 4 2 6 5 2 1 3 7 2 1 3
Câu 2 (2 điểm). Cho hai ma trận: A 2 1 2 ; B 0 2 1 3 3 8 2 0 2
1) Tìm ma trận nghịch đảo của ma trận A(nếu có). AøX Yù B 2) Tìm X, Y sao cho ø ý X Y þ ùA B
Câu 3 (1 điểm). Tính giới hạn: lim ø1 xùlnx. x 0
Câu 4 (1 điểm). Khai triển Maclaurin của hàm số trên tới lũy thừa bậc 4: f øx ù arctan x dx
Câu 5 (1 điểm). Tính tích phân suy rộng: . 2 x 6x 109 x
Câu 6 (1 điểm). Cho hàm số: f (x, y) arctan
. Tính vi phân toàn phần cấp 1 của hàm y
số trên tại điểm (1, 1).
Câu 7 (1 điểm). Tìm cực trị của hàm f øx, yù x 3y, với ràng buộc 2 2 x 9y 288. y
Câu 8 (1 điểm). Giải phương trình vi phân: / y 0 với y(1) 4. 2 x 231 Đề số 09 Câu 1 (2 điểm). x1 2x 2 x 3 7
1) Giải hệ phương trình tuyến tính sau: ý2x x 4x 17 1 2 3 þ3 1 x 2x2 2x3 m 1 5 4 3 1 2 1 2 1 0
2) Tìm hạng của ma trận sau: A 5 3 8 1 1 4 9 10 5 2 Câu 2 (2 điểm). 1 2 1
1) Tìm ma trận nghịch đảo của ma trận A 2 2 1 . 3 3 2 1 0 2) Cho A
. Tìm ma trận B sao cho AB BA. 1 1 9 2x 5
Câu 3 (1 điểm). Tính giới hạn: lim . 3 x 8 x 2
Câu 4 (1 điểm). Khai triển Taylor của hàm số sau tới lũy thừa bậc 4 ø ù 1 f x tại x 1 x 1 0 1
Câu 5 (1 điểm). Tính tích phân suy rộng: I dx. x(x 1) 1
Câu 6 (1 điểm). Cho hàm số: y f (x) thỏa mãn đẳng thức 3 2 y x x e ln y 2018, với f ø ù 1 1. Tính / f (1).
Câu 7 (1 điểm). Tìm cực trị của hàm f øx, yù 8x 15y 28, với ràng buộc 2 2 2x 3y 107 .
Câu 8 (1 điểm). Giải phương trình vi phân: // / 2 y 3y 2y x . Đề số 10 Câu 1 (2 điểm). 232 1 x 2x2 x3 7
1) Giải hệ phương trình tuyến tính sau : ý2x x 4x m 1 2 3 3x 2x 2x 14 þ 1 2 3 1 5 4 3 1 2 1 2 1 0
2) Tìm hạng của ma trận sau: A 5 3 8 1 1 6 8 12 4 2 Câu 2 (2 điểm). 1 2 6
1) Tìm ma trận nghịch đảo của ma trận A (nếu có), với A 4 3 8 2 2 5 1 1 2) Cho A
. Tìm ma trận B sao cho AB BA. 1 0 2 1 cos x
Câu 3 (1 điểm). Tính giới hạn: lim . 2 x 0 x
Câu 4 (1 điểm). Khai triển Taylor của hàm số sau tới lũy thừa bậc 4 ø ù 1 f x tại x 1 x 1 0 dx
Câu 5 (1 điểm). Tính tích phân suy rộng: . 2 x 3x 2 1
Câu 6 (1 điểm). Cho hàm số: y f (x) thỏa mãn đẳng thức 3 3 2x 4y 6xy 2018, với f ø1ù 2. Tính / f (1).
Câu 7 (1 điểm). Tìm cực trị của hàm f øx, yù 2x 9y 1, với ràng buộc 2 2 x 3y 31.
Câu 8 (1 điểm). Giải phương trình vi phân: // / 2 y 4y 3y x . Đề số 11 Câu 1 (2 điểm). 3x 4x x 2x 0 1 2 3 4
1) Giải hệ phương trình tuyến tính sau: ý2x1 3x2 3x3 x4 0 þ5x 7x 4x x 0 1 2 3 4 233 3 0 2 3 2 0 5 1
2) Tính định thức của ma trận sau: 1 2 4 5 m 1 0 0 1 2 6
Câu 2 (2 điểm). Cho ma trận A 4 3 8 . 3 4 11
1) Tìm ma trận nghịch đảo của ma trận A (nếu có).
2) Tìm ma trận X sao cho ø ù 1 T 13 A 2X A . 2 x
Câu 3 (1 điểm). Tính giới hạn: lim . 5 x 0 1 5x x 1 x
Câu 4 (1 điểm). Khai triển Taylor đến cấp 3 của f (x) tại x 2 . x 1 0 2 dx
Câu 5 (1 điểm). Tính tích phân suy rộng: . 2 2x 4x 20 u u
Câu 6 (1 điểm). Cho hàm số: ø 2 2 u ln x
xy y ù. Chứng minh rằng: x y 2 . x y
Câu 7 (1 điểm). Tìm cực trị của hàm số sau: ø ù 3 3 f x, y x 2xy 8y 2018 .
Câu 8 (1 điểm). Giải phương trình vi phân: / y 4y 3x 2 với y(0) 1 . Đề số 12 Câu 1 (2 điểm). x x 2x 3x 0 1 2 3 4
1) Giải hệ phương trình tuyến tính sau: ý3 1 x 4x2 x3 2x4 0 2x 3x 3x x 0 þ 1 2 3 4 1 0 2 3 2 0 3 0
2) Tính định thức của ma trận sau: 3 3 4 5 m 1 0 0 1 2 6
Câu 2 (2 điểm). Cho ma trận A 3 5 14 . 2 2 5 234
1) Tìm ma trận nghịch đảo của ma trận A (nếu có).
2) Tìm ma trận X sao cho ø ù 1 T 13 A X 2A .
Câu 3 (1 điểm). Tính giới hạn: x lim 1 arctan 2x. x 0
Câu 4 (1 điểm). Khai triển Maclaurin đến cấp 4 của hàm số: f (x) ln(1 x) . 1
Câu 5 (1 điểm). Tính tích phân suy rộng: dx . x(x 1) 1
Câu 6 (1 điểm). Cho hàm số: y f (x) thỏa mãn đẳng thức 3 2 y x x e 2ln y 2018 . Tính / y ( /
y là đạo hàm của y theo x). x x
Câu 7 (1 điểm). Tìm cực trị của hàm sau: ø ù 3 2 f x, y x 3xy 15x 12y 2018 với x, y 0 .
Câu 8 (1 điểm). Giải phương trình vi phân: / 2x y 2y 4xe với y(0) 10 . Đề số 13 Câu 1 (2 điểm). 2x x x x 0 1 2 3 4
1) Giải hệ phương trình tuyến tính sau : ý 1 x x2 x3 2x4 0 5x x 3x 2x 0 þ 1 2 3 4 1 0 3 2 0 2 2 0
2) Tính định thức của ma trận sau : A 3 2 3 1 0 3 0 4 Câu 2 (2 điểm). 2 2 1
1) Tìm ma trận nghịch đảo của ma trận A 1 1 0 (nếu có). 1 0 1 1 1 2) Cho ma trận A
. Tìm ma trận B sao cho AB BA. 0 1
Câu 3 (1 điểm). Tính giới hạn: lim ø1 xùlnx. x 0 235 2x e 1 khi x 0
Câu 4 (1 điểm). Cho hàm số f øx ù 2 x ý x m 3 khi x 0 þ
Tìm m để hàm f liên tục tại x 0. Với m tìm được hãy tính / f ø0 ù, (nếu có). dx
Câu 5 (1 điểm). Tính tích phân suy rộng: . 2 3x 12x 39 1
Câu 6 (1 điểm). Cho hàm số: 2 2 u ln x y . Chứng minh rằng: u u x y 1 . x y
Câu 7 (1 điểm). Tìm cực trị của hàm f øx, yù 2x 3y , với ràng buộc 2 2 x 9y 180. 2
Câu 8 (1 điểm). Giải phương trình vi phân: / x y 2xy 3xe với y(0) 1. Đề số 14 Câu 1 (2 điểm). 2x1 x2 x3 x4 0
1) Giải hệ phương trình tuyến tính : ý3x 2x 2x x 0 1 2 3 4 þ5 1 x x2 3x3 2x4 0 1 2 0 3 0 2 2 0
2) Tính định thức của ma trận sau : A 1 2 3 1 0 3 0 4 Câu 2 (2 điểm). 2 2 1
1) Tìm ma trận nghịch đảo của ma trận : A 3 3 1 (nếu có). 1 2 0 1 0
2) Tìm ma trận B sao cho AB BA với A 1 0
Câu 3 (1 điểm). Tính giới hạn: x lim 1 tan x . x 0 3x e 1 khi x 0
Câu 4 (1 điểm). Cho hàm số f øx ù 2 x ý x þ m 2 khi x 0
Tìm m để hàm f liên tục tại x 0 . Với m tìm được hãy tính / f ø0 ù, (nếu có). 236 dx
Câu 5 (1 điểm). Tính tích phân suy rộng: . 2 3x 12x 39 1 x u u
Câu 6 (1 điểm). Cho hàm số: u arctan . Chứng minh rằng : y x 1. y x y
Câu 7 (1 điểm). Tìm cực trị của hàm f øx,yù 3x y , với ràng buộc 2 2 9x y 162 . 2
Câu 8 (1 điểm). Giải phương trình vi phân: / 2x y 4xy xe với y(0) 5 . Đề số 15 Câu 1 (2 điểm). 2x x x x 0 1 2 3 4
1) Giải hệ phương trình tuyến tính sau : ý 1 x x2 x3 2x4 0 7x 2x 4x x 0 þ 1 2 3 4 1 2 0 2 0 2 2 0
2) Tính định thức của ma trận sau : A 2 1 3 1 0 5 0 4 Câu 2 (2 điểm). 2 2 1
1) Tìm ma trận nghịch đảo của ma trận A 4 3 3 (nếu có). 3 2 2 1 2 2) Cho ma trận A
. Tìm ma trận B sao cho AB BA. 1 1
Câu 3 (1 điểm). Tính giới hạn: 2 x lim cos 2x . x 0 ln x
Câu 4 (1 điểm). Khảo sát tính tăng, giảm và cực trị của hàm số sau: f (x) x 2 dx
Câu 5 (1 điểm). Tính tích phân suy rộng: . 2 2x 4x 20
Câu 6 (1 điểm). Cho hàm số: y f (x) thỏa mãn đẳng thức 3 3 x y 6xy 2018 . Tính / y ( /
y là đạo hàm của y theo x). x x
Câu 7 (1 điểm). Tìm cực trị của hàm f øx,yù x 3y , với ràng buộc 2 2 x 9y 288 . 2
Câu 8 (1 điểm). Giải phương trình vi phân: / x y 2xy 3xe với y(0) 2 . 237
Phụ lục 1. Tập số, tổng, tích hữu hạn, hằng đẳng thức, bất đẳng thức,
chứng minh bằng phương pháp quy nạp 1. Các ký hiệu tập số
1.1. Tập số tự nhiên (natural integer) Ký hiệu: * 0,1, 2,... ; 1, 2,... \ 0
1.2. Tập số nguyên (relative integer) Ký hiệu: ..., 2, 1,0,1,2,...
1.3. Tập số hữu tỷ (rational number) Ký hiệu: m * m ,n n
1.4. Tập số thực (real number): Ký hiệu:
1.5. Tập số phức (complex number) Ký hiệu: 2 a bi a, b , i 1 2. Tổng, tích hữu hạn 2.1. Ký hiệu tổng, tích Cho a , a ,...,a 1 2 n n n 1 a a2 ... an ai ; 1 a a2 ... an ai i 1 i 1
2.2. Tổng, tích được định nghĩa bằng quy nạp n 1 n n 1 n ai ai an 1; ai ai an 1. i 1 i 1 i 1 i 1 1 1 Quy ước: a a ; a a . i 1 1 1 i 1 i 1 3. Hằng đẳng thức n a. øa bùn k n k k C a b n (Nhị thức newton) k 0 238 n b. n n a b øa bù n k k 1 a b k 1 với k n! C n k!(n k)! Hệ quả n a. øa bùn k k n k k Cn ( 1) a b i 0 n b. Nếu n lẻ: n n a b øa b ù k 1 n k k 1 ( 1) a b . k 1 4. Bất đẳng thức
4.1. Bất đẳng thức Cauchy Cho a , a ,...,a 0 , ta có 1 2 n a1 a2 ... an n a a ...a 1 2 n n
Dấu “=” xảy ra khi và chỉ khi a a a . 1 2 n 4.2. Bất đẳng thức BCS
Cho a 1,a 2,...,a n, b1,b 2,..., b n 2 n n n 2 2 a b a b i i i i i 1 i 1 i 1 a a a
Dấu “=” xảy ra khi và chỉ khi 1 2 n . 1 b b2 bn
4.3. Bất đẳng thức Bernoulli Cho a 1 . Ta có ø ùn n , 1 a 1 na
Dấu “=” xảy ra khi và chỉ khi n 0 n 1,a 1.
5. Chứng minh bằng phương pháp quy nạp Xét hàm mệnh đề: * p(n), n Nếu + p(1) đúng + p(n) đúng p(n 1) đúng 239 Thì p(n) đúng với * n .
Ví dụ. Chứng minh đẳng thức sau bằng phương pháp quy nạp n(n 1) 1 2 n 2 Giải Đặt n(n 1) p(n) :1 2 n 2 1(1 1) +) Với n 1, p(1) :1 là đẳng thức đúng. 2
+) Với n bất kỳ, nếu p(n) đúng, nghĩa là đẳng thức n(n 1) 1 2 n 2 đúng thì khi đó, ta có n(n 1) (n 1)(n 2) 1 2 n (n 1) (n 1) 2 2
nghĩa là p(n 1) cũng là mệnh đề đúng. Nói khác đi n , p(n) p(n 1) là mệnh đề đúng.
Do nguyên lý quy nạp, đẳng thức n(n 1) 1 2 n 2 đúng với mọi n .
Chú ý rằng nguyên lý quy nạp không đơn thuần là một phép chứng minh. Nó còn
dùng trong các phép suy luận.
Tổng quát hơn, nguyên lý quy nạp còn dùng để chứng minh hàm mệnh đề sau:
Xét hàm mệnh đề: n n , p(n) 0 Nếu +) p(n 0) đúng và +) n n , p(n) đúng 0 p(n 1) đúng Thì n n 0, p(n) đúng. 240
Phụ lục 2. Tập hợp và ánh xạ 1. Tập hợp 1.1. Khái niệm tập hợp
Tập hợp là một khái niệm cơ bản, không định nghĩa. Thông thường, một tập hợp bao
gồm nhiều đối tượng, mỗi đối tượng đó được gọi là một phần tử của tập hợp. Ta chỉ có thể
nhận biết được tập hợp thông qua các phần tử của nó.
Ví dụ 1. Tập hợp các môn mà sinh viên năm thứ nhất của trường Đại học Tài chính –
Marketing phải học; tập hợp các mặt hàng mà công ty đang bán,…
Người ta thường kí hiệu tập hợp bằng các chữ cái in hoa A, B, C,…và các phần tử
của tập hợp bằng các chữ cái in thường a, c, b,…. Một tập hợp A chứa phần tử a (hay phần
tử a thuộc tập hợp A) được kí hiệu là a A. Tập hợp không chứa phần tử nào được gọi là tập rỗng, ký hiệu .
Để biểu diễn một tập hợp A, người ta còn dùng giản đồ Venn với một đường cong
đơn khép kín, chia mặt phẳng làm hai miền, miền phía bên trong đường cong dành cho các
phần tử thuộc về tập hợp A và miền phía bên ngoài mặt phẳng dành cho các phần tử không
thuộc về tập hợp A. Chẳng hạn, với giản đồ Venn sau mô tả 1,2,3 A và 4,5 A .
Có hai cách để xác định một tập hợp. Cách thứ nhất là liệt kê các phần tử của nó.
Trong toán học, người ta liệt kê các phần tử của một tập hợp giữa hai ngoặc nhọn (“{” và
“}”), không chú ý thứ tự liệt kê và mỗi phần tử chỉ được liệt kê một lần. Cách thứ hai là
mô tả tính chất của các phần tử của tập hợp đó.
Ví dụ 2. Một số tập hợp số thường dùng
Tập hợp các số tự nhiên, ký hiệu ={0,1,2,...} ; tập hợp các số tự nhiên khác 0, kí hiệu * .
Tập hợp các số nguyên, ký hiệu ={...,-2,-1,0,1,2,...}
Tập hợp các số hữu tỷ, ký hiệu m ={ |m ; n ;n 0 } . n 241
Tập hợp các số thực, ký hiệu {x | x
x I} ; tập hợp các số thực khác 0, ký
hiệu * ; tập hợp các số thực không âm, ký hiệu là
; tập các số thực không dương ký hiệu ,…
Tập hợp các số phức, ký hiệu 2 {a bi | a,b ;i 1}.
1.2. Các phép toán trên tập hợp
1.2.1. Phép lấy phần bù.
Phần bù của A trong X, ký hiệu CXA (hay A ), là tập con của X gồm những phần tử
không thuộc về A, nghĩa là : A x X x A .
1.2.2. Phép lấy phần hợp.
Phần hợp của A với B, ký hiệu A B , là tập con của X gồm những phần tử thuộc về
A hay thuộc về B, nghĩa là : A B x X x A x B .
1.2.3. Phép lấy phần giao.
Phần giao của A với B, ký hiệu A B , là tập con của X gồm những phần tử nằm
trong A và nằm trong B, nghĩa là : A B x X x A x B
1.2.4. Phép lấy phần hiệu.
Phần hiệu của A với B , ký hiệu A \ B, là tập con của X gồm những phần tử nằm
trong A và không nằm trong B, nghĩa là : A \ B x X x A x B . 242 Chú ý: A \ B A B .
Ví dụ 3. Cho tập X= 0,1,2,3,...,8,9
và hai tập hợp A = 0,2,4,6,8 ;B = 0,2,4 ta
tìm được A= 1,3,5,7,9 ; A B= 0,1,2,3,4,6,8 ; A B= 0,2,4 ; A\ B= 6,8 .
1.3. Các tính chất tập hợp Với mọi tập hợp A,B, C X. Ta có : i) ø ù A A ii) A B B A ; A B B A iii) øA B ù C A
øB C ù; øA B ù C A øB C ù
iv) A øB Cù øA B ù øA C ù;A øB C ù øA B ù øA C ù v) øA ù B A B; øA ù B A B vi) A A A ; A A A vii) A A ; A X A viii) A X X ; A ix) A A X ; A A x) A øA ù B A ; A øA ù B A. 2. Ánh xạ 2.1. Định nghĩa
Với hai tập hợp không rỗng X, Y, một ánh xạ f từ X vào Y là một sự liên kết giữa
các phần tử của X và Y sao cho mỗi phần tử x X đều được liên kết với duy nhất một
phần tử y Y , ký hiệu y f ø ù
x , gọi là ảnh của x qua ánh xạ f. Ta còn viết f : X Y x y f ø ù x
Tập X được gọi là miền xác định của f, tập Y được gọi là miền ảnh của f. Người ta
có thể dùng giản đồ Venn để mô tả ánh xạ. 243
Ví dụ 4. Để mô tả ánh xạ f :X
Y , với X= 1,2,3 , Y= a,b và f ø ù 1 =a ; fø ù
2 =f ø3 ù=b ta có thể mô tả như hình vẽ sau :
Ảnh của A X qua f , ký hiệu f ø ù
A , là tập hợp các phần tử y Y sao cho nó là
ảnh của một phần tử x A , nghĩa là : f øA ù y Y x A, y f øx ù . Đặc biệt, f ø ù
X được gọi là ảnh của f, ký hiệu Imf .
Ảnh ngược của B Y qua f , ký hiệu 1 f ø ù
B , là tập hợp gồm các phần tử x sao cho f ø ù x B, nghĩa là : 1 f øB ù x X f øx ù B
Đặc biệt, với y Y , ta ký hiệu 1 f ø ù y thay cho 1 f ø y ù .
Một số ánh xạ đặc biệt :
i) Với tập X bất kỳ, ánh xạ f :X X xác định bởi fø ù
x =x , với mọi x X , được
gọi là ánh xạ đồng nhất của X, ký hiệu i X d .
ii) Với mỗi tập con không rỗng A của một tập hợp X, hàm chỉ tiêu của A, ký hiệu , là ánh xạ f : X xác định bởi : A f ø ù ü1 khi x A x = ý , với mọi x X þ0 khi x A 2.2. Phân loại ánh xạ Xét ánh xạ f : X Y . Ta nói :
i) f là một toàn ánh khi Im f
Y , nghĩa là khi mọi phần tử y Y đều là ảnh của ít
nhất một phần tử x X . Nói khác đi, khi 1 f ø ù
y có ít nhất một phần tử, với mọi y Y.
ii) f là một đơn ánh khi ø 1 f ù
y có nhiều nhất một phần tử, với mọi y Y , nghĩa là với mọi x,x Xta có f ø ù x f øx ù thì x x . 244
iii) f là một song ánh khi nó vừa là một đơn ánh và là một toàn ánh. Nói khác đi, f là một song ánh khi 1 f ø ù
y luôn luôn có đúng một phần tử, với mọi y Y . Ví dụ 5. Ánh xạ f : xác định bởi ø ù 2 f x
x không là đơn ánh, cũng không là toàn ánh. Ánh xạ g : xác định bởi ø ù 2 g x
x không là toàn ánh nhưng là đơn ánh. Ánh xạ h : xác định bởi ø ù 2 h x
x không là đơn ánh nhưng là toàn ánh. Ánh xạ : xác định bởi ø ù 2 x
x vừa là toàn ánh, vừa là đơn ánh nên là song ánh. 2.3. Ánh xạ ngược Cho song ánh f : X
Y , khi đó ánh xạ đi từ Y vào X, liên kết phần tử y Y với
phần tử (duy nhất) x X sao cho f ø ù x
y được gọi là ánh xạ ngược của f, ký hiệu 1 f .
Ví dụ 6. Ánh xạ f cho bởi giản đồ Venn
là một song ánh và có ánh xạ ngược là xác định bởi 1 f ø ù a 2 (vì f ø ù 2 a ), 1 f ø ù b 3 (vì f ø ù 3 b ), 1 f ø ù c 1 (vì f ø ù 1 c ). 245 2.4. Ánh xạ hợp. Xét hai ánh xạ f : X Y và g : Y
Z . Ánh xạ có miền xác định X, miền ảnh Z,
liên kết phần tử x X với phần tử z g f øxù
Z được gọi là ánh xạ hợp của f với g, ký hiệu g f , g f : X Z x g f øxù Ví dụ 7.
i) Với các ánh xạ f và g cho bởi giản đồ Venn
ta được ánh xạ hợp g f
ii) Với các ánh xạ f ,g : xác định bởi ø ù 2 f x x và gø ù x x 1, ta có các
ánh xạ hợp g f , f g, f f , g g : xác định bởi : ø ù ø ø ù ø 2ù 2 g f x g f x g x x 1; x ø ù ø ø ù ø ù ø ù2 f g x f g x f x 1 x 1 ; x ø ù ø ø ùù ø ù ø ù2 2 2 4 f f x f f x f x x x ; x g gø ù x g øg ø ù
x ù gøx 1ù øx 1 ù 1 x 2 , x
Định lý. Với các ánh xạ f : X Y và g : Y X , ta có 1
g f nếu và chỉ nếu f g id Y và g f id . X 246
Phụ lục 3. Tính toán ma trận bằng máy tính cá nhân
Trong phần này chúng tôi chỉ hướng dẫn sử dụng máy tính cá nhân FX 570 ES Plus
II loại VINACAL để tính toán một số phép tính của ma trận còn các phép tính khác các
bạn đều đã được học dưới cấp 3. Các loại máy tính 570 khác cách làm tương tự. Cụ thể cho hai ma trận 1 2 2 3 0 1 A 2 0 3 ; B 2 1 2 3 1 5 1 2 4
Sử dụng máy tính FX 570 ES Plus II. Tính 1 1
2A, 3A 4B, AB, BA, A , B , A , B .
Bước 1. Vào chức năng ma trận Nhấn Mode
chọn MATRIX nhấn 6 (các máy tính khác có thể ký hiệu số khác) AC . Bước 2. Nhập ma trận +) Nhấn Shift 4
chọn cấp ma trận (DIM) nhấn 1 chọn ma trận A nhấn 1
Chọn cấp ma trận nếu chưa thấy cấp thì nhấn
di chuyển phím mũi tên xuống dưới
tìm cấp ma trận nhấn 3 3 nhập ma trận A AC . +) Nhấn Shift 4
chọn cấp ma trận (DIM) nhấn 1 chọn ma trận B nhấn 2
Chọn cấp ma trận nếu chưa thấy cấp thì nhấn
di chuyển phím mũi tên xuống dưới
tìm cấp ma trận nhấn 3 3 nhập ma trận B AC .
Bước 3. Khai thác kết quả +) Tính 2A Nhấn 2 Shift 3 ta được kết quả 2 4 4 2A 4 0 6 6 4 10 +) Tính 3A 4B Nhấn 3 Shift 3 4 Shift 4 ta được kết quả 247 15 6 10 3A 4B 14 4 17 13 11 31 +) Tính AB Nhấn Shift 3 Shift 4 ta được kết quả 9 6 13 AB 9 6 14 16 11 25 +) Tính BA Nhấn Shift 4 Shift 3 ta được kết quả 6 7 11 BA 10 6 17 17 6 28 +) Tính A Nhấn Shift 4 7 Shift 3 ta được kết quả A 1 +) Tính B Nhấn Shift 4 7 Shift 4 ta được kết quả B 3 +) Tính 1 A Nhấn Shift 4 3 1 x ta được kết quả 3 8 6 1 A 1 1 1 2 5 4 +) Tính 1 B Nhấn Shift 4 4 1 x ta được kết quả 2 1 0 3 3 11 4 1 B 2 3 3 1 2 1 248 TÀI LIỆU THAM KHẢO
[1] Nguyễn Huy Hoàng (chủ biên), Lê Thị Anh, Phùng Minh Đức, Bùi Quốc Hoàn,
Phạm Bảo Lâm, Nguyễn Mai Quyên, Đoàn Trọng Tuyến, Hoàng Văn Thắng –
Hướng dẫn giải bài tập Toán cao cấp cho các nhà kinh tế, NXB ĐHKTQD, 2006& NXB Thống kê, 2007
[2] Bộ môn toán cơ bản – Bài tập toán cao cấp, NXB Đại học Kinh tế Quốc dân, 2008.
[3] Nguyễn Huy Hoàng – Toán cơ sở cho kinh tế, NXB Thông tin và Truyền thông, 2011& NXB GD, 2014.
[4] Nguyễn Thị An, Nguyễn Huy Hoàng, Giới thiệu đề thi tuyển sinh Sau đại học
(2006 – 2012), Môn Toán Kinh tế (Phần Toán cơ sở cho Kinh tế), NXB Chính trị – Hành chính, 2012.
[5] Laurence D. Hoffmann, Gerald L. Bradley, Applied Calculus For Business,
Economics, and the Social and Life Sciences, The Mc. Graw - Hill Companies, Inc (Expanded 10th ed), 2010.
[6] Michael Hoy, John Livernois, Chris Mc Kenna, Ray Rees, Thanasis Stengos,
Mathematics for Economics, The MIT Press Cambrige, Massachusetts, London,
England (second edition), 2011.
[7] Michael Hoy, John Livernois, Chris Mc Kenna, Ray Rees, Thanasis Stengos,
Solutions Manual Mathematics for Economics, The MIT Press Cambrige,
Massachusetts, London, England (second edition), 2011.
[8] A. C. Chiang, Fundamental Methods of Mathematical Economics, Mc GrawHill, Inc., 3rd edition, 1984.
[9] A. C. Chiang, Instructor’s Manual to accompany Fundamental Methods of
Mathematical Economics, Mc GrawHill, Inc., 4rd edition, 2005. 249


