Hμm mét biÕn
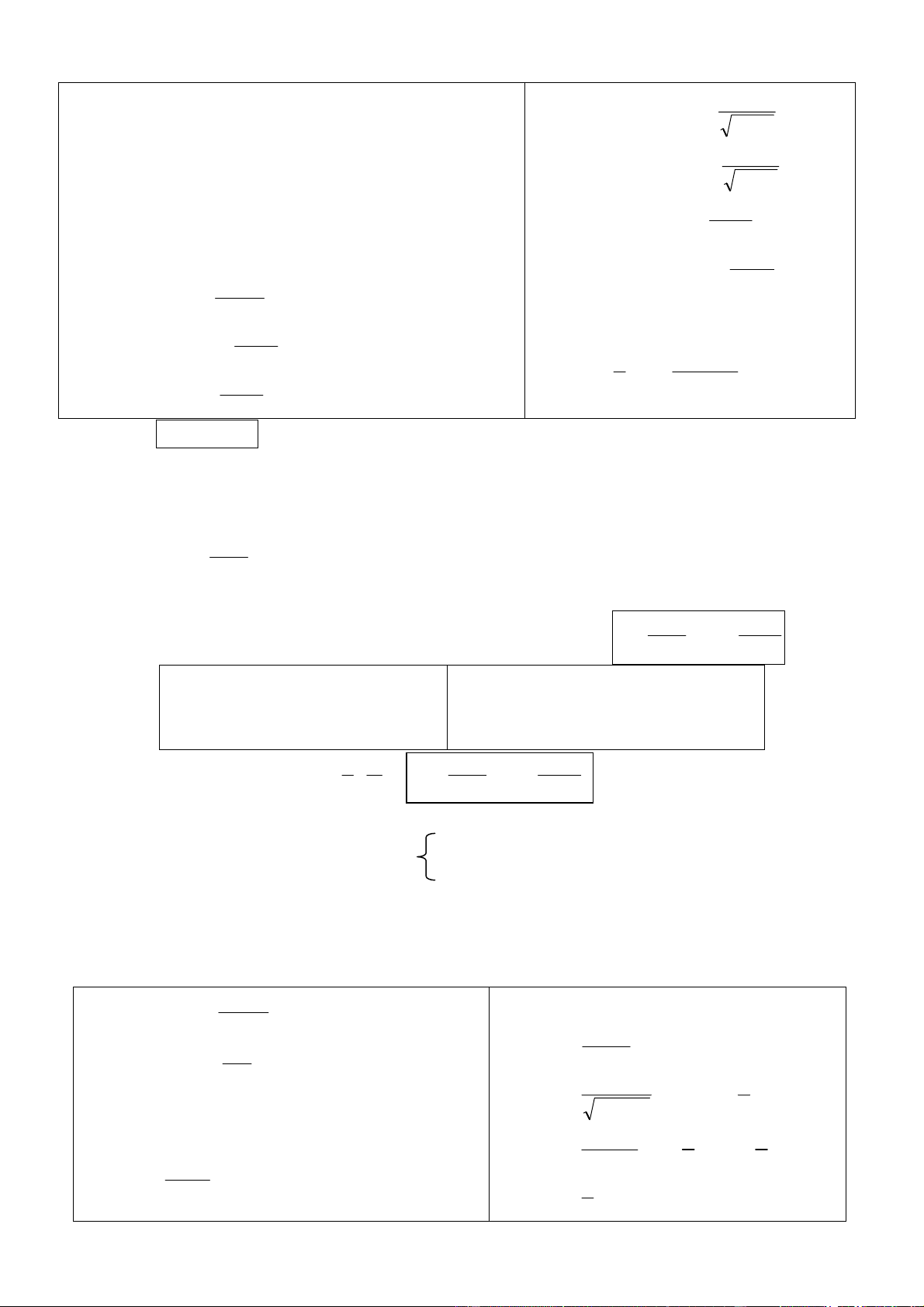
1. C«ng thøc tÝnh ®¹o hµm • α α
(u )’ = α .u’.u -1 (α: H»ng sè, U: Hµm • u' (arcsin u)’ = ; sè) 2 1− u
• (aU)’ = u’.ln a.aU (a: H»ng sè, U: Hµm • − u' (arccos u)’ = sè) 2 1− u • (eU)’ = u’.eU • u' • (arctg u)’ = ;
(Sin u)’ = u’.cos u 2 1+ u
• Cos u)’ = - u’.sin u • − u' (arccotg u)’ = 2 + • u' 1 u (Tg u)’= ; Cos2u
• (u ± v)’=u’ ± v’ • − u' • (Cotg u)’= (u.v)’= u’v+v’u Sin2u • u
u'v − v'u ( )’ = • u' 2 (Log u)’ = v v a u.ln a
2. Vi ph©n du = u’.dx 3. Giíi h¹n
- V« cïng bÐ t−¬ng ®−¬ng :
Limα (x) = 0 => α(x) ®−îcgäi lµ v« cïng bÐ khi x->a x→a α(x) Lim
= 1 --> α(x) vµ β(x) lµ hai v« cïng bÐ t−¬ng ®−¬ng khi x->a
x→a β (x) Ký
hiÖu : α(x) ∼β(x) khi x->a α(x) α (x)
§Þnh lý : NÕu α(x) ∼α (x) vµ β (x) ∼β (x)khi x->a th× 1 Lim = Lim 1 1
x→a β (x)
x→a β (x) 1 Sin x ∼ x khi x->0 ArcTg x ∼ x khi x->0 ArcSin x ∼ x khi x->0 ex-1 ∼ x khi x->0 Tg x ∼ x khi x->0 ln(1+x) ∼ x khi x->0 0 ∞ f (x) f '(x)
- C«ng thøc Lopital khö d¹ng ; : Lim = Lim 0 ∞
x→a g(x)
x→a g'(x)
4. TÝnh liªn tôc cña hµm sè
Hµm sè: y = f(x) liªn tôc t¹i x = x nÕu : + f(x ) x¸c ®Þnh vµ h÷u h¹n 0 0
+ Lim f (x) = f (x ) 0 x→ 0 x
(NÕu hµm sè kh«ng liªn tôc t¹i x th× x ®c gäi lµ ®iÓm gi¸m ®o¹n) 0 0
Hµm sè s¬ cÊp y = f(x) sÏ liªn tôc t¹i mäi ®iÓm mµ hµm sè x¸c ®Þnh 5. TÝch ph©n
a. C«ng thøc nguyªn hµm • α 1 • x dx = xα+ + C ∫ 1 . cos x dx . = − x + C ∫ sin (α (α>0) + ) 1 • 1 dx . • 1 ∫ = tg u + C axdx = ax + C ∫ . cos2 x ln a 1 x • • . = + exdx ex = + C dx ∫ C ∫ arcsin a2 − x2 a • sin x dx . = x + C ∫ cos • 1 1 x ∫ dx . = .arctg +C a2 + x2 a a • 1 ∫ dx .
= -cotg x + C sin2 x • 1 dx . = x + C ∫ ln x 1
b. TÝch ph©n tõng phÇn: ∫u dv . = u v . − ∫vdu Hμm nhiÒu biÕn
7. §¹o hµm riªng vµ vi ph©n toµn phÇn • ' f ∂ (x , y ) f (x + x
Δ , y ) − f (x , y )
f (x , y ) = 0 0 = Lim 0 0 0 0 x 0 0 x x ∂ Δ →0 x Δ • ' f ∂ (x , y )
f (x , y + Δy) − f (x , y )
f (x , y ) = 0 0 = Lim 0 0 0 0 y 0 0 y y ∂ Δ →0 Δy
• Vi ph©n toµn phÇn cÊp 1: df (x, y) = f '(x, y)dx + f '(x, y)dy x y
• Vi ph©n toµn phÇn cÊp 2: 2 2 2 2 2 2
d f (x, y) = f (x, y)dx + 2 f (x, y)dxdy + f (x, y)dy xx xy yy
• C«ng thøc tÝnh gÇn ®óng: f(x+Δx, y+Δy) = f(x,y) + f ’(x,y). Δx + f ’(x,y). Δy x y
• §¹o hµm cña hµm hîp: F(u,v), trong ®ã u =u(x,y); v=v(x,y) : ⎧∂F
∂F ∂u ∂F ∂ = + v ⎪⎪ ∂x ∂u ∂x ∂v ∂x ⎨ ⎪∂F
∂F ∂u ∂F ∂ = + v
⎪⎩ ∂y ∂u ∂y ∂v ∂y
• §¹o hµm cña hµm Èn : ' F (x, y)
*NÕu F(x,y) = 0 ; y= y(x): => y'(x) x = − ' F (x, y) y '
F (x, y, z) '
F (x, y, z)
*NÕu F(x,y,z) = 0 ; z= z(x,y): => z'(x) x = − ; z'( y) x = − '
F (x, y, z) '
F (x, y, z) x y
8. Cù trÞ hµm nhiÒu biÕn ⎪⎧ '
f (x, y) = 0
B−íc1: T×m ®iÓm c¸c ®iÓm dõng M(x ,y ) lµ nghiÖm cña hÖ PT: ⎨ x i i ⎪ '
⎩ f (x, y) = 0 y
B−íc2: KiÓm tra ®iÓm M(x ,y ) cã lµ cùc trÞ i i
A=f ”(x ,y ); B=f ”(x ,y ); C=f ”(x ,y ); xx i i xy i i yy i i
A<0: M(x ,y )--- Cùc ®¹i B2-AC < 0 i i
A>0: M(x ,y )--- Cùc tiÓu i i B2-AC > 0
M(x ,y )--- kh«ng lµ cùc trÞ i i B2-AC = 0
M(x ,y )--- Ch−a kÕt luËn ®−îc i i
Cùc trÞ cã ®iÒu kiÖn: T×m cùc trÞ hµm: u=f(x,y,z) víi ®k: g(x,y,z)=0 ⎧ ' ' ' f f x y f ⎪ = = z Gi¶i hÖ PT: ⎨ ' ' ' g g
g => NghiÖm M(x,y,z) x y z ⎪
⎩g(x, y, z) = 0 9. TÝch ph©n kÐp
a. Trong hÖ täa ®é ®Ò c¸c:
- NÕu miÒn D lµ h×nh ch÷ nhËt x¸c ®Þnh bëi: a ≤ x ≤b vµ c ≤ y ≤d th×: b d
f (x, y)dxdy
dx f (x, y)dy ∫∫ =∫ ∫ D a c
- NÕu miÒn D lµ h×nh ch÷ nhËt x¸c ®Þnh bëi: a ≤ x ≤b vµ y (x) ≤ y ≤y 1 2(x) th×: b y ( x) 2
f (x, y)dxdy dx
f (x, y)dy ∫∫ =∫ ∫ D a y ( x) 1 2
b. §æi biÕn trong tÝch ph©n kÐp: x=x(u,v) ; y=y(u,v)
f (x, y)dxdy
| J | . f [x u ( , v), y u ( , v dudv )] ∫∫ =∫∫ D D ' ' D(x, y) x x trong ®ã: J= u v = ' ' D(u, v) y y u v
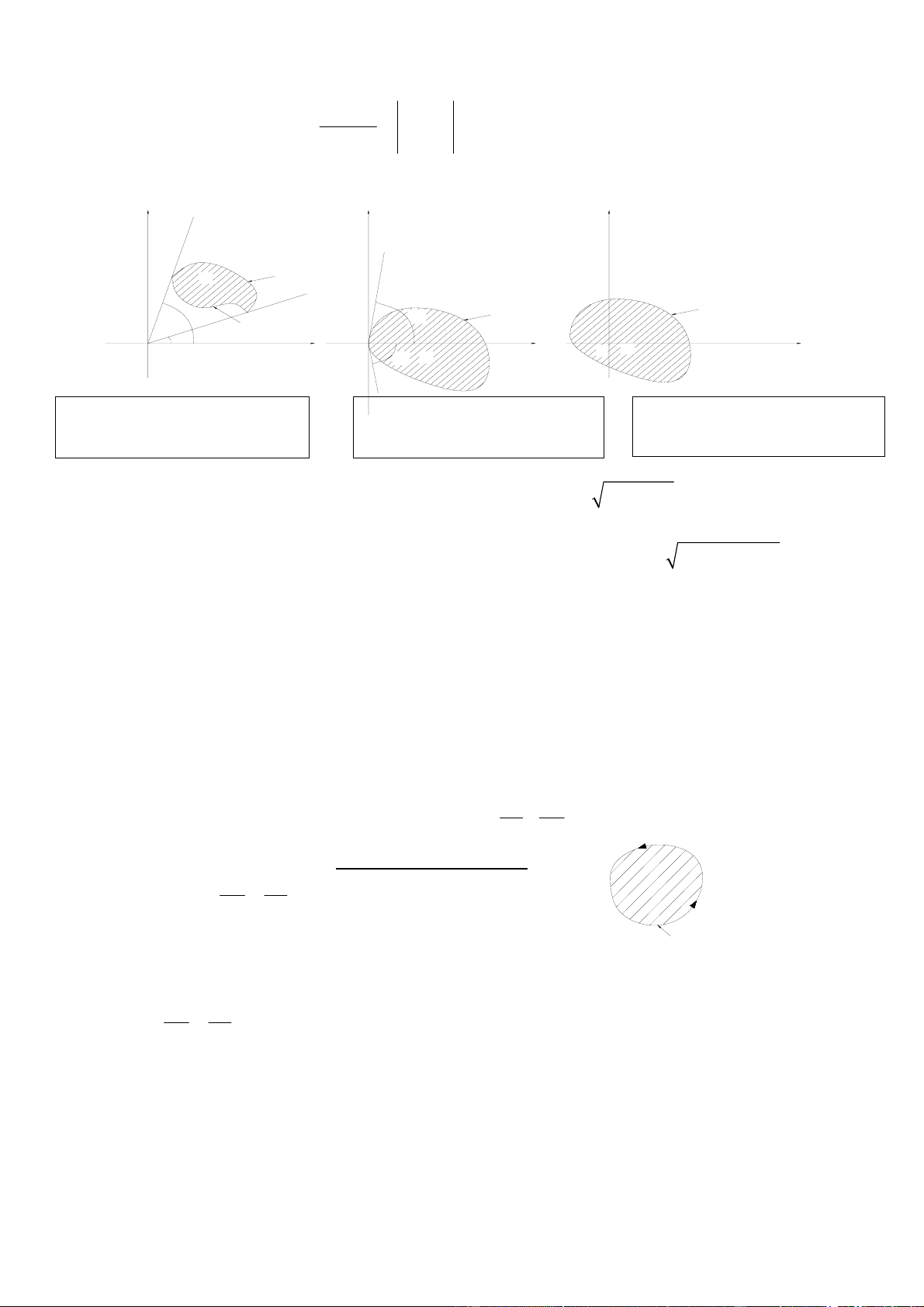
c. Trong hÖ täa ®é cùc: I=
f (x, y)dxdy
f (r cosϕ, r sin ϕ).r.drdϕ (x= r.cosϕ; y= r.sinϕ) ∫∫ =∫∫ D D' y y y D r=g2(ϕ) r=g(ϕ) ϕ2 ϕ2 r=g(ϕ) r=g1(ϕ) ϕ1 0 x 0 x ϕ1 0 D x D ϕ 2 g 2(ϕ ) ϕ 2 g (ϕ ) 2π g (ϕ ) I = ∫ ϕ d
∫ f (rcosϕ,rsinϕ).r.dr I = ϕ d
f (r cosϕ, r sinϕ).r.dr
I = ∫ dϕ ∫ f (r cosϕ,r sinϕ).r.dr ∫ ∫ ϕ g ϕ ϕ 10. TÝch p 1 h ( 1 ©n ® ) −êng lo¹i 1 1 0 0 0 b
- NÕu: y=y(x), a ≤ x ≤b th×: 2
f (x, y)ds = f (x, y(x)) 1+ y ' (x).dx ∫ ∫ AB a t2
- NÕu: x=x(t), y=y(x), t ≤ t ≤t 2 2
f (x, y)ds = f (x(t), y(t)). x ' (t) + y ' (t).dt ∫ ∫ 1 2 th×: AB 1 t
11. TÝch ph©n ®−êng lo¹i 2 - NÕu
AB ®−îc cho bëi: y=y(x), a,b lµ hoµnh ®é cña A vµ B th× b
P(x, y)dx + Q(x, y)dy = [P(x, y(x)) Q
+ (x, y(x)).y '(x)]dx ∫ ∫ AB a - NÕu
AB cho bëi: x=x(t), y=y(t), t=t (t¹i A), t=t (t¹i B) th× B : A B tB
P(x, y)dx + Q(x, y)dy = [P(x(t), y(t)).x '(t) Q
+ (x(t), y(t)).y '(t)]dt ∫ ∫ AB tA P ∂ Q ∂
- C«ng thøc Green : P(x, y)dx + Q(x, y)dy = ( − )dxdy ∫ ∫∫ x ∂ y ∂ L D
(L- lµ miÒn biªn cña D và lµ mét ®−êng khÐp kÝn) Q ∂ P ∂ HÖ qu¶: NÕu =
trong D th×: P(x, y)dx + Q(x, y)dy = 0 D ∫ x ∂ y ∂ L
• §Þnh lý 4 mÖnh ®Ò t−¬ng ®−¬ng: L
Cho P(x,y) vµ Q(x,y) liªn tôc, cã ®¹o hµm riªng cÊp 1 trong miÒn D. Khi ®ã, 4 mÖnh ®Ò sau lµ t−¬ng ®−¬ng: Q ∂ P ∂ (1) = x ∂ y ∂ (2)
∃ u(x,y) sao cho: du(x,y)= P(x,y)dx+Q(x,y)dy (3) Mäi
®−êng cong kÝn L ⊂ D th×: P(x, y)dx + Q(x, y)dy = 0 ∫ L+
(L+ - ®Þnh h−íng d−¬ng, do c«ng thøc Green) (4) TÝch ph©n
P(x, y)dx + Q(x, y)dy kh«ng phô thuéc vµo ®−êng cong nèi 2 ®iÓm A,B ∫AB 3
Ph−¬ng tr×nh vi ph©n
12. Ph−¬ng tr×nh vi ph©n cÊp 1: F(x,y,y’) = 0 hoÆc y’= f(x,y) − f (x) dy − f x
(1) Ph−¬ng tr×nh ph©n ly: y ' = ⇔ ( ) =
⇔ f (x)dx + g( y)dy = 0 g( y) dx g( y)
- TÝch ph©n 2 vÕ: f (x)dx + f ( y)dy C ∫ ∫ = ⇔ F(x)+ G(x) = C ⎛ y ⎞
(2) Ph−¬ng tr×nh ®¼ng cÊp: y ' = f ⎜ ⎟ ⎝ x ⎠ y - §Æt u(x) =
⇒ y = u(x).x ⇒ y’= u(x)+ u’(x).x Thay vµo PT ta cã: x du u+u’.x= f(u)
⇔ x.u’ = f(u) – u hay .x
= f (u) − u dx
* NÕu f(u) – u = 0: x.u’= 0 ⇒ u’= 0 ⇒ u= C ⇒ y = C.x - lµ 1 hä nghiÖm dx du * NÕu f(u) – u ≠ 0: =
(®©y lµ mét PT ph©n ly). TÝch ph©n hai vÕ : x
f (u) − u dx du y φ = ∫ ∫
⇒ ln | x |= φ(u) + ln | C | ⇒ ( ) = . x x C e x
f (u) − u 1
(Φ(u) lµ mét nguyªn hµm cña )
f (u) − u
(3) Ph−¬ng tr×nh tuyÕn tÝnh: y’+p(x).y=q(x)
Ph−¬ng tr×nh thuÇn nhÊt: y’+p(x).y=0 P( x)dx P( x)dx
C«ng thøc nghiÖm tæng qu¸t: y e∫ .(C Q(x).e∫ = + dx) ∫
(4) Ph−¬ng tr×nh Becnuly: y ' p(x).y q(x).yα + =
(α ≠ 0, α ≠ 1)
(Ph−¬ng ph¸p gi¶i: ®−a vÒ ph−¬ng tr×nh tuyÕn tÝnh)
• α>0: y= 0 lµ 1 nghiÖm cña ph−¬ng tr×nh • α α
Víi y ≠ 0 chia c¶ 2 vÕ cho y vµ ®Æt z(x) = y1-α ⇒ z’(x) = (1-α).y’.y thay vµo PT
z'+(1-α).p(x).z=(1-α).q(x) --- Lµ mét ph−¬ng tr×nh vi ph©n tuyÕn tÝnh P ∂ Q ∂
(5) Ph−¬ng tr×nh vi ph©n toµn phÇn: P(x,y)dx + Q(x,y)dy = 0 (trong ®ã: = ) y ∂ x ∂ x y
NghiÖm tæng qu¸t: u(x, y) = P(x, y )dx + Q(x, y)dy = C ∫ 0 ∫ 0 x 0 y x y
Hay : u(x, y) = P(x, y)dx + Q(x , y)dy = C ∫ ∫ 0 0 x 0 y
( trong ®ã (x ,y ) bÊt kú ∈ D). §Ó ®¬n gi¶n chän x = 0, y = 0, nÕu (0,0) ∈ D 0 0 0 0 P ∂ Q ∂
* Trong tr−êng hîp ≠
®−a vÒ ph−¬ng tr×nh vi ph©n toµn phÇn b»ng c¸ch y ∂ x ∂
nh©n hai vÕ víi μ(x,y): μ(x,y).P(x,y)dx + μ(x,y).Q(x,y)dy = 0. P ∂ Q ∂ − y ∂ x ∂ ϕ ( ). - NÕu = ϕ(x) th× μ( , ) μ − ( ) x dx x y x e ∫ = = Q P ∂ Q ∂ − y ∂ x ∂ ϕ ( ). ∫ - NÕu
= ϕ(y) th× μ( , ) = μ( ) y dy x y y = e P
13. Ph−¬ng tr×nh vi ph©n cÊp 2: F(x,y,y’,y’’) = 0 hoÆc y’= f(x,y,y’)
(1) Ph−¬ng tr×nh khuyÕt (ph−¬ng ph¸p gi¶i: H¹ cÊp => ph−¬ng tr×nh vi ph©n cÊp 1):
• KhuyÕt y vµ y’: f(x,y’’) = 0 hay y’’= f(x) -> tÝch ph©n 2 lÇn 4
NghiÖm tæng qu¸t: y = ( f (x).dx)dx + C x + C ∫ ∫ 1 2
• KhuyÕt y: f(x,y’,y’’) = 0. §Æt z(x) = y’ ⇒ y’’ = z’(x).
Ph−¬ng tr×nh trë thµnh: f(x,z,z’) = 0 => PTVP cÊp 1 víi z(x) • dy ' dz( y) dz dy dz dz
KhuyÕt x: f(y,y’,y’’) = 0. §Æt z(y) = y’ => y '' = = = . = .y ' = z. dx dx dy dx dy dy dz
Ph−¬ng tr×nh trë thµnh: f ( y, z, z.
) = 0 => PTVP cÊp 1 víi z(y) dy
(2) Ph−¬ng tr×nh vi ph©n tuyÕn tÝnh cÊp 2 cã hÖ sè h»ng :
a.y’’+b.y’+c.y= f(x) (1) ( Trong ®ã a,b,c lµ c¸c h»ng sè)
PT thuÇn nhÊt: a.y’’+b.y’+c.y= 0 (2)
NghiÖm tæng qu¸t cña (1) lµ: y = y + y * trong ®ã : y* - lµ nghiÖm riªng cña (1)
y - lµ nghiÖm TQ cña (2)
B−íc 1 : T×m nghiÖm tæng qu¸t cña PTTN(2)
Ph−¬ng tr×nh thuÇn nhÊt : a.y’’+b.y’+c.y= 0 (2)
NghiÖm TQ: y = C .y (x)+ C .y (x) (C , C 1 1 2 2 1 2 : H.sè)
PT ®Æc tr−ng : a.k2 + b.k+ c = 0 (3) Δ=b2- 4ac Δ > 0 Δ = 0 Δ < 0 PT (3) cã 2 no: k , k PT (3) cã no kÐp: k = k =k
PT (3) cã 2 no phøc: k = α ± β.i 1 2 1 2 1,2 + α 1 ( ) k x y x = e + ( ) kx y x = e + ( ) x
y x = e .cos β x 1 1 1 + α 2 ( ) k x y x = e + ( ) = . kx y x x e + ( ) x
y x = e .sin β x 2 2 1
y = C .ek1.x+ C .ek2.x y = C .ek.x+ C .x.ek.x α.x 1 2 1 2
y = e (C .cosβx+ C .sinβx) 1 2
B−íc 2 : T×m nghiÖm riªng cña PTKTN(1)
Ph−¬ng tr×nh vi ph©n tuyÕn tÝnh: a.y’’+b.y’+c.y= f(x) (1) ( Trong ®ã a,b,c lµ c¸c h»ng sè) T×m nghiÖm riªng : y*
Ph−¬ng ph¸p biÕn thiªn h»ng sè
C¨n cø d¹ng ®Æc biÖt cña vÕ tr¸i Lagrange α
D¹ng 1: f(x)=P (x).e x (P (x) lµ ®a thøc bËc n) n n
NghiÖm riªng cña (1) cã d¹ng: XÐt: α
D¹ng cÇn tÝnh cña nghiÖm riªng y*= C (x).y (x)+ C (x).y (x) 1 1 2 2 αx
( y (x), y (x) lµ 2 nghiÖm riªng ®éc lËp
Ko lµ no cña y* = Q (x). e n 1 2 PT§T(3)
cña PT thuÇn nhÊt (2) ë trªn)
(Q (x) cïng bËc víi P (x)) n n
Trong ®ã C (x), C (x) lµ c¸c hµm tho¶ L lµ no ®¬n αx 1 2 y* = x.Q (x). e n m·n hÖ: cña PT§T(3) ' ' C
⎧⎪ (x).y (x) + C (x).y (x) = 0 α 1 1 2 2 x ⎨ L lµ no kÐp y* = x2. Q (x). e n ' ' ' ' C
⎪ (x).y (x) + C (x).y (x) = f (x) ⎩ cña PT§T(3) 1 1 2 2 α
D¹ng 2 : f(x)=e x.(P (x).cosβx+Q (x).sinβx) n m XÐt: α±β.i
D¹ng cÇn tÝnh cña nghiÖm riªng α
Ko lµ no cña y*= e x.(K (x).cosβx+Q (x).sinβx) t t PT§T(3) (t=max(m,n)) α Lµ no cña
y*=x.e x.(K (x).cosβx+Q (x).sinβx) t t PT§T(3) (t=max(m,n)) 5
Chó ý: NÕu a.y’’+b.y’+c.y= f(x)+g(x) th× nghiÖm riªng: y*=y *+ y * trong ®ã y *, y * lÇn l−ît 1 2 1 2
lµ 2 nghiÖm riªng cña 2 PT: a.y’’+b.y’+c.y= f(x) vµ a.y’’+b.y’+c.y= g(x). Chuçi 14. Chuçi sè +∞ n
• Chuçi héi tô : Chuçi sè : ∑u S = ∑u
n - Héi tô nÕu tæng riªng thø n : n
k dÇn tíi mét giíi h¹n n 1 = k 1 =
h÷u h¹n khi n→∞.
• Chuçi ph©n kú : nÕu nã kh«ng héi tô. +∞ • Chuçi n
∑q héi tô nÕu |q|<1; phÇn kú nÕu |q|≥ 1 n=0 +∞ • 1 chuçi ∑
héi tô nÕu α >1; phÇn kú nÕu α ≤ 1 n 1 = nα
a. §K ®Ó mét chuçi héi tô : ∞ - NÕu chuçi ∑u
Lim u = 0 ( Lim u = 0 =>kh«ng kh¼ng ®Þnh ®−îc chuçi n héi tô th× n n n→+∞ n→+∞ n 1 = ∞ ∑u héi tô) n n 1 = ∞
- NÕu Lim u ≠ 0 th× chuçi ∑un ph©n kú n n→+∞ n 1 =
• C¸c quy t¾c kh¶o s¸t tÝnh héi tô cña chuçi sè ∞ U
- Quy t¾c D’lembert: chuçi d−¬ng ∑u , n 1 Lim
+ = k k<1: héi tô, k>1: ph©n kú n n→+∞ n 1 = Un ∞
- Quy t¾c Cauchy: chuçi d−¬ng ∑u , n
Lim U = k k<1: héi tô, k>1: ph©n kú n n n→+∞ n 1 = 15. Chuçi hµm
*T×m miÒn héi tô cña chuçi hµm U (x): n U (x)
b1: T×m giíi h¹n: l(x) n 1 = Lim + hoÆc n
l(x) = Lim U (x) n
n→+∞ U (x) n→+∞ n
b2: Gi¶i bÊt ph−¬ng tr×nh: l(x) < 1 ®Ó t×m kho¶ng héi tô cña chuçi hµm
b3: T¹i x = x mµ l(x)=1 ta thay x = x ®Ó xÐt trùc tiÕp 0 0
b4: KÕt luËn miÒn héi tô cña hµm 6