Giáo trình vật lý đại cương 1 | Trường Đại học Bách Khoa TPHCM

VẬT LÝ ĐẠI CƢƠNG 1 TS. Phạm Thị Hải Miền
Bộ môn Vật lý Ứng dụng – Khoa Khoa học Ứng dụng Đại học Bách Khoa Tp.HCM 1 TÀI LIỆU THAM KHẢO
[1] Vật lý đại cương A1, Nguyễn Thị Bé Bảy, Đại học Bách
khoa Tp.HCM (Giáo trình nội bộ), 2009.
[2] Bài Tập Vật lý đại cương A1 , Trần Văn Lượng (chủ
biên), NXB ĐHQG TP HCM, 2016. 2 NỘI DUNG MÔN HỌC
1. Động học chất điểm.
2. Động lực học chất điểm.
3. Cơ học hệ chất điểm – vật rắn.
4. Các định luật thực nghiệm về chất khí.
5. Các nguyên lý nhiệt động học.
6. Trường tĩnh điện trong chân không.
7. Điện trường trong không gian có điện môi – vật dẫn.
8. Trường tĩnh từ trong chân không.
9. Hiện tượng cảm ứng điện từ. 3 CHƢƠNG 1
ĐỘNG HỌC CHẤT ĐIỂM
1. ĐẠI LƢỢNG CƠ BẢN. 1.1. Vecto vị trí. 1.2. Vecto vận tốc. 1.3. Vecto gia tốc.
1.4. Phép biến đổi vận tốc và gia tốc.
1.5. Mối quan hệ giữa các đại lƣợng.
2. CHUYỂN ĐỘNG CỦA CHẤT ĐIỂM.
2.1. Chuyển động thẳng.
2.2. Chuyển động tròn.
2.3. Chuyển động parabol. 4 1.1. VECTO VỊ TRÍ
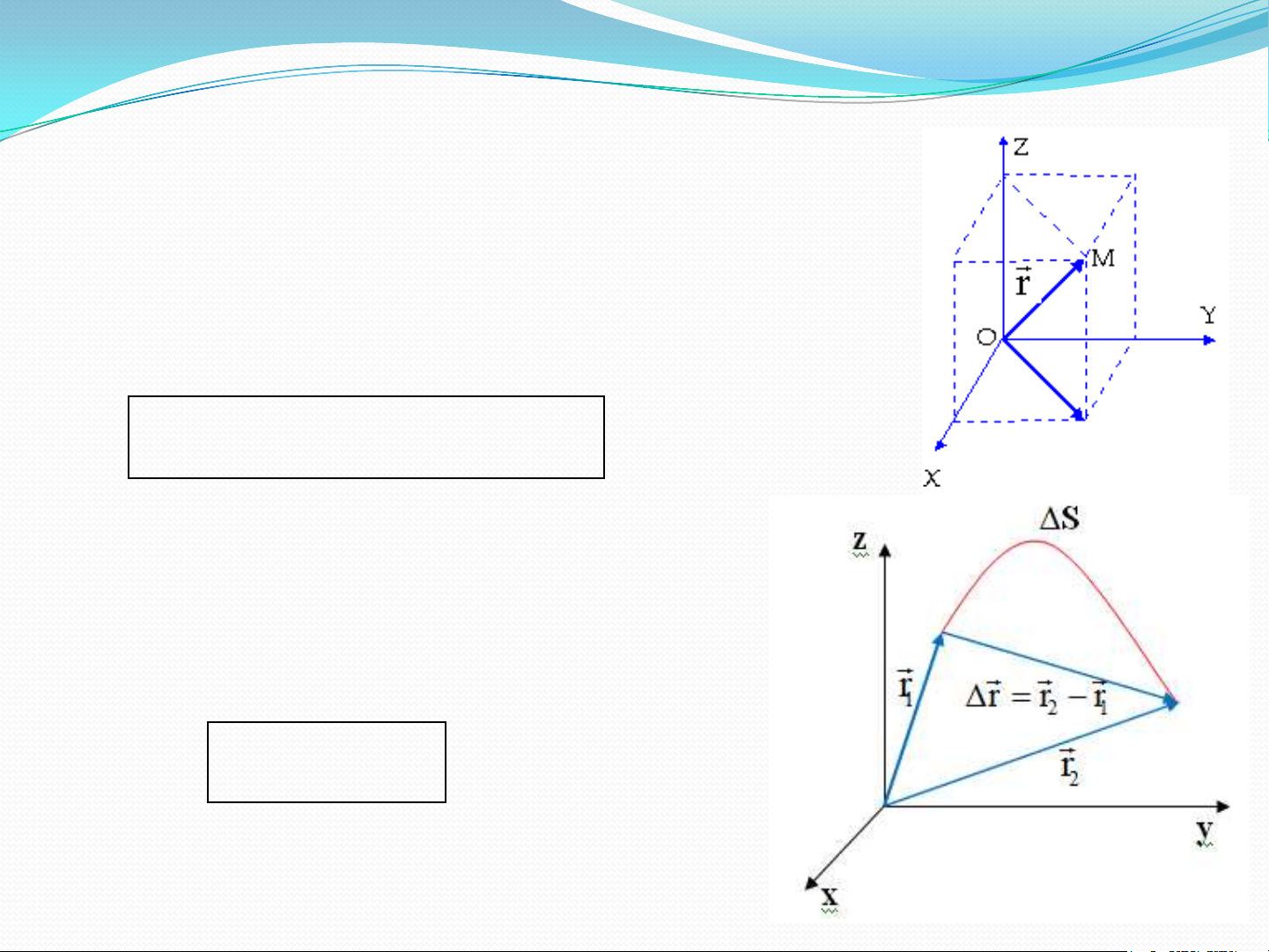
• Để xác định vị trí của một chất điểm M
trong không gian, người ta thường gắn vào
một hệ trục tọa độ (thường là hệ tọa độ
Descartes Oxyz). Vị trí của chất điểm M
được xác định bởi vecto vị trí:      OM  r  xi  yj  zk 
• Tại thời điểm t chất điểm có vecto vị trí 1 r  Tại thời điểm 1
t chất điểm có vecto vị trí 2 r2
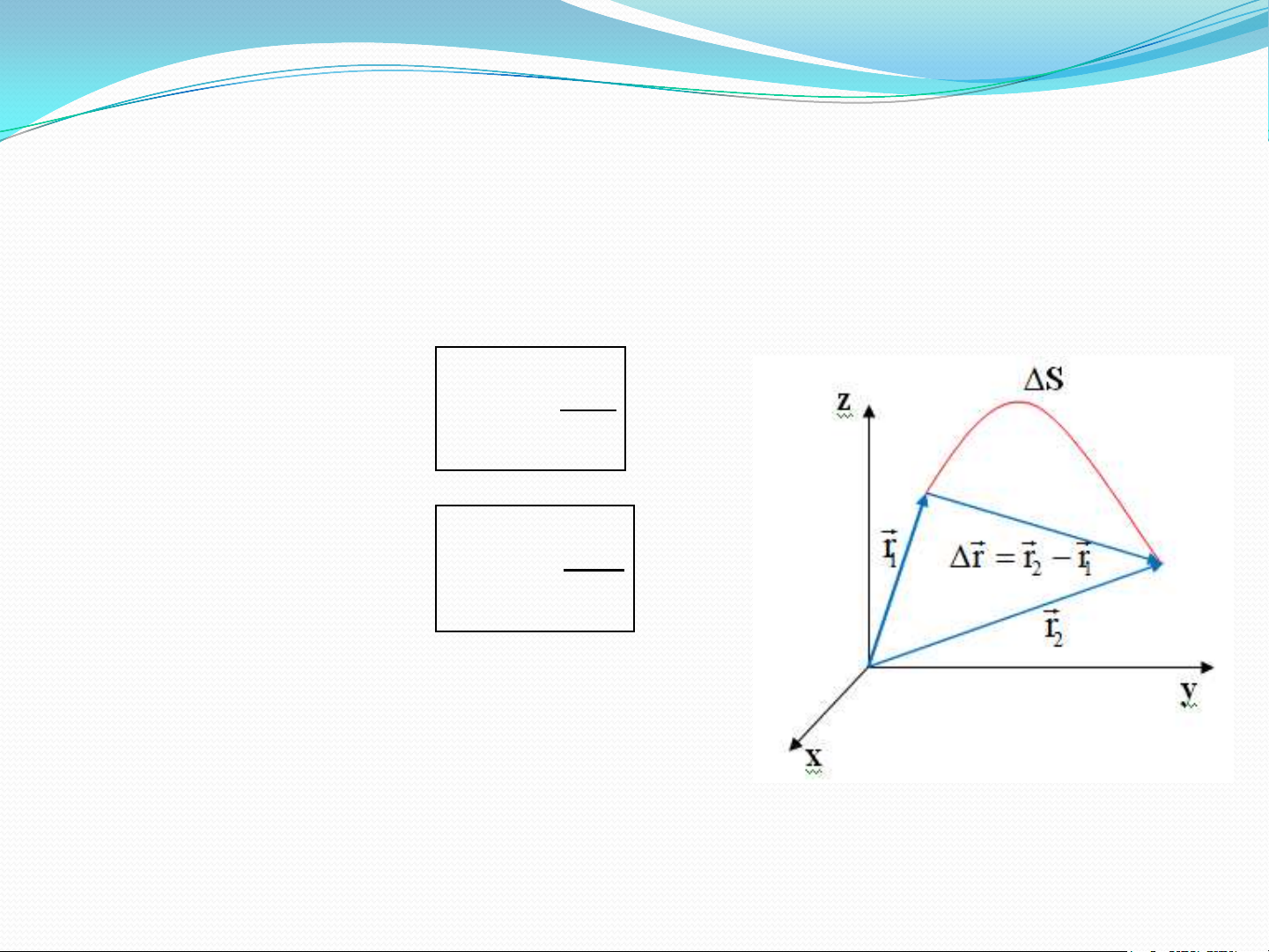
Độ dịch chuyển của chất điểm trong
khoảng thời gian ∆t = t - t : 2 1    r  r  r 2 1
Quãng đƣờng chất điểm đi được trong
khoảng thời gian ∆t = t - t là ∆S. 2 1 5 1.2. VECTO VẬN TỐC
a) Vecto vận tốc trung bình: • Tại thời điểm  
t và t chất điểm có vecto vị trí r và 1 2 r 1 2
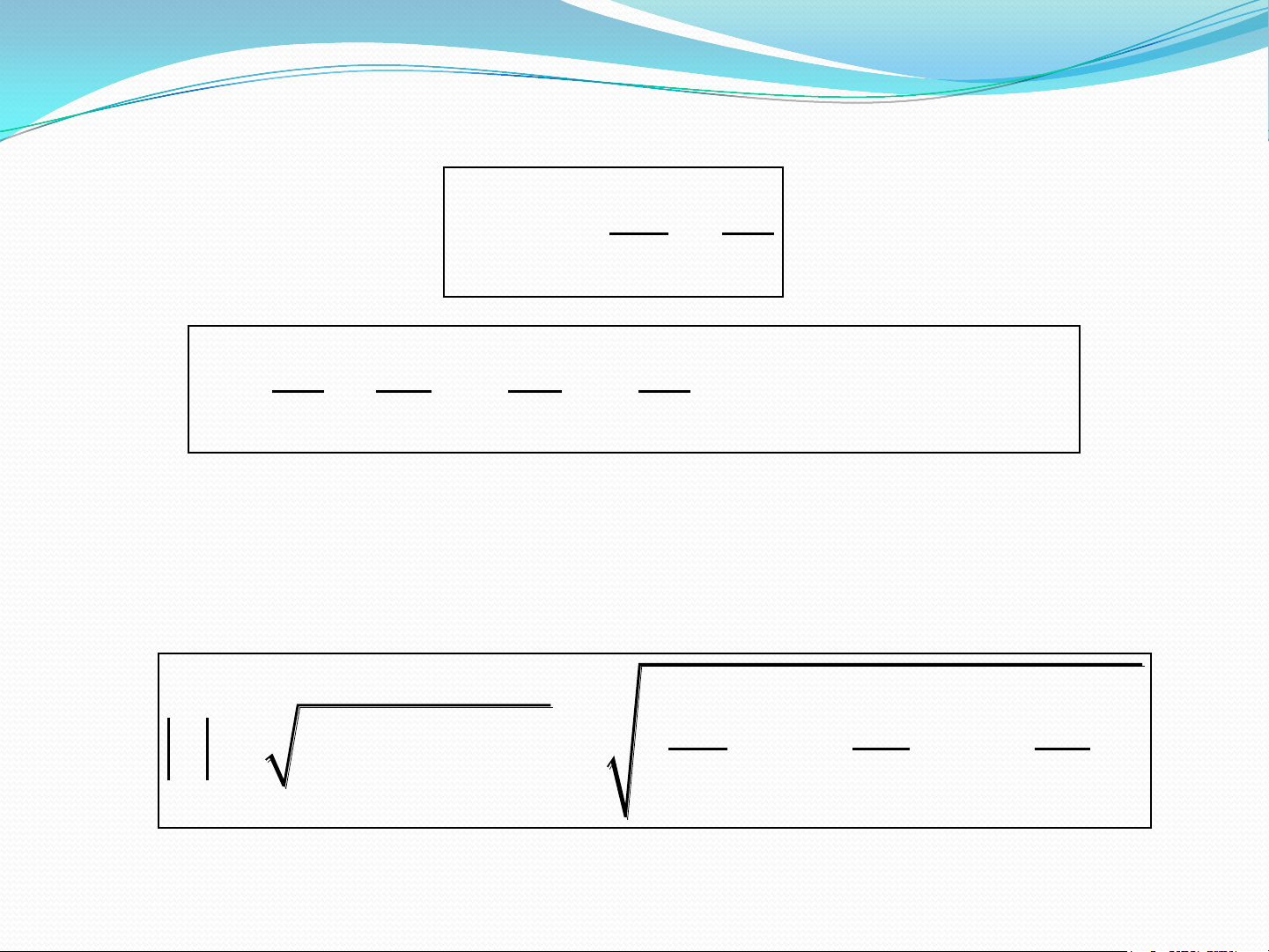
• Vecto vận tốc trung bình trong khoảng thời gian ∆t = t - t là: 2 1   r v  TB t   • Tốc độ S trung bình: v  TB t 
• Nếu sau khoảng thời gian ∆t chất điểm
trở lại vị trí ban đầu thì:   r  0  v  0 TB S   0  v  0 TB 6 BÀI TẬP VÍ DỤ 1
Một canô xuôi dòng từ bến A đến bến B với tốc độ v = 30 km/h, rồi 1
ngược dòng từ B về A với tốc độ v = 20 km/h. Tìm: 2
a) Vận tốc trung bình của cano trên cả quãng đường.
b) Tốc độ trung bình của cano trên cả quãng đường. HƢỚNG DẪN GiẢI 
a) Cano đi được một quãng đường khép kín nên r  0
Vì vậy vận tốc trung bình của cano bằng 0.
b) Tốc độ trung bình của cano: S  S  S 2S 2v v AB BA AB 1 2 v      24 km / h TB t  t  t S S  AB AB v v AB BA 1 2  v v 1 2 7
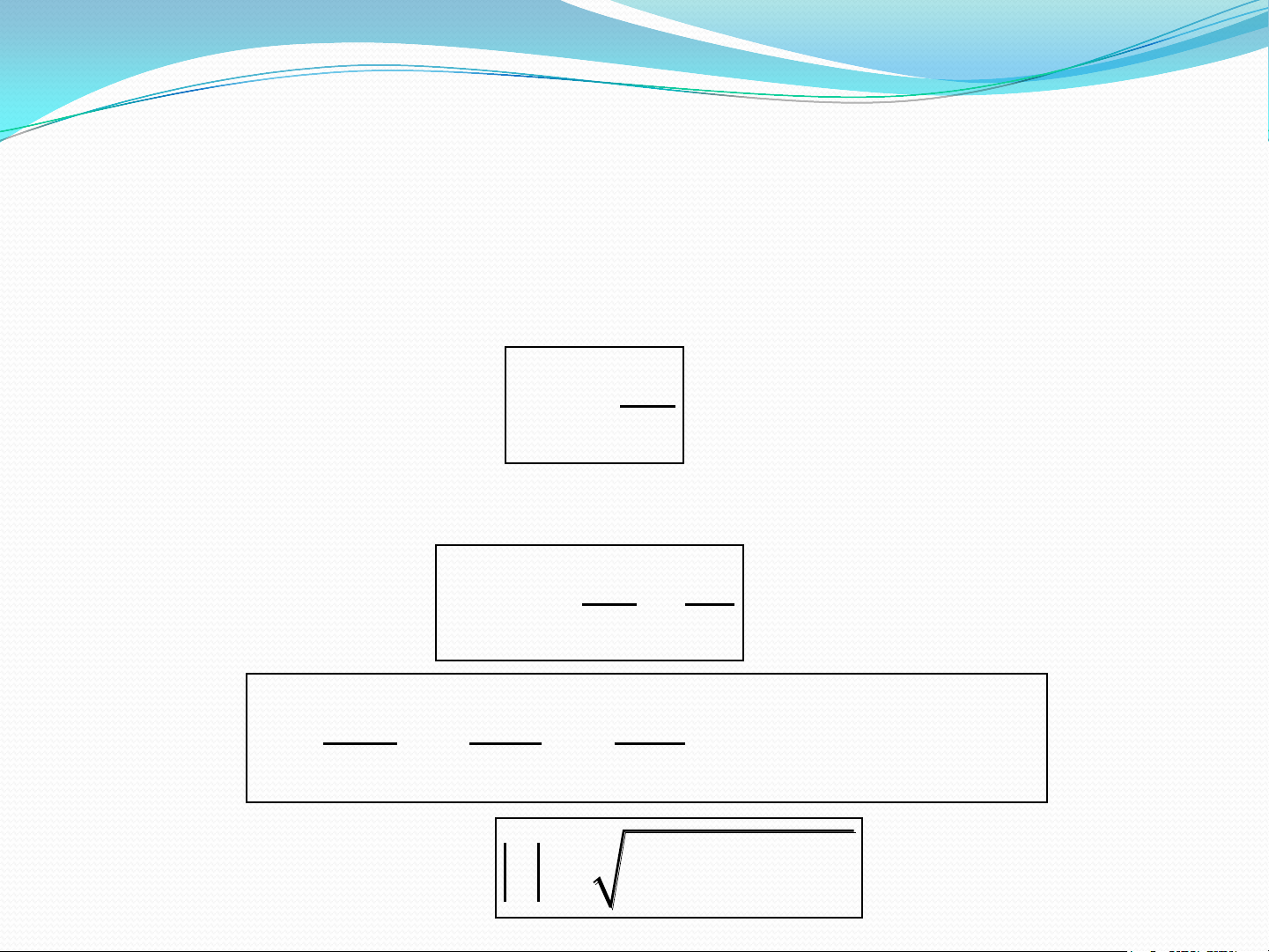
b) Vecto vận tốc tức thời: là giới hạn của vecto vận tốc trung bình khi ∆t  0.    r dr v  lim  t  0 t  dt   dr dx  dy  dz     v   i  j  k  v i  v j  v k x y z dt dt dt dt 
• v tiếp tuyến với quỹ đạo và hướng theo chiều chuyển động.
• Độ lớn của vecto vận tốc: 2 2 2   dx   dy   dz  2 2 2 v  v  v  v    x y z        dt   dt   dt  8 BÀI TẬP VÍ DỤ 2
Một chất điểm chuyển động trên trục Ox với vận tốc v  2 x (m/s)
theo chiều dương và bắt đầu từ gốc tọa độ O với vận tốc đầu bằng
không. Tìm vận tốc của chất điểm tại thời điểm t = 5 s. HƢỚNG DẪN GiẢI • Theo đề bài: 2 v  2 x  v  4x (1)
• Lấy đạo hàm 2 vế của (1) theo thời gian: d  dx dv 2 v   4  2v  4v  dv  2dt (2) dt dt dt
• Lấy tích phân 2 vế của (2): v 5 5
dv  2dt  v  2t  10 m / s   0 0 0 9 1.3. VECTO GIA TỐC
a) Vecto gia tốc trung bình • Tại thời điểm  
t và t chất điểm có vận tốc lần lượt là v và v 1 2 1 2   
 độ biến thiên vận tốc v   v  v 2 1
• Vecto gia tốc trung bình trong khoảng thời gian ∆t = t - t là: 2 1   v  a  TB t 
b) Vecto gia tốc tức thời: là giới hạn của vecto gia tốc trung bình khi ∆t    0.  v  dv a  lim  t  0 t  dt     dv  dv      y dv x z a  i  j  k  a i  a j  a k x y z dt dt dt • Độ lớn của vectơ  gia tốc: 2 2 2 a  a  a  a x y z 10
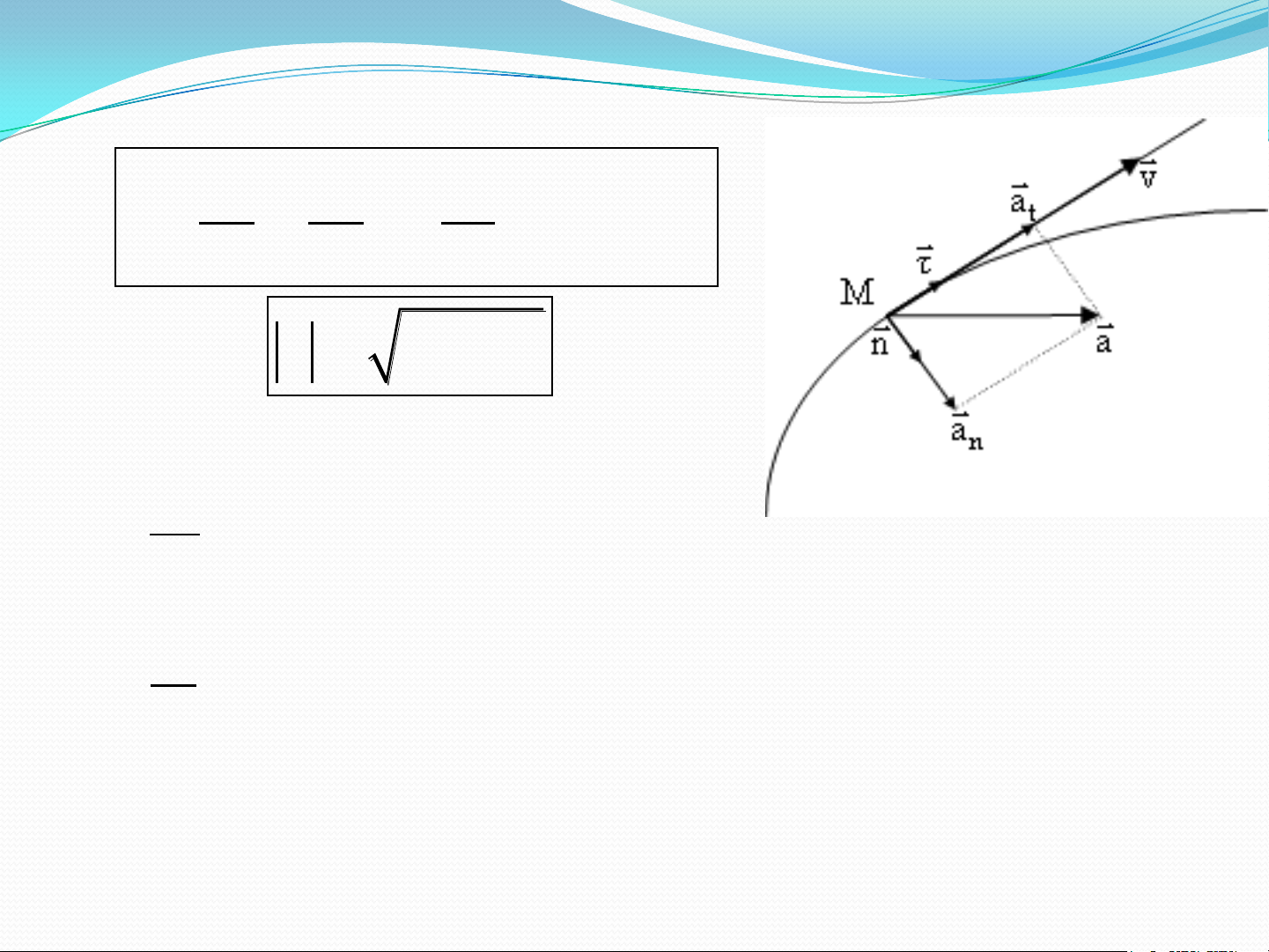
c) Vectơ gia tốc tiếp tuyến và pháp tuyến  2  dv dv  v    a     n  a  a t n dt dt R  2 2 a  a  a t n Trong đó: •  dv  a 
 là vectơ gia tốc tiếp tuyến t dt
đặc trưng cho sự thay đổi độ lớn của vectơ vận tốc. 2 •  v  a  n là n
vectơ gia tốc pháp tuyến đặc trưng cho sự thay đổi R
phương của vectơ vận tốc.
• R là bán kính cong của quĩ đạo. 11
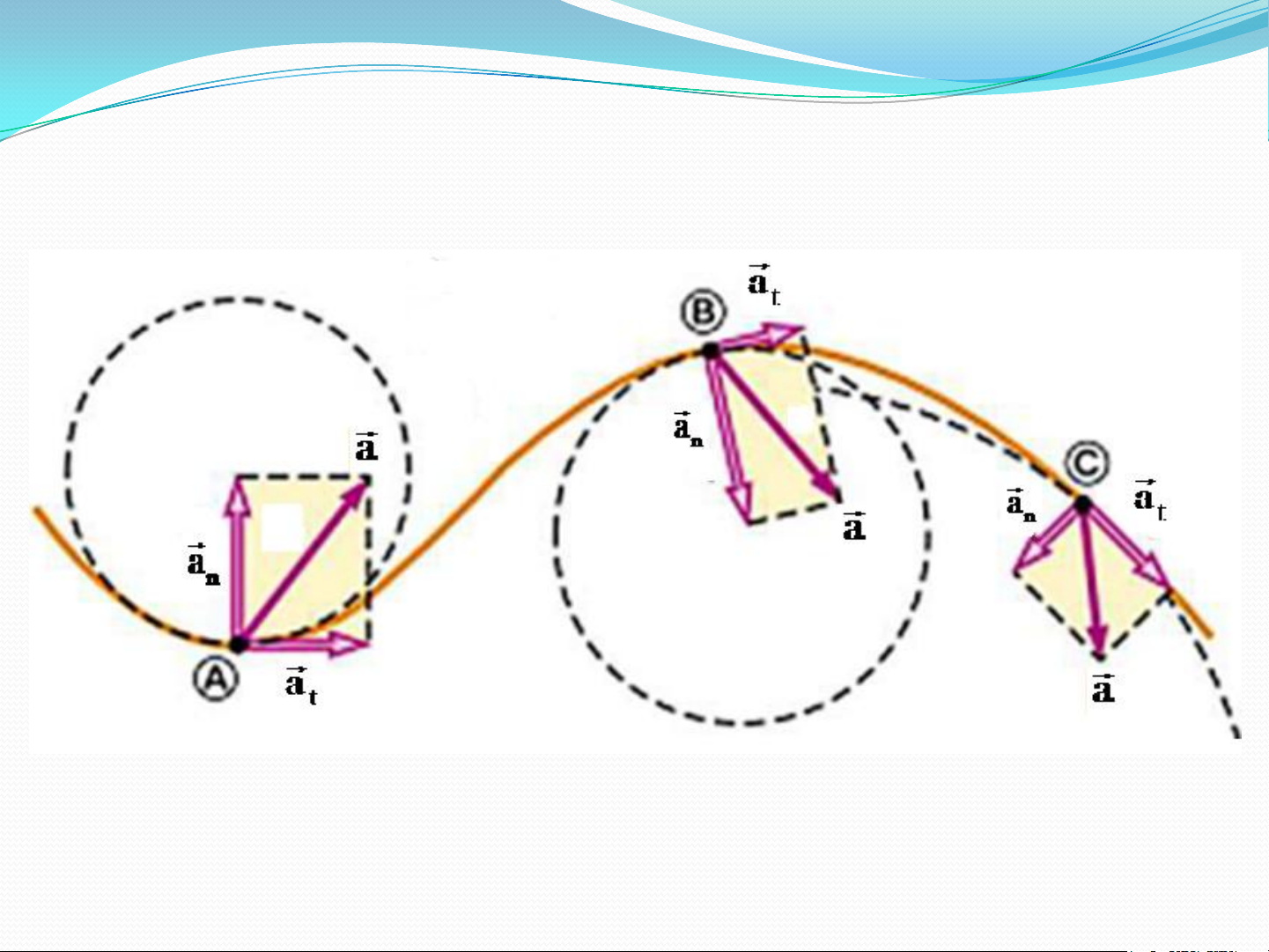
Gia tốc tiếp tuyến và pháp tuyến của chất điểm chuyển động
trên quỹ đạo cong bất kỳ 12
1.4. PHÉP BIẾN ĐỔI VẬN TỐC VÀ GIA TỐC
• Chuyển động có tính tương đối nên vận tốc của chất điểm phụ thuộc vào hệ qui chiếu.
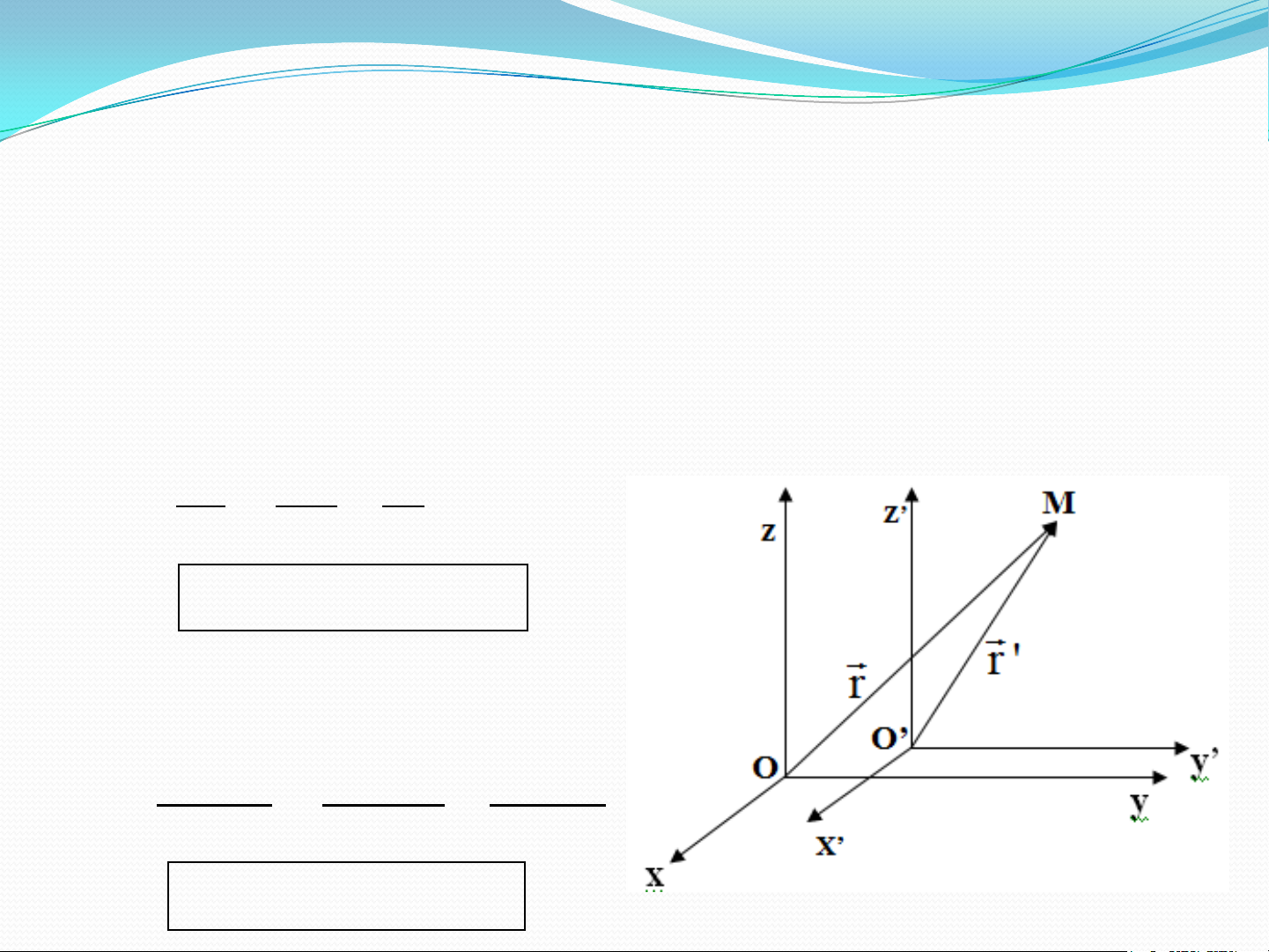
• Xét 2 HQC K (Oxyz) và K’ (O’x’y’z’).  
• Tọa độ của chất điểm M trong 2 HQC lần lượt là OM và O'M
     
OM  OO'  O' M  r  OO'  r ' (1)
• Lấy đạo hàm (1) theo thời gian ta được phép biến đổi vận tốc:   dr dr ' d    OO' dt dt dt    v  v  v (2) M/K M/K ' K '/K
• Lấy đạo hàm (2) theo thời gian ta được phép biến đổi gia tốc:    dv dv dv M/ K M/ K ' K '/ K   dt dt dt    a  a  a M/K M/K ' K '/K 13 BÀI TẬP VÍ DỤ 3
Một máy bay bay về hướng Đông với tốc độ v = 400 km/h đối với gió.
Gió thổi về hướng Bắc với tốc độ u = 75 km/h đối với mặt đất. Xác
định độ lớn và hướng của vận tốc máy bay đối với mặt đất. HƢỚNG DẪN GiẢI
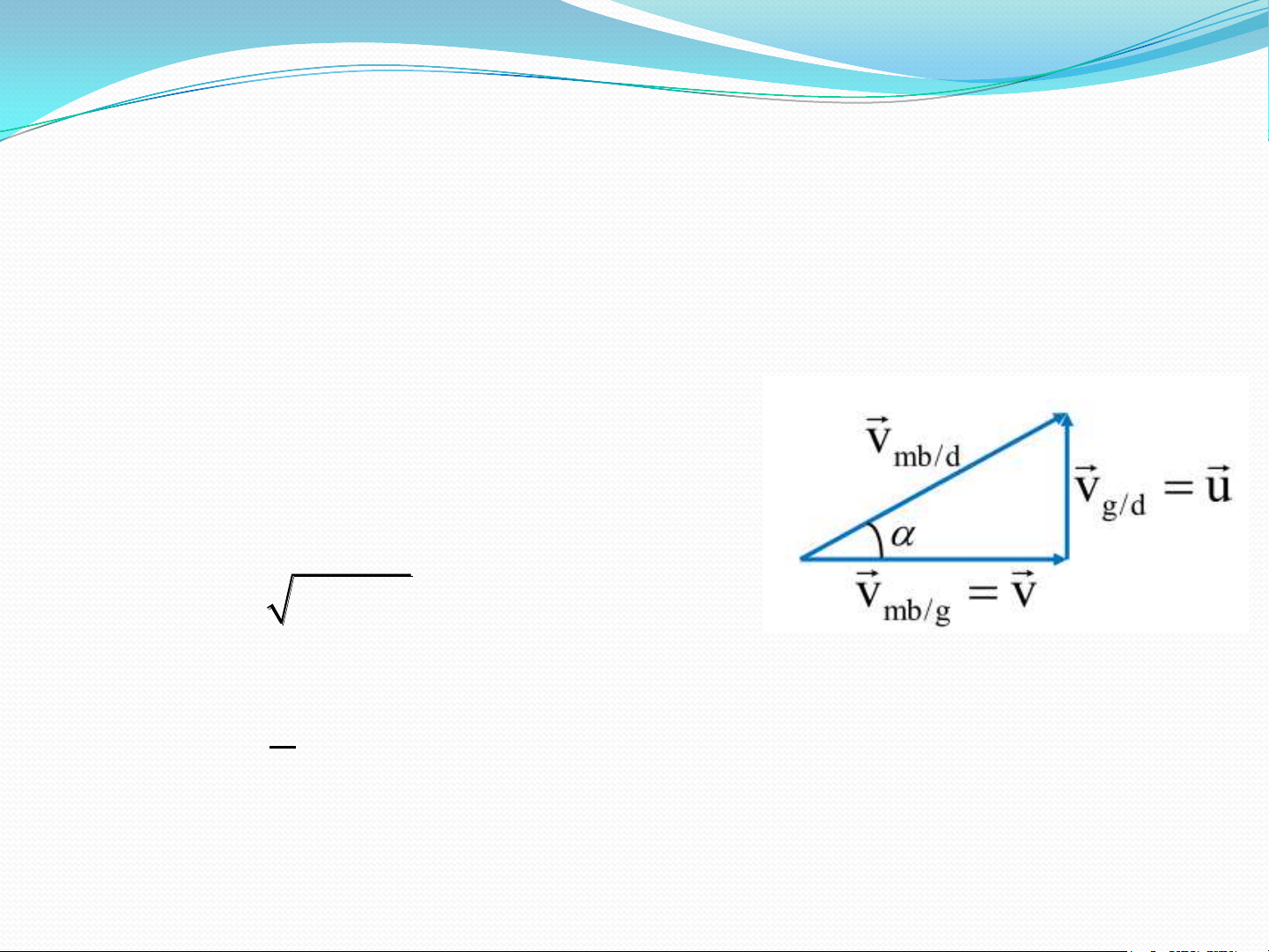
• Theo quy tắc cộng vận tốc ta có:    v  v  v mb/d mb/g g/d
• Vận tốc của máy bay đối với mặt đất: 2 2 v  v  u  407 km / h mb/g
• Hướng bay được xác định bởi: u 0 tan    0,1875   10,6 v
 Máy bay có vận tốc đối với mặt đất là 407 km/h và hướng theo
hướng Đông Bắc, lệch so với hướng Đông một góc α = 10,60. 14
1.5. MỐI QUAN HỆ GIỮA CÁC ĐẠI LƢỢNG
• Từ định nghĩa vận tốc tức thời ta có:  t  dr      v 
 dr  vdt  r  r  v(t)dt  (1) 0 dt • Từ định nghĩa 0 gia tốc tức thời ta có:  t  dv      a 
 dv  adt  v  v  a(t)dt  (2) 0 dt 0 
• Nếu vectơ gia tốc là hằng số ( a  const ), thế (2) vào (1) ta có:   v  v   at
(phƣơng trình vận tốc) 0    1  2 r  r  v t  at ( 0 0
phƣơng trình chuyển động) 2
• Phƣơng trình quỹ đạo có dạng f (x, y, z) = 0. 15
2.1. CHUYỂN ĐỘNG THẲNG
• Vận tốc không thay đổi phương nên gia tốc pháp tuyến luôn bằng
không, gia tốc toàn phần bằng gia tốc tiếp tuyến:    a  0 a  a n t a) Thẳng đều 
• Gia tốc bằng không: a  0 
• Vận tốc không đổi cả phương chiều và độ lớn: v  const
• Phương trình chuyển động: x  x  vt 0
trong đó x là tọa độ ban đầu của chất điểm tại thời điểm t = 0. 0
• Các đại lượng x và v trong PT trên là giá trị đại số, có thể âm hoặc
dương tùy thuộc vào chiều của trục Ox được chọn. Quy ước này áp
dụng cho tất cả các PT chuyển động khác trong mục 2.1 và 2.2. 16
b) Thẳng biến đổi đều
• Gia tốc không đổi: a  const  
Chuyển động nhanh dần đều: a.v  0  
Chuyển động chậm dần đều: a.v  0
• Vận tốc thay đổi theo quy luật: v  v  at (1) 0 • Phương 1 trình chuyển động: 2 x  x  v t  at (2) 0 0 2 • Mối 2 2
liên hệ giữa các đại lượng: v  v  2a(x  x ) (3) 0 0 17 BÀI TẬP VÍ DỤ 4
Một hòn đá được ném đứng từ mặt đất lên cao với vận tốc v =10 m/s. 0
Tìm độ cao cực đại và thời gian chuyển động của hòn đá. Lấy g = 10 m/s2. HƢỚNG DẪN GiẢI
• Chọn trục Oy hướng lên, gốc O tại mặt đất.
• Phương trình chuyển động và phương trình vận tốc của hòn đá: 1 2 y  v t  gt (1) 0 2 v  v  gt (2) 0
• Hòn đá đạt đến độ cao cực đại khi vận tốc bằng 0: v0
(2)  v  v  gt  0  t  1 m / s 0 g
• Độ cao cực đại của hòn đá: (1)  y(t 1)  5 m
• Sau khi hòn đá đạt đến độ cao cực đại, nó sẽ rơi tự do. Thời gian rơi
chạm đất = thời gian đạt độ cao cực đại
 Thời gian chuyển động của hòn đá là 2 giây. 18
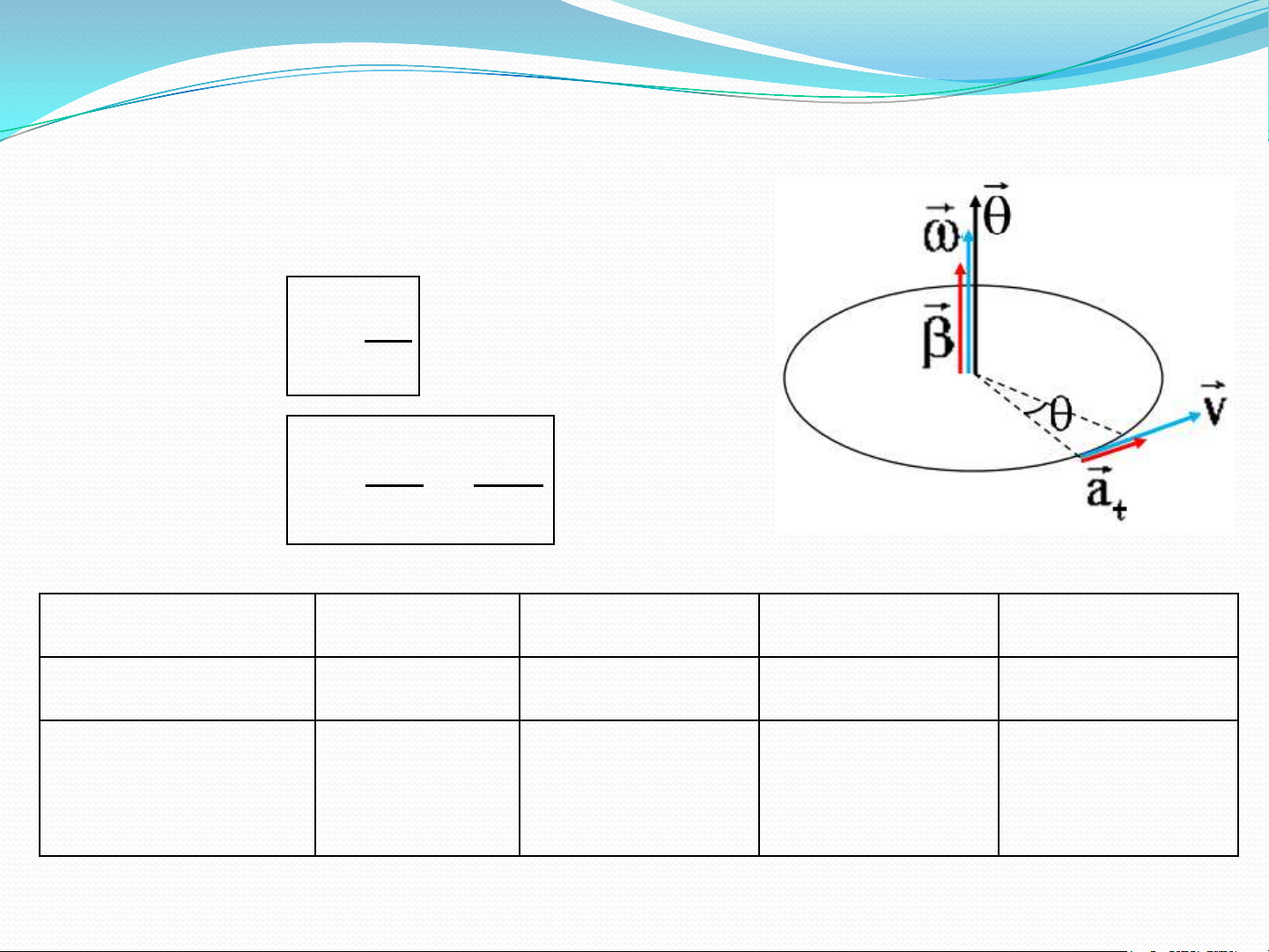
2.2. CHUYỂN ĐỘNG TRÒN Các đại lƣợng góc:
• Góc quay: θ (radian).  • Vận tốc  d góc:   (rad/s) dt  2    • d d Gia tốc góc:    (rad/ s2) 2 dt dt Đại lượng dài S v a a t n Đại lượng góc θ ω β s = R.θ v = R.ω a = R. β Mối t       a    = Rω2 liên hệ n s   ,  R v   ,  R     a   ,  R t   19 a) Tròn đều • 
Gia tốc pháp tuyến có độ lớn không đổi: a  const n 
• Gia tốc tiếp tuyến bằng 0: a  0 t 
• Gia tốc góc bằng 0:   0
• Vận tốc góc không đổi:   const
• Phương trình chuyển động:     t  0  • 2 Chu kỳ: ( T  giây)   • Tần số 1 : ( f   Hz) T 2 20