BỘ GIÁO DỤC VÀ ĐÀO TẠO
TRƯỜNG ĐẠI HỌC BÁCH KHOA TPHCM
KHOA KHOA HỌC ỨNG DỤNG Đề 07
Bài tập 27: Vẽ quỹ đạo của
vật khi có phương trình
chuyển động
Giáo viên hướng dẫn: Lê Quốc Khải MỤC LỤC 1. Giới thiệu đề tài 2. Cơ sở lý thuyết
3. Code MATLAB và diễn giải chi tiết a. Code MATLAB
b. Các hàm sử dụng trong đoạn code c. Diễn giải chi tiết
4. Kết quả và bàn luận 5. Kết luận
1. Giới thiệu đề tài
Phương trình chuyển động dạng động học thường được biểu diễn bởi hệ
phương trình: . Qua đó, khi biểu diễn y=y(x), ta có phương trình quỹ đạo của vật.
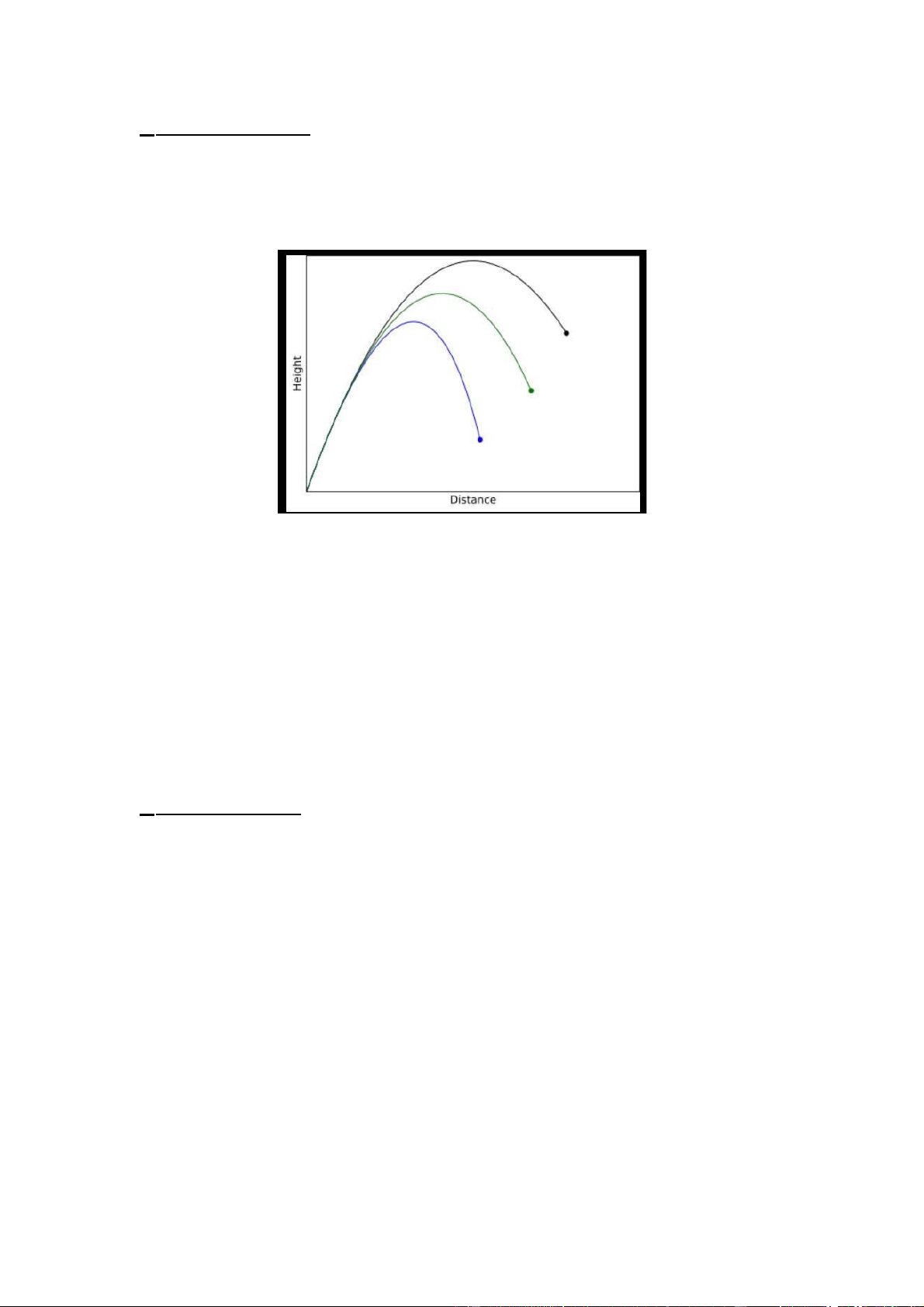
Hình 1: Quỹ đạo của vật
Dự án này chúng ta sử dụng Matlab để vẽ quỹ đạo của vật khi có phương trình
chuyển động và xác định bán kính cong quỹ đạo ở thời điểm bất kì, cụ thể là :
“Chất điểm chuyển động với phương trình: .
a. Vẽ quỹ đạo của vật trong khoảng thời gian từ t=0 đến t=5s.
b. Xác định bán kính cong của quỹ đạo lúc t = 1 s.
2. Cơ sở lý thuyết
a. Phương trình chuyển động: là các phương trình mô tả hành vi của một hệ
vận động về chuyển động của nó như một hàm số theo thời gian.
b. Phương trình quỹ đạo : phương trình quỹ đạo của một chất điểm chuyển
động là phương trình mô tả những điểm mà chất điểm đi qua, còn gọi là quỹ
đạo hay quỹ tích: y=y(x).
c. Vectơ vị trí: Trong hình học, một vị trí hoặc vector vị trí, còn được gọi là tọa
độ vector hoặc bán kính vector, là một vectơ đại diện cho vị trí của một điểm P
trong không gian liên quan đến một hệ quy chiếu gốc O tùy ý. Thường được ký
hiệu là x, r hoặc s, nó tương ứng với đoạn thẳng từ O đến P. Nói cách khác, nó
là li độ hoặc phép tịnh tiến từ gốc đến P:
d. Vectơ vận tốc :là đạo hàm của vectơ vị trí theo thời gian, có gốc đặt tại điểm
chuyển động, phương tiếp tuyến với quỹ đạo tại điểm đó, chiều là chiều chuyển
động và có độ lớn là v:
e. Vectơ gia tốc :là đạo hàm của vectơ vận tốc theo thời gian :
Gia tốc gồm 2 thành phần:
ốc tiếp tuyến: là thành phần làm thay đổi độ lớn của vectơ vận tốc và - Gia t
nằm trên phương vectơ vận tốc
- Gia tốc pháp tuyến: là thành phần làm thay đổi phương chiều vectơ vận tốc và
luôn hướng về tâm của quỹ đạo chuyển động
f. Bán kính quỹ đạo:
Sử dụng các phép toán trong Matlab, từ phương trình chuyển động ta vẽ được
phương trình quỹ đạo và tính được bán kính cong tại thời điểm xác định.
3. Code MATLAB và diễn giải chi tiết a. Code MATLAB:
1. %Khai bao bien va nhap phuong trinh 2. syms t;
3. x=input('nhap phuong trinh chuyen dong theo chieu x: x= ');
4. y=input('nhap phuong trinh chuyen dong theo chieu y: y= ');
5. t1=input('nhap thoi gian ban dau t1= ');
6. t2=input('nhap thoi gian t2= ');
7. t0=input('nhap thoi gian de tinh ban kinh quy tai tai thoi diem do: t0= '); 8. %Phuong trinh van toc 9. vx=diff(x,1); 10. vy=diff(y,1); 11. v=sqrt((vx^2)+(vy^2)); 12. %Phuong trinh gia toc 13. ax=diff(x,2); 14. ay=diff(y,2); 15. a=sqrt((ax^2)+(ay^2)); 16. %Tim Ban kinh cong 17. at=diff(v,1); 18. an=sqrt(a^2-at^2); 19. Bankinh_R=subs(v^2/an,1);
20. Bankinh_R=double(Bankinh_R) 21. %Ve quy dao cua vat 22. t=linspace(t1,t2); 23. x=eval(vectorize(x)); 24. y=eval(vectorize(y));
25. figure('name','Ve quy dao vat trong khong gian','numbertitle','off'); 26. hold on
27. title('Quy dao cua vat'); grid on; box on;
28. plot(x,y); xlabel('x'); ylabel('y'); 29. axis([0 10 -0.5 5])
b. Các hàm sử dụng trong đoạn code: Hàm Ý nghĩa Syms Khai báo biến X=input(‘….’)
Nhập một gia trị cho biến x Diff(f,n)
Đạo hàm cấp n của hàm f Sqrt(x) Lấy căn bậc 2 của x Subs(f,a)
Đổi biến của hàm f với một số a Double(a)
Chuyển đổi số a sang dạng số thập phân X=Linspace(a,b)
Lập vectơ x trong khoảng a đến b Eval(…)
Thực hiện lệnh bên trong dấu ngoặc Vectorize(f)
Vectơ hóa biểu thức trong ngoặc Figure
Đặt tên cho cửa sổ vẽ đồ thị Title Đặt tên cho đồ thị Plot(x,y) Vẽ đồ thị Xlabel, ylabel
Đặt tên cho trục x và y axis Thiết lập trục c. Diễn giải chi tiết: Dòng 2: khai báo biến t
Dòng 3-4: Nhập phương trình chuyển động Dòng 5-7: Nhập thời gian
Dòng 9-10: tìm vận tốc theo từng trục bằng đạo hàm cấp 1
Dòng 11: vận tốc bằng căn của tổng bình phương vận tốc theo trục x,y
Dòng 13-14: tìm phương trình gia tốc theo từng trục bằng đạo hàm cấp 2
phương trình chuyển động
Dòng 15: tìm gia tốc toàn phần bằng căn của tổng bình phương gia tốc theo trục x, y
Dòng 17: tìm gia tốc tiếp tuyến bằng đạo hàm cấp 1 vận tốc toàn phần
Dòng 18: tìm gia tốc pháp tuyến bằng căn của hiệu gia tốc toàn phần và gia tốc tiếp tuyến
Dòng 19-20: tính bán kính cong quỹ đạo
Dòng 22: tạo vector t từ đến
Dòng 23-24: vectơ hóa phương trình x và y
Dòng 25-29: vẽ quỹ đạo của vật từ đến
4. Kết quả và bàn luận
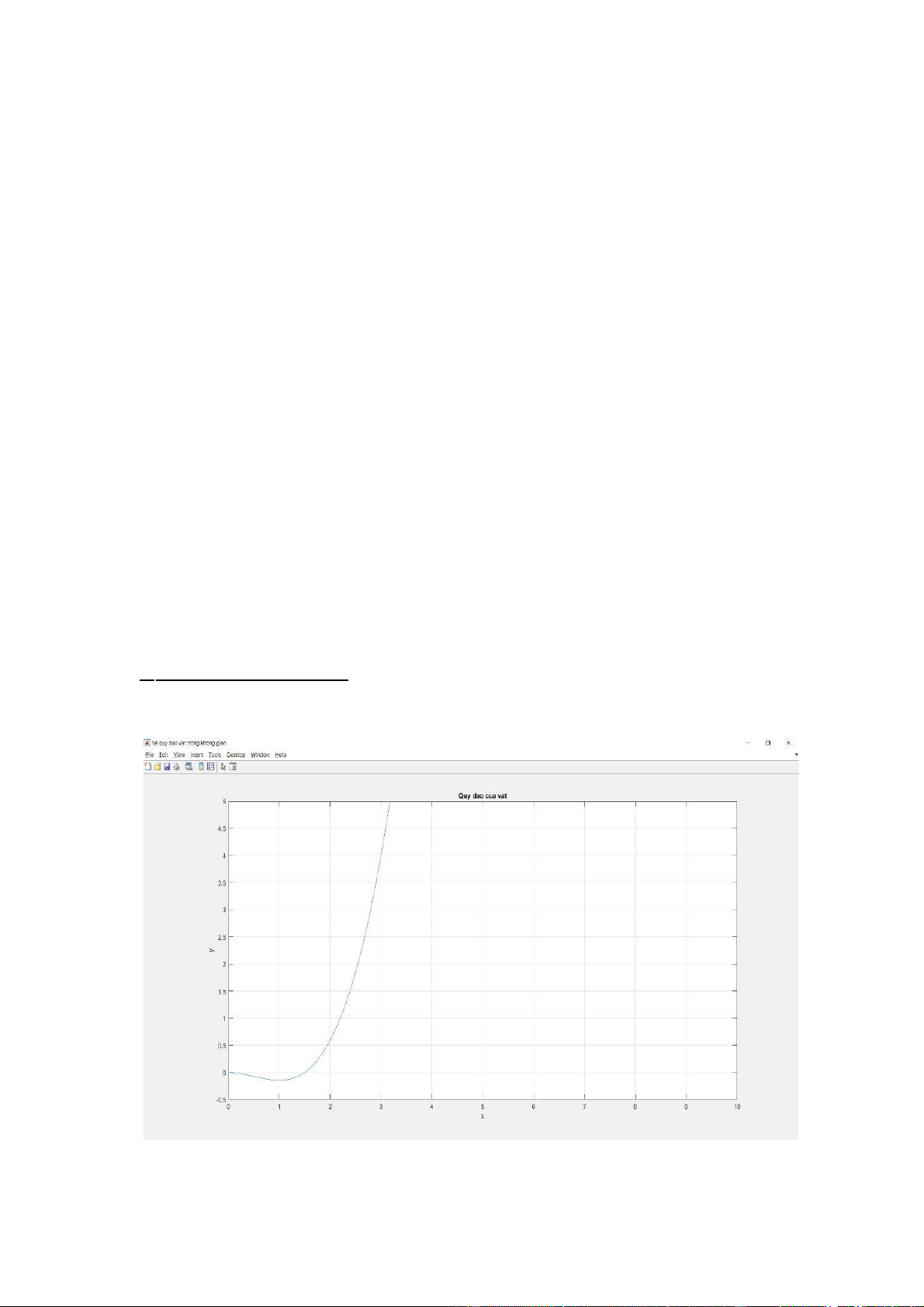
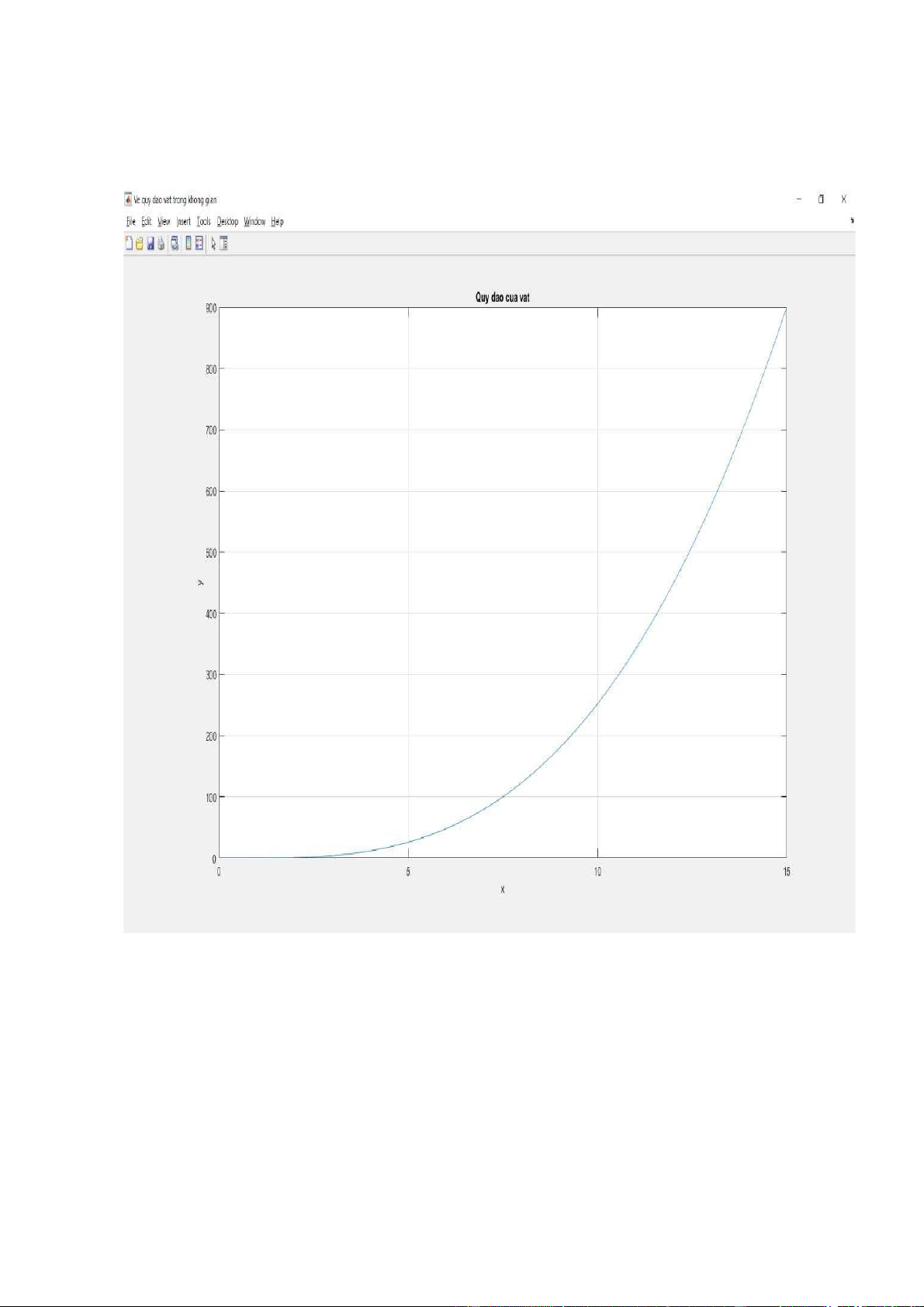
Hình 2: Quỹ đạo của vật ở những giây đầu
Hình 3: Quỹ đạo của vật từ 0s đến 5s
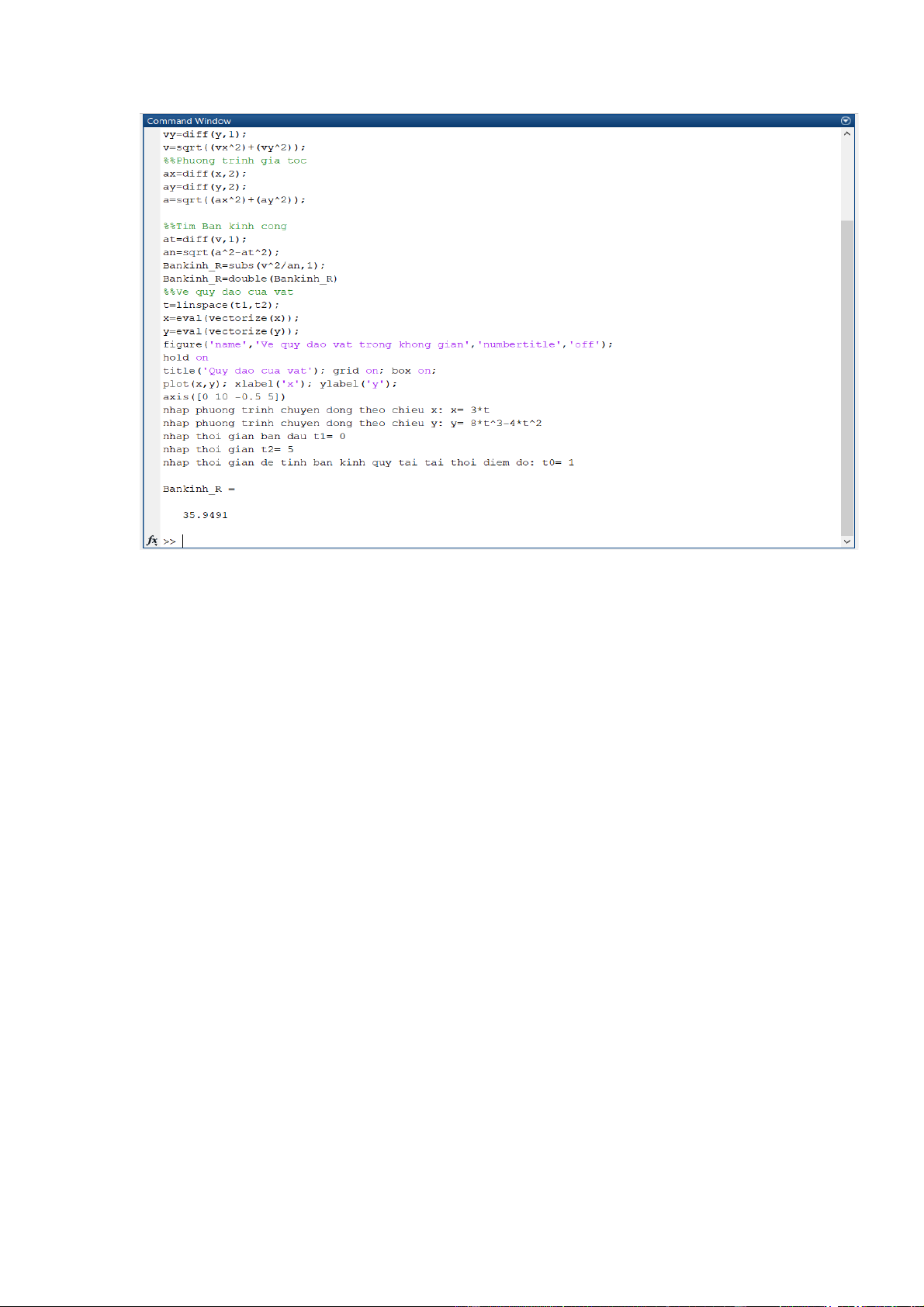
Hình 4: Kết quả tính bán kính quỹ đạo Cách thực hiện: Nhập x = 3*t Nhập y = 8*t^3 – 4*t^2
Nhập thời gian t1=0, t2=5, t0=1
Tính toán: Sau khi nhập các thông số.
Đạo hàm x và y sẽ được vận tốc theo phương x và y. Tính
Đạo hàm bậc 2 sẽ được gia tốc theo phương x và y. Gia tốc toàn phần:
Đạo hàm vận tốc toàn phần ta được gia tốc tiếp tuyến:
Gia tốc pháp tuyến được tính bằng công thức:
Bán kính R được tính bằng
Kết quả: Sau khi tính toán bằng Matlab, ta được kết quả là R=35.9491
Quỹ đạo của vật có dạng của đồ thị hàm số : với
Kết quả trùng khớp với kết quả tính toán thủ công.
Với Matlab, chúng ta có thể thay thế nhiều giá trị khác của đại lượng để tính
toán các trường hợp khác. 5. Kết luận
Với MATLAB, ta đã tính toán được bán kính cong của vật tại thời điểm xác
định và vẽ được quỹ đạo của vật trong không gian Oxy.
Với công cụ này, chúng ta có thể giải quyết bài toán phức tạp một cách nhanh chóng và chính xác.
Tài liệu tham khảo: Giáo trình vật lý A1