Giới hạn, hàm số liên tục Toán 11 GDPT 2018

Tài liệu gồm 171 trang, bao gồm kiến thức trọng tâm, các dạng toán thường gặp và bài tập chuyên đề giới hạn, hàm số liên tục môn Toán 11 chương trình GDPT 2018.

 

50 25 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Chương 5: Giới hạn. Hàm số liên tục (KNTT)

Môn: Toán 11

Thông tin:

171 trang 8 tháng trước

Tác giả:

Profile Kim Oanh
Chương 3. Giới hạn. Hàm số liên tục
Biết làm, làm đúng, làm nhanh
331
GIỚI HẠN. HÀM SỐ LIÊN TỤC
3
Chûúng
GIỚI HẠN. HÀM SỐ LIÊN TỤC
331/764 331/764
Toán 11 theo chương trình GDPT2018
1. Giới hạn của dãy số
Biết làm, làm đúng, làm nhanh
332
GIỚI HẠN CỦA DÃY SỐ
1
Baâi söë
A–GIỚI HẠN HỮU HẠN CỦA DÃY SỐ
1. Định nghĩa
c Định nghĩa 1.1. Dãy số (u
n
) có giới hạn bằng 0 khi n dần tới dương vô cực nếu |u
n
| có thể nhỏ hơn một
số dương bé tùy ý, kể từ một số hạng nào đó trở đi, kí hiệu L = lim
n→+∞
u
n
= 0.
Ngoài kí hiệu lim
n→+∞
u
n
= 0 ta cũng sử dụng các kí hiệu sau: lim u
n
= 0 hay u
n
→ 0 khi n → +∞.
Nhận xét. Nếu u
n
ngày càng gần tới 0 khi n càng lớn thì lim u
n
= 0.
c Định nghĩa 1.2. Dãy số (u
n
) có giới hạn hữu hạn là a khi n dần tới dương vô cực nếu lim
n→+∞
(u
n
− a) = 0,
kí hiệu lim
n→+∞
u
n
= a.
Ngoài kí hiệu lim
n→+∞
u
n
= a ta cũng sử dụng các kí hiệu sau: lim u
n
= a hay u
n
→ a khi n → +∞.
○ Một dãy số có giới hạn thì giới hạn đó là duy nhất.
○ Không phải dãy số nào cũng có giới hạn, chẳng hạn như dãy số (u
n
) với u
n
= (−1)
n
.
2. Một số giới hạn cơ bản
○ lim
1
n
= 0; lim
1
n
k
= 0 với k là số nguyên dương cho trước.
○ lim
c
n
= 0; lim
c
n
k
= 0 với c là hằng số, k là số nguyên dương cho trước.
○ Nếu |q| < 1 thì lim q
n
= 0.
○ Dãy số (u
n
) với u
n
=
Å
1 +
1
n
ã
n
có giới hạn là một số vô tỉ và gọi giới hạn đó là e,
e = lim
Å
1 +
1
n
ã
n
·
Một giá trị gần đúng của e là 2, 718281828459045.
B–ĐỊNH LÍ VỀ GIỚI HẠN HỮU HẠN
c Định lí 1.1.
○ Nếu lim u
n
= a và lim v
n
= b thì:
lim (u
n
+ v
n
) = a + b;
lim (u
n
− v
n
) = a − b;
lim (u
n
· v
n
) = a · b;
lim
u
n
v
n
=
a
b
(v
n
= 0, b = 0) .
○ Nếu u
n
≥ 0 với mọi n và lim u
n
= a thì a ≥ 0 và lim
√
u
n
=
√
a.
332/764 332/764
Toán 11 theo chương trình GDPT2018
Chương 3. Giới hạn. Hàm số liên tục
Biết làm, làm đúng, làm nhanh
333
C–TỔNG CỦA CẤP SỐ NHÂN LÙI VÔ HẠN
c Định nghĩa 1.3. Cấp số nhân vô hạn u
1
, u
1
q, ..., u
1
q
n−1
, ... có công bội q thỏa mãn |q| < 1 được gọi là cấp
số nhân lùi vô hạn. Tổng của cấp số nhân lùi vô hạn đã cho là
S = u
1
+ u
1
q + u
1
q
2
+ ... =
u
1
1 − q
.
D–GIỚI HẠN VÔ CỰC
c Định nghĩa 1.4.
a) Dãy số (u
n
) có giới hạn +∞ khi n → +∞, nếu u
n
có thể lớn hơn một số dương bất kì, kể từ một số
hạng nào đó trở đi.
Kí hiệu lim
n→+∞
u
n
= +∞ hay lim u
n
= +∞ hay u
n
→ +∞ khi n → +∞.
b) Dãy số (u
n
) có giới hạn −∞ khi n → +∞ nếu lim
n→+∞
(−u
n
) = +∞.
Kí hiệu lim
n→+∞
u
n
= −∞ hay lim u
n
= −∞ hay u
n
→ −∞ khi n → +∞.
Nhận xét. Một số giới hạn cơ bản
○ lim n
k
= +∞ với k là một số nguyên dương cho trước.
○ lim q
n
= +∞ với q > 1 là một số thực cho trước.
○ Nếu lim u
n
= a và lim v
n
= +∞ (hoặc lim v
n
= −∞) thì lim
u
n
v
n
= 0.
○ Nếu lim u
n
= a, a > 0 và lim v
n
= 0, v
n
> 0 với mọi n thì lim
u
n
v
n
= +∞.
○ lim u
n
= +∞ ⇔ lim (−u
n
) = −∞.
E–CÁC DẠNG TOÁN THƯỜNG GẶP
Dạng 1. Tính giới hạn dãy số bằng cách dùng định nghĩa, định lí về giới hạn dãy số
Cho lim u
n
= a, lim v
n
= b và c là hằng số. Khi đó
○ lim(u
n
+ v
n
) = a + b
○ lim(u
n
· v
n
) = a · b
○ lim(u
n
− v
n
) = a − b
○ lim(c · u
n
) = c · a
○ lim
u
n
v
n
=
a
b
, (b = 0).
○ Nếu u
n
≥ 0, ∀n ∈ N
∗
thì a ≥ 0 và lim
√
u
n
=
√
a.
1. Ví dụ mẫu
Ví dụ 1 (Cánh Diều). Cho dãy số (u
n
) với u
n
=
(−1)
n
n
. Giả sử h là số dương bé tùy ý cho trước.
Tìm số tự nhiên n để |u
n
| < h;a) Tính lim
(−1)
n
n
·b)
333/764 333/764
Toán 11 theo chương trình GDPT2018
1. Giới hạn của dãy số
Biết làm, làm đúng, làm nhanh
334
Lời giải.
a) Ta có |u
n
| =
(−1)
n
n
=
1
n
. Do đó |u
n
| < h ⇔
1
n
< h ⇔ n >
1
h
.
b) Vì |u
n
| < h là số dương bé tùy ý kể từ số hạng n >
1
h
nên lim
(−1)
n
n
= 0.
□
Ví dụ 2 (Cánh Diều). Chứng minh rằng lim
Å
−
1
2
ã
n
= 0.
Lời giải.
Do
−
1
2
=
1
2
< 1 nên lim
Å
−
1
2
ã
n
= 0. □
Ví dụ 3 (KNTT). Xét dãy số u
n
=
1
n
2
. Giải thích vì sao dãy số này có giới hạn là 0.
Lời giải.
Dãy số này có giới hạn là 0, bởi vì |u
n
| =
1
n
2
có thể nhỏ hơn một số dương bé tuỳ ý khi n đủ lớn. Chẳng hạn, để
|u
n
| < 0, 0001 tức là
1
n
2
< 10
−4
, ta cần n
2
> 10000 hay n > 100. Như vậy, các số hạng của dãy, kể từ số hạng thứ
101 đều có giá trị tuyệt đối nhỏ hơn 0,0001. □
Ví dụ 4 (CTST). Áp dụng giới hạn cơ bản, tìm lim
1
Ä
√
3
ä
n
.
Lời giải.
Ta có
1
Ä
√
3
ä
n
=
Å
1
√
3
ã
n
.
Do
1
√
3
< 1 nên lim
1
Ä
√
3
ä
n
= lim
Å
1
√
3
ã
n
= 0. □
Ví dụ 5 (Cánh Diều). Chứng minh rằng:
lim c = c với c là hằng số;a) lim
6n + 1
n
= 6.b)
Lời giải.
a) Do lim(c − c) = lim 0 = 0 nên theo định nghĩa về dãy số có giới hạn hữu hạn, ta có lim c = c.
b) Do lim
Å
6n + 1
n
− 6
ã
= lim
1
n
= 0 nên lim
6n + 1
n
= 6.
□
Ví dụ 6 (KNTT). Xét dãy số (u
n
) với u
n
=
2n + 1
n
. Chứng minh rằng lim
n→+∞
u
n
= 2.
Lời giải.
Ta có u
n
− 2 =
2n + 1
n
− 2 =
(2n + 1) −2n
n
=
1
n
→ 0 khi n → +∞. Do vậy lim
n→+∞
u
n
= 2. □
Ví dụ 7 (CTST). Dùng định nghĩa, tìm giới hạn lim
3n
2
+ 1
n
2
.
Lời giải.
Đặt u
n
=
3n
2
+ 1
n
2
. Ta có u
n
= 3 +
1
n
2
hay u
n
− 3 =
1
n
2
.
Suy ra lim (u
n
− 3) = lim
1
n
2
= 0.
Theo định nghĩa, ta có lim u
n
= 3. Vậy lim
3n
2
+ 1
n
2
= 3. □
334/764 334/764
Toán 11 theo chương trình GDPT2018
Chương 3. Giới hạn. Hàm số liên tục
Biết làm, làm đúng, làm nhanh
335
2. Bài tập tự luyện
Bài 1. Cho hai dãy số (u
n
), (v
n
) với u
n
= 3 +
1
n
; v
n
= 5 −
2
n
2
. Tính các giới hạn sau:
a) lim u
n
, lim v
n
.
b) lim (u
n
+ v
n
), lim (u
n
− v
n
), lim (u
n
· v
n
), lim
u
n
v
n
.
Lời giải.
a) Ta có
lim u
n
= lim
Å
3 +
1
n
ã
= lim 3 + lim
Å
1
n
ã
= 3 + 0 = 3.
lim v
n
= lim
Å
5 −
2
n
2
ã
= lim 5 − lim
Å
2
n
2
ã
= 5 − 0 = 5.
b) Ta có
lim (u
n
+ v
n
) = lim u
n
+ lim v
n
= 3 + 5 = 8.
lim (u
n
− v
n
) = lim u
n
− lim v
n
= 3 − 5 = −2.
lim (u
n
· v
n
) = lim u
n
· lim v
n
= 3 · 5 = 15.
lim
u
n
v
n
=
3
5
.
□
Bài 2. Cho hai dãy số không âm (u
n
) và (v
n
) với lim
n→+∞
u
n
= 2 và lim
n→+∞
v
n
= 3. Tìm các giới hạn sau
lim
n→+∞
u
2
n
v
n
− u
n
;a) lim
n→+∞
√
u
n
+ 2v
n
.b)
Lời giải.
a) lim
n→+∞
u
2
n
v
n
− u
n
=
lim
n→+∞
u
2
n
lim
n→+∞
v
n
− lim
n→+∞
u
n
=
Å
lim
n→+∞
u
n
ã
2
lim
n→+∞
v
n
− lim
n→+∞
u
n
=
2
2
3 − 2
= 4 ;
b) lim
n→+∞
√
u
n
+ 2v
n
=
q
lim
n→+∞
u
n
+ lim
n→+∞
2v
n
=
q
lim
n→+∞
u
n
+ 2 lim
n→+∞
v
n
=
√
2 + 2 ·3 = 2
√
2.
□
Bài 3. Cho hai dãy số (u
n
), (v
n
) với u
n
= 5 +
6
n
3
; v
n
= 3 +
7
n
4
. Tính các giới hạn sau:
a) lim u
n
, lim v
n
.
b) lim (u
n
+ v
n
), lim (u
n
− v
n
), lim (u
n
· v
n
), lim
u
n
v
n
.
Lời giải.
a) Ta có
lim u
n
= lim
Å
3 +
1
n
ã
= lim 3 + lim
Å
1
n
ã
= 3 + 0 = 3.
lim v
n
= lim
Å
5 −
2
n
2
ã
= lim 5 − lim
Å
2
n
2
ã
= 5 − 0 = 5.
b) Ta có
lim (u
n
+ v
n
) = lim u
n
+ lim v
n
= 3 + 5 = 8.
lim (u
n
− v
n
) = lim u
n
− lim v
n
= 3 − 5 = −2.
lim (u
n
· v
n
) = lim u
n
· lim v
n
= 3 · 5 = 15.
lim
u
n
v
n
=
3
5
.
335/764 335/764
Toán 11 theo chương trình GDPT2018
1. Giới hạn của dãy số
Biết làm, làm đúng, làm nhanh
336
□
Bài 4. Cho hai dãy số không âm (u
n
) và (v
n
) với lim
n→+∞
u
n
= 5 và lim
n→+∞
v
n
= −6. Tìm các giới hạn sau
lim (u
n
+ v
n
), lim (u
n
− v
n
), lim (u
n
· v
n
), lim
u
n
v
n
.a) lim
n→+∞
u
2
n
v
n
− u
n
;a)
lim
n→+∞
√
u
n
+ 2v
n
.b)
Lời giải.
a) lim
n→+∞
u
2
n
v
n
− u
n
=
lim
n→+∞
u
2
n
lim
n→+∞
v
n
− lim
n→+∞
u
n
=
Å
lim
n→+∞
u
n
ã
2
lim
n→+∞
v
n
− lim
n→+∞
u
n
=
2
2
3 − 2
= 4 ;
b) lim
n→+∞
√
u
n
+ 2v
n
=
q
lim
n→+∞
u
n
+ lim
n→+∞
2v
n
=
q
lim
n→+∞
u
n
+ 2 lim
n→+∞
v
n
=
√
2 + 2 ·3 = 2
√
2.
□
3. Bài tập trắc nghiệm
Câu 1. Giá trị của lim
1
n
bằng
A 0. B 1. C +∞. D −∞.
Lời giải.
lim
1
n
= 0.
Chọn đáp án A □
Câu 2. Giá trị của lim
1
n
k
với k ∈ Z
+
bằng
A 1. B +∞. C −∞. D 0.
Lời giải.
lim
1
n
k
= 0.
Chọn đáp án D □
Câu 3. Dãy số nào sau đây có giới hạn 0?
A u
n
=
n
2
. B u
n
=
2
n
. C u
n
= n. D u
n
=
√
n.
Lời giải.
lim
2
n
= 0.
Chọn đáp án B □
Câu 4. Giá trị của lim
−5
n
k
với k ∈ Z
+
bằng
A 5. B −1. C 0. D −∞.
Lời giải.
lim
−5
n
k
= 0.
Chọn đáp án C □
Câu 5. Giá trị của lim q
n
với |q| < 1 bằng
A 1. B 0. C +∞. D −∞.
Lời giải.
Với |q| < 1 thì lim q
n
= 0.
Chọn đáp án B □
336/764 336/764
Toán 11 theo chương trình GDPT2018
Chương 3. Giới hạn. Hàm số liên tục
Biết làm, làm đúng, làm nhanh
337
Câu 6. Dãy số (u
n
) có giới hạn là số thực L nếu
A lim
n→+∞
(u
n
− L) = 0. B lim
n→+∞
(u
n
) = 0. C lim
n→+∞
L = 0. D lim
n→+∞
(u
n
+ L) = 0.
Lời giải.
Theo định nghĩa giới hạn dãy số ta có (u
n
) có giới hạn là số thực L nếu lim
n→+∞
(u
n
− L) = 0.
Chọn đáp án A □
Câu 7. Giả sử lim u
n
= L, khẳng định nào sau đây là đúng?
A lim
√
u
n
= L. B lim
√
u
n
=
√
L. C lim
3
√
u
n
= L. D lim
3
√
u
n
=
3
√
L.
Lời giải.
Nếu lim u
n
= L thì lim
3
√
u
n
=
3
√
L.
Chọn đáp án D □
Câu 8. Dãy số nào sau đây có giới hạn bằng 0?
A (0,999)
n
. B (−1,01)
n
. C (1,01)
n
. D (−2,001)
n
.
Lời giải.
Vì |0,999| < 1 nên lim(0,999)
n
= 0.
Chọn đáp án A □
Câu 9. Dãy số nào sau đây có giới hạn bằng 0?
A
Å
5
4
ã
n
. B
π
3
n
. C
−
π
4
n
. D
Å
−
4
3
ã
n
.
Lời giải.
Vì
−
π
4
≈ 0,78 < 1 nên lim
−
π
4
n
= 0.
Chọn đáp án C □
Câu 10. Cho hai dãy (u
n
) và (v
n
) thỏa mãn lim u
n
= 1 và lim v
n
= −2. Giá trị của lim (u
n
+ v
n
) bằng
A −1. B −2. C 3. D −3.
Lời giải.
lim (u
n
+ v
n
) = lim u
n
+ lim v
n
= 1 + (−2) = −1.
Chọn đáp án
A □
Câu 11. Cho hai dãy (u
n
) và (v
n
) thỏa mãn lim u
n
= 6 và lim v
n
= 12. Giá trị của lim (u
n
− v
n
) bằng
A 2. B 72. C 18. D −6.
Lời giải.
lim (u
n
− v
n
) = lim u
n
− lim v
n
= 6 − 12 = −6.
Chọn đáp án D □
Câu 12. Cho hai dãy (u
n
) và (v
n
) thỏa mãn lim u
n
= 4 và lim v
n
= 7. Giá trị của lim (u
n
· v
n
) bằng
A
4
7
. B
7
4
. C 28. D 11.
Lời giải.
lim (u
n
· v
n
) = lim u
n
· lim v
n
= 4 · 7 = 28.
Chọn đáp án
C □
Câu 13. Cho hai dãy (u
n
) và (v
n
) thỏa mãn lim u
n
=
√
3 và lim v
n
= 2. Giá trị của lim
u
n
v
n
bằng
A 2
√
3. B
√
3
2
. C 2 +
√
3. D −2 +
√
3.
Lời giải.
lim
u
n
v
n
=
lim u
n
lim v
n
=
√
3
2
.
Chọn đáp án B □
Câu 14. Cho hai dãy (u
n
) thỏa mãn lim u
n
= 12. Giá trị của lim (6 + 3u
n
) bằng
A 30. B 108. C 36. D 42.
Lời giải.
lim (6 + 3u
n
) = lim 6 + lim 3 ·lim u
n
= 6 + 3 ·12 = 42.
Chọn đáp án D □
337/764 337/764
Toán 11 theo chương trình GDPT2018
1. Giới hạn của dãy số
Biết làm, làm đúng, làm nhanh
338
Câu 15. Biết lim u
n
= 3. Chọn mệnh đề đúng trong các mệnh đề sau
A lim
3u
n
− 1
u
n
+ 1
= 3. B lim
3u
n
− 1
u
n
+ 1
= −1. C lim
3u
n
− 1
u
n
+ 1
= 2. D lim
3u
n
− 1
u
n
+ 1
= 1.
Lời giải.
lim
3u
n
− 1
u
n
+ 1
= 2 =
lim 3 · lim u
n
− lim 1
lim u
n
+ lim 1
=
3 · 3 −1
3 + 1
= 2.
Chọn đáp án C □
Dạng 2. Tính giới hạn L = lim
P (n)
Q(n)
Rút lũy thừa bậc cao nhất của tử và mẫu, rồi sử dụng các công thức:
lim
c
n
k
= 0, (k ∈ N
∗
, c ∈ R).• lim n
k
= +∞, (k ∈ N
∗
).•
®
lim u
n
= +∞
lim v
n
= a > 0
⇒ lim(u
n
· v
n
) = +∞.•
®
lim u
n
= −∞
lim v
n
= a > 0
⇒ lim(u
n
· v
n
) = −∞.•
®
lim u
n
= +∞
lim v
n
= a < 0
⇒ lim(u
n
· v
n
) = −∞.•
®
lim u
n
= −∞
lim v
n
= a < 0
⇒ lim(u
n
· v
n
) = +∞.•
○ Áp dụng lim q
n
= 0 với |q| < 1.
○ Sử dụng công thức mũ, rồi chia cả tử và mẫu cho a
n
với |a| là cơ số lớn nhất.
○ Công thức mũ cần nhớ
a
m+n
= a
m
· a
n
và a
m−n
=
a
m
a
n
.
Nhận xét. Ta chia cho a
n
với |a| là cơ số lớn nhất vì sau khi chia luôn tạo ra cơ số có trị tuyệt đối nhỏ hơn 1
để áp dụng công thức lim q
n
= 0 với |q| < 1.
Nhận xét. Các công thức cần nhớ về cấp số nhân
u
k+1
u
k
= q (q là công bội).a) S
n
= u
1
+ u
2
+ ··· + u
n
= u
1
·
q
n
− 1
q − 1
.b)
u
n
= u
1
· q
n−1
.c) u
k+1
· u
k−1
= u
2
k
với k ≥ 2.d)
Nhận xét. Nếu bậc tử P (n) bằng bậc mẫu Q(n) thì lim
P (n)
Q(n)
=
Hệ số bậc cao nhất của tử
Hệ số bậc cao nhất của mẫu
.
Nhận xét. Với bài toán có lũy thừa cao, ta thường rút bậc cao trong từng dấu ngoặc, sau đó áp dụng công
thức (a · b)
n
= a
n
· b
n
và tính toán tương tự như các bài trước.
Nhận xét. Nếu bậc tử P (n) lớn hơn bậc mẫu Q(n) thì L = lim
P (n)
Q(n)
= ±∞. Để biết là +∞ hay −∞ ta dựa
vào dấu của giới hạn hai nhân tử trong tích theo quy tắc “cùng dấu thì tích dương, trái dấu thì tích âm”. Thông
thường, sẽ để trống = ··· và xét dấu sẽ điền vào sau. Vế trắc nghiệm, đó chính là dấu của tích hệ số bậc cao nhất
của tử và mẫu.
1. Ví dụ mẫu
Ví dụ 8 (Cánh Diều). Tính các giới hạn sau
lim
Å
2 +
1
n
2
ã
;a) lim
4n − 3
n
;b) lim
Å
5 +
1
n
ãÅ
6 −
1
4
n
ã
.c)
Lời giải.
338/764 338/764
Toán 11 theo chương trình GDPT2018
Chương 3. Giới hạn. Hàm số liên tục
Biết làm, làm đúng, làm nhanh
339
a) lim
Å
2 +
1
n
2
ã
= lim 2 + lim
1
n
2
= 2 + 0 = 2.
b) lim
4n − 3
n
= lim
Å
4n
n
−
3
n
ã
= lim 4 − lim
3
n
= 4 − 0 = 4.
c) lim
Å
5 +
1
n
ãÅ
6 −
1
4
n
ã
= lim
Å
5 +
1
n
ã
· lim
ï
6 −
Å
1
4
ã
n
ò
= 5 · 6 = 30.
□
Ví dụ 9 (CTST). Tìm các giới hạn sau
lim
3n + 2
2n − 1
.a) lim
√
9n
2
+ 1
n
.b)
Lời giải.
a) Ta có
3n + 2
2n − 1
=
3 +
2
n
2 −
1
n
(Chia cả tử và mẫu cho n).
Từ đó lim
3n + 2
2n − 1
= lim
3 + 2 ·
1
n
2 −
1
n
=
lim
Å
3 + 2 ·
1
n
ã
lim
Å
2 −
1
n
ã
=
lim 3 + 2 lim
1
n
lim 2 − lim
1
n
=
3 + 2 ·0
2 − 0
=
3
2
.
b) Ta có
√
9n
2
+ 1
n
=
√
9n
2
+ 1
√
n
2
=
…
9n
2
+ 1
n
2
=
…
9 +
1
n
2
.
Từ đó lim
√
9n
2
+ 1
n
= lim
…
9 +
1
n
2
=
lim
Å
9 +
1
n
2
ã
=
…
lim 9 + lim
1
n
2
=
√
9 + 0 = 3.
□
Ví dụ 10 (KNTT). Tìm lim
n→+∞
n
2
+ n + 1
2n
2
− 1
.
Lời giải.
Để tính giới hạn của dãy số dạng phân thức, ta chia cả tử thức và mẫu thức cho luỹ thừa cao nhất của n, rồi áp
dụng các quy tắc tính giới hạn.
Áp dụng các quy tắc tính giới hạn, ta được
lim
n→+∞
n
2
+ n + 1
2n
2
− 1
= lim
n→+∞
1 +
1
n
+
1
n
2
2 −
1
n
2
=
lim
n→+∞
Å
1 +
1
n
+
1
n
2
ã
lim
n→+∞
Å
2 −
1
n
2
ã
=
1
2
.
□
Ví dụ 11 (CTST). Tìm các giới hạn sau
lim
3n + 2
2n − 1
.a) lim
√
9n
2
+ 1
n
.b)
Lời giải.
a) Ta có
3n + 2
2n − 1
=
3 +
2
n
2 −
1
n
(Chia cả tử và mẫu cho n).
Từ đó lim
3n + 2
2n − 1
= lim
3 + 2 ·
1
n
2 −
1
n
=
lim
Å
3 + 2 ·
1
n
ã
lim
Å
2 −
1
n
ã
=
lim 3 + 2 lim
1
n
lim 2 − lim
1
n
=
3 + 2 ·0
2 − 0
=
3
2
.
339/764 339/764
Toán 11 theo chương trình GDPT2018
1. Giới hạn của dãy số
Biết làm, làm đúng, làm nhanh
340
b) Ta có
√
9n
2
+ 1
n
=
√
9n
2
+ 1
√
n
2
=
…
9n
2
+ 1
n
2
=
…
9 +
1
n
2
.
Từ đó lim
√
9n
2
+ 1
n
= lim
…
9 +
1
n
2
=
lim
Å
9 +
1
n
2
ã
=
…
lim 9 + lim
1
n
2
=
√
9 + 0 = 3.
□
Ví dụ 12 (Cánh Diều). Tính các giới hạn sau
lim
Å
5 +
1
6
n
ã
;a) lim
4
n
− 2 ·3
n
5 + 6 ·4
n
;b) lim
3 −
6
n
2
2
n
.c)
Lời giải.
a) Ta có lim
Å
5 +
1
6
n
ã
= lim 5 + lim
Å
1
6
n
ã
= 5 + 0 = 5.
b) Ta có lim
4
n
− 2 ·3
n
5 + 6 ·4
n
= lim
1 − 2 ·
Å
3
4
ã
n
5 ·
Å
1
4
ã
n
+ 6
=
1
6
.
c) Vì lim
Å
3 −
6
n
2
ã
= 3 và lim 2
n
= +∞ nên
3 −
6
n
2
2
n
= 0.
□
Ví dụ 13. Tìm giới hạn sau lim
3
n+1
− 4
n
4
n−1
+ 3
.
Lời giải.
lim
3
n+1
− 4
n
4
n−1
+ 3
= lim
9 · 3
n−1
− 4 ·4
n−1
4
n−1
+ 3
= lim
9 ·
Å
3
4
ã
n−1
− 4
1 + 3 ·
Å
1
4
ã
n−1
= −4.
□
Ví dụ 14. Tìm giới hạn sau lim
1 + 2 + 2
2
+ ··· + 2
n
1 + 3 + 3
2
+ ··· + 3
n
.
Lời giải.
lim
1 + 2 + 2
2
+ ··· + 2
n
1 + 3 + 3
2
+ ··· + 3
n
= lim
1 − 2
n+1
−1
1 − 3
n+1
−2
= lim
1 − 2
n+1
· 2
1 − 3
n+1
= lim
Ç
Å
1
3
ã
n+1
−
Å
2
3
ã
n+1
å
· 2
Å
1
3
ã
n+1
− 1
= 0.
□
2. Bài tập tự luyện
Bài 5. Tính các giới hạn sau:
lim
5n + 1
2n
;a) lim
6n
2
+ 8n + 1
5n
2
+ 3
;b) lim
√
n
2
+ 5n + 3
6n + 2
;c)
lim
Å
2 −
1
3
n
ã
;d) lim
3
n
+ 2
n
4 · 3
n
;e) lim
2 +
1
n
3
n
.f)
Lời giải.
a) Ta có lim
5n + 1
2n
= lim
5 +
1
n
2
=
5
2
.
340/764 340/764
Toán 11 theo chương trình GDPT2018
Chương 3. Giới hạn. Hàm số liên tục
Biết làm, làm đúng, làm nhanh
341
b) Ta có lim
6n
2
+ 8n + 1
5n
2
+ 3
= lim
6 +
8
n
+
1
n
2
5 +
3
n
2
=
6
5
.
c) Ta có lim
√
n
2
+ 5n + 3
6n + 2
= lim
…
1 +
5
n
+
3
n
2
6 +
2
n
=
1
6
.
d) Ta có lim
Å
2 −
1
3
n
ã
= lim 2 − lim
Å
1
3
n
ã
= 2 − 0 = 2.
e) Ta có lim
3
n
+ 2
n
4 · 3
n
= lim
1 +
Å
2
3
ã
n
4
=
1
4
.
f) Vì lim
Å
2 +
1
n
ã
= 2 và lim 3
n
= +∞ nên lim
2 +
1
n
3
n
= 0.
□
Bài 6. Tìm giới hạn sau lim
2n
3
− 2n + 3
1 − 4n
3
.
Lời giải.
lim
2n
3
− 2n + 3
1 − 4n
3
= lim
2 −
2
n
2
+
3
n
3
1
n
3
− 4
= −
1
2
.
□
Bài 7. Tìm giới hạn sau lim
√
n
4
+ 2n + 2
n
2
+ 1
.
Lời giải.
lim
√
n
4
+ 2n + 2
n
2
+ 1
= lim
…
1 +
2
n
3
+
2
n
4
1 +
1
n
2
= 1.
□
Bài 8. Tìm giới hạn sau lim
3
n+1
− 4
n
4
n−1
+ 3
.
Lời giải.
lim
3
n+1
− 4
n
4
n−1
+ 3
= lim
9 · 3
n−1
− 4 ·4
n−1
4
n−1
+ 3
= lim
9 ·
Å
3
4
ã
n−1
− 4
1 + 3 ·
Å
1
4
ã
n−1
= −4.
□
Bài 9. Tìm giới hạn sau lim
1 + 2 + 2
2
+ ··· + 2
n
1 + 3 + 3
2
+ ··· + 3
n
.
Lời giải.
lim
1 + 2 + 2
2
+ ··· + 2
n
1 + 3 + 3
2
+ ··· + 3
n
= lim
1 − 2
n+1
−1
1 − 3
n+1
−2
= lim
1 − 2
n+1
· 2
1 − 3
n+1
= lim
Ç
Å
1
3
ã
n+1
−
Å
2
3
ã
n+1
å
· 2
Å
1
3
ã
n+1
− 1
= 0.
□
Bài 10. Tìm các giới hạn sau
341/764 341/764
Toán 11 theo chương trình GDPT2018
1. Giới hạn của dãy số
Biết làm, làm đúng, làm nhanh
342
lim
n→+∞
n
2
+ n + 1
2n
2
+ 1
.a) lim
n→+∞
Ä
√
n
2
+ 2n −n
ä
.b)
Lời giải.
a) lim
n→+∞
n
2
+ n + 1
2n
2
+ 1
= lim
n→+∞
1 +
1
n
+
1
n
2
2 +
1
n
2
=
lim
n→+∞
Å
1 +
1
n
+
1
n
2
ã
lim
n→+∞
Å
2 +
1
n
2
ã
=
1
2
.
b) lim
n→+∞
Ä
√
n
2
+ 2n −n
ä
= lim
n→+∞
n
2
+ 2n −n
2
√
n
2
+ 2n + n
= lim
n→+∞
2
…
1 +
2
n
+ 1
=
2
lim
n→+∞
Ç
…
1 +
2
n
+ 1
å
= 1.
□
Bài 11. Tính các giới hạn sau:
lim
2
n
+ 3 ·4
n
4
n
− 5 ·3
n
.a) T = lim
3 · 7
n
+ 2 ·4
n
4 · 5
n
+ 7
n
.b)
Lời giải.
a) lim
2
n
+ 3 ·4
n
4
n
− 5 ·3
n
= lim
Å
1
2
ã
n
+ 3
1 − 5
Å
3
4
ã
n
= 3.
b) Ta có T = lim
3 · 7
n
+ 2 ·4
n
4 · 5
n
+ 7
n
= lim
3 + 2 ·
Å
4
7
ã
n
4 ·
Å
5
7
ã
n
+ 1
= 3.
□
Bài 12. Tìm các giới hạn sau
lim
−2n + 1
n
;a) lim
√
16n
2
− 2
n
;b) lim
4
2n + 1
;c) lim
n
2
− 2n + 3
2n
2
.d)
Lời giải.
a) Ta có lim
−2n + 1
n
= lim
−2 +
1
n
1
=
2 + 0
1
= −1.
b) lim
√
16n
2
− 2
n
= lim
…
16 −
2
n
2
1
= lim
…
16 −
2
n
2
=
√
16 − 0 = 4.
c) Ta có lim
4
2n + 1
= lim
4
n
2 +
1
n
=
0
2 + 0
= 0.
d) Ta có L = lim
n
2
− 2n + 3
2n
2
= lim
n
2
Å
1 −
2
n
+
3
n
2
ã
2n
2
= lim
1 −
2
n
+
3
n
2
2
=
1
2
.
□
Bài 13. Tính các giới hạn sau:
342/764 342/764
Toán 11 theo chương trình GDPT2018
Chương 3. Giới hạn. Hàm số liên tục
Biết làm, làm đúng, làm nhanh
343
lim
7n + 1
3n − 1
;a) lim
5n
2
+ 2n + 4
9n
2
+ 3n −3
;b) lim
√
2n
2
+ 3n + 3
7n + 2
;c)
lim
Å
12 −
1
5
n
ã
;d) lim
5
n
+ 3
n
4 · 5
n
;e) lim
2 +
1
n
4
n
.f)
Lời giải.
a) Ta có lim
5n + 1
2n
= lim
5 +
1
n
2
=
5
2
.
b) Ta có lim
6n
2
+ 8n + 1
5n
2
+ 3
= lim
6 +
8
n
+
1
n
2
5 +
3
n
2
=
6
5
.
c) Ta có lim
√
n
2
+ 5n + 3
6n + 2
= lim
…
1 +
5
n
+
3
n
2
6 +
2
n
=
1
6
.
d) Ta có lim
Å
2 −
1
3
n
ã
= lim 2 − lim
Å
1
3
n
ã
= 2 − 0 = 2.
e) Ta có lim
3
n
+ 2
n
4 · 3
n
= lim
1 +
Å
2
3
ã
n
4
=
1
4
.
f) Vì lim
Å
2 +
1
n
ã
= 2 và lim 3
n
= +∞ nên lim
2 +
1
n
3
n
= 0.
□
Bài 14. Tìm các giới hạn sau
lim
n→+∞
3n
2
+ 5n + 10
3n
2
+ 7
.a) lim
n→+∞
Ä
√
4n
2
+ 2n −2n
ä
.b)
Lời giải.
a) lim
n→+∞
n
2
+ n + 1
2n
2
+ 1
= lim
n→+∞
1 +
1
n
+
1
n
2
2 +
1
n
2
=
lim
n→+∞
Å
1 +
1
n
+
1
n
2
ã
lim
n→+∞
Å
2 +
1
n
2
ã
=
1
2
.
b) lim
n→+∞
Ä
√
n
2
+ 2n −n
ä
= lim
n→+∞
n
2
+ 2n −n
2
√
n
2
+ 2n + n
= lim
n→+∞
2
…
1 +
2
n
+ 1
=
2
lim
n→+∞
Ç
…
1 +
2
n
+ 1
å
= 1.
□
Bài 15. Tìm giới hạn của các dãy số cho bởi
u
n
=
n
2
+ 1
2n − 1
.a) v
n
=
√
2n
2
+ 1 −n.b)
Lời giải.
343/764 343/764
Toán 11 theo chương trình GDPT2018
1. Giới hạn của dãy số
Biết làm, làm đúng, làm nhanh
344
a) u
n
=
n
2
+ 1
2n − 1
= n ·
1 +
1
n
2
2 −
1
n
.
Hơn nữa lim
n→+∞
n = +∞ và lim
n→+∞
1 +
1
n
2
2 −
1
n
=
1 + lim
n→+∞
1
n
2
2 − lim
n→+∞
1
n
=
1
2
.
Do đó, lim
n→+∞
u
n
= +∞.
b) v
n
=
√
2n
2
+ 1 −n = n ·
Ç
…
2 +
1
n
2
− 1
å
.
Hơn nữa lim
n→+∞
n = +∞ và lim
n→+∞
Ç
…
2 +
1
n
2
− 1
å
=
√
2 − 1 > 0.
Do đó, lim
n→+∞
v
n
= +∞.
□
Bài 16. Tính giới hạn L = lim
4n
2
− n −1
3 + 2n
2
.
Lời giải.
Ta có L = lim
n
2
Å
4 −
1
n
−
1
n
2
ã
n
2
Å
3
n
2
+ 2
ã
= lim
4 −
1
n
−
1
n
2
3
n
2
+ 2
=
4 − 0 −0
0 + 2
= 2. □
Nhận xét. Nếu bậc tử P (n) bằng bậc mẫu Q(n) thì lim
P (n)
Q(n)
=
Hệ số bậc cao nhất của tử
Hệ số bậc cao nhất của mẫu
.
Bài 17. Tính giới hạn L = lim
2n
2
− n
5
· (4n −1)
4
20n
6
· (2n
2
− n + 1)
4
.
Lời giải.
L = lim
ï
n
2
Å
2 −
1
n
ãò
5
ï
n
Å
4 −
2
n
ãò
4
20n
6
ï
n
2
Å
2 −
3
n
+
1
n
2
ãò
4
= lim
n
10
Å
2 −
1
n
ã
5
n
4
Å
4 −
2
n
ã
4
20n
6
n
8
Å
2 −
3
n
+
1
n
2
ã
4
= lim
Å
2 −
1
n
ã
5
Å
4 −
2
n
ã
4
20
Å
2 −
3
n
+
1
n
2
ã
4
=
(2 − 0)
5
· (4 −0)
4
20 · (2 −0 + 0)
4
=
128
5
.
□
Nhận xét. Với bài toán có lũy thừa cao, ta thường rút bậc cao trong từng dấu ngoặc, sau đó áp dụng công
thức (a · b)
n
= a
n
· b
n
và tính toán tương tự như các bài trước.
Bài 18. Tính giới hạn L = lim
n
2
− n + 3
n
3
+ 2n
.
Lời giải.
344/764 344/764
Toán 11 theo chương trình GDPT2018
Chương 3. Giới hạn. Hàm số liên tục
Biết làm, làm đúng, làm nhanh
345
Ta có L = lim
n
2
Å
1 −
1
n
+
3
n
2
ã
n
3
Å
1 +
2
n
2
ã
= lim
Ö
1
n
·
1 −
1
n
+
3
n
2
1 +
2
n
2
è
= 0 ·
1 − 0 + 0
1 + 0
= 0. □
Nhận xét. Nếu bậc tử P (n) nhỏ hơn bậc mẫu Q(n) thì L = lim
P (n)
Q(n)
= 0.
Bài 19. Tính giới hạn L = lim
2n
3
− 11n + 1
n
2
− 2
.
Lời giải.
L = lim
n
3
Å
2 −
11
n
2
+
1
n
3
ã
n
2
Å
1 −
2
n
2
ã
= lim
Ö
n ·
2 −
11
n
2
+
1
n
3
1 −
2
n
2
è
= +∞ Vì lim n = +∞ và lim
2 −
11
n
2
+
1
n
3
1 −
2
n
2
= 2 > 0. □
Nhận xét. Nếu bậc tử P (n) lớn hơn bậc mẫu Q(n) thì L = lim
P (n)
Q(n)
= ±∞. Để biết là +∞ hay −∞ ta dựa
vào dấu của giới hạn hai nhân tử trong tích theo quy tắc “cùng dấu thì tích dương, trái dấu thì tích âm”. Thông
thường, sẽ để trống = ··· và xét dấu sẽ điền vào sau. Vế trắc nghiệm, đó chính là dấu của tích hệ số bậc cao nhất
của tử và mẫu.
Bài 20. Tính giới hạn L = lim
1 + 3 + 5 + 7 + 9 + ···+ (2n + 1)
3n
2
+ 4
.
Lời giải.
Xét cấp số cộng: 1, 3, 5, 7, 9, . . . , 2n + 1 có số hạng đầu tiên u
1
= 1, công sai d = 2 và số hạng cuối là u
m
= 2n + 1,
ta có
u
1
+ (m −1)d = 2n + 1 ⇔ 1 + 2(m − 1) = 2n + 1 ⇔ m = n + 1.
Vậy cấp số cộng có n + 1 số hạng. Suy ra tổng
S = 1 + 3 + 5 + ··· + 2n + 1 =
m
2
(u
1
+ u
m
) =
n + 1
2
(1 + 2n + 1) = n
2
+ 2n + 1.
Vì thế
L = lim
n
2
+ 2n + 1
3n
2
+ 4
= lim
n
2
Å
1 +
2
n
+
1
n
2
ã
n
2
Å
3 +
4
n
2
ã
= lim
1 +
2
n
+
1
n
2
3 +
4
n
2
=
1 + 0 + 0
3 + 0
=
1
3
.
□
Nhận xét. Cần nhớ công thức cấp số cộng:
u
k+1
− u
k
= d, với d là công sai.• u
n
= u
1
+ (n −1)d, với d là công sai.•
u
k+1
+ u
k−1
= 2u
k
, với k ≥ 2.• S
n
= u
1
+ u
2
+ ··· + u
n
=
n
2
(u
1
+ u
n
).•
Bài 21. Tính giới hạn L = lim
ï
1
1 · 2
+
1
2 · 3
+
1
3 · 4
+
1
4 · 5
+ ··· +
1
n(n + 1)
ò
.
Lời giải.
345/764 345/764
Toán 11 theo chương trình GDPT2018
1. Giới hạn của dãy số
Biết làm, làm đúng, làm nhanh
346
Số hạng tổng quát
1
k(k + 1)
=
1
k
−
1
k + 1
; (∀k = 1, 2, . . . , n). Do đó
L = lim
Å
1 −
1
2
+
1
2
−
1
3
+
1
3
−
1
4
+
1
4
−
1
5
+ ··· +
1
n
−
1
n + 1
ã
= lim
Å
1 −
1
n + 1
ã
= lim
n
n + 1
= lim
n
n
Å
1 +
1
n
ã
= lim
1
1 +
1
n
=
1
1 + 0
= 1.
□
Nhận xét. Phân tích
1
k(k + 1)
=
a
k
+
b
k + 1
với a =
1
k + 1
k=0
= 1 và b =
1
k
k=−1
= −1.
Bài 22. Tính giới hạn L = lim
3n
2
+ n −5
2n
2
+ 1
.
Lời giải.
Ta có
L = lim
n
2
Å
3 +
1
n
−
5
n
2
ã
n
2
Å
2 +
1
n
2
ã
= lim
3 +
1
n
−
5
n
2
2 +
1
n
2
=
3 + 0 −0
2 + 0
=
3
2
.
□
Bài 23. Tính giới hạn L = lim
n
3
− n + 3
2n
2
+ 3n
3
− 1
.
Lời giải.
Ta có
L = lim
n
3
Å
1 −
1
n
2
+
3
n
3
ã
n
3
Å
2
n
+ 3 −
1
n
3
ã
= lim
1 −
1
n
2
+
3
n
3
2
n
+ 3 −
1
n
3
=
1 − 0 + 0
0 + 3 −0
=
1
3
.
□
346/764 346/764
Toán 11 theo chương trình GDPT2018
Chương 3. Giới hạn. Hàm số liên tục
Biết làm, làm đúng, làm nhanh
347
Bài 24. Tính giới hạn L = lim
6n
3
− 2n + 1
5n
3
− n (n
2
+ n −1)
.
Lời giải.
Ta có
L = lim
6n
3
− 2n + 1
4n
3
− n
2
+ n
= lim
n
3
Å
6 −
2
n
2
+
1
n
3
ã
n
3
Å
4 −
1
n
+
1
n
2
ã
= lim
6 −
2
n
2
+
1
n
3
4 −
1
n
+
1
n
2
=
6 − 0 + 0
4 − 0 + 0
=
3
2
.
□
Bài 25. Tính giới hạn L = lim
2n
4
+ 1
2
(n + 2)
9
n
17
+ 1
.
Lời giải.
L = lim
ï
n
4
Å
2 +
1
n
4
ãò
2
ï
n
Å
1 +
2
n
ãò
9
n
17
Å
1 +
1
n
17
ã
= lim
n
8
Å
2 +
1
n
4
ã
2
n
9
Å
1 +
2
n
9
ã
9
n
17
Å
1 +
1
n
17
ã
= lim
Å
2 +
1
n
4
ã
2
Å
1 +
2
n
9
ã
9
Å
1 +
1
n
17
ã
=
(2 + 0)
2
· (1 + 0)
9
(1 + 0)
= 4.
□
Bài 26. Tính giới hạn L = lim
(2n − 1)
2
3 − 4n
3
(4n + 2)
3
(2 − n)
2
.
Lời giải.
L = lim
ï
n
Å
2 −
1
n
ãò
2
ï
n
3
Å
3
n
3
− 4
ãò
ï
n
Å
4 +
2
n
ãò
3
ï
n
Å
2
n
− 1
ãò
2
= lim
n
2
Å
2 −
1
n
ã
2
n
3
Å
3
n
3
− 4
ã
n
3
Å
4 +
2
n
ã
3
n
2
Å
2
n
− 1
ã
2
= lim
Å
2 −
1
n
ã
2
Å
3
n
3
− 4
ã
Å
4 +
2
n
ã
3
Å
2
n
− 1
ã
2
347/764 347/764
Toán 11 theo chương trình GDPT2018
1. Giới hạn của dãy số
Biết làm, làm đúng, làm nhanh
348
=
(2 − 0)
2
· (0 −4)
(4 + 0)
3
· (0 −1)
2
= −
1
4
.
□
Bài 27. Tính giới hạn L = lim
3n
2
− 1
3
(2n + 5)
2
(9n + 4)
(2n − 4)
4
(2n
3
+ 1) (2n
2
− 7)
.
Lời giải.
L = lim
ï
n
2
Å
3 −
1
n
2
ãò
3
ï
n
Å
2 +
5
n
ãò
2
ï
n
Å
9 +
4
n
ãò
ï
n
Å
2 −
4
n
ãò
4
ï
n
3
Å
2 +
1
n
3
ãòï
n
2
Å
2 −
7
n
2
ãò
= lim
n
6
Å
3 −
1
n
2
ã
3
n
2
Å
2 +
5
n
ã
2
n
Å
9 +
4
n
ã
n
4
Å
2 −
4
n
ã
4
n
3
Å
2 +
1
n
3
ã
n
2
Å
2 −
7
n
2
ã
= lim
Å
3 −
1
n
2
ã
3
Å
2 +
5
n
ã
2
Å
9 +
4
n
ã
Å
2 −
4
n
ã
4
Å
2 +
1
n
3
ãÅ
2 −
7
n
2
ã
=
(3 − 0)
3
· (2 + 0)
2
· (9 + 0)
(2 − 0)
4
· (2 + 0) · (2 − 0)
=
243
16
.
□
Bài 28. Tính giới hạn L = lim
n
2
+ 2
(n − 1)
3
(n + 1) (2n
2
+ 3)
2
.
Lời giải.
L = lim
ï
n
2
Å
1 +
2
n
2
ãòï
n
Å
1 −
1
n
ãò
3
ï
n
Å
1 +
1
n
ãòï
n
2
Å
2 +
3
n
2
ãò
2
= lim
n
2
Å
1 +
2
n
2
ã
n
3
Å
1 −
1
n
ã
3
n
Å
1 +
1
n
ã
n
4
Å
2 +
3
n
2
ã
2
= lim
Å
1 +
2
n
2
ãÅ
1 −
1
n
ã
3
Å
1 +
1
n
ãÅ
2 +
3
n
2
ã
2
=
(1 + 0) ·(1 − 0)
3
(1 + 0) ·(2 + 0)
2
=
1
4
.
□
Bài 29. Tính giới hạn I = lim
Ä
√
n
2
− 2n + 3 − n
ä
.
Lời giải.
348/764 348/764
Toán 11 theo chương trình GDPT2018
Chương 3. Giới hạn. Hàm số liên tục
Biết làm, làm đúng, làm nhanh
349
Ta có
I = lim
Ä
p
n
2
− 2n + 3 − n
ä
= lim
n
2
− 2n + 3 − n
2
√
n
2
− 2n + 3 + n
= lim
−2n + 3
√
n
2
− 2n + 3 + n
= lim
−2 +
3
n
»
1 −
2
n
+
3
n
2
+ 1
=
−2
√
1 + 1
= −1
□
Bài 30. Tính giới hạn I = lim
Ä
√
n
2
+ 7 −
√
n
2
+ 5
ä
.
Lời giải.
Ta có
I = lim
Ä
p
n
2
+ 7 −
p
n
2
+ 5
ä
= lim
n
2
+ 7 −(n
2
+ 5)
√
n
2
+ 7 +
√
n
2
+ 5
= lim
2
√
n
2
+ 7 +
√
n
2
+ 5
= 0
□
Bài 31. Tính giới hạn I = lim
Ä
√
n
2
+ 2n −
√
n
2
− 2n
ä
.
Lời giải.
Ta có
I = lim
Ä
p
n
2
+ 2n −
p
n
2
− 2n
ä
= lim
n
2
+ 2n −(n
2
− 2n)
√
n
2
+ 2n +
√
n
2
− 2n
= lim
4n
√
n
2
+ 2n +
√
n
2
− 2n
= lim
4
»
1 +
2
n
+
»
1 −
2
n
=
4
√
1 +
√
1
= 2
□
Bài 32. Tính giới hạn I = lim
Ä
√
2n
2
− n + 1 −
√
2n
2
− 3n + 2
ä
.
Lời giải.
Ta có
I = lim
Ä
p
2n
2
− n + 1 −
p
2n
2
− 3n + 2
ä
= lim
2n
2
− n + 1 − (2n
2
− 3n + 2)
√
2n
2
− n + 1 +
√
2n
2
− 3n + 2
= lim
2n − 1
√
2n
2
− n + 1 +
√
2n
2
− 3n + 2
= lim
2 −
1
n
»
2 −
1
n
+
1
n
2
+
»
2 −
3
n
+
2
n
2
=
2
√
2 +
√
2
=
1
√
2
349/764 349/764
Toán 11 theo chương trình GDPT2018
1. Giới hạn của dãy số
Biết làm, làm đúng, làm nhanh
350
□
Bài 33. Tính giới hạn L = lim
Ä
√
9n
2
+ 3n −4 − 3n + 20
ä
.
Lời giải.
Ta có:
L = lim 20 + lim
Ä
p
9n
2
+ 3n −4 − 3n
ä
= 20 + lim
3n − 4
√
9n
2
+ 3n −4 + 3n
= 20 + lim
n
Å
3 −
4
n
ã
n
…
9 +
3
n
−
4
n
2
+ 3n
= 20 + lim
3 −
4
n
…
9 +
3
n
−
4
n
2
+ 3
= 20 +
3 − 0
9 + 0 −0
+ 3
=
41
2
.
□
Bài 34. Tính giới hạn L = lim
7n
3
+ 2n
2
+ 1
n
4
+ 5n
3
+ n
.
Lời giải.
Ta có
L = lim
n
3
Å
7 +
2
n
+
1
n
3
ã
n
4
Å
1 +
5
n
+
1
n
3
ã
= lim
Ö
1
n
·
7 +
2
n
+
1
n
3
1 +
5
n
+
1
n
3
è
= 0.
Vì lim
1
n
= 0 và lim
7 +
2
n
+
1
n
3
1 +
5
n
+
1
n
3
= 7. □
Bài 35. Tính giới hạn L = lim
7n + 3
2n
2
+ 3n
3
+ 4
.
Lời giải.
Ta có
L = lim
n
Å
7 +
3
n
ã
n
3
Å
2
n
+ 3 +
4
n
3
ã
= lim
Ö
1
n
2
·
7 +
3
n
2
n
+ 3 +
4
n
3
è
= 0.
350/764 350/764
Toán 11 theo chương trình GDPT2018
Chương 3. Giới hạn. Hàm số liên tục
Biết làm, làm đúng, làm nhanh
351
Vì lim
1
n
2
= 0 và lim
7 +
3
n
2
n
+ 3 +
4
n
3
=
7
3
. □
Bài 36. Tính giới hạn L = lim
n
2
+ 4n −5
3n
3
+ n
2
+ 7
.
Lời giải.
Ta có
L = lim
n
2
Å
1 +
4
n
−
5
n
2
ã
n
3
Å
3 +
1
n
+
7
n
3
ã
= lim
Ö
1
n
·
1 +
4
n
−
5
n
2
3 +
1
n
+
7
n
3
è
= 0.
Vì lim
1
n
= 0 và lim
1 +
4
n
−
5
n
2
3 +
1
n
+
7
n
3
=
1
3
. □
Bài 37. Tính giới hạn L = lim
−2n
3
+ 3n
2
+ 4
n
4
+ 4n
3
+ n
.
Lời giải.
Ta có
L = lim
n
3
Å
−2 +
3
n
+
4
n
3
ã
n
4
Å
1 +
4
n
+
1
n
3
ã
= lim
Ö
1
n
·
−2 +
3
n
+
4
n
3
1 +
4
n
+
1
n
3
è
= 0.
Vì lim
1
n
= 0 và lim
−2 +
3
n
+
4
n
3
1 +
4
n
+
1
n
3
= −2. □
Bài 38. Tính giới hạn L = lim
−2n
2
+ n + 2
3n
4
+ 5
.
Lời giải.
Ta có
L = lim
n
2
Å
−2 +
1
n
+
2
n
2
ã
n
4
Å
3 +
5
n
4
ã
= lim
Ö
1
n
2
·
−2 +
1
n
+
2
n
2
3 +
5
n
4
è
= 0.
Vì lim
1
n
2
= 0 và lim
−2 +
1
n
+
2
n
2
3 +
5
n
4
= −
2
3
. □
351/764 351/764
Toán 11 theo chương trình GDPT2018
1. Giới hạn của dãy số
Biết làm, làm đúng, làm nhanh
352
3. Câu hỏi trắc nghiệm
Câu 16. Tính giới hạn I = lim
2n + 2023
3n + 2024
.
A I =
2
3
. B I =
3
2
. C I =
2023
2024
. D I = 1.
Lời giải.
Ta có I = lim
2n + 2023
3n + 2024
= lim
2 +
2017
n
3 +
2018
n
=
2
3
.
Chọn đáp án A □
Câu 17. Phát biểu nào sau đây là sai?
A lim u
n
= c (u
n
= c là hằng số). B lim q
n
= 0 (|q| > 1).
C lim
1
n
= 0. D lim
1
n
k
= 0 (k > 1).
Lời giải.
Theo định nghĩa giới hạn hữu hạn của dãy số thì lim q
n
= 0 (|q| < 1).
Chọn đáp án B □
Câu 18. Giá trị của lim
2 − n
n + 1
bằng
A 1. B 2. C −1. D 0.
Lời giải.
Ta có lim
2 − n
n + 1
= lim
2
n
− 1
1 +
1
n
=
0 − 1
1 + 0
= −1.
Chọn đáp án C □
Câu 19. Tính giới hạn lim
4n + 2024
2n + 1
.
A
1
2
. B 4. C 2. D 2024.
Lời giải.
Ta có lim
4n + 2024
2n + 1
= lim
4 +
2024
n
2 +
1
n
= 2.
Chọn đáp án C □
Câu 20. lim
2n
2
− 3
n
6
+ 5n
5
bằng
A 2. B 0. C
−3
5
. D −3.
Lời giải.
Ta có lim
2n
2
− 3
n
6
+ 5n
5
= lim
2
n
4
−
3
n
6
1 +
5
n
= 0.
Chọn đáp án B □
Câu 21. Tính lim
2n + 1
1 + n
được kết quả là
A 2. B 0. C
1
2
. D 1.
Lời giải.
Ta có lim
2n + 1
1 + n
= lim
n
Å
2 +
1
n
ã
n
Å
1
n
+ 1
ã
= lim
2 +
1
n
1
n
+ 1
=
2 + 0
0 + 1
= 2.
352/764 352/764
Toán 11 theo chương trình GDPT2018
Chương 3. Giới hạn. Hàm số liên tục
Biết làm, làm đúng, làm nhanh
353
Chọn đáp án A □
Câu 22. Dãy số nào sau đây có giới hạn khác 0?
A
1
n
. B
1
√
n
. C
n + 1
n
. D
sin n
√
n
.
Lời giải.
Có lim
n + 1
n
= lim 1 + lim
1
n
= 1.
Chọn đáp án C □
Câu 23. Giới hạn lim
√
n
2n
2
+ 3
có kết quả là
A 2. B 0. C +∞. D 4.
Lời giải.
lim
√
n
2n
2
+ 3
= lim
…
1
n
3
2 +
3
n
2
=
0
2 + 0
= 0.
Chọn đáp án B □
Câu 24. Dãy số (u
n
) với u
n
=
1
2n
, chọn M =
1
100
, để
1
2n
<
1
100
thì n phải lấy từ số hạng thứ bao nhiêu trở
đi?
A 51. B 49. C 48. D 50.
Lời giải.
Ta có
1
2n
<
1
100
⇔ 2n > 100 ⇔ n > 50.
Vậy n phải lấy từ số hạng thứ 51 trở đi.
Chọn đáp án A □
Câu 25. Giới hạn lim
3
n
+ 2
n
4
n
có kết quả là
A 0. B
5
4
. C
3
4
. D +∞.
Lời giải.
Ta có lim
3
n
+ 2
n
4
n
= lim
Å
3
4
ã
n
+
Å
2
4
ã
n
1
= 0.
Chọn đáp án A □
Câu 26. Tính giới hạn lim
ï
1
1 · 2
+
1
2 · 3
+
1
3 · 4
+ ··· +
1
n(n + 1)
ò
.
A 0. B 2. C 1. D
3
2
.
Lời giải.
Ta có
1
1 · 2
+
1
2 · 3
+
1
3 · 4
+ ··· +
1
n(n + 1)
=
1
1
−
1
2
+
1
2
−
1
3
+ ··· +
1
n − 1
−
1
n
+
1
n
−
1
n + 1
= 1 −
1
n + 1
.
Vậy lim
ï
1
1 · 2
+
1
2 · 3
+
1
3 · 4
+ ··· +
1
n(n + 1)
ò
= lim
Å
1 −
1
n + 1
ã
= 1.
Chọn đáp án C □
Câu 27. Tính giới hạn I = lim
Ä
√
n
2
+ 2n + 3 − n
ä
A 1. B 0. C 2. D 3.
Lời giải.
Ta có I = lim
Ä
√
n
2
+ 2n + 3 − n
ä
= lim
2n + 3
√
n
2
+ 2n + 3 + n
= lim
2 +
3
n
»
1 +
2
n
+
3
n
2
+ 1
= 1
Chọn đáp án A □
Câu 28. Tính giới hạn I = lim
Ä
√
n
2
+ 1 −
√
n
2
− 2
ä
353/764
353/764
Toán 11 theo chương trình GDPT2018
1. Giới hạn của dãy số
Biết làm, làm đúng, làm nhanh
354
A 3. B 0. C
√
3. D
3
2
.
Lời giải.
Ta có I = lim
Ä
√
n
2
+ 1 −
√
n
2
− 2
ä
= lim
3
√
n
2
+ 1 +
√
n
2
− 2
= 0
Chọn đáp án B □
Câu 29. Tính giới hạn I = lim
Ä
n −
√
n
2
+ 2n −3
ä
A 0. B - 2. C - 1. D 2.
Lời giải.
Ta có I = lim
Ä
n −
√
n
2
+ 2n −3
ä
= lim
−2n + 3
n +
√
n
2
+ 2n −3
= lim
−2 +
3
n
1 +
»
1 +
2
n
−
3
n
2
= −1
Chọn đáp án C □
Câu 30. Tính giới hạn I = lim
Ä
√
n
2
− n + 1 − n
ä
A
1
2
. B 1. C −
1
2
. D 0.
Lời giải.
Ta có I = lim
Ä
√
n
2
− n + 1 − n
ä
= lim
−n + 1
√
n
2
− n + 1 + n
= lim
−1 +
1
n
»
1 −
1
n
+
1
n
2
+ 1
= −
1
2
Chọn đáp án C □
Câu 31. Tính giới hạn I = lim
Ä
3
√
n
3
− n
2
− n
ä
A −
1
3
. B
1
3
. C 1. D 0.
Lời giải.
Ta có I = lim
Ä
3
√
n
3
− n
2
− n
ä
) = lim
−n
2
3
p
(n
3
− n
2
)
2
+ n
3
p
(n
3
− n
2
) + n
2
= lim
−1
3
»
1 −
1
n
2
+
3
»
1 −
1
n
+ 1
= −
1
3
Chọn đáp án A □
Câu 32. Tính giới hạn I = lim
Ä
√
2n
2
+ 2n −1 −
√
2n
2
+ n
ä
A 0. B
1
4
. C
1
2
. D
1
2
√
2
.
Lời giải.
Ta có I = lim
Ä
√
2n
2
+ 2n −1 −
√
2n
2
+ n
ä
= lim
n
√
2n
2
+ 2n −1 +
√
2n
2
+ n
= lim
1
»
2 +
2
n
−
1
n
2
+
»
2 +
2
n
=
1
2
√
2
Chọn đáp án D □
Câu 33. Tính giới hạn I = lim n
Ä
√
n
2
+ n + 1 −
√
n
2
+ n −8
ä
A 0. B ∞. C 2. D
9
2
.
Lời giải.
Ta có I = lim n
Ä
√
n
2
+ n + 1 −
√
n
2
+ n −8
ä
= lim
9n
√
n
2
+ n + 1 +
√
n
2
+ n −8
= lim
9
»
1 +
1
n
+
1
n
2
+
»
1 +
1
n
−
8
n
2
=
9
2
Chọn đáp án D □
Câu 34. Giới hạn lim
(2n − 1)(3 −n)
2
(4n − 5)
3
có kết quả bằng
A 0. B
1
32
. C
3
2
. D
1
2
.
Lời giải.
354/764 354/764
Toán 11 theo chương trình GDPT2018
Chương 3. Giới hạn. Hàm số liên tục
Biết làm, làm đúng, làm nhanh
355
lim
(2n − 1)(3 −n)
2
(4n − 5)
3
= lim
Å
2 −
1
n
ãÅ
3
n
− 1
ã
2
Å
4 −
5
n
ã
3
=
2
4
3
=
1
32
.
Chọn đáp án B □
—————————————————————————-
Dạng 3. Phương pháp lượng liên hợp (lim hữu hạn)
Sử dụng các hằng đẳng thức
○
√
a − b =
(
√
a − b) (
√
a + b)
(
√
a + b)
=
a − b
2
(
√
a + b)
.
○
√
a −
√
b =
Ä
√
a −
√
b
äÄ
√
a +
√
b
ä
Ä
√
a +
√
b
ä
=
a − b
Ä
√
a +
√
b
ä
.
1. Ví dụ mẫu
Ví dụ 15 (KNTT). Tìm giới hạn sau lim
n→+∞
Ä
√
n
2
+ 2n −n
ä
.
Lời giải.
lim
n→+∞
Ä
√
n
2
+ 2n −n
ä
= lim
n→+∞
n
2
+ 2n −n
2
√
n
2
+ 2n + n
= lim
n→+∞
2
…
1 +
2
n
+ 1
=
2
lim
n→+∞
Ç
…
1 +
2
n
+ 1
å
= 1. □
Ví dụ 16. Tìm giới hạn sau lim
Ä
√
3n
2
− 2n −
√
3n
2
+ 6n −1
ä
.
Lời giải.
lim
Ä
p
3n
2
− 2n −
p
3n
2
+ 6n −1
ä
= lim
3n
2
− 2n −3n
2
− 6n + 1
√
3n
2
− 2n +
√
3n
2
+ 6n −1
= lim
−8n + 1
√
3n
2
− 2n +
√
3n
2
+ 6n −1
= lim
−8 +
1
n
…
3 −
2
n
+
…
3 +
6
n
−
1
n
2
= −
4
√
3
.
□
Ví dụ 17. Tìm giới hạn sau lim n
Ä
√
n
2
+ 1 −
√
n
2
− 3
ä
.
Lời giải.
lim n
Ä
p
n
2
+ 1 −
p
n
2
− 3
ä
= lim
n
n
2
+ 1 −n
2
+ 3
√
n
2
+ 1 +
√
n
2
− 3
= lim
4n
√
n
2
+ 1 +
√
n
2
− 3
= lim
4
…
1 +
1
n
2
+
…
1 −
3
n
2
=
4
2
= 2.
□
355/764 355/764
Toán 11 theo chương trình GDPT2018
1. Giới hạn của dãy số
Biết làm, làm đúng, làm nhanh
356
Ví dụ 18. Tính giới hạn sau lim
1
√
9n
2
− n −3n
.
Lời giải.
lim
1
√
9n
2
− n −3n
= lim
√
9n
2
− n + 3n
9n
2
− n −(3n)
2
= lim
√
9n
2
− n + 3n
−n
= lim
…
9 −
1
n
+ 3
−1
= −6.
□
Ví dụ 19. Tính giới hạn sau lim
Ä
√
n
2
+ 3n + 2 − n + 2
ä
.
Lời giải.
lim
Ä
p
n
2
+ 3n + 2 − n + 2
ä
= lim
n
2
+ 3n + 2 − (n − 2)
2
√
n
2
+ 3n + 2 + (n − 2)
= lim
n
2
+ 3n + 2 − (n
2
− 4n + 1)
√
n
2
+ 3n + 2 + n − 2
= lim
7n + 1
√
n
2
+ 3n + 2 + n − 2
= lim
7 +
1
n
…
1 +
3
n
+
2
n
2
+ 1 −
2
n
=
7
2
.
□
2. Bài tập rèn luyện
Bài 39. Tìm giới hạn sau lim
Ä
√
n
2
− 3n −n
ä
.
Lời giải.
lim
Ä
p
n
2
− 3n −n
ä
= lim
n
2
− 3n −n
2
√
n
2
− 3n + n
= lim
−3
…
1 −
3
n
+ 1
= −
3
2
.
□
Bài 40. Tính giới hạn sau lim
Ä
√
5n
2
+ 3 −
√
5n
2
− 6n
ä
.
Lời giải.
lim
Ä
p
5n
2
+ 3 −
p
5n
2
− 6n
ä
= lim
5n
2
+ 3 −5n
2
+ 6n
√
5n
2
+ 3 +
√
5n
2
− 6n
= lim
3
n
+ 6
…
5 +
3
n
2
+
…
5 −
6
n
=
3
√
5
5
.
□
356/764 356/764
Toán 11 theo chương trình GDPT2018
Chương 3. Giới hạn. Hàm số liên tục
Biết làm, làm đúng, làm nhanh
357
Bài 41. Tính giới hạn sau lim n
Ä
n −
√
n
2
+ 2
ä
.
Lời giải.
lim n
Ä
n −
p
n
2
+ 2
ä
= lim
n
n
2
− n
2
− 2
n +
√
n
2
+ 2
= lim
−2n
n +
√
n
2
+ 2
= lim
−2
1 +
…
1 +
2
n
2
= −1.
□
Bài 42. Tính giới hạn sau lim
2
Ä
2n + 1 −
√
4n
2
− 3n
ä
.
Lời giải.
lim
2
Ä
2n + 1 −
√
4n
2
− 3n
ä
= lim
2
Ä
2n + 1 +
√
4n
2
− 3n
ä
(2n + 1)
2
− (4n
2
− 3n)
= lim
2
Ä
2n + 1 +
√
4n
2
− 3n
ä
4n
2
+ 4n + 1 − 4n
2
+ 3n
= lim
2
Ç
2 +
1
n
+
…
4 −
3
n
å
7 +
1
n
=
8
7
.
□
Bài 43. Tính giới hạn sau lim
√
n
2
+ 1 −
√
n + 1
3n + 2
.
Lời giải.
lim
√
n
2
+ 1 −
√
n + 1
3n + 2
= lim
n
2
− n
(3n + 2)
Ä
√
n
2
+ 1 +
√
n + 1
ä
= lim
1 −
1
n
Å
3 +
2
n
ã
Ç
…
1 +
1
n
2
+
…
1
n
+
1
n
2
å
=
1
3
.
□
3. Bài tập trắc nghiệm
Câu 35. Tìm giới hạn sau lim
Ä
√
n
2
+ 1 −n
ä
A 0. B +∞. C 1. D
1
2
.
Lời giải.
lim
Ä
p
n
2
+ 1 −n
ä
= lim
n
2
+ 1 −n
2
√
n
2
+ 1 + n
= lim
1
n
…
1 +
1
n
+ 1
= 0.
Chọn đáp án
A
□
357/764 357/764
Toán 11 theo chương trình GDPT2018
1. Giới hạn của dãy số
Biết làm, làm đúng, làm nhanh
358
Câu 36. Tìm giới hạn sau lim
Ä
√
4n
2
− 3 −2n
ä
A −∞. B −3. C 0. D −
3
4
.
Lời giải.
lim
Ä
p
4n
2
− 3 −2n
ä
= lim
4n
2
− 3 −(2n)
2
√
4n
2
− 3 + 2n
= lim
−
3
n
…
4 −
3
n
+ 2
= 0.
Chọn đáp án C □
Câu 37. Tính các giới hạn sau lim
√
n + 3 −
√
n
.
A +∞. B −∞. C 0. D
3
2
.
Lời giải.
lim
Ä
√
n + 3 −
√
n
ä
= lim
n + 3 −n
√
n + 3 −
√
n
= lim
3
√
n
…
1 +
3
n
+ 1
= 0.
Chọn đáp án C □
Câu 38. Tìm giới hạn sau lim
Ä
√
4n
2
+ 3n −2n
ä
.
A
3
4
. B +∞. C
1
2
. D 0.
Lời giải.
lim
Ä
p
4n
2
+ 3n −2n
ä
= lim
4n
2
+ 3n −(2n)
2
√
4n
2
+ 3n + 2n
= lim
3
n
…
4 +
3
n
+ 2
= 0.
Chọn đáp án D □
Câu 39. Tìm giới hạn sau lim
−3
√
16n
2
− 5n −4n
.
A −
24
5
. B +∞. C
24
5
. D −∞.
Lời giải.
lim
−3
√
16n
2
− 5n −4n
= lim
−3
Ä
√
16n
2
− 5n + 4n
ä
16n
2
− 5n −(4n)
2
= lim
−3
Ç
…
16 −
5
n
+ 4
å
−5
=
24
5
.
Chọn đáp án C □
Câu 40. Tìm giới hạn sau lim
Ä
√
9n
2
− n −3n
ä
.
A 0. B
1
6
. C −∞. D −
1
6
.
358/764 358/764
Toán 11 theo chương trình GDPT2018
Chương 3. Giới hạn. Hàm số liên tục
Biết làm, làm đúng, làm nhanh
359
Lời giải.
lim
Ä
p
9n
2
− n −3n
ä
= lim
9n
2
− n −(3n)
2
√
9n
2
− n + 3n
= lim
−1
…
9 −
1
n
+ 3
= −
1
6
.
Chọn đáp án D □
Câu 41. Tìm giới hạn sau lim
Ä
n −
√
n
2
+ 2n
ä
.
A 1. B −∞. C −1. D 0.
Lời giải.
lim
Ä
n −
p
n
2
+ 2n
ä
= lim
n
2
−
n
2
+ 2n
n +
√
n
2
+ 2n
= lim
−2
1 +
…
1 +
2
n
= −1.
Chọn đáp án C □
Câu 42. Tính giới hạn I = lim
Ä
√
n
2
− 2n + 3 − n
ä
.
A I = 1. B I = −1. C I = 0. D I = +∞.
Lời giải.
I = lim
Ä
p
n
2
− 2n + 3 − n
ä
= lim
n
2
− 2n + 3
− n
2
√
n
2
− 2n + 3 + n
= lim
−2 +
3
n
…
1 −
2
n
+
3
n
2
+ 1
= −1.
Chọn đáp án B □
Câu 43. Tìm giới hạn sau lim
Ä
n + 2 −
√
n
2
− 4n
ä
.
A 0. B 4. C +∞. D −∞.
Lời giải.
lim
Ä
n + 2 −
p
n
2
− 4n
ä
= lim
(n + 2)
2
−
n
2
− 4n
(n + 2) +
√
n
2
− 4n
= lim
n
2
+ 4n + 4 − n
2
+ 4n
n + 2 +
√
n
2
− 4n
= lim
8 +
4
n
1 +
2
n
+
…
1 −
4
n
= 4.
Chọn đáp án B □
Câu 44. Tính giới hạn lim
Ä
√
9n
2
+ 2n −3n + 8
ä
ta được kết quả
A
25
3
. B −∞. C
1
3
. D +∞.
Lời giải.
lim
Ä
p
9n
2
+ 2n −3n + 8
ä
= lim
9n
2
+ 2n −(3n − 8)
2
√
9n
2
+ 2n + (3n − 8)
359/764 359/764
Toán 11 theo chương trình GDPT2018
1. Giới hạn của dãy số
Biết làm, làm đúng, làm nhanh
360
= lim
9n
2
+ 2n −9n
2
+ 48n −64
√
9n
2
+ 2n + (3n − 8)
= lim
50 −
64
n
…
9 +
2
n
+ 3 −
8
n
=
50
6
=
25
3
.
Chọn đáp án A □
Câu 45. Tìm giới hạn sau lim
2
2n − 3 −
√
4n
2
+ 3n
.
A 0. B +∞. C −
8
15
. D −
8
9
.
Lời giải.
lim
2
2n − 3 −
√
4n
2
+ 3n
= lim
2
Ä
2n − 3 +
√
4n
2
+ 3n
ä
(2n − 3)
2
− (4n
2
+ 3n)
= lim
2
Ä
2n − 3 +
√
4n
2
+ 3n
ä
4n
2
− 12n + 9 − 4n
2
− 3n
= lim
2
Ç
2 −
3
n
+
…
4 +
3
n
å
−15
= −
8
15
.
Chọn đáp án C □
Câu 46. Biết lim
Ç
…
n
2
−
1
11
n + 3 −n
å
= a, với a ∈ Q. Tính P = a
2
+ 1.
A
485
484
. B
483
484
. C
1
121
. D
1
484
.
Lời giải.
lim
Ç
…
n
2
−
1
11
n + 3 −n
å
= lim
−
1
11
n + 3
…
n
2
−
1
11
n + 3 + n
= lim
−
1
11
+
3
n
…
1 −
1
11n
+
3
n
2
+ 1
= −
1
22
.
Vậy P = a
2
+ 1 =
Å
−
1
22
ã
2
+ 1 =
485
484
.
Chọn đáp án A □
Câu 47. Biết giới hạn lim
î
n
Ä
√
9n
2
+ 3 −
√
9n
2
+ 2
äó
=
a
b
với a, b ∈ N và
a
b
là phân số tối giản. Khi đó, giá trị
a
2
+ b bằng
A 31. B 7. C 84. D 37.
Lời giải.
Ta có lim
î
n
Ä
√
9n
2
+ 3 −
√
9n
2
+ 2
äó
= lim
n
√
9n
2
+ 3 +
√
9n
2
+ 2
= lim
1
…
9 +
3
n
2
+
…
9 +
2
n
2
=
1
6
.
Suy ra a = 1, b = 6. Do đó a
2
+ b = 1
2
+ 6 = 7.
Chọn đáp án B □
Câu 48. Biết lim
Ä
2n −
√
4n
2
+ an + 3
ä
= 1, giá trị của a thuộc khoảng nào sau đây?
A (−5; 0). B (1; 5). C (0; 1). D (−1; 3).
Lời giải.
lim
Ä
2n −
p
4n
2
+ an + 3
ä
= lim
−an − 3
2n +
√
4n
2
+ an + 3
= lim
−a −
3
n
2 +
…
4 +
a
n
+
3
n
2
=
−a
4
360/764 360/764
Toán 11 theo chương trình GDPT2018
Chương 3. Giới hạn. Hàm số liên tục
Biết làm, làm đúng, làm nhanh
361
Suy ra −
a
4
= 1 ⇒ a = −4. Vậy a ∈ (−5; 0).
Chọn đáp án A □
Câu 49. Biết L = lim
Ä
√
4n
2
+ 3n −
√
an
2
+ bn
ä
= 1. Tính S = a + b.
A S = 3. B S = −4. C S = 7. D S = −7.
Lời giải.
L = lim
Ä
p
4n
2
+ 3n −
p
an
2
+ bn
ä
= lim
(4 − a)n
2
+ (3 −b)n
n
Ç
…
4 +
3
n
+
…
a +
b
n
å
= lim
(4 − a)n + 3 − b
…
4 +
3
n
+
…
a +
b
n
.
Mà L = 1 ⇒
4 − a = 0
3 − b
2 +
√
a
= 1
⇔
®
a = 4
b = −1
⇒ S = 3.
Chọn đáp án A □
Dạng 4. Giới hạn vô cực
Ta nói dãy {u
n
} có giới hạn là +∞ khi n → +∞, nếu u
n
có thể lớn hơn một số dương bất kì, kể từ một số
hạng nào đó trở đi.
Kí hiệu: lim u
n
= +∞ hay u
n
→ +∞ khi n → +∞.
Dãy số {u
n
} có giới hạn là −∞ khi n → +∞, nếu lim −u
n
= +∞.
Kí hiệu: lim u
n
= −∞ hay u
n
→ −∞ khi n → +∞.
Một số giới hạn đặc biệt và định lí về giới hạn dãy số
Giới hạn đặc biệt:
lim
n→+∞
√
n = +∞
lim
n→+∞
n
k
= +∞ với k là số nguyên dương.
lim
n→+∞
q
n
= +∞ nếu q > 1
Định lý :
Nếu lim u
n
= a > 0 và lim v
n
= 0 với v
n
> 0 thì lim
u
n
v
n
= +∞
Nếu lim u
n
= +∞ và lim v
n
= a > 0 thì lim u
n
v
n
= +∞
1. Ví dụ mẫu
Ví dụ 20. Chứng minh rằng lim n
2
= +∞.
Lời giải.
Xét dãy số (u
n
) = n
2
. Với M là số dương bất kì, ta thấy: u
n
> M ⇔ n
2
> M ⇔ n >
√
M.
Vậy với các số tự nhiên n >
√
M thì u
n
> M. Do đó, lim n
2
= +∞. □
Ví dụ 21. Tinh lim
n→+∞
n
2
− 2n
.
Lời giải.
Ta có n
2
− 2n = n
2
Å
1 −
2
n
ã
. Hơn nữa lim
n→+∞
n
2
= +∞ và lim
n→+∞
Å
1 −
2
n
ã
= 1.
Do đó, lim
n→+∞
n
2
− 2n
= +∞. □
Ví dụ 22 (CTST). Tìm giới hạn lim q
n
với q > 1.
Lời giải.
Từ q > 1 suy ra 0 <
1
q
< 1. Do đó, lim
1
q
n
= lim
Å
1
q
ã
n
= 0.
Mà q
n
> 0 với mọi n nên lim q
n
= +∞. □
361/764 361/764
Toán 11 theo chương trình GDPT2018
1. Giới hạn của dãy số
Biết làm, làm đúng, làm nhanh
362
Ví dụ 23 (Cùng khám phá). Tìm lim(−n
4
).
Lời giải.
Vì lim(n
4
) = +∞ nên lim(−n
4
) = −∞. □
2. Bài tập tự luyện
Bài 44. Tìm giới hạn
lim(n
3
+ n
2
+ n + 1).a) lim
n
2
− n
√
n + 1
.b)
Lời giải.
a) lim(n
3
+ n
2
+ n + 1) = lim n
3
Å
1 +
1
n
+
1
n
2
+
1
n
3
ã
= +∞.
b) lim
n
2
− n
√
n + 1
= lim n
2
Å
1 −
1
√
n
+
1
n
2
ã
= +∞.
□
Bài 45. Tìm giới hạn
lim
n
5
+ n
4
− n −2
4n
3
+ 6n
2
+ 9
.a) lim
3
√
n
6
− 7n
3
− 5n + 8
n + 12
.b) lim
Ä
n +
√
n
2
− n + 1
ä
.c)
Lời giải.
a) lim
n
5
+ n
4
− n −2
4n
3
+ 6n
2
+ 9
= lim
n
2
+ n −
1
n
2
−
2
n
3
4 +
6
n
+
9
n
3
= lim
n
2
+ n
4
= +∞.
b) lim
3
√
n
6
− 7n
3
− 5n + 8
n + 12
= lim
n
2
3
»
1 −
7
n
3
−
5
n
5
+
8
n
6
n + 12
= lim
n
3
»
1 −
7
n
3
−
5
n
5
+
8
n
6
1 +
12
n
= +∞.
c) lim
Ä
n +
√
n
2
− n + 1
ä
= n
Ä
1 +
»
1 −
1
n
+
1
n
2
ä
= lim 2n = +∞
□
Bài 46. Tìm giới hạn
lim
√
5n
2
− 8n + 7.a) lim
√
n
3
− 5n + 6.b)
Lời giải.
a) lim
√
5n
2
− 8n + 7 = lim n
…
5 −
8
n
+
7
n
2
= +∞.
b) lim
√
n
3
− 5n + 6 = lim n
√
n
…
1 −
5
n
2
+
6
n
3
= +∞.
□
Bài 47. Tìm giới hạn
lim
√
5n
4
− 8n
2
+ 10
4n + 5
.a) lim
n
2
− 15n + 11
√
n
2
− 8n + 7
.b)
Lời giải.
a) lim
√
5n
4
− 8n
2
+ 10
4n + 5
= lim
n
2
»
5 −
8
n
2
+
10
n
4
4n + 5
=
n
»
5 −
8
n
2
+
10
n
4
4 +
5
n
= lim
n
√
5
4
= +∞.
b) lim
n
2
− 15n + 11
√
n
2
− 8n + 7
= lim
n − 15 +
11
n
»
1 −
8
n
+
7
n
2
= +∞.
□
362/764 362/764
Toán 11 theo chương trình GDPT2018
Chương 3. Giới hạn. Hàm số liên tục
Biết làm, làm đúng, làm nhanh
363
3. Bài tập trắc nghiệm
Câu 50. Tính giới hạn L = lim
n
3
− 2n
3n
2
+ n −2
.
A L = +∞. B L = 0. C L =
1
3
. D L = −∞.
Lời giải.
Ta có L = lim
n
3
− 2n
3n
2
+ n −2
= lim
n
3
Å
1 −
2
n
2
ã
n
2
Å
3 +
1
n
−
2
n
2
ã
= lim
n ·
Ö
1 −
2
n
2
3 +
1
n
−
2
n
2
è
= +∞
vì
lim n = +∞
lim
1 −
2
n
2
3 +
1
n
−
2
n
2
=
1 − 2 ·0
3 + 0 −2 · 0
=
1
3
> 0.
Chọn đáp án A □
Câu 51. Kết quả của lim
Å
4
3
ã
n
bằng
A 0. B 3. C 4. D +∞.
Lời giải.
Ta có lim
Å
4
3
ã
n
= +∞.
Chọn đáp án D □
Câu 52. lim(2n + 3) bằng
A +∞. B 3. C 5. D −∞.
Lời giải.
lim(2n + 3) = lim
ï
n
Å
2 +
3
n
ãò
= +∞.
Chọn đáp án A □
Câu 53. Trong bốn giới hạn sau đây, giới hạn nào bằng dương vô cực?
A lim
n
3
+ 2n −1
n − 2n
3
. B lim
n
2
+ 3n
3
+ 2
n
2
+ n
. C lim
2n
2
− 3n
n
3
+ 3n
. D lim
n
2
− n + 1
1 − 2n
.
Lời giải.
Ta có
○ lim
n
3
+ 2n −1
n − 2n
3
= lim
1 +
2
n
−
1
n
3
1
n
2
− 2
= −
1
2
.
○ lim
n
2
+ 3n
3
+ 2
n
2
+ n
= lim n ·
1
n
+ 3 +
2
n
3
1
n
+ 1
= +∞ (do
lim n = +∞
lim
1
n
+ 3 +
2
n
3
1
n
+ 1
= 3 > 0.
○ lim
2n
2
− 3n
n
3
+ 3n
= lim
2
n
−
3
n
2
1 +
3
n
2
= 0.
○ lim
n
2
− n + 1
1 − 2n
= lim n ·
1 −
1
n
+
1
n
2
1
n
− 2
= −∞ (do
lim n = +∞
lim
1 −
1
n
+
1
n
2
1
n
− 2
= −
1
2
< 0.
363/764 363/764
Toán 11 theo chương trình GDPT2018
1. Giới hạn của dãy số
Biết làm, làm đúng, làm nhanh
364
Chọn đáp án B □
Câu 54. Trong các giới hạn sau, giới hạn nào bằng −∞?
A lim
1 + 2
n+1
1 − 3
n
. B lim
Å
1
n
−
√
n
n + 1
ã
.
C lim n
√
n + 1 −
√
2n + 1
. D lim
1 − 3n
2
2n
3
+ 1
.
Lời giải.
Xét L = lim n
√
n + 1 −
√
2n + 1
= lim n
√
n
Ç
…
1 +
1
n
−
…
2 +
1
n
å
có
○ lim n
√
n = +∞.
○ lim
Ç
…
1 +
1
n
−
…
2 +
1
n
å
= 1 −
√
2 < 0.
Suy ra L = −∞.
Chọn đáp án C □
Câu 55. Tính lim(3 + 2n + n
3
).
A −∞. B +∞. C 1. D −1.
Lời giải.
Ta có lim(3 + 2n + n
3
) = lim
ï
n
3
Å
3
n
3
+
2
n
2
+ 1
ãò
= +∞ vì
lim n
3
= +∞
lim
Å
3
n
3
+
2
n
2
+ 1
ã
= 1 > 0.
Chọn đáp án B □
Câu 56. Tính lim
2n
3
− 11n + 1
−n
2
− 2
.
A 0. B −2. C +∞. D −∞.
Lời giải.
Ta có lim
n
3
Å
2 −
11
n
2
+
1
n
3
ã
n
2
Å
−1 −
2
n
2
ã
= lim n ·
2 −
11
n
2
+
1
n
3
−1 −
2
2n
2
= −∞.
Vì
lim n = +∞
lim
2 −
11
n
2
+
1
n
3
−1 −
2
n
2
= −2
Chọn đáp án D □
Câu 57. Tìm mệnh đề đúng trong các mệnh đề dưới đây.
A lim
−3n
4
+ 3
= −∞. B lim
−3n
4
+ 3
= 0.
C lim
−n
4
+ 2
= +∞. D lim
5n
4
− 2
= −∞.
Lời giải.
Ta có lim
−3n
4
+ 3
= −∞ là mệnh đề đúng.
lim
−3n
4
+ 3
= −∞.
lim
−n
4
+ 2
= −∞.
lim
5n
4
− 2
= +∞
Chọn đáp án A □
Câu 58. lim (3
n
− 4
n
) có giá trị bằng
A 1. B +∞. C −∞. D
4
3
.
Lời giải.
Ta có lim (3
n
− 4
n
) = lim 4
n
·
ïÅ
3
4
ã
n
− 1
ò
= −∞.
364/764 364/764
Toán 11 theo chương trình GDPT2018
Chương 3. Giới hạn. Hàm số liên tục
Biết làm, làm đúng, làm nhanh
365
Chọn đáp án C □
Câu 59. lim(2 − 3n)
4
(n + 1)
3
có giá trị bằng
A −∞. B +∞. C 2. D 81.
Lời giải.
Ta có lim(2 −3n)
4
(n + 1)
3
= lim n
7
Å
2
n
− 3
ã
4
Å
1 +
1
n
ã
3
= 81 lim n
7
= +∞.
Chọn đáp án B □
Câu 60. Tìm giới hạn lim
Ä
√
n
2
+ 1 −2n
ä
.
A +∞. B 0. C −
2
3
. D −∞.
Lời giải.
○ Cách 1. lim
Ä
√
n
2
+ 1 −2n
ä
= lim n
Ç
…
1 +
1
n
2
− 2
å
= −∞
(vì lim n = +∞ và lim
Ç
…
1 +
1
n
2
− 2
å
= −1 < 0).
○ Cách 2. lim
Ä
√
n
2
+ 1 −2n
ä
= lim
n
2
+ 1 −4n
2
√
n
2
+ 1 + 2n
= lim
−3n +
1
n
…
1 +
1
n
2
+ 2
= −∞.
Chọn đáp án D □
Dạng 5. Tính tổng của dãy cấp số nhân lùi vô hạn
c Định nghĩa 1.5. Cấp số nhân vô hạn u
1
, u
1
q, ..., u
1
q
n−1
, ... có công bội q thỏa mãn |q| < 1 được gọi là
cấp số nhân lùi vô hạn. Tổng của cấp số nhân lùi vô hạn đã cho là
S = u
1
+ u
1
q + u
1
q
2
+ ... =
u
1
1 − q
.
1. Ví dụ mẫu
Ví dụ 24 (Cánh diều). Cho cấp số nhân (u
n
), với u
1
= 1 và công bội q =
1
2
.
a) So sánh |q| với 1.
b) Tính S
n
= u
1
+ u
2
+ ··· + u
n
từ đó hãy tính lim S
n
.
Lời giải.
a) Ta có |q| =
1
2
=
1
2
< 1.
b) Ta có S
n
=
u
1
(1 − q
n
)
1 − q
=
1 ·
ï
1 −
Å
1
2
ã
n
ò
1 −
1
2
= 2 ·
Å
1 −
1
2
n
ã
= 2 −
1
2
n−1
.
Khi đó lim S
n
= lim
Å
2 −
1
2
n−1
ã
= 2.
□
Ví dụ 25 (Cánh diều). Tính tổng T = 1 +
1
3
+
1
3
2
+ . . . +
1
3
n
+ . . .
Lời giải.
365/764 365/764
Toán 11 theo chương trình GDPT2018
1. Giới hạn của dãy số
Biết làm, làm đúng, làm nhanh
366
Các số hạn của tổng lập thành câp số nhân (u
n
), có u
1
= 1, q =
1
3
nên
T = 1 +
1
3
+
1
3
2
+ . . . +
1
3
n
+ . . . =
1
1 −
1
3
=
2
3
·
□
Ví dụ 26 (Cánh diều). Biểu diễn số thập phân vô hạn tuần hoàn 0, (3) dưới dạng phân số.
Lời giải.
Ta có 0,(3) =
3
10
+
3
10
2
+ . . . +
3
10
n
+ . . . =
3
10
1 −
1
10
=
1
3
· □
Ví dụ 27 (CTST). Tính tổng của cấp số nhân lùi vô hạn: 1 −
1
4
+
1
16
−
1
64
+ ··· +
Å
−
1
4
ã
n
+ ···.
Lời giải.
Tổng trên là tổng của cấp số nhân lùi vô hạn có số hạng đầu u
1
= 1 và công bội q = −
1
4
nên
1 −
1
4
+
1
16
−
1
64
+ ··· +
Å
−
1
4
ã
n
+ ··· =
1
1 −
Å
−
1
4
ã
=
4
5
.
□
Ví dụ 28 (CTST). Biết rằng có thể coi số thập phân vô hạn tuần hoàn 0,666 . . . là tổng của một cấp số nhân lùi
vô hạn:
0,666 . . . = 0,6 + 0,06 + 0,006 + ··· = 0,6 + 0,6 ·
1
10
+ 0,6 ·
1
10
2
+ ··· .
Hãy viết 0,666 . . . dưới dạng phân số.
Lời giải.
Số 0,666 . . . là tổng của cấp số nhân lùi vô hạn có số hạng đầu bằng 0,6 và công bội bằng
1
10
.
Do đó 0,666 . . . =
0,6
1 −
1
10
=
6
9
=
2
3
. □
Ví dụ 29. Tính tổng S = 1 −
1
2
+
1
4
−
1
8
+ . . . +
Å
−
1
2
ã
n−1
+ . . ..
Lời giải.
Đây là tổng của cấp số nhân lùi vô hạn với u
1
= 1 và q = −
1
2
. Do đó S =
u
1
1 − q
=
1
1 −
Å
−
1
2
ã
=
2
3
. □
Ví dụ 30. Biểu diễn số thập phân vô hạn tuần hoàn 2,222 . . . dưới dạng phân số.
Lời giải.
Ta có 2,222 . . . = 2 + 0,2 + 0,02 + 0,002 + . . . = 2 + 2 ·10
−1
+ 2 ·10
−2
+ 2 ·10
−3
+ . . ..
Đây là tổng của cấp số nhân lùi vô hạn với u
1
= 2, q = 10
−1
nên
2,222 . . . =
u
1
1 − q
=
2
1 −
1
10
=
20
9
.
□
Ví dụ 31 (Cùng khám phá). Tính tổng của cấp số nhân lùi vô hạn S = 2 +
1
2
+
1
8
+
1
32
+ . . .
Lời giải.
S là tổng của cấp số nhân lùi vô hạn có số hạng đầu u
1
= 2 và công bội q =
1
4
.
Vậy S =
u
1
1 − q
=
2
1 −
1
4
=
8
3
. □
366/764 366/764
Toán 11 theo chương trình GDPT2018
Chương 3. Giới hạn. Hàm số liên tục
Biết làm, làm đúng, làm nhanh
367
2. Bài tập tự luyện
Bài 48. Cho cấp số nhân (u
n
), với u
1
= 1 và công bội q =
1
2
.
a) So sánh |q| với 1.
b) Tính S
n
= u
1
+ u
2
+ ··· + u
n
từ đó hãy tính lim S
n
.
Lời giải.
a) Ta có |q| =
1
2
=
1
2
< 1.
b) Ta có S
n
=
u
1
(1 − q
n
)
1 − q
=
1 ·
ï
1 −
Å
1
2
ã
n
ò
1 −
1
2
= 2 ·
Å
1 −
1
2
n
ã
= 2 −
1
2
n−1
.
Khi đó lim S
n
= lim
Å
2 −
1
2
n−1
ã
= 2.
□
Bài 49. Tính tổng T = 1 +
1
3
+
1
3
2
+ . . . +
1
3
n
+ . . .
Lời giải.
Các số hạn của tổng lập thành câp số nhân (u
n
), có u
1
= 1, q =
1
3
nên
T = 1 +
1
3
+
1
3
2
+ . . . +
1
3
n
+ . . . =
1
1 −
1
3
=
2
3
·
□
Bài 50. Tính tổng S = 1 −
1
2
+
1
4
−
1
8
+ . . . +
Å
−
1
2
ã
n−1
+ . . ..
Lời giải.
Đây là tổng của cấp số nhân lùi vô hạng với u
1
= 1 và q = −
1
2
. Do đó S =
u
1
1 − q
=
1
1 −
Å
−
1
2
ã
=
2
3
. □
Bài 51. Biểu diễn số thập phân vô hạn tuần hoàn 2,222 . . . dưới dạng phân số.
Lời giải.
Ta có 2,222 . . . = 2 + 0,2 + 0,02 + 0,002 + . . . = 2 + 2 ·10
−1
+ 2 ·10
−2
+ 2 ·10
−3
+ . . ..
Đây là tổng của cấp số nhân lùi vô hạn với u
1
= 2, q = 10
−1
nên
2,222 . . . =
u
1
1 − q
=
2
1 −
1
10
=
20
9
.
□
Bài 52. Biểu diễn số thập phân vô hạn tuần hoàn 0, (3) dưới dạng phân số.
Lời giải.
Ta có 0, (3) =
3
10
+
3
10
2
+ . . . +
3
10
n
+ . . . =
3
10
1 −
1
10
=
1
3
· □
Bài 53. Tính tổng của cấp số nhân lùi vô hạn 1 −
1
4
+
1
16
−
1
64
+ . . . +
Å
−
1
4
ã
n
+ . . ..
Lời giải.
367/764 367/764
Toán 11 theo chương trình GDPT2018
1. Giới hạn của dãy số
Biết làm, làm đúng, làm nhanh
368
Tổng trên là tổng của cấp số nhân lùi vô hạn có số hạng đầu u
1
= 1 và công bội q = −
1
4
nên
1 −
1
4
+
1
16
−
1
64
+ . . . +
Å
−
1
4
ã
n
+ . . . =
1
1 −
Å
−
1
4
ã
=
4
5
.
□
Bài 54. Biết rằng có thể coi số thập phân vô hạn tuần hoàn 0,666 . . . là tổng của một cấp số nhân lùi vô hạn
0,666 . . . = 0,6 + 0,06 + 0,006 + . . . = 0,6 + 0,6 ·
1
10
+ 0,6 ·
1
10
2
+ . . . .
Hãy viết 0,666 . . . dưới dạng phân số.
Lời giải.
Số 0,666 . . . là tổng của cấp số nhân lùi vô hạn có số hạng đầu bằng 0,6 và công bội bằng
1
10
.
Do đó 0,666 . . . =
0,6
1 −
1
10
=
6
9
=
2
3
. □
Bài 55. Tính tổng của cấp số nhân lùi vô hạn 1 +
1
3
+
Å
1
3
ã
2
+ . . . +
Å
1
3
ã
n
+ . . ..
Lời giải.
Tổng trên là tổng của cấp số nhân lùi vô hạn có số hạng đầu u
1
= 1 và công bội q =
1
3
nên
1 +
1
3
+
Å
1
3
ã
2
+ . . . +
Å
1
3
ã
n
+ . . . =
1
1 −
1
3
=
3
2
.
□
3. Câu hỏi trắc nghiệm
Câu 61. Cho cấp số nhân u
1
, u
2
, . . . với công bội q thỏa điều kiện |q| < 1. Lúc đó, ta nói cấp số nhân đã cho là
lùi vô hạn. Tổng của cấp số nhân đã cho là S = u
1
+ u
2
+ u
3
+ ··· + u
n
+ ··· bằng
A
u
1
q − 1
. B
u
1
(q
n
− 1)
q − 1
. C
u
1
1 + q
. D
u
1
1 − q
.
Lời giải.
Theo định nghĩa cấp số nhân lùi vô hạn ta chứng minh được.
S = u
1
+ u
2
+ u
3
+ ··· + u
n
+ ··· = u
1
+ u
1
q
1
+ u
1
q
2
+ ··· + u
1
q
n−1
+ ··· =
u
1
1 − q
.
Chọn đáp án D □
Câu 62. Gọi S =
1
3
−
1
9
+ ··· +
(−1)
n+1
3
n
. Khi đó, lim S bằng
A
3
4
. B
1
4
. C
1
2
. D 1.
Lời giải.
Ta có
S =
1
3
−
1
9
+ ··· +
(−1)
n+1
3
n
⇔ S = −
Å
−
1
3
+
1
9
+ ··· +
(−1)
n
3
n
ã
⇔ S =
1
3
·
1 −
Å
−1
3
ã
n
1 −
−1
3
⇔ S =
1
4
·
Å
1 −
Å
−1
3
ã
n
ã
.
368/764 368/764
Toán 11 theo chương trình GDPT2018
Chương 3. Giới hạn. Hàm số liên tục
Biết làm, làm đúng, làm nhanh
369
Suy ra lim S = lim
1
4
·
Å
1 −
Å
−1
3
ã
n
ã
=
1
4
.
Chọn đáp án B □
Câu 63. Tổng S =
1
3
+
1
3
2
+ ··· +
1
3
n
+ ··· có giá trị là
A
1
3
. B
1
2
. C
1
9
. D
1
4
.
Lời giải.
Ta có S =
1
3
+
1
3
2
+ ··· +
1
3
n
+ ··· =
1
3
·
1
1 −
1
3
=
1
2
.
Chọn đáp án B □
Câu 64. Tính S = 9 + 3 + 1 +
1
3
+
1
9
+ ··· +
1
3
n−3
+ ···. Kết quả là
A
27
2
. B 14. C 16. D 15.
Lời giải.
Ta có S = 9 + 3 + 1 +
1
3
+
1
9
+ ··· +
1
3
n−3
+ ··· = 13 +
1
3
·
1
1 −
1
3
= 13 +
1
2
=
27
2
.
Chọn đáp án A □
Câu 65. Tổng các cấp số nhân vô hạn: 1, −
1
2
,
1
4
, −
1
8
, . . . ,
(−1)
n+1
2
n−1
, . . . là
A
3
2
. B
2
3
. C −
2
3
. D 2.
Lời giải.
Ta có S = 1 −
1
2
+
1
4
−
1
8
+ ··· +
(−1)
n+1
2
n−1
+ ··· = 1 −
1
2
·
1
1 +
1
2
= 1 −
1
3
=
2
3
.
Chọn đáp án B □
Câu 66. Gọi S = 1 +
2
3
+
4
9
+ ··· +
2
n
3
n
+ ···. Giá trị của S bằng
A 3. B 5. C 6. D 4.
Lời giải.
Ta có S = 1 +
2
3
+
4
9
+ ··· +
2
n
3
n
+ ··· = 1 +
2
3
·
1
1 −
2
3
= 1 + 2 = 3.
Chọn đáp án A □
Câu 67. Số thập phân vô hạn tuần hoàn 0,233333 . . . biểu diễn dưới dạng số là
A
1
23
. B
2333
10000
. C
23333
10
5
. D
7
30
.
Lời giải.
0,233333 . . . = 0,2 + 3
Å
1
10
2
+
1
10
3
+ . . .
ã
= 0,2 + 3 ·
1
100
·
1
1 −
1
10
=
1
5
+
1
30
=
7
30
.
Chọn đáp án D □
Câu 68. Số thập phân vô hạn tuần hoàn 0,212121 . . . biểu diễn dưới dạng phân số là
A
2121
10
4
. B
1
21
. C
7
33
. D
212121
10
6
.
Lời giải.
0,212121 . . . = 21
Å
1
10
2
+
1
10
4
+ . . .
ã
= 21 ·
1
10
2
·
1
1 −
1
100
=
7
33
.
Chọn đáp án C □
Câu 69. Số thập phân vô hạn tuần hoàn 0,271414 . . . được biểu diễn bằng phân số:
A
2714
9900
. B
2617
9900
. C
2786
9900
. D
2687
9900
.
Lời giải.
0,271414 ··· = 0,27 + 14
Å
1
10
4
+
1
10
6
. . .
ã
= 0,27 + 14 ·
1
10
4
·
1
1 −
1
100
=
27
100
+
7
4950
=
2687
9900
.
369/764 369/764
Toán 11 theo chương trình GDPT2018
1. Giới hạn của dãy số
Biết làm, làm đúng, làm nhanh
370
Chọn đáp án D □
Câu 70. Tổng của cấp số nhân lùi vô hạn: −
1
2
,
1
4
,
1
8
, . . . ,
(−1)
n
2
n
, . . . là
A −
1
3
. B −
1
4
. C −1. D
1
2
.
Lời giải.
Từ −
1
2
,
1
4
,
1
8
, . . . ,
(−1)
n
2
n
, . . . có u
1
= −
1
2
và q = −
1
2
.
Có S = −
1
2
+
1
4
+
1
8
+ ··· +
(−1)
n
2
n
+ ··· =
−
1
2
1 −
−
1
2
= −
1
3
.
Chọn đáp án A □
Câu 71. Số thập phân vô hạn tuần hoàn 0,511111 ··· được biểu diễn bởi phân số
A
47
90
. B
46
90
. C
6
11
. D
43
90
.
Lời giải.
Ta có
0,511111 ··· = 0,5 +
1
10
2
+
1
10
3
. . . =
1
2
+
1
10
2
·
1
1 −
1
10
=
1
2
+
1
90
=
23
45
.
Chọn đáp án B □
Câu 72. Tổng của cấp số nhân vô hạn
1
2
, −
1
4
,
1
8
, . . .
(−1)
n+1
2
n
, . . . là
A −
2
3
. B 1. C −
1
3
. D
1
3
.
Lời giải.
Ta có S =
1
2
−
1
4
+
1
8
+ ··· +
(−1)
n+1
2
n
+ ··· =
1
2
·
1
1 +
1
2
=
1
3
.
Chọn đáp án D □
Câu 73. Tổng của cấp số nhân lùi vô hạn
1
2
, −
1
6
,
1
18
, . . . ,
(−1)
n+1
2 · 3
n−1
, . . . là
A
3
4
. B
8
3
. C
2
3
. D
3
8
.
Lời giải.
Cấp số nhân có u
1
=
1
2
, q = −
1
3
. Do đó tổng cần tìm là
S =
u
1
1 − q
=
1
2
1 +
1
3
=
1
2
·
3
4
=
3
8
.
Chọn đáp án D □
Câu 74. Tổng của cấp số nhân lùi vô hạn
1
3
, −
1
9
,
1
27
, . . . ·,
(−1)
n+1
3
n
, . . . là
A 4. B
1
2
. C
3
4
. D
1
4
.
Lời giải.
Cấp số nhân có u
1
=
1
3
, q = −
1
3
. Do đó tổng cần tìm là
S =
u
1
1 − q
=
1
3
1 +
1
3
=
1
3
·
3
4
=
1
4
.
Chọn đáp án D □
Câu 75. Số thập phân vô hạn tuần hoàn 0,17232323 . . . được biểu diễn bởi phân số?
A
1706
9900
. B
153
990
. C
164
990
. D
853
4950
.
Lời giải.
370/764 370/764
Toán 11 theo chương trình GDPT2018
Chương 3. Giới hạn. Hàm số liên tục
Biết làm, làm đúng, làm nhanh
371
0,17232323 . . . = 0,17 + 23
Å
1
10
4
+
1
10
6
+ . . .
ã
=
17
100
+ 23 ·
1
10
4
·
1
1 −
1
100
=
17
100
+
23
9900
=
853
4950
.
Chọn đáp án D □
Dạng 6. Toán thực tế, liên môn liên quan đến giới hạn dãy số
S = u
1
+ u
1
q + u
1
q
2
+ ... =
u
1
1 − q
.
1. Ví dụ mẫu
Ví dụ 32 (Cánh diều).
Từ hình vuông có độ dài cạnh bằng 1, người ta nối các trung điểm của cạnh hình vuông
để tạo ra hình vuông mới như hình bên. Tiếp tục quá trình này đến vô hạn.
a) Tính diện tích S
n
của hình vuông được tạo thành từ bước thứ n.
b) Tính tổng diện tích của tất cả các hình vuông được tạo thành.
1
Lời giải.
a) Từ giả thiết suy ra diện tích hình vuông sau bằng
1
2
diện tích hình vuông trước.
Khi đó diện tích của các hình vuông tạo thành một cấp số nhân lùi vô hạn với số hạng đầu S
1
= 1 và công
bội q =
1
2
.
Diện tích S
n
của hình vuông được tạo thành từ bước thứ n là S
n
= S
1
· q
n−1
=
Å
1
2
ã
n−1
.
b) Tổng diện tích của tất cả các hình vuông được tạo thành là:
S =
u
1
1 − q
=
1
1 −
1
2
= 2.
□
Ví dụ 33 (CTST). Từ tờ giấy, cắt một hình tròn bán kính R (cm) như Hình 3a. Tiếp theo, cắt hai hình tròn bán
kính
R
2
rồi chồng
lên hình tròn đầu tiên như Hình 3b. Tiếp theo, cắt
bốn hình tròn bán kính
R
4
rồi chồng lên các hình
trước như Hình 3c. Cứ thế tiếp tục mãi. Tính tổng
diện tích của các hình tròn.
a) b) c)
Hình 3
Lời giải.
Diện tích của các hình tròn trong các lần cắt là
a) Lần thứ 1: S
1
= πR
2
.
b) Lần thứ 2: S
2
= 2 · π
Å
R
2
ã
2
=
πR
2
2
.
c) Lần thứ 3: S
2
= 4 · π
Å
R
4
ã
2
=
πR
2
2
2
.
371/764 371/764
Toán 11 theo chương trình GDPT2018
1. Giới hạn của dãy số
Biết làm, làm đúng, làm nhanh
372
d) Lần thứ n: S
n
=
πR
2
2
n−1
.
Do đó diện tích các hình tròn lập thành một cấp số nhân lùi vô hạn có số hạng đầu S
1
= πR
2
và công bội q =
1
2
nên tổng diện tích các hình tròn là
S
1
+ S
2
+ ··· =
πR
2
1 −
1
2
= 2πR
2
.
□
Ví dụ 34.
Cho hình vuông cạnh 1 (đơn vị độ dài). Chia hình vuông đó thành bốn hình
vuông nhỏ bằng nhau, sau đó tô màu hình vuông nhỏ góc dưới bên trái (Hình
vẽ bên). Lặp lại các thao tác này với hình vuông nhỏ góc trên bên phải. Giả
sử quá trình trên tiếp diễn vô hạn lần. Gọi u
1
, u
2
, . . . , u
n
, . . . lần lượt là độ dài
cạnh của các hình vuông được tô màu.
a) Tính tổng S
n
= u
1
+ u
2
+ . . . + u
n
.
b) Tìm S = lim
n→+∞
S
n
.
Lời giải.
a) Độ của các hình vuông sau khi tô màu
○ Lần thứ 1: u
1
=
1
2
· 1 =
1
2
;
○ Lần thứ 2: u
2
=
1
2
·
1
2
=
1
4
;
○ Lần thứ 3: u
3
=
1
2
·
1
4
=
1
8
;
○ Lần thứ n: u
n
=
Å
1
2
ã
n
· 1 =
Å
1
2
ã
n
.
Vậy S
n
= u
1
+ u
2
+ . . . + u
n
=
1
2
+
1
4
+ . . . +
Å
1
2
ã
n
.
b) Độ dài các cạnh hình vuông lập thành một cấp số nhân lùi vô hạn có số hạng đầu u
1
=
1
2
và công bội q =
1
2
.
S = lim
n→+∞
S
n
=
u
1
1 − q
=
1
2
1 −
1
2
= 1.
□
2. Bài tập tự luyện
Bài 56. Từ tờ giấy, cắt một hình tròn bán kính R (cm) như Hình 3a. Tiếp theo, cắt hai hình tròn bán kính
R
2
rồi chồng lên hình tròn đầu tiên như Hình 3b. Tiếp theo, cắt bốn hình tròn bán kính
R
4
rồi chồng lên các hình
trước như Hình 3c. Cứ thế tiếp tục mãi. Tính tổng diện tích của các hình tròn.
a) b)
Hình 3
c)
372/764 372/764
Toán 11 theo chương trình GDPT2018
Chương 3. Giới hạn. Hàm số liên tục
Biết làm, làm đúng, làm nhanh
373
Lời giải.
Diện tích của hình tròn bán kính R là S
1
= π · R
2
cm
2
.
Diện tích của hình tròn bán kính
R
2
là S
2
= π ·
Å
R
2
ã
2
cm
2
.
Diện tích của hình tròn bán kính
R
4
là S
3
= π ·
Å
R
4
ã
2
cm
2
.
Tổng diện tích của các hình tròn là
S
n
= S
1
+ 2 ·S
2
+ 4 ·S
3
+ . . . = π · R
2
+ π · R
2
·
1
2
+ π · R
2
·
1
4
+ ···
Tổng trên là tổng của cấp số nhân lùi vô hạn có số hạng đầu u
1
= π·R
2
và công bội q =
1
2
nên S
n
=
π · R
2
1 −
1
2
= 2π·R
2
.
□
Bài 57.
Từ hình vuông có độ dài cạnh bằng 1, người ta nối các trung điểm của cạnh hình vuông
để tạo ra hình vuông mới như hình bên. Tiếp tục quá trình này đến vô hạn.
a) Tính diện tích S
n
của hình vuông được tạo thành từ bước thứ n.
b) Tính tổng diện tích của tất cả các hình vuông được tạo thành.
1
Lời giải.
a) Từ giả thiết suy ra diện tích hình vuông sau bằng
1
2
diện tích hình vuông trước.
Khi đó diện tích của các hình vuông tạo thành một cấp số nhân lùi vô hạn với số hạng đầu S
1
= 1 và công
bội q =
1
2
.
Diện tích S
n
của hình vuông được tạo thành từ bước thứ n là S
n
= S
1
· q
n−1
=
Å
1
2
ã
n−1
.
b) Tổng diện tích của tất cả các hình vuông được tạo thành là:
S =
u
1
1 − q
=
1
1 −
1
2
= 2.
□
Bài 58. Có 1 kg chất phóng xạ độc hại. Biết rằng, cứ sau một khoảng thời gian T = 24000 năm thì một nửa số
chất phóng xạ này bị phân rã thành chất khác không độc hại đối với sức khỏe của con người (T được gọi là chu
kì bán rã ).
(Nguồn: Đại số và giải tích 11, NXB GD Việt Nam, 2021 )
Gọi u
n
là khối lượng chất phóng xạ còn lại sau chu kì thứ n.
a) Tìm số hạng tổng quát u
n
của dãy số (u
n
).
b) Chứng minh rằng (u
n
) có giới hạn là 0.
c) Từ kết quả câu 2, chứng tỏ rằng sau một số năm nào đó khối lượng phóng xạ đã cho ban đầu không còn
độc hại với con người, biết rằng chất phóng xạ này sẽ không độc hại nữa nếu khối lượng chất phóng xạ còn
lại bé hơn 10
−6
g.
Lời giải.
373/764 373/764
Toán 11 theo chương trình GDPT2018
1. Giới hạn của dãy số
Biết làm, làm đúng, làm nhanh
374
a) Khối lượng chất phóng xạ còn lại sau chu kì bán rã thứ 1 là u
1
=
1
2
· 1 = 1 kg.
Khối lượng chất phóng xạ còn lại sau chu kì bán rã thứ 2 là u
2
=
1
2
· u
1
=
1
2
·
1
2
=
1
2
2
kg.
Khối lượng chất phóng xạ còn lại sau chu kì bán rã thứ 3 là u
3
=
1
2
· u
2
=
1
2
·
1
4
=
1
2
3
kg.
Khối lượng chất phóng xạ còn lại sau chu kì bán rã thứ n là u
n
=
1
2
n
kg.
b) lim u
n
= lim
1
2
n
= lim
Å
1
2
ã
n
= 0.
c) Chất phóng xạ sẽ không độc hại nữa nếu khối lượng chất phóng xạ còn lại bé hơn 10
−6
g = 10
−9
kg
⇔ u
n
< 10
−9
⇔
1
2
n
< 10
−9
⇔ 2
n
> 10
9
⇔ n ≥ 30.
Vậy sau ít nhất 30 chu kì bằng 30 ·24000 = 720000 năm thì khối lượng phóng xạ đã cho ban đầu không còn
độc hại với con người nữa.
□
Bài 59. Gọi C là nữa đường tròn đường kính AB = 2R.
C
1
là đường gồm hai nửa đường tròn đường kính
AB
2
,
C
2
là đường gồm bốn nửa đường tròn đường kính
AB
4
, ···
C
n
là đường gồm 2
n
nửa đường tròn đường kính
AB
2
n
, ···
Gọi p
n
là độ dài của C
n
, S
n
là diện tích hình phẳng giới hạn bởi C
n
và
đoạn thẳng AB.
a) Tính p
n
, S
n
.
b) Tính giới hạn của các dãy số (p
n
) và (S
n
).
C
C
1
C
2
C
3
AB
Lời giải.
a) Ta có
p
n
= 2
n
· πr = 2
n
· π ·
AB
2 · 2
n
=
πAB
2
=
π · 2R
2
= πR.
S
n
= 2
n
·
1
2
πr
2
= 2
n
·
1
2
π
Å
AB
2 · 2
n
ã
2
= 2
n
·
1
2
π
Å
2R
2 · 2
n
ã
2
= 2
n
·
1
2
π
R
2
(2
n
)
2
=
πR
2
2
n+1
.
374/764 374/764
Toán 11 theo chương trình GDPT2018
Chương 3. Giới hạn. Hàm số liên tục
Biết làm, làm đúng, làm nhanh
375
b) lim p
n
= lim (πR) = πR.
lim S
n
= lim
πR
2
2
n+1
= 0 (Vì lim
πR
2
= πR
2
và lim 2
n+1
= +∞).
□
Bài 60.
Từ độ cao 55, 8 m của tháp nghiêng Pisa nước Ý, người ta
thả một quả bóng cao su chạm xuống đất hình bên dưới.
Giả sử mỗi lần chạm đất quả bóng lại nảy lên độ cao bằng
1
10
độ cao mà quả bóng đạt được trước đó. Gọi S
n
là tổng
độ dài quãng đường di chuyển của quả bóng tính từ lúc thả
ban đầu cho đến khi quả bóng đó chạm đất n lần. Tính
lim S
n
.
Lời giải.
Mỗi khi chạm đất quả bóng lại nảy lên một độ cao bằng
1
10
độ cao của lần rơi ngay trước đó và sau đó lại rơi
xuống từ độ cao thứ hai này. Do đó, độ dài hành trình của quả bóng kể từ thời điểm rơi ban đầu đến:
Thời điểm chạm đất lần thứ nhất là d
1
= 55,8.
Thời điềm chạm đất lần thứ hai là d
2
= 55,8 + 2 ·
55,8
10
.
Thời điểm chạm đất lần thứ ba là d
3
= 55,8 + 2 ·
55,8
10
+ 2 ·
55,8
10
2
.
Thời điểm chạm đất lần thứ tư là d
4
= 55,8 + 2 ·
55,8
10
+ 2 ·
55, 8
10
2
+ 2 ·
55,8
10
3
.
. . .
Thời điểm chạm đất lần thứ n (n > 1) là
d
n
= 55,8 + 2 ·55,8 + 2 ·
55,8
10
2
+ 2 ·
55,8
10
3
+ . . . + 2 ·
55,8
10
n−1
.
Do đó, quãng đường mà quả bóng đi được kể từ thời điềm rơi đến khi nằm yên trên mặt đất là:
d = 55,8 + 2.55,8 + 2 ·
55,8
10
2
+ 2 ·
55,8
10
3
+ . . . + 2 ·
55,8
10
n−1
+ . . . = lim d
n
.
Vì 2 ·
55,8
10
; 2 ·
55,8
10
2
; 2 ·
55,8
10
3
; . . . ; 2 ·
55,8
10
n−1
; . . . là một cấp số nhân lùi vô hạn với công bội q =
1
10
nên ta có:
2 ·
55, 8
10
+ 2 ·
55,8
10
2
+ 2 ·
55,8
10
3
+ . . . + 2 ·
55,8
10
n−1
+ . . . =
2 ·
55,8
10
1 −
1
10
= 12,4.
Vậy d = 55,8 + 12,4 = 68,2 m. □
Bài 61. Cho một tam giác đều ABC cạnh a. Tam giác A
1
B
1
C
1
có các đỉnh là trung điểm các cạnh của tam giác
ABC, tam giác A
2
B
2
C
2
có các đỉnh là trung điểm các cạnh của tam giác A
1
B
1
C
1
, . . ., tam giác A
n+1
B
n+1
C
n+1
có các đỉnh là trung điểm các cạnh của tam giác A
n
B
n
C
n
, . . . Gọi p
1
, p
2
, . . . , p
n
, . . . và S
1
, S
2
, . . . , S
n
, . . . theo thứ
tự là chu vi và diện tích của các tam giác A
1
B
1
C
1
, A
2
B
2
C
2
, . . . , A
n
B
n
C
n
, . . ..
a) Tìm giới hạn của các dãy số (p
n
) và (S
n
).
b) Tìm các tổng p
1
+ p
2
+ . . . + p
n
+ . . . và S
1
+ S
2
+ . . . + S
n
+ . . ..
375/764 375/764
Toán 11 theo chương trình GDPT2018
1. Giới hạn của dãy số
Biết làm, làm đúng, làm nhanh
376
Lời giải.
a) Ta có p
1
, p
2
, . . . , p
n
, . . . lần lượt là chu vi của các tam giác A
1
B
1
C
1
, A
2
B
2
C
2
, . . . , A
n
B
n
C
n
, . . .
p
1
= 3a
p
2
= 3 ·
1
2
a
. . .
p
n
= 3 ·
1
2
n−1
a
suy ra lim p
n
= lim 3 ·
1
2
n−1
a = 0.
S
1
=
a
2
√
3
4
S
2
=
1
4
a
2
√
3
4
. . .
S
n
=
1
4
n−1
·
a
2
√
3
4
suy ra lim S
n
= lim
1
4
n−1
·
a
2
√
3
4
= 0.
b) Dựa vào dữ kiện đề bài suy ra tổng (p
n
) là tổng của cấp số nhân lùi vô hạn với công bội q =
1
2
và
p
1
+ p
2
+ . . . + p
n
+ . . . = lim (p
n
) =
p
1
1 − q
=
3a
1 −
1
2
= 6a.
Dựa vào dữ kiện đề bài suy ra tổng (S
n
) là tổng của cấp số nhân lùi vô hạn với công bội q =
1
4
và
S
1
+ S
2
+ . . . + S
n
+ . . . = lim (S
n
) =
S
1
1 − q
=
a
2
√
3
4
1 −
1
4
=
a
2
√
3
12
.
□
Bài 62.
Từ hình vuông đầu tiên có cạnh bằng 1 (đơn vị độ dài), nối các trung điểm của
bốn cạnh để có hình vuông thứ hai. Tiếp tục nối các trung điểm của bốn cạnh của
hình vuông thứ hai để được hình vuông thứ ba. Cứ tiếp tục làm như thế, nhận
được một dãy hình vuông (xem Hình 5).
Hình 5
a) Kí hiệu a
n
là diện tích của hình vuông thứ n và S
n
là tổng diện tích của n hình vuông đầu tiên. Viết công
thức tính a
n
, S
n
(n = 1, 2, 3, . . .) và tìm lim S
n
(giới hạn này nếu có được gọi là tổng diện tích của các hình
vuông).
b) Kí hiệu p
n
là chu vi của hình vuông thứ n và Q
n
là tổng chu vi của n hình vuông đầu tiên. Viết công thức
tính p
n
và Q
n
(n = 1, 2, 3, . . .) và tìm lim Q
n
(giới hạn này nếu có được gọi là tổng chu vi của các hình
vuông).
Lời giải.
a) Ta có hình vuông thứ nhất có cạnh bằng 1, hình vuông thứ hai có cạnh bằng
√
2
2
.
Hình vuông thứ ba có cạnh bằng
1
2
.
Suy ra hình vuông thứ n có cạnh bằng
Ç
√
2
2
å
n−1
.
376/764 376/764
Toán 11 theo chương trình GDPT2018
Chương 3. Giới hạn. Hàm số liên tục
Biết làm, làm đúng, làm nhanh
377
Diện tích của hình vuông thứ n là a
n
=
Ç
√
2
2
å
n−1
·
Ç
√
2
2
å
n−1
=
Å
1
2
ã
n−1
.
Tổng diện tích của n hình vuông đầu tiên là tổng của cấp số nhân có số hạng đầu a
1
= 1 và công bội q =
1
2
nên
S
n
=
a
1
(1 − q
n
)
1 − q
=
1 −
Å
1
2
ã
n
1 −
1
2
= 2
ï
1 −
Å
1
2
ã
n
ò
.
lim S
n
= lim 2
ï
1 −
Å
1
2
ã
n
ò
= 2
ï
lim 1 − lim
Å
1
2
ã
n
ò
= 2.
b) Hình vuông thứ nhất có chu vi bằng 4, hình vuông thứ 2 có chu vi là 2
√
2, hình vuông thứ 3 có chu vi là 2.
Suy ra hình vuông thứ n có chu vi bằng p
n
= 4 ·
Ç
√
2
2
å
n−1
. Tổng chu vi của n hình vuông đầu tiên là tổng
của cấp số nhân có số hạng đầu p
1
= 4 và công bội q =
√
2
2
nên
Q
n
=
p
1
(1 − q
n
)
1 − q
=
4
Ç
1 −
Ç
√
2
2
å
n
å
1 −
√
2
2
=
Ä
8 + 4
√
2
ä
ñ
1 −
Ç
√
2
2
å
n
ô
.
lim Q
n
=
Ä
8 + 4
√
2
ä
lim
ñ
1 −
Ç
√
2
2
å
n
ô
=
Ä
8 + 4
√
2
ä
(1 − 0) = 8 + 4
√
2.
□
Bài 63. Xét quá trình tạo ra hình có chu vi vô cực và diện tích bằng 0 như sau:
Bắt đầu bằng một hình vuông H
0
cạnh bằng 1 đơn vị độ dài (xem Hình 6a). Chia hình vuông H
0
thành chín hình
vuông bằng nhau, bỏ đi bốn hình vuông, nhận được hình H
1
(xem Hình 6b). Tiếp theo, chia mỗi hình vuông của
H
1
thành chín hình vuông, rồi bỏ đi bốn hình vuông, nhận được hình H
2
(xem Hình 6c). Tiếp tục quá trình này,
ta nhận được một dãy hình H
n
(n = 1, 2, 3, . . .).
H
0
a)
H
1
b)
H
2
c)
H
3
d)
Hình 6
Ta có: H
1
có 5 hình vuông, mỗi hình vuông có cạnh bằng
1
3
;
Ta có: H
2
có 5 · 5 = 5
2
hình vuông, mỗi hình vuông có cạnh bằng
1
3
·
1
3
=
1
3
2
; . . ..
Từ đó, nhận được H
n
có 5
n
hình vuông, mỗi hình vuông có cạnh bằng
1
3
n
.
a) Tính diện tích S
n
của H
n
và tính lim S
n
.
b) Tính chu vi p
n
của H
n
và tính lim p
n
.
(Quá trình trên tạo nên một hình, gọi là một fractal, được coi là có diện tích lim S
n
và chu vi lim p
n
).
Lời giải.
377/764 377/764
Toán 11 theo chương trình GDPT2018
1. Giới hạn của dãy số
Biết làm, làm đúng, làm nhanh
378
a) Hình vuông H
1
có diện tích S
1
= 5 ·
Å
1
3
ã
2
=
5
9
.
Hình vuông H
2
có diện tích S
2
= 5
2
·
Å
1
3
2
ã
2
=
Å
5
9
ã
2
.
Hình vuông H
n
có diện tích S
n
= 5
n
·
Å
1
3
n
ã
2
=
Å
5
9
ã
n
.
lim S
n
= lim
Å
5
9
ã
n
= 0.
b) Hình vuông H
1
có chu vi p
1
= 5 · 4 ·
1
3
= 4 ·
5
3
.
Hình vuông H
2
có chu vi p
2
= 5
2
· 4 ·
1
3
2
= 4 ·
Å
5
3
ã
2
.
Hình vuông H
n
có diện tích p
n
= 5
n
· 4 ·
1
3
n
= 4 ·
Å
5
3
ã
n
.
lim p
n
= lim 4 ·
Å
5
3
ã
n
= +∞.
□
Bài 64.
Cho tam giác đều có cạnh bằng a, gọi là tam giác H
1
. Nối các trung
điểm của H
1
để tạo thành tam giác H
2
. Tiếp theo, nối các trung
điểm của H
2
để tạo thành tam giác H
3
(Hình bên). Cứ tiếp tục như
vậy, nhận được dãy tam giác H
1
, H
2
, H
3
, . . .
Tính tổng chu vi và tổng diện tích các tam giác của dãy.
a
Lời giải.
Gọi S
i
và C
i
(i = 1, 2, . . .) lần lượt là diện tích và chu vi của tam giác H
i
, i = 1, 2, . . ..
Khi đó ta có
• S
1
=
a
2
√
3
4
; S
2
=
a
2
2
√
3
4
=
a
2
√
3
16
=
S
1
4
; S
3
=
1
4
S
2
, . . ..
Do đó (S
n
) là một cấp số nhân lùi vô hạn với S
1
=
a
2
√
3
4
và q
1
=
1
4
.
Tổng diện tích S = S
1
+ S
2
+ ··· =
S
1
1 − q
1
=
a
2
√
3
3
.
• C
1
= 3a; C
2
=
3a
2
=
1
2
C
1
, . . .
Do đó (C
n
) là một cấp số nhân lùi vô hạn với C
1
= 3a; q
2
=
1
2
.
Tổng chu vi là C = C
1
+ C
2
+ ··· =
C
1
1 − q
2
= 6a.
□
Bài 65. Một thấu kính hội tụ có tiêu cự là f. Gọi d và d
′
lần lượt là khoảng cách từ một vật thật AB và từ ảnh
A
′
B
′
của nó tới quang tâm O của thấu kính như hình vẽ bên dưới. Công thức thấu kính là
1
d
+
1
d
=
1
f
.
A
′
f f
d
d
′
B
′
F
′
F
A
B
O
a) Tìm biểu thức xác định hàm số d
′
= φ(d).
378/764 378/764
Toán 11 theo chương trình GDPT2018
Chương 3. Giới hạn. Hàm số liên tục
Biết làm, làm đúng, làm nhanh
379
b) Tìm lim
d→f
+
φ(d), lim
d→f
−
φ(d) và lim
d→f
φ(d). Giải thích ý nghĩa của các kết quả tìm được.
Lời giải.
a) Ta có
1
d
+
1
d
′
=
1
f
⇔ d
′
=
df
d − f
.
Vậy φ(d) =
df
d − f
.
b) Vì lim
d→f
+
df = f
2
; lim
d→f
+
(d − f) = 0; d → f
+
⇒ d −f > 0 nên lim
d→f
+
df
d − f
= +∞.
Vậy lim
d→f
+
φ(d) = lim
d→f
+
df
d − f
= +∞.
Ý nghĩa: Khi đặt vật nằm ngoài tiêu cự và tiến dần đến tiêu điểm thì cho ảnh thật ngược chiều với vật ở
vô cùng.
Vì lim
d→f
−
df = f
2
; lim
d→f
+
(d − f) = 0; d → f
−
⇒ d −f < 0 nên lim
d→f
+
df
d − f
= −∞.
Vậy lim
d→f
+
φ(d) = lim
d→f
+
df
d − f
= −∞.
Ý nghĩa: Khi đặt vật nằm trong tiêu cự và tiến dần đến tiêu điểm thì cho ảnh ảo cùng chiều với vật và
nằm ở vô cùng.
Vì không tồn tại lim
d→f
+
φ(d) và lim
d→f
−
φ(d) nên không tồn tại lim
d→f
φ(d).
□
3. Bài tập trắc nghiệm
Câu 76. Có 1 kg chất phóng xạ độc hại. Biết rằng, cứ sau một khoảng thời gian T = 24000 năm thì một nửa số
chất phóng xạ này bị phân rã thành chất khác không độc hại đối với sức khỏe của con người (T được gọi là chu
kì bán rã ). Gọi u
n
là khối lượng chất phóng xạ còn lại sau chu kì thứ n. Sau ít nhất bao nhiêu chu kì bán rã thì
khối lượng phóng xạ đã cho ban đầu không còn độc hại với con người, biết rằng chất phóng xạ này sẽ không độc
hại nữa nếu khối lượng chất phóng xạ còn lại bé hơn 10
−6
g.
A 24. B 30. C 100. D 15.
Lời giải.
Chất phóng xạ sẽ không độc hại nữa nếu khối lượng chất phóng xạ còn lại bé hơn 10
−6
g = 10
−9
kg
⇔ u
n
< 10
−9
⇔
1
2
n
< 10
−9
⇔ 2
n
> 10
9
⇔ n ≥ 30.
Vậy sau ít nhất 30 chu kì thì khối lượng phóng xạ đã cho ban đầu không còn độc hại với con người nữa.
Chọn đáp án B □
Câu 77. Có 1 kg chất phóng xạ độc hại. Biết rằng, cứ sau một khoảng thời gian T = 24000 năm thì một nửa
số chất phóng xạ này bị phân rã thành chất khác không độc hại đối với sức khỏe của con người (T được gọi là
chu kì bán rã ). Gọi u
n
là khối lượng chất phóng xạ còn lại sau chu kì thứ n. Sau ít nhất bao nhiêu năm thì khối
lượng phóng xạ đã cho ban đầu không còn độc hại với con người, biết rằng chất phóng xạ này sẽ không độc hại
nữa nếu khối lượng chất phóng xạ còn lại bé hơn 10
−6
g.
A 30. B 2400. C 720000. D 10000.
Lời giải.
Chất phóng xạ sẽ không độc hại nữa nếu khối lượng chất phóng xạ còn lại bé hơn 10
−6
g = 10
−9
kg
⇔ u
n
< 10
−9
⇔
1
2
n
< 10
−9
⇔ 2
n
> 10
9
⇔ n ≥ 30.
Vậy sau ít nhất 30 chu kì bằng 30 · 24000 = 720000 năm thì khối lượng phóng xạ đã cho ban đầu không còn độc
hại với con người nữa.
Chọn đáp án C □
379/764 379/764
Toán 11 theo chương trình GDPT2018
1. Giới hạn của dãy số
Biết làm, làm đúng, làm nhanh
380
Câu 78. Từ hình vuông có độ dài cạnh bằng 1, người ta nối các trung điểm của cạnh hình vuông để tạo ra hình
vuông mới như hình bên. Tiếp tục quá trình này đến vô hạn. Tính tổng diện tích của tất cả các hình vuông được
tạo thành.
A 1. B 2. C 3. D 4.
Lời giải.
Từ giả thiết suy ra diện tích hình vuông sau bằng
1
2
diện tích hình vuông trước.
Khi đó diện tích của các hình vuông tạo thành một cấp số nhân lùi vô hạn với số hạng đầu S
1
= 1 và công bội
q =
1
2
.
Diện tích S
n
của hình vuông được tạo thành từ bước thứ n là S
n
= S
1
· q
n−1
=
Å
1
2
ã
n−1
.
Tổng diện tích của tất cả các hình vuông được tạo thành là:
S =
u
1
1 − q
=
1
1 −
1
2
= 2.
Chọn đáp án B □
Câu 79. Từ hình vuông đầu tiên có cạnh bằng 1 (đơn vị độ dài), nối các trung điểm của bốn cạnh để có hình
vuông thứ hai. Tiếp tục nối các trung điểm của bốn cạnh của hình vuông thứ hai để được hình vuông thứ ba. Cứ
tiếp tục làm như thế, nhận được một dãy hình vuông. Tính tổng chu vi của dãy các hình vuông trên.
A 8 +
√
2. B 2 +
√
2. C 8 + 4
√
2. D 4 + 4
√
2.
Lời giải.
Hình vuông thứ nhất có chu vi bằng 4, hình vuông thứ 2 có chu vi là 2
√
2, hình vuông thứ 3 có chu vi là 2.
Suy ra hình vuông thứ n có chu vi bằng p
n
= 4 ·
Ç
√
2
2
å
n−1
. Tổng chu vi của n hình vuông đầu tiên là tổng của
cấp số nhân có số hạng đầu p
1
= 4 và công bội q =
√
2
2
nên
Q
n
=
p
1
(1 − q
n
)
1 − q
=
4
Ç
1 −
Ç
√
2
2
å
n
å
1 −
√
2
2
=
Ä
8 + 4
√
2
ä
ñ
1 −
Ç
√
2
2
å
n
ô
.
lim Q
n
=
Ä
8 + 4
√
2
ä
lim
ñ
1 −
Ç
√
2
2
å
n
ô
=
Ä
8 + 4
√
2
ä
(1 − 0) = 8 + 4
√
2.
Chọn đáp án C □
Câu 80. Bạn An thả quả bóng từ độ cao 6 m so với mặt đất xuống theo phương thẳng đứng sau đó bóng nảy lên
rồi lại rơi xuống cứ như vậy cho đến khi bóng dừng lại trên mặt đất. Tính quãng đường mà bóng đã di chuyển
biết rằng sau mỗi lần chạm đất bóng lại nảy lên đến độ cao bằng
3
4
độ cao của lần ngay trước đó.
A 30 m. B 18 m. C 24 m. D 48 m.
Lời giải.
Ta thấy độ cao của quả bóng mỗi lần nảy lên là một cấp số nhân với u
1
= 6, q =
3
4
. Tổng của cấp số nhân lùi vô
hạn đó là quãng đường mà quả bóng đã di chuyển đến khi dừng lại, khi đó
S =
u
1
1 − q
=
6
1 −
3
4
= 24 m.
Chọn đáp án C □
Câu 81. Từ độ cao 55, 8 m của tháp nghiêng Pisa nước Ý, người ta thả một quả bóng cao su chạm xuống đất
hình bên dưới. Giả sử mỗi lần chạm đất quả bóng lại nảy lên độ cao bằng
1
10
độ cao mà quả bóng đạt được trước
380/764 380/764
Toán 11 theo chương trình GDPT2018
Chương 3. Giới hạn. Hàm số liên tục
Biết làm, làm đúng, làm nhanh
381
đó. Gọi S
n
là tổng độ dài quãng đường di chuyển của quả bóng tính từ lúc thả ban đầu cho đến khi quả bóng đó
chạm đất n lần. Tính lim S
n
.
A 58,8. B 67,2. C 68. D 68,2.
Lời giải.
Mỗi khi chạm đất quả bóng lại nảy lên một độ cao bằng
1
10
độ cao của lần rơi ngay trước đó và sau đó lại rơi
xuống từ độ cao thứ hai này. Do đó, độ dài hành trình của quả bóng kể từ thời điểm rơi ban đầu đến:
Thời điểm chạm đất lần thứ nhất là d
1
= 55,8.
Thời điềm chạm đất lần thứ hai là d
2
= 55,8 + 2 ·
55,8
10
.
Thời điểm chạm đất lần thứ ba là d
3
= 55,8 + 2 ·
55,8
10
+ 2 ·
55,8
10
2
.
Thời điểm chạm đất lần thứ tư là d
4
= 55,8 + 2 ·
55,8
10
+ 2 ·
55, 8
10
2
+ 2 ·
55,8
10
3
.
. . .
Thời điểm chạm đất lần thứ n (n > 1) là
d
n
= 55,8 + 2 ·55,8 + 2 ·
55,8
10
2
+ 2 ·
55,8
10
3
+ . . . + 2 ·
55,8
10
n−1
.
Do đó, quãng đường mà quả bóng đi được kể từ thời điềm rơi đến khi nằm yên trên mặt đất là:
d = 55,8 + 2.55,8 + 2 ·
55,8
10
2
+ 2 ·
55,8
10
3
+ . . . + 2 ·
55,8
10
n−1
+ . . . = lim d
n
.
Vì 2 ·
55,8
10
; 2 ·
55,8
10
2
; 2 ·
55,8
10
3
; . . . ; 2 ·
55,8
10
n−1
; . . . là một cấp số nhân lùi vô hạn với công bội q =
1
10
nên ta có:
2 ·
55, 8
10
+ 2 ·
55,8
10
2
+ 2 ·
55,8
10
3
+ . . . + 2 ·
55,8
10
n−1
+ . . . =
2 ·
55,8
10
1 −
1
10
= 12,4.
Vậy d = 55,8 + 12,4 = 68,2 m.
Chọn đáp án D □
Câu 82. Cho tam giác đều ABC cạnh a. Lấy A
1
, B
1
, C
1
lần lượt là trung điểm của đoạn BC, CA, AB; A
2
,
B
2
, C
2
lần lượt là trung điểm của đoạn B
1
C
1
, C
1
A
1
, A
1
B
1
; . . . ; cứ tiếp tục như thế cho đến A
n+1
, B
n+1
, C
n+1
lần lượt là trung điểm của đoạn B
n
C
n
, C
n
A
n
, A
n
B
n
. Gọi S
1
, S
2
, S
3
, .. . lần lượt là diện tích của các tam giác
A
1
B
1
C
1
, A
2
B
2
C
2
,. . . , A
n
B
n
C
n
,. . . . Tính tổng S = S
1
+ S
2
+ ··· + S
n
+ ···.
A
a
2
√
3
8
. B
a
2
√
3
15
. C
a
2
√
3
12
. D
a
2
√
3
3
.
Lời giải.
Vì dãy các tam giác A
1
B
1
C
1
, A
2
B
2
C
2
,···, A
n
B
n
C
n
,··· là các tam giác đều nên
diện tích của các tam giác bằng
√
3a
2
4
.
A
B C
A
1
B
1
C
1
A
2
B
2
C
2
○ Tam giác A
1
B
1
C
1
có cạnh
1
2
a nên S
1
=
Å
1
2
a
ã
2
·
√
3
4
=
a
2
√
3
16
.
○ Tam giác A
2
B
2
C
2
có cạnh
1
4
a =
1
2
2
a nên S
2
=
Å
1
2
2
a
ã
2
·
√
3
4
=
1
4
·
a
2
√
3
16
.
○ Tam giác A
3
B
3
C
3
có cạnh
1
8
a =
1
2
3
a nên S
3
=
Å
1
2
3
a
ã
2
·
√
3
4
=
1
4
2
·
a
2
√
3
16
.
381/764 381/764
Toán 11 theo chương trình GDPT2018
1. Giới hạn của dãy số
Biết làm, làm đúng, làm nhanh
382
○ ···
○ Như vậy tam giác A
n
B
n
C
n
có cạnh
1
2
n
a nên S
n
=
Å
1
2
n
a
ã
2
·
√
3
4
=
1
4
n−1
·
a
2
√
3
16
.
○ ···
Khi đó, dãy S
1
, S
2
, S
3
,··· là một cấp số nhân lùi vô hạn với số hạng đầu u
1
= S
1
=
a
2
√
3
16
và công bội q =
1
4
nên
S = S
1
+ S
2
+ ··· + S
n
+ ··· =
u
1
1 − q
=
a
2
√
3
16
1 −
1
4
=
a
2
√
3
12
.
Vậy S =
a
2
√
3
12
.
Chọn đáp án C □
Câu 83.
Tam giác mà ba đỉnh của nó là ba trung điểm ba cạnh của tam giác ABC
được gọi là tam giác trung bình của tam giác ABC. Ta xây dựng dãy các tam
giác A
1
B
1
C
1
, A
2
B
2
C
2
, A
3
B
3
C
3
, . . . sao cho A
1
B
1
C
1
là một tam giác giác đều
cạnh bằng 3 và với mỗi số nguyên dương n ≥ 2, tam giác A
n
B
n
C
n
là tam giác
trung bình của tam giác A
n−1
B
n−1
C
n−1
. Với mỗi số nguyên dương n, kí hiệu
S
n
tương ứng là diện tích hình tròn ngoại tiếp tam giác A
n
B
n
C
n
. Tính tổng
S = S
1
+ S
2
+ ··· + S
n
+ ···.
A
B C
A
1
B
1
C
1
A
2
B
2
C
2
A 4π. B 10π. C 11π. D 6π.
Lời giải.
Ta có: S
1
= π ·
Ç
3 ·
√
3
3
å
2
= 3π;
S
2
= π ·
Ç
3
2
·
√
3
3
å
2
=
3π
4
=
1
4
· S
1
;
S
3
= π ·
Ç
3
4
·
√
3
3
å
2
=
3π
16
=
1
4
· S
2
Ta có S
1
; S
2
; S
3
;. . . ;S
n
; . . . tạo thành cấp số nhân lùi vô hạn với số hạng đầu là S
1
= 3π và công bội q =
1
4
.
Suy ra S = S
1
+ S
2
+ ··· + S
n
+ ··· =
S
n
1 − q
=
3π
1 −
1
4
= 4π.
Chọn đáp án A □
Câu 84. Từ một hình vuông có diện tích là 1m
2
. Gọi A, B, C, D lần lượt là trung điểm bốn cạnh của hình
vuông, bạn Hùng dùng bút chì vẽ theo hình vuông ABCD để được hình vuông thứ hai. Bạn Hùng lại tiếp tục vẽ
theo bốn trung điểm các cạnh của hình vuông ABCD để được hình vuông thứ ba, và cứ tiếp tục như vậy. Tính
tổng diện tích tất cả các hình vuông đã có.
A 4. B 2. C 3. D
1
2
.
Lời giải.
382/764 382/764
Toán 11 theo chương trình GDPT2018
Chương 3. Giới hạn. Hàm số liên tục
Biết làm, làm đúng, làm nhanh
383
Đặt a = 1 là độ dài cạnh hình vuông, S
1
= 1 là diện tích hình
vuông ban đầu.
Do M , N là trung điểm hai cạnh của hình vuông nên MN =
a
√
2
2
⇒ S
2
= MN
2
=
a
2
2
=
S
1
2
=
1
2
.
Lại lấy trung điểm các cạnh của hình vuông MNP Q để
tiếp tục, khi đó, hình vuông mới sinh ra có diện tích là
S
3
=
Ç
MN
√
2
2
å
2
=
MN
2
2
=
S
1
4
=
1
4
.
Vậy các hình vuông sinh ra có diện tích lần lượt là 1,
1
2
,
1
4
, . . .,
1
2
n
, . . ..
Vậy tổng diện tích các hình vuông tạo thành là
S = 1 ·
1
1 −
1
2
= 2.
A C
B
D
Chọn đáp án B □
Câu 85. Người ta xếp các hình vuông kề với nhau như trong hình dưới đây, mỗi hình vuông có độ dài cạnh bằng
nửa độ dài cạnh của hình vuông trước nó. Nếu hình vuông đầu tiên có cạnh dài 10 cm thì trên tia Ax cần có một
đoạn thẳng dài bao nhiêu xentimet để có thể xếp được tất cả các hình vuông đó?
A
x
A 22. B 15. C 18. D 20.
Lời giải.
Tổng các cạnh nằm trên tia Ax của các hình vuông đó là
10 + 5 +
5
2
+
5
2
2
+ . . . =
10
1 −
1
2
= 20 cm.
Chọn đáp án D □
Câu 86.
Cho hình vuông C
1
có cạnh bằng a. Chia mỗi cạnh của hình vuông thành bốn
phần bằng nhau và nối các điểm chia một cách thích hợp để có hình vuông C
2
.
Từ hình vuông C
2
lại tiếp tục làm như trên ta nhận được dãy các hình vuông
C
1
, C
2
, C
3
,. . . Gọi S
i
là diện tích của hình vuông C
i
(i ∈ {1; 2; 3; . . .}). Đặt S =
S
1
+ S
2
+ ··· + S
n
+ ···. Biết S =
32
3
, tính a.
A 2. B
5
2
. C
√
2. D 2
√
2.
Lời giải.
Ta có S
1
= a
2
, hình vuông C
2
có cạnh bằng
Å
3a
4
ã
2
+
a
4
2
=
a
√
10
4
, do đó S
2
=
10a
2
16
. Bằng quy nạp ta chứng
383/764 383/764
Toán 11 theo chương trình GDPT2018
1. Giới hạn của dãy số
Biết làm, làm đúng, làm nhanh
384
minh được (S
n
) là một cấp số nhân lùi vô hạn với công bội q =
S
2
S
1
=
5
8
. Nên
S =
a
2
1 −
5
8
=
8a
2
3
=
32
3
⇔ a = 2.
Chọn đáp án A □
384/764 384/764
Toán 11 theo chương trình GDPT2018
Chương 3. Giới hạn. Hàm số liên tục
Biết làm, làm đúng, làm nhanh
385
GIỚI HẠN CỦA HÀM SỐ
2
Baâi söë
A–GIỚI HẠN HỮU HẠN CỦA HÀM SỐ TẠI MỘT ĐIỂM
1. Định nghĩa
c Định nghĩa 2.1. Cho khoảng K chứa điểm x
0
và hàm số f(x) xác định trên K hoặc trên K \{x
0
}. Hàm số
f(x) có giới hạn là số L khi x dần tới x
0
nếu với dãy số (x
n
) bất kì, x
n
∈ K \{x
0
} và x
n
→ x
0
thì f (x
n
) → L.
Kí hiệu lim
x→x
0
f(x) = L hay f(x) → L khi x → x
0
.
Nhận xét. lim
x→x
0
x = x
0
; lim
x→x
0
c = c, với c là hằng số.
Hàm số f(x) có thể không xác định tại x = x
0
nhưng vẫn tồn tại giới hạn của hàm số đó khi x dần tới x
0
.
2. Phép toán trên giới hạn hữu hạn của hàm số
c Định lí 2.1. Ta thừa nhận định lí sau:
a) Nếu lim
x→x
0
f(x) = L và lim
x→x
0
g(x) = M (L, M ∈ R) thì
• lim
x→x
0
[f(x) + g(x)] = L + M;
• lim
x→x
0
[f(x) − g(x)] = L − M;
• lim
x→x
0
[f(x) · g(x)] = L · M;
• lim
x→x
0
f(x)
g(x)
=
L
M
(nếu M = 0).
b) Nếu f(x) ≥ 0 và lim
x→x
0
f(x) = L thì L ≥ 0 và lim
x→x
0
p
f(x) =
√
L.
3. Giới hạn một phía
c Định nghĩa 2.2. Trong trường hợp tổng quát, ta có các định nghĩa sau:
• Cho hàm số y = f (x) xác định trên khoảng (a; x
0
).
Số L được gọi là giới hạn bên trái của hàm số y = f(x) khi x → x
0
nếu với dãy số (x
n
) bất kì, a < x
n
< x
0
và x
n
→ x
0
, ta có f (x
n
) → L.
Kí hiệu lim
x→x
−
0
f(x) = L.
• Cho hàm số y = f (x) xác định trên khoảng (x
0
; b).
Số L được gọi là giới hạn bên phải của hàm số y = f (x) khi x → x
0
nếu với dãy số (x
n
) bất kì,
x
0
< x
n
< b và x
n
→ x
0
, ta có f (x
n
) → L.
Kí hiệu lim
x→x
+
0
f(x) = L.
c Định lí 2.2. Định lí sau đây cho ta mối liên hệ giữa “giới hạn hai phía” lim
x→x
0
f(x) với giới hạn bên trái
lim
x→x
−
0
f(x) và giới hạn bên phải lim
x→x
+
0
f(x).
lim
x→x
0
f(x) = L khi và chỉ khi lim
x→x
−
0
f(x) = lim
x→x
+
0
f(x) = L.
385/764 385/764
Toán 11 theo chương trình GDPT2018
2. Giới hạn của hàm số
Biết làm, làm đúng, làm nhanh
386
B–GIỚI HẠN HỮU HẠN CỦA HÀM SỐ TẠI VÔ CỰC
c Định nghĩa 2.3. Trong trường hợp tổng quát, ta có định nghĩa sau
a) Cho hàm số y = f(x) xác định trên khoảng (a; +∞).
Ta nói hàm số y = f(x) có giới hạn là số L khi x → +∞ nếu với dãy số (x
n
) bất kì, x
n
> a và x
n
→ +∞,
ta có f (x
n
) → L.
Kí hiệu lim
x→+∞
f(x) = L hay f(x) → L khi x → +∞.
b) Cho hàm số y = f(x) xác định trên khoảng (−∞; a).
Ta nói hàm số y = f(x) có giới hạn là số L khi x → −∞ nếu với dãy số (x
n
) bất kì, x
n
< a và x
n
→ −∞,
ta có f (x
n
) → L.
Kí hiệu lim
x→−∞
f(x) = L hay f(x) → L khi x → −∞.
○ Với c, k là các hằng số và k nguyên dương, ta luôn có
lim
x→+∞
c = c; lim
x→−∞
c = c; lim
x→+∞
c
x
k
= 0; lim
x→−∞
c
x
k
= 0.
○ Các phép toán trên giới hạn hữu hạn của hàm số khi x → x
0
vẫn còn đúng khi x → +∞ hoặc x → −∞.
Ví dụ 1. Tính lim
x→+∞
2x + 1
x − 1
.
Lời giải.
Ta có
lim
x→+∞
2x + 1
x − 1
= lim
x→+∞
x
Å
2 +
1
x
ã
x
Å
1 −
1
x
ã
= lim
x→+∞
2 +
1
x
1 −
1
x
=
lim
x→+∞
2 + lim
x→+∞
1
x
lim
x→+∞
1 − lim
x→+∞
1
x
=
2 + 0
1 − 0
= 2.
□
C–GIỚI HẠN VÔ CỰC (MỘT PHÍA) CỦA HÀM SỐ TẠI MỘT ĐIỂM
c Định nghĩa 2.4. Trong trường hợp tổng quát, ta có định nghĩa sau:
a) Cho hàm số y = f(x) xác định trên khoảng (a; +∞).
Ta nói hàm số y = f(x) có giới hạn là +∞ khi x → a
+
nếu với dãy số (x
n
) bất kì, x
n
> a và x
n
→ a, ta
có f (x
n
) → +∞.
Kí hiệu lim
x→a
+
f(x) = +∞ hay f(x) → +∞ khi x → a
+
.
b) Các trường hợp lim
x→a
+
f(x) = −∞; lim
x→a
−
f(x) = +∞; lim
x→a
−
f(x) = −∞ được định nghĩa tương tự.
386/764 386/764
Toán 11 theo chương trình GDPT2018
Chương 3. Giới hạn. Hàm số liên tục
Biết làm, làm đúng, làm nhanh
387
Ta có hai giới hạn cơ bản sau
lim
x→a
+
1
x − a
= +∞; lim
x→a
−
1
x − a
= −∞.
Ví dụ 2. Tính lim
x→2
+
1
x − 2
.
Lời giải.
Ta có lim
x→2
+
1
x − 2
= +∞. □
D–GIỚI HẠN VÔ CỰC CỦA HÀM SỐ TẠI VÔ CỰC
c Định nghĩa 2.5. Trong trường hợp tổng quát, ta có định nghĩa sau
a) Cho hàm số y = f(x) xác định trên khoảng (a; +∞).
Ta nói hàm số y = f(x) có giới hạn là +∞ khi x → +∞ nếu với dãy số (x
n
) bất kì, x
n
> a và x
n
→ +∞,
ta có f (x
n
) → +∞.
Kí hiệu lim
x→+∞
f(x) = +∞ hay f(x) → +∞ khi x → +∞.
b) Các trường hợp lim
x→+∞
f(x) = −∞; lim
x→−∞
f(x) = +∞; lim
x→−∞
f(x) = −∞ được định nghĩa tương tự.
Ta có ba giới hạn cơ bản sau
○ lim
x→+∞
x
k
= +∞ với k là số nguyên dương.
○ lim
x→−∞
x
k
= +∞ với k là số nguyên dương chẵn.
○ lim
x→−∞
x
k
= −∞ với k là số nguyên dương lẻ.
Ví dụ 3. Tính lim
x→+∞
x
3
; lim
x→−∞
x
3
.
Lời giải.
Ta có lim
x→+∞
x
3
= +∞; lim
x→−∞
x
3
= −∞. □
E–CÁC DẠNG TOÁN THƯỜNG GẶP
Dạng 1. Tính giới hạn bằng định nghĩa
Áp dụng các định nghĩa về giới hạn hàm số.
1. Ví dụ mẫu
Ví dụ 4. Xét hàm số f (x) =
x
2
− 9
x − 3
(x = 3). Chứng minh rằng lim
x→3
f(x) = 6.
Lời giải.
Giả sử (x
n
) là dãy số bất kì, thoả mãn x
n
= 3 và lim x
n
= 3.
Ta có
lim f (x
n
) = lim
x
2
n
− 9
x
n
− 3
= lim
(x
n
− 3) (x
n
+ 3)
x
n
− 3
= lim (x
n
+ 3)
= lim x
n
+ lim 3
387/764 387/764
Toán 11 theo chương trình GDPT2018
2. Giới hạn của hàm số
Biết làm, làm đúng, làm nhanh
388
= 3 + 3
= 6.
Vậy lim
x→3
f(x) = 6. □
Ví dụ 5 (CTST). Cho hàm số f(x) =
x
2
− 4
x + 2
. Tìm lim
x→−2
f(x).
Lời giải.
Hàm số y = f(x) xác định trên R \ {−2}.
Giả sử (x
n
) là dãy số bất kì, thỏa mãn x
n
= −2 với mọi n và x
n
→ −2 khi n → +∞. Ta có
lim f (x
n
) = lim
x
2
n
− 4
x
n
+ 2
= lim
(x
n
− 2)(x
n
+ 2)
x
n
+ 2
= lim(x
n
− 2) = lim x
n
− 2 = −2 −2 = −4.
Vậy lim
x→−2
f(x) = −4. □
Ví dụ 6 (KNTT). Cho hàm số f(x) =
x − 1
x
2
− 1
. Chứng tỏ rằng lim
x→1
f(x) =
1
2
.
Lời giải.
Lấy dãy số (x
n
) bất kì sao cho x
n
= 1 và x
n
→ 1. Ta có f (x
n
) =
x
n
− 1
x
2
n
− 1
=
1
x
n
+ 1
.
Do đó lim
n→+∞
f (x
n
) = lim
n→+∞
1
x
n
+ 1
=
1
2
. Vậy lim
x→1
f(x) =
1
2
. □
Ví dụ 7 (CTST). Tìm các giới hạn sau:
lim
x→3
(2x
2
− x);a) lim
x→−1
x
2
+ 2x + 1
x + 1
.b)
Lời giải.
a) Đặt g(x) = 2x
2
− x.
Hàm số y = g(x) xác định trên R.
Giả sử (x
n
) là dãy số bất kì, thỏa mãn x
n
→ 3 khi n → +∞. Ta có
lim g(x
n
) = lim(2x
2
n
− x
n
) = 2 · (lim x
n
)
2
− lim x
n
= 2 · 3
2
− 3 = 15.
Vậy lim
x→3
g(x) = 15.
b) Đặt h(x) =
x
2
+ 2x + 1
x + 1
.
Hàm số y = h(x) xác định trên R \ {−1}.
Giả sử (x
n
) là dãy số bất kì, thỏa mãn x
n
= −1 với mọi n và x
n
→ −1 khi n → +∞. Ta có
lim h(x
n
) = lim
x
2
n
+ 2x
n
+ 1
x
n
+ 1
= lim(x
n
+ 1) = lim x
n
+ 1 = −1 + 1 = 0.
Vậy lim
x→−1
h(x) = 0.
□
2. Bài tập tự luận
Bài 1. Sử dụng định nghĩa, tìm các giới hạn sau
lim
x→−3
x
2
.a) lim
x→5
x
2
− 25
x − 5
.b)
Lời giải.
388/764 388/764
Toán 11 theo chương trình GDPT2018
Chương 3. Giới hạn. Hàm số liên tục
Biết làm, làm đúng, làm nhanh
389
a) Giả sử (x
n
) là dãy số bất kì, thõa mãn lim x
n
= −3. Ta có
lim x
2
n
= lim x
n
· lim x
n
= (−3) · (−3)
= 9.
Vậy lim
x→−3
x
2
= 9.
b) Giả sử (x
n
) là dãy số bất kì, thõa mãn x
n
= 5 và lim x
n
= 5. Ta có
lim
x
2
n
− 25
x
n
− 5
= lim
(x
n
− 5) (x
n+5
)
x
n
− 5
= lim(x
n
+ 5)
= lim x
n
+ lim 5
= 5 + 5
= 10.
Vậy lim
x→5
x
2
− 25
x − 5
= 10.
□
Bài 2. Cho hàm số f (x) =
x
2
− 4
x + 2
. Tìm lim
x→−2
f(x).
Lời giải.
Hàm số y = f(x) xác định trên R \ {−2}.
Giả sử (x
n
) là dãy số bất kì, thỏa mãn x
n
= −2 với mọi n và x
n
→ −2 khi n → +∞.
Ta có lim f(x
n
) = lim
x
2
n
− 4
x
n
+ 2
= lim
(x
n
− 2)(x
n
+ 2)
x
n
+ 2
= lim(x
n
− 2) = −2 −2 = −4.
Vậy lim
x→−2
f(x) = −4. □
Bài 3. Cho hàm số f (x) =
2x − 1
x + 2
. Tìm lim
x→+∞
f(x).
Lời giải.
Hàm số xác định trên (−∞; −2) và (−2; +∞).
Giả sử (x
n
) là dãy số sao cho x
n
> −2 và x
n
→ +∞. Ta có
lim f (x
n
) = lim
2x
n
− 1
x
n
+ 2
= lim
2 −
1
x
n
1 +
2
x
n
=
2 − lim
1
x
n
1 + lim
2
x
n
=
2 − 0
1 + 0
= 2.
Vậy lim
x→+∞
f(x) = 2. □
Dạng 2. Các phép toán về giới hạn hàm số
a) Nếu lim
x→x
0
f(x) = L và lim
x→x
0
g(x) = M (L, M ∈ R) thì
• lim
x→x
0
[f(x) + g(x)] = L + M;
• lim
x→x
0
[f(x) − g(x)] = L − M;
• lim
x→x
0
[f(x) · g(x)] = L · M;
• lim
x→x
0
f(x)
g(x)
=
L
M
(nếu M = 0).
b) Nếu f(x) ≥ 0 và lim
x→x
0
f(x) = L thì L ≥ 0 và lim
x→x
0
p
f(x) =
√
L.
c) Các phép toán trên giới hạn hữu hạn của hàm số khi x → x
0
vẫn còn đúng khi x → +∞ hoặc x → −∞.
389/764 389/764
Toán 11 theo chương trình GDPT2018
2. Giới hạn của hàm số
Biết làm, làm đúng, làm nhanh
390
1. Ví dụ mẫu
Ví dụ 8 (Cánh Diều). Tính:
lim
x→2
x
2
+ x −6
;a) lim
x→1
x
2
+ 2x + 3
2x − 1
.b)
Lời giải.
a)
lim
x→2
x
2
+ x −6
= lim
x→2
x
2
+ lim
x→2
x − lim
x→2
6
= 4 + 2 − 6
= 0.
b)
lim
x→1
x
2
+ 2x + 3
2x − 1
=
lim
x→1
x
2
+ 2x + 3
lim
x→1
(2x − 1)
=
lim
x→1
x
2
+ lim
x→1
(2x) + lim
x→1
3
lim
x→1
(2x) − lim
x→1
1
=
1 + 2 + 3
2 − 1
= 6.
□
Ví dụ 9 (CTST). Tính các giới hạn sau:
lim
x→1
(x
2
− 4x + 2);a) lim
x→2
3x − 2
2x + 1
.b)
Lời giải.
a) lim
x→1
(x
2
− 4x + 2) = lim
x→1
x
2
− lim
x→1
(4x) + lim
x→1
2 = 1
2
− 4 lim
x→1
x + 2 = 1 −4 · 1 + 2 = −1;
b) lim
x→2
3x − 2
2x + 1
=
lim
x→2
(3x − 2)
lim
x→2
(2x + 1)
=
3 lim
x→2
x − 2
2 lim
x→2
x + 1
=
3 · 2 −2
2 · 2 + 1
=
4
5
.
□
Ví dụ 10 (CTST). Tính các giới hạn sau (khử dạng vô định):
lim
x→2
x
2
− 4
x − 2
;a) lim
x→3
√
x + 1 −2
x − 3
.b)
Lời giải.
a) lim
x→2
x
2
− 4
x − 2
= lim
x→2
(x − 2)(x + 2)
x − 2
= lim
x→2
(x + 2) = lim
x→2
x + lim
x→2
2 = 2 + 2 = 4.
b) lim
x→3
√
x + 1 −2
x − 3
.
lim
x→3
√
x + 1 −2
x − 3
= lim
x→3
√
x + 1 −2
√
x + 1 + 2
(x − 3)
√
x + 1 + 2
Ä
nhân cả tử và mẫu cho
Ä
√
x + 1 + 2
ää
= lim
x→3
(x + 1) −4
(x − 3)
√
x + 1 + 2
= lim
x→3
1
√
x + 1 + 2
=
1
lim
x→3
√
x + 1 + 2
=
1
lim
x→3
√
x + 1 + 2
=
1
q
lim
x→3
(x + 1) + 2
=
1
√
3 + 1 + 2
=
1
4
.
390/764 390/764
Toán 11 theo chương trình GDPT2018
Chương 3. Giới hạn. Hàm số liên tục
Biết làm, làm đúng, làm nhanh
391
□
Ví dụ 11 (CTST). Tính các giới hạn sau:
lim
x→−2
(x
2
+ 5x −2);a) lim
x→1
x
2
− 1
x − 1
.b)
Lời giải.
a) lim
x→−2
(x
2
+ 5x −2) = ( lim
x→−2
x)
2
+ lim
x→−2
(5x) − lim
x→−2
2 = (−2)
2
+ 5 ·(−2) − 2 = −8.
b) lim
x→1
x
2
− 1
x − 1
= lim
x→1
(x − 1)(x + 1)
(x − 1)
= lim
x→1
(x + 1) = lim
x→1
x + 1 = 1 + 1 = 2.
□
Ví dụ 12 (TH). Tính giới hạn lim
x→+∞
x
4
+ 7
x
4
+ 1
.
Lời giải.
Ta có lim
x→+∞
x
4
+ 7
x
4
+ 1
= lim
x→+∞
x
4
Å
1 +
7
x
4
ã
x
4
Å
1 +
1
x
4
ã
= lim
x→+∞
1 +
7
x
4
1 +
1
x
4
= 1. □
Ví dụ 13 (TH). Tìm giới hạn lim
x→+∞
x
2
+ 1
2x
4
+ x
2
− 3
.
Lời giải.
Ta có lim
x→+∞
x
2
+ 1
2x
4
+ x
2
− 3
= lim
x→+∞
x
x
2
·
Œ
1
x
2
+
1
x
4
2 +
1
x
2
−
3
x
4
= lim
x→+∞
1
x
·
Œ
1
x
2
+
1
x
4
2 +
1
x
2
−
3
x
4
= 0. □
Ví dụ 14 (TH). Tính giới hạn lim
x→1
Å
1
1 − x
−
3
1 − x
3
ã
.
Lời giải.
lim
x→1
Å
1
1 − x
−
3
1 − x
3
ã
= lim
x→1
1 + x + x
2
− 3
1 − x
3
= lim
x→1
(x − 1)(x + 2)
(1 − x) (1 + x + x
2
)
= lim
x→1
−(x + 2)
1 + x + x
2
= −1. □
Ví dụ 15 (VDT). Cho m, n là các số thực khác 0. Nếu giới hạn lim
x→−5
x
2
+ mx + n
x + 5
= 3, hãy tìm mn.
Lời giải.
Vì lim
x→−5
x
2
+ mx + n
x − 5
= 3 nên x = −5 là nghiệm của phương trình x
2
+ mx + n = 0.
⇒ −5m + n + 25 = 0 ⇔ n = 5m −25.
Khi đó lim
x→−5
x
2
+ mx + n
x − 1
= lim
x→−5
x
2
+ mx + 5m − 25
x + 5
= lim
x→−5
(x + 5)(x −5 + m)
x + 5
= lim
x→−5
(x − 5 + m) = m − 10.
Ta có m −10 = 3 ⇔ m = 13 ⇒ n = 40.
Vậy mn = 13 · 40 = 520. □
Ví dụ 16 (VDT). Tìm số thực a thỏa mãn lim
x→+∞
a
√
2x
2
+ 3 + 2024
2x + 2023
=
1
2
.
Lời giải.
Ta có lim
x→+∞
a
√
2x
2
+ 3 + 2024
2x + 2023
=
1
2
⇔ lim
x→+∞
a
…
2 +
3
x
2
+
2024
x
2 +
2023
x
=
1
2
⇔
a
√
2
2
=
1
2
⇔ a =
√
2
2
. □
391/764 391/764
Toán 11 theo chương trình GDPT2018
2. Giới hạn của hàm số
Biết làm, làm đúng, làm nhanh
392
2. Bài tập tự luận
Bài 4. Biết rằng hàm số f (x) thoả mãn lim
x→2
−
f(x) = 3 và lim
x→2
+
f(x) = 5. Trong trường hợp này có tồn tại giới
hạn lim
x→2
f(x) hay không? Giải thích.
Lời giải.
Ta có lim
x→2
−
f(x) = 3 và lim
x→2
+
f(x) = 5, do đó lim
x→2
−
f(x) = lim
x→2
+
f(x).
Vậy không tồn tại lim
x→2
f(x). □
Bài 5. Tính các giới hạn sau
lim
x→2
x
2
− 4x + 3
;a) lim
x→3
x
2
− 5x + 6
x − 3
;b) lim
x→1
√
x − 1
x − 1
.c)
Lời giải.
a)
lim
x→2
x
2
− 4x + 3
= lim
x→2
x
2
− lim
x→2
(4x) + lim
x→2
3
= 4 − 8 + 3
= −1.
b)
lim
x→3
x
2
− 5x + 6
x − 3
lim
x→3
(x − 2)(x −3)
x − 3
= lim
x→3
(x − 2)
= lim
x→3
x − lim
x→3
2
= 3 − 2
= 1.
c)
lim
x→1
√
x − 1
x − 1
= lim
x→1
√
x − 1
(
√
x + 1) (
√
x − 1)
= lim
x→1
1
√
x + 1
=
lim
x→1
1
lim
x→1
√
x + lim
x→1
1
=
1
1 + 1
=
1
2
.
□
Bài 6. Tính các giới hạn sau
lim
x→+∞
9x + 1
3x − 4
;a) lim
x→−∞
7x − 11
2x + 3
;b) lim
x→+∞
√
x
2
+ 1
x
;c)
lim
x→−∞
√
x
2
+ 1
x
;d) lim
x→6
−
1
x − 6
;e) lim
x→7
+
1
x − 7
.f)
Lời giải.
392/764 392/764
Toán 11 theo chương trình GDPT2018
Chương 3. Giới hạn. Hàm số liên tục
Biết làm, làm đúng, làm nhanh
393
a)
lim
x→+∞
9x + 1
3x − 4
= lim
x→+∞
x
Å
9 +
1
x
ã
x
Å
3 −
4
x
ã
= lim
x→+∞
9 +
1
x
3 −
4
x
=
lim
x→+∞
9 + lim
x→+∞
1
x
lim
x→+∞
3 − lim
x→+∞
4
x
=
9 + 0
3 − 0
= 3.
b)
lim
x→−∞
7x − 11
2x + 3
= lim
x→−∞
x
Å
7 −
11
x
ã
x
Å
2 +
3
x
ã
= lim
x→−∞
=
7 −
11
x
2 +
3
x
=
lim
x→−∞
7 − lim
x→−∞
11
x
lim
x→−∞
2 + lim
x→−∞
3
x
=
7 − 0
2 + 0
=
7
2
.
c)
lim
x→+∞
√
x
2
+ 1
x
= lim
x→+∞
x
…
1 +
1
x
2
x
= lim
x→+∞
…
1 +
1
x
2
=
lim
x→+∞
1 + lim
x→+∞
1
x
2
=
√
1 + 0
= 1.
d)
lim
x→−∞
√
x
2
+ 1
x
= lim
x→−∞
−x
…
1 +
1
x
2
x
= lim
x→−∞
−
…
1 +
1
x
2
393/764 393/764
Toán 11 theo chương trình GDPT2018
2. Giới hạn của hàm số
Biết làm, làm đúng, làm nhanh
394
= −
lim
x→−∞
1 + lim
x→−∞
1
x
2
= −
√
1 + 0
= −1.
e) lim
x→6
−
1
x − 6
= −∞
f) lim
x→7
+
1
x − 7
= +∞.
□
Bài 7. Tìm các giới hạn sau
lim
x→−2
(x
2
− 7x + 4);a) lim
x→3
x − 3
x
2
− 9
;b) lim
x→1
3 −
√
x + 8
x − 1
.c)
Lời giải.
a) lim
x→−2
(x
2
− 7x + 4) = lim
x→−2
x
2
− 7 lim
x→−2
x + lim
x→−2
4 = (−2)
2
− 7 ·(−2) + 4 = 22.
b) lim
x→3
x − 3
x
2
− 9
= lim
x→3
x − 3
(x − 3)(x + 3)
= lim
x→3
1
x + 3
=
1
lim
x→3
(x + 3)
=
1
lim
x→3
x + 3
=
1
3 + 3
=
1
6
.
c) Ta có
lim
x→1
3 −
√
x + 8
x − 1
= lim
x→1
3 −
√
x + 8
3 +
√
x + 8
(x − 1)
3 +
√
x + 8
= lim
x→1
9 − (x + 8)
(x − 1)
3 +
√
x + 8
= lim
x→1
−1
3 +
√
x + 8
=
−1
lim
x→1
3 +
√
x + 8
=
−1
3 + lim
x→1
√
x + 8
=
−1
3 +
√
1 + 8
=
−1
3 + 3
=
−1
6
.
□
Bài 8. Tìm các giới hạn sau
lim
x→+∞
4x + 3
2x
;a) lim
x→−∞
2
3x + 1
;b) lim
x→+∞
√
x
2
+ 1
x + 1
.c)
Lời giải.
a) lim
x→+∞
4x + 3
2x
= lim
x→+∞
4 +
3
x
2
=
lim
x→+∞
Å
4 +
3
x
ã
lim
x→+∞
2
=
4 + lim
x→+∞
3
x
2
=
4 + 0
2
= 2.
394/764 394/764
Toán 11 theo chương trình GDPT2018
Chương 3. Giới hạn. Hàm số liên tục
Biết làm, làm đúng, làm nhanh
395
b) lim
x→−∞
2
3x + 1
= lim
x→−∞
2
x
3 +
1
x
=
lim
x→−∞
2
x
3 + lim
x→−∞
1
x
=
0
3 + 0
= 0.
c) Ta có
lim
x→+∞
√
x
2
+ 1
x + 1
= lim
x→+∞
|x|
…
1 +
1
x
2
x + 1
= lim
x→+∞
x
…
1 +
1
x
2
x
Å
1 +
1
x
ã
= lim
x→+∞
…
1 +
1
x
2
1 +
1
x
=
lim
x→+∞
…
1 +
1
x
2
lim
x→+∞
Å
1 +
1
x
ã
=
…
1 + lim
x→+∞
1
x
2
1 + lim
x→+∞
1
x
=
√
1 + 0
1 + 0
= 1.
□
Bài 9. Tính các giới hạn sau
lim
x→+∞
9x + 1
3x − 4
;a) lim
x→−∞
7x − 11
2x + 3
;b) lim
x→+∞
√
x
2
+ 1
x
;c)
lim
x→−∞
√
x
2
+ 1
x
;d) lim
x→6
−
1
x − 6
;e) lim
x→7
+
1
x − 7
.f)
Lời giải.
a)
lim
x→+∞
9x + 1
3x − 4
= lim
x→+∞
x
Å
9 +
1
x
ã
x
Å
3 −
4
x
ã
= lim
x→+∞
9 +
1
x
3 −
4
x
=
lim
x→+∞
9 + lim
x→+∞
1
x
lim
x→+∞
3 − lim
x→+∞
4
x
=
9 + 0
3 − 0
= 3.
b)
lim
x→−∞
7x − 11
2x + 3
= lim
x→−∞
x
Å
7 −
11
x
ã
x
Å
2 +
3
x
ã
= lim
x→−∞
=
7 −
11
x
2 +
3
x
395/764 395/764
Toán 11 theo chương trình GDPT2018
2. Giới hạn của hàm số
Biết làm, làm đúng, làm nhanh
396
=
lim
x→−∞
7 − lim
x→−∞
11
x
lim
x→−∞
2 + lim
x→−∞
3
x
=
7 − 0
2 + 0
=
7
2
.
c)
lim
x→+∞
√
x
2
+ 1
x
= lim
x→+∞
x
…
1 +
1
x
2
x
= lim
x→+∞
…
1 +
1
x
2
=
lim
x→+∞
1 + lim
x→+∞
1
x
2
=
√
1 + 0
= 1.
d)
lim
x→−∞
√
x
2
+ 1
x
= lim
x→−∞
−x
…
1 +
1
x
2
x
= lim
x→−∞
−
…
1 +
1
x
2
= −
lim
x→−∞
1 + lim
x→−∞
1
x
2
= −
√
1 + 0
= −1.
e) lim
x→6
−
1
x − 6
= −∞
f) lim
x→7
+
1
x − 7
= +∞.
□
Bài 10. Tính các giới hạn sau:
a) lim
x→+∞
1 − 2x
√
x
2
+ 1
.
b) lim
x→+∞
Ä
√
x
2
+ x + 2 − x
ä
.
Lời giải.
a) Ta có
lim
x→+∞
1 − 2x
√
x
2
+ 1
= − lim
x→+∞
4x
2
− 4x + 1
x
2
+ 1
= − lim
x→+∞
…
4 −
4x
x
2
+ 1
+
1
x
2
+ 1
396/764 396/764
Toán 11 theo chương trình GDPT2018
Chương 3. Giới hạn. Hàm số liên tục
Biết làm, làm đúng, làm nhanh
397
= −
4 − lim
x→+∞
4x
x
2
+ 1
+ lim
x→+∞
1
x
2
+ 1
= −
Œ
4 − lim
x→+∞
4
x
1 +
1
x
2
+ lim
x→+∞
1
x
2
1 +
1
x
2
= −2.
b) Ta có
p
x
2
+ x + 2 − x =
Ä
√
x
2
+ x + 2
ä
2
− x
2
√
x
2
+ x + 2 + x
=
x + 2
√
x
2
+ x + 2 + x
=
x ·
Å
1 +
2
x
ã
x ·
Ç
…
1 +
1
x
+
2
x
2
+ 1
å
=
1 +
2
x
…
1 +
1
x
+
2
x
2
+ 1
.
Khi đó lim
x→+∞
Ä
√
x
2
+ x + 2 − x
ä
= lim
x→+∞
1 +
2
x
…
1 +
1
x
+
2
x
2
+ 1
=
1
1 + 1
=
1
2
.
□
Bài 11. Tính các giới hạn sau:
a) lim
x→0
(x + 2)
2
− 4
x
.
b) lim
x→0
√
x
2
+ 9 −3
x
2
.
Lời giải.
a) lim
x→0
(x + 2)
2
− 4
x
= lim
x→0
x
2
+ 4x
x
= lim
x→0
(x + 4) = 4.
b) lim
x→0
√
x
2
+ 9 −3
x
2
= lim
x→0
x
2
x
2
·
Ä
√
x
2
+ 9 + 3
ä
= lim
x→0
1
√
x
2
+ 9 + 3
=
1
6
.
□
Bài 12. Tính các giới hạn sau
lim
x→1
(x
2
− 4x + 2);a) lim
x→2
3x − 2
2x + 1
.b)
Lời giải.
a) lim
x→1
(x
2
− 4x + 2) = lim
x→1
x
2
− lim
x→1
(4x) + lim
x→1
2 = 1
2
− 4 lim
x→1
x + 2 = 1 −4 · 1 + 2 = −1;
b) lim
x→2
3x − 2
2x + 1
=
lim
x→2
(3x − 2)
lim
x→2
(2x + 1)
=
3 lim
x→2
x − 2
2 lim
x→2
x + 1
=
3 · 2 −2
2 · 2 + 1
=
4
5
.
□
Bài 13. Tìm các giới hạn sau
lim
x→3
x
2
x
3
− x −6
.a) lim
x→−2
3
2x
4
+ 3x + 2
x
2
− x + 2
.b)
397/764 397/764
Toán 11 theo chương trình GDPT2018
2. Giới hạn của hàm số
Biết làm, làm đúng, làm nhanh
398
Lời giải.
a) lim
x→3
x
2
x
3
− x −6
; do lim
x→3
x
2
x
3
− x −6
=
3
2
3
3
− 3 −6
=
1
2
> 0
⇒ lim
x→3
x
2
x
3
− x −6
=
…
1
2
=
√
2
2
.
b) lim
x→−2
3
2x
4
+ 3x + 2
x
2
− x + 2
; do lim
x→−2
2x
4
+ 3x + 2
x
2
− x + 2
=
7
2
⇒ lim
x→−2
3
2x
4
+ 3x + 2
x
2
− x + 2
=
3
…
7
2
=
3
√
28
2
.
□
Bài 14. Cho f(x) là một đa thức thỏa mãn lim
x→1
f(x) − 16
x − 1
= 24. Tính giới hạn sau
lim
x→1
f(x) − 16
(x − 1)
Ä
p
2f(x) + 4 + 6
ä
.
Lời giải.
Vì lim
x→1
f(x) − 16
x − 1
= 24 nên f(1) = 16. Khi đó
lim
x→1
f(x) − 16
(x − 1)
Ä
p
2f(x) + 4 + 6
ä
=
1
12
· lim
x→1
f(x) − 16
x − 1
= 2.
□
Bài 15. Tính các giới hạn sau:
lim
x→−2
(x
2
+ 5x −2);a) lim
x→1
x
2
− 1
x − 1
.b)
Lời giải.
a) lim
x→−2
(x
2
+ 5x −2) = ( lim
x→−2
x)
2
+ lim
x→−2
(5x) − lim
x→−2
2 = (−2)
2
+ 5 ·(−2) − 2 = −8.
b) lim
x→1
x
2
− 1
x − 1
= lim
x→1
(x − 1)(x + 1)
(x − 1)
= lim
x→1
(x + 1) = lim
x→1
x + 1 = 1 + 1 = 2.
□
Bài 16. Tính các giới hạn sau
lim
x→−1
(3x
2
− 2x + 1).a) lim
x→2
(x
3
− 3x)(x + 1)
x
2
+ 3
.b)
Lời giải.
a) lim
x→−1
(3x
2
− 2x + 1) = 3 lim
x→−1
x
2
− 2 lim
x→−1
x + lim
x→−1
1 = 3(1)
2
− 2 ·1 + 1 = 2.
b) Do lim
x→2
(x
2
+ 3) = 2
2
+ 3 = 7 = 0 và
lim
x→2
(x
3
− 3x)(x + 1) = lim
x→2
(x
3
− 3x) · lim
x→2
(x + 1) = (2
3
− 3 ·2) · (2 + 1) = 6
Nên lim
x→2
(x
3
− 3x)(x + 1)
x
2
+ 3
=
6
7
.
□
Bài 17. Tìm các giới hạn sau
lim
x→2
…
2
x
2
− x + 3
.a) lim
x→−3
3
…
−5
x
2
+ x −12
.b)
398/764 398/764
Toán 11 theo chương trình GDPT2018
Chương 3. Giới hạn. Hàm số liên tục
Biết làm, làm đúng, làm nhanh
399
Lời giải.
a) lim
x→2
…
x
x
2
− x + 3
; do lim
x→2
2
x
2
− x + 3
=
2
2
2
− 2 + 3
=
2
5
> 0
⇒ lim
x→2
…
2
x
2
− x + 3
=
…
2
5
=
√
10
5
.
b) lim
x→−3
3
…
−5
x
2
+ x −12
; do lim
x→−3
−5
x
2
+ x −12
=
5
6
⇒ lim
x→−3
3
…
−5
x
2
+ x −12
=
3
…
5
6
=
3
√
180
6
.
□
Bài 18. Cho f(x) = x − 1 và g(x) = x
3
. Tính các giới hạn sau:
a) lim
x→1
[3f(x) − g(x)].
b) lim
x→1
[f(x)]
2
g(x)
.
Lời giải.
Ta có lim
x→1
f(x) = lim
x→1
(x − 1) = lim
x→1
x − lim
x→1
1 = 1 − 1 = 0. Mặt khác, ta thấy lim
x→1
g(x) = lim
x→1
x
3
= 1.
a) Ta có
lim
x→1
[3f(x) − g(x)] = lim
x→1
[3f(x)] − lim
x→1
g(x) = lim
x→1
3 · lim
x→1
f(x) − lim
x→1
g(x) = 3 ·0 −1 = −1.
b) Ta có
lim
x→1
[f(x)]
2
g(x)
=
lim
x→1
[f(x)]
2
lim
x→1
g(x)
=
lim
x→1
f(x) · lim
x→1
f(x)
lim
x→1
g(x)
=
0
1
= 0.
□
Bài 19 (NB). Tính giới hạn lim
x→3
x
2
− 9
x − 3
.
Lời giải.
Ta có lim
x→3
x
2
− 9
x − 3
= lim
x→3
(x − 3)(x + 3)
x − 3
= lim
x→3
(x + 3) = 6. □
Bài 20 (TH). Tính giới hạn I = lim
x→2
x
2
− 5x + 6
x − 2
.
Lời giải.
I = lim
x→2
x
2
− 5x + 6
x − 2
= lim
x→2
(x − 2)(x −3)
x − 2
= lim
x→2
(x − 3) = −1. □
Bài 21 (TH). Tính giới hạn lim
x→+∞
x
4
+ 7
x
4
+ 1
.
Lời giải.
Ta có lim
x→+∞
x
4
+ 7
x
4
+ 1
= lim
x→+∞
x
4
Å
1 +
7
x
4
ã
x
4
Å
1 +
1
x
4
ã
= lim
x→+∞
1 +
7
x
4
1 +
1
x
4
= 1. □
Bài 22 (TH). Tìm giới hạn lim
x→+∞
x
2
+ 1
2x
4
+ x
2
− 3
.
Lời giải.
Ta có lim
x→+∞
x
2
+ 1
2x
4
+ x
2
− 3
= lim
x→+∞
x
x
2
·
Œ
1
x
2
+
1
x
4
2 +
1
x
2
−
3
x
4
= lim
x→+∞
1
x
·
Œ
1
x
2
+
1
x
4
2 +
1
x
2
−
3
x
4
= 0. □
399/764 399/764
Toán 11 theo chương trình GDPT2018
2. Giới hạn của hàm số
Biết làm, làm đúng, làm nhanh
400
Bài 23 (TH). Tính giới hạn lim
x→1
Å
1
1 − x
−
3
1 − x
3
ã
.
Lời giải.
lim
x→1
Å
1
1 − x
−
3
1 − x
3
ã
= lim
x→1
1 + x + x
2
− 3
1 − x
3
= lim
x→1
(x − 1)(x + 2)
(1 − x) (1 + x + x
2
)
= lim
x→1
−(x + 2)
1 + x + x
2
= −1. □
Bài 24 (VDT). Cho m, n là các số thực khác 0. Nếu giới hạn lim
x→−5
x
2
+ mx + n
x + 5
= 3, hãy tìm mn.
Lời giải.
Vì lim
x→−5
x
2
+ mx + n
x − 5
= 3 nên x = −5 là nghiệm của phương trình x
2
+ mx + n = 0.
⇒ −5m + n + 25 = 0 ⇔ n = 5m −25.
Khi đó lim
x→−5
x
2
+ mx + n
x − 1
= lim
x→−5
x
2
+ mx + 5m − 25
x + 5
= lim
x→−5
(x + 5)(x −5 + m)
x + 5
= lim
x→−5
(x − 5 + m) = m − 10.
Ta có m −10 = 3 ⇔ m = 13 ⇒ n = 40.
Vậy mn = 13 · 40 = 520. □
Bài 25 (VDT). Tìm số thực a thỏa mãn lim
x→+∞
a
√
2x
2
+ 3 + 2024
2x + 2023
=
1
2
.
Lời giải.
Ta có lim
x→+∞
a
√
2x
2
+ 3 + 2024
2x + 2023
=
1
2
⇔ lim
x→+∞
a
…
2 +
3
x
2
+
2024
x
2 +
2023
x
=
1
2
⇔
a
√
2
2
=
1
2
⇔ a =
√
2
2
. □
Bài 26 (NB). Tính lim
x→2
x
2
− 4
x − 2
.
Lời giải.
lim
x→2
x
2
− 4
x − 2
= lim
x→2
(x − 2)(x + 2)
x − 2
= lim
x→2
(x + 2) = 2 + 2 = 4. □
Bài 27 (NB). Tính lim
x→5
x
2
− 12x + 35
25 − 5x
.
Lời giải.
Ta có lim
x→5
x
2
− 12x + 35
25 − 5x
= lim
x→5
(x − 7)(x −5)
5(5 − x)
= lim
x→5
7 − x
5
=
2
5
.
Vậy lim
x→5
x
2
− 12x + 35
25 − 5x
=
2
5
. □
Bài 28 (TH). Tính giới hạn I = lim
x→2
x
3
− 8
x
2
− 4
.
Lời giải.
Ta có I = lim
x→2
x
3
− 8
x
2
− 4
= lim
x→2
(x − 2)
x
2
+ 2x + 4
(x − 2)(x + 2)
= lim
x→2
x
2
+ 2x + 4
x + 2
=
12
4
= 3. □
Bài 29 (TH). Tìm giới hạn A = lim
x→2
x
4
− 5x
2
+ 4
x
3
− 8
.
Lời giải.
Ta có
A = lim
x→2
x
4
− 5x
2
+ 4
x
3
− 8
= lim
x→2
x
2
− 1
x
2
− 4
x
3
− 2
3
= lim
x→2
x
2
− 1
(x − 2) (x + 2)
(x − 2) (x
2
+ 2x + 4)
= lim
x→2
x
2
− 1
(x + 2)
x
2
+ 2x + 4
400/764 400/764
Toán 11 theo chương trình GDPT2018
Chương 3. Giới hạn. Hàm số liên tục
Biết làm, làm đúng, làm nhanh
401
= 1.
□
Bài 30 (TH). Tìm giới hạn lim
x→−∞
1 + 3x
√
2x
2
+ 3
.
Lời giải.
Ta có lim
x→−∞
1 + 3x
√
2x
2
+ 3
= lim
x→−∞
x ·
Å
1
x
+ 3
ã
−x ·
Ç
…
2 +
3
x
å
= lim
x→−∞
1
x
+ 3
−
…
2 +
3
x
= −
3
√
2
2
. □
Bài 31 (TH). Tìm giới hạn lim
x→+∞
2x −
√
3x
2
+ 2
5x +
√
x
2
+ 2
.
Lời giải.
Ta có lim
x→+∞
2x −
√
3x
2
+ 2
5x +
√
x
2
+ 2
= lim
x→+∞
x
x
·
2 −
…
3 +
2
x
2
5 +
…
1 +
2
x
2
= lim
x→+∞
2 −
…
3 +
2
x
2
5 +
…
1 +
2
x
2
=
2 −
√
3
6
. □
Bài 32 (VDT). Giá trị của lim
x→1
x
2024
+ x −2
x
2023
+ x −2
bằng
a
b
, với
a
b
là phân số tối giản. Tính giá trị của a
2
− b
2
.
Lời giải.
Ta có
lim
x→1
x
2024
+ x −2
x
2023
+ x −2
= lim
x→1
x
2024
− 1 + x − 1
x
2023
− 1 + x − 1
= lim
x→1
(x − 1)(x
2023
+ x
2022
··· + x + 1) + x − 1
(x − 1)(x
2022
+ x
2021
+ ··· + x + 1) + x − 1
= lim
x→1
x
2023
+ x
2022
··· + x + 2
x
2022
+ x
2021
+ ··· + x + 2
=
1 + 1 + ···+ 1 + 2
1 + 1 + ···+ 1 + 2
=
2025
2024
.
Vậy a
2
− b
2
= 2025
2
− 2024
2
= 4049. □
Bài 33 (VDT). Cho giới hạn lim
x→3
x
2
+ ax + b
x − 3
= 3. Tìm a, b.
Lời giải.
Để lim
x→3
x
2
+ ax + b
x − 3
= 3 thì ta phải có x
2
+ ax + b = (x − 3)(x −m).
Khi đó 3 − m = 3 ⇔ m = 0. Vậy x
2
+ ax + b = (x − 3)x = x
2
− 3x.
Suy ra a = −3 và b = 0. □
Bài 34 (VDT). Tìm m để lim
x→−∞
√
4x
2
+ x + 1 + 4
mx − 2
=
1
2
.
Lời giải.
Ta có lim
x→−∞
√
4x
2
+ x + 1 + 4
mx − 2
= lim
x→−∞
−x
x
·
…
4 +
1
x
+
1
x
2
−
4
x
m −
2
x
= lim
x→−∞
−
…
4 +
1
x
+
1
x
2
+
4
x
m −
2
x
= −
2
m
.
Theo bài ra ta có −
2
m
=
1
2
⇔ m = −4. □
Bài 35 (VDC). Tính giới hạn lim
x→1
Å
m
1 − x
m
−
n
1 − x
n
ã
, m, n ∈ N
∗
.
Lời giải.
lim
x→1
Å
m
1 − x
m
−
n
1 − x
n
ã
= lim
x→1
ïÅ
m
1 − x
m
−
1
1 − x
ã
−
Å
n
1 − x
n
−
1
1 − x
ãò
401/764 401/764
Toán 11 theo chương trình GDPT2018
2. Giới hạn của hàm số
Biết làm, làm đúng, làm nhanh
402
= lim
x→1
Å
m
1 − x
m
−
1
1 − x
ã
− lim
x→1
Å
n
1 − x
n
−
1
1 − x
ã
= A − B.
A = lim
x→1
Å
m
1 − x
m
−
1
1 − x
ã
= lim
x→1
m −
1 + x + x
2
+ ··· + x
m−1
1 − x
m
= lim
x→1
(1 − x) +
1 − x
2
+ ··· +
1 − x
m−1
1 − x
m
= lim
x→1
(1 − x)
1 + (1 + x) + ··· +
1 + x + ···+ x
m−2

(1 − x) (1 + x + ···+ x
m−1
)
= lim
x→1
1 + (1 + x) + ··· +
1 + x + ···+ x
m−2
1 + x + ···+ x
m−1
= lim
x→1
1 + 2 + ···+ m − 1
m
=
m − 1
2
.
Tương tự, ta tính được B =
n − 1
2
.
Vậy lim
x→1
Å
m
1 − x
m
−
n
1 − x
n
ã
= A − B =
m − n
2
. □
Bài 36. Cho P = lim
x→2
√
x + 2 −2
x − 2
. Tính P .
A P =
1
4
. B P =
1
2
. C P = 1. D P = 0.
Lời giải.
Ta có: lim
x→2
√
x + 2 −2
x − 2
= lim
x→2
x − 2
(x − 2)
√
x + 2 + 2
= lim
x→2
1
√
x + 2 + 2
=
1
4
.
Vậy P =
1
4
.
Chọn đáp án A □
Bài 37. Cho m là hằng số. Tính lim
x→1
√
x + 3 −2
x
2
+ mx −x − m
.
A
1
m
. B 1. C
1
4
. D
1
4(m + 1)
.
Lời giải.
lim
x→1
√
x + 3 −2
x
2
+ mx −x − m
= lim
x→1
x − 1
(x − 1)(x + m)
√
x + 3 + 2
=
1
4(m + 1)
.
Chọn đáp án D □
Bài 38. Biết lim
x→−∞
Ä
√
x
2
+ 1 + x + 1
ä
= a. Tính 2a + 1.
A −1. B −3. C 0. D 3.
Lời giải.
lim
x→−∞
Ä
p
x
2
+ 1 + x + 1
ä
= lim
x→−∞
−2x
√
x
2
+ 1 −(x + 1)
= lim
x→−∞
−2
−
…
1 +
1
x
2
−
Å
1 +
1
x
ã
= 1
⇒ a = 1.
Vậy 2a + 1 = 3.
Chọn đáp án D □
402/764 402/764
Toán 11 theo chương trình GDPT2018
Chương 3. Giới hạn. Hàm số liên tục
Biết làm, làm đúng, làm nhanh
403
Bài 39. Biết lim
x→+∞
Ä
√
4x
2
− 3x + 1 − (ax + b)
ä
= 0. Tính giá trị biểu thức T = a − 4b.
A T = −2. B T = 5. C T = −1. D T = 3.
Lời giải.
Từ giả thiết, đường thẳng y = ax + b là tiệm cận xiên của đồ thị hàm số y =
√
4x
2
− 3x + 1, khi x → +∞. Từ đó,
a = lim
x→+∞
√
4x
2
− 3x + 1
x
= 2,
b = lim
x→+∞
Ä
√
4x
2
− 3x + 1 − 2x
ä
= lim
x→+∞
−3x + 1
√
4x
2
− 3x + 1 + 2x
= lim
x→+∞
−3 +
1
x
»
4 −
3
x
+
1
x
2
+ 2
= −
3
4
.
Suy ra a − 4b = 5.
Chọn đáp án B □
Bài 40. Cho f(x) là hàm đa thức thỏa lim
x→2
f(x) + 1
x − 2
= a và tồn tại lim
x→2
p
f(x) + 2x + 1 −x
x
2
− 4
= T . Chọn đẳng
thức đúng
A T =
a + 2
16
. B T =
a + 2
8
. C T =
a − 2
8
. D T =
a − 2
16
.
Lời giải.
Vì f(x) là đa thức và lim
x→2
f(x) + 1
x − 2
= a nên suy ra f (x) + 1 = (x − 2)g(x), g(2) = a.
Do đó
T = lim
x→2
p
(x − 2)g(x) + 2x − x
x
2
− 4
= lim
x→2
(x − 2)g(x) + 2x − x
2
(x − 2)(x + 2)
î
p
(x − 2)g(x) + 2x + x
ó
= lim
x→2
g(x) −x
(x + 2)
î
p
(x − 2)g(x) + 2x + x
ó
=
a − 2
16
.
Chọn đáp án D □
3. Câu hỏi trắc nghiệm
Câu 1. Biết lim
x→+∞
f(x) = m, lim
x→+∞
g(x) = n. Tính lim
x→+∞
[f(x) + g(x)].
A m + n. B m − n. C mn. D
m
n
.
Lời giải.
Ta có lim
x→+∞
[f(x) + g(x)] = lim
x→+∞
f(x) + lim
x→+∞
g(x) = m + n.
Chọn đáp án A □
Câu 2. Khẳng định nào sau đây là đúng?
A lim
x→x
0
3
p
f(x) + g(x) =
3
q
lim
x→x
0
f(x) +
3
q
lim
x→x
0
g(x). B lim
x→x
0
3
p
f(x) + g(x) = lim
x→x
0
3
p
f(x) + lim
x→x
0
3
p
g(x).
C lim
x→x
0
3
p
f(x) + g(x) =
3
q
lim
x→x
0
[f(x) + g(x)]. D lim
x→x
0
3
p
f(x) + g(x) = lim
x→x
0
î
3
p
f(x) +
3
p
g(x)
ó
.
Lời giải.
Theo định lý về giới hạn của thì lim
x→x
0
3
p
f(x) + g(x) =
3
q
lim
x→x
0
[f(x) + g(x)].
Chọn đáp án C □
403/764 403/764
Toán 11 theo chương trình GDPT2018
2. Giới hạn của hàm số
Biết làm, làm đúng, làm nhanh
404
Câu 3. Cho các giới hạn lim
x→x
0
f(x) = 2, lim
x→x
0
g(x) = 3. Tính M = lim
x→x
0
[3f(x) − 4g(x)].
A M = 5. B M = 2. C M = −6. D M = 3.
Lời giải.
Ta có M = lim
x→x
0
[3f(x) − 4g(x)] = 3 lim
x→x
0
f(x) − 4 lim
x→x
0
g(x) = 6 −12 = −6.
Chọn đáp án C □
Câu 4. Biết lim
x→+∞
f(x) = m, lim
x→+∞
g(x) = n. Tính lim
x→+∞
[f(x) − g(x)].
A m + n. B m − n. C mn. D
m
n
.
Lời giải.
Ta có lim
x→+∞
[f(x) − g(x)] = lim
x→+∞
f(x) − lim
x→+∞
g(x) = m −n.
Chọn đáp án B □
Câu 5. Cho lim
x→a
f(x) = −∞, kết quả của lim
x→a
[−3 · f(x)] bằng
A +∞. B 0. C 3. D −∞.
Lời giải.
Có lim
x→a
[−3 · f(x)] = −3 · lim
x→a
f(x) = +∞.
Chọn đáp án A □
Câu 6. Cho k ∈ Z, kết quả của lim
x→−∞
x
2k+1
bằng
A 0. B −∞. C +∞. D 5.
Lời giải.
Theo tính chất của giới hạn hàm số, ta có lim
x→−∞
x
2k+1
= −∞.
Chọn đáp án B □
Câu 7. Cho lim
x→3
f(x) = −2. Giá trị lim
x→3
[f(x) + 4x − 1] bằng
A 5. B 6. C −11. D 9.
Lời giải.
lim
x→3
[f(x) + 4x − 1] = lim
x→3
f(x) + lim
x→3
4x − 1 = −2 + 4 · 3 − 1 = 9.
Chọn đáp án D □
Câu 8. Cho lim
x→2
f(x) = 3. Giá trị của lim
x→2
[f(x) + x] bằng
A 5. B 6. C 1. D 4.
Lời giải.
Ta có lim
x→2
[f(x) + x] = lim
x→2
f(x) + lim
x→2
x = 3 + 2 = 5.
Chọn đáp án A □
Câu 9. Với k là số nguyên dương. Kết quả của giới hạn lim
x→+∞
x
2k
là
A +∞. B 0. C −∞. D 1.
Lời giải.
Với k nguyên dương thì lim
x→+∞
x
k
= +∞ ⇒ lim
x→+∞
x
2k
= +∞.
Chọn đáp án A □
Câu 10. Cho c là hằng số, k là số nguyên dương. Khẳng định nào sau đây sai?
A lim
x→+∞
c = +∞. B lim
x→+∞
c
x
k
= 0. C lim
x→x
0
c = c. D lim
x→x
0
x = x
0
.
Lời giải.
Theo định lý về giới hạn, khẳng định sai là lim
x→+∞
c = +∞.
Chọn đáp án A □
404/764 404/764
Toán 11 theo chương trình GDPT2018
Chương 3. Giới hạn. Hàm số liên tục
Biết làm, làm đúng, làm nhanh
405
Câu 11. Cho lim
x→+∞
f(x) = a, lim
x→+∞
g(x) = b. Hỏi mệnh đề nào sau đây là mệnh đề sai?
A lim
x→+∞
[f(x) · g(x)] = ab. B lim
x→+∞
[f(x) − g(x)] = a − b.
C lim
x→+∞
[f(x) + g(x)] = a + b. D lim
x→+∞
f(x)
g(x)
=
a
b
.
Lời giải.
Khi lim
x→+∞
g(x) = b = 0 thì lim
x→+∞
f(x)
g(x)
=
a
b
không đúng. □
Câu 12. Với k là số nguyên dương thì lim
x→−∞
1
x
k
bằng
A +∞. B −∞. C x. D 0.
Lời giải.
Vì
lim
x→−∞
1 = 1
lim
x→−∞
x
k
= ±∞
nên lim
x→−∞
1
x
k
= 0.
Chọn đáp án D □
Câu 13. Tính I = lim
x→2
x
2
+ x −6
.
A 0. B 1. C 2. D 3.
Lời giải.
lim
x→2
x
2
+ x −6
= lim
x→2
x
2
+ lim
x→2
x − lim
x→2
6
= 4 + 2 − 6
= 0.
Chọn đáp án A □
Câu 14. Tính I = lim
x→1
x
2
+ 2x + 3
2x − 1
.
A 4. B 5. C 6. D 7.
Lời giải.
lim
x→1
x
2
+ 2x + 3
2x − 1
=
lim
x→1
x
2
+ 2x + 3
lim
x→1
(2x − 1)
=
lim
x→1
x
2
+ lim
x→1
(2x) + lim
x→1
3
lim
x→1
(2x) − lim
x→1
1
=
1 + 2 + 3
2 − 1
= 6.
Chọn đáp án C □
Câu 15. Tính I = lim
x→0
|x|
x
.
A 1. B −1. C Không tồn tại . D 0.
Lời giải.
Ta có :
lim
x→0
+
|x|
x
= lim
x→0
+
x
x
= lim
x→0
+
1 = 1.
lim
x→0
−
|x|
x
= lim
x→0
−
(−x)
x
= lim
x→0
−
(−1) = −1.
Vậy không tồn tại lim
x→0
|x|
x
.
Chọn đáp án C □
405/764
405/764
Toán 11 theo chương trình GDPT2018
2. Giới hạn của hàm số
Biết làm, làm đúng, làm nhanh
406
Câu 16. Tìm lim
x→3
9 − x
2
x
2
− 4x + 3
. Kết quả là
A −3. B 4. C −4. D 3.
Lời giải.
Ta có lim
x→3
9 − x
2
x
2
− 4x + 3
= lim
x→3
(3 − x)(3 + x)
(x − 3)(x −1)
= lim
x→3
−(x + 3)
x − 1
= −3.
Chọn đáp án A □
Câu 17. Tìm lim
x→4
x
2
− 16
x − 4
. Kết quả là
A 7. B 8. C 5. D 6.
Lời giải.
Ta có lim
x→4
x
2
− 16
x − 4
= lim
x→4
(x − 4)(x + 4)
x − 4
= lim
x→4
(x + 4) = 8.
Chọn đáp án B □
Câu 18. Tính giới hạn A = lim
x→1
x
3
− 1
x − 1
.
A A = −∞. B A = 0. C A = 3. D A = +∞.
Lời giải.
Ta có A = lim
x→1
x
3
− 1
x − 1
= lim
x→1
(x − 1)
x
2
+ x + 1
x − 1
= lim
x→1
x
2
+ x + 1
= 3.
Chọn đáp án C □
Câu 19. Chọn kết quả đúng trong các kết quả sau của lim
x→−1
x
2
+ 2x + 1
2x + 2
là
A −∞. B 0. C
1
2
. D +∞.
Lời giải.
lim
x→−1
x
2
+ 2x + 1
2x + 2
= lim
x→−1
(x + 1)
2
2(x + 1)
= lim
x→−1
x + 1
2
= 0.
Chọn đáp án
B □
Câu 20. Giới hạn lim
x→4
x
2
+ 2x −15
x − 3
bằng
A
1
8
. B 9. C +∞. D 8.
Lời giải.
lim
x→4
x
2
+ 2x −15
x − 3
= lim
x→4
(x − 3)(x + 5)
x − 3
= 9.
Chọn đáp án B □
Câu 21. Tính giới hạn I = lim
x→−∞
3x − 2
2x + 1
.
A I = −2. B I = −
3
2
. C I = 2. D I =
3
2
.
Lời giải.
Ta có I = lim
x→−∞
3x − 2
2x + 1
= lim
x→−∞
x
Å
3 −
2
x
ã
x
Å
2 +
1
x
ã
= lim
x→−∞
3 −
2
x
2 +
1
x
=
3
2
.
Chọn đáp án D □
Câu 22. lim
x→+∞
x − 2
x + 3
bằng
A −
2
3
. B 1. C 2. D −3.
Lời giải.
406/764 406/764
Toán 11 theo chương trình GDPT2018
Chương 3. Giới hạn. Hàm số liên tục
Biết làm, làm đúng, làm nhanh
407
Ta có lim
x→+∞
x − 2
x + 3
= lim
x→+∞
x
Å
1 −
2
x
ã
x
Å
1 +
3
x
ã
= lim
x→+∞
1 −
2
x
1 +
3
x
=
1
1
= 1.
Chọn đáp án B □
Câu 23. Giới hạn lim
x→1
x
2
− 3x + 2
x
3
− x
2
+ x −1
bằng
A −2. B −1. C −
1
2
. D
1
2
.
Lời giải.
Ta có lim
x→1
x
2
− 3x + 2
x
3
− x
2
+ x −1
= lim
x→1
(x − 1)(x −2)
(x − 1)(x
2
+ 1)
= lim
x→1
x − 2
x
2
+ 1
= −
1
2
.
Chọn đáp án C □
Câu 24. Giới hạn T = lim
x→1
x
4
− 3x + 2
x
3
+ 2x −3
bằng
A
2
9
. B
2
5
. C
1
5
. D +∞.
Lời giải.
T = lim
x→1
x
4
− 3x + 2
x
3
+ 2x −3
= lim
x→1
(x − 1)
x
3
+ x
2
+ x −2
(x − 1) (x
2
+ x + 3)
= lim
x→1
x
3
+ x
2
+ x −2
x
2
+ x + 3
=
1
3
+ 1
2
+ 1 −2
1
2
+ 1 + 3
=
1
5
.
Chọn đáp án C □
Câu 25. Giới hạn lim
x→2
x
2
− 5x + 6
x
3
− x
2
− x −2
bằng
A 0. B −
1
7
. C −7. D +∞.
Lời giải.
Ta có lim
x→2
x
2
− 5x + 6
x
3
− x
2
− x −2
= lim
x→2
(x − 2)(x −3)
(x − 2) (x
2
+ x + 1)
= lim
x→2
x − 3
x
2
+ x + 1
=
−1
7
.
Chọn đáp án B □
Câu 26. Tìm lim
x→1
x
4
− 3x
2
+ 2
x
3
+ 2x −3
.
A −
5
2
. B −
2
5
. C
1
5
. D +∞.
Lời giải.
lim
x→1
x
4
− 3x
2
+ 2
x
3
+ 2x −3
= lim
x→1
(x − 1)(x + 1)
x
2
− 2
(x − 1) (x
2
+ x + 3)
= lim
x→1
(x + 1)
x
2
− 2
x
2
+ x + 3
= −
2
5
.
Chọn đáp án B □
Câu 27. Tính lim
x→2
Å
1
x
2
− 3x + 2
+
1
x
2
− 5x + 6
ã
.
A 2. B +∞. C −2. D 0.
Lời giải.
lim
x→2
Å
1
x
2
− 3x + 2
+
1
x
2
− 5x + 6
ã
= lim
x→2
2x
2
− 8x + 8
(x
2
− 3x + 2) (x
2
− 5x + 6)
= lim
x→2
2(x − 2)
2
(x − 1)(x −2)(x − 2)(x − 3)
= lim
x→2
2
(x − 1)(x −3)
= −2.
Chọn đáp án C □
Câu 28. Giới hạn lim
x→+∞
√
x
2
+ 2 −2
x − 2
bằng
A −∞. B 1. C +∞. D −1.
Lời giải.
407/764 407/764
Toán 11 theo chương trình GDPT2018
2. Giới hạn của hàm số
Biết làm, làm đúng, làm nhanh
408
lim
x→+∞
√
x
2
+ 2 −2
x − 2
= lim
x→+∞
x
…
1 +
2
x
2
− 2
x − 2
= lim
x→+∞
…
1 +
2
x
2
−
2
x
1 −
2
x
= 1.
Chọn đáp án B □
Câu 29. Cho hàm số f (x) =
(4x + 1)
3
(2x + 1)
4
(3 + 2x)
7
. Tính lim
x→−∞
f(x).
A 2. B 8. C 4. D 0.
Lời giải.
lim
x→−∞
f(x) = lim
x→−∞
(4x + 1)
3
(2x + 1)
4
(3 + 2x)
7
= lim
x→−∞
Å
4 +
1
x
ã
3
Å
2 +
1
x
ã
4
Å
3
x
+ 2
ã
7
= 2
3
= 8.
Chọn đáp án B □
Câu 30. Biết lim
x→3
x
2
+ bx + c
x − 3
= 8, (b, c ∈ R). Tính P = b + c.
A P = −13. B P = −11. C P = 5. D P = −12.
Lời giải.
Vì lim
x→3
x
2
+ bx + c
x − 3
= 8 là hữu hạn nên tam thức x
2
+ bx + c có nghiệm x = 3.
⇒ 3b + c + 9 = 0 ⇔ c = −9 −3b.
Khi đó lim
x→3
x
2
+ bx + c
x − 3
= lim
x→3
x
2
+ bx −9 − 3b
x − 3
= lim
x→3
(x − 3)(x + 3 + b)
x − 3
= lim
x→3
(x + 3 + b) = 8 ⇔ 6 + b = 8 ⇔ b = 2 ⇒ c = −15.
Vậy P = b + c = −13.
Chọn đáp án A □
Câu 31. Cho a, b là số nguyên và lim
x→1
ax
2
+ bx −5
x − 1
= 7. Tính a
2
+ b
2
+ a + b.
A 18. B 1. C 15. D 5.
Lời giải.
Vì lim
x→1
ax
2
+ bx −5
x − 1
= 7 hữu hạn nên x = 1 phải là nghiệm của phương trình ax
2
+ bx −5 = 0 suy ra a + b −5 =
0 ⇒ b = 5 − a.
Khi đó lim
x→1
ax
2
+ (5 −a) x − 5
x − 1
= lim
x→1
(x − 1) (ax + 5)
x − 1
= a + 5 = 7 ⇒ a = 2 nên b = 3.
Suy ra a
2
+ b
2
+ a + b = 18.
Chọn đáp án A □
Câu 32. Biết rằng lim
x→+∞
Å
x
2
+ 1
x − 2
+ ax −b
ã
= −5. Tính tổng a + b.
A 6. B 7. C 8. D 5.
Lời giải.
lim
x→+∞
Å
x
2
+ 1
x − 2
+ ax −b
ã
= lim
x→+∞
Å
(a + 1)x
2
− (2a + b)x + 2b + 1
x − 2
ã
= −5
⇔
®
a + 1 = 0
2a + b = 5
⇔
®
a = −1
b = 7.
Vậy a + b = 6.
Chọn đáp án A □
Câu 33. Cho hai số thực a và b thỏa mãn lim
x→+∞
Å
4x
2
− 3x + 1
x + 2
− ax −b
ã
= 0. Khi đó a + b bằng
A −4. B 4. C 7. D −7.
Lời giải.
408/764 408/764
Toán 11 theo chương trình GDPT2018
Chương 3. Giới hạn. Hàm số liên tục
Biết làm, làm đúng, làm nhanh
409
lim
x→+∞
Å
4x
2
− 3x + 1
x + 2
− ax −b
ã
= 0 ⇔ lim
x→+∞
Å
(4 − a) x − b −11 +
23
x + 2
ã
= 0.
⇒
®
4 − a = 0
− 11 −b = 0
⇔
®
a = 4
b = −11
⇒ a + b = −7.
Chọn đáp án D
□
Câu 34. Cho lim
x→1
f(x) + 1
x − 1
= −1. Tính lim
x→1
x
2
+ x
f(x) + 2
x − 1
.
A I = 5. B I = −4. C I = 4. D I = −5.
Lời giải.
lim
x→1
x
2
+ x
f(x) + 2
x − 1
= lim
x→1
x
2
+ x
(f(x) + 1) − x
2
− x + 2
x − 1
= lim
x→1
Ç
x
2
+ x
(f(x) + 1)
x − 1
− x −2
å
= −5.
Chọn đáp án D □
Câu 35. Gọi A là giới hạn của hàm số f(x) =
x + x
2
+ x
3
+ ··· + x
50
− 50
x − 1
khi x tiến đến 1. Tính giá trị của
A.
A A không tồn tại. B A = 1725. C A = 1527. D A = 1275.
Lời giải.
Ta có
lim
x→1
f(x) = lim
x→1
x + x
2
+ x
3
+ ··· + x
50
− 50
x − 1
= lim
x→1
1 + (x + 1) +
x
2
+ x + 1
+ ··· +
x
49
+ x
48
+ ··· + 1

= 1 + 2 + 3 + ···+ 50 = 25(1 + 50) = 1275.
Vậy A = lim
x→1
f(x) = 1275.
Chọn đáp án
D □
Câu 36. Biết lim
x→+∞
Ä
p
x
2
+ ax −1 − x
ä
= 5. Khi đó giá trị của tham số a là
A 10. B −6. C 6. D −10.
Lời giải.
lim
x→+∞
Ä
p
x
2
+ ax −1 − x
ä
= lim
x→+∞
x
2
+ ax −1 − x
2
√
x
2
+ ax −1 + x
= lim
x→+∞
a −
1
x
…
1 +
a
x
−
1
x
2
+ 1
=
a
2
= 5.
Suy ra a = 10.
Chọn đáp án A □
Câu 37. Có tất cả bao nhiêu giá trị nguyên của tham số m để lim
x→+∞
(
p
x
2
+ m
2
x − x) =
1
2
?
A 0. B 1. C 2. D 4.
Lời giải.
Ta có
lim
x→+∞
Ä
p
x
2
+ m
2
x − x
ä
= lim
x→+∞
m
2
x
√
x
2
+ m
2
x + x
= lim
x→+∞
m
2
»
1 +
m
2
x
+ 1
=
m
2
2
.
Do đó lim
x→+∞
(
p
x
2
+ m
2
x − x) =
1
2
⇔
m
2
2
=
1
2
⇔ m = ±1. Vậy có hai giá trị nguyên của tham số m thỏa mãn
yêu cầu của bài toán.
Chọn đáp án C □
409/764 409/764
Toán 11 theo chương trình GDPT2018
2. Giới hạn của hàm số
Biết làm, làm đúng, làm nhanh
410
Câu 38. Tính L = lim
x→−∞
Ä
√
x
2
− 7x + 1 −
√
x
2
− 3x + 2
ä
.
A L = +∞. B L = −∞. C L = 2. D L = −2.
Lời giải.
L = lim
x→−∞
−4x − 1
√
x
2
− 7x + 1 +
√
x
2
− 3x + 2
= lim
x→−∞
−4x − 1
−x
…
1 −
7
x
+
1
x
2
− x
…
1 −
3
x
+
2
x
2
= lim
x→−∞
−4 −
1
x
−
…
1 −
7
x
+
1
x
2
−
…
1 −
3
x
+
2
x
2
= 2.
Chọn đáp án C □
Câu 39. Giá trị của lim
x→1
√
2x + 1 −
√
x + 2
x − 1
là
A −
√
3
5
. B −
√
3
6
. C
√
3
6
. D
√
3
5
.
Lời giải.
Ta có
lim
x→1
√
2x + 1 +
√
x + 2
x − 1
= lim
x→1
x − 1
(x − 1)
√
2x + 1 −
√
x + 2
= lim
x→1
1
√
2x + 1 +
√
x + 2
=
1
2
√
3
.
Chọn đáp án C □
Câu 40. Cho lim
x→0
1 −
3
√
1 − x
x
=
m
n
, trong đó m, n là các số nguyên và
m
n
tối giản.
Tính A = 2m −n.
A A = 1. B A = −1. C A = 0. D A = −2.
Lời giải.
Ta có lim
x→0
1 −
3
√
1 − x
x
= lim
x→0
x
x ·
Ä
1 +
3
√
1 − x +
3
p
(1 − x)
2
ä
=
1
3
.
Vậy A = 2m − n = 2 · 1 −3 = −1.
Chọn đáp án B □
Câu 41. Giới hạn lim
x→3
x + 1 −
√
5x + 1
x −
√
4x − 3
=
a
b
, với a, b ∈ Z, b > 0 và
a
b
là phân số tối giản. Giá trị của a −b là
A
1
9
. B −1. C
9
8
. D 1.
Lời giải.
Ta có
lim
x→3
x + 1 −
√
5x + 1
x −
√
4x − 3
= lim
x→3
(x + 1)
2
− (5x + 1)
x + 1 +
√
5x + 1
x
2
− (4x −3)
x +
√
4x − 3
= lim
x→3
x +
√
4x − 3
(x − 3)x
x + 1 +
√
5x + 1
(x − 3)(x −1)
= lim
x→3
x
x +
√
4x − 3
x + 1 +
√
5x + 1
(x − 1)
=
9
8
.
Vậy a = 9, b = 8, suy ra a − b = 1.
Chọn đáp án D □
410/764 410/764
Toán 11 theo chương trình GDPT2018
Chương 3. Giới hạn. Hàm số liên tục
Biết làm, làm đúng, làm nhanh
411
Câu 42. Cho lim
x→4
√
3x + 4 −4
x − 4
=
a
b
, với
a
b
là phân số tối giản. Tính 2a + b
2
.
A 22. B 66. C 14. D 70.
Lời giải.
Có lim
x→4
√
3x + 4 −4
x − 4
= lim
x→4
3 (x − 4)
(x − 4)
√
3x + 4 + 4
= lim
x→4
3
√
3x + 4 + 4
=
3
8
.
⇒ 2a + b
2
= 6 + 64 = 70.
Chọn đáp án D □
Câu 43. Tính lim
x→+∞
Ä
√
x
2
+ 3x + 2 − x
ä
.
A −
3
2
. B
3
2
. C
7
2
. D −
7
2
.
Lời giải.
lim
x→+∞
Ä
p
x
2
+ 3x + 2 − x
ä
= lim
x→+∞
3x + 2
√
x
2
+ 3x + 2 + x
= lim
x→+∞
x
Å
3 +
2
x
ã
|x|
…
1 +
3
x
+
2
x
2
+ x
= lim
x→+∞
x
Å
3 +
2
x
ã
x
Ç
…
1 +
3
x
+
2
x
2
+ 1
å
= lim
x→+∞
3 +
2
x
…
1 +
3
x
+
2
x
2
+ 1
=
3
2
.
Chọn đáp án B □
Câu 44. Tìm giới hạn M = lim
x→−∞
Ä
√
x
2
− 4x −
√
x
2
− x
ä
.
A M = −
1
2
. B M =
3
2
. C M = −
3
2
. D M =
1
2
.
Lời giải.
Ta có
M = lim
x→−∞
Ä
p
x
2
− 4x −
p
x
2
− x
ä
= lim
x→−∞
−3x
√
x
2
− 4x +
√
x
2
− x
= lim
x→−∞
−3x
|x|
Ç
…
1 −
4
x
+
…
1 −
1
x
å
= lim
x→−∞
3
…
1 −
4
x
+
…
1 −
1
x
=
3
2
.
Chọn đáp án B □
Câu 45. Biết rằng lim
x→−∞
Ä
√
2x
2
− 3x + 1 + x
√
2
ä
=
a
b
√
2, (a, b ∈ Z, b > 0,
a
b
tối giản). Tổng a + b có giá trị
là
A 5. B 4. C 7. D 1.
Lời giải.
411/764 411/764
Toán 11 theo chương trình GDPT2018
2. Giới hạn của hàm số
Biết làm, làm đúng, làm nhanh
412
Ta có
lim
x→−∞
Ä
p
2x
2
− 3x + 1 + x
√
2
ä
= lim
x→−∞
2x
2
− 3x + 1 − 2x
2
√
2x
2
− 3x + 1 − x
√
2
= lim
x→−∞
−3x + 1
√
2x
2
− 3x + 1 − x
√
2
= lim
x→−∞
−3 +
1
x
−
…
2 −
3
x
+
1
x
2
−
√
2
=
3
4
·
√
2.
Vậy a = 3, b = 4. Tổng a + b = 7.
Chọn đáp án C □
Câu 46. Tìm giới hạn I = lim
x→+∞
Ä
x + 1 −
√
x
2
− x + 2
ä
.
A I =
1
2
. B I =
46
31
. C I =
17
11
. D I =
3
2
.
Lời giải.
Ta có: I = lim
x→+∞
Ä
x + 1 −
√
x
2
− x + 2
ä
= lim
x→+∞
Å
x
2
− x
2
+ x −2
x +
√
x
2
− x + 2
+ 1
ã
= lim
x→+∞
Å
x − 2
x +
√
x
2
− x + 2
+ 1
ã
= lim
x→+∞
Ü
1 −
2
x
1 +
…
1 −
1
x
+
2
x
2
+ 1
ê
=
3
2
.
Chọn đáp án D □
Câu 47. Cho f(x) là một đa thức thỏa mãn lim
x→2
f(x) − 15
x − 2
= 3. Tính
lim
x→2
f(x) − 15
(x
2
− 4)
Ä
p
2f(x) + 6 + 3
ä
.
A
1
10
. B
1
6
. C
1
12
. D
1
8
.
Lời giải.
Do lim
x→2
f(x) − 15
x − 2
= 3 và lim
x→2
(x − 2) = 0 nên lim
x→2
(f(x) − 15) = 0 ⇒ f(2) = 15.
Ta có
lim
x→2
f(x) − 15
(x
2
− 4)
Ä
p
2f(x) + 6 + 3
ä
= lim
x→2
f(x) − 15
x − 2
·
1
(x + 2)
Ä
p
2f(x) + 6 + 3
ä
= 3 ·
1
4 · (
√
2 · 15 + 6 + 3)
=
1
12
.
Chọn đáp án C □
Câu 48. Biết rằng b > 0, a + b = 5 và lim
x→0
3
√
ax + 1 −
√
1 − bx
x
= 2. Khẳng định nào dưới đây là sai?
A a
2
+ b
2
> 10. B a
2
− b
2
> 6. C a − b ≥ 0. D 1 ≤ a ≤ 3.
Lời giải.
Ta có
lim
x→0
3
√
ax + 1 −
√
1 − bx
x
= lim
x→0
3
√
ax + 1 −1
x
− lim
x→0
√
1 − bx −1
x
.
412/764 412/764
Toán 11 theo chương trình GDPT2018
Chương 3. Giới hạn. Hàm số liên tục
Biết làm, làm đúng, làm nhanh
413
Với L
1
= lim
x→0
3
√
ax + 1 −1
x
= lim
x→0
ax
x
Ä
3
p
(ax + 1)
2
+
3
√
ax + 1 + 1
ä
=
a
3
.
Với lim
x→0
√
1 − bx −1
x
= lim
x→0
−bx
x
√
1 − bx + 1
= −
b
2
.
Từ giả thiết bài toán ta có
L = L
1
− L
2
= 2 ⇔
a
3
+
b
2
= 2 ⇔ 2a + 3b = 12.
Ta có hệ phương trình
®
a + b = 5
2a + 3b = 12
⇔
®
a = 3
b = 2.
Kiểm tra trực tiếp từng đáp án ta thấy a
2
− b
2
> 6 là sai.
Chọn đáp án B □
Dạng 3. Phương pháp đặt thừa số chung - kết quả vô cực
Để tìm giới hạn của hàm số ta cần nhớ
○ lim
x→+∞
x
k
= +∞; lim
x→−∞
x
k
=
®
+ ∞, k = 2n
− ∞, k = 2n + 1.
○ lim
x→±∞
c = c; lim
x→±∞
c
x
k
= 0; lim
x→0
1
x
= ∞.
1. Ví dụ mẫu
Ví dụ 17 (NB). Tính lim
x→+∞
x
3
.
Lời giải.
Ta có lim
x→+∞
x
3
= +∞. □
Ví dụ 18 (TH). Tính lim
x→−∞
x
3
+ 3x + 1
.
Lời giải.
Ta có lim
x→−∞
x
3
+ 3x + 1
= lim
x→−∞
ï
x
3
Å
1 +
3
x
2
+
1
x
3
ãò
= −∞.
Vì lim
x→−∞
x
3
= −∞; lim
x→−∞
Å
1 +
3
x
2
+
1
x
3
ã
= 1 > 0. □
Ví dụ 19 (TH). Tính lim
x→−∞
−4x
5
− 3x
3
+ x + 1
.
Lời giải.
Ta có lim
x→−∞
−4x
5
− 3x
3
+ x + 1
= lim
x→−∞
x
5
Å
−4 −
3
x
2
+
1
x
4
+
1
x
5
ã
= +∞.
Vì
lim
x→−∞
Å
−4 −
3
x
2
+
1
x
4
+
1
x
5
ã
= −4 < 0
lim
x→−∞
x
5
= −∞.
□
Ví dụ 20 (TH). Tính giới hạn lim
x→−3
x + 2
(x + 3)
2
.
Lời giải.
Ta có lim
x→−3
x + 2
(x + 3)
2
= −∞.
Vì lim
x→−3
(x + 2) = −3 + 2 = −1 < 0, lim
x→−3
(x + 3)
2
= 0 và (x + 3)
2
> 0 khi x = −3. □
Ví dụ 21 (VDT). Tìm tất cả các giá trị nguyên của tham số m để I = lim
x→+∞
(m
2
− 1)x
3
+ 2x
= −∞.
Lời giải.
413/764 413/764
Toán 11 theo chương trình GDPT2018
2. Giới hạn của hàm số
Biết làm, làm đúng, làm nhanh
414
Ta có lim
x→+∞

m
2
− 1
x
3
+ 2x
= lim
x→+∞
x
3
ï
m
2
− 1 +
2
x
2
ò
.
Vì lim
x→+∞
x
3
= +∞ nên I = −∞ ⇔ lim
x→+∞
ï
m
2
− 1 +
2
x
2
ò
< 0 ⇔ m
2
− 1 < 0 ⇔ −1 < m < 1.
Do m ∈ Z nên m = 0. □
2. Bài tập rèn luyện
Bài 41 (NB). Tính lim
x→−∞
x
2
.
Lời giải.
Ta có lim
x→−∞
x
2
= +∞. □
Bài 42 (NB). Tính lim
x→−∞
Å
−x
4
−
1
x
ã
.
Lời giải.
Ta có lim
x→−∞
−x
4
= −∞ và lim
x→−∞
1
x
= 0. Suy ra lim
x→−∞
Å
−x
4
−
1
x
ã
= −∞. □
Bài 43 (TH). Tính giới hạn lim
x→+∞
−x
3
+ 5x
2
+ 2x + 1
.
Lời giải.
Ta có lim
x→+∞
−x
3
+ 5x
2
+ 2x + 1
= lim
x→+∞
ï
x
3
Å
−1 +
5
x
+
2
x
2
+
1
x
3
ãò
.
Do lim
x→+∞
x
3
= +∞; lim
x→+∞
Å
−1 +
5
x
+
2
x
2
+
1
x
3
ã
= −1 < 0 nên lim
x→+∞
−x
3
+ 5x
2
+ 2x + 1
= −∞. □
Bài 44 (TH). Tính lim
x→+∞
3x
2
− x
x + 1
.
Lời giải.
Ta có lim
x→+∞
3x
2
− x
x + 1
= lim
x→+∞
x
2
x
·
Ö
3 −
1
x
1 +
1
x
è
= lim
x→+∞
x ·
Ö
3 −
1
x
1 +
1
x
è
= +∞.
Vì lim
x→+∞
x = +∞ và lim
x→+∞
3 −
1
x
1 +
1
x
= 3. □
Bài 45 (TH). Giá trị của giới hạn lim
x→+∞
Ä
√
1 + 2x
2
− x
ä
là bao nhiêu?
Lời giải.
Ta có lim
x→+∞
Ä
√
1 + 2x
2
− x
ä
= lim
x→+∞
x
Ç
…
1
x
2
+ 2 −1
å
= +∞.
Vì lim
x→+∞
x = +∞; lim
x→+∞
Ç
…
1
x
2
+ 2 −1
å
=
√
2 − 1 > 0. □
Bài 46 (TH). Tính lim
x→3
Å
1
x
−
1
3
ã
1
(x − 3)
3
.
Lời giải.
lim
x→3
Å
1
x
−
1
3
ã
1
(x − 3)
3
= lim
x→3
3 − x
3x
·
1
(x − 3)
3
= lim
x→3
−1
3x(x − 3)
2
= −∞. □
Bài 47 (VDT). Có bao nhiêu giá trị m nguyên thuộc đoạn [−20; 20] để lim
x→+∞
Ä
√
4x
2
− 3x + 2 + mx − 1
ä
= −∞?
Lời giải.
Ta có lim
x→+∞
Ä
p
4x
2
− 3x + 2 + mx − 1
ä
= lim
x→+∞
Ç
x
…
4 −
3
x
+
2
x
2
+ mx −1
å
= lim
x→+∞
x
Ç
…
4 −
3
x
+
2
x
2
+ m −
1
x
å
.
414/764 414/764
Toán 11 theo chương trình GDPT2018
Chương 3. Giới hạn. Hàm số liên tục
Biết làm, làm đúng, làm nhanh
415
Mà lim
x→+∞
x = +∞ và lim
x→+∞
Ç
…
4 −
3
x
+
2
x
2
+ m −
1
x
å
= 2 + m nên lim
x→+∞
Ä
√
4x
2
− 3x + 2 + mx − 1
ä
= −∞ khi
2 + m < 0 ⇔ m < −2.
Do m nguyên thuộc đoạn [−20; 20] nên m ∈ {−20; −19; −18; . . . ; −3}.
Vậy có 18 giá trị m nguyên thuộc đoạn [−20; 20] thỏa bài toán. □
3. Câu hỏi trắc nghiệm
Câu 49. Giá trị của lim
x→−∞
(−x
3
) bằng
A +∞. B −∞. C 1. D −1.
Lời giải.
Ta có lim
x→−∞
(−x
3
) = +∞.
Chọn đáp án A □
Câu 50. Giới hạn lim
x→−∞
Ä
3x
3
+ 5x
2
− 9
√
3x − 2022
ä
bằng
A −∞. B 3. C −3. D +∞.
Lời giải.
Ta có lim
x→−∞
Ä
3x
3
+ 5x
2
− 9
√
3x − 2022
ä
= lim
x→−∞
x
3
Å
3 + 5 ·
1
x
− 9
√
3 ·
1
x
2
− 2022 ·
1
x
3
ã
= −∞.
Chọn đáp án A □
Câu 51. Tính lim
x→−∞
(x
3
+ 3x −3).
A 2. B 1. C −∞. D +∞.
Lời giải.
Ta có lim
x→−∞
x
3
+ 3x −3
= lim
x→−∞
ï
x
3
Å
1 +
3
x
2
−
3
x
3
ãò
= −∞.
Vì lim
x→−∞
x
3
= −∞; lim
x→−∞
Å
1 +
3
x
2
−
3
x
3
ã
= 1 > 0.
Chọn đáp án C □
Câu 52. Với k là số nguyên dương chẵn. Kết quả của lim
x→−∞
−3x
k
là
A 0. B −∞. C −3x
k
0
. D +∞.
Lời giải.
Ta có lim
x→−∞
x
k
= +∞ khi k là số nguyên dương chẵn.
Suy ra lim
x→−∞
−3x
k
= −∞.
Chọn đáp án B □
Câu 53. Cho hai hàm số f (x), g(x) thỏa mãn lim
x→1
f(x) = 2 và lim
x→1
g(x) = +∞. Giá trị của lim
x→1
[f(x) · g(x)]
bằng
A +∞. B −∞. C 2. D −2.
Lời giải.
Theo quy tắc giới hạn vô cực ta có lim
x→1
f(x) = 2 > 0 và lim
x→1
g(x) = +∞ thì lim
x→1
[f(x) · g(x)] = +∞.
Chọn đáp án A □
Câu 54. Giới hạn lim
x→−2
x + 1
(x + 2)
2
bằng
A −∞. B
3
16
. C 0. D +∞.
Lời giải.
Ta có lim
x→−2
x + 1
(x + 2)
2
= −∞.
Vì lim
x→−2
(x + 1) = −2 + 1 = −1 < 0, lim
x→−2
(x + 2)
2
= 0 và (x + 2)
2
> 0 khi x = −2.
Chọn đáp án A □
415/764 415/764
Toán 11 theo chương trình GDPT2018
2. Giới hạn của hàm số
Biết làm, làm đúng, làm nhanh
416
Câu 55. lim
x→−∞
−3x
3
+ 2x
bằng
A −∞. B +∞. C 1. D −1.
Lời giải.
Ta có lim
x→−∞
−3x
3
+ 2x
= lim
x→−∞
x
3
Å
−3 +
2
x
2
ã
= +∞.
Vì lim
x→−∞
x
3
= −∞ và lim
x→−∞
Å
−3 +
2
x
2
ã
= −3 < 0.
Chọn đáp án B □
Câu 56. Tìm L = lim
x→−1
2x
2
+ x −3
(x + 1)
2
.
A L = +∞. B L = 2.
C Không tồn tại lim
x→−1
2x
2
+ x −3
(x + 1)
2
. D L = −∞.
Lời giải.
lim
x→−1
2x
2
+ x −3
(x + 1)
2
= −∞ vì
lim
x→−1
(2x
2
+ x −3) = −2
lim
x→−1
(x + 1)
2
= 0
x → −1 ⇒ (x + 1)
2
> 0.
Chọn đáp án D □
Câu 57. lim
x→+∞
−2x
3
− 2x
bằng
A −∞. B +∞. C 2. D −2.
Lời giải.
Ta có lim
x→+∞
−2x
3
− 2x
= lim
x→+∞
x
3
Å
−2 −
2
x
2
ã
.
Mà lim
x→+∞
x
3
= +∞; lim
x→+∞
(−2 −
2
x
2
) = −2 < 0 nên lim
x→+∞
x
3
Å
−2 −
2
x
2
ã
= −∞.
Vậy lim
x→+∞
−2x
3
− 2x
= −∞.
Chọn đáp án A □
Câu 58. Tính giới hạn lim
x→−∞
x
2
+ 1
x − 2
.
A 1. B −
1
2
. C +∞. D −∞.
Lời giải.
lim
x→−∞
x
2
+ 1
x − 2
= lim
x→−∞
x
2
x
·
1 +
1
x
2
1 −
2
x
= lim
x→−∞
x ·
1 +
1
x
2
1 −
2
x
.
Do lim
x→−∞
x = −∞ và lim
x→−∞
1 +
1
x
2
1 −
2
x
= 1 nên lim
x→−∞
x
2
+ 1
x − 2
= −∞.
Chọn đáp án D □
Câu 59. Trong các mệnh đề sau, mệnh đề nào đúng?
A lim
x→−∞
√
x
4
− x
1 − 2x
= +∞. B lim
x→−∞
√
x
4
− x
1 − 2x
= 1.
C lim
x→−∞
√
x
4
− x
1 − 2x
= −∞. D lim
x→−∞
√
x
4
− x
1 − 2x
= 0.
Lời giải.
Vì lim
x→−∞
√
x
4
− x
1 − 2x
= lim
x→−∞
x
2
·
…
1 −
1
x
3
x ·
Å
1
x
− 2
ã
= lim
x→−∞
x ·
…
1 −
1
x
3
1
x
− 2
= +∞.
416/764 416/764
Toán 11 theo chương trình GDPT2018
Chương 3. Giới hạn. Hàm số liên tục
Biết làm, làm đúng, làm nhanh
417
Chọn đáp án A □
Câu 60. Biết lim
x→−2
f(x) = −1. Khi đó lim
x→−2
f(x)
(x + 2)
4
bằng
A −1. B +∞. C −∞. D 0.
Lời giải.
Ta có lim
x→−2
f(x) = −1 < 0; lim
x→−2
(x + 2)
4
= 0 và ∀x = −2 thì (x + 2)
4
> 0.
Suy ra lim
x→−2
f(x)
(x + 2)
4
= −∞.
Chọn đáp án C □
Câu 61. Biết lim
x→1
f(x) = −2. Khi đó lim
x→1
f(x)
(x − 1)
2
bằng
A −∞. B 0. C +∞. D −2.
Lời giải.
Có lim
x→1
f(x) = −2 < 0, lim
x→1
(x − 1)
2
= 0 và (x −1)
2
> 0, ∀x = 1 nên lim
x→1
f(x)
(x − 1)
2
= −∞.
Chọn đáp án A □
Câu 62. Có bao nhiêu giá trị nguyên của tham số m thuộc [−5; 5] để L = lim
x→+∞
x − 2(m
2
− 4)x
3
= −∞?
A 5. B 10. C 3. D 6.
Lời giải.
Ta có lim
x→+∞
x − 2
m
2
− 4
x
3
= lim
x→+∞
x
3
ï
1
x
2
− 2
m
2
− 4
ò
.
Ta có
lim
x→+∞
x
3
= +∞ ⇒ L = −∞ ⇔ lim
x→+∞
ï
1
x
2
− 2
m
2
− 4
ò
< 0
⇔ −2(m
2
− 4) < 0 ⇔ m
2
− 4 > 0 ⇔
ñ
m > 2
m < −2.
Lại có m thuộc đoạn [−5; 5] nên các giá trị nguyên thỏa mãn bài toán của m là {−5; −4; −3; 3; 4; 5}.
Vậy có 6 số nguyên thỏa mãn bài toán.
Chọn đáp án D □
Câu 63. Có bao nhiêu giá trị m nguyên thuộc đoạn [−20; 20] để lim
x→−∞
Ä
√
4x
2
− 3x + 2 + mx − 1
ä
= −∞?
A 21. B 22. C 18. D 41.
Lời giải.
Ta có lim
x→−∞
Ä
√
4x
2
− 3x + 2 + mx − 1
ä
= lim
x→−∞
x
Ç
−
…
4 −
3
x
+
2
x
2
+ m −
1
x
å
.
Có lim
x→−∞
x = −∞ và lim
x→−∞
Ç
−
…
4 −
3
x
+
2
x
2
+ m −
1
x
å
= m − 2
Để lim
x→−∞
Ä
√
4x
2
− 3x + 2 + mx − 1
ä
= −∞ suy ra m − 2 > 0 ⇔ m > 2.
Với m ∈ Z và m ∈ [−20; 20] có m ∈ {3; 4; 5; . . . ; 20} thỏa mãn yêu cầu bài toán.
Kết luận: Vậy có 18 giá trị nguyên của m thỏa mãn yêu cầu bài toán.
Chọn đáp án C □
Dạng 4. Giới hạn một phía
c Định lí 2.3. Định lí sau đây cho ta mối liên hệ giữa “giới hạn hai phía” lim
x→x
0
f(x) với giới hạn bên trái
lim
x→x
−
0
f(x) và giới hạn bên phải lim
x→x
+
0
f(x).
lim
x→x
0
f(x) = L khi và chỉ khi lim
x→x
−
0
f(x) = lim
x→x
+
0
f(x) = L.
417/764 417/764
Toán 11 theo chương trình GDPT2018
2. Giới hạn của hàm số
Biết làm, làm đúng, làm nhanh
418
1. Ví dụ mẫu
Ví dụ 22 (Cánh Diều). Tính: lim
x→2
−
√
2 − x.
Lời giải.
Với dãy số (x
n
) bất kì, x
n
< 2 và x
n
→ 2, ta có
lim
x
n
→2
−
√
2 − x
n
=
…
lim
x
n
→2
−
(2 − x
n
)
=
q
2 − lim
x
n
→2
−
x
n
=
√
2 − 2
= 0.
Vậy lim
x
n
→2
−
√
2 − x = 0. □
Ví dụ 23 (Cánh Diều). Cho hàm số f(x) =
− 1 nếu x < 0
0 nếu x = 0
1 nếu x > 0.
Chứng tỏ rằng không tồn tại lim
x→0
f(x).
Lời giải.
Ta có lim
x→0
−
f(x) = −1 và lim
x→0
+
f(x) = 1.
Suy ra lim
x→0
−
f(x) = lim
x→0
+
f(x).
Vậy không tồn tại lim
x→0
f(x). □
Ví dụ 24 (CTST). Cho hàm số f(x) =
®
0 khi x < 0
1 khi x > 0.
Tìm các giới hạn lim
x→0
+
f(x) và lim
x→0
−
f(x).a) Có tồn tại lim
x→0
f(x)?b)
Lời giải.
a) Giả sử (x
n
) là dãy số bất kì, x
n
> 0 và x
n
→ 0. Khi đó f(x
n
) = 1 nên lim f(x
n
) = lim 1 = 1.
Vậy lim
x→0
+
f(x) = 1.
Giả sử (x
n
) là dãy số bất kì, x
n
< 0 và x
n
→ 0. Khi đó f(x
n
) = 0 nên lim f(x
n
) = lim 0 = 0.
Vậy lim
x→0
−
f(x) = 0.
b) Vì lim
x→0
+
f(x) = lim
x→0
−
f(x) nên không tồn tại lim
x→0
f(x).
□
Ví dụ 25 (CTST). Cho hàm số f(x) =
®
1 − 2x khi x ≤ −1
x
2
+ 2 khi x > −1.
Tìm các giới hạn lim
x→−1
+
f(x) và lim
x→−1
−
f(x) và lim
x→−1
f(x) (nếu có).
Lời giải.
+ Giả sử (x
n
) là dãy số bất kì, x
n
< −1 và x
n
→ −1. Khi đó lim f(x
n
) = lim(1 − 2x
n
) = 3.
Vậy lim
x→−1
−
f(x) = 3.
Giả sử (x
n
) là dãy số bất kì, x
n
> −1 và x
n
→ −1. Khi đó lim f(x
n
) = lim(x
2
n
+ 2) = 3.
Vậy lim
x→−1
+
f(x) = 3.
+ Vì lim
x→−1
+
f(x) = lim
x→−1
−
f(x) nên tồn tại lim
x→−1
f(x) và lim
x→−1
f(x) = 3.
□
418/764 418/764
Toán 11 theo chương trình GDPT2018
Chương 3. Giới hạn. Hàm số liên tục
Biết làm, làm đúng, làm nhanh
419
Ví dụ 26 (KNTT). Cho hàm số f(x) =
®
x
2
nếu 0 < x < 1
x + 1 nếu 1 ≤ x < 2.
Tính lim
x→1
−
f(x) và lim
x→1
+
f(x).
Lời giải.
Với dãy số (x
n
) bất kì sao cho 0 < x
n
< 1 và x
n
→ 1, ta có f (x
n
) = x
2
n
.
Do đó lim
x→1
−
f(x) = lim
n→+∞
f (x
n
) = 1.
Tương tự, với dãy số (x
n
) bất kì mà 1 < x
n
< 2, x
n
→ 1, ta có f (x
n
) = x
n
+1, cho nên lim
x→1
+
f(x) = lim
n→+∞
f (x
n
) =
2. □
2. Bài tập tự luận
Bài 48. Cho hàm số f (x) =
®
0 khi x < 0
1 khi x > 0.
a) Tính các giới hạn lim
x→0
+
f(x) và lim
x→0
−
f(x).
b) Có tồn tại giới hạn lim
x→0
f(x)?
Lời giải.
a) Giả sử (x
n
) là dãy số bất kì, x
n
> 0 và x
n
→ 0 khi n → +∞. Khi đó f(x
n
) = 1 nên lim f(x
n
) = lim 1 = 1.
Vậy lim
x→0
+
f(x) = 1.
Giả sử (x
n
) là dãy số bất kì, x
n
< 0 và x
n
→ 0 khi n → +∞. Khi đó f(x
n
) = 0 nên lim f(x
n
) = lim 0 = 0.
Vậy lim
x→0
−
f(x) = 0.
b) Vì lim
x→0
+
f(x) = lim
x→0
−
f(x) nên không tồn tại giới hạn lim
x→0
f(x).
□
Bài 49. Cho hàm số f (x) =
®
1 − 2x khi x ≤ −1
x
2
+ 2 khi x > −1.
Tìm các giới hạn lim
x→−1
+
f(x) và lim
x→−1
−
f(x) và lim
x→−1
f(x) (nếu có).
Lời giải.
○ Giả sử (x
n
) là dãy số bất ki, x
n
≤ −1 và x
n
→ −1 khi n → +∞.
Khi đó f(x
n
) = 1 − 2x
n
nên lim f(x
n
) = lim(1 − 2x
n
) = 1 − 2(−1) = 3.
Vậy lim
x→−1
−
f(x) = 3.
○ Giả sử (x
n
) là dãy số bất ki, x
n
> −1 và x
n
→ −1 khi n → +∞.
Khi đó f(x
n
) = x
2
n
+ 2 nên lim f(x
n
) = lim(x
2
n
+ 2) = (−1)
2
+ 2 = 3.
Vậy lim
x→−1
+
f(x) = 3.
○ Vì lim
x→−1
+
f(x) = lim
x→−1
−
f(x) = 3 nên lim
x→−1
f(x) = 3.
□
Bài 50. Tìm các giới hạn sau
a) lim
x→2
+
1 − 2x
x − 2
;
b) lim
x→−∞
(x
2
+ 1).
Lời giải.
a) Ta có lim
x→2
+
(1 − 2x) = 1 −2 lim
x→2
+
x = 1 −2 · 2 = −3; lim
x→2
+
1
x − 2
= +∞.
Do đó lim
x→2
+
1 − 2x
x − 2
= lim
x→2
+
ï
(1 − 2x) ·
1
x − 2
ò
= −∞.
419/764 419/764
Toán 11 theo chương trình GDPT2018
2. Giới hạn của hàm số
Biết làm, làm đúng, làm nhanh
420
b) Viết (x
2
+ 1) = x
2
Å
1 +
1
x
2
ã
. Ta có lim
x→−∞
x
2
= +∞; lim
x→−∞
Å
1 +
1
x
2
ã
= 1 + lim
x→−∞
1
x
2
= 1 + 0 = 1.
Do đó lim
x→−∞
(x
2
+ 1) = lim
x→−∞
ï
x
2
Å
1 +
1
x
2
ãò
= +∞.
□
Bài 51. Tìm các giới hạn sau
a) lim
x→3
−
2x
x − 3
;
b) lim
x→+∞
(3x − 1).
Lời giải.
a) Ta có lim
x→3
−
(2x) = 2 lim
x→3
−
x = 2 ·3 = 6; lim
x→3
−
1
x − 3
= −∞.
Do đó lim
x→3
−
2x
x − 3
= lim
x→3
−
ï
(2x) ·
1
x − 3
ò
= −∞.
b) Viết (3x − 1) = x
Å
3 −
1
x
ã
. Ta có lim
x→+∞
x = +∞; lim
x→+∞
Å
3 −
1
x
ã
= 3 − lim
x→+∞
1
x
= 3 − 0 = 3.
Do đó lim
x→+∞
(3x − 1) = lim
x→−∞
x
Å
3 −
1
x
ã
= +∞.
□
Bài 52. Cho hàm số f (x) =
®
− x
2
khi x < 1
x khi x ≥ 1.
Tìm các giới hạn lim
x→1
+
f(x); lim
x→1
−
f(x); lim
x→1
f(x) (nếu có).
Lời giải.
Ta có lim
x→1
+
f(x) = lim
x→1
+
x = 1.
lim
x→1
−
f(x) = lim
x→1
−
(−x
2
) = −1
2
= −1.
Vì lim
x→1
+
f(x) = lim
x→1
−
f(x) nên không tồn tại lim
x→1
f(x). □
Bài 53. Biết rằng hàm số f(x) thoả mãn lim
x→2
−
f(x) = 3 và lim
x→2
+
f(x) = 5. Trong trường hợp này có tồn tại giới
hạn lim
x→2
f(x) hay không? Giải thích.
Lời giải.
Ta có lim
x→2
−
f(x) = 3 và lim
x→2
+
f(x) = 5, do đó lim
x→2
−
f(x) = lim
x→2
+
f(x).
Vậy không tồn tại lim
x→2
f(x). □
Bài 54. Cho hàm số f (x) =
2
(x − 1)(x −2)
. Tìm lim
x→2
+
f(x) và lim
x→2
−
f(x).
Lời giải.
Viết
2
(x − 1)(x −2)
=
2
x − 1
·
1
x − 2
, ta có lim
x→2
+
2
x − 1
= 2 > 0.
Hơn nữa lim
x→2
+
1
x − 2
= +∞ do x − 2 > 0 khi x > 2.
Áp dụng quy tắc tìm giới hạn của tích, ta được lim
x→2
+
2
(x − 1)(x −2)
= +∞.
Lí luận tương tự, ta có lim
x→2
−
1
x(1 − x)
= −∞. □
Bài 55. Tính các giới hạn sau
lim
x→−1
+
1
x + 1
;a) lim
x→−∞
(1 − x
2
);b) lim
x→3
−
x
3 − x
.c)
Lời giải.
420/764 420/764
Toán 11 theo chương trình GDPT2018
Chương 3. Giới hạn. Hàm số liên tục
Biết làm, làm đúng, làm nhanh
421
a) Ta có lim
x→−1
+
1 = 1; lim
x→−1
+
(x + 1) = 0.
Do đó lim
x→−1
+
1
x + 1
= +∞.
b) Viết (1 − x
2
) = x
2
Å
1
x
2
− 1
ã
.
Vì lim
x→−∞
x
2
= +∞; lim
x→−∞
Å
1
x
2
− 1
ã
= lim
x→−∞
1
x
2
− 1 = 0 −1 = −1.
Nên lim
x→−∞
(1 − x
2
) = −∞.
c) Ta viết
x
3 − x
=
−x
x − 3
.
Vì lim
x→3
−
(−x) = −3 < 0; lim
x→3
−
1
x − 3
= −∞
nên lim
x→3
−
x
3 − x
= lim
x→3
−
ï
−x ·
1
x − 3
ò
= +∞.
□
3. Câu hỏi trắc nghiệm
Câu 64. Trong các giới hạn sau đây, giới hạn nào sau đây có kết quả bằng +∞.
A lim
x→4
+
2x − 1
4 − x
. B lim
x→−∞
x
3
− 1
2x
2
+ x −1
. C lim
x→+∞
−x
3
+ x
2
+ 2
. D lim
x→4
−
2x − 1
4 − x
.
Lời giải.
Ta có lim
x→4
−
2x − 1
4 − x
= +∞ vì lim
x→4
−
(2x−1)=7>0
= và 4 − x > 0 với mọi x ∈ (−∞; 4).
Chọn đáp án D □
Câu 65. Cho hàm số f (x) =
®
2x + 1 khi x < 1
x
2
+ mx −2m khi x ≥ 1
. Hàm số có giới hạn khi x → 1 nếu
Lời giải.
Ta có lim
x→1
−
f(x) = lim
x→1
−
(2x + 1) = 3.
Mặt khác lim
x→1
+
f(x) = lim
x→1
+
x
2
+ mx −2m
= 1 − m.
Hàm số có giới hạn khi x → 1 khi và chỉ khi lim
x→1
−
f(x) = lim
x→1
+
f(x) ⇔ 1 − m = 3 ⇔ m = −2. □
Câu 66. Mệnh đề nào sau đây đúng?
A lim
x→(−3)
−
2x
2
+ 5x −3
(x + 3)
2
= −∞. B lim
x→(−3)
−
2x
2
+ 5x −3
(x + 3)
2
= 2.
C lim
x→(−3)
−
2x
2
+ 5x −3
(x + 3)
2
= −2. D lim
x→(−3)
−
2x
2
+ 5x −3
(x + 3)
2
= +∞.
Lời giải.
Ta có lim
x→(−3)
−
2x
2
+ 5x −3
(x + 3)
2
= lim
x→(−3)
−
(x + 3)(2x −1)
(x + 3)
2
= lim
x→(−3)
−
2x + 1
x + 3
= +∞.
Chọn đáp án D □
Câu 67. Tính lim
x→−1
−
1 − x
x + 1
.
A 1. B +∞. C −∞. D −1.
Lời giải.
Vì
lim
x→−1
−
(1 − x) = 2 > 0
lim
x→−1
−
(x + 1) = 0
x → −1
−
⇒ x < −1 ⇒ x + 1 < 0
nên lim
x→−1
−
1 − x
x + 1
= −∞.
Chọn đáp án C □
421/764 421/764
Toán 11 theo chương trình GDPT2018
2. Giới hạn của hàm số
Biết làm, làm đúng, làm nhanh
422
Câu 68. Tính giới hạn lim
x→(−2)
−
3 + 2x
x + 2
.
A +∞. B
3
2
. C −∞. D 2.
Lời giải.
Ta có: lim
x→(−2)
−
(3 + 2x) = −1 < 0 và lim
x→(−2)
−
(x + 2) = 0; x + 2 < 0 khi x → (−2)
−
.
Suy ra lim
x→(−2)
−
3 + 2x
x + 2
= +∞.
Chọn đáp án A □
Câu 69. Mệnh đề sao sau đây sai?
A lim
x→4
x − 4
√
x − 2
= 4. B lim
x→4
+
x − 4
(
√
x − 2)
2
= 0. C lim
x→4
x
2
− 4x
x − 4
= 4. D lim
x→4
x
2
− 4x
2
x − 4
= 0.
Lời giải.
• lim
x→4
x
2
− 4x
2
x − 4
lim
x→4
(x − 4) x
2
= 0.
• lim
x→4
+
x − 4
(
√
x − 2)
2
= lim
x→4
+
√
x + 2
√
x − 2
= +∞.
• lim
x→4
x − 4
√
x − 2
= lim
x→4
(
√
x + 2) = 4.
• lim
x→4
x
2
− 4x
x − 4
= lim
x→4
x = 4.
Chọn đáp án B □
Câu 70. Tính lim
x→1
−
√
x
3
− 3x + 2
x
2
− 7x + 4
.
A −
1
5
. B −
√
3
3
. C
√
3
3
. D
1
5
.
Lời giải.
Ta có
lim
x→1
−
√
x
3
− 3x + 2
x
2
− 7x + 4
= lim
x→1
−
p
(x − 1)
2
(x + 2)
(x − 1)(x −4)
= lim
x→1
−
−(x − 1)
√
x + 2
(x − 1)(x −4)
= lim
x→1
−
−
√
x + 2
x − 4
=
√
3
3
.
Chọn đáp án C □
Câu 71. Cho f(x) =
®
√
x − 2 + 3 nếu x ≥ 2
ax − 1 nếu x < 2
và lim
x→2
f(x) tồn tại. Tính a.
A 1. B −2. C 3. D 2.
Lời giải.
Ta có
○ lim
x→2
+
f(x) = lim
x→2
+
√
x − 2 + 3
= 3.
○ lim
x→2
−
f(x) = lim
x→2
−
(ax − 1) = 2a −1.
Vì lim
x→2
f(x) tồn tại nên lim
x→2+
f(x) = lim
x→2
−
f(x) ⇔ 2a − 1 = 3 ⇔ a = 2.
Chọn đáp án D □
422/764 422/764
Toán 11 theo chương trình GDPT2018
Chương 3. Giới hạn. Hàm số liên tục
Biết làm, làm đúng, làm nhanh
423
Câu 72. Tính giới hạn lim
x→2
x
2
− 2
x − 2
.
A −∞. B 2. C +∞. D Không tồn tại.
Lời giải.
- Ta có lim
x→2
−
x
2
− 2
x − 2
= −∞ và lim
x→2
+
x
2
− 2
x − 2
= +∞.
- Vì lim
x→2
−
x
2
− 2
x − 2
= lim
x→2
+
x
2
− 2
x − 2
nên không tồn tại giới hạn của hàm số tại x = 2.
Chọn đáp án D □
Câu 73. Tính lim
x→2
+
√
x − 2 −|x − 2|
|4 − x
2
|
.
A −∞. B +∞. C
1
4
. D 0.
Lời giải.
lim
x→2
+
√
x − 2 −|x − 2|
|4 − x
2
|
= lim
x→2
+
1 −
√
x − 2
√
x − 2|x + 2|
= +∞.
Vì lim
x→2
+
(1 −
√
x − 2) = 1, lim
x→2
+
√
x − 2|x + 2| = 0 và
√
x − 2|x + 2| > 0 ∀x > 2.
Chọn đáp án B □
Câu 74. Cho hàm số f (x) =
√
x + 4 −2
x
, x > 0
mx + m +
1
4
, x ≤ 0
m là tham số. Tìm giá trị của tham số m để hàm số có giới
hạn tại x = 0.
A m =
21
2
. B m = 1. C m =
−1
2
. D m = 0.
Lời giải.
Hàm số có giới hạn tại x = 0 ⇔ lim
x→0
+
f(x) = lim
x→0
−
f(x).
Vậy lim
x→0
+
√
x + 4 −2
x
= lim
x→0
−
Å
mx + m +
1
4
ã
⇔
1
4
= m +
1
4
⇔ m = 0.
Chọn đáp án D □
Câu 75. Gọi a, b là các giá trị để hàm số f(x) =
x
2
+ ax + b
x
2
− 4
khi x < −2
x + 1 khi x ≥ −2
có giới hạn hữu hạn khi x dần tới
−2. Tính 3a − b.
A 12. B 4. C 24. D 8.
Lời giải.
lim
x→−2
+
f(x) = lim
x→−2
+
(x + 1) = −1.
Suy ra f(x) có giới hạn hữu hạn khi x dần tới −2 khi và chỉ khi
lim
x→−2
−
f(x) = −1 ⇔ lim
x→−2
−
x
2
+ ax + b
x
2
− 4
= −1 ⇔ lim
x→−2
−
2x
2
+ ax + b − 4
x
2
− 4
= 0. (∗)
Do lim
x→−2
−
(x
2
− 4) = 0 nên điều kiện cần để có (*) là lim
x→−2
−
(2x
2
+ ax + b − 4) = 0 ⇒ 2a − b = 4.
Ngược lại, với 2a −b = 4 ta có
lim
x→−2
−
2x
2
+ ax + b − 4
x
2
− 4
= 0 ⇔ lim
x→−2
−
2x
2
+ ax + 2a − 8
x
2
− 4
= 0
⇔ lim
x→−2
−
2x + a −4
x − 2
= 0
⇔ a = 8.
Suy ra f(x) có giới hạn hữu hạn khi x dần tới −2 ⇔
®
a = 8
b = 12.
Vậy 3a −b = 12.
423/764 423/764
Toán 11 theo chương trình GDPT2018
2. Giới hạn của hàm số
Biết làm, làm đúng, làm nhanh
424
Chọn đáp án A □
Dạng 5. Bài toán thực tế về giới hạn hàm số
1. Ví dụ mẫu
Ví dụ 27 (KNTT). Một cái hồ đang chứa 200 m
3
nước mặn với nồng độ muối 10 kg/m
3
. Người ta ngọt hóa nước
trong hồ bằng cách bơm nước ngọt vào hồ với vận tốc 2 m
3
/phút.
a) Viết biểu thức C(t) biểu thị nồng độ muối trong hồ sau t phút kể từ khi bắt đầu bơm.
b) Tìm giới hạn lim
t→+∞
C(t) và giải thích ý nghĩa.
Lời giải.
a) Sau thời gian t phút, số m
3
nước trong hồ là 200 + 2t (m
3
).
Số kilôgam muối là 200 ·10 = 2000 (kg).
Nồng độ muối của nước trong hồ sau t phút khi bắt đầu bơm là
C(t) =
2000
200 + 2t
=
1000
100 + t
(kg/m
3
).
b) Khi t → +∞, ta xét giới hạn
lim
t→+∞
C(t) = lim
t→+∞
1000
100 + t
= 0.
□
Ví dụ 28 (KNTT). Trong Thuyết tương đối của Einstein, khối lượng của vật chuyển động với vận tốc v cho bởi
công thức
m =
m
0
…
1 −
v
2
c
2
.
trong đó m
0
là khối lượng của vật khi nó đứng yên, c là vận tốc ánh sáng. Chuyện gì xảy ra với khối lượng của
vật khi vận tốc của vật gần với vận tốc ánh sáng?
Lời giải.
Từ công thức khối lượng
m =
m
0
…
1 −
v
2
c
2
ta thấy m là một hàm số của v, với tập xác định là nửa khoảng [0; c). Rõ ràng khi v tiến gần tới vận tốc ánh
sáng, tức là v → c
−
, ta có
…
1 −
v
2
c
2
→ 0. Do đó lim
v→c
−
m(v) = +∞, nghĩa là khối lượng m của vật trở nên vô cùng
lớn khi vận tốc của vật gần với vận tốc ánh sáng. □
2. Bài tập tự luận
Bài 56. Một công ty sản xuất máy tính đã xác định được rằng, tính trung bình một nhân viên có thể lắp ráp được
N(t) =
50t
t + 4
(t ≥ 0) bộ phận mỗi ngày sau t ngày đào tạo. Tính lim
t→+∞
N(t) và cho biết ý nghĩa của kết quả.
Lời giải.
Ta có
lim
t→+∞
N(t) = lim
t→+∞
50t
t + 4
= lim
t→+∞
50t
t
Å
1 +
4
t
ã
= lim
t→+∞
50
1 +
4
t
424/764 424/764
Toán 11 theo chương trình GDPT2018
Chương 3. Giới hạn. Hàm số liên tục
Biết làm, làm đúng, làm nhanh
425
=
lim
t→+∞
50
lim
t→+∞
1 + lim
t→+∞
4
t
=
50
1 + 0
= 50.
Ý nghĩa của kết quả: năng suất lao động cao nhất trong một ngày của một nhân viên là 50. □
Bài 57. Chi phí (đơn vị: nghìn đồng) để sản xuất x sản phẩm của một công ty được xác định bởi hàm số
C(x) = 50000 + 105x.
a) Tính chi phí trung bình C(x) để sản xuất một sản phẩm.
b) Tính lim
x→+∞
C(x) và cho biết ý nghĩa của kết quả.
Lời giải.
a) Chi phí trung bình để sản xuất một sản phẩm là
C(x) =
50000 + 105x
x
.
b) Ta có
lim
x→+∞
C(x) = lim
x→+∞
50000 + 105x
x
= lim
x→+∞
Å
105 +
50000
x
ã
= lim
x→+∞
105 + lim
x→+∞
50000
x
= 105.
Ý nghĩa của kết quả: số lượng sản phẩm càng nhiều thì chi phí sản xuất sẽ càng giảm, chi phí thấp nhất là 105
nghìn đồng. □
Bài 58. Chiều dài một loài động vật nhỏ được tính theo công công thức h(t) =
300
1 + 9 ·(0,8)
t
mm, trong đó t số
ngày sau khi sinh của loài động vật đó. Tính chiều dài cuối cùng của nó (chiều dài khi t → +∞).
Lời giải.
Ta có lim
t→+∞
300
1 + 9 ·(0,8)
t
= 300.
Vậy chiều dài cuối cùng của loài động vật là 300 mm. □
Bài 59. Theo thuyết tương đối, khối lượng m của một hạt phụ thuộc vào vận tốc v của nó, theo công thức
m =
m
0
…
1 −
v
2
c
2
trong đó m
0
là khối lượng khi hạt đứng yên và c là tốc độ ánh sáng. Tìm giới hạn của khối lượng khi v tiến đến
c
−
.
Lời giải.
Với m
0
= 0 thì lim
v→c
−
= 0.
Với m
0
= 0.
Khi c → c
−
thì
1 −
v
2
c
2
→ 0
1 −
v
2
c
2
> 0
suy ra lim
v→c
−
m
0
…
1 −
v
2
c
2
= +∞.
Vậy nếu một hạt có khối lượng nghỉ khác 0 thì khối lượng của hạt sẽ lớn vô cùng khi vận tốc tiến gần vận tốc
ánh sáng. □
425/764 425/764
Toán 11 theo chương trình GDPT2018
2. Giới hạn của hàm số
Biết làm, làm đúng, làm nhanh
426
Bài 60. Một chất điểm chuyển động thẳng với phương trình s(t). Khi đó vận tốc tức thời tại thời điểm t
0
được định
nghĩa là lim
∆t
s(t
0
+ ∆t) −s(t
0
)
∆t
. Tính vận tốc tức thời của chất điểm với phương trình chuyển động s(t) = 3t
2
−2t+3
(s(t) có đơn vị là m, t đơn vị là giây), tại thời điểm t = 4 giây.
Lời giải.
Vận tốc tức thời của chất điểm tại thời điểm t = 4 giây là
lim
∆t→0
s(4 + ∆t) −s(4)
∆t
= lim
∆t→0
3(4 + ∆t)
2
− 2(4 + ∆t) + 3 − 43
∆t
= lim
∆t→0
3(∆t)
2
+ 22∆t
∆t
= 22 m/s.
□
Bài 61. Số lượng đơn vị hàng tồn kho trong một công ty được cho bởi
N(t) = 200
Å
3
ï
t + 3
3
ò
− t
ã
trong đó t là thời gian tính bằng ngày, [x] là số nguyên lớn nhất không vượt quá x (ví dụ [−1,5] = −2, [8,8] = 8).
a) Tính lim
t→55
+
N(t).
b) Tính lim
t→201
−
N(t).
Lời giải.
a) Khi t → 55
+
, ta có
ï
t + 3
3
ò
= 19.
Suy ra lim
t→55
+
N(t) = lim
t→55
+
200
Å
3
ï
t + 3
3
ò
− t
ã
= 200(3 · 19 −55) = 400.
b) Khi t → 201
−
, ta có
ï
t + 3
3
ò
= 201.
Suy ra lim
t→201
−
N(t) = lim
t→201
−
200
Å
3
ï
t + 3
3
ò
− t
ã
= 200 · 0 = 0.
□
Bài 62. Một chất điểm chuyển động thẳng với vận tốc v(t). Khi đó gia tốc tức thời tại thời điểm t
0
được định
nghĩa là lim
∆t→0
v(t
0
+ ∆t) −v(t
0
)
∆t
. Một chất điểm chuyển động với vận tốc v(t) = 0,1t
2
− 0,4t + 1 (m/s), tính gia
tốc tức thời tại thời điểm t = 8 giây.
Lời giải.
Gia tốc tức thời của chất điểm tại thời điểm t = 8 giây là
lim
∆t→0
v(8 + ∆t) −v(8)
∆t
= lim
∆t→0
0,1(8 + ∆t)
2
− 0,4(8 + ∆t) + 1 − 4,2
∆t
= lim
∆t→0
0,1(∆t)
2
+ 1,2∆t
∆t
= lim
∆t→0
(0,1∆t + 1,2)
= 1,2.
Vậy gia tốc tức thời của chất điểm tại thời điểm t = 8 giây là 1,2 (m/s
2
). □
Bài 63. Một người lái xe từ thành phố A đến thành phố B với vận tốc trung bình là x km/h. Trên chuyến trở về,
vận tốc trung bình là y km/h. Vận tốc trung bình của cả đi và về là 60 km/h. (Giả sử người lái xe đi trên cùng
một con đường trên cả chuyến đi và về).
a) Chứng minh rằng y =
30x
x − 30
.
426/764 426/764
Toán 11 theo chương trình GDPT2018
Chương 3. Giới hạn. Hàm số liên tục
Biết làm, làm đúng, làm nhanh
427
b) Tìm giới hạn của y khi x → 30
+
.
Lời giải.
a) Gọi khoảng cách giữa A và B là s km.
Thời gian chuyến đi là
s
x
, thời gian chuyến trở về là
s
y
.
Suy ra
2s
60
=
s
x
+
s
y
⇔
1
y
=
1
30
−
1
x
⇔ y =
30x
x − 30
.
b) Ta có lim
x→30
+
y = lim
x→30
+
30x
x − 30
= +∞.
□
Bài 64. Một hình elip với bán trục lớn a và bán trục nhỏ b thì diện tích được tính theo công thức S = πab. Tính
giới hạn diện tích của elip khi tiêu cự gần tới 0.
Lời giải.
Ta có S = πab = πa
√
a
2
− c
2
.
Vậy lim
c→0
S = lim
c→0
πa
√
a
2
− c
2
= πa
2
.
Ta thấy khi c → 0, thì giới hạn diện tích của elip là diện tích hình tròn bán kính R = a. □
Bài 65. Các nhà vật lý thấy rằng thuyết tương đối hẹp của Einstein quy về cơ học Newton khi c → +∞, trong
đó c là tốc độ ánh sáng. Điều này được minh họa bởi ví dụ: Một hòn đá được ném thẳng đứng từ mặt đất để nó
quay trở lại trái đất một giây sau đó. Sử dụng các định luật Newton, chúng ta thấy rằng chiều cao tối đa của hòn
đá là h =
g
8
mét (g = 9,8m/s
2
). Theo thuyết tương đối hẹp, khối lượng của hòn đá phụ thuộc vào vận tốc của nó
chia cho c, và có chiều cao cực đại là
h(c) = c
c
2
g
2
+
1
4
−
c
2
g
.
Tính lim
c→+∞
h(c).
Lời giải.
Ta có
lim
c→+∞
c
c
2
g
2
+
1
4
−
c
2
g
= lim
c→+∞
c
Å
c
2
g
2
+
1
4
−
c
2
g
2
ã
c
2
g
2
+
1
4
+
c
g
= lim
c→+∞
1
4
1
g
2
+
1
4c
2
+
1
g
=
g
8
.
□
Bài 66. Thế Lennard-Jones có dạng
U(r) =
B
r
12
−
A
r
6
trong đó A, B là các hằng số và r là khoảng cách giữa các hạt. Tính lim
r→+∞
U(r).
Lời giải.
Ta có
lim
r→+∞
U(r) = lim
r→+∞
Å
B
r
12
−
A
r
6
ã
= 0.
□
Bài 67. Trong thuyết tương đối, chiều dài của một vật thể đối với người quan sát phụ thuộc vào tốc độ mà vật
thể đang chuyển động đối với người quan sát. Nếu người quan sát đo chiều dài của vật thể là L
0
khi đứng yên,
thì ở tốc độ v chiều dài là
L = L
0
1 −
v
2
c
2
trong đó c là tốc độ ánh sáng trong chân không. Tìm lim
v→c
−
L.
Lời giải.
Ta có lim
v→c
−
L = lim
v→c
−
L
0
1 −
v
2
c
2
= lim
v→c
−
L
0
1 −
c
2
c
2
= 0. □
427/764 427/764
Toán 11 theo chương trình GDPT2018
2. Giới hạn của hàm số
Biết làm, làm đúng, làm nhanh
428
Bài 68. Trong kỹ thuật ứng dụng, chúng ta thường xuyên ghi nhận được các hàm số mà giá trị của nó thay đổi
đột ngột tại một thời điểm t xác định. Ví dụ: Sự thay đổi điện áp của một mạch điện tại thời điểm t khi đóng
hoặc ngắt mạch. Thông thường, giá trị t = 0 luôn được chọn là thời điểm bắt đầu cho việc đóng hoặc ngắt điện
áp. Quá trình đóng, ngắt mạch trên có thể mô tả bằng mô hình toán học bởi hàm Heaviside
u(t) =
®
0 nếu t < 0
1 nếu t ≥ 0.
Có tồn tại giới hạn lim
t→0
u(t) hay không?
Lời giải.
Ta có lim
t→0
+
u(t) = lim
t→0
+
1 = 1; lim
t→0
−
u(t) = lim
t→0
−
0 = 0.
Vậy giới hạn lim
t→0
u(t) không tồn tại. □
Bài 69. Trong một cuộc thi các môn thể thao trên tuyết, người ta muốn thiết kế một đường trượt bằng băng cho
nội dung đổ dốc tốc độ đường dài.
x
y
5 10 15 20 25 30 35 40 45
15
O
Vận động viên sẽ xuất phát từ vị trí (0; 15) cao 15 m so với mặt đất (trục Ox). Đường trượt phải thoả mãn yêu
cầu là càng ra xa thì càng gần mặt đất để tiết kiệm lượng tuyết nhân tạo. Một nhà thiết kế đề nghị sử dụng
đường cong là đồ thị hàm số y = f(x) =
150
x + 10
, với x ≥ 0. Hãy kiểm tra xem hàm số y = f(x) có thoả mãn các
điều kiện dưới đây hay không:
a) Có đồ thị qua điểm (0; 15);
b) Giảm trên [0; +∞);
c) Càng ra xa (x càng lớn), đồ thị của hàm số càng gần trục Ox với khoảng cách nhỏ tuỳ ý.
Lời giải.
a) Ta có f(0) =
150
10
nên đồ thị hàm số f(x) đi qua điểm (0; 15).
b) Chọn bất kì x
1
, x
2
∈ [0; +∞] và x
1
= x
2
.
Ta có
f(x
2
) − f(x
1
)
x
2
− x
1
=
150
x
2
+ 10
−
150
x
1
+ 10
x
2
− x
1
=
x
1
− x
2
(x
2
− x
1
)(x
1
+ 10)(x
2
+ 10)
= −
1
(x
1
+ 10)(x
2
+ 10)
< 0.
Suy ra hàm số nghịch biến trên [0; +∞) hay hàm số giảm trên [0; +∞).
c) Ta có lim
x→+∞
f(x) = lim
x→+∞
150
x + 10
= 0.
Vậy khi x càng lớn, đồ thị của hàm số càng gần trục Ox với khoảng cách nhỏ tuỳ ý.
□
Bài 70. Chiều dài một loài động vật nhỏ được tính theo công công thức h(t) =
100
2 + 3 ·(0,4)
t
mm, trong đó t số
ngày sau khi sinh của loài động vật đó. Tính chiều dài cuối cùng của nó (chiều dài khi t → +∞).
Lời giải.
Ta có lim
t→+∞
h(t) =
100
2 + 3 ·(0,4)
t
= 100.
Vậy chiều dài của loài động vật khi trưởng thành là 100 mm. □
428/764 428/764
Toán 11 theo chương trình GDPT2018
Chương 3. Giới hạn. Hàm số liên tục
Biết làm, làm đúng, làm nhanh
429
Bài 71. Một chất điểm chuyển động thẳng với phương trình s(t). Khi đó vận tốc tức thời tại thời điểm t
0
được định
nghĩa là lim
∆t
s(t
0
+ ∆t) −s(t
0
)
∆t
. Tính vận tốc tức thời của chất điểm với phương trình chuyển động s(t) = 4t
2
−3t+1
(s(t) có đơn vị là m, t đơn vị là giây), tại thời điểm t = 8 giây.
Lời giải.
Vận tốc tức thời của chất điểm tại thời điểm t = 8 giây là
lim
∆t→0
s(8 + ∆t) −s(8)
∆t
= lim
∆t→0
4(8 + ∆t)
2
− 3(8 + ∆t) + 1 − 233
∆t
= lim
∆t→0
4(∆t)
2
+ 61∆t
∆t
= 61 m/s.
□
Bài 72. Bỏ qua lực cản của không khí, độ cao tối đa mà tên lửa đạt được khi phóng với vận tốc ban đầu v
0
là
h =
v
2
0
R
19,6R − v
2
0
, trong đó R là bán kính của trái đất. Tính lim
R→+∞
h.
Lời giải.
Ta có
lim
R→+∞
h = lim
R→+∞
v
2
0
R
19,6R − v
2
0
= lim
R→+∞
v
2
0
19,6 −
v
2
0
R
=
v
2
0
19,6
.
□
Bài 73. Một hình elip với bán trục lớn a và bán trục nhỏ b thì diện tích được tính theo công thức S = πab. Cho
elip có bán trục nhỏ bằng 30 cm, tính giới hạn diện tích của elip khi tiêu cự gần tới 0.
Lời giải.
Ta có S = πab = πb
√
b
2
+ c
2
.
Vậy lim
c→0
S = lim
c→0
πb
√
b
2
+ c
2
= πb
2
= 900π cm
2
. □
Bài 74. Số lượng đơn vị hàng tồn kho trong một công ty nhỏ được cho bởi
N(t) = 25
Å
2
ï
t + 2
2
ò
− t
ã
trong đó t là thời gian tính bằng tháng, [x] là số nguyên lớn nhất không vượt quá x (ví dụ [2,4] = 2, [−2,7] = −3).
a) Tính lim
t→8
+
N(t).
b) Tính lim
t→16
−
N(t).
Lời giải.
a) Khi t → 8
+
, ta có
ï
t + 2
2
ò
= 5.
Suy ra lim
t→8
+
N(t) = lim
t→8
+
25
2
t+2
2
− t
= 50.
b) Khi t → 16
−
, ta có
ï
t + 2
2
ò
= 8.
Suy ra lim
t→16
−
N(t) = lim
t→16
−
25
2
t+2
2
− t
= 0.
□
Bài 75. Định luật Boyle được phát biểu: “Đối với một lượng khí ở nhiệt độ không đổi, áp suất P tỷ lệ nghịch với
thể tích V ”. Tìm giới hạn của P là V → 0
+
.
Lời giải.
Ta có P =
k
V
với k là số thực dương không đổi.
Khi đó lim
V →0
+
P =
k
V
= +∞. □
429/764 429/764
Toán 11 theo chương trình GDPT2018
2. Giới hạn của hàm số
Biết làm, làm đúng, làm nhanh
430
Bài 76. Một vật khối lượng m (không đổi) bắt đầu chuyển động với vận tốc v
0
= 0, được gia tốc bởi một lực F
không đổi trong t giây. Theo định luật Newton về chuyển động, vật tốc của vật là v
N
=
F t
m
. Theo thuyết tương
đối Einstein, vật có vận tốc v
E
=
F ct
√
m
2
c
2
+ F
2
t
2
, với c là vận tốc ánh sáng. Tính lim
t→+∞
v
N
và lim
t→+∞
v
E
.
Lời giải.
Ta có
lim
t→+∞
v
N
= lim
t→+∞
F t
m
= +∞;
lim
t→+∞
v
E
= lim
t→+∞
F ct
√
m
2
c
2
+ F
2
t
2
= lim
t→+∞
F c
…
m
2
c
2
t
2
+ F
2
=
c
F
.
□
Bài 77.
Gọi S là diện tích hình phẳng giới hạn bởi đường tròn bán kính 10 và tam giác
vuông (hình vẽ bên).
a) Đặt S = f(φ), với f (φ) là hàm số của φ (Đơn vị rad). Tìm công thức của
f(φ) với 0 < φ <
π
2
.
b) Tính giới hạn của f (φ) khi φ →
π
2
−
.
φ
A
B
C
D
Lời giải.
a) Diện tích tam giác ABC là S
ABC
=
1
2
AB · AC =
1
2
· 4 ·4 tan φ = 8 tan φ.
Diện tích hình quạt ABD là S
q
=
4
2
φ
2
= 8φ.
Diện tích hình phẳng S là S = f(φ) = S
ABC
− S
q
= 8(tan φ − φ).
b) Khi φ →
π
2
−
thì
®
cos φ → 0
cos φ > 0.
Suy ra lim
φ→
π
2
−
f(φ) = lim
φ→
π
2
−
8
Å
sin φ
cos φ
− φ
ã
= +∞.
□
Bài 78. Trên một chuyến đi dài d km đến một thành phố khác, vận tốc trung bình của một tài xế xe tải là x
km/h. Trên chuyến trở về, vận tốc trung bình là y km/h. Vận tốc trung bình của cả đi và về là 50 km/h.
a) Chứng minh rằng y =
25x
x − 25
.
b) Tìm giới hạn của y khi x → 25
+
và giải thích ý nghĩa của nó.
Lời giải.
a) Thời gian chuyến đi là
d
x
, thời gian chuyến trở về là
d
y
.
Suy ra
2d
50
=
d
x
+
d
y
⇔
1
y
=
1
25
−
1
x
⇔ y =
25x
x − 25
.
b) Ta có lim
x→25
+
y = lim
x→25
+
25x
x − 25
= +∞.
Khi vận tốc trung bình chuyến đi bằng 25 km/h, thì vận tốc trung bình chuyến của cả chuyến đi và về không
thể là 50 km/h.
□
430/764 430/764
Toán 11 theo chương trình GDPT2018
Chương 3. Giới hạn. Hàm số liên tục
Biết làm, làm đúng, làm nhanh
431
Bài 79. Một chất điểm chuyển động thẳng với vận tốc v(t). Khi đó gia tốc tức thời tại thời điểm t
0
được định
nghĩa là lim
∆t→0
v(t
0
+ ∆t) −v(t
0
)
∆t
. Một chất điểm chuyển động với vận tốc v(t) = 5 sin (4πt) (m/s), tính gia tốc
tức thời tại thời điểm t = 5 giây. (Biết lim
x→0
sin x
x
= 1).
Lời giải.
Gia tốc tức thời của chất điểm tại thời điểm t = 5 giây là
lim
∆t→0
v(5 + ∆t) −s(5)
∆t
= lim
∆t→0
5 sin(20π + 4π∆t) − 5 sin(20π)
∆t
= lim
∆t→0
5 sin(4π∆t)
∆t
= lim
∆t→0
20π sin(4π∆t)
4π∆t
= 20π.
Vậy gia tốc tức thời của chất điểm tại thời điểm t = 5 giây là 20π (m/s
2
). □
Bài 80. Một bể chứa 5000 lít nước tinh khiết. Nước muối chứa 30 g muối trên một lít nước được bơm vào bể với
tốc độ 25 lít/phút. Gọi nồng độ của muối sau t phút (tính bằng gam trên lít) là C(t). Tính lim
t→+∞
C(t). Giải thích
ý nghĩa của giới hạn này.
Lời giải.
Số lít nước muối được bơm vào bể sau t phút là 25t lít.
Số g muối có trong 25t lít nước muối là 30 ·25t = 750t gam.
Nồng độ của muối trong bể sau t phút là
750t
25t + 5000
=
30t
t + 200
gam/lít.
Ta có lim
t→+∞
C(t) = lim
t→+∞
30t
t + 200
= 30 gam/lít.
Khi thời gian tiến tới vô hạn thì nồng độ của muối trong bể bằng nồng độ của nước muối bơm vào bể. □
Bài 81. Một thấu kính hội tụ có tiêu cự f = 30 cm. Trong Vật lí, ta biết rằng nếu đặt vật thật AB cách quang
tâm của thấu kính một khoảng d > 30 (cm) thì được ảnh thật A
′
B
′
cách quang tâm của thấu kính một khoảng
d
′
(cm) (Hình vẽ dưới). Ngược lại, nếu 0 < d < 30, ta có ảnh ảo. Công thức của thấu kính là
1
d
+
1
d
′
=
1
30
.
30 30
d
d
′
A
B
A
′
B
′
O
F
F
′
a) Từ công thức của thấu kính, hãy tìm biểu thức xác định hàm số d
′
= h(d).
b) Tìm các giới hạn lim
d→30
+
h(d); lim
d→30
−
h(d) và lim
d→+∞
h(d). Sử dụng các kết quả này để giải thích ý nghĩa đã biết
trong Vật lí.
Lời giải.
a) Ta có
1
d
+
1
d
′
=
1
30
⇔
1
d
′
=
1
30
−
1
d
=
d − 30
30d
⇔ d
′
=
30d
d − 30
.
Vậy d
′
= h(d) =
30d
d − 30
.
431/764 431/764
Toán 11 theo chương trình GDPT2018
2. Giới hạn của hàm số
Biết làm, làm đúng, làm nhanh
432
b) Khi d → 30
+
, ta có d − 30 → 0, d − 30 > 0 và 30d → 900.
Suy ra lim
d→30
+
h(d) = lim
d→30
+
30d
d − 30
= +∞.
Khi d → 30
−
, ta có d − 30 → 0, d − 30 < 0 và 30d → 900.
Suy ra lim
d→30
−
h(d) = lim
d→30
−
30d
d − 30
= −∞.
Ta có lim
d→+∞
h(d) = lim
d→+∞
30d
d − 30
= lim
d→+∞
30
1 −
30
d
= 30.
Vậy
○ Khi vị trí của vật tiến gần tiêu điểm F (d > f) thì vị trí ảnh thật của vật dần ra xa vô cực.
○ Khi vị trí của vật tiến gần tiêu điểm F (d < f) thì vị trí ảnh ảo của vật dần ra xa vô cực.
○ Khi vị trí của vật tiến ra xa vô cực thì ảnh thật của vật dần tới tiêu điểm.
□
432/764 432/764
Toán 11 theo chương trình GDPT2018
Chương 3. Giới hạn. Hàm số liên tục
Biết làm, làm đúng, làm nhanh
433
HÀM SỐ LIÊN TỤC
3
Baâi söë
A–KHÁI NIỆM
1. Hàm số liên tục tại một điểm
c Định nghĩa 3.1. Cho hàm số y = f(x) xác định trên khoảng (a; b) và x
0
∈ (a; b). Hàm số y = f(x) được
gọi là liên tục tại x
0
nếu lim
x→x
0
f(x) = f (x
0
).
Nhận xét. Hàm số y = f(x) không liên tục tại x
0
được gọi là gián đoạn tại x
0
.
2. Hàm số liên tục trên một khoảng hoặc một đoạn
c Định nghĩa 3.2.
○ Hàm số y = f(x) được gọi là liên tục trên khoảng (a; b) nếu hàm số liên tục tại mọi điểm thuộc khoảng
đó.
○ Hàm số y = f(x) được gọi là liên tục trên đoạn [a; b] nếu hàm số đó liên tục trên khoảng (a; b) và
lim
x→a
+
f(x) = f (a); lim
x→b
−
f(x) = f (b).
Khái niệm hàm số liên tục trên các tập hợp có dạng (a; b], [a; b), (a; +∞), [a; +∞), (−∞; a), (−∞; a],
(−∞; +∞) được định nghĩa tương tự.
Nhận xét. Đồ thị hàm số liên tục trên một khoảng là “đường liền” trên khoảng đó.
B–MỘT SỐ ĐỊNH LÍ CƠ BẢN
1.
Tính liên tục của một số hàm số sơ cấp cơ bản
Các hàm đa thức, hàm phần thức hữu tỉ (thương của hai đa thức), hàm căn thức, hàm số lượng giác là những
hàm sơ cấp cơ bản. Sau đây, ta sẽ xét tính liên tục của những hàm số đó.
c Định lí 3.1.
○ Các hàm đa thức và hai hàm số lượng giác y = sin x, y = cos x liên tục trên R.
○ Các hàm phân thức hữu tỉ và hai hàm số lượng giác y = tan x, y = cot x liên tục trên từng khoảng xác
định của chúng.
○ Hàm căn thức y =
√
x liên tục trên nửa khoảng [0; +∞).
2. Tính liên tục của tổng, hiệu, tích, thương của hai hàm số liên tục
c Định lí 3.2. Giả sử y = f(x) và y = g(x) là hai hàm số liên tục tại điểm x
0
. Khi đó:
a) Các hàm số f(x) + g(x); f(x) − g(x) và f(x) · g(x) liên tục tại x
0
;
b) Hàm số y =
f(x)
g(x)
liên tục tại x
0
nếu g(x
0
) = 0.
433/764 433/764
Toán 11 theo chương trình GDPT2018
3. Hàm số liên tục
Biết làm, làm đúng, làm nhanh
434
C–CÁC DẠNG TOÁN THƯỜNG GẶP
Dạng 1. Câu hỏi lý thuyết
1. Ví dụ mẫu
Ví dụ 1 (CD). Bạn Nam cho rằng: “Nếu hàm số y = f (x) liên tục tại điểm x
0
, còn hàm số y = g(x) không liên
tục tại x
0
, thì hàm số y = f (x) + g(x) không liên tục tại x
0
”. Theo em, ý kiến của bạn Nam đúng hay sai? Giải
thích.
Lời giải.
Giả sử hàm số h(x) = f (x) + g(x) là hàm số liên tục tại x
0
.
Khi đó, hàm số g(x) = h(x) − f(x) là hiệu của hai hàm số liên tục tại x
0
nên hàm số g(x) là hàm số liên tục tại
x
0
. Điều này mâu thuẫn với giả thiết là g(x) không liên tục tại x
0
.
Vậy ý kiến trên là đúng. □
2. Bài tập trắc nghiệm
Câu 1. Cho hàm số y = f(x) xác định trên khoảng K và x
0
∈ K. Hàm số y = f(x) liên tục tại x
0
khi và chỉ
khi
A lim
x→x
0
f(x) = +∞. B lim
x→x
0
f(x) = −∞. C lim
x→x
0
f(x) = f (x
0
). D lim
x→x
+
0
f(x) = f (x
0
).
Lời giải.
Hàm số y = f(x) được gọi là liên tục tại x
0
nếu lim
x→x
0
f(x) = f (x
0
).
Chọn đáp án C □
Câu 2. Cho hàm số y = f (x) liên tục trên khoảng (a; b). Điều kiện cần và đủ để hàm số liên tục trên đoạn [a; b]
là
A lim
x→a
+
f(x) = f (a) và lim
x→b
−
f(x) = f (b). B lim
x→a
−
f(x) = f (a) và lim
x→b
+
f(x) = f (b).
C lim
x→a
+
f(x) = f (a) và lim
x→b
+
f(x) = f (b). D lim
x→a
−
f(x) = f (a) và lim
x→b
−
f(x) = f (b).
Lời giải.
Hàm số f xác định trên đoạn [a; b] được gọi là liên tục trên đoạn [a; b] nếu nó liên tục trên khoảng (a; b), đồng
thời lim
x→a
+
f(x) = f (a) và lim
x→b
−
f(x) = f (b) .
Chọn đáp án A □
Câu 3. Trong các mệnh đề sau, mệnh đề nào đúng?
A Hàm số đồng biến trên (a; b) có đồ thị là đường đi xuống từ trái sang phải trên (a; b).
B Hàm số nghịch biến trên (a; b) có đồ thị là đường đi lên từ trái sang phải trên (a; b).
C Hàm số y = 0 là hàm số không chẵn, không lẻ trên R.
D Hàm số liên tục trên (a; b) có đồ thị là đường liền nét trên (a; b).
Lời giải.
Hàm số liên tục trên (a; b) có đồ thị là đường liền nét trên (a; b).
Chọn đáp án D □
Câu 4. Trong các loại hàm số sau, hàm số nào luôn liên tục trên tập hợp các số thực R?
A Hàm số lượng giác. B Hàm số đa thức.
C Hàm số phân thức hữu tỉ. D Hàm số có chứa căn bậc hai.
Lời giải.
Hàm số đa thức luôn liên tục trên tập số thực R.
Chọn đáp án B □
Câu 5. Hàm số y = f(x) liên tục tại điểm x
0
khi nào?
A lim
x→x
0
f(x) = f (x). B lim
x→x
0
f(x) = f (x
0
). C lim
x→x
0
f(x) = f (0). D f(x
0
) = 0.
434/764 434/764
Toán 11 theo chương trình GDPT2018
Chương 3. Giới hạn. Hàm số liên tục
Biết làm, làm đúng, làm nhanh
435
Lời giải.
Theo định nghĩa hàm số liên tục, ta có lim
x→x
0
f(x) = f (x
0
).
Chọn đáp án B □
Câu 6. Cho hàm số f (x) thỏa mãn lim
x→x
0
f(x) = f (x
0
). Khẳng định nào sau đây đúng?
A Hàm số f(x) không xác định tại x
0
. B lim
x→x
−
0
f(x) = lim
x→x
+
0
f(x).
C Hàm số f(x) liên tục tại x
0
. D f(x) có giá trị 0 tại x
0
.
Lời giải.
Theo định nghĩa hàm số liên tục, ta có: do lim
x→x
0
f(x) = f (x
0
) nên hàm số f (x) không liên tục tại x
0
. Vì lim
x→x
0
f(x)
tồn tại nên lim
x→x
−
0
f(x) = lim
x→x
+
0
f(x).
Chọn đáp án B □
Câu 7. Xét các mệnh đề sau
a) Nếu hàm số f(x) có đạo hàm tại điểm x = x
0
thì f(x) liên tục tại điểm đó.
b) Nếu hàm số f(x) liên tục tại điểm x = x
0
thì f(x) có đạo hàm tại điểm đó.
c) Nếu f(x) không liên tục tại x
0
thì chắc chắn f(x) không có đạo hàm tại điểm đó.
d) f(x) có đạo hàm tại x
0
khi và chỉ khi f(x) liên tục tại x
0
.
Trong các mệnh đề trên, có bao nhiêu mệnh đề đúng?
A 2. B 1. C 4. D 3.
Lời giải.
Theo định lý thì mệnh đề thứ nhất và mệnh đề thứ ba đúng.
Xét hàm số f(x) = |x| ta có: lim
x→0
+
f(x) = 0 và lim
x→0
−
f(x) = 0 nên hàm số liên tục tại x = 0.
Mặt khác lim
x→0
+
f(x) − f(0)
x − 0
= 1 và lim
x→0
−
f(x) − f(0)
x − 0
= −1 nên hàm số không có đạo hàm tại x = 0. Vậy hai
mệnh đề còn lại sai.
Chọn đáp án A □
Câu 8. Cho hàm số f (x) xác định trên [a; b]. Trong các mệnh đề sau, mệnh đề nào đúng?
A Nếu hàm số f(x) liên tục trên đoạn [a; b] và f(a) · f (b) > 0 thì phương trình f(x) = 0 không có nghiệm
trong khoảng (a; b).
B Nếu hàm số f (x) liên tục trên đoạn [a; b] và f(a) ·f(b) < 0 thì phương trình f(x) = 0 có ít nhất một nghiệm
trong khoảng (a; b).
C Nếu phương trình f (x) = 0 có nghiệm trong khoảng (a; b), thì hàm số f(x) phải liên tục trên khoảng (a; b).
D Nếu f(a) · f(b) < 0 thì phương trình f(x) = 0 có nghiệm trong khoảng (a; b).
Lời giải.
Nếu hàm số f(x) liên tục trên đoạn [a; b] và f(a) · f (b) < 0 thì phương trình f(x) = 0 có ít nhất một nghiệm
trong khoảng (a; b).
Chọn đáp án B □
Câu 9. Tìm khẳng định đúng trong hai khẳng định sau
I. f(x) liên tục trên [a, b] và f(a) · f(b) > 0 thì tồn tại ít nhất số c ∈ (a, b) sao cho f(c) = 0.
II. f(x) liên tục trên (a, b) và (b, c) nhưng không liên tục trên (a, c).
A Chỉ I đúng. B Chỉ II đúng. C Cả I và II đều sai. D Cả I và II đều đúng.
Lời giải.
Chọn đáp án C □
435/764 435/764
Toán 11 theo chương trình GDPT2018
3. Hàm số liên tục
Biết làm, làm đúng, làm nhanh
436
Câu 10. Cho lim
x→a
f(x) = L. Khẳng định nào sau đây đúng?
A f (a) = L. B Hàm số liên tục tại x = a.
C Hàm số xác định tại x = a. D Không đáp án nào đúng.
Lời giải.
Chọn đáp án D □
Câu 11. Cho lim
x→3
−
f(x) = −1, lim
x→3
+
f(x) = −1. Khẳng định nào sau đây đúng?
A lim
x→3
f(x) = −1. B Hàm số liên tục tại x = 3.
C f (3) = −1. D f(3) không xác định.
Lời giải.
lim
x→3
−
f(x) = lim
x→3
+
f(x) = −1 ⇒ lim
x→3
f(x) = −1.
Chọn đáp án A □
Câu 12. Trong các mệnh đề sau, mệnh đề nào sai?
A Nếu hàm số f(x) liên tục trên khoảng (a; b) thì f(x) cũng liên tục trên mọi khoảng con của (a; b).
B Mọi hàm số đa thức đều liên tục trên khoảng (−∞; +∞).
C Mọi hàm số phân thức hữu tỉ đều liên tục trên mọi khoảng mà nó xác định.
D Nếu hàm số f (x) liên tục trên hai khoảng liên tiếp (a; b) và (b; c) thì f(x) cũng liên tục trên khoảng (a; c).
Lời giải.
Xét hàm số f(x) =
®
√
x − 1 nếu x ≥ 1
2x + 3 nếu x < 1.
Ta thấy f(x) liên tục trên các khoảng (0; 1) và (1; 2) nhưng không liên tục trên (0; 2).
Chọn đáp án D □
Câu 13. Cho f(x) là một hàm số liên tục trên khoảng (a; b). Trong các mệnh đề sau, mệnh đề nào sai?
A Hàm số g(x) = (f(x))
2
liên tục trên khoảng (a; b). B Hàm số h(x) =
3
p
f(x) liên tục trên khoảng (a; b).
C Hàm số k(x) =
1
f(x)
liên tục trên khoảng (a; b). D Hàm số u(x) = |f(x)| liên tục trên khoảng (a; b).
Lời giải.
Đối với hàm số k(x) =
1
f(x)
, cần thêm điều kiện f(x) = 0, ∀x ∈ (a; b).
Chọn đáp án C □
Câu 14. Cho f (x) và g(x) là hai hàm số liên tục trên khoảng (a; b). Tìm mệnh đề sai trong các mệnh đề sau?
A Hàm số h(x) = f(x) − g(x) liên tục trên khoảng (a; b).
B Hàm số k(x) = f(x).g(x) liên tục trên khoảng (a; b).
C Hàm số u(x) =
f(x)
g(x)
liên tục trên khoảng (a; b).
D Hàm số v(x) = af(x) + bg(x) liên tục trên khoảng (a; b) với a, b là các hằng số.
Lời giải.
Hàm số u(x) =
f(x)
g(x)
liên tục trên khoảng (a; b) khi g(x) = 0, ∀x ∈ (a; b).
Chọn đáp án C □
Câu 15. Tìm khẳng định đúng trong các khẳng định sau
I. f(x) liên tục trên đoạn [a; b] và f (a) · f(b) < 0 thì phương trình f(x) = 0 có nghiệm.
II. f(x) không liên tục trên [a; b] và f(a) · f(b) ≥ 0 thì phương trình f(x) = 0 vô nghiệm.
A Chỉ I đúng. B Chỉ II đúng. C Cả I và II đúng. D Cả I và II sai.
Lời giải.
Chọn đáp án A □
436/764 436/764
Toán 11 theo chương trình GDPT2018
Chương 3. Giới hạn. Hàm số liên tục
Biết làm, làm đúng, làm nhanh
437
Câu 16. Cho hàm số f(x) liên tục trên đoạn [a; b] và m ≤ f(x) ≤ M , ∀x ∈ [a; b] . Tìm mệnh đề sai trong các
mệnh đề sau?
A Luôn tồn tại x
1
∈ [a; b] sao cho f(x) ≥ f(x
1
), ∀x ∈ [a; b].
B Luôn tồn tại x
2
∈ [a; b] sao cho f(x) ≤ f(x
2
), ∀x ∈ [a; b].
C Với mọi k ∈ [m; M] , luôn tồn tại c ∈ [a; b] sao cho f(c) = k.
D Đồ thị của hàm số là một đường liền nét trên đoạn [a; b].
Lời giải.
f(x
1
) chính là giá trị nhỏ nhất của hàm số f(x) trên đoạn [a; b].
f(x
2
) chính là giá trị lớn nhất của hàm số f(x) trên đoạn [a; b].
Hàm số f(x) liên tục trên đoạn [a; b] nên có đồ thị là một đường liền nét trên đoạn [a; b].
Ngoài ra, m và M chưa chắc là giá trị nhỏ nhất và giá trị lớn nhất của f(x) trên đoạn [a; b].
Chọn đáp án
C □
Dạng 2. Dựa vào đồ thị xét tính liên tục của hàm số tại một điểm, một khoảng.
Để xét tính liên tục của hàm số khi biết đồ thị, ta cần nhớ:
○ Đồ thị của hàm số liên tục trên một khoảng là một đường liền nét trên khoảng đó.
○ Hàm số y = f(x) liên tục tại x
0
khi và chỉ khi lim
x→x
0
+
f(x) = lim
x→x
0
−
f(x) = f (x
0
).
1. Ví dụ mẫu
Ví dụ 2. Quan sát đồ thị hàm số trong Hình 12a và Hình 12b, xác định f(0) và lim
x→0
f(x). Từ đó cho biết mỗi
hàm số đó liên tục tại x = 0 hay không? Giải thích.
Lời giải.
Trong Hình 12a ta có f(0) = 0, lim
x→0
f(x) = lim
x→0
x
2
= 0.
x
y
−2 −1
1 2
O
x
y
−1
−1
1
1
O
a) Đồ thị hàm số f(x) = x
2
b) Đồ thị hàm số f(x) =
− 1 nếu x < 0
0 nếu x = 0
1 nếu x > 0
Hình 12
Như vậy lim
x→0
f(x) = f (0) nên hàm số liên tục tại x = 0.
Trong Hình 12b ta có lim
x→0
−
f(x) = −1, lim
x→0
+
f(x) = 1.
Do đó không tồn tại lim
x→0
f(x).
Vậy hàm số f(x) không liên tục tại x = 0. □
Ví dụ 3. Trong các hàm số có đồ thị ở Hình 15a, 15b, 15c hàm số nào liên tục trên tập xác định của hàm số đó?
Giải thích.
437/764 437/764
Toán 11 theo chương trình GDPT2018
3. Hàm số liên tục
Biết làm, làm đúng, làm nhanh
438
x
y
O
1
2
3
1 2 3
x
y
O
−1
1
−1
1
x
y
−1
1
−1
1
O
a) Đồ thị hàm số
f(x) = x
2
− 2x
b) Đồ thị hàm số
g(x) =
x
x − 1
c) Đồ thị hàm số
h(x) =
®
− 2x nếu x < −1
x + 1 nếu x ≥ 1
Hình 15
Lời giải.
Hàm số liên tục trên tập xác định là f(x) = x
2
− 2x. Vì đồ thị hàm số ở hình Hình 15a là một đường liền nét
trên mặt phẳng tọa độ. □
Ví dụ 4.
Cho hàm số y = f(x) có đồ thị như hình vẽ bên.
Xét tính liên tục của hàm số y = f(x) trên khoảng (0; 2).
O
x
y
1 2
y = f(x)
Lời giải.
Đồ thị hàm số là một đường liền nét trên khoảng (0; 2) nên hàm số đã cho liên tục trên khoảng (0; 2). □
Ví dụ 5.
Cho hàm số y = f(x) có đồ thị như hình vẽ bên.
Xét tính liên tục của hàm số y = f(x) trên khoảng (−2; 2).
O
x
y
−2
2
y = f(x)
Lời giải.
Đồ thị hàm số là một đường liền nét trên khoảng (−2; 2) nên hàm số đã cho liên tục trên khoảng (−2; 2). □
Ví dụ 6.
Cho hàm số y = f(x) có đồ thị như hình vẽ bên.
Xét tính liên tục của hàm số y = f(x) trên khoảng (0; 2).
O
x
y
1 2
1
2
y = f(x)
Lời giải.
○ Đồ thị hàm số là các đường liền nét trên các khoảng (0; 1), (1; 2) do đó hàm số liên tục trên các khoảng này.
○ Đồ thị hàm số không liền nét tại điểm x = 1 do đó hàm số đã cho gián đoạn tại điểm này.
□
Ví dụ 7.
438/764 438/764
Toán 11 theo chương trình GDPT2018
Chương 3. Giới hạn. Hàm số liên tục
Biết làm, làm đúng, làm nhanh
439
Cho hàm số y = f(x) có đồ thị như hình vẽ bên.
Xét tính liên tục của hàm số y = f(x) trên khoảng (0; 2).
O
x
y
1 2
1
2
y = f(x)
Lời giải.
○ Đồ thị hàm số là các đường liền nét trên các khoảng (0; 1), (1; 2) do đó hàm số liên tục trên các khoảng này.
○ Ta có lim
x→1
−
f(x) > f(1) = 1 và lim
x→1
+
f(x) = f (1) = 1.
Do đó lim
x→1
−
f(x) = lim
x→1
+
f(x).
Vậy hàm số đã cho gián đoạn tại x = 1.
□
Ví dụ 8.
Cho hàm số y = f (x) có tập xác định D = R \ {0} và có đồ thị như hình bên. Xét
tính liên tục của hàm số y = f(x) trên D .
O
x
y
y = f(x)
Lời giải.
Vì hàm số đã cho có tập xác định D = R \{0} nên
○ f(x) xác định trên khoảng (−∞; 0) nên liên tục trên khoảng này.
○ f(x) xác định trên khoảng (0; +∞) nên liên tục trên khoảng này.
○ f(x) không xác định tại điểm x = 0 nên gián đoạn tại điểm này.
□
2. Bài tập tự luận
Bài 1.
Cho hàm số y = f(x) xác định trên D = R và có đồ thị như hình vẽ bên.
Xét tính liên tục của hàm số y = f(x) trên D .
O
x
y
y = f(x)
Lời giải.
Do đồ thị hàm số là một đường liền nét trên D nên hàm số y = f (x) liên tục trên D = R. □
Bài 2.
Cho hàm số y = f(x) xác định trên D = R và có đồ thị như hình vẽ bên. Xét tính
liên tục của hàm số y = f (x) trên D.
O
x
y
y = f(x)
Lời giải.
Do đồ thị hàm số là một đường liền nét trên D nên hàm số y = f (x) liên tục trên D = R. □
Bài 3.
439/764 439/764
Toán 11 theo chương trình GDPT2018
3. Hàm số liên tục
Biết làm, làm đúng, làm nhanh
440
Cho hàm số y = f(x) xác định trên D = R và có đồ thị như hình vẽ bên.
Xét tính liên tục của hàm số y = f(x) trên D .
O
x
y
y = f(x)
2
Lời giải.
Do đồ thị hàm số là một đường liền nét trên D nên hàm số y = f (x) liên tục trên D = R. □
Bài 4.
Cho hàm số y = f(x) có đồ thị như hình vẽ bên.
Xét tính liên tục của hàm số y = f(x) tại điểm x
0
= 2.
O
x
y
y = f(x)
2
2
Lời giải.
Ta có lim
x→2
−
f(x) > 2 và lim
x→2
+
f(x) = 2. Do đó lim
x→2
−
f(x) = lim
x→2
+
f(x). Vậy hàm số đã cho gián đoạn tại x
0
= 2.
□
Bài 5.
Cho hàm số y = f(x) có đồ thị như hình vẽ bên.
Xét tính liên tục của hàm số y = f(x) tại điểm x
0
= 1.
O
x
y
1
y = f(x)
Lời giải.
Ta có lim
x→1
−
f(x) = −∞ và lim
x→1
+
f(x) = +∞. Do đó lim
x→1
−
f(x) = lim
x→1
+
f(x).
Vậy hàm số đã cho gián đoạn tại x
0
= 1. □
3. Bài tập trắc nghiệm
Câu 17. Cho đồ thị hàm số y = f(x) có đồ thị như hình vẽ bên. Chọn mệnh đề đúng
trong các mệnh đề sau:
A Hàm số y = f(x) liên tục trên R.
B Hàm số y = f(x) liên tục trên khoảng (0, +∞).
C Hàm số y = f(x) liên tục tại điểm x
0
= 0.
D lim
x→0
+
f(x) = +∞.
O
x
y
y = f(x)
Lời giải.
Đồ thị hàm số là một đường liền nét trên khoảng (0, +∞) nên liên tục trên khoảng này.
Chọn đáp án B □
440/764 440/764
Toán 11 theo chương trình GDPT2018
Chương 3. Giới hạn. Hàm số liên tục
Biết làm, làm đúng, làm nhanh
441
Câu 18. Cho đồ thị hàm số y = f (x) có đồ thị như hình vẽ bên. Chọn mệnh đề sai
trong các mệnh đề sau:
A lim
x→+∞
f(x) = −∞.
B Hàm số y = f(x) liên tục trên R.
C lim
x→+∞
f(x) = +∞.
D lim
x→−∞
f(x) = −∞.
O
x
y
y = f(x)
Lời giải.
Quan sát đồ thị hàm số, ta có
○ Hàm số y = f(x) liên tục trên R.
○ lim
x→+∞
f(x) = +∞.
○ lim
x→−∞
f(x) = −∞.
Chọn đáp án A □
Câu 19. Cho đồ thị hàm số y = f(x) có đồ thị như hình vẽ bên. Chọn mệnh đề
đúng trong các mệnh đề sau:
A lim
x→+∞
f(x) = −∞.
B Hàm số y = f(x) liên tục trên khoảng (0; +∞).
C Hàm số y = f(x) liên tục tại điểm x
0
= 0.
D Hàm số y = f(x) liên tục trên R.
O
x
y
y = f(x)
Lời giải.
Quan sát đồ thị hàm số, thấy đồ thị hàm số là một đường liền nét trên khoảng (0; +∞) do đó hàm số đã cho liên
tục trên khoảng này.
Chọn đáp án B □
Câu 20. Cho đồ thị hàm số y = f(x) có đồ thị như hình vẽ bên. Chọn mệnh đề sai
trong các mệnh đề sau:
A Hàm số gián đoạn tại điểm x
0
= 0.
B Hàm số liên tục trên khoảng (−∞; 0).
C Hàm số y = f(x) liên tục trên R.
D Hàm số liên tục trên khoảng (0; +∞).
O
x
y
−1
y = f(x)
Lời giải.
Quan sát đồ thị hàm số, ta có
○ Hàm số gián đoạn tại điểm x
0
= 0.
○ Hàm số liên tục trên khoảng (−∞; 0).
○ Hàm số liên tục trên khoảng (0; +∞).
Chọn đáp án C □
441/764 441/764
Toán 11 theo chương trình GDPT2018
3. Hàm số liên tục
Biết làm, làm đúng, làm nhanh
442
Câu 21. Cho đồ thị hàm số y = f (x) có đồ thị như hình vẽ bên. Chọn mệnh đề sai
trong các mệnh đề sau:
A Hàm số gián đoạn tại điểm x
0
= 1.
B Hàm số liên tục trên khoảng (−∞; 1).
C Hàm số y = f(x) liên tục trên R.
D Hàm số liên tục trên khoảng (1; +∞).
O
x
y
1
1
y = f(x)
Lời giải.
Quan sát đồ thị hàm số, ta có
○ Hàm số gián đoạn tại điểm x
0
= 1.
○ Hàm số liên tục trên khoảng (−∞; 1).
○ Hàm số liên tục trên khoảng (1; +∞).
Chọn đáp án C □
Câu 22.
Cho đồ thị hàm số y = f(x) có đồ thị như hình vẽ bên. Chọn mệnh đề đúng
trong các mệnh đề sau:
A Hàm số y = f(x) liên tục trên R.
B lim
x→+∞
f(x) = −∞.
C Hàm số liên tục tại điểm x
0
= −2.
D Hàm số gián đoạn tại điểm x
0
= −2.
O
x
y
y = f(x)
−2
2
Lời giải.
Quan sát đồ thị hàm số, ta có
○ Đồ thị hàm số là các đường liền nét trên các khoảng (−∞; −2), (−2; +∞) do đó hàm số liên tục trên các
khoảng này.
○ lim
x→+∞
f(x) = +∞
○ Ta có lim
x→(−2)
−
f(x) < f(−2) = 2 và lim
x→(−2)
+
f(x) = f (−2) = 2. Do đó lim
x→(−2)
−
f(x) = lim
x→(−2)
+
f(x).
Vậy hàm số đã cho gián đoạn tại x
0
= −2.
Chọn đáp án D □
Câu 23. Cho đồ thị hàm số y = f(x) có đồ thị như hình vẽ bên. Chọn mệnh đề đúng
trong các mệnh đề sau:
A lim
x→1
+
f(x) = +∞.
B Hàm số y = f(x) liên tục trên R.
C lim
x→1
+
f(x) = −∞.
D lim
x→1
−
f(x) = +∞.
O
x
y
1
−1
y = f(x)
Lời giải.
Quan sát đồ thị hàm số, ta có
○ Đồ thị hàm số là các đường liền nét trên các khoảng (−∞; 1), (1; +∞) do đó hàm số liên tục trên các khoảng
này.
442/764 442/764
Toán 11 theo chương trình GDPT2018
Chương 3. Giới hạn. Hàm số liên tục
Biết làm, làm đúng, làm nhanh
443
○ lim
x→+∞
f(x) = −1.
○ Ta có lim
x→1
−
f(x) = −∞ và lim
x→1
+
f(x) = +∞. Do đó lim
x→1
−
f(x) = lim
x→1
+
f(x).
Vậy hàm số đã cho gián đoạn tại x
0
= 1.
Chọn đáp án A □
Câu 24. Cho đồ thị hàm số y = f(x) có đồ thị như hình vẽ bên. Chọn mệnh đề
đúng trong các mệnh đề sau:
A Hàm số y = f(x) gián đoạn tại x
0
= 0.
B lim
x→+∞
f(x) = −1.
C lim
x→−∞
f(x) = −1.
D Hàm số y = f(x) liên tục trên R.
O
x
y
y = f(x)
Lời giải.
Quan sát đồ thị hàm số, ta có
○ Đồ thị hàm số là các đường liền nét trên khoảng (−∞; +∞) do đó hàm số liên tục trên R.
○ lim
x→+∞
f(x) = −∞.
○ lim
x→−∞
f(x) = −∞.
Chọn đáp án D □
Câu 25. Cho đồ thị hàm số y = f (x) có đồ thị như hình
vẽ bên. Chọn mệnh đề đúng trong các mệnh đề sau:
A Hàm số y = f(x) liên tục trên R.
B Hàm số y = f(x) liên tục tại x
0
= −3.
C lim
x→−∞
f(x) = −∞.
D Hàm số y = f(x) gián đoạn tại x
0
= 3.
O
x
y
−3
3
y = f(x)
Lời giải.
Quan sát đồ thị hàm số, ta có
○ Đồ thị hàm số là các đường liền nét trên khoảng (−∞; −3), (−3; 3), (3; +∞) do đó hàm số liên tục trên các
khoảng này.
○ lim
x→−∞
f(x) = 0.
○ Hàm số y = f(x) gián đoạn tại các điểm x
0
= 3 và x
0
= −3.
Chọn đáp án D □
Câu 26. Cho đồ thị hàm số y = f(x) có đồ thị như hình vẽ
bên. Chọn mệnh đề đúng trong các mệnh đề sau:
A Hàm số y = f(x) liên tục trên R.
B Hàm số y = f(x) liên tục tại điểm x
0
=
π
2
.
C Hàm số y = f(x) liên tục tại điểm x
0
= −
π
2
.
D Hàm số y = f(x) gián đoạn tại điểm x
0
=
π
2
.
x
y
O
y = f(x)y = f(x)y = f(x)
−π/2 π/2
443/764 443/764
Toán 11 theo chương trình GDPT2018
3. Hàm số liên tục
Biết làm, làm đúng, làm nhanh
444
Lời giải.
Quan sát đồ thị hàm số, ta có
○ Đồ thị hàm số là các đường liền nét trên khoảng (−
π
2
; 0), (0;
π
2
) do đó hàm số liên tục trên các khoảng này.
○ Hàm số y = f(x) gián đoạn tại các điểm x
0
=
π
2
và x
0
= −
π
2
.
Chọn đáp án D □
Dạng 3. Xét tính liên tục của hàm số tại một điểm
Để kiểm tra tính liên tục của hàm số y = f(x) tại điểm x = x
0
ta cần làm như sau:
○ Bước 1: Tính lim
x→x
0
f (x) .
○ Bước 2: Tính = f (x
0
) . Nếu lim
x→x
0
f (x) = f (x
0
) thì kết luận hàm số f (x) liên tục tại x = x
0
. Nếu
lim
x→x
0
f (x) = f (x
0
) thì kết luận hàm số f(x) liên tục tại x = x
0
.
1. Ví dụ mẫu
Ví dụ 9 (CD). Dùng định nghĩa xét tính liên tục của hàm số f (x) = 2x
3
+ x + 1 tại điểm x = 2.
Lời giải.
Hàm số trên là hàm sơ cấp nên liên tục trên R.
Ta có f(2) = 2 · 2
3
+ 2 + 1 = 19.
lim
x→2
f(x) = lim
x→2
2x
3
+ x + 1
= 2 · 2
3
+ 2 + 1 = 19.
Vậy lim
x→2
f(x) = f (2) = 19 nên hàm số y = 2x
3
+ x + 1 liên tục tại x = 2. □
Ví dụ 10 (TH). Hàm số f (x) =
3 khi x = −1
x
4
+ x
x
2
+ x
khi x = −1, x = 0
1 khi x = 0
. Xét tính liên tục của hàm số tại x = −1, x = 0.
Lời giải.
Hàm số y = f (x) có tập xác định D = R.
Dễ thấy hàm số y = f (x) liên tục trên mỗi khoảng (−∞; −1) , (−1; 0) và (0; +∞).
(i) Xét tại x = −1, ta có
lim
x→−1
f (x) = lim
x→−1
x
4
+ x
x
2
+ x
= lim
x→−1
x (x + 1)
x
2
− x + 1
x (x + 1)
= lim
x→−1
x
2
− x + 1
= 3 = f (−1) . Vậy hàm số y =
f (x) liên tục tại x = −1.
(ii) Xét tại x = 0, ta có
lim
x→0
f (x) = lim
x→0
x
4
+ x
x
2
+ x
= lim
x→0
x (x + 1)
x
2
− x + 1
x (x + 1)
= lim
x→0
x
2
− x + 1
= 1 = f (0) . Vậy hàm số y = f (x) liên
tục tại x = 0. □
Ví dụ 11 (TH). Tìm số điểm gián đoạn của hàm số f (x) =
0, 5 khi x = −1
x (x + 1)
x
2
− 1
khi x = −1, x = 1
1 khi x = 1
?
Lời giải.
Hàm số y = f (x) có tập xác định D = R.
Hàm số f (x) =
x (x + 1)
x
2
− 1
liên tục trên mỗi khoảng (−∞; −1), (−1; 1) và (1; +∞).
(i) Xét tại x = −1, ta có lim
x→−1
f (x) = lim
x→−1
x (x + 1)
x
2
− 1
= lim
x→−1
x
x − 1
=
1
2
= f (−1) ⇒ Hàm số liên tục tại x = −1.
444/764 444/764
Toán 11 theo chương trình GDPT2018
Chương 3. Giới hạn. Hàm số liên tục
Biết làm, làm đúng, làm nhanh
445
(ii) Xét tại x = 1, ta có
lim
x→1
+
f (x) = lim
x→1
+
x (x + 1)
x
2
− 1
= lim
x→1
+
x
x − 1
= +∞
lim
x→1
−
f (x) = lim
x→1
−
x (x + 1)
x
2
− 1
= lim
x→1
−
x
x − 1
= −∞
⇒Hàm số y = f (x) gián đoạn tại
x = 1. □
Ví dụ 12 (KNTT). Xét tính liên tục của hàm số f(x) =
x nếu x > 0
0 nếu x = 0
− x nếu x < 0
tại điểm x
0
= 0.
Lời giải.
Ta có f(0) = 0, lim
x→0
+
f(x) = lim
x→0
+
x
2
= 0, lim
x→0
−
f(x) = lim
x→0
−
(−x) = 0.
Suy ra f(0) = lim
x→0
+
f(x) = lim
x→0
−
f(x).
Vậy hàm số liên tục tại điểm x
0
= 0. □
Ví dụ 13 (CTST). Xét tính liên tục của hàm số
a) f(x) = x
2
− 2x + 3 tại điểm x
0
= 2.
b) f(x) =
®
x
2
+ 2 khi x > 0
2x khi x ≤ 0
tại điểm x
0
= 0.
Lời giải.
a) Ta có f(2) = 3 và lim
x→2
f(x) = lim
x→2
x
2
− 2x + 3
= 2
2
− 2 ·2 + 3 = 3, suy ra lim
x→2
f(x) = f (2).
Vậy hàm số y = f(x) liên tục tại x
0
= 2.
b) Ta có f(0) = 2 · 0 = 0, lim
x→0
−
f(x) = lim
x→0
−
(2x) = 2 · 0 = 0,
lim
x→0
+
f(x) = lim
x→0
+
x
2
+ 2
= 0 + 2 = 2.
Do lim
x→0
−
f(x) = lim
x→0
+
f(x) nên không tồn tại lim
x→0
f(x).
Vậy hàm số y = f(x) không liên tục tại điểm x
0
= 0.
□
2. Bài tập tự luyện
Bài 6. Xét tính liên tục của hàm số:
a) f(x) = x
2
− 2x + 3 tại điểm x
0
= 2;
b) f(x) =
®
x
2
+ 2 khi x > 0
2x khi x ≤ 0
tại điểm x
0
= 0.
Lời giải.
a) Ta có f(2) = 3 và lim
x→2
f(x) = lim
x→2
(x
2
− 2x + 3) = 2
2
− 2 · 2 + 3 = 3, suy ra lim
x→2
f(x) = f(2). Vậy hàm số
y = f(x) liên tục tại điểm x
0
= 2.
b) Ta có:
f(2) = 2 · 0 = 0;
lim
x→0
−
f(x) = lim
x→0
−
(2x) = 2 · lim
x→0
−
x = 2 ·0 = 0;
lim
x→0
+
f(x) = lim
x→0
+
(x
2
+ 2) = 0 + 2 = 2.
Suy ra không tồn tại lim
x→0
f(x). Vậy hàm số không liên tục tại điểm x
0
= 0.
445/764 445/764
Toán 11 theo chương trình GDPT2018
3. Hàm số liên tục
Biết làm, làm đúng, làm nhanh
446
x
y
O
−1
−2
2
1
3
□
Bài 7 (VD). Cho hàm số y =
x
2
− 7x + 12
x − 3
khi x = 3
− 1 khi x = 3
. Hàm số đã cho có đạo hàm tại x = 3 không?
Lời giải.
lim
x→3
x
2
− 7x + 12
x − 3
= lim
x→3
(x − 4) = −1 = y (3) nên hàm số liên tục tại x
0
= 3.
lim
x→3
x
2
− 7x + 12
−
3
2
− 7.3 + 12
x − 3
= lim
x→3
x
2
− 7x + 12
x − 3
= lim
x→3
(x − 4) = −1 ⇒ y
′
(3) = −1. □
Bài 8. Xét tính liên tục của hàm dấu s(x) =
1 nếu x > 0
0 nếu x = 0
− 1 nếu x < 0
tại điểm x
0
= 0.
Lời giải.
Ta thấy rằng lim
x→0
+
s(x) = 1 và lim
x→0
−
s(x) = −1. Do đó, không tồn tại giới hạn lim
x→0
s(x).
Vậy hàm số không liên tục tại x = 0. □
Bài 9. Xét tính liên tục của hàm số
a) f(x) = 1 − x
2
tại điểm x
0
= 3;
b) f(x) =
®
x
2
+ 1 khi x > 1
−x khi x ≤ 1
tại điểm x = 1.
Lời giải.
a) Ta có f(3) = −8 và lim
x→3
f(x) = lim
x→3
(1 − x
2
) = 1 − 3
2
= −8, suy ra lim
x→3
f(x) = f (3). Vậy hàm số y = f(x) liên
tục tại điểm x
0
= 3.
b) Ta có:
f(1) = −1;
lim
x→1
−
f(x) = lim
x→1
−
(−x) = −1;
lim
x→1
+
f(x) = lim
x→1
+
(x
2
+ 1) = 1 + 2 = 3.
Suy ra không tồn tại lim
x→1
f(x). Vậy hàm số không liên tục tại điểm x
0
= 1.
□
446/764 446/764
Toán 11 theo chương trình GDPT2018
Chương 3. Giới hạn. Hàm số liên tục
Biết làm, làm đúng, làm nhanh
447
Bài 10. Xét tính liên tục của hàm số f(x) =
x nếu x > 0
0 nếu x = 0
− x nếu x < 0
tại điểm x
0
= 0.
Lời giải.
Ta có f(0) = 0, lim
x→0
+
f(x) = lim
x→0
+
x
2
= 0, lim
x→0
−
f(x) = lim
x→0
−
(−x) = 0.
Suy ra f(0) = lim
x→0
+
f(x) = lim
x→0
−
f(x).
Vậy hàm số liên tục tại điểm x
0
= 0. □
Bài 11. Xét tính liên tục của hàm số:
a) f(x) =
®
x
2
+ 1 khi x ≥ 0
1 − x khi x < 0
tại điểm x = 0;
b) f(x) =
®
x
2
+ 2 khi x ≥ 1
x khi x < 1
tại điểm x = 1.
Lời giải.
a) Ta có
f(0) = 1;
lim
x→0
−
f(x) = lim
x→0
−
(1 − x) = 1 −0 = 1;
lim
x→0
+
f(x) = lim
x→0
+
(x
2
+ 1) = 0
2
+ 1 = 1.
Do đó, lim
x→0
f(x) = f (0) nên hàm số liên tục tại x
0
= 0.
b) Ta có
f(1) = 3;
lim
x→1
−
f(x) = lim
x→1
−
(x) = 1.
Do đó, không thể xảy ra lim
x→1
f(x) = f (1) nên hàm số gián đoạn tại x
0
= 1.
□
Bài 12. Dùng định nghĩa xét tính liên tục của hàm số f(x) = 2x
3
+ x + 1 tại điểm x = 2.
Lời giải.
Hàm số trên là hàm sơ cấp nên liên tục trên R.
Ta có f(2) = 2 · 2
3
+ 2 + 1 = 19.
lim
x→2
f(x) = lim
x→2
2x
3
+ x + 1
= 2 · 2
3
+ 2 + 1 = 19.
Vậy lim
x→2
f(x) = f (2) = 19 nên hàm số y = 2x
3
+ x + 1 liên tục tại x = 2. □
3. Bài tập trắc nghiệm
Câu 27. Cho hàm số f (x) =
2x − 1
x
3
− x
. Kết luận nào sau đây đúng?
A Hàm số liên tục tại x = −1. B Hàm số liên tục tại x = 0.
C Hàm số liên tục tại x = 1. D Hàm số liên tục tại x =
1
2
.
Lời giải.
Tại x =
1
2
, ta có lim
x→
1
2
f (x) = lim
x→
1
2
2x − 1
x
3
− 1
= 0 = f
Å
1
2
ã
. Vậy hàm số liên tục tại x = 2.
Chọn đáp án D □
447/764 447/764
Toán 11 theo chương trình GDPT2018
3. Hàm số liên tục
Biết làm, làm đúng, làm nhanh
448
Câu 28. Hàm số nào sau đây liên tục tại x = 1 :
A f (x) =
x
2
+ x + 1
x − 1
. B f (x) =
x
2
− x −2
x
2
− 1
. C f (x) =
x
2
+ x + 1
x
. D f (x) =
x + 1
x − 1
.
Lời giải.
• f (x) =
x
2
+ x + 1
x − 1
lim
x→1
+
f (x) = +∞ suy ra f (x) không liên tục tại x = 1.
• f (x) =
x
2
− x −2
x
2
− 1
lim
x→1
+
f (x) = lim
x→1
+
x − 2
x − 1
= −∞ suy ra f (x) không liên tục tại x = 1.
• f (x) =
x
2
+ x + 1
x
lim
x→1
f (x) = lim
x→1
x
2
+ x + 1
x
= 3 = f (1) suy ra f (x) liên tục tại x = 1.
• f (x) =
x + 1
x − 1
lim
x→1
+
f (x) = lim
x→1
+
x + 1
x − 1
= +∞ suy ra f (x) không liên tục tại x = 1.
Chọn đáp án C □
Câu 29. Hàm số nào dưới đây gián đoạn tại điểm x
0
= −1.
A y = (x + 1)
x
2
+ 2
. B y =
2x − 1
x + 1
. C y =
x
x − 1
. D y =
x + 1
x
2
+ 1
.
Lời giải.
Ta có y =
2x − 1
x + 1
không xác định tại x
0
= −1 nên gián đoạn tại x
0
= −1.
Chọn đáp án B □
Câu 30. Hàm số nào sau đây gián đoạn tại x = 2?
A y =
3x − 4
x − 2
. B y = sin x. C y = x
4
− 2x
2
+ 1. D y = tan x.
Lời giải.
Ta có y =
3x − 4
x − 2
có tập xác định D = R \{2}, do đó gián đoạn tại x = 2.
Chọn đáp án A □
Câu 31. Hàm số y =
x
x + 1
gián đoạn tại điểm x
0
bằng?
A x
0
= 2018. B x
0
= 1. C x
0
= 0. D x
0
= −1.
Lời giải.
Vì hàm số y =
x
x + 1
có tập xác định D = R \{−1} nên hàm số gián đoạn tại điểm x
0
= −1.
Chọn đáp án D □
Câu 32. Cho hàm số y =
x − 3
x
2
− 1
. Mệnh đề nào sau đây đúng?
A Hàm số không liên tục tại các điểm x = ±1. B Hàm số liên tục tại mọi x ∈ R.
C Hàm số liên tục tại các điểm x = −1. D Hàm số liên tục tại các điểm x = 1.
Lời giải.
Hàm số y =
x − 3
x
2
− 1
có tập xác định R \ {±1}. Do đó hàm số không liên tục tại các điểm x = ±1.
Chọn đáp án A □
Câu 33. Để hàm số y =
x
2
+ 3x + 2
khi
x ≤ −1
4x + a
khi
x > −1
liên tục tại điểm x = −1 thì giá trị của a là
A −4. B 4. C 1. D −1.
Lời giải.
448/764 448/764
Toán 11 theo chương trình GDPT2018
Chương 3. Giới hạn. Hàm số liên tục
Biết làm, làm đúng, làm nhanh
449
Hàm số liên tục tại x = −1 khi và chỉ khi lim
x→−1
+
y = lim
x→−1
−
y = y (−1) .
⇔ lim
x→−1
+
(4x + a) = lim
x→−1
−
x
2
+ 3x + 2
= y (−1) ⇔ a − 4 = 0 ⇔ a = 4.
Chọn đáp án B □
Câu 34. Tìm giá trị thực của tham số m để hàm số f (x) =
x
3
− x
2
+ 2x −2
x − 1
khi x = 1
3x + m khi x = 1
liên tục tại x = 1.
A m = 0. B m = 6. C m = 4. D m = 2.
Lời giải.
Ta có f (1) = m + 3.
lim
x→1
f (x) = lim
x→1
x
3
− x
2
+ 2x −2
x − 1
= lim
x→1
(x − 1)
x
2
+ 2
x − 1
= lim
x→1
x
2
+ 2
= 3.
Để hàm số f (x) liên tục tại x = 1 thì lim
x→1
f (x) = f (1) ⇔ 3 = m + 3 ⇔ m = 0.
Chọn đáp án A □
Câu 35. Cho hàm số f (x) =
x
2016
+ x −2
√
2018x + 1 −
√
x + 2018
khi x = 1
k khi x = 1
. Tìm k để hàm số f (x) liên tục tại x = 1.
A k = 2
√
2019. B k =
2017.
√
2018
2
. C k = 1. D k =
20016
2017
√
2019.
Lời giải.
Ta có lim
x→1
x
2016
+ x −2
√
2018x + 1 −
√
x + 2018
= lim
x→1
x
2016
− 1 + x − 1
√
2018x + 1 +
√
x + 2018
2017x − 2017
= lim
x→1
(x − 1)
x
2015
+ x
2014
+ ... + x + 1 + 1
√
2018x + 1 +
√
x + 2018
2017 (x − 1)
= 2
√
2019.
Để hàm số liên tục tại x = 1 ⇔ lim
x→1
f (x) = f (1) ⇔ k = 2
√
2019.
Chọn đáp án A □
Câu 36. Cho hàm số f (x) =
√
x − 1
x − 1
khi x = 1
a khi x = 1
. Tìm a để hàm số liên tục tại x
0
= 1.
A a = 0. B a = −
1
2
. C a =
1
2
. D a = 1.
Lời giải.
Ta có lim
x→1
f (x) = lim
x→1
√
x − 1
x − 1
= lim
x→1
√
x − 1
(
√
x − 1) (
√
x + 1)
= lim
x→1
1
√
x + 1
=
1
2
.
Để hàm số liên tục tại x
0
= 1 khi lim
x→1
f (x) = f (1) ⇔ a =
1
2
.
Chọn đáp án C □
Câu 37. Biết hàm số f (x) =
®
3x + b khi x ≤ −1
x + a khi x > −1
liên tục tại x = −1. Mệnh đề nào dưới đây đúng?
A a = b −2. B a = −2 −b. C a = 2 − b. D a = b + 2.
Lời giải.
lim
x →−1
−
f (x) = f (−1) = b −3; lim
x →−1
+
f (x) = a −1. Để hàm số liên tục tại x = −1 thì b −3 = a −1 ⇔ a = b −2.
Chọn đáp án A □
Câu 38. Cho hàm số f (x) =
3 − x
√
x + 1 −2
khi x = 3
m khi x = 3
. Hàm số đã cho liên tục tại x = 3 khi m bằng bao nhiêu?
A −1. B 1. C 4. D −4.
Lời giải.
449/764 449/764
Toán 11 theo chương trình GDPT2018
3. Hàm số liên tục
Biết làm, làm đúng, làm nhanh
450
f (3) = m lim
x→3
f (x) = lim
x→3
3 − x
√
x + 1 −2
= lim
x→3
(3 − x)
√
x + 1 + 2
x − 3
= lim
x→3
−
√
x + 1 −2
= −4.
Để hàm số liên tục tại x = 3 thì lim
x→3
f (x) = f (3).
Suy ra m = −4.
Chọn đáp án D □
Câu 39. Biết hàm số f (x) =
®
ax
2
+ bx −5 khi x ≤ 1
2ax − 3b khi x > 1
liên tục tại x = 1 Tính giá trị của biểu thức P =
a − 4b.
A P = −4. B P = −5. C P = 5. D P = 4.
Lời giải.
Ta có lim
x→1
−
f (x) = lim
x→1
−
ax
2
+ bx −5
= a + b −5 = f (1).
lim
x→1
+
f (x) = lim
x→1
+
(2ax − 3b) = 2a −3b. Vì hàm số liên tục tại x = 1 nên a + b − 5 = 2a − 3b ⇒ a − 4b = −5.
Chọn đáp án B □
Câu 40. Tìm m để hàm số f(x) =
x
2
− x
x − 1
khi x = 1
m − 1 khi
x
= 1
liên tục tại x = 1?
A m = 0. B m = −1. C m = 1. D m = 2.
Lời giải.
Tập xác định D = R
Ta có lim
x→1
f(x) = lim
x→1
x
2
− x
x − 1
= lim
x→1
x = 1 và f (1) = m − 1.
Hàm số liên tục tại x = 1 ⇔ m − 1 = 1 ⇔ m = 2.
Chọn đáp án D □
Câu 41. Có bao nhiêu số tự nhiên m để hàm số f (x) =
x
2
− 3x + 2
x − 1
khi x = 1
m
2
+ m −1 khi x = 1
liên tục tại điểm x = 1?
A 0. B 3. C 2. D 1.
Lời giải.
lim
x→1
x
2
− 3x + 2
x − 1
= lim
x→1
(x − 1) (x − 2)
x − 1
= lim
x→1
(x − 2) = −1.
Vì hàm số f (x) liên tục tại điểm x = 1 nên lim
x→1
f (x) = f (1)
⇔ m
2
+ m −1 = −1 ⇔ m
2
+ m = 0 ⇔
ñ
m = 0 (Thoả mãn)
m = −1 (Loại).
Chọn đáp án D □
Câu 42. Tìm a để hàm số f (x) =
√
x + 2 −2
x − 2
khi x = 2
2x + a khi x = 2
liên tục tại x = 2?
A
15
4
. B −
15
4
. C
1
4
. D 1.
Lời giải.
Ta có f (2) = 4 + a.
Ta tính được lim
x→2
f (x) = lim
x→2
x + 2 −4
(x − 2)
√
x + 2 + 2
= lim
x→2
1
√
x + 2 + 2
=
1
4
.
Hàm số đã cho liên tục tại x = 2 khi và chỉ khi f (2) = lim
x→2
f (x) ⇔ 4 + a =
1
4
⇔ a = −
15
4
.
Vậy hàm số liên tục tại x = 2 khi a = −
15
4
.
Chọn đáp án B □
450/764 450/764
Toán 11 theo chương trình GDPT2018
Chương 3. Giới hạn. Hàm số liên tục
Biết làm, làm đúng, làm nhanh
451
Câu 43. Cho hàm số f (x) =
x
2
− 3x + 2
√
x + 2 −2
khi x > 2
m
2
x − 4m + 6 khi x ≤ 2
, m là tham số. Có bao nhiêu giá trị của m để hàm số
đã cho liên tục tại x = 2?
A 3. B 0. C 2. D 1.
Lời giải.
Ta có
lim
x→2
+
f(x) = lim
x→2
+
x
2
− 3x + 2
√
x + 2 −2
= lim
x→2
+
(x − 2) (x − 1)
√
x + 2 + 2
x − 2
= lim
x→2
+
(x − 1)
√
x + 2 + 2
= 4.
lim
x→2
−
f(x) = lim
x→2
−
m
2
x − 4m + 6
= 2m
2
− 4m + 6.
f(2) = 2m
2
− 4m + 6.
Để hàm số liên tục tại x = 2 thì lim
x→2
+
f(x) = lim
x→2
−
f(x) = f (2) ⇔ 2m
2
−4m+6 = 4 ⇔ 2m
2
−4m+2 = 0 ⇔ m = 1.
Vậy có một giá trị của m thỏa mãn hàm số đã cho liên tục tại x = 2.
Chọn đáp án D □
Câu 44. Cho hàm số f (x) =
√
3x
2
+ 2x −1 − 2
x
2
− 1
, x = 1
4 − m, x = 1
. Hàm số f (x) liên tục tại x
0
= 1 khi
A m = 3. B m = −3. C m = 7. D m = −7.
Lời giải.
Tập xác định D = R, x
0
= 1 ∈ R.
Ta có f (1) = 4 − m.
lim
x→1
f (x) = lim
x→1
√
3x
2
+ 2x −1 − 2
(x + 1) (x − 1)
= lim
x→1
(x − 1) (3x + 5)
(x + 1) (x − 1)
Ä
√
3x
2
+ 2x −1 + 2
ä
= lim
x→1
3x + 5
(x + 1)
Ä
√
3x
2
+ 2x −1 + 2
ä
= 1.
Hàm số f (x) liên tục tại x
0
= 1 khi và chỉ khi lim
x→1
(x) = f (1) ⇔ 4 − m = 1 ⇔ m = 3.
Chọn đáp án A □
Câu 45. Tìm giá trị của tham số m để hàm số f (x) =
x
2
+ 3x + 2
x
2
− 1
khi x < −1
mx + 2 khi x ≥ −1
liên tục tại x = −1.
A m =
−3
2
. B m =
−5
2
. C m =
3
2
. D m =
5
2
.
Lời giải.
Ta có
• f (−1) = −m + 2.
• lim
x→(−1)
+
f (x) = −m + 2.
• lim
x→(−1)
−
f (x) = lim
x→(−1)
−
x
2
+ 3x + 2
x
2
− 1
= lim
x→(−1)
−
(x + 1) (x + 2)
(x − 1) (x + 1)
= lim
x→(−1)
−
x + 2
x − 1
=
−1
2
.
Hàm số liên tục tại x = −1 ⇔ f (−1) = lim
x→(−1)
+
f (x) = lim
x→(−1)
−
f (x) ⇔ −m + 2 =
−1
2
⇔ m =
5
2
.
Chọn đáp án D □
Câu 46. Cho hàm số f(x) =
√
x
2
+ 4 −2
x
2
khi x = 0
2a −
5
4
khi x = 0
. Tìm giá trị thực của tham số a để hàm số f(x) liên
tục tại x = 0.
A a = −
3
4
. B a =
4
3
. C a = −
4
3
. D a =
3
4
.
Lời giải.
Tập xác định D = R.
451/764 451/764
Toán 11 theo chương trình GDPT2018
3. Hàm số liên tục
Biết làm, làm đúng, làm nhanh
452
lim
x→0
f(x) = lim
x→0
√
x
2
+ 4 −2
x
2
= lim
x→0
Ä
√
x
2
+ 4 −2
äÄ
√
x
2
+ 4 + 2
ä
x
2
Ä
√
x
2
+ 4 + 2
ä
= lim
x→0
x
2
+ 4 −4
x
2
(
√
x
2
+ 4 + 2)
= lim
x→0
1
√
x
2
+ 4 + 2
=
1
4
.
f(0) = 2a −
5
4
.
Hàm số f(x) liên tục tại x = 0 ⇔ lim
x→0
f(x) = f (0) ⇔ 2a −
5
4
=
1
4
⇔ a =
3
4
.
Vậy a =
3
4
.
Chọn đáp án D □
Câu 47. Cho hàm số f (x) =
®
x
2
− 2x + 3 khi x = 1
3x + m −1 khi x = 1
. Tìm m để hàm số liên tục tại x
0
= 1.
A m = 1. B m = 3. C m = 0. D m = 2.
Lời giải.
Tập xác định D = R.
Ta có f (1) = 2 + m.
lim
x→1
f (x) = lim
x→1
x
2
− 2x + 3
= 2.
Hàm số liên tục tại x
0
= 1 ⇔ lim
x→1
f (x) = f (1) ⇔ 2 = m + 2 ⇔ m = 0.
Chọn đáp án C □
Câu 48. Cho hàm số f (x) =
x
2
− 3x + 2
x − 2
khi x = 2
a khi x = 2
. Hàm số liên tục tại x = 2 khi a bằng
A 1. B 0. C 2. D −1.
Lời giải.
Hàm số liên tục tại x = 2 khi và chỉ khi lim
x→2
f(x) = f (2).
Ta có f(2) = a, lim
x→2
f(x) = lim
x→2
x
2
− 3x + 2
x − 2
= lim
x→2
(x − 1) = 1. Do đó a = 1.
Chọn đáp án A □
Dạng 4. Hàm số liên tục trên khoảng, đoạn
○ Hàm số y = f(x) được gọi là liên tục trên một khoảng nếu nó liên tục tại mọi điểm của khoảng đó.
○ Hàm số y = f(x) được gọi là liên tục trên đoạn [a, b] nếu nó liên tục trên khoảng (a, b) và
lim
x→a
+
f (x) = f (a) , lim
x→b
−
f (x) = f (b) .
○ Đồ thị của hàm số liên tục trên một khoảng là một đường liền nét trên khoảng đó.
1. Ví dụ mẫu
Ví dụ 14 (Cánh Diều).
a) Hàm số f(x) = 2x + 3 có liên tục trên đoạn [3; 4] hay không?
b) Hàm số f(x) =
x + 1
x − 2
(x = 2) có liên tục trên khoảng (1; 3) hay không?
Lời giải.
a) Với mỗi x
0
∈ (3; 4) ta có lim
x→x
0
f(x) = lim
x→x
0
(2x + 3) = 2x
0
+ 3 = f (x
0
).
Ta lại có
452/764 452/764
Toán 11 theo chương trình GDPT2018
Chương 3. Giới hạn. Hàm số liên tục
Biết làm, làm đúng, làm nhanh
453
lim
x→3
+
f(x) = lim
x→3
+
(2x + 3) = 9 = f(3).
lim
x→4
−
f(x) = lim
x→4
−
(2x + 3) = 11 = f(4).
Vậy hàm số đã cho liên tục trên đoạn [3; 4].
b) Hàm số f(x) =
x + 1
x − 2
không xác định tại x = 2 nên hàm số không liên tục tại x = 2.
Do 2 ∈ (1; 3) nên hàm số đã cho không liên tục trên khoảng (1; 3).
□
Ví dụ 15 (Cánh Diều). Cho hàm số f(x) = x
3
+ 2x +
6
x − 2
.
a) Xét tính liên tục của hàm số f(x) tại x = 3.
b) Xét tính liên tục của hàm số f(x) trên tập xác định của hàm số đó.
Lời giải.
Tập xác định của hàm số là R \ {2}.
a) Ta thấy
lim
x→3
f(x) = lim
x→3
Å
x
3
+ 2x +
6
x − 2
ã
= lim
x→3
x
3
+ lim
x→3
(2x) + lim
x→3
Å
6
x − 2
ã
= 3
3
+ 2 ·3 +
6
3 − 2
= f (3)
Vậy hàm số f(x) liên tục tại x = 3.
b) Hàm số g(x) = x
3
+ 2x là hàm đa thức nên liên tục trên R. Do đó hàm số g(x) liên tục trên mỗi khoảng
(−∞; 2) và (2; +∞).
Hàm số h(x) là hàm số phân thức hữu tỉ nên liên tục trên mỗi khoảng xác định (−∞; 2) và (2; +∞).
Vậy hàm số f(x) = g(x) + h(x) liên tục trên mỗi khoảnh (−∞; 2) và (2; +∞).
c)
□
Ví dụ 16 (KNTT). Xét tính liên tục của hàm số f(x) =
®
x − 1 nếu x ∈ (0; 1)
0 nếu x = 1
trên nửa khoảng (0; 1].
Lời giải.
Ta có f(x) = x − 1 với x ∈ (0; 1). Với x
0
∈ (0; 1) bất kì, ta có
lim
x→x
0
(x − 1) = x
0
− 1 = f (x
0
) .
Do đó, hàm số đã cho liên tục trên khoảng (0; 1).
Hơn nữa, ta có
lim
x→1
−
f(x) = lim
x→1
−
(x − 1) = 0 = f(1)
nên f(x) liên tục trên nửa khoảng (0; 1]. □
Ví dụ 17 (KNTT). Cho hàm số f(x) =
x + 1
x − 1
. Tìm các khoảng liên tục của hàm số f(x).
Lời giải.
○ Tập xác định của hàm số đã cho là D = (−∞; 1) ∪(1; +∞).
453/764 453/764
Toán 11 theo chương trình GDPT2018
3. Hàm số liên tục
Biết làm, làm đúng, làm nhanh
454
○ Với mọi x
0
∈ (−∞; 1), ta có
lim
x→x
0
f(x) = lim
x→x
0
x + 1
x − 1
=
x
0
+ 1
x
0
− 1
= f(x
0
).
Do đó hàm số f (x) liên tục tại x = x
0
hay f(x) liên tục trên khoảng (−∞; 1).
○ Tương tự, hàm số f(x) liên tục trên khoảng (1; +∞).
Vậy, hàm số đã cho liên tục trên các khoảng (−∞; 1) và (1; +∞) . □
Ví dụ 18 (CTST). Xét tính liên tục của hàm số f(x) =
√
1 − x
2
trên đoạn [−1; 1].
Lời giải.
Với mọi x
0
∈ (−1; 1), ta có lim
x→x
0
f(x) = lim
x→x
0
√
1 − x
2
=
»
1 − x
2
0
= f (x
0
).
Do đó hàm số f (x) liên tục tại mọi điểm x
0
∈ (−1; 1).
Ta lại có
lim
x→(−1)
+
f(x) = lim
x→(−1)
+
√
1 − x
2
=
p
1 − (−1)
2
= 0 = f(−1).
lim
x→1
−
f(x) = lim
x→1
−
√
1 − x
2
=
√
1 − 1
2
= 0 = f(1).
Vậy hàm số f(x) liên tục trên đoạn [−1; 1].
x
y
O
1
−1
y =
√
1 − x
2
□
2. Bài tập tự luyện
Bài 13. Xét tính liên tục của hàm số y =
sin x
x + 1
.
Lời giải.
Tập xác định của hàm số D = (−∞; −1) ∪ (−1; +∞).
Các hàm số y = sin x và y = x + 1 liên tục tại mọi điểm x
0
∈ R. Do đó hàm số y =
sin x
x + 1
liên tục tại mọi
điểm x
0
= −1 (hay liên tục trên các khoảng (−∞; −1) và (−1; +∞).
□
Bài 14. Xét tính liên tục của các hàm số
a) y =
√
x
2
+ 1 + 3 − x.
b) y =
x
2
− 1
x
· cos x.
Lời giải.
a)
Tập xác định của hàm số S = R.
Các hàm số y =
√
x
2
+ 1 và y = 3 − x liên tục tại mọi điểm x
0
∈ R. Do đó hàm số y =
√
x
2
+ 1 + 3 − x
liên tục tại mọi điểm x
0
∈ R hay liên tục trên R.
b)
Tập xác định của hàm số D = (−∞; 0) ∪ (0; +∞).
Các hàm số y =
x
2
− 1
x
liên tục tại mọi điểm x
0
= 0 và hàm số y = cos x liên tục tại mọi điểm x
0
∈ R.
Do đó hàm số y =
x
2
− 1
x
. cos x liên tục tại mọi điểm x
0
= 0 (hay liên tục trên các khoảng (−∞; 0) và
(0; +∞)).
□
Bài 15. Xét tính liên tục của các hàm số sau:
454/764 454/764
Toán 11 theo chương trình GDPT2018
Chương 3. Giới hạn. Hàm số liên tục
Biết làm, làm đúng, làm nhanh
455
a) y = 3x
3
− 4x
2
+ 5x + 2;
b) y =
3x
2
+ x −1
x − 2
.
Lời giải.
a) y = 3x
3
− 4x
2
+ 5x = 2 hàm số đa thức nên nó liên tục trên R.
b) y =
3x
2
+ x −1
x − 2
là hàm số phân thức, có tập xác định là (−∞; 2) ∪ (2; +∞) nên nó liên tục trên các khoảng
(−∞; 2), (2; +∞).
□
Bài 16. Tìm các khoảng liên tục của hàm số f(x) =
x
2
+ 1
x + 2
.
Lời giải.
Tập xác định của hàm số f(x) là (−∞, −2) ∪ (−2, +∞). Vậy hàm số liên tục trên các khoảng (−∞, −2) và
(−2, +∞). □
Bài 17.
a) Hàm số f(x) = 2x + 3 có liên tục trên đoạn [3; 4] hay không?
b) Hàm số f(x) =
x + 1
x − 2
(x = 2) có liên tục trên khoảng (1; 3) hay không?
Lời giải.
a) Với mỗi x
0
∈ (3; 4) ta có lim
x→x
0
f(x) = lim
x→x
0
(2x + 3) = 2x
0
+ 3 = f (x
0
).
Ta lại có
lim
x→3
+
f(x) = lim
x→3
+
(2x + 3) = 9 = f(3).
lim
x→4
−
f(x) = lim
x→4
−
(2x + 3) = 11 = f(4).
Vậy hàm số đã cho liên tục trên đoạn [3; 4].
b) Hàm số f(x) =
x + 1
x − 2
không xác định tại x = 2 nên hàm số không liên tục tại x = 2.
Do 2 ∈ (1; 3) nên hàm số đã cho không liên tục trên khoảng (1; 3).
□
Bài 18. Cho hàm số f (x) = x
3
+ 2x +
6
x − 2
.
a) Xét tính liên tục của hàm số f(x) tại x = 3.
b) Xét tính liên tục của hàm số f(x) trên tập xác định của hàm số đó.
Lời giải.
Tập xác định của hàm số là R \ {2}.
a) Ta thấy
lim
x→3
f(x) = lim
x→3
Å
x
3
+ 2x +
6
x − 2
ã
= lim
x→3
x
3
+ lim
x→3
(2x) + lim
x→3
Å
6
x − 2
ã
= 3
3
+ 2 ·3 +
6
3 − 2
= f (3)
Vậy hàm số f(x) liên tục tại x = 3.
455/764 455/764
Toán 11 theo chương trình GDPT2018
3. Hàm số liên tục
Biết làm, làm đúng, làm nhanh
456
b) Hàm số g(x) = x
3
+ 2x là hàm đa thức nên liên tục trên R. Do đó hàm số g(x) liên tục trên mỗi khoảng
(−∞; 2) và (2; +∞).
Hàm số h(x) là hàm số phân thức hữu tỉ nên liên tục trên mỗi khoảng xác định (−∞; 2) và (2; +∞).
Vậy hàm số f(x) = g(x) + h(x) liên tục trên mỗi khoảnh (−∞; 2) và (2; +∞).
□
Bài 19. Xét tính liên tục của hàm số f(x) =
x − 1
x + 1
tại điểm x
0
= 2.
Lời giải.
Rõ ràng, hàm số đã cho xác định trên R \{1}, do đó x
0
= 2 thuộc tập xác định của hàm số.
Ta có
lim
x→2
f(x) = lim
x→2
x − 1
x + 1
= 3 = f(2).
Do đó, hàm số f (x) liên tục tại x
0
= 2. □
Bài 20. Cho hàm số f (x) =
x + 1
x − 1
. Tìm các khoảng liên tục của hàm số f(x).
Lời giải.
Tập xác định của hàm số đã cho là D = (−∞; 1) ∪(1; +∞). Vậy, hàm số đã cho liên tục trên các khoảng (−∞; 1)
và (1; +∞) . □
Bài 21. Xét tính liên tục của hàm số y =
√
x
2
− 4.
Lời giải.
Hàm số y =
√
x
2
− 4 là hàm số sơ cấp có tập xác định là (−∞; −2] ∪ [2; +∞) nên nó liên tục trên (−∞; 2] và
[2; +∞). □
Bài 22. Tìm các khoảng liên tục của hàm số f(x) =
x
2
+ 1
x + 2
.
Lời giải.
Tập xác định của hàm số f(x) là (−∞, −2) ∪ (−2, +∞). Vậy hàm số liên tục trên các khoảng (−∞, −2) và
(−2, +∞). □
Bài 23 (TH). Cho hàm số f (x) =
x
2
− 3x + 2
√
x + 2 −2
khi x > 2
m
2
x − 4m + 6 khi x ≤ 2
, m là tham số. Với giá trị nào của m thì hàm số
đã cho liên tục tại x = 2?
Lời giải.
Ta có
lim
x→2
+
f(x) = lim
x→2
+
x
2
− 3x + 2
√
x + 2 −2
= lim
x→2
+
(x − 2) (x − 1)
√
x + 2 + 2
x − 2
= lim
x→2
+
(x − 1)
√
x + 2 + 2
= 4.
lim
x→2
−
f(x) = lim
x→2
−
m
2
x − 4m + 6
= 2m
2
− 4m + 6.
f(2) = 2m
2
− 4m + 6.
Để hàm số liên tục tại x = 2 thì lim
x→2
+
f(x) = lim
x→2
−
f(x) = f (2) ⇔ 2m
2
−4m+6 = 4 ⇔ 2m
2
−4m+2 = 0 ⇔ m = 1.
Vậy có một giá trị của m thỏa mãn hàm số đã cho liên tục tại x = 2. □
Bài 24 (TH). Tìm giá trị của tham số m để hàm số f (x) =
x
2
+ 3x + 2
x
2
− 1
khi x < −1
mx + 2 khi x ≥ −1
liên tục tại x = −1?
Lời giải.
Ta có
• f (−1) = −m + 2.
• lim
x→(−1)
+
f (x) = −m + 2.
• lim
x→(−1)
−
f (x) = lim
x→(−1)
−
x
2
+ 3x + 2
x
2
− 1
= lim
x→(−1)
−
(x + 1) (x + 2)
(x − 1) (x + 1)
= lim
x→(−1)
−
x + 2
x − 1
=
−1
2
.
Hàm số liên tục tại x = −1 ⇔ f (−1) = lim
x→(−1)
+
f (x) = lim
x→(−1)
−
f (x) ⇔ −m + 2 =
−1
2
⇔ m =
5
2
. □
456/764 456/764
Toán 11 theo chương trình GDPT2018
Chương 3. Giới hạn. Hàm số liên tục
Biết làm, làm đúng, làm nhanh
457
Bài 25 (TH). Tìm m để hàm số f (x) =
x
2
− 16
x − 4
khi x > 4
mx + 1 khi x ≤ 4
liên tục tại điểm x = 4.
Lời giải.
Ta có lim
x→4
−
f (x) = f (4) = 4m + 1; lim
x→4
+
f (x) = lim
x→4
+
x
2
− 16
x − 4
= lim
x→4
+
(x + 4) = 8.
Hàm số liên tục tại điểm x = 4 ⇔ lim
x→4
−
f (x) = lim
x→4
+
f (x) = f (4) ⇔ 4m + 1 = 8 ⇔ m =
7
4
. □
Bài 26 (TH). Tìm m để hàm số f(x) =
x
2
− x −2
x + 1
khix > −1
mx − 2m
2
khi x ≤ −1
liên tục tại x = −1.
Lời giải.
Tập xác định D = R.
• f(−1) = −m − 2m
2
• lim
x→−1
−
f(x) = lim
x→−1
−
(mx − 2m
2
) = −m − 2m
2
.
• lim
x→−1
+
f(x) = lim
x→−1
+
x
2
− x −2
x + 1
= lim
x→−1
+
(x + 1)(x −2)
x + 1
= lim
x→−1
+
(x − 2) = −3.
Hàm số liên tục tại x = −1 khi và chỉ khi lim
x→−1
−
f(x) = lim
x→−1
+
f(x) = f (−1)
⇔ −m −2m
2
= −3 ⇔ 2m
2
+ m −3 = 0 ⇔
m = 1
m = −
3
2
.
Vậy các giá trị của m là m ∈
ß
1; −
3
2
™
. □
Bài 27 (VD). Tìm giá trị của m để hàm số f (x) =
√
1 − x −
√
1 + x
x
khi x < 0
m +
1 − x
1 + x
khi x ≥ 0
liên tục tại x = 0?
Lời giải.
Ta có
lim
x→0
+
f (x) = lim
x→0
+
Å
m +
1 − x
1 + x
ã
= m+1. lim
x→0
−
f (x) = lim
x→0
−
Ç
√
1 − x −
√
1 + x
x
å
= lim
x→0
−
−2x
x
√
1 − x +
√
1 + x
=
lim
x→0
−
−2
√
1 − x +
√
1 + x
= −1.
f (0) = m + 1.
Để hàm liên tục tại x = 0 thì lim
x→0
+
f (x) = lim
x→0
−
f (x) = f (0) ⇔ m + 1 = −1 ⇒ m = −2. □
Bài 28 (TH). Cho hàm số f (x) =
√
x + 3 −2
x − 1
khi (x > 1)
m
2
+ m +
1
4
khi (x ≤ 1)
. Tìm tất cả các giá trị của tham số thực m để hàm
số f (x) liên tục tại x = 1?
Lời giải.
Ta có lim
x→1
+
f (x) = lim
x→1
+
√
x + 3 −2
x − 1
= lim
x→1
+
1
√
x + 3 + 2
=
1
4
; f (1) = lim
x→1
−
f (x) = m
2
+ m +
1
4
.
Để hàm số f (x) liên tục tại x = 1 thì m
2
+ m +
1
4
=
1
4
⇔
ñ
m = −1
m = 0
. □
Bài 29 (TH). Tìm a để hàm số f (x) =
2x + a khi x ≤ 1
x
3
− x
2
+ 2x −2
x − 1
khi x > 1
liên tục trên R?
Lời giải.
Khi x < 1 thì f (x) = 2x + a là hàm đa thức nên liên tục trên khoảng (−∞; 1).
Khi x > 1 thì f (x) =
x
3
− x
2
+ 2x −2
x − 1
là hàm phân thức hữu tỉ xác định trên khoảng (1; +∞) nên liên tục trên
457/764 457/764
Toán 11 theo chương trình GDPT2018
3. Hàm số liên tục
Biết làm, làm đúng, làm nhanh
458
khoảng (1; +∞).
Xét tính liên tục của hàm số tại điểm x = 1, ta có
+ f (1) = 2 + a.
+ lim
x →1
−
f (x) = lim
x →1
−
(2x + a) = 2 + a.
+ lim
x →1
+
f (x) = lim
x →1
+
x
3
− x
2
+ 2x −2
x − 1
= lim
x →1
+
(x − 1)
x
2
+ 2
x − 1
= lim
x →1
+
x
2
+ 2
= 3.
Hàm số f (x) liên tục trên R ⇔ hàm số f (x) liên tục tại x = 1.
lim
x →1
−
f (x) = lim
x →1
+
f (x) = f (1) → 2a + 1 = 3 → a = 1. □
Bài 30 (TH). Tìm m để hàm số f(x) =
x
2
+ 4x + 3
x + 1
khi x > −1
mx + 2 khi x ≤ −1
liên tục tại điểm x = −1.
Lời giải.
Ta có lim
x→(−1)
+
f (x) = lim
x→(−1)
+
x
2
+ 4x + 3
x + 1
= lim
x→(−1)
+
(x + 1) (x + 3)
x + 1
= lim
x→(−1)
+
(x + 3) = 2.
lim
x→(−1)
−
f (x) = lim
x→(−1)
−
(mx + 2) = −m + 2.
f (−1) = −m + 2.
Để hàm số đã cho liên tục tại điểm x = −1 thì lim
x→(−1)
+
f (x) = lim
x→(−1)
−
f (x) = f (−1) ⇔ 2 = −m + 2 ⇔ m = 0.
□
Bài 31 (VD). Cho hàm số f (x) =
®
sin πx khi |x| ≤ 1
x + 1 khi |x| > 1
. Tìm các khoảng liên tục của hàm số? Lệnh này giờ vô
dụng Hàm số liên tục trên các khoảng (−∞; 1) và (1; +∞).
Lời giải.
Ta có lim
x→1
+
(x + 1) = 2 và lim
x→1
−
sin πx = 0 ⇒ lim
x→1
+
f (x) = lim
x→1
−
f (x) do đó hàm số gián đoạn tại x = 1.
Tương tự lim
x→(−1)
−
(x + 1) = 0 và lim
x→(−1)
+
sin πx = 0
⇒ lim
x→(−1)
+
f (x) = lim
x→(−1)
−
f (x) = lim
x→−1
f (x) = f (−1) do đó hàm số liên tục tại x = −1.
Với x = ±1 thì hàm số liên tục trên tập xác định.
Vậy hàm số đã cho liên tục trên các khoảng (−∞; 1) và (1; +∞). □
Bài 32 (TH). Cho hàm số f (x) =
®
sin x nếu cos x ≥ 0
1 + cos x nếu cos x < 0
. Hỏi hàm số f có tất cả bao nhiêu điểm gián đoạn
trên khoảng (0; 2018)?
Lời giải.
Vì f là hàm lượng giác nên hàm số f gián đoạn khi và chỉ khi hàm số f gián đoạn tại x làm cho cos x = 0 ⇔ x =
π
2
+ kπ (k ∈ Z) ∈ (0; 2018) ⇔ 0 <
π
2
+ kπ < 2018 ⇔ 0 <
1
2
+ k <
2018
π
⇔ −
1
2
< k <
2018
π
−
1
2
⇔ 0 ≤ k ≤ 641. □
Bài 33 (TH). Tìm m để hàm số y = f (x) =
®
x
2
+ 2
√
x − 2 khi x ≥ 2
5x − 5m + m
2
khi x < 2
liên tục trên R?
Lời giải.
Tập xác định R .
+ Xét trên (2; +∞) khi đó f (x) = x
2
+ 2
√
x − 2.
∀x
0
∈ (2; +∞) , lim
x→x
0
x
0
2
+ 2
√
x
0
− 2
= x
2
0
+ 2
√
x
0
− 2 = f (x
0
) ⇒hàm số liên tục trên (2; +∞).
+ Xét trên (−∞; 2) khi đó f (x) = 5x −5m + m
2
là hàm đa thức liên tục trên R ⇒ hàm số liên tục trên (−∞; 2).
+ Xét tại x
0
= 2, ta có f (2) = 4.
lim
x→2
+
f (x) = lim
x→2
+
x
2
+ 2
√
x − 2
= 4; lim
x→2
−
f (x) = lim
x→2
−
5x − 5m + m
2
= m
2
− 5m + 10. Để hàm số đã cho
liên tục trên R thì nó phải liên tục tại x
0
= 2.
⇔ lim
x→2
+
f (x) = lim
x→2
−
f (x) = f (2) ⇔ m
2
− 5m + 10 = 4 ⇔ m
2
− 5m + 6 = 0 ⇔
ñ
m = 2
m = 3
. □
458/764 458/764
Toán 11 theo chương trình GDPT2018
Chương 3. Giới hạn. Hàm số liên tục
Biết làm, làm đúng, làm nhanh
459
Bài 34 (VD). Cho hàm số f (x) =
3x + a −1 khi x ≤ 0
√
1 + 2x −1
x
khi x > 0
. Tìm tất cả giá trị thực của a để hàm số đã cho liên
tục trên R.
Lời giải.
Hàm số liên tục tại mọi điểm x = 0 với mọi a.
Với x = 0, ta có f (0) = a −1.
lim
x→0
−
f (x) = lim
x→0
−
(3x + a −1) = a − 1.
lim
x→0
+
f (x) = lim
x→0
+
√
1 + 2x −1
x
= lim
x→0
+
2x
x
√
1 + 2x + 1
= lim
x→0
+
2
√
1 + 2x + 1
= 1.
Hàm số liên tục trên R khi và chỉ khi hàm số liên tục tại x = 0 ⇔ a −1 = 1 ⇔ a = 2. □
Bài 35 (TH). Có bao nhiêu giá trị thực của tham số m để hàm số f (x) =
®
m
2
x
2
khi x ≤ 2
(1 − m) x khi x > 2
liên tục trên
R?
Lời giải.
Ta có hàm số luôn liên tục với ∀x = 2.
Tại x = 2, ta có lim
x→2
+
f (x) = lim
x→2
−
(1 − m) x = (1 − m) 2;
lim
x→2
−
f (x) = lim
x→2
−
m
2
x
2
= 4m
2
; f (2) = 4m
2
.
Hàm số liên tục tại x = 2 khi và chỉ khi
lim
x→2
+
f (x) = lim
x→2
+
f (x) = f (2) ⇔ 4m
2
= (1 − m) 2 ⇔ 4m
2
+ 2m −2 = 0. (1)
Phương trình luôn có hai nghiệm thực phân biệt. Vậy có hai giá trị của m.
□
Bài 36. Xét tính liên tục của các hàm số sau:
a) f(x) =
x
x
2
− 4
;
b) g(x) =
√
9 − x
2
;
c) h(x) = cos x + tan x.
Lời giải.
a) f(x) là hàm phân thức nên nó liên tục trên tập xác định hay hay liên tục trên R\{−2; 2}.
b) g(x) là hàm sơ cấp nên nó liên tục trên tập xác định hay liên tục trên [−3; 3].
c) Ta có:
y = cos x liên tục trên R.
y = tan x liên tục trên R\
n
π
2
+ kπ với k ∈ Z
o
.
Do đó, hàm số h(x) liên tục trên R\
n
π
2
+ kπ với k ∈ Z
o
.
□
Bài 37. Bạn Nam cho rằng: “Nếu hàm số y = f(x) liên tục tại điểm x
0
, còn hàm số y = g(x) không liên tục tại
x
0
, thì hàm số y = f(x) + g(x) không liên tục tại x
0
”. Theo em, ý kiến của bạn Nam đúng hay sai? Giải thích.
Lời giải.
Giả sử hàm số h(x) = f (x) + g(x) là hàm số liên tục tại x
0
.
Khi đó, hàm số g(x) = h(x) − f(x) là hiệu của hai hàm số liên tục tại x
0
nên hàm số g(x) là hàm số liên tục tại
x
0
. Điều này mâu thuẫn với giả thiết là g(x) không liên tục tại x
0
.
Vậy ý kiến trên là đúng. □
Bài 38. Xét tính liên tục của mỗi hàm số sau trên tập xác định của hàm số đó
459/764 459/764
Toán 11 theo chương trình GDPT2018
3. Hàm số liên tục
Biết làm, làm đúng, làm nhanh
460
f(x) = x
2
+ sin x.a) g(x) = x
4
− x
2
+
6
x − 1
.b) h(x) =
2x
x − 3
+
x − 1
x + 4
.c)
Lời giải.
a) Hàm số y = x
2
và hàm số y = sin x liên tục trên R nên hàm số f(x) = x
2
+ sin x là tổng của hai hàm số
trên cũng liên tục trên R.
b) Tập xác định của hàm số là R \ {1}.
Vậy hàm số f(x) liên tục trên các khoảng (−∞; 1) và (1; +∞).
c) Tập xác định của hàm số là R \ {−4; 3}.
Vậy hàm số f(x) liên tục trên các khoảng (−∞; −4); (-4;3) và (3; +∞).
□
Bài 39. Cho hàm số f (x) =
®
x
2
+ x + 1 nếu x = 4
2a + 1 nếu x = 4.
a) Với a = 0, xét lính liên tục của hàm số tại x = 4.
b) Với giá trị nào của a thì hàm số liên tục tại x = 4.
c) Với giá trị nào của a thì hàm số liên tục trên tập xác định của nó?
Lời giải.
a) Hàm số trên là hàm đa thức nên liên tục trên R.
Ta có f(4) = 2a + 1 = 1 (do a = 0).
lim
x→4
f(x) = lim
x→4
x
2
+ x + 1
= 4
2
+ 4 + 1 = 21.
Vì lim
x→4
f(x) = f (4) nên hàm số trên không liên tục tại x = 4 khi a = 0.
b) Hàm số trên là hàm đa thức nên liên tục trên R.
Ta có f(4) = 2a + 1.
lim
x→4
f(x) = lim
x→4
x
2
+ x + 1
= 4
2
+ 4 + 1 = 21.
Để hàm số liên tục tại x = 4 thì lim
x→4
f(x) = f (4) ⇔ 2a + 1 = 21 ⇔ a = 10.
Vậy a = 10 thì hàm số liên tục tại x = 4.
c) Tập xác định của hàm số là R.
○ TH1: x = 4, hàm số trên là hàm đa thức nên liên tục trên R.
○ TH2: x = 4, hàm số trên là hàm hằng nên liên tục trên R.
Vậy hàm số trên liên tục trên R.
□
Bài 40. Tìm P để hàm số y =
x
2
− 4x + 3
x − 1
khi x > 1
6P x −3 khi x ≤ 1
liên tục trên R.
Lời giải.
Hàm số y = f (x) liên tục trên R ⇒ y = f (x) liên tục tại x = 1 ⇒ lim
x→1
+
f (x) = lim
x→1
−
f (x) = f (1).
lim
x→1
+
f (x) = lim
x→1
+
x
2
− 4x + 3
x − 1
= lim
x→1
+
(x − 3) = −2.
lim
x→1
−
f (x) = lim
x→1
−
(6P x −3) = 6P − 3.
f (1) = 6P − 3.
Do đó lim
x→1
+
f (x) = lim
x→1
−
f (x) = f (1) ⇔ 6P − 3 = −2 ⇔ P =
1
6
. □
460/764 460/764
Toán 11 theo chương trình GDPT2018
Chương 3. Giới hạn. Hàm số liên tục
Biết làm, làm đúng, làm nhanh
461
Bài 41 (TH). Hàm số f(x) =
®
ax + b + 1, khi x > 0
a cos x + b sin x , khi x ≤ 0
liên tục trên R khi và chỉ khi
Lời giải.
Khi x < 0 thì f (x) = a cos x + b sin x liên tục với x < 0.
Khi x > 0 thì f (x) = ax + b + 1 liên tục với mọi x > 0.
Tại x = 0 ta có f (0) = a.
lim
x→0
+
f (x)= lim
x→0
+
(ax + b + 1)= b + 1.
lim
x→0
−
f (x)= lim
x→0
−
(a cos x + b sin x)= a.
Để hàm số liên tục tại x = 0 thì lim
x→0
+
f (x)= lim
x→0
−
f (x) = f (0) ⇔ a = b + 1 ⇔ a − b = 1. □
Bài 42 (TH). Cho hàm số y =
®
3x + 1 khi x ≥ −1
x + m khi x < −1
, m là tham số. Tìm m để hàm số liên tục trên R.
Lời giải.
Ta có hàm số liên tục trên các khoảng (−∞; −1) và (−1; +∞).
Xét tính liên tục của hàm số tại x = −1.
Có y (−1) = −2 = lim
x→−1
+
y và lim
x→−1
−
y = −1 + m.
Để hàm số liên tục trên R thì y (−1) = lim
x→−1
+
y = lim
x→−1
−
y ⇔ −2 = −1 + m ⇔ m = −1. □
Bài 43. Xét tính liên tục của các hàm số sau trên tập xác định của chúng:
f(x) =
x
x
2
+ 5x + 6
;a) f(x) =
®
1 + x
2
nếu x < 1
4 − x nếu x ≥ 1.
b)
Lời giải.
a) Tập xác định của hàm số đã cho là R \{−2; −3}. Do đó hàm số đã cho liên tục trên các khoảng (−∞; −3),
(−3; −2) và (−2, +∞);
b) Hàm số đã cho xác định trên R. Với x < 1, ta có f(x) = 1 + x
2
là hàm đa thức, do đó liên tục trên khoảng
(−∞; 1). Với x > 1, ta có f(x) = 4 −x cũng là hàm đa thức, do đó liên tục trên khoảng (1; +∞). Tại x = 1,
ta có
○ lim
x→1
−
f(x) = lim
x→1
−
(1 + x
2
) = 2.
○ lim
x→1
+
f(x) = lim
x→1
+
(4 − x) = 3.
Vì lim
x→1
+
f(x) = lim
x→1
−
f(x) do đó hàm số đã cho không liên tục tại x = 1. Vậy hàm số đã cho liên tục trên
các khoảng (−∞; 1) và (1; +∞).
□
Bài 44. Tìm giá trị của tham số m để hàm số
f(x) =
®
sin x nếu x ≥ 0
− x + m nếu x < 0
liên tục trên R.
Lời giải.
Hàm số đã cho liên tục trên các khoảng (−∞; 0) và (0; +∞).
Xét tại x = 0.
Ta có
○ f(0) = sin 0 = 0.
○ lim
x→0
+
f(x) = lim
x→0
+
sin x = 0.
○ lim
x→0
−
f(x) = lim
x→0
−
(−x + m) = m.
461/764 461/764
Toán 11 theo chương trình GDPT2018
3. Hàm số liên tục
Biết làm, làm đúng, làm nhanh
462
Hàm số đã cho liên tục trên R khi và chỉ khi f(0) = lim
x→0
+
f(x) = lim
x→0
−
f(x) ⇔ m = 0. □
Bài 45. Cho hàm số f (x) =
x
2
− 4
x + 2
khi x = −2
a khi x = −2.
.Tìm a để hàm số y = f (x) liên tục trên R.
Lời giải.
Với x
0
∈ (−∞; −2) ∪ (−2; +∞), ta có:
f(x) =
x
2
− 4
x + 2
là hàm số liên tục trên x
0
∈ (−∞; −2)∪(−2; +∞) nên f(x) liên tục trên (−∞; −2)∪(−2; +∞).
Do đó, để hàm số liên tục trên R khi và chỉ khi hàm số liên tục tại x
0
= −2, ta có
f(−2) = a;
lim
x→−2
f(x) = lim
x→−2
x
2
− 4
x + 2
= lim
x→−2
(x + 2)(x −2)
x + 2
= lim
x→−2
(x + 2) = 0.
Do đó, để hàm số liên tục tại x
0
= −2 thì a = 0.
□
Bài 46. Một bảng giá cước taxi được cho như sau:
Giá mở cửa (0, 5 km đầu) Giá cước các km tiếp theo đến 30 km Giá cước từ km thứ 31
10 000 đồng 13 500 đồng 11 000 đồng
a) Viết công thức hàm số mô tả số tiền khách phải trả theo quãng đường di chuyển.
b) Xét tính liên tục của hàm số ở câu a.
Lời giải.
a) Gọi x là quãng đường di chuyển, f(x) là giá tiền tính theo quãng đường.
○ 0 ≤ x ≤ 0,5, ta có f(x) = 10000 đồng.
○ 0,5 < x ≤ 30, f(x) = 10000 + 13500(x −0,5) đồng.
○ x > 30, f(x) = 408250 + 11000(x − 30) đồng.
Vậy f(x) =
10000 nếu 0 ≤ x ≤ 0,5
10000 + 13500(x −0,5) nếu 0,5 < x ≤ 30
408250 + 11000(x −30) nếu x > 30.
b) Hàm số f(x) liên tục trên các khoảng (0; 0,5), (0,5; 30) và (30; +∞).
Tại x = 0,5, ta có f(0,5) = 10000, lim
x→0,5
+
f(x) = 10000, lim
x→0,5
−
f(x) = 10000.
Vì f(0, 5) = lim
x→0,5
+
f(x) = lim
x→0,5
−
f(x), do đó f(x) liên tục tại x = 0, 5.
Tại x = 30, ta có f(30) = 408250, lim
x→30
−
f(x) = 408250, lim
x→30
+
f(x) = 408250.
Vì f(30) = lim
x→30
−
f(x) = lim
x→30
+
f(x), do đóf(x) liên tục tại x = 30.
Vậy f(x) liên tục trên khoảng (0; +∞). □
Bài 47. Một bãi đậu xe ô tô đưa ra giá C(x) (đồng) khi thời gian đậu xe là x (giờ) như sau:
C(x) =
60000 khi 0 < x ≤ 2
100000 khi 2 < x ≤ 4
200000 khi 4 < x ≤ 24.
Xét tính liên tục của hàm số C(x).
Lời giải.
Tập xác định D = (0; 24]
462/764 462/764
Toán 11 theo chương trình GDPT2018
Chương 3. Giới hạn. Hàm số liên tục
Biết làm, làm đúng, làm nhanh
463
Khi 0 < x < 2 thì C(x) = 60000 là hàm đa thức liên tục trên R nên C(x) liên tục trên (0; 2).
Khi 2 < x < 4 thì C(x) = 100000 là hàm đa thức liên tục trên R nên C(x) liên tục trên (2; 4).
Khi 4 < x ≤ 24 thì C(x) = 200000 là hàm đa thức liên tục trên R nên C(x) liên tục trên (4; 24].
Khi x
0
= 2, ta có
f(2) = 60000;
lim
x→2
−
f(x) = lim
x→2
−
60000 = 60000;
lim
x→2
+
f(x) = lim
x→2
+
100000 = 100000.
Do dó hàm số không có giới hạn tại 2 nên không liên tục tại 2.
Khi x
0
= 4, ta có
f(4) = 100000;
lim
x→4
−
f(x) = lim
x→4
−
100000 = 100000;
lim
x→4
+
f(x) = lim
x→4
+
200000 = 200000.
Do dó hàm số không có giới hạn tại 4 nên không liên tục tại 4.
Vậy hàm số liên tục trên (0; 24]\{2; 4}
□
Bài 48. Lực hấp dẫn do Trái Đất tác dụng lên một đơn vị khối lượng ở khoảng cách r tính từ tâm của nó là
F (r) =
GMr
R
3
khi 0 < r < R
GM
r
2
khi r ≥ R,
trong đó M là khối lượng, R là bán kính của Trái Đất, G là hằng số hấp dẫn. Hàm số F (r) có liên tục trên
(0; +∞) không?
Lời giải.
Khi 0 < r < R thì F (r) =
GMr
R
3
là hàm đa thức liên tục trên R nên F (r) liên tục trên (0; R).
Khi R < r thì F (r) =
GM
r
2
là hàm phân thức liên tục trên R\{0} nên F (r) liên tục trên (R; +∞).
Tại r = R, ta có:
F (R) =
GM
R
2
;
lim
x→R
−
F (r) = lim
x→R
−
GMr
R
3
=
GM
R
2
;
lim
x→R
+
F (r) = lim
x→R
+
GM
r
2
=
GM
R
2
.
Do đó, hàm số liên tục tại R.
Vậy hàm số liên tục trên (0; +∞).
□
463/764 463/764
Toán 11 theo chương trình GDPT2018
3. Hàm số liên tục
Biết làm, làm đúng, làm nhanh
464
Bài 49.
Hình bên cạnh biểu thị độ cao h (m) của một quả bóng được đá lên thời gian t (s),
trong đó h(t) = −2t
2
+ 8t.
a) Chứng tỏ hàm số h(t) liên tục trên tập xác định.
b) Dựa và đồ thì hãy xác định lim
t→2
−2t
2
+ 8t
.
t(s)
h(m)
O
4
8
2
Lời giải.
a) Hàm số trên là hàm đa thức nên liên tục trên R.
b) Dựa vào đồ thị ta có lim
t→2
−2t
2
+ 8t
= 8.
□
Bài 50. Một hãng taxi đưa ra giá cước T (x) (đồng) khi quãng đường x (km) cho loại xe 4 chỗ như sau:
T (x) =
10000 khi 0 < x ≤ 0.7
10000 + (x −0,7).14000 khi 0,7 < x ≤ 20
280200 + (x −20).12000 khi x > 20
Xét tính liên tục của hàm số T (x).
Lời giải.
Khi 0 < x < 0,7, T (x) = 1000 là hàm số đa thức liên tục trên R nên T (x) liên tục trên (0; 0,7).
Khi 0,7 < x < 20, T (x) = 10000 + (x − 0,7).14000 là hàm số đa thức liên tục trên R nên T (x) liên tục trên
(0,7; 20).
Khi 20 < x, T (x) = 280200 + (x − 20).12000 là hàm số đa thức liên tục trên R nên T (x) liên tục trên
(20; +∞).
Tại x = 0,7. Ta có
f(0,7) = 10000;
lim
x→0,7
+
f(x) = lim
x→0,7
+
10000 = 10000;
lim
x→0,7
−
f(x) = lim
x→0,7
−
[10000 + (x −0, 7).14000] = 10000 + (0,7 −0,7).14000 = 10000.
Do đó, T (x) liên tục tại x = 0,7.
Tại x = 20. Ta có:
f(20) = 280200;
lim
x→20
+
f(x) = lim
x→0,7
+
[10000 + (x −0,7).14000] = 280200;
lim
x→0,7
−
f(x) = lim
x→0,7
−
[280200 + (x −20).12000] = 280200 + (20 − 20).12000 = 280200,.
Do đó, T (x) liên tục tại x = 0,7.
Từ những điều trên, T (x) liên tục trên R.
□
464/764 464/764
Toán 11 theo chương trình GDPT2018
Chương 3. Giới hạn. Hàm số liên tục
Biết làm, làm đúng, làm nhanh
465
3. Bài tập trắc nghiệm
Câu 49. Cho hàm số y = f (x) liên tục trên (a; b). Điều kiện cần và đủ để hàm số liên tục trên [a; b] là
A lim
x→a
+
f (x) = f (a) và lim
x→b
+
f (x) = f (b). B lim
x→a
−
f (x) = f (a) và lim
x→b
−
f (x) = f (b).
C lim
x→a
+
f (x) = f (a) và lim
x→b
−
f (x) = f (b). D lim
x→a
−
f (x) = f (a) và lim
x→b
+
f (x) = f (b).
Lời giải.
Theo định nghĩa hàm số liên tục trên đoạn [a; b]. Chọn lim
x→a
+
f (x) = f (a) và lim
x→b
−
f (x) = f (b).
Chọn đáp án C □
Câu 50. Cho đồ thị của hàm số y = f (x) như hình vẽ sau:
f(x)
x
y
O
Chọn mệnh đề đúng.
A Hàm số y = f (x) có đạo hàm tại điểm x = 0 nhưng không liên tục tại điểm x = 0.
B Hàm số y = f (x)liên tục tại điểm x = 0 nhưng không có đạo hàm tại điểm x = 0.
C Hàm số y = f (x) liên tục và có đạo hàm tại điểm x = 0.
D Hàm số y = f (x) không liên tục và không có đạo hàm tại điểm x = 0.
Lời giải.
Đồ thị là một đường liền nét, nhưng bị “gãy” tại điểm x = 0 nên nó liên tục tại điểm x = 0 nhưng không có đạo
hàm tại điểm x = 0.
Chọn đáp án B □
Câu 51. Hình nào trong các hình dưới đây là đồ thị của hàm số không liên tục tại x = 1?
A
−3 −2 −1
1 2 3
1
2
3
4
f(x)
x
y
O
. B
−3 −2 −1
1 2 3
1
2
3
4
f(x)
x
y
O
.
C
−3 −2 −1
1 2 3
1
2
3
4
f(x)
x
y
O
. D
−2 −1
1 2 3 4
1
2
3
4
f(x)
x
y
O
.
Lời giải.
Vì lim
x→1
+
y = lim
x→1
−
y nên hàm số không liên tục tại x = 1. □
465/764 465/764
Toán 11 theo chương trình GDPT2018
3. Hàm số liên tục
Biết làm, làm đúng, làm nhanh
466
Câu 52. Cho hàm số y =
1 − x
3
1 − x
, khi x < 1
1 , khi x ≥ 1
. Hãy chọn kết luận đúng
A y liên tục phải tại x = 1. B y liên tục tại x = 1.
C y liên tục trái tại x = 1. D y liên tục trên R.
Lời giải.
Ta có y (1) = 1.
Ta có lim
x→1
+
y = 1; lim
x→1
−
y = lim
x→1
−
1 − x
3
1 − x
= lim
x→1
−
(1 − x)
1 + x + x
2
1 − x
= lim
x→1
−
1 + x + x
2
= 4.
Nhận thấy lim
x→1
+
y = y (1), suy ra y liên tục phải tại x = 1.
Chọn đáp án A □
Câu 53. Trong các hàm số sau, hàm số nào liên tục trên R?
A y = x
3
− x. B y = cot x. C y =
2x − 1
x − 1
. D y =
√
x
2
− 1.
Lời giải.
Vì y = x
3
− x là đa thức nên liên tục trên R.
Chọn đáp án A □
Câu 54. Trong các hàm số sau, hàm số nào liên tục trên R?
A f (x) = tan x + 5. B f (x) =
x
2
+ 3
5 − x
. C f (x) =
√
x − 6. D f (x) =
x + 5
x
2
+ 4
.
Lời giải.
Hàm số f (x) =
x + 5
x
2
+ 4
là hàm phân thức hữu tỉ và có tập xác định là D = R do đó hàm số f (x) =
x + 5
x
2
+ 4
liên
tục trên R.
Chọn đáp án D □
Câu 55. Cho hàm số y =
®
− x
2
+ x + 3 khi x ≥ 2
5x + 2 khi x < 2
. Chọn mệnh đề sai trong các mệnh đề sau:
A Hàm số liên tục tại x
0
= 1.
B Hàm số liên tục trên R.
C
Hàm số liên tục trên các khoảng (−∞; 2) , (2; +∞).
D Hàm số gián đoạn tại x
0
= 2.
Lời giải.
+ Với x > 2, ta có f (x) = −x
2
+ x + 3 là hàm đa thức ⇒ hàm số f (x) liên tục trên khoảng (2; +∞).
+ Với x < 2, ta có f (x) = 5x + 2 là hàm đa thức ⇒ hàm số f (x) liên tục trên khoảng (−∞; 2).
+ Tại x = 2.
lim
x→2
+
f (x) = lim
x→2
+
−x
2
+ x + 3
= 1 lim
x→2
−
f (x) = lim
x→2
−
(5x + 2) = 12 ⇒ lim
x→2
+
f (x) = lim
x→2
−
f (x). Do đó không
tồn tại lim
x→2
f (x) . Vậy hàm số gián đoạn tại x
0
= 2 hay Hàm số không liên tục trên R.
Chọn đáp án B □
Câu 56. Hàm số nào sau đây liên tục trên R?
A f (x) =
√
x. B f (x) = x
4
− 4x
2
. C f (x) =
x
4
− 4x
2
x + 1
. D f (x) =
x
4
− 4x
2
x + 1
.
Lời giải.
Vì hàm số f (x) = x
4
− 4x
2
có dạng đa thức với D = R nên hàm số này liên tục trên R
Chọn đáp án B □
Câu 57. Tìm tất cả các giá trị thực của m để hàm số f(x) =
√
x + 1 −1
x
khi x > 0
p
x
2
+ 1 −m khi x ≤ 0
liên tục trên R.
A m =
3
2
. B m =
1
2
. C m = −2. D m = −
1
2
.
Lời giải.
466/764 466/764
Toán 11 theo chương trình GDPT2018
Chương 3. Giới hạn. Hàm số liên tục
Biết làm, làm đúng, làm nhanh
467
Khi x > 0, ta có f(x) =
√
x + 1 −1
x
liên tục trên khoảng (0; +∞).
Khi x < 0, ta có f(x) =
√
x
2
+ 1 −m liên tục trên khoảng (−∞; 0).
Hàm số liên tục trên R khi và chỉ khi hàm số liên tục tại x = 0.
Ta có lim
x→0
+
f(x) = lim
x→0
+
√
x + 1 −1
x
= lim
x→0
+
1
√
x + 1 + 1
=
1
2
.
lim
x→0
−
f(x) = lim
x→0
−
Ä
√
x
2
+ 1 −m
ä
= 1 − m = f (0). Do đó hàm số liên tục tại x = 0 khi và chỉ khi
1
2
= 1 − m ⇔
m =
1
2
.
Chọn đáp án B □
Câu 58. Tìm tất cả các giá trị thực của tham số m để hàm số f (x) =
x
2
− 16
x − 4
khi x > 4
mx + 1 khi x ≤ 4
liên tục trên
R.
A m = 8 hoặc m = −
7
4
. B m =
7
4
. C m = −
7
4
. D m = −8 hoặc m =
7
4
.
Lời giải.
*) Với x > 4 thì f (x) =
x
2
− 16
x − 4
là hàm phân thức nên liên tục trên tập xác định của nó ⇒ f (x) liên tục trên
(4; +∞).
*) Với x < 4 thì f (x) = mx + 1 là hàm đa thức nên liên tục trên R ⇒ f (x) liên tục trên (−∞; 4).
Do vậy hàm số f (x) đã liên tục trên các khoảng (4; +∞), (−∞; 4).
Suy ra hàm số f (x) liên tục trên R khi và chỉ khi f (x) liên tục tại x = 4.Do đó
lim
x→4
+
f (x) = lim
x→4
−
f (x) = f (4) ⇔ lim
x→4
+
x
2
− 16
x − 4
= lim
x→4
−
(mx + 1) = 4m+1 ⇔ lim
x→4
+
(x + 4) = 4m+1 ⇔ 4m+ 1 =
8 ⇔ m =
7
4
.
Chọn đáp án B □
Câu 59. Nếu hàm số f (x) =
x
2
+ ax + b khi x < −5
x + 17 khi −5 ≤ x ≤ 10
ax + b + 10 khi x > 10
liên tục trên R thì a + b bằng
A −1. B 0. C 1. D 2.
Lời giải.
Với x < −5 ta có f (x) = x
2
+ ax + b, là hàm đa thức nên liên tục trên (−∞; −5).
Với −5 < x < 10 ta có f (x) = x + 7, là hàm đa thức nên liên tục trên (−5; 10).
Với x > 10 ta có f (x) = ax + b + 10, là hàm đa thức nên liên tục trên (10; +∞).
Để hàm số liên tục trên R thì hàm số phải liên tục tại x = −5 và x = 10.
Ta có
f (−5) = 12;f (10) = 17.
lim
x→−5
−
f (x) = lim
x→−5
−
x
2
+ ax + b
= −5a + b + 25.
lim
x→−5
+
f (x) = lim
x→−5
+
(x + 17) = 12. lim
x→10
−
f (x) = lim
x→10
−
(x + 17) = 27. lim
x→10
+
f (x) = lim
x→10
+
(ax + b + 10) =
10a + b + 10. Hàm số liên tục tại x = −5 và x = 10 khi
®
5a + b + 25 = 12
10a + b + 10 = 27
⇔
®
− 5a + b = −13
10a + b = 17
⇔
®
a = 2
b = −3
⇒ a + b = −1.
Chọn đáp án A □
Dạng 5. Bài toán có chứa tham số
1. Ví dụ mẫu
Ví dụ 19 (Cánh Diều). Cho hàm số f(x) =
®
x + 1 nếu x = 3
a nếu x = 3
. Tìm a để hàm số f(x) liên tục trên R.
467/764 467/764
Toán 11 theo chương trình GDPT2018
3. Hàm số liên tục
Biết làm, làm đúng, làm nhanh
468
Lời giải.
Do f(x) = x + 1 nếu x = 3 nên hàm số đó liên tục trên mỗi khoảng (−∞; 3) và (3; +∞).
Với x = 3 thì f(3) = a.
Ta có lim
x→3
f(x) = lim
x→3
(x + 1) = 3 + 1 = 4.
Vậy hàm số f(x) liên tục trên R khi hàm số f(x) liên tục tại điểm x = 3 khi và chỉ khi
lim
x→3
f(x) = f (3) = 4 ⇔ a = 4.
□
Ví dụ 20. Cho hàm số f (x) =
®
x + 1 nếu x = 3
a nếu x = 3
. Tìm a để hàm số f(x) liên tục trên R.
Lời giải.
Do f(x) = x + 1 nếu x = 3 nên hàm số đó liên tục trên mỗi khoảng (−∞; 3) và (3; +∞).
Với x = 3 thì f(3) = a.
Ta có lim
x→3
f(x) = lim
x→3
(x + 1) = 3 + 1 = 4.
Vậy hàm số f(x) liên tục trên R khi hàm số f(x) liên tục tại điểm x = 3 khi và chỉ khi
lim
x→3
f(x) = f (3) = 4 ⇔ a = 4.
□
Ví dụ 21. Tìm giá trị của tham số m để hàm số
f(x) =
®
sin x nếu x ≥ 0
− x + m nếu x < 0
liên tục trên R.
Lời giải.
Hàm số đã cho liên tục trên các khoảng (−∞; 0) và (0; +∞).
Xét tại x = 0.
Ta có
○ f(0) = sin 0 = 0.
○ lim
x→0
+
f(x) = lim
x→0
+
sin x = 0.
○ lim
x→0
−
f(x) = lim
x→0
−
(−x + m) = m.
Hàm số đã cho liên tục trên R khi và chỉ khi f(0) = lim
x→0
+
f(x) = lim
x→0
−
f(x) ⇔ m = 0. □
2. Bài tập rèn luyện
Bài 51. Tìm giá trị của tham số m để hàm số f(x) =
x + 1
x − m
liên tục trên khoảng (1; 2).
Lời giải.
Tập xác định D = R \ {m}.
Hàm số f(x) là hàm phân thức hữu tỷ nên hàm số liên tục trên (−∞; m) và (m; +∞).
Vậy để hàm số f(x) liên tục trên khoảng (1; 2) thì
ñ
(1; 2) ⊂ (−∞; m)
(1; 2) ⊂ (m; +∞)
⇔
ñ
m ≥ 2
m ≤ 1.
□
468/764 468/764
Toán 11 theo chương trình GDPT2018
Chương 3. Giới hạn. Hàm số liên tục
Biết làm, làm đúng, làm nhanh
469
Bài 52. Tìm giá trị của tham số a sao cho hàm số f(x) =
®
x + 2 nếu x = 2
a nếu x = 2
liên tục trên R.
Lời giải.
Tập xác định D = R.
Với x = 2, f (x) = x + 2 là hàm đa thức nên hàm số f(x) liên trục trên (−∞; 2) và (2; +∞).
Vậy để hàm số f(x) liên tục trên R thì hàm số f(x) cần liên tục tại x = 2, điều này tương đương với
lim
x→2
f(x) = f (2) ⇔ lim
x→2
(x + 2) = a ⇔ 2 + 2 = a ⇔ a = 4.
□
Bài 53. Tìm các giá trị nguyên của tham số m để hàm số f(x) =
√
9 − x
2
liên tục trên khoảng (m; 2m + 1).
Lời giải.
Hàm số f(x) =
√
9 − x
2
là hàm số căn thức nên hàm số f(x) liên tục trên tập xác định D = [−3; 3].
Suy ra hàm số f (x) =
√
9 − x
2
liên tục trên khoảng (m; 2m + 1) khi và chỉ khi
(m; 2m + 1) ⊂ [−3; 3] ⇔
®
m ≥ −3
2m + 1 ≤ 3
⇔ −3 ≥ m ≤ 1.
Vậy có 5 giá trị nguyên của tham số m thoả mãn yêu cầu bài toán. □
Bài 54. Tìm m để f (x) =
x
2
+ 5x −6
6 + x
khi x = −6
√
mx + 4 + mx − 5 khi x = −6
liên tục tại x
0
= −6.
Lời giải.
Ta có lim
x→−6
f(x) = lim
x→−6
x
2
+ 5x −6
6 + x
= lim
x→−6
(x + 6)(x −1)
6 + x
= lim
x→−6
(x − 1) = −6 −1 = −7.
Mặt khác f(−6) =
√
−6m + 4 −6m − 5 nên hàm số liên tục tại x
0
= 6 tương đương với
lim
x→−6
f(x) = f (−6)
⇔
√
−6m + 4 −6m − 5 = −7
⇔
√
−6m + 4 = 6m −2
⇔
®
6m − 2 ≥ 0
− 6m + 4 = 36m
2
− 24m + 4
⇔
m ≥
1
3
36m
2
− 18m = 0
⇔ m =
1
2
.
Vậy m =
1
2
thỏa mãn yêu cầu bài toán. □
Bài 55. Tìm a để hàm số f(x) =
x
3
+ 2x
2
− 5x −6
x
3
− 4x
khi x = 2
1
8
(a + x) khi x = 2
liên tục tại x
0
= 2.
Lời giải.
○ f(2) =
1
8
(a + 2).
○ lim
x→2
f(x) = lim
x→2
x
3
+ 2x
2
− 5x −6
x
3
− 4x
= lim
x→2
(x − 2)(x
2
+ 4x + 3)
x(x − 2)(x + 2)
= lim
x→2
x
2
+ 4x + 3
x(x + 2)
=
15
8
.
Hàm số liên tục tại x
0
= 2 ⇔ f(2) = lim
x→2
f(x) ⇔
1
8
(a + 2) =
15
8
⇔ a = 13. □
469/764 469/764
Toán 11 theo chương trình GDPT2018
3. Hàm số liên tục
Biết làm, làm đúng, làm nhanh
470
3. Bài tập trắc nghiệm
Câu 60. Tất cả giá trị của tham số m để hàm số f(x) =
√
x − 1 liên tục trên khoảng (m; m + 2) là
A m ≥ 1. B m > 1. C m > −1. D m ≥ −1.
Lời giải.
Hàm số f(x) =
√
x − 1 là hàm số dạng căn thức nên hàm số f(x) liên tục trên tập xác định D = [1; +∞).
Vậy hàm số f(x) =
√
x − 1 liên tục trên khoảng (m; m + 2) khi và chỉ khi
(m; m + 2) ⊂ [1; +∞) ⇔ m ≥ 1.
Chọn đáp án A □
Câu 61. Cho hàm số f(x) =
®
2x − 2 khi x = 3
2m khi x = 3
(m là tham số). Tìm giá trị thực của tham số m để hàm số đã
cho liên tục tại x
0
= 3.
A m = 4. B m = 2. C m = 3. D m = 1.
Lời giải.
Tập xác định D = R.
Ta có lim
x→3
f(x) = lim
x→3
(2x − 2) = 4, f(3) = 2m. Để hàm số liên tục tại x
0
= 3 thì lim
x→3
f(x) = f(3) ⇔ 4 = 2m ⇔
m = 2.
Chọn đáp án B □
Câu 62. Hàm số f(x) =
®
ax + 5 khi x ≥ 2
5 khi x < 2
liên tục trên R nếu a bằng
A 0. B 3. C −1. D 7.
Lời giải.
Hàm số đã cho liên tục trên (2; +∞) và (−∞; 2), từ đó suy ra hàm số liên tục trên R nếu nó liên tục tại x = 2.
Ta có lim
x→2
+
f(x) = lim
x→2
+
(ax + 5) = 2a + 5; lim
x→2
−
f(x) = lim
x→2
+
(3x − 1) = 5.
Từ đó suy ra hàm số liên tục trên R nếu 2a + 5 = 5 ⇒ a = 0.
Chọn đáp án A □
Câu 63. Cho số thực a và hàm số f(x) =
®
x + 2 nếu x ≤ a
2x − 1 nếu x > a
. Giá trị của a để hàm số f (x) liên tục trên R
là
A 0. B 1. C 2. D 3.
Lời giải.
Hàm số có dạng đa thức trên các khoảng (−∞; a) và (a; +∞) nên hàm số f(x) hiển nhiên liên tục trên (−∞; a)
và (a; +∞).
Vậy hàm số f(x) liên tục trên R khi và chỉ khi hàm số liên tục tại x = a, điều này tương đương với
lim
x→a
+
f(x) = lim
x→a
−
f(x) = f (a) ⇔ a + 2 = 2a −1 ⇔ a = 3.
Chọn đáp án D □
Câu 64. Cho hàm số f (x) =
®
x
2
+ m khi x ≥ 2
3x − 1 khi x < 2
(m là tham số). Tìm giá trị thực của tham số m để hàm số đã
cho liên tục tại x
0
= 2.
A m = 2. B m = 1. C m = 0. D m = 3.
Lời giải.
Xét tính liên tục tại x
0
= 2:
Ta có lim
x→2
+
f(x) = lim
x→2
+
x
2
+ m
= 4 + m = f(2) và lim
x→2
−
f(x) = lim
x→2
−
(3x − 1) = 5.
Khi đó hàm số đã cho liên tục tại x
0
= 2 khi và chỉ khi
lim
x→2
+
f(x) = lim
x→2
−
f(x) = f (2) ⇔ 4 − m = 5 ⇔ m = 1.
Chọn đáp án B □
470/764 470/764
Toán 11 theo chương trình GDPT2018
Chương 3. Giới hạn. Hàm số liên tục
Biết làm, làm đúng, làm nhanh
471
Câu 65. Biết hàm số y = f(x) =
®
3x + b khi x ⩽ −1
x + a khi x > −1
liên tục trên R. Khi đó giá trị của a − b bằng
A 1. B −1. C 2. D −2.
Lời giải.
Ta có lim
x→−1
+
f(x) = lim
x→−1
+
(x + a) = a −1 và lim
x→−1
−
f(x) = lim
x→−1
−
(3x + b) = b −3.
Vì hàm số liên tục trên R nên ta có a − 1 = b − 3 ⇔ a − b = −2.
Chọn đáp án
D □
Câu 66. Cho hàm số f (x) =
®
x
3
+ x
2
+ 7 khi x = −1
2x + m −1 khi x = −1
. Tìm m để hàm số liên tục tại điểm x
0
= −1.
A m = 12. B m = 8. C m = −10. D m = 10.
Lời giải.
Ta có lim
x→−1
(x
3
+ x
2
+ 7) = 7 và f(−1) = m − 3.
Để hàm số liên tục tại điểm x
0
= −1 thì m − 3 = 7 ⇔ m = 10.
Chọn đáp án D □
Câu 67. Cho hàm số y = f(x) =
x
3
− x
2
x − 1
khi x > 1
n khi x = 1
mx + 1 khi x < 1
. Biết hàm số f(x) liên tục tại x
0
= 1. Giá trị của m, n
là
A n = 1, m = 0. B n = 0, m = 1. C n = m = 1. D n = −1, m = 0.
Lời giải.
Ta có
○ lim
x→1
+
f(x) = lim
x→1
+
x
3
− x
2
x − 1
= lim
x→1
+
x
2
= 1;
○ lim
x→1
−
f(x) = lim
x→1
−
(mx + 1) = m + 1;
○ f(1) = n.
Do hàm số f(x) liên tục tại x = 1 nên ta có lim
x→1
−
f(x) = lim
x→1
+
f(x) = f (1) ⇔ m + 1 = 1 = n.
Suy ra n = 1, m = 0.
Chọn đáp án A □
Câu 68. Tìm giá trị của m để hàm số f(x) =
4 − x
√
x + 5 −3
khi x = 4
1 − m khi x = 4
liên tục tại x = 4.
A m = 7. B m = 0. C m = 2. D m = −5.
Lời giải.
Ta có lim
x→4
4 − x
√
x + 5 −3
= lim
x→4
(4 − x)
√
x + 5 + 3
x − 4
= − lim
x→4
√
x + 5 + 3
= −6.
Để hàm số liên tục tại x = 4 thì −6 = 1 −m ⇔ m = 7.
Chọn đáp án A □
Câu 69. Cho các tham số a, b thoả mãn hàm số f(x) =
ax
2
− bx + 4
x − 1
khi x = 1
3 khi x = 1
liên tục trên R. Giá trị của
biểu thức P = a + b là
A 27. B 28. C 29. D 30.
Lời giải.
Do hàm số f(x) liên tục trên R nên hàm số f (x) liên tục tại x = 1, điều này tương đương với
lim
x→1
ax
2
− bx + 4
x − 1
= 3 ⇔ lim
x→1
Å
ax + a −b +
a − b + 4
x − 1
ã
= 3 ⇔
®
a − b + 4 = 0
2a − b = 3
⇔
®
a = 7
b = 11.
471/764 471/764
Toán 11 theo chương trình GDPT2018
3. Hàm số liên tục
Biết làm, làm đúng, làm nhanh
472
Vậy a + b = 28.
Chọn đáp án B □
Dạng 6. Toán thực tế, liên môn về hàm số liên tục
1. Ví dụ
Ví dụ 22.
Hình bên cạnh biểu thị độ cao h (m) của một quả bóng được đá lên thời gian t (s),
trong đó h(t) = −2t
2
+ 8t.
a) Chứng tỏ hàm số h(t) liên tục trên tập xác định.
b) Dựa và đồ thì hãy xác định lim
t→2
−2t
2
+ 8t
.
t(s)
h(m)
O
4
8
2
Lời giải.
a) Hàm số trên là hàm đa thức nên liên tục trên R.
b) Dựa vào đồ thị ta có lim
t→2
−2t
2
+ 8t
= 8.
□
Ví dụ 23. Một bãi đậu xe ô-tô đưa ra giá C(x) (đồng) khi thời gian đậu xe là x (giờ) như sau:
C(x) =
60.000 khi 0 < x ≤ 2
100.000 khi 2 < x ≤ 4
200.000 khi 4 < x ≤ 24.
Xét tính liên tục của hàm số C(x).
Lời giải.
○ Hàm số C(x) là hàm hằng trên từng khoảng (0; 2), (2; 4), (4; 6) nên liên tục trên từng khoảng đó.
○ Ta có
lim
x→2
−
C(x) = 60.000
lim
x→2
+
C(x) = 100.000
⇒ không tồn tại lim
x→2
C(x), vậy C(x) không liên tục tại x
0
= 2.
○ Ta có
lim
x→4
−
C(x) = 100.000
lim
x→4
+
C(x) = 200.000
⇒ không tồn tại lim
x→4
C(x), vậy C(x) không liên tục tại x
0
= 4.
Vậy hàm số C(x) liên tục trên từng khoảng (0; 2), (2; 4), (4; 6). □
Ví dụ 24. Lực hấp dẫn do Trái Đất tác dụng lên một đơn vị khối lượng ở khoảng cách r tính từ tâm của nó là
F (r) =
GMr
R
3
khi 0 < r ≤ R
GM
r
2
khi r ≥ R
, trong đó M là khối lượng, R là bán kính của Trái Đất, G là hằng số hấp dẫn.
Hàm số F (r) có liên tục trên (0; +∞) không?
Lời giải.
○ Với mọi r ∈ (0; R), hàm số F (r) =
GMr
R
3
luôn xác định nên liên tục tại đó.
472/764 472/764
Toán 11 theo chương trình GDPT2018
Chương 3. Giới hạn. Hàm số liên tục
Biết làm, làm đúng, làm nhanh
473
○ Với mọi r ∈ (R; +∞), hàm số F (r) =
GM
r
2
luôn xác định nên liên tục tại đó.
○ Ta có
lim
r→R
−
F (r) = lim
r→R
−
GMr
R
3
=
GM
R
2
lim
x→R
+
F (r) = lim
x→R
+
GM
r
2
=
GM
R
2
F (R) =
GM
R
2
nên hàm số F (r) liên tục tại r = R.
Vậy hàm số F (r) liên tục trên (0; +∞). □
Ví dụ 25. Một bảng giá cước taxi được cho như sau:
Giá mở cửa (0, 5 km đầu) Giá cước các km tiếp theo đến 30 km Giá cước từ km thứ 31
10 000 đồng 13 500 đồng 11 000 đồng
a) Viết công thức hàm số mô tả số tiền khách phải trả theo quãng đường di chuyển.
b) Xét tính liên tục của hàm số ở câu a.
Lời giải.
a) Gọi x là quãng đường di chuyển, f(x) là giá tiền tính theo quãng đường.
○ 0 ≤ x ≤ 0,5, ta có f(x) = 10000 đồng.
○ 0,5 < x ≤ 30, f(x) = 10000 + 13500(x −0,5) đồng.
○ x > 30, f(x) = 408250 + 11000(x − 30) đồng.
Vậy f(x) =
10000 nếu 0 ≤ x ≤ 0,5
10000 + 13500(x −0,5) nếu 0,5 < x ≤ 30
408250 + 11000(x −30) nếu x > 30.
b) Hàm số f(x) liên tục trên các khoảng (0; 0,5), (0,5; 30) và (30; +∞).
Tại x = 0,5, ta có f(0,5) = 10000, lim
x→0,5
+
f(x) = 10000, lim
x→0,5
−
f(x) = 10000.
Vì f(0, 5) = lim
x→0,5
+
f(x) = lim
x→0,5
−
f(x), do đó f(x) liên tục tại x = 0, 5.
Tại x = 30, ta có f(30) = 408250, lim
x→30
−
f(x) = 408250, lim
x→30
+
f(x) = 408250.
Vì f(30) = lim
x→30
−
f(x) = lim
x→30
+
f(x), do đóf(x) liên tục tại x = 30.
Vậy f(x) liên tục trên khoảng (0; +∞). □
Dạng 7. Bài toán phương trình có nghiệm
1. Ví dụ mẫu
Ví dụ 26. Chứng minh rằng phương trình x
5
+ x
3
− 10 = 0 có nghiệm thuộc khoảng (0; 2).
Lời giải.
Xét hàm số f(x) = x
5
+ x
3
− 10 với x ∈ R. Ta có
○ Vì f(x) là hàm số đa thức nên f(x) liên tục trên R.
○ f(0) = −1 < 0, f(2) = 30 > 0. Suy ra f(0)f(2) < 0.
Suy ra f(x) = 0 có nghiệm thuộc khoảng (0; 2). □
Ví dụ 27. Chứng minh rằng phương trình x
3
− 3x + 1 = 0 có đúng 3 nghiệm thực phân biệt.
Lời giải.
Ta có
○ Hàm số f (x) = x
3
− 3x + 1 có dạng đa thức nên hàm số f(x) liên tục trên R.
473/764 473/764
Toán 11 theo chương trình GDPT2018
3. Hàm số liên tục
Biết làm, làm đúng, làm nhanh
474
○ f(−2) < 0, f(−1) > 0, f (1) < 0, f(2) > 0 nên f(−2)f(−1) < 0, f(−1)f(1) < 0 và f(1)f(2) < 0.
Do đó hàm số có 3 nghiệm phân biệt lần lượt thuộc các khoảng (−2; −1), (−1, 1) và (1; 2).
Mặt khác hàm số f (x) là đa thức bậc 3 nên có tối đa 3 nghiệm thực.
Vậy phương trình f(x) = 0 có đúng 3 nghiệm thực phân biệt. □
2. Bài tập rèn luyện
Bài 56. Chứng minh phương trình 4x
3
− 8x
2
+ 1 = 0 có nghiệm trong khoảng (−1; 2).
Lời giải.
Đặt f(x) = 4x
3
− 8x
2
+ 1 và f(x) là hàm đa thức nên liên tục trên R, suy ra liên tục trên [−1; 2].
Ta có
®
f(−1) = −11
f(2) = 1
⇒ f(−1) · f(2) = −11 < 0 ⇒ ∃x
0
∈ (−1; 2) : f (x
0
) = 0, nghĩa là phương trình f (x) = 0 có
ít nhất một nghiệm trong khoảng (−1; 2). □
Bài 57. Chứng minh rằng phương trình x
3
+ x + 1 = 0 có ít nhất một nghiệm âm lớn hơn −1.
Lời giải.
Đặt f(x) = x
3
+ x + 1 và f(x) là hàm đa thức nên liên tục trên R, suy ra liên tục trên [−1; 0].
Ta có
®
f(−1) = −1
f(0) = 1
⇒ f(−1) · f(0) = −1 < 0 ⇒ ∃x
0
∈ (−1; 0) : f (x
0
) = 0, nghĩa là phương trình f (x) = 0 có ít
nhất một nghiệm trong khoảng (−1; 0). □
Bài 58. Chứng minh phương trình x
3
− 3x + 1 = 0 có đúng ba nghiệm phân biệt .
Lời giải.
Đặt f(x) = x
3
− 3x + 1 và f (x) là hàm đa thức nên liên tục trên R, suy ra hàm số f (x) liên tục trên các đoạn
[−2; 0], [0; 1], [1; 2].
○ Ta có
®
f(−2) = −1
f(0) = 1
⇒ f(−2) · f(0) = −1 < 0 ⇒ Phương trình f (x) = 0 có ít nhất một nghiệm thuộc
khoảng (−2; 0). (1)
○ Ta có
®
f(0) = 1
f(1) = −1
⇒ f(0) · f(1) = −1 < 0 ⇒ Phương trình f(x) = 0 có ít nhất một nghiệm thuộc khoảng
(0; 1). (2)
○ Ta có
®
f(1) = −1
f(2) = 3
⇒ f(1) · f(2) = −3 < 0 ⇒ Phương trình f(x) = 0 có ít nhất một nghiệm thuộc khoảng
(1; 2). (3)
Từ (1), (2), (3), suy ra phương trình có ít nhất ba nghiệm phân biệt thuộc các khoảng (−2; 0), (0; 1), (1; 2). Mà
f(x) là đa thức bậc ba nên phương trình f(x) = 0 có tối đa ba nghiệm. Suy ra phương trình đã cho có đúng ba
nghiệm phân biệt.
Nhận xét. Với sự hỗ trợ của chức năng Table trong Casio, ta dễ dàng tìm được các khoảng (−2; 0), (0; 1), (1; 2)
như trên. Công việc còn lại là trình bày sao cho đúng ngôn ngữ.
□
Bài 59. Chứng minh phương trình
1 − m
2
x
5
− 3x −1 = 0 luôn có nghiệm với mọi m.
Lời giải.
Đặt f(x) =
1 − m
2
x
5
− 3x −1 và f(x) là hàm đa thức nên liên tục trên R ⇒ f(x) liên tục trên đoạn [−1; 0].
Ta có
®
f(0) = −1
f(−1) = m
2
+ 3 > 0
⇒ f(−1) · f(0) < 0 ⇒ ∃x
0
∈ (−1; 0): f(x
0
) = 0.
Do đó phương trình f (x) =
1 − m
2
x
5
− 3x −1 = 0 luôn có nghiệm ∀m. □
Bài 60. Chứng minh rằng phương trình (x −a)(x −b) + (x −b)(x −c) + (x −c)(x −a) = 0 có ít nhất một nghiệm
với mọi số thực a, b, c.
Lời giải.
Đặt f(x) = (x −a)(x −b) + (x − b)(x −c) + (x − c)(x − a) và f(x) là hàm đa thức nên sẽ liên tục trên R.
Không mất tính tổng quát, có thể giả sử a ≤ b ≤ c.
474/764 474/764
Toán 11 theo chương trình GDPT2018
Chương 3. Giới hạn. Hàm số liên tục
Biết làm, làm đúng, làm nhanh
475
○ Nếu a = b hoặc b = c thì f (b) = (b − a)(b − c) = 0 ⇒ Phương trình có nghiệm x = b.
○ Nếu a < b < c thì
®
f(a) = (a − b)(a − c) > 0
f(b) = (b − a)(b − c) < 0
⇒ f(a) ·f(b) < 0. Do đó phương trình có ít nhất một nghiệm
trong khoảng (a; b).
Suy ra phương trình có ít nhất một nghiệm. □
3. Bài tập trắc nghiệm
Câu 70. Chứng minh rằng phương trình x
3
− x + 3 = 0 có ít nhất một nghiệm.
Một bạn học sinh trình bày lời giải như sau:
Bước 1: Xét hàm số y = f(x) = x
3
− x + 3 liên tục trên R.
Bước 2: Ta có f (0) = 3 và f(−2) = −3.
Bước 3: Suy ra f(0)f(−2) > 0
Bước 4: Vậy phương trình đã cho có ít nhất một nghiệm.
Học sinh trên giải sai tại
A Bước 1. B Bước 2. C Bước 3. D Bước 4.
Lời giải.
Ta có f(0)f(−2) < 0 do đó bài giải sai ở Bước 3.
Chọn đáp án C □
Câu 71. Biết rằng trong khoảng (−4; 0), phương trình x
3
− 12x + 1 = 0 có đúng 1 nghiệm. Nghiệm đó thuộc
khoảng
A (−4; −3). B (−3; −2). C (−2; −1). D (−1; 0).
Lời giải.
Hàm số f(x) = x
3
−12x + 1 là hàm đa thức nên liên tục trên R và f(−4)f(−3) < 0 nên nghiệm của phương trình
f(x) = 0 thuộc khoảng (−4; −3).
Chọn đáp án A □
Câu 72. Biết rằng phương trình x
5
−4x
2
+ x + 1 = 0 có nghiệm thuộc đúng 3 khoảng trong các khoảng 4 khoảng
(−1; 0), (0; 1), (1; 2) và (2; 3). Khoảng không chứa nghiệm của phương trình x
5
− 4x
2
+ x + 1 = 0 là
A (−1; 0). B (0; 1). C (1; 2). D (2; 3).
Lời giải.
Hàm số f(x) = x
5
− 4x
2
+ x + 1 là hàm đa thức nên liên tục trên R.
Do f(−1)f(0) < 0, f(0)f(1) < 0 và f(1)f(2) < 0 nên phương trình f(x) = 0 có nghiệm trong các khoảng (−1; 0),
(0; 1) và (1; 2).
Vậy phương trình x
5
− 4x
2
+ x + 1 = 0 không có nghiệm thuộc khoảng (2; 3).
Chọn đáp án D □
Câu 73. Cho hàm số f (x) =
x + 2
x
√
4 − x
. Chọn khẳng định sai trong các khẳng định dưới đây.
A Hàm số f(x) xác định trên tập hợp K = (−∞; 0) ∪(0; 4).
B Hàm số f (x) liên tục tại x = 2.
C Hàm số f(x) gián đoạn tại x = 0 và x = 4.
D Vì f(−1) = −
1
√
5
; f(2) =
√
2 nên f(−1)f(2) < 0, suy ra phương trình f(x) = 0 có ít nhất 1 nghiệm thuộc
khoảng (−1; 2).
Lời giải.
Tập xác định D = (−∞; 0) ∪(0; 4).
Suy ra hàm số f (x) liên tục trên các khoảng (−∞; 0) và (0; 4).
Từ đó tính chất liên tục trên đoạn [−1; 2] của hàm số không xảy ra.
Vậy không thể suy ra phương trình f(x) = 0 có ít nhất 1 nghiệm thuộc khoảng (−1; 2).
Chọn đáp án D □
Câu 74. Khẳng định nào sau đây đúng với phương trình 2x
3
− 3x
2
+ 2 = 0?
A Phương trình có ít nhất một nghiệm thuộc khoảng (−1; 0).
475/764 475/764
Toán 11 theo chương trình GDPT2018
3. Hàm số liên tục
Biết làm, làm đúng, làm nhanh
476
B Phương trình có ít nhất một nghiệm thuộc khoảng (1; 2).
C Phương trình có 3 nghiệm thực phân biệt.
D Phương trình có ít nhất một nghiệm thuộc khoảng (−2; −1).
Lời giải.
Đặt f(x) = 2x
3
− 3x
2
+ 2 là hàm đa thức nên hàm số f(x) liên tục trên R.
Do f(−1) · f(0) = −6 < 0 nên phương trình có ít nhất một nghiệm thuộc khoảng (−1; 0).
Chọn đáp án A □
Câu 75. Phương trình nào dưới đây có nghiệm trong khoảng (0; 1)?
A 2x
2
− 3x + 4 = 0. B (x − 1)
5
− x
7
− 2 = 0. C 3x
4
− 4x
2
+ 5 = 0. D 3x
2017
− 8x + 4 = 0.
Lời giải.
Xét hàm số f(x) = 3x
2017
− 8x + 4 = 0 liên tục trên R.
Do f (0) = 4; f(1) = −1 nên f(0) · f (1) = −4 < 0, suy ra phương trình f(x) = 0 có ít nhất một nghiệm thuộc
khoảng (0; 1).
Chọn đáp án D □
Câu 76. Xét các mệnh đề sau
(1) Phương trình x
3
+ 4x + 4 = 0 không có nghiệm trên khoảng (−1; 1).
(2) Phương trình x
3
+ x −1 = 0 không có nghiệm dương bé hơn 1.
Chọn đáp án đúng.
A Cả mệnh đề (1) và (2) đều đúng. B Mệnh đề (1) và (2) đều sai.
C Chỉ có mệnh đề (2) đúng. D Chỉ có mệnh đề (1) đúng.
Lời giải.
Đặt f(x) = x
3
+ 4x + 4, g(x) = x
3
+ x −1.
Nhận xét: f(x) và g(x) là hàm đa thức nên liên tục trên R.
Mặt khác
○ f(−1) = −1, f(1) = 9 ⇒ f(−1) · f(1) < 0 nên phương trình f (x) = 0 có nghiệm trên khoảng (−1; 1).
○ g(0) = −1, g(1) = 1 ⇒ g(0) · g(1) < 0 nên phương trình g(x) = 0 có nghiệm trên khoảng (0; 1).
Do đó phương trình g(x) = 0 có nghiệm dương bé hơn 1.
Chọn đáp án B □
Câu 77. Cho phương trình ax
2
+ bx + c = 0 thỏa mãn a = 0 và 2a + 6b + 19c = 0. Biết phương trình có nghiệm
x
0
, khẳng định nào sau đây đúng?
A x
0
∈
ï
0;
1
3
ò
. B x
0
∈
ï
−
1
3
; −
1
2
ò
. C x
0
∈
ï
2
3
; 1
ò
. D x
0
∈ [1; 2].
Lời giải.
Ta có 2a + 6b + 19c = 0 ⇔ 2a + 6b = −19c ⇔ a + 3b =
−19c
2
.
Lại có f(0)f
Å
1
3
ã
=
1
9
c(a + 3b + 9c) =
1
9
c
−1
2
c =
−1
18
c
2
≤ 0.
Vậy phương trình luôn có nghiệm x
0
∈
ï
0;
1
3
ò
.
Chọn đáp án A □
Câu 78. Tìm tất cả giá trị thực của tham số m để phương trình (m
2
−3m + 2)x
3
−3x + 1 = 0 có nghiệm.
A m ∈ R. B m ∈ {1; 2}. C m ∈ R \ {1; 2}. D m ∈ ∅.
Lời giải.
Trường hợp 1. Với m = 1 hoặc m = 2 thì phương trình có nghiệm là x =
1
3
.
Trường hợp 2. Với m
2
− 3m + 2 = 0.
Đặt f(x) = (m
2
− 3m + 2)x
3
− 3x + 1 là hàm đa thức nên liên tục trên R (1).
Khi đó lim
x→−∞
f(x) = −∞ hoặc lim
x→+∞
f(x) = −∞. Từ đó, tồn tại A < 0 và x
0
∈ R sao cho f(x
0
) = A < 0.
Mặt khác f(0) = 1 nên f(0) · f(x
0
) < 0 (2).
476/764 476/764
Toán 11 theo chương trình GDPT2018
Chương 3. Giới hạn. Hàm số liên tục
Biết làm, làm đúng, làm nhanh
477
Từ (1) và (2) suy ra phương trình f(x) = 0 luôn có nghiệm nằm giữa 0 và x
0
.
Từ hai trường hợp trên suy ra phương trình luôn có nghiệm với mọi m ∈ R.
Chọn đáp án A □
Câu 79. Cho phương trình x
12
+1 = 4x
4
.
√
x
n
− 1, (n ∈ Z
+
). Tìm số n nhỏ nhất để phương trình có nghiệm.
A n = 3. B n = 5. C n = 2. D n = 10.
Lời giải.
Với n chẵn thì ta có |x| ≥ 1, nếu x
0
là nghiệm của phương trình thì −x
0
cũng là nghiệm của phương trình.
Với n lẻ thì ta có x ≥ 1. Lại có x = 1 không là nghiệm của phương trình nên ta chỉ cần xét x > 1.
Áp dụng bất đẳng thức AM-GM ta có:
x
4
+ 1 ≥ 2x
2
x
8
− x
4
+ 1 =
x
4
− 1
2
+ x
4
≥ 2x
2
p
x
4
− 1.
Suy ra x
12
+ 1 ≥ 4x
4
√
x
4
− 1.
Dấu bằng không xảy ra nên ta có: x
12
+ 1 > 4x
4
√
x
4
− 1 ≥ 4x
4
√
x
n
− 1 với mọi n ≤ 4.
Với n = 5 ta xét hàm số f(x) = x
12
+ 1 −4x
4
√
x
5
− 1.
Ta có: f(1) = 2, f
Ä
5
√
2
ä
= 1 + 4
5
√
4 − 4
5
√
16 < 0 nên phương trình f(x) = 0 có nghiệm thuộc
Ä
1;
5
√
2
ä
.
Vậy n = 5 là giá trị cần tìm.
Chọn đáp án B □
477/764 477/764
Toán 11 theo chương trình GDPT2018
4. Bài tập cuối chương III
Biết làm, làm đúng, làm nhanh
478
BÀI TẬP CUỐI CHƯƠNG III
4
Baâi söë
A–BÀI TẬP TỰ LUẬN
Bài 1. Tính các giới hạn sau:
lim
2n
2
+ 6n + 1
8n
2
+ 5
;a) lim
4n
2
− 3n + 1
−3n
3
+ 5n
2
− 2
;b)
lim
√
4n
2
− n + 3
8n − 5
;c) lim
Å
4 −
2
n+1
3
n
ã
;d)
lim
4.5
n
+ 2
n+2
6.5
n
;e) lim
2 +
4
n
3
6
n
.f)
Lời giải.
a) lim
2n
2
+ 6n + 1
8n
2
+ 5
= lim
2 +
6
n
+
1
n
2
8 +
5
n
2
=
1
4
.
b) lim
4n
2
− 3n + 1
−3n
3
+ 5n
2
− 2
= lim
4
n
−
3
n
2
+
1
n
3
−3 +
5
n
−
2
n
3
= 0.
c) lim
√
4n
2
− n + 3
8n − 5
= lim
…
4 −
1
n
+
3
n
2
8 −
5
n
=
1
4
.
d) lim
Å
4 −
2
n+1
3
n
ã
= lim
Å
4 −
2 · 2
n
3
n
ã
= lim
Å
4 − 2
Å
2
3
ã
n
ã
= 4.
e) lim
Å
4 · 5
n
+ 2
n+2
6 · 5
n
ã
= lim
Ç
4 + 4 ·
2
5
n
6
å
=
2
3
.
f) lim
Ç
2 +
4
n
3
6
n
å
= lim
Ö
2
6
n
+
4
n
3
· 6
n
1
è
= 0.
□
Bài 2. Tính các giới hạn sau:
lim
x→−3
4x
2
− 5x + 6
;a) lim
x→2
2x
2
− 5x + 2
x − 2
;b) lim
x→4
√
x − 2
x
2
− 16
.c)
Lời giải.
a) lim
x→−3
4x
2
− 5x + 6
= 4(−3)
2
− 5(−3) + 6 = 57.
b) lim
x→2
2x
2
− 5x + 2
x − 2
= lim
x→2
(2x − 1)(x −2)
x − 2
= lim
x→2
(2x − 1) = 3.
c) lim
x→4
√
x − 2
x
2
− 16
= lim
x→4
√
x − 2
(
√
x − 2)(
√
x + 2)(x + 4)
= lim
x→4
1
(
√
x + 2)(x + 4)
=
1
32
.
□
478/764 478/764
Toán 11 theo chương trình GDPT2018
Chương 3. Giới hạn. Hàm số liên tục
Biết làm, làm đúng, làm nhanh
479
Bài 3. Tính các giới hạn sau:
lim
x→−∞
6x + 8
5x − 2
;a) lim
x→+∞
6x + 8
5x − 2
;b) lim
x→+∞
√
9x
2
− x + 1
3x − 2
;c)
lim
x→−∞
√
9x
2
− x + 1
3x − 2
;d) lim
x→−2
−
3x
2
+ 4
2x + 4
;e) lim
x→−2
+
3x
2
+ 4
2x + 4
.f)
Lời giải.
a) lim
x→−∞
6x + 8
5x − 2
=
6
5
.
b) lim
x→+∞
6x + 8
5x − 2
=
6
5
.
c) lim
x→−∞
√
9x
2
− x + 1
3x − 2
= lim
x→−∞
−x
…
9 −
1
x
+
1
x
2
x
Å
3 −
2
x
ã
= −1.
d) lim
x→+∞
√
9x
2
− x + 1
3x − 2
= lim
x→+∞
x
…
9 −
1
x
+
1
x
2
x
Å
3 −
2
x
ã
= 1.
e) Vì lim
x→2
−
3x
2
+ 4
= 16 > 0; lim
x→2
−
(x + 2) = 0 và x → −2
−
⇒ x + 2 < 0 nên
lim
x→−2
−
3x
2
+ 4
2x + 4
= −∞
f) Vì lim
x→2
+
3x
2
+ 4
= 16 > 0; lim
x→2
+
(x + 2) = 0 và x → −2
+
⇒ x + 2 > 0 nên
lim
x→−2
−
3x
2
+ 4
2x + 4
= +∞
□
Bài 4. Cho hàm số f (x) =
2x + a nếu x < 2
4 nếu x = 2
−3x + b nếu x > 2
a) Với a = 0, b = 1, xét tính liên tục của hàm số tại x = 2.
b) Với giá trị nào của a, b thì hàm số liên tục tại x = 2 ?
c) Với giá trị nào của a, b thì hàm số liên tục trên tập xác định?
Lời giải.
a) Với a = 0; b = 1, ta có:
f(x) =
2x nếu x < 2
4 nếu x = 2
−3x + 1 nếu x > 2.
Ta có
lim
x→2
−
f(x) = lim
x→2
−
(2x) = 4 và lim
x→2
+
f(x) = lim
x→2
+
(−3x + 1) = −5.
Vì lim
x→2
−
f(x) = lim
x→2
+
f(x) nên không tồn tại lim
x→2
f(x).
479/764 479/764
Toán 11 theo chương trình GDPT2018
4. Bài tập cuối chương III
Biết làm, làm đúng, làm nhanh
480
b) Ta có
lim
x→2
−
f(x) = lim
x→2
−
(2x + a) = 4 + a và lim
x→2
+
f(x) = lim
x→2
+
(−3x + b) = −6 + b.
Hàm số liên tục của hàm số tại x = 2 khi và chỉ khi tồn tại lim
x→2
f(x) và lim
x→2
f(x) = f (2)
⇔
®
4 + a = 4
−6 + b = 4
⇔
®
a = 0
b = 10.
Vậy a = 0; b = 10 thoả mãn yêu cầu bài toán.
c) Để hàm số liên tục trên tập xác định điều kiện cần và đủ là hàm số liên tục tại x = 2. Do đó với a = 0, b = 10
thì hàm số liên tục trên tập xác định.
□
Bài 5.
Từ độ cao 55, 8 m của tháp nghiêng Pisa nước Ý, người ta
thả một quả bóng cao su chạm xuống đất hình bên dưới.
Giả sử mỗi lần chạm đất quả bóng lại nảy lên độ cao bằng
1
10
độ cao mà quả bóng đạt được trước đó. Gọi S
n
là tổng
độ dài quãng đường di chuyển của quả bóng tính từ lúc thả
ban đầu cho đến khi quả bóng đó chạm đất n lần. Tính
lim S
n
.
Lời giải.
Mỗi khi chạm đất quả bóng lại nảy lên một độ cao bằng
1
10
độ cao của lần rơi ngay trước đó và sau đó lại rơi
xuống từ độ cao thứ hai này. Do đó, độ dài hành trình của quả bóng kể từ thời điểm rơi ban đầu đến:
Thời điểm chạm đất lần thứ nhất là d
1
= 55,8.
Thời điềm chạm đất lần thứ hai là d
2
= 55,8 + 2 ·
55,8
10
.
Thời điểm chạm đất lần thứ ba là d
3
= 55,8 + 2 ·
55,8
10
+ 2 ·
55,8
10
2
.
Thời điểm chạm đất lần thứ tư là d
4
= 55,8 + 2 ·
55,8
10
+ 2 ·
55, 8
10
2
+ 2 ·
55,8
10
3
.
. . .
Thời điểm chạm đất lần thứ n (n > 1) là
d
n
= 55,8 + 2 ·55,8 + 2 ·
55,8
10
2
+ 2 ·
55,8
10
3
+ . . . + 2 ·
55,8
10
n−1
.
Do đó, quãng đường mà quả bóng đi được kể từ thời điềm rơi đến khi nằm yên trên mặt đất là:
d = 55,8 + 2.55,8 + 2 ·
55,8
10
2
+ 2 ·
55,8
10
3
+ . . . + 2 ·
55,8
10
n−1
+ . . . = lim d
n
.
Vì 2 ·
55,8
10
; 2 ·
55,8
10
2
; 2 ·
55,8
10
3
; . . . ; 2 ·
55,8
10
n−1
; . . . là một cấp số nhân lùi vô hạn với công bội q =
1
10
nên ta có:
2 ·
55, 8
10
+ 2 ·
55,8
10
2
+ 2 ·
55,8
10
3
+ . . . + 2 ·
55,8
10
n−1
+ . . . =
2 ·
55,8
10
1 −
1
10
= 12,4.
Vậy d = 55,8 + 12,4 = 68,2 m. □
480/764 480/764
Toán 11 theo chương trình GDPT2018
Chương 3. Giới hạn. Hàm số liên tục
Biết làm, làm đúng, làm nhanh
481
Bài 6. Cho một tam giác đều ABC cạnh a. Tam giác A
1
B
1
C
1
có các đỉnh là trung điểm các cạnh của tam giác
ABC, tam giác A
2
B
2
C
2
có các đỉnh là trung điểm các cạnh của tam giác A
1
B
1
C
1
, . . ., tam giác A
n+1
B
n+1
C
n+1
có các đỉnh là trung điểm các cạnh của tam giác A
n
B
n
C
n
, . . . Gọi p
1
, p
2
, . . . , p
n
, . . . và S
1
, S
2
, . . . , S
n
, . . . theo thứ
tự là chu vi và diện tích của các tam giác A
1
B
1
C
1
, A
2
B
2
C
2
, . . . , A
n
B
n
C
n
, . . ..
a) Tìm giới hạn của các dãy số (p
n
) và (S
n
).
b) Tìm các tổng p
1
+ p
2
+ . . . + p
n
+ . . . và S
1
+ S
2
+ . . . + S
n
+ . . ..
Lời giải.
a) Ta có p
1
, p
2
, . . . , p
n
, . . . lần lượt là chu vi của các tam giác A
1
B
1
C
1
, A
2
B
2
C
2
, . . . , A
n
B
n
C
n
, . . .
p
1
= 3a
p
2
= 3 ·
1
2
a
. . .
p
n
= 3 ·
1
2
n−1
a
suy ra lim p
n
= lim 3 ·
1
2
n−1
a = 0.
S
1
=
a
2
√
3
4
S
2
=
1
4
a
2
√
3
4
. . .
S
n
=
1
4
n−1
·
a
2
√
3
4
suy ra lim S
n
= lim
1
4
n−1
·
a
2
√
3
4
= 0.
b) Dựa vào dữ kiện đề bài suy ra tổng (p
n
) là tổng của cấp số nhân lùi vô hạn với công bội q =
1
2
và
p
1
+ p
2
+ . . . + p
n
+ . . . = lim (p
n
) =
p
1
1 − q
=
3a
1 −
1
2
= 6a.
Dựa vào dữ kiện đề bài suy ra tổng (S
n
) là tổng của cấp số nhân lùi vô hạn với công bội q =
1
4
và
S
1
+ S
2
+ . . . + S
n
+ . . . = lim (S
n
) =
S
1
1 − q
=
a
2
√
3
4
1 −
1
4
=
a
2
√
3
12
.
□
Bài 7. Một thấu kính hội tụ có tiêu cự là f. Gọi d và d
′
lần lượt là khoảng cách từ một vật thật AB và từ ảnh
A
′
B
′
của nó tới quang tâm O của thấu kính như hình vẽ bên dưới. Công thức thấu kính là
1
d
+
1
d
=
1
f
.
A
′
f f
d
d
′
B
′
F
′
F
A
B
O
a) Tìm biểu thức xác định hàm số d
′
= φ(d).
b) Tìm lim
d→f
+
φ(d), lim
d→f
−
φ(d) và lim
d→f
φ(d). Giải thích ý nghĩa của các kết quả tìm được.
481/764 481/764
Toán 11 theo chương trình GDPT2018
4. Bài tập cuối chương III
Biết làm, làm đúng, làm nhanh
482
Lời giải.
a) Ta có
1
d
+
1
d
′
=
1
f
⇔ d
′
=
df
d − f
.
Vậy φ(d) =
df
d − f
.
b) Vì lim
d→f
+
df = f
2
; lim
d→f
+
(d − f) = 0; d → f
+
⇒ d −f > 0 nên lim
d→f
+
df
d − f
= +∞.
Vậy lim
d→f
+
φ(d) = lim
d→f
+
df
d − f
= +∞.
Ý nghĩa: Khi đặt vật nằm ngoài tiêu cự và tiến dần đến tiêu điểm thì cho ảnh thật ngược chiều với vật ở
vô cùng.
Vì lim
d→f
−
df = f
2
; lim
d→f
+
(d − f) = 0; d → f
−
⇒ d −f < 0 nên lim
d→f
+
df
d − f
= −∞.
Vậy lim
d→f
+
φ(d) = lim
d→f
+
df
d − f
= −∞.
Ý nghĩa: Khi đặt vật nằm trong tiêu cự và tiến dần đến tiêu điểm thì cho ảnh ảo cùng chiều với vật và
nằm ở vô cùng.
Vì không tồn tại lim
d→f
+
φ(d) và lim
d→f
−
φ(d) nên không tồn tại lim
d→f
φ(d).
□
B–BÀI TẬP TRẮC NGHIỆM
Câu 1. Cho hàm số y = f (x) xác định trên khoảng (a; b) và x
0
∈ (a; b). Điều kiện cần và đủ để hàm số y = f(x)
liên tục tại x
0
là
A lim
x→x
+
0
f(x) = f (x
0
). B lim
x→x
−
0
f(x) = f (x
0
).
C lim
x→x
+
0
f(x) = lim
x→x
−
0
f(x). D lim
x→x
+
0
f(x) = lim
x→x
−
0
f(x) = f (x
0
).
Lời giải.
Theo định nghĩa về hàm số liên tục ta có điều kiện cần và đủ để hàm số y = f(x) liên tục tại x
0
là lim
x→x
+
0
f(x) =
lim
x→x
−
0
f(x) = f (x
0
).
Chọn đáp án D □
Câu 2. Trong các giới hạn sau, giới hạn nào bằng 0?
A lim(n
3
− 3n + 1). B lim
n
2
+ n
n
3
+ 1
. C lim
n
2
+ n + 1
4n + 1
. D lim
2
n
− 3
n
3
n
+ 2
.
Lời giải.
Ta có lim
n
2
+ n
n
3
+ 1
= lim
1
n
+
1
n
2
1 +
1
n
3
= 0.
Chọn đáp án B □
Câu 3. Trong các khẳng định dưới đây, khẳng định nào sai?
A lim
n→+∞
q
n
= 0.
B lim
n→+∞
1
n
k
= 0 với k nguyên dương.
C lim
n→+∞
1
n
= 0.
D Nếu u
n
= c (c là hằng số) thì lim
n→+∞
u
n
= lim c = c.
Lời giải.
482/764 482/764
Toán 11 theo chương trình GDPT2018
Chương 3. Giới hạn. Hàm số liên tục
Biết làm, làm đúng, làm nhanh
483
Ta có lim
n→+∞
q
n
= 0 khi |q| < 1; lim
n→+∞
q
n
= +∞ khi q > 1.
Chọn đáp án A □
Câu 4. Tính lim
n
2
+ 1
2n
2
+ n + 1
ta được kết quả là
A lim
n
2
+ 1
2n
2
+ n + 1
= 0. B lim
n
2
+ 1
2n
2
+ n + 1
=
1
2
.
C lim
n
2
+ 1
2n
2
+ n + 1
= +∞. D lim
n
2
+ 1
2n
2
+ n + 1
= 1.
Lời giải.
Ta có lim
n
2
+ 1
2n
2
+ n + 1
= lim
1 +
1
n
2
2 +
1
n
+
1
n
2
=
1
2
.
Chọn đáp án B □
Câu 5. lim
2023
n
+ 2024
n
2025
n
có giá trị bằng
A
3
5
. B +∞. C 0. D 1.
Lời giải.
Ta có lim
2023
n
+ 2024
n
2025
n
= lim
Å
2023
2025
ã
n
+ lim
Å
2024
2025
ã
n
= 0 + 0 = 0.
Chọn đáp án C □
Câu 6. Tìm lim
Ä
√
n
2
+ 1 −2n
ä
ta được kết quả là
A −∞. B +∞. C 0. D −
2
3
.
Lời giải.
○ Cách 1: lim
Ä
√
n
2
+ 1 −2n
ä
= lim n
Ç
…
1 +
1
n
2
− 2
å
= −∞
(vì lim n = +∞ và lim
Ç
…
1 +
1
n
2
− 2
å
= −1 < 0).
○ Cách 2: lim
Ä
√
n
2
+ 1 −2n
ä
= lim
n
2
+ 1 −4n
2
√
n
2
+ 1 + 2n
= lim
−3n +
1
n
…
1 +
1
n
2
+ 2
= −∞.
Chọn đáp án A □
Câu 7. Tính tổng vô hạn S = 9 + 3 + 1 +
1
3
+ ··· +
1
3
n−3
+ ···
A S = 14. B S = 15. C S =
27
2
. D S = 16.
Lời giải.
Dãy số (u
n
) : 9; 3; 1;
1
3
; ··· ;
1
3
n−3
; ··· là một cấp số nhân lùi vô hạn với số hạng đầu u
1
= 9, công bội q =
1
3
.
Do đó tổng của dãy là S = 9 + 3 + 1 +
1
3
+ ··· +
1
3
n−3
+ ··· =
u
1
1 − q
=
9
1 −
1
3
=
27
2
.
Chọn đáp án C □
Câu 8. Trong các mệnh đề sau, mệnh đề nào là mệnh đề sai?
A lim
n→+∞
1
n
= 0. B lim
n→+∞
2n + 1
n − 3
= 2.
C lim
n→+∞
(n
2
− 2n + 1) = +∞. D lim
n→+∞
n
k
= −∞ (k ∈ N
∗
).
Lời giải.
Ta có lim
n→+∞
n
k
= +∞ (k ∈ N
∗
).
483/764 483/764
Toán 11 theo chương trình GDPT2018
4. Bài tập cuối chương III
Biết làm, làm đúng, làm nhanh
484
Chọn đáp án D □
Câu 9. Tính lim n
Ä
√
4n
2
+ 3 −
3
√
8n
3
+ n
ä
.
A
2
3
. B +∞. C −∞. D 1.
Lời giải.
Ta có
lim n
Ä
p
4n
2
+ 3 −
3
p
8n
3
+ n
ä
= lim n
îÄ
p
4n
2
+ 3 −2n
ä
+
Ä
2n −
3
p
8n
3
+ n
äó
= lim n
ñ
3
√
4n
2
+ 3 + 2n
+
−n
(2n)
2
+ 2n ·
3
√
8n
3
+ n +
3
√
8n
3
+ n
2
ô
= lim
3
…
4 +
3
n
2
+ 2
+
−1
2
2
+ 2
3
…
8 +
1
n
2
+
3
…
8 +
1
n
2
2
=
2
3
.
Chọn đáp án A □
Câu 10. Dãy số (u
n
) với u
n
=
√
2n
3
+ n + 3n − 1
√
6n
3
+ 2n
2
+ n
có giới hạn bằng
…
a
b
, a > 0, b > 0 và ƯCLN(a, b = 1). Hãy
tính giá trị của a
2
+ b
2
.
A 5. B 40. C 9. D 10.
Lời giải.
Ta có
lim u
n
= lim
√
2n
3
+ n + 3n − 1
√
6n
3
+ 2n
2
+ n
= lim
…
2 +
1
n
2
+
3
√
n
−
1
n
√
n
…
6 +
2
n
+
1
√
n
=
…
1
3
.
Suy ra a = 1, b = 3 ⇒ a
2
+ b
2
= 10.
Chọn đáp án D □
Câu 11. Tìm tất cả các giá trị thực của tham số b để biểu thức A = lim
9 − b
2
n
2
11n
2
+ 3
< 0.
A b ≤ 0. B b = 0. C b < 0. D b > 0.
Lời giải.
Ta có A = lim
9 − b
2
n
2
11n
2
+ 3
= lim
n
2
Å
9
n
2
− b
2
ã
n
2
Å
11 +
3
n
2
ã
= lim
9
n
2
− b
2
11 +
3
n
2
= −
b
2
11
.
Yêu cầu bài toán xảy ra khi −
b
2
11
< 0 ⇔ b
2
> 0 ⇔ b = 0.
Chọn đáp án B □
Câu 12. Cho các giới hạn: lim
x→x
0
f(x) = 2, lim
x→x
0
g(x) = 3. Tính M = lim
x→x
0
[3f(x) − 4g(x)].
A M = 5. B M = 2. C M = −6. D M = 3.
Lời giải.
Ta có M = lim
x→x
0
[3f(x) − 4g(x)] = 3 lim
x→x
0
f(x) − 4 lim
x→x
0
g(x) = 6 −12 = −6.
Chọn đáp án C □
Câu 13. Giá trị của lim
x→−2
x
3
− x
2
+ 1
bằng
A −11. B 12. C 5. D 0.
484/764 484/764
Toán 11 theo chương trình GDPT2018
Chương 3. Giới hạn. Hàm số liên tục
Biết làm, làm đúng, làm nhanh
485
Lời giải.
Ta có lim
x→−2
x
3
− x
2
+ 1
= lim
x→−2
(−2)
3
− (−2)
2
+ 1
= −11.
Chọn đáp án A □
Câu 14. Giá trị của lim
x→−∞
Ä
√
x
2
+ 5 −x
ä
là
A +∞. B −∞. C 1. D 0.
Lời giải.
Ta có
lim
x→−∞
Ä
p
x
2
+ 5 −x
ä
= lim
x→−∞
x
Ç
−
…
1 +
5
x
2
− 1
å
= +∞.
Chọn đáp án A □
Câu 15. Giá trị của lim
x→−∞
2x
2
− x + 1
x + 2
là
A −∞. B +∞. C −2. D 1.
Lời giải.
Ta có lim
x→−∞
2x
2
− x + 1
x + 2
= lim
x→−∞
x
2
Å
2 −
1
x
+
1
x
2
ã
x
Å
1 +
2
x
ã
= lim
x→−∞
x ·
Å
2 −
1
x
+
1
x
2
ã
1 +
2
x
= −∞.
Chọn đáp án A □
Câu 16. Giả sử lim
x→x
0
f(x) = +∞ và lim
x→x
0
g(x) = −∞. Ta xét các mệnh đề sau
lim
x→x
0
[f(x) + g(x)] = 0.(1) lim
x→x
0
f(x)
g(x)
= −1.(2) lim
x→x
0
|f(x)| = lim
x→x
0
|g(x)| = +∞.(3)
Trong các mệnh đề trên có tất cả bao nhiêu mệnh đề đúng?
A Có một mệnh đề đúng. B Có hai mệnh đề đúng.
C Có ba mệnh đề đúng. D Không có mệnh đề nào đúng.
Lời giải.
○ Mệnh đề (1), (2) sai nếu ta chọn lim
x→x
0
f(x) = lim
x→1
3
(x − 1)
2
và lim
x→x
0
g(x) = lim
x→1
−2
(x − 1)
2
. Khi đó
lim
x→1
[f(x) + g(x)] = +∞ và lim
x→x
0
f(x)
g(x)
=
−3
2
.
○ Mệnh đề (3) sai vì lim
x→x
0
|f(x)| = +∞ và lim
x→x
0
|g(x)| = +∞ nhưng lim
x→x
0
|f(x)| = lim
x→x
0
|g(x)|.
Chọn đáp án D □
Câu 17. Cho a là số thực khác 0. Tính lim
x→a
x
4
− a
4
x − a
.
A a
3
. B 4a
3
. C 2a
3
. D 3a
3
.
Lời giải.
Ta có lim
x→a
x
4
− a
4
x − a
= lim
x→a
(x − a)(x + a)
x
2
+ a
2
x − a
= lim
x→a

x
2
+ a
2
(x + a)
= 2a
2
· 2a = 4a
3
.
Chọn đáp án B □
Câu 18. Cho 2a + b = 2 và lim
x→2
ax
2
+ bx −4
x − 2
= 5. Khẳng định nào sau đây là đúng?
A a = −1, b = 4. B a = 1, b = 0. C a =
3
2
, b = −1. D a = −2, b = 6.
Lời giải.
485/764 485/764
Toán 11 theo chương trình GDPT2018
4. Bài tập cuối chương III
Biết làm, làm đúng, làm nhanh
486
Ta có 2a + b = 2 ⇔ b = 2 − 2a.
Khi đó ta có
lim
x→2
ax
2
+ bx −4
x − 2
= 5 ⇔ lim
x→2
ax
2
+ (2 −2a)x − 4
x − 2
= 5 ⇔ lim
x→2
(ax + 2)(x −2)
x − 2
= 5
⇔ lim
x→2
(ax + 2) = 5 ⇔ 2a + 2 = 5 ⇔ a =
3
2
⇒ b = −1.
Chọn đáp án C □
Câu 19. Tính lim
x→2
3
√
3x + 2 + x − 4
x
2
− 3x + 2
ta được kết quả là
A
1
2
. B
1
3
. C
5
4
. D
1
5
.
Lời giải.
lim
x→2
3
√
3x + 2 + x − 4
x
2
− 3x + 2
= lim
x→2
3x + 2 + (x − 4)
3
(x
2
− 3x + 2)
î
3
p
(3x + 2)
2
− (x −4)
3
√
3x + 2 + (x − 4)
2
ó
= lim
x→2
x
3
− 12x
2
+ 51x −62
(x
2
− 3x + 2)
î
3
p
(3x + 2)
2
− (x −4)
3
√
3x + 2 + (x − 4)
2
ó
= lim
x→2
(x − 2)(x
2
− 10x + 31)
(x − 2)(x −1)
î
3
p
(3x + 2)
2
− (x −4)
3
√
3x + 2 + (x − 4)
2
ó
= lim
x→2
x
2
− 10x + 31
(x − 1)
î
3
p
(3x + 2)
2
− (x −4)
3
√
3x + 2 + (x − 4)
2
ó
=
5
4
.
Chọn đáp án C □
Câu 20. Tính lim
x→0
√
1 + x
2
− 1
2x
3
− 3x
2
ta được kết quả là
A −
1
2
. B −
1
4
. C −
1
6
. D −
1
8
.
Lời giải.
lim
x→0
√
1 + x
2
− 1
2x
3
− 3x
2
= lim
x→0
x
2
(2x
3
− 3x
2
)
Ä
√
1 + x
2
+ 1
ä
= lim
x→0
1
(2x − 3)
Ä
√
1 + x
2
+ 1
ä
= −
1
6
.
Chọn đáp án C □
Câu 21. Kết quả của lim
x→0
√
x + 9 +
√
x + 16 −7
x
là
A
7
23
. B
7
24
. C
7
25
. D
7
26
.
Lời giải.
lim
x→0
√
x + 9 +
√
x + 16 −7
x
= lim
x→0
√
x + 9 −3
+
√
x + 16 −4
x
= lim
x→0
ñ
√
x + 9 −3
x
+
√
x + 16 −4
x
ô
= lim
x→0
ñ
x
x
√
x + 9 + 3
+
x
x
√
x + 16 + 4
ô
= lim
x→0
ï
1
√
x + 9 + 3
+
1
√
x + 16 + 4
ò
=
1
6
+
1
8
=
7
24
.
Chọn đáp án B □
486/764 486/764
Toán 11 theo chương trình GDPT2018
Chương 3. Giới hạn. Hàm số liên tục
Biết làm, làm đúng, làm nhanh
487
Câu 22. Giới hạn lim
x→−∞
Ä
√
x
2
− 4x −
√
x
2
− x
ä
bằng
A −
3
2
. B
1
2
. C
3
2
. D −
1
2
.
Lời giải.
Ta có
lim
x→−∞
Ä
p
x
2
− 4x −
p
x
2
− x
ä
= lim
x→−∞
−3x
√
x
2
− 4x +
√
x
2
− x
= lim
x→−∞
3x
x
Ç
…
1 −
4
x
+
…
1 −
1
x
å
=
3
2
.
Chọn đáp án C □
Câu 23. Giới hạn lim
x→+∞
2x − 3a
3x + 2a
(với a là tham số) có giá trị bằng
A 2. B −1. C
3
2
. D
2
3
.
Lời giải.
Ta có lim
x→+∞
2x − 3a
3x + 2a
= lim
x→+∞
2 −
3a
x
3 +
2a
x
=
2
3
.
Chọn đáp án D □
Câu 24. Tìm giới hạn I = lim
x→+∞
Ä
x + 1 −
√
x
2
− x −2
ä
.
A I =
3
2
. B I =
1
2
. C I =
17
11
. D I =
46
31
.
Lời giải.
I = lim
x→+∞
Ä
x + 1 −
p
x
2
− x −2
ä
= lim
x→+∞
Ä
x + 1 −
√
x
2
− x −2
äÄ
x + 1 +
√
x
2
− x −2
ä
x + 1 +
√
x
2
− x −2
= lim
x→+∞
(x + 1)
2
−
x
2
− x −2
x + 1 +
√
x
2
− x −2
= lim
x→+∞
3x + 3
x + 1 +
√
x
2
− x −2
= lim
x→+∞
x
Å
3 +
3
x
ã
x
Ç
1 +
1
x
+
…
1 −
1
x
−
2
x
2
å
= lim
x→+∞
3 +
3
x
1 +
1
x
+
…
1 −
1
x
−
2
x
2
=
3
2
.
Chọn đáp án A □
Câu 25. Giá trị của giới hạn lim
x→+∞
Ä
√
x
2
+ x + 1 −
√
x
2
− x + 1
ä
là
A 0. B 1. C 2. D 3.
Lời giải.
Ta có
lim
x→+∞
Ä
p
x
2
+ x + 1 −
p
x
2
− x + 1
ä
= lim
x→+∞
2x
√
x
2
+ x + 1 +
√
x
2
− x + 1
= lim
x→+∞
2
…
1 +
1
x
+
1
x
2
+
…
1 −
1
x
+
1
x
2
= 1.
Chọn đáp án B □
487/764 487/764
Toán 11 theo chương trình GDPT2018
4. Bài tập cuối chương III
Biết làm, làm đúng, làm nhanh
488
Câu 26. Cho lim
x→1
√
x + 3 −2
x
2
− 1
=
a
b
, trong đó
a
b
là phân số tối giản. Tổng a + b có giá trị bằng
A 9. B 8. C 7. D 6.
Lời giải.
Ta có
lim
x→1
√
x + 3 −2
x
2
− 1
= lim
x→1
√
x + 3 −2
√
x + 3 + 2
(x
2
− 1)
√
x + 3 + 2
= lim
x→1
x + 3 −4
(x − 1)(x + 1)
√
x + 3 + 2
= lim
x→1
x − 1
(x − 1)(x + 1)
√
x + 3 + 2
= lim
x→1
1
(x + 1)
√
x + 3 + 2
=
1
(1 + 1)
√
1 + 3 + 2
=
1
8
.
Từ đó suy ra a + b = 1 + 8 = 9.
Chọn đáp án A □
Câu 27. Tính I = lim
x→1
+
3x + 2
1 − x
ta được kết quả là
A I = +∞. B I = −∞. C I = 0. D I = −3.
Lời giải.
Ta có lim
x→1
+
(3x + 2) = 5, lim
x→1
+
(1 − x) = 0 và 1 − x < 0 khi x > 1.
Nên lim
x→1
+
3x + 2
1 − x
= −∞.
Chọn đáp án B □
Câu 28. Tính lim
x→3
+
−x
2
+ 5
x − 3
ta được kết quả là
A −∞. B +∞. C 1. D Không tồn tại.
Lời giải.
Ta có lim
x→3
+
(−x
2
+ 5) = −4 < 0, lim
x→3
+
(x − 3) = 0 và x − 3 > 0, ∀x > 3.
Do đó lim
x→3
+
−x
2
+ 5
x − 3
= −∞.
Chọn đáp án A □
Câu 29. Tính lim
x→(−2)
+
x
2
− 4
x + 2
ta được kết quả là
A 1. B 4. C 2. D 3D.
Lời giải.
Ta có lim
x→−2
+
|x
2
− 4|
x + 2
= lim
x→−2
+
4 − x
2
x + 2
= lim
x→−2
+
(2 − x) = 4.
Chọn đáp án B □
Câu 30. Tính lim
x→1
2x + 1
x − 1
ta được kết quả là
A 0. B +∞. C −∞. D Không tồn tại.
Lời giải.
Ta có lim
x→1
−
(2x + 1) = 3 > 0; lim
x→1
−
(x − 1) = 0 và x − 1 < 0, ∀x < 1 nên lim
x→1
−
2x + 1
x − 1
= −∞.
Tương tự, ta cũng có lim
x→1
+
(2x + 1) = 3 > 0; lim
x→1
+
(x − 1) = 0 và x − 1 > 0, ∀x > 1 nên lim
x→1
+
2x + 1
x − 1
= +∞.
Vì lim
x→1
−
2x + 1
x − 1
= lim
x→1
+
2x + 1
x − 1
nên không tồn tại lim
x→1
2x + 1
x − 1
.
Chọn đáp án D □
488/764 488/764
Toán 11 theo chương trình GDPT2018
Chương 3. Giới hạn. Hàm số liên tục
Biết làm, làm đúng, làm nhanh
489
Câu 31. Giá trị của lim
x→a
x
2
− (a + 1) x + a
x
3
− a
3
(a = 0) là
A +∞. B
a + 1
3a
2
. C
a − 1
3a
. D
a − 1
3a
2
.
Lời giải.
Ta có
lim
x→a
x
2
− (a + 1)x + a
x
3
− a
3
= lim
x→a
(x − a)(x −1)
(x − a)(x
2
+ ax + a
2
)
=
a − 1
3a
2
.
Chọn đáp án D □
Câu 32. Cho hàm số y = f(x) liên tục trên khoảng (a; b). Hàm số y = f(x) liên tục trên đoạn [a; b] nếu điều kiện
nào sau đây xảy ra?
A lim
x→a
−
f (x) = f (a) , lim
x→b
+
f (x) = f (b). B lim
x→a
+
f (x) = f (a) , lim
x→b
−
f (x) = f (b).
C lim
x→a
−
f (x) = a, lim
x→b
+
f (x) = b. D lim
x→a
+
f (x) = a, lim
x→b
−
f (x) = b.
Lời giải.
Hàm số y = f(x) được gọi là liên tục trên đoạn [a; b] nếu nó liên tục trên khoảng (a; b) và lim
x→a
+
f (x) =
f (a) , lim
x→b
−
f (x) = f (b).
Chọn đáp án B □
Câu 33. Trong các hàm số sau, hàm số nào liên tục tại điểm x = 0?
A y =
x
2
− 2x + 3
x
. B y = x
3
− 2x
2
− x + 1. C y = cot x. D y =
√
2x
2
− 1.
Lời giải.
○ Hàm số y =
x
2
− 2x + 3
x
có tập xác định là D = R \{0} nên bị gián đoạn tại điểm x = 0.
○ Hàm số y = x
3
− 2x
2
− x + 1 là hàm đa thức, liên tục trên R nên nó liên tục tại điểm x = 0.
○ Hàm số y = cot x có tập xác định là D = R \{kπ, k ∈ Z} nên bị gián đoạn tại điểm x = 0.
○ Hàm số y =
√
2x
2
− 1 có tập xác định là D =
Ç
−∞; −
√
2
2
ô
∪
ñ
√
2
2
; +∞
å
nên bị gián đoạn tại điểm x = 0.
Chọn đáp án B □
Câu 34. Chọn khẳng định đúng trong các khẳng định sau
A Nếu hàm số f (x) liên tục trên [a; b] và f(a)f(b) < 0 thì phương trình f (x) = 0 có ít nhất một nghiệm trên
(a; b).
B Nếu phương trình f(x) = 0 có nghiệm trong khoảng (a; b) thì hàm số f(x) liên tục trên [a; b] và f(a)f(b) < 0.
C Nếu hàm số f(x) liên tục trên [a; b] và f(a)f(b) < 0 thì phương trình f(x) = 0 có đúng một nghiệm trên
(a; b).
D Nếu hàm số f (x) liên tục trên [a; b] và f(a)f(b) < 0 thì phương trình f(x) = 0 có một nghiệm trên [a; b].
Lời giải.
Định lí về sự tồn tại nghiệm của phương trình trên một khoảng.
Chọn đáp án A □
Câu 35.
Cho hàm số y = f(x) có đồ thị dưới đây, trên khoảng (−2; 3) hàm số gián đoạn tại điểm
nào?
A x = 0. B x = 1. C x = 2. D x = 3.
x
y
2
1
1
3
O
−1
Lời giải.
489/764 489/764
Toán 11 theo chương trình GDPT2018
4. Bài tập cuối chương III
Biết làm, làm đúng, làm nhanh
490
Dựa vào đồ thị hàm số ta thấy lim
x→1
−
f(x) = 3 và lim
x→1
+
f(x) = 0, suy ra lim
x→1
−
f(x) = lim
x→1
+
f(x). Do đó hàm số
gián đoạn tại x = 1.
Chọn đáp án B □
Câu 36. Cho hàm số f (x) =
x
2
− 3x + 2
x − 1
, khi x > 1
2x + 1 , khi x ≤ 1
. Chọn khẳng định đúng.
A Hàm số f(x) liên tục tại điểm x = 1.
B Hàm số f (x) gián đoạn tại điểm x = 1 vì lim
x→1
f(x) = f (1).
C Hàm số f(x) gián đoạn tại điểm x = 1 vì không tồn tại lim
x→1
f(x).
D Hàm số f(x) không xác định tại x = 1.
Lời giải.
Ta có
○ lim
x→1
+
f(x) = lim
x→1
+
x
2
− 3x + 2
x − 1
= lim
x→1
+
(x − 1)(x −2)
x − 1
= lim
x→1
+
(x − 2) = −1.
○ lim
x→1
−
f(x) = lim
x→1
−
(2x + 1) = 3.
Vì lim
x→1
+
f(x) = lim
x→1
−
f(x) nên không tồn tại lim
x→1
f(x).
Do đó hàm số gián đoạn tại điểm x = 1 vì không tồn tại lim
x→1
f(x).
Chọn đáp án C □
Câu 37. Hàm số nào sau đây liên tục trên R?
A y = cos
3
x
. B y = cot 3x. C y =
1 − x
x
2
+ 4
. D y =
√
x + 2.
Lời giải.
○ Hàm số y = cos
3
x
có tập xác định là D = R \{0} nên không liên tục trên R.
○ Hàm số y = cot 3x có tập xác định là D = R \
n
k
π
3
, k ∈ Z
o
nên không liên tục trên R.
○ Hàm số y =
1 − x
x
2
+ 4
là hàm sơ cấp nên có tập xác định R nên liên tục trên R.
○ Hàm số y =
√
x + 2 có tập xác định là D = [−2; +∞) nên không liên tục trên R.
Chọn đáp án C □
Câu 38. Cho hàm số f (x) =
x
2
+ 3
x
2
− 5x + 6
. Hàm số f(x) liên tục trên khoảng nào dưới đây?
A (2; 3). B (−3; 3). C (−3; +∞). D (−∞; 3).
Lời giải.
Hàm số xác định trên tập D = (−∞; 2) ∪(2; 3) ∪ (3; +∞), suy ra hàm số liên tục trên khoảng (2; 3).
Chọn đáp án A □
Câu 39. Cho hàm số y =
x + 4
x − 3
. Mệnh đề nào sau đây là đúng?
A Hàm số liên tục tại x = 3. B Hàm số liên tục trên (−∞; +∞).
C Hàm số liên tục tại x = 2 và x = 3. D Hàm số liên tục trên (−∞; 3) và (3; +∞).
Lời giải.
Với x
0
= 3, ta có lim
x→x
0
f(x) = f (x
0
) suy ra hàm số liên tục (−∞; 3) và (3; +∞).
Chọn đáp án D □
490/764 490/764
Toán 11 theo chương trình GDPT2018
Chương 3. Giới hạn. Hàm số liên tục
Biết làm, làm đúng, làm nhanh
491
Câu 40. Cho hàm số y = f(x) =
x
3
− x
2
x − 1
khi x > 1
n khi x = 1
mx + 1 khi x < 1
. Biết hàm số f(x) liên tục tại x
0
= 1. Giá trị của m, n
là
A n = 1, m = 0. B n = 0, m = 1. C n = m = 1. D n = −1, m = 0.
Lời giải.
Ta có
○ lim
x→1
+
f(x) = lim
x→1
+
x
3
− x
2
x − 1
= lim
x→1
+
x
2
= 1.
○ lim
x→1
−
f(x) = lim
x→1
−
(mx + 1) = m + 1.
○ f(1) = n.
Do hàm số f(x) liên tục tại x = 1 nên ta có
lim
x→1
−
f(x) = lim
x→1
+
f(x) = f (1) ⇔ m + 1 = 1 = n.
Suy ra n = 1, m = 0.
Chọn đáp án A □
Câu 41. Cho hàm số f (x) =
®
x
3
+ x
2
+ 7 khi x = −1
2x + m −1 khi x = −1
. Tìm m để hàm số liên tục tại điểm x
0
= −1.
A m = 12. B m = 8. C m = −10. D m = 10.
Lời giải.
Ta có lim
x→−1
(x
3
+ x
2
+ 7) = 7 và f(−1) = m − 3.
Để hàm số liên tục tại điểm x
0
= −1 thì m − 3 = 7 ⇔ m = 10.
Chọn đáp án D □
Câu 42. Tìm tất cả các giá trị thực của m để phương trình m(x −1)
3
(x − 2) + 2x − 3 = 0 vô nghiệm.
A ∀m ∈ R. B m = 1. C Không có giá trị m. D m = 0.
Lời giải.
Đặt f(x) = m(x − 1)
3
(x − 2) + 2x − 3 xác định và liên tục trên R.
Ta có f(1) = −1, f(2) = 1 ⇒ f(1) · f(2) < 0, ∀m ∈ R suy ra phương trình luôn có nghiệm ∀m ∈ R.
Chọn đáp án C □
Câu 43. Phương trình nào dưới đây có nghiệm trong khoảng (0; 1)?
A 2x
2
− 3x + 4 = 0. B (x − 1)
5
− x
7
− 2 = 0. C 3x
4
− 4x
2
+ 5 = 0. D 3x
2024
− 8x + 4 = 0.
Lời giải.
Xét hàm số f(x) = 3x
2024
− 8x + 4 = 0 liên tục trên R.
Ta có f(0) = 4; f(1) = −1 ⇒ f(0) · f(1) = −4 < 0 suy ra phương trình có ít nhất một nghiệm thuộc khoảng
(0; 1).
Chọn đáp án D □
Câu 44. Hàm số nào sau đây gián đoạn tại x = −
√
2 ?
A y = cos x. B y =
3x + 2
√
2
x
2
− 2
. C y = x +
√
2. D y = tan x.
Lời giải.
Ta có lim
x→
(
−
√
2
)
−
3x + 2
√
2
x
2
− 2
= −∞ và lim
x→
(
−
√
2
)
+
3x + 2
√
2
x
2
− 2
= +∞ nên hàm số y =
3x + 2
√
2
x
2
− 2
gián đoạn tại x = −
√
2.
Chọn đáp án B □
Câu 45. Tìm m để hàm số f(x) =
√
x
2
+ 1 −1
x
khi x = 0
2m + 2 khi x = 0
liên tục tại x = 0.
491/764
491/764
Toán 11 theo chương trình GDPT2018
4. Bài tập cuối chương III
Biết làm, làm đúng, làm nhanh
492
A m = 2. B m = 1. C m = −1. D m = −2.
Lời giải.
Ta có lim
x→0
f(x) = lim
x→0
√
x
2
+ 1 −1
x
= lim
x→0
x
√
x
2
+ 1 + 1
= 0, f(0) = 2m + 2.
Hàm số liên tục tại x = 0 ⇔ lim
x→0
f(x) = f (0) ⇔ 2m + 2 = 0 ⇔ m = −1.
Chọn đáp án C
□
Câu 46. Hàm số nào sau đây không liên tục trên R?
A f (x) =
x + 1
x
2
+ 1
. B f(x) =
x + 1
x − 1
.
C f (x) = sin
x −
π
5
. D f(x) = x
3
− 2x
2
+ x −7.
Lời giải.
○ Hàm số f (x) =
x + 1
x
2
+ 1
là hàm sơ cấp nên có tập xác định R nên liên tục trên R.
○ Hàm số f (x) =
x + 1
x − 1
có tập xác định R \ {1} nên hàm số không liên tục trên R.
○ Hàm số sin
x −
π
5
là hàm sơ cấp nên có tập xác định R nên liên tục trên R.
○ Hàm số f (x) = x
3
− 2x
2
+ x −7 là hàm đa thức nên liên tục trên R.
Chọn đáp án B □
Câu 47. Cho hàm số f(x) chưa xác định tại x = 0, f (x) =
x
3
+ 2x
2
x
2
. Để hàm số f(x) liên tục tại x = 0 thì phải
gán cho f(0) giá trị bằng bao nhiêu?
A 3. B 2. C 1. D 0.
Lời giải.
Ta có lim
x→0
f(x) = lim
x→0
x
3
+ 2x
2
x
2
= lim
x→0
(x + 2) = 2.
Do đó, để hàm số f(x) liên tục tại x = 0 thì phải gán cho f(0) = 2.
Chọn đáp án B □
Câu 48. Cho hàm số f (x) =
3 − x
√
x + 1 −2
nếu x = 3
m nếu x = 3
. Hàm số đã cho liên tục tại x = 3 khi m bằng
A 1. B 4. C −1. D −4.
Lời giải.
Ta có lim
x→3
3 − x
√
x + 1 −2
= lim
x→3
(3 − x)(
√
x + 1 + 2)
x − 3
= lim
x→3
(−
√
x + 1 −2) = −4.
Hàm số liên tục tại x = 3 khi và chỉ khi lim
x→3
3 − x
√
x + 1 −2
= f(3) ⇔ −4 = m ⇔ m = −4.
Chọn đáp án D □
Câu 49. Cho hàm số f(x) =
x
2
− 16
x − 4
khi x = 4
ax − 1 khi x = 4
. Tập hợp các giá trị của a để hàm số liên tục tại x = 4 là
A
ß
9
4
™
. B
ß
−
9
4
™
. C {8}. D {0}.
Lời giải.
Ta có:
○ f(4) = a · 4 −1 = 4a − 1.
○ lim
x→4
f(x) = lim
x→4
x
2
− 16
x − 4
= lim
x→4
(x − 4)(x + 4)
x − 4
= lim
x→4
(x + 4) = 8.
492/764 492/764
Toán 11 theo chương trình GDPT2018
Chương 3. Giới hạn. Hàm số liên tục
Biết làm, làm đúng, làm nhanh
493
Do đó, điều kiện cần và đủ để hàm số đã cho liên tục tại x = 4 là
lim
x→4
f(x) = f (4) ⇔ 8 = 4a − 1 ⇔ a =
9
4
.
Chọn đáp án A □
Câu 50. Tìm m để hàm số f(x) =
3
√
x − 2 + 2x − 1
x − 1
khi x = 1
3m − 2 khi x = 1
liên tục trên R.
A m = 1. B m =
4
3
. C m = 2. D m = 0.
Lời giải.
Với x = 1, ta có f(x) =
3
√
x − 2 + 2x − 1
x − 1
nên hàm số liên tục trên các khoảng (−∞; 1) và (1; +∞).
Do đó, để hàm số liên tục trên R thì hàm số liên tục tại x = 1.
Ta có f(1) = 3m − 2.
Ta có
lim
x→1
f(x) = lim
x→1
3
√
x − 2 + 2x − 1
x − 1
= lim
x→1
1 +
x
3
+ x −2
(x − 1)
Ä
x
2
− x
3
√
x − 2 +
3
p
(x − 2)
2
ä
= lim
x→1
ñ
1 +
x
2
+ x + 2
x
2
− x
3
√
x − 2 +
3
p
(x − 2)
2
ô
= 2.
Nên hàm số liên tục tại x = 1 khi và chỉ khi lim
x→1
f(x) = f (1) ⇔ 3m − 2 = 2 ⇔ m =
4
3
.
Vậy m =
4
3
.
Chọn đáp án B □
Câu 51. Có bao nhiêu giá trị thực của tham số m để hàm số f (x) =
®
m
2
x
2
khi x ≤ 2
(1 − m)x khi x > 2
liên tục trên R?
A 0. B 2. C 3. D 4.
Lời giải.
Ta có hàm số luôn liên tục ∀x = 2 .
Tại x = 2 , ta có
○ lim
x→2
+
f (x) = lim
x→2
−
(1 − m) x = (1 − m) ·2 = 2 − 2m;
○ lim
x→2
−
f (x) = lim
x→2
−
m
2
x
2
= 4m
2
;
○ f (2) = 4m
2
.
Hàm số liên tục tại x = 2 khi và chỉ khi
lim
x→2
+
f (x) = lim
x→2
−
f (x) = f (2) ⇔ 4m
2
= 2 − 2m ⇔ 4m
2
+ 2m −2 = 0 ⇔
m =
1
2
m = −1.
Vậy có hai giá trị của m.
Chọn đáp án B □
493/764 493/764
Toán 11 theo chương trình GDPT2018
4. Bài tập cuối chương III
Biết làm, làm đúng, làm nhanh
494
C–ĐỀ ÔN TẬP
1. Phần Trắc nghiệm (7 điểm)
Câu 1. Khẳng định nào sau đây sai?
A lim
Ä
−
√
3
ä
2n
= −∞. B lim
Ä
√
2
ä
n
= +∞. C lim
Å
2
3
ã
n
= 0. D lim
Å
−
1
2
ã
n
= 0.
Lời giải.
Vì
2
3
< 1 nên lim
Å
2
3
ã
n
= 0.
Chọn đáp án C □
Câu 2. Cho q là số thực thỏa q > 1, kết quả của lim q
n
bằng
A 0. B −∞. C +∞. D q.
Lời giải.
Theo tính chất giới hạn ta có q là số thực thỏa q > 1 thì lim q
n
= +∞.
Chọn đáp án C □
Câu 3. Dãy nào sau đây có giới hạn bằng 0?
A u
n
=
Å
1
2
ã
n
. B u
n
=
Å
3
2
ã
n
. C u
n
= 2
n
. D u
n
= 2023
n
.
Lời giải.
Vì 0 <
1
2
< 1 nên lim
Å
1
2
ã
n
= 0.
Chọn đáp án A □
Câu 4. Tính giới hạn lim
1 + n −3n
2
n
2
+ 2n
.
A 1. B −
3
2
. C
1
2
. D −3.
Lời giải.
lim
1 + n −3n
2
n
2
+ 2n
= lim
1
n
2
+
1
n
− 3
1 +
2
n
= −3.
Chọn đáp án D □
Câu 5. Giới hạn lim
−3n + 2
n + 3
bằng
A 3. B 0. C −3. D
2
3
.
Lời giải.
lim
−3n + 2
n + 3
= lim
−3 +
2
n
1 +
3
n
= −3.
Chọn đáp án C □
Câu 6. Giá trị của lim
n + 1
n
2
+ 2
bằng bao nhiêu?
A 1. B
1
2
. C 0. D 2.
Lời giải.
Ta có lim
n + 1
n
2
+ 2
= lim
n
2
Å
1
n
+
1
n
2
ã
n
2
Å
1 +
2
n
2
ã
= lim
1
n
+
1
n
2
1 +
2
n
2
= 0.
Chọn đáp án C □
Câu 7. Tính giới hạn lim
x→2
2x + 1
x − 1
.
A −1. B 2. C 0. D 5.
494/764 494/764
Toán 11 theo chương trình GDPT2018
Chương 3. Giới hạn. Hàm số liên tục
Biết làm, làm đúng, làm nhanh
495
Lời giải.
lim
x→2
2x + 1
x − 1
=
2 · 2 + 1
2 − 1
= 5.
Chọn đáp án D □
Câu 8. Tính giới hạn I = lim
x→1
(x
2
+ x + 1).
A I = 3. B I = 1. C I = +∞. D I = 2.
Lời giải.
Ta có I = lim
x→1
(x
2
+ x + 1) = 1
2
+ 1 + 1 = 3.
Chọn đáp án A □
Câu 9. Tính giá trị của lim
x→2
(x − 2).
A 1. B −2. C 4. D 0.
Lời giải.
Ta có lim
x→2
(x − 2) = 2 −2 = 0.
Chọn đáp án D □
Câu 10. Tính giới hạn L = lim
x→3
x − 3
x + 3
.
A L = 1. B L = −∞. C L = 0. D L = +∞.
Lời giải.
Ta có lim
x→3
x − 3
x + 3
=
0
6
= 0.
Chọn đáp án C □
Câu 11. Tính giới hạn lim
x→1
3x − 1
x
2
− 2x + 2
.
A −
1
2
. B 2. C −2. D
1
2
.
Lời giải.
lim
x→1
3x − 1
x
2
− 2x + 2
=
3 − 1
1
2
− 2 + 2
= 2.
Chọn đáp án B □
Câu 12. Tính giới hạn lim
x→3
+
x + 1
2x − 6
.
A
1
2
. B
1
6
. C −∞. D +∞.
Lời giải.
Ta thấy khi x → 3
+
thì (x + 1) → 4 còn (2x −6) → 0
+
.
Từ đó suy ra lim
x→3
+
x + 1
2x − 6
= +∞.
Chọn đáp án D □
Câu 13. Giới hạn lim
x→2
+
f(x) = lim
x→2
−
5 − x
x − 2
có kết quả bằng
A −∞. B
1
2
. C +∞. D −1.
Lời giải.
lim
x→2
−
(x − 2) = 0, x − 2 < 0 với mọi x < 2 và lim
x→2
+
(5 − x) = 3 > 0.
Do đó, lim
x→2
+
5 − x
x − 2
= −∞.
Chọn đáp án A □
Câu 14. Tính giới hạn lim
x→−∞
x
4
+ 2x
2
+ 1
.
A 0. B +∞. C −∞. D 1.
Lời giải.
495/764 495/764
Toán 11 theo chương trình GDPT2018
4. Bài tập cuối chương III
Biết làm, làm đúng, làm nhanh
496
lim
x→−∞
x
4
+ 2x
2
+ 1
= lim
x→−∞
x
4
Å
1 +
2
x
2
+
1
x
4
ã
= +∞.
Chọn đáp án B □
Câu 15. Tính giới hạn H = lim
x→+∞
x
3
.
A H = 0. B H = −∞. C H = 3. D H = +∞.
Lời giải.
Ta có giới hạn đặc biệt lim
x→+∞
x
k
= +∞ với k nguyên dương.
Áp dụng với k = 3, ta có H = lim
x→+∞
x
3
= +∞.
Chọn đáp án D □
Câu 16. Tính lim
x→+∞
x + 1
x + 2
.
A 1. B 2. C 3. D 4.
Lời giải.
Ta có lim
x→+∞
x + 1
x + 2
= lim
x→+∞
x
Å
1 +
1
x
ã
x
Å
1 +
2
x
ã
= lim
x→+∞
1 +
1
x
1 +
2
x
= 1.
Chọn đáp án A □
Câu 17. Hàm số y = f(x) liên tục tại điểm x
0
khi nào?
A lim
x→x
0
f(x) = f (x). B lim
x→x
0
f(x) = f (x
0
). C lim
x→x
0
f(x) = f (0). D f(x
0
) = 0.
Lời giải.
Theo định nghĩa hàm số liên tục, ta có lim
x→x
0
f(x) = f (x
0
).
Chọn đáp án B □
Câu 18. Cho hàm số f (x) thỏa mãn lim
x→x
0
f(x) = f (x
0
). Chọn khẳng định đúng.
A Hàm số f(x) không xác định tại x
0
. B Hàm số f(x) gián đoạn tại x
0
.
C Hàm số f(x) liên tục tại x
0
. D f(x) có giá trị 0 tại x
0
.
Lời giải.
Theo định nghĩa hàm số liên tục, ta có, do lim
x→x
0
f(x) = f (x
0
) nên hàm số f (x) gián đoạn tại x
0
.
Chọn đáp án B □
Câu 19. Trong các loại hàm số sau, hàm số nào luôn liên tục trên tập hợp các số thực R?
A Hàm số lượng giác. B Hàm số đa thức.
C Hàm số phân thức hữu tỉ. D Hàm số có chứa căn bậc hai.
Lời giải.
Hàm số đa thức luôn liên tục trên tập số thực R.
Chọn đáp án B □
Câu 20. Trong các hàm số sau, hàm số nào liên tục trên R?
A y =
√
x. B y =
2x − 1
x − 1
. C y = cot x. D y = x
4
− x.
Lời giải.
Hàm số y = x
4
− x là hàm số đa thức nên liên tục trên R.
Chọn đáp án D □
Câu 21. Cho hàm số f (x) =
x − 3
x
2
− 1
. Mệnh đề nào sau đây đúng?
A Hàm số liên tục tại x = 1. B Hàm số không liên tục tại các điểm x = ±1.
C Hàm số liên tục tại mọi x ∈ R. D Hàm số liên tục tại x = −1.
Lời giải.
Hàm số đã cho có tập xác định là D = R \{±1}. Do đó, hàm số không liên tục tại các điểm x = ±1.
Chọn đáp án
B □
496/764 496/764
Toán 11 theo chương trình GDPT2018
Chương 3. Giới hạn. Hàm số liên tục
Biết làm, làm đúng, làm nhanh
497
Câu 22. Cho hai dãy số (u
n
), (v
n
) thỏa mãn lim u
n
= 2, lim v
n
= 1. Tính lim(2u
n
− 3v
n
).
A 1. B 2. C 3. D 7.
Lời giải.
Ta có lim(2u
n
− 3v
n
) = lim 2u
n
− lim 3v
n
= 2 · 2 −3 · 1 = 1.
Chọn đáp án A
□
Câu 23. Trong các dãy số sau, dãy số nào có giới hạn khác 0?
A u
n
=
2n − 1
n
. B u
n
=
1
n(n + 1)
. C u
n
=
Å
1
3
ã
n
. D u
n
=
1
√
n
2
+ 1
.
Lời giải.
○ lim
2n − 1
n
= lim
2 −
1
n
1
=
2
1
= 2 = 0.
○ lim
1
n(n + 1)
= 0.
○ lim
Å
1
3
ã
n
= 0.
○ lim
1
√
n
2
+ 1
= 0.
Chọn đáp án A □
Câu 24. Giá trị lim
x→−2
2|x + 1|−5
√
x
2
− 3
2x + 3
bằng
A
1
3
. B
1
7
. C 7. D 3.
Lời giải.
lim
x→−2
2|x + 1|−5
√
x
2
− 3
2x + 3
=
2| − 2 + 1| − 5
p
(−2)
2
− 3
2 · (−2) + 3
= 3.
Chọn đáp án D □
Câu 25. Cho biết lim
x→1
x +
√
x
2
+ 1
x + 1
= a + b
√
2 (với a, b ∈ Q). Giá trị của a + b bằng
A 1. B 2. C 5. D 0.
Lời giải.
Ta có lim
x→1
x +
√
x
2
+ 1
x + 1
=
1 +
√
1
2
+ 1
1
2
+ 1
=
1
2
+
1
2
·
√
2.
Suy ra a =
1
2
, b =
1
2
. Vậy a + b = 1.
Chọn đáp án A □
Câu 26. Giới hạn lim
x→2
√
x + 2 −
√
8 − 2x
x − 2
bằng
A +∞. B −∞. C 0. D
3
4
.
Lời giải.
lim
x→2
√
x + 2 −
√
8 − 2x
x − 2
= lim
x→2
−6 + 3x
(x − 2)
√
x + 2 +
√
8 − 2x
= lim
x→2
3(x − 2)
(x − 2)
√
x + 2 +
√
8 − 2x
= lim
x→2
3
√
x + 2 +
√
8 − 2x
=
3
4
.
Chọn đáp án D □
497/764 497/764
Toán 11 theo chương trình GDPT2018
4. Bài tập cuối chương III
Biết làm, làm đúng, làm nhanh
498
Câu 27. Tính lim
x→−1
x
2
+ 2x + 1
2x
3
+ 2
.
A +∞. B −∞. C
1
2
. D 0.
Lời giải.
lim
x→−1
x
2
+ 2x + 1
2x
3
+ 2
= lim
x→−1
(x + 1)
2
2(x + 1)(x
2
− x + 1)
=
x + 1
2(x
2
− x + 1)
= 0.
Chọn đáp án D □
Câu 28. Biết rằng lim
x→−∞
Ä
√
2x
2
− 3x + 1 + x
√
2
ä
=
a
b
√
2, (a, b ∈ Z,
a
b
tối giản). Tổng a + b có giá trị là
A 1. B 5. C 4. D 7.
Lời giải.
Ta có
lim
x→−∞
Ä
p
2x
2
− 3x + 1 + x
√
2
ä
= lim
x→−∞
2x
2
− 3x + 1 − 2x
2
√
2x
2
− 3x + 1 − x
√
2
= lim
x→−∞
−3x + 1
√
2x
2
− 3x + 1 − x
√
2
= lim
x→−∞
−3 +
1
x
−
…
2 −
3
x
+
1
x
2
−
√
2
=
3
4
·
√
2.
Vậy a = 3, b = 4. Tổng a + b = 7.
Chọn đáp án D □
Câu 29. Tính giới hạn lim
x→2
+
x
2
+ 3x + 1
2x − 4
.
A
1
2
. B 0. C +∞. D −∞.
Lời giải.
Ta có lim
x→2
+
(x
2
+ 3x + 1) = 11 > 0.
Và lim
x→2
+
(2x − 4) = 0.
Mà khi x → 2
+
thì 2x − 4 > 0.
Vậy lim
x→+∞
x
2
+ 3x + 1
2x − 4
= +∞.
Chọn đáp án C □
Câu 30. Cho dãy số (u
n
) xác định bởi
u
1
= 2
u
n+1
=
2u
n
+ 1
5
. Tìm giới hạn I = lim u
n
.
A I =
1
3
. B I =
2
5
. C I =
√
2
5
. D I = +∞.
Lời giải.
Nhận xét: (u
n
) là dãy giảm và bị chặn trên bởi 2.
Giả sử lim u
n
= L.
Ta có u
n+1
=
2u
n
+ 1
5
⇔ L =
2L + 1
5
⇔ L =
1
3
.
Vậy I =
1
3
.
Chọn đáp án A □
Câu 31. Biết rằng lim
x→−∞
Ä
√
2x
2
+ 2x −1 + x
√
2
ä
=
a
√
b
c
(a là số nguyên; b, c là số nguyên tố). Tính tổng S =
a + b + c.
A S = 5. B S = 9. C S = 10. D S = 3.
498/764 498/764
Toán 11 theo chương trình GDPT2018
Chương 3. Giới hạn. Hàm số liên tục
Biết làm, làm đúng, làm nhanh
499
Lời giải.
lim
x→−∞
Ä
p
2x
2
+ 2x −1 + x
√
2
ä
= lim
x→−∞
(2x
2
+ 2x −1) − (2x
2
)
√
2x
2
+ 2x −1 − x
√
2
= lim
x→−∞
2x − 1
√
2x
2
+ 2x −1 − x
√
2
= lim
x→−∞
x
Å
2 −
1
x
ã
−x
Ç
…
2 +
2
x
−
1
x
2
+
√
2
å
=
√
2
2
.
Suy ra a = 1; b = 2; c = 2. Vậy S = 5.
Chọn đáp án A □
Câu 32. Biết rằng lim
x→∞
Å
x
2
+ 1
x − 2
+ ax −b
ã
= −5. Tính tổng a + b.
A 6. B 7. C 8. D 5.
Lời giải.
Ta có
lim
x→∞
Å
x
2
+ 1
x − 2
+ ax −b
ã
= lim
x→∞
x
2
+ 1 + ax
2
− 2ax −bx + 2b
x − 2
= lim
x→∞
(1 + a)x
2
− (2a + b)x + 2b + 1
x − 2
.
Vì kết quả giới hạn bằng −5 nên từ đó ta có hệ
®
a = −1
2a + b = 5
⇔
®
a = −1
b = 7.
Vậy a + b = 6.
Chọn đáp án A □
Câu 33. Giá trị của giới hạn lim
x→+∞
Ä
√
x
2
+ x −
3
√
x
3
− x
2
ä
là
A −1. B +∞. C −∞. D
5
6
.
Lời giải.
Ta có
lim
x→+∞
Ä
p
x
2
+ x −
3
p
x
3
− x
2
ä
= lim
x→+∞
Ä
p
x
2
+ x −x
ä
+ lim
x→+∞
Ä
x −
3
p
x
3
− x
2
ä
.
Mà
lim
x→+∞
Ä
p
x
2
+ x −x
ä
= lim
x→+∞
x
√
x
2
+ x + x
= lim
x→+∞
1
»
1 +
1
x
+ 1
=
1
2
,
và
lim
x→+∞
Ä
x −
3
p
x
3
− x
2
ä
= lim
x→+∞
1
1 +
3
»
1 −
1
x
+
3
»
1 −
1
x
2
=
1
3
,
nên
lim
x→+∞
Ä
p
x
2
+ x −
3
p
x
3
− x
2
ä
=
1
2
+
1
3
=
5
6
.
Chọn đáp án D □
Câu 34. Cho lim
x→−∞
2x +
√
3x
2
− 2
√
4x
2
+ 1 −|x|
=
√
3 + b
c
. Tính giá trị của A = b · c.
A A = 6. B A = −6. C A = 2. D A = −2.
Lời giải.
499/764 499/764
Toán 11 theo chương trình GDPT2018
4. Bài tập cuối chương III
Biết làm, làm đúng, làm nhanh
500
Ta có lim
x→−∞
2x + |x|
…
3 −
2
x
2
|x|
…
4 +
1
x
2
+ x
= lim
x→−∞
2 −
…
3 −
2
x
2
−
…
4 +
1
x
2
+ 1
=
2 −
√
3
−2 + 1
=
√
3 − 2
1
.
Vậy b = −2, c = 1 ⇒ A = b · c = −2.
Chọn đáp án D □
Câu 35. Cho f(x) là hàm đa thức thỏa lim
x→2
f(x) + 1
x − 2
= a và tồn tại lim
x→2
p
f(x) + 2x + 1 −x
x
2
− 4
= T . Chọn đẳng
thức đúng.
A T =
a − 2
16
. B T =
a + 2
16
. C T =
a − 2
8
. D T =
a + 2
8
.
Lời giải.
Vì f(x) là đa thức và lim
x→2
f(x) + 1
x − 2
= a nên suy ra f (x) + 1 = (x − 2)g(x), g(2) = a.
Do đó, Ta có
T = lim
x→2
p
(x − 2)g(x) + 2x − x
x
2
− 4
= lim
x→2
(x − 2)g(x) + 2x − x
2
(x − 2)(x + 2)
î
p
(x − 2)g(x) + 2x + x
ó
= lim
x→2
g(x) −x
(x + 2)
î
p
(x − 2)g(x) + 2x + x
ó
=
a − 2
16
.
Chọn đáp án A □
2. Phần Tự luận (3 điểm)
Bài 1. Tính các giới hạn sau:
lim
√
4n
2
− n + 3
8n − 5
;a) lim
x→4
√
x − 2
x
2
− 16
;b)
lim
x→+∞
6x + 8
5x − 2
;c) lim
x→−2
+
3x
2
+ 4
2x + 4
.d)
Lời giải.
a) lim
√
4n
2
− n + 3
8n − 5
= lim
…
4 −
1
n
+
3
n
2
8 −
5
n
=
1
4
.
b) lim
x→4
√
x − 2
x
2
− 16
= lim
x→4
√
x − 2
(
√
x − 2)(
√
x + 2)(x + 4)
= lim
x→4
1
(
√
x + 2)(x + 4)
=
1
32
.
c) lim
x→+∞
6x + 8
5x − 2
=
6
5
.
d) Vì lim
x→2
+
3x
2
+ 4
= 16 > 0; lim
x→2
+
(x + 2) = 0 và x → −2
+
⇒ x + 2 > 0 nên lim
x→−2
−
3x
2
+ 4
2x + 4
= +∞.
□
Bài 2. Cho hàm số f (x) =
x
2
− 25
x − 5
khi x = 5
a khi x = 5.
Tìm a để hàm số y = f (x) liên tục trên R.
500/764 500/764
Toán 11 theo chương trình GDPT2018
Chương 3. Giới hạn. Hàm số liên tục
Biết làm, làm đúng, làm nhanh
501
Lời giải.
Với x = 5 thì f(x) =
x
2
− 25
x − 5
= x + 5 là hàm liên tục.
Do đó, để hàm số liên tục trên R thì hàm số phải liên tục tại x = 5.
Tức là lim
x→5
f(x) = f (5) ⇔ lim
x→5
(x + 5) = a ⇔ a = 10.
Vậy với a = 10 thì hàm số liên tục trên R. □
Bài 3. Chứng minh rằng giới hạn lim
x→0
|x|
x
không tồn tại.
Lời giải.
○ lim
x→0
−
|x|
x
= lim
x→0
−
−x
x
= lim
x→0
−
(−1) = −1.
○ lim
x→0
+
|x|
x
= lim
x→0
+
x
x
= lim
x→0
+
1 = 1.
Vậy lim
x→0
−
|x|
x
= lim
x→0
+
|x|
x
nên giới hạn lim
x→0
|x|
x
không tồn tại. □
501/764 501/764
Toán 11 theo chương trình GDPT2018
| 1/171
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

331
Chương 3. Giới hạn. Hàm số liên tục
Biết làm, làm đúng, làm nhanh Chûúng 3
GIỚI HẠN. HÀM SỐ LIÊN TỤC
GIỚI HẠN. HÀM SỐ LIÊN TỤC 331/764 331/764
Toán 11 theo chương trình GDPT2018 332
1. Giới hạn của dãy số
Biết làm, làm đúng, làm nhanh Baâi söë 1
GIỚI HẠN CỦA DÃY SỐ
A – GIỚI HẠN HỮU HẠN CỦA DÃY SỐ 1. Định nghĩa
c Định nghĩa 1.1. Dãy số (un) có giới hạn bằng 0 khi n dần tới dương vô cực nếu |un| có thể nhỏ hơn một
số dương bé tùy ý, kể từ một số hạng nào đó trở đi, kí hiệu L = lim un = 0. n→+∞ Ngoài kí hiệu
lim un = 0 ta cũng sử dụng các kí hiệu sau: lim un = 0 hay un → 0 khi n → +∞. n→+∞
Nhận xét. Nếu un ngày càng gần tới 0 khi n càng lớn thì lim un = 0.
c Định nghĩa 1.2. Dãy số (un) có giới hạn hữu hạn là a khi n dần tới dương vô cực nếu lim (un − a) = 0, n→+∞ kí hiệu lim un = a. n→+∞ Ngoài kí hiệu
lim un = a ta cũng sử dụng các kí hiệu sau: lim un = a hay un → a khi n → +∞. n→+∞
○ Một dãy số có giới hạn thì giới hạn đó là duy nhất.
○ Không phải dãy số nào cũng có giới hạn, chẳng hạn như dãy số (un) với un = (−1)n. 2.
Một số giới hạn cơ bản 1 1 ○ lim = 0; lim
= 0 với k là số nguyên dương cho trước. n nk c c ○ lim = 0; lim
= 0 với c là hằng số, k là số nguyên dương cho trước. n nk
○ Nếu |q| < 1 thì lim qn = 0. Å 1 ãn
○ Dãy số (un) với un = 1 +
có giới hạn là một số vô tỉ và gọi giới hạn đó là e, n Å 1 ãn e = lim 1 + · n
Một giá trị gần đúng của e là 2, 718281828459045.
B – ĐỊNH LÍ VỀ GIỚI HẠN HỮU HẠN c Định lí 1.1.
○ Nếu lim un = a và lim vn = b thì: lim (un + vn) = a + b; lim (un − vn) = a − b; lim (un · vn) = a · b; un a lim = (vn ̸= 0, b ̸= 0) . vn b √ √
○ Nếu un ≥ 0 với mọi n và lim un = a thì a ≥ 0 và lim un = a. 332/764 332/764
Toán 11 theo chương trình GDPT2018 333
Chương 3. Giới hạn. Hàm số liên tục
Biết làm, làm đúng, làm nhanh
C – TỔNG CỦA CẤP SỐ NHÂN LÙI VÔ HẠN
c Định nghĩa 1.3. Cấp số nhân vô hạn u1, u1q, ..., u1qn−1, ... có công bội q thỏa mãn |q| < 1 được gọi là cấp
số nhân lùi vô hạn. Tổng của cấp số nhân lùi vô hạn đã cho là u1 S = u1 + u1q + u1q2 + ... = . 1 − q
D – GIỚI HẠN VÔ CỰC c Định nghĩa 1.4.
a) Dãy số (un) có giới hạn +∞ khi n → +∞, nếu un có thể lớn hơn một số dương bất kì, kể từ một số hạng nào đó trở đi. Kí hiệu
lim un = +∞ hay lim un = +∞ hay un → +∞ khi n → +∞. n→+∞
b) Dãy số (un) có giới hạn −∞ khi n → +∞ nếu lim (−un) = +∞. n→+∞ Kí hiệu
lim un = −∞ hay lim un = −∞ hay un → −∞ khi n → +∞. n→+∞
Nhận xét. Một số giới hạn cơ bản
○ lim nk = +∞ với k là một số nguyên dương cho trước.
○ lim qn = +∞ với q > 1 là một số thực cho trước. u ○ n
Nếu lim un = a và lim vn = +∞ (hoặc lim vn = −∞) thì lim = 0. vn u ○ n
Nếu lim un = a, a > 0 và lim vn = 0, vn > 0 với mọi n thì lim = +∞. vn
○ lim un = +∞ ⇔ lim (−un) = −∞.
E – CÁC DẠNG TOÁN THƯỜNG GẶP
Dạng 1. Tính giới hạn dãy số bằng cách dùng định nghĩa, định lí về giới hạn dãy số
Cho lim un = a, lim vn = b và c là hằng số. Khi đó ○ lim(un + vn) = a + b ○ lim(un − vn) = a − b ○ lim(un · vn) = a · b ○ lim(c · un) = c · a u a ○ n lim = , (b ̸= 0). vn b √ √ ○ Nếu u ∗ n ≥ 0, ∀n ∈ N thì a ≥ 0 và lim un = a. 1. Ví dụ mẫu (−1)n
Ví dụ 1 (Cánh Diều). Cho dãy số (un) với un =
. Giả sử h là số dương bé tùy ý cho trước. n (−1)n
a) Tìm số tự nhiên n để |un| < h; b) Tính lim · n 333/764 333/764
Toán 11 theo chương trình GDPT2018 334
1. Giới hạn của dãy số
Biết làm, làm đúng, làm nhanh Lời giải. (−1)n 1 1 1 a) Ta có |u n| = = . Do đó |un| < h ⇔ < h ⇔ n > . n n n h 1 (−1)n
b) Vì |un| < h là số dương bé tùy ý kể từ số hạng n > nên lim = 0. h n □ Å 1 ãn
Ví dụ 2 (Cánh Diều). Chứng minh rằng lim − = 0. 2 Lời giải. 1 1 Å 1 ãn Do − = < 1 nên lim − = 0. □ 2 2 2 1
Ví dụ 3 (KNTT). Xét dãy số un =
. Giải thích vì sao dãy số này có giới hạn là 0. n2 Lời giải. 1
Dãy số này có giới hạn là 0, bởi vì |un| =
có thể nhỏ hơn một số dương bé tuỳ ý khi n đủ lớn. Chẳng hạn, để n2 1 |un| < 0, 0001 tức là
< 10−4, ta cần n2 > 10000 hay n > 100. Như vậy, các số hạng của dãy, kể từ số hạng thứ n2
101 đều có giá trị tuyệt đối nhỏ hơn 0,0001. □ 1
Ví dụ 4 (CTST). Áp dụng giới hạn cơ bản, tìm lim √ Ä än . 3 Lời giải. 1 Å 1 ãn Ta có √ √ . Ä än = 3 3 1 1 Å 1 ãn Do √ √ < 1 nên lim √ = 0. □ Ä än = lim 3 3 3
Ví dụ 5 (Cánh Diều). Chứng minh rằng: 6n + 1
a) lim c = c với c là hằng số; b) lim = 6. n Lời giải.
a) Do lim(c − c) = lim 0 = 0 nên theo định nghĩa về dãy số có giới hạn hữu hạn, ta có lim c = c. Å 6n + 1 ã 1 6n + 1 b) Do lim − 6 = lim = 0 nên lim = 6. n n n □ 2n + 1
Ví dụ 6 (KNTT). Xét dãy số (un) với un = . Chứng minh rằng lim un = 2. n n→+∞ Lời giải. 2n + 1 (2n + 1) − 2n 1 Ta có un − 2 = − 2 = = → 0 khi n → +∞. Do vậy lim un = 2. □ n n n n→+∞ 3n2 + 1
Ví dụ 7 (CTST). Dùng định nghĩa, tìm giới hạn lim . n2 Lời giải. 3n2 + 1 1 1 Đặt un = . Ta có un = 3 + hay un − 3 = . n2 n2 n2 1 Suy ra lim (un − 3) = lim = 0. n2 3n2 + 1
Theo định nghĩa, ta có lim un = 3. Vậy lim = 3. □ n2 334/764 334/764
Toán 11 theo chương trình GDPT2018 335
Chương 3. Giới hạn. Hàm số liên tục
Biết làm, làm đúng, làm nhanh 2. Bài tập tự luyện 1 2
Bài 1. Cho hai dãy số (un), (vn) với un = 3 + ; vn = 5 − . Tính các giới hạn sau: n n2 a) lim un, lim vn. un
b) lim (un + vn), lim (un − vn), lim (un · vn), lim . vn Lời giải. a) Ta có Å 1 ã Å 1 ã lim un = lim 3 + = lim 3 + lim = 3 + 0 = 3. n n Å 2 ã Å 2 ã lim vn = lim 5 − = lim 5 − lim = 5 − 0 = 5. n2 n2 b) Ta có
lim (un + vn) = lim un + lim vn = 3 + 5 = 8.
lim (un − vn) = lim un − lim vn = 3 − 5 = −2.
lim (un · vn) = lim un · lim vn = 3 · 5 = 15. un 3 lim = . vn 5 □
Bài 2. Cho hai dãy số không âm (un) và (vn) với lim un = 2 và lim vn = 3. Tìm các giới hạn sau n→+∞ n→+∞ u2 √ a) lim n ; b) lim un + 2vn. n→+∞ vn − un n→+∞ Lời giải. Å ã2 lim u2 lim u u2 n n n→+∞ n→+∞ 22 a) lim n = = = = 4 ; n→+∞ vn − un lim vn − lim un lim vn − lim un 3 − 2 n→+∞ n→+∞ n→+∞ n→+∞ √ √ √ b) lim
un + 2vn = q lim un + lim 2vn = q lim un + 2 lim vn = 2 + 2 · 3 = 2 2. n→+∞ n→+∞ n→+∞ n→+∞ n→+∞ □ 6 7
Bài 3. Cho hai dãy số (un), (vn) với un = 5 + ; vn = 3 + . Tính các giới hạn sau: n3 n4 a) lim un, lim vn. un
b) lim (un + vn), lim (un − vn), lim (un · vn), lim . vn Lời giải. a) Ta có Å 1 ã Å 1 ã lim un = lim 3 + = lim 3 + lim = 3 + 0 = 3. n n Å 2 ã Å 2 ã lim vn = lim 5 − = lim 5 − lim = 5 − 0 = 5. n2 n2 b) Ta có
lim (un + vn) = lim un + lim vn = 3 + 5 = 8.
lim (un − vn) = lim un − lim vn = 3 − 5 = −2.
lim (un · vn) = lim un · lim vn = 3 · 5 = 15. un 3 lim = . vn 5 335/764 335/764
Toán 11 theo chương trình GDPT2018 336
1. Giới hạn của dãy số
Biết làm, làm đúng, làm nhanh □
Bài 4. Cho hai dãy số không âm (un) và (vn) với lim un = 5 và lim vn = −6. Tìm các giới hạn sau n→+∞ n→+∞ un u2 a) lim (u n
n + vn), lim (un − vn), lim (un · vn), lim . a) lim ; vn n→+∞ vn − un √ b) lim un + 2vn. n→+∞ Lời giải. Å ã2 lim u2 lim u u2 n n n→+∞ n→+∞ 22 a) lim n = = = = 4 ; n→+∞ vn − un lim vn − lim un lim vn − lim un 3 − 2 n→+∞ n→+∞ n→+∞ n→+∞ √ √ √ b) lim
un + 2vn = q lim un + lim 2vn = q lim un + 2 lim vn = 2 + 2 · 3 = 2 2. n→+∞ n→+∞ n→+∞ n→+∞ n→+∞ □ 3.
Bài tập trắc nghiệm 1 Câu 1. Giá trị của lim bằng n A 0. B 1. C +∞. D −∞. Lời giải. 1 lim = 0. n Chọn đáp án A □ 1 Câu 2. Giá trị của lim với k ∈ + Z bằng nk A 1. B +∞. C −∞. D 0. Lời giải. 1 lim = 0. nk Chọn đáp án D □
Câu 3. Dãy số nào sau đây có giới hạn 0? n 2 √ A un = . B un = . C un = n. D un = n. 2 n Lời giải. 2 lim = 0. n Chọn đáp án B □ −5 Câu 4. Giá trị của lim với k ∈ + Z bằng nk A 5. B −1. C 0. D −∞. Lời giải. −5 lim = 0. nk Chọn đáp án C □
Câu 5. Giá trị của lim qn với |q| < 1 bằng A 1. B 0. C +∞. D −∞. Lời giải.
Với |q| < 1 thì lim qn = 0. Chọn đáp án B □ 336/764 336/764
Toán 11 theo chương trình GDPT2018 337
Chương 3. Giới hạn. Hàm số liên tục
Biết làm, làm đúng, làm nhanh
Câu 6. Dãy số (un) có giới hạn là số thực L nếu A lim (un − L) = 0. B lim (un) = 0. C lim L = 0. D lim (un + L) = 0. n→+∞ n→+∞ n→+∞ n→+∞ Lời giải.
Theo định nghĩa giới hạn dãy số ta có (un) có giới hạn là số thực L nếu lim (un − L) = 0. n→+∞ Chọn đáp án A □
Câu 7. Giả sử lim un = L, khẳng định nào sau đây là đúng? √ √ √ √ √ √ A lim un = L. B lim un = L. C lim 3 un = L. D lim 3 un = 3 L. Lời giải. √ √
Nếu lim un = L thì lim 3 un = 3 L. Chọn đáp án D □
Câu 8. Dãy số nào sau đây có giới hạn bằng 0? A (0,999)n. B (−1,01)n. C (1,01)n. D (−2,001)n. Lời giải.
Vì |0,999| < 1 nên lim(0,999)n = 0. Chọn đáp án A □
Câu 9. Dãy số nào sau đây có giới hạn bằng 0? Å 5 ãn Å ãn π n π n 4 A . B . C − . D − . 4 3 4 3 Lời giải. π π n
Vì − ≈ 0,78 < 1 nên lim − = 0. 4 4 Chọn đáp án C □
Câu 10. Cho hai dãy (un) và (vn) thỏa mãn lim un = 1 và lim vn = −2. Giá trị của lim (un + vn) bằng A −1. B −2. C 3. D −3. Lời giải.
lim (un + vn) = lim un + lim vn = 1 + (−2) = −1. Chọn đáp án A □
Câu 11. Cho hai dãy (un) và (vn) thỏa mãn lim un = 6 và lim vn = 12. Giá trị của lim (un − vn) bằng A 2. B 72. C 18. D −6. Lời giải.
lim (un − vn) = lim un − lim vn = 6 − 12 = −6. Chọn đáp án D □
Câu 12. Cho hai dãy (un) và (vn) thỏa mãn lim un = 4 và lim vn = 7. Giá trị của lim (un · vn) bằng 4 7 A . B . C 28. D 11. 7 4 Lời giải.
lim (un · vn) = lim un · lim vn = 4 · 7 = 28. Chọn đáp án C □ √ u Câu 13. n
Cho hai dãy (un) và (vn) thỏa mãn lim un =
3 và lim vn = 2. Giá trị của lim bằng vn √ √ 3 √ √ A 2 3. B . C 2 + 3. D −2 + 3. 2 Lời giải. √ un lim un 3 lim = = . vn lim vn 2 Chọn đáp án B □
Câu 14. Cho hai dãy (un) thỏa mãn lim un = 12. Giá trị của lim (6 + 3un) bằng A 30. B 108. C 36. D 42. Lời giải.
lim (6 + 3un) = lim 6 + lim 3 · lim un = 6 + 3 · 12 = 42. Chọn đáp án D □ 337/764 337/764
Toán 11 theo chương trình GDPT2018 338
1. Giới hạn của dãy số
Biết làm, làm đúng, làm nhanh
Câu 15. Biết lim un = 3. Chọn mệnh đề đúng trong các mệnh đề sau 3u 3u 3u 3u A n − 1 n − 1 n − 1 n − 1 lim = 3. B lim = −1. C lim = 2. D lim = 1. un + 1 un + 1 un + 1 un + 1 Lời giải. 3un − 1 lim 3 · lim un − lim 1 3 · 3 − 1 lim = 2 = = = 2. un + 1 lim un + lim 1 3 + 1 Chọn đáp án C □ P (n)
Dạng 2. Tính giới hạn L = lim Q(n)
Rút lũy thừa bậc cao nhất của tử và mẫu, rồi sử dụng các công thức: c • lim = 0, (k ∈ ∗ ∗ N , c ∈ R). • lim nk = +∞, (k ∈ N ). nk ® lim u ® n = +∞ lim un = −∞ • ⇒ lim(un · vn) = +∞. • ⇒ lim(un · vn) = −∞. lim vn = a > 0 lim vn = a > 0 ® lim u ® n = +∞ lim un = −∞ • ⇒ lim(un · vn) = −∞. • ⇒ lim(un · vn) = +∞. lim vn = a < 0 lim vn = a < 0
○ Áp dụng lim qn = 0 với |q| < 1.
○ Sử dụng công thức mũ, rồi chia cả tử và mẫu cho an với |a| là cơ số lớn nhất.
○ Công thức mũ cần nhớ am am+n = am · an và am−n = . an
Nhận xét. Ta chia cho an với |a| là cơ số lớn nhất vì sau khi chia luôn tạo ra cơ số có trị tuyệt đối nhỏ hơn 1
để áp dụng công thức lim qn = 0 với |q| < 1.
Nhận xét. Các công thức cần nhớ về cấp số nhân uk+1 qn − 1 a) = q (q là công bội).
b) Sn = u1 + u2 + · · · + un = u1 · . uk q − 1 c) un = u1 · qn−1.
d) uk+1 · uk−1 = u2 với k ≥ 2. k P (n)
Hệ số bậc cao nhất của tử
Nhận xét. Nếu bậc tử P (n) bằng bậc mẫu Q(n) thì lim = . Q(n)
Hệ số bậc cao nhất của mẫu
Nhận xét. Với bài toán có lũy thừa cao, ta thường rút bậc cao trong từng dấu ngoặc, sau đó áp dụng công
thức (a · b)n = an · bn và tính toán tương tự như các bài trước. P (n)
Nhận xét. Nếu bậc tử P (n) lớn hơn bậc mẫu Q(n) thì L = lim
= ±∞. Để biết là +∞ hay −∞ ta dựa Q(n)
vào dấu của giới hạn hai nhân tử trong tích theo quy tắc “cùng dấu thì tích dương, trái dấu thì tích âm”. Thông
thường, sẽ để trống = · · · và xét dấu sẽ điền vào sau. Vế trắc nghiệm, đó chính là dấu của tích hệ số bậc cao nhất của tử và mẫu. 1. Ví dụ mẫu
Ví dụ 8 (Cánh Diều). Tính các giới hạn sau Å 1 ã 4n − 3 Å 1 ã Å 1 ã a) lim 2 + ; b) lim ; c) lim 5 + 6 − . n2 n n 4n Lời giải. 338/764 338/764
Toán 11 theo chương trình GDPT2018 339
Chương 3. Giới hạn. Hàm số liên tục
Biết làm, làm đúng, làm nhanh Å 1 ã 1 a) lim 2 + = lim 2 + lim = 2 + 0 = 2. n2 n2 4n − 3 Å 4n 3 ã 3 b) lim = lim − = lim 4 − lim = 4 − 0 = 4. n n n n Å 1 ã Å 1 ã Å 1 ã ï Å 1 ãnò c) lim 5 + 6 − = lim 5 + · lim 6 − = 5 · 6 = 30. n 4n n 4 □
Ví dụ 9 (CTST). Tìm các giới hạn sau √ 3n + 2 9n2 + 1 a) lim . b) lim . 2n − 1 n Lời giải. 2 3n + 2 3 + a) Ta có =
n (Chia cả tử và mẫu cho n). 2n − 1 1 2 − n Å ã 1 1 1 lim 3 + 2 · 3n + 2 3 + 2 · lim 3 + 2 lim n 3 + 2 · 0 3 Từ đó lim = lim n = = n = = . 2n − 1 1 Å 1 ã 1 2 − 0 2 2 − lim 2 − lim 2 − lim n n n √ √ … 9n2 + 1 9n2 + 1 9n2 + 1 … 1 b) Ta có = √ = = 9 + . n n2 n2 n2 √ 9n2 + 1 … 1 Å 1 ã … 1 √ Từ đó lim = lim 9 + = lim 9 + = lim 9 + lim = 9 + 0 = 3. n n2 n2 n2 □ n2 + n + 1
Ví dụ 10 (KNTT). Tìm lim . n→+∞ 2n2 − 1 Lời giải.
Để tính giới hạn của dãy số dạng phân thức, ta chia cả tử thức và mẫu thức cho luỹ thừa cao nhất của n, rồi áp
dụng các quy tắc tính giới hạn.
Áp dụng các quy tắc tính giới hạn, ta được Å ã 1 1 1 1 lim 1 + + n2 + n + 1 1 + + n→+∞ n n2 1 lim = lim n n2 = = . n→+∞ 2n2 − 1 n→+∞ 1 Å 1 ã 2 2 − lim 2 − n2 n→+∞ n2 □
Ví dụ 11 (CTST). Tìm các giới hạn sau √ 3n + 2 9n2 + 1 a) lim . b) lim . 2n − 1 n Lời giải. 2 3n + 2 3 + a) Ta có =
n (Chia cả tử và mẫu cho n). 2n − 1 1 2 − n Å ã 1 1 1 lim 3 + 2 · 3n + 2 3 + 2 · lim 3 + 2 lim n 3 + 2 · 0 3 Từ đó lim = lim n = = n = = . 2n − 1 1 Å 1 ã 1 2 − 0 2 2 − lim 2 − lim 2 − lim n n n 339/764 339/764
Toán 11 theo chương trình GDPT2018 340
1. Giới hạn của dãy số
Biết làm, làm đúng, làm nhanh √ √ … 9n2 + 1 9n2 + 1 9n2 + 1 … 1 b) Ta có = √ = = 9 + . n n2 n2 n2 √ 9n2 + 1 … 1 Å 1 ã … 1 √ Từ đó lim = lim 9 + = lim 9 + = lim 9 + lim = 9 + 0 = 3. n n2 n2 n2 □
Ví dụ 12 (Cánh Diều). Tính các giới hạn sau 6 Å 1 ã 4n − 2 · 3n 3 − a) lim 5 + ; b) lim ; c) lim n2 . 6n 5 + 6 · 4n 2n Lời giải. Å 1 ã Å 1 ã a) Ta có lim 5 + = lim 5 + lim = 5 + 0 = 5. 6n 6n Å 3 ãn 1 − 2 · 4n − 2 · 3n 4 1 b) Ta có lim = lim = . 5 + 6 · 4n Å 1 ãn 6 5 · + 6 4 6 Å 6 ã 3 − c) Vì lim 3 − = 3 và lim 2n = +∞ nên n2 = 0. n2 2n □ 3n+1 − 4n
Ví dụ 13. Tìm giới hạn sau lim . 4n−1 + 3 Lời giải. Å 3 ãn−1 9 · − 4 3n+1 − 4n 9 · 3n−1 − 4 · 4n−1 4 lim = lim = lim = −4. 4n−1 + 3 4n−1 + 3 Å 1 ãn−1 1 + 3 · 4 □ 1 + 2 + 22 + · · · + 2n
Ví dụ 14. Tìm giới hạn sau lim . 1 + 3 + 32 + · · · + 3n Lời giải. ÇÅ ãn+1 Å ãn+1 å 1 − 2n+1 1 2 − · 2 1 + 2 + 22 + · · · + 2n −1 1 − 2n+1 · 2 3 3 lim = lim = lim = lim = 0. 1 + 3 + 32 + · · · + 3n 1 − 3n+1 1 − 3n+1 Å 1 ãn+1 − 1 −2 3 □ 2. Bài tập tự luyện
Bài 5. Tính các giới hạn sau: √ 5n + 1 6n2 + 8n + 1 n2 + 5n + 3 a) lim ; b) lim ; c) lim ; 2n 5n2 + 3 6n + 2 1 Å 1 ã 3n + 2n 2 + d) lim 2 − ; e) lim ; f) lim n . 3n 4 · 3n 3n Lời giải. 1 5n + 1 5 + 5 a) Ta có lim = lim n = . 2n 2 2 340/764 340/764
Toán 11 theo chương trình GDPT2018 341
Chương 3. Giới hạn. Hàm số liên tục
Biết làm, làm đúng, làm nhanh 8 1 6n2 + 8n + 1 6 + + 6 b) Ta có lim = lim n n2 = . 5n2 + 3 3 5 5 + n2 … √ 5 3 1 + + n2 + 5n + 3 n n2 1 c) Ta có lim = lim = . 6n + 2 2 6 6 + n Å 1 ã Å 1 ã d) Ta có lim 2 − = lim 2 − lim = 2 − 0 = 2. 3n 3n Å 2 ãn 1 + 3n + 2n 3 1 e) Ta có lim = lim = . 4 · 3n 4 4 1 Å 1 ã 2 + f) Vì lim 2 + = 2 và lim 3n = +∞ nên lim n = 0. n 3n □ 2n3 − 2n + 3
Bài 6. Tìm giới hạn sau lim . 1 − 4n3 Lời giải. 2 3 2n3 − 2n + 3 2 − + 1 lim = lim n2 n3 = − . 1 − 4n3 1 2 − 4 n3 □ √n4 + 2n + 2
Bài 7. Tìm giới hạn sau lim . n2 + 1 Lời giải. … √ 2 2 1 + + n4 + 2n + 2 n3 n4 lim = lim = 1. n2 + 1 1 1 + n2 □ 3n+1 − 4n
Bài 8. Tìm giới hạn sau lim . 4n−1 + 3 Lời giải. Å 3 ãn−1 9 · − 4 3n+1 − 4n 9 · 3n−1 − 4 · 4n−1 4 lim = lim = lim = −4. 4n−1 + 3 4n−1 + 3 Å 1 ãn−1 1 + 3 · 4 □ 1 + 2 + 22 + · · · + 2n
Bài 9. Tìm giới hạn sau lim . 1 + 3 + 32 + · · · + 3n Lời giải. ÇÅ ãn+1 Å ãn+1 å 1 − 2n+1 1 2 − · 2 1 + 2 + 22 + · · · + 2n −1 1 − 2n+1 · 2 3 3 lim = lim = lim = lim = 0. 1 + 3 + 32 + · · · + 3n 1 − 3n+1 1 − 3n+1 Å 1 ãn+1 − 1 −2 3 □
Bài 10. Tìm các giới hạn sau 341/764 341/764
Toán 11 theo chương trình GDPT2018 342
1. Giới hạn của dãy số
Biết làm, làm đúng, làm nhanh n2 + n + 1 √ Ä ä a) lim . b) lim n2 + 2n − n . n→+∞ 2n2 + 1 n→+∞ Lời giải. Å ã 1 1 1 1 lim 1 + + n2 + n + 1 1 + + n→+∞ n n2 1 a) lim = lim n n2 = = . n→+∞ 2n2 + 1 n→+∞ 1 Å 1 ã 2 2 + lim 2 + n2 n→+∞ n2 √ Ä ä n2 + 2n − n2 2 2 b) lim n2 + 2n − n = lim √ = lim = = 1. n→+∞ n→+∞ Ç å n2 + 2n + n n→+∞ … 2 … 2 1 + + 1 lim 1 + + 1 n n→+∞ n □
Bài 11. Tính các giới hạn sau: 2n + 3 · 4n 3 · 7n + 2 · 4n a) lim . b) T = lim . 4n − 5 · 3n 4 · 5n + 7n Lời giải. Å 1 ãn + 3 2n + 3 · 4n 2 a) lim = lim 4n − 5 · 3n Å 3 ãn = 3. 1 − 5 4 Å 4 ãn 3 + 2 · 3 · 7n + 2 · 4n 7 b) Ta có T = lim = lim = 3. 4 · 5n + 7n Å 5 ãn 4 · + 1 7 □
Bài 12. Tìm các giới hạn sau √ −2n + 1 16n2 − 2 4 n2 − 2n + 3 a) lim ; b) lim ; c) lim ; d) lim . n n 2n + 1 2n2 Lời giải. 1 −2n + 1 −2 + 2 + 0 a) Ta có lim = lim n = = −1. n 1 1 … √ 2 16 − 16n2 − 2 … n2 2 √ b) lim = lim = lim 16 − = 16 − 0 = 4. n 1 n2 4 4 0 c) Ta có lim = lim n = = 0. 2n + 1 1 2 + 0 2 + n Å 2 3 ã 2 3 n2 1 − + n2 − 2n + 3 1 − + n n2 1 d) Ta có L = lim = lim = lim n n2 = . 2n2 2n2 2 2 □
Bài 13. Tính các giới hạn sau: 342/764 342/764
Toán 11 theo chương trình GDPT2018 343
Chương 3. Giới hạn. Hàm số liên tục
Biết làm, làm đúng, làm nhanh √ 7n + 1 5n2 + 2n + 4 2n2 + 3n + 3 a) lim ; b) lim ; c) lim ; 3n − 1 9n2 + 3n − 3 7n + 2 1 Å 1 ã 5n + 3n 2 + d) lim 12 − ; e) lim ; f) lim n . 5n 4 · 5n 4n Lời giải. 1 5n + 1 5 + 5 a) Ta có lim = lim n = . 2n 2 2 8 1 6n2 + 8n + 1 6 + + 6 b) Ta có lim = lim n n2 = . 5n2 + 3 3 5 5 + n2 … √ 5 3 1 + + n2 + 5n + 3 n n2 1 c) Ta có lim = lim = . 6n + 2 2 6 6 + n Å 1 ã Å 1 ã d) Ta có lim 2 − = lim 2 − lim = 2 − 0 = 2. 3n 3n Å 2 ãn 1 + 3n + 2n 3 1 e) Ta có lim = lim = . 4 · 3n 4 4 1 Å 1 ã 2 + f) Vì lim 2 + = 2 và lim 3n = +∞ nên lim n = 0. n 3n □
Bài 14. Tìm các giới hạn sau 3n2 + 5n + 10 √ Ä ä a) lim . b) lim 4n2 + 2n − 2n . n→+∞ 3n2 + 7 n→+∞ Lời giải. Å ã 1 1 1 1 lim 1 + + n2 + n + 1 1 + + n→+∞ n n2 1 a) lim = lim n n2 = = . n→+∞ 2n2 + 1 n→+∞ 1 Å 1 ã 2 2 + lim 2 + n2 n→+∞ n2 √ Ä ä n2 + 2n − n2 2 2 b) lim n2 + 2n − n = lim √ = lim = = 1. n→+∞ n→+∞ Ç å n2 + 2n + n n→+∞ … 2 … 2 1 + + 1 lim 1 + + 1 n n→+∞ n □
Bài 15. Tìm giới hạn của các dãy số cho bởi n2 + 1 √ a) un = . b) vn = 2n2 + 1 − n. 2n − 1 Lời giải. 343/764 343/764
Toán 11 theo chương trình GDPT2018 344
1. Giới hạn của dãy số
Biết làm, làm đúng, làm nhanh 1 n2 + 1 1 + a) u n2 n = = n · . 2n − 1 1 2 − n 1 1 1 + 1 + lim n→+∞ n2 1 Hơn nữa lim n = +∞ và lim n2 = = . n→+∞ n→+∞ 1 1 2 2 − 2 − lim n n→+∞ n Do đó, lim un = +∞. n→+∞ √ Ç… å 1 b) vn = 2n2 + 1 − n = n · 2 + − 1 . n2 Ç… å 1 √ Hơn nữa lim n = +∞ và lim 2 + − 1 = 2 − 1 > 0. n→+∞ n→+∞ n2 Do đó, lim vn = +∞. n→+∞ □ 4n2 − n − 1
Bài 16. Tính giới hạn L = lim . 3 + 2n2 Lời giải. Å 1 1 ã 1 1 n2 4 − − 4 − − n n2 4 − 0 − 0 Ta có L = lim = lim n n2 = = 2. □ Å 3 ã 3 0 + 2 n2 + 2 + 2 n2 n2 P (n)
Hệ số bậc cao nhất của tử
Nhận xét. Nếu bậc tử P (n) bằng bậc mẫu Q(n) thì lim = . Q(n)
Hệ số bậc cao nhất của mẫu 2n2 − n5 · (4n − 1)4
Bài 17. Tính giới hạn L = lim . 20n6 · (2n2 − n + 1)4 Lời giải. ï Å 1 ãò5 ï Å 2 ãò4 n2 2 − n 4 − n n L = lim ï Å 3 1 ãò4 20n6 n2 2 − + n n2 Å 1 ã5 Å 2 ã4 n10 2 − n4 4 − n n = lim Å 3 1 ã4 20n6n8 2 − + n n2 Å 1 ã5 Å 2 ã4 2 − 4 − n n = lim Å 3 1 ã4 20 2 − + n n2 (2 − 0)5 · (4 − 0)4 = 20 · (2 − 0 + 0)4 128 = . 5 □
Nhận xét. Với bài toán có lũy thừa cao, ta thường rút bậc cao trong từng dấu ngoặc, sau đó áp dụng công
thức (a · b)n = an · bn và tính toán tương tự như các bài trước. n2 − n + 3
Bài 18. Tính giới hạn L = lim . n3 + 2n Lời giải. 344/764 344/764
Toán 11 theo chương trình GDPT2018 345
Chương 3. Giới hạn. Hàm số liên tục
Biết làm, làm đúng, làm nhanh Å 1 3 ã Ö 1 3 è n2 1 − + 1 − + n n2 1 1 − 0 + 0 Ta có L = lim = lim · n n2 = 0 · = 0. □ Å 2 ã n 2 1 + 0 n3 1 + 1 + n2 n2 P (n)
Nhận xét. Nếu bậc tử P (n) nhỏ hơn bậc mẫu Q(n) thì L = lim = 0. Q(n) 2n3 − 11n + 1
Bài 19. Tính giới hạn L = lim . n2 − 2 Lời giải. Å 11 1 ã Ö 11 1 è 11 1 n3 2 − + 2 − + 2 − + n2 n3 L = lim = lim n · n2 n3
= +∞ Vì lim n = +∞ và lim n2 n3 = 2 > 0. □ Å 2 ã 2 2 n2 1 − 1 − 1 − n2 n2 n2 P (n)
Nhận xét. Nếu bậc tử P (n) lớn hơn bậc mẫu Q(n) thì L = lim
= ±∞. Để biết là +∞ hay −∞ ta dựa Q(n)
vào dấu của giới hạn hai nhân tử trong tích theo quy tắc “cùng dấu thì tích dương, trái dấu thì tích âm”. Thông
thường, sẽ để trống = · · · và xét dấu sẽ điền vào sau. Vế trắc nghiệm, đó chính là dấu của tích hệ số bậc cao nhất của tử và mẫu.
1 + 3 + 5 + 7 + 9 + · · · + (2n + 1)
Bài 20. Tính giới hạn L = lim . 3n2 + 4 Lời giải.
Xét cấp số cộng: 1, 3, 5, 7, 9, . . . , 2n + 1 có số hạng đầu tiên u1 = 1, công sai d = 2 và số hạng cuối là um = 2n + 1, ta có
u1 + (m − 1)d = 2n + 1 ⇔ 1 + 2(m − 1) = 2n + 1 ⇔ m = n + 1.
Vậy cấp số cộng có n + 1 số hạng. Suy ra tổng m n + 1
S = 1 + 3 + 5 + · · · + 2n + 1 = (u1 + um) = (1 + 2n + 1) = n2 + 2n + 1. 2 2 Vì thế Å 2 1 ã 2 1 n2 1 + + n2 + 2n + 1 1 + + n n2 1 + 0 + 0 1 L = lim = lim = lim n n2 = = . 3n2 + 4 Å 4 ã 4 3 + 0 3 n2 3 + 3 + n2 n2 □
Nhận xét. Cần nhớ công thức cấp số cộng:
• uk+1 − uk = d, với d là công sai.
• un = u1 + (n − 1)d, với d là công sai. n
• uk+1 + uk−1 = 2uk, với k ≥ 2.
• Sn = u1 + u2 + · · · + un = (u1 + un). 2 ï 1 1 1 1 1 ò
Bài 21. Tính giới hạn L = lim + + + + · · · + . 1 · 2 2 · 3 3 · 4 4 · 5 n(n + 1) Lời giải. 345/764 345/764
Toán 11 theo chương trình GDPT2018 346
1. Giới hạn của dãy số
Biết làm, làm đúng, làm nhanh 1 1 1 Số hạng tổng quát = −
; (∀k = 1, 2, . . . , n). Do đó k(k + 1) k k + 1 Å 1 1 1 1 1 1 1 1 1 ã L = lim 1 − + − + − + − + · · · + − 2 2 3 3 4 4 5 n n + 1 Å 1 ã = lim 1 − n + 1 n = lim n + 1n = lim Å 1 ã n 1 + n 1 = lim 1 1 + n 1 = = 1. 1 + 0 □ 1 a b 1 1 Nhận xét. Phân tích = + với a = = 1 và b = = −1. k(k + 1) k k + 1 k + 1 k k=0 k=−1 3n2 + n − 5
Bài 22. Tính giới hạn L = lim . 2n2 + 1 Lời giải. Ta có Å 1 5 ã n2 3 + − n n2 L = lim Å 1 ã n2 2 + n2 1 5 3 + − = lim n n2 1 2 + n2 3 + 0 − 0 = 2 + 0 3 = . 2 □ n3 − n + 3
Bài 23. Tính giới hạn L = lim . 2n2 + 3n3 − 1 Lời giải. Ta có Å 1 3 ã n3 1 − + n2 n3 L = lim Å 2 1 ã n3 + 3 − n n3 1 3 1 − + = lim n2 n3 2 1 + 3 − n n3 1 − 0 + 0 1 = = . 0 + 3 − 0 3 □ 346/764 346/764
Toán 11 theo chương trình GDPT2018 347
Chương 3. Giới hạn. Hàm số liên tục
Biết làm, làm đúng, làm nhanh 6n3 − 2n + 1
Bài 24. Tính giới hạn L = lim . 5n3 − n (n2 + n − 1) Lời giải. Ta có 6n3 − 2n + 1 L = lim 4n3 − n2 + n Å 2 1 ã n3 6 − + n2 n3 = lim Å 1 1 ã n3 4 − + n n2 2 1 6 − + = lim n2 n3 1 1 4 − + n n2 6 − 0 + 0 3 = = . 4 − 0 + 0 2 □ 2n4 + 12 (n + 2)9
Bài 25. Tính giới hạn L = lim . n17 + 1 Lời giải. ï Å 1 ãò2 ï Å 2 ãò9 n4 2 + n 1 + n4 n L = lim Å 1 ã n17 1 + n17 Å 1 ã2 Å 2 ã9 n8 2 + n9 1 + n4 n9 = lim Å 1 ã n17 1 + n17 Å 1 ã2 Å 2 ã9 2 + 1 + n4 n9 = lim Å 1 ã 1 + n17 (2 + 0)2 · (1 + 0)9 = = 4. (1 + 0) □ (2n − 1)2 3 − 4n3
Bài 26. Tính giới hạn L = lim . (4n + 2)3(2 − n)2 Lời giải. ï Å 1 ãò2 ï Å 3 ãò n 2 − n3 − 4 n n3 L = lim ï Å 2 ãò3 ï Å 2 ãò2 n 4 + n − 1 n n Å 1 ã2 Å 3 ã n2 2 − n3 − 4 n n3 = lim Å 2 ã3 Å 2 ã2 n3 4 + n2 − 1 n n Å 1 ã2 Å 3 ã 2 − − 4 n n3 = lim Å 2 ã3 Å 2 ã2 4 + − 1 n n 347/764 347/764
Toán 11 theo chương trình GDPT2018 348
1. Giới hạn của dãy số
Biết làm, làm đúng, làm nhanh (2 − 0)2 · (0 − 4) 1 = = − . (4 + 0)3 · (0 − 1)2 4 □ 3n2 − 13 (2n + 5)2(9n + 4)
Bài 27. Tính giới hạn L = lim .
(2n − 4)4 (2n3 + 1) (2n2 − 7) Lời giải. ï Å 1 ãò3 ï Å 5 ãò2 ï Å 4 ãò n2 3 − n 2 + n 9 + n2 n n L = lim ï Å 4 ãò4 ï Å 1 ãò ï Å 7 ãò n 2 − n3 2 + n2 2 − n n3 n2 Å 1 ã3 Å 5 ã2 Å 4 ã n6 3 − n2 2 + n 9 + n2 n n = lim Å 4 ã4 Å 1 ã Å 7 ã n4 2 − n3 2 + n2 2 − n n3 n2 Å 1 ã3 Å 5 ã2 Å 4 ã 3 − 2 + 9 + n2 n n = lim Å 4 ã4 Å 1 ã Å 7 ã 2 − 2 + 2 − n n3 n2
(3 − 0)3 · (2 + 0)2 · (9 + 0)
= (2 − 0)4 · (2 + 0) · (2 − 0) 243 = . 16 □ n2 + 2 (n − 1)3
Bài 28. Tính giới hạn L = lim . (n + 1) (2n2 + 3)2 Lời giải. ï Å 2 ãò ï Å 1 ãò3 n2 1 + n 1 − n2 n L = lim ï Å 1 ãò ï Å 3 ãò2 n 1 + n2 2 + n n2 Å 2 ã Å 1 ã3 n2 1 + n3 1 − n2 n = lim Å 1 ã Å 3 ã2 n 1 + n4 2 + n n2 Å 2 ã Å 1 ã3 1 + 1 − n2 n = lim Å 1 ã Å 3 ã2 1 + 2 + n n2 (1 + 0) · (1 − 0)3 = (1 + 0) · (2 + 0)2 1 = . 4 □ √ Ä ä
Bài 29. Tính giới hạn I = lim n2 − 2n + 3 − n . Lời giải. 348/764 348/764
Toán 11 theo chương trình GDPT2018 349
Chương 3. Giới hạn. Hàm số liên tục
Biết làm, làm đúng, làm nhanh Ta có Äp ä I = lim n2 − 2n + 3 − n n2 − 2n + 3 − n2 = lim √n2 − 2n + 3 + n −2n + 3 = lim √n2 − 2n + 3 + n −2 + 3 = lim n »1 − 2 + 3 + 1 n n2 −2 = √ = −1 1 + 1 □ √ √ Ä ä
Bài 30. Tính giới hạn I = lim n2 + 7 − n2 + 5 . Lời giải. Ta có Äp p ä I = lim n2 + 7 − n2 + 5 n2 + 7 − (n2 + 5) = lim √ √ n2 + 7 + n2 + 5 2 = lim √ √ n2 + 7 + n2 + 5 = 0 □ √ √ Ä ä
Bài 31. Tính giới hạn I = lim n2 + 2n − n2 − 2n . Lời giải. Ta có Äp p ä I = lim n2 + 2n − n2 − 2n n2 + 2n − (n2 − 2n) = lim √ √ n2 + 2n + n2 − 2n 4n = lim √ √ n2 + 2n + n2 − 2n 4 = lim » » 1 + 2 + 1 − 2 n n 4 = √ √ = 2 1 + 1 □ √ √ Ä ä
Bài 32. Tính giới hạn I = lim 2n2 − n + 1 − 2n2 − 3n + 2 . Lời giải. Ta có Äp p ä I = lim 2n2 − n + 1 − 2n2 − 3n + 2
2n2 − n + 1 − (2n2 − 3n + 2) = lim √ √ 2n2 − n + 1 + 2n2 − 3n + 2 2n − 1 = lim √ √ 2n2 − n + 1 + 2n2 − 3n + 2 2 − 1 = lim n » » 2 − 1 + 1 + 2 − 3 + 2 n n2 n n2 2 1 = √ √ = √ 2 + 2 2 349/764 349/764
Toán 11 theo chương trình GDPT2018 350
1. Giới hạn của dãy số
Biết làm, làm đúng, làm nhanh □ √ Ä ä
Bài 33. Tính giới hạn L = lim 9n2 + 3n − 4 − 3n + 20 . Lời giải. Ta có: Äp ä L = lim 20 + lim 9n2 + 3n − 4 − 3n 3n − 4 =
20 + lim √9n2 + 3n − 4 + 3n Å 4 ã n 3 − n = 20 + lim … 3 4 n 9 + − + 3n n n2 4 3 − = 20 + lim n … 3 4 9 + − + 3 n n2 3 − 0 = 20 + + 3 9 + 0 − 0 41 = . 2 □ 7n3 + 2n2 + 1
Bài 34. Tính giới hạn L = lim . n4 + 5n3 + n Lời giải. Ta có Å 2 1 ã n3 7 + + n n3 L = lim Å 5 1 ã n4 1 + + n n3 Ö 2 1 è 1 7 + + = lim · n n3 n 5 1 1 + + n n3 = 0. 2 1 1 7 + + Vì lim = 0 và lim n n3 = 7. □ n 5 1 1 + + n n3 7n + 3
Bài 35. Tính giới hạn L = lim . 2n2 + 3n3 + 4 Lời giải. Ta có Å 3 ã n 7 + n L = lim Å 2 4 ã n3 + 3 + n n3 Ö 3 è 1 7 + = lim · n n2 2 4 + 3 + n n3 = 0. 350/764 350/764
Toán 11 theo chương trình GDPT2018 351
Chương 3. Giới hạn. Hàm số liên tục
Biết làm, làm đúng, làm nhanh 3 1 7 + 7 Vì lim = 0 và lim n = . □ n2 2 4 3 + 3 + n n3 n2 + 4n − 5
Bài 36. Tính giới hạn L = lim . 3n3 + n2 + 7 Lời giải. Ta có Å 4 5 ã n2 1 + − n n2 L = lim Å 1 7 ã n3 3 + + n n3 Ö 4 5 è 1 1 + − = lim · n n2 n 1 7 3 + + n n3 = 0. 4 5 1 1 + − 1 Vì lim = 0 và lim n n2 = . □ n 1 7 3 3 + + n n3 −2n3 + 3n2 + 4
Bài 37. Tính giới hạn L = lim . n4 + 4n3 + n Lời giải. Ta có Å 3 4 ã n3 −2 + + n n3 L = lim Å 4 1 ã n4 1 + + n n3 Ö 3 4 è 1 −2 + + = lim · n n3 n 4 1 1 + + n n3 = 0. 3 4 1 −2 + + Vì lim = 0 và lim n n3 = −2. □ n 4 1 1 + + n n3 −2n2 + n + 2
Bài 38. Tính giới hạn L = lim . 3n4 + 5 Lời giải. Ta có Å 1 2 ã n2 −2 + + n n2 L = lim Å 5 ã n4 3 + n4 Ö 1 2 è 1 −2 + + = lim · n n2 n2 5 3 + n4 = 0. 1 2 1 −2 + + 2 Vì lim = 0 và lim n n2 = − . □ n2 5 3 3 + n4 351/764 351/764
Toán 11 theo chương trình GDPT2018 352
1. Giới hạn của dãy số
Biết làm, làm đúng, làm nhanh 3.
Câu hỏi trắc nghiệm 2n + 2023
Câu 16. Tính giới hạn I = lim . 3n + 2024 2 3 2023 A I = . B I = . C I = . D I = 1. 3 2 2024 Lời giải. 2017 2n + 2023 2 + 2 Ta có I = lim = lim n = . 3n + 2024 2018 3 3 + n Chọn đáp án A □
Câu 17. Phát biểu nào sau đây là sai?
A lim un = c (un = c là hằng số).
B lim qn = 0 (|q| > 1). 1 1 C lim = 0. D lim = 0 (k > 1). n nk Lời giải.
Theo định nghĩa giới hạn hữu hạn của dãy số thì lim qn = 0 (|q| < 1). Chọn đáp án B □ 2 − n Câu 18. Giá trị của lim bằng n + 1 A 1. B 2. C −1. D 0. Lời giải. 2 2 − n − 1 0 − 1 Ta có lim = lim n = = −1. n + 1 1 1 + 0 1 + n Chọn đáp án C □ 4n + 2024
Câu 19. Tính giới hạn lim . 2n + 1 1 A . B 4. C 2. D 2024. 2 Lời giải. 2024 4n + 2024 4 + Ta có lim = lim n = 2. 2n + 1 1 2 + n Chọn đáp án C □ 2n2 − 3 Câu 20. lim bằng n6 + 5n5 −3 A 2. B 0. C . D −3. 5 Lời giải. 2 3 2n2 − 3 − Ta có lim = lim n4 n6 = 0. n6 + 5n5 5 1 + n Chọn đáp án B □ 2n + 1 Câu 21. Tính lim được kết quả là 1 + n 1 A 2. B 0. C . D 1. 2 Lời giải. Å 1 ã 1 n 2 + 2n + 1 2 + n 2 + 0 Ta có lim = lim = lim n = = 2. 1 + n Å 1 ã 1 0 + 1 n + 1 + 1 n n 352/764 352/764
Toán 11 theo chương trình GDPT2018 353
Chương 3. Giới hạn. Hàm số liên tục
Biết làm, làm đúng, làm nhanh Chọn đáp án A □
Câu 22. Dãy số nào sau đây có giới hạn khác 0? 1 1 n + 1 sin n A . B √ . C . D √ . n n n n Lời giải. n + 1 1 Có lim = lim 1 + lim = 1. n n Chọn đáp án C □ √n Câu 23. Giới hạn lim có kết quả là 2n2 + 3 A 2. B 0. C +∞. D 4. Lời giải. … √ 1 n n3 0 lim = lim = = 0. 2n2 + 3 3 2 + 0 2 + n2 Chọn đáp án B □ 1 1 1 1
Câu 24. Dãy số (un) với un = , chọn M = , để <
thì n phải lấy từ số hạng thứ bao nhiêu trở 2n 100 2n 100 đi? A 51. B 49. C 48. D 50. Lời giải. 1 1 Ta có < ⇔ 2n > 100 ⇔ n > 50. 2n 100
Vậy n phải lấy từ số hạng thứ 51 trở đi. Chọn đáp án A □ 3n + 2n Câu 25. Giới hạn lim có kết quả là 4n 5 3 A 0. B . C . D +∞. 4 4 Lời giải. Å 3 ãn Å 2 ãn + 3n + 2n 4 4 Ta có lim = lim = 0. 4n 1 Chọn đáp án A □ ï 1 1 1 1 ò
Câu 26. Tính giới hạn lim + + + · · · + . 1 · 2 2 · 3 3 · 4 n(n + 1) 3 A 0. B 2. C 1. D . 2 Lời giải. 1 1 1 1 1 1 1 1 1 1 1 1 1 Ta có + + + · · · + = − + − + · · · + − + − = 1 − . 1 · 2 2 · 3 3 · 4 n(n + 1) 1 2 2 3 n − 1 n n n + 1 n + 1 ï 1 1 1 1 ò Å 1 ã Vậy lim + + + · · · + = lim 1 − = 1. 1 · 2 2 · 3 3 · 4 n(n + 1) n + 1 Chọn đáp án C □ √ Ä ä
Câu 27. Tính giới hạn I = lim n2 + 2n + 3 − n A 1. B 0. C 2. D 3. Lời giải. √ Ä ä 2n + 3 2 + 3 Ta có I = lim n2 + 2n + 3 − n = lim √ = lim n = 1 n2 + 2n + 3 + n »1 + 2 + 3 + 1 n n2 Chọn đáp án A □ √ √ Ä ä
Câu 28. Tính giới hạn I = lim n2 + 1 − n2 − 2 353/764 353/764
Toán 11 theo chương trình GDPT2018 354
1. Giới hạn của dãy số
Biết làm, làm đúng, làm nhanh √ 3 A 3. B 0. C 3. D . 2 Lời giải. √ √ Ä ä 3 Ta có I = lim n2 + 1 − n2 − 2 = lim √ √ = 0 n2 + 1 + n2 − 2 Chọn đáp án B □ √ Ä ä
Câu 29. Tính giới hạn I = lim n − n2 + 2n − 3 A 0. B - 2. C - 1. D 2. Lời giải. √ Ä ä −2n + 3 −2 + 3 Ta có I = lim n − n2 + 2n − 3 = lim √ = lim n = −1 n + n2 + 2n − 3 » 1 + 1 + 2 − 3 n n2 Chọn đáp án C □ √ Ä ä
Câu 30. Tính giới hạn I = lim n2 − n + 1 − n 1 1 A . B 1. C − . D 0. 2 2 Lời giải. √ Ä ä −n + 1 −1 + 1 1 Ta có I = lim n2 − n + 1 − n = lim √ = lim n = − n2 − n + 1 + n »1 − 1 + 1 + 1 2 n n2 Chọn đáp án C □ √ Ä ä
Câu 31. Tính giới hạn I = lim 3 n3 − n2 − n 1 1 A − . B . C 1. D 0. 3 3 Lời giải. √ Ä ä −n2 −1 1 Ta có I = lim 3 n3 − n2 − n ) = lim = lim = − 3 p(n3 − n2)2 + n 3 p(n3 − n2) + n2 » 3 » 1 − 1 2 + 3 1 − 1 + 1 3 n n Chọn đáp án A □ √ √ Ä ä
Câu 32. Tính giới hạn I = lim 2n2 + 2n − 1 − 2n2 + n 1 1 1 A 0. B . C . D √ . 4 2 2 2 Lời giải. √ √ Ä ä n 1 Ta có I = lim 2n2 + 2n − 1 − 2n2 + n = lim √ √ = lim = 2n2 + 2n − 1 + 2n2 + n » » 2 + 2 − 1 + 2 + 2 n n2 n 1 √ 2 2 Chọn đáp án D □ √ √ Ä ä
Câu 33. Tính giới hạn I = lim n n2 + n + 1 − n2 + n − 8 9 A 0. B ∞. C 2. D . 2 Lời giải. √ √ Ä ä 9n Ta có I = lim n n2 + n + 1 − n2 + n − 8 = lim √ √ n2 + n + 1 + n2 + n − 8 9 9 = lim = » » 1 + 1 + 1 + 1 + 1 − 8 2 n n2 n n2 Chọn đáp án D □ (2n − 1)(3 − n)2 Câu 34. Giới hạn lim có kết quả bằng (4n − 5)3 1 3 1 A 0. B . C . D . 32 2 2 Lời giải. 354/764 354/764
Toán 11 theo chương trình GDPT2018 355
Chương 3. Giới hạn. Hàm số liên tục
Biết làm, làm đúng, làm nhanh Å 1 ã Å 3 ã2 2 − − 1 (2n − 1)(3 − n)2 n n 2 1 lim = lim = = . (4n − 5)3 Å 5 ã3 43 32 4 − n Chọn đáp án B □
—————————————————————————-
Dạng 3. Phương pháp lượng liên hợp (lim hữu hạn)
Sử dụng các hằng đẳng thức √ √ √ ( a − b) ( a + b) a − b2 ○ a − b = √ = √ . ( a + b) ( a + b) √ √ Ä√ ä Ä√ ä √ √ a − b a + b a − b ○ a − b = √ = √ . Ä√ ä Ä√ ä a + b a + b 1. Ví dụ mẫu √ Ä ä
Ví dụ 15 (KNTT). Tìm giới hạn sau lim n2 + 2n − n . n→+∞ Lời giải. √ Ä ä n2 + 2n − n2 2 2 lim n2 + 2n − n = lim √ = lim = = 1. □ n→+∞ n→+∞ Ç å n2 + 2n + n n→+∞ … 2 … 2 1 + + 1 lim 1 + + 1 n n→+∞ n √ √ Ä ä
Ví dụ 16. Tìm giới hạn sau lim 3n2 − 2n − 3n2 + 6n − 1 . Lời giải. Äp p ä lim 3n2 − 2n − 3n2 + 6n − 1 3n2 − 2n − 3n2 − 6n + 1 = lim √ √ 3n2 − 2n + 3n2 + 6n − 1 −8n + 1 = lim √ √ 3n2 − 2n + 3n2 + 6n − 1 1 −8 + 4 = lim n = − √ . … 2 … 6 1 3 3 − + 3 + − n n n2 □ √ √ Ä ä
Ví dụ 17. Tìm giới hạn sau lim n n2 + 1 − n2 − 3 . Lời giải. Äp p ä lim n n2 + 1 − n2 − 3 n n2 + 1 − n2 + 3 = lim √ √ n2 + 1 + n2 − 3 4n = lim √ √ n2 + 1 + n2 − 3 4 4 = lim = = 2. … 1 … 3 2 1 + + 1 − n2 n2 □ 355/764 355/764
Toán 11 theo chương trình GDPT2018 356
1. Giới hạn của dãy số
Biết làm, làm đúng, làm nhanh 1
Ví dụ 18. Tính giới hạn sau lim √ . 9n2 − n − 3n Lời giải. 1 lim √9n2 − n − 3n √9n2 − n + 3n = lim 9n2 − n − (3n)2 √9n2 − n + 3n = lim −n … 1 9 − + 3 n = lim = −6. −1 □ √ Ä ä
Ví dụ 19. Tính giới hạn sau lim n2 + 3n + 2 − n + 2 . Lời giải. Äp ä lim n2 + 3n + 2 − n + 2 n2 + 3n + 2 − (n − 2)2 = lim √n2 + 3n + 2 + (n − 2)
n2 + 3n + 2 − (n2 − 4n + 1) = lim √n2 + 3n + 2 + n − 2 7n + 1 = lim √n2 + 3n + 2 + n − 2 1 7 + 7 = lim n = . … 3 2 2 2 1 + + + 1 − n n2 n □ 2. Bài tập rèn luyện √ Ä ä
Bài 39. Tìm giới hạn sau lim n2 − 3n − n . Lời giải. Äp ä n2 − 3n − n2 lim n2 − 3n − n = lim √n2 − 3n + n −3 3 = lim = − . … 3 2 1 − + 1 n □ √ √ Ä ä
Bài 40. Tính giới hạn sau lim 5n2 + 3 − 5n2 − 6n . Lời giải. Äp p ä 5n2 + 3 − 5n2 + 6n lim 5n2 + 3 − 5n2 − 6n = lim √ √ 5n2 + 3 + 5n2 − 6n 3 √ + 6 3 5 = lim n = . … 3 … 6 5 5 + + 5 − n2 n □ 356/764 356/764
Toán 11 theo chương trình GDPT2018 357
Chương 3. Giới hạn. Hàm số liên tục
Biết làm, làm đúng, làm nhanh √ Ä ä
Bài 41. Tính giới hạn sau lim n n − n2 + 2 . Lời giải. Ä p ä n n2 − n2 − 2 lim n n − n2 + 2 = lim √ n + n2 + 2 −2n = lim √ n + n2 + 2 −2 = lim = −1. … 2 1 + 1 + n2 □ 2
Bài 42. Tính giới hạn sau lim √ . Ä ä 2n + 1 − 4n2 − 3n Lời giải. √ Ä ä 2 2 2n + 1 + 4n2 − 3n lim √ = lim Ä ä 2n + 1 − 4n2 − 3n (2n + 1)2 − (4n2 − 3n) √ Ä ä 2 2n + 1 + 4n2 − 3n = lim 4n2 + 4n + 1 − 4n2 + 3n Ç å 1 … 3 2 2 + + 4 − n n 8 = lim = . 1 7 7 + n □ √ √ n2 + 1 − n + 1
Bài 43. Tính giới hạn sau lim . 3n + 2 Lời giải. √ √ n2 + 1 − n + 1 n2 − n lim = lim √ √ 3n + 2 Ä ä (3n + 2) n2 + 1 + n + 1 1 1 − 1 = lim n = . Å å 2 ã Ç… 1 … 1 1 3 3 + 1 + + + n n2 n n2 □ 3.
Bài tập trắc nghiệm √ Ä ä
Câu 35. Tìm giới hạn sau lim n2 + 1 − n 1 A 0. B +∞. C 1. D . 2 Lời giải. Äp ä n2 + 1 − n2 lim n2 + 1 − n = lim √n2 + 1 + n 1 = lim n = 0. … 1 1 + + 1 n Chọn đáp án A □ 357/764 357/764
Toán 11 theo chương trình GDPT2018 358
1. Giới hạn của dãy số
Biết làm, làm đúng, làm nhanh √ Ä ä
Câu 36. Tìm giới hạn sau lim 4n2 − 3 − 2n 3 A −∞. B −3. C 0. D − . 4 Lời giải. Äp ä 4n2 − 3 − (2n)2 lim 4n2 − 3 − 2n = lim √4n2 − 3 + 2n 3 − = lim n = 0. … 3 4 − + 2 n Chọn đáp án C □ √ √
Câu 37. Tính các giới hạn sau lim n + 3 − n. 3 A +∞. B −∞. C 0. D . 2 Lời giải. √ √ Ä ä n + 3 − n lim n + 3 − n = lim √ √ n + 3 − n 3 √n = lim = 0. … 3 1 + + 1 n Chọn đáp án C □ √ Ä ä
Câu 38. Tìm giới hạn sau lim 4n2 + 3n − 2n . 3 1 A . B +∞. C . D 0. 4 2 Lời giải. Äp ä 4n2 + 3n − (2n)2 lim 4n2 + 3n − 2n = lim √4n2 + 3n + 2n 3 = lim n = 0. … 3 4 + + 2 n Chọn đáp án D □ −3
Câu 39. Tìm giới hạn sau lim √ . 16n2 − 5n − 4n 24 24 A − . B +∞. C . D −∞. 5 5 Lời giải. √ Ä ä −3 −3 16n2 − 5n + 4n lim √ = lim 16n2 − 5n − 4n 16n2 − 5n − (4n)2 Ç… å 5 −3 16 − + 4 n 24 = lim = . −5 5 Chọn đáp án C □ √ Ä ä
Câu 40. Tìm giới hạn sau lim 9n2 − n − 3n . 1 1 A 0. B . C −∞. D − . 6 6 358/764 358/764
Toán 11 theo chương trình GDPT2018 359
Chương 3. Giới hạn. Hàm số liên tục
Biết làm, làm đúng, làm nhanh Lời giải. Äp ä 9n2 − n − (3n)2 lim 9n2 − n − 3n = lim √9n2 − n + 3n −1 1 = lim = − . … 1 6 9 − + 3 n Chọn đáp án D □ √ Ä ä
Câu 41. Tìm giới hạn sau lim n − n2 + 2n . A 1. B −∞. C −1. D 0. Lời giải. Ä p ä n2 − n2 + 2n lim n − n2 + 2n = lim √ n + n2 + 2n −2 = lim = −1. … 2 1 + 1 + n Chọn đáp án C □ √ Ä ä
Câu 42. Tính giới hạn I = lim n2 − 2n + 3 − n . A I = 1. B I = −1. C I = 0. D I = +∞. Lời giải. Äp ä n2 − 2n + 3 − n2 I = lim n2 − 2n + 3 − n = lim √n2 − 2n + 3 + n 3 −2 + = lim n = −1. … 2 3 1 − + + 1 n n2 Chọn đáp án B □ √ Ä ä
Câu 43. Tìm giới hạn sau lim n + 2 − n2 − 4n . A 0. B 4. C +∞. D −∞. Lời giải. Ä p ä (n + 2)2 − n2 − 4n lim n + 2 − n2 − 4n = lim √ (n + 2) + n2 − 4n n2 + 4n + 4 − n2 + 4n = lim √ n + 2 + n2 − 4n 4 8 + = lim n = 4. 2 … 4 1 + + 1 − n n Chọn đáp án B □ √ Ä ä
Câu 44. Tính giới hạn lim
9n2 + 2n − 3n + 8 ta được kết quả 25 1 A . B −∞. C . D +∞. 3 3 Lời giải. Äp ä 9n2 + 2n − (3n − 8)2 lim 9n2 + 2n − 3n + 8 = lim √9n2 + 2n + (3n − 8) 359/764 359/764
Toán 11 theo chương trình GDPT2018 360
1. Giới hạn của dãy số
Biết làm, làm đúng, làm nhanh 9n2 + 2n − 9n2 + 48n − 64 = lim √9n2 + 2n + (3n − 8) 64 50 − 50 25 = lim n = = . … 2 8 6 3 9 + + 3 − n n Chọn đáp án A □ 2
Câu 45. Tìm giới hạn sau lim √ . 2n − 3 − 4n2 + 3n 8 8 A 0. B +∞. C − . D − . 15 9 Lời giải. √ Ä ä 2 2 2n − 3 + 4n2 + 3n lim √ = lim 2n − 3 − 4n2 + 3n (2n − 3)2 − (4n2 + 3n) √ Ä ä 2 2n − 3 + 4n2 + 3n =
lim 4n2 − 12n + 9 − 4n2 − 3n Ç å 3 … 3 2 2 − + 4 + n n 8 = lim = − . −15 15 Chọn đáp án C □ Ç… å 1 Câu 46. Biết lim n2 − n + 3 − n
= a, với a ∈ Q. Tính P = a2 + 1. 11 485 483 1 1 A . B . C . D . 484 484 121 484 Lời giải. 1 1 3 Ç… å 1 − n + 3 − + 1 lim n2 − n + 3 − n = lim 11 = lim 11 n = − . 11 … 1 … 1 3 22 n2 − n + 3 + n 1 − + + 1 11 11n n2 Å 1 ã2 485 Vậy P = a2 + 1 = − + 1 = . 22 484 Chọn đáp án A □ √ √ î Ä äó a a
Câu 47. Biết giới hạn lim n 9n2 + 3 − 9n2 + 2 = với a, b ∈ N và
là phân số tối giản. Khi đó, giá trị b b a2 + b bằng A 31. B 7. C 84. D 37. Lời giải. √ √ î Ä äó n 1 1 Ta có lim n 9n2 + 3 − 9n2 + 2 = lim √ √ = lim = . 9n2 + 3 + 9n2 + 2 … 3 … 2 6 9 + + 9 + n2 n2
Suy ra a = 1, b = 6. Do đó a2 + b = 12 + 6 = 7. Chọn đáp án B □ √ Ä ä Câu 48. Biết lim 2n −
4n2 + an + 3 = 1, giá trị của a thuộc khoảng nào sau đây? A (−5; 0). B (1; 5). C (0; 1). D (−1; 3). Lời giải. Ä p ä −an − 3 lim 2n − 4n2 + an + 3 = lim √ 2n + 4n2 + an + 3 3 −a − −a = lim n = … a 3 4 2 + 4 + + n n2 360/764 360/764
Toán 11 theo chương trình GDPT2018 361
Chương 3. Giới hạn. Hàm số liên tục
Biết làm, làm đúng, làm nhanh a Suy ra −
= 1 ⇒ a = −4. Vậy a ∈ (−5; 0). 4 Chọn đáp án A □ √ √ Ä ä Câu 49. Biết L = lim 4n2 + 3n − an2 + bn = 1. Tính S = a + b. A S = 3. B S = −4. C S = 7. D S = −7. Lời giải. Äp p ä (4 − a)n2 + (3 − b)n L = lim 4n2 + 3n − an2 + bn = lim Ç… å 3 … b n 4 + + a + n n (4 − a)n + 3 − b = lim . … 3 … b 4 + + a + n n 4 − a = 0 ®  a = 4 Mà L = 1 ⇒ 3 − b ⇔ ⇒ S = 3. √ = 1 b = −1  2 + a Chọn đáp án A □
Dạng 4. Giới hạn vô cực
Ta nói dãy {un} có giới hạn là +∞ khi n → +∞, nếu un có thể lớn hơn một số dương bất kì, kể từ một số hạng nào đó trở đi.
Kí hiệu: lim un = +∞ hay un → +∞ khi n → +∞.
Dãy số {un} có giới hạn là −∞ khi n → +∞, nếu lim −un = +∞.
Kí hiệu: lim un = −∞ hay un → −∞ khi n → +∞.
Một số giới hạn đặc biệt và định lí về giới hạn dãy số Giới hạn đặc biệt : √ lim n = +∞ n→+∞
lim nk = +∞ với k là số nguyên dương. n→+∞ lim qn = +∞ nếu q > 1 n→+∞ Định lý : un
Nếu lim un = a > 0 và lim vn = 0 với vn > 0 thì lim = +∞ vn
Nếu lim un = +∞ và lim vn = a > 0 thì lim unvn = +∞ 1. Ví dụ mẫu
Ví dụ 20. Chứng minh rằng lim n2 = +∞. Lời giải. √
Xét dãy số (un) = n2. Với M là số dương bất kì, ta thấy: un > M ⇔ n2 > M ⇔ n > M . √
Vậy với các số tự nhiên n >
M thì un > M . Do đó, lim n2 = +∞. □ Ví dụ 21. Tinh lim n2 − 2n. n→+∞ Lời giải. Å 2 ã Å 2 ã Ta có n2 − 2n = n2 1 − . Hơn nữa lim n2 = +∞ và lim 1 − = 1. n n→+∞ n→+∞ n Do đó, lim n2 − 2n = +∞. □ n→+∞
Ví dụ 22 (CTST). Tìm giới hạn lim qn với q > 1. Lời giải. 1 1 Å 1 ãn Từ q > 1 suy ra 0 < < 1. Do đó, lim = lim = 0. q qn q
Mà qn > 0 với mọi n nên lim qn = +∞. □ 361/764 361/764
Toán 11 theo chương trình GDPT2018 362
1. Giới hạn của dãy số
Biết làm, làm đúng, làm nhanh
Ví dụ 23 (Cùng khám phá). Tìm lim(−n4). Lời giải.
Vì lim(n4) = +∞ nên lim(−n4) = −∞. □ 2. Bài tập tự luyện
Bài 44. Tìm giới hạn √ a) lim(n3 + n2 + n + 1). b) lim n2 − n n + 1. Lời giải. Å 1 1 1 ã
a) lim(n3 + n2 + n + 1) = lim n3 1 + + + = +∞. n n2 n3 √ Å 1 1 ã
b) lim n2 − n n + 1 = lim n2 1 − √ + = +∞. n n2 □
Bài 45. Tìm giới hạn √ n5 + n4 − n − 2 3 n6 − 7n3 − 5n + 8 √ Ä ä a) lim . b) lim . c) lim n + n2 − n + 1 . 4n3 + 6n2 + 9 n + 12 Lời giải. n5 + n4 − n − 2 n2 + n − 1 − 2 n2 + n a) lim = lim n2 n3 = lim = +∞. 4n3 + 6n2 + 9 4 + 6 + 9 4 n n3 √ » » 3 n6 − 7n3 − 5n + 8 n2 3 1 − 7 − 5 + 8 n 3 1 − 7 − 5 + 8 b) lim = lim n3 n5 n6 = lim n3 n5 n6 = +∞. n + 12 n + 12 1 + 12 n √ Ä ä Ä » ä c) lim n + n2 − n + 1 = n 1 + 1 − 1 + 1 = lim 2n = +∞ n n2 □
Bài 46. Tìm giới hạn √ √ a) lim 5n2 − 8n + 7. b) lim n3 − 5n + 6. Lời giải. √ … 8 7 a) lim 5n2 − 8n + 7 = lim n 5 − + = +∞. n n2 √ √ … 5 6 b) lim n3 − 5n + 6 = lim n n 1 − + = +∞. n2 n3 □
Bài 47. Tìm giới hạn √5n4 − 8n2 + 10 n2 − 15n + 11 a) lim . b) lim √ . 4n + 5 n2 − 8n + 7 Lời giải. √ » √ 5n4 − 8n2 + 10 n2»5 − 8 + 10 n 5 − 8 + 10 n 5 a) lim = lim n2 n4 = n2 n4 = lim = +∞. 4n + 5 4n + 5 4 + 5 4 n n2 − 15n + 11 n − 15 + 11 b) lim √ = lim n = +∞. n2 − 8n + 7 »1 − 8 + 7 n n2 □ 362/764 362/764
Toán 11 theo chương trình GDPT2018 363
Chương 3. Giới hạn. Hàm số liên tục
Biết làm, làm đúng, làm nhanh 3.
Bài tập trắc nghiệm n3 − 2n
Câu 50. Tính giới hạn L = lim . 3n2 + n − 2 1 A L = +∞. B L = 0. C L = . D L = −∞. 3 Lời giải. Å 2 ã  Ö 2 è n3 1 − n3 − 2n 1 − n2 Ta có L = lim = lim = lim n2 n ·  = +∞ 3n2 + n − 2 Å 1 2 ã  1 2  n2 3 + − 3 + − n n2 n n2  lim n = +∞     2  vì 1 − 1 − 2 · 0 1 lim n2 = = > 0.   1 2  3 + 0 − 2 · 0 3  3 + −  n n2 Chọn đáp án A □ Å 4 ãn Câu 51. Kết quả của lim bằng 3 A 0. B 3. C 4. D +∞. Lời giải. Å 4 ãn Ta có lim = +∞. 3 Chọn đáp án D □ Câu 52. lim(2n + 3) bằng A +∞. B 3. C 5. D −∞. Lời giải. ï Å 3 ãò lim(2n + 3) = lim n 2 + = +∞. n Chọn đáp án A □
Câu 53. Trong bốn giới hạn sau đây, giới hạn nào bằng dương vô cực? n3 + 2n − 1 n2 + 3n3 + 2 2n2 − 3n n2 − n + 1 A lim . B lim . C lim . D lim . n − 2n3 n2 + n n3 + 3n 1 − 2n Lời giải. Ta có 2 1 n3 + 2n − 1 1 + − 1 ○ lim = lim n n3 = − . n − 2n3 1 2 − 2 n2  lim n = +∞ 1 2    n2 + 3n3 + 2 + 3 +  1 2  ○ lim = lim n · n n3 = +∞ (do + 3 + n2 + n 1 n n3 + 1 lim = 3 > 0.   1 n   + 1  n 2 3 2n2 − 3n − ○ lim = lim n n2 = 0. n3 + 3n 3 1 + n2  lim n = +∞ 1 1    n2 − n + 1 1 − +  1 1  ○ lim = lim n · n n2 = −∞ (do 1 − + 1 1 − 2n 1 n n2 − 2 lim = − < 0.   1 n  2  − 2  n 363/764 363/764
Toán 11 theo chương trình GDPT2018 364
1. Giới hạn của dãy số
Biết làm, làm đúng, làm nhanh Chọn đáp án B □
Câu 54. Trong các giới hạn sau, giới hạn nào bằng −∞? √ 1 + 2n+1 Å 1 n ã A lim . B lim − . 1 − 3n n n + 1 √ √ 1 − 3n2 C lim n n + 1 − 2n + 1. D lim . 2n3 + 1 Lời giải. √ √ √ Ç… å 1 … 1 Xét L = lim n n + 1 − 2n + 1 = lim n n 1 + − 2 + có n n √ ○ lim n n = +∞. Ç… å 1 … 1 √ ○ lim 1 + − 2 + = 1 − 2 < 0. n n Suy ra L = −∞. Chọn đáp án C □
Câu 55. Tính lim(3 + 2n + n3). A −∞. B +∞. C 1. D −1. Lời giải.  lim n3 = +∞ ï Å 3 2 ãò 
Ta có lim(3 + 2n + n3) = lim n3 + + 1 = +∞ vì Å 3 2 ã n3 n2 lim + + 1 = 1 > 0.  n3 n2 Chọn đáp án B □ 2n3 − 11n + 1 Câu 56. Tính lim . −n2 − 2 A 0. B −2. C +∞. D −∞. Lời giải. Å 11 1 ã 11 1 n3 2 − + 2 − + n2 n3 Ta có lim = lim n · n2 n3 = −∞. Å 2 ã 2 n2 −1 − −1 − n2 2n2  lim n = +∞     11 1  Vì 2 − + lim n2 n3 = −2   2   −1 −  n2 Chọn đáp án D □
Câu 57. Tìm mệnh đề đúng trong các mệnh đề dưới đây.
A lim −3n4 + 3 = −∞. B lim −3n4 + 3 = 0. C lim −n4 + 2 = +∞.
D lim 5n4 − 2 = −∞. Lời giải.
Ta có lim −3n4 + 3 = −∞ là mệnh đề đúng. lim −3n4 + 3 = −∞. lim −n4 + 2 = −∞. lim 5n4 − 2 = +∞ Chọn đáp án A □
Câu 58. lim (3n − 4n) có giá trị bằng 4 A 1. B +∞. C −∞. D . 3 Lời giải. ïÅ 3 ãn ò
Ta có lim (3n − 4n) = lim 4n · − 1 = −∞. 4 364/764 364/764
Toán 11 theo chương trình GDPT2018 365
Chương 3. Giới hạn. Hàm số liên tục
Biết làm, làm đúng, làm nhanh Chọn đáp án C □
Câu 59. lim(2 − 3n)4(n + 1)3 có giá trị bằng A −∞. B +∞. C 2. D 81. Lời giải. Å 2 ã4 Å 1 ã3
Ta có lim(2 − 3n)4(n + 1)3 = lim n7 − 3 1 + = 81 lim n7 = +∞. n n Chọn đáp án B □ √ Ä ä Câu 60. Tìm giới hạn lim n2 + 1 − 2n . 2 A +∞. B 0. C − . D −∞. 3 Lời giải. √ Ç… å 1 ○ Ä ä Cách 1. lim n2 + 1 − 2n = lim n 1 + − 2 = −∞ n2 Ç… å 1 (vì lim n = +∞ và lim 1 + − 2 = −1 < 0). n2 1 √ n2 + 1 − 4n2 −3n + ○ Ä ä Cách 2. lim n2 + 1 − 2n = lim √ = lim n = −∞. n2 + 1 + 2n … 1 1 + + 2 n2 Chọn đáp án D □
Dạng 5. Tính tổng của dãy cấp số nhân lùi vô hạn
c Định nghĩa 1.5. Cấp số nhân vô hạn u1, u1q, ..., u1qn−1, ... có công bội q thỏa mãn |q| < 1 được gọi là
cấp số nhân lùi vô hạn. Tổng của cấp số nhân lùi vô hạn đã cho là u1 S = u1 + u1q + u1q2 + ... = . 1 − q 1. Ví dụ mẫu 1
Ví dụ 24 (Cánh diều). Cho cấp số nhân (un), với u1 = 1 và công bội q = . 2 a) So sánh |q| với 1.
b) Tính Sn = u1 + u2 + · · · + un từ đó hãy tính lim Sn. Lời giải. 1 1 a) Ta có |q| = = < 1. 2 2 ï Å 1 ãnò 1 · 1 − u Å ã 1 (1 − qn) 2 1 1 b) Ta có Sn = = = 2 · 1 − = 2 − . 1 − q 1 2n 2n−1 1 − 2 Å 1 ã Khi đó lim Sn = lim 2 − = 2. 2n−1 □ 1 1 1
Ví dụ 25 (Cánh diều). Tính tổng T = 1 + + + . . . + + . . . 3 32 3n Lời giải. 365/764 365/764
Toán 11 theo chương trình GDPT2018 366
1. Giới hạn của dãy số
Biết làm, làm đúng, làm nhanh 1
Các số hạn của tổng lập thành câp số nhân (un), có u1 = 1, q = nên 3 1 1 1 1 2 T = 1 + + + . . . + + . . . = = · 3 32 3n 1 3 1 − 3 □
Ví dụ 26 (Cánh diều). Biểu diễn số thập phân vô hạn tuần hoàn 0, (3) dưới dạng phân số. Lời giải. 3 3 3 3 1 Ta có 0,(3) = + + . . . + + . . . = 10 = · □ 10 102 10n 1 3 1 − 10 1 1 1 Å 1 ãn
Ví dụ 27 (CTST). Tính tổng của cấp số nhân lùi vô hạn: 1 − + − + · · · + − + · · · . 4 16 64 4 Lời giải. 1
Tổng trên là tổng của cấp số nhân lùi vô hạn có số hạng đầu u1 = 1 và công bội q = − nên 4 1 1 1 Å 1 ãn 1 4 1 − + − + · · · + − + · · · = = . 4 16 64 4 Å 1 ã 5 1 − − 4 □
Ví dụ 28 (CTST). Biết rằng có thể coi số thập phân vô hạn tuần hoàn 0,666 . . . là tổng của một cấp số nhân lùi vô hạn: 1 1
0,666 . . . = 0,6 + 0,06 + 0,006 + · · · = 0,6 + 0,6 · + 0,6 · + · · · . 10 102
Hãy viết 0,666 . . . dưới dạng phân số. Lời giải. 1
Số 0,666 . . . là tổng của cấp số nhân lùi vô hạn có số hạng đầu bằng 0,6 và công bội bằng . 10 0,6 6 2 Do đó 0,666 . . . = = = . □ 1 9 3 1 − 10 1 1 1 Å 1 ãn−1
Ví dụ 29. Tính tổng S = 1 − + − + . . . + − + . . .. 2 4 8 2 Lời giải. 1 u1 1 2
Đây là tổng của cấp số nhân lùi vô hạn với u1 = 1 và q = − . Do đó S = = = . □ 2 1 − q Å 1 ã 3 1 − − 2
Ví dụ 30. Biểu diễn số thập phân vô hạn tuần hoàn 2,222 . . . dưới dạng phân số. Lời giải.
Ta có 2,222 . . . = 2 + 0,2 + 0,02 + 0,002 + . . . = 2 + 2 · 10−1 + 2 · 10−2 + 2 · 10−3 + . . ..
Đây là tổng của cấp số nhân lùi vô hạn với u1 = 2, q = 10−1 nên u1 2 20 2,222 . . . = = = . 1 − q 1 9 1 − 10 □ 1 1 1
Ví dụ 31 (Cùng khám phá). Tính tổng của cấp số nhân lùi vô hạn S = 2 + + + + . . . 2 8 32 Lời giải. 1
S là tổng của cấp số nhân lùi vô hạn có số hạng đầu u1 = 2 và công bội q = . 4 u1 2 8 Vậy S = = = . □ 1 − q 1 3 1 − 4 366/764 366/764
Toán 11 theo chương trình GDPT2018 367
Chương 3. Giới hạn. Hàm số liên tục
Biết làm, làm đúng, làm nhanh 2. Bài tập tự luyện 1
Bài 48. Cho cấp số nhân (un), với u1 = 1 và công bội q = . 2 a) So sánh |q| với 1.
b) Tính Sn = u1 + u2 + · · · + un từ đó hãy tính lim Sn. Lời giải. 1 1 a) Ta có |q| = = < 1. 2 2 ï Å 1 ãnò 1 · 1 − u Å ã 1 (1 − qn) 2 1 1 b) Ta có Sn = = = 2 · 1 − = 2 − . 1 − q 1 2n 2n−1 1 − 2 Å 1 ã Khi đó lim Sn = lim 2 − = 2. 2n−1 □ 1 1 1
Bài 49. Tính tổng T = 1 + + + . . . + + . . . 3 32 3n Lời giải. 1
Các số hạn của tổng lập thành câp số nhân (un), có u1 = 1, q = nên 3 1 1 1 1 2 T = 1 + + + . . . + + . . . = = · 3 32 3n 1 3 1 − 3 □ 1 1 1 Å 1 ãn−1
Bài 50. Tính tổng S = 1 − + − + . . . + − + . . .. 2 4 8 2 Lời giải. 1 u1 1 2
Đây là tổng của cấp số nhân lùi vô hạng với u1 = 1 và q = − . Do đó S = = = . □ 2 1 − q Å 1 ã 3 1 − − 2
Bài 51. Biểu diễn số thập phân vô hạn tuần hoàn 2,222 . . . dưới dạng phân số. Lời giải.
Ta có 2,222 . . . = 2 + 0,2 + 0,02 + 0,002 + . . . = 2 + 2 · 10−1 + 2 · 10−2 + 2 · 10−3 + . . ..
Đây là tổng của cấp số nhân lùi vô hạn với u1 = 2, q = 10−1 nên u1 2 20 2,222 . . . = = = . 1 − q 1 9 1 − 10 □
Bài 52. Biểu diễn số thập phân vô hạn tuần hoàn 0, (3) dưới dạng phân số. Lời giải. 3 3 3 3 1 Ta có 0, (3) = + + . . . + + . . . = 10 = · □ 10 102 10n 1 3 1 − 10 1 1 1 Å 1 ãn
Bài 53. Tính tổng của cấp số nhân lùi vô hạn 1 − + − + . . . + − + . . .. 4 16 64 4 Lời giải. 367/764 367/764
Toán 11 theo chương trình GDPT2018 368
1. Giới hạn của dãy số
Biết làm, làm đúng, làm nhanh 1
Tổng trên là tổng của cấp số nhân lùi vô hạn có số hạng đầu u1 = 1 và công bội q = − nên 4 1 1 1 Å 1 ãn 1 4 1 − + − + . . . + − + . . . = = . 4 16 64 4 Å 1 ã 5 1 − − 4 □
Bài 54. Biết rằng có thể coi số thập phân vô hạn tuần hoàn 0,666 . . . là tổng của một cấp số nhân lùi vô hạn 1 1
0,666 . . . = 0,6 + 0,06 + 0,006 + . . . = 0,6 + 0,6 · + 0,6 · + . . . . 10 102
Hãy viết 0,666 . . . dưới dạng phân số. Lời giải. 1
Số 0,666 . . . là tổng của cấp số nhân lùi vô hạn có số hạng đầu bằng 0,6 và công bội bằng . 10 0,6 6 2 Do đó 0,666 . . . = = = . □ 1 9 3 1 − 10 1 Å 1 ã2 Å 1 ãn
Bài 55. Tính tổng của cấp số nhân lùi vô hạn 1 + + + . . . + + . . .. 3 3 3 Lời giải. 1
Tổng trên là tổng của cấp số nhân lùi vô hạn có số hạng đầu u1 = 1 và công bội q = nên 3 1 Å 1 ã2 Å 1 ãn 1 3 1 + + + . . . + + . . . = = . 3 3 3 1 2 1 − 3 □ 3.
Câu hỏi trắc nghiệm
Câu 61. Cho cấp số nhân u1, u2, . . . với công bội q thỏa điều kiện |q| < 1. Lúc đó, ta nói cấp số nhân đã cho là
lùi vô hạn. Tổng của cấp số nhân đã cho là S = u1 + u2 + u3 + · · · + un + · · · bằng u u u u A 1 1 (qn − 1) 1 1 . B . C . D . q − 1 q − 1 1 + q 1 − q Lời giải.
Theo định nghĩa cấp số nhân lùi vô hạn ta chứng minh được. u1
S = u1 + u2 + u3 + · · · + un + · · · = u1 + u1q1 + u1q2 + · · · + u1qn−1 + · · · = . 1 − q Chọn đáp án D □ 1 1 (−1)n+1 Câu 62. Gọi S = − + · · · + . Khi đó, lim S bằng 3 9 3n 3 1 1 A . B . C . D 1. 4 4 2 Lời giải. Ta có 1 1 (−1)n+1 S = − + · · · + 3 9 3n Å 1 1 (−1)n ã ⇔ S = − − + + · · · + 3 9 3n Å −1 ãn 1 − 1 3 ⇔ S = · 3 −1 1 − 3 1 Å Å −1 ãnã ⇔ S = · 1 − . 4 3 368/764 368/764
Toán 11 theo chương trình GDPT2018 369
Chương 3. Giới hạn. Hàm số liên tục
Biết làm, làm đúng, làm nhanh 1 Å Å −1 ãnã 1 Suy ra lim S = lim · 1 − = . 4 3 4 Chọn đáp án B □ 1 1 1 Câu 63. Tổng S = + + · · · + + · · · có giá trị là 3 32 3n 1 1 1 1 A . B . C . D . 3 2 9 4 Lời giải. 1 1 1 1 1 1 Ta có S = + + · · · + + · · · = · = . 3 32 3n 3 1 − 1 2 3 Chọn đáp án B □ 1 1 1 Câu 64. Tính S = 9 + 3 + 1 + + + · · · + + · · · . Kết quả là 3 9 3n−3 27 A . B 14. C 16. D 15. 2 Lời giải. 1 1 1 1 1 1 27 Ta có S = 9 + 3 + 1 + + + · · · + + · · · = 13 + · = 13 + = . 3 9 3n−3 3 1 − 1 2 2 3 Chọn đáp án A □ 1 1 1 (−1)n+1
Câu 65. Tổng các cấp số nhân vô hạn: 1, − , , − , . . . , , . . . là 2 4 8 2n−1 3 2 2 A . B . C − . D 2. 2 3 3 Lời giải. 1 1 1 (−1)n+1 1 1 1 2 Ta có S = 1 − + − + · · · + + · · · = 1 − · = 1 − = . 2 4 8 2n−1 2 1 + 1 3 3 2 Chọn đáp án B □ 2 4 2n Câu 66. Gọi S = 1 + + + · · · +
+ · · · . Giá trị của S bằng 3 9 3n A 3. B 5. C 6. D 4. Lời giải. 2 4 2n 2 1 Ta có S = 1 + + + · · · + + · · · = 1 + · = 1 + 2 = 3. 3 9 3n 3 1 − 23 Chọn đáp án A □
Câu 67. Số thập phân vô hạn tuần hoàn 0,233333 . . . biểu diễn dưới dạng số là 1 2333 23333 7 A . B . C . D . 23 10000 105 30 Lời giải. Å 1 1 ã 1 1 1 1 7 0,233333 . . . = 0,2 + 3 + + . . . = 0,2 + 3 · · = + = . 102 103 100 1 − 1 5 30 30 10 Chọn đáp án D □
Câu 68. Số thập phân vô hạn tuần hoàn 0,212121 . . . biểu diễn dưới dạng phân số là 2121 1 7 212121 A . B . C . D . 104 21 33 106 Lời giải. Å 1 1 ã 1 1 7 0,212121 . . . = 21 + + . . . = 21 · · = . 102 104 102 1 − 1 33 100 Chọn đáp án C □
Câu 69. Số thập phân vô hạn tuần hoàn 0,271414 . . . được biểu diễn bằng phân số: 2714 2617 2786 2687 A . B . C . D . 9900 9900 9900 9900 Lời giải. Å 1 1 ã 1 1 27 7 2687 0,271414 · · · = 0,27 + 14 + . . . = 0,27 + 14 · · = + = . 104 106 104 1 − 1 100 4950 9900 100 369/764 369/764
Toán 11 theo chương trình GDPT2018 370
1. Giới hạn của dãy số
Biết làm, làm đúng, làm nhanh Chọn đáp án D □ 1 1 1 (−1)n
Câu 70. Tổng của cấp số nhân lùi vô hạn: − , , , . . . , , . . . là 2 4 8 2n 1 1 1 A − . B − . C −1. D . 3 4 2 Lời giải. 1 1 1 (−1)n 1 1 Từ − , , , . . . , , . . . có u1 = − và q = − . 2 4 8 2n 2 2 1 1 1 (−1)n − 1 1 Có S = − + + + · · · + + · · · = 2 = − . 2 4 8 2n 1 − − 1 3 2 Chọn đáp án A □
Câu 71. Số thập phân vô hạn tuần hoàn 0,511111 · · · được biểu diễn bởi phân số 47 46 6 43 A . B . C . D . 90 90 11 90 Lời giải. Ta có 1 1 1 1 1 1 1 23 0,511111 · · · = 0,5 + + . . . = + · = + = . 102 103 2 102 1 − 1 2 90 45 10 Chọn đáp án B □ 1 1 1 (−1)n+1
Câu 72. Tổng của cấp số nhân vô hạn , − , , . . . , . . . là 2 4 8 2n 2 1 1 A − . B 1. C − . D . 3 3 3 Lời giải. 1 1 1 (−1)n+1 1 1 1 Ta có S = − + + · · · + + · · · = · = . 2 4 8 2n 2 1 + 1 3 2 Chọn đáp án D □ 1 1 1 (−1)n+1
Câu 73. Tổng của cấp số nhân lùi vô hạn , − , , . . . , , . . . là 2 6 18 2 · 3n−1 3 8 2 3 A . B . C . D . 4 3 3 8 Lời giải. 1 1 Cấp số nhân có u1 =
, q = − . Do đó tổng cần tìm là 2 3 1 u1 1 3 3 S = = 2 = · = . 1 − q 1 + 1 2 4 8 3 Chọn đáp án D □ 1 1 1 (−1)n+1
Câu 74. Tổng của cấp số nhân lùi vô hạn , − , , . . . ·, , . . . là 3 9 27 3n 1 3 1 A 4. B . C . D . 2 4 4 Lời giải. 1 1 Cấp số nhân có u1 =
, q = − . Do đó tổng cần tìm là 3 3 1 u1 1 3 1 S = = 3 = · = . 1 − q 1 + 1 3 4 4 3 Chọn đáp án D □
Câu 75. Số thập phân vô hạn tuần hoàn 0,17232323 . . . được biểu diễn bởi phân số? 1706 153 164 853 A . B . C . D . 9900 990 990 4950 Lời giải. 370/764 370/764
Toán 11 theo chương trình GDPT2018 371
Chương 3. Giới hạn. Hàm số liên tục
Biết làm, làm đúng, làm nhanh Å 1 1 ã 17 1 1 17 23 853 0,17232323 . . . = 0,17 + 23 + + . . . = + 23 · · = + = . 104 106 100 104 1 − 1 100 9900 4950 100 Chọn đáp án D □
Dạng 6. Toán thực tế, liên môn liên quan đến giới hạn dãy số u1 S = u1 + u1q + u1q2 + ... = . 1 − q 1. Ví dụ mẫu Ví dụ 32 (Cánh diều).
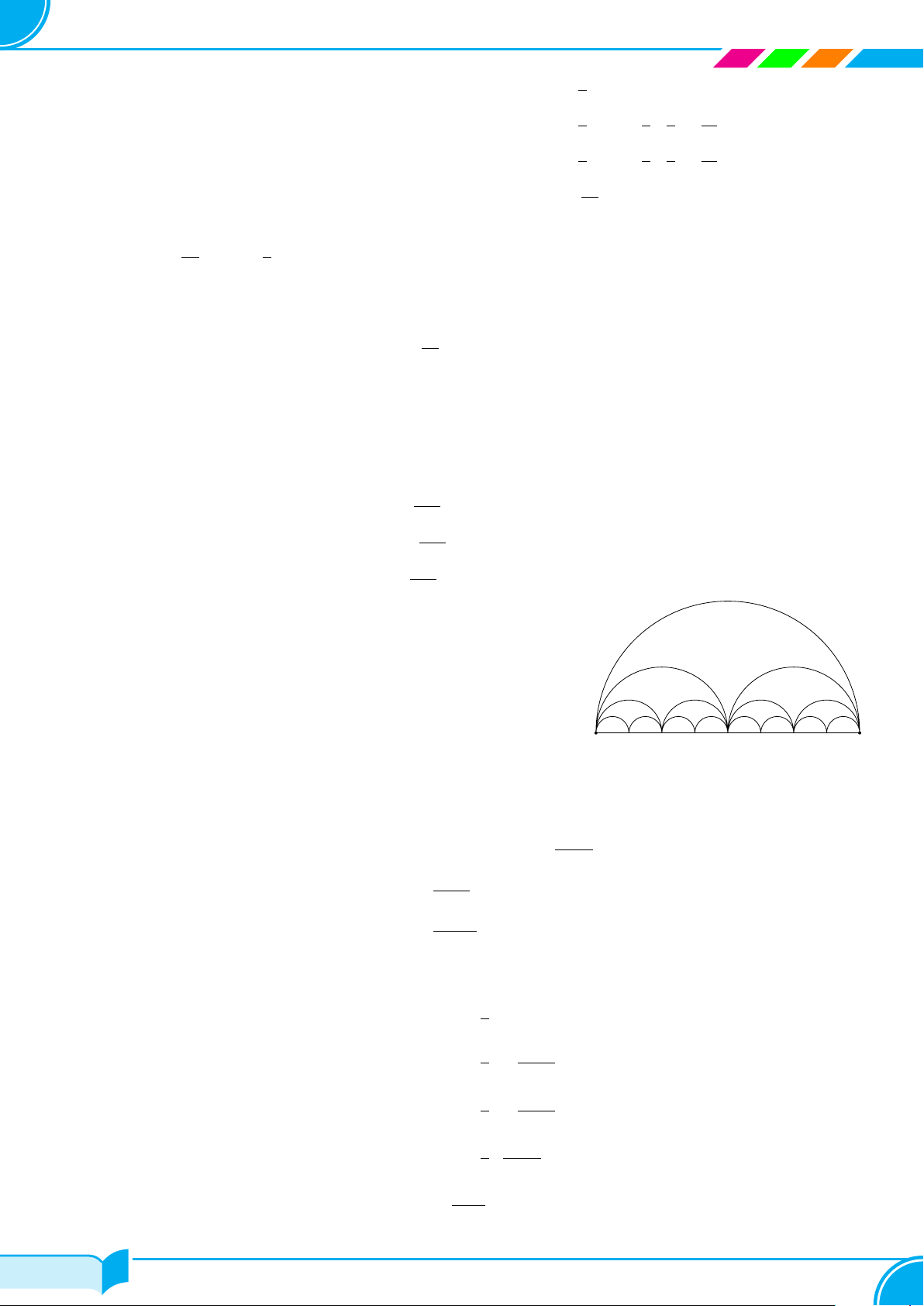
Từ hình vuông có độ dài cạnh bằng 1, người ta nối các trung điểm của cạnh hình vuông
để tạo ra hình vuông mới như hình bên. Tiếp tục quá trình này đến vô hạn.
a) Tính diện tích Sn của hình vuông được tạo thành từ bước thứ n.
b) Tính tổng diện tích của tất cả các hình vuông được tạo thành. 1 Lời giải. 1
a) Từ giả thiết suy ra diện tích hình vuông sau bằng
diện tích hình vuông trước. 2
Khi đó diện tích của các hình vuông tạo thành một cấp số nhân lùi vô hạn với số hạng đầu S1 = 1 và công 1 bội q = . 2 Å 1 ãn−1
Diện tích Sn của hình vuông được tạo thành từ bước thứ n là Sn = S1 · qn−1 = . 2
b) Tổng diện tích của tất cả các hình vuông được tạo thành là: u1 1 S = = = 2. 1 − q 1 1 − 2 □
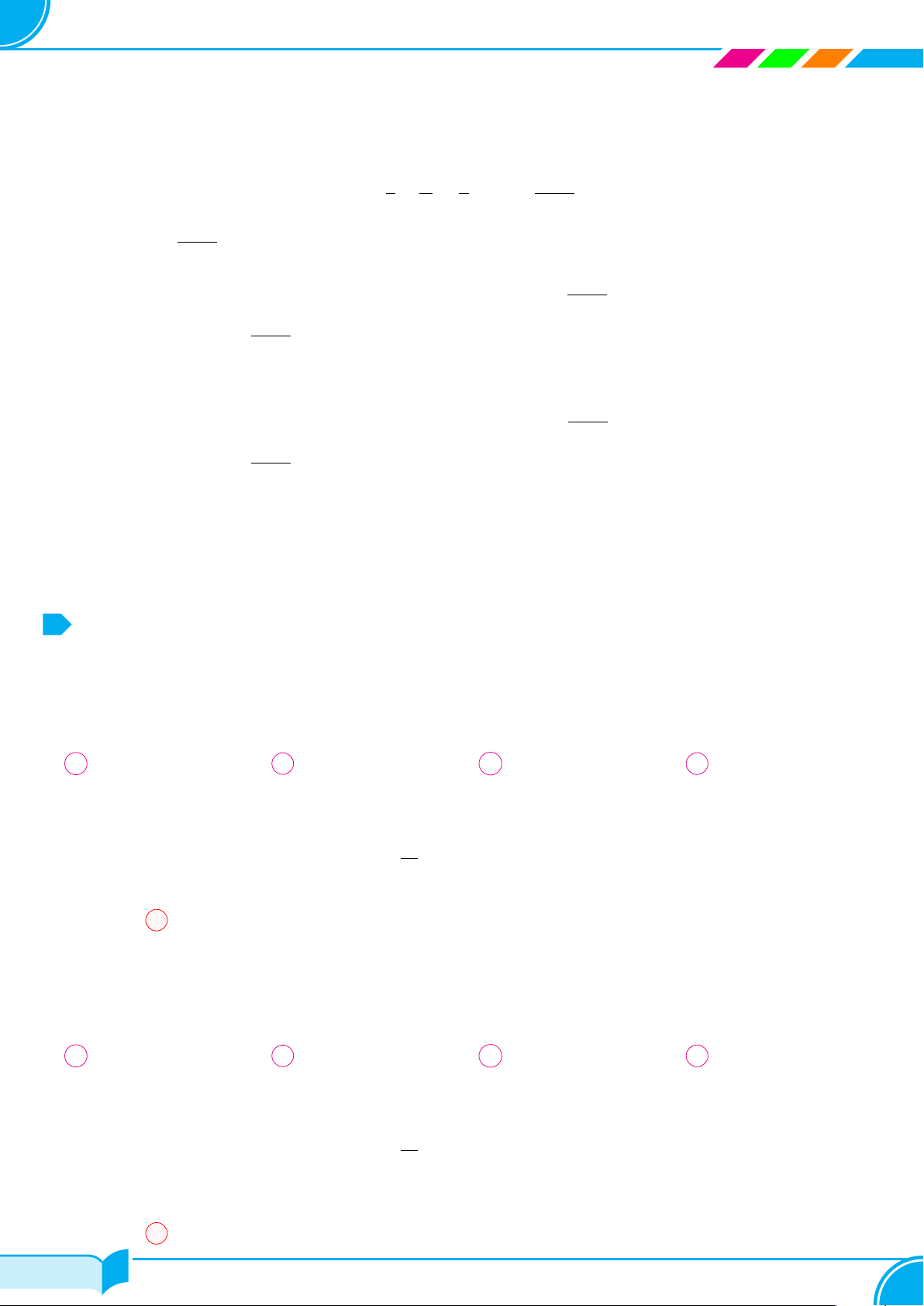
Ví dụ 33 (CTST). Từ tờ giấy, cắt một hình tròn bán kính R (cm) như Hình 3a. Tiếp theo, cắt hai hình tròn bán R kính rồi chồng 2
lên hình tròn đầu tiên như Hình 3b. Tiếp theo, cắt R bốn hình tròn bán kính rồi chồng lên các hình 4
trước như Hình 3c. Cứ thế tiếp tục mãi. Tính tổng
diện tích của các hình tròn. a) b) c) Hình 3 Lời giải.
Diện tích của các hình tròn trong các lần cắt là a) Lần thứ 1: S1 = πR2. Å R ã2 πR2 b) Lần thứ 2: S2 = 2 · π = . 2 2 Å R ã2 πR2 c) Lần thứ 3: S2 = 4 · π = . 4 22 371/764 371/764
Toán 11 theo chương trình GDPT2018 372
1. Giới hạn của dãy số
Biết làm, làm đúng, làm nhanh πR2 d) Lần thứ n: Sn = . 2n−1 1
Do đó diện tích các hình tròn lập thành một cấp số nhân lùi vô hạn có số hạng đầu S1 = πR2 và công bội q = 2
nên tổng diện tích các hình tròn là πR2 S1 + S2 + · · · = = 2πR2. 1 1 − 2 □ Ví dụ 34.
Cho hình vuông cạnh 1 (đơn vị độ dài). Chia hình vuông đó thành bốn hình
vuông nhỏ bằng nhau, sau đó tô màu hình vuông nhỏ góc dưới bên trái (Hình
vẽ bên). Lặp lại các thao tác này với hình vuông nhỏ góc trên bên phải. Giả
sử quá trình trên tiếp diễn vô hạn lần. Gọi u1, u2, . . . , un, . . . lần lượt là độ dài
cạnh của các hình vuông được tô màu.
a) Tính tổng Sn = u1 + u2 + . . . + un. b) Tìm S = lim Sn. n→+∞ Lời giải.
a) Độ của các hình vuông sau khi tô màu 1 1 ○ Lần thứ 1: u1 = · 1 = ; 2 2 1 1 1 ○ Lần thứ 2: u2 = · = ; 2 2 4 1 1 1 ○ Lần thứ 3: u3 = · = ; 2 4 8 Å 1 ãn Å 1 ãn ○ Lần thứ n: un = · 1 = . 2 2 1 1 Å 1 ãn
Vậy Sn = u1 + u2 + . . . + un = + + . . . + . 2 4 2 1 1
b) Độ dài các cạnh hình vuông lập thành một cấp số nhân lùi vô hạn có số hạng đầu u1 = và công bội q = . 2 2 1 u1 S = lim S 2 n = = = 1. n→+∞ 1 − q 1 1 − 2 □ 2. Bài tập tự luyện R
Bài 56. Từ tờ giấy, cắt một hình tròn bán kính R (cm) như Hình 3a. Tiếp theo, cắt hai hình tròn bán kính 2 R
rồi chồng lên hình tròn đầu tiên như Hình 3b. Tiếp theo, cắt bốn hình tròn bán kính rồi chồng lên các hình 4
trước như Hình 3c. Cứ thế tiếp tục mãi. Tính tổng diện tích của các hình tròn. a) b) c) Hình 3 372/764 372/764
Toán 11 theo chương trình GDPT2018 373
Chương 3. Giới hạn. Hàm số liên tục
Biết làm, làm đúng, làm nhanh Lời giải.
Diện tích của hình tròn bán kính R là S1 = π · R2 cm2. R Å R ã2
Diện tích của hình tròn bán kính là S2 = π · cm2. 2 2 R Å R ã2
Diện tích của hình tròn bán kính là S3 = π · cm2. 4 4
Tổng diện tích của các hình tròn là 1 1
Sn = S1 + 2 · S2 + 4 · S3 + . . . = π · R2 + π · R2 · + π · R2 · + · · · 2 4 1 π · R2
Tổng trên là tổng của cấp số nhân lùi vô hạn có số hạng đầu u1 = π·R2 và công bội q = nên Sn = = 2π·R2. 2 1 1 − 2 □ Bài 57.
Từ hình vuông có độ dài cạnh bằng 1, người ta nối các trung điểm của cạnh hình vuông
để tạo ra hình vuông mới như hình bên. Tiếp tục quá trình này đến vô hạn.
a) Tính diện tích Sn của hình vuông được tạo thành từ bước thứ n.
b) Tính tổng diện tích của tất cả các hình vuông được tạo thành. 1 Lời giải. 1
a) Từ giả thiết suy ra diện tích hình vuông sau bằng
diện tích hình vuông trước. 2
Khi đó diện tích của các hình vuông tạo thành một cấp số nhân lùi vô hạn với số hạng đầu S1 = 1 và công 1 bội q = . 2 Å 1 ãn−1
Diện tích Sn của hình vuông được tạo thành từ bước thứ n là Sn = S1 · qn−1 = . 2
b) Tổng diện tích của tất cả các hình vuông được tạo thành là: u1 1 S = = = 2. 1 − q 1 1 − 2 □
Bài 58. Có 1 kg chất phóng xạ độc hại. Biết rằng, cứ sau một khoảng thời gian T = 24000 năm thì một nửa số
chất phóng xạ này bị phân rã thành chất khác không độc hại đối với sức khỏe của con người (T được gọi là chu kì bán rã ).
(Nguồn: Đại số và giải tích 11, NXB GD Việt Nam, 2021 )
Gọi un là khối lượng chất phóng xạ còn lại sau chu kì thứ n.
a) Tìm số hạng tổng quát un của dãy số (un).
b) Chứng minh rằng (un) có giới hạn là 0.
c) Từ kết quả câu 2, chứng tỏ rằng sau một số năm nào đó khối lượng phóng xạ đã cho ban đầu không còn
độc hại với con người, biết rằng chất phóng xạ này sẽ không độc hại nữa nếu khối lượng chất phóng xạ còn lại bé hơn 10−6 g. Lời giải. 373/764 373/764
Toán 11 theo chương trình GDPT2018 374
1. Giới hạn của dãy số
Biết làm, làm đúng, làm nhanh 1
a) Khối lượng chất phóng xạ còn lại sau chu kì bán rã thứ 1 là u1 = · 1 = 1 kg. 2 1 1 1 1
Khối lượng chất phóng xạ còn lại sau chu kì bán rã thứ 2 là u2 = · u1 = · = kg. 2 2 2 22 1 1 1 1
Khối lượng chất phóng xạ còn lại sau chu kì bán rã thứ 3 là u3 = · u2 = · = kg. 2 2 4 23 1
Khối lượng chất phóng xạ còn lại sau chu kì bán rã thứ n là un = kg. 2n 1 Å 1 ãn b) lim un = lim = lim = 0. 2n 2
c) Chất phóng xạ sẽ không độc hại nữa nếu khối lượng chất phóng xạ còn lại bé hơn 10−6 g = 10−9 kg 1 ⇔ un < 10−9 ⇔
< 10−9 ⇔ 2n > 109 ⇔ n ≥ 30. 2n
Vậy sau ít nhất 30 chu kì bằng 30 · 24000 = 720000 năm thì khối lượng phóng xạ đã cho ban đầu không còn
độc hại với con người nữa. □
Bài 59. Gọi C là nữa đường tròn đường kính AB = 2R. AB
C1 là đường gồm hai nửa đường tròn đường kính , 2 AB
C2 là đường gồm bốn nửa đường tròn đường kính , · · · 4 AB
Cn là đường gồm 2n nửa đường tròn đường kính , · · · 2n
Gọi pn là độ dài của Cn, Sn là diện tích hình phẳng giới hạn bởi Cn và C đoạn thẳng AB. a) Tính pn, Sn. C1
b) Tính giới hạn của các dãy số (pn) và (Sn). C2 C3 B A Lời giải. a) Ta có AB
pn = 2n · πr = 2n · π · 2 · 2n πAB = 2 π · 2R = 2 = πR. 1 Sn = 2n · πr2 2 1 Å AB ã2 = 2n · π 2 2 · 2n 1 Å 2R ã2 = 2n · π 2 2 · 2n 1 R2 = 2n · π 2 (2n)2 πR2 = . 2n+1 374/764 374/764
Toán 11 theo chương trình GDPT2018 375
Chương 3. Giới hạn. Hàm số liên tục
Biết làm, làm đúng, làm nhanh b) lim pn = lim (πR) = πR. πR2 lim Sn = lim
= 0 (Vì lim πR2 = πR2 và lim 2n+1 = +∞). 2n+1 □ Bài 60.
Từ độ cao 55, 8 m của tháp nghiêng Pisa nước Ý, người ta
thả một quả bóng cao su chạm xuống đất hình bên dưới.
Giả sử mỗi lần chạm đất quả bóng lại nảy lên độ cao bằng
1 độ cao mà quả bóng đạt được trước đó. Gọi Sn là tổng 10
độ dài quãng đường di chuyển của quả bóng tính từ lúc thả
ban đầu cho đến khi quả bóng đó chạm đất n lần. Tính lim Sn. Lời giải. 1
Mỗi khi chạm đất quả bóng lại nảy lên một độ cao bằng
độ cao của lần rơi ngay trước đó và sau đó lại rơi 10
xuống từ độ cao thứ hai này. Do đó, độ dài hành trình của quả bóng kể từ thời điểm rơi ban đầu đến:
Thời điểm chạm đất lần thứ nhất là d1 = 55,8. 55,8
Thời điềm chạm đất lần thứ hai là d2 = 55,8 + 2 · . 10 55,8 55,8
Thời điểm chạm đất lần thứ ba là d3 = 55,8 + 2 · + 2 · . 10 102 55,8 55, 8 55,8
Thời điểm chạm đất lần thứ tư là d4 = 55,8 + 2 · + 2 · + 2 · . 10 102 103 . . .
Thời điểm chạm đất lần thứ n (n > 1) là 55,8 55,8 55,8 dn = 55,8 + 2 · 55,8 + 2 · + 2 · + . . . + 2 · . 102 103 10n−1
Do đó, quãng đường mà quả bóng đi được kể từ thời điềm rơi đến khi nằm yên trên mặt đất là: 55,8 55,8 55,8 d = 55,8 + 2.55,8 + 2 · + 2 · + . . . + 2 · + . . . = lim dn. 102 103 10n−1 55,8 55,8 55,8 55,8 1 Vì 2 · ; 2 · ; 2 · ; . . . ; 2 ·
; . . . là một cấp số nhân lùi vô hạn với công bội q = nên ta có: 10 102 103 10n−1 10 55,8 55, 8 55,8 55,8 55,8 2 · 2 · + 2 · + 2 · + . . . + 2 · + . . . = 10 = 12,4. 10 102 103 10n−1 1 1 − 10
Vậy d = 55,8 + 12,4 = 68,2 m. □
Bài 61. Cho một tam giác đều ABC cạnh a. Tam giác A1B1C1 có các đỉnh là trung điểm các cạnh của tam giác
ABC, tam giác A2B2C2 có các đỉnh là trung điểm các cạnh của tam giác A1B1C1, . . ., tam giác An+1Bn+1Cn+1
có các đỉnh là trung điểm các cạnh của tam giác AnBnCn, . . . Gọi p1, p2, . . . , pn, . . . và S1, S2, . . . , Sn, . . . theo thứ
tự là chu vi và diện tích của các tam giác A1B1C1, A2B2C2, . . . , AnBnCn, . . ..
a) Tìm giới hạn của các dãy số (pn) và (Sn).
b) Tìm các tổng p1 + p2 + . . . + pn + . . . và S1 + S2 + . . . + Sn + . . .. 375/764 375/764
Toán 11 theo chương trình GDPT2018 376
1. Giới hạn của dãy số
Biết làm, làm đúng, làm nhanh Lời giải.
a) Ta có p1, p2, . . . , pn, . . . lần lượt là chu vi của các tam giác A1B1C1, A2B2C2, . . . , AnBnCn, . . . p1 = 3a 1 p2 = 3 · a 2 . . . 1 pn = 3 · a 2n−1 1 suy ra lim pn = lim 3 · a = 0. 2n−1 √ a2 3 S1 = 4 √ 1 a2 3 S2 = 4 4 . . . √ 1 a2 3 Sn = · 4n−1 4 √ 1 a2 3 suy ra lim Sn = lim · = 0. 4n−1 4 1
b) Dựa vào dữ kiện đề bài suy ra tổng (pn) là tổng của cấp số nhân lùi vô hạn với công bội q = và 2 p1 3a
p1 + p2 + . . . + pn + . . . = lim (pn) = = = 6a. 1 − q 1 − 12 1
Dựa vào dữ kiện đề bài suy ra tổng (Sn) là tổng của cấp số nhân lùi vô hạn với công bội q = và √ 4 √ S a2 3 1 a2 3 S 4
1 + S2 + . . . + Sn + . . . = lim (Sn) = = = . 1 − q 1 − 1 12 4 □ Bài 62.
Từ hình vuông đầu tiên có cạnh bằng 1 (đơn vị độ dài), nối các trung điểm của
bốn cạnh để có hình vuông thứ hai. Tiếp tục nối các trung điểm của bốn cạnh của
hình vuông thứ hai để được hình vuông thứ ba. Cứ tiếp tục làm như thế, nhận
được một dãy hình vuông (xem Hình 5). Hình 5
a) Kí hiệu an là diện tích của hình vuông thứ n và Sn là tổng diện tích của n hình vuông đầu tiên. Viết công
thức tính an, Sn (n = 1, 2, 3, . . .) và tìm lim Sn (giới hạn này nếu có được gọi là tổng diện tích của các hình vuông).
b) Kí hiệu pn là chu vi của hình vuông thứ n và Qn là tổng chu vi của n hình vuông đầu tiên. Viết công thức
tính pn và Qn (n = 1, 2, 3, . . .) và tìm lim Qn (giới hạn này nếu có được gọi là tổng chu vi của các hình vuông). Lời giải. √2
a) Ta có hình vuông thứ nhất có cạnh bằng 1, hình vuông thứ hai có cạnh bằng . 2 1
Hình vuông thứ ba có cạnh bằng . 2 √ Ç ån−1 2
Suy ra hình vuông thứ n có cạnh bằng . 2 376/764 376/764
Toán 11 theo chương trình GDPT2018 377
Chương 3. Giới hạn. Hàm số liên tục
Biết làm, làm đúng, làm nhanh √ √ Ç ån−1 Ç ån−1 2 2 Å 1 ãn−1
Diện tích của hình vuông thứ n là an = · = . 2 2 2 1
Tổng diện tích của n hình vuông đầu tiên là tổng của cấp số nhân có số hạng đầu a1 = 1 và công bội q = 2 nên Å 1 ãn 1 − a ï Å ãn ò 1 (1 − qn) 2 1 Sn = = = 2 1 − . 1 − q 1 2 1 − 2 ï Å 1 ãnò ï Å 1 ãnò lim Sn = lim 2 1 − = 2 lim 1 − lim = 2. 2 2 √
b) Hình vuông thứ nhất có chu vi bằng 4, hình vuông thứ 2 có chu vi là 2 2, hình vuông thứ 3 có chu vi là 2. √ Ç ån−1 2
Suy ra hình vuông thứ n có chu vi bằng pn = 4 ·
. Tổng chu vi của n hình vuông đầu tiên là tổng 2 √2
của cấp số nhân có số hạng đầu p1 = 4 và công bội q = nên 2 √ Ç Ç ån å 2 4 1 − √ ñ Ç ån ô p 2 √ 1 (1 − qn) Ä ä 2 Qn = = √ = 8 + 4 2 1 − . 1 − q 2 2 1 − 2 √ √ ñ Ç ån ô √ √ Ä ä 2 Ä ä lim Qn = 8 + 4 2 lim 1 − = 8 + 4 2 (1 − 0) = 8 + 4 2. 2 □
Bài 63. Xét quá trình tạo ra hình có chu vi vô cực và diện tích bằng 0 như sau:
Bắt đầu bằng một hình vuông H0 cạnh bằng 1 đơn vị độ dài (xem Hình 6a). Chia hình vuông H0 thành chín hình
vuông bằng nhau, bỏ đi bốn hình vuông, nhận được hình H1 (xem Hình 6b). Tiếp theo, chia mỗi hình vuông của
H1 thành chín hình vuông, rồi bỏ đi bốn hình vuông, nhận được hình H2 (xem Hình 6c). Tiếp tục quá trình này,
ta nhận được một dãy hình Hn (n = 1, 2, 3, . . .). H0 H1 H2 H3 a) b) c) d) Hình 6 1
Ta có: H1 có 5 hình vuông, mỗi hình vuông có cạnh bằng ; 3 1 1 1
Ta có: H2 có 5 · 5 = 52 hình vuông, mỗi hình vuông có cạnh bằng · = ; . . .. 3 3 32 1
Từ đó, nhận được Hn có 5n hình vuông, mỗi hình vuông có cạnh bằng . 3n
a) Tính diện tích Sn của Hn và tính lim Sn.
b) Tính chu vi pn của Hn và tính lim pn.
(Quá trình trên tạo nên một hình, gọi là một fractal, được coi là có diện tích lim Sn và chu vi lim pn). Lời giải. 377/764 377/764
Toán 11 theo chương trình GDPT2018 378
1. Giới hạn của dãy số
Biết làm, làm đúng, làm nhanh Å 1 ã2 5
a) Hình vuông H1 có diện tích S1 = 5 · = . 3 9 Å 1 ã2 Å 5 ã2
Hình vuông H2 có diện tích S2 = 52 · = . 32 9 Å 1 ã2 Å 5 ãn
Hình vuông Hn có diện tích Sn = 5n · = . 3n 9 Å 5 ãn lim Sn = lim = 0. 9 1 5
b) Hình vuông H1 có chu vi p1 = 5 · 4 · = 4 · . 3 3 1 Å 5 ã2
Hình vuông H2 có chu vi p2 = 52 · 4 · = 4 · . 32 3 1 Å 5 ãn
Hình vuông Hn có diện tích pn = 5n · 4 · = 4 · . 3n 3 Å 5 ãn lim pn = lim 4 · = +∞. 3 □ Bài 64.
Cho tam giác đều có cạnh bằng a, gọi là tam giác H1. Nối các trung
điểm của H1 để tạo thành tam giác H2. Tiếp theo, nối các trung
điểm của H2 để tạo thành tam giác H3 (Hình bên). Cứ tiếp tục như a
vậy, nhận được dãy tam giác H1, H2, H3, . . .
Tính tổng chu vi và tổng diện tích các tam giác của dãy. Lời giải.
Gọi Si và Ci (i = 1, 2, . . .) lần lượt là diện tích và chu vi của tam giác Hi, i = 1, 2, . . .. Khi đó ta có √ √ √ a2 3 a 2 3 a2 3 S 1 • 1 S1 = ; S2 = = = ; S3 = S2, . . .. 4 2 4 16 4 4 √ a2 3 1
Do đó (Sn) là một cấp số nhân lùi vô hạn với S1 = và q1 = . √ 4 4 S1 a2 3
Tổng diện tích S = S1 + S2 + · · · = = . 1 − q1 3 3a 1 • C1 = 3a; C2 = = C1, . . . 2 2 1
Do đó (Cn) là một cấp số nhân lùi vô hạn với C1 = 3a; q2 = . 2 C1
Tổng chu vi là C = C1 + C2 + · · · = = 6a. 1 − q2 □
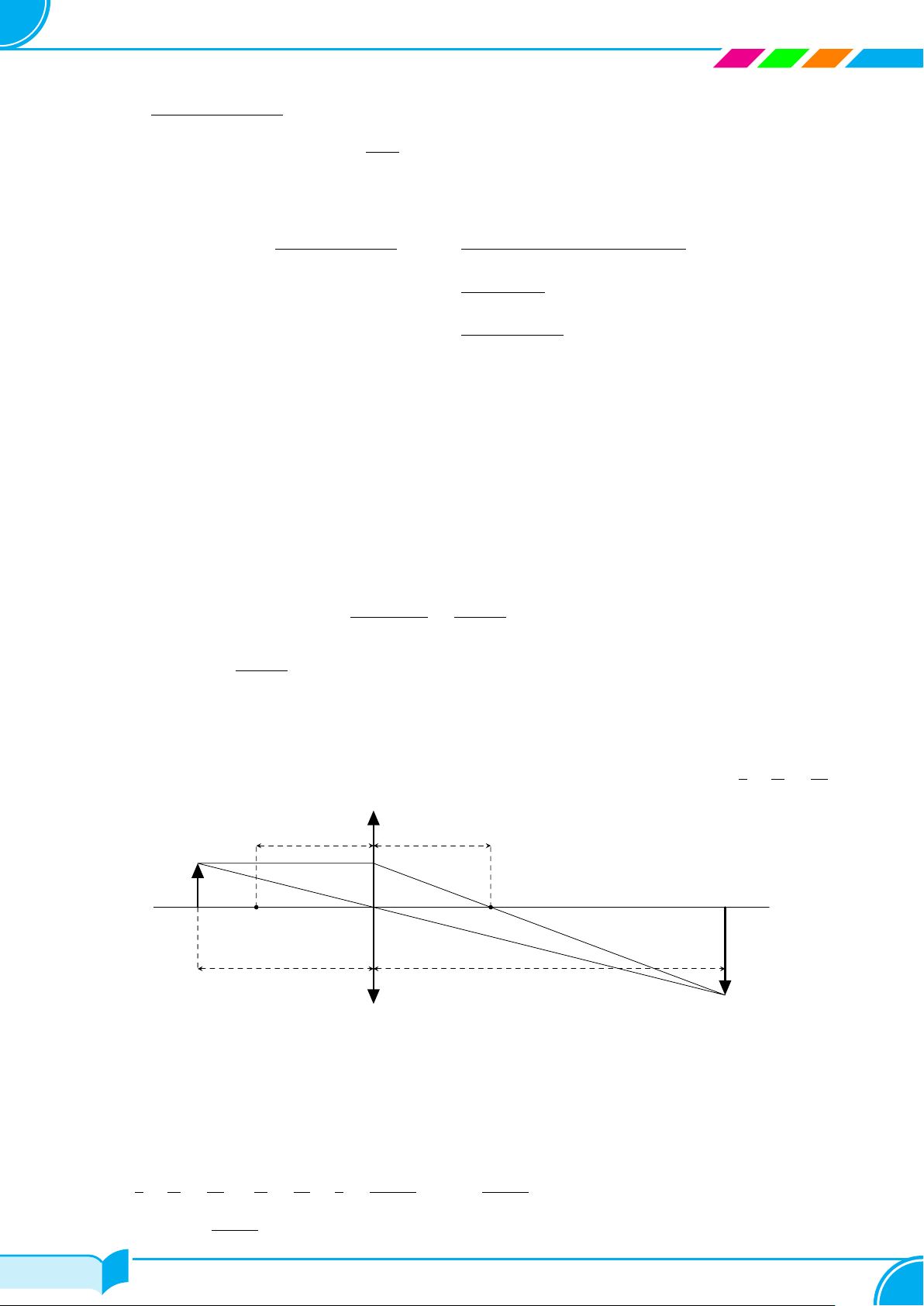
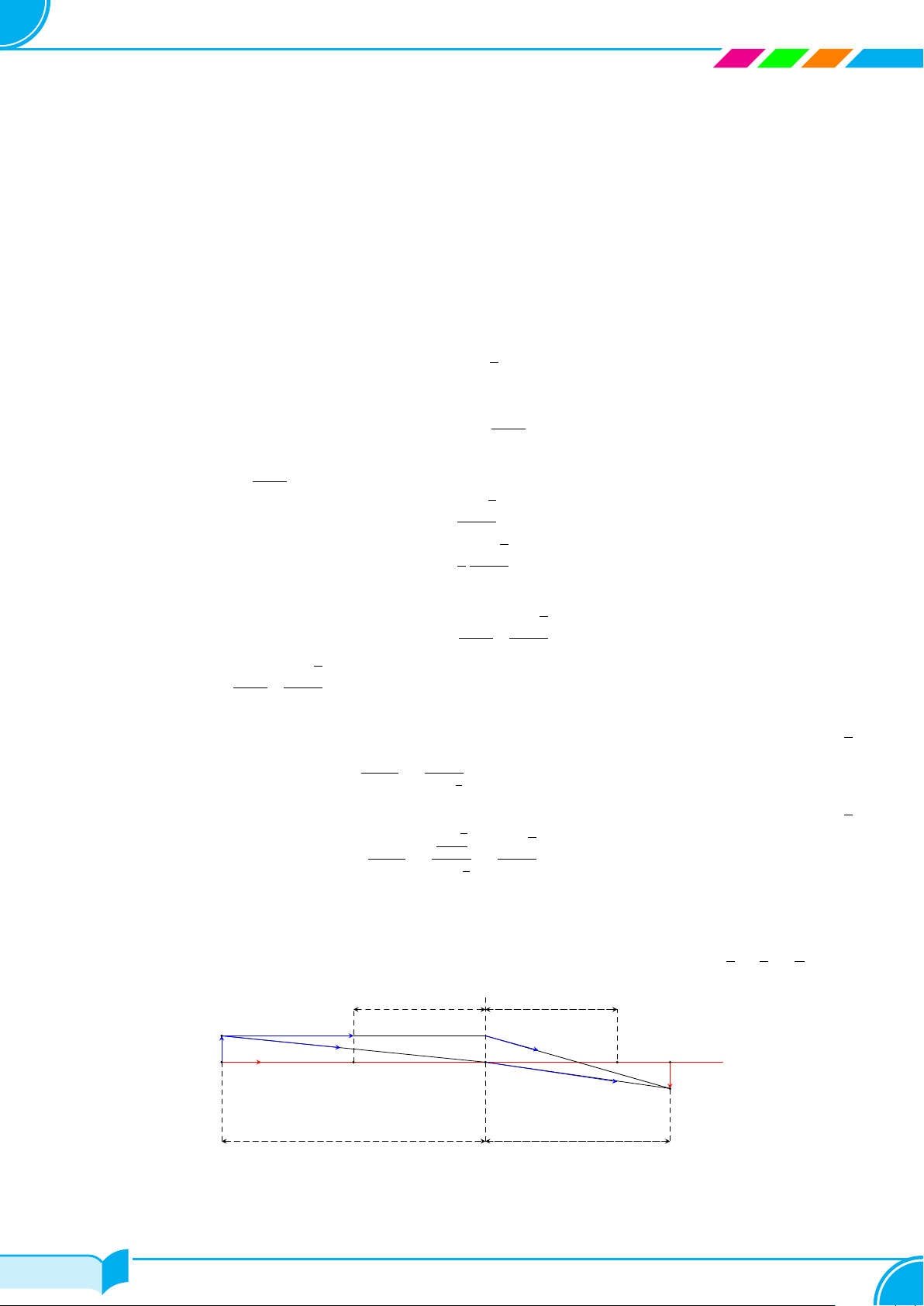
Bài 65. Một thấu kính hội tụ có tiêu cự là f . Gọi d và d′ lần lượt là khoảng cách từ một vật thật AB và từ ảnh 1 1 1
A′B′ của nó tới quang tâm O của thấu kính như hình vẽ bên dưới. Công thức thấu kính là + = . d d f f f B F ′ A′ A F O B′ d d′
a) Tìm biểu thức xác định hàm số d′ = φ(d). 378/764 378/764
Toán 11 theo chương trình GDPT2018 379
Chương 3. Giới hạn. Hàm số liên tục
Biết làm, làm đúng, làm nhanh
b) Tìm lim φ(d), lim φ(d) và lim φ(d). Giải thích ý nghĩa của các kết quả tìm được. d→f + d→f − d→f Lời giải. a) Ta có 1 1 1 df + = ⇔ d′ = . d d′ f d − f df Vậy φ(d) = . d − f df
b) Vì lim df = f 2; lim (d − f ) = 0; d → f + ⇒ d − f > 0 nên lim = +∞. d→f + d→f + d→f + d − f df Vậy lim φ(d) = lim = +∞. d→f + d→f + d − f
Ý nghĩa: Khi đặt vật nằm ngoài tiêu cự và tiến dần đến tiêu điểm thì cho ảnh thật ngược chiều với vật ở vô cùng. df
Vì lim df = f 2; lim (d − f ) = 0; d → f − ⇒ d − f < 0 nên lim = −∞. d→f − d→f + d→f + d − f df Vậy lim φ(d) = lim = −∞. d→f + d→f + d − f
Ý nghĩa: Khi đặt vật nằm trong tiêu cự và tiến dần đến tiêu điểm thì cho ảnh ảo cùng chiều với vật và nằm ở vô cùng.
Vì không tồn tại lim φ(d) và lim φ(d) nên không tồn tại lim φ(d). d→f + d→f − d→f □ 3.
Bài tập trắc nghiệm
Câu 76. Có 1 kg chất phóng xạ độc hại. Biết rằng, cứ sau một khoảng thời gian T = 24000 năm thì một nửa số
chất phóng xạ này bị phân rã thành chất khác không độc hại đối với sức khỏe của con người (T được gọi là chu
kì bán rã ). Gọi un là khối lượng chất phóng xạ còn lại sau chu kì thứ n. Sau ít nhất bao nhiêu chu kì bán rã thì
khối lượng phóng xạ đã cho ban đầu không còn độc hại với con người, biết rằng chất phóng xạ này sẽ không độc
hại nữa nếu khối lượng chất phóng xạ còn lại bé hơn 10−6 g. A 24. B 30. C 100. D 15. Lời giải.
Chất phóng xạ sẽ không độc hại nữa nếu khối lượng chất phóng xạ còn lại bé hơn 10−6 g = 10−9 kg 1 ⇔ un < 10−9 ⇔
< 10−9 ⇔ 2n > 109 ⇔ n ≥ 30. 2n
Vậy sau ít nhất 30 chu kì thì khối lượng phóng xạ đã cho ban đầu không còn độc hại với con người nữa. Chọn đáp án B □
Câu 77. Có 1 kg chất phóng xạ độc hại. Biết rằng, cứ sau một khoảng thời gian T = 24000 năm thì một nửa
số chất phóng xạ này bị phân rã thành chất khác không độc hại đối với sức khỏe của con người (T được gọi là
chu kì bán rã ). Gọi un là khối lượng chất phóng xạ còn lại sau chu kì thứ n. Sau ít nhất bao nhiêu năm thì khối
lượng phóng xạ đã cho ban đầu không còn độc hại với con người, biết rằng chất phóng xạ này sẽ không độc hại
nữa nếu khối lượng chất phóng xạ còn lại bé hơn 10−6 g. A 30. B 2400. C 720000. D 10000. Lời giải.
Chất phóng xạ sẽ không độc hại nữa nếu khối lượng chất phóng xạ còn lại bé hơn 10−6 g = 10−9 kg 1 ⇔ un < 10−9 ⇔
< 10−9 ⇔ 2n > 109 ⇔ n ≥ 30. 2n
Vậy sau ít nhất 30 chu kì bằng 30 · 24000 = 720000 năm thì khối lượng phóng xạ đã cho ban đầu không còn độc
hại với con người nữa. Chọn đáp án C □ 379/764 379/764
Toán 11 theo chương trình GDPT2018 380
1. Giới hạn của dãy số
Biết làm, làm đúng, làm nhanh
Câu 78. Từ hình vuông có độ dài cạnh bằng 1, người ta nối các trung điểm của cạnh hình vuông để tạo ra hình
vuông mới như hình bên. Tiếp tục quá trình này đến vô hạn. Tính tổng diện tích của tất cả các hình vuông được tạo thành. A 1. B 2. C 3. D 4. Lời giải. 1
Từ giả thiết suy ra diện tích hình vuông sau bằng
diện tích hình vuông trước. 2
Khi đó diện tích của các hình vuông tạo thành một cấp số nhân lùi vô hạn với số hạng đầu S1 = 1 và công bội 1 q = . 2 Å 1 ãn−1
Diện tích Sn của hình vuông được tạo thành từ bước thứ n là Sn = S1 · qn−1 = . 2
Tổng diện tích của tất cả các hình vuông được tạo thành là: u1 1 S = = = 2. 1 − q 1 1 − 2 Chọn đáp án B □
Câu 79. Từ hình vuông đầu tiên có cạnh bằng 1 (đơn vị độ dài), nối các trung điểm của bốn cạnh để có hình
vuông thứ hai. Tiếp tục nối các trung điểm của bốn cạnh của hình vuông thứ hai để được hình vuông thứ ba. Cứ
tiếp tục làm như thế, nhận được một dãy hình vuông. Tính tổng chu vi của dãy các hình vuông trên. √ √ √ √ A 8 + 2. B 2 + 2. C 8 + 4 2. D 4 + 4 2. Lời giải. √
Hình vuông thứ nhất có chu vi bằng 4, hình vuông thứ 2 có chu vi là 2 2, hình vuông thứ 3 có chu vi là 2. √ Ç ån−1 2
Suy ra hình vuông thứ n có chu vi bằng pn = 4 ·
. Tổng chu vi của n hình vuông đầu tiên là tổng của 2 √2
cấp số nhân có số hạng đầu p1 = 4 và công bội q = nên 2 √ Ç Ç ån å 2 4 1 − √ ñ Ç ån ô p 2 √ 1 (1 − qn) Ä ä 2 Qn = = √ = 8 + 4 2 1 − . 1 − q 2 2 1 − 2 √ √ ñ Ç ån ô √ √ Ä ä 2 Ä ä lim Qn = 8 + 4 2 lim 1 − = 8 + 4 2 (1 − 0) = 8 + 4 2. 2 Chọn đáp án C □
Câu 80. Bạn An thả quả bóng từ độ cao 6 m so với mặt đất xuống theo phương thẳng đứng sau đó bóng nảy lên
rồi lại rơi xuống cứ như vậy cho đến khi bóng dừng lại trên mặt đất. Tính quãng đường mà bóng đã di chuyển 3
biết rằng sau mỗi lần chạm đất bóng lại nảy lên đến độ cao bằng
độ cao của lần ngay trước đó. 4 A 30 m. B 18 m. C 24 m. D 48 m. Lời giải. 3
Ta thấy độ cao của quả bóng mỗi lần nảy lên là một cấp số nhân với u1 = 6, q =
. Tổng của cấp số nhân lùi vô 4
hạn đó là quãng đường mà quả bóng đã di chuyển đến khi dừng lại, khi đó u1 6 S = = = 24 m. 1 − q 3 1 − 4 Chọn đáp án C □
Câu 81. Từ độ cao 55, 8 m của tháp nghiêng Pisa nước Ý, người ta thả một quả bóng cao su chạm xuống đất 1
hình bên dưới. Giả sử mỗi lần chạm đất quả bóng lại nảy lên độ cao bằng
độ cao mà quả bóng đạt được trước 10 380/764 380/764
Toán 11 theo chương trình GDPT2018 381
Chương 3. Giới hạn. Hàm số liên tục
Biết làm, làm đúng, làm nhanh
đó. Gọi Sn là tổng độ dài quãng đường di chuyển của quả bóng tính từ lúc thả ban đầu cho đến khi quả bóng đó
chạm đất n lần. Tính lim Sn. A 58,8. B 67,2. C 68. D 68,2. Lời giải. 1
Mỗi khi chạm đất quả bóng lại nảy lên một độ cao bằng
độ cao của lần rơi ngay trước đó và sau đó lại rơi 10
xuống từ độ cao thứ hai này. Do đó, độ dài hành trình của quả bóng kể từ thời điểm rơi ban đầu đến:
Thời điểm chạm đất lần thứ nhất là d1 = 55,8. 55,8
Thời điềm chạm đất lần thứ hai là d2 = 55,8 + 2 · . 10 55,8 55,8
Thời điểm chạm đất lần thứ ba là d3 = 55,8 + 2 · + 2 · . 10 102 55,8 55, 8 55,8
Thời điểm chạm đất lần thứ tư là d4 = 55,8 + 2 · + 2 · + 2 · . 10 102 103 . . .
Thời điểm chạm đất lần thứ n (n > 1) là 55,8 55,8 55,8 dn = 55,8 + 2 · 55,8 + 2 · + 2 · + . . . + 2 · . 102 103 10n−1
Do đó, quãng đường mà quả bóng đi được kể từ thời điềm rơi đến khi nằm yên trên mặt đất là: 55,8 55,8 55,8 d = 55,8 + 2.55,8 + 2 · + 2 · + . . . + 2 · + . . . = lim dn. 102 103 10n−1 55,8 55,8 55,8 55,8 1 Vì 2 · ; 2 · ; 2 · ; . . . ; 2 ·
; . . . là một cấp số nhân lùi vô hạn với công bội q = nên ta có: 10 102 103 10n−1 10 55,8 55, 8 55,8 55,8 55,8 2 · 2 · + 2 · + 2 · + . . . + 2 · + . . . = 10 = 12,4. 10 102 103 10n−1 1 1 − 10
Vậy d = 55,8 + 12,4 = 68,2 m. Chọn đáp án D □
Câu 82. Cho tam giác đều ABC cạnh a. Lấy A1, B1, C1 lần lượt là trung điểm của đoạn BC, CA, AB; A2,
B2, C2 lần lượt là trung điểm của đoạn B1C1, C1A1, A1B1; . . . ; cứ tiếp tục như thế cho đến An+1, Bn+1, Cn+1
lần lượt là trung điểm của đoạn BnCn, CnAn, AnBn. Gọi S1, S2, S3, . . . lần lượt là diện tích của các tam giác
A1B1C1, A2B2C2,. . . , AnBnCn,. . . . Tính tổng S = S1 + S2 + · · · + Sn + · · · . √ √ √ √ a2 3 a2 3 a2 3 a2 3 A . B . C . D . 8 15 12 3 Lời giải.
Vì dãy các tam giác A1B1C1, A2B2C2,· · · , AnBnCn,· · · là các tam giác đều nên √ A 3a2
diện tích của các tam giác bằng . 4 A2 C1 B1 B2 C2 B C A1 √ √ 1 Å 1 ã2 3 a2 3
○ Tam giác A1B1C1 có cạnh a nên S1 = a · = . 2 2 4 16 √ √ 1 1 Å 1 ã2 3 1 a2 3
○ Tam giác A2B2C2 có cạnh a = a nên S2 = a · = · . 4 22 22 4 4 16 √ √ 1 1 Å 1 ã2 3 1 a2 3
○ Tam giác A3B3C3 có cạnh a = a nên S3 = a · = · . 8 23 23 4 42 16 381/764 381/764
Toán 11 theo chương trình GDPT2018 382
1. Giới hạn của dãy số
Biết làm, làm đúng, làm nhanh ○ · · · √ √ 1 Å 1 ã2 3 1 a2 3
○ Như vậy tam giác AnBnCn có cạnh a nên Sn = a · = · . 2n 2n 4 4n−1 16 ○ · · · √ a2 3 1
Khi đó, dãy S1, S2, S3,· · · là một cấp số nhân lùi vô hạn với số hạng đầu u1 = S1 = và công bội q = nên √ 16 4 a2 3 √ u1 a2 3 S = S 16
1 + S2 + · · · + Sn + · · · = = = . 1 − q 1 12 1 − √ 4 a2 3 Vậy S = . 12 Chọn đáp án C □ Câu 83.
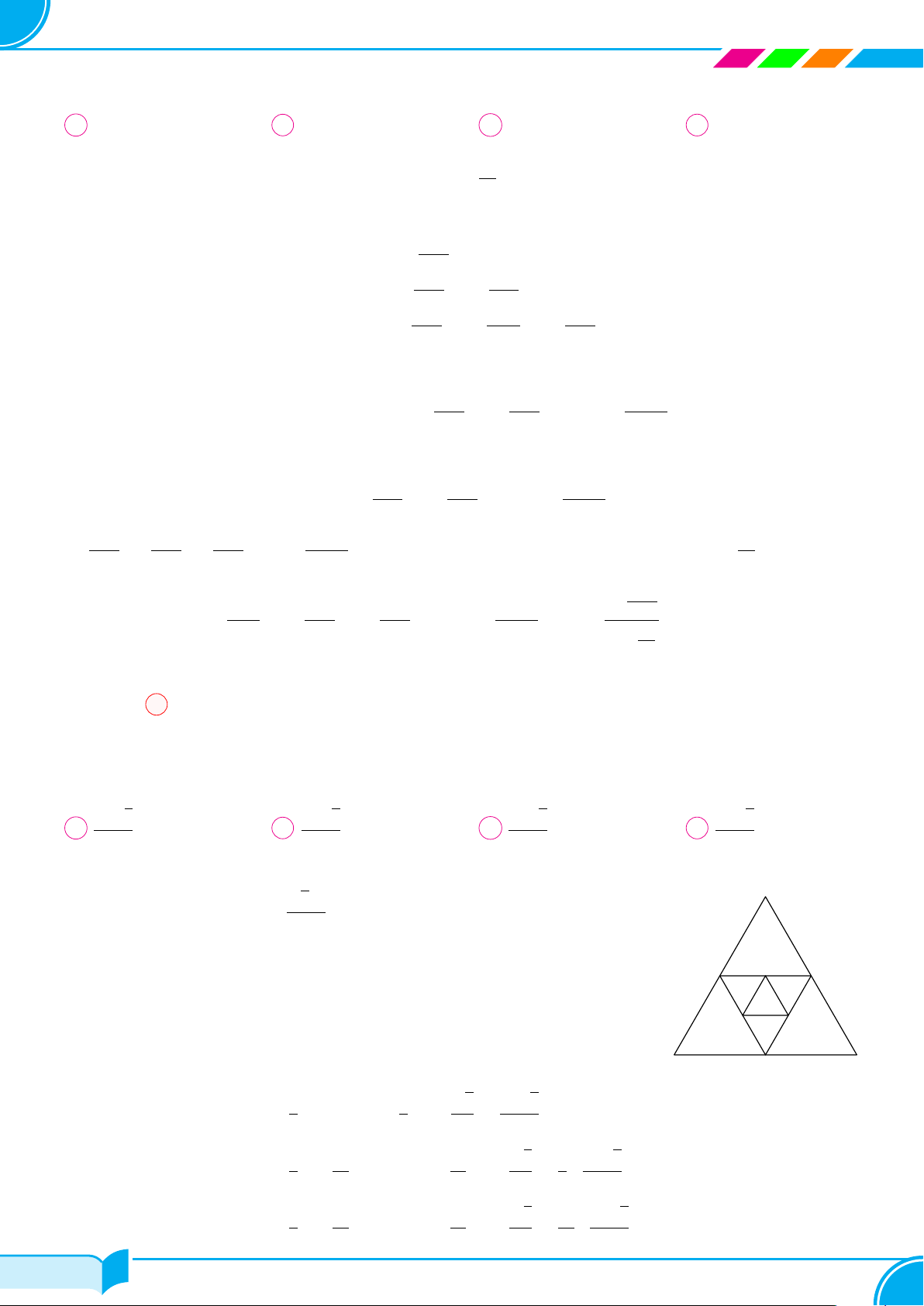
Tam giác mà ba đỉnh của nó là ba trung điểm ba cạnh của tam giác ABC A
được gọi là tam giác trung bình của tam giác ABC. Ta xây dựng dãy các tam
giác A1B1C1, A2B2C2, A3B3C3, . . . sao cho A1B1C1 là một tam giác giác đều
cạnh bằng 3 và với mỗi số nguyên dương n ≥ 2, tam giác AnBnCn là tam giác
trung bình của tam giác An−1Bn−1Cn−1. Với mỗi số nguyên dương n, kí hiệu A2 C1 B S 1
n tương ứng là diện tích hình tròn ngoại tiếp tam giác AnBnCn. Tính tổng
S = S1 + S2 + · · · + Sn + · · · . B2 C2 B C A1 A 4π. B 10π. C 11π. D 6π. Lời giải. √ Ç å2 3 Ta có: S1 = π · 3 · = 3π; 3 √ Ç å2 3 3 3π 1 S2 = π · · = = · S1; 2 3 4 4 √ Ç å2 3 3 3π 1 S3 = π · · = = · S2 4 3 16 4 1
Ta có S1; S2; S3;. . . ;Sn; . . . tạo thành cấp số nhân lùi vô hạn với số hạng đầu là S1 = 3π và công bội q = . 4 Sn 3π
Suy ra S = S1 + S2 + · · · + Sn + · · · = = = 4π. 1 − q 1 1 − 4 Chọn đáp án A □
Câu 84. Từ một hình vuông có diện tích là 1m2. Gọi A, B, C, D lần lượt là trung điểm bốn cạnh của hình
vuông, bạn Hùng dùng bút chì vẽ theo hình vuông ABCD để được hình vuông thứ hai. Bạn Hùng lại tiếp tục vẽ
theo bốn trung điểm các cạnh của hình vuông ABCD để được hình vuông thứ ba, và cứ tiếp tục như vậy. Tính
tổng diện tích tất cả các hình vuông đã có. 1 A 4. B 2. C 3. D . 2 Lời giải. 382/764 382/764
Toán 11 theo chương trình GDPT2018 383
Chương 3. Giới hạn. Hàm số liên tục
Biết làm, làm đúng, làm nhanh
Đặt a = 1 là độ dài cạnh hình vuông, S1 = 1 là diện tích hình D vuông ban đầu.
Do M , N là trung điểm hai cạnh của hình vuông nên M N = √ a 2 a2 S 1 ⇒ 1 S2 = M N 2 = = = . 2 2 2 2
Lại lấy trung điểm các cạnh của hình vuông M N P Q để
tiếp tục, khi đó, hình vuông mới sinh ra có diện tích là √ Ç å2 M N 2 M N 2 S1 1 S3 = = = = . 2 2 4 4 A C 1 1
Vậy các hình vuông sinh ra có diện tích lần lượt là 1, , , . . ., 2 4 1 , . . .. 2n
Vậy tổng diện tích các hình vuông tạo thành là 1 S = 1 · = 2. 1 − 12 B Chọn đáp án B □
Câu 85. Người ta xếp các hình vuông kề với nhau như trong hình dưới đây, mỗi hình vuông có độ dài cạnh bằng
nửa độ dài cạnh của hình vuông trước nó. Nếu hình vuông đầu tiên có cạnh dài 10 cm thì trên tia Ax cần có một
đoạn thẳng dài bao nhiêu xentimet để có thể xếp được tất cả các hình vuông đó? A x A 22. B 15. C 18. D 20. Lời giải.
Tổng các cạnh nằm trên tia Ax của các hình vuông đó là 5 5 10 10 + 5 + + + . . . = = 20 cm. 2 22 1 1 − 2 Chọn đáp án D □ Câu 86.
Cho hình vuông C1 có cạnh bằng a. Chia mỗi cạnh của hình vuông thành bốn
phần bằng nhau và nối các điểm chia một cách thích hợp để có hình vuông C2.
Từ hình vuông C2 lại tiếp tục làm như trên ta nhận được dãy các hình vuông
C1, C2, C3,. . . Gọi Si là diện tích của hình vuông Ci (i ∈ {1; 2; 3; . . .}). Đặt S = 32
S1 + S2 + · · · + Sn + · · · . Biết S = , tính a. 3 5 √ √ A 2. B . C 2. D 2 2. 2 Lời giải. √ Å 3aã2 a 2 a 10 10a2
Ta có S1 = a2, hình vuông C2 có cạnh bằng + = , do đó S2 = . Bằng quy nạp ta chứng 4 4 4 16 383/764 383/764
Toán 11 theo chương trình GDPT2018 384
1. Giới hạn của dãy số
Biết làm, làm đúng, làm nhanh S2 5
minh được (Sn) là một cấp số nhân lùi vô hạn với công bội q = = . Nên S1 8 a2 8a2 32 S = = = ⇔ a = 2. 1 − 5 3 3 8 Chọn đáp án A □ 384/764 384/764
Toán 11 theo chương trình GDPT2018 385
Chương 3. Giới hạn. Hàm số liên tục
Biết làm, làm đúng, làm nhanh Baâi söë 2
GIỚI HẠN CỦA HÀM SỐ
A – GIỚI HẠN HỮU HẠN CỦA HÀM SỐ TẠI MỘT ĐIỂM 1. Định nghĩa
c Định nghĩa 2.1. Cho khoảng K chứa điểm x0 và hàm số f(x) xác định trên K hoặc trên K \ {x0}. Hàm số
f (x) có giới hạn là số L khi x dần tới x0 nếu với dãy số (xn) bất kì, xn ∈ K \ {x0} và xn → x0 thì f (xn) → L.
Kí hiệu lim f (x) = L hay f (x) → L khi x → x0. x→x0
Nhận xét. lim x = x0; lim c = c, với c là hằng số. x→x0 x→x0
Hàm số f (x) có thể không xác định tại x = x0 nhưng vẫn tồn tại giới hạn của hàm số đó khi x dần tới x0. 2.
Phép toán trên giới hạn hữu hạn của hàm số
c Định lí 2.1. Ta thừa nhận định lí sau:
a) Nếu lim f (x) = L và lim g(x) = M (L, M ∈ R) thì x→x0 x→x0
• lim [f (x) + g(x)] = L + M ;
• lim [f (x) · g(x)] = L · M ; x→x0 x→x0 f (x) L
• lim [f (x) − g(x)] = L − M ; • lim = (nếu M ̸= 0). x→x x→x g(x) M 0 0 √
b) Nếu f (x) ≥ 0 và lim f (x) = L thì L ≥ 0 và lim pf (x) = L. x→x0 x→x0 3.
Giới hạn một phía
c Định nghĩa 2.2. Trong trường hợp tổng quát, ta có các định nghĩa sau:
• Cho hàm số y = f (x) xác định trên khoảng (a; x0).
Số L được gọi là giới hạn bên trái của hàm số y = f (x) khi x → x0 nếu với dãy số (xn) bất kì, a < xn < x0
và xn → x0, ta có f (xn) → L. Kí hiệu lim f (x) = L. x→x− 0
• Cho hàm số y = f (x) xác định trên khoảng (x0; b).
Số L được gọi là giới hạn bên phải của hàm số y = f (x) khi x → x0 nếu với dãy số (xn) bất kì,
x0 < xn < b và xn → x0, ta có f (xn) → L. Kí hiệu lim f (x) = L. x→x+ 0
c Định lí 2.2. Định lí sau đây cho ta mối liên hệ giữa “giới hạn hai phía” lim f (x) với giới hạn bên trái x→x0
lim f (x) và giới hạn bên phải lim f (x). x→x− x→x+ 0 0
lim f (x) = L khi và chỉ khi lim f (x) = lim f (x) = L. x→x0 x→x− x→x+ 0 0 385/764 385/764
Toán 11 theo chương trình GDPT2018 386
2. Giới hạn của hàm số
Biết làm, làm đúng, làm nhanh
B – GIỚI HẠN HỮU HẠN CỦA HÀM SỐ TẠI VÔ CỰC
c Định nghĩa 2.3. Trong trường hợp tổng quát, ta có định nghĩa sau
a) Cho hàm số y = f (x) xác định trên khoảng (a; +∞).
Ta nói hàm số y = f (x) có giới hạn là số L khi x → +∞ nếu với dãy số (xn) bất kì, xn > a và xn → +∞, ta có f (xn) → L. Kí hiệu
lim f (x) = L hay f (x) → L khi x → +∞. x→+∞
b) Cho hàm số y = f (x) xác định trên khoảng (−∞; a).
Ta nói hàm số y = f (x) có giới hạn là số L khi x → −∞ nếu với dãy số (xn) bất kì, xn < a và xn → −∞, ta có f (xn) → L. Kí hiệu
lim f (x) = L hay f (x) → L khi x → −∞. x→−∞
○ Với c, k là các hằng số và k nguyên dương, ta luôn có c c lim c = c; lim c = c; lim = 0; lim = 0. x→+∞ x→−∞ x→+∞ xk x→−∞ xk
○ Các phép toán trên giới hạn hữu hạn của hàm số khi x → x0 vẫn còn đúng khi x → +∞ hoặc x → −∞. 2x + 1 Ví dụ 1. Tính lim . x→+∞ x − 1 Lời giải. Ta có Å 1 ã x 2 + 2x + 1 x lim = lim x→+∞ x − 1 x→+∞ Å 1 ã x 1 − x 1 2 + = lim x x→+∞ 1 1 − x 1 lim 2 + lim x→+∞ x→+∞ x = 1 lim 1 − lim x→+∞ x→+∞ x 2 + 0 = 1 − 0 = 2. □
C – GIỚI HẠN VÔ CỰC (MỘT PHÍA) CỦA HÀM SỐ TẠI MỘT ĐIỂM
c Định nghĩa 2.4. Trong trường hợp tổng quát, ta có định nghĩa sau:
a) Cho hàm số y = f (x) xác định trên khoảng (a; +∞).
Ta nói hàm số y = f (x) có giới hạn là +∞ khi x → a+ nếu với dãy số (xn) bất kì, xn > a và xn → a, ta có f (xn) → +∞.
Kí hiệu lim f (x) = +∞ hay f (x) → +∞ khi x → a+. x→a+
b) Các trường hợp lim f (x) = −∞; lim f (x) = +∞; lim f (x) = −∞ được định nghĩa tương tự. x→a+ x→a− x→a− 386/764 386/764
Toán 11 theo chương trình GDPT2018 387
Chương 3. Giới hạn. Hàm số liên tục
Biết làm, làm đúng, làm nhanh
Ta có hai giới hạn cơ bản sau 1 1 lim = +∞; lim = −∞. x→a+ x − a x→a− x − a 1 Ví dụ 2. Tính lim . x→2+ x − 2 Lời giải. 1 Ta có lim = +∞. □ x→2+ x − 2
D – GIỚI HẠN VÔ CỰC CỦA HÀM SỐ TẠI VÔ CỰC
c Định nghĩa 2.5. Trong trường hợp tổng quát, ta có định nghĩa sau
a) Cho hàm số y = f (x) xác định trên khoảng (a; +∞).
Ta nói hàm số y = f (x) có giới hạn là +∞ khi x → +∞ nếu với dãy số (xn) bất kì, xn > a và xn → +∞, ta có f (xn) → +∞. Kí hiệu
lim f (x) = +∞ hay f (x) → +∞ khi x → +∞. x→+∞ b) Các trường hợp
lim f (x) = −∞; lim f (x) = +∞; lim f (x) = −∞ được định nghĩa tương tự. x→+∞ x→−∞ x→−∞
Ta có ba giới hạn cơ bản sau ○
lim xk = +∞ với k là số nguyên dương. x→+∞ ○
lim xk = +∞ với k là số nguyên dương chẵn. x→−∞ ○
lim xk = −∞ với k là số nguyên dương lẻ. x→−∞
Ví dụ 3. Tính lim x3; lim x3. x→+∞ x→−∞ Lời giải. Ta có
lim x3 = +∞; lim x3 = −∞. □ x→+∞ x→−∞
E – CÁC DẠNG TOÁN THƯỜNG GẶP
Dạng 1. Tính giới hạn bằng định nghĩa
Áp dụng các định nghĩa về giới hạn hàm số. 1. Ví dụ mẫu x2 − 9
Ví dụ 4. Xét hàm số f (x) =
(x ̸= 3). Chứng minh rằng lim f (x) = 6. x − 3 x→3 Lời giải.
Giả sử (xn) là dãy số bất kì, thoả mãn xn ̸= 3 và lim xn = 3. Ta có x2 − 9 lim f (x n n) = lim xn − 3 (xn − 3) (xn + 3) = lim xn − 3 = lim (xn + 3) = lim xn + lim 3 387/764 387/764
Toán 11 theo chương trình GDPT2018 388
2. Giới hạn của hàm số
Biết làm, làm đúng, làm nhanh = 3 + 3 = 6. Vậy lim f (x) = 6. □ x→3 x2 − 4
Ví dụ 5 (CTST). Cho hàm số f (x) = . Tìm lim f (x). x + 2 x→−2 Lời giải.
Hàm số y = f (x) xác định trên R \ {−2}.
Giả sử (xn) là dãy số bất kì, thỏa mãn xn ̸= −2 với mọi n và xn → −2 khi n → +∞. Ta có x2 − 4 (xn − 2)(xn + 2) lim f (x n n) = lim = lim
= lim(xn − 2) = lim xn − 2 = −2 − 2 = −4. xn + 2 xn + 2 Vậy lim f (x) = −4. □ x→−2 x − 1 1
Ví dụ 6 (KNTT). Cho hàm số f (x) =
. Chứng tỏ rằng lim f (x) = . x2 − 1 x→1 2 Lời giải. xn − 1 1
Lấy dãy số (xn) bất kì sao cho xn ̸= 1 và xn → 1. Ta có f (xn) = = . x2 − n 1 xn + 1 1 1 1 Do đó lim f (xn) = lim = . Vậy lim f (x) = . □ n→+∞ n→+∞ xn + 1 2 x→1 2
Ví dụ 7 (CTST). Tìm các giới hạn sau: x2 + 2x + 1 a) lim (2x2 − x); b) lim . x→3 x→−1 x + 1 Lời giải. a) Đặt g(x) = 2x2 − x.
Hàm số y = g(x) xác định trên R.
Giả sử (xn) là dãy số bất kì, thỏa mãn xn → 3 khi n → +∞. Ta có lim g(xn) = lim(2x2 − n
xn) = 2 · (lim xn)2 − lim xn = 2 · 32 − 3 = 15. Vậy lim g(x) = 15. x→3 x2 + 2x + 1 b) Đặt h(x) = . x + 1
Hàm số y = h(x) xác định trên R \ {−1}.
Giả sử (xn) là dãy số bất kì, thỏa mãn xn ̸= −1 với mọi n và xn → −1 khi n → +∞. Ta có x2 lim h(x n + 2xn + 1 n) = lim
= lim(xn + 1) = lim xn + 1 = −1 + 1 = 0. xn + 1 Vậy lim h(x) = 0. x→−1 □ 2. Bài tập tự luận
Bài 1. Sử dụng định nghĩa, tìm các giới hạn sau x2 − 25 a) lim x2. b) lim . x→−3 x→5 x − 5 Lời giải. 388/764 388/764
Toán 11 theo chương trình GDPT2018 389
Chương 3. Giới hạn. Hàm số liên tục
Biết làm, làm đúng, làm nhanh
a) Giả sử (xn) là dãy số bất kì, thõa mãn lim xn = −3. Ta có lim x2n = lim xn · lim xn = (−3) · (−3) = 9. Vậy lim x2 = 9. x→−3
b) Giả sử (xn) là dãy số bất kì, thõa mãn xn ̸= 5 và lim xn = 5. Ta có x2 − 25 (xn − 5) (xn+5) lim n = lim xn − 5 xn − 5 = lim(xn + 5) = lim xn + lim 5 = 5 + 5 = 10. x2 − 25 Vậy lim = 10. x→5 x − 5 □ x2 − 4
Bài 2. Cho hàm số f (x) = . Tìm lim f (x). x + 2 x→−2 Lời giải.
Hàm số y = f (x) xác định trên R \ {−2}.
Giả sử (xn) là dãy số bất kì, thỏa mãn xn ̸= −2 với mọi n và xn → −2 khi n → +∞. x2 − 4 (xn − 2)(xn + 2) Ta có lim f (x n n) = lim = lim
= lim(xn − 2) = −2 − 2 = −4. xn + 2 xn + 2 Vậy lim f (x) = −4. □ x→−2 2x − 1
Bài 3. Cho hàm số f (x) = . Tìm lim f (x). x + 2 x→+∞ Lời giải.
Hàm số xác định trên (−∞; −2) và (−2; +∞).
Giả sử (xn) là dãy số sao cho xn > −2 và xn → +∞. Ta có 1 1 2 − 2 − lim 2xn − 1 x x 2 − 0 lim f (x n n n) = lim = lim = = = 2. x 2 2 n + 2 1 + 0 1 + 1 + lim xn xn Vậy lim f (x) = 2. □ x→+∞
Dạng 2. Các phép toán về giới hạn hàm số
a) Nếu lim f (x) = L và lim g(x) = M (L, M ∈ R) thì x→x0 x→x0
• lim [f (x) + g(x)] = L + M ;
• lim [f (x) · g(x)] = L · M ; x→x0 x→x0 f (x) L
• lim [f (x) − g(x)] = L − M ; • lim = (nếu M ̸= 0). x→x x→x g(x) M 0 0 √
b) Nếu f (x) ≥ 0 và lim f (x) = L thì L ≥ 0 và lim pf (x) = L. x→x0 x→x0
c) Các phép toán trên giới hạn hữu hạn của hàm số khi x → x0 vẫn còn đúng khi x → +∞ hoặc x → −∞. 389/764 389/764
Toán 11 theo chương trình GDPT2018 390
2. Giới hạn của hàm số
Biết làm, làm đúng, làm nhanh 1. Ví dụ mẫu
Ví dụ 8 (Cánh Diều). Tính: x2 + 2x + 3 a) lim x2 + x − 6; b) lim . x→2 x→1 2x − 1 Lời giải. a) lim x2 + x − 6 = lim x2 + lim x − lim 6 x→2 x→2 x→2 x→2 = 4 + 2 − 6 = 0. b) lim x2 + 2x + 3 x2 + 2x + 3 lim = x→1 x→1 2x − 1 lim (2x − 1) x→1 lim x2 + lim (2x) + lim 3 = x→1 x→1 x→1 lim (2x) − lim 1 x→1 x→1 1 + 2 + 3 = 2 − 1 = 6. □
Ví dụ 9 (CTST). Tính các giới hạn sau: 3x − 2 a) lim (x2 − 4x + 2); b) lim . x→1 x→2 2x + 1 Lời giải.
a) lim (x2 − 4x + 2) = lim x2 − lim (4x) + lim 2 = 12 − 4 lim x + 2 = 1 − 4 · 1 + 2 = −1; x→1 x→1 x→1 x→1 x→1 lim (3x − 2) 3 lim x − 2 3x − 2 3 · 2 − 2 4 b) lim = x→2 = x→2 = = . x→2 2x + 1 lim (2x + 1) 2 lim x + 1 2 · 2 + 1 5 x→2 x→2 □
Ví dụ 10 (CTST). Tính các giới hạn sau (khử dạng vô định): √ x2 − 4 x + 1 − 2 a) lim ; b) lim . x→2 x − 2 x→3 x − 3 Lời giải. x2 − 4 (x − 2)(x + 2) a) lim = lim
= lim (x + 2) = lim x + lim 2 = 2 + 2 = 4. x→2 x − 2 x→2 x − 2 x→2 x→2 x→2 √x + 1 − 2 b) lim . x→3 x − 3 √ √ √ x + 1 − 2 x + 1 − 2 x + 1 + 2 √ Ä Ä ää lim = lim √ nhân cả tử và mẫu cho x + 1 + 2 x→3 x − 3 x→3 (x − 3) x + 1 + 2 (x + 1) − 4 1 = lim √ = lim √ x→3 (x − 3) x + 1 + 2 x→3 x + 1 + 2 1 1 = √ = √ lim x + 1 + 2 lim x + 1 + 2 x→3 x→3 1 1 1 = = √ = . q lim(x + 1) + 2 3 + 1 + 2 4 x→3 390/764 390/764
Toán 11 theo chương trình GDPT2018 391
Chương 3. Giới hạn. Hàm số liên tục
Biết làm, làm đúng, làm nhanh □
Ví dụ 11 (CTST). Tính các giới hạn sau: x2 − 1 a) lim (x2 + 5x − 2); b) lim . x→−2 x→1 x − 1 Lời giải. a)
lim (x2 + 5x − 2) = ( lim x)2 + lim (5x) − lim 2 = (−2)2 + 5 · (−2) − 2 = −8. x→−2 x→−2 x→−2 x→−2 x2 − 1 (x − 1)(x + 1) b) lim = lim
= lim (x + 1) = lim x + 1 = 1 + 1 = 2. x→1 x − 1 x→1 (x − 1) x→1 x→1 □ x4 + 7
Ví dụ 12 (TH). Tính giới hạn lim . x→+∞ x4 + 1 Lời giải. Å 7 ã 7 x4 1 + x4 + 7 1 + x4 Ta có lim = lim = lim x4 = 1. □ x→+∞ x4 + 1 x→+∞ Å 1 ã x→+∞ 1 x4 1 + 1 + x4 x4 x2 + 1
Ví dụ 13 (TH). Tìm giới hạn lim . x→+∞ 2x4 + x2 − 3 Lời giải. Œ Œ 1 1 1 1 x2 + 1 x + 1 + Ta có lim = lim · x2 x4 = lim · x2 x4 = 0. □ x→+∞ 2x4 + x2 − 3 x→+∞ x2 1 3 x→+∞ x 1 3 2 + − 2 + − x2 x4 x2 x4 Å 1 3 ã
Ví dụ 14 (TH). Tính giới hạn lim − . x→1 1 − x 1 − x3 Lời giải. Å 1 3 ã 1 + x + x2 − 3 (x − 1)(x + 2) −(x + 2) lim − = lim = lim = lim = −1. □ x→1 1 − x 1 − x3 x→1 1 − x3 x→1 (1 − x) (1 + x + x2) x→1 1 + x + x2 x2 + mx + n
Ví dụ 15 (VDT). Cho m, n là các số thực khác 0. Nếu giới hạn lim = 3, hãy tìm mn. x→−5 x + 5 Lời giải. x2 + mx + n Vì lim
= 3 nên x = −5 là nghiệm của phương trình x2 + mx + n = 0. x→−5 x − 5
⇒ −5m + n + 25 = 0 ⇔ n = 5m − 25. x2 + mx + n x2 + mx + 5m − 25 Khi đó lim = lim x→−5 x − 1 x→−5 x + 5 (x + 5)(x − 5 + m) = lim x→−5 x + 5
= lim (x − 5 + m) = m − 10. x→−5
Ta có m − 10 = 3 ⇔ m = 13 ⇒ n = 40. Vậy mn = 13 · 40 = 520. □ √ a 2x2 + 3 + 2024 1
Ví dụ 16 (VDT). Tìm số thực a thỏa mãn lim = . x→+∞ 2x + 2023 2 Lời giải. … √ 3 2024 a 2 + + √ √ a 2x2 + 3 + 2024 1 x2 x 1 a 2 1 2 Ta có lim = ⇔ lim = ⇔ = ⇔ a = . □ x→+∞ 2x + 2023 2 x→+∞ 2023 2 2 2 2 2 + x 391/764 391/764
Toán 11 theo chương trình GDPT2018 392
2. Giới hạn của hàm số
Biết làm, làm đúng, làm nhanh 2. Bài tập tự luận
Bài 4. Biết rằng hàm số f (x) thoả mãn lim f (x) = 3 và lim f (x) = 5. Trong trường hợp này có tồn tại giới x→2− x→2+
hạn lim f (x) hay không? Giải thích. x→2 Lời giải.
Ta có lim f (x) = 3 và lim f (x) = 5, do đó lim f (x) ̸= lim f (x). x→2− x→2+ x→2− x→2+
Vậy không tồn tại lim f (x). □ x→2
Bài 5. Tính các giới hạn sau √ x2 − 5x + 6 x − 1 a) lim x2 − 4x + 3; b) lim ; c) lim . x→2 x→3 x − 3 x→1 x − 1 Lời giải. a) lim x2 − 4x + 3 = lim x2 − lim (4x) + lim 3 x→2 x→2 x→2 x→2 = 4 − 8 + 3 = −1. b) x2 − 5x + 6 (x − 2)(x − 3) lim lim = lim (x − 2) x→3 x − 3 x→3 x − 3 x→3 = lim x − lim 2 x→3 x→3 = 3 − 2 = 1. c) √ √ x − 1 x − 1 lim = lim √ √ x→1 x − 1 x→1 ( x + 1) ( x − 1) 1 = lim √ x→1 x + 1 lim 1 = x→1 √ lim x + lim 1 x→1 x→1 1 = 1 + 1 1 = . 2 □
Bài 6. Tính các giới hạn sau √ 9x + 1 7x − 11 x2 + 1 a) lim ; b) lim ; c) lim ; x→+∞ 3x − 4 x→−∞ 2x + 3 x→+∞ x √x2 + 1 1 1 d) lim ; e) lim ; f) lim . x→−∞ x x→6− x − 6 x→7+ x − 7 Lời giải. 392/764 392/764
Toán 11 theo chương trình GDPT2018 393
Chương 3. Giới hạn. Hàm số liên tục
Biết làm, làm đúng, làm nhanh a) Å 1 ã x 9 + 9x + 1 x lim = lim x→+∞ 3x − 4 x→+∞ Å 4 ã x 3 − x 1 9 + = lim x x→+∞ 4 3 − x 1 lim 9 + lim x→+∞ x→+∞ x = 4 lim 3 − lim x→+∞ x→+∞ x 9 + 0 = 3 − 0 = 3. b) Å 11 ã x 7 − 7x − 11 x lim = lim x→−∞ 2x + 3 x→−∞ Å 3 ã x 2 + x 11 7 − = lim = x x→−∞ 3 2 + x 11 lim 7 − lim x→−∞ x→−∞ x = 3 lim 2 + lim x→−∞ x→−∞ x 7 − 0 = 2 + 0 7 = . 2 c) … √ 1 x 1 + x2 + 1 x2 lim = lim x→+∞ x x→+∞ x … 1 = lim 1 + x→+∞ x2 1 = lim 1 + lim x→+∞ x→+∞ x2 √ = 1 + 0 = 1. d) … √ 1 −x 1 + x2 + 1 x2 lim = lim x→−∞ x x→−∞ x … 1 = lim − 1 + x→−∞ x2 393/764 393/764
Toán 11 theo chương trình GDPT2018 394
2. Giới hạn của hàm số
Biết làm, làm đúng, làm nhanh 1 = − lim 1 + lim x→−∞ x→−∞ x2 √ = − 1 + 0 = −1. 1 e) lim = −∞ x→6− x − 6 1 f) lim = +∞. x→7+ x − 7 □
Bài 7. Tìm các giới hạn sau √ x − 3 3 − x + 8 a) lim (x2 − 7x + 4); b) lim ; c) lim . x→−2 x→3 x2 − 9 x→1 x − 1 Lời giải. a)
lim (x2 − 7x + 4) = lim x2 − 7 lim x + lim 4 = (−2)2 − 7 · (−2) + 4 = 22. x→−2 x→−2 x→−2 x→−2 x − 3 x − 3 1 1 1 1 1 b) lim = lim = lim = = = = . x→3 x2 − 9 x→3 (x − 3)(x + 3) x→3 x + 3 lim (x + 3) lim x + 3 3 + 3 6 x→3 x→3 c) Ta có √ √ √ 3 − x + 8 3 − x + 8 3 + x + 8 lim = lim √ x→1 x − 1 x→1 (x − 1) 3 + x + 8 9 − (x + 8) = lim √ x→1 (x − 1) 3 + x + 8 −1 = lim √ x→1 3 + x + 8 −1 = √ lim 3 + x + 8 x→1 −1 = √ 3 + lim x + 8 x→1 −1 = √ 3 + 1 + 8 −1 = 3 + 3 −1 = . 6 □
Bài 8. Tìm các giới hạn sau √ 4x + 3 2 x2 + 1 a) lim ; b) lim ; c) lim . x→+∞ 2x x→−∞ 3x + 1 x→+∞ x + 1 Lời giải. Å ã 3 3 3 lim 4 + 4 + lim 4x + 3 4 + x→+∞ x x→+∞ x 4 + 0 a) lim = lim x = = = = 2. x→+∞ 2x x→+∞ 2 lim 2 2 2 x→+∞ 394/764 394/764
Toán 11 theo chương trình GDPT2018 395
Chương 3. Giới hạn. Hàm số liên tục
Biết làm, làm đúng, làm nhanh 2 2 lim 2 x→−∞ x 0 b) lim = lim x = = = 0. x→−∞ 3x + 1 x→−∞ 1 1 3 + 0 3 + 3 + lim x x→−∞ x c) Ta có … … √ 1 1 |x| 1 + x 1 + x2 + 1 x2 x2 lim = lim = lim x→+∞ x + 1 x→+∞ x + 1 x→+∞ Å 1 ã x 1 + x … 1 … 1 1 + lim 1 + x2 x→+∞ x2 = lim = x→+∞ 1 Å 1 ã 1 + lim 1 + x x→+∞ x … 1 1 + lim √ x→+∞ x2 1 + 0 = = = 1. 1 1 + 0 1 + lim x→+∞ x □
Bài 9. Tính các giới hạn sau √ 9x + 1 7x − 11 x2 + 1 a) lim ; b) lim ; c) lim ; x→+∞ 3x − 4 x→−∞ 2x + 3 x→+∞ x √x2 + 1 1 1 d) lim ; e) lim ; f) lim . x→−∞ x x→6− x − 6 x→7+ x − 7 Lời giải. a) Å 1 ã x 9 + 9x + 1 x lim = lim x→+∞ 3x − 4 x→+∞ Å 4 ã x 3 − x 1 9 + = lim x x→+∞ 4 3 − x 1 lim 9 + lim x→+∞ x→+∞ x = 4 lim 3 − lim x→+∞ x→+∞ x 9 + 0 = 3 − 0 = 3. b) Å 11 ã x 7 − 7x − 11 x lim = lim x→−∞ 2x + 3 x→−∞ Å 3 ã x 2 + x 11 7 − = lim = x x→−∞ 3 2 + x 395/764 395/764
Toán 11 theo chương trình GDPT2018 396
2. Giới hạn của hàm số
Biết làm, làm đúng, làm nhanh 11 lim 7 − lim x→−∞ x→−∞ x = 3 lim 2 + lim x→−∞ x→−∞ x 7 − 0 = 2 + 0 7 = . 2 c) … √ 1 x 1 + x2 + 1 x2 lim = lim x→+∞ x x→+∞ x … 1 = lim 1 + x→+∞ x2 1 = lim 1 + lim x→+∞ x→+∞ x2 √ = 1 + 0 = 1. d) … √ 1 −x 1 + x2 + 1 x2 lim = lim x→−∞ x x→−∞ x … 1 = lim − 1 + x→−∞ x2 1 = − lim 1 + lim x→−∞ x→−∞ x2 √ = − 1 + 0 = −1. 1 e) lim = −∞ x→6− x − 6 1 f) lim = +∞. x→7+ x − 7 □
Bài 10. Tính các giới hạn sau: 1 − 2x a) lim √ . x→+∞ x2 + 1 √ Ä ä b) lim x2 + x + 2 − x . x→+∞ Lời giải. a) Ta có 1 − 2x 4x2 − 4x + 1 lim √ = − lim x→+∞ x2 + 1 x→+∞ x2 + 1 … 4x 1 = − lim 4 − + x→+∞ x2 + 1 x2 + 1 396/764 396/764
Toán 11 theo chương trình GDPT2018 397
Chương 3. Giới hạn. Hàm số liên tục
Biết làm, làm đúng, làm nhanh 4x 1 = − 4 − lim + lim x→+∞ x2 + 1 x→+∞ x2 + 1 Œ 4 1 = − 4 − lim x + lim x2 x→+∞ 1 x→+∞ 1 1 + 1 + x2 x2 = −2. b) Ta có √ Ä ä2 x2 + x + 2 − x2 p x + 2 x2 + x + 2 − x = √ = √ x2 + x + 2 + x x2 + x + 2 + x Å 2 ã 2 x · 1 + 1 + x = = x . Ç… å 1 2 … 1 2 x · 1 + + + 1 1 + + + 1 x x2 x x2 2 √ 1 + Ä ä 1 1 Khi đó lim x2 + x + 2 − x = lim x = = . x→+∞ x→+∞ … 1 2 1 + 1 2 1 + + + 1 x x2 □
Bài 11. Tính các giới hạn sau: (x + 2)2 − 4 a) lim . x→0 x √x2 + 9 − 3 b) lim . x→0 x2 Lời giải. (x + 2)2 − 4 x2 + 4x a) lim = lim = lim (x + 4) = 4. x→0 x x→0 x x→0 √x2 + 9 − 3 x2 1 1 b) lim = lim √ = lim √ = . Ä ä x→0 x2 x→0 x2 · x2 + 9 + 3 x→0 x2 + 9 + 3 6 □
Bài 12. Tính các giới hạn sau 3x − 2 a) lim (x2 − 4x + 2); b) lim . x→1 x→2 2x + 1 Lời giải.
a) lim (x2 − 4x + 2) = lim x2 − lim (4x) + lim 2 = 12 − 4 lim x + 2 = 1 − 4 · 1 + 2 = −1; x→1 x→1 x→1 x→1 x→1 lim (3x − 2) 3 lim x − 2 3x − 2 3 · 2 − 2 4 b) lim = x→2 = x→2 = = . x→2 2x + 1 lim (2x + 1) 2 lim x + 1 2 · 2 + 1 5 x→2 x→2 □
Bài 13. Tìm các giới hạn sau x2 2x4 + 3x + 2 a) lim . b) lim 3 . x→3 x3 − x − 6 x→−2 x2 − x + 2 397/764 397/764
Toán 11 theo chương trình GDPT2018 398
2. Giới hạn của hàm số
Biết làm, làm đúng, làm nhanh Lời giải. x2 x2 32 1 a) lim ; do lim = = > 0 x→3 x3 − x − 6 x→3 x3 − x − 6 33 − 3 − 6 2 √ x2 … 1 2 ⇒ lim = = . x→3 x3 − x − 6 2 2 √ 2x4 + 3x + 2 2x4 + 3x + 2 7 2x4 + 3x + 2 … 7 3 28 b) lim 3 ; do lim = ⇒ lim 3 = 3 = . x→−2 x2 − x + 2 x→−2 x2 − x + 2 2 x→−2 x2 − x + 2 2 2 □ f (x) − 16
Bài 14. Cho f (x) là một đa thức thỏa mãn lim = 24. Tính giới hạn sau x→1 x − 1 f (x) − 16 lim . Ä ä
x→1 (x − 1) p2f (x) + 4 + 6 Lời giải. f (x) − 16 Vì lim = 24 nên f (1) = 16. Khi đó x→1 x − 1 f (x) − 16 1 f (x) − 16 lim = · lim = 2. Ä ä
x→1 (x − 1) p2f (x) + 4 + 6 12 x→1 x − 1 □
Bài 15. Tính các giới hạn sau: x2 − 1 a) lim (x2 + 5x − 2); b) lim . x→−2 x→1 x − 1 Lời giải. a)
lim (x2 + 5x − 2) = ( lim x)2 + lim (5x) − lim 2 = (−2)2 + 5 · (−2) − 2 = −8. x→−2 x→−2 x→−2 x→−2 x2 − 1 (x − 1)(x + 1) b) lim = lim
= lim (x + 1) = lim x + 1 = 1 + 1 = 2. x→1 x − 1 x→1 (x − 1) x→1 x→1 □
Bài 16. Tính các giới hạn sau (x3 − 3x)(x + 1) a) lim (3x2 − 2x + 1). b) lim . x→−1 x→2 x2 + 3 Lời giải. a)
lim (3x2 − 2x + 1) = 3 lim x2 − 2 lim x + lim 1 = 3(1)2 − 2 · 1 + 1 = 2. x→−1 x→−1 x→−1 x→−1
b) Do lim (x2 + 3) = 22 + 3 = 7 ̸= 0 và x→2
lim (x3 − 3x)(x + 1) = lim (x3 − 3x) · lim (x + 1) = (23 − 3 · 2) · (2 + 1) = 6 x→2 x→2 x→2 (x3 − 3x)(x + 1) 6 Nên lim = . x→2 x2 + 3 7 □
Bài 17. Tìm các giới hạn sau … 2 … −5 a) lim . b) lim 3 . x→2 x2 − x + 3 x→−3 x2 + x − 12 398/764 398/764
Toán 11 theo chương trình GDPT2018 399
Chương 3. Giới hạn. Hàm số liên tục
Biết làm, làm đúng, làm nhanh Lời giải. … x 2 2 2 a) lim ; do lim = = > 0 x→2 x2 − x + 3 x→2 x2 − x + 3 22 − 2 + 3 5 √ … 2 … 2 10 ⇒ lim = = . x→2 x2 − x + 3 5 5 √ … −5 −5 5 … −5 … 5 3 180 b) lim 3 ; do lim = ⇒ lim 3 = 3 = . x→−3 x2 + x − 12 x→−3 x2 + x − 12 6 x→−3 x2 + x − 12 6 6 □
Bài 18. Cho f (x) = x − 1 và g(x) = x3. Tính các giới hạn sau: a) lim [3f (x) − g(x)]. x→1 [f (x)]2 b) lim . x→1 g(x) Lời giải.
Ta có lim f (x) = lim (x − 1) = lim x − lim 1 = 1 − 1 = 0. Mặt khác, ta thấy lim g(x) = lim x3 = 1. x→1 x→1 x→1 x→1 x→1 x→1 a) Ta có
lim [3f (x) − g(x)] = lim [3f (x)] − lim g(x) = lim 3 · lim f (x) − lim g(x) = 3 · 0 − 1 = −1. x→1 x→1 x→1 x→1 x→1 x→1 b) Ta có lim [f (x)]2 lim f (x) · lim f (x) [f (x)]2 0 lim = x→1 = x→1 x→1 = = 0. x→1 g(x) lim g(x) lim g(x) 1 x→1 x→1 □ x2 − 9
Bài 19 (NB). Tính giới hạn lim . x→3 x − 3 Lời giải. x2 − 9 (x − 3)(x + 3) Ta có lim = lim = lim (x + 3) = 6. □ x→3 x − 3 x→3 x − 3 x→3 x2 − 5x + 6
Bài 20 (TH). Tính giới hạn I = lim . x→2 x − 2 Lời giải. x2 − 5x + 6 (x − 2)(x − 3) I = lim = lim = lim (x − 3) = −1. □ x→2 x − 2 x→2 x − 2 x→2 x4 + 7
Bài 21 (TH). Tính giới hạn lim . x→+∞ x4 + 1 Lời giải. Å 7 ã 7 x4 1 + x4 + 7 1 + x4 Ta có lim = lim = lim x4 = 1. □ x→+∞ x4 + 1 x→+∞ Å 1 ã x→+∞ 1 x4 1 + 1 + x4 x4 x2 + 1
Bài 22 (TH). Tìm giới hạn lim . x→+∞ 2x4 + x2 − 3 Lời giải. Œ Œ 1 1 1 1 x2 + 1 x + 1 + Ta có lim = lim · x2 x4 = lim · x2 x4 = 0. □ x→+∞ 2x4 + x2 − 3 x→+∞ x2 1 3 x→+∞ x 1 3 2 + − 2 + − x2 x4 x2 x4 399/764 399/764
Toán 11 theo chương trình GDPT2018 400
2. Giới hạn của hàm số
Biết làm, làm đúng, làm nhanh Å 1 3 ã
Bài 23 (TH). Tính giới hạn lim − . x→1 1 − x 1 − x3 Lời giải. Å 1 3 ã 1 + x + x2 − 3 (x − 1)(x + 2) −(x + 2) lim − = lim = lim = lim = −1. □ x→1 1 − x 1 − x3 x→1 1 − x3 x→1 (1 − x) (1 + x + x2) x→1 1 + x + x2 x2 + mx + n
Bài 24 (VDT). Cho m, n là các số thực khác 0. Nếu giới hạn lim = 3, hãy tìm mn. x→−5 x + 5 Lời giải. x2 + mx + n Vì lim
= 3 nên x = −5 là nghiệm của phương trình x2 + mx + n = 0. x→−5 x − 5
⇒ −5m + n + 25 = 0 ⇔ n = 5m − 25. x2 + mx + n x2 + mx + 5m − 25 Khi đó lim = lim x→−5 x − 1 x→−5 x + 5 (x + 5)(x − 5 + m) = lim x→−5 x + 5
= lim (x − 5 + m) = m − 10. x→−5
Ta có m − 10 = 3 ⇔ m = 13 ⇒ n = 40. Vậy mn = 13 · 40 = 520. □ √ a 2x2 + 3 + 2024 1
Bài 25 (VDT). Tìm số thực a thỏa mãn lim = . x→+∞ 2x + 2023 2 Lời giải. … √ 3 2024 a 2 + + √ √ a 2x2 + 3 + 2024 1 x2 x 1 a 2 1 2 Ta có lim = ⇔ lim = ⇔ = ⇔ a = . □ x→+∞ 2x + 2023 2 x→+∞ 2023 2 2 2 2 2 + x x2 − 4 Bài 26 (NB). Tính lim . x→2 x − 2 Lời giải. x2 − 4 (x − 2)(x + 2) lim = lim = lim (x + 2) = 2 + 2 = 4. □ x→2 x − 2 x→2 x − 2 x→2 x2 − 12x + 35 Bài 27 (NB). Tính lim . x→5 25 − 5x Lời giải. x2 − 12x + 35 (x − 7)(x − 5) 7 − x 2 Ta có lim = lim = lim = . x→5 25 − 5x x→5 5(5 − x) x→5 5 5 x2 − 12x + 35 2 Vậy lim = . □ x→5 25 − 5x 5 x3 − 8
Bài 28 (TH). Tính giới hạn I = lim . x→2 x2 − 4 Lời giải. x3 − 8 (x − 2) x2 + 2x + 4 x2 + 2x + 4 12 Ta có I = lim = lim = lim = = 3. □ x→2 x2 − 4 x→2 (x − 2)(x + 2) x→2 x + 2 4 x4 − 5x2 + 4
Bài 29 (TH). Tìm giới hạn A = lim . x→2 x3 − 8 Lời giải. Ta có x4 − 5x2 + 4 x2 − 1 x2 − 4 A = lim = lim x→2 x3 − 8 x→2 x3 − 23 x2 − 1 (x − 2) (x + 2) = lim x→2 (x − 2) (x2 + 2x + 4) x2 − 1 (x + 2) = lim x→2 x2 + 2x + 4 400/764 400/764
Toán 11 theo chương trình GDPT2018 401
Chương 3. Giới hạn. Hàm số liên tục
Biết làm, làm đúng, làm nhanh = 1. □ 1 + 3x
Bài 30 (TH). Tìm giới hạn lim √ . x→−∞ 2x2 + 3 Lời giải. Å 1 ã 1 x · + 3 √ 1 + 3x + 3 x 3 2 Ta có lim √ = lim = lim x = − . □ x→−∞ Ç å 2x2 + 3 x→−∞ … 3 x→−∞ … 3 2 −x · 2 + − 2 + x x √ 2x − 3x2 + 2
Bài 31 (TH). Tìm giới hạn lim √ . x→+∞ 5x + x2 + 2 Lời giải. … … √ 2 2 2 − 3 + 2 − 3 + √ 2x − 3x2 + 2 x x2 x2 2 − 3 Ta có lim √ = lim · = lim = . □ x→+∞ 5x + x2 + 2 x→+∞ x … 2 x→+∞ … 2 6 5 + 1 + 5 + 1 + x2 x2 x2024 + x − 2 a a
Bài 32 (VDT). Giá trị của lim bằng , với
là phân số tối giản. Tính giá trị của a2 − b2. x→1 x2023 + x − 2 b b Lời giải. Ta có x2024 + x − 2 x2024 − 1 + x − 1 lim = lim x→1 x2023 + x − 2 x→1 x2023 − 1 + x − 1
(x − 1)(x2023 + x2022 · · · + x + 1) + x − 1 = lim
x→1 (x − 1)(x2022 + x2021 + · · · + x + 1) + x − 1 x2023 + x2022 · · · + x + 2 = lim
x→1 x2022 + x2021 + · · · + x + 2 1 + 1 + · · · + 1 + 2 2025 = = . 1 + 1 + · · · + 1 + 2 2024
Vậy a2 − b2 = 20252 − 20242 = 4049. □ x2 + ax + b
Bài 33 (VDT). Cho giới hạn lim = 3. Tìm a, b. x→3 x − 3 Lời giải. x2 + ax + b Để lim
= 3 thì ta phải có x2 + ax + b = (x − 3)(x − m). x→3 x − 3
Khi đó 3 − m = 3 ⇔ m = 0. Vậy x2 + ax + b = (x − 3)x = x2 − 3x. Suy ra a = −3 và b = 0. □ √4x2 + x + 1 + 4 1
Bài 34 (VDT). Tìm m để lim = . x→−∞ mx − 2 2 Lời giải. … … √ 1 1 4 1 1 4 4 + + − − 4 + + + 4x2 + x + 1 + 4 −x x x2 x x x2 x 2 Ta có lim = lim · = lim = − . x→−∞ mx − 2 x→−∞ x 2 x→−∞ 2 m m − m − x x 2 1 Theo bài ra ta có − = ⇔ m = −4. □ m 2 Å m n ã
Bài 35 (VDC). Tính giới hạn lim − , m, n ∈ ∗ N . x→1 1 − xm 1 − xn Lời giải. Å m n ã ïÅ m 1 ã Å n 1 ãò lim − = lim − − − x→1 1 − xm 1 − xn x→1 1 − xm 1 − x 1 − xn 1 − x 401/764 401/764
Toán 11 theo chương trình GDPT2018 402
2. Giới hạn của hàm số
Biết làm, làm đúng, làm nhanh Å m 1 ã Å n 1 ã = lim − − lim − = A − B. x→1 1 − xm 1 − x x→1 1 − xn 1 − x Å m 1 ã A = lim − x→1 1 − xm 1 − x
m − 1 + x + x2 + · · · + xm−1 = lim x→1 1 − xm
(1 − x) + 1 − x2 + · · · + 1 − xm−1 = lim x→1 1 − xm
(1 − x) 1 + (1 + x) + · · · + 1 + x + · · · + xm−2 = lim x→1
(1 − x) (1 + x + · · · + xm−1)
1 + (1 + x) + · · · + 1 + x + · · · + xm−2 = lim x→1 1 + x + · · · + xm−1 1 + 2 + · · · + m − 1 = lim x→1 m m − 1 = . 2 n − 1
Tương tự, ta tính được B = . 2 Å m n ã m − n Vậy lim − = A − B = . □ x→1 1 − xm 1 − xn 2 √x + 2 − 2 Bài 36. Cho P = lim . Tính P . x→2 x − 2 1 1 A P = . B P = . C P = 1. D P = 0. 4 2 Lời giải.√x+2−2 x − 2 1 1 Ta có: lim = lim √ = lim √ = . x→2 x − 2 x→2 (x − 2) x + 2 + 2 x→2 x + 2 + 2 4 1 Vậy P = . 4 Chọn đáp án A □ √x + 3 − 2
Bài 37. Cho m là hằng số. Tính lim . x→1 x2 + mx − x − m 1 1 1 A . B 1. C . D . m 4 4(m + 1) Lời giải. √x + 3 − 2 x − 1 1 lim = lim √ = . x→1 x2 + mx − x − m x→1 (x − 1)(x + m) x + 3 + 2 4(m + 1) Chọn đáp án D □ √ Ä ä Bài 38. Biết lim
x2 + 1 + x + 1 = a. Tính 2a + 1. x→−∞ A −1. B −3. C 0. D 3. Lời giải. Äp ä −2x lim x2 + 1 + x + 1 = lim √ x→−∞ x→−∞ x2 + 1 − (x + 1) −2 = lim x→−∞ … 1 Å 1 ã − 1 + − 1 + x2 x = 1 ⇒ a = 1. Vậy 2a + 1 = 3. Chọn đáp án D □ 402/764 402/764
Toán 11 theo chương trình GDPT2018 403
Chương 3. Giới hạn. Hàm số liên tục
Biết làm, làm đúng, làm nhanh √ Ä ä Bài 39. Biết lim
4x2 − 3x + 1 − (ax + b) = 0. Tính giá trị biểu thức T = a − 4b. x→+∞ A T = −2. B T = 5. C T = −1. D T = 3. Lời giải. √
Từ giả thiết, đường thẳng y = ax + b là tiệm cận xiên của đồ thị hàm số y =
4x2 − 3x + 1, khi x → +∞. Từ đó, √4x2 − 3x + 1 a = lim = 2, x→+∞ x √ Ä ä b = lim 4x2 − 3x + 1 − 2x x→+∞ −3x + 1 = lim √ x→+∞ 4x2 − 3x + 1 + 2x −3 + 1 3 = lim x = − . x→+∞ »4 − 3 + 1 + 2 4 x x2 Suy ra a − 4b = 5. Chọn đáp án B □ f (x) + 1 pf(x) + 2x + 1 − x
Bài 40. Cho f (x) là hàm đa thức thỏa lim = a và tồn tại lim = T . Chọn đẳng x→2 x − 2 x→2 x2 − 4 thức đúng a + 2 a + 2 a − 2 a − 2 A T = . B T = . C T = . D T = . 16 8 8 16 Lời giải. f (x) + 1
Vì f (x) là đa thức và lim
= a nên suy ra f (x) + 1 = (x − 2)g(x), g(2) = a. x→2 x − 2 Do đó p(x − 2)g(x) + 2x − x T = lim x→2 x2 − 4 (x − 2)g(x) + 2x − x2 = lim î ó
x→2 (x − 2)(x + 2) p(x − 2)g(x) + 2x + x g(x) − x = lim î ó
x→2 (x + 2) p(x − 2)g(x) + 2x + x a − 2 = . 16 Chọn đáp án D □ 3.
Câu hỏi trắc nghiệm
Câu 1. Biết lim f (x) = m, lim g(x) = n. Tính lim [f (x) + g(x)]. x→+∞ x→+∞ x→+∞ m A m + n. B m − n. C mn. D . n Lời giải. Ta có
lim [f (x) + g(x)] = lim f (x) + lim g(x) = m + n. x→+∞ x→+∞ x→+∞ Chọn đáp án A □
Câu 2. Khẳng định nào sau đây là đúng? A q q lim 3 pf(x) + g(x) = 3 p 3 p 3 p 3 lim f (x) + 3 lim g(x). B lim f (x) + g(x) = lim f (x) + lim g(x). x→x0 x→x0 x→x0 x→x0 x→x0 x→x0 î ó C q lim 3 pf(x) + g(x) = 3 p 3 p 3 lim [f (x) + g(x)]. D lim f (x) + g(x) = lim f (x) + 3 pg(x) . x→x0 x→x0 x→x0 x→x0 Lời giải. q
Theo định lý về giới hạn của thì lim 3
pf(x) + g(x) = 3 lim [f(x) + g(x)]. x→x0 x→x0 Chọn đáp án C □ 403/764 403/764
Toán 11 theo chương trình GDPT2018 404
2. Giới hạn của hàm số
Biết làm, làm đúng, làm nhanh
Câu 3. Cho các giới hạn lim f (x) = 2, lim g(x) = 3. Tính M = lim [3f (x) − 4g(x)]. x→x0 x→x0 x→x0 A M = 5. B M = 2. C M = −6. D M = 3. Lời giải.
Ta có M = lim [3f (x) − 4g(x)] = 3 lim f (x) − 4 lim g(x) = 6 − 12 = −6. x→x0 x→x0 x→x0 Chọn đáp án C □
Câu 4. Biết lim f (x) = m, lim g(x) = n. Tính lim [f (x) − g(x)]. x→+∞ x→+∞ x→+∞ m A m + n. B m − n. C mn. D . n Lời giải. Ta có
lim [f (x) − g(x)] = lim f (x) − lim g(x) = m − n. x→+∞ x→+∞ x→+∞ Chọn đáp án B □
Câu 5. Cho lim f (x) = −∞, kết quả của lim [−3 · f (x)] bằng x→a x→a A +∞. B 0. C 3. D −∞. Lời giải.
Có lim [−3 · f (x)] = −3 · lim f (x) = +∞. x→a x→a Chọn đáp án A □
Câu 6. Cho k ∈ Z, kết quả của lim x2k+1 bằng x→−∞ A 0. B −∞. C +∞. D 5. Lời giải.
Theo tính chất của giới hạn hàm số, ta có lim x2k+1 = −∞. x→−∞ Chọn đáp án B □
Câu 7. Cho lim f (x) = −2. Giá trị lim [f (x) + 4x − 1] bằng x→3 x→3 A 5. B 6. C −11. D 9. Lời giải.
lim [f (x) + 4x − 1] = lim f (x) + lim 4x − 1 = −2 + 4 · 3 − 1 = 9. x→3 x→3 x→3 Chọn đáp án D □
Câu 8. Cho lim f (x) = 3. Giá trị của lim [f (x) + x] bằng x→2 x→2 A 5. B 6. C 1. D 4. Lời giải.
Ta có lim [f (x) + x] = lim f (x) + lim x = 3 + 2 = 5. x→2 x→2 x→2 Chọn đáp án A □
Câu 9. Với k là số nguyên dương. Kết quả của giới hạn lim x2k là x→+∞ A +∞. B 0. C −∞. D 1. Lời giải. Với k nguyên dương thì
lim xk = +∞ ⇒ lim x2k = +∞. x→+∞ x→+∞ Chọn đáp án A □
Câu 10. Cho c là hằng số, k là số nguyên dương. Khẳng định nào sau đây sai? c A lim c = +∞. B lim = 0. C lim c = c. D lim x = x0. x→+∞ x→+∞ xk x→x0 x→x0 Lời giải.
Theo định lý về giới hạn, khẳng định sai là lim c = +∞. x→+∞ Chọn đáp án A □ 404/764 404/764
Toán 11 theo chương trình GDPT2018 405
Chương 3. Giới hạn. Hàm số liên tục
Biết làm, làm đúng, làm nhanh
Câu 11. Cho lim f (x) = a, lim g(x) = b. Hỏi mệnh đề nào sau đây là mệnh đề sai? x→+∞ x→+∞ A lim [f (x) · g(x)] = ab. B
lim [f (x) − g(x)] = a − b. x→+∞ x→+∞ f (x) a C lim [f (x) + g(x)] = a + b. D lim = . x→+∞ x→+∞ g(x) b Lời giải. f (x) a Khi lim g(x) = b = 0 thì lim = không đúng. □ x→+∞ x→+∞ g(x) b 1
Câu 12. Với k là số nguyên dương thì lim bằng x→−∞ xk A +∞. B −∞. C x. D 0. Lời giải.  lim 1 = 1  x→−∞ 1 Vì nên lim = 0. lim xk = ±∞ x→−∞ xk  x→−∞ Chọn đáp án D □
Câu 13. Tính I = lim x2 + x − 6. x→2 A 0. B 1. C 2. D 3. Lời giải. lim x2 + x − 6 = lim x2 + lim x − lim 6 x→2 x→2 x→2 x→2 = 4 + 2 − 6 = 0. Chọn đáp án A □ x2 + 2x + 3 Câu 14. Tính I = lim . x→1 2x − 1 A 4. B 5. C 6. D 7. Lời giải. lim x2 + 2x + 3 x2 + 2x + 3 lim = x→1 x→1 2x − 1 lim (2x − 1) x→1 lim x2 + lim (2x) + lim 3 = x→1 x→1 x→1 lim (2x) − lim 1 x→1 x→1 1 + 2 + 3 = 2 − 1 = 6. Chọn đáp án C □ |x| Câu 15. Tính I = lim . x→0 x A 1. B −1. C Không tồn tại . D 0. Lời giải. Ta có : |x| x lim = lim = lim 1 = 1. x→0+ x x→0+ x x→0+ |x| (−x) lim = lim = lim (−1) = −1. x→0− x x→0− x x→0− |x| Vậy không tồn tại lim . x→0 x Chọn đáp án C □ 405/764 405/764
Toán 11 theo chương trình GDPT2018 406
2. Giới hạn của hàm số
Biết làm, làm đúng, làm nhanh 9 − x2 Câu 16. Tìm lim . Kết quả là x→3 x2 − 4x + 3 A −3. B 4. C −4. D 3. Lời giải. 9 − x2 (3 − x)(3 + x) −(x + 3) Ta có lim = lim = lim = −3. x→3 x2 − 4x + 3 x→3 (x − 3)(x − 1) x→3 x − 1 Chọn đáp án A □ x2 − 16 Câu 17. Tìm lim . Kết quả là x→4 x − 4 A 7. B 8. C 5. D 6. Lời giải. x2 − 16 (x − 4)(x + 4) Ta có lim = lim = lim (x + 4) = 8. x→4 x − 4 x→4 x − 4 x→4 Chọn đáp án B □ x3 − 1
Câu 18. Tính giới hạn A = lim . x→1 x − 1 A A = −∞. B A = 0. C A = 3. D A = +∞. Lời giải. x3 − 1 (x − 1) x2 + x + 1 Ta có A = lim = lim = lim x2 + x + 1 = 3. x→1 x − 1 x→1 x − 1 x→1 Chọn đáp án C □ x2 + 2x + 1
Câu 19. Chọn kết quả đúng trong các kết quả sau của lim là x→−1 2x + 2 1 A −∞. B 0. C . D +∞. 2 Lời giải. x2 + 2x + 1 (x + 1)2 x + 1 lim = lim = lim = 0. x→−1 2x + 2 x→−1 2(x + 1) x→−1 2 Chọn đáp án B □ x2 + 2x − 15 Câu 20. Giới hạn lim bằng x→4 x − 3 1 A . B 9. C +∞. D 8. 8 Lời giải. x2 + 2x − 15 (x − 3)(x + 5) lim = lim = 9. x→4 x − 3 x→4 x − 3 Chọn đáp án B □ 3x − 2
Câu 21. Tính giới hạn I = lim . x→−∞ 2x + 13 3 A I = −2. B I = − . C I = 2. D I = . 2 2 Lời giải. Å 2 ã 2 x 3 − 3x − 2 3 − x 3 Ta có I = lim = lim = lim x = . x→−∞ 2x + 1 x→−∞ Å 1 ã x→−∞ 1 2 x 2 + 2 + x x Chọn đáp án D □ x − 2 Câu 22. lim bằng x→+∞ x + 3 2 A − . B 1. C 2. D −3. 3 Lời giải. 406/764 406/764
Toán 11 theo chương trình GDPT2018 407
Chương 3. Giới hạn. Hàm số liên tục
Biết làm, làm đúng, làm nhanh Å 2 ã 2 x 1 − x − 2 1 − x 1 Ta có lim = lim = lim x = = 1. x→+∞ x + 3 x→+∞ Å 3 ã x→+∞ 3 1 x 1 + 1 + x x Chọn đáp án B □ x2 − 3x + 2 Câu 23. Giới hạn lim bằng x→1 x3 − x2 + x − 1 1 1 A −2. B −1. C − . D . 2 2 Lời giải. x2 − 3x + 2 (x − 1)(x − 2) x − 2 1 Ta có lim = lim = lim = − . x→1 x3 − x2 + x − 1 x→1 (x − 1)(x2 + 1) x→1 x2 + 1 2 Chọn đáp án C □ x4 − 3x + 2 Câu 24. Giới hạn T = lim bằng x→1 x3 + 2x − 3 2 2 1 A . B . C . D +∞. 9 5 5 Lời giải. x4 − 3x + 2 (x − 1) x3 + x2 + x − 2 x3 + x2 + x − 2 13 + 12 + 1 − 2 1 T = lim = lim = lim = = . x→1 x3 + 2x − 3 x→1 (x − 1) (x2 + x + 3) x→1 x2 + x + 3 12 + 1 + 3 5 Chọn đáp án C □ x2 − 5x + 6 Câu 25. Giới hạn lim bằng x→2 x3 − x2 − x − 2 1 A 0. B − . C −7. D +∞. 7 Lời giải. x2 − 5x + 6 (x − 2)(x − 3) x − 3 −1 Ta có lim = lim = lim = . x→2 x3 − x2 − x − 2 x→2 (x − 2) (x2 + x + 1) x→2 x2 + x + 1 7 Chọn đáp án B □ x4 − 3x2 + 2 Câu 26. Tìm lim . x→1 x3 + 2x − 3 5 2 1 A − . B − . C . D +∞. 2 5 5 Lời giải. x4 − 3x2 + 2 (x − 1)(x + 1) x2 − 2 (x + 1) x2 − 2 2 lim = lim = lim = − . x→1 x3 + 2x − 3 x→1 (x − 1) (x2 + x + 3) x→1 x2 + x + 3 5 Chọn đáp án B □ Å 1 1 ã Câu 27. Tính lim + . x→2 x2 − 3x + 2 x2 − 5x + 6 A 2. B +∞. C −2. D 0. Lời giải. Å 1 1 ã 2x2 − 8x + 8 lim + = lim x→2 x2 − 3x + 2 x2 − 5x + 6
x→2 (x2 − 3x + 2) (x2 − 5x + 6) 2(x − 2)2 2 = lim = lim = −2.
x→2 (x − 1)(x − 2)(x − 2)(x − 3) x→2 (x − 1)(x − 3) Chọn đáp án C □ √x2 + 2 − 2 Câu 28. Giới hạn lim bằng x→+∞ x − 2 A −∞. B 1. C +∞. D −1. Lời giải. 407/764 407/764
Toán 11 theo chương trình GDPT2018 408
2. Giới hạn của hàm số
Biết làm, làm đúng, làm nhanh … … √ 2 2 2 x 1 + − 2 1 + − x2 + 2 − 2 x2 x2 x lim = lim = lim = 1. x→+∞ x − 2 x→+∞ x − 2 x→+∞ 2 1 − x Chọn đáp án B □ (4x + 1)3(2x + 1)4 Câu 29. Cho hàm số f (x) = . Tính lim f (x). (3 + 2x)7 x→−∞ A 2. B 8. C 4. D 0. Lời giải. Å 1 ã3 Å 1 ã4 4 + 2 + (4x + 1)3(2x + 1)4 x x lim f (x) = lim = lim = 23 = 8. x→−∞ x→−∞ (3 + 2x)7 x→−∞ Å 3 ã7 + 2 x Chọn đáp án B □ x2 + bx + c Câu 30. Biết lim
= 8, (b, c ∈ R). Tính P = b + c. x→3 x − 3 A P = −13. B P = −11. C P = 5. D P = −12. Lời giải. x2 + bx + c Vì lim
= 8 là hữu hạn nên tam thức x2 + bx + c có nghiệm x = 3. x→3 x − 3
⇒ 3b + c + 9 = 0 ⇔ c = −9 − 3b. x2 + bx + c x2 + bx − 9 − 3b (x − 3)(x + 3 + b) Khi đó lim = lim = lim x→3 x − 3 x→3 x − 3 x→3 x − 3
= lim (x + 3 + b) = 8 ⇔ 6 + b = 8 ⇔ b = 2 ⇒ c = −15. x→3 Vậy P = b + c = −13. Chọn đáp án A □ ax2 + bx − 5
Câu 31. Cho a, b là số nguyên và lim = 7. Tính a2 + b2 + a + b. x→1 x − 1 A 18. B 1. C 15. D 5. Lời giải. ax2 + bx − 5 Vì lim
= 7 hữu hạn nên x = 1 phải là nghiệm của phương trình ax2 + bx − 5 = 0 suy ra a + b − 5 = x→1 x − 1 0 ⇒ b = 5 − a. ax2 + (5 − a) x − 5 (x − 1) (ax + 5) Khi đó lim = lim
= a + 5 = 7 ⇒ a = 2 nên b = 3. x→1 x − 1 x→1 x − 1 Suy ra a2 + b2 + a + b = 18. Chọn đáp án A □ Å x2 + 1 ã Câu 32. Biết rằng lim + ax − b = −5. Tính tổng a + b. x→+∞ x − 2 A 6. B 7. C 8. D 5. Lời giải. Å x2 + 1 ã
Å (a + 1)x2 − (2a + b)x + 2b + 1 ã lim + ax − b = lim = −5 x→+∞ x − 2 x→+∞ x − 2 ®a + 1 = 0 ®a = −1 ⇔ ⇔ 2a + b = 5 b = 7. Vậy a + b = 6. Chọn đáp án A □ Å 4x2 − 3x + 1 ã
Câu 33. Cho hai số thực a và b thỏa mãn lim − ax − b = 0. Khi đó a + b bằng x→+∞ x + 2 A −4. B 4. C 7. D −7. Lời giải. 408/764 408/764
Toán 11 theo chương trình GDPT2018 409
Chương 3. Giới hạn. Hàm số liên tục
Biết làm, làm đúng, làm nhanh Å 4x2 − 3x + 1 ã Å 23 ã lim − ax − b = 0 ⇔ lim (4 − a) x − b − 11 + = 0. x→+∞ x + 2 x→+∞ x + 2 ®4 − a = 0 ®a = 4 ⇒ ⇔ ⇒ a + b = −7. − 11 − b = 0 b = −11 Chọn đáp án D □ f (x) + 1 x2 + x f (x) + 2 Câu 34. Cho lim = −1. Tính lim . x→1 x − 1 x→1 x − 1 A I = 5. B I = −4. C I = 4. D I = −5. Lời giải. x2 + x f (x) + 2
x2 + x (f (x) + 1) − x2 − x + 2 Ç x2 + x (f (x) + 1) å lim = lim = lim − x − 2 = −5. x→1 x − 1 x→1 x − 1 x→1 x − 1 Chọn đáp án D □
x + x2 + x3 + · · · + x50 − 50
Câu 35. Gọi A là giới hạn của hàm số f (x) =
khi x tiến đến 1. Tính giá trị của x − 1 A. A A không tồn tại. B A = 1725. C A = 1527. D A = 1275. Lời giải. Ta có
x + x2 + x3 + · · · + x50 − 50 lim f (x) = lim x→1 x→1 x − 1 =
lim 1 + (x + 1) + x2 + x + 1 + · · · + x49 + x48 + · · · + 1 x→1 =
1 + 2 + 3 + · · · + 50 = 25(1 + 50) = 1275. Vậy A = lim f (x) = 1275. x→1 Chọn đáp án D □ Äp ä Câu 36. Biết lim
x2 + ax − 1 − x = 5. Khi đó giá trị của tham số a là x→+∞ A 10. B −6. C 6. D −10. Lời giải. 1 a − Äp ä x2 + ax − 1 − x2 a lim x2 + ax − 1 − x = lim √ = lim x = = 5. x→+∞ x→+∞ x2 + ax − 1 + x x→+∞ … a 1 2 1 + − + 1 x x2 Suy ra a = 10. Chọn đáp án A □ p 1
Câu 37. Có tất cả bao nhiêu giá trị nguyên của tham số m để lim ( x2 + m2x − x) = ? x→+∞ 2 A 0. B 1. C 2. D 4. Lời giải. Ta có Äp ä m2x lim x2 + m2x − x = lim √ x→+∞ x→+∞ x2 + m2x + x m2 = lim x→+∞ »1 + m2 + 1 x m2 = . 2 p 1 m2 1 Do đó lim ( x2 + m2x − x) = ⇔ =
⇔ m = ±1. Vậy có hai giá trị nguyên của tham số m thỏa mãn x→+∞ 2 2 2 yêu cầu của bài toán. Chọn đáp án C □ 409/764 409/764
Toán 11 theo chương trình GDPT2018 410
2. Giới hạn của hàm số
Biết làm, làm đúng, làm nhanh √ √ Ä ä Câu 38. Tính L = lim x2 − 7x + 1 − x2 − 3x + 2 . x→−∞ A L = +∞. B L = −∞. C L = 2. D L = −2. Lời giải. −4x − 1 L = lim √ √ x→−∞ x2 − 7x + 1 + x2 − 3x + 2 −4x − 1 = lim x→−∞ … 7 1 … 3 2 −x 1 − + − x 1 − + x x2 x x2 1 −4 − = lim x x→−∞ … 7 1 … 3 2 − 1 − + − 1 − + x x2 x x2 = 2. Chọn đáp án C □ √ √ 2x + 1 − x + 2 Câu 39. Giá trị của lim là x→1 x − 1 √ √ √ √ 3 3 3 3 A − . B − . C . D . 5 6 6 5 Lời giải. Ta có √ √ 2x + 1 + x + 2 x − 1 1 1 lim = lim √ √ = lim √ √ = √ . x→1 x − 1 x→1 (x − 1) 2x + 1 − x + 2 x→1 2x + 1 + x + 2 2 3 Chọn đáp án C □ √ 1 − 3 1 − x m m Câu 40. Cho lim =
, trong đó m, n là các số nguyên và tối giản. x→0 x n n Tính A = 2m − n. A A = 1. B A = −1. C A = 0. D A = −2. Lời giải. √ 1 − 3 1 − x x 1 Ta có lim = lim √ = . Ä x→0 x x→0 x · 1 + 3 1 − x + 3 p(1 − x)2ä 3
Vậy A = 2m − n = 2 · 1 − 3 = −1. Chọn đáp án B □ √ x + 1 − 5x + 1 a a Câu 41. Giới hạn lim √ =
, với a, b ∈ Z, b > 0 và
là phân số tối giản. Giá trị của a − b là x→3 x − 4x − 3 b b 1 9 A . B −1. C . D 1. 9 8 Lời giải. Ta có (x + 1)2 − (5x + 1) √ √ x + 1 − 5x + 1 x + 1 + 5x + 1 lim √ = lim x→3 x − 4x − 3 x→3 x2 − (4x − 3) √ x + 4x − 3 √ x + 4x − 3 (x − 3)x = lim √ x→3 x + 1 + 5x + 1 (x − 3)(x − 1) √ x x + 4x − 3 9 = lim √ = . x→3 x + 1 + 5x + 1 (x − 1) 8
Vậy a = 9, b = 8, suy ra a − b = 1. Chọn đáp án D □ 410/764 410/764
Toán 11 theo chương trình GDPT2018 411
Chương 3. Giới hạn. Hàm số liên tục
Biết làm, làm đúng, làm nhanh √3x + 4 − 4 a a Câu 42. Cho lim = , với
là phân số tối giản. Tính 2a + b2. x→4 x − 4 b b A 22. B 66. C 14. D 70. Lời giải. √3x + 4 − 4 3 (x − 4) 3 3 Có lim = lim √ = lim √ = . x→4 x − 4 x→4 (x − 4) 3x + 4 + 4 x→4 3x + 4 + 4 8 ⇒ 2a + b2 = 6 + 64 = 70. Chọn đáp án D □ √ Ä ä Câu 43. Tính lim x2 + 3x + 2 − x . x→+∞ 3 3 7 7 A − . B . C . D − . 2 2 2 2 Lời giải. Äp ä 3x + 2 lim x2 + 3x + 2 − x = lim √ x→+∞ x→+∞ x2 + 3x + 2 + x Å 2 ã x 3 + x = lim x→+∞ … 3 2 |x| 1 + + + x x x2 Å 2 ã x 3 + x = lim x→+∞ Ç… å 3 2 x 1 + + + 1 x x2 2 3 + 3 = lim x = . x→+∞ … 3 2 2 1 + + + 1 x x2 Chọn đáp án B □ √ √ Ä ä
Câu 44. Tìm giới hạn M = lim x2 − 4x − x2 − x . x→−∞ 1 3 3 1 A M = − . B M = . C M = − . D M = . 2 2 2 2 Lời giải. Ta có Äp p ä M = lim x2 − 4x − x2 − x x→−∞ −3x = lim √ √ x→−∞ x2 − 4x + x2 − x −3x = lim x→−∞ Ç… å 4 … 1 |x| 1 − + 1 − x x 3 3 = lim = . x→−∞ … 4 … 1 2 1 − + 1 − x x Chọn đáp án B □ √ √ √ Ä ä a a Câu 45. Biết rằng lim 2x2 − 3x + 1 + x 2 = 2, (a, b ∈ Z, b > 0,
tối giản). Tổng a + b có giá trị x→−∞ b b là A 5. B 4. C 7. D 1. Lời giải. 411/764 411/764
Toán 11 theo chương trình GDPT2018 412
2. Giới hạn của hàm số
Biết làm, làm đúng, làm nhanh Ta có √ Äp ä 2x2 − 3x + 1 − 2x2 lim 2x2 − 3x + 1 + x 2 = lim √ √ x→−∞ x→−∞ 2x2 − 3x + 1 − x 2 −3x + 1 = lim √ √ x→−∞ 2x2 − 3x + 1 − x 2 1 −3 + = lim x x→−∞ … 3 1 √ − 2 − + − 2 x x2 3 √ = · 2. 4
Vậy a = 3, b = 4. Tổng a + b = 7. Chọn đáp án C □ √ Ä ä
Câu 46. Tìm giới hạn I = lim x + 1 − x2 − x + 2 . x→+∞ 1 46 17 3 A I = . B I = . C I = . D I = . 2 31 11 2 Lời giải. √ Å ã Ä ä x2 − x2 + x − 2 Ta có: I = lim x + 1 − x2 − x + 2 = lim √ + 1 x→+∞ x→+∞ x + x2 − x + 2 Ü 2 ê Å x − 2 ã 1 − 3 = lim √ + 1 = lim x + 1 = . x→+∞ x + x2 − x + 2 x→+∞ … 1 2 2 1 + 1 − + x x2 Chọn đáp án D □ f (x) − 15
Câu 47. Cho f (x) là một đa thức thỏa mãn lim = 3. Tính x→2 x − 2 f (x) − 15 lim . Ä ä
x→2 (x2 − 4) p2f (x) + 6 + 3 1 1 1 1 A . B . C . D . 10 6 12 8 Lời giải. f (x) − 15 Do lim
= 3 và lim (x − 2) = 0 nên lim (f (x) − 15) = 0 ⇒ f (2) = 15. x→2 x − 2 x→2 x→2 Ta có   f (x) − 15 f (x) − 15 1 lim = lim · Ä ä  Ä ä 
x→2 (x2 − 4) p2f (x) + 6 + 3 x→2 x − 2 (x + 2) p2f (x) + 6 + 3 1 1 = 3 · √ = . 4 · ( 2 · 15 + 6 + 3) 12 Chọn đáp án C □ √ √ 3 ax + 1 − 1 − bx
Câu 48. Biết rằng b > 0, a + b = 5 và lim
= 2. Khẳng định nào dưới đây là sai? x→0 x A a2 + b2 > 10. B a2 − b2 > 6. C a − b ≥ 0. D 1 ≤ a ≤ 3. Lời giải. Ta có √ √ √ √ 3 ax + 1 − 1 − bx 3 ax + 1 − 1 1 − bx − 1 lim = lim − lim . x→0 x x→0 x x→0 x 412/764 412/764
Toán 11 theo chương trình GDPT2018 413
Chương 3. Giới hạn. Hàm số liên tục
Biết làm, làm đúng, làm nhanh √ 3 ax + 1 − 1 ax a Với L1 = lim = lim √ = . Ä ä x→0 x x→0 x 3 p(ax + 1)2 + 3 ax + 1 + 1 3 √1 − bx − 1 −bx b Với lim = lim √ = − . x→0 x x→0 x 1 − bx + 1 2
Từ giả thiết bài toán ta có a b L = L1 − L2 = 2 ⇔ + = 2 ⇔ 2a + 3b = 12. 3 2 ®a + b = 5 ®a = 3 Ta có hệ phương trình ⇔ 2a + 3b = 12 b = 2.
Kiểm tra trực tiếp từng đáp án ta thấy a2 − b2 > 6 là sai. Chọn đáp án B □
Dạng 3. Phương pháp đặt thừa số chung - kết quả vô cực
Để tìm giới hạn của hàm số ta cần nhớ ® + ∞, k = 2n ○ lim xk = +∞; lim xk = x→+∞ x→−∞ − ∞, k = 2n + 1. c 1 ○ lim c = c; lim = 0; lim = ∞. x→±∞ x→±∞ xk x→0 x 1. Ví dụ mẫu
Ví dụ 17 (NB). Tính lim x3. x→+∞ Lời giải. Ta có lim x3 = +∞. □ x→+∞
Ví dụ 18 (TH). Tính lim x3 + 3x + 1. x→−∞ Lời giải. ï Å 3 1 ãò Ta có lim x3 + 3x + 1 = lim x3 1 + + = −∞. x→−∞ x→−∞ x2 x3 Å 3 1 ã Vì lim x3 = −∞; lim 1 + + = 1 > 0. □ x→−∞ x→−∞ x2 x3
Ví dụ 19 (TH). Tính lim −4x5 − 3x3 + x + 1. x→−∞ Lời giải. Å 3 1 1 ã Ta có lim
−4x5 − 3x3 + x + 1 = lim x5 −4 − + + = +∞. x→−∞ x→−∞ x2 x4 x5  Å 3 1 1 ã  lim −4 − + + = −4 < 0  Vì x→−∞ x2 x4 x5 □  lim x5 = −∞.  x→−∞ x + 2
Ví dụ 20 (TH). Tính giới hạn lim . x→−3 (x + 3)2 Lời giải. x + 2 Ta có lim = −∞. x→−3 (x + 3)2
Vì lim (x + 2) = −3 + 2 = −1 < 0, lim (x + 3)2 = 0 và (x + 3)2 > 0 khi x ̸= −3. □ x→−3 x→−3
Ví dụ 21 (VDT). Tìm tất cả các giá trị nguyên của tham số m để I = lim (m2 − 1)x3 + 2x = −∞. x→+∞ Lời giải. 413/764 413/764
Toán 11 theo chương trình GDPT2018 414
2. Giới hạn của hàm số
Biết làm, làm đúng, làm nhanh ï 2 ò Ta có
lim m2 − 1 x3 + 2x = lim x3 m2 − 1 + . x→+∞ x→+∞ x2 ï 2 ò Vì
lim x3 = +∞ nên I = −∞ ⇔ lim m2 − 1 +
< 0 ⇔ m2 − 1 < 0 ⇔ −1 < m < 1. x→+∞ x→+∞ x2 Do m ∈ Z nên m = 0. □ 2. Bài tập rèn luyện
Bài 41 (NB). Tính lim x2. x→−∞ Lời giải. Ta có lim x2 = +∞. □ x→−∞ Å 1 ã Bài 42 (NB). Tính lim −x4 − . x→−∞ x Lời giải. 1 Å 1 ã Ta có lim −x4 = −∞ và lim = 0. Suy ra lim −x4 − = −∞. □ x→−∞ x→−∞ x x→−∞ x
Bài 43 (TH). Tính giới hạn lim −x3 + 5x2 + 2x + 1. x→+∞ Lời giải. ï Å 5 2 1 ãò Ta có lim −x3 + 5x2 + 2x + 1 = lim x3 −1 + + + . x→+∞ x→+∞ x x2 x3 Å 5 2 1 ã Do lim x3 = +∞; lim −1 + + + = −1 < 0 nên lim −x3 + 5x2 + 2x + 1 = −∞. □ x→+∞ x→+∞ x x2 x3 x→+∞ 3x2 − x Bài 44 (TH). Tính lim . x→+∞ x + 1 Lời giải. Ö 1 è Ö 1 è 3x2 − x x2 3 − 3 − Ta có lim = lim · x = lim x · x = +∞. x→+∞ x + 1 x→+∞ x 1 x→+∞ 1 1 + 1 + x x 1 3 − Vì lim x = +∞ và lim x = 3. □ x→+∞ x→+∞ 1 1 + x √ Ä ä
Bài 45 (TH). Giá trị của giới hạn lim 1 + 2x2 − x là bao nhiêu? x→+∞ Lời giải. √ Ç… å Ä ä 1 Ta có lim 1 + 2x2 − x = lim x + 2 − 1 = +∞. x→+∞ x→+∞ x2 Ç… å 1 √ Vì lim x = +∞; lim + 2 − 1 = 2 − 1 > 0. □ x→+∞ x→+∞ x2 Å 1 1 ã 1 Bài 46 (TH). Tính lim − . x→3 x 3 (x − 3)3 Lời giải. Å 1 1 ã 1 3 − x 1 −1 lim − = lim · = lim = −∞. □ x→3 x 3 (x − 3)3 x→3 3x (x − 3)3 x→3 3x(x − 3)2 √ Ä ä
Bài 47 (VDT). Có bao nhiêu giá trị m nguyên thuộc đoạn [−20; 20] để lim
4x2 − 3x + 2 + mx − 1 = −∞? x→+∞ Lời giải. Ç … å Äp ä 3 2 Ta có lim
4x2 − 3x + 2 + mx − 1 = lim x 4 − + + mx − 1 x→+∞ x→+∞ x x2 Ç… å 3 2 1 = lim x 4 − + + m − . x→+∞ x x2 x 414/764 414/764
Toán 11 theo chương trình GDPT2018 415
Chương 3. Giới hạn. Hàm số liên tục
Biết làm, làm đúng, làm nhanh Ç… å 3 2 1 √ Ä ä Mà lim x = +∞ và lim 4 − + + m − = 2 + m nên lim
4x2 − 3x + 2 + mx − 1 = −∞ khi x→+∞ x→+∞ x x2 x x→+∞ 2 + m < 0 ⇔ m < −2.
Do m nguyên thuộc đoạn [−20; 20] nên m ∈ {−20; −19; −18; . . . ; −3}.
Vậy có 18 giá trị m nguyên thuộc đoạn [−20; 20] thỏa bài toán. □ 3.
Câu hỏi trắc nghiệm
Câu 49. Giá trị của lim (−x3) bằng x→−∞ A +∞. B −∞. C 1. D −1. Lời giải. Ta có lim (−x3) = +∞. x→−∞ Chọn đáp án A □ √ Ä ä Câu 50. Giới hạn lim
3x3 + 5x2 − 9 3x − 2022 bằng x→−∞ A −∞. B 3. C −3. D +∞. Lời giải. √ Å √ ã Ä ä 1 1 1 Ta có lim
3x3 + 5x2 − 9 3x − 2022 = lim x3 3 + 5 · − 9 3 · − 2022 · = −∞. x→−∞ x→−∞ x x2 x3 Chọn đáp án A □
Câu 51. Tính lim (x3 + 3x − 3). x→−∞ A 2. B 1. C −∞. D +∞. Lời giải. ï Å 3 3 ãò Ta có lim x3 + 3x − 3 = lim x3 1 + − = −∞. x→−∞ x→−∞ x2 x3 Å 3 3 ã Vì lim x3 = −∞; lim 1 + − = 1 > 0. x→−∞ x→−∞ x2 x3 Chọn đáp án C □
Câu 52. Với k là số nguyên dương chẵn. Kết quả của lim −3xk là x→−∞ A 0. B −∞. C −3xk. D +∞. 0 Lời giải. Ta có
lim xk = +∞ khi k là số nguyên dương chẵn. x→−∞ Suy ra lim −3xk = −∞. x→−∞ Chọn đáp án B □
Câu 53. Cho hai hàm số f (x), g(x) thỏa mãn lim f (x) = 2 và lim g(x) = +∞. Giá trị của lim [f (x) · g(x)] x→1 x→1 x→1 bằng A +∞. B −∞. C 2. D −2. Lời giải.
Theo quy tắc giới hạn vô cực ta có lim f (x) = 2 > 0 và lim g(x) = +∞ thì lim [f (x) · g(x)] = +∞. x→1 x→1 x→1 Chọn đáp án A □ x + 1 Câu 54. Giới hạn lim bằng x→−2 (x + 2)2 3 A −∞. B . C 0. D +∞. 16 Lời giải. x + 1 Ta có lim = −∞. x→−2 (x + 2)2
Vì lim (x + 1) = −2 + 1 = −1 < 0, lim (x + 2)2 = 0 và (x + 2)2 > 0 khi x ̸= −2. x→−2 x→−2 Chọn đáp án A □ 415/764 415/764
Toán 11 theo chương trình GDPT2018 416
2. Giới hạn của hàm số
Biết làm, làm đúng, làm nhanh Câu 55. lim −3x3 + 2x bằng x→−∞ A −∞. B +∞. C 1. D −1. Lời giải. Å 2 ã Ta có lim −3x3 + 2x = lim x3 −3 + = +∞. x→−∞ x→−∞ x2 Å 2 ã Vì lim x3 = −∞ và lim −3 + = −3 < 0. x→−∞ x→−∞ x2 Chọn đáp án B □ 2x2 + x − 3 Câu 56. Tìm L = lim . x→−1 (x + 1)2 A L = +∞. B L = 2. 2x2 + x − 3
C Không tồn tại lim . D L = −∞. x→−1 (x + 1)2 Lời giải.  lim (2x2 + x − 3) = −2   x→−1 2x2 + x − 3   lim = −∞ vì lim (x + 1)2 = 0 x→−1 (x + 1)2 x→−1   
x → −1 ⇒ (x + 1)2 > 0. Chọn đáp án D □ Câu 57. lim −2x3 − 2x bằng x→+∞ A −∞. B +∞. C 2. D −2. Lời giải. Å 2 ã Ta có lim
−2x3 − 2x = lim x3 −2 − . x→+∞ x→+∞ x2 2 Å 2 ã Mà lim x3 = +∞; lim (−2 − ) = −2 < 0 nên lim x3 −2 − = −∞. x→+∞ x→+∞ x2 x→+∞ x2 Vậy lim −2x3 − 2x = −∞. x→+∞ Chọn đáp án A □ x2 + 1
Câu 58. Tính giới hạn lim . x→−∞ x − 2 1 A 1. B − . C +∞. D −∞. 2 Lời giải. 1 1 x2 + 1 x2 1 + 1 + lim = lim · x2 = lim x · x2 . x→−∞ x − 2 x→−∞ x 2 x→−∞ 2 1 − 1 − x x 1 1 + x2 + 1 Do lim x = −∞ và lim x2 = 1 nên lim = −∞. x→−∞ x→−∞ 2 x→−∞ x − 2 1 − x Chọn đáp án D □
Câu 59. Trong các mệnh đề sau, mệnh đề nào đúng? √ √ x4 − x x4 − x A lim = +∞. B lim = 1. x→−∞ 1 − 2x x→−∞ 1 − 2x √ √ x4 − x x4 − x C lim = −∞. D lim = 0. x→−∞ 1 − 2x x→−∞ 1 − 2x Lời giải. … … √ 1 1 x2 · 1 − 1 − x4 − x x3 x3 Vì lim = lim = lim x · = +∞. x→−∞ 1 − 2x x→−∞ Å 1 ã x→−∞ 1 x · − 2 − 2 x x 416/764 416/764
Toán 11 theo chương trình GDPT2018 417
Chương 3. Giới hạn. Hàm số liên tục
Biết làm, làm đúng, làm nhanh Chọn đáp án A □ f (x)
Câu 60. Biết lim f (x) = −1. Khi đó lim bằng x→−2 x→−2 (x + 2)4 A −1. B +∞. C −∞. D 0. Lời giải.
Ta có lim f (x) = −1 < 0; lim (x + 2)4 = 0 và ∀x ̸= −2 thì (x + 2)4 > 0. x→−2 x→−2 f (x) Suy ra lim = −∞. x→−2 (x + 2)4 Chọn đáp án C □ f (x)
Câu 61. Biết lim f (x) = −2. Khi đó lim bằng x→1 x→1 (x − 1)2 A −∞. B 0. C +∞. D −2. Lời giải. f (x)
Có lim f (x) = −2 < 0, lim (x − 1)2 = 0 và (x − 1)2 > 0, ∀x ̸= 1 nên lim = −∞. x→1 x→1 x→1 (x − 1)2 Chọn đáp án A □
Câu 62. Có bao nhiêu giá trị nguyên của tham số m thuộc [−5; 5] để L = lim x − 2(m2 − 4)x3 = −∞? x→+∞ A 5. B 10. C 3. D 6. Lời giải. ï 1 ò Ta có
lim x − 2 m2 − 4 x3 = lim x3 − 2 m2 − 4 . x→+∞ x→+∞ x2 Ta có ï 1 ò
lim x3 = +∞ ⇒ L = −∞ ⇔ lim − 2 m2 − 4 < 0 x→+∞ x→+∞ x2 ñm > 2
⇔ −2(m2 − 4) < 0 ⇔ m2 − 4 > 0 ⇔ m < −2.
Lại có m thuộc đoạn [−5; 5] nên các giá trị nguyên thỏa mãn bài toán của m là {−5; −4; −3; 3; 4; 5}.
Vậy có 6 số nguyên thỏa mãn bài toán. Chọn đáp án D □ √ Ä ä
Câu 63. Có bao nhiêu giá trị m nguyên thuộc đoạn [−20; 20] để lim
4x2 − 3x + 2 + mx − 1 = −∞? x→−∞ A 21. B 22. C 18. D 41. Lời giải. √ Ç … å Ä ä 3 2 1 Ta có lim
4x2 − 3x + 2 + mx − 1 = lim x − 4 − + + m − . x→−∞ x→−∞ x x2 x Ç … å 3 2 1 Có lim x = −∞ và lim − 4 − + + m − = m − 2 x→−∞ x→−∞ x x2 x √ Ä ä Để lim
4x2 − 3x + 2 + mx − 1 = −∞ suy ra m − 2 > 0 ⇔ m > 2. x→−∞
Với m ∈ Z và m ∈ [−20; 20] có m ∈ {3; 4; 5; . . . ; 20} thỏa mãn yêu cầu bài toán.
Kết luận: Vậy có 18 giá trị nguyên của m thỏa mãn yêu cầu bài toán. Chọn đáp án C □
Dạng 4. Giới hạn một phía
c Định lí 2.3. Định lí sau đây cho ta mối liên hệ giữa “giới hạn hai phía” lim f (x) với giới hạn bên trái x→x0
lim f (x) và giới hạn bên phải lim f (x). x→x− x→x+ 0 0
lim f (x) = L khi và chỉ khi lim f (x) = lim f (x) = L. x→x0 x→x− x→x+ 0 0 417/764 417/764
Toán 11 theo chương trình GDPT2018 418
2. Giới hạn của hàm số
Biết làm, làm đúng, làm nhanh 1. Ví dụ mẫu √
Ví dụ 22 (Cánh Diều). Tính: lim 2 − x. x→2− Lời giải.
Với dãy số (xn) bất kì, xn < 2 và xn → 2, ta có √ … lim 2 − xn = lim (2 − xn) xn→2− xn→2− = q2 − lim xn xn→2− √ = 2 − 2 = 0. √ Vậy lim 2 − x = 0. □ xn→2−  − 1 nếu x < 0  
Ví dụ 23 (Cánh Diều). Cho hàm số f (x) = 0 nếu x = 0  1 nếu x > 0.
Chứng tỏ rằng không tồn tại lim f (x). x→0 Lời giải.
Ta có lim f (x) = −1 và lim f (x) = 1. x→0− x→0+
Suy ra lim f (x) ̸= lim f (x). x→0− x→0+
Vậy không tồn tại lim f (x). □ x→0 ®0 khi x < 0
Ví dụ 24 (CTST). Cho hàm số f (x) = 1 khi x > 0.
a) Tìm các giới hạn lim f (x) và lim f (x). b) Có tồn tại lim f (x)? x→0+ x→0− x→0 Lời giải.
a) Giả sử (xn) là dãy số bất kì, xn > 0 và xn → 0. Khi đó f (xn) = 1 nên lim f (xn) = lim 1 = 1. Vậy lim f (x) = 1. x→0+
Giả sử (xn) là dãy số bất kì, xn < 0 và xn → 0. Khi đó f (xn) = 0 nên lim f (xn) = lim 0 = 0. Vậy lim f (x) = 0. x→0−
b) Vì lim f (x) ̸= lim f (x) nên không tồn tại lim f (x). x→0+ x→0− x→0 □ ®1 − 2x khi x ≤ −1
Ví dụ 25 (CTST). Cho hàm số f (x) = x2 + 2 khi x > −1. Tìm các giới hạn lim f (x) và
lim f (x) và lim f (x) (nếu có). x→−1+ x→−1− x→−1 Lời giải.
+ Giả sử (xn) là dãy số bất kì, xn < −1 và xn → −1. Khi đó lim f (xn) = lim(1 − 2xn) = 3. Vậy lim f (x) = 3. x→−1−
Giả sử (xn) là dãy số bất kì, xn > −1 và xn → −1. Khi đó lim f (xn) = lim(x2n + 2) = 3. Vậy lim f (x) = 3. x→−1+ + Vì lim f (x) =
lim f (x) nên tồn tại lim f (x) và lim f (x) = 3. x→−1+ x→−1− x→−1 x→−1 □ 418/764 418/764
Toán 11 theo chương trình GDPT2018 419
Chương 3. Giới hạn. Hàm số liên tục
Biết làm, làm đúng, làm nhanh ®x2 nếu 0 < x < 1
Ví dụ 26 (KNTT). Cho hàm số f (x) = x + 1 nếu 1 ≤ x < 2. Tính lim f (x) và lim f (x). x→1− x→1+ Lời giải.
Với dãy số (xn) bất kì sao cho 0 < xn < 1 và xn → 1, ta có f (xn) = x2n. Do đó lim f (x) = lim f (xn) = 1. x→1− n→+∞
Tương tự, với dãy số (xn) bất kì mà 1 < xn < 2, xn → 1, ta có f (xn) = xn +1, cho nên lim f (x) = lim f (xn) = x→1+ n→+∞ 2. □ 2. Bài tập tự luận ®0 khi x < 0
Bài 48. Cho hàm số f (x) = 1 khi x > 0.
a) Tính các giới hạn lim f (x) và lim f (x). x→0+ x→0−
b) Có tồn tại giới hạn lim f (x)? x→0 Lời giải.
a) Giả sử (xn) là dãy số bất kì, xn > 0 và xn → 0 khi n → +∞. Khi đó f (xn) = 1 nên lim f (xn) = lim 1 = 1. Vậy lim f (x) = 1. x→0+
Giả sử (xn) là dãy số bất kì, xn < 0 và xn → 0 khi n → +∞. Khi đó f (xn) = 0 nên lim f (xn) = lim 0 = 0. Vậy lim f (x) = 0. x→0−
b) Vì lim f (x) ̸= lim f (x) nên không tồn tại giới hạn lim f (x). x→0+ x→0− x→0 □ ®1 − 2x khi x ≤ −1
Bài 49. Cho hàm số f (x) = x2 + 2 khi x > −1. Tìm các giới hạn lim f (x) và
lim f (x) và lim f (x) (nếu có). x→−1+ x→−1− x→−1 Lời giải.
○ Giả sử (xn) là dãy số bất ki, xn ≤ −1 và xn → −1 khi n → +∞.
Khi đó f (xn) = 1 − 2xn nên lim f (xn) = lim(1 − 2xn) = 1 − 2(−1) = 3. Vậy lim f (x) = 3. x→−1−
○ Giả sử (xn) là dãy số bất ki, xn > −1 và xn → −1 khi n → +∞.
Khi đó f (xn) = x2n + 2 nên lim f(xn) = lim(x2n + 2) = (−1)2 + 2 = 3. Vậy lim f (x) = 3. x→−1+
○ Vì lim f (x) = lim f (x) = 3 nên lim f (x) = 3. x→−1+ x→−1− x→−1 □
Bài 50. Tìm các giới hạn sau 1 − 2x a) lim ; b) lim (x2 + 1). x→−∞ x→2+ x − 2 Lời giải. 1
a) Ta có lim (1 − 2x) = 1 − 2 lim x = 1 − 2 · 2 = −3; lim = +∞. x→2+ x→2+ x→2+ x − 2 1 − 2x ï 1 ò Do đó lim = lim (1 − 2x) · = −∞. x→2+ x − 2 x→2+ x − 2 419/764 419/764
Toán 11 theo chương trình GDPT2018 420
2. Giới hạn của hàm số
Biết làm, làm đúng, làm nhanh Å 1 ã Å 1 ã 1 b) Viết (x2 + 1) = x2 1 + . Ta có lim x2 = +∞; lim 1 + = 1 + lim = 1 + 0 = 1. x2 x→−∞ x→−∞ x2 x→−∞ x2 ï Å 1 ãò Do đó lim (x2 + 1) = lim x2 1 + = +∞. x→−∞ x→−∞ x2 □
Bài 51. Tìm các giới hạn sau 2x a) lim ; b) lim (3x − 1). x→+∞ x→3− x − 3 Lời giải. 1
a) Ta có lim (2x) = 2 lim x = 2 · 3 = 6; lim = −∞. x→3− x→3− x→3− x − 3 2x ï 1 ò Do đó lim = lim (2x) · = −∞. x→3− x − 3 x→3− x − 3 Å 1 ã Å 1 ã 1 b) Viết (3x − 1) = x 3 − . Ta có lim x = +∞; lim 3 − = 3 − lim = 3 − 0 = 3. x x→+∞ x→+∞ x x→+∞ x Å 1 ã Do đó lim (3x − 1) = lim x 3 − = +∞. x→+∞ x→−∞ x □ ® − x2 khi x < 1
Bài 52. Cho hàm số f (x) = x khi x ≥ 1.
Tìm các giới hạn lim f (x); lim f (x); lim f (x) (nếu có). x→1+ x→1− x→1 Lời giải. Ta có lim f (x) = lim x = 1. x→1+ x→1+
lim f (x) = lim (−x2) = −12 = −1. x→1− x→1−
Vì lim f (x) ̸= lim f (x) nên không tồn tại lim f (x). □ x→1+ x→1− x→1
Bài 53. Biết rằng hàm số f (x) thoả mãn lim f (x) = 3 và lim f (x) = 5. Trong trường hợp này có tồn tại giới x→2− x→2+
hạn lim f (x) hay không? Giải thích. x→2 Lời giải.
Ta có lim f (x) = 3 và lim f (x) = 5, do đó lim f (x) ̸= lim f (x). x→2− x→2+ x→2− x→2+
Vậy không tồn tại lim f (x). □ x→2 2
Bài 54. Cho hàm số f (x) =
. Tìm lim f (x) và lim f (x). (x − 1)(x − 2) x→2+ x→2− Lời giải. 2 2 1 2 Viết = · , ta có lim = 2 > 0. (x − 1)(x − 2) x − 1 x − 2 x→2+ x − 1 1 Hơn nữa lim
= +∞ do x − 2 > 0 khi x > 2. x→2+ x − 2 2
Áp dụng quy tắc tìm giới hạn của tích, ta được lim = +∞. x→2+ (x − 1)(x − 2) 1
Lí luận tương tự, ta có lim = −∞. □ x→2− x(1 − x)
Bài 55. Tính các giới hạn sau 1 x a) lim ; b) lim (1 − x2); c) lim . x→−1+ x + 1 x→−∞ x→3− 3 − x Lời giải. 420/764 420/764
Toán 11 theo chương trình GDPT2018 421
Chương 3. Giới hạn. Hàm số liên tục
Biết làm, làm đúng, làm nhanh a) Ta có lim 1 = 1; lim (x + 1) = 0. x→−1+ x→−1+ 1 Do đó lim = +∞. x→−1+ x + 1 Å 1 ã b) Viết (1 − x2) = x2 − 1 . x2 Å 1 ã 1 Vì lim x2 = +∞; lim − 1 = lim − 1 = 0 − 1 = −1. x→−∞ x→−∞ x2 x→−∞ x2 Nên lim (1 − x2) = −∞. x→−∞ x −x c) Ta viết = . 3 − x x − 3 1
Vì lim (−x) = −3 < 0; lim = −∞ x→3− x→3− x − 3 x ï 1 ò nên lim = lim −x · = +∞. x→3− 3 − x x→3− x − 3 □ 3.
Câu hỏi trắc nghiệm
Câu 64. Trong các giới hạn sau đây, giới hạn nào sau đây có kết quả bằng +∞. 2x − 1 x3 − 1 2x − 1 A lim . B lim . C lim −x3 + x2 + 2. D lim . x→4+ 4 − x x→−∞ 2x2 + x − 1 x→+∞ x→4− 4 − x Lời giải. 2x − 1 Ta có lim = +∞ vì lim
= và 4 − x > 0 với mọi x ∈ (−∞; 4). x→4− 4 − x x→4−(2x−1)=7>0 Chọn đáp án D □ ®2x + 1 khi x < 1 Câu 65. Cho hàm số f (x) =
. Hàm số có giới hạn khi x → 1 nếu x2 + mx − 2m khi x ≥ 1 Lời giải.
Ta có lim f (x) = lim (2x + 1) = 3. x→1− x→1− Mặt khác lim f (x) = lim x2 + mx − 2m = 1 − m. x→1+ x→1+
Hàm số có giới hạn khi x → 1 khi và chỉ khi lim f (x) = lim f (x) ⇔ 1 − m = 3 ⇔ m = −2. □ x→1− x→1+
Câu 66. Mệnh đề nào sau đây đúng? 2x2 + 5x − 3 2x2 + 5x − 3 A lim = −∞. B lim = 2. x→(−3)− (x + 3)2 x→(−3)− (x + 3)2 2x2 + 5x − 3 2x2 + 5x − 3 C lim = −2. D lim = +∞. x→(−3)− (x + 3)2 x→(−3)− (x + 3)2 Lời giải. 2x2 + 5x − 3 (x + 3)(2x − 1) 2x + 1 Ta có lim = lim = lim = +∞. x→(−3)− (x + 3)2 x→(−3)− (x + 3)2 x→(−3)− x + 3 Chọn đáp án D □ 1 − x Câu 67. Tính lim . x→−1− x + 1 A 1. B +∞. C −∞. D −1. Lời giải.  lim (1 − x) = 2 > 0   x→−1−   1 − x Vì lim (x + 1) = 0 nên lim = −∞. x→−1− x→−1− x + 1   
x → −1− ⇒ x < −1 ⇒ x + 1 < 0 Chọn đáp án C □ 421/764 421/764
Toán 11 theo chương trình GDPT2018 422
2. Giới hạn của hàm số
Biết làm, làm đúng, làm nhanh 3 + 2x Câu 68. Tính giới hạn lim . x→(−2)− x + 2 3 A +∞. B . C −∞. D 2. 2 Lời giải. Ta có: lim (3 + 2x) = −1 < 0 và lim
(x + 2) = 0; x + 2 < 0 khi x → (−2)−. x→(−2)− x→(−2)− 3 + 2x Suy ra lim = +∞. x→(−2)− x + 2 Chọn đáp án A □
Câu 69. Mệnh đề sao sau đây sai? x − 4 x − 4 x2 − 4x x2 − 4x2 A lim √ = 4. B lim √ = 0. C lim = 4. D lim = 0. x→4 x − 2 x→4+ ( x − 2)2 x→4 x − 4 x→4 x − 4 Lời giải. x2 − 4x2 • lim lim (x − 4) x2 = 0. x→4 x − 4 x→4 √ x − 4 x + 2 • lim √ = lim √ = +∞. x→4+ ( x − 2)2 x→4+ x − 2 x − 4 √ • lim √ = lim ( x + 2) = 4. x→4 x − 2 x→4 x2 − 4x • lim = lim x = 4. x→4 x − 4 x→4 Chọn đáp án B □ √x3 − 3x + 2 Câu 70. Tính lim . x→1− x2 − 7x + 4 √ √ 1 3 3 1 A − . B − . C . D . 5 3 3 5 Lời giải. Ta có √x3 − 3x + 2 p(x − 1)2(x + 2) lim = lim x→1− x2 − 7x + 4 x→1− (x − 1)(x − 4) √ −(x − 1) x + 2 = lim x→1− (x − 1)(x − 4) √ − x + 2 = lim x→1− x − 4 √3 = . 3 Chọn đáp án C □ √ ® x − 2 + 3 nếu x ≥ 2 Câu 71. Cho f (x) =
và lim f (x) tồn tại. Tính a. ax − 1 nếu x < 2 x→2 A 1. B −2. C 3. D 2. Lời giải. Ta có √ ○ lim f (x) = lim x − 2 + 3 = 3. x→2+ x→2+
○ lim f (x) = lim (ax − 1) = 2a − 1. x→2− x→2−
Vì lim f (x) tồn tại nên lim f (x) = lim f (x) ⇔ 2a − 1 = 3 ⇔ a = 2. x→2 x→2+ x→2− Chọn đáp án D □ 422/764 422/764
Toán 11 theo chương trình GDPT2018 423
Chương 3. Giới hạn. Hàm số liên tục
Biết làm, làm đúng, làm nhanh x2 − 2
Câu 72. Tính giới hạn lim . x→2 x − 2 A −∞. B 2. C +∞. D Không tồn tại. Lời giải. x2 − 2 x2 − 2 - Ta có lim = −∞ và lim = +∞. x→2− x − 2 x→2+ x − 2 x2 − 2 x2 − 2 - Vì lim ̸= lim
nên không tồn tại giới hạn của hàm số tại x = 2. x→2− x − 2 x→2+ x − 2 Chọn đáp án D □ √x − 2 − |x − 2| Câu 73. Tính lim . x→2+ |4 − x2| 1 A −∞. B +∞. C . D 0. 4 Lời giải. √ √ x − 2 − |x − 2| 1 − x − 2 lim = lim √ = +∞. x→2+ |4 − x2| x→2+ x − 2|x + 2| √ √ √ Vì lim (1 − x − 2) = 1, lim x − 2|x + 2| = 0 và
x − 2|x + 2| > 0 ∀x > 2. x→2+ x→2+ Chọn đáp án B □ √  x + 4 − 2  , x > 0  Câu 74. Cho hàm số f (x) = x
m là tham số. Tìm giá trị của tham số m để hàm số có giới 1  mx + m + , x ≤ 0 4 hạn tại x = 0. 21 −1 A m = . B m = 1. C m = . D m = 0. 2 2 Lời giải.
Hàm số có giới hạn tại x = 0 ⇔ lim f (x) = lim f (x). x→0+ x→0− √x + 4 − 2 Å 1 ã 1 1 Vậy lim = lim mx + m + ⇔ = m + ⇔ m = 0. x→0+ x x→0− 4 4 4 Chọn đáp án D □  x2 + ax + b  khi x < −2
Câu 75. Gọi a, b là các giá trị để hàm số f (x) = x2 − 4
có giới hạn hữu hạn khi x dần tới x + 1 khi x ≥ −2 −2. Tính 3a − b. A 12. B 4. C 24. D 8. Lời giải. lim f (x) = lim (x + 1) = −1. x→−2+ x→−2+
Suy ra f (x) có giới hạn hữu hạn khi x dần tới −2 khi và chỉ khi x2 + ax + b 2x2 + ax + b − 4 lim f (x) = −1 ⇔ lim = −1 ⇔ lim = 0. (∗) x→−2− x→−2− x2 − 4 x→−2− x2 − 4 Do
lim (x2 − 4) = 0 nên điều kiện cần để có (*) là
lim (2x2 + ax + b − 4) = 0 ⇒ 2a − b = 4. x→−2− x→−2−
Ngược lại, với 2a − b = 4 ta có 2x2 + ax + b − 4 2x2 + ax + 2a − 8 lim = 0 ⇔ lim = 0 x→−2− x2 − 4 x→−2− x2 − 4 2x + a − 4 ⇔ lim = 0 x→−2− x − 2 ⇔ a = 8. ®a = 8
Suy ra f (x) có giới hạn hữu hạn khi x dần tới −2 ⇔ b = 12. Vậy 3a − b = 12. 423/764 423/764
Toán 11 theo chương trình GDPT2018 424
2. Giới hạn của hàm số
Biết làm, làm đúng, làm nhanh Chọn đáp án A □
Dạng 5. Bài toán thực tế về giới hạn hàm số 1. Ví dụ mẫu
Ví dụ 27 (KNTT). Một cái hồ đang chứa 200 m3 nước mặn với nồng độ muối 10 kg/m3. Người ta ngọt hóa nước
trong hồ bằng cách bơm nước ngọt vào hồ với vận tốc 2 m3/phút.
a) Viết biểu thức C(t) biểu thị nồng độ muối trong hồ sau t phút kể từ khi bắt đầu bơm.
b) Tìm giới hạn lim C(t) và giải thích ý nghĩa. t→+∞ Lời giải.
a) Sau thời gian t phút, số m3 nước trong hồ là 200 + 2t (m3).
Số kilôgam muối là 200 · 10 = 2000 (kg).
Nồng độ muối của nước trong hồ sau t phút khi bắt đầu bơm là 2000 1000 C(t) = = (kg/m3). 200 + 2t 100 + t
b) Khi t → +∞, ta xét giới hạn 1000 lim C(t) = lim = 0. t→+∞ t→+∞ 100 + t □
Ví dụ 28 (KNTT). Trong Thuyết tương đối của Einstein, khối lượng của vật chuyển động với vận tốc v cho bởi công thức m0 m = . … v2 1 − c2
trong đó m0 là khối lượng của vật khi nó đứng yên, c là vận tốc ánh sáng. Chuyện gì xảy ra với khối lượng của
vật khi vận tốc của vật gần với vận tốc ánh sáng? Lời giải.
Từ công thức khối lượng m0 m = … v2 1 − c2
ta thấy m là một hàm số của v, với tập xác định là nửa khoảng [0; c). Rõ ràng khi v tiến gần tới vận tốc ánh … v2
sáng, tức là v → c−, ta có 1 −
→ 0. Do đó lim m(v) = +∞, nghĩa là khối lượng m của vật trở nên vô cùng c2 v→c−
lớn khi vận tốc của vật gần với vận tốc ánh sáng. □ 2. Bài tập tự luận
Bài 56. Một công ty sản xuất máy tính đã xác định được rằng, tính trung bình một nhân viên có thể lắp ráp được 50t N (t) =
(t ≥ 0) bộ phận mỗi ngày sau t ngày đào tạo. Tính lim N (t) và cho biết ý nghĩa của kết quả. t + 4 t→+∞ Lời giải. Ta có 50t 50t lim N (t) = lim = lim t→+∞ t→+∞ t + 4 t→+∞ Å 4 ã t 1 + t 50 = lim t→+∞ 4 1 + t 424/764 424/764
Toán 11 theo chương trình GDPT2018 425
Chương 3. Giới hạn. Hàm số liên tục
Biết làm, làm đúng, làm nhanh lim 50 t→+∞ = 4 lim 1 + lim t→+∞ t→+∞ t 50 = 1 + 0 = 50.
Ý nghĩa của kết quả: năng suất lao động cao nhất trong một ngày của một nhân viên là 50. □
Bài 57. Chi phí (đơn vị: nghìn đồng) để sản xuất x sản phẩm của một công ty được xác định bởi hàm số C(x) = 50000 + 105x.
a) Tính chi phí trung bình C(x) để sản xuất một sản phẩm. b) Tính
lim C(x) và cho biết ý nghĩa của kết quả. x→+∞ Lời giải. 50000 + 105x
a) Chi phí trung bình để sản xuất một sản phẩm là C(x) = . x b) Ta có 50000 + 105x lim C(x) = lim x→+∞ x→+∞ x Å 50000 ã = lim 105 + x→+∞ x 50000 = lim 105 + lim x→+∞ x→+∞ x = 105.
Ý nghĩa của kết quả: số lượng sản phẩm càng nhiều thì chi phí sản xuất sẽ càng giảm, chi phí thấp nhất là 105 nghìn đồng. □ 300
Bài 58. Chiều dài một loài động vật nhỏ được tính theo công công thức h(t) = mm, trong đó t số 1 + 9 · (0,8)t
ngày sau khi sinh của loài động vật đó. Tính chiều dài cuối cùng của nó (chiều dài khi t → +∞). Lời giải. 300 Ta có lim = 300. t→+∞ 1 + 9 · (0,8)t
Vậy chiều dài cuối cùng của loài động vật là 300 mm. □
Bài 59. Theo thuyết tương đối, khối lượng m của một hạt phụ thuộc vào vận tốc v của nó, theo công thức m0 m = … v2 1 − c2
trong đó m0 là khối lượng khi hạt đứng yên và c là tốc độ ánh sáng. Tìm giới hạn của khối lượng khi v tiến đến c−. Lời giải. Với m0 = 0 thì lim = 0. v→c− Với m0 ̸= 0.   v2   1 − → 0   c2 m0 Khi c → c− thì suy ra lim = +∞. … v→c−  v2  v2  1 −  1 − > 0  c2 c2
Vậy nếu một hạt có khối lượng nghỉ khác 0 thì khối lượng của hạt sẽ lớn vô cùng khi vận tốc tiến gần vận tốc ánh sáng. □ 425/764 425/764
Toán 11 theo chương trình GDPT2018 426
2. Giới hạn của hàm số
Biết làm, làm đúng, làm nhanh
Bài 60. Một chất điểm chuyển động thẳng với phương trình s(t). Khi đó vận tốc tức thời tại thời điểm t0 được định s(t0 + ∆t) − s(t0) nghĩa là lim
. Tính vận tốc tức thời của chất điểm với phương trình chuyển động s(t) = 3t2−2t+3 ∆t ∆t
(s(t) có đơn vị là m, t đơn vị là giây), tại thời điểm t = 4 giây. Lời giải.
Vận tốc tức thời của chất điểm tại thời điểm t = 4 giây là s(4 + ∆t) − s(4)
3(4 + ∆t)2 − 2(4 + ∆t) + 3 − 43 lim = lim ∆t→0 ∆t ∆t→0 ∆t 3(∆t)2 + 22∆t = lim = 22 m/s. ∆t→0 ∆t □
Bài 61. Số lượng đơn vị hàng tồn kho trong một công ty được cho bởi Å ï t + 3 ò ã N (t) = 200 3 − t 3
trong đó t là thời gian tính bằng ngày, [x] là số nguyên lớn nhất không vượt quá x (ví dụ [−1,5] = −2, [8,8] = 8). a) Tính lim N (t). t→55+ b) Tính lim N (t). t→201− Lời giải. ï t + 3 ò a) Khi t → 55+, ta có = 19. 3 Å ï t + 3 ò ã Suy ra lim N (t) = lim 200 3 − t = 200(3 · 19 − 55) = 400. t→55+ t→55+ 3 ï t + 3 ò b) Khi t → 201−, ta có = 201. 3 Å ï t + 3 ò ã Suy ra lim N (t) = lim 200 3 − t = 200 · 0 = 0. t→201− t→201− 3 □
Bài 62. Một chất điểm chuyển động thẳng với vận tốc v(t). Khi đó gia tốc tức thời tại thời điểm t0 được định v(t0 + ∆t) − v(t0) nghĩa là lim
. Một chất điểm chuyển động với vận tốc v(t) = 0,1t2 − 0,4t + 1 (m/s), tính gia ∆t→0 ∆t
tốc tức thời tại thời điểm t = 8 giây. Lời giải.
Gia tốc tức thời của chất điểm tại thời điểm t = 8 giây là v(8 + ∆t) − v(8)
0,1(8 + ∆t)2 − 0,4(8 + ∆t) + 1 − 4,2 lim = lim ∆t→0 ∆t ∆t→0 ∆t 0,1(∆t)2 + 1,2∆t = lim ∆t→0 ∆t = lim (0,1∆t + 1,2) ∆t→0 = 1,2.
Vậy gia tốc tức thời của chất điểm tại thời điểm t = 8 giây là 1,2 (m/s2). □
Bài 63. Một người lái xe từ thành phố A đến thành phố B với vận tốc trung bình là x km/h. Trên chuyến trở về,
vận tốc trung bình là y km/h. Vận tốc trung bình của cả đi và về là 60 km/h. (Giả sử người lái xe đi trên cùng
một con đường trên cả chuyến đi và về). 30x a) Chứng minh rằng y = . x − 30 426/764 426/764
Toán 11 theo chương trình GDPT2018 427
Chương 3. Giới hạn. Hàm số liên tục
Biết làm, làm đúng, làm nhanh
b) Tìm giới hạn của y khi x → 30+. Lời giải.
a) Gọi khoảng cách giữa A và B là s km. s s Thời gian chuyến đi là
, thời gian chuyến trở về là . x y Suy ra 2s s s 1 1 1 30x = + ⇔ = − ⇔ y = . 60 x y y 30 x x − 30 30x b) Ta có lim y = lim = +∞. x→30+ x→30+ x − 30 □
Bài 64. Một hình elip với bán trục lớn a và bán trục nhỏ b thì diện tích được tính theo công thức S = πab. Tính
giới hạn diện tích của elip khi tiêu cự gần tới 0. Lời giải. √
Ta có S = πab = πa a2 − c2. √
Vậy lim S = lim πa a2 − c2 = πa2. c→0 c→0
Ta thấy khi c → 0, thì giới hạn diện tích của elip là diện tích hình tròn bán kính R = a. □
Bài 65. Các nhà vật lý thấy rằng thuyết tương đối hẹp của Einstein quy về cơ học Newton khi c → +∞, trong
đó c là tốc độ ánh sáng. Điều này được minh họa bởi ví dụ: Một hòn đá được ném thẳng đứng từ mặt đất để nó
quay trở lại trái đất một giây sau đó. Sử dụng các định luật Newton, chúng ta thấy rằng chiều cao tối đa của hòn g đá là h =
mét (g = 9,8m/s2). Theo thuyết tương đối hẹp, khối lượng của hòn đá phụ thuộc vào vận tốc của nó 8
chia cho c, và có chiều cao cực đại là c2 1 c2 h(c) = c + − . g2 4 g Tính lim h(c). c→+∞ Lời giải. Ta có Å c2 1 c2 ã 1 c + − c2 1 c2 g2 4 g2 g lim c + − = lim = lim 4 = . c→+∞ g2 4 g c→+∞ c2 1 c c→+∞ 1 1 1 8 + + + + g2 4 g g2 4c2 g □
Bài 66. Thế Lennard-Jones có dạng B A U (r) = − r12 r6
trong đó A, B là các hằng số và r là khoảng cách giữa các hạt. Tính lim U (r). r→+∞ Lời giải. Ta có Å B A ã lim U (r) = lim − = 0. r→+∞ r→+∞ r12 r6 □
Bài 67. Trong thuyết tương đối, chiều dài của một vật thể đối với người quan sát phụ thuộc vào tốc độ mà vật
thể đang chuyển động đối với người quan sát. Nếu người quan sát đo chiều dài của vật thể là L0 khi đứng yên,
thì ở tốc độ v chiều dài là v2 L = L0 1 − c2
trong đó c là tốc độ ánh sáng trong chân không. Tìm lim L. v→c− Lời giải. v2 c2 Ta có lim L = lim L0 1 − = lim L0 1 − = 0. □ v→c− v→c− c2 v→c− c2 427/764 427/764
Toán 11 theo chương trình GDPT2018 428
2. Giới hạn của hàm số
Biết làm, làm đúng, làm nhanh
Bài 68. Trong kỹ thuật ứng dụng, chúng ta thường xuyên ghi nhận được các hàm số mà giá trị của nó thay đổi
đột ngột tại một thời điểm t xác định. Ví dụ: Sự thay đổi điện áp của một mạch điện tại thời điểm t khi đóng
hoặc ngắt mạch. Thông thường, giá trị t = 0 luôn được chọn là thời điểm bắt đầu cho việc đóng hoặc ngắt điện
áp. Quá trình đóng, ngắt mạch trên có thể mô tả bằng mô hình toán học bởi hàm Heaviside ®0 nếu t < 0 u(t) = 1 nếu t ≥ 0.
Có tồn tại giới hạn lim u(t) hay không? t→0 Lời giải.
Ta có lim u(t) = lim 1 = 1; lim u(t) = lim 0 = 0. t→0+ t→0+ t→0− t→0−
Vậy giới hạn lim u(t) không tồn tại. □ t→0
Bài 69. Trong một cuộc thi các môn thể thao trên tuyết, người ta muốn thiết kế một đường trượt bằng băng cho
nội dung đổ dốc tốc độ đường dài. y 15 O x 5 10 15 20 25 30 35 40 45
Vận động viên sẽ xuất phát từ vị trí (0; 15) cao 15 m so với mặt đất (trục Ox). Đường trượt phải thoả mãn yêu
cầu là càng ra xa thì càng gần mặt đất để tiết kiệm lượng tuyết nhân tạo. Một nhà thiết kế đề nghị sử dụng 150
đường cong là đồ thị hàm số y = f (x) =
, với x ≥ 0. Hãy kiểm tra xem hàm số y = f (x) có thoả mãn các x + 10
điều kiện dưới đây hay không:
a) Có đồ thị qua điểm (0; 15); b) Giảm trên [0; +∞);
c) Càng ra xa (x càng lớn), đồ thị của hàm số càng gần trục Ox với khoảng cách nhỏ tuỳ ý. Lời giải. 150 a) Ta có f (0) =
nên đồ thị hàm số f (x) đi qua điểm (0; 15). 10
b) Chọn bất kì x1, x2 ∈ [0; +∞] và x1 ̸= x2. 150 150 − f (x2) − f (x1) x x x1 − x2 1 Ta có = 2 + 10 1 + 10 = = − < 0. x2 − x1 x2 − x1 (x2 − x1)(x1 + 10)(x2 + 10) (x1 + 10)(x2 + 10)
Suy ra hàm số nghịch biến trên [0; +∞) hay hàm số giảm trên [0; +∞). 150 c) Ta có lim f (x) = lim = 0. x→+∞ x→+∞ x + 10
Vậy khi x càng lớn, đồ thị của hàm số càng gần trục Ox với khoảng cách nhỏ tuỳ ý. □ 100
Bài 70. Chiều dài một loài động vật nhỏ được tính theo công công thức h(t) = mm, trong đó t số 2 + 3 · (0,4)t
ngày sau khi sinh của loài động vật đó. Tính chiều dài cuối cùng của nó (chiều dài khi t → +∞). Lời giải. 100 Ta có lim h(t) = = 100. t→+∞ 2 + 3 · (0,4)t
Vậy chiều dài của loài động vật khi trưởng thành là 100 mm. □ 428/764 428/764
Toán 11 theo chương trình GDPT2018 429
Chương 3. Giới hạn. Hàm số liên tục
Biết làm, làm đúng, làm nhanh
Bài 71. Một chất điểm chuyển động thẳng với phương trình s(t). Khi đó vận tốc tức thời tại thời điểm t0 được định s(t0 + ∆t) − s(t0) nghĩa là lim
. Tính vận tốc tức thời của chất điểm với phương trình chuyển động s(t) = 4t2−3t+1 ∆t ∆t
(s(t) có đơn vị là m, t đơn vị là giây), tại thời điểm t = 8 giây. Lời giải.
Vận tốc tức thời của chất điểm tại thời điểm t = 8 giây là s(8 + ∆t) − s(8)
4(8 + ∆t)2 − 3(8 + ∆t) + 1 − 233 lim = lim ∆t→0 ∆t ∆t→0 ∆t 4(∆t)2 + 61∆t = lim = 61 m/s. ∆t→0 ∆t □
Bài 72. Bỏ qua lực cản của không khí, độ cao tối đa mà tên lửa đạt được khi phóng với vận tốc ban đầu v0 là v2R h = 0
, trong đó R là bán kính của trái đất. Tính lim h. 19,6R − v2 R→+∞ 0 Lời giải. Ta có v2R lim h = lim 0 R→+∞ R→+∞ 19,6R − v2 0 v2 v2 = lim 0 = 0 . R→+∞ v2 19,6 19,6 − 0 R □
Bài 73. Một hình elip với bán trục lớn a và bán trục nhỏ b thì diện tích được tính theo công thức S = πab. Cho
elip có bán trục nhỏ bằng 30 cm, tính giới hạn diện tích của elip khi tiêu cự gần tới 0. Lời giải. √ Ta có S = πab = πb b2 + c2. √
Vậy lim S = lim πb b2 + c2 = πb2 = 900π cm2. □ c→0 c→0
Bài 74. Số lượng đơn vị hàng tồn kho trong một công ty nhỏ được cho bởi Å ï t + 2 ò ã N (t) = 25 2 − t 2
trong đó t là thời gian tính bằng tháng, [x] là số nguyên lớn nhất không vượt quá x (ví dụ [2,4] = 2, [−2,7] = −3). a) Tính lim N (t). t→8+ b) Tính lim N (t). t→16− Lời giải. ï t + 2 ò a) Khi t → 8+, ta có = 5. 2 Suy ra lim N (t) = lim t→8+ 25 2 t+2 − t = 50. 2 t→8+ ï t + 2 ò b) Khi t → 16−, ta có = 8. 2 Suy ra lim N (t) = lim t→16− 25 2 t+2 − t = 0. 2 t→16− □
Bài 75. Định luật Boyle được phát biểu: “Đối với một lượng khí ở nhiệt độ không đổi, áp suất P tỷ lệ nghịch với
thể tích V ”. Tìm giới hạn của P là V → 0+. Lời giải. k Ta có P =
với k là số thực dương không đổi. V k Khi đó lim P = = +∞. □ V →0+ V 429/764 429/764
Toán 11 theo chương trình GDPT2018 430
2. Giới hạn của hàm số
Biết làm, làm đúng, làm nhanh
Bài 76. Một vật khối lượng m (không đổi) bắt đầu chuyển động với vận tốc v0 = 0, được gia tốc bởi một lực F F t
không đổi trong t giây. Theo định luật Newton về chuyển động, vật tốc của vật là vN = . Theo thuyết tương m F ct
đối Einstein, vật có vận tốc vE = √
, với c là vận tốc ánh sáng. Tính lim vN và lim vE. m2c2 + F 2t2 t→+∞ t→+∞ Lời giải. Ta có F t lim vN = lim = +∞; t→+∞ t→+∞ m F ct F c c lim vE = lim √ = lim = . t→+∞ t→+∞ m2c2 + F 2t2 t→+∞ … m2c2 F + F 2 t2 □ Bài 77.
Gọi S là diện tích hình phẳng giới hạn bởi đường tròn bán kính 10 và tam giác C vuông (hình vẽ bên). D
a) Đặt S = f (φ), với f (φ) là hàm số của φ (Đơn vị rad). Tìm công thức của π f (φ) với 0 < φ < . 2 π − φ
b) Tính giới hạn của f (φ) khi φ → . 2 A B Lời giải. 1 1
a) Diện tích tam giác ABC là SABC = AB · AC = · 4 · 4 tan φ = 8 tan φ. 2 2 42φ
Diện tích hình quạt ABD là Sq = = 8φ. 2
Diện tích hình phẳng S là S = f (φ) = SABC − Sq = 8(tan φ − φ). ® cos φ → 0 b) Khi φ → π − thì 2 cos φ > 0. Å sin φ ã Suy ra lim f (φ) = lim 8 − φ = +∞. π − π − cos φ φ→ φ→ 2 2 □
Bài 78. Trên một chuyến đi dài d km đến một thành phố khác, vận tốc trung bình của một tài xế xe tải là x
km/h. Trên chuyến trở về, vận tốc trung bình là y km/h. Vận tốc trung bình của cả đi và về là 50 km/h. 25x a) Chứng minh rằng y = . x − 25
b) Tìm giới hạn của y khi x → 25+ và giải thích ý nghĩa của nó. Lời giải. d d
a) Thời gian chuyến đi là
, thời gian chuyến trở về là . x y Suy ra 2d d d 1 1 1 25x = + ⇔ = − ⇔ y = . 50 x y y 25 x x − 25 25x b) Ta có lim y = lim = +∞. x→25+ x→25+ x − 25
Khi vận tốc trung bình chuyến đi bằng 25 km/h, thì vận tốc trung bình chuyến của cả chuyến đi và về không thể là 50 km/h. □ 430/764 430/764
Toán 11 theo chương trình GDPT2018 431
Chương 3. Giới hạn. Hàm số liên tục
Biết làm, làm đúng, làm nhanh
Bài 79. Một chất điểm chuyển động thẳng với vận tốc v(t). Khi đó gia tốc tức thời tại thời điểm t0 được định v(t0 + ∆t) − v(t0) nghĩa là lim
. Một chất điểm chuyển động với vận tốc v(t) = 5 sin (4πt) (m/s), tính gia tốc ∆t→0 ∆t sin x
tức thời tại thời điểm t = 5 giây. (Biết lim = 1). x→0 x Lời giải.
Gia tốc tức thời của chất điểm tại thời điểm t = 5 giây là v(5 + ∆t) − s(5)
5 sin(20π + 4π∆t) − 5 sin(20π) lim = lim ∆t→0 ∆t ∆t→0 ∆t 5 sin(4π∆t) = lim ∆t→0 ∆t 20π sin(4π∆t) = lim ∆t→0 4π∆t = 20π.
Vậy gia tốc tức thời của chất điểm tại thời điểm t = 5 giây là 20π (m/s2). □
Bài 80. Một bể chứa 5000 lít nước tinh khiết. Nước muối chứa 30 g muối trên một lít nước được bơm vào bể với
tốc độ 25 lít/phút. Gọi nồng độ của muối sau t phút (tính bằng gam trên lít) là C(t). Tính lim C(t). Giải thích t→+∞
ý nghĩa của giới hạn này. Lời giải.
Số lít nước muối được bơm vào bể sau t phút là 25t lít.
Số g muối có trong 25t lít nước muối là 30 · 25t = 750t gam.
Nồng độ của muối trong bể sau t phút là 750t 30t = gam/lít. 25t + 5000 t + 200 30t Ta có lim C(t) = lim = 30 gam/lít. t→+∞ t→+∞ t + 200
Khi thời gian tiến tới vô hạn thì nồng độ của muối trong bể bằng nồng độ của nước muối bơm vào bể. □
Bài 81. Một thấu kính hội tụ có tiêu cự f = 30 cm. Trong Vật lí, ta biết rằng nếu đặt vật thật AB cách quang
tâm của thấu kính một khoảng d > 30 (cm) thì được ảnh thật A′B′ cách quang tâm của thấu kính một khoảng 1 1 1
d′ (cm) (Hình vẽ dưới). Ngược lại, nếu 0 < d < 30, ta có ảnh ảo. Công thức của thấu kính là + = . d d′ 30 30 30 B A′ A O F F ′ d d′ B′
a) Từ công thức của thấu kính, hãy tìm biểu thức xác định hàm số d′ = h(d).
b) Tìm các giới hạn lim h(d); lim h(d) và lim h(d). Sử dụng các kết quả này để giải thích ý nghĩa đã biết d→30+ d→30− d→+∞ trong Vật lí. Lời giải. 1 1 1 1 1 1 d − 30 30d a) Ta có + = ⇔ = − = ⇔ d′ = . d d′ 30 d′ 30 d 30d d − 30 30d Vậy d′ = h(d) = . d − 30 431/764 431/764
Toán 11 theo chương trình GDPT2018 432
2. Giới hạn của hàm số
Biết làm, làm đúng, làm nhanh
b) Khi d → 30+, ta có d − 30 → 0, d − 30 > 0 và 30d → 900. 30d Suy ra lim h(d) = lim = +∞. d→30+ d→30+ d − 30
Khi d → 30−, ta có d − 30 → 0, d − 30 < 0 và 30d → 900. 30d Suy ra lim h(d) = lim = −∞. d→30− d→30− d − 30 30d 30 Ta có lim h(d) = lim = lim = 30. d→+∞ d→+∞ d − 30 d→+∞ 30 1 − d Vậy
○ Khi vị trí của vật tiến gần tiêu điểm F (d > f ) thì vị trí ảnh thật của vật dần ra xa vô cực.
○ Khi vị trí của vật tiến gần tiêu điểm F (d < f ) thì vị trí ảnh ảo của vật dần ra xa vô cực.
○ Khi vị trí của vật tiến ra xa vô cực thì ảnh thật của vật dần tới tiêu điểm. □ 432/764 432/764
Toán 11 theo chương trình GDPT2018 433
Chương 3. Giới hạn. Hàm số liên tục
Biết làm, làm đúng, làm nhanh Baâi söë 3 HÀM SỐ LIÊN TỤC A – KHÁI NIỆM 1.
Hàm số liên tục tại một điểm
c Định nghĩa 3.1. Cho hàm số y = f(x) xác định trên khoảng (a; b) và x0 ∈ (a; b). Hàm số y = f(x) được
gọi là liên tục tại x0 nếu lim f (x) = f (x0). x→x0
Nhận xét. Hàm số y = f (x) không liên tục tại x0 được gọi là gián đoạn tại x0. 2.
Hàm số liên tục trên một khoảng hoặc một đoạn c Định nghĩa 3.2.
○ Hàm số y = f (x) được gọi là liên tục trên khoảng (a; b) nếu hàm số liên tục tại mọi điểm thuộc khoảng đó.
○ Hàm số y = f (x) được gọi là liên tục trên đoạn [a; b] nếu hàm số đó liên tục trên khoảng (a; b) và
lim f (x) = f (a); lim f (x) = f (b). x→a+ x→b−
Khái niệm hàm số liên tục trên các tập hợp có dạng (a; b], [a; b), (a; +∞), [a; +∞), (−∞; a), (−∞; a],
(−∞; +∞) được định nghĩa tương tự.
Nhận xét. Đồ thị hàm số liên tục trên một khoảng là “đường liền” trên khoảng đó.
B – MỘT SỐ ĐỊNH LÍ CƠ BẢN 1.
Tính liên tục của một số hàm số sơ cấp cơ bản
Các hàm đa thức, hàm phần thức hữu tỉ (thương của hai đa thức), hàm căn thức, hàm số lượng giác là những
hàm sơ cấp cơ bản. Sau đây, ta sẽ xét tính liên tục của những hàm số đó. c Định lí 3.1.
○ Các hàm đa thức và hai hàm số lượng giác y = sin x, y = cos x liên tục trên R.
○ Các hàm phân thức hữu tỉ và hai hàm số lượng giác y = tan x, y = cot x liên tục trên từng khoảng xác định của chúng. √ ○ Hàm căn thức y =
x liên tục trên nửa khoảng [0; +∞). 2.
Tính liên tục của tổng, hiệu, tích, thương của hai hàm số liên tục
c Định lí 3.2. Giả sử y = f (x) và y = g(x) là hai hàm số liên tục tại điểm x0. Khi đó:
a) Các hàm số f (x) + g(x); f (x) − g(x) và f (x) · g(x) liên tục tại x0; f (x) b) Hàm số y =
liên tục tại x0 nếu g(x0) ̸= 0. g(x) 433/764 433/764
Toán 11 theo chương trình GDPT2018 434 3. Hàm số liên tục
Biết làm, làm đúng, làm nhanh
C – CÁC DẠNG TOÁN THƯỜNG GẶP
Dạng 1. Câu hỏi lý thuyết 1. Ví dụ mẫu
Ví dụ 1 (CD). Bạn Nam cho rằng: “Nếu hàm số y = f (x) liên tục tại điểm x0, còn hàm số y = g(x) không liên
tục tại x0, thì hàm số y = f (x) + g(x) không liên tục tại x0”. Theo em, ý kiến của bạn Nam đúng hay sai? Giải thích. Lời giải.
Giả sử hàm số h(x) = f (x) + g(x) là hàm số liên tục tại x0.
Khi đó, hàm số g(x) = h(x) − f (x) là hiệu của hai hàm số liên tục tại x0 nên hàm số g(x) là hàm số liên tục tại
x0. Điều này mâu thuẫn với giả thiết là g(x) không liên tục tại x0.
Vậy ý kiến trên là đúng. □ 2.
Bài tập trắc nghiệm
Câu 1. Cho hàm số y = f (x) xác định trên khoảng K và x0 ∈ K. Hàm số y = f (x) liên tục tại x0 khi và chỉ khi A lim f (x) = +∞. B lim f (x) = −∞. C lim f (x) = f (x0). D lim f (x) = f (x0). x→x0 x→x0 x→x0 x→x+ 0 Lời giải.
Hàm số y = f (x) được gọi là liên tục tại x0 nếu lim f (x) = f (x0). x→x0 Chọn đáp án C □
Câu 2. Cho hàm số y = f (x) liên tục trên khoảng (a; b). Điều kiện cần và đủ để hàm số liên tục trên đoạn [a; b] là A
lim f (x) = f (a) và lim f (x) = f (b). B
lim f (x) = f (a) và lim f (x) = f (b). x→a+ x→b− x→a− x→b+
C lim f (x) = f (a) và lim f (x) = f (b). D
lim f (x) = f (a) và lim f (x) = f (b). x→a+ x→b+ x→a− x→b− Lời giải.
Hàm số f xác định trên đoạn [a; b] được gọi là liên tục trên đoạn [a; b] nếu nó liên tục trên khoảng (a; b), đồng
thời lim f (x) = f (a) và lim f (x) = f (b) . x→a+ x→b− Chọn đáp án A □
Câu 3. Trong các mệnh đề sau, mệnh đề nào đúng?
A Hàm số đồng biến trên (a; b) có đồ thị là đường đi xuống từ trái sang phải trên (a; b).
B Hàm số nghịch biến trên (a; b) có đồ thị là đường đi lên từ trái sang phải trên (a; b).
C Hàm số y = 0 là hàm số không chẵn, không lẻ trên R.
D Hàm số liên tục trên (a; b) có đồ thị là đường liền nét trên (a; b). Lời giải.
Hàm số liên tục trên (a; b) có đồ thị là đường liền nét trên (a; b). Chọn đáp án D □
Câu 4. Trong các loại hàm số sau, hàm số nào luôn liên tục trên tập hợp các số thực R?
A Hàm số lượng giác. B Hàm số đa thức.
C Hàm số phân thức hữu tỉ.
D Hàm số có chứa căn bậc hai. Lời giải.
Hàm số đa thức luôn liên tục trên tập số thực R. Chọn đáp án B □
Câu 5. Hàm số y = f (x) liên tục tại điểm x0 khi nào? A lim f (x) = f (x). B lim f (x) = f (x0). C lim f (x) = f (0). D f (x0) = 0. x→x0 x→x0 x→x0 434/764 434/764
Toán 11 theo chương trình GDPT2018 435
Chương 3. Giới hạn. Hàm số liên tục
Biết làm, làm đúng, làm nhanh Lời giải.
Theo định nghĩa hàm số liên tục, ta có lim f (x) = f (x0). x→x0 Chọn đáp án B □
Câu 6. Cho hàm số f (x) thỏa mãn lim f (x) ̸= f (x0). Khẳng định nào sau đây đúng? x→x0
A Hàm số f (x) không xác định tại x0. B lim f (x) = lim f (x). x→x− x→x+ 0 0
C Hàm số f (x) liên tục tại x0.
D f (x) có giá trị 0 tại x0. Lời giải.
Theo định nghĩa hàm số liên tục, ta có: do lim f (x) ̸= f (x0) nên hàm số f (x) không liên tục tại x0. Vì lim f (x) x→x0 x→x0
tồn tại nên lim f (x) = lim f (x). x→x− x→x+ 0 0 Chọn đáp án B □
Câu 7. Xét các mệnh đề sau
a) Nếu hàm số f (x) có đạo hàm tại điểm x = x0 thì f (x) liên tục tại điểm đó.
b) Nếu hàm số f (x) liên tục tại điểm x = x0 thì f (x) có đạo hàm tại điểm đó.
c) Nếu f (x) không liên tục tại x0 thì chắc chắn f (x) không có đạo hàm tại điểm đó.
d) f (x) có đạo hàm tại x0 khi và chỉ khi f (x) liên tục tại x0.
Trong các mệnh đề trên, có bao nhiêu mệnh đề đúng? A 2. B 1. C 4. D 3. Lời giải.
Theo định lý thì mệnh đề thứ nhất và mệnh đề thứ ba đúng.
Xét hàm số f (x) = |x| ta có: lim f (x) = 0 và lim f (x) = 0 nên hàm số liên tục tại x = 0. x→0+ x→0− f (x) − f (0) f (x) − f (0) Mặt khác lim = 1 và lim
= −1 nên hàm số không có đạo hàm tại x = 0. Vậy hai x→0+ x − 0 x→0− x − 0 mệnh đề còn lại sai. Chọn đáp án A □
Câu 8. Cho hàm số f (x) xác định trên [a; b]. Trong các mệnh đề sau, mệnh đề nào đúng?
A Nếu hàm số f (x) liên tục trên đoạn [a; b] và f (a) · f (b) > 0 thì phương trình f (x) = 0 không có nghiệm trong khoảng (a; b).
B Nếu hàm số f (x) liên tục trên đoạn [a; b] và f (a) · f (b) < 0 thì phương trình f (x) = 0 có ít nhất một nghiệm trong khoảng (a; b).
C Nếu phương trình f (x) = 0 có nghiệm trong khoảng (a; b), thì hàm số f (x) phải liên tục trên khoảng (a; b).
D Nếu f (a) · f (b) < 0 thì phương trình f (x) = 0 có nghiệm trong khoảng (a; b). Lời giải.
Nếu hàm số f (x) liên tục trên đoạn [a; b] và f (a) · f (b) < 0 thì phương trình f (x) = 0 có ít nhất một nghiệm trong khoảng (a; b). Chọn đáp án B □
Câu 9. Tìm khẳng định đúng trong hai khẳng định sau
I. f (x) liên tục trên [a, b] và f (a) · f (b) > 0 thì tồn tại ít nhất số c ∈ (a, b) sao cho f (c) = 0.
II. f (x) liên tục trên (a, b) và (b, c) nhưng không liên tục trên (a, c). A Chỉ I đúng. B Chỉ II đúng.
C Cả I và II đều sai.
D Cả I và II đều đúng. Lời giải. Chọn đáp án C □ 435/764 435/764
Toán 11 theo chương trình GDPT2018 436 3. Hàm số liên tục
Biết làm, làm đúng, làm nhanh
Câu 10. Cho lim f (x) = L. Khẳng định nào sau đây đúng? x→a A f (a) = L.
B Hàm số liên tục tại x = a.
C Hàm số xác định tại x = a.
D Không đáp án nào đúng. Lời giải. Chọn đáp án D □
Câu 11. Cho lim f (x) = −1, lim f (x) = −1. Khẳng định nào sau đây đúng? x→3− x→3+ A lim f (x) = −1.
B Hàm số liên tục tại x = 3. x→3 C f (3) = −1.
D f (3) không xác định. Lời giải.
lim f (x) = lim f (x) = −1 ⇒ lim f (x) = −1. x→3− x→3+ x→3 Chọn đáp án A □
Câu 12. Trong các mệnh đề sau, mệnh đề nào sai?
A Nếu hàm số f (x) liên tục trên khoảng (a; b) thì f (x) cũng liên tục trên mọi khoảng con của (a; b).
B Mọi hàm số đa thức đều liên tục trên khoảng (−∞; +∞).
C Mọi hàm số phân thức hữu tỉ đều liên tục trên mọi khoảng mà nó xác định.
D Nếu hàm số f (x) liên tục trên hai khoảng liên tiếp (a; b) và (b; c) thì f (x) cũng liên tục trên khoảng (a; c). Lời giải. √ ® x − 1 nếu x ≥ 1 Xét hàm số f (x) = 2x + 3 nếu x < 1.
Ta thấy f (x) liên tục trên các khoảng (0; 1) và (1; 2) nhưng không liên tục trên (0; 2). Chọn đáp án D □
Câu 13. Cho f (x) là một hàm số liên tục trên khoảng (a; b). Trong các mệnh đề sau, mệnh đề nào sai?
A Hàm số g(x) = (f (x))2 liên tục trên khoảng (a; b). B Hàm số h(x) = 3
pf (x) liên tục trên khoảng (a; b). 1 C Hàm số k(x) =
liên tục trên khoảng (a; b).
D Hàm số u(x) = |f (x)| liên tục trên khoảng (a; b). f (x) Lời giải. 1 Đối với hàm số k(x) =
, cần thêm điều kiện f (x) ̸= 0, ∀x ∈ (a; b). f (x) Chọn đáp án C □
Câu 14. Cho f (x) và g(x) là hai hàm số liên tục trên khoảng (a; b). Tìm mệnh đề sai trong các mệnh đề sau?
A Hàm số h(x) = f (x) − g(x) liên tục trên khoảng (a; b).
B Hàm số k(x) = f (x).g(x) liên tục trên khoảng (a; b). f (x) C Hàm số u(x) =
liên tục trên khoảng (a; b). g(x)
D Hàm số v(x) = af (x) + bg(x) liên tục trên khoảng (a; b) với a, b là các hằng số. Lời giải. f (x) Hàm số u(x) =
liên tục trên khoảng (a; b) khi g(x) ̸= 0, ∀x ∈ (a; b). g(x) Chọn đáp án C □
Câu 15. Tìm khẳng định đúng trong các khẳng định sau
I. f (x) liên tục trên đoạn [a; b] và f (a) · f (b) < 0 thì phương trình f (x) = 0 có nghiệm.
II. f (x) không liên tục trên [a; b] và f (a) · f (b) ≥ 0 thì phương trình f (x) = 0 vô nghiệm. A Chỉ I đúng. B Chỉ II đúng. C Cả I và II đúng. D Cả I và II sai. Lời giải. Chọn đáp án A □ 436/764 436/764
Toán 11 theo chương trình GDPT2018 437
Chương 3. Giới hạn. Hàm số liên tục
Biết làm, làm đúng, làm nhanh
Câu 16. Cho hàm số f (x) liên tục trên đoạn [a; b] và m ≤ f (x) ≤ M , ∀x ∈ [a; b] . Tìm mệnh đề sai trong các mệnh đề sau?
A Luôn tồn tại x1 ∈ [a; b] sao cho f (x) ≥ f (x1), ∀x ∈ [a; b].
B Luôn tồn tại x2 ∈ [a; b] sao cho f (x) ≤ f (x2), ∀x ∈ [a; b].
C Với mọi k ∈ [m; M ] , luôn tồn tại c ∈ [a; b] sao cho f (c) = k.
D Đồ thị của hàm số là một đường liền nét trên đoạn [a; b]. Lời giải.
f (x1) chính là giá trị nhỏ nhất của hàm số f (x) trên đoạn [a; b].
f (x2) chính là giá trị lớn nhất của hàm số f (x) trên đoạn [a; b].
Hàm số f (x) liên tục trên đoạn [a; b] nên có đồ thị là một đường liền nét trên đoạn [a; b].
Ngoài ra, m và M chưa chắc là giá trị nhỏ nhất và giá trị lớn nhất của f (x) trên đoạn [a; b]. Chọn đáp án C □
Dạng 2. Dựa vào đồ thị xét tính liên tục của hàm số tại một điểm, một khoảng.
Để xét tính liên tục của hàm số khi biết đồ thị, ta cần nhớ:
○ Đồ thị của hàm số liên tục trên một khoảng là một đường liền nét trên khoảng đó.
○ Hàm số y = f (x) liên tục tại x0 khi và chỉ khi lim f(x) = lim f(x) = f(x0). x→x + − 0 x→x0 1. Ví dụ mẫu
Ví dụ 2. Quan sát đồ thị hàm số trong Hình 12a và Hình 12b, xác định f (0) và lim f (x). Từ đó cho biết mỗi x→0
hàm số đó liên tục tại x = 0 hay không? Giải thích. Lời giải.
Trong Hình 12a ta có f (0) = 0, lim f (x) = lim x2 = 0. x→0 x→0 y y 1 −1 O x 1 −2 −1 −1 O x 1 2  − 1 nếu x < 0
a) Đồ thị hàm số f (x) = x2  
b) Đồ thị hàm số f (x) = 0 nếu x = 0  1 nếu x > 0 Hình 12
Như vậy lim f (x) = f (0) nên hàm số liên tục tại x = 0. x→0
Trong Hình 12b ta có lim f (x) = −1, lim f (x) = 1. x→0− x→0+
Do đó không tồn tại lim f (x). x→0
Vậy hàm số f (x) không liên tục tại x = 0. □
Ví dụ 3. Trong các hàm số có đồ thị ở Hình 15a, 15b, 15c hàm số nào liên tục trên tập xác định của hàm số đó? Giải thích. 437/764 437/764
Toán 11 theo chương trình GDPT2018 438 3. Hàm số liên tục
Biết làm, làm đúng, làm nhanh y y y 3 1 2 1 1 1 −1 O x 1 O 1 2 3 x −1 −1 O x −1 a) Đồ thị hàm số b) Đồ thị hàm số c) Đồ thị hàm số x ® f (x) = x2 − 2x − 2x nếu x < −1 g(x) = x − 1 h(x) = x + 1 nếu x ≥ 1 Hình 15 Lời giải.
Hàm số liên tục trên tập xác định là f (x) = x2 − 2x. Vì đồ thị hàm số ở hình Hình 15a là một đường liền nét
trên mặt phẳng tọa độ. □ Ví dụ 4.
Cho hàm số y = f (x) có đồ thị như hình vẽ bên. y y = f (x)
Xét tính liên tục của hàm số y = f (x) trên khoảng (0; 2). O 1 2 x Lời giải.
Đồ thị hàm số là một đường liền nét trên khoảng (0; 2) nên hàm số đã cho liên tục trên khoảng (0; 2). □ Ví dụ 5.
Cho hàm số y = f (x) có đồ thị như hình vẽ bên. y
Xét tính liên tục của hàm số y = f (x) trên khoảng (−2; 2). y = f (x) −2 O 2 x Lời giải.
Đồ thị hàm số là một đường liền nét trên khoảng (−2; 2) nên hàm số đã cho liên tục trên khoảng (−2; 2). □ Ví dụ 6.
Cho hàm số y = f (x) có đồ thị như hình vẽ bên. y
Xét tính liên tục của hàm số y = f (x) trên khoảng (0; 2). y = f (x) 2 1 O 1 2 x Lời giải.
○ Đồ thị hàm số là các đường liền nét trên các khoảng (0; 1), (1; 2) do đó hàm số liên tục trên các khoảng này.
○ Đồ thị hàm số không liền nét tại điểm x = 1 do đó hàm số đã cho gián đoạn tại điểm này. □ Ví dụ 7. 438/764 438/764
Toán 11 theo chương trình GDPT2018 439
Chương 3. Giới hạn. Hàm số liên tục
Biết làm, làm đúng, làm nhanh
Cho hàm số y = f (x) có đồ thị như hình vẽ bên. y
Xét tính liên tục của hàm số y = f (x) trên khoảng (0; 2). y = f (x) 2 1 O 1 2 x Lời giải.
○ Đồ thị hàm số là các đường liền nét trên các khoảng (0; 1), (1; 2) do đó hàm số liên tục trên các khoảng này.
○ Ta có lim f (x) > f (1) = 1 và lim f (x) = f (1) = 1. x→1− x→1+
Do đó lim f (x) ̸= lim f (x). x→1− x→1+
Vậy hàm số đã cho gián đoạn tại x = 1. □ Ví dụ 8.
Cho hàm số y = f (x) có tập xác định D = R \ {0} và có đồ thị như hình bên. Xét y
tính liên tục của hàm số y = f (x) trên D. y = f (x) O x Lời giải.
Vì hàm số đã cho có tập xác định D = R \ {0} nên
○ f (x) xác định trên khoảng (−∞; 0) nên liên tục trên khoảng này.
○ f (x) xác định trên khoảng (0; +∞) nên liên tục trên khoảng này.
○ f (x) không xác định tại điểm x = 0 nên gián đoạn tại điểm này. □ 2. Bài tập tự luận Bài 1.
Cho hàm số y = f (x) xác định trên D = R và có đồ thị như hình vẽ bên. y
Xét tính liên tục của hàm số y = f (x) trên D. y = f (x) O x Lời giải.
Do đồ thị hàm số là một đường liền nét trên D nên hàm số y = f (x) liên tục trên D = R. □ Bài 2.
Cho hàm số y = f (x) xác định trên D = R và có đồ thị như hình vẽ bên. Xét tính y
liên tục của hàm số y = f (x) trên D. y = f (x) O x Lời giải.
Do đồ thị hàm số là một đường liền nét trên D nên hàm số y = f (x) liên tục trên D = R. □ Bài 3. 439/764 439/764
Toán 11 theo chương trình GDPT2018 440 3. Hàm số liên tục
Biết làm, làm đúng, làm nhanh
Cho hàm số y = f (x) xác định trên D = R và có đồ thị như hình vẽ bên. y
Xét tính liên tục của hàm số y = f (x) trên D. y = f (x) O 2 x Lời giải.
Do đồ thị hàm số là một đường liền nét trên D nên hàm số y = f (x) liên tục trên D = R. □ Bài 4.
Cho hàm số y = f (x) có đồ thị như hình vẽ bên. y
Xét tính liên tục của hàm số y = f (x) tại điểm x0 = 2. 2 y = f (x) O 2 x Lời giải.
Ta có lim f (x) > 2 và lim f (x) = 2. Do đó lim f (x) ̸= lim f (x). Vậy hàm số đã cho gián đoạn tại x0 = 2. x→2− x→2+ x→2− x→2+ □ Bài 5.
Cho hàm số y = f (x) có đồ thị như hình vẽ bên. y
Xét tính liên tục của hàm số y = f (x) tại điểm x0 = 1. O 1 x y = f (x) Lời giải.
Ta có lim f (x) = −∞ và lim f (x) = +∞. Do đó lim f (x) ̸= lim f (x). x→1− x→1+ x→1− x→1+
Vậy hàm số đã cho gián đoạn tại x0 = 1. □ 3.
Bài tập trắc nghiệm
Câu 17. Cho đồ thị hàm số y = f (x) có đồ thị như hình vẽ bên. Chọn mệnh đề đúng y trong các mệnh đề sau:
A Hàm số y = f (x) liên tục trên R. O x
B Hàm số y = f (x) liên tục trên khoảng (0, +∞). y = f (x)
C Hàm số y = f (x) liên tục tại điểm x0 = 0. D lim f (x) = +∞. x→0+ Lời giải.
Đồ thị hàm số là một đường liền nét trên khoảng (0, +∞) nên liên tục trên khoảng này. Chọn đáp án B □ 440/764 440/764
Toán 11 theo chương trình GDPT2018 441
Chương 3. Giới hạn. Hàm số liên tục
Biết làm, làm đúng, làm nhanh
Câu 18. Cho đồ thị hàm số y = f (x) có đồ thị như hình vẽ bên. Chọn mệnh đề sai y trong các mệnh đề sau: A lim f (x) = −∞. x→+∞
B Hàm số y = f (x) liên tục trên R. O C lim f (x) = +∞. x→+∞ x D y = f (x) lim f (x) = −∞. x→−∞ Lời giải.
Quan sát đồ thị hàm số, ta có
○ Hàm số y = f (x) liên tục trên R. ○ lim f (x) = +∞. x→+∞ ○ lim f (x) = −∞. x→−∞ Chọn đáp án A □
Câu 19. Cho đồ thị hàm số y = f (x) có đồ thị như hình vẽ bên. Chọn mệnh đề y
đúng trong các mệnh đề sau: A lim f (x) = −∞. x→+∞
B Hàm số y = f (x) liên tục trên khoảng (0; +∞). y = f (x)
C Hàm số y = f (x) liên tục tại điểm x0 = 0.
D Hàm số y = f (x) liên tục trên R. O x Lời giải.
Quan sát đồ thị hàm số, thấy đồ thị hàm số là một đường liền nét trên khoảng (0; +∞) do đó hàm số đã cho liên tục trên khoảng này. Chọn đáp án B □
Câu 20. Cho đồ thị hàm số y = f (x) có đồ thị như hình vẽ bên. Chọn mệnh đề sai y trong các mệnh đề sau:
A Hàm số gián đoạn tại điểm x0 = 0. y = f (x)
B Hàm số liên tục trên khoảng (−∞; 0).
C Hàm số y = f (x) liên tục trên R. O x
D Hàm số liên tục trên khoảng (0; +∞). −1 Lời giải.
Quan sát đồ thị hàm số, ta có
○ Hàm số gián đoạn tại điểm x0 = 0.
○ Hàm số liên tục trên khoảng (−∞; 0).
○ Hàm số liên tục trên khoảng (0; +∞). Chọn đáp án C □ 441/764 441/764
Toán 11 theo chương trình GDPT2018 442 3. Hàm số liên tục
Biết làm, làm đúng, làm nhanh
Câu 21. Cho đồ thị hàm số y = f (x) có đồ thị như hình vẽ bên. Chọn mệnh đề sai y trong các mệnh đề sau:
A Hàm số gián đoạn tại điểm x0 = 1.
B Hàm số liên tục trên khoảng (−∞; 1). 1
C Hàm số y = f (x) liên tục trên R. O 1 x
D Hàm số liên tục trên khoảng (1; +∞). y = f (x) Lời giải.
Quan sát đồ thị hàm số, ta có
○ Hàm số gián đoạn tại điểm x0 = 1.
○ Hàm số liên tục trên khoảng (−∞; 1).
○ Hàm số liên tục trên khoảng (1; +∞). Chọn đáp án C □ Câu 22.
Cho đồ thị hàm số y = f (x) có đồ thị như hình vẽ bên. Chọn mệnh đề đúng y trong các mệnh đề sau: 2
A Hàm số y = f (x) liên tục trên R. B lim f (x) = −∞. y = f (x) x→+∞
C Hàm số liên tục tại điểm x0 = −2. −2 O x
D Hàm số gián đoạn tại điểm x0 = −2. Lời giải.
Quan sát đồ thị hàm số, ta có
○ Đồ thị hàm số là các đường liền nét trên các khoảng (−∞; −2), (−2; +∞) do đó hàm số liên tục trên các khoảng này. ○ lim f (x) = +∞ x→+∞ ○ Ta có lim f (x) < f (−2) = 2 và lim f (x) = f (−2) = 2. Do đó lim f (x) ̸= lim f (x). x→(−2)− x→(−2)+ x→(−2)− x→(−2)+
Vậy hàm số đã cho gián đoạn tại x0 = −2. Chọn đáp án D □
Câu 23. Cho đồ thị hàm số y = f (x) có đồ thị như hình vẽ bên. Chọn mệnh đề đúng y trong các mệnh đề sau: y = f (x) A lim f (x) = +∞. x→1+ O 1 x
B Hàm số y = f (x) liên tục trên R. −1 C lim f (x) = −∞. x→1+ D lim f (x) = +∞. x→1− Lời giải.
Quan sát đồ thị hàm số, ta có
○ Đồ thị hàm số là các đường liền nét trên các khoảng (−∞; 1), (1; +∞) do đó hàm số liên tục trên các khoảng này. 442/764 442/764
Toán 11 theo chương trình GDPT2018 443
Chương 3. Giới hạn. Hàm số liên tục
Biết làm, làm đúng, làm nhanh ○ lim f (x) = −1. x→+∞
○ Ta có lim f (x) = −∞ và lim f (x) = +∞. Do đó lim f (x) ̸= lim f (x). x→1− x→1+ x→1− x→1+
Vậy hàm số đã cho gián đoạn tại x0 = 1. Chọn đáp án A □
Câu 24. Cho đồ thị hàm số y = f (x) có đồ thị như hình vẽ bên. Chọn mệnh đề y
đúng trong các mệnh đề sau:
A Hàm số y = f (x) gián đoạn tại x0 = 0. B lim f (x) = −1. x→+∞ C lim f (x) = −1. x→−∞ O x
D Hàm số y = f (x) liên tục trên R. y = f (x) Lời giải.
Quan sát đồ thị hàm số, ta có
○ Đồ thị hàm số là các đường liền nét trên khoảng (−∞; +∞) do đó hàm số liên tục trên R. ○ lim f (x) = −∞. x→+∞ ○ lim f (x) = −∞. x→−∞ Chọn đáp án D □
Câu 25. Cho đồ thị hàm số y = f (x) có đồ thị như hình y
vẽ bên. Chọn mệnh đề đúng trong các mệnh đề sau:
A Hàm số y = f (x) liên tục trên R. y = f (x)
B Hàm số y = f (x) liên tục tại x0 = −3. O C lim f (x) = −∞. −3 3 x x→−∞
D Hàm số y = f (x) gián đoạn tại x0 = 3. Lời giải.
Quan sát đồ thị hàm số, ta có
○ Đồ thị hàm số là các đường liền nét trên khoảng (−∞; −3), (−3; 3), (3; +∞) do đó hàm số liên tục trên các khoảng này. ○ lim f (x) = 0. x→−∞
○ Hàm số y = f (x) gián đoạn tại các điểm x0 = 3 và x0 = −3. Chọn đáp án D □
Câu 26. Cho đồ thị hàm số y = f (x) có đồ thị như hình vẽ y
bên. Chọn mệnh đề đúng trong các mệnh đề sau:
A Hàm số y = f (x) liên tục trên R. π
B Hàm số y = f (x) liên tục tại điểm x0 = . 2 O π
C Hàm số y = f (x) liên tục tại điểm x −π/2 π/2 x 0 = − . 2 π D y = f (x ( )
Hàm số y = f (x) gián đoạn tại điểm x0 = . 2 443/764 443/764
Toán 11 theo chương trình GDPT2018 444 3. Hàm số liên tục
Biết làm, làm đúng, làm nhanh Lời giải.
Quan sát đồ thị hàm số, ta có π π
○ Đồ thị hàm số là các đường liền nét trên khoảng (− ; 0), (0; ) do đó hàm số liên tục trên các khoảng này. 2 2 π π
○ Hàm số y = f (x) gián đoạn tại các điểm x0 = và x0 = − . 2 2 Chọn đáp án D □
Dạng 3. Xét tính liên tục của hàm số tại một điểm
Để kiểm tra tính liên tục của hàm số y = f (x) tại điểm x = x0 ta cần làm như sau:
○ Bước 1: Tính lim f (x) . x→x0
○ Bước 2: Tính = f (x0) . Nếu lim f (x) = f (x0) thì kết luận hàm số f(x) liên tục tại x = x0. Nếu x→x0
lim f (x) ̸= f (x0) thì kết luận hàm số f (x) liên tục tại x = x0. x→x0 1. Ví dụ mẫu
Ví dụ 9 (CD). Dùng định nghĩa xét tính liên tục của hàm số f (x) = 2x3 + x + 1 tại điểm x = 2. Lời giải.
Hàm số trên là hàm sơ cấp nên liên tục trên R.
Ta có f (2) = 2 · 23 + 2 + 1 = 19.
lim f (x) = lim 2x3 + x + 1 = 2 · 23 + 2 + 1 = 19. x→2 x→2
Vậy lim f (x) = f (2) = 19 nên hàm số y = 2x3 + x + 1 liên tục tại x = 2. □ x→2  3 khi x = −1     x4 + x
Ví dụ 10 (TH). Hàm số f (x) =
khi x ̸= −1, x ̸= 0 . Xét tính liên tục của hàm số tại x = −1, x = 0. x2 + x     1 khi x = 0 Lời giải.
Hàm số y = f (x) có tập xác định D = R.
Dễ thấy hàm số y = f (x) liên tục trên mỗi khoảng (−∞; −1) , (−1; 0) và (0; +∞).
(i) Xét tại x = −1, ta có x4 + x x (x + 1) x2 − x + 1 lim f (x) = lim = lim = lim
x2 − x + 1 = 3 = f (−1) . Vậy hàm số y = x→−1 x→−1 x2 + x x→−1 x (x + 1) x→−1
f (x) liên tục tại x = −1. (ii) Xét tại x = 0, ta có x4 + x x (x + 1) x2 − x + 1 lim f (x) = lim = lim
= lim x2 − x + 1 = 1 = f (0) . Vậy hàm số y = f (x) liên x→0 x→0 x2 + x x→0 x (x + 1) x→0 tục tại x = 0. □  0, 5 khi x = −1    x (x + 1)
Ví dụ 11 (TH). Tìm số điểm gián đoạn của hàm số f (x) = khi x ̸= −1, x ̸= 1 ? x2 − 1    1 khi x = 1 Lời giải.
Hàm số y = f (x) có tập xác định D = R. x (x + 1) Hàm số f (x) =
liên tục trên mỗi khoảng (−∞; −1), (−1; 1) và (1; +∞). x2 − 1 x (x + 1) x 1
(i) Xét tại x = −1, ta có lim f (x) = lim = lim =
= f (−1) ⇒ Hàm số liên tục tại x = −1. x→−1 x→−1 x2 − 1 x→−1 x − 1 2 444/764 444/764
Toán 11 theo chương trình GDPT2018 445
Chương 3. Giới hạn. Hàm số liên tục
Biết làm, làm đúng, làm nhanh  x (x + 1) x  lim f (x) = lim = lim = +∞   x→1+ x→1+ x2 − 1 x→1+ x − 1 (ii) Xét tại x = 1, ta có
⇒Hàm số y = f (x) gián đoạn tại x (x + 1) x   lim f (x) = lim = lim = −∞  x→1− x→1− x2 − 1 x→1− x − 1 x = 1. □ x nếu x > 0  
Ví dụ 12 (KNTT). Xét tính liên tục của hàm số f (x) = 0
nếu x = 0 tại điểm x0 = 0.   − x nếu x < 0 Lời giải.
Ta có f (0) = 0, lim f (x) = lim x2 = 0, lim f (x) = lim (−x) = 0. x→0+ x→0+ x→0− x→0−
Suy ra f (0) = lim f (x) = lim f (x). x→0+ x→0−
Vậy hàm số liên tục tại điểm x0 = 0. □
Ví dụ 13 (CTST). Xét tính liên tục của hàm số
a) f (x) = x2 − 2x + 3 tại điểm x0 = 2. ®x2 + 2 khi x > 0 b) f (x) = tại điểm x0 = 0. 2x khi x ≤ 0 Lời giải.
a) Ta có f (2) = 3 và lim f (x) = lim x2 − 2x + 3 = 22 − 2 · 2 + 3 = 3, suy ra lim f (x) = f (2). x→2 x→2 x→2
Vậy hàm số y = f (x) liên tục tại x0 = 2.
b) Ta có f (0) = 2 · 0 = 0, lim f (x) = lim (2x) = 2 · 0 = 0, x→0− x→0− lim f (x) = lim x2 + 2 = 0 + 2 = 2. x→0+ x→0+
Do lim f (x) ̸= lim f (x) nên không tồn tại lim f (x). x→0− x→0+ x→0
Vậy hàm số y = f (x) không liên tục tại điểm x0 = 0. □ 2. Bài tập tự luyện
Bài 6. Xét tính liên tục của hàm số:
a) f (x) = x2 − 2x + 3 tại điểm x0 = 2; ® x2 + 2 khi x > 0 b) f (x) = tại điểm x0 = 0. 2x khi x ≤ 0 Lời giải.
a) Ta có f (2) = 3 và lim f (x) = lim (x2 − 2x + 3) = 22 − 2 · 2 + 3 = 3, suy ra lim f (x) = f (2). Vậy hàm số x→2 x→2 x→2
y = f (x) liên tục tại điểm x0 = 2. b) Ta có: f (2) = 2 · 0 = 0;
lim f (x) = lim (2x) = 2 · lim x = 2 · 0 = 0; x→0− x→0− x→0−
lim f (x) = lim (x2 + 2) = 0 + 2 = 2. x→0+ x→0+
Suy ra không tồn tại lim f (x). Vậy hàm số không liên tục tại điểm x0 = 0. x→0 445/764 445/764
Toán 11 theo chương trình GDPT2018 446 3. Hàm số liên tục
Biết làm, làm đúng, làm nhanh y 3 2 −1 O 1 x −2 □  x2 − 7x + 12  khi x ̸= 3
Bài 7 (VD). Cho hàm số y = x − 3
. Hàm số đã cho có đạo hàm tại x = 3 không?  − 1 khi x = 3 Lời giải. x2 − 7x + 12 lim
= lim (x − 4) = −1 = y (3) nên hàm số liên tục tại x0 = 3. x→3 x − 3 x→3
x2 − 7x + 12 − 32 − 7.3 + 12 x2 − 7x + 12 lim = lim
= lim (x − 4) = −1 ⇒ y′ (3) = −1. □ x→3 x − 3 x→3 x − 3 x→3 1 nếu x > 0  
Bài 8. Xét tính liên tục của hàm dấu s(x) = 0
nếu x = 0 tại điểm x0 = 0.   − 1 nếu x < 0 Lời giải.
Ta thấy rằng lim s(x) = 1 và lim s(x) = −1. Do đó, không tồn tại giới hạn lim s(x). x→0+ x→0− x→0
Vậy hàm số không liên tục tại x = 0. □
Bài 9. Xét tính liên tục của hàm số
a) f (x) = 1 − x2 tại điểm x0 = 3; ® x2 + 1 khi x > 1 b) f (x) = tại điểm x = 1. −x khi x ≤ 1 Lời giải.
a) Ta có f (3) = −8 và lim f (x) = lim (1 − x2) = 1 − 32 = −8, suy ra lim f (x) = f (3). Vậy hàm số y = f (x) liên x→3 x→3 x→3 tục tại điểm x0 = 3. b) Ta có: f (1) = −1; lim f (x) = lim (−x) = −1; x→1− x→1−
lim f (x) = lim (x2 + 1) = 1 + 2 = 3. x→1+ x→1+
Suy ra không tồn tại lim f (x). Vậy hàm số không liên tục tại điểm x0 = 1. x→1 □ 446/764 446/764
Toán 11 theo chương trình GDPT2018 447
Chương 3. Giới hạn. Hàm số liên tục
Biết làm, làm đúng, làm nhanh x nếu x > 0  
Bài 10. Xét tính liên tục của hàm số f (x) = 0
nếu x = 0 tại điểm x0 = 0.   − x nếu x < 0 Lời giải.
Ta có f (0) = 0, lim f (x) = lim x2 = 0, lim f (x) = lim (−x) = 0. x→0+ x→0+ x→0− x→0−
Suy ra f (0) = lim f (x) = lim f (x). x→0+ x→0−
Vậy hàm số liên tục tại điểm x0 = 0. □
Bài 11. Xét tính liên tục của hàm số: ® x2 + 1 khi x ≥ 0 a) f (x) = tại điểm x = 0; 1 − x khi x < 0 ® x2 + 2 khi x ≥ 1 b) f (x) = tại điểm x = 1. x khi x < 1 Lời giải. a) Ta có f (0) = 1;
lim f (x) = lim (1 − x) = 1 − 0 = 1; x→0− x→0−
lim f (x) = lim (x2 + 1) = 02 + 1 = 1. x→0+ x→0+
Do đó, lim f (x) = f (0) nên hàm số liên tục tại x0 = 0. x→0 b) Ta có f (1) = 3; lim f (x) = lim (x) = 1. x→1− x→1−
Do đó, không thể xảy ra lim f (x) ̸= f (1) nên hàm số gián đoạn tại x0 = 1. x→1 □
Bài 12. Dùng định nghĩa xét tính liên tục của hàm số f (x) = 2x3 + x + 1 tại điểm x = 2. Lời giải.
Hàm số trên là hàm sơ cấp nên liên tục trên R.
Ta có f (2) = 2 · 23 + 2 + 1 = 19.
lim f (x) = lim 2x3 + x + 1 = 2 · 23 + 2 + 1 = 19. x→2 x→2
Vậy lim f (x) = f (2) = 19 nên hàm số y = 2x3 + x + 1 liên tục tại x = 2. □ x→2 3.
Bài tập trắc nghiệm 2x − 1 Câu 27. Cho hàm số f (x) =
. Kết luận nào sau đây đúng? x3 − x
A Hàm số liên tục tại x = −1.
B Hàm số liên tục tại x = 0. 1
C Hàm số liên tục tại x = 1.
D Hàm số liên tục tại x = . 2 Lời giải. 1 2x − 1 Å 1 ã Tại x = , ta có lim f (x) = lim = 0 = f
. Vậy hàm số liên tục tại x = 2. 2 1 1 x3 − 1 2 x→ x→ 2 2 Chọn đáp án D □ 447/764 447/764
Toán 11 theo chương trình GDPT2018 448 3. Hàm số liên tục
Biết làm, làm đúng, làm nhanh
Câu 28. Hàm số nào sau đây liên tục tại x = 1 : x2 + x + 1 x2 − x − 2 x2 + x + 1 x + 1 A f (x) = . B f (x) = . C f (x) = . D f (x) = . x − 1 x2 − 1 x x − 1 Lời giải. x2 + x + 1 • f (x) = x − 1
lim f (x) = +∞ suy ra f (x) không liên tục tại x = 1. x→1+ x2 − x − 2 • f (x) = x2 − 1 x − 2 lim f (x) = lim
= −∞ suy ra f (x) không liên tục tại x = 1. x→1+ x→1+ x − 1 x2 + x + 1 • f (x) = x x2 + x + 1 lim f (x) = lim
= 3 = f (1) suy ra f (x) liên tục tại x = 1. x→1 x→1 x x + 1 • f (x) = x − 1 x+1 lim f (x) = lim
= +∞ suy ra f (x) không liên tục tại x = 1. x→1+ x→1+ x − 1 Chọn đáp án C □
Câu 29. Hàm số nào dưới đây gián đoạn tại điểm x0 = −1. 2x − 1 x x + 1 A y = (x + 1) x2 + 2. B y = . C y = . D y = . x + 1 x − 1 x2 + 1 Lời giải. 2x − 1 Ta có y =
không xác định tại x0 = −1 nên gián đoạn tại x0 = −1. x + 1 Chọn đáp án B □
Câu 30. Hàm số nào sau đây gián đoạn tại x = 2? 3x − 4 A y = . B y = sin x. C y = x4 − 2x2 + 1. D y = tan x. x − 2 Lời giải. 3x − 4 Ta có y =
có tập xác định D = R \ {2}, do đó gián đoạn tại x = 2. x − 2 Chọn đáp án A □ x Câu 31. Hàm số y =
gián đoạn tại điểm x0 bằng? x + 1 A x0 = 2018. B x0 = 1. C x0 = 0. D x0 = −1. Lời giải. x Vì hàm số y =
có tập xác định D = R \ {−1} nên hàm số gián đoạn tại điểm x0 = −1. x + 1 Chọn đáp án D □ x − 3 Câu 32. Cho hàm số y =
. Mệnh đề nào sau đây đúng? x2 − 1
A Hàm số không liên tục tại các điểm x = ±1.
B Hàm số liên tục tại mọi x ∈ R.
C Hàm số liên tục tại các điểm x = −1.
D Hàm số liên tục tại các điểm x = 1. Lời giải. x − 3 Hàm số y =
có tập xác định R \ {±1}. Do đó hàm số không liên tục tại các điểm x = ±1. x2 − 1 Chọn đáp án A □ x2 + 3x + 2  khi x ≤ −1 Câu 33. Để hàm số y =
liên tục tại điểm x = −1 thì giá trị của a là 4x + a khi x > −1 A −4. B 4. C 1. D −1. Lời giải. 448/764 448/764
Toán 11 theo chương trình GDPT2018 449
Chương 3. Giới hạn. Hàm số liên tục
Biết làm, làm đúng, làm nhanh
Hàm số liên tục tại x = −1 khi và chỉ khi lim y = lim y = y (−1) . x→−1+ x→−1− ⇔ lim (4x + a) = lim
x2 + 3x + 2 = y (−1) ⇔ a − 4 = 0 ⇔ a = 4. x→−1+ x→−1− Chọn đáp án B □  x3 − x2 + 2x − 2  khi x ̸= 1
Câu 34. Tìm giá trị thực của tham số m để hàm số f (x) = x − 1 liên tục tại x = 1. 3x + m khi x = 1 A m = 0. B m = 6. C m = 4. D m = 2. Lời giải. Ta có f (1) = m + 3. x3 − x2 + 2x − 2 (x − 1) x2 + 2 lim f (x) = lim = lim = lim x2 + 2 = 3. x→1 x→1 x − 1 x→1 x − 1 x→1
Để hàm số f (x) liên tục tại x = 1 thì lim f (x) = f (1) ⇔ 3 = m + 3 ⇔ m = 0. x→1 Chọn đáp án A □  x2016 + x − 2   √ √ khi x ̸= 1 Câu 35. Cho hàm số f (x) = 2018x + 1 − x + 2018
. Tìm k để hàm số f (x) liên tục tại x = 1.  k khi x = 1 √ √ 2017. 2018 20016 √ A k = 2 2019. B k = . C k = 1. D k = 2019. 2 2017 Lời giải. √ √ x2016 + x − 2 x2016 − 1 + x − 1 2018x + 1 + x + 2018 Ta có lim √ √ = lim x→1 2018x + 1 − x + 2018 x→1 2017x − 2017 √ √
(x − 1) x2015 + x2014 + ... + x + 1 + 1 2018x + 1 + x + 2018 √ = lim = 2 2019. x→1 2017 (x − 1) √
Để hàm số liên tục tại x = 1 ⇔ lim f (x) = f (1) ⇔ k = 2 2019. x→1 Chọn đáp án A □ √  x − 1  khi x ̸= 1 Câu 36. Cho hàm số f (x) = x − 1
. Tìm a để hàm số liên tục tại x0 = 1. a khi x = 1 1 1 A a = 0. B a = − . C a = . D a = 1. 2 2 Lời giải. √ √ x − 1 x − 1 1 1 Ta có lim f (x) = lim = lim √ √ = lim √ = . x→1 x→1 x − 1 x→1 ( x − 1) ( x + 1) x→1 x + 1 2 1
Để hàm số liên tục tại x0 = 1 khi lim f (x) = f (1) ⇔ a = . x→1 2 Chọn đáp án C □ ®3x + b khi x ≤ −1
Câu 37. Biết hàm số f (x) =
liên tục tại x = −1. Mệnh đề nào dưới đây đúng? x + a khi x > −1 A a = b − 2. B a = −2 − b. C a = 2 − b. D a = b + 2. Lời giải. lim f (x) = f (−1) = b − 3; lim
f (x) = a − 1. Để hàm số liên tục tại x = −1 thì b − 3 = a − 1 ⇔ a = b − 2. x → −1− x → −1+ Chọn đáp án A □  3 − x  √ khi x ̸= 3 Câu 38. Cho hàm số f (x) = x + 1 − 2
. Hàm số đã cho liên tục tại x = 3 khi m bằng bao nhiêu? m khi x = 3 A −1. B 1. C 4. D −4. Lời giải. 449/764 449/764
Toán 11 theo chương trình GDPT2018 450 3. Hàm số liên tục
Biết làm, làm đúng, làm nhanh √ 3 − x (3 − x) x + 1 + 2 √ f (3) = m lim f (x) = lim √ = lim = lim − x + 1 − 2 = −4. x→3 x→3 x + 1 − 2 x→3 x − 3 x→3
Để hàm số liên tục tại x = 3 thì lim f (x) = f (3). x→3 Suy ra m = −4. Chọn đáp án D □ ®ax2 + bx − 5 khi x ≤ 1
Câu 39. Biết hàm số f (x) =
liên tục tại x = 1 Tính giá trị của biểu thức P = 2ax − 3b khi x > 1 a − 4b. A P = −4. B P = −5. C P = 5. D P = 4. Lời giải. Ta có lim f (x) = lim
ax2 + bx − 5 = a + b − 5 = f (1). x→1− x→1−
lim f (x) = lim (2ax − 3b) = 2a − 3b. Vì hàm số liên tục tại x = 1 nên a + b − 5 = 2a − 3b ⇒ a − 4b = −5. x→1+ x→1+ Chọn đáp án B □  x2 − x  khi x ̸= 1
Câu 40. Tìm m để hàm số f (x) = x − 1 liên tục tại x = 1? m − 1 khi x = 1 A m = 0. B m = −1. C m = 1. D m = 2. Lời giải. Tập xác định D = R x2 − x Ta có lim f (x) = lim
= lim x = 1 và f (1) = m − 1. x→1 x→1 x − 1 x→1
Hàm số liên tục tại x = 1 ⇔ m − 1 = 1 ⇔ m = 2. Chọn đáp án D □  x2 − 3x + 2  khi x ̸= 1
Câu 41. Có bao nhiêu số tự nhiên m để hàm số f (x) = x − 1
liên tục tại điểm x = 1? m2 + m − 1 khi x = 1 A 0. B 3. C 2. D 1. Lời giải. x2 − 3x + 2 (x − 1) (x − 2) lim = lim = lim (x − 2) = −1. x→1 x − 1 x→1 x − 1 x→1
Vì hàm số f (x) liên tục tại điểm x = 1 nên lim f (x) = f (1) x→1 ñm = 0 (Thoả mãn)
⇔ m2 + m − 1 = −1 ⇔ m2 + m = 0 ⇔ m = −1 (Loại). Chọn đáp án D □ √  x + 2 − 2  khi x ̸= 2
Câu 42. Tìm a để hàm số f (x) = x − 2 liên tục tại x = 2? 2x + a khi x = 2 15 15 1 A . B − . C . D 1. 4 4 4 Lời giải. Ta có f (2) = 4 + a. x + 2 − 4 1 1
Ta tính được lim f (x) = lim √ = lim √ = . x→2 x→2 (x − 2) x + 2 + 2 x→2 x + 2 + 2 4 1 15
Hàm số đã cho liên tục tại x = 2 khi và chỉ khi f (2) = lim f (x) ⇔ 4 + a = ⇔ a = − . x→2 4 4 15
Vậy hàm số liên tục tại x = 2 khi a = − . 4 Chọn đáp án B □ 450/764 450/764
Toán 11 theo chương trình GDPT2018 451
Chương 3. Giới hạn. Hàm số liên tục
Biết làm, làm đúng, làm nhanh  x2 − 3x + 2   √ khi x > 2 Câu 43. Cho hàm số f (x) = x + 2 − 2
, m là tham số. Có bao nhiêu giá trị của m để hàm số  m2x − 4m + 6 khi x ≤ 2
đã cho liên tục tại x = 2? A 3. B 0. C 2. D 1. Lời giải. Ta có √ x2 − 3x + 2 (x − 2) (x − 1) x + 2 + 2 √ lim f (x) = lim √ = lim = lim (x − 1) x + 2 + 2 = 4. x→2+ x→2+ x + 2 − 2 x→2+ x − 2 x→2+ lim f (x) = lim
m2x − 4m + 6 = 2m2 − 4m + 6. x→2− x→2− f (2) = 2m2 − 4m + 6.
Để hàm số liên tục tại x = 2 thì lim f (x) = lim f (x) = f (2) ⇔ 2m2 −4m+6 = 4 ⇔ 2m2 −4m+2 = 0 ⇔ m = 1. x→2+ x→2−
Vậy có một giá trị của m thỏa mãn hàm số đã cho liên tục tại x = 2. Chọn đáp án D □ √  3x2 + 2x − 1 − 2   , x ̸= 1 Câu 44. Cho hàm số f (x) = x2 − 1
. Hàm số f (x) liên tục tại x0 = 1 khi  4 − m, x = 1 A m = 3. B m = −3. C m = 7. D m = −7. Lời giải.
Tập xác định D = R, x0 = 1 ∈ R. Ta có f (1) = 4 − m. √3x2 + 2x − 1 − 2 (x − 1) (3x + 5) lim f (x) = lim = lim √ Ä ä x→1 x→1 (x + 1) (x − 1) x→1 (x + 1) (x − 1) 3x2 + 2x − 1 + 2 3x + 5 = lim √ = 1. Ä ä x→1 (x + 1) 3x2 + 2x − 1 + 2
Hàm số f (x) liên tục tại x0 = 1 khi và chỉ khi lim (x) = f (1) ⇔ 4 − m = 1 ⇔ m = 3. x→1 Chọn đáp án A □  x2 + 3x + 2  khi x < −1
Câu 45. Tìm giá trị của tham số m để hàm số f (x) = x2 − 1 liên tục tại x = −1. mx + 2 khi x ≥ −1 −3 −5 3 5 A m = . B m = . C m = . D m = . 2 2 2 2 Lời giải. Ta có • f (−1) = −m + 2. • lim f (x) = −m + 2. x→(−1)+ x2 + 3x + 2 (x + 1) (x + 2) x + 2 −1 • lim f (x) = lim = lim = lim = . x→(−1)− x→(−1)− x2 − 1
x→(−1)− (x − 1) (x + 1) x→(−1)− x − 1 2 −1 5
Hàm số liên tục tại x = −1 ⇔ f (−1) = lim f (x) = lim f (x) ⇔ −m + 2 = ⇔ m = . x→(−1)+ x→(−1)− 2 2 Chọn đáp án D □ √  x2 + 4 − 2   khi x ̸= 0 Câu 46. Cho hàm số f (x) = x2
. Tìm giá trị thực của tham số a để hàm số f (x) liên 5  2a − khi x = 0 4 tục tại x = 0. 3 4 4 3 A a = − . B a = . C a = − . D a = . 4 3 3 4 Lời giải. Tập xác định D = R. 451/764 451/764
Toán 11 theo chương trình GDPT2018 452 3. Hàm số liên tục
Biết làm, làm đúng, làm nhanh √ √ √ Ä ä Ä ä x2 + 4 − 2 x2 + 4 − 2 x2 + 4 + 2 x2 + 4 − 4 1 lim f (x) = lim = lim √ = lim √ = lim √ = ä x→0 x→0 x2 x→0 x2 Ä x2 + 4 + 2 x→0 x2( x2 + 4 + 2) x→0 x2 + 4 + 2 1 . 4 5 f (0) = 2a − . 4 5 1 3
Hàm số f (x) liên tục tại x = 0 ⇔ lim f (x) = f (0) ⇔ 2a − = ⇔ a = . x→0 4 4 4 3 Vậy a = . 4 Chọn đáp án D □ ®x2 − 2x + 3 khi x ̸= 1 Câu 47. Cho hàm số f (x) =
. Tìm m để hàm số liên tục tại x0 = 1. 3x + m − 1 khi x = 1 A m = 1. B m = 3. C m = 0. D m = 2. Lời giải. Tập xác định D = R. Ta có f (1) = 2 + m. lim f (x) = lim x2 − 2x + 3 = 2. x→1 x→1
Hàm số liên tục tại x0 = 1 ⇔ lim f (x) = f (1) ⇔ 2 = m + 2 ⇔ m = 0. x→1 Chọn đáp án C □  x2 − 3x + 2  khi x ̸= 2 Câu 48. Cho hàm số f (x) = x − 2
. Hàm số liên tục tại x = 2 khi a bằng a khi x = 2 A 1. B 0. C 2. D −1. Lời giải.
Hàm số liên tục tại x = 2 khi và chỉ khi lim f (x) = f (2). x→2 x2 − 3x + 2
Ta có f (2) = a, lim f (x) = lim
= lim (x − 1) = 1. Do đó a = 1. x→2 x→2 x − 2 x→2 Chọn đáp án A □
Dạng 4. Hàm số liên tục trên khoảng, đoạn
○ Hàm số y = f (x) được gọi là liên tục trên một khoảng nếu nó liên tục tại mọi điểm của khoảng đó.
○ Hàm số y = f (x) được gọi là liên tục trên đoạn [a, b] nếu nó liên tục trên khoảng (a, b) và
lim f (x) = f (a) , lim f (x) = f (b) . x→a+ x→b−
○ Đồ thị của hàm số liên tục trên một khoảng là một đường liền nét trên khoảng đó. 1. Ví dụ mẫu
Ví dụ 14 (Cánh Diều).
a) Hàm số f (x) = 2x + 3 có liên tục trên đoạn [3; 4] hay không? x + 1 b) Hàm số f (x) =
(x ̸= 2) có liên tục trên khoảng (1; 3) hay không? x − 2 Lời giải.
a) Với mỗi x0 ∈ (3; 4) ta có lim f (x) = lim (2x + 3) = 2x0 + 3 = f (x0). x→x0 x→x0 Ta lại có 452/764 452/764
Toán 11 theo chương trình GDPT2018 453
Chương 3. Giới hạn. Hàm số liên tục
Biết làm, làm đúng, làm nhanh
lim f (x) = lim (2x + 3) = 9 = f (3). x→3+ x→3+
lim f (x) = lim (2x + 3) = 11 = f (4). x→4− x→4−
Vậy hàm số đã cho liên tục trên đoạn [3; 4]. x + 1 b) Hàm số f (x) =
không xác định tại x = 2 nên hàm số không liên tục tại x = 2. x − 2
Do 2 ∈ (1; 3) nên hàm số đã cho không liên tục trên khoảng (1; 3). □ 6
Ví dụ 15 (Cánh Diều). Cho hàm số f (x) = x3 + 2x + . x − 2
a) Xét tính liên tục của hàm số f (x) tại x = 3.
b) Xét tính liên tục của hàm số f (x) trên tập xác định của hàm số đó. Lời giải.
Tập xác định của hàm số là R \ {2}. a) Ta thấy Å 6 ã lim f (x) = lim x3 + 2x + x→3 x→3 x − 2 Å 6 ã = lim x3 + lim (2x) + lim x→3 x→3 x→3 x − 2 6 = 33 + 2 · 3 + 3 − 2 = f (3)
Vậy hàm số f (x) liên tục tại x = 3.
b) Hàm số g(x) = x3 + 2x là hàm đa thức nên liên tục trên R. Do đó hàm số g(x) liên tục trên mỗi khoảng (−∞; 2) và (2; +∞).
Hàm số h(x) là hàm số phân thức hữu tỉ nên liên tục trên mỗi khoảng xác định (−∞; 2) và (2; +∞).
Vậy hàm số f (x) = g(x) + h(x) liên tục trên mỗi khoảnh (−∞; 2) và (2; +∞). c) □ ®x − 1 nếu x ∈ (0; 1)
Ví dụ 16 (KNTT). Xét tính liên tục của hàm số f (x) = trên nửa khoảng (0; 1]. 0 nếu x = 1 Lời giải.
Ta có f (x) = x − 1 với x ∈ (0; 1). Với x0 ∈ (0; 1) bất kì, ta có
lim (x − 1) = x0 − 1 = f (x0) . x→x0
Do đó, hàm số đã cho liên tục trên khoảng (0; 1). Hơn nữa, ta có
lim f (x) = lim (x − 1) = 0 = f (1) x→1− x→1−
nên f (x) liên tục trên nửa khoảng (0; 1]. □ x + 1
Ví dụ 17 (KNTT). Cho hàm số f (x) =
. Tìm các khoảng liên tục của hàm số f (x). x − 1 Lời giải.
○ Tập xác định của hàm số đã cho là D = (−∞; 1) ∪ (1; +∞). 453/764 453/764
Toán 11 theo chương trình GDPT2018 454 3. Hàm số liên tục
Biết làm, làm đúng, làm nhanh
○ Với mọi x0 ∈ (−∞; 1), ta có x + 1 x0 + 1 lim f (x) = lim = = f (x0). x→x0 x→x0 x − 1 x0 − 1
Do đó hàm số f (x) liên tục tại x = x0 hay f (x) liên tục trên khoảng (−∞; 1).
○ Tương tự, hàm số f (x) liên tục trên khoảng (1; +∞).
Vậy, hàm số đã cho liên tục trên các khoảng (−∞; 1) và (1; +∞) . □ √
Ví dụ 18 (CTST). Xét tính liên tục của hàm số f (x) =
1 − x2 trên đoạn [−1; 1]. Lời giải. √ »
Với mọi x0 ∈ (−1; 1), ta có lim f (x) = lim 1 − x2 = 1 − x2 = f (x0). y x→x 0 0 x→x0 √
Do đó hàm số f (x) liên tục tại mọi điểm x0 ∈ (−1; 1). y = 1 − x2 Ta lại có √ lim f (x) = lim
1 − x2 = p1 − (−1)2 = 0 = f (−1). x→(−1)+ x→(−1)+ √ √ lim f (x) = lim 1 − x2 = 1 − 12 = 0 = f (1). x −1 O 1 x→1− x→1−
Vậy hàm số f (x) liên tục trên đoạn [−1; 1]. □ 2. Bài tập tự luyện sin x
Bài 13. Xét tính liên tục của hàm số y = . x + 1 Lời giải.
Tập xác định của hàm số D = (−∞; −1) ∪ (−1; +∞). sin x
Các hàm số y = sin x và y = x + 1 liên tục tại mọi điểm x0 ∈ R. Do đó hàm số y = liên tục tại mọi x + 1
điểm x0 ̸= −1 (hay liên tục trên các khoảng (−∞; −1) và (−1; +∞). □
Bài 14. Xét tính liên tục của các hàm số √ a) y = x2 + 1 + 3 − x. x2 − 1 b) y = · cos x. x Lời giải. a)
Tập xác định của hàm số S = R. √ √ Các hàm số y =
x2 + 1 và y = 3 − x liên tục tại mọi điểm x0 ∈ R. Do đó hàm số y = x2 + 1 + 3 − x
liên tục tại mọi điểm x0 ∈ R hay liên tục trên R. b)
Tập xác định của hàm số D = (−∞; 0) ∪ (0; +∞). x2 − 1 Các hàm số y =
liên tục tại mọi điểm x0 ̸= 0 và hàm số y = cos x liên tục tại mọi điểm x0 ∈ R. x x2 − 1 Do đó hàm số y =
. cos x liên tục tại mọi điểm x0 ̸= 0 (hay liên tục trên các khoảng (−∞; 0) và x (0; +∞)). □
Bài 15. Xét tính liên tục của các hàm số sau: 454/764 454/764
Toán 11 theo chương trình GDPT2018 455
Chương 3. Giới hạn. Hàm số liên tục
Biết làm, làm đúng, làm nhanh a) y = 3x3 − 4x2 + 5x + 2; 3x2 + x − 1 b) y = . x − 2 Lời giải.
a) y = 3x3 − 4x2 + 5x = 2 hàm số đa thức nên nó liên tục trên R. 3x2 + x − 1 b) y =
là hàm số phân thức, có tập xác định là (−∞; 2) ∪ (2; +∞) nên nó liên tục trên các khoảng x − 2 (−∞; 2), (2; +∞). □ x2 + 1
Bài 16. Tìm các khoảng liên tục của hàm số f (x) = . x + 2 Lời giải.
Tập xác định của hàm số f (x) là (−∞, −2) ∪ (−2, +∞). Vậy hàm số liên tục trên các khoảng (−∞, −2) và (−2, +∞). □ Bài 17.
a) Hàm số f (x) = 2x + 3 có liên tục trên đoạn [3; 4] hay không? x + 1 b) Hàm số f (x) =
(x ̸= 2) có liên tục trên khoảng (1; 3) hay không? x − 2 Lời giải.
a) Với mỗi x0 ∈ (3; 4) ta có lim f (x) = lim (2x + 3) = 2x0 + 3 = f (x0). x→x0 x→x0 Ta lại có
lim f (x) = lim (2x + 3) = 9 = f (3). x→3+ x→3+
lim f (x) = lim (2x + 3) = 11 = f (4). x→4− x→4−
Vậy hàm số đã cho liên tục trên đoạn [3; 4]. x + 1 b) Hàm số f (x) =
không xác định tại x = 2 nên hàm số không liên tục tại x = 2. x − 2
Do 2 ∈ (1; 3) nên hàm số đã cho không liên tục trên khoảng (1; 3). □ 6
Bài 18. Cho hàm số f (x) = x3 + 2x + . x − 2
a) Xét tính liên tục của hàm số f (x) tại x = 3.
b) Xét tính liên tục của hàm số f (x) trên tập xác định của hàm số đó. Lời giải.
Tập xác định của hàm số là R \ {2}. a) Ta thấy Å 6 ã lim f (x) = lim x3 + 2x + x→3 x→3 x − 2 Å 6 ã = lim x3 + lim (2x) + lim x→3 x→3 x→3 x − 2 6 = 33 + 2 · 3 + 3 − 2 = f (3)
Vậy hàm số f (x) liên tục tại x = 3. 455/764 455/764
Toán 11 theo chương trình GDPT2018 456 3. Hàm số liên tục
Biết làm, làm đúng, làm nhanh
b) Hàm số g(x) = x3 + 2x là hàm đa thức nên liên tục trên R. Do đó hàm số g(x) liên tục trên mỗi khoảng (−∞; 2) và (2; +∞).
Hàm số h(x) là hàm số phân thức hữu tỉ nên liên tục trên mỗi khoảng xác định (−∞; 2) và (2; +∞).
Vậy hàm số f (x) = g(x) + h(x) liên tục trên mỗi khoảnh (−∞; 2) và (2; +∞). □ x − 1
Bài 19. Xét tính liên tục của hàm số f (x) = tại điểm x0 = 2. x + 1 Lời giải.
Rõ ràng, hàm số đã cho xác định trên R \ {1}, do đó x0 = 2 thuộc tập xác định của hàm số. Ta có x − 1 lim f (x) = lim = 3 = f (2). x→2 x→2 x + 1
Do đó, hàm số f (x) liên tục tại x0 = 2. □ x + 1
Bài 20. Cho hàm số f (x) =
. Tìm các khoảng liên tục của hàm số f (x). x − 1 Lời giải.
Tập xác định của hàm số đã cho là D = (−∞; 1) ∪ (1; +∞). Vậy, hàm số đã cho liên tục trên các khoảng (−∞; 1) và (1; +∞) . □ √
Bài 21. Xét tính liên tục của hàm số y = x2 − 4. Lời giải. √ Hàm số y =
x2 − 4 là hàm số sơ cấp có tập xác định là (−∞; −2] ∪ [2; +∞) nên nó liên tục trên (−∞; 2] và [2; +∞). □ x2 + 1
Bài 22. Tìm các khoảng liên tục của hàm số f (x) = . x + 2 Lời giải.
Tập xác định của hàm số f (x) là (−∞, −2) ∪ (−2, +∞). Vậy hàm số liên tục trên các khoảng (−∞, −2) và (−2, +∞). □  x2 − 3x + 2   √ khi x > 2
Bài 23 (TH). Cho hàm số f (x) = x + 2 − 2
, m là tham số. Với giá trị nào của m thì hàm số  m2x − 4m + 6 khi x ≤ 2
đã cho liên tục tại x = 2? Lời giải. Ta có √ x2 − 3x + 2 (x − 2) (x − 1) x + 2 + 2 √ lim f (x) = lim √ = lim = lim (x − 1) x + 2 + 2 = 4. x→2+ x→2+ x + 2 − 2 x→2+ x − 2 x→2+ lim f (x) = lim
m2x − 4m + 6 = 2m2 − 4m + 6. x→2− x→2− f (2) = 2m2 − 4m + 6.
Để hàm số liên tục tại x = 2 thì lim f (x) = lim f (x) = f (2) ⇔ 2m2 −4m+6 = 4 ⇔ 2m2 −4m+2 = 0 ⇔ m = 1. x→2+ x→2−
Vậy có một giá trị của m thỏa mãn hàm số đã cho liên tục tại x = 2. □  x2 + 3x + 2  khi x < −1
Bài 24 (TH). Tìm giá trị của tham số m để hàm số f (x) = x2 − 1 liên tục tại x = −1? mx + 2 khi x ≥ −1 Lời giải. Ta có • f (−1) = −m + 2. • lim f (x) = −m + 2. x→(−1)+ x2 + 3x + 2 (x + 1) (x + 2) x + 2 −1 • lim f (x) = lim = lim = lim = . x→(−1)− x→(−1)− x2 − 1
x→(−1)− (x − 1) (x + 1) x→(−1)− x − 1 2 −1 5
Hàm số liên tục tại x = −1 ⇔ f (−1) = lim f (x) = lim f (x) ⇔ −m + 2 = ⇔ m = . □ x→(−1)+ x→(−1)− 2 2 456/764 456/764
Toán 11 theo chương trình GDPT2018 457
Chương 3. Giới hạn. Hàm số liên tục
Biết làm, làm đúng, làm nhanh  x2 − 16  khi x > 4
Bài 25 (TH). Tìm m để hàm số f (x) = x − 4
liên tục tại điểm x = 4. mx + 1 khi x ≤ 4 Lời giải. x2 − 16
Ta có lim f (x) = f (4) = 4m + 1; lim f (x) = lim = lim (x + 4) = 8. x→4− x→4+ x→4+ x − 4 x→4+ 7
Hàm số liên tục tại điểm x = 4 ⇔ lim f (x) = lim f (x) = f (4) ⇔ 4m + 1 = 8 ⇔ m = . □ x→4− x→4+ 4  x2 − x − 2  khix > −1
Bài 26 (TH). Tìm m để hàm số f (x) = x + 1 liên tục tại x = −1. mx − 2m2 khi x ≤ −1 Lời giải. Tập xác định D = R. • f (−1) = −m − 2m2 • lim f (x) =
lim (mx − 2m2) = −m − 2m2. x→−1− x→−1− x2 − x − 2 (x + 1)(x − 2) • lim f (x) = lim = lim = lim (x − 2) = −3. x→−1+ x→−1+ x + 1 x→−1+ x + 1 x→−1+
Hàm số liên tục tại x = −1 khi và chỉ khi lim f (x) = lim f (x) = f (−1) x→−1− x→−1+ m = 1
⇔ −m − 2m2 = −3 ⇔ 2m2 + m − 3 = 0 ⇔  3 . m = − 2 ß 3 ™
Vậy các giá trị của m là m ∈ 1; − . □ 2 √ √  1 − x − 1 + x   khi x < 0
Bài 27 (VD). Tìm giá trị của m để hàm số f (x) = x liên tục tại x = 0? 1 − x  m + khi x ≥ 0  1 + x Lời giải. Ta có √ √ Å Ç å 1 − x ã 1 − x − 1 + x −2x lim f (x) = lim m + = m+1. lim f (x) = lim = lim √ √ = x→0+ x→0+ 1 + x x→0− x→0− x x→0− x 1 − x + 1 + x −2 lim √ √ = −1. x→0− 1 − x + 1 + x f (0) = m + 1.
Để hàm liên tục tại x = 0 thì lim f (x) = lim f (x) = f (0) ⇔ m + 1 = −1 ⇒ m = −2. □ x→0+ x→0− √  x + 3 − 2   khi (x > 1) 
Bài 28 (TH). Cho hàm số f (x) = x − 1
. Tìm tất cả các giá trị của tham số thực m để hàm 1  m2 + m + khi (x ≤ 1)  4
số f (x) liên tục tại x = 1? Lời giải. √x + 3 − 2 1 1 1 Ta có lim f (x) = lim = lim √ = ; f (1) = lim f (x) = m2 + m + . x→1+ x→1+ x − 1 x→1+ x + 3 + 2 4 x→1− 4 ñ 1 1 m = −1
Để hàm số f (x) liên tục tại x = 1 thì m2 + m + = ⇔ . □ 4 4 m = 0 2x + a khi x ≤ 1 
Bài 29 (TH). Tìm a để hàm số f (x) = x3 − x2 + 2x − 2 liên tục trên R?  khi x > 1 x − 1 Lời giải.
Khi x < 1 thì f (x) = 2x + a là hàm đa thức nên liên tục trên khoảng (−∞; 1). x3 − x2 + 2x − 2 Khi x > 1 thì f (x) =
là hàm phân thức hữu tỉ xác định trên khoảng (1; +∞) nên liên tục trên x − 1 457/764 457/764
Toán 11 theo chương trình GDPT2018 458 3. Hàm số liên tục
Biết làm, làm đúng, làm nhanh khoảng (1; +∞).
Xét tính liên tục của hàm số tại điểm x = 1, ta có + f (1) = 2 + a.
+ lim f (x) = lim (2x + a) = 2 + a. x → 1− x → 1− x3 − x2 + 2x − 2 (x − 1) x2 + 2 + lim f (x) = lim = lim = lim x2 + 2 = 3. x → 1+ x → 1+ x − 1 x → 1+ x − 1 x → 1+
Hàm số f (x) liên tục trên R ⇔ hàm số f (x) liên tục tại x = 1.
lim f (x) = lim f (x) = f (1) → 2a + 1 = 3 → a = 1. □ x → 1− x → 1+  x2 + 4x + 3  khi x > −1
Bài 30 (TH). Tìm m để hàm số f (x) = x + 1
liên tục tại điểm x = −1. mx + 2 khi x ≤ −1 Lời giải. x2 + 4x + 3 (x + 1) (x + 3) Ta có lim f (x) = lim = lim = lim (x + 3) = 2. x→(−1)+ x→(−1)+ x + 1 x→(−1)+ x + 1 x→(−1)+ lim f (x) = lim (mx + 2) = −m + 2. x→(−1)− x→(−1)− f (−1) = −m + 2.
Để hàm số đã cho liên tục tại điểm x = −1 thì lim f (x) = lim
f (x) = f (−1) ⇔ 2 = −m + 2 ⇔ m = 0. x→(−1)+ x→(−1)− □ ®sin πx khi |x| ≤ 1
Bài 31 (VD). Cho hàm số f (x) =
. Tìm các khoảng liên tục của hàm số? Lệnh này giờ vô x + 1 khi |x| > 1
dụng Hàm số liên tục trên các khoảng (−∞; 1) và (1; +∞). Lời giải.
Ta có lim (x + 1) = 2 và lim sin πx = 0 ⇒ lim f (x) ̸= lim f (x) do đó hàm số gián đoạn tại x = 1. x→1+ x→1− x→1+ x→1− Tương tự lim (x + 1) = 0 và lim sin πx = 0 x→(−1)− x→(−1)+ ⇒ lim f (x) = lim
f (x) = lim f (x) = f (−1) do đó hàm số liên tục tại x = −1. x→(−1)+ x→(−1)− x→−1
Với x ̸= ±1 thì hàm số liên tục trên tập xác định.
Vậy hàm số đã cho liên tục trên các khoảng (−∞; 1) và (1; +∞). □ ® sin x nếu cos x ≥ 0
Bài 32 (TH). Cho hàm số f (x) =
. Hỏi hàm số f có tất cả bao nhiêu điểm gián đoạn 1 + cos x nếu cos x < 0 trên khoảng (0; 2018)? Lời giải.
Vì f là hàm lượng giác nên hàm số f gián đoạn khi và chỉ khi hàm số f gián đoạn tại x làm cho cos x = 0 ⇔ x = π π 1 2018 1 2018 1
+ kπ (k ∈ Z) ∈ (0; 2018) ⇔ 0 < + kπ < 2018 ⇔ 0 < + k < ⇔ − < k < − ⇔ 0 ≤ k ≤ 641. □ 2 2 2 π 2 π 2 √ ®x2 + 2 x − 2 khi x ≥ 2
Bài 33 (TH). Tìm m để hàm số y = f (x) = liên tục trên R? 5x − 5m + m2 khi x < 2 Lời giải. Tập xác định R . √
+ Xét trên (2; +∞) khi đó f (x) = x2 + 2 x − 2. √ √ ∀x 2 0 ∈ (2; +∞) , lim x0 + 2 x0 − 2 = x2 + 2 x 0
0 − 2 = f (x0) ⇒hàm số liên tục trên (2; +∞). x→x0
+ Xét trên (−∞; 2) khi đó f (x) = 5x − 5m + m2 là hàm đa thức liên tục trên R ⇒ hàm số liên tục trên (−∞; 2).
+ Xét tại x0 = 2, ta có f (2) = 4. √ lim f (x) = lim
x2 + 2 x − 2 = 4; lim f (x) = lim
5x − 5m + m2 = m2 − 5m + 10. Để hàm số đã cho x→2+ x→2+ x→2− x→2−
liên tục trên R thì nó phải liên tục tại x0 = 2. ñm = 2
⇔ lim f (x) = lim f (x) = f (2) ⇔ m2 − 5m + 10 = 4 ⇔ m2 − 5m + 6 = 0 ⇔ . □ x→2+ x→2− m = 3 458/764 458/764
Toán 11 theo chương trình GDPT2018 459
Chương 3. Giới hạn. Hàm số liên tục
Biết làm, làm đúng, làm nhanh  3x + a − 1 khi x ≤ 0  Bài 34 (VD). √ Cho hàm số f (x) = 1 + 2x − 1
. Tìm tất cả giá trị thực của a để hàm số đã cho liên  khi x > 0 x tục trên R. Lời giải.
Hàm số liên tục tại mọi điểm x ̸= 0 với mọi a.
Với x = 0, ta có f (0) = a − 1.
lim f (x) = lim (3x + a − 1) = a − 1. x→0− x→0− √1 + 2x − 1 2x 2 lim f (x) = lim = lim √ = lim √ = 1. x→0+ x→0+ x x→0+ x 1 + 2x + 1 x→0+ 1 + 2x + 1
Hàm số liên tục trên R khi và chỉ khi hàm số liên tục tại x = 0 ⇔ a − 1 = 1 ⇔ a = 2. □ ® m2x2 khi x ≤ 2
Bài 35 (TH). Có bao nhiêu giá trị thực của tham số m để hàm số f (x) = liên tục trên (1 − m) x khi x > 2 R? Lời giải.
Ta có hàm số luôn liên tục với ∀x ̸= 2.
Tại x = 2, ta có lim f (x) = lim (1 − m) x = (1 − m) 2; x→2+ x→2− lim f (x) = lim m2x2 = 4m2; f (2) = 4m2. x→2− x→2−
Hàm số liên tục tại x = 2 khi và chỉ khi
lim f (x) = lim f (x) = f (2) ⇔ 4m2 = (1 − m) 2 ⇔ 4m2 + 2m − 2 = 0. (1) x→2+ x→2+
Phương trình luôn có hai nghiệm thực phân biệt. Vậy có hai giá trị của m. □
Bài 36. Xét tính liên tục của các hàm số sau: x a) f (x) = ; x2 − 4 √ b) g(x) = 9 − x2; c) h(x) = cos x + tan x. Lời giải.
a) f (x) là hàm phân thức nên nó liên tục trên tập xác định hay hay liên tục trên R\{−2; 2}.
b) g(x) là hàm sơ cấp nên nó liên tục trên tập xác định hay liên tục trên [−3; 3]. c) Ta có: y = cos x liên tục trên R. n π o y = tan x liên tục trên R\ + kπ với k ∈ Z . 2 n π o
Do đó, hàm số h(x) liên tục trên R\ + kπ với k ∈ Z . 2 □
Bài 37. Bạn Nam cho rằng: “Nếu hàm số y = f (x) liên tục tại điểm x0, còn hàm số y = g(x) không liên tục tại
x0, thì hàm số y = f (x) + g(x) không liên tục tại x0”. Theo em, ý kiến của bạn Nam đúng hay sai? Giải thích. Lời giải.
Giả sử hàm số h(x) = f (x) + g(x) là hàm số liên tục tại x0.
Khi đó, hàm số g(x) = h(x) − f (x) là hiệu của hai hàm số liên tục tại x0 nên hàm số g(x) là hàm số liên tục tại
x0. Điều này mâu thuẫn với giả thiết là g(x) không liên tục tại x0.
Vậy ý kiến trên là đúng. □
Bài 38. Xét tính liên tục của mỗi hàm số sau trên tập xác định của hàm số đó 459/764 459/764
Toán 11 theo chương trình GDPT2018 460 3. Hàm số liên tục
Biết làm, làm đúng, làm nhanh 6 2x x − 1 a) f (x) = x2 + sin x. b) g(x) = x4 − x2 + . c) h(x) = + . x − 1 x − 3 x + 4 Lời giải.
a) Hàm số y = x2 và hàm số y = sin x liên tục trên R nên hàm số f (x) = x2 + sin x là tổng của hai hàm số
trên cũng liên tục trên R.
b) Tập xác định của hàm số là R \ {1}.
Vậy hàm số f (x) liên tục trên các khoảng (−∞; 1) và (1; +∞).
c) Tập xác định của hàm số là R \ {−4; 3}.
Vậy hàm số f (x) liên tục trên các khoảng (−∞; −4); (-4;3) và (3; +∞). □ ®x2 + x + 1 nếu x ̸= 4
Bài 39. Cho hàm số f (x) = 2a + 1 nếu x = 4.
a) Với a = 0, xét lính liên tục của hàm số tại x = 4.
b) Với giá trị nào của a thì hàm số liên tục tại x = 4.
c) Với giá trị nào của a thì hàm số liên tục trên tập xác định của nó? Lời giải.
a) Hàm số trên là hàm đa thức nên liên tục trên R.
Ta có f (4) = 2a + 1 = 1 (do a = 0).
lim f (x) = lim x2 + x + 1 = 42 + 4 + 1 = 21. x→4 x→4
Vì lim f (x) ̸= f (4) nên hàm số trên không liên tục tại x = 4 khi a = 0. x→4
b) Hàm số trên là hàm đa thức nên liên tục trên R. Ta có f (4) = 2a + 1.
lim f (x) = lim x2 + x + 1 = 42 + 4 + 1 = 21. x→4 x→4
Để hàm số liên tục tại x = 4 thì lim f (x) = f (4) ⇔ 2a + 1 = 21 ⇔ a = 10. x→4
Vậy a = 10 thì hàm số liên tục tại x = 4.
c) Tập xác định của hàm số là R.
○ TH1: x ̸= 4, hàm số trên là hàm đa thức nên liên tục trên R.
○ TH2: x = 4, hàm số trên là hàm hằng nên liên tục trên R.
Vậy hàm số trên liên tục trên R. □  x2 − 4x + 3  khi x > 1
Bài 40. Tìm P để hàm số y = x − 1 liên tục trên R. 6P x − 3 khi x ≤ 1 Lời giải.
Hàm số y = f (x) liên tục trên R ⇒ y = f (x) liên tục tại x = 1 ⇒ lim f (x) = lim f (x) = f (1). x→1+ x→1− x2 − 4x + 3 lim f (x) = lim = lim (x − 3) = −2. x→1+ x→1+ x − 1 x→1+
lim f (x) = lim (6P x − 3) = 6P − 3. x→1− x→1− f (1) = 6P − 3. 1
Do đó lim f (x) = lim f (x) = f (1) ⇔ 6P − 3 = −2 ⇔ P = . □ x→1+ x→1− 6 460/764 460/764
Toán 11 theo chương trình GDPT2018 461
Chương 3. Giới hạn. Hàm số liên tục
Biết làm, làm đúng, làm nhanh ®ax + b + 1, khi x > 0
Bài 41 (TH). Hàm số f (x) =
liên tục trên R khi và chỉ khi
a cos x + b sin x , khi x ≤ 0 Lời giải.
Khi x < 0 thì f (x) = a cos x + b sin x liên tục với x < 0.
Khi x > 0 thì f (x) = ax + b + 1 liên tục với mọi x > 0. Tại x = 0 ta có f (0) = a.
lim f (x)= lim (ax + b + 1)= b + 1. x→0+ x→0+
lim f (x)= lim (a cos x + b sin x)= a. x→0− x→0−
Để hàm số liên tục tại x = 0 thì lim f (x)= lim f (x) = f (0) ⇔ a = b + 1 ⇔ a − b = 1. □ x→0+ x→0− ®3x + 1 khi x ≥ −1
Bài 42 (TH). Cho hàm số y =
, m là tham số. Tìm m để hàm số liên tục trên R. x + m khi x < −1 Lời giải.
Ta có hàm số liên tục trên các khoảng (−∞; −1) và (−1; +∞).
Xét tính liên tục của hàm số tại x = −1. Có y (−1) = −2 = lim y và lim y = −1 + m. x→−1+ x→−1−
Để hàm số liên tục trên R thì y (−1) = lim y = lim y ⇔ −2 = −1 + m ⇔ m = −1. □ x→−1+ x→−1−
Bài 43. Xét tính liên tục của các hàm số sau trên tập xác định của chúng: ® x 1 + x2 nếu x < 1 a) f (x) = ; b) f (x) = x2 + 5x + 6 4 − x nếu x ≥ 1. Lời giải.
a) Tập xác định của hàm số đã cho là R \ {−2; −3}. Do đó hàm số đã cho liên tục trên các khoảng (−∞; −3), (−3; −2) và (−2, +∞);
b) Hàm số đã cho xác định trên R. Với x < 1, ta có f (x) = 1 + x2 là hàm đa thức, do đó liên tục trên khoảng
(−∞; 1). Với x > 1, ta có f (x) = 4 − x cũng là hàm đa thức, do đó liên tục trên khoảng (1; +∞). Tại x = 1, ta có
○ lim f (x) = lim (1 + x2) = 2. x→1− x→1−
○ lim f (x) = lim (4 − x) = 3. x→1+ x→1+
Vì lim f (x) ̸= lim f (x) do đó hàm số đã cho không liên tục tại x = 1. Vậy hàm số đã cho liên tục trên x→1+ x→1−
các khoảng (−∞; 1) và (1; +∞). □
Bài 44. Tìm giá trị của tham số m để hàm số ® sin x nếu x ≥ 0 f (x) = − x + m nếu x < 0 liên tục trên R. Lời giải.
Hàm số đã cho liên tục trên các khoảng (−∞; 0) và (0; +∞). Xét tại x = 0. Ta có ○ f (0) = sin 0 = 0. ○ lim f (x) = lim sin x = 0. x→0+ x→0+
○ lim f (x) = lim (−x + m) = m. x→0− x→0− 461/764 461/764
Toán 11 theo chương trình GDPT2018 462 3. Hàm số liên tục
Biết làm, làm đúng, làm nhanh
Hàm số đã cho liên tục trên R khi và chỉ khi f (0) = lim f (x) = lim f (x) ⇔ m = 0. □ x→0+ x→0−  x2 − 4  khi x ̸= −2
Bài 45. Cho hàm số f (x) = x + 2
.Tìm a để hàm số y = f (x) liên tục trên R. a khi x = −2. Lời giải.
Với x0 ∈ (−∞; −2) ∪ (−2; +∞), ta có: x2 − 4 f (x) =
là hàm số liên tục trên x0 ∈ (−∞; −2)∪(−2; +∞) nên f (x) liên tục trên (−∞; −2)∪(−2; +∞). x + 2
Do đó, để hàm số liên tục trên R khi và chỉ khi hàm số liên tục tại x0 = −2, ta có f (−2) = a; x2 − 4 (x + 2)(x − 2) lim f (x) = lim = lim = lim (x + 2) = 0. x→−2 x→−2 x + 2 x→−2 x + 2 x→−2
Do đó, để hàm số liên tục tại x0 = −2 thì a = 0. □
Giá mở cửa (0, 5 km đầu)
Giá cước các km tiếp theo đến 30 km Giá cước từ km thứ 31
Bài 46. Một bảng giá cước taxi được cho như sau: 10 000 đồng 13 500 đồng 11 000 đồng
a) Viết công thức hàm số mô tả số tiền khách phải trả theo quãng đường di chuyển.
b) Xét tính liên tục của hàm số ở câu a. Lời giải.
a) Gọi x là quãng đường di chuyển, f (x) là giá tiền tính theo quãng đường.
○ 0 ≤ x ≤ 0,5, ta có f (x) = 10000 đồng.
○ 0,5 < x ≤ 30, f (x) = 10000 + 13500(x − 0,5) đồng.
○ x > 30, f (x) = 408250 + 11000(x − 30) đồng. 10000 nếu 0 ≤ x ≤ 0,5   Vậy f (x) = 10000 + 13500(x − 0,5) nếu 0,5 < x ≤ 30 
408250 + 11000(x − 30) nếu x > 30.
b) Hàm số f (x) liên tục trên các khoảng (0; 0,5), (0,5; 30) và (30; +∞).
Tại x = 0,5, ta có f (0,5) = 10000, lim f (x) = 10000, lim f (x) = 10000. x→0,5+ x→0,5− Vì f (0, 5) = lim f (x) =
lim f (x), do đó f (x) liên tục tại x = 0, 5. x→0,5+ x→0,5−
Tại x = 30, ta có f (30) = 408250, lim f (x) = 408250, lim f (x) = 408250. x→30− x→30+
Vì f (30) = lim f (x) = lim f (x), do đóf (x) liên tục tại x = 30. x→30− x→30+
Vậy f (x) liên tục trên khoảng (0; +∞). □
Bài 47. Một bãi đậu xe ô tô đưa ra giá C(x) (đồng) khi thời gian đậu xe là x (giờ) như sau:  60000 khi 0 < x ≤ 2   C(x) = 100000 khi 2 < x ≤ 4   200000 khi 4 < x ≤ 24.
Xét tính liên tục của hàm số C(x). Lời giải. Tập xác định D = (0; 24] 462/764 462/764
Toán 11 theo chương trình GDPT2018 463
Chương 3. Giới hạn. Hàm số liên tục
Biết làm, làm đúng, làm nhanh
Khi 0 < x < 2 thì C(x) = 60000 là hàm đa thức liên tục trên R nên C(x) liên tục trên (0; 2).
Khi 2 < x < 4 thì C(x) = 100000 là hàm đa thức liên tục trên R nên C(x) liên tục trên (2; 4).
Khi 4 < x ≤ 24 thì C(x) = 200000 là hàm đa thức liên tục trên R nên C(x) liên tục trên (4; 24]. Khi x0 = 2, ta có f (2) = 60000; lim f (x) = lim 60000 = 60000; x→2− x→2−
lim f (x) = lim 100000 = 100000. x→2+ x→2+
Do dó hàm số không có giới hạn tại 2 nên không liên tục tại 2. Khi x0 = 4, ta có f (4) = 100000;
lim f (x) = lim 100000 = 100000; x→4− x→4−
lim f (x) = lim 200000 = 200000. x→4+ x→4+
Do dó hàm số không có giới hạn tại 4 nên không liên tục tại 4.
Vậy hàm số liên tục trên (0; 24]\{2; 4} □
Bài 48. Lực hấp dẫn do Trái Đất tác dụng lên một đơn vị khối lượng ở khoảng cách r tính từ tâm của nó là  GM r  khi 0 < r < R   R3  F (r) =   GM   khi r ≥ R, r2
trong đó M là khối lượng, R là bán kính của Trái Đất, G là hằng số hấp dẫn. Hàm số F (r) có liên tục trên (0; +∞) không? Lời giải. GM r
Khi 0 < r < R thì F (r) =
là hàm đa thức liên tục trên R nên F (r) liên tục trên (0; R). R3 GM Khi R < r thì F (r) =
là hàm phân thức liên tục trên R\{0} nên F (r) liên tục trên (R; +∞). r2 Tại r = R, ta có: GM F (R) = ; R2 GM r GM lim F (r) = lim = ; x→R− x→R− R3 R2 GM GM lim F (r) = lim = . x→R+ x→R+ r2 R2
Do đó, hàm số liên tục tại R.
Vậy hàm số liên tục trên (0; +∞). □ 463/764 463/764
Toán 11 theo chương trình GDPT2018 464 3. Hàm số liên tục
Biết làm, làm đúng, làm nhanh Bài 49.
Hình bên cạnh biểu thị độ cao h (m) của một quả bóng được đá lên thời gian t (s), h(m) trong đó h(t) = −2t2 + 8t. 8
a) Chứng tỏ hàm số h(t) liên tục trên tập xác định.
b) Dựa và đồ thì hãy xác định lim −2t2 + 8t. t→2 4 O 2 t(s) Lời giải.
a) Hàm số trên là hàm đa thức nên liên tục trên R.
b) Dựa vào đồ thị ta có lim −2t2 + 8t = 8. t→2 □
Bài 50. Một hãng taxi đưa ra giá cước T (x) (đồng) khi quãng đường x (km) cho loại xe 4 chỗ như sau:  10000 khi 0 < x ≤ 0.7   T (x) = 10000 + (x − 0,7).14000 khi 0,7 < x ≤ 20   280200 + (x − 20).12000 khi x > 20
Xét tính liên tục của hàm số T (x). Lời giải.
Khi 0 < x < 0,7, T (x) = 1000 là hàm số đa thức liên tục trên R nên T (x) liên tục trên (0; 0,7).
Khi 0,7 < x < 20, T (x) = 10000 + (x − 0,7).14000 là hàm số đa thức liên tục trên R nên T (x) liên tục trên (0,7; 20).
Khi 20 < x, T (x) = 280200 + (x − 20).12000 là hàm số đa thức liên tục trên R nên T (x) liên tục trên (20; +∞). Tại x = 0,7. Ta có f (0,7) = 10000; lim f (x) = lim 10000 = 10000; x→0,7+ x→0,7+ lim f (x) =
lim [10000 + (x − 0, 7).14000] = 10000 + (0,7 − 0,7).14000 = 10000. x→0,7− x→0,7−
Do đó, T (x) liên tục tại x = 0,7. Tại x = 20. Ta có: f (20) = 280200; lim f (x) =
lim [10000 + (x − 0,7).14000] = 280200; x→20+ x→0,7+ lim f (x) =
lim [280200 + (x − 20).12000] = 280200 + (20 − 20).12000 = 280200,. x→0,7− x→0,7−
Do đó, T (x) liên tục tại x = 0,7.
Từ những điều trên, T (x) liên tục trên R. □ 464/764 464/764
Toán 11 theo chương trình GDPT2018 465
Chương 3. Giới hạn. Hàm số liên tục
Biết làm, làm đúng, làm nhanh 3.
Bài tập trắc nghiệm
Câu 49. Cho hàm số y = f (x) liên tục trên (a; b). Điều kiện cần và đủ để hàm số liên tục trên [a; b] là A
lim f (x) = f (a) và lim f (x) = f (b). B
lim f (x) = f (a) và lim f (x) = f (b). x→a+ x→b+ x→a− x→b−
C lim f (x) = f (a) và lim f (x) = f (b). D
lim f (x) = f (a) và lim f (x) = f (b). x→a+ x→b− x→a− x→b+ Lời giải.
Theo định nghĩa hàm số liên tục trên đoạn [a; b]. Chọn lim f (x) = f (a) và lim f (x) = f (b). x→a+ x→b− Chọn đáp án C □
Câu 50. Cho đồ thị của hàm số y = f (x) như hình vẽ sau : y f (x) O x Chọn mệnh đề đúng.
A Hàm số y = f (x) có đạo hàm tại điểm x = 0 nhưng không liên tục tại điểm x = 0.
B Hàm số y = f (x)liên tục tại điểm x = 0 nhưng không có đạo hàm tại điểm x = 0.
C Hàm số y = f (x) liên tục và có đạo hàm tại điểm x = 0.
D Hàm số y = f (x) không liên tục và không có đạo hàm tại điểm x = 0. Lời giải.
Đồ thị là một đường liền nét, nhưng bị “gãy” tại điểm x = 0 nên nó liên tục tại điểm x = 0 nhưng không có đạo hàm tại điểm x = 0. Chọn đáp án B □
Câu 51. Hình nào trong các hình dưới đây là đồ thị của hàm số không liên tục tại x = 1? y y 4 4 3 f (x) 3 f (x) 2 2 1 1 −3 −2 −1 1 2 3 O x −3 −2 −1 1 2 3 O x A . B . y 4 3 y 4 2 f (x) 3 1 f (x) 2 −2 −1 1 2 3 4 O x 1 −3 −2 −1 1 2 3 O x C . D . Lời giải.
Vì lim y ̸= lim y nên hàm số không liên tục tại x = 1. □ x→1+ x→1− 465/764 465/764
Toán 11 theo chương trình GDPT2018 466 3. Hàm số liên tục
Biết làm, làm đúng, làm nhanh  1 − x3  , khi x < 1 Câu 52. Cho hàm số y = 1 − x
. Hãy chọn kết luận đúng 1 , khi x ≥ 1
A y liên tục phải tại x = 1.
B y liên tục tại x = 1.
C y liên tục trái tại x = 1.
D y liên tục trên R. Lời giải. Ta có y (1) = 1. 1 − x3 (1 − x) 1 + x + x2 Ta có lim y = 1; lim y = lim = lim = lim 1 + x + x2 = 4. x→1+ x→1− x→1− 1 − x x→1− 1 − x x→1−
Nhận thấy lim y = y (1), suy ra y liên tục phải tại x = 1. x→1+ Chọn đáp án A □
Câu 53. Trong các hàm số sau, hàm số nào liên tục trên R? 2x − 1 √ A y = x3 − x. B y = cot x. C y = . D y = x2 − 1. x − 1 Lời giải.
Vì y = x3 − x là đa thức nên liên tục trên R. Chọn đáp án A □
Câu 54. Trong các hàm số sau, hàm số nào liên tục trên R? x2 + 3 √ x + 5 A f (x) = tan x + 5. B f (x) = . C f (x) = x − 6. D f (x) = . 5 − x x2 + 4 Lời giải. x + 5 x + 5 Hàm số f (x) =
là hàm phân thức hữu tỉ và có tập xác định là D = R do đó hàm số f (x) = liên x2 + 4 x2 + 4 tục trên R. Chọn đáp án D □ ® − x2 + x + 3 khi x ≥ 2 Câu 55. Cho hàm số y =
. Chọn mệnh đề sai trong các mệnh đề sau : 5x + 2 khi x < 2
A Hàm số liên tục tại x0 = 1.
B Hàm số liên tục trên R.
C Hàm số liên tục trên các khoảng (−∞; 2) , (2; +∞).
D Hàm số gián đoạn tại x0 = 2. Lời giải.
+ Với x > 2, ta có f (x) = −x2 + x + 3 là hàm đa thức ⇒ hàm số f (x) liên tục trên khoảng (2; +∞).
+ Với x < 2, ta có f (x) = 5x + 2 là hàm đa thức ⇒ hàm số f (x) liên tục trên khoảng (−∞; 2). + Tại x = 2. lim f (x) = lim
−x2 + x + 3 = 1 lim f (x) = lim (5x + 2) = 12 ⇒ lim f (x) ̸= lim f (x). Do đó không x→2+ x→2+ − x→2 x→2− x→2+ x→2−
tồn tại lim f (x) . Vậy hàm số gián đoạn tại x0 = 2 hay Hàm số không liên tục trên R. x→2 Chọn đáp án B □
Câu 56. Hàm số nào sau đây liên tục trên R? √ x4 − 4x2 x4 − 4x2 A f (x) = x. B f (x) = x4 − 4x2. C f (x) = . D f (x) = . x + 1 x + 1 Lời giải.
Vì hàm số f (x) = x4 − 4x2 có dạng đa thức với D = R nên hàm số này liên tục trên R Chọn đáp án B □ √  x + 1 − 1   khi x > 0
Câu 57. Tìm tất cả các giá trị thực của m để hàm số f (x) = x liên tục trên R. p   x2 + 1 − m khi x ≤ 0 3 1 1 A m = . B m = . C m = −2. D m = − . 2 2 2 Lời giải. 466/764 466/764
Toán 11 theo chương trình GDPT2018 467
Chương 3. Giới hạn. Hàm số liên tục
Biết làm, làm đúng, làm nhanh √x + 1 − 1 Khi x > 0, ta có f (x) =
liên tục trên khoảng (0; +∞). √ x Khi x < 0, ta có f (x) =
x2 + 1 − m liên tục trên khoảng (−∞; 0).
Hàm số liên tục trên R khi và chỉ khi hàm số liên tục tại x = 0. √x + 1 − 1 1 1 Ta có lim f (x) = lim = lim √ = . x→0+ x→0+ x x→0+ x + 1 + 1 2 √ Ä ä 1 lim f (x) = lim
x2 + 1 − m = 1 − m = f (0). Do đó hàm số liên tục tại x = 0 khi và chỉ khi = 1 − m ⇔ x→0− x→0− 2 1 m = . 2 Chọn đáp án B □  x2 − 16  khi x > 4
Câu 58. Tìm tất cả các giá trị thực của tham số m để hàm số f (x) = x − 4 liên tục trên  mx + 1 khi x ≤ 4 R. 7 7 7 7
A m = 8 hoặc m = − . B m = . C m = − . D m = −8 hoặc m = . 4 4 4 4 Lời giải. x2 − 16 *) Với x > 4 thì f (x) =
là hàm phân thức nên liên tục trên tập xác định của nó ⇒ f (x) liên tục trên x − 4 (4; +∞).
*) Với x < 4 thì f (x) = mx + 1 là hàm đa thức nên liên tục trên R ⇒ f (x) liên tục trên (−∞; 4).
Do vậy hàm số f (x) đã liên tục trên các khoảng (4; +∞), (−∞; 4).
Suy ra hàm số f (x) liên tục trên R khi và chỉ khi f (x) liên tục tại x = 4.Do đó x2 − 16
lim f (x) = lim f (x) = f (4) ⇔ lim
= lim (mx + 1) = 4m + 1 ⇔ lim (x + 4) = 4m + 1 ⇔ 4m + 1 = x→4+ x→4− x→4+ x − 4 x→4− x→4+ 7 8 ⇔ m = . 4 Chọn đáp án B □ x2 + ax + b khi x < −5  
Câu 59. Nếu hàm số f (x) = x + 17
khi − 5 ≤ x ≤ 10 liên tục trên R thì a + b bằng  ax + b + 10 khi x > 10 A −1. B 0. C 1. D 2. Lời giải.
Với x < −5 ta có f (x) = x2 + ax + b, là hàm đa thức nên liên tục trên (−∞; −5).
Với −5 < x < 10 ta có f (x) = x + 7, là hàm đa thức nên liên tục trên (−5; 10).
Với x > 10 ta có f (x) = ax + b + 10, là hàm đa thức nên liên tục trên (10; +∞).
Để hàm số liên tục trên R thì hàm số phải liên tục tại x = −5 và x = 10. Ta có f (−5) = 12;f (10) = 17. lim f (x) = lim x2 + ax + b = −5a + b + 25. x→−5− x→−5− lim f (x) = lim (x + 17) = 12. lim f (x) = lim (x + 17) = 27. lim f (x) = lim (ax + b + 10) = x→−5+ x→−5+ x→10− x→10− x→10+ x→10+
10a + b + 10. Hàm số liên tục tại x = −5 và x = 10 khi ®5a + b + 25 = 12 ® − 5a + b = −13 ®a = 2 ⇔ ⇔ ⇒ a + b = −1. 10a + b + 10 = 27 10a + b = 17 b = −3 Chọn đáp án A □
Dạng 5. Bài toán có chứa tham số 1. Ví dụ mẫu ®x + 1 nếu x ̸= 3
Ví dụ 19 (Cánh Diều). Cho hàm số f (x) =
. Tìm a để hàm số f (x) liên tục trên R. a nếu x = 3 467/764 467/764
Toán 11 theo chương trình GDPT2018 468 3. Hàm số liên tục
Biết làm, làm đúng, làm nhanh Lời giải.
Do f (x) = x + 1 nếu x ̸= 3 nên hàm số đó liên tục trên mỗi khoảng (−∞; 3) và (3; +∞). Với x = 3 thì f (3) = a.
Ta có lim f (x) = lim (x + 1) = 3 + 1 = 4. x→3 x→3
Vậy hàm số f (x) liên tục trên R khi hàm số f (x) liên tục tại điểm x = 3 khi và chỉ khi
lim f (x) = f (3) = 4 ⇔ a = 4. x→3 □ ®x + 1 nếu x ̸= 3
Ví dụ 20. Cho hàm số f (x) =
. Tìm a để hàm số f (x) liên tục trên R. a nếu x = 3 Lời giải.
Do f (x) = x + 1 nếu x ̸= 3 nên hàm số đó liên tục trên mỗi khoảng (−∞; 3) và (3; +∞). Với x = 3 thì f (3) = a.
Ta có lim f (x) = lim (x + 1) = 3 + 1 = 4. x→3 x→3
Vậy hàm số f (x) liên tục trên R khi hàm số f (x) liên tục tại điểm x = 3 khi và chỉ khi
lim f (x) = f (3) = 4 ⇔ a = 4. x→3 □
Ví dụ 21. Tìm giá trị của tham số m để hàm số ® sin x nếu x ≥ 0 f (x) = − x + m nếu x < 0 liên tục trên R. Lời giải.
Hàm số đã cho liên tục trên các khoảng (−∞; 0) và (0; +∞). Xét tại x = 0. Ta có ○ f (0) = sin 0 = 0. ○ lim f (x) = lim sin x = 0. x→0+ x→0+
○ lim f (x) = lim (−x + m) = m. x→0− x→0−
Hàm số đã cho liên tục trên R khi và chỉ khi f (0) = lim f (x) = lim f (x) ⇔ m = 0. □ x→0+ x→0− 2. Bài tập rèn luyện x + 1
Bài 51. Tìm giá trị của tham số m để hàm số f (x) =
liên tục trên khoảng (1; 2). x − m Lời giải.
Tập xác định D = R \ {m}.
Hàm số f (x) là hàm phân thức hữu tỷ nên hàm số liên tục trên (−∞; m) và (m; +∞).
Vậy để hàm số f (x) liên tục trên khoảng (1; 2) thì ñ(1; 2) ⊂ (−∞; m) ñm ≥ 2 ⇔ (1; 2) ⊂ (m; +∞) m ≤ 1. □ 468/764 468/764
Toán 11 theo chương trình GDPT2018 469
Chương 3. Giới hạn. Hàm số liên tục
Biết làm, làm đúng, làm nhanh ®x + 2 nếu x ̸= 2
Bài 52. Tìm giá trị của tham số a sao cho hàm số f (x) = liên tục trên R. a nếu x = 2 Lời giải. Tập xác định D = R.
Với x ̸= 2, f (x) = x + 2 là hàm đa thức nên hàm số f (x) liên trục trên (−∞; 2) và (2; +∞).
Vậy để hàm số f (x) liên tục trên R thì hàm số f (x) cần liên tục tại x = 2, điều này tương đương với
lim f (x) = f (2) ⇔ lim (x + 2) = a ⇔ 2 + 2 = a ⇔ a = 4. x→2 x→2 □ √
Bài 53. Tìm các giá trị nguyên của tham số m để hàm số f (x) =
9 − x2 liên tục trên khoảng (m; 2m + 1). Lời giải. √ Hàm số f (x) =
9 − x2 là hàm số căn thức nên hàm số f (x) liên tục trên tập xác định D = [−3; 3]. √ Suy ra hàm số f (x) =
9 − x2 liên tục trên khoảng (m; 2m + 1) khi và chỉ khi ®m ≥ −3 (m; 2m + 1) ⊂ [−3; 3] ⇔ ⇔ −3 ≥ m ≤ 1. 2m + 1 ≤ 3
Vậy có 5 giá trị nguyên của tham số m thoả mãn yêu cầu bài toán. □  x2 + 5x − 6  khi x ̸= −6
Bài 54. Tìm m để f (x) = 6 + x liên tục tại x √ 0 = −6.  mx + 4 + mx − 5 khi x = −6 Lời giải. x2 + 5x − 6 (x + 6)(x − 1) Ta có lim f (x) = lim = lim
= lim (x − 1) = −6 − 1 = −7. x→−6 x→−6 6 + x x→−6 6 + x x→−6 √ Mặt khác f (−6) =
−6m + 4 − 6m − 5 nên hàm số liên tục tại x0 = 6 tương đương với lim f (x) = f (−6) x→−6 √ ⇔ −6m + 4 − 6m − 5 = −7 √ ⇔ −6m + 4 = 6m − 2 ®6m − 2 ≥ 0 ⇔ − 6m + 4 = 36m2 − 24m + 4  1 m ≥ ⇔ 3 36m2 − 18m = 0 1 ⇔ m = . 2 1 Vậy m =
thỏa mãn yêu cầu bài toán. □ 2  x3 + 2x2 − 5x − 6   khi x ̸= 2 
Bài 55. Tìm a để hàm số f (x) = x3 − 4x liên tục tại x0 = 2. 1   (a + x) khi x = 2  8 Lời giải. 1 ○ f (2) = (a + 2). 8 x3 + 2x2 − 5x − 6 (x − 2)(x2 + 4x + 3) x2 + 4x + 3 15 ○ lim f (x) = lim = lim = lim = . x→2 x→2 x3 − 4x x→2 x(x − 2)(x + 2) x→2 x(x + 2) 8 1 15
Hàm số liên tục tại x0 = 2 ⇔ f (2) = lim f (x) ⇔ (a + 2) = ⇔ a = 13. □ x→2 8 8 469/764 469/764
Toán 11 theo chương trình GDPT2018 470 3. Hàm số liên tục
Biết làm, làm đúng, làm nhanh 3.
Bài tập trắc nghiệm √
Câu 60. Tất cả giá trị của tham số m để hàm số f (x) =
x − 1 liên tục trên khoảng (m; m + 2) là A m ≥ 1. B m > 1. C m > −1. D m ≥ −1. Lời giải. √ Hàm số f (x) =
x − 1 là hàm số dạng căn thức nên hàm số f (x) liên tục trên tập xác định D = [1; +∞). √ Vậy hàm số f (x) =
x − 1 liên tục trên khoảng (m; m + 2) khi và chỉ khi
(m; m + 2) ⊂ [1; +∞) ⇔ m ≥ 1. Chọn đáp án A □ ®2x − 2 khi x ̸= 3 Câu 61. Cho hàm số f (x) =
(m là tham số). Tìm giá trị thực của tham số m để hàm số đã 2m khi x = 3 cho liên tục tại x0 = 3. A m = 4. B m = 2. C m = 3. D m = 1. Lời giải. Tập xác định D = R.
Ta có lim f (x) = lim (2x − 2) = 4, f (3) = 2m. Để hàm số liên tục tại x0 = 3 thì lim f (x) = f (3) ⇔ 4 = 2m ⇔ x→3 x→3 x→3 m = 2. Chọn đáp án B □ ®ax + 5 khi x ≥ 2 Câu 62. Hàm số f (x) =
liên tục trên R nếu a bằng 5 khi x < 2 A 0. B 3. C −1. D 7. Lời giải.
Hàm số đã cho liên tục trên (2; +∞) và (−∞; 2), từ đó suy ra hàm số liên tục trên R nếu nó liên tục tại x = 2.
Ta có lim f (x) = lim (ax + 5) = 2a + 5; lim f (x) = lim (3x − 1) = 5. x→2+ x→2+ x→2− x→2+
Từ đó suy ra hàm số liên tục trên R nếu 2a + 5 = 5 ⇒ a = 0. Chọn đáp án A □ ®x + 2 nếu x ≤ a
Câu 63. Cho số thực a và hàm số f (x) =
. Giá trị của a để hàm số f (x) liên tục trên R 2x − 1 nếu x > a là A 0. B 1. C 2. D 3. Lời giải.
Hàm số có dạng đa thức trên các khoảng (−∞; a) và (a; +∞) nên hàm số f (x) hiển nhiên liên tục trên (−∞; a) và (a; +∞).
Vậy hàm số f (x) liên tục trên R khi và chỉ khi hàm số liên tục tại x = a, điều này tương đương với
lim f (x) = lim f (x) = f (a) ⇔ a + 2 = 2a − 1 ⇔ a = 3. x→a+ x→a− Chọn đáp án D □ ®x2 + m khi x ≥ 2 Câu 64. Cho hàm số f (x) =
(m là tham số). Tìm giá trị thực của tham số m để hàm số đã 3x − 1 khi x < 2 cho liên tục tại x0 = 2. A m = 2. B m = 1. C m = 0. D m = 3. Lời giải.
Xét tính liên tục tại x0 = 2: Ta có lim f (x) = lim
x2 + m = 4 + m = f (2) và lim f (x) = lim (3x − 1) = 5. x→2+ x→2+ x→2− x→2−
Khi đó hàm số đã cho liên tục tại x0 = 2 khi và chỉ khi
lim f (x) = lim f (x) = f (2) ⇔ 4 − m = 5 ⇔ m = 1. x→2+ x→2− Chọn đáp án B □ 470/764 470/764
Toán 11 theo chương trình GDPT2018 471
Chương 3. Giới hạn. Hàm số liên tục
Biết làm, làm đúng, làm nhanh ®3x + b khi x ⩽ −1
Câu 65. Biết hàm số y = f (x) =
liên tục trên R. Khi đó giá trị của a − b bằng x + a khi x > −1 A 1. B −1. C 2. D −2. Lời giải. Ta có lim f (x) = lim (x + a) = a − 1 và lim f (x) = lim (3x + b) = b − 3. x→−1+ x→−1+ x→−1− x→−1−
Vì hàm số liên tục trên R nên ta có a − 1 = b − 3 ⇔ a − b = −2. Chọn đáp án D □ ®x3 + x2 + 7 khi x ̸= −1 Câu 66. Cho hàm số f (x) =
. Tìm m để hàm số liên tục tại điểm x0 = −1. 2x + m − 1 khi x = −1 A m = 12. B m = 8. C m = −10. D m = 10. Lời giải.
Ta có lim (x3 + x2 + 7) = 7 và f (−1) = m − 3. x→−1
Để hàm số liên tục tại điểm x0 = −1 thì m − 3 = 7 ⇔ m = 10. Chọn đáp án D □  x3 − x2   khi x > 1   x − 1
Câu 67. Cho hàm số y = f (x) = n
khi x = 1 . Biết hàm số f (x) liên tục tại x0 = 1. Giá trị của m, n    mx + 1 khi x < 1 là A n = 1, m = 0. B n = 0, m = 1. C n = m = 1. D n = −1, m = 0. Lời giải. Ta có x3 − x2 ○ lim f (x) = lim = lim x2 = 1; x→1+ x→1+ x − 1 x→1+
○ lim f (x) = lim (mx + 1) = m + 1; x→1− x→1− ○ f (1) = n.
Do hàm số f (x) liên tục tại x = 1 nên ta có lim f (x) = lim f (x) = f (1) ⇔ m + 1 = 1 = n. x→1− x→1+ Suy ra n = 1, m = 0. Chọn đáp án A □  4 − x  √ khi x ̸= 4
Câu 68. Tìm giá trị của m để hàm số f (x) = x + 5 − 3 liên tục tại x = 4. 1 − m khi x = 4 A m = 7. B m = 0. C m = 2. D m = −5. Lời giải. √ 4 − x (4 − x) x + 5 + 3 √ Ta có lim √ = lim = − lim x + 5 + 3 = −6. x→4 x + 5 − 3 x→4 x − 4 x→4
Để hàm số liên tục tại x = 4 thì −6 = 1 − m ⇔ m = 7. Chọn đáp án A □  ax2 − bx + 4  khi x ̸= 1
Câu 69. Cho các tham số a, b thoả mãn hàm số f (x) = x − 1
liên tục trên R. Giá trị của 3 khi x = 1 biểu thức P = a + b là A 27. B 28. C 29. D 30. Lời giải.
Do hàm số f (x) liên tục trên R nên hàm số f (x) liên tục tại x = 1, điều này tương đương với ® ® ax2 − bx + 4 Å a − b + 4 ã a − b + 4 = 0 a = 7 lim = 3 ⇔ lim ax + a − b + = 3 ⇔ ⇔ x→1 x − 1 x→1 x − 1 2a − b = 3 b = 11. 471/764 471/764
Toán 11 theo chương trình GDPT2018 472 3. Hàm số liên tục
Biết làm, làm đúng, làm nhanh Vậy a + b = 28. Chọn đáp án B □
Dạng 6. Toán thực tế, liên môn về hàm số liên tục 1. Ví dụ Ví dụ 22.
Hình bên cạnh biểu thị độ cao h (m) của một quả bóng được đá lên thời gian t (s), h(m) trong đó h(t) = −2t2 + 8t. 8
a) Chứng tỏ hàm số h(t) liên tục trên tập xác định.
b) Dựa và đồ thì hãy xác định lim −2t2 + 8t. t→2 4 O 2 t(s) Lời giải.
a) Hàm số trên là hàm đa thức nên liên tục trên R.
b) Dựa vào đồ thị ta có lim −2t2 + 8t = 8. t→2 □
Ví dụ 23. Một bãi đậu xe ô-tô đưa ra giá C(x) (đồng) khi thời gian đậu xe là x (giờ) như sau: 60.000 khi 0 < x ≤ 2   C(x) = 100.000 khi 2 < x ≤ 4  200.000 khi 4 < x ≤ 24.
Xét tính liên tục của hàm số C(x). Lời giải.
○ Hàm số C(x) là hàm hằng trên từng khoảng (0; 2), (2; 4), (4; 6) nên liên tục trên từng khoảng đó.  lim C(x) = 60.000  ○ x→2− Ta có
⇒ không tồn tại lim C(x), vậy C(x) không liên tục tại x0 = 2. lim C(x) = 100.000 x→2  x→2+  lim C(x) = 100.000  ○ x→4− Ta có
⇒ không tồn tại lim C(x), vậy C(x) không liên tục tại x0 = 4. lim C(x) = 200.000 x→4  x→4+
Vậy hàm số C(x) liên tục trên từng khoảng (0; 2), (2; 4), (4; 6). □
Ví dụ 24. Lực hấp dẫn do Trái Đất tác dụng lên một đơn vị khối lượng ở khoảng cách r tính từ tâm của nó là  GM r  khi 0 < r ≤ R  F (r) = R3
, trong đó M là khối lượng, R là bán kính của Trái Đất, G là hằng số hấp dẫn. GM   khi r ≥ R r2
Hàm số F (r) có liên tục trên (0; +∞) không? Lời giải. GM r
○ Với mọi r ∈ (0; R), hàm số F (r) =
luôn xác định nên liên tục tại đó. R3 472/764 472/764
Toán 11 theo chương trình GDPT2018 473
Chương 3. Giới hạn. Hàm số liên tục
Biết làm, làm đúng, làm nhanh GM
○ Với mọi r ∈ (R; +∞), hàm số F (r) =
luôn xác định nên liên tục tại đó. r2  GM r GM  lim F (r) = lim =    r→R− r→R− R3 R2    ○ GM GM Ta có lim F (r) = lim =
nên hàm số F (r) liên tục tại r = R. r2 R2  x→R+ x→R+    GM  F (R) =  R2
Vậy hàm số F (r) liên tục trên (0; +∞). □
Giá mở cửa (0, 5 km đầu)
Giá cước các km tiếp theo đến 30 km Giá cước từ km thứ 31
Ví dụ 25. Một bảng giá cước taxi được cho như sau: 10 000 đồng 13 500 đồng 11 000 đồng
a) Viết công thức hàm số mô tả số tiền khách phải trả theo quãng đường di chuyển.
b) Xét tính liên tục của hàm số ở câu a. Lời giải.
a) Gọi x là quãng đường di chuyển, f (x) là giá tiền tính theo quãng đường.
○ 0 ≤ x ≤ 0,5, ta có f (x) = 10000 đồng.
○ 0,5 < x ≤ 30, f (x) = 10000 + 13500(x − 0,5) đồng.
○ x > 30, f (x) = 408250 + 11000(x − 30) đồng. 10000 nếu 0 ≤ x ≤ 0,5   Vậy f (x) = 10000 + 13500(x − 0,5) nếu 0,5 < x ≤ 30 
408250 + 11000(x − 30) nếu x > 30.
b) Hàm số f (x) liên tục trên các khoảng (0; 0,5), (0,5; 30) và (30; +∞).
Tại x = 0,5, ta có f (0,5) = 10000, lim f (x) = 10000, lim f (x) = 10000. x→0,5+ x→0,5− Vì f (0, 5) = lim f (x) =
lim f (x), do đó f (x) liên tục tại x = 0, 5. x→0,5+ x→0,5−
Tại x = 30, ta có f (30) = 408250, lim f (x) = 408250, lim f (x) = 408250. x→30− x→30+
Vì f (30) = lim f (x) = lim f (x), do đóf (x) liên tục tại x = 30. x→30− x→30+
Vậy f (x) liên tục trên khoảng (0; +∞). □
Dạng 7. Bài toán phương trình có nghiệm 1. Ví dụ mẫu
Ví dụ 26. Chứng minh rằng phương trình x5 + x3 − 10 = 0 có nghiệm thuộc khoảng (0; 2). Lời giải.
Xét hàm số f (x) = x5 + x3 − 10 với x ∈ R. Ta có
○ Vì f (x) là hàm số đa thức nên f (x) liên tục trên R.
○ f (0) = −1 < 0, f (2) = 30 > 0. Suy ra f (0)f (2) < 0.
Suy ra f (x) = 0 có nghiệm thuộc khoảng (0; 2). □
Ví dụ 27. Chứng minh rằng phương trình x3 − 3x + 1 = 0 có đúng 3 nghiệm thực phân biệt. Lời giải. Ta có
○ Hàm số f (x) = x3 − 3x + 1 có dạng đa thức nên hàm số f (x) liên tục trên R. 473/764 473/764
Toán 11 theo chương trình GDPT2018 474 3. Hàm số liên tục
Biết làm, làm đúng, làm nhanh
○ f (−2) < 0, f (−1) > 0, f (1) < 0, f (2) > 0 nên f (−2)f (−1) < 0, f (−1)f (1) < 0 và f (1)f (2) < 0.
Do đó hàm số có 3 nghiệm phân biệt lần lượt thuộc các khoảng (−2; −1), (−1, 1) và (1; 2).
Mặt khác hàm số f (x) là đa thức bậc 3 nên có tối đa 3 nghiệm thực.
Vậy phương trình f (x) = 0 có đúng 3 nghiệm thực phân biệt. □ 2. Bài tập rèn luyện
Bài 56. Chứng minh phương trình 4x3 − 8x2 + 1 = 0 có nghiệm trong khoảng (−1; 2). Lời giải.
Đặt f (x) = 4x3 − 8x2 + 1 và f (x) là hàm đa thức nên liên tục trên R, suy ra liên tục trên [−1; 2]. ®f (−1) = −11 Ta có
⇒ f (−1) · f (2) = −11 < 0 ⇒ ∃x0 ∈ (−1; 2) : f (x0) = 0, nghĩa là phương trình f (x) = 0 có f (2) = 1
ít nhất một nghiệm trong khoảng (−1; 2). □
Bài 57. Chứng minh rằng phương trình x3 + x + 1 = 0 có ít nhất một nghiệm âm lớn hơn −1. Lời giải.
Đặt f (x) = x3 + x + 1 và f (x) là hàm đa thức nên liên tục trên R, suy ra liên tục trên [−1; 0]. ®f (−1) = −1 Ta có
⇒ f (−1) · f (0) = −1 < 0 ⇒ ∃x0 ∈ (−1; 0) : f (x0) = 0, nghĩa là phương trình f (x) = 0 có ít f (0) = 1
nhất một nghiệm trong khoảng (−1; 0). □
Bài 58. Chứng minh phương trình x3 − 3x + 1 = 0 có đúng ba nghiệm phân biệt . Lời giải.
Đặt f (x) = x3 − 3x + 1 và f (x) là hàm đa thức nên liên tục trên R, suy ra hàm số f (x) liên tục trên các đoạn [−2; 0], [0; 1], [1; 2]. ®f (−2) = −1 ○ Ta có
⇒ f (−2) · f (0) = −1 < 0 ⇒ Phương trình f (x) = 0 có ít nhất một nghiệm thuộc f (0) = 1 khoảng (−2; 0). (1) ®f (0) = 1 ○ Ta có
⇒ f (0) · f (1) = −1 < 0 ⇒ Phương trình f (x) = 0 có ít nhất một nghiệm thuộc khoảng f (1) = −1 (0; 1). (2) ®f (1) = −1 ○ Ta có
⇒ f (1) · f (2) = −3 < 0 ⇒ Phương trình f (x) = 0 có ít nhất một nghiệm thuộc khoảng f (2) = 3 (1; 2). (3)
Từ (1), (2), (3), suy ra phương trình có ít nhất ba nghiệm phân biệt thuộc các khoảng (−2; 0), (0; 1), (1; 2). Mà
f (x) là đa thức bậc ba nên phương trình f (x) = 0 có tối đa ba nghiệm. Suy ra phương trình đã cho có đúng ba nghiệm phân biệt.
Nhận xét. Với sự hỗ trợ của chức năng Table trong Casio, ta dễ dàng tìm được các khoảng (−2; 0), (0; 1), (1; 2)
như trên. Công việc còn lại là trình bày sao cho đúng ngôn ngữ. □
Bài 59. Chứng minh phương trình 1 − m2 x5 − 3x − 1 = 0 luôn có nghiệm với mọi m. Lời giải.
Đặt f (x) = 1 − m2 x5 − 3x − 1 và f (x) là hàm đa thức nên liên tục trên R ⇒ f (x) liên tục trên đoạn [−1; 0]. ®f (0) = −1 Ta có
⇒ f (−1) · f (0) < 0 ⇒ ∃x0 ∈ (−1; 0) : f (x0) = 0. f (−1) = m2 + 3 > 0
Do đó phương trình f (x) = 1 − m2 x5 − 3x − 1 = 0 luôn có nghiệm ∀m. □
Bài 60. Chứng minh rằng phương trình (x − a)(x − b) + (x − b)(x − c) + (x − c)(x − a) = 0 có ít nhất một nghiệm
với mọi số thực a, b, c. Lời giải.
Đặt f (x) = (x − a)(x − b) + (x − b)(x − c) + (x − c)(x − a) và f (x) là hàm đa thức nên sẽ liên tục trên R.
Không mất tính tổng quát, có thể giả sử a ≤ b ≤ c. 474/764 474/764
Toán 11 theo chương trình GDPT2018 475
Chương 3. Giới hạn. Hàm số liên tục
Biết làm, làm đúng, làm nhanh
○ Nếu a = b hoặc b = c thì f (b) = (b − a)(b − c) = 0 ⇒ Phương trình có nghiệm x = b.
®f (a) = (a − b)(a − c) > 0 ○ Nếu a < b < c thì
⇒ f (a) · f (b) < 0. Do đó phương trình có ít nhất một nghiệm
f (b) = (b − a)(b − c) < 0 trong khoảng (a; b).
Suy ra phương trình có ít nhất một nghiệm. □ 3.
Bài tập trắc nghiệm
Câu 70. Chứng minh rằng phương trình x3 − x + 3 = 0 có ít nhất một nghiệm.
Một bạn học sinh trình bày lời giải như sau:
Bước 1: Xét hàm số y = f (x) = x3 − x + 3 liên tục trên R.
Bước 2: Ta có f (0) = 3 và f (−2) = −3.
Bước 3: Suy ra f (0)f (−2) > 0
Bước 4: Vậy phương trình đã cho có ít nhất một nghiệm.
Học sinh trên giải sai tại A Bước 1. B Bước 2. C Bước 3. D Bước 4. Lời giải.
Ta có f (0)f (−2) < 0 do đó bài giải sai ở Bước 3. Chọn đáp án C □
Câu 71. Biết rằng trong khoảng (−4; 0), phương trình x3 − 12x + 1 = 0 có đúng 1 nghiệm. Nghiệm đó thuộc khoảng A (−4; −3). B (−3; −2). C (−2; −1). D (−1; 0). Lời giải.
Hàm số f (x) = x3 − 12x + 1 là hàm đa thức nên liên tục trên R và f (−4)f (−3) < 0 nên nghiệm của phương trình
f (x) = 0 thuộc khoảng (−4; −3). Chọn đáp án A □
Câu 72. Biết rằng phương trình x5 − 4x2 + x + 1 = 0 có nghiệm thuộc đúng 3 khoảng trong các khoảng 4 khoảng
(−1; 0), (0; 1), (1; 2) và (2; 3). Khoảng không chứa nghiệm của phương trình x5 − 4x2 + x + 1 = 0 là A (−1; 0). B (0; 1). C (1; 2). D (2; 3). Lời giải.
Hàm số f (x) = x5 − 4x2 + x + 1 là hàm đa thức nên liên tục trên R.
Do f (−1)f (0) < 0, f (0)f (1) < 0 và f (1)f (2) < 0 nên phương trình f (x) = 0 có nghiệm trong các khoảng (−1; 0), (0; 1) và (1; 2).
Vậy phương trình x5 − 4x2 + x + 1 = 0 không có nghiệm thuộc khoảng (2; 3). Chọn đáp án D □ x + 2 Câu 73. Cho hàm số f (x) = √
. Chọn khẳng định sai trong các khẳng định dưới đây. x 4 − x
A Hàm số f (x) xác định trên tập hợp K = (−∞; 0) ∪ (0; 4).
B Hàm số f (x) liên tục tại x = 2.
C Hàm số f (x) gián đoạn tại x = 0 và x = 4. 1 √
D Vì f (−1) = − √ ; f (2) =
2 nên f (−1)f (2) < 0, suy ra phương trình f (x) = 0 có ít nhất 1 nghiệm thuộc 5 khoảng (−1; 2). Lời giải.
Tập xác định D = (−∞; 0) ∪ (0; 4).
Suy ra hàm số f (x) liên tục trên các khoảng (−∞; 0) và (0; 4).
Từ đó tính chất liên tục trên đoạn [−1; 2] của hàm số không xảy ra.
Vậy không thể suy ra phương trình f (x) = 0 có ít nhất 1 nghiệm thuộc khoảng (−1; 2). Chọn đáp án D □
Câu 74. Khẳng định nào sau đây đúng với phương trình 2x3 − 3x2 + 2 = 0?
A Phương trình có ít nhất một nghiệm thuộc khoảng (−1; 0). 475/764 475/764
Toán 11 theo chương trình GDPT2018 476 3. Hàm số liên tục
Biết làm, làm đúng, làm nhanh
B Phương trình có ít nhất một nghiệm thuộc khoảng (1; 2).
C Phương trình có 3 nghiệm thực phân biệt.
D Phương trình có ít nhất một nghiệm thuộc khoảng (−2; −1). Lời giải.
Đặt f (x) = 2x3 − 3x2 + 2 là hàm đa thức nên hàm số f (x) liên tục trên R.
Do f (−1) · f (0) = −6 < 0 nên phương trình có ít nhất một nghiệm thuộc khoảng (−1; 0). Chọn đáp án A □
Câu 75. Phương trình nào dưới đây có nghiệm trong khoảng (0; 1)? A 2x2 − 3x + 4 = 0.
B (x − 1)5 − x7 − 2 = 0. C 3x4 − 4x2 + 5 = 0.
D 3x2017 − 8x + 4 = 0. Lời giải.
Xét hàm số f (x) = 3x2017 − 8x + 4 = 0 liên tục trên R.
Do f (0) = 4; f (1) = −1 nên f (0) · f (1) = −4 < 0, suy ra phương trình f (x) = 0 có ít nhất một nghiệm thuộc khoảng (0; 1). Chọn đáp án D □
Câu 76. Xét các mệnh đề sau
(1) Phương trình x3 + 4x + 4 = 0 không có nghiệm trên khoảng (−1; 1).
(2) Phương trình x3 + x − 1 = 0 không có nghiệm dương bé hơn 1. Chọn đáp án đúng.
A Cả mệnh đề (1) và (2) đều đúng.
B Mệnh đề (1) và (2) đều sai.
C Chỉ có mệnh đề (2) đúng.
D Chỉ có mệnh đề (1) đúng. Lời giải.
Đặt f (x) = x3 + 4x + 4, g(x) = x3 + x − 1.
Nhận xét: f (x) và g(x) là hàm đa thức nên liên tục trên R. Mặt khác
○ f (−1) = −1, f (1) = 9 ⇒ f (−1) · f (1) < 0 nên phương trình f (x) = 0 có nghiệm trên khoảng (−1; 1).
○ g(0) = −1, g(1) = 1 ⇒ g(0) · g(1) < 0 nên phương trình g(x) = 0 có nghiệm trên khoảng (0; 1).
Do đó phương trình g(x) = 0 có nghiệm dương bé hơn 1. Chọn đáp án B □
Câu 77. Cho phương trình ax2 + bx + c = 0 thỏa mãn a ̸= 0 và 2a + 6b + 19c = 0. Biết phương trình có nghiệm
x0, khẳng định nào sau đây đúng? ï 1 ò ï 1 1 ò ï 2 ò A x0 ∈ 0; . B x0 ∈ − ; − . C x0 ∈ ; 1 . D x0 ∈ [1; 2]. 3 3 2 3 Lời giải. −19c
Ta có 2a + 6b + 19c = 0 ⇔ 2a + 6b = −19c ⇔ a + 3b = . 2 Å 1 ã 1 1 −1 −1 Lại có f (0)f = c(a + 3b + 9c) = c c = c2 ≤ 0. 3 9 9 2 18 ï 1 ò
Vậy phương trình luôn có nghiệm x0 ∈ 0; . 3 Chọn đáp án A □
Câu 78. Tìm tất cả giá trị thực của tham số m để phương trình (m2 − 3m + 2)x3 − 3x + 1 = 0 có nghiệm. A m ∈ R. B m ∈ {1; 2}. C m ∈ R \ {1; 2}. D m ∈ ∅. Lời giải. 1
Trường hợp 1. Với m = 1 hoặc m = 2 thì phương trình có nghiệm là x = . 3
Trường hợp 2. Với m2 − 3m + 2 ̸= 0.
Đặt f (x) = (m2 − 3m + 2)x3 − 3x + 1 là hàm đa thức nên liên tục trên R (1). Khi đó lim f (x) = −∞ hoặc
lim f (x) = −∞. Từ đó, tồn tại A < 0 và x0 ∈ R sao cho f (x0) = A < 0. x→−∞ x→+∞
Mặt khác f (0) = 1 nên f (0) · f (x0) < 0 (2). 476/764 476/764
Toán 11 theo chương trình GDPT2018 477
Chương 3. Giới hạn. Hàm số liên tục
Biết làm, làm đúng, làm nhanh
Từ (1) và (2) suy ra phương trình f (x) = 0 luôn có nghiệm nằm giữa 0 và x0.
Từ hai trường hợp trên suy ra phương trình luôn có nghiệm với mọi m ∈ R. Chọn đáp án A □ √
Câu 79. Cho phương trình x12 + 1 = 4x4. xn − 1, (n ∈ +
Z ). Tìm số n nhỏ nhất để phương trình có nghiệm. A n = 3. B n = 5. C n = 2. D n = 10. Lời giải.
Với n chẵn thì ta có |x| ≥ 1, nếu x0 là nghiệm của phương trình thì −x0 cũng là nghiệm của phương trình.
Với n lẻ thì ta có x ≥ 1. Lại có x = 1 không là nghiệm của phương trình nên ta chỉ cần xét x > 1.
Áp dụng bất đẳng thức AM-GM ta có: x4 + 1 ≥ 2x2
x8 − x4 + 1 = x4 − 12 + x4 ≥ 2x2px4 − 1. √
Suy ra x12 + 1 ≥ 4x4 x4 − 1. √ √
Dấu bằng không xảy ra nên ta có: x12 + 1 > 4x4 x4 − 1 ≥ 4x4 xn − 1 với mọi n ≤ 4. √
Với n = 5 ta xét hàm số f (x) = x12 + 1 − 4x4 x5 − 1. √ √ √ √ Ä ä Ä ä Ta có: f (1) = 2, f
5 2 = 1 + 4 5 4 − 4 5 16 < 0 nên phương trình f (x) = 0 có nghiệm thuộc 1; 5 2 .
Vậy n = 5 là giá trị cần tìm. Chọn đáp án B □ 477/764 477/764
Toán 11 theo chương trình GDPT2018 478
4. Bài tập cuối chương III
Biết làm, làm đúng, làm nhanh Baâi söë 4
BÀI TẬP CUỐI CHƯƠNG III
A – BÀI TẬP TỰ LUẬN
Bài 1. Tính các giới hạn sau: 2n2 + 6n + 1 4n2 − 3n + 1 a) lim ; b) lim ; 8n2 + 5 −3n3 + 5n2 − 2 √4n2 − n + 3 Å 2n+1 ã c) lim ; d) lim 4 − ; 8n − 5 3n 4.5n + 2n+2 2 + 4 e) lim ; f) lim n3 . 6.5n 6n Lời giải. 6 1 2n2 + 6n + 1 2 + + 1 a) lim = lim n n2 = . 8n2 + 5 5 4 8 + n2 4 3 1 4n2 − 3n + 1 − + b) lim = lim n n2 n3 = 0. −3n3 + 5n2 − 2 5 2 −3 + − n n3 … √ 1 3 4 − + 4n2 − n + 3 n n2 1 c) lim = lim = . 8n − 5 5 4 8 − n Å 2n+1 ã Å 2 · 2n ã Å Å 2 ãnã d) lim 4 − = lim 4 − = lim 4 − 2 = 4. 3n 3n 3 Å Ç å 4 · 5n + 2n+2 ã 4 + 4 · 2 n 2 e) lim = lim 5 = . 6 · 5n 6 3 Ö 2 4 è Ç 2 + 4 å + f) lim n3 = lim 6n n3 · 6n = 0. 6n 1 □
Bài 2. Tính các giới hạn sau: √ 2x2 − 5x + 2 x − 2 a) lim 4x2 − 5x + 6; b) lim ; c) lim . x→−3 x→2 x − 2 x→4 x2 − 16 Lời giải. a) lim
4x2 − 5x + 6 = 4(−3)2 − 5(−3) + 6 = 57. x→−3 2x2 − 5x + 2 (2x − 1)(x − 2) b) lim = lim = lim (2x − 1) = 3. x→2 x − 2 x→2 x − 2 x→2 √ √ x − 2 x − 2 1 1 c) lim = lim √ √ = lim √ = . x→4 x2 − 16 x→4 ( x − 2)( x + 2)(x + 4) x→4 ( x + 2)(x + 4) 32 □ 478/764 478/764
Toán 11 theo chương trình GDPT2018 479
Chương 3. Giới hạn. Hàm số liên tục
Biết làm, làm đúng, làm nhanh
Bài 3. Tính các giới hạn sau: √ 6x + 8 6x + 8 9x2 − x + 1 a) lim ; b) lim ; c) lim ; x→−∞ 5x − 2 x→+∞ 5x − 2 x→+∞ 3x − 2 √9x2 − x + 1 3x2 + 4 3x2 + 4 d) lim ; e) lim ; f) lim . x→−∞ 3x − 2 x→−2− 2x + 4 x→−2+ 2x + 4 Lời giải. 6x + 8 6 a) lim = . x→−∞ 5x − 2 5 6x + 8 6 b) lim = . x→+∞ 5x − 2 5 … √ 1 1 −x 9 − + 9x2 − x + 1 x x2 c) lim = lim = −1. x→−∞ 3x − 2 x→−∞ Å 2 ã x 3 − x … √ 1 1 x 9 − + 9x2 − x + 1 x x2 d) lim = lim = 1. x→+∞ 3x − 2 x→+∞ Å 2 ã x 3 − x e) Vì lim
3x2 + 4 = 16 > 0; lim (x + 2) = 0 và x → −2− ⇒ x + 2 < 0 nên x→2− x→2− 3x2 + 4 lim = −∞ x→−2− 2x + 4 f) Vì lim
3x2 + 4 = 16 > 0; lim (x + 2) = 0 và x → −2+ ⇒ x + 2 > 0 nên x→2+ x→2+ 3x2 + 4 lim = +∞ x→−2− 2x + 4 □  2x + a nếu x < 2  
Bài 4. Cho hàm số f (x) = 4 nếu x = 2   −3x + b nếu x > 2
a) Với a = 0, b = 1, xét tính liên tục của hàm số tại x = 2.
b) Với giá trị nào của a, b thì hàm số liên tục tại x = 2 ?
c) Với giá trị nào của a, b thì hàm số liên tục trên tập xác định? Lời giải. a) Với a = 0; b = 1, ta có: 2x nếu x < 2   f (x) = 4 nếu x = 2  −3x + 1 nếu x > 2. Ta có
lim f (x) = lim (2x) = 4 và lim f (x) = lim (−3x + 1) = −5. x→2− x→2− x→2+ x→2+
Vì lim f (x) ̸= lim f (x) nên không tồn tại lim f (x). x→2− x→2+ x→2 479/764 479/764
Toán 11 theo chương trình GDPT2018 480
4. Bài tập cuối chương III
Biết làm, làm đúng, làm nhanh b) Ta có
lim f (x) = lim (2x + a) = 4 + a và lim f (x) = lim (−3x + b) = −6 + b. x→2− x→2− x→2+ x→2+
Hàm số liên tục của hàm số tại x = 2 khi và chỉ khi tồn tại lim f (x) và lim f (x) = f (2) x→2 x→2 ® 4 + a = 4 ® a = 0 ⇔ ⇔ −6 + b = 4 b = 10.
Vậy a = 0; b = 10 thoả mãn yêu cầu bài toán.
c) Để hàm số liên tục trên tập xác định điều kiện cần và đủ là hàm số liên tục tại x = 2. Do đó với a = 0, b = 10
thì hàm số liên tục trên tập xác định. □ Bài 5.
Từ độ cao 55, 8 m của tháp nghiêng Pisa nước Ý, người ta
thả một quả bóng cao su chạm xuống đất hình bên dưới.
Giả sử mỗi lần chạm đất quả bóng lại nảy lên độ cao bằng
1 độ cao mà quả bóng đạt được trước đó. Gọi Sn là tổng 10
độ dài quãng đường di chuyển của quả bóng tính từ lúc thả
ban đầu cho đến khi quả bóng đó chạm đất n lần. Tính lim Sn. Lời giải. 1
Mỗi khi chạm đất quả bóng lại nảy lên một độ cao bằng
độ cao của lần rơi ngay trước đó và sau đó lại rơi 10
xuống từ độ cao thứ hai này. Do đó, độ dài hành trình của quả bóng kể từ thời điểm rơi ban đầu đến:
Thời điểm chạm đất lần thứ nhất là d1 = 55,8. 55,8
Thời điềm chạm đất lần thứ hai là d2 = 55,8 + 2 · . 10 55,8 55,8
Thời điểm chạm đất lần thứ ba là d3 = 55,8 + 2 · + 2 · . 10 102 55,8 55, 8 55,8
Thời điểm chạm đất lần thứ tư là d4 = 55,8 + 2 · + 2 · + 2 · . 10 102 103 . . .
Thời điểm chạm đất lần thứ n (n > 1) là 55,8 55,8 55,8 dn = 55,8 + 2 · 55,8 + 2 · + 2 · + . . . + 2 · . 102 103 10n−1
Do đó, quãng đường mà quả bóng đi được kể từ thời điềm rơi đến khi nằm yên trên mặt đất là: 55,8 55,8 55,8 d = 55,8 + 2.55,8 + 2 · + 2 · + . . . + 2 · + . . . = lim dn. 102 103 10n−1 55,8 55,8 55,8 55,8 1 Vì 2 · ; 2 · ; 2 · ; . . . ; 2 ·
; . . . là một cấp số nhân lùi vô hạn với công bội q = nên ta có: 10 102 103 10n−1 10 55,8 55, 8 55,8 55,8 55,8 2 · 2 · + 2 · + 2 · + . . . + 2 · + . . . = 10 = 12,4. 10 102 103 10n−1 1 1 − 10
Vậy d = 55,8 + 12,4 = 68,2 m. □ 480/764 480/764
Toán 11 theo chương trình GDPT2018 481
Chương 3. Giới hạn. Hàm số liên tục
Biết làm, làm đúng, làm nhanh
Bài 6. Cho một tam giác đều ABC cạnh a. Tam giác A1B1C1 có các đỉnh là trung điểm các cạnh của tam giác
ABC, tam giác A2B2C2 có các đỉnh là trung điểm các cạnh của tam giác A1B1C1, . . ., tam giác An+1Bn+1Cn+1
có các đỉnh là trung điểm các cạnh của tam giác AnBnCn, . . . Gọi p1, p2, . . . , pn, . . . và S1, S2, . . . , Sn, . . . theo thứ
tự là chu vi và diện tích của các tam giác A1B1C1, A2B2C2, . . . , AnBnCn, . . ..
a) Tìm giới hạn của các dãy số (pn) và (Sn).
b) Tìm các tổng p1 + p2 + . . . + pn + . . . và S1 + S2 + . . . + Sn + . . .. Lời giải.
a) Ta có p1, p2, . . . , pn, . . . lần lượt là chu vi của các tam giác A1B1C1, A2B2C2, . . . , AnBnCn, . . . p1 = 3a 1 p2 = 3 · a 2 . . . 1 pn = 3 · a 2n−1 1 suy ra lim pn = lim 3 · a = 0. 2n−1 √ a2 3 S1 = 4 √ 1 a2 3 S2 = 4 4 . . . √ 1 a2 3 Sn = · 4n−1 4 √ 1 a2 3 suy ra lim Sn = lim · = 0. 4n−1 4 1
b) Dựa vào dữ kiện đề bài suy ra tổng (pn) là tổng của cấp số nhân lùi vô hạn với công bội q = và 2 p1 3a
p1 + p2 + . . . + pn + . . . = lim (pn) = = = 6a. 1 − q 1 − 12 1
Dựa vào dữ kiện đề bài suy ra tổng (Sn) là tổng của cấp số nhân lùi vô hạn với công bội q = và √ 4 √ S a2 3 1 a2 3 S 4
1 + S2 + . . . + Sn + . . . = lim (Sn) = = = . 1 − q 1 − 1 12 4 □
Bài 7. Một thấu kính hội tụ có tiêu cự là f . Gọi d và d′ lần lượt là khoảng cách từ một vật thật AB và từ ảnh 1 1 1
A′B′ của nó tới quang tâm O của thấu kính như hình vẽ bên dưới. Công thức thấu kính là + = . d d f f f B F ′ A′ A F O B′ d d′
a) Tìm biểu thức xác định hàm số d′ = φ(d).
b) Tìm lim φ(d), lim φ(d) và lim φ(d). Giải thích ý nghĩa của các kết quả tìm được. d→f + d→f − d→f 481/764 481/764
Toán 11 theo chương trình GDPT2018 482
4. Bài tập cuối chương III
Biết làm, làm đúng, làm nhanh Lời giải. a) Ta có 1 1 1 df + = ⇔ d′ = . d d′ f d − f df Vậy φ(d) = . d − f df
b) Vì lim df = f 2; lim (d − f ) = 0; d → f + ⇒ d − f > 0 nên lim = +∞. d→f + d→f + d→f + d − f df Vậy lim φ(d) = lim = +∞. d→f + d→f + d − f
Ý nghĩa: Khi đặt vật nằm ngoài tiêu cự và tiến dần đến tiêu điểm thì cho ảnh thật ngược chiều với vật ở vô cùng. df
Vì lim df = f 2; lim (d − f ) = 0; d → f − ⇒ d − f < 0 nên lim = −∞. d→f − d→f + d→f + d − f df Vậy lim φ(d) = lim = −∞. d→f + d→f + d − f
Ý nghĩa: Khi đặt vật nằm trong tiêu cự và tiến dần đến tiêu điểm thì cho ảnh ảo cùng chiều với vật và nằm ở vô cùng.
Vì không tồn tại lim φ(d) và lim φ(d) nên không tồn tại lim φ(d). d→f + d→f − d→f □
B – BÀI TẬP TRẮC NGHIỆM
Câu 1. Cho hàm số y = f (x) xác định trên khoảng (a; b) và x0 ∈ (a; b). Điều kiện cần và đủ để hàm số y = f (x) liên tục tại x0 là A lim f (x) = f (x0). B lim f (x) = f (x0). x→x+ x→x− 0 0
C lim f (x) = lim f (x). D
lim f (x) = lim f (x) = f (x0). x→x+ x→x− x→x+ x→x− 0 0 0 0 Lời giải.
Theo định nghĩa về hàm số liên tục ta có điều kiện cần và đủ để hàm số y = f (x) liên tục tại x0 là lim f (x) = x→x+ 0 lim f (x) = f (x0). x→x− 0 Chọn đáp án D □
Câu 2. Trong các giới hạn sau, giới hạn nào bằng 0? n2 + n n2 + n + 1 2n − 3n A lim(n3 − 3n + 1). B lim . C lim . D lim . n3 + 1 4n + 1 3n + 2 Lời giải. 1 1 n2 + n + Ta có lim = lim n n2 = 0. n3 + 1 1 1 + n3 Chọn đáp án B □
Câu 3. Trong các khẳng định dưới đây, khẳng định nào sai? A lim qn = 0. n→+∞ 1 B lim = 0 với k nguyên dương. n→+∞ nk 1 C lim = 0. n→+∞ n
D Nếu un = c (c là hằng số) thì lim un = lim c = c. n→+∞ Lời giải. 482/764 482/764
Toán 11 theo chương trình GDPT2018 483
Chương 3. Giới hạn. Hàm số liên tục
Biết làm, làm đúng, làm nhanh Ta có lim qn = 0 khi |q| < 1; lim qn = +∞ khi q > 1. n→+∞ n→+∞ Chọn đáp án A □ n2 + 1 Câu 4. Tính lim ta được kết quả là 2n2 + n + 1 n2 + 1 n2 + 1 1 A lim = 0. B lim = . 2n2 + n + 1 2n2 + n + 1 2 n2 + 1 n2 + 1 C lim = +∞. D lim = 1. 2n2 + n + 1 2n2 + n + 1 Lời giải. 1 n2 + 1 1 + 1 Ta có lim = lim n2 = . 2n2 + n + 1 1 1 2 2 + + n n2 Chọn đáp án B □ 2023n + 2024n Câu 5. lim có giá trị bằng 2025n 3 A . B +∞. C 0. D 1. 5 Lời giải. 2023n + 2024n Å 2023 ãn Å 2024 ãn Ta có lim = lim + lim = 0 + 0 = 0. 2025n 2025 2025 Chọn đáp án C □ √ Ä ä Câu 6. Tìm lim
n2 + 1 − 2n ta được kết quả là 2 A −∞. B +∞. C 0. D − . 3 Lời giải. √ Ç… å 1 ○ Ä ä Cách 1: lim n2 + 1 − 2n = lim n 1 + − 2 = −∞ n2 Ç… å 1 (vì lim n = +∞ và lim 1 + − 2 = −1 < 0). n2 1 √ n2 + 1 − 4n2 −3n + ○ Ä ä Cách 2: lim n2 + 1 − 2n = lim √ = lim n = −∞. n2 + 1 + 2n … 1 1 + + 2 n2 Chọn đáp án A □ 1 1
Câu 7. Tính tổng vô hạn S = 9 + 3 + 1 + + · · · + + · · · 3 3n−3 27 A S = 14. B S = 15. C S = . D S = 16. 2 Lời giải. 1 1 1
Dãy số (un) : 9; 3; 1; ; · · · ;
; · · · là một cấp số nhân lùi vô hạn với số hạng đầu u1 = 9, công bội q = . 3 3n−3 3 1 1 u1 9 27
Do đó tổng của dãy là S = 9 + 3 + 1 + + · · · + + · · · = = = . 3 3n−3 1 − q 1 2 1 − 3 Chọn đáp án C □
Câu 8. Trong các mệnh đề sau, mệnh đề nào là mệnh đề sai? 1 2n + 1 A lim = 0. B lim = 2. n→+∞ n n→+∞ n − 3 C lim (n2 − 2n + 1) = +∞. D lim nk = −∞ (k ∈ ∗ N ). n→+∞ n→+∞ Lời giải. Ta có lim nk = +∞ (k ∈ ∗ N ). n→+∞ 483/764 483/764
Toán 11 theo chương trình GDPT2018 484
4. Bài tập cuối chương III
Biết làm, làm đúng, làm nhanh Chọn đáp án D □ √ √ Ä ä Câu 9. Tính lim n 4n2 + 3 − 3 8n3 + n . 2 A . B +∞. C −∞. D 1. 3 Lời giải. Ta có Äp ä lim n 4n2 + 3 − 3 p8n3 + n îÄp ä Ä äó = lim n 4n2 + 3 − 2n + 2n − 3 p8n3 + n ñ ô 3 −n = lim n √ + √ √ 4n2 + 3 + 2n 2
(2n)2 + 2n · 3 8n3 + n + 3 8n3 + n    3 −1  = lim  +   … 3 … … 2   1 1 4 + + 2  22 + 2 3 8 + + 3 8 + n2 n2 n2 2 = . 3 Chọn đáp án A □ √2n3 + n + 3n − 1 … a
Câu 10. Dãy số (un) với un = √ có giới hạn bằng
, a > 0, b > 0 và ƯCLN(a, b = 1). Hãy 6n3 + 2n2 + n b
tính giá trị của a2 + b2. A 5. B 40. C 9. D 10. Lời giải. Ta có … √ 1 3 1 2 + + √ − √ 2n3 + n + 3n − 1 … n2 n n n 1 lim un = lim √ = lim = . 6n3 + 2n2 + n … 2 1 3 6 + + √ n n
Suy ra a = 1, b = 3 ⇒ a2 + b2 = 10. Chọn đáp án D □ 9 − b2n2
Câu 11. Tìm tất cả các giá trị thực của tham số b để biểu thức A = lim < 0. 11n2 + 3 A b ≤ 0. B b ̸= 0. C b < 0. D b > 0. Lời giải. Å 9 ã 9 n2 − b2 9 − b2n2 − b2 n2 b2 Ta có A = lim = lim = lim n2 = − . 11n2 + 3 Å 3 ã 3 11 n2 11 + 11 + n2 n2 b2
Yêu cầu bài toán xảy ra khi −
< 0 ⇔ b2 > 0 ⇔ b ̸= 0. 11 Chọn đáp án B □
Câu 12. Cho các giới hạn: lim f (x) = 2, lim g(x) = 3. Tính M = lim [3f (x) − 4g(x)]. x→x0 x→x0 x→x0 A M = 5. B M = 2. C M = −6. D M = 3. Lời giải.
Ta có M = lim [3f (x) − 4g(x)] = 3 lim f (x) − 4 lim g(x) = 6 − 12 = −6. x→x0 x→x0 x→x0 Chọn đáp án C □ Câu 13. Giá trị của lim x3 − x2 + 1 bằng x→−2 A −11. B 12. C 5. D 0. 484/764 484/764
Toán 11 theo chương trình GDPT2018 485
Chương 3. Giới hạn. Hàm số liên tục
Biết làm, làm đúng, làm nhanh Lời giải. Ta có lim x3 − x2 + 1 = lim
(−2)3 − (−2)2 + 1 = −11. x→−2 x→−2 Chọn đáp án A □ √ Ä ä Câu 14. Giá trị của lim x2 + 5 − x là x→−∞ A +∞. B −∞. C 1. D 0. Lời giải. Ta có Ç … å Äp ä 5 lim x2 + 5 − x = lim x − 1 + − 1 = +∞. x→−∞ x→−∞ x2 Chọn đáp án A □ 2x2 − x + 1 Câu 15. Giá trị của lim là x→−∞ x + 2 A −∞. B +∞. C −2. D 1. Lời giải. Å 1 1 ã  Å 1 1 ã  x2 2 − + 2 − + 2x2 − x + 1 x x2 x x2 Ta có lim = lim = lim   x ·  = −∞. x→−∞ x + 2 x→−∞ Å 2 ã x→−∞ 2   x 1 + 1 + x x Chọn đáp án A □
Câu 16. Giả sử lim f (x) = +∞ và lim g(x) = −∞. Ta xét các mệnh đề sau x→x0 x→x0 f (x) (1) lim [f (x) + g(x)] = 0. (2) lim = −1.
(3) lim |f (x)| = lim |g(x)| = +∞. x→x0 x→x0 g(x) x→x0 x→x0
Trong các mệnh đề trên có tất cả bao nhiêu mệnh đề đúng?
A Có một mệnh đề đúng.
B Có hai mệnh đề đúng.
C Có ba mệnh đề đúng.
D Không có mệnh đề nào đúng. Lời giải. 3 −2
○ Mệnh đề (1), (2) sai nếu ta chọn lim f (x) = lim và lim g(x) = lim . Khi đó x→x0 x→1 (x − 1)2 x→x0 x→1 (x − 1)2 f (x) −3
lim [f (x) + g(x)] = +∞ và lim = . x→1 x→x0 g(x) 2
○ Mệnh đề (3) sai vì lim |f (x)| = +∞ và lim |g(x)| = +∞ nhưng lim |f (x)| ̸= lim |g(x)|. x→x0 x→x0 x→x0 x→x0 Chọn đáp án D □ x4 − a4
Câu 17. Cho a là số thực khác 0. Tính lim . x→a x − a A a3. B 4a3. C 2a3. D 3a3. Lời giải. x4 − a4 (x − a)(x + a) x2 + a2 Ta có lim = lim
= lim x2 + a2 (x + a) = 2a2 · 2a = 4a3. x→a x − a x→a x − a x→a Chọn đáp án B □ ax2 + bx − 4
Câu 18. Cho 2a + b = 2 và lim
= 5. Khẳng định nào sau đây là đúng? x→2 x − 2 3 A a = −1, b = 4. B a = 1, b = 0. C a = , b = −1. D a = −2, b = 6. 2 Lời giải. 485/764 485/764
Toán 11 theo chương trình GDPT2018 486
4. Bài tập cuối chương III
Biết làm, làm đúng, làm nhanh
Ta có 2a + b = 2 ⇔ b = 2 − 2a. Khi đó ta có ax2 + bx − 4 ax2 + (2 − 2a)x − 4 (ax + 2)(x − 2) lim = 5 ⇔ lim = 5 ⇔ lim = 5 x→2 x − 2 x→2 x − 2 x→2 x − 2 3 ⇔
lim (ax + 2) = 5 ⇔ 2a + 2 = 5 ⇔ a = ⇒ b = −1. x→2 2 Chọn đáp án C □ √ 3 3x + 2 + x − 4 Câu 19. Tính lim ta được kết quả là x→2 x2 − 3x + 2 1 1 5 1 A . B . C . D . 2 3 4 5 Lời giải. √ 3 3x + 2 + x − 4 3x + 2 + (x − 4)3 lim = lim √ î x→2 x2 − 3x + 2 x→2 (x2 − 3x + 2) 3
p(3x + 2)2 − (x − 4) 3 3x + 2 + (x − 4)2ó x3 − 12x2 + 51x − 62 = lim √ î x→2 (x2 − 3x + 2) 3
p(3x + 2)2 − (x − 4) 3 3x + 2 + (x − 4)2ó (x − 2)(x2 − 10x + 31) = lim √ î x→2 (x − 2)(x − 1) 3
p(3x + 2)2 − (x − 4) 3 3x + 2 + (x − 4)2ó x2 − 10x + 31 = lim √ î x→2 (x − 1) 3
p(3x + 2)2 − (x − 4) 3 3x + 2 + (x − 4)2ó 5 = . 4 Chọn đáp án C □ √1 + x2 − 1 Câu 20. Tính lim ta được kết quả là x→0 2x3 − 3x2 1 1 1 1 A − . B − . C − . D − . 2 4 6 8 Lời giải. √1 + x2 − 1 x2 1 1 lim = lim √ = lim √ = − . Ä ä Ä ä x→0 2x3 − 3x2 x→0 (2x3 − 3x2) 1 + x2 + 1 x→0 (2x − 3) 1 + x2 + 1 6 Chọn đáp án C □ √ √ x + 9 + x + 16 − 7 Câu 21. Kết quả của lim là x→0 x 7 7 7 7 A . B . C . D . 23 24 25 26 Lời giải. √ √ √ √ √ √ ñ ô x + 9 + x + 16 − 7 x + 9 − 3 + x + 16 − 4 x + 9 − 3 x + 16 − 4 lim = lim = lim + x→0 x x→0 x x→0 x x ñ ô x x = lim √ + √ x→0 x x + 9 + 3 x x + 16 + 4 ï 1 1 ò = lim √ + √ x→0 x + 9 + 3 x + 16 + 4 1 1 7 = + = . 6 8 24 Chọn đáp án B □ 486/764 486/764
Toán 11 theo chương trình GDPT2018 487
Chương 3. Giới hạn. Hàm số liên tục
Biết làm, làm đúng, làm nhanh √ √ Ä ä Câu 22. Giới hạn lim x2 − 4x − x2 − x bằng x→−∞ 3 1 3 1 A − . B . C . D − . 2 2 2 2 Lời giải. Ta có Äp p ä −3x 3x 3 lim x2 − 4x − x2 − x = lim √ √ = lim = . x→−∞ x→−∞ Ç å x2 − 4x + x2 − x x→−∞ … 4 … 1 2 x 1 − + 1 − x x Chọn đáp án C □ 2x − 3a Câu 23. Giới hạn lim
(với a là tham số) có giá trị bằng x→+∞ 3x + 2a 3 2 A 2. B −1. C . D . 2 3 Lời giải. 3a 2x − 3a 2 − 2 Ta có lim = lim x = . x→+∞ 3x + 2a x→+∞ 2a 3 3 + x Chọn đáp án D □ √ Ä ä
Câu 24. Tìm giới hạn I = lim x + 1 − x2 − x − 2 . x→+∞ 3 1 17 46 A I = . B I = . C I = . D I = . 2 2 11 31 Lời giải. √ √ Ä ä Ä ä x + 1 − x2 − x − 2 x + 1 + x2 − x − 2 Ä p ä I = lim x + 1 − x2 − x − 2 = lim √ x→+∞ x→+∞ x + 1 + x2 − x − 2 (x + 1)2 − x2 − x − 2 = lim √ x→+∞ x + 1 + x2 − x − 2 3x + 3 = lim √ x→+∞ x + 1 + x2 − x − 2 Å 3 ã x 3 + x = lim x→+∞ Ç å 1 … 1 2 x 1 + + 1 − − x x x2 3 3 + 3 = lim x = . x→+∞ 1 … 1 2 2 1 + + 1 − − x x x2 Chọn đáp án A □ √ √ Ä ä
Câu 25. Giá trị của giới hạn lim x2 + x + 1 − x2 − x + 1 là x→+∞ A 0. B 1. C 2. D 3. Lời giải. Ta có Äp p ä 2x lim x2 + x + 1 − x2 − x + 1 = lim √ √ x→+∞ x→+∞ x2 + x + 1 + x2 − x + 1 2 = lim = 1. x→+∞ … 1 1 … 1 1 1 + + + 1 − + x x2 x x2 Chọn đáp án B □ 487/764 487/764
Toán 11 theo chương trình GDPT2018 488
4. Bài tập cuối chương III
Biết làm, làm đúng, làm nhanh √x + 3 − 2 a a Câu 26. Cho lim = , trong đó
là phân số tối giản. Tổng a + b có giá trị bằng x→1 x2 − 1 b b A 9. B 8. C 7. D 6. Lời giải. Ta có √ √ √ x + 3 − 2 x + 3 − 2 x + 3 + 2 lim = lim √ x→1 x2 − 1 x→1 (x2 − 1) x + 3 + 2 x + 3 − 4 = lim √ x→1 (x − 1)(x + 1) x + 3 + 2 x − 1 = lim √ x→1 (x − 1)(x + 1) x + 3 + 2 1 = lim √ x→1 (x + 1) x + 3 + 2 1 1 = √ = . (1 + 1) 1 + 3 + 2 8
Từ đó suy ra a + b = 1 + 8 = 9. Chọn đáp án A □ 3x + 2 Câu 27. Tính I = lim ta được kết quả là x→1+ 1 − x A I = +∞. B I = −∞. C I = 0. D I = −3. Lời giải.
Ta có lim (3x + 2) = 5, lim (1 − x) = 0 và 1 − x < 0 khi x > 1. x→1+ x→1+ 3x + 2 Nên lim = −∞. x→1+ 1 − x Chọn đáp án B □ −x2 + 5 Câu 28. Tính lim ta được kết quả là x→3+ x − 3 A −∞. B +∞. C 1. D Không tồn tại. Lời giải.
Ta có lim (−x2 + 5) = −4 < 0, lim (x − 3) = 0 và x − 3 > 0, ∀x > 3. x→3+ x→3+ −x2 + 5 Do đó lim = −∞. x→3+ x − 3 Chọn đáp án A □ x2 − 4 Câu 29. Tính lim ta được kết quả là x→(−2)+ x + 2 A 1. B 4. C 2. D 3D. Lời giải. |x2 − 4| 4 − x2 Ta có lim = lim = lim (2 − x) = 4. x→−2+ x + 2 x→−2+ x + 2 x→−2+ Chọn đáp án B □ 2x + 1 Câu 30. Tính lim ta được kết quả là x→1 x − 1 A 0. B +∞. C −∞. D Không tồn tại. Lời giải. 2x + 1
Ta có lim (2x + 1) = 3 > 0; lim (x − 1) = 0 và x − 1 < 0, ∀x < 1 nên lim = −∞. x→1− x→1− x→1− x − 1 2x + 1
Tương tự, ta cũng có lim (2x + 1) = 3 > 0; lim (x − 1) = 0 và x − 1 > 0, ∀x > 1 nên lim = +∞. x→1+ x→1+ x→1+ x − 1 2x + 1 2x + 1 2x + 1 Vì lim ̸= lim nên không tồn tại lim . x→1− x − 1 x→1+ x − 1 x→1 x − 1 Chọn đáp án D □ 488/764 488/764
Toán 11 theo chương trình GDPT2018 489
Chương 3. Giới hạn. Hàm số liên tục
Biết làm, làm đúng, làm nhanh x2 − (a + 1) x + a Câu 31. Giá trị của lim (a ̸= 0) là x→a x3 − a3 a + 1 a − 1 a − 1 A +∞. B . C . D . 3a2 3a 3a2 Lời giải. Ta có x2 − (a + 1)x + a (x − a)(x − 1) a − 1 lim = lim = . x→a x3 − a3 x→a (x − a)(x2 + ax + a2) 3a2 Chọn đáp án D □
Câu 32. Cho hàm số y = f (x) liên tục trên khoảng (a; b). Hàm số y = f (x) liên tục trên đoạn [a; b] nếu điều kiện nào sau đây xảy ra? A
lim f (x) = f (a) , lim f (x) = f (b). B
lim f (x) = f (a) , lim f (x) = f (b). x→a− x→b+ x→a+ x→b−
C lim f (x) = a, lim f (x) = b. D lim f (x) = a, lim f (x) = b. x→a− x→b+ x→a+ x→b− Lời giải.
Hàm số y = f (x) được gọi là liên tục trên đoạn [a; b] nếu nó liên tục trên khoảng (a; b) và lim f (x) = x→a+ f (a) , lim f (x) = f (b). x→b− Chọn đáp án B □
Câu 33. Trong các hàm số sau, hàm số nào liên tục tại điểm x = 0? x2 − 2x + 3 √ A y = .
B y = x3 − 2x2 − x + 1. C y = cot x. D y = 2x2 − 1. x Lời giải. x2 − 2x + 3 ○ Hàm số y =
có tập xác định là D = R \ {0} nên bị gián đoạn tại điểm x = 0. x
○ Hàm số y = x3 − 2x2 − x + 1 là hàm đa thức, liên tục trên R nên nó liên tục tại điểm x = 0.
○ Hàm số y = cot x có tập xác định là D = R \ {kπ, k ∈ Z} nên bị gián đoạn tại điểm x = 0. √ √ √ Ç ô ñ å 2 2 ○ Hàm số y =
2x2 − 1 có tập xác định là D = −∞; − ∪ ; +∞
nên bị gián đoạn tại điểm x = 0. 2 2 Chọn đáp án B □
Câu 34. Chọn khẳng định đúng trong các khẳng định sau
A Nếu hàm số f (x) liên tục trên [a; b] và f (a)f (b) < 0 thì phương trình f (x) = 0 có ít nhất một nghiệm trên (a; b).
B Nếu phương trình f (x) = 0 có nghiệm trong khoảng (a; b) thì hàm số f (x) liên tục trên [a; b] và f (a)f (b) < 0.
C Nếu hàm số f (x) liên tục trên [a; b] và f (a)f (b) < 0 thì phương trình f (x) = 0 có đúng một nghiệm trên (a; b).
D Nếu hàm số f (x) liên tục trên [a; b] và f (a)f (b) < 0 thì phương trình f (x) = 0 có một nghiệm trên [a; b]. Lời giải.
Định lí về sự tồn tại nghiệm của phương trình trên một khoảng. Chọn đáp án A □ Câu 35.
Cho hàm số y = f (x) có đồ thị dưới đây, trên khoảng (−2; 3) hàm số gián đoạn tại điểm y nào? 3 A x = 0. B x = 1. C x = 2. D x = 3. 1 −1 O 1 2 x Lời giải. 489/764 489/764
Toán 11 theo chương trình GDPT2018 490
4. Bài tập cuối chương III
Biết làm, làm đúng, làm nhanh
Dựa vào đồ thị hàm số ta thấy lim f (x) = 3 và lim f (x) = 0, suy ra lim f (x) ̸= lim f (x). Do đó hàm số x→1− x→1+ x→1− x→1+ gián đoạn tại x = 1. Chọn đáp án B □  x2 − 3x + 2  , khi x > 1 Câu 36. Cho hàm số f (x) = x − 1
. Chọn khẳng định đúng. 2x + 1 , khi x ≤ 1
A Hàm số f (x) liên tục tại điểm x = 1.
B Hàm số f (x) gián đoạn tại điểm x = 1 vì lim f (x) ̸= f (1). x→1
C Hàm số f (x) gián đoạn tại điểm x = 1 vì không tồn tại lim f (x). x→1
D Hàm số f (x) không xác định tại x = 1. Lời giải. Ta có x2 − 3x + 2 (x − 1)(x − 2) ○ lim f (x) = lim = lim = lim (x − 2) = −1. x→1+ x→1+ x − 1 x→1+ x − 1 x→1+
○ lim f (x) = lim (2x + 1) = 3. x→1− x→1−
Vì lim f (x) ̸= lim f (x) nên không tồn tại lim f (x). x→1+ x→1− x→1
Do đó hàm số gián đoạn tại điểm x = 1 vì không tồn tại lim f (x). x→1 Chọn đáp án C □
Câu 37. Hàm số nào sau đây liên tục trên R? 3 1 − x √ A y = cos . B y = cot 3x. C y = . D y = x + 2. x x2 + 4 Lời giải. 3 ○ Hàm số y = cos
có tập xác định là D = R \ {0} nên không liên tục trên R. x n π o
○ Hàm số y = cot 3x có tập xác định là D = R \ k , k ∈ Z nên không liên tục trên R. 3 1 − x ○ Hàm số y =
là hàm sơ cấp nên có tập xác định R nên liên tục trên R. x2 + 4 √ ○ Hàm số y =
x + 2 có tập xác định là D = [−2; +∞) nên không liên tục trên R. Chọn đáp án C □ x2 + 3 Câu 38. Cho hàm số f (x) =
. Hàm số f (x) liên tục trên khoảng nào dưới đây? x2 − 5x + 6 A (2; 3). B (−3; 3). C (−3; +∞). D (−∞; 3). Lời giải.
Hàm số xác định trên tập D = (−∞; 2) ∪ (2; 3) ∪ (3; +∞), suy ra hàm số liên tục trên khoảng (2; 3). Chọn đáp án A □ x + 4 Câu 39. Cho hàm số y =
. Mệnh đề nào sau đây là đúng? x − 3
A Hàm số liên tục tại x = 3.
B Hàm số liên tục trên (−∞; +∞).
C Hàm số liên tục tại x = 2 và x = 3.
D Hàm số liên tục trên (−∞; 3) và (3; +∞). Lời giải.
Với x0 ̸= 3, ta có lim f (x) = f (x0) suy ra hàm số liên tục (−∞; 3) và (3; +∞). x→x0 Chọn đáp án D □ 490/764 490/764
Toán 11 theo chương trình GDPT2018 491
Chương 3. Giới hạn. Hàm số liên tục
Biết làm, làm đúng, làm nhanh  x3 − x2   khi x > 1   x − 1
Câu 40. Cho hàm số y = f (x) =
. Biết hàm số f (x) liên tục tại x n khi x = 1 0 = 1. Giá trị của m, n    mx + 1 khi x < 1 là A n = 1, m = 0. B n = 0, m = 1. C n = m = 1. D n = −1, m = 0. Lời giải. Ta có x3 − x2 ○ lim f (x) = lim = lim x2 = 1. x→1+ x→1+ x − 1 x→1+
○ lim f (x) = lim (mx + 1) = m + 1. x→1− x→1− ○ f (1) = n.
Do hàm số f (x) liên tục tại x = 1 nên ta có
lim f (x) = lim f (x) = f (1) ⇔ m + 1 = 1 = n. x→1− x→1+ Suy ra n = 1, m = 0. Chọn đáp án A □ ®x3 + x2 + 7 khi x ̸= −1 Câu 41. Cho hàm số f (x) =
. Tìm m để hàm số liên tục tại điểm x0 = −1. 2x + m − 1 khi x = −1 A m = 12. B m = 8. C m = −10. D m = 10. Lời giải.
Ta có lim (x3 + x2 + 7) = 7 và f (−1) = m − 3. x→−1
Để hàm số liên tục tại điểm x0 = −1 thì m − 3 = 7 ⇔ m = 10. Chọn đáp án D □
Câu 42. Tìm tất cả các giá trị thực của m để phương trình m(x − 1)3(x − 2) + 2x − 3 = 0 vô nghiệm. A ∀m ∈ R. B m = 1.
C Không có giá trị m. D m = 0. Lời giải.
Đặt f (x) = m(x − 1)3(x − 2) + 2x − 3 xác định và liên tục trên R.
Ta có f (1) = −1, f (2) = 1 ⇒ f (1) · f (2) < 0, ∀m ∈ R suy ra phương trình luôn có nghiệm ∀m ∈ R. Chọn đáp án C □
Câu 43. Phương trình nào dưới đây có nghiệm trong khoảng (0; 1)? A 2x2 − 3x + 4 = 0.
B (x − 1)5 − x7 − 2 = 0. C 3x4 − 4x2 + 5 = 0.
D 3x2024 − 8x + 4 = 0. Lời giải.
Xét hàm số f (x) = 3x2024 − 8x + 4 = 0 liên tục trên R.
Ta có f (0) = 4; f (1) = −1 ⇒ f (0) · f (1) = −4 < 0 suy ra phương trình có ít nhất một nghiệm thuộc khoảng (0; 1). Chọn đáp án D □ √
Câu 44. Hàm số nào sau đây gián đoạn tại x = − 2 ? √ 3x + 2 2 √ A y = cos x. B y = . C y = x + 2. D y = tan x. x2 − 2 Lời giải. √ √ √ 3x + 2 2 3x + 2 2 3x + 2 2 √ Ta có lim = −∞ và lim = +∞ nên hàm số y = gián đoạn tại x = − 2. √ x2 − 2 √ x2 − 2 x2 − 2 x→(− 2)− x→(− 2)+ Chọn đáp án B □ √  x2 + 1 − 1  khi x ̸= 0
Câu 45. Tìm m để hàm số f (x) = x liên tục tại x = 0. 2m + 2 khi x = 0 491/764 491/764
Toán 11 theo chương trình GDPT2018 492
4. Bài tập cuối chương III
Biết làm, làm đúng, làm nhanh A m = 2. B m = 1. C m = −1. D m = −2. Lời giải. √x2 + 1 − 1 x Ta có lim f (x) = lim = lim √ = 0, f (0) = 2m + 2. x→0 x→0 x x→0 x2 + 1 + 1
Hàm số liên tục tại x = 0 ⇔ lim f (x) = f (0) ⇔ 2m + 2 = 0 ⇔ m = −1. x→0 Chọn đáp án C □
Câu 46. Hàm số nào sau đây không liên tục trên R? x + 1 x + 1 A f (x) = . B f (x) = . x2 + 1 x − 1 π C f (x) = sin x − .
D f (x) = x3 − 2x2 + x − 7. 5 Lời giải. x + 1 ○ Hàm số f (x) =
là hàm sơ cấp nên có tập xác định R nên liên tục trên R. x2 + 1 x + 1 ○ Hàm số f (x) =
có tập xác định R \ {1} nên hàm số không liên tục trên R. x − 1 π ○ Hàm số sin x −
là hàm sơ cấp nên có tập xác định R nên liên tục trên R. 5
○ Hàm số f (x) = x3 − 2x2 + x − 7 là hàm đa thức nên liên tục trên R. Chọn đáp án B □ x3 + 2x2
Câu 47. Cho hàm số f (x) chưa xác định tại x = 0, f (x) =
. Để hàm số f (x) liên tục tại x = 0 thì phải x2
gán cho f (0) giá trị bằng bao nhiêu? A 3. B 2. C 1. D 0. Lời giải. x3 + 2x2 Ta có lim f (x) = lim = lim (x + 2) = 2. x→0 x→0 x2 x→0
Do đó, để hàm số f (x) liên tục tại x = 0 thì phải gán cho f (0) = 2. Chọn đáp án B □  3 − x  √ nếu x ̸= 3 Câu 48. Cho hàm số f (x) = x + 1 − 2
. Hàm số đã cho liên tục tại x = 3 khi m bằng m nếu x = 3 A 1. B 4. C −1. D −4. Lời giải. √ 3 − x (3 − x)( x + 1 + 2) √ Ta có lim √ = lim
= lim (− x + 1 − 2) = −4. x→3 x + 1 − 2 x→3 x − 3 x→3 3 − x
Hàm số liên tục tại x = 3 khi và chỉ khi lim √
= f (3) ⇔ −4 = m ⇔ m = −4. x→3 x + 1 − 2 Chọn đáp án D □  x2 − 16  khi x ̸= 4 Câu 49. Cho hàm số f (x) = x − 4
. Tập hợp các giá trị của a để hàm số liên tục tại x = 4 là ax − 1 khi x = 4 ß 9 ™ ß 9 ™ A . B − . C {8}. D {0}. 4 4 Lời giải. Ta có:
○ f (4) = a · 4 − 1 = 4a − 1. x2 − 16 (x − 4)(x + 4) ○ lim f (x) = lim = lim = lim (x + 4) = 8. x→4 x→4 x − 4 x→4 x − 4 x→4 492/764 492/764
Toán 11 theo chương trình GDPT2018 493
Chương 3. Giới hạn. Hàm số liên tục
Biết làm, làm đúng, làm nhanh
Do đó, điều kiện cần và đủ để hàm số đã cho liên tục tại x = 4 là 9
lim f (x) = f (4) ⇔ 8 = 4a − 1 ⇔ a = . x→4 4 Chọn đáp án A □ √  3 x − 2 + 2x − 1  khi x ̸= 1
Câu 50. Tìm m để hàm số f (x) = x − 1 liên tục trên R. 3m − 2 khi x = 1 4 A m = 1. B m = . C m = 2. D m = 0. 3 Lời giải. √ 3 x − 2 + 2x − 1 Với x ̸= 1, ta có f (x) =
nên hàm số liên tục trên các khoảng (−∞; 1) và (1; +∞). x − 1
Do đó, để hàm số liên tục trên R thì hàm số liên tục tại x = 1. Ta có f (1) = 3m − 2. Ta có √ 3 x − 2 + 2x − 1 lim f (x) = lim x→1 x→1 x − 1   x3 + x − 2 = lim 1 + √ Ä  x→1
(x − 1) x2 − x 3 x − 2 + 3 p(x − 2)2ä ñ ô x2 + x + 2 = lim 1 + √ = 2. x→1 x2 − x 3 x − 2 + 3 p(x − 2)2 4
Nên hàm số liên tục tại x = 1 khi và chỉ khi lim f (x) = f (1) ⇔ 3m − 2 = 2 ⇔ m = . x→1 3 4 Vậy m = . 3 Chọn đáp án B □ ®m2x2 khi x ≤ 2
Câu 51. Có bao nhiêu giá trị thực của tham số m để hàm số f (x) = liên tục trên R? (1 − m)x khi x > 2 A 0. B 2. C 3. D 4. Lời giải.
Ta có hàm số luôn liên tục ∀x ̸= 2 . Tại x = 2 , ta có
○ lim f (x) = lim (1 − m) x = (1 − m) · 2 = 2 − 2m; x→2+ x→2−
○ lim f (x) = lim m2x2 = 4m2; x→2− x→2− ○ f (2) = 4m2.
Hàm số liên tục tại x = 2 khi và chỉ khi  1 m =
lim f (x) = lim f (x) = f (2) ⇔ 4m2 = 2 − 2m ⇔ 4m2 + 2m − 2 = 0 ⇔ 2  x→2+ x→2− m = −1.
Vậy có hai giá trị của m. Chọn đáp án B □ 493/764 493/764
Toán 11 theo chương trình GDPT2018 494
4. Bài tập cuối chương III
Biết làm, làm đúng, làm nhanh C – ĐỀ ÔN TẬP 1.
Phần Trắc nghiệm (7 điểm)
Câu 1. Khẳng định nào sau đây sai? √ √ Å ãn Å ãn Ä ä2n Ä än 2 1 A lim − 3 = −∞. B lim 2 = +∞. C lim = 0. D lim − = 0. 3 2 Lời giải. 2 Å 2 ãn Vì < 1 nên lim = 0. 3 3 Chọn đáp án C □
Câu 2. Cho q là số thực thỏa q > 1, kết quả của lim qn bằng A 0. B −∞. C +∞. D q. Lời giải.
Theo tính chất giới hạn ta có q là số thực thỏa q > 1 thì lim qn = +∞. Chọn đáp án C □
Câu 3. Dãy nào sau đây có giới hạn bằng 0? Å 1 ãn Å 3 ãn A un = . B un = . C un = 2n. D un = 2023n. 2 2 Lời giải. 1 Å 1 ãn Vì 0 < < 1 nên lim = 0. 2 2 Chọn đáp án A □ 1 + n − 3n2 Câu 4. Tính giới hạn lim . n2 + 2n 3 1 A 1. B − . C . D −3. 2 2 Lời giải. 1 1 1 + n − 3n2 + − 3 lim = lim n2 n = −3. n2 + 2n 2 1 + n Chọn đáp án D □ −3n + 2 Câu 5. Giới hạn lim bằng n + 3 2 A 3. B 0. C −3. D . 3 Lời giải. −3n + 2 −3 + 2 lim = lim n = −3. n + 3 1 + 3n Chọn đáp án C □ n + 1 Câu 6. Giá trị của lim bằng bao nhiêu? n2 + 2 1 A 1. B . C 0. D 2. 2 Lời giải. Å 1 1 ã 1 1 n2 + n + 1 + n n2 Ta có lim = lim = lim n n2 = 0. n2 + 2 Å 2 ã 2 n2 1 + 1 + n2 n2 Chọn đáp án C □ 2x + 1 Câu 7. Tính giới hạn lim . x→2 x − 1 A −1. B 2. C 0. D 5. 494/764 494/764
Toán 11 theo chương trình GDPT2018 495
Chương 3. Giới hạn. Hàm số liên tục
Biết làm, làm đúng, làm nhanh Lời giải. 2x + 1 2 · 2 + 1 lim = = 5. x→2 x − 1 2 − 1 Chọn đáp án D □
Câu 8. Tính giới hạn I = lim (x2 + x + 1). x→1 A I = 3. B I = 1. C I = +∞. D I = 2. Lời giải.
Ta có I = lim (x2 + x + 1) = 12 + 1 + 1 = 3. x→1 Chọn đáp án A □
Câu 9. Tính giá trị của lim (x − 2). x→2 A 1. B −2. C 4. D 0. Lời giải.
Ta có lim (x − 2) = 2 − 2 = 0. x→2 Chọn đáp án D □ x − 3
Câu 10. Tính giới hạn L = lim . x→3 x + 3 A L = 1. B L = −∞. C L = 0. D L = +∞. Lời giải. x − 3 0 Ta có lim = = 0. x→3 x + 3 6 Chọn đáp án C □ 3x − 1
Câu 11. Tính giới hạn lim . x→1 x2 − 2x + 2 1 1 A − . B 2. C −2. D . 2 2 Lời giải. 3x − 1 3 − 1 lim = = 2. x→1 x2 − 2x + 2 12 − 2 + 2 Chọn đáp án B □ x + 1
Câu 12. Tính giới hạn lim . x→3+ 2x − 6 1 1 A . B . C −∞. D +∞. 2 6 Lời giải.
Ta thấy khi x → 3+ thì (x + 1) → 4 còn (2x − 6) → 0+. x + 1 Từ đó suy ra lim = +∞. x→3+ 2x − 6 Chọn đáp án D □ 5 − x
Câu 13. Giới hạn lim f (x) = lim có kết quả bằng x→2+ x→2− x − 2 1 A −∞. B . C +∞. D −1. 2 Lời giải.
lim (x − 2) = 0, x − 2 < 0 với mọi x < 2 và lim (5 − x) = 3 > 0. x→2− x→2+ 5 − x Do đó, lim = −∞. x→2+ x − 2 Chọn đáp án A □
Câu 14. Tính giới hạn lim x4 + 2x2 + 1. x→−∞ A 0. B +∞. C −∞. D 1. Lời giải. 495/764 495/764
Toán 11 theo chương trình GDPT2018 496
4. Bài tập cuối chương III
Biết làm, làm đúng, làm nhanh Å 2 1 ã lim x4 + 2x2 + 1 = lim x4 1 + + = +∞. x→−∞ x→−∞ x2 x4 Chọn đáp án B □
Câu 15. Tính giới hạn H = lim x3. x→+∞ A H = 0. B H = −∞. C H = 3. D H = +∞. Lời giải.
Ta có giới hạn đặc biệt
lim xk = +∞ với k nguyên dương. x→+∞
Áp dụng với k = 3, ta có H = lim x3 = +∞. x→+∞ Chọn đáp án D □ x + 1 Câu 16. Tính lim . x→+∞ x + 2 A 1. B 2. C 3. D 4. Lời giải. Å 1 ã 1 x 1 + x + 1 1 + x Ta có lim = lim = lim x = 1. x→+∞ x + 2 x→+∞ Å 2 ã x→+∞ 2 x 1 + 1 + x x Chọn đáp án A □
Câu 17. Hàm số y = f (x) liên tục tại điểm x0 khi nào? A lim f (x) = f (x). B lim f (x) = f (x0). C lim f (x) = f (0). D f (x0) = 0. x→x0 x→x0 x→x0 Lời giải.
Theo định nghĩa hàm số liên tục, ta có lim f (x) = f (x0). x→x0 Chọn đáp án B □
Câu 18. Cho hàm số f (x) thỏa mãn lim f (x) ̸= f (x0). Chọn khẳng định đúng. x→x0
A Hàm số f (x) không xác định tại x0.
B Hàm số f (x) gián đoạn tại x0.
C Hàm số f (x) liên tục tại x0.
D f (x) có giá trị 0 tại x0. Lời giải.
Theo định nghĩa hàm số liên tục, ta có, do lim f (x) ̸= f (x0) nên hàm số f (x) gián đoạn tại x0. x→x0 Chọn đáp án B □
Câu 19. Trong các loại hàm số sau, hàm số nào luôn liên tục trên tập hợp các số thực R?
A Hàm số lượng giác. B Hàm số đa thức.
C Hàm số phân thức hữu tỉ.
D Hàm số có chứa căn bậc hai. Lời giải.
Hàm số đa thức luôn liên tục trên tập số thực R. Chọn đáp án B □
Câu 20. Trong các hàm số sau, hàm số nào liên tục trên R? √ 2x − 1 A y = x. B y = . C y = cot x. D y = x4 − x. x − 1 Lời giải.
Hàm số y = x4 − x là hàm số đa thức nên liên tục trên R. Chọn đáp án D □ x − 3 Câu 21. Cho hàm số f (x) =
. Mệnh đề nào sau đây đúng? x2 − 1
A Hàm số liên tục tại x = 1.
B Hàm số không liên tục tại các điểm x = ±1.
C Hàm số liên tục tại mọi x ∈ R.
D Hàm số liên tục tại x = −1. Lời giải.
Hàm số đã cho có tập xác định là D = R \ {±1}. Do đó, hàm số không liên tục tại các điểm x = ±1. Chọn đáp án B □ 496/764 496/764
Toán 11 theo chương trình GDPT2018 497
Chương 3. Giới hạn. Hàm số liên tục
Biết làm, làm đúng, làm nhanh
Câu 22. Cho hai dãy số (un), (vn) thỏa mãn lim un = 2, lim vn = 1. Tính lim(2un − 3vn). A 1. B 2. C 3. D 7. Lời giải.
Ta có lim(2un − 3vn) = lim 2un − lim 3vn = 2 · 2 − 3 · 1 = 1. Chọn đáp án A □
Câu 23. Trong các dãy số sau, dãy số nào có giới hạn khác 0? 2n − 1 1 Å 1 ãn 1 A un = . B un = . C un = . D un = √ . n n(n + 1) 3 n2 + 1 Lời giải. 1 2n − 1 2 − 2 ○ lim = lim n = = 2 ̸= 0. n 1 1 1 ○ lim = 0. n(n + 1) Å 1 ãn ○ lim = 0. 3 1 ○ lim √ = 0. n2 + 1 Chọn đáp án A □ √ 2|x + 1| − 5 x2 − 3 Câu 24. Giá trị lim bằng x→−2 2x + 3 1 1 A . B . C 7. D 3. 3 7 Lời giải. √ 2|x + 1| − 5 x2 − 3
2| − 2 + 1| − 5p(−2)2 − 3 lim = = 3. x→−2 2x + 3 2 · (−2) + 3 Chọn đáp án D □ √ x + x2 + 1 √ Câu 25. Cho biết lim
= a + b 2 (với a, b ∈ Q). Giá trị của a + b bằng x→1 x + 1 A 1. B 2. C 5. D 0. Lời giải. √ √ x + x2 + 1 1 + 12 + 1 1 1 √ Ta có lim = = + · 2. x→1 x + 1 12 + 1 2 2 1 1 Suy ra a = , b = . Vậy a + b = 1. 2 2 Chọn đáp án A □ √ √ x + 2 − 8 − 2x Câu 26. Giới hạn lim bằng x→2 x − 2 3 A +∞. B −∞. C 0. D . 4 Lời giải. √ √ x + 2 − 8 − 2x −6 + 3x lim = lim √ √ x→2 x − 2 x→2 (x − 2) x + 2 + 8 − 2x 3(x − 2) = lim √ √ x→2 (x − 2) x + 2 + 8 − 2x 3 3 = lim √ √ = . x→2 x + 2 + 8 − 2x 4 Chọn đáp án D □ 497/764 497/764
Toán 11 theo chương trình GDPT2018 498
4. Bài tập cuối chương III
Biết làm, làm đúng, làm nhanh x2 + 2x + 1 Câu 27. Tính lim . x→−1 2x3 + 2 1 A +∞. B −∞. C . D 0. 2 Lời giải. x2 + 2x + 1 (x + 1)2 x + 1 lim = lim = = 0. x→−1 2x3 + 2
x→−1 2(x + 1)(x2 − x + 1) 2(x2 − x + 1) Chọn đáp án D □ √ √ √ Ä ä a a Câu 28. Biết rằng lim 2x2 − 3x + 1 + x 2 = 2, (a, b ∈ Z,
tối giản). Tổng a + b có giá trị là x→−∞ b b A 1. B 5. C 4. D 7. Lời giải. Ta có √ Äp ä 2x2 − 3x + 1 − 2x2 lim 2x2 − 3x + 1 + x 2 = lim √ √ x→−∞ x→−∞ 2x2 − 3x + 1 − x 2 −3x + 1 = lim √ √ x→−∞ 2x2 − 3x + 1 − x 2 1 −3 + = lim x x→−∞ … 3 1 √ − 2 − + − 2 x x2 3 √ = · 2. 4
Vậy a = 3, b = 4. Tổng a + b = 7. Chọn đáp án D □ x2 + 3x + 1
Câu 29. Tính giới hạn lim . x→2+ 2x − 4 1 A . B 0. C +∞. D −∞. 2 Lời giải.
Ta có lim (x2 + 3x + 1) = 11 > 0. x→2+ Và lim (2x − 4) = 0. x→2+
Mà khi x → 2+ thì 2x − 4 > 0. x2 + 3x + 1 Vậy lim = +∞. x→+∞ 2x − 4 Chọn đáp án C □ u1 = 2 
Câu 30. Cho dãy số (un) xác định bởi 2u . Tìm giới hạn I = lim u n + 1 n. un+1 = 5 √ 1 2 2 A I = . B I = . C I = . D I = +∞. 3 5 5 Lời giải.
Nhận xét: (un) là dãy giảm và bị chặn trên bởi 2. Giả sử lim un = L. 2un + 1 2L + 1 1 Ta có un+1 = ⇔ L = ⇔ L = . 5 5 3 1 Vậy I = . 3 Chọn đáp án A □ √ √ √ Ä ä a b Câu 31. Biết rằng lim 2x2 + 2x − 1 + x 2 =
(a là số nguyên; b, c là số nguyên tố). Tính tổng S = x→−∞ c a + b + c. A S = 5. B S = 9. C S = 10. D S = 3. 498/764 498/764
Toán 11 theo chương trình GDPT2018 499
Chương 3. Giới hạn. Hàm số liên tục
Biết làm, làm đúng, làm nhanh Lời giải. √ Äp ä (2x2 + 2x − 1) − (2x2) lim 2x2 + 2x − 1 + x 2 = lim √ √ x→−∞ x→−∞ 2x2 + 2x − 1 − x 2 2x − 1 = lim √ √ x→−∞ 2x2 + 2x − 1 − x 2 Å 1 ã x 2 − √ x 2 = lim = . x→−∞ Ç… å 2 1 √ 2 −x 2 + − + 2 x x2
Suy ra a = 1; b = 2; c = 2. Vậy S = 5. Chọn đáp án A □ Å x2 + 1 ã Câu 32. Biết rằng lim + ax − b = −5. Tính tổng a + b. x→∞ x − 2 A 6. B 7. C 8. D 5. Lời giải. Ta có Å x2 + 1 ã
x2 + 1 + ax2 − 2ax − bx + 2b lim + ax − b = lim x→∞ x − 2 x→∞ x − 2
(1 + a)x2 − (2a + b)x + 2b + 1 = lim . x→∞ x − 2
Vì kết quả giới hạn bằng −5 nên từ đó ta có hệ ®a = −1 ®a = −1 ⇔ 2a + b = 5 b = 7. Vậy a + b = 6. Chọn đáp án A □ √ √ Ä
Câu 33. Giá trị của giới hạn lim x2 + x − 3 x3 − x2ä là x→+∞ 5 A −1. B +∞. C −∞. D . 6 Lời giải. Ta có Äp Äp ä Ä lim x2 + x − 3 px3 − x2ä = lim x2 + x − x + lim x − 3 px3 − x2ä . x→+∞ x→+∞ x→+∞ Mà Äp ä x 1 1 lim x2 + x − x = lim √ = lim = , x→+∞ x→+∞ x2 + x + x x→+∞ »1 + 1 + 1 2 x và Ä 1 1 lim x − 3 px3 − x2ä = lim = , x→+∞ x→+∞ » » 2 3 1 + 3 1 − 1 + 3 1 − 1 x x nên Äp 1 1 5 lim x2 + x − 3 px3 − x2ä = + = . x→+∞ 2 3 6 Chọn đáp án D □ √ √ 2x + 3x2 − 2 3 + b Câu 34. Cho lim √ =
. Tính giá trị của A = b · c. x→−∞ 4x2 + 1 − |x| c A A = 6. B A = −6. C A = 2. D A = −2. Lời giải. 499/764 499/764
Toán 11 theo chương trình GDPT2018 500
4. Bài tập cuối chương III
Biết làm, làm đúng, làm nhanh … 2 … 2 2x + |x| 3 − 2 − 3 − √ √ x2 x2 2 − 3 3 − 2 Ta có lim = lim = = . x→−∞ … 1 x→−∞ … 1 −2 + 1 1 |x| 4 + + x − 4 + + 1 x2 x2
Vậy b = −2, c = 1 ⇒ A = b · c = −2. Chọn đáp án D □ f (x) + 1 pf(x) + 2x + 1 − x
Câu 35. Cho f (x) là hàm đa thức thỏa lim = a và tồn tại lim = T . Chọn đẳng x→2 x − 2 x→2 x2 − 4 thức đúng. a − 2 a + 2 a − 2 a + 2 A T = . B T = . C T = . D T = . 16 16 8 8 Lời giải. f (x) + 1
Vì f (x) là đa thức và lim
= a nên suy ra f (x) + 1 = (x − 2)g(x), g(2) = a. x→2 x − 2 Do đó, Ta có p(x − 2)g(x) + 2x − x T = lim x→2 x2 − 4 (x − 2)g(x) + 2x − x2 = lim î ó
x→2 (x − 2)(x + 2) p(x − 2)g(x) + 2x + x g(x) − x = lim î ó
x→2 (x + 2) p(x − 2)g(x) + 2x + x a − 2 = . 16 Chọn đáp án A □ 2.
Phần Tự luận (3 điểm)
Bài 1. Tính các giới hạn sau: √ √ 4n2 − n + 3 x − 2 a) lim ; b) lim ; 8n − 5 x→4 x2 − 16 6x + 8 3x2 + 4 c) lim ; d) lim . x→+∞ 5x − 2 x→−2+ 2x + 4 Lời giải. … √ 1 3 4 − + 4n2 − n + 3 n n2 1 a) lim = lim = . 8n − 5 5 4 8 − n √ √ x − 2 x − 2 1 1 b) lim = lim √ √ = lim √ = . x→4 x2 − 16 x→4 ( x − 2)( x + 2)(x + 4) x→4 ( x + 2)(x + 4) 32 6x + 8 6 c) lim = . x→+∞ 5x − 2 5 3x2 + 4 d) Vì lim
3x2 + 4 = 16 > 0; lim (x + 2) = 0 và x → −2+ ⇒ x + 2 > 0 nên lim = +∞. x→2+ x→2+ x→−2− 2x + 4 □  x2 − 25  khi x ̸= 5
Bài 2. Cho hàm số f (x) = x − 5 a khi x = 5.
Tìm a để hàm số y = f (x) liên tục trên R. 500/764 500/764
Toán 11 theo chương trình GDPT2018 501
Chương 3. Giới hạn. Hàm số liên tục
Biết làm, làm đúng, làm nhanh Lời giải. x2 − 25 Với x ̸= 5 thì f (x) = = x + 5 là hàm liên tục. x − 5
Do đó, để hàm số liên tục trên R thì hàm số phải liên tục tại x = 5.
Tức là lim f (x) = f (5) ⇔ lim (x + 5) = a ⇔ a = 10. x→5 x→5
Vậy với a = 10 thì hàm số liên tục trên R. □ |x|
Bài 3. Chứng minh rằng giới hạn lim không tồn tại. x→0 x Lời giải. |x| −x ○ lim = lim = lim (−1) = −1. x→0− x x→0− x x→0− |x| x ○ lim = lim = lim 1 = 1. x→0+ x x→0+ x x→0+ |x| |x| |x| Vậy lim ̸= lim nên giới hạn lim không tồn tại. □ x→0− x x→0+ x x→0 x 501/764 501/764
Toán 11 theo chương trình GDPT2018