Đề kiểm tra cuối học kì 1 môn Toán lớp 12 năm học 2025 - 2026 Trường THPT Thống Nhất - Đồng Nai

SỞ GD&ĐT ĐỒNG NAI
HDG ĐỀ ÔN KIỂM TRA HỌC KỲ I NĂM HỌC 2025 – 2026
TRƯỜNG THPT THỐNG NHẤT MÔN: TOÁN LỚP 12
(Đề thi có 05 trang)
Thời gian làm bài: 90 (không kể thời gian phát đề)
Họ và tên: ............................................................................ Số báo danh: ....... Mã đề 124
PHẦN I. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án đúng. Câu 1.
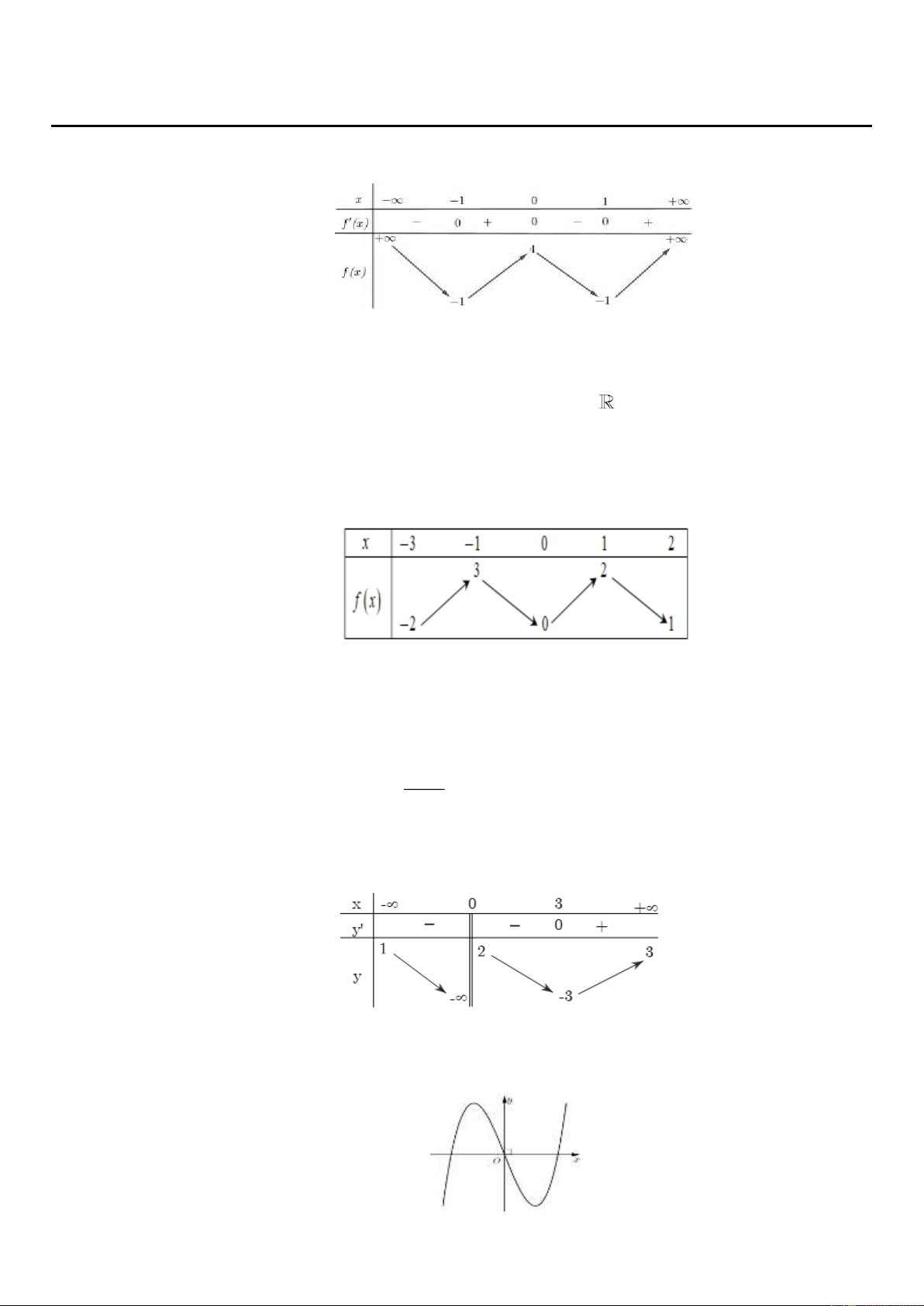
Cho hàm số f x có bảng biến thiên như sau:
Hàm số đã cho đồng biến trên khoảng nào dưới đây? A.  ;    1 . B. 0  ;1 . C.  1  ;  1 . D.  1  ;0 Đáp án: D Câu 2.
Cho hàm số f  x có đạo hàm f  x  x x   x  3 1 4 , x
  . Số điểm cực đại của hàm số đã cho là A. 3 . B. 4 . C. 2 . D. 1. Đáp án: D Câu 3.
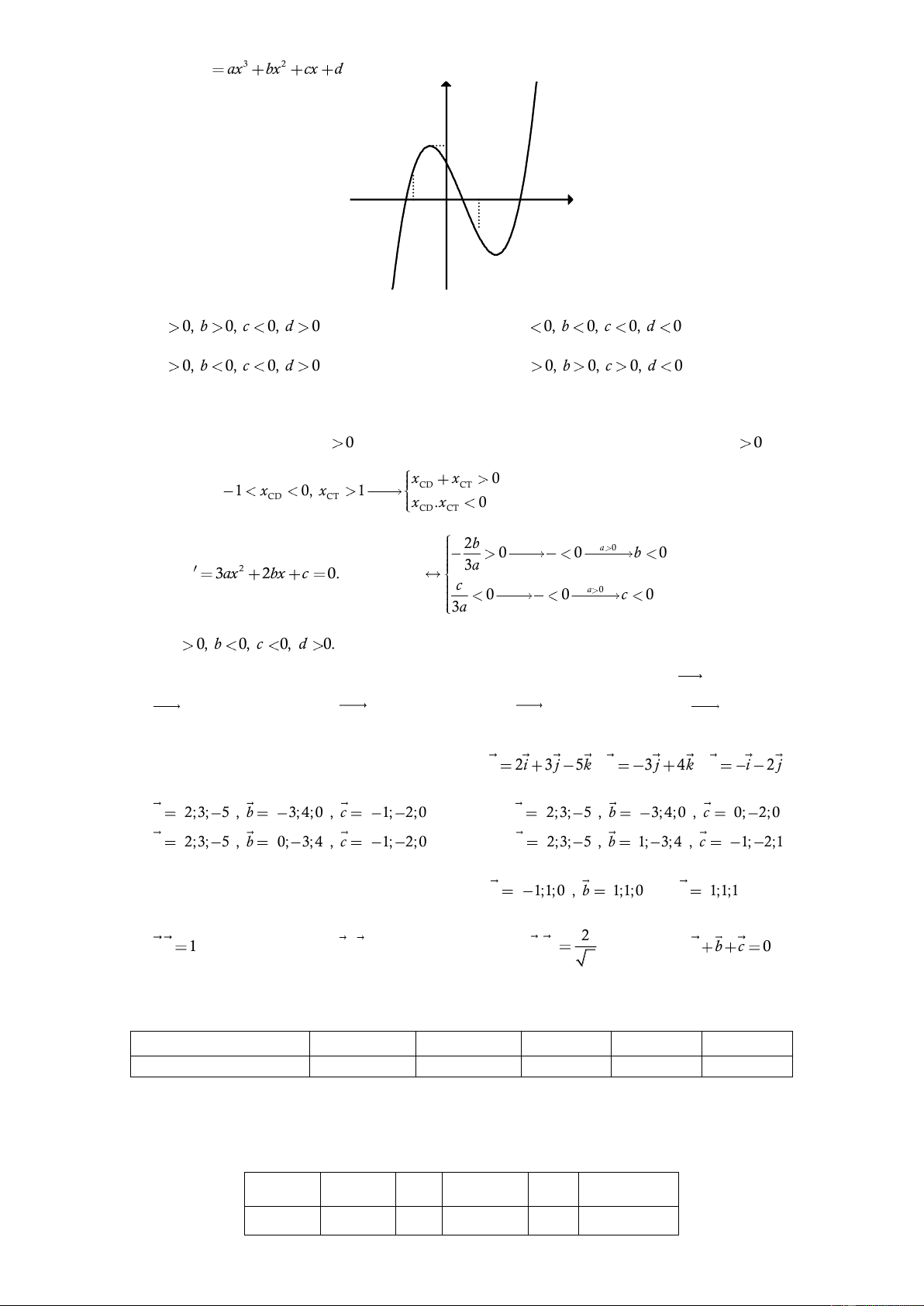
Cho hàm số y  f  x liên tục trên  3
 ;2 và có bảng biến thiên như sau.
Gọi M , m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y  f  x trên đoạn  1  ;  2 . Tính M  m . A. 1 . B. 2 . C. 3 . D. 4 . Đáp án: C x  2 Câu 4.
Tiệm cận ngang của đồ thị hàm số y  x  là 1 A. y  2  .
B. y 1. C. x  1  .
D. x  2 . Đáp án: A Câu 5.
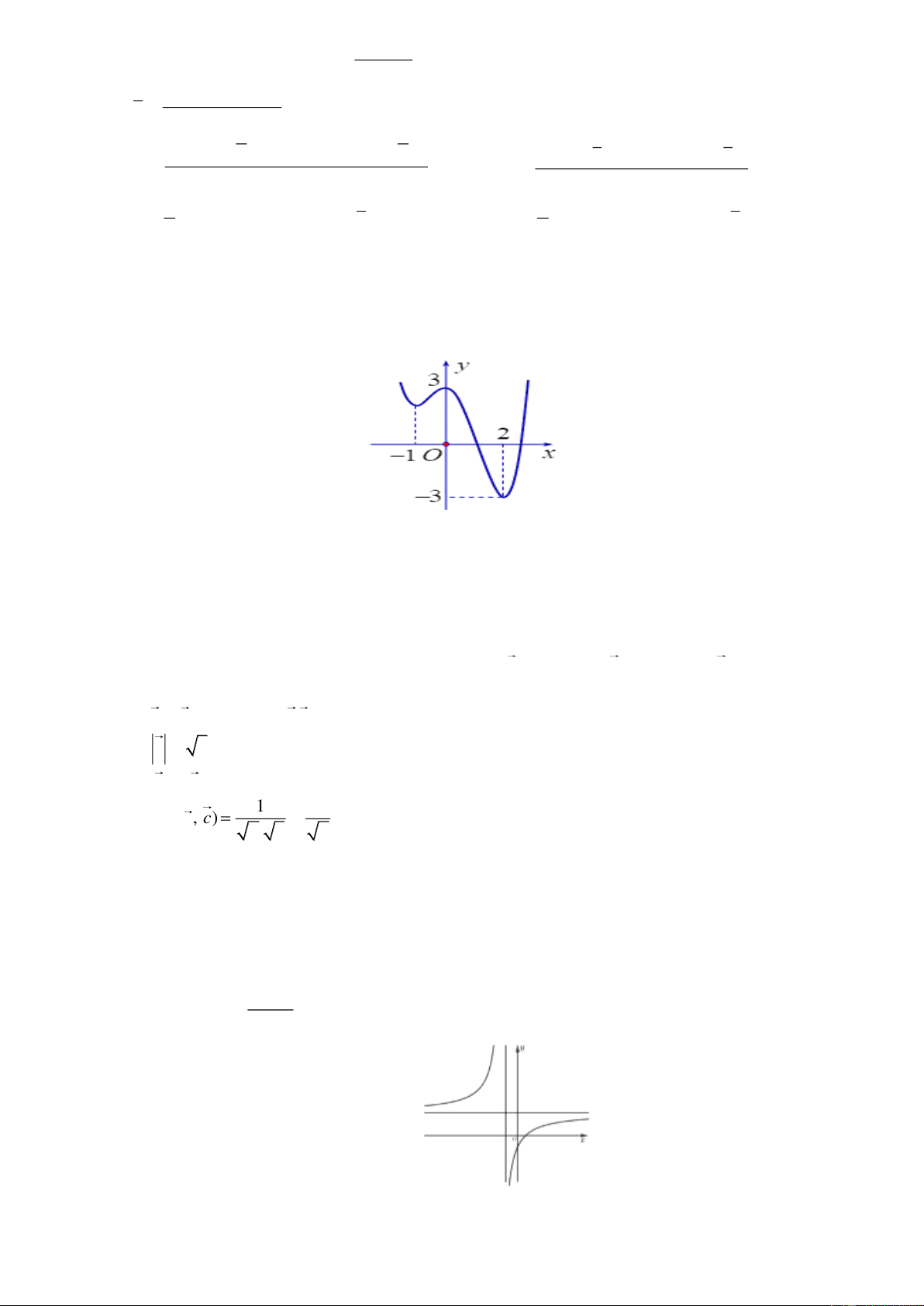
Cho hàm số y  f  x có báng biến thiên như sau:
Tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho là: A. 2. B. 3. C. 4. D. 1. Đáp án: B Câu 6.
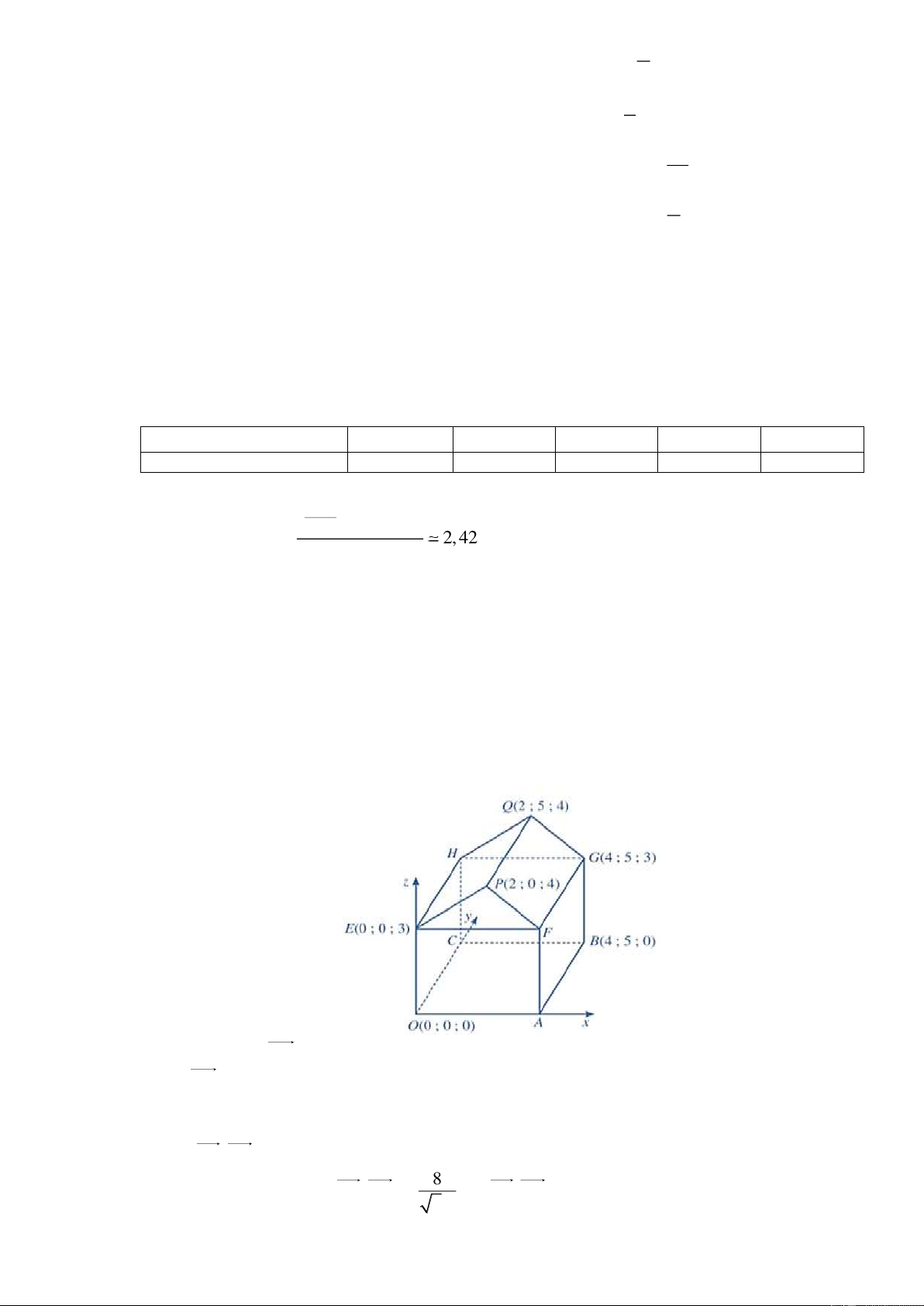
Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình bên? 3 3
A. y  x  3x .
B. y  x  3x . C. 3 2
y  x  3x 1. D. 3 2
y  x  3x . Đáp án: B Câu 7. Hàm số 3 2 y ax bx
cx d có đồ thị như hình vẽ bên. y 2 x 1 -1 O
Mệnh đề nào sau đây là đúng
A. a 0, b 0, c 0, d 0 .
B. a 0, b 0, c 0, d 0 .
C. a 0, b 0, c 0, d 0 .
D. a 0, b 0, c 0, d 0 . Lời giải.
Đồ thị hàm số thể hiện a 0; cắt trục tung tại điểm có tung độ dương nên d 0 . x x 0 Hàm số có CD CT 1 x 0, x 1 . * CD CT x .x 0 CD CT 2b b a 0 0 0 b 0 Ta có 2 y 3ax 2bx c 0. Do đó 3 * a a . c c a 0 0 0 c 0 3a a
Vậy a 0, b 0, c 0, d 0. Chọn C. Câu 8.
Cho hình hộp chữ nhật ABC . D A B  C  D
  .Vectơ nào sau đây cùng phương với BC ? A. DC B. DA
C. BB D. C C  Đáp án: B Câu 9.
Trong không gian với hệ tọa độ Oxyz , cho ba vectơ a
2i 3 j 5k , b
3 j 4k , c i 2 j .
Khẳng định nào sau đây đúng? A. a 2;3; 5 , b 3;4;0 , c 1; 2;0 . B. a 2;3; 5 , b 3;4;0 , c 0; 2;0 . C. a 2;3; 5 , b 0; 3;4 , c 1; 2;0 . D. a 2;3; 5 , b 1; 3;4 , c 1; 2;1 . Đáp án: C
Câu 10. Trong không gian với hệ tọa độ Oxyz , cho ba vectơ a 1;1;0 , b 1;1;0 và c 1;1;1 . Trong các khẳng
định sau, khẳng định nào đúng? 2 A. . a c 1 .
B. a, b cùng phương. C. cos b,c . D. a b c 0 . 6 Đáp án: C
Câu 11. Cô Hà thống kê lại đường kính thân gỗ của một số cây xoan đào 6 năm tuổi được trồng ở một lâm trường ở bảng sau. Đường kính ( ) cm [40;45) [45;50) [50;55) [55;60) [60;65) Tần số 5 20 18 7 3
Hãy tìm khoảng biến thiên của mẫu số liệu ghép nhóm trên. A. 25. B. 30. C. 6. D. 69,8. Đáp án: A
Câu 12. Cho mẫu số liệu ghép nhóm: Nhóm
a ;a  a ;a   a ; a k k 1   ; i 1   1 2  Tần số m  m  m 1 i k a  a trong đó, i i 1
n  m  m ; x   với i 1, 2, ,
 k là giá trị đại diện cho nhóm a ;a và i i 1   1 k i 2
m x  m x 1 1 k k x 
là số trung bình của mẫu số liệu ghép nhóm.Xét mệnh đề sau : n
m  x  x 2  m x  x m x  x
 m x  x 2 1  1 2 k  k 2 k  k 2 1 1 s  (I ) s  (II ) n n 1 1 s   2 2
m  x  m  x  x III 2 s   2 2
m  x  m  x  (x) (IV ) 1 1 k k  2 k k  2 ( ) ( ) 1 1 n n
Phương sai của mẫu số liệu ghép nhóm là:
A. (I);(II)
B. (III );(II )
C. (II );(IV )
D. (III );(IV ) Đáp án: C
PHẦN II. Thí sinh trả lời từ câu 1 đến câu 2. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai. Câu 1.
Cho hàm số y  f  x có đồ thị như hình vẽ bên. Khi đó
a) Đồng biến trên khoảng  1  ;0 : Đúng
b) Giá trị lớn nhất của hàm số trên  1
 ;2 là 2 : Đúng Sai ( là 3 ) c) Điểm  3
 ;2 thuộc đồ thị hàm số : Đúng
d) Phương trình f ( )
x  m có 2 nghiệm trên khoảng 0; 2 : Sai ( 1 nghiệm) Câu 2.
Trong không gian với hệ tọa độ Oxyz , cho các vec tơ a   1
 ;1;0 ; b  1;1;0 và c  1;1;  1 . Xét tính
đúng sai của các mệnh đề sau:
a) c  b : Sai ( vỉ .
c b 11 0  2  0 ) b) c  3 : Đúng
c) 3a  2b có toạ độ (-5;1;0) : Đúng 1 1
d) cos(a, c)   : sai 2. 3 6
PHẦN III. Thí sinh trả lời đáp án từ câu 1 đến câu 4. Câu 1. Cho hàm số 3
y  x  3x  2 . Tính tổng giá trị lớn nhất và nhỏ nhất của hàm số trên [0;2] Đáp án: 4 x  1 3 2
y  x  3x  2  y '  3x  3  y '  0 
 f (0)  2; f (1)  0; f (2)  4  x  1 
Vậy tổng giá trị lớn nhất và nhỏ nhất của hàm số trên [0;2] là 4 ax  b Câu 2. Cho hàm số y 
có đồ thị như trong hình bên dưới. cx  d
Biết rằng a là số thực dương, hỏi trong các số , b ,
c d có tất cả bao nhiêu số dương? Đáp án: 3  d   0  c  a  0  c   b 
Theo đồ thị thì tiệm cận đứng có giá trị am, ngang có giá trị dương nên:  ox  :
 0  b  0;c  0;d  0 a   b oy  :  0  d  a  0(gt)      Câu 3.
Cho hình hộp chữ nhật OABC O A B C có cạnh OA 4, OC 6, OO  
 3. Chọn hệ trục tọa độ Oxyz có
gốc tọa độ O ; các điểm ,
A C,O lần lượt nằm trên các tia O , x O , y Oz . ’ B  ; a ;
b cthì S  a  b  c bằng Đáp án: ’
B 4;6;3 nên S  a  b  c  6 Câu 4.
Người ta theo dõi sự thay đổi cân nặng, được tính bằng hiệu cân nặng trước và sau ba tháng áp dụng chế độ
ăn kiêng của một số người cho kết quả như sau:
Thay đổi cân nặng (kg) [ 1  ;0) [0;1) [1;2) [2;3) [3; 4) Số người 2 3 5 3 2
Hãy tìm tứ phân vị thứ 3 15.3 ( 10)(3 2) Đáp án: 2,42 4 Q  2  2, 42 3 3
PHẦN IV: TỰ LUẬN. Thí sinh làm bài trên giấy câu 1 đến câu 3. Câu 1.
Trong 5 giây đầu tiên, một chất điểm chuyển động theo phương trình 3 2
s(t)  t
  6t  t  5 trong đó t tính
bằng giây và s tính bằng mét.
a.Tính vận tốc tại thời điểm t= 3s
b.Chất điểm có vận tốc tức thời lớn nhất bằng bao nhiêu trong 5 giây đầu tiên đó? a. Đáp án: 10(m/s) 3 2 2
s(t)  t
  6t  t  5  v  3
 t 12t 1 v(3)  2
 7  36 1 10(m / s) b. Đáp án: 2s v '  6
 t 12  v'  0  t  2 lập BBT ta được vận tốc tức thời lớn nhất bằng 13(m/s) khi t = 2. Câu 2.
Hình minh hoạ sơ đồ một ngôi nhà trong hệ trục tọa độ Oxyz , trong đó nền nhà, bốn bức tường và hai mái
nhà đều là hình chữ nhật.
a) Xác định toạ độ OF
Đáp án: OF  (4;0;3)
b) Tính góc dốc của mái nhà, tức là số đo của góc nhị diện có cạnh là đường thẳng FG , hai mặt lần lượt là (FGQ )
P và (FGHE) (làm tròn kết quả đến hàng phần mười của độ) Đáp án: 0
(EP, EF )  26 .3' 8 0
((FGQP), FG, (FGHE))  (EP, EF ) 
 (EP, EF)  26 ,34' 5.4 Câu 3.
Mai và Ngọc cùng sử dụng vòng đeo tay thông minh để ghi lại số bước chân hai bạn đi mỗi ngày trong một
tháng. Kết quả được ghi lại ở bảng sau:
Số bước (đơn vị: nghìn) [3;5) [5;7) [7;9) [9;11) [11;13) Mai 6 7 6 6 5 Ngọc 2 5 13 8 2
a) Hãy tính số trung bình của mẫu số liệu ghép nhóm trên.
b) Tính độ lệch chuẩn của mẫu số liệu ghép nhóm trên. Nếu so sánh theo độ lệch chuẩn thì bạn nào có số
lượng bước chân đi mỗi ngày đều đặn hơn? Kết quả các phép tính làm tròn đến hàng phần nghìn. Lời giải Giá trị đại diện 4 6 8 10 12 Mai 6 7 6 6 5 Ngọc 2 5 13 8 2
a) Cỡ mẫu: n  30
- Xét mẫu số liệu của Mai:
6.4  7.6  6.8  6.10  5.12 Số trung bình: x   7,8 1 30  2 2 2 2 2
6.4  7.6  6.8  6.10  5.12 2  b) Phương sai: 2 S   7,8  7,56 1 30
Độ lệch chuẩn:   7,56  2,75 1
- Xét mẫu số liệu của Ngọc:
2.4  5.6 13.8  8.10  2.12 Số trung bình: x   8,2 2 30  2 2 2 2 2
2.4  5.6 13.8  8.10  2.12 2  Phương sai: 2 S  8,2  3,83 2 30
Độ lệch chuẩn:   3,83 1,96 2
Nếu so sánh theo độ lệch chuẩn thì bạn Ngọc có số lượng bước chân đi mỗi ngày đều đặn hơn.