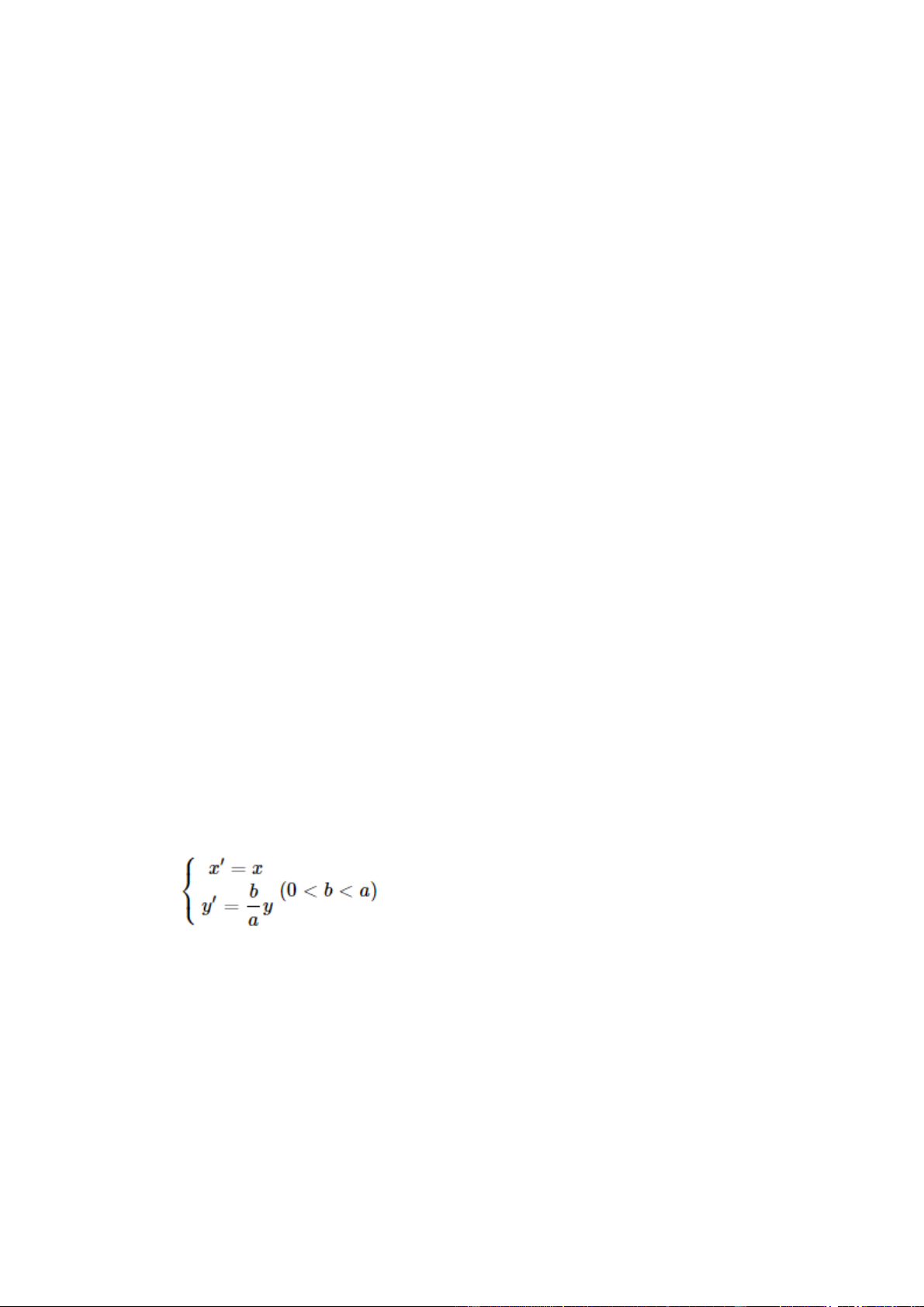




Preview text:
Hình elip là gì ? Xem là hiểu ngay
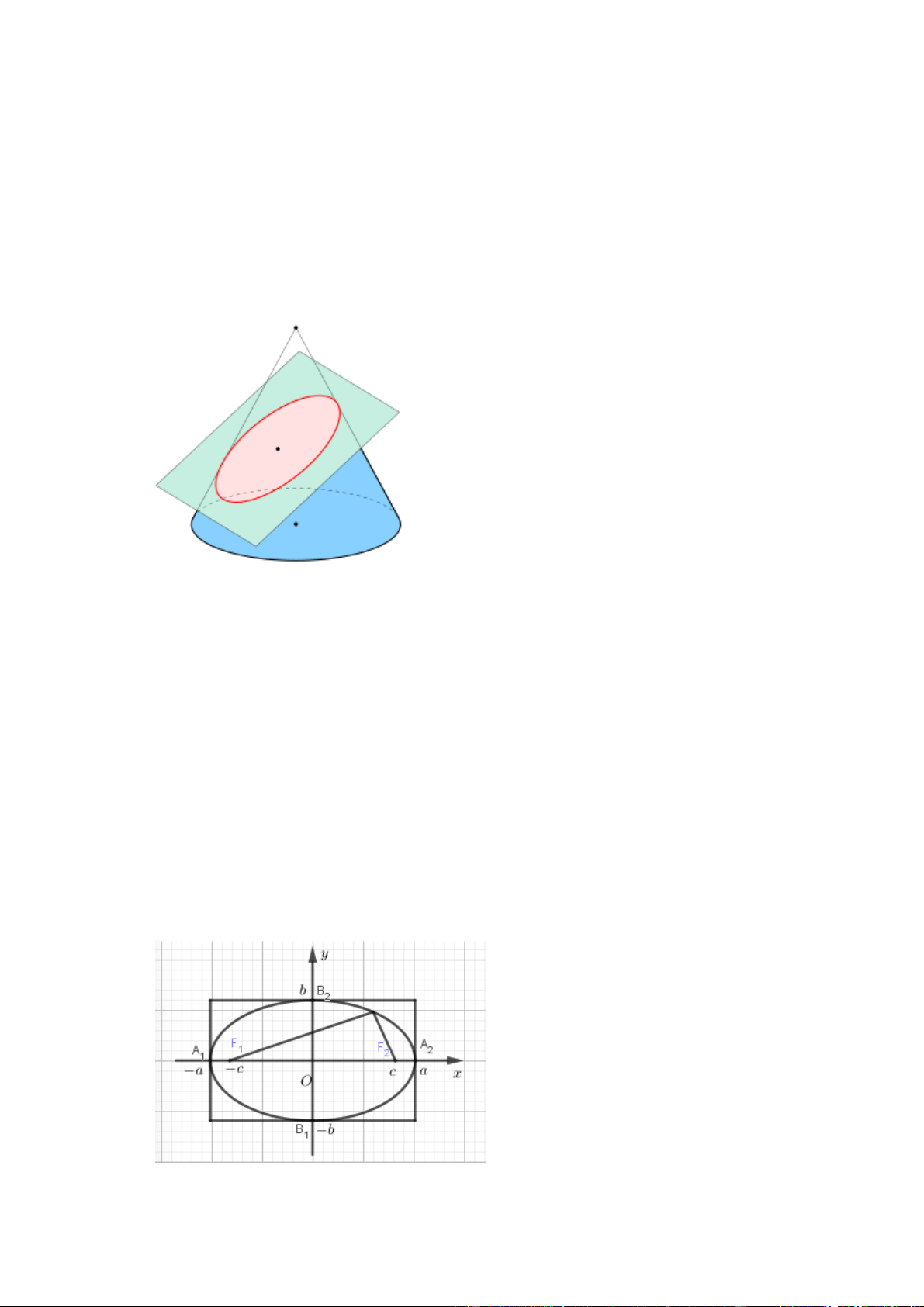
1. Định nghĩa hình elip?
- Theo wikipedia: Một hình elip là một đường cong phẳng xung quanh hai tiêu điểm, sao
cho với mọi điểm trên đường cong, tổng khoảng cách đến hai tiêu điểm là hằng số. Hình tròn
là trường hợp đặc biệt của đường elip khi hai tiêu điểm trùng nhau. Độ dẹt của hình elip được
biểu diễn bằng tâm sai e của nó, chạy tưd e = 0 (trường hợp của đường tròn) đến e = 1 ( độ dẹt
vô hạn, không còn là elip mà là một parabol)
- Theo định nghĩa Toán học:
Cho 2 điểm cố định F1, F2 với F1.F2 = 2c ( c>0) và hằng số a > c. Elip (E) là tập hợp các
điểm M thỏa mãn MF1 + MF2 = 2a.
Các điểm F1, F2 là tiêu điểm của (E)
Khoảng cách F1.F2 = 2c là tiêu cự của (E)
MF1, MF2 được gọi là bán kính qua tiêu.
2. Phương trình chính tắc của elip - Với F1 (-c; 0), F2 (x;0)
M(x;y) thuộc (E) <=> x2 / a 2 + y2 / b2 = 1 (1) trong đó b2 = a2 - c2
(1) được gọi là phương trình chính tắc của (E)
3. Hình dạng và tính chất hình elip
Elip có phương trình (1) nhận các trục tọa độ là trục đối xứng và gốc toạ độ làm tâm đối xứng
- Tiêu điểm: Tiêu điểm tráu F1(-c; 0), tiêu điểm phải F2 (x;0)
- Các đỉnh: A1 (-a;0); A2 (a;0); B1(0;-b); B2 (0;b)
- Trục lớn: A1.A2 = 2a, nằm trên trục Ox; trục nhỏ: B1.B2 = 2b, nằm trên trục Oy
- Hình chữ nhật tạo bởi các đường thẳng x = + - a, y = + - b gọi là hình chữ nhật cơ sở. - Tâm sai: e = c / a <1
- Bán kính qua tiêu điểm của điểm M (xm; ym) thuộc (E) là:
MF1 = a + exM = a + (c / a )xM, MF2 = a - exM = a = (- c / a)xM
4. Độ lệch tâm của hình elip
- Tỷ lệ khoảng cách từ tâm của hình elip từ một trong hai tiêu điểm đến bán trục chính
của elip được định nghĩa là độ lệch tâm của elip.
- Độ lệch tâm của elip, e = c / a
- Trong đó c là tiêu cự và a là độ dài của bán trục chính
- Vì c <= a nên độ lệch tâm luôn lớn hơn 1 trong trường hợp hình elip
5. Liên hệ giữa đường tròn và đường elip
- Từ hệ thức: b2 = a2 - c2 ta thấy nếu tiêu cụ của elip càng nhỏ thì b càng gần bằng a, tức
là trục nhỏ của elip càng gần bằng trực lớn. Lúc đo elip có dạng gần như đường tròn.
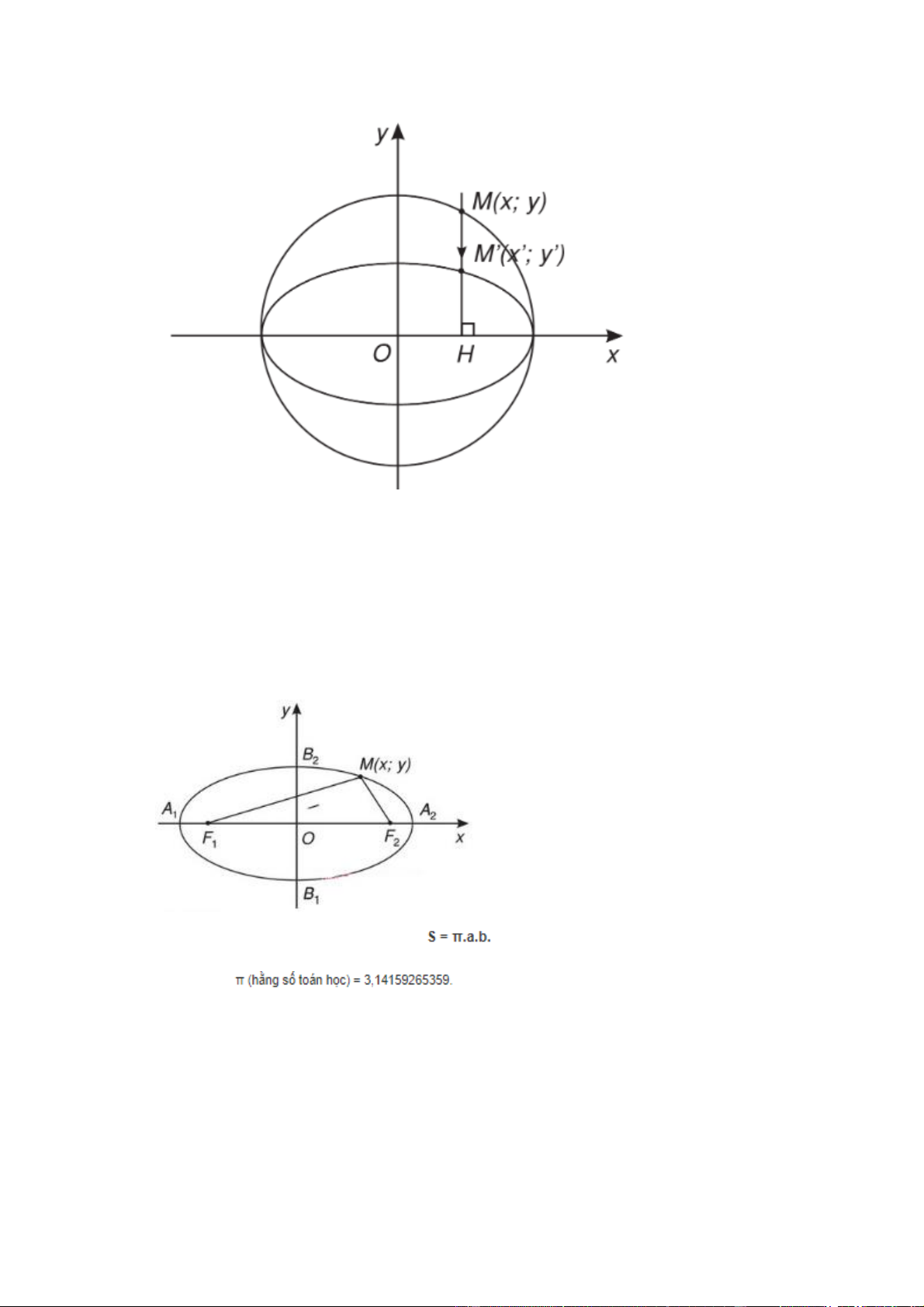
- Trong mặt phẳng Oxy cho đường tròn (C) có phương trình: x2 + y2 = a2
Với mỗi điểm M(x;y) thuộc đường tròn ta xét điểm M'(x';y') sao cho:
thì tập hợp các điểm M' có tọa độ thỏa mãn phương trình x2 / a2 + y2 / b2 = 1 là một elip (E)
Khi đó ta nói đường tròn (C) được co thành elip (E)
6. Diện tích hình elip
Hình elip có hai trục đối xứng A1A2 và B1B2 vuông góc với nhau, cắt tại tâm đối xứng
O, cắt đường elip tại trực lớn A1A2 và trục nhỏ B1B2. Nửa chiều dài trục lớn gọi là (a), trục
nhỏ là (B). Từ tâm elip O đến tiêu điểm F1, F2 gọi là bán tiêu cự (c).
Do đó, ta có: A1, A1, B1, B2 là đỉnh của hình Elip; B1B2 là trục nhỏ (2a); A1A2 là trục
lớn (2b); F1F2 là tiêu cực của hình Elip (2c).
- Công thức tính diện tích hình Elip: Trong đó,
Do đó, khi biét được độ dài trục lớn và trục nhỏ, bạn dễ dàng tính ra diện tích của hình elip.
7. Một số bài tập về hình elip
Bài 1. Cho Elip (E): x2 / 16 + y2 / 12 = 1 và điểm M nằm trên (E). Giả sử điểm M có
hoành độ bằng 1 thì các khoảng cách từ M tới 2 tiêu điểm của (E) bằng bao nhiêu? Giải: Ta có: a2 = 16, b2 = 12 nên c2 = a2 - b2 = 4
-> a = 4; c = 2 và hai tiêu điểm F1(-2;0); F2 (2;0)
Điểm M thuộc (E) và xM = 1=>
Tâm sai của elip e = c / q => e = 2 / 4 = 1 / 2
=> MF1 = a + exM = 4 + 0.5 = 4.5 MF2 = a - exM = 4 - 0.5 = 3.5
Bài 2. Trong mặt phẳng tọa độ Oxy, viết phương trình chính tắc của elip (E) có tâm sai bằng
và độ dài đường chéo hình chữ nhật cơ sở bằng . Lời giải:
Gọi phương trình chính tắc của elip (E) có dạng với a > b > 0 Tâm sai: e = c / a =
Độ dài đường chép hình chữ nhật:
<=> a2 + b2 = 5 <=> b2 = 5 - a2
Khi đó: a2 = b2 + c2 <=> a2 = 5 - a2 + a2 / 3 <=> a2 = 3 => b2 = 2
Vậy phương trình chính tắc của elip (E) cần lập là x2 / 3 + y2 / 2 = 1
Bài 3. Trong mặt phẳng tọa độ Oxy. Viết phương trình chính tắc của elip (E) biết rằng
elip (E) có hai tiêu điểm F1, F2 với
và có một điểm M thuộc (E) để tam giác
F1MF2 vuông tại M và có S = 1. Lời giải:
Gọi phương trình chính tắc của elip (E) có dạng: x2 / a2 + y2 / b2 với a > b > 0 Với , suy ra c =
=> a2 - b2 - c2 = 3 hay a2 = b2 + 3 (1) Gọi M(x0;y0) Khi đó: <=> <=> X 2 2 0 - 3 + y0 = 0 <=> x 2 2 0 + y0 = 3
Ta có: S F1MF2 = 1 / 2 d (M,Ox).F1F2 = <=> y 2 0 = 1 / 3 => x 2 0 = 8 / 3
Mặt khác M (x0;y0) thuộc E <=> x 2 2 0 / a2 + y0 / b2 = 1
<=> 8 / 3a2 + 1 / 3b2 = 1 (2)
Thay (1) vào (2) ta được: ( do b > 0) => a2 = 4
Vậy phương trình chính tắc của elip (E) cần lập là: x2 / 4 + y2 = 1
Bài 4. Trong mặt phẳng tọa độ Oxy, cho đường tròn (C): x2 + y2 = 8. Biết (E) có độ dài
trục lớn bằng 8 và (E) cắt (C) tại bốn điểm tạo thành bốn đỉnh của hình vuông. Hãy viết phương trình chính tắc elip (E) Lời giải:
Ta có phương trình chính tắc của elip (E) có dạng: x2 / a2 + y2 / b2 = 1
- (E) có độ dài trục lớn bằng 8 nên suy ra 2a =8 => a = 4
- (E) cắt (C) tại 4 điểm phân biệt tạo thành 4 đỉnh của một hình vuông => 4 đỉnh nằm
trên hai đường phân giác thuộc góc phần tư thứ nhất và thứ hai.
Ta giả sử A là một giao điểm của (E) và (C) thuộc đường phân giác denta: y = x
- Gọi A(t;t) thuộc denta ( t > 0). ta có: A thuộc (C) => t2 + t2 = 8 <=> t = 2 (vì t > 0) => A (2;2)
- Mà A thuộc (E) => 22 / 42 + 22 / b2 = 1 => b2 = 16 / 3
Vậy phương trình chính tắc của elip (E) là:
Bài 5. Trong mặt phẳng tọa độ Oxy, cho elip (E) có hai tiêu điểm và đi qua điểm
. Hãy lập phương trình chính tắc của (E) và với mọi điểm M thuộc
(E), hãy tính giá trị biểu thức: P = MF12 + MF22 - 3OM2 - MF1MF2. Lời giải:
- Gọi phương trình chính tắc của elip (E) có dạng: x2 / a2 + y2 / b2 = 1 với a > b > 0 (E) có hai tiêu điểm suy ra c =
- Khi đó a2 - b2 = c2 = 3 <=> a2 = b2 + 3=> (E): - Với thuộc (E) : - Với thuộc (E) <=>
<=> ab2 - b2 - 3 = 0 <=> (4b2 +3)(b2 - 1) = 0 <=> b2 = 1 => a2 = 4
Vậy Phương trình chính tắc của (E) là: x2 / 4 + y2 = 1 M(x0;y0) thuộc (E) => Khi đó: P = + - 3(x 2 0 + y02) - = x + - 3(x 2 2 0 +y0 ) = 4 + 9 / 4 . x 2 2 2 0 - 3(x0 + y0 ) = 4 - 3(x 2 2 0 / 4 + y0 ) = 4 - 3 = 1 Vậy P = 1
Bài 6. Cho elip (E) có tiêu cự là 2c, độ dài trục lớn và trục nhỏ lần lượt là 2a và 2b. Trong
các mệnh đề sau, mệnh đề nào đúng ? A. c < b < a B. c < a < b C. c > b > a D. c < a và b < a Đáp án: Phương pháp giải:
Áp dụng lý thuyết phương trình chính tắc của elip
Phương trình chính tắc của elip có dạng x2 / a2 + y2 / b2 = 1 Với a > b và a2 = b2 + c2 với 2c là tiêu cự của (E). Lời giải chi tiết:
Vì a2 = b2 + c2 và a, b, c > 0 nên ta có a2 > c2 <=> a > c. Hiển nhiên b < a Chọn đáp án D.




