hinh-hoc-hoa-hinh_pham-van-son_hinhhoacuoiki - [cuuduongthancongcom]

Hình học họa hình Huỳnh Quý Tuyển
TRƯỜNG ĐẠI HỌC BÁCH KHOA  ÔN TẬP HÌNH HỌA
Họ và tên:……………………………
Lớp:…………………………………. 2019 1 CuuDuongThanCong.com
https://fb.com/tailieudientucntt
Hình học họa hình Huỳnh Quý Tuyển
Chương 1: Cần nắm rõ các tính chất của phép chiếu vuông góc
( trường hợp đặc biệt của phép chiếu song song). Chương 2:
- Nắm rõ các mối tương quan giữa các hình chiếu của một điểm (độ
cao, độ xa, độ xa cạnh).
- Biểu diễn được các điểm nằm trong các góc phần tư, nằm trên
mppg1, 2 (chú ý hình chiếu đối xứng qua trục x và trùng nhau).
- Tìm được hình chiếu thứ 3 khi biết được 2 hình chiếu. Chương 3:
- Biểu diễn được các đường thẳng có vị trí đặc biệt so với các mphc
(đường bằng, đường mặt, đường cạnh; đường thẳng chiếu bằng,
đường thẳng chiếu đứng, đường thẳng chiếu cạnh).
- Bài toán điểm thuộc đường thẳng.
- Vết của đường thẳng (cần nhớ hình chiếu nào của vết nằm trên trục x).
- Vị trí tương đối của 2 đường thẳng (chú ý trường hợp có đường thẳng đặc biệt). Chương 4:
- Biểu diễn được mặt phẳng trong các trường hợp khác nhau, mặt phẳng bằng vết.
- Các mặt phẳng có vị trí đặc biệt so với các mphc (vị trí vuông góc, song song).
- Thuộc làu 2 bài toán cơ bản của mặt phẳng (sử dụng liên tục trong các phần sau).
- Điêu kiện để 2 mặt phẳng song song, đường thẳng song song với mặt phẳng.
- Bài toán giao của 2 mặt phảng trong trường hợp đặc biệt (một
trong hai là mặt phẳng chiếu) --> xem như biết trước một hình
chiếu của giao tuyến, trùng với hình chiếu suy biến của mặt phẳng
chiếu, để tìm hình chiếu còn lại sử dụng bài toán cơ bản.
- Giao 2 mặt phẳng cho bằng vết (trường hợp tổng quát) cũng xem
như đặc biệt vì đã biết trước 2 điểm chung của 2 mặt phẳng.
- Giao của đường thẳng và mặt phẳng trong trường hợp đặc biệt
(một trong hai là đối tượng chiếu) --> xem như biết trước một hình
chiếu của giao điểm, trùng với hình chiếu suy biến của đường thẳng
chiếu (hoặc giao của hình chiếu suy biến của mặt phẳng chiếu với 2 CuuDuongThanCong.com
https://fb.com/tailieudientucntt
Hình học họa hình Huỳnh Quý Tuyển
hình chiếu tương ứng của đường thẳng), để tìm hình chiếu còn lại
sử dụng bài toán cơ bản (hoặc bài toán điểm thuộc đường thẳng). Chương 5:
- Cần nắm rõ các tính chất của các đối tượng đặc biệt để biết vị trí
của mặt phẳng thay đổi nằm ở đâu. Nếu không nắm rõ sẽ không làm được. Chương 6:
- Biểu diễn được đường tròn nằm trên mặt phẳng chiếu. Để xác
định được elip thì cần biết gì?
- Biểu diễn được mặt đa diện và điểm thuộc mặt đa diện ( thực chất
là bài toán cơ bản xét trên nhiều miếng phẳng).
- Biểu diễn các mặt cong tròn xoay bậc 2 (nhớ quỹ tích của mặt
cong bậc 2) và điểm thuộc mặt cong này (chú ý cách gắn điểm).
Chương 7: Trong chương này chia ra 3 phần
7.1. Phần 1: Giao của mặt phẳng với mặt (chỉ xét trường hợp đặc biệt).
- Giao của mặt phẳng với đa diện, giao tuyến là giác. Biết trước 1
hình chiếu của đa giác trùng với hình chiếu suy biến của mặt phẳng
chiếu (nằm trong phạm vi của đa diện) hoặc trùng với hình chiếu
của lăng trụ. Để tìm hình chiếu còn lại của giao tuyến xét bài toán
điểm thuộc mặt hoặc bài toán cơ bản.
- Giao của mặt phẳng với mặt cong tròn xoay bậc 2, tùy vào vị trí
của mặt phẳng, giao có thể là điểm, đường thẳng, đường cong bậc 2
( đường tròn, elip, parabol, hypebol). Biết trước 1 hình chiếu của
giao trùng với hình chiếu suy biến của mặt phẳng chiếu (nằm trong
phạm vi của mặt cong tròn xoay bậc 2) hoặc trùng với hình chiếu
của trụ. Để tìm hình chiếu còn lại của giao tuyến xét bài toán điểm
thuộc mặt cong tròn xoay bậc 2 hoặc bài toán cơ bản.
7.2. Phần 2: Giao của đường thẳng với mặt
- Trường hợp đặc biệt: luôn biết trước 1 hình chiếu của giao điểm
trùng với hình chiếu suy biến của đường thẳng hoặc giao của hình
chiếu suy biến của mặt với hình chiếu của đường thẳng tương ứng.
Tìm hình chiếu còn lại sử dụng bài toán điểm thuộc mặt hoặc điểm thuộc đường thẳng. 3 CuuDuongThanCong.com
https://fb.com/tailieudientucntt
Hình học họa hình Huỳnh Quý Tuyển
- Trường hợp tổng quát: sử dụng phương pháp mặt phẳng phụ trợ
(chú ý chọn mặt phẳng phụ trợ chứa đường thẳng và có vị trí thuận
lợi để dễ tìm giao tuyến).
* Bài toán tổng quát: Cần có suy luận để tìm hướng giải quyết của
bài toán, sau đó dựng bài toán và tiến hành giải. Thông thường liên
quan đến một số dạng quỹ tích sau:
- Những điểm cách đều 2 điểm cho trước --> mặt phảng trung trực của 2 điểm đó.
- Những điểm cách 1 điểm cho trước khoảng không đổi, những
điểm nhìn 2 điểm cho trước dưới góc vuông --> mặt cầu.
- Những điểm cách đường thẳng cho trước khoảng không đổi,
những đường thẳng song song và cách đường thẳng cho trước
khoảng không đổi --> mặt trụ tròn xoay.
- Những điểm, đường thẳng đi quan một điểm cố định và nghiêng
với mặt phẳng cho trước 1 góc không đổi --> mặt nón tròn xoay.
- Ngoài ra chú ý giao với mặt phẳng phân giác.
Phần 3: Giao của hai mặt: Chỉ xét bài toán trong trường hợp đặc
biệt, biết trước 1 hình chiếu của giao tuyến (chú ý giao hoàn toàn
hay không hoàn toàn), để tìm hình chiếu còn lại xét bài toán điểm
thuộc mặt, để nối giao tuyến cần xét thấy khuất.
- Dạng 1- Giao hai đa diện: giao tuyến là 1 đường gấp khúc kín
(giao không hoàn toàn), 2 đường gấp khúc kín (giao hoàn toàn)
gồm các đoạn thẳng. Biết trước 1 hình chiếu của giao tuyến trùng
với hình chiếu suy biến của đa diện chiếu (trong phạm vi của đa
diện còn lai). Để tìm hình chiếu còn lại xét bài toán điểm thuộc mặt.
- Dạng 2- Giao đa diện và mặt cong:
Giao tuyến là đường gấp khúc kín gồm các thẳng, cong.
- Dạng 3- Giao 2 mặt cong: Giao tuyến là đường cong ghềnh bậc 4
(Nguồn: Thầy Nguyễn Đức Sỹ)
Trên là những lưu ý của các bạn để đạt điểm cao, các bạn cần cố
gắng luyện tập để thành thạo và giải quyết nhiều bài toàn. 4 CuuDuongThanCong.com
https://fb.com/tailieudientucntt
Hình học họa hình Huỳnh Quý Tuyển CẤU TRÚC ĐỀ THI Câu 1: (4 điểm)
- Xoay quanh các bài toán về Quỹ tích , một số bài về số bài về
đường và mặt, đa phần giống thi giữa kỳ.
- Vẽ giao tuyến với đường và mặt, giao tuyến với MP phân giác 1, 2..vv..
Đây là phần khó trong đề thi. Câu 2: (6 điểm)
- Xác định giao tuyến của mặt và mặt, xét thấy khuất ..vv :
Mặt cầu với nón, mặt cầu với trụ tròn, lăng trụ với lăng trụ ..vv..
Đây là phần dễ của bài thi, cần làm trước, cẩn thận, tỉ mỉ kể cả
từng dấu mũi tên. Ăn chắc 6 điểm.
(Tham khảo các tài liệu và bài tập của thầy Phan Tường thầy
Nguyễn Đức Sỹ và thầy Dương Thọ) 5 CuuDuongThanCong.com
https://fb.com/tailieudientucntt
Hình học họa hình Huỳnh Quý Tuyển
Phần 1: ÔN TẬP CÂU 6 ĐIỂM I. Vẽ một điểm :
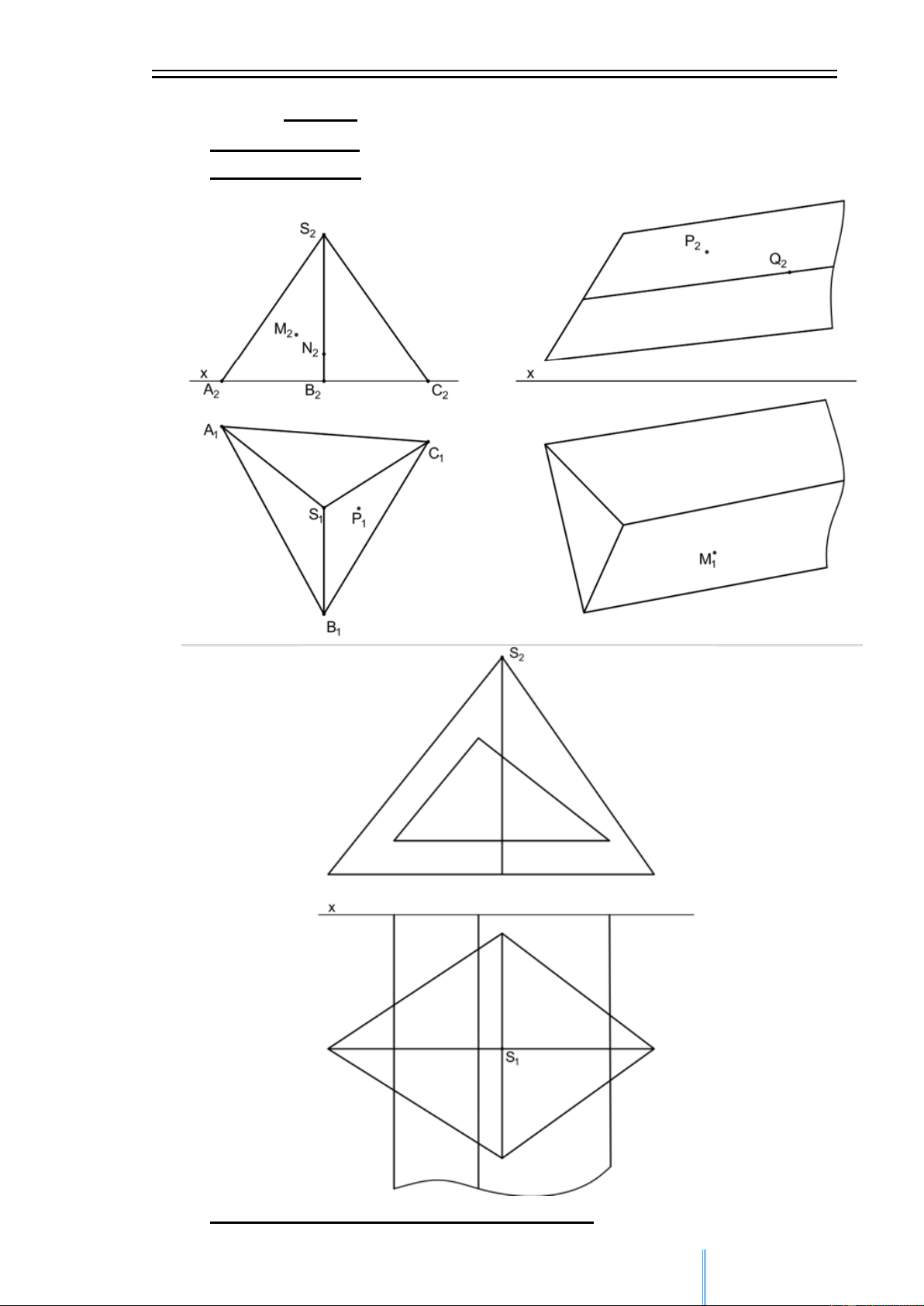
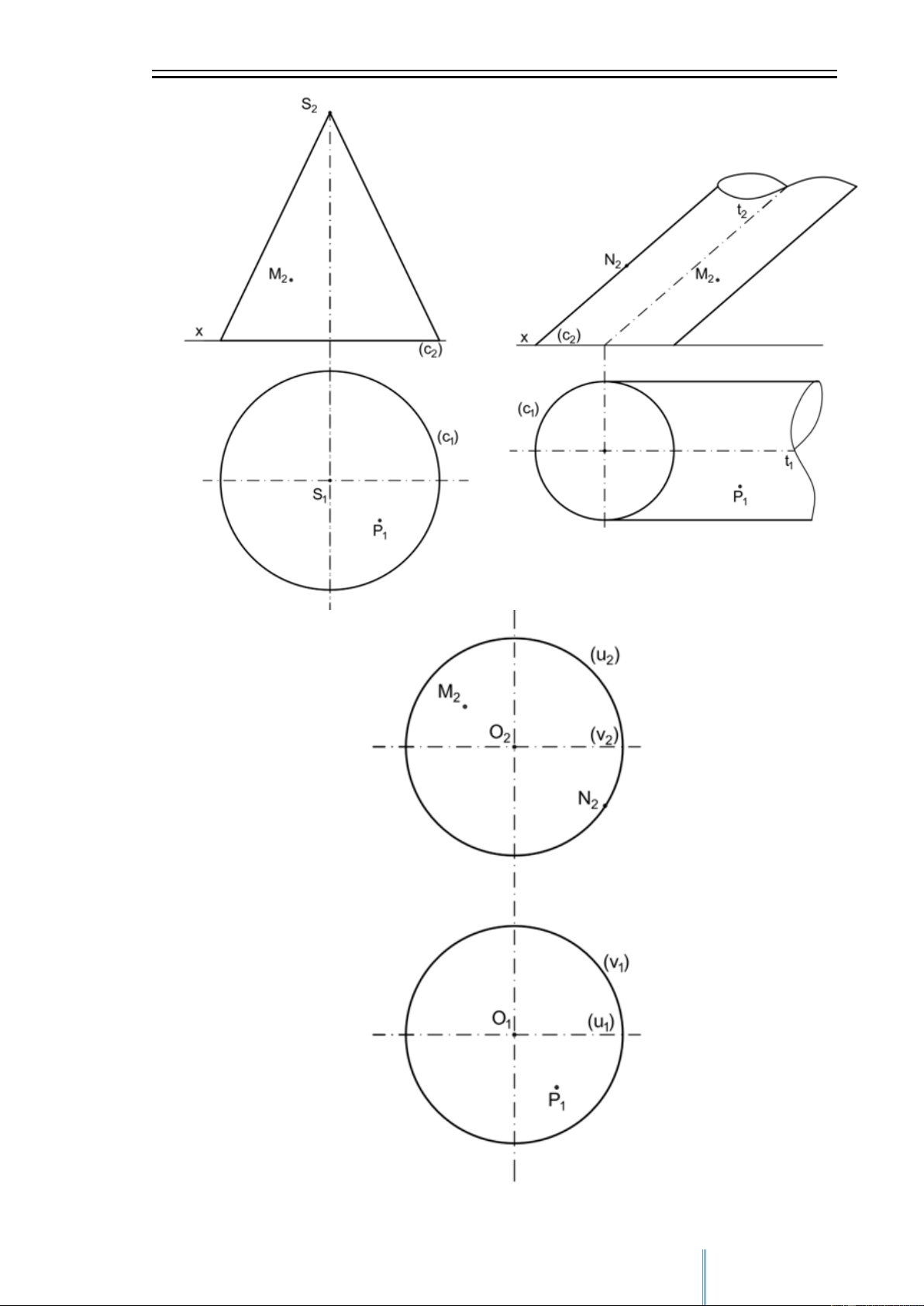
1. Thuộc đa diện
2. Thuộc nón và thuộc trụ tròn và cầu: 6 CuuDuongThanCong.com
https://fb.com/tailieudientucntt
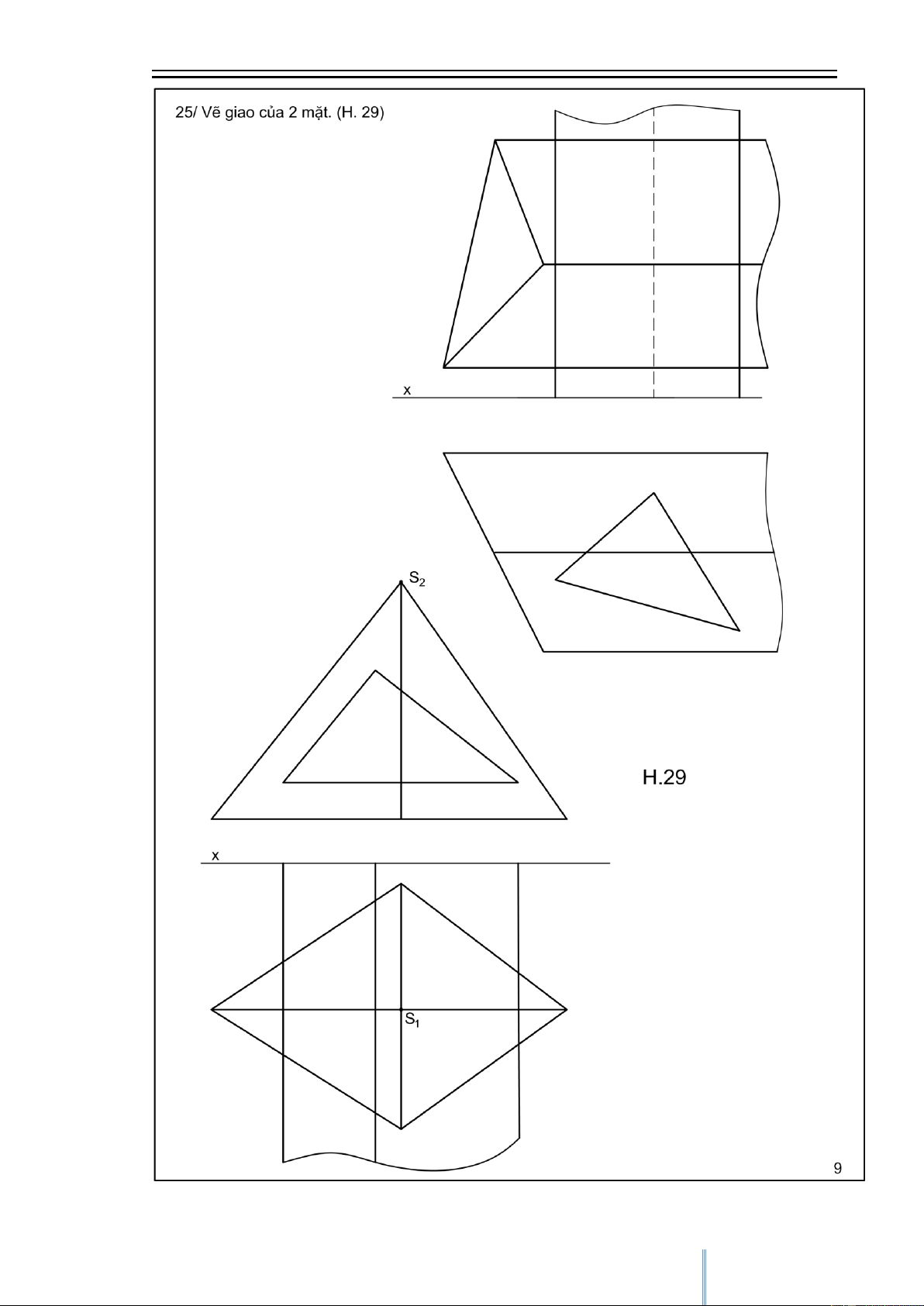
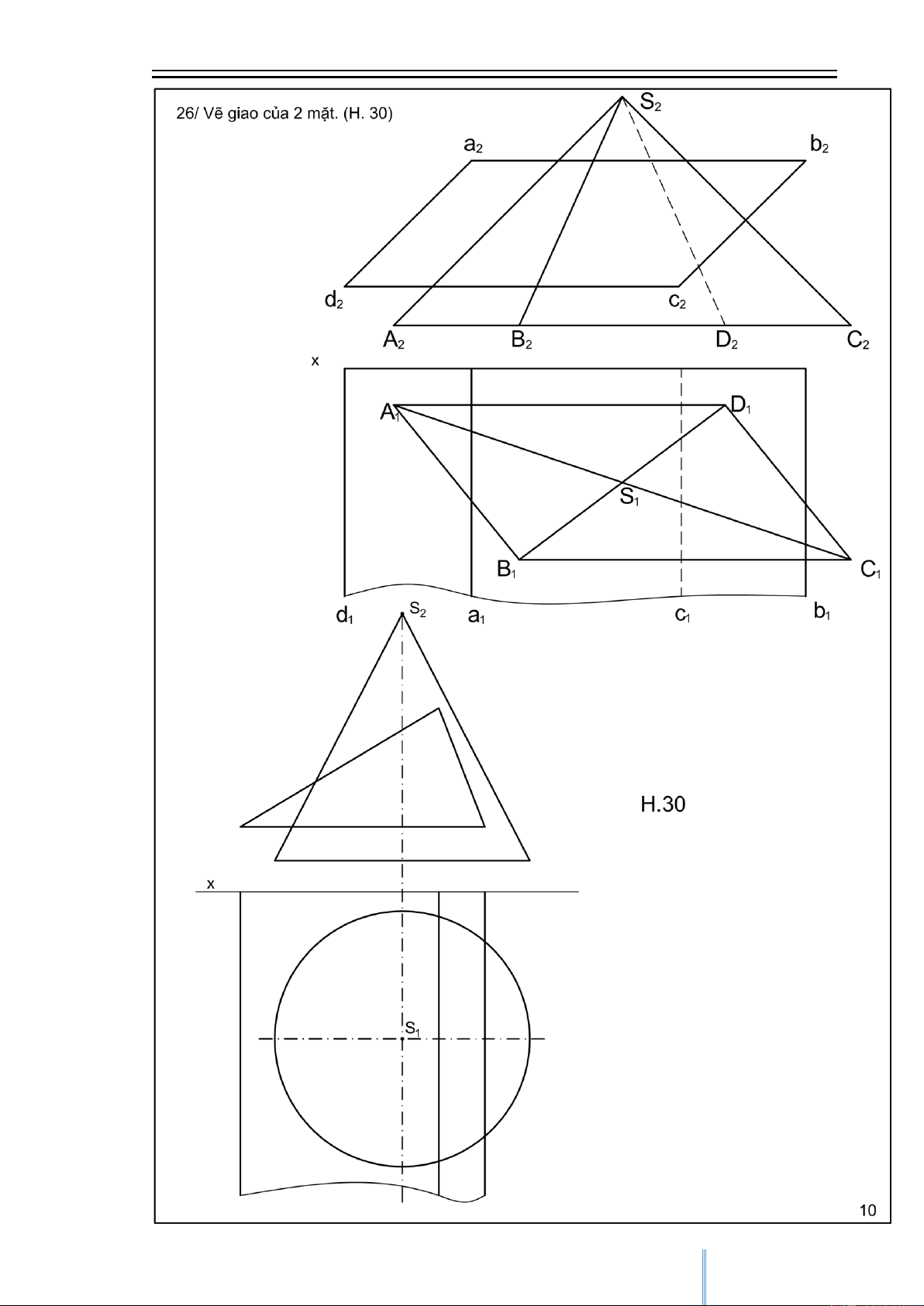
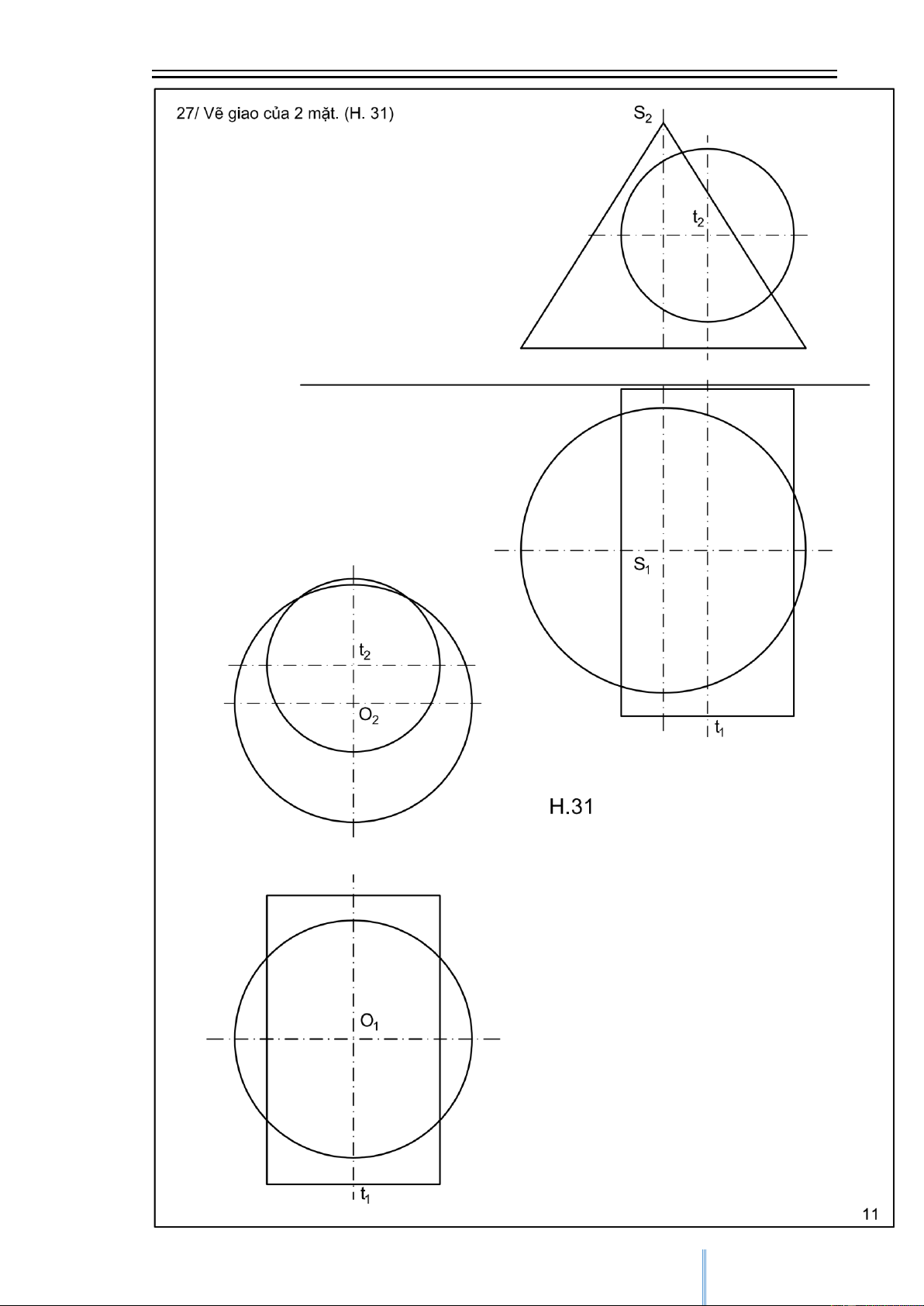
Hình học họa hình Huỳnh Quý Tuyển Các bài tập mẫu 7 CuuDuongThanCong.com
https://fb.com/tailieudientucntt
Hình học họa hình Huỳnh Quý Tuyển 8 CuuDuongThanCong.com
https://fb.com/tailieudientucntt
Hình học họa hình Huỳnh Quý Tuyển 9 CuuDuongThanCong.com
https://fb.com/tailieudientucntt
Hình học họa hình Huỳnh Quý Tuyển 10 CuuDuongThanCong.com
https://fb.com/tailieudientucntt
Hình học họa hình Huỳnh Quý Tuyển
Phần 2: Bài giải mẫu:
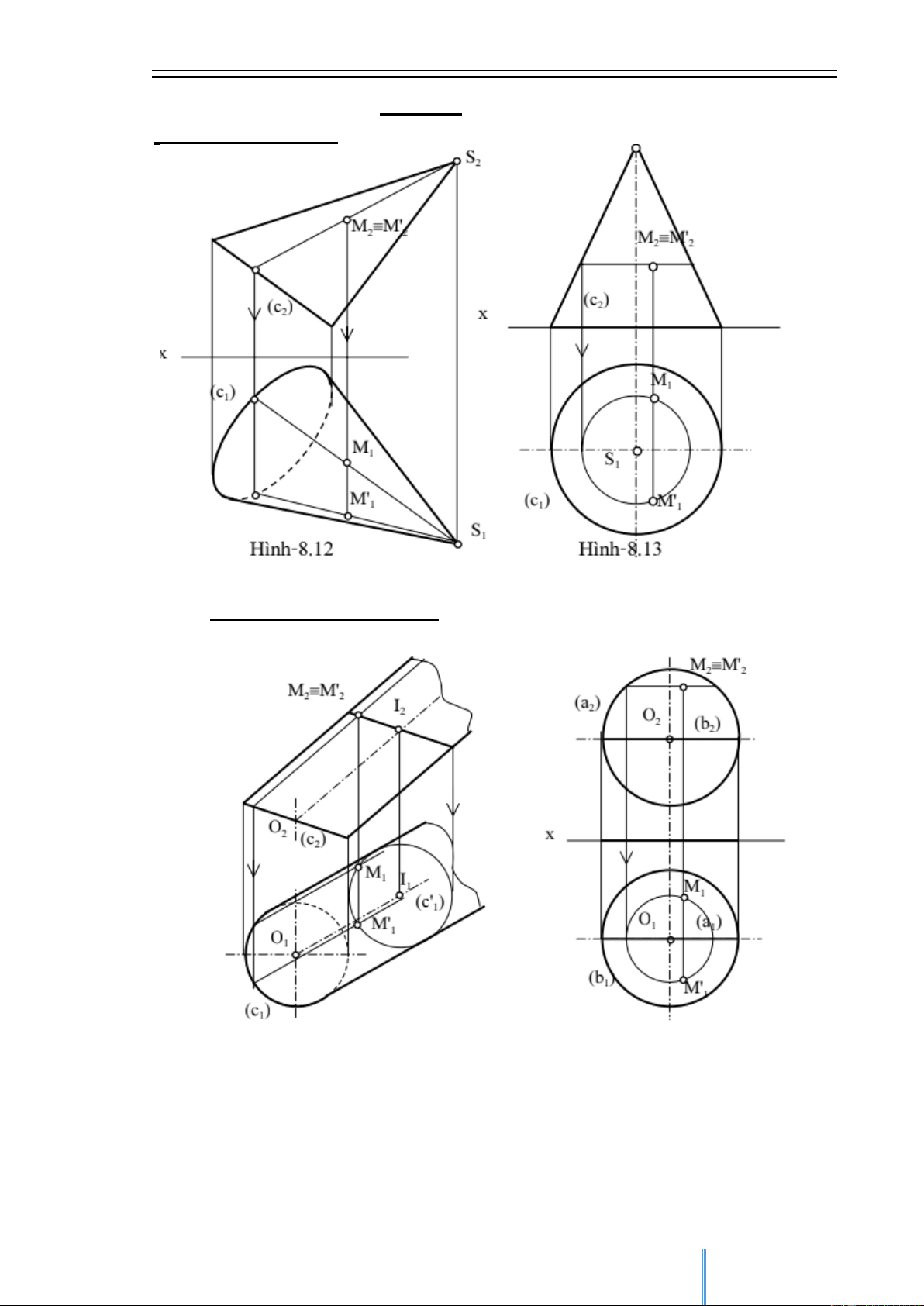
1.Điểm thuộc nón
3. Điểm thuộc trụ và cầu 11 CuuDuongThanCong.com
https://fb.com/tailieudientucntt
Hình học họa hình Huỳnh Quý Tuyển 4.
Mặt phằng anpha 12 CuuDuongThanCong.com
https://fb.com/tailieudientucntt
Hình học họa hình Huỳnh Quý Tuyển 5.
Lăng trụ giao với lăng trụ 13 CuuDuongThanCong.com
https://fb.com/tailieudientucntt