Học bài & tổng hợp kiến thức căn bản môn Toán cao cấp C1 | Trường Đại học Duy Tân

Kí hiệu: MTH101 Tín chỉ: 3 (LEC 2, REC 1) Giáo viên: Nguyễn Thị Ngọc Châu 0935317657 nguyentngocbich@dtu.edu.vn
Phòng 707 ( Cơ sở 3 Quang Trung) Thứ 5 (14h-16h)
Sách: Giải tích cho kinh tế, quản trị, khoa học sự sống và xã hội (Phòng 607 Phan Thanh)
Calculus for business, economics, emd the social and life science. Mục tiêu: Ghi nhớ Giải quyết Áp dụng 19/10/22: I.
Hàm số và đồ thị 1. Hàm số 1.Hàm số: • Khái niệm: •
Hàm: 1 quy tắc cho tương ứng mỗi phần tử thuộc tập A với 1 và chỉ 1 phần tử thuộc tập B. • Tập A: TXĐ • Tập B: miền giá trị •
Nếu A, B là các tập số thì hàm được gọi là hàm số. • Các cách biểu diễn: • Công thức: y = f(x). • x: biến độc lập • y: biến phụ thuộc
f(x): giá trị của hàm f tại x Bảng giá trị: Năm 2010 2011 2012 2013 2014 Số dân 86,93 87,8 90,4 91,5 92,5 • Phương trình: • 2y-10=x y=10+12x
→ Phương trình trên xác định y là hàm theo x • x2+ y2=9
→ Phương trình này không xác định y là hàm theo x (Vì x=0 y=3) Biểu diễn bằng lời:
Với mỗi người công dân đều có mỗi mã số CCCD riêng tương ứng với mỗi người. •
Định nghĩa miền xác định: • Kí hiệu: D •
Miền xác định của hàm số y = f(x) là tập hợp các số thực x sao cho f(x) xác định
→ Tính được giá trị f(x) tại x • Cho y=x
x=1f(1) =1 ⇒ f(x) xác định
x=-9 f(-9) không tính được ⇒ f(x) không xác định • Cho f(x)=x+10 a. Tìm D?
f(x) xác định với ∀x ∈ R ⇒ D = R b.
Tính f(2), f(5)? f(2) = 12 f(5) = 15 Cho f(x)=xx+3-4x a. Tìm D? f(x) xác định x+30x-3 ⇒ D = R \ {3}
b. f(0) = 0 f(-3) không xác định vì x = 3 ∉ D • Cho f(x)=4-x2+10x a. Tìm D? f(x) xác định 4-x20-2x2 ⇒ D = 〔-2;2〕 b. Tính f(0), f(3), f(-4)? f(0) = 2
f(3) không xác định vì x = 3 ∉ D f(-
4) không xác định vì x = -4 ∉ D •
Tổng chi phí sản xuất x đvsp của mặt hàng: C(x)=x2+25x+200(đô)
a. Tính chi phí sản xuất 5 đơn vị? C(5) = 350(đô)
b. Tính chi phí sản xuất đvsp thứ 5? C(5) - C(4) = 34(đô)
c. Tính chi phí trung bình mỗi đvsp khi 5 đvsp được sản xuất? C(5)5=70(đô) •
Khi sản xuất x(đvsp) thì tổng doanh thu là R(x)=-x2+40(triệu đồng)
a. Tính doanh thu khi sản xuất 5 đvsp? R(5) = 175(triệu đồng)
b. Tính doanh thu khi sản xuất đvsp thứ 7?
R(7) - R(6) = 27(triệu đồng)
c. Cần sản xuất bao nhiêu đvsp để doanh thu đạt 300(triệu đồng) -
x2+40x=300300 x = 10(đvsp)(chọn) x = 30(đvsp) •
Dân số của thành phố A sau t năm tính từ đầu năm 2022 là:
P(t) = 5t + 120(nghìn người)
a. Dân số của thành phố A vào đầu năm 2025 là bao nhiêu? P(3) = 135(nghìn người)
b. Dân số của thành phố A tăng bao nhiêu trong suốt năm 2025?
P(4) - P(3) = 5(nghìn người)
c. Khi nào dân số thành phố A đạt 200 nghìn người?
5t + 120 = 200 ⇔ t = 16(năm) ⇒ vào năm 2038 • BTVN: •
Khi sản xuất và bán ra x(đvsp) thì giá bán của 1 đvsp là p(x) =
30003x+25+4(đvtt). Xác định số đvsp cần sản xuất và bán ra để giá bán của 1 đvsp là 5,2(đvtt)
3003x+25+4=5,23003x+25+12x+1003x+25=785x+1303x+25 300+12x+100=785x+130 -185x=-270 x=75(đvsp) Doanh số bán hàng sau t tháng tính
từ 2/2021 được cho bởi công thức s(t) = 1204+t(đvsp). Tính doanh số bán hàng vào 7/2021?
s(6) - s(5) = 19,47331922(đvsp) •
Người ta ước tính rằng sau t năm tính từ bây giờ, dân số ở 1 vùng ngoại ô sẽ là
P(t) = 20-6t+1(nghìn người)
a. Dân số của vùng sau 5 năm? P(5) = 19(nghìn người)
b. Dân số thay đổi như thế nào trong năm thứ 2?
P(2) - P(1) = 1(nghìn người) ⇒ Tăng 1 nghìn người
c. Dân số tăng bao nhiêu trong 4 năm đầu? P(4) - P(0) = 14(triệu người) 23/10/22:
2. 1 số hàm trong kinh tế: •
Hàm giá: p = ax + b Trong đó: •
x là số đơn vị sản xuất (cung/cầu) •
p là giá bán của 1 đơn vị • a, b ∈ R • Vd: p(20) = 50
→ Khi sản xuất 20 đơn vị sản phẩm thì giá bán của 1 đơn vị sản phẩm là 50＄ • Hàm chi phí:
C = chi phí 1 đơn vị * số đơn vị + chi phí cố định (nếu có) Trong đó:
• Chi phí đơn vị * số đơn vị: chi phí sản xuất
• Chi phí cố định: chi phí ban đầu Hàm doanh thu:
R = giá bán * số đơn vị Hàm lợi nhuận: • P = R - C •
P = (giá bán - chi phí 1 đơn vị) * số đơn vị •
Giá bán - chi phí 1 đơn vị: lợi nhuận 1 đơn vị • Vd: •
Tổng chi phí mỗi tuần của công ty A gồm chi phí cố định là 500(triệu đồng),
chi phí sản xuất mỗi đơn vị là 60,000(đ). Lập hàm tổng chi phí mỗi tuần của
công ty A khi sản xuất ra x đơn vị sản phẩm.
C(x) = 0.06x + 500 (triệu đồng) •
Công ty A nhận định rằng, khi sản xuất x đơn vị sản phẩm thì giá của mỗi
sản phẩm là p(x) = 140 - x.
a. Lập hàm doanh thu của công ty A? R=p(x)*x(140-x)*x -x2+140x
b. Nếu phí sản xuất x đơn vị sản phẩm là: C(x) = 5x +3,000. Hãy
lập hàm lợi nhuận hằng ngày của công ty A? P=-x2+140-5x-3,000 =-x2+135x-3,000 •
Khi sản xuất x đơn vị sản phẩm mỗi tháng thì giá bán của mỗi đơn vị sản phẩm
là: p(x) = -2x + 100(＄). Biết rằng chi phí sản xuất mỗi đơn vị sản phẩm là 4＄.
Tìm lợi nhuận khi xuất 30 đơn vị sản phẩm mỗi tháng? P(x) = (-2x+100-4) *x =-2x2+96x P(30)=1080(＄)
Hàm trung bình mỗi đơn vị: •
Nếu C(x) là chi phí sản xuất x đơn vị thì chi phí sản xuất trung bình mỗi đơn vị
được ký hiệu và xác định bởi: C(x)=C(x)x •
Ví dụ: Doanh thu khi sản xuất x máy tính: R(x)=-x2+120x (triệu đồng) a.
Tìm hàm doanh thu trung bình? R(x)=R(x)x=-x2+120xx=-x+120 b.
Tính doanh thu trung bình của mỗi máy tình khi sản xuất 80
máy? R(80)=40 (triệu đồng / máy) 86 (SGK 16): a. b. p(11) = 1,340 ($) p(18) = 920 ($) 1.2. Hàm số 1. Đồ thị của hàm số: •
Khái niệm: Đồ thị của hàm số y = f(x) là tập hợp tất cả các điểm (x, y); trong đó x
thuộc miền xác định của f và y = f(x). •
Đồ thị của y = f(x) là 1 đường thẳng hoặc cong trên trục tọa độ xOy. •
Phương pháp vẽ đồ thị của hàm số y = f(x): • Bước 1: Tìm TXĐ. •
Bước 2: Lập bảng giá trị (chọn x và tính giá trị y tương ứng). •
Bước 3: Vẽ các cặp điểm (x, y) lên mặt phẳng tọa độ Oxy. •
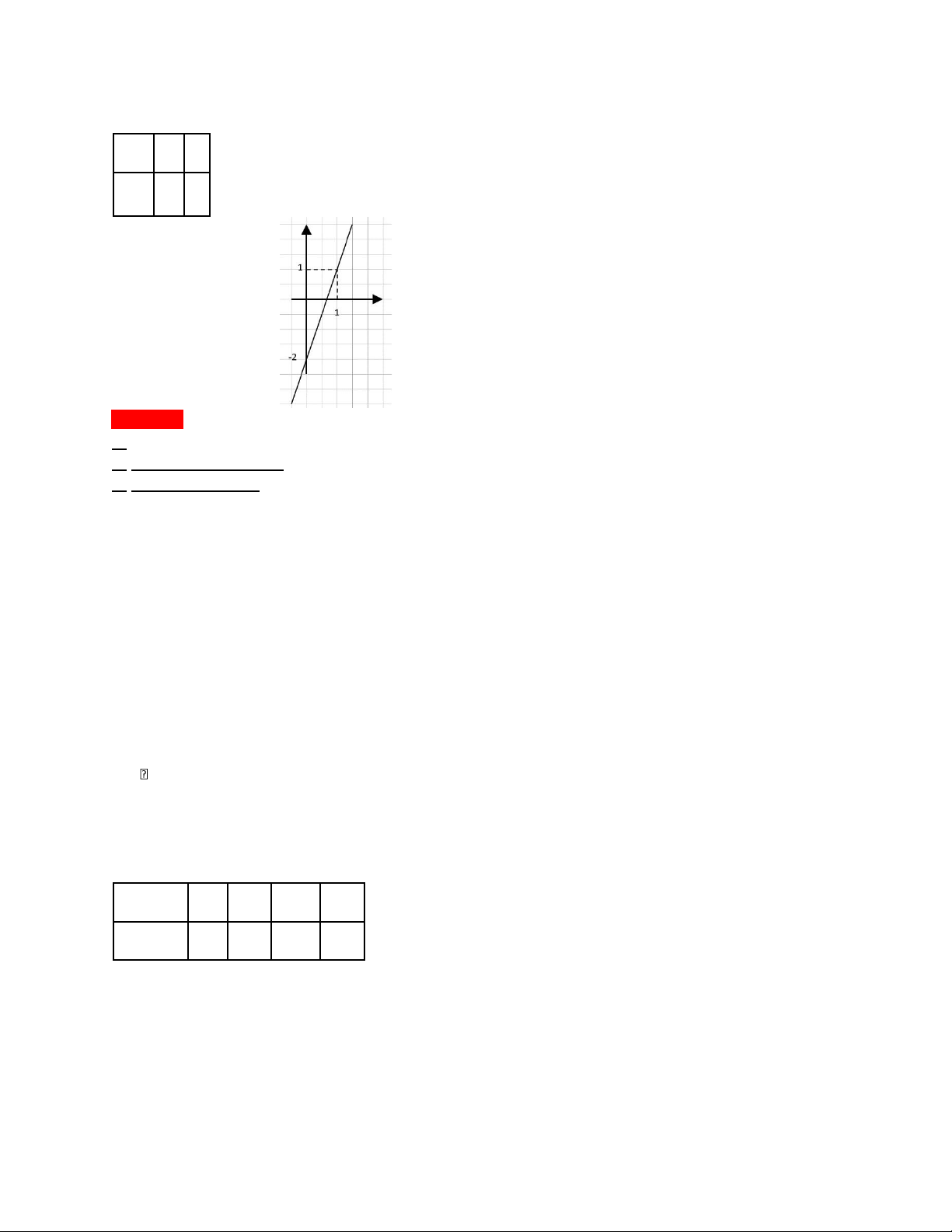
Bước 4: Nối các điểm trong bước 3 bằng 1 đường trơn (thẳng hoặc cong). • Vẽ đồ thị: a. f(x) = 3x - 2. D = R. x 0 1 - f(x) 1 2 26/10/22: 2. Hàm 2. Hàm sơ cấp (Sách): 3. Hàm từng mảnh: •
Hàm từng mảnh là hàm có nhiều hơn 1 công thức. • Có dạng:
f(x) = công thức 1 nếu điều kiện 1.
công thức 2 nếu điều kiện
2. ….. công thức n nếu điều kiện n. •
Vd: f(x) = 4x - 1 nếu x < 2. x2 + 2 nếu x 2. a. Tìm D? D = (-;2) [2;+) = R
b. Tính f(-2), f(1), f(2), f(4)? f(-2) = -9. f(1) = 3. f(2) = 6. f(4) = 18. 69 (28):
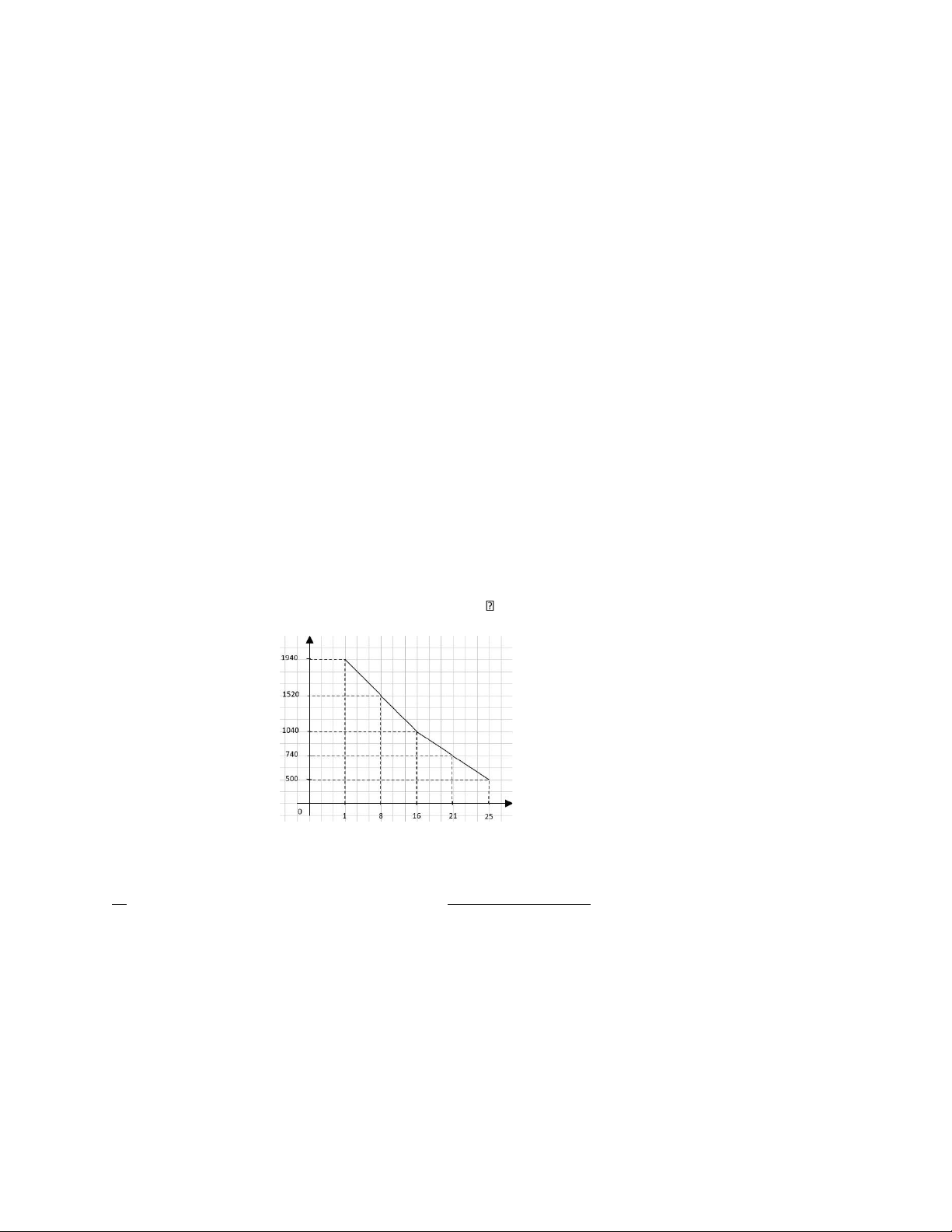
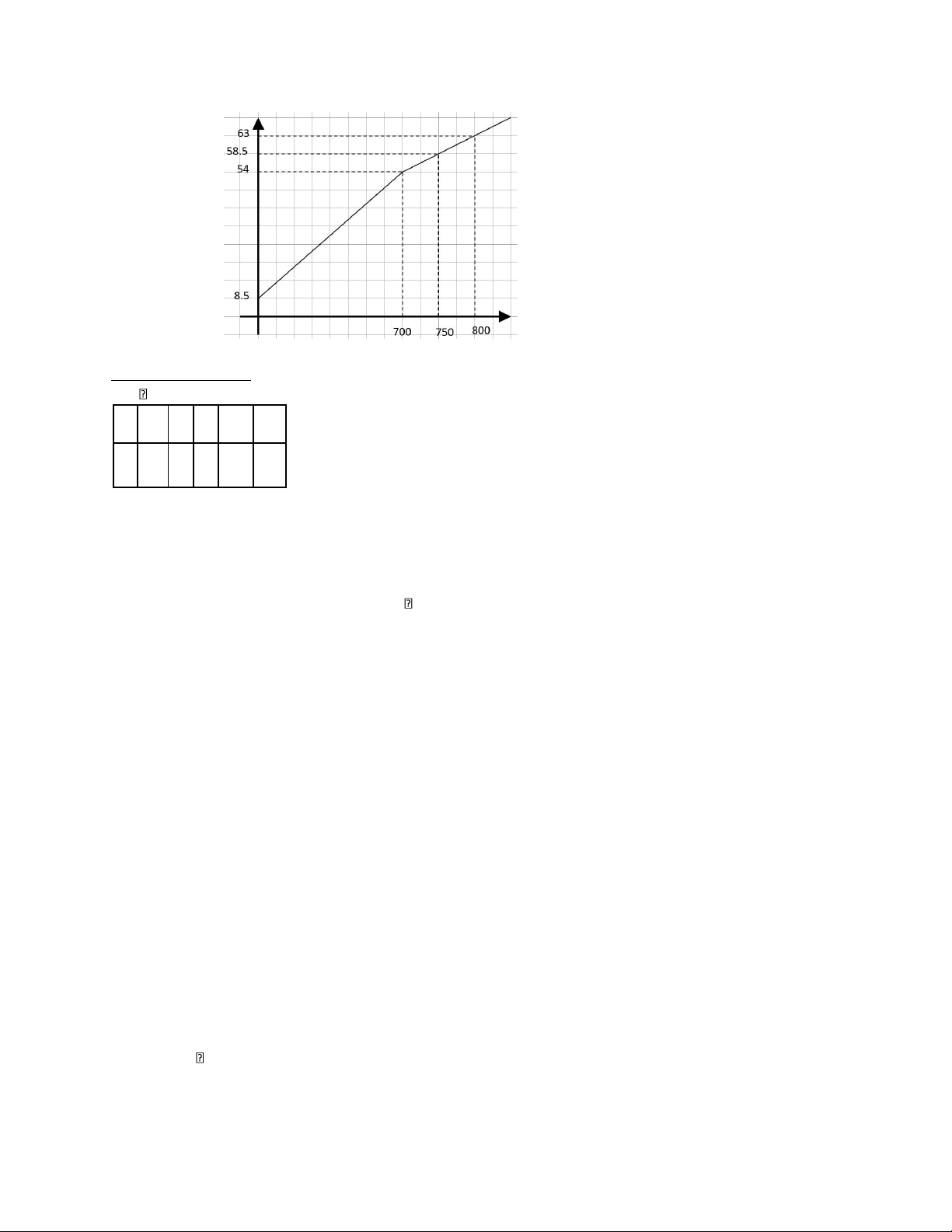
a. f(x) = 8.5 + 0.065x nếu 0 x 700. -9 + 0.09x nếu x > 700. b. x (kWh) 0 700 750 800 S(x) ($) 8.5 54 58.5 63 1.3.
Hàm tuyến tính và hàm bậc hai 1. Hàm tuyến tính: Vd: x 0 1 2 3 … - y 2 6 10 … 2 Nhận xét: x 1 y 4. y là hàm tuyến tính. • Khái niệm: •
Hàm tuyến tính là 1 hàm mà giá trị của nó thay đổi (tăng/giảm) với 1 tốc độ
không đổi với biến độc lập.
Công thức: y = ax + b (a 0)
a: hệ số góc = tốc độ thay đổi. • a > 0 thì y . • a < 0 thì y . •
Ý nghĩa: nếu x 1 thì y a đơn vị. •
Hệ số góc của hàm tuyến tính đi qua 2 điểm A (x1;y1) và B (x2;y2). a = y2-y1x2-x1. • Vd: A (1;5), B (2, 10) a = 5. • Vd: •
Giả sử giá trị sản phẩm A đang giảm với 1 tốc độ không đổi là 100 (nghìn
đồng/tháng). Hãy xác định hệ số góc của hàm biểu diễn giá mặt hàng A theo thời gian.
Vì giá giảm với tốc độ không đổi là 100 nghìn đồng/tháng a = -100. •
Giá trị của 1 mảnh đất đang tăng với tốc độ không đổi trong các năm gần
đây. Hiện tại giá trị mảnh đất là 400 (triệu đồng) và sau 3 năm giá trị của
mảnh đất là 900 (triệu đồng). Hãy xác định tốc độ tăng giá mỗi năm của mảnh đất đó. Theo bài ra ta có: A (0,400) B (3,900) a = 166.7 (triệu đồng).
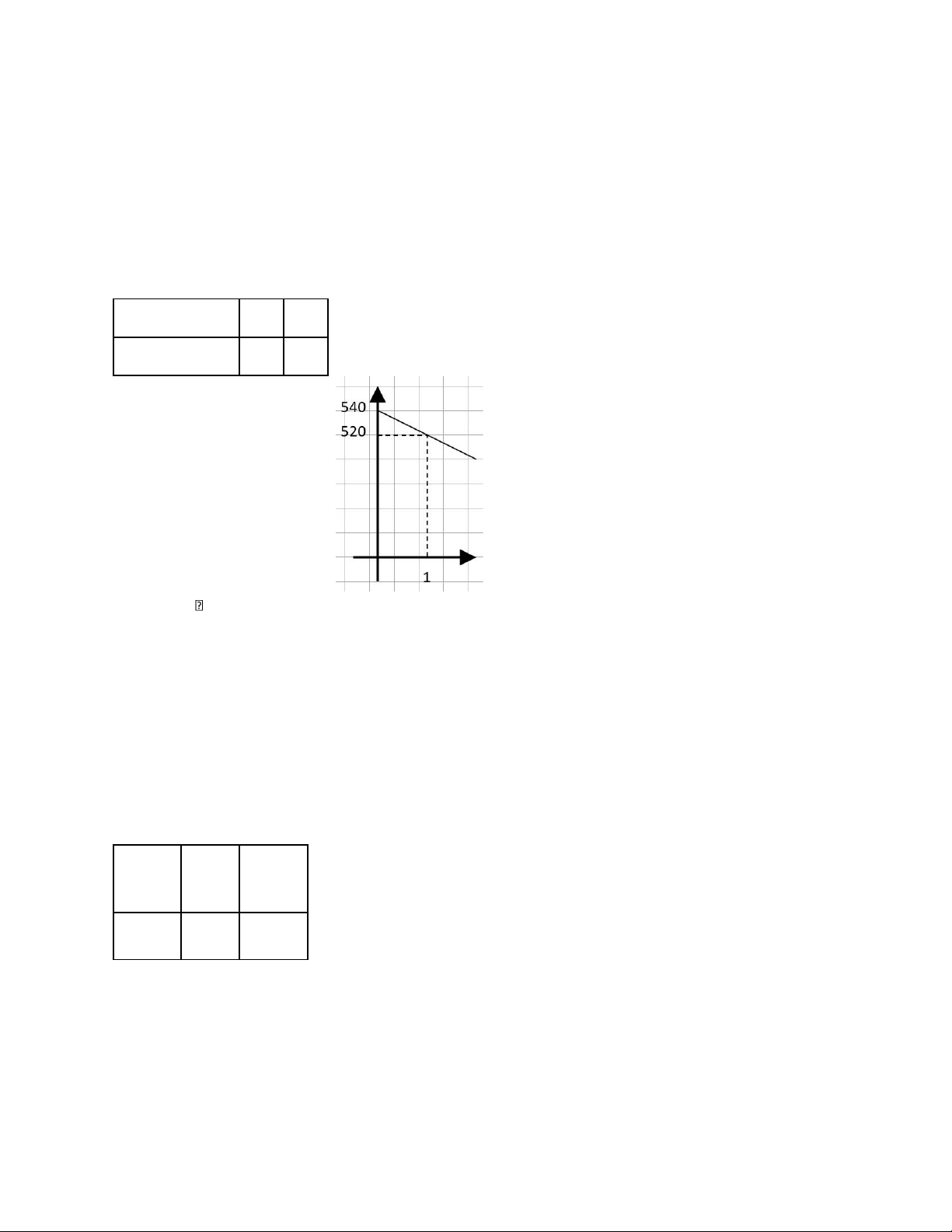
Vd1: Vào đầu năm, giá của sản phẩm A trên thị trường nội địa đang giảm với tốc
độ không đổi là 20 nghìn đồng/tháng. Đầu tháng 3, giá sản phẩm A là 500 nghìn đồng.
a. Hãy biểu diễn giá của sản phẩm A bằng 1 hàm theo thời gian, vẽ đồ thị? Ta có: a = -20.
x: số tháng trôi qua từ đầu năm (x 0)
y: giá sản phẩm A tương ứng.
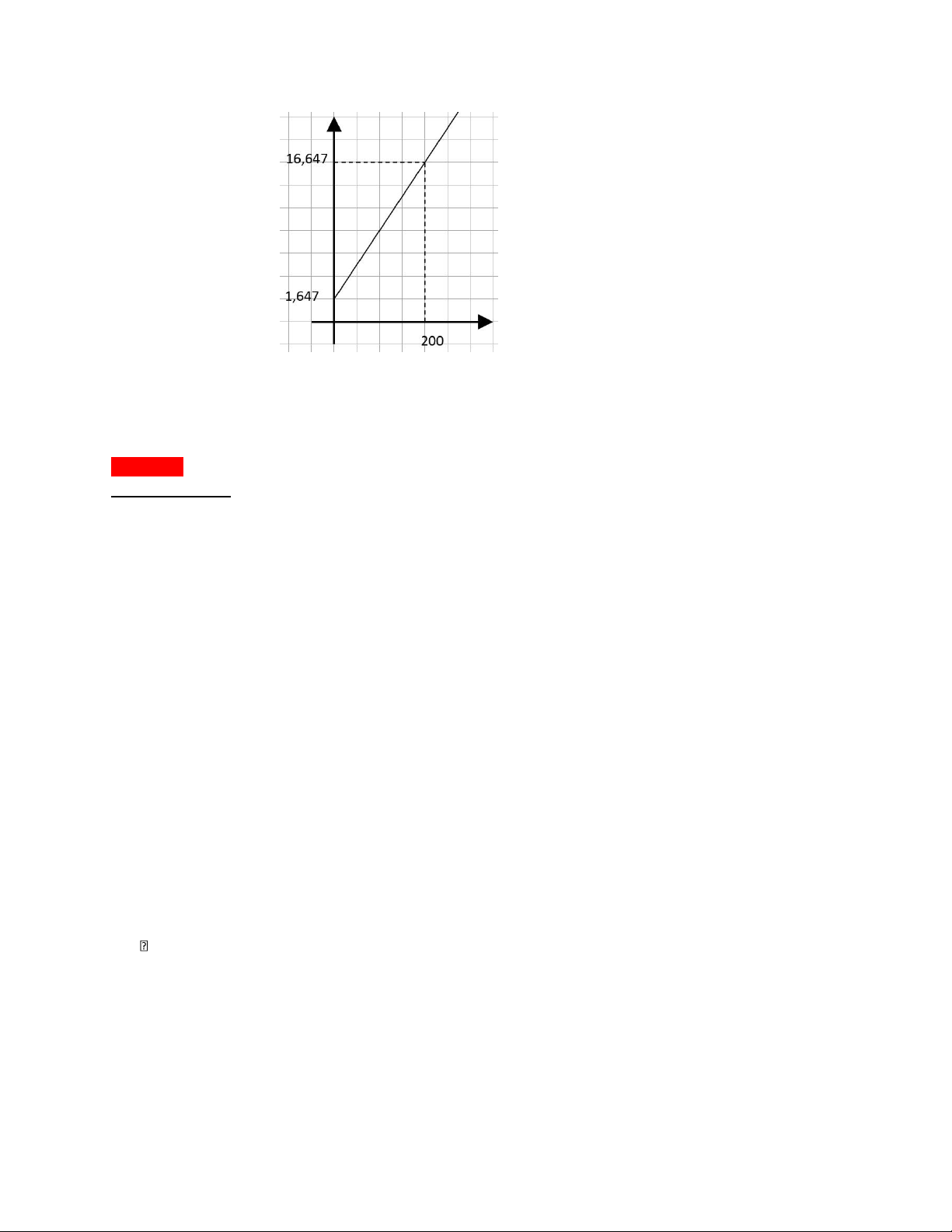
Vì giá sản phẩm A giảm với tốc độ không đổi nên giá là hàm giá trị. ax + b = y -20 * 2 + b = 500. b = 540. x (tháng) 0 1 y (nghìn đồng) 540 520 63 (46): a. Theo bài ra ta có: A (80; 7,647) B (100; 9,147) a = 0.075. Ta có hệ phương trình: a = 0.075x = 80 y = 7,647. a = 0.075 80a + b = 7,647. b = 1,647. y = 0.075x + 1,647. b. x 0 200 (gậy) y ($) 1,647 16,647
c. Hệ số góc a = 0.075: Nếu sản xuất thêm 1 gậy đánh golf thì chi phí hàng ngày tăng 0.075$.
Giao điểm của hàm chi phí với trục y là điểm A (0; 1,647): Nếu chi phí cố
định mỗi ngày của công ty là 1,647$. 30/10/22: 2. Hàm bậc hai: •
Hàm bậc hai là hàm có dạng: f(x) = ax2 + bx + c (a 0). •
Đồ thị của hàm bậc hai là 1 parabol. •
Nếu a < 0 thì f(x) đạt cực đại tại đỉnh x = -b2a. •
Nếu a > 0 thì f(x) đạt cực tiểu tại đỉnh x = -b2a. • Vd: y = 2x2 - 8x + 10.
Vì y là hàm bậc hai có a = 2 > 0 y đạt cực đại
tại đỉnh x = 2 và ymin = y(2) = 2. •
Vd1: Cho hàm giá - nhu cầu: p = 100 - 2x. Xác định số sản phẩm cần sản xuất để doanh thu lớn nhất. R = p*x. = -2x2 + 100x.
Vì R là hàm bậc hai có a = -2 < 0
y đạt cực đại tại đỉnh x = 25.
Vậy để doanh thu lớn nhất thì cần sản xuất 25 sản phẩm.
Vd: Cho phương trình giá - cung: 4x + 2p = 1500. Tìm giá bán để doanh thu lớn nhất. p(x) = -2x + 750. R(x) = -2x2 + 750x.
Vì R(x) là hàm bậc hai có a = -2 < 0
R(x) đạt cực đại tại đỉnh x = 187.5 và p = 375.
Vậy để doanh thu lớn nhất thì nên bán với giá 375 (đvtt).
Vd: Khách sạn A có 90 phòng hoạt động hết công suất mỗi đêm khi giá cho thuê mỗi
phòng 4 triệu đồng. Khách sạn ước tính rằng cứ mỗi lần tăng giá cho thuê thêm 0.2
triệu đồng thì sẽ có 3 phòng bị bỏ trống.Hãy tìm giá cho thuê của mỗi phòng để tổng
doanh thu mỗi đêm của khách sạn lớn nhất? Tìm doanh thu lớn nhất đó?
Gọi x: số lần tăng 0.2 triệu đồng. Giá thuê mới: 4 + 0.2x.
Số phòng được thuê: 90 - 3x. Vật hàm doanh thu: R = (4 + 0.2x)(90 - 3x) = 360 - 12x + 18x - 0.6x2 = -0.6x2 + 6x + 360.
Vì R là hàm bậc hai có a = -0.6 < 0 nên R đạt cực đại tại đỉnh x = 5 và Rmax = 375, p = 5.
Vậy tổng doanh thu mỗi đêm của khách sạn lớn nhất khi p = 5 triệu đồng và
doanh thu lớn nhất Rmax = 375 triệu đồng.
Vd: 1 quán cà phê bán 1 ly cà phê với giá 2.4$ thì mỗi ngày sẽ bán 600 ly. Họ ước tính
rằng cứ mỗi lần giảm 0.1$ từ giá bán ban đầu thì mỗi ngày sẽ bán thêm 60 ly. Xác định
giá bán để doanh thu lớn nhất.
Gọi x là số lần giá bán giảm
0.1$. Nên giá bán mới là 2.4 -
0.1x số ly bán ra là 600 + 60x Ta có hàm doanh thu: R = (2.4 - 0.1x)(600 + 60x) = 1440 + 144x - 60x - 6x2 = -6x2 + 84x + 1440
Vì hàm R là hàm bậc hai có a = -6 < 0 nên R đạt cực đại tại đỉnh x = -b2a = 7 và p = 1.7$.
BTVN: 1 nhà máy sản xuất băng đĩa với chi phí 2 USD/đĩa. Họ đã ước tính rằng, nếu
bán đĩa với giá 8 USD/đĩa thì mỗi tháng nhà máy sẽ bán được 4000 đĩa. Nhà sản xuất
dự định tăng giá bán và họ ước tính rằng cứ mỗi 1 USD tăng lên trong giá bán thì mỗi
tháng sẽ bán ít hơn 200 đĩa. Tìm giá bán để lợi nhuận của nhà sản xuất là lớn nhất. Tìm
lợi nhuận lớn nhất tương ứng.
Gọi x là số lần tăng 1$.
Ta có: Giá bán mới: 8 + x.
Số đĩa bán ra: 4000 - 200x. Chi phí: 2. Ta có hàm lợi nhuận: P = (8 + x - 2)(4000 - 200x)
= 32000 - 1600x + 4000x - 200x2 - 8000 + 400x = -200x2 + 2800x + 24000.
Vì P là hàm bậc hai có a = -200 < 0 nên P là hàm cực đại tại đỉnh x = 7 và p = 15$, Pmax = 33800$. 2/11/22: 1.4.
Hàm mũ và hàm logarit 1. Hàm mũ - hàm logarit: •
y = ax: a là cơ số (a > 0, a 1). xác định với x ∈ R. Nếu a = e thì y = ex. Nếu a > 1 thì y = ax .
Nếu 0 < a < 1 thì y = ax . • Hàm logarit: • y = logax: 0 < a 1. xác định với x > 0. •
Nếu a = e thì y = logex = lnx. • Vd: log5x. y = ln(x + 1). •
Mối quan hệ của hàm mũ và hàm logarit: •
Vd: y = 2x ⇄ x = log2y. y = 2x ⇄ x = logay.
2. Ứng dụng hàm mũ và hàm logarit:
Bài toán: Tháng 8/2021 bạn gửi tiết kiệm 200 triệu đồng, với lãi suất hằng năm là 6%. Tính số
tiền (số dư) bạn nhận được đến tháng 8/2022 nếu: a. Tiền lãi tính 1 lần? b. Tiền lãi tính 2 lần?
Làm: Số dư = tiền gốc + tiền lãi.
= tiền gốc + tiền gốc * lãi suất.
a. Số dư có được đến 8/2022 là:
200 + 200*6% = 212 (triệu đồng).
b. Số dư có được ở lần 1 là:
200 + 200*3% = 206 (triệu đồng).
Số dư có được ở lần 2 là:
206 + 206*3% = 212,18 (triệu đồng). 3. Công thức lãi kép:
Gọi: P là tiền vốn ban đầu (tiền gốc) (giá trị hiện tại).
t là số năm đầu tiên. r là lãi suất hằng năm.
A là số dư (tiền vốn và tiền lãi) (giá trị tương lai).
m là số kỳ tính lãi trong năm.
Nếu lãi tính m kỳ trong năm:
Vì lãi suất hằng năm là r và lãi được tính m kỳ, nên lãi suất trong mỗi kỳ là rm.
Số dư tại cuối kỳ thứ nhất là: P1 = P + P * rm = P (1+rm)
Số dư tại cuối kỳ thứ 2 là:
P2 = P1 + P1 * rm = P1 (1 + rm) = P (1 + rm)
Số dư tại kỳ thứ m là: Pm = P (1+rm)m Số dư sau t năm: A = P (1+rm)m*t Nếu lãi tính liên tục: A = P * er*t. •
1 số giá trị thường gặp của m: •
Nếu lãi tính theo năm thì m = 1. •
Nếu lãi tính theo quý thì m = 4. •
Nếu lãi tính theo tháng thì m = 12. •
Nếu lãi tính theo tuần thì m = 52. •
Nếu lãi tính theo ngày thì m = 365. •
Nếu lãi tính 4 tháng 1 lần thì m = 3. •
Chú ý: m không phụ thuộc vào thời gian gửi tiền t. •
Vd1: Tìm giá trị của vốn đầu tư 10000$ trong 12 năm, với lãi suất hằng năm là
3,95% nếu tiền lãi được tính liên tục.
Vì lãi tính liên tục nên: A = P * er*t = 10000 * e3,95%*12 = 16.064,07$
Vd2: 1 người mong muốn có 900 triệu đồng tiền mặt để mua 1 chiếc xe mới sau 2 năm
kể từ bây giờ. Hỏi ngay từ bây giờ người đó phải gửi tiết kiệm bao nhiêu để thực hiện
điều đó. Biết rằng lãi suất hằng năm là 8,4% và kỳ hạn tính lãi theo: a. Liên tục?
Vì lãi tính liên tục nên: A = P * er*t 900 = P * e8,4%*2
P = 760,82 (triệu đồng). b. 2 tháng 1 lần?
Vì lãi tính 2 tháng 1 lần nên: A = P (1+rm)m*t 900 = P (1 + 8,4%6)6*2 P = 761,71 (triệu đồng). • 48 (71): A = 32.542,7 ($). • 49 (71): a. A = 2.633,56 ($). b. A = 7.079,54 ($) 50 (71): a. A = 4121,75 ($). b. A = 7285,95 ($). • 51 (71): P = 10.705,6 ($). • 52 (71): P = 15.705,54 ($). • 53 (71): a. A = 10.095,41 ($). b. A = 10.080,32 ($).
c. A = 10.085,27 ($). 54 (71): a. A = 10.697,09 ($). b. A = 10.671,21 ($). c. A = 10.644,93 ($). 6/11/22: 1.5.
Hàm mũ và hàm logarit
Vd5: Ban quản lý ngân hàng Agribank đưa ra chiến lược kinh doanh nhằm thu hút
khách hàng như sau: “Tiền gửi tiết kiệm tại ngân hàng sẽ tăng 30% trong 2 năm”. Hãy
tìm mức lãi suất hằng năm của ngân hàng, biết tiền lãi được tính theo: a. 4 tháng 1 lần? b. Liên tục? Giải: Ta có: t = 2. A = P + 30%P = 1,3P.
a. Vì lãi tính 4 tháng 1 lần m = 3. A = P (1+rm)m*t 1,3P = P (1+r3)3*2 1,3 = (1+r3)3*2 r = 0,1341.
Vậy lãi suất hằng năm là 0,1341%.
b. Vì lãi tính liên tục: A = P * er*t 1,3P = P * er*2 1,3 = er*2 r = 0,1312.
Vậy lãi suất hằng năm là 0,1312%. II.
Đạo hàm và ứng dụng 2.1. Đạo hàm
1. Tốc độ thay đổi trung bình - Tốc độ thay đổi tức thời: •
Cho đại lượng y = f(x) xác định trên D:
Tốc độ thay đổi trung bình của f(x) khi x = a đến x = a + h là:
fx=f(a+h)-f(a)a+h-a=f(a+h)-f(a)h (h 0) •
Vd: Chi phí sản xuất ra x (đvsp) là: C(x) = 12x2 + 10x + 50 ($). Tính tốc độ thay đổi trung
bình trong chi phí khi lượng sản xuất thay đổi từ: a. 10 15 đvsp.
Cx=C(15) - C(10)15-10=22,5 ($/đvsp). b. 10 11 đvsp.
Tốc độ thay đổi trung bình trong chi phí là:
Cx=C(11) - C(10)11-10=20,5 ($/đvsp). c. 10 10,2 đvsp.
Cx=C(10,2) - C(10)10,2-10=20,1 ($/đvsp).
Tốc độ thay đổi tức thời của f(x) tại x = a là: h0f(a+h)-f(a)h= f'(a)
Tức là tốc độ thay đổi (tức thời) của đại lượng f(x) là f’(x). 2. Đạo hàm: • Khái niệm:
Cho hàm số y = f(x). Đạo hàm của hàm số ký hiệu là f’(x) được cho bởi công thức: f’(x) = h0f(x+h)-f(x)h •
Vd: Dùng định nghĩa đạo hàm tìm f’(x) nếu: f(x) = 5 - 10x. f’(x) = h0f(x+h)-f(x)h. = h05-10(x+h)-5+10xh. = h0-10hh. = h0(-10). = -10. •
Ký hiệu của đạo hàm: f’(x) hay dfdx. • Đơn vị của đạo hàm:
Đơn vị của f’(x) = đơn vị của f(x)đơn vị của x.
3. Quy tắc tính đạo hàm: • 1 số đạo hàm cơ bản:
(k)’ = 0 (k là hằng số). (kn)’ = n*kn-1 (a ∈ R). (x)’ = 12x (x > 0). (1x)’ = -1x2 (x 0). (ex)’ = ex. (lnx)’ = 1x. •
Phép toán của đạo hàm:
Cho u, v là các hàm khả vi và k ∈ R. Khi đó: 1. (k * u)’ = k*u’. 2. (u + v)’ = u’ v’.
3. (u * v)’ = u’ * v + u * v’.
4. (uv)’ = u' * v - u * v'v2. Vd: Tìm f’(x), nếu:
a. f(x) = 10 + 6x + 1x f’(x) = 6 - 1x2.
b. f(t) = et (2t + 7) f’(t) = et (2t + 7) + 2 * et.
c. f(x) = 10 - 2xx2+1 f’(x) = -2
(x2+1)-2x(10-2x)(x2+1)2 = -2x2 - 2 - 20x - 4x2x4+2x2+1 = 2x220x- 2x4+2x2+1.
d. f(x) = 10x3 + 3x + lnx = 10x-3 +
x13 + lnx f’(x) = -30x-40 + 13x-23 + 1x
3. Ý nghĩa của đạo hàm: •
Ý nghĩa thực tiễn: f’(x) là tốc độ thay đổi của đại lượng f(x). •
Chú ý: tốc độ thay đổi = tốc độ thay đổi tức thời = f’(x). •
Vd4: Giả sử doanh thu của công ty A khi sản xuất q đơn vị sản phẩm là R(q) = 12q2+50q (triệu đồng).
a. Tính tốc độ thay đổi tức thời của doanh thu của công ty khi sản xuất 30 đơn vị sản phẩm?
b. Tính tốc độ thay đổi của doanh thu khi sản xuất 60 (đvsp)? Làm: Ta có: R’(x) = -q + 50.
a. Tốc độ thay đổi của doanh thu khi sản xuất 30 đvsp là:
R’(30) = 20 (triệu đồng/đvsp).
Vậy doanh thu tăng với tốc độ 20 triệu đồng/đvsp.
b. Tốc độ thay đổi của doanh thu khi sản xuất 60 đvsp là:
R’(60) = -10 (triệu đồng/đvsp).
Vậy doanh thu giảm với tốc độ 10 triệu đồng/đvsp. 9/11/22:
4. Tốc độ thay đổi phần trăm: •
Tốc độ thay đổi phần trăm: •
Tốc độ thay đổi phần trăm của f(x) là: 100f'(x)f(x). •
Vd7: Giả sử GDP (tỷ USD) của 1 quốc gia nào đó sau t năm tính từ đầu năm
2015 là: P(t) = 5t2 + 3t + 250.
a. Tính tốc độ tăng trưởng GDP của quốc gia đó vào đầu năm 2021.
b. Tính tốc độ tăng trưởng phần trăm GDP của quốc gia đó vào đầu năm 2021. Làm: Ta có: P’(t) = 10t + 3.
a. P’(6) = 63 (tỷ $/năm).
b. 100P'(6)P(6) = 14,76 (%/năm).
Vd: Doanh thu khi sản xuất x đvsp là R(x) = -2x2 + 100x ($).
a. Tính tốc độ thay đổi doanh thu khi sản xuất 10 đvsp?
b. Tính tốc độ thay đổi phần trăm doanh thu khi sản xuất 10 đvsp? Làm: Ta có: R’(x) = -4x + 100.
a. Tốc độ thay đổi doanh thu khi sản xuất 10 đvsp: R’(10) = 60 ($/đvsp).
b. Tốc độ thay đổi phần trăm doanh thu khi sản xuất 10 đvsp:
100R'(10)R(10) = 7,5 (%/đvsp). 5. Đạo hàm hàm hợp: • Khái niệm:
Cho các hàm f(u) và u(x). Hàm hợp f(u(x)) là hàm theo x nhận được bằng cách
thay u = u(x) vào công thức f(u). • Vd: 1. Cho
f(u) = u3 + 5u - 2. u(x) = 3 - 6x. Tìm f(u(x))? f(u(x)) = (3- 6x)3+5(3-6x)-2
2. Cho f(x) = 5x2 + 10 và x(t) = t2 + 4t.
Tìm f(x(1))? f(x(t)) = 5 (5t2+4t)2 + 10 f(x(1)) = 135. •
Vd2: Tổng chi phí khi sản xuất q sản phẩm là C(q) = 0.1q2 + 5q + 60 (triệu đồng). Biết
rằng số sản phẩm sản xuất sau t giờ được xác định bởi: q(t) = 30t (sản phẩm). Xác định
tổng chi phí sau 5 giờ sản xuất.
Tổng chi phí sau 5 giờ sản xuất:
C(q(t)) = 0.1(30t)2 + 5(30t) + 60.
C(q(5)) = 3.060 (triệu đồng). • Đạo hàm hàm hợp:
Cho 2 hàm số f(u) và u = u(x) khả vi. Khi đó, hàm hợp f(u(x)) có đạo hàm theo
biến x được tính theo công thức sau: f’(u(x)) = f’(u) * u’(x). • Vd3:
1. Cho f(u) = 3u2 + 10u - 5 với u(x) = 6x - x2. Tìm f’(u(x))?
f’(u(x)) = (6u + 10)(6 - 2x)
= [6(6x - x2) + 10](6 - 2x) 2. Cho
f(x) = x + 10 và x(t) = 2t + 4. Tìm f’(x(4))? f’(x(t)) = 12x * 2 = 1x = 12x+4 f’(x(4)) = 36. •
1 số quy tắc tính đạo hàm hàm hợp: Cho u là hàm khả vi theo x: (un)’ = n * un-1 * u’ (u)’ = u2u (eu)' = eu * u’ [1u]’ = -u'u2 (lnx)’ = u'u • Vd4:
1. f(x) = (5x+4)3 f’(x) = 3(5x+4)2 * 5 = 15(5x+4)2
2. f(x) = x3+6 f’(x) = 3x22x3+6
3. f(x) = 52x2+4x-1 f’(x) = - 5(4x+4)(2x2+4x-1)2 = - 20x+20(2x2+4x-1)2
4. f(x) = e3x+6 f’(x) = 3e3x+6
5. f(x) = 10(2x+5)6 = 10 * (2x+5)-6
f’(x) = 10 * -6(2x+5)-7 * 2 = - 120(2x+5)-7 •
Vd5: Công ty A nhận định rằng, tổng chi phí (USD) sản xuất ra q sản phẩm và số
sản phẩm sản xuất sau t giờ lần lượt là: C(q) = q2 + 5q + 300; q(t) = t2 + 4t. Hãy tìm
tốc độ thay đổi của tổng chi phí sản xuất sau 1 giờ?
C(q(t)) = (t2+4t)2+5(t2+4t)+300
C’(q(t)) = 2(t2 + 4t)(2t + 4) + 5(2t + 4)
C’(q(1)) = 90 ($/sản phẩm). 16/11/22: • 72(195):
Số dư trong tài khoản sau t năm:
A = P * er*t = 25000 * e8,4%*t.
a. Tốc độ thay đổi tức thời của số dư trong tài khoản sau 2 năm: A’(2) = 2484,17 ($/năm).
b. Thời gian để số dư trong tài khoản bằng 30000$: 30000 = 25000 * e8,4%*t t = 2,17 (năm).
Tốc độ thay đổi tức thời của số dư trong tài khoản tại thời gian 2,17 năm là: A’(2,17) = 2520 ($/năm). 2.2.
Công thức gần đúng - Phân tích cận biên trong kinh tế 1. Công thức gần đúng: •
Cho hàm số f(x) khả vi tại x0, theo định nghĩa đạo hàm ta có: f’(x0) =
h0f(x0+ h)-f(x0)h Khi h nhỏ ta có:
f’(x0) f(x0+h) - f(x0)h f(x0 + h) - f(x0) f’(x0) * h. • Khi h = x thì:
f(x0 + x) - f(x0) f’(x0) * x f f’(x0) * x. f
Y = f(x) x: sự thay đổi trong x. f: sự thay đổi trong f. •
Công thức: Nếu f(x) là hàm khả vi và x thay đổi từ a đến b thì: •
Thay đổi chính xác trong f là: f = f(b) - f(a).
Thay đổi gần đúng trong f: f f’(a) * x; x = b - a.
Vd: Cho f(x) = 12x2 + 10x. Nếu x thay đổi từ 3 đến 3,7 đơn vị. Hãy tính:
a. Thay đổi chính xác trong f?
f = f(3,7) - f(3) = 9,345 (đơn vị).
Vậy f tăng chính xác 9,35 đơn vị.
b. Thay đổi gần đúng trong f? f = f’(3) * (3,7 - 3) = 9,1 (đơn vị).
Vậy f tăng xấp xỉ 9,1 đơn vị. •
Vd2: Tổng chi phí sản xuất ($) của công ty A khi sản xuất q đơn vị là:
C(q) = 0,2q3 - 0,5q2 + 500q + 100.
Mức sản xuất hiện tại là 5 đơn vị, công ty dự định tăng mức này lên 5,2 đơn vị.
Dùng công thức gần đúng, hãy tính tổng chi phí sẽ thay đổi như thế nào? C C’(a) * (b - a) 102 ($).
Vậy tổng chi phí tăng xấp xỉ 102 $. •
Vd3: Đầu ra (đvsp) hằng ngày của nhà máy A là: Q(k) = 600k14
Trong đó k là vốn đầu tư của nhà máy. Biết vốn đầu tư hiện tại là 400 triệu đồng.
Tính thay đổi gần đúng trong đầu ra của nhà máy khi vốn đầu tư của nhà máy giảm đi 50 triệu đồng?
Q Q(a) * (b - a) -83,85 (đvsp).
Vậy đầu ra của nhà máy giảm 83,85 đvsp.
Vd4: GDP của quốc gia A sau t năm tính từ đầu
năm 2020 là: P(t) = 13t3 + 50t + 100 (tỉ $)
Hãy tính thay đổi gần đúng trong GDP vào: a. Quý I năm 2025.
P P’(5) * (5,25 - 5) 18,75 (tỉ $). b. Quý II năm 2025.
P P’(5,25) * (5,5 - 5,25) 19,39 (tỉ $). c. 6 tháng cuối năm 2025.
P P’(5,5) * (6 - 5,5) 40,13 (tỉ $).
2. Chi phí, doanh thu và lợi nhuận cận biên: •
Định nghĩa: Nếu C(x), R(x) và P(x) lần lượt là các hàm chi phí, hàm doanh thu và
hàm lợi nhuận khi sản xuất x đvsp, thì: •
Hàm chi phí cận biên là: MC(x) = C’(x). •
Hàm doanh thu cận biên là: MR(x) = R’(x). •
Hàm lợi nhuận cận biên là: MP(x) = P’(x).
Tổng quát: Hàm cận biên của f(x) là f’(x). •
Chú ý: Tốc độ thay đổi = Hàm cận biên = Đạo hàm. • Công thức cận biên:
Cho C(x) là chi phí sản xuất x (đvsp). Khi đó: •
Chi phí (chính xác) sản xuất đơn vị thứ x + 1 là: C(x + 1) - C(x). •
Theo định nghĩa đạo hàm, ta có: C’(x) = h0C(x+h)-C(x)h.
Khi h nhỏ, thì: C’(x) = C(x+h)-C(h)h. Cho h = 1, ta được: C’(x) = C(x + 1) - C(x). • Ý nghĩa hàm cận biên: •
Công thức: C’(x) = MC(x) C(x + 1) - C(x). •
Ý nghĩa: Chi phí cận biên tại x Chi phí chính xác của đơn vị thứ x + 1. • Giải thích MC(x): •
Tại mức sản xuất x đơn vị, nếu tăng mức sản xuất thêm 1 đơn vị thì chi phí sẽ
thay đổi (tăng hoặc giảm) xấp xỉ C’(x). • Vd: C(4) - C(3) C’(3). •
C(4) - C(3): chi phí chính xác sản phẩm thứ 4. •
C’(3): chi phí gần đúng sản phẩm thứ 4. •
Vd1: 1 công ty sản xuất hộp số tự động cho xe ô tô. Tổng chi phí hằng tuần (tính
bằng $) sản xuất x hộp số được cho bởi: C(x) = 60000 + 400x - 0,5x2.
a. Tìm hàm chi phí cận biên: MC(x) = C’(x) = 400 - x.
b. Tìm chi phí biên tại mức sản xuất 50 hộp số. Giải thích. C’(50) = 350 ($).
Tại mức sản xuất 50 đơn vị, nếu tăng mức sản xuất thêm 1 hộp thì chi phí sẽ tăng xấp xỉ 350$.
c. Dùng hàm chi phí biến, tính chi phí gần đúng khi sản xuất hộp số thứ 91. C’(90) = 310 ($).
d. Tính chính xác chi phí sản xuất hộp số thứ 91. C(91) - C(90) = 309,5 ($). •
BTVN: 45 - 52 / 162 - 163. 33 - 44 / 171 - 172. 20/11/22: • 45 (162): • x: 10 - 11 (ngàn $). N N’(10) * 1 40 (đvsp). x: 20 - 21 (ngàn $). N N’(20) * 1 20 (đvsp). 46 (162):
D = D’(3) * (0,2) = -48 (pound). • 47 (162): • x: 20 - 25 (vợt).
C = (C)’(20) * 5 -2,5 (đvtt). x: 40 - 45 (vợt).
C = (C)’(40) * 5 1,25 (đvtt). • 49 (162): • x: 1500 - 1510 (TV).
C C’(1500) * 10 600 (đvtt).
R R’(1500) * 10 1000 (đvtt). x: 4500 - 4510 (TV).
C C’(4500) * 10 600 (đvtt).
R R’(4500) * 10 -1000 (đvtt). 36 (171): a. C(1000) = 30 ($).
b. C'(1000) = -0,02 ($/cuốn).
Tại mức sản xuất 1000 từ điển, nếu tăng mức sản xuất thêm 1 đơn vị thì chi phí
trung bình sẽ giảm 0,02 $. c. 30 - 0,02 = 29,98 ($). 38 (171): a. P(26) - P(25) = 14,7 ($). b. P’(25) = 15 ($). 2.4. Đạo hàm hàm ẩn 1. Hàm ẩn: Khái niệm hàm ẩn:
Phương trình f(x,y) = 0, trong đó ẩn y là 1 hàm theo biến x, và hàm y không
được viết dưới dạng tường minh theo biến x thì hàm y được gọi là hàm ẩn.
2. Phương pháp tìm đạo hàm hàm ẩn: •
Cho phương trình f(x,y) = 0, trong đó ẩn y là 1 hàm khả vi theo biến x. Để tìm dydx ta làm như sau: •
Bước 1: Đạo hàm cả 2 vế của phương trình theo x (chú ý dùng quy tắc đạo hàm
hàm hợp khi tính đạo hàm các số hạng chứa y). •
Bước 2: Giải phương trình trong bước 1, suy ra dydx. • Vd: 1. x2 - y2 = 5y - 4.
Lấy đạo hàm 2 vế theo x: x2 - y2 = 5y - 4. 2x - 2y * y’ = 5y’. 5y’ + 2y *y’ = 2x. y’ (5 + 2y) = 2x. y’ = 2x5+2y. 2. 6y2 - 3xy = 10.
12y * y’ - 3y + 3x * y’ = 0. y’ (12y + 3x) = 3y. y’ = 3y12y+3x. 3. x3 - 4y = e5y - 7. 3x2 - 4y’ = 5y’ * e5y. 3x2 = 5y’ * e5y + 4y’. y’ = 3x5e5y+4.
4. (1+y)2 + y = x + 7 (A(2,1)). 2y’ * (1 + y) + y’ = 1. y’ = 12(1+y)+1 = 12.
5. lny = 2y2 - x (A(2,1)). y'y = 4y * y’ - 1. y’ * y-1 - 4y * y’ = -1. y’ = -1y-1-4y = 13. Vd: 1. x3 - 5y2 = 10x - 2y.
3x2 * xt’ - 10y * yt' = 10xt' - 2yt'. -
10y * yt' + 2yt' = 10xt' - 3x2 * xt'. yt' = (10-3x2)xt'-10y+2. 2. x2y - 6y = 2x - 10.
2xy * xt' + x2 * yt' - 6yt' = 2xt'. yt' = (2-2xy)xt'x2-6. • BTVN: 33 - 38 (225). • 33 (225):
Ta có x và C, R, P là hàm ẩn theo thời gian t và x = 6000; xt' = 500. a. Tìm Ct'. b. Tìm Rt'. c. Tìm Pt'. 23/11/22: 2.5.
Cực trị của hàm một biến
1. Cực trị tương đối: • Khái niệm:
Cho hàm số y = f(x) xác định trên D và x0 D. Khi đó: •
f(x) được gọi là đạt cực đại tương đối tại x0, nếu: f(x0) f(x), với mọi x thuộc lân cận của x0. •
f(x) được gọi là đạt cực tiểu tương đối tại x0, nếu: f(x0) f(x), với mọi x thuộc lân cận của x0. •
Cực đại và cực tiểu tương đối được gọi là cực trị tuyệt đối. • Tính chất:
o Cực trị tương đối (nếu có) của hàm số y = f(x) chỉ xuất hiện tại x0 D, sao cho
f’(x0) = 0 hoặc f’(x0) không tồn tại.
o Khi đó x0 được gọi là điểm tới hạn của hàm số y = f(x).
o Vd: Tìm điểm tới hạn của: f(x) = x2 + 10x - 5. f’(x) = 2x + 10. f’(x) = 0 x = -5.
Vậy f(x) có 1 điểm tới hạn A(-5,-30). •
Dấu hiệu nhận biết cực trị: o Định lí 1:
Giả sử x0 D là điểm tới hạn của hàm số y = f(x). Khi đó:
Nếu f’(x) đổi dấu từ + sang - khi đi qua x0 thì f(x) đạt cực đại tương đối tại x0.
Nếu f’(x) đổi dấu từ - sang + khi đi qua x0 thì f(x) đạt cực tiểu tương đối tại x0. o Định lí 2:
Giả sử x0 D là điểm tới hạn của hàm số y = f(x). Khi đó:
Nếu f’ (x0) < 0 thì f(x) đạt cực đại tương đối tại x0.
Nếu f’ (x0) > 0 thì f(x) đạt cực tiểu tương đối tại x0. •
Phương pháp tìm cực trị của y = f(x):
o Bước 1: Tìm điều kiện của x.
o Bước 2: Tìm f’(x) và cho f’(x) = 0.
Điểm tới hạn x0 điều kiện. o Bước 3:
Cách 1: Lập bảng biến thiên.
Cách 2: Tìm f’ (x0) và tính f’ (x0). o Bước 4: Kết luận. • Vd: Tìm cực trị của:
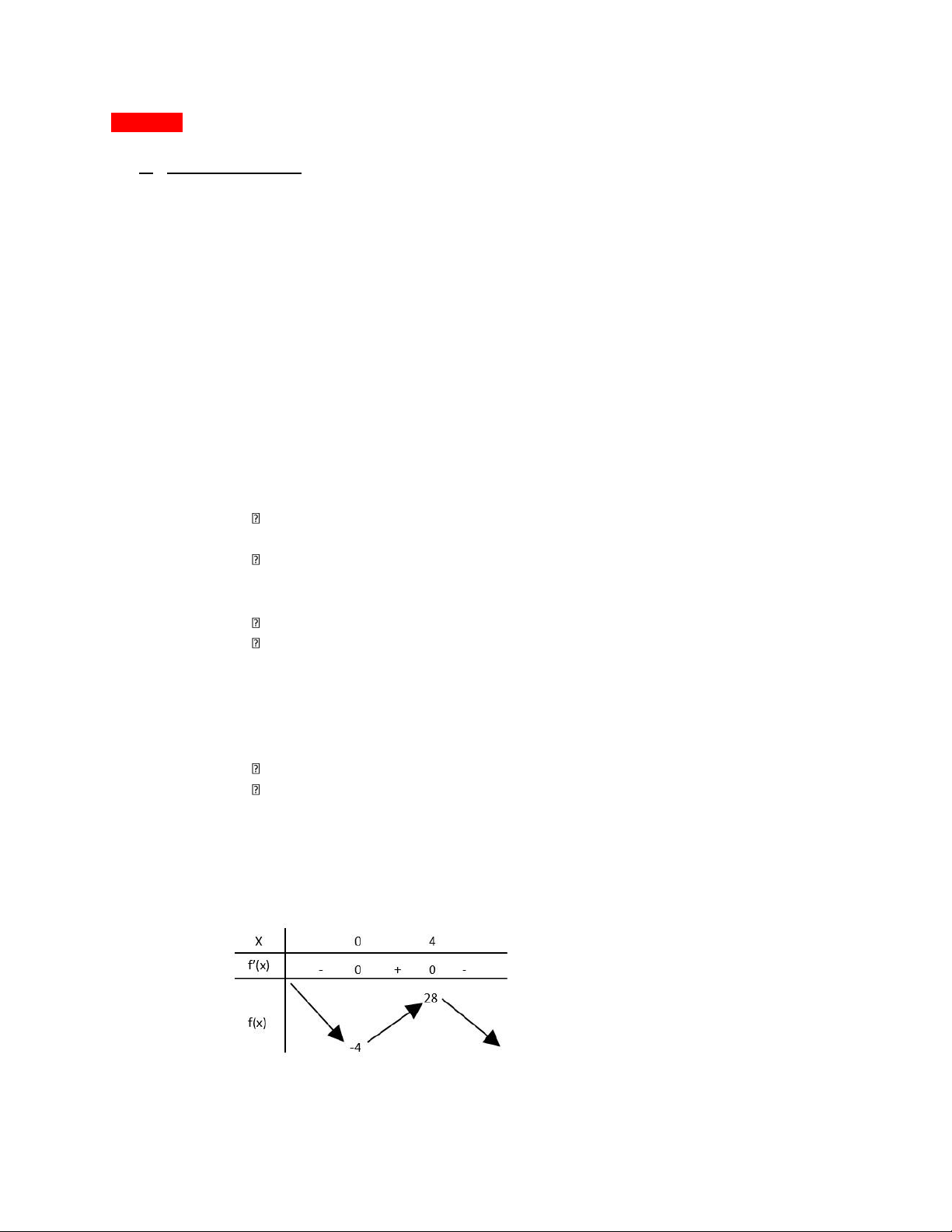
1. f(x) = -x3 + 6x2 - 4. D = R.
f’(x) = -2x2 + 12x. f’(x) = 0 x = 4 hoặc x = 0. BBT:
2. f(x) = x + 9x, x > 1. D = (1;
+∞). f’(x) = 1 - 9x2. f’(x) =
0 x = 3 hoặc x = -3 (loại).
f’ (x) = 18xx4 f’ (3) = 23 > 0.
2. Cực trị tuyệt đối (tương tự cực trị tương đối): •
Chú ý: o Cực trị tuyệt đối có thể xuất hiện tại điểm tới hạn hoặc tại các điểm biên. •
Vd: Tìm cực trị tuyệt đối của: f(x) = x2 + 8x - 3, 4 x < 9. D = R. f’(x) = 2x + 8. f’(x) = 0 x = -4 (loại). BBT:
Vậy f(x) đạt cực tiểu tuyệt đối tại x = 4 với f(4) = 45. •
BTVN: o 19 - 30 (310 - 311). o 21 (310).
Bài tập ôn thi giữa kỳ - MTH 101 I. Lý thuyết:
1. Một số nội dung thường gặp: •
Hàm chi phí: C = chi phí 1 đơn vị * số đơn vị + chi phí cố định (nếu có). •
Hàm doanh thu: R = giá bán mỗi đơn vị * số đơn vị. •
Hàm lợi nhuận: P = R - C = (giá bán - chi phí mỗi đơn vị) * số đơn vị. Hàm
trung bình mỗi đơn vị: C(x) = C(x)x.
2. Hàm tuyến tính - Hàm bậc hai: • Hàm tuyến tính: •
Giá trị của hàm thay đổi với tốc độ không đổi. • Công thức: f(x) = ax + b. •
a: Hệ số góc = Tốc độ thay đổi của hàm. •
Nếu đồ thị hàm tuyến tính đi qua 2 điểm A(x1,y1); B(x2,y2) thì a = y2y1x2-x1. • Hàm bậc hai: •
Công thức: f(x) = ax2 + bx + c; a 0. •
Nếu a < 0 thì f(x) đạt cực đại tại đỉnh x = -b2a. •
Nếu a > 0 thì f(x) đạt cực tiểu tại đỉnh x = -b2a.
3. Công thức lãi kép - lãi kép liên tục: •
P: Tiền gốc (giá trị hiện tại). •
A: Số dư (giá trị tương lai). •
t: Thời gian đầu tư (tính bằng năm). • r: Lãi suất hằng năm. •
m: Số lần tính lãi trong năm. • Lãi tính m kỳ: A = P (1 +rm)mt. Lãi tính liên tục: