https://thcs.toanmath.com/2022/07/de-tuyen-sinh-lop-10-mon-toan-nam-2022-truong-thuc-hanh-cao-nguyen-dak-lak.html

Giới thiệu đến quý thầy, cô giáo và các em học sinh lớp 10 đề thi chính thức kỳ thi tuyển sinh vào lớp 10 THPT môn Toán năm học 2022 – 2023 trường THPT Thực Hành Cao Nguyên, tỉnh Đắk Lắk; kỳ thi được diễn ra vào ngày 18 tháng 06 năm 2022; đề thi có đáp án và lời giải chi tiết. Mời bạn đọc đón xem!

43 22 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề thi vào 10 môn Toán năm 2023-2024

Môn: Môn Toán

Thông tin:

4 trang 8 tháng trước

Tác giả:

Profile Vũ Hường
trang
1
TRƯỜNG THPT THỰC HÀNH
CAO NGUYÊN
HỘI ĐỒNG TUYỂN SINH
ĐỀ THI CHÍNH THỨC
KỲ THI TUYỂN SINH LỚP 10
NĂM 2022
MÔN THI: TOÁN
(Thời gian 120 phút không kể thời gian phát đề)
Ngày thi 18/6/2022
Bài 1: (2,0 điểm)
Rút gọn các biểu thức sau:
1.
27 3 12 2 3 : 3 A
2.
1 5 6 2
:
9
3 3 3
B
x
x x x
với
0, 9 x x
.
Bài 2: (2,0 điểm)
1) Không sử dụng máy tính cầm tay, giải hệ phương trình sau:
2 4
2 7
x y
x y
.
2) Một ô tô và một xc máy khởi hành cùng một lúc từ hai tinh cách nhau 200 km đi
ngược chiều và gặp nhau sau 2 giờ. Tìm vận tốc của ô tô và xe máy, biết rằng nếu vận tốc
của ô tô tăng thêm 10 km/h và vận tốc của xe máy giảm đi 5 km/h thì vận tốc của ô tô sẽ
gấp 2 lần vận tốc của xe máy.
Bài 3: (2,0 điểm)
Cho đường thẳng
2
: 2 1 d y mx m
với m là tham số và parabol
2
: P y x
.
1) Chứng minh
d
luôn cắt
P
tại hai điềm phân biệt nằm về hai phía của trục
tung.
2) Gọi
1 2
,x x
là hoành độ các giao điểm của
d
và
P
. Tim
m
thỏa mãn
1 2
1 2
1 2
3
0
x x
x x
x x
.
Bài 4: (3,5 điểm)
Cho đường tròn tâm
O
đường kính
AB
. Gọi
,C D
là hai điểm thuộc
O
và nằm
khác phía đối với đường thẳng
AB
. Gọi
,E F
lần lượt là trung điểm hai dây
AC
và
AD
.
1) Tính tổng
2 2
AC BC
biết bán kính đường tròn
O
bằng 3cm.
2) Chứng minh bốn điểm
, , ,A O E F
cùng thuộc một đường tròn.
3) Đường thẳng
EF
cắt đường tròn ngoại tiếp tam giác
ADE
tại điểm
K
khác
E
.
Chửng minh đường thẳng
DK
là tiếp tuyến của đường tròn
.
Bài 5: (0,5 điểm)
Cho ba số thực dương a, b, c. Chứng minh rằng:
3 3 3
2 2 2 2 2 2
3
a b c a b c
a ab b b bc c c ca a
.
----------------- Hết -----------------
trang
2
SƠ LƯỢC BÀI GIẢI
Bài 1: (2,0 điểm)
Rút gọn các biểu thức sau:
1.
27 3 12 2 3 : 3 A
2.
1 5 6 2
:
9
3 3 3
B
x
x x x
với
0, 9 x x
.
1)
27 3 12 2 3 : 3 9 3 3 4 3 2 3 : 3 A
.
3 3 6 3 2 3 : 3 7 3 : 3 7
.
2)
3 5 3 6 6 3
1 5 6 2 3
: 3
9 2
3 3 3
3 3 2 3
x x x
x
B
x
x x x
x x x
.
Bài 2: (2,0 điểm)
1) Không sử dụng máy tính cầm tay, giải hệ phương trình sau:
2 4
2 7
x y
x y
.
2) Một ô tô và một xc máy khởi hành cùng một lúc từ hai tinh cách nhau 200 km đi
ngược chiều và gặp nhau sau 2 giờ. Tìm vận tốc của ô tô và xe máy, biết rằng nếu vận tốc
của ô tô tăng thêm 10 km/h và vận tốc của xe máy giảm đi 5 km/h thì vận tốc của ô tô sẽ
gấp 2 lần vận tốc của xe máy.
1)
2 4
2 4 2 4 2
2 2 4 7
2 7 5 15 3
y x
x y y x y
x x
x y x x
.
2) Gọi
, /x y km h
lần lượt là vận tốc của ô tô, xe máy
0; 5 x y
.
Khi đó: Quãng đường ô tô đi được trong 2 giờ là
2x km
.
Quãng đường xe máy đi được trong 2 giờ là
2y km
.
Vì sau 2 giờ hai xe gặp nhau, nên ta có phương trình:
2 2 200 100 x y x y
.
Vận tốc của ô tô sau khi tăng là
10 /x km h
.
Vận tốc của xe máy sau khi giảm là
5 /y km h
.
Vì vận tốc của ô tô gấp 2 lần vận tốc của xe máy, nên có phương trình:
10 2 5 2 20 x y x y
.
Ta có hệ phương trình:
100 3 120 40
2 20 100 60
x y y y
x y x y x
(TMĐK).
Vậy vận tốc ô tô là 60 km/h; xe máy là 40 km/h.
Bài 3: (2,0 điểm)
Cho đường thẳng
2
: 2 1 d y mx m
với m là tham số và parabol
2
: P y x
.
1) Chứng minh
d
luôn cắt
P
tại hai điềm phân biệt nằm về hai phía của trục
tung.
2) Gọi
1 2
,x x
là hoành độ các giao điểm của
d
và
P
. Tim
m
thỏa mãn
1 2
1 2
1 2
3
0
x x
x x
x x
.
trang
3
1) Phương trình hoành độ giao điểm của
d
và
P
là:
2 2 2 2
2 1 2 1 0 * x mx m x mx m
.
Ta có
2
1 0; ac m m
. Nên phương trình
*
luôn có 2 nghiệm trái dấu với mọi
m
.
Vậy
d
luôn cắt
P
tại hai điềm phân biệt nằm về hai phía của trục tung.
2) Vì phương trình
*
luôn có 2 nghiệm trái dấu với mọi
m
(theo câu 1).
Nên theo Viét, ta có:
1 2
2
1 2
2
1
x x m
x x m
.
Khi đó
2
2
1 2
1 2
1 2
3 1
3 7 3
0 2 0 0 2 0 0
2 2
m
x x m
x x m m m
x x m m
.
(do
2
7 3 0; m m
).
Bài 4: (3,5 điểm)
Cho đường tròn tâm
O
đường kính
AB
. Gọi
,C D
là hai điểm thuộc
O
và nằm
khác phía đối với đường thẳng
AB
. Gọi
,E F
lần lượt là trung điểm hai dây
AC
và
AD
.
1) Tính tổng
2 2
AC BC
biết bán kính đường tròn
O
bằng 3cm.
2) Chứng minh bốn điểm
, , ,A O E F
cùng thuộc một đường tròn.
3) Đường thẳng
EF
cắt đường tròn ngoại tiếp tam giác
ADE
tại điểm
K
khác
E
.
Chửng minh đường thẳng
DK
là tiếp tuyến của đường tròn
.
1) Tính tổng
2 2
AC BC
biết bán kính đường tròn
O
bằng 3cm.
Xét
ABC
, ta có:
0
90
ACB
(góc nội tiếp chắn nửa đường tròn (O))
2
2 2 2 2
2 3 36 AC BC AB cm
.
2) Chứng minh bốn điểm
, , ,A O E F
cùng thuộc một đường tròn.
Ta có
1
2
AE CE AC gt OE AC
. (quan hệ giữa đường kính và dây)
1
2
AF DF AD gt OF AD
. (quan hệ giữa đường kính và dây)
Xét tứ giác
AEOF
, ta có:
0
90 , AEO AFO do OE AC OF AD
.
Vậy tứ giác
AEOF
là tứ giác nội tiếp
trang
4
3) Chửng minh đường thẳng
DK
là tiếp tuyến của đường tròn
O
.
Ta có
0
90 ACB ADB
(góc nội tiếp chắn nửa đường tròn (O))
hay
; BC AC BD AD
, mà
; / / ; / /
OE AC OF AD cmt OE BC OF BD
.
Xét
ABC
, ta có:
/ /
AE AO
OE BC cmt
AC AB
(định lí Ta lét)
Xét
ABD
, ta có:
/ /
AF AO
OF BD cmt
AD AB
(định lí Ta lét)
Do đó
AE AF
AC AD
. Xét
ACD
, ta có:
/ /
AE AF
cmt CD EF
AC AD
(định lí Ta lét đảo)
AEK ACD
(đồng vị).
Lại có:
AEK ADK
.(góc nội tiếp cùng chắn cung
AK
của đường tròn ngoại tiếp
ADE
)
ABD ACD
(góc nội tiếp cùng chắn cung
AD
của đường tròn
O
).
ABD ODB
(
: OBD OB OD
, nên
OBD
cân tại
O
).
0
90 ADK ODB ADK ADO ODB ADO KDO ADB
, hay
DK OD
.
Vậy đường thẳng
DK
là tiếp tuyến của đường tròn
O
.
Bài 5: (0,5 điểm)
Cho ba số thực dương a, b, c. Chứng minh rằng:
3 3 3
2 2 2 2 2 2
3
a b c a b c
a ab b b bc c c ca a
.
Ta có:
2
2 2 2 2
0 a b a ab b ab a b a ab b ab a b
.
3 3 2 2 3 3 3 3 2 2
3 a b a b ab a a b a a b ab
.
3 2 2 2 2 3 2 2
3 3 2
a a b a ab b a a ab b a a b a ab b
.
3
2 2
2 2
2
, 0 0; 0; ,
3
a a b
do a b a b a ab b a b
a ab b
.
Tương tự:
3 3
2 2 2 2
2 2
;
3 3
b b c c c a
b bc c c ca a
Do đó
3 3 3
2 2 2 2 2 2
2 2 2
3 3 3 3
a b c a b b c c a a b c
a ab b b bc c c ca a
.
Đẳng thức xảy ra khi
a b c
.
| 1/4
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

TRƯỜNG THPT THỰC HÀNH
KỲ THI TUYỂN SINH LỚP 10 CAO NGUYÊN NĂM 2022 HỘI ĐỒNG TUYỂN SINH MÔN THI: TOÁN
(Thời gian 120 phút không kể thời gian phát đề) Ngày thi 18/6/2022 ĐỀ THI CHÍNH THỨC Bài 1: (2,0 điểm)
Rút gọn các biểu thức sau:
1. A   27  3 12  2 3: 3  1 5 6  2 2. B    :   với x  0, x  9 .  x  3 x  3 x  9  x  3 Bài 2: (2,0 điểm) 2x  y  4
1) Không sử dụng máy tính cầm tay, giải hệ phương trình sau:  . x  2y  7
2) Một ô tô và một xc máy khởi hành cùng một lúc từ hai tinh cách nhau 200 km đi
ngược chiều và gặp nhau sau 2 giờ. Tìm vận tốc của ô tô và xe máy, biết rằng nếu vận tốc
của ô tô tăng thêm 10 km/h và vận tốc của xe máy giảm đi 5 km/h thì vận tốc của ô tô sẽ
gấp 2 lần vận tốc của xe máy. Bài 3: (2,0 điểm) Cho đường thẳng d  2
: y  2mx  m 1 với m là tham số và parabol P 2 : y  x .
1) Chứng minh d  luôn cắt P tại hai điềm phân biệt nằm về hai phía của trục tung.
2) Gọi x , x là hoành độ các giao điểm của d  và P . Tim m thỏa mãn 1 2 3x x 1 2  x  x  0 . 1 2 x  x 1 2 Bài 4: (3,5 điểm)
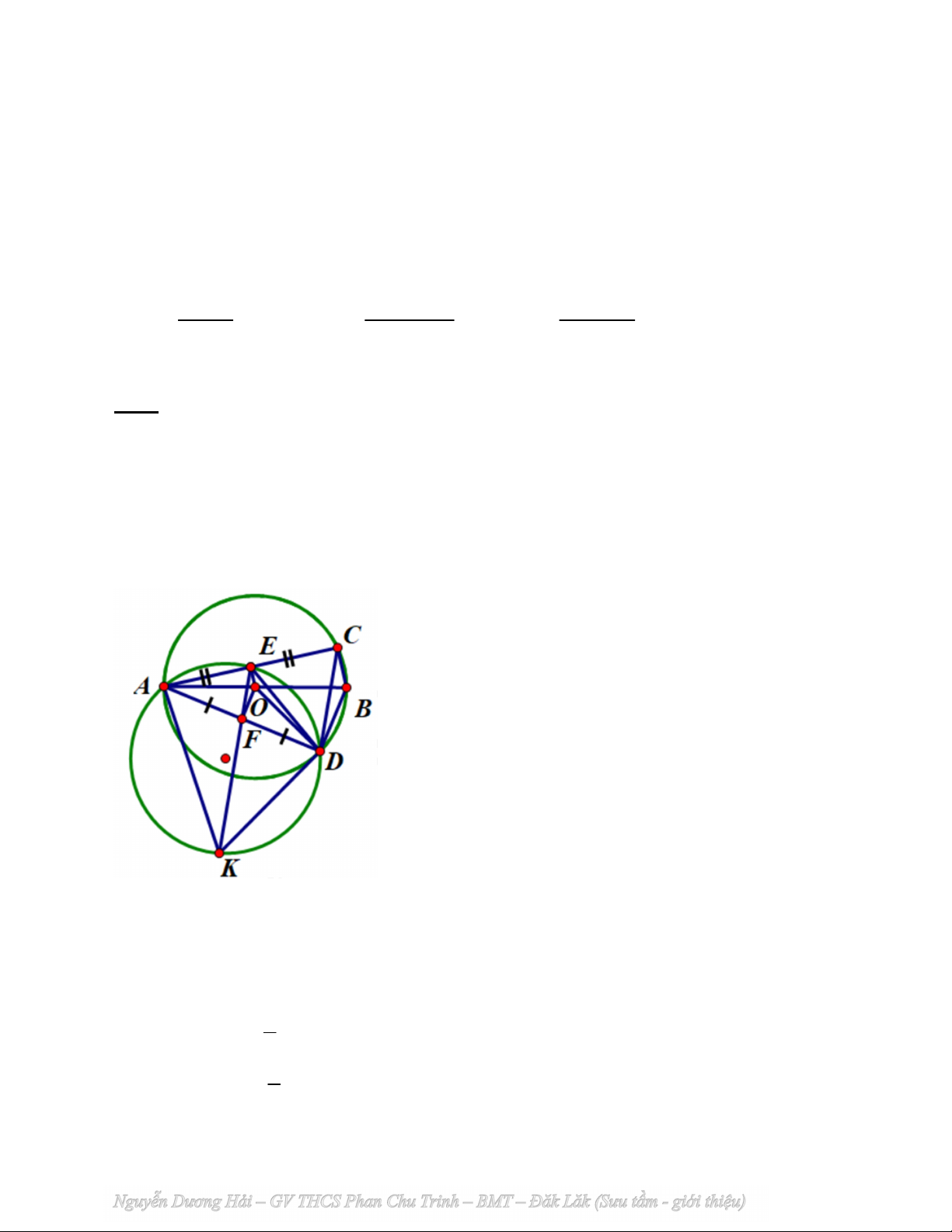
Cho đường tròn tâm O đường kính AB . Gọi C, D là hai điểm thuộc O và nằm
khác phía đối với đường thẳng AB . Gọi E, F lần lượt là trung điểm hai dây AC và AD . 1) Tính tổng 2 2
AC  BC biết bán kính đường tròn O bằng 3cm.
2) Chứng minh bốn điểm , A ,
O E, F cùng thuộc một đường tròn.
3) Đường thẳng EF cắt đường tròn ngoại tiếp tam giác ADE tại điểm K khác E .
Chửng minh đường thẳng DK là tiếp tuyến của đường tròn O. Bài 5: (0,5 điểm)
Cho ba số thực dương a, b, c. Chứng minh rằng: 3 3 3 a b c a  b     c . 2 2 2 2 2 2 a  ab  b b  bc  c c  ca  a 3
----------------- Hết ----------------- trang 1 SƠ LƯỢC BÀI GIẢI Bài 1: (2,0 điểm)
Rút gọn các biểu thức sau:
1. A   27  3 12  2 3: 3  1 5 6  2 2. B    :   với x  0, x  9 .  x  3 x  3 x  9  x  3
1) A   27  3 12  2 3: 3   93  3 43  2 3: 3 .
 3 3  6 3  2 3: 3  7 3 : 3  7 . x  3  5    x 36 6 x   x 3 1 5 6 2 3  2) B    :       .  x  3 x  3 x   x  3  x 3 x 3 2 x  3 3 9 2 Bài 2: (2,0 điểm) 2x  y  4
1) Không sử dụng máy tính cầm tay, giải hệ phương trình sau:  . x  2y  7
2) Một ô tô và một xc máy khởi hành cùng một lúc từ hai tinh cách nhau 200 km đi
ngược chiều và gặp nhau sau 2 giờ. Tìm vận tốc của ô tô và xe máy, biết rằng nếu vận tốc
của ô tô tăng thêm 10 km/h và vận tốc của xe máy giảm đi 5 km/h thì vận tốc của ô tô sẽ
gấp 2 lần vận tốc của xe máy. 2x  y  4  y  2x  4 y  2x  4  y  2 1)        . x  2y  7 x  2 
2x  4  7 5x 15  x  3
2) Gọi x, y km / h lần lượt là vận tốc của ô tô, xe máy  x  0; y  5 . Khi đó:
Quãng đường ô tô đi được trong 2 giờ là 2x km .
Quãng đường xe máy đi được trong 2 giờ là 2y km .
Vì sau 2 giờ hai xe gặp nhau, nên ta có phương trình: 2x  2y  200  x  y 100.
Vận tốc của ô tô sau khi tăng là x 10 km / h .
Vận tốc của xe máy sau khi giảm là y  5 km / h .
Vì vận tốc của ô tô gấp 2 lần vận tốc của xe máy, nên có phương trình:
x 10  2 y  5  x  2y  20.  x  y 100 3  y 120  y  40
Ta có hệ phương trình:      (TMĐK). x  2y  20  x 100  y x  60
Vậy vận tốc ô tô là 60 km/h; xe máy là 40 km/h. Bài 3: (2,0 điểm) Cho đường thẳng d  2
: y  2mx  m 1 với m là tham số và parabol P 2 : y  x .
1) Chứng minh d  luôn cắt P tại hai điềm phân biệt nằm về hai phía của trục tung.
2) Gọi x , x là hoành độ các giao điểm của d  và P . Tim m thỏa mãn 1 2 3x x 1 2  x  x  0 . 1 2 x  x 1 2 trang 2
1) Phương trình hoành độ giao điểm của d  và P là: 2 2 2 2
x  2mx  m 1  x  2mx  m 1  0 *. Ta có 2
ac  m 1 0; m . Nên phương trình * luôn có 2 nghiệm trái dấu với mọi m .
Vậy d  luôn cắt P tại hai điềm phân biệt nằm về hai phía của trục tung.
2) Vì phương trình * luôn có 2 nghiệm trái dấu với mọi m (theo câu 1).  x  x  2m Nên theo Viét, ta có: 1 2  . 2 x x  m 1  1 2 3x x 3 m 1 7  m  3 1 2  2  2 Khi đó  x  x  0   2m  0 
 0  2m  0  m  0. 1 2 x  x 2m 2m 1 2 (do 2 7  m  3  0; m ). Bài 4: (3,5 điểm)
Cho đường tròn tâm O đường kính AB . Gọi C, D là hai điểm thuộc O và nằm
khác phía đối với đường thẳng AB . Gọi E, F lần lượt là trung điểm hai dây AC và AD . 1) Tính tổng 2 2
AC  BC biết bán kính đường tròn O bằng 3cm.
2) Chứng minh bốn điểm , A ,
O E, F cùng thuộc một đường tròn.
3) Đường thẳng EF cắt đường tròn ngoại tiếp tam giác ADE tại điểm K khác E .
Chửng minh đường thẳng DK là tiếp tuyến của đường tròn O. 1) Tính tổng 2 2
AC  BC biết bán kính đường tròn O bằng 3cm. Xét ABC , ta có:  0
ACB  90 (góc nội tiếp chắn nửa đường tròn (O))
 AC  BC  AB    2 2 2 2   2 2 3 36 cm .
2) Chứng minh bốn điểm , A ,
O E, F cùng thuộc một đường tròn. 1
Ta có AE  CE  AC  gt  OE  AC . (quan hệ giữa đường kính và dây) 21
AF  DF  AD  gt  OF  AD . (quan hệ giữa đường kính và dây) 2
Xét tứ giác AEOF , ta có:  AEO   0 AFO  90 do OE  AC,OF  AD.
Vậy tứ giác AEOF là tứ giác nội tiếp trang 3
3) Chửng minh đường thẳng DK là tiếp tuyến của đường tròn O. Ta có  ACB   0
ADB  90 (góc nội tiếp chắn nửa đường tròn (O))
hay BC  AC; BD  AD , mà OE  AC;OF  AD cmt  OE / /BC; OF / /BD . AE AO
Xét ABC , ta có: OE / /BC cmt   (định lí Ta lét) AC AB AF AO
Xét ABD , ta có: OF / /BD cmt   (định lí Ta lét) AD AB AE AF AE AF Do đó  . Xét ACD , ta có: 
cmt  CD / /EF (định lí Ta lét đảo) AC AD AC AD   AEK   ACD (đồng vị). Lại có:  AEK  
ADK .(góc nội tiếp cùng chắn cung 
AK của đường tròn ngoại tiếp ADE )  ABD  
ACD (góc nội tiếp cùng chắn cung 
AD của đường tròn O).  ABD  
ODB ( OBD : OB  OD , nên OBD cân tại O ).   ADK   ODB   ADK   ADO   ODB   ADO   KDO   0 ADB  90 , hay DK  OD .
Vậy đường thẳng DK là tiếp tuyến của đường tròn O. Bài 5: (0,5 điểm)
Cho ba số thực dương a, b, c. Chứng minh rằng: 3 3 3 a b c a  b     c . 2 2 2 2 2 2 a  ab  b b  bc  c c  ca  a 3 Ta có: a  b2 2 2
  a  ab  b  ab  a  b 2 2 0
a  ab  b   aba  b. 3 3 2 2 3
 a  b  a b  ab  a   3 3 a  b    3 2 2 3 a  a b  ab . 3  a  a  b 2 2 a  ab  b   a 2 2 a  ab  b  3  a   a  b 2 2 3 3 2 a  ab  b . 3 a 2a    b  2 2
do a,b  0  a  b  0; a  ab  b  0; a,b . 2 2  a  ab  b 3 3 3 b 2b  c c 2c  a Tương tự:  ;  2 2 2 2 b  bc  c 3 c  ca  a 3 3 3 3 a b c 2a  b 2b  c 2c  a a  b  c Do đó       . 2 2 2 2 2 2 a  ab  b b  bc  c c  ca  a 3 3 3 3
Đẳng thức xảy ra khi a  b  c . trang 4