Hướng dẫn bài tập Chương IV: lý thuyết hành vi người tiêu dùng | Môn Kinh tế vi mô - Trường Đại học Kinh tế, Đại học Huế

lOMoAR cPSD| 58797173
CHƯƠNG IV: LÝ THUYẾT HÀNH VI NGƯỜI TIÊU DÙNG
Câu 1: Giả sử một người tiêu dùng có thu nhập bằng tiền I = 60$ dùng để mua 2 hàng hóa
X, Y với giá PX = 3$, PY = 1$. Biết hàm tổng lới ích TU = X.Y.
a. Viết phương trình đường ngân sách (BL)
b. Xác định hàm MUX, MUY và MRSX/Y.
c. Xác định lượng hàng hoá X và Y mà người tiêu dùng mua để tối đa hoá lợi ích? Xác định lợi ích tối đa?
d. Nếu Px giảm xuống = 2$, điểm tiêu dùng tối ưu là bao nhiêu? Viết phương trình đường
cầu hh X (biết đường cầu là tuyến tính) Giải = 3$, I = 60$ X : P X Y: PY = 1$ TU = X.Y
a. Phương trình đường ngân sách X.Px + Y.Py = I 3X + 1Y = 60 b.
+ MUx = TU’x = (X.Y)’x = Y
+ MUy = TU’y = (X.Y)’y = X
+ MRS = MUx/MUy = Y/X c. MU X MUY = PX PY
X .P X+Y . PY =I Y/3 = X/1 3X + Y = 60 X = 10 Y = 30
Vậy, X = 10 và Y = 30 thì TU = X.Y = 10*30 = 300 (đơn vị lợi ích)
d. Nếu Px giảm xuống = 2$, điểm tiêu dùng tối ưu lOMoAR cPSD| 58797173
- Trong trường hợp này, ta có : + I, Py không đổi
+ Px thay đổi : trước đây Px = 3, bây giờ Px = 2 (giá Px giảm -> người tiêu dùng mua
NHIỀU HƠN) MU X MUY = PX PY
X .P X+Y . PY =I Y/2 = X/1 2X + Y = 60 X = 15 Y = 30
+ Tổng lợi ích: Lấy X = 15 và Y = 30 thay vào hàm tổng lợi ích:
TU = X.Y = 15 *30 = 450 (đơn vị lợi ích)
+ Giả sử phương trình hàm cầu hàng hóa X tuyến tính có dạng Qd = aP + b (a<0)
+ Với Px = 3, ta có X = 10 (Qd = 10)
+ Với Px = 2, ta có X = 15 (Qd = 15) 10 = 3a + b 15 = 2a + b a
= -5 (thỏa mãn điều kiện) b = 25
Vậy, phương trình hàm cầu hàng hóa X: Qd = - 5P + 25
Câu 3: Hàm hữu dụng của một người tiêu dùng được cho như sau : U(X,Y) = X.Y a)
Sở thích ban đầu của người tiêu dùng là 6 đơn vị X và 2 đơn vị Y. Với sở thích không
đổi (U = 12) hãy vẽ đường đồng mức thỏa mãn của người tiêu dùng trên. b)
Giá của X là 10.000đ/đơn vị giá của Y là 30.000đ/ đơn vị. Người tiêu dùng có
120.000đ để chi tiêu cho hàng hóa X và hàng hóa Y, hãy vẽ đường ngân sách của người tiêu
dùng. c) Sự lựa chọn tối ưu của người tiêu dùng được thực hiện như thế nào?
Giải a) Với X = 6 và Y = 2
Đường đồng mức thỏa mãn: cùng lợi ích -> đường bàng quan: U = X.Y = 6*2 = 12 X Y 1 12 2 6 3 4 lOMoAR cPSD| 58797173 6 2
b) Phương trình đường ngân sách X.Px + Y.Py = I
10.000X + 30.000Y = 120.000 c)
+ MUx = TU’x = (X.Y)’x = Y
+ MUy = TU’y = (X.Y)’y = X
+ MRS = MUx/MUy = Y/X MU X MUY = Ta có
: PX PY X .P X+Y . PY =I X = 6 Y = 2
Câu 4: Giả sử một người tiêu dùng có thu nhập: I = 60$ dùng để mua 2 hàng hóa X, Y với
giá PX = 2$, PY = 1$. Hàm tổng lới ích U (X,Y) = 2X + Y
a. Viết phương trình đường ngân sách (BL)
b. Xác định hàm MUX, MUY và MRSX/Y.
c. Xác định lượng hàng hoá X và Y mà người tiêu dùng mua để tối đa hoá lợi ích?
d. Nếu Py tăng lên bằng 2$ thì điểm tiêu dùng tối ưu là bao nhiêu?
e. Nếu Py giảm xuống còn 0,5$, điểm tiêu dùng tối ưu là bao nhiêu? Giải
a. Phương trình đường ngân sách
X.Px + Y.Py = I 2X + Y = 60 b. + MUx = 2 + MUy = 1 + MRS = MUx/MUy = 2/1 = 2 MU X MUY = c. PX PY
X .P X+Y . PY =I
2/2 = 1/1 (luôn luôn đúng) 2X + 1*Y = 60 lOMoAR cPSD| 58797173
Với mọi X và Y thỏa mãn phương trình đường ngân sách sẽ giúp người tiêu dùng tối đa
hóa lợi ích Trường hợp này :
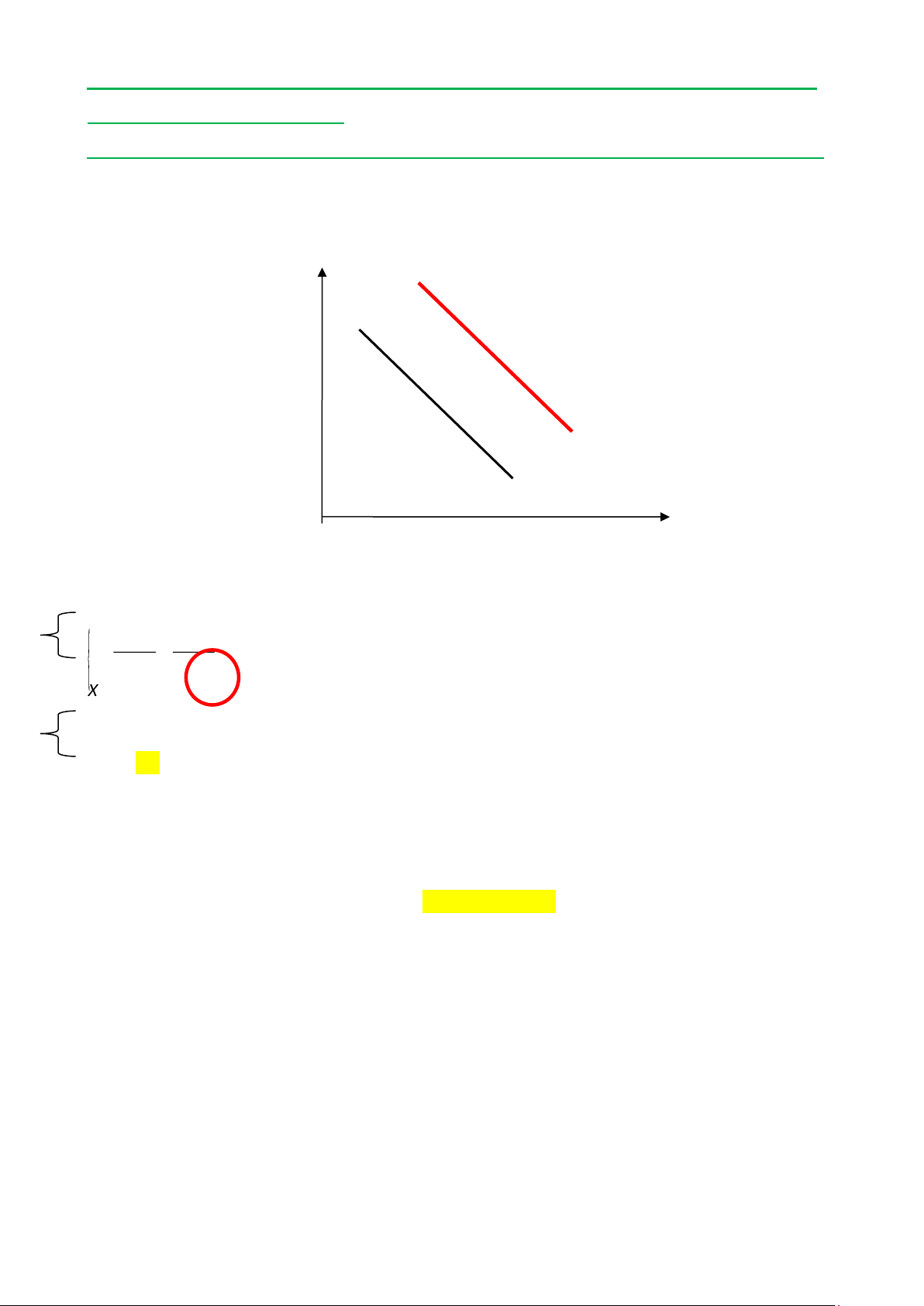
+ Đường BL trùng đường IC + Hình dạng 2 đường là đường thẳng, hệ số góc không đổi
Ngân sách (BL) : Y = 60 - 2X
Bàng quang (IC) : Y = U(X,Y) - 2X <=> U(X, Y) = 60 Y BL IC X
d. Nếu Py tăng lên bằng 2$ thì điểm tiêu dùng tối ưu là bao nhiêu? MU X MUY = PX PY
X .P X+Y . PY =I 2/2 = 1/2 (vô lý) 2X + 2Y =60 Ta có 1 > 0,5 2X + 2Y =60
Vậy, chúng ta sẽ sử dụng toàn bộ I = 60$ để mua tòa bộ X với X = 30 đơn vị sản phẩm.
Lưu ý: + Đường bàng quan: độ dốc MRS = MUx/MUy = 2
+ Đường ngân sách: Px/Py = 2/2 = 1
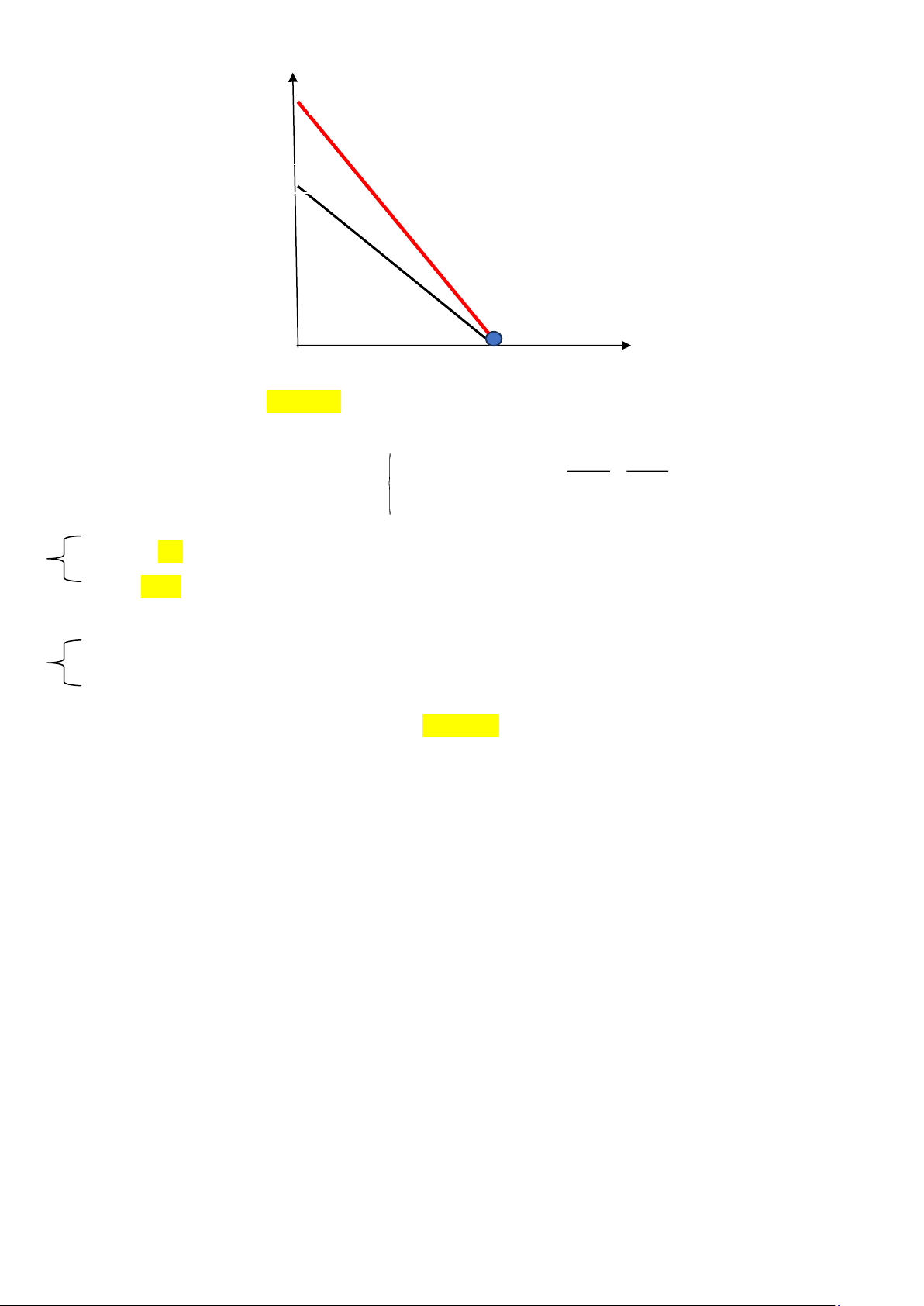
Trường hợp này, cả hai đường bàng quan và ngân sách đều là đường thẳng, khác nhau độ
dốc. Giao điểm của 2 đường chính là chấm (màu xanh) trên đồ thị. Tại chấm màu xanh => X = 30 và Y = 0 lOMoAR cPSD| 58797173 Y BL IC X
e.Nếu Py giảm xuống còn 0,5$, điểm tiêu dùng tối ưu là bao nhiêu? MU X MUY = PX PY
X .P X+Y . PY =I 2/2 = 1/0,5 (vô lý) 2X + 0,5Y = 60 Ta có : 1 < 2 2X + 0,5Y = 60
Vậy, chúng ta sẽ sử dụng toàn bộ I = 60$ để mua Y với Y = 120 đơn vị sản phẩm.
Thực hành xác định MUx và MUy
1) TU = 9X(Y - 2) = 9XY - 18X + MUx = 9Y - 18 + MUy = 9X + MRS = MUx/MUy 2) TU = X2.Y + 2Y + 19 + MUx = 2XY + 0 + 0 + MUy = X2 + 2 + 0 + MRS = MUx/MUy