Hướng dẫn báo cáo môn Thực hành vật lý đại cương( cho
khoa ngoài) dành cho sinh viên Đại học Khoa học Tự nhiên.
Lưu ý các số liệu trong các bài có thể bị sai sót và tài liệu chỉ
mang tính chất tham khảo. Họ và tên: MSV: Lớp:
BÁO CÁO THỰC HÀNH BÀI 1:
KHẢO SÁT HIỆN TƯỢNG VA CHẠM
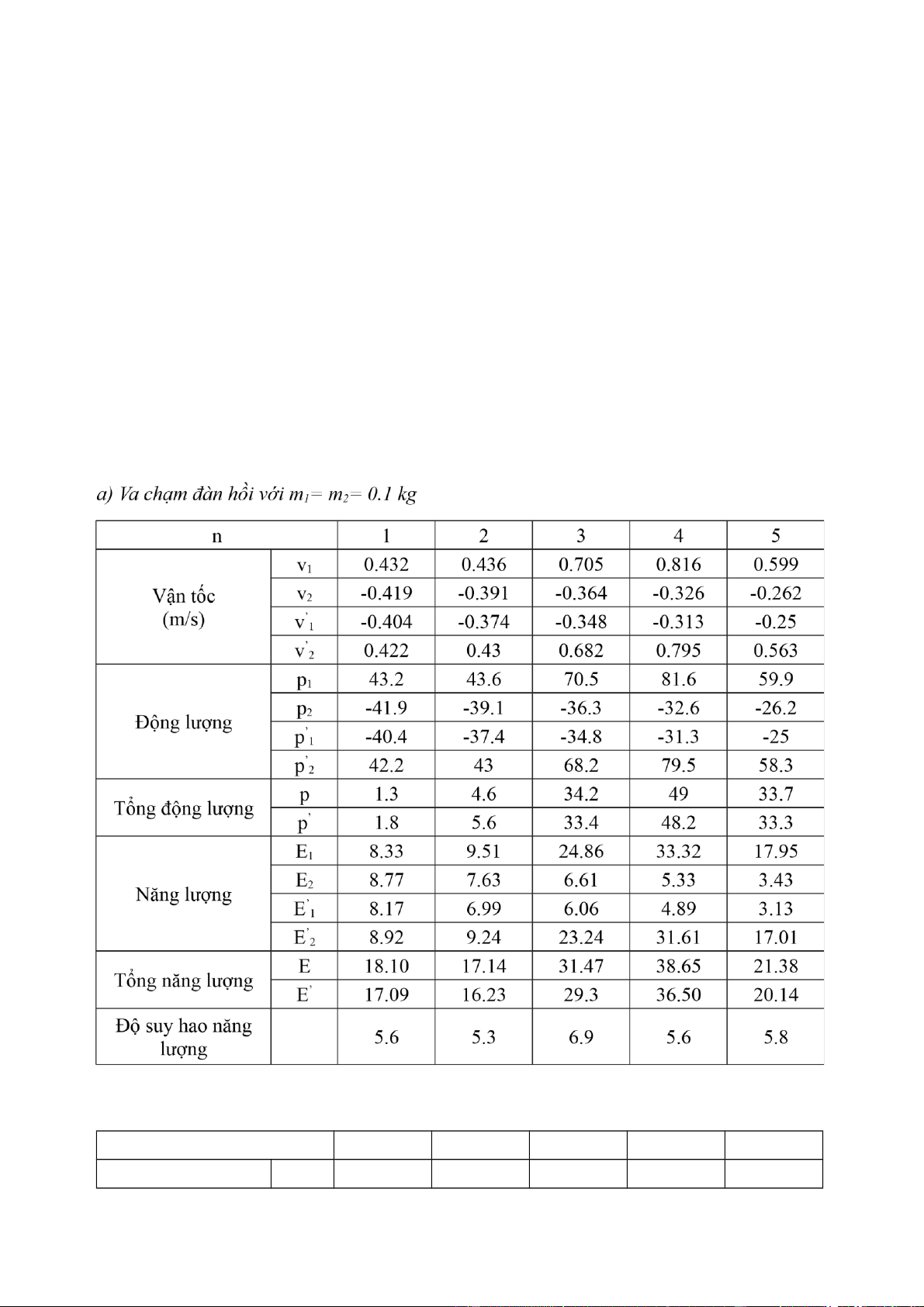
1.Va chạm đàn hồi.
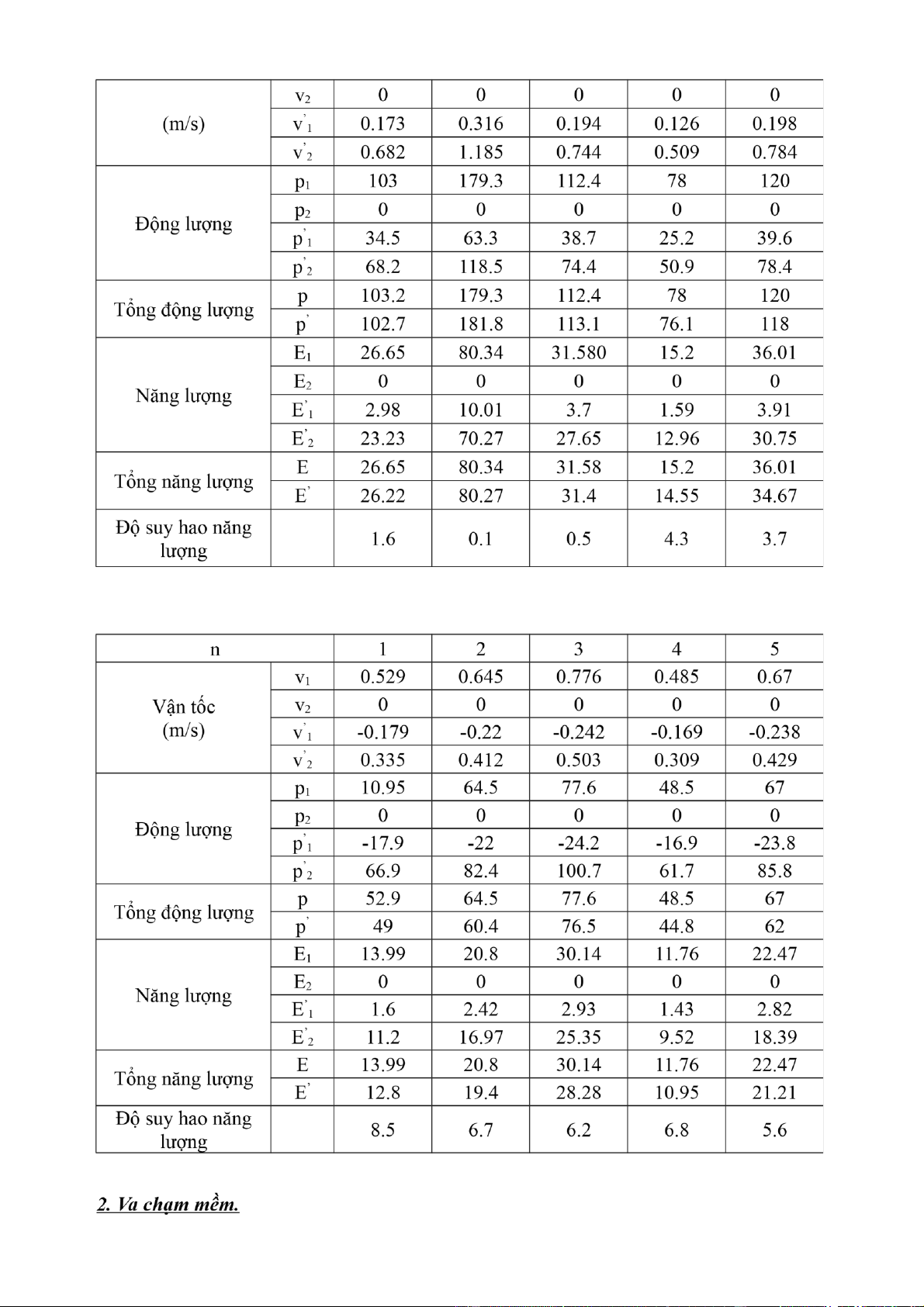
b) Va chạm đàn hồi với m1=0.2 kg; m2=0.1 kg n 1 2 3 4 5 Vận tốc v 1 0.516 0.896 0.562 0.39 0.6
c) Va chạm đàn hồi với m1=0.1 kg; m2=0.2 kg
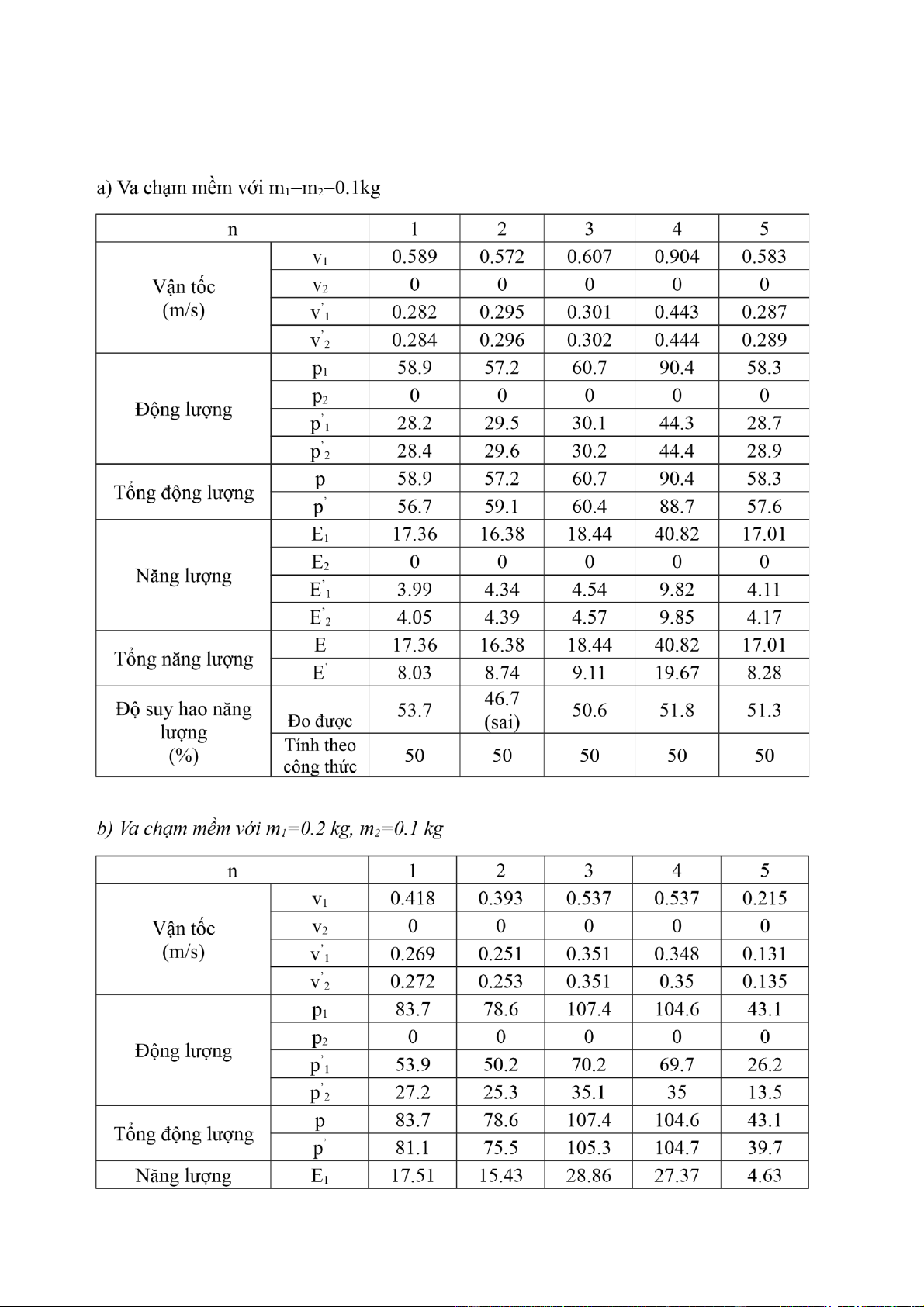
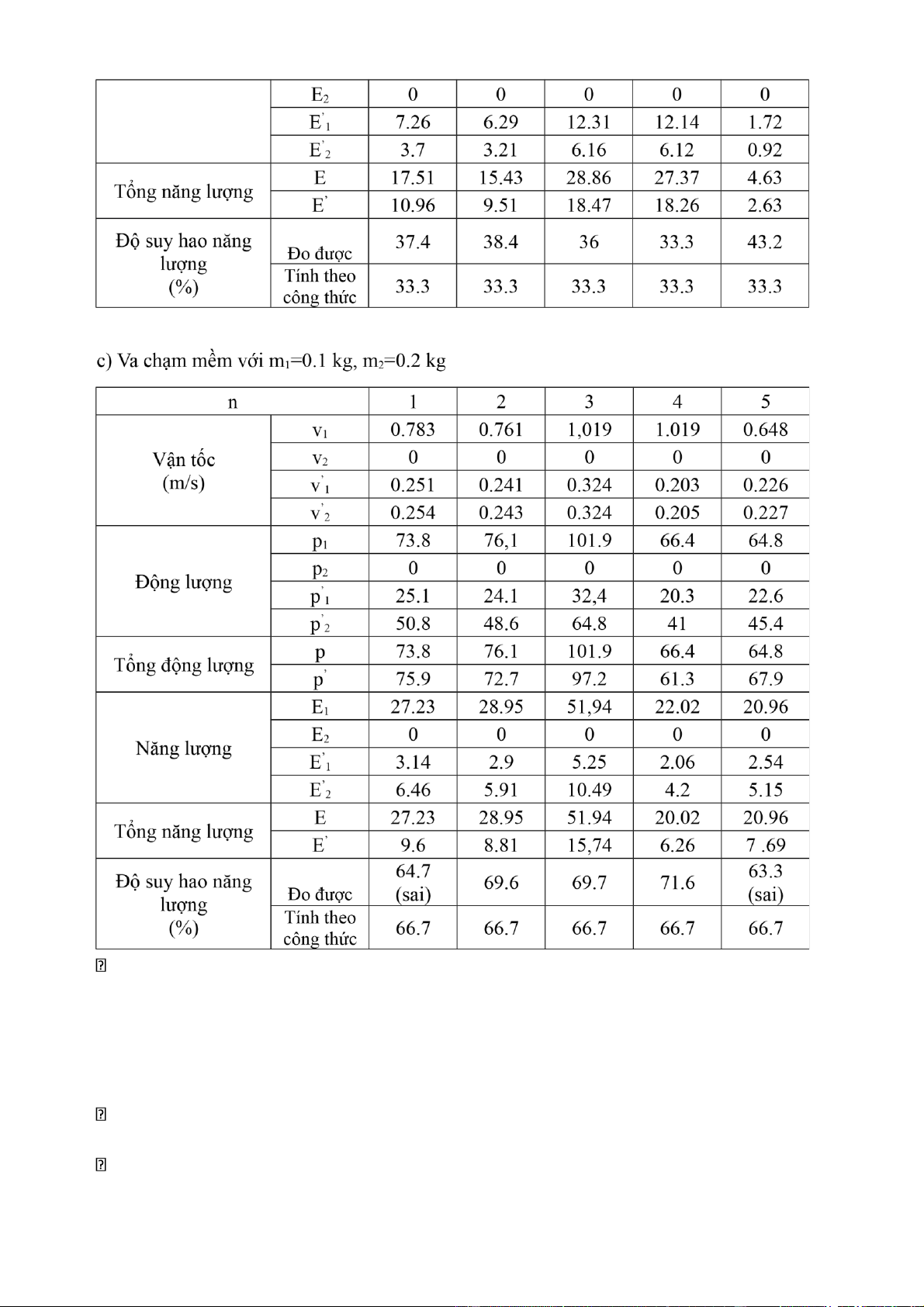
Công thức tính độ suy hao năng lượng trong va chạm mềm là: H = = x
Phân biệt va chạm đàn hồi và va chạm mềm:
- Va chạm đàn hồi là va chạm các vật tách rời nhau, động lượng của hệ và động năng của
hệ được bảo toàn. Sau va chạm 2 vật chuyển động với vận tốc riêng biệt v1’;v2’.
- Va chạm mềm là va chạm không đàn hồi, động lượng của hệ được bảo toàn, động năng
của hệ không bảo toàn. Sau va chạm 2 vật dính vào nhau và chuyển động với cùng vận tốc.
Định luật bảo toàn động lượng không có nghiệm đúng vì trong các thí nghiệm trên hệ
không kín, không lý tưởng.
Định luật bảo toàn năng lượng không được nghiệm đúng vì khi va chạm sẽ mất đi một
phần năng lượng triệt tiêu nhau để vật đổi chiều chuyển động. Khối lượng xe đứng yên
càng lớn thì năng lượng tiêu hao đi càng lớn.
Các kết quả tính toán lại cho thấy kết quả gần chính xác với kết quả thực nghiệm vì: hệ
không kín, do sai số thiết bị, do thao tác thực hành chưa chuẩn xác.
*** BÁO CÁO THỰC HÀNH BÀI 2: NHIỄU XẠ ÁNH SÁNG QUA MỘT
KHE VÀ QUA NHIỀU KHE HẸP
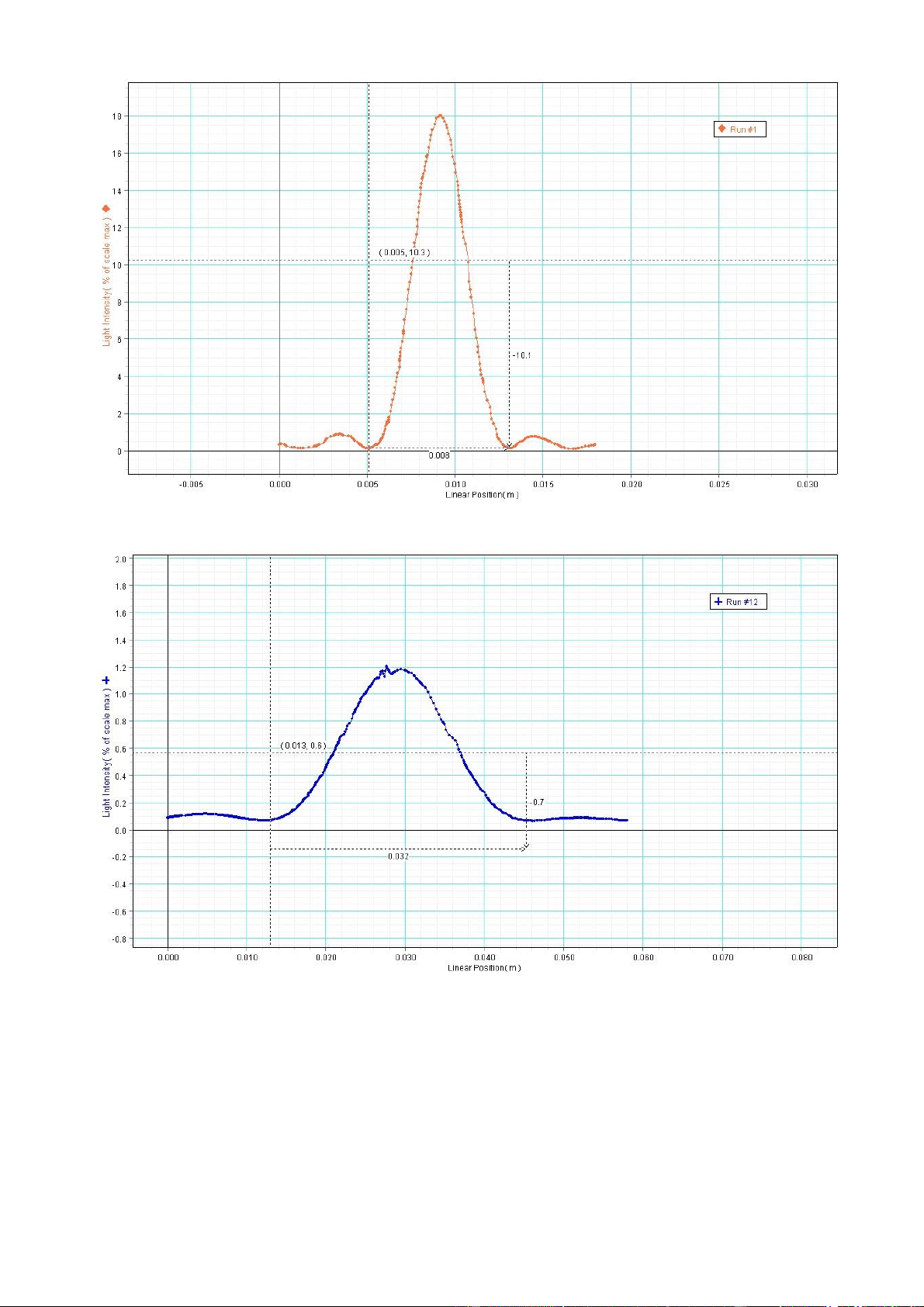
1. Nhiễu xạ qua một khe hẹp với các độ rộng khe khác nhau *Kết
quả thực nghiệm: Độ rộng khe
Khoảng cách giữa 2 vân cực tiểu bậc 1 (mm) a (mm) Lần 1 Lần 2 Lần 3 TB 0.16 8 8 8 8 0.04 32 32 32 32 0.08 16 16 16 16
Ta có công thức: a.sin = m.λ
Với góc rất nhỏ ta có: sin tan = x/2d
λ = a Với d = 93cm = 930mm a, Với a = 0.16 => λ =
0.16 x = 6.88 x 10-4 mm = 688 nm b, Với a = 0.04 => λ =
0.04 x = 6.88 x 10-4 mm = 688 nm c, Với a = 0.08 => λ =
0.08 x = 6.88 x 10-4 mm = 688 nm
Nhận xét: Ta thấy bước sóng thực tế λ = 688 nm > bước sóng lí thuyết λ = 632.8 nm
Qua các anh nhiễu xạ ta thấy khi độ rộng khe giảm góc nhiễu xạ tăng, từ trung tâm thoải
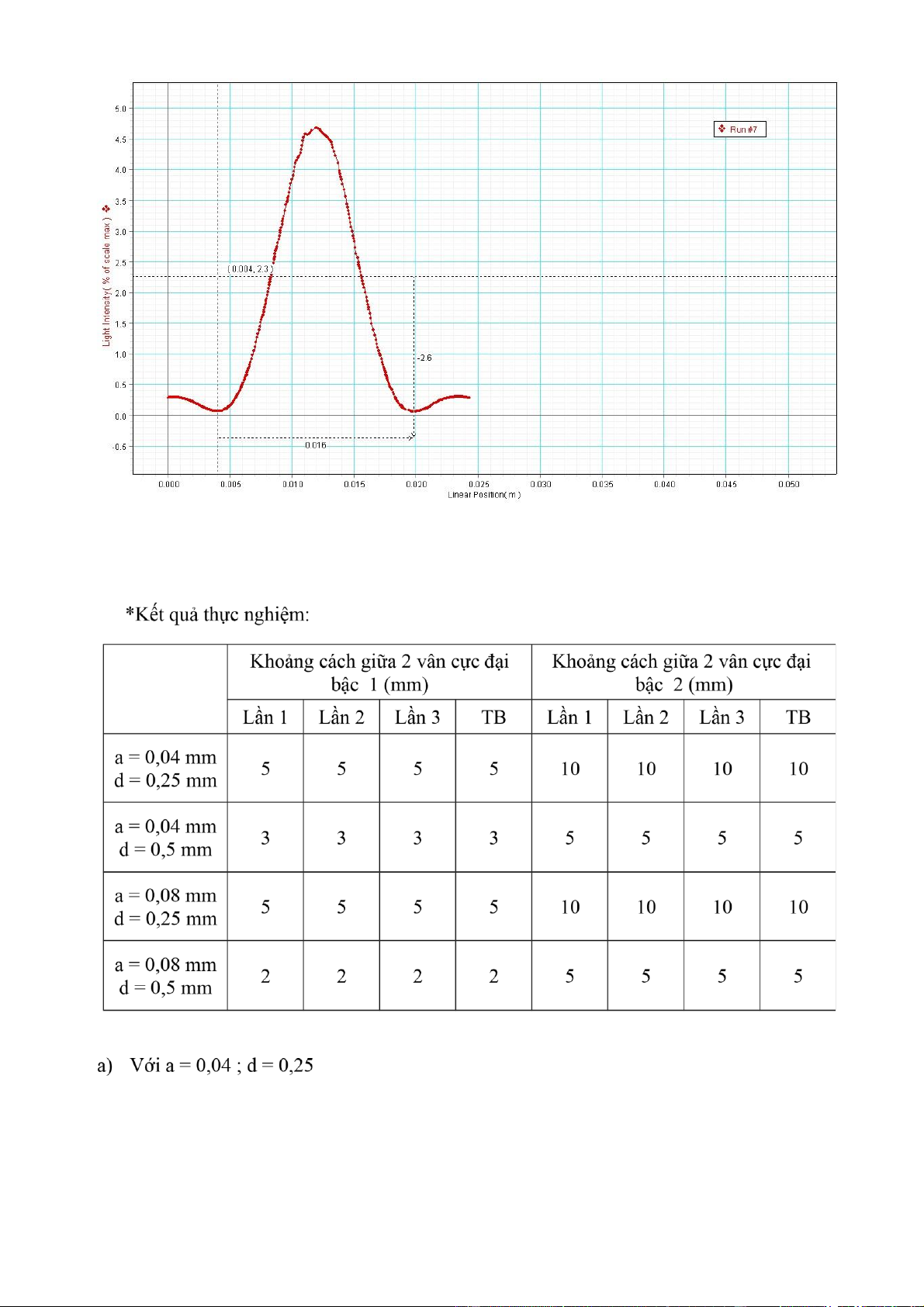
dần về hai phía và chiếm toàn bộ màn quan sát. a) a = 0,16 b) a = 0,04 c) Với a = 0,08
2. Nhiễu xạ nhiều khe hẹp
a) Nhiễu xạ qua hai khe hẹp với các độ rộng a và khoảng cách giữa các khe d khác nhau b) a = 0,04 ; d = 0,5 c) a = 0,08 ; d = 0,25 d) a = 0,08 ; d = 0,5
*Nhận xét: Quan sát đồ thị và qua bảng số liệu ta rút ra được: Với cùng một khoảng cách
d trên cùng đồ thị, độ rộng a càng nhỏ thì các vân sáng (hoặc tối) càng gần nhau (hay
khoảng cách giữa hai vân sáng càng nhỏ)
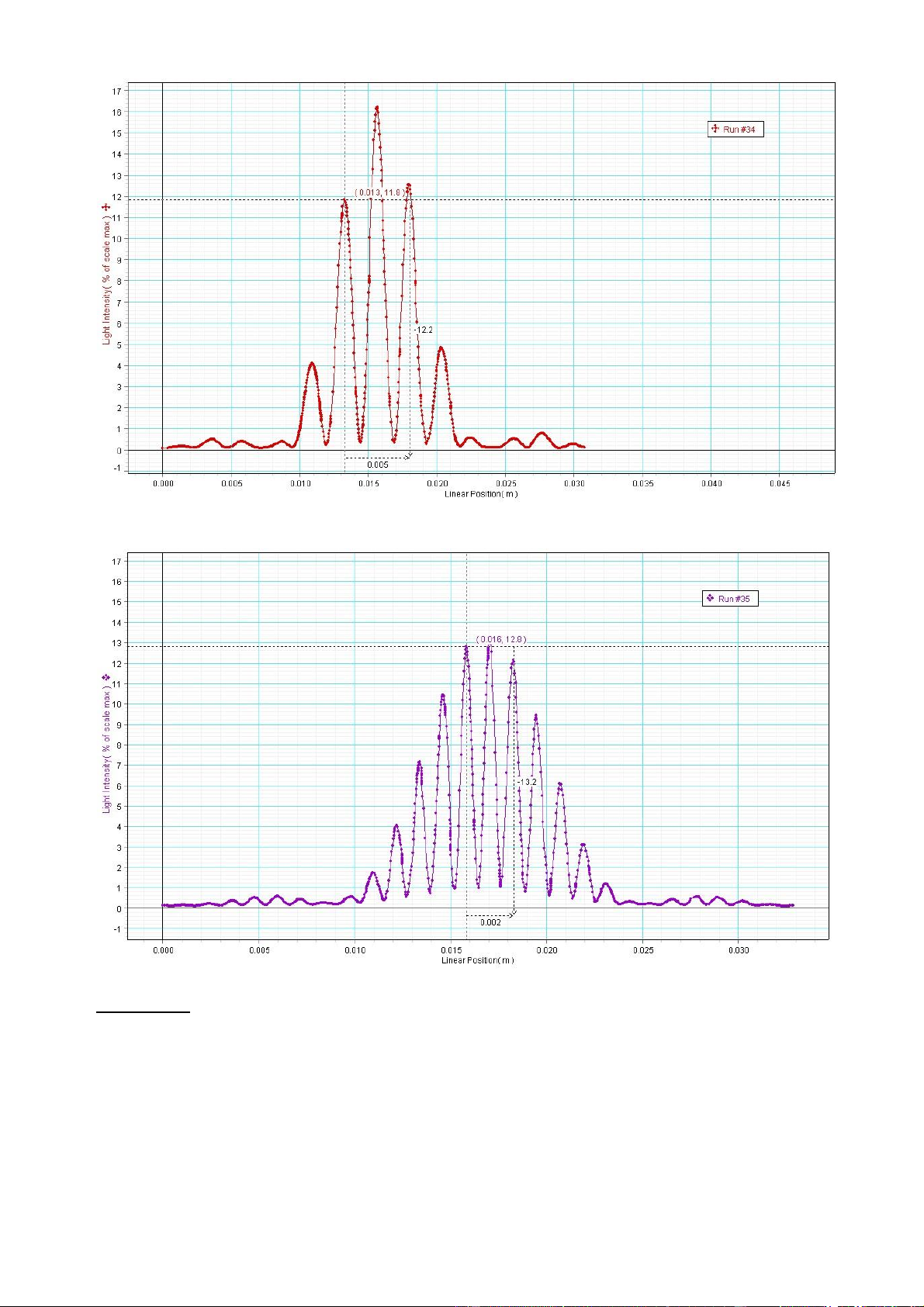
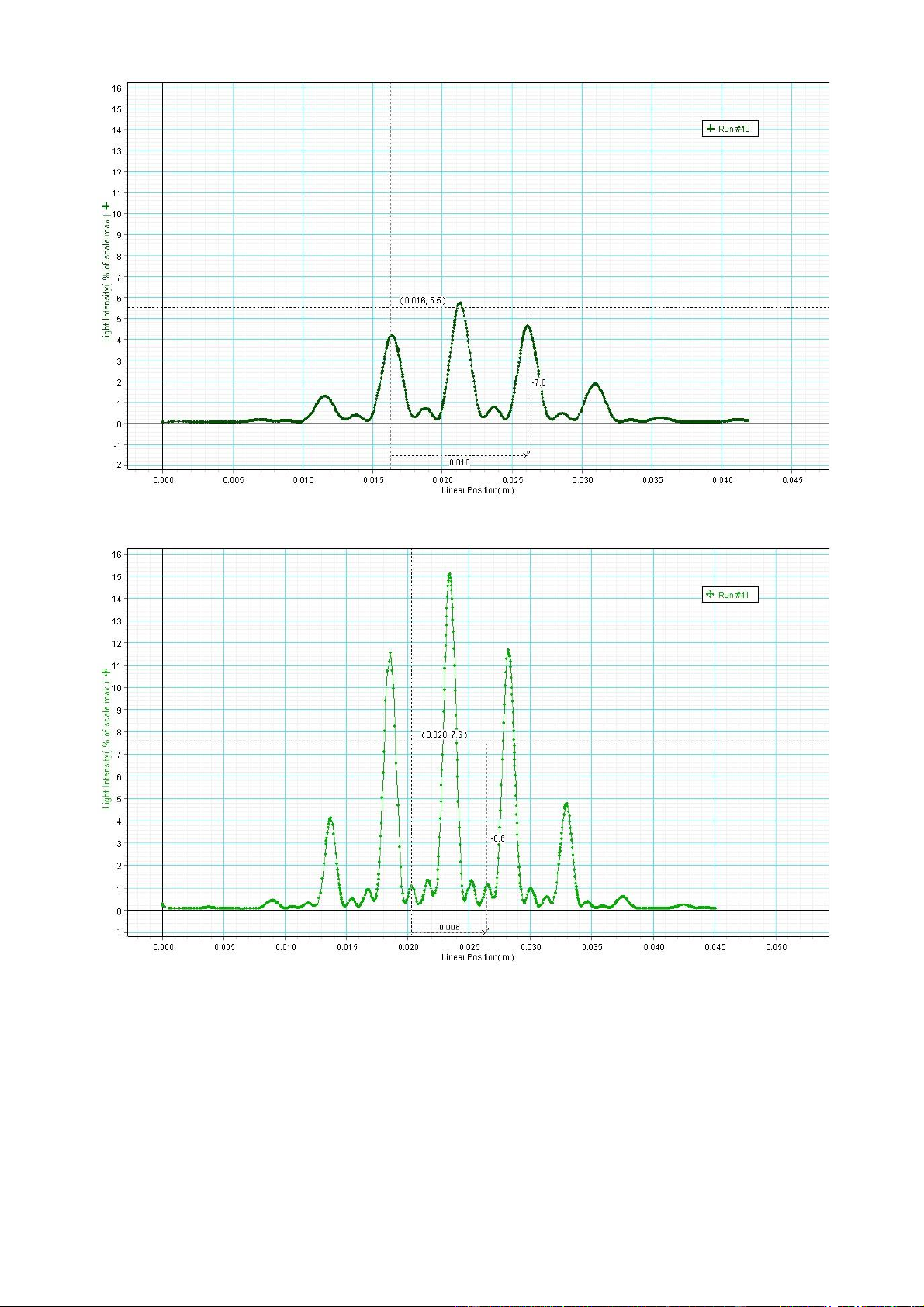
b)Nhiễu xạ qua nhiều khe hẹp với các độ rộng a và khoảng cách giữa các khe d giống nhau.
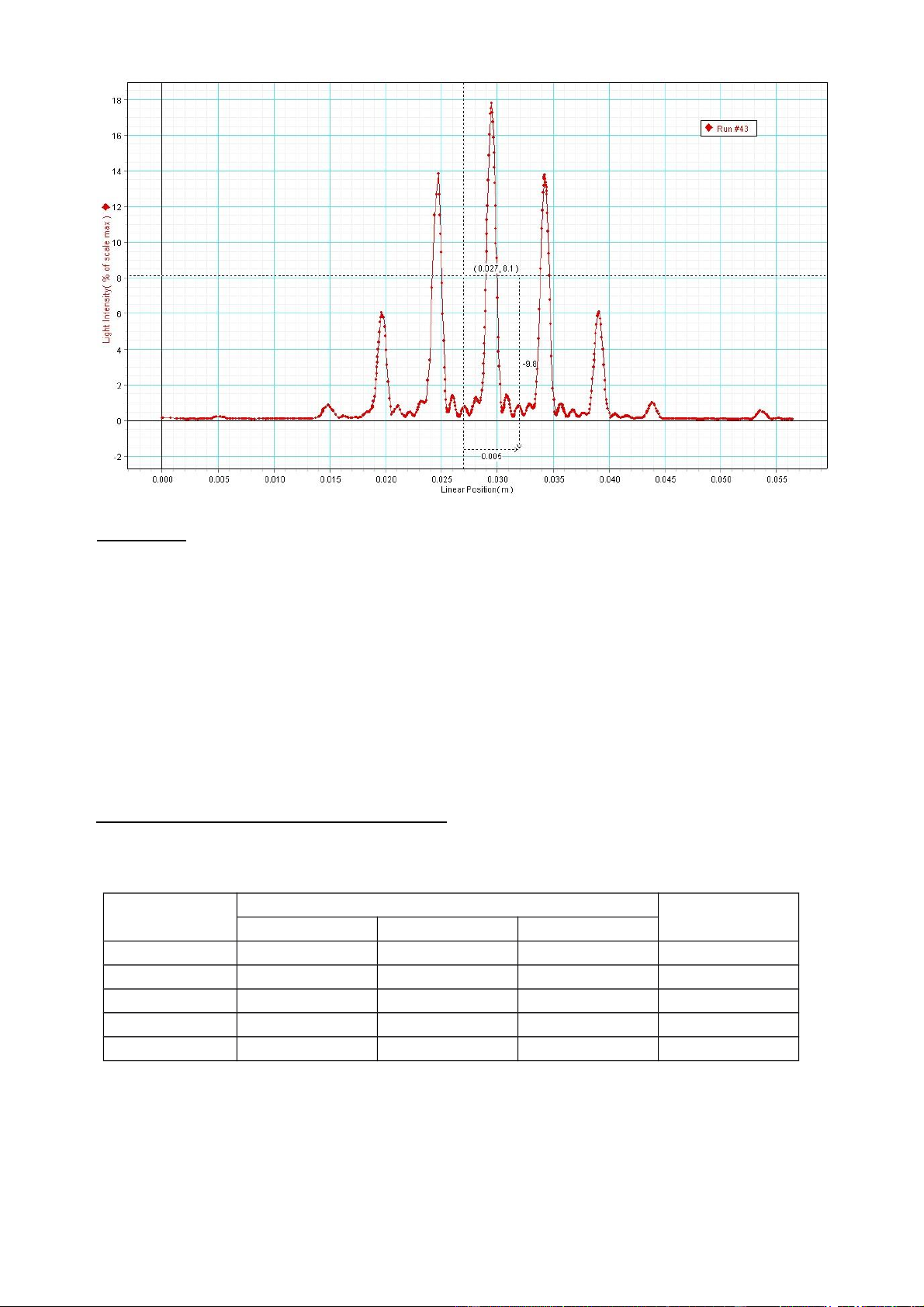
* Nhiễu xạ hệ gồm 3 khe:
*Nhiễu xạ hệ gồm 4 khe:
*Nhiễu xạ hệ gồm 5 khe: *Nhận xét:
Sự khác nhau giữa các phổ nhiễu xạ qua 3,4 và 5 khe trên cùng 1 đồ thị có phù hợp
với lý thuyết. Theo lý thuyết giữa hai cực đại chính liên tiếp có (N-2) cực đại phụ và (N1)
cực tiểu phụ. Trên thực tế đồ thị với N = 3 có giữa hai cực đại chính có đúng 1 cực đại
phụ và 2 cực tiểu phụ.
Tương tự với N = 4 và N = 5 cũng đúng với lý thuyết. ***
BÁO CÁO THỰC HÀNH BÀI 3: GIAO THOA KẾ MICHELSON
I, Xác định bước sóng của ánh sáng laze:
1, Bảng số liệu biểu thị số vân giao thoa Z và quãng đường dịch chuyển tương ứng của gương M1: Z () ( tb ) Lần 1 Lần 2 Lần 3 () 30 11 11 10 11 40 15 15 13 14 50 18 18 17 18 60 21 21 21 21 70 24 24 24 24
Qua bảng số liệu tính được: λ30 = 0,73.10-6 m λ60 = 0,7.10-6 m λ40 = 0,7.10-6 m λ70 = 0,69.10-6 m λ50 = 0,72.10-6 m λTB = 0,7.10-6 m
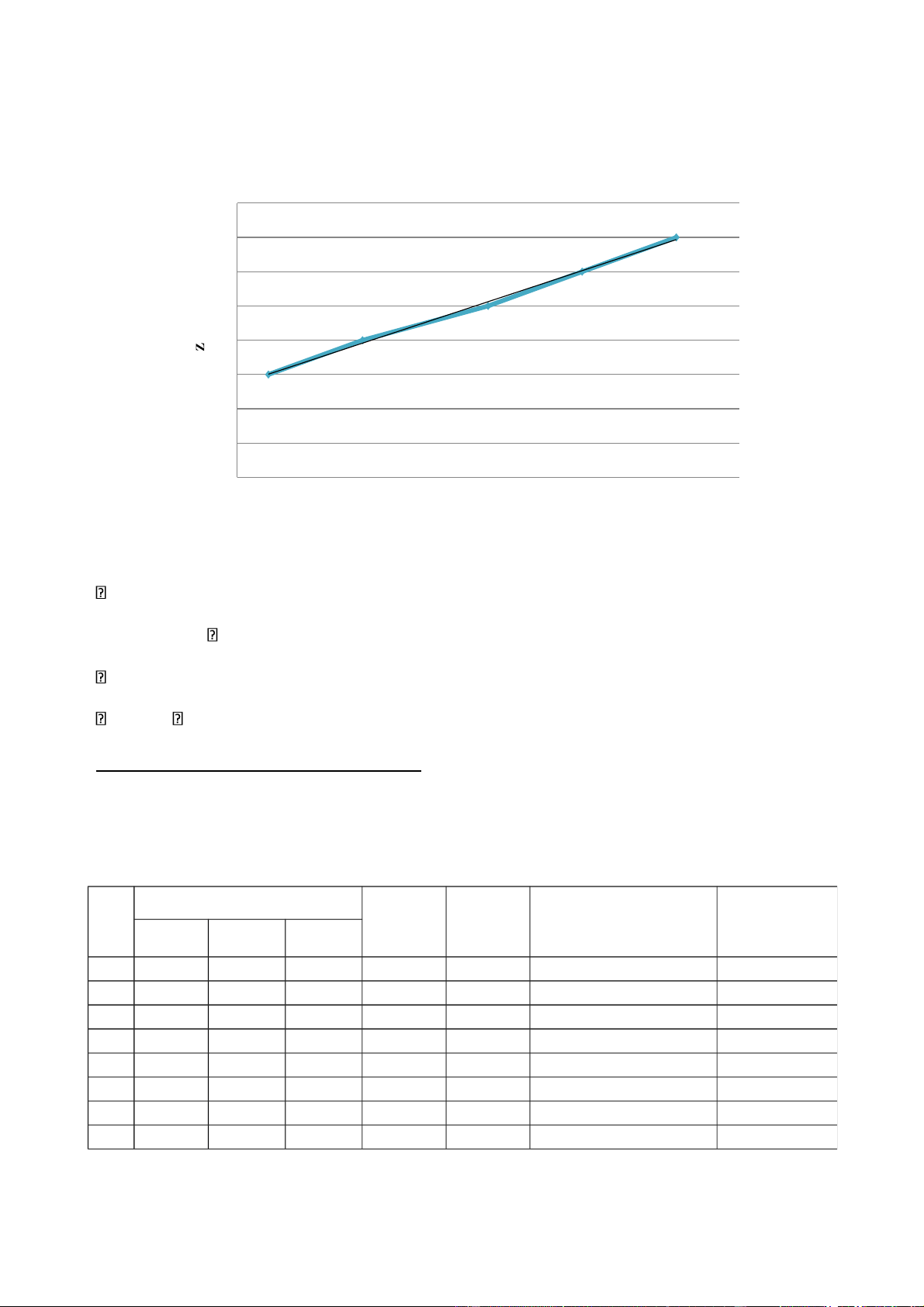
2, Đồ thị biểu diễn sự phụ thuộc của số vân giao thoa Z vào quãng đường dịch chuyển :
Đồ thị mô tả sự phụ thuộc của số vân giao thoa dịch chuyển Z vào quãng
đường dịch chuyển ∆S 80 70 f(x) = 3.02 x − 3.19 60 R² = 1 50 40 30 20 10 0 10 12 14 16 18 20 22 24 26 ∆S (µm) Nhận xét: Ta thấy: λ=2 Z=
Giá trị của chính bằng giá trị hệ số góc của đường thẳng trên.
= 3.022 λ= 0.662 = 0.662 10-6 m
II, Xác định chiết suất của không khí:
1, Bảng biểu diễn giá trị số vân giao thoa dịch chuyển phụ thuộc vào áp suất trong bình khí: P(inHg) P(tb) P(tb) Áp suất thực tế Z trong bình(P=PKQ - n Lần 1 Lần 2 Lần 3 (inHg) (cmHg) Pđo được)
1 1.5 1.5 2 1.67 4.24 71.76 1.0000044 2 2.5 3.5 4 3.33 8.46 67.54 1.0000041 3 4 4.7 5
4.57 11.61 64.39 1.0000039 4 5.5 6 6.4 5.97 15.16 60.84 1.0000037 5 7 7.9 7.7 7.53 19.13 56.87 1.0000035
6 8.5 9.1 9.4 9 22.86 53.14 1.0000033 7 10 10.4 10.5 10.3 26.16 49.84 1.0000031 8 11.5 12 12 11.83 30.05 45.95 1.0000028 9 13
13.2 13.6 13.27 33.71 42.29 1.0000026 10 14 15 15 14.67 37.26 38.74 1.0000024 11
15.5 16.4 16.4 16.1 40.89 35.11 1.0000021 12 17
17.5 17.6 17.37 44.12 31.88 1.0000020 13 18
18.9 18.5 18.47 46.91 29.09 1.0000018 14 19.5 20.4 20 19.97 50.72 25.28 1.0000015 15
21 21.8 22 21.6 54.86 21.14 1.0000013 16 22 22.9 23.1 22.67 57.58 18.42 1.0000011 17 23 24 24.4 23.8 60.45 15.55 1.0000010
- Đổi đơn vị: 1 cmHg = 0.393702 inHg ; 1 inHg = 2.53999 cmHg
- Đổi số liệu: PKQ = 76cmHg
- Ta có: n(p) = n(P = 0) + với n(P = 0) = 1, P = PKQ - Pđo được Và ta cũng có: với s = 3cm, = 0.662 10-6 m
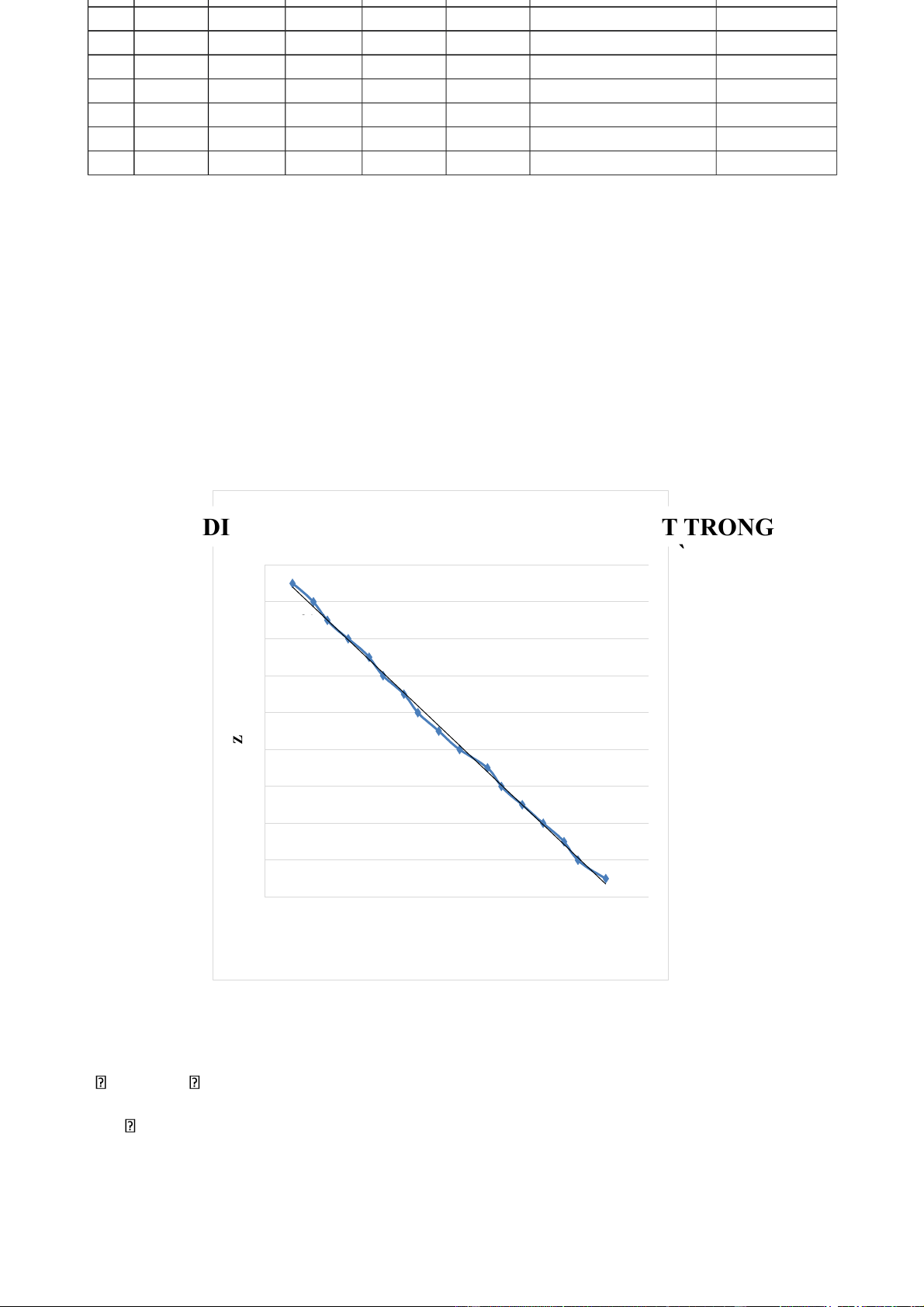
2, Đồ thị biểu diễn sự phụ thuộc của số vân giao thoa dịch chuyển vào áp suất trong bình khí:
ĐỒ THỊ DIỄN SỰ PHỤ THUỘC CỦA SỐ VÂN G T IA TRO O TH NG OA BIỂU 1 VÀO ÁP SUẤ BÌNH 8 1 f(x) = − 0.28 x + 6 21 R .² 04 = 1 1 4 1 2 1 0 8 6 4 2 0 1 2 3 4 5 6 7 8 0 0 0 0 0 0 0 0 P (cmHg)
Nhận xét: Từ đồ thị ta thấy giá trị của chính bằng giá trị hệ số góc của đồ thị.
= - 0.282 = 0.282 = 6.22 10-8 n(P) = 1+ 6.22 10-8P
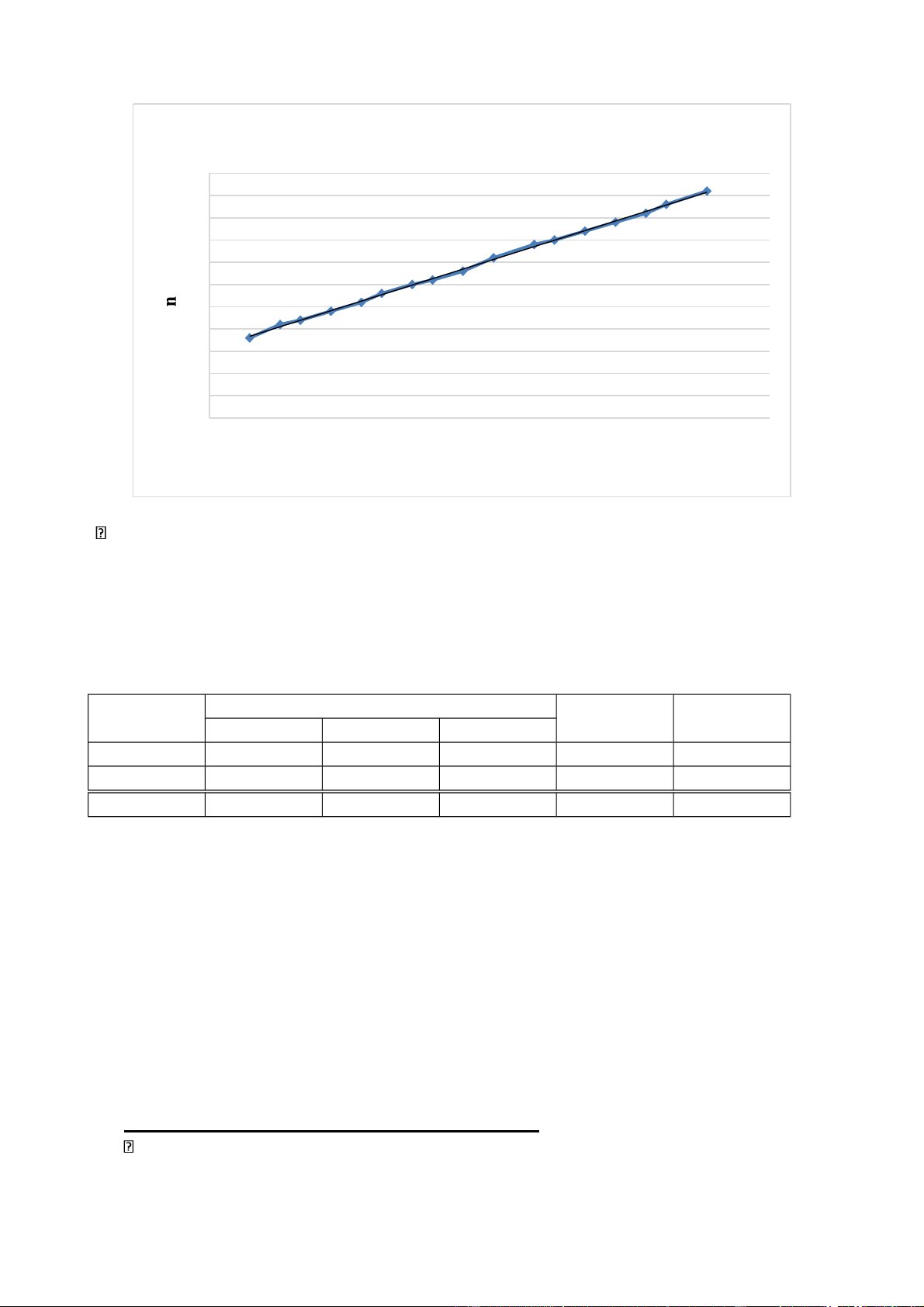
3, Đồ thị biểu diễn sự phụ thuộc của chiết suất váo áp suất không khí trong bình:
Đồ thị biểu diễn sự phụ thuộc của chiết suất vào áp suất không khí 1 1 f(x) = 0 x + 1 1 R² = 1 1 1 1 1 1 1 1 1 1 10 20 30 40 50 60 70 80 P (cmHg) Nhận xét:
Đường đồ thị này cho ta thấy rằng cứ với 1 giá trị P thì sẽ có 1 giá trị chiết suất n tương
ứng. Khi P giảm thì giá trị chiết suất n giảm và ngược lại.
III, Xác định chiết suất tấm thủy tinh: 1, Bảng số liệu: Z ( tb ) n tt Lần 1 Lần 2 Lần 3 80 9.2 9.4 9.1 9.2 1.691 100 10.4 10.4 10.1 10.3 1.686 120 11.4 11.4 11.1 11.3 1.681
Ta có: ntt = với t là độ dày của tấm thủy tinh. = 0.662 x 10-6 m ; t = 5mm. *** BÁO CÁO THỰC HÀNH
BÀI 4: KHẢO SÁT HIỆN TƯỢNG PHÂN CỰC ÁNH SÁNG
1. Phân biệt ánh sáng tự nhiên và ánh sáng phân cực Ánh sáng tự nhiên:
+ Là ánh sáng có vector cường độ điện trường (vector sóng sáng) dao động đều đặn theo
mọi phương vuông góc với tia sáng
+ Khi một ánh sáng tự nhiên đi qua 1 môi trường bất đẳng hướng về mặt quang học thì tác
dụng của môi trường lên ánh sáng tự nhiên có thể làm cho vector cường độ điện trường chỉ
còn dao động theo một hướng nhất định.
+ Anh sáng tự nhiên có thể coi là tập hợp của vô số ánh sáng phân cực toàn phần. Tia sáng phân cực:
+ Ánh sáng phân cực toàn phần (ánh sáng phân cực thẳng): ánh sáng có vector cường độ
điện trường dao động chỉ theo một phương xác định.
+ Ánh sáng phân cực một phần: ánh sáng có vector cường độ điện trường dao động theo
mọi phương vuông góc với tia sáng nhưng có phương dao động mạnh và có phương dao động yếu. 2. Vẽ đồ thị
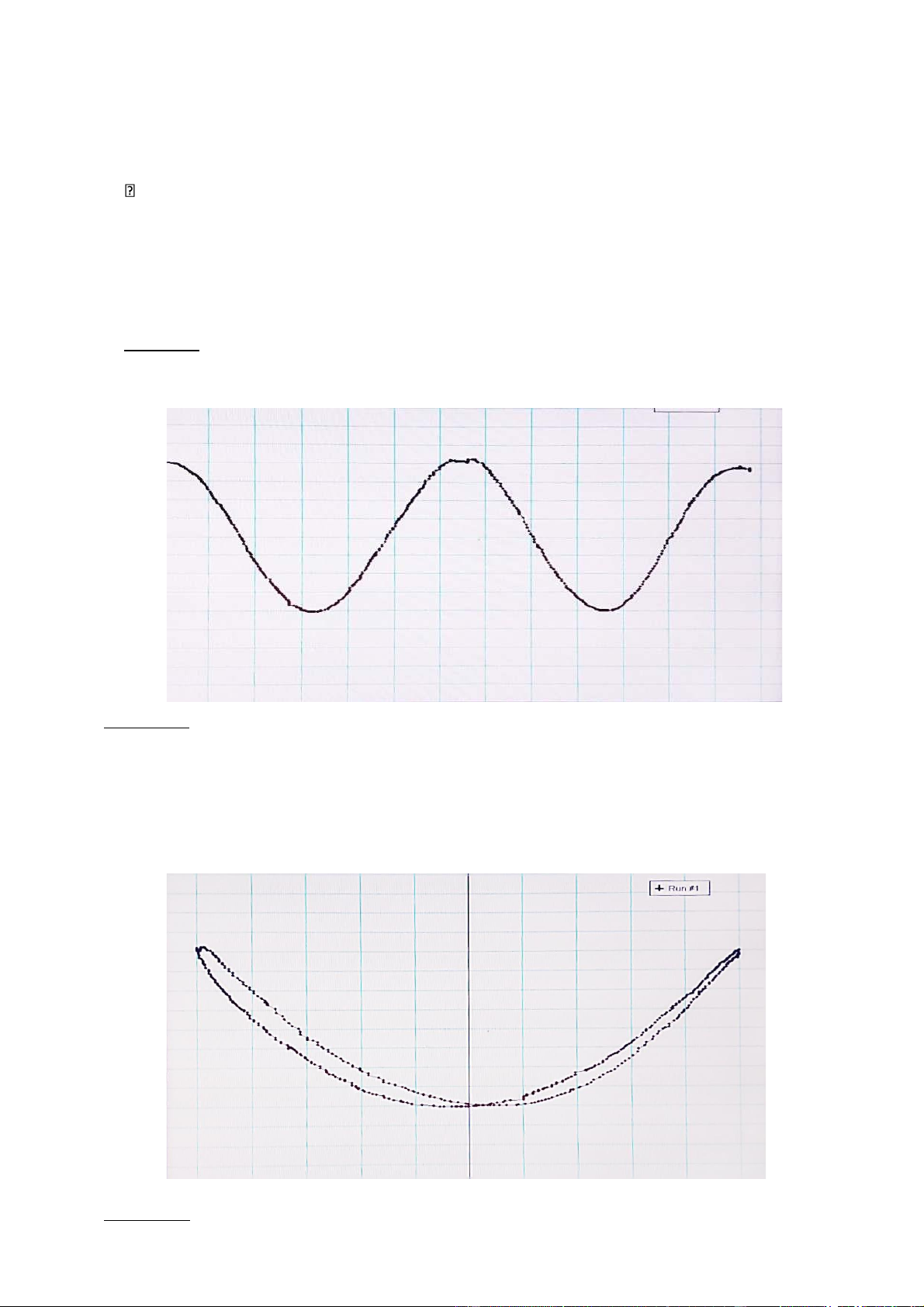
a) Đồ thị mô tả sự phụ thuộc của cường độ ánh sáng I sau khi đi qua kính phân tích vào vị trí
góc x (góc tạo bởi hai trục quang T1 và T2) *Nhận xét:
Từ đồ thị ta thấy cường độ I của tia ló giảm khi góc x tăng
+ Giá trị I = 0 khi góc x = 900 (khi 2 quang trục của 2 kính vuông góc với nhau).
+ Giá trị I sau đó tăng dần đến giá trị cực đại khi góc x = 1800.
+ Sau đó giá trị I lại giảm khi x = 2700, nó đạt giá trị cực đại khi góc x = 3600.
b) Đồ thị mô tả sự phụ thuộc của cường độ ánh sáng I sau khi đi qua kính phân tích vào cosx *Nhận xét:
- Định luật Malus: I = I0.cos2x được nghiệm đúng
- Đồ thị mô tả sự phụ thuộc của cường độ ánh sáng I sau khi đi qua kính phân tích vào cosxlà một đường cong Parabol.
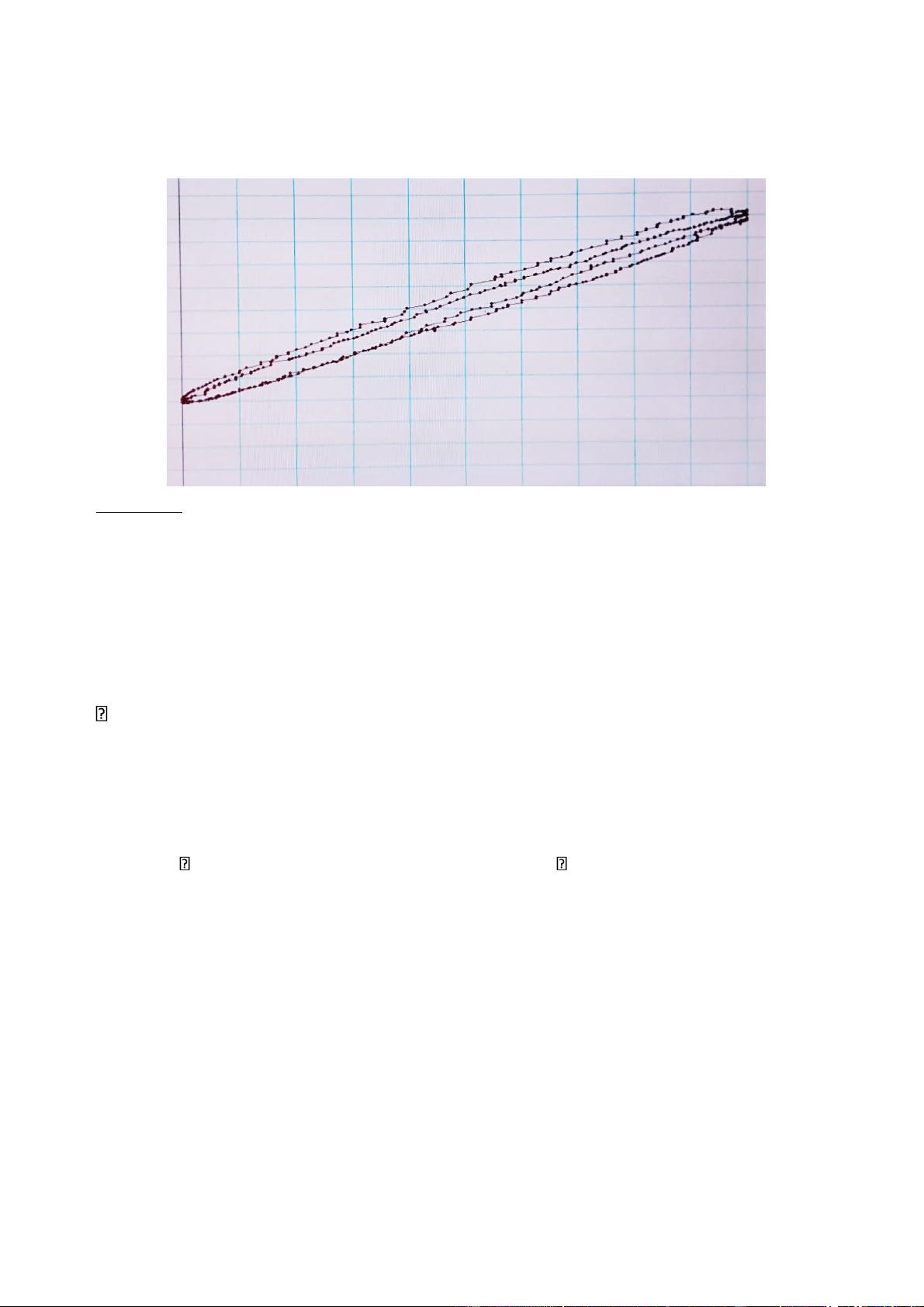
c) Đồ thị mô tả sự phụ thuộc của cường độ ánh sáng I sau khi đi qua kính phân tích vào cos2x
*Nhận xét: Đồ thị mô tả sự phụ thuộc của cường độ ánh sáng I sau khi đi qua kính phân tích
vào cos2x là một đường thẳng
Định luật Malus được nghiệm đúng. Vì cường độ ánh sáng I sau khi đi qua kính phân tích phụ
thuộc tuyến tính vào cos2x. ***
BÁO CÁO THỰC HÀNH BÀI 6: ĐỘNG CƠ NHIỆT STIRLING Lý thuyết
- Động cơ nhiệt thực hiện công trong thời gian T và điện áp đốt U là W + tần số quay: f = 1/T
+ công suất : P = W/T = W.f
Đổi 104 hPa*cm3 = 1J => 1 hPa*cm3 = 10-4J Giản
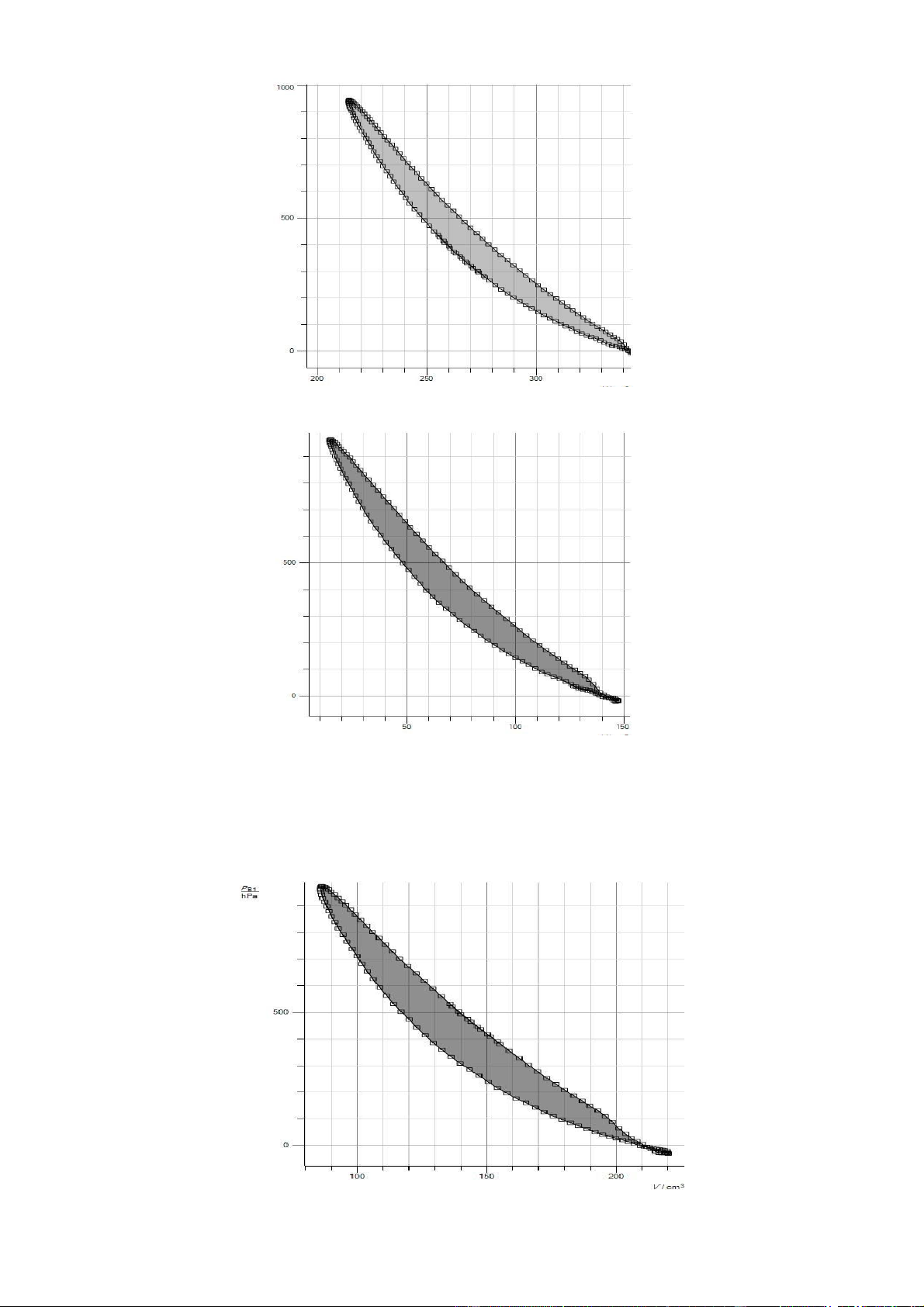
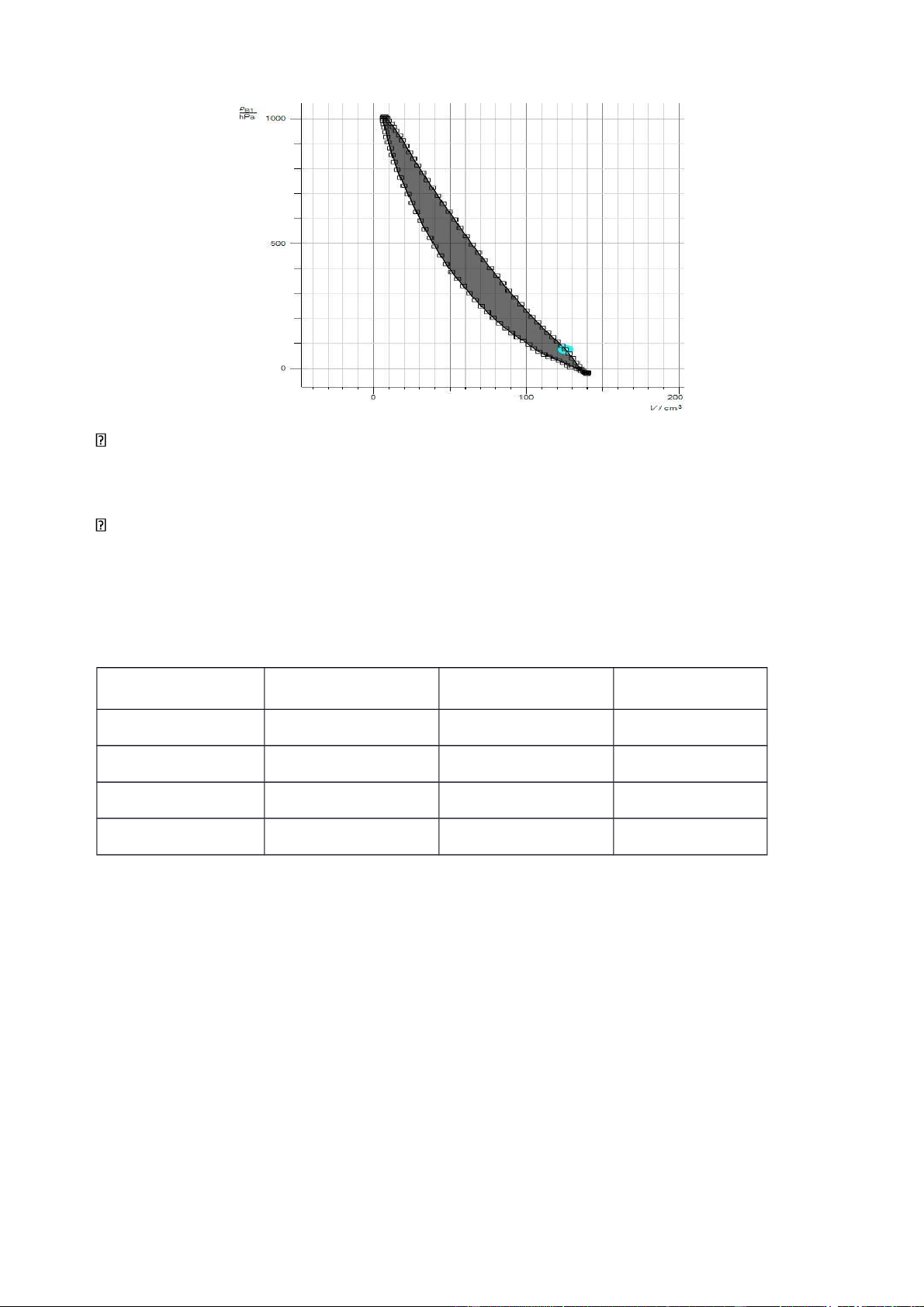
đồ pV với các điện áp đốt khác nhau:
a) Với điện áp : U = 10V, T = 0.34s thì W = 1.3320 (J)
b) Với điện áp U = 12V, T = 0.28s thì W = 1.5190 (J)
c) Với điện áp U = 14V, T = 0.25s thì W = 1.7390 (J)
d) Với điện áp U = 16V , T = 0.21s thì W = 2.0010 (J)
Nhận xét: từ hình ảnh giản đồ pV cho thấy kết quả thực nghiệm khác với lý thuyết. Hai
quá trình đẳng tích theo lí thuyết sẽ là 2 đường thẳng song song với nhau và vuông góc
với trục V, nhưng trên thực tế khác. Giải thích:
+ Do sự hoạt động của piston động cơ chuyển động hình sin nên trạng thái đẳng tích
không như trường hợp lí tưởng.
+ Một phần nhiệt lượng tỏa ra môi trường và làm nóng động cơ.
Bảng 2: Công cơ học W (J) của một vòng, tần số quay và công suất theo điện áp đốt:
Điện áp đốt U(V) Công cơ học W(J)
Tần số quay f(Hz) Công suất P(W) 10 1,332 /0, 1 34 3,918 12 1,519 1 /0, 28 5,425 14 1,739 1 /0, 25 6,956 16 2,001 1 /0, 21 9,529 ***
BÁO CÁO THỰC HÀNH BÀI 7: ĐỊNH LUẬT ÔM (OHM)
1. Khảo sát sự phụ thuộc của dòng điện vào hiệu điện thế của các dây dẫn có tiết diện khác nhau.
Bảng 1: Các giá trị tương ứng giữa U và I của các dây constantan có cùng chiều dài l = 1
m với các đường kính khác nhau. d = 1 mm
d = 0,7 mm d = 0,5 mm d = 0,35 mm A = 0,8 mm2 A = 0,4 mm2 A = 0,2 mm2 A = 0,1 mm2 U(V) I(A) U(V) I(A) U(V) I(A) U(V) I(A) 0,1 0,158 0,2 0,152 0,4 0,158 0,8 0,156 0,2 0,312 0,4 0,303 0,8 0,317 1,6 0,314 0,3 0,471 0,6 0,457 1,2 0,476 2,4 0,471 0,4 0,625 0,8 0,607 1,6 0,634 3,2 0,629 0,5 0,788 1,0 0,759 2,0 0,794 4,0 0,787 0,6 0,945 1,2 0,912 2,4 0,952 0,7 1,097 1,4 1,064 2,8 1,112 0,8 1,258 1,6 1,216 3,2 1,271 0,9 1,409 1,8 1,370 3,6 1,430 1,0 1,568 2,0 1,518 1,1 1,726 2,2 1,672 1,2 1,884
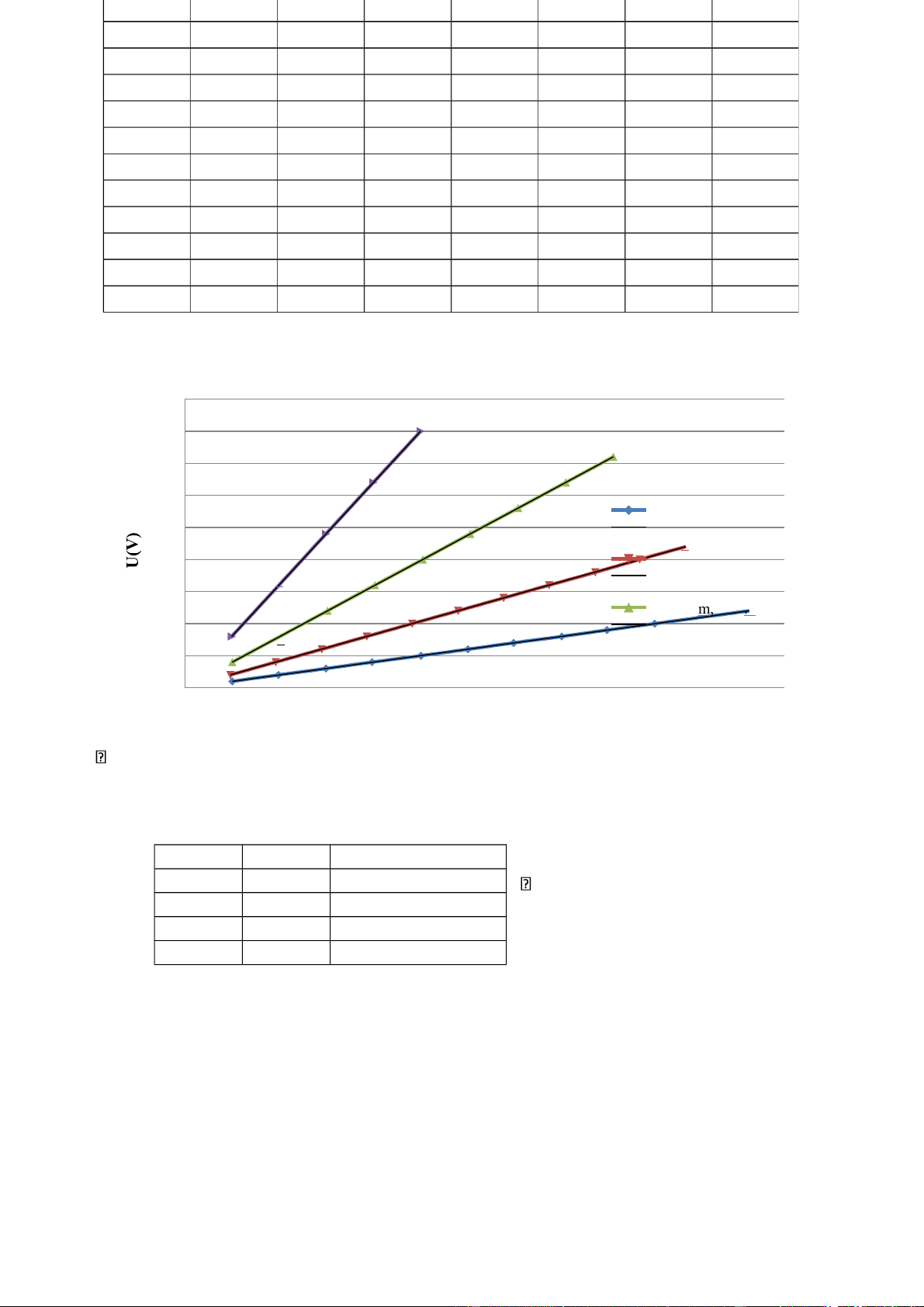
Đồ thị U(I) theo các dây dẫn có tiết diện khác nhau 4.5 4 f(x) = 5.07 x + 0.01 3.5 R² = 1 f(x) = 2.52 x + 0 3 R² = 1 d=1mm, A=0.8mm2 2.5 Linear (d=1mm, A=0. 8mm2) 2 f(x) = 1.32 x + 0 d=0.7mm, A=0.4mm2 R² = 1 Linear (d=0.7mm, 1.5 A=0.4mm2) d=0.5m , m A=0 mm .2 1 f(x) = 0.64 x − 0 Linear (d=0.5mm, R² = 1 A=0.2mm) 0.5 0 0 0.2 0.4 0.6 0.8 1 1.2 1.4 1.6 1.8 2 I(A)
Nhận xét: A càng lớn thì giá trị của I tăng càng chậm khi mà tăng U.
Các đồ thị U, I là những đường thẳng có hệ số góc chính bằng giá trị của điển trở R ứng
với các trường hợp (theo định luật Ôm: U = R.I). Ta có bảng sau: A(mm 2 ) R(Ω) 1 /A( mm -2 ) 0.1 5.1 10
Nhận xét: Độ lớn tiết diện 0.2 2.5 5
của dây dẫn tỉ lệ nghịch với 0.4 1.3 2.5
giá trị điện trở của dây. 0.8 0.6 1.25
Bảng 2: Các giá trị điện trở tương ứng với các tiết diện khác nhau của dây Constantan có
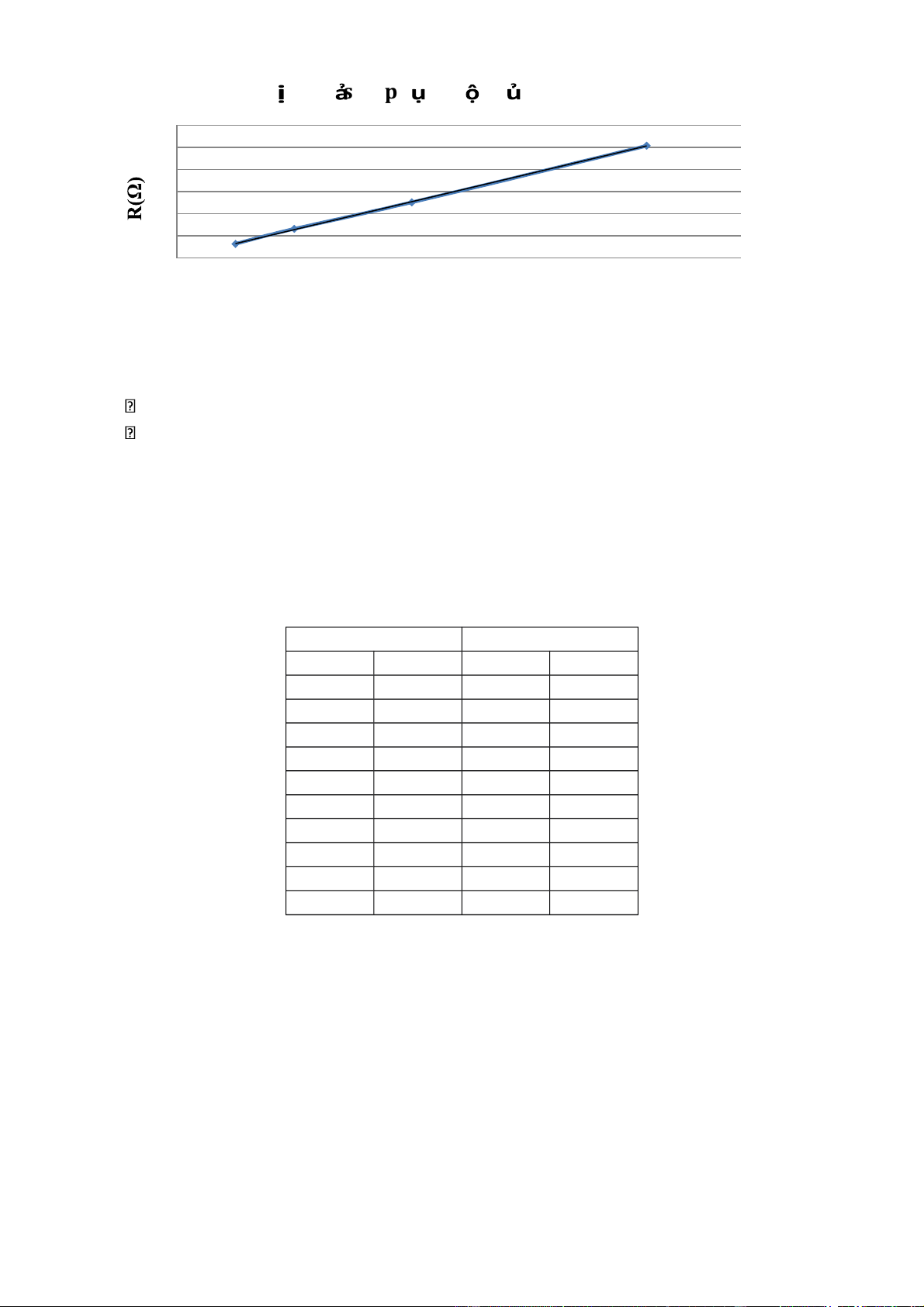
l =1m. Từ bảng trên ta có đồ thị: Đồồ th m
ồ t s ph th u c c a R vào 1/A 6 5 4 f(x) = 0.5 x + 0.02 R² = 1 3 2 1 0 0 2 4 6 8 10 12 1/A (mm-2)
Hệ số góc của đường thẳng R (1/A) chính bằng l.ρ vì R = l.ρ.
l(mm).ρ(Ω.mm) = 0.5046 (Ω.mm2) = 0.5046x10-6(Ω.m2) ρ = 0.5046x10-6(Ω.m)
Điện trở suất của dây constantan đã được công bố là: 0.5x10-6 (Ω.m).
Như vậy, kết quả thu được từ thí nghiệm phù hợp. 2.
Khảo sát sự phụ thuộc của dòng điện vào hiệu điện thế của các dây dẫn có
chiềudài khác nhau.
Bảng 3: Các giá trị tương ứng của U và I với các dây dẫn có chiều dài khác nhau. l = 1 m l = 2 m U(V) I(A) U(V) I(A) 0.2 0,152 0.4 0.150 0.4 0,303 0.8 0.298 0.6 0,457 1.2 0.448 0.8 0,607 1.6 0.598 1.0 0,759 2.0 0.746 1.2 0,912 2.4 0.896 1.4 1,064 2.8 1.045 1.8 1,370 3.3 1.232 2.0 1,518 3.6 1.344 2.2 1,672 4.0 1.495