






Preview text:
CHƯƠNG 7
ĐƯỜNG THẲNG VÀ MẶT PHẲNG
TRONG KHÔNG GIAN BÀI 1.
ĐẠI CƯƠNG VỀ ĐƯỜNG THẲNG VÀ MẶT PHẲNG A TÓM TẮT LÝ THUYẾT 1
Mở đầu về hình học không gian. Đối tượng cơ bản:
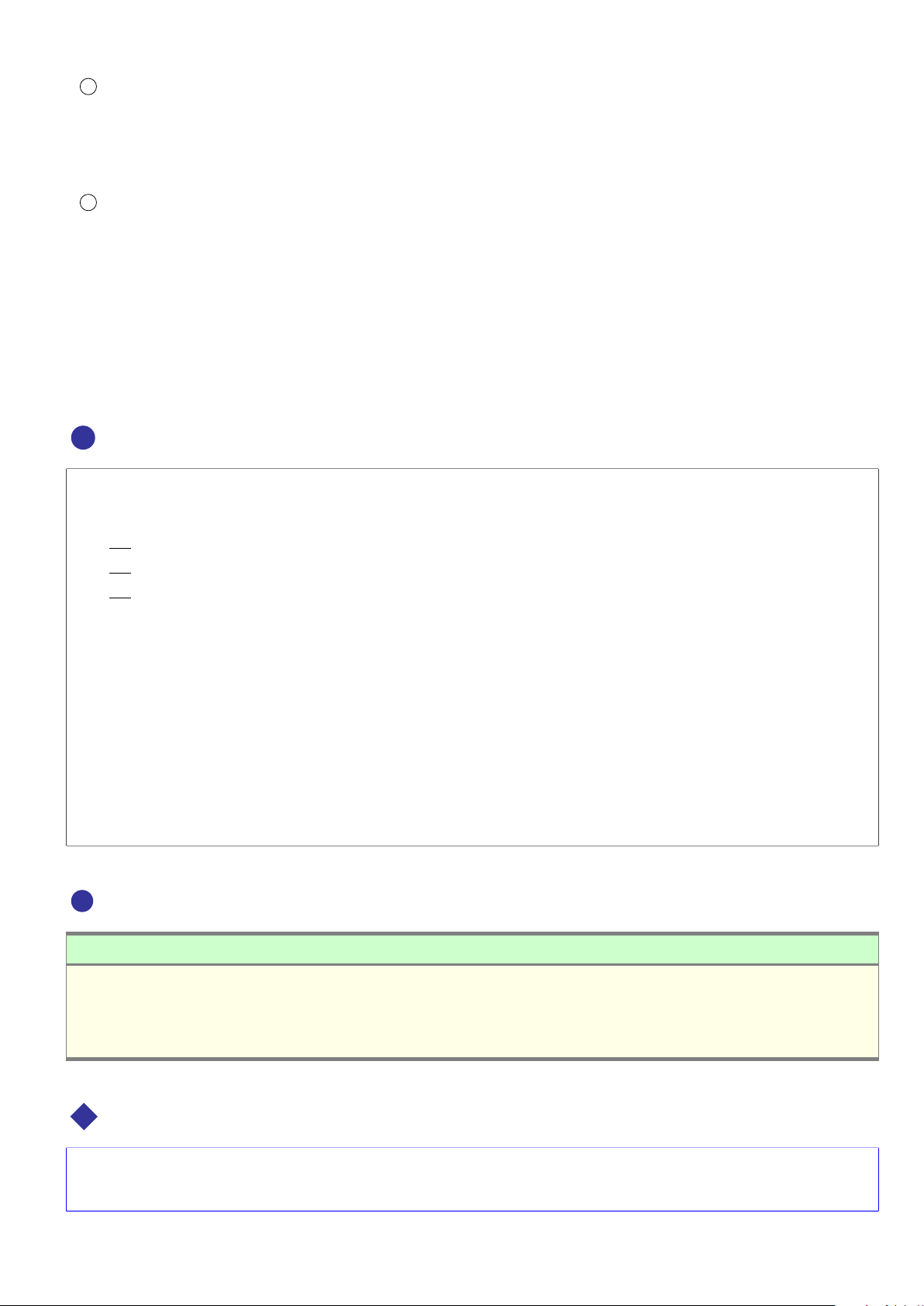
. Điểm: kí hiệu A, B, C, ... d
. Đường thẳng: kí hiệu a, b, c, d, ... A
. Mặt phẳng: kí hiệu (P), (Q), (α), (β), ... B P Quan hệ cơ bản:
. Thuộc: kí hiệu ∈. Ví dụ A ∈ d, M ∈ (P) ...
. Chứa, nằm trong: kí hiệu ⊂. Ví dụ: d ⊂ (P), b ⊂ (α).
Hình biểu diễn của một hình trong không gian:
. Đường thẳng được biểu diễn bởi đường thẳng. Đoạn thẳng biểu diễn bởi đoạn thẳng.
. Hai đường thẳng song song (hoặc cắt nhau) được biểu diễn bởi hai đường thẳng song song (hoặc cắt nhau).
. Hai đoạn thẳng song song hoặc bằng nhau được biểu diễn bởi hai đoạn thẳng song song và bằng nhau.
. Dùng nét vẽ liền để biểu diễn cho những đường trông thấy và dùng nét đứt đoạn (- - - -) để biểu diễn
cho những đường bị che khuất. 2
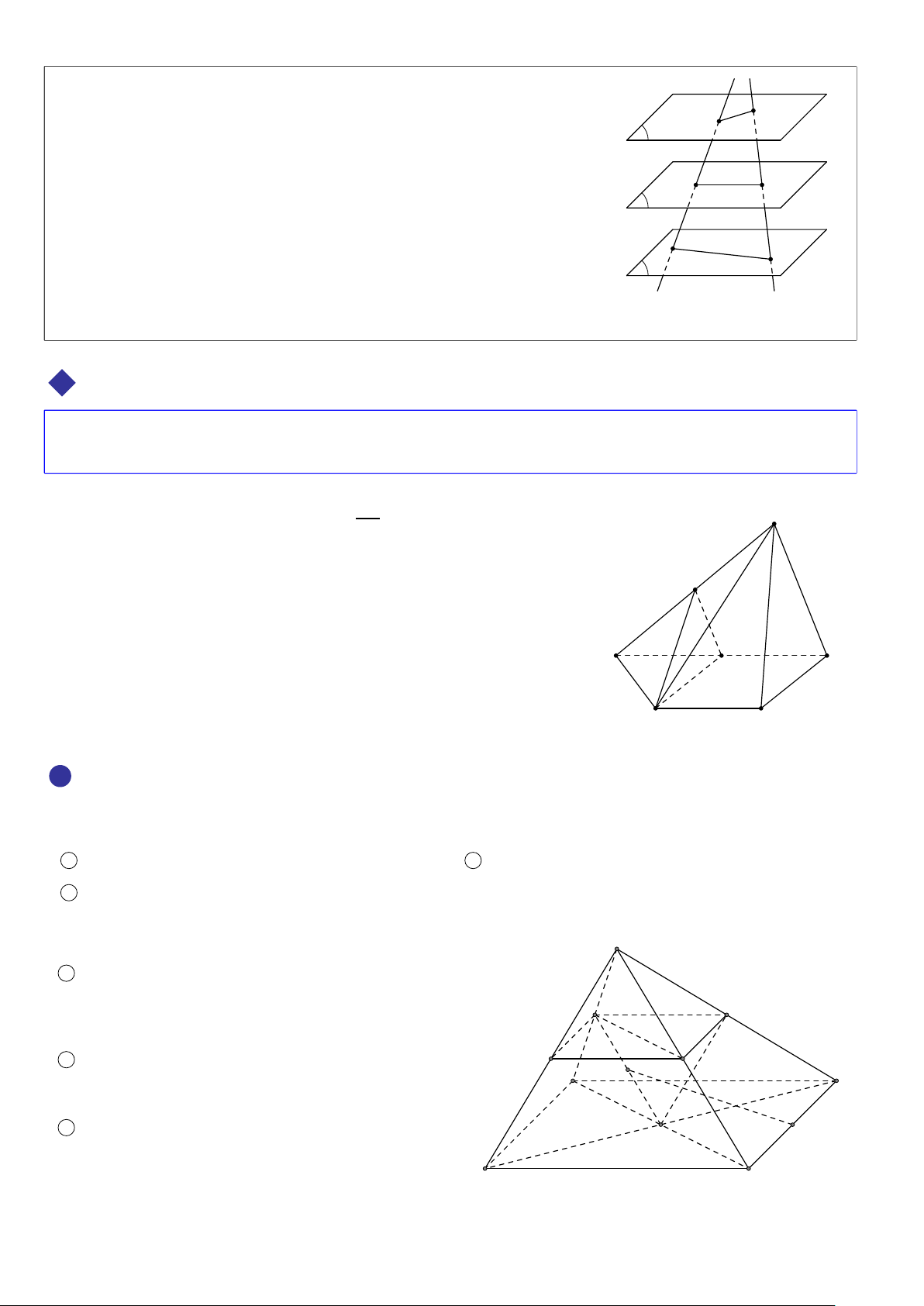
Các tính chất thừa nhận trong hình học không gian.
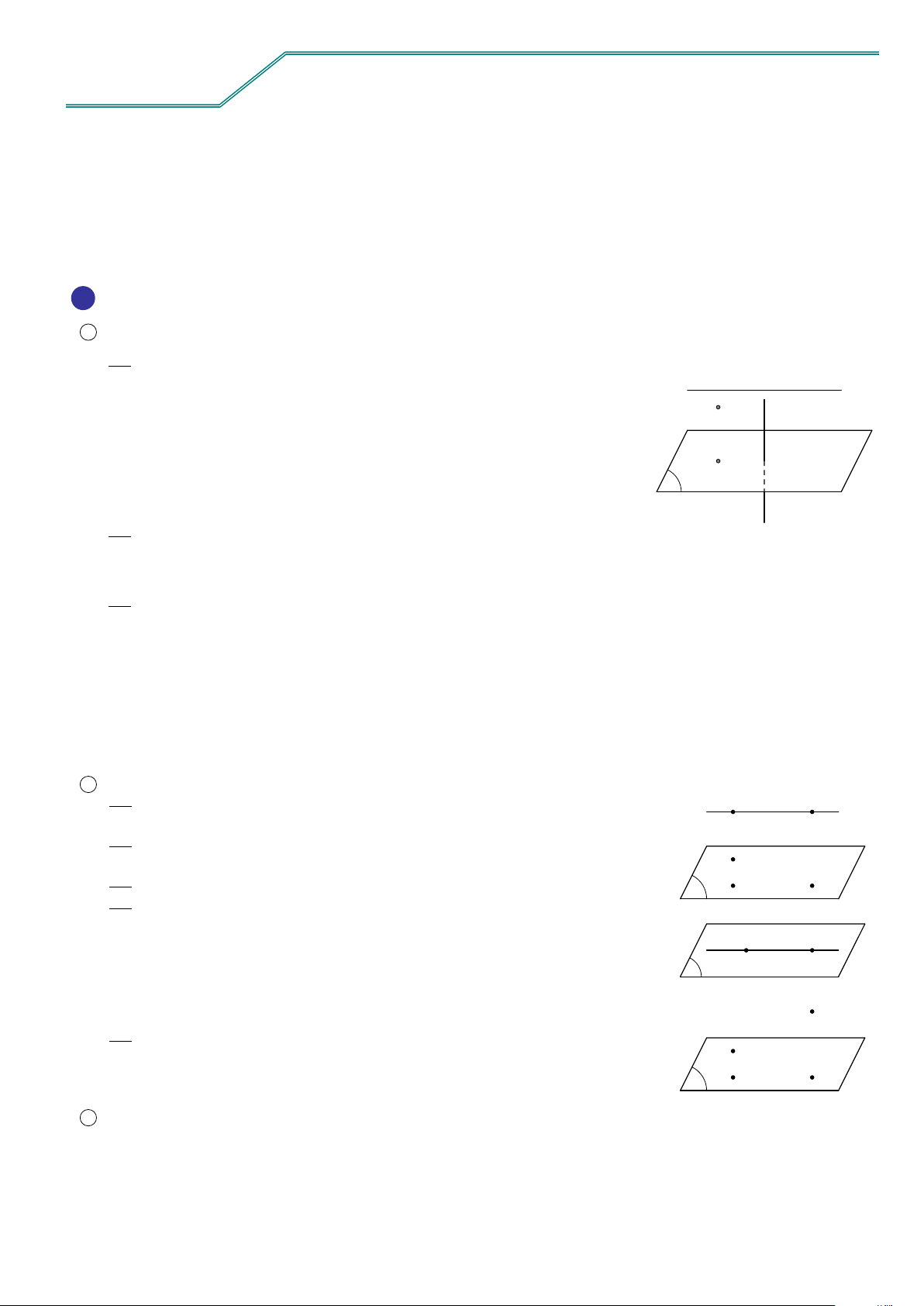
Có một và chỉ một mặt phẳng đi qua ba điểm phân biệt không thẳng d hàng cho trước. E G
Nếu một đường thẳng có hai điểm phân biệt thuộc một mặt phẳng
thì mọi điểm của đường thẳng đều thuộc mặt phẳng đó. A
Tồn tại bốn điểm không cùng thuộc một mặt phẳng. B C α
Nếu hai mặt phẳng phân biệt có một điểm chung thì chúng còn có
một điểm chung khác nữa.
Từ tính chất này suy ra: Nếu hai mặt phẳng phân biệt có một điểm d
chung thì chúng sẽ có một đường thẳng chung đi qua điểm chung A B α
ấy. Đường thẳng chung là duy nhất chứa tất cả các điểm chung của
hai mặt phẳng đó. Đường thẳng chung đó được gọi là giao tuyến D của hai mặt phẳng.
Trên mỗi mặt phẳng, các kết quả đã biết trong hình học phẳng đều A đúng. B C α 3
Điều kiện xác định mặt phẳng.
. Mặt phẳng được hoàn toàn xác định khi biết nó đi qua ba điểm không thẳng hàng.
. Mặt phẳng được hoàn toàn xác định khi biết nó đi qua một điểm và chứa một đường thẳng không đi qua điểm đó.
. Mặt phẳng được hoàn toàn xác định khi biết nó chứa hai đường thẳng cắt nhau.
Mặt phẳng hoàn toàn có thể mở rộng ra đến vô cực. 311 312
CHƯƠNG 7. ĐƯỜNG THẲNG VÀ MẶT PHẲNG TRONG KHÔNG GIAN 4
Hình chóp và hình tứ diện.
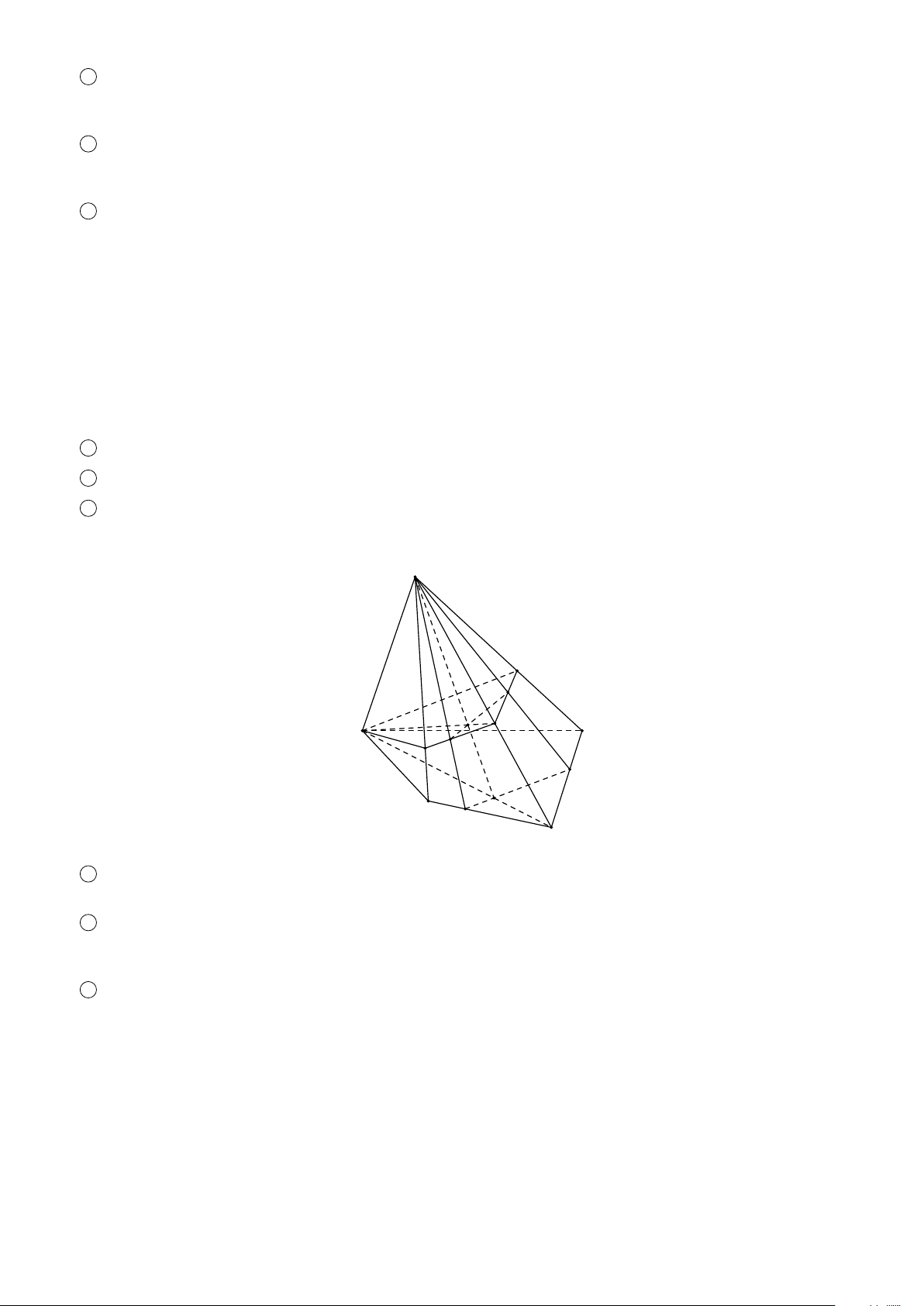
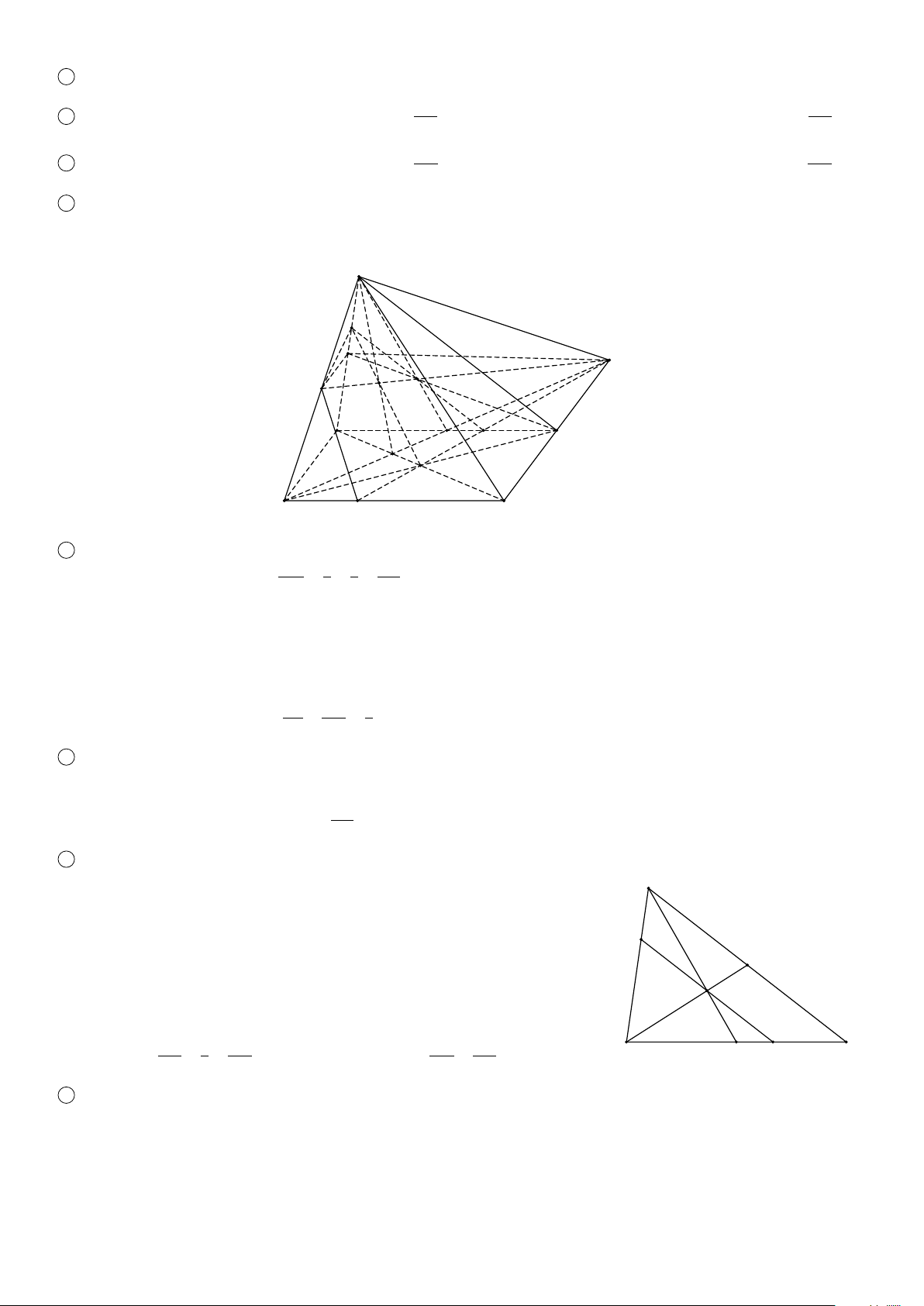
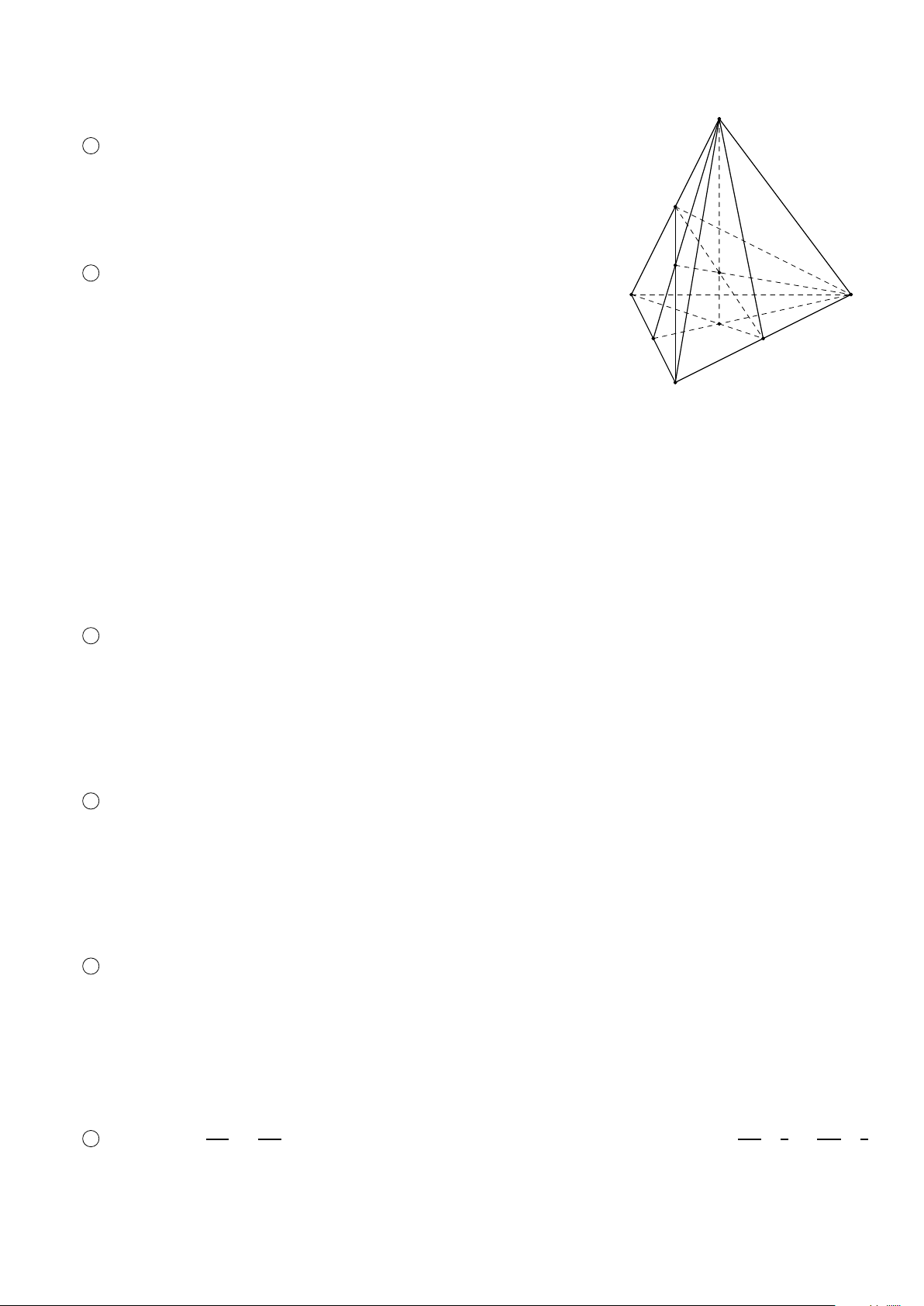
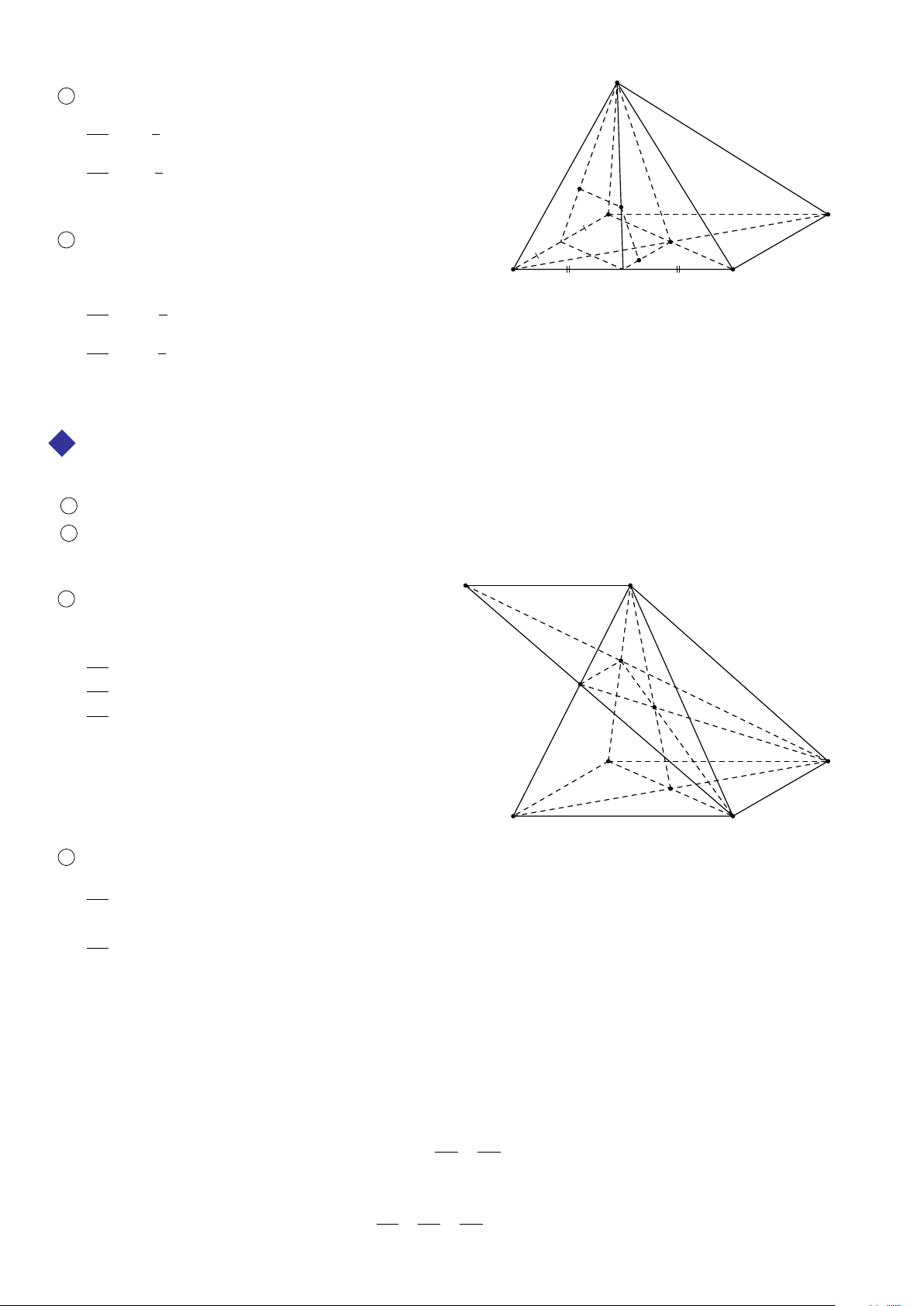
Cho đa giác A1 A2 A3...An nằm trong mặt phẳng (α) và điểm S ∉ (α). Lần lượt nối điểm S với các đỉnh
A1 A2 A3...An ta được n tam giác S A1 A2, S A2 A32, ... S An A1. Hình gồm đa giác A1 A2 A3...An và n tam giác
S A1 A2, S A2 A3, ... S An A1 được gọi là hình chóp, kí hiệu hình chóp này là S.A1 A2 A3...An. Khi đó ta gọi:
. S là đỉnh của hình chóp.
. A1 A2 A3...An là mặt đáy của hình chóp.
. Các tam giác S A1 A2, S A2 A3, ... S An A1 được gọi là các mặt bên.
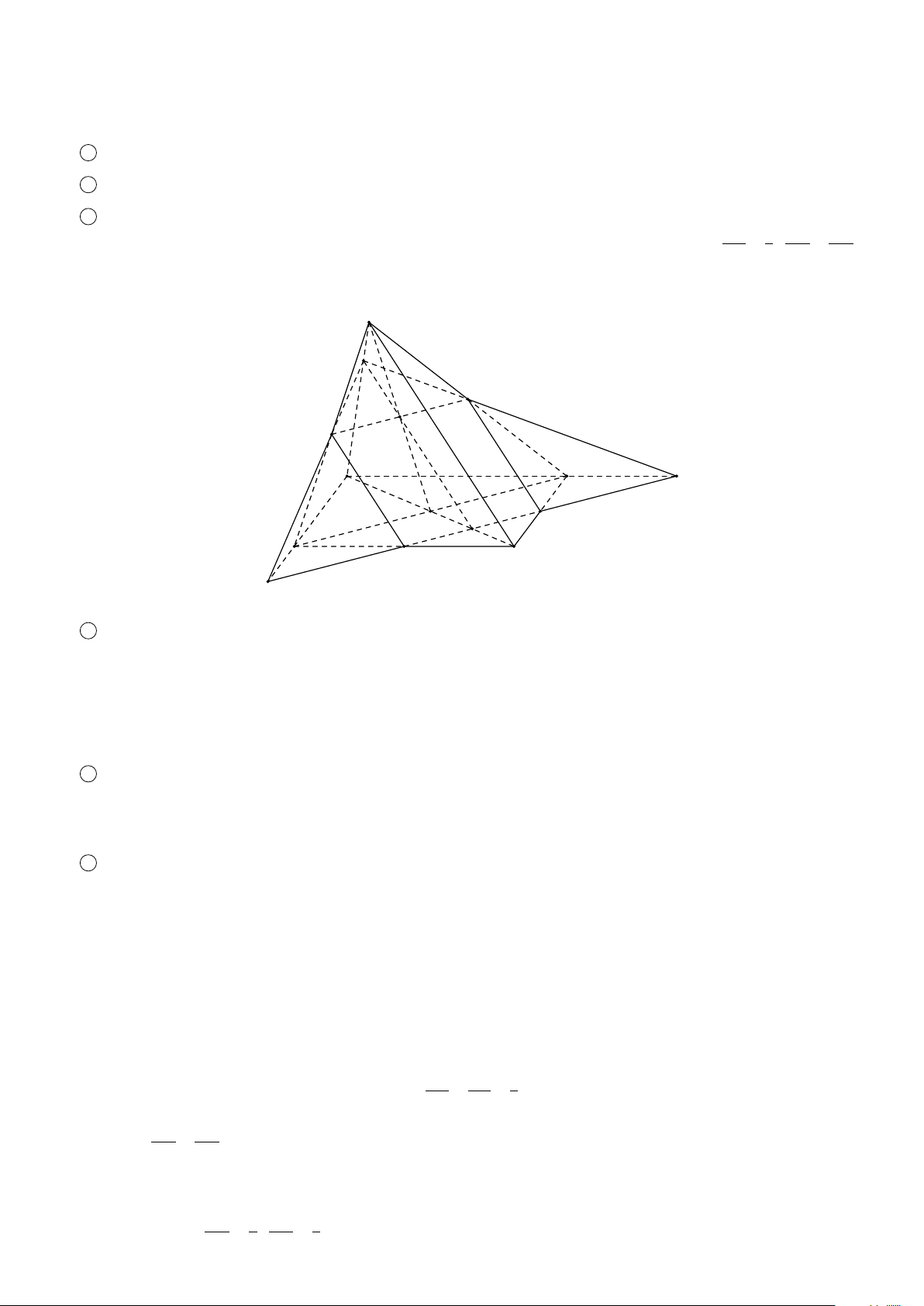
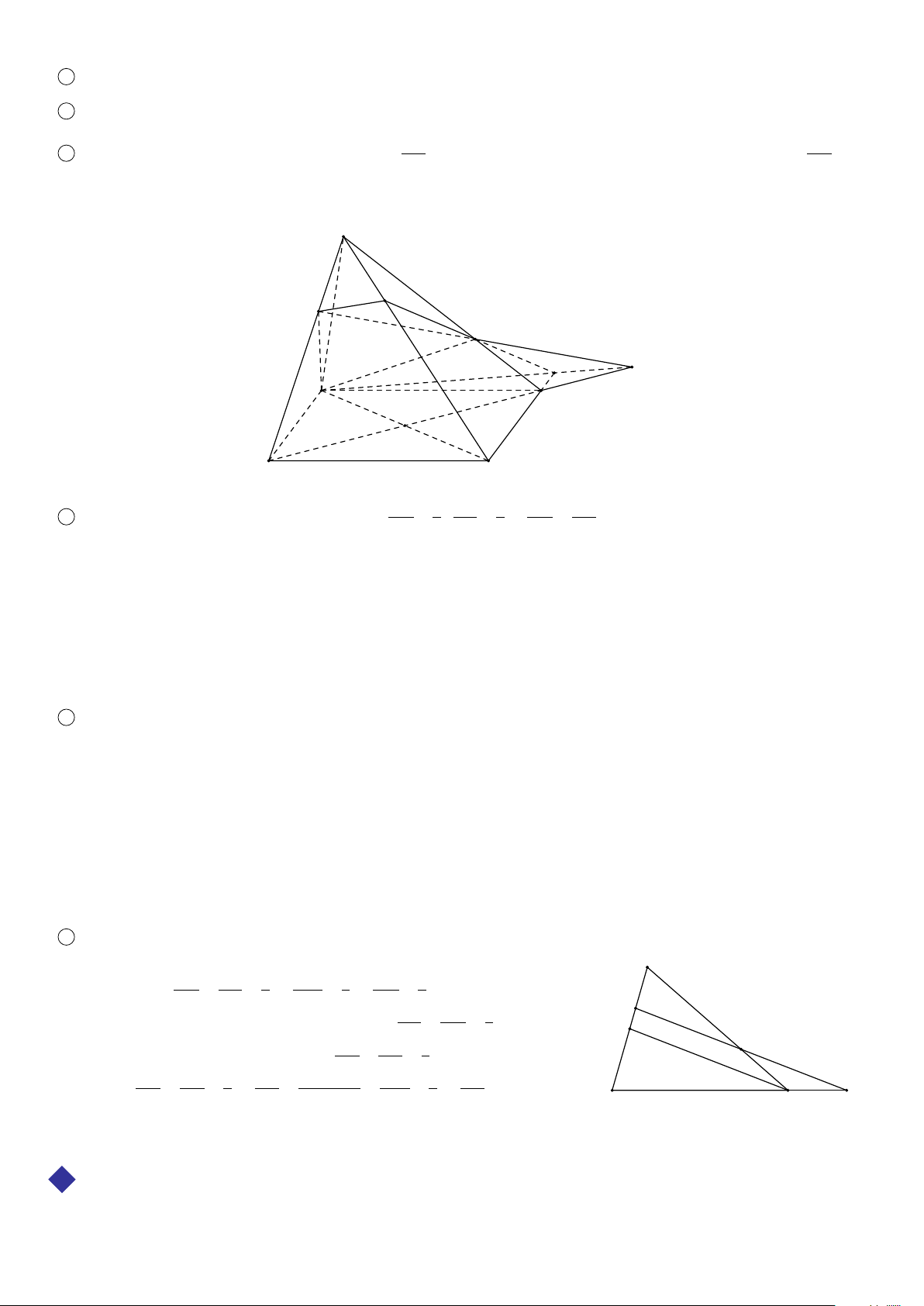
Ta gọi hình chóp có đáy là tam giác, tứ giác, ngũ giác,..., lần lượt là hình chóp tam giác, hình chóp tứ giác, hình chóp ngũ giác, ....
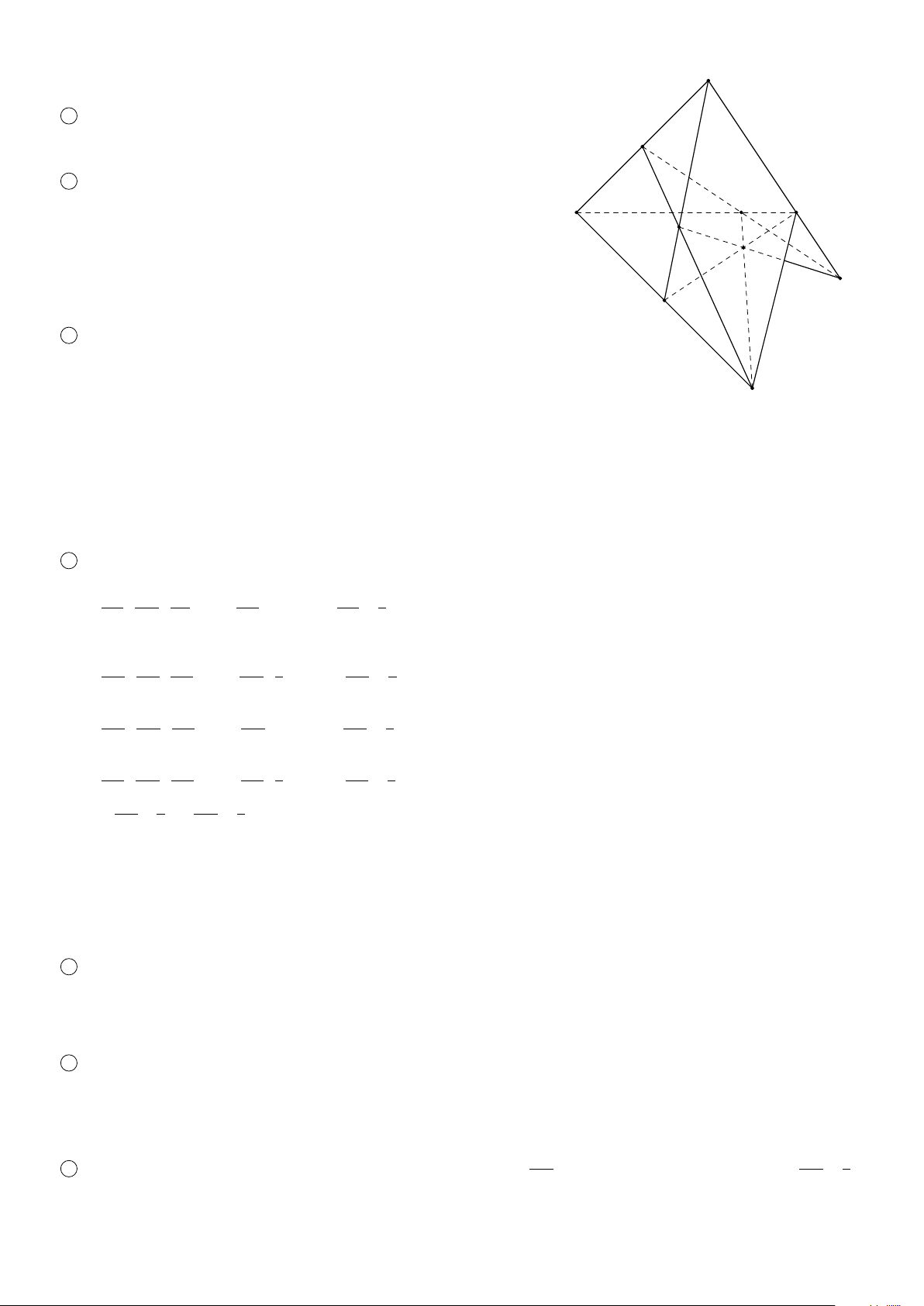
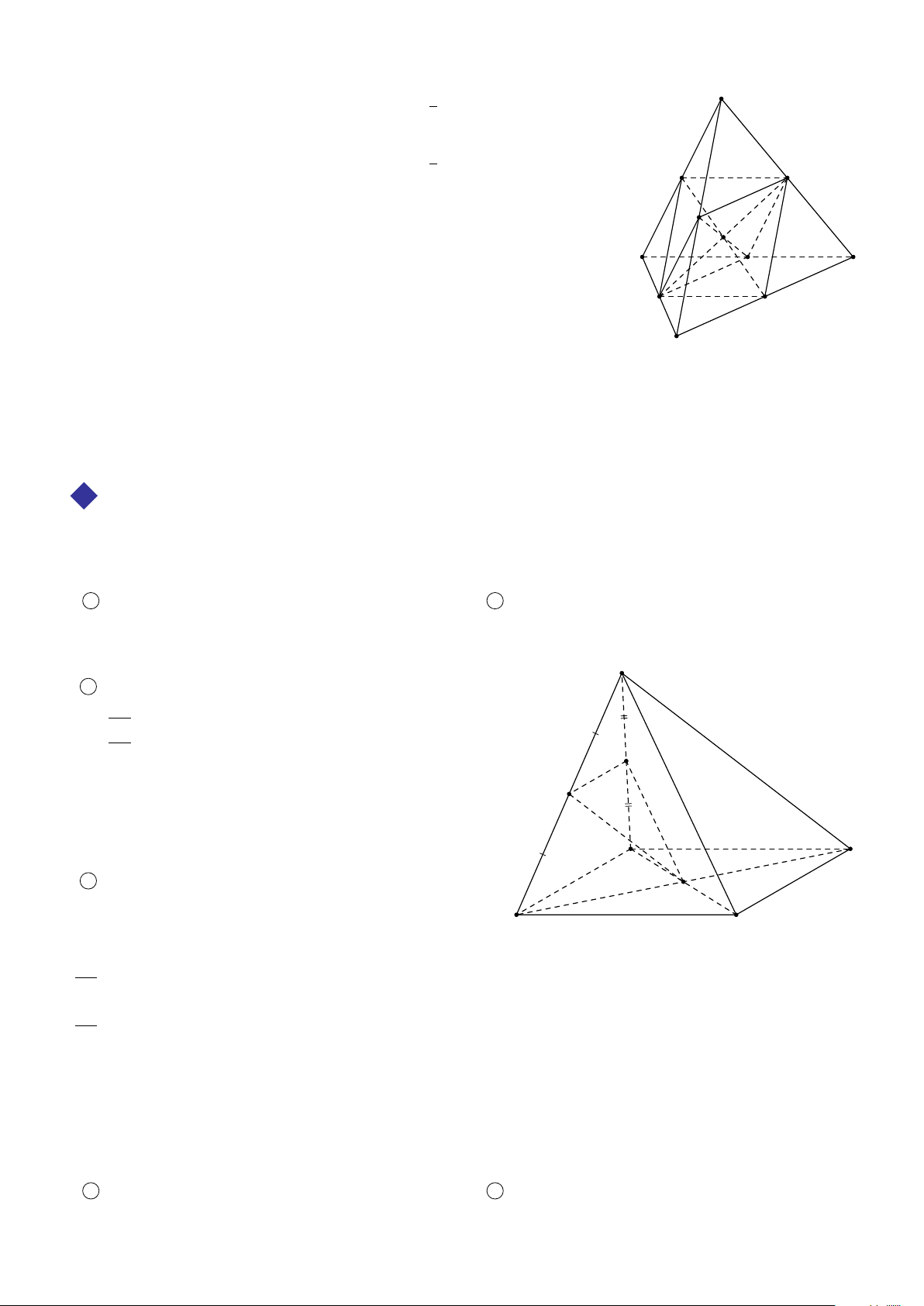
Cho bốn điểm A, B, C, D không đồng phẳng. Hình gồm 4 tam giác ABC, ACD, BCD, ABD gọi là hình tứ
diện (hay ngắn gọn gọi là tứ diện) và được kí hiệu là ABCD.
. Các điểm A, B, C, D là bốn đỉnh của tứ diện.
. Các đoạn thẳng AB, BC, CD, D A, C A, BD gọi là các cạnh của tứ diện.
. Hai cạnh không đi qua một đỉnh gọi là hai cạnh đối diện của tứ diện.
. Các tam giác ABC, ACD, ABD, BCD gọi là các mặt của tứ diện.
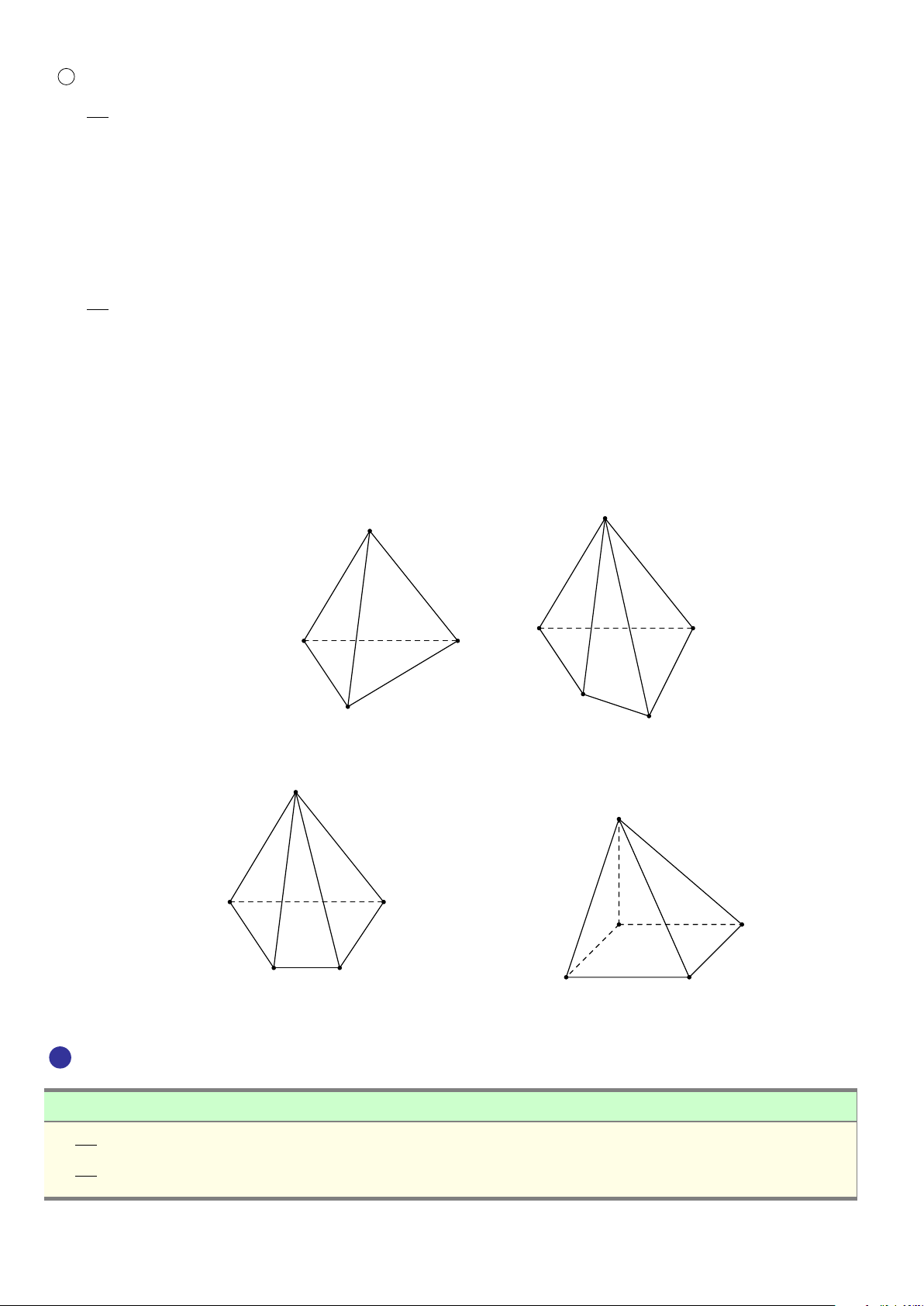
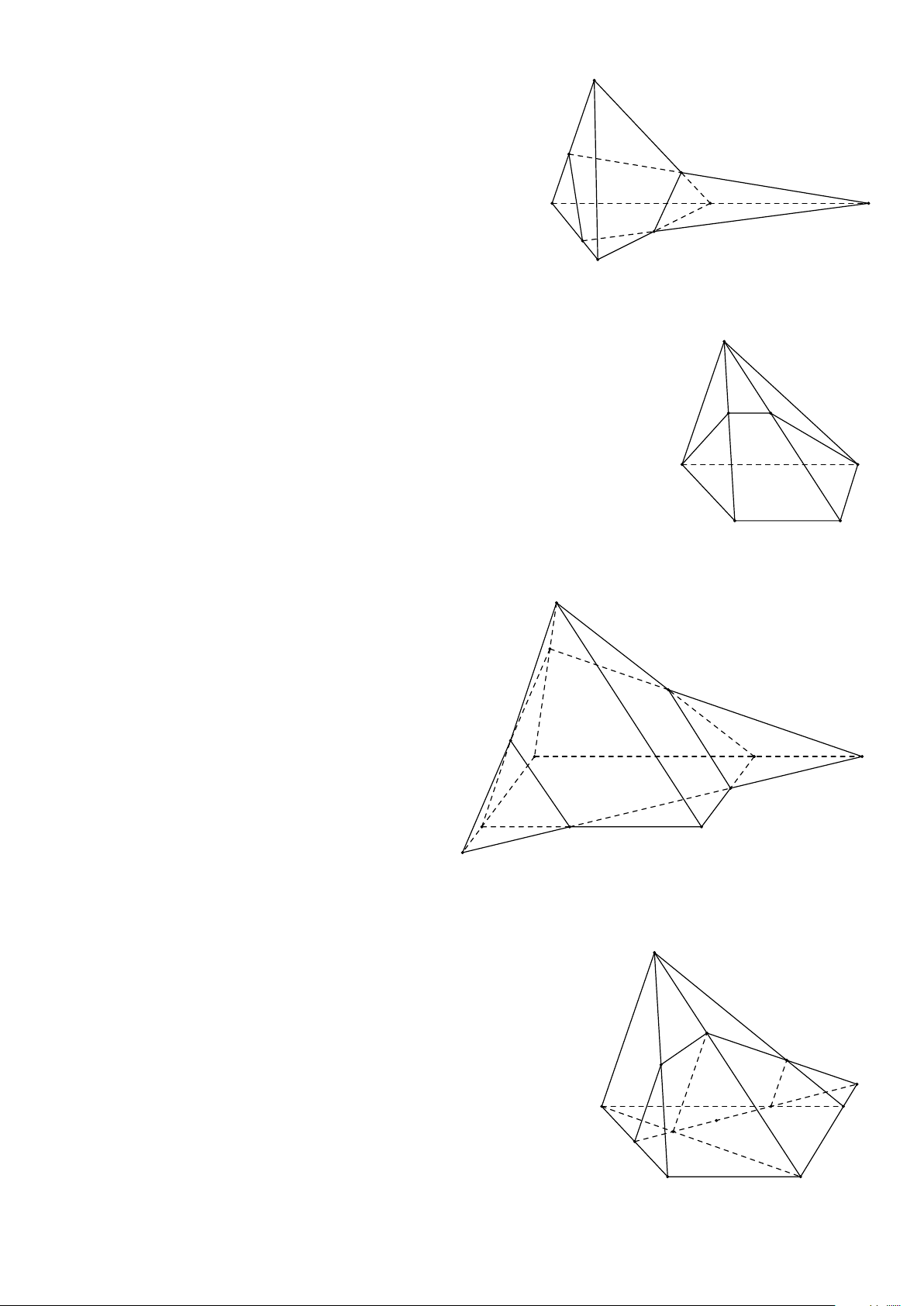
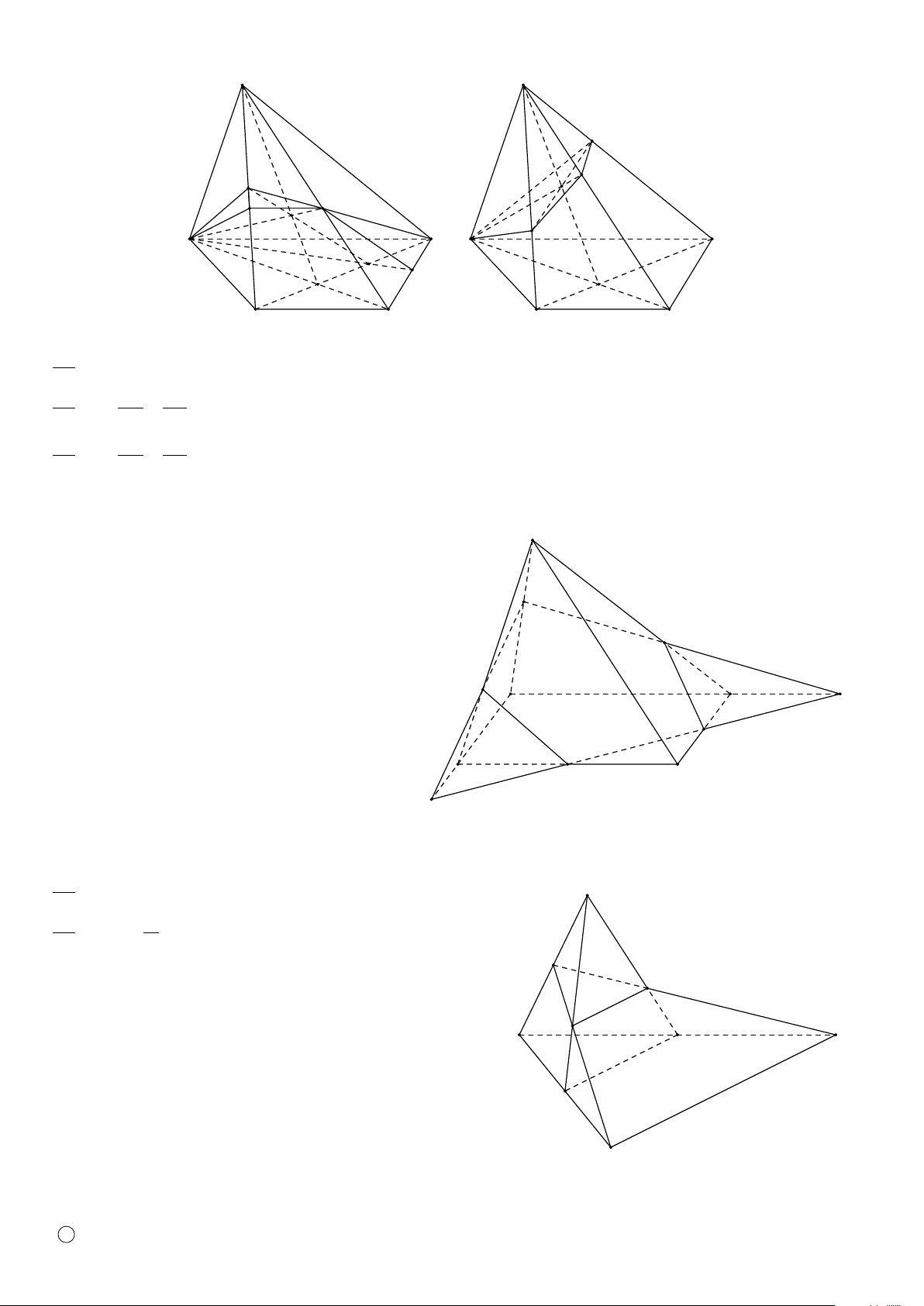
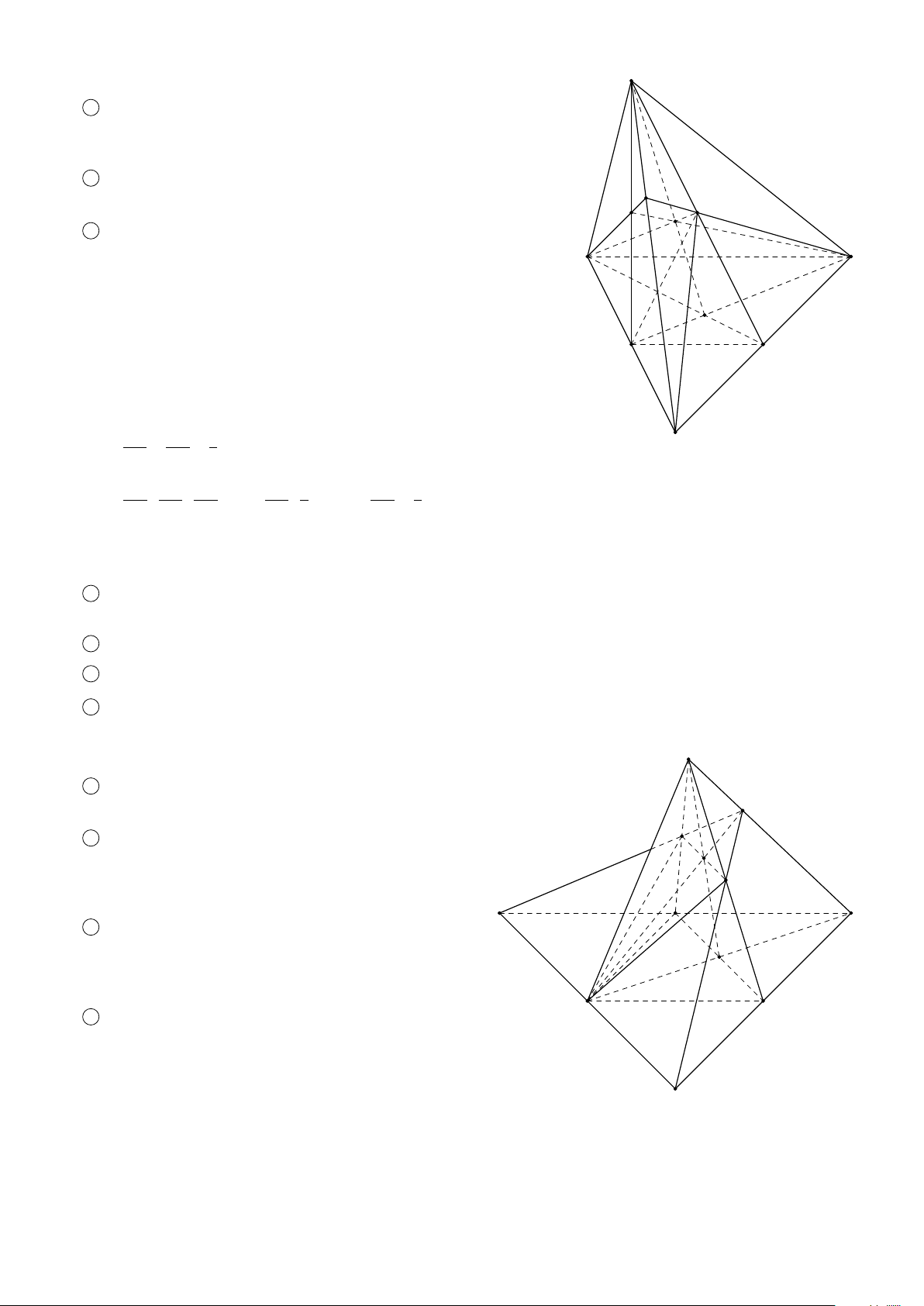
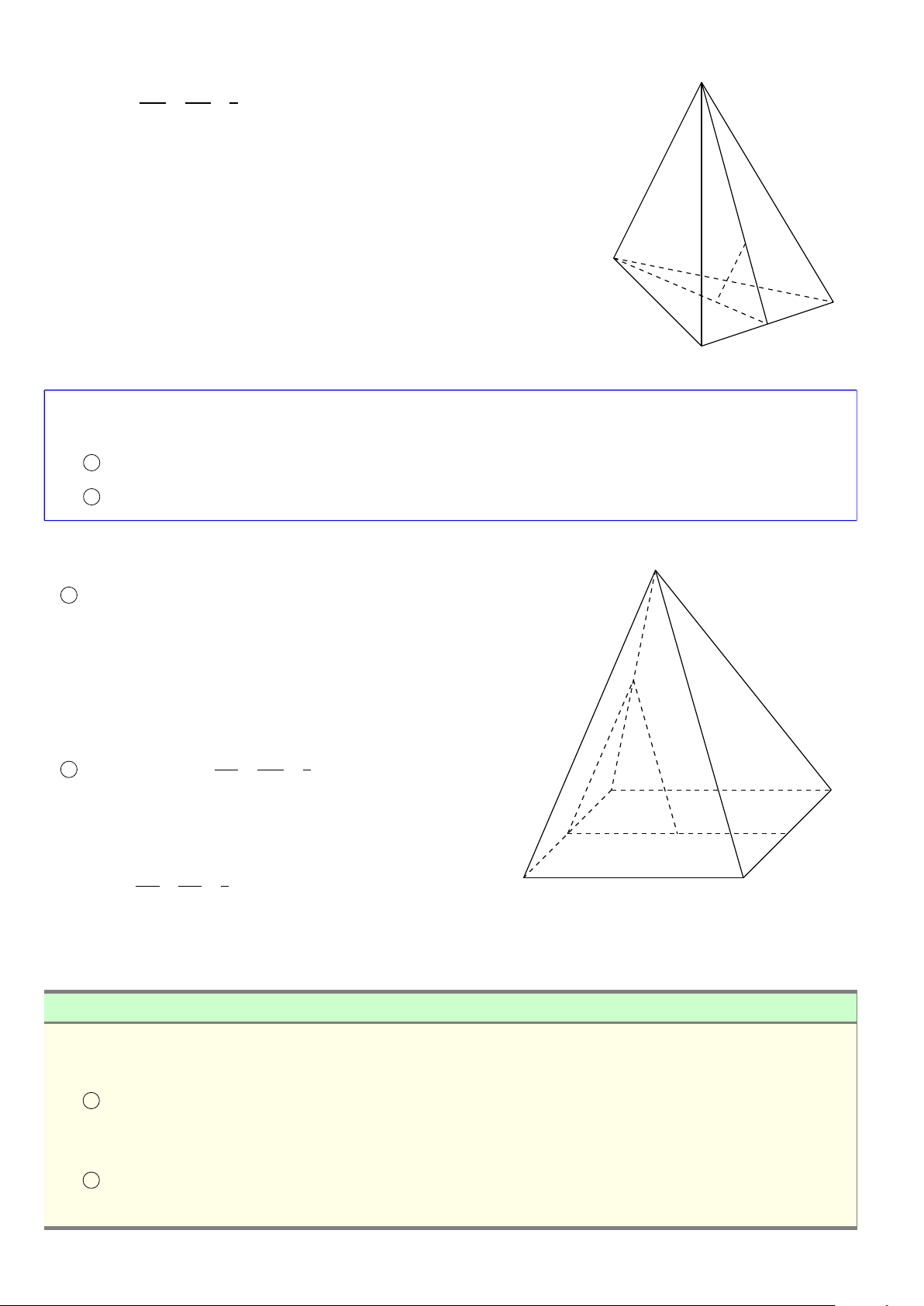
Hình tứ diện có bốn mặt là các tam giác đều gọi là hình tứ diện đều. S A A B B C D D C
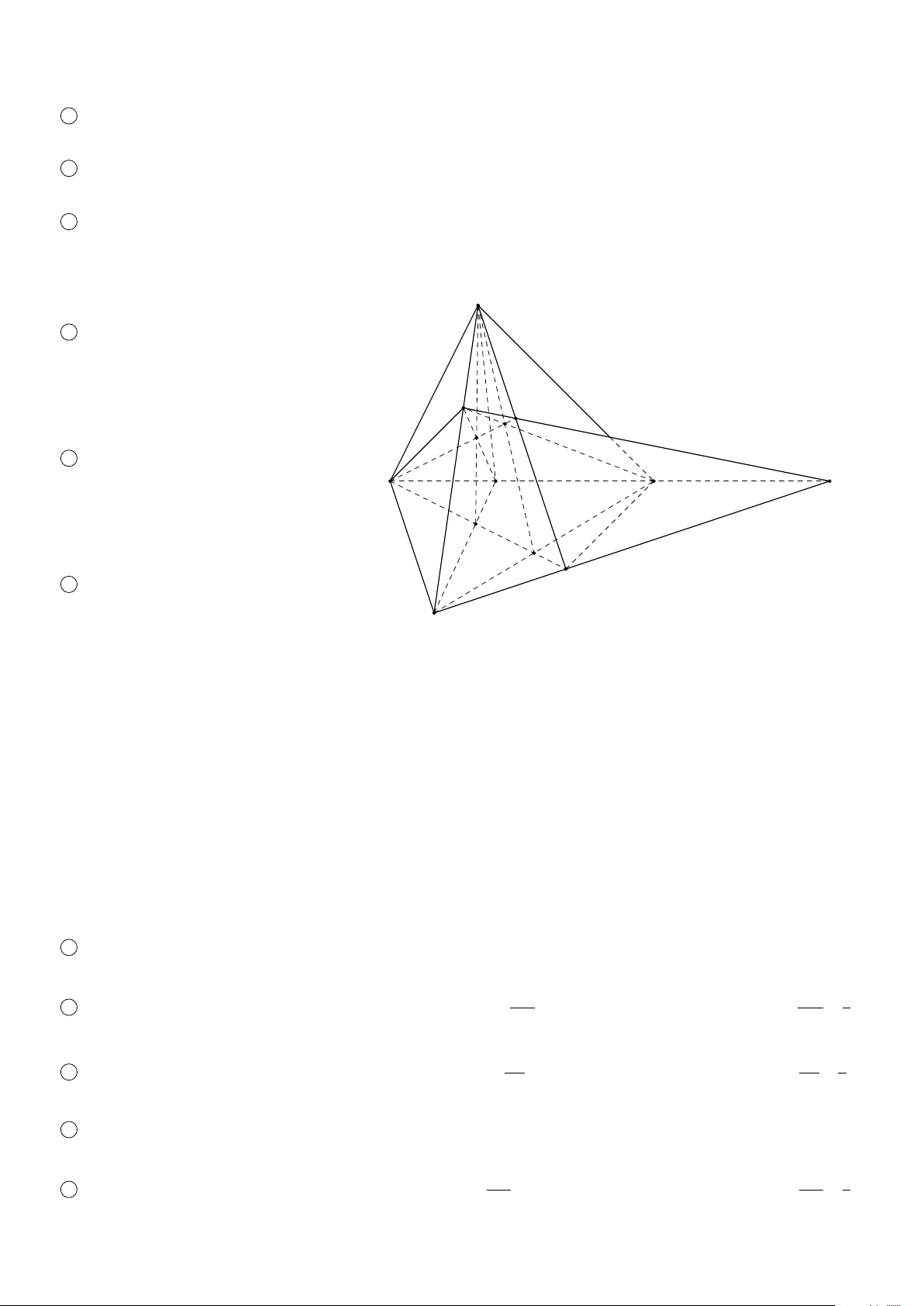
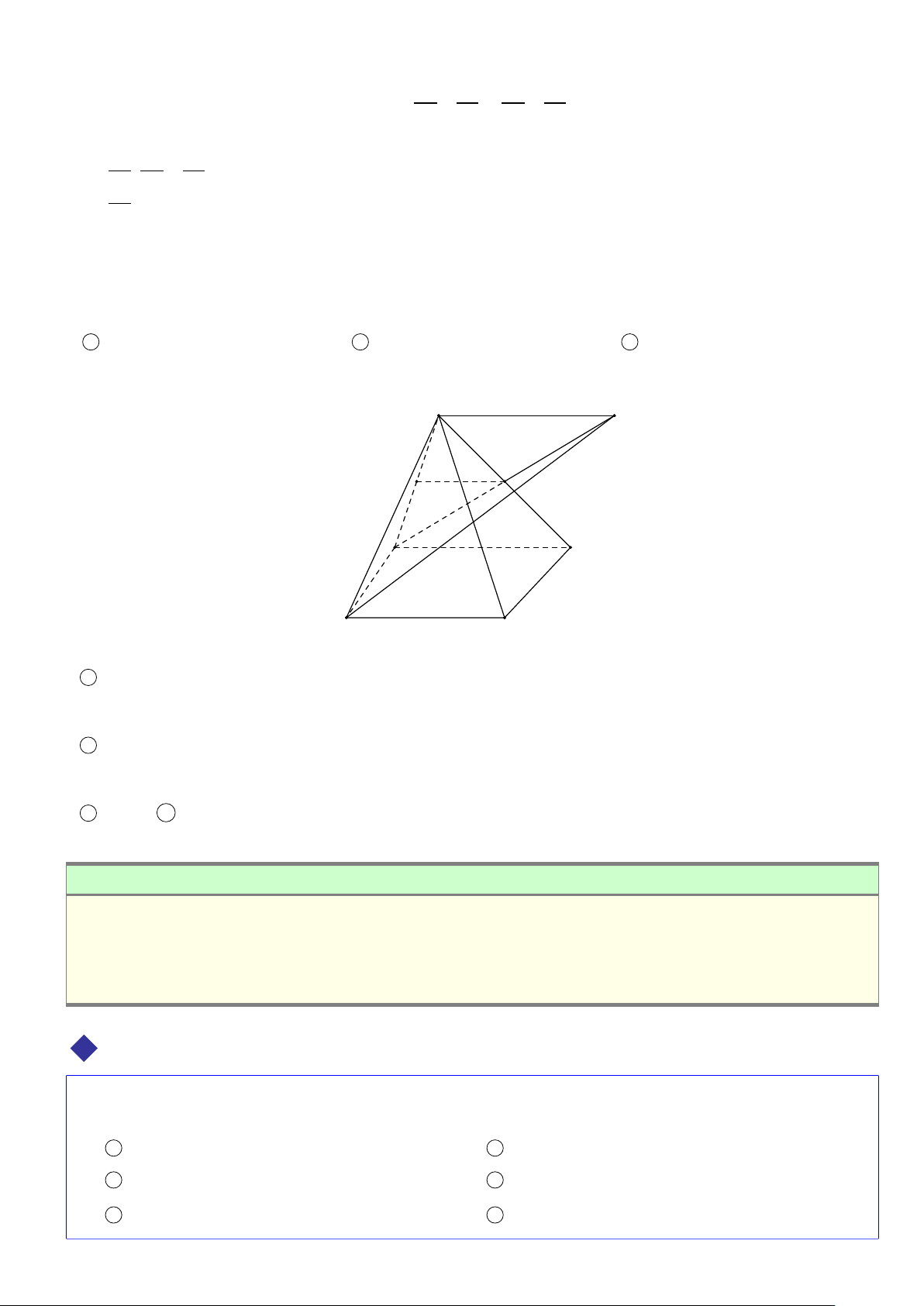
Hình chóp tam giác (Tứ diện) Hình chóp tứ giác S S A B A B C D D C
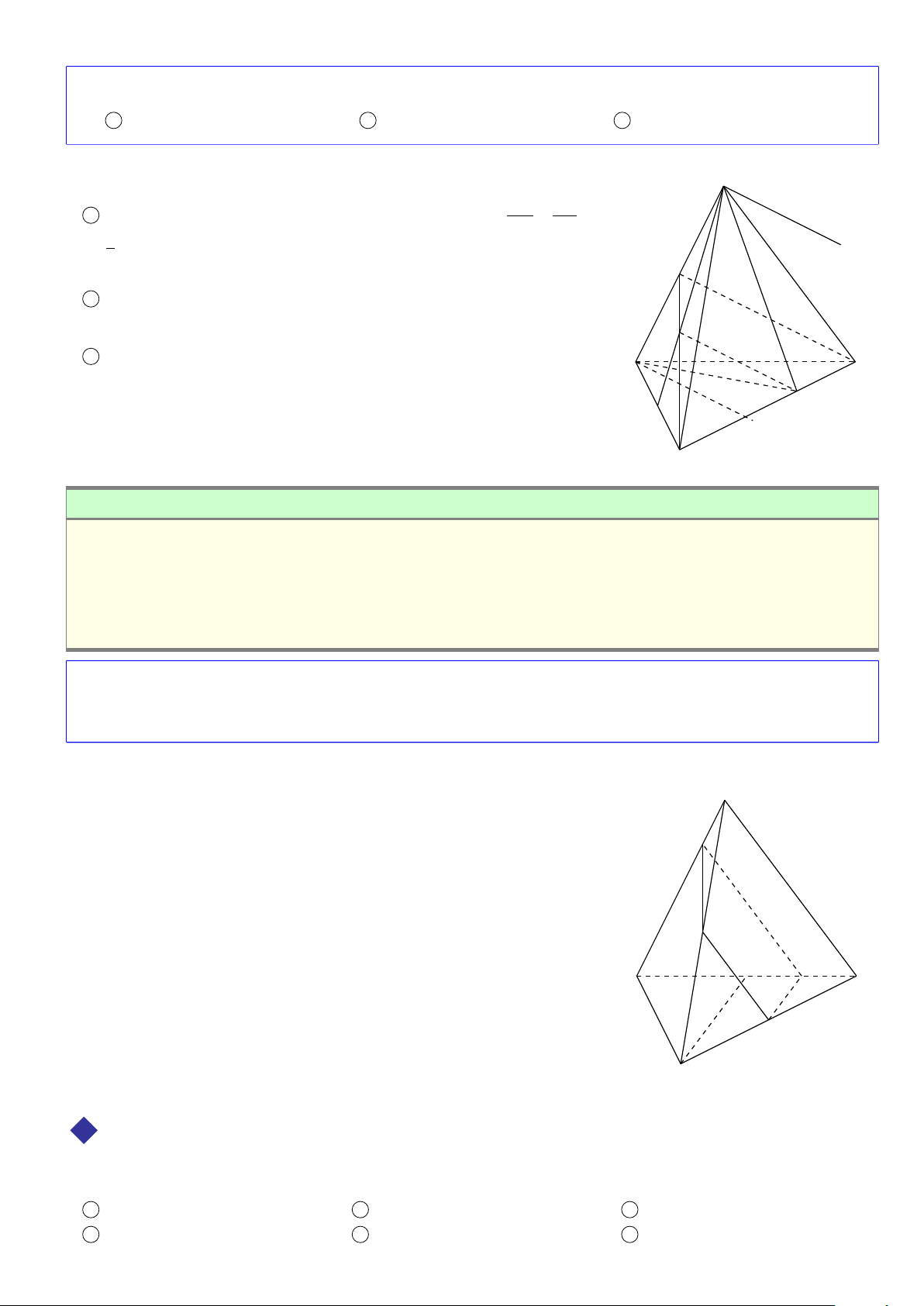
Hình chóp tứ giác có đáy là hình thang
Hình chóp tứ giác có đáy là hình bình hành B
DẠNG TOÁN VÀ BÀI TẬP
{ DẠNG 1.1. Xác định giao tuyến của hai mặt phẳng
Tìm hai điểm chung phân biệt của hai mặt phẳng.
Đường thẳng nối hai điểm đó là giao tuyến của chúng.
1. ĐẠI CƯƠNG VỀ ĐƯỜNG THẲNG VÀ MẶT PHẲNG 313 1 VÍ DỤ
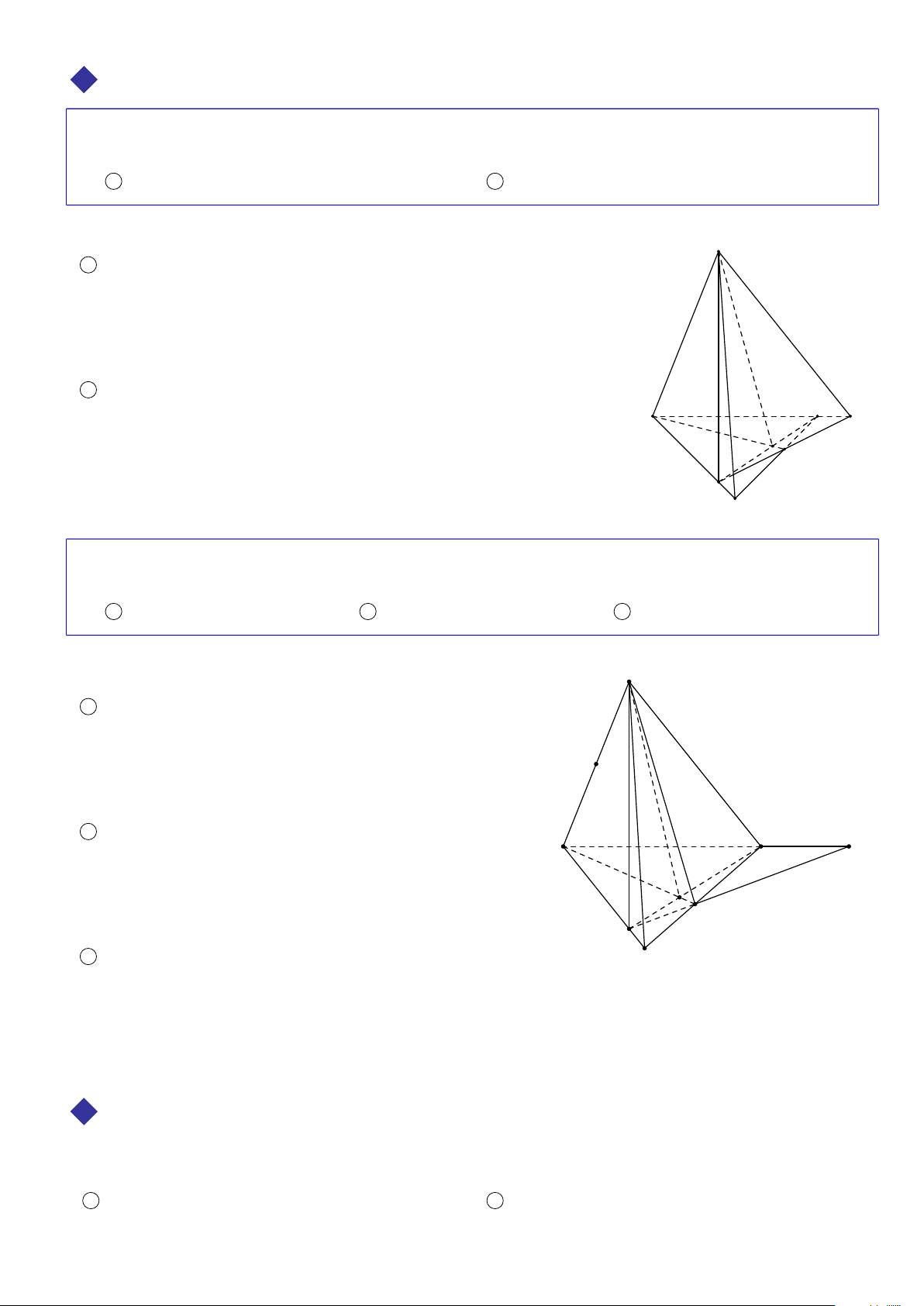
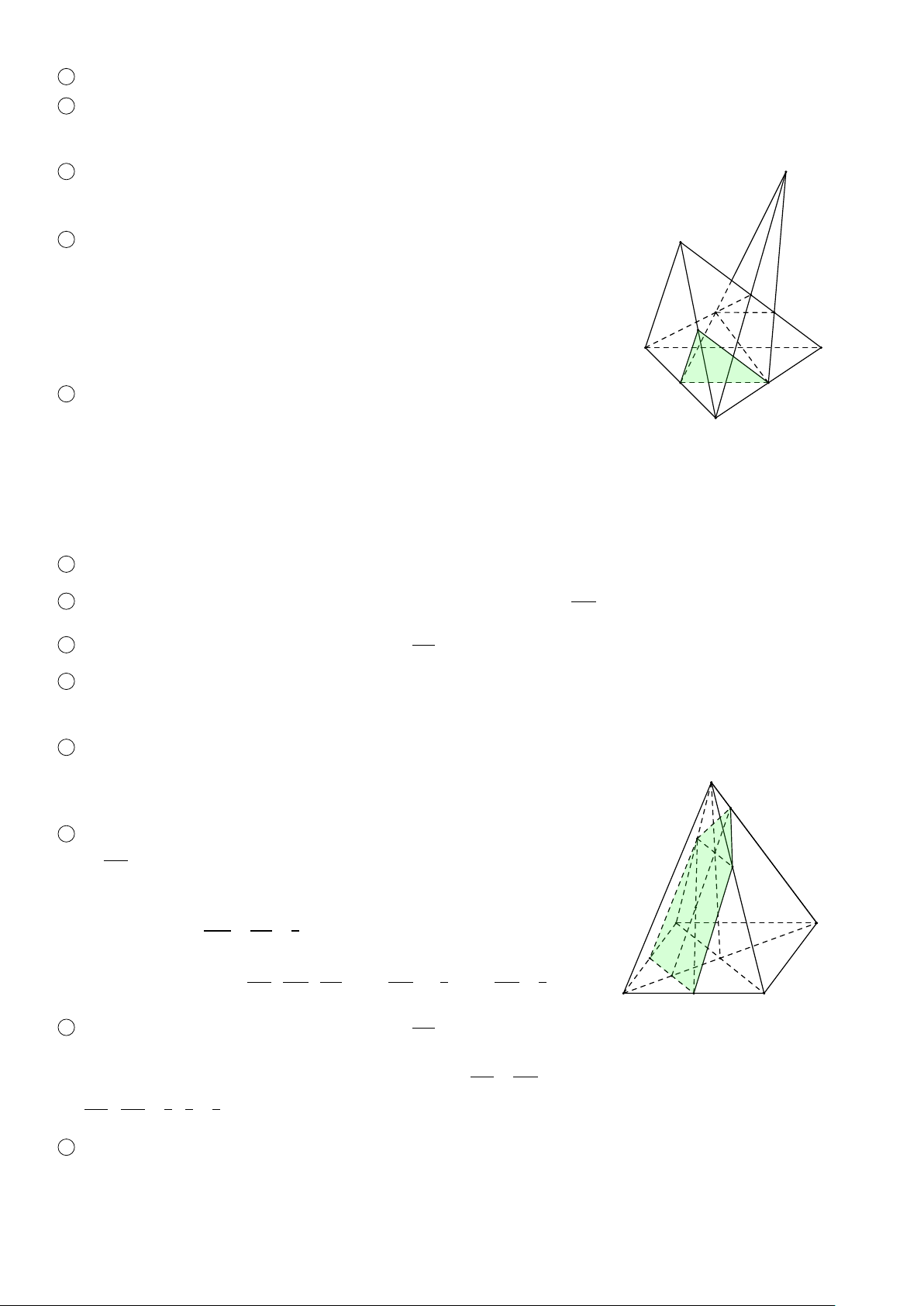
VÍ DỤ 1. Cho tứ diện S ABC. Gọi M, N lần lượt là hai điểm trên cạnh AB và BC sao cho M N không song song
với AC. Tìm giao tuyến của các cặp mặt phẳng sau 1 (S M N) và (S AC); 2 (S A N) và (SCM). Lời giải. S 1
Trong (ABC), gọi K = MN ∩ AC, ta có (S ∈ (SMN) ∩ (SAC)S K ∈ (SMN) ∩ (S AC).
Vậy giao tuyến của hai mặt phẳng là đường thẳng SK. 2
Trong (ABC), gọi H = AN ∩ CM, ta có A M B (S ∈ (SAN) ∩ (SCM) H H ∈ (S AN) ∩ (SCM). N
Vậy giao tuyến của hai mặt phẳng là đường thẳng SH. C K ä
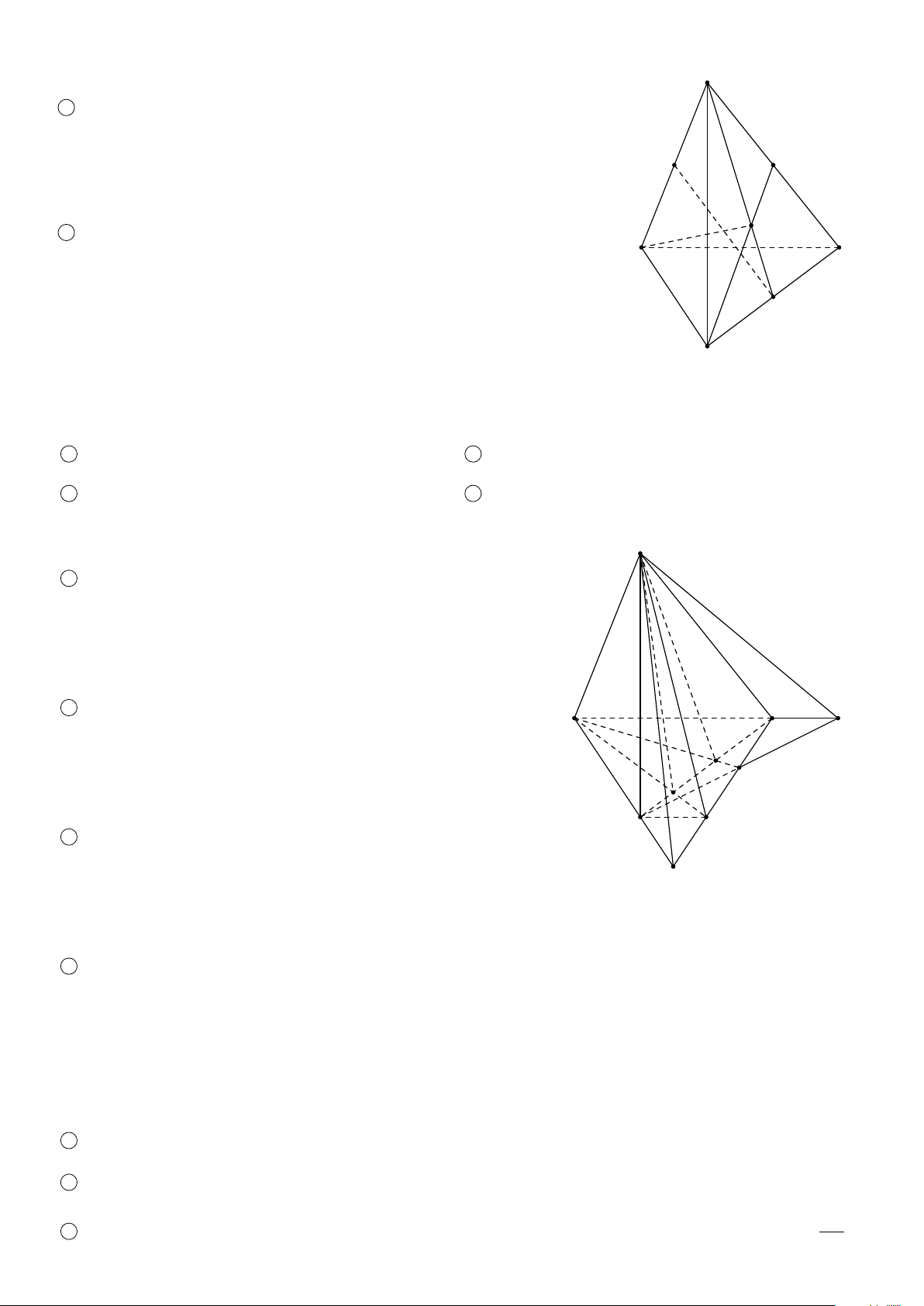
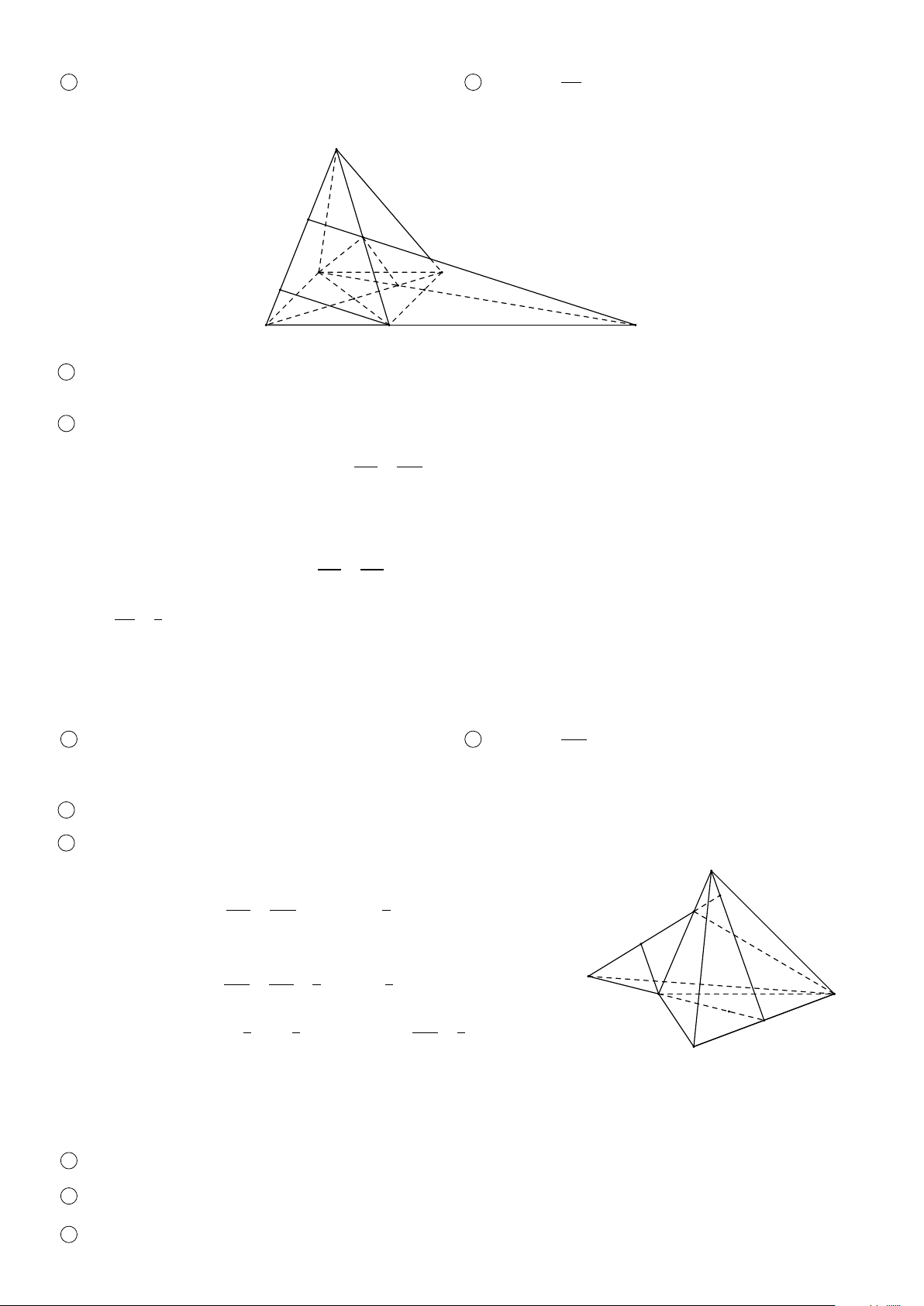
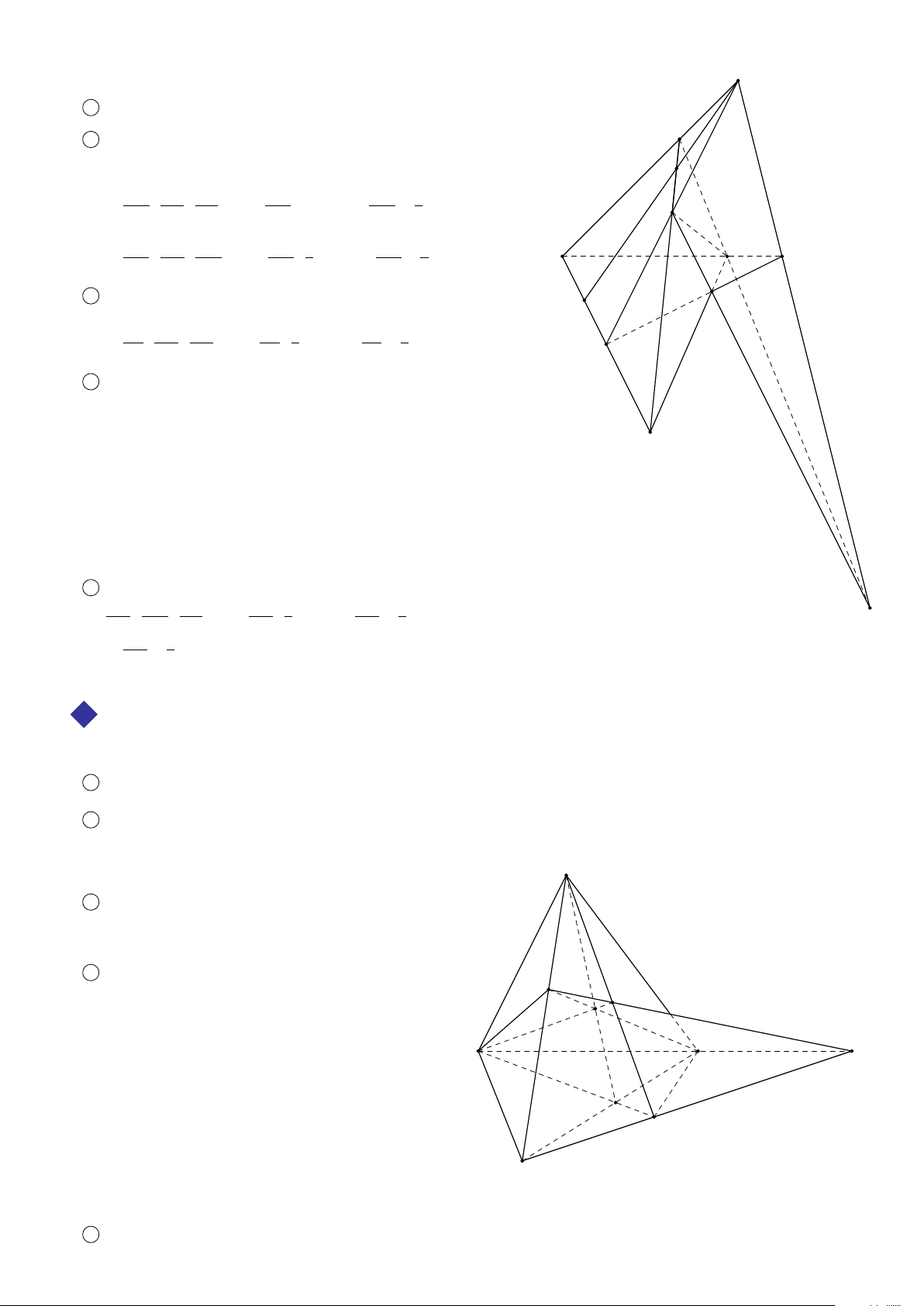
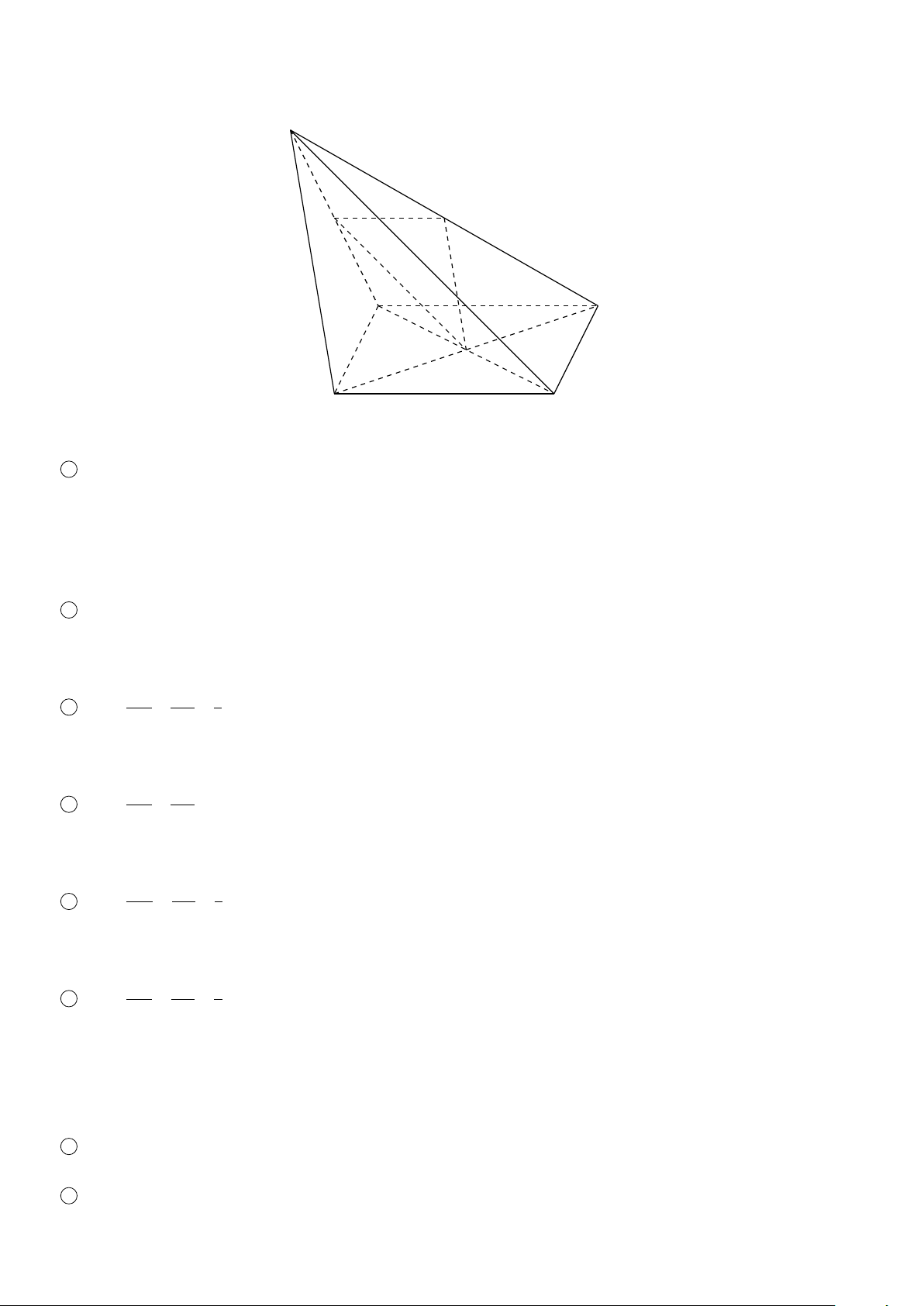
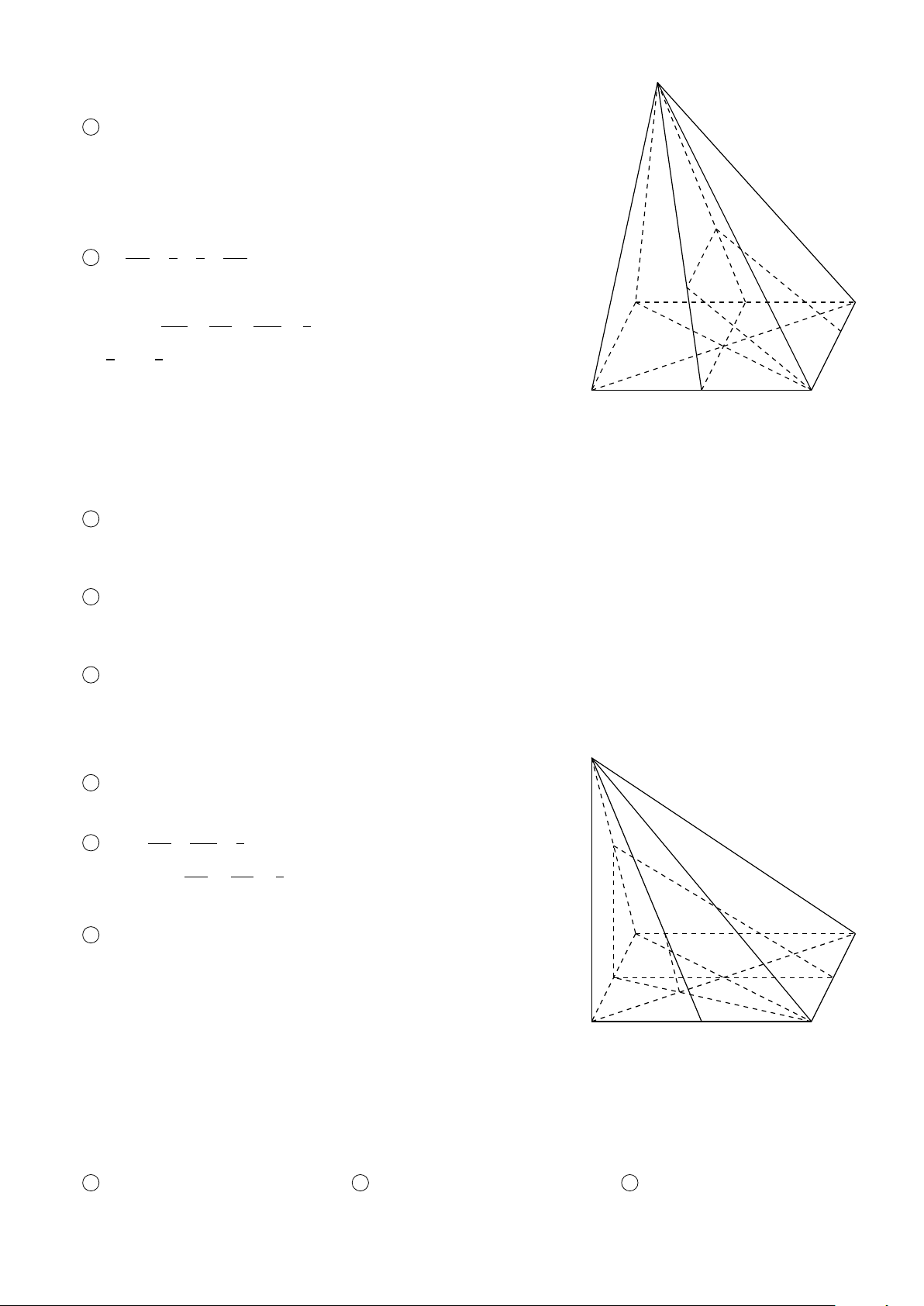
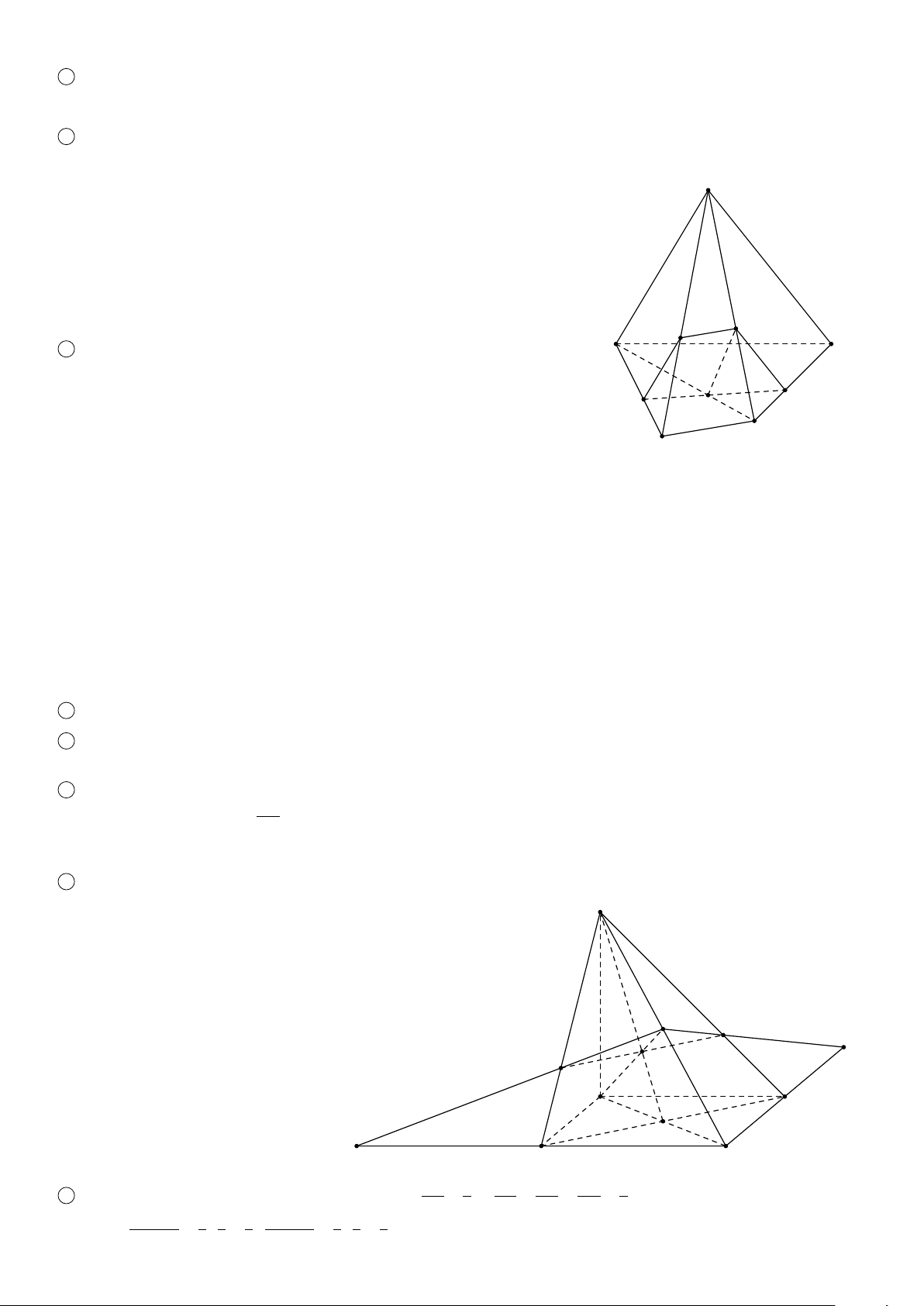
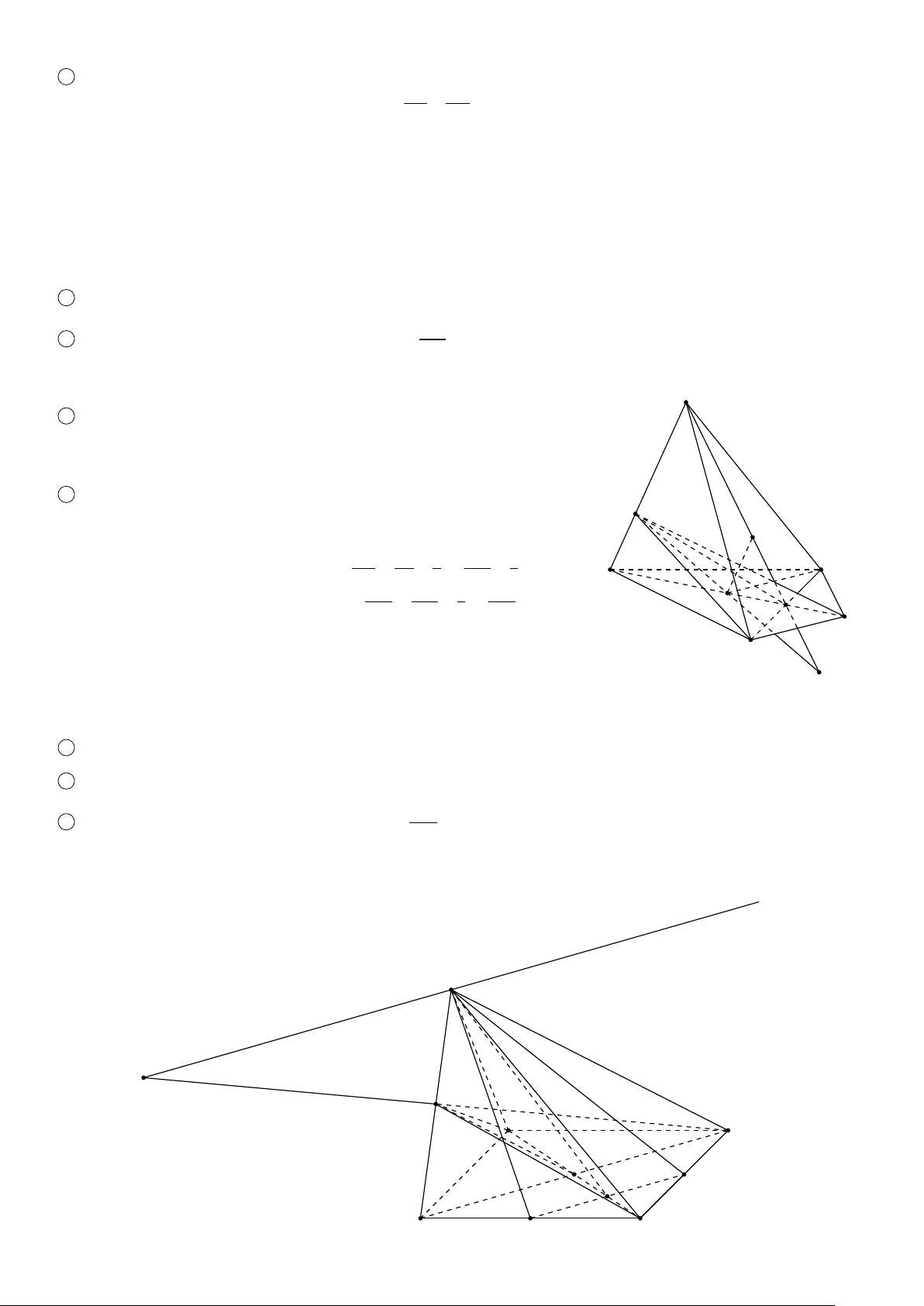
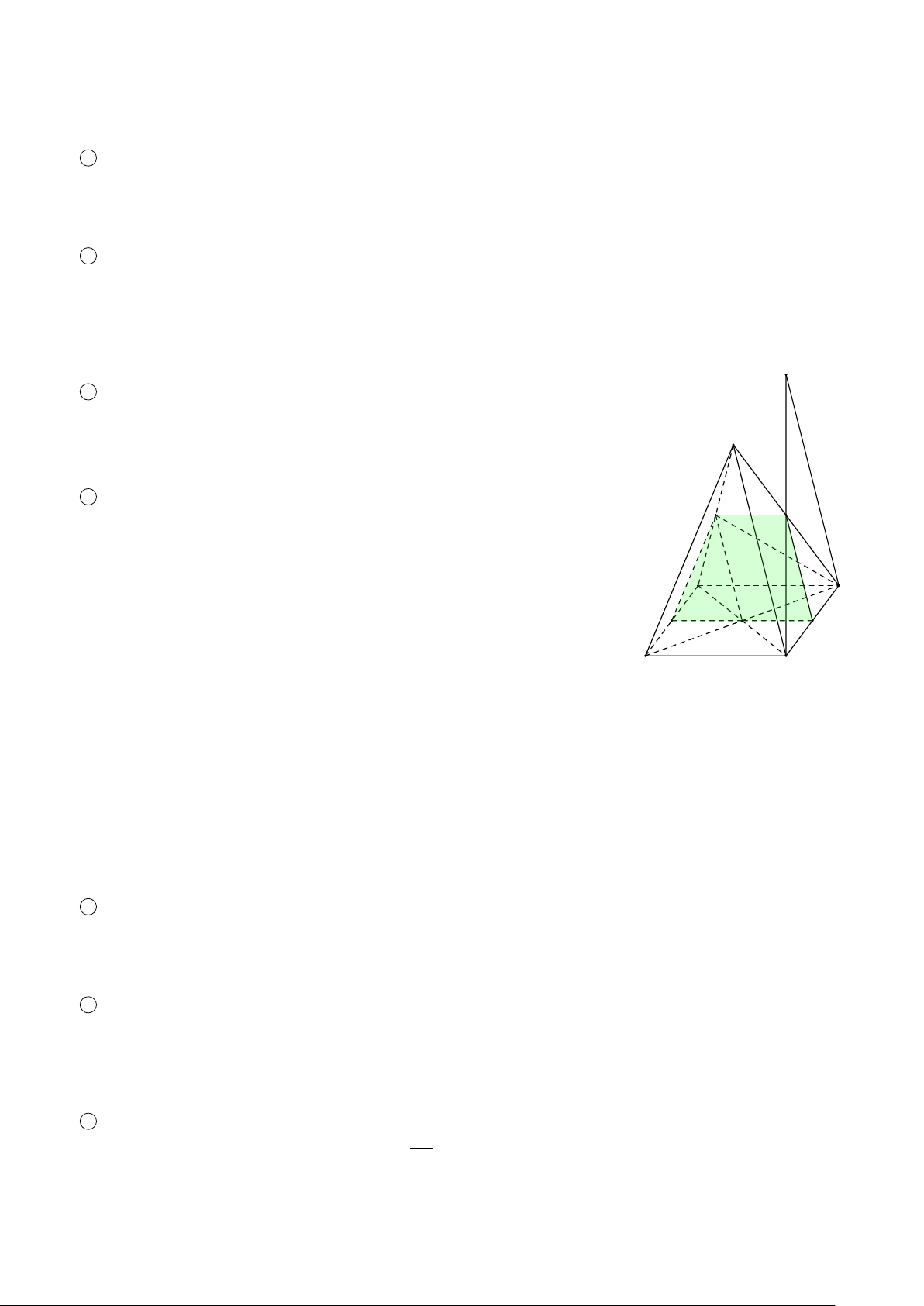
VÍ DỤ 2. Cho hình chóp S.ABCD, trong đó mặt đáy ABCD có các cặp cạnh đối không song song. Gọi điểm M
thuộc cạnh S A. Tìm giao tuyến của các cặp mặt phẳng sau 1 (S AC) và (SBD); 2 (S AB) và (SCD); 3 (MBC) và (S AD). Lời giải. S 1
Trong (ABCD), gọi E = AC ∩ BD, ta có (S ∈ (SAC) ∩ (SBD) M E ∈ (S AC) ∩ (SBD).
Vậy đường thẳng giao tuyến là SE. 2
Trong (ABCD), gọi F = AB ∩ CD, ta có A D K (S ∈ (SAB) ∩ (SCD) F ∈ (S AB) ∩ (SCD). E C
Vậy giao tuyến của hai mặt phẳng là SF. B 3
Trong (ABCD), gọi K = AD ∩ CB, ta có F (M ∈ (MBC) ∩ (SAD) K ∈ (MBC) ∩ (S AD).
Vậy giao tuyến của hai mặt phẳng là MK. ä 2 BÀI TẬP ÁP DỤNG
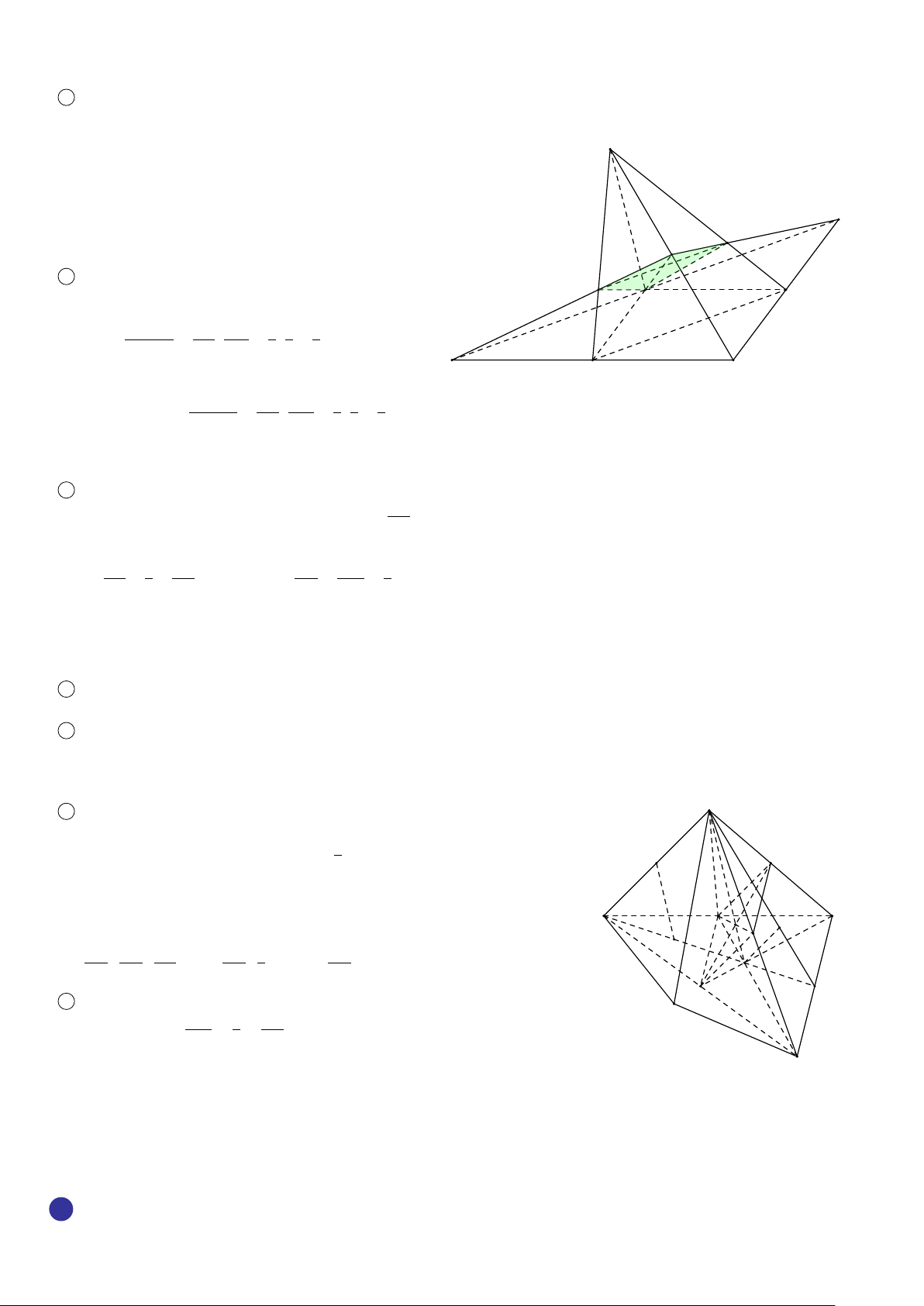
BÀI 1. Cho tứ diện S ABC. Gọi K , M lần lượt là hai điểm trên cạnh S A và SC. Gọi N là trung điểm của cạnh BC.
Tìm giao tuyến của các cặp mặt phẳng sau 1 (S A N) và (ABM); 2 (S A N) và (BCK ). Lời giải. 314
CHƯƠNG 7. ĐƯỜNG THẲNG VÀ MẶT PHẲNG TRONG KHÔNG GIAN S 1
Trong (SBC), gọi E = SN ∩ BM, ta có ( A ∈ (SAN) ∩ (ABM) K M E ∈ (S AN) ∩ (ABM).
Vậy đường thẳng giao tuyến là AE. E 2 Ta có A (N ∈ (SAN) ∩ (BCK) C K ∈ (S AN) ∩ (BCK).
Suy ra giao tuyến của hai mặt phẳng là K N. N B ä
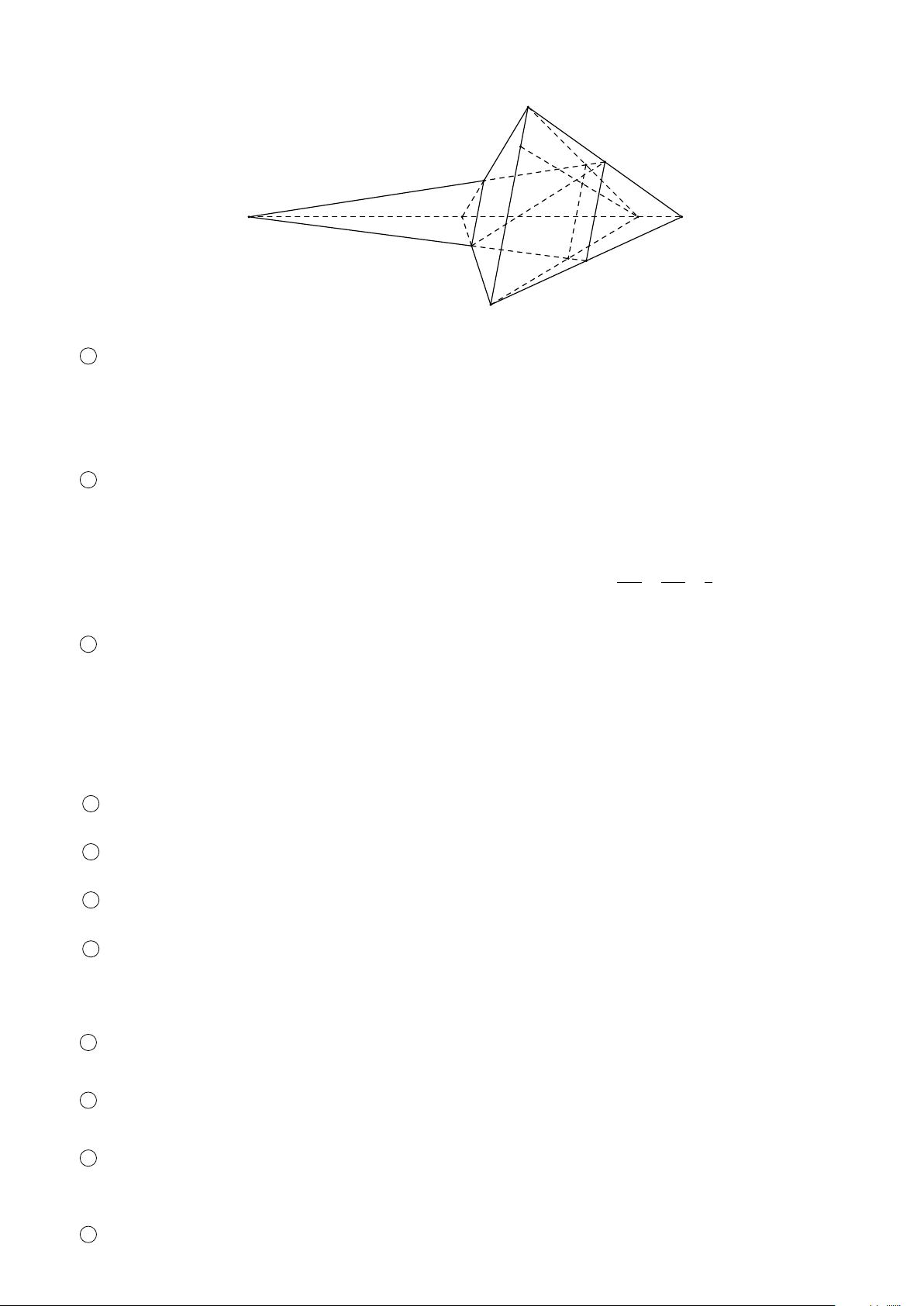
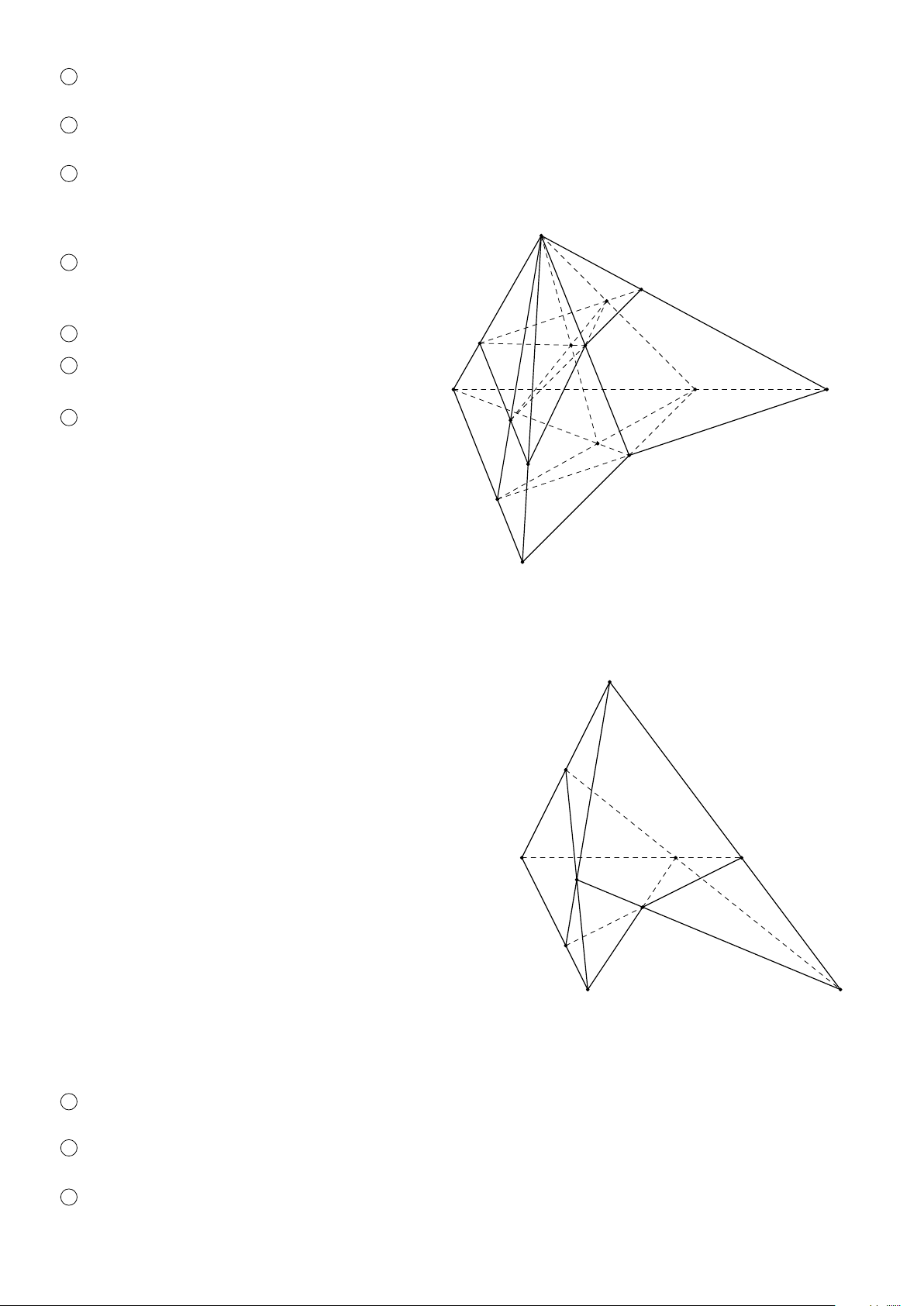
BÀI 2. Cho hình chóp S ABCD có đáy ABCD là hình thang với AB ∥ CD và AB > CD. Lấy điểm M trên đoạn BC. Tìm
giao tuyến của các cặp mặt phẳng sau đây: 1 (S AC) và (SBD); 2 (S AD) và (SBC); 3 (S A M) và (SBD); 4 (SD M) và (S AB). Lời giải. S
1 Trong (ABCD), gọi E = AC ∩ BD, ta có (S ∈ (SAC) ∩ (SBD) E ∈ (S AC) ∩ (SBD).
Vậy đường thẳng giao tuyến là SE.
2 Trong (ABCD), gọi K = AD ∩ CB, ta có A B H (S ∈ (SBC) ∩ (SAD) K ∈ (S AD) ∩ (SBC). M F
Vậy giao tuyến của hai mặt phẳng là SK. E D C
3 Trong (ABCD), gọi F = AM ∩ DB, ta có (S ∈ (SAM) ∩ (SBD) K F ∈ (S AM) ∩ (SBD).
Vậy giao tuyến của hai mặt phẳng là SF.
4 Trong (ABCD), gọi = DM ∩ AB, ta có (S ∈ (SDM) ∩ (SAB) H ∈ (SDM) ∩ (S AB).
Vậy giao tuyến của hai mặt phẳng là SH. ä
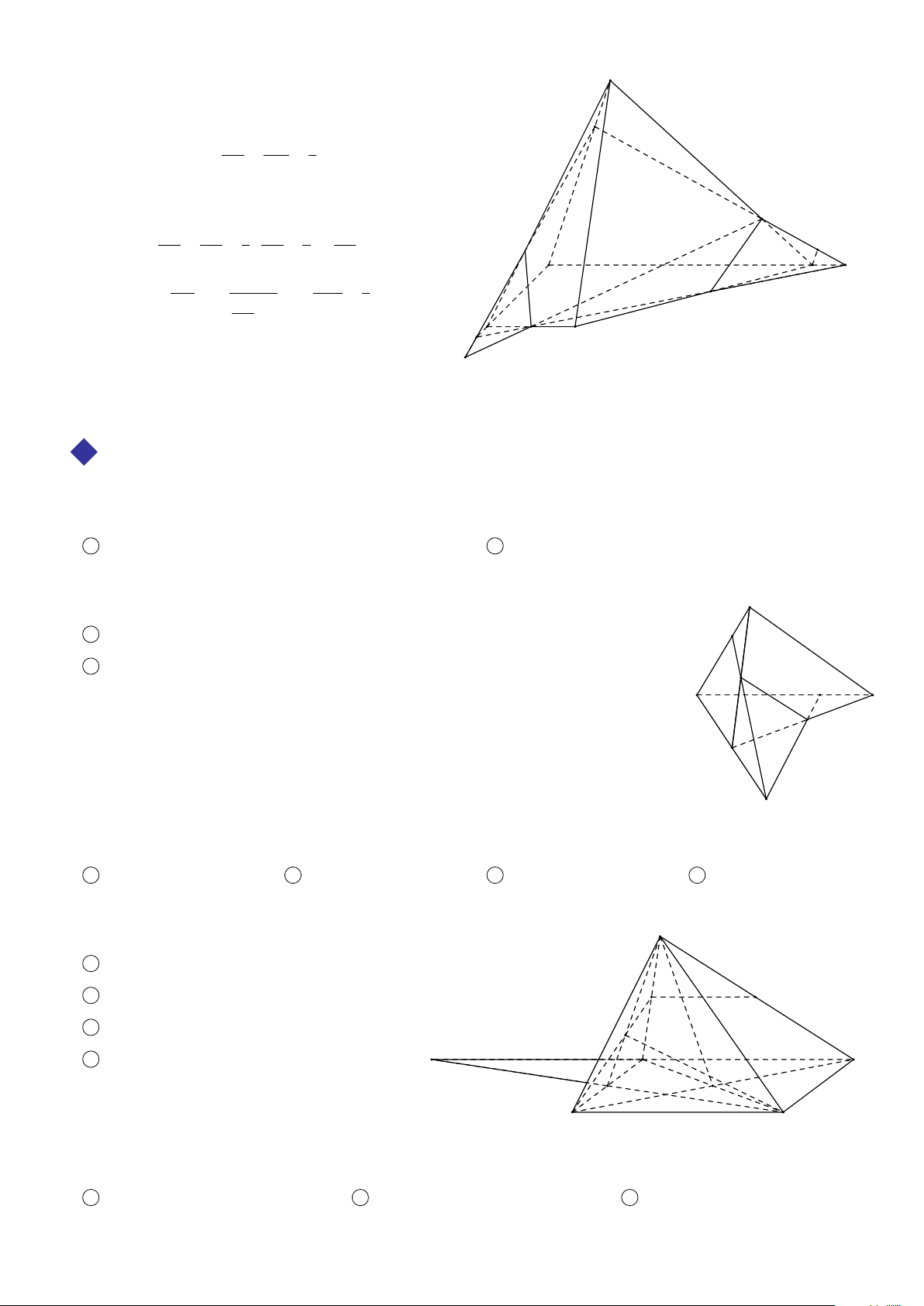
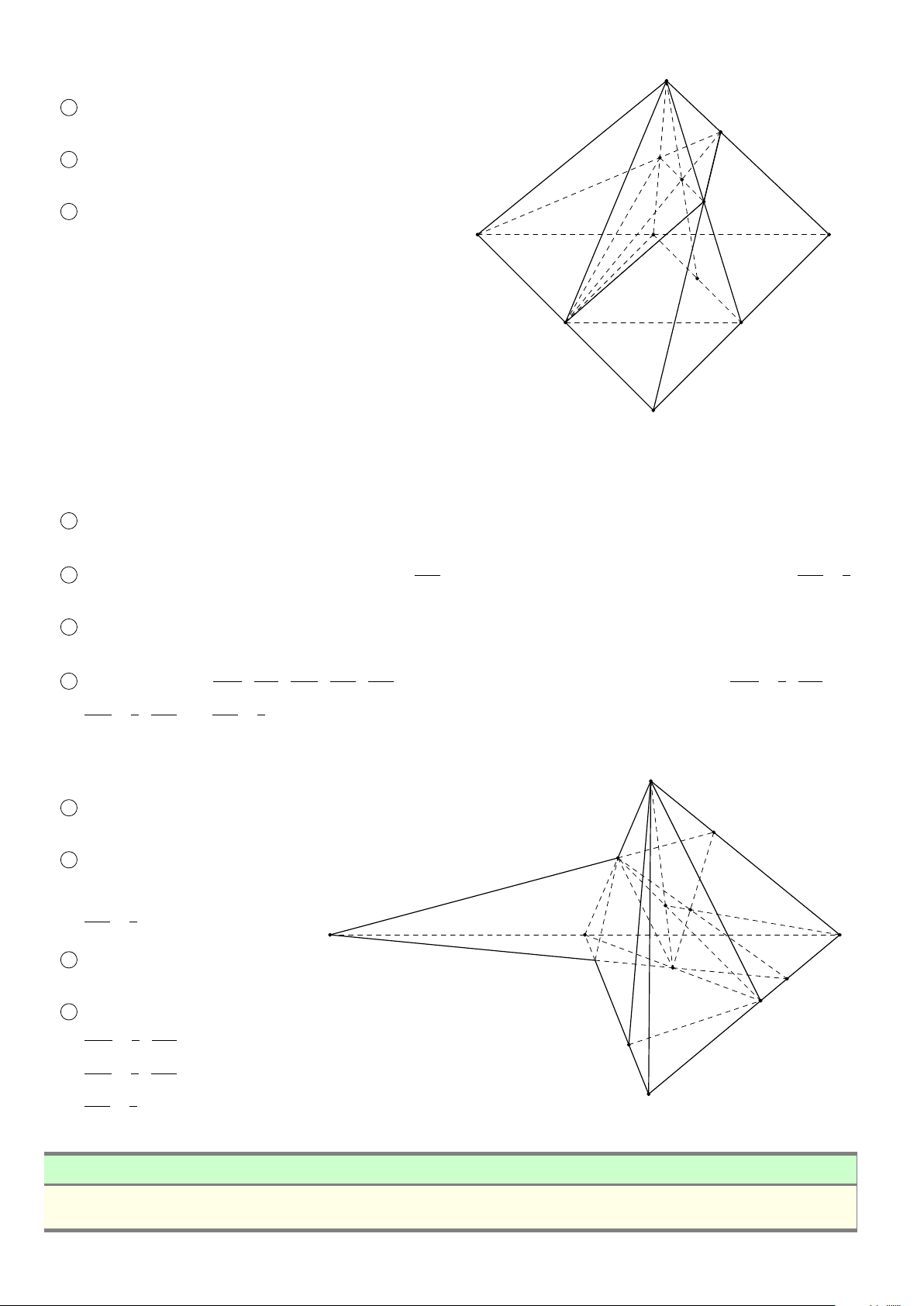
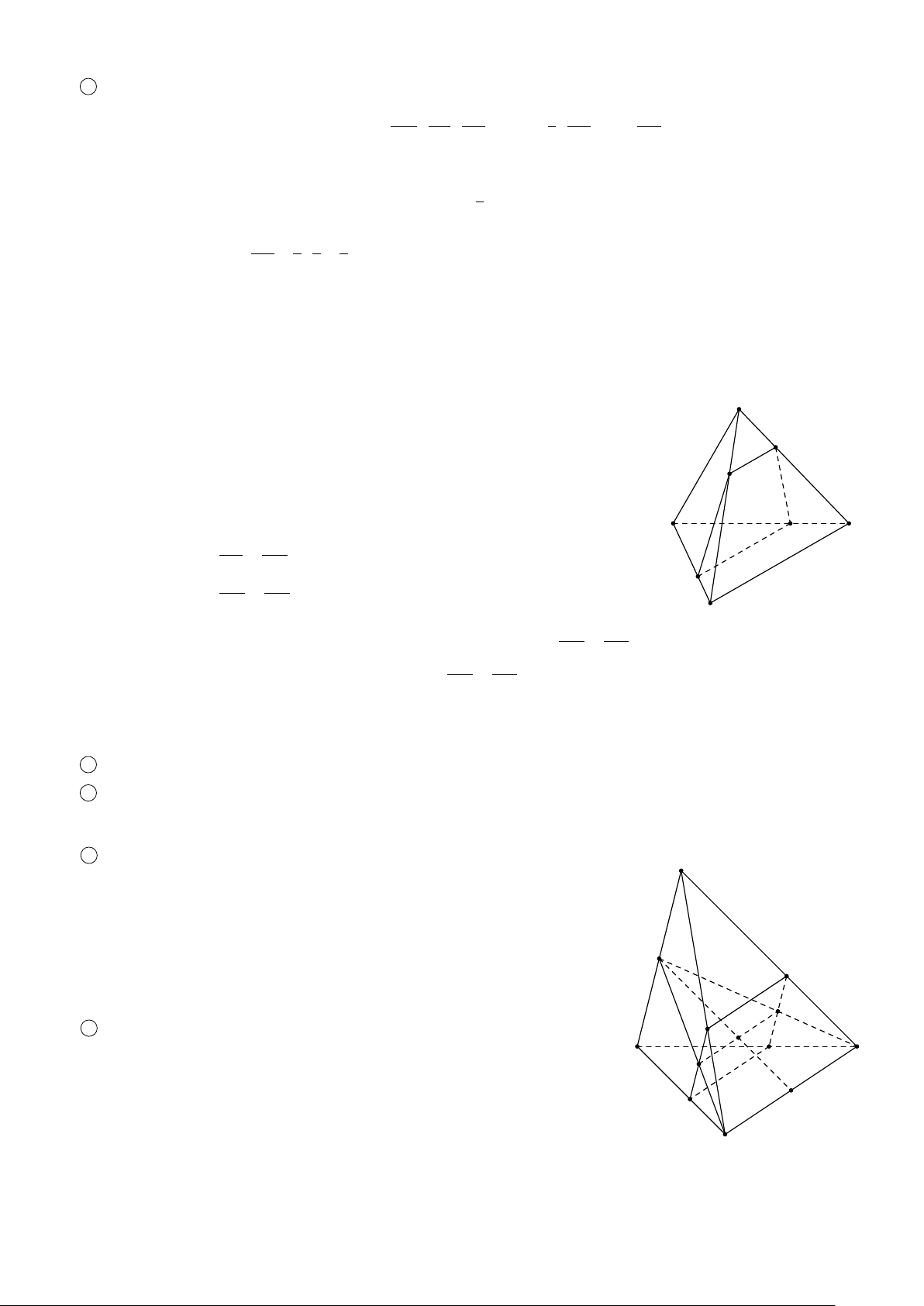
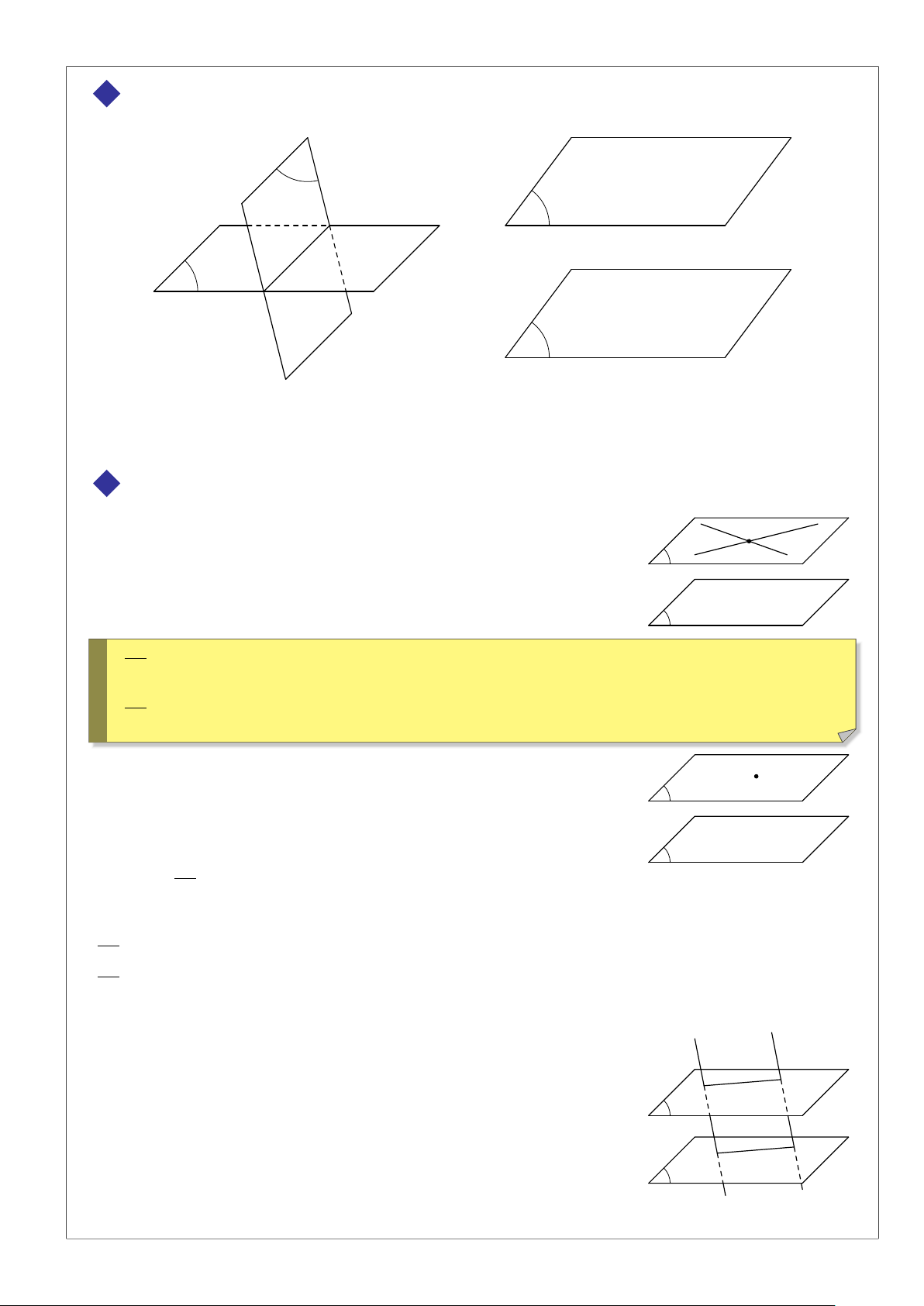
BÀI 3. Cho tứ diện S ABC. Gọi D, E, F lần lượt là trung điểm của AB, BC, S A.
1 Tìm giao tuyến SH của hai mặt phẳng (SCD) và (S AE);
2 Tìm giao tuyến C I của hai mặt phẳng (SCD) và (BFC); OH
3 SH và C I có cắt nhau không? Giải thích? Nếu có, gọi giao điểm đó là O, chứng minh I H ∥ SC. Tính tỉ số . OS
1. ĐẠI CƯƠNG VỀ ĐƯỜNG THẲNG VÀ MẶT PHẲNG 315 Lời giải. S
1 Trong (ABC), gọi H = AE ∩ CD ≡ H.
Ta có giao tuyến của (SCD) và (S AE) là SH. F
2 Trong (S AB), gọi I = SD ∩ BF.
Ta có giao tuyến của hai mặt phẳng (SCD) và (BFC) là CI.
3 Ta có C I và SH cùng nằm trong mặt phẳng (SCD). O I
Xét tam giác SCD có I ∈ SD; H ∈ CD nên CI và SH cắt nhau tại O. A I D 1
Ta có I là trọng tâm tam giác S AB suy ra = . C SD 3 DH 1
H là trọng tâm tam giác ABC suy ra H = . CD 3 D E I D DH Suy ra = ⇔ IH ∥ SC. SD CD OH I H I D 1 Vậy B = = = . OS SC SD 3 ä 3 BÀI TẬP TỰ LUYỆN
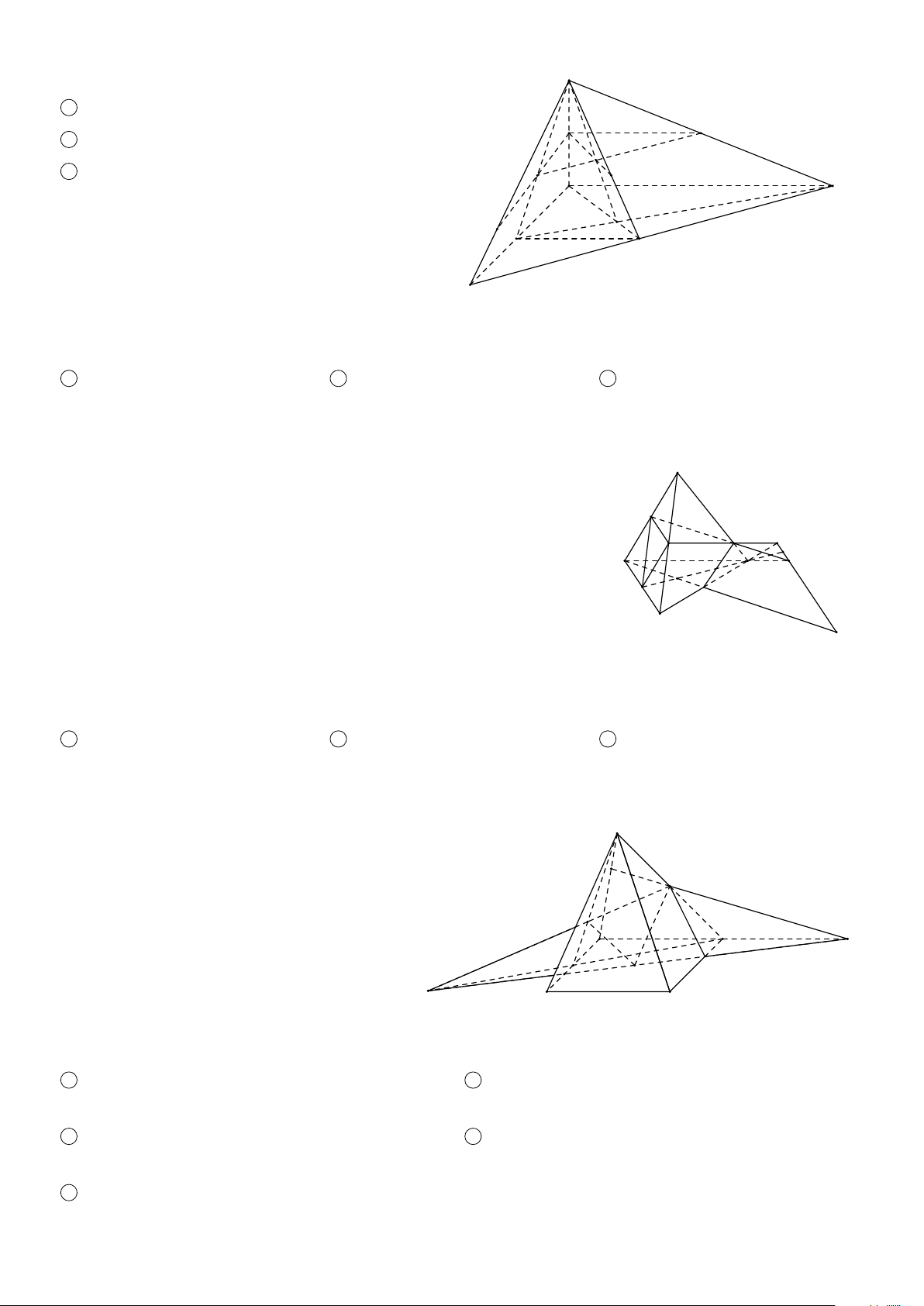
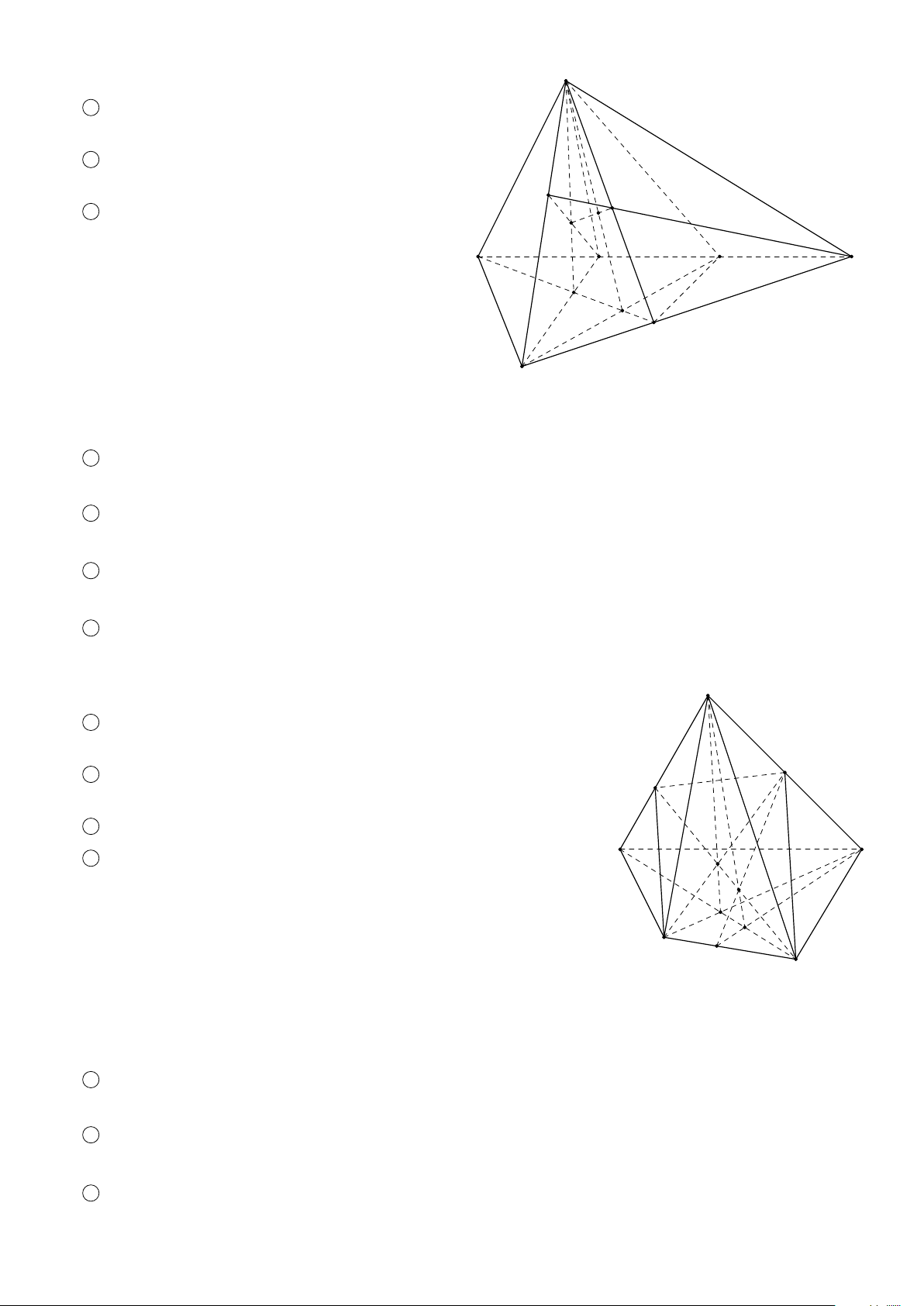
BÀI 4. Cho hình chóp S ABCD có đáy ABCD là tứ giác lồi. Trên cạnh S A lấy điểm M. Tìm giao tuyến của các cặp mặt phẳng sau đây: 1 (S AC) và (SBD). 2 (BC M) và (S AD). 3 (CD M) và (S AB). 4 (BD M) và (S AC).
BÀI 5. Cho hình chóp S ABCD có đáy ABCD là hình bình hành. Trung điểm của CD là M. Tìm giao tuyến của các cặp mặt phẳng sau đây: 1 (S AC) và (SBD). 2 (SBM) và (S AC). 3 (SBM) và (S AD). 4 (S A M) và (SBC).
BÀI 6. Cho hình chóp S ABCD có đáy ABCD là hình thang với AB ∥ CD và AB > CD. Lấy điểm M nằm trên đoạn
S A. Hãy tìm giao tuyến của các cặp mặt phẳng sau đây: 1 (BD M) và (S AC). 2 (BC M) và (S AD). 3 (BC M) và (SCD).
BÀI 7. Cho hình chóp S ABCD có đáy ABCD là hình bình hành tâm O. Lấy điểm M trên cạnh S A, trung điểm CD
là N. Tìm giao tuyến của các cặp mặt phẳng sau đây: 1 (BM N) và (S AC). 2 (BM N) và (S AD). 3 (MCD) và (SBD). 4 (MCD) và (S AB).
BÀI 8. Cho hình chóp S ABCD có đáy ABCD là tứ giác có hai cạnh đối diện không song song. Lấy điểm M thuộc
miền trong tam giác SCD. Tìm giao tuyến của các cặp mặt phẳng sau đây: 1 (SBM) và (SCD). 2 (ABM) và (SCD). 3 (ABM) và (S AC).
BÀI 9. Cho hình chóp S ABCD có đáy ABCD là tứ giác lồi. Lấy I thuộc cạnh S A, J thuộc cạnh SB sao cho I J không
song song với AB. Lấy K là một điểm thuộc miền trong tứ giác ABCD. Tìm giao tuyến của các cặp mặt phẳng sau đây: 1 (I JK ) và (ABCD). 2 (I JK ) và (S AB). 3 (I JK ) và (S AD). 4 (I JK ) và (S AC). 5 (I JK ) và (SBD).
BÀI 10. Cho hình chóp S ABC. Trên cạnh S A, SC lấy điểm M, N sao cho M N không song song với AC. Gọi K là trung
điểm của BC. Tìm giao tuyến của các cặp mặt phẳng sau đây: 316
CHƯƠNG 7. ĐƯỜNG THẲNG VÀ MẶT PHẲNG TRONG KHÔNG GIAN 1 (M N K ) và (ABC). 2 (M N K ) và (S AB).
BÀI 11. Cho hình chóp S ABC. Trên cạnh S A, SC lấy điểm M, N sao cho M N không song song với AC. Gọi O là điểm
thuộc miền trong của tam giác ABC. Tìm giao tuyến của các cặp mặt phẳng sau đây: 1 (M NO) và (ABC). 2 (M NO) và (S AB). 3 (S MO) và (SBC). 4 (ONC) và (S AB).
BÀI 12. Cho tứ diện ABCD có M là điểm trên cạnh AB, N là điểm trên cạnh AD sao cho MB = 2M A, AN = 2ND. Gọi
P là điểm nằm trong tam giác BCD. Tìm giao tuyến của các cặp mặt phẳng sau đây: 1 (C M N) và (BCD). 2 (M N P) và (S AD). 3 (M N P) và (ABC).
BÀI 13. Cho tứ diện ABCD. Gọi M là điểm nằm trong tam giác ABC, N là điểm nằm trong tam giác ACD. Tìm giao
tuyến của các cặp mặt phẳng sau đây: 1 (CD M) và (ABD). 2 (BC N) và (ABD). 3 (C M N) và (BCD).
BÀI 14. Cho tứ diện S AC. Lấy điểm E, F lần lượt trên đoạn S A, SB và điểm G là trọng tâm tam giác ABC. Tìm giao
tuyến của các cặp mặt phẳng sau đây: 1 (EFG) và (ABC). 2 (EFG) và (SBC). 3 (EFG) và (SGC).
BÀI 15. Cho hình chóp S.ABCD. Hai điểm G, H lần lượt là trọng tâm 4S AB,4SCD. Tìm giao tuyến của các cặp mặt phẳng sau đây: 1 (SG H) và (ABCD). 2 (S AC) và (SGH). 3 (S AC) và (BGH). 4 (SCD) và (BGH).
BÀI 16. Cho hình chóp S.ABCD có đáy ABCD là hình thang có AB ∥ CD. Gọi I là giao điểm của AD và BC. Lấy M
thuộc cạnh SC. Tìm giao tuyến của các cặp mặt phẳng sau đây: 1 (S AC) và (SBD). 2 (S AD) và (SBC). 3 (AD M) và (SBC).
BÀI 17. Cho hình chóp S.ABCD có đáy là hình bình hành tâm O. Gọi M, N,Q lần lượt là trung điểm của các cạnh
BC, CD, S A. Hãy tìm giao tuyến của các cặp mặt phẳng sau đây: 1 (M N P) và (S AB). 2 (M N P) và (S AD). 3 (M N P) và (SBC). 4 (M N P) và (SCD).
BÀI 18. Cho hình chóp S.ABC. Gọi H, K lần lượt là trọng tâm tam giác S AB, SBC và M là trung điểm cạnh AC,
I ∈ SM sao cho SI > SM . Tìm giao tuyến của các cặp mặt phẳng sau đây: 1 (I HK ) và (ABC). 2 (I HK ) và (SBC).
1. ĐẠI CƯƠNG VỀ ĐƯỜNG THẲNG VÀ MẶT PHẲNG 317
{ DẠNG 1.2. Tìm giao điểm của đường thẳng d và mặt phẳng (α) β d I u α
Tìm một mặt phẳng phụ (β) chứa d sao cho dễ tạo giao tuyến với (α). Mặt phẳng này thường xác định
bởi d và một điểm của (α).
Tìm giao tuyến u của (α) và (β).
Trong (β), d cắt u tại I, mà u ⊂ (α). Vậy d cắt (α) tại I. 1 VÍ DỤ
VÍ DỤ 1. Cho tứ diện S ABC có M là điểm nằm trên tia đối của tia S A, O là điểm nằm trong tam giác ABC. Tìm các giao điểm của 1
Đường thẳng BC và mặt phẳng (SO A); 2
Đường thẳng MO và mặt phẳng (SBC); 3
Đường thẳng AB và mặt phẳng (MOC); 4
Đường thẳng SB và mặt phẳng (MOC). Lời giải. M 1
Trong mặt phẳng (ABC), kéo dài AO cắt BC tại I. ( I ∈ BC Ta có
⇒ I là giao điểm của BC và (SO A). S I ∈ AO ⊂ (SOA) H 2
Chọn mặt phẳng phụ chứa MO là (SO A), ta có (SO A) ∩ (SBC) = SI. J
Trong (SO A) ≡ (SMI), gọi J là giao điểm của SI và MO. ( J ∈ MO Ta có
⇒ J là giao điểm của MO và (SBC). A C J ∈ SI ⊂ (SBC) O K I 3
Trong mặt phẳng (ABC), kéo dài CO cắt AB tại K. B (K ∈ AB Ta có
⇒ K là giao điểm của AB và (MOC). K ∈ CO ⊂ (MOC) 4
Chọn mặt phẳng phụ chứa SB là (S AB), ta có (S AB) ∩ (MOC) = MK.
Trong (S AB) ≡ (M AB), gọi H là giao điểm của SB và MK. (H ∈ SB Ta có
⇒ H là giao điểm của SB và (MOC). H ∈ MK ⊂ (MOC) ä
VÍ DỤ 2. Cho tứ diện S ABC có hai điểm M, N lần lượt thuộc hai cạnh S A, SB và O là điểm nằm trong tam
giác ABC. Xác định giao điểm của 1
Đường thẳng AB và mặt phẳng (SOC); 2
Đường thẳng MN và mặt phẳng (SOC); 318
CHƯƠNG 7. ĐƯỜNG THẲNG VÀ MẶT PHẲNG TRONG KHÔNG GIAN 3
Đường thẳng SO và mặt phẳng (CMN). Lời giải. S 1
Trong mặt phẳng (ABC), kéo dài CO cắt AB tại I. ( I ∈ AB Ta có
⇒ I là giao điểm của AB và (SOC). N I ∈ CO ⊂ (SOC) K 2
Chọn mặt phẳng phụ chứa MN là (S AB), ta có (S AB) ∩ (SOC) = SI. H M
Trong (S AB), gọi K là giao điểm của SI và MN. (K ∈ MN Ta có
⇒ K là giao điểm của MN và (SOC). A C K ∈ SI ⊂ (SOC) O I 3
Chọn mặt phẳng phụ chứa SO là (SIC), ta có (SIC) ∩ (CMN) = KC. B
Trong (SIC), gọi H là giao điểm của K C và SO. (H ∈ SO Ta có
⇒ H là giao điểm của SO và (CMN). H ∈ KC ⊂ (CMN) ä 2 BÀI TẬP ÁP DỤNG
BÀI 1. Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm của AC và BC. Lấy điểm P trên cạnh BD sao cho
PB > PD. Tìm giao điểm của 1 CD và (M N P). 2 AD và (M N P). Lời giải. A M E Q D C N P B NB PB 1
Trong mặt phẳng (BCD), xét tam giác BCD có = 1 6=
nên NP và DC cắt nhau giả sử tại Q. Rõ ràng NC PC
Q ∈ CD theo cách dựng. Lại có Q ∈ NP ⊂ (MNP) nên Q ∈ (MNP). Vậy Q = CD ∩ (MNP). 2
Trong mặt phẳng (ACD) nối Q với M cắt AD tại E. Dễ thấy E ∈ AD theo cách dựng. Lại có E ∈ MQ ⊂ (MNP)
nên E ∈ (MNP). Vậy E = AD ∩ (MNP). ä
BÀI 2. Cho tứ diện ABCD. Trên AC và AD lần lượt lấy các điểm M, N sao cho M N không song song với CD. Gọi O
là điểm thuộc miền trong 4BCD. Tìm giao điểm của 1 BD và (OM N). 2 BC và (OM N). 3 M N và (ABO). 4 AO và (BM N). Lời giải.
Trong mặt phẳng (ACD), vì MN không song song với CD nên ta giả A
sử MN cắt CD tại E. Trong mặt phẳng (BCD), nối E với O kéo dài
cắt BD và BC lần lượt tại F và G. M 1
Ta có F ∈ OE ⊂ (OMN) và F ∈ BD. Suy ra F = BD ∩ (OMN). I 2
Theo cách dựng thì G ∈ BC và G ∈ OE ⊂ (OMN). Vậy G = BC ∩ J G B C (OM N). N O 3
Trong mặt phẳng (BCD) kéo dài BO cắt DC tại H. Trong mặt F H
phẳng (ADC) nối H với A cắt MN tại I. Vì H ∈ BO ⊂ (ABO) nên E D
AH ⊂ (ABO). Suy ra I ∈ (ABO). Vậy I = MN ∩ (ABO). 4
Trong mặt phẳng (ABH) nối B với I cắt AO tại J. Rõ ràng J ∈ AO theo cách dựng và J ∈ BI ⊂ (BMN). Vậy J = AO ∩ (BMN).
1. ĐẠI CƯƠNG VỀ ĐƯỜNG THẲNG VÀ MẶT PHẲNG 319 ä
BÀI 3. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M là trung điểm SB, N là trọng tâm 4SCD.
Xác định giao điểm của 1 M N và (ABCD). 2 M N và (S AC). 3 SC và (AM N). 4 S A và (CM N). Lời giải.
Gọi I và J lần lượt là trung điểm của các cạnh SD và DC. Trọng S
tâm của tam giác SCD là N = SJ ∩ CI. 1
Trong mặt phẳng (ABCD) nối B với J cắt AC và AD lần lượt G I
tại E và K. Vì DK ∥ BC nên theo Hệ quả của Định lý Talet ta có H M JB JC N = = 1 ⇒ JC = JD. F JK JD K A D
Vậy 4SCD và 4SBK có chung đường trung tuyến là SJ. Vì
thế trọng tâm N của 4SCD cũng là trọng tâm của 4SBK. J E
Suy ra K ∈ MN. Lúc đó K = MN ∩ (ABCD). B C 2
Trong mặt phẳng (SBJ) nối S với E cắt MN tại F. Ta có F = M N ∩ (S AC). 3
Trong mặt phẳng (SCD) nối N với D kéo dài cắt SC tại H. Vì D ∈ AK ⊂ (AMN) nên ND ⊂ (AMN). Suy ra
H ∈ (AMN). Vậy H = SC ∩ (AMN). 4
Theo cách dựng ta thấy IK = (CMN) ∩ (S AD). Trong mặt phẳng (S AD) kéo dài IK cắt S A tại G. Lúc đó G = S A ∩ (CMN). ä
BÀI 4. Cho hình chóp S.ABCD có đáy hình bình hành tâm O. Trên S A, SB lần lượt lấy hai điểm M và N.
1 Tìm giao điểm của SO và (CM N).
2 Tìm giao tuyến của (S AD) và (CM N). Lời giải.
Trong mặt phẳng (S AC) nối S với O cắt MC tại I. Trong mặt phẳng (SBD) kéo dài S
I N cắt SD tại J. Lúc đó M 1 I = SO ∩ (CMN). J N I 2
J ∈ (S AD) ∩ (CMN). Lại có M ∈ (S AD) ∩ (CMN). Vậy JM = (S AD) ∩ (CMN). A B O D C ä
BÀI 5. Cho hình chóp S.ABCD. Gọi M, N lần lượt là trung điểm của cạnh S A, SD và P là điểm thuộc cạnh SB sao cho SP = 3PB.
1 Tìm giao điểm Q của SC và (M N P).
2 Tìm giao tuyến của (M N P) và (ABCD). Lời giải.
Gọi O là giao điểm của AC và BD. Trong mặt phẳng (SBD) gọi I là giao điểm của S
N P với SO. Lúc đó I ∈ (MNP) và M I ⊂ (S AC). 1
Trong mặt phẳng (S AC) gọi Q là giao điểm của M I và SC. Vì Q ∈ MI nên M P Q = SC ∩ (MNP). H N I 2
Trong mặt phẳng (S AC) gọi G là giao điểm của M I và AC. Lúc đó G ∈ B A
(M N P) ∩ (ABCD). Trong mặt phẳng (S AB), vì O MS P S 1 = 6= = 3 G D C M A PB Q
nên MP và AB cắt nhau. Gọi H là giao điểm của MP và AB. Ta có H ∈
(M N P) ∩ (ABCD). Vậy GH = (MNP) ∩ (ABCD). . ä
BÀI 6. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành, M là trung điểm của SC, N là trung điểm của OB
với O là giao điểm của AC và BD. 320
CHƯƠNG 7. ĐƯỜNG THẲNG VÀ MẶT PHẲNG TRONG KHÔNG GIAN S I
1 Tìm giao điểm I của SD với (AM N). 2 Tính tỉ số . I D Lời giải. S I M A B P O N L D C J 1
Trong mặt phẳng (ABCD) nối A với N kéo dài cắt DC tại J và cắt BC tại L. Trong mặt phẳng (SDC) nối J với
M kéo dài cắt SD tại I. Vì J ∈ AN ⊂ (AMN) nên M J ⊂ (AMN). Suy ra I ∈ (AMN). Vậy I = SD ∩ (AMN). 2
Trong mặt phẳng (ABCD), vì AB ∥ D J nên 4N AB đồng dạng với 4N JD. Suy ra D J D N = = 3 ⇒ D J = 3AB = 3DC. AB NB
Trên cạnh SD lấy điểm P sao cho I là trung điểm của SP. Ta có I M là đường trung bình của 4SPC nên
I M ∥ PC ⇒ I M ∥ I J. Áp dụng Định lý Talet trong 4DI J ta có D I D J =
= 3 ⇒ D I = 3DP và SI = P I = 2DP. DP DC S I 2 Vậy = . I D 3 ä
BÀI 7. Cho hình chóp S.ABC có G là trọng tâm tam giác ABC. Gọi M là điểm trên cạnh S A sao cho M A = 2MS, K
là trung điểm BC và D là điểm đối xứng của G qua A. HK
1 Tìm giao điểm H của SK với (MCD). 2 Tính tỉ số . SK Lời giải. 1
Trong mặt phẳng (SDK) kéo dài DM cắt SK tại H. Lúc đó H = SK ∩ (MCD). 2
Trong mặt phẳng (SDK) vẽ đường thẳng qua A và song song với S
SK cắt DH tại E. Vì AE ∥ SH nên theo Hệ quả của Định lý Talet ta có AE M A 1 M = = 2 ⇒ SH = AE. H SH MS 2 E
Trong 4DHK ta có AE ∥ HK nên theo Định lý Talet thì AE D A 2 5 D = = ⇒ HK = AE. HK DK 5 2 C A G 1 5 HK 5
Ta có SK = SH + HK = AE + AE = 3AE. Vậy = . K 2 2 SK 6 B ä
BÀI 8. Cho tứ diện ABCD. Gọi I và J lần lượt là trung điểm của AC và BC. Trên cạnh BD lấy điểm K sao cho BK = 2K D.
1 Tìm giao điểm E của CD với (I JK ). Chứng minh: DE = DC.
2 Tìm giao điểm F của AD với (I JK ). Chứng minh: F A = 2FD và FK ∥ I J.
3 Gọi M và N là hai điểm bất kì lần lượt nằm trên hai cạnh AB và CD. Tìm giao điểm của M N với (I JK ).
1. ĐẠI CƯƠNG VỀ ĐƯỜNG THẲNG VÀ MẶT PHẲNG 321 Lời giải. A M I P F H E N C D Q K J B 1
Trong mặt phẳng (BCD) kéo dài JK cắt CD tại E. Lúc đó, dễ thấy E ∈ CD theo cách dựng. Lại có E ∈ K J ⊂ (I JK). Suy ra E = CD ∩ (I JK).
Trong mặt phẳng (BCD) lấy điểm E0 thuộc đường thẳng DC sao cho D là trung điểm của E0C. Xét 4E0BC có
BD và E0 J là các đường trung tuyến. Vì BK = 2K D nên K là trọng tâm 4E0BC. Suy ra E0, K, J thẳng hàng. Từ
đây có E0 = DC ∩ K J. Vậy E0 ≡ E. Suy ra DE = DC. 2
Trong mặt phẳng (ACD), nối I với E cắt AD tại F. Lúc đó rõ ràng F ∈ AD và vì F ∈ EI ⊂ (I JK) nên F ∈ (I JK). Vậy F = AD ∩ (I JK).
Trong 4AEC, vì các điểm D, I lần lượt là trung điểm của EC và AC nên F = AD ∩ EI chính là trọng tâm của
4AEC. Theo tính chất trọng tâm tam giác ta có F A = 2FD. DK DF 1
Vì I J là đường trung bình của tam giác ABC nên I J ∥ AB. Mặt khác, vì = = nên theo Định lý Talet DB D A 3
ta có FK ∥ AB. Từ đó suy ra FK ∥ I J. 3
Trong mặt phẳng (BCD) nối B với N cắt K J tại Q. Ta có Q ∈ (I JK). Trong mặt phẳng (ADC) nối A với N cắt EI
tại P. Vì (I JK) ≡ (IEJ) nên P ∈ EI ⊂ (IEJ) ⇒ P ∈ (I JK). Trong mặt phẳng (ABN) nối P với Q cắt MN tại H. Lúc
đó, vì H ∈ PQ ⊂ (I JK) nên H ∈ (I JK). Vậy H = MN ∩ (I JK). ä
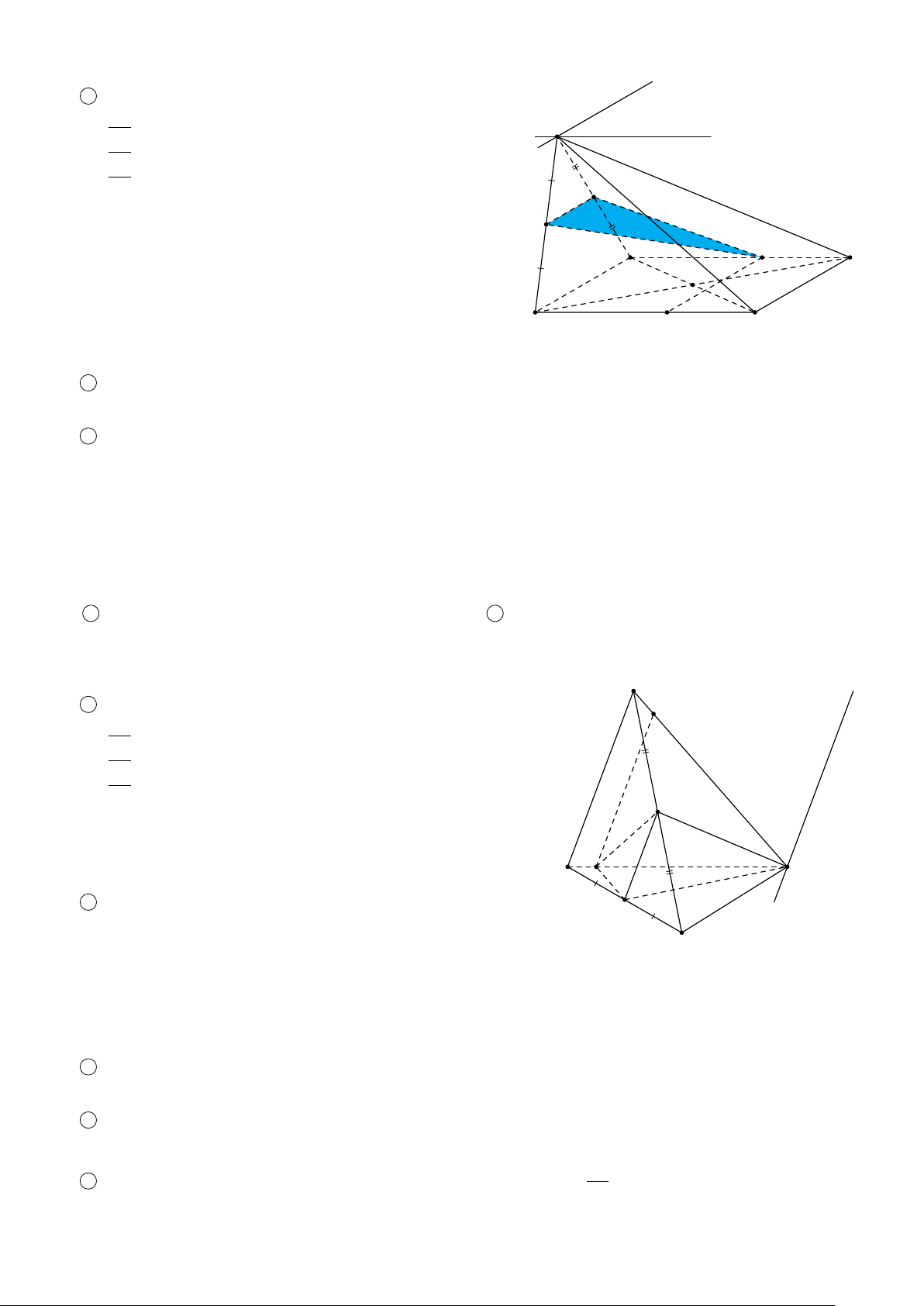
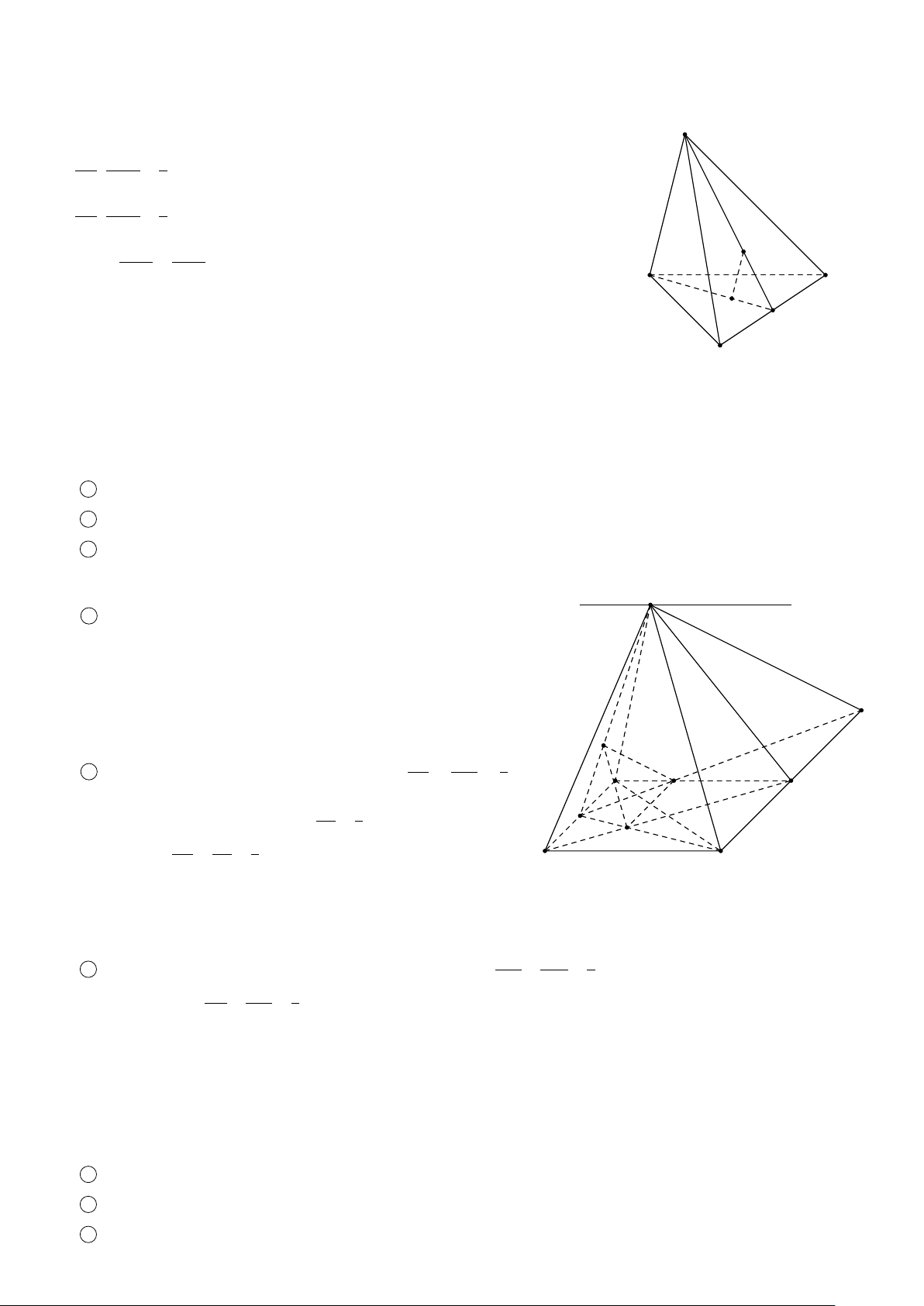
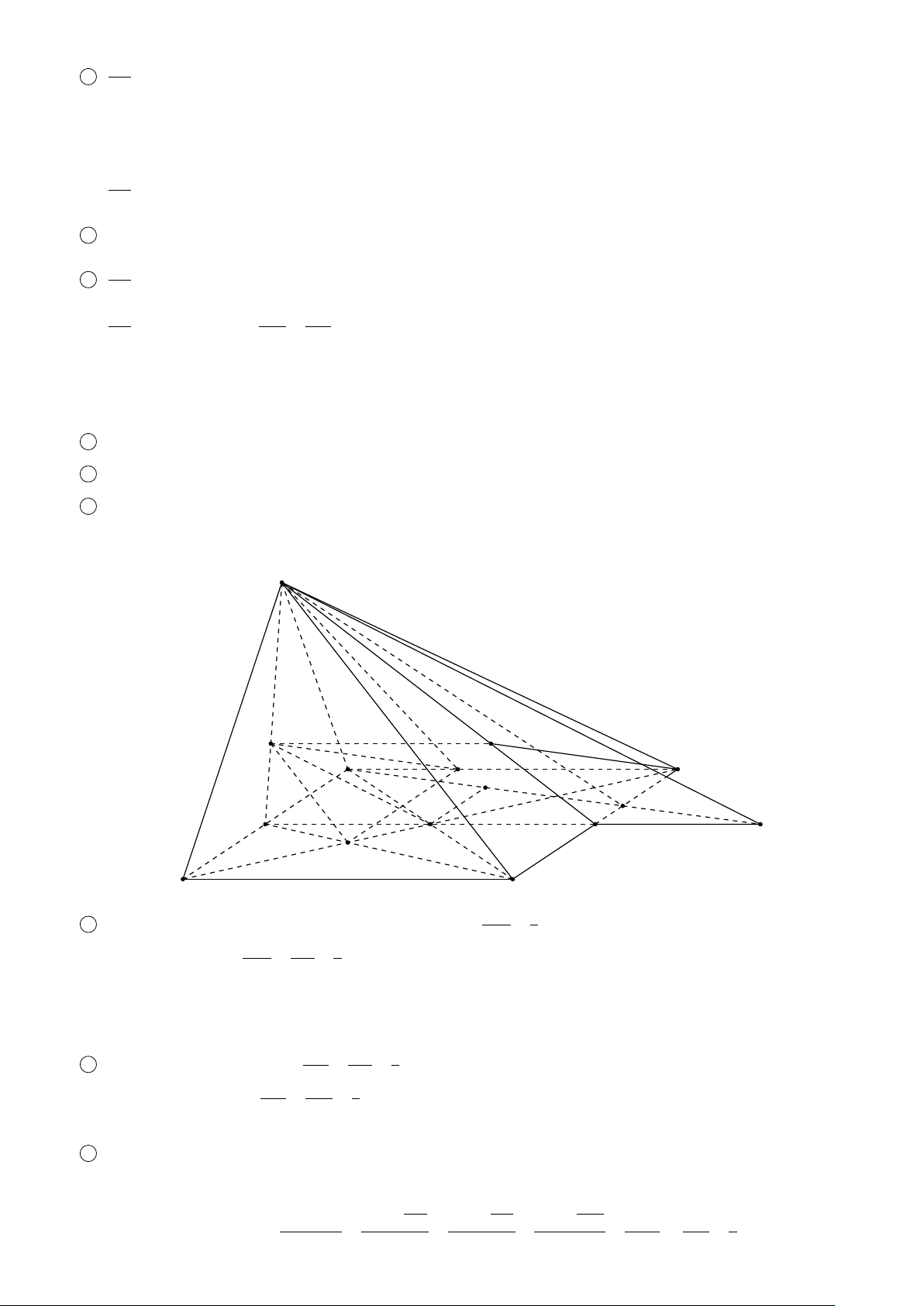
BÀI 9. Cho hình chóp S.ABCD có đáy ABCD là hình thang với AD ∥ BC và AD = 2BC, E là trung điểm của S A. Gọi
N là điểm thuộc đoạn AB sao cho NB = 2N A và M là điểm thuộc đoạn CD sao cho MD = 2MC.
1 Tìm giao tuyến của hai mặt phẳng (EM N) và (S AD).
2 Tìm giao tuyến của hai mặt phẳng (EM N)và (SCD).
3 Tìm giao điểm L của đường thẳng EM và mặt phẳng (SBC).
4 Tìm giao tuyến của (CDE) và (S AB). Giao tuyến này cắt SB tại P và cắt AB tại I. Chứng minh: 2SB = 3SP và S4IDE = 3S4ICP. Lời giải. 1
Trong mặt phẳng (ABCD) kéo dài MN và AD cắt nhau tại J. Lúc đó J ∈ AD ⊂ (S AD) và J ∈ MN ⊂ (EMN). Vì
thế J ∈ (S AD) ∩ (EMN). Dễ thấy E ∈ (S AD) ∩ (EMN). Vậy EJ = (EMN) ∩ (S AD). 2
Trong mặt phẳng (S AD) kéo dài JE cắt SD tại Q. Vì JE ⊂ (EJM) ≡ (EMN) nên Q ∈ (EMN). Lúc đó QM = (EM N) ∩ (SCD). 3
Trong mặt phẳng (S AB) kéo dài NE và SB cắt nhau tại K. Lúc đó K ∈ (EMN) ∩ (SBC). Trong mặt phẳng
(ABCD) kéo dài M N và BC cắt nhau tại H. Ta có H ∈ (EMN) ∩ (SBC). Suy ra GH = (EMN) ∩ (SBC). Trong mặt
phẳng (EMN) kéo dài K H và EM cắt nhau tại L. Vì K H ⊂ (SBC) nên L ∈ (SBC). Vậy L = EM ∩ (SBC). 4
Trong mặt phẳng (ABCD) kéo dài CD và AB cắt nhau tại 322
CHƯƠNG 7. ĐƯỜNG THẲNG VÀ MẶT PHẲNG TRONG KHÔNG GIAN
I. Lúc đó IE = (CDE) ∩ (S AB). K
Trong mặt phẳng (ABCD) vì BC ∥ AD nên áp dụng Định lý Talet với 4I AD ta có IB IC BC 1 = = = ⇒ IB = AB và ID = 2IC. I A I D AD 2
Trong mặt phẳng (S AB) xét 4SI A có B và E lần lượt là
trung điểm các cạnh I A và S A. Lúc đó P = IE∩SB là trọng S
tâm 4SI A. Theo tính chất trọng tâm thì Q 3 I E = IP và 2SB = 3SP. E 2 Ta có J A 1 1 3 P D S N 4IDE = I E · ID · sin EID I P E I D = · · 2IC · sin 2 2 2 M 1 = 3 · · IP · IC · sin P IC = 3S 2 4ICP . B C H Vậy S4IDE = 3S4ICP. I L ä
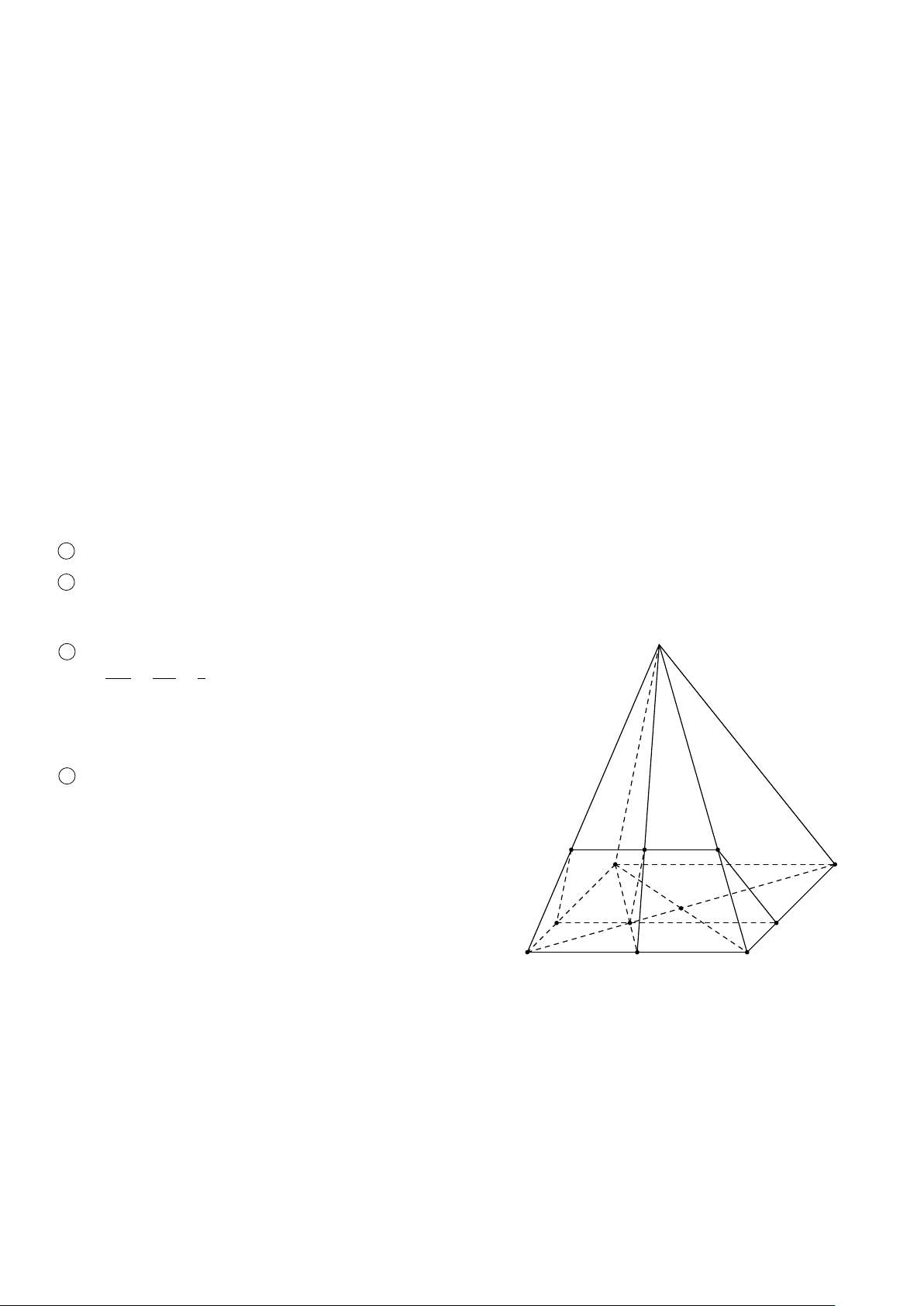
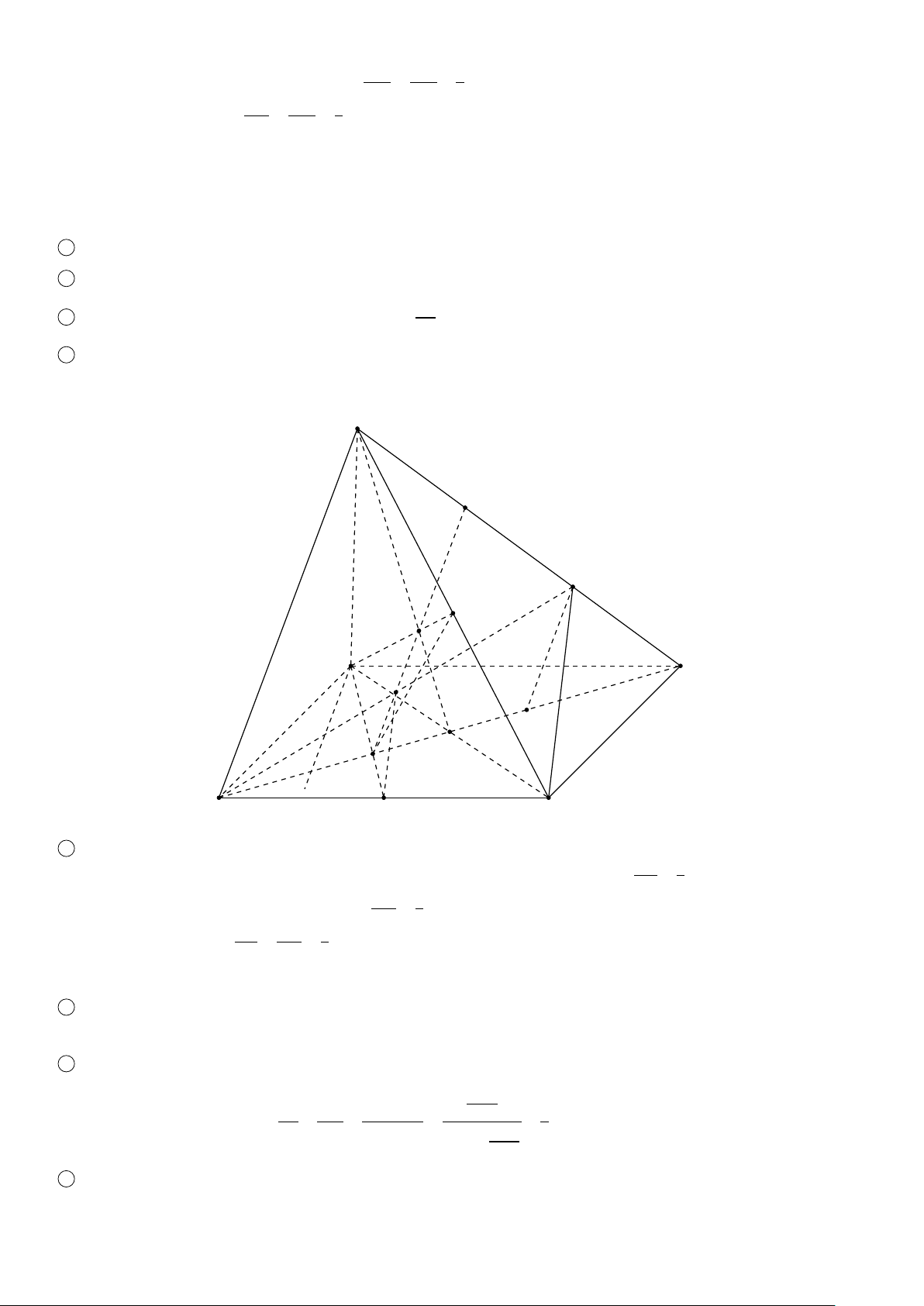
BÀI 10. Cho hình chóp S.ABCD có đáy ABCD là hình thang, AB đáy lớn và AB = 3CD. Gọi N là trung điểm của
CD, M là điểm trên cạnh SB thỏa SM = 3MB, điểm I trên cạnh S A và thỏa AI = 3IS.
1 Tìm giao điểm của đường thẳng M N với (S AD). HB
2 Gọi H là giao điểm của CB với (I M N). Tính tỉ số . HC Lời giải. 1 I S MS Trong mặt phẳng (S AB) vì = 6=
= 3 nên I M và AB cắt nhau. Gọi J là giao điểm của I M và AB. Trong mặt 3 A I MB
phẳng (ABCD) nối J, N cắt AD tại P. Trong mặt phẳng (I MN) nối M, N cắt IP tại K. 1
Theo cách dựng, dễ thấy K ∈ MN. Vì K ∈ IP ⊂ (S AD) nên K ∈ (S AD). Vậy K = MN ∩ (S AD). 2
Vì H là giao điểm của CB với (I MN) nên H = CB ∩ N J. 1 1 Ta có NC = DC = AB. 2 6
Vì NC ∥ BJ nên theo Hệ quả của Định lý Talet ta có: HB BJ HB BJ BJ 1 = ⇒ = 6 · = 6 · = 6 · . HC NC HC AB J A − BJ J A −1 BJ
1. ĐẠI CƯƠNG VỀ ĐƯỜNG THẲNG VÀ MẶT PHẲNG 323
Trong mặt phẳng (S AB) vẽ đường thẳng qua B S
và song song với S A cắt I J tại O.
Vì BO ∥ SI nên áp dụng Hệ quả Định lý Talet ta có I BO BM 1 = = . S I MS 3
Vì BO ∥ AI nên áp dụng Định lý Talet trong 4J AI ta có M JB BO 1 BO 1 J A = = · = ⇒ = 9. O J A I A 3 S I 9 BJ J B A HB 1 1 3 Từ đó có = 6 · = 6 · = . HC J A 9 − 1 4 H − 1 BJ D P N C K ä 3 BÀI TẬP RÈN LUYỆN
BÀI 11. Cho hình chóp S.ABC. Trên cạnh S A lấy M sao cho S A = 3SM, trên cạnh SC lấy điểm N sao cho SC = 2SN.
Điểm P thuộc cạnh AB. Tìm giao điểm của: 1 M N và (ABC). 2 BC và (M N P). ĐS: S 1 M N ∩ (ABC) = I. M 2 BC ∩ (MNP) = J. N P A J C I
BÀI 12. Cho hình chóp S.ABCD có đáy hình bình hành tâm O. Gọi G là trọng tâm tam giác S AB. Hãy tìm: 1 (SGC) ∩ (ABCD) =?. 2 AD ∩ (SGC) =?. 3 SO ∩ (SGB) =?. 4 SD ∩ (BCG) =?. ĐS: S
1 (SGC) ∩ (ABCD) = MC. I J 2 AD ∩ (SGC) = N. 3 SO ∩ (SGB) = S. G A 4 SD ∩ (BCG) = J. D N M O B C
BÀI 13. Cho hình chóp S.ABCD có đáy ABCD là hình thang, đáy lớn AB. Gọi I, J lần lượt là trung điểm S A và SB.
Lấy điểm M tùy ý trên SD. Tìm giao điểm của 1 I M với (SBC). 2 J M với (S AC). 3 SC với (I J M). ĐS: 324
CHƯƠNG 7. ĐƯỜNG THẲNG VÀ MẶT PHẲNG TRONG KHÔNG GIAN S 1 I M ∩ (SBC) = H. I J 2 J M ∩ (S AC) = K. 3 SC ∩ (I J M) = P. K P M B A H O D C G
BÀI 14. Cho tứ diện O ABC. Gọi M, N, P lần lượt là trung điểm của O A, OB và AB. Trên cạnh OC lấy điểm Q sao
cho OQ > QC. Gọi G là trọng tâm tam giác ABC. Tìm giao điểm 1 E = BC ∩ (MNQ). 2 F = CP ∩ (MNQ). 3 K = BG ∩ (MNQ). ĐS: O N Q H M F B G C E P A K
BÀI 15. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Gọi M là trung điểm của SB và G là trọng
tâm của tam giác S AD. Tìm giao điểm: 1 K = GM ∩ (ABCD). 2 F = AD ∩ (OMG). 3 E = S A ∩ (OMG). ĐS: S E M G B J A N O K F D C
BÀI 16. Cho tứ diện S.ABC, lấy điểm M là trung điểm S A, lấy điểm N là trọng tâm 4SBC và P nằm trong 4ABC.
1 Tìm giao điểm của M N và (ABC). 2 SB ∩ (MNP) =?. 3 SC ∩ (MNP) =?. 4 N P ∩ (S AB) =?.
5 Tứ giác ABIC là hình gì ? ĐS:
1. ĐẠI CƯƠNG VỀ ĐƯỜNG THẲNG VÀ MẶT PHẲNG 325 K 1 M N ∩ (ABC) = I. 2 SB ∩ (MNP) = J. 3 SC ∩ (MNP) = K. O S 4 N P ∩ (S AB) = O. J
5 Tứ giác ABIC là hình bình hành. M N A B H Q P I C
BÀI 17. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành, M là trung điểm của SD.
1 Tìm I = BM ∩ (S AC). Chứng minh: BI = 2I M.
2 Tìm E = S A ∩ (BCM). Chứng minh: E là trung điểm của S A. ĐS: S E M I A B O D C
BÀI 18. Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật tâm O. Gọi M là trung điểm của SB, N là điểm
thuộc đoạn SD sao cho SN = 2ND.
1 Tìm giao tuyến của hai mặt phẳng (SBD) và (S AC). EN
2 Tìm giao điểm E của đường thẳng M N và mặt phẳng (ABCD). Tính . EM JK
3 Tìm giao điểm K của đường thẳng SC và mặt phẳng (AM N). Gọi J giao điểm của AK và SO. Tính tỉ số: . J A ĐS: S
1 (SBD) ∩ (S AC) = SO. EN 2 K M 2 = . EM 3 J JK 2 N 3 = . J A 5 B A O D C E
BÀI 19. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N, lần lượt là trung điểm của S A và CD.
1 Tìm giao điểm E của AD với (BM N).
2 Tìm giao điểm F của SD và (BM N). Chứng minh rằng: F S = 2FD. 326
CHƯƠNG 7. ĐƯỜNG THẲNG VÀ MẶT PHẲNG TRONG KHÔNG GIAN ĐS: S M F A B C D N E
BÀI 20. Cho tứ diện ABCD. Gọi I, M lần lượt là trung điểm của AB và BC, G là trọng tâm tam giác ACD. PC
1 Tìm giao điểm P của CD và (I MG). 2 Tính tỉ số: . P D ĐS: A PC 1 • = . I P D 2 G J B D M P C
BÀI 21. Cho tứ diện ABCD. Gọi I và J lần lượt là trung điểm của AC và BC. Trên cạnh BD lấy điểm K sao cho BK = 2K D.
1 Tìm giao điểm E của đường thẳng CD và (I JK ). Chứng minh: DE = DC. F A
2 Tìm giao điểm F của đường thẳng AD và (I JK ). Tính tỉ số . F D ĐS: A F A • = 2. I F D J B C F K D E
{ DẠNG 1.3. Tìm thiết diện của hình chóp khi cắt bởi mặt phẳng (α).
Phương pháp giải: Ta tìm các đoạn giao tuyến nối tiếp nhau của mặt phẳng (α) với các mặt của hình chóp cho
đến khi khép kín thành một đa giác phẳng. Đa giác đó là thiết diện cần tìm và các đoạn giao tuyến chính là
các cạnh của thiết diện.
1. ĐẠI CƯƠNG VỀ ĐƯỜNG THẲNG VÀ MẶT PHẲNG 327 1 VÍ DỤ
VÍ DỤ 1. Cho tứ diện ABCD, trên các đoạn C A, CB, BD lấy lần lượt các điểm M, N, P sao cho M N không
song song với AB. Gọi (α) là mặt phẳng xác định bởi ba điểm M, N, P. Xác định thiết diện tạo bởi (α) và tứ diện ABCD? Lời giải.
Trong mặt phẳng (ABC), do MN và AB không song E
song nên chúng cắt nhau giả sử tại E. Khi đó điểm E A A nằm ngoài đoạn AB.
Trong mặt phẳng (ABD), gọi Q là giao điểm của EP và AD. Ta có N Q • (MNP) ∩ (ABC) = MN. Q • (MNP) ∩ (BCD) = MP. N B D B D P • (MNP) ∩ (ABD) = PQ. P M • (MNP) ∩ (ACD) = QN. M C E C
Vậy thiết diện cắt tứ diện ABCD bởi mặt phẳng
(M N P) là tứ giác M NQP. Hay hiết diện cắt tứ diện
ABCD bởi mặt phẳng (α) là tứ giác MNQP. ä
VÍ DỤ 2. Cho tứ diện S ABC và O là một điểm thuộc miền trong tam giác ABC. Gọi M, N lần lượt là hai điểm
nằm trên cạnh S A và SC sao cho MN không song song với AC. Xác định thiết diện cắt tứ diện S ABC bởi mặt phẳng (MNO)? Lời giải.
Trong mặt phẳng (S AC), do MN và AC không song song nên chúng cắt nhau S
giả sử tại E. Khi đó điểm E nằm ngoài đoạn AC.
Trong mặt phẳng (ABC), gọi P, Q lần lượt là giao điểm của EO với BC và AB. M Ta có N • (MNO) ∩ (S AC) = MN. • (MNO) ∩ (SBC) = NP. C A E • (MNO) ∩ (ABC) = PQ. P O Q • (MNO) ∩ (S AB) = QM. B
Vậy thiết diện cắt tứ diện S ABC bởi mặt phẳng (MNO) là tứ giác MNPQ. ä 2 BÀI TẬP ÁP DỤNG
BÀI 1. Cho hình chóp S.ABC. Trên các cạnh S A, SB lần lượt lấy các điểm M, N sao cho M N không song song với
AB. Gọi P là điểm thuộc miền trong tam giác ABC. Xác định giao tuyến của (M NP) và (ABC) từ đó suy ra thiết diện
khi cắt hình chóp S.ABC bởi mặt phẳng (MNP). Lời giải.
Trong mặt phẳng (S AB), do MN không song song với AB nên chúng cắt nhau giả sử S
tại E. Khi đó E nằm ngoài đoạn AB.
Trong mặt phẳng (ABC), gọi K, H lần lượt là giao điểm của EP với các đoạn BC, AC M
(Vì P thuộc miền trong tam giác (ABC)). Khi đó ta có • (MNP) ∩ (S AB) = MN. • (MNP) ∩ (SBC) = NK. N H A C • (MNP) ∩ (ABC) = K H. P K • (MNP) ∩ (S AC) = HM. B
Vậy thiết diện cắt hình chóp S.ABC bởi mặt phẳng (MNP) là tứ giác MNK H. E ä 328
CHƯƠNG 7. ĐƯỜNG THẲNG VÀ MẶT PHẲNG TRONG KHÔNG GIAN
BÀI 2. Cho tứ diện S ABC. Gọi K , N lần lượt là trung điểm của S A, BC và M là điểm thuộc đoạn SC sao cho 3SM = 2MC. 1
Tìm thiết diện của hình chóp và mặt phẳng (K MN). I A I A 2 2
Mặt phẳng (K MN) cắt AB tại I. Tính tỉ số . ĐS: = IB IB 3 Lời giải. S M K P E A C I H N B SM 2 SM 2 1 SK 1
Trong mặt phẳng (S AC), vì = ⇒ = 6= =
nên K M không song song với AC. Gọi E là giao điểm MC 3 SC 5 2 S A của K M và AC.
Trong mặt phẳng (ABC), gọi I là giao điểm của EN và AB, khi đó I là giao điểm của AB với (K MN). Ta có • (K MN) ∩ (S AC) = MK. • (K MN) ∩ (S AB) = K I. • (K MN) ∩ (ABC) = I N. • (K MN) ∩ (SBC) = N M.
Vậy thiết diện cắt tứ diện S ABC bởi mặt phẳng (K MN) là tứ giác MN IK. 2
Trên SC lấy điểm P sao cho M là trung điểm của SP. Khi đó ta có AC PC 1
• AP ∥ K M theo tính chất đường trung bình của tam giác S AP nên AP ∥ EM ⇒ = = . AE P M 2
• Gọi H là trung điểm của AB, khi đó NH ∥ AC (Tính chất đường trung bình). I H N H 1 4 2 A I 2 Do đó = = ⇒ AI = AH = AB ⇒ = . I A AE 4 5 5 BI 3 ä
BÀI 3. Cho hình chóp S.ABCD có đáy ABCD là hình thang thỏa mãn AB ∥ CD, AB > CD. Gọi I, J theo thứ tự là
trung điểm của các cạnh SB, SC. 1
Xác định giao tuyến của hai mặt phẳng (S AD) và (SBC). 2
Tìm giao điểm của đường thẳng SD với (AI J). 3
Xác định thiết diện của hình chóp S.ABCD cắt bởi mặt phẳng (AI J). Lời giải. S d I J A D B C
1. ĐẠI CƯƠNG VỀ ĐƯỜNG THẲNG VÀ MẶT PHẲNG 329 1
Hai mặt phẳng (S AD) và (SBC) có S là một điểm chung.
Lại có AD ∥ BC theo giả thiết và S ∉ (ABCD) nên giao tuyến của (S AD) và (SBC) là đường thẳng d đi qua S và song song với AD, BC. 2
Do I J là đường trung bình của tam giác SBC nên I J ∥ BC mà I ∉ (ABCD) ⇒ I J ∥ AD. Vì vậy A, D, I, J xác định
mặt phẳng (AD J I) hay D ∈ (AI J).
Mặt khác D ∈ SD nên D là giao điểm của SD với (AI J). 3 Từ kết quả trên ta có • (AI J) ∩ (ABCD) = AD. • (AI J) ∩ (SCD) = D J. • (AI J) ∩ (SBC) = J I. • (AI J) ∩ (S AB) = I A.
Vậy thiết diện của hình chóp S.ABCD cắt bởi mặt phẳng (AI J) là hình thang AD J I. ä
BÀI 4. Cho hình chóp S.ABCD. Lấy một điểm M thuộc miền trong tam giác SBC. Lấy điểm N thuộc miền trong tam giác SCD. 1
Tìm giao điểm của MN và mặt phẳng (S AC). 2
Tìm giao điểm của SC và mặt phẳng (AMN). 3
Tìm thiết diện của hình chóp S.ABCD cắt bởi mặt phẳng (AMN). Lời giải. S Q N I P A D M R F B O E C 1
Trong mặt phẳng (ABCD), gọi O là giao điểm của AC và EF. Khi đó SO = (S AC) ∩ (SEF).
Trong mặt phẳng (SEF), gọi {I} = MN ∩ SO. Ta có I ∈ SO ⇒ I ∈ (S AC). Mà I ∈ MN nên {I} = MN ∩ (S AC). 2
Theo chứng minh trên ta suy ra AI = (AMN) ∩ (S AC).
Trong mặt phẳng (S AC) gọi P là giao điểm của AI và SC. Khi đó do P ∈ AI ⇒ P ∈ (AMN). Mà P ∈ SC nên {P} = SC ∩ (AMN). 3
Do M, P ∈ (SBC) nên trong mặt phẳng (SBC), gọi R là giao điểm của P M với SB. Ta có P M ⊂ (AMN) nên R ∈ (AMN).
Tương tự, trong mặt phẳng (SCD), gọi Q là giao điểm của P N với SD ta có Q ∈ (AMN). Vì vậy • (AMN) ∩ (S AB) = AR. • (AMN) ∩ (SBC) = RP. • (AMN) ∩ (SCD) = PQ. • (AMN) ∩ (S AD) = Q A.
Vậy thiết diện cắt hình chóp S.ABCD bởi mặt phẳng (AMN) là tứ giác ARPQ. ä
BÀI 5. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Gọi M là trung điểm của SB và G là trọng tâm tam giác S AD. 330
CHƯƠNG 7. ĐƯỜNG THẲNG VÀ MẶT PHẲNG TRONG KHÔNG GIAN 1
Tìm giao điểm I của GM với (ABCD). Chứng minh I thuộc đường thẳng CD và IC = 2ID. J A J A 2
Tìm giao điểm J của AD và (OMG). Tính tỉ số . ĐS: = 2 JD JD K A K A 3
Tìm giao điểm K của S A và (OMG). Tính tỉ số . ĐS: = 2 K S K S 4
Tìm thiết diện cắt hình chóp S.ABCD bởi mặt phẳng (OMG). Lời giải. S K I N M G H A D E J F O B P C 1
Gọi E, N lần lượt là trung điểm của AD, S A. Ta có M là trung điểm của SB, G là trọng tâm của tam giác S AD. SM 1 2 SG Trong mặt phẳng (SBE) có = 6= =
suy ra MG và BE không song song. Do đó MG và BE cắt nhau. SB 2 3 SE
Lại do BE ⊂ (ABCD), {I} = MG ∩ (ABCD) nên I ∈ BE.
Vậy giao điểm I của MG và (ABCD) là giao điểm I của MG và BE.
Do MN là đường trung bình của tam giác S AB nên MN ∥ AB ⇒ MN ∥ CD. Suy ra MN, CD xác định mặt phẳng (M N DC).
Lại do G là trọng tâm tam giác S AD nên G ∈ ND ⇒ G ∈ (MNDC), I ∈ MG ⇒ I ∈ (MNDC).
Mặt khác (MNDC) ∩ (ABCD) = CD, I ∈ (MNDC), I ∈ (ABCD) nên I ∈ CD. I D ED 1
Mà AD ∥ BC nên ED ∥ BC ⇒ = = ⇒ IC = 2ID. IC BC 2 2
Dễ thấy I ∈ (OMG). Trong mặt phẳng (ABCD), gọi J0 là giao điểm của AD và OI. Vì OI ⊂ (OMG) ⇒ J0 ∈ (OMG) nên AD ∩ (OMG) = {J0}.
Mà J là giao điểm của AD và (OMG) (gt) nên J0 ≡ J. Vậy J là giao điểm của IO và AD. J A
Dễ thấy J là trọng tâm 4I AC nên = 2. JD 3
Trong mặt phẳng (ABCD), gọi F là giao điểm của BI và AC suy ra (SBI) ∩ (S AC) = SF.
Trong mặt phẳng (SBI), gọi H là giao điểm của M I và SF. Ta có H ∈ MG ⇒ S
OH ⊂ (OMG) và H thuộc (S AC).
Trong mặt phẳng (S AC), gọi K0 là giao điểm của OH và S A. Khi đó do
K 0 ∈ OH ⇒ K0 ∈ (OMG) ⇒ S A ∩(OMG) = {K0} hay K0 ≡ K. Vậy K là giao điểm K của OH với S A. Q
Lại có K, G, J là các điểm chung của hai mặt phẳng (OMG) và (S AD) nên K , G, J thẳng hàng. G
Gọi Q là trung điểm của SD, vì J là trọng tâm 4I AC. Xét 4S AD có AG 2 A J K A J A = =
⇒ G J ∥ SD ⇒ K J ∥ SD ⇒ = = 2. A E J D AQ 3 AD K S JD 4
Từ chứng minh trên ta suy ra • (OMG) ∩ (S AB) = K M. • (OMG) ∩ (SBC) = MP. • (OMG) ∩ (ABCD) = P J. • (OMG) ∩ (S AD) = JK.
Vậy thiết diện cắt hình chóp S.ABCD bởi mặt phẳng (OMG) là tứ giác K MP J.
1. ĐẠI CƯƠNG VỀ ĐƯỜNG THẲNG VÀ MẶT PHẲNG 331 ä
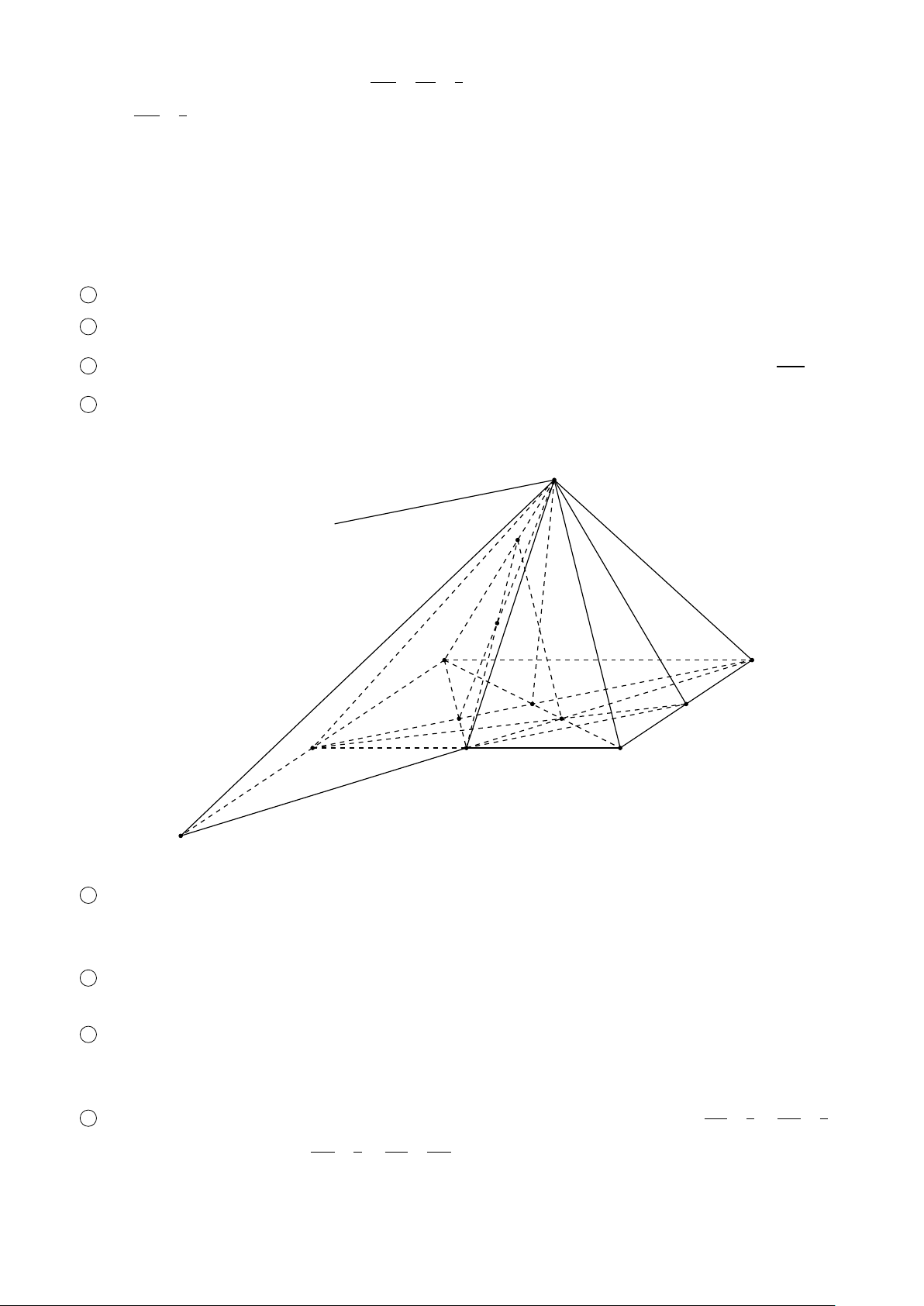
BÀI 6. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Gọi M, N, P lần lượt là trung điểm của SB, SD và OC. 1
Tìm giao tuyến của mặt phẳng (MNP) với các mặt phẳng (S AC) và (ABCD). 2
Tìm giao điểm của S A với mặt phẳng (MNP). 3
Xác định thiết diện của hình chóp S.ABCD với mặt phẳng (MNP). Tính tỉ số mà mặt phẳng (MNP) chia các ES 1 HB K D cạnh S A, BC và CD. ĐS: = , = = 1 E A 3 HC K C Lời giải. S E N I M D A G O K P B H C F 1
Do M, N lần lượt là trung điểm của SB, SD nên MN là đường trung bình của tam giác SBD, suy ra MN ∥ BD. Ta có (P MN) ∩ (SBD) = MN.
Trong mặt phẳng (SBD), gọi I là giao điểm của MN và SO. Khi đó vì I ∈ SO ⇒ I ∈ (S AC), P ∈ AC ⇒ P ∈ (S AC)
suy ra (P MN) ∩ (S AC) = P I.
Hai mặt phẳng (P MN) và (ABCD) có P là một điểm chung. Mà MN ∥ BD, P ∉ MN, P ∉ BD nên giao tuyến của
(P M N) và (ABCD) là đường thẳng qua P, song song với M N và song song với BD, cắt các cạnh BC, CD lần lượt tại H và K. 2
Trong mặt phẳng (S AC), gọi E là giao điểm của P I và S A. Ta có
• E ∈ P I, P I ⊂ (P MN) ⇒ E ∈ (P MN).
• Mà E ∈ S A nên E là giao điểm của S A với (P MN). 3
Ta có (P MN) lần lượt giao với các cạnh S A, SB, BC, CD, SD tại các điểm E, M, H, K, N nên • (P MN) ∩ (S AB) = EM. • (P MN) ∩ (SBC) = MH. • (P MN) ∩ (ABCD) = HK. • (P MN) ∩ (SCD) = K N. • (P MN) ∩ (S AD) = NE.
Vậy thiết diện của hình chóp S.ABCD với mặt phẳng (P MN) là ngũ giác EMHK N. Vì MN là đường trung bình
trong tam giác ABD nên I là trung điểm của SO.
Trong tam giác SOC có IP là đường trung bình nên IP ∥ SC. ES PC 1
Do đó trong tam giác S AC có PE ∥ SC suy ra = = . E A P A 3
Lại có P là trung điểm của OC, HK qua P và HK ∥ BD nên HK là đường trung bình của tam giác BCD. HB K D Do đó = = 1. HC K C ä
BÀI 7. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Trên các cạnh SB, SD ta lần lượt lấy các SM 1 SN 2 điểm M, N sao cho = , = . SB 3 SD 3 332
CHƯƠNG 7. ĐƯỜNG THẲNG VÀ MẶT PHẲNG TRONG KHÔNG GIAN 1
Tìm giao tuyến của hai mặt phẳng (AMN) và (SCD). 2
Tìm giao điểm I của SC và mặt phẳng (AMN). Suy ra thiết diện của mặt phẳng (AMN) và hình chóp S.ABCD. K C K C 3
Gọi K là giao điểm của I N và CD. Tính tỉ số . ĐS: = 5 K D K D Lời giải. S I M N K E A D O B C SM 1 SN 2 SM SN 1
Trong mặt phẳng (SBD). Theo bài ra ta có = , = ⇒ 6=
. Do đó MN cắt BD giả sử tại E. SB 3 SD 3 SB SD
Hai mặt phẳng (AMN) và (ABCD) có hai điểm chung A và E nên (AMN) ∩ (ABCD) = AE.
Trong mặt phẳng (ABCD), gọi K là giao điểm của AE và CD. Khi đó • K ∈ AE ⇒ K ∈ (AMN).
• K ∈ CD ⇒ K ∈ (SCD). Suy ra K là một điểm chung của (AMN) và (SCD).
• Mặt khác (AMN) và (SCD) có điểm N chung (vì N ∈ SD).
Vậy giao tuyến của hai mặt phẳng (AMN) và (SCD) là đường thẳng K N. 2
Trong mặt phẳng (SCD), gọi I là giao điểm của K N và SC. Khi đó I ∈ K N ⇒ I ∈ (AMN). Vậy I là giao điểm của SC và (AM N).
Do (AMN) cắt các cạnh S A, SB, SC, SD lần lượt tại các điểm A, M, I, N nên • (AMN) ∩ (S AB) = AM. • (AMN) ∩ (SBC) = M I. • (AMN) ∩ (SCD) = I N. • (AMN) ∩ (S AD) = N A.
Suy ra thiết diện của mặt phẳng (AMN) và hình chóp S.ABCD là tứ giác AM I N. 3
Ta có K ∈ CD và K, I, N thẳng hàng.
Lấy điểm P trên cạnh SB sao cho PD ∥ MN. S SM SN 2 MP 1 MP 1 Khi đó ta có = = ⇒ = ⇒ = vì BM = 2SM. SP SD 3 M M 2 MB 4 ED MP 1 M
Xét tam giác BME, ta cũng có PD ∥ ME nên = = . EB MB 4 P K D ED 1 N
Xét tam giác ABE, có K D ∥ AB nên = = . AB EB 4 K D K D 1 K D K D 1 1 K C Suy ra = = ⇒ = = = ⇒ = 5. DC AB 4 K C K D + DC 1 + 4 5 K D B D E ä 3 BÀI TẬP TỰ LUYỆN
BÀI 8. Cho tứ diện ABCD. Trên AB lấy điểm M. Trên cạnh BC lấy điểm N thỏa mãn BN = 2NC. Gọi P là trung
điểm của CD. Xác định thiết diện của tứ diện ABCD khi cắt bởi mặt phẳng (MNP). ĐS:
1. ĐẠI CƯƠNG VỀ ĐƯỜNG THẲNG VÀ MẶT PHẲNG 333
Thiết diện là tứ giác MNPQ. A M Q B D E P N C
BÀI 9. Cho hình chóp S.ABCD có đáy ABCD là hình thang đáy lớn AD. Lấy điểm M trên cạnh SB. Tìm thiết diện
của hình chóp cắt bởi mặt phẳng (AMD). ĐS:
Thiết diện là hình thang AMND. S M N A D B C
BÀI 10. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N, P là các điểm lần lượt nằm trên các
cạnh BC, CD, S A. Tìm thiết diện của hình chóp S.ABCD cắt bởi mặt phẳng (MNP). ĐS:
Thiết diện là ngũ giác MN HPG. S P H G A F D N B M C E
BÀI 11. Cho hình chóp S.ABCD có đáy ABCD là hình thang đáy lớn AD. Gọi H, K lần lượt là trung điểm của các
cạnh SB và AB và M là một điểm nằm trong hình thang ABCD sao cho đường thẳng K M cắt hai đường thẳng AD
và CD. Tìm thiết diện của hình chóp S.ABCD khi cắt bởi mặt phẳng (HK M). ĐS:
Thiết diện là ngũ giác HK PQ J. S J Q H N A D P M I K B C
BÀI 12. Cho hình chóp S.ABCD có đáy ABCD là hình thang đáy lớn AB. Lấy các điểm M, N lần lượt trên các cạnh
SC và SD. Tìm thiết diện của hình chóp S.ABCD với các mặt phẳng (ABM) và (AM N). ĐS: 334
CHƯƠNG 7. ĐƯỜNG THẲNG VÀ MẶT PHẲNG TRONG KHÔNG GIAN S S Q M N I M P I A B A N B J Q O O D C D C Hình 1 Hình 2
Thiết diện cắt bởi (ABM) là hình thang ABMP. SM SN Nếu >
thì thiết diện cắt hình chóp S.ABCD bởi (AMN) là tứ giác AN MQ (Hình 1). SC SD SM SN Nếu <
thì thiết diện cắt hình chóp S.ABCD bởi (AMN) là tứ giác AN MQ (Hình 2). SC SD
BÀI 13. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi H, K lần lượt là trung điểm của BC và CD.
Lấy điểm M bất kỳ trên cạnh S A. Tìm thiết diện của hình chóp S.ABCD với mặt phẳng (MHK). ĐS:
Thiết diện là ngũ giác P MQK H. S M Q P A F D K B H C E
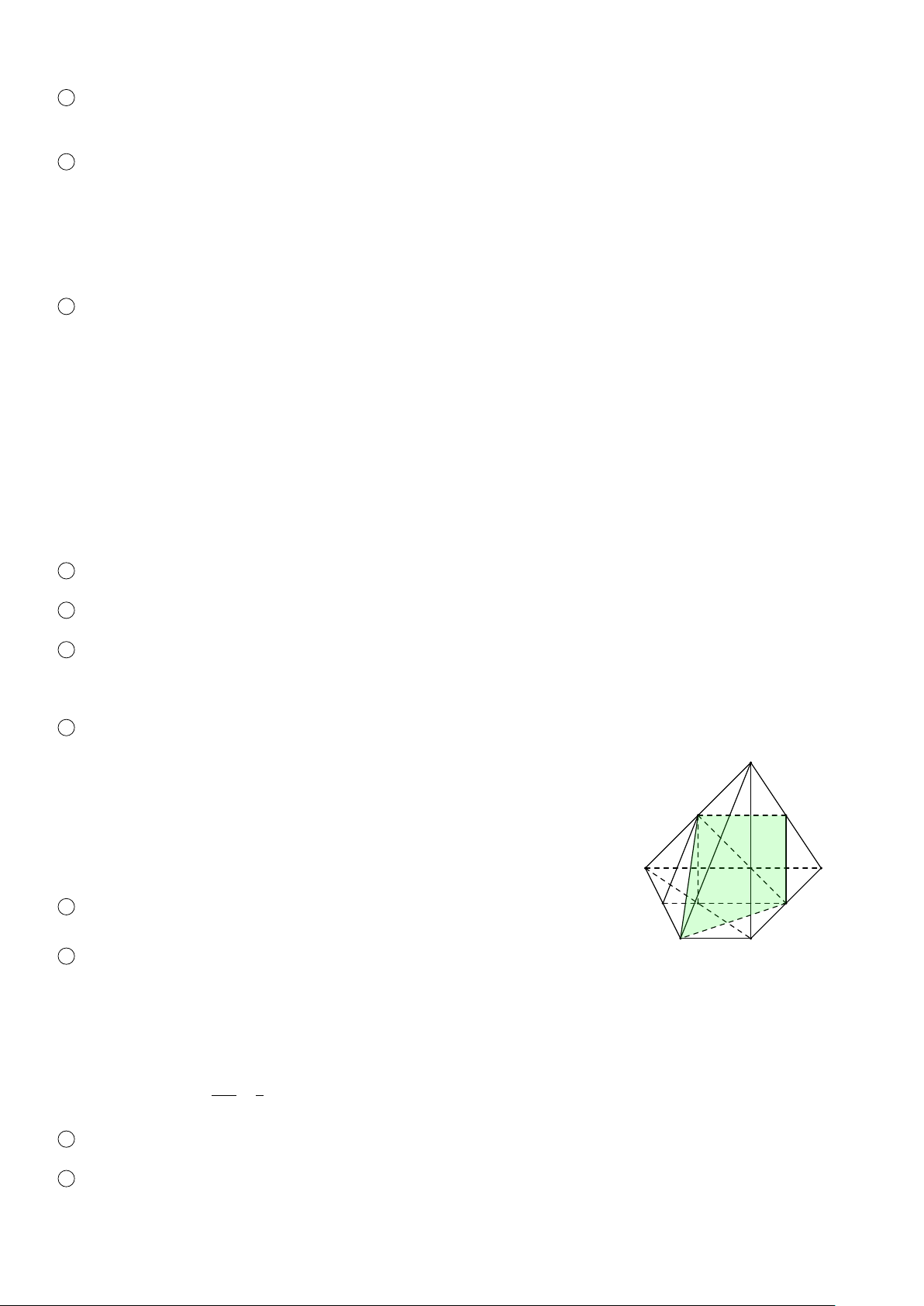
BÀI 14. Cho tứ diện đều ABCD có cạnh bằng a. Gọi I là trung điểm của AD, J là điểm đối xứng với D qua C, K là
điểm đối xứng với D qua B. Xác định thiết diện của tứ diện ABCD khi cắt bởi mặt phẳng (I JK) và tính diện tích của thiết diện này. ĐS:
Thiết diện là tam giác IEF cân tại I. A a2 S4IEF = . 6 I E F D K B C J
BÀI 15. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi K là trọng tâm của tam giác S AC. Gọi I, J
lần lượt là trung điểm của CD và SD. 1
Tìm giao điểm H của đường thẳng IK với mặt phẳng (S AB).
1. ĐẠI CƯƠNG VỀ ĐƯỜNG THẲNG VÀ MẶT PHẲNG 335 2
Xác định thiết diện của hình chóp với mặt phẳng (I JK). ĐS: S 1 {H} = SP ∩ IK. 2
Thiết diện của hình chóp với mặt phẳng (I JK) là ngũ giác G I JG MF. M H J K A B P O F E D I C
BÀI 16. Cho hình chóp S.ABCD có đáy ABCD không là hình thang, điểm P nằm trong tam giác S AB và điểm M
thuộc cạnh SD sao cho MD = 2MS. 1
Tìm giao tuyến của hai mặt phẳng (S AB) và (PCD). 2
Tìm giao điểm của SC với mặt phẳng (ABM). 3
Gọi N là trung điểm của AD. Tìm thiết diện tạo bởi mặt phẳng (MNP) và hình chóp S.ABCD. ĐS: S S S M R M Q E0 P I P F A D F0 A D A D N G B J0 O H I0 C B L C C B E Hình 1. Hình 2. Hình 3. 1
Giao tuyến của hai mặt phẳng (S AB) và (PCD) là đường thẳng PE. 2
Giao điểm của SC với mặt phẳng (ABM) là điểm F. 3
Thiết diện tạo bởi mặt phẳng (MNP) và hình chóp S.ABCD là ngũ giác MN HQR.
{ DẠNG 1.4. Chứng minh ba điểm thẳng hàng Phương pháp giải
Giả sử chứng minh ba điểm I, J, K thẳng hàng.
Xét hai mặt phẳng (P) và (Q). Chứng minh ba điểm I, J, K là ba điểm chung của (P) và (Q).
Khi đó I, J, K thuộc giao tuyến của (P) và (Q) hay I, J, K thẳng hàng. 1 VÍ DỤ
VÍ DỤ 1. Cho tứ diện S ABC. Trên các cạnh S A, SB, SC lần lượt lấy M, N, P sao cho M N cắt AB tại I, NP
cắt BC tại J và MP cắt AC tại K. Chứng minh rằng ba điểm I, J, K thẳng hàng. Lời giải. 336
CHƯƠNG 7. ĐƯỜNG THẲNG VÀ MẶT PHẲNG TRONG KHÔNG GIAN
Xét hai mặt phẳng (ABC) và (MNP). Ta có S
( I ∈ AB ⊂ (ABC) ⇒ I ∈(ABC)∩(MNP). (1) I ∈ MN ⊂ (MNP) M
( J ∈ BC ⊂ (ABC) ⇒ J ∈(ABC)∩(MNP). (2) P J ∈ NP ⊂ (MNP) N J (K ∈ AC ⊂ (ABC) A ⇒ K ∈ (ABC) ∩ (MNP). (3) C K K ∈ MP ⊂ (MNP)
Từ (1), (2), (3) suy ra I, J, K cùng thuộc đường thẳng giao tuyến của (ABC) và (M NP). B
Vậy ba điểm I, J, K thẳng hàng. I ä
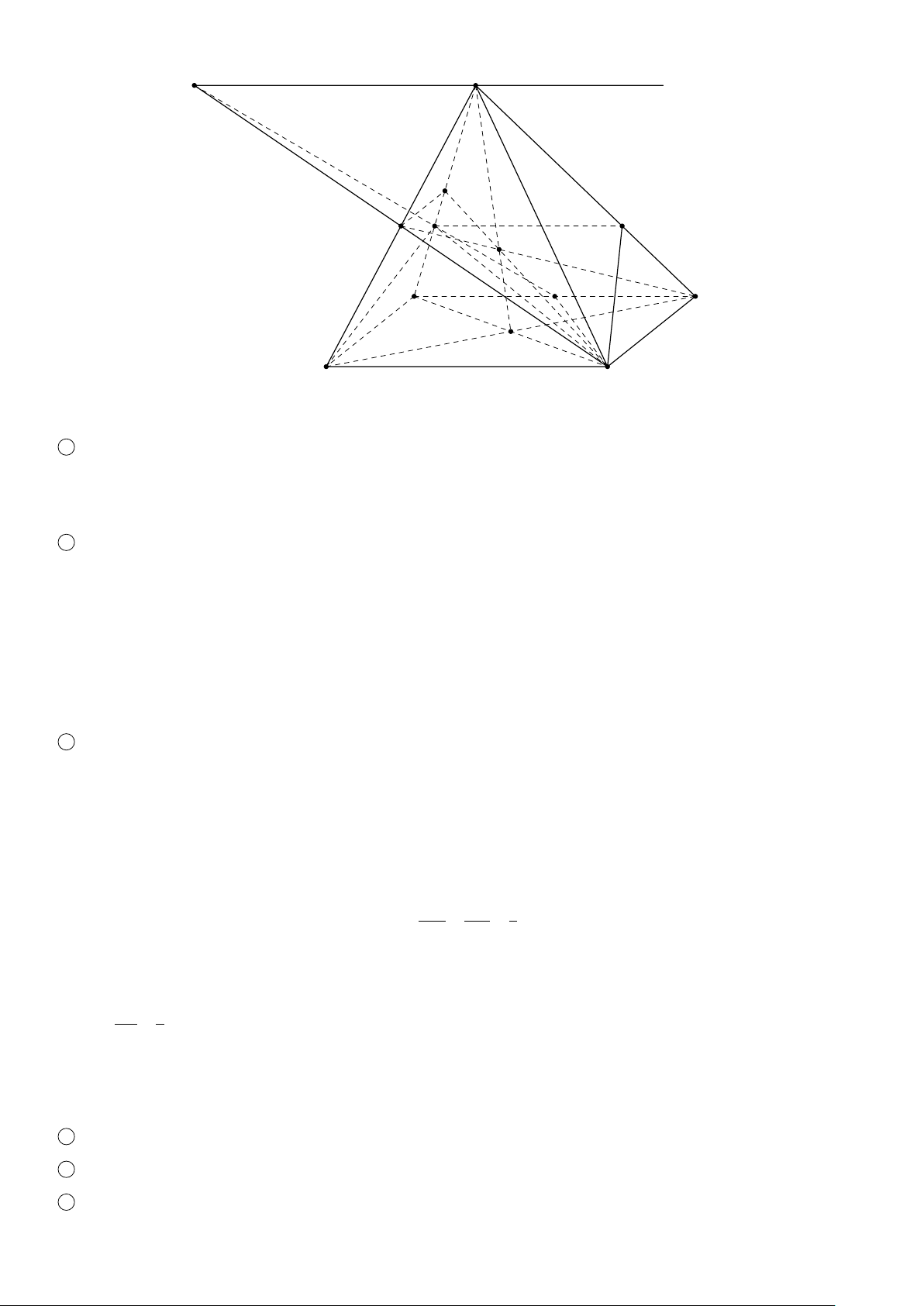
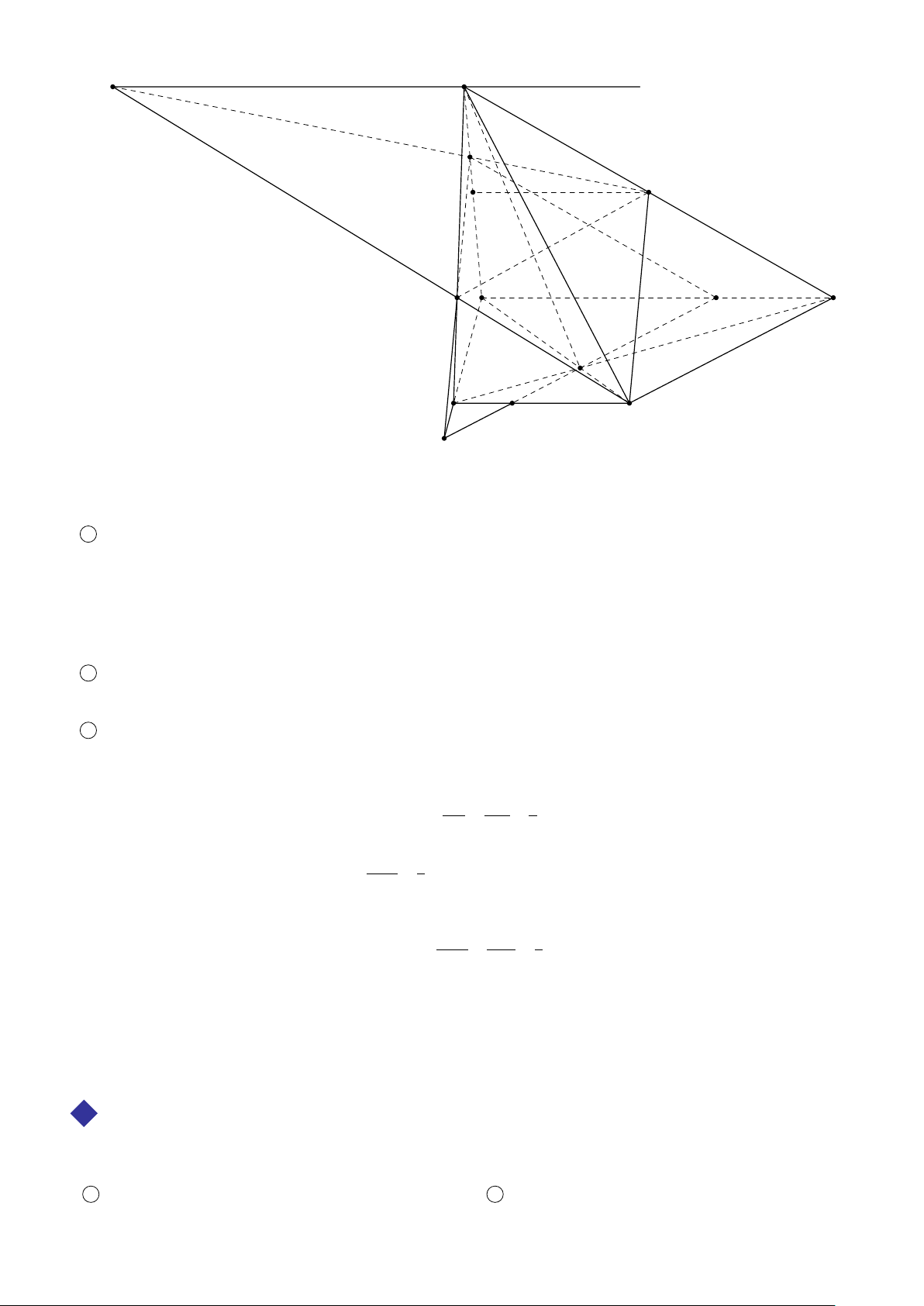
VÍ DỤ 2. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O hai điểm, M, N lần lượt là trung
điểm của SB, SD, điểm P thuộc SC và không là trung điểm của SC. 1
Tìm giao điểm I của SO với mặt phẳng (MNP). 2
Tìm giao điểm Q của S A với mặt phẳng (MNP). 3
Gọi F, G, H lần lượt là giao điểm của QM và AB, QP và AC, QN và AD. Chứng minh ba điểm F, G, H thẳng hàng. S 1
Trong mặt phẳng (SBD), gọi I = SO ∩ MN. ( I ∈ SO Ta có ⇒ I = SO ∩ (MNP). I ∈ MN ⊂ (MNP) P N 2
Trong mặt phẳng (S AC), gọi Q = S A ∩ IP. I (Q ∈ SA M Ta có ⇒ Q = S A ∩ (MNP). Q ∈ IP ⊂ (MNP) A D H 3
Xét hai mặt phẳng (ABCD) và (MNPQ). Ta có F G (F ∈ AB ⊂ (ABCD) O F ∈ QM ⊂ (MNPQ) Q ⇒ F ∈ (ABCD) ∩ (MNPQ). (1) B C (G ∈ AC ⊂ (ABCD) G ∈ QP ⊂ (MNPQ) ⇒ G ∈ (ABCD) ∩ (MNPQ). (2) (H ∈ AD ⊂ (ABCD) H ∈ QN ⊂ (MNPQ) ⇒ H ∈ (ABCD) ∩ (MNPQ). (3)
Từ (1), (2), (3) suy ra F, G, H cùng thuộc đường thẳng giao
tuyến của (ABCD) và (MNPQ).
Vậy ba điểm F, G, H thẳng hàng. 2 BÀI TẬP ÁP DỤNG
BÀI 1. Cho tứ diện ABCD có G là trọng tâm tam giác BCD. Gọi M, N, P lần lượt là trung điểm của AB, BC, CD.
1 Tìm giao tuyến của (AD N) và (ABP).
2 Gọi I = AG ∩ MP và J = CM ∩ AN. Chứng minh D, I, J thẳng hàng.
1. ĐẠI CƯƠNG VỀ ĐƯỜNG THẲNG VÀ MẶT PHẲNG 337 Lời giải. A
1 Ta có A ∈ (ADN) ∩ (ABP). (1) (G ∈ DN ∈ (ADN) Mặt khác G ∈ BP ∈ (ABP) M ⇒ G ∈ (ADN) ∩ (ABP). (2)
Từ (1) và (2) suy ra (ADN) ∩ (ABP) = AG. J I
2 Xét hai mặt phẳng (CD M) và (AD N). Ta có + D ∈ (CDM) ∩ (ADN). (3) B D ( I ∈ JD ⊂ (CDM) + I ∈ AG ⊂ (AND) N G P ⇒ I ∈ (CDM) ∩ (ADN). (4) ( J ∈ CM ⊂ (CDM) + C J ∈ AN ⊂ (AND) ⇒ J ∈ (CDM) ∩ (ADN). (5)
Từ (3), (4), (5) suy ra D, I, J thẳng hàng. ä
BÀI 2. Cho tứ diện ABCD có K là trung điểm của AB. Lấy I, J lần lượt thuộc AC, BD sao cho I A = 2IC và JB = 3JD.
1 Tìm giao điểm E của AD và (I JK ).
2 Tìm giao tuyến d của (I JK ) và (BCD).
3 Gọi O là giao điểm của d với CD. Chứng minh I, O, E thẳng hàng. OI OC OI 2 OC 3 4 Tính các tỉ số và . ĐS: = và = . OE OD OE 3 OD 2 Lời giải. 338
CHƯƠNG 7. ĐƯỜNG THẲNG VÀ MẶT PHẲNG TRONG KHÔNG GIAN A (E ∈ AD
1 Trong (ABD), gọi AD ∩ K J = E. Ta có E ∈ K J ⊂ (I JK) ⇒ E = AD ∩ (I JK). K
2 Trong (ABC), gọi K I ∩ BC = F. Ta có ( J ∈ (I JK) J + ⇒ J ∈ (I JK) ∩ (BCD). (1) B D J ∈ BD ⊂ (BCD) I (F ∈ K I ⊂ (I JK) O + ⇒ F ∈ (I JK) ∩ (BCD). (2) F ∈ BC ⊂ (BCD) E
Từ (1) và (2) suy ra (I JK) ∩ (BCD) = F J hay d ≡ F J. C
3 Trong (BCD), O = F J ∩ CD.
Xét hai mặt phẳng (I JK) và (ACD). Ta có ( I ∈ (I JK) + ⇒ I ∈ (I JK) ∩ (ACD). (3) I ∈ AC ⊂ (ACD) F (O ∈ F J ⊂ (I JK) + ⇒ O ∈ (I JK) ∩ (ACD). (4) O ∈ CD ⊂ (ACD) (E ∈ K J ⊂ (I JK) + ⇒ E ∈ (I JK) ∩ (ACD). (5) E ∈ AD ⊂ (ACD)
Từ (3), (4), (5) suy ra I, O, E thẳng hàng.
4 Áp dụng định lí Menelaus trong các tam giác sau.
Tam giác ABC có K, I, F thẳng hàng FC K B I A FC FC 1 ⇒ · · = 1 ⇔ · 1 · 2 = 1 ⇒ = FB K A IC FB FB 2
⇒ C là trung điểm của BF.
Tam giác BCD có F, O, J thẳng hàng OC JD FB OC 1 OC 3 ⇒ · · = 1 ⇔ · · 2 = 1 ⇔ = . OD JB FC OD 3 OD 2
Tam giác ABD có K, J, E thẳng hàng ED K A JB ED ED 1 ⇒ · · = 1 ⇔ · 1 · 3 = 1 ⇔ = . E A K B JD E A E A 3
Tam giác AIE có C, O, D thẳng hàng OI DE C A OI 1 OI 2 ⇒ · · = 1 ⇔ · · 3 = 1 ⇔ = . OE D A C I OE 2 OE 3 OI 2 OC 3 Vậy = và = . OE 3 OD 2 ä
BÀI 3. Cho hình chóp S.ABCD có đáy ABCD là hình thang, AD là đáy lớn và AD = 2BC. Gọi M, N lần lượt là trung
điểm của SB, SC và O = AC ∩ BD.
1 Tìm giao tuyến của (ABN) và (SCD).
ĐS: (ABN) ∩ (SCD) = EN với E = AB ∩ CD
2 Tìm giao điểm P của D N và (S AB). ĐS: P = DN ∩ SE K S K S 3
3 Gọi K = AN ∩ DM. Chứng minh S, K, O thẳng hàng. Tính tỉ số . ĐS: = K O K O 2 Lời giải.
1. ĐẠI CƯƠNG VỀ ĐƯỜNG THẲNG VÀ MẶT PHẲNG 339 S
1 Ta có N ∈ (ABN) ∩ (SCD).
Trong (ABCD), gọi AB ∩ CD = E ⇒ E ∈ (ABN) ∩ (SCD). Suy ra (ABN) ∩ (SCD) = EN.
2 Trong (SCD), gọi D N ∩ SE = P ⇒ P = DN ∩ (S AB). P N M K
3 Xét hai mặt phẳng (S AC) và (SBD) có + S ∈ (S AC) ∩ (SBD). (1) A D (K ∈ AN ⊂ (SAC) + K ∈ MD ⊂ (SBD) ⇒ K ∈ (S AC) ∩ (SBD). (2) O (O ∈ AC ⊂ (SAC) + B O ∈ BD ⊂ (SBD) C ⇒ O ∈ (S AC) ∩ (SBD). (3)
Từ (1), (2), (3) suy ra S, K, O thẳng hàng.
Vì AD ∥ BC nên 4OAD ∼ 4OCB OC BC 1 ⇒ = = . E O A AD 2
Áp dụng định lí Menenalus vào 4SOC có A, K, N thẳng hàng K S AO NC K S 2 K S 3 ⇒ · · = 1 ⇔ · · 1 = 1 ⇔ = . K O AC N S K O 3 K O 2 ä
BÀI 4. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Gọi M, N lần lượt là trung điểm của S A, SC.
1 Tìm giao tuyến của (BM N) với các mặt phẳng (S AB) và (SBC).
ĐS: (BMN) ∩ (S AB) = BM và (BM N) ∩ (SBC) = BN
2 Tìm I = SO ∩ (BMN) và K = SD ∩ (BMN).
ĐS: SO ∩ MN = I và SD ∩ BI = K
3 Tìm E = AD ∩ (BMN) và F = CD ∩ (BMN).
ĐS: MK ∩ AD = E và NK ∩ CD = F
4 Chứng minh rằng ba điểm B, E, F thẳng hàng.
ĐS: B, E, F là điểm chung của (ABCD) và (MNP) Lời giải. S
1 Ta có (BM N) ∩ (S AB) = BM và (BM N) ∩ (SBC) = BN. K
2 Trong (S AC), gọi SO ∩ MN = I M ⇒ I = SO ∩ (BMN). I
Trong (SBD), gọi SD ∩ BI = K N ⇒ K = SD ∩ (BMN). E A D
3 Trong (S AD), gọi MK ∩ AD = E ⇒ E = AD ∩ (BMN).
Trong (SCD), gọi NK ∩ CD = F O ⇒ F = CD ∩ (BMN). B C
4 Xét hai mặt phẳng (ABCD) và (BM N) có (B ∈ (ABCD) + ⇒ B ∈ (ABCD) ∩ (BMN). (1) B ∈ (BMN) (E ∈ AD ⊂ (ABCD) + F E ∈ (BMN) ⇒ E ∈ (ABCD) ∩ (BMN). (2) (F ∈ CD ⊂ (ABCD) + F ∈ (BMN) ⇒ F ∈ (ABCD) ∩ (BMN). (3)
Từ (1), (2), (3) suy ra B, E, F thẳng hàng. ä 340
CHƯƠNG 7. ĐƯỜNG THẲNG VÀ MẶT PHẲNG TRONG KHÔNG GIAN
BÀI 5. Cho hình chóp S.ABCD. Gọi I và J là hai điểm trên hai cạnh AD, SB.
1 Tìm giao tuyến của (SBI) và (S AC). Tìm giao điểm K của I J và (S AC).
2 Tìm giao tuyến của (SBD) và (S AC). Tìm giao điểm L của D J và (S AC).
3 Gọi O = AD ∩ BC, M = OJ ∩ SC. Chứng minh rằng A, K, L, M thẳng hàng. ĐS: A, K, L, M là điểm chung của (S AC) và (AO J) Lời giải. S
1 Ta có S ∈ (SBI) ∩ (S AC).
Trong (ABCD), gọi BI ∩ AC = E ⇒ E ∈ (SBI) ∩ (S AC) Suy ra (SBI) ∩ (S AC) = SE.
Trong (SBI), gọi I J ∩ SE = K J M ⇒ K = I J ∩ (S AC). K L
2 Ta có S ∈ (SBD) ∩ (S AC).
Trong (ABCD), gọi AC ∩ BD = F A O ⇒ F ∈ (SBD) ∩ (S AC). I D Suy ra (SBD) ∩ (S AC) = SF.
Trong (SBD), gọi D J ∩ SF = L E ⇒ L = D J ∩ (S AC). F
3 Xét (S AC) và (AO J) có C + A ∈ (S AC) ∩ (AOJ). (1) B (K ∈ SE ⊂ (SAC) + K ∈ I J ⊂ (AOJ) ⇒ K ∈ (S AC) ∩ (AOJ). (2) (L ∈ SF ⊂ (SAC) + L ∈ JD ⊂ (AOJ) ⇒ L ∈ (S AC) ∩ (AOJ). (3) (M ∈ SC ⊂ (SAC) + M ∈ OJ ⊂ (AOJ) ⇒ M ∈ (S AC) ∩ (AOJ). (4)
Từ (1), (2), (3), (4) suy ra A, K, L, M thẳng hàng. ä
BÀI 6. Cho tứ diện ABCD. Trên các cạnh AB, AC, BD lần lượt lấy ba điểm E, F, G sao cho AB = 3AE, AC = 2AF, DB = 4DG.
1 Tìm giao tuyến của hai mặt phẳng (EFG) và (BCD). HC HC 3
2 Tìm giao điểm H của đường thẳng CD với (EFG). Tính tỉ số . ĐS: = HD HD 2 I A I A 3
3 Tìm giao điểm I của đường thẳng AD với (EFG). Tính tỉ số . ĐS: = . I D I D 2
4 Chứng minh ba điểm F, H, I thẳng hàng. AK AK 2
5 Gọi J là trung điểm của BC, A J cắt EF tại K . Tính tỉ số . ĐS: = A J A J 5 Lời giải.
1. ĐẠI CƯƠNG VỀ ĐƯỜNG THẲNG VÀ MẶT PHẲNG 341 A
1 Trong (ABC), gọi EF ∩ BC = M ⇒ (EFG) ∩ (BCD) = MG.
2 Trong (BCD), gọi MG ∩ CD = H ⇒ H = CD ∩ (EFG). E
Áp dụng định lí Menenalus với các tam giác sau. K
Tam giác ABC có E, F, M thẳng hàng MC EB F A MC MC 1 ⇒ · · = 1 ⇔ · 2 · 1 = 1 ⇔ = . MB E A FC MB MB 2 F
Tam giác BCD có M, H, G thẳng hàng HC GD MB HC 1 HC 3 G ⇒ · · = 1 ⇔ · · 2 = 1 ⇔ = . B D HD GB MC HD 3 HD 2
3 Trong (ABD), goij AD ∩ EG = I ⇒ I = AD ∩ (EFG). H J
Tam giacs ABD cos E, G, I thẳng hàng I A GD EB I A 1 I A 3 ⇒ · · = 1 ⇔ · · 2 = 1 ⇔ = . C I D GB E A I D 3 I D 2
4 Xét hai mặt phẳng (ACD) và (EFG) có (F ∈ AC ⊂ (ACD) + ⇒ F ∈ (ACD) ∩ (EFG). (1) F ∈ (EFG) M (H ∈ CD ⊂ (ACD) + ⇒ H ∈ (ACD) ∩ (EFG). (2) H ∈ (EFG) ( I ∈ AD ⊂ (ACD) + ⇒ I ∈ (ACD) ∩ (EFG). (3) I ∈ (EFG)
Từ (1), (2), (3) suy ra F, H, I thẳng hàng.
5 Tam giác A JC có K , F, M thẳng hàng K A M J FC K A 3 K A 2 I · · = 1 ⇔ · · 1 = 1 ⇔ = K J MC F A K J 2 K J 3 AK 2 ⇒ = . A J 5 ä 3 BÀI TẬP RÈN LUYỆN
BÀI 7. Cho hình chóp S.ABCD có AD không song song với BC. Lấy M thuộc SB và O là giao điểm AC với BD.
1 Tìm giao điểm N của SC với (AMD).
2 Gọi I = AN ∩ DM. Chứng minh S, I, O thẳng hàng. Lời giải. S
1 Trong (ABCD), gọi AD ∩ BC = E.
Trong (SBC), gọi SC ∩ ME = N ⇒ N = SC ∩ (AMD).
2 Xét (S AC) và (SBD) có + S ∈ (S AC) ∩ (SBD). M N ( I ∈ AN ⊂ (SAC) + I I ∈ DM ⊂ (SBD) ⇒ I ∈ (S AC) ∩ (SBD). A E (O ∈ AC ⊂ (SAC) D + O ∈ BD ⊂ (SBD) ⇒ O ∈ (S AC) ∩ (SBD). O Suy ra S, I, O thẳng hàng. C B ä
BÀI 8. Cho hình chóp S.ABCD. Gọi E, F, H lần lượt là các điểm thuộc cạnh S A, SB, SC.
1 Tìm giao điểm K = SD ∩ (EF H). 342
CHƯƠNG 7. ĐƯỜNG THẲNG VÀ MẶT PHẲNG TRONG KHÔNG GIAN
2 Gọi O = AC ∩ BD và I = EH ∩ FK. Chứng minh S, I, O thẳng hàng.
3 Gọi M = AD ∩ BC và N = EK ∩ F H. Chứng minh S, M, N thẳng hàng.
4 Gọi P = AB ∩ CD và Q = EF ∩ HK. Chứng minh S, P, Q thẳng hàng. Lời giải. S
1 Trong (S AC), gọi I = EH ∩ SO.
Trong (SBD), gọi F I ∩ SD = K K N ⇒ K = SD ∩ (EF H).
2 Hiển nhiên S, I, O thẳng hàng. E I H
3 Chứng minh S, M, N là điểm chung của (S AD) và (SBC). A M D
4 Chứng minh S, P, Q là điểm chung của (S AB) F và (SCD). O Q C B P ä
BÀI 9. Cho tứ diện ABCD. Gọi M, N, P lần lượt là các điểm thuộc cạnh AB, AC, BD và M N ∩ BC = I, MP ∩ AD = J,
N J ∩ IP = K. Chứng minh C, D, K thẳng hàng. Lời giải.
Chứng minh C, D, K là điểm chung của hai mặt phẳng (ACD) A và (BCD). M B D P N K C I J ä
BÀI 10. Cho tứ giác ABCD có các cạnh đối đôi một không song song và điểm S ∉ (ABCD). Lấy điểm I thuộc cạnh
AD, lấy điểm J thuộc cạnh SB.
1 Tìm K = I J ∩ (S AC).
2 Tìm L = D J ∩ (S AC).
3 Gọi O = AD ∩ BC, M = OJ ∩ SC. Chứng minh rằng K, L, M thẳng hàng. Lời giải.
1. ĐẠI CƯƠNG VỀ ĐƯỜNG THẲNG VÀ MẶT PHẲNG 343 S
1 Gọi AC ∩ BI = E; I J ∩ SE = K ⇒ K = I J ∩ (S AC).
2 Gọi AC ∩ BD = F; D J ∩ SF = L ⇒ L = D J ∩ (S AC). J M
3 Chứng minh K , L, M là điểm chung của (S AC) K L và (AOJ). A O I D E F C B ä
BÀI 11. Cho hình chóp S.ABCD. Gọi M, N là 2 điểm lần lượt nằm trên 2 cạnh BC và SD.
1 Tìm giao điểm I của BN và (S AC).
2 Tìm giao điểm J của M N và (S AC).
3 Chứng minh I, J, C thẳng hàng.
4 Xác định thiết diện của mặt phẳng (BCN) với hình chóp. Lời giải. S
1 Gọi AC ∩ BD = O; BN ∩ SO = I ⇒ I = BN ∩ (S AC).
2 Gọi AC ∩ MD = E; MN ∩ SE = J N ⇒ J = MN ∩ (S AC). P
3 Chứng minh I, J, C là điểm chung của (S AC) và (BCN). A
4 Gọi C I ∩ S A = P. I D
Thiết diện của mặt phẳng (BCN) với hình chóp là tứ giác BCNP. J O B E M C ä
BÀI 12. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Gọi M, N lần lượt là trung điểm của S A,
SC. Gọi (P) là mặt phẳng qua M, N và B.
1 Tìm giao tuyến của (P) với các mặt phẳng (S AB), (SBC), (S AD), (SDC).
2 Tìm I = SO ∩ (P), K = SD ∩ (P), E = D A ∩ (P), F = DC ∩ (P).
3 Chứng minh rằng ba điểm E, B, F thẳng hàng.
ĐS: E, B, F là điểm chung của (P) và (ABCD) Lời giải. 344
CHƯƠNG 7. ĐƯỜNG THẲNG VÀ MẶT PHẲNG TRONG KHÔNG GIAN S
1 Ta có (P) ∩ (S AB) = BM; (P) ∩ (SBC) = BN;
(P) ∩ (S AD) = MK; (P) ∩ (SCD) = NK. K
2 I = SO ∩ MN; K = BI ∩ SD; E = D A ∩ MK; F = DC ∩ M N K . I N
3 Chứng minh E, B, F là điểm chung của (P) và (ABCD). E A D O B C F ä
BÀI 13. Cho hình chóp S.ABCD có đáy ABCD là tứ giác có các cặp cạnh đối không song song nhau. Gọi M, E là
trung điểm S A, AC và F ∈ CD sao cho CD = 3CF.
1 Tìm giao tuyến của (S AB) và (SCD). N S N S 1
2 Tìm giao điểm N của SD và (MEF). Tính tỉ số . ĐS: = N D N D 2
3 Gọi H = SE ∩ CM và K = MF ∩ NE. Chứng minh D, H, K thẳng hàng. H M HS K M K N K H H M 1 HS
4 Tính các tỉ số sau ; ; ; ; . ĐS: = ; = 2; HC HE K F K E K D HC 2 HE K M 1 K N K H 1 = ; = 1; = K F 2 K E K D 4 Lời giải. S 1 Gọi AB ∩ CD = I ⇒ (S AB) ∩ (SCD) = SI. N M 2 Gọi AD ∩ EF = J, SD ∩ JM = N ⇒ N = SD ∩ (MEF). K N S 1 H = N D 2 A J D
3 Chứng minh D, H, K là điểm chung của (MCD) và (SED). E F 4 Ta có C H M 1 HS = ; = 2; HC 2 HE B K M 1 K N = ; = 1; K F 2 K E K H 1 = . I K D 4 ä
{ DẠNG 1.5. Chứng minh ba đường thẳng đồng quy
Phương pháp: Tìm giao của hai đường thẳng, sau đó chứng minh đường thẳng thứ ba đi qua giao điểm đó.
1. ĐẠI CƯƠNG VỀ ĐƯỜNG THẲNG VÀ MẶT PHẲNG 345 1 VÍ DỤ
VÍ DỤ 1. Cho tứ diện ABCD. Lấy M, N, P lần lượt trên các cạnh AB, AC, BD sao cho M N cắt BC tại I, MP
cắt AD tại J. Chứng minh P I, N J, CD đồng quy. Lời giải. A (K ∈ P I, P I ⊂ (MI J)
Trong (BCD) : Gọi K = P I ∩ CD ⇒ K ∈ CD, CD ⊂ (ACD) M ⇒ K ∈ (M I J) ∩ (ACD) ⇒ K ∈ N J. N
Vậy P I, N J, CD đồng quy tại K. P B D K C I J ä 2 BÀI TẬP ÁP DỤNG
BÀI 1. Cho hình chóp S.ABCD có AB không song song CD. Gọi M là trung điểm SC và O là giao điểm của AC và BD. 1
Tìm giao điểm N của SD và (M AB). 2
Chứng minh ba đường thẳng SO, AM, BN đồng quy. Lời giải. S 1
Trong (S AC): Gọi K = AM ∩ SO. N (N ∈ BK, BK ⊂ (M AB)
Trong (SBD) : Gọi N = BK ∩ SD ⇒ N ∈ SD ⇒ N = SD ∩ (M AB). 2
Ta có K = AM ∩ SO ⇒ SO, AM đi qua K. M
Mà N = BK ∩ SD ⇒ BN cũng đi qua K.
Vậy ba đường thẳng SO, AM, BN đồng quy tại K. K A D O B C ä
BÀI 2. Cho hình chóp S.ABCD. Trên cạnh SC lấy một điểm E không trùng với S và C. 1
Tìm giao điểm F của đường thẳng SD và (ABE). 2
Giả sử AB không song song CD. Chứng minh ba đường thẳng AB, CD, EF đồng quy. Lời giải. 346
CHƯƠNG 7. ĐƯỜNG THẲNG VÀ MẶT PHẲNG TRONG KHÔNG GIAN S 1
Trong (ABCD): Gọi I = AC ∩ BD. F
Trong (S AC): Gọi J = AE ∩ SI. (F ∈ BJ, BJ ⊂ (ABE)
Trong (SBD) : Gọi F = BJ ∩ SD ⇒ F ∈ SD ⇒ F = SD ∩ (ABE). E 2 Ta có J
(E ∈ (ABE) ∩ (SCD) ⇒(ABE)∩(SCD)=EF. F ∈ (ABE) ∩ (SCD) A D (K ∈ AB, AB ⊂ (ABE)
Trong (ABCD) : Gọi K = AB ∩ CD ⇒ K ∈ CD, CD ⊂ (SCD) B I ⇒ K ∈ (ABE) ∩ (SCD) C ⇒ K ∈ EF. K
Vậy AB, CD, EF đồng quy tại K. ä
BÀI 3. Cho hình chóp S.ABCD có đáy ABCD là tứ giác lồi. Lấy điểm M trên cạnh SC. Gọi N là giao điểm của SB
và (ADM). Gọi O là giao điểm của AC và BD. Chứng minh SO, AM, DN đồng quy. Lời giải.
Ta có S ∈ (S AB) ∩ (SCD). (1) S ( I ∈ AB, AB ⊂ (SAB)
Trong (ABCD) : Gọi I = AB ∩ CD ⇒ I ∈ CD, CD ⊂ (SCD) ⇒ I ∈ (S AB) ∩ (SCD). (2)
Từ (1) và (2) ⇒ (S AB) ∩ (SCD) = SI.
Trong (SID): Gọi J = DM ∩ SI. J M (N ∈ AJ, AJ ⊂ (ADM)
Trong (S AI) : Gọi N = AJ ∩ SB ⇒ N N ∈ SB K ⇒ N = SB ∩ (ADM). A D (S ∈ (SAC) ∩ (SBD) Ta có : ⇒ (S AC) ∩ (SBD) = SO. O ∈ (S AC) ∩ (SBD) O B (K ∈ AM, AM ⊂ (SAC)
Trong (A JD) : Gọi K = AM ∩ DN ⇒ C K ∈ DN, DN ⊂ (SBD) ⇒ K ∈ (S AC) ∩ (SBD) I ⇒ K ∈ SO.
Vậy SO, AM, DN đồng quy tại K. ä
BÀI 4. Cho hình chóp S.ABCD có AB ∩ CD = E và AD ∩ BC = K. Gọi M, N, P lần lượt là trung điểm của S A, SB, SC. 1
Tìm giao tuyến của (S AC) và (SBD). 2
Tìm giao tuyến của (MNP) và (SBD). 3
Tìm giao điểm Q của SD và (MNP). 4
Gọi H = MN ∩ PQ. Chứng minh S, H, E thẳng hàng. 5
Chứng minh SK, QM, NP đồng quy. Lời giải.
1. ĐẠI CƯƠNG VỀ ĐƯỜNG THẲNG VÀ MẶT PHẲNG 347 S 1 Ta có S ∈ (S AC) ∩ (SBD). (1) ( I ∈ AC, AC ⊂ (SAC) Trong (ABCD) : I = AC ∩ BD ⇒ I ∈ BD, BD ⊂ (SBD) M F Q J ⇒ I ∈ (S AC) ∩ (SBD). (2) N
Từ (1) và (2) ⇒ (S AB) ∩ (SCD) = SI. P A H 2 Ta có N ∈ (MNP) ∩ (SBD). (3) K D ( I J ∈ MP, MP ⊂ (MNP)
Trong (S AC) : Gọi J = MP ∩ SI ⇒ J ∈ SI, SI ⊂ (SBD) B ⇒ J ∈ (MNP) ∩ (SBD). (4) C
Từ (3) và (4) ⇒ (MNP) ∩ (SBD) = N J. 3 E (Q ∈ N J, N J ⊂ (MNP)
Trong (SBD) : GọiQ = N J ∩ SD ⇒ Q ∈ SD ⇒ Q = SD ∩ (MNP). 4 (H ∈ MN, MN ⊂ (SAB) Trong (MNPQ) : H = MN ∩ PQ ⇒ H ∈ PQ, PQ ⊂ (SCD) ⇒ H ∈ (S AB) ∩ (SCD) ⇒ H ∈ SE. Suy ra S, H, E thẳng hàng. 5 Ta có S ∈ (S AD) ∩ (SBC). (5) (K ∈ AD, AD ⊂ (SAD) Trong (ABCD) : K = AD ∩ BC ⇒ K ∈ BC, BC ⊂ (SBC) ⇒ K ∈ (S AD) ∩ (SBC). (6)
Từ (5) và (6) ⇒ (S AD) ∩ (SBC) = SK. (F ∈ QM, QM ⊂ (SAD)
Trong (MNPQ) : Gọi F = QM ∩ P N ⇒ F ∈ P N, P N ⊂ (SBC) ⇒ F ∈ (S AD) ∩ (SBC) ⇒ F ∈ SK.
Suy ra SK, QM, NP đồng quy tại F. ä 3 BÀI TẬP RÈN LUYỆN
BÀI 5. Cho tứ diện S.ABC với I là trung điểm của S A, J là trung điểm của BC. Gọi M là điểm di động trên I J và
N là điểm di động trên SC. 1
Xác định giao điểm P của MC và (S AB). 2
Tìm giao tuyến của (SMP) và (ABC). 3
Tìm giao điểm E của MN và (ABC). 4
Gọi F = I N ∩ AC. Chứng minh đường thẳng EF luôn đi qua một điểm cố định khi M, N di động. 348
CHƯƠNG 7. ĐƯỜNG THẲNG VÀ MẶT PHẲNG TRONG KHÔNG GIAN
BÀI 6. Cho tứ diện ABCD. Gọi I, K lần lượt là trung điểm của AB, CD. Gọi J là một điểm trên đoạn AD sao cho AD = 3JD. 1
Tìm giao điểm F của I J và (BCD). EB EB 2
Tìm giao điểm E của (I JK) và đường thẳng BC. Tính tỉ số . ĐS: = 2 EC EC HC HC 3
Chứng minh ba đường thẳng AC, K J, IE đồng quy tại điểm H. Tính tỉ số . ĐS: = 2 H A H A 4
Chứng minh E J ∥ HF và đường thẳng IK đi qua trung điểm của đoạn HF. 5
Gọi O là trung điểm IK và G là trọng tâm của tam giác BCD. Chứng minh ba điểm A, O,G thẳng hàng. Tính O A O A tỉ số . ĐS: = 3 OG OG CHƯƠNG 8
ĐƯỜNG THẲNG VÀ MẶT PHẲNG
TRONG KHÔNG GIAN. QUAN HỆ SONG SONG BÀI 1.
HAI ĐƯỜNG THẲNG SONG SONG. A TÓM TẮT LÝ THUYẾT 1
Vị trí tương đối của hai đường thẳng phân biệt a
Cho hai đường thẳng phân biệt a, b. a a I b b b Định nghĩa 1.
• Hai đường thẳng gọi là đồng phẳng nếu chúng cùng nằm trong một mặt phẳng.
• Hai đường thẳng gọi là chéo nhau nếu chúng không đồng phẳng.
• Hai đường thẳng gọi là song song nếu chúng đồng phẳng và không có điểm chung. 2
Tính chất hai đường thẳng song song
Định lí 1. Trong không gian, qua một điểm không nằm trên đường thẳng cho trước, có một và chỉ một
đường thẳng song song với đường thẳng đã cho.
Định lí 2 (Định lí về giao tuyến của ba mặt phẳng). Nếu ba mặt phẳng phân biệt đôi một cắt nhau
theo ba giao tuyến phân biệt thì ba giao tuyến ấy hoặc đồng quy hoặc đôi một song song với nhau. c c β β α α b b a a γ γ
Hệ quả 1. Nếu hai mặt phẳng phân biệt lần lượt chứa hai đường thẳng song song thì giao tuyến của
chúng (nếu có) cũng song song với hai đường thẳng đó hoặc trùng với một trong hai đường thẳng đó. β β β α α α d d00 d d d0 d00 d00 d0 d0
Định lí 3. Hai đường thẳng phân biệt cùng song song với đường thẳng thứ ba thì song song với nhau. 349 350
CHƯƠNG 8. ĐƯỜNG THẲNG VÀ MẶT PHẲNG TRONG KHÔNG GIAN. QUAN HỆ SONG SONG. c β α b a γ B
DẠNG TOÁN VÀ BÀI TẬP
{ DẠNG 1.1. Chứng minh hai đường thẳng song song. Phương pháp giải:
Cách 1. Chứng minh hai đường thẳng a, b đồng phẳng, rồi dùng các định lí trong hình học phẳng, chẳng
hạn định lí đường trung bình, định lí đảo Thales, . . . để chứng minh a ∥ b.
Cách 2. Chứng minh hai đường thẳng đó cùng song song với đường thẳng thứ ba. Chẳng hạn, chứng minh ( c ∥ a ⇒a∥ b. c ∥ b
Cách 3. Áp dụng định lí về giao tuyến của ba mặt phẳng và hệ quả của nó. Chẳng hạn, chứng minh b ∥ c a ∥ b ∥ c
b ⊂ (α), c ⊂ (β) ⇒ a ≡ b
(α) ∩ (β) = a a ≡ c. 1 VÍ DỤ
VÍ DỤ 1. Cho tứ diện ABCD có I, J lần lượt là trọng tâm của tam giác ABC và ABD. Chứng minh rằng I J ∥ CD. Lời giải. ( I ∈ CE
Gọi E là trung điểm AB. Ta có
⇒ I J và CD đồng phẳng. A J ∈ DE
Vì I, J lần lượt là trọng tâm của tam giác ABC và ABD nên E I E J 1 E J = = . EC ED 3 I
Theo định lí đảo Thales suy ra I J ∥ CD (đpcm). B D C ä
VÍ DỤ 2. Cho tứ diện ABCD. Gọi M, N, P, Q, R, S lần lượt là trung điểm của AB, CD, BC, AD, AC, BD.
Chứng minh MP NQ là hình bình hành. Từ đó suy ra ba đoạn thẳng MN, PQ, RS cắt nhau tại trung điểm G của mỗi đoạn. Lời giải.
1. HAI ĐƯỜNG THẲNG SONG SONG. 351 MP ∥ AC
Vì MP là đường trung bình của 4ABC nên A 1 (1) M P = AC. 2 NQ ∥ AC
Vì NQ là đường trung bình của 4ACD nên 1 (2) N Q = AC. Q 2 M (MP ∥ NQ Từ (1) và (2) suy ra MP = NQ. R G
Do đó, MP NQ là hình bình hành. Suy ra MN, PQ cắt nhau tại trung điểm G của mỗi đoạn. B D
Chứng minh tương tự ta được PSQR là hình bình hành nên PQ, RS cắt S
nhau tại trung điểm G của mỗi đoạn.
Vậy MN, PQ, RS cắt nhau tại trung điểm G của mỗi đoạn. P N C ä
Nhận xét. Điểm G nói trên được gọi là trọng tâm của tứ diện.
Trọng tâm của tứ diện là điểm đồng qui của các đoạn nối trung điểm của các cạnh đối, nó cũng là trung điểm của các cạnh này. 2 BÀI TẬP ÁP DỤNG
BÀI 1. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Gọi M, N lần lượt là trung điểm của S A, SD. Chứng minh
1 M N ∥ AD và MN ∥ BC;
2 MO ∥ SC và NO ∥ SB. Lời giải. S 1 Xét tam giác S AD có
M là trung điểm của S A (giả thiết);
N là trung điểm của SD (giả thiết). M
Suy ra MN là đường trung bình của 4S AD. Do đó M N ∥ AD. N
(MN ∥ AD (chứng minh trên) Ta có ⇒ MN ∥
BC ∥ AD (ABCD là hình bình hành) BC. A B 2 Xét tam giác ASC có O D C
M là trung điểm của S A (giả thiết);
O là trung điểm của AC (O là tâm của hình bình hành ABCD).
Suy ra OM là đường trung bình của 4S AC. Do đó MO ∥ SC.
Tương tự, NO là đường trung bình của 4SDB nên NO ∥ SB. ä
BÀI 2. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Gọi M, N lần lượt là trung điểm của AB,
AD. Gọi I, J, G lần lượt là trọng tâm của các tam giác S AB, S AD và AOD. Chứng minh 1 I J ∥ MN;
2 I J ∥ BD và G J ∥ SO. Lời giải. 352
CHƯƠNG 8. ĐƯỜNG THẲNG VÀ MẶT PHẲNG TRONG KHÔNG GIAN. QUAN HỆ SONG SONG. S 1 Xét tam giác SMN có 2
S I = SM (I là trọng tâm của 4S AB); 3 2
S J = SN (J là trọng tâm của 4S AD). 3 I J
suy ra I J ∥ MN (định lý Ta-lét đảo). C B 2
Vì MN là đường trung bình của 4ABD nên MN ∥ BD. M
Mà I J ∥ MN (chứng minh trên) nên I J ∥ BD. O G Xét tam giác A SON có N D 1
NG = NO (G là trọng tâm của 4AOD); 3 1
N J = SN (J là trọng tâm của 4S AD). 3
suy ra G J ∥ SO (định lý Ta-lét đảo). ä 3 BÀI TẬP RÈN LUYỆN
BÀI 3. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O và I là một điểm trên cạnh SO.
1 Tìm giao điểm E và F của mặt phẳng (ICD) lần lượt với các đường S A, SB. Chứng minh EF ∥ AB;
2 Gọi K là giao điểm của DE và CF. Chứng minh SK ∥ BC. Lời giải. S K 1
Vì I ∈ SO mà SO ⊂ (SBD) nên I ∈ (SBD). Do đó
F = DI ∩ SB và E = CI ∩ S A. Ta có F (CD I) ∩ (ABCD) = CD; (S AB) ∩ (ABCD) = AB; E (CD I) ∩ (S AB) = EF. I
Mà AB ∥ CD (ABCD là hình bình hành) nên
EF ∥ AB ∥ CD (tính chất giao tuyến của ba mặt C B phẳng). O A D 2 Cách 1. Ta có
(K ∈ ED ⊂ (SAD) ⇒K là điểm chung thứ nhất của hai mặt phẳng (SAD) và (SBC). K ∈ FE ⊂ (SBC)
(S ∈ (SAD) ⇒S là điểm chung thứ hai của hai mặt phẳng (SAD) và (SBC). S ∈ (SBC)
Suy ra SK là giao tuyến của hai mặt phẳng (S AD) và (SBC). (S AD) ∩ (ABCD) = AD (SBC) ∩ ( ABCD) = BC Ta có ⇒ SK ∥ BC ∥ AD. (S AD) ∩ (SBC) = SK AD ∥ BC Vậy SK ∥ BC.
Cách 2. Trong 4SCD có EF ∥ CD nên theo định lý Ta-lét ta có K F EF = . (1) K C CD
Tương tự, trong 4S AB có EF ∥ AB nên SF EF EF = = (AB = CD). (2) SB AB CD
1. HAI ĐƯỜNG THẲNG SONG SONG. 353 Từ (1) và (2) suy ra K F SF K F SF = ⇔ = . K C SB FC FB Xét 4FSK và 4FBC có K F SF = (chứng minh trên); FC FB SF K = BFC (đối đỉnh).
Do đó 4FSK v 4FBC (cạnh - góc - cạnh) suy ra SK ∥ BC. ä
BÀI 4. Cho hình chóp S ABCD có đáy ABCD là hình thang đáy lớn AB. Gọi E, F lần lượt là trung điểm của S A và SB.
1 Chứng minh EF ∥ CD.
2 Tìm I = AF ∩ (SCD).
3 Chứng minh S I ∥ AB ∥ CD. Lời giải. S I F E A B D C 1
Ta có EF là đường trung bình của tam giác S AB nên EF ∥ AB
mà AB ∥ CD (hai đáy của hình thang) nên EF ∥ CD. 2
Hai mặt phẳng (S AB) và (SCD) có AB ∥ CD nên giao tuyến là đường thẳng Sx ∥ AB ∥ CD. Kéo dài AF cắt Sx tại I.
Ta thấy I là điểm chung của AF và (SCD). 3 Theo ý 2 . ä
{ DẠNG 1.2. Tìm giao tuyến của hai mặt phẳng chứa hai đường thẳng song song. Phương pháp giải:
A ∈ (α) ∩ (β)
a ⊂ (α), b ⊂ (β) ⇒ (α) ∩ (β) = Ax với Ax ∥ a ∥ b. a ∥ b 1 VÍ DỤ
VÍ DỤ 1. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Điểm M thuộc cạnh S A. Điểm E, F lần
lượt là trung điểm của AB và BC.
1 Tìm (S AB) ∩ (SCD).
2 Tìm (MBC) ∩ (S AD).
3 Tìm (MEF) ∩ (S AC). 4 Tìm AD ∩ (MEF). 5 Tìm SD ∩ (MEF).
6 Tìm thiết diện của hình chóp cắt bởi (MEF). 354
CHƯƠNG 8. ĐƯỜNG THẲNG VÀ MẶT PHẲNG TRONG KHÔNG GIAN. QUAN HỆ SONG SONG. Lời giải. S S ∈ (S AB) ∩ (SCD) 1 AB ⊂ (S AB), CD ⊂ (SCD) N AB ∥ CD
⇒ (S AB) ∩ (SCD) = Sx với Sx ∥ AB ∥ CD. y M M x ∈ (MBC) ∩ (S AD) 2 BC ⊂ (MBC), AD ⊂ (S AD) K BC ∥ AD z
⇒ (MBC) ∩ (S AD) = M y với M y ∥ BC ∥ AD. M ∈ (MEF) ∩ (S AC) A I D 3 EF ⊂ (MEF), AC ⊂ (S AC) EF ∥ AC
⇒ (MEF) ∩ (S AC) = M z với M z ∥ EF ∥ AC. E 4
Trong (ABCD), gọi I = EF ∩ AD.
Mà EF ⊂ (MEF) nên AD ∩ (MEF) = I. B F C 5
Trong (S AD), gọi N = SD ∩ I M.
Mà I M ⊂ (MEF) nên SD ∩ (MEF) = N. 6
Thiết diện của hình chóp cắt bởi (MEF) là ngũ giác M N K F E. ä
VÍ DỤ 2. Cho hình chóp S.ABCD. Mặt đáy là hình thang có cạnh đáy lớn AD, AB cắt CD tại điểm K . Gọi M
là điểm nằm trên cạnh SD. 1
Tìm d = (S AD) ∩ (SBC) và N = K M ∩ (SBC). 2
Chứng minh rằng AM, BN và d đồng qui. Lời giải. S E d S ∈ (S AD) ∩ (SBC) 1
• AD ⊂ (S AD), BC ⊂ (SBC) M AD ∥ BC
⇒ (S AD) ∩ (SBC) = d với S ∈ d, d ∥ AD ∥ BC.
• Trong (SCD), gọi N = K M ∩ SC.
Mà SC ⊂ (SBC) nên N = K M ∩ (SBC). (SBC) ∩ (S AD) = d N 2 (SBC) ∩ (M AB) = BN A D (M AB) ∩ (S AD) = AM
Theo định lí về giao tuyến của 3 mặt phẳng, suy ra AM, BN
và d hoặc đồng qui hoặc đôi một song song.
Mà AM, d cắt nhau nên AM, BN và d phải đồng qui. B C K ä 2 BÀI TẬP ÁP DỤNG
BÀI 1. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N lần lượt là trung điểm của S A, SB. Gọi
P là một điểm trên cạnh BC. Tìm giao tuyến của 1 (SBC) và (S AD); 2 (S AB) và (SCD); 3 (M N P) và (ABCD). Lời giải.
1. HAI ĐƯỜNG THẲNG SONG SONG. 355 y 1 Ta có (SBC) ∩ (ABCD) = BC; S x (S AD) ∩ (ABCD) = AD;
AD ∥ BC (ABCD là hình bình hành). N
Mà S là điểm chung của 2 mặt phẳng (SBC) và (S AD)
nên giao tuyến của 2 mặt phẳng (SBC) và (S AD) là M
đường thẳng Sx ∥ BC ∥ AD. P B C O D A Q 2
Giao tuyến của hai mặt phẳng (S AB) và (SCD) là đường thẳng S y ∥ AB ∥ CD. 3
Vì MN ∥ AB (MN là đường trung bình của 4S AB) nên qua P kẻ PQ ∥ AB (Q ∈ AD). Khi đó giao tuyến của hai
mặt phẳng (MNP) và (ABCD) là đường thẳng PQ. ä
BÀI 2. Cho tứ diện S ABC. Gọi E và F lần lượt là trung điểm của các cạnh SB và AB, G là một điểm trên cạnh AC.
Tìm giao tuyến của các cặp mặt phẳng sau 1 (S AC) và (EFC); 2 (S AC) và (EFG). Lời giải. S x 1 Ta có H (S AC) ∩ (S AB) = S A; (EFC) ∩ (S AB) = EF;
S A ∥ EF (EF là đường trung bình của 4S AB). E
Do đó giao tuyến của 2 mặt phẳng (S AC) và (EFC) sẽ song song với S A và EF.
Mà C là điểm chung của 2 mặt phẳng (S AC) và (EFC) nên G
giao tuyến của chúng là đường thẳng Cx ∥ S A ∥ EF. A C 2
Vì EF ∥ S A (EF là đường trung bình của 4S AB) nên qua G F
kẻ GH ∥ S A (H ∈ SC). Khi đó giao tuyến của hai mặt phẳng
(S AC) và (EFG) là đường thẳng GH. B ä
BÀI 3. Cho hình chóp S.ABCD có O là tâm của hình bình hành ABCD, điểm M thuộc cạnh S A sao cho SM = 2M A, N là trung điểm của AD. 1
Tìm giao tuyến của mặt phẳng (S AD) và (MBC). 2
Tìm giao điểm I của SB và (CMN), giao điểm J của S A và (ICD). SE 3
Chứng minh ba đường thẳng ID, JC, SO đồng quy tại E. Tính tỉ số . SO Lời giải. 356
CHƯƠNG 8. ĐƯỜNG THẲNG VÀ MẶT PHẲNG TRONG KHÔNG GIAN. QUAN HỆ SONG SONG. F S t J M P I E N A D O B C M ∈ (MBC) ∩ (S AD) 1 Vì BC ⊂ (MBC) và AD ⊂ (S AD) BC ∥ AD
nên (S AD) ∩ (MBC) = MP ∥ BC ∥ AD (với P ∈ SD). S ∈ (S AD) ∩ (SBC) 2 Vì AD ⊂ (S AD) và BC ⊂ (SBC) AD ∥ BC
nên (S AD) ∩ (SBC) = St ∥ AD ∥ BC.
Gọi F = MN ∩ St; I = CF ∩ SB. ( I ∈ SB Vì nên I = SB ∩ (CMN). I ∈ CF ⊂ (CMN)
Qua I kẻ đường thẳng song song với AB cắt S A tại J. ( J ∈ SA Vì nên J = S A ∩ (ICD).
J ∈ J I ⊂ (ICD)(vì I J ∥ CD ⇒ (I JCD) ≡ (ICD)) 3
Xét 3 mặt phẳng (S AC), (SBD) và (CD J I), ta có SO = (S AC) ∩ (SBD) I D = (SBD) ∩ (CD J I) JC = (S AC) ∩ (CD J I).
Do đó ba đường thẳng ID, JC, SO đồng quy. Gọi điểm đồng quy là E.
Trong mặt phẳng (SF AD), áp dụng định lý Thales (để ý rằng AN ∥ SF) ta có M A AN 1 = = . MS SF 2
Suy ra SF = AD = BC và SFBC là hình bình hành.
I = SB ∩ CF nên I là trung điểm của SB.
4SBD có D I và SO là trung tuyến nên E là trọng tâm của 4SBD. SE 2 Vậy = . SO 3 ä
BÀI 4. Cho hình chóp S.ABCD có đáy ABCD là hình thang với AD là đáy lớn và AD = 2BC. Gọi M, N, P lần lượt
thuộc các đoạn S A, AD, BC sao cho M A = 2MS, N A = 2ND, PC = 2PB. 1
Tìm giao tuyến của các cặp mặt phẳng sau: (S AD) và (SBC), (S AC) và (SBD). 2
Xác định giao điểm Q của SB với (MNP). 3
Gọi K là trung điểm của SD. Chứng minh CK = (MQK) ∩ (SCD). Lời giải.
1. HAI ĐƯỜNG THẲNG SONG SONG. 357 F ≡ F0 S t M K K 0 A N D Q O B P C E S ∈ (S AD) ∩ (SBC) 1 Vì AD ⊂ (S AD) và BC ⊂ (SBC) AD ∥ BC
nên (S AD) ∩ (SBC) = St ∥ AD ∥ BC. (O ∈ AC ⊂ (SAC) Gọi O = AC ∩ BD ⇒ suy ra SO = (S AC) ∩ (SBD). O ∈ BD ⊂ (SBD) (Q ∈ SB 2
Gọi E = NP ∩ AB và Q = EM ∩ SB. Vì nên Q = SB ∩ (MNP). Q ∈ ME ⊂ (MNP) 3
Gọi F = MK ∩ St và F0 = QC ∩ St. Dựa vào các vị trí các điểm Q, C, M và K của giả thiết cho, dễ thấy F và F0
cùng nằm về một phía so với mặt phẳng (S AB).
Trong mặt phẳng (SF0BC), áp dụng định lý Thales (để ý rằng SF0 ∥ BC) ta có QS BC 1 = = . (1) QB SF0 2 MK 0 1
Gọi K0 là trung điểm của S A. suy ra = . MS 2
Trong mặt phẳng (SF AD), áp dụng định lý Thales (để ý rằng SF ∥ K K0) ta có MK 0 K K 0 1 = = . (2) MS SF 2
Từ (1), (2) và AD = 2BC suy ra SF = SF0. Do đó F ≡ F0, suy ra bốn điểm Q, C, M và K đồng phẳng. Vậy CK = (MQK) ∩ (SCD). ä 3 BÀI TẬP RÈN LUYỆN
BÀI 5. Cho tứ diện ABCD. Gọi G, J lần lượt là trọng tâm tam giác BCD và ACD.
1 Chứng minh G J ∥ AB.
2 Tìm (ABD) ∩ (G JD). Lời giải. 358
CHƯƠNG 8. ĐƯỜNG THẲNG VÀ MẶT PHẲNG TRONG KHÔNG GIAN. QUAN HỆ SONG SONG. A x J B D G M C 1 Gọi M là trung điểm CD. MG M J 1 Xét tam giác ABM có = = MB M A 3 Suy ra G J ∥ AB. 2
Hai mặt phẳng (ABD) và (G JD) có điểm D chung và G J ∥ AB nên giao tuyến là đường thẳng Dx ∥ G J ∥ AB. ä
BÀI 6. Cho tứ diện ABCD. Gọi I, J lần lượt là trọng tâm 4ABC, 4ABD và E, F lần lượt là trung điểm BC, AC.
1 Chứng minh I J ∥ CD. 2 Tìm (DEF) ∩ (ABD). Lời giải. A x F J I M B D E C 1 Gọi M là trung điểm BD. A I A J 1 Tam giác AEM có = = nên I J ∥ ME. AE AM 3
Mà ME ∥ CD (đường trung bình) Suy ra I J ∥ CD. 2
Hai mặt phẳng (DEF) và (ABD) có điểm chung D và EF ∥ AB nên giao tuyến là đường thẳng Dx ∥ AB ∥ EF. ä
BÀI 7. Cho hình chóp S ABCD có đáy ABCD là hình bình hành. Gọi M là trung điểm của SC và N là trọng tâm tam giác ABC.
1 Tìm I = SD ∩ (AMN).
2 Chứng minh N I ∥ SB.
3 Tìm (AM N) ∩ (S AD). Lời giải.
1. HAI ĐƯỜNG THẲNG SONG SONG. 359 S I M E A D O N B C 1
Gọi O là giao điểm AC và BD, E là giao điểm SO và AM.
Khi đó NE và SD cắt nhau tại I.
Ta thấy I ∈ SD và I ∈ NE ⊂ (AMN) nên I = SD ∩ (AMN). OE ON 1 2 Tam giác SOB có = = nên NE ∥ SB. OS OB 3 Suy ra N I ∥ SB. 3
Hai mặt phẳng (AMN) và (S AD) có hai điểm chung A, I nên (AMN) ∩ (S AD) = AI. ä
BÀI 8. Cho hình chóp S ABCD có đáy ABCD là hình thang (AB ∥ CD) với CD = 2AB. Gọi O là giao điểm của AC và
BD, K là trung điểm SC, G là trọng tâm tam giác SCD.
1 Chứng minh OG ∥ BK. 2 Tìm (ACG) ∩ (SBC). Lời giải. x S K G A B O D C 1 Ta có 4OCD v 4OAB do COD = AOB và ODC = OB A. OD OC CD Suy ra = = = 2. OB O A AB 2 Suy ra OD = DB. 3 DG DO 2 Tam giác DBK có = = nên OG ∥ BK. DK DB 3 2
Hai mặt phẳng (SBC) và (ACG) có điểm C chung và OG ∥ BK nên giao tuyến là đường thẳng Cx ∥ OG ∥ BK. ä
BÀI 9. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành và O là giao điểm hai đường chéo AC và BD. Lấy
điểm E trên cạnh SC sao cho EC = 2ES. 360
CHƯƠNG 8. ĐƯỜNG THẲNG VÀ MẶT PHẲNG TRONG KHÔNG GIAN. QUAN HỆ SONG SONG. 1
Tìm giao tuyến của hai mặt phẳng (S AB) và (SCD) 2
Tìm giao điểm M của đường thẳng AE và mặt phẳng (SBD). Chứng minh M là trung điểm của đoạn thẳng SO. Lời giải. S S ∈ (S AB) ∩ (SCD) F 1 Vì AB ⊂ (S AB) và CD ⊂ (SCD) t AB ∥ CD
nên (S AB) ∩ (SCD) = St ∥ AB ∥ CD. E 2 Gọi M = AE ∩ SO. ( M M ∈ AE I Vì nên M = AE ∩ (SBD). M ∈ SO ∩ (SBD) E I 1
Gọi I là trung điểm SC, suy ra = . ES 2 Gọi F A
= OI ∩ AE. Trong mặt phẳng (S AC), áp dụng D
định lý Thales (để ý rằng OI ∥ S A) O F I E I 1 = = . B C S A ES 2 S A Suy ra F I = OI =
, từ đó dẫn đến SFO A là hình bình hành. Vậy M là trung điểm của SO. 2 ä
BÀI 10. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành, gọi M, N, P lần lượt là trung điểm của SD, CD, BC. 1
Tìm giao tuyến của các cặp mặt phẳng sau: (S AC) và (SBC), (AMN) và (SBC). 2
Tìm giao điểm I của (P MN) và AC, K của (P MN) và S A. 3
Gọi F là trung điểm của P M, chứng minh ba điểm K, F, I thẳng hàng. Lời giải. S K M t F A D N I B P C E 1
Dễ thấy SC = (S AC) ∩ (SBC). Gọi E = BC ∩ AN E ∈ (SBC) ∩ (AMN) Ta có SC ⊂ (SBC) và MN ⊂ (AMN) SC ∥ MN
suy ra (SBC) ∩ (AMN) = Et ∥ SC ∥ MN.
2. ĐƯỜNG THẲNG SONG SONG VỚI MẶT PHẲNG 361 ( I ∈ AC 2 Gọi I = AC ∩ P N ⇒ ⇒ I = AC ∩ (P MN). I ∈ P N ⊂ (P MN)
Gọi K là giao điểm của S A với đường thẳng đi qua I và song song với SC. (K ∈ SA Vì nên K = S A ∩ (P MN).
K ∈ IK ⊂ (P MN) (vì MN ∥ SC) 3
Theo cách dựng ta có IK ∥ MN. (1)
ABCD là hình bình hành nên AC và BD cắt nhau tại trung điểm mỗi đường. Mà P N là đường trung bình của
4CBD nên AC cũng cắt P N tại I là trung điểm của P N.
Suy ra IF là đường trung bình của 4P MN ⇒ IF ∥ MN. (2)
(1) và (2) suy ra K, F, I thẳng hàng. ä BÀI 2.
ĐƯỜNG THẲNG SONG SONG VỚI MẶT PHẲNG A TÓM TẮT LÝ THUYẾT
1 Vị trí tương đối của hai đường thẳng phân biệt Cho đường thẳng d và mặt phẳng (P). Có ba trường hợp xảy ra:
Đường thẳng d và (P) có 2 điểm chung phân biệt ⇒ d ⊂ (P).
Đường thẳng d và (P) có 1 điểm chung duy nhất ⇒ d ∩ (P) = A.
Đường thẳng d và (P) không có điểm chung nào ⇒ d ∥ (P).
Định nghĩa 1. Đường thẳng d và mặt phẳng (P) gọi là song song với nhau nếu chúng không có điểm chung. 2 Các định lý
Định lí 1. Nếu đường thẳng d không nằm trong mặt phẳng (α) và d song song với đường thẳng d0 nằm
trong (α) thì d song song với (α).
Định lí 2. Cho đường thẳng a song song với mặt phẳng (α). Nếu mặt phẳng (β) chứa a và cắt (α) theo giao
tuyến b thì b song song với (α).
Hệ quả 1. Nếu hai mặt phẳng phân biệt cắt nhau và cùng song song với một đương thẳng thì giao tuyến
của chúng (nếu có) cũng song song với đường thẳng đó.
Định lí 3. Cho hai đường thẳng chéo nhau. Có duy nhất một mặt phẳng chứa đường thẳng này và song
song với đường thẳng kia. B
DẠNG TOÁN VÀ BÀI TẬP
{ DẠNG 2.1. Chứng minh dường thẳng a song song với mặt phẳng (P) a ∥ b
Phương pháp: Chứng minh
b ⊂ (P) ⇒ a ∥ (P). a ∉ (P) 1 VÍ DỤ
VÍ DỤ 1. Cho tứ diện ABCD. Gọi M vàN lần lượt là trọng tâm của các tam giác ACD và BCD. Chứng minh
rằng MN song song với các mặt phẳng (ABC) và (ABD). Lời giải. 362
CHƯƠNG 8. ĐƯỜNG THẲNG VÀ MẶT PHẲNG TRONG KHÔNG GIAN. QUAN HỆ SONG SONG.
Gọi P, Q lần lượt là trung điểm của BC và CD. A Q M Q N 1 Khi đó, ta có = = ⇒ MN ∥ AB. M A NB 3 M N 6⊂ (ABC) Vì
AB ⊂ (ABC) nên MN ∥ (ABC). M N ∥ AB M N 6⊂ (ABD) Tương tự, ta có
AB ⊂ (ABD) nên MN ∥ (ABD). M N ∥ AB M B P D N Q C ä
VÍ DỤ 2. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N lần lượt là trung điểm của các cạnh AB và CD.
1 Chứng minh M N song song với các mặt phẳng (SBC) và (S AD).
2 Gọi E là trung điểm của S A. Chứng minh SB và SC đều song song với mặt phẳng (M N E). Lời giải. S
1 Từ giả thiết, ta suy ra M N ∥ BC và MN ∥ AD. M N 6⊂ (SBC) Vì
BC ⊂ (SBC) nên MN ∥ (SBC). M N ∥ BC M N 6⊂ (S AD) E Tương tự, ta có
AD ⊂ (S AD) nên MN ∥ (S AD). M N ∥ AD AE AM 1
2 Từ giả thiết, ta có = = ⇒ ME ∥ SB. AS AB 2 SB 6⊂ (MNE) A D Vì
ME ⊂ (MNE) nên SB ∥ (MNE). M N ME ∥ SB O
Tương tự, gọi O là tâm của hình bình hành. AO AE 1 B C Khi đó = = ⇒ EO ∥ SC. AC AS 2 SC 6⊂ (MNE) Vì
EO ⊂ (MNE) nên SC ∥ (MNE). EO ∥ SC ä
{ DẠNG 2.2. Tìm giao tuyến của hai mặt phẳng
Phương pháp: Áp dụng một trong hai cách sau a ∥ (P) 1 Cách 1: a ⊂ (Q)
⇒ (P) ∩ (Q) = Mx ∥ a. M ∈ (P) ∩ (Q) a ∥ (P) 2 Cách 2: a ∥ (Q)
⇒ (P) ∩ (Q) = Mx ∥ a. M ∈ (P) ∩ (Q)
2. ĐƯỜNG THẲNG SONG SONG VỚI MẶT PHẲNG 363
VÍ DỤ 1. Cho tứ diện ABCD có G là trọng tâm 4ABC, M ∈ CD với MC = 2MD.
1 Chứng minh MG ∥ (ABD). 2 Tìm (ABD) ∩ (BGM). 3 Tìm (ABD) ∩ (AGM). Lời giải. A CM CG
1 Gọi N là trung điểm của AB. Trong tam giác CD N, ta có = = CD CN 2 y
⇒ GM ∥ ND. Vì ND ⊂ (ABD), GM 6⊂ (ABD) nên GM ∥ (ABD). 3 N (GM ∥ (ABD) 2 Vì
⇒ (ABD) ∩ (BGM) = Bx ∥ GM ∥ ND. B ∈ (ABD) ∩ (BGM) G (GM ∥ (ABD) 3 Vì
⇒ (ABD) ∩ (BGM) = A y ∥ GM ∥ ND. A ∈ (ABD) ∩ (AGM) B D M x C ä
{ DẠNG 2.3. Tìm thiết diện song song với một đường thẳng
Phương pháp: Để tìm thiết diện của mặt phẳng song song với mặt phẳng (α) đi qua một điểm và song song
với hai đường thẳng chéo nhau hoặc (α) chứa một đường thẳng và song song với một đường thẳng sử dụng
M ∈ (α) ∩ (β) tích chất sau: d ∥ (α)
⇒ (α) ∩ (β) = a ∥ d , (vớiM ∈ a). d ⊂ (β)
VÍ DỤ 1. Cho tứ diện ABCD. Gọi M, I lần lượt là trung điểm của BC, AC. Mặt phẳng (P) đi qua điểm M,
song song với BI và SC. Xác định trên hình vẽ các giao điểm của (P) với các cạnh AC, S A, SB. Từ đó suy ra
thiết diện của (P) cắt hình chóp. Lời giải. ((P) ∥ SC Vì
⇒ (P) ∩ (SBC) = MN ∥ SC, N ∈ SB (1) S M ∈ (P) ∩ (SBC) ((P) ∥ BI Tương tự,
⇒ (P) ∩ (ABC) = MH ∥ BI, H ∈ AC (2) M ∈ (P) ∩ (ABC) K ((P) ∥ (SC) Mặt khác,
⇒ (P) ∩ (S AC) = HK ∥ SC, K ∈ S A (3) Từ (1), (2) N ∈ (P)cap(S AC)
và (3) ta có thiết diện của (P) với tư diện ABCD là tứ giác MNK H. N I H A C M B ä 1 BÀI TẬP ÁP DỤNG
BÀI 550. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Gọi M, N lần lượt là trung điểm S A, SD. Chứng minh rằng: 1 BC ∥ (S AD). 2 AD ∥ (SBC). 3 M N ∥ (ABCD). 4 M N ∥ (SBC). 5 MO ∥ (SCD). 6 NO ∥ (SBC). 364
CHƯƠNG 8. ĐƯỜNG THẲNG VÀ MẶT PHẲNG TRONG KHÔNG GIAN. QUAN HỆ SONG SONG. Lời giải. S M N A D O B C 1 BC ∥ (S AD) BC ∥ AD Ta có
AD ⊂ (S AD) ⇒ BC ∥ (S AD). BC 6⊂ (S AD) AD ∥ BC 2 Ta có BC ⊂ (SBC) ⇒ AD ∥ (SBC). AD 6⊂ (SBC) M N ∥ AD SM SN 1 3 Ta có = = ⇒ MN ∥ AD. Khi đó
AD ⊂ (ABCD) ⇒ MN ∥ (ABCD). S A SD 2 M N 6⊂ (ABCD) M N ∥ BC SM SN 4 Ta có =
⇒ MN ∥ AD, vì AD ∥ BC nên MN ∥ BC Khi đó BC ⊂ (SBC) ⇒ MN ∥ (SBC). S A SD M N 6⊂ (SBC) MO ∥ SC AM AO 1 5 Ta có = = ⇒ MO ∥ SC. Vì SC ⊂ (SCD) ⇒ MO ∥ (SCD). AS AC 2 MO 6⊂ (SCD) NO ∥ SB D N DO 1 6 Ta có = = ⇒ NO ∥ SB. Vì SB ⊂ (SBC) ⇒ NO ∥ (SBC). DS DC 2 NO 6⊂ (SBC) ä
BÀI 551. Cho hình chóp S.ABCD có dáy ABCD là hình chữ nhật. Gọi G là trọng tâm tam giác S AD và E là điểm
trên cạnh DC sao cho DC = 3DE, I là trung điểm AD.
1 Chứng minh OI ∥ (S AB) và OI ∥ (SCD).
2 Tìm giao điểm P của I E và (SBC). Chứng minh GE ∥ (SBC). Lời giải.
2. ĐƯỜNG THẲNG SONG SONG VỚI MẶT PHẲNG 365 S OI ∥ AB 1 Ta có
AB ⊂ (S AB) ⇒ OI ∥ (S AB). OI 6⊂ (S AB) OI ∥ CD Tương tự, CD ⊂ (SCD) ⇒ OI ∥ (SCD). OI 6⊂ (SCD) G D I 1 1 DE 2 Vì = 6= =
nên IE không song song với AC. Trong hình D A 2 3 DC
chữ nhật ABCD, gọi P = IE ∩ BC ⇒ P = IE ∩ (SBC). G0
Gọi K là trung điểm của BC, G0 là trọng tâm tam giác SBC. A D SG0 SG G0G 2 I Khi đó = = =
,suy ra G0G ∥ K I ∥ CE và ⇒ G0G = SK S I K I 3 E 2 2
K I = CD = CE. Do dó tứ giác G0GEC là hình bình hành, suy O 3 3
ra CG0 ∥ CE ⇒ CG ∥ (SBC). B K C ä
BÀI 552. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N lần lượt là trung điểm AB và CD.
1 Chứng minh M N ∥ (SBC) và MN ∥ (S AD).
2 Gọi P là trung điểm cạnh S A. Chứng minh SB ∥ (MNP) và SC ∥ (MNP).
3 Gọi G, I là trọng tâm của tam giác ABC và SBC. Chứng minh G I ∥ (MNP). Lời giải. S
1 Từ giả thiết, ta có M N ∥ AD ∥ BC. Vì MN 6⊂ (SBC), MN 6⊂ (S AD)
nên MN ∥ (SBC) và MN ∥ (S AD). AP AM 1 2 Ta có = =
⇒ SB ∥ P M ⇒ SB ∥ (MNP). P AS AB 2 AO AP 1 Tương tự, = =
⇒ PO ∥ SC vì OP ⊂ (MNP) nên SC ∥ AC AS 2 (M N P). 3 A D I M N O G B C ä
BÀI 553. Cho hình chóp S.ABCD có đáy là hình thang đáy lớn AB, với AB = 2CD. Gọi O là giao điểm của AC và
BD, I là trung điểm của S A, G là trọng tâm của tam giác SBC và E là một điểm trên cạnh SD sao cho 3SE = 2SD. Chứng minh: 1 D I ∥ (SBC). 2 GO ∥ (SCD). 3 SB ∥ (ACE). Lời giải. 366
CHƯƠNG 8. ĐƯỜNG THẲNG VÀ MẶT PHẲNG TRONG KHÔNG GIAN. QUAN HỆ SONG SONG. S 1
1 Gọi N là trung điểm SB, khi đó I N ∥ AB và I N = AB. Suy ra 2
I N ∥ CD, I N = DC suy ra tứ giác I NCD là hình bình hành, do
đó ID ∥ NC. Vậy ID ∥ (SBC). 2 GO ∥ (SCD) I N
Gọi P là trung điểm của SC, khi đó GO ∥ PD, suy ra GO ∥ (SCD).
3 Ta có EO ∥ SB, suy ra SB ∥ (ACE). P G E A B M O D C ä
BÀI 554. Cho hình chóp S.ABCD có đáy là hình bình hành tâm O. Gọi M, N là trung điểm của các cạnh AB, AD. S I S J 2
Gọi I, J thuộc SM, SN sao cho = = . Chứng minh SM SN 3 1 M N ∥ (SBD). 2 I J ∥ (SBD). 3 SC ∥ (I JO). Lời giải. 1
Ta có M, N là trung điểm của các cạnh AB, AD. S
Suy ra MN ∥ BD, mà BD ⊂ (SBD). Nên MN ∥ (SBD). S I S J 2 2 Ta có = =
⇒ I J ∥ MN. Hay I J ∥ BD. SM SN 3
Mà BD ⊂ (SBD). Nên I J ∥ (SBD). 3
Trong mặt phẳng (ABCD), gọi H là giao điểm của MN và K J AC. I
Trong mặt phẳng (SMN) gọi K là giao điểm của I J và SH. HO 1 A D
Dễ thấy H là trung điểm của AO, suy ra = . N HC 3 HK M I 1 H M
Lại có I J ∥ MN ⇒ IK ∥ MH ⇒ = = . O SH SM 3 HK HO 1 Do đó = = ⇒ KO ∥ SC. B HS HC 3 C
Mà KO ⊂ (I JO) ⇒ SC ∥ (I JO). ä
BÀI 555. Cho tứ diện ABCD, G là trọng tâm của tam giác ABD và I là điểm trên cạnh BC sao cho BI = 2IC. Chứng minh IG ∥ (ACD). Lời giải.
Gọi H là trung điểm của BD. Trong mặt phẳng (BCD), gọi K là A giao điểm của H I và CD. BH IC K D 1 K D Theo định lý Menelaus có · · = 1 ⇔ 1 · · = 1 ⇔ HD BI K C 2 K C K K D = 2. K C
Suy ra C là trung điểm của K D, suy ra BC là trung tuyến của G 4BDK. B C I
Mà BI = 2IC, suy ra I là trọng tâm của 4BDK. H I 1 HG 1 Suy ra
= . Lại có G là trọng tâm của 4ABD ⇒ = . H HK 3 HK 3
Do đó, G I ∥ AK, mà AK ⊂ (ACD) ⇒ IG ∥ (ACD). D ä
BÀI 556. Cho tứ diện ABCD. Gọi G và P lần lượt là trọng tâm của tam giác ACD và ABC. Chứng minh rằng GP ∥ (BCD), GP ∥ (ABD).
2. ĐƯỜNG THẲNG SONG SONG VỚI MẶT PHẲNG 367 Lời giải.
Gọi K, H lần lượt là trung điểm của BC và CD. Suy ra K H ∥ BD (1). A
Ta có G, P lần lượt là trọng tâm của 4ACD,4ABC. AP 2 AG 2 Suy ra = , = ⇒ PG ∥ HK (2). AK 3 AH 3
Từ (1) và (2), suy ra GP ∥ BD.
Mà BD ⊂ (BCD), BD ⊂ (ABD), suy ra GP ∥ (BCD),GP ∥ (ABD). P G B D K H C ä
BÀI 557. Cho hình chóp S.ABCD có đáy là hình bình hành, O là giao điểm của AC và BD, M là trung điểm của S A. 1 Chứng minh OM ∥ (SCD). 2
Gọi (α) là mặt phẳng đi qua M, đồng thời song song với SC và AD. Tìm thiết diện của mặt phẳng (α) với hình chóp S.ABCD. Lời giải. 1
Ta có M, O là trung điểm của S A và AC, suy ra MO ∥ SC. S
Mà SC ⊂ (SCD) ⇒ OM ∥ (SCD). 2
Vì MO ∥ SC ⇒ O ∈ (α).
O ∈ (α) ∩ (ABCD) M Ta có AD ∥ (α)
⇒ (α) ∩ (ABCD) = PQ. N AD ⊂ (ABCD)
Với PQ ∥ AD,O ∈ PQ,Q ∈ AB, P ∈ CD. P ∈ (α) ∩ (SCD) Lại có SC ∥ (α)
⇒ (α) ∩ (SCD) = P N, với P N ∥ SC. A D SC ⊂ (SCD) Q P
Có (α) ∩ (S AD) = MN,(α) ∩ (S AB) = MQ. O B
Nhận thấy P,Q là trung điểm của CD và AB. Suy ra N là trung điểm C của SD.
Suy ra MN ∥ PQ. Vậy thiết diện là hình thang MNPQ. ä
BÀI 558. Cho hình chóp S.ABCD có đáy ABCD là hình thang đáy lớn AB. Gọi M là trung điểm của CD, (α) là mặt
phẳng qua M, đồng thời song song với S A và BC. Tìm thiết điện của (α) với hình chóp S.ABCD. Thiết diện là hình gì? Lời giải.
M ∈ (α) ∩ (ABCD) Ta có BC ∥ (α)
⇒ (α) ∩ (ABCD) = MK, S BC ⊂ (ABCD) với MK ∥ BC, K ∈ AB.
K ∈ (α) ∩ (S AB) Có S A ∥ (α)
⇒ (α) ∩ (S AB) = K H, với K H ∥ S A. H S A ⊂ (S AB) H ∈ (α) ∩ (SBC) A B K Lại có BC ∥ (α)
⇒ (α) ∩ (SBC) = H I, với H I ∥ BC. BC ⊂ (SBC) I
Do đó, α ∩ (SCD) = I M, mà MK, HI đều song song với BC.
Vậy thiết diện của hình chóp là hình thang MK H I. D M C ä
BÀI 559. Cho hình chóp S.ABCD. Gọi M, N thuộc cạnh AB, CD. Gọi (α) là mặt phẳng qua MN và song song với S A. 1
Tìm thiết diện của (α) với hình chóp. 368
CHƯƠNG 8. ĐƯỜNG THẲNG VÀ MẶT PHẲNG TRONG KHÔNG GIAN. QUAN HỆ SONG SONG. 2
Tìm điều kiện của MN để thiết diện là hình thang. Lời giải. 1
M ∈ (α) ∩ (S AB) Ta có S A ∥ (α)
⇒ (α) ∩ (S AB) = MP, với MP ∥ S A. S S A ⊂ (S AB)
Trong mặt phẳng (ABCD), gọi R = MN ∩ AC.
R ∈ (α) ∩ (S AC) Ta có S A ∥ (α)
⇒ (α) ∩ (S AC) = RQ, với RQ ∥ S A. S A ⊂ (S AC)
Ta có (α) ∩ (SCD) = QN. Vậy thiết diện là tứ giác MNQP. " Q MP ∥ QN (1) A P 2
Ta có MNQP là hình thang ⇒ . D M N ∥ PQ (2) (S A ∥ MP Xét (1) ta có ⇒ S A ∥ QN. N MP ∥ QN M R (S A ∥ QN Do đó ⇒ S A ∥ (SCD) (vô lý). C Q N ⊂ (SCD) B BC = (ABCD) ∩ (SBC) Xét (2) ta có M N ⊂ (ABCD) ⇒ MN ∥ BC. PQ ⊂ (SBC) PQ = (α) ∩ (SBC)
Ngược lại, nếu MN ∥ BC thì M N ⊂ (α) ⇒ MN ∥ PQ. BC ⊂ (SBC)
Vậy để thiết diện là hình thang thì MN ∥ PQ. ä
BÀI 560. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M là trung điểm của cạnh SC. (P) là mặt
phẳng qua AM và song song với BD. 1
Xác định thiết diện của hình chóp khi cắt bởi mặt phẳng (P). 2
Gọi E, F lần lượt là giao điểm của (P) với các cạnh SB, SD. Tìm tỉ số diện tích của 4SME với 4SBC và tỉ số
diện tích của 4SMF với 4SCD. 3
Gọi K là giao điểm của ME và CB, J là giao của MF và CD. Chứng minh K, A, J nằm trên đường thẳng song EF
song với EF và tìm tỉ số . K J Lời giải. 1
Trong mặt phẳng (ABCD) gọi S AC ∩ BD = O,
trong mặt phẳng (S AC), gọi AM ∩ SO = I. I ∈ (P) ∩ (SBD) Ta có BD ∥ (P) BD ⊂ (SBD) M F
⇒ (P) ∩ (SBD) = EF, với I ∈ J EF, E ∈ SB, F ∈ SD. E I
Ta có (P) ∩ (S AB) = AE,(P) ∩ A (SBC) = EM,(P) ∩ (SCD) = MF. D
Vậy thiết diện là tứ giác AEMF. O K B C S I 2 SE SF EF 2 2
Trong 4S AC, có I là trọng tâm của tam giác ⇒ = ⇒ = = = (1). SO 3 SB SD BD 3 S 2 1 1 S 2 1 1 Do đó 4AME = · = , 4SMF = · = . S4SBC 3 2 3 S4SCD 3 2 3
2. ĐƯỜNG THẲNG SONG SONG VỚI MẶT PHẲNG 369 ((MEF) ∩ (ABCD) = AK 3 Ta có ⇒ K, A, J thẳng hàng. (MEF) ∩ (ABCD) = AJ MS EB K C 1 K C K C
Theo định lý Menelaus, xét 4SBC ta có · · = 1 ⇔ 1 · · = 1 ⇔ = 2. MC ES K B 2 K B K B
Hay B là trung điểm của K C. Tương tự, ta có D là trung điểm của C J. BD ∥ K J
Do đó, BD là đường trung bình của 4KCJ ⇒ 1 . BD = · K J (2) 2
Mà BD ∥ EF. Vậy A, K, J nằm trên đường song song với EF. EF 2 1 1 Từ (1) và (2), suy ra = · = . K J 3 2 3 ä
BÀI 561. Cho tứ diện ABCD. Gọi M và N là hai điểm lần lượt nằm trên cạnh BC và AD. Xác định thiết diện của
tứ diện cắt bởi mặt phẳng (α) qua MN và song song với CD. Xác định vị trí của hai điểm M, N để thiết diện là hình bình hành. Lời giải. M = (α) ∩ (BCD) Ta có CD ∥ (α)
⇒ (α) ∩ (BCD) = M I, với M I ∥ CD. A CD ⊂ (BCD) N = (α) ∩ (ACD) N CD ∥ (α)
⇒ (α) ∩ (ACD) = NK, với NK ∥ CD. K CD ⊂ (ACD)
Ta có (α) ∩ (ABD) = N I,(α) ∩ (ABC) = MK.
Vậy thiết diện là hình thang M I NK, (vì M I ∥ NK). B D I M I BM ( M I ∥ CD = CD CB Lại có ⇒ . M K N ∥ CD K N AN = CD AD C BM AN
Để thiết diện M I NK là hình bình hành khi và chỉ khi M I = NK ⇔ = . CD AD BM AN
Vậy M, N lần lượt là hai điểm nằm trên BC và AD và = . CD AD ä
BÀI 562. Cho tứ diện ABCD. Gọi I, J lần lượt là trung điểm của AB và CD, M là một điểm trên đoạn I J. Gọi (P) là
mặt phẳng qua M và song song với AB và CD. 1
Tìm giao tuyến của mặt phẳng (P) và (ICD). 2
Xác định thiết diện của tứ diện với mặt phẳng (P). Thiết diện là hình gì? Lời giải. 1
Gọi ∆1 = (P) ∩ (ICD), ta có A (M ∈ (P) ⇒ M ∈ ∆1. M ∈ I J, I J ⊂ (ICD) (P) ∥ CD CD ⊂ (ICD) ⇒ ∆1 ∥ CD. I (P) ∩ (ICD) = ∆1 P
Vậy ∆1 là đường thẳng qua M và song song với CD. Gọi E = ∆ F
1 ∩ I C, F = ∆1 ∩ T D, ta được (P) ∩ (I CD) = EF . 2
Gọi ∆2 = (P) ∩ (ABD), ta có Q M (F ∈ (P) B D ⇒ F ∈ ∆2. G F ∈ ID, ID ⊂ (ABD) E (P) ∥ AB J AB ⊂ (ABD) ⇒ ∆ H 2 ∥ AB. (P) ∩ (ABD) = ∆2 C
Vậy ∆2 là đường thẳng qua F và song song với AB.
Gọi G = ∆2 ∩ BD, P = ∆2 ∩ AD, ta được (P) ∩ (ICD) = GP.
Gọi ∆3 = (P) ∩ (ABC), ta có (E ∈ (P) ⇒ E ∈ ∆3. E ∈ IC, IC ⊂ (ABC) 370
CHƯƠNG 8. ĐƯỜNG THẲNG VÀ MẶT PHẲNG TRONG KHÔNG GIAN. QUAN HỆ SONG SONG. Ta có (P) ∥ AB AB ⊂ (ABC) ⇒ ∆3 ∥ AB. (P) ∩ (ABC) = ∆3
Vậy ∆3 là đường thẳng qua E và song song với AB.
Gọi H = ∆3 ∩ BC,Q = ∆3 ∩ AC, ta được (P) ∩ (ABC) = HQ.
Giao tuyến của (P) với các mặt phẳng (BCD), (ABD), (ACD), (ABC) lần lượt là GH, GP, PQ, QH. Do đó thiết
diện của tứ diện với mặt phẳng (P) là tứ giác HGPQ. Ta có (P) ∥ CD CD ⊂ (ACD) ⇒ PQ ∥ CD (P) ∩ (ACD) = PQ và (P) ∥ CD CD ⊂ (BCD) ⇒ HG ∥ CD. (P) ∩ (BCD) = HG
(HG ∥ PQ (cùng song song vớiCD) Ta có
⇒ tứ giác HGPQ là hình bình hành.
HQ ∥ PG (cùng song song với AB) ä
BÀI 563. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Gọi K và J lần lượt là trọng tâm của các tam giác ABC và SBC. 1 Chứng minh K J ∥ (S AB). 2
Gọi (P) là mặt phẳng chứa K J và song song với AD. Tìm thiết diện của hình chóp cắt bởi mặt phẳng (P). Lời giải. S 1
Gọi H là trung điểm BC, theo tính chất trọng tâm ta HK H J 1 có = =
⇒ K J ∥ S A (Định lý Ta-lét đảo). Ta có H A HS 3 K J ∥ S A
S A ⊂ (S AB) ⇒ K J ∥ (S AB). K J 6⊂ (S AB) 2
Gọi ∆1 = (P) ∩ (ABCD), ta có
(K ∈ K J, K J ⊂ (P) ⇒K ∈∆1. K ∈ (ABCD) (P) ∥ AD J M N AD ⊂ (ABCD) ⇒ ∆1 ∥ AD. A D (P) ∩ (ABCD) = ∆1 O
Vậy ∆1 là đường thẳng qua K và song song với AD. K
Gọi E = ∆1 ∩ AB, F = ∆1 ∩ CD, ta được E F (P) ∩ (ABCD) = EF. C B H
Gọi ∆2 = (P) ∩ (SBC), ta có
( J ∈ K J, K J ⊂ (P) ⇒K ∈∆2. J ∈ (SBC) Và (P) ∥ AD ∥ BC BC ⊂ (ABCD) ⇒ ∆2 ∥ BC. (P) ∩ (ABCD) = ∆2
Vậy ∆2 là đường thẳng qua J và song song với BC.
Gọi M = ∆2 ∩ SB, N = ∆1 ∩ SD, ta được (P) ∩ (SBC) = MN.
Ta có giao tuyến của (P) với các mặt phẳng (ABCD), (SCD), (SBC), (S AB) lần lượt là EF, F N, N M, NE, do đó
thiết diện của hình chóp cắt bởi mặt phẳng (P) là tứ giác MNFE. ä
2. ĐƯỜNG THẲNG SONG SONG VỚI MẶT PHẲNG 371
BÀI 564. Cho tứ diện ABCD. Gọi G1, G2 lần lượt là trọng tâm của các tam giác ACD và BCD. Chứng minh rằng
G1G2 ∥ (ABC) và G1G2 ∥ (ABD). Lời giải. A Xét tam giác ABM ta có MG2 1 = (G2 là trọng tâm 4BCD). MB 3 MG1 1 = (G1 là trọng tâm 4ACD). M A 3 MG2 MG1 G1 Suy ra =
⇒ G1G2 ∥ AB (Định lý Ta-lét đảo). MB M A B D G1G2 ∥ AB Ta có AB ⊂ (ABC) ⇒ G1G2 ∥ (ABC). G2 M G1G2 6⊂ (ABC) G1G2 ∥ AB C Ta có AB ⊂ (ABD) ⇒ G1G2 ∥ (ABD). G1G2 6⊂ (ABD) ä
BÀI 565. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi G là trọng tâm của 4S AB, I là trung điểm
AB, lấy điểm M trong đoạn AD sao cho AD = 3AM. 1
Tìm giao tuyến của hai mặt phẳng (S AD) và (SBC). 2
Đường thẳng qua M và song song với AB cắt CI tại N. Chứng minh NG ∥ (SCD). 3 Chứng minh MG ∥ (SCD). Lời giải. ∆ S 1
Gọi ∆ = (S AD) ∩ (SBC), ta có S ∈ ∆. AD ∥ BC A D ⊂ (S AD) Ta có ⇒ ∆ ∥ AD. BC ⊂ (SBC) (S AD) ∩ (SBC) = ∆ E
Vậy ∆ là đường thẳng qua S và song song với AD. G I N AM 1 2
Hình thang AICD có MN ∥ AI ∥ CD nên = = M IC AD 3 A D (Định lí Ta-lét). IG 1
4S AB có G là trọng tâm nên = . I I S 3 I N IG 1 N 4ISC có = =
⇒ NG ∥ SC (Định lý Ta-lét đảo). IC I S 3 B C NG ∥ SC Ta có SC ⊂ (SCD) ⇒ NG ∥ (SCD). NG 6⊂ (SCD) I M AM 1 3
Gọi E là giao điểm của I M và CD. Vì AI ∥ DE nên ta có = = (Định lý Ta-lét). ME MD 2 IG I M 1 Xét 4ASE có = = ⇒ GM ∥ SE. GS ME 2 MG ∥ SE Ta có SE ⊂ (SCD) ⇒ MG ∥ (SCD). MG 6⊂ (SCD) ä
BÀI 566. Cho hình chóp S.ABCD có đáy ABCD là hình thang với đáy lớn AD và AD = 2BC. Gọi O là giao điểm của
AC và BD, G là trọng tâm của tam giác SCD. 1 Chứng minh OG ∥ (SBC). 2
Cho M là trung điểm của SD. Chứng minh CM ∥ (S AB). 3
Gọi I là điểm trên cạnh SC sao cho 2SC = 3SI. Chứng minh S A ∥ (BDI). 372
CHƯƠNG 8. ĐƯỜNG THẲNG VÀ MẶT PHẲNG TRONG KHÔNG GIAN. QUAN HỆ SONG SONG. Lời giải. S NG 1 1
Gọi N là trung điểm SC, vì G là trọng tâm 4SCD nên = . GD 2 BO CO BC 1 Ta có BC ∥ AD ⇒ = = = (Định lí Ta-lét). OD AO AD 2 NG BO 1 4BND có = =
⇒ OG ∥ BN (Định lí Ta-lét đảo). E GD OD 2 M OG ∥ BN N Ta có BN ⊂ (SBC) ⇒ OG ∥ (SBC). OG 6⊂ (SBC) I G A 2
Gọi E là trung điểm của S A, theo tính chất đường trung bình D 1 ta có ME ∥ AD và ME = AD. 2 1 O M E = BC = AD 2
⇒ Tứ giác MEBC là hình bình hành. B C ME ∥ BC (∥ AD) Suy ra CM ∥ BE. CM ∥ BE Ta có
BE ⊂ (S AB) ⇒ CM ∥ (S AB). CM 6⊂ (S AB) 3
Ta có 2SC = 3SI ⇔ 2SI + 2IC = 3SI ⇔ SI = 2IC. C I CO 1 Xét 4S AC có = =
⇒ OI ∥ S A (Định lí Ta-lét đảo). I S O A 2 S A ∥ BI Ta có BI ⊂ (BDI) ⇒ AB ∥ (BDI). AB 6⊂ (BD I) ä
BÀI 567. Cho hình chóp S.ABCD, đáy ABCD là hình bình hành. Gọi M, N, P lần lượt là trung điểm của các cạnh AB, AD, SB. 1 Chứng minh BD ∥ (MNP). 2
Tìm giao điểm của (MNP) với BC. 3
Tìm giao tuyến của hai mặt phẳng (MNP) và (SBD). 4
Tìm thiết diện của hình chóp với (MNP). Lời giải. S K Q P N A D M H C B 1 1
4ABD có MN là đường trung bình nên MN ∥ BD và MN = BD. 2 BD ∥ MN Ta có
M N ⊂ (MNP) ⇒ BD ∥ (MNP). BD 6⊂ (MNP)
2. ĐƯỜNG THẲNG SONG SONG VỚI MẶT PHẲNG 373 2
Trong (ABCD), dựng H = MN ∩ BC, ta có (H ∈ BC ⇒ H = (MNP) ∩ BC. H ∈ MN, MN ⊂ (MNP) (P ∈ (SBD) 3
Gọi ∆ = (MNP) ∩ (SBD), ta có ⇒ P ∈ ∆. P ∈ (MNP) Ta có M N ∥ BD
M N ⊂ (MNP), (BD) ⊂ (SBD) ⇒ ∆ ∥ MN. (M N P) ∩ (SBD) = ∆
Vậy ∆ là đường thẳng qua P và song song với MN.
Gọi Q = ∆ ∩ SD, ta được (MNP) ∩ (SBD) = PQ. 4
Trong (SBC), dựng K = HP∩SC. Giao tuyến của (MNP) với các mặt phẳng (ABCD), (S AB), (SBC), (SCD), (SD A)
lần lượt là MN, P M, PK, KQ, QN. Vậy thiết diện của hình chóp với (MNP) là ngũ giác P MNQK. ä
BÀI 568. Cho tứ diện ABCD. Gọi M là điểm thuộc BC sao cho MC = 2MB. Gọi N, P lần lượt trung điểm của BD và AD. 1 Chứng minh NP ∥ (ABC). Q A 2
Tìm giao điểm Q của AC với (MNP) và tính
. Suy ra thiết diện của hình chóp bị cắt bởi (MNP). QC 3
Chứng minh MG ∥ (ABD), với G là trọng tâm của tam giác ACD. Lời giải. 1
4ABD có NP là đường trung bình nên NP ∥ AB và NP = A 1 AB. 2 NP ∥ AB Ta có AB ⊂ (ABC) ⇒ NP ∥ (ABC). N P 6⊂ (ABC) Q P 2
Gọi ∆ = (MNP) ∩ (ABC), ta có (M ∈ (SBD) ⇒ M ∈ ∆. G M ∈ BC, BC ⊂ (ABC) NP ∥ (ABC) B D N N P ⊂ (MNP) ⇒ ∆ ∥ AB. M (M N P) ∩ (ABC) = ∆
Vậy ∆ là đường thẳng qua M và song song với AB.
Trong (ABC) dựng Q = ∆ ∩ AC, ta có (Q ∈ AC C ⇒ Q = AC ∩ (MNP). Q ∈ ∆, ∆ ⊂ (MNP) MB 1
Ta có MC = 2MB ⇔ MC + MB = 3MB ⇔ BC = 3MB ⇔ = . BC 3 Q A BM 1 Xét 4ABC có QM ∥ AB ⇒ = = . QC BC 3
Ta có giao tuyến của (MNP) với các mặt phẳng (ABC), (ACD), (ABD), (BCD) lần lượt là QM, QP, P N, MN. Vậy
thiết diện cùa hình chóp bị cắt bởi (MNP) là tứ giác MNPQ. PG 1 3
Vì G là trọng tâm 4ACD nên = . PC 3 PG BM 1 Xét 4BCP có = =
⇒ MG ∥ BP (Định lí Ta-lét đảo). PC BC 3 MG ∥ BP Ta có BP ⊂ (ABD) ⇒ MG ∥ (ABD). MG 6⊂ (ABD) ä 374
CHƯƠNG 8. ĐƯỜNG THẲNG VÀ MẶT PHẲNG TRONG KHÔNG GIAN. QUAN HỆ SONG SONG.
BÀI 569. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. 1
Tìm giao tuyến của (S AC) và (SBD); (S AB) và (SCD). 2
Một mặt phẳng qua BC và song song với AD cắt S A tại E, (E 6= S, E 6= A), cắt SD tại F, (F 6= S, F 6= D). Tứ giác BEFC là hình gì? 3
Gọi M thuộc đoạn AD sao cho AD = 3AM và G là trọng tâm tam giác S AB, I là trung điểm AB. Đường thẳng
qua M và song song AB cắt CI tại N. Chứng minh NG ∥ (SCD) và MG ∥ (SCD). Lời giải. S ∆ H F E G A M D O I N B C 1 Ta có S ∈ (S AC) ∩ (SBD)
Trong (ABCD), dựng O = AC ∩ BD, ta có
(O ∈ AC, AC ⊂ (SAC) ⇒O ∈(SAC)∩(SBD). O ∈ BD, BD ⊂ (SBD) Vậy (S AC) ∩ (SBD) = SO.
Gọi ∆ = (S AB) ∩ (SCD), ta có S ∈ ∆ AB ∥ CD AB ⊂ (S AB) Ta có ⇒ ∆ ∥ AB. CD ⊂ (SCD) (S AB) ∩ (SCD) = ∆
Vậy ∆ là đường thẳng qua S và song song với AB. 2 Ta có BC ∥ AD BC ⊂ (BCF E) ⇒ EF ∥ AD ∥ BC. AD ⊂ (S AD) (BCF E) ∩ (S AD) = EF
Vậy tứ giác BCFE là hình thang. AM I N 1 3
Xét hình thang AICD có MN ∥ AI ⇒ = = (Định lí Ta-lét). AD IC 3 IG 1
Vì G là trọng tâm tam giác S AB nên = . I S 3 Xét 4ISC ta có IG I N 1 = =
⇒ GN ∥ SC (Định lí Ta-lét đảo). I S IC 3
2. ĐƯỜNG THẲNG SONG SONG VỚI MẶT PHẲNG 375 Ta có G N ∥ SC SC ⊂ (SCD) ⇒ NG ∥ (SCD). NG 6⊂ (SCD) I M AM 1
Trong (ABCD), dựng H = I M ∩ CD. Vì AI ∥ DM nên ta có = = (Định lí Ta-lét). I H AD 3 Xét 4ISH ta có IG I M 1 = =
⇒ GM ∥ SH (Định lí Ta-lét đảo). I S I H 3 Ta có MG ∥ SH SH ⊂ (SCD) ⇒ MG ∥ (SCD). MG 6⊂ (SCD) ä
BÀI 570. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Gọi M, N, P lần lượt là trung điểm của S A, BC, CD. 1
Tìm giao tuyến của hai mặt phẳng (S AC) và (SBD). 2
Tìm giao tuyến của hai mặt phẳng (S AB) và (SCD). 3
Tìm giao điểm E của SB và (MNP). 4 Chứng minh NE ∥ (S AP). Lời giải. S M A D E F O P B C N Q (O ∈ AC ⊂ (SAC) 1
Ta có O = AC ∩ BD ⇒ O ∈ BC ⊂(SBD).
Do đó O là điểm chung của hai mặt phẳng (S AC) và (SBD)
mà S là điểm chung thứ hai của hai mặt phẳng (S AC) và (SBD) nên SO = (S AC) ∩ (SBD). AB ∥ CD AB ⊂ (S AB) 2 Ta có
⇒ (S AB) ∩ (SCD) = Sx ∥ AB và Sx ∥ CD. CD ⊂ (SCD) S ∈ (S AB) ∩ (SCD) 3
Gọi Q = NP ∩ AB ⇒ Q là điểm chung của (S AB) và (MNP)
mà M là điểm chung thứ hai nên (S AB) ∩ (MNP) = MQ.
Trong mặt phẳng (S AB) gọi E = MQ ∩ SB. (E ∈ SB Ta có ⇒ E = SB ∩ (MNP). E ∈ MQ ⊂ (MNP) 376
CHƯƠNG 8. ĐƯỜNG THẲNG VÀ MẶT PHẲNG TRONG KHÔNG GIAN. QUAN HỆ SONG SONG. 4
Ta có N là trung điểm của BC và BQ ∥ CP nên BQ = CP và NQ = NP (1). AB CD
Gọi F là trung điểm của AB, ta có AF = BF = = = CP = BQ. 2 2
Ta có M, F là trung điểm của S A và AB nên MF là đường trung bình tam giác S AB nên MF ∥ SB.
Trong tam giác QMF có B là trung điểm QF và BE ∥ MF nên E là trung điểm MQ (2).
Từ (1) và (2) ta có EN là đường trung bình tam giác QMP ⇒ EN ∥ MP.
Mặt khác, do MP ⊂ (S AP) nên NE ∥ (S AP). ä
BÀI 571. Cho tứ diện ABCD. Lấy điểm M trên cạnh AB sau cho AM = 2MB. Gọi G là trọng tâm 4BCD và I là trung
điểm CD, H là điểm đối xứng của G qua I. 1 Chứng minh GD ∥ (MCH). GK 2
Tìm giao điểm K của MG với (ACD). Tính tỉ số . G M Lời giải. A 1
Ta có IC = ID và IG = IH nên GDHC là hình bình hành. Do đó GD ∥ CH
mà CH ⊂ (MCH) nên GD ∥ (MCH). (K ∈ AI ⊂ (ACD) 2
Trong mp(ABI), gọi K = AI ∩ MG, ta có K ∈ MG M ⇒ K = MG ∩ (ACD).
Trong mp(ABI), kẻ GE ∥ AB, (E ∈ AI). E GE IG 1 GE 1
Xét tam giác ABI, có GE ∥ AB, suy ra = = ⇒ = . B D AB IB 3 AM 2 KG GE 1 GK
Xét tam giác AK M, có GE ∥ AM, suy ra = = ⇒ = 1. G K M AM 2 G M I H C K ä
BÀI 572. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi I, K lần lượt là trung điểm của BC và CD. 1
Tìm giao tuyến của (SIK) và (S AC), (SIK) và (SBD). 2
Gọi M là trung điểm của SB. Chứng minh SD ∥ (ACM). MF 3
Tìm giao điểm F của DM và (SIK). Tính tỉ số . MD Lời giải. x S F M A D K O E B C I
2. ĐƯỜNG THẲNG SONG SONG VỚI MẶT PHẲNG 377 1 Ta có S ∈ (SIK) ∩ (S AC). (E ∈ IK ⊂ (SIK)
Trong mp(ABCD), gọi E = IK ∩ AC ⇒ ⇒ E ∈ (SIK) ∩ (S AC). E ∈ AC ⊂ (S AC) Suy ra SE = (SIK) ∩ (S AC). (S ∈ (SIK) ∩ (SBD) Ta có
⇒ (SIK) ∩ (SBD) = Sx, (với Sx ∥ BD ∥ IK).
BD ∈ (SBD), IK ∈ (SIK), BD ∥ IK 2
Trong mp(ABCD), gọi O = AC ∩ BD, ta có SD ∥ MO. Mà MO ⊂ (ACM), suy ra SD ∥ (ACM). (S ∈ DM 3
Trong mp(SBD), gọi F = Sx ∩ DM ⇒ ⇒ F = DM ∩ (SIK). S ∈ Sx ⊂ (SIK) MF MS Ta có SF ∥ BD ⇒ = = 1. MD MB ä
BÀI 573. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Gọi G là trọng tâm 4S AB, trên AD lấy
điểm E sao cho AD = 3AE. Gọi M là trung điểm AB. 1 Chứng minh EG ∥ (SCD). 2
Đường thẳng qua E song song AB cắt MC tại F. Chứng minh GF ∥ (SCD). 3
Gọi I là điểm thuộc cạnh CD sao cho CI = 2ID. Chứng minh GO ∥ (S AI). Lời giải. S H G E A D L I M K O N F B C GH 2 1
Gọi H là trọng tâm tam giác SCD, ta có GH ∥ MN và = . M N 3 ED ED 2 Lại có ED ∥ MN và = = . M N AD 3
Suy ra GH ∥ ED và GH = ED. Suy ra GHDE là hình bình hành. (EG ∥ DH Ta có ⇒ EG ∥ (SCD). DH ⊂ (SCD) MF AE 1 2
Ta có M A ∥ EF ∥ CD, suy ra = = . MC AD 3 MF MG 1 Xét tam giác MSC có = = , suy ra GF ∥ SC. MC MS 3
Mà SC ⊂ (SCD). Vậy GF ∥ (SCD). 3
Trong mp(ABCD), gọi K = AI ∩ MN. Ta có SK = (SMN) ∩ (S AI).
Gọi L là trung điểm của AI, ta có OL là đường trung bình của hình thang AMN I, suy ra CD AB AM AM AM AM AM + N I + + + 6 6 3 2AM OL 2 OL = = = = = ⇒ = . 2 2 2 2 3 AM 3 378
CHƯƠNG 8. ĐƯỜNG THẲNG VÀ MẶT PHẲNG TRONG KHÔNG GIAN. QUAN HỆ SONG SONG. K O OL 2
Xét tam giác AK M, có OL ∥ AM, suy ra = = . K M AM 3 SG K O 2 Xét tam giác SMK, có = = , suy ra GO ∥ SK. SM K M 3
Mà SK ⊂ (S AI). Vậy GO ∥ (S AI). ä
BÀI 574. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M là trung điểm của SC và N là trọng tâm tam giác ABC. 1 Chứng minh SB ∥ (AMN). 2
Tìm giao tuyến (AMN) và (S AB). I S 3
Tìm giao điểm I của SD với (AMN). Tính tỉ số . I D 4
Gọi Q là trung điểm của ID. Chứng minh QC ∥ (AMN). Lời giải. S I Q M E A D F T O N x B C G 1
Trong mp(ABCD), gọi O = AC ∩ BD. OE 1
Trong mp(S AC), gọi E = AM ∩ SO, ta có E là trọng tâm tam giác S AC. Suy ra = . OS 3 ON 1
Ta có N là trọng tâm tam giác ABC nên = . OB 3 OE ON 1 Xét tam giác OSB có = = . Suy ra NE ∥ SB. OS OB 3
Mà NE ⊂ (AMN). Vậy SB ∥ (AMN). ( A ∈ (SAB) ∩ (AMN) 2 Ta có
⇒ (S AB) ∩ (AMN) = Ax, (với Ax ∥ SB). SB ⊂ (S AB), SB ∥ (AMN) ( I ∈ NE ⊂ (AMN) 3
Trong mp(SBD), gọi I = NE ∩ SD ⇒ ⇒ I = SD ∩ (AMN). I ∈ SD 2BO I S BN BN 3 1
Ta có NE ∥ SB ⇒ N I ∥ SB ⇒ = = = = . I D N D BD − BN 2BO 2 2BO − 3 4
Trong mp(SBD), gọi F = NE ∩ BQ.
Trong mp(ABCD), gọi G = AN ∩ BC, vì N là trọng tâm tam giác ABC nên G là trung điểm của BC. Ta có FG = (AMN) ∩ (BQC). Kẻ QT ∥ F N, (T ∈ BD). (1)
2. ĐƯỜNG THẲNG SONG SONG VỚI MẶT PHẲNG 379 N T IQ 1
Xét tam giác DN I có QT ∥ N I, suy ra = = D N D I 2 BN 1 Mà =
nên BN = NT, hay N là trung điểm của BT. (2) N D 2
Từ (1) và (2), ta có F là trung điểm của BQ.
Do đó GF là đường trung bình của tam giác BQC. Suy ra QC ∥ GF.
Mà GF ⊂ (AMN). Vậy QC ∥ (AMN). ä
BÀI 575. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N lần lượt là trung điểm của BC, CD. 1
Tìm giao tuyến của (SMD) và (S AB). 2
Tìm giao tuyến của (SMN) và (SBD). K H 3
Gọi H là điểm trên cạnh S A sao cho H A = 2HS. Tìm giao điểm K của MH và (SBD). Tính tỉ số . K M 4
Gọi G là giao điểm của BN và DM. Chứng minh HG ∥ (SBC). Lời giải. S x H K A D N F O G B C M E (E ∈ MD ⊂ (SMD) 1
Trong mp(ABCD), gọi E = MD ∩ AB ⇒ ⇒ E ∈ (SMD) ∩ (S AB). E ∈ AB ⊂ (S AB)
mà S ∈ (S AB) ∩ (SMD) ⇒ SE = (S AB) ∩ (SMD). M N ∥ BD 2 Ta có
M N ⊂ (SMN), BD ⊂ (SBD) ⇒ (SMN) ∩ (SBD) = Sx ∥ BD ∥ MN. S ∈ (SMN) ∩ (SBD) 3
Trong mp(ABCD), gọi F = AM ∩ BD. (K ∈ SF ⊂ (SBD)
Trong mp(S AM), gọi K = MH ∩ SF ⇒ ⇒ K = MH ∩ (SBD). K ∈ MH GC 2 GC 1 4
Trong tam giác BCD, BN và DM là hai trung tuyến nên G là trọng tâm. Từ đó ta có = ⇒ = . CO 3 AC 3 HS 1 GC HS Mặt khác, do H A = 2HS nên = ⇒ =
⇒ HG ∥ SC ⇒ HG ∥ (SBC). S A 3 AC S A ä
BÀI 576. Cho hình chóp S.ABCD có đáy ABCD là hình thang với AD là đáy lớn và AD = 2BC. Gọi O là giao điểm
của AC và BD, G là trọng tâm của tam giác SCD. 380
CHƯƠNG 8. ĐƯỜNG THẲNG VÀ MẶT PHẲNG TRONG KHÔNG GIAN. QUAN HỆ SONG SONG. 1 Chứng minh OG ∥ (SBC). 2
Gọi M là trung điểm của cạnh SD. Chứng minh CM ∥ (S AB). 3
Giả sử điểm I trên đoạn SC sao cho 2SC = 3SI. Chứng minh S A ∥ (BID). K B 4
Xác định giao điểm K của BG và mặt phẳng (S AC). Tính tỉ số . KG Lời giải. S M P N G I A D O B C OD AD 1 Ta có AD ∥ BC ⇒ = = 2. OB BC GD
Mặt khác, gọi N là trung điểm SC. Vì G là trọng tâm 4SCD nên = 2 G N GD OD ⇒ =
⇒ OG ∥ BN ⇒ OG ∥ (SBC). G N OB 2
Gọi P là trung điểm S A, ta có ngay P M là đường trung bình của 4S AD. AD Suy ra P M =
= BC và P M ∥ AD ∥ BC. Do đó P MCB là hình bình hành. 2
Vậy CM ∥ BP ⇒ CM ∥ (S AB). O A 3 Ta có AD ∥ BC ⇒ = 2. OC S I S I O A
Mặt khác, vì 2SC = 3SI nên = 2 ⇒ =
⇒ OI ∥ S A ⇒ S A ∥ (BID). IC IC OC 4
Trong mp(BCMP), gọi K = BG ∩ CP
mà CP ∈ (S AC) ⇒ K = BG ∩ (S AC). K B BP CM 3 Ta lại có CG ∥ BP ⇒ = = = . KG CG CG 2 ä
BÀI 577. Cho hình chóp S.ABC Gọi M, P, I lần lượt là trung điểm của AB, SC, SB. Một mặt phẳng (α) qua MP và
song song với AC và cắt các cạnh S A, BC tại N, Q. 1 Chứng minh BC ∥ (I MP). 2
Xác định thiết diện của (α) với hình chóp. Thiết diện này là hình gì? 3
Tìm giao điểm của đường thẳng CN và mặt phẳng (SMQ). Lời giải.
2. ĐƯỜNG THẲNG SONG SONG VỚI MẶT PHẲNG 381 x D S N P I A C Q M B 1
Ta có IP là đường trung bình của tam giác SBC nên IP ∥ BC ⇒ BC ∥ (I MP). 2
Ta có (α) cắt BC tại Q nên (α) ∩ (SBC) = PQ và (α) ∩ (ABC) = MQ.
Ta lại có (α) cắt S A tại N nên (α) ∩ (S AB) = MN và (α) ∩ (S AC) = P N.
Vậy thiết diện cần tìm là tứ giác MNPQ. ((α) ∥ AC Mặt khác, do
⇒ (α) ∩ (ABC) = MQ ∥ AC ⇒ Q là trung điểm BC. AC ⊂ (ABC)
Tương tự ta chứng minh được NP ∥ AC và N là trung điểm S A. AC
Lúc này NP và MQ là đường trung bình tam giác S AC và ABC nên NP = MQ = và NP ∥ MQ. 2
Suy ra MNPQ là hình bình hành. AC ∥ MQ 3 Ta có
AC ⊂ (S AC), MQ ⊂ (SMQ) ⇒ (S AC) ∩ (SMQ) = Sx ∥ AC. S ∈ (S AC) ∩ (SMQ)
Trong mp(S AC), gọi D = CN ∩ Sx. Ta có D ∈ Sx ⊂ (SMQ) và D ∈ CN nên D = CN ∩ (SMQ). ä
BÀI 578. Cho hình chóp S.ABCD có đáy là một hình tứ giác lồi. Gọi M, N là trung điểm của SC và CD. Gọi (α) là
mặt phẳng qua M, N và song song với đường thẳng AC. 1
Tìm giao tuyến của (α) với (ABCD). 2
Tìm giao điểm của SB và (α). 3
Tìm thiết diện của hình chóp cắt bởi mặt phẳng (α). Lời giải. S z y Q H M A D P K N B C 382
CHƯƠNG 8. ĐƯỜNG THẲNG VÀ MẶT PHẲNG TRONG KHÔNG GIAN. QUAN HỆ SONG SONG. AC ∥ (α) 1 Ta có AC ⊂ (ABCD)
⇒ (α) ∩ (ABCD) = N x ∥ AC. Gọi P = N x ∩ AD ta có (α) ∩ (ABCD) = NP.
N ∈ (α) ∩ (ABCD) 2
Ta có MN là đường trung bình của tam giác SCD nên SD ∥ MN ⇒ SD ⇒ SD ∥ (α). SD ∥ (α) Gọi K = NP ∩ BD, ta có SD ⊂ (SBD)
⇒ (α) ∩ (SBD) = K y ∥ SD. Gọi H = K y ∩ SB. K ∈ (α) ∩ (SBD)
Ta có H ∈ K y ⊂ (α) và H ∈ SB ⇒ H = SB ∩ (α). SD ∥ (α) 3 Ta có SD ⊂ (S AD)
⇒ (α) ∩ (SBD) = P z ∥ SD. Gọi Q = P z ∩ S A.
P ∈ (α) ∩ (S AD)
(α) và (S AB) có H, Q là điểm chung nên giao tuyến là QH.
(α) và (S AD) có P, Q là điểm chung nên giao tuyến là PQ.
(α) và (ABCD) có P, N là điểm chung nên giao tuyến là P N.
(α) và (SCD) có M, N là điểm chung nên giao tuyến là MN.
(α) và (SBC) có H, M là điểm chung nên giao tuyến là HM.
Vậy thiết diện cần tìm là ngũ giác MNPQH. ä
BÀI 579. Cho hình chóp S.ABCD có đáy ABCD là hình thang với AB ∥ CD. Gọi M, N, I, lần lượt là trung điểm của AD, BC, S A. 1
Tìm giao tuyến của hai mặt phẳng (I MN) và (S AC); (I MN) và (S AB). 2
Tìm giao điểm của SB và (I MN). 3
Tìm thiết diện của mặt phẳng (IDN) với hình chóp S.ABCD. Lời giải. 1
Tìm giao tuyến của hai mặt phẳng (I MN) và (S AC); (I MN) và (S AB).
(a) Tìm giao tuyến của (I MN) và (S AC). S
Ta có I ∈ (S AC) ∩ (I MN).
Trong (ABCD) gọi E = AC ∩ MN ⇒ E ∈ (S AC) ∩ (I MN). I a J Vậy IE = (I MN) ∩ (S AC). I
(b) Ta có I ∈ (I MN)∩(S AB) và MN là đường trung bình của hình thang
ABCD nên M N ∥ AB. Nên giao tuyến của (I MN) và (S AB) là đường A B
thẳng a đi qua I song song với AB. 2
Ta thấy SB ⊂ (S AB) và a = (I MN) ∩ (S AB). Gọi J = SB ∩ a, vậy J = SB ∩ M E N (I M N). D C 3 Ta thấy
I J = (S AB)∩(IDN), ID = (S AD)∩(IDN), DN = (ABCD)∩(IDN), N J = (SBC)∩(IDN).
Vậy thiết diện của (IDN) và hình chóp S.ABCD là tứ giác I J ND. ä
BÀI 580. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Gọi G là trọng tâm 4S AB; N là một điểm AN 1 thuộc đoạn AC sao cho
= ; I là trung điểm của AB. AC 3 1
Chứng minh OI ∥ (S AD) và GN ∥ SD. 2
Gọi (α) là mặt phẳng đi qua O, song song với S A và BC. Mặt phẳng (α) cắt SB, SC lần lượt tại L và K. Xác
định thiết diện cắt bởi mặt phẳng (α) với hình chóp. Lời giải.
2. ĐƯỜNG THẲNG SONG SONG VỚI MẶT PHẲNG 383 1
Chứng minh OI ∥ (S AD) và GN ∥ SD.
(a) Chứng minh OI ∥ (S AD). S
Ta có OI ∥ BC (OI là đường trung bình trong 4ABC) nên OI ∥
AD (vì AD ∥ BC) mà AD ⊂ (S AD) suy ra OI ∥ (S AD). (b) Chứng minh GN ∥ SD. L AN 1 AN 2 Do = ⇒ =
suy ra N là trọng tâm 4ABD. Từ đó ta AC 3 AO 3 K I N 1 IG G có = = ⇒ GN ∥ SD. I D 3 I S A 2
Xác định giao điểm L = SB ∩ (α). I B N
Ta thấy (α) là (K IH) với H, K lần lượt là trung điểm CD, SC. Ta
thấy SB ⊂ (SBC), K = (α) ∩ (SBC) và IH ∥ BC nên giao tuyến của O
(α) và (SBC) là đường thẳng d đi qua K song song với BC. Khi đó L D H C
= d ∩ SB suy ra L là trung điểm SB. Ta thấy
(α) ∩ (ABCD) = H I, (α) ∩ (SBC) = K L, (α) ∩ (S AB) = LI.
Vậy thiết diện của (α) với hình chóp là hình thang LK HI. ä
BÀI 581. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Gọi H, K lần lượt là trung điểm các cạnh
S A, SB và M là điểm thuộc cạnh CD, (M khác C và D). 1
Tìm giao tuyến của (K AM) và (SBC), (SBC) và (S AD). 2
Tìm thiết diện tạo bởi (HKO) với hình chóp S.ABCD. Thiết diện là hình gì? 3
Gọi L là trung điểm đoạn HK. Tìm I = OL ∩ (SBC). Chứng minh SI ∥ BC. Lời giải. I 1
Tìm giao tuyến của (K AM) và (SBC), (SBC) và (S AD).
Tìm giao tuyến của (K AM) và (SBC). S
Ta có K ∈ (K AM) ∩ (SBC). Trong (ABCD) gọi F = AM ∩ BC, nên d
F ∈ (K AM) ∩ (SBC). Suy ra K F = (K AM) ∩ (SBC).
Tìm giao tuyến của (SBC) và (S AD). L
Ta thấy S ∈ (SBC) ∩ (S AD), mà BC ∥ AD nên giao tuyến của H K
(SBC) và (S AD) là đường thẳng d đi qua S song song với AD và BC. 2
Tìm thiết diện tạo bởi (HKO) với hình chóp S.ABCD. Thiết diện là A J B hình gì? O
Ta thấy (HKO) và (ABCD) chứa có chung điểm O và lần lượt chứa E G
HK và AB song song với nhau nên giao tuyến là đường thẳng a đi
qua O song song với AB cắt AD và BC lần lượt tại E và G. Ta thấy D M C
(HK O) ∩ (ABCD) = EG, (HKO) ∩ (S AD) = HE,
(HK O)∩(S AB) = HK,(HKO)∩(SBC) = KG. Vậy thiết diện của (HKO)
và hình chóp là hình thang HKGE do HK ∥ AB mà AB ∥ EG nên F HK ∥ EG. 3
Tìm I = OL ∩ (SBC). Chứng minh SI ∥ BC.
Trong (HKGE) gọi I = OL ∩ GK
mà GK ⊂ (SBC) ⇒ I ∈ OL ∩ (SBC).
Trong (S AB) gọi J = SL ∩ AB khi đó L là trung điểm của AB do HK ∥ AB.
Xét (S JO) và (SBC) ta thấy có S là điểm chung và OJ ∥ BC nên giao
tuyến là đường thẳng đi d đi qua S và song song với BC. Mặt khác
I ∈ (SJO) ∩ (SBC) nên SI ≡ d. Vậy SI ∥ BC. ä
BÀI 582. Cho tứ diện ABCD, có M, N lần lượt là trung điểm của AB, BC và G là trọng tâm của tam giác ACD. 1
Tìm giao điểm E của MG và (BCD). 384
CHƯƠNG 8. ĐƯỜNG THẲNG VÀ MẶT PHẲNG TRONG KHÔNG GIAN. QUAN HỆ SONG SONG. 2
Tìm d = (MNG) ∩ (BCD). Giả sử d ∩ CD = P. Chứng minh GP ∥ (ABC). 3
Gọi (α) là mặt phẳng chứa MN và song song với AD. Tìm thiết diện của (α) với tứ diện. Lời giải. E 1
Tìm giao điểm E của MG và (BCD).
Ta thấy (ABF) chứa MG với F là trung điểm của DC và BF = (ABF) ∩
(BCD). Gọi E = MG ∩ BF ⇒ E = MG ∩ (BCD). D 2
Tìm d = (MNG) ∩ (BCD). Giả sử d ∩ CD = P. Chứng minh GP ∥ (ABC).
Ta có N ∈ (BCD) ∩ (MNG) và E ∈ MG ⊂ (MNG); E ∈ BF ⊂ (BCD). Suy ra d ≡ NE = (MNG) ∩ (BCD). F Ta thấy G P
(ABC) ∩ (EMN) = MN, (D AC) ∩ (ABC) = AC, (EMN) ∩ (D AC) = GP K A C
mà MN ∥ AC nên GP ∥ AC ⇒ GP ∥ (ABC). 3
Gọi K là trung điểm của BD, do (α) chứa MN và song song với AD nên M N
(α) đi qua K. Ta thấy B
(α) ∩ (ABD) = NK, (α) ∩ (ABC), (α) ∩ (BCD) = K N.
Vậy thiết diện của (α) và hình chóp là tam giác MNK. ä
BÀI 583. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Điểm M thuộc cạnh S A thỏa mãn 3M A = 2MS.
Hai điểm E và F lần lượt là trung điểm của AB và BC. 1
Xác định giao tuyến của hai mặt phẳng (MEF) và (S AC). K S 2
Xác định giao điểm K của mặt phẳng (MEF) với cạnh SD. Tính tỉ số . K D I M 3
Tìm giao điểm I của MF với (SBD). Tính tỉ số . I F 4
Tìm thiết diện tạo bởi mặt phẳng (MEF) với hình chóp S.ABCD. Lời giải. 1
Xác định giao tuyến của hai mặt phẳng (MEF) và (S AC).
Ta thấy M ∈ (MEF)∩(S AC) và EF ∥ AC với EF ⊂ (MEF), AC ∥ (S AC) S
nên giao tuyến của (MEF) và (S AC) là đường thẳng d đi qua M song song với AC. K 2
Xác định giao điểm K của mặt phẳng (MEF) với cạnh SD. Tính tỉ M K S L số . K D N
Ta thấy SD ⊂ (SBD), gọi H = EF ∩ BD, O = AC ∩ BD, L = d ∩ SO. Khi
đó HL = (MEF) ∩ (SBD), gọi K = HL ∩ SD ⇒ K = SD ∩ (MEF). I M A LO 3 Do D ML ∥ AC nên = = . MS LS 2 A
Xét tam giác SOD trong (SBD) vì K, L, H thẳng hàng nên theo SK HD LO SK 3 SK 2 E O định lí Menelaus ta có · · = 1 ⇒ · 3 · = 1 ⇒ = . K D HO LS K D 2 K D 9 H B F C I M 3
Tìm giao điểm I của MF với (SBD). Tính tỉ số . I F
Trong (MEF) gọi I = HL ∩ MF mà HL ⊂ (SBD) ⇒ I = MF ∩ (SBD). I M ML
Do ML ∥ AC và EF ∥ AC nên ML ∥ EF. Từ đó ta suy ra = = I F HF HL HF 2 1 4 : = : = . AO AO 5 2 5 4
Tìm thiết diện tạo bởi mặt phẳng (MEF) với hình chóp S.ABCD.
Gọi N = ML ∩ SC. Ta thấy (MEF) ∩ (S AB) = EM,
(MEF) ∩ (ABCD) = EF, (MEF) ∩ (S AD) = MK,
(MEF) ∩ (SCD) = K N, (MEF) ∩ (SBC) = NF. Vậy thiết diện của
(MEF) với hình chóp là ngũ giác EMK NF. ä
2. ĐƯỜNG THẲNG SONG SONG VỚI MẶT PHẲNG 385
BÀI 584. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Gọi M, N là trung điểm của S A, SD. 1
Xác định giao điểm của NC và (OMD). 2
Xác định thiết diện của hình chóp với mặt phẳng (P) qua MN và song song với SC. Lời giải. K 1
Xác định giao điểm của NC và (OMD).
Ta thấy CN ⊂ (SCD), OM ∥ SC mà OM ⊂ (OMD), SC ⊂ (SCD) và
O ∈ (OMD) ∩ (SCD) nên giao tuyến của (OMD) và (SCD) là đường S
thẳng d đi qua D và song song với OM, SC. Gọi K = d ∩ NC ⇒ K = NC ∩ (OMD). 2
Xác định thiết diện của hình chóp với mặt phẳng (P) qua MN và M N song song với SC. Ta thấy (P) ≡ (OMN).
Xác định giao tuyến của (OMN) và (SCD).
Ta thấy N ∈ (OMN) ∩ (SCD) và OM ∥ SC nên giao tuyến của (OMN)
và (SCD) là đường thẳng đi qua N song song với SC cắt CD tại I là A D trung điểm CD.
Gọi J = OI ∩ AB. Ta thấy (OMN) ∩ (S AB) = JM, J O I
(OM N) ∩ (S AD) = MN, (OMN) ∩ (SCD) = I N, (OMN) ∩ (ABCD). Vậy
thiết diện của mặt phẳng (P) với hình chóp là hình thang MN I J. B C ä
BÀI 585. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M là trung điểm của SC, (P) là mặt phẳng qua AM và song song với BD. 1
Xác định thiết diện của hình chóp khi cắt bởi mặt phẳng (P). 2
Gọi E, F lần lượt là giao điểm của (P) với cạnh SB và SD. Hãy tìm tỉ số diện tích của tam giác SME với diện
tích tam giác SBC và tỉ số diện tích của tam giác SMF và diện tích tam giác SCD. 3
Gọi K là giao điểm của ME và CB, J là giao điểm của MF và CD. Chứng minh ba điểm K, A, J nằm trên một EF
đường thẳng song song với EF và tìm tỉ số . K J Lời giải. 386
CHƯƠNG 8. ĐƯỜNG THẲNG VÀ MẶT PHẲNG TRONG KHÔNG GIAN. QUAN HỆ SONG SONG. 1
Xác định thiết diện của hình chóp khi cắt bởi mặt phẳng (P).
Trong (ABCD) qua A kẻ đường thẳng song song S
BD cắt BC và CD lần lượt tại K và J. Khi đó
(P) ≡ (MK J). Gọi E = MK ∩ SB, F = CD ∩ SD.
Khi đó, ta thấy (P) ∩ (S AB) = E A, (P) ∩ (SBC) =
EM, (P) ∩ (SCD) = MF, (P) ∩ (S AD) = AF. Vậy J
thiết diện của (P) với hình chóp là tứ giác F AEMF. M 2
Tính tỉ số diện tích của tam giác SME với diện E
tích tam giác SBC và tỉ số diện tích của tam A D
giác SMF và diện tích tam giác SCD. S SE SM 2 1 1 Ta có 4SME = · = · = . (Vì E là giao S4SBC SB SC 3 2 3
điểm của hai đường trung tuyến K M và SB nên K B C
E là trọng tâm của tam giác SCK .) S SF SM 2 1 1 Tương tự ta có 4SMF = · = · = . (Vì S4SCD SD SC 3 2 3
F là giao điểm của hai đường trung tuyến J M
và SD nên F là trọng tâm của tam giác SC J.) 3
Chứng minh ba điểm K, A, J nằm trên một EF
đường thẳng song song với EF và tìm tỉ số . K J Ta có SE 2 SF EF ME 1 = = ⇒ EF ∥ K J ⇒ = = . SB 3 SD K J MK 3 ä
BÀI 586. Cho hình chóp S.ABCD có G là trọng tâm 4ABC. Gọi M, N, P, Q, R, H lần lượt là trung điểm của S A, SC, CB, BA, Q N, AG. 1
Chứng minh rằng S, R, G thẳng hàng và SG = 2MH = 4RG. 2
Gọi G0 là trọng tâm 4SBC. Chứng minh rằng GG0 ∥ (S AB) và GG0 ∥ (S AC). Lời giải. S 1
Chứng minh rằng S, R, G thẳng hàng và SG = 2MH = 4RG.
Gọi E, F lần lượt là trung điểm của AC và SB khi đó ta có QENF 1
là hình bình hành (do EQ = NF = BC, EQ ∥ BC ∥ NF) nên R là M F 2
trung điểm của EF. Ta thấy S ∈ (SQC) ∩ (SEB), G ∈ (SQC) ∩ (SEB),
R ∈ (SQC) ∩ (SEB) suy ra S, R, G thẳng hàng. Q
Vì M, H lần lượt là trung điểm của S A, AG nên SG = 2MH. A B R G0
Xét 4SGB vì E, R, F thẳng hàng nên theo định lí Menelaus ta có N RS EG FB RS 1 RS H · · = 1 ⇒ · · 1 = 1 ⇒ = 3 ⇒ SG = 4RG. RG EB F S RG 3 RG G P 2
Chứng minh rằng GG0 ∥ (S AB) và GG0 ∥ (S AC). E PG0 1 PG D Xét 4S AP có = =
⇒ GG0 ∥ S A mà S A ⊂ (S AB) và S A ⊂ P S 3 P A
(S AC) nên suy ra GG0 ∥ (S AB), GG0 ∥ (S AC). C ä BÀI 3.
HAI MẶT PHẲNG SONG SONG A TÓM TẮT LÝ THUYẾT 3. HAI MẶT PHẲNG SONG SONG 387 1
VỊ TRÍ TƯƠNG ĐỐI CỦA HAI MẶT PHẲNG PHÂN BIỆT
Cho đường thẳng d và mặt phẳng (P). Có ba trường hợp xảy ra: Q P P Q
(P), (Q) có 1 điểm chung: (P) ∩ (Q) = a
(P), (Q) không có điểm chung: (P) ∥ (Q)
Định nghĩa 1. Hai mặt phẳng được gọi là song song nếu chúng không có điểm chung. 2 CÁC ĐỊNH LÍ M
Định lí 1. Nếu mặt phẳng (α) chứa hai đường thẳng cắt nhau a, b và a, b a b α
cùng song song với mặt phẳng (β) thì (α) song song với (β). β
Muốn chứng minh hai mặt phẳng song song, ta phải chứng minh có hai đường thẳng cắt nhau !
thuộc mặt phẳng này lần lượt song song với mặt phẳng kia.
Muốn chứng minh đường thẳng a ∥ (Q), ta chứng minh đường thẳng a nằm trong mặt phẳng (P) ∥ (Q). A
Định lí 2. Qua một điểm nằm ngoài một mặt phẳng cho trước có một và chỉ α
một mặt phẳng song song với mặt phẳng đã cho. β Hệ quả 1.
Nếu đường thẳng d song song với mặt phẳng (α) thì trong (α) có một đường thẳng song song
với d và qua d có duy nhất một mặt phẳng song song với (α). Do đó đường thẳng d song song với (α) ta
phải chứng minh d thuộc mặt phẳng (β) và có (α) ∥ (β) ⇒ d ∥ (α).
Hai mặt phẳng phân biệt cùng song song với mặt phẳng thứ ba thì song song với nhau.
Cho điểm A không nằm trên mặt phẳng (α). Mọi đường thẳng đi qua A và song song với (α) đều nằm
trong mặt phẳng đi qua A và song song với (α). a b
Định lí 3. Cho hai mặt phẳng song song. Nếu một mặt phẳng cắt mặt phẳng
này thì cũng cắt mặt phẳng kia và hai giao tuyến song song với nhau. A0 A α B B0 β
Hệ quả 2. Hai mặt phẳng song song chắn trên hai cát tuyến song song những đoạn thẳng bằng nhau. 388
CHƯƠNG 8. ĐƯỜNG THẲNG VÀ MẶT PHẲNG TRONG KHÔNG GIAN. QUAN HỆ SONG SONG.
Định lí 4. Định lí Thales: Ba mặt phẳng đôi một song song chắn trên hai A0
cát tuyến bất kì những đoạn thẳng tương ứng tỉ lệ. A α B B0 β C γ C0 3 VÍ DỤ
VÍ DỤ 1. Cho hình chóp S.ABCD với đáy ABCD là hình thang mà AD ∥ BC và AD = 2BC. Gọi M, N lần lượt
là trung điểm của S A và AD. Chứng minh: (BMN) ∥ (SCD). Lời giải. AD
Vì N là trung điểm của AD nên N A = ND = = BC. S 2
Tứ giác NBCD có ND = BC và ND ∥ BC nên NBCD là hình bình hành, suy ra NB ∥ CD ⇒ NB ∥ (SCD).
Tam giác S AD có M, N lần lượt là trung điểm của AS và AD nên MN là M
đường trung bình của 4ADS, suy ra MN ∥ SD ⇒ MN ∥ (SCD). (MN ∥ (SCD), MN ⊂ (BMN) Từ ⇒ (BMN) ∥ (SCD). BN ∥ (SCD), BN ⊂ (BMN) A D N B C ä B BÀI TẬP ÁP DỤNG
BÀI 587. Cho hình chóp S.ABCD có đáy là hình bình hành tâm O. Gọi M, N, P lần lượt là trung điểm S A, SB, SD
và K, I là trung điểm của BC, OM.
1 Chứng minh (OM N) ∥ (SCD).
2 Chứng minh (P M N) ∥ (ABCD).
3 Chứng minh K I ∥ (SCD). Lời giải. S 1
Ta có O, M lần lượt là trung điểm của AC và S A
nên OM ∥ SC, suy ra OM ∥ (SCD). Tương tự ON ∥ (SCD). M N Khi đó (OMN) ∥ (SCD). 2
Ta có N, M lần lượt là trung điểm của SB và S A P Q I B
nên MN ∥ AB, suy ra MN ∥ (ABCD). Tương tự P M ∥
(ABCD). Vậy (P M N) ∥ (ABCD). A O 3
Ta có O, K lần lượt là trung điểm của AC và BC K
nên OK ∥ AB, suy ra OK ∥ MN. Khi đó 5 điểm M, N, K, O, I đồng phẳng. D C
Từ câu trên (OMN) ∥ (SCD), thì K I ∥ (SCD). ä
BÀI 588. Cho hình chóp S.ABCD có đáy là hình bình hành tâm O. Gọi M, N lần lượt là trung điểm S A, SD 3. HAI MẶT PHẲNG SONG SONG 389 1 Chứng minh (OMN) ∥ (SBC). 2
Gọi P, Q, R lần lượt là trung điểm của AB, ON, SB. Chứng minh PQ ∥ (SBC) và (ROM) ∥ (SCD). Lời giải. S 1
Ta có O, M lần lượt là trung điểm của AC và S A
nên OM ∥ SC, suy ra OM ∥ (SBC). Tương tự ON ∥ (SBC). M R Khi đó (OMN) ∥ (SBC). 2
Ta có O, P lần lượt là trung điểm của AC và BA N P B
nên OP ∥ CB, suy ra OP ∥ (SBC) hay P ∈ (OMN). Mặt khác Q ∈ (OMN). A Q
Theo trên (OMN) ∥ (SBC) thì PQ ∥ (SBC).
Ta có R, O lần lượt là trung điểm của SB và BD O
nên RO ∥ SD, suy ra RO ∥ (SCD).
Theo trên OM ∥ SC nên OM ∥ (SCD). D C Vậy (ROM) ∥ (SCD). ä
BÀI 589. Cho hai hình bình hành ABCD và ABEF có chung cạnh AB và không đồng phẳng. Gọi I, J, K lần lượt là
trung điểm AB, CD, EF. Chứng minh 1 (ADF) ∥ (BCE). 2 (D I K ) ∥ (JBE). Lời giải. F K E 1
Ta có AD ∥ BC, suy ra AD ∥ (BCE). Tương tự AF ∥ (BCE). Khi đó (ADF) ∥ (BCE). 2
Trong hình bình hành ABCD có I, J lần lượt
là trung điểm của AB và CD nên BI = D J. I
Do đó IBJD là hình bình hành. Suy ra D I ∥ A B BJ nên D I ∥ (JBE).
Trong hình bình hành ABEF có I, K lần lượt
là trung điểm của AB và EF nên IK ∥ EF, suy ra IK ∥ (JBE). Vậy (D IK) ∥ (JBE). D C J ä
BÀI 590. Cho hai hình bình hành ABCD và ABEF nằm trên hai mặt phẳng khác nhau. Trên các đường chéo AC,
BF lấy các điểm M, N sao cho MC = 2AM, NF = 2BN. Qua M, N lần lượt kẻ các đường thẳng song song với cạnh AB,
cắt các cạnh AD, AF theo thứ tự tại M1, N1. Chứng minh rằng 1 M N ∥ DE. 2 M1 N1 ∥ (DEF).
3 (M N M1 N1) ∥ (DEF). Lời giải. F E N1 N A B M1 M C I D 390
CHƯƠNG 8. ĐƯỜNG THẲNG VÀ MẶT PHẲNG TRONG KHÔNG GIAN. QUAN HỆ SONG SONG. BM AM 1 BN 1 1
Gọi I là giao điểm của BM với CD. Khi đó ta có = = . Mặt khác = . M I MC 2 N F 2 Khi đó MN ∥ IF. AM 1 AB 1 Theo trên = nên = . Suy ra D I = CD = AB. MC 2 C I 2
Lại có D I ∥ EF. Do đó DEF I là hình bình hành, hay F I ∥ DE. Vậy MN ∥ DE. 2
Theo giả thiết thì MM1 ∥ N N1 (vì cùng song song với AB) nên M, M1, N,N1 đồng phẳng.
Lại có MM1 ∥ (DEF) (vì MM1 ∥ CD ∥ AB) và theo câu trên thì MN ∥ DE nên MN ∥ (DEF).
Vậy (MM1N1N) ∥ (DEF), suy ra M1N1 ∥ (DEF). 3 Đã chứng minh ở câu 2. ä
BÀI 591. Cho hai hình bình hành ABCD và ABEF nằm trên hai mặt phẳng phân biệt. Gọi I, J, K theo thứ tự là
trọng tâm các tam giác ADF, ADC, BCE. Chứng minh rằng (I JK) ∥ (CDFE). Lời giải.
Ta có CD ∥ EF ∥ AB nên CD và EF đồng F E phẳng.
Gọi M, N lần lượt là trung điểm của DF,
CD. Khi đó, vì I, J lần lượt là trọng tâm tam giác ADF, ADC nên A I 2 A J M P = =
⇒ I J ∥ MN ⇒ I J ∥ (CDEF). K AM 3 AN I B
Mặt khác, gọi P là trung điểm CE. Khi đó A BK 2 = . BP 3 J
Ta có ABCD, ABEF là hình bình hành nên
CDF E cũng là hình bình hành. Khi đó với D C
M, P là trung điểm của hai cạnh đối của N
hình bình hành CDFE nên MP ∥ CD ∥ AB
suy ra IK ∥ MP ∥ AB. Do đó ABPK cũng là A I 2 BK hình bình hành. Ta có = = . Suy AM 3 BP
ra IK ∥ MN. Khi đó IK ∥ (CDFE). Vậy (I JK) ∥ (CDFE). ä
BÀI 592. Cho hình chóp S.ABCD có đáy là hình bình hành tâm O. Gọi M, N, P lần lượt là trung điểm S A, BC, CD. 1
Tìm giao tuyến của hai mặt phẳng (S AD) và (MOP). 2
Gọi E là trung điểm của SC và I là điểm trên cạnh S A thỏa AI = 3IS. Tìm K = IE ∩ (ABC) và H = AB ∩ (EI N). AH Tính tỉ số . AB 3
Gọi G là trọng tâm tam giác SBC. Tìm thiết diện hình chóp S.ABC bị cắt bởi (I MG). Lời giải. S I M E Q G A H B N O D P C K 3. HAI MẶT PHẲNG SONG SONG 391 1
Ta có O, P lần lượt là trung điểm của AC và CD nên OP ∥ AD, suy ra OP ∥ (S AD).
Khi đó giao tuyến của (S AD) và (OMP) là đường thẳng qua M và song song với AD và cắt SD tại trung điểm Q của SD. S I 1 1 SE 2 Xét mặt phẳng (S AC) có = 6= = suy ra IE cắt AC tại K. S A 4 2 SC Khi đó K = IE ∩ (ABC).
Áp dụng định lý Menelaus trong tam giác S AC với ba điểm K, E, I thẳng hàng có K C I A ES K C 3 K C 1 · · = 1 ⇔ · · 1 = 1 ⇔ = . K A I S EC K A 1 K A 3
Áp dụng định lý Menelaus trong tam giác ABC với ba điểm K, N, H thẳng hàng có K C H A NB 1 H A H A · · = 1 ⇔ · · 1 = 1 ⇔ = 3. K A HB NC 3 HB HB AH 3 Khi đó = . AB 4 3
Ta thấy mặt phẳng (I MG) cũng chính là mặt phẳng (S AG).
Vì G là trọng tâm tam giác SBC và N là trung điểm BC nên (I MG) ∩ (SBC) = SN.
Vậy thiết diện hình chóp S.ABC bị cắt bởi (I MG) là tam giác S AN. ä
BÀI 593. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Gọi M, N lần lượt là trung điểm của S A
và CD. Gọi E là giao điểm của AD và (BMN), I là trung điểm của ME và G = AN ∩ BD.
1 Tìm điểm E và giao điểm F của SD với mặt phẳng (BM N). Chứng minh F S = 2FD.
2 Chứng minh FG ∥ (S AB) và (CD I) ∥ (S AB).
3 Gọi H là giao điểm của M N và SG. Chứng minh OH ∥ GF. Lời giải. S M F I H A E D G O N B C 1
Trong mặt phẳng (ABCD) kéo dài BN cắt đường thẳng AD tại E. Khi đó E là giao điểm của (BMN) với AD.
Gọi F là giao điểm của ME với SD. Khi đó F là giao điểm của SD với (BMN). ED D N 1 Vì = =
nên D là trung điểm của đoạn AE. Từ đó suy ra SD và EM là các đường trung tuyến của E A AB 2
tam giác S AE. Suy ra F là trọng tâm tam giác S AE. Vậy FS = 2FD. GD D N 1 2
Tam giác DGN và tam giác BG A đồng dạng nên = = . GB B A 2 GD F D Từ đó suy ra =
. Nên FG ∥ SB ⇒ FG ∥ (S AB). GB F S
Ta có CD ∥ AB và DI ∥ M A. Từ đó suy ra (CDI) ∥ (S AB). 3
Ta có G là trọng tâm tam giác ACD. Áp dụng định lý Menelaus cho tam giác S AG với bộ ba điểm thẳng hàng M, H, N, ta có NG M A HS 1 HS HS · · = 1 ⇔ · 1 · = 1 ⇔ = 3. N A MS HG 3 HG HG OG OG 1 Ta cũng có = = ⇒ OH ∥ SB. OB OD 3
Theo chứng minh trên ta cũng có GF ∥ SB. Vậy OH ∥ GF. ä 392
CHƯƠNG 8. ĐƯỜNG THẲNG VÀ MẶT PHẲNG TRONG KHÔNG GIAN. QUAN HỆ SONG SONG.
BÀI 594. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Gọi M là trung điểm của SC, N là điểm
trên đường chéo BD sao cho BD = 3BN. T M T M 1
1 Xác định giao tuyến của mặt phẳng (SCD) và (S AB) và tìm T = DM ∩ (S AB). Tính . ĐS: = T D T D 2
2 Gọi K = AN ∩ BC. Chứng minh rằng MK ∥ (SBD). LS SIK M LS 1 SIK M 3
3 Gọi I = AN ∩ DC, L = I M ∩ SD. Tính tỉ số và . ĐS: = ; = LD SI AL LD 2 SI AL 8 Lời giải. d S T L M D A N O C B K I 1
Mặt phẳng (S AB) và (SCD) lần lượt chứa hai đường thẳng song song là AB và CD nên giao tuyến của
chúng là đường thẳng d qua S và d ∥ AB ∥ CD.
Trong mặt phẳng (SCD) kéo dài DM cắt d tại T. Khi đó T ∈ d ⇒ T ∈ (S AB). Vậy T = DM ∩ (S AB). MT MS T M 1
Do CD ∥ ST nên hai tam giác MCD và MST đồng dạng. Do đó = = 1. Vậy = . MD MC T D 2 BN 1 BN 2 2 Vì = ⇒
= . Do đó N là trọng tâm tam giác ABC. BD 3 BO 3
Suy ra K là trung điểm của BC. Dẫn đến MK là đường trung bình của tam giác SBC.
Nên MK ∥ SB ⇒ MK ∥ (SBD). IC K C 1 3
Tam giác IK C và tam giác I AD đồng dạng nên = = . I D AD 2
Áp dụng định lý Menelaus trong tam giác SCD với bộ điểm thẳng hàng I, M, L ta có LS I D MC LS LS 1 · · = 1 ⇔ · 2 · 1 = 1 ⇔ = . LD IC MS LD LD 2
Áp dụng định lý Menelaus cho tam giác IDL với ba điểm thẳng hàng S, M, C ta có SD ML C I ML ML 1 · · = 1 ⇔ 3 · · 1 = 1 ⇔ = . SL M I CD M I M I 3 3 Từ đó suy ra I M = IL. 4 h I M 3
Gọi h, k là lượt là độ dài đường cao các tam giác IK M và I AL kẻ từ M và L. Dễ thấy rằng = = . k I L 4 Vậy 1 S h I K M · IK 3 1 3 = 2 = · = . S 1 I AL 4 2 8 k · I A 2 ä
BÀI 595. Cho hai hình vuông ABCD và ABEF ở trong hai mặt phẳng phân biệt. Trên các đường chéo AC và BF lần
lượt lấy các điểm M, N sao cho AM = BN. Các đường thẳng song song với AB vẽ từ M, N lần lượt cắt AD và AF tại M0 và N0. 3. HAI MẶT PHẲNG SONG SONG 393
1 Chứng minh rằng (ADF) ∥ (BCE).
2 Chứng minh rằng (CDF) ∥ (MM0N0N). Lời giải. F E N N0 A B M0 M D C AD ∥ BC 1 Ta có AF ∥ BE ⇒ (ADE) ∥ (BCF). AD ∩ AF = A 2 Ta có AM AM0 M M0 ∥ CD ⇒ = (1) AC AD Ta cũng có BN AN0 N N0 ∥ AB ⇒ = (2) BF AF Mà từ giả thiết ta có AM BN AM0 AN0 = ⇒ = (3) AC BF AD AF
Từ (3) suy ra M0N0 ∥ DF. Ta cũng có MM0 ∥ N N0 ∥ DC ∥ FE. Vậy (CDF) ∥ (MM0N0N). ä
BÀI 596. Cho hình lăng trụ ABC.A0B0C0. Gọi I, J, K lần lượt là trọng tâm các tam giác ABC, ACC0, A0B0C0. Chứng
minh rằng (I JK) ∥ (BCC0B0) và (A0 JK) ∥ (AIB0). Lời giải. A0 C0 K P B0 N J A C I M B 1
Gọi M, N, P lần lượt là trung điểm của BC, CC0 và B0C0. Theo tính chất của trọng tâm tam giác ta có A I A J = ⇒ I J ∥ MN. AM AN A I AK 2
Tứ giác AMP A0 là hình bình hành và có = = ⇒ IK ∥ MP. AM AP 3 Vậy (I JK) ∥ (BCC0B0). 2
Chú ý rằng mặt phẳng (AIB0) chính là mặt phẳng (AMB0). Mặt phẳng (A0 JK) chính là mặt phẳng (A0CP).
Vì AM ∥ A0P, MB0 ∥ CP (do tứ giác B0MCP là hình bình hành). Vậy ta có (A0 JK) ∥ (AIB0). ä 394
CHƯƠNG 8. ĐƯỜNG THẲNG VÀ MẶT PHẲNG TRONG KHÔNG GIAN. QUAN HỆ SONG SONG.
BÀI 597. Cho hình chóp S.ABCD có đáy ABCD là hình thang với đáy lớn AD và AD = 2BC, M ∈ BC. Gọi (P) là mặt
phẳng đi qua M, (P) ∥ CD,(P) ∥ SC, (P) cắt AD, S A ,SB lần lượt tại N, P, Q.
1 Chứng minh rằng NQ ∥ (SCD) và NP ∥ SD.
2 Gọi H, K lần lượt là trung điểm của SD và AD. Chứng minh rằng (CHK ) ∥ (S AB). Lời giải. S P H Q A D K N B M C E 1
- Từ M ta kẻ đường thẳng song song với CD cắt AD tại N và cắt AB tại E.
Từ M kẻ đường thẳng song song với SC cắt SB tại Q. Kéo dài EQ cắt S A tại P.
Theo cách dựng ta suy ra (EP N) ∥ (SCD) và NQ ⊂ (EP N). Vậy NQ ∥ (SCD).
- Do (P) ∥ (SCD) và hai mặt phẳng này cùng cắt (S AD) theo các giao tuyến là NP và SD. Do đó ta suy ra N P ∥ SD. 2
Ta có HK là đường trung bình của tam giác S AD nên HK ∥ S A (1)
Vì K là trung điểm của AD nên AK = BC. Do đó tứ giác ABCK là hình bình hành. Suy ra CK ∥ AB (2)
Từ (1) và (2) suy ra (CK H) ∥ (S AB). ä
BÀI 598. Cho hình chóp S ABC có G là trọng tâm tam giác ABC. Trên đoạn S A lấy hai điểm M, N sao cho SM = M N = N A.
1 Chứng minh rằng G M ∥ (SBC).
2 Gọi D là điểm đối xứng với A qua G. Chứng minh rằng (MCD) ∥ (NBG).
3 Gọi H = DM ∩ (SBC). Chứng minh rằng H là trọng tâm tam giác SBC. Lời giải. S M N H A C G E D B AG AM 2 1
Gọi E là trung điểm của BC. Khi đó ta có = =
⇒ GM ∥ SE. Vậy GM ∥ (SBC). AE AS 3 3. HAI MẶT PHẲNG SONG SONG 395 2
Từ giả thiết ta suy ra G, N lần lượt là trung điểm của AD và AM. Do đó NG ∥ MD (1) (1)
Từ giác BDCG có E là trung điểm của hai đường chéo nên đó là hình bình hành. Suy ra BG ∥ CD (2)
Từ (1) và (2) suy ra (MCD) ∥ (NBG). 3
Ta có AE là đường trung tuyến của tam giác SBC (3)
Áp dụng định lý Menelaus cho tam giác S AE với ba điểm thẳng hàng M, H, D ta có HS DE M A HS 1 HS · · · = 1 ⇔ · · 2 = 1 ⇔ = 2 (4) HE D A MS HE 4 HE
Từ (3) và (4) suy ra H là trọng tâm tam giác SBC. ä 396
CHƯƠNG 8. ĐƯỜNG THẲNG VÀ MẶT PHẲNG TRONG KHÔNG GIAN. QUAN HỆ SONG SONG. BÀI 4.
BÀI TẬP ÔN CUỐI CHƯƠNG 2
BÀI 1. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O.
1 Tìm giao tuyến của (S AB) và (SCD).
2 Gọi E là trung điểm của SC. Chứng minh OE ∥ (S AB). SM
3 Gọi F là điểm trên đoạn BD sao cho 3BF = 2BD. Tìm giao điểm M của SB và (AEF). Tính tỉ số . SB Lời giải. S AB ∥ (SCD) 1 Ta có AB ⊂ (S AB)
⇒ (S AB) ∩ (SCD) = Sx ∥ AB. S ∈ (S AB) ∩ (SCD) M OE ∥ S A (đường trung bình) x 2 Ta có S A ⊂ (S AB) ⇒ OE ∥ (S AB). E OE 6⊂ (S AB) I
3 Trong mặt phẳng (S AC) có I = SO ∩ AE. A D ( I ∈ (SBF) Suy ra . F I ∈ (AEF) O SB ⊂ (SBF)
F I = (SBF) ∩ (AEF) ⇒ M ∈ SB ∩ (AEF). C B M = F I ∩ SB Ta có 3BF = 2BD ⇒ 3(OB + OF) = 4OD ⇒ 3OD + 3OF = 4OD ⇒ 3OF = OD OF 1 ⇒ = . (8.1) OD 3 OE OI 1
Mặt khác 4IOE v 4ISM (g.g), suy ra = = suy ra SM S I 2 OI 1 = (2) OS 3
Từ (1) và (2) suy ra F I ∥ SD, suy ra MF ∥ AD. 2 1 1
Mà FD = OD = BD, suy ra SM = SB. 3 3 3 SM 1 Vậy = . SB 3 ä
BÀI 2. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Gọi I, J lần lượt là trọng tâm tam giác S AB
và S AD. Gọi M, N lần lượt là trung điểm của S A, SB.
1 Chứng minh I J ∥ (ABCD).
2 Chứng minh (OM N) ∥ (SDC).
3 Tìm giao tuyến của (S AB) và (SDC).
4 Tìm giao điểm của BC và (OM N). Lời giải.
4. BÀI TẬP ÔN CUỐI CHƯƠNG 2 397 S
1 Gọi P, Q lần lượt là trung điểm của AB và AD, ta có: S I S J 2 = = . SP SQ 3 M Suy ra I J ∥ PQ. I J x ∥ PQ J N
PQ ⊂ (ABCD) ⇒ I J ∥ (ABCD). I J I 6⊂ (SBCD) Q A D
2 Xét hai mặt phẳng (OM N) và (SCD) có: M N ∥ CD (cùng song song AB) M N ∥ (SCD) P O MO ∥ SC ⇒ MO ∥ (SCD) ⇒ (OMN) ∥ M = MN ∩ MO M = MN ∩ MO C B R (SCD). AB ∥ (SCD) 3 Ta có AB ⊂ (S AB)
⇒ (S AB) ∩ (SCD) = Sx ∥ AB. S ∈ (S AB) ∩ (SCD)
4 Gọi R là trung điểm BC, dễ dàng chứng minh M N ∥ RQ. BC ⊂ (ABCD) Ta có
(OM N) ∩ (ABCD) = RQ ⇒ R = BC ∩ (OMN). R = BC ∩ RQ ä
BÀI 3. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Gọi H, I, K , L lần lượt là trung điểm của S A, SC, OB, SD.
1 Xác định giao tuyến của mặt phẳng (S AC) và (SBD); (H I K ) và (SBD).
2 Chứng minh OL song song với (H I K ).
3 Xác định thiết diện của hình chóp S.ABCD bị cắt bởi mặt phẳng (H I K ). Lời giải. 398
CHƯƠNG 8. ĐƯỜNG THẲNG VÀ MẶT PHẲNG TRONG KHÔNG GIAN. QUAN HỆ SONG SONG. S (SO ⊂ (SAC) 1 Ta có ⇒ SO = (S AC) ∩ (SBD). Q SO ⊂ (SBD)
Gọi M là giao điểm của SO và H I, ta có: K ∈ BO ⊂ (SBD) L H K ∈ (H I K ) ⇒ MK = (H IK) ∩ (SBD). M M ∈ SO ⊂ (SBD) I M ∈ H I ⊂ (H IK) A D
2 Trong tam giác S AC có H I ∥ AC nên theo định lí Talet ta có SM 1
= , suy ra M là trung điểm SO. SO 2 N O
Trong tam giác SOB có MK ∥ SB (tính chất trung bình), trong
tam giác SBD có OL ∥ SB (tính chất trung bình). Do đó, OL ∥ K C MK . B P OL ∥ MK Ta có
MK ⊂ (H IK) ⇒ OL ∥ (HIK). OL 6⊂ (H IK)
3 Gọi N, P lần lượt là trung điểm của AB và BC, từ đó dễ dàng
chứng minh được N, K, P thẳng hàng. Gọi Q là giao điểm của MK và SD.
Suy ra NP ∥ AC ⇒ NP ∥ HI (tính chất trung bình). HN = (HIK) ∩ (SAB) P I = (H I K ) ∩ (SBC) Ta có Q I = (H IK) ∩ (SCD) HQ = (H I K ) ∩ (S AD) N P = (H I K ) ∩ (ABCD).
Do đó, thiết diện tạo bởi (H IK) và hình chóp S.ABCD là ngũ giác HNP IQ. ä
BÀI 4. Cho hình chóp S.ABCD có đáy ABCD là hình thang cạnh đáy lớn AD. Gọi E, F lần lượt là các điểm trên hai SE SF 1
cạnh S A, SD thỏa mãn điều kiện =
= . Gọi G là trọng tâm tam giác ABC. S A SD 3
1 Tìm giao tuyến của (S AB) và (SCD), của (S AD) và (SBC).
2 Tìm giao điểm H của CD và (EFG).
3 Chứng minh EG ∥ (SBC).
4 Xác định thiết diện của hình chóp S.ABCD bị cắt bởi (EFG). Nó là hình gì? Lời giải.
4. BÀI TẬP ÔN CUỐI CHƯƠNG 2 399 S x
1 Gọi I là giao điểm của AB và CD, ta có: F S ∈ (SAB) E S ∈ (SCD) ⇒ SI = (S AB) ∩ (SCD). I ∈ AB ⊂ (S AB) I ∈ CD ⊂ (SCD) BC ∥ AD A D A D ⊂ (S AD) Ta có
⇒ (S AD) ∩ (SBC) = Sx ∥ BC. BC K G ⊂ (SBC) H S ∈ (S AB) ∩ (SBC) C B AK 2
2 Theo định lí Talet thì EF ∥ AD, lấy điểm K trên AB sao cho = , do AB 3 đó:
Cũng theo định lí Talet thì KG ∥ BC mà BC ∥ AB nên EF ∥ KG. I
Gọi H là giao điểm của KG và CD, ta có: (H ∈ CD ⇒ H ∈ CD ∩ (EFG). H ∈ K H ⊂ (EFG) EF ∥ BC ⊂ (SBC) 3 Ta có
EK ∥ SB ⊂ (SBC) ⇒ (EFG) ∥ (SBC) ⇒ EG ∥ (SBC). E = EF ∩ EK EF = (EFG) ∩ (S AD) F H = (EFG) ∩ (SBD) K H = (EFG) ∩ ( ABCD) 4 Ta có EK = (EFG) ∩ (S AB) ∅ = (EFG) ∩ (SBC) EF.
Vậy mặt phẳng (EFG) cắt hình chóp S.ABCD là hình thang EF HK. ä
BÀI 5. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi G là trọng tâm 4S AB. Lấy điểm M thuộc cạnh AD sao cho AD = 3AM.
1 Tìm giao tuyến của hai mặt phẳng (S AD) và (GCD).
2 Tìm giao điểm I của CD và mặt phẳng (SG M).
3 Chứng minh MG song song (SCD). Lời giải. 400
CHƯƠNG 8. ĐƯỜNG THẲNG VÀ MẶT PHẲNG TRONG KHÔNG GIAN. QUAN HỆ SONG SONG. S 2
1 Lấy điểm N trên S A sao cho SN = S A, ta có: 3
(GN ∥ AB ⇒GN ∥CD ⇒GN ⊂(GCD). I AB ∥ CD N N ∈ SA ⊂ (SAD) G M N ∈ G D ⊂ (GCD) Do đó, ⇒ ND = (GCD) ∩ (S AD). D A D ∈ (S AD) D ∈ (GCD) P O
2 Gọi P là trung điểm AB và I là giao điểm của P M và CD, ta có: C ( I ∈ CD B ⇒ I ∈ CD ∩ (SGM). I ∈ P M ⊂ (SGM) CD ∥ GN 3 Ta có
G N ⊂ (GMN) ⇒ CD ∥ (GMN). (1) CD 6⊂ (GMN) AN AM 1 =
= , theo định lí Talet ta được MN ∥ SD. AS AD 3 SD ∥ MN
M N ⊂ (GMN) ⇒ SD ∥ (GMN). (2) SD 6⊂ (GMN)
Từ (1) và (2) suy ra, (SCD) ∥ (GMN) ⇒ GM ∥ (SCD). ä
BÀI 6. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N lần lượt là trung điểm S A, SB.
1 Tìm giao tuyến của (MBC) và (S AD).
2 Chứng minh (M N ∥ (SCD).
3 Gọi I = DM ∩ CN. Chứng minh SI ∥ (N AD). Lời giải. S I
1 Gọi P là trung điểm của SD, ta có:
(MP ∥ AD ⇒ MP ∥BC ⇒ MP ⊂(MBC). P AD ∥ BC M M ∈ (MBC) N M ∈ (S AD) ⇒ MP = (MBC) ∩ (S AD). P A ∈ SD ⊂ (S AD) D P ∈ MP ⊂ (MBC) M N ∥ AB ∥ CD O 2 Ta có CD ⊂ (SCD) ⇒ MN ∥ (SCD). C B M N 6⊂ (SCD) 1 1 3 Ta có M N = AB =
CD suy ra M N là đường trung 2 2
bình của 4ICD, do đó M là trung điểm ID.
Dễ dàng chứng minh 4MSI = 4M AD (c.g.c). Suy ra S I M =
AD M ⇒ SI ∥ AD (so le trong). S I ∥ AD
AD ⊂ (N AD) ⇒ SI ∥ (N AD). S I 6⊂ (N AD) ä
Document Outline
- I Đại số - Giải tích
- Hàm số lượng giác - Phương trình lượng giác
- Công thức lượng giác cần nắm
- Tóm tắt lý thuyết
- Hàm số lượng giác
- Tóm tắt lý thuyết
- Các dạng toán thường gặp
- violetDạng 2.1. Tìm tập xác định của hàm số lượng giác
- Bài tập vận dụng
- Bài tập tự luyện
- violetDạng 2.2. Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số lượng giác
- Ví dụ
- Bài tập áp dụng
- Bài tập rèn luyện
- violetDạng 2.3. Xét tính chẵn lẻ của hàm số lượng giác
- Ví dụ
- Bài tập áp dụng
- Bài tập rèn luyện
- Hàm số lượng giác - phương trình lượng giác
- Phương trình lượng giác
- Phương trình lượng giác cơ bản
- Ví dụ
- Bài tập áp dụng
- Bài tập rèn luyện
- Một số kỹ năng giải phương trình lượng giác
- violetDạng 1.1. Sử dụng thành thạo cung liên kết
- Ví dụ
- Bài tập áp dụng
- Bài tập rèn luyện
- violetDạng 1.2. Ghép cung thích hợp để áp dụng công thức tích thành tổng
- Ví dụ
- Bài tập áp dụng
- Bài tập rèn luyện
- violetDạng 1.3. Hạ bậc khi gặp bậc chẵn của sin và cos
- Ví dụ
- Bài tập áp dụng
- Bài tập rèn luyện
- violetDạng 1.4. Xác định nhân tử chung để đưa về phương trình tích
- Ví dụ
- Bài tập áp dụng
- Bài tập rèn luyện
- Hàm số lượng giác - phương trình lượng giác
- Phương trình lượng giác đưa về bậc hai và bậc cao cùng một hàm lượng giác
- Tóm tắt lý thuyết
- Dạng toán và bài tập
- Ví dụ
- Bài tập vận dụng
- Bài tập tự luyện
- Phương trình bậc nhất đối với sin và cos
- Tóm tắt lý thuyết
- Ví dụ và bài tập
- Ví dụ
- Bài tập áp dụng
- Bài tập rèn luyện
- Phương trình lượng giác đẳng cấp (bậc 2, bậc 3, bậc 4)
- Tóm tắt lý thuyết
- Ví dụ
- Bài tập áp dụng
- Phương trình lượng giác đối xứng
- Tóm tắt lý thuyết
- Ví dụ
- Bài tập áp dụng
- Bài tập rèn luyện
- Một số phương trình lượng giác khác
- Tóm tắt lý thuyết
- Ví dụ
- Bài tập áp dụng
- Bài tập rèn luyện
- Phương trình lượng giác có cách giải đặc biệt
- Tóm tắt lý thuyết
- Ví dụ
- Bài tập áp dụng
- Bài tập rèn luyện
- Bài tập ôn cuối chương I
- Phương trình lượng giác đưa về bậc hai và bậc cao cùng một hàm lượng giác
- Tổ hợp và xác suất
- Các quy tắc đếm cơ bản
- Tóm tắt lý thuyết
- Dạng toán và bài tập
- Ví dụ
- violetDạng 1.1. Bài toán sử dụng quy tắc cộng
- violetDạng 1.2. Bài toán sử dụng quy tắc nhân
- violetDạng 1.3. Bài toán sử dụng quy tắc bù trừ
- Bài tập áp dụng
- Hoán vị - Chỉnh hợp - Tổ hợp
- Tóm tắt lý thuyết
- Ví dụ minh họa
- Dạng toán và bài tập
- violetDạng 2.1. Giải phương trình, bất phương trình, hệ phương trình
- Ví dụ
- Bài tập áp dụng
- Bài tập rèn luyện
- violetDạng 2.2. Các bài toán sử dụng hoán vị
- Ví dụ
- Bài tập áp dụng
- Bài tập rèn luyện
- violetDạng 2.3. Các bài toán sử dụng chỉnh hợp
- Ví dụ
- Bài tập áp dụng
- Bài tập rèn luyện
- violetDạng 2.4. Các bài toán sử dụng tổ hợp
- Ví dụ
- Bài tập áp dụng
- Bài tập rèn luyện
- Nhị thức Newton
- Nhị thức Newton
- Tam giác Pascal
- Dạng toán và bài tập
- violetDạng 3.1. Tìm hệ số hoặc số hạng thỏa mãn điều kiện cho trước
- Ví dụ minh họa
- Bài tập áp dụng
- Bài tập rèn luyện
- violetDạng 3.2. Tìm hệ số trong khai triển nhị thức Niu-tơn (a+b)n
- Ví dụ
- Bài tập áp dụng
- Bài tập rèn luyện
- violetDạng 3.3. Chứng minh hoặc tính tổng
- Ví dụ
- Bài tập áp dụng
- Bài tập rèn luyện
- Biến cố và xác suất của biến cố
- Phép thử
- Biến cố
- Xác suất
- violetDạng 4.1. Chọn hoặc sắp xếp đồ vật
- Lí thuyết
- Ví dụ
- Bài tập rèn luyện
- Bài tập tự luyện
- violetDạng 4.2. Chọn hoặc sắp xếp người
- Lí thuyết
- Ví dụ
- Bài tập rèn luyện
- Bài tập tự luyện
- violetDạng 4.3. Chọn hoặc sắp xếp số
- Lí thuyết
- Ví dụ
- Bài tập rèn luyện
- Bài tập tự luyện
- Các quy tắc tính xác suất
- Tóm tắt lý thuyết
- Quy tắc cộng xác suất
- Quy tắc nhân xác suất
- Bài tập áp dụng
- Tóm tắt lý thuyết
- Bài tập ôn chương 2
- Dãy số - Cấp số cộng - Cấp số nhân
- Phương pháp quy nạp toán học
- Tóm tắt lý thuyết
- Dạng toán và bài tập
- violetDạng 1.1. Chứng minh mệnh đề P(n) đúng với mọi số tự nhiên n
- Ví dụ
- Bài tập áp dụng
- Bài tập rèn luyện
- Dãy số
- Tóm tắt lý thuyết
- Định nghĩa
- Cách cho một dãy số
- Dãy số tăng, dãy số giảm
- Dãy số bị chặn
- Dạng toán và bài tập
- violetDạng 2.1. Tìm số hạng của dãy số cho trước
- Ví dụ
- Bài tập áp dụng
- Bài tập rèn luyện
- violetDạng 2.2. Xét tính tăng, giảm của dãy số
- Ví dụ
- Bài tập áp dụng
- Bài tập rèn luyện
- violetDạng 2.3. Tính bị chặn của dãy số
- Ví dụ
- Bài tập áp dụng
- Bài tập rèn luyện
- Cấp số cộng
- Tóm tắt lý thuyết
- Dạng toán và bài tập
- Ví dụ
- Bài tập áp dụng
- Cấp số nhân
- Tóm tắt lý thuyết
- Dạng toán và bài tập
- Ví dụ
- Bài tập áp dụng
- Bài tập rèn luyện
- II Hình học
- Phép biến hình
- Mở đầu về phép biến hình
- Tóm tắt lý thuyết
- Phép tịnh tiến
- Tóm tắt lý thuyết
- Dạng toán và bài tập
- violetDạng 2.1. Xác định ảnh của một hình qua phép tịnh tiến
- Ví dụ
- Bài tập áp dụng
- Bài tập rèn luyện
- violetDạng 2.2. Xác định phép tịnh tiến khi biết ảnh và tạo ảnh
- Ví dụ
- Bài tập áp dụng
- Bài tập rèn luyện
- violetDạng 2.3. Các bài toán ứng dụng của phép tịnh tiến
- Ví dụ
- Bài tập áp dụng
- Bài tập rèn luyện
- Phép đối xứng trục (Bài đọc thêm)
- Định nghĩa
- Biểu thức tọa độ
- Tính chất
- Trục đối xứng của một hình
- Phép quay
- Tóm tắt lý thuyết
- Dạng toán và bài tập
- violetDạng 4.1. Tìm tọa độ ảnh của một điểm qua phép quay
- Ví dụ
- Bài tập áp dụng
- Bài tập rèn luyện
- violetDạng 4.2. Tìm phương trình ảnh của một đường tròn qua phép quay
- Ví dụ
- Bài tập áp dụng
- Bài tập rèn luyện
- Phép đối xứng tâm
- Tóm tắt lý thuyết
- Phép vị tự và phép đồng dạng
- Tóm tắt lý thuyết
- Dạng toán và bài tập
- violetDạng 6.1. Phép vị tự trong hệ tọa độ Oxy
- Ví dụ
- Bài tập áp dụng
- Đường thẳng và mặt phẳng trong không gian
- Đại cương về đường thẳng và mặt phẳng
- Tóm tắt lý thuyết
- Dạng toán và bài tập
- violetDạng 1.1. Xác định giao tuyến của hai mặt phẳng
- Ví dụ
- Bài tập áp dụng
- Bài tập tự luyện
- violetDạng 1.2. Tìm giao điểm của đường thẳng d và mặt phẳng ()
- Ví dụ
- Bài tập áp dụng
- Bài tập rèn luyện
- violetDạng 1.3. Tìm thiết diện của hình chóp khi cắt bởi mặt phẳng ().
- Ví dụ
- Bài tập áp dụng
- Bài tập tự luyện
- violetDạng 1.4. Chứng minh ba điểm thẳng hàng
- Ví dụ
- Bài tập áp dụng
- Bài tập rèn luyện
- violetDạng 1.5. Chứng minh ba đường thẳng đồng quy
- Ví dụ
- Bài tập áp dụng
- Bài tập rèn luyện
- Đường thẳng và mặt phẳng trong không gian. Quan hệ song song.
- Hai đường thẳng song song.
- Tóm tắt lý thuyết
- Dạng toán và bài tập
- violetDạng 1.1. Chứng minh hai đường thẳng song song.
- Ví dụ
- Bài tập áp dụng
- Bài tập rèn luyện
- violetDạng 1.2. Tìm giao tuyến của hai mặt phẳng chứa hai đường thẳng song song.
- Ví dụ
- Bài tập áp dụng
- Bài tập rèn luyện
- Đường thẳng song song với mặt phẳng
- Tóm tắt lý thuyết
- Dạng toán và bài tập
- violetDạng 2.1. Chứng minh dường thẳng a song song với mặt phẳng (P)
- Ví dụ
- violetDạng 2.2. Tìm giao tuyến của hai mặt phẳng
- violetDạng 2.3. Tìm thiết diện song song với một đường thẳng
- Bài tập áp dụng
- Hai mặt phẳng song song
- Tóm tắt lý thuyết
- Vị trí tương đối của hai mặt phẳng phân biệt
- Các định lí
- Ví dụ
- Bài tập áp dụng
- Tóm tắt lý thuyết
- Bài tập ôn cuối chương 2
- violetDạng 2.3. Tìm thiết diện song song với một đường thẳng
- Hai đường thẳng song song.
- Đại cương về đường thẳng và mặt phẳng
- Mở đầu về phép biến hình
- Phép biến hình
- Tóm tắt lý thuyết
- Phương pháp quy nạp toán học
- violetDạng 1.3. Bài toán sử dụng quy tắc bù trừ
- violetDạng 1.2. Bài toán sử dụng quy tắc nhân
- Các quy tắc đếm cơ bản
- Phương trình lượng giác cơ bản
- Phương trình lượng giác
- Công thức lượng giác cần nắm
- Hàm số lượng giác - Phương trình lượng giác




