Hướng dẫn giải toán chuyên đề dãy số – Nguyễn Minh Hải

Tài liệu gồm 23 trang hướng dẫn giải toán chuyên đề dãy số, tài liệu được biên soạn bởi thầy Nguyễn Minh Hải.

Phần 1. Một số vấn đề về lý thuyết
I – Phương pháp quy nạp toán học

34 17 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Chương 5: Giới hạn. Hàm số liên tục (KNTT)

Môn: Toán 11

Thông tin:

23 trang 7 tháng trước

Tác giả:

Profile Kim Oanh
NguyÔn Minh H¶i. THPT Lª Xoay - VÜnh Têng - VÜnh phóc
VT. 05 - 2009
1
Lêi nãi ®Çu
Mét trong nh÷ng ph¬ng ph¸p rÊt m¹nh trong to¸n häc dïng nghiªn cøu vµ
chøng minh c¸c gi¶ thiÕt lµ nguyªn lý quy n¹p to¸n häc. Ph¬ng ph¸p quy n¹p
®îc ¸p dông s©u réng vµo hÇu hÕt c¸c d¹ng to¸n: Sè häc, D·y sè, H×nh häc,
B§T, Tæ hîp,…Trong b¸o c¸o nµy t«i chØ ®Ò cËp ®Õn ¸p dông cña ph¬ng ph¸p
quy n¹p vµo mét sè d¹ng to¸n vÒ d·y sè.
Trong ch¬ng tr×nh to¸n phæ th«ng th× to¸n vÒ d·y sè ®îc ph©n phèi thêi
lîng kh«ng nhiÒu, ®Æc biÖt trong ch¬ng tr×nh to¸n ph©n ban hiÖn nay ®· lîc
bá nhiÒu ®Þnh lý quan träng.Trong phÇn lín c¸c kú thi th× d¹ng to¸n nµy hÇu nh
kh«ng cã. To¸n vÒ d·y sè thêng chØ giµnh cho nh÷ng häc sinh kh¸ giái trong
c¸c kú thi cÊp TØnh vµ Quèc gia, do vËy nã cµng Ýt ®îc häc sinh vµ c¶ gi¸o viªn
quan t©m ®Õn. PhÇn v× d¹ng to¸n nµy còng t¬ng ®èi khã vµ trõu tîng ®èi víi
häc sinh, häc sinh gÆp nhiÒu khã kh¨n vµ rÊt ng¹i khi gÆp d¹ng to¸n nµy.
Trong thêi gian võa qua t«i ®· thu thËp, tÝch lòy vµ hÖ thèng ®îc mét sè d¹ng
to¸n vÒ d·y sè nh»m phôc vô cho c«ng t¸c gi¶ng d¹y, båi dìng häc sinh giái cña
m×nh. Víi môc ®Ých gióp häc sinh tiÕp cËn mét sè d¹ng to¸n ®Æc trng vÒ d·y sè
do ®ã t«i lùa chän ®Ò tµi nµy. C¸c bµi to¸n ®îc lùa chän chñ yÕu cho nh÷ng häc
sinh kh¸, giái. Sù ph©n chia thµnh c¸c d¹ng to¸n vµ nh÷ng ®¸nh gi¸ cña t«i lµ
theo quan ®iÓm chñ quan cña m×nh, do ®ã kh«ng tr¸nh khái nh÷ng thiÕu sãt.
KÝnh mong c¸c thÇy c« vµ c¸c b¹n ®ång nghiÖp ®äc vµ cho ý kiÕn gãp ý ®Ó tµi
liÖu nµy ®îc hoµn thiÖn h¬n.
Xin ch©n thµnh c¸m ¬n !
VÜnh Têng 5 . 2009
T¸c gi¶: NguyÔn Minh H¶i
NguyÔn Minh H¶i. THPT Lª Xoay - VÜnh Têng - VÜnh phóc
VT. 05 - 2009
2
Môc lôc
TT Néi dung Trang
Lêi nãi ®Çu 1
PhÇn 1 Mét sè vÊn ®Ò vÒ lý thuyÕt
I
Ph¬ng ph
¸p quy n¹p to¸n häc 3
II
M
ét sè vÊn ®Ò vÒ d·y sè 5
III
M
ét sè d¹ng to¸n vÒ d·y sè thêng gÆp 6
PhÇn 2
¸p dông gi¶i to¸n
I
Chøng minh
d·y sè t¨ng, gi¶m vµ bÞ chÆn 8
II
C«ng thøc
tæng qu¸t cña d·y sè 10
III
T×m giíi h¹n cña d·y sè 12
IV
Mét sè d¹ng to¸n kh¸c 18
PhÇn 3 Bµi tËp tổng hîp 21
Tµi liÖu tham kh¶o 23
NguyÔn Minh H¶i. THPT Lª Xoay - VÜnh Têng - VÜnh phóc
VT. 05 - 2009
3
PhÇn
1
. Mét
sè vÊn ®Ò vÒ nguyªn lý Quy n¹p to¸n häc vµ D·y sè
.
I.
Ph¬ng ph¸p quy n¹p to¸
n häc
Sau ®©y
lµ ba d¹ng cña nguyªn lÝ quy n¹p to¸n häc thêng ®îc dïng trong nh÷n
g
bµi to¸n
ë THP
T.
1. §Þnh lÝ 1
.
Cho n
0
lµ
mét sè nguyªn d¬ng vµ P(n) lµ mÖnh ®Ò cã nghÜa víi mäi sè t
ù
nhiªn
0
.
n n
NÕu: 1
0
. P(n
0
) lµ
mÖnh ®Ò ®óng
2
0
.
NÕu P(k) ®óng th× P(k+1) còng ®óng víi mçi sè tù nhiª
n
0
.
k n
Khi ®ã mÖnh ®Ó P(n) ®óng víi mäi sè tù nhiªn
0
.
n n
VÝ dô 1. Cho d·y sè (u
n
) x¸c ®inh bëi: u
n
= n
2
.
CMR tång cña n phÇn tö ®Çu tiªn cña d·y ®îc tÝnh:
(
1)(2 1)
6
n
n
n n
S
Chøng minh
.
Víi n = 1. §¼ng thøc ®óng.
Gi¶ sö §T ®óng víi n = k ( k ≥ 1), tøc lµ cã:
(
1)(2 1)
.
6
k
k
k k
S
Ta chøng minh §T ®óng víi n = k+1, tøc CM:
1
(
1)( 2)(2 3)
.
6
k
k
k k
S
ThËt
vËy. Ta cã
2
2
1
( 1)(2 1) ( 1)( 2)(2 3)
( 1) ( 1) .
6
6
k
k
k k k k k k
S S k k
VËy §T ®óng víi mäi sè nguyªn d¬ng.
2. §Þnh lÝ 2
.
Cho p lµ sè nguyªn d¬ng vµ d·y c¸c mÖnh ®Ò: P(1), P(2), …,
P(n),…
NÕu: 1
0
. P(1),
P(2), …, P(p) lµ nh÷ng mÖnh ®Ò ®óng
2
0
.
Víi mçi sè tù nhiªn
k
p
c¸c mÖnh ®Ò
(
1), ( 2), ..., ( )
P
k p P k p P k
®óng,
suy ra mÖnh ®Ò P(k+1) còng
®óng.
Khi ®ã mÖnh ®Ó P(n) ®óng víi mäi sè nguyªn d¬ng n.
VÝ dô 2
.
Cho
0
1
2, 3
v v
vµ víi mçi sè tù nhiªn k cã ®¼ng thøc:
1
1
3 2 .
k
k k
v v v
CMR:
2
1.
n
n
v
Chøng m
inh
.
- DÔ
thÊy mÖnh ®Ò ®óng víi n = 0, 1.
NguyÔn Minh H¶i. THPT Lª Xoay - VÜnh Têng - VÜnh phóc
VT. 05 - 2009
4
- Gi¶ sö
víi mçi sè tù nhiªn
2
k
m®
®óng víi n = k vµ n = k –
1.
Tøc lµ cã:
1
1
2 1, 2 1.
k
k
k k
v v
-Ta
chøng minh m® ®óng víi n = k +
1.
TV. Theo CT truy håi
1 1
1 1
3 2 3(2 1) 2(2 1) 2 1. ( )
k k k
k k k
v v v dpcm
VËy bµi to¸n ®îc chøng minh.
3. §Þnh lÝ 3. Cho d·y c¸c mÖnh ®Ò: P(1), P(2), …, P(n),…
NÕu: 1
0
. P(1) lµ
nh÷ng mÖnh ®Ò ®óng
2
0
.
Víi mçi sè tù nhiªn
1
k
c¸c mÖnh ®Ò
(
1), (2), ..., ( )
P
P P k
®óng,
suy ra mÖnh ®Ò P(k+1) còng ®óng.
Khi ®ã mÖnh ®Ó P(n) ®óng víi mäi sè nguyªn d¬ng n.
D¹ng quy n¹p nµy m¹nh h¬n d¹ng thø hai ë bíc quy n¹p.
VÝ dô 3
.
Cho d·y sè (u
n
) x¸c ®inh
bëi:
*
*
1
1
,
, . .
n
n
n
U
x n N x N U Z
x
CMR (u
n
) lµ d·y c¸c sè nguyªn.
Chøng minh
Víi n = 1 mÖnh ®Ò hiÓn nhiªn ®óng.
Gi¶ sö víi mäi sè tù nhiªn tõ 1 ®Õn k, u
k
lµ
sè nguyªn. Ta CM u
k+1
còng nguyªn.
TV.
1
1
1 1 1
1 1
1
1 1 1
( )( ) ( ) .
k
k k
k k k
k k k
u
x x x x u u u Z
x x x x
VËy (u
n
) lµ
d·y c¸c sè nguyªn.
NguyÔn Minh H¶i. THPT Lª Xoay - VÜnh Têng - VÜnh phóc
VT. 05 - 2009
5
II. M
ét sè vÊn ®Ò vÒ d·y sè
.
2.1.
D·y sè t¨ng, gi¶m (®¬n ®iÖu).
§N. D·y sè (u
n
) ®îc gäi lµ d·y t¨ng nÕu víi mäi
*
n
N
ta cã u
n
< u
n+1
.
D·y sè (u
n
) ®îc
gäi lµ d·y gi¶m nÕu víi mäi
*
n
N
ta
cã u
n
> u
n+1
.
D·y sè t¨ng vµ d·y gi¶m ®îc gäi chung lµ d·y ®¬n ®iÖu.
2.2. D·y bÞ chÆn.
§N
+) D·y sè (u
n
) ®îc
gäi lµ d·y bÞ chÆn trªn, nÕu tån t¹i mét sè M sao c
ho
*
,
.
n
u
M n N
+) D·y sè (u
n
) ®îc
gäi lµ d·y bÞ chÆn díi, nÕu tån t¹i mét sè m sao cho
*
,
.
n
u
m n N
+) D·y sè (u
n
) ®îc
gäi lµ d·y bÞ chÆn nÕu nã võa bÞ chÆn trªn võa bÞ chÆn díi,
tøc lµ tån t¹i c¸c sè m, M sao cho
*
, .
n
m u M n N
*
(
0 : , )
n
M
u M n N
2.
3. Giíi h¹n d·y sè.
§N 1. D·y sè (u
n
) cã giíi h¹n 0 nÕu víi mçi sè d¬ng nhá tuú ý cho tríc, mäi sè
h¹ng cña d·y sè, kÓ tõ mét sè h¹ng nµo ®ã trë ®i, ®Òu cã gi¸ trÞ tuyÖt ®èi nhá
h¬n sè d¬ng ®ã. Ta viÕt lim(u
n
)
= 0 hoÆc limu
n
= 0 hoÆc u
n
0.
C¸ch ph¸t biÓu míi nµy gióp häc sinh h×nh dung ®îc d·y sè cã giíi h¹n 0 mét c¸ch
thuËn lîi h¬n, tuy nhiªn ®Þnh nghÜa nµy khã diÔn ®¹t trong khi chøng minh mét sè ®Þnh
lý vÒ giíi h¹n. Do vËy t«i xin trë l¹i ®Þnh nghÜa tríc ®©y:
§N 2
.
Ta nãi r»ng d·y sè (u
n
) cã
giíi h¹n 0 nÕu víi mçi sè d¬ng
bÊt kú, tån t¹i
mét sè nguyªn d¬ng N sao cho
*
n
n
N , n N | u | .
Ta viÕt lim(u
n
) =
0 hoÆc limu
n
= 0 hoÆc u
n
0.
§N 3
.
Ta nãi d·y sè (u
n
) cã
giíi h¹n lµ sè thùc L nÕu lim(u
n
– L) = 0.
Ta viÕt lim(u
n
) =
L hoÆc limu
n
=
L hoÆc u
n
L.
§N 4
.
- Ta nãi d·y
sè (u
n
) cã
giíi h¹n +
nÕu
víi mçi sè d¬ng tuú ý cho tríc, mäi
sè
h¹ng cña d·y sè, kÓ tõ mét sè h¹ng nµo ®ã trë ®i, ®Òu lín h¬n sè d¬ng ®ã.
NguyÔn Minh H¶i. THPT Lª Xoay - VÜnh Têng - VÜnh phóc
VT. 05 - 2009
6
- Ta nãi d·y sè (u
n
) cã
giíi h¹n -
nÕu víi mçi sè ©m tuú ý cho tríc, mäi s
è
h¹ng cña d·y sè, kÓ tõ mét sè h¹ng nµo ®ã trë ®i, ®Òu nhá h¬n sè d¬ng ®ã.
§Þnh lÝ 1
.
Cho hai d·y sè (u
n
) vµ
(v
n
).
NÕu | u
n
| v
n
víi mäi n vµ limv
n
=
0 th× limu
n
= 0.
§Þnh lÝ 2
.
NÕu | q| < 1 th× lim q
n
=
0.
§Þnh lÝ 3
.
Gi¶ sö lim u
n
=
L. Khi
®ã:
a) lim |
u
n
| = | L | vµ
3
3
n
l
im u L.
b) NÕu u
n
0 víi mäi n th× L 0 vµ
n
l
im u L.
§Þnh lÝ 4
.
Gi¶ sö lim u
n
= L, lim v
n
= M
vµ c lµ mét h»ng sè. Khi
®ã:
lim( ) .
n
n
u v L M
lim( . ) .
n
n
u v L M
n
lim(c.u ) c.L
l
im
n
n
u
L
v
M
nÕu M 0.
§Þnh lÝ 5
.
NÕu lim |u
n
|
= + th×
n
1
l
im 0.
u
VËn dông c¸c kÕt qu¶ trªn, ta cã thÓ chóng minh ®îc c¸c ®Þnh lý sau:
§Þnh lÝ 6
.
(§iÒu kiÖn cÇn) Mét d·y sè cã giíi h¹n th× nã bÞ chÆn.
§Þnh lÝ 7. (Duy nhÊt) Mét d·y sè cã giíi h¹n th× giíi h¹n ®ã lµ duy nhÊt.
§Þnh lÝ 8
.
(Giíi h¹n kÑp) Cho ba d·y sè (u
n
),
(v
n
),
(w
n
) tháa m·n:
0
*
1
. , .
n
n n
v
u w n N
0
2
. lim lim
n
n
v
w A
th× lim u
n
= A.
Ta thõa nhËn ®Þnh lÝ sau ®©y.
§Þnh lÝ 9
.
(§iÒu kiÖn ®ñ- §Þnh lÝ Waiesstr
as)
Mét d·y t¨ng vµ bÞ chÆn trªn th× cã giíi h¹n.
Mét d·y gi¶m vµ bÞ chÆn díi th× cã giíi h¹n.
HiÖn nay bèn §Þnh lý trªn kh«ng ®îc giíi thiÖu trong ch¬ng tr×nh, tuy nhiªn cã
thÓ chøng minh ®îc §Þnh lÝ 6, 7, 8 tõ c¸c ®Þnh lý cã s½n. Trong b¸o c¸o nµy t«i vÉn
xin ®îc sö dông ®Ó c¸c d¹ng to¸n ®îc ®a d¹ng h¬n.
NguyÔn Minh H¶i. THPT Lª Xoay - VÜnh Têng - VÜnh phóc
VT. 05 - 2009
7
2.4.
CÊp sè céng.
§Þnh nghÜa
.
CÊp sè céng lµ mét d·y sè, trong ®ã, kÓ tõ sè h¹ng thø hai mçi sè
h¹ng
®Òu lµ tæng cña sè h¹ng liÒn tríc víi mét sè kh«ng ®æi gäi lµ c«ng sai.
TÝnh chÊt
. Cho cÊp sè céng ( u
n
) c«ng sai d, khi ®ã
*
n
N
ta cã:
0
1
1
1
. ; ( 1) .
n
n n
u
u d u u n d
0
2
1
2
. .
2
n
n
n
u u
u
0
1
2 1 1
3
. ... ( ) 2 ( 1) .
2 2
n
n n
n
n
S
u u u u u u n d
2.5.
CÊp sè nh©n.
§Þnh nghÜa
.
CÊp sè nh©n lµ mét d·y sè, trong ®ã, kÓ tõ sè h¹ng thø hai mçi sè
h¹ng
®Òu lµ tÝch cña sè h¹ng liÒn tríc víi mét sè kh«ng ®æi gäi lµ c«ng béi.
TÝnh chÊt
.
Cho cÊp sè nh©n ( u
n
)
c«ng béi q, ta cã:
0
1
1
1
1 . . ; . .
n
n
n n
u u q u u q
0
1
2
2 . .
n
n n
u u u
0
1
2 1
1
3
. ... . ; ( 1)
1
n
n
n
q
S u u u u q
q
Tæng cña cÊp sè nh©n v« h¹n c«ng béi q (q <1)
1
1
1
lim
lim . . ( 1)
1 1
n
n
u
q
S S u q
q q
III. Mét
sè d¹ng to¸n vÒ d·y sè thêng gÆp.
1. Chøng m
inh d·y sè t¨ng, gi¶m, bÞ chÆn, d·y cã
giíi h¹n.
2. Chøng m
inh d·y sè lËp thµnh cÊp sè céng, cÊp sè nh©n, tÝnh chÊt cña cÊp sè.
3. T×m c«ng thøc tæng qu¸t cña d·y sè.
4. Chøng minh d·y sè cã giíi h¹n vµ t×m giíi h¹n d·y sè.
5. Mét sè d¹ng kh¸c: B§T vÒ d·y sè, chøng minh tÝnh chÊt chia hÕt, chøng min
h
d·y
sè nguyªn…..
NguyÔn Minh H¶i. THPT Lª Xoay - VÜnh Têng - VÜnh phóc
VT. 05 - 2009
8
PhÇn
2
. ¸
p dông trong gi¶i to¸n
I. Ch
øng minh d·y sè t¨ng, gi¶m vµ bÞ chÆn.
Bµi
1.1
Cho d·y (u
n
):
1
2
1 2
1
, 2.
2
, 3.
n
n n
u
u
u u u n
CMR:
*
5
,
.
2
n
n
u
n N
Gi¶i
ë
bµi to¸n nµy u
n
cho bëi c«ng thøc truy håi, ®îc tÝnh theo u
n-1
vµ u
n-2
do ®ã ta
vËn dông
nguyªn lÝ quy n¹p thø hai ®Ó chøng minh.
- Víi
n = 1, n = 2 mÖnh ®Ò ®óng.
- Gi¶
sö m® ®óng víi n = k – 1, vµ n = k ( k >1), tøc lµ cã:
1
1
5 5
,
.
2
2
n
n
n
n
u
u
- Ta
chøng minh m® ®óng víi n = k +
1.
TV. Ta cã:
1
1
1
2
5
5 5
2
2. .
2
2 2
n
n n
n n n
u
u u
(®pc
m)
Bµi 1.2 Cho d·y (u
n
):
1
*
1
1.
3( 2)
, .
2( 1) 2( 1)
n
n
u
n n
u u n N
n n
a). CM d·y sè bÞ chÆn trªn.
b). CM d·y sè t¨ng.
Gi¶i
§©y
lµ bµi to¸n kh«ng khã nÕu dù ®o¸n ®îc d·y sè bÞ chÆn trªn bëi sè
nµo thÝch
hîp
nhÊt? Ta cã thÓ xuÊt ph¸t tõ yªu cÇu thø hai cña bµi to¸n:
Cã:
1
(
3 )( 2)
0
3.
1
n
n
n n
u
n
u u u
n
a). Ta CM quy n¹p theo nguyªn lÝ thø nhÊt:
*
3
, .
n
u
n N
- Gi¶
sö m® ®óng víi n = k khi ®ã
cã:
1
3
( 2) 3 3( 2)
3.
2(
1) 2( 1) 2( 2) 2( 1)
k
k
k
k k k
u u
k k k k
- VËy
m® ®óng víi n = k +
1.
b).
Theo phÇn (a) cã:
1
(3
)( 2)
0.
1
n
n
n
u
n
u u
n
VËy d·y (u
n
) t¨ng
vµ bÞ chÆn trªn.
NguyÔn Minh H¶i. THPT Lª Xoay - VÜnh Têng - VÜnh phóc
VT. 05 - 2009
9
Bµi
1.3
Chøng minh d·y
1
(
1 )
n
n
u
n
lµ d·y t¨ng vµ bÞ chÆn trªn.
Gi¶i
+) Ta chøng minh
*
3
, .
n
u
n N
- Víi n = 1, n = 2. B§T hiÓn nhiªn
®óng.
- Víi n ≥ 3,
ta chøng minh B§T phô sau
®©y:
2
2
1
(
1 ) 1 , :1 . (1)
k
k k
k k n
n
n n
TV. – Víi k = 1, B§T ®óng .
- Gi¶ sö
(1) ®óng víi k (
1
1
k
n
),
tøc
:
2
2
1
(
1 ) 1 .
k
k k
n
n n
Khi ®ã:
2 2 2
1
2
2 3
1
1 1 1 1
(
1 ) (1 )(1 ) (1 )(1 ) 1 .
k
k
k
k k k k k
n
n n n n n n n n
MÆt kh¸c dÔ dµng CM:
2
2 2
2
3 2
(
1)
.
k
k k k
n
n n
2
1
2
1 1 ( 1)
(
1 ) 1 .
1
( 1)
k
k k
n n n
VË
y B§T ®óng víi k + 1.
KL. B§T (1) ®óng víi mäi sè nguyªn d¬ng k, (
1
k n
)
-) Víi k = n ta cã :
2
2
1
(
1 ) 1 3.
n
n n
n
n n
+
) Chøng minh d·y t¨ng.
¸p dông B§T Cauchy cho n + 1 sè d¬ng kh«ng ®ång thêi b»ng nhau, ta ®îc:
1
1
1 1 1
1
(1 ) (1 ) ... (1 ) ( 1) (1 ) .
n
n
n
n
n n n
1
*
1
1
1 1 1 1
1
(1 ) (1 ) (1 ) , .
1
1
n
n n
n
n n
u
u n N
n
n n n
Bµi 1.5
XÐt tÝnh ®¬n ®iÖu, bÞ chÆn cña c¸c d·y sè sau:
1
0
*
1
2
1
.
1
,
.
2
n
n
u
u
u
n N
1
0
*
1
2
2
.
2
, .
n
n
u
u
u n N
Gi¶i
1
0
. B»
ng quy n¹p ta chøng minh (u
n
) lµ d·y
gi¶m vµ bÞ chÆn díi bëi 0.
2
0
. B»
ng quy n¹p ta chøng minh (u
n
) lµ d·y
t¨ng vµ bÞ chÆn trªn bëi 2.
NguyÔn Minh H¶i. THPT Lª Xoay - VÜnh Têng - VÜnh phóc
VT. 05 - 2009
10
II. C«
ng thøc tæng qu¸t cña d·y sè
.
Bµi
2.1
Cho d·y (u
n
):
1 2
1 1
2
, 3.
3 2 , 2.
n n n
u
u
u u u n
CMR
1
2
1.
n
n
u
T
ính S
n
.
Gi¶i
Quy n¹p. Víi n =1; n = 2. §óng.
Gi¶ sö m® ®óng víi k-1 vµ k (k > 1), ta chøng minh m® ®óng víi n = k + 1.
ThËt vËy: Cã
2
1 1 2 2
1 1
2
1, 2 1 3(2 1) 2(2 1) 4.2 1 2 1.
k
k k k k k
k k k
u
u u
MÖnh ®Ò ®îc chøng minh.
Khi ®ã:
1
1
2
.
.. 1 (1 2) ... (1 2 ) 2 1.
n
n
n n
S
u u u n
Bµi
2.2
Cho d·y (u
n
):
1
*
1
2
, .
1
n
n
n
u
u
u n N
u
a) CMR:
*
0
, .
n
u
n N
b) §Æt
1
.
n
n
n
u
v
u
C
MR
n
3
v
n, n.
2
c). T×m CTTQ tÝnh
n
n 1 2 n
u ,S u u ...u .
Gi¶i
a). Chøng minh b»ng quy n¹p.
- Víi
n = 1 m® ®óng.
- Gi¶
sö m® ®óng víi n = k ( k
1),
tøc
0.
k
u
Khi
®ã
1
0
,1 0 0.
1
k
k
k k
k
u
u
u u
u
- VËy
m® ®óng víi n = k +1
.
b). Ta cã:
1
1 1
.
.
1
n
n
n n n n
n
u
u
u u u u
u
1
1
1
1 1
1
1
1.
.
n
n n n
n n
n n n n
u
u u u
v v
u u u u
1
1 ( )
n
n n
v v v
lµ
CSC c«ng sai d = -1,
1
1
1
1
2 1 1
.
2 2
u
v
u
1
1 3
( 1) ( 1)( 1) .
2 2
n
v v n d n n
Tõ
1
1
2
.
1
2 1
n
n
n
n n
u
v
u
u v n
C¸ch 2. CM quy n¹p.
NguyÔn Minh H¶i. THPT Lª Xoay - VÜnh Têng - VÜnh phóc
VT. 05 - 2009
11
Bµi
2.4
Cho d·y (u
n
):
1
2
1 1
1, 2.
2
2, 2.
n
n n
u u
u u u n
CMR:
2
(
1) 1.
n
u
n
T
×m S
n
?
Gi¶i
- HiÓn
nhiªn c«ng thøc ®óng víi n = 1,
n = 2.
- Gi¶
sö c«ng thøc ®óng víi n = k - 1, n =
k tøc:
2
2
1
( 2) 1; ( 1) 1
k
k
u k u k
Khi
®ã:
2 2 2 2
1 1
2
2 2[( 1) 1] [( 2) 1] 2 1 [( 1) 1] 1
k k k
u
u u k k k k
VËy c«ng thøc ®óng víi n = k + 1.
Khi ®ã:
2
2 2
(
1)(2 1)
( 1) ( 2) ... 1 .
6
n
n
n n
S n n n n
Chó ý
:
NÕu bµi to¸n yªu cÇu chøng minh
1
n
u
lµ
sè chÝnh ph¬ng th× c¸ch lµm
hoµn toµn vÉn nh vËy.
Bµi 2.5
Cho d·y (u
n
):
1
2
1 1
3
, 2.
3 2 1, 2.
n
n n
u
u
u u u n
CMR:
1
1
1
2
2 4.
1
n
n
n
q
u v n n
q
TÝnh S
n
?
Gi¶i
Quy
n¹p: Gi¶ sö:
1
1
2
( 1) 4; 2 4
k
k
k k
u
k u k
1
1 1
1 1
3
2 1 3[ 2 4] 2[ 2 3] 1 8.2 5 2 ( 1) 4
k
k k k
n n n
u
u u k k k k
Bµi
2.6
Cho d·y (u
n
):
*
1
0
1
1
, , .
2.
1 2
n
n
n
u
u u n N
u
n
T×m CTTQ cña u
n
?
Gi¶i
- NÕu
0
0 0, .
n
u u n N
- NÕu
0
0.
u
B»ng quy n¹p ta chøng minh ®îc
0, .
n
u n N
Khi ®ã:
1
1
2
1
1
1
2 .
n
n
n n
u
u
u u
§Æt
1
1
2
n n n n
n
v
v v v
u
lµ CSC c«ng sai
2.
d
0
0
0
0
1 1
2 .
2
. 1
n
n
n
u
v
v nd n u
u v n u
NguyÔn Minh H¶i. THPT Lª Xoay - VÜnh Têng - VÜnh phóc
VT. 05 - 2009
12
III. T×
m giíi h¹n cña
d·y sè.
NÕu d·y sè cho bëi CTTQ th× ta thêng sö dông c¸c ph¬ng ph¸p tÝnh giíi h¹n cña
d·y sè ®Ó tÝnh. Trong nhiÒu trêng hîp ta ph¶i biÕn ®æi CTTQ ®ã vÒ d¹ng ®¬n gi¶n
h¬n tríc khi tÝnh giíi h¹n.
Mét sè ph¬ng ph¸p tÝnh giíi h¹n cña d·y sè:
- Nh©n liªn hîp, ®èi víi giíi h¹n d¹ng
-
- Chia c
¶ tö vµ mÉu cho lòy thõa bËc cao nhÊt cña n, ®èi víi giíi h¹n d¹ng
- KÕ
t hîp hai ph¬ng ph¸p trªn cho giíi h¹
n d¹ng
0
;
; ; .
0
- Sö dôn
g ®Þnh lý giíi h¹n kÑ
p
- Sö dôn
g ®iÒu kiÖn ®ñ ®Ó d·y sè cã giíi h¹n, thiÕt lËp biÓu thøc vÒ
giíi h¹n.
K
Õt qu¶ giíi h¹n lµ nghiÖm cña mét ph¬ng tr×nh nµo ®ã.
Bµi 3.1
TÝnh c¸c giíi h¹n sau:
3
2
3
lim
( )
A
n n n
2
3
4
1
lim
n n
B
n n n
3
2
6
4
2
1
lim
1
n n
C
n n
1
3
2
l
im
2
5.3
n n
n
n
D
1
4.3
7
lim
2.
5 7
n n
n
n
E
2
2
4 1 2 1
l
im
4 1
n n
F
n n n
HD.
1 1 1
; ; 0; ; 7; .
3
5 2
A B C D E F
Bµi
3.2
TÝnh giíi h¹n cña c¸c d·y sè sau
1 1 1
lim ...
1.2 2.3 ( 1)
A
n n
1 1 1
lim ...
1.2.3 2.3.4 ( 1)( 2)
B
n n n
2
2 2
1
1 1
l
im(1 )(1 )...(1 )
2 3
C
n
2 2 2 2
1
3 5 2 1
lim ...
n
D
n n n n
1
1 1 1
l
im ( ... )
1
3 3 5 2 1 2 1
E
n
n n
{§
Ò thi HSG líp 11 n¨m 2007}
NguyÔn Minh H¶i. THPT Lª Xoay - VÜnh Têng - VÜnh phóc
VT. 05 - 2009
13
Häc sinh thêng ¸p dông sai c«ng thøc tÝnh giíi h¹n cña tæng vµ tÝch c¸c d·y sè.
Hai c«ng thøc nµy chØ ¸p dông ®èi víi tæng vµ tÝch h÷u h¹n c¸c d·y sè. Häc sinh
thêng ¸p dông cho tæng, tÝch v« h¹n dÉn ®Õn kÕt qu¶ sai.
Gi¶i
a). NhËn xÐt:
*
1 ( 1) 1 1
,
( 1) ( 1) 1
n n
n
N
n
n n n n n
1
1 1 1 1 1 1 1 1
...
(1 ) ( ) ... ( ) 1
1.2 2.3 ( 1) 2 2 3 1
n
u
n n n n n
1
l
im lim(1 ) 1.
n
A
u
n
b). NhËn xÐt:
*
1 ( 2) 1 1 1
( ),
( 1)( 2) 2 ( 1) 2 ( 1) ( 1)( 2)
n n
n
N
n
n n n n n n n n
1
1 1 1 1 1 1 1 1 1
...
[( ) ( ) ... ( )]
1.2.3 2.3.4 ( 1)( 2) 2 1.2 2.3 2.3 3.4 ( 1) ( 1)( 2)
n
u
n
n n n n n n
1
1 1
.
4
2( 1)( 2) 4
n
u B
n n
c
).
2
2 2
2 2 2
2
1 3 1 1 1.3 2.4 ( 1)( 1) 1 1
.
..... . .... .
2
3 2.2 3.3 . 2 2
n
n
n n n
u C
n
n n n
d).
2
2
2
1
3 5 ... (2 1)
1.
n
n
n
u D
n n
e
). Ta cã:
1 2 1 2 1 2 1 2 1
, 1.
(2 1) (2 1) 2 2
2 1 2 1
n n n n
n
n n
n n
1
1 1 1
(
... )
1
3 3 5 2 1 2 1
n
u
n
n n
1 3 1 5 3 2 1 2 1 1 2 1 1
.
[( ) ( ) ... ( )] .
2 2 2 2 2 2 2
n n n
n n
2 1 1 2
lim lim .
2
2
n
n
E u
n
Bµi
3.3
TÝnh c¸c giíi h¹n sau
2
1
2 3 ...
lim
2
3
n
A
n
n
2
2 2
3
1
2 3 ...
lim
4
1
n
B
n
3
3 3
4
2
1
2 3 ...
lim
3
1
n
C
n
n
2
2 2
3
1
3 5 ... (2 1)
l
im
3
4
n
C
n
n
NguyÔn Minh H¶i. THPT Lª Xoay - VÜnh Têng - VÜnh phóc
VT. 05 - 2009
14
Gi¶i
§
Ó ®¬n gi¶n biÓu thøc ta chøng minh quy n¹p c¸c c«ng thøc
sau:
0
( 1)
1 . 1 2 3 ...
2
n n
n
0
2 2 2
( 1)(2 1)
2 . 1 2 3 ...
6
n n n
n
0
3 3 3
(
1)( 2) ( 1)( 2)( 3)( 4)
3
. 1 2 3 ... 1 8( 1) 19 ( 1)( 2)( 3)
2
4
n
n n n n n
n n n n n
0
2 2 3
1
4
. 1 3 5 ... (2 1) (2 1)(2 1).
3
n
n n n
- Khi ®ã ta cã ®îc c¸c kÕt qu¶ sau:
1
1 1 4
.
. . .
4
12 4 9
A
B C D
Trong n
hiÒu bµi to¸n ta kh«ng thÓ ®¬n gi¶n ®îc CTTQ ®Ó sö dông hai ph¬ng ph¸p
nh©n liªn hîp, hoÆc chia cho lòy thõa cña n. Khi ®ã h·y nghÜ ®Õn
§
Þnh lÝ giíi h¹n kÑp
Bµi
3.4
TÝnh giíi h¹n sau.
2
2 2
1 1 1
lim ...
1 2
A
n n n n
1.3.5.7.
....(2 1)
lim
2.4.6.....(2 )
n
B
n
Gi¶i
a). Ta cã:
2 2 2
1
1 1
,
,1 .
1
k
N k n
n
n n k n
2
2 2 2 2
1
1 1
... ,
1 2 1
n
n
n
u
n n n n n n n
mµ
2 2
lim lim 1
1
n
n
n n n
lim 1 1.
n
u A
b). §Æt
2
2 2 2
2
2 2 2 2 2 2 2
1.
3.5.7.....(2 1) 1.3 .5 .7 .....(2 1) 1.3 3.5 (2
1
).(2 1) 1
.
... .
2.
4.6.....(2 ) 2 .4 .6 .....(2 ) 2 4 (2 ) 2 1
n
n
n
n n n
u u
n
n n n
2
1
1
0
0 ,
2
1
2
1
n
n
u
u
n
n
mµ
1
l
im 0 lim 0.
2
1
n
B
u
n
§èi víi nh÷ng bµi to¸n mµ d·y sè cho bëi c«ng thøc truy håi, hoÆc cho mét hÖ thøc
liªn hÖ gi÷a c¸c phÇn tö th× ta tiÕn hµnh nh sau:
- T×m CTTQ cña d·y sè sau ®ã t×m giíi h¹n
.
- NÕu
kh«ng t×m ®îc CTTQ th× ta sö dông ®iÒu kiÖn ®ñ ®Ó d·y sè cã
giíi h¹n.
NguyÔn Minh H¶i. THPT Lª Xoay - VÜnh Têng - VÜnh phóc
VT. 05 - 2009
15
Chøng m
inh d·y t¨ng vµ bÞ chÆn trªn hoÆc gi¶m vµ bÞ chÆn díi. Sau ®ã ®Æt giíi
h¹n vµo c«ng thøc truy håi hoÆc hÖ thøc liªn hÖ gi÷a c¸c phÇn tö ta thu ®îc mét
ph¬ng tr×nh víi Èn lµ giíi h¹n cÇn t×m.
Bµi 3.5
Cho d·y (u
n
):
1
1
1
(
), 2.
2
n
n
n
a
u
u n
u
1
0,
.
a
u a
CMR (u
n
) cã
giíi h¹n. TÝnh giíi h¹n ®ã.
Gi¶i
- CM
quy n¹p
*
,
.
n
u
a n N
B§T Cauchy:
1
1
1 1
1
1
(
) .2 . .
2 2
n
n n
n n
a
a
u
u u a
u u
DÊu b»ng kh«ng x¶y ra.
.
n
u
a
-
Ta chøng minh (u
n
) lµ
d·y gi¶m.
Ta cã:
1
1
1
2
1
1 1
2
1
( )
1 1 1 1
1 , 1 ( )
2
2 2 2
n
n
n
n
n n
n
n n
u
u u
u u n u
u
u u
lµ
d·y gi¶m.
lim 0.
n
L u
Ta
cã:
1
1
2
1
lim lim ( ) .
2 2
n
n
n
L
a
L
L u u L a
u
VËy
lim .
n
u a
Chó ý
: ë bµi
to¸n trªn, thùc ra chØ cÇn gi¶ thiÕt
1
0, 0.
a u
Khi ®ã
viÖc chøng minh
hoµn toµn t¬ng tù.
- NÕu
*
1
,
lim .
n n
u
a u a n N u a
- NÕu
1
,
1 0, .
n
n
u
a u a n u n
lim
.
n
u
a
Bµi
3.6
Cho d·y (u
n
):
1
2
1
1
(
2 ), 2.
3
n
n
n
a
u
u n
u
3
1
0, .
a u a
CMR (u
n
) cã
giíi h¹n. TÝnh giíi h¹n ®ã.
Gi¶i
- T¬ng
tù bµi 4.6 ta CM quy n¹p.
*
3
,
; ( )
n
n
u
a n N u
lµ
d·y t¨ng.
- §Æ
t
lim 0.
n
L u
Theo
gt cã:
2
3
1
2
1
2
1
lim lim (2 ) .
3 3
n
n
n
a
L
a
L
L u u L a
u
VËy
3
l
im .
n
u
a
NguyÔn Minh H¶i. THPT Lª Xoay - VÜnh Têng - VÜnh phóc
VT. 05 - 2009
16
Chó ý: ë
bµi to¸n trªn, thùc ra chØ cÇn gi¶ thiÕt
1
0, 0.
a u
Khi ®ã
viÖc chøng minh
hoµn toµn t¬ng tù.
- NÕu
*
3
3 3
1
,
lim .
n
n
u
a u a n N u a
- NÕ
u
3 3
1
,
1 0, .
n
n
u
a u a n u n
3
lim
.
n
u
a
Bµi
3.7
Cho d·y (u
n
):
0 1
n
u
vµ
1
1
(1 ) .
4
n
n
u u
TÝnh limu
n
?
Gi¶i
- Chøng minh d·y (u
n
) t¨ng
vµ bÞ chÆn
trªn.
Theo
gt hiÓn nhiªn (u
n
) bÞ
chÆn
trªn.
¸p dông B§T Cauchy:
*
1
1 1
1
(
1 ) 2 (1 ) 2. 1 , .
2
n
n n n n n
u
u u u u u n N
(u
n
) t¨ng
VËy (u
n
) cã
giíi h¹n, ®Æt
lim .
n
a u
1
1
1 1
lim
[ (1 )] (1 ) .
4 4 2
n
n
u
u a a a
Bµi
3.8
Cho d·y (u
n
):
2
1
1
3, 3 4, 1.
n
n n
u u u u n
a). CMR (u
n
) lµ
d·y ®¬n ®iÖu nhng kh«ng bÞ chÆn.
b). D·y (v
n
) x®:
1
2
1
1 1
... , 1.
1
1 1
n
n
v n
u u u
cã giíi h¹n, tÝnh giíi h¹n ®ã.
Gi¶i
a). Quy n¹p. - Ta cã:
2
2
1 1 1
3 4 4 3 .
u u u u
- Gi¶ sö
1
.
n n
u u
Ta
CM
1
. (*)
n n
u u
TV.
2
2
1
(
*) 3 4 ( 2) 0
n
n n n n
u
u u u u
(®óng). VËy (u
n
) lµ
d·y t¨ng.
+) Gi¶ sö (u
n
) lµ
d·y bÞ chÆn khi ®ã (u
n
) l
µ d·y cã giíi h¹n, ®Æt
lim .
n
u a
Khi ®ã -). (u
n
) lµ d·y t¨ng,
3, lim 3.
n
n
u n N a u
-).
2
2
1
lim
lim( 3 4) 3 4 2.
n
n n
a
u u u a a a
( V«
lý)
VËy (u
n
) lµ
d·y kh«ng bÞ chÆn.
lim .
n
u

b). Tõ
2
1 1
1
1
1 1 1
3
4 2 ( 1)( 2) .
( 1)( 2) 2 1
n
n n n n n
n n n n n
u
u u u u u
u u u u u
1
1
1 1
1 2 2
n
n n
u u u
NguyÔn Minh H¶i. THPT Lª Xoay - VÜnh Têng - VÜnh phóc
VT. 05 - 2009
17
1
2 1 2 2 3 1
1 1 1 1 1 1 1 1 1
... ...
1
1 1 2 2 2 2 2 2
n
n
n n
v
u
u u u u u u u u
1
1 1
1 1 1
0
( ) / .
2
2 2
n
n
n
v
v b c
u
u u
- V×
3 ( )
n
n
u v
lµ
d·y t¨ng.
-
1 1 1
1 1 1
l
im lim( ) 1.
2
2 2
n
n
v
u
u u
NguyÔn Minh H¶i. THPT Lª Xoay - VÜnh Têng - VÜnh phóc
VT. 05 - 2009
18
IV.
Mét sè d¹ng to¸n kh¸c
Bµi
4.1
Cho d·y (u
n
):
2
1
*
0, .
n n n
n
u
u u
u n N
*
1
:
, .
n
C
MR u n N
n
Gi¶i
Chøng minh Quy n¹p.
- Víi n = 1, cã:
2
1
1 2 1 1 1 1
(
1) 0 1. ( 0, )
n
u
u u u u u u do u n
VËy m® ®óng víi n = 1.
- Víi n = 2, cã:
2
2 2
1 1 2 1 2 1 1 1
1 1 1 1
( ) .
4
2 4 2
u u u u u u u u
VËy m® ®óng víi n = 2.
- Gi¶ sö cã:
1
, ( 2)
n
u n
n
.
Hµm sè
2
( )
f x x x
®ång biÕn trªn ®o¹n
1
[0, ].
2
Do
2
2 2
1
1 1 1 1 1 1 1 1 1
0
( ) ( )
( 1) ( 1) 1 ( 1) ( 1) ( 1)
n
n
n
n
u f u f
n n n n n n n n n n n n n n n
1
2
1 1 1
(
) .
1
( 1) 1
n
n
u
f u
n n n n
VËy
m® ®óng víi n +1.
MÖnh ®Ò ®îc chøng minh.
Bµi 4.2
Cho hai d·y (a
n
) vµ
(b
n
) x¸c ®Þnh
bëi:
1
1 1
1
;
, 0.
n
n
n
a
a a b
b
*
1
1
,
.
n
n
n
b
b n N
a
:
2 2 , 2.
n n
C
MR a b n n
Gi¶i
Chøng mi
nh b»ng Quy n¹p.
- DÔ rµng chøng minh
*
,
0, .
n n
a
b n N
- Víi
n = 3 ta cã:
2
2 1 1 1 1
1 1 1 1
1
1 1
.
( ).( ) . 2 4.
.
a
b a b a b
b a a b
3
3 2 2 2 2
2 2 2 2
1
1 1 1
. ( ).( ) . 2 . 4 2 6.
a b a b a b
b a a b
3
3 3 3
2
. 2 2.3
a
b a b
VËy m® ®óng víi n = 3.
- Gi¶ sö m® ®óng víi n = k ( k >2),
tøc:
2
2 .
k
k
a
b k
- Ta
chøng minh m® ®óng víi n = k + 1.
NguyÔn Minh H¶i. THPT Lª Xoay - VÜnh Têng - VÜnh phóc
VT. 05 - 2009
19
TV.
Ta cã:
2 2 2 2 2 2
1 1
2 2
1
1 1 1
(
) 2 ; ( ) 2 .
k
k
k
k k k k k
k
k k k k k
a
b
a
a a b b b
b
b b a a a
1 1
2
2
. 2 . 4
.
k k k k
k
k
a
b a b
a
b
Suy ra:
2 2 2 2
1 1
1
1
( ) ( ) ( ) 4 . 4 ( ) 4 4 8 8.
C
osi
k k k k k k k k
k k
a b a b a b a b k
a b
2
2( 1).
k
k
a
b k
VËy m® ®óng víi n = k + 1. KÕt luËn.
2
2 , 2.
n
n
a
b n n
Bµi
4.3
Cho d·y(u
n
):
2
1
1
1
1
,
.
2
o
k k k
u
u u u
n
1
:
1 1.
n
C
MR u
n
Gi¶i
+
) Ta cã:
2
1
1
1
.
k
k k
u u u
n
B»ng quy n¹p chøng minh ®îc
1
,
1.
k
k
u
u k n
2
1 1 1
1
1
1 1
1 1 1
. .
.
. .
k k k k
k k k
k
k k k k k
u
u u u
u u u
n
u u n u u u n u
Do
1
1
2 1 0 1
1
1 1 1 1 1 1 1 1
,
1. ; ;... ; .
k
k
k k k k
u
u k n
u
u n u u n u u n
0 0 1 1 2 1
1 1 1 1 1 1 1 1
(
) ( ) ... ( ) 1.
k k k
k
u u u u u u u u n
1
2
1 1.
k
k
u
u
+) L¹i cã:
1
1
2
1 1 1 1
1
1 1 1
.
. . 1
k
k
k k k k k k
u
u
u u n u n u u n u n
1 2 1 0 1 0
1
1 1 1 1 1 1 1 1 1 1 1
; ;...; 1 .
1
1 1 1 1
k k k k k
n
u
u n u u n u u n u u n n
1
1 1
1
1 .
2 2
k
n
u
n n n
VËy m® ®îc chøng minh.
Bµi 4.4 Cho d·y sè x¸c ®Þnh:
4 15 1; 10 18 28.
n
n
n n
u n v n
: 9; 27, .
n
n
CMR u v n N
Gi¶i
+) Chøng minh
9.
n
u
- DÔ
thÊy m® ®óng víi n = 0, n = 1.
- Gi¶ sö m® ®óng víi n = k, cã nghÜa
9.
k
u
K
hi ®ã:
1
1
4
15( 1) 1 4(4 15 1) 18 4. 18 9
k
k
k k
u
k k u
VËy m® ®óng víi n = k+1.
Bµi 4.5
Gi¶ sö p/t:
2
a
x bx c 0 (a 0)
cã hai nghiÖm
1 2
x , x .
§Æt
n
n *
n
1 2
S
x x , n N .
NguyÔn Minh H¶i. THPT Lª Xoay - VÜnh Têng - VÜnh phóc
VT. 05 - 2009
20
a. CMR:
n
n 1 n 2
a.S b.S c.S 0, n N, n 3.
b. Gi¶
sö a = c = 1, b = - 4. CMR:
n
S
kh«ng chi hÕt cho 3.
Gi¶i.
a. Ta
cã:
2
n n 1 n 2
1 1 1 1 1
2 n n 1 n 2
2 2 2 2 2
ax bx c 0 ax bx cx 0
ax bx c 0 ax bx cx 0
n
n n 1 n 1 n 2 n 2
1 2 1 2 1 2 n n 1 n 2
a
(x x ) b(x x ) c(x x ) a.S b.S c.S 0, n N, n 3.
b. Ta
cã:
1
1 2
S x x 4
. kh«ng chia hÕt cho 3.
2
2 2
2 1 2 1 2 1 2
S
x x (x x ) 2x x 16 2 14
kh«ng chia hÕt cho 3.
Gi¶ sö S
k-1
,
S
k
(k >1)kh«ng chia hÕt cho 3, ta chøng minh S
k+1
còng kh«ng
chia hÕt cho 3. ThËt vËy. Theo (a) cã:
k
k 1 k 2
S 4S S
kh«ng
chia hÕt cho 3.
Bµi 4.6
Gi¶ sö
1
2
x , x .
lµ
hai nghiÖm cña p/t:
2
x x 5 0.
CMR:
20
09 2009
1 2
x
x Z.
Gi¶i.
Chøng minh quy n¹p:
n
n *
n
1 2
S
x x Z, n N .
Sử dông kÕt qu¶ bµi 5.9:
n
n 1 n 2
S S 5S 0, n N,n 3.
Trong
®ã: S
1
=1;
S
2
=11.
Bµi
4.7
TÝnh giíi h¹n cña d·y sè
2
2 2
1) . .....
2
2 2
2
2 ... 2
n
u
2 2 ... 2
2)
2 2 ... 3
n
u
Gi¶i. Trong bµi nµy ta thõa nhËn kÕt qu¶:
0
sin
l
im 1.
x
x
x
1. Quy
n¹p
CT:
1
2 1
, .
cos
2 2 ... 2
2
n
n
Khi ®ã:
1
1
1
1
sin
1 1 1
2
. ..... 2 .sin lim lim .
2 2 2
cos cos cos
4 8 2 2
n
n
n
n
n
n n
u u
2. Quy
n¹p CT:
2
2 ... 2 2.cos ; 2 2 ... 3 2.cos
2
3.2
n
n
1
1
2
2 cos
sin
1
2
2
l
im .
3
2
2 cos sin
3.
2 3.2
n
n
n
n
n n
u
u
NguyÔn Minh H¶i. THPT Lª Xoay - VÜnh Têng - VÜnh phóc
VT. 05 - 2009
21
PhÇ
n 3
. Bµi
tËp t¬ng tù
Bµi 1. CMR:
3
5 2 1
3
3 3 ... 3 30.
n
n
u
2
1 2
12
11 133
n
n
n
v
Bµi 2
. Cho x
1
, x
2
lµ nghiÖm cña ph¬ng tr×nh
2
27
14 0.
x
x
CMR
1 2
,
.
n
n
n
S
x x n N
kh«ng chia hÕt cho 715.
Bµi 3
.
Ký hiÖu
2
2 2 ... 2
n
R
c
©n bËc hai n lÇn.
1
2
1
1
:
cos , sin 2 .
2
2 2 2
n
n
n n
C
MR R R
Bµi
4
.
Cho d·y (a
n
) x¸c ®Þnh
:
2
*
2 1 2
( 2)( 1) 0, , 0, 1.
n
n
n n a n a n N a a
T×m a
n
?
Bµi 5
.
Cho d·y (S
n
):
2
3
*
1
1
2 2 2
(2 ... ), .
2
2 3
n
n
n
n
S n N
n
CM d·y (S
n
) ®¬n
®iÖu gi¶m vµ bÞ chÆn díi.
Bµi 6
.
Cho c¸c sè nguyªn a, b, c tháa m·n ®iÒu kiÖn
2
1.
a
b
D·y sè (u
n
) ®îc x¸c ®Þnh:
2 2
0 1
0, . , .
n
n n
u u au b u c n N
CMR mäi sè h¹ng cña d·y ®Òu lµ sè chÝnh ph¬ng.
Bµi 7
.
Cho hai d·y sè
2
1 1 2 1 1 *
2
2 1; 2 2 1, .
n
n n n
n n
a
b n N
CMR víi mçi n chØ cã mét vµ chØ mét trong hai sè a
n
,
b
n
chia hÕt cho 5.
Bµi 8
.
D·y(a
n
) lµ
mét CSC,
*
0
, .
n
a
n N
Gi¶ sö:
1
2
... ;
n
a a a
1
2
1
1 1
... .
n
a
a a
TÝnh
1
2
. .....
n
P a a a
theo
, .
Bµi
9. Cho d·y (u
n
):
1
1
4. 5; ( 1), 1.
n
n
u u n u
X¸c ®Þnh CTTQ tÝnh u
n
? S
n
?
Bµi 10
.
Cho d·y (u
n
):
1
2
1 1
, .
.
( ) , 2.
n
n n
u u
a u a b u bu c n
T×m CTTQ cña u
n
, S
n
?
Bµi 11
.
Ba sè
2, 3, 5
cã thÓ cïng cã mÆt trong mét CSC hay CSN ®îc hay kh«ng?
Bµi 12
.
CMR
*
n
N
cã
:
2
2 2
1
1 1 5
1.
... .
1
2 3
n
1
1 1 1
2.
... 2.
2
3
2 4 3 ( 1)n n
Bµi
13
.
T×m CTTQ cña c¸c d·y sè sau:
1
1
1
)
( 1), 1.
n
n
u
a
u
u n n n
1
2
2 1
1
)
.
, 0.
n
n n
u
u
b
u u u n
NguyÔn Minh H¶i. THPT Lª Xoay - VÜnh Têng - VÜnh phóc
VT. 05 - 2009
22
1
2
2 1
2
, 5
).
5 6 , 0.
n
n n
u
u
c
u u u n
1
2
1 2
1
,
0
).
2
2
1 0, 2.
n
n n
u
u
d
u u u n
Bµi
14
.
Cho d·y (u
n
) x®:
1
1
1
2
2 3
, 1.
2
n
n
u
n
u u n
n
CMR:
1.
n
limS
Bµi
15
.
§Æt
2
2 *
( ) ( 1) 1, .
f n n n n N
D·y (u
n
) x®:
*
(
1). (3)..... (2 1)
,
.
(2). (4)..... (2 )
n
f
f f n
u
n N
f f f n
1
:
lim .
2
n
C
MR n u
Bµi
16
.
Cho d·y sè (u
n
) cã
tÝnh chÊt:
1
1
2 , ( ) 1.
n
n n
u u u K Const n
TÝnh giíi h¹n
2
l
im ?
n
u
n
Bµi
17
.
Cho d·y (u
n
):
*
1
2
0
2
2.
0, .
n
n
n n
u
u
u u n N
*
1
: ( ) 2, .
n
n
CMR n u u n N
Bµi
18.
Cho d·y (u
n
):
1
3
2
1
2
3.
2 9 9 3, 1.
n
n
u
u
u n n n n
CMR víi p lµ sè nguyªn tè th×
1
.
p
S
p
Bµi
19
Cho d·y (a
n
):
2 *
1
1
1
, 2. 1, .
n
n
a
a a n N
CMR:
1
2 1
n
n n
a
b
.
Bµi
20
Cho d·y (a
n
):
1
2
1 2
2 1
.
1
1
,
, .
2 3 3. 2.
n
n
n
n n
a
a
a a a
a a
CMR:
*
1
1
,
.
2
1
n
n
a
n N
Bµi
21
Cho d·y (u
n
):
1
*
1
1
8
, .
5
n
n
u
u
u n N
vµ
d·y (v
n
): v
n
= u
n
– 2,
*
n
N
CMR:
1
( )
5
n
n
v
Bµi
22
Cã tån t¹i CSN chøa ®ång thêi 3 phÇn tö: 2, 3, 5 kh«ng ?
Cã tån t¹i CSC chøa ®ång thêi 3 phÇn tö: 1,
3
,
3 kh«ng ?
Bµi 23 Cho
1
2
, ,..., 0; 2
k
a a a k
tháa m·n:
1
2
... .
k
a a a k
§Æt
*
1
2
... , .
n
n n
n k
u a a a n N
CMR (u
n
) lµ
d·y t¨ng.
NguyÔn Minh H¶i. THPT Lª Xoay - VÜnh Têng - VÜnh phóc
VT. 05 - 2009
23
Tµi liÖu tham kh¶o
1. SGK §
¹i sè líp 11. ( Ch¬ng tr×nh kh«ng ph©n ba
n)
2. SGK §
¹i sè líp 11. ( Ch¬ng tr×nh ph©n ba
n)
3. Ph¬ng
ph¸p quy n¹p to¸n häc. NguyÔn H÷u
§iÓn
4. Mét sè bµi to¸n chän läc vÒ d·y sè. NguyÔn V¨n MËu
5. C¬ së
lý thuyÕt vµ mét sè bµi to¸n vÒ d·y sè. Vâ Giang Gia
i
6. 10.
000 bµi to¸n s¬ cÊp – D·y sè vµ giíi h¹n. Phan Huy Kh¶
i
7. BÊ
t ®¼ng thøc.Phan §øc C
hÝnh.
8. N©ng c
ao gi¶i tÝch 12. Phan Huy Kh¶
i.
9.
Bå
i dìng ®¹i sè 11. Phan Huy Kh¶i.
10.
TuyÓn tË
p ®Ò thi OLIMPIC 30-4, lÇn X – 2004.
11.
TuyÓn tË
p ®Ò thi OLIMPIC 30-4, lÇn XI – 2005.
12.
TuyÓn tË
p ®Ò thi OLIMPIC 30-4, lÇn XII – 2006.
13.
TuyÓn tËp ®Ò thi OLIMPIC 30-4, lÇn XIII – 2007.
14.
TuyÓn tË
p ®Ò thi OLIMPIC 30-4, lÇn XIII – 2008.
15.
B¸o T
o¸n häc vµ tuæi trÎ.
| 1/23
| | Tải xuống

Có thể bạn quan tâm:

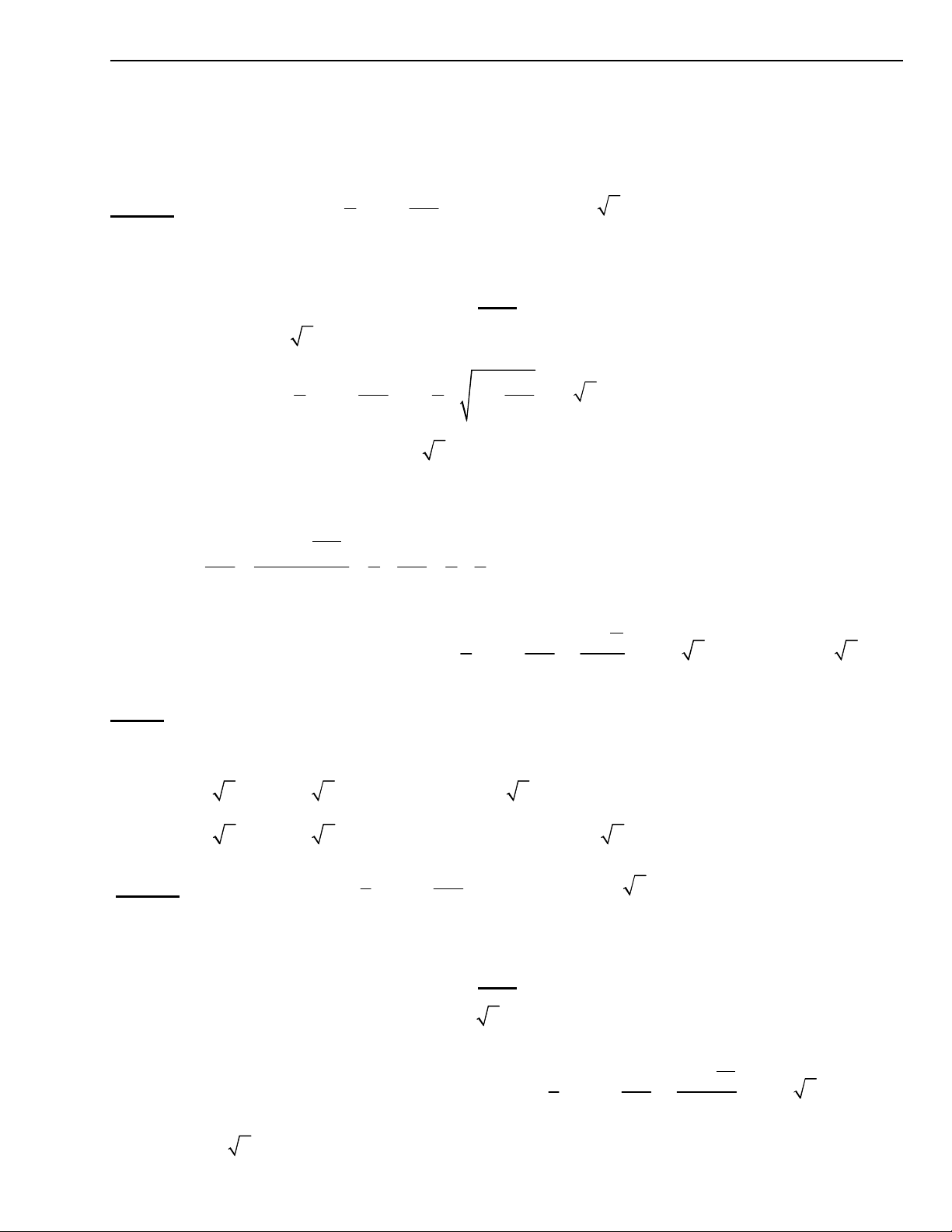
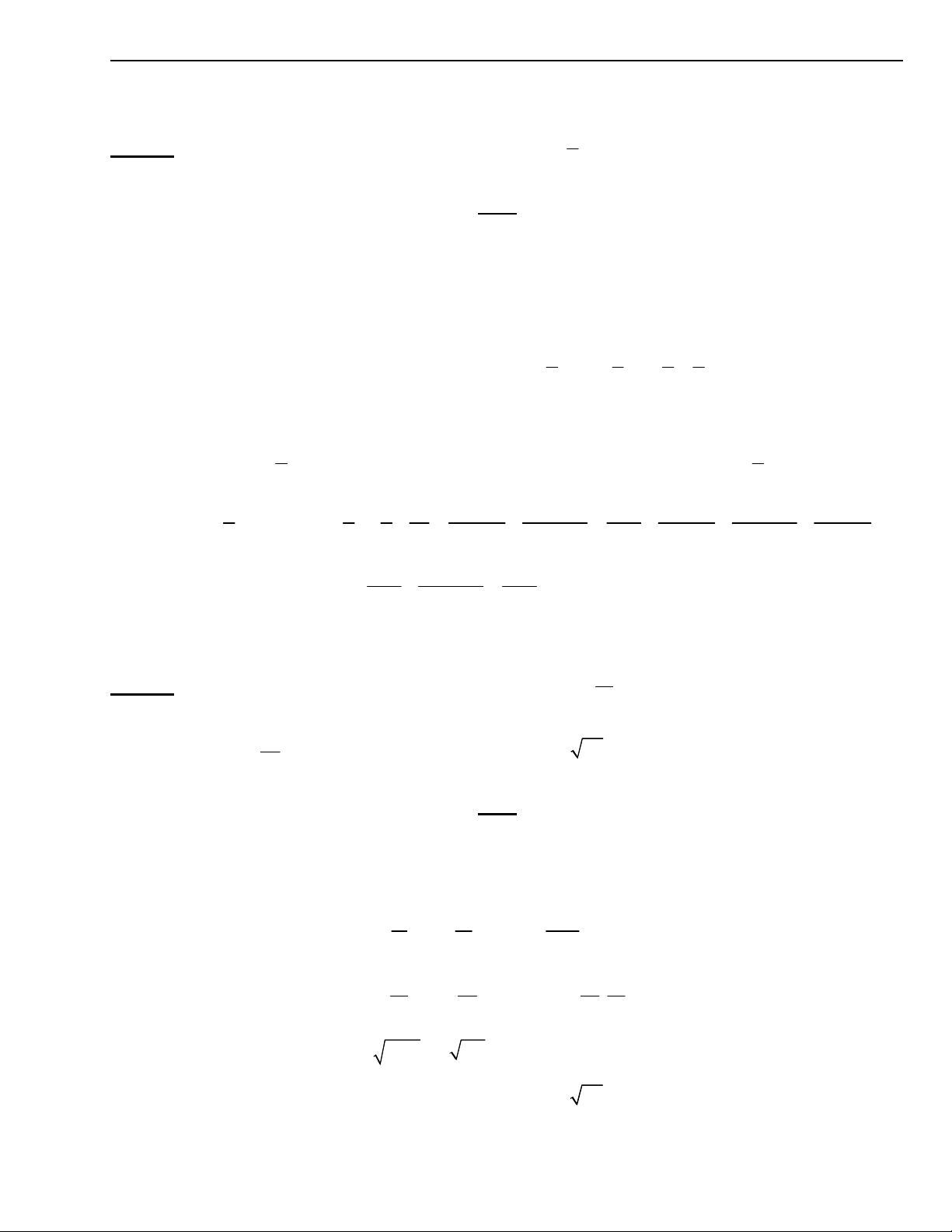
Preview text:

NguyÔn Minh H¶i. THPT Lª Xoay - VÜnh T­êng - VÜnh phóc Lêi nãi ®Çu
Mét trong nh÷ng ph­¬ng ph¸p rÊt m¹nh trong to¸n häc dïng nghiªn cøu vµ
chøng minh c¸c gi¶ thiÕt lµ nguyªn lý quy n¹p to¸n häc. Ph­¬ng ph¸p quy n¹p
®­îc ¸p dông s©u réng vµo hÇu hÕt c¸c d¹ng to¸n: Sè häc, D·y sè, H×nh häc,
B§T, Tæ hîp,…Trong b¸o c¸o nµy t«i chØ ®Ò cËp ®Õn ¸p dông cña ph­¬ng ph¸p
quy n¹p vµo mét sè d¹ng to¸n vÒ d·y sè.
Trong ch­¬ng tr×nh to¸n phæ th«ng th× to¸n vÒ d·y sè ®­îc ph©n phèi thêi
l­îng kh«ng nhiÒu, ®Æc biÖt trong ch­¬ng tr×nh to¸n ph©n ban hiÖn nay ®· l­îc
bá nhiÒu ®Þnh lý quan träng.Trong phÇn lín c¸c kú thi th× d¹ng to¸n nµy hÇu nh­
kh«ng cã. To¸n vÒ d·y sè th­êng chØ giµnh cho nh÷ng häc sinh kh¸ giái trong
c¸c kú thi cÊp TØnh vµ Quèc gia, do vËy nã cµng Ýt ®­îc häc sinh vµ c¶ gi¸o viªn
quan t©m ®Õn. PhÇn v× d¹ng to¸n nµy còng t­¬ng ®èi khã vµ trõu t­îng ®èi víi
häc sinh, häc sinh gÆp nhiÒu khã kh¨n vµ rÊt ng¹i khi gÆp d¹ng to¸n nµy.
Trong thêi gian võa qua t«i ®· thu thËp, tÝch lòy vµ hÖ thèng ®­îc mét sè d¹ng
to¸n vÒ d·y sè nh»m phôc vô cho c«ng t¸c gi¶ng d¹y, båi d­ìng häc sinh giái cña
m×nh. Víi môc ®Ých gióp häc sinh tiÕp cËn mét sè d¹ng to¸n ®Æc tr­ng vÒ d·y sè
do ®ã t«i lùa chän ®Ò tµi nµy. C¸c bµi to¸n ®­îc lùa chän chñ yÕu cho nh÷ng häc
sinh kh¸, giái. Sù ph©n chia thµnh c¸c d¹ng to¸n vµ nh÷ng ®¸nh gi¸ cña t«i lµ
theo quan ®iÓm chñ quan cña m×nh, do ®ã kh«ng tr¸nh khái nh÷ng thiÕu sãt.
KÝnh mong c¸c thÇy c« vµ c¸c b¹n ®ång nghiÖp ®äc vµ cho ý kiÕn gãp ý ®Ó tµi
liÖu nµy ®­îc hoµn thiÖn h¬n.
Xin ch©n thµnh c¸m ¬n !
VÜnh T­êng 5 . 2009
T¸c gi¶: NguyÔn Minh H¶i VT. 05 - 2009 1
NguyÔn Minh H¶i. THPT Lª Xoay - VÜnh T­êng - VÜnh phóc Môc lôc TT Néi dung Trang Lêi nãi ®Çu 1 PhÇn 1
Mét sè vÊn ®Ò vÒ lý thuyÕt
I Ph­¬ng ph¸p quy n¹p to¸n häc 3
II Mét sè vÊn ®Ò vÒ d·y sè 5
III Mét sè d¹ng to¸n vÒ d·y sè th­êng gÆp 6 PhÇn 2 ¸p dông gi¶i to¸n
I Chøng minh d·y sè t¨ng, gi¶m vµ bÞ chÆn 8
II C«ng thøc tæng qu¸t cña d·y sè 10
III T×m giíi h¹n cña d·y sè 12 IV Mét sè d¹ng to¸n kh¸c 18 PhÇn 3 Bµi tËp tổng hîp 21 Tµi liÖu tham kh¶o 23 VT. 05 - 2009 2
NguyÔn Minh H¶i. THPT Lª Xoay - VÜnh T­êng - VÜnh phóc
PhÇn 1. Mét sè vÊn ®Ò vÒ nguyªn lý Quy n¹p to¸n häc vµ D·y sè.
I.Ph­¬ng ph¸p quy n¹p to¸n häc
Sau ®©y lµ ba d¹ng cña nguyªn lÝ quy n¹p to¸n häc th­êng ®­îc dïng trong nh÷ng
bµi to¸n ë THPT.
1. §Þnh lÝ 1. Cho n lµ mét sè nguyªn d­¬ng vµ P(n) lµ mÖnh ®Ò cã nghÜa víi mäi sè tù 0
nhiªn n n . 0
NÕu: 10. P(n ) lµ mÖnh ®Ò ®óng 0
20. NÕu P(k) ®óng th× P(k+1) còng ®óng víi mçi sè tù nhiªn k n . 0
Khi ®ã mÖnh ®Ó P(n) ®óng víi mäi sè tù nhiªn n n . 0
VÝ dô 1. Cho d·y sè (u ) x¸c ®inh bëi: u = n2. n n
n(n 1)(2n 1)
CMR tång cña n phÇn tö ®Çu tiªn cña d·y ®­îc tÝnh: S  . n 6 Chøng minh.
Víi n = 1. §¼ng thøc ®óng.
k(k 1)(2k 1)
Gi¶ sö §T ®óng víi n = k ( k ≥ 1), tøc lµ cã: S  . k 6
(k 1)(k  2)(2k  3)
Ta chøng minh §T ®óng víi n = k+1, tøc CM: S  . k 1  6
k (k  1)(2k 1)
(k 1)(k  2)(2k  3) ThËt vËy. Ta cã 2 2 S
S  (k 1)   (k 1)  . k 1  k 6 6
VËy §T ®óng víi mäi sè nguyªn d­¬ng.
2. §Þnh lÝ 2. Cho p lµ sè nguyªn d­¬ng vµ d·y c¸c mÖnh ®Ò: P(1), P(2), …, P(n),…
NÕu: 10. P(1), P(2), …, P(p) lµ nh÷ng mÖnh ®Ò ®óng
20. Víi mçi sè tù nhiªn k p c¸c mÖnh ®Ò P(k p 1), P(k p  2), ..., P(k)
®óng, suy ra mÖnh ®Ò P(k+1) còng ®óng.
Khi ®ã mÖnh ®Ó P(n) ®óng víi mäi sè nguyªn d­¬ng n.
VÝ dô 2. Cho v  2, v  3 vµ víi mçi sè tù nhiªn k cã ®¼ng thøc: v  3v  2v . 0 1 k 1  k k 1 
CMR: v  2n 1. n Chøng minh.
- DÔ thÊy mÖnh ®Ò ®óng víi n = 0, 1. VT. 05 - 2009 3
NguyÔn Minh H¶i. THPT Lª Xoay - VÜnh T­êng - VÜnh phóc
- Gi¶ sö víi mçi sè tù nhiªn k  2 m® ®óng víi n = k vµ n = k – 1. Tøc lµ cã: k k 1 v  2 1, v  2  1. k k 1 
-Ta chøng minh m® ®óng víi n = k + 1. TV. Theo CT truy håi k k 1  k 1 v  3v  2v  3(2 1)  2(2
1)  2  1. (dpcm) k 1  k k 1 
VËy bµi to¸n ®­îc chøng minh.
3. §Þnh lÝ 3. Cho d·y c¸c mÖnh ®Ò: P(1), P(2), …, P(n),…
NÕu: 10. P(1) lµ nh÷ng mÖnh ®Ò ®óng
20. Víi mçi sè tù nhiªn k  1 c¸c mÖnh ®Ò P(1), P(2), ..., P(k) ®óng,
suy ra mÖnh ®Ò P(k+1) còng ®óng.
Khi ®ã mÖnh ®Ó P(n) ®óng víi mäi sè nguyªn d­¬ng n.
D¹ng quy n¹p nµy m¹nh h¬n d¹ng thø hai ë b­íc quy n¹p. n 1
VÝ dô 3. Cho d·y sè (u ) x¸c ®inh bëi: * * U x
, n N , x N . U Z. n n n 1 x
CMR (u ) lµ d·y c¸c sè nguyªn. n Chøng minh
Víi n = 1 mÖnh ®Ò hiÓn nhiªn ®óng.
Gi¶ sö víi mäi sè tù nhiªn tõ 1 ®Õn k, u lµ sè nguyªn. Ta CM u còng nguyªn. k k+1 k  1 1 k 1 k  1 TV. 1 1 ux
 (x  )(x  )  (x
)  u .u uZ k 1  k 1  k k 1  1 k k 1  x x x x
VËy (u ) lµ d·y c¸c sè nguyªn. n VT. 05 - 2009 4
NguyÔn Minh H¶i. THPT Lª Xoay - VÜnh T­êng - VÜnh phóc
II. Mét sè vÊn ®Ò vÒ d·y sè.
2.1. D·y sè t¨ng, gi¶m (®¬n ®iÖu).
§N. D·y sè (u ) ®­îc gäi lµ d·y t¨ng nÕu víi mäi *
n N ta cã u < u . n n n+1
D·y sè (u ) ®­îc gäi lµ d·y gi¶m nÕu víi mäi *
n N ta cã u > u . n n n+1
D·y sè t¨ng vµ d·y gi¶m ®­îc gäi chung lµ d·y ®¬n ®iÖu.
2.2. D·y bÞ chÆn.
§N +) D·y sè (u ) ®­îc gäi lµ d·y bÞ chÆn trªn, nÕu tån t¹i mét sè M sao cho n *
u M , n N . n
+) D·y sè (u ) ®­îc gäi lµ d·y bÞ chÆn d­íi, nÕu tån t¹i mét sè m sao cho n * u  ,
m n N . n
+) D·y sè (u ) ®­îc gäi lµ d·y bÞ chÆn nÕu nã võa bÞ chÆn trªn võa bÞ chÆn d­íi, n
tøc lµ tån t¹i c¸c sè m, M sao cho *
m u M ,n N . n *
(  M  0 : u M ,n N ) n
2.3. Giíi h¹n d·y sè.
§N 1. D·y sè (u ) cã giíi h¹n 0 nÕu víi mçi sè d­¬ng nhá tuú ý cho tr­íc, mäi sè n
h¹ng cña d·y sè, kÓ tõ mét sè h¹ng nµo ®ã trë ®i, ®Òu cã gi¸ trÞ tuyÖt ®èi nhá
h¬n sè d­¬ng ®ã. Ta viÕt lim(u ) = 0 hoÆc limu = 0 hoÆc u 0. n n n
C¸ch ph¸t biÓu míi nµy gióp häc sinh h×nh dung ®­îc d·y sè cã giíi h¹n 0 mét c¸ch
thuËn lîi h¬n, tuy nhiªn ®Þnh nghÜa nµy khã diÔn ®¹t trong khi chøng minh mét sè ®Þnh
lý vÒ giíi h¹n. Do vËy t«i xin trë l¹i ®Þnh nghÜa tr­íc ®©y:
§N 2. Ta nãi r»ng d·y sè (u ) cã giíi h¹n 0 nÕu víi mçi sè d­¬ng bÊt kú, tån t¹i n
mét sè nguyªn d­¬ng N sao cho * n   N , n  N |  u | .  n
Ta viÕt lim(u ) = 0 hoÆc limu = 0 hoÆc u 0. n n n
§N 3. Ta nãi d·y sè (u ) cã giíi h¹n lµ sè thùc L nÕu lim(u – L) = 0. n n
Ta viÕt lim(u ) = L hoÆc limu = L hoÆc u L. n n n §N 4.
- Ta nãi d·y sè (u ) cã giíi h¹n + nÕu víi mçi sè d­¬ng tuú ý cho tr­íc, mäi sè n
h¹ng cña d·y sè, kÓ tõ mét sè h¹ng nµo ®ã trë ®i, ®Òu lín h¬n sè d­¬ng ®ã. VT. 05 - 2009 5
NguyÔn Minh H¶i. THPT Lª Xoay - VÜnh T­êng - VÜnh phóc
- Ta nãi d·y sè (u ) cã giíi h¹n - nÕu víi mçi sè ©m tuú ý cho tr­íc, mäi sè n
h¹ng cña d·y sè, kÓ tõ mét sè h¹ng nµo ®ã trë ®i, ®Òu nhá h¬n sè d­¬ng ®ã.
§Þnh lÝ 1. Cho hai d·y sè (u ) vµ (v ). n n
NÕu | u |  v víi mäi n vµ limv = 0 th× limu = 0. n n n n
§Þnh lÝ 2. NÕu | q| < 1 th× lim qn = 0.
§Þnh lÝ 3. Gi¶ sö lim u = L. Khi ®ã: n a) lim | u | = | L | vµ 3 3 lim u  L. n n
b) NÕu u  0 víi mäi n th× L  0 vµ lim u  L. n n
§Þnh lÝ 4. Gi¶ sö lim u = L, lim v = M vµ c lµ mét h»ng sè. Khi ®ã: n n
lim(u v )  L M .
lim(u .v )  . L M n n n n u L lim(c.u )  c.L lim n  nÕu M  0. n v M n 1
§Þnh lÝ 5. NÕu lim |u | = + th× lim  0. n un
VËn dông c¸c kÕt qu¶ trªn, ta cã thÓ chóng minh ®­îc c¸c ®Þnh lý sau:
§Þnh lÝ 6.(§iÒu kiÖn cÇn) Mét d·y sè cã giíi h¹n th× nã bÞ chÆn.
§Þnh lÝ 7. (Duy nhÊt) Mét d·y sè cã giíi h¹n th× giíi h¹n ®ã lµ duy nhÊt.
§Þnh lÝ 8. (Giíi h¹n kÑp) Cho ba d·y sè (u ), (v ), (w ) tháa m·n: n n n 0 * 1 .
v u w , n N . n n n 0
2 . lim v  lim w A th× lim u = A. n n n
Ta thõa nhËn ®Þnh lÝ sau ®©y.
§Þnh lÝ 9. (§iÒu kiÖn ®ñ- §Þnh lÝ Waiesstras)
Mét d·y t¨ng vµ bÞ chÆn trªn th× cã giíi h¹n.
Mét d·y gi¶m vµ bÞ chÆn d­íi th× cã giíi h¹n.
HiÖn nay bèn §Þnh lý trªn kh«ng ®­îc giíi thiÖu trong ch­¬ng tr×nh, tuy nhiªn cã
thÓ chøng minh ®­îc §Þnh lÝ 6, 7, 8 tõ c¸c ®Þnh lý cã s½n. Trong b¸o c¸o nµy t«i vÉn
xin ®­îc sö dông ®Ó c¸c d¹ng to¸n ®­îc ®a d¹ng h¬n. VT. 05 - 2009 6
NguyÔn Minh H¶i. THPT Lª Xoay - VÜnh T­êng - VÜnh phóc 2.4. CÊp sè céng.
§Þnh nghÜa. CÊp sè céng lµ mét d·y sè, trong ®ã, kÓ tõ sè h¹ng thø hai mçi sè h¹ng
®Òu lµ tæng cña sè h¹ng liÒn tr­íc víi mét sè kh«ng ®æi gäi lµ c«ng sai.
TÝnh chÊt. Cho cÊp sè céng ( u ) c«ng sai d, khi ®ã *
n N ta cã: n 0 1 . u
u d; u u  (n 1)d. n 1  n n 1 u u 0 n n 2 2 . u   . n 1  2 n n 0 3 .
S u u  ...  u  (u u ) 
2u  (n 1)d . n 1 2 n 1 n  1  2 2
2.5. CÊp sè nh©n.
§Þnh nghÜa. CÊp sè nh©n lµ mét d·y sè, trong ®ã, kÓ tõ sè h¹ng thø hai mçi sè h¹ng
®Òu lµ tÝch cña sè h¹ng liÒn tr­íc víi mét sè kh«ng ®æi gäi lµ c«ng béi.
TÝnh chÊt. Cho cÊp sè nh©n ( u ) c«ng béi q, ta cã: n 0 n 1 1 . u
u .q; u u .q  . n 1  n n 1 0 2 . uu .u n 1  n n2 n q 1 0 3 .
S u u  ...  u u . ; (q  1) n 1 2 n 1 q 1
Tæng cña cÊp sè nh©n v« h¹n c«ng béi q (q <1) n q 1 u 1
S  lim S  lim u .  . (q  1) n 1 q 1 1 q
III. Mét sè d¹ng to¸n vÒ d·y sè th­êng gÆp.
1. Chøng minh d·y sè t¨ng, gi¶m, bÞ chÆn, d·y cã giíi h¹n.
2. Chøng minh d·y sè lËp thµnh cÊp sè céng, cÊp sè nh©n, tÝnh chÊt cña cÊp sè.
3. T×m c«ng thøc tæng qu¸t cña d·y sè.
4. Chøng minh d·y sè cã giíi h¹n vµ t×m giíi h¹n d·y sè.
5. Mét sè d¹ng kh¸c: B§T vÒ d·y sè, chøng minh tÝnh chÊt chia hÕt, chøng minh
d·y sè nguyªn….. VT. 05 - 2009 7
NguyÔn Minh H¶i. THPT Lª Xoay - VÜnh T­êng - VÜnh phóc
PhÇn 2. ¸p dông trong gi¶i to¸n
I. Chøng minh d·y sè t¨ng, gi¶m vµ bÞ chÆn. n
u  1, u  2.  5 Bµi 1.1  Cho d·y (u ): 1 2 CMR: * u  ,n N . n  n   u  2uu , n  3.   2 n n 1  n2  Gi¶i
ë bµi to¸n nµy u cho bëi c«ng thøc truy håi, ®­îc tÝnh theo u vµ u do ®ã ta n n-1 n-2
vËn dông nguyªn lÝ quy n¹p thø hai ®Ó chøng minh.
- Víi n = 1, n = 2 mÖnh ®Ò ®óng. n 1  n  5   5 
- Gi¶ sö m® ®óng víi n = k – 1, vµ n = k ( k >1), tøc lµ cã: u  , u  . n 1       2 n   2 
- Ta chøng minh m® ®óng víi n = k + 1. n 1  n n 1   5   5   5 
TV. Ta cã: u  2uu  2.   . (®pcm) n n 1  n2        2   2   2   u  1. 1 
Bµi 1.2 Cho d·y (u ): n  n 3(n  2) * uu  , n N . n 1   2(n  1) n 2(n 1) 
a). CM d·y sè bÞ chÆn trªn. b). CM d·y sè t¨ng. Gi¶i
§©y lµ bµi to¸n kh«ng khã nÕu dù ®o¸n ®­îc d·y sè bÞ chÆn trªn bëi sè nµo thÝch
hîp nhÊt? Ta cã thÓ xuÊt ph¸t tõ yªu cÇu thø hai cña bµi to¸n:
(3  u )(n  2) Cã: n uu   0  u  3. n 1  n n 1 n
a). Ta CM quy n¹p theo nguyªn lÝ thø nhÊt: *
u  3,n N . n
- Gi¶ sö m® ®óng víi n = k khi ®ã cã: k 3(k  2) 3k 3(k  2) uu     3. k 1  2(k 1) k 2(k 1) 2(k  2) 2(k 1)
- VËy m® ®óng víi n = k +1.
(3  u )(n  2) b). Theo phÇn (a) cã: n uu   0. n 1  n n 1
VËy d·y (u ) t¨ng vµ bÞ chÆn trªn. n VT. 05 - 2009 8
NguyÔn Minh H¶i. THPT Lª Xoay - VÜnh T­êng - VÜnh phóc 1
Bµi 1.3 Chøng minh d·y u  (1 )n lµ d·y t¨ng vµ bÞ chÆn trªn. n n Gi¶i +) Ta chøng minh *
u  3, n N . n -
Víi n = 1, n = 2. B§T hiÓn nhiªn ®óng. 2 1 k k -
Víi n ≥ 3, ta chøng minh B§T phô sau ®©y: (1 )k  1  , k  :1  k  . n (1) 2 n n n
TV. – Víi k = 1, B§T ®óng . 2 1 k k
- Gi¶ sö (1) ®óng víi k (1  k n 1), tøc : (1 )k  1  . 2 n n n 2 2 2 1    k k k k k k k 1 1 k 1 1 Khi ®ã: 1 (1 )
 (1 )(1 )  (1 )(1  )  1   . 2 2 3 n n n n n n n n n 2 2 2 k k k (k 1) MÆt kh¸c dÔ dµng CM:   . 2 3 2 n n n 2 1    k k k 1 ( 1) 1  (1 )  1 
. VËy B§T ®óng víi k + 1. 2 n n 1 (n 1)
KL. B§T (1) ®óng víi mäi sè nguyªn d­¬ng k, (1  k n ) 2 1 n n
-) Víi k = n ta cã : (1 )n  1   3. 2 n n n +) Chøng minh d·y t¨ng.
¸p dông B§T Cauchy cho n + 1 sè d­¬ng kh«ng ®ång thêi b»ng nhau, ta ®­îc: 1 1 1 1 n n 1 1 (1 ) (1 ) ... (1 ) (n 1)           (1 ) . n n n n 1 1 n 1 n 1 1 n * n 1  1    (1 )  (1 )  (1 )  u
u ,n N . n 1 n 1 n n  1  n n
Bµi 1.5 XÐt tÝnh ®¬n ®iÖu, bÞ chÆn cña c¸c d·y sè sau:  u  2 1   u  2  0 1 . 0  u 1 1 2 .  n * u  , n N . *  n 1  u
2  u , n N .   2 1   n n Gi¶i
10. B»ng quy n¹p ta chøng minh (u ) lµ d·y gi¶m vµ bÞ chÆn d­íi bëi 0. n
20. B»ng quy n¹p ta chøng minh (u ) lµ d·y t¨ng vµ bÞ chÆn trªn bëi 2. n VT. 05 - 2009 9
NguyÔn Minh H¶i. THPT Lª Xoay - VÜnh T­êng - VÜnh phóc
II. C«ng thøc tæng qu¸t cña d·y sè. 
u  2, u  3.
Bµi 2.1 Cho d·y (u ): 1 2 CMR n 1 u 2   1. Tính S n  n. u  3u  2u , n  2. nn 1  n n 1  Gi¶i
Quy n¹p. Víi n =1; n = 2. §óng.
Gi¶ sö m® ®óng víi k-1 vµ k (k > 1), ta chøng minh m® ®óng víi n = k + 1.
ThËt vËy: Cã k 2 k 1  k 1  k 2 k 2 u  2 1, u  2 1  u  3(2 1)  2(2  1)  4.2 1  2k 1. k 1  k k 1 
MÖnh ®Ò ®­îc chøng minh. Khi ®ã: n 1 S u u ... u 1 (1 2) ... (1 2           
)  2n n 1. n 1 2 nu  2  1 
Bµi 2.2 Cho d·y (u ): n  un * u  ,n N . n 1   1  un a) CMR: *
u  0,n N . n u 1 3 b) §Æt n v  . CMR v   n, n.  n u n 2 n
c). T×m CTTQ tÝnh u ,S  u  u  ...u . n n 1 2 n Gi¶i
a). Chøng minh b»ng quy n¹p. - Víi n = 1 m® ®óng. u
- Gi¶ sö m® ®óng víi n = k ( k  1), tøc u  0. Khi ®ã u  0,1 u  0 ku   0. k k k k 1  1 uk
- VËy m® ®óng víi n = k +1. u u 1 u 1 u u b). Ta cã: n u   u .uuu . n 1  n n n 1  vv      1.  n 1  n n 1  n 1 1  nu n 1  n u u u .u n n 1  n n n 1  u 1 2  1 1  v
v 1  (v ) lµ CSC c«ng sai d = -1, 1 v    . n 1  n n 1 u 2  2 1 1 3
v v  (n 1)d   (n 1)( 1  )   . n n 1 2 2 u 1 1 2  Tõ n v   u   . n n u v 1 2n 1 n n
C¸ch 2. CM quy n¹p. VT. 05 - 2009 10
NguyÔn Minh H¶i. THPT Lª Xoay - VÜnh T­êng - VÜnh phóc 
u  1, u  2.
Bµi 2.4 Cho d·y (u ): 1 2 CMR: 2
u  (n 1) 1. T×m S ? n
u  2u u  2,n  2. n n  n 1  n n 1  Gi¶i -
HiÓn nhiªn c«ng thøc ®óng víi n = 1, n = 2. -
Gi¶ sö c«ng thøc ®óng víi n = k - 1, n = k tøc: 2 2 u
 (k  2) 1;u  (k 1) 1 k 1  k Khi ®ã: 2 2 2 2 u  2u u
 2  2[(k 1) 1]  [(k  2)  1]  2  k 1  [(k 1) 1] 1 k 1  k k 1 
VËy c«ng thøc ®óng víi n = k + 1.
n(n 1)(2n 1) Khi ®ã: 2 2 2
S  (n 1)  (n  2)  ... 1  n   . n n 6
Chó ý: NÕu bµi to¸n yªu cÇu chøng minh u 1 lµ sè chÝnh ph­¬ng th× c¸ch lµm n
hoµn toµn vÉn nh­ vËy. 
u  3, u  2.
Bµi 2.5 Cho d·y (u ): 1 2 n
u  3u  2u 1,n  2.  n 1  n n 1  n 1  q 1 CMR: u
v n  2  2n n  4. TÝnh S ? n 1 q 1 n Gi¶i
Quy n¹p: Gi¶ sö: k 1 u  2  
 (k 1)  4; u  2
k k  4 k 1  k k k 1  k 1  k 1  u  3u  2u 1  3[ 2   k  4]  2[2
k  3] 1  8.2
k  5  2   (k 1)  4 n 1  n n 1  u 1 
Bµi 2.6 Cho d·y (u ): n 1  * u  ,u
,n N . T×m CTTQ cña u ? n n 0 n 2.u 1 2n n 1  Gi¶i
- NÕu u  0  u  0,n N. 0 n
- NÕu u  0. B»ng quy n¹p ta chøng minh ®­îc u  0,n N. 0 n 1 2u 1 1 Khi ®ã: n 1    2  . u u u n n 1  n 1 §Æt v
v  2  vv
lµ CSC c«ng sai d  2. n n n 1  n un 1 1 u 0
v v nd   2n u   . n 0 n u v 2 . n u 1 0 n 0 VT. 05 - 2009 11
NguyÔn Minh H¶i. THPT Lª Xoay - VÜnh T­êng - VÜnh phóc
III. T×m giíi h¹n cña d·y sè.
NÕu d·y sè cho bëi CTTQ th× ta th­êng sö dông c¸c ph­¬ng ph¸p tÝnh giíi h¹n cña
d·y sè ®Ó tÝnh. Trong nhiÒu tr­êng hîp ta ph¶i biÕn ®æi CTTQ ®ã vÒ d¹ng ®¬n gi¶n
h¬n tr­íc khi tÝnh giíi h¹n.
Mét sè ph­¬ng ph¸p tÝnh giíi h¹n cña d·y sè: -
Nh©n liªn hîp, ®èi víi giíi h¹n d¹ng -  -
Chia c¶ tö vµ mÉu cho lòy thõa bËc cao nhÊt cña n, ®èi víi giíi h¹n d¹ng ;         0 -
KÕt hîp hai ph­¬ng ph¸p trªn cho giíi h¹n d¹ng ; ; ; .        0 -
Sö dông ®Þnh lý giíi h¹n kÑp -
Sö dông ®iÒu kiÖn ®ñ ®Ó d·y sè cã giíi h¹n, thiÕt lËp biÓu thøc vÒ giíi h¹n.
KÕt qu¶ giíi h¹n lµ nghiÖm cña mét ph­¬ng tr×nh nµo ®ã.
Bµi 3.1 TÝnh c¸c giíi h¹n sau: 2 3 n  1  n 2 3
A  lim( n n n) B  lim 4 3
n n n 2 3 6 n  1 n n n 1 3 2   C  lim D  lim 4 2 n n n 1  n 2  5.3 n n 1 4.3 7   2
4n 1  2n 1 E  lim F  lim 2.5n  7n 2
n  4n 1  n HD. 1 1 1 A  ; B  ;  C  0; D  ; E  7; F   . 3 5 2
Bµi 3.2 TÝnh giíi h¹n cña c¸c d·y sè sau  1 1 1   1 1 1  A  lim   ...    B  lim   ...    1.2 2.3 n(n 1)   1.2.3 2.3.4
n(n 1)(n  2)   1 1 1  1 3 5 2n 1  C  lim(1 )(1 )...(1 ) D  lim    ...  2 2 2   2 3 n 2 2 2 2  n n n n  1 1 1 1 E  lim (   ... 
) {§Ò thi HSG líp 11 n¨m 2007} n 1  3 3  5
2n 1  2n 1 VT. 05 - 2009 12
NguyÔn Minh H¶i. THPT Lª Xoay - VÜnh T­êng - VÜnh phóc
Häc sinh th­êng ¸p dông sai c«ng thøc tÝnh giíi h¹n cña tæng vµ tÝch c¸c d·y sè.
Hai c«ng thøc nµy chØ ¸p dông ®èi víi tæng vµ tÝch h÷u h¹n c¸c d·y sè. Häc sinh
th­êng ¸p dông cho tæng, tÝch v« h¹n dÉn ®Õn kÕt qu¶ sai. Gi¶i 1 (n 1)  n 1 1 a). NhËn xÐt: *    ,n N n(n 1) ( n n 1) n n 1 1 1 1 1 1 1 1 1 1  u    ... 
 (1 )  (  )  ...  (  )  1 n 1.2 2.3 ( n n 1) 2 2 3 n 1 n n 1
A  lim u  lim(1 )  1. n n 1 (n  2)  n 1 1 1 b). NhËn xÐt: *   (  ),n N
n(n 1)(n  2) 2n(n 1) 2 n(n 1)
(n 1)(n  2) 1 1 1 1 1 1 1 1 1 1  u    ...   [(  )  (  )  ...  (  )] n 1.2.3 2.3.4 (
n n 1)(n  2) 2 1.2 2.3 2.3 3.4 ( n n 1)
(n 1)(n  2) 1 1 1  u    B  . n 4
2(n  1)(n  2) 4 2 2 2 2 1 3 1 n 1 1.3 2.4 (n 1)(n 1) n 1 1 c). u  . .....  . ....   C  . n 2 2 2 2 3 n 2.2 3.3 . n n 2n 2 2
1 3  5  ...  (2n 1) n d). u    D  1. n 2 2 n n 1
2n  1  2n 1 2n  1 2n 1 e). Ta cã:    , n   1.
2n 1  2n 1
(2n 1)  (2n 1) 2 2 1 1 1 1  u  (   ...  ) n n 1  3 3  5
2n 1  2n 1 1 3 1 5 3 2n 1  2n 1  1 2n 1  1   .[(  ) (   ) .  . (   )]  . n 2 2 2 2 2 2 n 2 2n  1 1 2  E  lim u  lim  . n 2 n 2
Bµi 3.3 TÝnh c¸c giíi h¹n sau
1 2  3  ...  n 2 2 2
1 2  3  ...  n A  lim B  lim 2 2n n  3 3 4n 1 3 3 3
1 2  3  ...  n 2 2 2
1 3  5  ...  (2n 1) C  lim C  lim 4 2 n  3n 1 3 3n n  4 VT. 05 - 2009 13
NguyÔn Minh H¶i. THPT Lª Xoay - VÜnh T­êng - VÜnh phóc Gi¶i
§Ó ®¬n gi¶n biÓu thøc ta chøng minh quy n¹p c¸c c«ng thøc sau: n(n  1)
n(n 1)(2n 1) 0
1 . 1 2  3  ...  n 0 2 2 2
2 . 1 2  3  ...  n  2 6
(n 1)(n  2)
(n 1)(n  2)(n  3)(n  4) 0 3 3 3
3 . 1 2  3  ...  n  1 8(n 1) 19
 (n 1)(n  2)(n  3)  2 4 1 0 2 2 3
4 . 1 3  5  ...  (2n 1) 
n(2n 1)(2n 1). 3
- Khi ®ã ta cã ®­îc c¸c kÕt qu¶ sau: 1 1 1 4 A  . B  . C  . D  . 4 12 4 9
Trong nhiÒu bµi to¸n ta kh«ng thÓ ®¬n gi¶n ®­îc CTTQ ®Ó sö dông hai ph­¬ng ph¸p
nh©n liªn hîp, hoÆc chia cho lòy thõa cña n. Khi ®ã h·y nghÜ ®Õn §Þnh lÝ giíi h¹n kÑp
Bµi 3.4 TÝnh giíi h¹n sau.  1 1 1  1.3.5.7.....(2n 1) A  lim    ...   B  lim 2 2 2  n 1 n  2 n n  2.4.6.....(2n) Gi¶i 1 1 1 a). Ta cã:  
, k N ,1  k  . n 2 2 2 n n n k n 1 n 1 1 1 n   u    ...   , n 2 2 2 2 2 n n n 1 n  2 n n n 1 n n mµ lim  lim  1
 lim u  1 A  1. n 2 2 n n n 1 2 2 2 2 1.3.5.7.....(2n 1)
1.3 .5 .7 .....(2n 1) 1.3 3.5
(2n 1).(2n 1) 1 b). §Æt 2 u   u   . ... . n n 2 2 2 2 2 2 2 2.4.6.....(2n) 2 .4 .6 .....(2n) 2 4 (2n) 2n 1 1 1 2  0  u   0  u  , n 2n 1 n 2n 1 1 mµ lim
 0  B  lim u  0. n 2n 1
§èi víi nh÷ng bµi to¸n mµ d·y sè cho bëi c«ng thøc truy håi, hoÆc cho mét hÖ thøc
liªn hÖ gi÷a c¸c phÇn tö th× ta tiÕn hµnh nh­ sau: -
T×m CTTQ cña d·y sè sau ®ã t×m giíi h¹n. -
NÕu kh«ng t×m ®­îc CTTQ th× ta sö dông ®iÒu kiÖn ®ñ ®Ó d·y sè cã giíi h¹n. VT. 05 - 2009 14
NguyÔn Minh H¶i. THPT Lª Xoay - VÜnh T­êng - VÜnh phóc
Chøng minh d·y t¨ng vµ bÞ chÆn trªn hoÆc gi¶m vµ bÞ chÆn d­íi. Sau ®ã ®Æt giíi
h¹n vµo c«ng thøc truy håi hoÆc hÖ thøc liªn hÖ gi÷a c¸c phÇn tö ta thu ®­îc mét
ph­¬ng tr×nh víi Èn lµ giíi h¹n cÇn t×m. 1 a
Bµi 3.5 Cho d·y (u ): u  (u  ), n
  2. a  0, u a. n n n 1 2  u 1 n 1 
CMR (u ) cã giíi h¹n. TÝnh giíi h¹n ®ã. n Gi¶i - CM quy n¹p * u
a , n N . n 1 a 1 a
B§T Cauchy: u  (u  )  .2 u .  a. n n 1  n 1 2 u 2  u n 1  n 1 
DÊu b»ng kh«ng x¶y ra.  u a. n
- Ta chøng minh (u ) lµ d·y gi¶m. n 2 1(u  ) n 1 uu 1 1 1 1 Ta cã: n n 1      
 1  u u
,n  1  (u ) lµ d·y gi¶m. 2 n n 1 u 2u 2 u 2 2  n n 1  n 1  n 1  2 L  1 a
  L  lim u  0. Ta cã:  lim  lim (  ) L L u u   L
a. VËy lim u a. n n n 1 2  u 2 n n 1 
Chó ý: ë bµi to¸n trªn, thùc ra chØ cÇn gi¶ thiÕt a  0, u  0. Khi ®ã viÖc chøng minh 1
hoµn toµn t­¬ng tù. - NÕu * u au
a, n N  lim u a. 1 n n
- NÕu u a u a,n  1  u  0,  .
n  lim u a. 1 n n n 1 a
Bµi 3.6 Cho d·y (u ): u  (2u  ), n   2. 3 a  0, u a. n n n 1  2 3 u 1 n 1 
CMR (u ) cã giíi h¹n. TÝnh giíi h¹n ®ã. n Gi¶i
- T­¬ng tù bµi 4.6 ta CM quy n¹p. 3 * u
a , n N ; (u ) lµ d·y t¨ng. n n a 2L  2 1 a
- §Æt   L  lim u  0. Theo gt cã: L 3
L  lim u  lim (2u  )   L a. n n n 1  2 3 u 3 n 1  VËy 3 lim u a. n VT. 05 - 2009 15
NguyÔn Minh H¶i. THPT Lª Xoay - VÜnh T­êng - VÜnh phóc
Chó ý: ë bµi to¸n trªn, thùc ra chØ cÇn gi¶ thiÕt a  0, u  0. Khi ®ã viÖc chøng minh 1
hoµn toµn t­¬ng tù. - NÕu 3 3 * 3 u au
a, n N  lim u a. 1 n n - NÕu 3 3 u a
u a , n  1  u  0,  . n 3  lim u a. 1 n n n 1
Bµi 3.7 Cho d·y (u ): 0  u  1 vµ u (1 u )  . TÝnh limu ? n n n 1  n 4 n Gi¶i
- Chøng minh d·y (u ) t¨ng vµ bÞ chÆn trªn. n
Theo gt hiÓn nhiªn (u ) bÞ chÆn trªn. n 1 ¸p dông B§T Cauchy: * u  (1 u )  2 u (1 u )  2.  1  u
u ,n N . n 1  n n 1  n n 1 2  n (u ) t¨ng n 1 1 1
VËy (u ) cã giíi h¹n, ®Æt a  lim u .  lim[u (1 u )] 
a(1 a)   a  . n n n 1  n 4 4 2
Bµi 3.8 Cho d·y (u ): 2 u  3, u
u  3u  4, n   1. n 1 n 1  n n
a). CMR (u ) lµ d·y ®¬n ®iÖu nh­ng kh«ng bÞ chÆn. n 1 1 1
b). D·y (v ) x®: v    ... 
, n  1. cã giíi h¹n, tÝnh giíi h¹n ®ã. n n u 1 u 1 u 1 1 2 n Gi¶i a). Quy n¹p. - Ta cã: 2
u u  3u  4  4  3  u . 2 1 1 1
- Gi¶ sö u u . Ta CM uu . (*) n n 1  n 1  n TV. 2 2 (*)  u
u  3u  4  u  (u  2)  0 (®óng). VËy (u ) lµ d·y t¨ng. n 1  n n n n n
+) Gi¶ sö (u ) lµ d·y bÞ chÆn khi ®ã (u ) lµ d·y cã giíi h¹n, ®Æt lim u  . a n n n
Khi ®ã -). (u ) lµ d·y t¨ng, u  3,n N a  lim u  3. n n n -). 2 2 a  lim u
 lim(u  3u  4)  a  3a  4  a  2.( V« lý) n 1  n n
VËy (u ) lµ d·y kh«ng bÞ chÆn.  lim u  .  n n 1 1 1 1 b). Tõ 2 u
u  3u  4  u
 2  (u 1)(u  2)     . n 1  n n n 1  n n u
(u 1)(u  2) u  2 u 1 n 1  n n n n 1 1 1    . u 1 u  2 u  2 n n n 1  VT. 05 - 2009 16
NguyÔn Minh H¶i. THPT Lª Xoay - VÜnh T­êng - VÜnh phóc 1 1 1  1 1   1 1   1 1   v    ...       ...   n       u 1 u 1 u 1 u  2 u  2 u  2 u  2 u  2 u  2 1 2 n  1 2   2 3   n n 1    1 1  1  0  v     (v ) b / . c n   u  2 u  2 u  2 n  1 n 1   1 -
V× u  3  (v ) lµ d·y t¨ng. n n 1 1 1 - lim v  lim(  )   1. n u  2 u  2 u  2 1 n 1  1 VT. 05 - 2009 17
NguyÔn Minh H¶i. THPT Lª Xoay - VÜnh T­êng - VÜnh phóc IV.Mét sè d¹ng to¸n kh¸c 2
u u u 1
Bµi 4.1 Cho d·y (u ): n n n 1  * CMR : u  , n N . n  * n
u  0, n N .  n n Gi¶i
Chøng minh Quy n¹p. - Víi n = 1, cã: 2
u u u u
u (u 1)  0  u  1. (do u  0, n  ) 1 1 2 1 1 1 1 n VËy m® ®óng víi n = 1. 1 1 1 1 - Víi n = 2, cã: 2 2 2
u u u u
u u u   (u  )   . 1 1 2 1 2 1 1 1 4 2 4 2 VËy m® ®óng víi n = 2. 1 1
- Gi¶ sö cã: u  , (n  2) . Hµm sè 2
f (x)  x x ®ång biÕn trªn ®o¹n [0, ]. n n 2 1 1 1 1 n 1 n 1 1 1 1 1 Do 0  u
f (u )  f ( )         n n 2 2 2 n n n n n(n 1) n (n 1) n 1 n(n 1) n (n 1) n(n 1) 1 1 1  uf (u )    . VËy m® ®óng víi n +1. n 1  n 2 n 1 n (n 1) n 1
MÖnh ®Ò ®­îc chøng minh. 1
Bµi 4.2 Cho hai d·y (a ) vµ (b ) x¸c ®Þnh bëi: aa  ; a ,b  0. n n n 1  n 1 1 bn 1 * bb  ,n N .
CMR : a b  2 2n, n   2. n 1  n a n n n Gi¶i
Chøng minh b»ng Quy n¹p. - DÔ rµng chøng minh *
a , b  0,n N . n n 1 1 1
- Víi n = 3 ta cã: a .b  (a  ).(b  )  a .b   2  4. 2 2 1 1 1 1 b a a .b 1 1 1 1 1 1 1 1
a .b  (a  ).(b
)  a .b  2  .  4  2  6. 3 3 2 2 2 2 b a a b 2 2 2 2
a b  2 a .b  2 2.3 VËy m® ®óng víi n = 3. 3 3 3 3 -
Gi¶ sö m® ®óng víi n = k ( k >2), tøc: a b  2 2k . k k -
Ta chøng minh m® ®óng víi n = k + 1. VT. 05 - 2009 18
NguyÔn Minh H¶i. THPT Lª Xoay - VÜnh T­êng - VÜnh phóc 1 1 a 1 1 b TV. Ta cã: 2 2 2 k 2 2 2 a  (a  )  a   2 ; b  (b  )  b   2 k . k 1  k k 2 k 1  k k 2 b b b a a a k k k k k k 2 2a .b
 2a .b  4  k 1  k 1  k k a .b k k  1 1 Cosi  Suy ra: 2 2 2 2 (ab
)  (a b )  (  )  4a .b
 4  (a b )  4  4  8k  8. k 1  k 1  k kk k k k a bk k
a b  2 2(k 1). VËy m® ®óng víi n = k + 1. KÕt luËn. a b  2 2n, n   2. k k n n 1 1 1 Bµi 4.3 Cho d·y(u ): 2 u  , u u  .u
CMR :1  u  1. n o k k 1  k 1 2 nn n Gi¶i 1 +) Ta cã: 2 u u  .u
B»ng quy n¹p chøng minh ®­îc u u , k   1.n k k 1  k 1 nk k 1  1 u u u 1 1 u 2 k k 1  k 1  k 1 u u  .u       . k k 1  k 1 nu .u . n u u u . n u k k 1  k k 1  k k 1 1 1 1 1 1 1 1 1
Do u u , k   1.n    ;   ;... ;   . k k 1  u u n u u n u u n k 1  k k 2 k 1  0 1 1 1 1 1 1 1 1 1 k 1    (  )  (  )  ...  (  )   1.  2   1  u  1. u u u u u u u u n k u 0 k 0 1 1 2 k 1  k k 1 1 u u 1 1 +) L¹i cã: k 1  k 1       . 2 u u . n u . n uu n u n 1 k 1  k k k 1  k 1  k 1  1 1 1 1 1 1 1 1 1 1 1 n 1    ;   ;...;       1 . u u n 1 u u n 1 u u n 1 u u n 1 n 1 k 1  k k 2 k 1  0 1 0 k n  1 1 1  u   1  1
. VËy m® ®­îc chøng minh. k n  2 n  2 n
Bµi 4.4 Cho d·y sè x¸c ®Þnh: u  4n 15n 1; v  10n 18n  28. n n
CMR : u 9; v 27, n N. n n Gi¶i
+) Chøng minh u 9. n -
DÔ thÊy m® ®óng víi n = 0, n = 1. -
Gi¶ sö m® ®óng víi n = k, cã nghÜa u 9. k Khi ®ã: k 1 u
 4   15(k 1) 1  4(4k 15k 1)  18  4.u 189 VËy m® ®óng víi n = k+1. k 1  k Bµi 4.5 Gi¶ sö p/t: 2
ax  bx  c  0 (a  0) cã hai nghiÖm x , x . §Æt n n * S  x  x , n  N . 1 2 n 1 2 VT. 05 - 2009 19
NguyÔn Minh H¶i. THPT Lª Xoay - VÜnh T­êng - VÜnh phóc a. CMR: a.S  b.S  c.S  0, n   N, n  3. n n 1  n 2
b. Gi¶ sö a = c = 1, b = - 4. CMR: S kh«ng chi hÕt cho 3. n Gi¶i. 2 n n 1  n2  ax  bx  c  0    ax  bx  cx  0 a. Ta cã: 1 1 1 1 1    2 n n 1  n2 ax  bx  c  0 ax  bx  cx  0  2 2    2 2 2 n n n 1  n 1  n2 n2  a(x  x )  b(x  x )  c(x  x )  a.S  b.S  c.S  0, n   N, n  3. 1 2 1 2 1 2 n n 1  n2
b. Ta cã: S  x  x  4 . kh«ng chia hÕt cho 3. 1 1 2 2 2 2
S  x  x  (x  x )  2x x  16  2  14 kh«ng chia hÕt cho 3. 2 1 2 1 2 1 2
Gi¶ sö S , S (k >1)kh«ng chia hÕt cho 3, ta chøng minh S còng kh«ng k-1 k k+1
chia hÕt cho 3. ThËt vËy. Theo (a) cã: S  4S  S kh«ng chia hÕt cho 3. k k 1  k2
Bµi 4.6 Gi¶ sö x , x .lµ hai nghiÖm cña p/t: 2 x  x  5  0. CMR: 2009 2009 x  x  Z. 1 2 1 2 Gi¶i. Chøng minh quy n¹p: n n * S  x  x  Z, n   N . n 1 2
Sử dông kÕt qu¶ bµi 5.9: S  S  5S  0, n
  N, n  3. Trong ®ã: S =1; S =11. n n 1  n 2 1 2
Bµi 4.7 TÝnh giíi h¹n cña d·y sè 2 2 2 2  2  ...  2 1) u  . ..... 2) u n n 2 2  2 2  2  ...  2 2  2  ...  3 sin x
Gi¶i. Trong bµi nµy ta thõa nhËn kÕt qu¶: lim  1. x0 x 2 1 1. Quy n¹p CT:  , . n  2  2  ...  2 cos 1 2n  sin n 1 1 1 1     Khi ®ã: n 2 u  . .....  2 .sin  lim u  lim  . n n 1    2  n 2  2 cos cos cos n 1  n 1 4 8 2 2   
2. Quy n¹p CT: 2  2  ... 2  2.cos ;
2  2  ...  3  2.cos 2n 3.2n   2  2 cos sin n n 1 2  1 2  u    lim u  . n n   3 2  2 cos sin n n 1 3.2 3.2  VT. 05 - 2009 20
NguyÔn Minh H¶i. THPT Lª Xoay - VÜnh T­êng - VÜnh phóc
PhÇn 3. Bµi tËp t­¬ng tù Bµi 1. CMR: 3 5 2n 1 u 3 3 3 ... 3       30. 2n 1  n2 v  12 11 133  n n
Bµi 2. Cho x , x lµ nghiÖm cña ph­¬ng tr×nh 2
x  27x 14  0. 1 2
CMR S n x n
x ,n N. kh«ng chia hÕt cho 715. n 1 2
Bµi 3. Ký hiÖu R  2  2  2  ... 2 c©n bËc hai n lÇn. n  1  1 CMR : cos  R , sin  2  R . n n 1  n n2 2 2 2 2
Bµi 4. Cho d·y (a ) x¸c ®Þnh : 2 *
(n  2)(n 1)a
n a  0,n N , a  0, a  1. T×m a ? n n2 n 1 2 n 2 3 n 1 2 2 2n Bµi 5. Cho d·y (S ): * S  (2    ...  ), n N . n n n 1 2  2 3 n
CM d·y (S ) ®¬n ®iÖu gi¶m vµ bÞ chÆn d­íi. n
Bµi 6. Cho c¸c sè nguyªn a, b, c tháa m·n ®iÒu kiÖn 2 a b 1.
D·y sè (u ) ®­îc x¸c ®Þnh: 2 2 u  0, uau  .
b u c ,n N. n 0 n 1  n n
CMR mäi sè h¹ng cña d·y ®Òu lµ sè chÝnh ph­¬ng.
Bµi 7. Cho hai d·y sè 2n 1  n 1  2n 1  n 1  * a  2  2 1; b  2  2
1,n N . n n
CMR víi mçi n chØ cã mét vµ chØ mét trong hai sè a , b chia hÕt cho 5. n n
Bµi 8. D·y(a ) lµ mét CSC, *
a  0, n N . n n 1 1 1
Gi¶ sö: a a  ...  a  ;   ... 
 . TÝnh P a .a .....a theo , . 1 2 n a a a 1 2 n 1 2 n
Bµi 9. Cho d·y (u ): u
 4.u  5; (n  1), u  1. X¸c ®Þnh CTTQ tÝnh u ? S ? n n 1  n 1 n n 
u   , u  .
Bµi 10. Cho d·y (u ): 1 2 T×m CTTQ cña u , S ? n
 .au  (a b)u bu  ,cn  2. n n  n 1  n n 1 
Bµi 11. Ba sè 2, 3, 5 cã thÓ cïng cã mÆt trong mét CSC hay CSN ®­îc hay kh«ng? 1 1 1 5 1 1 1 1 Bµi 12. CMR *
n N cã : 1.   ...   . 2.    ...   2. 2 2 2 1 2 n 3 2 3 2 4 3 (n 1) n
Bµi 13. T×m CTTQ cña c¸c d·y sè sau:  u  1  u u  1 1 a)  1 2 b).  u
u n(n 1), n   1.  uuu , n  0. n 1  nn2 n 1  n VT. 05 - 2009 21
NguyÔn Minh H¶i. THPT Lª Xoay - VÜnh T­êng - VÜnh phóc  1  u  2, u  5  u  , u  0 1 2 c).  1 2 d ).  2 u  5u
 6u , n  0.  n2 n 1  n u   u  2u 1  0, n  2.  n n 1  n2
Bµi 14. Cho d·y (u ) x®: n  1 u  1   2  CMR: limS  1. 2n  3 n u   u , n   1. n n 1   2nBµi 15. §Æt 2 2 *
f (n)  (n n 1) 1,n N . D·y (u ) x®: n
f (1). f (3)..... f (2n 1) 1 * u  ,n N .
CMR : lim n u  . n
f (2). f (4)..... f (2 ) n n 2
Bµi 16. Cho d·y sè (u ) cã tÝnh chÊt: u  2u u
K , (Const) n   1. n n 1  n n 1  u
TÝnh giíi h¹n lim n  ? 2 n  0  u  2
Bµi 17. Cho d·y (u ): n *
CMR : n(u u
)  2,n N . n  * u  2.uu
 0, n N . n n 1   n n 1  n2  u  2
Bµi 18. Cho d·y (u ): 1 n  3 2 u  3.u
 2n  9n  9n  3, n  1.  n n 1 
CMR víi p lµ sè nguyªn tè th× S  . p p 1  Bµi 19 Cho d·y (a ): 2 *
a  1, a  2.a
1, n N .
CMR: a b 1  2n 1 . n 1 n n 1  n n 1 1 a .a 1 Bµi 20 Cho d·y (a ): n 1  n2 a  , a  , a  . CMR: * a  , n N . n 1 2 2 3 n 3.a  2.a n n 1 2   1 n2 n 1   u  1 1  Bµi 21 Cho d·y (u ): vµ d·y (v ): v = u – 2, * n N . n  u  8 n * n n n u  ,n N .  n 1   5 1
CMR: v  ( )n n 5
Bµi 22 Cã tån t¹i CSN chøa ®ång thêi 3 phÇn tö: 2, 3, 5 kh«ng ?
Cã tån t¹i CSC chøa ®ång thêi 3 phÇn tö: 1, 3, 3 kh«ng ?
Bµi 23 Cho a , a ,..., a  0;k  2 tháa m·n: a a  ... a k. 1 2 k 1 2 k §Æt n n n *
u a a  ...  a , n N . CMR (u ) lµ d·y t¨ng. n 1 2 k n VT. 05 - 2009 22
NguyÔn Minh H¶i. THPT Lª Xoay - VÜnh T­êng - VÜnh phóc Tµi liÖu tham kh¶o
1. SGK §¹i sè líp 11. ( Ch­¬ng tr×nh kh«ng ph©n ban)
2. SGK §¹i sè líp 11. ( Ch­¬ng tr×nh ph©n ban)
3. Ph­¬ng ph¸p quy n¹p to¸n häc. NguyÔn H÷u §iÓn
4. Mét sè bµi to¸n chän läc vÒ d·y sè. NguyÔn V¨n MËu
5. C¬ së lý thuyÕt vµ mét sè bµi to¸n vÒ d·y sè. Vâ Giang Giai
6. 10.000 bµi to¸n s¬ cÊp – D·y sè vµ giíi h¹n. Phan Huy Kh¶i
7. BÊt ®¼ng thøc.Phan §øc ChÝnh.
8. N©ng cao gi¶i tÝch 12. Phan Huy Kh¶i.
9. Båi d­ìng ®¹i sè 11. Phan Huy Kh¶i.
10. TuyÓn tËp ®Ò thi OLIMPIC 30-4, lÇn X – 2004.
11. TuyÓn tËp ®Ò thi OLIMPIC 30-4, lÇn XI – 2005.
12. TuyÓn tËp ®Ò thi OLIMPIC 30-4, lÇn XII – 2006.
13. TuyÓn tËp ®Ò thi OLIMPIC 30-4, lÇn XIII – 2007.
14. TuyÓn tËp ®Ò thi OLIMPIC 30-4, lÇn XIII – 2008.
15. B¸o To¸n häc vµ tuæi trÎ. VT. 05 - 2009 23