Inbound Decision Variables and Simplex Method Analysis | Môn Deterministic Models in Operations Research - Trường Đại học Quốc tế, Đại học Quốc gia Thành phố Hồ Chí Minh

lOMoAR cPSD| 58583460 Question 1 Decision variables
𝑥𝑖𝑗: 𝑛𝑢𝑚𝑏𝑒𝑟 𝑜𝑓 𝑝𝑟𝑜𝑑𝑢𝑐𝑡𝑠 𝑖 𝑝𝑟𝑜𝑑𝑢𝑐𝑒𝑑 𝑜𝑛 𝑚𝑎𝑐ℎ𝑖𝑛𝑒 𝑗
Maximize: 𝑍 = 150(𝑥11 + 𝑥12 + 𝑥13) + 120(𝑥21 + 𝑥22 + 𝑥23) + 125(𝑥31 + 𝑥32 + 𝑥33) St:
+ 4𝑥21 + 2𝑥31 <= 400 + 2𝑥 + 𝑥 <= 300 𝑥
35 𝑜𝑟 𝑥31 + 𝑥32 + 𝑥33 = 35 𝑥𝑖𝑗
𝑖𝑗 𝑖𝑛𝑡𝑒𝑔𝑒𝑟 Question 2 - Parameters
(demand, capacity, transportation cost)
𝐹: set of factories 𝑖 = 1,2,3
𝐶: set of customers 𝑗 = 1,2
𝑃: set of products 𝑘 = 1, 2
𝐷𝑗𝑘: demand quantity of product 𝑘 of customer 𝑗
𝐾𝑖𝑘: capacity of factory 𝑖 to produce product 𝑘
𝑐𝑖𝑗: transportation cost per unit from factory 𝑖 to customer 𝑗 - Decision variables
(quantity produced of each product at each factory)
𝑥𝑖𝑗𝑘: quantity of product 𝑘 is produced in factory 𝑖 and transport to customer 𝑗 - Objective function
(minimize production cost + transportation cost)
Min: 𝑖,𝑗,𝑘 𝑐𝑖𝑗𝑥𝑖𝑗𝑘 - Constraints
(demand constraints, capacity constraints) 𝑖 𝑥𝑖𝑗𝑘 𝑗𝑘
forall 𝑗 𝑖𝑛 𝐶, 𝑘 𝑖𝑛 𝑃 𝑗 𝑥𝑖𝑗𝑘 𝑖𝑘
forall 𝑖 𝑖𝑛 𝐹, 𝑘 𝑖𝑛 𝑃 𝑥𝑖𝑗𝑘
forall 𝑖 𝑖𝑛 𝐹, 𝑗 𝑖𝑛 𝐶, 𝑘 𝑖𝑛 𝑃 lOMoAR cPSD| 58583460 Question 2
a. Using revised simplex method to complete the final tableau (optimal solution) in Table
above. Given that the basic variable are x2, s2, s3. Show your calculation! Iteration Equation BS x1 x2 x3 s1 s2 s3 RHS 0 Z 0 0 2/5 1/2 0 0 5 1 x2 1/3 1 2/3 1/3 0 0 10/3 s2 1 2 -5/3 0 2/3 4/3 1 0 43/3 3 s3 5/3 0 4/3 -1/3 0 1 5/3
b. Is this a special case in simplex method? If yes, what is this? Explain why?
We are at an optimal point and there are non-basic variables with reduced cost equal to 0, so
there are multiple values for the decision variables that allow obtaining the optimal value of Z =
5, which are contained in the segment of the line: 1/2X1 + 3/2X2 + 3/5X3 = 5. One of the
solutions is: X1= 0, X2= 10/3, X3= 0, S1= 0, S2= 43/3, S3= 5/3 lOMoAR cPSD| 58583460 Question 3
a. Use the revised simplex method step by step to identify the entering variable
and leaving variable for iteration 1 (iteration 0 is the initial iteration)
b. Use Fundamental insight to identify the missing numbers in the following table and show your calculations?
c. What are the special cases in the Linear Programming model? What special
case does the given model belong to? (If any) Justify your choice. lOMoAR cPSD| 58583460 Question 4
Because we have one non-basic variable having coefficient in the objective
function equal to 0. Therefore, we can conclude that this model has multiple solutions
a. Using two phase method to solve this problem. Max z = 3x1 + 2x2 + 3x3 St 2x1 + x2 + x3 + A1 = 4 x1 + 3x2 + x3 + A2 = 12 3x1 + 4x2 + 2x3 + A3 = 16
x1,x2,x3,A1,A2,A3 >= 0 Phase 1: Min z = A1 + A2 + A3 St 2x1 + x2 + x3 + A1 = 4 x1 + 3x2 + x3 + A2 = 12 3x1 + 4x2 + 2x3 + A3 = 16
x1,x2,x3,A1,A2,A3 >= 0 Phase 2: Max z = 3x1 + 2x2 + 3x3 St 2x1 + x2 + x3 + A1 = 4 x1 + 3x2 + x3 + A2 = 12 3x1 + 4x2 + 2x3 + A3 = 16 x1,x2,x3,A1,A2,A3 >= 0 Transform Z in phase 1:
Z = 32 – 6x1 – 8x2 – 4x3
Objective max (-Z) – 6x1 – 8x2 – 4x3 = -32 lOMoAR cPSD| 58583460 Question 5 lOMoAR cPSD| 58583460 Iteration Equation BS x1 x2 x3 A1 A2 A3 RHS Ratio 0 Z -6 -8 -4 0 0 0 -32 4 1 A1 2 1 1 1 0 0 4 4 0 2 A2 1 3 1 0 1 0 12 4 3 A3 3 4 2 0 0 1 16 4 0 Z -10 0 -4 -8 0 0 0 0 1 x2 2 1 1 1 0 0 4 2 1 2 A2 5 0 2 3 -1 0 0 0 3 A3 5 0 2 4 0 -1 0 0 0 Z 0 0 0 2 2 0 0 1 x2 0 1 0.2 -0.2 0.4 0 4 2 2 x1 1 0 0.4 0.6 -0.2 0 0 3 A3 0 0 0 1 1 -1 0
Drop A1, A2, A3, then we move to the phase 2 0 Z -3 -2 -3 0 1 x2 0 1 0.2 4 20 0 2 x1 1 0 0.4 0 0 3 A3 0 0 0 0 - 0 Z 4.5 -2 0 0 1 x2 -0.5 1 0 4 4 1 2 x3 2.5 0 1 0 - 3 A3 0 0 0 0 - 0 Z 3.5 0 0 0 0 0 8 1 x2 -0.5 1 0 4 2 2 x3 2.5 0 1 0 3 A3 0 0 0 0
b. Convert this problem to BigM method.
Max z = 3x1 + 2x2 + 3x3 – MA1 – MA2 – MA3 St 2x1 + x2 + x3 + A1 = 4 x1 + 3x2 + x3 + A2 = 12 3x1 + 4x2 + 2x3 + A3 = 16 x1,x2,x3,A1,A2,A3 >= 0 Transforming Z:
Max Z = (3 + 6M)x1 + (2 + 8M)x2 + (3 + 4M)x3 - 32M lOMoAR cPSD| 58583460 Question 6
a. Assumed that you are known that x1, x2 are the basic solution of the optimal problem in the
final tableau. Using fundamental insight through matrix multiplication to show the final tableau. Show your calculation. Iteration Equation BS x1 x2 x3 s1 s2 RHS 0 Z x1 0 0 9 2 2 12 2 1 1 0 4 0 1 4 2 x2 0 1 6 -1 2 6
b. If the RHS of the constraint (2) is increase by 1 unit, how the objective function will change? Old optimal value: 𝑍 New optimal value: 𝑍 Then, ∆𝑍∗ = 2 lOMoAR cPSD| 58583460 Question 7
a. Reformulate this problem to fit our standard form in simplex method.
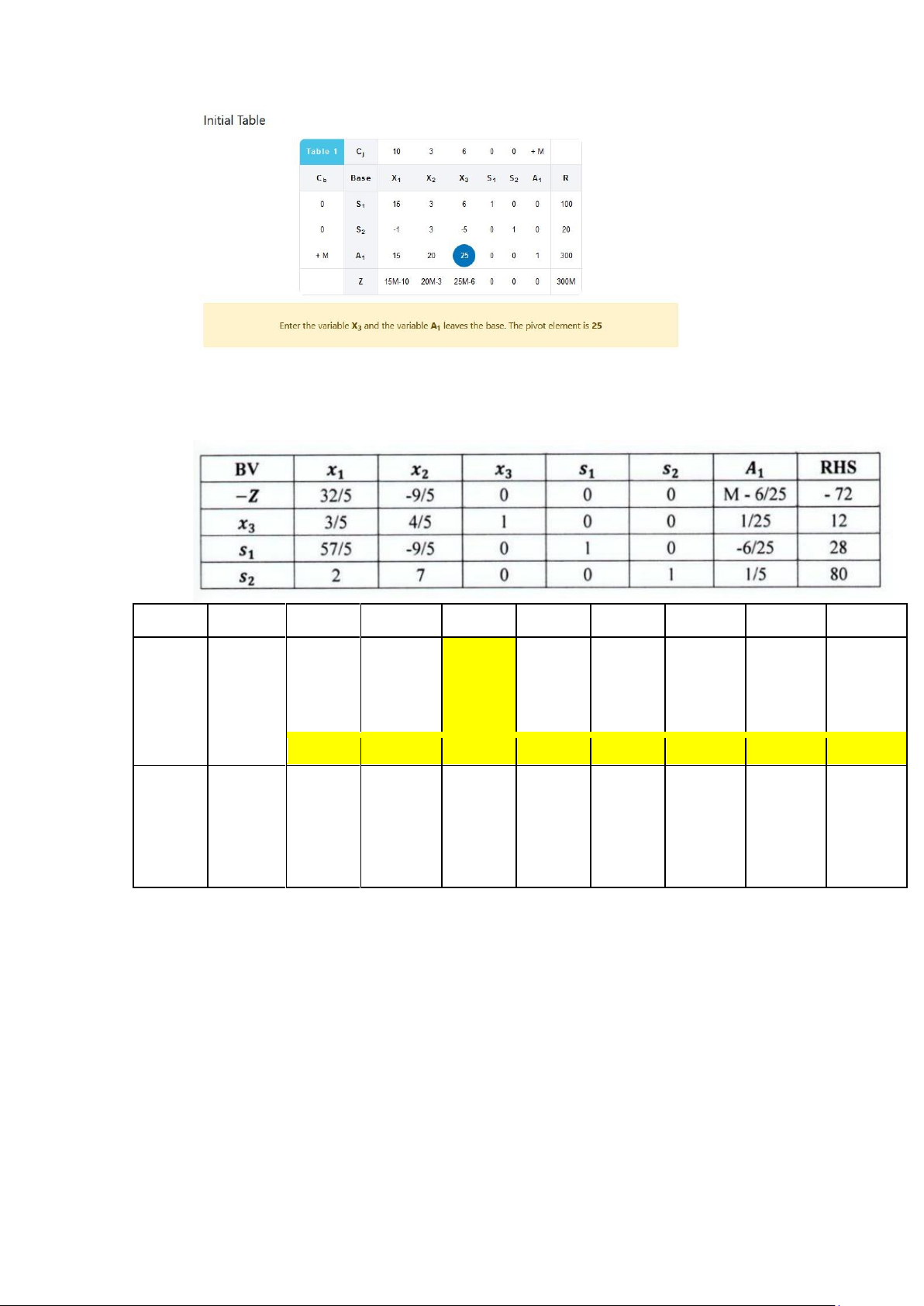
Minimize Z=15M-10x1+20M-3x2+25M-6x3-300M subject to: 15x1+3x2+6x3+s1=100 -x1+3x2-5x3+s2=20
15x1+20x2+25x3+A1=300 x1,x2,x3,s1,s2,A1≥0
b. Reformulate this problem to equivalent to TWO-PHASE method. Phase 1: Minimize Z=A1 subject to 15x1+3x2+6x3+s1=100 -x1+3x2-5x3+s2=20 15x1+20x2+25x3+A1=300 x1, x2, x3,s1,s2,A1≥0 Phase 2: Minimize Z=10x1+3x2+6x3 subject to 15x1+3x2+6x3+s1=100 -x1+3x2-5x3+s2=20
15x1+20x2+25x3=300 x1,x2,x3,s1,s2≥0
c. Using Big M method, construct the initial tableau for simplex method and identify the
corresponding initial (artificial) BF solution? lOMoAR cPSD| 58583460
Initial solution: Z=300M, s1=100,s2=20,A1=300, x1=x2=x3=0
d. Using the Big M method, all the artificial variables are removed from the below. Utilize this
table, let find optimal solution by using TWO-PHASE method. Iteration Equation BS x1 x2 x3 s1 s2 RHS Ratio 0 -Z 6.4 -1.8 0 0 0 -72 - 1 x3 s1 0.8 1 0 0 12 15 0.8 0 2 11.4 0 1 0 28 -15.5556 3 -1.8 s2 2 7 0 0 1 80 11.42857 0 -Z 6.914286 0 0 0 0.257143 -51.4286 1 x3 s1 0.571429 0 1 0 -0.11429 2.857143 1 2 11.91429 0 0 1 0.257143 48.57143 3 x2 0.285714 1 0 0 0.142857 11.42857
Optimal solution: Z = 360/7 ; x1 = 0 ; x2 = 80/7 ; x3 = 20/7; s1 = 340/7; s2 = 0